
Title: Scientific American Supplement, No. 441, June 14, 1884.
Author: Various
Release date: May 16, 2005 [eBook #15833]
Most recently updated: December 14, 2020
Language: English
Credits: Produced by Juliet Sutherland and the Online Distributed
Proofreading Team at www.pgdp.net.
The object of the apparatus shown in the accompanying engraving is to effect a separation of the tough epidermis of the sugar-cane from the internal spongy pith which is to be pressed. Its function consists in isolating and separating the cells from their cortex, and in putting them in direct contact with the rollers or cylinders of the mill. After their passage into the apparatus, which is naturally placed in a line with the endless chain that carries them to the mill, the canes arrive in less compact layers, pass through much narrower spaces, and finally undergo a more efficient pressure, which is shown by an abundant flow of juice. The first trials of the machine were made in 1879 at the Pointe Simon Works, at Martinique, with the small type that was shown at the Paris Exhibition of 1878. These experiments, which were applied to a work of 3,000 kilos of cane per hour, gave entire satisfaction, and decided the owners of three of the colonial works (Pointe Simon, Larcinty, and Marin) to adopt it for the season of 1880.
The apparatus is shown in longitudinal section in Fig. 1, and in plan in Fig. 2.
Fig. 3 gives a transverse section passing through the line 3-4, and Fig. 4 an external view on the side whence the decorticated canes make their exit from the apparatus.
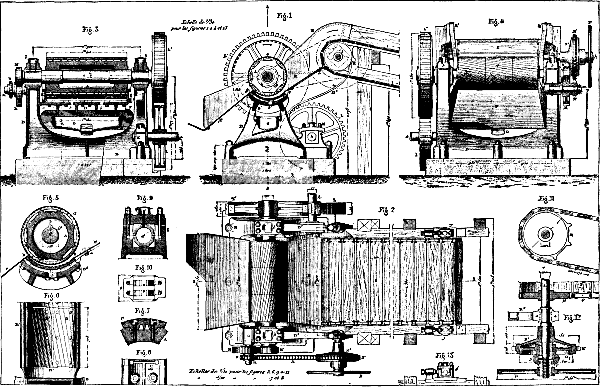
FAURE'S MACHINE FOR DECORTICATING SUGAR CANE.
The other figures relate to details that will be referred to further along.
The Decorticating Cylinder.—The principal part of the apparatus is a hollow drum, A, of cast iron, 430 mm. in internal diameter by 1.41 m. in length, which is keyed at its two extremities to the shaft, a. Externally, this drum (which is represented apart in transverse section in Fig. 5) has the form of an octagonal prism with well dressed projections between which are fixed the eight plates, C, that constitute the decorticating cylinder. These plates, which are of tempered cast iron, and one of which is shown in transverse section in Fig. 7, when once in place form a cylindrical surface provided with 48 helicoidal, dentate channels. The length of these plates is 470 mm. There are three of them in the direction of the generatrices of the cylinder, and this makes a total of 24. All are strengthened by ribs (as shown in Fig. 8), and each is fixed by 4 bolts, c, 20mm. in diameter. The pitch of the helices of each tooth is very elongated, and reaches about 7.52 m. The depth of the toothing is 18 mm.
Frame and Endless Chain.—The cylinder thus constructed rotates with a velocity of 50 revolutions per minute over a cylindrical vessel, B', cast in a piece with the frame, B. This vessel is lined with two series of tempered cast iron plates, D and D', called exit and entrance plates, which rest thereon, through the intermedium of well dressed pedicels, and which are held in place by six 20-millimeter bolts. Their length is 708 mm. The entrance plates, D, are provided with 6 spiral channels, whose pitch is equal to that of the channels of the decorticating cylinder, C, and in the same direction. The depth of the toothing is 10 mm.
The exit plates, D', are provided with 7 spiral channels of the same pitch and direction as those of the preceding, but the depth of which increases from 2 to 10 mm. The axis of the decorticating cylinder does not coincide with that of the vessel, B', so that the free interval for the passage of the cane continues to diminish from the entrance to the exit.
The passage of the cane to the decorticator gives rise to a small quantity of juice, which flows through two orifices, b', into a sort of cast iron trough, G, suspended beneath the vessel. The cane, which is brought to the apparatus by an endless belt, empties in a conduit formed of an inclined bottom, E, of plate iron, and two cast iron sides provided with ribs. These sides rest upon the two ends of the vessel, B', and are cross-braced by two flat bars, e, to which is bolted the bottom, E. This conduit is prolonged beyond the decorticating cylinder by an inclined chute, F, the bottom of which is made of plate iron 7 mm. thick and the sides of the same material 9 mm. thick. The hollow frame, B, whose general form is like that of a saddle, carries the bearings, b, in which revolves the shaft, a. One of these bearings is represented in detail in Figs. 9 and 10. It will be seen that the cap is held by bolts with sunken heads, and that the bearing on the bushes is through horizontal surfaces only. In a piece with this frame are cast two similar brackets, B², which support the axle, h, of the endless chain. To this axle, whose diameter is 100 mm., are keyed, toward the extremities, the pinions, H, to which correspond the endless pitch chains, i. These latter are formed, as may be seen in Figs. 11 and 12, of two series of links. The shorter of these latter are only 100 mm. in length, while the longer are 210 mm., and are hollowed out so as to receive the butts of the boards, I. The chain thus formed passes over two pitch pinions, J, like the pinions, H, that are mounted at the extremities of an axle, j, that revolves in bearings, I', whose position with regard to the apparatus is capable of being varied so as to slacken or tauten the chain, I. This arrangement is shown in elevation in Fig. 13.
Transmission.—The driving shaft, k, revolves in a pillow block, K, cast in a piece with the frame, B. It is usually actuated by a special motor, and carries a fly-wheel (not shown in the figure for want of space). It receives in addition a cog-wheel, L, which transmits its motion to the decorticating cylinder through, the intermedium of a large wooden-toothed gear wheel, L'. The shaft, a, whose diameter is 228 mm., actuates in its turn, through the pinions, M' and M, the pitch pinion, N, upon whose prolonged hub is keyed the pinion, M. This latter is mounted loosely upon the intermediate axle, m. Motion is transmitted to the driving shaft, h, of the endless chain, I, by an ordinary pitch chain, through a gearing which is shown in Fig. 12. The pitch pinion, N', is cast in a piece with a hollow friction cone, N², which is mounted loosely upon the shaft, h, and to which corresponds a second friction cone, O. This latter is connected by a key to a socket, o, upon which it slides, and which is itself keyed to the shaft, h. The hub of the cone, O, is connected by a ring with a bronze nut, p, mounted at the threaded end of the shaft, h, and carrying a hand-wheel, P. It is only necessary to turn this latter in one direction or the other in order to throw the two cones into or out of gear.
If we allow that the motor has a velocity of 70 revolutions per minute, the decorticating cylinder will run at the rate of 50, and the sugar-cane will move forward at the rate of 12 meters per minute.
This new machine is a very simple and powerful one. The decortication is effected with wonderful rapidity, and the canes, opened throughout their entire length and at all points of their circumference, leave the apparatus in a state that allows of no doubt as to what the result of the pressure will be that they have to undergo. There is no tearing, no trituration, no loss of juice, but merely a simple preparation for a rational pressure effected under most favorable conditions.
The apparatus, which is made in several sizes, has already received numerous applications in Martinique, Trinidad, Cuba, Antigua, St. Domingo, Peru, Australia, the Mauritius Islands, and Brazil.—Publication Industrielle.
An interesting piece of engineering work has recently been accomplished at Bristol, England, which consisted in the moving of a foot-bridge 134 feet in length, bodily, down the river a considerable distance. The pontoons by means of which the bridge was floated to its new position consisted of four 80-ton barges, braced together so as to form one solid structure 64 feet in width, and were placed in position soon after the tide commenced to rise. At six o'clock A.M. the top of the stages, which was 24 feet above the water, touched the under part of the bridge, and in a quarter of an hour later both ends rose from their foundations. When the tide had risen 4 ft. the stage and bridge were floated to the new position, when at 8.30 the girders dropped on to their beds.
It will not be necessary to commence this lecture by explaining the origin of fuel; it will be sufficient if I remind you that it is to the action of the complex rays of the sun upon the foliage of plants that we mainly owe our supply of combustibles. The tree trunks and branches of our forests, as well as the subterranean deposits of coal and naphtha, at one time formed portions of the atmosphere in the form of carbonic acid gas; that gas was decomposed by the energy of the solar rays, the carbon and the oxygen were placed in positions of advantage with respect to each other—endowed with potential energy; and it is my duty this evening to show how we can best make use of these relations, and by once more combining the constituents of fuel with the oxygen of the air, reverse the action which caused the growth of the plants, that is to say, by destroying the plant reproduce the heat and light which fostered it. The energy which can be set free by this process cannot be greater than that derived originally from the sun, and which, acting through the frail mechanism of green leaves, tore asunder the strong bonds of chemical affinity wherein the carbon and oxygen were hound, converting the former into the ligneous portions of the plants and setting the latter free for other uses. The power thus silently exerted is enormous; for every ton of carbon separated in twelve hours necessitates an expenditure of energy represented by at least 1,058 horse power, but the action is spread over an enormous area of leaf surface, rendered necessary by the small proportion of carbonic acid contained in the air, by measure only 1/2000 part, and hence the action is silent and imperceptible. It is now conceded on all hands that what is termed heat is the energy of molecular motion, and that this motion is convertible into various kinds and obeys the general laws relating to motion. Two substances brought within the range of chemical affinity unite with more or less violence; the motion of transition of the particles is transformed, wholly or in part, into a vibratory or rotary motion, either of the particles themselves or the interatomic ether; and according to the quality of the motions we are as a rule, besides other effects, made conscious of heat or light, or of both. When these emanations come to be examined they are found to be complex in the extreme, intimately bound up together, and yet capable of being separated and analyzed.
As soon as the law of definite chemical combination was firmly established, the circumstance that changes of temperature accompanied most chemical combinations was noticed, and chemists were not long in suspecting that the amount of heat developed or absorbed by chemical reaction should be as much a property of the substances entering into combination as their atomic weights. Solid ground for this expectation lies in the dynamic theory of heat. A body of water at a given height is competent by its fall to produce a definite and invariable quantity of heat or work, and in the same way two substances falling together in chemical union acquire a definite amount of kinetic energy, which, if not expended in the work of molecular changes, may also by suitable arrangements be made to manifest a definite and invariable quantity of heat.
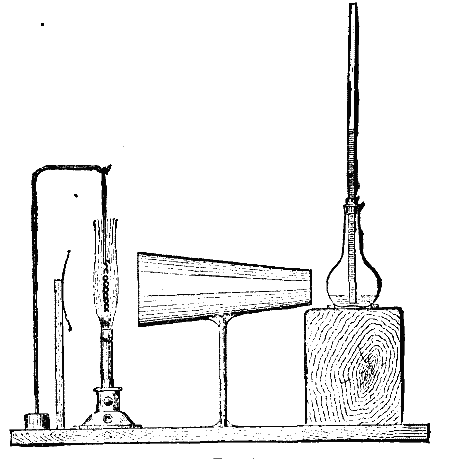
At the end of last century Lavoisier and Laplace, and after them, down to our own time, Dulong, Desprez, Favre and Silbermann, Andrews, Berthelot, Thomson, and others, devoted much time and labor to the experimental determination of the heat of combustion and the laws which governed its development. Messrs. Favre and Silbermann, in particular, between the years 1845 and 1852, carried out a splendid series of experiments by means of the apparatus partly represented in Fig. 1 (opposite), which is a drawing one-third the natural size of the calorimeter employed. It consisted essentially of a combustion chamber formed of thin copper, gilt internally. The upper part of the chamber was fitted with a cover through which the combustible could be introduced, with a pipe for a gas jet, with a peep hole closed by adiathermanous but transparent substances, alum and glass, and with a branch leading to a thin copper coil surrounding the lower part of the chamber and descending below it. The whole of this portion of the apparatus was plunged into a thin copper vessel, silvered internally and filled with water, which was kept thoroughly mixed by means of agitators. This second vessel stood inside a third one, the sides and bottom of which were covered with the skins of swans with the down on, and the whole was immersed in a fourth vessel tilled with water, kept at the average temperature of the laboratory. Suitable thermometers of great delicacy were provided, and all manner of precautions were taken to prevent loss of heat.
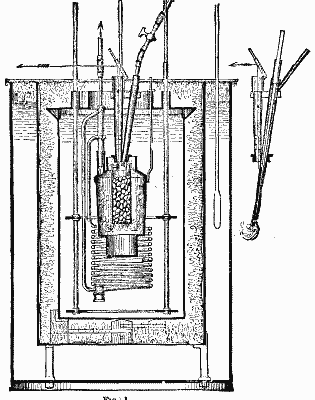
THE GENERATION OF STEAM. Fig 1.
It is impossible not to admire the ingenuity and skill exhibited in the details of the apparatus, in the various accessories for generating and storing the gases used, and for absorbing and weighing the products of combustion; but it is a matter of regret that the experiments should have been carried out on so small a scale. For example, the little cage which held the solid fuel tested was only 5/8 inch diameter by barely 2 inches high, and held only 38 grains of charcoal, the combustion occupying about sixteen minutes. Favre and Silbermann adopted the plan of ascertaining the weight of the substances consumed by calculation from the weight of the products of combustion. Carbonic acid was absorbed by caustic potash, as also was carbonic oxide, after having been oxidized to carbonic acid by heated oxide of copper, and the vapor of water was absorbed by concentrated sulphuric acid. The adoption of this system showed that it was in any case necessary to analyze the products of combustion in order to,m detect imperfect action. Thus, in the case of substances containing carbon, carbonic oxide was always present to a variable extent with the carbonic acid, and corrections were necessary in order to determine the total heat due to the complete combination of the substance with oxygen. Another advantage gained was that the absorption of the products of combustion prevents any sensible alteration in the volumes during the process, so that corrections for the heat absorbed in the work of displacing the atmosphere were not required. The experiments on various substances were repeated many times. The mean results for those in which we are immediately interested are given in Table I., next column.
Comparison with later determinations have established their substantial accuracy. The general conclusion arrived at is thus stated:
"As a rule there is an equality between the heat disengaged or absorbed in the acts, respectively, of chemical combination or decomposition of the same elements, so that the heat evolved during the combination of two simple or com-pound substances is equal to the heat absorbed at the time of their chemical segregation."
TABLE I.—SUBSTANCES ENTERING INTO THE COMPOSITION OF FUEL.
| Symbol and Atomic Weight. | Heat evolved in the Combustion of 1 lb. of Fuel. | |||||
|---|---|---|---|---|---|---|
| Before Combustion | After Combustion | In British Thermal Units. | In Pounds of Water Evaporated from and at 212°. | |||
| Hydrogen burned in oxygen. | H | 1 | H2O | 18 | 62,032 | 64.21 |
| Carbon burned to carbonic oxide. | C | 12 | CO | 28 | 4,451 | 4.61 |
| Carbon burned to carbonic acid. | C | 12 | CO2 | 44 | 14,544 | 15.06 |
| Carbonic oxide burned to carbonic acid. | CO | 28 | CO2 | 44 | 4,326 | 4.48 |
| Olefiant gas (ethylene) burnt in oxygen. | C2H4 2H2O | 28 | 2CO2 | 124 | 21,343 | 22.09 |
| Marsh gas (methane) burnt in oxygen. | CH4 | 16 | 2CO2 2H2O | 80 | 23,513 | 24.34 |
Composition of air—
| { | by volume 0.788 N + 0.197 O + 0.001 CO2 + 0.014 H2O |
| by weight 0.771 N + 0.218 O + 0.009 CO2 + 0.017 H2O |
This law is, however, subject to some apparent exceptions. Carbon burned in protoxide of nitrogen, or laughing gas, N2O, produces about 38 per cent. more heat than the same substance burned in pure oxygen, notwithstanding that the work of decomposing the protoxide of nitrogen has to be performed. In marsh gas, or methane, CH4, again, the energy of combustion is considerably less than that due to the burning of its carbon and hydrogen separately. These exceptions probably arise from the circumstance that the energy of chemical action is absorbed to a greater or less degree in effecting molecular changes, as, for example, the combustion of 1 pound of nitrogen to form protoxide of nitrogen results in the absorption of 1,157 units of heat. Berthelot states, as one of the fundamental principles of thermochemistry, "that the quantity of heat evolved is the measure of the sum of the chemical and physical work accomplished in the reaction"; and such a law will no doubt account for the phenomena above noted. The equivalent heat of combustion of the compounds we have practically to deal with has been experimentally determined, and therefore constitutes a secure basis on which to establish calculations of the caloric value of fuel; and in doing so, with respect to substances composed of carbon, hydrogen, and oxygen, it is convenient to reduce the hydrogen to its heat-producing equivalent of carbon. The heat of combustion of hydrogen being 62,032 units, that of carbon 14,544 units, it follows that 4.265 times the weight of hydrogen will represent an equivalent amount of carbon. With respect to the oxygen, it is found that it exists in combination with the hydrogen in the form of water, and, being combined already, abstracts its combining equivalent of hydrogen from the efficient ingredients of the fuel; and hence hydrogen, to the extent of 1/8 of the weight of the oxygen, must be deducted. The general formula then becomes:
Heat of combustion = 14,544 {C + 4.265 (H-(O/8))},
and water evaporated from and at 212°, taking 966 units as the heat necessary to evaporate 1 pound of water,
lb. evaporated = 15.06 {C + 4.265 (H-(O/8))},
carbon, hydrogen, and oxygen being taken at their weight per cent. in the fuel. Strictly speaking, marsh gas should be separately determined. It often happens that available energy is not in a form in which it can be applied directly to our needs. The water flowing down from the mountains in the neighborhood of the Alpine tunnels was competent to provide the power necessary for boring through them, but it was not in a form in which it could be directly applied. The kinetic energy of the water had first to be changed into the potential energy of air under pressure, then, in that form, by suitable mechanism, it was used with signal success to disintegrate and excavate the hard rock of the tunnels. The energy resulting from combustion is also incapable of being directly transformed into useful motive power; it must first be converted into potential force of steam or air at high temperature and pressure, and then applied by means of suitable heat engines to produce the motions we require. It is probably to this circumstance that we must attribute the slowness of the human race to take advantage of the energy of combustion. The history of the steam engine hardly dates back 200 years, a very small fraction of the centuries during which man has existed, even since historic times.
The apparatus by means of which the potential energy of fuel with respect to oxygen is converted into the potential energy of steam, we call a steam boiler; and although it has neither cylinder nor piston, crank nor fly wheel, I claim for it that it is a veritable heat engine, because it transmits the undulations and vibrations caused by the energy of chemical combination in the fuel to the water in the boiler; these motions expend themselves in overcoming the liquid cohesion of the water and imparting to its molecules that vigor of motion which converts them into the molecules of a gas which, impinging on the surfaces which confine it and form the steam space, declare their presence and energy in the shape of pressure and temperature. A steam pumping engine, which furnishes water under high pressure to raise loads by means of hydraulic cranes, is not more truly a heat engine than a simple boiler, for the latter converts the latent energy of fuel into the latent energy of steam, just as the pumping engine converts the latent energy of steam into the latent energy of the pumped-up accumulator or the hoisted weight.
If I am justified in taking this view, then I am justified in applying to my heat engine the general principles laid down in 1824 by Sadi Carnot, namely, that the proportion of work which can be obtained out of any substance working between two temperatures depends entirely and solely upon the difference between the temperatures at the beginning and end of the operation; that is to say, if T be the higher temperature at the beginning, and t the lower temperature at the end of the action, then the maximum possible work to be got out of the substance will be a function of (T-t). The greatest range of temperature possible or conceivable is from the absolute temperature of the substance at the commencement of the operation down to absolute zero of temperature, and the fraction of this which can be utilized is the ratio which the range of temperature through which the substance is working bears to the absolute temperature at the commencement of the action. If W = the greatest amount of effect to be expected, T and t the absolute temperatures, and H the total quantity of heat (expressed in foot pounds or in water evaporated, as the case may be) potential in the substance at the higher temperature, T, at the beginning of the operation, then Carnot's law is expressed by the equation:
| W = H ( | T - t | ) |
| T |
I will illustrate this important doctrine in the manner which Carnot himself suggested.
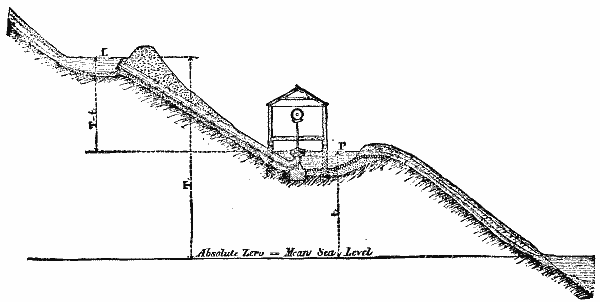
THE GENERATION OF STEAM. Fig 2.
Fig. 2 represents a hillside rising from the sea. Some distance up there is a lake, L, fed by streams coming down from a still higher level. Lower down on the slope is a millpond, P, the tail race from which falls into the sea. At the millpond is established a factory, the turbine driving which is supplied with water by a pipe descending from the lake, L. Datum is the mean sea level; the level of the lake is T, and of the millpond t. Q is the weight of water falling through the turbine per minute. The mean sea level is the lowest level to which the water can possibly fall; hence its greatest potential energy, that of its position in the lake, = QT = H. The water is working between the absolute levels, T and t; hence, according to Carnot, the maximum effect, W, to be expected is—
| W = H ( | T - t T |
) | |
| but H = QT ∴ | W = QT ( | T - t | ) |
| T | |||
| W = Q (T - t), | |||
that is to say, the greatest amount of work which can be expected is found by multiplying the weight of water into the clear fall, which is, of course, self-evident.
Now, how can the quantity of work to be got out of a given weight of water be increased without in any way improving the efficiency of the turbine? In two ways:
1. By collecting the water higher up the mountain, and by that means increasing T.
2. By placing the turbine lower down, nearer the sea, and by that means reducing t.
Now, the sea level corresponds to the absolute zero of temperature, and the heights T and t to the maximum and minimum temperatures between which the substance is working; therefore similarly, the way to increase the efficiency of a heat engine, such as a boiler, is to raise the temperature of the furnace to the utmost, and reduce the heat of the smoke to the lowest possible point. It should be noted, in addition, that it is immaterial what liquid there may be in the lake; whether water, oil, mercury, or what not, the law will equally apply, and so in a heat engine, the nature of the working substance, provided that it does not change its physical state during a cycle, does not affect the question of efficiency with which the heat being expended is so utilized. To make this matter clearer, and give it a practical bearing, I will give the symbols a numerical value, and for this purpose I will, for the sake of simplicity, suppose that the fuel used is pure carbon, such as coke or charcoal, the heat of combustion of which is 14,544 units, that the specific heat of air, and of the products of combustion at constant pressure, is 0.238, that only sufficient air is passed through the fire to supply the quantity of oxygen theoretically required for the combustion of the carbon, and that the temperature of the air is at 60° Fahrenheit = 520° absolute. The symbol T represents the absolute temperature of the furnace, a value which is easily calculated in the following manner: 1 lb. of carbon requires 2-2/3 lb. of oxygen to convert it into carbonic acid, and this quantity is furnished by 12.2 lb. of air, the result being 13.2 lb. of gases, heated by 14,544 units of heat due to the energy of combustion; therefore:
| T = 520° + | 14,544 units | = 5,150° absolute. |
| 13.2 lb. × 0.238 |
The lower temperature, t, we may take as that of the feed water, say at 100° or 560° absolute, for by means of artificial draught and sufficiently extending the heating surface, the temperature of the smoke may be reduced to very nearly that of the feed water. Under such circumstances the proportion of heat which can be realized is
| = | 5,150° - 560° | = 0.891; |
| 5,150° |
that is to say, under the extremely favorable if not impracticable conditions assumed, there must be a loss of 11 per cent. Next, to give a numerical value to the potential energy, H, to be derived from a pound of carbon, calculating from absolute zero, the specific heat of carbon being 0.25, and absolute temperature of air 520°:
| Units. | ||
| 1 lb. of carbon × 0.25 × 520 | = | 130 |
| 12.2 of air × 0.238 × 520 | = | 1,485 |
| Heat of combustion | = | 14,544 |
| 16,159 | ||
| Deduct heat equivalent to work of displacing atmosphere by products of combustion raised from 60° to 100°, or from 149.8 cubic feet to 161.3 cubic feet, | 32 | |
| Total units of heat available | 16,127 | |
Equal to 16.69 lb. of water evaporated from and at 212°. Hence the greatest possible evaporation from and at 212° from a lb. of carbon—
| W = | 16,159 u. × 0.891 - 32 u. | = 14.87 lb. |
| 966 u. |
I will now take a definite case, and compare the potential energy of a certain kind of fuel with the results actually obtained. For this purpose the boiler of the eight-horse portable engine, which gained the first prize at the Cardiff show of the Royal Agricultural Society in 1872, will serve very well, because the trials, all the details of which are set forth very fully in vol. ix. of the Journal of the Society, were carried out with great care and skill by Sir Frederick Bramwell and the late Mr. Menelaus; indeed, the only fact left undetermined was the temperature of the furnace, an omission due to the want of a trustworthy pyrometer, a want which has not been satisfied to this day.2 The data necessary for our purpose are:
| Steam pressure 80 lb. temperature | 324° = 784° | absolute. |
| Mean temperature of smoke | 389° = 849° | " |
| Water evaporated per 1 lb of coal, from and at 212° | 11.83 lb. | |
| Temperature of the air | 60° = 520° | absolute. |
| Temperature of feed water | 209° = 669° | " |
| Heating surface | 220 square feet. | |
| Grate surface | 3.29 feet. | |
| Coal burnt per hour | 41 lb. |
The fuel used was a smokeless Welsh coal, from the Llangennech colleries. It was analyzed by Mr. Snelus, of the Dowlais Ironworks, and in Table II. are exhibited the details of its composition, and the weight and volume of air required for its combustion. The total heat of combustion in 1 lb of water evaporated:
= 15.06 × (0.8497 + 4.265 × (0.426 - 0.035/8))
= 15.24 lb. of water from and at 212°
= 14,727 units of heat.
TABLE II.—PROPERTIES OF LLANGENNECH COAL.
| Analyses of 1 lb. of Coal. | Oxygen required for Combustion. Pounds. | Products of Combustion at 32° F. | ||
|---|---|---|---|---|
| Cubic feet. | Volume per cent. | |||
| Carbon | 0.8497 | 2.266 | 25.3 | 11.1 |
| Hydrogen | 0.0426 | 0.309 | 7.6 | 3.4 |
| Oxygen | 0.0350 | — | — | — |
| Sulphur | 0.0042 | — | — | — |
| Nitrogen | 0.1045 | — | 0.18 | }85.5 |
| Ash | 0.0540 | — | — | |
| Total | 1.0000 | 2.572 | — | |
| 9-1/3.lb nitrogen | — | — | 118.9 | |
| 6 lb. excess of air. | — | — | 71.4 | |
| Total cubic feet of products per 1 lb. of coal | — | — | 226.4 | 100.0 |
The temperature of the furnace not having been determined, we must calculate it on the supposition, which will be justified later on, that 50 per cent more air was admitted than was theoretically necessary to supply the oxygen required for perfect combustion. This would make 18 lb. of air per 1 lb. of coal; consequently 19 lb. of gases would be heated by 14,727 units of heat. Hence:
| T = | 14,727 u. | = 3,257° |
| 19 lb. × 0.238 |
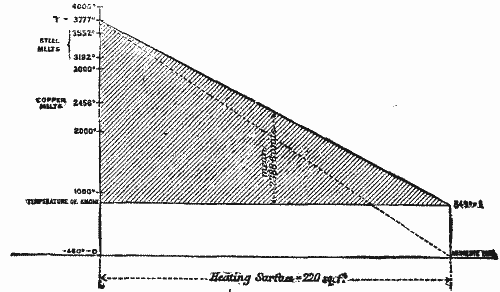
above the temperatures of the air, or 3,777° absolute. The temperature of the smoke, t, was 849° absolute; hence the maximum duty would be
| 3,777° - 849° | = 0.7752. |
| 3,777° |
The specific heat of coal is very nearly that of gases at constant pressure, and may, without sensible error, be taken as such. The potential energy of 1 lb. of coal, therefore, with reference to the oxygen with which it will combine, and calculated from absolute zero, is:
| Units. | |
| 19 lb. of coal and air at the temperature of the air contained 19 lb. × 520° × 0.238 | 2,350 |
| Heat of combustion | 14,727 |
| 17,078 | |
| Deduct heat expended in displacing atmosphere 151 cubic feet | - 422 |
| Total potential energy | 16,656 |
Hence work to be expected from the boiler:
| 17,078 units × ( | 3,777° - 849° | ) - 422 units | ||
| 3,777° | ||||
| = | ————————————————— | = 13.27 lb. | ||
| 966 units | ||||
of water evaporated from and at 212°, corresponding to 12,819 units. The actual result obtained was 11.83 lb.; hence the efficiency of this boiler was
| 11.83 | = 0.892. |
| 13.27 |
I have already claimed for a boiler that it is a veritable heat engine, and I have ventured to construct an indicator diagram to illustrate its working. The rate of transfer of heat from the furnace to the water in the boiler, at any given point, is some way proportional to the difference of temperature, and the quantity of heat in the gases is proportional to their temperatures. Draw a base line representing -460° Fahr., the absolute zero of temperature. At one end erect an ordinate, upon which set off T = 3,777°, the temperature of the furnace. At 849° = t, on the scale of temperature, draw a line parallel to the base, and mark on it a length proportional to the heating surface of the boiler; join T by a diagonal with the extremity of this line, and drop a perpendicular on to the zero line. The temperature of the water in the boiler being uniform, the ordinates bounded by the sloping line, and by the line, t, will at any point be approximately proportional to the rate of transmission of heat, and the shaded area above t will be proportional to the quantity of heat imparted to the water. Join T by another diagonal with extremity of the heating surface on the zero line, then the larger triangle, standing on the zero line, will represent the whole of the heat of combustion, and the ratio of the two triangles will be as the lengths of their respective bases, that is, as (T-t) / T, which is the expression we have already used. The heating surface was 220 square feet, and it was competent to transmit the energy developed by 41 lb. of coal consumed per hour = 12,819 u. × 41 u. = 525,572 units, equal to an average of 2,389 units per square foot per hour; this value will correspond to the mean pressure in an ordinary diagram, for it is a measure of the energy with which molecular motion is transferred from the heated gases to the boiler-plate, and so to the water. The mean rate of transmission, multiplied by the area of heating surface, gives the area of the shaded portion of the figure, which is the total work which should have been done, that is to say, the work of evaporating 544 lb. of water per hour. The actual work done, however, was only 485 lb. To give the speculations we have indulged in a practical turn, it will be necessary to examine in detail the terms of Carnot's formula. Carnot labored under great disadvantages. He adhered to the emission theory of heat; he was unacquainted with its dynamic equivalent; he did not know the reason of the difference between the specific heat of air at constant pressure and at constant volume, the idea of an absolute zero of temperature had not been broached; but the genius of the man, while it made him lament the want of knowledge which he felt must be attainable, also enabled him to penetrate the gloom by which he was surrounded, and enunciate propositions respecting the theory of heat engines, which the knowledge we now possess enables us to admit as true. His propositions are:
1. The motive power of heat is independent of the agents employed to develop it, and its quantity is determined solely by the temperature of the bodies between which the final transfer of caloric takes place.
2. The temperature of the agent must in the first instance be raised to the highest degree possible in order to obtain a great fall of caloric, and as a consequence a large production of motive power.
3. For the same reason the cooling of the agent must be carried to as low a degree as possible.
4. Matters must be so arranged that the passage of the elastic agent from the higher to the lower temperature must be due to an increase of volume, that is to say, the cooling of the agent must be caused by its rarefaction.
This last proposition indicates the defective information which Carnot possessed. He knew that expansion of the elastic agent was accompanied by a fall of temperature, but he did not know that that fall was due to the conversion of heat into work. We should state this clause more correctly by saying that "the cooling of the agent must be caused by the external work it performs." In accordance with these propositions, it is immaterial what the heated gases or vapors in the furnace of a boiler may be, provided that they cool by doing external work and, in passing over the boiler surfaces, impart their heat energy to the water. The temperature of the furnace, it follows, must be kept as high as possible. The process of combustion is usually complex. First, in the case of coal, close to the fire-bars complete combustion of the red hot carbon takes place, and the heat so developed distills the volatile hydrocarbons and moisture in the upper layers of the fuel. The inflammable gases ignite on or near the surface of the fuel, if there be a sufficient supply of air, and burn with a bright flame for a considerable distance around the boiler. If the layer of fuel be thin, the carbonic acid formed in the first instance passes through the fuel and mixes with the other gases. If, however, the layer of fuel be thick, and the supply of air through the bars insufficient, the carbonic acid is decomposed by the red hot coke, and twice the volume of carbonic oxide is produced, and this, making its way through the fuel, burns with a pale blue flame on the surface, the result, as far as evolution of heat is concerned, being the same as if the intermediate decomposition of carbonic acid had not taken place. This property of coal has been taken advantage of by the late Sir W. Siemens in his gas producer, where the supply of air is purposely limited, in order that neither the hydrocarbons separated by distillation, nor the carbonic oxide formed in the thick layer of fuel, may be consumed in the producer, but remain in the form of crude gas, to be utilized in his regenerative furnaces.
THE GENERATION OF STEAM. Fig 3.
THE GENERATION OF STEAM. Fig 4.
THE GENERATION OF STEAM. Fig 5.
THE GENERATION OF STEAM. Fig 6.
THE GENERATION OF STEAM. Fig 7.
(To be continued.)
Lecture delivered at the Institution of Civil Engineers, session 1883-84. For the illustrations we are indebted to the courtesy of Mr. J. Forrest, the secretary.
In the fifty-second volume of the Proceedings (1887-78), page 154, will be found a remarkable experiment on the evaporative power of a vertical boiler with internal circulating pipes. The experiment was conducted by Sir Frederick Bramwell and Dr. Russell, and is remarkable in this respect, that the quantity of air admitted to the fuel, the loss by convection and radiation, and the composition of the smoke were determined. The facts observed were as follows:
| Steam pressure 53 lb | = 300.6° F. |
| lb. | |
| Fuel—Water in coke and wood | 26.08 |
| Ash | 10.53 |
| Hydrogen, oxygen, nitrogen, and sulphur | 7.18 |
| ——— | |
| Total non-combustible | 43.79 |
| Carbon, being useful combustible | 194.46 |
| ——— | |
| Total fuel | 238.25 |
| Air per pound of carbon | 17-1/8 lb. |
| Time of experiment | 4 h. 12 min. |
| Water evaporated from 60° into steam at 53 lb. pressure | 1,620 lb. |
| Heat lost by radiation and convection | 70,430 units. |
| Mean temperature of chimney | 700° F. |
| Mean temperature of air | 70° F. |
No combustible gas was found in the chimney.
I will apply Carnot's doctrine to this case.
Potential energy of the fuel with respect to absolute zero:
| Units. | |
| 239.25 lb. × 530° abs. × 0.238 | = 30,053 |
| 194.46 lb. × 17-1/8 × 530° × 0.238, the weight and heat of air | 420,660 |
| 194.46 × 14,544 units heat of combustion of carbon | 2,828,200 |
| ———— | |
| Total energy | 3,278,813 |
| Heat absorbed in evaporating 26.08 lb. of water in fuel | -29,888 |
| ———— | |
| Available energy | 3,248,425 |
Temperature of furnace—
The whole of the fuel was heated up, but the heat absorbed in the evaporation of the water lowered the temperature of the furnace, and must be deducted from the heat of combustion.
| Units. | |
| Heat of combustion | 2,828,200 |
| Heat of evaporation of 26.08 lb. water | -29,888 |
| ——— | |
| Available heat of combustion | 2,798,312 |
| Dividing by 238.25 lb. gives the heat per 1 lb. of fuel used | = 11,745 units. |
And temperature of furnace:
| 11,745 units (18.125 lb. × 0.238) | + 530° | = 3,253° |
| Temperature of chimney 700° + 460° | = 1,160° | |
| Maximum duty | (3,253° - 1,160°) 3,253° | = 0.643° |
Work of displacing atmosphere by smoke at 700°:
| Cubic feet. | |
| Volumes of gases at 70° | = 228.3 |
| Volumes of gases at 700° | = 499.8 |
| ——— | |
| Increase of volume | 271.5 |
| Work done= | Units. |
| (194.46 lb. × 271.5 cub. ft. × 144 sq. in. × 15 lb.) 722 units | = 147,720 |
| Maximum amount of work to be expected = 3,248,425 × 0.643 | = 2,101,700 |
| Deduct work of displacing atmosphere | = 147,720 |
| ———— | |
| Available work | 1,953,980 |
Actual work done:
| Units. | |
| 1,620 lb. of water raised from 60° and turned into steam at 53 lb | = 1,855,900 |
| Loss by radiation and convection | 70,430 |
| 10½ lb. ashes left, say at 500° | 1,129 |
| ———— | |
| Total work actually done | 1,927,459 |
| Unaccounted for | 26,521 |
| ———— | |
| Calculated available work | 1,953,980 |
The unaccounted-for work, therefore, amounts to only 1½ per cent. of the calculated available work.
Sir Frederick Bramwell ingeniously arranged his data in the form of a balance sheet, and showed 253,979 units unaccounted for; but if from this we deduct the work lost in displacing the air, the unaccounted-for heat falls to less than 4 per cent. of the total heat of combustion. These results show how extremely accurate the observations must have been, and that the loss mainly arises from convection and radiation from the boiler.
[Continued from SUPPLEMENT No. 437, page 6970.]
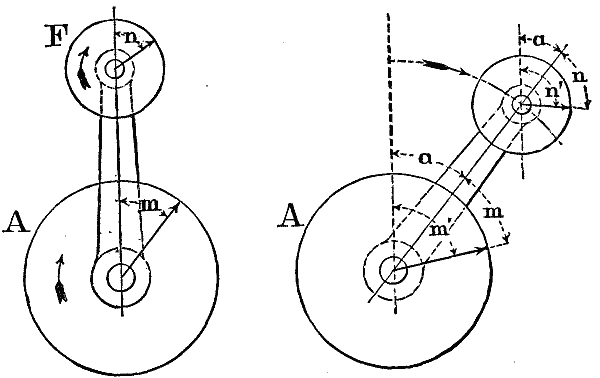
PLANETARY WHEEL TRAINS. Fig. 14
It has already been shown that the rotations of all the wheels of a planetary train, relatively to the train-arm, are the same when the arm is in motion as they would be if it were fixed. Now, in Fig. 14, let A be the first and F the last wheel of an incomplete train, that is, one having but one sun-wheel. As before, let these be so connected by intermediate gearing that, when T is stationary, a rotation of A through m degrees shall drive F through n degrees: and also as before, let T in the same time move through a degrees. Then, if m' represent the total motion of A, we have again,
m' = m + a, or m = m' - a.
This is, clearly, the motion of A relatively to the fixed frame of the machine; and is measured from a fixed vertical line through the center of A. Now, if we wish to express the total motion of F relatively to the same fixed frame, we must measure it from a vertical line through the center of F, wherever that maybe; which gives in this case:
n' = n + a, or n = n' - a.
but with respect to the train-arm when at rest, we have:
| ang. vel. A ang. vel. F |
= | n m | , whence again, |
| n' - a m' - a |
= | n m | . |
This is the manner in which the equation is deduced by Prof. Willis, who expressly states that it applies whether the last wheel F is or is not concentric with the first wheel A, and also that the train may be composed of any combinations which transmit rotation with both a constant velocity ratio and a constant directional relation. He designates the quantities m', n', absolute revolutions, as distinguished from the relative revolutions (that is, revolutions relatively to the train-arm), indicated by the quantities m, n: adding, "Hence it appears that the absolute revolutions of the wheels of epicyclic trains are equal to the sum of their relative revolutions to the arm, and of the arm itself, when they take place in the same direction, and equal to the difference of these revolutions when in the opposite direction."
In this deduction of the formula, as in that of Prof. Rankine, all the motions are supposed to have the same direction, corresponding to that of the hands of the clock; and in its application to any given train, the signs of the terms must be changed in case of any contrary motion, as explained in the preceding article.
And both the deduction and the application, in reference to these incomplete trains in which the last wheel is carried by the train-arm, clearly involve and depend upon the resolving of a motion of revolution into the components of a circular translation and a rotation, in the manner previously discussed.
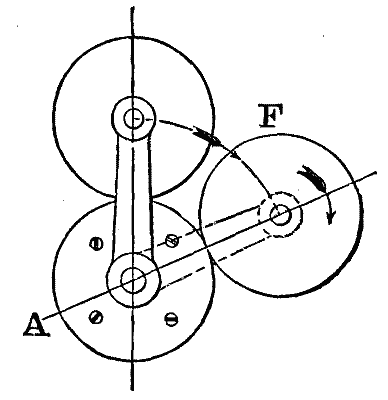
PLANETARY WHEEL TRAINS. Fig. 15
To illustrate: Take the simple case of two equal wheels, Fig. 15, of which the central one A is fixed. Supposing first A for the moment released and the arm to be fixed, we see that the two wheels will turn in opposite directions with equal velocities, which gives n/m = -1; but when A is fixed and T revolves, we have m' = 0, whence in the general formula
| n' - a -a |
= -1, or n' = 2 a; |
which means, being interpreted, that F makes two rotations about its axis during one revolution of T, and in the same direction. Again, let A and F be equal in the 3-wheel train, Fig. 16, the former being fixed as before. In this case we have:
| n m |
= 1, m' = 0, which gives |
| n' - a -a |
= 1, ∴ n' = 0; |
that is to say, the wheel F, which now evidently has a motion of circular translation, does not rotate at all about its axis during the revolution of the train-arm.
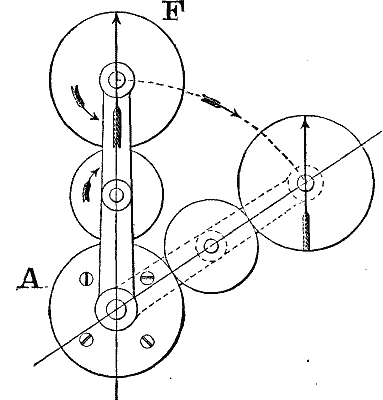
PLANETARY WHEEL TRAINS. Fig. 16
All this is perfectly consistent, clearly, with the hypothesis that the motion of circular translation is a simple one, and the motion of revolution about a fixed axis is a compound one.
Whether the hypothesis was made to substantiate the formula, or the formula constructed to suit the hypothesis, is not a matter of consequence. In either case, no difficulty will arise so long as the equation is applied only to cases in which, as in those here mentioned, that motion of revolution can be resolved into those components.
When the definition of an epicyclic train is restricted as it is by Prof. Rankine, the consideration of the hypothesis in question is entirely eliminated, and whether it be accepted or rejected, the whole matter is reduced to merely adding the motion of the train-arm to the rotation of each sun-wheel.
But in attempting to apply this formula in analyzing the action of an incomplete train, we are required to add this motion of the train-arm, not only to that of a sun-wheel, but to that of a planet-wheel. This is evidently possible in the examples shown in Figs. 15 and 16, because the motions to be added are in all respects similar: the trains are composed of spur-wheels, and the motions, whether of revolution, translation, or rotation, take place in parallel planes perpendicular to parallel axes. This condition, which we have emphasized, be it observed, must hold true with regard to the motions of the first and last wheels and the train-arm, in order to make this addition possible. It is not essential that spur-wheels should be used exclusively or even at all; for instance, in Fig. 16, A and F may be made bevel or screw-wheels, without affecting the action or the analysis; but the train-arm in all cases revolves around the central axis of the system, that is, about the axis of A, and to this the axis of F must be parallel, in order to render the deduction of the formula, as made by Prof. Willis, and also by Prof. Goodeve, correct, or even possible.
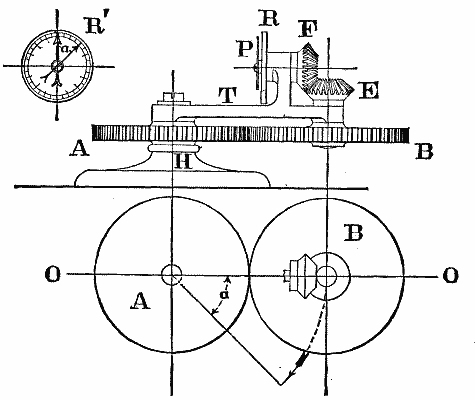
PLANETARY WHEEL TRAINS. Fig. 17
This will be seen by an examination of Fig. 17; in which A and B are two equal spur-wheels, E and F two equal bevel wheels, B and E being secured to the same shaft, and A being fixed to the frame H. As the arm T goes round, B will also turn in its bearings in the same direction: let this direction be that of the clock, when the apparatus is viewed from above, then the motion of F will also have the same direction, when viewed from the central vertical axis, as shown at F': and let these directions be considered as positive. It is perfectly clear that F will turn in its bearings, in the direction indicated, at a rate precisely equal to that of the train-arm. Let P be a pointer carried by F, and R a dial fixed to T; and let the pointer be vertical when OO is the plane containing the axes of A, B, and E. Then, when F has gone through any angle a measured from OO, the pointer will have turned from its original vertical position through an equal angle, as shown also at F'.
Now, there is no conceivable sense in which the motion of T can be said to be added to the rotation of F about its axis, and the expression "absolute revolution," as applied to the motion of the last wheel in this train, is absolutely meaningless.
Nevertheless, Prof. Goodeve states (Elements of Mechanism, p. 165) that "We may of course apply the general formula in the case of bevel wheels just as in that of spur wheels." Let us try the experiment; when the train-arm is stationary, and A released and turned to the right, F turns to the left at the same rate, whence:
| n m |
= -1; also m'= 0 when A is fixed, |
and the equation becomes
| n' - a - a |
= -1, ∴ n' = 2 a: |
or in other words F turns twice on its axis during one revolution of T: a result too palpably absurd to require any comment. We have seen that this identical result was obtained in the case of Fig. 15, and it would, of course, be the same were the formula applied to Figs. 5 and 6; whereas it has never, so far as we are aware, been pretended that a miter or a bevel wheel will make more than one rotation about its axis in rolling once around an equal fixed one.
Again, if the formula be general, it should apply equally well to a train of screw wheels: let us take, for example, the single pair shown in Fig. 8, of which, when T is fixed, the velocity ratio is unity. The directional relation, however, depends upon the direction in which the wheels are twisted: so that in applying the formula, we shall have n/m = +1, if the helices of both wheels are right handed, and n/m = -1, if they are both left handed. Thus the formula leads to the surprising conclusion, that when A is fixed and T revolves, the planet-wheel B will revolve about its axis twice as fast as T moves, in one case, while in the other it will not revolve at all.
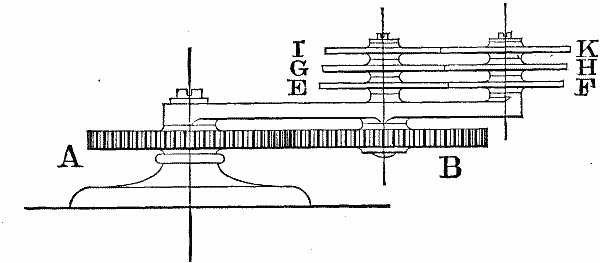
PLANETARY WHEEL TRAINS. Fig. 18
A favorite illustration of the peculiarities of epicyclic mechanism, introduced both by Prof. Willis and Prof. Goodeve, is found in the contrivance known as Ferguson's Mechanical Paradox, shown in Fig. 18. This consists of a fixed sun-wheel A, engaging with a planet-wheel B of the same diameter. Upon the shaft of B are secured the three thin wheels E, G, I, each having 20 teeth, and in gear with the three others F, H, K, which turn freely upon a stud fixed in the train-arm, and have respectively 19, 20, and 21 teeth. In applying the general formula, we have the following results:
| For the wheel | F, | n m |
= | 20 19 |
= | n' - a -a |
∴ n' = | - | 1 19 | a. | |
| " | H, | n m | = | 1 | = | n' - a -a |
∴ n' = | 0. | |||
| " | K, | n m |
= | 21 20 |
= | n' - a -a |
∴ n' = | + | 1 21 | a. |
The paradoxical appearance, then, consists in this, that although the drivers of the three last wheels each have the same number of teeth, yet the central one, H, having a motion of circular translation, remains always parallel to itself, and relatively to it the upper one seems to turn in the same direction as the train-arm, and the lower in the contrary direction. And the appearance is accepted, too, as a reality; being explained, agreeably to the analysis just given, by saying that H has no absolute rotation about its axis, while the other wheels have; that of F being positive and that of K negative.
The Mechanical Paradox, it is clear, may be regarded as composed of three separate trains, each of which is precisely like that of Fig. 16: and that, again, differs from the one of Fig. 15 only in the addition of a third wheel. Now, we submit that the train shown in Fig. 17 is mechanically equivalent to that of Fig. 15; the velocity ratio and the directional relation being the same in both. And if in Fig. 17 we remove the index P, and fix upon its shaft three wheels like E, G, and I of Fig. 18, we shall have a combination mechanically equivalent to Ferguson's Paradox, the three last wheels rotating in vertical planes about horizontal axes. The relative motions of those three wheels will be the same, obviously, as in Fig. 18; and according to the formula their absolute motions are the same, and we are invited to perceive that the central one does not rotate at all about its axis.
But it does rotate, nevertheless; and this unquestioned fact is of itself enough to show that there is something wrong with the formula as applied to trains like those in question. What that something is, we think, has been made clear by what precedes; since it is impossible in any sense to add together motions which are unlike, it will be seen that in order to obtain an intelligible result in cases like these, the equation must be of the form n'/(m'-a) = n/m. We shall then have:
| For the wheel F, | n m |
= | 20 19 |
= | n' -a |
, ∴ n' = - | 20 19 |
a. |
| For the wheel H, | n m |
= | 1 | = | n' -a |
, ∴ n' = - | a; | |
| For the wheel K, | n m |
= | 21 20 |
= | n' -a |
, ∴ n' = - | 21 20 |
a, |
which corresponds with the actual state of things; all three wheels rotate in the same direction, the central one at the same rate as the train arm, one a little more rapidly and the third a little more slowly.
It is, then, absolutely necessary to make this modification in the general formula, in order to apply it in determining the rotations of any wheel of an epicyclic train whose axis is not parallel to that of the sun-wheels. And in this modified form it applies equally well to the original arrangement of Ferguson's paradox, if we abandon the artificial distinction between "absolute" and "relative" rotations of the planet-wheels, and regard a spur-wheel, like any other, as rotating on its axis when it turns in its bearings; the action of the device shown in Fig. 18 being thus explained by saying that the wheel H turns once backward during each forward revolution of the train-arm, while F turns a little more and K a little less than once, in the same direction. In this way the classification and analysis of these combinations are made more simple and consistent, and the incongruities above pointed out are avoided; since, without regard to the kind of gearing employed or the relative positions of the axes, we have the two equations:
| I. | n' - a m' - a |
= | n m | , for all complete trains; |
| II. | n' m' - a |
= | n m | , for all incomplete trains. |
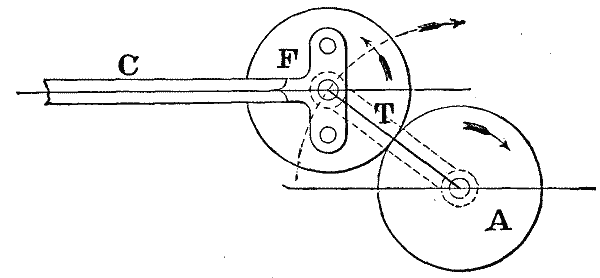
PLANETARY WHEEL TRAINS. Fig. 19
As another example of the difference in the application of these formulæ, let us take Watt's sun and planet wheels, Fig. 19. This device, as is well known, was employed by the illustrious inventor as a substitute for the crank, which some one had succeeded in patenting. It consists merely of two wheels A and F connected by the link T; A being keyed on the shaft of the engine and F being rigidly secured to the connecting-rod. Suppose the rod to be of infinite length, so as to remain always parallel to itself, and the two wheels to be of equal size.
Then, according to Prof. Willis' analysis, we shall have—
| n' - a m' - a |
= | n m |
= -1, n' = 0, ∴ | -a m' - a |
= -1, whence |
-a = a - m', or m = 2a.
The other view of the question is, that F turns once backward in its bearings during each forward revolution of T; whence in Eq. 2 we have—
| n' m' - a |
= | n m |
= -1, n' = - a, |
| ∴ | -a m' - a |
= -1 which gives -a = a - m', or m' = 2a, |
as before.
It is next to be remarked, that the errors which arise from applying Eq. I. to incomplete trains may in some cases counterbalance and neutralize each other, so that the final result is correct.
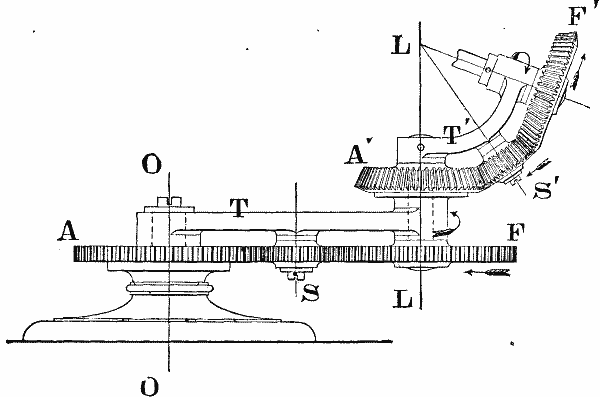
PLANETARY WHEEL TRAINS. Fig. 20
For example, take the combination shown in Fig. 20. This consists of a train-arm T revolving about the vertical axis OO of the fixed wheel A, which is equal in diameter to F, which receives its motion by the intervention of one idle wheel carried by a stud S fixed in the arm. The second train-arm T' is fixed to the shaft of F and turns with it; A' is secured to the arm T, and F' is actuated by A' also through a single idler carried by T'.
We have here a compound train, consisting of two simple planetary trains, A—F and A'—F'; and its action is to be determined by considering them separately. First suppose T' to be removed and find the motion of F; next suppose F to be removed and T fixed, and find the rotation of F'; and finally combine these results, noting that the motion of T' is the same as that of F, and the motion of A' the same as that of T.
Then, according to the analysis of Prof. Willis, we shall have (substituting the symbol t for a in the equation of the second train, in order to avoid confusion):
| 1. Train A—F. | n | = 1 = | m' - a | ; m' = 0, |
| m | m' - a | |||
| whence | n' - a | = 1, n' = 0, = rot. of F. | ||
| - a | ||||
| 2. Train A'—F'. | n | = 1 = | m' - t | ; m' = 0, |
| m | m' - t | |||
| whence again | n' - t | = 1, t = 0, = rot. of F'. | ||
| - t | ||||
Of these results, the first is explicable as being the absolute rotation of F, but the second is not; and it will be readily seen that the former would have been equally absurd, had the axis LL been inclined instead of vertical. But in either case we should find the errors neutralized upon combining the two, for according to the theory now under consideration, the wheel A', being fixed to T, turns once upon its axis each time that train arm revolves, and in the same direction; and the revolutions of T' equal the rotations of F, whence finally in train A'—F' we have:
| 3. | n | = 1 = | n' - t | ; in which t = 0, m' = a, |
| m | m' - t | |||
| which gives | n' - 0 | = 1, or n' = a. | ||
| a - 0 | ||||
This is, unquestionably, correct; and indeed it is quite obvious that the effect upon F' is the same, whether we say that during a revolution of T the wheel A' turns once forward and T' not at all, or adopt the other view and assert that T' turns once backward and A' not at all. But the latter view has the advantage of giving concordant results when the trains are considered separately, and that without regard to the relative positions of the axes or the kind of gearing employed. Analyzing the action upon this hypothesis, we have:
| In train A—F: | n | = 1 = | n' | ; m' = 0, ∴ | n' | = 1, or n' = -a; |
| m | m' - a | -a | ||||
| In train A'—F': | n' | = 1 = | n' | ; m' = 0, ∴ | n' | = 1, or n' = -t; |
| m | m' - t | -t |
In combining, we have in the latter train m' = 0, t = -a, whence
| n m | = 1 = | n' m' - t |
gives | n' +a |
= 1, or n' = a, as before. |
Now it happens that the only examples given by Prof. Willis of incomplete trains in which the axis of a planet-wheel whose motion is to be determined is not parallel to the central axis of the system, are similar to the one just discussed; the wheel in question being carried by a secondary train-arm which derives its motion from a wheel of the primary train.
The application of his general equation in these cases gives results which agree with observed facts; and it would seem that this circumstance, in connection doubtless with the complexity of these compound trains, led him to the too hasty conclusion that the formula would hold true in all cases; although we are still left to wonder at his overlooking the fact that in these very cases the "absolute" and the "relative" rotations of the last wheel are identical.
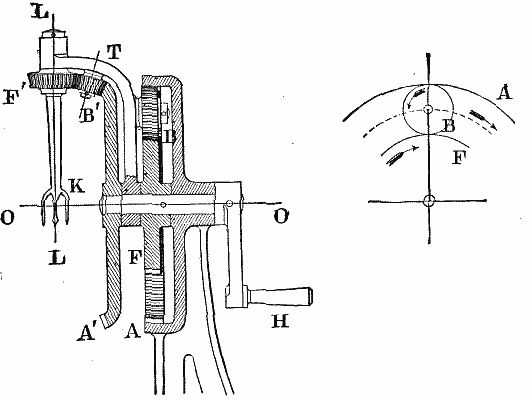
PLANETARY WHEEL TRAINS. Fig. 21
In Fig. 21 is shown a combination consisting also of two distinct trains, in which, however, there is but one train-arm T turning freely upon the horizontal shaft OO, to which shaft the wheels A', F, are secured; the train-arm has two studs, upon which turn the idlers B B', and also carries the bearings of the last wheel F'; the first wheel A is annular, and fixed to the frame of the machine. Let it be required to determine the results of one revolution of the crank H, the numbers of teeth being assigned as follows:
A = 60, F = 30, A' = 60, F' = 10.
We shall then have, for the train ABF (Eq. I.),
| n | = - | 60 | = -2 = | n' - a | , in which n' = 1, m' = 0, |
| m | 30 | m' - a' |
| whence -2 = | 1 - a -a |
, 2a = 1 - a, 3a - 1, a = | 1 3 | . |
And for the train A'B'F' (Eq. II.),
| n | = | 60 | = 6 = | n' | , in which a = | 1 | , m' = 1, |
| m | 10 | m' - a' | 3 |
| whence 6 = | n' | , or n' = 4. |
| 1 - (1/3) |
That is, the last wheel F' turns four times about the axis LL during one revolution of the crank H. But according to Profs. Willis and Goodeve, we should have for the second train:
| n | = | 60 | = 6 = | n' - a | , in which a = | 1 | , m' = 1, |
| m | 10 | m' - a' | 3 |
| which gives 6 = | n' - (1/3) | , n' - | 1 | = 4, n' = 4 | 1 | , |
| 1 - (1/3) | 3 | 3 |
or four and one-third revolutions of F' for one of H.
This result, no doubt, might be near enough to the truth to serve all practical purposes in the application of this mechanism to its original object, which was that of paring apples, impaled upon the fork K; but it can hardly be regarded as entirely satisfactory in a general way; nor can the analysis which renders such a result possible.
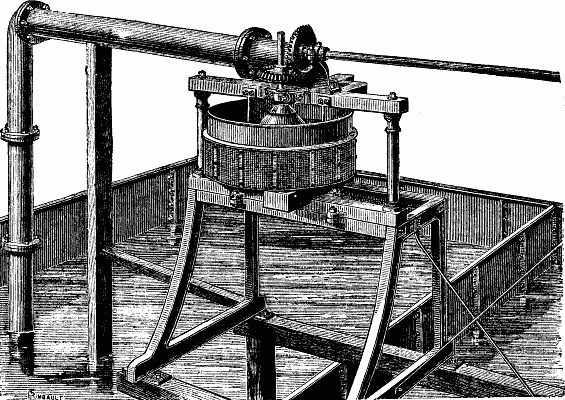
The need of irrigating prairies, inundating vines, drying marshes, and accumulating electricity cheaply has, for some time past, led to a search for some means of utilizing the forces of nature better than has ever hitherto been done. Wind, which figures in the first rank as a force, has thus far, with all the mills known to us, rendered services that are much inferior to those that we have a right to expect from it with improved apparatus; for the work produced, whatever the velocity of the wind, has never been greater than that that could be effected by wind of seven meters per second. But, thanks to the experiments of recent years, we are now obtaining an effective performance double that which we did with apparatus on the old system.
Desirous of making known the efforts that have been made in this direction, we lately described Mr. Dumont's atmospheric turbine. In speaking of this apparatus we stated that aerial motors generally stop or are destroyed in high winds. Recently, Mr. Sanderson has communicated to us the result of some experiments that he has been making for years back by means of an apparatus which he styles a pantanemone.
The engraving that we give of this machine shows merely a cabinet model of it; and it goes without saying that it is simply designed to exhibit the principle upon which its construction is based.
Two plane surfaces in the form of semicircles are mounted at right angles to each other upon a horizontal shaft, and at an angle of 45° with respect to the latter. It results from this that the apparatus will operate (even without being set) whatever be the direction of the wind, except when it blows perpendicularly upon the axle, thus permitting (owing to the impossibility of reducing the surfaces) of three-score days more work per year being obtained than can be with other mills. Three distinct apparatus have been successively constructed. The first of these has been running for nine years in the vicinity of Poissy, where it lifts about 40,000 liters of water to a height of 20 meters every 24 hours, in a wind of a velocity of from 7 to 8 meters per second. The second raises about 150,000 liters of water to the Villejuif reservoir, at a height of 10 meters, every 24 hours, in a wind of from 5 to 6 meters. The third supplies the laboratory of the Montsouris observatory.
The first is not directible, the second may be directed by hand, and the third is directed automatically. These three machines defied the hurricane of the 26th of last January.—La Nature.
The Spanish and Portuguese papers have recently made known some interesting experiments that have been made by Mr. Carlos Relvas with a new life-boat which parts the waves with great facility and exhibits remarkable stability. This boat, which is shown in front view in one of the corners of our engraving, is T-shaped, and consists of a very thin keel connected with the side-timbers by iron rods. Cushions of cork and canvas are adapted to the upper part, and, when the boat is on the sea, it has the appearance of an ordinary canoe, although, as may be seen, it differs essentially therefrom in the submerged part. When the sea is heavy, says Mr. Relvas, and the high waves are tumbling over each other, they pass over my boat, and are powerless to capsize it. My boat clears waves that others are obliged to recoil before. It has the advantage of being able to move forward, whatever be the fury of the sea, and is capable, besides, of approaching rocks without any danger of its being broken.
A committee was appointed by the Portuguese government to examine this new life-boat, and comparative experiments were made with it and an ordinary life-boat at Porto on a very rough sea. Mr. Relvas's boat was manned by eight rowers all provided with cork girdles, while the government life-boat was manned by twelve rowers and a pilot, all likewise wearing cork girdles. The chief of the maritime department, an engineer of the Portuguese navy and a Portuguese deputy were present at the trial in a pilot boat. The three boats proceeded to the entrance of the bar, where the sea was roughest, and numerous spectators collected upon the shore and wharfs followed their evolutions from afar.
The experiments began at half past three o'clock in the afternoon. The two life-boats shot forward to seek the most furious waves, and were seen from afar to surmount the billows and then suddenly disappear. It was a spectacle as moving as it was curious. It was observed that Mr. Relvas's boat cleft the waves, while the other floated upon their surface like a nut-shell. After an hour's navigation the two boats returned to their starting point.
The official committee that presided over these experiments has again found in this new boat decided advantages, and has pointed out to its inventor a few slight modifications that will render it still more efficient.—La Nature.
The series of experiments we are about to describe has recently been made by Mr. Horatio Phillips, a practical gun maker of London. The results will no doubt prove of interest to those concerned in the use or manufacture of firearms.
The reason that the two barrels of a shot gun or rifle will, if put together parallel, throw their charges in diverging lines has never yet been satisfactorily accounted for, although many plausible and ingenious theories have been advanced for the purpose. The natural supposition would be that this divergence resulted from the axes of the barrels not being in the same vertical plane as the center line of the stock. That this is not the true explanation of the fact, the following experiment would tend to prove.
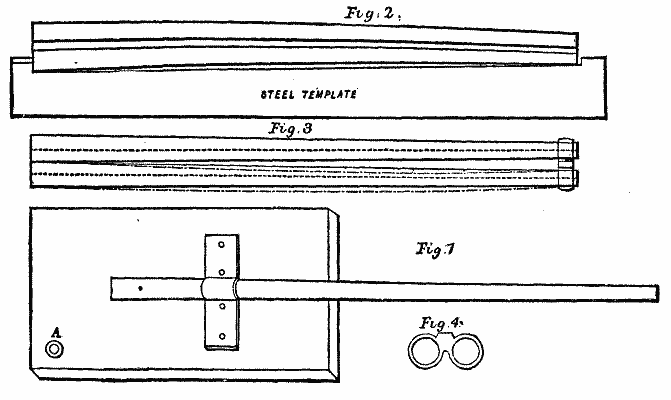
EXPERIMENTS WITH DOUBLE-BARRELLED GUNS.
Fig. 1 represents a single barrel fitted with sights and firmly attached to a heavy block of beech. This was placed on an ordinary rifle rest, being fastened thereto by a pin at the corner, A, the block and barrel being free to revolve upon the pin as a center. Several shots were fired both with the pin in position and with it removed, the barrel being carefully pointed at the target each time. No practical difference in the accuracy of fire was discernible under either condition. When the pin was holding the corner of the block, the recoil caused the barrel to move from right to left in a circular path; but when the pin was removed, so that the block was not attached to the rest in any way, the recoil took place in a line with the axis of the bore. It will be observed that the conditions which are present when a double barreled gun is fired in the ordinary way from the shoulder were in some respects much exaggerated in the apparatus, for the pin was a distance of 3 in. laterally from the axis of the barrel, whereas the center of resistance of the stock of a gun against the shoulder would ordinarily be about one-sixth of this distance from the axis of the barrel. This experiment would apparently tend to prove that the recoil does not appreciably affect the path of the projectile, as it would seem that the latter must clear the muzzle before any considerable movement of the barrel takes place.
With a view to obtain a further confirmation of the result of this experiment, it was repeated in a different form by a number of shots being fired from a "cross-eyed" rifle,1 in which the sights were fixed in the center of the rib. Very accurate shooting was obtained with this arm.
A second theory, often broached, in order to account for the divergence of the charge, is that the barrel which is not being fired, by its vis inertia in some way causes the shot to diverge. In order to test this, Mr. Phillips took a single rifle and secured it near the muzzle to a heavy block of metal, when the accuracy of the shooting was in no way impaired.
So far the experiments were of a negative character, and the next step was made with a view to discover the actual cause of the divergence referred to. A single barrel was now taken, to which a template was fitted, in order to record its exact length. The barrel was then subjected to a heavy internal hydrostatic pressure. Under this treatment it expanded circumferentially and at the same time was reduced in length. This, it was considered, gave a clew to the solution of the problem. A pair of barrels was now taken and a template fitted accurately to the side of the right-hand one. As the template fitted the barrel when the latter was not subject to internal pressure, upon such pressure being applied any alterations that might ensue in the length or contour of the barrel could be duly noted. The right-hand barrel was then subjected to internal hydrostatic pressure. The result is shown in an exaggerated form in Fig. 2. It will be seen that both barrels are bent into an arched form. This would be caused by the barrel under pressure becoming extended circumferentially, and thereby reduced in length, because the metal that is required to supply the increased circumference is taken to some extent from the length, although the substance of metal in the walls of the barrel by its expansion contributes also to the increased diameter. A simple illustration of this effect is supplied by subjecting an India-rubber tube to internal pressure. Supposing the material to be sufficiently elastic and the pressure strong enough, the tube would ultimately assume a spherical form. It is a well known fact that heavy barrels with light charges give less divergence than light barrels with heavy charges.
After the above experiments it was hoped that, if a pair of barrels were put together parallel and soldered only for a space of 3 in. at the breech end, and were then coupled by two encircling rings joined together as in Fig. 4, the left-hand ring only being soldered to the barrel, very accurate shooting would be obtained. For, it was argued, that by these means the barrel under fire would be able to contract without affecting or being affected by the other barrel; that on the right-hand, it will be seen by the illustration, was the one to slide in its ring.
A pair of able 0.500 bore express rifle barrels were accordingly fitted in this way. Fig. 3 shows the arrangement with the rings in position. Upon firing these barrels with ordinary express charges it was found that the lines of fire from each barrel respectively crossed each other, the bullet from the right-hand barrel striking the target 10 in. to the left of the bull's eye, while the left barrel placed its projectile a similar distance in the opposite direction; or, as would be technically said, the barrels crossed 20 in. at 100 yards, the latter distance being the range at which the experiment was made. These last results have been accounted for in the following manner: The two barrels were rigidly joined for a space of 3 in., and for that distance they would behave in a manner similar to that illustrated in Fig. 2, and were they not coupled at the muzzles by the connecting rings they would shoot very wide, the charges taking diverging courses. When the connecting rings are fitted on, the barrel not being fired will remain practically straight, and, as it is coupled to the barrel being fired by the rings, the muzzle of the latter will be restrained from pointing outward.
The result will be as shown in an exaggerated manner by the dotted lines on the right barrel in Fig. 3.
It would appear from these experiments that when very accurate shooting is required at long ranges with double-barreled rifles, they should be mounted in a manner similar to that adopted in the manufacture of the Nordenfelt machine gun, in which weapon the barrels are fitted into a plate at the extreme breech end, the muzzles projecting through holes bored to receive them in a metal plate. No unequal expansion would then take place, and the barrels would be free to become shorter independently of each other. We give the above experiments on the authority of their author, who, we believe, has taken great pains to render them as exhaustive as possible, so far as they go.—Engineering.
A cross-eyed rifle is one made with a crooked stock for the purpose of shooting from the right shoulder, aim being taken with the left eye.
The distinguishing feature in the ball turning machine shown opposite is that the tool is stationary, while the work revolves in two directions simultaneously. In the case of an ordinary spherical object, such as brass clack ball, the casting is made from a perfect pattern having two small caps or shanks, in which the centers are also marked to avoid centering by hand. It is fixed in the machine between two centers carried on a face plate or chuck, with which they revolve. One of these centers, when the machine is in motion, receives a continuous rotary motion about its axis from a wormwheel, D. This is driven by a worm, C, carried on a shaft at the back of the chuck, and driven itself by a wormwheel, B, which gears with a screw which rides loosely upon the mandrel, and is kept from rotating by a finger on the headstock. This center, in its rotation, carries with it the ball, which is thus slowly moved round an axis parallel to the face plate, at the same time that it revolves about the axis of the mandrel, the result being that the tool cuts upon the ball a scroll, of which each convolution is approximately a circle, and lies in a plane parallel to the line of centers.
When the chuck is set for one size of ball, which may be done in a few minutes, any quantity of that diameter may be turned without further adjustment. A roughing cut for a 2 in. ball may be done in one minute, and a finishing cut leaving the ball quite bright in the same time. The two paps are cut off within one-sixteenth of an inch and then broken off, and the ball finished in the usual way. On account of the work being geometrically true, the finishing by the ferrule tool is done in one quarter of the time usually required.
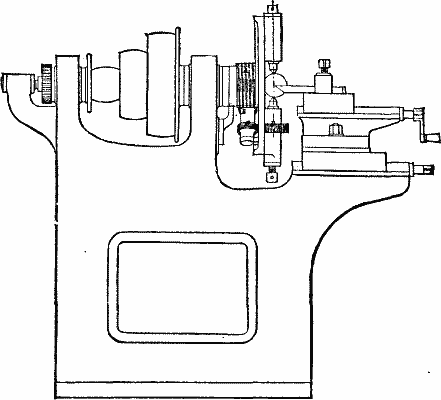
IMPROVED BALL TURNING MACHINE.
The chuck may be applied to an ordinary lathe or may be combined with a special machine tool, as show in our illustration. In the latter case everything is arranged in the most handy way for rapid working, and six brass balls of 2 in. in diameter can be turned and finished in an hour. The machine is specially adapted for turning ball valves for pumps, pulsometers, and the like, and in the larger sizes for turning governor balls and spherical nuts for armor plates, and is manufactured by Messrs. Wilkinson and Lister, of Bradford Road Iron Works, Keighley.—Engineering.
It often happens in towns and where manufactories are crowded together, that the supply of water for condensing purposes is very small, and consequently that it attains an inconveniently high temperature under unfavorable conditions of weather, resulting in the deterioration of the vacuum and a consequent increase in the consumption of fuel. To remedy or to diminish this difficulty, Messrs. Boase and Miller, of London, have brought out the water cooler illustrated above. This consists, says Engineering, of a revolving basket of wire gauze surrounding an inner stationary vessel pierced with numerous small holes, through which the heated water discharged by the air pump finds its way into the basket, to be thrown out in the form of fine spray to a distance of 20 ft. at each side. The drops are received in the tank or pond, and in their rapid passage through the air are sufficiently cooled to be again injected into the condenser.
The illustration shows a cooler having a basket three feet in diameter, revolving at 300 revolutions per minute, and discharging into a tank 40 ft. square. It requires 3 to 4 indicated horse-power to drive it, and will cool 300 gallons per minute. The following decrease of temperature has been observed in actual practice: Water entering at 95 deg. fell 20 deg. in temperature; water entering at 100 deg. to 110 deg. fell 25 deg.; and water entering at 110 deg. to 120 deg. fell 30 deg. The machine with which these trials were made was so placed that the top of the basket was four ft. from the surface of the water in the pond. With a greater elevation, as shown in the engraving, better results can be obtained.
IMPROVED WATER COOLING APPARATUS.
The advantages claimed for the cooler are that by its means the temperature of the injection water can be reduced, the cost and size of cooling ponds can be diminished, and condensing engines can be employed where hitherto they have not been possible. The apparatus has been for two years in operation at several large factories, and there is every reason to believe that its use will extend, as it supplies a real want in a very simple and ingenious manner. Messrs. Duncan Brothers, of Dundee and 32 Queen Victoria Street, E.C., are the manufacturers.
This is a pulley recently introduced by Messrs. J. and E. Hall, of Dartford Eng. With the exception of the boss, which is cast, it is composed entirely of steel or sheet iron. In place of the usual arms a continuous web of corrugated sheet metal connects the boss to the rim; this web is attached to the boss by means of Spence's metal. Inside the rim, which is flanged inward, a double hoop iron ring is fixed for strengthening purposes. The advantageous disposition of metal obtained by means of the corrugated web enables the pulley to be made of a given strength with less weight of material, and from this cause and also on account of being accurately balanced these pulleys are well adapted for high speeds.

Although the electric telegraph is, comparatively speaking, a recent invention, yet methods of communication at a distance, by means of signals, have probably existed in all ages and in all nations. There is reason to believe that among the Greeks a system of telegraphy was in use, as the burning of Troy was certainly known in Greece very soon after it happened, and before any person had returned from Troy. Polybius names the different instruments used by the ancients for communicating information—"pyrsia," because the signals were always made by means of fire lights. At first they communicated information of events in an imperfect manner, but a new method was invented by Cleoxenus, which was much improved by Polybius, as he himself informs us, and which may be described as follows:
Take the letters of the alphabet and arrange them on a board in five columns, each column containing five letters; then the man who signals would hold up with his left hand a number of torches which would represent the number of the column from which the letter is to be taken, and with his right hand a number of torches that will represent the particular letter in that column that is to be taken. It is thus easy to understand how the letters of a short sentence are communicated from station to station as far as required. This is the pyrsia or telegraph of Polybius.
It seems that the Romans had a method of telegraphing in their walled cities, either by a hollow formed in the masonry, or by a tube fixed thereto so as to confine the sound, in order to convey information to any part they liked. This method of communicating is in the present age frequently employed in the well known speaking tubes. It does not appear that the moderns had thought of such a thing as a telegraph until 1661, when the Marquis of Worcester, in his "Century of Inventions," affirmed that he had discovered a method by which a man could hold discourse with his correspondent as far as they could reach, by night as well as by day; he did not, however, describe this invention.
Dr. Hooke delivered a discourse before the Royal Society in 1684, showing how to communicate at great distances. In this discourse he asserts the possibility of conveying intelligence from one place to another at a distance of 120 miles as rapidly as a man can write what he would have sent. He takes to his aid the then recent invention of the telescope, and explains how characters exposed at one station on the top of one hill may be made visible to the next station on the top of the next hill. He invented twenty-four simple characters, each formed of a combination of three deal boards, each character representing a letter by the use of cords; these characters were pushed from behind a screen and exposed, and then withdrawn behind the screen again. It was not, however, until the French revolution that the telegraph was applied to practical purposes; but about the end of 1703 telegraphic communication was established between Paris and the frontiers, and shortly afterward telegraphs were introduced into England.
The history of the invention and introduction of the electric telegraph by Prof. Morse is one of inexhaustible interest, and every incident relating to it is worthy of preservation. The incidents described below will be found of special interest. The article is from the pen of the late Judge Neilson Poe, and was the last paper written by him. He prepared it during his recent illness, the letter embodied in it from Mr. Latrobe being of course obtained at the time of its date. It is as follows:
On the 5th of April, 1843, when the monthly meeting of the directors of the Baltimore & Ohio Railroad Company was about to adjourn, the President, the Hon. Louis McLane, rose with a paper in his hand which he said he had almost overlooked, and which the Secretary would read. It proved to be an application from Prof. Morse for the privilege of laying the wires of his electric telegraph along the line of the railroad between Baltimore and Washington, and was accompanied by a communication from B.H. Latrobe, Esq., Chief Engineer, recommending the project as worthy of encouragement.
On motion of John Spear Nicholas, seconded by the Hon. John P. Kennedy, the following resolution was then considered:
Resolved, "That the President be authorized to afford Mr. Morse such facilities as may be requisite to give his invention a proper trial upon the Washington road, provided in his opinion and in that of the engineer it can be done without injury to the road and without embarrassment to the operations of the company, and provided Mr. Morse will concede to the company the use of the telegraph upon the road without expense, and reserving to the company the right of discontinuing the use if, upon experiment, it should prove in any manner injurious."
"Whatever," said Mr. McLane, "may be our individual opinions as to the feasibility of Mr. Morse's invention, it seems to me that it is our duty to concede to him the privilege he asks, and to lend him all the aid in our power, especially as the resolution carefully protects the company against all present or future injury to its works, and secures us the right of requiring its removal at any time."
[In view of the fact that no railroad can now be run safely without the aid of the telegraph, the cautious care with which the right to remove it if it should become a nuisance was reserved, strikes one at this day as nearly ludicrous.]
A short pause ensued, and the assent of the company was about to be assumed, when one of the older directors, famed for the vigilance with which he watched even the most trivial measure, begged to be heard.
He admitted that the rights and interests of the work were all carefully guarded by the terms of the resolution, and that the company was not called upon to lay out any of its means for the promotion of the scheme. But notwithstanding all this, he did not feel, as a conscientious man, that he could, without further examination, give his vote for the resolution. He knew that this idea of Mr. Morse, however plausible it might appear to theorists and dreamers, and so-called men of science, was regarded by all practical people as destined, like many other similar projects, to certain failure, and must consequently result in loss and possibly ruin to Mr. Morse. For one, he felt conscientiously scrupulous in giving a vote which would aid or tempt a visionary enthusiast to ruin himself.
Fortunately, the views of this cautious, practical man did not prevail. A few words from the mover of the resolution, Mr. Nicholas, who still lives to behold the wonders he helped to create, and from Mr. Kennedy, without whose aid the appropriation would not have passed the House of Representatives, relieved the other directors from all fear of contributing to Mr. Morse's ruin, and the resolution was adopted. Of the President and thirty directors who took part in this transaction, only three, Samuel W. Smith, John Spear Nicholas, and the writer, survive. Under it Morse at once entered upon that test of his invention whose fruits are now enjoyed by the people of all the continents.
It was not, however, until the spring of 1844 that he had his line and its appointments in such a condition as to allow the transmission of messages between the two cities, and it was in May of that year that the incident occurred which has chiefly led to the writing of this paper.
MY DEAR MR. POE: Agreeably to my promise, this morning I put on paper my recollection of the introduction of the magnetic telegraph between Baltimore and Washington. I was counsel of the Baltimore & Ohio Railroad Co. at the time, and calling on Mr. Louis McLane, the President, on some professional matter, was asked in the course of conversation whether I knew anything about an electric telegraph which the inventor, who had obtained an appropriation from Congress, wanted to lay down on the Washington branch of the road. He said he expected Mr. Morse, the inventor, to call on him, when he would introduce me to him, and would be glad if I took an opportunity to go over the subject with him and afterward let him, Mr. McLane, know what I thought about it. While we were yet speaking, Mr. Morse made his appearance, and when Mr. McLane introduced me he referred to the fact that, as I had been educated at West Point, I might the more readily understand the scientific bearings of Mr. Morse's invention. The President's office being no place for prolonged conversation, it was agreed that Mr. Morse should take tea at my dwelling, when we would go over the whole subject. We met accordingly, and it was late in the night before we parted. Mr. Morse went over the history of his invention from the beginning with an interest and enthusiasm that had survived the wearying toil of an application to Congress, and with the aid of diagrams drawn on the instant made me master of the matter, and wrote for me the telegraphic alphabet which is still in use over the world. Not a small part of what Mr. Morse said on this occasion had reference to the future of his invention, its influence upon communities and individuals, and I remember regarding as the wild speculations of an active imagination what he prophesied in this connection, and which I have lived to see even more than realized. Nor was his conversation confined to his invention. A distinguished artist, an educated gentleman, an observant traveler, it was delightful to hear him talk, and at this late day I recall few more pleasant evenings than the only one I passed in his company.
Of course, my first visit the next morning was to Mr. McLane to make my report. By this time I had become almost as enthusiastic as Mr. Morse himself, and repeated what had passed between us. I soon saw that Mr. McLane was becoming as eager for the construction of the line to Washington as Mr. Morse could desire. He entered warmly into the spirit of the thing, and laughed heartily, if not incredulously, when I told him that although he had been Minister to England, Secretary of State, and Secretary of the Treasury, his name would be forgotten, while that of Morse would never cease to be remembered with gratitude and praise. We then considered the question as to the right of the company to permit the line to be laid in the bed of the road—the plan of construction at that time being to bury in a trench some eight or ten inches deep a half inch leaden tube containing the wrapped wire that was to form the electric circuit. About this there was, in my opinion, no doubt, and it was not long after that the work of construction commenced. I met Mr. Morse from time to time while he lived, and often recurred to the evening's discussion at my house in Baltimore.
The above is the substance of what I have more than once related to other persons. I hope you will persist in your design of putting on paper your own very interesting recollections in this connection, and if what I have contributed of mine is of service to you, I shall be much pleased.
Most truly yours,
JOHN H.B. LATROBE.
March 3, 1881.
At the origin of every science, of whatever nature it may be, there is always a fruitless period, of greater or less length, characterized by the warfare of a few superior minds against general apathy. The finest discoveries pass unperceived, so to speak, since they cannot cross the limits of a narrow circle; and it often happens that they fall into oblivion before they have been seriously judged. Meanwhile, a slow progress is imperceptibly made, and, in measure as theoretical principles more clearly disengage themselves, a few industrial applications spring up and have the effect of awakening curiosity. An impulse is thus given, and from this moment a movement in advance goes on increasing at a headlong pace from day to day.
With electricity this period has been of comparatively short duration, since scarcely a century and a half separate us from the first experiments made in this line of research. Now that it has truly taken its place in a rank with the other sciences, we like to go back to the hesitations of the first hour, and trace, step by step, the history of the progress made, so as to assign to each one that portion of the merit that belongs to him in the common work. When we thus cast a retrospective glance we find ourselves in the presence of one strange fact, and that is the simultaneousness of discoveries. That an absolutely original idea, fertile in practical consequences, should rise at a given moment in a fine brain is well; we admire the discovery, and, in spite of us, a little surprise mingles with our admiration. But is it not a truly curious thing that several individuals should have had at nearly the same time that idea that was so astonishing in one? This, however, is a fact that the history of electrical inventions offers more than one example of. No one ignores the fact that the invention of the telephone gave rise to a notorious lawsuit, two inventors having had this ingenious apparatus patented on the same day and at nearly the same hour. This is one example among a thousand. In the history of dynamo-electric machines it is an equally delicate matter to fix upon the one to whom belongs the honor of having first clearly conceived the possibility of engendering continuous currents.
We do not wish to take up this debate nor to go over the history of the question again. Every one knows that the first continuous current electric generator whose form was practical is due to Zenobius Gramme, and dates back to July, 1871, an epoch at which appeared a memoir (entitled "Note upon a magneto-electric machine that produces continuous currents") that was read to the Academy of Sciences by Mr. Jamin. Ten years previous, Pacinotti had had a glimpse of the phenomenon, and of its practical realization, but was unfortunately unable to appreciate the importance of his discovery and the benefit that might be reaped from it. It is of slight consequence whether Gramme knew of this experiment or not, for the glory that attaches to his name could not be diminished for all that. But an interesting fact that we propose to dwell upon now has recently been brought to light in an electrical review published at Vienna.1 It results from documents whose authenticity cannot be doubted that, as far back as 1867, Mr. L. Pfaundler, a professor at Innsbruck, very clearly announced the reversibility of a magneto-electric motor constructed by Kravogl, a mechanician of the same place, and that he succeeded some time before Gramme in obtaining continuous currents.
The Kravogl motor that figured at the Universal Exhibition of 1867 is but little known, and it is now very difficult to obtain drawings of it. What is certain is that this motor is an application of the properties of the solenoid, and, from this standpoint, resembles the Bessolo motor that was patented in 1855. We may figure the apparatus to our mind very well if we suppose that in the Gramme ring a half and almost two-thirds of the core are removed, and the spirals are movable around the said core. If a current be sent into a portion of the spirals only, and in such a way that only half of the core be exposed, the latter will move with respect to the bobbin or the bobbin with respect to the core, according as we suppose the solenoid or the bobbin fixed. In the first case we have a Bessolo motor, and in the second a Kravogl one.
In order to obtain a continuous motion it is only necessary to allow the current to circulate successively in the different portions of the solenoid. It is difficult to keep the core in place, since it is unreachable, being placed in the interior of the bobbin. Kravogl solved this difficulty by constructing a hollow core into which he poured melted lead. This heavy piece, mounted upon rollers, assumed a position of equilibrium that resulted from its weight, from friction, and from magnetic attraction. But for a current of given intensity this position, once reached, did not vary, and so necessitated a simple adjustment of the rubbers. Under such circumstances, with a somewhat large number of sections, the polarity of the core was nearly constant. The spirals as a whole were attached to a soft iron armature that had the effect of closing up the lines of forces and forming a shell, so to speak.
Like Bessolo, Kravogl never thought of making anything but a motor, and did not perceive that his machine was reversible. It results from some correspondence between Dr. A. Von Waltenhofen and Mr. L. Pfaundler at this epoch that the latter clearly saw the possibility of utilizing this motor as a current generator. Under date of November 9, 1867, he wrote, in speaking of the Kravogl motor, which had just been taken to Innsbruck in order to send it to Paris. "I regret that I shall not be able to see it any more, for I should have liked to try to make it act in an opposite direction, that is to say, to produce a current or an electric light by means of mechanical work." A little more than two years later these experiments were carried out on a larger motor constructed by Kravogl in 1869, and Mr. Pfaundler was enabled to write as follows: "Upon running the machine by hand we obtain a current whose energy is that of one Bunsen element." This letter is dated February 11, 1870, that is to say, it is a year anterior to the note of Gramme.
FIG. 1.
In the presence of the historic interest that attaches to the question, we do not think it will be out of place to reproduce here the considerations that guided Prof. Pfaundler in the researches that led him to convert the Kravogl motor into a dynamo-electric machine. Let us consider two magnetized bars, db and bd', placed end to end and surrounded by a cylindrical armature forming a shell, this armature being likewise supposed to be a permanent magnet and to present poles of contrary direction opposite the poles of the bars. For the sake of greater simplicity this shell is represented by a part only in the figure, s n n s. If, into a magnetic field thus formed, we pass a spiral from left to right, the spiral will be traversed by a current whose direction will change according to the way in which the moving is done. It is only necessary to apply Lenz's law to see that a reversal of the currents will occur at the points, a and c, the direction of the current being represented by arrows in the figure. If we suppose a continual displacement of the spirals from left to right, we shall collect a continuous current by placing two rubbers at a and c. Either the core or the shell may be replaced by a piece of soft iron. In such a case this piece will move with the spiral and keep its poles that are developed by induction fixed in space. From this, in order to reach a dynamo-electric machine it is necessary to try to develop the energy of the magnetic field by the action of the current itself. If we suppose the core to be of soft iron, and make a closer study of the action of the current as regards the polarity that occurs under the influence of the poles, s, n, s, we shall see that from d to a and from b to c the current is contrary, while that from a to b and from c to d' it is favorable to the development of such polarity. In short, with a spiral moving from d to d' the resulting effect is nil, a fact, moreover, that is self-evident. Under such circumstances, if we suppose the shell, as well as the core, to be of soft iron, we shall obtain a feeble current due to the presence of remanent magnetism; but this magnetism will not be able to continue increasing under the influence of the current. To solve this difficulty two means present themselves: (1) to cause a, favorable magnetic current and act upon the armature, and (2) to suppress such portions of the current in the spirals as are injurious in effect. The first solution was thought of by Gramme in 1871, and is represented diagramatically in Fig. 2. The second is due to Prof. Pfaundler, and dates back to 1870. The core is cut through the center (Fig. 3), and the portion to the right is suppressed; the current is interrupted between da and cd', and is closed only between a and c (v, Fig. 1). It results from this arrangement that, under the action of the current, the polarity due to remanent magnetism does nothing but increase. It suffices then for but little remanent magnetism to prime the machine; the polarity of the shell continues to increase, and the energy of the magnetic field, and consequently of the current, has for a limit only the saturation of the soft iron. If, now, we curve the core, the spirals, and the armature into a circle, we have a Gramme or a Pfaundler machine, according as we consider Fig. 2 or Fig. 3.
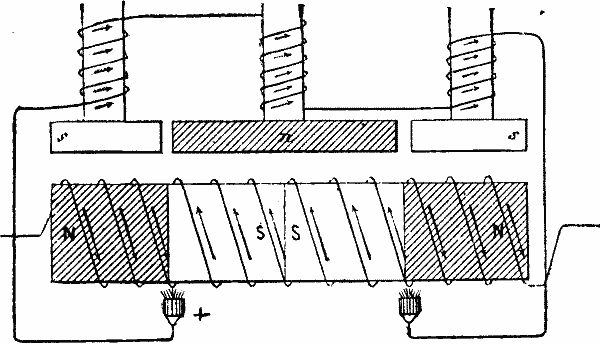
FIG. 2.
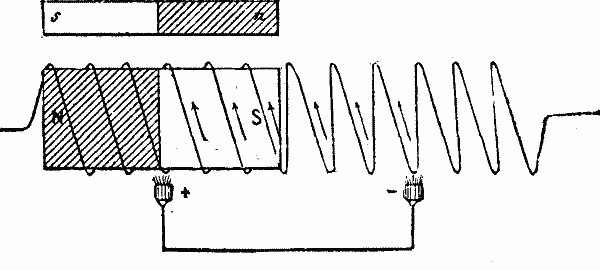
FIG. 3.
This latter apparatus has in this case the form shown in Fig. 4.
FIG. 4.
The spiral, s m b, is movable, and the core, N o s, is kept in a position of equilibrium by virtue of its weight, and is provided with rollers. For the sake of greater clearness, the front part of the armature is supposed to be removed. The current does not circulate in the spirals to the right of the diameter, W O, which latter is not absolutely vertical. The position of the rubbers and armature is regulated once for all. We do not know just what were the means devised by Kravogl to suppress the current in the spheres to the right. At all events, it is probable that the system has grown old since Gramme invented his collector. In the application of the Kravogl motor to the generation of continuous currents, Professor Pfaundler now proposes to ingeniously utilize the Gramme collector. In such a case the arrangement shown in Fig. 5 would be adopted. Let us suppose an ordinary collector having as many plates as there are sections in the ring, these plates being connected as usual with the entrance and exit wires of the sections. The diametrically opposite touches that are in the line, W O, are divided, and one of the halves is connected at the entrance, c a' (Fig. 4), with the corresponding section, while the other communicates with the exit, c' a, of the neighboring section. Each of these halves is prolonged by a piece of metal bent into the form of an arc of a circle and embracing a little less than a semi-circumference. Between these prolongations there is an insulating part. In the rotary motion of the spiral, at least one of the touches is always outside of the arc comprised between the brushes, R. In order to secure a continuity of the circuit in the effective arc, W S o, it is only necessary to arrange a rubber, M, in such a way as to establish a communication between the two parts of the divided touch as soon as this latter enters the arc under consideration.
In order to produce a current in the direction of the arrows shown in Fig. 4, the spiral and axle must revolve from right to left. In this case the rubber, M, occupies the position shown in the same figure, the brushes embracing an arc of a little less than 180°. As soon as the lower touch comes in contact with the brush, R, when the revolution is being effected from left to right, the rubber, M, establishes a communication between the two halves that have until now been isolated, and the current is no longer interrupted. The second touch during this time is at any point whatever of the arc, W N o, and the spirals corresponding to the latter arc outside of the circuit. In short, thanks to the rubber, M, we have an ordinary Gramme collector in that portion of the circuit comprised between the brushes, and a collector with a breakage of the circuit in the portion to the right.
FIG. 5.
This type of machine is entirely theoretical. In the apparatus used for Prof. Pfaundler's experiments in 1870, the armature revolved with the solenoid. The core and armature were of soft iron, and the core was arranged in a manner analogous to the preceding, and remained in place under the action of its weight, and the shell, forming a complete circle, revolved with poles fixed in space.
Practically, the machine that we have just described would prove inconvenient to realize, and would present serious inconveniences. In the first place, it seems to us quite difficult to transmit the motion of the solenoid to the axle, supposing the former to revolve within the armature. In the second place, considerable friction would surely occur between the spirals and core, and the axle, being submitted to a lateral stress, would be placed in a poor condition for work. It is even allowable to doubt whether such a type could be practically got up. At all events, no trial has as yet been made of it.
Compared with the Gramme machine, from an absolutely theoretical point of view, the Pfaundler apparatus presents undoubted advantages. A theoretically perfect dynamo electric machine would be one in which there was a complete reciprocity between the magnetizing action of the current and the inductive action of the magnetic field. Now, such is not the case in the Gramme machine. In this apparatus the soft iron core is at the same time a magnet through favorable induction and a disadvantageous electro-magnet. This double polarization is only remedied to a certain extent by the adjustment of the brushes. In the Pfaundler machine, on the contrary, the electro-magnetism and magnetism through induction act in the same direction, and concur in effecting a polarization that favors the production of the current. Looked at it in this light, the latter machine more nearly approaches the type of perfection than does that of Gramme.
But we must not forget that such qualities are purely theoretical. In practice the best machine is that in which the copper is best utilized, that is to say, that which with a given weight of this metal furnishes the most work. Now, this is certainly not the case in the Pfaundler machine, for here half or more than half of the ring is inert—a defect which is apparent at first sight. It results from this that as soon as we propose to obtain an electromotive force, however slight it be, we must get it with machines of large dimensions. Now, it is permissible to believe that under such circumstances (taking into consideration the complication of mechanical means that the construction of such apparatus necessitates, and the great friction that occurs) it would be impossible to obtain practical rotary velocities. Comparing his machine with Gramme's, Prof. Pfaundler expresses the idea that between them there is the same analogy as there is between a constant pressure and an expansion engine. With cylinders of equal diameters the work performed by the former of these is greater than that done by the second, but in the latter the expansive force of the steam is better utilized. This comparison seems to us to be more ingenious than exact. Would it not be coming nearer to the truth if we were to suppose a case of a hydraulic motor whose performance continued diminishing with the height of the fall, and would it not be advantageous under such circumstances to utilize only a portion of the fall for the purpose of increasing the motor's performance?
This machine, however, as before stated, has never as yet been constructed, so that experimental data relative to its mode of working are wanting. It is especially interesting as regards its origin, which dates back to an epoch at which researches on the dynamo electric machine were at their heat. It is in its historical aspect that it is proper to regard it, and it is from such a point of view that we have deemed it well to say a few words about it in this place.—La Lumiere Electrique.
Zeitschrift des Electrotechnischen Vereines in Wien, July, 1883.
We shall not attempt to pass in review the several apparatus that have hitherto been devised for igniting blasts in mining operations, but shall simply describe in this place a machine recently invented for this purpose by Mr. Bornhardt, an engineer to the Grand Duke of Brunswick.
This apparatus (shown in the accompanying engravings) consists essentially of two hard-rubber disks, A (Figs. 2 and 3), keyed to an iron axle, and of two rubbers, B, that are formed of skin and are held against the disks by small springs, R; motion is communicated to the axle, a, by means of a pair of gearings, a and b, and a crank, f.
BORNHARDT'S ELECTRIC MACHINE FOR BLASTING IN MINES.
Each disk revolves between two metallic rings, c, provided with points that attract and collect in Leyden jars, D, the electricity produced by the friction. For discharging the condensers there is employed a manipulator formed of a rod, mm, which can be acted upon, from the exterior, by means of a button, k. Upon bringing the ball, m, of the rod in contact with the ball, p, of the condenser, the lever (which then takes the position shown by the dotted line) continues to remain in connection with a small ring, q, through a special spring. Another ring, t, is connected in the same way with the external armature of the condenser. Upon connecting the rings, p and t, by a wire to which cartridges are attached, any number of the latter may be ignited.
The parts that we have just enumerated are inclosed in a tin box covered with a wooden casing, P. Between the two there is inserted a sheet of hard rubber in order to prevent a loss of electricity; the whole is held in place by strong springs.
In order to show the normal state of the condenser, a scale consisting of 15 metallic buttons to give the dimensions of the sparks, is arranged at X. This scale is capable of being connected with the rings, q and t, by means of chains; when the spark obtained after 15 or 20 revolutions considerably exceeds the intervals of the scale, it is a sure thing that the machine is in a proper state.
In order to prepare the apparatus for carriage, the winch is taken off and placed in the compartment, m, which is closed by means of a door, Q.
Figs. 5 and 6 show the arrangement of the dynamite cartridges and wires in the blast hole. Figs. 7 to 10 show different arrangements of the igniting wires. Figs. 11 and 12 give the general arrangement for igniting a number of cartridges simultaneously by means of the electric machine. Fig. 13 shows the arrangement where powder is employed. Fig. 14 shows the arrangement of a horizontal hole.—Annales Industrielles.
The object of this apparatus is to close an electric circuit when the temperature of a room rises above a certain point. Many devices have been invented for effecting this object, each of which have their own advantages or disadvantages. The invention of Mr. Pritchett enables the required result to be obtained in a very satisfactory manner. The apparatus consists (as shown by the figure) of a long glass vessel containing air; connected to this vessel there is a glass tube filled with mercury. The whole is mounted on a metal cradle, which turns on pivots. According to the position which the glass vessel and its adjuncts occupy in the cradle (this position being adjustable by means of a thumb-screw, seen at the upper part of the cradle), so will the same have a tendency to rock longitudinally over to one side or the other. Now, if we suppose the position to be such that the right hand end of the glass vessel is depressed, and the left hand end raised, then if the vessel becomes subjected to an elevation of temperature, the air inside the same will become expanded, and the mercury column in the tube will be driven over to the left, and will rise in the turned up end of the tube. This will cause the left hand branch of the glass vessel, and its attachments, to become increased in weight, while the right hand branch will become proportionally lighter; the consequence of this will be that the vessel and its cradle will cant over, and by falling on an electrical contact will close a circuit and sound an alarm. It is obvious that the apparatus is equally well adapted for indicating a diminution as well as an increase of temperature, for if the electrical contact be placed under the right hand portion of the cradle, and the latter be adjusted so that in its normal position its left hand portion is depressed, then when the glass vessel becomes cooled, the air in it will contract, and the mercury will fall in the turned-up portion of the tube before referred to, and will rise in the limb connected to the vessel, consequently the cradle and glass vessel will cant over in the reverse way to that which it did in the first case.
Owing to the surface which the glass vessel exposes, the air inside quickly responds to any external change of temperature, consequently the apparatus is very sensitive. Another important feature is the fact that the cradle and vessel in canting over acquires a certain momentum, and thus the contact made becomes very certain.
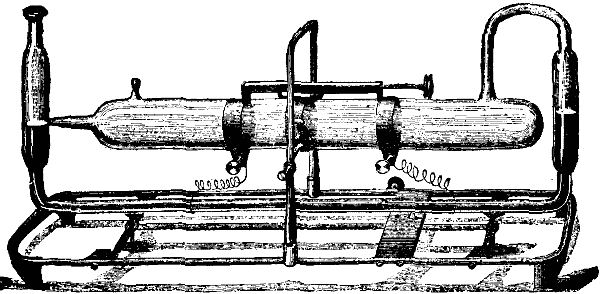
PRITCHETT'S ELECTRIC FIRE ALARM.
Mr. Pritchett proposes that his apparatus shall give external evidence outside the house by ringing a gong, and by dropping a semaphore arm released by an electromagnet. He also proposes (as has often been suggested) that a water supply shall be automatically turned on.—Electrical Review.
Dr. G. Gore, F.R.S., has invented an improved thermopile for measuring small electromotive forces. It consists of about 300 pairs of horizontal, slender, parallel wires of iron and German silver, the former being covered with cotton. They are mounted on a wooden frame. About 1½ in. of the opposite ends of the wires are bent downward to a vertical position to enable them to dip into liquids at different temperatures contained in long narrow troughs; the liquids being non-conductors, such as melted paraffin for the hot junctions, and the non-volatile petroleum, known as thin machinery oil. The electromotive force obtained varies with the temperature; a pile of 295 pairs having a resistance of 95.6 ohms at 16 deg. Cent. gave with a difference of temperature of 100 deg. Cent. an electromotive force of 0.7729 volts, or with 130 deg. Cent. an electromotive force of 1.005 volt. Each element, therefore, equaled 0.0000262 volt for each degree Cent. difference of temperature. On having been verified with a standard voltaic cell the apparatus becomes itself a standard, especially for small electromotive forces. It is capable of measuring the 1/34861 part of a volt. For higher electromotive forces than a volt, several of these piles would have to be connected in series. The fractional electromotive force is obtained by means of a sliding contact which cuts out so many pairs as is required.
The annual meeting of the French Society of Physics, the success of which is continually increasing, took place this year in the salons of the Observatory, which were kindly placed at the Society's disposal by Admiral Mouchez.
There were three consecutive sessions, the one of Tuesday, April 15, being set apart for the members of the Association, the one of the 16th for the invited guests of Admiral Mouchez, and that of the 17th for the invited guests of the Society. The salons were partially lighted by the Siemens differential arc, continuous current lamps, and partially by the Swan incandescent lamp supplied by a distributing machine that permitted of the lamps being lighted and extinguished at will without changing the normal operation of all the rest. Many apparatus figured at this exhibition, but we shall on the present occasion merely call attention to those that presented a certain character of novelty or of originality.
Among the apparatus that we shall reserve a description of for the present was Messrs. Richard Bros.' registering thermometer designed for the Concarneau laboratory, an instrument which, when sunk at one mile from the coast, and to a depth of 40 meters, will give a diagram of the temperature of the ocean at that depth; and Mr. Hospitalier's continuous electrical indicators, designed for making known from a distance such mechanical or physical phenomena as velocities, levels, temperatures, pressures, etc.
Among the most important of the apparatus exhibited we must reckon Mr. Cailletet's devices for liquefying gases, and those of Mr. Mascart for determining the ohm. The results obtained by Mr. Mascart (which have been submitted to the Committee on Unities of the Congress of Electricians now in session at Paris), are sensibly concordant with those obtained independently in England by Lord Rayleigh. Everything leads to the hope, then, that a rapid and definite solution will be given of this important question of electric unities, and that nothing further will prevent the international development of the C.G.S. system.
Mr. Jules Duboscq** made a number of very successful projections, and we particularly remarked the peculiar experiment made in conjunction with Mr. Parinaud, that gave in projection two like spectra produced by the same prism, and which, through superposition, were capable of increasing the intensity of the colors, or, on the contrary, of reconstituting white light.
Among the optical applications we may cite Mr. Leon Laurent's apparatus for controlling plane, parallel, perpendicular, and oblique surfaces, and magic mirrors obtained with an ordinary light; Mr. S.P. Thompson's apparatus for demonstrating the propagation of electro-magnetic waves in ether (according to Maxwell's theory), as well as some new polarizing prisms; and a mode of lighting the microscope (presented by Mr. Yvon), that was quite analogous to the one employed more than a year ago by Dr. Van Heurck, director of the Botanical Garden of Anvers.
Acoustics were represented by an electro-magnetic brake siren of Mr. Bourbouze; Konig's apparatus for the synthesis of sounds; and Mr. S.P. Thompson's cymatograph—a pendulum apparatus for demonstrating the phenomena of beats.
It was electricity again that occupied the largest space in the programme of the session.
Apparatus for teaching are assuming greater and greater importance every day, and the exhibit of Mr. Ducretet included a large number of the most interesting of these. The house of Breguet exhibited on a reduced scale the magnificent experiments of Gaston Plante, wherein 320 leaden wire secondary elements charged for quantity with 3 Daniell elements, and afterward coupled for tension, served to charge a rheostatic machine formed of 50 condensers coupled for quantity. These latter, coupled anew for tension, furnished upon being discharged a spark due to a difference of potential of about 32,000 volts that presented all the characters of the spark produced by induction coils on the machines so improperly called "static." Finally, we may cite the apparatus arranged by Mr. S.P. Thompson for studying the development of currents in magneto-electric machines. The inventor studies the influence of the forms of the inductors and armatures of machines by means of an arrangement that allows him to change the rings or armatures at will and to take out the induced bobbins in order to sound every part of the magnetic field. Upon giving the armature an angular motion limited by two stops, there develops a certain quantity of electricity that may be measured by causing it to traverse an appropriate ballistic galvanometer. Messrs. Deprez and D'Arsonval's galvanometer answers very well for this purpose, and its aperiodicity, which causes it quickly to return to zero as soon as the induced current ceases, permits of a large number of readings being taken within a very short space of time.
Measuring apparatus were represented by a new and very elegant arrangement of Sir William Thomson's reflecting galvanometers, due to Mr. J. Carpentier. The mounting adopted by Mr. Carpentier permits of an easy removal of the bobbins and of an instantaneous substitution therefor. The galvanometric part, composed of the needles and mirror, therefore remains entirely free, thus allowing of its being verified, and making it convenient to attach the silken fiber. Mr. Carpentier has, moreover, adopted for all the minor apparatus a transparent celluloid scale which simplifies them, facilitates observations, and renders the use of reflection almost industrial.
We shall complete our enumeration of the measuring apparatus by citing Ducretet's non-oscillating galvanometer, Sir William Thomson's amperemeters, voltameters, ohmmeters, and mhosmeters, constructed and exhibited by Breguet, and a new aperiodic galvanoscope of Mr. Maiche. Mr. Baudot exhibited the recent improvements that he has made in his multiplex printing telegraph, and M. Boudet of Paris showed a new system of telephone transmission by submarine cables.
FIG. 1.—DIAGRAM EXHIBITING THE ARRANGEMENT FOR TELEPHONIC TRANSMISSIONS WITHOUT A RECEIVER.
Finally, we shall conclude our enumeration by referring to the curiosities. The house of Siemens exhibited a miniature electric railway actuated by a new model of Reynier accumulators; M. Maiche operated a system of musical telephonic auditions that differed only in detail from those instituted by Mr. Ader at the exhibition of 1881; and Mr. Hospitalier presented a new form of an experiment devised by Mr. Giltay, consisting of a telephonic transmission of sounds without the use of receivers. Mr. Giltay's experiment is nothing but Mr. Dunand's speaking condenser without the condenser. A glance at Fig. 1 will show how things are arranged for the experiment. The transmitting system comprises two distinct circuits, viz.: (1) one formed of a pile, P, of 2 or 3 Leclanche elements, or of 1 or 2 small sized accumulators, an Ader microphane transmitter, M, and the inducting wire of a small induction coil, B; and (2) the other formed of the induced wire of the coil, B, of a pile, P', of 10 or 12 Leclanche elements, and of a line whose extremities terminate at R, in two ordinary electro-medical handles. With this arrangement the experiment performed is as follows: When any one speaks or sings in front of the transmitter, T, while two persons, A and B, each having one hand gloved, are holding the handles in the ungloved hand, it is only necessary for A to place his gloved hand upon B's ear, or for the latter to place his hand upon A's, or for each to place his hand on the other's ear simultaneously, in order that A or B, or A and B simultaneously, may hear a voice issuing from the glove. Under these circumstances, Mr. Giltay's experiment is explained like Dunand's speaking condenser—the hand of A and the ear of B here constituting the armature of an elementary condenser in which the glove performs the role of dielectric.
Upon repeating this experiment at the laboratory of the School of Physics and Industrial Chemistry of Paris, it has been found that the glove maybe replaced by a sheet of plain or paraffined paper. In this case, when two persons are holding the handles, and have their ears applied, one against the other, if a sheet of paper be interposed, airs or words will be heard to proceed therefrom. Finally, it has been found possible to entirely suppress the paper, or dielectric, and to hear directly, by simply interposing the auditor or auditors in the circuit. One of the most curious forms of the experiment is the one shown in Fig. 2. Here a third person, C, hears the hands of A and B speak when a circuit is formed by means of three persons, A, B, and C, the two former, A and B, each holding one of the wires of the circuit and applying his free hand to the ear of C. Although the experiment is one that requires entire silence, and could not on that account be performed at the laboratory, a sort of telephonic chain can be formed in which five or six persons may hear at the same time. A, putting his hand on the ear of B, the latter putting his to that of C, and so on up to the last person, who closes the circuit by grasping one of the handles, the other one being held by A.

EXPERIMENT ON TELEPHONIC TRANSMISSION WITHOUT RECEIVING APPARATUS.
It is difficult in the present state of science to explain very clearly how these telephonic transmissions are effected without a receiver. All that we can conclude from it so far is that the ear is an instrument of incomparable delicacy and of exquisite sensitiveness, since it perceives vibrations in which the energy developer, particularly in the telephonic chain, is exceedingly feeble.
Without any desire to seek an application for an experiment that is simply curious, we yet believe that there is here a phenomenon of a nature to be studied by physicists. Discoveries in telephony and microphony have certainly opened up to science, as regards both theory and practice, new horizons that still promise other surprises for the future. But to return to the observatory: The success obtained by the exhibition of the French Society of Physics shows that these reunions respond to a genuine need—that of instructing in and popularizing science. While warmly congratulating the organizers of these meetings, we may express a wish that the good example set by the Society of Physics may be followed by other societies. We are convinced in advance that an equal success awaits them.—La Nature.
In telegraphy, as well as in the question of lightning rods, attention has been but incidentally paid to the improvement of ground conductors, and this point has not been the object of that careful study that has been bestowed upon the establishment of aerial lines. It is only recently that the interest created by lightning rods has given rise to new forms of conductors differing from those formerly used. The publications of the Prussian Academy of Sciences of from 1876 to 1880 contain some information of special importance in regard to this. It is stated therein that the effect of ground conductors may be notably increased by the division of the earth plates and the use of metallic rods, without necessitating a greater output of material. These facts, however, have not as yet been put to profit in practice for the reason, perhaps, that the considerations, which have remained general, have not at once permitted of obtaining forms what could be employed with perfect knowledge of the results. This is what led Mr. Ulbricht, of Dresden, to make calculations for a few forms of conductors, and to test their approximate values. The results of these researches are printed in the Elektrotechnischen Zeitschrift for 1883 (p. 18).
The equations found show, in the first place, that there exist three means of obtaining a considerable effect, as regards the ground conductor, with a slight expenditure of material: The cylindrical electrode may be drawn out into the form of a bar or wire; the plate may be rendered narrow, and elongated in the form of a ribbon; and, besides, the annular plate may be enlarged in lessening the metallic surface.
Finally, a short, open cylinder with a vertical axis may be formed by curving a narrow plate or ribbon. It is not necessary to see the formula to recognize the fact that this cylinder must behave like a ribbon and a flat ring. The radius increasing, and the surface remaining constant, the resistance of the earth here likewise approaches zero.
As the resistance of the earth is inversely proportional to the diameter of the plates, the zero resistance can also be reached by dividing a plate ad infinitum. As the parts of the plate may be brought quite close to each other without perceptibly interfering with the action, a network has finally been reached by a division carried very far, yet limited, and by connecting the parts with one another by conducting cylinders.
If we seek to determine what forms of ground conductors are efficient and economical under given conditions, we shall have to begin by informing ourselves as to the choice of material to be used for the electrode, and shall then have to ascertain whether putting it in the ground will or will not necessitate much outlay. The most suitable material is copper, which may be used with advantage, in that it lasts pretty well underground, and that the facility which it may be worked permits of easily giving it more appropriate forms than those that can be obtained with cast iron, which is of itself less costly.
If the burying in the ground requires little or no labor, as when there exist ponds, rivers, and wells, or subterranean strata of water near the surface of the earth, elongated forms of conductors will be employed, such as the solid or hollow cylinder, the wire, the ribbon, the narrow ring, and the network. Plates approaching a square or circular shape are not advantageous. But if the ground has to be dug deeply in order to sink the conductor, the form of the electrode must be more condensed, and selected in such a way that the necessary action may be obtained with a minimum output of copper and labor. For great depths, and when the ground will permit of boring, an elongated and narrow cylinder will be used. Such a system, however, can only be employed when the cylinder is surrounded by spring water, since, without that, an intimate contact with earth that is only moist, cannot be obtained with certainty. In earth that is only moist and for moderate depths, preference may be given to an electrode laid down flat. The digging necessary in this case is onerous, it is true, but it permits of very accurately determining the state of the earth beneath and of obtaining a very perfect adherence of the electrode therewith. Two forms, the annular ribbon or the flat ring and the network, present themselves, according to calculations, as a substitute for copper plates, which are so expensive; and these forms are satisfactory on condition that the labor of digging be not notably increased. These forms should always have a diameter a little greater than that of the plate. The flat ring and the network, however, offer one weak point, which they possess in common with the plate, and that is, their dimensions cannot be easily adapted to the nature of the ground met with without a notable increase in the expense. Now, if the ground should offer a conductivity less than what was anticipated, and it were desired to increase the plate, say by one-third, it would be impossible to do so as a consequence of the closed form.
One important advantage is realized in this respect by combining the ring and the network in the form of a reticulated ring having a diameter of from 1 to 1½ meters. On cutting this ring at a given place and according to a certain radius we obtain the reticulated ribbon shown in the accompanying figure. The thickness of the wires is 2.5 mm., and their weight is 0.475 kilo. per meter. L, L, and L are the points at which the conducting cable is soldered. A reticulated ribbon of copper can be made in advance of any length whatever, and, according to local exigencies, it may be easily curved and given the form of a flat or cylindrical ring of varying width. Even though the ribbon has already been cut for a ring of given diameter, it may be still further enlarged by drawing it out and leaving a bit of the ring open, so as to thus obtain a nearly corresponding diminution in the resistance. Such a resistance may be still further diminished by rendering the ring higher, that is to say, by employing an annular cylindrical form.
After assuring himself, by experiments on a small scale, that calculation and observation gave concordant results for the flat ring, the author made an experiment on a larger scale with the annular network. For practical reasons he employed for this purpose a copper wire 2.5 mm. in diameter, which may be expected to last as long as one of iron plate 2 mm. in thickness. Calculation showed that in a ribbon 160 mm. wide, meshes 40 mm. in breadth were advantageous and favorable as regards rigidity. A reticulated ribbon like this, 4 meters in length, was made and formed into a flat ring having an external diameter of 1.42 m. and an internal one of 1.10 m. The resistance of this ring was found to be W = 0.3485 1/k, and that of a plate one meter square, W0 = 0.368 1/k.
As the conductivity of the earth is very variable, and as we cannot have an absolute guarantee that the ramming will be uniform, it seemed proper to make the measurements of the resistance by fixing the plate and the ring in succession to the lower surface of a small raft, in such a way that the contact with the water should correspond as well as possible to the suppositions made for the calculation. As a second ground conductor, a system of water pipes was used, and, after this, a lightning rod conductor, etc.
Repeated and varied experiments gave, for the calculation of the values of the resistances, equations so concordant that the following results may be considered very approximate.
The square plate had a resistance of 35.5 Siemens units, and the reticulated ring one of 32.5. From the first figure we deduce k = 1/91.12, that is to say, the specific conductivity of river-water is 1:91120000. Calculation, then, gives as the resistance of the earth in Siemens units:
| Calculated | Observed. | |
|---|---|---|
| Square plate. | 33.5 | 33.5 |
| Annular ring. | 31.76 | 32.5 |
These figures prove the accuracy of the calculations that had been made in an approximate way.
The experiments were performed upon the Elba, above Dresden. Other experiments still had reference to the influence of immersion. In order to diminish polarization, only instantaneous currents from the measuring pile were employed. It was to be supposed that the current of water through which the bubbles of gas were removed from the electrodes would not have permitted of a notable resistance of polarization. Later measurements, made upon a ribbon buried, like the plates, in the earth, gave likewise most favorable results.
As a result of these experiments, the State railways of Saxony have, in such cases as were practicable, introduced the annular network of copper. There are some manufacturers, too, who seem desirous of adopting this system, although it has hardly emerged from the period of experiment. The pecuniary advantages that will result from an application of it ought, it would seem, to dispel a large proportion of the criticisms directed against the erection of lightning rods, from the standpoint of expense, and contribute to extend an arrangement which may be considered as a very happy one.
If we compare the square plate with the equivalent annular network, constructed as above indicated, and which should possess, according to the author an external diameter of 1.26 m. and of 3.45 m., we find that:
| The square plate, | 1 mm. thick | weighs 8.9 kilos. |
| " | 2 mm. thick | weighs 17.8 kilos. |
| The annular network | weighs 1.64 kilos. | |
The cost of reticulated ribbon per meter amounts to about 4.4 francs, supposing it to be arranged as shown in the cut.
As term of comparison, we may admit that the following forms are nearly the equivalent of a horizontal, unburied plate one meter square.
| Length. | Diameter. | ||
|---|---|---|---|
| Vertical cylinder | buried | 1.40 m. | 0.13 m. |
| " | " | 1.80 m. | 0.06 m. |
| Vertical bar | " | 2.60 m. | 0.013 m. |
| Horizontal bar | " | 5.20 m. | 0.013 m. |
Horizontal flat ring 1.32 m. in external diameter, and 1.08 m. internal.
Horizontal network 1.01 m. square, and having meshes of the same size as those of the reticulated ribbon.
Horizontal reticulated ribbon 3 m. in length and of the structure described.
Horizontal annular ring 1.26 m. in external diameter, 0.94 m. internal.
In conclusion, let us meet an objection that might be made to the accuracy of the hypotheses that serve as a base to the preceding calculations, in cases where ground plates for lightning rods and not for telegraphs are concerned. Between the two ground plates of a telegraph line there is generally a distance such that the curves of the current undergo no deviation in the vicinity of one of the electrodes (the only part important for integrations) through the influence of the other. But it might be admitted that such would prove the case with a lightning rod in a storm, at the time of the passage of the fluid into the earth. The ground plate here is one of the electrodes, and the other is replaced by the surface of the earth strongly charged to a great distance under the storm clouds. If we suppose (what may be admitted in a good lightning rod) that there no longer occurs any spark from the point downward, the curves of the current, in starting perpendicularly from the ground plate, would be obliged to leave their rectilinear trajectory and strike the surface of the earth at right angles. When the electricity flows through a plane surface into an infinite body, it is only when such surface presents a very great development that the respective potentials decrease very slowly in the vicinity of the said surface. No notable modification occurs, then, in the curves of equal potential, in the vicinity of the ground plate through the action of this extended charge, nor consequently any modification in the curves of the current; but the electricity which spreads has but a short distance to travel in order to overcome the most important resistances.
The calculations of resistances given above have, then, the same value for discharges of atmospheric electricity.—Bull. du Musee de l'Industrie.
Concerning the separations which take place at the positive pole, the composition of the peroxides, and the manner of their determination, relatively little has been done.
If solutions of the salts of lead, thallium, silver, bismuth, nickel, and cobalt are decomposed by the current between platinum electrodes, metal is deposited at the negative, and oxide at the positive electrode. Manganese is precipitated only as peroxide. The formation of peroxide is, of course, effected by the ozone found in the electrolytic oxygen at the positive pole; the oxide existing in solution is brought to a higher degree of oxidation, and is separated out. Its formation may be decreased or entirely prevented by the addition of readily oxidizible bodies, such as organic acids, lactose, glycerine, and preferably by an excess of oxalic acid; but only until the organic matter is transformed into carbonic acid. In this manner Classen separates other metals from manganese in order to prevent the saline solutions from being retained by the peroxide.
With solutions of silver, bismuth, nickel, and cobalt, it is often practicable to prevent the separation of oxide by giving the current a greater resistance—increasing the distance between the electrodes.
The proportion between the quantities of metal and of peroxide deposited is not constant, and even if we disregard the concentration of the solution, the strength of the current and secondary influences (action of nascent hydrogen) is different in acid and in alkaline solutions. In acid solutions much peroxide is formed; in alkaline liquids, little or none. The reason of the difference is that ozone is evolved principally in acid solutions, but appears in small quantities only in alkaline liquids, or under certain circumstances not at all. The quantity of peroxide deposited depends also on the temperature of the saline solution; at ordinary temperatures the author obtained more peroxide—the solution, the time, and the strength of current being equal—than from a heated liquid. The cause is that ozone is destroyed by heat and converted into ordinary oxygen. With the exception of lead and thallium the quantity of metal deposited from an acid solution is always greater than that of the peroxide.
Lead.—Luckow has shown that from acid solutions—no matter what may be the acid—lead is deposited at the anode as a mixture of anhydrous and hydrated peroxide of variable composition. Only very strongly acid solutions let all their lead fall down as peroxide; the precipitation is rapid immediately on closing the circuit, and complete separation is effected only in presence of at least 10 per cent. of free nitric acid. As the current becomes stronger with the increase of free acid, there is deposited upon the first compact layer a new stratum of loosely adhering peroxide.
In presence of small quantities of other metals which are thrown down by the current in the metallic state, such as copper, mercury, etc., peroxide alone is deposited from a solution of lead containing small quantities only of free nitric acid.
The lead peroxide deposited is at first light brown or dark red, and becomes constantly darker and finally taking a velvet-black. As its stratification upon the platinum is unequal, it forms beautifully colored rings.
Experiments show that the quantity of peroxide deposited depends on the nature of the solution and the strength of the current. In case of very feeble currents and slight acidity, its quantity is so small that it does not need to be taken into consideration. If the lead solution is very dilute scarcely any current is observed, lead solutions per se being very bad conductors of electricity.
Faintly acid concentrated lead solutions give loose peroxide along with much spongy metallic lead. Free alkali decreases the separation of peroxide; feebly alkaline solutions, concentrated and dilute, yield relatively much peroxide along with metallic lead, while strongly alkaline solutions deposit no peroxide.
Dried lead peroxide is so sparingly hygroscopic that it may be weighed as such; its weight remains constant upon the balance for a long time. In order to apply the peroxide for quantitative determinations, a large surface must be exposed to action. As positive electrode a platinum capsule is convenient, and a platinum disk as negative pole. The capsule shape is necessary because the peroxide when deposited in large quantities adheres only partially, and falls in part in thin loose scales. It is necessary to siphon off the nitric solution, since, like all peroxides, that of lead is not absolutely insoluble in nitric acid. The methods of Riche and May give results which are always too high, since portions of saline solution are retained by the spongy deposit and can be but very imperfectly removed by washing. This is especially the case in presence of free alkali.
The author has proceeded as follows: The lead peroxide is dried in the capsule, and there is passed over it pure dry gaseous sulphurous acid in a strong current from a rather narrow delivery tube. Lead sulphate is formed with evolution of heat; it is let cool under the exsiccator, and weighed as such. Or he ignites the peroxide along with finely pulverized ammonium sulphite; the mass must have a pure white color. After the conclusion of the reaction it is ignited for about 20 minutes. The results are too high. The proportion of actual lead peroxide in the deposit ranges from 94 to 94.76 per cent. The peroxide precipitated from a nitric solution may, under certain circumstances, be anhydrous. This result is due to the secondary influences at the positive pole, where the free acid gradually withdraws water from the peroxide.
The peroxide thrown down from alkaline solutions retains alkali so obstinately that it cannot be removed by washing; the peroxide plays here the part of an acid. The lead nitrate mechanically inclosed in the peroxide is resolved by ignition into oxide, hyponitric acid, and oxygen; this small proportion of lead oxide does not exert an important influence on the final result. The quantity of matter mechanically inclosed is relatively high, as in the precipitation of much lead peroxide there is relatively more saline matter occluded than when a few centigrammes are deposited. The peroxide incloses also more foreign matter if it is thrown down upon a small surface than if it is deposited in a thin layer over a broad surface. From numerous analyses the author concludes that in presence of much free nitric acid the proportion of water is increased; with free alkali the reverse holds good.
Thallium behaves similarly to lead. From a nitric acid solution it is thrown down, according to the proportion of free acid, either as sesquioxide only or in small quantities as silvery, metallic leaflets; from alkaline solutions it is deposited as sesquioxide and metal, the latter of a lead-gray color. Thallium solutions conduct the electric current badly. Thallium oxide resembles lead peroxide in color; at a strong heat it melts, becomes darker, and is converted into peroxide, in which state it can be weighed.
Silver.—All solutions of silver salts, except the nitrate, and those containing a very large quantity of free nitric acid or nitrates, deposit electrolytically merely metallic silver. In the above mentioned exceptional cases there is formed a small quantity of peroxide which adheres to the anode as a blackish-gray deposit. The greatest quantity of peroxide is obtained on employing a concentrated, strongly acid solution of the nitrate, and a strong current. If the solution is very dilute we obtain no peroxide, or mere traces which disappear again toward the end of the process. The peroxide is deposited at first in small, dark, shining octahedral crystals; subsequently, in an amorphous state. At 110° it evolves oxygen suddenly, and is converted into metallic silver. It dissolves in ammonia with a violent escape of nitrogen. In nitric acid it dissolves without decomposition and with a red color.
The author uses a galvanic current for reducing silver residues, consisting of sulphocyanide. The salt is mixed with sulphuric acid in a roomy platinum capsule, and a fine platinum wire gauze is used as positive electrode.
Bismuth.—The current resolves bismuth solutions into metal and bismutic acid. The latter is deposited at the positive pole, and in thin layers appears of a golden-yellow, but in thick strata is darker, approaching to red. Its formation is very gradual, and in time it disappears again, owing to secondary actions of the current. On ignition it becomes lemon yellow, and transitorily darker, even brown, and passes into the sexquioxide.
Nickel and Cobalt.—On the electrolysis of the ammonical solution the sesquioxide appears at the positive pole. Its formation is prevented by an excess of ammonia. The author never obtains more than 3½ per cent. of the quantity of the metal. The sesquioxides dissolve in ammonia without escape of nitrogen, and are usually anhydrous.
Manganese.—Manganese is the only metal which is precipitated only as peroxide. It is deposited at once on closing the circuit, and is at first brown, then black and shining. Organic acids, ferrous oxide, chromic oxide, ammonium salts, etc., prevent the formation of peroxide and the red color produced by permanganic acid. In very dilute strongly acid nitric solutions there is formed only permanganic acid, which according to Riche is plainly visible in solutions containing 1/1000000 grm. manganese. On electrolyzing a manganiferous solution of copper nitrate, red permanganic acid appeared in a stratum floating above the platinum disk coated with brown peroxide. No manganese peroxide was deposited. The peroxide adheres firmly to the platinum when the proportion of free acid is small, not exceeding 3 per cent., and the current is not too strong. If the action of the current is prolonged after the peroxide is thrown down, it falls off in laminæ. According to Riche, in a nitric solution the manganese is deposited as peroxide, also at the negative pole. This formation is not directly due to the current, but is a precipitate occasioned by the production of ammonia by the reduction of nitric acid. To determine the manganese in peroxide electrolytically precipitated, it is heated to bright redness in the platinum capsule until the weight becomes constant. The results are too high.
Selenium and Tellurium.—Both these bodies are readily and completely reduced by the current either in acid or alkaline solutions. Selenium is thrown down at first of a fine brownish red, which gradually becomes darker. The deposit of tellurium is of a bluish black color. If the current is feeble, the deposit of selenium is moderately compact; that of tellurium is always loose, and it often floats on the liquid. A strong current precipitates both as powders. The positive pole is coated during electrolysis with a film of a dark color in case of selenium, but of a lemon yellow with tellurium. As in case of arsenic and antimony, the hydrogen evolved at the negative pole combines with the reduced substances, forming hydrogen, selenide, or telluride, which remain in part in solution in the liquid. The reduced metal separates out at the anode in a friable condition.—Zeitschrift fur Analytische Chemie, and Chemical News.
A very careful and important determination of the electrochemical equivalent of silver has been made at the observatory of the Physical Institute of Würzbourg, and the results are that an ampere current flowing for a second, or a coulomb of electricity deposits 1.1183 milligrammes of silver or 0.3281 milligramme of copper, and decomposes 0.09328 milligramme of water, a result agreeing closely with that of Lord Rayleigh recently communicated to the Physical Society. An ampere therefore deposits 4.0259 grammes of silver per hour; Kohlrausch's value is 4.0824, a value hitherto accepted universally. This value is so useful in measuring electric currents with accuracy, and free from the disturbances of magnetism, etc., that it is eminently satisfactory to find the German value agree with that of Lord Rayleigh, which will probably be adopted by English electricians.
Herr Hefner-Alteneck has suggested a new standard light for photometric purposes, which promises to be very simple and effective in operation. The light is produced by an open flame of amyl-acetate burning from a wick of cotton fiber which fills a tube of German silver 1 in. long and 316 mils. internal diameter; the external diameter being 324 mils. The flame is 1.58 in. high from top to bottom; and it should be lighted at least ten minutes before using the light for testing. A cylindrical glass chimney surrounds it to ward off air currents. About 2 per cent. of the light is absorbed by the glass. The power of the flame is that of a standard English candle; and experiments have shown that amyl acetate, which besides is not expensive, is the best fuel for steadiness and brilliance. Neither the substitution of commercial amyl-acetate for pure nor the use of a wick of cotton thread for loose cotton fiber alters the illuminating power; but the wick should be trimmed square across the mouth of the tube, for if it project and droop the illuminating power is increased.
[NATURE.]
In a recent number of the Zeitschrift fur Instrumentenkunde (iv., 42-50, February, 1884), Dr. K. Feussner of Karlsruhe has given a detailed description of a polarizing prism lately devised by him, which presents several points of novelty, and for which certain advantages are claimed. The paper also contains an account, although not an exhaustive one, of the various polarizing prisms which have from time to time been constructed by means of different combinations of Iceland spar. The literature of this subject is scattered and somewhat difficult of access, and moreover only a small part of it has hitherto been translated into English; and it would appear therefore that a brief abstract of the paper may not be without service to those among the readers of Nature who may be unacquainted with the original memoirs, or who may not have the necessary references at hand.
Following the order adopted by Dr. Feussner, the subject may be divided into two parts:
In comparing the various forms of polarizing prisms, the main points which need attention are—the angular extent of the field of view, the direction of the emergent polarized ray, whether it is shifted to one side of, or remains symmetrical to the long axis of the prism; the proportion which the length of the prism bears to its breadth; and lastly, the position of the terminal faces, whether perpendicular or inclined to the long axis. These requirements are fulfilled in different degrees by the following methods of construction:
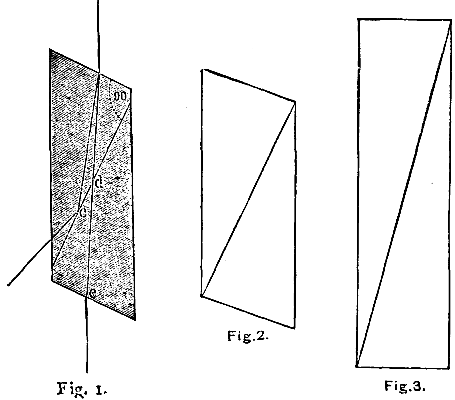
Figs. 1., 2., and 3.
1. The Nicol Prism (Edin. New Phil. Journal, 1828, vi., 83).—This (Fig. 1), as is well known, is constructed from a rhombohedron of Iceland spar, the length of which must be fully three times as great as the width. The end faces are cut off in such a manner that the angle of 72° which they originally form with the lateral edge of the rhombohedron is reduced to 68°. The prism is then cut in two in a plane perpendicular to the new end surfaces, the section being carried obliquely from one obtuse corner of the prism to the other, in the direction of its length. The surfaces of this section, after having been carefully polished, are cemented together again by means of Canada balsam. A ray of light, on entering the prism, is separated by the double refraction of the calc-spar into an ordinary and an extraordinary ray; the former undergoes total reflection at the layer of balsam at an incidence which allows the extraordinary ray to be transmitted; the latter, therefore, passes through unchanged. This principle of obtaining a single polarized ray by means of total reflection of the other is common to all the forms of prism now to be described.
Dr. Feussner gives a mathematical analysis of the paths taken by the two polarized rays within the Nicol prism, and finds that the emergent extraordinary ray can include an angular field of 29°, but that this extreme value holds good only for rays incident upon that portion of the end surface which is near to the obtuse corner, and that from thence it gradually decreases until the field includes an angle of only about half the previous amount. He finds, moreover, that, although of course the ray emerges parallel to its direction of incidence, yet that the zone of polarized light is shifted to one side of the central line. Also that the great length of the Nicol—3.28 times its breadth—is not only an inconvenience, but owing to the large pieces of spar thus required for its construction, prisms of any but small size become very expensive. To this it may be added that there is a considerable loss of light by reflection from the first surface, owing to its inclined position in regard to the long axis of the prism.
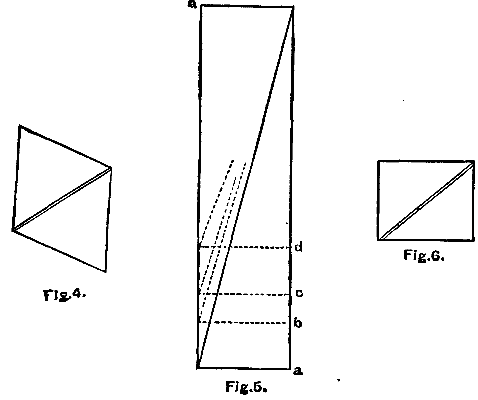
Figs. 4., 5., and 6.
It is with the view of obviating these defects that the modifications represented in Figs. 2 to 6 have been devised.
2. The Shortened Nicol Prism.—This arrangement of the Nicol prism is constructed by Dr. Steeg and Reuter of Homburg v.d.H. For the sake of facility of manufacture, the end surfaces are cleavage planes, and the oblique cut, instead of being perpendicular, makes with these an angle of about 84°. By this alteration the prism becomes shorter, and is now only 2.83 times its breadth; but if Canada balsam is still used as the cement, the field will occupy a very unsymmetrical position in regard to the long axis. If balsam of copaiba is made use of, the index of refraction of which is 1.50, a symmetrical field of about 24° will be obtained. A prism of this kind has also been designed by Prof. B. Hasert of Eisenach (Pogg. Ann., cxiii., 189), but its performance appears to be inferior to the above.
3. The Nicol Prism with Perpendicular Ends.—The terminal surfaces in this prism are perpendicular to the long axis, and the sectional cut makes with them an angle of about 75°. The length of the prism is 3.75 times its breadth, and if the cement has an index of refraction of 1.525, the field is symmetrically disposed, and includes an angle of 27°. Prisms of this kind have been manufactured by Dr. Steeg, Mr. C.D. Ahrens, and others.
4. The Foucault Prism (Comptes Rendus, 1857, xlv., 238).—This construction differs from all those hitherto mentioned, in that a film of air is employed between the two cut surfaces as the totally reflecting medium instead of a layer of cement. The two halves of the prism are kept in position, without touching each other, by means of the mounting. The length of the prism is in this way much reduced, and amounts to only 1.528 times its breadth. The end surfaces are cleavage planes, and the sectional cut makes with them an angle of 59°. The field, however, includes not more than about 8°, so that this prism can be used only in the case of nearly parallel rays; and in addition to this the pictures which may be seen through it are to some extent veiled and indistinct, owing to repeated internal reflection.
5. The Hartnack Prism (Ann. de Ch. et de Physique, ser. iv., vii., 181).—This form of prism was devised in 1866 by MM. Hartnack and Prazmowiski; the original memoir is a valuable one; a translation of it, with some additions, has lately been published (Journ. of the R. Microscopical Soc., June, 1883, 428). It is considered by Dr. Feussner to be the most perfect prism capable of being prepared from calc-spar. The ends of the prism are perpendicular to its length; the section carried through it is in a plane perpendicular to the principal axis of the crystal. The cementing medium is linseed oil, the index of refraction of which is 1.485. This form of prism is certainly not so well known in this country as it deserves to be; a very excellent one, supplied to the present writer by Dr. Steeg is of rectangular form throughout, the terminal surfaces are 19 × 15 mm., and the length 41 mm. The lateral shifting of the field is scarcely perceptible, the prism is perfectly colorless and transparent, and its performance is far superior to that of the ordinary Nicol. The field of view afforded by this construction depends upon the cementing substance used, and also upon the inclination of the sectional cut in regard to the end of the prism; it may vary from 20° to 41°. If the utmost extent of field is not required, the prism may be shortened by lessening the angle of the section, at the expense, however, of interfering with the symmetrical disposition of the field.
6. The Glan Prism (Carl's "Repertorium," xvi., 570, and xvii., 195).—This is a modification of the Foucault, and in a similar manner includes a film of air between the sectional surfaces. The end surfaces and also the cut carried through the prism are parallel to the principal axis of the calc-spar. The ends are normal to the length, and the field includes about 8°. This prism is very short, and may indeed be even shorter than it is broad. It is subject to the same defect as that mentioned in the case of the Foucault, although perhaps not quite to the same extent.
This prism differs very considerably from the preceding forms, and consists of a thin plate of a doubly refracting crystal cemented between two wedge-shaped pieces of glass, the terminal faces of which are normal to the length. The external form of the prism may thus be similar to the Hartnack, the calc-spar being replaced by glass. The indices of refraction of the glass and of the cementing medium should correspond with the greater index of refraction of the crystal, and the directions of greatest and least elasticity in the latter must stand in a plane perpendicular to the direction of the section. One of the advantages claimed for the new prism is that, it dispenses with the large and valuable pieces of spar hitherto found necessary; a further advantage being that other crystalline substances may be used in this prism instead of calc-spar. The latter advantage, however, occurs only when the difference between the indices of refraction for the ordinary and extraordinary rays in the particular crystal made use of is greater than in calc-spar. When this is the case, the field becomes enlarged, and the length of the prism is reduced.
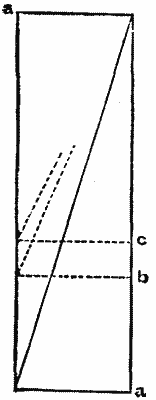
Fig. 7.
The substance which Dr. Feussner has employed as being most suitable for the separating crystal plate is nitrate of soda (natronsalpeter), in which the above-mentioned values are ω = 1.587 and η = 1.336. It crystallizes in similar form to calcite, and in both cases thin plates obtained by cleavage may be used.
As the cementing substance for the nitrate of soda, a mixture of gum dammar with monobromonaphthalene was used, which afforded an index of refraction of 1.58. In the case of thin plates of calcite, a solid cementing substance of sufficiently high refractive power was not available, and a fluid medium was therefore employed. For this purpose the whole prism was inclosed in a short glass tube with airtight ends, which was filled with monobromonaphthalene. In an experimental prism a mixture of balsam of tolu was made use of, giving a cement with an index of refraction of 1.62, but the low refractive power resulted in a very considerable reduction of the field. The extent and disposition of the field may be varied by altering the inclination at which the crystal lamina is inserted (Fig. 7), and thereby reducing the length of the prism, as in the case of the Hartnack.
In order to obviate the effects of reflection from the internal side surfaces if the prism, the wedge-shaped blocks of glass of which it is built up may be made much broader than would otherwise be necessary; the edges of this extra width are cut obliquely and suitably blackened.
The accompanying diagram (Fig. 8) represents a prism of cylindrical external form constructed in this manner, the lower surface being that of the incident light. In this the field amounts to 30°, and the breadth is about double the length.
Fig. 8.
Dr. Feussner remarks that a prism similar in some respects to his new arrangement was devised in 1869 by M. Jamin (Comptes Rendus, lxviii., 221), who used a thin plate of calc-spar inclosed in a cell filled with bisulphide of carbon; and also by Dr. Zenker, who replaced the liquid in M. Jamin's construction by wedges of flint glass.
Among others, the carefully considered modifications of the Nicol prism which have recently been devised by Prof. S.P. Thompson (Phil. Mag., November, 1881, 349, and Jour. R. Micros. Soc., August, 1883, 575), and by Mr. R.T. Glazebrook (Phil. Mag., May, 1883, 352), do not appear to have been known to Dr. Feussner.
The following tabular view of different forms of polarizing prisms is taken from the conclusion of Dr. Feussner's paper:
| Field. | Inclination of section in regard to long axis. | Ratio of length to clear width. | Fig. | ||
|---|---|---|---|---|---|
| I. THE OLD POLARISING PRISMS. | ° | ° | |||
| 1. Nicol's prism. | 29 | 22 | 3.28 | 1 | |
| 2. Shortened Nicol prism— | |||||
| a. Cemented with Canada balsam. | 13 | 25 | 2.83 | 2 | |
| b. Cemented with copaiba balsam. | 24 | 25 | 2.83 | 2 | |
| 3. Nicol with perpendicular ends— | |||||
| a. With Canada balsam. | 20 | 15 | 3.73 | 3 | |
| b. With cement of index of refraction of 1.525. | 27 | 15 | 3.73 | 3 | |
| 4. Foucault's prism. | 8 | 40 | 1.528 | 4 | |
| 5. Hartnack's prism— | |||||
| a. Original form. | 35 | 15.9 | 3.51 | 5ab | |
| b. With largest field. | 41.9 | 13.9 | 4.04 | 5aa | |
| c. With field of 30°. | 30 | 17.4 | 3.19 | 5ac | |
| d. With field of 20°. | 20 | 20.3 | 2.70 | 5ad | |
| 6. Glan's prism. | 7.9 | 50.3 | 0.831 | 6 | |
| II. THE NEW POLARISING PRISM. | |||||
| 1. With calc-spar: | largest field. | 44 | 13.2 | 4.26 | 5aa |
| 2. " | field of 30°. | 30 | 17.4 | 3.19 | 5ac |
| 3. " | field of 20°. | 20 | 20.3 | 2.70 | 5ad |
| 4. With nitrate of soda: | largest field. | 54 | 16.7 | 3.53 | 7aa |
| 5. " | field of 30°. | 30 | 24 | 2.25 | 7ab |
| 6. " | field of 20°. | 20 | 27 | 1.96 | 7ac |
As an analyzing prism of about 6 mm. clear width, and 13.5 mm. long, the new prism is stated by its inventor to be of the most essential service, and it would certainly appear that the arrangement is rather better adapted for small prisms than for those of considerable size. Any means by which a beam of polarized light of large diameter—say 3 to 3½ inches—could be obtained with all the convenience of a Nicol would be a real advance, for spar of sufficient size and purity for such a purpose has become so scarce and therefore so valuable that large prisms are difficult to procure at all. So far as an analyzer is concerned, the experience of the writer of this notice would lead to the opinion that improvements are to be looked for rather in the way of the discovery of an artificial crystal which absorbs one of the polarized rays than by further modifications depending upon total reflection. The researches of Dr. Herapath on iodosulphate of quinine (Phil. Mag., March, 1852, 161, and November, 1853, 346) are in this direction; but crystals of the so-called herapathite require great manipulative skill for their production. If these could be readily obtained of sufficient size, they would be invaluable as analyzers.
This opinion is supported by the existence of an inconvenience which attends every form of analyzing prism. It is frequently, and especially in projecting apparatus, required to be placed at the focus of a system of lenses, so that the rays may cross in the interior of the prism. This is an unfavorable position for a prismatic analyzer, and in the case of a powerful beam of light, such as that from the electric arc, the crossing of the rays within the prism is not unattended with danger to the cementing substance, and to the surfaces in contact with it.
PHILIP R. SLEEMAN.
Finely ground zircon is quickly rendered soluble if fused with a mixture of potassium borofluoride and potassium carbonate. The author takes two parts of the former to three of the latter, and prepares an intimate, finely divided mixture, which is kept ready for use.
Of this mixture four parts are taken to one of zircon, thoroughly mixed, and melted in a platinum crucible at a red heat. The mass fuses readily, froths at first and gives off bubbles of gas, and flows then quietly, forming a very fluid melt. If the zircon is finely ground, 15 minutes are sufficient for this operation. The loss of weight is 16 per cent., and is not notably increased on prolonged fusion. It corresponds approximately to the weight of the carbonic anhydride present in the potassium carbonate.
As pungent vapors are given off during fusion, the operation should be conducted under a draught hood. The activity of the mixture in attacking zircon appears from the following experiment: Two zircon crystals, each weighing ½ grm., were introduced into the melted mixture and subjected to prolonged heat. In a short time they decreased perceptibly in size; each of them broke up into two fragments, and within an hour they were entirely dissolved. The melted mass is poured upon a dry metal plate, and when congealed is thrown into water. It is at once intersected with a number of fissures, which facilitate pulverization. This process is the more necessary as the unbroken mass is very slowly attacked by water even on prolonged boiling. The powder is boiled in a large quantity of water so as to remove everything soluble. There is obtained a faintly alkaline solution and a sediment insoluble in water. From the filtrate alkalies throw down zirconium hydroxide, free from iron.
The portion insoluble in water is readily dissolved in hydrofluoric acid, and is converted into zircon potassium fluoride. The chief bulk of the zirconium is found in the aqueous solution in the state of double fluorides. The platinum crucible is not in the least attacked during melting. On the contrary, dirty platinum crucibles may be advantageously cleaned by melting in them a little of the above mentioned mixture.
If finely divided zircon is boiled for a long time with caustic lye, it is perceptibly attacked. It is very probable that in this manner zircon might be entirely dissolved under a pressure of 10 atmospheres.
Potassium borofluoride may be readily prepared from cryolite. Crucibles of nickel seem especially well adapted for the fusion of zircon in caustic alkalies.—Ber. Bœhm. Gesell. Wissenschaft; Chem. News.
The numerous direct processes which have been patented and brought before the iron masters of the world, differ materially from that now introduced by Mr. Wilson. After a careful examination of his process, I am convinced that Mr. Wilson has succeeded in producing good blooms from iron ore, and I think that I am able to point out theoretically the chief reasons of the success of his method.
Without going deeply into the history of the metal, I may mention the well known fact that wrought iron was extensively used in almost all quarters of the globe, before pig or cast iron was ever produced. Without entering into the details of the processes by which this wrought iron was made, it suffices for my present purpose to say that they were crude, wasteful, and expensive, so that they can be employed to-day only in a very few localities favored with good and cheap ore, fuel, and labor.
The construction of larger furnaces and the employment of higher temperatures led to the production of a highly carbonized, fusible metal, without any special design on the part of the manufacturers in producing it. This pig iron, however, could be used only for a few purposes for which metallic iron was needed; but it was produced cheaply and with little loss of metal, and the attempt to decarbonize this product and bring it into a state in which it could be hammered and welded was soon successfully made. This process of decarbonization, or some modification of it, has successfully held the field against all so-called, direct processes up to the present time. Why? Because the old fashioned bloomeries and Catalan forges could produce blooms only at a high cost, and because the new processes introduced failed to turn out good blooms. Those produced were invariably "red short," that is, they contained unreduced oxide of iron, which prevented the contact of the metallic particles, and rendered the welding together of these particles to form a solid bloom impossible.
The process of puddling cast iron, and transforming it by decarbonization into wrought iron, has, as everybody knows, been in successful practical operation for many years, and the direct process referred to so closely resembles this, that a short description of the theory of puddling is not out of place here.
The material operated on in puddling is iron containing from 2½ to 4 per cent. of carbon. During the first stage of the process this iron is melted down to a fluid bath in the bottom of a reverberatory furnace. Then the oxidation of the carbon contained in the iron commences, and at the same time a fluid, basic cinder, or slag, is produced, which covers a portion of the surface of the metal bath, and prevents too hasty oxidation. This slag results from the union of oxides of iron with the sand adhering to the pigs, and the silica resulting from the oxidation of the silicon contained in the iron.
This cinder now plays a very important part in the process. It takes up the oxides of iron formed by the contact of the oxidizing flame with the exposed portion of the metal bath, and at the same time the carbon of the iron, coming in contact with the under surface of the cinder covering, where it is protected from oxidizing influences, reduces these oxides from the cinder and restores them to the bath in metallic form. This alternate oxidation of exposed metal, and its reduction by the carbon of the cast iron, continues till the carbon is nearly exhausted, when the iron assumes a pasty condition, or "comes to nature," as the puddlers call this change. The charge is then worked up into balls, and removed for treatment in the squeezer, and then hammered or rolled. In the Wilson process the conditions which we have noted in the puddling operation are very closely approximated. Iron ore reduced to a coarse sand is mixed with the proper proportion of charcoal or coke dust, and the mixture fed into upright retorts placed in the chimney of the puddling furnace. By exposure for 24 hours to the heat of the waste gases from the furnace, in the presence of solid carbon, a considerable portion of the oxygen of the ore is removed, but little or no metallic iron is formed. The ore is then drawn from the deoxidizer into the rear or second hearth of the puddling furnace, situated below it, where it is exposed for 20 minutes to a much higher temperature than that of the deoxidizer. Here the presence of the solid carbon, mixed with the ore, prevents any oxidizing action, and the temperature of the mass is raised to a point at which the cinder begins to form. Then the charge is carried forward by the workmen to the front hearth, in which the temperature of a puddling furnace prevails. Here the cinder melts, and at the same time the solid carbon reacts on the oxygen remaining combined with the ore, and forms metallic iron; but by this time the molten cinder is present to prevent undue oxidation of the metal formed, and solid carbon is still present in the mixture to play the same role, of reducing protoxide of iron from the cinder, as the carbon of the cast iron does in the ordinary puddling process. I have said that the cast iron used as the material for puddling contains about 3 per cent. of carbon; but in this process sufficient carbon is added to effect the reduction of the ore to a metallic state, and leave enough in the mass to play the part of the carbon of the cast iron when the metallic stage has been reached.
It would be interesting to compare the Wilson with the numerous other direct processes to which allusion has already been made, but there have been so many of them, and the data concerning them are so incomplete, that this is impossible. Two processes, however, the Blair and the Siemens, have attracted sufficient attention, and are sufficiently modern to deserve notice. In the Blair process a metallic iron sponge was made from the ore in a closed retort, this sponge cooled down in receptacles from which the air was excluded, to the temperature of the atmosphere, then charged into a puddling furnace and heated for working. In this way (and the same plan essentially has been followed by other inventors), the metallic iron, in the finest possible state of subdivision, is subjected to the more or less oxidizing influences of the flame, without liquid slag to save it from oxidation, and with no carbon present to again reduce the iron oxides from the cinder after it is formed. The loss of metal is consequently very large, but oxides of iron being left in the metal the blooms are invariably "red short."
In the Siemens process pieces of ore of the size of beans or peas, mixed with lime or other fluxing material, form the charge, which is introduced into a rotating furnace; and when this charge has become heated to a bright-red heat, small coal of uniform size is added in sufficient quantity to effect the reduction of the ore.
The size of the pieces of the material employed prevents the intimate mixture of the particles of iron with the particles of carbon, and hence we would, on theoretical grounds, anticipate just what practice has proved, viz., that the reduction is incomplete, and the resulting metal being charged with oxides is red-short. In practice, blooms made by this process have been so red-short that they could not be hammered at all.
It would be impracticable in this process to employ ore and carbon in as fine particles as Wilson does, as a very large portion of the charge would be carried off by the draught, and a sticking of the material to the sides of the rotating furnace could scarcely be avoided. I do not imagine that a division of the material into anything like the supposed size of molecules is necessary; we know that the graphitic carbon in the pig-iron employed in puddling is not so finely divided, but it is much smaller particles than bean or pea size, and by approximating the size of the graphite particles in pig iron, Wilson has succeeded in obtaining good results.
If we examine the utilization of the heat developed by the combustion of a given quantity of coal in this process, and compare it with the result of the combustion of an equivalent amount of fuel in a blast furnace, we shall soon see the theoretical economy of the process. The coal is burned on the grate of the puddling-furnace, to carbonic acid, and the flame is more fully utilized than in an ordinary puddling-furnace, for besides the ordinary hearth there is the second or rear hearth, where additional heat is taken up, and then the products of combustion are further utilized in heating the retorts in which the ore is partly reduced. After this the heat is still further utilized by passing it under the boilers for the generation of steam, and the heat lost in the gases, when they finally escape, is very small. In a blast furnace the carbon is at first burned only to carbonic oxide, and the products of combustion issue mainly in this form from the top of the furnace. Then a portion of the heat resulting from the subsequent burning of these gases is pretty well utilized in making steam to supply the power required about the works, but the rest of the gas can only be utilized for heating the blast, and here there is an enormous waste, the amount of heat returned to the furnace by the heated blast being very small in proportion to the amount generated by the burning of that portion of carbonic oxide expended in heating it, and the gases escape from both the hot-blast and the boilers at a high temperature.
In the direct process under consideration the fuel burned is more completely utilized than in the puddling process, to which the cast iron from the blast furnace is subjected to convert it into wrought iron.
The economy claimed for this process, over the blast furnace and puddling practice for the production of wrought iron, is that nearly all the fuel used in the puddling operation is saved, and that with about the same amount of fuel used in the blast furnace to produce a ton of pig iron, a ton of wrought iron blooms can be made. I had no opportunity of weighing the charges of ore and coal used, but I saw the process in actual operation at Rockaway, N.J. The iron produced was hammered up into good solid blooms, containing but little cinder. The muck-bar made from the blooms was fibrous in fracture, and showed every appearance of good iron. I am informed by the manager of the Sanderson Brothers' steel works, at Syracuse, N.Y., that they purchased blooms made by the Wilson process in 1881-1882, that none of them showed red-shortness, and that they discontinued their use only on account of the injurious action of the titanium they contained on the melting pots. These blooms were made from magnetic sands from the Long Island and Connecticut coasts.
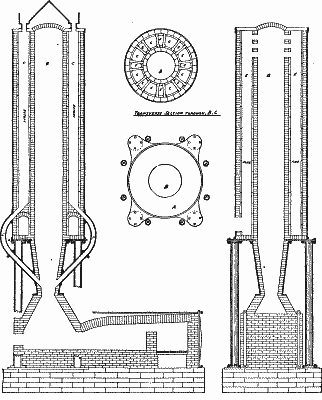
NEW PROCESS FOR MAKING WROUGHT IRON FROM THE ORE.
The drawing given shows the construction of the furnace employed. I quote from the published description:
"The upper part, or deoxidizer, is supported on a strong mantel plate resting on four cast iron columns.
"The retorts and flues are made entirely of fire-brick, from special patterns. The outside is protected by a wrought iron jacket made of No. 14 iron. The puddling furnace is of the ordinary construction, except in the working bottom, which is made longer to accommodate two charges of ore, and thus utilize more of the waste heat in reducing the ore to metallic iron.
"The operation of the furnace is as follows: The pulverized ore is mixed with 20 per cent. of pulverized charcoal or coke, and is fed into an elevator which discharges into the hopper on the deoxidizer leading into the retorts marked C. These retorts are proportioned so that they will hold ore enough to run the puddling furnace 24 hours, the time required for perfect deoxidation. After the retorts are filled, a fire is started in the furnace, and the products of combustion pass up through the main flue, or well, B, where they are deflected by the arch, and pass out through suitable openings, as indicated by arrows, into the down-takes marked E, and out through an annular flue, where they are passed under a boiler.
"It will be noticed that the ore is exposed to the waste heat on three sides of the retorts, and owing to the great surface so exposed, the ore is very thoroughly deoxidized, and reduced in the retorts before it is introduced into the puddling furnace for final reduction. The curved cast iron pipes marked D are provided with slides, and are for the purpose of introducing the deoxidized ore into the second bottom of the furnace. As before stated, the furnace is intended to accommodate two charges of ore, and as fast as it is balled up and taken out of the working bottom, the charge remaining in the second bottom is worked up in the place occupied by the first charge, and a new charge is introduced. As fast as the ore is drawn out from the retorts the elevator supplies a new lot, so that the retorts are always filled, thus making the process continuous."
The temperature of the charge in the deoxidizer is from 800° to 1,000° F.—Amer. Engineer.
A paper read at the Cincinnati Meeting of the American Institute of Mining Engineers, by Willard P. Ward, A.M., M.E., February, 1884.
Having had occasion some short time ago to examine a hard water which owed half its hardness to salts of magnesium, I noticed that the soap test, applied in the usual way, gave a result which differed very much from that obtained by the quantitative estimation of calcium and magnesium. A perfectly normal lather was obtained when soap had been added in quantities sufficient to neutralize 14° of hardness, whereas the water contained salts of calcium and magnesium equivalent, on Clark's scale, to a hardness of 27°.
Although I was aware that similar observations had been made before, I thought that it might be useful to determine the conditions under which the soap test could not be depended upon for reliable results.
I found with waters containing calcium or magnesium alone that, whenever salts of either of these metals were in solution in quantities sufficient to give 23° of hardness on Clark's scale, no dependence could be placed upon the results given by the soap test. In the case of waters containing salts of both calcium and magnesium, I found that if the salts of the latter metal were in solution in quantities sufficient to give more than 10° of hardness, no evidence could be obtained of their presence so long as the salts of calcium in the same water exceeded 6°; in such a case a perfect and permanent lather was produced when soap had been added equivalent to 7° of hardness.
If any water be diluted so as to reduce the proportions of the salts of calcium and magnesium below those stated above, perfectly reliable results will of course be obtained.
Instead of dilution I found that heating the water to about 70° C. was sufficient to cause a complete reaction between the soap and the salts of calcium and magnesium, even if these were present in far larger quantities than any given here.
The experiments so far had all been made with a solution of Castile soap of the strength suggested by Mr. Wanklyn in his book on "Water Analysis." My attention was next directed to the use of any one of the compounds of which such a soap is composed. I commenced with sodium oleate, and found that by employing this substance in a moderately pure condition, perfectly reliable results could be obtained in very hard waters without the trouble of either diluting or heating. I was unable to try sodium stearate directly because of the slight solubility of this substance in cold water or dilute alcohol; but I found that a mixture of sodium oleate and stearate behaved in exactly the same manner as the Castile soap.
I am not prepared at present to state the exact reaction which takes place between salts of calcium and magnesium and a compound soap containing sodium oleate and stearate. I publish these results because I have not noticed anywhere the fact that some waters show a greater hardness with soap when their temperatures approach the boiling point than they do at the average temperature of the air, it being, I believe, the ordinary impression that cold water wastes more soap than hot water before a good and useful lather can be obtained, whereas with very many waters the case is quite the reverse. Neither am I aware at present whether it is well known that the use of sodium oleate unmixed with sodium stearate dispenses with the process of dilution even in very hard waters.—Chem. News.
MM. Berthelot and Vielle have recently been studying the influence of the density of detonating gaseous mixtures upon the pressure developed. The measure of pressure developed by the same gaseous system, taken under two initial states of different density to which the same quantity of heat is communicated, is an important matter in thermodynamics. If the pressures vary in the same ratio as the densities, we may conclude, independently of all special hypotheses on the laws of gases, first, that the specific heat of the system is independent of its density (that is to say, of its initial pressure), and depends only on the absolute temperature, whatever that may mean; and secondly, that the relative variation of the pressure at constant volume, produced by the introduction of a determinate quantity of heat, is also independent of the pressure, and a function only of the temperature. Lastly, the pressure itself will vary proportionally with the absolute temperature, as defined by the theory of a perfect gas, and will serve to determine it. MM. Berthelot and Vielle operated with a bomb, at first kept at ordinary temperatures in the air, and afterward heated in an oil bath to 153 deg. Cent. They also employed isomeric mixtures of the gases; methylic ether, cyanogen, hydrogen, acetylene, and other gases were experimented upon, and the general conclusions are as follows: 1. The same quantity of heat being furnished to a gaseous system, the pressure of the system varies proportionally to the density of the system. 2. The specific heat of the gas is sensibly independent of the density as well toward very high temperatures as about deg. Cent. This is all true for densities near to those that the gas possesses cold under normal pressure, and which varied in the experiment to double the original value. 3. The pressure increases with the quantity of heat furnished to the same system. 4. The apparent specific heat increases parallel with this quantity of heat. These conclusions are independent of all hypotheses on the nature and laws of gases, and were simply drawn from the experiments in question.
The Turkish bath has become an established institution in this country; men of all classes now use it for sanitary as well as remedial purposes. Athletes of various descriptions find it invaluable in "training," and all the distinguished jockeys and light weights keep themselves in condition by its use.
It was thought probable that what was good for man might also be good for the horse, and the fact has been proved. Messrs. Pickford, the eminent carriers, in their hospital for horses at Finchley, have had a bath in operation over eleven years, and find the horses derive great benefit from its use. The bath is put in operation three days a week, and is administered to over twenty horses in this time. The value of the bath having been thus proved, it is rather strange that it has not been more generally adopted by the large carrying firms. However, the Great Northern Railway Company at their new hospital for horses at Totteridge, are erecting a very complete Turkish bath. It consists of three rooms. First, a large wash room or grooming room, from which is entered the first hot room, or tepidarium, from 140° to 150° Fahr.; from this room, the horse, after being thoroughly acclimated, can, if necessary, pass to the hottest room, or calidarium, from 160° to 170° Fahr., and without any turning round can pass on into the grooming and washing room again. This last room is slightly heated from the two other rooms, and in each are stocks in which the animal can he fastened if required. The heating is done most economically by Constantine's convoluted stove, and thorough ventilation is secured from the large volume of hot air constantly supplied, which passes through the baths, and as it becomes vitiated is drawn off by specially designed outlets. The wash room is supplied with hot and cold water, which can, of course, be mixed to any required temperature.—Building News.
In a very interesting account of a journey from the Pacific Ocean through Asia to the United States, by Lieutenant B.H. Buckingham and Ensigns George C. Foulk and Walter McLean,2 United States navy, I find an affection of the nervous system described which, on account of its remarkable characteristics, as well as by reason of certain known analogies, I think should be brought to the special notice of the medical profession. I quote from the work referred to, the following account of this disease. The party is on the Ussuri River not far from its junction with the Amur in Eastern Siberia: "While we were walking on the bank here we observed our messmate, the captain of the general staff (of the Russian army), approach the steward of the boat suddenly, and, without any apparent reason or remark, clap his hands before his face; instantly the steward clapped his hands in the same manner, put on an angry look, and passed on. The incident was somewhat curious, as it involved a degree of familiarity with the steward hardly to have been expected. After this we observed a number of queer performances of the steward, and finally comprehended the situation. It seemed that he was afflicted with a peculiar mental or nervous disease, which forced him to imitate everything suddenly presented to his senses. Thus, when the captain slapped the paddle-box suddenly in the presence of the steward, the latter instantly gave it a similar thump; or, if any noise were made suddenly, he seemed compelled against his will to imitate it instantly, and with remarkable accuracy. To annoy him, some of the passengers imitated pigs grunting, or called out absurd names; others clapped their hands and shouted, jumped, or threw their hats on the deck suddenly, and the poor steward, suddenly startled, would echo them all precisely, and sometimes several consecutively. Frequently he would expostulate, begging people not to startle him, and again would grow furiously angry, but even in the midst of his passion he would helplessly imitate some ridiculous shout or motion directed at him by his pitiless tormenters. Frequently he shut himself up in his pantry, which was without windows, and locked the door, but even there he could be heard answering the grunts, shouts, or pounds on the bulkhead outside. He was a man of middle age, fair physique, rather intelligent in facial expression, and without the slightest indication in appearance of his disability. As we descended the bank to go on board the steamer, some one gave a loud shout and threw his cap on the ground; looking about for the steward, for the shout was evidently made for his benefit, we saw him violently throw his cap, with a shout, into a chicken-coop, into which he was about to put the result of his foraging expedition among the houses of the stanitza.
"We afterward witnessed an incident which illustrated the extent of his disability. The captain of the steamer, running up to him, suddenly clapping his hands at the same time, accidentally slipped and fell hard on the deck; without having been touched by the captain, the steward instantly clapped his bands and shouted, and then, in powerless imitation, he too fell as hard and almost precisely in the same manner and position as the captain. In speaking of the steward's disorder, the captain of the general staff stated that it was not uncommon in Siberia; that he had seen a number of cases of it, and that it was commonest about Yakutsk, where the winter cold is extreme. Both sexes were subject to it, but men much less than women. It was known to Russians by the name of 'miryachit'".
So far as I am aware—and I have looked carefully through several books of travel in Siberia—no account of this curious disease has been hitherto published.
The description given by the naval officers at once, however, brings to mind the remarks made by the late Dr. George M. Beard, before the meeting of the American Neurological Association in 1880, relative to the "Jumpers" or "Jumping Frenchmen" of Maine and northern New Hampshire.3
In June, 1880, Dr. Beard visited Moosehead Lake, found the "Jumpers," and experimented with them. He ascertained that whatever order was given them was at once obeyed. Thus, one of the jumpers who was sitting in a chair with a knife in his hand was told to throw it, and he threw it quickly, so that it stuck in a beam opposite; at the same time he repeated the order to throw it with a cry of alarm not unlike that of hysteria or epilepsy. He also threw away his pipe, which he was filling with tobacco, when he was slapped upon the shoulder. Two jumpers standing near each other were told to strike, and they struck each other very forcibly. One jumper, when standing by a window, was suddenly commanded by a person on the other side of the window to jump, and he jumped up half a foot from the floor, repeating the order. When the commands are uttered in a quick, loud voice, the jumper repeats the order. When told to strike he strikes, when told to throw he throws whatever he may happen to have in his hand. Dr. Beard tried this power of repetition with the first part of the first line of Virgil's "Æneid" and the first part of the first line of Homer's "Iliad," and out-of-the-way words of the English language with which the jumper could not be familiar, and he repeated or echoed the sound of the word as it came to him in a quick, sharp voice, at the same time he jumped, or struck, or threw, or raised his shoulders, or made some other violent muscular motion. They could not help repeating the word or sound that came from the person that ordered them, any more than they could help striking, dropping, throwing, jumping, or starting; all of these phenomena were indeed but parts of the general condition known as jumping. It was not necessary that the sound should come from a human being; any sudden or unexpected noise, as the explosion of a gun or pistol, the falling of a window, or the slamming of a door—provided it was unexpected and loud enough—would cause these jumpers to exhibit some one or all of these phenomena. One of these jumpers came very near cutting his throat, while shaving, on hearing a door slam. They had been known to strike their fists against a red-hot stove, to jump into the fire and into water. They could not help striking their best friend if near them when ordered. The noise of a steam whistle was especially obnoxious to them. One of these jumpers, when taking some bromide of sodium in a tumbler, was told to throw it, and he dashed the tumbler upon the floor. It was dangerous to startle them in any way when they had an ax or an knife in their hands. All of the jumpers agreed that it tired them to be jumped, and they dreaded it, but they were constantly annoyed by their companions.
From this description it will at once, I think, be perceived that there are striking analogies between "miryachit" and this disorder of the "Jumping Frenchmen" of Maine. Indeed, it appears to me that, if the two affections were carefully studied, it would be found that they were identical, or that, at any rate, the phenomena of the one could readily be developed into those of the others. It is not stated that the subjects of miryachit do what they are told to do. They require an example to reach their brains through the sense of sight or that of hearing, whereas the "Jumpers" do not apparently perform an act which is executed before them, but they require a command. It seems, however, that a "Jumper" starts whenever any sudden noise reaches his ears.
In both classes of cases a suggestion of some kind is required, and then the act takes place independently of the will. There is another analogous condition known by the Germans as Schlaftrunkenheit, and to English and American neurologists as somnolentia, or sleep-drunkenness. In this state an individual, on being suddenly awakened, commits some incongruous act of violence, ofttimes a murder. Sometimes this appears to be excited by a dream, but in others no such cause could be discovered.
Thus, a sentry fell asleep during his watch, and, being suddenly aroused by the officer in command, attacked the latter with his sword, and would have killed him but for the interposition of the bystanders. The result of the medical examination was that the act was involuntary, being the result of a violent confusion of mind consequent upon the sudden awaking from a profound sleep. Other cases are cited by Wharton and Stille in their work on medical jurisprudence, by Hoffbauer, and by myself in "Sleep and its Derangements."
The following cases among others have occurred in my own experience:
A gentleman was roused one night by his wife, who heard the street-door bell ring. He got up, and, without paying attention to what she said, dragged the sheets off of the bed, tore them hurriedly into strips, and proceeded to tie the pieces together. She finally succeeded in bringing him to himself, when he said he had thought the house was on fire, and he was providing means for their escape. He did not recollect having had any dream of the kind, but was under the impression that the idea had occurred to him at the instant of his awaking.
Another was suddenly aroused from a sound sleep by the slamming of a window-shutter by the wind. He sprang instantly from his bed, and, seizing a chair that was near, hurled it with all his strength against the window. The noise of the breaking of glass fully awakened him. He explained that he imagined some one was trying to get into the room and had let his pistol fall on the floor, thereby producing the noise which had startled him.
In another case a man dreamed that he heard a voice telling him to jump out of the window. He at once arose, threw open the sash, and jumped to the ground below, fortunately only a distance of about ten feet, so that he was not injured beyond receiving a violent shock. Such a case as this appears to me to be very similar to those described by Dr. Beard in all its essential aspects.
A few years ago I had a gentleman under my charge who would attempt to execute any order given him while he was asleep by a person whispering into his ear. Thus, if told in this way to shout, he shouted as loud as he could; if ordered to get up, he at once jumped from the bed; if directed to repeat certain words, he said them, and so on.
I am not able to give any certain explanation of the phenomena of miryachit or of the "Jumpers," or of certain of those cases of sleep-drunkenness which seem to be of like character. But they all appear to be due to the fact a motor impulse is excited by perceptions without the necessary concurrence of the volition of the individual to cause the discharge. They are, therefore, analogous to reflex actions, and especially to certain epileptic paroxysms due to reflex irritations. It would seem as though the nerve cells were very much in the condition of a package of dynamite or nitro glycerin, in which a very slight impression is sufficient to effect a discharge of nerve force. They differ, however, from the epileptic paroxysm in the fact that the discharge is consonant with the perception—which is in these cases an irritation—and is hence an apparently logical act, whereas in epilepsy the discharge is more violent, is illogical, and does not cease with the cessation of the irritation.
Certainly the whole subject is of sufficient importance to demand the careful study of competent observers.
Read before the New York Neurological Society, February 5, 1884.
"Observations upon the Korean Coast, Japanese-Korean Ports, and Siberia, made during a journey from the Asiatic Station to the United States, through Siberia to Europe, June 3 to September 8, 1882." Published by the United States Navy Department, Washington, 1883, pp. 51.
"Journal of Nervous and Mental Diseases," vol. vii., 1880, p. 487.
An essay by Dr. Beijerinck, on the contagion of the gum disease in plants, lately published by the Royal Academy of Sciences at Amsterdam, contains some useful facts. The gum disease (gummosis, gum-flux) is only too well known to all who grow peaches, apricots, plums, cherries, or other stone fruits. A similar disease produces gum arabic, gum tragacanth, and probably many resins and gum resins. It shows itself openly in the exudation of thick and sticky or hard and dry lumps of gum, which cling on branches of any of these trees where they have been cracked or wounded through the bark. Dr. Beijerinck was induced to make experimental inoculations of the gum disease by suspicions that, like some others observed in plants, it was due to bacteria. He ascertained that it is in a high degree contagious, and can easily be produced by inserting the gum under the edge of a wound through the bark of any of the trees above named. The observation that heated or long boiled pieces of gum lose their contagious property made it most probable that a living organism was concerned in the contagions; and he then found that only those pieces of the gum conveyed contagion in which, whether with or without bacteria, there were spores of a relatively highly organized fungus, belonging to the class of Ascomycetes; and that these spores, inserted by themselves under the bark, produced the same pathological changes as did the pieces of gum. The fungus thus detected, was examined by Professor Oudemans, who ascertained it to be a new species of Coryneum, and has named it Coryneum Beijerincki. The inoculation experiments are best made by means of incisions through the bark of young branches of healthy peach trees or cherry trees, and by slightly raising the cut edge of the bark and putting under it little bits of gum from a diseased tree of the same kind. In nearly every instance these wounds become the seats of acute gum disease, while similar wounds in the same or other branches of the same tree, into which no gum is inserted, remain healthy, unless, by chance, gum be washed into them during rain. The inoculation fails only when the inserted pieces of gum contain no Coryneum. By similar inoculations similar diseases can be produced in plum, almond, and apricot trees, and with the gum of any one of these trees any other can be infected; but of many other substances which Beijerinck tried, not one produced any similar disease. The inoculation with the gum is commonly followed by the death of more or less of the adjacent structures; first of the bark, then of the wood. Small branches or leaf stalks thus infected in winter, or in many places at the same time, may be completely killed; but, in the more instructive experiments the first symptom of the gum disease is the appearance of a beautiful red color around the wound. It comes out in spots like those which often appear spontaneously on the green young branches of peach trees that have the gum disease; and in these spots it is usual to find Coryneum stromata or mycelium filaments. The color is due to the formation of a red pigment in one or more of the layers of the cells of the bark. But in its further progress the disease extends beyond the parts at which the Coryneum or any structures derived from it can be found; and this extension, Beijerinck believes, is due to the production of a fluid of the nature of a ferment, produced by the Coryneum, and penetrating the adjacent structures. This, acting on the cell walls, the starch granules, and other constituents of the cells, transforms them into gum, and even changes into gum the Coryneum itself, reminding the observer of the self-digestion of a stomach.
In the cells of the cambium, the same fluid penetrating unites with the protoplasm, and so alters it that the cells produced from it form, not good normal wood, but a morbid parenchymatous structure. The cells of this parenchyma, well known among the features of gum disease, are cubical or polyhedral, thin walled, and rich in protoplasm. This, in its turn, is transformed into gum, such as fills the gum channels and other cavities found in wood, and sometimes regarded as gum glands. And from this also the new ferment fluid constantly produced, and tracking along the tissues of the branches, conveys the Coryneum infection beyond the places in which its mycelium can be found.
Communicated to the Medical Times by Sir James Paget.
Drinkstone has long been distinguished on account of the successful cultivation of remarkable plants. It lies some eight miles southeast from Bury St. Edmund's, and is the seat of T.H. Powell, Esq. The mansion or hall is a large old-fashioned edifice, a large portion of its south front being covered by a magnificent specimen of the Magnolia grandiflora, not less than 40 feet in height, while other portions of its walls are covered with the finest varieties of climbing roses and other suitable plants. The surrounding country, although somewhat flat, is well wooded, and the soil is a rich loam upon a substratum of gravel, and is consequently admirably suited to the development of the finer kinds of coniferous and other ornamental trees and shrubs, so that the park and grounds contain a fine and well selected assortment of such plants.

THE SNOWFLAKE, LEUCOJUM VERNUM, AT DRINKSTONE PARK.
Coniferous trees are sometimes considered as out of place in park scenery; this, however, does not hold good at Drinkstone, where Mr. Powell has been displayed excellent taste in the way of improving the landscape and creating a really charming effect by so skillfully blending the dressed grounds with the rich greensward of the park that it is not easy to tell where the one terminates or the other commences.
The park, which covers some 200 acres, including a fine lake over eight acres in extent, contains also various large groups or clumps of such species as the Sequoia gigantea, Taxodium sempervirens, Cedres deodora, Picea douglasii, Pinsapo, etc., interspersed with groups of ornamental deciduous trees, producing a warm and very pleasing effect at all seasons of the year. Among species which are conspicuous in the grounds are fine, well-grown examples of Araucaria imbricata, some 30 feet high; Cedrus deodara, 60 feet in height; Abies pinsapo, 40 feet; and fine specimens of Abies grandis, A. nobilis, and A. nordmanniana, etc., together with Abies albertiana or mertensiana, a fine, free-growing species; also Libocedrus gigantea, Thuiopsis borealis, Thuia lobbii, Juniperus recurva, Taxas adpressa, fine plants; with fine golden yews and equally fine examples of the various kinds of variegated hollies, etc.

ODONTOGLOSSUM ROSSI MAJOR VAR. RUBESCENS, AT DRINKSTONE
PARK.
Particular attention is here paid to early spring flowers. Drinkstone is also celebrated as a fruit growing establishment, more particularly as regards the grape vine; the weight and quality of the crops of grapes which are annually produced here are very remarkable.—The Gardeners' Chronicle.
The recently published number of the Royal Agricultural Society's Journal contains some information upon the subject of silage which appears to me of considerable interest to those chemists who are at present investigating the changes which take place in the conversion of grass into silage. The data1 are, so far as I know, unique, and though the analytical work is not my own, yet it is that of an agricultural chemist, Mr. A. Smetham, of Liverpool, whose work I know from personal experience to be thoroughly careful and reliable. I have therefore no hesitation in basing my remarks upon it.
We have here for the first time an accurate account of the quantity of grass put into a silo, of the quantity of silage taken out, and of the exact composition both of the grass and resulting silage. I desire merely to place myself in the position of, so to speak, a "chemical accountant."
The ensilage has been analyzed at three depths, or rather in three layers, the first being 1 foot, the second 1 ft. to 1 ft. 6 in., and the third 1 ft. 6 in. to 2 ft. from the bottom of the silo. By doubling the figures of the bottom layer analysis, adding these to the second and third layer analysis, and dividing by 4, we obtain a fair representation of the average composition of the silage taken throughout the silo, for by so doing we obtain the average of the analyses of each 6-inch layer of silage. The results of the analyses are as follows, calculated on the dry matter. The moisture was practically the same, being 70.48 per cent, in the grass and 72.97 in the silage.
Composition of Grass and Silage (dried at 100°C.).
| Grass. | Ensilage. | |
|---|---|---|
| Fat (ether extract) | 2.80 | 5.38 |
| Soluble albuminous compounds | 3.06 | 5.98 |
| Insoluble albuminous compounds | 6.94 | 3.77 |
| Mucilage, sugar, and extractives, etc. | 11.65 | 4.98 |
| Digestible fiber | 36.24 | 33.37 |
| Indigestible woody fiber | 32.33 | 31.79 |
| —— | —— | |
| 93.02 | 85.27 | |
| Soluble mineral matters | 5.24 | 12.62 |
| Insoluble mineral matters | 1.74 | 2.11 |
| —— | —— | |
| 100.00 | 100.00 |
The striking difference in the mineral matter of the grass and silage I will merely draw attention to; it is not due to the salt added to the silage. I may say, however, that other analysts and I myself have found similar striking differences. For instance, Prof. Kinch 2 found in grass 8.50 per cent. mineral matter, in silage 10.10 per cent., which, as be points out, is equivalent, to a "loss of about 18 per cent. of combustible constituents"—a loss which we have no proof of having taken place. In Mr. Smetham's sample the loss would have to be 50 per cent., which did not occur, and in fact is not possible. What is the explanation?
I am, however, considering now the organic constituents. Calculating the percentages of these in the grass and silage, we obtain the following figures:
Percentage Composition of Organic Compounds.
| Grass. | Ensilage. | ||
|---|---|---|---|
| Fat (ether extract) | 3.01 | 6.31 | |
| Soluble albuminous compounds | 8.29 | } 10.75 11.43 { | 7.01 |
| Insoluble albuminous compounds | 7.46 | 4.42 | |
| Mucilage, sugar, and extractives | 12.52 | 5.84 | |
| Digestible fiber | 38.96 | 39.14 | |
| Indigestible woody fiber | 34.76 | 37.28 | |
| ——— | ——— | ||
| 100.00 | 100.00 |
The difference in the total nitrogen in the grass and silage is equal to 0.68 per cent. of albuminoids. Practically it is a matter of impossibility that the nitrogen could have increased in the silo, and it will be a very safe premise upon which to base any further calculations that the total amount of nitrogen in the silage was identical with that in the grass. There may have been a loss, but that is not yet proved. Arguing then upon the first hypothesis, it is evident that 100 parts of the organic matters of silage represent more than 100 parts of the organic matter of grass, and by the equation we obtain 10.75:11.43 :: 100:106 approximately. If now we calculate the composition of 106 parts organic matter of grass, it will represent exactly the organic matter which has gone to form 100 parts of that present in silage.
The following table gives these results, and also the loss or gain in the various constitutents arising from the conversion into silage:
Organic Matter.
| In 106 pts. Grass. | In 100 pts. Silage. | Loss or Gain. | |
|---|---|---|---|
| Fat (ether extract) | 3.19 | 6.31 | +3.12 |
| Soluble albuminous compounds | 3.49 | 7.01 | +3.52 |
| Insoluble albuminous compounds | 7.91 | 4.42 | -3.49 |
| Mucilage | 13.27 | 5.84 | -7.43 |
| Digestible Fiber | 41.30 | 39.14 | -2.16 |
| Indigestible woody fiber | 36.84 | 37.28 | +0.44 |
| ——— | ——— | ||
| 106.00 | 100.00 |
These calculations show, provided my reasoning be correct, that the chief changes which take place are in the albuminous compounds, which has already been pointed out by Professors Voelcker, Kinch, and others; and in the starch, gum, mucilage, sugar, and those numerous bodies termed extractives, which was to be expected. But they show most conclusively that the "decrease in the amount of indigestible fiber and increase in digestible" so much spoken of is, so far as our present very imperfect methods of analyzing these compounds permit us to judge, a myth; and I have not yet found any sufficient evidence to support this statement. A loss, then, of 6 parts of organic matter out of every 106 parts put into the silo has in this instance taken place, due chiefly to the decomposition of starch, sugar, and mucilage, etc. And as the grass contained 70 parts of water when put into the silo, the total loss would only be 1.7 per cent. of the total weight. This theoretical deduction was found by practical experience correct, for Mr. Smith, agent to Lord Egerton, upon whose estate this silage was made, in his report to Mr. Jenkins says the "actual weight out of the silo corresponds exactly with the weight we put into the same."
In my judgment these figures are of interest to the agricultural chemist for many reasons. First, they will clear the ground for future workers and eliminate from their researches what would have greatly complicated them—changes in the cellulose bodies.
Secondly, they are of interest because our present methods of distinguishing between and estimating digestible and indigestible fiber is most rough, and probably inaccurate, and may not in the least represent the power of an animal—say a cow—to digest these various substances; and most of us know that when a new method of analysis becomes a necessity, a new method is generally discovered. Lastly, they are of interest to the agriculturist, for they point out, I believe for the first time, the exact amount of loss which grass—or at least one sample—has undergone in conversion into silage, and also that much of the nitrogenous matter is changed, and so far as we know at present, lost its nutritive value. This, however, is only comparing silage with grass. What is wanted is to compare silage with hay—both made out of the same grass. Then, and then only, will it be possible to sum up the relative advantages or disadvantages of the two methods of preserving grass as food for cattle.—Chem. News.
Royal Agricultural Society's Journal, vol. xx., part i., pp. 175 and 380.
Journ. Chem. Society, March, 1884, p. 124.
Dr. Percy Frankland has obtained results which may be thus briefly summarized: (1.) That pure ethylene, when burnt at the rate of 5 cubic feet per hour from a Referee's Argand burner, emits a light of 68.5 standard candles. (2.) That the illuminating power of equal volumes of mixtures of ethylene with either hydrogen carbonic oxide or marsh-gas is less than that of pure ethylene. (3.) That when the proportion of ethylene in such mixtures is above 63 per cent. the illuminating power of the mixture is but slightly affected by the nature of the diluent. When, on the other hand, the proportion of ethylene in such mixtures is low, the illuminating power of the mixture is considerably the highest when marsh-gas is the diluent, and the lowest when the ethylene is mixed with carbonic oxide. (4.) That if 5 cubic feet of ethylene be uniformly consumed irrespectively of the composition of the mixture, the calculated illuminating power is in every case equal to or actually greater than that of pure ethylene until a certain degree of dilution is attained. This intrinsic luminosity of ethylene remains almost constant when the latter is diluted with carbonic oxide, until the ethylene forms only 40 per cent. of the mixture, after which it rapidly diminishes to zero when the ethylene forms only 20 per cent. of the mixture. When the ethylene is diluted with hydrogen, its intrinsic luminosity rises to 81 candles when the ethylene constitutes 30 per cent. of the mixture, after which it rapidly falls to zero when the ethylene amounts to only 10 per cent. In the case of mixtures of ethylene and marsh-gas, the intrinsic luminosity of the former is augmented with increasing rapidity as the proportion of marsh gas rises, the intrinsic luminosity of ethylene, in a mixture containing 10 per cent. of the latter, being between 170 and 180 candles.
The reality of the sun's corona having been cast in doubt by a leading observer of the last total eclipse, who, from the erratic display observed in the spectroscope, has declared it a subjective phenomenon of diffraction, has led me to an examination and inquiry as to the bearing of an obscurely considered and heretofore only casually observed phenomenon seen to take place during total solar eclipses. This phenomenon, it seems to me, ought to account for, and will possibly satisfy, the spectroscopic conditions observed just before, during, and after totality; which has probably led to the epithet used by some leading observers—"the fickle corona." The peculiar phenomenon observed in the spectroscope, the flickering bands or lines of the solar spectrum flashing upon and across the coronal spectrum, has caused no little speculation among observers.
The diffraction or interference bands projected by the passage of a strong beam of light by a solid body, as discovered long since by Grimaldi, and investigated later by Newton, Fresnel, and Fraunhofer, are explained and illustrated in our text books; but the grand display of this phenomenon in a total solar eclipse, where the sun is the source of light and the moon the intercepting body, has as yet received but little attention from observers, and is not mentioned to my knowledge in our text books.
In the instructions issued from the United States Naval Observatory and the Signal Office at Washington for the observation of the eclipse of July 29, 1878, attention was casually directed to this phenomenon, and a few of the observers at Pike's Peak, Central City, Denver, and other places have given lucid and interesting descriptions of the flight of the diffraction bands as seen coursing over the face of the earth at the speed of the moon's shadow, at the apparent enormous velocity of thirty-three miles per minute, or fifty times the speed of a fast railway train.
From a known optical illusion derived from interference or fits of perception, as illustrated in quick moving shadows, this great speed was not realized to the eye, as the observed motion of these shadows was apparently far less rapid than their reality.
The ultra or diffraction bands outside of the shadow were distinctly seen and described by Mr. J.E. Keeler at Central City, both before and after totality. He estimates the shadow bands at 8 inches wide and 4 feet apart.
Professor E.S. Holden, also at Central City, estimated the dark bands as about 3 feet apart, and variable.
From estimates which he obtained from other observers of his party, the distances between the bands varied from 6 to l½ feet, but so quickly did they pass that they baffled all attempts to count even the number that passed in one second.
He observed the time of continuance of their passage from west to east as forty-eight seconds, which indicates a width of 33 miles of diffraction bands stretching outward from the edge of the shadow to the number of many thousands.
Mr. G.W. Hill, at Denver, a little to the north of the central track of the shadow, observed the infra or bands within the shadow, alluding to the fact that they must be moving at the same rate as the shadow, although their apparent motion was much slower, or like the shadows of flying clouds. He attributes the discrepancy to optical illusion.
At Virginia City the colors of the ultra bands were observed, and estimated at five seconds' duration from the edge of the shadow, which is equal to about 4 miles in width. These are known to be the strongest color bands in the diffraction spectrum, which accounts for their being generally observed.
Mr. W.H. Bush, observing at Central City, in a communication to Prof. Holden alludes to the brilliancy of the colors of these bands as seen through small clouds floating near the sun's place during totality, and of the rapid change of their rainbow colors as observed dashing across the clouds with the rapidity of thought.
All of these bands, both ultra and infra, as seen in optical experiments, are colored in reverse order, being from violet to red for each band outward and inward from the edge of the shadow.
It is very probable that the velocity of the passage of all the bands during a total eclipse very much modifies the distinctness of the colors or possibly obliterates them by optically blending so as to produce the dull white and black bands which occupied so large a portion of this grand panorama.
The phenomenon of these faint colored bands, with the observed light and dark shadows, may be attributed to one or all of the following causes:
1. A change in the direction of a small portion of the sun's light passing by the solid body of the moon, it being deflected outward by repulsion or reflection from its surface, and other portions being deflected inward after passing the body by mutual repulsion of its own elements toward a light vacuum or space devoid of the element of vibration.
2. The colored spectral bands being the direct result of the property of interference, or the want of correspondence of the wave lengths due to divergence; the same phenomenon being also observed in convergent light. This is practically illustrated in the hazy definition of the reduced aperture of telescopes, and its peculiarities shown in the spectral rings within and beyond the focus.
3. Chromatic dispersion by our atmosphere, together with selective absorption, also by our atmosphere and its vapors, have been suggested as causes in this curious and complicated phenomena.
In none of the reports descriptive of the phenomena of polarization of the corona is there the slightest allusion to the influence that the diffraction bands may possibly have in modifying or producing the various conditions of polarization observed; although these observations have been made and commented upon during the past twenty-five years.
Investigations now in progress of the modifying relation of the phenomenon of diffraction in its effect upon not only the physical aspect of the corona, but also in some strange spectroscopic anomalies that have been observed near the sun at other times than during a total solar eclipse, will, it is hoped, result in a fuller interpretation of the physical nature of one of the grandest elements of creation—light; let there be more of it.
A paper read before the American Astronomical Society, May 5, 1884.
A CATALOGUE containing brief notices of many important scientific papers heretofore published in the SUPPLEMENT, may be had gratis at this office.
Terms of Subscription, $5 a Year.
Sent by mail, postage prepaid, to subscribers in any part of the United States or Canada. Six dollars a year, sent, prepaid, to any foreign country.
All the back numbers of THE SUPPLEMENT, from the commencement, January 1, 1876, can be had. Price, 10 cents each.
All the back volumes of THE SUPPLEMENT can likewise be supplied. Two volumes are issued yearly. Price of each volume, $2.50, stitched in paper, or $3.50, bound in stiff covers.
COMBINED RATES—One copy of SCIENTIFIC AMERICAN and one copy of SCIENTIFIC AMERICAN SUPPLEMENT, one year, postpaid, $7.00.
A liberal discount to booksellers, news agents, and canvassers.
MUNN & CO., Publishers,
361 Broadway, New York, N.Y.
In connection with the Scientific American, Messrs MUNN & Co. are Solicitors of American and Foreign Patents, have had 39 years' experience, and now have the largest establishment in the world. Patents are obtained on the best terms.
A special notice is made in the Scientific American of all Inventions patented through this Agency, with the name and residence of the Patentee. By the immense circulation thus given, public attention is directed to the merits of the new patent, and sales or introduction often easily effected.
Any person who has made a new discovery or invention can ascertain, free of charge, whether a patent can probably be obtained, by writing to MUNN & Co.
We also send free our Hand Book about the Patent Laws, Patents, Caveats, Trade Marks, their costs, and how procured. Address
MUNN & CO., 361 Broadway, New York.
Branch Office, cor. F and 7th Sts., Washington. D.C.