 PLATE I.
PLATE I.THE PLANET SATURN,
IN 1872.
Title: The Story of the Heavens
Author: Robert S. Ball
Release date: December 1, 2008 [eBook #27378]
Language: English
Credits: Produced by K. Nordquist, Brenda Lewis, Stephen Hope, Greg
Bergquist and the Online Distributed Proofreading Team at
http://www.pgdp.net (This file was produced from images
generously made available by The Internet Archive/American
Libraries.)
Transcriber’s Note
The punctuation and spelling from the original text have been faithfully preserved. Only obvious typographical errors have been corrected.
THE
Story of the Heavens
SIR ROBERT STAWELL BALL, LL.D. D.Sc.
Author of "Star-Land"
FELLOW OF THE ROYAL SOCIETY OF LONDON, HONORARY FELLOW OF THE ROYAL SOCIETY OF
EDINBURGH, FELLOW OF THE ROYAL ASTRONOMICAL SOCIETY, SCIENTIFIC ADVISER TO THE
COMMISSIONERS OF IRISH LIGHTS, LOWNDEAN PROFESSOR OF ASTRONOMY AND
GEOMETRY IN THE UNIVERSITY OF CAMBRIDGE, AND FORMERLY
ROYAL ASTRONOMER OF IRELAND
WITH TWENTY-FOUR COLOURED PLATES AND NUMEROUS
ILLUSTRATIONS
NEW AND REVISED EDITION
CASSELL and COMPANY, Limited
LONDON, PARIS, NEW YORK & MELBOURNE
1900
ALL RIGHTS RESERVED

I have to acknowledge the kind aid which I have received in the preparation of this book.
Mr. Nasmyth has permitted me to use some of the beautiful drawings of the Moon, which have appeared in the well-known work published by him in conjunction with Mr. Carpenter. To this source I am indebted for Plates VII., VIII., IX., X., and Figs. 28, 29, 30.
Professor Pickering has allowed me to copy some of the drawings made at Harvard College Observatory by Mr. Trouvelot, and I have availed myself of his kindness for Plates I., IV., XII., XV.
I am indebted to Professor Langley for Plate II., to Mr. De la Rue for Plates III. and XIV., to Mr. T.E. Key for Plate XVII., to Professor Schiaparelli for Plate XVIII., to the late Professor C. Piazzi Smyth for Fig. 100, to Mr. Chambers for Fig. 7, which has been borrowed from his "Handbook of Descriptive Astronomy," to Dr. Stoney for Fig. 78, and to Dr. Copeland and Dr. Dreyer for Fig. 72. I have to acknowledge the valuable assistance derived from Professor Newcomb's "Popular Astronomy," and Professor Young's "Sun." In revising the volume I have had the kind aid of the Rev. Maxwell Close.
I have also to thank Dr. Copeland and Mr. Steele for their kindness in reading through the entire proofs; while I have also occasionally availed myself of the help of Mr. Cathcart.
ROBERT S. BALL.
Observatory, Dunsink, Co. Dublin.
12th May, 1886.
I have taken the opportunity in the present edition to revise the work in accordance with the recent progress of astronomy. I am indebted to the Royal Astronomical Society for the permission to reproduce some photographs from their published series, and to Mr. Henry F. Griffiths, for beautiful drawings of Jupiter, from which Plate XI. was prepared.
ROBERT S. BALL.
Cambridge,
1st May, 1900.
| page | ||
| Introduction | 1 | |
| chapter | ||
| I. | The Astronomical Observatory | 9 |
| II. | The Sun | 29 |
| III. | The Moon | 70 |
| IV. | The Solar System | 107 |
| V. | The Law of Gravitation | 122 |
| VI. | The Planet of Romance | 150 |
| VII. | Mercury | 155 |
| VIII. | Venus | 167 |
| IX. | The Earth | 192 |
| X. | Mars | 208 |
| XI. | The Minor Planets | 229 |
| XII. | Jupiter | 245 |
| XIII. | Saturn | 268 |
| XIV. | Uranus | 298 |
| XV. | Neptune | 315 |
| XVI. | Comets | 336 |
| XVII. | Shooting Stars | 372 |
| XVIII. | The Starry Heavens | 409 |
| XIX. | The Distant Suns | 425 |
| XX. | Double Stars | 434 |
| XXI. | The Distances of the Stars | 441 |
| XXII. | Star Clusters and Nebulæ | 461 |
| XXIII. | The Physical Nature of the Stars | 477 |
| XXIV. | The Precession and Nutation of the Earth's Axis | 492 |
| XXV. | The Aberration of Light | 503 |
| XXVI. | The Astronomical Significance of Heat | 513 |
| XXVII. | The Tides | 531 |
| Appendix | 558 | |
| PLATE | ||||
| I. | The Planet Saturn | Frontispiece | ||
| II. | A Typical Sun-spot | To face page | 9 | |
| A. | The Sun | " | " | 44 |
| III. | Spots and Faculæ on the Sun | " | " | 37 |
| IV. | Solar Prominences or Flames | " | " | 57 |
| V. | The Solar Corona | " | " | 62 |
| VI. | Chart of the Moon's Surface | " | " | 81 |
| B. | Portion of the Moon | " | " | 88 |
| VII. | The Lunar Crater Triesnecker | " | " | 93 |
| VIII. | A Normal Lunar Crater | " | " | 97 |
| IX. | The Lunar Crater Plato | " | " | 102 |
| X. | The Lunar Crater Tycho | " | " | 106 |
| XI. | The Planet Jupiter | " | " | 254 |
| XII. | Coggia's Comet | " | " | 340 |
| C. | Comet A., 1892, 1 Swift | " | " | 358 |
| XIII. | Spectra of the Sun and of three Stars | " | " | 47 |
| D. | The Milky Way, near Messier II. | " | " | 462 |
| XIV. | The Great Nebula in Orion | " | " | 466 |
| XV. | The Great Nebula in Andromeda | " | " | 468 |
| E. | Nebulæ in the Pleiades | " | " | 472 |
| F. | ω Centauri | " | " | 474 |
| XVI. | Nebulæ observed with Lord Rosse's Telescope | " | " | 476 |
| XVII. | The Comet of 1882 | " | " | 357 |
| XVIII. | Schiaparelli's Map of Mars | " | " | 221 |
| FIG. | PAGE | |
| 1. | Principle of the Refracting Telescope | 11 |
| 2. | Dome of the South Equatorial at Dunsink Observatory, Co. Dublin | 12 |
| 3. | Section of the Dome of Dunsink Observatory | 13 |
| 4. | The Telescope at Yerkes Observatory, Chicago | 15 |
| 5. | Principle of Herschel's Reflecting Telescope | 16 |
| 6. | South Front of the Yerkes Observatory, Chicago | 17 |
| 7. | Lord Rosse's Telescope | 18 |
| 8. | Meridian Circle | 20 |
| 9. | The Great Bear | 27 |
| 10. | Comparative Sizes of the Earth and the Sun | 30 |
| 11. | The Sun, photographed September 22, 1870 | 33 |
| 12. | Photograph of the Solar Surface | 35 |
| 13. | An ordinary Sun-spot | 36 |
| 14. | Scheiner's Observations on Sun-spots | 38 |
| 15. | Zones on the Sun's Surface in which Spots appear | 39 |
| 16. | Texture of the Sun and a small Spot | 43 |
| 17. | The Prism | 45 |
| 18. | Dispersion of Light by the Prism | 46 |
| 19. | Prominences seen in Total Eclipses | 53 |
| 20. | View of the Corona in a Total Eclipse | 62 |
| 21. | View of Corona during Eclipse of January 22, 1898 | 63 |
| 22. | The Zodiacal Light in 1874 | 69 |
| 23. | Comparative Sizes of the Earth and the Moon | 73 |
| 24. | The Moon's Path around the Sun | 76 |
| 25. | The Phases of the Moon | 76 |
| 26. | The Earth's Shadow and Penumbra | 78 |
| 27. | Key to Chart of the Moon (Plate VI.) | 81 |
| 28. | Lunar Volcano in Activity: Nasmyth's Theory | 97 |
| 29. | Lunar Volcano: Subsequent Feeble Activity | 97 |
| 30. | Lunar Volcano: Formation of the Level Floor by Lava | 98 |
| 31. | Orbits of the Four Interior Planets | 115 |
| 32. | The Earth's Movement | 116 |
| 33. | Orbits of the Four Giant Planets | 117 |
| 34. | Apparent Size of the Sun from various Planets | 118 |
| 35. | Comparative Sizes of the Planets | 119 |
| 36. | Illustration of the Moon's Motion | 130 |
| 37. | Drawing an Ellipse | 137 |
| 38. | Varying Velocity of Elliptic Motion | 140 |
| 39. | Equal Areas in Equal Times | 141 |
| 40. | Transit of the Planet of Romance | 153 |
| 41. | Variations in Phase and apparent Size of Mercury | 160 |
| 42. | Mercury as a Crescent | 161 |
| 43. | Venus, May 29, 1889 | 170 |
| 44. | Different Aspects of Venus in the Telescope | 171 |
| 45. | Venus on the Sun at the Transit of 1874 | 177 |
| 46. | Paths of Venus across the Sun in the Transits of 1874 and 1882 | 179 |
| 47. | A Transit of Venus, as seen from Two Localities | 183 |
| 48. | Orbits of the Earth and of Mars | 210 |
| 49. | Apparent Movements of Mars in 1877 | 212 |
| 50. | Relative Sizes of Mars and the Earth | 216 |
| 51, 52. | Drawings of Mars | 217 |
| 53. | Elevations and Depressions on the Terminator of Mars | 217 |
| 54. | The Southern Polar Cap on Mars | 217 |
| 55. | The Zone of Minor Planets between Mars and Jupiter | 234 |
| 56. | Relative Dimensions of Jupiter and the Earth | 246 |
| 57–60. | The Occultation of Jupiter | 255 |
| 61. | Jupiter and his Four Satellites | 258 |
| 62. | Disappearances of Jupiter's Satellites | 259 |
| 63. | Mode of Measuring the Velocity of Light | 264 |
| 64. | Saturn | 270 |
| 65. | Relative Sizes of Saturn and the Earth | 273 |
| 66. | Method of Measuring the Rotation of Saturn's Rings | 288 |
| 67. | Method of Measuring the Rotation of Saturn's Rings | 289 |
| 68. | Transit of Titan and its Shadow | 295 |
| 69. | Parabolic Path of a Comet | 339 |
| 70. | Orbit of Encke's Comet | 346 |
| 71. | Tail of a Comet directed from the Sun | 363 |
| 72. | Bredichin's Theory of Comets' Tails | 366 |
| 73. | Tails of the Comet of 1858 | 367 |
| 74. | The Comet of 1744 | 368 |
| 75. | The Path of the Fireball of November 6, 1869 | 375 |
| 76. | The Orbit of a Shoal of Meteors | 378 |
| 77. | Radiant Point of Shooting Stars | 381 |
| 78. | The History of the Leonids | 385 |
| 79. | Section of the Chaco Meteorite | 398 |
| 80. | The Great Bear and Pole Star | 410 |
| 81. | The Great Bear and Cassiopeia | 411 |
| 82. | The Great Square of Pegasus | 413 |
| 83. | Perseus and its Neighbouring Stars | 415 |
| 84. | The Pleiades | 416 |
| 85. | Orion, Sirius, and Neighbouring Stars | 417 |
| 86. | Castor and Pollux | 418 |
| 87. | The Great Bear and the Lion | 419 |
| 88. | Boötes and the Crown | 420 |
| 89. | Virgo and Neighbouring Constellations | 421 |
| 90. | The Constellation of Lyra | 422 |
| 91. | Vega, the Swan, and the Eagle | 423 |
| 92. | The Orbit of Sirius | 426 |
| 93. | The Parallactic Ellipse | 444 |
| 94. | 61 Cygni and the Comparison Stars | 447 |
| 95. | Parallax in Declination of 61 Cygni | 450 |
| 96. | Globular Cluster in Hercules | 463 |
| 97. | Position of the Great Nebula in Orion | 466 |
| 98. | The Multiple Star θ Orionis | 467 |
| 99. | The Nebula N.G.C. 1499 | 471 |
| 100. | Star-Map, showing Precessional Movement | 493 |
| 101. | Illustration of the Motion of Precession | 495 |
THE
Story of the Heavens.
"The Story of the Heavens" is the title of our book. We have indeed a wondrous story to narrate; and could we tell it adequately it would prove of boundless interest and of exquisite beauty. It leads to the contemplation of grand phenomena in nature and great achievements of human genius.
Let us enumerate a few of the questions which will be naturally asked by one who seeks to learn something of those glorious bodies which adorn our skies: What is the Sun—how hot, how big, and how distant? Whence comes its heat? What is the Moon? What are its landscapes like? How does our satellite move? How is it related to the earth? Are the planets globes like that on which we live? How large are they, and how far off? What do we know of the satellites of Jupiter and of the rings of Saturn? How was Uranus discovered? What was the intellectual triumph which brought the planet Neptune to light? Then, as to the other bodies of our system, what are we to say of those mysterious objects, the comets? Can we discover the laws of their seemingly capricious movements? Do we know anything of their nature and of the marvellous tails with which they are often decorated? What can be told about the shooting-stars which so often dash into our atmosphere and perish in a streak of splendour? What is the nature of those constellations of bright stars which have been recognised from all antiquity, and of the host of smaller stars which our telescopes disclose? Can it be true that these countless orbs are really majestic suns, sunk to an appalling[Pg 2] depth in the abyss of unfathomable space? What have we to tell of the different varieties of stars—of coloured stars, of variable stars, of double stars, of multiple stars, of stars that seem to move, and of stars that seem at rest? What of those glorious objects, the great star clusters? What of the Milky Way? And, lastly, what can we learn of the marvellous nebulæ which our telescopes disclose, poised at an immeasurable distance? Such are a few of the questions which occur when we ponder on the mysteries of the heavens.
The history of Astronomy is, in one respect, only too like many other histories. The earliest part of it is completely and hopelessly lost. The stars had been studied, and some great astronomical discoveries had been made, untold ages before those to which our earliest historical records extend. For example, the observation of the apparent movement of the sun, and the discrimination between the planets and the fixed stars, are both to be classed among the discoveries of prehistoric ages. Nor is it to be said that these achievements related to matters of an obvious character. Ancient astronomy may seem very elementary to those of the present day who have been familiar from childhood with the great truths of nature, but, in the infancy of science, the men who made such discoveries as we have mentioned must have been sagacious philosophers.
Of all the phenomena of astronomy the first and the most obvious is that of the rising and the setting of the sun. We may assume that in the dawn of human intelligence these daily occurrences would form one of the first problems to engage the attention of those whose thoughts rose above the animal anxieties of everyday existence. A sun sets and disappears in the west. The following morning a sun rises in the east, moves across the heavens, and it too disappears in the west; the same appearances recur every day. To us it is obvious that the sun, which appears each day, is the same sun; but this would not seem reasonable to one who thought his senses showed him that the earth was a flat plain of indefinite extent, and that around the inhabited regions on all sides extended, to vast distances, either desert wastes or trackless oceans. How could that same sun, which plunged into the ocean at a fabulous distance in the west,[Pg 3] reappear the next morning at an equally great distance in the east? The old mythology asserted that after the sun had dipped in the western ocean at sunset (the Iberians, and other ancient nations, actually imagined that they could hear the hissing of the waters when the glowing globe was plunged therein), it was seized by Vulcan and placed in a golden goblet. This strange craft with its astonishing cargo navigated the ocean by a northerly course, so as to reach the east again in time for sunrise the following morning. Among the earlier physicists of old it was believed that in some manner the sun was conveyed by night across the northern regions, and that darkness was due to lofty mountains, which screened off the sunbeams during the voyage.
In the course of time it was thought more rational to suppose that the sun actually pursued his course below the solid earth during the course of the night. The early astronomers had, moreover, learned to recognise the fixed stars. It was noticed that, like the sun, many of these stars rose and set in consequence of the diurnal movement, while the moon obviously followed a similar law. Philosophers thus taught that the various heavenly bodies were in the habit of actually passing beneath the solid earth.
By the acknowledgment that the whole contents of the heavens performed these movements, an important step in comprehending the constitution of the universe had been decidedly taken. It was clear that the earth could not be a plane extending to an indefinitely great distance. It was also obvious that there must be a finite depth to the earth below our feet. Nay, more, it became certain that whatever the shape of the earth might be, it was at all events something detached from all other bodies, and poised without visible support in space. When this discovery was first announced it must have appeared a very startling truth. It was so difficult to realise that the solid earth on which we stand reposed on nothing! What was to keep it from falling? How could it be sustained without tangible support, like the legendary coffin of Mahomet? But difficult as it may have been to receive this doctrine, yet its necessary truth in due time[Pg 4] commanded assent, and the science of Astronomy began to exist. The changes of the seasons and the recurrence of seed-time and harvest must, from the earliest times, have been associated with certain changes in the position of the sun. In the summer at mid-day the sun rises high in the heavens, in the winter it is always low. Our luminary, therefore, performs an annual movement up and down in the heavens, as well as a diurnal movement of rising and setting. But there is a third species of change in the sun's position, which is not quite so obvious, though it is still capable of being detected by a few careful observations, if combined with a philosophical habit of reflection. The very earliest observers of the stars can hardly have failed to notice that the constellations visible at night varied with the season of the year. For instance, the brilliant figure of Orion, though so well seen on winter nights, is absent from the summer skies, and the place it occupied is then taken by quite different groups of stars. The same may be said of other constellations. Each season of the year can thus be characterised by the sidereal objects that are conspicuous by night. Indeed, in ancient days, the time for commencing the cycle of agricultural occupations was sometimes indicated by the position of the constellations in the evening.
By reflecting on these facts the early astronomers were enabled to demonstrate the apparent annual movement of the sun. There could be no rational explanation of the changes in the constellations with the seasons, except by supposing that the place of the sun was altering, so as to make a complete circuit of the heavens in the course of the year. This movement of the sun is otherwise confirmed by looking at the west after sunset, and watching the stars. As the season progresses, it may be noticed each evening that the constellations seem to sink lower and lower towards the west, until at length they become invisible from the brightness of the sky. The disappearance is explained by the supposition that the sun appears to be continually ascending from the west to meet the stars. This motion is, of course, not to be confounded with the ordinary diurnal rising and setting, in which all the heavenly bodies participate. It is to be understood[Pg 5] that besides being affected by the common motion our luminary has a slow independent movement in the opposite direction; so that though the sun and a star may set at the same time to-day, yet since by to-morrow the sun will have moved a little towards the east, it follows that the star must then set a few minutes before the sun.[1]
The patient observations of the early astronomers enabled the sun's track through the heavens to be ascertained, and it was found that in its circuit amid the stars and constellations our luminary invariably followed the same path. This is called the ecliptic, and the constellations through which it passes form a belt around the heavens known as the zodiac. It was anciently divided into twelve equal portions or "signs," so that the stages on the sun's great journey could be conveniently indicated. The duration of the year, or the period required by the sun to run its course around the heavens, seems to have been first ascertained by astronomers whose names are unknown. The skill of the early Oriental geometers was further evidenced by their determination of the position of the ecliptic with regard to the celestial equator, and by their success in the measurement of the angle between these two important circles on the heavens.
The principal features of the motion of the moon have also been noticed with intelligence at an antiquity more remote than history. The attentive observer perceives the important truth that the moon does not occupy a fixed position in the heavens. During the course of a single night the fact that the moon has moved from west to east across the heavens can be perceived by noting its position relatively to adjacent stars. It is indeed probable that the motion of the moon was a discovery prior to that of the annual motion of the sun, inasmuch as it is the immediate consequence of a simple observation, and involves but little exercise of any intellectual power. In prehistoric times also, the time of revolution of the moon had been ascertained, and the phases of our satellite had been correctly attributed to the varying aspect[Pg 6] under which the sun-illuminated side is turned towards the earth.
But we are far from having exhausted the list of great discoveries which have come down from unknown antiquity. Correct explanations had been given of the striking phenomenon of a lunar eclipse, in which the brilliant surface is plunged temporarily into darkness, and also of the still more imposing spectacle of a solar eclipse, in which the sun itself undergoes a partial or even a total obscuration. Then, too, the acuteness of the early astronomers had detected the five wandering stars or planets: they had traced the movements of Mercury and Venus, Mars, Jupiter, and Saturn. They had observed with awe the various configurations of these planets: and just as the sun, and in a lesser degree the moon, were intimately associated with the affairs of daily life, so in the imagination of these early investigators the movements of the planets were thought to be pregnant with human weal or human woe. At length a certain order was perceived to govern the apparently capricious movements of the planets. It was found that they obeyed certain laws. The cultivation of the science of geometry went hand in hand with the study of astronomy: and as we emerge from the dim prehistoric ages into the historical period, we find that the theory of the phenomena of the heavens possessed already some degree of coherence.
Ptolemy, following Pythagoras, Plato, and Aristotle, acknowledged that the earth's figure was globular, and he demonstrated it by the same arguments that we employ at the present day. He also discerned how this mighty globe was isolated in space. He admitted that the diurnal movement of the heavens could be accounted for by the revolution of the earth upon its axis, but unfortunately he assigned reasons for the deliberate rejection of this view. The earth, according to him, was a fixed body; it possessed neither rotation round an axis nor translation through space, but remained constantly at rest in what he supposed to be the centre of the universe. According to Ptolemy's theory the sun and the moon moved in circular orbits around the earth in the centre. The [Pg 7]explanation of the movements of the planets he found to be more complicated, because it was necessary to account for the fact that a planet sometimes advanced and that it sometimes retrograded. The ancient geometers refused to believe that any movement, except revolution in a circle, was possible for a celestial body: accordingly a contrivance was devised by which each planet was supposed to revolve in a circle, of which the centre described another circle around the earth.
Although the Ptolemaic doctrine is now known to be framed on quite an extravagant estimate of the importance of the earth in the scheme of the heavens, yet it must be admitted that the apparent movements of the celestial bodies can be thus accounted for with considerable accuracy. This theory is described in the great work known as the "Almagest," which was written in the second century of our era, and was regarded for fourteen centuries as the final authority on all questions of astronomy.
Such was the system of Astronomy which prevailed during the Middle Ages, and was only discredited at an epoch nearly simultaneous with that of the discovery of the New World by Columbus. The true arrangement of the solar system was then expounded by Copernicus in the great work to which he devoted his life. The first principle established by these labours showed the diurnal movement of the heavens to be due to the rotation of the earth on its axis. Copernicus pointed out the fundamental difference between real motions and apparent motions; he proved that the appearances presented in the daily rising and setting of the sun and the stars could be accounted for by the supposition that the earth rotated, just as satisfactorily as by the more cumbrous supposition of Ptolemy. He showed, moreover, that the latter supposition must attribute an almost infinite velocity to the stars, so that the rotation of the entire universe around the earth was clearly a preposterous supposition. The second great principle, which has conferred immortal glory on Copernicus, assigned to the earth its true position in the universe. Copernicus transferred the centre, about which all the planets revolve, from the earth to the sun; and he established the[Pg 8] somewhat humiliating truth, that our earth is merely a planet pursuing a track between the paths of Venus and of Mars, and subordinated like all the other planets to the supreme sway of the Sun.
This great revolution swept from astronomy those distorted views of the earth's importance which arose, perhaps not unnaturally, from the fact that we happen to be domiciled on that particular planet. The achievements of Copernicus were soon to be followed by the invention of the telescope, that wonderful instrument by which the modern science of astronomy has been created. To the consideration of this important subject we shall devote the first chapter of our book.
Early Astronomical Observations—The Observatory of Tycho Brahe—The Pupil of the Eye—Vision of Faint Objects—The Telescope—The Object-Glass—Advantages of Large Telescopes—The Equatorial—The Observatory—The Power of a Telescope—Reflecting Telescopes—Lord Rosse's Great Reflector at Parsonstown—How the mighty Telescope is used—Instruments of Precision—The Meridian Circle—The Spider Lines—Delicacy of pointing a Telescope—Precautions necessary in making Observations—The Ideal Instrument and the Practical One—The Elimination of Error—Greenwich Observatory—The ordinary Opera-Glass as an Astronomical Instrument—The Great Bear—Counting the Stars in the Constellation—How to become an Observer.
The earliest rudiments of the Astronomical Observatory are as little known as the earliest discoveries in astronomy itself. Probably the first application of instrumental observation to the heavenly bodies consisted in the simple operation of measuring the shadow of a post cast by the sun at noonday. The variations in the length of this shadow enabled the primitive astronomers to investigate the apparent movements of the sun. But even in very early times special astronomical instruments were employed which possessed sufficient accuracy to add to the amount of astronomical knowledge, and displayed considerable ingenuity on the part of the designers.
Professor Newcomb[2] thus writes: "The leader was Tycho Brahe, who was born in 1546, three years after the death of Copernicus. His attention was first directed to the study of astronomy by an eclipse of the sun on August 21st, 1560, which was total in some parts of Europe. Astonished that such a phenomenon could be predicted, he devoted himself to a study of the methods of observation and calculation by[Pg 10] which the prediction was made. In 1576 the King of Denmark founded the celebrated observatory of Uraniborg, at which Tycho spent twenty years assiduously engaged in observations of the positions of the heavenly bodies with the best instruments that could then be made. This was just before the invention of the telescope, so that the astronomer could not avail himself of that powerful instrument. Consequently, his observations were superseded by the improved ones of the centuries following, and their celebrity and importance are principally due to their having afforded Kepler the means of discovering his celebrated laws of planetary motion."
The direction of the telescope to the skies by Galileo gave a wonderful impulse to the study of the heavenly bodies. This extraordinary man is prominent in the history of astronomy, not alone for his connection with this supreme invention, but also for his achievements in the more abstract parts of astronomy. He was born at Pisa in 1564, and in 1609 the first telescope used for astronomical observation was constructed. Galileo died in 1642, the year in which Newton was born. It was Galileo who laid with solidity the foundations of that science of Dynamics, of which astronomy is the most splendid illustration; and it was he who, by promulgating the doctrines taught by Copernicus, incurred the wrath of the Inquisition.
The structure of the human eye in so far as the exquisite adaptation of the pupil is concerned presents us with an apt illustration of the principle of the telescope. To see an object, it is necessary that the light from it should enter the eye. The portal through which the light is admitted is the pupil. In daytime, when the light is brilliant, the iris decreases the size of the pupil, and thus prevents too much light from entering. At night, or whenever the light is scarce, the eye often requires to grasp all it can. The pupil then expands; more and more light is admitted according as the pupil grows larger. The illumination of the image on the retina is thus effectively controlled in accordance with the requirements of vision.
A star transmits to us its feeble rays of light, and from[Pg 11] those rays the image is formed. Even with the most widely-opened pupil, it may, however, happen that the image is not bright enough to excite the sensation of vision. Here the telescope comes to our aid: it catches all the rays in a beam whose original dimensions were far too great to allow of its admission through the pupil. The action of the lenses concentrates those rays into a stream slender enough to pass through the small opening. We thus have the brightness of the image on the retina intensified. It is illuminated with nearly as much light as would be collected from the same object through a pupil as large as the great lenses of the telescope.
In astronomical observatories we employ telescopes of two entirely different classes. The more familiar forms are those known as refractors, in which the operation of condensing the rays of light is conducted by refraction. The character of the refractor is shown in Fig. 1. The rays from the star fall upon the object-glass at the end of the telescope, and on passing through they become refracted into a converging beam, so that all intersect at the focus. Diverging from thence, the rays encounter the eye-piece, which has the effect of restoring them to parallelism. The large cylindrical beam which poured down on the object-glass has been thus condensed into a small one, which can enter the pupil. It should, however, be added that the composite nature of light requires a more complex form of object-glass than the simple lens here shown. In a refracting telescope we have to employ what is known as the achromatic combination, consisting of one lens of flint glass and one of crown glass, adjusted to suit each other with extreme care.
The appearance of an astronomical observatory, designed to accommodate an instrument of moderate dimensions, is shown in the adjoining figures. The first (Fig. 2) represents the dome erected at Dunsink Observatory for the equatorial telescope, the object-glass of which was presented to the Board of Trinity College, Dublin, by the late Sir James South. The main part of the building is a cylindrical wall, on the top of which reposes a hemispherical roof. In this roof is a shutter, which can be opened so as to allow the telescope in the interior to obtain a view of the heavens. The dome is capable of revolving so that the opening may be turned towards that part of the sky where the object happens to be situated. The next view (Fig. 3) exhibits a section through the dome, showing the machinery by which the attendant causes it to revolve, as well as the telescope itself. The eye of the observer is placed at the eye-piece, and he is represented in the act of turning a handle, which has the power of slowly moving the telescope, in order to adjust the instrument accurately on the celestial body which it is desired to observe. The two lenses which together form the object-glass of this instrument are twelve inches in diameter, and the quality of the telescope mainly depends on the accuracy with which[Pg 14] these lenses have been wrought. The eye-piece is a comparatively simple matter. It consists merely of one or two small lenses; and various eye-pieces can be employed, according to the magnifying power which may be desired. It is to be observed that for many purposes of astronomy high magnifying powers are not desirable. There is a limit, too, beyond which the magnification cannot be carried with advantage. The object-glass can only collect a certain quantity of light from the star; and if the magnifying power be too great, this limited amount of light will be thinly dispersed over too large a surface, and the result will be found unsatisfactory. The unsteadiness of the atmosphere still further limits the extent to which the image may be advantageously magnified, for every increase of power increases in the same degree the atmospheric disturbance.
A telescope mounted in the manner here shown is called an equatorial. The convenience of this peculiar style of supporting the instrument consists in the ease with which the telescope can be moved so as to follow a star in its apparent journey across the sky. The necessary movements of the tube are given by clockwork driven by a weight, so that, once the instrument has been correctly pointed, the star will remain in the observer's field of view, and the effect of the apparent diurnal movement will be neutralised. The last refinement in this direction is the application of an electrical arrangement by which the driving of the instrument is controlled from the standard clock of the observatory.
 Fig. 4.—The Telescope at Yerkes Observatory, Chicago.
Fig. 4.—The Telescope at Yerkes Observatory, Chicago.The power of a refracting telescope—so far as the expression has any definite meaning—is to be measured by the diameter of its object-glass. There has, indeed, been some honourable rivalry between the various civilised nations as to which should possess the greatest refracting telescope. Among the notable instruments that have been successfully completed is that erected in 1881 by Sir Howard Grubb, of Dublin, at the splendid observatory at Vienna. Its dimensions may be estimated from the fact that the object-glass is two feet and three inches in diameter. Many ingenious contrivances help to lessen the inconvenience incident to the use of an instrument possessing such vast proportions. Among them we may here notice the method by which the graduated circles attached to the telescope are brought within view of the observer. These circles are necessarily situated at parts of the instrument which lie remote from the eye-piece where the observer is stationed. The delicate marks and figures are, however, easily read from a distance by a small auxiliary telescope, which, by suitable reflectors, conducts the rays of light from the circles to the eye of the observer.
Numerous refracting telescopes of exquisite perfection have been produced by Messrs. Alvan Clark, of Cambridgeport, Boston, Mass. One of their most famous telescopes is the great Lick Refractor now in use on Mount Hamilton in California. The diameter of this object-glass is thirty-six inches, and its focal length is fifty-six feet two inches. A still greater effort has recently been made by the same firm in the refractor of forty inches aperture for the Yerkes Observatory of the University of Chicago. The telescope, which is seventy-five feet in length, is mounted under a revolving dome ninety feet in diameter, and in order to enable the observer to reach the eye-piece without using very large step-ladders, the floor of the room can be raised and lowered through a range of twenty-two feet by electric motors. This is shown in Fig. 4, while the south front of the Yerkes Observatory is represented in Fig. 6.
 Fig. 6.—South Front of the Yerkes Observatory, Chicago.
Fig. 6.—South Front of the Yerkes Observatory, Chicago.Within the last few years two fine telescopes have been added to the instrumental equipment of the Royal Observatory, Greenwich, both by Sir H. Grubb. One of these, containing a 28-inch object-glass, has been erected on a mounting originally constructed for a smaller instrument by Sir G. Airy. The other, presented by Sir Henry Thompson, is of 26 inches aperture, and is adapted for photographic work.
There is a limit to the size of the refractor depending upon the material of the object-glass. Glass manufacturers seem to experience unusual difficulties in their attempts to form large discs of optical glass pure enough and uniform enough to be suitable for telescopes. These difficulties are enhanced with every increase in the size of the discs, so that the cost has a tendency to increase at a very much greater rate. It may be mentioned in illustration that the price paid for the object-glass of the Lick telescope exceeded ten thousand pounds.
There is, however, an alternative method of constructing a telescope, in which the difficulty we have just mentioned does not arise. The principle of the simplest form of reflector is shown in Fig. 5, which represents what is called the Herschelian instrument. The rays of light from the star under observation fall on a mirror which is both carefully shaped and highly polished. After reflection, the rays proceed to a focus, and diverging from thence, fall on the eye-piece, by which they are restored to parallelism, and thus become adapted for reception in the eye. It was essentially on this principle (though with a secondary flat mirror at the upper end of the tube reflecting the rays at a right angle to the side of the tube, where the eye-piece is placed) that Sir Isaac Newton constructed the little reflecting telescope which is now treasured by the Royal Society. A famous instrument of the Newtonian type was built, half a century ago, by the late Earl of Rosse, at Parsonstown. It is represented in Fig. 7. The colossal aperture of this instrument has never been surpassed; it has, indeed, never been rivalled. The mirror or speculum, as it is often called, is a thick metallic disc, composed of a mixture of two parts of copper with one of tin. This alloy is so hard and brittle as to make the necessary mechanical operations difficult to manage. The material admits, however, of a brilliant polish, and of receiving and retaining an accurate figure. The Rosse speculum—six feet in diameter and three tons in weight—reposes at the lower end of a telescope fifty-five feet long. The tube is suspended between two massive castellated walls, which form an imposing feature on the lawn at Birr Castle. This instrument cannot be turned about towards every part of the sky, like the equatorials we have recently been considering. The great tube is only capable of elevation in altitude along the meridian, and of a small lateral movement east and west of the meridian. Every star or nebula visible in the latitude of Parsonstown (except those very near the pole) can, however, be observed in the great telescope, if looked for at the right time.
Before the object reaches the meridian, the telescope must be adjusted at the right elevation. The necessary power is transmitted by a chain from a winch at the northern end of the walls to a point near the upper end of the tube. By this contrivance the telescope can be raised or lowered, and an ingenious system of counterpoises renders the movement equally easy at all altitudes. The observer then takes his station in one of the galleries which give access to the eye-piece; and when the right moment has arrived, the star enters the field of view. Powerful mechanism drives the great instrument, so as to counteract the diurnal movement, and thus the observer can retain the object in view until he has made his measurements or finished his drawing.
Of late years reflecting telescopes have been generally made with mirrors of glass covered with a thin film of silver, which is capable of reflecting much more light than the surface of a metallic mirror. Among great reflectors of this kind we may mention two, of three and five feet aperture respectively, with which Dr. Common has done valuable work.
We must not, however, assume that for the general work in an observatory a colossal instrument is the most suitable. The mighty reflector, or refractor, is chiefly of use where unusually faint objects are being examined. For work in which accurate measurements are made of objects not particularly difficult to see, telescopes of smaller dimensions are more suitable. The fundamental facts about the heavenly bodies have been chiefly learned from observations obtained with instruments of moderate optical power, specially furnished so as to enable precise measures of position to be secured. Indeed, in the early stages of astronomy, important determinations of position were effected by contrivances[Pg 22] which showed the direction of the object without any telescopic aid.
Perhaps the most valuable measurements obtained in our modern observatories are yielded by that instrument of precision known as the meridian circle. It is impossible, in any adequate account of the Story of the Heavens, to avoid some reference to this indispensable aid to astronomical research, and therefore we shall give a brief account of one of its simpler forms, choosing for this purpose a great instrument in the Paris Observatory, which is represented in Fig. 8.
The telescope is attached at its centre to an axis at right angles to its length. Pivots at each extremity of this axis rotate upon fixed bearings, so that the movements of the telescope are completely restricted to the plane of the meridian. Inside the eye-piece of the telescope extremely fine vertical fibres are stretched. The observer watches the moon, or star, or planet enter the field of view; and he notes by the clock the exact time, to the fraction of a second, at which the object passes over each of the lines. A silver band on the circle attached to the axis is divided into degrees and subdivisions of a degree, and as this circle moves with the telescope, the elevation at which the instrument is pointed will be indicated. For reading the delicately engraved marks and figures on the silver, microscopes are necessary. These are shown in the sketch, each one being fixed into an aperture in the wall which supports one end of the instrument. At the opposite side is a lamp, the light from which passes through the perforated axis of the pivot, and is thence ingeniously deflected by mirrors so as to provide the requisite illumination for the lines at the focus.
The fibres which the observer sees stretched over the field of view of the telescope demand a few words of explanation. We require for this purpose a material which shall be very fine and fairly durable, as well as somewhat elastic, and of no appreciable weight. These conditions cannot be completely fulfilled by any metallic wire, but they are exquisitely realised in the beautiful thread which is spun by the spider. The[Pg 23] delicate fibres are stretched with nice skill across the field of view of the telescope, and cemented in their proper places. With instruments so beautifully appointed we can understand the precision attained in modern observations. The telescope is directed towards a star, and the image of the star is a minute point of light. When that point coincides with the intersection of the two central spider lines the telescope is properly sighted. We use the word sighted designedly, because we wish to suggest a comparison between the sighting of a rifle at the target and the sighting of a telescope at a star. Instead of the ordinary large bull's-eye, suppose that the target only consisted of a watch-dial, which, of course, the rifleman could not see at the distance of any ordinary range. But with the telescope of the meridian circle the watch-dial would be visible even at the distance of a mile. The meridian circle is indeed capable of such precision as a sighting instrument that it could be pointed separately to each of two stars which subtend at the eye an angle no greater than that subtended by an adjoining pair of the sixty minute dots around the circumference of a watch-dial a mile distant from the observer.
This power of directing the instrument so accurately would be of but little avail unless it were combined with arrangements by which, when once the telescope has been pointed correctly, the position of the star can be ascertained and recorded. One element in the determination of the position is secured by the astronomical clock, which gives the moment when the object crosses the central vertical wire; the other element is given by the graduated circle which reads the angular distance of the star from the zenith or point directly overhead.
Superb meridian instruments adorn our great observatories, and are nightly devoted to those measurements upon which the great truths of astronomy are mainly based. These instruments have been constructed with refined skill; but it is the duty of the painstaking astronomer to distrust the accuracy of his instrument in every conceivable way. The great tube may be as rigid a structure as mechanical engineers can produce; the graduations on the circle may[Pg 24] have been engraved by the most perfect of dividing machines; but the conscientious astronomer will not be content with mere mechanical precision. That meridian circle which, to the uninitiated, seems a marvellous piece of workmanship, possessing almost illimitable accuracy, is viewed in a very different light by the astronomer who makes use of it. No one can appreciate more fully than he the skill of the artist who has made that meridian circle, and the beautiful contrivances for illumination and reading off which give to the instrument its perfection; but while the astronomer recognises the beauty of the actual machine he is using, he has always before his mind's eye an ideal instrument of absolute perfection, to which the actual meridian circle only makes an approximation.
Contrasted with the ideal instrument, the finest meridian circle is little more than a mass of imperfections. The ideal tube is perfectly rigid, the actual tube is flexible; the ideal divisions of the circle are perfectly uniform, the actual divisions are not uniform. The ideal instrument is a geometrical embodiment of perfect circles, perfect straight lines, and perfect right angles; the actual instrument can only show approximate circles, approximate straight lines, and approximate right angles. Perhaps the spider's part of the work is on the whole the best; the stretched web gives us the nearest mechanical approach to a perfectly straight line; but we mar the spider's work by not being able to insert those beautiful threads with perfect uniformity, while our attempts to adjust two of them across the field of view at right angles do not succeed in producing an angle of exactly ninety degrees.
Nor are the difficulties encountered by the meridian observer due solely to his instrument. He has to contend against his own imperfections; he has often to allow for personal peculiarities of an unexpected nature; the troubles that the atmosphere can give are notorious; while the levelling of his instrument warns him that he cannot even rely on the solid earth itself. We learn that the earthquakes, by which the solid ground is sometimes disturbed, are merely[Pg 25] the more conspicuous instances of incessant small movements in the earth which every night in the year derange the delicate adjustment of the instrument.
When the existence of these errors has been recognised, the first great step has been taken. By an alliance between the astronomer and the mathematician it is possible to measure the discrepancies between the actual meridian circle and the instrument that is ideally perfect. Once this has been done, we can estimate the effect which the irregularities produce on the observations, and finally, we succeed in purging the observations from the grosser errors by which they are contaminated. We thus obtain results which are not indeed mathematically accurate, but are nevertheless close approximations to those which would be obtained by a perfect observer using an ideal instrument of geometrical accuracy, standing on an earth of absolute rigidity, and viewing the heavens without the intervention of the atmosphere.
In addition to instruments like those already indicated, astronomers have other means of following the motions of the heavenly bodies. Within the last fifteen years photography has commenced to play an important part in practical astronomy. This beautiful art can be utilised for representing many objects in the heavens by more faithful pictures than the pencil of even the most skilful draughtsman can produce. Photography is also applicable for making charts of any region in the sky which it is desired to examine. When repeated pictures of the same region are made from time to time, their comparison gives the means of ascertaining whether any star has moved during the interval. The amount and direction of this motion may be ascertained by a delicate measuring apparatus under which the photographic plate is placed.
If a refracting telescope is to be used for taking celestial photographs, the lenses of the object-glass must be specially designed for this purpose. The rays of light which imprint an image on the prepared plate are not exactly the same as those which are chiefly concerned in the production of the image on the retina of the human eye. A reflecting mirror, however, brings all the rays, both those which are chemically[Pg 26] active and those which are solely visual, to one and the same focus. The same reflecting instrument may therefore be used either for looking at the heavens or for taking pictures on a photographic plate which has been substituted for the observer's eye.
A simple portrait camera has been advantageously employed for obtaining striking photographs of larger areas of the sky than can be grasped in a long telescope; but for purposes of accurate measurement those taken with the latter are incomparably better.
It is needless to say that the photographic apparatus, whatever it may be, must be driven by delicately-adjusted clockwork to counteract the apparent daily motion of the stars caused by the rotation of the earth. The picture would otherwise be spoiled, just as a portrait is ruined if the sitter does not remain quiet during the exposure.
Among the observatories in the United Kingdom the Royal Observatory at Greenwich is of course the most famous. It is specially remarkable among all the similar institutions in the world for the continuity of its labours for several generations. Greenwich Observatory was founded in 1675 for the promotion of astronomy and navigation, and the observations have from the first been specially arranged with the object of determining with the greatest accuracy the positions of the principal fixed stars, the sun, the moon, and the planets. In recent years, however, great developments of the work of the Observatory have been witnessed, and the most modern branches of the science are now assiduously pursued there.
The largest equatorial at Greenwich is a refractor of twenty-eight inches aperture and twenty-eight feet long, constructed by Sir Howard Grubb. A remarkable composite instrument from the same celebrated workshop has also been recently added to our national institution. It consists of a great refractor specially constructed for photography, of twenty-six inches aperture (presented by Sir Henry Thompson) and a reflector of thirty inches diameter, which is the product of Dr. Common's skill. The huge volume published[Pg 27] annually bears witness to the assiduity with which the Astronomer Royal and his numerous staff of assistant astronomers make use of the splendid means at their disposal.
The southern part of the heavens, most of which cannot be seen in this country, is watched from various observatories in the southern hemisphere. Foremost among them is the Royal Observatory at the Cape of Good Hope, which is furnished with first-class instruments. We may mention a great photographic telescope, the gift of Mr. M'Clean. Astronomy has been greatly enriched by the many researches made by Dr. Gill, the director of the Cape Observatory.
It is not, however, necessary to use such great instruments to obtain some idea of the aid the telescope will afford. The most suitable instrument for commencing astronomical studies is within ordinary reach. It is the well-known binocular that a captain uses on board ship; or if that cannot be had, then the common opera-glass will answer nearly as well. This is, no doubt, not so powerful as a telescope, but it has some compensating advantages. The opera-glass will enable us to survey a large region of the sky at one glance, while a telescope, generally speaking, presents a much smaller field of view.
Let us suppose that the observer is provided with an opera-glass and is about to commence his astronomical studies.[Pg 28] The first step is to become acquainted with the conspicuous group of seven stars represented in Fig. 9. This group is often called the Plough, or Charles's Wain, but astronomers prefer to regard it as a portion of the constellation of the Great Bear (Ursa Major). There are many features of interest in this constellation, and the beginner should learn as soon as possible to identify the seven stars which compose it. Of these the two marked α and β, at the head of the Bear, are generally called the "pointers." They are of special use, because they serve to guide the eye to that most important star in the whole sky, known as the "pole star."
Fix the attention on that region in the Great Bear, which forms a sort of rectangle, of which the stars α β γ δ are the corners. The next fine night try to count how many stars are visible within that rectangle. On a very fine night, without a moon, perhaps a dozen might be perceived, or even more, according to the keenness of the eyesight. But when the opera-glass is directed to the same part of the constellation an astonishing sight is witnessed. A hundred stars can now be seen with the greatest ease.
But the opera-glass will not show nearly all the stars in this region. Any good telescope will reveal many hundreds too faint for the feebler instrument. The greater the telescope the more numerous the stars: so that seen through one of the colossal instruments the number would have to be reckoned in thousands.
We have chosen the Great Bear because it is more generally known than any other constellation. But the Great Bear is not exceptionally rich in stars. To tell the number of the stars is a task which no man has accomplished; but various estimates have been made. Our great telescopes can probably show at least 50,000,000 stars.
The student who uses a good refracting telescope, having an object-glass not less than three inches in diameter, will find occupation for many a fine evening. It will greatly increase the interest of his work if he have the charming handbook of the heavens known as Webb's "Celestial Objects for Common Telescopes."
The vast Size of the Sun—Hotter than Melting Platinum—Is the Sun the Source of Heat for the Earth?—The Sun is 92,900,000 miles distant—How to realise the magnitude of this distance—Day and Night—Luminous and Non-Luminous Bodies—Contrast between the Sun and the Stars—The Sun a Star—Granulated Appearance of the Sun—The Spots on the Sun—Changes in the Form of a Spot—The Faculæ—The Rotation of the Sun on its Axis—View of a Typical Sun-Spot—Periodicity of the Sun-Spots—Connection between the Sun-Spots and Terrestrial Magnetism—Principles of Spectrum Analysis—Substances present in the Sun—Spectrum of a Spot—The Prominences surrounding the Sun—Total Eclipse of the Sun—Size and Movement of the Prominences—Their connection with the Spots—Spectroscopic Measurement of Motion on the Sun—The Corona surrounding the Sun—Constitution of the Sun.
In commencing our examination of the orbs which surround us, we naturally begin with our peerless sun. His splendid brilliance gives him the pre-eminence over all other celestial bodies.
The dimensions of our luminary are commensurate with his importance. Astronomers have succeeded in the difficult task of ascertaining the exact figures, but they are so gigantic that the results are hard to realise. The diameter of the orb of day, or the length of the axis, passing through the centre from one side to the other, is 866,000 miles. Yet this bare statement of the dimensions of the great globe fails to convey an adequate idea of its vastness. If a railway were laid round the sun, and if we were to start in an express train moving sixty miles an hour, we should have to travel for five years without intermission night or day before we had accomplished the journey.
When the sun is compared with the earth the bulk of our luminary becomes still more striking. Suppose his globe[Pg 30] were cut up into one million parts, each of these parts would appreciably exceed the bulk of our earth. Fig. 10 exhibits a large circle and a very small one, marked S and E respectively. These circles show the comparative sizes of the two bodies. The mass of the sun does not, however, exceed that of the earth in the same proportion. Were the sun placed in one pan of a mighty weighing balance, and were 300,000 bodies as heavy as our earth placed in the other, the luminary would turn the scale.
The sun has a temperature far surpassing any that we artificially produce, either in our chemical laboratories or our metallurgical establishments. We can send a galvanic current through a piece of platinum wire. The wire first becomes red hot, then white hot; then it glows with a brilliance almost dazzling until it fuses and breaks. The temperature of the melting platinum wire could hardly be surpassed in the most elaborate furnaces, but it does not attain the temperature of the sun.
It must, however, be admitted that there is an apparent discrepancy between a fact of common experience and the[Pg 31] statement that the sun possesses the extremely high temperature that we have just tried to illustrate. "If the sun were hot," it has been said, "then the nearer we approach to him the hotter we should feel; yet this does not seem to be the case. On the top of a high mountain we are nearer to the sun, and yet everybody knows that it is much colder up there than in the valley beneath. If the mountain be as high as Mont Blanc, then we are certainly two or three miles nearer the glowing globe than we were at the sea-level; yet, instead of additional warmth, we find eternal snow." A simple illustration may help to lessen this difficulty. In a greenhouse on a sunshiny day the temperature is much hotter than it is outside. The glass will permit the hot sunbeams to enter, but it refuses to allow them out again with equal freedom, and consequently the temperature rises. The earth may, from this point of view, be likened to a greenhouse, only, instead of the panes of glass, our globe is enveloped by an enormous coating of air. On the earth's surface, we stand, as it were, inside the greenhouse, and we benefit by the interposition of the atmosphere; but when we climb very high mountains, we gradually pass through some of the protecting medium, and then we suffer from the cold. If the earth were deprived of its coat of air, it seems certain that eternal frost would reign over whole continents as well as on the tops of the mountains.
The actual distance of the sun from the earth is about 92,900,000 miles; but by merely reciting the figures we do not receive a vivid impression of the real magnitude. It would be necessary to count as quickly as possible for three days and three nights before one million was completed; yet this would have to be repeated nearly ninety-three times before we had counted all the miles between the earth and the sun.
Every clear night we see a vast host of stars scattered over the sky. Some are bright, some are faint, some are grouped into remarkable forms. With regard to this multitude of brilliant points we have now to ask an important question. Are they bodies which shine by their own light like the sun,[Pg 32] or do they only shine with borrowed light like the moon? The answer is easily stated. Most of those bodies shine by their own light, and they are properly called stars.
Suppose that the sun and the multitude of stars, properly so called, are each and all self-luminous brilliant bodies, what is the great distinction between the sun and the stars? There is, of course, a vast and obvious difference between the unrivalled splendour of the sun and the feeble twinkle of the stars. Yet this distinction does not necessarily indicate that our luminary has an intrinsic splendour superior to that of the stars. The fact is that we are nestled up comparatively close to the sun for the benefit of his warmth and light, while we are separated from even the nearest of the stars by a mighty abyss. If the sun were gradually to retreat from the earth, his light would decrease, so that when he had penetrated the depths of space to a distance comparable with that by which we are separated from the stars, his glory would have utterly departed. No longer would the sun seem to be the majestic orb with which we are familiar. No longer would he be a source of genial heat, or a luminary to dispel the darkness of night. Our great sun would have shrunk to the insignificance of a star, not so bright as many of those which we see every night.
Momentous indeed is the conclusion to which we are now led. That myriad host of stars which studs our sky every night has been elevated into vast importance. Each one of those stars is itself a mighty sun, actually rivalling, and in many cases surpassing, the splendour of our own luminary. We thus open up a majestic conception of the vast dimensions of space, and of the dignity and splendour of the myriad globes by which that space is tenanted.
There is another aspect of the picture not without its utility. We must from henceforth remember that our sun is only a star, and not a particularly important star. If the sun and the earth, and all which it contains, were to vanish, the effect in the universe would merely be that a tiny star had ceased its twinkling. Viewed simply as a star, the sun must retire to a position of insignificance in the mighty fabric[Pg 33] of the universe. But it is not as a star that we have to deal with the sun. To us his comparative proximity gives him an importance incalculably transcending that of all the other stars. We imagined ourselves to be withdrawn from the sun to obtain his true perspective in the universe; let us now draw near, and give him that attention which his supreme importance to us merits.
To the unaided eye the sun appears to be a flat circle. If, however, it be examined with the telescope, taking care of course to interpose a piece of dark-coloured glass, or to employ some similar precaution to screen the eye from injury, it will then be perceived that the sun is not a flat surface, but a veritable glowing globe.
The first question which we must attempt to answer[Pg 34] enquires whether the glowing matter which forms the globe is a solid mass, or, if not solid, which is it, liquid or gaseous? At the first glance we might think that the sun cannot be fluid, and we might naturally imagine that it was a solid ball of some white-hot substance. But this view is not correct; for we can show that the sun is certainly not a solid body in so far at least as its superficial parts are concerned.
A general view of the sun as shown by a telescope of moderate dimensions may be seen in Fig. 11, which is taken from a photograph obtained by Mr. Rutherford at New York on the 22nd of September, 1870. It is at once seen that the surface of the luminary is by no means of uniform texture or brightness. It may rather be described as granulated or mottled. This appearance is due to the luminous clouds which float suspended in a somewhat less luminous layer of gas. It is needless to say that these solar clouds are very different from the clouds which we know so well in our own atmosphere. Terrestrial clouds are, of course, formed from minute drops of water, while the clouds at the surface of the sun are composed of drops of one or more chemical elements at an exceedingly high temperature.
The granulated appearance of the solar surface is beautifully shown in the remarkable photographs on a large scale which M. Janssen, of Meudon, has succeeded in obtaining during the last twenty years. We are enabled to reproduce one of them in Fig. 12. It will be observed that the interstices between the luminous dots are of a greyish tint, the general effect (as remarked by Professor Young) being much like that of rough drawing paper seen from a little distance. We often notice places over the surface of such a plate where the definition seems to be unsatisfactory. These are not, however, the blemishes that might at first be supposed. They arise neither from casual imperfections of the photographic plate nor from accidents during the development; they plainly owe their origin to some veritable cause in the sun itself, nor shall we find it hard to explain what that cause must be. As we shall have occasion to mention further on, the velocities with which the glowing gases on the sun are animated must be exceedingly great. Even in the hundredth part of a second (which is about the duration of the exposure of this plate) the movements of the solar clouds are sufficiently great to produce the observed indistinctness.
Irregularly dispersed over the solar surface small dark objects called sun-spots are generally visible. These spots vary greatly both as to size and as to number. Sun-spots were first noticed in the beginning of the seventeenth century, shortly after the invention of the telescope. Their general appearance is shown in Fig. 13, in which the dark central nucleus appears in sharp contrast with the lighter margin or penumbra. Fig. 16 shows a small spot developing out of one of the pores or interstices between the granules.
The earliest observers of these spots had remarked that they seem to have a common motion across the sun. In Fig. 14 we give a copy of a remarkable drawing by Father Scheiner, showing the motion of two spots observed by him in March, 1627. The figure indicates the successive positions assumed by the spots on the several days from the 2nd to the 16th March. Those marks which are merely given in outline represent the assumed positions on the 11th and the 13th, on which days it happened that the weather was cloudy, so that no observations could be made. It is invariably found that these objects move in the same direction—namely, from the eastern to the western limb[3] of the sun. They complete the journey across the face of the sun in twelve or thirteen days, after which they remain invisible for about the same length of time until they reappear at the eastern limb. These early observers were quick to discern the true import of their discovery. They deduced from these simple observations the remarkable fact that the sun, like the earth, performs a rotation on its axis, and in the same direction. But there is the important difference between these rotations that whereas the earth takes only twenty-four hours to turn once round, the solar globe takes about twenty-six days to complete one of its much more deliberate rotations.
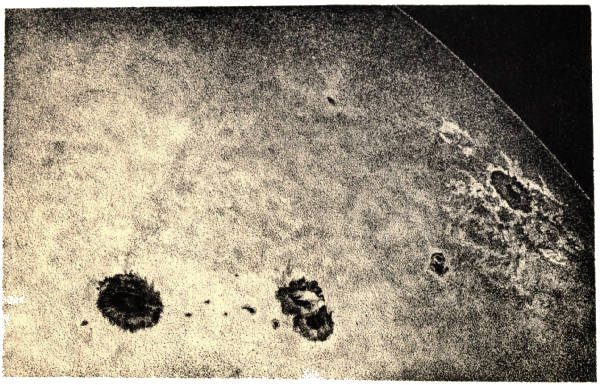 PLATE III.
PLATE III.If we examine sun-spots under favourable atmospheric conditions and with a telescope of fairly large aperture, we perceive a great amount of interesting detail which is full of information with regard to the structure of the sun. The penumbra of a spot is often found to be made up of filaments directed towards the middle of the spot, and generally brighter at their inner ends, where they adjoin the nucleus. In a regularly formed spot the outline of the penumbra is of the same general form as that of the nucleus, but astronomers are frequently deeply interested by witnessing vast spots of very irregular figure. In such cases the bright surface-covering of the sun (the photosphere, as it is called) often encroaches on the nucleus and forms a peninsula stretching out into, or even bridging across, the gloomy interior. This is well shown in Professor Langley's fine drawing (Plate II.) of a very irregular spot which he observed on December 23–24, 1873.
The details of a spot vary continually; changes may often be noticed even from day to day, sometimes from hour to hour. A similar remark may be made with respect to the bright streaks or patches which are frequently to be observed especially in the neighbourhood of spots. These bright marks are known by the name of faculæ (little torches). They are most distinctly seen near the margin of the sun, where the light from its surface is not so bright as it is nearer to the centre of the disc. The reduction of light at the margin is due to the greater thickness of absorbing atmosphere round the sun, through which the light emitted from the regions near the margin has to pass in starting on its way towards us.
None of the markings on the solar disc constitute permanent features on the sun. Some of these objects may no doubt last for weeks. It has, indeed, occasionally happened that the same spot has marked the solar globe for many months; but after an existence of greater or less duration those on one part of the sun may disappear, while as frequently fresh marks of the same kind become visible in other places. The inference from these various facts is[Pg 38] irresistible. They tell us that the visible surface of the sun is not a solid mass, is not even a liquid mass, but that the globe, so far as we can see it, consists of matter in the gaseous, or vaporous, condition.
It often happens that a large spot divides into two or more separate portions, and these have been sometimes seen to fly apart with a velocity in some cases not less than a thousand miles an hour. "At times, though very rarely" (I quote here Professor Young,[4] to whom I am frequently indebted), "a different phenomenon of the most surprising and startling character appears in connection with these objects: patches of intense brightness suddenly break out, remaining visible for a few minutes, moving, while they[Pg 39] last, with velocities as great as one hundred miles a second."
"One of these events has become classical. It occurred on the forenoon (Greenwich time) of September 1st, 1859, and was independently witnessed by two well-known and reliable observers—Mr. Carrington and Mr. Hodgson—whose accounts of the matter may be found in the Monthly Notices of the Royal Astronomical Society for November, 1859. Mr. Carrington at the time was making his usual daily observations upon the position, configuration, and size of the spots by means of an image of the solar disc upon a screen—being then engaged upon that eight years' series of observations which lie at the foundation of so much of our present solar science. Mr. Hodgson, at a distance of many miles, was at the same time sketching details of sun-spot structure by means of a solar eye-piece and shade-glass. They simultaneously saw two luminous objects, shaped something like two new moons, each about eight thousand miles in length and two thousand wide, at a distance of some twelve thousand miles from each other. These burst suddenly into sight at the edge of a great sun-spot with a dazzling brightness at least five or six times that of the neighbouring portions of the photosphere, and moved eastward over the spot in parallel lines, growing smaller and fainter, until in about five minutes they disappeared, after traversing a course of nearly thirty-six thousand miles."
The sun-spots do not occur at all parts of the sun's surface indifferently. They are mainly found in two zones (Fig. 15) on each side of the solar equator between the latitudes of 10° and 30°. On the equator the spots are rare except, curiously enough, near the time when there are few spots elsewhere. In high latitudes they are never seen. Closely connected with these peculiar principles of their distribution[Pg 40] is the remarkable fact that spots in different latitudes do not indicate the same values for the period of rotation of the sun. By watching a spot near the sun's equator Carrington found that it completed a revolution in twenty-five days and two hours. At a latitude of 20° the period is about twenty-five days and eighteen hours, at 30° it is no less than twenty-six days and twelve hours, while the comparatively few spots observed in the latitude of 45° require twenty-seven and a half days to complete their circuit.
As the sun, so far at least as its outer regions are concerned, is a mass of gas and not a solid body, there would be nothing incredible in the supposition that spots are occasionally endowed with movements of their own like ships on the ocean. It seems, however, from the facts before us that the different zones on the sun, corresponding to what we call the torrid and temperate zones on the earth, persist in rotating with velocities which gradually decrease from the equator towards the poles. It seems probable that the interior parts of the sun do not rotate as if the whole were a rigidly connected mass. The mass of the sun, or at all events its greater part, is quite unlike a rigid body, and the several portions are thus to some extent free for independent motion. Though we cannot actually see how the interior parts of the sun rotate, yet here the laws of dynamics enable us to infer that the interior layers of the sun rotate more rapidly than the outer layers, and thus some of the features of the spot movements can be accounted for. But at present it must be confessed that there are great difficulties in the way of accounting for the distribution of spots and the law of rotation of the sun.
In the year 1826 Schwabe, a German astronomer, commenced to keep a regular register of the number of spots visible on the sun. After watching them for seventeen years he was able to announce that the number of spots seemed to fluctuate from year to year, and that there was a period of about ten years in their changes. Subsequent observations have confirmed this discovery, and old books and manuscripts have been thoroughly searched for information of early date.[Pg 41] Thus a more or less complete record of the state of the sun as regards spots since the beginning of the seventeenth century has been put together. This has enabled astronomers to fix the period of the recurring maximum with greater accuracy.
The course of one of the sun-spot cycles may be described as follows: For two or three years the spots are both larger and more numerous than on the average; then they begin to diminish, until in about six or seven years from the maximum they decline to a minimum; the number of the spots then begins to increase, and in about four and a half years the maximum is once more attained. The length of the cycle is, on an average, about eleven years and five weeks, but both its length and the intensity of the maxima vary somewhat. For instance, a great maximum occurred in the summer of 1870, after which a very low minimum occurred in 1879, followed by a feeble maximum at the end of 1883; next came an average minimum about August, 1889, followed by the last observed maximum in January, 1894. It is not unlikely that a second period of about sixty or eighty years affects the regularity of the eleven-year period. Systematic observations carried on through a great many years to come will be required to settle this question, as the observations of sun-spots previous to 1826 are far too incomplete to decide the issues which arise.
A curious connection seems to exist between the periodicity of the spots and their distribution over the surface of the sun. When a minimum is about to pass away the spots generally begin to show themselves in latitudes about 30° north and south of the sun's equator; they then gradually break out somewhat nearer to the equator, so that at the time of maximum frequency most of them appear at latitudes not greater than 16°. This distance from the sun's equator goes on decreasing till the time of minimum. Indeed, the spots linger on very close to the equator for a couple of years more, until the outbreak signalising the commencement of another period has commenced in higher latitudes.
We have still to note an extraordinary feature which[Pg 42] points to an intimate connection between the phenomena of sun-spots and the purely terrestrial phenomena of magnetism. It is of course well known that the needle of a compass does not point exactly to the north, but diverges from the meridian by an angle which is different in different places and is not even constant at the same place. For instance, at Greenwich the needle at present points in a direction 17° West of North, but this amount is subject to very slow and gradual changes, as well as to very small daily oscillations. It was found about fifty years ago by Lamont (a Bavarian astronomer, but a native of Scotland) that the extent of this daily oscillation increases and decreases regularly in a period which he gave as 10-1⁄3 years, but which was subsequently found to be 11-1⁄10 years, exactly the same as the period of the spots on the sun. From a diligent study of the records of magnetic observations it has been found that the time of sun-spot maximum always coincides almost exactly with that of maximum daily oscillation of the compass needle, while the minima agree similarly. This close relationship between the periodicity of sun-spots and the daily movements of the magnetic needle is not the sole proof we possess that there is a connection of some sort between solar phenomena and terrestrial magnetism. A time of maximum sun-spots is a time of great magnetic activity, and there have even been special cases in which a peculiar outbreak on the sun has been associated with remarkable magnetic phenomena on the earth. A very interesting instance of this kind is recorded by Professor Young, who, when observing at Sherman on the 3rd August, 1872, perceived a very violent disturbance of the sun's surface. He was told the same day by a member of his party, who was engaged in magnetic observations and who was quite in ignorance of what Professor Young had seen, that he had been obliged to desist from his magnetic work in consequence of the violent motion of his magnet. It was afterwards found from the photographic records at Greenwich and Stonyhurst that the magnetic "storm" observed in America had simultaneously been felt in England. A similar connection between sun-spots and the aurora borealis has[Pg 43] also been noticed, this fact being a natural consequence of the well-known connection between the aurora and magnetic disturbances. On the other hand, it must be confessed that many striking magnetic storms have occurred without any corresponding solar disturbance,[5] but even those who are inclined to be sceptical as to the connection between these two classes of phenomena in particular cases can hardly doubt the remarkable parallelism between the general rise and fall in the number of sun-spots and the extent of the daily movements of the compass needle.
We have now described the principal solar phenomena with which the telescope has made us acquainted. But there are many questions connected with the nature of the sun which not even the most powerful telescope would enable us to solve, but which the spectroscope has given us the means of investigating.
What we receive from the sun is warmth and light. The intensely heated mass of the sun radiates forth its beams in[Pg 44] all directions with boundless prodigality. Each beam we feel to be warm, and we see to be brilliantly white, but a more subtle analysis than mere feeling or mere vision is required. Each sunbeam bears marks of its origin. These marks are not visible until a special process has been applied, but then the sunbeam can be made to tell its story, and it will disclose to us much of the nature of the constitution of the great luminary.
We regard the sun's light as colourless, just as we speak of water as tasteless, but both of those expressions relate rather to our own feelings than to anything really characteristic of water or of sunlight. We regard the sunlight as colourless because it forms, as it were, the background on which all other colours are depicted. The fact is, that white is so far from being colourless that it contains every known hue blended together in certain proportions. The sun's light is really extremely composite; Nature herself tells us this if we will but give her the slightest attention. Whence come the beautiful hues with which we are all familiar? Look at the lovely tints of a garden; the red of the rose is not in the rose itself. All the rose does is to grasp the sunbeams which fall upon it, extract from these beams the red which they contain, and radiate that red light to our eyes. Were there not red rays conveyed with the other rays in the sunbeam, there could be no red rose to be seen by sunlight.
The principle here involved has many other applications; a lady will often say that a dress which looks very well in the daylight does not answer in the evening. The reason is that the dress is intended to show certain colours which exist in the sunlight; but these colours are not contained to the same degree in gaslight, and consequently the dress has a different hue. The fault is not in the dress, the fault lies in the gas; and when the electric light is used it sends forth beams more nearly resembling those from the sun, and the colours of the dress appear with all their intended beauty.
The most glorious natural indication of the nature of the sunlight is seen in the rainbow. Here the sunbeams are refracted and reflected from tiny globes of water in the clouds; these convey to us the sunlight, and in doing so decompose the white beams into the seven primary hues—red, orange, yellow, green, blue, indigo, and violet.
The bow set in the cloud is typical of that great department of modern science of which we shall now set forth the principles. The globes of water decompose the solar beams; and we follow the course suggested by the rainbow, and analyse the sunlight into its constituents. We are enabled to do this with scientific accuracy when we employ that remarkable key to Nature's secrets known as the spectroscope. The beams of white sunlight consist of innumerable beams of every hue in intimate association. Every shade of red, of yellow, of blue, and of green, can be found in a sunbeam. The magician's wand, with which we strike the sunbeam and sort the tangled skein into perfect order, is the simple instrument known as the glass prism. We have represented this instrument in its simplest form in the adjoining figure (Fig. 17). It is a piece of pure and homogeneous glass in the shape of a wedge. When a ray of light from the sun or from any source falls upon the prism, it passes through the transparent glass and emerges on the other side; a remarkable change is, however, impressed on the ray by the influence of the glass. It is bent by refraction from the path it originally pursued, and is compelled to follow a different path. If, however, the prism bent all rays of light equally, then it would be of no service in the analysis of light; but it fortunately happens that the prism acts with varying efficiency on the rays of different hues. A red ray is not refracted so much as a yellow ray; a yellow ray is not refracted so much as a blue one. It consequently happens that when the composite beam of sunlight, in which all the different rays are blended, passes through the prism, they emerge in the manner shown in the annexed figure (Fig. 18). Here then we have the source of the analysing[Pg 46] power of the prism; it bends the different hues unequally and consequently the beam of composite sunlight, after passing through the prism, no longer shows mere white light, but is expanded into a coloured band of light, with hues like the rainbow, passing from deep red at one end through every intermediate grade to the violet.
We have in the prism the means of decomposing the light from the sun, or the light from any other source, into its component parts. The examination of the quality of the light when analysed enables us to learn something of the constitution of the body from which this light has emanated. Indeed, in some simple cases the mere colour of a light will be sufficient to indicate the source from which it has come. There is, for instance, a splendid red light sometimes seen in displays of fireworks, due to the metal strontium. The eye can identify the element by the mere colour of the flame. There is also a characteristic yellow light produced by the flame of common salt burned with spirits of wine. Sodium is the important constituent of salt, so here we recognise another substance merely by the colour it emits when burning. We may also mention a third substance, magnesium, which burns with a brilliant white light, eminently characteristic of the metal.
The three metals, strontium, sodium, and magnesium, may thus be identified by the colours they produce when incandescent. In this simple observation lies the germ of the modern method of research known as spectrum analysis. We may now examine with the prism the colours of the sun and the colours of the stars, and from this examination we can learn something of the materials which enter into their composition. We are not restricted to the use of merely a single prism, but we may arrange that the light which it is desired to analyse shall pass through several prisms in succession in order to increase the dispersion or the spreading out of the different colours. To enter the spectroscope the light first passes through a narrow slit, and the rays are then rendered parallel by passing through a lens; these parallel rays next pass through one or more prisms, and are finally viewed through a small telescope, or they may be intercepted by a photographic plate on which a picture will then be made. If the beam of light passing through the slit has radiated from an incandescent solid or liquid body, or from a gas under high pressure, the coloured band or spectrum is found to contain all the colours indicated on Plate XIII., without any interruption between the colours. This is known as a continuous spectrum. But if we examine light from a gas under low pressure, as can be done by placing a small quantity of the gas in a glass tube and making it glow by an electric current, we find that it does not emit rays of all colours, but only rays of certain distinct colours which are different for different gases. The spectrum of a gas, therefore, consists of a number of detached luminous lines.
When we study the sunlight through the prism, it is found that the spectrum does not extend quite continuously from one end to the other, but is shaded over by a multitude of dark lines, only a few of which are shown in the adjoining plate. (Plate XIII.) These lines are a permanent feature in the solar spectrum. They are as characteristic of the sunlight as the prismatic colours themselves, and are full of interest and information with regard to the sun. These lines are the characters in which the history and the nature of the sun are written. Viewed through an instrument of adequate power, dark lines are to be found crossing the solar spectrum[Pg 48] in hundreds and in thousands. They are of every variety of strength and faintness; their distribution seems guided by no simple law. At some parts of the spectrum there are but few lines; in other regions they are crowded so closely together that it is difficult to separate them. They are in some places exquisitely fine and delicate, and they never fail to excite the admiration of every one who looks at this interesting spectacle in a good instrument.
There can be no better method of expounding the rather difficult subject of spectrum analysis than by actually following the steps of the original discovery which first gave a clear demonstration of the significance of the dark "Fraunhofer" lines. Let us concentrate our attention specially upon that line of the solar spectrum marked D. This, when seen in the spectroscope, is found to consist of two lines, very delicately separated by a minute interval, one of these lines being slightly thicker than the other. Suppose that while the attention is concentrated on these lines the flame of an ordinary spirit-lamp coloured by common salt be held in front of the instrument, so that the ray of direct solar light passes through the flame before entering the spectroscope. The observer sees at once the two lines known as D flash out with a greatly increased blackness and vividness, while there is no other perceptible effect on the spectrum. A few trials show that this intensification of the D lines is due to the vapour of sodium arising from the salt burning in the lamp through which the sunlight has passed.
It is quite impossible that this marvellous connection between sodium and the D lines of the spectrum can be merely casual. Even if there were only a single line concerned, it would be in the highest degree unlikely that the coincidence should arise by accident; but when we find the sodium affecting both of the two close lines which form D, our conviction that there must be some profound connection between these lines and sodium rises to absolute certainty. Suppose that the sunlight be cut off, and that all other light is excluded save that emanating from the glowing vapour of[Pg 49] sodium in the spirit flame. We shall then find, on looking through the spectroscope, that we no longer obtain all the colours of the rainbow; the light from the sodium is concentrated into two bright yellow lines, filling precisely the position which the dark D lines occupied in the solar spectrum, and the darkness of which the sodium flame seemed to intensify.
We must here endeavour to remove what may at first sight appear to be a paradox. How is it, that though the sodium flame produces two bright lines when viewed in the absence of other light, yet it actually appears to intensify the two dark lines in the sun's spectrum? The explanation of this leads us at once to the cardinal doctrine of spectrum analysis. The so-called dark lines in the solar spectrum are only dark by contrast with the brilliant illumination of the rest of the spectrum. A good deal of solar light really lies in the dark lines, though not enough to be seen when the eye is dazzled by the brilliancy around. When the flame of the spirit-lamp charged with sodium intervenes, it sends out a certain amount of light, which is entirely localised in these two lines. So far it would seem that the influence of the sodium flame ought to be manifested in diminishing the darkness of the lines and rendering them less conspicuous. As a matter of fact, they are far more conspicuous with the sodium flame than without it. This arises from the fact that the sodium flame possesses the remarkable property of cutting off the sunlight which was on its way to those particular lines; so that, though the sodium contributes some light to the lines, yet it intercepts a far greater quantity of the light that would otherwise have illuminated those lines, and hence they became darker with the sodium flame than without it.
We are thus conducted to a remarkable principle, which has led to the interpretation of the dark lines in the spectrum of the sun. We find that when the sodium vapour is heated, it gives out light of a very particular type, which, viewed through the prism, is concentrated in two lines. But the sodium vapour possesses also this property, that light from[Pg 50] the sun can pass through it without any perceptible absorption, except of those particular rays which are of the same characters as the two lines in question. In other words, we say that if the heated vapour of a substance gives a spectrum of bright lines, corresponding to lights of various kinds, this same vapour will act as an opaque screen to lights of those special kinds, while remaining transparent to light of every other description.
This principle is of such importance in the theory of spectrum analysis that we add a further example. Let us take the element iron, which in a very striking degree illustrates the law in question. In the solar spectrum some hundreds of the dark lines are known to correspond with the spectrum of iron. This correspondence is exhibited in a vivid manner when, by a suitable contrivance, the light of an electric spark from poles of iron is examined in the spectroscope side by side with the solar spectrum. The iron lines in the sun are identical in position with the lines in the spectrum of glowing iron vapour. But the spectrum of iron, as here described, consists of bright lines; while those with which it is compared in the sun are dark on a bright background. They can be completely understood if we suppose the vapour arising from intensely heated iron to be present in the atmosphere which surrounds the luminous strata on the sun. This vapour would absorb or stop precisely the same rays as it emits when incandescent, and hence we learn the important fact that iron, no less than sodium, must, in one form or another, be a constituent of the sun.
Such is, in brief outline, the celebrated discovery of modern times which has given an interpretation to the dark lines of the solar spectrum. The spectra of a large number of terrestrial substances have been examined in comparison with the solar spectrum, and thus it has been established that many of the elements known on the earth are present in the sun. We may mention calcium, iron, hydrogen, sodium, carbon, nickel, magnesium, cobalt, aluminium, chromium, strontium, manganese, copper, zinc, cadmium, silver, tin, lead, potassium. Some of the elements which are of the greatest importance[Pg 51] on the earth would appear to be missing from the sun. Sulphur, phosphorus, mercury, gold, nitrogen may be mentioned among the elements which have hitherto given no indication of their being solar constituents.
It is also possible that the lines of a substance in the sun's atmosphere may be so very bright that the light of the continuous spectrum, on which they are superposed, is not able to "reverse" them—i.e. turn them into dark lines. We know, for instance, that the bright lines of sodium vapour may be made so intensely bright that the spectrum of an incandescent lime-cylinder placed behind the sodium vapour does not reverse these lines. If, then, we make the sodium lines fainter, they may be reduced to exactly the intensity prevailing in that part of the spectrum of the lime-light, in which case the lines, of course, could not be distinguished. The question as to what elements are really missing from the sun must therefore, like many other questions concerning our great luminary, at present be considered an open one. We shall shortly see that an element previously unknown has actually been discovered by means of a line representing it in the solar spectrum.
Let us now return to the sun-spots and see what the spectroscope can teach us as to their nature. We attach a powerful spectroscope to the eye-end of a telescope in order to get as much light as possible concentrated on the slit; the latter has therefore to be placed exactly at the focus of the object-glass. The instrument is then pointed to a spot, so that its image falls on the slit, and the presence of the dark central part called the umbra reveals itself by a darkish stripe which traverses the ordinary sun-spectrum from end to end. It is bordered on both sides by the spectrum of the penumbra, which is much brighter than that of the umbra, but fainter than that of the adjoining regions of the sun.
From the fact that the spectrum is darkened we learn that there is considerable general absorption of light in the umbra. This absorption is not, however, such as would be caused by the presence of volumes of minute solid or liquid particles like those which constitute smoke or cloud. This is indicated[Pg 52] by the fact, first discovered by Young in 1883, that the spectrum is not uniformly darkened as it would be if the absorption were caused by floating particles. In the course of examination of many large and quiescent spots, he perceived that the middle green part of the spectrum was crossed by countless fine, dark lines, generally touching each other, but here and there separated by bright intervals. Each line is thicker in the middle (corresponding to the centre of the spot) and tapers to a fine thread at each end; indeed, most of these lines can be traced across the spectrum of the penumbra and out on to that of the solar surface. The absorption would therefore seem to be caused by gases at a much lower temperature than that of the gases present outside the spot.
In the red and yellow parts of the spot-spectrum, which have been specially studied for many years by Sir Norman Lockyer at the South Kensington Observatory, interesting details are found which confirm this conclusion. Many of the dark lines are not thicker and darker in the spot than they are in the ordinary sun-spectrum, while others are very much thickened in the spot-spectrum, such as the lines of iron, calcium, and sodium. The sodium lines are sometimes both widened and doubly reversed—that is, on the thick dark line a bright line is superposed. The same peculiarity is not seldom seen in the notable calcium lines H and K at the violet end of the spectrum. These facts indicate the presence of great masses of the vapours of sodium and calcium over the nucleus. The observations at South Kensington have also brought to light another interesting peculiarity of the spot-spectra. At the time of minimum frequency of spots the lines of iron and other terrestrial elements are prominent among the most widened lines; at the maxima these almost vanish, and the widening is found only amongst lines of unknown origin.
The spectroscope has given us the means of studying other interesting features on the sun, which are so faint that in the full blaze of sunlight they cannot be readily observed with a mere telescope. We can, however, see them easily enough when the brilliant body of the sun is obscured during the rare occurrence of a total eclipse. The conditions necessary[Pg 53] for the occurrence of an eclipse will be more fully considered in the next chapter. For the present it will be sufficient to observe that by the movement of the moon it may so happen that the moon completely hides the sun, and thus for certain parts of the earth produces what we call a total eclipse. The few minutes during which a total eclipse lasts are of much interest to the astronomer. Darkness reigns over the landscape, and in that darkness rare and beautiful sights are witnessed.
We have in Fig. 19 a diagram of a total eclipse, showing some of the remarkable objects known as prominences (a, b, c, d, e) which project from behind the dark body of the moon. That they do not belong to the moon, but are solar appendages of some sort, is easily demonstrated. They first appear on the eastern limb at the commencement of totality. Those first seen are gradually more or less covered by the advancing moon, while others peep out behind the western limb of the moon, until totality is over and the sunlight bursts out again, when they all instantly vanish.
The first total eclipse which occurred after the spectroscope had been placed in the hands of astronomers was in 1868. On the 18th August in that year a total eclipse was visible in India. Several observers, armed with spectroscopes, were on the look-out for the prominences, and were able to announce that their spectrum consisted of detached bright lines, thus demonstrating that these objects were masses of glowing gas. On the following day the illustrious astronomer, Janssen, one of the observers of the eclipse, succeeded in seeing the lines in full sunlight, as he now knew exactly where to look for them. Many months before the eclipse Sir Norman Lockyer had been preparing to search for the prominences, as he expected them to yield[Pg 54] a line spectrum which would be readily visible, if only the sun's ordinary light could be sufficiently winnowed away. He proposed to effect this by using a spectroscope of great dispersion, which would spread out the continuous spectrum considerably and make it fainter. The effect of the great dispersion on the isolated bright lines he expected to see would be only to widen the intervals between them without interfering with their brightness. The new spectroscope, which he ordered to be constructed for this purpose, was not completed until some weeks after the eclipse was over, though before the news of Janssen's achievement reached Europe from India. When that news did arrive Sir N. Lockyer had already found the spectrum of unseen prominences at the sun's limb. The honour of the practical application of a method of observing solar prominences without the help of an eclipse must therefore be shared between the two astronomers.
When a spectroscope is pointed to the margin of the sun so that the slit is radial, certain short luminous lines become visible which lie exactly in the prolongation of the corresponding dark lines in the solar spectrum. From due consideration of the circumstances it can be shown that the gases which form the prominences are also present as a comparatively shallow atmospheric layer all round the great luminary. This layer is about five or six thousand miles deep, and is situated immediately above the dense layer of luminous clouds which forms the visible surface of the sun and which we call the photosphere. The gaseous envelope from which the prominences spring has been called the chromosphere on account of the coloured lines displayed in its spectrum. Such lines are very numerous, but those pertaining to the single substance, hydrogen, predominate so greatly that we may say the chromosphere consists chiefly of this element. It is, however, to be noted that calcium and one other element are also invariably present, while iron, manganese and magnesium are often apparent. The remarkable element, of which we have not yet mentioned the name, has had an astonishing history.
During the eclipse of 1868 a fine yellow line was noticed among the lines of the prominence spectrum, and it was not unnaturally at first assumed that it must be the yellow sodium line. But when careful observations were afterwards made without hurry in full sunshine, and accurate measures were obtained, it was at once remarked that this line was not identical with either of the components of the double sodium line. The new line was, no doubt, quite close to the sodium lines, but slightly towards the green part of the spectrum. It was also noticed there was not generally any corresponding line to be seen among the dark lines in the ordinary solar spectrum, though a fine dark one has now and then been detected, especially near a sun-spot. Sir Norman Lockyer and Sir Edward Frankland showed that this was not produced by any known terrestrial element. It was, therefore, supposed to be caused by some hitherto unknown body to which the name of helium, or the sun element, was given. About a dozen less conspicuous lines were gradually identified in the spectrum of the prominences and the chromosphere, which appeared also to be caused by this same mysterious helium. These same remarkable lines have in more recent years also been detected in the spectra of various stars.
This gas so long known in the heavens was at last detected on earth. In April, 1895, Professor Ramsay, who with Lord Rayleigh had discovered the new element argon, detected the presence of the famous helium line in the spectrum of the gas liberated by heating the rare mineral known as cleveite, found in Norway. Thus this element, the existence of which had first been detected on the sun, ninety-three million miles away, has at last been proved to be a terrestrial element also.
When it was announced by Runge that the principal line in the spectrum of the terrestrial helium had a faint and very close companion line on the red-ward side, some doubt seemed at first to be cast on the identity of the new terrestrial gas discovered by Ramsay with the helium of the chromosphere. The helium line of the latter had never been noticed to be double. Subsequently, however, several observers provided[Pg 56] with very powerful instruments found that the famous line in the chromosphere really had a very faint companion line. Thus the identity between the celestial helium and the gas found on our globe was established in the most remarkable manner. Certain circumstances have seemed to indicate that the new gas might possibly be a mixture of two gases of different densities, but up to the present this has not been proved to be the case.
After it had been found possible to see the spectra of prominences without waiting for an eclipse, Sir W. Huggins, in an observation on the 13th of February, 1869, successfully applied a method for viewing the remarkable solar objects themselves instead of their mere spectra in full sunshine. It is only necessary to adjust the spectroscope so that one of the brightest lines—e.g. the red hydrogen line—is in the middle of the field of the viewing telescope, and then to open wide the slit of the spectroscope. A red image of the prominence will then be displayed instead of the mere line. In fact, when the slit is opened wide, the prisms produce a series of detached images of the prominence under observation, one for each kind of light which the object emits.
We have spoken of the spectroscope as depending upon the action of glass prisms. It remains to be added that in the highest class of spectroscopes the prisms are replaced by ruled gratings from which the light is reflected. The effect of the ruling is to produce by what is known as diffraction the required breaking up of the beam of light into its constituent parts.
Majestic indeed are the proportions of some of those mighty prominences which leap from the luminous surface; yet they flicker, as do our terrestrial flames, when we allow them time comparable to their gigantic dimensions. Drawings of the same prominence made at intervals of a few hours, or even less, often show great changes. The magnitude of the displacements that have been noticed sometimes attains many thousands of miles, and the actual velocity with which such masses move frequently exceeds 100 miles a second. Still more violent are the convulsions when, from the surface of the chromosphere, as from a mighty furnace, vast incandescent masses of gas are projected upwards. Plate IV. gives a view of a number of prominences as seen by Trouvelot at Harvard College Observatory, Cambridge, U.S.A. Trouvelot has succeeded in exhibiting in the different pictures the wondrous variety of aspect which these objects assume. The dimensions of the prominences may be inferred from the scale appended to the plate. The largest of those here shown is fully 80,000 miles high; and trustworthy observers have recorded prominences of an altitude even much greater. The rapid changes which these objects sometimes undergo are well illustrated in the two sketches on the left of the lowest line, which were drawn on April 27th, 1872. These are both drawings of the same prominence taken at an interval no greater than twenty minutes. This mighty flame is so vast that its length is ten times as great as the diameter of the earth, yet in this brief period it has completely changed its aspect; the upper part of the flame has, indeed, broken away, and is now shown in that part of the drawing between the two figures on the line above. The same plate also shows various instances of the remarkable spike-like objects, taken, however, at different times and at various parts of the sun. These spikes attain altitudes not generally greater than 20,000 miles, though sometimes they soar aloft to stupendous distances.
We may refer to one special object of this kind, the remarkable history of which has been chronicled by Professor Young. On October 7th, 1880, a prominence was seen, at about 10.30 a.m., on the south-east limb of the sun. It was then about 40,000 miles high, and attracted no special attention. Half an hour later a marvellous transformation had taken place. During that brief interval the prominence became very brilliant and doubled its length. For another hour the mighty flame still soared upwards, until it attained the unprecedented elevation of 350,000 miles—a distance more than one-third the diameter of the great luminary itself. At this climax the energy of the mighty outbreak seems to have at last become exhausted: the flame broke up into fragments,[Pg 58] and by 12.30—an interval of only two hours from the time when it was first noticed—the phenomenon had completely faded away.
No doubt this particular eruption was exceptional in its vehemence, and in the vastness of the changes of which it was an indication. The velocity of upheaval must have been at least 200,000 miles an hour, or, to put it in another form, more than fifty miles a second. This mighty flame leaped from the sun with a velocity more than 100 times as great as that of the swiftest bullet ever fired from a rifle.
The prominences may be generally divided into two classes. We have first those which are comparatively quiescent, and in form somewhat resemble the clouds which float in our earth's atmosphere. The second class of prominences are best described as eruptive. They are, in fact, thrown up from the chromosphere like gigantic jets of incandescent material. These two classes of objects differ not only in appearance but also in the gases of which they are composed. The cloud-like prominences consist mainly of hydrogen, with helium and calcium, while many metals are present in the eruptive discharges. The latter are never seen in the neighbourhood of the sun's poles, but generally appear close to a sun-spot, thus confirming the conclusion that the spots are associated with violent disturbances on the surface of the sun. When a spot has reached the limb of the sun it is frequently found to be surrounded by prominences. It has even been possible in a few instances to detect powerful gaseous eruptions in the neighbourhood of a spot, the spectroscope rendering them visible against the background of the solar surface just as the prominences are observed at the limb against the background of the sky.
In order to photograph a prominence we have, of course, to substitute a photographic plate for the observer's eye. Owing, however, to the difficulty of preventing the feeble light from the prominence from being overpowered by extraneous light, the photography of these bodies was not very successful until Professor Hale, of Chicago, designed his spectro-heliograph. In this instrument there is (in addition to the[Pg 59] usual slit through which the light falls on the prisms, or grating,) a second slit immediately in front of the photographic plate through which the light of a given wave-length can be permitted to pass to the exclusion of all the rest. The light chosen for producing an image of the prominences is that radiated in the remarkable "K line," due to calcium. This lies at the extreme end of the violet. The light from that part of the spectrum, though it is invisible to the eye, is much more active photographically than the light from the red, yellow, or green parts of the spectrum. The front slit is adjusted so that the K line falls upon the second slit, and as the front slit is slowly swept by clockwork over the whole of a prominence, the second slit keeps pace with it by a mechanical contrivance.
If the image of the solar disc is hidden by a screen of exactly the proper size, the slits may be made to sweep over the whole sun, thus giving us at one exposure a picture of the chromospheric ring round the sun's limb with its prominences. The screen may now be withdrawn, and the slits may be made to sweep rapidly over the disc itself. They reveal the existence of glowing calcium vapours in many parts of the surface of the sun. Thus we get a striking picture of the sun as drawn by this particular light. In this manner Professor Hale confirmed the observation made long before by Professor Young, that the spectra of faculæ always show the two great calcium bands.
The velocity with which a prominence shoots upward from the sun's limb can, of course, be measured directly by observations of the ordinary kind with a micrometer. The spectroscope, however, enables us to estimate the speed with which disturbances at the surface of the sun travel in the direction towards the earth or from the earth. We can measure this speed by watching the peculiar behaviour of the spectral lines representing the rapidly moving masses. This opens up a remarkable line of investigation with important applications in many branches of astronomy.
It is, of course, now generally understood that the sensation of light is caused by waves or undulations which impinge[Pg 60] on the retina of the eye after having been transmitted through that medium which we call the ether. To the different colours correspond different wave-lengths—that is to say, different distances between two successive waves. A beam of white light is formed by the union of innumerable different waves whose lengths have almost every possible value lying between certain limits. The wave-length of red light is such that there are 33,000 waves in an inch, while that of violet light is but little more than half that of red light. The position of a line in the spectrum depends solely on the wave-length of the light to which it is due. Suppose that the source of light is approaching directly towards the observer; obviously the waves follow each other more closely than if the source were at rest, and the number of undulations which his eye receives in a second must be proportionately increased. Thus the distance between two successive ether waves will be very slightly diminished. A well-known phenomenon of a similar character is the change of pitch of the whistle of a locomotive engine as it rushes past. This is particularly noticeable if the observer happens to be in a train which is moving rapidly in the opposite direction. In the case of sound, of course, the vibrations or waves take place in the air and not in the ether. But the effect of motion to or from the observer is strictly analogous in the two cases. As, however, light travels 186,000 miles a second, the source of light will also have to travel with a very high velocity in order to produce even the smallest perceptible change in the position of a spectral line.
We have already seen that enormously high velocities are by no means uncommon in some of these mighty disturbances on the sun; accordingly, when we examine the spectrum of a sun-spot, we often see that some of the lines are shifted a little towards one end of the spectrum and sometimes towards the other, while in other cases the lines are seen to be distorted or twisted in the most fantastic manner, indicating very violent local commotions. If the spot happens to be near the centre of the sun's disc, the gases must be shooting upwards or downwards to produce[Pg 61] these changes in the lines. The velocities indicated in observations of this class sometimes amount to as much as two or even three hundred miles per second. We find it difficult to conceive the enormous internal pressures which are required to impel such mighty masses of gases aloft from the photosphere with speeds so terrific, or the conditions which bring about the downrush of such gigantic masses of vapour from above. In the spectra of the prominences on the sun's limb also we often see the bright lines bent or shifted to one side. In such cases what we witness is evidently caused by movements along the surface of the chromosphere, conveying materials towards us or away from us.
An interesting application of this beautiful method of measuring the speed of moving bodies has been made in various attempts to determine the period of rotation of the sun spectroscopically. As the sun turns round on its axis, a point on the eastern limb is moving towards the observer and a point on the western limb is moving away from him. In each case the velocity is a little over a mile per second. At the eastern limb the lines in the solar spectrum are very slightly shifted towards the violet end of the spectrum, while the lines in the spectrum of the western limb are equally shifted towards the red end. By an ingenious optical contrivance it is possible to place the spectra from the two limbs side by side, which doubles the apparent displacement, and thus makes it much more easy to measure. Even with this contrivance the visual quantities to be measured remain exceedingly minute. All the parts of the instrument have to be most accurately adjusted, and the observations are correspondingly delicate. They have been attempted by various observers. Among the most successful investigations of this kind we may mention that of the Swedish astronomer, Dunér, who, by pointing his instrument to a number of places on the limb, found values in good agreement with the peculiar law of rotation which has been deduced from the motion of sun-spots. This result is specially interesting, as it shows that the atmospheric layers, in which that absorption takes[Pg 62] place which produces the dark lines in the spectrum, shares in the motion of the photosphere at the same latitude.
We have yet to mention one other striking phenomenon which is among the chief attractions to observers of total eclipses, and which it has hitherto not been found possible to see in full daylight. This is the corona or aureole of light which is suddenly seen to surround the sun in an eclipse when the moon has completely covered the last remaining crescent of the sun. A general idea of the appearance of the corona is given in Fig. 20, and we further present in Plate V. the drawing of the corona made by Professor Harkness from a comparison of a large number of photographs obtained at different places in the United States during the total eclipse of July 29th, 1878. In Fig. 21 we are permitted by the kindness of Mr. and Mrs. Maunder to reproduce the remarkable photograph of the corona which they obtained in India during the eclipse of January 22nd, 1898.
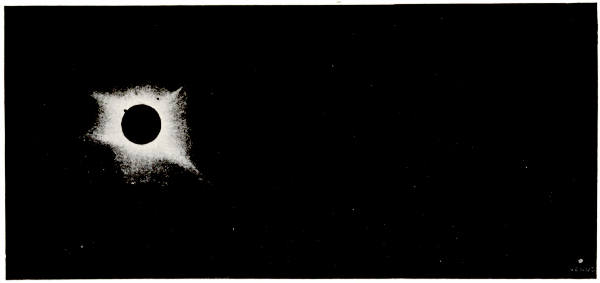 Fig. 21.—View of Corona during the Eclipse of Jan. 22nd,
1898
Fig. 21.—View of Corona during the Eclipse of Jan. 22nd,
1898The part of the corona nearest the sun is very bright, though not so brilliant as the prominences, which (as Professor Young says) blaze through it like[Pg 64] carbuncles. This inner portion is generally of fairly regular outline, forming a white ring about a tenth part of the solar diameter in width. The outer parts of the corona are usually very irregular and very extensive. They are often interrupted by narrow "rifts," or narrow dark bands, which reach from the limb of the sun through the entire corona. On the other hand, there are also sometimes narrow bright streamers, inclined at various angles to the limb of the sun and not seldom curved. In the eclipses of 1867, 1878, and 1889, all of which occurred at periods of sun-spot minimum, the corona showed long and faint streamers nearly in the direction of the sun's equator, and short but distinct brushes of light near the poles. In the eclipses of 1870, 1882, and 1893, near sun-spot maxima, the corona was more regularly circular, and chiefly developed over the spot zones. We have here another proof (if one were necessary) of the intimate connection between the periodicity of the spots and the development of all other solar phenomena.
In the spectrum of the corona there is a mysterious line in the green, as to the origin of which nothing is at present certainly known. It is best seen during eclipses occurring near the time of sun-spot maximum. It is presented in the ordinary solar spectrum as a very thin, dark line, which generally remains undisturbed even when lines of hydrogen and other substances are twisted and distorted by the violent rush of disturbed elements. The line is always present among the bright lines of the chromosphere spectrum. In addition to it the corona shows a few other bright lines, belonging, no doubt, to the same unknown element ("coronium"), and also a faint continuous spectrum, in which even a few of the more prominent dark lines of the solar spectrum have been sometimes detected. This shows that in addition to glowing gas (represented by the bright lines) the corona also contains a great deal of matter like dust, or fog, the minute particles of which are capable of reflecting the sunlight and thereby producing a feeble continuous spectrum. This matter seems to form the principal constituent of the long coronal rays and streamers, as the latter are not visible in the[Pg 65] detached images of the corona which appear instead of the bright lines when the corona is viewed, or photographed, during an eclipse, in a spectroscope without a slit. If the long rays were composed of the gas or gases which constitute the inner corona, it is evident that they ought to appear in these detached images. As to the nature of the forces which are continually engaged in shooting out these enormously long streamers, we have at present but little information. It is, however, certain that the extensive atmospheric envelope round the sun, which shows itself as the inner corona, must be extremely attenuated. Comets have on several occasions been known to rush through this coronal atmosphere without evincing the slightest appreciable diminution in their speed from the resistance to which they were exposed.
We have accumulated by observation a great number of facts concerning the sun, but when we try to draw from these facts conclusions as to the physical constitution of that great body, it cannot be denied that the difficulties seem to be very great indeed. We find that the best authorities differ considerably in the opinions they entertain as to its nature. We shall here set forth the principal conclusions as to which there is little or no controversy.
We shall see in a following chapter that astronomers have been able to determine the relative densities of the bodies in the solar system; in other words, they have found the relation between the quantities of matter contained in an equally large volume of each. It has thus been ascertained that the average density of the sun is about a quarter that of the earth. If we compare the weight of the sun with that of an equally great globe of water, we find that the luminary would be barely one and a half times as heavy as the water. Of course, the actual mass of the sun is very enormous; it is no less than 330,000 times as great as that of the earth. The solar material itself is, however, relatively light, so that the sun is four times as big as it would have to be if, while its weight remained the same, its density equalled that of the earth. Bearing in mind this lightness of the sun, and also the exceedingly high temperature which we know to prevail[Pg 66] there, no other conclusion seems possible than that the body of the sun must be in a gaseous state. The conditions under which such gases exist in the sun are, no doubt, altogether different from those with which we are acquainted on the earth. At the surface of the sun the force of gravity is more than twenty-seven times as great as it is on the earth. A person who on the earth could just lift twenty-seven equal pieces of metal would, if he were transferred to the sun, only be able to lift one of the pieces at a time. The pressure of the gases below the surface must therefore be very great, and it might be supposed that they would become liquefied in consequence. It was, however, discovered by Andrews that so long as a gas is kept at a temperature higher than a certain point, known as the "critical temperature" (which is different for different gases), the gas will not be turned into a liquid however great be the pressure to which it is submitted. The temperature on the sun cannot be lower than the critical temperatures of the gases there existing; so it would seem that even the enormous pressure can hardly reduce the gases in the great luminary to the liquid form.
Of the interior of the sun we can, of course, expect to learn little or nothing. What we observe is the surface-layer, the so-called photosphere, in which the cold of space produces the condensation of the gases into those luminous clouds which we see in our drawings and photographs as "rice grains" or "willow leaves." It has been suggested by Dr. Johnstone Stoney (and afterwards by Professor Hastings, of Baltimore) that these luminous clouds are mainly composed of carbon with those of the related elements silicon and boron, the boiling points of which are much higher than those of other elements which might be considered likely to form the photospheric clouds. The low atomic weight of carbon must also have the effect of giving the molecules of this element a very high velocity, and thereby enabling them to work their way into the upper regions, where the temperature has so fallen that the vapour becomes chilled into cloud. A necessary consequence of the rapid cooling of these clouds, and the consequent[Pg 67] radiation of heat on a large scale, would be the formation of what we may perhaps describe as smoke, which settles by degrees through the intervals between the clouds (making these intervals appear darker) until it is again volatilised on reaching a level of greater heat below the clouds. This same smoke is probably the cause of the well-known fact that the solar limb is considerably fainter than the middle of the disc. This seems to arise from the greater absorption caused by the longer distance which a ray of light from a point near the limb has to travel through this layer of smoke before reaching the earth. It is shown that this absorption cannot be attributed to a gaseous atmosphere, since this would have the effect of producing more dark absorption lines in the spectrum. There would thus be a marked difference between the solar spectrum from a part near the middle of the disc and the spectrum from a part near the limb. This, however, we do not find to be the case.
With regard to the nature of sun-spots, the idea first suggested by Secchi and Lockyer, that they represent down rushes of cooler vapours into the photosphere (or to its surface), seems on the whole to accord best with the observed phenomena. We have already mentioned that the spots are generally accompanied by faculæ and eruptive prominences in their immediate neighbourhood, but whether these eruptions are caused by the downfall of the vapour which makes the photospheric matter "splash up" in the vicinity, or whether the eruptions come first, and by diminishing the upward pressure from below form a "sink," into which overlying cooler vapour descends, are problems as to which opinions are still much divided.
A remarkable appendage to the sun, which extends to a distance very much greater than that of the corona, produces the phenomenon of the zodiacal light. A pearly glow is sometimes seen in the spring to spread over a part of the sky in the vicinity of the point where the sun has disappeared after sunset. The same spectacle may also be witnessed before sunrise in the autumn, and it would seem as if the material producing the zodiacal light, whatever it may be, had a[Pg 68] lens-shaped form with the sun in the centre. The nature of this object is still a matter of uncertainty, but it is probably composed of a kind of dust, as the faint spectrum it affords is of a continuous type. A view of the zodiacal light is shown in Fig. 22.
In all directions the sun pours forth, with the most prodigal liberality, its torrents of light and of heat. The earth can only grasp the merest fraction, less than the 2,000,000,000th part of the whole. Our fellow planets and the moon also intercept a trifle; but how small is the portion of the mighty flood which they can utilise! The sip that a flying swallow takes from a river is as far from exhausting the water in the river as are the planets from using all the heat which streams from the sun.
The sun's gracious beams supply the magic power that enables the corn to grow and ripen. It is the heat of the sun which raises water from the ocean in the form of vapour, and then sends down that vapour as rain to refresh the earth and to fill the rivers which bear our ships down to the ocean. It is the heat of the sun beating on the large continents which gives rise to the breezes and winds that waft our vessels across the deep; and when on a winter's evening we draw around the fire and feel its invigorating rays, we are only enjoying sunbeams which shone on the earth countless ages ago. The heat in those ancient sunbeams developed the mighty vegetation of the coal period, and in the form of coal that heat has slumbered for millions of years, till we now call it again into activity. It is the power of the sun stored up in coal that urges on our steam-engines. It is the light of the sun stored up in coal that beams from every gaslight in our cities.
For the power to live and move, for the plenty with which we are surrounded, for the beauty with which nature is adorned, we are immediately indebted to one body in the countless hosts of space, and that body is the sun.
The Moon and the Tides—The Use of the Moon in Navigation—The Changes of the Moon—The Moon and the Poets—Whence the Light of the Moon?—Sizes of the Earth and the Moon—Weight of the Moon—Changes in Apparent Size—Variations in its Distance—Influence of the Earth on the Moon—The Path of the Moon—Explanation of the Moon's Phases—Lunar Eclipses—Eclipses of the Sun, how produced—Visibility of the Moon in a Total Eclipse—How Eclipses are Predicted—Uses of the Moon in finding Longitude—The Moon not connected with the Weather—Topography of the Moon—Nasmyth's Drawing of Triesnecker—Volcanoes on the Moon—Normal Lunar Crater—Plato—The Shadows of Lunar Mountains—The Micrometer—Lunar Heights—Former Activity on the Moon—Nasmyth's View of the Formation of Craters—Gravitation on the Moon—Varied Sizes of the Lunar Craters—Other Features of the Moon—Is there Life on the Moon?—Absence of Water and of Air—Dr. Stoney's Theory—Explanation of the Rugged Character of Lunar Scenery—Possibility of Life on Distant Bodies in Space.
If the moon were suddenly struck out of existence, we should be immediately apprised of the fact by a wail from every seaport in the kingdom. From London and from Liverpool we should hear the same story—the rise and fall of the tide had almost ceased. The ships in dock could not get out; the ships outside could not get in; and the maritime commerce of the world would be thrown into dire confusion.
The moon is the principal agent in causing the daily ebb and flow of the tide, and this is the most important work which our satellite has to do. The fleets of fishing boats around the coasts time their daily movements by the tide, and are largely indebted to the moon for bringing them in and out of harbour. Experienced sailors assure us that the tides are of the utmost service to navigation. The question as to how the moon causes the tides is postponed to a future chapter, in which we shall also sketch the marvellous part which[Pg 71] the tides seem to have played in the early history of our earth.
Who is there that has not watched, with admiration, the beautiful series of changes through which the moon passes every month? We first see her as an exquisite crescent of pale light in the western sky after sunset. If the night is fine, the rest of the moon is visible inside the crescent, being faintly illumined by light reflected from our own earth. Night after night she moves further and further to the east, until she becomes full, and rises about the same time that the sun sets. From the time of the full the disc of light begins to diminish until the last quarter is reached. Then it is that the moon is seen high in the heavens in the morning. As the days pass by, the crescent shape is again assumed. The crescent wanes thinner and thinner as the satellite draws closer to the sun. Finally she becomes lost in the overpowering light of the sun, again to emerge as the new moon, and again to go through the same cycle of changes.
The brilliance of the moon arises solely from the light of the sun, which falls on the not self-luminous substance of the moon. Out of the vast flood of light which the sun pours forth with such prodigality into space the dark body of the moon intercepts a little, and of that little it reflects a small fraction to illuminate the earth. The moon sheds so much light, and seems so bright, that it is often difficult at night to remember that the moon has no light except what falls on it from the sun. Nevertheless, the actual surface of the brightest full moon is perhaps not much brighter than the streets of London on a clear sunshiny day. A very simple observation will suffice to show that the moon's light is only sunlight. Look some morning at the moon in daylight, and compare the moon with the clouds. The brightness of the moon and of the clouds are directly comparable, and then it can be readily comprehended how the sun which illuminates the clouds has also illumined the moon. An attempt has been made to form a comparative estimate of the brightness of the sun and the full moon. If 600,000 full moons were shining at once, their collective brilliancy would equal that of the sun.[Pg 72]
The beautiful crescent moon has furnished a theme for many a poet. Indeed, if we may venture to say so, it would seem that some poets have forgotten that the moon is not to be seen every night. A poetical description of evening is almost certain to be associated with the appearance of the moon in some phase or other. We may cite one notable instance in which a poet, describing an historical event, has enshrined in exquisite verse a statement which cannot be correct. Every child who speaks our language has been taught that the burial of Sir John Moore took place
"By the struggling moonbeams' misty light."
There is an appearance of detail in this statement which wears the garb of truth. We are not inclined to doubt that the night was misty, nor as to whether the moonbeams had to struggle into visibility; the question at issue is a much more fundamental one. We do not know who was the first to raise the point as to whether any moon shone on that memorable event at all or not; but the question having been raised, the Nautical Almanac immediately supplies an answer. From it we learn in language, whose truthfulness constitutes its only claim to be poetry, that the moon was new at one o'clock in the morning of the day of the battle of Corunna (16th January, 1809). The ballad evidently implies that the funeral took place on the night following the battle. We are therefore assured that the moon can hardly have been a day old when the hero was consigned to his grave. But the moon in such a case is practically invisible, and yields no appreciable moonbeams at all, misty or otherwise. Indeed, if the funeral took place at the "dead of night," as the poet asserts, then the moon must have been far below the horizon at the time.[6]
In alluding to this and similar instances, Mr. Nasmyth gives a word of advice to authors or to artists who desire to bring the moon on a scene without knowing as a matter of fact[Pg 73] that our satellite was actually present. He recommends them to follow the example of Bottom in A Midsummer's Night's Dream, and consult "a calendar, a calendar! Look in the almanac; find out moonshine, find out moonshine!"
Among the countless host of celestial bodies—the sun, the moon, the planets, and the stars—our satellite enjoys one special claim on our attention. The moon is our nearest permanent neighbour. It is just possible that a comet may occasionally approach the earth more closely than the moon but with this exception the other celestial bodies are all many hundreds or thousands, or even many millions, of times further from us than the moon.
It is also to be observed that the moon is one of the smallest visible objects which the heavens contain. Every one of the thousands of stars that can be seen with the unaided eye is enormously larger than our satellite. The brilliance and apparent vast proportions of the moon arise from the fact that it is only 240,000 miles away, which is a distance almost[Pg 74] immeasurably small when compared with the distances between the earth and the stars.
Fig. 23 exhibits the relative sizes of the earth and its attendant. The small globe shows the moon, while the larger globe represents the earth. When we measure the actual diameters of the two globes, we find that of the earth to be 7,918 miles and of the moon 2,160 miles, so that the diameter of the earth is nearly four times greater than the diameter of the moon. If the earth were cut into fifty pieces, all equally large, then one of these pieces rolled into a globe would equal the size of the moon. The superficial extent of the moon is equal to about one thirteenth part of the surface of the earth. The hemisphere our neighbour turns towards us exhibits an area equal to about one twenty-seventh part of the area of the earth. This, to speak approximately, is about double the actual extent of the continent of Europe. The average materials of the earth are, however, much heavier than those contained in the moon. It would take more than eighty globes, each as ponderous as the moon, to weigh down the earth.
Amid the changes which the moon presents to us, one obvious fact stands prominently forth. Whether our satellite be new or full, at first quarter or at last, whether it be high in the heavens or low near the horizon, whether it be in process of eclipse by the sun, or whether the sun himself is being eclipsed by the moon, the apparent size of the latter is nearly constant. We can express the matter numerically. A globe one foot in diameter, at a distance of 111 feet from the observer, would under ordinary circumstances be just sufficient to hide the disc of the moon; occasionally, however, the globe would have to be brought in to a distance of only 103 feet, or occasionally it might have to be moved out to so much as 118 feet, if the moon is to be exactly hidden. It is unusual for the moon to approach either of its extreme limits of position, so that the distance from the eye at which the globe must be situated so as to exactly cover the moon is usually more than 105 feet, and less than 117 feet. These fluctuations in the apparent size of our satellite are contained within such narrow limits that in the first glance at the[Pg 75] subject they may be overlooked. It will be easily seen that the apparent size of the moon must be connected with its real distance from the earth. Suppose, for the sake of illustration, that the moon were to recede into space, its size would seem to dwindle, and long ere it had reached the distance of even the very nearest of the other celestial bodies it would have shrunk into insignificance. On the other hand, if the moon were to come nearer to the earth, its apparent size would gradually increase until, when close to our globe, it would seem like a mighty continent stretching over the sky. We find that the apparent size of the moon is nearly constant, and hence we infer that the average distance of the same body is also nearly constant. The average value of that distance is 239,000 miles. In rare circumstances it may approach to a distance but little more than 221,000 miles, or recede to a distance hardly less than 253,000 miles, but the ordinary fluctuations do not exceed more than about 13,000 miles on either side of its mean value.
From the moon's incessant changes we perceive that she is in constant motion, and we now further see that whatever these movements may be, the earth and the moon must at present remain at nearly the same distance apart. If we further add that the path pursued by the moon around the heavens lies nearly in a plane, then we are forced to the conclusion that our satellite must be revolving in a nearly circular path around the earth at the centre. It can, indeed, be shown that the constant distance of the two bodies involves as a necessary condition the revolution of the moon around the earth. The attraction between the moon and the earth tends to bring the two bodies together. The only way by which such a catastrophe can be permanently avoided is by making the satellite move as we actually find it to do. The attraction between the earth and the moon still exists, but its effect is not then shown in bringing the moon in towards the earth. The attraction has now to exert its whole power in restraining the moon in its circular path; were the attraction to cease, the moon would start off in a straight line, and recede never to return.
The fact of the moon's revolution around the earth is easily demonstrated by observations of the stars. The rising and setting of our satellite is, of course, due to the rotation of the earth, and this apparent diurnal movement the moon possesses in common with the sun and with the stars. It will, however, be noticed that the moon is continually changing its place among the stars. Even in the course of a single night the displacement will be conspicuous to a careful observer without the aid of a telescope. The moon completes each revolution around the earth in a period of 27·3 days.
In Fig. 24 we have a view of the relative positions of the earth, the sun, and the moon, but it is to be observed that, for the convenience of illustration, we have been obliged to represent the orbit of the moon on a much larger scale than it ought to be in comparison with the distance of the sun. That half of the moon which is turned towards the sun is brilliantly illuminated, and, according as we see more or less of that brilliant half, we say that the moon is more or less full, the several "phases" being visible in the succession shown by the numbers in Fig. 25. A beginner sometimes finds [Pg 77]considerable difficulty in understanding how the light on the full moon at night can have been derived from the sun. "Is not," he will say, "the earth in the way? and must it not intercept the sunlight from every object on the other side of the earth to the sun?" A study of Fig. 24 will explain the difficulty. The plane in which the moon revolves does not coincide with the plane in which the earth revolves around the sun. The line in which the plane of the earth's motion is intersected by that of the moon divides the moon's path into two semicircles. We must imagine the moon's path to be tilted a little, so that the upper semicircle is somewhat above the plane of the paper, and the other semicircle below. It thus follows that when the moon is in the position marked full, under the circumstances shown in the figure, the moon will be just above the line joining the earth and the sun; the sunlight will thus pass over the earth to the moon, and the moon will be illuminated. At new moon, the moon will be under the line joining the earth and the sun.
As the relative positions of the earth and the sun are changing, it happens twice in each revolution that the sun comes into the position of the line of intersection of the two planes. If this occurs at the time of full moon, the earth lies directly between the moon and the sun; the moon is thus plunged into the shadow of the earth, the light from the sun is intercepted, and we say that the moon is eclipsed. The moon sometimes only partially enters the earth's shadow, in which case the eclipse is a partial one. When, on the other hand, the sun is situated on the line of intersection at the time of new moon, the moon lies directly between the earth and the sun, and the dark body of the moon will then cut off the sunlight from the earth, producing a solar eclipse. Usually only a part of the sun is thus obscured, forming the well-known partial eclipse; if, however, the moon pass centrally over the sun, then we must have one or other of two very remarkable kinds of eclipse. Sometimes the moon entirely blots out the sun, and thus is produced the sublime spectacle of a total eclipse, which tells us so much as to the nature of the sun, and to which we have already referred in the last[Pg 78] chapter. Even when the moon is placed centrally over the sun, a thin rim of sunlight is occasionally seen round the margin of the moon. We then have what is known as an annular eclipse.
It is remarkable that the moon is sometimes able to hide the sun completely, while on other occasions it fails to do so. It happens that the average apparent size of the moon is nearly equal to the average apparent size of the sun, but, owing to the fluctuations in their distances, the actual apparent sizes of both bodies undergo certain changes. On certain occasions the apparent size of the moon is greater than that of the sun. In this case a central passage produces a total eclipse; but it may also happen that the apparent size of the sun exceeds that of the moon, in which case a central passage can only produce an annular eclipse.
 Fig. 26.—Form of the Earth's Shadow, showing the
Penumbra, or partially shaded region. Within the Penumbra, the Moon is
visible; in the Shadow it is nearly invisible.
Fig. 26.—Form of the Earth's Shadow, showing the
Penumbra, or partially shaded region. Within the Penumbra, the Moon is
visible; in the Shadow it is nearly invisible.
There are hardly any more interesting celestial phenomena than the different descriptions of eclipses. The almanac will always give timely notice of the occurrence, and the more striking features can be observed without a telescope. In an eclipse of the moon (Fig. 26) it is interesting to note the moment when the black shadow is first detected, to watch its gradual encroachment over the bright surface of the moon, to follow it, in case the eclipse is total, until there is only a thin crescent of moonlight left, and to watch the final extinction of that crescent when the whole moon is plunged into the shadow. But now a spectacle of great interest and beauty is often manifested; for though the moon is so hidden behind the[Pg 79] earth that not a single direct ray of the sunlight could reach its surface, yet we often find that the moon remains visible, and, indeed, actually glows with a copper-coloured hue bright enough to permit several of the markings on the surface to be discerned.
This illumination of the moon even in the depth of a total eclipse is due to the sunbeams which have just grazed the edge of the earth. In doing so they have become bent by the refraction of the atmosphere, and have thus been turned inwards into the shadow. Such beams have passed through a prodigious thickness of the earth's atmosphere, and in this long journey through hundreds of miles of air they have become tinged with a ruddy or copper-like hue. Nor is this property of our atmosphere an unfamiliar one. The sun both at sunrise and at sunset glows with a light which is much more ruddy than the beams it dispenses at noonday. But at sunset or at sunrise the rays which reach our eyes have much more of our atmosphere to penetrate than they have at noon, and accordingly the atmosphere imparts to them that ruddy colour so characteristic and often so lovely. If the spectrum of the sun when close to the horizon is examined it is seen to be filled with numerous dark lines and bands situated chiefly towards the blue and violet end. These are caused by the increased absorption which the light suffers in the atmosphere, and give rise to the preponderating red light on the sun under such conditions. In the case of the eclipsed moon, the sunbeams have to take an atmospheric journey more than double as long as that at sunrise or sunset, and hence the ruddy glow of the eclipsed moon may be accounted for.
The almanacs give the full particulars of each eclipse that happens in the corresponding year. These predictions are reliable, because astronomers have been carefully observing the moon for ages, and have learned from these observations not only how the moon moves at present, but also how it will move for ages to come. The actual calculations are so complicated that we cannot here discuss them. There is, however, one leading principle about eclipses which is so simple that we must refer to it. The eclipses occurring this year have no[Pg 80] very obvious relation to the eclipses that occurred last year, or to those that will occur next year. Yet, when we take a more extended view of the sequence of these phenomena, a very definite principle becomes manifest. If we observe all the eclipses in a period of eighteen years, or nineteen years, then we can predict, with at least an approximation to the truth, all the future eclipses for many years. It is only necessary to recollect that in 6,585-1⁄3 days after one eclipse a nearly similar eclipse follows. For instance, a beautiful eclipse of the moon occurred on the 5th of December, 1881. If we count back 6,585 days from that date, or, that is, eighteen years and eleven days, we come to November 24th, 1863, and a similar eclipse of the moon took place then. Again, there were four eclipses in the year 1881. If we add 6,585-1⁄3 days to the date of each eclipse, it will give the dates of all the four eclipses in the year 1899. It was this rule which enabled the ancient astronomers to predict the recurrence of eclipses, at a time when the motions of the moon were not understood nearly so well as they now are.
During a long voyage, and perhaps in critical circumstances, the moon will often render invaluable information to the sailor. To navigate a ship, suppose from Liverpool to China, the captain must frequently determine the precise position which his ship then occupies. If he could not do this, he would never find his way across the trackless ocean. Observations of the sun give him his latitude and tell him his local time, but the captain further requires to know the Greenwich time before he can place his finger at a point of the chart and say, "My ship is here." To ascertain the Greenwich time the ship carries a chronometer which has been carefully rated before starting, and, as a precaution, two or three chronometers are usually provided to guard against the risk of error. An unknown error of a minute in the chronometer might perhaps lead the vessel fifteen miles from its proper course.
It is important to have the means of testing the chronometers during the progress of the voyage; and it would be a great convenience if every captain, when he wished, could actually consult some infallible standard of Greenwich time. We want, in fact, a Greenwich clock which may be visible over the whole globe. There is such a clock; and, like any other clock, it has a face on which certain marks are made, and a hand which travels round that face. The great clock at Westminster shrinks into insignificance when compared with the mighty clock which the captain uses for setting his chronometer. The face of this stupendous dial is the face of the heavens. The numbers engraved on the face of a clock are replaced by the twinkling stars; while the hand which moves over the dial is the beautiful moon herself.[Pg 82] When the captain desires to test his chronometer, he measures the distance of the moon from a neighbouring star. For example, he may see that the moon is three degrees from the star Regulus. In the Nautical Almanac he finds the Greenwich time at which the moon was three degrees from Regulus. Comparing this with the indications of the chronometer, he finds the required correction.
There is one widely-credited myth about the moon which must be regarded as devoid of foundation. The idea that our satellite and the weather bear some relation has no doubt been entertained by high authority, and appears to be an article in the belief of many an excellent mariner. Careful comparison between the state of the weather and the phases of the moon has, however, quite discredited the notion that any connection of the kind does really exist.
We often notice large blank spaces on maps of Africa and of Australia which indicate our ignorance of parts of the interior of those great continents. We can find no such blank spaces in the map of the moon. Astronomers know the surface of the moon better than geographers know the interior of Africa. Every spot on the face of the moon which is as large as an English parish has been mapped, and all the more important objects have been named.
A general map of the moon is shown in Plate VI. It has been based upon drawings made with small telescopes, and it gives an entire view of that side of our satellite which is presented towards us. The moon is shown as it appears in an astronomical telescope, which inverts everything, so that the south is at the top and the north at the bottom (to show objects upright a telescope requires an additional pair of lenses in the eye-piece, and as this diminishes the amount of light reaching the eye they are dispensed with in astronomical telescopes). We can see on the map some of the characteristic features of lunar scenery. Those dark regions so conspicuous in the ordinary full moon are easily recognised on the map. They were thought to be seas by astronomers before the days of telescopes, and indeed the name "Mare" is still retained, though it is obvious that they contain no[Pg 83] water at present. The map also shows certain ridges or elevated portions, and when we apply measurement to these objects we learn that they must be mighty mountain ranges. But the most striking features on the moon are those ring-like objects which are scattered over the surface in profusion. These are known as the lunar craters.
To facilitate reference to the chief points of interest we have arranged an index map (Fig. 27) which will give a clue to the names of the several objects depicted upon the plate. The so-called seas are represented by capital letters; so that A is the Mare Crisium, and H the Oceanus Procellarum. The ranges of mountains are indicated by small letters; thus a on the index is the site of the so-called Caucasus mountains, and similarly the Apennines are denoted by c. The numerous craters are distinguished by numbers; for example, the feature on the map corresponding to 20 on the index is the crater designated Ptolemy.
A. Mare Crisium.
B. Mare Fœcunditatis.
C. Mare Tranquillitatis.
D. Mare Serenitatis.
E. Mare Imbrium.
F. Sinus Iridum.
G. Mare Vaporum.
H. Oceanus Procellarum.
I. Mare Humorum.
J. Mare Nubium.
K. Mare Nectaris.
a. Caucasus.
b. Alps.
c. Apennines.
d. Carpathians.
f. Cordilleras & D'Alembert mountains.
g. Rook mountains.
h. Dœrfel mountains.
i. Leibnitz mountains.
1. Posidonius.
2. Linné.
3. Aristotle.
4. Great Valley of the Alps.
5. Aristillus.
6. Autolycus.
7. Archimedes.
8. Plato.
9. Eratosthenes.
10. Copernicus.
11. Kepler.
12. Aristarchus.
13. Grimaldi.
14. Gassendi.
15. Schickard.
16. Wargentin.
17. Clavius.
18. Tycho.
19. Alphonsus.
20. Ptolemy.
21. Catharina.
22. Cyrillus.
23. Theophilus.
24. Petavius.
25. Hyginus.
26. Triesnecker.
In every geographical atlas there is a map showing the two hemispheres of the earth, the eastern and the western. In the case of the moon we can only give a map of one hemisphere, for the simple reason that the moon always turns the same side towards us, and accordingly we never get a view of the other side. This is caused by the interesting circumstance that the moon takes exactly the same time to turn[Pg 84] once round its own axis as it takes to go once round the earth. The rotation is, however, performed with uniform speed, while the moon does not move in its orbit with a perfectly uniform velocity (see Chapter IV.). The consequence is that we now get a slight glimpse round the east limb, and now a similar glimpse round the west limb, as if the moon were shaking its head very gently at us. But it is only an insignificant margin of the far side of the moon which this libration permits us to examine.
Lunar objects are well suited for observation when the sunlight falls upon them in such a manner as to exhibit strongly contrasted lights and shadows. It is impossible to observe the moon satisfactorily when it is full, for then no conspicuous shadows are cast. The most opportune moment for seeing any particular lunar object is when it lies just at the illuminated side of the boundary between light and shade, for then the features are brought out with exquisite distinctness.
Plate VII.[7] gives an illustration of lunar scenery, the object represented being known to astronomers by the name of Triesnecker. The district included is only a very small fraction of the entire surface of the moon, yet the actual area is very considerable, embracing as it does many hundreds of square miles. We see in it various ranges of lunar mountains, while the central object in the picture is one of those remarkable lunar craters which we meet with so frequently in every lunar landscape. This crater is about twenty miles in diameter, and it has a lofty mountain in the centre, the peak of which is just illuminated by the rising sun in that phase of our satellite which is represented in the picture.
A typical view of a lunar crater is shown in Plate VIII. This is, no doubt, a somewhat imaginary sketch. The point of view from which the artist is supposed to have taken the picture is one quite unattainable by terrestrial astronomers, yet there can be little doubt that it is a fair representation of objects on the moon. We should, however, recollect the scale on which it is drawn. The vast crater must be many miles across, and the mountain at its centre must be thousands of feet high. The telescope will, even at its best, only show the moon as well as we could see it with the unaided eye if it were 250 miles away instead of being 240,000. We must not, therefore, expect to see any details on the moon even with the finest telescopes, unless they were coarse enough to be visible at a distance of 250 miles. England from such a point of view would only show London as a coloured spot, in contrast with the general surface of the country.
We return, however, from a somewhat fancy sketch to a more prosaic examination of what the telescope does actually reveal. Plate IX. represents the large crater Plato, so well known to everyone who uses a telescope. The floor of this remarkable object is nearly flat, and the central mountain, so often seen in other craters, is entirely wanting. We describe it more fully in the general list of lunar objects.
The mountain peaks on the moon throw long, well-defined shadows, characterised by a sharpness which we do not find in the shadows of terrestrial objects. The difference between the two cases arises from the absence of air from the moon. Our atmosphere diffuses a certain amount of light, which mitigates the blackness of terrestrial shadows and tends to soften their outline. No such influences are at work on the moon, and the sharpness of the shadows is taken advantage of in our attempts to measure the heights of the lunar mountains.
It is often easy to compute the altitude of a church steeple, a lofty chimney, or any similar object, from the length of its shadow. The simplest and the most accurate process is to measure at noon the number of feet from the base of the object[Pg 86] to the end of the shadow. The elevation of the sun at noon on the day in question can be obtained from the almanac, and then the height of the object follows by a simple calculation. Indeed, if the observations can be made either on the 6th of April or the 6th of September, at or near the latitude of London, then calculations would be unnecessary. The noonday length of the shadow on either of the dates named is equal to the altitude of the object. In summer the length of the noontide shadow is less than the altitude; in winter the length of the shadow exceeds the altitude. At sunrise or sunset the shadows are, of course, much longer than at noon, and it is shadows of this kind that we observe on the moon. The necessary measurements are made by that indispensable adjunct to the equatorial telescope known as the micrometer.
This word denotes an instrument for measuring small distances. In one sense the term is not a happy one. The objects to which the astronomer applies the micrometer are usually anything but small. They are generally of the most transcendent dimensions, far exceeding the moon or the sun, or even our whole system. Still, the name is not altogether inappropriate, for, vast though the objects may be, they generally seem minute, even in the telescope, on account of their great distance.
We require for such measurements an instrument capable of the greatest nicety. Here, again, we invoke the aid of the spider, to whose assistance in another department we have already referred. In the filar micrometer two spider lines are parallel, and one intersects them at right angles. One or both of the parallel lines can be moved by means of screws, the threads of which have been shaped by consummate workmanship. The distance through which the line has been moved is accurately indicated by noting the number of revolutions and parts of a revolution of the screw. Suppose the two lines be first brought into coincidence, and then separated until the apparent length of the shadow of the mountain on the moon is equal to the distance between the lines: we then know the number of revolutions of the micrometer screw which is equivalent to the length of the shadow. The number of miles on[Pg 87] the moon which correspond to one revolution of the screw has been previously ascertained by other observations, and hence the length of the shadow can be determined. The elevation of the sun, as it would have appeared to an observer at this point of the moon, at the moment when the measures were being made, is also obtainable, and hence the actual elevation of the mountain can be calculated. By measurements of this kind the altitudes of other lunar objects, such, for example, as the height of the rampart surrounding a circular-walled plane, can be determined.
The beauty and interest of the moon as a telescopic object induces us to give to the student a somewhat detailed account of the more remarkable features which it presents. Most of the objects we are to describe can be effectively exhibited with very moderate telescopic power. It is, however, to be remembered that all of them cannot be well seen at one time. The region most distinctly shown is the boundary between light and darkness. The student will, therefore, select for observation such objects as may happen to lie near that boundary at the time when he is observing.
1. Posidonius.—The diameter of this large crater is nearly 60 miles. Although its surrounding wall is comparatively slender, it is so distinctly marked as to make the object very conspicuous. As so frequently happens in lunar volcanoes, the bottom of the crater is below the level of the surrounding plain, in the present instance to the extent of nearly 2,500 feet.
2. Linné.—This small crater lies in the Mare Serenitatis. About sixty years ago it was described as being about 6-1⁄2 miles in diameter, and seems to have been sufficiently conspicuous. In 1866 Schmidt, of Athens, announced that the crater had disappeared. Since then an exceedingly small shallow depression has been visible, but the whole object is now very inconsiderable. This seems to be the most clearly attested case of change in a lunar object. Apparently the walls of the crater have tumbled into the interior and partly filled it up, but many astronomers doubt that a change has really taken place, as Schröter, a Hanoverian observer at the end of the eighteenth century, appears not to have seen any[Pg 88] conspicuous crater in the place, though it must be admitted that his observations are rather incomplete. To give some idea of Schmidt's amazing industry in lunar researches, it may be mentioned that in six years he made nearly 57,000 individual settings of his micrometer in the measurement of lunar altitudes. His great chart of the mountains in the moon is based on no less than 2,731 drawings and sketches, if those are counted twice that may have been used for two divisions of the map.
3. Aristotle.—This great philosopher's name has been attached to a grand crater 50 miles in diameter, the interior of which, although very hilly, shows no decidedly marked central cone. But the lofty wall of the crater, exceeding 10,500 feet in height, overshadows the floor so continuously that its features are never seen to advantage.
4. The Great Valley of the Alps.—A wonderfully straight valley, with a width ranging from 3-1⁄2 to 6 miles, runs right through the lunar Alps. It is, according to Mädler, at least 11,500 feet deep, and over 80 miles in length. A few low ridges which are parallel to the sides of the valley may possibly be the result of landslips.
5. Aristillus.—Under favourable conditions Lord Rosse's great telescope has shown the exterior of this magnificent crater to be scored with deep gullies radiating from its centre. Aristillus is about 34 miles wide and 10,000 feet in depth.
6. Autolycus is somewhat smaller than the foregoing, to which it forms a companion in accordance with what Mädler thought a well-defined relation amongst lunar craters, by which they frequently occurred in pairs, with the smaller one more usually to the south. Towards the edge this arrangement is generally rather apparent than real, and is merely a result of foreshortening.
7. Archimedes.—This large plain, about 50 miles in diameter, has its vast smooth interior divided by unequally bright streaks into seven distinct zones, running east and west. There is no central mountain or other obvious internal sign of former activity, but its irregular wall rises into abrupt towers, and is marked outside by decided terraces.
8. Plato.—We have already referred to this extensive circular plain, which is noticeable with the smallest telescope. The average height of the rampart is about 3,800 feet on the eastern side; the western side is somewhat lower, but there is one peak rising to the height of nearly 7,300 feet. The plain girdled by this vast rampart is of ample proportions. It is a somewhat irregular circle, about 60 miles in diameter, and containing an area of 2,700 square miles. On its floor the shadows of the western wall are shown in Plate IX., as are also three of the small craters, of which a large number have been detected by persevering observers. The narrow sharp line leading from the crater to the left is one of those remarkable "clefts" which traverse the moon in so many directions. Another may be seen further to the left. Above Plato are several detached mountains, the loftiest of which is Pico, about 8,000 feet in height. Its long and pointed shadow would at first sight lead one to suppose that it must be very steep; but Schmidt, who specially studied the inclinations of the lunar slopes, is of opinion that it cannot be nearly so steep as many of the Swiss mountains that are frequently ascended. As many as thirty minute craters have been carefully observed on the floor of Plato, and variations have been thought by Mr. W.H. Pickering to be perceptible.
9. Eratosthenes.—This profound crater, upwards of 37 miles in diameter, lies at the end of the gigantic range of the Apennines. Not improbably, Eratosthenes once formed the volcanic vent for the stupendous forces that elevated the comparatively craterless peaks of these great mountains.
10. Copernicus.—Of all the lunar craters this is one of the grandest and best known. The region to the west is dotted over with innumerable minute craterlets. It has a central many-peaked mountain about 2,400 feet in height. There is good reason to believe that the terracing shown in its interior is mainly due to the repeated alternate rise, partial congelation, and subsequent retreat of a vast sea of lava. At full moon the crater of Copernicus is seen to be surrounded by radiating streaks.
11. Kepler.—Although the internal depth of this crater is scarcely less than 10,000 feet, it has but a very low surrounding wall, which is remarkable for being covered with the same glistening substance that also forms a system of bright rays not unlike those surrounding the last object.
12. Aristarchus is the most brilliant of the lunar craters, being specially vivid with a low power in a large telescope. So bright is it, indeed, that it has often been seen on the dark side just after new moon, and has thus given rise to marvellous stories of active lunar volcanoes. To the south-east lies another smaller crater, Herodotus, north of which is a narrow, deep valley, nowhere more than 2-1⁄2 miles broad, which makes a remarkable zigzag. It is one of the largest of the lunar "clefts."
13. Grimaldi calls for notice as the darkest object of its size in the moon. Under very exceptional circumstances it has been seen with the naked eye, and as its area has been estimated at nearly 14,000 square miles, it gives an idea of how little unaided vision can discern in the moon; it must, however, be added that we always see Grimaldi considerably foreshortened.
14. The great crater Gassendi has been very frequently mapped on account of its elaborate system of "clefts." At its northern end it communicates with a smaller but much deeper crater, that is often filled with black shadow after the whole floor of Gassendi has been illuminated.
15. Schickard is one of the largest walled plains on the moon, about 134 miles in breadth. Within its vast expanse Mädler detected 23 minor craters. With regard to this object Chacornac pointed out that, owing to the curvature of the surface of the moon, a spectator at the centre of the floor "would think himself in a boundless desert," because the surrounding wall, although in one place nearly 10,000 feet high, would lie entirely beneath his horizon.
16. Close to the foregoing is Wargentin. There can be little doubt that this is really a huge crater almost filled with congealed lava, as there is scarcely any fall towards the interior.
17. Clavius.—Near the 60th parallel of lunar south latitude lies this enormous enclosure, the area of which is not less than 16,500 square miles. Both in its interior and on its walls are many peaks and secondary craters. The telescopic view of a sunrise upon the surface of Clavius is truly said by Mädler to be indescribably magnificent. One of the peaks rises to a height of 24,000 feet above the bottom of one of the included craters. Mädler even expressed the opinion that in this wild neighbourhood there are craters so profound that no ray of sunlight ever penetrated their lowest depths, while, as if in compensation, there are peaks whose summits enjoy a mean day almost twice as long as their night.
18. If the full moon be viewed through an opera-glass or any small hand-telescope, one crater is immediately seen to be conspicuous beyond all others, by reason of the brilliant rays or streaks that radiate from it. This is the majestic Tycho, 17,000 feet in depth and 50 miles in diameter (Plate X.). A peak 6,000 feet in height rises in the centre of its floor, while a series of terraces diversity its interior slopes; but it is the mysterious bright rays that chiefly surprise us. When the sun rises on Tycho, these streaks are utterly invisible; indeed, the whole object is then so obscure that it requires a practised eye to recognise Tycho amidst its mountainous surroundings. But as soon as the sun has attained a height of about 30° above its horizon, the rays emerge from their obscurity and gradually increase in brightness until the moon becomes full, when they are the most conspicuous objects on her surface. They vary in length, from a few hundred miles to two or, in one instance, nearly three thousand miles. They extend indifferently across vast plains, into the deepest craters, or over the loftiest elevations. We know of nothing on our earth to which they can be compared. As these rays are only seen about the time of full moon, their visibility obviously depends on the light falling more or less closely in the line of sight, quite regardless of the inclination of the surfaces, mountains or valleys, on which they appear. Each small portion of the surface of the streak must therefore be of a form which is symmetrical to the spectator[Pg 92] from whatever point it is seen. The sphere alone appears to fulfil this condition, and Professor Copeland therefore suggests that the material constituting the surface of the streak must be made up of a large number of more or less completely spherical globules. The streaks must represent parts of the lunar surface either pitted with minute cavities of spherical figure, or strewn over with minute transparent spheres.[8]
Near the centre of the moon's disc is a fine range of ring plains fully open to our view under all illuminations. Of these, two may be mentioned—Alphonsus (19), the floor of which is strangely characterised by two bright and several dark markings which cannot be explained by irregularities in the surface.—Ptolemy (20). Besides several small enclosed craters, its floor is crossed by numerous low ridges, visible when the sun is rising or setting.
21, 22, 23.—When the moon is five or six days old this beautiful group of three craters will be favourably placed for observation. They are named Catharina, Cyrillus, and Theophilus. Catharina, the most southerly of the group, is more than 16,000 feet deep, and connected with Cyrillus by a wide valley; but between Cyrillus and Theophilus there is no such connection. Indeed, Cyrillus looks as if its huge surrounding ramparts, as high as Mont Blanc, had been completely finished before the volcanic forces commenced the formation of Theophilus, the rampart of which encroaches considerably on its older neighbour. Theophilus stands as a well-defined circular crater about 64 miles in diameter, with an internal depth of 14,000 to 18,000 feet, and a beautiful central group of mountains, one-third of that height, on its floor. Although Theophilus is the deepest crater we can see in the moon, it has suffered little or no deformation from secondary eruptions, while the floor and wall of Catharina show complete sequences of lesser craters of various sizes that have broken in upon and partly destroyed each other. In the spring of the year, when the moon is somewhat before the first quarter, this instructive group of extinct volcanoes can be seen to great advantage at a convenient hour in the evening.
24. Petavius is remarkable not only for its great size, but also for the rare feature of having a double rampart. It is a beautiful object soon after new moon, or just after full moon, but disappears absolutely when the sun is more than 45° above its horizon. The crater floor is remarkably convex, culminating in a central group of hills intersected by a deep cleft.
25. Hyginus is a small crater near the centre of the moon's disc. One of the largest of the lunar chasms passes right through it, making an abrupt turn as it does so.
26. Triesnecker.—This fine crater has been already described, but is again alluded to in order to draw attention to the elaborate system of chasms so conspicuously shown in Plate VII. That these chasms are depressions is abundantly evident by the shadows inside. Very often their margins are appreciably raised. They seem to be fractures in the moon's surface.
Of the various mountains that are occasionally seen as projections on the actual edge of the moon, those called after Leibnitz (i) seem to be the highest. Schmidt found the highest peak to be upwards of 41,900 feet above a neighbouring valley. In comparing these altitudes with those of mountains on our earth, we must for the latter add the depth of the sea to the height of the land. Reckoned in this way, our highest mountains are still higher than any we know of in the moon.
We must now discuss the important question as to the origin of these remarkable features on the surface of the moon. We shall admit at the outset that our evidence on this subject is only indirect. To establish by unimpeachable evidence the volcanic origin of the remarkable lunar craters, it would seem almost necessary that volcanic outbursts should have been witnessed on the moon, and that such outbursts should have been seen to result in the formation of the well-known ring, with or without the mountain rising from the[Pg 94] centre. To say that nothing of the kind has ever been witnessed would be rather too emphatic a statement. On certain occasions careful observers have reported the occurrence of minute local changes on the moon. As we have already remarked, a crater named Linné, of dimensions respectable, no doubt, to a lunar inhabitant, but forming a very inconsiderable telescopic object, was thought to have undergone some change. On another occasion a minute crater was thought to have arisen near the well-known object named Hyginus. The mere enumeration of such instances gives real emphasis to the statement that there is at the present time no appreciable source of disturbance of the moon's surface. Even were these trifling cases of suspected change really established—and this is perhaps rather farther than many astronomers would be willing to go—they are still insignificant when compared with the mighty phenomena that gave rise to the host of great craters which cover so large a portion of the moon's surface.
We are led inevitably to the conclusion that our satellite must have once possessed much greater activity than it now displays. We can also give a reasonable, or, at all events, a plausible, explanation of the cessation of that activity in recent times. Let us glance at two other bodies of our system, the earth and the sun, and compare them with the moon. Of the three bodies, the sun is enormously the largest, while the moon is much less than the earth. We have also seen that though the sun must have a very high temperature, there can be no doubt that it is gradually parting with its heat. The surface of the earth, formed as it is of solid rocks and clay, or covered in great part by the vast expanse of ocean, bears but few obvious traces of a high temperature. Nevertheless, it is highly probable from ordinary volcanic phenomena that the interior of the earth still possesses a temperature of incandescence.
A large body when heated takes a longer time to cool than does a small body raised to the same temperature. A large iron casting will take days to cool; a small casting will become cold in a few hours. Whatever may have been the[Pg 95] original source of heat in our system—a question which we are not now discussing—it seems demonstrable that the different bodies were all originally heated, and have now for ages been gradually cooling. The sun is so vast that he has not yet had time to cool; the earth, of intermediate bulk, has become cold on the outside, while still retaining vast stores of internal heat; while the moon, the smallest body of all, has lost its heat to such an extent that changes of importance on its surface can no longer be originated by internal fires.
We are thus led to refer the origin of the lunar craters to some ancient epoch in the moon's history. We have no moans of knowing the remoteness of that epoch, but it is reasonable to surmise that the antiquity of the lunar volcanoes must be extremely great. At the time when the moon was sufficiently heated to originate those convulsions, of which the mighty craters are the survivals, the earth must also have been much hotter than it is at present. When the moon possessed sufficient heat for its volcanoes to be active, the earth was probably so hot that life was impossible on its surface. This supposition would point to an antiquity for the lunar craters far too great to be estimated by the centuries and the thousands of years which are adequate for such periods as those with which the history of human events is concerned. It seems not unlikely that millions of years may have elapsed since the mighty craters of Plato or of Copernicus consolidated into their present form.
We shall now attempt to account for the formation of the lunar craters. The most probable views on the subject seem to be those which have been set forth by Mr. Nasmyth, though it must be admitted that his doctrines are by no means free from difficulty. According to his theory we can explain how the rampart around the lunar crater has been formed, and how the great mountain arose which so often adorns the centre of the plain. The view in Fig. 28 contains an imaginary sketch of a volcanic vent on the moon in the days when the craters were active. The eruption is[Pg 96] here shown in the fulness of its energy, when the internal forces are hurling forth ashes or stones which fall at a considerable distance from the vent. The materials thus accumulated constitute the rampart surrounding the crater.
The second picture (Fig. 29) depicts the crater in a later stage of its history. The prodigious explosive power has now been exhausted, and has perhaps been intermitted for some time. Again, the volcano bursts into activity, but this time with only a small part of its original energy. A comparatively feeble eruption now issues from the same vent, deposits materials close around the orifice, and raises a mountain in the centre. Finally, when the activity has subsided, and the volcano is silent and still, we find the evidence of the early energy testified to by the rampart which surrounds the ancient crater, and by the mountain which adorns the interior. The flat floor which is found in some of the craters may not improbably have arisen from an outflow of lava which has afterwards consolidated. Subsequent outbreaks have also occurred in many cases.
One of the principal difficulties attending this method of accounting for the structure of a crater arises from the great size which some of these objects attain. There are ancient volcanoes on the moon forty or fifty miles in diameter; indeed, there is one well-formed ring, with a mountain rising in the centre, the diameter of which is no less than seventy-eight miles (Petavius). It seems difficult to conceive how a blowing cone at the centre could convey the materials to such a distance as the thirty-nine miles between the centre of Petavius and the rampart. The explanation is, however, facilitated when it is borne in mind that the force of gravitation is much less on the moon than on the earth.
Have we not already seen that our satellite is so much smaller than the earth that eighty moons rolled into one would not weigh as much as the earth? On the earth an ounce weighs an ounce and a pound weighs a pound; but a weight of six ounces here would only weigh one ounce on the moon, and a weight of six pounds here would only weigh one pound on the moon. A labourer who can carry one sack of corn on the earth could, with the same exertion, carry six sacks of corn on the moon. A cricketer who can throw a ball 100 yards on the earth could with precisely the same exertion throw the same ball 600 yards on the moon. Hiawatha could shoot ten arrows into the air one[Pg 98] after the other before the first reached the ground; on the moon he might have emptied his whole quiver. The volcano, which on the moon drove projectiles to the distance of thirty-nine miles, need only possess the same explosive power as would have been sufficient to drive the missiles six or seven miles on the earth. A modern cannon properly elevated would easily achieve this feat.
It must also be borne in mind that there are innumerable craters on the moon of the same general type but of the most varied dimensions; from a tiny telescopic object two or three miles in diameter, we can point out gradually ascending stages until we reach the mighty Petavius just considered. With regard to the smaller craters, there is obviously little or no difficulty in attributing to them a volcanic origin, and as the continuity from the smallest to the largest craters is unbroken, it seems quite reasonable to suppose that even the greatest has arisen in the same way.
It should, however, be remarked that some lunar features might be explained by actions from without rather than from within. Mr. G.K. Gilbert has marshalled the evidence in support of the belief that lunar sculptures arise from the impact of bodies falling on the moon. The Mare Imbrium, according to this view, has been the seat of a collision to which the surrounding lunar scenery is due. Mr. Gilbert explains the furrows as hewn out by mighty projectiles moving with such velocities as meteors possess.
The lunar landscapes are excessively weird and rugged.[Pg 99] They always remind us of sterile deserts, and we cannot fail to notice the absence of grassy plains or green forests such as we are familiar with on our globe. In some respects the moon is not very differently circumstanced from the earth. Like it, the moon has the pleasing alternations of day and night, though the day in the moon is as long as twenty-nine of our days, and the night of the moon is as long as twenty-nine of our nights. We are warmed by the rays of the sun; so, too, is the moon; but, whatever may be the temperature during the long day on the moon, it seems certain that the cold of the lunar night would transcend that known in the bleakest regions of our earth. The amount of heat radiated to us by the moon has been investigated by Lord Rosse, and more recently by Professor Langley. Though every point on the moon's surface is exposed to the sunlight for a fortnight without any interruption, the actual temperature to which the soil is raised cannot be a high one. The moon does not, like the earth, possess a warm blanket, in the shape of an atmosphere, which can keep in and accumulate the heat received.
Even our largest telescopes can tell nothing directly as to whether life can exist on the moon. The mammoth trees of California might be growing on the lunar mountains, and elephants might be walking about on the plains, but our telescopes could not show them. The smallest object that we can see on the moon must be about as large as a good-sized cathedral, so that organised beings resembling in size any that we are familiar with, if they existed, could not make themselves visible as telescopic objects.
We are therefore compelled to resort to indirect evidence as to whether life would be possible on the moon. We may say at once that astronomers believe that life, as we know it, could not exist. Among the necessary conditions of life, water is one of the first. Take every form of vegetable life, from the lichen which grows on the rock to the giant tree of the forest, and we find the substance of every plant contains water, and could not exist without it. Nor is water less necessary to the existence of animal life. Deprived of this element, all organic life, the life of man himself, would be inconceivable.
Unless, therefore, water be present in the moon, we shall be bound to conclude that life, as we know it, is impossible. If anyone stationed on the moon were to look at the earth through a telescope, would he be able to see any water here? Most undoubtedly he would. He would see the clouds and he would notice their incessant changes, and the clouds alone would be almost conclusive evidence of the existence of water. An astronomer on the moon would also see our oceans as coloured surfaces, remarkably contrasted with the land, and he would perhaps frequently see an image of the sun, like a brilliant star, reflected from some smooth portion of the sea. In fact, considering that much more than half of our globe is covered with oceans, and that most of the remainder is liable to be obscured by clouds, the lunar astronomer in looking at our earth would often see hardly anything but water in one form or other. Very likely he would come to the conclusion that our globe was only fitted to be a residence for amphibious animals.
But when we look at the moon with our telescopes we see no direct evidence of water. Close inspection shows that the so-called lunar seas are deserts, often marked with small craters and rocks. The telescope reveals no seas and no oceans, no lakes and no rivers. Nor is the grandeur of the moon's scenery ever impaired by clouds over her surface. Whenever the moon is above our horizon, and terrestrial clouds are out of the way, we can see the features of our satellite's surface with distinctness. There are no clouds in the moon; there are not even the mists or the vapours which invariably arise wherever water is present, and therefore astronomers have been led to the conclusion that the surface of the globe which attends the earth is a sterile and a waterless desert.
Another essential element of organic life is also absent from the moon. Our globe is surrounded with a deep clothing of air resting on the surface, and extending above our heads to the height of about 200 or 300 miles. We need hardly say how necessary air is to life, and therefore we turn with interest to the question as to whether the moon can be surrounded with an atmosphere. Let us clearly understand the problem[Pg 101] we are about to consider. Imagine that a traveller started from the earth on a journey to the moon; as he proceeded, the air would gradually become more and more rarefied, until at length, when he was a few hundred miles above the earth's surface, he would have left the last perceptible traces of the earth's envelope behind him. By the time he had passed completely through the atmosphere he would have advanced only a very small fraction of the whole journey of 240,000 miles, and there would still remain a vast void to be traversed before the moon would be reached. If the moon were enveloped in the same way as the earth, then, as the traveller approached the end of his journey, and came within a few hundred miles of the moon's surface, he would meet again with traces of an atmosphere, which would gradually increase in density until he arrived at the moon's surface. The traveller would thus have passed through one stratum of air at the beginning of his journey, and through another at the end, while the main portion of the voyage would have been through space more void than that to be found in the exhausted receiver of an air-pump.
Such would be the case if the moon were coated with an atmosphere like that surrounding our earth. But what are the facts? The traveller as he drew near the moon would seek in vain for air to breathe at all resembling ours. It is possible that close to the surface there are faint traces of some gaseous material surrounding the moon, but it can only be equal to a very small fractional part of the ample clothing which the earth now enjoys. For all purposes of respiration, as we understand the term, we may say that there is no air on the moon, and an inhabitant of our earth transferred thereto would be as certainly suffocated as he would be in the middle of space.
It may, however, be asked how we learn this. Is not air transparent, and how, therefore, could our telescopes be expected to show whether the moon really possessed such an envelope? It is by indirect, but thoroughly reliable, methods of observation that we learn the destitute condition of our satellite. There are various arguments to be adduced; but the most[Pg 102] conclusive is that obtained on the occurrence of what is called an "occultation." It sometimes happens that the moon comes directly between the earth and a star, and the temporary extinction of the latter is an "occultation." We can observe the moment when the phenomenon takes place, and the suddenness of the disappearance of the star is generally remarked. If the moon were enveloped in a copious atmosphere, the interposition of this gaseous mass by the movement of the moon would produce a gradual evanescence of the star wholly wanting the abruptness which marks the obscuration.[9]
Let us consider how we can account for the absence of an atmosphere from the moon. What we call a gas has been found by modern research to be a collection of an immense number of molecules, each of which is in exceedingly rapid motion. This motion is only pursued for a short distance in one direction before a molecule comes into collision with some other molecule, whereby the directions and velocities of the individual molecules are continually changed. There is a certain average speed for each gas which is peculiar to the molecules of that gas at a certain temperature. When several gases are mixed, as oxygen and nitrogen are in our atmosphere, the molecules of each gas continue to move with their own characteristic velocities. So far as we can estimate the temperature at the boundary of the earth's atmosphere, we may assume that the average of the velocities of the oxygen molecules there found is about a quarter of a mile per second. The velocities for nitrogen are much the same, while the average speed of a molecule of hydrogen is about one mile per second, being, in fact, by far the greatest molecular velocity possessed by any gas.
A stone thrown into the air soon regains the earth. A rifle bullet fired vertically upwards will ascend higher and higher, until at length its motion ceases, it begins to return, and falls to the ground. Let us for the moment suppose that we had a rifle of infinite strength and gunpowder of unlimited power. As we increase the charge we find that the bullet will ascend higher and higher, and each time it will take a longer period before it returns to the ground. The descent of the bullet is due to the attraction of the earth. Gravitation must necessarily act on the projectile throughout its career, and it gradually lessens the velocity, overcomes the upward motion, and brings the bullet back. It must be remembered that the efficiency of the attraction decreases when the height is increased. Consequently when the body has a prodigiously great initial velocity, in consequence of which it ascends to an enormous height, its return is retarded by a twofold cause. In the first place, the distance through which it has to be recalled is greatly increased, and in the second place the efficiency of gravitation in effecting its recall has decreased. The greater the velocity, the feebler must be the capacity of gravitation for bringing back the body. We can conceive the speed to be increased to that point at which the gravitation, constantly declining as the body ascends, is never quite able to neutralise the velocity, and hence we have the remarkable case of a body projected away never to return.
It is possible to exhibit this reasoning in a numerical form, and to show that a velocity of six or seven miles a second directed upwards would suffice to convey a body entirely away from the gravitation of the earth. This speed is far beyond the utmost limits of our artillery. It is, indeed, at least a dozen times as swift as a cannon shot; and even if we could produce it, the resistance of the air would present an insuperable difficulty. Such reflections, however, do not affect the conclusion that there is for each planet a certain specific velocity appropriate to that body, and depending solely upon its size and mass, with which we should have to discharge a projectile, in order to prevent the attraction of that body from pulling the projectile back again.
It is a simple matter of calculation to determine this "critical velocity" for any celestial body. The greater the body the greater in general must be the initial speed which will enable the projectile to forsake for ever the globe from[Pg 104] which it has been discharged. As we have already indicated, this speed is about seven miles per second on the earth. It would be three on the planet Mercury, three and a half on Mars, twenty-two on Saturn, and thirty-seven on Jupiter; while for a missile to depart from the sun without prospect of return, it must leave the brilliant surface at a speed not less than 391 miles per second.
Supposing that a quantity of free hydrogen was present in our atmosphere, its molecules would move with an average velocity of about one mile per second. It would occasionally happen by a combination of circumstances that a molecule would attain a speed which exceeded seven miles a second. If this happened on the confines of the atmosphere where it escaped collision with other molecules, the latter object would fly off into space, and would not be recaptured by the earth. By incessant repetitions of this process, in the course of countless ages, all the molecules of hydrogen gas would escape from the earth, and in this manner we may explain the fact that there is no free hydrogen present in the earth's atmosphere.[10]
The velocities which can be attained by the molecules of gases other than hydrogen are far too small to permit of their escape from the attraction of the earth. We therefore find oxygen, nitrogen, water vapour, and carbon dioxide remaining as permanent components of our air. On the other hand, the enormous mass of the sun makes the "critical velocity" at the surface of that body to be so great (391 miles per second) that not even the molecules of hydrogen can possibly emulate it. Consequently, as we have seen, hydrogen is a most important component of the sun's atmospheric envelope.
If we now apply this reasoning to the moon, the critical velocity is found by calculation to be only a mile and a half per second. This seems to be well within the maximum velocities attainable by the molecules of oxygen, nitrogen, and other gases. It therefore follows that none of these gases[Pg 105] could remain permanently to form an atmosphere at the surface of so small a body as the moon. This seems to be the reason why there are no present traces of any distinct gaseous surroundings to our satellite.
The absence of air and of water from the moon explains the sublime ruggedness of the lunar scenery. We know that on the earth the action of wind and of rain, of frost and of snow, is constantly tending to wear down our mountains and reduce their asperities. No such agents are at work on the moon. Volcanoes sculptured the surface into its present condition, and, though they have ceased to operate for ages, the traces of their handiwork seem nearly as fresh to-day as they were when the mighty fires were extinguished.
"The cloud-capped towers, the gorgeous palaces, the solemn temples" have but a brief career on earth. It is chiefly the incessant action of water and of air that makes them vanish like the "baseless fabric of a vision." On the moon these causes of disintegration and of decay are all absent, though perhaps the changes of temperature in the transition from lunar day to lunar night would be attended with expansions and contractions that might compensate in some slight degree for the absence of more potent agents of dissolution.
It seems probable that a building on the moon would remain for century after century just as it was left by the builders. There need be no glass in the windows, for there is no wind and no rain to keep out. There need not be fireplaces in the rooms, for fuel cannot burn without air. Dwellers in a lunar city would find that no dust could rise, no odours be perceived, no sounds be heard.
Man is a creature adapted for life under circumstances which are very narrowly limited. A few degrees of temperature more or less, a slight variation in the composition of air, the precise suitability of food, make all the difference between health and sickness, between life and death. Looking beyond the moon, into the length and breadth of the universe, we find countless celestial globes with every conceivable variety of temperature and of constitution. Amid this vast number of worlds with which space is tenanted, are there any inhabited by living[Pg 106] beings? To this great question science can make no response: we cannot tell. Yet it is impossible to resist a conjecture. We find our earth teeming with life in every part. We find life under the most varied conditions that can be conceived. It is met with under the burning heat of the tropics and in the everlasting frost at the poles. We find life in caves where not a ray of light ever penetrates. Nor is it wanting in the depths of the ocean, at the pressure of tons on the square inch. Whatever may be the external circumstances, Nature generally provides some form of life to which those circumstances are congenial.
It is not at all probable that among the million spheres of the universe there is a single one exactly like our earth—like it in the possession of air and of water, like it in size and in composition. It does not seem probable that a man could live for one hour on any body in the universe except the earth, or that an oak-tree could live in any other sphere for a single season. Men can dwell on the earth, and oak-trees can thrive therein, because the constitutions of the man and of the oak are specially adapted to the particular circumstances of the earth.
Could we obtain a closer view of some of the celestial bodies, we should probably find that they, too, teem with life, but with life specially adapted to the environment—life in forms strange and weird; life far stranger to us than Columbus found it to be in the New World when he first landed there. Life, it may be, stranger than ever Dante described or Doré sketched. Intelligence may also have a home among those spheres no less than on the earth. There are globes greater and globes less—atmospheres greater and atmospheres less. The truest philosophy on this subject is crystallised in the language of Tennyson:—
"This truth within thy mind rehearse,
That in a boundless universe
Is boundless better, boundless worse.
"Think you this mould of hopes and fears
Could find no statelier than his peers
In yonder hundred million spheres?"
Exceptional Importance of the Sun and Moon—The Course to be pursued—The Order of Distance—The Neighbouring Orbs—How are they to be discriminated?—The Planets Venus and Jupiter attract Notice by their Brilliancy—Sirius not a Neighbour—The Planets Saturn and Mercury—Telescopic Planets—The Criterion as to whether a Body is to be ranked as a Neighbour—Meaning of the word Planet—Uranus and Neptune—Comets—The Planets are illuminated by the Sun—The Stars are not—The Earth is really a Planet—The Four Inner Planets, Mercury, Venus, the Earth, and Mars—Velocity of the Earth—The Outer Planets, Jupiter, Saturn, Uranus, Neptune—Light and Heat received by the Planets from the Sun—Comparative Sizes of the Planets—The Minor Planets—The Planets all revolve in the same Direction—The Solar System—An Island Group in Space.
In the two preceding chapters of this work we have endeavoured to describe the heavenly bodies in the order of their relative importance to mankind. Could we doubt for a moment as to which of the many orbs in the universe should be the first to receive our attention? We do not now allude to the intrinsic significance of the sun when compared with other bodies or groups of bodies scattered through space. It may be that numerous globes rival the sun in real splendour, in bulk, and in mass. We shall, in fact, show later on in this volume that this is the case; and we shall then be in a position to indicate the true rank of the sun amid the countless hosts of heaven. But whatever may be the importance of the sun, viewed merely as one of the bodies which teem through space, there can be no hesitation in asserting how immeasurably his influence on the earth surpasses that of all other bodies in the universe together. It was therefore natural—indeed inevitable—that our first examination of the orbs of heaven should be directed to that mighty body which is the source of our life itself.
Nor could there be much hesitation as to the second step[Pg 108] which ought to be taken. The intrinsic importance of the moon, when compared with other celestial bodies, may be small; it is, indeed, as we shall afterwards see, almost infinitesimal. But in the economy of our earth the moon has played, and still plays, a part second only in importance to that of the sun himself. The moon is so close to us that her brilliant rays pale to invisibility countless orbs of a size and an intrinsic splendour incomparably greater than her own. The moon also occupies an exceptional position in the history of astronomy; for the law of gravitation, the greatest discovery that science has yet witnessed, was chiefly accomplished by observations of the moon. It was therefore natural that an early chapter in our Story of the Heavens should be devoted to a body the interest of which approximated so closely to that of the sun himself.
But the sun and the moon having been partly described (we shall afterwards have to refer to them again), some hesitation is natural in the choice of the next step. The two great luminaries being abstracted from our view, there remains no other celestial body of such exceptional interest and significance as to make it quite clear what course to pursue; we desire to unfold the story of the heavens in the most natural manner. If we made the attempt to describe the celestial bodies in the order of their actual magnitude, our ignorance must at once pronounce the task to be impossible. We cannot even make a conjecture as to which body in the heavens is to stand first on the list. Even if that mightiest body be within reach of our telescopes (in itself a highly improbable supposition), we have not the least idea in what part of the heavens it is to be sought. And even if this were possible—if we were able to arrange all the visible bodies rank by rank in the order of their magnitude and their splendour—still the scheme would be impracticable, for of most of them we know little or nothing.
We are therefore compelled to adopt a different method of procedure, and the simplest, as well as the most natural, will be to follow as far as possible the order of distance of the different bodies. We have already spoken of the moon as[Pg 109] the nearest neighbour to the earth; we shall next consider some of the other celestial bodies which are comparatively near to us; then, as the subject unfolds, we shall discuss the objects further and further away, until towards the close of the volume we shall be engaged in considering the most distant bodies in the universe which the telescope has yet revealed to us.
Even when we have decided on this principle, our course is still not free from ambiguity. Many of the bodies in the heavens are in motion, so that their relative distances from the earth are in continual change; this is, however, a difficulty which need not detain us. We shall make no attempt to adhere closely to the principle in all details. It will be sufficient if we first describe those great bodies—not a very numerous class—which are, comparatively speaking, in our vicinity, though still at varied distances; and then we shall pass on to the uncounted bodies which are separated from us by distances so vast that the imagination is baffled in the attempt to realise them.
Let us, then, scan the heavens to discover those orbs which lie in our neighbourhood. The sun has set, the moon has not risen; a cloudless sky discloses a heaven glittering with countless gems of light. Some are grouped together into well-marked constellations; others seem scattered promiscuously, with every degree of lustre, from the very brightest down to the faintest point that the eye can just glimpse. Amid all this host of objects, how are we to identify those which lie nearest to the earth? Look to the west: and there, over the spot where the departing sunbeams still linger, we often see the lovely evening star shining forth. This is the planet Venus—a beauteous orb, twin-sister to the earth. The brilliancy of this planet, its rapid changes both in position and in lustre, would suggest at once that it was much nearer to the earth than other star-like objects. This presumption has been amply confirmed by careful measurements, and therefore Venus is to be included in the list of the orbs which constitute our neighbours.
Another conspicuous planet—almost rivalling Venus in lustre, and vastly surpassing Venus in the magnificence of its proportions and its retinue—has borne from antiquity the majestic name of Jupiter. No doubt Jupiter is much more distant from us than Venus. Indeed, he is always at least twice as far, and sometimes as much as ten times. But still we must include Jupiter among our neighbours. Compared with the host of stars which glitter on the heavens, Jupiter must be regarded as quite contiguous. The distance of the great planet requires, it is true, hundreds of millions of miles for its expression; yet, vast as is that distance, it would have to be multiplied by tens of thousands, or hundreds of thousands, before it would be long enough to span the abyss which intervenes between the earth and the nearest of the stars.
Venus and Jupiter have invited our attention by their exceptional brilliancy. We should, however, fall into error if we assumed generally that the brightest objects were those nearest to the earth. An observer unacquainted with astronomy might not improbably point to the Dog Star—or Sirius, as astronomers more generally know it—as an object whose exceptional lustre showed it to be one of our neighbours. This, however, would be a mistake. We shall afterwards have occasion to refer more particularly to this gem of our southern skies, and then it will appear that Sirius is a mighty globe far transcending our own sun in size as well as in splendour, but plunged into the depths of space to such an appalling distance that his enfeebled rays, when they reach the earth, give us the impression, not of a mighty sun, but only of a brilliant star.
The principle of selection, by which the earth's neighbours can be discriminated, will be explained presently; in the meantime, it will be sufficient to observe that our list is to be augmented first by the addition of the unique object known as Saturn, though its brightness is far surpassed by that of Sirius, as well as by a few other stars. Then we add Mars, an object which occasionally approaches so close to the earth that it shines with a fiery radiance which would[Pg 111] hardly prepare us for the truth that this planet is intrinsically one of the smallest of the celestial bodies. Besides the objects we have mentioned, the ancient astronomers had detected a fifth, known as Mercury—a planet which is usually invisible amid the light surrounding the sun. Mercury, however, occasionally wanders far enough from our luminary to be seen before sunrise or after sunset. These five—Mercury, Venus, Mars, Jupiter, and Saturn—comprised the planets known from remote antiquity.
We can, however, now extend the list somewhat further by adding to it the telescopic objects which have in modern times been found to be among our neighbours. Here we must no longer postpone the introduction of the criterion by which we can detect whether a body is near the earth or not. The brighter planets can be recognised by the steady radiance of their light as contrasted with the incessant twinkling of the stars. A little attention devoted to any of the bodies we have named will, however, point out a more definite contrast between the planets and the stars.
Observe, for instance, Jupiter, on any clear night when the heavens can be well seen, and note his position with regard to the constellations in his neighbourhood—how he is to the right of this star, or to the left of that; directly between this pair, or directly pointed to by that. We then mark down the place of Jupiter on a celestial map, or we make a sketch of the stars in the neighbourhood showing the position of the planet. After a month or two, when the observations are repeated, the place of Jupiter is to be compared again with those stars by which it was defined. It will be found that, while the stars have preserved their relative positions, the place of Jupiter has changed. Hence this body is with propriety called a planet, or a wanderer, because it is incessantly moving from one part of the starry heavens to another. By similar comparisons it can be shown that the other bodies we have mentioned—Venus and Mercury, Saturn and Mars—are also wanderers, and belong to that group of heavenly bodies known as planets. Here, then, we have the simple criterion by which the earth's neighbours are readily to be[Pg 112] discriminated from the stars. Each of the bodies near the earth is a planet, or a wanderer, and the mere fact that a body is a wanderer is alone sufficient to prove it to be one of the class which we are now studying.
Provided with this test, we can at once make an addition to our list of neighbours. Amid the myriad orbs which the telescope reveals, we occasionally find one which is a wanderer. Two other mighty planets, known as Uranus and Neptune, must thus be added to the five already mentioned, making in all a group of seven great planets. A vastly greater number may also be reckoned when we admit to our view bodies which not only seem to be minute telescopic objects, but really are small globes when compared with the mighty bulk of our earth. These lesser planets, to the number of more than four hundred, are also among the earth's neighbours.
We should remark that another class of heavenly bodies widely differing from the planets must also be included in our system. These are the comets, and, indeed, it may happen that one of these erratic bodies will sometimes draw nearer to the earth than even the closest approach ever made by a planet. These mysterious visitors will necessarily engage a good deal of our attention later on. For the present we confine our attention to those more substantial globes, whether large or small, which are always termed planets.
Imagine for a moment that some opaque covering could be clasped around our sun so that all his beams were extinguished. That our earth would be plunged into the darkness of midnight is of course an obvious consequence. A moment's consideration will show that the moon, shining as it does by the reflected rays of the sun, would become totally invisible. But would this extinction of the sunlight have any other effect? Would it influence the countless brilliant points that stud the heavens at midnight? Such an obscuration of the sun would indeed produce a remarkable effect on the sky at night, which a little attention would disclose. The stars, no doubt, would not exhibit the slightest change in brilliancy. Each star shines by its own light and is not indebted to the sun. The constellations would thus twinkle on as before,[Pg 113] but a wonderful change would come over the planets. Were the sun to be obscured, the planets would also disappear from view. The midnight sky would thus experience the effacement of the planets one by one, while the stars would remain unaltered. It may seem difficult to realise how the brilliancy of Venus or the lustre of Jupiter have their origin solely in the beams which fall upon these bodies from the distant sun. The evidence is, however, conclusive on the question; and it will be placed before the reader more fully when we come to discuss the several planets in detail.
Suppose that we are looking at Jupiter high in mid-heavens on a winter's night, it might be contended that, as the earth lies between Jupiter and the sun, it must be impossible for the rays of the sun to fall upon the planet. This is, perhaps, not an unnatural view for an inhabitant of this earth to adopt until he has become acquainted with the relative sizes of the various bodies concerned, and with the distances by which those bodies are separated. But the question would appear in a widely different form to an inhabitant of the planet Jupiter. If such a being were asked whether he suffered much inconvenience by the intrusion of the earth between himself and the sun, his answer would be something of this kind:—"No doubt such an event as the passage of the earth between me and the sun is possible, and has occurred on rare occasions separated by long intervals; but so far from the transit being the cause of any inconvenience, the whole earth, of which you think so much, is really so minute, that when it did come in front of the sun it was merely seen as a small telescopic point, and the amount of sunlight which it intercepted was quite inappreciable."
The fact that the planets shine by the sun's light points at once to the similarity between them and our earth. We are thus led to regard our sun as a central fervid globe associated with a number of much smaller bodies, each of which, being dark itself, is indebted to the sun both for light and for heat.
That was, indeed, a grand step in astronomy which demonstrated the nature of the solar system. The discovery that our[Pg 114] earth must be a globe isolated in space was in itself a mighty exertion of human intellect; but when it came to be recognised that this globe was but one of a whole group of similar objects, some smaller, no doubt, but others very much larger, and when it was further ascertained that these bodies were subordinated to the supreme control of the sun, we have a chain of discoveries that wrought a fundamental transformation in human knowledge.
We thus see that the sun presides over a numerous family. The members of that family are dependent upon the sun, and their dimensions are suitably proportioned to their subordinate position. Even Jupiter, the largest member of that family, does not contain one-thousandth part of the material which forms the vast bulk of the sun. Yet the bulk of Jupiter alone would exceed that of the rest of the planets were they all rolled together.
Around the central luminary in Fig. 31 we have drawn four circles in dotted lines which sufficiently illustrate the orbits in which the different bodies move. The innermost of these four paths represents the orbit of the planet Mercury. The planet moves around the sun in this path, and regains the place from which it started in eighty-eight days.
The next orbit, proceeding outwards from the sun, is that of the planet Venus, which we have already referred to as the well-known Evening Star. Venus completes the circuit of its path in 225 days. One step further from the sun and we come to the orbit of another planet. This body is almost the same size as Venus, and is therefore much larger than Mercury. The planet now under consideration accomplishes each revolution in 365 days. This period sounds familiar to our ears. It is the length of the year; and the planet is the earth on which we stand. There is an impressive way in which to realise the length of the road along which the earth has to travel in each annual journey. The circumference of a circle is about three and one-seventh times the diameter of the same figure; so that taking the distance from the earth to the centre of the sun as 92,900,000 miles, the diameter of the circle which the earth describes around the sun will be 185,800,000 miles, and consequently[Pg 115] the circumference of the mighty circle in which the earth moves round the sun is fully 583,000,000 miles. The earth has to travel this distance every year. It is merely a sum in division to find how far we have to move each second in order to accomplish this long journey in a twelvemonth. It will appear that the earth must actually complete eighteen miles every second, as otherwise it would not finish its journey within the allotted time.
Pause for a moment to think what a velocity of eighteen miles a second really implies. Can we realise a speed so tremendous? Let us compare it with our ordinary types of rapid movement. Look at that express train how it crashes under the bridge, how, in another moment, it is lost to view! Can any velocity be greater than that? Let us try it by figures. The train moves a mile a minute; multiply that velocity by eighteen and it becomes eighteen miles a[Pg 116] minute, but we must further multiply it by sixty to make it eighteen miles a second. The velocity of the express train is not even the thousandth part of the velocity of the earth. Let us take another illustration. We stand at the rifle ranges to see a rifle fired at a target 1,000 feet away, and we find that a second or two is sufficient to carry the bullet over that distance. The earth moves nearly one hundred times as fast as the rifle bullet.
Viewed in another way, the stupendous speed of the earth does not seem immoderate. The earth is a mighty globe, so great indeed that even when moving at this speed it takes almost eight minutes to pass over its own diameter. If a steamer required eight minutes to traverse a distance equal to its own length, its pace would be less than a mile an hour. To illustrate this method of considering the subject, we show here a view of the progress made by the earth (Fig. 32). The distance between the centres of these circles is about six times the diameter; and, accordingly, if they be taken to represent the earth, the time required to pass from one position to the other is about forty-eight minutes.
Outside the path of the earth, we come to the orbit of the fourth planet, Mars, which requires 687 days, or nearly two years, to complete its circuit round the sun. With our arrival at Mars we have gained the limit to the inner portion of the solar system.
The four planets we have mentioned form a group in themselves, distinguished by their comparative nearness to the sun. They are all bodies of moderate dimensions. Venus and the Earth are globes of about the same size. Mercury and Mars are both smaller objects which lie, so far as bulk is concerned, between the earth and the moon. The four planets which come nearest to the sun are vastly surpassed in bulk and weight by the giant bodies of our system—the[Pg 117] stately group of Jupiter and Saturn, Uranus and Neptune.
These giant planets enjoy the sun's guidance equally with their weaker brethren. In the diagram on this page (Fig. 33) parts of the orbits of the great outer planets are represented. The sun, as before, presides at the centre, but the inner planets would on this scale be so close to the sun that it is only possible to represent the orbit of Mars. After the orbit of Mars comes a considerable interval, not, however, devoid of planetary activity, and then follow the orbits of Jupiter and Saturn; further still, we have Uranus, a great globe on the verge of unassisted vision; and, lastly, the whole system is bounded by the grand orbit of Neptune—a planet of which we shall have a marvellous story to narrate.
The various circles in Fig. 34 show the apparent sizes of the sun as seen from the different planets. Taking the circle corresponding to the earth to represent the amount[Pg 118] of heat and light which the earth derives from the sun then the other circles indicate the heat and the light enjoyed by the corresponding planets. The next outer planet to the earth is Mars, whose share of solar blessings is not so very inferior to that of the earth; but we fail to see how bodies so remote as Jupiter or Saturn can enjoy climates at all comparable with those of the planets which are more favourably situated.
Fig. 35 shows a picture of the whole family of planets[Pg 119] surrounding the sun—represented on the same scale, so as to exhibit their comparative sizes. Measured by bulk, Jupiter is more than 1,200 times as great as the earth, so that it would take at least 1,200 earths rolled into one to form a globe equal to the globe of Jupiter. Measured by weight, the disparity between the earth and Jupiter, though still enormous, is not quite so great; but this is a matter to be discussed more fully in a later chapter.
Even in this preliminary survey of the solar system we[Pg 120] must not omit to refer to the planets which attract our attention, not by their bulk, but by their multitude. In the ample zone bounded on the inside by the orbit of Mars and on the outside by the orbit of Jupiter it was thought at one time that no planet revolved. Modern research has shown that this region is tenanted, not by one planet, but by hundreds. The discovery of these planets is a charge which has been undertaken by various diligent astronomers of the present day, while the discussion of their movements affords labour to other men of science. We shall find something to learn from the study of these tiny bodies, and especially from another small planet called Eros, which lies nearer to the earth than the limit above indicated. A chapter will be devoted to these objects.
But we do not propose to enter deeply into the mere statistics of the planetary system at present. Were such our intention, the tables at the end of the volume would show that ample materials are available. Astronomers have taken an inventory of each of the planets. They have measured their distances, the shapes of their orbits and the positions of those orbits, their times of revolution, and, in the case of all the larger planets, their sizes and their weights. Such results are of interest for many purposes. It is, however, the more general features of the science which at present claim our attention.
Let us, in conclusion, note one or two important truths with reference to our planetary system. We have seen that all the planets revolve in nearly circular paths around the sun. We have now to add another fact possessing much significance. Each of the planets pursues its path in the same direction. It thus happens that one such body may overtake another, but it can never happen that two planets pass by each other as do the trains on adjacent lines of railway. We shall subsequently find that the whole welfare of our system, nay, its continuous existence, is dependent upon this remarkable uniformity taken in conjunction with other features of the system.
Such is our solar system; a mighty organised group of[Pg 121] planets circulating under the control of the sun, and completely isolated from all external interference. No star, no constellation, has any appreciable influence on our solar system. We constitute a little island group, separated from the nearest stars by the most amazing distances. It may be that as the other stars are suns, so they too may have systems of planets circulating around them; but of this we know nothing. Of the stars we can only say that they appear to us as points of light, and any planets they may possess must for ever remain invisible to us, even if they were many times larger than Jupiter.
We need not repine at this limitation to our possible knowledge, for just as we find in the solar system all that is necessary for our daily bodily wants, so shall we find ample occupation for whatever faculties we may possess in endeavouring to understand those mysteries of the heavens which lie within our reach.
Gravitation—The Falling of a Stone to the Ground—All Bodies fall equally, Sixteen Feet in a Second—Is this true at Great Heights?—Fall of a Body at a Height of a Quarter of a Million Miles—How Newton obtained an Answer from the Moon—His Great Discovery—Statement of the Law of Gravitation—Illustrations of the Law—How is it that all the Bodies in the Universe do not rush Together?—The Effect of Motion—How a Circular Path can be produced by Attraction—General Account of the Moon's Motion—Is Gravitation a Force of Great Intensity?—Two Weights of 50 lbs.—Two Iron Globes, 53 Yards in Diameter, and a Mile apart, attract with a Force of 1 lb.—Characteristics of Gravitation—Orbits of the Planets not strictly Circles—The Discoveries of Kepler—Construction of an Ellipse—Kepler's First Law—Does a Planet move Uniformly?—Law of the Changes of Velocity—Kepler's Second Law—The Relation between the Distances and the Periodic Times—Kepler's Third Law—Kepler's Laws and the Law of Gravitation—Movement in a Straight Line—A Body unacted on by Disturbing Forces would move in a Straight Line with Constant Velocity—Application to the Earth and the Planets—The Law of Gravitation deduced from Kepler's Laws—Universal Gravitation.
Our description of the heavenly bodies must undergo a slight interruption, while we illustrate with appropriate detail an important principle, known as the law of gravitation, which underlies the whole of astronomy. By this law we can explain the movements of the moon around the earth, and of the planets around the sun. It is accordingly incumbent upon us to discuss this subject before we proceed to the more particular account of the separate planets. We shall find, too, that the law of gravitation sheds some much-needed light on the nature of the stars situated at the remotest distances in space. It also enables us to cast a glance through the vistas of time past, and to trace with plausibility, if not with certainty, certain early phases in the history of our system. The sun and the moon, the planets and the comets, the stars and the nebulæ, all alike are subject to this universal law, which is now to engage our attention.
What is more familiar than the fact that when a stone is dropped it will fall to the ground? No one at first thinks the matter even worthy of remark. People are often surprised at seeing a piece of iron drawn to a magnet. Yet the fall of a stone to the ground is the manifestation of a force quite as interesting as the force of magnetism. It is the earth which draws the stone, just as the magnet draws the iron. In each case the force is one of attraction; but while the magnetic attraction is confined to a few substances, and is of comparatively limited importance, the attraction of gravitation is significant throughout the universe.
Let us commence with a few very simple experiments upon the force of gravitation. Hold in the hand a small piece of lead, and then allow it to drop upon a cushion. The lead requires a certain time to move from the fingers to the cushion, but that time is always the same when the height is the same. Take now a larger piece of lead, and hold one piece in each hand at the same height. If both are released at the same moment, they will both reach the cushion simultaneously. It might have been thought that the heavy body would fall more quickly than the light body; but when the experiment is tried, it is seen that this is not the case. Repeat the experiment with various other substances. An ordinary marble will be found to fall in the same time as the piece of lead. With a piece of cork we again try the experiment, and again obtain the same result. At first it seems to fail when we compare a feather with the piece of lead; but that is solely on account of the air, which resists the feather more than it resists the lead. If, however, the feather be placed upon the top of a penny, and the penny be horizontal when dropped, it will clear the air out of the way of the feather in its descent, and then the feather will fall as quickly as the penny, as quickly as the marble, or as quickly as the lead.
If the observer were in a gallery when trying these experiments, and if the cushion were sixteen feet below his hands, then the time the marble would take to fall through the sixteen feet would be one second. The time occupied by the cork or by the lead would be the same; and even the feather[Pg 124] itself would fall through sixteen feet in one second, if it could be screened from the interference of the air. Try this experiment where we like, in London, or in any other city, in any island or continent, on board a ship at sea, at the North Pole, or the South Pole, or the equator, it will always be found that any body, of any size or any material, will fall about sixteen feet in one second of time.
Lest any erroneous impression should arise, we may just mention that the distance traversed in one second does vary slightly at different parts of the earth, but from causes which need not at this moment detain us. We shall for the present regard sixteen feet as the distance through which any body, free from interference, would fall in one second at any part of the earth's surface. But now let us extend our view above the earth's surface, and enquire how far this law of sixteen feet in a second may find obedience elsewhere. Let us, for instance, ascend to the top of a mountain and try the experiment there. It would be found that at the top of the mountain a marble would take a little longer to fall through sixteen feet than the same marble would if let fall at its base. The difference would be very small; but yet it would be measurable, and would suffice to show that the power of the earth to pull the marble to the ground becomes somewhat weakened at a point high above the earth's surface. Whatever be the elevation to which we ascend, be it either the top of a high mountain, or the still greater altitudes that have been reached in balloon ascents, we shall never find that the tendency of bodies to fall to the ground ceases, though no doubt the higher we go the more is that tendency weakened. It would be of great interest to find how far this power of the earth to draw bodies towards it can really extend. We cannot attain more than about five or six miles above the earth's surface in a balloon; yet we want to know what would happen if we could ascend 500 miles, or 5,000 miles, or still further, into the regions of space.
Conceive that a traveller were endowed with some means of soaring aloft for miles and thousands of miles, still up[Pg 125] and up, until at length he had attained the awful height of nearly a quarter of a million of miles above the ground. Glancing down at the surface of that earth, which is at such a stupendous depth beneath, he would be able to see a wonderful bird's-eye view. He would lose, no doubt, the details of towns and villages; the features in such a landscape would be whole continents and whole oceans, in so far as the openings between the clouds would permit the earth's surface to be exposed.
At this stupendous elevation he could try one of the most interesting experiments that was ever in the power of a philosopher. He could test whether the earth's attraction was felt at such a height, and he could measure the amount of that attraction. Take for the experiment a cork, a marble, or any other object, large or small; hold it between the fingers, and let it go. Everyone knows what would happen in such a case down here; but it required Sir Isaac Newton to tell what would happen in such a case up there. Newton asserts that the power of the earth to attract bodies extends even to this great height, and that the marble would fall. This is the doctrine that we can now test. We are ready for the experiment. The marble is released, and, lo! our first exclamation is one of wonder. Instead of dropping instantly, the little object appears to remain suspended. We are on the point of exclaiming that we must have gone beyond the earth's attraction, and that Newton is wrong, when our attention is arrested; the marble is beginning to move, so slowly that at first we have to watch it carefully. But the pace gradually improves, so that the attraction is beyond all doubt, until, gradually acquiring more and more velocity, the marble speeds on its long journey of a quarter of a million of miles to the earth.
But surely, it will be said, such an experiment must be entirely impossible; and no doubt it cannot be performed in the way described. The bold idea occurred to Newton of making use of the moon itself, which is almost a quarter of a million of miles above the earth, for the purpose of answering the question. Never was our satellite put to such[Pg 126] noble use before. It is actually at each moment falling in towards the earth. We can calculate how much it is deflected towards the earth in each second, and thus obtain a measure of the earth's attractive power. From such enquiries Newton was able to learn that a body released at the distance of 240,000 miles above the surface of the earth would still be attracted by the earth, that in virtue of the attraction the body would commence to move off towards the earth—not, indeed, with the velocity with which a body falls in experiments on the surface, but with a very much lesser speed. A body dropped down from the distance of the moon would commence its long journey so slowly that a minute, instead of a second, would have elapsed before the distance of sixteen feet had been accomplished.[11]
It was by pondering on information thus won from the moon that Newton made his immortal discovery. The gravitation of the earth is a force which extends far and wide through space. The more distant the body, the weaker the gravitation becomes; here Newton found the means of determining the great problem as to the law according to which the intensity of the gravitation decreased. The information derived from the moon, that a body 240,000 miles away requires a minute to fall through a space equal to that through which it would fall in a second down here, was of paramount importance. In the first place, it shows that the attractive power of the earth, by which it draws all bodies earthwards, becomes weaker at a distance. This might, indeed, have been anticipated. It is as reasonable to suppose that as we retreated further and further into the depths of space the power of attraction should diminish, as that the lustre of light should diminish as we recede from it; and it is remarkable that the law according to which the attraction of gravitation decreases with the increase of distance is[Pg 127] precisely the same as the law according to which the brilliancy of a light decreases as its distance increases.
The law of nature, stated in its simplest form, asserts that the intensity of gravitation varies inversely as the square of the distance. Let me endeavour to elucidate this somewhat abstract statement by one or two simple illustrations. Suppose a body were raised above the surface of the earth to a height of nearly 4,000 miles, so as to be at an altitude equal to the radius of the earth. In other words, a body so situated would be twice as far from the centre of the earth as a body which lay on the surface. The law of gravitation says that the intensity of the attraction is then to be decreased to one-fourth part, so that the pull of the earth on a body 4,000 miles high is only one quarter of the pull of the earth on that body so long as it lies on the ground. We may imagine the effect of this pull to be shown in different ways. Allow the body to fall, and in the interval of one second it will only drop through four feet, a mere quarter of the distance that gravity would cause near the earth's surface.
We may consider the matter in another way by supposing that the attraction of the earth is measured by one of those little weighing machines known as a spring balance. If a weight of four pounds be hung on such a contrivance, at the earth's surface, the index of course shows a weight of four pounds; but conceive this balance, still bearing the weight appended thereto, were to be carried up and up, the indicated strain would become less and less, until by the time the balance reached 4,000 miles high, where it was twice as far away from the earth's centre as at first, the indicated strain would be reduced to the fourth part, and the balance would only show one pound. If we could imagine the instrument to be carried still further into the depths of space, the indication of the scale would steadily continue to decline. By the time the apparatus had reached a distance of 8,000 miles high, being then three times as far from the earth's centre as at first, the law of gravitation tells us that the attraction must have decreased to one-ninth part. The strain[Pg 128] thus shown on the balance would be only the ninth part of four pounds, or less than half a pound. But let the voyage be once again resumed, and let not a halt be made this time until the balance and its four-pound weight have retreated to that orbit which the moon traverses in its monthly course around the earth. The distance thus attained is about sixty times the radius of the earth, and consequently the attraction of gravitation is diminished in the proportion of one to the square of sixty; the spring will then only be strained by the inappreciable fraction of 1-3,600 part of four pounds. It therefore appears that a weight which on the earth weighed a ton and a half would, if raised 240,000 miles, weigh less than a pound. But even at this vast distance we are not to halt; imagine that we retreat still further and further; the strain shown by the balance will ever decrease, but it will still exist, no matter how far we go. Astronomy appears to teach us that the attraction of gravitation can extend, with suitably enfeebled intensity, across the most profound gulfs of space.
The principle of gravitation is of far wider scope than we have yet indicated. We have spoken merely of the attraction of the earth, and we have stated that this force extends throughout space. But the law of gravitation is not so limited. Not only does the earth attract every other body, and every other body attract the earth, but each of these bodies attracts the other; so that in its more complete shape the law of gravitation announces that "every body in the universe attracts every other body with a force which varies inversely as the square of the distance."
It is impossible for us to over-estimate the importance of this law. It supplies the clue by which we can unravel the complicated movements of the planets. It has led to marvellous discoveries, in which the law of gravitation has enabled us to anticipate the telescope, and to feel the existence of bodies before those bodies have even been seen.
An objection which may be raised at this point must first be dealt with. It seems to be, indeed, a plausible one. If the earth attracts the moon, why does not the moon tumble[Pg 129] down on the earth? If the earth is attracted by the sun, why does it not tumble into the sun? If the sun is attracted by other stars, why do they not rush together with a frightful collision? It may not unreasonably be urged that if all these bodies in the heavens are attracting each other, it would seem that they must all rush together in consequence of that attraction, and thus weld the whole material universe into a single mighty mass. We know, as a matter of fact, that these collisions do not often happen, and that there is extremely little likelihood of their taking place. We see that although our earth is said to have been attracted by the sun for countless ages, yet the earth is just as far from the sun as ever it was. Is not this in conflict with the doctrine of universal gravitation? In the early days of astronomy such objections would be regarded, and doubtless were regarded, as well-nigh insuperable; even still we occasionally hear them raised, and it is therefore the more incumbent on us to explain how it happens that the solar system has been able to escape from the catastrophe by which it seems to be threatened.
There can be no doubt that if the moon and the earth had been initially placed at rest, they would have been drawn together by their mutual attraction. So, too, if the system of planets surrounding the sun had been left initially at rest they would have dashed into the sun, and the system would have been annihilated. It is the fact that the planets are moving, and that the moon is moving, which has enabled these bodies successfully to resist the attraction in so far, at least, as that they are not drawn thereby to total destruction.
It is so desirable that the student should understand clearly how a central attraction is compatible with revolution in a nearly circular path, that we give an illustration to show how the moon pursues its monthly orbit under the guidance and the control of the attracting earth.
The imaginary sketch in Fig. 36 denotes a section of the earth with a high mountain thereon.[12] If a cannon were stationed on the top of the mountain at C, and if the cannonball were fired off in the direction C E with a moderate charge of powder, the ball would move down along the first curved path. If it be fired a second time with a heavier charge, the path will be along the second curved line, and the ball would again fall to the ground. But let us try next time with a charge still further increased, and, indeed, with a far stronger cannon than any piece of ordnance ever yet made. The velocity of the projectile must now be assumed to be some miles per second, but we can conceive that the speed shall be so adjusted that the ball shall move along the path C D, always at the same height above the earth, though still curving, as every projectile must curve, from the horizontal line in which it moved at the first moment. Arrived at D, the ball will still be at the same height above the surface, and its velocity must be unabated. It will therefore continue in its path and move round another quadrant of the circle without getting nearer to the surface. In this manner the projectile will travel completely round the whole globe, coming back again to C and then taking another start in the same path. If we could abolish the mountain and the cannon at[Pg 131] the top, we should have a body revolving for ever around the earth in consequence of the attraction of gravitation.
Make now a bold stretch of the imagination. Conceive a terrific cannon capable of receiving a round bullet not less than 2,000 miles in diameter. Discharge this enormous bullet with a velocity of about 3,000 feet per second, which is two or three times as great as the velocity actually attainable in modern artillery. Let this notable bullet be fired horizontally from some station nearly a quarter of a million miles above the surface of the earth. That fearful missile would sweep right round the earth in a nearly circular orbit, and return to where it started in about four weeks. It would then commence another revolution, four weeks more would find it again at the starting point, and this motion would go on for ages.
Do not suppose that we are entirely romancing. We cannot indeed show the cannon, but we can point to a great projectile. We see it every month; it is the beautiful moon herself. No one asserts that the moon was ever shot from such a cannon; but it must be admitted that she moves as if she had been. In a later chapter we shall enquire into the history of the moon, and show how she came to revolve in this wonderful manner.
As with the moon around the earth, so with the earth around the sun. The illustration shows that a circular or nearly circular motion harmonises with the conception of the law of universal gravitation.
We are accustomed to regard gravitation as a force of stupendous magnitude. Does not gravitation control the moon in its revolution around the earth? Is not even the mighty earth itself retained in its path around the sun by the surpassing power of the sun's attraction? No doubt the actual force which keeps the earth in its path, as well as that which retains the moon in our neighbourhood, is of vast intensity, but that is because gravitation is in such cases associated with bodies of enormous mass. No one can deny that all bodies accessible to our observation appear to attract each other in accordance with the law of gravitation; but[Pg 132] it must be confessed that, unless one or both of the attracting bodies is of gigantic dimensions, the intensity is almost immeasurably small.
Let us attempt to illustrate how feeble is the gravitation between masses of easily manageable dimensions. Take, for instance, two iron weights, each weighing about 50lb., and separated by a distance of one foot from centre to centre. There is a certain attraction of gravitation between these weights. The two weights are drawn together, yet they do not move. The attraction between them, though it certainly exists, is an extremely minute force, not at all comparable as to intensity with magnetic attraction. Everyone knows that a magnet will draw a piece of iron with considerable vigour, but the intensity of gravitation is very much less on masses of equal amount. The attraction between these two 50lb. weights is less than the ten-millionth part of a single pound. Such a force is utterly infinitesimal in comparison with the friction between the weights and the table on which they stand, and hence there is no response to the attraction by even the slightest movement. Yet, if we can conceive each of these weights mounted on wheels absolutely devoid of friction, and running on absolutely perfect horizontal rails, then there is no doubt that the bodies would slowly commence to draw together, and in the course of time would arrive in actual contact.
If we desire to conceive gravitation as a force of measurable intensity, we must employ masses immensely more ponderous than those 50lb. weights. Imagine a pair of globes, each composed of 417,000 tons of cast iron, and each, if solid, being about 53 yards in diameter. Imagine these globes placed at a distance of one mile apart. Each globe attracts the other by the force of gravitation. It does not matter that buildings and obstacles of every description intervene; gravitation will pass through such impediments as easily as light passes through glass. No screen can be devised dense enough to intercept the passage of this force. Each of these iron globes will therefore under all circumstances attract the other; but, notwithstanding their ample[Pg 133] proportions, the intensity of that attraction is still very small, though appreciable. The attraction between these two globes is a force no greater than the pressure exerted by a single pound weight. A child could hold back one of these massive globes from its attraction by the other. Suppose that all was clear, and that friction could be so neutralised as to permit the globes to follow the impulse of their mutual attractions. The two globes will then commence to approach, but the masses are so large, while the attraction is so small, that the speed will be accelerated very slowly. A microscope would be necessary to show when the motion has actually commenced. An hour and a half must elapse before the distance is diminished by a single foot; and although the pace improves subsequently, yet three or four days must elapse before the two globes will come together.
The most remarkable characteristic of the force of gravitation must be here specially alluded to. The intensity appears to depend only on the quantity of matter in the bodies, and not at all on the nature of the substances of which these bodies are composed. We have described the two globes as made of cast iron, but if either or both were composed of lead or copper, of wood or stone, of air or water, the attractive power would still be the same, provided only that the masses remain unaltered. In this we observe a profound difference between the attraction of gravitation and magnetic attraction. In the latter case the attraction is not perceptible at all in the great majority of substances, and is only considerable in the case of iron.
In our account of the solar system we have represented the moon as revolving around the earth in a nearly circular path, and the planets as revolving around the sun in orbits which are also approximately circular. It is now our duty to give a more minute description of these remarkable paths; and, instead of dismissing them as being nearly circles, we must ascertain precisely in what respects they differ therefrom.
If a planet revolved around the sun in a truly circular path, of which the sun was always at the centre, it is[Pg 134] then obvious that the distance from the sun to the planet, being always equal to the radius of the circle, must be of constant magnitude. Now, there can be no doubt that the distance from the sun to each planet is approximately constant; but when accurate observations are made, it becomes clear that the distance is not absolutely so. The variations in distance may amount to many millions of miles, but, even in extreme cases, the variation in the distance of the planet is only a small fraction—usually a very small fraction—of the total amount of that distance. The circumstances vary in the case of each of the planets. The orbit of the earth itself is such that the distance from the earth to the sun departs but little from its mean value. Venus makes even a closer approach to perfectly circular movement; while, on the other hand, the path of Mars, and much more the path of Mercury, show considerable relative fluctuations in the distance from the planet to the sun.
It has often been noticed that many of the great discoveries in science have their origin in the nice observation and explanation of minute departures from some law approximately true. We have in this department of astronomy an excellent illustration of this principle. The orbits of the planets are nearly circles, but they are not exactly circles. Now, why is this? There must be some natural reason. That reason has been ascertained, and it has led to several of the grandest discoveries that the mind of man has ever achieved in the realms of Nature.
In the first place, let us see the inferences to be drawn from the fact that the distance of a planet from the sun is not constant. The motion in a circle is one of such beauty and simplicity that we are reluctant to abandon it, unless the necessity for doing so be made clearly apparent. Can we not devise any way by which the circular motion might be preserved, and yet be compatible with the fluctuations in the distance from the planet to the sun? This is clearly impossible with the sun at the centre of the circle. But suppose the sun did not occupy the centre, while the planet, as before, revolved around the sun. The distance between the two[Pg 135] bodies would then necessarily fluctuate. The more eccentric the position of the sun, the larger would be the proportionate variation in the distance of the planet when at the different parts of its orbit. It might further be supposed that by placing a series of circles around the sun the various planetary orbits could be accounted for. The centre of the circle belonging to Venus is to coincide very nearly with the centre of the sun, and the centres of the orbits of all the other planets are to be placed at such suitable distances from the sun as will render a satisfactory explanation of the gradual increase and decrease of the distance between the two bodies.
There can be no doubt that the movements of the moon and of the planets would be, to a large extent, explained by such a system of circular orbits; but the spirit of astronomical enquiry is not satisfied with approximate results. Again and again the planets are observed, and again and again the observations are compared with the places which the planets would occupy if they moved in accordance with the system here indicated. The centres of the circles are moved hither and thither, their radii are adjusted with greater care; but it is all of no avail. The observations of the planets are minutely examined to see if they can be in error; but of errors there are none at all sufficient to account for the discrepancies. The conclusion is thus inevitable—astronomers are forced to abandon the circular motion, which was thought to possess such unrivalled symmetry and beauty, and are compelled to admit that the orbits of the planets are not circular.
Then if these orbits be not circles, what are they? Such was the great problem which Kepler proposed to solve, and which, to his immortal glory, he succeeded in solving and in proving to demonstration. The great discovery of the true shape of the planetary orbits stands out as one of the most conspicuous events in the history of astronomy. It may, in fact, be doubted whether any other discovery in the whole range of science has led to results of such far-reaching interest.
We must here adventure for a while into the field of science known as geometry, and study therein the nature of[Pg 136] that curve which the discovery of Kepler has raised to such unparalleled importance. The subject, no doubt, is a difficult one, and to pursue it with any detail would involve us in many abstruse calculations which would be out of place in this volume; but a general sketch of the subject is indispensable, and we must attempt to render it such justice as may be compatible with our limits.
The curve which represents with perfect fidelity the movements of a planet in its revolution around the sun belongs to that well-known group of curves which mathematicians describe as the conic sections. The particular form of conic section which denotes the orbit of a planet is known by the name of the ellipse: it is spoken of somewhat less accurately as an oval. The ellipse is a curve which can be readily constructed. There is no simpler method of doing so than that which is familiar to draughtsmen, and which we shall here briefly describe.
We represent on the next page (Fig. 37) two pins passing through a sheet of paper. A loop of twine passes over the two pins in the manner here indicated, and is stretched by the point of a pencil. With a little care the pencil can be guided so as to keep the string stretched, and its point will then describe a curve completely round the pins, returning to the point from which it started. We thus produce that celebrated geometrical figure which is called an ellipse.
It will be instructive to draw a number of ellipses, varying in each case the circumstances under which they are formed. If, for instance, the pins remain placed as before, while the length of the loop is increased, so that the pencil is farther away from the pins, then it will be observed that the ellipse has lost some of its elongation, and approaches more closely to a circle. On the other hand, if the length of the cord in the loop be lessened, while the pins remain as before, the ellipse will be found more oval, or, as a mathematician would say, its eccentricity is increased. It is also useful to study the changes which the form of the ellipse undergoes when one of the pins is altered, while the length of the loop remains unchanged. If the two pins be brought[Pg 137] nearer together the eccentricity will decrease, and the ellipse will approximate more closely to the shape of a circle. If the pins be separated more widely the eccentricity of the ellipse will be increased. That the circle is an extreme form of ellipse will be evident, if we suppose the two pins to draw in so close together that they become coincident; the point will then simply trace out a circle as the pencil moves round the figure.
The points marked by the pins obviously possess very remarkable relations with respect to the curve. Each one is called a focus, and an ellipse can only have one pair of foci. In other words, there is but a single pair of positions possible for the two pins, when an ellipse of specified size, shape, and position is to be constructed.
The ellipse differs principally from a circle in the circumstance that it possesses variety of form. We can have large and small ellipses just as we can have large and small circles, but we can also have ellipses of greater or less eccentricity. If the ellipse has not the perfect simplicity of the circle it has, at least, the charm of variety which the circle has not. The oval curve has also the beauty derived from an outline of perfect grace and an association with ennobling conceptions.
The ancient geometricians had studied the ellipse: they had noticed its foci; they were acquainted with its geometrical relations; and thus Kepler was familiar with the ellipse at the time when he undertook his celebrated researches on the movements of the planets. He had found, as we have already indicated, that the movements of the planets could not be reconciled with circular orbits. What shape of orbit should next be tried? The ellipse was ready to hand, its properties were known, and the comparison could be made; memorable, indeed, was the consequence of this comparison. Kepler found that the movement of the planets could be explained, by supposing that the path in which each one revolved was an ellipse. This in itself was a discovery of the most commanding importance. On the one hand it reduced to order the movements of the great globes which circulate round the sun; while on the other, it took that beautiful class of curves which had exercised the geometrical talents of the ancients, and assigned to them the dignity of defining the highways of the universe.
But we have as yet only partly enunciated the first discovery of Kepler. We have seen that a planet revolves in an ellipse around the sun, and that the sun is, therefore, at some point in the interior of the ellipse—but at what point? Interesting, indeed, is the answer to this question. We have pointed out how the foci possess a geometrical significance which no other points enjoy. Kepler showed that the sun must be situated in one of the foci of the ellipse in which each planet revolves. We thus enunciate the first law of planetary motion in the following words:—
Each planet revolves around the sun in an elliptic path, having the sun at one of the foci.
We are now enabled to form a clear picture of the orbits of the planets, be they ever so numerous, as they revolve around the sun. In the first place, we observe that the ellipse is a plane curve; that is to say, each planet must, in the course of its long journey, confine its movements to one plane. Each planet has thus a certain plane appropriated to it. It is true that all these planes are very nearly coincident,[Pg 139] at least in so far as the great planets are concerned; but still they are distinct, and the only feature in which they all agree is that each one of them passes through the sun. All the elliptic orbits of the planets have one focus in common, and that focus lies at the centre of the sun.
It is well to illustrate this remarkable law by considering the circumstances of two or three different planets. Take first the case of the earth, the path of which, though really an ellipse, is very nearly circular. In fact, if it were drawn accurately to scale on a sheet of paper, the difference between the elliptic orbit and the circle would hardly be detected without careful measurement. In the case of Venus the ellipse is still more nearly a circle, and the two foci of the ellipse are very nearly coincident with the centre of the circle. On the other hand, in the case of Mercury, we have an ellipse which departs from the circle to a very marked extent, while in the orbits of some of the minor planets the eccentricity is still greater. It is extremely remarkable that every planet, no matter how far from the sun, should be found to move in an ellipse of some shape or other. We shall presently show that necessity compels each planet to pursue an elliptic path, and that no other form of path is possible.
Started on its elliptic path, the planet pursues its stately course, and after a certain duration, known as the periodic time, regains the position from which its departure was taken. Again the planet traces out anew the same elliptic path, and thus, revolution after revolution, an identical track is traversed around the sun. Let us now attempt to follow the body in its course, and observe the history of its motion during the time requisite for the completion of one of its circuits. The dimensions of a planetary orbit are so stupendous that the planet must run its course very rapidly in order to finish the journey within the allotted time. The earth, as we have already seen, has to move eighteen miles a second to accomplish one of its voyages round the sun in the lapse of 365-1⁄4 days. The question then arises as to whether the rate at which a planet moves is uniform or not. Does the earth, for instance, actually move at all times with the velocity of[Pg 140] eighteen miles a second, or does our planet sometimes move more rapidly and sometimes more slowly, so that the average of eighteen miles a second is still maintained? This is a question of very great importance, and we are able to answer it in the clearest and most emphatic manner. The velocity of a planet is not uniform, and the variations of that velocity can be explained by the adjoining figure (Fig. 38).
Let us first of all imagine the planet to be situated at that part of its path most distant from the sun towards the right of the figure. In this position the body's velocity is at its lowest; as the planet begins to approach the sun the speed gradually improves until it attains its mean value. After this point has been passed, and the planet is now rapidly hurrying on towards the sun, the velocity with which it moves becomes gradually greater and greater, until at length, as it dashes round the sun, its speed attains a maximum. After passing the sun, the distance of the planet from the luminary increases, and the velocity of the motion begins to abate; gradually it declines until the mean value is again reached, and then it falls still lower, until the body recedes to its greatest distance from the sun, by which time the velocity has abated to the value from which we supposed it to commence. We thus observe that the nearer the planet is to the sun the quicker[Pg 141] it moves. We can, however, give numerical definiteness to the principle according to which the velocity of the planet varies. The adjoining figure (Fig. 39) shows a planetary orbit, with, of course, the sun at the focus S. We have taken two portions, A B and C D, round the ellipse, and joined their extremities to the focus. Kepler's second law may be stated in these words:—
"Every planet moves round the sun with such a velocity at every point, that a straight line drawn from it to the sun passes over equal areas in equal times."
For example, if the two shaded portions, A B S and D C S, are equal in area, then the times occupied by the planet in travelling over the portions of the ellipse, A B and C D, are equal. If the one area be greater than the other, then the times required are in the proportion of the areas.
This law being admitted, the reason of the increase in the planet's velocity when it approaches the sun is at once apparent. To accomplish a definite area when near the sun, a larger arc is obviously necessary than at other parts of the path. At the opposite extremity, a small arc suffices for a large area, and the velocity is accordingly less.
These two laws completely prescribe the motion of a planet round the sun. The first defines the path which the planet pursues; the second describes how the velocity of the body varies at different points along its path. But Kepler added to these a third law, which enables us to compare the movements[Pg 142] of two different planets revolving round the same sun. Before stating this law, it is necessary to explain exactly what is meant by the mean distance of a planet. In its elliptic path the distance from the sun to the planet is constantly changing; but it is nevertheless easy to attach a distinct meaning to that distance which is an average of all the distances. This average is called the mean distance. The simplest way of finding the mean distance is to add the greatest of these quantities to the least, and take half the sum. We have already defined the periodic time of the planet; it is the number of days which the planet requires for the completion of a journey round its path. Kepler's third law establishes a relation between the mean distances and the periodic times of the various planets. That relation is stated in the following words:—
"The squares of the periodic times are proportional to the cubes of the mean distances."
Kepler knew that the different planets had different periodic times; he also saw that the greater the mean distance of the planet the greater was its periodic time, and he was determined to find out the connection between the two. It was easily found that it would not be true to say that the periodic time is merely proportional to the mean distance. Were this the case, then if one planet had a distance twice as great as another, the periodic time of the former would have been double that of the latter; observation showed, however, that the periodic time of the more distant planet exceeded twice, and was indeed nearly three times, that of the other. By repeated trials, which would have exhausted the patience of one less confident in his own sagacity, and less assured of the accuracy of the observations which he sought to interpret, Kepler at length discovered the true law, and expressed it in the form we have stated.
To illustrate the nature of this law, we shall take for comparison the earth and the planet Venus. If we denote the mean distance of the earth from the sun by unity then the mean distance of Venus from the sun is 0·7233. Omitting decimals beyond the first place, we can represent the periodic[Pg 143] time of the earth as 365·3 days, and the periodic time of Venus as 224·7 days. Now the law which Kepler asserts is that the square of 365·3 is to the square of 224·7 in the same proportion as unity is to the cube of 0·7233. The reader can easily verify the truth of this identity by actual multiplication. It is, however, to be remembered that, as only four figures have been retained in the expressions of the periodic times, so only four figures are to be considered significant in making the calculations.
The most striking manner of making the verification will be to regard the time of the revolution of Venus as an unknown quantity, and deduce it from the known revolution of the earth and the mean distance of Venus. In this way, by assuming Kepler's law, we deduce the cube of the periodic time by a simple proportion, and the resulting value of 224·7 days can then be obtained. As a matter of fact, in the calculations of astronomy, the distances of the planets are usually ascertained from Kepler's law. The periodic time of the planet is an element which can be measured with great accuracy; and once it is known, then the square of the mean distance, and consequently the mean distance itself, is determined.
Such are the three celebrated laws of Planetary Motion, which have always been associated with the name of their discoverer. The profound skill by which these laws were elicited from the mass of observations, the intrinsic beauty of the laws themselves, their widespread generality, and the bond of union which they have established between the various members of the solar system, have given them quite an exceptional position in astronomy.
As established by Kepler, these planetary laws were merely the results of observation. It was found, as a matter of fact, that the planets did move in ellipses, but Kepler assigned no reason why they should adopt this curve rather than any other. Still less was he able to offer a reason why these bodies should sweep over equal areas in equal times, or why that third law was invariably obeyed. The laws as they came from Kepler's hands stood out as three[Pg 144] independent truths; thoroughly established, no doubt, but unsupported by any arguments as to why these movements rather than any others should be appropriate for the revolutions of the planets.
It was the crowning triumph of the great law of universal gravitation to remove this empirical character from Kepler's laws. Newton's grand discovery bound together the three isolated laws of Kepler into one beautiful doctrine. He showed not only that those laws are true, but he showed why they must be true, and why no other laws could have been true. He proved to demonstration in his immortal work, the "Principia," that the explanation of the famous planetary laws was to be sought in the attraction of gravitation. Newton set forth that a power of attraction resided in the sun, and as a necessary consequence of that attraction every planet must revolve in an elliptic orbit round the sun, having the sun as one focus; the radius of the planet's orbit must sweep over equal areas in equal times; and in comparing the movements of two planets, it was necessary to have the squares of the periodic times proportional to the cubes of the mean distances.
As this is not a mathematical treatise, it will be impossible for us to discuss the proofs which Newton has given, and which have commanded the immediate and universal acquiescence of all who have taken the trouble to understand them. We must here confine ourselves only to a very brief and general survey of the subject, which will indicate the character of the reasoning employed, without introducing details of a technical character.
Let us, in the first place, endeavour to think of a globe freely poised in space, and completely isolated from the influence of every other body in the universe. Let us imagine that this globe is set in motion by some impulse which starts it forward on a rapid voyage through the realms of space. When the impulse ceases the globe is in motion, and continues to move onwards. But what will be the path which it pursues? We are so accustomed to see a stone thrown into the air moving in a curved path, that we might[Pg 145] naturally think a body projected into free space will also move in a curve. A little consideration will, however, show that the cases are very different. In the realms of free space we find no conception of upwards or downwards; all paths are alike; there is no reason why the body should swerve to the right or to the left; and hence we are led to surmise that in these circumstances a body, once started and freed from all interference, would move in a straight line. It is true that this statement is one which can never be submitted to the test of direct experiment. Circumstanced as we are on the surface of the earth, we have no means of isolating a body from external forces. The resistance of the air, as well as friction in various other forms, no less than the gravitation towards the earth itself, interfere with our experiments. A stone thrown along a sheet of ice will be exposed to but little resistance, and in this case we see that the stone will take a straight course along the frozen surface. A stone similarly cast into empty space would pursue a course absolutely rectilinear. This we demonstrate, not by any attempts at an experiment which would necessarily be futile, but by indirect reasoning. The truth of this principle can never for a moment be doubted by one who has duly weighed the arguments which have been produced in its behalf.
Admitting, then, the rectilinear path of the body, the next question which arises relates to the velocity with which that movement is performed. The stone gliding over the smooth ice on a frozen lake will, as everyone has observed, travel a long distance before it comes to rest. There is but little friction between the ice and the stone, but still even on ice friction is not altogether absent; and as that friction always tends to stop the motion, the stone will at length be brought to rest. In a voyage through the solitudes of space, a body experiences no friction; there is no tendency for the velocity to be reduced, and consequently we believe that the body could journey on for ever with unabated speed. No doubt such a statement seems at variance with our ordinary experience. A sailing ship makes no progress on the sea when the[Pg 146] wind dies away. A train will gradually lose its velocity when the steam has been turned off. A humming-top will slowly expend its rotation and come to rest. From such instances it might be plausibly argued that when the force has ceased to act, the motion that the force generated gradually wanes, and ultimately vanishes. But in all these cases it will be found, on reflection, that the decline of the motion is to be attributed to the action of resisting forces. The sailing ship is retarded by the rubbing of the water on its sides; the train is checked by the friction of the wheels, and by the fact that it has to force its way through the air; and the atmospheric resistance is mainly the cause of the stopping of the humming-top, for if the air be withdrawn, by making the experiment in a vacuum, the top will continue to spin for a greatly lengthened period. We are thus led to admit that a body, once projected freely in space and acted upon by no external resistance, will continue to move on for ever in a straight line, and will preserve unabated to the end of time the velocity with which it originally started. This principle is known as the first law of motion.
Let us apply this principle to the important question of the movement of the planets. Take, for instance, the case of our earth, and let us discuss the consequences of the first law of motion. We know that the earth is moving each moment with a velocity of about eighteen miles a second, and the first law of motion assures us that if this globe were submitted to no external force, it would for ever pursue a straight track through the universe, nor would it depart from the precise velocity which it possesses at the present moment. But is the earth moving in this manner? Obviously not. We have already found that our globe is moving round the sun, and the comprehensive laws of Kepler have given to that motion the most perfect distinctness and precision. The consequence is irresistible. The earth cannot be free from external force. Some potent influence on our globe must be in ceaseless action. That influence, whatever it may be, constantly deflects the earth from the rectilinear path which it tends to pursue, and constrains it to trace out an ellipse instead of a straight line.
The great problem to be solved is now easily stated. There must be some external agent constantly influencing the earth. What is that agent, whence does it proceed, and to what laws is it submitted? Nor is the question confined to the earth. Mercury and Venus, Mars, Jupiter, and Saturn, unmistakably show that, as they are not moving in rectilinear paths, they must be exposed to some force. What is this force which guides the planets in their paths? Before the time of Newton this question might have been asked in vain. It was the splendid genius of Newton which supplied the answer, and thus revolutionised the whole of modern science.
The data from which the question is to be answered must be obtained from observation. We have here no problem which can be solved by mere mathematical meditation. Mathematics is no doubt a useful, indeed, an indispensable, instrument in the enquiry; but we must not attribute to mathematics a potency which it does not possess. In a case of this kind, all that mathematics can do is to interpret the results obtained by observation. The data from which Newton proceeded were the observed phenomena in the movement of the earth and the other planets. Those facts had found a succinct expression by the aid of Kepler's laws. It was, accordingly, the laws of Kepler which Newton took as the basis of his labours, and it was for the interpretation of Kepler's laws that Newton invoked the aid of that celebrated mathematical reasoning which he created.
The question is then to be approached in this way: A planet being subject to some external influence, we have to determine what that influence is, from our knowledge that the path of each planet is an ellipse, and that each planet sweeps round the sun over equal areas in equal times. The influence on each planet is what a mathematician would call a force, and a force must have a line of direction. The most simple conception of a force is that of a pull communicated along a rope, and the direction of the rope is in this case the direction of the force. Let us imagine that the force exerted on each planet is imparted by an invisible rope. Kepler's[Pg 148] laws will inform us with regard to the direction of this rope and the intensity of the strain transmitted through it.
The mathematical analysis of Kepler's laws would be beyond the scope of this volume. We must, therefore, confine ourselves to the results to which they lead, and omit the details of the reasoning. Newton first took the law which asserted that the planet moved over equal areas in equal times, and he showed by unimpeachable logic that this at once gave the direction in which the force acted on the planet. He showed that the imaginary rope by which the planet is controlled must be invariably directed towards the sun. In other words, the force exerted on each planet was at all times pointed from the planet towards the sun.
It still remained to explain the intensity of the force, and to show how the intensity of that force varied when the planet was at different points of its path. Kepler's first law enables this question to be answered. If the planet's path be elliptic, and if the force be always directed towards the sun at one focus of that ellipse, then mathematical analysis obliges us to say that the intensity of the force must vary inversely as the square of the distance from the planet to the sun.
The movements of the planets, in conformity with Kepler's laws, would thus be accounted for even in their minutest details, if we admit that an attractive power draws the planet towards the sun, and that the intensity of this attraction varies inversely as the square of the distance. Can we hesitate to say that such an attraction does exist? We have seen how the earth attracts a falling body; we have seen how the earth's attraction extends to the moon, and explains the revolution of the moon around the earth. We have now learned that the movement of the planets round the sun can also be explained as a consequence of this law of attraction. But the evidence in support of the law of universal gravitation is, in truth, much stronger than any we have yet presented. We shall have occasion to dwell on this matter further on. We shall show not only how the sun attracts the planets, but how the planets attract each other; and we shall find how this mutual attraction of the planets has led to remarkable discoveries,[Pg 149] which have elevated the law of gravitation beyond the possibility of doubt.
Admitting the existence of this law, we can show that the planets must revolve around the sun in elliptic paths with the sun in the common focus. We can show that they must sweep over equal areas in equal times. We can prove that the squares of the periodic times must be proportional to the cubes of their mean distances. Still further, we can show how the mysterious movements of comets can be accounted for. By the same great law we can explain the revolutions of the satellites. We can account for the tides, and for other phenomena throughout the Solar System. Finally, we shall show that when we extend our view beyond the limits of our Solar System to the beautiful starry systems scattered through space, we find even there evidence of the great law of universal gravitation.
Outline of the Subject—Is Mercury the Planet nearest the Sun?—Transit of an Interior Planet across the Sun—Has a Transit of Vulcan ever been seen?—Visibility of Planets during a Total Eclipse of the Sun—Professor Watson's Researches in 1878.
Provided with a general survey of the Solar System, and with such an outline of the law of universal gravitation as the last chapter has afforded us, we commence the more detailed examination of the planets and their satellites. We shall begin with the planets nearest to the sun, and then we shall gradually proceed outwards to one planet after another, until we reach the confines of the system. We shall find much to occupy our attention. Each planet is itself a globe, and it will be for us to describe as much as is known of it. The satellites by which so many of the planets are accompanied possess many points of interest. The circumstances of their discovery, their sizes, their movements, and their distances must be duly considered. It will also be found that the movements of the planets present much matter for reflection and examination. We shall have occasion to show how the planets mutually disturb each other, and what remarkable consequences have arisen from these influences. We must also occasionally refer to the important problems of celestial measuring and celestial weighing. We must show how the sizes, the weights, and the distances of the various members of our system are to be discovered. The greater part of our task will fortunately lead us over ground which is thoroughly certain, and where the results have been confirmed by frequent observation. It happens, however, that at the very outset of[Pg 151] our course we are obliged to deal with observations which are far from certain. The existence of a planet much closer to the sun than those hitherto known has been asserted by competent authority. The question is still unsettled, but the planet cannot at present be found. Hence it is that we have called the subject of this chapter, The Planet of Romance.
It had often been thought that Mercury, long supposed to be the nearest planet to the sun, was perhaps not really the body entitled to that distinction. Mercury revolves round the sun at an average distance of about 36,000,000 miles. In the interval between it and the sun there might have been one or many other planets. There might have been one revolving at ten million miles, another at fifteen, and so on. But did such planets exist? Did even one planet revolve inside the orbit of Mercury? There were certain reasons for believing in such a planet. In the movements of Mercury indications were perceptible of an influence that it was at one time thought might have been accounted for by the supposition of an interior planet.[13] But there was necessarily a great difficulty about seeing this object. It must always be close to the sun, and even in the best telescope it is generally impossible to see a star-like point in that position. Nor could such a planet be seen after sunset, for under the most favourable conditions it would set almost immediately after the sun, and a like difficulty would make it invisible at sunrise.
Our ordinary means of observing a planet have therefore completely failed. We are compelled to resort to extraordinary methods if we would seek to settle the great question as to the existence of the intra-Mercurial planets. There are at least two lines of observation which might be expected to answer our purpose.
An opportunity for the first would arise when it happened that the unknown planet came directly between the earth and the sun. In the diagram (Fig. 40) we show the sun at the centre; the internal dotted circle denotes the orbit of the unknown planet, which has received the name of Vulcan before even its very existence has been at all satisfactorily established. The outer circle denotes the orbit of the earth. As Vulcan moves more rapidly than the earth, it will frequently happen that the planet will overtake the earth, so that the three bodies will have the positions represented in the diagram. It would not, however, necessarily follow that Vulcan was exactly between the earth and the luminary. The path of the planet may be tilted, so that, as seen from the earth, Vulcan would be over or under the sun, according to circumstances.
If, however, Vulcan really does exist, we might expect that sometimes the three bodies will be directly in line, and this would then give the desired opportunity of making the telescopic discovery of the planet. We should expect on such an occasion to observe the planet as a dark spot, moving slowly across the face of the sun. The two other planets interior to the earth, namely, Mercury and Venus, are occasionally seen in the act of transit; and there cannot be a doubt that if Vulcan exists, its transits across the sun must be more numerous than those of Mercury, and far more numerous than those of Venus. On the other hand, it may reasonably be anticipated that Vulcan is a small globe, and as it will be much more distant from us than Mercury at the time of its transit, we could not expect that the transit of the planet of romance would be at all comparable as a spectacle with those of either of the two other bodies we have named.
The question arises as to whether telescopic research has ever disclosed anything which can be regarded as a transit of Vulcan. On this point it is not possible to speak with any certainty. It has, on more than one occasion, been asserted by observers that a spot has been seen traversing the sun, and from its shape and general appearance they have presumed it to have been an intra-Mercurial planet. But a close examination of the circumstances in which such observations[Pg 153] have been made has not tended to increase confidence in this presumption. Such discoveries have usually been made by persons little familiar with telescopic observations. It is certainly a significant fact that, notwithstanding the diligent scrutiny to which the sun has been subjected during the past century by astronomers who have specially devoted themselves to this branch of research, no telescopic discovery of Vulcan on the sun has been announced by any really experienced astronomer. The last announcement of a planet having crossed the sun dates from 1876, and was made by a German amateur, but what he thought to have been a planet was promptly shown to have been a small sun-spot, which had been photographed at Greenwich in the course of the daily routine work, and had also been observed at Madrid. From an examination of the whole subject, we are inclined to believe that there is not at this moment any reliable telescopic evidence of the transit of an intra-Mercurial planet over the face of the central luminary.
But there is still another method by which we might reasonably hope to detect new planets in the vicinity of the sun. This method is, however, but seldom available. It is only possible when the sun is totally eclipsed.
When the moon is interposed directly between the earth and the sun, the brightness of day is temporarily exchanged for the gloom of night. If the sky be free from clouds the stars spring forth, and can be seen around the obscured sun. Even if a planet were quite close to the luminary it would be visible on such an occasion if its magnitude were comparable with that of Mercury. Careful preparation is necessary when it is proposed to make a trial of this kind. The danger to be specially avoided is that of confounding the planet with the ordinary stars, which it will probably resemble. The late distinguished American astronomer, Professor Watson, specially prepared to devote himself to this research during the notable total eclipse in 1878. When the eclipse occurred the light of the sun vanished and the stars burst forth. Among them Professor Watson saw an object which to him seemed to be the long-sought intra-Mercurial planet. We should add that this zealous observer saw another object which he at first took to be the star known as Zeta in the constellation Cancer. When he afterwards found that the recorded place of this object did not agree so well as he expected with the known position of this star, he came to the conclusion that it could not be Zeta but must be some other unknown planet. The relative positions of the two objects which he took to be planets agree, however, sufficiently well, considering the difficulties of the observation, with the relative positions of the stars Theta and Zeta Cancri, and it can now hardly be doubted that Watson merely saw these two stars. He maintained, however, that he had noticed Theta Cancri as well as the two planets, but without recording its position. There is, however, a third star, known as 20 Cancri, near the same place, and this Watson probably mistook for Theta. It is necessary to record that Vulcan has not been observed, though specially looked for, during the eclipses which have occurred since 1878, and it is accordingly the general belief among astronomers that no planet has yet been detected within the orbit of Mercury.
The Ancient Astronomical Discoveries—How Mercury was first found—Not easily seen—Mercury was known from the earliest ages—Skill necessary in the Discovery—The Distinction of Mercury from a Star—Mercury in the East and in the West—The Prediction—How to Observe Mercury—Its Telescopic Appearance—Difficulty of Observing its Appearance—Orbit of Mercury—Velocity of the Planet—Can there be Life on the Planet?—Changes in its Temperature—Transit of Mercury over the Sun—Gassendi's Observations—Rotation of Mercury—The Weight of Mercury.
Long and glorious is the record of astronomical discovery. The discoveries of modern days have succeeded each other with such rapidity, they have so often dazzled our imaginations with their brilliancy, that we are sometimes apt to think that astronomical discovery is a purely modern product. But no idea could be more fundamentally wrong. While we appreciate to the utmost the achievements of modern times, let us endeavour to do justice to the labours of the astronomers of antiquity.
And when we speak of the astronomers of antiquity, let us understand clearly what is meant. The science is now growing so rapidly that each century witnesses a surprising advance; each generation, each decade, each year, has its own rewards for those diligent astronomers by whom the heavens are so carefully scanned. We must, however, project our glance to a remote epoch in time past, if we would view the memorable discovery of Mercury. Compared with it, the discoveries of Newton are to be regarded as very modern achievements; even the announcement of the Copernican system of the heavens is itself a recent event in comparison with the detection of this planet now to be discussed.
By whom was this great discovery made? Let us see if the question can be answered by the examination of astronomical records. At the close of his memorable life Copernicus was heard to express his sincere regret that he never enjoyed an opportunity of beholding the planet Mercury. He had specially longed to see this body, the movements of which were to such a marked extent illustrative of the theory of the celestial motions which it was his immortal glory to have established, but he had never been successful. Mercury is not generally to be seen so easily as are some of the other planets, and it may well have been that the vapours from the immense lagoon at the mouth of the Vistula obscured the horizon at Frauenburg, where Copernicus dwelt, and thus his opportunities of viewing Mercury were probably even rarer than they are at other places.
The existence of Mercury was certainly quite a familiar fact in the time of Copernicus, and therefore we must look to some earlier epoch for its discovery. In the scanty astronomical literature of the Middle Ages we find occasional references to the existence of this object. We can trace observations of Mercury through remote centuries to the commencement of our era. Records from dates still earlier are not wanting, until at length we come on an observation which has descended to us for more than 2,000 years, having been made in the year 265 before the Christian era. It is not pretended, however, that this observation records the discovery of the planet. Earlier still we find the chief of the astronomers at Nineveh alluding to Mercury in a report which he made to Assurbanipal, the King of Assyria. It does not appear in the least degree likely that the discovery was even then a recent one. It may have been that the planet was independently discovered in two or more localities, but all records of such discoveries are totally wanting; and we are ignorant alike of the names of the discoverers, of the nations to which they belonged, and of the epochs at which they lived.
Although this discovery is of such vast antiquity, although it was made before correct notions were entertained as to the[Pg 157] true system of the universe, and, it is needless to add, long before the invention of the telescope, yet it must not be assumed that the detection of Mercury was by any means a simple or obvious matter. This will be manifest when we try to conceive the manner in which the discovery must probably have been made.
Some primæval astronomer, long familiar with the heavens, had learned to recognise the various stars and constellations. Experience had impressed upon him the permanence of these objects; he had seen that Sirius invariably appeared at the same seasons of the year, and he had noticed how it was placed with regard to Orion and the other neighbouring constellations. In the same manner each of the other bright stars was to him a familiar object always to be found in a particular region of the heavens. He saw how the stars rose and set in such a way, that though each star appeared to move, yet the relative positions of the stars were incapable of alteration. No doubt this ancient astronomer was acquainted with Venus; he knew the evening star; he knew the morning star; and he may have concluded that Venus was a body which oscillated from one side of the sun to the other.
We can easily imagine how the discovery of Mercury was made in the clear skies over an Eastern desert. The sun has set, the brief twilight has almost ceased, when lo, near that part of the horizon where the glow of the setting sun still illuminates the sky, a bright star is seen. The primæval astronomer knows that there is no bright star at this place in the heavens. If the object of his attention be not a star, what, then, can it be? Eager to examine this question, the heavens are watched next night, and there again, higher above the horizon, and more brilliant still, is the object seen the night before. Each successive night the body gains more and more lustre, until at length it becomes a conspicuous gem. Perhaps it will rise still higher and higher; perhaps it will increase till it attains the brilliancy of Venus itself. Such were the surmises not improbably made by those who first watched this object; but they were not realised. After a few nights of exceptional splendour the lustre of this[Pg 158] mysterious orb declines. The planet again draws near the horizon at sunset, until at length it sets so soon after the sun that it has become invisible. Is it lost for ever? Years may elapse before another opportunity of observing the object after sunset may be available; but then again it will be seen to run through the same series of changes, though, perhaps, under very different circumstances. The greatest height above the horizon and the greatest brightness both vary considerably.
Long and careful observations must have been made before the primæval astronomer could assure himself that the various appearances might all be attributed to a single body. In the Eastern deserts the phenomena of sunrise must have been nearly as familiar as those of sunset, and in the clear skies, at the point where the sunbeams were commencing to dawn above the horizon, a bright star-like point might sometimes be perceived. Each successive day this object rose higher and higher above the horizon before the moment of sunrise, and its lustre increased with the distance; then again it would draw in towards the sun, and return for many months to invisibility. Such were the data which were presented to the mind of the primitive astronomer. One body was seen after sunset, another body was seen before sunrise. To us it may seem an obvious inference from the observed facts that the two bodies were identical. The inference is a correct one, but it is in no sense an obvious one. Long and patient observation established the remarkable law that one of these bodies was never seen until the other had disappeared. Hence it was inferred that the phenomena, both at sunrise and at sunset, were due to the same body, which oscillated to and fro about the sun.
We can easily imagine that the announcement of the identity of these two objects was one which would have to be carefully tested before it could be accepted. How are the tests to be applied in a case of this kind? There can hardly be a doubt that the most complete and convincing demonstration of scientific truth is found in the fulfilment of prediction. When Mercury had been observed for years, a certain regularity in the recurrence of its visibility was noticed. Once a periodicity[Pg 159] had been fully established, prediction became possible. The time when Mercury would be seen after sunset, the time when it would be seen before sunrise, could be foretold with accuracy! When it was found that these predictions were obeyed to the letter—that the planet was always seen when looked for in accordance with the predictions—it was impossible to refuse assent to the hypothesis on which these predictions were based. Underlying that hypothesis was the assumption that all the various appearances arose from the oscillations of a single body, and hence the discovery of Mercury was established on a basis as firm as the discovery of Jupiter or of Venus.
In the latitudes of the British Islands it is generally possible to see Mercury some time during the course of the year. It is not practicable to lay down, within reasonable limits, any general rule for finding the dates at which the search should be made; but the student who is determined to see the planet will generally succeed with a little patience. He must first consult an almanac which gives the positions of the body, and select an occasion when Mercury is stated to be an evening or a morning star. Such an occasion during the spring months is especially suitable, as the elevation of Mercury above the horizon is usually greater then than at other seasons; and in the evening twilight, about three-quarters of an hour after sunset, a view of this shy but beautiful object will reward the observer's attention.
To those astronomers who are provided with equatorial telescopes such instructions are unnecessary. To enjoy a telescopic view of Mercury, we first turn to the Nautical Almanac, and find the position in which the planet lies. If it happen to be above the horizon, we can at once direct the telescope to the place, and even in broad daylight the planet will very often be seen. The telescopic appearance of Mercury is, however, disappointing. Though it is much larger than the moon, yet it is sufficiently far off to seem insignificant. There is, however, one feature in a view of this planet which would immediately attract attention. Mercury is not usually observed to be a circular object, but more or less crescent-shaped,[Pg 160] like a miniature moon. The phases of the planet are also to be accounted for on exactly the same principles as the phases of the moon. Mercury is a globe composed, like our earth, of materials possessing in themselves no source of illumination. One hemisphere of the planet must necessarily be turned towards the sun, and this side is accordingly lighted up brilliantly by the solar rays. When we look at Mercury we see nothing of the non-illuminated side, and the crescent is due to the foreshortened view which we obtain of the illuminated part. The planet is such a small object that, in the glitter of the naked-eye view, the shape of the luminous body cannot be defined. Indeed, even in the much larger crescent of Venus, the aid of the telescope has to be invoked before the characteristic form can be observed. Beyond, however, the fact that Mercury is a crescent, and that it undergoes varying phases in correspondence with the changes in its relative position to the earth and the sun, we cannot see much of the planet. It is too small and too bright to admit of easy delineation of details on its surface. No doubt attempts have been made, and observations have been recorded, as to certain very faint and indistinct markings on the planet, but such statements must be received with great hesitation.
The facts which have been thoroughly established with regard to Mercury are mainly numerical statements as to the path it describes around the sun. The time taken by the planet to complete one of its revolutions is eighty-eight days nearly. The average distance from the sun is about 36,000,000 miles, and the mean velocity with which the body moves is over twenty-nine miles a second. We have already alluded to the most characteristic and remarkable feature of the orbit of Mercury. That orbit differs from the paths of all the other large planets by its much greater departure from the circular form. In the majority of cases the planetary orbits are so little elliptic that a diagram of the orbit drawn accurately to scale would not be perceived to differ from a circle unless careful measurements were made. In the case of Mercury the circumstances are different. The elliptic form of the path would be quite unmistakable by the most casual observer. The distance from the sun to the planet fluctuates between very considerable limits. The lowest value it can attain is about 30,000,000 miles; the highest value is about 43,000,000 miles. In accordance with Kepler's second law, the velocity of the planet must exhibit corresponding changes. It must sweep rapidly around that part of his path near the sun, and more slowly round the remote parts of his path. The greatest[Pg 162] velocity is about thirty-five miles a second, and the least is twenty-three miles a second.
For an adequate conception of the movements of Mercury we ought not to dissociate the velocity from the true dimensions of the body by which it is performed. No doubt a speed of twenty-nine miles a second is enormous when compared with the velocities with which daily life makes us familiar. The speed of the planet is not less than a hundred times as great as the velocity of the rifle bullet. But when we compare the sizes of the bodies with their velocities, the velocity of Mercury seems relatively much less than that of the bullet. A rifle bullet traverses a distance equal to its own diameter many thousands of times in a second. But even though Mercury is moving so much faster, yet the dimensions of the planet are so considerable that a period of two minutes will be required for it to move through a distance equal to its diameter. Viewing the globe of the planet as a whole, the velocity of its movement is but a stately and dignified progress appropriate to its dimensions.
As we can learn little or nothing of the true surface of Mercury, it is utterly impossible for us to say whether life can exist on the surface of that planet. We may, however, reasonably conclude that there cannot be life on Mercury in any respect analogous to the life which we know on the earth. The heat of the sun and the light of the sun beat down on Mercury with an intensity many times greater than that which we experience. When this planet is at its utmost distance from the sun the intensity of solar radiation is even then more than four times greater than the greatest heat which ever reaches the earth. But when Mercury, in the course of its remarkable changes of distance, draws in to the warmest part of its orbit, it is exposed to a terrific scorching. The intensity of the sun's heat must then be not less than nine times as great as the greatest radiation to which we are exposed.
These tremendous climatic changes succeed each other much more rapidly than do the variations of our seasons. On Mercury the interval between midsummer and midwinter[Pg 163] is only forty-four days, while the whole year is only eighty-eight days. Such rapid variations in solar heat must in themselves exercise a profound effect on the habitability of Mercury. Mr. Ledger well remarks, in his interesting work,[14] that if there be inhabitants on Mercury the notions of "perihelion" and "aphelion," which are here often regarded as expressing ideas of an intricate or recondite character, must on the surface of that planet be familiar to everybody. The words imply "near the sun," and "away from the sun;" but we do not associate these expressions with any obvious phenomena, because the changes in the distance of the earth from the sun are inconsiderable. But on Mercury, where in six weeks the sun rises to more than double his apparent size, and gives more than double the quantity of light and of heat, such changes as are signified by perihelion and aphelion embody ideas obviously and intimately connected with the whole economy of the planet.
It is nevertheless rash to found any inferences as to climate merely upon the proximity or the remoteness of the sun. Climate depends upon other matters besides the sun's distance. The atmosphere surrounding the earth has a profound influence on heat and cold, and if Mercury have an atmosphere—as has often been supposed—its climate may be thereby modified to any necessary extent. It seems, however, hardly possible to suppose that any atmosphere could form an adequate protection for the inhabitants from the violent and rapid fluctuations of solar radiation. All we can say is, that the problem of life in Mercury belongs to the class of unsolved, and perhaps unsolvable, mysteries.
It was in the year 1629 that Kepler made an important announcement as to impending astronomical events. He had been studying profoundly the movements of the planets; and from his study of the past he had ventured to predict the future. Kepler announced that in the year 1631 the planets Venus and Mercury would both make a transit across the sun, and he assigned the dates to be November 7th for Mercury, and December 6th for Venus. This was at the time a very[Pg 164] remarkable prediction. We are so accustomed to turn to our almanacs and learn from them all the astronomical phenomena which are anticipated during the year, that we are apt to forget how in early times this was impossible. It has only been by slow degrees that astronomy has been rendered so perfect as to enable us to foretell, with accuracy, the occurrence of the more delicate phenomena. The prediction of those transits by Kepler, some years before they occurred, was justly regarded at the time as a most remarkable achievement.
The illustrious Gassendi prepared to apply the test of actual observation to the announcements of Kepler. We can now assign the time of the transit accurately to within a few minutes, but in those early attempts equal precision was not practicable. Gassendi considered it necessary to commence watching for the transit of Mercury two whole days before the time indicated by Kepler, and he had arranged an ingenious plan for making his observations. The light of the sun was admitted into a darkened room through a hole in the shutter, and an image of the sun was formed on a white screen by a lens. This is, indeed, an admirable and a very pleasing way of studying the surface of the sun, and even at the present day, with our best telescopes, one of the methods of viewing our luminary is founded on the same principle.
Gassendi commenced his watch on the 5th of November, and carefully studied the sun's image at every available opportunity. It was not, however, until five hours after the time assigned by Kepler that the transit of Mercury actually commenced. Gassendi's preparations had been made with all the resources which he could command, but these resources seem very imperfect when compared with the appliances of our modern observatories. He was anxious to note the time when the planet appeared, and for this purpose he had stationed an assistant in the room beneath, who was to observe the altitude of the sun at the moment indicated by Gassendi. The signal to the assistant was to be conveyed by a very primitive apparatus. Gassendi was to stamp on the floor when the critical moment had arrived. In spite of the long[Pg 165] delay, which exhausted the patience of the assistant, some valuable observations were obtained, and thus the first passage of a planet across the sun was observed.
The transits of Mercury are not rare phenomena (there have been thirteen of them during the nineteenth century), and they are chiefly of importance on account of the accuracy which their observation infuses into our calculations of the movements of the planet. It has often been hoped that the opportunities afforded by a transit would be available for procuring information as to the physical character of the globe of Mercury, but these hopes have not been realised.
Spectroscopic observations of Mercury are but scanty. They seem to indicate that water vapour is a probable constituent in the atmosphere of Mercury, as it is in our own.
A distinguished Italian astronomer, Professor Schiaparelli, some years ago announced a remarkable discovery with respect to the rotation of the planet Mercury. He found that the planet rotates on its axis in the same period as it revolves around the sun. The practical consequence of the identity between these two periods is that Mercury always turns the same face to the sun. If our earth were to rotate in a similar fashion, then the hemisphere directed to the sun would enjoy eternal day, while the opposite hemisphere would be relegated to perpetual night. According to this discovery, Mercury revolves around the sun in the same way as the moon revolves around the earth. As the velocity with which Mercury travels round the sun is very variable, owing to the highly elliptic shape of its orbit, while the rotation about its axis is performed with uniform speed, it follows that rather more than a hemisphere (about five-eighths of the surface) enjoys more or less the light of the sun in the course of a Mercurial year.
This important discovery of Schiaparelli has lately been confirmed by an American astronomer, Mr. Lowell, of Arizona, U.S.A., who observed the planet under very favourable conditions with a refractor of twenty-four inches aperture. He has detected on the globe of Mercury certain narrow, dark lines, the very slow shifting of which points to a period of rotation[Pg 166] about its axis exactly coincident with the period of revolution round the sun. The same observer shows that the axis of rotation of Mercury is perpendicular to the plane of the orbit. Mr. Lowell has perceived no sign of clouds or obscurations, and indeed no indication of any atmospheric envelope; the surface of Mercury is colourless, "a geography in black and white."
We may assert that, there is a strong à priori probability in favour of the reality of Schiaparelli's discovery. Mercury, being one of the planets devoid of a moon, will be solely influenced by the sun in so far as tidal phenomena are concerned. Owing, moreover, to the proximity of Mercury to the sun, the solar tides on that planet possess an especial vehemence. As the tendency of tides is to make Mercury present a constant face to the sun, there need be little hesitation in accepting testimony that tides have wrought exactly the result that we know they were competent to perform.
Here we take leave of the planet Mercury—an interesting and beautiful object, which stimulates our intellectual curiosity, while at the same time it eludes our attempts to make a closer acquaintance. There is, however, one point of attainable knowledge which we must mention in conclusion. It is a difficult, but not by any means an impossible, task to weigh Mercury in the celestial balance, and determine his mass in comparison with the other globes of our system. This is a delicate operation, but it leads us through some of the most interesting paths of astronomical discovery. The weight of the planet, as recently determined by Von Asten, is about one twenty-fourth part of the weight of the earth, but the result is more uncertain than the determinations of the mass of any of the other larger planets.
Interest attaching to this Planet—The Unexpectedness of its Appearance—The Evening Star—Visibility in Daylight—Lighted only by the Sun—The Phases of Venus—Why the Crescent is not Visible to the Unaided Eye—Variations in the Apparent Size of the Planet—The Rotation of Venus—Resemblance of Venus to the Earth—The Transit of Venus—Why of such Especial Interest—The Scale of the Solar System—Orbits of the Earth and Venus not in the same Plane—Recurrence of the Transits in Pairs—Appearance of Venus in Transit—Transits of 1874 and 1882—The Early Transits of 1631 and 1639—The Observations of Horrocks and Crabtree—The Announcement of Halley—How the Track of the Planet differs from Different Places—Illustrations of Parallax—Voyage to Otaheite—The Result of Encke—Probable Value of the Sun's Distance—Observations at Dunsink of the Last Transit of Venus—The Question of an Atmosphere to Venus—Other Determinations of the Sun's Distance—Statistics about Venus.
It might, for one reason, have been not inappropriate to have commenced our review of the planetary system by the description of the planet Venus. This body is not especially remarkable for its size, for there are other planets hundreds of times larger. The orbit of Venus is no doubt larger than that of Mercury, but it is much smaller than that of the outer planets. Venus has not even the splendid retinue of minor attendants which gives such dignity and such interest to the mighty planets of our system. Yet the fact still remains that Venus is peerless among the planetary host. We speak not now of celestial bodies only seen in the telescope; we refer to the ordinary observation which detected Venus ages before telescopes were invented.
Who has not been delighted with the view of this glorious object? It is not to be seen at all times. For months together the star of evening is hidden from mortal gaze. Its beauties[Pg 168] are even enhanced by the caprice and the uncertainty which attend its appearance. We do not say that there is any caprice in the movements of Venus, as known to those who diligently consult their almanacs. The movements of the lovely planet are there prescribed with a prosaic detail hardly in harmony with the character usually ascribed to the Goddess of Love. But to those who do not devote particular attention to the stars, the very unexpectedness of its appearance is one of its greatest charms. Venus has not been noticed, not been thought of, for many months. It is a beautifully clear evening; the sun has just set. The lover of nature turns to admire the sunset, as every lover of nature will. In the golden glory of the west a beauteous gem is seen to glitter; it is the evening star—the planet Venus. A few weeks later another beautiful sunset is seen, and now the planet is no longer a point low down in the western glow; it has risen high above the horizon, and continues a brilliant object long after the shades of night have descended. Again, a little later, and Venus has gained its full brilliancy and splendour. All the heavenly host—even Sirius and even Jupiter—must pale before the splendid lustre of Venus, the unrivalled queen of the firmament.
After weeks of splendour, the height of Venus at sunset diminishes, and its lustre begins gradually to decline. It sinks to invisibility, and is forgotten by the great majority of mankind; but the capricious goddess has only moved from one side of the sky to the other. Ere the sun rises, the morning star will be seen in the east. Its splendour gradually augments until it rivals the beauty of the evening star. Then again the planet draws near to the sun, and remains lost to view for many months, until the same cycle of changes recommences, after an interval of a year and seven months.
When Venus is at its brightest it can be easily seen in broad daylight with the unaided eye. This striking spectacle proclaims in an unmistakable manner the unrivalled supremacy of this planet as compared with its fellow-planets and with the fixed stars. Indeed, at this time Venus is from forty[Pg 169] to sixty times more brilliant than any stellar object in the northern heavens.
The beautiful evening star is often such a very conspicuous object that it may seem difficult at first to realise that the body is not self-luminous. Yet it is impossible to doubt that the planet is really only a dark globe, and to that extent resembles our own earth. The brilliance of the planet is not so very much greater than that of the earth on a sunshiny day. The splendour of Venus entirely arises from the reflected light of the sun, in the manner already explained with respect to the moon.
We cannot distinguish the characteristic crescent shape of the planet with the unaided eye, which merely shows a brilliant point too small to possess sensible form. This is to be explained on physiological grounds. The optical contrivances in the eye form an image of the planet on the retina which is necessarily very small. Even when Venus is nearest to the earth the diameter of the planet subtends an angle not much more than one minute of arc. On the delicate membrane a picture of Venus is thus drawn about one six-thousandth part of an inch in diameter. Great as may be the delicacy of the retina, it is not adequate to the perception of form in a picture so minute. The nervous structure, which has been described as the source of vision, forms too coarse a canvas for the reception of the details of this tiny picture. Hence it is that to the unaided eye the brilliant Venus appears merely as a bright spot. Ordinary vision cannot tell what shape it has; still less can it reveal the true beauty of the crescent.
If the diameter of Venus were several times as great as it actually is; were this body, for instance, as large as Jupiter or some of the other great planets, then its crescent could be readily discerned by the unaided eye. It is curious to speculate on what might have been the history of astronomy had Venus only been as large as Jupiter. Were everyone able to see the crescent form without a telescope, it would then have been an elementary and almost obvious truth that Venus must be a dark body revolving round the sun. The analogy[Pg 170] between Venus and our earth would have been at once perceived; and the doctrine which was left to be discovered by Copernicus in comparatively modern times might not improbably have been handed down to us with the other discoveries which have come from the ancient nations of the East.
Perhaps the most perfect drawing of Venus that has been hitherto obtained is that made (Fig. 43) by Professor E.E. Barnard, on 29th May, 1889, with a 12-inch equatorial, at the Lick Observatory, which for this purpose and on this occasion Professor Barnard found to be superior to the 36-inch. The markings shown seem undoubtedly to exist on the planet, and in 1897 Professor Barnard writes: "The circumstances under which this drawing was made are memorable with me, for I never afterwards had such perfect conditions to observe Venus."
In Fig. 44 we show three views of Venus under different aspects. The planet is so much closer to the earth when the crescent is seen, that it appears to be part of a much larger circle than that made by Venus when more nearly full. This drawing shows the different aspects of the globe in their true relative proportions. It is very difficult to perceive distinctly any markings on the brilliantly lighted surface. Sometimes observers have seen spots or other features, and occasionally the pointed extremities of the horns have been irregular, as if to show that the surface of Venus is not smooth. Some observers report having seen white spots at the poles of Venus, in some degree resembling the more conspicuous features of the same character to be seen on Mars.
As it is so very difficult to see any markings on Venus, we are hardly yet able to give a definite answer to the important question as to the period of rotation of this planet round its axis. Various observers during the last two hundred years have from very insufficient data concluded that Venus rotated in about twenty-three hours. Schiaparelli, of Milan, turned his attention to this planet in 1877 and noticed a dark shade and two bright spots, all situated not far from the southern end of the crescent. This most painstaking astronomer watched[Pg 172] these markings for three months, and found that there was no change perceptible in the position which they occupied. This was particularly the case when he continued his watch for some consecutive hours. This fact seemed to show conclusively that Venus could not rotate in twenty-three hours nor in any other short period. Week after week the spots remained unaltered, until Schiaparelli felt convinced that his observations could only be reconciled with a period of rotation between six and nine months. He naturally concluded that the period was 225 days—that is to say, the period which Venus takes to complete one revolution round the sun; in other words, Venus always turns the same face to the sun.
This remarkable result was confirmed by observations made at Nice; but it has been vigorously assailed by several observers, who maintain that their own drawings can only agree with a period about equal to that of the rotation of our own earth. Schiaparelli's result is, however, well supported by the letters of Mr. Lowell. He has published a number of drawings of Venus made with his 24-inch refractor, and he finds that the rotation is performed in the same time as the planet's orbital revolution, the axis of rotation being perpendicular to the plane of the orbit. The markings seen by Mr. Lowell were long and streaky, and they were always visible whenever his own atmospheric conditions were fairly good.
We have seen that the moon revolves so as to keep the same face always turned towards the earth. We have now seen that the planets Venus and Mercury each appear to revolve in such a way that they keep the same face towards the sun. All these phenomena are of profound interest in the higher departments of astronomical research. They are not mere coincidences. They arise from the operation of the tides, in a manner that will be explained in a later chapter.
It happens that our earth and Venus are very nearly equal in bulk. The difference is hardly perceptible, but the earth has a diameter a few miles greater than that of Venus. There are indications of the existence of an atmosphere around Venus, and the evidence of the spectroscope shows that water vapour is there present.
If there be oxygen in the atmosphere of Venus, then it would seem possible that there might be life on that globe not essentially different in character from some forms of life on the earth. No doubt the sun's heat on Venus is greatly in excess of the sun's heat with which we are acquainted, but this is not an insuperable difficulty. We see at present on the earth, life in very hot regions and life in very cold regions. Indeed, with each approach to the Equator we find life more and more exuberant; so that, if water be present on the surface of Venus and if oxygen be a constituent of its atmosphere, we might expect to find in that planet a luxuriant tropical life, of a kind perhaps analogous in some respects to life on the earth.
In our account of the planet Mercury, as well as in the brief description of the hypothetical planet Vulcan, it has been necessary to allude to the phenomena presented by the transit of a planet over the face of the sun. Such an event is always of interest to astronomers, and especially so in the case of Venus. We have in recent years had the opportunity of witnessing two of these rare occurrences. It is perhaps not too much to assert that the transits of 1874 and 1882 have received a degree of attention never before accorded to any astronomical phenomenon.
The transit of Venus cannot be described as a very striking or beautiful spectacle. It is not nearly so fine a sight as a great comet or a shower of shooting stars. Why is it, then, that it is regarded as of so much scientific importance? It is because the phenomenon helps us to solve one of the greatest problems which has ever engaged the mind of man. By the transit of Venus we may determine the scale on which our solar system is constructed. Truly this is a noble problem. Let us dwell upon it for a moment. In the centre of our system we have the sun—a majestic globe more than a million times as large as the earth. Circling round the sun we have the planets, of which our earth is but one. There are hundreds of small planets. There are a few comparable with our earth; there are others vastly surpassing the earth. Besides the planets there are other bodies in our system.[Pg 174] Many of the planets are accompanied by systems of revolving moons. There are hundreds, perhaps thousands, of comets. Each member of this stupendous host moves in a prescribed orbit around the sun, and collectively they form the solar system.
It is comparatively easy to learn the proportions of this system, to measure the relative distances of the planets from the sun, and even the relative sizes of the planets themselves. Peculiar difficulties are, however, experienced when we seek to ascertain the actual size of the system as well as its shape. It is this latter question which the transit of Venus offers us a method of solving.
Look, for instance, at an ordinary map of Europe. We see the various countries laid down with precision; we can tell the courses of the rivers; we can say that France is larger than England, and Russia larger than France; but no matter how perfectly the map be constructed, something else is necessary before we can have a complete conception of the dimensions of the country. We must know the scale on which the map is drawn. The map contains a reference line with certain marks upon it. This line is to give the scale of the map. Its duty is to tell us that an inch on the map corresponds with so many miles on the actual surface. Unless it be supplemented by the scale, the map would be quite useless for many purposes. Suppose that we consulted it in order to choose a route from London to Vienna, we can see at once the direction to be taken and the various towns and countries to be traversed; but unless we refer to the little scale in the corner, the map will not tell how many miles long the journey is to be.
A map of the solar system can be readily constructed. We can draw on it the orbits of some of the planets and of their satellites, and we can include many of the comets. We can assign to the planets and to the orbits their proper proportions. But to render the map quite efficient something more is necessary. We must have the scale which is to tell us how many millions of miles on the heavens correspond to one inch of the map. It is at this point we encounter a difficulty.[Pg 175] There are, however, several ways of solving the problem, though they are all difficult and laborious. The most celebrated method (though far from the best) is that presented on an occasion of the transit of Venus. Herein, then, lies the importance of this rare event. It is one of the best-known means of finding the actual scale on which our system is constructed. Observe the full importance of the problem. Once the scale has been determined, then all is known. We know the size of the sun; we know his distance; we know the bulk of Jupiter, and the distances at which his satellites revolve; we know the dimensions of the comets, and the number of miles to which they recede in their wanderings; we know the velocity of the shooting stars; and we learn the important lesson that our earth is but one of the minor members of the sun's family.
As the path of Venus lies inside that of the earth, and as Venus moves more quickly than the earth, it follows that the earth is frequently passed by the planet, and just at the critical moment it will sometimes happen that the earth, the planet, and the sun lie in the same straight line. We can then see Venus on the face of the sun, and this is the phenomenon which we call the transit of Venus. It is, indeed, quite plain that if the three bodies were exactly in a line, an observer on the earth, looking at the planet, would see it brought out vividly against the brilliant background of the sun.
Considering that the earth is overtaken by Venus once every nineteen months, it might seem that the transits of the planet should occur with corresponding frequency. This is not the case; the transit of Venus is an exceedingly rare occurrence, and a hundred years or more will often elapse without a single one taking place. The rarity of these phenomena arises from the fact that the path of the planet is inclined to the plane of the earth's orbit; so that for half of its path Venus is above the plane of the earth's orbit, and in the other half it is below. When Venus overtakes the earth, the line from the earth to Venus will therefore usually pass over or under the sun. If, however, it should[Pg 176] happen that Venus overtakes the earth at or near either of the points in which the plane of the orbit of Venus passes through that of the earth, then the three bodies will be in line, and a transit of Venus will be the consequence. The rarity of the occurrence of a transit need no longer be a mystery. The earth passes through one of the critical parts every December, and through the other every June. If it happens that the conjunction of Venus occurs on, or close to, June 6th or December 7th, then a transit of Venus will occur at that conjunction, but in no other circumstances.
The most remarkable law with reference to the repetition of the phenomenon is the well-known eight-year interval. The transits may be all grouped together into pairs, the two transits of any single pair being separated by an interval of eight years. For instance, a transit of Venus took place in 1761, and again in 1769. No further transits occurred until those witnessed in 1874 and in 1882. Then, again, comes a long interval, for another transit will not occur until 2004, but it will be followed by another in 2012.
This arrangement of the transits in pairs admits of a very simple explanation. It happens that the periodic time of Venus bears a remarkable relation to the periodic time of the earth. The planet accomplishes thirteen revolutions around the sun in very nearly the same time that the earth requires for eight revolutions. If, therefore, Venus and the earth were in line with the sun in 1874, then in eight years more the earth will again be found in the same place; and so will Venus, for it has just been able to accomplish thirteen revolutions. A transit of Venus having occurred on the first occasion, a transit must also occur on the second.
It is not, however, to be supposed that every eight years the planets will again resume the same position with sufficient precision for a regular eight-year transit interval. It is only approximately true that thirteen revolutions of Venus are coincident with eight revolutions of the earth. Each recurrence of conjunction takes place at a slightly different position of the planets, so that when the two planets came together again in the year 1890 the point of conjunction[Pg 177] was so far removed from the critical point that the line from the earth to Venus did not intersect the sun, and thus, although Venus passed very near the sun, yet no transit took place.
Fig. 45 represents the transit of Venus in 1874. It is taken from a photograph obtained, during the occurrence, by M. Janssen. His telescope was directed towards the sun during the eventful minutes while it lasted, and thus an image of the sun was depicted on the photographic plate placed in the telescope. The lighter circle represents the disc of the sun. On that disc we see the round, sharp image[Pg 178] of Venus, showing the characteristic appearance of the planet during the progress of the transit. The only other features to be noticed are a few of the solar spots, rather dimly shown, and a network of lines which were marked on a glass plate across the field of view of the telescope to facilitate measurements.
The adjoining sketch (Fig. 46) exhibits the course which the planet pursued in its passage across the sun on the two occasions in 1874 and 1882. Our generation has had the good fortune to witness the two occurrences indicated on this picture. The white circle denotes the disc of the sun; the planet encroaches on the white surface, and at first is like a bite out of the sun's margin. Gradually the black spot steals in front of the sun, until, after nearly half an hour, the black disc is entirely visible. Slowly the planet wends its way across, followed by hundreds of telescopes from every accessible part of the globe whence the phenomenon is visible, until at length, in the course of a few hours, it emerges at the other side.
It will be useful to take a brief retrospect of the different transits of Venus of which there is any historical record. They are not numerous. Hundreds of such phenomena have occurred since man first came on the earth. It was not until the approach of the year 1631 that attention began to be directed to the matter, though the transit which undoubtedly occurred in that year was not noticed by anyone. The success of Gassendi in observing the transit of Mercury, to which we have referred in the last chapter, led him to hope that he would be equally fortunate in observing the transit of Venus, which Kepler had also foretold. Gassendi looked at the sun on the 4th, 5th, and 6th December. He looked at it again on the 7th, but he saw no sign of the planet. We now know the reason. The transit of Venus took place during the night, between the 6th and the 7th, and must therefore have been invisible to European observers.
Kepler had not noticed that another transit would occur in 1639. This discovery was made by another astronomer, and it is the one with which the history of the subject may[Pg 179] be said to commence. It was the first occasion on which the phenomenon was ever actually witnessed; nor was it then seen by many. So far as is known, it was witnessed by only two persons.
A young and ardent English astronomer, named Horrocks, had undertaken some computations about the motions of Venus. He made the discovery that the transit of Venus would be repeated in 1639, and he prepared to verify the fact. The sun rose bright on the morning of the day—which happened to be a Sunday. The clerical profession, which Horrocks followed, here came into collision with his desires as an astronomer. He tells us that at nine he was called away by business of the highest importance—referring, no doubt, to his official duties; but the service was quickly performed, and a little before ten he was again on the watch, only to find the brilliant face of the sun without any unusual feature. It was marked with a spot, but nothing that could[Pg 180] be mistaken for a planet. Again, at noon, came an interruption; he went to church, but he was back by one. Nor were these the only impediments to his observations. The sun was also more or less clouded over during part of the day. However, at a quarter past three in the afternoon his clerical work was over; the clouds had dispersed, and he once more resumed his observations. To his intense delight he then saw on the sun the round, dark spot, which was at once identified as the planet Venus. The observations could not last long; it was the depth of winter, and the sun was rapidly setting. Only half an hour was available, but he had made such careful preparations beforehand that it sufficed to enable him to secure some valuable measurements.
Horrocks had previously acquainted his friend, William Crabtree, with the impending occurrence. Crabtree was therefore on the watch, and succeeded in seeing the transit; a striking picture of Crabtree's famous observation is shown in one of the beautiful frescoes in the Town Hall at Manchester. But to no one else had Horrocks communicated the intelligence; as he says, "I hope to be excused for not informing other of my friends of the expected phenomenon, but most of them care little for trifles of this kind, rather preferring their hawks and hounds, to say no worse; and although England is not without votaries of astronomy, with some of whom I am acquainted, I was unable to convey to them the agreeable tidings, having myself had so little notice."
It was not till long afterwards that the full importance of the transit of Venus was appreciated. Nearly a century had rolled away when the great astronomer, Halley (1656–1742), drew attention to the subject. The next transit was to occur in 1761, and forty-five years before that event Halley explained his celebrated method of finding the distance of the sun by means of the transit of Venus.[15] He was then a man sixty years of age; he could have no expectation that he would live to witness the event; but in noble[Pg 181] language he commends the problem to the notice of the learned, and thus addresses the Royal Society of London:—"And this is what I am now desirous to lay before this illustrious Society, which I foretell will continue for ages, that I may explain beforehand to young astronomers, who may, perhaps, live to observe these things, a method by which the immense distance of the sun may be truly obtained.... I recommend it, therefore, again and again to those curious astronomers who, when I am dead, will have an opportunity of observing these things, that they would remember this my admonition, and diligently apply themselves with all their might in making the observations, and I earnestly wish them all imaginable success—in the first place, that they may not by the unseasonable obscurity of a cloudy sky be deprived of this most desirable sight, and then that, having ascertained with more exactness the magnitudes of the planetary orbits, it may redound to their immortal fame and glory." Halley lived to a good old age, but he died nineteen years before the transit occurred.
The student of astronomy who desires to learn how the transit of Venus will tell the distance from the sun must prepare to encounter a geometrical problem of no little complexity. We cannot give to the subject the detail that would be requisite for a full explanation. All we can attempt is to render a general account of the method, sufficient to enable the reader to see that the transit of Venus really does contain all the elements necessary for the solution of the problem.
We must first explain clearly the conception which is known to astronomers by the name of parallax; for it is by parallax that the distance of the sun, or, indeed, the distance of any other celestial body, must be determined. Let us take a simple illustration. Stand near a window whence you can look at buildings, or the trees, the clouds, or any distant objects. Place on the glass a thin strip of paper vertically in the middle of one of the panes. Close the right eye, and note with the left eye the position of the strip of paper relatively to the objects in the background. Then, while still remaining in the same position, close the left eye and[Pg 182] again observe the position of the strip of paper with the right eye. You will find that the position of the paper on the background has changed. As I sit in my study and look out of the window I see a strip of paper, with my right eye, in front of a certain bough on a tree a couple of hundred yards away; with my left eye the paper is no longer in front of that bough, it has moved to a position near the outline of the tree. This apparent displacement of the strip of paper, relatively to the distant background, is what is called parallax.
Move closer to the window, and repeat the observation, and you find that the apparent displacement of the strip increases. Move away from the window, and the displacement decreases. Move to the other side of the room, the displacement is much less, though probably still visible. We thus see that the change in the apparent place of the strip of paper, as viewed with the right eye or the left eye, varies in amount as the distance changes; but it varies in the opposite way to the distance, for as either becomes greater the other becomes less. We can thus associate with each particular distance a corresponding particular displacement. From this it will be easy to infer that if we have the means of measuring the amount of displacement, then we have the means of calculating the distance from the observer to the window.
It is this principle, applied on a gigantic scale, which enables us to measure the distances of the heavenly bodies. Look, for instance, at the planet Venus; let this correspond to the strip of paper, and let the sun, on which Venus is seen in the act of transit, be the background. Instead of the two eyes of the observer, we now place two observatories in distant regions of the earth; we look at Venus from one observatory, we look at it from the other; we measure the amount of the displacement, and from that we calculate the distance of the planet. All depends, then, on the means which we have of measuring the displacement of Venus as viewed from the two different stations. There are various ways of accomplishing this, but the most simple is that originally proposed by Halley.
From the observatory at A Venus seems to pursue the upper of the two tracks shown in the adjoining figure (Fig. 47). From the observatory at B it follows the lower track, and it is for us to measure the distance between the two tracks. This can be accomplished in several ways. Suppose the observer at A notes the time that Venus has occupied in crossing the disc, and that similar observations be made at B. As the track seen from B is the larger, it must follow that the time observed at B will be greater than that at A. When the observations from the different hemispheres are compared, the times observed will enable the lengths of the tracks to be calculated. The lengths being known, their places on the circular disc of the sun are determined, and hence the amount of displacement of Venus in transit is ascertained. Thus it is that the distance of Venus is measured, and the scale of the solar system is known.
 Fig. 47.—To Illustrate the Observation of the Transit of
Venus from Two Localities, A and B, on the Earth.
Fig. 47.—To Illustrate the Observation of the Transit of
Venus from Two Localities, A and B, on the Earth.
The two transits to which Halley's memorable researches[Pg 184] referred occurred in the years 1761 and 1769. The results of the first were not very successful, in spite of the arduous labours of those who undertook the observations. The transit of 1769 is of particular interest, not only for the determination of the sun's distance, but also because it gave rise to the first of the celebrated voyages of Captain Cook. It was to see the transit of Venus that Captain Cook was commissioned to sail to Otaheite, and there, on the 3rd of June, on a splendid day in that exquisite climate, the phenomenon was carefully observed and measured by different observers. Simultaneously with these observations others were obtained in Europe and elsewhere, and from the combination of all the observations an approximate knowledge of the sun's distance was gained. The most complete discussion of these observations did not, however, take place for some time. It was not until the year 1824 that the illustrious Encke computed the distance of the sun, and gave as the definite result 95,000,000 miles.
For many years this number was invariably adopted, and many of the present generation will remember how they were taught in their school-days that the sun was 95,000,000 miles away. At length doubts began to be whispered as to the accuracy of this result. The doubts arose in different quarters, and were presented with different degrees of importance; but they all pointed in one direction, they all indicated that the distance of the sun was not really so great as the result which Encke had obtained. It must be remembered that there are several ways of finding the distance of the sun, and it will be our duty to allude to some other methods later on. It has been ascertained that the result obtained by Encke from the observations made in 1761 and 1769, with instruments inferior to our modern ones, was too great, and that the distance of the sun may probably be now stated at 92,000,000 miles.
I venture to record our personal experience of the last transit of Venus, which we had the good fortune to view from Dunsink Observatory on the afternoon of the 6th of December, 1882.
The morning of the eventful day appeared to be about as unfavourable for a grand astronomical spectacle as could well be imagined. Snow, a couple of inches thick, covered the ground, and more was falling, with but little intermission, all the forenoon. It seemed almost hopeless that a view of the phenomenon could be obtained from that observatory; but it is well in such cases to bear in mind the injunction given to the observers on a celebrated eclipse expedition. They were instructed, no matter what the day should be like, that they were to make all their preparations precisely as they would have done were the sun shining with undimmed splendour. By this advice no doubt many observers have profited; and we acted upon it with very considerable success.
There were at that time at the observatory two equatorials, one of them an old, but tolerably good, instrument, of about six inches aperture; the other the great South equatorial, of twelve inches aperture, already referred to. At eleven o'clock the day looked worse than ever; but we at once proceeded to make all ready. I stationed Mr. Rambaut at the small equatorial, while I myself took charge of the South instrument. The snow was still falling when the domes were opened; but, according to our prearranged scheme, the telescopes were directed, not indeed upon the sun, but to the place where we knew the sun was, and the clockwork was set in motion which carried round the telescopes, still constantly pointing towards the invisible sun. The predicted time of the transit had not yet arrived.
The eye-piece employed on the South equatorial must also receive a brief notice. It will, of course, be obvious that the full glare of the sun has to be greatly mitigated before the eye can view it with impunity. The light from the sun falls upon a piece of transparent glass inclined at a certain angle, and the chief portion of the sun's heat, as well as a certain amount of its light, pass through the glass and are lost. A certain fraction of the light is, however, reflected from the glass, and enters the eye-piece. This light is already much reduced in intensity, but it undergoes as much further[Pg 186] reduction as we please by an ingenious contrivance. The glass which reflects the light does so at what is called the polarising angle, and between the eye-piece and the eye is a plate of tourmaline. This plate of tourmaline can be turned round by the observer. In one position it hardly interferes with the polarised light at all, while in the position at right angles thereto it cuts off nearly the whole of it. By simply adjusting the position of the tourmaline, the observer has it in his power to render the image of any brightness that may be convenient, and thus the observations of the sun can be conducted with the appropriate degree of illumination.
But such appliances seemed on this occasion to be a mere mockery. The tourmaline was all ready, but up to one o'clock not a trace of the sun could be seen. Shortly after one o'clock, however, we noticed that the day was getting lighter; and, on looking to the north, whence the wind and the snow were coming, we saw, to our inexpressible delight, that the clouds were clearing. At length, the sky towards the south began to improve, and at last, as the critical moment approached, we could detect the spot where the sun was becoming visible. But the predicted moment arrived and passed, and still the sun had not broken through the clouds, though every moment the certainty that it would do so became more apparent. The external contact was therefore missed. We tried to console ourselves by the reflection that this was not, after all, a very important phase, and hoped that the internal contact would be more successful.
At length the struggling beams pierced the obstruction, and I saw the round, sharp disc of the sun in the finder, and eagerly glanced at the point on which attention was concentrated. Some minutes had now elapsed since the predicted moment of first contact, and, to my delight, I saw the small notch in the margin of the sun showing that the transit had commenced, and that the planet was then one-third on the sun. But the critical moment had not yet arrived. By the expression "first internal contact" we are to understand the moment when the planet has completely entered on the sun. This first contact was timed to occur twenty-one minutes[Pg 187] later than the external contact already referred to. But the clouds again disappointed our hope of seeing the internal contact. While steadily looking at the exquisitely beautiful sight of the gradual advance of the planet, I became aware that there were other objects besides Venus between me and the sun. They were the snowflakes, which again began to fall rapidly. I must admit the phenomenon was singularly beautiful. The telescopic effect of a snowstorm with the sun as a background I had never before seen. It reminded me of the golden rain which is sometimes seen falling from a flight of sky-rockets during pyrotechnic displays; I would gladly have dispensed with the spectacle, for it necessarily followed that the sun and Venus again disappeared from view. The clouds gathered, the snowstorm descended as heavily as ever, and we hardly dared to hope that we should see anything more; 1 hr. 57 min. came and passed, the first internal contact was over, and Venus had fully entered on the sun. We had only obtained a brief view, and we had not yet been able to make any measurements or other observations that could be of service. Still, to have seen even a part of a transit of Venus is an event to remember for a lifetime, and we felt more delight than can be easily expressed at even this slight gleam of success.
But better things were in store. My assistant came over with the report that he had also been successful in seeing Venus in the same phase as I had. We both resumed our posts, and at half-past two the clouds began to disperse, and the prospect of seeing the sun began to improve. It was now no question of the observations of contact. Venus by this time was well on the sun, and we therefore prepared to make observations with the micrometer attached to the eye-piece. The clouds at length dispersed, and at this time Venus had so completely entered on the sun that the distance from the edge of the planet to the edge of the sun was about twice the diameter of the planet. We measured the distance of the inner edge of Venus from the nearest limb of the sun. These observations were repeated as frequently as possible, but it should be added that they were only made with very[Pg 188] considerable difficulty. The sun was now very low, and the edges of the sun and of Venus were by no means of that steady character which is suitable for micrometrical measurement. The margin of the luminary was quivering, and Venus, though no doubt it was sometimes circular, was very often distorted to such a degree as to make the measures very uncertain.
We succeeded in obtaining sixteen measures altogether; but the sun was now getting low, the clouds began again to interfere, and we saw that the pursuit of the transit must be left to the thousands of astronomers in happier climes who had been eagerly awaiting it. But before the phenomena had ceased I spared a few minutes from the somewhat mechanical work at the micrometer to take a view of the transit in the more picturesque form which the large field of the finder presented. The sun was already beginning to put on the ruddy hues of sunset, and there, far in on its face, was the sharp, round, black disc of Venus. It was then easy to sympathise with the supreme joy of Horrocks, when, in 1639, he for the first time witnessed this spectacle. The intrinsic interest of the phenomenon, its rarity, the fulfilment of the prediction, the noble problem which the transit of Venus helps us to solve, are all present to our thoughts when we look at this pleasing picture, a repetition of which will not occur again until the flowers are blooming in the June of A.D. 2004.
The occasion of a transit of Venus also affords an opportunity of studying the physical nature of the planet, and we may here briefly indicate the results that have been obtained. In the first place, a transit will throw some light on the question as to whether Venus is accompanied by a satellite. If Venus were attended by a small body in close proximity, it would be conceivable that in ordinary circumstances the brilliancy of the planet would obliterate the feeble beam of rays from the minute companion, and thus the satellite would remain undiscovered. It was therefore a matter of great interest to scrutinise the vicinity of the planet while in the act of transit. If a satellite existed—and the existence of one or more of such bodies has often been suspected—then it would[Pg 189] be capable of detection against the brilliant background of the sun. Special attention was directed to this point during the recent transits, but no satellite of Venus was to be found. It seems, therefore, to be very unlikely that Venus can be attended by any companion globe of appreciable dimensions.
The observations directed to the investigation of the atmosphere surrounding Venus have been more successful. If the planet were devoid of an atmosphere, then it would be totally invisible just before commencing to enter on the sun, and would relapse into total invisibility as soon as it had left the sun. The observations made during the transits are not in conformity with such suppositions. Special attention has been directed to this point during the recent transits. The result has been very remarkable, and has proved in the most conclusive manner the existence of an atmosphere around Venus. As the planet gradually moved off the sun, the circular edge of the planet extending out into the darkness was seen to be bounded by a circular arc of light, and Dr. Copeland, who observed this transit in very favourable circumstances, was actually able to follow the planet until it had passed entirely away from the sun, at which time the globe, though itself invisible, was distinctly marked by the girdle of light by which it was surrounded. This luminous circle is inexplicable save by the supposition that the globe of Venus is surrounded by an atmospheric shell in the same way as the earth.
It may be asked, what is the advantage of devoting so much time and labour to a celestial phenomenon like the transit of Venus which has so little bearing on practical affairs? What does it matter whether the sun be 95,000,000 miles off, or whether it be only 93,000,000, or any other distance? We must admit at once that the enquiry has but a slender bearing on matters of practical utility. No doubt a fanciful person might contend that to compute our nautical almanacs with perfect accuracy we require a precise knowledge of the distance of the sun. Our vast commerce depends on skilful navigation, and one factor necessary for success is the reliability of the "Nautical Almanac." The increased[Pg 190] perfection of the almanac must therefore bear some relation to increased perfection in navigation. Now, as good authorities tell us that in running for a harbour on a tempestuous night, or in other critical emergencies, even a yard of sea-room is often of great consequence, so it may conceivably happen that to the infinitesimal influence of the transit of Venus on the "Nautical Almanac" is due the safety of a gallant vessel.
But the time, the labour, and the money expended in observing the transit of Venus are really to be defended on quite different grounds. We see in it a fruitful source of information. It tells us the distance of the sun, which is the foundation of all the great measurements of the universe. It gratifies the intellectual curiosity of man by a view of the true dimensions of the majestic solar system, in which the earth is seen to play a dignified, though still subordinate, part; and it leads us to a conception of the stupendous scale on which the universe is constructed.
It is not possible for us, with a due regard to the limits of this volume, to protract any longer our discussion of the transit of Venus. When we begin to study the details of the observations, we are immediately confronted with a multitude of technical and intricate matters. Unfortunately, there are very great difficulties in making the observations with the necessary precision. The moments when Venus enters on and leaves the solar disc cannot be very accurately observed, partly owing to a peculiar optical illusion known as "the black drop," whereby Venus seems to cling to the sun's limb for many seconds, partly owing to the influence of the planet's atmosphere, which helps to make the observed time of contact uncertain. These circumstances make it difficult to determine the distance of the sun from observations of transits of Venus with the accuracy which modern science requires. It seems therefore likely that the final determination of the sun's distance will be obtained in quite a different manner. This will be explained in Chapter XI., and hence we feel the less reluctance in passing any from the consideration of the transit of Venus as a method of celestial surveying.
We must now close our description of this lovely planet;[Pg 191] but before doing so, let us add—or in some cases repeat—a few statistical facts as to the size and the dimensions of the planet and its orbit.
The diameter of Venus is about 7,660 miles, and the planet shows no measurable departure from the globular form, though we can hardly doubt that its polar diameter must really be somewhat shorter than the equatorial diameter. This diameter is only about 258 miles less than that of the earth. The mass of Venus is about three-quarters of the mass of the earth; or if, as is more usual, we compare the mass of Venus with the sun, it is to be represented by the fraction 1 divided by 425,000. It is to be observed that the mass of Venus is not quite so great in comparison with its bulk as might have been expected. The density of this planet is about 0·850 of that of the earth. Venus would weigh 4·81 times as much as a globe of water of equal size. The gravitation at its surface will, to a slight extent, be less than the gravitation at the surface of the earth. A body here falls sixteen feet in a second; a body let fall at the surface of Venus would fall about three feet less. It seems not unlikely that the time of rotation of Venus may be equal to the period of its revolution around the sun.
The orbit of Venus is remarkable for the close approach which it makes to a circle. The greatest distance of this planet from the sun does not exceed the least distance by one per cent. Its mean distance from the sun is about 67,000,000 miles, and the movement in the orbit amounts to a mean velocity of nearly 22 miles per second, the entire journey being accomplished in 224·70 days.
The Earth is a great Globe—How the Size of the Earth is Measured—The Base Line—The Latitude found by the Elevation of the Pole—A Degree of the Meridian—The Earth not a Sphere—The Pendulum Experiment—Is the Motion of the Earth slow or fast?—Coincidence of the Axis of Rotation and the Axis of Figure—The Existence of Heat in the Earth—The Earth once in a Soft Condition—Effects of Centrifugal Force—Comparison with the Sun and Jupiter—The Protuberance of the Equator—The Weighing of the Earth—Comparison between the Weight of the Earth and an equal Globe of Water—Comparison of the Earth with a Leaden Globe—The Pendulum—Use of the Pendulum in Measuring the Intensity of Gravitation—The Principle of Isochronism—Shape of the Earth measured by the Pendulum.
That the earth must be a round body is a truth immediately suggested by simple astronomical considerations. The sun is round, the moon is round, and telescopes show that the planets are round. No doubt comets are not round, but then a comet seems to be in no sense a solid body. We can see right through one of these frail objects, and its weight is too small for our methods of measurement to appreciate. If, then, all the solid bodies we can see are round globes, is it not likely that the earth is a globe also? But we have far more direct information than mere surmise.
There is no better way of actually seeing that the surface of the ocean is curved than by watching a distant ship on the open sea. When the ship is a long way off and is still receding, its hull will gradually disappear, while the masts will remain visible. On a fine summer's day we can often see the top of the funnel of a steamer appearing above the sea, while the body of the steamer is below. To see this best the eye should be brought as close as possible to the surface of the sea. If the sea were perfectly flat, there would be nothing to obscure[Pg 193] the body of the vessel, and it would therefore be visible so long as the funnel remains visible. If the sea be really curved, the protuberant part intercepts the view of the hull, while the funnel is still to be seen.
We thus learn how the sea is curved at every part, and therefore it is natural to suppose that the earth is a sphere. When we make more careful measurements we find that the globe is not perfectly round. It is flattened to some extent at each of the poles. This may be easily illustrated by an indiarubber ball, which can be compressed on two opposite sides so as to bulge out at the centre. The earth is similarly flattened at the poles, and bulged out at the equator. The divergence of the earth from the truly globular form is, however, not very great, and would not be noticed without very careful measurements.
The determination of the size of the earth involves operations of no little delicacy. Very much skill and very much labour have been devoted to the work, and the dimensions of the earth are known with a high degree of accuracy, though perhaps not with all the precision that we may ultimately hope to attain. The scientific importance of an accurate measurement of the earth can hardly be over-estimated. The radius of the earth is itself the unit in which many other astronomical magnitudes are expressed. For example, when observations are made with the view of finding the distance of the moon, the observations, when discussed and reduced, tell us that the distance of the moon is equal to fifty-nine times the equatorial radius of the earth. If we want to find the distance of the moon in miles, we require to know the number of miles in the earth's radius.
A level part of the earth's surface having been chosen, a line a few miles long is measured. This is called the base, and as all the subsequent measures depend ultimately on the base, it is necessary that this measurement shall be made with scrupulous accuracy. To measure a line four or five miles long with such precision as to exclude any errors greater than a few inches demands the most minute precautions. We do not now enter upon a description of the operations that are[Pg 194] necessary. It is a most laborious piece of work, and many ponderous volumes have been devoted to the discussion of the results. But when a few base lines have been obtained in different places on the earth's surface, the measuring rods are to be laid aside, and the subsequent task of the survey of the earth is to be conducted by the measurement of angles from one station to another and trigonometrical calculations based thereon. Starting from a base line a few miles long, distances of greater length are calculated, until at length stretches 100 miles long, or even more, can be accomplished. It is thus possible to find the length of a long line running due north and south.
So far the work has been merely that of the terrestrial surveyor. The distance thus ascertained is handed over to the astronomer to deduce from it the dimensions of the earth. The astronomer fixes his observatory at the northern end of the long line, and proceeds to determine his latitude by observation. There are various ways by which this can be accomplished. They will be found fully described in works on practical astronomy. We shall here only indicate in a very brief manner the principle on which such observations are to be made.
Everyone ought to be familiar with the Pole Star, which, though by no means the most brilliant, is probably the most important star in the whole heavens. In these latitudes we are accustomed to find the Pole Star at a considerable elevation, and there we can invariably find it, always in the same place in the northern sky. But suppose we start on a voyage to the southern hemisphere: as we approach the equator we find, night after night, the Pole Star coming closer to the horizon. At the equator it is on the horizon; while if we cross the line, we find on entering the southern hemisphere that this useful celestial body has become invisible. This is in itself sufficient to show us that the earth cannot be the flat surface that untutored experience seems to indicate.
On the other hand, a traveller leaving England for Norway observes that the Pole Star is every night higher in the heavens than he has been accustomed to see it. If he extend[Pg 195] his journey farther north, the same object will gradually rise higher and higher, until at length, when approaching the pole of the earth, the Pole Star is high up over his head. We are thus led to perceive that the higher our latitude, the higher, in general, is the elevation of the Pole Star. But we cannot use precise language until we replace the twinkling point by the pole of the heavens itself. The pole of the heavens is near the Pole Star, which itself revolves around the pole of the heavens, as all the other stars do, once every day. The circle described by the Pole Star is, however, so small that, unless we give it special attention, the motion will not be perceived. The true pole is not a visible point, but it is capable of being accurately defined, and it enables us to state with the utmost precision the relation between the pole and the latitude. The statement is, that the elevation of the pole above the horizon is equal to the latitude of the place.
The astronomer stationed at one end of the long line measures the elevation of the pole above the horizon. This is an operation of some delicacy. In the first place, as the pole is invisible, he has to obtain its position indirectly. He measures the altitude of the Pole Star when that altitude is greatest, and repeats the operation twelve hours later, when the altitude of the Pole Star is least; the mean between the two, when corrected in various ways which it is not necessary for us now to discuss, gives the true altitude of the pole. Suffice it to say that by such operations the latitude of one end of the line is determined. The astronomer then, with all his equipment of instruments, moves to the other end of the line. He there repeats the process, and he finds that the pole has now a different elevation, corresponding to the different latitude. The difference of the two elevations thus gives him an accurate measure of the number of degrees and fractional parts of a degree between the latitudes of the two stations. This can be compared with the actual distance in miles between the two stations, which has been ascertained by the trigonometrical survey. A simple calculation will then show the number of miles and fractional parts of a mile[Pg 196] corresponding to one degree of latitude—or, as it is more usually expressed, the length of a degree of the meridian.
This operation has to be repeated in different parts of the earth—in the northern hemisphere and in the southern, in high latitudes and in low. If the sea-level over the entire earth were a perfect sphere, an important consequence would follow—the length of a degree of the meridian would be everywhere the same. It would be the same in Peru as in Sweden, the same in India as in England. But the lengths of the degrees are not all the same, and hence we learn that our earth is not really a sphere. The measured lengths of the degrees enable us to see to what extent the shape of the earth departs from a perfect sphere. Near the pole the length of a degree is longer than near the equator. This shows that the earth is flattened at the poles and protuberant at the equator, and it provides the means by which we may calculate the actual lengths of the polar and the equatorial axes. In this way the equatorial diameter has been found equal to 7,927 miles, while the polar diameter is 27 miles shorter.
The polar axis of the earth may be defined as the diameter about which the earth rotates. This axis intersects the surface at the north and south poles. The time which the earth occupies in making a complete rotation around this axis is called a sidereal day. The sidereal day is a little shorter than the ordinary day, being only 23 hours, 56 minutes, and 4 seconds. The rotation is performed just as if a rigid axis passed through the centre of the earth; or, to use the old and homely illustration, the earth rotates just as a ball of worsted may be made to rotate around a knitting-needle thrust through its centre.
It is a noteworthy circumstance that the axis about which the earth rotates occupies a position identical with that of the shortest diameter of the earth as found by actual surveying. This is a coincidence which would be utterly inconceivable if the shape of the earth was not in some way physically connected with the fact that the earth is rotating. What connection can then be traced? Let us enquire into the[Pg 197] subject, and we shall find that the shape of the earth is a consequence of its rotation.
The earth at the present time is subject, at various localities, to occasional volcanic outbreaks. The phenomena of such eruptions, the allied occurrence of earthquakes, the well-known fact that the heat increases the deeper we descend into the earth, the existence of hot springs, the geysers found in Iceland and elsewhere, all testify to the fact that heat exists in the interior of the earth. Whether that heat be, as some suppose, universal in the interior of the earth, or whether it be merely local at the several places where its manifestations are felt, is a matter which need not now concern us. All that is necessary for our present purpose is the admission that heat is present to some extent.
This internal heat, be it much or little, has obviously a different origin from the heat which we know on the surface. The heat we enjoy is derived from the sun. The internal heat cannot have been derived from the sun; its intensity is far too great, and there are other insuperable difficulties attending the supposition that it has come from the sun. Where, then, has this heat come from? This is a question which at present we can hardly answer—nor, indeed, does it much concern our argument that we should answer it. The fact being admitted that the heat is there, all that we require is to apply one or two of the well-known thermal laws to the interpretation of the facts. We have first to consider the general principle by which heat tends to diffuse itself and spread away from its original source. The heat, deep-seated in the interior of the earth, is transmitted through the superincumbent rocks, and slowly reaches the surface. It is true that the rocks and materials with which our earth is covered are not good conductors of heat; most of them are, indeed, extremely inefficient in this way; but, good or bad, they are in some shape conductors, and through them the heat must creep to the surface.
It cannot be urged against this conclusion that we do not feel this heat. A few feet of brickwork will so confine the heat of a mighty blast furnace that but little will escape[Pg 198] through the bricks; but some heat does escape, and the bricks have never been made, and never could be made, which would absolutely intercept all the heat. If a few feet of brickwork can thus nearly mask the heat of a furnace, cannot some scores of miles of rock nearly mask the heat in the depths of the earth, even though that heat were seven times hotter than the mightiest furnace that ever existed? The heat would escape slowly, and perhaps imperceptibly, but, unless all our knowledge of nature is a delusion, no rocks, however thick, can prevent, in the course of time, the leakage of the heat to the surface. When this heat arrives at the surface of the earth it must, in virtue of another thermal law, gradually radiate away and be lost to the earth.
It would lead us too far to discuss fully the objections which may perhaps be raised against what we have here stated. It is often said that the heat in the interior of the earth is being produced by chemical combination or by mechanical process, and thus that the heat may be constantly renewed as fast or even faster than it escapes. This, however, is more a difference in form than in substance. If heat be produced in the way just supposed (and there can be no doubt that there may be such an origin for some of the heat in the interior of the globe) there must be a certain expenditure of chemical or mechanical energies that produces a certain exhaustion. For every unit of heat which escapes there will either be a loss of an unit of heat from the globe, or, what comes nearly to the same thing, a loss of an unit of heat-making power from the chemical or the mechanical energies. The substantial result is the same; the heat, actual or potential, of the earth must be decreasing. It should, of course, be observed that a great part of the thermal losses experienced by the earth is of an obvious character, and not dependent upon the slow processes of conduction. Each outburst of a volcano discharges a stupendous quantity of heat, which disappears very speedily from the earth; while in the hot springs found in so many places there is a perennial discharge of the same kind, which in the course of years attains enormous proportions.
The earth is thus losing heat, while it never acquires any fresh supplies of the same kind to replace the losses. The consequence is obvious; the interior of the earth must be growing colder. No doubt this is an extremely slow process; the life of an individual, the life of a nation, perhaps the life of the human race itself, has not been long enough to witness any pronounced change in the store of terrestrial heat. But the law is inevitable, and though the decline in heat may be slow, yet it is continuous, and in the lapse of ages must necessarily produce great and important results.
It is not our present purpose to offer any forecast as to the changes which must necessarily arise from this process. We wish at present rather to look back into past time and see what consequences we may legitimately infer. Such intervals of time as we are familiar with in ordinary life, or even in ordinary history, are for our present purpose quite inappreciable. As our earth is daily losing internal heat, or the equivalent of heat, it must have contained more heat yesterday than it does to-day, more last year than this year, more twenty years ago than ten years ago. The effect has not been appreciable in historic time; but when we rise from hundreds of years to thousands of years, from thousands of years to hundreds of thousands of years, and from hundreds of thousands of years to millions of years, the effect is not only appreciable, but even of startling magnitude.
There must have been a time when the earth contained much more heat than at present. There must have been a time when the surface of the earth was sensibly hot from this source. We cannot pretend to say how many thousands or millions of years ago this epoch must have been; but we may be sure that earlier still the earth was even hotter, until at length we seem to see the temperature increase to a red heat, from a red heat we look back to a still earlier age when the earth was white hot, back further till we find the surface of our now solid globe was actually molten. We need not push the retrospect any further at present, still less is it necessary for us to attempt to assign the probable origin of that heat. This, it will be observed, is not required[Pg 200] in our argument. We find heat now, and we know that heat is being lost every day. From this the conclusion that we have already drawn seems inevitable, and thus we are conducted back to some remote epoch in the abyss of time past when our solid earth was a globe molten and soft throughout.
A dewdrop on the petal of a flower is nearly globular; but it is not quite a globe, because the gravitation presses it against the flower and somewhat distorts the shape. A falling drop of rain is a globe; a drop of oil suspended in a liquid with which it does not mix forms a globe. Passing from small things to great things, let us endeavour to conceive a stupendous globe of molten matter. Let that globe be as large as the earth, and let its materials be so soft as to obey the forces of attraction exerted by each part of the globe on all the other parts. There can be no doubt as to the effect of these attractions; they would tend to smooth down any irregularities on the surface just in the same way as the surface of the ocean is smooth when freed from the disturbing influences of the wind. We might, therefore, expect that our molten globe, isolated from all external interference, would assume the form of a sphere.
But now suppose that this great sphere, which we have hitherto assumed to be at rest, is made to rotate round an axis passing through its centre. We need not suppose that this axis is a material object, nor are we concerned with any supposition as to how the velocity of rotation was caused. We can, however, easily see what the consequence of the rotation would be. The sphere would become deformed, the centrifugal force would make the molten body bulge out at the equator and flatten down at the poles. The greater the velocity of rotation the greater would be the bulging. To each velocity of rotation a certain degree of bulging would be appropriate. The molten earth thus bulged out to an extent which was dependent upon the fact that it turned round once a day. Now suppose that the earth, while still rotating, commences to pass from the liquid to the solid state. The form which the earth would assume on consolidation would, no doubt, be very irregular on the surface; it would be irregular[Pg 201] in consequence of the upheavals and the outbursts incident to the transformation of so mighty a mass of matter; but irregular though it be, we can be sure that, on the whole, the form of the earth's surface would coincide with the shape which it had assumed by the movement of rotation. Hence we can explain the protuberant form of the equator of the earth, and we can appeal to that form in corroboration of the view that this globe was once in a soft or molten condition.
The argument may be supported and illustrated by comparing the shape of our earth with the shapes of some of the other celestial bodies. The sun, for instance, seems to be almost a perfect globe. No measures that we can make show that the polar diameter of the sun is shorter than the equatorial diameter. But this is what we might have expected. No doubt the sun is rotating on its axis, and, as it is the rotation that causes the protuberance, why should not the rotation have deformed the sun like the earth? The probability is that a difference really does exist between the two diameters of the sun, but that the difference is too small for us to measure. It is impossible not to connect this with the slowness of the sun's rotation. The sun takes twenty-five days to complete a rotation, and the protuberance appropriate to so low a velocity is not appreciable.
On the other hand, when we look at one of the quickly-rotating planets, we obtain a very different result. Let us take the very striking instance which is presented in the great planet Jupiter. Viewed in the telescope, Jupiter is at once seen not to be a globe. The difference is so conspicuous that accurate measures are not necessary to show that the polar diameter of Jupiter is shorter than the equatorial diameter. The departure of Jupiter from the truly spherical shape is indeed much greater than the departure of the earth. It is impossible not to connect this with the much more rapid rotation of Jupiter. We shall presently have to devote a chapter to the consideration of this splendid orb. We may, however, so far anticipate what we shall then say as to state that the time of Jupiter's rotation is under ten hours, and this notwithstanding the fact that Jupiter is more than one[Pg 202] thousand times greater than the earth. His enormously rapid rotation has caused him to bulge out at the equator to a remarkable extent.
The survey of our earth and the measurement of its dimensions having been accomplished, the next operation for the astronomer is the determination of its weight. Here, indeed, is a problem which taxes the resources of science to the very uttermost. Of the interior of the earth we know little—I might almost say we know nothing. No doubt we sink deep mines into the earth. These mines enable us to penetrate half a mile, or even a whole mile, into the depths of the interior. But this is, after all, only a most insignificant attempt to explore the interior of the earth. What is an advance of one mile in comparison with the distance to the centre of the earth? It is only about one four-thousandth part of the whole. Our knowledge of the earth merely reaches to an utterly insignificant depth below the surface, and we have not a conception of what may be the nature of our globe only a few miles below where we are standing. Seeing, then, our almost complete ignorance of the solid contents of the earth, does it not seem a hopeless task to attempt to weigh the entire globe? Yet that problem has been solved, and the result is known—not, indeed, with the accuracy attained in other astronomical researches, but still with tolerable approximation.
It is needless to enunciate the weight of the earth in our ordinary units. The enumeration of billions of tons does not convey any distinct impression. It is a far more natural course to compare the mass of the earth with that of an equal globe of water. We should be prepared to find that our earth was heavier than a like volume of water. The rocks which form its surface are heavier, bulk for bulk, than the oceans which repose on those rocks. The abundance of metals in the earth, the gradual increase in the density of the earth, which must arise from the enormous pressure at great depths—all these considerations will prepare us to learn that the earth is very much heavier than a globe of water of equal size.
Newton supposed that the earth was between five and six times as heavy as an equal bulk of water. Nor is it hard to see that such a suggestion is plausible. The rocks and materials on the surface are usually about two or three times as heavy as water, but the density of the interior must be much greater. There is good reason to believe that down in the remote depths of the earth there is a very large proportion of iron. An iron earth would weigh about seven times as much as an equal globe of water. We are thus led to see that the earth's weight must be probably more than three, and probably less than seven, times an equal globe of water; and hence, in fixing the density between five and six, Newton adopted a result plausible at the moment, and since shown to be probably correct. Several methods have been proposed by which this important question can be solved with accuracy. Of all these methods we shall here only describe one, because it illustrates, in a very remarkable manner, the law of universal gravitation.
In the chapter on Gravitation it was pointed out that the intensity of this force between two masses of moderate dimensions was extremely minute, and the difficulty in weighing the earth arises from this cause. The practical application of the process is encumbered by multitudinous details, which it will be unnecessary for us to consider at present. The principle of the process is simple enough. To give definiteness to our description, let us conceive a large globe about two feet in diameter; and as it is desirable for this globe to be as heavy as possible, let us suppose it to be made of lead. A small globe brought near the large one is attracted by the force of gravitation. The amount of this attraction is extremely small, but, nevertheless, it can be measured by a refined process which renders extremely small forces sensible. The intensity of the attraction depends both on the masses of the globes and on their distance apart, as well as on the force of gravitation. We can also readily measure the attraction of the earth upon the small globe. This is, in fact, nothing more nor less than the weight of the small globe in the[Pg 204] ordinary acceptation of the word. We can thus compare the attraction exerted by the leaden globe with the attraction exerted by the earth.
If the centre of the earth and the centre of the leaden globe were at the same distance from the attracted body, then the intensity of their attractions would give at once the ratio of their masses by simple proportion. In this case, however, matters are not so simple: the leaden ball is only distant by a few inches from the attracted ball, while the centre of the earth's attraction is nearly 4,000 miles away at the centre of the earth. Allowance has to be made for this difference, and the attraction of the leaden sphere has to be reduced to what it would be were it removed to a distance of 4,000 miles. This can fortunately be effected by a simple calculation depending upon the general law that the intensity of gravitation varies inversely as the square of the distance. We can thus, partly by calculation and partly by experiment, compare the intensity of the attraction of the leaden sphere with the attraction of the earth. It is known that the attractions are proportional to the masses, so that the comparative masses of the earth and of the leaden sphere have been measured; and it has been ascertained that the earth is about half as heavy as a globe of lead of equal size would be. We may thus state finally that the mass of the earth is about five and a half times as great as the mass of a globe of water equal to it in bulk.
In the chapter on Gravitation we have mentioned the fact that a body let fall near the surface of the earth drops through sixteen feet in the first second. This distance varies slightly at different parts of the earth. If the earth were a perfect sphere, then the attraction would be the same at every part, and the body would fall through the same distance everywhere. The earth is not round, so the distance which the body falls in one second differs slightly at different places. At the pole the radius of the earth is shorter than at the equator, and accordingly the attraction of the earth at the pole is greater than at the equator. Had we accurate measurements showing the distance a body would fall in one second[Pg 205] both at the pole and at the equator, we should have the means of ascertaining the shape of the earth.
It is, however, difficult to measure correctly the distance a body will fall in one second. We have, therefore, been obliged to resort to other means for determining the force of attraction of the earth at the equator and other accessible parts of its surface. The methods adopted are founded on the pendulum, which is, perhaps, the simplest and certainly one of the most useful of philosophical instruments. The ideal pendulum is a small and heavy weight suspended from a fixed point by a fine and flexible wire. If we draw the pendulum aside from its vertical position and then release it, the weight will swing to and fro.
For its journey to and fro the pendulum requires a small period of time. It is very remarkable that this period does not depend appreciably on the length of the circular arc through which the pendulum swings. To verify this law we suspend another pendulum beside the first, both being of the same length. If we draw both pendulums aside and then release them, they swing together and return together. This might have been expected. But if we draw one pendulum a great deal to one side, and the other only a little, the two pendulums still swing sympathetically. This, perhaps, would not have been expected. Try it again, with even a still greater difference in the arc of vibration, and still we see the two weights occupy the same time for the swing.
We can vary the experiment in another way. Let us change the weights on the pendulums, so that they are of unequal size, though both of iron. Shall we find any difference in the periods of vibration? We try again: the period is the same as before; swing them through different arcs, large or small, the period is still the same. But it may be said that this is due to the fact that both weights are of the same material. Try it again, using a leaden weight instead of one of the iron weights; the result is identical. Even with a ball of wood the period of oscillation is the same as that of the ball of iron, and this is true no matter what be the arc through which the vibration takes place.[Pg 206]
If, however, we change the length of the wire by which the weight is supported, then the period will not remain unchanged. This can be very easily illustrated. Take a short pendulum with a wire only one-fourth of the length of that of the long one; suspend the two close together, and compare the periods of vibration of the short pendulum with that of the long one, and we find that the former has a period only half that of the latter. We may state the result generally, and say that the time of vibration of a pendulum is proportional to the square root of its length. If we quadruple the length of the suspending cord we double the time of its vibration; if we increase the length of the pendulum ninefold, we increase its period of vibration threefold.
It is the gravitation of the earth which makes the pendulum swing. The greater the attraction, the more rapidly will the pendulum oscillate. This may be easily accounted for. If the earth pulls the weight down very vigorously, the time will be short; if the power of the earth's attraction be lessened, then it cannot pull the weight down so quickly, and the period will be lengthened.
The time of vibration of the pendulum can be determined with great accuracy. Let it swing for 10,000 oscillations, and measure the time that these oscillations have consumed. The arc through which the pendulum swings may not have remained quite constant, but this does not appreciably affect the time of its oscillation. Suppose that an error of a second is made in the determination of the time of 10,000 oscillations; this will only entail an error of the ten-thousandth part of the second in the time of a single oscillation, and will afford a correspondingly accurate determination of the force of gravity at the place where the experiment was made.
Take a pendulum to the equator. Let it perform 10,000 oscillations, and determine carefully the time that these oscillations have required. Bring the same pendulum to another part of the earth, and repeat the experiment. We have thus a means of comparing the gravitation at the two places. There are, no doubt, a multitude of precautions[Pg 207] to be observed which need not here concern us. It is not necessary to enter into details as to the manner in which the motion of the pendulum is to be sustained, nor as to the effect of changes of temperature in the alteration of its length. It will suffice for us to see how the time of the pendulum's swing can be measured accurately, and how from that measurement the intensity of gravitation can be calculated.
The pendulum thus enables us to make a gravitational survey of the surface of the earth with the highest degree of accuracy. We cannot, however, infer that gravity alone affects the oscillations of the pendulum. We have seen how the earth rotates on its axis, and we have attributed the bulging of the earth at the equator to this influence. But the centrifugal force arising from the rotation has the effect of decreasing the apparent weight of bodies, and the change is greatest at the equator, and lessens gradually as we approach the poles. From this cause alone the attraction of the pendulum at the equator is less than elsewhere, and therefore the oscillations of the pendulum will take a longer time there than at other localities. A part of the apparent change in gravitation is accordingly due to the centrifugal force; but there is, in addition, a real alteration.
In a work on astronomy it does not come within our scope to enter into further detail on the subject of our planet. The surface of the earth, its contour and its oceans, its mountain chains and its rivers, are for the physical geographer; while its rocks and their contents, its volcanoes and its earthquakes, are to be studied by the geologists and the physicists.
Our nearer Neighbours in the Heavens—Surface of Mars can be Examined in the Telescope—Remarkable Orbit of Mars—Resemblance of Mars to a Star—Meaning of Opposition—The Eccentricity of the Orbit of Mars—Different Oppositions of Mars—Apparent Movements of the Planet—Effect of the Earth's Movement—Measurement of the Distance of Mars—Theoretical Investigation of the Sun's Distance—Drawings of the Planet—Is there Snow on Mars?—The Rotation of the Planet—Gravitation on Mars—Has Mars any Satellites?—Prof. Asaph Hall's great Discovery—The Revolutions of the Satellites—Deimos and Phobos—"Gulliver's Travels."
The special relation in which we stand to one planet of our system has necessitated a somewhat different treatment of that globe from the treatment appropriate to the others. We discussed Mercury and Venus as distant objects known chiefly by telescopic research, and by calculations of which astronomical observations were the foundation. Our knowledge of the earth is of a different character, and attained in a different way. Yet it was necessary for symmetry that we should discuss the earth after the planet Venus, in order to give to the earth its true position in the solar system. But now that the earth has been passed in our outward progress from the sun, we come to the planet Mars; and here again we resume, though in a somewhat modified form, the methods that were appropriate to Venus and to Mercury.
Venus and Mars have, from one point of view, quite peculiar claims on our attention. They are our nearest planetary neighbours, on either side. We may naturally expect to learn more of them than of the other planets farther off. In the case of Venus, however, this anticipation can hardly be realised, for, as we have already pointed[Pg 209] out, its dense atmosphere prevents us from making a satisfactory telescopic examination. When we turn to our other planetary neighbour, Mars, we are enabled to learn a good deal with regard to his appearance. Indeed, with the exception of the moon, we are better acquainted with the details of the surface of Mars than with those of any other celestial body.
This beautiful planet offers many features for consideration besides those presented by its physical structure. The orbit of Mars is one of remarkable proportions, and it was by the observations of this orbit that the celebrated laws of Kepler were discovered. During the occasional approaches of Mars to the earth it has been possible to measure its distance with accuracy, and thus another method of finding the sun's distance has arisen which, to say the least, may compete in precision with that afforded by the transit of Venus. It must also be observed that the greatest achievement in pure telescopic research which this century has witnessed was that of the discovery of the satellites of Mars.
To the unaided eye this planet generally appears like a star of the first magnitude. It is usually to be distinguished by its ruddy colour, but the beginner in astronomy cannot rely on its colour only for the identification of Mars. There are several stars nearly, if not quite, as ruddy as this globe. The bright star Aldebaran, the brightest star in the constellation of the Bull, has often been mistaken for the planet. It often resembles Betelgeuze, a brilliant point in the constellation of Orion. Mistakes of this kind will be impossible if the learner has first studied the principal constellations and the more brilliant stars. He will then find great interest in tracing out the positions of the planets, and in watching their ceaseless movements.
The position of each orb can always be ascertained from the almanac. Sometimes the planet will be too near the sun to be visible. It will rise with the sun and set with the sun, and consequently will not be above the horizon during the night. The best time for seeing one of the planets situated like Mars will be during what is called its opposition. This state of things occurs when the earth intervenes directly between the planet and the sun. In this case, the distance from Mars to the earth is less than at any other time. There is also another advantage in viewing Mars during opposition. The planet is then at one side of the earth and the sun at the opposite side, so that when Mars is high in the heavens the sun is directly beneath the earth; in other words, the planet is then at its greatest elevation above the horizon at midnight. Some oppositions of Mars are, however, much more favourable than others. This is distinctly shown in Fig. 48, which represents the orbit of Mars and the orbit of the Earth[Pg 211] accurately drawn to scale. It will be seen that while the orbit of the earth is very nearly circular, the orbit of Mars has a very decided degree of eccentricity; indeed, with the exception of the orbit of Mercury, that of Mars has the greatest eccentricity of any orbit of the larger planets in our system.
The value of an opposition of Mars for telescopic purposes will vary greatly according to circumstances. The favourable oppositions will be those which occur as near as possible to the 26th of August. The other extreme will be found in an opposition which occurs near the 22nd of February. In the latter case the distance between the planet and the earth is nearly twice as great as the former. The last opposition which was suitable for the highest class of work took place in the year 1877. Mars was then a magnificent object, and received much, and deserved, attention. The favourable oppositions follow each other at somewhat irregular intervals; the last occurred in the year 1892, and another will take place in the year 1909.
The apparent movements of Mars are by no means simple. We can imagine the embarrassment of the early astronomer who first undertook the task of attempting to decipher these movements. The planet is seen to be a brilliant and conspicuous object. It attracts the astronomer's attention; he looks carefully, and he sees how it lies among the constellations with which he is familiar. A few nights later he observes the same body again; but is it exactly in the same place? He thinks not. He notes more carefully than before the place of the planet. He sees how it is situated with regard to the stars. Again, in a few days, his observations are repeated. There is no longer a trace of doubt about the matter—Mars has decidedly changed his position. It is veritably a wanderer.
Night after night the primitive astronomer is at his post. He notes the changes of Mars. He sees that it is now moving even more rapidly than it was at first. Is it going to complete the circuit of the heavens? The astronomer determines to watch the orb and see whether this surmise is justified. He pursues his task night after night, and at[Pg 212] length he begins to think that the body is not moving quite so rapidly as at first. A few nights more, and he is sure of the fact: the planet is moving more slowly. Again a few nights more, and he begins to surmise that the motion may cease; after a short time the motion does cease, and the object seems to rest; but is it going to remain at rest for ever? Has its long journey been finished? For many nights this seems to be the case, but at length the astronomer suspects that the planet must be commencing to move backwards. A few nights more, and the fact is confirmed beyond possibility of doubt, and the extraordinary discovery of the direct and the retrograde movement of Mars has been accomplished.
In the greater part of its journey around the heavens Mars seems to move steadily from the west to the east. It moves backwards, in fact, as the moon moves and as the sun moves. It is only during a comparatively small part of its[Pg 213] path that those elaborate movements are accomplished which presented such an enigma to the primitive observer. We show in the adjoining picture (Fig. 49) the track of the actual journey which Mars accomplished in the opposition of 1877. The figure only shows that part of its path which presents the anomalous features; the rest of the orbit is pursued, not indeed with uniform velocity, but with unaltered direction.
This complexity of the apparent movements of Mars seems at first sight fatal to the acceptance of any simple and elementary explanation of the planetary motion. If the motion of Mars were purely elliptic, how, it may well be said, could it perform this extraordinary evolution? The elucidation is to be found in the fact that the earth on which we stand is itself in motion. Even if Mars were at rest, the fact that the earth moves would make the planet appear to move. The apparent movements of Mars are thus combined with the real movements. This circumstance will not embarrass the geometer. He is able to disentangle the true movement of the planet from its association with the apparent movement, and to account completely for the complicated evolutions exhibited by Mars. Could we transfer our point of view from the ever-shifting earth to an immovable standpoint, we should then see that the shape of the orbit of Mars was an ellipse, described around the sun in conformity with the laws which Kepler discovered by observations of this planet.
Mars takes 687 days to travel round the sun, its average distance from that body being 141,500,000 miles. Under the most favourable circumstances the planet, at the time of opposition, may approach the earth to a distance not greater than about 35,500,000 miles. No doubt this seems an enormous distance, when estimated by any standard adapted for terrestrial measurements; it is, however, hardly greater than the distance of Venus when nearest, and it is much less than the distance from the earth to the sun.
We have explained how the form of the solar system is known from Kepler's laws, and how the absolute size of the system and of its various parts can be known when the direct[Pg 214] measurement of any one part has been accomplished. A close approach of Mars affords a favourable opportunity for measuring his distance, and thus, in a different way, solving the same problem as that investigated by the transit of Venus. We are thus led a second time to a knowledge of the distance of the sun and the distances of the planets generally, and to many other numerical facts about the solar system.
On the occasion of the opposition of Mars in 1877 a successful attempt was made to apply this refined process to the solution of the problem of celestial measurement. It cannot be said to have been the first occasion on which this method was suggested, or even practically attempted. The observations of 1877 were, however, conducted with such skill and with such minute attention to the necessary precautions as to render them an important contribution to astronomy. Dr. David Gill, now her Majesty's Astronomer at the Cape of Good Hope, undertook a journey to the Island of Ascension for the purpose of observing the parallax of Mars in 1877. On this occasion Mars approached to the earth so closely as to afford an admirable opportunity for the application of the method. Dr. Gill succeeded in obtaining a valuable series of measurements, and from them he concluded the distance of the sun with an accuracy somewhat superior to that attainable by the transit of Venus.
There is yet another method by which Mars can be made to give us information as to the distance of the sun. This method is one of some delicacy, and is interesting from its connection with the loftiest enquiries in mathematical astronomy. It was foreshadowed in the Dynamical theory of Newton, and was wrought to perfection by Le Verrier. It is based upon the great law of gravitation, and is intimately associated with the splendid discoveries in planetary perturbation which form so striking a chapter in modern astronomical discovery.
There is a certain relation between two quantities which at first sight seems quite independent. These quantities are the mass of the earth and the distance of the sun. The distance of the sun bears to a certain distance (which can[Pg 215] be calculated when we know the intensity of gravitation at the earth's surface, the size of the earth and the length of the year) the same proportion that the cube root of the sun's mass bears to the cube root of that of the earth. There is no uncertainty about this result, and the consequence is obvious. If we have the means of weighing the earth in comparison with the sun, then the distance of the sun can be immediately deduced. How are we to place our great earth in the weighing scales? This is the problem which Le Verrier has shown us how to solve, and he does so by invoking the aid of the planet Mars.
If Mars in his revolution around the sun were solely swayed by the attraction of the sun, he would, in accordance with the well-known laws of planetary motion, follow for ever the same elliptic path. At the end of one century, or even of many centuries, the shape, the size, and the position of that ellipse would remain unaltered. Fortunately for our present purpose, a disturbance in the orbit of Mars is produced by the earth. Although the mass of our globe is so much less than that of the sun, yet the earth is still large enough to exercise an appreciable attraction on Mars. The ellipse described by the planet is consequently not invariable. The shape of that ellipse and its position gradually change, so that the position of the planet depends to some extent upon the mass of the earth. The place in which the planet is found can be determined by observation; the place which the planet would have had if the earth were absent can be found by calculation. The difference between the two is due to the attraction of the earth, and, when it has been measured, the mass of the earth can be ascertained. The amount of displacement increases from one century to another, but as the rate of growth is small, ancient observations are necessary to enable the measures to be made with accuracy.
A remarkable occurrence which took place more than two centuries ago fortunately enables the place of Mars to be determined with great precision at that date. On the 1st of October, 1672, three independent observers witnessed the occultation of a star in Aquarius by the ruddy planet.[Pg 216] The place of the star is known with accuracy, and hence we are provided with the means of indicating the exact point in the heavens occupied by Mars on the day in question. From this result, combined with the modern meridian observations, we learn that the displacement of Mars by the attraction of the earth has, in the lapse of two centuries, grown to about five minutes of arc (294 seconds). It has been maintained that this cannot be erroneous to the extent of more than a second, and hence it would follow that the earth's mass is determined to about one three-hundredth part of its amount. If no other error were present, this would give the sun's distance to about one nine-hundredth part.
Notwithstanding the intrinsic beauty of this method, and the very high auspices under which it has been introduced, it is, we think, at present hardly worthy of reliance in comparison with some of the other methods. As the displacement of Mars, due to the perturbing influence of the earth, goes on increasing continually, it will ultimately attain sufficient magnitude to give a very exact value of the earth's mass, and then this method will give us the distance of the sun with great precision. But interesting and beautiful though this method may be, we must as yet rather regard it as a striking confirmation of the law of gravitation than as affording an accurate means of measuring the sun's distance.
The close approaches of Mars to the earth afford us opportunities for making a careful telescopic scrutiny of his surface. It must not be expected that the details on Mars could be inspected with the same minuteness as those on the moon. Even under the most favourable circumstances, Mars is still more than a hundred times as far as the moon, and, therefore, the features of the planet have to be at least one hundred times as large if they are to be seen as distinctly as the features on the moon. Mars is much smaller than the earth. The diameter of the planet is 4,200 miles, but little more than half that of the earth.[Pg 218] Fig. 50 shows the comparative sizes of the two bodies. We here reproduce two of the remarkable drawings[16] of Mars made by Professor William H. Pickering at the Lowell Observatory, Flagstaff A.T. Fig. 51 was taken on the 30th of July, 1894, and Fig. 52 on the 16th of August, 1894.
The southern polar cap on Mars, as seen by Professor William H. Pickering at Lowell Observatory on the 1st of July, 1894, is represented in Fig. 54.[17] The remarkable black mark intruding into the polar area will be noticed. In Fig. 53 are shown a series of unusually marked elevations and depressions upon the "terminator" of the planet, drawn as accurately as possible to scale by the same skilful hand on the 24th of August, 1894.
In making an examination of the planet it is to be observed that it does not, like the moon, always present the same face towards the observer. Mars rotates upon an axis in exactly the same manner as the earth. It is not a little remarkable that the period required by Mars for the completion of one rotation should be only about half an hour greater than the period of rotation of the earth. The exact period is 24 hours, 37 minutes, 22-3⁄4 seconds. It therefore follows that the aspect of the planet changes from hour to hour. The western side gradually sinks from view, the eastern side gradually assumes prominence. In twelve hours the aspect of the planet is completely changed. These changes, together with the inevitable effects of foreshortening, render it often difficult to correlate the objects on the planet with those on the maps. The latter, it must be confessed, fall short of the maps of the moon in definiteness and in certainty; yet there is no doubt that the main features of the planet are to be regarded as thoroughly established, and some astronomers have given names to all the prominent objects.
The markings on the surface of Mars are of two classes. Some of them are of an iron-grey hue verging on green, while the others are generally dark yellow or orange,[Pg 219] occasionally verging on white. The former have usually been supposed to represent the tracts of ocean, the latter the continental masses on the ruddy planet. We possess a great number of drawings of Mars, the earliest being taken in the middle of the seventeenth century. Though these early sketches are very rough, and are not of much value for the solution of questions of topography, they have been found very useful in aiding us to fix the period of rotation of the planet on its axis by comparison with our modern drawings.
Early observers had already noticed that each of the poles of Mars is distinguished by a white spot. It is, however, to William Herschel that we owe the first systematic study of these remarkable polar caps. This illustrious astronomer was rewarded by a very interesting discovery. He found that these arctic tracts on Mars vary both in extent and distinctness with the seasons of the hemisphere on which they are situated. They attain a maximum development from three to six months after the winter solstice on that planet, and then diminish until they are smallest about three to six months after the summer solstice. The analogy with the behaviour of the masses of snow and ice which surround our own poles is complete, and there has until lately been hardly any doubt that the white polar spots of Mars are somewhat similarly constituted.
As the period of revolution of Mars around the sun is so much longer than our year, 687 days instead of 365, the seasons of the planet are, of course, also much longer than the terrestrial seasons. In the northern hemisphere of Mars the summer lasts for no fewer than 381 days, and the winter must be 306 days. In both hemispheres the white polar cap in the course of the long winter season increases until it reaches a diameter of 45° to 50°, while the long summer reduces it to a small area only 4° or 5° in diameter. It is remarkable that one of these white regions—that at the south pole—seems not to be concentric with the pole, but is placed so much to one side that the south pole of Mars appears to be quite free from ice or snow once a year.
Although many valuable observations of Mars were made in the course of the nineteenth century, it is only since the very favourable opposition of 1877 that the study of the surface of Mars has made that immense progress which is one of the most remarkable features of modern astronomy. Among the observers who produced valuable drawings of the planet in 1877 we may mention Mr. Green, whose exquisite pictures were published by the Royal Astronomical Society, and Professor Schiaparelli, of Milan, who almost revolutionised our knowledge of this planet. Schiaparelli had a refractor of only eight inches aperture at his disposal, but he was doubtless much favoured by the purity of the Italian sky, which enabled him to detect in the bright portions of the surface of Mars a considerable number of long, narrow lines. To these he gave the name of canals, inasmuch as they issued from the so-called oceans, and could be traced across the reputed continents for considerable distances, which sometimes reached thousands of miles.
The canals seemed to form a kind of network, which connected the various seas with each other. A few of the more conspicuous of these so-called canals appeared indeed on some of the drawings made by Dawes and others before Schiaparelli's time. It was, however, the illustrious Italian astronomer who detected that these narrow lines are present in such great numbers as to form a notable feature of the planet. Some of these remarkable features are shown in Figs. 51 and 52, which are copied from drawings made by Professor William H. Pickering at the Lowell Observatory in 1894.
Great as had been the surprise of astronomers when Schiaparelli first proclaimed the discovery of these numerous canals, it was, perhaps, surpassed by the astonishment with which his announcement was received in 1882 that most of the canals had become double. Between December, 1881, and February, 1882, thirty of these duplications appear to have taken place. Nineteen of these were cases of a well-traced parallel line being formed near a previously existing canal. The remaining canals were less certainly established, or were cases where the two lines did not seem to be quite parallel. A copy of the map of Mars which Schiaparelli formed from his observations of 1881–82 is given in Plate XVIII. It brings out clearly these strange double canals, so unlike any features that we know on any other globe.
Subsequent observations by Schiaparelli and several other observers seem to indicate that this phenomenon of the duplication of the canals is of a periodic character. It is produced about the times when Mars passes through its equinoxes. One of the two parallel lines is often superposed as exactly as possible upon the track of the old canal. It does, however, sometimes happen that both the lines occupy opposite sides of the former canal and are situated on entirely new ground. The distance between the two lines varies from about 360 miles as a maximum down to the smallest limit distinguishable in our large telescopes, which is something less than thirty miles. The breadth of each of these remarkable channels may range from the limits of visibility, say, up to more than sixty miles.
The duplication of the canals is perhaps the most difficult problem which Mars offers to us for solution. Even if we admit that the canals themselves represent inlets or channels through which the melted polar snow makes its way across the equatorial continents, it is not easy to see how the duplicate canals can arise. This is especially true in those cases where the original channel seems to vanish and to be replaced by two quite new canals, each about the breadth of the English Channel, and lying one on each side of the course of the old one. The very obvious explanation that the whole duplication is an optical illusion has been brought forward more than once, but never in a conclusive manner. We must, perhaps, be content to let the solution of this matter rest for the present, in the hope that the extraordinary attention which this planet is now receiving will in due time explain the present enigma.
The markings on the surface of this planet are, generally speaking, of a permanent character, so that when we compare drawings made one or two hundred years ago with drawings[Pg 222] made more recently we can recognise in each the same features. This permanence is, however, not nearly so absolute as it is in the case of the moon. In addition to the canals which we have already considered, many other parts of the surface of Mars alter their outlines from time to time. This is particularly the case with those dark spots which we call oceans, the contours of which sometimes undergo modifications in matters of detail which are quite unmistakable. Changes of colour are often observed on parts of the planet, and though some of these observations may perhaps be attributed to the influence of our own atmosphere on the planet's appearance, they cannot be all thus accounted for. Some of the phenomena must certainly be due to actual changes which have taken place on the surface of Mars.
As an example of such changes, we may refer to the north-western part of the notable feature, to which Schiaparelli has given the name of Syrtis major.[18] This has at various times been recorded as grey, green, blue, brown, and even violet. When this region (about the time of the autumnal equinox of the northern hemisphere) is situated in the middle of the visible disc, the eastern part is distinctly greener than the western. As the season progresses this characteristic colour gets feebler, until the green tint is to be perceived only on the shores of the Syrtis. The atmosphere of Mars is usually very transparent, and fortunately allows us to scrutinise the surface of the planet without putting obstacles in the way m the shape of Martian clouds. Such clouds, however, are not invariably absent. Our view of the surface is occasionally obstructed in such a manner as to make it certain that clouds or mist in the atmosphere of Mars must be the cause of the trouble.
Would we form an idea of the physical constitution of the surface of Mars, then the question as to the character of the atmosphere of the planet is among the first to be considered. Spectroscopic observations do not in this case render[Pg 223] us much assistance. Of course, we know that the planet has no intrinsic light. It merely shines by reflected sunlight. The hemisphere which is turned towards the sun is bright, and the hemisphere which is turned away from the sun is dark. The spectrum ought, therefore, like that of the moon, to be an exact though faint copy of the solar spectrum, unless the sun's rays, by passing twice through the atmosphere of Mars, suffered some absorption which could give rise to additional dark lines. Some of the earlier observers thought that they could distinctly make out some such lines due, as was supposed, to water vapour. The presence of such lines is, however, denied by Mr. Campbell, of the Lick Observatory, and Professor Keeler, at the Allegheny Observatory,[19] who, with their unrivalled opportunities, both instrumental and climatic, could find no difference between the spectra of Mars and the moon. If Mars had an atmosphere of appreciable extent, its absorptive effect should be noticeable, especially at the limb of the planet; but Mr. Campbell's observations do not show any increased absorption at the limb. It would therefore seem that Mars cannot have an extensive atmosphere, and this conclusion is confirmed in several other ways.
The distinctness with which we see the surface of this planet tends to show that the atmosphere must be very thin as compared with our own. There can hardly be any doubt that an observer on Mars with a good telescope would be unable to distinguish much of the features of the earth's surface. This would be the case not only by reason of the strong absorption of the light during the double passage through our atmosphere, but also on account of the great diffusion of the light caused by this same atmosphere. Also, it is needless to say, the great amount of cloud generally floating over the earth would totally obscure many parts of our planet from a Martian observer. But though, as already mentioned, we occasionally find parts of Mars rendered indistinct, it must be acknowledged that the clouds on Mars are very slight. We should expect that the polar caps, if composed of snow, would, when melting, produce clouds which[Pg 224] would more or less hide the polar regions from our inspection; yet nothing of the kind has ever been seen.
We have seen that there are very grave doubts as to the existence of water on Mars. No doubt we have frequently spoken of the dark markings as "oceans" and of the bright parts as "continents." That this language was just has been the opinion of astronomers for a very long time. A few years ago Mr. Schaeberle, of the Lick Observatory, came to the very opposite conclusion. He contended that the dark parts were the continents and the bright ones were the oceans of water, or some other fluid. He pointed to the irregular shading of the dark parts, which does not suggest the idea of light reflected from a spherical surface of water, especially as the contrasts between light and shade are strongest about the middle of the disc.
It is also to be noticed that the dark regions are not infrequently traversed by still darker streaks, which can be traced for hundreds of miles almost in straight lines, while the so-called canals in the bright parts often seem to be continuations of these same lines. Mr. Schaeberle therefore suggests that the canals may be chains of mountains stretching over sea and land! The late Professor Phillips and Mr. H.D. Taylor have pointed out that if there were lakes or seas in the tropical regions of Mars we should frequently see the sun directly reflected from them, thus producing a bright, star-like point which could not escape observation. Even moderately disturbed water would make its presence known in this manner, and yet nothing of the kind has ever been recorded.
On the question as to the possibility of life on Mars a few words may be added. If we could be certain of the existence of water on Mars, then one of the fundamental conditions would be fulfilled; and even though the atmosphere on Mars had but few points of resemblance either in composition or in density to the atmosphere of the earth, life might still be possible. Even if we could suppose that a man would find suitable nutriment for his body and suitable air for his respiration, it seems very doubtful whether he would be able to live. Owing to the small size of Mars and[Pg 225] the smallness of its mass in comparison with the earth, the intensity of the gravitation on the neighbouring planet would be different from the attraction on the surface of the earth. We have already alluded to the small gravitation on the moon, and in a lesser degree the same remarks will apply to Mars. A body which weighs on the earth two pounds would on the surface of Mars weigh rather less than one pound. Nearly the same exertion which will raise a 56-lb. weight on the earth would lift two similar weights on Mars.
The earth is attended by one moon. Jupiter is attended by four conspicuous moons. Mars is a planet revolving between the orbits of the earth and of Jupiter. It is a body of the same general type as the earth and Jupiter. It is ruled by the same sun, and all three planets form part of the same system; but as the earth has one moon and Jupiter four moons, why should not Mars also have a moon? No doubt Mars is a small body, less even than the earth, and much less than Jupiter. We could not expect Mars to have large moons, but why should it be unlike its two neighbours, and not have any moon at all? So reasoned astronomers, but until modern times no satellite of Mars could be found. For centuries the planet has been diligently examined with this special object, and as failure after failure came to be recorded, the conclusion seemed almost to be justified that the chain of analogical reasoning had broken down. The moonless Mars was thought to be an exception to the rule that all the great planets outside Venus were dignified by an attendant retinue of satellites. It seemed almost hopeless to begin again a research which had often been tried, and had invariably led to disappointment; yet, fortunately, the present generation has witnessed still one more attack, conducted with perfect equipment and with consummate skill This attempt has obtained the success it so well merited, and the result has been the memorable detection of two satellites of Mars.
This discovery was made by Professor Asaph Hall, the distinguished astronomer at the observatory of Washington. Mr. Hall was provided with an instrument of colossal [Pg 226]proportions and of exquisite workmanship, known as the great Washington refractor. It is the product of the celebrated workshop of Messrs. Alvan Clark and Sons, from which so many large telescopes have proceeded, and in its noble proportions far surpassed any other telescope ever devoted to the same research. The object-glass measures twenty-six inches in diameter, and is hardly less remarkable for the perfection of its definition than for its size. But even the skill of Mr. Hall, and the space-penetrating power of his telescope, would not have been able on ordinary occasions to discover the satellites of Mars. Advantage was accordingly taken of that memorable opposition of Mars in 1877, when, as we have already described, the planet came unusually near the earth.
Had Mars been attended by a moon one-hundredth part of the bulk of our moon it must long ago have been discovered. Mr. Hall, therefore, knew that if there were any satellites they must be extremely small bodies, and he braced himself for a severe and diligent search. The circumstances were all favourable. Not only was Mars as near as it well could be to the earth; not only was the great telescope at Washington the most powerful refractor then in existence; but the situation of Washington is such that Mars was seen from the observatory at a high elevation. It was while the British Association were meeting at Plymouth, in 1877, that a telegram flashed across the Atlantic. Brilliant success had rewarded Mr. Hall's efforts. He had hoped to discover one satellite. The discovery of even one would have made the whole scientific world ring; but fortune smiled on Mr. Hall. He discovered first one satellite, and then he discovered a second; and, in connection with these satellites, he further discovered a unique fact in the solar system.
Deimos, the outer of the satellites, revolves around the planet in the period of 30 hours, 17 mins., 54 secs.; it is the inner satellite, Phobos, which has commanded the more special attention of every astronomer in the world. Mars turns round on his axis in a Martial day, which is very nearly the same length as our day of twenty-four hours. The inner satellite of Mars moves round in 7 hours, 39 mins., 14 secs. Phobos,[Pg 227] in fact, revolves three times round Mars in the same time that Mars can turn round once. This circumstance is unparalleled in the solar system; indeed, as far as we know, it is unparalleled in the universe. In the case of our own planet, the earth rotates twenty-seven times for one revolution of the moon. To some extent the same may be said of Jupiter and of Saturn; while in the great system of the sun himself and the planets, the sun rotates on his axis several times for each revolution of even the most rapidly moving of the planets. There is no other known case where the satellite revolves around the primary more quickly than the primary rotates on its axis. The anomalous movement of the satellite of Mars has, however, been accounted for. In a subsequent chapter we shall again allude to this, as it is connected with an important department of modern astronomy.
The satellites are so small that we are unable to measure their diameters directly, but from observations of their brightness it is evident that their diameters cannot exceed twenty or thirty miles, and may be even smaller. Owing to their rapid motion the two satellites must present some remarkable peculiarities to an observer on Mars. Phobos rises in the west, passes across the heavens, and sets in the east after about five and a half hours, while Deimos rises in the east and remains more than two days above the horizon.
As the satellites revolve in paths vertically above the equator of their primary, the one less than 4,000 miles and the other only some 14,500 miles above the surface, it follows that they can never be visible from the poles of Mars; indeed, to see Phobos, the observer's planetary latitude must not be above 68-3⁄4°. If it were so, the satellite would be hidden by the body of Mars, just as we, in the British Islands, would be unable to see an object revolving round the earth a few hundred miles above the equator.
Before passing from the attractive subject of the satellites, we may just mention two points of a literary character. Mr. Hall consulted his classical friends as to the designation to be conferred on the two satellites. Homer was referred to, and a passage in the "Iliad" suggested the names of[Pg 228] Deimos and Phobos. These personages were the attendants of Mars, and the lines in which they occur have been thus construed by my friend Professor Tyrrell:—
"Mars spake, and called Dismay and Rout
To yoke his steeds, and he did on his harness sheen."
A curious circumstance with respect to the satellites of Mars will be familiar to those who are acquainted with "Gulliver's Travels." The astronomers on board the flying Island of Laputa had, according to Gulliver, keen vision and good telescopes. The traveller says that they had found two satellites to Mars, one of which revolved around him in ten hours, and the other in twenty-one and a half. The author has thus not only made a correct guess about the number of the satellites, but he actually stated the periodic time with considerable accuracy! We do not know what can have suggested the latter guess. A few years ago any astronomer reading the voyage to Laputa would have said this was absurd. There might be two satellites to Mars, no doubt; but to say that one of them revolves in ten hours would be to assert what no one could believe. Yet the truth has been even stranger than the fiction.
And now we must bring to a close our account of this beautiful and interesting planet. There are many additional features over which we are tempted to linger, but so many other bodies claim our attention in the solar system, so many other bodies which exceed Mars in size and intrinsic importance, that we are obliged to desist. Our next step will not, however, at once conduct us to the giant planets. We find outside Mars a host of objects, small indeed, but of much interest; and with these we shall find abundant occupation for the following chapter.
The Lesser Members of our System—Bode's Law—The Vacant Region in the Planetary System—The Research—The Discovery of Piazzi—Was the small Body a Planet?—The Planet becomes Invisible—Gauss undertakes the Search by Mathematics—The Planet Recovered—Further Discoveries—Number of Minor Planets now known—The Region to be Searched—The Construction of the Chart for the Search for Small Planets—How a Minor Planet is Discovered—Physical Nature of the Minor Planets—Small Gravitation on the Minor Planets—The Berlin Computations—How the Minor Planets tell us the Distance of the Sun—Accuracy of the Observations—How they may be Multiplied—Victoria and Sappho—The most Perfect Method.
In our chapters on the Sun and Moon, on the Earth and Venus, and on Mercury and Mars, we have been discussing the features and the movements of globes of vast dimensions. The least of all these bodies is the moon, but even that globe is 2,000 miles from one side to the other. In approaching the subject of the minor planets we must be prepared to find objects of dimensions quite inconsiderable in comparison with the great spheres of our system. No doubt these minor planets are all of them some few miles, and some of them a great many miles, in diameter. Were they close to the earth they would be conspicuous, and even splendid, objects; but as they are so distant they do not, even in our greatest telescopes, become very remarkable, while to the unaided eye they are almost all invisible.
In the diagram (p. 234) of the orbits of the various planets, it is shown that a wide space exists between the orbit of Mars and that of Jupiter. It was often surmised that this ample region must be tenanted by some other planet. The presumption became much stronger when a remarkable law was discovered which exhibited, with considerable accuracy, the[Pg 230] relative distances of the great planets of our system. Take the series of numbers, 0, 3, 6, 12, 24, 48, 96, whereof each number (except the second) is double of the number which precedes it. If we now add four to each, we have the series 4, 7, 10, 16, 28, 52, 100. With the exception of the fifth of these numbers (28), they are all sensibly proportional to the distances of the various planets from the sun. In fact, the distances are as follows:—Mercury, 3·9; Venus, 7·2; Earth, 10; Mars, 15·2; Jupiter, 52·9; Saturn, 95·4. Although we have no physical reason to offer why this law—generally known as Bode's—should be true, yet the fact that it is so nearly true in the case of all the known planets tempts us to ask whether there may not also be a planet revolving around the sun at the distance represented by 28.
So strongly was this felt at the end of the eighteenth century that some energetic astronomers decided to make a united effort to search for the unknown planet. It seemed certain that the planet could not be a large one, as otherwise it must have been found long ago. If it should exist, then means were required for discriminating between the planet and the hosts of stars strewn along its path.
The search for the small planet was soon rewarded by a success which has rendered the evening of the first day in the nineteenth century memorable in astronomy. It was in the pure skies of Palermo that the observatory was situated where the memorable discovery of the first known minor planet was made by Piazzi. This laborious and accomplished astronomer had organised an ingenious system of exploring the heavens which was eminently calculated to discriminate a planet among the starry host. On a certain night he would select a series of stars to the number of fifty, more or less, according to circumstances. With his meridian circle he determined the places of the chosen objects. The following night, or, at all events, as soon as convenient, he re-observed the whole fifty stars with the same instrument and in the same manner, and the whole operation was afterwards repeated on two, or perhaps more, nights. When the observations were compared together he was in possession of some four or more places of each[Pg 231] one of the stars on different nights, and the whole series was complete. He was persevering enough to carry on these observations for very many groups, and at length he was rewarded by a success which amply compensated him for all his toil.
It was on the 1st of January, 1801, that Piazzi commenced for the one hundred and fifty-ninth time to observe a new series. Fifty stars this night were viewed in his telescope, and their places were carefully recorded. Of these objects the first twelve were undoubtedly stellar, and so to all appearance was the thirteenth, a star of the eighth magnitude in the constellation of Taurus. There was nothing to distinguish the telescopic appearance of this object from all the others which preceded or followed it. The following night Piazzi, according to his custom, re-observed the whole fifty stars, and he did the same again on the 3rd of January, and once again on the 4th. He then, as usual, brought together the four places he had found for each of the several bodies. When this was done it was at once seen that the thirteenth object on the list was quite a different body from the remainder and from all the other stars which he had ever observed before. The four places of this mysterious object were all different; in other words, it was in movement, and was therefore a planet.
A few days' observation sufficed to show how this little body, afterwards called Ceres, revolved around the sun, and how it circulated in that vacant path intermediate between the path of Mars and the path of Jupiter. Great, indeed, was the interest aroused by this discovery and the influence which it has exercised on the progress of astronomy. The majestic planets of our system had now to admit a much more humble object to a share of the benefits dispensed by the sun.
After Piazzi had obtained a few further observations, the season for observing this part of the heavens passed away, and the new planet of course ceased to be visible. In a few months, no doubt, the same part of the sky would again be above the horizon after dark, and the stars would of course be[Pg 232] seen as before. The planet, however, was moving, and would continue to move, and by the time the next season had arrived it would have passed off into some distant region, and would be again confounded with the stars which it so closely resembled. How, then, was the planet to be pursued through its period of invisibility and identified when it again came within reach of observation?
This difficulty attracted the attention of astronomers, and they sought for some method by which the place of the planet could be recovered so as to prevent Piazzi's discovery from falling into oblivion. A young German mathematician, whose name was Gauss, opened his distinguished career by a successful attempt to solve this problem. A planet, as we have shown, describes an ellipse around the sun, and the sun lies at a focus of that curve. It can be demonstrated that when three positions of a planet are known, then the ellipse in which the planet moves is completely determined. Piazzi had on each occasion measured the place which it then occupied. This information was available to Gauss, and the problem which he had to solve may be thus stated. Knowing the place of the planet on three nights, it is required, without any further observations, to tell what the place of the planet will be on a special occasion some months in the future. Mathematical calculations, based on the laws of Kepler, will enable this problem to be solved, and Gauss succeeded in solving it. Gauss demonstrated that though the telescope of the astronomer was unable to detect the wanderer during its season of invisibility, yet the pen of the mathematician could follow it with unfailing certainty. When, therefore, the progress of the seasons permitted the observations to be renewed, the search was recommenced. The telescope was directed to the point which Gauss's calculations indicated, and there was the little Ceres. Ever since its re-discovery, the planet has been so completely bound in the toils of mathematical reasoning that its place every night of the year can be indicated with a fidelity approaching to that attainable in observing the moon or the great planets of our system.
The discovery of one minor planet was quickly followed by similar successes, so that within seven years Pallas, Juno, and Vesta were added to the solar system. The orbits of all these bodies lie in the region between the orbit of Mars and of Jupiter, and for many years it seems to have been thought that our planetary system was now complete. Forty years later systematic research was again commenced. Planet after planet was added to the list; gradually the discoveries became a stream of increasing volume, until in 1897 the total number reached about 430. Their distribution in the solar system is somewhat as represented in Fig. 55. By the improvement of astronomical telescopes, and by the devotion with which certain astronomers have applied themselves to this interesting research, a special method of observing has been created for the distinct purpose of searching out these little objects.
It is known that the paths in which all the great planets move through the heavens coincide very nearly with the path which the sun appears to follow among the stars, and which is known as the ecliptic. It is natural to assume that the small planets also move in the same great highway, which leads them through all the signs of the zodiac in succession. Some of the small planets, no doubt, deviate rather widely from the track of the sun, but the great majority are approximately near it. This consideration at once simplifies the search for new planets. A certain zone extending around the heavens is to be examined, but there is in general little advantage in pushing the research into other parts of the sky.
The next step is to construct a map containing all the stars in this region. This is a task of very great labour; the stars visible in the large telescopes are so numerous that many tens of thousands, perhaps we should say hundreds of thousands, are included in the region so narrowly limited. The fact is that many of the minor planets now known are objects of extreme minuteness; they can only be seen with very powerful telescopes, and for their detection it is necessary to use charts on which even the faintest stars have[Pg 234] been depicted. Many astronomers have concurred in the labour of producing these charts; among them may be mentioned Palisa, of Vienna, who by means of his charts has found eighty-three minor planets, and the late Professor Peters, of Clinton, New York, who in a similar way found forty-nine of these bodies.
The astronomer about to seek for a new planet directs his telescope towards that part of the sun's path which is on the meridian at midnight; there, if anywhere, lies the chance of success, because that is the region in which such a body is nearer to the earth than at any other part of its course. He steadfastly compares his chart with the heavens, and usually finds the stars in the heavens and the stars in the chart to correspond; but sometimes it will happen that a[Pg 235] point in the heavens is missing from the chart. His attention is at once arrested; he follows the object with care, and if it moves it is a planet. Still he cannot be sure that he has really made a discovery; he has found a planet, no doubt, but it may be one of the large number already known. To clear up this point he must undertake a further, and sometimes a very laborious, enquiry; he must search the Berlin Year-Book and other ephemerides of such planets and see whether it is possible for one of them to have been in the position on the night in question. If he can ascertain that no previously discovered body could have been there, he is then entitled to announce to his brother astronomers the discovery of a new member of the solar system. It seems certain that all the more important of the minor planets have been long since discovered. The recent additions to the list are generally extremely minute objects, beyond the powers of small telescopes.
Since 1891 the method of searching for minor planets which we have just described has been almost abandoned in favour of a process greatly superior. It has been found feasible to employ photography for making charts of the heavens. A photographic plate is exposed in the telescope to a certain region of the sky sufficiently long to enable very faint telescopic stars to imprint their images. Care has to be taken that the clock which moves the camera shall keep pace most accurately with the rotation of the earth, so that fixed stars appear on the plate as sharp points. If, on developing the plate, a star is found to have left a trail, it is evident that this star must during the time of exposure (generally some hours) have had an independent motion of its own; in other words, it must be a planet. For greater security a second picture is generally taken of the same region after a short interval. If the place occupied by the trail on the first plate is now vacant, while on the second plate a new trail appears in a line with the first one, there remains no possible doubt that we have genuine indications of a planet, and that we have not been led astray by some impurity on the plate or by a few minute stars which happened to lie very closely[Pg 236] together. Wolf, of Heidelberg, and following in his footsteps Charlois, of Nice, have in this manner discovered a great number of new minor planets, while they have also recovered a good many of those which had been lost sight of owing to an insufficiency of observations.
On the 13th of August, 1898, Herr G. Witt, of the observatory of Urania in Berlin, discovered a new asteroid by the photographic method. This object was at first regarded merely as forming an addition of no special importance to the 432 asteroids whose discovery had preceded it. It received, as usual, a provisional designation in accordance with a simple alphabetical device. This temporary label affixed to Witt's asteroid was "D Q." But the formal naming of the asteroid has now superseded this label. Herr Witt has given to his asteroid the name of "Eros." This has been duly accepted by astronomers, and thus for all time the planet is to be known.
The feature which makes the discovery of Eros one of the most remarkable incidents in recent astronomy is that on those rare occasions when this asteroid comes nearest to the earth it is closer to the earth than the planet Mars can ever be. Closer than the planet Venus can ever be. Closer than any other known asteroid can ever be. Thus we assign to Eros the exceptional position of being our nearest planetary neighbour in the whole host of heaven. Under certain circumstances it will have a distance from the earth not exceeding one-seventh of the mean distance of the sun.
Of the physical composition of the asteroids and of the character of their surfaces we are entirely ignorant. It may be, for anything we can tell, that these planets are globes like our earth in miniature, diversified by continents and by oceans. If there be life on such bodies, which are often only a few miles in diameter, that life must be something totally different from anything with which we are familiar. Setting aside every other difficulty arising from the possible absence of water and from the great improbability of finding there an atmosphere of a density and a composition suitable for respiration, gravitation itself would prohibit organic beings adapted for this earth from residing on a minor planet.
Let us attempt to illustrate this point, and suppose that we take the case of a minor planet eight miles in diameter, or, in round numbers, one-thousandth part of the diameter of the earth. If we further suppose that the materials of the planet are of the same nature as the substances in the earth, it is easy to prove that the gravity on the surface of the planet will be only one-thousandth part of the gravity of the earth. It follows that the weight of an object on the earth would be reduced to the thousandth part if that object were transferred to the planet. This would not be disclosed by an ordinary weighing scales, where the weights are to be placed in one pan and the body to be weighed in the other. Tested in this way, a body would, of course, weigh precisely the same anywhere; for if the gravitation of the body is altered, so is also in equal proportion the gravitation of the counterpoising weights. But, weighed with a spring balance, the change would be at once evident, and the effort with which a weight could be raised would be reduced to one-thousandth part. A load of one thousand pounds could be lifted from the surface of the planet by the same effort which would lift one pound on the earth; the effects which this would produce are very remarkable.
In our description of the moon it was mentioned (p. 103) that we can calculate the velocity with which it would be necessary to discharge a projectile so that it would never again fall back on the globe from which it was expelled. We applied this reasoning to explain why the moon has apparently altogether lost any atmosphere it might have once possessed.
If we assume for the sake of illustration that the densities of all planets are identical, then the law which expresses the critical velocity for each planet can be readily stated. It is, in fact, simply proportional to the diameter of the globe in question. Thus, for a minor planet whose diameter was one-thousandth part of that of the earth, or about eight miles, the critical velocity would be the thousandth part of six miles a second—that is, about thirty feet per second. This is a low velocity compared with ordinary standards. A child easily tosses a ball up fifteen or sixteen feet high, yet to carry it[Pg 238] up this height it must be projected with a velocity of thirty feet per second. A child, standing upon a planet eight miles in diameter, throws his ball vertically upwards; up and up the ball will soar to an amazing elevation. If the original velocity were less than thirty feet per second, the ball would at length cease to move, would begin to turn, and fall with a gradually accelerating pace, until at length it regained the surface with a speed equal to that with which it had been projected. If the original velocity had been as much as, or more than, thirty feet per second, then the ball would soar up and up never to return. In a future chapter it will be necessary to refer again to this subject.
A few of the minor planets appear in powerful telescopes as discs with appreciable dimensions, and they have even been measured with the micrometer. In this way Professor Barnard, late of the Lick Observatory, determined the following values for the diameters of the four first discovered minor planets:—
| Ceres | 485 miles. |
| Pallas | 304 miles. |
| Juno | 118 miles. |
| Vesta | 243 miles. |
The value for Juno is, however, very uncertain, and by far the greater number of the minor planets are very much smaller than the figures here given would indicate. It is possible by a certain calculation to form an estimate of the aggregate mass of all the minor planets, inasmuch as observations disclose to us the extent of their united disturbing influences on the motion of Mars. In this manner Le Verrier concluded that the collected mass of the small planets must be about equal to one-fourth of the mass of the earth. Harzer, repeating the enquiry in an improved manner, deduced a collected mass one-sixth of that of the earth. There can be no doubt that the total mass of all the minor planets at present known is not more than a very small fraction of the amount to which these calculations point. We therefore conclude that there must be a vast number of minor planets which have not yet been recognised in the observatory. These unknown planets must be extremely minute.
The orbits of this group of bodies differ in remarkable characteristics from those of the larger planets. Some of them are inclined at angles of 30° to the plane of the earth's orbit, the inclinations of the great planets being not more than a few degrees. Some of the orbits of the minor planets are also greatly elongated ellipses, while, of course, the orbits of the large planets do not much depart from the circular form. The periods of revolution of these small objects round the sun range from three years to nearly nine years.
A great increase in the number of minor planets has rewarded the zeal of those astronomers who have devoted their labours to this subject. Their success has entailed a vast amount of labour on the computers of the "Berlin Year-Book." That useful work occupies in this respect a position which has not been taken by our own "Nautical Almanac," nor by the similar publications of other countries. A skilful band of computers make it their duty to provide for the "Berlin Year-Book" detailed information as to the movements of the minor planets. As soon as a few complete observations have been obtained, the little object passes into the secure grasp of the mathematician; he is able to predict its career for years to come, and the announcements with respect to all the known minor planets are to be found in the annual volumes of the work referred to.
The growth of discovery has been so rapid that the necessary labour for the preparation of such predictions is now enormous. It must be confessed that many of the minor planets are very faint and otherwise devoid of interest, so that astronomers are sometimes tempted to concur with the suggestion that a portion of the astronomical labour now devoted to the computation of the paths of these bodies might be more profitably applied. For this it would be only necessary to cast adrift all the less interesting members of the host, and allow them to pursue their paths unwatched by the telescope, or by the still more ceaseless tables of the mathematical computer.
The sun, which controls the mighty orbs of our system,[Pg 240] does not disdain to guide, with equal care, the tiny globes which form the minor planets. At certain times some of them approach near enough to the earth to merit the attention of those astronomers who are specially interested in determining the dimensions of the solar system. The observations are of such a nature that they can be made with considerable precision; they can also be multiplied to any extent that may be desired. Some of these little bodies have consequently a great astronomical future, inasmuch as they seem destined to indicate the true distance from the earth to the sun more accurately than Venus or than Mars. The smallest of these planets will not answer for this purpose; they can only be seen in powerful telescopes, and they do not admit of being measured with the necessary accuracy. It is also obvious that the planets to be chosen for observation must come as near the earth as possible. In favourable circumstances, some of the minor planets will approach the earth to a distance which is about three-quarters of the distance of the sun. These various conditions limit the number of bodies available for this purpose to about a dozen, of which one or two will usually be suitably placed each year.
For the determination of the sun's distance this method by the minor planets offers unquestionable advantages. The orb itself is a minute star-like point in the telescope, and the measures are made from it to the stars which are seen near it. A few words will, perhaps, be necessary at this place as to the nature of the observations referred to. When we speak of the measures from the planet to the star, we do not refer to what would be perhaps the most ordinary acceptation of the expression. We do not mean the actual measurement of the number of miles in a straight line between the planet and the star. This element, even if attainable, could only be the result of a protracted series of observations of a nature which will be explained later on when we come to speak of the distances of the stars. The measures now referred to are of a more simple character; they are merely to ascertain the apparent distance of the objects expressed in angular measure. This angular[Pg 241] measurement is of a wholly different character from the linear measurement, and the two methods may, indeed, lead to results that would at first seem paradoxical.
We may take, as an illustration, the case of the group of stars forming the Pleiades, and those which form the Great Bear. The latter is a large group, the former is a small one. But why do we think the words large and small rightly applied here? Each pair of stars of the Great Bear makes a large angle with the eye. Each pair of stars in the Pleiades makes a small angle, and it is these angles which are the direct object of astronomical measurement. We speak of the distance of two stars, meaning thereby the angle which is bounded by the two lines from the eye to the two stars. This is what our instruments are able to measure, and it is to be observed that no reference to linear magnitude is implied. Indeed, if we are to mention actual dimensions, it is quite possible, for anything we can tell, that the Pleiades may form a much larger group than the Great Bear, and that the apparent superiority of the latter is merely due to its being closer to us. The most accurate of these angular measures are obtained when two stars, or two star-like points, are so close together as to enable them to be included in one field of view of the telescope. There are special forms of apparatus which enable the astronomer in this case to give to his observations a precision unattainable in the measurement of objects less definitely marked, or at a greater apparent distance. The determination of the distance of the small star-like planet from a star is therefore characterised by great accuracy.
But there is another and, perhaps, a weightier argument in favour of the determination of the scale of the solar system by this process. The real strength of the minor planet method rests hardly so much on the individual accuracy of the observations, as on the fact that from the nature of the method a considerable number of repetitions can be concentrated on the result. It will, of course, be understood that when we speak of the accuracy of an observation, it is not to be presumed that it can ever be[Pg 242] entirely free from error. Errors always exist, and though they may be small, yet if the quantity to be measured is minute, an error of intrinsic insignificance may amount to an appreciable fraction of the whole. The one way by which their effect can be subdued is by taking the mean of a large number of observations. This is the real source of the value of the minor planet method. We have not to wait for the occurrence of rare events like the transit of Venus. Each year will witness the approach of some one or more minor planets sufficiently close to the earth to render the method applicable. The varied circumstances attending each planet, and the great variety of the observations which may be made upon it, will further conduce to eliminate error.
As the planet pursues its course through the sky, which is everywhere studded over with countless myriads of minute stars, it is evident that this body, itself so like a star, will always have some stars in its immediate neighbourhood. As the movements of the planet are well known, we can foretell where it will be on each night that it is to be observed. It is thus possible to prearrange with observers in widely-different parts of the earth as to the observations to be made on each particular night.
An attempt has been made, on the suggestion of Dr. Gill, to carry out this method on a scale commensurate with its importance. The planets Iris, Victoria, and Sappho happened, in the years 1888 and 1889, to approach so close to the earth that arrangements were made for simultaneous measurements in both the northern and the southern hemispheres. A scheme was completely drawn up many months before the observations were to commence. Each observer who participated in the work was thus advised beforehand of the stars which were to be employed each night. Viewed from any part of the earth, from the Cape of Good Hope or from Great Britain, the positions of the stars remain absolutely unchanged. Their distance is so stupendous that a change of place on the earth displaces them to no appreciable extent. But the case is different with a minor planet. It is hardly one-millionth part of the distance of the stars[Pg 243], and the displacement of the planet when viewed from the Cape and when viewed from Europe is a measurable quantity.
The magnitude we are seeking is to be elicited by comparison between the measurements made in the northern hemisphere with those made in the southern. The observations in the two localities must be as nearly simultaneous as possible, due allowance being made for the motion of the planet in whatever interval may have elapsed. Although every precaution is taken to eliminate the errors of each observation, yet the fact remains that we compare the measures made by observers in the northern hemisphere with those made by different observers, using of course different instruments, thousands of miles away. But in this respect we are at no greater disadvantage than in observing the transit of Venus.
It is, however, possible to obviate even this objection, and thus to give the minor planet method a supremacy over its rival which cannot be disputed. The difficulty would be overcome if we could arrange that an astronomer, after making a set of observations on a fine night in the northern hemisphere, should be instantly transferred, instruments and all, to the southern station, and there repeat the observations. An equivalent transformation can be effected without any miraculous agency, and in it we have undoubtedly the most perfect mode of measuring the sun's distance with which we are acquainted. This method has already been applied with success by Dr. Gill in the case of Juno, and there are other members of the host of minor planets still more favourably circumstanced.
Consider, for instance, a minor planet, which sometimes approaches to within 70,000,000 miles of the earth. When the opposition is drawing near, a skilled observer is to be placed at some suitable station near the equator. The instrument he is to use should be that marvellous piece of mechanical and optical skill known as the heliometer.[20] It[Pg 244] can be used to measure the angular distance between objects too far apart for the filar micrometer. The measurements are to be made in the evening as soon as the planet has risen high enough to enable it to be seen distinctly. The observer and the observatory are then to be transferred to the other side of the earth. How is this to be done? Say, rather, how we could prevent it from being done. Is not the earth rotating on its axis, so that in the course of a few hours the observatory on the equator is carried bodily round for thousands of miles? As the morning approaches the observations are to be repeated. The planet is found to have changed its place very considerably with regard to the stars. This is partly due to its own motion, but it is also largely due to the parallactic displacement arising from the rotation of the earth, which may amount to so much as twenty seconds. The measures on a single night with the heliometer should not have a mean error greater than one-fifth of a second, and we might reasonably expect that observations could be secured on about twenty-five nights during the opposition. Four such groups might be expected to give the sun's distance without any uncertainty greater than the thousandth part of the total amount. The chief difficulty of the process arises from the movement of the planet during the interval which divides the evening from the morning observations. This drawback can be avoided by diligent and repeated measurements of the place of the planet with respect to the stars among which it passes.
In the monumental piece of work which issued in 1897 from the Cape Observatory, under the direction of Dr. Gill, the final results from the observations of Iris, Victoria, and Sappho have been obtained. From this it appears that the angle which the earth's equatorial radius subtends at the centre of the sun when at its mean distance has the value 8´´·802. If we employ the best value of the earth's equatorial radius we obtain 92,870,000 miles as the mean distance of the centre of the sun from the centre of the earth. This is probably the most accurate determination of the scale of the solar system which has yet been made.
The Great Size of Jupiter—Comparison of his Diameter with that of the Earth—Dimensions of the Planet and his Orbit—His Rotation—Comparison of his Weight and Bulk with that of the Earth—Relative Lightness of Jupiter—How Explained—Jupiter still probably in a Heated Condition—The Belts on Jupiter—Spots on his Surface—Time of Rotation of different Spots various—Storms on Jupiter—Jupiter not Incandescent—The Satellites—Their Discovery—Telescopic Appearance—Their Orbits—The Eclipses and Occultations—A Satellite in Transit—The Velocity of Light Discovered—How is this Velocity to be Measured Experimentally?—Determination of the Sun's Distance by the Eclipses of Jupiter's Satellites—Jupiter's Satellites demonstrating the Copernican System.
In our exploration of the beautiful series of bodies which form the solar system, we have proceeded step by step outwards from the sun. In the pursuit of this method we have now come to the splendid planet Jupiter, which wends its majestic way in a path immediately outside those orbits of the minor planets which we have just been considering. Great, indeed, is the contrast between these tiny globes and the stupendous globe of Jupiter. Had we adopted a somewhat different method of treatment—had we, for instance, discussed the various bodies of our planetary system in the order of their magnitude—then the minor planets would have been the last to be considered, while the leader of the host would be Jupiter. To this position Jupiter is entitled without an approach to rivalry. The next greatest on the list, the beautiful and interesting Saturn, comes a long distance behind. Another great descent in the scale of magnitude has to be made before we reach Uranus and Neptune, while still another step downwards must be made[Pg 246] before we reach that lesser group of planets which includes our earth. So conspicuously does Jupiter tower over the rest, that even if Saturn were to be augmented by all the other globes of our system rolled into one, the united mass would still not equal the great globe of Jupiter.
The adjoining picture (Fig. 56) shows the relative dimensions of Jupiter and the earth, and it conveys to the eye a more vivid impression of the enormous bulk of Jupiter than we can readily obtain by merely considering the numerical statements by which his bulk is to be accurately estimated. As, however, it will be necessary to place the numerical facts before our readers, we do so at the outset of this chapter.
Jupiter revolves in an elliptic orbit around the sun in the focus, at a mean distance of 483,000,000 miles. The path of Jupiter is thus about 5·2 times as great in diameter as the path pursued by the earth. The shape of Jupiter's orbit departs very appreciably from a circle, the greatest distance from the sun being 5·45, while the least distance is about 4·95, the earth's distance from the sun being taken as unity.[Pg 247] In the most favourable circumstances for seeing Jupiter at opposition, it must still be about four times as far from the earth as the earth is from the sun. This great globe will also illustrate the law that the more distant a planet is, the slower is the velocity with which its orbital motion is accomplished. While the earth passes over eighteen miles each second, Jupiter only accomplishes eight miles. Thus for a twofold reason the time occupied by an exterior planet in completing a revolution is greater than the period of the earth. Not only has the outer planet to complete a longer course than the earth, but the speed is less; it thus happens that Jupiter requires 4,332·6 days, or about fifty days less than twelve years, to make a circuit of the heavens.
The mean diameter of the great planet is about 87,000 miles. We say the mean diameter, because there is a conspicuous difference in the case of Jupiter between his equatorial and his polar diameters. We have already seen that there is a similar difference in the case of the earth, where we find the polar diameter to be shorter than the equatorial; but the inequality of these two dimensions is very much larger in Jupiter than in the earth. The equatorial diameter of Jupiter is 89,600 miles, while the polar is not more than 84,400 miles. The ellipticity of Jupiter indicated by these figures is sufficiently marked to be obvious without any refined measures. Around the shortest diameter the planet spins with what must be considered an enormous velocity when we reflect on the size of the globe. Each rotation is completed in about 9 hrs. 55 mins.
We may naturally contrast the period of rotation of Jupiter with the much slower rotation of our earth in twenty-four hours. The difference becomes much more striking if we consider the relative speeds at which an object on the equator of the earth and on that of Jupiter actually moves. As the diameter of Jupiter is nearly eleven times that of the earth, it will follow that the speed of the equator on Jupiter must be about twenty-seven times as great as that on the earth. It is no doubt to this high velocity of rotation that we must ascribe the extraordinary ellipticity of Jupiter; the rapid[Pg 248] rotation causes a great centrifugal force, and this bulges out the pliant materials of which he seems to be formed.
Jupiter is not, so far as we can see, a solid body. This is an important circumstance; and therefore it will be necessary to discuss the matter at some little length, as we here perceive a wide contrast between this great planet and the other planets which have previously occupied our attention. From the measurements already given it is easy to calculate the bulk or the volume of Jupiter. It will be found that this planet is about 1,300 times as large as the earth; in other words, it would take 1,300 globes, each as large as our earth, all rolled into one, to form a single globe as large as Jupiter.
If the materials of which Jupiter is composed were of a nature analogous to the materials of the earth, we might expect that the weight of the planet would exceed the weight of the earth in something like the proportion of their volumes. This is the matter now proposed to be brought to trial. Here we may at once be met with the query, as to how we are to find the weight of Jupiter. It is not even an easy matter to weigh the earth on which we stand. How, then, can we weigh a mighty planet vastly larger than the earth, and distant from us by some hundreds of millions of miles? Truly, this is a bold problem. Yet the intellectual resources of man have proved sufficient to achieve this feat of celestial engineering. They are not, it is true, actually able to make the ponderous weighing scales in which the great planet is to be cast, but they are able to divert to this purpose certain natural phenomena which yield the information that is required.
Such investigations are based on the principle of universal gravitation. The mass of Jupiter attracts other masses in the solar system. The efficiency of that attraction is more particularly shown on the bodies which are near the planet. In virtue of this attraction certain movements are performed by those bodies. We can observe their character with our telescopes, we can ascertain their amount, and from our measurements we can calculate the mass of the body by which the movements have been produced. This is the sole method which we possess for the investigation of the masses[Pg 249] of the planets; and though it may be difficult in its application—not only from the observations which are required, but also from the intricacy and the profundity of the calculations to which those observations must be submitted—yet, in the case of Jupiter at least, there is no uncertainty about the result.
The task is peculiarly simplified in the case of the greatest planet of our system by the beautiful system of moons with which he is attended. These little moons revolve under the guidance of Jupiter, and their movements are not otherwise interfered with so as to prevent their use for our present purpose. It is from the observations of the satellites of Jupiter that we are enabled to measure his attractive power, and thence to calculate the mass of the mighty planet.
To those not specially conversant with the principles of mechanics, it may seem difficult to realise the degree of accuracy of which such a method is capable. Yet there can be no doubt that his moons inform us of the mass of Jupiter, and do not leave a margin of inaccuracy so great as one hundredth part of the total amount. If other confirmation be needed, then it is forthcoming in abundance. A minor planet occasionally draws near the orbit of Jupiter and experiences his attraction; the planet is forced to swerve from its path, and the amount of the deviation can be measured. From that measurement the mass of Jupiter can be computed by a calculation, of which it would be impossible to give an account in this place. The mass of Jupiter, as determined by this method, agrees with the mass obtained in a totally different manner from the satellites.
Nor have we yet exhausted the resources of astronomy in its bearing on this question. We can discard the planetary system, and invite the assistance of a comet which, flashing through the orbits of the planets, occasionally experiences large and sometimes enormous disturbances. For the present it suffices to remark, that on one or two occasions it has happened that venturous comets have been near enough to Jupiter to be much disturbed by his attraction, and then to proclaim in their altered movements the magnitude of the[Pg 250] mass which has affected them. The satellites of Jupiter, the minor planets, and the comets, all tell the weight of the giant orb; and, as they all concur in the result (at least within extremely narrow limits), we cannot hesitate to conclude that the mass of the greatest planet of our system has been determined with accuracy.
The results of these measures must now be stated. They show, of course, that Jupiter is vastly inferior to the sun—that, in fact, it would take about 1,047 Jupiters, all rolled into one, to form a globe equal in weight to the sun. They also show us that it would take 316 globes as heavy as our Earth to counterbalance the weight of Jupiter.
No doubt this proves Jupiter to be a body of magnificent proportions; but the remarkable circumstance is not that Jupiter should be 316 times as heavy as the earth, but that he is not a great deal more. Have we not stated that Jupiter is 1,300 times as large as the earth? How then comes it that he is only 316 times as heavy? This points at once to some fundamental contrast between the constitution of Jupiter and of the earth. How are we to account for this difference? We can conceive of two explanations. In the first place, it might be supposed that Jupiter is constituted of materials partly or wholly unknown on the earth. There is, however, an alternative supposition at once more philosophical and more consistent with the evidence. It is true that we know little or nothing of what the elementary substances on Jupiter may be, but one of the great discoveries of modern astronomy has taught us something of the elementary bodies present in other bodies of the universe, and has demonstrated that to a large extent they are identical with the elementary bodies on the earth. If Jupiter be composed of bodies resembling those on the earth, there is one way, and only one, in which we can account for the disparity between his size and his mass. Perhaps the best way of stating the argument will be found in a glance at the remote history of the earth itself, for it seems not impossible that the present condition of Jupiter was itself foreshadowed by the condition of our earth countless ages ago.
In a previous chapter we had occasion to point out how the earth seemed to be cooling from an earlier and highly heated condition. The further we look back, the hotter our globe seems to have been; and if we project our glance back to an epoch sufficiently remote, we see that it must once have been so hot that life on its surface would have been impossible. Back still earlier, we find the heat to have been such that water could not rest on the earth; and hence it seems likely that at some incredibly remote epoch all the oceans now reposing in the deeps on the surface, and perhaps a considerable portion of its now solid crust, must have been in a state of vapour. Such a transformation of the globe would not alter its mass, for the materials weigh the same whatever be their condition as to temperature, but it would alter the size of our globe to a very considerable extent. If these oceans were transformed into vapour, then the atmosphere, charged with mighty clouds, would have a bulk some hundreds of times greater than that which it has at present. Viewed from a distant planet, the cloud-laden atmosphere would indicate the visible size of our globe, and its average density would accordingly appear to be very much less than it is at present.
From these considerations it will be manifest that the discrepancy between the size and the weight of Jupiter, as contrasted with our earth, would be completely removed if we supposed that Jupiter was at the present day a highly heated body in the condition of our earth countless ages ago. Every circumstance of the case tends to justify this argument. We have assigned the smallness of the moon as a reason why the moon has cooled sufficiently to make its volcanoes silent and still. In the same way the smallness of the earth, as compared with Jupiter, accounts for the fact that Jupiter still retains a large part of its original heat, while the smaller earth has dissipated most of its store. This argument is illustrated and strengthened when we introduce other planets into the comparison. As a general rule we find that the smaller bodies, like the earth and Mars, have a high density, indicative of a low temperature,[Pg 252] while the giant planets, like Jupiter and Saturn, have a low density, suggesting that they still retain a large part of their original heat. We say "original heat" for the want, perhaps, of a more correct expression; it will, however, indicate that we do not in the least refer to the solar heat, of which, indeed, the great outer planets receive much less than those nearer the sun. Where the original heat may have come from is a matter still confined to the province of speculation.
A complete justification of these views with regard to Jupiter is to be found when we make a minute telescopic scrutiny of its surface; and it fortunately happens that the size of the planet is so great that, even at a distance of more millions of miles than there are days in the year, we can still trace on its surface some significant features.
Plate XI. gives a series of four different views of Jupiter. They have been taken from a series of admirable drawings of the great planet made by Mr. Griffiths in 1897. The first picture shows the appearance of the globe at 10h. 20m. Greenwich time on February 17th, 1897, through a powerful refracting telescope. We at once notice in this drawing that the outline of Jupiter is distinctly elliptical. The surface of the planet usually shows the remarkable series of belts here represented. They are nearly parallel to each other and to the planet's equator.
When Jupiter is observed for some hours, the appearance of the belts undergoes certain changes. These are partly due to the regular rotation of the planet on its axis, which, in a period of less than five hours, will completely carry away the hemisphere we first saw, and replace it by the hemisphere originally at the other side. But besides the changes thus arising, the belts and other features on the planet are also very variable. Sometimes new stripes or marks appear, and old ones disappear; in fact, a thorough examination of Jupiter will demonstrate the remarkable fact that there are no permanent features whatever to be discerned. We are here immediately struck by the contrast between Jupiter and Mars; on the smaller planet the main[Pg 253] topographical outlines are almost invariable, and it has been feasible to construct maps of the surface with tolerably accurate detail; a map of Jupiter is, however, an impossibility—the drawing of the planet which we make to-night will be different from the drawing of the same hemisphere made a few weeks hence.
It should, however, be noticed that objects occasionally appear on the planet which seem of a rather more persistent character than the belts. We may especially mention the object known as the great oblong Red Spot, which has been a very remarkable feature upon the southern hemisphere of Jupiter since 1878. This object, which has attracted a great deal of attention from observers, is about 30,000 miles long by about 7,000 in breadth. Professor Barnard remarks that the older the spots on Jupiter are, the more ruddy do they tend to become.
The conclusion is irresistibly forced upon us that when we view the surface of Jupiter we are not looking at any solid body. The want of permanence in the features of the planet would be intelligible if what we see be merely an atmosphere laden with clouds of impenetrable density. The belts especially support this view; we are at once reminded of the equatorial zones on our own earth, and it is not at all unlikely that an observer sufficiently remote from the earth to obtain a just view of its appearance would detect upon its surface more or less perfect cloud-belts suggestive of those on Jupiter. A view of our earth would be, as it were, intermediate between a view of Jupiter and of Mars. In the latter case the appearance of the permanent features of the planet is only to a trifling extent obscured by clouds floating over the surface. Our earth would always be partly, and often perhaps very largely, covered with cloud, while Jupiter seems at all times completely enveloped.
From another class of observations we are also taught the important truth that Jupiter is not, superficially at least, a solid body. The period of rotation of the planet around its axis is derived from the observation of certain marks, which present sufficient definiteness and sufficient[Pg 254] permanence to be suitable for the purpose. Suppose one of these objects to lie at the centre of the planet's disc; its position is carefully measured, and the time is noted. As the hours pass on, the mark moves to the edge of the disc, then round the other side of the planet, and back again to the visible disc. When it has returned to the position originally occupied the time is again taken, and the interval which has elapsed is called the period of rotation of the spot.
If Jupiter were a solid, and if these features were engraved upon its surface, then it is perfectly clear that the time of rotation as found by any one spot must coincide precisely with the time yielded by any other spot; but this is not observed to be the case. In fact, it would be nearer the truth to say that each spot gives a special period of its own. Nor are the differences very minute. It has been found that the time in which the red spot (the latitude of which is about 25° south) is carried round is five minutes longer than that required by some peculiar white marks near the equator. The red spot has now been watched for about twenty years, and during most of that time has had a tendency to rotate more and more slowly, as may be seen from the following values of its rotation period:—
| In 1879, 9h. 55m. 33·9s. |
| In 1886, 9h. 55m. 40·6s. |
| In 1891, 9h. 55m. 41·7s. |
Since 1891 this tendency seems to have ceased, while the spot has been gradually fading away. Generally speaking, we may say that the equatorial regions rotate in about 9h. 50m. 20s., and the temperate zones in about 9h. 55m. 40s. Remarkable exceptions are occasionally met with. Some small black spots in north latitude 22°, which broke out in 1880 and again in 1891, rotated in 9h. 48m. to 9h. 49-1⁄2m. It may, therefore, be regarded as certain that the globe of Jupiter, so far as we can see it, is not a solid body. It consists, on the exterior at all events, of clouds and vaporous masses, which seem to be agitated by storms of the utmost intensity, if we are to judge from the ceaseless changes of the planet's surface.
Various photographs of Jupiter have been obtained; those which have been taken at the Lick Observatory being specially interesting and instructive. Pictures of the planet obtained with the camera in remarkable circumstances are represented in Figs. 57–60, which were taken by Professor Wm. H. Pickering at Arequipa, Peru, on the 12th of August, 1892.[21] The small object with the belts is the planet Jupiter. The[Pg 256] large advancing disc (of which only a small part can be shown) is the moon. The phenomenon illustrated is called the "occultation" of the planet. The planet is half-way behind the moon in Fig. 59, while in Fig. 60 half of the planet is still hidden by the dark limb of the moon.
It is well known that the tempests by which the atmosphere surrounding the earth is convulsed are to be ultimately attributed to the heat of the sun. It is the rays from the great luminary which, striking on the vast continents, warm the air in contact therewith. This heated air becomes lighter, and rises, while air to supply its place must flow in along the surface. The currents so produced form a breeze or a wind; while, under exceptional circumstances, we have the phenomena of cyclones and hurricanes, all originated by the sun's heat. Need we add that the rains, which so often accompany the storms, have also arisen from the solar beams, which have distilled from the wide expanse of ocean the moisture by which the earth is refreshed?
The storms on Jupiter seem to be vastly greater than those on the earth. Yet the intensity of the sun's heat on Jupiter is only a mere fraction—less, indeed, than the twenty-fifth part—of that received by the earth. It is incredible that the motive power of the appalling tempests on the great planet can be entirely, or even largely, due to the feeble influence of solar heat. We are, therefore, led to seek for some other source of such disturbances. What that source is to be will appear obvious when we admit that Jupiter still retains a large proportion of primitive internal heat. Just as the sun itself is distracted by violent tempests as an accompaniment of its intense internal fervour, so, in a lesser degree, do we observe the same phenomena in Jupiter. It may also be noticed that the spots on the sun usually lie in more or less regular zones, parallel to its equator, the arrangement being in this respect not dissimilar to that of the belts on Jupiter.
It being admitted that the mighty planet still retains some of its internal heat, the question remains as to how much. It is, of course, obvious that the heat of the planet is [Pg 257]inconsiderable when compared with the heat of the sun. The brilliance of Jupiter, which makes it an object of such splendour in our midnight sky, is derived from the same great source which illuminates the earth, the moon, or the other planets. Jupiter, in fact, shines by reflected sunlight, and not in virtue of any intrinsic light in his globe. A beautiful proof of this truth is familiar to every user of a telescope. The little satellites of the planet sometimes intrude between him and the sun, and cast a shadow on Jupiter. The shadow is black, or, at all events, it seems black, relatively to the brilliant surrounding surface of the planet. It must, therefore, be obvious that Jupiter is indebted to the sun for its brilliancy. The satellites supply another interesting proof of this truth. One of these bodies sometimes enters the shadow of Jupiter and lo! the little body vanishes. It does so because Jupiter has cut off the supply of sunlight which previously rendered the satellite visible. But the planet is not himself able to offer the satellite any light in compensation for the sunlight which he has intercepted.[22]
Enough, however, has been demonstrated to enable us to pronounce on the question as to whether the globe of Jupiter can be inhabited by living creatures resembling those on this earth. Obviously this cannot be so. The internal heat and the fearful tempests seem to preclude the possibility of organic life on the great planet, even were there not other arguments tending to the same conclusion. It may, however, be contended, with perhaps some plausibility, that Jupiter has in the distant future the prospect of a glorious career as the residence of organic life. The time will assuredly come when the internal heat must decline, when the clouds will gradually condense into oceans. On the surface dry land may then appear, and Jupiter be rendered habitable.
From this sketch of the planet itself we now turn to the interesting and beautiful system of five satellites by which Jupiter is attended. We have, indeed, already found it necessary to allude more than once to these little bodies, but not[Pg 258] to such an extent as to interfere with the more formal treatment which they are now to receive.
The discovery of the four chief satellites may be regarded as an important epoch in the history of astronomy. They are objects situated in a remarkable manner on the border-line which divides the objects visible to the unaided eye from those which require telescopic aid. It has been frequently asserted that these objects have been seen with the unaided eye; but without entering into any controversy on the matter, it is sufficient to recite the well-known fact that, although Jupiter had been a familiar object for countless centuries, yet the sharpest eyes under the clearest skies never discovered the satellites until Galileo turned the newly invented telescope upon them. This tube was no doubt a very feeble instrument, but very little power suffices to show objects so dose to the limit of visibility.
The view of the planet and its elaborate system of satellites as shown in a telescope of moderate power, is represented in Fig. 61. We here see the great globe, and nearly in a line parsing through its centre lie four small objects, three on one side and one on the other. These little bodies resemble stars, but they can be distinguished therefrom by their ceaseless movements around the planet, which they never fail to accompany during his entire circuit of the heavens. There is no more pleasing spectacle for the student than to follow with his telescope the movements of this beautiful system.
In Fig. 62 we have represented some of the various phenomena which the satellites present. The long black shadow is that produced by the interposition of Jupiter in the path of the sun's rays. In consequence of the great distance of the sun this shadow will extend, in the form of a very elongated cone, to a distance far beyond the orbit of the outer satellite. The second satellite is immersed in this shadow, and consequently eclipsed. The eclipse of a satellite must not be attributed to the intervention of the body of Jupiter between the satellite and the earth. Such an occurrence is called an occultation, and the third satellite is shown in this condition. The second and the third satellites are thus alike invisible, but the cause of the invisibility is quite different in the two cases. The eclipse is much the more striking phenomenon of the two, because the satellite, at the moment it plunges into the darkness, may be still at some apparent distance from the edge of the planet, and is thus seen up to the moment of the eclipse. In an occultation the satellite in passing behind the planet is, at the time of disappearance,[Pg 260] close to the planet's bright edge, and the extinction of the light from the small body cannot be observed with the same impressiveness as the occurrence of an eclipse.
A satellite also assumes another remarkable situation when in the course of transit over the face of the planet. The satellite itself is not always very easy to see in such circumstances, but the beautiful shadow which it casts forms a sharp black spot on the brilliant orb: the satellite will, indeed, frequently cast a visible shadow when it passes between the planet and the sun, even though it be not actually at the moment in front of the planet, as it is seen from the earth.
The periods in which the four principal moons of Jupiter revolve around their primary are respectively, 1 day 18 hrs. 27 min. 34 secs. for the first; 3 days 13 hrs. 13 min. 42 secs., for the second; 7 days 3 hrs. 42 min. 33 secs, for the third; and 16 days 16 hrs. 32 min. 11 secs. for the fourth. We thus observe that the periods of Jupiter's satellites are decidedly briefer than that of our moon. Even the satellite most distant from the great planet requires for each revolution less than two-thirds of an ordinary lunar month. The innermost of these bodies, revolving as it does in less than two days, presents a striking series of ceaseless and rapid changes, and it becomes eclipsed during every revolution. The distance from the centre of Jupiter to the orbit of the innermost of these four attendants is a quarter of a million miles, while the radius of the outermost is a little more than a million miles. The second of the satellites proceeding outwards from the planet is almost the same size as our moon; the other three bodies are larger; the third being the greatest of all (about 3,560 miles in diameter). Owing to the minuteness of the satellites as seen from the earth, it is extremely difficult to perceive any markings on their surfaces, but the few observations made seem to indicate that the satellites (like our moon) always turn the same face towards their primary. Professor Barnard has, with the great Lick refractor, seen a white equatorial belt on the first satellite, while its poles were very dark. Mr. Douglass, observing with Mr. Lowell's great refractor, has also reported certain streaky markings on the third satellite.
A very interesting astronomical discovery was that made by Professor E.E. Barnard in 1892. He detected with the 36-inch Lick refractor an extremely minute fifth satellite to Jupiter at a distance of 112,400 miles, and revolving in a period of 11 hrs. 57 min. 22·6 secs. It can only be seen with the most powerful telescopes.
The eclipses of Jupiter's satellites had been observed for many years, and the times of their occurrence had been recorded. At length it was perceived that a certain order reigned among the eclipses of these bodies, as among all other astronomical phenomena. When once the laws according to which the eclipses recurred had been perceived, the usual consequence followed. It became possible to foretell the time at which the eclipses would occur in future. Predictions were accordingly made, and it was found that they were approximately verified. Further improvements in the calculations were then perfected, and it was sought to predict the times with still greater accuracy. But when it came to naming the actual minute at which the eclipse should occur, expectations were not always realised. Sometimes the eclipse was five or ten minutes too soon. Sometimes it was five or ten minutes too late. Discrepancies of this kind always demand attention. It is, indeed, by the right use of them that discoveries are often made, and one of the most interesting examples is that now before us.
The irregularity in the occurrence of the eclipses was at length perceived to observe certain rules. It was noticed that when the earth was near to Jupiter the eclipse generally occurred before the predicted time; while when the earth happened to be at the side of its orbit away from Jupiter, the eclipse occurred after the predicted time. Once this was proved, the great discovery was quickly made by Roemer, a Danish astronomer, in 1675. When the satellite enters the shadow, its light gradually decreases until it disappears. It is the last ray of light from the eclipsed satellite that gives the time of the eclipse; but that ray of light has to travel from the satellite to the earth, and enter our telescope, before we can note the occurrence. It used to be thought that[Pg 262] light travelled instantaneously, so that the moment the eclipse occurred was assumed to be the moment when the eclipse was seen in the telescope. This was now perceived to be incorrect. It was found that light took time to travel. When the earth was comparatively near Jupiter the light had only a short journey, the intelligence of the eclipse arrived quickly, and the eclipse was seen sooner than the calculations indicated. When the earth occupied a position far from Jupiter, the light had a longer journey, and took more than the average time, so that the eclipse was later than the prediction. This simple explanation removed the difficulty attending the predictions of the eclipses of the satellites. But the discovery had a significance far more momentous. We learned from it that light had a measurable velocity, which, according to recent researches, amounts to 186,300 miles per second.
One of the most celebrated attempts to ascertain the distance of the sun is derived from a combination of experiments on the velocity of light with astronomical measurements. This is a method of considerable refinement and interest, and although it does not so fulfil all the necessary conditions as to make it perfectly satisfactory, yet it is impossible to avoid some reference to it here. Notwithstanding that the velocity of light is so stupendous, it has been found possible to measure that velocity by actual trial. This is one of the most delicate experimental researches that have ever been undertaken. If it be difficult to measure the speed of a rifle bullet, what shall we say of the speed of a ray of light, which is nearly a million times as great? How shall we devise an apparatus subtle enough to determine the velocity which would girdle the earth at the equator no less than seven times in a single second of time? Ordinary contrivances for measurement are here futile; we have to devise an instrument of a wholly different character.
In the attempt to discover the speed of a moving body we first mark out a certain distance, and then measure the time which the body requires to traverse that distance. We determine the velocity of a railway train by the time it takes to pass from one mile-post to the next. We learn the speed[Pg 263] of a rifle bullet by an ingenious contrivance really founded on the same principle. The greater the velocity, the more desirable is it that the distance traversed during the experiment shall be as large as possible. In dealing with the measurement of the velocity of light, we therefore choose for our measured distance the greatest length that may be convenient. It is, however, necessary that the two ends of the line shall be visible from each other. A hill a mile or two away will form a suitable site for the distant station, and the distance of the selected point on the hill from the observer must be carefully measured.
The problem is now easily stated. A ray of light is to be sent from the observer to the distant station, and the time occupied by that ray in the journey is to be measured. We may suppose that the observer, by a suitable contrivance, has arranged a lantern from which a thin ray of light issues. Let us assume that this travels all the way to the distant station, and there falls upon the surface of a reflecting mirror. Instantly it will be diverted by reflection into a new direction depending upon the inclination of the mirror. By suitable adjustment the latter can be so placed that the light shall fall perpendicularly upon it, in which case the ray will of course return along the direction in which it came. Let the mirror be fixed in this position throughout the course of the experiments. It follows that a ray of light starting from the lantern will be returned to the lantern after it has made the journey to the distant station and back again. Imagine, then, a little shutter placed in front of the lantern. We open the shutter, the ray streams forth to the remote reflector, and back again through the opening. But now, after having allowed the ray to pass through the shutter, suppose we try and close it before the ray has had time to get back again. What fingers could be nimble enough to do this? Even if the distant station were ten miles away, so that the light had a journey of ten miles in going to the mirror and ten miles in coming back, yet the whole course would be accomplished in about the nine-thousandth part of a second—a[Pg 264] period so short that even were it a thousand times as long it would hardly enable manual dexterity to close the aperture. Yet a shutter can be constructed which shall be sufficiently delicate for the purpose.
The principle of this beautiful method will be sufficiently obvious from the diagram on this page (Fig. 63), which has been taken from Newcomb's "Popular Astronomy." The figure exhibits the lantern and the observer, and a large wheel with projecting teeth. Each tooth as it passes round eclipses the beam of light emerging from the lantern, and also the eye, which is of course directed to the mirror at the distant station. In the position of the wheel here shown the ray from the lantern will pass to the mirror and back so as to be visible to the eye; but if the wheel be rotating, it may so happen that the beam after leaving the lantern will not have time to return before the next tooth of the wheel comes in front of the eye and screens it. If the wheel be urged still faster, the next tooth may have passed the eye, so that the ray again becomes visible. The speed at which the wheel is rotating can be measured. We can thus determine the time taken by one of the teeth to pass in front of the eye; we have accordingly a measure of the time occupied by the ray of light in the double journey, and hence we have a measurement of the velocity of light.
It thus appears that we can tell the velocity of light either[Pg 265] by the observations of Jupiter's satellites or by experimental enquiry. If we take the latter method, then we are entitled to deduce remarkable astronomical consequences. We can, in fact, employ this method for solving that great problem so often referred to—the distance from the earth to the sun—though it cannot compete in accuracy with some of the other methods.
The dimensions of the solar system are so considerable that a sunbeam requires an appreciable interval of time to span the abyss which separates the earth from the sun. Eight minutes is approximately the duration of the journey, so that at any moment we see the sun as it appeared eight minutes earlier to an observer in its immediate neighbourhood. In fact, if the sun were to be suddenly blotted out it would still be seen shining brilliantly for eight minutes after it had really disappeared. We can determine this period from the eclipses of Jupiter's satellites.
So long as the satellite is shining it radiates a stream of light across the vast space between Jupiter and the earth. When the eclipse has commenced, the little orb is no longer luminous, but there is, nevertheless, a long stream of light on its way, and until all this has poured into our telescopes we still see the satellite shining as before. If we could calculate the moment when the eclipse really took place, and if we could observe the moment at which the eclipse is seen, the difference between the two gives the time which the light occupies on the journey. This can be found with some accuracy; and, as we already know the velocity of light, we can ascertain the distance of Jupiter from the earth; and hence deduce the scale of the solar system. It must, however, be remarked that at both extremities of the process there are characteristic sources of uncertainty. The occurrence of the eclipse is not an instantaneous phenomenon. The satellite is large enough to require an appreciable time in crossing the boundary which defines the shadow, so that the observation of an eclipse cannot be sufficiently precise to form the basis of an important and accurate measurement.[23] Still[Pg 266] greater difficulties accompany the attempt to define the true moment of the occurrence of the eclipse as it would be seen by an observer in the vicinity of the satellite. For this we should require a far more perfect theory of the movements of Jupiter's satellites than is at present attainable. This method of finding the sun's distance holds out no prospect of a result accurate to the one-thousandth part of its amount, and we may discard it, inasmuch as the other methods available seem to admit of much higher accuracy.
The four chief satellites of Jupiter have special interest for the mathematician, who finds in them a most striking instance of the universality of the law of gravitation. These bodies are, of course, mainly controlled in their movements by the attraction of the great planet; but they also attract each other, and certain curious consequences are the result.
The mean motion of the first satellite in each day about the centre of Jupiter is 203°·4890. That of the second is 101°·3748, and that of the third is 50°·3177. These quantities are so related that the following law will be found to be observed:
The mean motion of the first satellite added to twice the mean motion of the third is exactly equal to three times the mean motion of the second.
There is another law of an analogous character, which is thus expressed (the mean longitude being the angle between a fixed line and the radius to the mean place of the satellite): If to the mean longitude of the first satellite we add twice the mean longitude of the third, and subtract three times the mean longitude of the second, the difference is always 180°.
It was from observation that these principles were first discovered. Laplace, however, showed that if the satellites revolved nearly in this way, then their mutual perturbations, in accordance with the law of gravitation, would preserve them in this relative position for ever.
We shall conclude with the remark, that the discovery of Jupiter's satellites afforded the great confirmation of the[Pg 267] Copernican theory. Copernicus had asked the world to believe that our sun was a great globe, and that the earth and all the other planets were small bodies revolving round the great one. This doctrine, so repugnant to the theories previously held, and to the immediate evidence of our senses, could only be established by a refined course of reasoning. The discovery of Jupiter's satellites was very opportune. Here we had an exquisite ocular demonstration of a system, though, of course, on a much smaller scale, precisely identical with that which Copernicus had proposed. The astronomer who had watched Jupiter's moons circling around their primary, who had noticed their eclipses and all the interesting phenomena attendant on them, saw before his eyes, in a manner wholly unmistakable, that the great planet controlled these small bodies, and forced them to revolve around him, and thus exhibited a miniature of the great solar system itself. "As in the case of the spots on the sun, Galileo's announcement of this discovery was received with incredulity by those philosophers of the day who believed that everything in nature was described in the writings of Aristotle. One eminent astronomer, Clavius, said that to see the satellites one must have a telescope which would produce them; but he changed his mind as soon as he saw them himself. Another philosopher, more prudent, refused to put his eye to the telescope lest he should see them and be convinced. He died shortly afterwards. 'I hope,' said the caustic Galileo, 'that he saw them while on his way to heaven'"[24]
The Position of Saturn in the System—Saturn one of the Three most Interesting Objects in the Heavens—Compared with Jupiter—Saturn to the Unaided Eye—Statistics relating to the Planet—Density of Saturn—Lighter than Water—The Researches of Galileo—What he found in Saturn—A Mysterious Object—The Discoveries made by Huyghens half a Century later—How the Existence of the Ring was Demonstrated—Invisibility of the Rings every Fifteen Years—The Rotation of the Planet—The Celebrated Cypher—The Explanation—Drawing of Saturn—The Dark Line—W. Herschel's Researches—Is the Division in the Ring really a Separation?—Possibility of Deciding the Question—The Ring in a Critical Position—Are there other Divisions in the Ring?—The Dusky Ring—Physical Nature of Saturn's Rings—Can they be Solid?—Can they even be Slender Rings?—A Fluid?—True Nature of the Rings—A Multitude of Small Satellites—Analogy of the Rings of Saturn to the Group of Minor Planets—Problems Suggested by Saturn—The Group of Satellites to Saturn—The Discoveries of Additional Satellites—The Orbit of Saturn not the Frontier of our System.
At a profound distance in space, which, on an average, is 886,000,000 miles, the planet Saturn performs its mighty revolution around the sun in a period of twenty-nine and a half years. This gigantic orbit formed the boundary to the planetary system, so far as it was known to the ancients.
Although Saturn is not so great a body as Jupiter, yet it vastly exceeds the earth in bulk and in mass, and is, indeed, much greater than any one of the planets, Jupiter alone excepted. But while Saturn must yield the palm to Jupiter so far as mere dimensions are concerned, yet it will be generally admitted that even Jupiter, with all the retinue by which he is attended, cannot compete in beauty with the marvellous system of Saturn. To the present writer it has always seemed that Saturn is one of the three most interesting celestial objects visible to observers in northern latitudes. The other two will[Pg 269] occupy our attention in future chapters. They are the great nebula in Orion, and the star cluster in Hercules.
So far as the globe of Saturn is concerned, we do not meet with any features which give to the planet any exceptional interest. The globe is less than that of Jupiter, and as the latter is also much nearer to us, the apparent size of Saturn is in a twofold way much smaller than that of Jupiter. It should also be noticed that, owing to the greater distance of Saturn from the sun, its intrinsic brilliancy is less than that of Jupiter. There are, no doubt, certain marks and bands often to be seen on Saturn, but they are not nearly so striking nor so characteristic as the ever-variable belts upon Jupiter. The telescopic appearance of the globe of Saturn must also be ranked as greatly inferior in interest to that of Mars. The delicacy of detail which we can see on Mars when favourably placed has no parallel whatever in the dim and distant Saturn. Nor has Saturn, regarded again merely as a globe, anything like the interest of Venus. The great splendour of Venus is altogether out of comparison with that of Saturn, while the brilliant crescent of the evening star is infinitely more pleasing than any telescopic view of the globe of Saturn. Yet even while we admit all this to the fullest extent, it does not invalidate the claim of Saturn to be one of the most supremely beautiful and interesting objects in the heavens. This interest is not due to his globe; it is due to that marvellous system of rings by which Saturn is surrounded—a system wonderful from every point of view, and, so far as our knowledge goes, without a parallel in the wide extent of the universe.
To the unaided eye Saturn usually appears like a star of the first magnitude. Its light alone would hardly be sufficient to discriminate it from many of the brighter fixed stars. Yet the ancients were acquainted with Saturn, and they knew it as a planet. It was included with the other four great planets—Mercury, Venus, Mars, and Jupiter—in the group of wanderers, which were bound to no fixed points of the sky like the stars. On account of the great distance of Saturn, its movements are much slower than those of the other planets known to the ancients. Twenty-nine years and a half are required for this distant object to complete its circuit of the heavens; and, though this movement is slow compared with the incessant changes of Venus, yet it is rapid enough to attract the attention of any careful observer. In a single year Saturn moves through a distance of about twelve degrees, a quantity sufficiently large to be conspicuous to casual observation. Even in a month, or sometimes in a week, the planet traverses an arc of the sky which can be detected by anyone who will take the trouble to mark the place of the planet with regard to the stars in its vicinity. Those who are privileged to use accurate astronomical instruments can readily detect the motion of Saturn in a few hours.
The average distance from the sun to Saturn is about 886 millions of miles. The path of Saturn, as of every other planet, is really an ellipse with the sun in one focus. In the case of Saturn the shape of this ellipse is very appreciably different from a purely circular path. Around this path Saturn moves with an average velocity of 5·96 miles per second.
The mean diameter of the globe of Saturn is about 71,000 miles. Its equatorial diameter is about 75,000 miles, and its polar diameter 67,000 miles—the ratio of these numbers being approximately that of 10 to 9. It is thus obvious that Saturn departs from the truly spherical shape to a very marked extent. The protuberance at its equator must, no doubt, be attributed to the high velocity with which the planet is rotating. The velocity of rotation of Saturn is more than double as fast as that of the earth, though it is not quite so fast as that of Jupiter. Saturn makes one complete rotation in about 10 hrs. 14 min. Mr. Stanley Williams has, however, observed with great care a number of spots which he has discovered, and he finds that some of these spots in about 27° north latitude indicate rotation in a period of 10 hrs. 14 mins. to 15 min., while equatorial spots require no more than 10 hrs. 12 min. to 13 min. There is, however, the peculiarity that spots in the same latitude, but at different parts of the planet, rotate at rates which differ by a minute or more, while the period found by various groups of spots seems to change from year to year.
These facts prove that Saturn and the spots do not form a rigid system. The lightness of this planet is such as to be wholly incompatible with the supposition that its globe is constituted of solid materials at all comparable with those of which the crust of our earth is composed. The satellites, which surround Saturn and form a system only less interesting than the renowned rings themselves, enable us to weigh the planet in comparison with the sun, and hence to deduce its actual mass relatively to the earth. The result is not a little remarkable. It appears that the density of the earth is eight times as great as that of Saturn. In fact, the density of the latter is less than that of water itself, so that a mighty globe of water, equal in bulk to Saturn, would actually weigh more. If we could conceive a vast ocean into which a globe equal to Saturn in size and weight were cast, the great globe would not sink like our earth or like any of the other planets; it would float buoyantly at the surface with one-fourth of its bulk out of the water.
We thus learn with high probability that what our telescopes show upon Saturn is not a solid surface, but merely a vast envelope of clouds surrounding a heated interior. It is impossible to resist the suggestion that this planet, like Jupiter, has still retained its heat because its mass is so large. We must, however, allude to a circumstance which perhaps may seem somewhat inconsistent with the view here taken. We have found that Jupiter and Saturn are, both of them, much less dense than the earth. When we compare the two planets together, it appears that Saturn is much less dense than Jupiter. In fact, every cubic mile of Jupiter weighs nearly twice as much as each cubic mile of Saturn. This would seem to point to the conclusion that Saturn is the more heated of the two bodies. Yet, as Jupiter is the larger, it might more reasonably have been expected to be hotter than the other planet. We do not attempt to reconcile this discrepancy; in fact, in our ignorance as to the material constitution of these bodies, it would be idle to discuss the question.
Even if we allow for the lightness of Saturn, as compared[Pg 273] bulk for bulk with the earth, yet the volume of Saturn is so enormous that the planet weighs more than ninety-five times as much as the earth. The adjoining view represents the relative sizes of Saturn and the earth (Fig. 65).
As the unaided eye discloses none of those marvels by which Saturn is surrounded, the interest which attaches to this planet may be said to commence from the time when it began to be observed with the telescope. The history must be briefly alluded to, for it was only by degrees that the real nature of this complicated object was understood. When Galileo completed his little refracting telescope, which, though it only magnified thirty times, was yet an enormous addition to the powers of unaided vision, he made with it his memorable review of the heavens. He saw the spots on the sun and the mountains on the moon; he noticed the crescent of Venus and the satellites of Jupiter. Stimulated and encouraged by such brilliant discoveries, he naturally sought to examine the other planets, and accordingly directed his telescope to Saturn. Here, again, Galileo at once made a discovery. He saw that Saturn presented a visible form like the other planets, but that it differed from any other telescopic object, inasmuch as it appeared to him to be composed[Pg 274] of three bodies which always touched each other and always maintained the same relative positions. These three bodies were in a line—the central one was the largest, and the two others were east and west of it. There was nothing he had hitherto seen in the heavens which filled his mind with such astonishment, and which seemed so wholly inexplicable.
In his endeavours to understand this mysterious object, Galileo continued his observations during the year 1610, and, to his amazement, he saw the two lesser bodies gradually become smaller and smaller, until, in the course of the two following years, they had entirely vanished, and the planet simply appeared with a round disc like Jupiter. Here, again, was a new source of anxiety to Galileo. He had at that day to contend against the advocates of the ancient system of astronomy, who derided his discoveries and refused to accept his theories. He had announced his observation of the composite nature of Saturn; he had now to tell of the gradual decline and the ultimate extinction of these two auxiliary globes, and he naturally feared that his opponents would seize the opportunity of pronouncing that the whole of his observations were illusory.[25] "What," he remarks, "is to be said concerning so strange a metamorphosis? Are the two lesser stars consumed after the manner of the solar spots? Have they vanished and suddenly fled? Has Saturn perhaps, devoured his own children? Or were the appearances indeed illusion or fraud, with which the glasses have so long deceived me, as well as many others to whom I have shown them? Now, perhaps, is the time come to revive the well-nigh withered hopes of those who, guided by more profound contemplations, have discovered the fallacy of the new observations, and demonstrated the utter impossibility of their existence. I do not know what to say in a case so surprising, so unlooked for, and so novel. The shortness of the time, the unexpected nature of the event, the weakness of my understanding, and the fear of being mistaken, have greatly confounded me."
But Galileo was not mistaken. The objects were really[Pg 275] there when he first began to observe, they really did decline, and they really disappeared; but this disappearance was only for a time—they again came into view. They were then subjected to ceaseless examination, until gradually their nature became unfolded. With increased telescopic power it was found that the two bodies which Galileo had described as globes on either side of Saturn were not really spherical—they were rather two luminous crescents with the concavity of each turned towards the central globe. It was also perceived that these objects underwent a remarkable series of periodic changes. At the beginning of such a series the planet was found with a truly circular disc. The appendages first appeared as two arms extending directly outwards on each side of the planet; then these arms gradually opened into two crescents, resembling handles to the globe, and attained their maximum width after about seven or eight years; then they began to contract, until after the lapse of about the same time they vanished again.
The true nature of these objects was at length discovered by Huyghens in 1655, nearly half a century after Galileo had first detected their appearance. He perceived the shadow thrown by the ring upon the globe, and his explanation of the phenomena was obtained in a very philosophical manner. He noticed that the earth, the sun, and the moon rotated upon their axes, and he therefore regarded it as a general law that each one of the bodies in the system rotates about an axis. It is true, observations had not yet been made which actually showed that Saturn was also rotating; but it would be highly, nay, indeed, infinitely, improbable that any planet should be devoid of such movement. All the analogies of the system pointed to the conclusion that the velocity of rotation would be considerable. One satellite of Saturn was already known to revolve in a period of sixteen days, being little more than half our month. Huyghens assumed—and it was a most reasonable assumption—that Saturn in all probability rotated rapidly on its axis. It was also to be observed that if these remarkable appendages were attached by an actual bodily connection to the planet they must rotate[Pg 276] with Saturn. If, however, the appendages were not actually attached it would still be necessary that they should rotate if the analogy of Saturn to other objects in the system were to be in any degree preserved. We see satellites near Jupiter which revolve around him. We see, nearer home, how the moon revolves around the earth. We see how all the planetary system revolves around the sun. All these considerations were present to Huyghens when he came to the conclusion that, whether the curious appendages were actually attached to the planet or were physically free from it, they must still be in rotation.
Provided with such reasonings, it soon became easy to conjecture the true nature of the Saturnian system. We have seen how the appendages declined to invisibility once every fifteen years, and then gradually reappeared in the form, at first, of rectilinear arms projecting outwards from the planet. The progressive development is a slow one, and for weeks and months, night after night, the same appearance is presented with but little change. But all this time both Saturn and the mysterious objects around him are rotating. Whatever these may be, they present the same appearance to the eye, notwithstanding their ceaseless motion of rotation.
What must be the shape of an object which satisfies the conditions here implied? It will obviously not suffice to regard the projections as two spokes diverging from the planet. They would change from visibility to invisibility in every rotation, and thus there would be ceaseless alterations of the appearance instead of that slow and gradual change which requires fifteen years for a complete period. There are, indeed, other considerations which preclude the possibility of the objects being anything of this character, for they are always of the same length as compared with the diameter of the planet. A little reflection will show that one supposition—and indeed only one—will meet all the facts of the case. If there were a thin symmetrical ring rotating in its own plane around the equator of Saturn, then the persistence of the object from night to night would be accounted for. This[Pg 277] at once removes the greater part of the difficulty. For the rest, it was only necessary to suppose that the ring was so thin that when turned actually edgewise to the earth it became invisible, and then as the illuminated side of the plane became turned more and more towards the earth the appendages to the planet gradually increased. The handle-shaped appearance which the object periodically assumed demonstrated that the ring could not be attached to the globe.
At length Huyghens found that he had the clue to the great enigma which had perplexed astronomers for the last fifty years. He saw that the ring was an object of astonishing interest, unique at that time, as it is, indeed, unique still. He felt, however, that he had hardly demonstrated the matter with all the certainty which it merited, and which he thought that by further attention he could secure. Yet he was loath to hazard the loss of his discovery by an undue postponement of its announcement, lest some other astronomer might intervene. How, then, was he to secure his priority if the discovery should turn out correct, and at the same time be enabled to perfect it at his leisure? He adopted the course, usual at the time, of making his first announcement in cipher, and accordingly, on March 5th, 1656, he published a tract, which contained the following proposition:—
| aaaaaaa iiiiiii oooo pp |
ccccc llll q rr |
d mm s ttttt |
eeeee g h nnnnnnnnn uuuuu |
Perhaps some of those curious persons whose successors now devote so much labour to double acrostics may have pondered on this renowned cryptograph, and even attempted to decipher it. But even if such attempts were made, we do not learn that they were successful. A few years of further study were thus secured to Huyghens. He tested his theory in every way that he could devise, and he found it verified in every detail. He therefore thought that it was needless for him any longer to conceal from the world his great discovery, and accordingly in the year 1659—about three years after the appearance of his cryptograph—he announced the interpretation of it. By[Pg 278] restoring the letters to their original arrangement the discovery was enunciated in the following words:—"Annulo cingitur, tenui, plano, nusquam cohærente, ad eclipticam inclinato," which may be translated into the statement:—"The planet is surrounded by a slender flat ring everywhere distinct from its surface, and inclined to the elliptic."
Huyghens was not content with merely demonstrating how fully this assumption explained all the observed phenomena. He submitted it to the further and most delicate test which can be applied to any astronomical theory. He attempted by its aid to make a prediction the fulfilment of which would necessarily give his theory the seal of certainty. From his calculations he saw that the planet would appear circular about July or August in 1671. This anticipation was practically verified, for the ring was seen to vanish in May of that year. No doubt, with our modern calculations founded on long-continued and accurate observation, we are now enabled to make forecasts as to the appearance or the disappearance of Saturn's ring with far greater accuracy; but, remembering the early stage in the history of the planet at which the prediction of Huyghens was made, we must regard its fulfilment as quite sufficient, and as confirming in a satisfactory manner the theory of Saturn and his ring.
The ring of Saturn having thus been thoroughly established as a fact in celestial architecture, each generation of astronomers has laboured to find out more and more of its marvellous features. In the frontispiece (Plate I.) we have a view of the planet as seen at the Harvard College Observatory, U.S.A., between July 28th and October 20th, 1872. It has been drawn by the skilful astronomer and artist—Mr. L. Trouvelot—and gives a faithful and beautiful representation of this unique object.
Fig. 64 is a drawing of the same object taken on July 2nd, 1894, by Prof. E.E. Barnard, at the Lick Observatory.
The next great discovery in the Saturnian system after those of Huyghens showed that the ring surrounding the planet was marked by a dark concentric line, which divided it into two parts—the outer being narrower than the inner. This line was first seen by J.D. Cassini, when Saturn emerged[Pg 279] from the rays of the sun in 1675. That this black line is not merely a black mark on the ring, but that it is actually a separation, was rendered very probable by the researches of Maraldi in 1715, followed many years later by those of Sir William Herschel, who, with that thoroughness which was a marked characteristic of the man, made a minute and scrupulous examination of Saturn. Night after night he followed it for hours with his exquisite instruments, and considerably added to our knowledge of the planet and his system.
Herschel devoted very particular attention to the examination of the line dividing the ring. He saw that the colour of this line was not to be distinguished from the colour of the space intermediate between the globe and the ring. He observed it for ten years on the northern face of the ring, and during that time it continued to present the same breadth and colour and sharpness of outline. He was then fortunate enough to observe the southern side of the ring. There again could the black line be seen, corresponding both in appearance and in position with the dark line as seen on the northern side. No doubt could remain as to the fact that Saturn was girdled by two concentric rings equally thin, the outer edge of one closely approaching to the inner edge of the other.
At the same time it is right to add that the only absolutely indisputable proof of the division between the rings has not yet been yielded by the telescope. The appearances noted by Herschel would be consistent with the view that the black line was merely a part of the ring extending through its thickness, and composed of materials very much less capable of reflecting light than the rest of the ring. It is still a matter of doubt how far it is ever possible actually to see through the dark line. There is apparently only one satisfactory method of accomplishing this. It would only occur in rare circumstances, and it does not seem that the opportunity has as yet arisen. Suppose that in the course of its motion through the heavens the path of Saturn happened to cross directly between the earth and a fixed star. The telescopic appearance of a star is merely a point of light much smaller than the globes and rings of Saturn. If the ring passed in front[Pg 280] of the star and the black line on the ring came over the star, we should, if the black line were really an opening, see the star shining through the narrow aperture.
Up to the present, we believe, there has been no opportunity of submitting the question of the duplex character of the ring to this crucial test. Let us hope that as there are now so many telescopes in use adequate to deal with the subject, there may, ere long, be observations made which will decide the question. It can hardly be expected that a very small star would be suitable. No doubt the smallness of the star would render the observations more delicate and precise if the star were visible; but we must remember that it will be thrown into contrast with the bright rings of Saturn on each margin so that unless the star were of considerable magnitude it would hardly answer. It has, however, been recently observed that the globe of the planet can be, in some degree, discerned through the dark line; this is practically a demonstration of the fact that the line is at all events partly transparent.
The outer ring is also divided into two by a line much fainter than that just described. It requires a good telescope and a fine night, combined with a favourable position of the planet, to render this line a well-marked object. It is most easily seen at the extremities of the ring most remote from the planet. To the present writer, who has examined the planet with the twelve-inch refractor of the South equatorial at Dunsink Observatory, this outer line appears as broad as the well-known line; but it is unquestionably fainter, and has a more shaded appearance. It certainly does not suggest the appearance of being actually an opening in the ring, and it is often invisible for a long time. It seems rather as if the ring were at this place thinner and less substantial without being actually void of substance.
On these points it may be expected that much additional information will be acquired when next the ring places itself in such a position that its plane, if produced, would pass between the earth and the sun. Such occasions are but rare, and even when they do occur it may happen that the planet will not[Pg 281] be well placed for observation. The next really good opportunity will not be till 1907. In this case the sunlight illuminates one side of the ring, while it is the other side of the ring that is presented towards the earth. Powerful telescopes are necessary to deal with the planet under such circumstances; but it may be reasonably hoped that the questions relating to the division of the ring, as well as to many other matters, will then receive some further elucidation.
Occasionally, other divisions of the ring, both inner and outer, have been recorded. It may, at all events, be stated that no such divisions can be regarded as permanent features. Yet their existence has been so frequently enunciated by skilful observers that it is impossible to doubt that they have been sometimes seen.
It was about 200 years after Huyghens had first explained the true theory of Saturn that another very important discovery was effected. It had, up to the year 1850, been always supposed that the two rings, divided by the well-known black line, comprised the entire ring system surrounding the planet. In the year just mentioned, Professor Bond, the distinguished astronomer of Cambridge, Mass., startled the astronomical world by the announcement of his discovery of a third ring surrounding Saturn. As so often happens in such cases, the same object was discovered independently by another—an English astronomer named Dawes. This third ring lies just inside the inner of the two well-known rings, and extends to about half the distance towards the body of the planet. It seems to be of a totally different character from the two other rings in so far as they present a comparatively substantial appearance. We shall, indeed, presently show that they are not solid—not even liquid bodies—but still, when compared with the third ring, the others were of a substantial character. They can receive and exhibit the deeply-marked shadow of Saturn, and they can throw a deep and black shadow upon Saturn themselves; but the third ring is of a much less compact texture. It has not the brilliancy of the others, it is rather of a dusky, semi-transparent appearance, and the expression "crape ring," by which it is often designated, is by no means inappropriate.[Pg 282] It is the faintness of this crape ring which led to its having been so frequently overlooked by the earlier observers of Saturn.
It has often been noticed that when an astronomical discovery has been made with a good telescope, it afterwards becomes possible for the same object to be observed with instruments of much inferior power. No doubt, when the observer knows what to look for, he will often be able to see what would not otherwise have attracted his attention. It may be regarded as an illustration of this principle, that the crape ring of Saturn has become an object familiar to those who are accustomed to work with good telescopes; but it may, nevertheless, be doubted whether the ease and distinctness with which the crape ring is now seen can be entirely accounted for by this supposition. Indeed, it seems possible that the crape ring has, from some cause or other, gradually become more and more visible. The supposed increased brightness of the crape ring is one of those arguments now made use of to prove that in all probability the rings of Saturn are at this moment undergoing gradual transformation; but observations of Hadley show that the crape ring was seen by him in 1720, and it was previously seen by Campani and Picard, as a faint belt crossing the planet. The partial transparency of the crape ring was beautifully illustrated in an observation by Professor Barnard of the eclipse of Iapetus on November 1st, 1889. The satellite was faintly visible in the shadow of the crape ring, while wholly invisible in the shadow of the better known rings.
The various features of the rings are well shown in the drawing of Trouvelot already referred to. We here see the inner and the outer ring, and the line of division between them. We see in the outer ring the faint traces of the line by which it is divided, and inside the inner ring we have a view of the curious and semi-transparent crape ring. The black shadow of the planet is cast upon the ring, thus proving that the ring, no less than the body of the planet, shines only in virtue of the sunlight which falls upon it. This shadow presents some anomalous features, but its[Pg 283] curious irregularity may be, to some extent, an optical illusion.
There can be no doubt that any attempt to depict the rings of Saturn only represents the salient features of that marvellous system. We are situated at such a great distance that all objects not of colossal dimensions are invisible. We have, indeed, only an outline, which makes us wish to be able to fill in the details. We long, for instance, to see the actual texture of the rings, and to learn of what materials they are made; we wish to comprehend the strange and filmy crape ring, so unlike any other object known to us in the heavens. There is no doubt that much may even yet be learned under all the disadvantageous conditions of our position; there is still room for the labour of whole generations of astronomers provided with splendid instruments. We want accurate drawings of Saturn under every conceivable aspect in which it may be presented. We want incessantly repeated measurements, of the most fastidious accuracy. These measures are to tell us the sizes and the shapes of the rings; they are to measure with fidelity the position of the dark lines and the boundaries of the rings. These measures are to be protracted for generations and for centuries; then and then only can terrestrial astronomers learn whether this elaborate system has really the attributes of permanence, or whether it may be undergoing changes.
We have been accustomed to find that the law of universal gravitation pervades every part of our system, and to look to gravitation for the explanation of many phenomena otherwise inexplicable. We have good reasons for knowing that in this marvellous Saturnian system the law of gravitation is paramount. There are satellites revolving around Saturn as well as a ring; these satellites move, as other satellites do, in conformity with the laws of Kepler; and, therefore, any theory as to the nature of Saturn's ring must be formed subject to the condition that it shall be attracted by the gigantic planet situated in its interior.
To a hasty glance nothing might seem easier than to reconcile the phenomena of the ring with the attraction of[Pg 284] the planet. We might suppose that the ring stands at rest symmetrically around the planet. At its centre the planet pulls in the ring equally on all sides, so that there is no tendency in it to move in one way rather than another; and, therefore, it will stay at rest. This will not do. A ring composed of materials almost infinitely rigid might possibly, under such circumstances, be for a moment at rest; but it could not remain permanently at rest any more than can a needle balanced vertically on its point. In each case the equilibrium is unstable. If the slightest cause of disturbance arise, the equilibrium is destroyed, and the ring would inevitably fall in upon the planet. Such causes of derangement are incessantly present, so that unstable equilibrium cannot be an appropriate explanation of the phenomena.
Even if this difficulty could be removed, there is still another, which would be quite insuperable if the ring be composed of any materials with which we are acquainted. Let us ponder for a moment on the matter, as it will lead up naturally to that explanation of the rings of Saturn which is now most generally accepted.
Imagine that you stood on the planet Saturn, near his equator; over your head stretches the ring, which sinks down to the horizon in the east and in the west. The half-ring above your horizon would then resemble a mighty arch, with a span of about a hundred thousand miles. Every particle of this arch is drawn towards Saturn by gravitation, and if the arch continue to exist, it must do so in obedience to the ordinary mechanical laws which regulate the railway arches with which we are familiar.
The continuance of these arches depends upon the resistance of the stones forming them to a crushing force. Each stone of an arch is subjected to a vast pressure, but stone is a material capable of resisting such pressure, and the arch remains. The wider the span of the arch the greater is the pressure to which each stone is exposed. At length a span is reached which corresponds to a pressure as great as the stones can safely bear, and accordingly we thus find the limiting span over which a single arch of masonry[Pg 285] can be constructed. Apply these principles to the stupendous arch formed by the ring of Saturn. It can be shown that the pressure on the materials of the arch capable of spanning an abyss of such awful magnitude would be something so enormous that no materials we know of would be capable of bearing it. Were the ring formed of the toughest steel that was ever made, the pressure would be so great that the metal would be squeezed like a liquid, and the mighty structure would collapse and fall down on the surface of the planet. It is not credible that any materials could exist capable of sustaining a stress so stupendous. The law of gravitation accordingly bids us search for a method by which the intensity of this stress can be mitigated.
One method is at hand, and is obviously suggested by analogous phenomena everywhere in our system. We have spoken of the ring as if it were at rest; let us now suppose it to be animated by a motion of rotation in its plane around Saturn as a centre. Instantly we have a force developed antagonistic to the gravitation of Saturn. This force is the so-called centrifugal force. If we imagine the ring to rotate, the centrifugal force at all points acts in an opposite direction to the attractive force, and hence the enormous stress on the ring can be abated and one difficulty can be overcome.
We can thus attribute to each ring a rotation which will partly relieve it from the stress the arch would otherwise have to sustain. But we cannot admit that the difficulty has been fully removed. Suppose that the outer ring revolve at such a rate as shall be appropriate to neutralise the gravitation on its outer edge, the centrifugal force will be less at the interior of the ring, while the gravitation will be greater; and hence vast stresses will be set up in the interior parts of the outer ring. Suppose the ring to rotate at such a rate as would be adequate to neutralise the gravitation at its inner margin; then the centrifugal force at the outer parts will largely exceed the gravitation, and there will be a tendency to disruption of the ring outwards.
To obviate this tendency we may assume the outer parts[Pg 286] of each ring to rotate more slowly than the inner parts. This naturally requires that the parts of the ring shall be mobile relatively to one another, and thus we are conducted to the suggestion that perhaps the rings are really composed of matter in a fluid state. The suggestion is, at first sight, a plausible one; each part of each ring would then move with an appropriate velocity, and the rings would thus exhibit a number of concentric circular currents with different velocities. The mathematician can push this inquiry a little farther, and he can study how this fluid would behave under such circumstances. His symbols can pursue the subject into the intricacies which cannot be described in general language. The mathematician finds that waves would originate in the supposed fluid, and that as these waves would lead to disruption of the rings, the fluid theory must be abandoned.
But we can still make one or two more suppositions. What if it be really true that the ring consist of an incredibly large number of concentric rings, each animated precisely with the velocity which would be suitable to the production of a centrifugal force just adequate to neutralise the attraction? No doubt this meets many of the difficulties: it is also suggested by those observations which have shown the presence of several dark lines on the ring. Here again dynamical considerations must be invoked for the reply. Such a system of solid rings is not compatible with the laws of dynamics.
We are, therefore, compelled to make one last attempt, and still further to subdivide the ring. It may seem rather startling to abandon entirely the supposition that the ring is in any sense a continuous body, but there remains no alternative. Look at it how we will, we seem to be conducted to the conclusion that the ring is really an enormous shoal of extremely minute bodies; each of these little bodies pursues an orbit of its own around the planet, and is, in fact, merely a satellite. These bodies are so numerous and so close together that they seem to us to be continuous, and they may be very minute—perhaps not larger than the globules of water found in an ordinary cloud over the surface of the[Pg 287] earth, which, even at a short distance, seems like a continuous body.
Until a few years ago this theory of the constitution of Saturn's rings, though unassailable from a mathematical point of view, had never been confirmed by observation. The only astronomer who maintained that he had actually seen the rings rotate was W. Herschel, who watched the motion of some luminous points on the ring in 1789, at which time the plane of the ring happened to pass through the earth. From these observations Herschel concluded that the ring rotated in ten hours and thirty-two minutes. But none of the subsequent observers, even though they may have watched Saturn with instruments very superior to that used by Herschel, were ever able to succeed in verifying his rotation of these appendages of Saturn. If the ring were composed of a vast number of small bodies, then the third law of Kepler will enable us to calculate the time which these tiny satellites would require to travel completely round the planet. It appears that any satellite situated at the outer edge of the ring would require as long a period as 13 hrs. 46 min., those about the middle would not need more than 10 hrs. 28 min., while those at the inner edge of the ring would accomplish their rotation in 7 hrs. 28 min. Even our mightiest telescopes, erected in the purest skies and employed by the most skilful astronomers, refuse to display this extremely delicate phenomenon. It would, indeed, have been a repetition on a grand scale of the curious behaviour of the inner satellite of Mars, which revolves round its primary in a shorter time than the planet itself takes to turn round on its own axis.
But what the telescope could not show, the spectroscope has lately demonstrated in a most effective and interesting manner. We have explained in the chapter on the sun how the motion of a source of light along the line of vision, towards or away from the observer, produces a slight shift in the position of the lines of the spectrum. By the measurement of the displacement of the lines the direction and amount of the motion of the source of light may be determined. We illustrated the method by showing how it had actually been used to measure the speed of rotation of the solar surface. In 1895 Professor Keeler,[26] Director of the Allegheny Observatory, succeeded in measuring the rotation of Saturn's ring in this manner. He placed the slit of his spectroscope across the ball, in the direction of the major axis of the elliptic figure which the effect of perspective gives the ring as shown by the parallel lines in Fig. 66 stretching[Pg 289] from E to W. His photographic plate should then show three spectra close together, that of the ball of Saturn in the middle, separated by dark intervals from the narrower spectra above and below it of the two handles (or ansæ, as they are generally called) of the ring. In Fig. 67 we have represented the behaviour of any one line of the spectrum under various suppositions as to rotation or non-rotation of Saturn and the ring. At the top (1) we see how each line would look if there was no rotatory motion; the three lines produced by ring, planet, and ring are in a straight line. Of course the spectrum, which is practically a very faint copy of the solar spectrum, shows the principal dark Fraunhofer lines, so that the reader must imagine these for himself, parallel to the one we show in the figure. But Saturn and the ring are not standing still, they are rotating, the eastern part (at E) moving towards us, and the western part (W) moving away[Pg 290] from us.[27] At E the line will therefore be shifted towards the violet end of the spectrum and at W towards the red, and as the actual linear velocity is greater the further we get away from the centre of Saturn (assuming ring and planet to rotate together), the lines would be turned as in Fig. 67 (2), but the three would remain in a straight line. If the ring consisted of two independent rings separated by Cassini's division and rotating with different velocities, the lines would be situated as in Fig. 67 (3), the lines due to the inner ring being more deflected than those due to the outer ring, owing to the greater velocity of the inner ring.
Finally, let us consider the case of the rings, consisting of innumerable particles moving round the planet in accordance with Kepler's third law. The actual velocities of these particles would be per second:—
| At outer edge of ring | 10·69 miles. |
| At middle of ring | 11·68 miles. |
| At inner edge of ring | 13·01 miles. |
| Rotation speed at surface of planet | 6·38 miles. |
The shifting of the lines of the spectrum should be in accordance with these velocities, and it is easy to see that the lines ought to lie as in the fourth figure. When Professor Keeler came to examine the photographed spectra, he found the lines of the three spectra tilted precisely in this manner, showing that the outer edge of the ring was travelling round the planet with a smaller linear velocity than the inner one, as it ought to do if the sources of light (or, rather, the reflectors of sunlight) were independent particles free to move according to Kepler's third law, and as it ought not to do if the ring, or rings, were rigid, in which case the outer edge would have the greatest linear speed, as it had to travel through the greatest distance. Here, at last, was the proof of the meteoritic composition of Saturn's ring. Professor Keeler's beautiful discovery has since been verified by repeated observations at[Pg 291] the Allegheny, Lick, Paris, and Pulkova Observatories; the actual velocities resulting from the observed displacements of the lines have been measured and found to agree well (within the limits of the errors of observation) with the calculated velocities, so that this brilliant confirmation of the mathematical deductions of Clerk Maxwell is raised beyond the possibility of doubt.
The spectrum of Saturn is so faint that only the strongest lines of the solar spectrum can be seen in it, but the atmosphere of the planet seems to exert a considerable amount of general absorption in the blue and violet parts of the spectrum, which is especially strong near the equatorial belt, while a strong band in the red testifies to the density of the atmosphere. This band is not seen in the spectrum of the rings, around which there can therefore be no atmosphere.
As Saturn's ring is itself unique, we cannot find elsewhere any very pertinent illustration of a structure so remarkable as that now claimed for the ring. Yet the solar system does show some analogous phenomena. There is, for instance, one on a very grand scale surrounding the sun himself. We allude to the multitude of minor planets, all confined within a certain region of the system. Imagine these planets to be vastly increased in number, and those orbits which are much inclined to the rest flattened down and otherwise adjusted, and we should have a ring surrounding the sun, thus producing an arrangement not dissimilar from that now attributed to Saturn.
It is tempting to linger still longer over this beautiful system, to speculate on the appearance which the ring would present to an inhabitant of Saturn, to conjecture whether it is to be regarded as a permanent feature of our system in the same way as we attribute permanence to our moon or to the satellites of Jupiter. Looked at from every point of view, the question is full of interest, and it provides occupation abundant for the labours of every type of astronomer. If he be furnished with a good telescope, then has he ample duties to fulfil in the task of surveying, of sketching, and of measuring. If he be one of those useful astronomers[Pg 292] who devote their energies not to actual telescopic work, but to forming calculations based on the observations of others, then the beautiful system of Saturn provides copious material. He has to foretell the different phases of the ring, to announce to astronomers when each feature can be best seen, and at what hour each element can be best determined. He has also to predict the times of the movements of Saturn's satellites, and the other phenomena of a system more elaborate than that of Jupiter.
Lastly, if the astronomer be one of that class—perhaps, from some points of view, the highest class of all—who employ the most profound researches of the human intellect to unravel the dynamical problems of astronomy, he, too, finds in Saturn problems which test to the utmost, even if they do not utterly transcend, the loftiest flights of analysis. He discovers in Saturn's ring an object so utterly unlike anything else, that new mathematical weapons have to be forged for the encounter. He finds in the system so many extraordinary features, and such delicacy of adjustment, that he is constrained to admit that if he did not actually see Saturn's rings before him, he would not have thought that such a system was possible. The mathematician's labours on this wondrous system are at present only in their infancy. Not alone are the researches of so abstruse a character as to demand the highest genius for this branch of science, but even yet the materials for the inquiry have not been accumulated. In a discussion of this character, observation must precede calculation. The scanty observations hitherto obtained, however they may illustrate the beauty of the system, are still utterly insufficient to form the basis of that great mathematical theory of Saturn which must eventually be written.
But Saturn possesses an interest for a far more numerous class of persons than those who are specially devoted to astronomy. It is of interest, it must be of interest, to every cultivated person who has the slightest love for nature. A lover of the picturesque cannot behold Saturn in a telescope without feelings of the liveliest emotion; while, if his reading and reflection have previously rendered him aware of the[Pg 293] colossal magnitude of the object at which he is looking, he will be constrained to admit that no more remarkable spectacle is presented in the whole of nature.
We have pondered so long over the fascinations of Saturn's ring that we can only give a very brief account of that system of satellites by which the planet is attended. We have already had occasion to allude more than once to these bodies; it only remains now to enumerate a few further particulars.
It was on the 25th of March, 1655, that the first satellite of Saturn was detected by Huyghens, to whose penetration we owe the discovery of the true form of the ring. On the evening of the day referred to, Huyghens was examining Saturn with a telescope constructed with his own hands, when he observed a small star-like object near the planet. The next night he repeated his observations, and it was found that the star was accompanying the planet in its progress through the heavens. This showed that the little object was really a satellite to Saturn, and further observations revealed the fact that it was revolving around him in a period of 15 days, 22 hours, 41 minutes. Such was the commencement of that numerous series of discoveries of satellites which accompany Saturn. One by one they were detected, so that at the present time no fewer than nine are known to attend the great planet through his wanderings. The subsequent discoveries were, however, in no case made by Huyghens, for he abandoned the search for any further satellites on grounds which sound strange to modern ears, but which were quite in keeping with the ideas of his time. It appears that from some principle of symmetry, Huyghens thought that it would accord with the fitness of things that the number of satellites, or secondary planets, should be equal in number to the primary planets themselves. The primary planets, including the earth, numbered six; and Huyghens' discovery now brought the total number of satellites to be also six. The earth had one, Jupiter had four, Saturn had one, and the system was complete.
Nature, however, knows no such arithmetical doctrines as those which Huyghens attributed to her. Had he been less[Pg 294] influenced by such prejudices, he might, perhaps, have anticipated the labours of Cassini, who, by discovering other satellites of Saturn, demonstrated the absurdity of the doctrine of numerical equality between planets and satellites. As further discoveries were made, the number of satellites was at first raised above the number of planets; but in recent times, when the swarm of minor planets came to be discovered, the number of planets speedily reached and speedily passed the number of their attendant satellites.
It was in 1671, about sixteen years after the discovery of the first satellite of Saturn, that a second was discovered by Cassini. This is the outermost of the older satellites; it takes 79 days to travel round Saturn. In the following year he discovered another; and twelve years later, in 1684, still two more; thus making a total of five satellites to this planet.
The complexity of the Saturnian system had now no rival in the heavens. Saturn had five satellites, and Jupiter had but four, while at least one of the satellites of Saturn, named Titan, was larger than any satellite of Jupiter.[28] Some of the discoveries of Cassini had been made with telescopes of quite monstrous dimensions. The length of the instrument, or rather the distance at which the object-glass was placed, was one hundred feet or more from the eye of the observer. It seemed hardly possible to push telescopic research farther with instruments of this cumbrous type. At length, however, the great reformation in the construction of astronomical instruments began to dawn. In the hands of Herschel, it was found possible to construct reflecting telescopes of manageable dimensions, which were both more powerful and more accurate than the long-focussed lenses of Cassini. A great instrument of this kind, forty feet long, just completed by Herschel, was directed to Saturn on the 28th of August, 1789. Never before had the wondrous planet been submitted to a scrutiny so minute. Herschel was familiar with the labours of his predecessors. He had often looked at Saturn and his five moons in inferior telescopes; now again he saw the five moons and a star-like object so near the plane of the ring that he conjectured this to be a sixth satellite. A speedy method of testing this conjecture was at hand. Saturn was then moving rapidly over the heavens. If this new object were in truth a satellite, then it must be carried on by Saturn. Herschel watched with anxiety to see whether this would be the case. A short time sufficed to answer the question; in two hours and a half the planet had moved to a distance quite appreciable, and had carried with him not only the five satellites already known, but also this sixth object. Had this been a star it would have been left behind; it was not left behind, and hence it, too, was a satellite. Thus, after the long lapse of a century, the telescopic discovery of satellites to Saturn recommenced. Herschel, as was his wont, observed this object with unremitting ardour, and discovered that it was much nearer to Saturn than any of the previously known satellites. In accordance with the general law, that the nearer the satellite the shorter the period of revolution, Herschel found that this little moon completed a revolution in about 1 day, 8 hours, 53 minutes. The same great telescope, used with the same unrivalled skill, soon led Herschel to a still more interesting discovery.[Pg 296] An object so small as only to appear like a very minute point in the great forty-foot reflector was also detected by Herschel, and was by him proved to be a satellite, so close to the planet that it completed a revolution in the very brief period of 22 hours and 37 minutes. This is an extremely delicate object, only to be seen by the best telescopes in the brief intervals when it is not entirely screened from view by the ring.
Again another long interval elapsed, and for almost fifty years the Saturnian system was regarded as consisting of the series of rings and of the seven satellites. The next discovery has a singular historical interest. It was made simultaneously by two observers—Professor Bond, of Cambridge, Mass., and Mr. Lassell, of Liverpool—for on the 19th September, 1848, both of these astronomers verified that a small point which they had each seen on previous nights was really a satellite. This object is, however, at a considerable distance from the planet, and requires 21 days, 7 hours, 28 minutes for each revolution; it is the seventh in order from the planet.
Yet one more extremely faint outer satellite was discerned by photography on the 16th, 17th, and 18th August, 1898, by Professor W.H. Pickering. This object is much more distant from the planet than the larger and older satellites. Its motion has not yet been fully determined, but probably it requires not less than 490 days to perform a single revolution.
From observations of the satellites it has been found that 3,500 globes as heavy as Saturn would weigh as much as the sun.
A law has been observed by Professor Kirkwood, which connects together the movements of the four interior satellites of Saturn. This law is fulfilled in such a manner as leads to the supposition that it arises from the mutual attraction of the satellites. We have already described a similar law relative to three of the satellites of Jupiter. The problem relating to Saturn, involving as it does no fewer than four satellites, is one of no ordinary complexity. It involves the theory of Perturbations to a greater degree than that to[Pg 297] which mathematicians are accustomed in their investigation of the more ordinary features of our system. To express this law it is necessary to have recourse to the daily movements of the satellites; these are respectively—
| Satellite. | Daily Movement. |
| I. | 382°·2. |
| II. | 262°·74. |
| III. | 190°·7. |
| IV. | 131°·4. |
The law states that if to five times the movement of the first satellite we add that of the third and four times that of the fourth, the whole will equal ten times the movement of the second satellite. The calculation stands thus:—
| 5 times I. equals 1911°·0 | ||
| III. equals 190°·7 | II. 262°·74 | |
| 4 times IV. equals 525°·6 | 10 | |
| ———— | ———— | |
| 2627°·3 | equal | 2627°·4 nearly. |
Nothing can be simpler than the verification of this law; but the task of showing the physical reason why it should be fulfilled has not yet been accomplished.
Saturn was the most distant planet known to the ancients. It revolves in an orbit far outside the other ancient planets, and, until the discovery of Uranus in the year 1781, the orbit of Saturn might well be regarded as the frontier of the solar system. The ringed planet was indeed a worthy object to occupy a position so distinguished. But we now know that the mighty orbit of Saturn does not extend to the frontiers of the solar system; a splendid discovery, leading to one still more splendid, has vastly extended the boundary, by revealing two mighty planets, revolving in dim telescopic distance, far outside the path of Saturn. These objects have not the beauty of Saturn; they are, indeed, in no sense effective telescopic pictures. Yet these outer planets awaken an interest of a most special kind. The discovery of each is a classical event in the history of astronomy, and the opinion has been maintained, and perhaps with reason, that the discovery of Neptune, the more remote of the two, is the greatest achievement in astronomy made since the time of Newton.
Contrast between Uranus and the other great Planets—William Herschel—His Birth and Parentage—Herschel's Arrival in England—His Love of Learning—Commencement of his Astronomical Studies—The Construction of Telescopes—Construction of Mirrors—The Professor of Music becomes an Astronomer—The Methodical Research—The 13th March, 1781—The Discovery of Uranus—Delicacy of Observation—Was the Object a Comet?—The Significance of this Discovery—The Fame of Herschel—George III. and the Bath Musician—The King's Astronomer at Windsor—The Planet Uranus—Numerical Data with reference thereto—The Four Satellites of Uranus—Their Circular Orbits—Early Observations of Uranus—Flamsteed's Observations—Lemonnier saw Uranus—Utility of their Measurements—The Elliptic Path—The Great Problem thus Suggested.
To the present writer it has always seemed that the history of Uranus, and of the circumstances attending its discovery, forms one of the most pleasing and interesting episodes in the whole history of science. We here occupy an entirely new position in the study of the solar system. All the other great planets were familiarly known from antiquity, however erroneous might be the ideas entertained in connection with them. They were conspicuous objects, and by their movements could hardly fail to attract the attention of those whose pursuits led them to observe the stars. But now we come to a great planet, the very existence of which was utterly unknown to the ancients; and hence, in approaching the subject, we have first to describe the actual discovery of this object, and then to consider what we can learn as to its physical nature.
We have, in preceding pages, had occasion to mention the revered name of William Herschel in connection with various branches of astronomy; but we have hitherto designedly postponed any more explicit reference to this extraordinary man[Pg 299] until we had arrived at the present stage of our work. The story of Uranus, in its earlier stages at all events, is the story of the early career of William Herschel. It would be alike impossible and undesirable to attempt to separate them.
William Herschel, the illustrious astronomer, was born at Hanover in 1738. His father was an accomplished man, pursuing, in a somewhat humble manner, the calling of a professor of music. He had a family of ten children, of whom William was the fourth; and it may be noted that all the members of the family of whom any record has been preserved inherited their father's musical talents, and became accomplished performers. Pleasing sketches have been given of this interesting family, of the unusual aptitude of William, of the long discussions on music and on philosophy, and of the little sister Caroline, destined in later years for an illustrious career. William soon learned all that his master could teach him in the ordinary branches of knowledge, and by the age of fourteen he was already a competent performer on the oboe and the viol. He was engaged in the Court orchestra at Hanover, and was also a member of the band of the Hanoverian Guards. Troublous times were soon to break up Herschel's family. The French invaded Hanover, the Hanoverian Guards were overthrown in the battle of Hastenbeck, and young William Herschel had some unpleasant experience of actual warfare. His health was not very strong, and he decided that he would make a change in his profession. His method of doing so is one which his biographers can scarcely be expected to defend; for, to speak plainly, he deserted, and succeeded in making his escape to England. It is stated on unquestionable authority that on Herschel's first visit to King George III., more than twenty years afterwards, his pardon was handed to him by the King himself, written out in due form.
At the age of nineteen the young musician began to seek his fortunes in England. He met at first with very considerable hardship, but industry and skill conquered all difficulties, and by the time he was twenty-six years of age he was thoroughly settled in England, and doing well in his profession. In the year 1766 we find Herschel occupying[Pg 300] a position of some distinction in the musical world; he had become the organist of the Octagon Chapel at Bath, and his time was fully employed in giving lessons to his numerous pupils, and with his preparation for concerts and oratorios.
Notwithstanding his busy professional life, Herschel still retained that insatiable thirst for knowledge which he had when a boy. Every moment he could snatch from his musical engagements was eagerly devoted to study. In his desire to perfect his knowledge of the more abstruse parts of the theory of music he had occasion to learn mathematics; from mathematics the transition to optics was a natural one; and once he had commenced to study optics, he was of course brought to a knowledge of the telescope, and thence to astronomy itself.
His beginnings were made on a very modest scale. It was through a small and imperfect telescope that the great astronomer obtained his first view of the celestial glories. No doubt he had often before looked at the heavens on a clear night, and admired the thousands of stars with which they were adorned; but now, when he was able to increase his powers of vision even to a slight extent, he obtained a view which fascinated him. The stars he had seen before he now saw far more distinctly; but, more than this, he found that myriads of others previously invisible were now revealed to him. Glorious, indeed, is this spectacle to anyone who possesses a spark of enthusiasm for natural beauty. To Herschel this view immediately changed the whole current of his life. His success as a professor of music, his oratorios, and his pupils were speedily to be forgotten, and the rest of his life was to be devoted to the absorbing pursuit of one of the noblest of the sciences.
Herschel could not remain contented with the small and imperfect instrument which first interested him. Throughout his career he determined to see everything for himself in the best manner which his utmost powers could command. He at once decided to have a better instrument, and he wrote to a celebrated optician in London with the view of making a purchase. But the price which the optician demanded seemed[Pg 301] more than Herschel thought he could or ought to give. Instantly his resolution was taken. A good telescope he must have, and as he could not buy one he resolved to make one. It was alike fortunate, both for Herschel and for science, that circumstances impelled him to this determination. Yet, at first sight, how unpromising was the enterprise! That a music teacher, busily employed day and night, should, without previous training, expect to succeed in a task where the highest mechanical and optical skill was required, seemed indeed unlikely. But enthusiasm and genius know no insuperable difficulties. From conducting a brilliant concert in Bath, when that city was at the height of its fame, Herschel would rush home, and without even delaying to take off his lace ruffles, he would plunge into his manual labours of grinding specula and polishing lenses. No alchemist of old was ever more deeply absorbed in a project for turning lead into gold than was Herschel in his determination to have a telescope. He transformed his home into a laboratory; of his drawing-room he made a carpenter's shop. Turning lathes were the furniture of his best bedroom. A telescope he must have, and as he progressed he determined, not only that he should have a good telescope, but a very good one; and as success cheered his efforts he ultimately succeeded in constructing the greatest telescope that the world had up to that time ever seen. Though it is as an astronomer that we are concerned with Herschel, yet we must observe even as a telescope maker also great fame and no small degree of commercial success flowed in upon him. When the world began to ring with his glorious discoveries, and when it was known that he used no other telescopes than those which were the work of his own hands, a demand sprang up for instruments of his construction. It is stated that he made upwards of eighty large telescopes, as well as many others of smaller size. Several of these instruments were purchased by foreign princes and potentates.[29] We have never heard that any of these illustrious personages became celebrated astronomers, but,[Pg 302] at all events, they seem to have paid Herschel handsomely for his skill, so that by the sale of large telescopes he was enabled to realise what may be regarded as a fortune in the moderate horizon of the man of science.
Up to the middle of his life Herschel was unknown to the public except as a laborious musician, with considerable renown in his profession, not only in Bath, but throughout the West of England. His telescope-making was merely the occupation of his spare moments, and was unheard of by most of those who knew and respected his musical attainments. It was in 1774 that Herschel first enjoyed a view of the heavens through an instrument built with his own hands. It was but a small one in comparison with those which he afterwards fashioned, but at once he experienced the advantage of being his own instrument maker. Night after night he was able to add the improvements which experience suggested; at one time he was enlarging the mirrors; at another he was reconstructing the mounting, or trying to remedy defects in the eye-pieces. With unwearying perseverance he aimed at the highest excellence, and with each successive advance he found that he was able to pierce further into the sky. His enthusiasm attracted a few friends who were, like himself, ardently attached to science. The mode in which he first made the acquaintance of Sir William Watson, who afterwards became his warmest friend, was characteristic of both. Herschel was observing the mountains in the moon, and as the hours passed on, he had occasion to bring his telescope into the street in front of his house to enable him to continue his work. Sir William Watson happened to pass by, and was[Pg 303] arrested by the unusual spectacle of an astronomer in the public street, at the dead of night, using a large and quaint-looking instrument. Having a taste for astronomy, Sir William stopped, and when Herschel took his eye from the telescope, asked if he might be allowed to have a look at the moon. The request was readily granted. Probably Herschel found but few in the gay city who cared for such matters; he was quickly drawn to Sir W. Watson, who at once reciprocated the feeling, and thus began a friendship which bore important fruit in Herschel's subsequent career.
At length the year 1781 approached, which was to witness his great achievement. Herschel had made good use of seven years' practical experience in astronomy, and he had completed a telescope of exquisite optical perfection, though greatly inferior in size to some of those which he afterwards erected. With this reflector Herschel commenced a methodical piece of observation. He formed the scheme of systematically examining all the stars which were above a certain degree of brightness. It does not quite appear what object Herschel proposed to himself when he undertook this labour, but, in any case, he could hardly have anticipated the extraordinary success with which the work was to be crowned. In the course of this review the telescope was directed to a star; that star was examined; then another was brought into the field of view, and it too was examined. Every star under such circumstances merely shows itself as a point of light; the point may be brilliant or not, according as the star is bright or not; the point will also, of course, show the colour of the star, but it cannot exhibit recognisable size or shape. The greater, in fact, the perfection of the telescope, the smaller is the telescopic image of a star.
How many stars Herschel inspected in this review we are not told; but at all events, on the ever-memorable night of the 13th of March, 1781, he was pursuing his self-allotted task among the hosts in the constellation Gemini. Doubtless, one star after another was admitted to view, and was allowed to pass away. At length, however, an object was placed in the field which differed from every other star. It was not a[Pg 304] mere point of light; it had a minute, but still a perfectly recognisable, disc. We say the disc was perfectly recognisable, but we should be careful to add that it was so in the excellent telescope of Herschel alone. Other astronomers had seen this object before. Its position had actually been measured no fewer than nineteen times before the Bath musician, with his home-made telescope, looked at it, but the previous observers had only seen it in small meridian instruments with low magnifying powers. Even after the discovery was made, and when well-trained observers with good instruments looked again under the direction of Herschel, one after another bore testimony to the extraordinary delicacy of the great astronomer's perception, which enabled him almost at the first glance to discriminate between it and a star.
If not a star, what, then, could it be? The first step to enable this question to be answered was to observe the body for some time. This Herschel did. He looked at it one night after another, and soon he discovered another fundamental difference between this object and an ordinary star. The stars are, of course, characterised by their fixity, but this object was not fixed; night after night the place it occupied changed with respect to the stars. No longer could there be any doubt that this body was a member of the solar system, and that an interesting discovery had been made; many months, however, elapsed before Herschel knew the real merit of his achievement. He did not realise that he had made the superb discovery of another mighty planet revolving outside Saturn; he thought that it could only be a comet. No doubt this object looked very different from a great comet, decorated with a tail. It was not, however, so entirely different from some forms of telescopic comets as to make the suggestion of its being a body of this kind unlikely; and the discovery was at first announced in accordance with this view. Time was necessary before the true character of the object could be ascertained. It must be followed for a considerable distance along its path, and measures of its position at different epochs must be effected, before it is practicable for the mathematician to calculate the path which the body pursues; once, however,[Pg 305] attention was devoted to the subject, many astronomers aided in making the necessary observations. These were placed in the hands of mathematicians, and the result was proclaimed that this body was not a comet, but that, like all the planets, it revolved in nearly a circular path around the sun, and that the path lay millions of miles outside the path of Saturn, which had so long been regarded as the boundary of the solar system.
It is hardly possible to over-estimate the significance of this splendid discovery. The five planets had been known from all antiquity; they were all, at suitable seasons, brilliantly conspicuous to the unaided eye. But it was now found that, far outside the outermost of these planets revolved another splendid planet, larger than Mercury or Mars, larger—far larger—than Venus and the earth, and only surpassed in bulk by Jupiter and by Saturn. This superb new planet was plunged into space to such a depth that, notwithstanding its noble proportions, it seemed merely a tiny star, being only on rare occasions within reach of the unaided eye. This great globe required a period of eighty-four years to complete its majestic path, and the diameter of that path was 3,600,000,000 miles.
Although the history of astronomy is the record of brilliant discoveries—of the labours of Copernicus, and of Kepler—of the telescopic achievements of Galileo, and the splendid theory of Newton—of the refined discovery of the aberration of light—of many other imperishable triumphs of intellect—yet this achievement of the organist at the Octagon Chapel occupies a totally different position from any other. There never before had been any historic record of the discovery of one of the bodies of the particular system to which the earth belongs. The older planets were no doubt discovered by someone, but we can say little more about these discoveries than we can about the discovery of the sun or of the moon; all are alike prehistoric. Here was the first recorded instance of the discovery of a planet which, like the earth, revolves around the sun, and, like our earth, may conceivably be an inhabited globe. So unique an achievement instantly arrested the[Pg 306] attention of the whole scientific world. The music-master at Bath, hitherto unheard of as an astronomer, was speedily placed in the very foremost rank of those entitled to the name. On all sides the greatest interest was manifested about the unknown philosopher. The name of Herschel, then unfamiliar to English ears, appeared in every journal, and a curious list has been preserved of the number of blunders which were made in spelling the name. The different scientific societies hastened to convey their congratulations on an occasion so memorable.
Tidings of the discovery made by the Hanoverian musician reached the ears of George III., and he sent for Herschel to come to the Court, that the King might learn what his achievement actually was from the discoverer's own lips. Herschel brought with him one of his telescopes, and he provided himself with a chart of the solar system, with which to explain precisely wherein the significance of the discovery lay. The King was greatly interested in Herschel's narrative, and not less in Herschel himself. The telescope was erected at Windsor, and, under the astronomer's guidance, the King was shown Saturn and other celebrated objects. It is also told how the ladies of the Court the next day asked Herschel to show them the wonders which had so pleased the King. The telescope was duly erected in a window of one of the Queen's apartments, but when evening arrived the sky was found to be overcast with clouds, and no stars could be seen. This was an experience with which Herschel, like every other astronomer, was unhappily only too familiar. But it is not every astronomer who would have shown the readiness of Herschel in escaping gracefully from the position. He showed to his lady pupils the construction of the telescope; he explained the mirror, and how he had fashioned it and given the polish; and then, seeing the clouds were inexorable, he proposed that, as he could not show them the real Saturn, he should exhibit an artificial one as the best substitute. The permission granted, Herschel turned the telescope away from the sky, and pointed it towards the wall of a distant garden. On looking into the telescope there was Saturn, his globe and[Pg 307] his system of rings, so faithfully shown that, says Herschel, even a skilful astronomer might have been deceived. The fact was that during the course of the day Herschel saw that the sky would probably be overcast in the evening, and he had provided for the emergency by cutting a hole in a piece of cardboard, the shape of Saturn, which was then placed against the distant garden wall, and illuminated by a lamp at the back.
This visit to Windsor was productive of consequences momentous to Herschel, momentous to science. He had made so favourable an impression, that the King proposed to create for him the special appointment of King's Astronomer at Windsor. The King was to provide the means for erecting the great telescopes, and he allocated to Herschel a salary of £200 a year, the figures being based, it must be admitted, on a somewhat moderate estimate of the requirements of an astronomer's household. Herschel mentioned these particulars to no one save to his constant and generous friend, Sir W. Watson, who exclaimed, "Never bought monarch honour so cheap." To other enquirers, Herschel merely said that the King had provided for him. In accepting this post, the great astronomer took no doubt a serious step. He at once sacrificed entirely his musical career, now, from many sources, a lucrative one; but his determination was speedily taken. The splendid earnest that he had already given of his devotion to astronomy was, he knew, only the commencement of a series of memorable labours. He had indeed long been feeling that it was his bounden duty to follow that path in life which his genius indicated. He was no longer a young man. He had attained middle age, and the years had become especially precious to one who knew that he had still a life-work to accomplish. He at one stroke freed himself from all distractions; his pupils and concerts, his whole connection at Bath, were immediately renounced; he accepted the King's offer with alacrity, and after one or two changes settled permanently at Slough, near Windsor.
It has, indeed, been well remarked that the most important event in connection with the discovery of Uranus was the[Pg 308] discovery of Herschel's unrivalled powers of observation. Uranus must, sooner or later, have been found. Had Herschel not lived, we would still, no doubt, have known Uranus long ere this. The really important point for science was that Herschel's genius should be given full scope, by setting him free from the engrossing details of an ordinary professional calling. The discovery of Uranus secured all this, and accordingly obtained for astronomy all Herschel's future labours.[30]
Uranus is so remote that even the best of our modern telescopes cannot make of it a striking picture. We can see, as Herschel did, that it has a measurable disc, and from measurements of that disc we conclude that the diameter of the planet is about 31,700 miles. This is about four times as great as the diameter of the earth, and we accordingly see that the volume of Uranus must be about sixty-four times as great as that of the earth. We also find that, like the other giant planets, Uranus seems to be composed of materials much lighter, on the whole, than those we find here; so that, though sixty-four times as large as the earth, Uranus is only fifteen times as heavy. If we may trust to the analogies of what we see everywhere else in our system, we can feel but little doubt that Uranus must rotate about an axis. The ordinary means of demonstrating this rotation can be hardly available in a body whose surface appears so small and so faint. The period of rotation is accordingly unknown. The spectroscope tells us that a remarkable atmosphere, containing apparently some gases foreign to our own, deeply envelops Uranus.
There is, however, one feature about Uranus which presents many points of interest to those astronomers who are possessed of telescopes of unusual size and perfection. Uranus is accompanied by a system of satellites, some of which are so faint as to require the closest scrutiny for their detection. The discovery of these satellites was one of the subsequent achievements of Herschel. It is, however, remarkable that even his penetration and care did not preserve him[Pg 309] from errors with regard to these very delicate objects. Some of the points which he thought to be satellites must, it would now seem, have been merely stars enormously more distant, which happened to lie in the field of view. It has been since ascertained that the known satellites of Uranus are four in number, and their movements have been made the subject of prolonged and interesting telescopic research. The four satellites bear the names of Ariel, Umbriel, Titania, and Oberon. Arranged in order of their distance from the central body, Ariel, the nearest, accomplishes its journey in 2 days and 12 hours. Oberon, the most distant, completes its journey in 13 days and 11 hours.
The law of Kepler declares that the path of a satellite around its primary, no less than of the primary around the sun, must be an ellipse. It leaves, however, boundless latitude in the actual eccentricity of the curve. The ellipse may be nearly a circle, it may be absolutely a circle, or it may be something quite different from a circle. The paths pursued by the planets are, generally speaking, nearly circles; but we meet with no exact circle among planetary orbits. So far as we at present know, the closest approach made to a perfectly circular movement is that by which the satellites of Uranus revolve around their primary. We are not prepared to say that these paths are absolutely circular. All that can be said is that our telescopes fail to show any measurable departure therefrom. It is also to be noted as an interesting circumstance that the orbits of the satellites of Uranus all lie in the same plane. This is not true of the orbits of the planets around the sun, nor is it true of the orbits of any other system of satellites around their primary. The most singular circumstance attending the Uranian system is, however, found in the position which this plane occupies. This is indeed almost as great an anomaly in our system as are the rings of Saturn themselves. We have already had occasion to notice that the plane in which the earth revolves around the sun is very nearly coincident with the planes in which all the other great planets revolve. The same is true, to a large extent, of the orbits of the minor planets; though here, no doubt, we[Pg 310] meet with a few cases in which the plane of the orbit is inclined at no inconsiderable angle to the plane in which the earth moves. The plane in which the moon revolves also approximates to this system of planetary planes. So, too, do the orbits of the satellites of Saturn and of Jupiter, while even the more recently discovered satellites of Mars form no exception to the rule. The whole solar system—at least so far as the great planets are concerned—would require comparatively little alteration if the orbits were to be entirely flattened down into one plane. There are, however, some notable exceptions to this rule. The satellites of Uranus revolve in a plane which is far from coinciding with the plane to which all other orbits approximate. In fact, the paths of the satellites of Uranus lie in a plane nearly at right angles to the orbit of Uranus. We are not in a position to give any satisfactory explanation of this circumstance. It is, however, evident that in the genesis of the Uranian system there must have been some influence of a quite exceptional and local character.
Soon after the discovery of the planet Uranus, in 1781, sufficient observations were accumulated to enable the orbit it follows to be determined. When the path was known, it was then a mere matter of mathematical calculation to ascertain where the planet was situated at any past time, and where it would be situated at any future time. An interesting enquiry was thus originated as to how far it might be possible to find any observations of the planet made previously to its discovery by Herschel. Uranus looks like a star of the sixth magnitude. Not many astronomers were provided with telescopes of the perfection attained by Herschel, and the personal delicacy of perception characteristic of Herschel was a still more rare possession. It was, therefore, to be expected that, if such previous observations existed, they would merely record Uranus as a star visible, and indeed bright, in a moderate telescope, but still not claiming any exceptional attention over thousands of apparently similar stars. Many of the early astronomers had devoted themselves to the useful and laborious work of forming catalogues of stars. In the preparation of a star catalogue, the telescope was directed to the heavens, the stars[Pg 311] were observed, their places were carefully measured, the brightness of the star was also estimated, and thus the catalogue was gradually compiled in which each star had its place faithfully recorded, so that at any future time it could be identified. The stars were thus registered, by hundreds and by thousands, at various dates from the birth of accurate astronomy till the present time. The suggestion was then made that, as Uranus looked so like a star, and as it was quite bright enough to have engaged the attention of astronomers possessed of even very moderate instrumental powers, there was a possibility that it had already been observed, and thus actually lay recorded as a star in some of the older catalogues. This was indeed an idea worthy of every attention, and pregnant with the most important consequences in connection with the immortal discovery to be discussed in our next chapter. But how was such an examination of the catalogues to be conducted? Uranus is constantly moving about; does it not seem that there is every element of uncertainty in such an investigation? Let us consider a notable example.
The great national observatory at Greenwich was founded in 1675, and the first Astronomer-Royal was the illustrious Flamsteed, who in 1676 commenced that series of observations of the heavenly bodies which has been continued to the present day with such incalculable benefits to science. At first the instruments were of a rather primitive description, but in the course of some years Flamsteed succeeded in procuring instruments adequate to the production of a catalogue of stars, and he devoted himself with extraordinary zeal to the undertaking. It is in this memorable work, the "Historia Cœlestis" of Flamsteed, that the earliest observation of Uranus is recorded. In the first place it was known that the orbit of this body, like the orbit of every other great planet, was inclined at a very small angle to the ecliptic. It hence follows that Uranus is at all times only to be met with along the ecliptic, and it is possible to calculate where the planet has been in each year. It was thus seen that in 1690 the planet was situated in that part of the ecliptic where Flamsteed was at the same date making his observations. It was natural to[Pg 312] search the observations of Flamsteed, and see whether any of the so-called stars could have been Uranus. An object was found in the "Historia Cœlestis" which occupied a position identical with that which Uranus must have filled on the same date. Could this be Uranus? A decisive test was at once available. The telescope was directed to the spot in the heavens where Flamsteed saw a sixth-magnitude star. If that were really a star, then would it still be visible. The trial was made: no such star could be found, and hence the presumption that this was really Uranus could hardly be for a moment doubted. Speedily other confirmation flowed in. It was shown that Uranus had been observed by Bradley and by Tobias Mayer, and it also became apparent that Flamsteed had observed Uranus not only once, but that he had actually measured its place four times in the years 1712 and 1715. Yet Flamsteed was never conscious of the discovery that lay so nearly in his grasp. He was, of course, under the impression that all these observations related to different stars. A still more remarkable case is that of Lemonnier, who had actually observed Uranus twelve times, and even recorded it on four consecutive days in January, 1769. If Lemonnier had only carefully looked over his own work; if he had perceived, as he might have done, how the star he observed yesterday was gone to-day, while the star visible to-day had moved away by to-morrow, there is no doubt that Uranus would have been discovered, and William Herschel would have been anticipated. Would Lemonnier have made as good use of his fame as Herschel did? This seems a question which can never be decided, but those who estimate Herschel as the present writer thinks he ought to be estimated, will probably agree in thinking that it was most fortunate for science that Lemonnier did not compare his observations.[31]
These early accidental observations of Uranus are not merely to be regarded as matters of historical interest or curiosity. That they are of the deepest importance with[Pg 313] regard to the science itself a few words will enable us to show. It is to be remembered that Uranus requires no less than eighty-four years to accomplish his mighty revolution around the sun. The planet has completed one entire revolution since its discovery, and up to the present time (1900) has accomplished more than one-third of another. For the careful study of the nature of the orbit, it was desirable to have as many measurements as possible, and extending over the widest possible interval. This was in a great measure secured by the identification of the early observations of Uranus. An approximate knowledge of the orbit was quite capable of giving the places of the planet with sufficient accuracy to identify it when met with in the catalogues. But when by their aid the actual observations have been discovered, they tell us precisely the place of Uranus; and hence, instead of our knowledge of the planet being limited to but little more than one revolution, we have at the present time information with regard to it extending over considerably more than two revolutions.
From the observations of the planet the ellipse in which it moves can be ascertained. We can compute this ellipse from the observations made during the time since the discovery. We can also compute the ellipse from the early observations made before the discovery. If Kepler's laws were rigorously verified, then, of course, the ellipse performed in the present revolution must differ in no respect from the ellipse performed in the preceding, or indeed in any other revolution. We can test this point in an interesting manner by comparing the ellipse derived from the ancient observations with that deduced from the modern ones. These ellipses closely resemble each other; they are nearly the same; but it is most important to observe that they are not exactly the same, even when allowance has been made for every known source of disturbance in accordance with the principles explained in the next chapter. The law of Kepler seems thus not absolutely true in the case of Uranus. Here is, indeed, a matter demanding our most earnest and careful attention. Have we not repeatedly laid down the universality of the laws of[Pg 314] Kepler in controlling the planetary motions? How then can we reconcile this law with the irregularities proved beyond a doubt to exist in the motions of Uranus?
Let us look a little more closely into the matter. We know that the laws of Kepler are a consequence of the laws of gravitation. We know that the planet moves in an elliptic path around the sun, in virtue of the sun's attraction, and we know that the ellipse will be preserved without the minutest alteration if the sun and the planet be left to their mutual attractions, and if no other force intervene. We can also calculate the influence of each of the known planets on the form and position of the orbit. But when allowance is made for all such perturbing influences it is found that the observed and computed orbits do not agree. The conclusion is irresistible. Uranus does not move solely in consequence of the sun's attraction and that of the planets of our system interior to Uranus; there must therefore be some further influence acting upon Uranus besides those already known. To the development of this subject the next chapter will be devoted.
Discovery of Neptune—A Mathematical Achievement—The Sun's Attraction—All Bodies attract—Jupiter and Saturn—The Planetary Perturbations—Three Bodies—Nature has simplified the Problem—Approximate Solution—The Sources of Success—The Problem Stated for the Earth—The Discoveries of Lagrange—The Eccentricity—Necessity that all the Planets revolve in the same Direction—Lagrange's Discoveries have not the Dramatic Interest of the more Recent Achievements—The Irregularities of Uranus—The Unknown Planet must revolve outside the Path of Uranus—The Data for the Problem—Le Verrier and Adams both investigate the Question—Adams indicates the Place of the Planet—How the Search was to be conducted—Le Verrier also solves the Problem—The Telescopic Discovery of the Planet—The Rival Claims—Early Observation of Neptune—Difficulty of the Telescopic Study of Neptune—Numerical Details of the Orbit—Is there any Outer Planet?—Contrast between Mercury and Neptune.
We describe in this chapter a discovery so extraordinary that the whole annals of science may be searched in vain for a parallel. We are not here concerned with technicalities of practical astronomy. Neptune was first revealed by profound mathematical research rather than by minute telescopic investigation. We must develop the account of this striking epoch in the history of science with the fulness of detail which is commensurate with its importance; and it will accordingly be necessary, at the outset of our narrative, to make an excursion into a difficult but attractive department of astronomy, to which we have as yet made little reference.
The supreme controlling power in the solar system is the attraction of the sun. Each planet of the system experiences that attraction, and, in virtue thereof, is constrained to revolve around the sun in an elliptic path. The efficiency of a body as an attractive agent is directly proportional to its mass, and[Pg 316] as the mass of the sun is more than a thousand times as great as that of Jupiter, which, itself, exceeds that of all the other planets collectively, the attraction of the sun is necessarily the chief determining force of the movements in our system. The law of gravitation, however, does not merely say that the sun attracts each planet. Gravitation is a doctrine much more general, for it asserts that every body in the universe attracts every other body. In obedience to this law, each planet must be attracted, not only by the sun, but by innumerable bodies, and the movement of the planet must be the joint effect of all such attractions. As for the influence of the stars on our solar system, it may be at once set aside as inappreciable. The stars are no doubt enormous bodies, in many cases possibly transcending the sun in magnitude, but the law of gravitation tells us that the intensity of the attraction decreases as the square of the distance increases. Most of the stars are a million times as remote as the sun, and consequently their attraction is so slight as to be absolutely inappreciable in the discussion of this question. The only attractions we need consider are those which arise from the action of one body of the system upon another. Let us take, for instance, the two largest planets of our system, Jupiter and Saturn. Each of these globes revolves mainly in consequence of the sun's attraction, but every planet also attracts every other, and the consequence is that each one is slightly drawn away from the position it would have otherwise occupied. In the language of astronomy, we would say that the path of Jupiter is perturbed by the attraction of Saturn; and, conversely, that the path of Saturn is perturbed by the attraction of Jupiter.
For many years these irregularities of the planetary motions presented problems with which astronomers were not able to cope. Gradually, however, one difficulty after another has been vanquished, and though there are no doubt some small irregularities still outstanding which have not been completely explained, yet all the larger and more important phenomena of the kind are well understood. The subject is one of the most difficult which the astronomer has to [Pg 317]encounter in the whole range of his science. He has here to calculate what effect one planet is capable of producing on another planet. Such calculations bristle with formidable difficulties, and can only be overcome by consummate skill in the loftiest branches of mathematics. Let us state what the problem really is.
When two bodies move in virtue of their mutual attraction, both of them will revolve in a curve which admits of being exactly ascertained. Each path is, in fact, an ellipse, and they must have a common focus at the centre of gravity of the two bodies, considered as a single system. In the case of a sun and a planet, in which the mass of the sun preponderates enormously over the mass of the planet, the centre of gravity of the two lies very near the centre of the sun; the path of the great body is in such a case very small in comparison with the path of the planet. All these matters admit of perfectly accurate calculation of a somewhat elementary character. But now let us add a third body to the system which attracts each of the others and is attracted by them. In consequence of this attraction, the third body is displaced, and accordingly its influence on the others is modified; they in turn act upon it, and these actions and reactions introduce endless complexity into the system. Such is the famous "problem of three bodies," which has engaged the attention of almost every great mathematician since the time of Newton. Stated in its mathematical aspect, and without having its intricacy abated by any modifying circumstances, the problem is one that defies solution. Mathematicians have not yet been able to deal with the mutual attractions of three bodies moving freely in space. If the number of bodies be greater than three, as is actually the case in the solar system, the problem becomes still more hopeless.
Nature, however, has in this matter dealt kindly with us. She has, it is true, proposed a problem which cannot be accurately solved; but she has introduced into the problem, as proposed in the solar system, certain special features which materially reduce the difficulty. We are still unable to make[Pg 318] what a mathematician would describe as a rigorous solution of the question; we cannot solve it with the completeness of a sum in arithmetic; but we can do what is nearly if not quite as useful. We can solve the problem approximately; we can find out what the effect of one planet on the other is very nearly, and by additional labour we can reduce the limits of uncertainty to as low a point as may be desired. We thus obtain a practical solution of the problem adequate for all the purposes of science. It avails us little to know the place of a planet with absolute mathematical accuracy. If we can determine what we want with so close an approximation to the true position that no telescope could possibly disclose the difference, then every practical end will have been attained. The reason why in this case we are enabled to get round the difficulties which we cannot surmount lies in the exceptional character of the problem of three bodies as exhibited in the solar system. In the first place, the sun is of such pre-eminent mass that many matters may be overlooked which would be of moment were he rivalled in mass by any of the planets. Another source of our success arises from the small inclinations of the planetary orbits to each other; while the fact that the orbits are nearly circular also greatly facilitates the work. The mathematicians who may reside in some of the other parts of the universe are not equally favoured. Among the sidereal systems we find not a few cases where the problem of three bodies, or even of more than three, would have to be faced without any of the alleviating circumstances which our system presents. In such groups as the marvellous star Θ Orionis, we have three or four bodies comparable in size, which must produce movements of the utmost complexity. Even if terrestrial mathematicians shall ever have the hardihood to face such problems, there is no likelihood of their being able to do so for ages to come; such researches must repose on accurate observations as their foundation; and the observations of these distant systems are at present utterly inadequate for the purpose.
The undisturbed revolution of a planet around the sun, in conformity with Kepler's law, would assure for that planet[Pg 319] permanent conditions of climate. The earth, for instance, if guided solely by Kepler's laws, would return each day of the year exactly to the same position which it had on the same day of last year. From age to age the quantity of heat received by the earth would remain constant if the sun continued unaltered, and the present climate might thus be preserved indefinitely. But since the existence of planetary perturbation has become recognised, questions arise of the gravest importance with reference to the possible effects which such perturbations may have. We now see that the path of the earth is not absolutely fixed. That path is deranged by Venus and by Mars; it is deranged, it must be deranged, by every planet in our system. It is true that in a year, or even in a century, the amount of alteration produced is not very great; the ellipse which represents the path of our earth this year does not differ considerably from the ellipse which represented the movement of the earth one hundred years ago. But the important question arises as to whether the slight difference which does exist may not be constantly increasing, and may not ultimately assume such proportions as to modify our climates, or even to render life utterly impossible. Indeed, if we look at the subject without attentive calculation, nothing would seem more probable than that such should be the fate of our system. This globe revolves in a path inside that of the mighty Jupiter. It is, therefore, constantly attracted by Jupiter, and when it overtakes the vast planet, and comes between him and the sun, then the two bodies are comparatively close together, and the earth is pulled outwards by Jupiter. It might be supposed that the tendency of such disturbances would be to draw the earth gradually away from the sun, and thus to cause our globe to describe a path ever growing wider and wider. It is not, however, possible to decide a dynamical question by merely superficial reasoning of this character. The question has to be brought before the tribunal of mathematical analysis, where every element in the case is duly taken into account. Such an enquiry is by no means a simple one. It worthily occupied[Pg 320] the splendid talents of Lagrange and Laplace, whose discoveries in the theory of planetary perturbation are some of the most remarkable achievements in astronomy.
We cannot here attempt to describe the reasoning which these great mathematicians employed. It can only be expressed by the formulæ of the mathematician, and would then be hardly intelligible without previous years of mathematical study. It fortunately happens, however, that the results to which Lagrange and Laplace were conducted, and which have been abundantly confirmed by the labours of other mathematicians, admit of being described in simple language.
Let us suppose the case of the sun, and of two planets circulating around him. These two planets are mutually disturbing each other, but the amount of the disturbance is small in comparison with the effect of the sun on each of them. Lagrange demonstrated that, though the ellipse in which each planet moved was gradually altered in some respects by the attraction of the other planet, yet there is one feature of the curve which the perturbation is powerless to alter permanently: the longest axis of the ellipse, and, therefore, the mean distance of the planet from the sun, which is equal to one-half of it, must remain unchanged. This is really a discovery as important as it was unexpected. It at once removes all fear as to the effect which perturbations can produce on the stability of the system. It shows that, notwithstanding the attractions of Mars and of Venus, of Jupiter and of Saturn, our earth will for ever continue to revolve at the same mean distance from the sun, and thus the succession of the seasons and the length of the year, so far as this element at least is concerned, will remain for ever unchanged.
But Lagrange went further into the enquiry. He saw that the mean distance did not alter, but it remained to be seen whether the eccentricity of the ellipse described by the earth might not be affected by the perturbations. This is a matter of hardly less consequence than that just referred to. Even though the earth preserved the same average distance from the sun, yet the greatest and least distance might be widely unequal: the earth might pass very close to the sun at one[Pg 321] part of its orbit, and then recede to a very great distance at the opposite part. So far as the welfare of our globe and its inhabitants is concerned, this is quite as important as the question of the mean distance; too much heat in one half of the year would afford but indifferent compensation for too little during the other half. Lagrange submitted this question also to his analysis. Again he vanquished the mathematical difficulties, and again he was able to give assurance of the permanence of our system. It is true that he was not this time able to say that the eccentricity of each path will remain constant; this is not the case. What he does assert, and what he has abundantly proved, is that the eccentricity of each orbit will always remain small. We learn that the shape of the earth's orbit gradually swells and gradually contracts; the greatest length of the ellipse is invariable, but sometimes it approaches more to a circle, and sometimes becomes more elliptical. These changes are comprised within narrow limits; so that, though they may probably correspond with measurable climatic changes, yet the safety of the system is not imperilled, as it would be if the eccentricity could increase indefinitely. Once again Lagrange applied the resources of his calculus to study the effect which perturbations can have on the inclination of the path in which the planet moves. The result in this case was similar to that obtained with respect to the eccentricities. If we commence with the assumption that the mutual inclinations of the planets are small, then mathematics assure us that they must always remain small. We are thus led to the conclusion that the planetary perturbations are unable to affect the stability of the solar system.
We shall perhaps more fully appreciate the importance of these memorable researches if we consider how easily matters might have been otherwise. Let us suppose a system resembling ours in every respect save one. Let that system have a sun, as ours has; a system of planets and of satellites like ours. Let the masses of all the bodies in this hypothetical system be identical with the masses in our system, and let the distances and the periodic times be the same in the two cases. Let all the planes of the orbits be similarly placed;[Pg 322] and yet this hypothetical system might contain seeds of decay from which ours is free. There is one point in the imaginary scheme which we have not yet specified. In our system all the planets revolve in the same direction around the sun. Let us suppose this law violated in the hypothetical system by reversing one planet on its path. That slight change alone would expose the system to the risk of destruction by the planetary perturbations. Here, then, we find the necessity of that remarkable uniformity of the directions in which the planets revolve around the sun. Had these directions not been uniform, our system must, in all probability, have perished ages ago, and we should not be here to discuss perturbations or any other subject.
Great as was the success of the eminent French mathematician who made these beautiful discoveries, it was left for this century to witness the crowning triumph of mathematical analysis applied to the law of gravitation. The work of Lagrange lacks the dramatic interest of the discovery made by Le Verrier and Adams, which gave still wider extent to the solar system by the discovery of the planet Neptune revolving far outside Uranus.
We have already alluded to the difficulties which were experienced when it was sought to reconcile the early observations of Uranus with those made since its discovery. We have shown that the path in which this planet revolved experienced change, and that consequently Uranus must be exposed to the action of some other force besides the sun's attraction.
The question arises as to the nature of these disturbing forces. From what we have already learned of the mutual deranging influence between any two planets, it seems natural to inquire whether the irregularities of Uranus could not be accounted for by the attraction of the other planets. Uranus revolves just outside Saturn. The mass of Saturn is much larger than the mass of Uranus. Could it not be that Saturn draws Uranus aside, and thus causes the changes? This is a question to be decided by the mathematician. He can compute what Saturn is able to do, and he finds, no[Pg 323] doubt, that Saturn is capable of producing some displacement of Uranus. In a similar manner Jupiter, with his mighty mass, acts on Uranus, and produces a disturbance which the mathematician calculates. When the figures had been worked out for all the known planets they were applied to Uranus, and we might expect to find that they would fully account for the observed irregularities of his path. This was, however, not the case. After every known source of disturbance had been carefully allowed for, Uranus was still shown to be influenced by some further agent; and hence the conclusion was established that Uranus must be affected by some unknown body. What could this unknown body be, and where must it be situated? Analogy was here the guide of those who speculated on this matter. We know no cause of disturbance of a planet's motion except it be the attraction of another planet. Could it be that Uranus was really attracted by some other planet at that time utterly unknown? This suggestion was made by many astronomers, and it was possible to determine some conditions which the unknown body should fulfil. In the first place its orbit must lie outside the orbit of Uranus. This was necessary, because the unknown planet must be a large and massive one to produce the observed irregularities. If, therefore, it were nearer than Uranus, it would be a conspicuous object, and must have been discovered long ago. Other reasonings were also available to show that if the disturbances of Uranus were caused by the attraction of a planet, that body must revolve outside the globe discovered by Herschel. The general analogies of the planetary system might also be invoked in support of the hypothesis that the path of the unknown planet, though necessarily elliptic, did not differ widely from a circle, and that the plane in which it moved must also be nearly coincident with the plane of the earth's orbit.
The measured deviations of Uranus at the different points of its orbit were the sole data available for the discovery of the new planet. We have to fit the orbit of the unknown globe, as well as the mass of the planet itself, in such a way as to account for the various perturbations. Let us, for[Pg 324] instance, assume a certain distance for the hypothetical body, and try if we can assign both an orbit and a mass for the planet, at that distance, which shall account for the perturbations. Our first assumption is perhaps too great. We try again with a lesser distance. We can now represent the observations with greater accuracy. A third attempt will give the result still more closely, until at length the distance of the unknown planet is determined. In a similar way the mass of the body can be also determined. We assume a certain value, and calculate the perturbations. If the results seem greater than those obtained by observations, then the assumed mass is too great. We amend the assumption, and recompute with a lesser amount, and so on until at length we determine a mass for the planet which harmonises with the results of actual measurement. The other elements of the unknown orbit—its eccentricity and the position of its axis—are all to be ascertained in a similar manner. At length it appeared that the perturbations of Uranus could be completely explained if the unknown planet had a certain mass, and moved in an orbit which had a certain position, while it was also manifest that no very different orbit or greatly altered mass would explain the observed facts.
These remarkable computations were undertaken quite independently by two astronomers—one in England and one in France. Each of them attacked, and each of them succeeded in solving, the great problem. The scientific men of England and the scientific men of France joined issue on the question as to the claims of their respective champions to the great discovery; but in the forty years which have elapsed since these memorable researches the question has gradually become settled. It is the impartial verdict of the scientific world outside England and France, that the merits of this splendid triumph of science must be divided equally between the late distinguished Professor J.C. Adams, of Cambridge, and the late U.J.J. Le Verrier, the director of the Paris Observatory.
Shortly after Mr. Adams had taken his degree at Cambridge, in 1843, when he obtained the distinction of Senior Wrangler, he turned his attention to the perturbations of Uranus, and,[Pg 325] guided by these perturbations alone, commenced his search for the unknown planet. Long and arduous was the enquiry—demanding an enormous amount of numerical calculation, as well as consummate mathematical resource; but gradually Mr. Adams overcame the difficulties. As the subject unfolded itself, he saw how the perturbations of Uranus could be fully explained by the existence of an exterior planet, and at length he had ascertained, not alone the orbit of this outer body, but he was even able to indicate the part of the heavens in which the unknown globe must be sought. With his researches in this advanced condition, Mr. Adams called on the Astronomer-Royal, Sir George Airy, at Greenwich, in October, 1845, and placed in his hands the computations which indicated with marvellous accuracy the place of the yet unobserved planet. It thus appears that seven months before anyone else had solved this problem Mr. Adams had conquered its difficulties, and had actually located the planet in a position but little more than a degree distant from the spot which it is now known to have occupied. All that was wanted to complete the discovery, and to gain for Professor Adams and for English science the undivided glory of this achievement, was a strict telescopic search through the heavens in the neighbourhood indicated.
Why, it may be said, was not such an enquiry instituted at once? No doubt this would have been done, if the observatories had been generally furnished forty years ago with those elaborate star-charts which they now possess. In the absence of a chart (and none had yet been published of the part of the sky where the unknown planet was) the search for the planet was a most tedious undertaking. It had been suggested that the new globe could be detected by its visible disc; but it must be remembered that even Uranus, so much closer to us, had a disc so small that it was observed nearly a score of times without particular notice, though it did not escape the eagle glance of Herschel. There remained then only one available method of finding Neptune. It was to construct a chart of the heavens in the neighbourhood indicated, and then to compare this chart night after night with the stars in the[Pg 326] heavens. Before recommending the commencement of a labour so onerous, the Astronomer-Royal thought it right to submit Mr. Adams's researches to a crucial preliminary test. Mr. Adams had shown how his theory rendered an exact account of the perturbations of Uranus in longitude. The Astronomer-Royal asked Mr. Adams whether he was able to give an equally clear explanation of the notable variations in the distance of Uranus. There can be no doubt that his theory would have rendered a satisfactory account of these variations also; but, unfortunately, Mr. Adams seems not to have thought the matter of sufficient importance to give the Astronomer-Royal any speedy reply, and hence it happened that no less than nine months elapsed between the time when Mr. Adams first communicated his results to the Astronomer-Royal and the time when the telescopic search for the planet was systematically commenced. Up to this time no account of Mr. Adams's researches had been published. His labours were known to but few besides the Astronomer-Royal and Professor Challis of Cambridge, to whom the duty of making the search was afterwards entrusted.
In the meantime the attention of Le Verrier, the great French mathematician and astronomer, had been specially directed by Arago to the problem of the perturbations of Uranus. With exhaustive analysis Le Verrier investigated every possible known source of disturbance. The influences of the older planets were estimated once more with every precision, but only to confirm the conclusion already arrived at as to their inadequacy to account for the perturbations. Le Verrier then commenced the search for the unknown planet by the aid of mathematical investigation, in complete ignorance of the labours of Adams. In November, 1845, and again on the 1st of June, 1846, portions of the French astronomer's results were announced. The Astronomer-Royal then perceived that his calculations coincided practically with those of Adams, insomuch that the places assigned to the unknown planet by the two astronomers were not more than a degree apart! This was, indeed, a remarkable result. Here was a planet unknown to human sight, yet felt, as it were, by mathematical analysis[Pg 327] with a certainty so great that two astronomers, each in total ignorance of the other's labours, concurred in locating the planet in almost the same spot of the heavens. The existence of the new globe was thus raised nearly to a certainty, and it became incumbent on practical astronomers to commence the search forthwith. In June, 1846, the Astronomer-Royal announced to the visitors of the Greenwich Observatory the close coincidence between the calculations of Le Verrier and of Adams, and urged that a strict scrutiny of the region indicated should be at once instituted. Professor Challis, having the command of the great Northumberland equatorial telescope at Cambridge, was induced to undertake the work, and on the 29th July, 1846, he began his labours.
The plan of search adopted by Professor Challis was an onerous one. He first took the theoretical place of the planet, as given by Mr. Adams, and after allowing a very large margin for the uncertainties of a calculation so recondite, he marked out a certain region of the heavens, near the ecliptic, in which it might be anticipated that the unknown planet must be found. He then determined to observe all the stars in this region and measure their relative positions. When this work was once done it was to be repeated a second time. His scheme even contemplated a third complete set of observations of the stars contained within this selected region. There could be no doubt that this process would determine the planet if it were bright enough to come within the limits of stellar magnitude which Professor Challis adopted. The globe would be detected by its motion relatively to the stars, when the three series of measures came to be compared. The scheme was organised so thoroughly that it must have led to the expected discovery—in fact, it afterwards appeared that Professor Challis did actually observe the planet more than once, and a subsequent comparison of its positions must infallibly have led to the detection of the new globe.
Le Verrier was steadily maturing his no less elaborate investigations in the same direction. He felt confident of the existence of the planet, and he went so far as to predict not only the situation of the globe but even its actual appearance.[Pg 328] He thought the planet would be large enough (though still of course only a telescopic object) to be distinguished from the stars by the possession of a disc. These definite predictions strengthened the belief that we were on the verge of another great discovery in the solar system, so much so that when Sir John Herschel addressed the British Association on the 10th of September, 1846, he uttered the following words:—"The past year has given to us the new planet Astræa—it has done more, it has given us the probable prospect of another. We see it as Columbus saw America from the shores of Spain. Its movements have been felt trembling along the far-reaching line of our analysis, with a certainty hardly inferior to ocular demonstration."
The time of the discovery was now rapidly approaching. On the 18th of September, 1846, Le Verrier wrote to Dr. Galle of the Berlin Observatory, describing the place of the planet indicated by his calculations, and asking him to make its telescopic discovery. The request thus preferred was similar to that made on behalf of Adams to Professor Challis. Both at Berlin and at Cambridge the telescopic research was to be made in the same region of the heavens. The Berlin astronomers were, however, fortunate in possessing an invaluable aid to the research which was not at the time in the hands of Professor Challis. We have mentioned how the search for a telescopic planet can be facilitated by the use of a carefully-executed chart of the stars. In fact, a mere comparison of the chart with the sky is all that is necessary. It happened that the preparation of a series of star charts had been undertaken by the Berlin Academy of Sciences some years previously. On these charts the place of every star, down even to the tenth magnitude, had been faithfully engraved. This work was one of much utility, but its originators could hardly have anticipated the brilliant discovery which would arise from their years of tedious labour. It was found convenient to publish such an extensive piece of surveying work by instalments, and accordingly, as the chart was completed, it issued from the press sheet by sheet. It happened that just before the news of Le Verrier's labours reached Berlin[Pg 329] the chart of that part of the heavens had been engraved and printed.
It was on the 23rd of September that Le Verrier's letter reached Dr. Galle at Berlin. The sky that night was clear, and we can imagine with what anxiety Dr. Galle directed his telescope to the heavens. The instrument was pointed in accordance with Le Verrier's instructions. The field of view showed a multitude of stars, as does every part of the heavens. One of these was really the planet. The new chart was unrolled, and, star by star, the heavens were compared with it. As the identification of the stars went on, one object after another was found to lie in the heavens as it was engraved on the chart, and was of course rejected. At length a star of the eighth magnitude—a brilliant object—was brought into review. The chart was examined, but there was no star there. This object could not have been in its present place when the chart was formed. The object was therefore a wanderer—a planet. Yet it was necessary to be cautious in such a matter. Many possibilities had to be guarded against. It was, for instance, at least conceivable that the object was really a star which, by some mischance, eluded the careful eye of the astronomer who had constructed the map. It was even possible that the star might be one of the large class of variables which alternate in brightness, and it might have been too faint to have been visible when the chart was made. Or it might be one of the minor planets moving between Mars and Jupiter. Even if none of these explanations would answer, it was still necessary to show that the object was moving with that particular velocity and in that particular direction which the theory of Le Verrier indicated. The lapse of a single day was sufficient to dissipate all doubts. The next night the object was again observed. It had moved, and when its motion was measured it was found to accord precisely with what Le Verrier had foretold. Indeed, as if no circumstance in the confirmation should be wanting, the diameter of the planet, as measured by the micrometers at Berlin, proved to be practically coincident with that anticipated by Le Verrier.
The world speedily rang with the news of this splendid achievement. Instantly the name of Le Verrier rose to a pinnacle hardly surpassed by that of any astronomer of any age or country. The circumstances of the discovery were highly dramatic. We picture the great astronomer buried in profound meditation for many months; his eyes are bent, not on the stars, but on his calculations. No telescope is in his hand; the human intellect is the instrument he alone uses. With patient labour, guided by consummate mathematical artifice, he manipulates his columns of figures. He attempts one solution after another. In each he learns something to avoid; by each he obtains some light to guide him in his future labours. At length he begins to see harmony in those results where before there was but discord. Gradually the clouds disperse, and he discerns with a certainty little short of actual vision the planet glittering in the far depths of space. He rises from his desk and invokes the aid of a practical astronomer; and lo! there is the planet in the indicated spot. The annals of science present no such spectacle as this. It was the most triumphant proof of the law of universal gravitation. The Newtonian theory had indeed long ere this attained an impregnable position; but, as if to place its truth in the most conspicuous light, this discovery of Neptune was accomplished.
For a moment it seemed as if the French were to enjoy the undivided honour of this splendid triumph; nor would it, indeed, have been unfitting that the nation which gave birth to Lagrange and to Laplace, and which developed the great Newtonian theory by their immortal labours, should have obtained this distinction. Up to the time of the telescopic discovery of the planet by Dr. Galle at Berlin, no public announcement had been made of the labours of Challis in searching for the planet, nor even of the theoretical researches of Adams on which those observations were based. But in the midst of the pæans of triumph with which the enthusiastic French nation hailed the discovery of Le Verrier, there appeared a letter from Sir John Herschel in the Athenæum for 3rd October, 1846, in which he announced the researches made by Adams, and claimed for him a participation in the glory[Pg 331] of the discovery. Subsequent enquiry has shown that this claim was a just one, and it is now universally admitted by all independent authorities. Yet it will easily be imagined that the French savants, jealous of the fame of their countryman, could not at first be brought to recognise a claim so put forward. They were asked to divide the unparalleled honour between their own illustrious countryman and a young foreigner of whom but few had ever heard, and who had not even published a line of his work, nor had any claim been made on his part until after the work had been completely finished by Le Verrier. The demand made on behalf of Adams was accordingly refused any acknowledgment in France; and an embittered controversy was the consequence. Point by point the English astronomers succeeded in establishing the claim of their countryman. It was true that Adams had not published his researches to the world, but he had communicated them to the Astronomer-Royal, the official head of the science in this country. They were also well known to Professor Challis, the Professor of Astronomy at Cambridge. Then, too, the work of Adams was published, and it was found to be quite as thorough and quite as successful as that of Le Verrier. It was also found that the method of search adopted by Professor Challis not only must have been eventually successful, but that it actually was in a sense already successful. When the telescopic discovery of the planet had been achieved, Challis turned naturally to see whether he had observed the new globe also. It was on the 1st October that he heard of the success of Dr. Galle, and by that time Challis had accumulated observations in connection with this research of no fewer than 3,150 stars. Among them he speedily found that an object observed on the 12th of August was not in the same place on the 30th of July. This was really the planet; and its discovery would thus have been assured had Challis had time to compare his measurements. In fact, if he had only discussed his observations at once, there cannot be much doubt that the entire glory of the discovery would have been awarded to Adams. He would then have been first, no less in the theoretical calculations than in the optical verification of the planet's[Pg 332] existence. It may also be remarked that Challis narrowly missed making the discovery of Neptune in another way. Le Verrier had pointed out in his paper the possibility of detecting the sought-for globe by its disc. Challis made the attempt, and before the intelligence of the actual discovery at Berlin had reached him he had made an examination of the region indicated by Le Verrier. About 300 stars passed through the field of view, and among them he selected one on account of its disc; it afterwards appeared that this was indeed the planet.
If the researches of Le Verrier and of Adams had never been undertaken it is certain that the distant Neptune must have been some time discovered; yet that might have been made in a manner which every true lover of science would now deplore. We hear constantly that new minor planets are observed, yet no one attaches to such achievements a fraction of the consequence belonging to the discovery of Neptune. The danger was, that Neptune should have been merely dropped upon by simple survey work, just as Uranus was discovered, or just as the hosts of minor planets are now found. In this case Theoretical Astronomy, the great science founded by Newton, would have been deprived of its most brilliant illustration.
Neptune had, in fact, a very narrow escape on at least one previous occasion of being discovered in a very simple way. This was shown when sufficient observations had been collected to enable the path of the planet to be calculated. It was then possible to trace back the movements of the planet among the stars and thus to institute a search in the catalogues of earlier astronomers to see whether they contained any record of Neptune, erroneously noted as a star. Several such instances have been discovered. I shall, however, only refer to one, which possesses a singular interest. It was found that the place of the planet on May 10th, 1795, must have coincided with that of a so-called star recorded on that day in the "Histoire Céleste" of Lalande. By actual examination of the heavens it further appeared that there was no star in the place indicated by Lalande, so the fact that here was[Pg 333] really an observation of Neptune was placed quite beyond doubt. When reference was made to the original manuscripts of Lalande, a matter of great interest was brought to light. It was there found that he had observed the same star (for so he regarded it) both on May 8th and on May 10th; on each day he had determined its position, and both observations are duly recorded. But when he came to prepare his catalogue and found that the places on the two occasions were different, he discarded the earlier result, and merely printed the latter.
Had Lalande possessed a proper confidence in his own observations, an immortal discovery lay in his grasp; had he manfully said, "I was right on the 10th of May and I was right on the 8th of May; I made no mistake on either occasion, and the object I saw on the 8th must have moved between that and the 10th," then he must without fail have found Neptune. But had he done so, how lamentable would have been the loss to science! The discovery of Neptune would then merely have been an accidental reward to a laborious worker, instead of being one of the most glorious achievements in the loftiest department of human reason.
Besides this brief sketch of the discovery of Neptune, we have but little to tell with regard to this distant planet. If we fail to see in Uranus any of those features which make Mars or Venus, Jupiter or Saturn, such attractive telescopic objects, what can we expect to find in Neptune, which is half as far again as Uranus? With a good telescope and a suitable magnifying power we can indeed see that Neptune has a disc, but no features on that disc can be identified. We are consequently not in a position to ascertain the period in which Neptune rotates around its axis, though from the general analogy of the system we must feel assured that it really does rotate. More successful have been the attempts to measure the diameter of Neptune, which is found to be about 35,000 miles, or more than four times the diameter of the earth. It would also seem that, like Jupiter and like Saturn, the planet must be enveloped with a vast cloud-laden atmosphere, for the mean density of the globe is only about one-fifth that[Pg 334] of the earth. This great globe revolves around the sun at a mean distance of no less than 2,800 millions of miles, which is about thirty times as great as the mean distance from the earth to the sun. The journey, though accomplished at the rate of more than three miles a second, is yet so long that Neptune requires almost 165 years to complete one revolution. Since its discovery, some fifty years ago, Neptune has moved through about one-third of its path, and even since the date when it was first casually seen by Lalande, in 1795, it has only had time to traverse three-fifths of its mighty circuit.
Neptune, like our earth, is attended by a single satellite; this delicate object was discovered by Mr. Lassell with his two-foot reflecting telescope shortly after the planet itself became known. The motion of the satellite of Neptune is nearly circular. Its orbit is inclined at an angle of about 35° to the Ecliptic, and it is specially noteworthy that, like the satellites of Uranus, the direction of the motion runs counter to the planetary movements generally. The satellite performs its journey around Neptune in a period of a little less than six days. By observing the motions of this moon we are enabled to determine the mass of the planet, and thus it appears that the weight of Neptune is about one nineteen-thousandth part of that of the sun.
No planets beyond Neptune have been seen, nor is there at present any good ground for believing in their existence as visual objects. In the chapter on the minor planets I have entered into a discussion of the way in which these objects are discovered. It is by minute and diligent comparison of the heavens with elaborate star charts that these bodies are brought to light. Such enquiries would be equally efficacious in searching for an ultra-Neptunian planet; in fact, we could design no better method to seek for such a body, if it existed, than that which is at this moment in constant practice at many observatories. The labours of those who search for small planets have been abundantly rewarded with discoveries now counted by hundreds. Yet it is a noteworthy fact that all these planets are limited to one region of the solar system. It has sometimes been [Pg 335]conjectured that time may disclose perturbations in the orbit of Neptune, and that these perturbations may lead to the discovery of a planet still more remote, even though that planet be so distant and so faint that it eludes all telescopic research. At present, however, such an enquiry can hardly come within the range of practical astronomy. Its movements have no doubt been studied minutely, but it must describe a larger part of its orbit before it would be feasible to conclude, from the perturbations of its path, the existence of an unknown and still more remote planet.
We have thus seen that the planetary system is bounded on one side by Mercury and on the other by Neptune. The discovery of Mercury was an achievement of prehistoric times. The early astronomer who accomplished that feat, when devoid of instrumental assistance and unsupported by accurate theoretical knowledge, merits our hearty admiration for his untutored acuteness and penetration. On the other hand, the discovery of the exterior boundary of the planetary system is worthy of special attention from the fact that it was founded solely on profound theoretical learning.
Though we here close our account of the planets and their satellites, we have still two chapters to add before we shall have completed what is to be said with regard to the solar system. A further and notable class of bodies, neither planets nor satellites, own allegiance to the sun, and revolve round him in conformity with the laws of universal gravitation. These bodies are the comets, and their somewhat more humble associates, the shooting stars. We find in the study of these objects many matters of interest, which we shall discuss in the ensuing chapters.
Comets contrasted with Planets in Nature as well as in their Movements—Coggia's Comet—Periodic Returns—The Law of Gravitation—Parabolic and Elliptic Orbits—Theory in Advance of Observations—Most Cometary Orbits are sensibly Parabolic—The Labours of Halley—The Comet of 1682—Halley's Memorable Prediction—The Retardation produced by Disturbance—Successive Returns of Halley's Comet—Encke's Comet—Effect of Perturbations—Orbit of Encke's Comet—Attraction of Mercury and of Jupiter—How the Identity of the Comet is secured—How to weigh Mercury—Distance from the Earth to the Sun found by Encke's Comet—The Disturbing Medium—Remarkable Comets—Spectrum of a Comet—Passage of a Comet between the Earth and the Stars—Can the Comet be weighed?—Evidence of the Small Mass of the Comet derived from the Theory of Perturbation—The Tail of the Comet—Its Changes—Views as to its Nature—Carbon present in Comets—Origin of Periodic Comets.
In our previous chapters, which treated of the sun and the moon, the planets and their satellites, we found in all cases that the celestial bodies with which we were concerned were nearly globular in form, and many are undoubtedly of solid substance. All these objects possess a density which, even if in some cases it be much less than that of the earth, is still hundreds of times greater than the density of merely gaseous materials. We now, however, approach the consideration of a class of objects of a widely different character. We have no longer to deal with globular objects possessing considerable mass. Comets are of altogether irregular shape; they are in large part, at all events, formed of materials in the utmost state of tenuity, and their masses are so small that no means we possess have enabled them to be measured. Not only are comets different in constitution from planets or from the other more solid bodies of our system, but the movements of[Pg 337] such bodies are quite distinct from the orderly return of the planets at their appointed seasons. The comets appear sometimes with almost startling unexpectedness; they rapidly swell in size to an extent that in superstitious ages called forth the utmost terror; presently they disappear, in many cases never again to return. Modern science has, no doubt, removed a great deal of the mystery which once invested the whole subject of comets. Their movements are now to a large extent explained, and some additions have been made to our knowledge of their nature, though we must still confess that what we do know bears but a very small proportion to what remains unknown.
Let me first describe in general terms the nature of a comet, in so far as its structure is disclosed by the aid of a powerful refracting telescope. We represent in Plate XII. two interesting sketches made at Harvard College Observatory of the great comet of 1874, distinguished by the name of its discoverer Coggia.
We see here the head of the comet, containing as its brightest spot what is called the nucleus, and in which the material of the comet seems to be much denser than elsewhere. Surrounding the nucleus we find certain definite layers of luminous material, the coma, or head, from 20,000 to 1,000,000 miles in diameter, from which the tail seems to stream away. This view may be regarded as that of a typical object of this class, but the varieties of structure presented by different comets are almost innumerable. In some cases we find the nucleus absent; in other cases we find the tail to be wanting. The tail is, no doubt, a conspicuous feature in those great comets which receive universal attention; but in the small telescopic objects, of which a few are generally found every year, this feature is usually absent. Not only do comets present great varieties in appearance, but even the aspect of a single object undergoes great change. The comet will sometimes increase enormously in bulk; sometimes it will diminish; sometimes it will have a large tail, or sometimes no tail at all. Measurements of a comet's size are almost futile; they may cease to be true even during the few hours[Pg 338] in which a comet is observed in the course of a night. It is, in fact, impossible to identify a comet by any description of its personal appearance. Yet the question as to identity of a comet is often of very great consequence. We must provide means by which it can be established, entirely apart from what the comet may look like.
It is now well known that several of these bodies make periodic returns. After having been invisible for a certain number of years, a comet comes into view, and again retreats into space to perform another revolution. The question then arises as to how we are to recognise the body when it does come back? The personal features of its size or brightness, the presence or absence of a tail, large or small, are fleeting characters of no value for such a purpose. Fortunately, however, the law of elliptic motion established by Kepler has suggested the means of defining the identity of a comet with absolute precision.
After Newton had made his discovery of the law of gravitation, and succeeded in demonstrating that the elliptic paths of the planets around the sun were necessary consequences of that law, he was naturally tempted to apply the same reasoning to explain the movements of comets. Here, again, he met with marvellous success, and illustrated his theory by completely explaining the movements of the remarkable body which was visible from December, 1680, to March, 1681.
There is a certain beautiful curve known to geometricians by the name of the parabola. Its form is shown in the adjoining figure; it is a curved line which bends in towards and around a certain point known as the focus. This would not be the occasion for any allusion to the geometrical properties of this curve; they should be sought in works on mathematics. It will here be only necessary to point to the connection which exists between the parabola and the ellipse. In a former chapter we have explained the construction of the latter curve, and we have shown how it possesses two foci. Let us suppose that a series of ellipses are drawn, each of which has a greater distance between its foci than the preceding one. Imagine the process carried on until at length the distance between the foci became enormously great in comparison with the distance from each focus to the curve, then each end of this long ellipse will practically have the same form as a parabola. We may thus look on the latter curve represented in Fig. 69 as being one end of an ellipse of which the other end is at an indefinitely great distance. In 1681 Doerfel, a clergyman of Saxony, proved that the great comet then recently observed moved in a parabola, in the focus of which the sun was situated. Newton showed that the law of gravitation would permit a body to move in an ellipse of this very extreme type no less than in one of the more ordinary proportions. An object revolving in a parabolic orbit about the sun at the focus moves in gradually towards the sun, sweeps around the great luminary, and then begins to retreat. There is a necessary distinction between parabolic and elliptic motion. In the latter case the body, after its retreat to[Pg 340] a certain distance, will turn round and again draw in towards the sun; in fact, it must make periodic circuits of its orbit, as the planets are found to do. But in the case of the true parabola the body can never return; to do so it would have to double the distant focus, and as that is infinitely remote, it could not be reached except in the lapse of infinite time.
The characteristic feature of the movement in a parabola may be thus described. The body draws in gradually towards the focus from an indefinitely remote distance on one side, and after passing round the focus gradually recedes to an indefinitely remote distance on the other side, never again to return. When Newton had perceived that parabolic motion of this type could arise from the law of gravitation, it at once occurred to him (independently of Doerfel's discovery, of which he was not aware) that by its means the movements of a comet might be explained. He knew that comets must be attracted by the sun; he saw that the usual course of a comet was to appear suddenly, to sweep around the sun and then retreat, never again to return. Was this really a case of parabolic motion? Fortunately, the materials for the trial of this important suggestion were ready to his hand. He was able to avail himself of the known movements of the comet of 1680, and of observations of several other bodies of the same nature which had been collected by the diligence of astronomers. With his usual sagacity, Newton devised a method by which, from the known facts, the path which the comet pursues could be determined. He found that it was a parabola, and that the velocity of the comet was governed by the law that the straight line from the sun to the comet swept over equal areas in equal times. Here was another confirmation of the law of universal gravitation. In this case, indeed, the theory may be said to have been actually in advance of calculation. Kepler had determined from observation that the paths of the planets were ellipses, and Newton had shown how this fact was a consequence of the law of gravitation. But in the case of the comets their highly erratic orbits had never been reduced to geometrical form until the theory of Newton showed him that they were parabolic, and then he invoked observation to verify the anticipations of his theory.
The great majority of comets move in orbits which cannot be sensibly discriminated from parabolæ, and any body whose orbit is of this character can only be seen at a single apparition. The theory of gravitation, though it admits the parabola as a possible orbit for a comet, does not assert that the path must necessarily be of this type. We have pointed out that this curve is only a very extreme type of ellipse, and it would still be in perfect accordance with the law of gravitation for a comet to pursue a path of any elliptical form, provided that the sun was placed at the focus, and that the comet obeyed the rule of describing equal areas in equal times. If a body move in an elliptic path, then it will return to the sun again, and consequently we shall have periodical visits from the same object.
An interesting field of enquiry was here presented to the astronomer. Nor was it long before the discovery of a periodic comet was made which illustrated, in a striking manner, the soundness of the anticipation just expressed. The name of the celebrated astronomer Halley is, perhaps, best known from its association with the great comet whose periodicity was discovered by his calculations. When Halley learned from the Newtonian theory the possibility that a comet might move in an elliptic orbit, he undertook a most laborious investigation; he collected from various records of observed comets all the reliable particulars that could be obtained, and thus he was enabled to ascertain, with tolerable accuracy, the nature of the paths pursued by about twenty-four large comets. One of these was the great body of 1682, which Halley himself observed, and whose path he computed in accordance with the principles of Newton. Halley then proceeded to investigate whether this comet of 1682 could have visited our system at any previous epoch. To answer this question he turned to the list of recorded comets which he had so carefully compiled, and he found that his comet very closely resembled, both in appearance and in orbit, a comet observed in 1607, and also another observed in 1531. Could these three bodies[Pg 342] be identical? It was only necessary to suppose that a comet, instead of revolving in a parabolic orbit, really revolved in an extremely elongated ellipse, and that it completed each revolution in a period of about seventy-five or seventy-six years. He submitted this hypothesis to every test that he could devise; he found that the orbits, determined on each of the three occasions, were so nearly identical that it would be contrary to all probability that the coincidence should be accidental. Accordingly, he decided to submit his theory to the most supreme test known to astronomy. He ventured to make a prediction which posterity would have the opportunity of verifying. If the period of the comet were seventy-five or seventy-six years, as the former observations seemed to show, then Halley estimated that, if unmolested, it ought to return in 1757 or 1758. There were, however, certain sources of disturbance which he pointed out, and which would be quite powerful enough to affect materially the time of return. The comet in its journey passes near the path of Jupiter, and experiences great perturbations from that mighty planet. Halley concluded that the expected return might be accordingly delayed till the end of 1758 or the beginning of 1759.
This prediction was a memorable event in the history of astronomy, inasmuch as it was the first attempt to foretell the apparition of one of those mysterious bodies whose visits seemed guided by no fixed law, and which were usually regarded as omens of awful import. Halley felt the importance of his announcement. He knew that his earthly course would have run long before the comet had completed its revolution; and, in language almost touching, the great astronomer writes: "Wherefore if it should return according to our prediction about the year 1758, impartial posterity will not refuse to acknowledge that this was first discovered by an Englishman."
As the time drew near when this great event was expected, it awakened the liveliest interest among astronomers. The distinguished mathematician Clairaut undertook to compute anew, by the aid of improved methods, the effect which would be wrought on the comet by the attraction of the planets.[Pg 343] His analysis of the perturbations was sufficient to show that the object would be kept back for 100 days by Saturn, and for 518 days by Jupiter. He therefore gave some additional exactness to the prediction of Halley, and finally concluded that this comet would reach the perihelion, or the point of its path nearest to the sun, about the middle of April, 1759. The sagacious astronomer (who, we must remember, lived long before the discovery of Uranus and of Neptune) further adds that as this body retreats so far, it may possibly be subject to influences of which we do not know, or to the disturbance even of some planet too remote to be ever perceived. He, accordingly, qualified his prediction with the statement that, owing to these unknown possibilities, his calculations might be a month wrong one way or the other. Clairaut made this memorable communication to the Academy of Sciences on the 14th of November, 1758. The attention of astronomers was immediately quickened to see whether the visitor, who last appeared seventy-six years previously, was about to return. Night after night the heavens were scanned. On Christmas Day in 1758 the comet was first detected, and it passed closest to the sun about midnight on the 12th of March, just a month earlier than the time announced by Clairaut, but still within the limits of error which he had assigned as being possible.
The verification of this prediction was a further confirmation of the theory of gravitation. Since then, Halley's comet has returned once again, in 1835, in circumstances somewhat similar to those just narrated. Further historical research has also succeeded in identifying Halley's comet with numerous memorable apparitions of comets in former times. It has even been shown that a splendid object, which appeared eleven years before the commencement of the Christian era, was merely Halley's comet in one of its former returns. Among the most celebrated visits of this body was that of 1066, when the apparition attracted universal attention. A picture of the comet on this occasion forms a quaint feature in the Bayeux Tapestry. The next return of Halley's comet is expected about the year 1910.
There are now several comets known which revolve in elliptic paths, and are, accordingly, entitled to be termed periodic. These objects are chiefly telescopic, and are thus in strong contrast to the splendid comet of Halley. Most of the other periodic comets have periods much shorter than that of Halley. Of these objects, by far the most celebrated is that known as Encke's comet, which merits our careful attention.
The object to which we refer has had a striking career during which it has provided many illustrations of the law of gravitation. We are not here concerned with the prosaic routine of a mere planetary orbit. A planet is mainly subordinated to the compelling sway of the sun's gravitation. It is also to some slight extent affected by the attractions which it experiences from the other planets. Mathematicians have long been accustomed to anticipate the movements of these globes by actual calculation. They know how the place of the planet is approximately decided by the sun's attraction, and they can discriminate the different adjustments which that place is to receive in consequence of the disturbances produced by the other planets. The capabilities of the planets for producing disturbance are greatly increased when the disturbed body follows the eccentric path of a comet. It is frequently found that the path of such a body comes very near the track of a planet, so that the comet may actually sweep by the planet itself, even if the two bodies do not actually run into collision. On such an occasion the disturbing effect is enormously augmented, and we therefore turn to the comets when we desire to illustrate the theory of planetary perturbations by some striking example.
Having decided to choose a comet, the next question is, What comet? There cannot here be much room for hesitation. Those splendid comets which appear so capriciously may be at once excluded. They are visitors apparently coming for the first time, and retreating without any distinct promise that mankind shall ever see them again. A comet of this kind moves in a parabolic path, sweeps once around the sun, and thence retreats into the space whence it came. We cannot[Pg 345] study the effect of perturbations on a comet completely until it has been watched during successive returns to the sun. Our choice is thus limited to the comparatively small class of objects known as periodic comets; and, from a survey of the entire group, we select the most suitable to our purpose. It is the object generally known as Encke's comet, for, though Encke was not the discoverer, yet it is to his calculations that the comet owes its fame. This body is rendered more suitable for our purpose by the researches to which it has recently given rise.
In the year 1818 a comet was discovered by the painstaking astronomer Pons at Marseilles. We are not to imagine that this body produced a splendid spectacle. It was a small telescopic object, not unlike one of those dim nebulæ which are scattered in thousands over the heavens. The comet is, however, readily distinguished from a nebula by its movement relatively to the stars, while the nebula remains at rest for centuries. The position of this comet was ascertained by its discoverer, as well as by other astronomers. Encke found from the observations that the comet returned to the sun once in every three years and a few months. This was a startling announcement. At that time no other comet of short period had been detected, so that this new addition to the solar system awakened the liveliest interest. The question was immediately raised as to whether this comet, which revolved so frequently, might not have been observed during previous returns. The historical records of the apparitions of comets are counted by hundreds, and how among this host are we to select those objects which were identical with the comet discovered by Pons?
We may at once relinquish any hope of identification from drawings of the object, but, fortunately, there is one feature of a comet on which we can seize, and which no fluctuations of the actual structure can modify or disguise. The path in which the body travels through space is independent of the bodily changes in its structure. The shape of that path and its position depend entirely upon those other bodies of the solar system which are specially involved in the theory of Encke's comet. In Fig. 70 we show the orbits of three of the planets. They have been chosen with such proportions as shall make the innermost represent the orbit of Mercury; the next is the orbit of the earth, while the outermost is the orbit of Jupiter. Besides these three we perceive in the figure a much more elliptical path, representing the orbit of Encke's comet, projected down on the plane of the earth's motion. The sun is situated at the focus of the ellipse. The comet is constrained to revolve in this curve by the attraction of the sun, and it requires a little more than three years to accomplish a complete revolution. It passes close to the sun at perihelion, at a point inside the path of Mercury, while[Pg 347] at its greatest distance it approaches the path of Jupiter. This elliptic orbit is mainly determined by the attraction of the sun. Whether the comet weighed an ounce, a ton, a thousand tons, or a million tons, whether it was a few miles, or many thousands of miles in diameter, the orbit would still be the same. It is by the shape of this ellipse, by its actual size, and by the position in which it lies, that we identify the comet. It had been observed in 1786, 1795, and 1805, but on these occasions it had not been noticed that the comet's path deviated from the parabola.
Encke's comet is usually so faint that even the most powerful telescope in the world would not show a trace of it. After one of its periodical visits, the body withdraws until it recedes to the outermost part of its path, then it will turn, and again approach the sun. It would seem that it becomes invigorated by the sun's rays, and commences to dilate under their genial influence. While moving in this part of its path the comet lessens its distance from the earth. It daily increases in splendour, until at length, partly by the intrinsic increase in brightness and partly by the decrease in distance from the earth, it comes within the range of our telescopes. We can generally anticipate when this will occur, and we can tell to what point of the heavens the telescope is to be pointed so as to discern the comet at its next return to perihelion. The comet cannot elude the grasp of the mathematician. He can tell when and where the comet is to be found, but no one can say what it will be like.
Were all the other bodies of the system removed, then the path of Encke's comet must be for ever performed in the same ellipse and with absolute regularity. The chief interest for our present purpose lies not in the regularity of its path, but in the irregularities introduced into that path by the presence of the other bodies of the solar system. Let us, for instance, follow the progress of the comet through its perihelion passage, in which the track lies near that of the planet Mercury. It will usually happen that Mercury is situated in a distant part of its path at the moment the comet is passing, and the[Pg 348] influence of the planet will then be comparatively small. It may, however, sometimes happen that the planet and the comet come close together. One of the most interesting instances of a close approach to Mercury took place on the 22nd November, 1848. On that day the comet and the planet were only separated by an interval of about one-thirtieth of the earth's distance from the sun, i.e. about 3,000,000 miles. On several other occasions the distance between Encke's comet and Mercury has been less than 10,000,000 miles—an amount of trifling import in comparison with the dimensions of our system. Approaches so close as this are fraught with serious consequences to the movements of the comet. Mercury, though a small body, is still sufficiently massive. It always attracts the comet, but the efficacy of that attraction is enormously enhanced when the comet in its wanderings comes near the planet. The effect of this attraction is to force the comet to swerve from its path, and to impress certain changes upon its velocity. As the comet recedes, the disturbing influence of Mercury rapidly abates, and ere long becomes insensible. But time cannot efface from the orbit of the comet the effect which the disturbance of Mercury has actually accomplished. The disturbed orbit is different from the undisturbed ellipse which the comet would have occupied had the influence of the sun alone determined its shape. We are able to calculate the movements of the comet as determined by the sun. We can also calculate the effects arising from the disturbance produced by Mercury, provided we know the mass of the latter.
Though Mercury is one of the smallest of the planets, it is perhaps the most troublesome to the astronomer. It lies so close to the sun that it is seen but seldom in comparison with the other great planets. Its orbit is very eccentric, and it experiences disturbances by the attraction of other bodies in a way not yet fully understood. A special difficulty has also been found in the attempt to place Mercury in the weighing scales. We can weigh the whole earth, we can weigh the sun, the moon, and even Jupiter and other planets, but Mercury presents difficulties of a peculiar character. Le Verrier, however, succeeded in devising a method of weighing it. He[Pg 349] demonstrated that our earth is attracted by this planet, and he showed how the amount of attraction may be disclosed by observations of the sun, so that, from an examination of the observations, he made an approximate determination of the mass of Mercury. Le Verrier's result indicated that the weight of the planet was about the fourteenth part of the weight of the earth. In other words, if our earth was placed in a balance, and fourteen globes, each equal to Mercury, were laid in the other, the scales would hang evenly. It was necessary that this result should be received with great caution. It depended upon a delicate interpretation of somewhat precarious measurements. It could only be regarded as of provisional value, to be discarded when a better one should be obtained.
The approach of Encke's comet to Mercury, and the elaborate investigations of Von Asten and Backlund, in which the observations of the body were discussed, have thrown much light on the subject; but, owing to a peculiarity in the motion of this comet, which we shall presently mention, the difficulties of this investigation are enormous. Backlund's latest result is, that the sun is 9,700,000 times as heavy as Mercury, and he considers that this is worthy of great confidence. There is a considerable difference between this result (which makes the earth about thirty times as heavy as Mercury) and that of Le Verrier; and, on the other hand, Haerdtl has, from the motion of Winnecke's periodic comet, found a value of the mass of Mercury which is not very different from Le Verrier's. Mercury is, however, the only planet about the mass of which there is any serious uncertainty, and this must not make us doubt the accuracy of this delicate weighing-machine. Look at the orbit of Jupiter, to which Encke's comet approaches so nearly when it retreats from the sun. It will sometimes happen that Jupiter and the comet are in close proximity, and then the mighty planet seriously disturbs the pliable orbit of the comet. The path of the latter bears unmistakable traces of the Jupiter perturbations, as well as of the Mercury perturbations. It might seem a hopeless task to discriminate between the influences of the two planets, overshadowed as they both are by the supreme control of the sun, but contrivances[Pg 350] of mathematical analysis are adequate to deal with the problem. They point out how much is due to Mercury, how much is due to Jupiter; and the wanderings of Encke's comet can thus be made to disclose the mass of Jupiter as well as that of Mercury. Here we have a means of testing the precision of our weighing appliances. The mass of Jupiter can be measured by his moons, in the way mentioned in a previous chapter. As the satellites revolve round and round the planet, they furnish a method of measuring his weight by the rapidity of their motion. They tell us that if the sun were placed in one scale of the celestial balance, it would take 1,047 bodies equal to Jupiter in the other to weigh him down. Hardly a trace of uncertainty clings to this determination, and it is therefore of great interest to test the theory of Encke's comet by seeing whether it gives an accordant result. The comparison has been made by Von Asten. Encke's comet tells us that the sun is 1,050 times as heavy as Jupiter; so the results are practically identical, and the accuracy of the indications of the comet are confirmed. But the calculation of the perturbations of Encke's comet is so extremely intricate that Asten's result is not of great value. From the motion of Winnecke's periodic comet, Haerdtl has found that the sun is 1,047·17 times as heavy as Jupiter, in perfect accordance with the best results derived from the attraction of Jupiter on his satellites and the other planets.
We have hitherto discussed the adventures of Encke's comet in cases where they throw light on questions otherwise more or less known to us. We now approach a celebrated problem, on which Encke's comet is our only authority. Every 1,210 days that comet revolves completely around its orbit, and returns again to the neighbourhood of the sun. The movements of the comet are, however, somewhat irregular. We have already explained how perturbations arise from Mercury and from Jupiter. Further disturbances arise from the attraction of the earth and of the other remaining planets; but all these can be allowed for, and then we are entitled to expect, if the law of gravitation be universally true, that the comet shall obey the calculations of mathematics. Encke's[Pg 351] comet has not justified this anticipation; at each revolution the period is getting steadily shorter! Each time the comet comes back to perihelion in two and a half hours less than on the former occasion. Two and a half hours is, no doubt, a small period in comparison with that of an entire revolution; but in the region of its path visible to us the comet is moving so quickly that its motion in two and a half hours is considerable. This irregularity cannot be overlooked, inasmuch as it has been confirmed by the returns during about twenty revolutions. It has sometimes been thought that the discrepancies might be attributed to some planetary perturbations omitted or not fully accounted for. The masterly analysis of Von Asten and Backlund has, however, disposed of this explanation. They have minutely studied the observations down to 1891, but only to confirm the reality of this diminution in the periodic time of Encke's comet.
An explanation of these irregularities was suggested by Encke long ago. Let us briefly attempt to describe this memorable hypothesis. When we say that a body will move in an elliptic path around the sun in virtue of gravitation, it is always assumed that the body has a free course through space. It is assumed that there is no friction, no air, or other source of disturbance. But suppose that this assumption should be incorrect; suppose that there really is some medium pervading space which offers resistance to the comet in the same way as the air impedes the flight of a rifle bullet, what effect ought such a medium to produce? This is the idea which Encke put forward. Even if the greater part of space be utterly void, so that the path of the filmy and almost spiritual comet is incapable of feeling resistance, yet in the neighbourhood of the sun it was supposed that there might be some medium of excessive tenuity capable of affecting so light a body. It can be demonstrated that a resisting medium such as we have supposed would lessen the size of the comet's path, and diminish the periodic time. This hypothesis has, however, now been abandoned. It has always appeared strange that no other comet showed the least sign of being retarded by the assumed resisting medium. But[Pg 352] the labours of Backlund have now proved beyond a doubt that the acceleration of the motion of Encke's comet is not a constant one, and cannot be accounted for by assuming a resisting medium distributed round the sun, no matter how we imagine this medium to be constituted with regard to density at different distances from the sun. Backlund found that the acceleration was fairly constant from 1819 to 1858; it commenced to decrease between 1858 and 1862, and continued to diminish till some time between 1868 and 1871, since which time it has remained fairly constant. He considers that the acceleration can only be produced by the comet encountering periodically a swarm of meteors, and if we could only observe the comet during its motion through the greater part of its orbit we should be able to point out the locality where this encounter takes place.
We have selected the comets of Halley and of Encke as illustrations of the class of periodic comets, of which, indeed, they are the most remarkable members. Another very remarkable periodic comet is that of Biela, of which we shall have more to say in the next chapter. Of the much more numerous class of non-periodic comets, examples in abundance may be cited. We shall mention a few which have appeared during the present century. There is first the splendid comet of 1843, which appeared suddenly in February of that year, and was so brilliant that it could be seen during full daylight. This comet followed a path which could not be certainly distinguished from a parabola, though there is no doubt that it might have been a very elongated ellipse. It is frequently impossible to decide a question of this kind, during the brief opportunities available for finding the place of the comet. We can only see the object during a very small arc of its orbit, and even then it is not a very well-defined point which admits of being measured with the precision attainable in observations of a star or a planet. This comet of 1843 is, however, especially remarkable for the rapidity with which it moved, and for the close approach which it made to the sun. The heat to which it was exposed during its passage around the sun must have been[Pg 353] enormously greater than the heat which can be raised in our mightiest furnaces. If the materials had been agate or cornelian, or the most infusible substances known on the earth, they would have been fused and driven into vapour by the intensity of the sun's rays.
The great comet of 1858 was one of the celestial spectacles of modern times. It was first observed on June 2nd of that year by Donati, whose name the comet has subsequently borne; it was then merely a faint nebulous spot, and for about three months it pursued its way across the heavens without giving any indications of the splendour which it was so soon to attain. The comet had hardly become visible to the unaided eye at the end of August, and was then furnished with only a very small tail, but as it gradually drew nearer and nearer to the sun in September, it soon became invested with splendour. A tail of majestic proportions was quickly developed, and by the middle of October, when the maximum brightness was attained, its length extended over an arc of forty degrees. The beauty and interest of this comet were greatly enhanced by its favourable position in the sky at a season when the nights were sufficiently dark.
On the 22nd May, 1881, Mr. Tebbutt, of Windsor, in New South Wales, discovered a comet which speedily developed into one of the most interesting celestial objects seen by this generation. About the 22nd of June it became visible from these latitudes in the northern sky at midnight. Gradually it ascended higher and higher until it passed around the pole. The nucleus of the comet was as bright as a star of the first magnitude, and its tail was about 20° long. On the 2nd of September it ceased to be visible to the unaided eye, but remained visible in telescopes until the following February. This was the first comet which was successfully photographed, and it may be remarked that comets possess very little actinic power. It has been estimated that moonlight possesses an intensity 300,000 times greater than that of a comet where the purposes of photography are concerned.
Another of the bodies of this class which have received great and deserved attention was that discovered in the[Pg 354] southern hemisphere early in September, 1882. It increased so much in brilliancy that it was seen in daylight by Mr. Common on the 17th of that month, while on the same day the astronomers at the Cape of Good Hope were fortunate enough to have observed the body actually approach the sun's limb, where it ceased to be visible. We know that the comet must have passed between the earth and the sun, and it is very interesting to learn from the Cape observers that it was totally invisible when it was actually projected on the sun's disc. The following day it was again visible to the naked eye in full daylight, not far from the sun, and valuable spectroscopic observations were secured at Dunecht and Palermo. At that time the comet was rushing through the part of its orbit closest to the sun, and about a week later it began to be visible in the morning before sunrise, near the eastern horizon, exhibiting a fine long tail. (See Plate XVII.) The nucleus gradually lengthened until it broke into four separate pieces, lying in a straight line, while the comet's head became enveloped in a sort of faint, nebulous tube, pointing towards the sun. Several small detached nebulous masses became also visible, which travelled along with the comet, though not with the same velocity. The comet became invisible to the naked eye in February, and was last observed telescopically in South America on the 1st June, 1883.
There is a remarkable resemblance between the orbit of this comet and the orbits in which the comet of 1668, the great comet of 1843, and a great comet seen in 1880 in the southern hemisphere, travelled round the sun. In fact, these four comets moved along very nearly the same track and rushed round the sun within a couple of hundred thousand miles of the surface of the photosphere. It is also possible that the comet which, according to Aristotle, appeared in the year 372 B.C. followed the same orbit. And yet we cannot suppose that all these were apparitions of one and the same comet, as the observations of the comet of 1882 give the period of revolution of that body equal to about 772 years. It is not impossible that the comets of 1843 and 1880 are one and the same, but in both years the observations extend over too short[Pg 355] a time to enable us to decide whether the orbit was a parabola or an ellipse. But as the comet of 1882 was in any case a distinct body, it seems more likely that we have here a family of comets approaching the sun from the same region of space and pursuing almost the same course. We know a few other instances of such resemblances between the orbits of distinct comets.
Of other interesting comets seen within the last few years we may mention one discovered by Mr. Holmes in London on the 6th November, 1892. It was then situated not far from the bright nebula in the constellation Andromeda, and like it was just visible to the naked eye. The comet became gradually fainter and more diffused, but on the 16th January following it appeared suddenly with a central condensation, like a star of the eighth magnitude, surrounded by a small coma. Gradually it expanded again, and grew fainter, until it was last observed on the 6th April.[32] The orbit was found to be an ellipse more nearly circular than the orbit of any other known comet, the period being nearly seven years. Another comet of 1892 is remarkable as having been discovered by Professor Barnard, of the Lick Observatory, on a photograph of a region in Aquila; he was at once able to distinguish the comet from a nebula by its motion.
Since 1864 the light of every comet which has made its appearance has been analysed by the spectroscope. The slight surface-brightness of these bodies renders it necessary to open the slit of the spectroscope rather wide, and the dispersion employed cannot be very great, which again makes accurate measurements difficult. The spectrum of a comet is chiefly characterised by three bright bands shading gradually off towards the violet, and sharply defined on the side towards the red. This appearance is caused by a large number of fine and close lines, whose intensity and distance apart decrease towards the violet. These three bands reveal the existence of hydrocarbon in comets.
The important rôle which we thus find carbon playing in the constitution of comets is especially striking when we reflect on the significance of the same element on the earth. We see it as the chief constituent of all vegetable life, we find it to be invariably present in animal life. It is an interesting fact that this element, of such transcendent importance on the earth, should now have been proved to be present in these wandering bodies. The hydrocarbon bands are, however, not always the only features visible in cometary spectra. In a comet seen in the spring months of 1882, Professor Copeland discovered that a new bright yellow line, coinciding in position with the D-line of sodium, had suddenly appeared, and it was subsequently, both by him and by other observers, seen beautifully double. In fact, sodium was so strongly represented in this comet, that both the head and the tail could be perfectly well seen in sodium light by merely opening the slit of the spectroscope very wide, just as a solar prominence may be seen in hydrogen light. The sodium line attained its greatest brilliance at the time when the comet was nearest to the sun, while the hydrocarbon bands were either invisible or very faint. The same connection between the intensity of the sodium line and the distance from the sun was noticed in the great September comet of 1882.
The spectrum of the great comet of 1882 was observed by Copeland and Lohse on the 18th September in daylight, and, in addition to the sodium line, they saw a number of other bright lines, which seemed to be due to iron vapour, while the only line of manganese visible at the temperature of a Bunsen burner was also seen. This very remarkable observation was made less than a day after the perihelion passage, and illustrates the wonderful activity in the interior of a comet when very close to the sun.
In addition to the bright lines comets generally show a faint continuous spectrum, in which dark Fraunhofer lines can occasionally be distinguished. Of course, this shows that the continuous spectrum is to a great extent due to reflected sunlight, but there is no doubt that part of it is often due to light actually developed in the comets. This was certainly the case in the first comet of 1884, as a sudden outburst of light in this body was accompanied by a considerable increase of brightness of the continuous spectrum. A change in the relative brightness of the three hydrocarbon bands indicated a considerable rise of temperature, during the continuance of which the comet emitted white light.
As comets are much nearer to the earth than the stars, it will occasionally happen that the comet must arrive at a position directly between the earth and a star. There is quite a similar phenomenon in the movement of the moon. A star is frequently occulted in this way, and the observations of such phenomena are familiar to astronomers; but when a comet passes in front of a star the circumstances are widely different. The star is indeed seen nearly as well through the comet as it would be if the comet were entirely out of the way. This has often been noticed. One of the most celebrated observations of this kind was made by the late Sir John Herschel on Biela's comet, which is one of the periodic class, and will be alluded to in the next chapter. The illustrious astronomer saw on one occasion this object pass over a star cluster. It consisted of excessively minute stars, which could only be seen by a powerful telescope, such as the one Sir John was using. The faintest haze or the merest trace of a cloud would have sufficed to hide all the stars. It was therefore with no little interest that the astronomer watched the progress of Biela's comet. Gradually the wanderer encroached on the group of stars, so that if it had any appreciable solidity the numerous twinkling points would have been completely screened. But what were the facts? Down to the most minute star in that cluster, down to the smallest point of light which the great telescope could show, every object in the group was distinctly seen to twinkle right through the mass of Biela's comet.
This was an important observation. We must recollect that the veil drawn between the cluster and the telescope was not a thin curtain; it was a volume of cometary substance many thousands of miles in thickness. Contrast, then, the almost inconceivable tenuity of a comet with the clouds to which we[Pg 358] are accustomed. A cloud a few hundred feet thick will hide not only the stars, but even the great sun himself. The lightest haze that ever floated in a summer sky would do more to screen the stars from our view than would one hundred thousand miles of such cometary material as was here interposed.
The great comet of Donati passed over many stars which were visible distinctly through its tail. Among these stars was a very bright one—the well-known Arcturus. The comet, fortunately, happened to pass over Arcturus, and though nearly the densest part of the comet was interposed between the earth and the star, yet Arcturus twinkled on with undiminished lustre through the thickness of this stupendous curtain. Recent observations have, however, shown that stars in some cases experience change in lustre when the denser part of the comet passes over them. It is, indeed, difficult to imagine that a star would remain visible if the nucleus of a really large comet passed over it; but it does not seem that an opportunity of testing this supposition has yet arisen.
As a comet contains transparent gaseous material we might expect that the place of a star would be deranged when the comet approached it. The refractive power of air is very considerable. When we look at the sunset, we see the sun appearing to pass below the horizon; yet the sun has actually sunk beneath the horizon before any part of its disk appears to have commenced its descent. The refractive power of the air bends the luminous rays round and shows the sun, though it is directly screened by the intervening obstacles. The refractive power of the material of comets has been carefully tested. A comet has been observed to approach two stars; one of which was seen through the comet, while the other could be observed directly. If the body had any appreciable quantity of gas in its composition the relative places of the two stars would be altered. This question has been more than once submitted to the test of actual measurement. It has sometimes been found that no appreciable change of position could be detected, and that accordingly in such cases the comet has no perceptible density. Careful measurements of the great comet in 1881 showed, however, that in the neighbourhood of the nucleus there was some refractive power, though quite insignificant in comparison with the refraction of our atmosphere.
From these considerations it will probably be at once admitted that the mass of a comet must be indeed a very small quantity in comparison with its bulk. When we attempt actually to weigh the comet, our efforts have proved abortive. We have been able to weigh the mighty planets Jupiter and Saturn; we have been even able to weigh the vast sun himself; the law of gravitation has provided us with a stupendous weighing apparatus, which has been applied in all these cases with success, but the same methods applied to comets are speedily seen to be illusory. No weighing machinery known to the astronomer is delicate enough to determine the weight of a comet. All that we can accomplish in any circumstances is to weigh one heavenly body in comparison with another. Comets seem to be almost imponderable when estimated by such robust masses as those of the earth, or any of the other great planets. Of course, it will be understood that when we say the weight of a comet is inappreciable, we mean with regard to the other bodies of our system. Perhaps no one now doubts that a great comet must really weigh tons; though whether those tons are to be reckoned in tens, in hundreds, in thousands, or in millions, the total seems quite insignificant when compared with the weight of a body like the earth.
The small mass of comets is also brought before us in a very striking way when we recall what has been said in the last chapter on the important subject of the planetary perturbations. We have there treated of the permanence of our system, and we have shown that this permanence depends upon certain laws which the planetary motions must invariably fulfil. The planets move nearly in circles, their orbits are all nearly in the same plane, and they all move in the same direction. The permanence of the system would be imperilled if any one of these[Pg 360] conditions was not fulfilled. In that discussion we made no allusion to the comets. Yet they are members of our system, and they far outnumber the planets. The comets repudiate these rules of the road which the planets so rigorously obey. Their orbits are never like circles; they are, indeed, more usually parabolic, and thus differ as widely as possible from the circular path. Nor do the planes of the orbits of comets affect any particular aspect; they are inclined at all sorts of angles, and the directions in which they move seem to be mere matters of caprice. All these articles of the planetary convention are violated by comets, but yet our system lasts; it has lasted for countless ages, and seems destined to last for ages to come. The comets are attracted by the planets, and conversely, the comets must attract the planets, and must perturb their orbits to some extent; but to what extent? If comets moved in orbits subject to the same general laws which characterise planetary motion, then our argument would break down. The planets might experience considerable derangements from cometary attraction, and yet in the lapse of time those disturbances would neutralise each other, and the permanence of the system would be unaffected. But the case is very different when we deal with the actual cometary orbits. If comets could appreciably disturb planets, those disturbances would not neutralise each other, and in the lapse of time the system would be wrecked by a continuous accumulation of irregularities. The facts, however, show that the system has lived, and is living, notwithstanding comets; and hence we are forced to the conclusion that their masses must be insignificant in comparison with those of the great planetary bodies.
These considerations exhibit the laws of universal gravitation and their relations to the permanence of our system in a very striking light. If we include the comets, we may say that the solar system includes many thousands of bodies, in orbits of all sizes, shapes, and positions, only agreeing in the fact that the sun occupies a focus common to all. The majority of these bodies are imponderable in comparison with planets, and their orbits are placed anyhow, so that, although they[Pg 361] may suffer much from the perturbations of the other bodies, they can in no case inflict any appreciable disturbance. There are, however, a few great planets capable of producing vast disturbances; and if their orbits were not properly adjusted, chaos would sooner or later be the result. By the mutual adaptations of their orbits to a nearly circular form, to a nearly coincident plane, and to a uniformity of direction, a permanent truce has been effected among the great planets. They cannot now permanently disorganise each other, while the slight mass of the comets renders them incompetent to do so. The stability of the great planets is thus assured; but it is to be observed that there is no guarantee of stability for comets. Their eccentric and irregular paths may undergo the most enormous derangements; indeed, the history of astronomy contains many instances of the vicissitudes to which a cometary career is exposed.
Great comets appear in the heavens in the most diverse circumstances. There is no part of the sky, no constellation or region, which is not liable to occasional visits from these mysterious bodies. There is no season of the year, no hour of the day or of the night when comets may not be seen above the horizon. In like manner, the size and aspect of the comets are of every character, from the dim spot just visible to an eye fortified by a mighty telescope, up to a gigantic and brilliant object, with a tail stretching across the heavens for a distance which is as far as from the horizon to the zenith. So also the direction of the tail of the comet seems at first to admit of every possible position: it may stand straight up in the heavens, as if the comet were about to plunge below the horizon; it may stream down from the head of the comet, as if the body had been shot up from below; it may slope to the right or to the left. Amid all this variety and seeming caprice, can we discover any feature common to the different phenomena? We shall find that there is a very remarkable law which the tails of comets obey—a law so true and satisfactory, that if we are given the place of a comet in the heavens, it is possible at once to point out in what direction the tail will lie.
A beautiful comet appears in summer in the northern sky. It is near midnight; we are gazing on the faintly luminous tail, which stands up straight and points towards the zenith; perhaps it may be curved a little or possibly curved a good deal, but still, on the whole, it is directed from the horizon to the zenith. We are not here referring to any particular comet. Every comet, large or small, that appears in the north must at midnight have its tail pointed up in a nearly vertical direction. This fact, which has been verified on numerous occasions, is a striking illustration of the law of direction of comets' tails. Think for one moment of the facts of the case. It is summer; the twilight at the north shows the position of the sun, and the tail of the comet points directly away from the twilight and away from the sun. Take another case. It is evening; the sun has set, the stars have begun to shine, and a long-tailed comet is seen. Let that comet be high or low, north or south, east or west, its tail invariably points away from that point in the west where the departing sunlight still lingers. Again, a comet is watched in the early morning, and if the eye be moved from the place where the first streak of dawn is appearing to the head of the comet, then along that direction, streaming away from the sun, is found the tail of the comet. This law is of still more general application. At any season, at any hour of the night, the tail of a comet is directed away from the sun.
More than three hundred years ago this fact in the movement of comets arrested the attention of those who pondered on the movements of the heavenly bodies. It is a fact patent to ordinary observation, it gives some degree of consistency to the multitudinous phenomena of comets, and it must be made the basis of our enquiries into the structure of the tails.
In the adjoining figure, Fig. 71, we show a portion of the parabolic orbit of a comet, and we also represent the position of the tail of the comet at various points of its path. It would be, perhaps, going too far to assert that throughout the whole vast journey of the comet, its tail must always be directed from the sun. In the first place, it must be recollected that we can only see the comet during that small part of its journey when it is[Pg 363] approaching to or receding from the sun. It is also to be remembered that, while actually passing round the sun, the brilliancy of the comet is so overpowered by the sun that the comet often becomes invisible, just as the stars are invisible in daylight. Indeed, in certain cases, jets of cometary material are actually projected towards the sun.
In a hasty consideration of the subject, it might be thought that as the comet was dashing along with enormous velocity the tail was merely streaming out behind, just as the shower of sparks from a rocket are strewn along the path which it follows. This would be an entirely erroneous analogy; the comet is moving not through an atmosphere, but through open space, where there is no medium sufficient to sweep the tail into the line of motion. Another very remarkable feature is the gradual growth of the tail as the comet approaches the sun. While the body is still at a great distance it has usually no perceptible tail, but as it draws in the tail gradually develops, and in some cases reaches stupendous dimensions. It is not to be supposed that this increase is a mere optical consequence of the diminution of distance. It can be shown that the growth of the tail takes place much more rapidly than it would be possible to explain in this way. We are thus led to connect the formation of the tail with the approach to the sun, and we are accordingly[Pg 364] in the presence of an enigma without any analogy among the other bodies of our system.
That the comet as a whole is attracted by the sun there can be no doubt whatever. The fact that the comet moves in an ellipse or in a parabola proves that the two bodies act and react on each other in obedience to the law of universal gravitation. But while this is true of the comet as a whole, it is no less certain that the tail of the comet is repelled by the sun. It is impossible to speak with certainty as to how this comes about, but the facts of the case seem to point to an explanation of the following kind.
We have seen that the spectroscope has proved with certainty the presence of hydrocarbon and other gases in comets. But we are not to conclude from this that comets are merely masses of gas moving through space. Though the total quantity of matter in a comet, as we have seen, is exceedingly small, it is quite possible that the comet may consist of a number of widely scattered particles of appreciable density; indeed, we shall see in the next chapter, when describing the remarkable relationship between comets and meteors, that we have reason to believe this to be the case. We may therefore look on a comet as a swarm of tiny solid particles, each surrounded by gas.
When we watch a great comet approaching the sun the nucleus is first seen to become brighter and more clearly defined; at a later stage luminous matter appears to be projected from it towards the sun, often in the shape of a fan or a jet, which sometimes oscillates to and fro like a pendulum. In the head of Halley's comet, for instance, Bessel observed in October, 1835, that the jet in the course of eight hours swung through an angle of 36°. On other occasions concentric arcs of light are formed round the nucleus, one after another, getting fainter as they travel further from the nucleus. Evidently the material of the fan or the arcs is repelled by the nucleus of the comet; but it is also repelled by the sun, and this latter repulsive force compels the luminous matter to overcome the attraction of gravitation, and to turn back all round the nucleus in the direction away from the sun. In[Pg 365] this manner the tail is formed. (See Plate XII.) The mathematical theory of the formation of comets' tails has been developed on the assumption that the matter which forms the tail is repelled both by the nucleus and by the sun. This investigation was first undertaken by the great astronomer Bessel, in his memoir on the appearance of Halley's comet in 1835, and it has since been considerably developed by Roche and the Russian astronomer Bredichin. Though we are, perhaps, hardly in a position to accept this theory as absolutely true, we can assert that it accounts well for the principal phenomena observed in the formation of comets' tails.
Professor Bredichin has conducted his labours in the philosophical manner which has led to many other great discoveries in science. He has carefully collated the measurements and drawings of the tails of various comets. One result has been obtained from this preliminary part of his enquiry, which possesses a value that cannot be affected even if the ulterior portion of his labours should be found to require qualification. In the examination of the various tails, he observed that the curvilinear shapes of the outlines fall into one or other of three special types. In the first we have the straightest tails, which point almost directly away from the sun. In the second are classed tails which, after starting away from the sun, are curved backwards from the direction towards which the comet is moving. In the third we find the appendage still more curved in towards the comet's path. It can be shown that the tails of comets can almost invariably be identified with one or other of these three types; and in cases where the comet exhibits two tails, as has sometimes happened, then they will be found to belong to two of the types.
The adjoining diagram (Fig. 72) gives a sketch of an imaginary comet furnished with tails of the three different types. The direction in which the comet is moving is shown by the arrow-head on the line passing through the nucleus. Bredichin concludes that the straightest of the three tails, marked as Type I., is most probably due to the element hydrogen; the[Pg 366] tails of the second form are due to the presence of some of the hydrocarbons in the body of the comet; while the small tails of the third type may be due to iron or to some other element with a high atomic weight. It will, of course, be understood that this diagram does not represent any actual comet.
An interesting illustration of this theory is afforded in the case of the celebrated comet of 1858 already referred to, of which a drawing is shown in Fig. 73. We find here, besides the great tail, which is the characteristic feature of the body, two other faint streaks of light. These are the edges of the hollow cone which forms a tail of Type I. When we look through the central regions it will be easily understood that the light is not sufficiently intense to be visible; at the edges, however, a sufficient thickness of the cometary matter is presented, and thus we have the appearance shown in this figure. It would seem that Donati's comet possessed one tail due to hydrogen, and another due to some of the compounds of carbon. The carbon compounds involved appear to be of considerable variety, and there is, in consequence, a disposition in the tails of the second type to a more indefinite outline than in the hydrogen tails. Cases have been recorded in which several tails have been seen simultaneously on the same comet. The most celebrated of these is that which appeared in the year 1744. Professor Bredichin has devoted special attention to the theory of this marvellous object, and he has shown with a high degree of probability how the multiform tail could be accounted for. The adjoining figure (Fig. 74) is from a sketch of this object made on the morning of the 7th March by Mademoiselle Kirch at the Berlin Observatory. The figure shows eleven streaks, of which the first ten (counting from the left) represent the bright edges of five of the tails, while the sixth and shortest tail is at the extreme right. Sketches of this rare phenomenon were also made by Chéseaux at Lausanne and De L'Isle at St. Petersburg.[Pg 368] Before the perihelion passage the comet had only had one tail, but a very splendid one.
It is possible to submit some of the questions involved to the test of calculation, and it can be shown that the repulsive force adequate to produce the straight tail of Type I. need only be about twelve times as large as the attraction of gravitation. Tails of the second type could be produced by a repulsive force which was about equal to gravitation, while tails of the third type would only require a repulsive force about one-quarter the power of gravitation.[33] The chief repulsive force known in nature is derived from electricity, and it has naturally been surmised that the phenomena of comets'[Pg 369] tails are due to the electric condition of the sun and of the comet. It would be premature to assert that the electric character of the comet's tail has been absolutely demonstrated; all that can be said is that, as it seems to account for the observed facts, it would be undesirable to introduce some mere hypothetical repulsive force. It must be remembered that on quite other grounds it is known that the sun is the seat of electric phenomena.
As the comet gradually recedes from the sun the repulsive force becomes weaker, and accordingly we find that the tail of the comet declines. If the comet be a periodic one, the same series of changes may take place at its next return to perihelion. A new tail is formed, which also gradually disappears as the comet regains the depths of space. If we may employ the analogy of terrestrial vapours to guide us in our reasoning, then it would seem that, as the comet retreats, its tail would condense into myriads of small particles. Over these small particles the law of gravitation would resume its undivided sway, no longer obscured by the superior efficiency of the repulsion. The mass of the comet is, however, so extremely small that it would not be able to recall these particles by the mere force of attraction. It follows that, as the comet at each perihelion passage makes a tail, it must on each occasion expend a corresponding quantity of tail-making material. Let us suppose that the comet was endowed in the beginning with a certain capital of those particular materials which are adapted for the production of tails. Each perihelion passage witnesses the formation of a tail, and the expenditure of a corresponding amount of the capital. It is obvious that this operation cannot go on indefinitely. In the case of the great majority of comets the visits to perihelion are so extremely rare that the consequences of the extravagance are not very apparent; but to those periodic comets which have short periods and make frequent returns, the consequences are precisely what might have been anticipated: the tail-making capital has been gradually squandered, and thus at length we have the spectacle of a comet without any tail at all. We can even conceive that a comet may in this[Pg 370] manner be completely dissipated, and we shall see in the next chapter how this fate seems to have overtaken Biela's periodic comet.
But as it sweeps through the solar system the comet may chance to pass very near one of the larger planets, and, in passing, its motion may be seriously disturbed by the attraction of the planet. If the velocity of the comet is accelerated by this disturbing influence, the orbit will be changed from a parabola into another curve known as a hyperbola, and the comet will swing round the sun and pass away never to return. But if the planet is so situated as to retard the velocity of the comet, the parabolic orbit will be changed into an ellipse, and the comet will become a periodic one. We can hardly doubt that some periodic comets have been "captured" in this manner and thereby made permanent members of our solar system, if we remark that the comets of short periods (from three to eight years) come very near the orbit of Jupiter at some point or other of their paths. Each of them must, therefore, have been near the giant planet at some moment during their past history. Similarly the other periodic comets of longer period approach near to the orbits of either Saturn, Uranus, or Neptune, the last-mentioned planet being probably responsible for the periodicity of Halley's comet. We have, indeed, on more than one occasion, actually witnessed the violent disturbance of a cometary orbit. The most interesting case is that of Lexell's comet. In 1770 the French astronomer Messier (who devoted himself with great success to the discovery of comets) detected a comet for which Lexell computed the orbit, and found an ellipse with a period of five years and some months. Yet the comet had never been seen before, nor did it ever come back again. Long afterwards it was found, from most laborious investigations by Burckhardt and Le Verrier, that the comet had moved in a totally different orbit previous to 1767. But at the beginning of the year 1767 it happened to come so close to Jupiter that the powerful attraction of this planet forced it into a new orbit, with a period of five and a half years. It passed the perihelion[Pg 371] on the 13th August, 1770, and again in 1776, but in the latter year it was not conveniently situated for being seen from the earth. In the summer of 1779 the comet was again in the neighbourhood of Jupiter, and was thrown out of its elliptic orbit, so that we have never seen it since, or, perhaps, it would be safer to say that we have not with certainty identified Lexell's comet with any comet observed since then. We are also, in the case of several other periodic comets, able to fix in a similar way the date when they started on their journeys in their present elliptic orbits.
Such is a brief outline of the principal facts known with regard to these interesting but perplexing bodies. We must be content with the recital of what we know, rather than hazard guesses about matters beyond our reach. We see that they are obedient to the great laws of gravitation, and afford a striking illustration of their truth. We have seen how modern science has dissipated the superstition with which, in earlier ages, the advent of a comet was regarded. We no longer regard such a body as a sign of impending calamity; we may rather look upon it as an interesting and a beautiful visitor, which comes to please us and to instruct us, but never to threaten or to destroy.
Small Bodies of our System—Their Numbers—How they are Observed—The Shooting Star—The Theory of Heat—A Great Shooting Star—The November Meteors—Their Ancient History—The Route followed by the Shoal—Diagram of the Shoal of Meteors—How the Shoal becomes Spread out along its Path—Absorption of Meteors by the Earth—The Discovery of the Relation between Meteors and Comets—The Remarkable Investigations concerning the November Meteors—Two Showers in Successive Years—No Particles have ever been Identified from the Great Shooting Star Showers—Meteoric Stones—Chladni's Researches—Early Cases of Stone-falls—The Meteorite at Ensisheim—Collections of Meteorites—The Rowton Siderite—Relative Frequency of Iron and Stony Meteorites—Fragmentary Character of Meteorites—Tschermak's Hypothesis—Effects of Gravitation on a Missile ejected from a Volcano—Can they have come from the Moon?—The Claims of the Minor Planets to the Parentage of Meteorites—Possible Terrestrial Origin—The Ovifak Iron.
In the preceding chapters we have dealt with the gigantic bodies which form the chief objects in what we know as the solar system. We have studied mighty planets measuring thousands of miles in diameter, and we have followed the movements of comets whose dimensions are often to be told by millions of miles. Once, indeed, in a previous chapter we have made a descent to objects much lower in the scale of magnitude, and we have examined that numerous class of small bodies which we call the minor planets. It is now, however, our duty to make a still further, and this time a very long step, downwards in the scale of magnitude. Even the minor planets must be regarded as colossal objects when compared with those little bodies whose presence is revealed to us in an interesting and sometimes in a striking manner.
These small bodies compensate in some degree for their minute size by the profusion in which they exist. No attempt,[Pg 373] indeed, could be made to tell in figures the myriads in which they swarm throughout space. They are probably of very varied dimensions, some of them being many pounds or perhaps tons in weight, while others seem to be not larger than pebbles, or even than grains of sand. Yet, insignificant as these bodies may seem, the sun does not disdain to undertake their control. Each particle, whether it be as small as the mote in a sunbeam or as mighty as the planet Jupiter, must perforce trace out its path around the sun in conformity with the laws of Kepler.
Who does not know that beautiful occurrence which we call a shooting star, or which, in its more splendid forms, is sometimes called a meteor or fireball? It is to objects of this class that we are now to direct our attention.
A small body is moving round the sun. Just as a mighty planet revolves in an ellipse, so even a small object will be guided round and round in an ellipse with the sun in the focus. There are, at the present moment, inconceivable myriads of such meteors moving in this manner. They are too small and too distant for our telescopes, and we never see them except under extraordinary circumstances.
When the meteor flashes into view it is moving with such enormous velocity that it often traverses more than twenty miles in a second of time. Such a velocity is almost impossible near the earth's surface: the resistance of the air would prevent it. Aloft, in the emptiness of space, there is no air to impede its flight. It may have been moving round and round the sun for thousands, perhaps for millions of years, without suffering any interference; but the supreme moment arrives, and the meteor perishes in a streak of splendour.
In the course of its wanderings the body comes near the earth, and within a few hundred miles of its surface begins to encounter the upper surface of the atmosphere with which the earth is enclosed. To a body moving with the appalling velocity of a meteor, a plunge into the atmosphere is usually fatal. Even though the upper layers of air are excessively attenuated, yet they suddenly check the velocity almost as a[Pg 374] rifle bullet would be checked when fired into water. As the meteor rushes through the atmosphere the friction of the air warms its surface; gradually it becomes red-hot, then white-hot, and is finally driven off into vapour with a brilliant light, while we on the earth, one or two hundred miles below, exclaim: "Oh, look, there is a shooting star!"
We have here an experiment illustrating the mechanical theory of heat. It may seem incredible that mere friction should be sufficient to generate heat enough to produce so brilliant a display, but we must recollect two facts: first, that the velocity of the meteor is, perhaps, one hundred times that of a rifle bullet; and, second, that the efficiency of friction in developing heat is proportional to the square of the velocity. The meteor in passing through the air may therefore develop by the friction of the air about ten thousand times as much heat as the rifle bullet. We do not make an exaggerated estimate in supposing that the latter missile becomes heated ten degrees by friction; yet if this be admitted, we must grant that there is such an enormous development of heat attending the flight of the meteor that even a fraction of it would be sufficient to drive the object into vapour.
Let us first consider the circumstances in which these external bodies are manifested to us, and, for the sake of illustration, we may take a remarkable fireball which occurred on November 6th, 1869. This body was seen from many different places in England; and by combining and comparing these observations, we obtain accurate information as to the height of the object and the velocity with which it travelled.
It appears that this meteor commenced to be visible at a point ninety miles above Frome, in Somersetshire, and that it vanished twenty-seven miles over the sea, near St. Ives, in Cornwall. The path of the body, and the principal localities from which it was observed, are shown in the map (Fig. 75). The whole length of its visible course was about 170 miles, which was performed in a period of five seconds, thus giving an average velocity of thirty-four miles per second. A remarkable feature in the appearance which this fireball presented was the long persistent streak of luminous cloud, about fifty miles long and four miles wide, which remained in sight for fully fifty minutes. We have in this example an illustration of the chief features of the phenomena of a shooting star presented on a very grand scale. It is, however, to be observed that the persistent luminous streak is not a universal, nor, indeed, a very common characteristic of a shooting star.
The small objects which occasionally flash across the field of the telescope show us that there are innumerable telescopic shooting stars, too small and too faint to be visible to the unaided eye. These objects are all dissipated in the way we have described; it is, in fact, only at the moment, and during the process of their dissolution, that we become aware of their existence. Small as these missiles probably are, their velocity is so prodigious that they would render the earth uninhabitable were they permitted to rain down unimpeded on its surface. We must, therefore, among the other good qualities of our atmosphere, not forget that it constitutes a kindly screen, which shields us from a tempest of missiles, the velocity of which no artillery could equal. It is, in fact, the very fury of these missiles which is the cause of their utter destruction. Their anxiety to strike us is so great, that friction dissolves them into harmless vapour.
Next to a grand meteor such as that we have just described, the most striking display in connection with shooting stars is what is known as a shower. These phenomena have attracted a great deal of attention within the last century, and they have abundantly rewarded the labour devoted to them by affording some of the most interesting astronomical discoveries of modern times.
The showers of shooting stars do not occur very frequently. No doubt the quickened perception of those who especially attend to meteors will detect a shower when others see only a few straggling shooting stars; but, speaking generally, we may say that the present generation can hardly have witnessed more than two or three such occurrences. I have myself seen two great showers, one of which, in November, 1866, has impressed itself on my memory as a glorious spectacle.
To commence the history of the November meteors it is necessary to look back for nearly a thousand years. On the 12th of October, in the year 902, occurred the death of a Moorish king, and in connection with this event an old chronicler relates how "that night there were seen, as it were lances, an infinite number of stars, which scattered[Pg 377] themselves like rain to right and left, and that year was called the Year of the Stars."
No one now believes that the heavens intended to commemorate the death of the king by that display. The record is, however, of considerable importance, for it indicates the year 902 as one in which a great shower of shooting stars occurred. It was with the greatest interest astronomers perceived that this was the first recorded instance of that periodical shower, the last of whose regular returns were seen in 1799, 1833, and 1866. Further diligent literary research has revealed here and there records of startling appearances in the heavens, which fit in with successive returns of the November meteors. From the first instance, in 902, to the present day there have been twenty-nine visits of the shower; and it is not unlikely that these may have all been seen in some parts of the earth. Sometimes they may have been witnessed by savages, who had neither the inclination nor the means to place on record an apparition which to them was a source of terror. Sometimes, however, these showers were observed by civilised communities. Their nature was not understood, but the records were made; and in some cases, at all events, these records have withstood the corrosion of time, and have now been brought together to illustrate this curious subject. We have altogether historical notices of twelve of these showers, collected mainly by the industry of Professor H.A. Newton whose labours have contributed so much to the advancement of our knowledge of shooting stars.
Let us imagine a swarm of small objects roaming through space. Think of a shoal of herrings in the ocean, extending over many square miles, and containing countless myriads of individuals; or think of those enormous flocks of wild pigeons in the United States of which Audubon has told us. The shoal of shooting stars is perhaps much more numerous than the herrings or the pigeons. The shooting stars are, however, not very close together; they are, on an average, probably some few miles apart. The actual bulk of the shoal is therefore prodigious; and its dimensions are to be measured by hundreds of thousands of miles.
The meteors cannot choose their own track, like the shoal of herrings, for they are compelled to follow the route which is prescribed to them by the sun. Each one pursues its own ellipse in complete independence of its neighbours, and accomplishes its journey, thousands of millions of miles in length, every thirty-three years. We cannot observe the meteors during the greater part of their flight. There are countless myriads of these bodies at this very moment coursing round their path. We never see them till the earth catches them. Every thirty-three years the earth makes a haul of these meteors just as successfully as the fisherman among the herrings, and in much the same way, for while the fisherman spreads his net in which the fishes meet their doom, so the earth has an atmosphere wherein the meteors perish. We are told that there is no fear of the herrings becoming exhausted, for those the fishermen catch are as nothing compared to the profusion in which they abound in ocean. We may say the same with regard to the meteors. They exist in such myriads, that though the earth swallows up millions every thirty-three years, plenty are left for future showers. The diagram (Fig. 76) will explain the way in which the[Pg 379] earth makes her captures. We there see the orbit in which our globe moves around the sun, as well as the elliptic path of the meteors, though it should be remarked that it is not convenient to draw the figure exactly to scale, so that the path of the meteors is relatively much larger than here represented. Once each year the earth completes its revolution, and between the 13th and the 16th of November crosses the track in which the meteors move. It will usually happen that the great shoal is not at this point when the earth is passing. There are, however, some stragglers all along the path, and the earth generally catches a few of these at this date. They dart into our atmosphere as shooting stars, and form what we usually speak of as the November meteors.
It will occasionally happen that when the earth is in the act of crossing the track it encounters the bulk of the meteors. Through the shoal our globe then plunges, enveloped, of course, with the surrounding coat of air. Into this net the meteors dash in countless myriads, never again to emerge. In a few hours' time, the earth, moving at the rate of eighteen miles a second, has crossed the track and emerges on the other side, bearing with it the spoils of the encounter. Some few meteors, which have only narrowly escaped capture, will henceforth bear evidence of the fray by moving in slightly different orbits, but the remaining meteors of the shoal continue their journey without interruption; perhaps millions have been taken, but probably hundreds of millions have been left.
Such was the occurrence which astonished the world on the night between November 13th and 14th, 1866. We then plunged into the middle of the shoal. The night was fine; the moon was absent. The meteors were distinguished not only by their enormous multitude, but by their intrinsic magnificence. I shall never forget that night. On the memorable evening I was engaged in my usual duty at that time of observing nebulæ with Lord Rosse's great reflecting telescope. I was of course aware that a shower of meteors had been predicted, but nothing that I had heard prepared me for the splendid spectacle so soon to be unfolded. It was about ten o'clock[Pg 380] at night when an exclamation from an attendant by my side made me look up from the telescope, just in time to see a fine meteor dash across the sky. It was presently followed by another, and then again by more in twos and in threes, which showed that the prediction of a great shower was likely to be verified. At this time the Earl of Rosse (then Lord Oxmantown) joined me at the telescope, and, after a brief interval, we decided to cease our observations of the nebulæ and ascend to the top of the wall of the great telescope (Fig. 7, p. 18), whence a clear view of the whole hemisphere of the heavens could be obtained. There, for the next two or three hours, we witnessed a spectacle which can never fade from my memory. The shooting stars gradually increased in number until sometimes several were seen at once. Sometimes they swept over our heads, sometimes to the right, sometimes to the left, but they all diverged from the east. As the night wore on, the constellation Leo ascended above the horizon, and then the remarkable character of the shower was disclosed. All the tracks of the meteors radiated from Leo. (See Fig. 74, p. 368.) Sometimes a meteor appeared to come almost directly towards us, and then its path was so foreshortened that it had hardly any appreciable length, and looked like an ordinary fixed star swelling into brilliancy and then as rapidly vanishing. Occasionally luminous trains would linger on for many minutes after the meteor had flashed across, but the great majority of the trains in this shower were evanescent. It would be impossible to say how many thousands of meteors were seen, each one of which was bright enough to have elicited a note of admiration on any ordinary night.
The adjoining figure (Fig. 77) shows the remarkable manner in which the shooting stars of this shower diverged from a point. It is not to be supposed that all these objects were in view at the same moment. The observer of a shower is provided with a map of that part of the heavens in which the shooting stars appear. He then fixes his attention on one particular shooting star, and observes carefully its track with respect to the fixed stars in its vicinity. He then draws[Pg 381] a line upon his map in the direction in which the shooting star moved. Repeating the same observation for several other shooting stars belonging to the shower, his map will hardly fail to show that their different tracks almost all tend from one point or region of the figure. There are, it is true, a few erratic ones, but the majority observe this law. It certainly looks, at first sight, as if all the shooting stars did actually dart from this point; but a little reflection will show that this is a case in which the real motion is different from the apparent. If there actually were a point from which these meteors diverged, then from different parts of the earth the point would be seen in different positions with respect to the fixed stars; but this is not the case. The radiant, as this point is called, is seen in the same part of the heavens from whatever station the shower is visible.
We are, therefore, led to accept the simple explanation afforded by the theory of perspective. Those who are acquainted with the principles of this science know that when a number of parallel lines in an object have to be represented[Pg 382] in a drawing, they must all be made to pass through the same point in the plane of the picture. When we are looking at the shooting stars, we see the projections of their paths upon the surface of the heavens. From the fact that those paths pass through the same point, we are to infer that the shooting stars belonging to the same shower are moving in parallel lines.
We are now able to ascertain the actual direction in which the shooting stars are moving, because a line drawn from the eye of the observer to the radiant point must be parallel to that direction. Of course, it is not intended to convey the idea that throughout all space the shooting stars of one shower are moving in parallel lines; all we mean is that during the short time in which we see them the motion of each of the shooting stars is sensibly a straight line, and that all these straight lines are parallel.
In the year 1883 the great meteor shoal of the Leonids (for so this shower is called) attained its greatest distance from the sun, and then commenced to return. Each year the earth crossed the orbit of the meteors; but the shoal was not met with, and no noteworthy shower of stars was perceived. Every succeeding year found the meteors approaching the critical point, and the year 1899 brought the shoal to the earth's track. In that year a brilliant meteoric shower was expected, but the result fell far short of expectation. The shoal of meteors is of such enormous length that it takes more than a year for the mighty procession to pass through the critical portion of its orbit which lies across the track of the earth. We thus see that the meteors cannot escape the earth. It may be that when the shoal begins to reach this neighbourhood the earth will have just left this part of its path, and a year will have elapsed before the earth gets round again. Those meteors that have the good fortune to be in the front of the shoal will thus escape the net, but some of those behind will not be so fortunate, and the earth will again devour an incredible host. It has sometimes happened that casts into the shoal have been obtained in two consecutive years. If the earth happened to pass through the front part in one year, then the shoal[Pg 383] is so long that the earth will have moved right round its orbit of 600,000,000 miles, and will again dash through the critical spot before the entire number have passed. History contains records of cases when, in two consecutive Novembers, brilliant showers of Leonids have been seen.
As the earth consumes such myriads of Leonids each thirty-three years, it follows that the total number must be decreasing. The splendour of the showers in future ages will, no doubt, be affected by this circumstance. They cannot be always so bright as they have been. It is also of interest to notice that the shape of the shoal is gradually changing. Each meteor of the shoal moves in its own ellipse round the sun, and is quite independent of the rest of these bodies. Each one has thus a special period of revolution which depends upon the length of the ellipse in which it happens to revolve. Two meteors will move around the sun in the same time if the lengths of their ellipses are exactly equal, but not otherwise. The lengths of these ellipses are many hundreds of millions of miles, and it is impossible that they can be all absolutely equal. In this may be detected the origin of a gradual change in the character of the shower. Suppose two meteors A and B be such that A travels completely round in thirty-three years, while B takes thirty-four years. If the two start together, then when A has finished the first round B will be a year behind; the next time B will be two years behind, and so on. The case is exactly parallel to that of a number of boys who start for a long race, in which they have to run several times round the course before the distance has been accomplished. At first they all start in a cluster, and perhaps for the first round or two they may remain in comparative proximity; gradually, however, the faster runners get ahead and the slower ones lag behind, so the cluster becomes elongated. As the race continues, the cluster becomes dispersed around the entire course, and perhaps the first boy will even overtake the last. Such seems the destiny of the November meteors in future ages. The cluster will in time come to be spread out around the whole of this mighty track, and no longer[Pg 384] will a superb display have to be recorded every thirty-three years.
It was in connection with the shower of November meteors in 1866 that a very interesting and beautiful discovery in mathematical astronomy was made by Professor Adams. We have seen that the Leonids must move in an elliptic path, and that they return every thirty-three years, but the telescope cannot follow them during their wanderings. All that we know by observation is the date of their occurrence, the point of the heavens from which they radiate, and the great return every thirty-three years. Putting these various facts together, it is possible to determine the ellipse in which the meteors move—not exactly: the facts do not go so far—they only tell us that the ellipse must be one of five possible orbits. These five possible orbits are—firstly, the immense ellipse in which we now know the meteorites do revolve, and for which they require the whole thirty-three years to complete a revolution; secondly, a nearly circular orbit, very little larger than the earth's path, which the meteors would traverse in a few days more than a year; another similar orbit, in which the time would be a few days short of the year; and two other small elliptical orbits lying inside the earth's orbit. It was clearly demonstrated by Professor Newton, of New Haven, U.S.A., that the observed facts would be explained if the meteors moved in any one of these paths, but that they could not be explained by any other hypothesis. It remained to see which of these orbits was the true one. Professor Newton himself made the suggestion of a possible method of solving the problem. The test he proposed was one of some difficulty, for it involved certain intricate calculations in the theory of perturbations. Fortunately, however, Professor Adams undertook the inquiry, and by his successful labours the path of the Leonids has been completely ascertained.
When the ancient records of the appearance of great Leonid showers were examined, it was found that the date of their occurrence undergoes a gradual and continuous change, which Professor Newton fixed at one day in seventy years. It follows as a necessary consequence that the point where the path of the meteors crosses the earth's track is not fixed, but that at each successive return they cross at a point about half a degree further on in the direction in which the earth is travelling. It follows that the orbit in which the meteors are revolving is undergoing change; the path they follow in one revolution varies slightly from that pursued in the next. As, however, these changes proceed in the same direction, they may gradually attain considerable dimensions; and the amount of change which is produced in the path of the meteors in the lapse of centuries may be estimated by the two ellipses shown in Fig. 78. The continuous line represents the orbit in A.D. 126; the dotted line represents it at present.
This unmistakable change in the orbit is one that astronomers attribute to what we have already spoken of as perturbation. It is certain that the elliptic motion of these bodies is due to the sun, and that if they were only acted on by the sun the ellipse would remain absolutely unaltered. We see, then, in this gradual change of the ellipse the influence of the attractions of the planets. It was shown that if the meteors moved in the large orbit, this shifting of the path must be due to the attraction of the planets Jupiter, Saturn, Uranus, and the Earth; while if the meteors followed one of the smaller orbits, the planets that would be near enough and massive enough to act sensibly on them would be the Earth, Venus, and Jupiter. Here, then, we see how the question may be answered by calculation. It is difficult, but it is possible, to calculate what the attraction of the planets would be capable of producing for each of the five different suppositions as to the orbit. This is what Adams did. He found that if the meteors moved in the great orbit, then the attraction of Jupiter would account for two-thirds of the observed change, while the remaining third was due to the influence of Saturn, supplemented by a small addition on account of Uranus. In this way the calculation showed that the large orbit was a possible one. Professor Adams also computed the amount of displacement in the path that could be produced if the meteors revolved in any of the four smaller ellipses. This investigation was one of an arduous character, but the results amply repaid the labour. It was shown that with the smaller ellipses it would be impossible to obtain a displacement even one-half of that which was observed. These four orbits must, therefore, be rejected. Thus the demonstration was complete that it is in the large path that the meteors revolve.
The movements in each revolution are guided by Kepler's laws. When at the part of its path most distant from the sun the velocity of a meteor is at its lowest, being then but little more than a mile a second; as it draws in, the speed gradually increases, until, when the meteor crosses the earth's track, its velocity is no less than twenty-six miles a second.[Pg 387] The earth is moving very nearly in the opposite direction at the rate of eighteen miles a second, so that, if the meteor happen to strike the earth's atmosphere, it does so with the enormous velocity of nearly forty-four miles a second. If a collision is escaped, then the meteor resumes its onward journey with gradually declining velocity, and by the time it has completed its circuit a period of thirty-three years and a quarter will have elapsed.
The innumerable meteors which form the Leonids are arranged in an enormous stream, of a breadth very small in comparison with its length. If we represent the orbit by an ellipse whose length is seven feet, then the meteor stream will be represented by a thread of the finest sewing-silk, about a foot and a half or two feet long, creeping along the orbit.[34] The size of this stream may be estimated from the consideration that even its width cannot be less than 100,000 miles. Its length may be estimated from the circumstance that, although its velocity is about twenty-six miles a second, yet the stream takes about two years to pass the point where its orbit crosses the earth's track. On the memorable night between the 13th and 14th of November, 1866, the earth plunged into this stream near its head, and did not emerge on the other side until five hours later. During that time it happened that the hemisphere of the earth which was in front contained the continents of Europe, Asia, and Africa, and consequently it was in the Old World that the great shower was seen. On that day twelvemonth, when the earth had regained the same spot, the shoal had not entirely passed, and the earth made another plunge. This time the American continent was in the van, and consequently it was there that the shower of 1867 was seen. Even in the following year the great shoal had not entirely passed, and since then a few stragglers along the route have been encountered at each annual transit of the earth across this meteoric highway.
The diagram is also designed to indicate a remarkable[Pg 388] speculation which was put forward on the high authority of Le Verrier, with the view of explaining how the shoal came to be introduced into the solar system. The orbit in which the meteors revolve does not intersect the paths of Jupiter, Saturn, or Mars, but it does intersect the orbit of Uranus. It must sometimes happen that Uranus is passing through this point of its path just as the shoal arrives there. Le Verrier has demonstrated that such an event took place in the year A.D. 126, but that it has not happened since. We thus seem to have a clue to a very wonderful history by which the meteors are shown to have come into our system in the year named. The expectations or a repetition of the great shower in 1899 which had been widely entertained, and on good grounds, were not realised. Hardly more than a few meteors of the ordinary type were observed.
Assuming that the orbit of the August meteors was a parabola, Schiaparelli computed the dimensions and position in space of this orbit, and when he had worked this out, he noticed that the orbit corresponded in every particular with the orbit of a fine comet which had appeared in the summer of 1862. This could not be a mere matter of accident. The plane in which the comet moved coincided exactly with that in which the meteors moved; so did the directions of the axes of their orbits, while the direction of the motion is the same, and the shortest distance from the sun to the orbit is also in the two cases identical. This proved to demonstration that there must be some profound physical connection between comets and swarms of meteors. And a further proof of this was shortly afterwards furnished, when Le Verrier had computed the orbit of the November meteors, for this was at once noticed to be precisely the same as the orbit of a comet which had passed its perihelion in January, 1866, and for which the period of revolution had been found to be thirty-three years and two months.
Among the Leonids we see occasionally fireballs brighter than Venus, and even half the apparent size of the moon, bursting out with lightning-like flashes, and leaving streaks which last from a minute to an hour or more. But the great[Pg 389] majority are only as bright as stars of the second, third, or fourth magnitude. As the amount of light given by a meteor depends on its mass and velocity, we can form some idea as to the actual weight of one of these meteors, and it appears that most of them do not weigh nearly as much as a quarter of an ounce; indeed, it is probable that many do not weigh a single grain. But we have seen that a comet in all probability is nothing but a very loose swarm of small particles surrounded by gas of very slight density, and we have also seen that the material of a comet must by degrees be more or less dissipated through space. We have still to tell a wonderful story of the breaking up of a comet and what appears to have become of the particles thereof.
A copious meteoric shower took place on the night of the 27th November, 1872. On this occasion the shooting stars diverged from a radiant point in the constellation of Andromeda. As a spectacle, it was unquestionably inferior to the magnificent display of 1866, but it is difficult to say which of the two showers has been of greater scientific importance.
It surely is a remarkable coincidence that the earth should encounter the Andromedes (for so this shower is called) at the very moment when it is crossing the track of Biela's comet. We have observed the direction from which the Andromedes come when they plunge into the atmosphere; we can ascertain also the direction in which Biela's comet is moving when it passes the earth's track, and we find that the direction in which the comet moves and the direction in which the meteors move are identical. This is, in itself, a strong and almost overwhelming presumption that the comet and the shooting stars are connected; but it is not all. We have observations of this swarm dating back to the eighteenth century, and we find that the date of its appearance has changed from the 6th or 7th of December to the end of November in perfect accordance with the retrograde motion of the crossing-point of the earth's orbit and the orbit of Biela's comet. This comet was[Pg 390] observed in 1772, and again in 1805–6, before its periodic return every seven years was discovered. It was discovered by Biela in 1826, and was observed again in 1832. In 1846 the astronomical world was startled to find that there were now two comets in place of one, and the two fragments were again perceived at the return in 1852. In 1859 Biela's comet could not be seen, owing to its unfavourable situation with regard to the earth. No trace of Biela's comet was seen in 1865–66, when its return was also due, nor has it ever been seen since. It therefore appears that in the autumn of 1872 the time had arrived for the return of Biela's comet, and thus the occurrence of the great shower of the Andromedes took place about the time when Biela's comet was actually due. The inference is irresistible that the shooting stars, if not actually a part of the comet itself, are at all events most intimately connected therewith. This shower is also memorable for the telegram sent from Professor Klinkerfues to Mr. Pogson at Madras. The telegram ran as follows:—"Biela touched earth on 27th. Search near Theta Centauri." Pogson did search and did find a comet, but, unfortunately, owing to bad weather he only secured observations of it on two nights. As we require three observations to determine the orbit of a planet or comet, it is not possible to compute the orbit of Pogson's, but it seems almost certain that the latter cannot be identical with either of the two components of Biela's comet. It is, however, likely that it really was a comet moving along the same track as Biela and the meteors.
Another display of the Biela meteors took place in 1885, just giving time for two complete revolutions of the swarm since 1872. The display on the 27th November, 1885, was magnificent; Professor Newton estimated that at the time of maximum the meteors came on at the rate of 75,000 per hour. In 1892 the comet ought again to have returned to perihelion, but in that year no meteors were seen on the 27th November, while many were seen on the 23rd from the same radiant. The change in the point of intersection between the orbit of the meteors and the orbit[Pg 391] of the earth indicated by this difference of four days was found by Bredichin to be due to the perturbing action of Jupiter on the motion of the swarm.
It is a noticeable circumstance that the great meteoric showers seem never yet to have projected a missile which has reached the earth's surface. Out of the myriads of Leonids, of Perseids, or of Andromedes, not one particle has ever been seized and identified.[35] Those bodies which fall from the sky to the earth, and which we call meteorites, do not seem to come from the great showers, so far as we know. They may, indeed, have quite a different origin from that of the periodic meteors.
It is somewhat curious that the belief in the celestial origin of meteorites is of modern growth. In ancient times there were, no doubt, rumours of wonderful stones which had fallen down from the heavens to the earth, but these reports seem to have obtained but little credit. They were a century ago regarded as perfectly fabulous, though there was abundant testimony on the subject. Eye-witnesses averred that they had seen the stones fall. The bodies themselves were unlike other objects in the neighbourhood, and cases were even authenticated where men had been killed by these celestial visitors.
No doubt the observations were generally made by ignorant and illiterate persons. The true parts of the record were so mixed up with imaginary additions, that cautious men refused to credit the statements that such objects really fell from the sky. Even at the present day it is often extremely difficult to obtain accurate testimony on such matters. For instance, the fall of a meteorite was observed by a Hindoo in the jungle. The stone was there, its meteoric character was undoubted, and the witness was duly examined as to the details of the occurrence; but he was so frightened by the noise and by the danger he believed[Pg 392] himself to have narrowly escaped, that he could tell little or nothing. He felt certain, however, that the meteorite had hunted him for two hours through the jungle before it fell to the earth!
In the year 1794 Chladni published an account of the remarkable mass of iron which the traveller Pallas had discovered in Siberia. It was then for the first time recognised that this object and others similar to it must have had a celestial origin. But even Chladni's reputation and the arguments he brought forward failed to procure universal assent. Shortly afterwards a stone of fifty-six pounds was exhibited in London, which several witnesses declared they had seen fall at Wold Cottage, in Yorkshire, in 1795. This body was subsequently deposited in our national collection, and is now to be seen in the Natural History Museum at South Kensington. The evidence then began to pour in from other quarters; portions of stone from Italy and from Benares were found to be of identical composition with the Yorkshire stone. The incredulity of those who had doubted the celestial origin of these objects began to give way. A careful memoir on the Benares meteorite, by Howard, was published in the "Philosophical Transactions" for 1802, while, as if to complete the demonstration, a great shower of stones took place in the following year at L'Aigle, in Normandy. The French Academy deputed the physicist Biot to visit the locality and make a detailed examination of the circumstances attending this memorable shower. His enquiry removed every trace of doubt, and the meteoric stones have accordingly been transferred from the dominions of geology to those of astronomy. It may be noted that the recognition of the celestial origin of meteorites happens to be simultaneous with the discovery of the first of the minor planets. In each case our knowledge of the solar system has been extended by the addition of numerous minute bodies, which, notwithstanding their insignificant dimensions, are pregnant with information.
When the possibility of stone-falls has been admitted, we can turn to the ancient records, and assign to them the[Pg 393] credit they merit, which was withheld for so many centuries. Perhaps the earliest of all these stone-falls which can be said to have much pretension to historical accuracy is that of the shower which Livy describes as having fallen, about the year 654 B.C., on the Alban Mount, near Rome. Among the more modern instances, we may mention one which was authenticated in a very emphatic manner. It occurred in the year 1492 at Ensisheim, in Alsace. The Emperor Maximilian ordered a minute narrative of the circumstances to be drawn up and deposited with the stone in the church. The stone was suspended in the church for three centuries, until in the French Revolution it was carried off to Colmar, and pieces were broken from it, one of which is now in our national collection. Fortunately, this interesting object has been restored to its ancient position in the church at Ensisheim, where it remains an attraction to sight-seers at this day. The account is as follows:—"In the year of the Lord 1492, on the Wednesday before St. Martin's Day, November 7th, a singular miracle occurred, for between eleven o'clock and noon there was a loud clap of thunder and a prolonged confused noise, which was heard at a great distance, and a stone fell from the air in the jurisdiction of Ensisheim which weighed 260 pounds, and the confused noise was at other places much louder than here. Then a boy saw it strike on ploughed ground in the upper field towards the Rhine and the Ill, near the district of Gisgang, which was sown with wheat, and it did no harm, except that it made a hole there; and then they conveyed it from the spot, and many pieces were broken from it, which the Land Vogt forbade. They therefore caused it to be placed in the church, with the intention of suspending it as a miracle, and there came here many people to see this stone, so there were many remarkable conversations about this stone; the learned said they knew not what it was, for it was beyond the ordinary course of nature that such a large stone should smite from the height of the air, but that it was really a miracle from God, for before that time never was anything heard like it, nor seen, nor written. When they found that stone, it had entered[Pg 394] into the earth to half the depth of a man's stature, which everybody explained to be the will of God that it should be found, and the noise of it was heard at Lucerne, at Villingen, and at many other places, so loud that the people thought that the houses had been overturned; and as the King Maximilian was here, the Monday after St. Catherine's Day of the same year, his Royal Excellency ordered the stone which had fallen to be brought to the castle, and after having conversed a long time about it with the noblemen, he said that the people of Ensisheim should take it and order it to be hung up in the church, and not to allow anybody to take anything from it. His Excellency, however, took two pieces of it, of which he kept one, and sent the other to Duke Sigismund of Austria, and there was a great deal of talk about the stone, which was suspended in the choir, where it still is, and a great many people came to see it."
Admitting the celestial origin of the meteorites, they surely claim our closest attention. They afford the only direct method we possess of obtaining a knowledge of the materials of bodies exterior to our planet. We can take a meteorite in our hands, we can analyse it, and find the elements of which it is composed. We shall not attempt to enter into any very detailed account of the structure of meteorites; it is rather a matter for the consideration of chemists and mineralogists than for astronomers. A few of the more obvious features will be all that we require. They will serve as a preliminary to the discussion of the probable origin of these bodies.
In the Natural History Museum at South Kensington we may examine a superb collection of meteorites. They have been brought together from all parts of the earth, and vary in size from bodies not much larger than a pin's head up to vast masses weighing many hundredweights. There are also models of celebrated meteorites, of which the originals are dispersed through various other museums.
Many meteorites have nothing very remarkable in their external appearance. If they were met with on the sea beach, they would be passed by without more notice than would be given to any other stone. Yet, what a history a meteorite[Pg 395] might tell us if we could only manage to obtain it! It fell; it was seen to fall from the sky; but what was its course anterior to that movement? Where was it 100 years ago, 1,000 years ago? Through what regions of space has it wandered? Why did it never fall before? Why has it actually now fallen? Such are some of the questions which crowd upon us as we ponder over these most interesting bodies. Some of these objects are composed of very characteristic materials; take, for example, one of the more recent arrivals, known as the Rowton siderite. This body differs very much from the more ordinary kind of stony meteorite. It is an object which even a casual passer-by would hardly pass without notice. Its great weight would also attract attention, while if it be scratched or rubbed with a file, it would appear to be a mass of nearly pure iron. We know the circumstances in which that piece of iron fell to the earth. It was on the 20th of April, 1876, about 3.40 p.m., that a strange rumbling noise, followed by a startling explosion, was heard over an area of several miles in extent among the villages in Shropshire, eight or ten miles north of the Wrekin. About an hour after this occurrence a farmer noticed that the ground in one of his grass-fields had been disturbed, and he probed the hole which the meteorite had made, and found it, still warm, about eighteen inches below the surface. Some men working at no great distance had heard the noise made in its descent. This remarkable object, weighs 7-3⁄4 lbs. It is an irregular angular mass of iron, though all its edges seem to have been rounded by fusion in its transit through the air. It is covered with a thick black pellicle of the magnetic oxide of iron, except at the point where it first struck the ground. The Duke of Cleveland, on whose property it fell, afterwards presented it to our national institution already referred to, where, as the Rowton siderite, it attracts the attention of everyone who is interested in these wonderful bodies.
This siderite is specially interesting on account of its distinctly metallic character. Falls of objects of this particular type are not so frequent as are those of the stony meteorites; in fact, there are only a few known instances of meteoric[Pg 396] irons having been actually seen to fall, while the observed falls of stony meteorites are to be counted in scores or in hundreds. The inference is that the iron meteorites are much less frequent than the stony ones. This is, however, not the impression that the visitor to the Museum would be likely to receive. In that extensive collection the meteoric irons are by far the most striking objects. The explanation is not difficult. Those gigantic masses of iron are unquestionably meteoric: no one doubts that this is the case. Yet the vast majority of them have never been seen to fall; they have simply been found, in circumstances which point unmistakably to their meteoric nature. Suppose, for instance, that a traveller on one of the plains of Siberia or of Central America finds a mass of metallic iron lying on the surface of the ground, what explanation can be rendered of such an occurrence? No one has brought the iron there, and there is no iron within hundreds of miles. Man never fashioned that object, and the iron is found to be alloyed with nickel in a manner that is always observed in known meteorites, and is generally regarded as a sure indication of a meteoric origin. Observe also, that as iron perishes by corrosion in our atmosphere, that great mass of iron cannot have lain where it is for indefinite ages; it must have been placed there at some finite time. Only one source for such an object is conceivable; it must have fallen from the sky. On the same plains the stony meteorites have also fallen in hundreds and in thousands, but they crumble away in the course of time, and in any case would not arrest the attention of the traveller as the irons are likely to do. Hence it follows, that although the stony meteorites seem to fall much more frequently, yet, unless they are actually observed at the moment of descent, they are much more liable to be overlooked than the meteoric irons. Hence it is that the more prominent objects of the British collection are the meteoric irons.
We have said that a noise accompanied the descent of the Rowton siderite, and it is on record that a loud explosion took place when the meteorite fell at Ensisheim. In this we have a characteristic feature of the phenomenon. Nearly[Pg 397] all the descents of meteorites that have been observed seem to have been ushered in by a detonation. We do not, however, assert that this is quite an invariable feature; and it is also the case that meteors often detonate without throwing down any solid fragments that have been collected. The violence associated with the phenomenon is forcibly illustrated by the Butsura meteorite. This object fell in India in 1861. A loud explosion was heard, several fragments of stone were collected from distances three or four miles apart; and when brought together, they were found to fit, so as to enable the primitive form of the meteorite to be reconstructed. A few of the pieces are wanting (they were, no doubt, lost by falling unobserved into localities from which they could not be recovered), but we have obtained pieces quite numerous enough to permit us to form a good idea of the irregular shape of the object before the explosion occurred which shattered it into fragments. This is one of the ordinary stony meteorites, and is thus contrasted with the Rowton siderite which we have just been considering. There are also other types of meteorites. The Breitenbach iron, as it is called, is a good representative of a class of these bodies which lie intermediate between the meteoric irons and the stones. It consists of a coarsely cellular mass of iron, the cavities being filled with mineral substances. In the Museum, sections of intermediate forms are shown in which this structure is exhibited.
Look first at the most obvious characteristic of these meteorites. We do not now allude to their chemical composition, but to their external appearance. What is the most remarkable feature in the shape of these objects?—surely it is that they are fragments. They are evidently pieces that are broken from some larger object. This is apparent by merely looking at their form; it is still more manifest when we examine their mechanical structure. It is often found that meteorites are themselves composed of smaller fragments. Such a structure may be illustrated by a section of an aërolite found on the Sierra of Chaco, weighing about 30 lbs. (Fig. 79).
The section here represented shows the composite structure of this object, which belongs to the class of stony meteorites. Its shape shows that it was really a fragment with angular edges and corners. No doubt it may have been much more considerable when it first dashed into the atmosphere. The angular edges now seen on the exterior may be due to an explosion which then occurred; but this will not account for the structure of the interior. We there see irregular pieces of varied form and material agglomerated into a single mass. If we would seek for analogous objects on the earth, we must look to some of the volcanic rocks, where we have multitudes of irregular angular fragments cemented together by a matrix in which they are imbedded. The evidence presented by this meteorite is conclusive as to one circumstance with regard to the origin of these objects. They must have come as fragments, from some body of considerable, if not of vast, dimensions. In this meteorite there are numerous small grains of iron mingled with mineral substances. The iron in many meteorites has, indeed, characters resembling those produced by the actual blasting of iron by dynamite. Thus, a large meteoric iron from Brazil has been found to have been actually shivered into fragments at some time anterior to its fall on the earth. These fragments have been cemented together again by irregular veins of mineral substances.
For an aërolite of a very different type we may refer to[Pg 399] the carbonaceous meteorite of Orgueil, which fell in France on the 14th May, 1864. On the occasion of its descent a splendid meteor was seen, rivalling the full moon in size. The actual diameter of this globe of fire must have been some hundreds of yards. Nearly a hundred fragments of the body were found scattered over a tract of country fifteen miles long. This object is of particular interest, inasmuch as it belongs to a rare group of aërolites, from which metallic iron is absent. It contains many of the same minerals which are met with in other meteorites, but in these fragments they are associated with carbon, and with substances of a white or yellowish crystallisable material, soluble in ether, and resembling some of the hydrocarbons. Such a substance, if it had not been seen falling to the earth, would probably be deemed a product resulting from animal or vegetable life!
We have pointed out how a body moving with great velocity and impinging upon the air may become red-hot and white-hot, or even be driven off into vapour. How, then, does it happen that meteorites escape this fiery ordeal, and fall down to the earth, with a great velocity, no doubt, but still, with very much less than that which would have sufficed to drive them off into vapour? Had the Rowton siderite, for instance, struck our atmosphere with a velocity of twenty miles a second, it seems unquestionable that it would have been dissipated by heat, though, no doubt, the particles would ultimately coalesce so as to descend slowly to the earth in microscopic beads of iron. How has the meteorite escaped this fate? It must be remembered that our earth is also moving with a velocity of about eighteen miles per second, and that the relative velocity with which the meteorite plunges into the air is that which will determine the degree to which friction is operating. If the meteorite come into direct collision with the earth, the velocity of the collision will be extremely great; but it may happen that though the actual velocities of the two bodies are both enormous, yet the relative velocity may be comparatively small. This is, at all events, one conceivable explanation of the arrival of a meteorite on the surface of the earth.
We have shown in the earlier parts of the chapter that the well-known star showers are intimately connected with comets. In fact, each star shower revolves in the path pursued by a comet, and the shooting star particles have, in all probability, been themselves derived from the comet. Showers of shooting stars have, therefore, an intimate connection with comets, but it is doubtful whether meteorites have any connection with comets. It has already been remarked that meteorites have never been known to fall in the great star showers. No particle of a meteorite is known to have dropped from the countless host of the Leonids or of the Perseids; as far as we know, the Lyrids never dropped a meteorite, nor did the Quadrantids, the Geminids, or the many other showers with which every astronomer is familiar. There is no reason to connect meteorites with these showers, and it is, therefore, doubtful whether we should connect meteorites with comets.
With reference to the origin of meteorites it is difficult to speak with any great degree of confidence. Every theory of meteorites presents difficulties, so it seems that the only course open to us is to choose that view of their origin which seems least improbable. It appears to me that this condition is fulfilled in the theory entertained by the Austrian mineralogist, Tschermak. He has made a study of the meteorites in the rich collection at Vienna, and he has come to the conclusion that the "meteorites have had a volcanic source on some celestial body." Let us attempt to pursue this reasoning and discuss the problem, which may be thus stated:—Assuming that at least some of the meteorites have been ejected from volcanoes, on what body or bodies in the universe must these volcanoes be situated? This is really a question for astronomers and mathematicians. Once the mineralogists assure us that these bodies are volcanic, the question becomes one of calculation and of the balance of probabilities.
The first step in the enquiry is to realise distinctly the dynamical conditions of the problem. Conceive a volcano to be located on a planet. The volcano is supposed to be in a state of eruption, and in one of its mighty throes projects[Pg 401] a missile aloft: this missile will ascend, it will stop, and fall down again. Such is the case at present in the eruptions of terrestrial volcanoes. Cotopaxi has been known to hurl prodigious stones to a vast height, but these stones assuredly return to earth. The gravitation of the earth has gradually overcome the velocity produced by the explosion, and down the body falls. But let us suppose that the eruption is still more violent, and that the stones are projected from the planet to a still greater height above its surface. Suppose, for instance, that the stone should be shot up to a height equal to the planet's radius, the attraction of gravitation will then be reduced to one-fourth of what it was at the surface, and hence the planet will find greater difficulty in pulling back the stone. Not only is the distance through which the stone has to be pulled back increased as the height increases, but the efficiency of gravitation is weakened, so that in a twofold way the difficulty of recalling the stone is increased. We have already more than once alluded to this subject, and we have shown that there is a certain critical velocity appropriate to each planet, and depending on its mass and its radius. If the missile be projected upwards with a velocity equal to or greater than this, then it will ascend never to return. We all recollect Jules Verne's voyage to the moon, in which he described the Columbiad, an imaginary cannon, capable of shooting out a projectile with a velocity of six or seven miles a second. This is the critical velocity for the earth. If we could imagine the air removed, then a cannon of seven-mile power would project a body upwards which would never fall down.
The great difficulty about Tschermak's view of the volcanic origin of the meteorites lies in the tremendous initial velocity which is required. The Columbiad is a myth, and we know no agent, natural or artificial, at the present time on the earth, adequate to the production of a velocity so appalling. The thunders of Krakatoa were heard thousands of miles away, but in its mightiest throes it discharged no missiles with a velocity of six miles a second. We are therefore led to enquire whether any of the other celestial[Pg 402] bodies are entitled to the parentage of the meteorites. We cannot see volcanoes on any other body except the moon; all the other bodies are too remote for an inspection so minute. Does it seem likely that volcanoes on the moon can ever launch forth missiles which fall upon the earth?
This belief was once sustained by eminent authority. The mass of the moon is about one-eightieth of the mass of the earth. It would not be true to assert that the critical velocity of projection varies directly as the mass of the planet. The correct law is, that it varies directly as the square root of the mass, and inversely as the square root of the radius. It is hence shown that the velocity required to project a missile away from the moon is only about one-sixth of that which would be required to project a missile away from the earth. If the moon had on its surface volcanoes of one-mile power, it is quite conceivable that these might be the source of meteorites. We have seen how the whole surface of the moon shows traces of intense volcanic activity. A missile thus projected from the moon could undoubtedly fall on the earth, and it is not impossible that some of the meteorites may really have come from this source. There is, however, one great difficulty about the volcanoes on the moon. Suppose an object were so projected, it would, under the attraction of the earth, in accordance with Kepler's laws, move around the earth as a focus. If we set aside the disturbances produced by all other bodies, as well as the disturbance produced by the moon itself, we see that the meteorite if it once misses the earth can never fall thereon. It would be necessary that the shortest distance of the earth's centre from the orbit of the projectile should be less than the radius of the earth, so that if a lunar meteorite is to fall on the earth, it must do so the first time it goes round. The journey of a meteorite from the moon to the earth is only a matter of days, and therefore, as meteorites are still falling, it would follow that they must still be constantly ejected from the moon. The volcanoes on the moon are, however, not now active; observers have long studied its surface, and they find no reliable traces[Pg 403] of volcanic activity at the present day. It is utterly out of the question, whatever the moon may once have been able to do, that at the present date she could still continue to launch forth meteorites. It is just possible that a meteorite expelled from the moon in remote antiquity, when its volcanoes were active, may, under the influence of the disturbances of the other bodies of the system, have its orbit so altered, that at length it comes within reach of the atmosphere and falls to the earth, but in no circumstances could the moon send us a meteorite at present. It is therefore reasonable to look elsewhere in our search for volcanoes fulfilling the conditions of the problem.
Let us now direct our attention to the planets, and examine the circumstances in which volcanoes located thereon could eject a meteorite which should ultimately tumble on the earth. We cannot see the planets well enough to tell whether they have or ever had any volcanoes; but the almost universal presence of heat in the large celestial masses seems to leave us in little doubt that some form of volcanic action might be found in the planets. We may at once dismiss the giant planets, such as Jupiter or Saturn: their appearance is very unlike a volcanic surface; while their great mass would render it necessary to suppose that the meteorites were expelled with terrific velocity if they should succeed in escaping from the gravitation of the planet. Applying the rule already given, a volcano on Jupiter would have to be five or six times as powerful as the volcano on the earth. To avoid this difficulty, we naturally turn to the smaller planets of the system; take, for instance, one of that innumerable host of minor planets, and let us enquire how far this body is likely to have ejected a missile which should fall upon the earth. Some of these globes are only a few miles in diameter. There are bodies in the solar system so small that a very moderate velocity would be sufficient to project a missile away from them altogether. We have, indeed, already illustrated this point in discussing the minor planets. It has been suggested that a volcano placed on one of the minor planets might be quite[Pg 404] powerful enough to start the meteorites on a long ramble through space until the chapter of accidents brought them into collision with the earth. There is but little difficulty in granting that there might be such volcanoes, and that they might be sufficiently powerful to drive bodies from the surface of the planet; but we must remember that the missiles are to fall on the earth, and dynamical considerations are involved which merit our close attention. To concentrate our ideas, we shall consider one of the minor planets, and for this purpose let us take Ceres. If a meteorite is to fall upon the earth, it must pass through the narrow ring, some 8,000 miles wide, which marks the earth's path; it will not suffice for the missile to pass through the ecliptic on the inside or on the outside of the ring, it must be actually through this narrow strip, and then if the earth happens to be there at the same moment the meteorite will fall. The first condition to be secured is, therefore, that the path of the meteorite shall traverse this narrow ring. This is to be effected by projection from some point in the orbit of Ceres. But it can be shown on purely dynamical grounds that although the volcanic energy sufficient to remove the projectile from Ceres may be of no great account, yet if that projectile is to cross the earth's track, the dynamical requirements of the case demand a volcano on Ceres at the very least of three-mile power. We have thus gained but little by the suggestion of a minor planet, for we have not found that a moderate volcanic power would be adequate. But there is another difficulty in the case of Ceres, inasmuch as the ring on the ecliptic is very narrow in comparison with the other dimensions of the problem. Ceres is a long way off, and it would require very great accuracy in volcanic practice on Ceres to project a missile so that it should just traverse this ring and fall neither inside nor outside, neither above nor below. There must be a great many misses for every hit. We have attempted to make the calculation by the aid of the theory of probabilities, and we find that the chances against this occurrence are about 50,000 to 1, so that out of every 50,000 projectiles hurled from a point in the orbit of Ceres[Pg 405] only a single one can be expected to satisfy even the first of the conditions necessary if it is ever to tumble on our globe. It is thus evident that there are two objections to Ceres (and the same may be said of the other minor planets) as a possible source of the meteorites. Firstly, that notwithstanding the small mass of the planet a very powerful volcano would still be required; and secondly, that we are obliged to assume that for every one which ever reached the earth at least 50,000 must have been ejected. It is thus plain that if the meteorites have really been driven from some planet of the solar system, large or small, the volcano must, from one cause or another, have been a very powerful one. We are thus led to enquire which planet possesses on other grounds the greatest probability in its favour.
We admit of course that at the present time the volcanoes on the earth are utterly devoid of the necessary power; but were the terrestrial volcanoes always so feeble as they are in these later days? Grounds are not wanting for the belief that in the very early days of geological time the volcanic energy on the earth was much greater than at present. We admit fully the difficulties of the view that the meteorites have really come from the earth; but they must have some origin, and it is reasonable to indicate the source which seems to have most probability in its favour. Grant for a moment that in the primæval days of volcanic activity there were some mighty throes which hurled forth missiles with the adequate velocity: these missiles would ascend, they would pass from the gravitation of the earth, they would be seized by the gravitation of the sun, and they would be compelled to revolve around the sun for ever after. No doubt the resistance of the air would be a very great difficulty, but this resistance would be greatly lessened were the crater at a very high elevation above the sea level, while, if a vast volume of ejected gases or vapours accompanied the more solid material, the effect of the resistance of the air would be still further reduced. Some of these objects might perhaps revolve in hyperbolic orbits, and retreat never to return; while others would be driven into elliptic paths.[Pg 406] Round the sun these objects would revolve for ages, but at each revolution—and here is the important point—they would traverse the point from which they were originally launched. In other words, every object so projected from the earth would at each revolution cross the track of the earth. We have in this fact an enormous probability in favour of the earth as contrasted with Ceres. Only one Ceres-ejected meteorite out of every 50,000 would probably cross the earth's track, while every earth-projected meteorite would necessarily do so.
If this view be true, then there must be hosts of meteorites traversing space in elliptic orbits around the sun. These orbits have one feature in common: they all intersect the track of the earth. It will sometimes happen that the earth is found at this point at the moment the meteorite is crossing; when this is the case the long travels of the little body are at an end, and it tumbles back on the earth from which it parted so many ages ago.
It is well to emphasise the contrast between the lunar theory of meteorites (which we think improbable) and the terrestrial theory (which appears to be probable). For the lunar theory it would, as we have seen, be necessary that some of the lunar volcanoes should be still active. In the terrestrial theory it is only necessary to suppose that the volcanoes on the earth once possessed sufficient explosive power. No one supposes that the volcanoes at present on the earth eject now the fragments which are to form future meteorites; but it seems possible that the earth may be now slowly gathering back, in these quiet times, the fragments she ejected in an early stage of her history. Assuming, therefore, with Tschermak, that many meteorites have had a volcanic origin on some considerable celestial body, we are led to agree with those who think that most probably that body is the earth.
It is interesting to notice a few circumstances which seem to corroborate the view that many meteorites are of ancient terrestrial origin. The most characteristic constituent of these bodies is the alloy of iron and nickel, which is almost[Pg 407] universally present. Sometimes, as in the Rowton siderite, the whole object consists of little else; sometimes this alloy is in grains distributed through the mass. When Nordenskjöld discovered in Greenland a mass of native iron containing nickel, this was at once regarded as a celestial visitor. It was called the Ovifak meteorite, and large pieces of the iron were conveyed to our museums. There is, for instance, in the national collection a most interesting exhibit of the Ovifak substance. Close examination shows that this so-called meteorite lies in a bed of basalt which has been vomited from the interior of the earth. Those who believe in the meteoric origin of the Ovifak iron are constrained to admit that shortly after the eruption of the basalt, and while it was still soft, this stupendous iron meteorite of gigantic mass and bulk happened to fall into this particular soft bed. The view is, however, steadily gaining ground that this great iron mass was no celestial visitor at all, but that it simply came forth from the interior of the earth with the basalt itself. The beautiful specimens in the British Museum show how the iron graduates into the basalt in such a way as to make it highly probable that the source of the iron is really to be sought in the earth and not external thereto. Should further research establish this, as now seems probable, a most important step will have been taken in proving the terrestrial origin of meteorites. If the Ovifak iron be really associated with the basalt, we have a proof that the iron-nickel alloy is indeed a terrestrial substance, found deep in the interior of the earth, and associated with volcanic phenomena. This being so, it will be no longer difficult to account for the iron in undoubted meteorites. When the vast volcanoes were in activity they ejected masses of this iron-alloy, which, having circulated round the sun for ages, have at last come back again. As if to confirm this view, Professor Andrews discovered particles of native iron in the basalt of the Giant's Causeway, while the probability that large masses of iron are there associated with the basaltic formation was proved by the researches on magnetism of the late Provost Lloyd.
Besides the more solid meteorites there can be no doubt that the débris of the ordinary shooting stars must rain down upon the earth in gentle showers of celestial dust. The snow in the Arctic regions has often been found stained with traces of dust which contains particles of iron. Similar particles have been found on the towers of cathedrals and in many other situations where it could only have been deposited from the air. There can be hardly a doubt that some of the motes in the sunbeam, and many of the particles which good housekeepers abhor as dust, have indeed a cosmical origin. In the famous cruise of the Challenger the dredges brought up from the depths of the Atlantic no "wedges of gold, great anchors, heaps of pearl," but among the mud which they raised are to be found numerous magnetic particles which there is every reason to believe fell from the sky, and thence subsided to the depths of the ocean. Sand from the deserts of Africa, when examined under the microscope, yield traces of minute iron particles which bear the marks of having experienced a high temperature.
The earth draws in this cosmic dust continuously, but the earth now never parts with a particle of its mass. The consequence is inevitable; the mass of the earth must be growing, and though the change may be a small one, yet to those who have studied Darwin's treatise on "Earth-worms," or to those who are acquainted with the modern theory of evolution, it will be manifest that stupendous results can be achieved by slight causes which tend in one direction. It is quite probable that an appreciable part of the solid substance of our globe may have been derived from meteoric matter which descends in perennial showers upon its surface.
The Constellations—The Great Bear and the Pointers—The Pole Star—Cassiopeia—Andromeda, Pegasus, and Perseus—The Pleiades: Auriga, Capella, Aldebaran—Taurus, Orion, Sirius; Castor and Pollux—The Lion—Boötes, Corona, and Hercules—Virgo and Spica—Vega and Lyra—The Swan.
The student of astronomy should make himself acquainted with the principal constellations in the heavens. This is a pleasing acquirement, and might well form a part of the education of every child in the kingdom. We shall commence our discussion of the sidereal system with a brief account of the principal constellations visible in the northern hemisphere, and we accompany our description with such outline maps of the stars as will enable the beginner to identify the chief features of the starry heavens.
In an earlier chapter we directed the attention of the student to the remarkable constellation of stars which is known to astronomers as Ursa Major, or the Great Bear. It forms the most conspicuous group in the northern skies, and in northern latitudes it never sets. At eleven p.m. in the month of April the Great Bear is directly overhead (for an observer in the United Kingdom); at the same hour in September it is low down in the north; at the same hour July it is in the west; by Christmas it is at the east. From the remotest antiquity this group of stars has attracted attention. The stars in the Great Bear were comprised in a great catalogue of stars, made two thousand years ago, which has been handed down to us. From the positions of the stars given in this catalogue it is possible to reconstruct the Great Bear as it appeared in those early days. This has been done,[Pg 410] and it appears that the seven principal stars have not changed in this lapse of time to any large extent, so that the configuration of the Great Bear remains practically the same now as it was then. The beginner must first obtain an acquaintance with this group of seven stars, and then his further progress in this branch of astronomy will be greatly facilitated. The Great Bear is, indeed, a splendid constellation, and its only rival is to be found in Orion, which contains more brilliant stars, though it does not occupy so large a region in the heavens.
In the first place, we observe how the Great Bear enables the Pole Star, which is the most important object in the northern heavens, to be readily found. The Pole Star is very conveniently indicated by the direction of the two stars, β and α, of the Great Bear, which are, accordingly, generally known as the "pointers." This use of the Great Bear is shown on the diagram in Fig. 80, in which the line β α, produced onwards and slightly curved, will conduct to the Pole Star. There is no likelihood of making any mistake in this star, as it is the only bright one in the neighbourhood. Once it has been seen it will be readily identified on future occasions, and the observer will not fail to notice how constant is the position which it preserves in the heavens. The other stars either rise or set, or, like the Great Bear, they dip down low in the north without actually setting, but the Pole Star exhibits no considerable changes. In summer or winter, by night or by day, the Pole Star is ever found in the same place—at least, so far as ordinary observation is concerned. No doubt, when we use the accurate instruments of the observatory the notion of the fixity of the Pole Star[Pg 412] is abandoned; we then see that it has a slow motion, and that it describes a small circle every twenty-four hours around the true pole of the heavens, which is not coincident with the Pole Star, though closely adjacent thereto. The distance is at present a little more than a degree, and it is gradually lessening, until, in the year A.D. 2095, the distance will be under half a degree.
The Pole Star itself belongs to another inconsiderable group of stars known as the Little Bear. The two principal members of this group, next in brightness to the Pole Star, are sometimes called the "Guards." The Great Bear and the Little Bear, with the Pole Star, form a group in the northern sky not paralleled by any similarly situated constellation in the southern heavens. At the South Pole there is no conspicuous star to indicate its position approximately—a circumstance disadvantageous to astronomers and navigators in the southern hemisphere.
It will now be easy to add a third constellation to the two already acquired. On the opposite side of the Pole Star to the Great Bear, and at about the same distance, lies a very pleasing group of five bright stars, forming a W. These are the more conspicuous members of the constellation Cassiopeia, which contains altogether about sixty stars visible to the naked eye. When the Great Bear is low down in the north, then Cassiopeia is high overhead. When the Great Bear is high overhead, then Cassiopeia is to be looked for low down in the north. The configuration of the leading stars is so striking that once the eye has recognised them future identification will be very easy—the more so when it is borne in mind that the Pole Star lies midway between Cassiopeia and the Great Bear (Fig. 81). These important constellations will serve as guides to the rest. We shall accordingly show how the learner may distinguish the various other groups visible from the British Islands or similar northern latitudes.
The next constellation to be recognised is the imposing group which contains the Great Square of Pegasus. This is not, like Ursa Major, or like Cassiopeia, said to be "circumpolar."[Pg 413] The Great Square of Pegasus sets and rises daily. It cannot be seen conveniently during the spring and the summer, but in autumn and in winter the four stars which mark the corners of the square can be easily recognised. There are certain small stars within the region so limited; perhaps about thirty can be counted by an unaided eye of ordinary power in these latitudes. In the south of Europe, with its pure and bright skies, the number of visible stars appears to be greatly increased. An acute observer at Athens has counted 102 in the same region.
The Great Square of Pegasus can be reached by a line from the Pole Star over the end of Cassiopeia. If it be produced about as far again it will conduct the eye to the centre of the Great Square of Pegasus (Fig. 82).
The line through β and α in Pegasus continued 45° to the south points out the important star Fomalhaut in the mouth of the Southern Fish. To the right of this line, nearly half-way down, is the rather vague constellation of Aquarius, where a small equilateral triangle with a star in the centre may be noticed.
The square of Pegasus is not a felicitous illustration of[Pg 414] the way in which the boundaries of the constellations should be defined. There can be no more naturally associated group than the four stars of this square, and they ought surely to be included in the same constellation. Three of the stars—marked α, β, γ—do belong to Pegasus; but that at the fourth corner—also marked α—is placed in a different figure, known as Andromeda, whereof it is, indeed, the brightest member. The remaining bright stars of Andromeda are marked β and γ, and they are readily identified by producing one side of the Square of Pegasus in a curved direction. We have thus a remarkable array of seven stars, which it is both easy to identify and easy to remember, notwithstanding that they are contributed to by three different constellations. They are respectively α, β, and γ of Pegasus; α, β, and γ of Andromeda; and α of Perseus. The three form a sort of handle, as it were, extending from one side of the square, and are a group both striking in appearance, and useful in the further identification of celestial objects. β Andromedæ, with two smaller stars, form the girdle of the unfortunate heroine.
α Persei lies between two other stars (γ and δ) of the same constellation. If we draw a curve through these three and prolong it in a bold sweep, we are conducted to one of the gems of the northern heavens—the beautiful star Capella, in Auriga (Fig. 83). Close to Capella are three small stars forming an isosceles triangle—these are the Hœdi or Kids. Capella and Vega are, with the exception of Arcturus, the two most brilliant stars in the northern heavens; and though Vega is probably the more lustrous of the two, yet the opposite opinion has been entertained. Different eyes will frequently form various estimates of the relative brilliancy of stars which approach each other in brightness. The difficulty of making a satisfactory comparison between Vega and Capella is greatly increased by the wide distance in the heavens at which they are separated, as well as by a slight difference in colour, for Vega is distinctly whiter than Capella. This contrast between the colour of stars is often a source of uncertainty in the attempt to compare[Pg 415] their relative brilliancy; so that when actual measurements have to be effected by instrumental means, it is necessary to compare the two stars alternately with some object of intermediate hue.
On the opposite side of the pole to Capella, but not quite so far away, will be found four small stars in a quadrilateral. They form the head of the Dragon, the rest of whose form coils right round the pole.
If we continue the curve formed by the three stars γ, α, and δ in Perseus, and if we bend round this curve gracefully into one of an opposite flexion, in the manner shown in Fig. 83, we are first conducted to two other principal stars in Perseus, marked ε and ζ. The region of Perseus is one of the richest in the heavens. We have here a most splendid portion of[Pg 416] the Milky Way, and the field of the telescope is crowded with stars beyond number. Even a small telescope or an opera-glass directed to this teeming constellation cannot fail to delight the observer, and convey to him a profound impression of the extent of the sidereal heavens. We shall give in a subsequent paragraph a brief enumeration of some of the remarkable telescopic objects in Perseus. Pursuing in the same figure the line ε and ζ, we are conducted to the remarkable little group known as the Pleiades.
The Pleiades form a group so universally known and so easily identified that it hardly seems necessary to give any further specific instructions for their discovery. It may, however, be observed that in these latitudes they cannot be seen before midnight during the summer. Let us suppose that the search is made at about 11 p.m. at night: on the 1st of January the Pleiades will be found high up in the sky in the south-west; on the 1st of March, at the same hour, they will be seen to be setting in the west. On the 1st of May they are not visible; on the 1st of July they are not visible; on the 1st of September they will be seen low down in the east. On the 1st of November they will be high in the heavens in the south-east. On the ensuing 1st of January the Pleiades will be in the same position as they were on the same date in the previous year, and so on from year to year. It need, perhaps, hardly be explained here that these changes are not really due to movements of the constellations; they are due, of course, to the apparent annual motion of the sun among the stars.
The Pleiades are shown in the figure (Fig. 84), where a group of ten stars is represented, this being about the number visible with the unaided eye to those who are gifted with very acute vision. The lowest telescopic power will increase the number of stars[Pg 418] to thirty or forty (Galileo saw more than forty with his first telescope), while with telescopes of greater power the number is largely increased; indeed, no fewer than 625 have been counted with the aid of a powerful telescope. The group is, however, rather too widely scattered to make an effective telescopic object, except with a large field and low power. Viewed through an opera-glass it forms a very pleasing spectacle.
If we draw a ray from the Pole Star to Capella, and produce it sufficiently far, as shown in Fig. 85, we come to the great constellation of our winter sky, the splendid group of Orion. The brilliancy of the stars in Orion, the conspicuous belt, and the telescopic objects which it contains, alike render this group remarkable, and place it perhaps at the head of the constellations. The leading star in Orion is known either as α Orionis, or as Betelgeuze, by which name it is here designated. It lies above the three stars, δ, ε, ζ, which form the belt. Betelgeuze is a star of the first magnitude, and so also is Rigel, on the opposite side of the belt. Orion thus enjoys the distinction of containing two stars of the first magnitude in its group, while the five other stars shown in Fig. 85 are of the second magnitude.
The neighbourhood of Orion contains some important stars. If we carry on the line of the belt upwards to the right, we are conducted to another star of the first magnitude, Aldebaran, which strongly resembles Betelgeuze in its ruddy[Pg 419] colour. Aldebaran is the brightest star in the constellation of Taurus. It is this constellation which contains the Pleiades already referred to, and another more scattered group known as the Hyades, which can be discovered near Aldebaran.
The line of the belt of Orion continued downwards to the left conducts the eye to the gem of the sky, the splendid Sirius, which is the most brilliant star in the heavens. It has, indeed, been necessary to create a special order of magnitude for the reception of Sirius alone; all the other first magnitude stars, such as Vega and Capella, Betelgeuze and Aldebaran, coming a long way behind. Sirius, with a few other stars of much less lustre, form the constellation of Canis Major.
It is useful for the learner to note the large configuration, of an irregular lozenge shape, of which the four corners are the first magnitude stars, Aldebaran, Betelgeuze, Sirius, and[Pg 420] Rigel (Fig. 85). The belt of Orion is placed symmetrically in the centre of the group, and the whole figure is so striking that once perceived it is not likely to be forgotten.
About half way from the Square of Pegasus to Aldebaran is the chief star in the Ram—a bright orb of the second magnitude; with two others it forms a curve, at the other end of which will be found γ of the same constellation, which was the first double star ever noticed.
We can again invoke the aid of the Great Bear to point out the stars in the constellation of Gemini (Fig. 86). If the diagonal joining the stars δ and β of the body of the Bear be produced in the direction opposite to the tail, it will lead to Castor and Pollux, two remarkable stars of the second magnitude. This same line carried a little further on passes near the star Procyon, of the first magnitude, which is the only conspicuous object in the constellation of the Little Dog.
The pointers in the Great Bear marked α β will also serve to indicate the constellation of the Lion. If we produce the line joining them in the direction opposite from that used in finding the Pole, we are brought into the body of the Lion. This group will be recognised by the star of the first magnitude called Regulus. It is one of a series of stars forming an object somewhat resembling a sickle: three of the group are of the second magnitude. The Sickle has a special claim on our notice because it contains the radiant point from which the periodic shooting star shower known as the Leonids diverges. Regulus lies alongside the sun's highway through the stars, at a point which he passes on the 21st of August every year.
Between Gemini and Leo the inconspicuous constellation of the Crab may be found; the most striking object it contains is the misty patch called Præsepe or the Bee-Hive, which the smallest opera-glass will resolve into its component stars.
The tail of the Great Bear, when prolonged with a continuation of the curve which it possesses, leads to a brilliant star of the first magnitude known as Arcturus, the principal star in the constellation of Boötes (Fig. 88). A few other stars, marked β, γ, δ, and ε in the same constellation, are also shown in the figure. Among the stars visible in these latitudes Arcturus is to be placed next to Sirius in point of brightness. Two stars in the southern hemisphere, invisible in these latitudes, termed α Centauri and Canopus, are nearly as bright as Vega and Capella, but not quite as bright as Arcturus.
In the immediate neighbourhood of Boötes is a striking[Pg 423] semicircular group known as the Crown or Corona Borealis. It will be readily found from its position as indicated in the figure, or it may be identified by following the curved line indicated by β, δ, ε, and ζ in the Great Bear.
The constellation of Virgo is principally characterised by the first magnitude star called Spica, or α Virginis. This may be found from the Great Bear; for if the line joining the two stars α and γ in that constellation be prolonged with a slight curve, it will conduct the eye to Spica. We may here notice another of those large configurations which are of great assistance in the study of the stars. There is a fine equilateral triangle, whereof Arcturus and Spica form two of the corners, while the third is indicated by Denebola, the bright star near the tail of the Lion (Fig. 89).
In the summer evenings when the Crown is overhead, a line from the Pole Star through its fainter edge, continued nearly to the southern horizon, encounters the brilliant red star Cor Scorpionis, or the Scorpion's Heart (Antares), which was the first star mentioned as having been seen with the telescope in the daytime.
The first magnitude star, Vega, in the constellation of the[Pg 424] Lyre, can be readily found at the corner of a bold triangle, of which the Pole Star and Arcturus form the base (Fig. 90). The brilliant whiteness of Vega will arrest the attention, while the small group of neighbouring stars which form the Lyre produces one of the best defined constellations.
Near Vega is another important constellation, known as the Swan or Cygnus. The brightest star will be identified as the vertex of a right-angled triangle, of which the line from Vega to the Pole Star is the base, as shown in Fig. 91. There are in Cygnus five principal stars, which form a constellation of rather remarkable form.
The last constellation which we shall here describe is that of Aquila or the Eagle, which contains a star of the first magnitude, known as Altair; this group can be readily found by a line from Vega over β Cygni, which passes near the line of three stars, forming the characteristic part of the Eagle.
We have taken the opportunity to indicate in these sketches of the constellations the positions of some other remarkable telescopic objects, the description of which we must postpone to the following chapters.
Sirius Contrasted with the Sun—Stars can be Weighed, but not in general Measured—The Companion of Sirius—Determination of the Weights of Sirius and his Companion—Dark Stars—Variable and Temporary Stars—Enormous Number of Stars.
The splendid pre-eminence of Sirius has caused it to be observed with minute care from the earliest times in the history of astronomy. Each generation of astronomers devoted time and labour to determine the exact places of the brightest stars in the heavens. A vast mass of observations as to the place of Sirius among the stars had thus been accumulated, and it was found that, like many other stars, Sirius had what astronomers call proper motion. Comparing the place of Sirius with regard to the other stars now with the place which it occupied one hundred years ago, there is a difference of two minutes (127´´) in its situation. This is a small quantity: it is so small that the unaided eye could not see it. Could we now see the sky as it appeared one century ago, we should still see this star in its well-known place to the left of Orion. Careful alignment by the eye would hardly detect that Sirius was moving in two, or even in three or in four centuries. But the accuracy of the meridian circle renders these minute quantities evident, and gives to them their true significance. To the eye of the astronomer, Sirius, instead of creeping along with a movement which centuries will not show, is pursuing its majestic course with a velocity appropriate to its dimensions.
Though the velocity of Sirius is about 1,000 miles a minute,[Pg 426] yet it is sometimes a little more and sometimes a little less than its mean value. To the astronomer this fact is pregnant with information. Were Sirius an isolated star, attended only by planets of comparative insignificance, there could be no irregularity in its motion. If it were once started with a velocity of 1,000 miles a minute, then it must preserve that velocity. Neither the lapse of centuries nor the mighty length of the journey could alter it. The path of Sirius would be inflexible in its direction; and it would be traversed with unalterable velocity.
The fact that Sirius had not been moving uniformly was of such interest that it arrested the attention of Bessel when he discovered the irregularities in 1844. Believing, as Bessel did, that there must be some adequate cause for these [Pg 427]disturbances, it was hardly possible to doubt what the cause must be. When motion is disturbed there must be force in action, and the only force that we recognise in such cases is that known as gravitation. But gravity can only act from one body to another body; so that when we seek for the derangement of Sirius by gravitation, we are obliged to suppose that there must be some mighty and massive body near Sirius. The question was taken up again by Peters and by Auwers, who were able to discover, from the irregularities of Sirius, the nature of the path of the disturbing body. They were able to show that it must revolve around Sirius in a period of about fifty years, and although they could not tell its distance from Sirius, yet they were able to point out the direction in which it must lie. Fig. 92 shows the orbit of Sirius as given by Mr. Burnham, of Yerkes Observatory.
The detection of the attendant of Sirius, and the measures which have been made thereon, enable us to determine the weight of this famous star. Let us attempt to illustrate this subject. It must, no doubt, be admitted that the numerical estimates we employ have to be received with a certain degree of caution. The companion of Sirius is a difficult object to observe, and previous to 1896 it had only been followed through an arc of 90°. We are, therefore, hardly as yet in a position to speak with absolute accuracy as to the periodic time in which the companion completes its revolution. We may, however, take this time to be fifty-two years. We also know the distance from Sirius to his companion, and we may take it to be about twenty-one times the distance from the earth to the sun. It is useful, in the first place, to compare the revolution of the companion around Sirius with the revolution of the planet Uranus around the sun. Taking the earth's distance as unity, the radius of the orbit of Uranus is about nineteen, and Uranus takes eighty-four years to accomplish a complete revolution. We have no planet in the solar system at a distance of twenty-one; but from Kepler's third law it may be shown that, if there were such a planet, its periodic time would be about ninety-nine years. We have now the necessary materials for making the comparison between the[Pg 428] mass of Sirius and the mass of the sun. A body revolving around Sirius at a certain distance completes its journey in fifty-two years. To revolve around the sun at the same distance a body should complete its journey in ninety-nine years. The quicker the body is moving the greater must be the centrifugal force, and the greater must be the attractive power of the central body. It can be shown from the principles of dynamics that the attractive power is inversely proportional to the square of the periodic time. Hence, then, the attractive power of Sirius must bear to the attractive power of the sun the proportion which the square of ninety-nine has to the square of fifty-two. As the distances are in each case supposed to be equal, the attractive powers will be proportional to the masses, and hence we conclude that the mass of Sirius, together with that of his companion, is to the mass of the sun, together with that of his planet, in the ratio of three and a half to one. We had already learned that Sirius was much brighter than the sun; now we have learned that it is also much more massive.
Before we leave the consideration of Sirius, there is one additional point of very great interest which it is necessary to consider. There is a remarkable contrast between the brilliancy of Sirius and his companion. Sirius is a star far transcending all other stars of the first magnitude, while his companion is extremely faint. Even if it were completely withdrawn from the dazzling proximity of Sirius, the companion would be only a small star of the eighth or ninth magnitude, far below the limits of visibility to the unaided eye. To put the matter in numerical language, Sirius is 5,000 times as bright as its companion, but only about twice as heavy! Here is a very great contrast; and this point will appear even more forcible if we contrast the companion of Sirius with our sun. The companion is slightly heavier than our sun; but in spite of its slightly inferior bulk, our sun is much more powerful as a light-giver. One hundred of the companions of Sirius would not give as much light as our sun! This is a result of very considerable significance. It teaches us that besides the great bodies in the universe which attract attention by their brilliancy, there are also other bodies[Pg 429] of stupendous mass which have but little brilliancy—probably some of them possess none at all. This suggests a greatly enhanced conception of the majestic scale of the universe. It also invites us to the belief that the universe which we behold bears but a small ratio to the far larger part which is invisible in the sombre shades of night. In the wide extent of the material universe we have here or there a star or a mass of gaseous matter sufficiently heated to be luminous, and thus to become visible from the earth; but our observation of these luminous points can tell us little of the remaining contents of the universe.
The most celebrated of all the variable stars is that known as Algol, whose position in the constellation of Perseus is shown in Fig. 83. This star is conveniently placed for observation, being visible every night in our latitude, and its interesting changes can be observed without any telescopic aid. Everyone who desires to become acquainted with the great truths of astronomy should be able to recognise this star, and should have also followed it during one of its periods of change. Algol is usually a star of the second magnitude; but in a period between two and three days, or, more accurately, in an interval of 2 days 20 hours 48 minutes and 55 seconds, its brilliancy goes through a most remarkable cycle of variations. The series commences with a gradual decline of the star's brightness, which in the course of four and a half hours falls from the second magnitude down to the fourth. At this lowest stage of brightness Algol remains for about twenty minutes, and then begins to increase, until in three and a half hours it regains the second magnitude, at which it continues for about 2 days 12 hours, when the same series commences anew. It seems that the period required by Algol to go through its changes is itself subject to a slow but certain variation. We shall see in a following chapter how it has been proved that the variability of Algol is due to the occasional interposition of a dark companion which cuts off a part of the lustre of the star. All the circumstances can thus be accounted for, and even the weight and the size of Algol and its dark companion be determined.
There are, however, other classes of variable stars, the fluctuation of whose light can hardly be due to occasional obscuration by dark bodies. This is particularly the case with those variables which are generally faint, but now and then flare up for a short time, after which temporary exaltation they again sink down to their original condition. The periods of such changes are usually from six months to two years. The best known example of a star of this class was discovered more than three hundred years ago. It is situated in the constellation Cetus, a little south of the equator. This object was the earliest known case of a variable star, except the so-called temporary stars, to which we shall presently refer. The variable in Cetus received the name of Mira, or the wonderful. The period of the fluctuations of Mira Ceti is about eleven months, during the greater part of which time the star is of the ninth magnitude, and consequently invisible to the naked eye. When the proper time has arrived, its brightness begins to increase rather suddenly. It soon becomes a conspicuous object of the second or third magnitude. In this condition it remains for eight or ten days, and then declines more slowly than it rose until it is reduced to its original faintness, about three hundred days after the rise commenced.
More striking to the general observer than the ordinary variable stars are the temporary stars which on rare occasions suddenly make their appearance in the heavens. The most famous object of this kind was that which blazed out in the beginning of November, 1572, and which when first seen was as bright as Venus at its maximum brightness. It could, indeed, be seen in full daylight by sharp-sighted people. As far as history can tell us, no other temporary star has ever been as bright as this one. It is specially associated with the name of Tycho Brahe, for although he was not the discoverer, he made the best observations of the object, and he proved that it was at a distance comparable with that of the ordinary fixed stars. Tycho described carefully the gradual decline of the wonderful star until it disappeared from his view about the end of March, 1574, for the telescope, by which it could doubtless have been followed further, had not yet[Pg 431] been invented. During the decline the colour of the object gradually changed; at first it was white, and by degrees became yellow, and in the spring of 1573 reddish, like Aldebaran. About May, 1573, we are told somewhat enigmatically that it "became like lead, or somewhat like Saturn," and so it remained as long as it was visible. What a fund of information our modern spectroscopes and other instruments would supply us with if so magnificent a star were to burst out in these modern days!
But though we have not in our own times been favoured with a view of a temporary star as splendid as the one seen by Tycho Brahe and his contemporaries, it has been our privilege to witness several minor outbursts of this kind. It seems likely that we should possess more records of temporary stars from former times if a better watch had been kept for them. That is at any rate the impression we get when we see how several of the modern stars of this kind have nearly escaped us altogether, notwithstanding the great number of telescopes which are now pointed to the sky on every clear night.
In 1866 a star of the second magnitude suddenly appeared in the constellation of the crown (Corona Borealis). It was first seen on the 12th May, and a few days afterwards it began to fade away. Argelander's maps of the northern heavens had been published some years previously, and when the position of the new star had been accurately determined, it was found that it was identical with an insignificant looking star marked on one of the maps as of the 9-1⁄2 magnitude. The star exists in the same spot to this day, and it is of the same magnitude as it was prior to its spasmodic outburst in 1866. This was the first new star which was spectroscopically examined. We shall give in Chapter XXIII. a short account of the features of its spectrum.
The next of these temporary bright stars, Nova Cygni, was first seen by Julius Schmidt at Athens on the 24th November, 1876, when it was between the third and fourth magnitudes, and he maintains that it cannot have been[Pg 432] conspicuous four days earlier, when he was looking at the same constellation. By some inadvertence the news of the discovery was not properly circulated, and the star was not observed elsewhere for about ten days, when it had already become considerably fainter. The decrease of brightness went on very slowly; in October, 1877, the star was only of the tenth magnitude, and it continued getting fainter until it reached the fifteenth magnitude; in other words, it became a minute telescopic star, and it is so still in the very same spot. As this star did not reach the first or second magnitude it would probably have escaped notice altogether if Schmidt had not happened to look at the Swan on that particular evening.
We are not so likely to miss seeing a new star since astronomers have pressed the photographic camera into their service. This became evident in 1892, when the last conspicuous temporary star appeared in Auriga. On the 24th January, Dr. Anderson, an astronomer in Edinburgh, noticed a yellowish star of the fifth magnitude in the constellation Auriga, and a week later, when he had compared a star-map with the heavens and made sure that the object was really a new star, he made his discovery public. In the case of this star we are able to fix fairly closely the moment when it first blazed out. In the course of the regular photographic survey of the heavens undertaken at the Harvard College Observatory (Cambridge, Massachusetts) the region of the sky where the new star appeared had been photographed on thirteen nights from October 21st to December 1st, 1891, and on twelve nights from December 10th to January 20th, 1892. On the first series of plates there was no trace of the Nova, while it was visible on the very first plate of the second series as a star of the fifth magnitude. Fortunately it turned out that Professor Max Wolf of Heidelberg, a most successful celestial photographer, had photographed the same region on the 8th December, and this photograph does not show the star, so that it cannot on that night have been as bright as the ninth magnitude. Nova Auriga must therefore have flared up suddenly between the 8th and the[Pg 433] 10th of December. According to the Harvard photographs, the first maximum of brightness occurred about the 20th of December, when the magnitude was 4-1⁄2. The decrease of the brightness was very irregular; the star fluctuated for the five weeks following the first of February between the fourth and the sixth magnitude, but after the beginning of March, 1892, the brightness declined very rapidly, and at the end of April the star was seen as an exceedingly faint one (sixteenth magnitude) with the great Lick Refractor. When this mighty instrument was again pointed to the Nova in the following August, it had risen nearly to the tenth magnitude, after which it gradually became extremely faint again, and is so still.
The temporary and the variable stars form but a very small section of the vast number of stars with which the vault of the heavens is studded. That the sun is no more than a star, and the stars are no less than suns, is a cardinal doctrine of astronomy. The imposing magnificence of this truth is only realised when we attempt to estimate the countless myriads of stars. This is a problem on which our calculations are necessarily vain. Let us, therefore, invoke the aid of the poet to attempt to express the innumerable, and conclude this chapter with the following lines of Mr. Allingham:—
"But number every grain of sand,
Wherever salt wave touches land;
Number in single drops the sea;
Number the leaves on every tree,
Number earth's living creatures, all
That run, that fly, that swim, that crawl;
Of sands, drops, leaves, and lives, the count
Add up into one vast amount,
And then for every separate one
Of all those, let a flaming SUN
Whirl in the boundless skies, with each
Its massy planets, to outreach
All sight, all thought: for all we see
Encircled with infinity,
Is but an island."
Interesting Stellar Objects—Stars Optically Double—The Great Discovery of the Binary Stars made by Herschel—The Binary Stars describe Elliptic Paths—Why is this so important?—The Law of Gravitation—Special Double Stars—Castor—Mizar—The Coloured Double Stars—β Cygni.
The sidereal heavens contain few more interesting objects for the telescope than can be found in the numerous class of double stars. They are to be counted in thousands; indeed, many thousands can be found in the catalogues devoted to this special branch of astronomy. Many of these objects are, no doubt, small and comparatively uninteresting, but some of them are among the most conspicuous stars in the heavens, such as Sirius, whose system we have already described. We shall in this brief account select for special discussion and illustration a few of the more remarkable double stars. We shall particularly notice some of those that can be readily observed with a small telescope, and we have indicated on the sketches of the constellations in a previous chapter how the positions of these objects in the heavens can be ascertained.
It had been shown by Cassini in 1678 that certain stars, which appeared to the unaided eye as single points of light, really consisted of two or more stars, so close together that the telescope was required for their separation.[36] The number of these objects was gradually increased by fresh discoveries, until in 1781 (the same year in which Herschel discovered Uranus) a list containing eighty double stars was published[Pg 435] by the astronomer Bode. These interesting objects claimed the attention of Herschel during his memorable researches. The list of known doubles rapidly swelled. Herschel's discoveries are to be enumerated by hundreds, while he also commenced systematic measurements of the distance by which the stars were separated, and the direction in which the line joining them pointed. It was these measurements which ultimately led to one of the most important and instructive of all Herschel's discoveries. When, in the course of years, his observations were repeated, Herschel found that in some cases the relative position of the stars had changed. He was thus led to the discovery that in many of the double stars the components are so related that they revolve around each other. Mark the importance of this result. We must remember that the stars are suns, comparable, it may be, with our sun in magnitude; so that here we have the astonishing spectacle of pairs of suns in mutual revolution. There is nothing very surprising in the fact that movements should be observed, for in all probability every body in the universe is in motion. It is the particular character of the movement which is specially interesting and instructive.
It had been imagined that the proximity of the two stars forming a double must be only accidental. It was thought that amid the vast host of stars in the heavens it not unfrequently happened that one star was so nearly behind another (as seen from the earth) that when the two were viewed in the telescope they produced the effect of a double star. No doubt many of the so-called double stars are produced in this way. Herschel's discovery shows that this explanation will not always answer, but that in many cases we really have two stars close together, and in motion round their common centre of gravity.
When the measurements of the distances and the positions of double stars had been accumulated during many years, they were taken over by the mathematicians to be treated by their methods. There is one peculiarity about double star observations: they have not—they cannot have—the[Pg 436] accuracy which the computer of an orbit demands. If the distance between the pair of stars forming a binary be four seconds, the orbit we have to scrutinise is only as large as the apparent size of a penny-piece at the distance of one mile. It would require very careful measurement to make out the form of a penny a mile off, even with good telescopes. If the penny were tilted a little, it would appear, not circular, but oval; and it would be possible, by measuring this oval, to determine how much the penny was tilted. All this requires skilful work: the errors, viewed intrinsically, may not be great, but viewed with reference to the whole size of the quantities under consideration, they are very appreciable. We therefore find the errors of observation far more prominent in observations of this class than is generally the case when the mathematician assumes the task of discussing the labours of the observer.
The interpretation of Herschel's discovery was not accomplished by himself; the light of mathematics was turned on his observations of the binary stars by Savary, and afterwards by other mathematicians. Under their searching enquiries the errors of the measurements were disclosed, and the observations were purified from the grosser part of their inaccuracy. Mathematicians could then apply to their corrected materials the methods of enquiry with which they were familiar; they could deduce with fair precision the actual shape of the orbit of the binary stars, and the position of the plane in which that orbit is contained. The result is not a little remarkable. It has been proved that the motion of each of the stars is performed in an ellipse which contains the centre of gravity of the two stars in its focus. This has been actually shown to be true in many binary stars; it is believed to be true in all. But why is this so important? Is not motion in an ellipse common enough? Does not the earth revolve in an ellipse round the sun? And do not the planets also revolve in ellipses?
It is this very fact that elliptic motion is so common in the planets of the solar system which renders its discovery in binary stars of such importance. From what does the elliptic[Pg 437] motion in the solar system arise? Is it not due to the law of attraction, discovered by Newton, which states that every mass attracts every other mass with a force which varies inversely as the square of the distance? That law of attraction had been found to pervade the whole solar system, and it explained the movements of the bodies of our system with marvellous fidelity. But the solar system, consisting of the sun, and the planets, with their satellites, the comets, and a host of smaller bodies, formed merely a little island group in the universe. In the economy of this tiny cosmical island the law of gravitation reigns supreme; before Herschel's discovery we never could have known whether that law was not merely a piece of local legislation, specially contrived for the exigencies of our particular system. This discovery gave us the knowledge which we could have gained from no other source. From the binary stars came a whisper across the vast abyss of space. That whisper told us that the law of gravitation was not peculiar to the solar system. It told us the law extended to the distant shores of the abyss in which our island is situated. It gives us grounds for believing that the law of gravitation is obeyed throughout the length, breadth, and depth of the entire visible universe.
One of the finest binary stars is that known as Castor, the brighter of the two principal stars in the constellation of Gemini. The position of Castor on the heavens is indicated in Fig. 86, page 418. Viewed by the unaided eye, Castor resembles a single star; but with a moderately good telescope it is found that what seems to be one star is really two separate stars, one of which is of the third magnitude, while the other is somewhat less. The angular distance of these two stars in the heavens is not so great as the angle subtended by a line an inch long viewed at a distance of half a mile. Castor is one of the double stars in which the components have been observed to possess a motion of revolution. The movement is, however, extremely slow, and the lapse of centuries will be required before a revolution is completely effected.
A beautiful double star can be readily identified in the[Pg 438] constellation of Ursa Major (see Fig. 80, page 410). It is known as Mizar, and is the middle star (ζ) of the three which form the tail. In the close neighbourhood of Mizar is the small star Alcor, which can be readily seen with the unaided eye; but when we speak of Mizar as a double star, it is not to be understood that Alcor is one of the components of the double. Under the magnifying power of the telescope Alcor is seen to be transferred a long way from Mizar, while Mizar itself is split up into two suns close together. These components are of the second and the fourth magnitudes respectively, and as the apparent distance is nearly three times as great as in Castor, they are observed with facility even in a small telescope. This is, indeed, the best double star in the heavens for the beginner to commence his observations upon. We cannot, however, assert that Mizar is a binary, inasmuch as observations have not yet established the existence of a motion of revolution. Still less are we able to say whether Alcor is also a member of the same group, or whether it may not merely be a star which happens to fall nearly in the line of vision. Recent spectroscopic observations have shown that the larger component of Mizar is itself a double, consisting of a pair of suns so close together that there is not the slightest possibility of their ever being seen separately by the most powerful telescope in the world.
A pleasing class of double stars is that in which we have the remarkable phenomenon of colours, differing in a striking degree from the colours of ordinary stars. Among the latter we find, in the great majority of cases, no very characteristic hue; some are, however, more or less tinged with red, some are decidedly ruddy, and some are intensely red. Stars of a bluish or greenish colour are much more rare,[37] and when a star of this character does occur, it is almost invariably as one of a pair which form a double. The other star of the double is sometimes of the same hue, but more usually it is yellow or ruddy.
One of the loveliest of these objects, which lies within reach of telescopes of very moderate pretensions, is that found in the constellation of the Swan, and known as β Cygni (Fig. 91). This exquisite object is composed of two stars. The larger, about the third magnitude, is of a golden-yellow, or topaz, colour; the smaller, of the sixth magnitude, is of a light blue. These colours are nearly complementary, but still there can be no doubt that the effect is not merely one of contrast. That these two stars are both tinged with the hues we have stated can be shown by hiding each in succession behind a bar placed in the field of view. It has also been confirmed in a very striking manner by spectroscopic investigation; for we see that the blue star has experienced a special absorption of the red rays, while the more ruddy light of the other star has arisen from the absorption of the blue rays. The contrast of the colours in this object can often be very effectively seen by putting the eye-piece out of focus. The discs thus produced show the contrast of colours better than when the telescope exhibits merely two stellar points.
Such are a few of these double and multiple stars. Their numbers are being annually augmented; indeed, one observer—Mr. Burnham, formerly on the staff of the Lick Observatory, and now an observer in the Yerkes Observatory—has added by his own researches more than 1,000 new doubles to the list of those previously known.
The interest in this class of objects must necessarily be increased when we reflect that, small as the stars appear to be in our telescopes, they are in reality suns of great size and splendour, in many cases rivalling our own sun, or, perhaps, even surpassing him. Whether these suns have planets attending upon them we cannot tell; the light reflected from the planet would be utterly inadequate to the penetration of the vast extent of space which separates us from the stars. If there be planets surrounding these objects, then, instead of a single sun, such planets will be illuminated by two, or, perhaps, even more suns. What wondrous effects of light and shade must be the result! Sometimes both suns will be[Pg 440] above the horizon together, sometimes only one sun, and sometimes both will be absent. Especially remarkable would be the condition of a planet whose suns were of the coloured type. To-day we have a red sun illuminating the heavens, to-morrow it would be a blue sun, and, perhaps, the day after both the red sun and the blue sun will be in the firmament together. What endless variety of scenery such a thought suggests! There are, however, grave dynamical reasons for doubting whether the conditions under which such a planet would exist could be made compatible with life in any degree resembling the life with which we are familiar. The problem of the movement of a planet under the influence of two suns is one of the most difficult that has ever been proposed to mathematicians, and it is, indeed, impossible in the present state of analysis to solve with accuracy all the questions which it implies. It seems not at all unlikely that the disturbances of the planet's orbit would be so great that it would be exposed to vicissitudes of light and of temperature far transcending those experienced by a planet moving, like the earth, under the supreme control of a single sun.
Sounding-line for Space—The Labours of Bessel—Meaning of Annual Parallax—Minuteness of the Parallactic Ellipse Illustrated—The Case of 61 Cygni—Different Comparison Stars used—The Proper Motion of the Star—Struve's Investigations—Can they be Reconciled?—Researches at Dunsink—Conclusion obtained—Accuracy which such Observations admit Examined—The Proper Motion of 61 Cygni—The Permanence of the Sidereal Heavens—The New Star in Cygnus—Its History—No Appreciable Parallax—A Mighty Outburst of Light—The Movement of the Solar System through Space—Herschel's Discovery—Journey towards Lyra—Probabilities.
We have long known the dimensions of the solar system with more or less accuracy. Our knowledge includes the distances of the planets and the comets from the sun, as well as their movements. We have also considerable knowledge of the diameters and the masses of many of the different bodies which belong to the solar system. We have long known, in fact, many details of the isolated group nestled together under the protection of the sun. The problem for consideration in the present chapter involves a still grander survey than is required for measures of our solar system. We propose to carry the sounding-line across the vast abyss which separates the group of bodies closely associated about our sun from the other stars which are scattered through the realms of space. For centuries the great problem of star distance has engaged the attention of those who have studied the heavens. It would be impossible to attempt here even an outline of the various researches which have been made on the subject. In the limited survey which we can make, we must glance first at the remarkable speculative efforts which have been directed to the problem, and then we shall refer to those labours which[Pg 442] have introduced the problem into the region of accurate astronomy.
No attempt to solve the problem of the absolute distances of the stars was successful until many years after Herschel's labours were closed. Fresh generations of astronomers, armed with fresh appliances, have for many years pursued the subject with unremitting diligence, but for a long time the effort seemed hopeless. The distances of the stars were so great that they could not be ascertained until the utmost refinements of mechanical skill and the most elaborate methods of mathematical calculation were brought to converge on the difficulty. At last it was found that the problem was beginning to yield. A few stars have been induced to disclose the secret of their distance. We are able to give some answer to the question—How far are the stars? though it must be confessed that our reply up to the present moment is both hesitating and imperfect. Even the little knowledge which has been gained possesses interest and importance. As often happens in similar cases, the discovery of the distance of a star was made independently about the same time by two or three astronomers. The name of Bessel stands out conspicuously in this memorable chapter of astronomy. Bessel proved (1840) that the distance of the star known as 61 Cygni was a measurable quantity. His demonstration possessed such unanswerable logic that universal assent could not be withheld. Almost simultaneously with the classical labours of Bessel we have Struve's measurement of the distance of Vega, and Henderson's determination of the distance of the southern star α Centauri. Great interest was excited in the astronomical world by these discoveries, and the Royal Astronomical Society awarded its gold medal to Bessel. It appropriately devolved on Sir John Herschel to deliver the address on the occasion of the presentation of the medal: that address is a most eloquent tribute to the labours of the three astronomers. We cannot resist quoting the few lines in which Sir John said:—[Pg 443]
"Gentlemen of the Royal Astronomical Society,—I congratulate you and myself that we have lived to see the great and hitherto impassable barrier to our excursion into the sidereal universe, that barrier against which we have chafed so long and so vainly—æstuantes angusto limite mundi—almost simultaneously overleaped at three different points. It is the greatest and most glorious triumph which practical astronomy has ever witnessed. Perhaps I ought not to speak so strongly; perhaps I should hold some reserve in favour of the bare possibility that it may be all an illusion, and that future researches, as they have repeatedly before, so may now fail to substantiate this noble result. But I confess myself unequal to such prudence under such excitement. Let us rather accept the joyful omens of the time, and trust that, as the barrier has begun to yield, it will speedily be effectually prostrated."
Before proceeding further, it will be convenient to explain briefly how the distance of a star can be measured. The problem is one of a wholly different character from that of the sun's distance, which we have already discussed in these pages. The observations for the determination of stellar parallax are founded on the familiar truth that the earth revolves around the sun. We may for our present purpose assume that the earth revolves in a circular path. The centre of that path is at the centre of the sun, and the radius of the path is 92,900,000 miles. Owing to our position on the earth, we observe the stars from a point of view which is constantly changing. In summer the earth is 185,800,000 miles distant from the position which it occupied in winter. It follows that the apparent positions of the stars, as projected on the background of the sky, must present corresponding changes. We do not now mean that the actual positions of the stars are really displaced. The changes are only apparent, and while oblivious of our own motion, which produces the displacements, we attribute the changes to the stars.
On the diagram in Fig. 93 is an ellipse with certain months—viz., January, April, July, October—marked upon its circumference. This ellipse may be regarded as a miniature picture of the earth's orbit around the sun. In January the earth[Pg 444] is at the spot so marked; in April it has moved a quarter of the whole journey; and so on round the whole circle, returning to its original position in the course of one year. When we look from the position of the earth in January, we see the star A projected against the point of the sky marked 1. Three months later the observer with his telescope is carried round to April; but he now sees the star projected to the position marked 2. Thus, as the observer moves around the whole orbit in the annual revolution of the earth, so the star appears to move round in an ellipse on the background of the sky. In the technical language of astronomers, we speak of this as the parallactic ellipse, and it is by measuring the major axis of this ellipse that we determine the distance of the star from the sun. Half of this major axis, or, what comes to the same thing, the angle which the radius of the earth's orbit subtends as seen from the star, is called the star's "annual parallax."
The figure shows another star, B, more distant from the earth and the solar system generally than the star previously considered. This star also describes an elliptic path. We cannot, however, fail to notice that the parallactic ellipse belonging to B is much smaller than that of A. The[Pg 445] difference in the sizes of the ellipses arises from the different distances of the stars from the earth. The nearer the star is to the earth the greater is the ellipse, so that the nearest star in the heavens will describe the largest ellipse, while the most distant star will describe the smallest ellipse. We thus see that the distance of the star is inversely proportional to the size of the ellipse, and if we measure the angular value of the major axis of the ellipse, then, by an exceedingly simple mathematical manipulation, the distance of the star can be expressed as a multiple of a radius of the earth's orbit. Assuming that radius to be 92,900,000 miles, the distance of the star is obtained by simple arithmetic. The difficulty in the process arises from the fact that these ellipses are so small that our micrometers often fail to detect them.
How shall we adequately describe the extreme minuteness of the parallactic ellipses in the case of even the nearest stars? In the technical language of astronomers, we may state that the longest diameter of the ellipse never subtends an angle of more than one and a half seconds. In a somewhat more popular manner, we would say that one thousand times the major axis of the very largest parallactic ellipse would not be as great as the diameter of the full moon. For a still more simple illustration, let us endeavour to think of a penny-piece placed at a distance of two miles. If looked at edgeways it will be linear, if tilted a little it would be elliptic; but the ellipse would, even at that distance, be greater than the greatest parallactic ellipse of any star in the sky. Suppose a sphere described around an observer, with a radius of two miles. If a penny-piece were placed on this sphere, in front of each of the stars, every parallactic ellipse would be totally concealed.
The star in the Swan known as 61 Cygni is not remarkable either for its size or for its brightness. It is barely visible to the unaided eye, and there are some thousands of stars which are apparently larger and brighter. It is, however, a very interesting example of that remarkable class of objects known as double stars. It consists of two nearly equal stars close[Pg 446] together, and evidently connected by a bond of mutual attraction. The attention of astronomers is also specially directed towards the star by its large proper motion. In virtue of that proper motion, the two components are carried together over the sky at the rate of five seconds annually. A proper motion of this magnitude is extremely rare, yet we do not say it is unparalleled, for there are some few stars which have a proper motion even more rapid; but the remarkable duplex character of 61 Cygni, combined with the large proper motion, render it an unique object, at all events, in the northern hemisphere.
When Bessel proposed to undertake the great research with which his name will be for ever connected, he determined to devote one, or two, or three years to the continuous observations of one star, with the view of measuring carefully its parallactic ellipse. How was he to select the object on which so much labour was to be expended? It was all-important to choose a star which should prove sufficiently near to reward his efforts by exhibiting a measurable parallax. Yet he could have but little more than surmise and analogy as a guide. It occurred to him that the exceptional features of 61 Cygni afforded the necessary presumption, and he determined to apply the process of observation to this star. He devoted the greater part of three years to the work, and succeeded in discovering its distance from the earth.
Since the date of Sir John Herschel's address, 61 Cygni has received the devoted and scarcely remitted attention of astronomers. In fact, we might say that each succeeding generation undertakes a new discussion of the distance of this star, with the view of confirming or of criticising the original discovery of Bessel. The diagram here given (Fig. 94) is intended to illustrate the recent history of 61 Cygni.
When Bessel engaged in his labours, the pair of stars forming the double were at the point indicated on the diagram by the date 1838. The next epoch occurred fifteen years later, when Otto Struve undertook his researches, and the[Pg 447] pair of stars had by that time moved to the position marked 1853. Finally, when the same object was more recently observed at Dunsink Observatory, the pair had made still another advance, to the position indicated by the date 1878. Thus, in forty years this double star had moved over an arc of the heavens upwards of three minutes in length. The actual path is, indeed, more complicated than a simple rectilinear movement. The two stars which form the double have a certain relative velocity, in consequence of their mutual attraction. It will not, however, be necessary to take this into account, as the displacement thus arising in the lapse of a single year is far too minute to produce any inconvenient effect on the parallactic ellipse.
The case of 61 Cygni is, however, exceptional. It is one of our nearest neighbours in the heavens. We can never find its distance accurately to one or two billions of miles; but still we have a consciousness that an uncertainty amounting to twenty billions is too large a percentage of the whole.[Pg 448] We shall presently show that we believe Struve was right, yet it does not necessarily follow that Bessel was wrong. The apparent paradox can be easily explained. It would not be easily explained if Struve had used the same comparison star as Bessel had done; but Struve's comparison star was different from either of Bessel's, and this is probably the cause of the discrepancy. It will be recollected that the essence of the process consists of the comparison of the small ellipse made by the distant star with the larger ellipse made by the nearer star. If the two stars were at the same distance, the process would be wholly inapplicable. In such a case, no matter how near the stars were to the earth, no parallax could be detected. For the method to be completely successful, the comparison star should be at least eight times as far as the principal star. Bearing this in mind, it is quite possible to reconcile the measures of Bessel with those of Struve. We need only assume that Bessel's comparison stars are about three times as far as 61 Cygni, while Struve's comparison star is at least eight or ten times as far. We may add that, as the comparison stars used by Bessel are brighter than that of Struve, there really is a presumption that the latter is the most distant of the three.
We have here a characteristic feature of this method of determining parallax. Even if all the observations and the reductions of a parallax series were mathematically correct, we could not with strict propriety describe the final result as the parallax of one star. It is only the difference between the parallax of the star and that of the comparison star. We can therefore only assert that the parallax sought cannot be less than the quantity determined. Viewed in this manner, the discrepancy between Struve and Bessel vanishes. Bessel asserted that the distance of 61 Cygni could not be more than sixty billions of miles. Struve did not contradict this—nay, he certainly confirmed it—when he showed that the distance could not be more than forty billions.
Nearly half a century has elapsed since Struve made his[Pg 449] observations. Those observations have certainly been challenged; but they are, on the whole, confirmed by other investigations. In a critical review of the subject Auwers showed that Struve's determination is worthy of considerable confidence. Yet, notwithstanding this authoritative announcement, the study of 61 Cygni has been repeatedly resumed. Dr. Brünnow, when Astronomer Royal of Ireland, commenced a series of observations on the parallax of 61 Cygni, which were continued and completed by the present writer, his successor. Brünnow chose a fourth comparison star (marked on the diagram), different from any of those which had been used by the earlier observers. The method of observing which Brünnow employed was quite different from that of Struve, though the filar micrometer was used in both cases. Brünnow sought to determine the parallactic ellipse by measuring the difference in declination between 61 Cygni and the comparison star.[38] In the course of a year it is found that the difference in declination undergoes a periodic change, and from that change the parallactic ellipse can be computed. In the first series of observations I measured the difference of declination between the preceding star of 61 Cygni and the comparison star; in the second series I took the other component of 61 Cygni and the same comparison star. We had thus two completely independent determinations of the parallax resulting from two years' work. The first of these makes the distance forty billions of miles, and the second makes it almost exactly the same. There can be no doubt that this work supports Struve's determination in correction of Bessel's, and therefore we may perhaps sum up the present state of our knowledge of this question by saying that the distance of 61 Cygni is much nearer to the forty billions of miles which Struve found than to the sixty billions which Bessel found.[39]
It is desirable to give the reader the means of forming[Pg 450] his own opinion as to the quality of the evidence which is available in such researches. The diagram in Fig. 95 here shown has been constructed with this object. It is intended to illustrate the second series of observations of difference of declination which I made at Dunsink. Each of the dots represents one night's observations. The height of the dot is the observed difference of declination between 61 (B) Cygni and the comparison star. The distance along the horizontal line—or the abscissa, as a mathematician would call it—represents the date. These observations are grouped more or less regularly in the vicinity of a certain curve. That curve expresses where the observations should have been, had they been absolutely perfect. The distances between the dots and the curve may be regarded as the errors which have been committed in making the observations.
Perhaps it will be thought that in many cases these errors appear to have attained very undesirable dimensions. Let us, therefore, hasten to say that it was precisely for the purpose[Pg 451] of setting forth these errors that this diagram has been shown; we have to exhibit the weakness of the case no less than its strength. The errors of the observations are not, however, intrinsically so great as might at first sight be imagined. To perceive this, it is only necessary to interpret the scale on which this diagram has been drawn by comparison with familiar standards. The distance from the very top of the curve to the horizontal line denotes an angle of only four-tenths of a second. This is about the apparent diameter of a penny-piece at a distance of ten miles! We can now appraise the true magnitude of the errors which have been made. It will be noticed that no one of the dots is distant from the curve by much more than half of the height of the curve. It thus appears that the greatest error in the whole series of observations amounts to but two or three tenths of a second. This is equivalent to our having pointed the telescope to the upper edge of a penny-piece fifteen or twenty miles off, instead of to the lower edge. This is not a great blunder. A rifle team whose errors in pointing were more than a hundred times as great might still easily win every prize at Bisley.
We have entered into the history of 61 Cygni with some detail, because it is the star whose distance has been most studied. We do not say that 61 Cygni is the nearest of all the stars; it would, indeed, be very rash to assert that any particular star was the nearest of all the countless millions in the heavenly host. We certainly know one star which seems nearer than 61 Cygni; it lies in one of the southern constellations, and its name is α Centauri. This star is, indeed, of memorable interest in the history of the subject. Its parallax was first determined at the Cape of Good Hope by Henderson; subsequent researches have confirmed his observations, and the elaborate investigations of Dr. Gill have proved that the parallax of this star is about three-quarters of a second, so that it is only two-thirds of the distance of 61 Cygni.
61 Cygni arrested our attention, in the first instance, by the circumstance that it had the large proper motion of five seconds annually. We have also ascertained that the annual[Pg 452] parallax is about half a second. The combination of these two statements leads to a result of considerable interest. It teaches us that 61 Cygni must each year traverse a distance of not less than ten times the radius of the earth's orbit. Translating this into ordinary figures, we learn that this star must travel nine hundred and twenty million miles per annum. It must move between two and three million miles each day, but this can only be accomplished by maintaining the prodigious velocity of thirty miles per second. There seems to be no escape from this conclusion. The facts which we have described, and which are now sufficiently well established, are inconsistent with the supposition that the velocity of 61 Cygni is less than thirty miles per second; the velocity may be greater, but less it cannot be.
For the last hundred and fifty years we know that 61 Cygni has been moving in the same direction and with the same velocity. Prior to the existence of the telescope we have no observation to guide us; we cannot, therefore, be absolutely certain as to the earlier history of this star, yet it is only reasonable to suppose that 61 Cygni has been moving from remote antiquity with a velocity comparable with that it has at present. If disturbing influences were entirely absent, there could be no trace of doubt about the matter. Some disturbing influence, however, there must be; the only question is whether that disturbing influence is sufficient to modify seriously the assumption we have made. A powerful disturbing influence might greatly alter the velocity of the star; it might deflect the star from its rectilinear course; it might even force the star to move around a closed orbit. We do not, however, believe that any disturbing influence of this magnitude need be contemplated, and there can be no reasonable doubt that 61 Cygni moves at present in a path very nearly straight, and with a velocity very nearly uniform.
As the distance of 61 Cygni from the sun is forty billions of miles, and its velocity is thirty miles a second, it is easy to find how long the star would take to accomplish a journey equal to its distance from the sun. The time required will be about 40,000 years. In the last 400,000 years[Pg 453] 61 Cygni will have moved over a distance ten times as great as its present distance from the sun, whatever be the direction of motion. This star must therefore have been about ten times as far from the earth 400,000 years ago as it is at present. Though this epoch is incredibly more remote than any historical record, it is perhaps not incomparable with the duration of the human race; while compared with the vast lapse of geological time, such periods seem trivial and insignificant. Geologists have long ago repudiated mere thousands of years; they now claim millions, and many millions of years, for the performance of geological phenomena. If the earth has existed for the millions of years which geologists assert, it becomes reasonable for astronomers to speculate on the phenomena which have transpired in the heavens in the lapse of similar ages. By the aid of our knowledge of star distances, combined with an assumed velocity of thirty miles per second, we can make the attempt to peer back into the remote past, and show how great are the changes which our universe seems to have undergone.
In a million years 61 Cygni will apparently have moved through a distance which is twenty-five times as great as its present distance from the sun. Whatever be the direction in which 61 Cygni is moving—whether it be towards the earth or from the earth, to the right or to the left, it must have been about twenty-five times as far off a million years ago as it is at present; but even at its present distance 61 Cygni is a small star; were it ten times as far it could only be seen with a good telescope; were it twenty-five times as far it would barely be a visible point in our greatest telescopes.
The conclusions arrived at with regard to 61 Cygni may be applied with varying degrees of emphasis to other stars. We are thus led to the conclusion that many of the stars with which the heavens are strewn are apparently in slow motion. But this motion though apparently slow may really be very rapid. When standing on the sea-shore, and looking at a steamer on the distant horizon, we can hardly notice that the steamer is moving. It is true that by looking again in a few minutes we can detect a change in its place; but[Pg 454] the motion of the steamer seems slow. Yet if we were near the steamer we would find that it was rushing along at the rate of many miles an hour. It is the distance which causes the illusion. So it is with the stars: they seem to move slowly because they are very distant, but were we near them, we could see that in the majority of cases their motions are a thousand times as fast as the quickest steamer that ever ploughed the ocean.
It thus appears that the permanence of the sidereal heavens, and the fixity of the constellations in their relative positions, are only ephemeral. When we rise to the contemplation of such vast periods of time as the researches of geology disclose, the durability of the constellations vanishes! In the lapse of those stupendous ages stars and constellations gradually dissolve from view, to be replaced by others of no greater permanence.
It not unfrequently happens that a parallax research proves abortive. The labour has been finished, the observations are reduced and discussed, and yet no value of the parallax can be obtained. The distance of the star is so vast that our base-line, although it is nearly two hundred millions of miles long, is too short to bear any appreciable ratio to the distance of the star. Even from such failures, however, information may often be drawn.
Let me illustrate this by an account derived from my own experience at Dunsink. We have already mentioned that on the 24th November, 1876, a well-known astronomer—Dr. Schmidt, of Athens—noticed a new bright star of the third magnitude in the constellation Cygnus. On the 20th of November Nova Cygni was invisible. Whether it first burst forth on the 21st, 22nd, or 23rd no one can tell; but on the 24th it was discovered. Its brilliancy even then seemed to be waning; so, presumably, it was brightest at some moment between the 20th and 24th of November. The outbreak must thus have been comparatively sudden, and we know of no cause which would account for such a phenomenon more simply than a gigantic collision. The decline in the brilliancy was much more tardy than its growth, and[Pg 455] more than a fortnight passed before the star relapsed into insignificance—two or three days (or less) for the rise, two or three weeks for the fall. Yet even two or three weeks was a short time in which to extinguish so mighty a conflagration. It is comparatively easy to suggest an explanation of the sudden outbreak; it is not equally easy to understand how it can have been subdued in a few weeks. A good-sized iron casting in one of our foundries takes nearly as much time to cool as sufficed to abate the celestial fires in Nova Cygni!
On this ground it seemed not unreasonable to suppose that perhaps Nova Cygni was not really a very extensive conflagration. But, if such were the case, the star must have been comparatively near to the earth, since it presented so brilliant a spectacle and attracted so much attention. It therefore appeared a plausible object for a parallax research; and consequently a series of observations were made some years ago at Dunsink. I was at the time too much engaged with other work to devote very much labour to a research which might, after all, only prove illusory. I simply made a sufficient number of micrometric measurements to test whether a large parallax existed. It has been already pointed out how each star appears to describe a minute parallactic ellipse, in consequence of the annual motion of the earth, and by measurement of this ellipse the parallax—and therefore the distance—of the star can be determined. In ordinary circumstances, when the parallax of a star is being investigated, it is necessary to measure the position of the star in its ellipse on many different occasions, distributed over a period of at least an entire year. The method we adopted was much less laborious. It was sufficiently accurate to test whether or not Nova Cygni had a large parallax, though it might not have been delicate enough to disclose a small parallax. At a certain date, which can be readily computed, the star is at one end of the parallactic ellipse, and six months later the star is at the other end. By choosing suitable times in the year for our observations, we can measure the star in those two positions when it is most deranged by parallax.[Pg 456] It was by observations of this kind that I sought to detect the parallax of Nova Cygni. Its distance from a neighbouring star was carefully measured by the micrometer at the two seasons when, if parallax existed, those distances should show their greatest discrepancy; but no certain difference between these distances could be detected. The observations, therefore, failed to reveal the existence of a parallactic ellipse—or, in other words, the distance of Nova Cygni was too great to be measured by observations of this kind.
It is certain that if Nova Cygni had been one of the nearest stars these observations would not have been abortive. We are therefore entitled to believe that Nova Cygni must be at least 20,000,000,000,000 miles from the solar system; and the suggestion that the brilliant outburst was of small dimensions must, it seems, be abandoned. The intrinsic brightness of Nova Cygni, when at its best, cannot have been greatly if at all inferior to the brilliancy of our sun himself. If the sun were withdrawn from us to the distance of Nova Cygni, it would seemingly have dwindled down to an object not more brilliant than the variable star. How the lustre of such a stupendous object declined so rapidly remains, therefore, a mystery not easy to explain. Have we not said that the outbreak of brilliancy in this star occurred between the 20th and the 24th of November, 1876? It would be more correct to say that the tidings of that outbreak reached our system at the time referred to. The real outbreak must have taken place at least three years previously. Indeed, at the time that the star excited such commotion in the astronomical world here, it had already relapsed again into insignificance.
In connection with the subject of the present chapter we have to consider a great problem which was proposed by Sir William Herschel. He saw that the stars were animated by proper motion; he saw also that the sun is a star, one of the countless host of heaven, and he was therefore led to propound the stupendous question as to whether the sun, like the other stars which are its peers, was also in motion. Consider all that this great question involves. The sun has[Pg 457] around it a retinue of planets and their attendant satellites, the comets, and a host of smaller bodies. The question is, whether all this superb system is revolving around the sun at rest in the middle, or whether the whole system—sun, planets, and all—is not moving on bodily through space.
Herschel was the first to solve this noble problem; he discovered that our sun and the splendid retinue by which it is attended are moving in space. He not only discovered this, but he ascertained the direction in which the system was moving, as well as the approximate velocity with which that movement was probably performed. It has been shown that the sun and his system is now hastening towards a point of the heavens near the constellation Lyra. The velocity with which the motion is performed corresponds to the magnitude of the system; quicker than the swiftest rifle-bullet that was ever fired, the sun, bearing with it the earth and all the other planets, is now sweeping onwards. We on the earth participate in that motion. Every half hour we are something like ten thousand miles nearer to the constellation of Lyra than we should have been if the solar system were not animated by this motion. As we are proceeding at this stupendous rate towards Lyra, it might at first be supposed that we ought soon to get there; but the distances of the stars in that neighbourhood seem not less than those of the stars elsewhere, and we may be certain that the sun and his system must travel at the present rate for far more than a million years before we have crossed the abyss between our present position and the frontiers of Lyra. It must, however, be acknowledged that our estimate of the actual speed with which our solar system is travelling is exceedingly uncertain, but this does not in the least affect the fact that we are moving in the direction first approximately indicated by Herschel (see Chapter XXIII.).
It remains to explain the method of reasoning which Herschel adopted, by which he was able to make this great discovery. It may sound strange to hear that the detection of the motion of the sun was not made by looking at the sun; all the observations of the luminary itself with all the telescopes in the world would never tell us of that motion,[Pg 458] for the simple reason that the earth, whence our observations must be made, participates in it. A passenger in the cabin of a ship usually becomes aware that the ship is moving by the roughness of the sea; but if the sea be perfectly calm, then, though the tables and chairs in the cabin are moving as rapidly as the ship, yet we do not see them moving, because we are also travelling with the ship. If we could not go out of the cabin, nor look through the windows, we would never know whether the ship was moving or at rest; nor could we have any idea as to the direction in which the ship was going, or as to the velocity with which that motion was performed.
The sun, with his attendant host of planets and satellites, may be likened to the ship. The planets may revolve around the sun just as the passengers may move about in the cabin, but as the passengers, by looking at objects on board, can never tell whither the ship is going, so we, by merely looking at the sun, or at the other planets or members of the solar system, can never tell if our system as a whole is in motion.
The conditions of a perfectly uniform movement along a perfectly calm sea are not often fulfilled on the waters with which we are acquainted, but the course of the sun and his system is untroubled by any disturbance, so that the majestic progress is conducted with absolute uniformity. We do not feel the motion; and as all the planets are travelling with us, we can get no information from them as to the common motion by which the whole system is animated.
The passengers are, however, at once apprised of the ship's motion when they go on deck, and when they look at the sea surrounding them. Let us suppose that their voyage is nearly accomplished, that the distant land appears in sight, and, as evening approaches, the harbour is discerned into which the ship is to enter. Let us suppose that the harbour has, as is often the case, a narrow entrance, and that its mouth is indicated by a lighthouse on each side. When the harbour is still a long way off, near the horizon, the two lights are seen close together, and now that the evening has closed in, and the night has become quite dark, these two lights are all[Pg 459] that remain visible. While the ship is still some miles from its destination the two lights seem close together, but as the distance decreases the two lights seem to open out; gradually the ship gets nearer, while the lights are still opening, till finally, when the ship enters the harbour, instead of the two lights being directly in front, as at the commencement, one of the lights is passed by on the right hand, while the other is similarly found on the left. If, then, we are to discover the motion of the solar system, we must, like the passenger, look at objects unconnected with our system, and learn our own motion by their apparent movements. But are there any objects in the heavens unconnected with our system? If all the stars were like the earth, merely the appendages of our sun, then we never could discover whether we were at rest or whether we were in motion: our system might be in a condition of absolute rest, or it might be hurrying on with an inconceivably great velocity, for anything we could tell to the contrary. But the stars do not belong to the system of our sun; they are, rather, suns themselves, and do not recognise the sway of our sun, as this earth is obliged to do. The stars will, therefore, act as the external objects by which we can test whether our system is voyaging through space.
With the stars as our beacons, what ought we to expect if our system be really in motion? Remember that when the ship was approaching the harbour the lights gradually opened out to the right and left. But the astronomer has also lights by which he can observe the navigation of that vast craft, our solar system, and these lights will indicate the path along which he is borne. If our solar system be in motion, we should expect to find that the stars were gradually spreading away from that point in the heavens towards which our motion tends. This is precisely what we do find. The stars in the constellations are gradually spreading away from a central point near the constellation of Lyra, and hence we infer that it is towards Lyra that the motion of the solar system is directed.
There is one great difficulty in the discussion of this question. Have we not had occasion to observe that the stars[Pg 460] themselves are in actual motion? It seems certain that every star, including the sun himself as a star, has each an individual motion of its own. The motions of the stars as we see them are partly apparent as well as partly real; they partly arise from the actual motion of each star and partly from the motion of the sun, in which we partake, and which produces an apparent motion of the star. How are these to be discriminated? Our telescopes and our observations can never effect this decomposition directly. To accomplish the analysis, Herschel resorted to certain geometrical methods. His materials at that time were but scanty, but in his hands they proved adequate, and he boldly announced his discovery of the movement of the solar system.
So astounding an announcement demanded the severest test which the most refined astronomical resources could suggest. There is a certain powerful and subtle method which astronomers use in the effort to interpret nature. Bishop Butler has said that probability is the guide of life. The proper motion of a star has to be decomposed into two parts, one real and the other apparent. When several stars are taken, we may conceive an infinite number of ways into which the movements of each star can be so decomposed. Each one of these conceivable divisions will have a certain element of probability in its favour. It is the business of the mathematician to determine the amount of that probability. The case, then, is as follows:—Among all the various systems one must be true. We cannot lay our finger for certain on the true one, but we can take that which has the highest degree of probability in its favour, and thus follow the precept of Butler to which we have already referred. A mathematician would describe his process by calling it the method of least squares. Since Herschel's discovery, one hundred years ago, many an astronomer using observations of hundreds of stars has attacked the same problem. Mathematicians have exhausted every refinement which the theory of probabilities can afford, but only to confirm the truth of that splendid theory which seems to have been one of the flashes of Herschel's genius.
Interesting Sidereal Objects—Stars not Scattered uniformly—Star Clusters—Their Varieties—The Cluster in Perseus—The Globular Cluster in Hercules—The Milky Way—A Cluster of Minute Stars—The Magellanic Clouds—Nebulæ distinct from Clouds—Number of known Nebulæ—The Constellation of Orion—The Position of the Great Nebula—The Wonderful Star θ Orionis—The Drawing of the Great Nebula in Lord Rosse's Telescope—Photographs of this Wonderful Object—The Great Nebula in Andromeda—The Annular Nebula in Lyra—Resemblance to Vortex Rings—Planetary Nebulæ—Drawings of Several Remarkable Nebulæ—Nature of Nebulæ—Spectra of Nebulæ—Their Distribution; the Milky Way.
We have already mentioned Saturn as one of the most glorious telescopic spectacles in the heavens. Setting aside the obvious claims of the sun and of the moon, there are, perhaps, two other objects visible from these latitudes which rival Saturn in the splendour and the interest of their telescopic picture. One of these objects is the star cluster in Hercules; the other is the great nebula in Orion. We take these objects as typical of the two great classes of bodies to be discussed in this chapter, under the head of Star Clusters and Nebulæ.
The stars, which to the number of several millions bespangle the sky, are not scattered uniformly. We can see that while some regions are comparatively barren, others contain stars in profusion. Sometimes we have a small group, like the Pleiades; sometimes we have a stupendous region of the heavens strewn over with stars, as in the Milky Way. Such objects are called star clusters. We find every variety in the clusters; sometimes the stars are remarkable for their brilliancy, sometimes for their enormous numbers, and sometimes for the remarkable form in which they are grouped. Sometimes a star cluster is adorned with brilliantly-coloured stars; sometimes the luminous[Pg 462] points are so close together that their separate rays cannot he disentangled; sometimes the stars are so minute or so distant that the cluster is barely distinguishable from a nebula.
Of the clusters remarkable at once both for richness and brilliancy of the individual stars, we may mention the cluster in the Sword-handle of Perseus. The position of this object is marked on Fig. 83, page 415. To the unaided eye a hazy spot is visible, which in the telescope expands into two clusters separated by a short distance. In each of them we have innumerable stars, crowded together so as to fill the field of view of the telescope. The splendour of this object may be appreciated when we reflect that each one of these stars is itself a brilliant sun, perhaps rivalling our own sun in lustre. There are, however, regions in the heavens near the Southern Cross, of course invisible from northern latitudes, in which parts of the Milky Way present a richer appearance even than the cluster in Perseus.
The most striking type of star cluster is well exhibited in the constellation of Hercules. In this case we have a group of minute stars apparently in a roughly globular form. Fig. 96 represents this object as seen in Lord Rosse's great telescope, and it shows three radiating streaks, in which the stars seem less numerous than elsewhere. It is estimated that this cluster must contain from 1,000 to 2,000 stars, all concentrated into an extremely small part of the heavens. Viewed in a very small telescope, this object resembles a nebula. The position of the cluster in Hercules is shown in a diagram previously given (Fig. 88, page 420). We have already referred to this glorious aggregation of stars as one of the three especially interesting objects in the heavens.
The Milky Way forms a girdle which, with more or less regularity, sweeps completely around the heavens; and when viewed with the telescope, is seen to consist of myriads of minute stars. In some places the stars are much more numerous than elsewhere. All these stars are incomparably more distant than the sun, which they surround, so it is evident that our sun and, of course, the system which attends him lie actually inside the Milky Way. It seems tempting to pursue the thought here suggested, and to reflect that the whole Milky Way may, after all, be merely a star cluster, comparable in size with some of the other star clusters which we see, and that, viewed from a remote point in space, the Milky Way would seem to be but one of the many clusters of stars containing our sun as an indistinguishable unit.
In the southern hemisphere there are two immense masses which are conspicuously visible to the naked eye, and resemble detached portions of the Milky Way. They cannot be seen by observers in our latitude, and are known as the Magellanic clouds or the two nubeculæ. Their structure, as revealed to an observer using a powerful telescope, is of great complexity. Sir John Herschel, who made a special study of these remarkable objects, gives the following description of them: "The[Pg 464] general ground of both consists of large tracts and patches of nebulosity in every stage of resolution, from light irresolvable, in a reflector of eighteen inches aperture, up to perfectly separated stars like the Milky Way, and clustering groups sufficiently insulated and condensed to come under the designation of irregular and in some cases pretty rich clusters. But besides these there are also nebulæ in abundance and globular clusters in every state of condensation." It can hardly be doubted that the two nubeculæ, which are, roughly speaking, round, or, rather, oval, are not formed accidentally by a vast number of very different objects being ranged at various distances along the same line of sight, but that they really represent two great systems of objects, widely different in constitution, which here are congregated in each other's neighbourhood, whereas they generally do not co-exist close to each other in the Milky Way, with which the mere naked-eye view would otherwise lead us to associate the Magellanic clouds.
When we direct a good telescope to the heavens, we shall occasionally meet with one of the remarkable celestial objects which are known as nebulæ. They are faint cloudy spots, or stains of light on the black background of the sky. They are nearly all invisible to the naked eye. These celestial objects must not for a moment be confounded with clouds, in the ordinary meaning of the word. The latter exist only suspended in the atmosphere, while nebulæ are immersed in the depths of space. Clouds shine by the light of the sun, which they reflect to us; nebulæ shine with no borrowed light; they are self-luminous. Clouds change from hour to hour; nebulæ do not change even from year to year. Clouds are far smaller than the earth; while the smallest nebula known to us is incomparably greater than the sun. Clouds are within a few miles of the earth; the nebulæ are almost inconceivably remote.
Immediately after Herschel and his sister had settled at Slough he commenced his review of the northern heavens in a systematic manner. For observations of this kind it is essential that the sky be free from cloud, while even the light of the moon is sufficient to obliterate the fainter and[Pg 465] more interesting objects. It was in the long and fine winter nights, when the stars were shining brilliantly and the pale path of the Milky Way extended across the heavens, that the labour was to be done. The telescope being directed to the heavens, the ordinary diurnal motion by which the sun and stars appear to rise and set carries the stars across the field of view in a majestic panorama. The stars enter slowly into the field of view, slowly move across it, and slowly leave it, to be again replaced by others. Thus the observer, by merely remaining passive at the eye-piece, sees one field after another pass before him, and is enabled to examine their contents. It follows, that even without moving the telescope a long narrow strip of the heavens is brought under review, and by moving the telescope slightly up and down the width of this strip can be suitably increased. On another night the telescope is brought into a different position, and another strip of the sky is examined; so that in the course of time the whole heavens can be carefully scrutinised.
Herschel stands at the eye-piece to watch the glorious procession of celestial objects. Close by, his sister Caroline sits at her desk, pen in hand, to take down the observations as they fall from her brother's lips. In front of her is a chronometer from which she can note the time, and a contrivance which indicates the altitude of the telescope, so that she can record the exact position of the object in connection with the description which her brother dictated. Such was the splendid scheme which this brother and sister had arranged to carry out as the object of their life-long devotion. The discoveries which Herschel was destined to make were to be reckoned not by tens or by hundreds, but by thousands. The records of these discoveries are to be found in the "Philosophical Transactions of the Royal Society," and they are among the richest treasures of those volumes. It was left to Sir John Herschel, the only son of Sir William, to complete his father's labour by repeating the survey of the northern heavens and extending it to the southern hemisphere. He undertook with this object a journey to the[Pg 466] Cape of Good Hope, and sojourned there for the years necessary to complete the great work.
As the result of the gigantic labours thus inaugurated and continued by other observers, there are now about eight thousand nebulæ known to us, and with every improvement of the telescope fresh additions are being made to the list. They differ from one another as eight thousand pebbles selected at random on a sea-beach might differ—namely, in form, size, colour, and material—but yet, like the pebbles, bear a certain generic resemblance to each other. To describe this class of bodies in any detail would altogether exceed the limits of this chapter; we shall merely select a few of the nebulæ, choosing naturally those of the most remarkable character, and also those which are representatives of the different groups into which nebulæ may be divided.
We have already stated that the great nebula in the constellation of Orion is one of the most interesting objects in the heavens. It is alike remarkable whether we consider its size or its brilliancy, the care with which it has been studied, or the success which has attended the efforts to learn something of its character. To find this object, we refer to Fig. 97 for the sketch of the chief stars in this constellation, where the letter A indicates the middle one of the three stars which form the sword-handle of Orion. Above the handle will be seen the three stars which form the well-known belt so conspicuous in the wintry sky. The star A, when viewed attentively with the unaided eye, presents a somewhat misty appearance. In the year 1618 Cysat directed a telescope to this star, and saw surrounding it a curious luminous haze, which proved to be the great nebula. Ever since his time this object has been diligently studied by many astronomers, so that very many observations have been made of the great nebula, and even whole volumes have been written which treat of nothing else. Any ordinary telescope will show the object to some extent, but the more powerful the telescope the more are the curious details revealed.
In the first place, the object which we have denoted by A (θ Orionis, also called the trapezium of Orion) is in itself the most striking multiple star in the whole heavens. It consists really of six stars, represented in the next diagram (Fig. 98). These points are so close together that their commingled rays cannot be distinguished without a telescope. Four of them are, however, easily seen in quite small instruments, but the two smaller stars require telescopes of considerable power. And yet these stars are suns, comparable, it may be, with our sun in magnitude.
It is not a little remarkable that this unrivalled group of six suns should be surrounded by the renowned nebula; the nebula or the multiple star would, either of them alone, be of exceptional interest, and here we have a combination of[Pg 468] the two. It seems impossible to resist drawing the conclusion that the multiple star really lies in the nebula, and not merely along the same line of vision. It would, indeed, seem to be at variance with all probability to suppose that the presentation of these two exceptional objects in the same field of view was merely accidental. If the multiple star be really in the nebula, then this object affords evidence that in one case at all events the distance of a nebula is a quantity of the same magnitude as the distance of a star. This is unhappily almost the entire extent of our knowledge of the distances of the nebulæ from the earth.
The great nebula of Orion surrounds the multiple star, and extends out to a vast distance into the neighbouring space. The dotted circle drawn around the star marked A in Fig. 97 represents approximately the extent of the nebula, as seen in a moderately good telescope. The nebula is of a faint bluish colour, impossible to represent in a drawing. Its brightness is much greater in some places than in others; the central parts are, generally speaking, the most brilliant, and the luminosity gradually fades away as the edge of the nebula is approached. In fact, we can hardly say that the nebula has any definite boundary, for with each increase of telescopic power faint new branches can be seen. There seems to be an empty space in the nebula immediately surrounding the multiple star, but this is merely an illusion, produced by the contrast of the brilliant light of the stars, as the spectroscopic examination of the nebula shows that the nebulous matter is continuous between the stars.
The plate of the great nebula in Orion which is here shown (Plate XIV.) represents, in a reduced form, the elaborate drawing of this object, which has been made with the Earl of Rosse's great reflecting telescope at Parsonstown.[40] A telescopic view of the nebula shows two hundred stars or more, scattered over its surface. It is not necessary to suppose that these stars are immersed in the substance of the nebula as the multiple star appears to be; they may be either in front of it, or, less probably, behind it, so as to be projected on the same part of the sky.
 PLATE XV.
PLATE XV.A considerable number of drawings of this unique object have been made by other astronomers. Among these we must mention that executed by Professor Bond, in Cambridge, Mass., which possesses a faithfulness in detail that every student of this object is bound to acknowledge. Of late years also successful attempts have been made to photograph the great nebula. The late Professor Draper was fortunate enough to obtain some admirable photographs. In England Mr. Common was the first to take most excellent photographs of the nebula, and superb photographs of the same object have also been obtained by Dr. Roberts and Mr. W.E. Wilson, which show a vast extension of the nebula into regions which it was not previously known to occupy.
The great nebula in Andromeda, which is faintly visible to the unaided eye, is shown in Plate XV., which has been copied with permission from one of the astonishing photographs that Dr. Isaac Roberts has obtained. Two dark channels in the nebula cannot fail to be noticed, and the number of faint stars scattered over its surface is also a point to which attention may be drawn. To find this object we must look out for Cassiopeia and the Great Square of Pegasus, and then the nebula will be easily perceived in the position shown on p. 413. In the year 1885 a new star of the seventh magnitude suddenly appeared close to the brightest part of the nebula, and declined again to invisibility after the lapse of a few months.
The nebula in Lyra is the most conspicuous ring nebula in the heavens, but it is not to be supposed that it is the only member of this class. Altogether, there are about a dozen of these objects. It seems difficult to form any adequate conception of the nature of such a body. It is, however, impossible to view the annular nebulæ without being, at all events, reminded of those elegant objects known as vortex rings. Who has not noticed a graceful ring of steam which occasionally escapes from the funnel of a locomotive, and ascends high into the air, only dissolving some time after the steam not so specialised has disappeared? Such vortex rings can be produced artificially by a cubical box, one open side of which is covered with[Pg 470] canvas, while on the opposite side of the box is a circular hole. A tap on the canvas will cause a vortex ring to start from the hole; and if the box be filled with smoke, this ring will be visible for many feet of its path. It would certainly be far too much to assert that the annular nebulæ have any real analogy to vortex rings; but there is, at all events, no other object known to us with which they can be compared.
The heavens contain a number of minute but brilliant objects known as the planetary nebulæ. They can only be described as globes of glowing bluish-coloured gas, often small enough to be mistaken for a star when viewed through a telescope. One of the most remarkable of these objects lies in the constellation Draco, and can be found half-way between the Pole Star and the star γ Draconis. Some of the more recently discovered planetary nebulæ are extremely small, and they have indeed only been distinguished from small stars by the spectroscope. It is also to be noticed that such objects are a little out of the stellar focus in the refracting telescope in consequence of their blue colour. This remark does not apply to a reflecting telescope, as this instrument conducts all the rays to a common focus.
There are many other forms of nebulæ: there are long nebulous rays; there are the wondrous spirals which have been disclosed in Lord Rosse's great reflector; there are the double nebulæ. But all these various objects we must merely dismiss with this passing reference. There is a great difficulty in making pictorial representations of such nebulæ. Most of them are very faint—so faint, indeed, that they can only be seen with close attention even in powerful instruments. In making drawings of these objects, therefore, it is impossible to avoid intensifying the fainter features if an intelligible picture is to be made. With this caution, however, we present Plate XVI., which exhibits several of the more remarkable nebulæ as seen through Lord Rosse's great telescope.
The actual nature of the nebulæ offers a problem of the greatest interest, which naturally occupied the mind of the first assiduous observer of nebulæ, William Herschel, for many years. At first he assumed all nebulæ to be nothing but dense aggregations of stars—a very natural conclusion for one who had so greatly advanced the optical power of telescopes,[Pg 472] and was accustomed to see many objects which in a small telescope looked nebulous become "resolved" into stars when scrutinised with a telescope of large aperture. But in 1864, when Sir William Huggins first directed a telescope armed with a spectroscope to one of the planetary nebulæ, it became evident that at least some nebulæ were really clouds of fiery mist and not star clusters.
We shall in our next chapter deal with the spectra of the fixed stars, but we may here in anticipation remark that these spectra are continuous, generally showing the whole length of spectrum, from red to violet, as in the sun's spectrum, though with many and important differences as to the presence of dark and bright lines. A star cluster must, of course, give a similar spectrum, resulting from the superposition of the spectra of the single stars in the cluster. Many nebulæ give a spectrum of this kind; for instance, the great nebula in Andromeda. But it does not by any means follow from this that these objects are only clusters of ordinary stars, as a continuous spectrum may be produced not only by matter in the liquid or solid state, or by gases at high pressure, but also by gases at lower pressure but high temperature under certain conditions. A continuous spectrum in the case of a nebula, therefore, need not indicate that the nebula is a cluster of bodies comparable in size and general constitution with our sun. But if a spectrum of bright lines is given by a nebula, we can be certain that gases at low pressure are present in the object under examination. And this was precisely what Sir William Huggins discovered to be the case in many nebulæ. When he first decided to study the spectra of nebulæ, he selected for observation those objects known as planetary nebulæ—small, round, or slightly oval discs, generally without central condensation, and looking like ill-defined planets. The colour of their light, which often is blue tinted with green, is remarkable, since this is a colour very rare among single stars. The spectrum was found to be totally different to that of any star, consisting merely of three or four bright lines. The brightest one is situated in the bluish-green part of the spectrum, and was at first thought to be identical with a line of the spectrum of nitrogen, but subsequent more accurate measures have shown that neither this nor the second nebular line correspond to any dark line in the solar spectrum, nor can they be produced experimentally in the laboratory, and we are therefore unable to ascribe them to any known element. The third and fourth lines were at once seen to be identical with the two hydrogen lines which in the solar spectrum are named F and g.
Spectrum analysis has here, as on so many other occasions, rendered services which no telescope could ever have done. The spectra of nebulæ have, after Huggins, been studied, both visually and photographically, by Vogel, Copeland, Campbell, Keeler, and others, and a great many very faint lines have been detected in addition to those four which an instrument of moderate dimensions shows. It is remarkable that the red C-line of hydrogen, ordinarily so bright, is either absent or excessively faint in the spectra of nebulæ, but experiments by Frankland and Lockyer have shown that under certain conditions of temperature and pressure the complicated spectrum of hydrogen is reduced to one green line, the F-line. It is, therefore, not surprising that the spectra of gaseous nebulæ are comparatively simple, as the probably low density of the gases in them and the faintness of these bodies would tend to reduce the spectra to a small number of lines. Some gaseous nebulæ also show faint continuous spectra, the place of maximum brightness of which is not in the yellow (as in the solar spectrum), but about the green. It is probable that these continuous spectra are really an aggregate of very faint luminous lines.
A list of all the nebulæ known to have a gaseous spectrum would now contain about eighty members. In addition to the planetary nebulæ, many large and more diffused nebulæ belong to this class, and this is also the case with the annular nebula in Lyra and the great nebula of Orion. It is needless to say that it is of special interest to find this grand object enrolled among the nebulæ of a gaseous nature. In this nebula Copeland detected the[Pg 474] wonderful D3 line of helium at a time when "helium" was a mere name, a hypothetical something, but which we now know to be an element very widely distributed through the universe. It has since been found in several other nebulæ. The ease with which the characteristic gaseous spectrum is recognised has suggested the idea of sweeping the sky with a spectroscope in order to pick up new planetary nebulæ, and a number of objects have actually been discovered by Pickering and Copeland in this manner, as also more recently by Pickering by examining spectrum photographs of various regions of the sky. Most of these new objects when seen through a telescope look like ordinary stars, and their real nature could never have been detected without the spectroscope.
When we look up at the starry sky on a clear night, the stars seem at first sight to be very irregularly distributed over the heavens. Here and there a few bright stars form characteristic groups, like Orion or the Great Bear, while other equally large tracts are almost devoid of bright stars and only contain a few insignificant ones. If we take a binocular, or other small telescope, and sweep the sky with it, the result seems to be the same—now we come across spaces rich in stars; now we meet with comparatively empty places. But when we approach the zone of the Milky Way, we are struck with the rapid increase of the number of stars which fill the field of the telescope; and when we reach the Milky Way itself, the eye is almost unable to separate the single points of light, which are packed so closely together that they produce the appearance to the naked eye of a broad, but very irregular, band of dim light, which even a powerful telescope in some places can hardly resolve into stars. How are we to account for this remarkable arrangement of the stars? What is the reason of our seeing so few at the parts of the heavens farthest from the Milky Way, and so very many in or near that wonderful belt? The first attempt to give an answer to these questions was made by Thomas Wright, an instrument maker in London, in a book published in 1750. He supposed the stars of our sidereal system to be distributed in a vast stratum of inconsiderable thickness compared with its length and breadth. If we had a big grindstone made of glass, in which had become uniformly imbedded a vast quantity of grains of sand or similar minute particles, and if we were able to place our eye somewhere near the centre of this grindstone, it is easy to see that we should see very few particles near the direction of the axle of the grindstone, but a great many if we looked towards any point of the circumference. This was Wright's idea of the structure of the Milky Way, and he supposed the sun to be situated not very far from the centre of this stellar stratum.
If the Milky Way itself did not exist—and we had simply the fact to build on that the stars appeared to increase rapidly in number towards a certain circle (almost a great circle) spanning the heavens—then the disc theory might have a good deal in its favour. But the telescopic study of the Milky Way, and even more the marvellous photographs of its complicated structure produced by Professor Barnard, have given the death blow to the old theory, and have made it most reasonable to conclude that the Milky Way is really, and not only apparently, a mighty stream of stars encircling the heavens. We shall shortly mention a few facts which point in this direction. A mere glance is sufficient to show that the Milky Way is not a single belt of light; near the constellation Aquila it separates into two branches with a fairly broad interval between them, and these branches do not meet again until they have proceeded far into the southern hemisphere. The disc theory had, in order to explain this, to assume that the stellar stratum was cleft in two nearly to the centre. But even if we grant this, how can we account for the numerous more or less dark holes in the Milky Way, the largest and most remarkable of which is the so-called "coal sack" in the southern hemisphere? Obviously we should have to assume the existence of a number of tunnels, drilled through the disc-like stratum, and by some strange sympathy all directed towards the spot where our solar system is situated. And the many small arms which stretch out[Pg 476] from the Milky Way would have to be either planes seen edgeways or the convexities of curved surfaces viewed tangentially. The improbability of these various assumptions is very great. But evidence is not wanting that the relatively bright stars are crowded together along the same zone where the excessively faint ones are so closely packed. The late Mr. Proctor plotted all the stars which occur in Argelander's great atlas of the northern hemisphere, 324,198 in number, on a single chart, and though these stars are all above the tenth magnitude, and thus superior in brightness to that innumerable host of stars of which the individual members are more or less lost in the galactic zone, and on the hypothesis of uniform distribution ought to be relatively near to us, the chart shows distinctly the whole course of the Milky Way by the clustering of these stars. This disposes sufficiently of the idea that the Milky Way is nothing but a disc-like stratum seen projected on the heavenly sphere; after this it is hardly necessary to examine Professor Barnard's photographs and see how fairly bright and very faint regions alternate without any attempt at regularity, in order to become convinced that the Milky Way is more probably a stream of stars clustered together, a stream or ring of incredibly enormous dimensions, inside which our solar system happens to be situated. But it must be admitted that it is premature to attempt to find the actual figure of this stream or to determine the relative distance of the various portions of it.
Star Spectroscopes—Classification of Stellar Spectra—Type I., with very Few Absorption Lines—Type II., like the Sun—Type III., with Strongly Marked Dark Bands—Distribution of these Classes over the Heavens—Motion in the Line of Sight—Orbital Motion Discovered with the Spectroscope: New Class of Binaries—Spectra of Temporary Stars—Nature of these Bodies.
We have frequently in the previous chapters had occasion to refer to the revelations of the spectroscope, which form an important chapter in the history of modern science. By its aid a mighty stride has been taken in our attempt to comprehend the physical constitution of the sun. In the present chapter we propose to give an account of what the spectroscope tells us about the physical constitution of the fixed stars.
Quite a new phase of astronomy is here opened up. Every improvement in telescopes revealed fainter and fainter objects, but all the telescopes in the world could not answer the question as to whether iron and other elements are to be found in the stars. The ordinary star is a mighty glowing globe, hotter than a Bessemer converter or a Siemens furnace; if iron is in the star, it must be not only white-hot and molten, but actually converted into vapour. But the vapour of iron is not visible in the telescope. How would you recognise it? How would you know if it commingled with the vapour of many other metals or other substances? It is, in truth, a delicate piece of analysis to discriminate iron in the glowing atmosphere of a star. But the spectroscope is adequate to the task, and it renders its analysis with an amount of evidence that is absolutely convincing.
That the spectra of the moon and planets are practically[Pg 478] nothing but faint reproductions of the spectrum of the sun was discovered by the great German optician Fraunhofer about the year 1816. By placing a prism in front of the object glass of a small theodolite (an instrument used for geodetic measurements) he was able to ascertain that Venus and Mars showed the same spectrum as the sun, while Sirius gave a very different one. This important observation encouraged him to procure better instrumental means with which to continue the work, and he succeeded in distinguishing the chief characteristics of the various types of stellar spectra. The form of instrument which Fraunhofer adopted for this work, in which the prism was placed outside the object glass of the telescope, has not been much used until within the last few years, owing to the difficulty of obtaining prisms of large dimensions (for it is obvious that the prism ought to be as large as the object glass if the full power of the latter is to be made use of), but this is the simplest form of spectroscope for observing spectra of objects of no sensible angular diameter, like the fixed stars. The parallel rays from the stars are dispersed by the prism into a spectrum, and this is viewed by means of the telescope. But as the image of the star in the telescope is nothing but a luminous point, its spectrum will be merely a line in which it would not be possible to distinguish any lines crossing it laterally such as those we see in the spectrum of the sun. A cylindrical lens is, therefore, placed before the eye-piece of the telescope, and as this has the effect of turning a point into a line and a line into a band, the narrow spectrum of the star is thereby broadened out into a luminous band in which we can distinguish any details that exist. In other forms of stellar spectroscope we require a slit which must be placed in the focus of the object glass, and the general arrangement is similar to that which we have described in the chapter on the sun, except that a cylindrical lens is required.
The study of the spectra of the fixed stars made hardly any progress until the principles of spectrum analysis had been established by Kirchhoff in 1859. When the dark[Pg 479] lines in the solar spectrum had been properly interpreted, it was at once evident that science had opened wide the gates of a new territory for human exploration, of the very existence of which hardly anyone had been aware up to that time. We have seen to what splendid triumphs the study of the sun has led the investigators in this field, and we have seen how very valuable results have been obtained by the new method when applied to observations of comets and nebulæ. We shall now give some account of what has been learned with regard to the constitution of the fixed stars by the researches which were inaugurated by Sir William Huggins and continued and developed by him, as well as by Secchi, Vogel, Pickering, Lockyer, Dunér, Scheiner and others. Here, as in the other modern branches of astronomy, photography has played a most important part, not only because photographed spectra of stars extend much farther at the violet end than the observer can follow them with his eye, but also because the positions of the lines can be very accurately measured on the photographs.
The first observer who reduced the apparently chaotic diversity of stellar spectra to order was Secchi, who showed that they might all be grouped according to four types. Within the last thirty years, however, so many modifications of the various types have been found that it has become necessary to subdivide Secchi's types, and most observers now make use of Vogel's classification, which we shall also for convenience adopt in this chapter.
Type I.—In the spectra of stars of this class the metallic lines, which are so very numerous and conspicuous in the sun's violet spectrum, are very faint and thin, or quite invisible, and the blue and white parts are very intensely bright. Vogel subdivides the class into three groups. In the first (I.a) the hydrogen lines are present, and are remarkably broad and intense; Sirius, Vega, and Regulus are examples of this group. The great breadth of the lines probably indicates that these stars are surrounded by hydrogen atmospheres of great dimensions. It is generally acknowledged that stars of this group must be the hottest of all, and support is lent to this[Pg 480] view by the appearance in their spectra of a certain magnesium line, which, as Sir Norman Lockyer showed many years ago, by laboratory experiments, does not appear in the ordinary spectrum of magnesium, but is indicative of the presence of the substance at a very high temperature. In the spectra of stars of Group I.b the hydrogen lines and the few metallic lines are of equal breadth, and the magnesium line just mentioned is the strongest of all. Rigel and several other bright stars in Orion belong to this group, and it is remarkable that helium is present at least in some of these stars, so that (as Professor Keeler remarks) the spectrum of Rigel may almost be regarded as the nebular spectrum reversed (lines dark instead of bright), except that the two chief nebular lines are not reversed in the star. This fact will doubtless eventually be of great importance to our understanding the successive development of a star from a nebula; and a star like Rigel is no doubt also of very high temperature. This is probably not the case with stars of the third subdivision of Type I. (I.c), the spectra of which are distinguished by the presence of bright hydrogen lines and the bright helium line D3. Among the stars having this very remarkable kind of spectrum is a very interesting variable star in the constellation Lyra (β) and the star known as γ Cassiopeiæ, both of which have been assiduously observed, their spectra possessing numerous peculiarities which render an explanation of the physical constitution of the stars of this subdivision a very difficult matter.
Passing to Type II., we find spectra in which the metallic lines are strong. The more refrangible end of the spectrum is fainter than in the previous Class, and absorption bands are sometimes found towards the red end. In its first subdivision (II.a) are contained spectra with a large number of strong and well-defined lines due to metals, the hydrogen lines being also well seen, though they are not specially conspicuous. Among the very numerous stars of this group are Capella, Aldebaran, Arcturus, Pollux, etc. The spectra of these stars are in fact practically identical with the spectrum of our own sun, as shown, for instance, by Dr. Scheiner, of the Potsdam Astrophysical Observatory, who has measured several hundred[Pg 481] lines on photographs of the spectrum of Capella, and found a very close agreement between these lines and corresponding ones in the solar spectrum. We can hardly doubt that the physical constitution of these stars is very similar to that of our sun. This cannot be the case with the stars of the second subdivision (II.b), the spectra of which are very complex, each consisting of a continuous spectrum crossed by numerous dark lines, on which is superposed a second spectrum of bright lines. Upwards of seventy stars are known to possess this extraordinary spectrum, the only bright one among them being a star of the third magnitude in the southern constellation Argus. Here again we have hydrogen and helium represented by bright lines, while the origin of the remaining bright lines is doubtful. With regard to the physical constitution of the stars of this group it is very difficult to come to a definite conclusion, but it would seem not unlikely that we have here to do with stars which are not only surrounded by an atmosphere of lower temperature, causing the dark lines, but which, outside of that, have an enormous envelope of hydrogen and other gases. In one star at least of this group Professor Campbell, of the Lick Observatory, has seen the F line as a long line extending a very appreciable distance on each side of the continuous spectrum, and with an open slit it was seen as a large circular disc about six seconds in diameter; two other principal hydrogen lines showed the same appearance. As far as this observation goes, the existence of an extensive gaseous envelope surrounding the star seems to be indicated.
Type III. contains comparatively few stars, and the spectra are characterised by numerous dark bands in addition to dark lines, while the more refrangible parts are very faint, for which reason the stars are more or less red in colour. This class has two strongly marked subdivisions. In the first (III.a) the principal absorption lines coincide with similar ones in the solar spectrum, but with great differences as to intensity, many lines being much stronger in these stars than in the sun, while many new lines also appear. These dissimilarities are, however, of less importance than the peculiar absorption bands in the red, yellow, and green parts of the spectrum, overlying the[Pg 482] metallic lines, and being sharply defined on the side towards the violet and shading off gradually towards the red end of the spectrum. Bands of this kind belong to chemical combinations, and this appears to show that somewhere in the atmospheres of these distant suns the temperature is low enough to allow stable chemical combinations to be formed. The most important star of this kind is Betelgeuze or α Orionis, the red star of the first magnitude in the shoulder of Orion; but it is of special importance to note that many variable stars of long period have spectra of Type III.a. Sir Norman Lockyer predicted in 1887 that bright lines, probably of hydrogen, would eventually be found to appear at the maximum of brightness, when the smaller swarm is supposed to pass through the larger one, and this was soon afterwards confirmed by the announcement that Professor Pickering had found a number of hydrogen lines bright on photographs, obtained at Harvard College Observatory, of the spectrum of the remarkable variable, Mira Ceti, at the time of maximum. Professor Pickering has since then reported that bright lines have been found on the plates of forty-one previously known variables of this class, and that more than twenty other stars have been detected as variables by this peculiarity of their spectrum; that is, bright lines being seen in them suggested that the stars were variable, and further photometric investigations corroborated the fact.
The second subdivision (III.b) contains only comparatively faint stars, of which none exceed the fifth magnitude, and is limited to a small number of red stars. The strongly marked bands in their spectra are sharply defined and dark on the red side, while they fade away gradually towards the violet, exactly the reverse of what we see in the spectra of III.a. These bands appear to arise from the absorption due to hydrocarbon vapours present in the atmospheres of these stars; but there are also some lines visible which indicate the presence of metallic vapours, sodium being certainly among these. There can be little doubt that these stars represent the last stage in the life of a sun, when it has cooled down considerably and is not very far from actual extinction, owing[Pg 483] to the increasing absorption of its remaining light in the atmosphere surrounding it.
The method employed for the spectroscopic determination of the motion of a star in the line of sight is the same as the method we have described in the chapter on the sun. The position of a certain line in the spectrum of a star is compared with the position of the corresponding bright line of an element in an artificially produced spectrum, and in this manner a displacement of the stellar line either towards the violet (indicating that the star is approaching us) or towards the red (indicating that it is receding) may be detected. The earliest attempt of this sort was made in 1867 by Sir William Huggins, who compared the F line in the spectrum of Sirius with the same line of the spectrum of hydrogen contained in a vacuum tube reflected into the field of his astronomical spectroscope, so that the two spectra appeared side by side. The work thus commenced and continued by him was afterwards taken up at the Greenwich Observatory; but the results obtained by these direct observations were never satisfactory, as remarkable discrepancies appeared between the values obtained by different observers, and even by the same observer on different nights. This is not to be wondered at when we bear in mind that the velocity of light is so enormous compared with any velocity with which a heavenly body may travel, that the change of wave length resulting from the latter motion can only be a very minute one, difficult to perceive, and still more difficult to measure. But since photography was first made use of for these investigations by Dr. Vogel, of Potsdam, much more accordant and reliable results have been obtained, though even now extreme care is required to avoid systematic errors. To give some idea of the results obtainable, we present in the following table the values of the velocity per second of a number of stars observed in 1896 and 1897 by Mr. H.F. Newall with the Bruce spectrograph attached to the great 25-inch Newall refractor of the Cambridge Observatory, and we have added the values found at Potsdam by Vogel and Scheiner. The results are expressed in kilometres (1 km. = 0·62 English[Pg 484] mile). The sign + means that the star is receding from us,-that it is approaching.
| Newall. | Vogel. | Scheiner. | |
| Aldebaran | + 49·2 | + 47·6 | + 49·4 |
| Betelgeuze | + 10·6 | + 15·6 | + 18·8 |
| Procyon | - 4·2 | - 7·2 | - 10·5 |
| Pollux | - 0·7 | + 1·9 | + 0·4 |
| γ Leonis | - 39·9 | - 36·5 | - 40·5 |
| Arcturus | - 6·4 | - 7·0 | - 8·3 |
These results have been corrected for the earth's orbital motion round the sun, but not for the sun's motion through space, as the amount of the latter is practically unknown, or at least very uncertain; so that the above figures really represent the velocity per second of the various stars relative to the sun. We may add that the direction and velocity of the sun's motion may eventually be ascertained from spectroscopic measures of a great number of stars, and it seems likely that the sun's velocity will be much more accurately found in this way than by the older method of combining proper motions of stars with speculations as to the average distances of the various classes of stars. This has already been attempted by Dr. Kempf, who from the Potsdam spectrographic observations found the sun's velocity to be 18·6 kilometres, or 11·5 miles per second, a result which is probably not far from the truth.
But the spectra of the fixed stars can also tell us something about orbital motion in these extremely distant systems. If one star revolved round another in a plane passing through the sun, it must on one side of the orbit move straight towards us and on the other side move straight away from us, while it will not alter its distance from us while it is passing in front of, or behind, the central body. If we therefore find from the spectroscopic observations that a star is alternately moving towards and away from the earth in a certain period, there can be no doubt that this star is travelling round some unseen body (or, rather, round the centre of gravity of both) in the period indicated by the shifting of the spectral lines. In Chapter XIX. we mentioned[Pg 485] the variable star Algol in the constellation Perseus, which is one of a class of variable stars distinguished by the fact that for the greater part of the period they remain of unaltered brightness, while for a very short time they become considerably fainter. That this was caused by some sort of an eclipse—or, in other words, by the periodic passage of a dark body in front of the star, hiding more or less of the latter from us—was the simplest possible hypothesis, and it had already years ago been generally accepted. But it was not possible to prove that this was the true explanation of the periodicity of stars like Algol until Professor Vogel, from the spectroscopic observations made at Potsdam, found that before every minimum Algol is receding from the sun, while it is approaching us after the minimum. Assuming the orbit to be circular, the velocity of Algol was found to be twenty-six miles per second. From this and the length of the period (2d. 22h. 48m. 55s.) and the time of obscuration it was easy to compute the size of the orbit and the actual dimensions of the two bodies. It was even possible to go a step further and to calculate from the orbital velocities the masses of the two bodies,[41] assuming them to be of equal density—an assumption which is no doubt very uncertain. The following are the approximate elements of the Algol system found by Vogel:—
| Diameter of Algol | 1,054,000 miles. |
| Diameter of companion | 825,000 miles. |
| Distance between their centres | 3,220,000 miles. |
| Orbital velocity of Algol | 26 miles per sec. |
| Orbital velocity of companion | 55 miles per sec. |
| Mass of Algol | 4⁄9 of sun's mass. |
| Mass of companion | 2⁄9 of sun's mass. |
The period of Algol has been gradually decreasing during the last century (by six or seven seconds), but whether this is caused by the motion of the pair round a third and very much more distant body, as suggested by Mr. Chandler, has still to be found out.
We have already mentioned that in order to produce eclipses, and thereby variations of light, it is necessary that[Pg 486] the line of sight should lie nearly in the plane of the orbit. It is also essential that there should be a considerable difference of brightness between the two bodies. These conditions must be fulfilled in the fifteen variable stars of the Algol class now known; but according to the theory of probability, there must be many more binary systems like that of Algol where these conditions are not fulfilled, and in those cases no variations will occur in the stars' brightness. Of course, we know many cases of a luminous star travelling round another, but there must also be cases of a large companion travelling round another at so small a distance that our telescopes are unable to "divide" the double star. This has actually been discovered by means of the spectroscope. If we suppose an extremely close double star to be examined with the spectroscope, the spectra of the two components will be superposed, and we shall not be aware that we really see two different spectra. But during the revolution of the two bodies round their common centre of gravity there must periodically come a time when one body is moving towards us and the other moving from us, and consequently the lines in the spectrum of the former will be subject to a minute, relative shift towards the violet end of the spectrum, and those of the other to a minute shift towards the red. Those lines which are common to the two spectra will therefore periodically become double. A discovery of this sort was first made in 1889 by Professor Pickering from photographs of the spectrum of Mizar, or ζ Ursa Majoris, the larger component of the well-known double star in the tail of the Great Bear. Certain of the lines were found to be double at intervals of fifty-two days. The maximum separation of the two components of each line corresponds to a relative velocity of one star as compared with the other of about a hundred miles per second, but subsequent observations have shown the case to be very complicated, either with a very eccentric elliptic orbit or possibly owing to the presence of a third body. The Harvard College photographs also showed periodic duplicity of lines in the star β Aurigæ, the period being remarkably short, only three days and twenty-three hours and thirty-seven minutes. In 1891 Vogel found,[Pg 487] from photographs of the spectrum of Spica, the first magnitude star in Virgo, that this star alternately recedes from and approaches to the solar system, the period being four days. Certain other "spectroscopic binaries" have since then been found, notably one component of Castor, with a period of three days, found by M. Belopolsky, and a star in the constellation Scorpio, with a period of only thirty-four hours, detected on the Harvard spectrograms.
Quite recently Mr. H.F. Newall, at Cambridge, and Mr. Campbell, of the Lick Observatory, have shown that α Aurigæ, or Capella, consists of a sun-like star and a Procyon-like star, revolving in 104 days.
At first sight there is something very startling in the idea of two suns circling round each other, separated by an interval which, in comparison with their diameters, is only a very small one. In the Algol system, for instance, we have two bodies, one the size of our own sun and the other slightly larger, moving round their common centre of gravity in less than three days, and at a distance between their surfaces equal to only twice the diameter of the larger one. Again, in the system of Spica we have two great suns swinging round each other in only four days, at a distance equal to that between Saturn and his sixth satellite. But although we have at present nothing analogous to this in our solar system, it can be proved mathematically that it is perfectly possible for a system of this kind to preserve its stability, if not for ever, at any rate for ages, and we shall see in our last chapter that there was in all probability a time when the earth and the moon formed a peculiar system of two bodies revolving rapidly at a very small distance compared to the diameters of the bodies.
It is possible that we have a more complicated system in the star known as β Lyræ. This is a variable star of great interest, having a period of twelve days and twenty-two hours, in which time it rises from magnitude 4-1⁄2 to a little above 3-1⁄2, sinks nearly to the fourth magnitude, rises again to fully 3-1⁄2, and finally falls to magnitude 4-1⁄2. In 1891 Professor Pickering discovered that the bright lines in the spectrum of this star[Pg 488] changed their position from time to time, appearing now on one side, now on the other side of corresponding dark lines. Obviously these bright lines change their wave length, the light-giving source alternately receding from and approaching to the earth, and the former appeared to be the case during one-half of the period of variation of the star's light, the latter during the other half. The spectrum of this star has been further examined by Belopolsky and others, who have found that the lines are apparently double, but that one of the components either disappears or becomes very narrow from time to time. On the assumption that these lines were really single (the apparent duplicity resulting from the superposition of a dark line), Belopolsky determined the amount of their displacement by measuring the distances from the two edges of a line of hydrogen (F) to the artificial hydrogen line produced by gas glowing in a tube and photographed along with the star-spectrum. Assuming the alternate approach and recession to be caused by orbital revolution, Belopolsky found that the body emitting the light of the bright lines moved with an orbital velocity of forty-one miles. He succeeded in 1897 in observing the displacement of a dark line due to magnesium, and found that the body emitting it was also moving in an orbit, but while the velocities given by the bright F line are positive after the principal minimum of the star's light, those given by the dark line are negative. Therefore, during the principal minimum it is a star giving the dark line which is eclipsed, and during the secondary minimum another star giving the bright line is eclipsed. This wonderful variable will, however, require more observations before the problem of its constitution is finally solved, and the same may be said of several variable stars, e.g. η Aquilæ and δ Cephei, in which a want of harmony has been found between the changes of velocity and the fluctuations of the light.
There are some striking analogies between the complicated spectrum of β Lyræ and the spectra of temporary stars. The first "new star" which could be spectroscopically examined was that which appeared in Corona Borealis in 1866, and which[Pg 489] was studied by Sir W. Huggins. It showed a continuous spectrum with dark absorption lines, and also the bright lines of hydrogen; practically the same spectrum as the stars of Type II.b. This was also the case with Schmidt's star of 1876, which showed the helium line (D3) and the principal nebula line in addition to the lines of hydrogen; but in the autumn of 1877, when the star had fallen to the tenth magnitude, Dr. Copeland was surprised to find that only one line was visible, the principal nebula line, in which almost the whole light of the star was concentrated, the continuous spectrum being hardly traceable. It seemed, in fact, that the star had been transformed into a planetary nebula, but later the spectrum seems to have lost this peculiar monochromatic character, the nebula line having disappeared and a faint continuous spectrum alone being visible, which is also the case with the star of 1866 since it sank down to the tenth magnitude. A continuous spectrum was all that could be seen of the new star which broke out in the nebula of Andromeda in 1885, much the same as the spectrum of the nebula itself.
When the new star in Auriga was announced, in February, 1892, astronomers were better prepared to observe it spectroscopically, as it was now possible by means of photography to study the ultra-violet part of the spectrum which to the eye is invisible. The visible spectrum was very like that of Nova Cygni of 1876, but when the wave-lengths of all the bright lines seen and photographed at the Lick Observatory and at Potsdam were measured, a strong resemblance to the bright line spectrum of the chromosphere of the sun became very evident. The hydrogen lines were very conspicuous, while the iron lines were very numerous, and calcium and magnesium were also represented. The most remarkable revelation made by the photographs was, however, that the bright lines were in many cases accompanied, on the side next the violet, by broad dark bands, while both bright and dark lines were of a composite character. Many of the dark lines had a thin bright line superposed in the middle, while on the other hand many of the bright lines had two or three points maxima of brightness. The results of the measures of motion in[Pg 490] the line of sight were of special importance. They showed that the source of light, whence came the thin bright lines within the dark ones, was travelling towards the sun at the enormous rate of 400 miles per second, and if the bright lines were actual "reversals" of the dark ones, then the source of the absorption spectrum must have been endowed with much the same velocity. On the other hand, if the two or three maxima of brightness in the bright lines really represent two or three separate bodies giving bright lines, the measures indicate that the principal one was almost at rest as regards the sun, while the others were receding from us at the extraordinary rates of 300 and 600 miles per second. And as if this were not sufficiently puzzling, the star on its revival in August, 1892, as a tenth magnitude star had a totally different spectrum, showing nothing but a number of the bright lines belonging to planetary nebulæ! It is possible that the principal ones of these were really present in the spectrum from the first, but that their wave lengths had been different owing to change of the motion in the line of sight, so that the nebula lines seen in the autumn were identical with others seen in the spring at slightly different places. Subsequent observations of these nebula lines seemed to point to a motion of the Nova towards the solar system (of about 150 miles per second) which gradually diminished.
But although we are obliged to confess our inability to say for certain why a temporary star blazes up so suddenly, we have every cause to think that these strange bodies will by degrees tell us a great deal about the constitution of the fixed stars. The great variety of spectra which we see in the starry universe, nebula spectra with bright lines, stellar spectra of the same general character, others with broad absorption bands, or numerous dark lines like our sun, or a few absorption lines only—all this shows us the universe as teeming with bodies in various stages of evolution. We shall have a few more words to say on this matter when we come to consider the astronomical significance of heat; but we have reached a point where man's[Pg 491] intellect can hardly keep pace with the development of our instrumental resources, and where our imagination stands bewildered when we endeavour to systematise the knowledge we have gained. That great caution will have to be exercised in the interpretation of the observed phenomena is evident from the recent experience of Professor Rowland, of Baltimore, from which we learn that spectral lines are not only widened by increased pressure of the light-giving vapour, but that they may be bodily shifted thereby. Dr. Zeeman's discovery, that a line from a source placed in a strong magnetic field may be both widened, broadened, and doubled, will also increase our difficulties in the interpretation of these obscure phenomena.
The Pole is not a Fixed Point—Its Effect on the Apparent Places of the Stars—The Illustration of the Peg-Top—The Disturbing Force which acts on the Earth—Attraction of the Sun on a Globe—The Protuberance at the Equator—The Attraction of the Protuberance by the Sun and by the Moon produces Precession—The Efficiency of the Precessional Agent varies inversely as the Cube of the Distance—The Relative Efficiency of the Sun and the Moon—How the Pole of the Earth's Axis revolves round the Pole of the Ecliptic—Variation of Latitude.
The position of the pole of the heavens is most conveniently indicated by the bright star known as the Pole Star, which lies in its immediate vicinity. Around this pole the whole heavens appear to rotate once in a sidereal day; and we have hitherto always referred to the pole as though it were a fixed point in the heavens. This language is sufficiently correct when we embrace only a moderate period of time in our review. It is no doubt true that the pole lies near the Pole Star at the present time. It did so during the lives of the last generation, and it will do so during the lives of the next generation. All this time, however, the pole is steadily moving in the heavens, so that the time will at length come when the pole will have departed a long way from the present Pole Star. This movement is incessant. It can be easily detected and measured by the instruments in our observatories, and astronomers are familiar with the fact that in all their calculations it is necessary to hold special account of this movement of the pole. It produces an apparent change in the position of a star, which is known by the term "precession."
The movement of the pole is very clearly shown in the accompanying figure (Fig. 100), for which I am indebted to the kindness of the late Professor C. Piazzi Smyth. The circle shows the track along which the pole moves among the stars.
The centre of the circle in the constellation of Draco is the pole of the ecliptic. A complete journey of the pole occupies the considerable period of about 25,867 years. The drawing shows the[Pg 494] position of the pole at the several dates from 4000 B.C. to 2000 A.D. A glance at this map brings prominently before us how casual is the proximity of the pole to the Pole Star. At present, indeed, the distance of the two is actually lessening, but afterwards the distance will increase until, when half of the revolution has been accomplished, the pole will be at a distance of twice the radius of the circle from the Pole Star. It will then happen that the pole will be near the bright star Vega or α Lyræ, so that our successors some 12,000 years hence may make use of Vega for many of the purposes for which the Pole Star is at present employed! Looking back into past ages, we see that some 2,000 or 3,000 years B.C. the star α Draconis was suitably placed to serve as the Pole Star, when β and δ of the Great Bear served as pointers. It need hardly be added, that since the birth of accurate astronomy the course of the pole has only been observed over a very small part of the mighty circle. We are not, however, entitled to doubt that the motion of the pole will continue to pursue the same path. This will be made abundantly clear when we proceed to render an explanation of this very interesting phenomenon.
The north pole of the heavens is the point of the celestial sphere towards which the northern end of the axis about which the earth rotates is directed. It therefore follows that this axis must be constantly changing its position. The character of the movement of the earth, so far as its rotation is concerned, may be illustrated by a very common toy with which every boy is familiar. When a peg-top is set spinning, it has, of course, a very rapid rotation around its axis; but besides this rotation there is usually another motion, whereby the axis of the peg-top does not remain in a constant direction, but moves in a conical path around the vertical line. The adjoining figure (Fig. 101) gives a view of the peg-top. It is, of course, rotating with great rapidity around its axis, while the axis itself revolves around the vertical line with a very deliberate motion. If we could imagine a vast peg-top which rotated on its axis once a day, and if that axis were inclined at an angle of twenty-three and a half degrees[Pg 495] to the vertical, and if the slow conical motion of the axis were such that the revolution of the axis were completed in about 26,000 years, then the movements would resemble those actually made by the earth. The illustration of the peg-top comes, indeed, very close to the actual phenomenon of precession. In each case the rotation about the axis is far more rapid than that of the revolution of the axis itself; in each case also the slow movement is due to an external interference. Looking at the figure of the peg-top (Fig. 101) we may ask the question, Why does it not fall down? The obvious effect of gravity would seem to say that it is impossible for the peg-top to be in the position shown in the figure. Yet everybody knows that this is possible so long as the top is spinning. If the top were not spinning, it would, of course, fall. It therefore follows that the effect of the rapid rotation of the top so modifies the effect of gravitation that the latter, instead of producing its apparently obvious consequence, causes the slow conical motion of the axis of rotation. This is, no doubt, a dynamical question of some difficulty, but it is easy to verify experimentally that it is the case. If a top be constructed so that the point about which it is spinning shall coincide with the centre of gravity, then there is no effect of gravitation on the top, and there is no conical motion perceived.
If the earth were subject to no external interference, then the direction of the axis about which it rotates must remain for ever constant; but as the direction of the axis does not remain constant, it is necessary to seek for a disturbing force adequate to the production of the phenomena which are observed. We have invariably found that the dynamical phenomena of astronomy can be accounted for by the law of universal gravitation. It is therefore natural to enquire how far gravitation will render an account of the phenomenon of precession; and to put the matter in its simplest form, let us consider the effect which a[Pg 496] distant attracting body can have upon the rotation of the earth.
To answer this question, it becomes necessary to define precisely what we mean by the earth; and as for most purposes of astronomy we regard the earth as a spherical globe, we shall commence with this assumption. It seems also certain that the interior of the earth is, on the whole, heavier than the outer portions. It is therefore reasonable to assume that the density increases as we descend; nor is there any sufficient ground for thinking that the earth is much heavier in one part than at any other part equally remote from the centre. It is therefore usual in such calculations to assume that the earth is formed of concentric spherical shells, each one of which is of uniform density; while the density decreases from each shell to the one exterior thereto.
A globe of this constitution being submitted to the attraction of some external body, let us examine the effects which that external body can produce. Suppose, for instance, the sun attracts a globe of this character, what movements will be the result? The first and most obvious result is that which we have already so frequently discussed, and which is expressed by Kepler's laws: the attraction will compel the earth to revolve around the sun in an elliptic path, of which the sun is in the focus. With this movement we are, however, not at this moment concerned. We must enquire how far the sun's attraction can modify the earth's rotation around its axis. It can be demonstrated that the attraction of the sun would be powerless to derange the rotation of the earth so constituted. This is a result which can be formally proved by mathematical calculation. It is, however, sufficiently obvious that the force of attraction of any distant point on a symmetrical globe must pass through the centre of that globe: and as the sun is only an enormous aggregate of attracting points, it can only produce a corresponding multitude of attractive forces; each of these forces passes through the centre of the earth, and consequently the resultant force which expresses the joint result of all the individual forces must also be directed through the centre of the earth. A[Pg 497] force of this character, whatever other potent influence it may have, will be powerless to affect the rotation of the earth. If the earth be rotating on an axis, the direction of that axis would be invariably preserved; so that as the earth revolves around the sun, it would still continue to rotate around an axis which always remained parallel to itself. Nor would the attraction of the earth by any other body prove more efficacious than that of the sun. If the earth really were the symmetrical globe we have supposed, then the attraction of the sun and moon, and even the influence of all the planets as well, would never be competent to make the earth's axis of rotation swerve for a single second from its original direction.
We have thus narrowed very closely the search for the cause of the "precession." If the earth were a perfect sphere, precession would be inexplicable. We are therefore forced to seek for an explanation of precession in the fact that the earth is not a perfect sphere. This we have already demonstrated to be the case. We have shown that the equatorial axis of the earth is longer than the polar axis, so that there is a protuberant zone girdling the equator. The attraction of external bodies is able to grasp this protuberance, and thereby force the earth's axis of rotation to change its direction.
There are only two bodies in the universe which sensibly contribute to the precessional movement of the earth's axis: these bodies are the sun and the moon. The shares in which the labour is borne by the sun and the moon are not what might have been expected from a hasty view of the subject. This is a point on which it will be desirable to dwell, as it illustrates a point in the theory of gravitation which is of very considerable importance.
The law of gravitation asserts that the intensity of the attraction which a body can exercise is directly proportional to the mass of that body, and inversely proportional to the square of its distance from the attracted point. We can thus compare the attraction exerted upon the earth by the sun and by the moon. The mass of the sun exceeds the mass[Pg 498] of the moon in the proportion of about 26,000,000 to 1. On the other hand, the moon is at a distance which, on an average, is about one-386th part of that of the sun. It is thus an easy calculation to show that the efficiency of the sun's attraction on the earth is about 175 times as great as the attraction of the moon. Hence it is, of course, that the earth obeys the supremely important attraction of the sun, and pursues an elliptic path around the sun, bearing the moon as an appendage.
But when we come to that particular effect of attraction which is competent to produce precession, we find that the law by which the efficiency of the attracting body is computed assumes a different form. The measure of efficiency is, in this case, to be found by taking the mass of the body and dividing it by the cube of the distance. The complete demonstration of this statement must be sought in the formulæ of mathematics, and cannot be introduced into these pages; we may, however, adduce one consideration which will enable the reader in some degree to understand the principle, though without pretending to be a demonstration of its accuracy. It will be obvious that the nearer the disturbing body approaches to the earth the greater is the leverage (if we may use the expression) which is afforded by the protuberance at the equator. The efficiency of a given force will, therefore, on this account alone, increase in the inverse proportion of the distance. The actual intensity of the force itself augments in the inverse square of the distance, and hence the capacity of the attracting body for producing precession will, for a double reason, increase when the distance decreases. Suppose, for example, that the disturbing body is brought to half its original distance from the disturbed body, the leverage is by this means doubled, while the actual intensity of the force is at the same time quadrupled according to the law of gravitation. It will follow that the effect produced in the latter case must be eight times as great as in the former case. And this is merely equivalent to the statement that the precession-producing capacity of a body varies inversely as the cube of the distance.
It is this consideration which gives to the moon an[Pg 499] importance as a precession-producing agent to which its mere attractive capacity would not have entitled it. Even though the mass of the sun be 26,000,000 times as great as the mass of the moon, yet when this number is divided by the cube of the relative value of the distances of the bodies (386), it is seen that the efficiency of the moon is more than twice as great as that of the sun. In other words, we may say that one-third of the movement of precession is due to the sun, and two-thirds to the moon.
For the study of the joint precessional effect due to the sun and the moon acting simultaneously, it will be advantageous to consider the effect produced by the two bodies separately; and as the case of the sun is the simpler of the two, we shall take it first. As the earth travels in its annual path around the sun, the axis of the earth is directed to a point in the heavens which is 23-1⁄2° from the pole of the ecliptic. The precessional effect of the sun is to cause this point—the pole of the earth—to revolve, always preserving the same angular distance from the pole of the ecliptic; and thus we have a motion of the type represented in the diagram. As the ecliptic occupies a position which for our present purpose we may regard as fixed in space, it follows that the pole of the ecliptic is a fixed point on the surface of the heavens; so that the path of the pole of the earth must be a small circle in the heavens, fixed in its position relatively to the surrounding stars. In this we find a motion strictly analogous to that of the peg-top. It is the gravitation of the earth acting upon the peg-top which forces it into the conical motion. The immediate effect of the gravitation is so modified by the rapid rotation of the top, that, in obedience to a profound dynamical principle, the axis of the top revolves in a cone rather than fall down, as it would do were the top not spinning. In a similar manner the immediate effect of the sun's attraction on the protuberance at the equator would be to bring the pole of the earth's axis towards the pole of the ecliptic, but the rapid rotation of the earth modifies this into the conical movement of precession.
The circumstances with regard to the moon are much more[Pg 500] complicated. The moon describes a certain orbit around the earth; that orbit lies in a certain plane, and that plane has, of course, a certain pole on the celestial sphere. The precessional effect of the moon would accordingly tend to make the pole of the earth's axis describe a circle around that point in the heavens which is the pole of the moon's orbit. This point is about 5° from the pole of the ecliptic. The pole of the earth is therefore solicited by two different movements—one a revolution around the pole of the ecliptic, the other a revolution about another point 5° distant, which is the pole of the moon's orbit. It would thus seem that the earth's pole should make a certain composite movement due to the two separate movements. This is really the case, but there is a point to be very carefully attended to, which at first seems almost paradoxical. We have shown how the potency of the moon as a precessional agent exceeds that of the sun, and therefore it might be thought that the composite movement of the earth's pole would conform more nearly to a rotation around the pole of the plane of the moon's orbit than to a rotation around the pole of the ecliptic; but this is not the case. The precessional movement is represented by a revolution around the pole of the ecliptic, as is shown in the figure. Here lies the germ of one of those exquisite astronomical discoveries which delight us by illustrating some of the most subtle phenomena of nature.
The plane in which the moon revolves does not occupy a constant position. We are not here specially concerned with the causes of this change in the plane of the moon's orbit, but the character of the movement must be enunciated. The inclination of this plane to the ecliptic is about 5°, and this inclination does not vary (except within very narrow limits); but the line of intersection of the two planes does vary, and, in fact, varies so quickly that it completes a revolution in about 18-2⁄3 years. This movement of the plane of the moon's orbit necessitates a corresponding change in the position of its pole. We thus see that the pole of the moon's orbit must be actually revolving around the pole of the ecliptic, always remaining at the same distance of 5°, and completing its revolution in 18-2⁄3[Pg 501] years. It will, therefore, be obvious that there is a profound difference between the precessional effect of the sun and of the moon in their action on the earth. The sun invites the earth's pole to describe a circle around a fixed centre; the moon invites the earth's pole to describe a circle around a centre which is itself in constant motion. It fortunately happens that the circumstances of the case are such as to reduce considerably the complexity of the problem. The movement of the moon's plane, only occupying about 18-2⁄3 years, is a very rapid motion compared with the whole precessional movement, which occupies about 26,000 years. It follows that by the time the earth's axis has completed one circuit of its majestic cone, the pole of the moon's plane will have gone round about 1,400 times. Now, as this pole really only describes a comparatively small cone of 5° in radius, we may for a first approximation take the average position which it occupies; but this average position is, of course, the centre of the circle which it describes—that is, the pole of the ecliptic.
We thus see that the average precessional effect of the moon simply conspires with that of the sun to produce a revolution around the pole of the ecliptic. The grosser phenomena of the movements of the earth's axis are to be explained by the uniform revolution of the pole in a circular path; but if we make a minute examination of the track of the earth's axis, we shall find that though it, on the whole, conforms with the circle, yet that it really traces out a sinuous line, sometimes on the inside and sometimes on the outside of the circle. This delicate movement arises from the continuous change in the place of the pole of the moon's orbit. The period of these undulations is 18-2⁄3 years, agreeing exactly with the period of the revolution of the moon's nodes. The amount by which the pole departs from the circle on either side is only about 9·2 seconds—a quantity rather less than the twenty-thousandth part of the radius of the sphere. This phenomenon, known as "nutation," was discovered by the beautiful telescopic researches of Bradley, in 1747. Whether we look at the theoretical interest of the subject or at the refinement of the observations involved, this achievement of the "Vir incomparabilis," as Bradley has[Pg 502] been called by Bessel, is one of the masterpieces of astronomical genius.
The phenomena of precession and nutation depend on movements of the earth itself, and not on movements of the axis of rotation within the earth. Therefore the distance of any particular spot on the earth from the north or south pole is not disturbed by either of these phenomena. The latitude of a place is the distance of the place from the earth's equator, and this quantity remains unaltered in the course of the long precession cycle of 26,000 years. But it has been discovered within the last few years that latitudes are subject to a small periodic change of a few tenths of a second of arc. This was first pointed out about 1880 by Dr. Küstner, of Berlin, and by a masterly analysis of all available observations, made in the course of many years past at various observatories, Dr. Chandler, of Boston, has shown that the latitude of every point on the earth is subject to a double oscillation, the period of one being 427 days and the other about a year, the mean amplitude of each being O´´·14. In other words, the spot in the arctic regions, directly in the prolongation of the earth's axis of rotation, is not absolutely fixed; the end of the imaginary axis moves about in a complicated manner, but always keeping within a few yards of its average position. This remarkable discovery is not only of value as introducing a new refinement in many astronomical researches depending on an accurate knowledge of the latitude, but theoretical investigations show that the periods of this variation are incompatible with the assumption that the earth is an absolutely rigid body. Though this assumption has in other ways been found to be untenable, the confirmation of this view by the discovery of Dr. Chandler is of great importance.
The Real and Apparent Movements of the Stars—How they can be Discriminated—Aberration produces Effects dependent on the Position of the Stars—The Pole of the Ecliptic—Aberration makes Stars seem to Move in a Circle, an Ellipse, or a Straight Line according to Position—All the Ellipses have Equal Major Axes—How is this Movement to be Explained?—How to be Distinguished from Annual Parallax—The Apex of the Earth's Way—How this is to be Explained by the Velocity of Light—How the Scale of the Solar System can be Measured by the Aberration of Light.
We have in this chapter to narrate a discovery of a recondite character, which illustrates in a forcible manner some of the fundamental truths of Astronomy. Our discussion of it will naturally be divided into two parts. In the first part we must describe the nature of the phenomenon, and then we must give the extremely elegant explanation afforded by the properties of light. The telescopic discovery of aberration, as well as its explanation, are both due to the illustrious Bradley.
The expression fixed star, so often used in astronomy, is to be received in a very qualified sense. The stars are, no doubt, well fixed in their places, so far as coarse observation is concerned. The lineaments of the constellations remain unchanged for centuries, and, in contrast with the ceaseless movements of the planets, the stars are not inappropriately called fixed. We have, however, had more than one occasion to show throughout the course of this work that the expression "fixed star" is not an accurate one when minute quantities are held in estimation. With the exact measures of modern instruments, many of these quantities are so perceptible that they have to be always reckoned with in astronomical enquiry. We can divide the[Pg 504] movements of the stars into two great classes: the real movements and the apparent movements. The proper motion of the stars and the movements of revolution of the binary stars constitute the real movements of these bodies. These movements are special to each star, so that two stars, although close together in the heavens, may differ in the widest degree as to the real movements which they possess. It may, indeed, sometimes happen that stars in a certain region are animated with a common movement. In this phenomenon we have traces of a real movement shared by a number of stars in a certain group. With this exception, however, the real movements of the stars seem to be governed by no systematic law, and the rapidly moving stars are scattered here and there indiscriminately over the heavens.
The apparent movements of the stars have a different character, inasmuch as we find the movement of each star determined by the place which it occupies in the heavens. It is by this means that we discriminate the real movements of the star from its apparent movements, and examine the character of both.
In the present chapter we are concerned with the apparent movements only, and of these there are three, due respectively to precession, to nutation, and to aberration. Each of these apparent movements obeys laws peculiar to itself, and thus it becomes possible to analyse the total apparent motion, and to discriminate the proportions in which the precession, the nutation, and the aberration have severally contributed. We are thus enabled to isolate the effect of aberration as completely as if it were the sole agent of apparent displacement, so that, by an alliance between mathematical calculation and astronomical observation, we can study the effects of aberration as clearly as if the stars were affected by no other motions.
Concentrating our attention solely on the phenomena of aberration we shall describe its particular effect upon stars in different regions of the sky, and thus ascertain the laws according to which the effects of aberration are exhibited. When this step has been taken, we shall be in a position to[Pg 505] give the beautiful explanation of those laws dependent upon the velocity of light.
At one particular region of the heavens the effect of aberration has a degree of simplicity which is not manifested anywhere else. This region lies in the constellation Draco, at the pole of the ecliptic. At this pole, or in its immediate neighbourhood, each star, in virtue of aberration, describes a circle in the heavens. This circle is very minute; it would take something like 2,000 of these circles together to form an area equal to the area of the moon. Expressed in the usual astronomical language, we should say that the diameter of this small circle is about 40·9 seconds of arc. This is a quantity which, though small to the unaided eye, is really of great relative magnitude in the present state of telescopic research. It is not only large enough to be perceived, but it can be measured, with an accuracy which actually does not admit of a doubt, to the hundredth part of the whole. It is also observed that each star describes its little circle in precisely the same period of time; and that period is one year, or, in other words, the time of the revolution of the earth around the sun. It is found that for all stars in this region, be they large stars or small, single or double, white or coloured, the circles appropriate to each have all the same size, and are all described in the same time. Even from this alone it would be manifest that the cause of the phenomenon cannot lie in the star itself. This unanimity in stars of every magnitude and distance requires some simpler explanation.
Further examination of stars in different regions sheds new light on the subject. As we proceed from the pole of the ecliptic, we still find that each star exhibits an annual movement of the same character as the stars just considered. In one respect, however, there is a difference. The apparent path of the star is no longer a circle; it has become an ellipse. It is, however, soon perceived that the shape and the position of this ellipse are governed by the simple law that the further the star is from the pole of the ecliptic the greater is the eccentricity of the ellipse. The apparent path of the stars[Pg 506] at the same distance from the pole have equal eccentricity, and of the axes of the ellipse the shorter is always directed to the pole, the longer being, of course, perpendicular to it. It is, however, found that no matter how great the eccentricity may become, the major axis always retains its original length. It is always equal to about 40·9 seconds—that is, to the diameter of the circle of aberration at the pole itself. As we proceed further and further from the pole of the ecliptic, we find that each star describes a path more and more eccentric, until at length, when we examine a star on the ecliptic, the ellipse has become so attenuated that it has flattened into a line. Each star which happens to lie on the ecliptic oscillates to and fro along the ecliptic through an amplitude of 40·9 seconds. Half a year accomplishes the journey one way, and the other half of the year restores the star to its original position. When we pass to stars on the southern side of the ecliptic, we see the same series of changes proceed in an inverse order. The ellipse, from being actually linear, gradually grows in width, though still preserving the same length of major axis, until at length the stars near the southern pole of the ecliptic are each found to describe a circle equal to the paths pursued by the stars at the north pole of the ecliptic.
The circumstance that the major axes of all those ellipses are of equal length suggests a still further simplification. Let us suppose that every star, either at the pole of the ecliptic or elsewhere, pursues an absolutely circular path, and that all these circles agree not only in magnitude, but also in being all parallel to the plane of the ecliptic: it is easy to see that this simple supposition will account for the observed facts. The stars at the pole of the ecliptic will, of course, show their circles turned fairly towards us, and we shall see that they pursue circular paths. The circular paths of the stars remote from the pole of the ecliptic will, however, be only seen somewhat edgewise, and thus the apparent paths will be elliptical, as we actually find them. We can even calculate the degree of ellipticity which this surmise would require, and we find that it coincides with[Pg 507] the observed ellipticity. Finally, when we observe stars actually moving in the ecliptic, the circles they follow would be seen edgewise, and thus the stars would have merely the linear movement which they are seen to possess. All the observed phenomena are thus found to be completely consistent with the supposition that every star of all the millions in the heavens describes once each year a circular path; and that, whether the star be far or near, this circle has always the same apparent diameter, and lies in a plane always parallel to the plane of the ecliptic.
We have now wrought the facts of observation into a form which enables us to examine into the cause of a movement so systematic. Why is it that each star should seem to describe a small circular path? Why should that path be parallel to the ecliptic? Why should it be completed exactly in a twelvemonth? We are at once referred to the motion of the earth around the sun. That movement takes place in the ecliptic. It is completed in a year. The coincidences are so obvious that we feel almost necessarily compelled to connect in some way this apparent movement of the stars with the annual movement of the earth around the sun. If there were no such connection, it would be in the highest degree improbable that the planes of the circles should be all parallel to the ecliptic, or that the time of revolution of each star in its circle should equal that of the revolution of the earth around the sun. As both these conditions are fulfilled, the probability of the connection rises to a value almost infinite.
The important question has then arisen as to why the movement of the earth around the sun should be associated in so remarkable a manner with this universal star movement. There is here one obvious point to be noticed and to be dismissed. We have in a previous chapter discussed the important question of the annual parallax of stars, and we have shown how, in virtue of annual parallax, each star describes an ellipse. It can further be demonstrated that these ellipses are really circles parallel to the ecliptic; so that we might hastily assume that annual parallax was the cause of the phenomenon discovered by Bradley. A single circumstance will, however, dispose of this[Pg 508] suggestion. The circle described by a star in virtue of annual parallax has a magnitude dependent on the distance of the star, so that the circles described by various stars are of various dimensions, corresponding to the varied distances of different stars. The phenomena of aberration, however, distinctly assert that the circular path of each star is of the same size, quite independently of what its distance may be, and hence annual parallax will not afford an adequate explanation. It should also be noticed that the movements of a star produced by annual parallax are much smaller than those due to aberration. There is not any known star whose circular path due to annual parallax has a diameter one-twentieth part of that of the circle due to aberration; indeed, in the great majority of cases the parallax of the star is an absolutely insensible quantity.
There is, however, a still graver and quite insuperable distinction between the parallactic path and the aberrational path. Let us, for simplicity, think of a star situated near the pole of the ecliptic, and thus appearing to revolve annually in a circle, whether we regard either the phenomenon of parallax or of aberration. As the earth revolves, so does the star appear to revolve; and thus to each place of the earth in its orbit corresponds a certain place of the star in its circle. If the movement arise from annual parallax, it is easy to see where the place of the star will be for any position of the earth. It is, however, found that in the movement discovered by Bradley the star never has the position which parallax assigns to it, but is, in fact, a quarter of the circumference of its little circle distant therefrom.
A simple rule will find the position of the star due to aberration. Draw from the centre of the ellipse a radius parallel to the direction in which the earth is moving at the moment in question, then the extremity of this radius gives the point on its ellipse where the star is to be found. Tested at all seasons, and with all stars, this law is found to be always verified, and by its means we are conducted to the true explanation of the phenomenon.
We can enunciate the effects of aberration in a somewhat different manner, which will show even more forcibly how the[Pg 509] phenomenon is connected with the motion of the earth in its orbit. As the earth pursues its annual course around the sun, its movement at any moment may be regarded as directed towards a certain point of the ecliptic. From day to day, and even from hour to hour, the point gradually moves along the ecliptic, so as to complete the circuit in a year. At each moment, however, there is always a certain point in the heavens towards which the earth's motion is directed. It is, in fact, the point on the celestial sphere towards which the earth would travel continuously if, at the moment, the attraction of the sun could be annihilated. It is found that this point is intimately connected with the phenomenon of aberration. In fact, the aberration is really equivalent to drawing each star from its mean place towards the Apex of the Earth's Way, as the point is sometimes termed. It can also be shown by observation that the amount of aberration depends upon the distance from the apex. A star which happened to lie on the ecliptic will not be at all deranged by aberration from its mean place when it happens that the apex coincides with the star. All the stars 10° from the apex will be displaced each by the same amount, and all directly in towards the apex. A star 20° from the apex will undergo a larger degree of displacement, though still in the same direction, exactly towards the apex; and all stars at the same distance will be displaced by the same amount. Proceeding thus from the apex, we come to stars at a distance of 90° therefrom. Here the amount of displacement will be a maximum. Each one will be about twenty seconds from its average place; but in every case the imperative law will be obeyed, that the displacement of the star from its mean place lies towards the apex of the earth's way. We have thus given two distinct descriptions of the phenomenon of aberration. In the first we find it convenient to speak of a star as describing a minute circular path; in the other we have regarded aberration as merely amounting to a derangement of the star from its mean place in accordance with specified laws. These descriptions are not inconsistent: they are, in fact, geometrically equivalent; but the latter is rather the more perfect, inasmuch as it assigns completely the direction and extent of the[Pg 510] derangement caused by aberration in any particular star at any particular moment.
The question has now been narrowed to a very definite form. What is it which makes each star seem to close in towards the point towards which the earth is travelling? The answer will be found when we make a minute enquiry into the circumstances in which we view a star in the telescope.
The beam of rays from a star falls on the object-glass of a telescope; those rays are parallel, and after they pass through the object-glass they converge to a focus near the eye end of the instrument. Let us first suppose that the telescope is at rest; then if the telescope be pointed directly towards the star, the rays will converge to a point at the centre of the field of view where a pair of cross wires are placed, whose intersection defines the axis of the telescope. The case will, however, be altered if the telescope be moved after the light has passed through the objective; the rays of light in the interior of the tube will pursue a direct path, as before, and will proceed to a focus at the same precise point as before. As, however, the telescope has moved, it will, of course, have carried with it the pair of cross wires; they will no longer be at the same point as at first, and consequently the image of the star will not now coincide with their intersection.
The movement of the telescope arises from its connection with the earth: for as the earth hurries along at a speed of eighteen miles a second, the telescope is necessarily displaced with this velocity. It might at first be thought, that in the incredibly small fraction of time necessary for light to pass from the object-glass to the eye-piece, the change in the position of the telescope must be too minute to be appreciable. Let us suppose, for instance, that the star is situated near the pole of the ecliptic, then the telescope will be conveyed by the earth's motion in a direction perpendicular to its length. If the tube of the instrument be about twenty feet long, it can be readily demonstrated that during the time the light travels down the tube the movement of the earth will convey the telescope through a distance of about one-fortieth of an inch.[42][Pg 511] This is a quantity very distinctly measurable with the magnifying power of the eye-piece, and hence this derangement of the star's place is very appreciable. It therefore follows that if we wish the star to be shown at the centre of the instrument, the telescope is not to be pointed directly at the star, as it would have to be were the earth at rest, but the telescope must be pointed a little in advance of the star's true position; and as we determine the apparent place of the star by the direction in which the telescope is pointed, it follows that the apparent place of the star is altered by the motion of the earth.
Every circumstance of the change in the star's place admits of complete explanation in this manner. Take, for instance, the small circular path which each star appears to describe. We shall, for simplicity, refer only to a star at the pole of the ecliptic. Suppose that the telescope is pointed truly to the place of the star, then, as we have shown, the image of the star will be at a distance of one-fortieth of an inch from the cross wires. This distance will remain constant, but each night the direction of the star from the cross wires will change, so that in the course of the year it completes a circle, and returns to its original position. We shall not pursue the calculations relative to other stars; suffice it here to say that the movement of the earth has been found adequate to account for the phenomena, and thus the doctrine of the aberration of light is demonstrated.
It remains to allude to one point of the utmost interest and importance. We have seen that the magnitude of the aberration can be measured by astronomical observation. The amount of this aberration depends upon the velocity of light, and on the velocity with which the earth's motion is performed. We can measure the velocity of light by independent measurements, in the manner already explained in Chapter XII. We are thus enabled to calculate what the velocity of the earth[Pg 512] must be, for there is only one particular velocity for the earth which, when combined with the measured velocity of light, will give the measured value of aberration. The velocity of the earth being thus ascertained, and the length of the year being known, it is easy to find the circumference of the earth's path, and therefore its radius; that is, the distance from the earth to the sun.
Here is indeed a singular result, and one which shows how profoundly the various phenomena of science are interwoven. We make experiments in our laboratory, and find the velocity of light. We observe the fixed stars, and measure the aberration. We combine these results, and deduce therefrom the distance from the earth to the sun! Although this method of finding the sun's distance is one of very great elegance, and admits of a certain amount of precision, yet it cannot be relied upon as a perfectly unimpeachable method of deducing the great constant. A perfect method must be based on the operations of mere surveying, and ought not to involve recondite physical considerations. We cannot, however, fail to regard the discovery of aberration by Bradley as a most pleasing and beautiful achievement, for it not only greatly improves the calculations of practical astronomy, but links together several physical phenomena of the greatest interest.
Heat and Astronomy—Distribution of Heat—The Presence of Heat in the Earth—Heat in other Celestial Bodies—Varieties of Temperature—The Law of Cooling—The Heat of the Sun—Can its Temperature be Measured?—Radiation connected with the Sun's Bulk—Can the Sun be Exhausting his Resources?—No marked Change has occurred—Geological Evidence as to the Changes of the Sun's Heat Doubtful—The Cooling of the Sun—The Sun cannot be merely an Incandescent Solid Cooling—Combustion will not Explain the Matter—Some Heat is obtained from Meteoric Matter, but this is not Adequate to the Maintenance of the Sun's Heat—The Contraction of a Heated Globe of Gas—An Apparent Paradox—The Doctrine of Energy—The Nebular Theory—Evidence in Support of this Theory—Sidereal Evidence of the Nebular Theory—Herschel's View of Sidereal Aggregation—The Nebulæ do not Exhibit Changes within the Limits of our Observation.
That a portion of a work on astronomy should bear the title placed at the head of this chapter will perhaps strike some of our readers as unusual, if not actually inappropriate. Is not heat, it may be said, a question merely of experimental physics? and how can it be legitimately introduced into a treatise upon the heavenly bodies and their movements? Whatever weight such objections might have once had need not now be considered. The recent researches on heat have shown not only that heat has important bearings on astronomy, but that it has really been one of the chief agents by which the universe has been moulded into its actual form. At the present time no work on astronomy could be complete without some account of the remarkable connection between the laws of heat and the astronomical consequences which follow from those laws.
In discussing the planetary motions and the laws of Kepler, or in discussing the movements of the moon, the proper motions of the stars, or the revolutions of the binary stars, we proceed[Pg 514] on the supposition that the bodies we are dealing with are rigid particles, and the question as to whether these particles are hot or cold does not seem to have any especial bearing. No doubt the ordinary periodic phenomena of our system, such as the revolution of the planets in conformity with Kepler's laws, will be observed for countless ages, whether the planets be hot or cold, or whatever may be the heat of the sun. It must, however, be admitted that the laws of heat introduce certain modifications into the statement of these laws. The effects of heat may not be immediately perceptible, but they exist—they are constantly acting; and in the progress of time they are adequate to effecting the mightiest changes throughout the universe.
Let us briefly recapitulate the circumstances of our system which give to heat its potency. Look first at our earth, which at present seems—on its surface, at all events—to be a body devoid of internal heat; a closer examination will dispel this idea. Have we not the phenomena of volcanoes, of geysers, and of hot springs, which show that in the interior of the earth heat must exist in far greater intensity than we find on the surface? These phenomena are found in widely different regions of the earth. Their origin is, no doubt, involved in a good deal of obscurity, but yet no one can deny that they indicate vast reservoirs of heat. It would indeed seem that heat is to be found everywhere in the deep inner regions of the earth. If we take a thermometer down a deep mine, we find it records a temperature higher than at the surface. The deeper we descend the higher is the temperature; and if the same rate of progress should be maintained through those depths of the earth which we are not able to penetrate, it can be demonstrated that at twenty or thirty miles below the surface the temperature must be as great as that of red-hot iron.
We find in the other celestial bodies abundant evidence of the present or the past existence of heat. Our moon, as we have already mentioned, affords a very striking instance of a body which must once have been very highly heated. The extraordinary volcanoes on its surface place this beyond any[Pg 515] doubt. It is equally true that those volcanoes have been silent for ages, so that, whatever may be the interior condition of the moon, the surface has now cooled down. Extending our view further, we see in the great planets Jupiter and Saturn evidence that they are still endowed with a temperature far in excess of that which the earth has retained; while, when we look at our sun, we see a body in a state of brilliant incandescence, and glowing with a fervour to which we cannot approximate in our mightiest furnaces. The various fixed stars are bodies which glow with heat, like our sun; while we have in the nebulæ objects the existence of which is hardly intelligible to us, unless we admit that they are possessed of heat.
From this rapid survey of the different bodies in our universe one conclusion is obvious. We may have great doubts as to the actual temperature of any individual body of the system; but it cannot be doubted that there is a wide range of temperature among the different bodies. Some are hotter than others. The stars and suns are perhaps the hottest of all; but it is not improbable that they may be immeasurably outnumbered by the cold and dark bodies of the universe, which are to us invisible, and only manifest their existence in an indirect and casual manner.
The law of cooling tells us that every body radiates heat, and that the quantity of heat which it radiates increases when the temperature of the body increases relatively to the surrounding medium. This law appears to be universal. It is obeyed on the earth, and it would seem that it must be equally obeyed by every other body in space. We thus see that each of the planets and each of the stars is continuously pouring forth in all directions a never-ceasing stream of heat. This radiation of heat is productive of very momentous consequences. Let us study them, for instance, in the case of the sun.
Our great luminary emits an incessant flood of radiant heat in all directions. A minute fraction of that heat is intercepted by our earth, and is, directly or indirectly, the source of all life, and of nearly all movement, on our earth. To pour forth heat as the sun does, it is necessary that his temperature[Pg 516] be enormously high. And there are some facts which permit us to form an estimate of what that temperature must actually be.
It is difficult to form any numerical statement of the actual temperature of the sun. The intensity of that temperature vastly transcends the greatest artificial heat, and any attempt to clothe such estimates in figures is necessarily very precarious. But assuming the greatest artificial temperature to be about 4,000° Fahr., we shall probably be well within the truth if we state the effective temperature of the sun to be about 14,000° Fahr. This is the result of a recent investigation by Messrs. Wilson and Gray, which seems to be entitled to considerable weight.
The copious outflow of heat from the sun corresponds with its enormous temperature. We can express the amount of heat in various ways, but it must be remembered that considerable uncertainty still attaches to such measurements. The old method of measuring heat by the quantity of ice melted may be used as an illustration. It is computed that a shell of ice 43-1⁄2 feet thick surrounding the whole sun would in one minute be melted by the sun's heat underneath. A somewhat more elegant illustration was also given by Sir John Herschel, who showed that if a cylindrical glacier 45 miles in diameter were to be continually flowing into the sun with the velocity of light, the end of that glacier would be melted as quickly as it advanced. From each square foot in the surface of the sun emerges a quantity of heat as great as could be produced by the daily combustion of sixteen tons of coal. This is, indeed, an amount of heat which, properly transformed into work, would keep an engine of many hundreds of horse-power running from one year's end to the other. The heat radiated from a few acres on the sun would be adequate to drive all the steam engines in the world. When we reflect on the vast intensity of the radiation from each square foot of the sun's surface, and when we combine with this the stupendous dimensions of the sun, imagination fails to realise how vast must be the actual expenditure of heat.
In presence of the prodigal expenditure of the sun's heat,[Pg 517] we are tempted to ask a question which has the most vital interest for the earth and its inhabitants. We live from hour to hour by the sun's splendid generosity; and, therefore, it is important for us to know what security we possess for the continuance of his favours. When we witness the terrific disbursement of the sun's heat each hour, we are compelled to ask whether our great luminary may not be exhausting its resources; and if so, what are the prospects of the future? This question we can partly answer. The whole subject is indeed of surpassing interest, and redolent with the spirit of modern scientific thought.
Our first attempt to examine this question must lie in an appeal to the facts which are attainable. We want to know whether the sun is showing any symptoms of decay. Are the days as warm and as bright now as they were last year, ten years ago, one hundred years ago? We can find no evidence of any change since the beginning of authentic records. If the sun's heat had perceptibly changed within the last two thousand years, we should expect to find corresponding changes in the distribution of plants and of animals; but no such changes have been detected. There is no reason to think that the climate of ancient Greece or of ancient Rome was appreciably different from the climates of the Greece and the Rome that we know at this day. The vine and the olive grow now where they grew two thousand years ago.
We must not, however, lay too much stress on this argument; for the effects of slight changes in the sun's heat may have been neutralised by corresponding adaptations in the pliable organisms of cultivated plants. All we can certainly conclude is that no marked change has taken place in the heat of the sun during historical time. But when we come to look back into much earlier ages, we find copious evidence that the earth has undergone great changes in climate. Geological records can on this question hardly be misinterpreted. Yet it is curious to note that these changes are hardly such as could arise from the gradual exhaustion of the sun's radiation. No doubt, in very early times we[Pg 518] have evidence that the earth's climate must have been much warmer than at present. We had the great carboniferous period, when the temperature must almost have been tropical in Arctic latitudes. Yet it is hardly possible to cite this as evidence that the sun was then much more powerful; for we are immediately reminded of the glacial period, when our temperate zones were overlaid by sheets of solid ice, as Northern Greenland is at present. If we suppose the sun to have been hotter than it is at present to account for the vegetation which produced coal, then we ought to assume the sun to be colder than it is now to account for the glacial period. It is not reasonable to attribute such phenomena to fluctuations in the radiation from the sun. The glacial periods prove that we cannot appeal to geology in aid of the doctrine that a secular cooling of the sun is now in progress. The geological variations of climate may have been caused by changes in the earth itself, or by changes in its actual orbit; but however they have been caused, they hardly tell us much with regard to the past history of our sun.
The heat of the sun has lasted countless ages; yet we cannot credit the sun with the power of actually creating heat. We must apply to the tremendous mass of the sun the same laws which we have found by our experiments on the earth. We must ask, whence comes the heat sufficient to supply this lavish outgoing? Let us briefly recount the various suppositions that have been made.
Place two red-hot spheres of iron side by side, a large one and a small one. They have been taken from the same fire; they were both equally hot; they are both cooling, but the small sphere cools more rapidly. It speedily becomes dark, while the large sphere is still glowing, and would continue to do so for some minutes. The larger the sphere, the longer it will take to cool; and hence it has been supposed that a mighty sphere of the prodigious dimensions of our sun would, if once heated, cool gradually, but the duration of the cooling would be so long that for thousands and for millions of years it could continue to be a source of light[Pg 519] and heat to the revolving system of planets. This suggestion will not bear the test of arithmetic. If the sun had no source of heat beyond that indicated by its high temperature, we can show that radiation would cool the sun a few degrees every year. Two thousand years would then witness a very great decrease in the sun's heat. We are certain that no such decrease can have taken place. The source of the sun's radiation cannot be found in the mere cooling of an incandescent mass.
Can the fires in the sun be maintained by combustion, analogous to that which goes on in our furnaces? Here we would seem to have a source of gigantic heat; but arithmetic also disposes of this supposition. We know that if the sun were made of even solid coal itself, and if that coal were burning in pure oxygen, the heat that could be produced would only suffice for 6,000 years. If the sun which shone upon the builders of the great Pyramid had been solid coal from surface to centre, it must by this time have been in great part burned away in the attempt to maintain its present rate of expenditure. We are thus forced to look to other sources for the supply of the sun's heat, since neither the heat of incandescence nor the heat of combustion will suffice.
There is probably—indeed, we may say certainly—one external source from which the heat of the sun is recruited. It will be necessary for us to consider this source with some care, though I think we shall find it to be merely an auxiliary of comparatively trifling moment. According to this view, the solar heat receives occasional accessions from the fall upon the sun's surface of masses of meteoric matter. There can be hardly a doubt that such masses do fall upon the sun; there is certainly no doubt that if they do, the sun must gain some heat thereby. We have experience on the earth of a very interesting kind, which illustrates the development of heat by meteoric matter. There lies a world of philosophy in a shooting star. Some of these myriad objects rush into our atmosphere and are lost; others, no doubt, rush into the sun with the same result. We also admit that the descent of a shooting star into the atmosphere of the sun[Pg 520] must be attended with a flash of light and of heat. The heat acquired by the earth from the flashing of the shooting stars through our air is quite insensible. It has been supposed, however, that the heat accruing to the sun from the same cause may be quite sensible—nay, it has been even supposed that the sun may be re-invigorated from this source.
Here, again, we must apply the cold principles of weights and measures to estimate the plausibility of this suggestion. We first calculate the actual weight of meteoric indraught to the sun which would be adequate to sustain the fires of the sun at their present vigour. The mass of matter that would be required is so enormous that we cannot usefully express it by imperial weights; we must deal with masses of imposing magnitude. It fortunately happens that the weight of our moon is a convenient unit. Conceive that our moon—a huge globe, 2,000 miles in diameter—were crushed into a myriad of fragments, and that these fragments were allowed to rain in on the sun; there can be no doubt that this tremendous meteoric shower would contribute to the sun rather more heat than would be required to supply his radiation for a whole year. If we take our earth itself, conceive it comminuted into dust, and allow that dust to fall on the sun as a mighty shower, each fragment would instantly give out a quantity of heat, and the whole would add to the sun a supply of heat adequate to sustain the present rate of radiation for nearly one hundred years. The mighty mass of Jupiter treated in the same way would generate a meteoric display greater in the ratio in which the mass of Jupiter exceeds the mass of earth. Were Jupiter to fall into the sun, enough heat would be thereby produced to scorch the whole solar system; while all the planets together would be capable of producing heat which, if properly economised, would supply the radiation of the sun for 45,000 years.
It must be remembered that though the moon could supply one year's heat, and Jupiter 30,000 years' heat, yet the practical question is not whether the solar system could supply the sun's heat, but whether it does. Is it likely that meteors equal in mass to the moon fall into the sun[Pg 521] every year? This is the real question, and I think we are bound to reply to it in the negative. It can be shown that the quantity of meteors which could be caught by the sun in any one year can be only an excessively minute fraction of the total amount. If, therefore, a moon-weight of meteors were caught every year, there must be an incredible mass of meteoric matter roaming at large through the system. There must be so many meteors that the earth would be incessantly pelted with them, and heated to such a degree as to be rendered uninhabitable. There are also other reasons which preclude the supposition that a stupendous quantity of meteoric matter exists in the vicinity of the sun. Such matter would produce an appreciable effect on the movement of the planet Mercury. There are, no doubt, some irregularities in the movements of Mercury not yet fully explained, but these irregularities are very much less than would be the case if meteoric matter existed in quantity adequate to the sustentation of the sun. Astronomers, then, believe that though meteors may provide a rate in aid of the sun's current expenditure, yet that the greater portion of that expenditure must be defrayed from other resources.
It is one of the achievements of modern science to have effected the solution of the problem—to have shown how it is that, notwithstanding the stupendous radiation, the sun still maintains its temperature. The question is not free from difficulty in its exposition, but the matter is one of such very great importance that we are compelled to make the attempt.
Let us imagine a vast globe of heated gas in space. This is not an entirely gratuitous supposition, inasmuch as there are globes apparently of this character; they have been already alluded to as planetary nebulæ. This globe will radiate heat, and we shall suppose that it emits more heat than it receives from the radiation of other bodies. The globe will accordingly lose heat, or what is equivalent thereto, but it will be incorrect to assume that the globe will necessarily fall in temperature. That the contrary is, indeed, the case is a result almost paradoxical at the first glance; but yet it can be shown to be a necessary consequence of the laws of heat and of gases.
Let us fix our attention on a portion of the gas lying on the surface of the globe. This is, of course, attracted by all the rest of the globe, and thus tends in towards the centre of the globe. If equilibrium subsists, this tendency must be neutralised by the pressure of the gas beneath; so that the greater the gravitation, the greater is the pressure. When the globe of gas loses heat by radiation, let us suppose that it grows colder—that its temperature accordingly falls; then, since the pressure of a gas decreases when the temperature falls, the pressure beneath the superficial layer of the gas will decrease, while the gravitation is unaltered. The consequence will inevitably be that the gravitation will now conquer the pressure, and the globe of gas will accordingly contract. There is, however, another way in which we can look at the matter. We know that heat is equivalent to energy, so that when the globe radiates forth heat, it must expend energy. A part of the energy of the globe will be due to its temperature; but another, and in some respects a more important, part is that due to the separation of its particles. If we allow the particles to come closer together we shall diminish the energy due to separation, and the energy thus set free can take the form of heat. But this drawing in of the particles necessarily involves a shrinking of the globe.
And now for the remarkable consequence, which seems to have a very important application in astronomy. As the globe contracts, a part of its energy of separation is changed into heat; that heat is partly radiated away, but not so rapidly as it is produced by the contraction. The consequence is, that although the globe is really losing heat and really contracting, yet that its temperature is actually rising.[43] A simple case will suffice to demonstrate this result, paradoxical as it may at first seem. Let us suppose that by contraction of the sphere it had diminished to one-half its diameter; and let us fix our attention on a cubic inch of the gaseous matter in any point of the mass. After the contraction has taken place each edge[Pg 523] of the cube would be reduced to half an inch, and the volume would therefore be reduced to one-eighth part of its original amount. The law of gases tells us that if the temperature be unaltered the pressure varies inversely as the volume, and consequently the internal pressure in the cube would in that case be increased eightfold. As, however, in the case before us, the distance between every two particles is reduced to one-half, it will follow that the gravitation between every two particles is increased fourfold, and as the area is also reduced to one-fourth, it will follow that the pressure inside the reduced cube is increased sixteenfold; but we have already seen that with a constant temperature it only increases eightfold, and hence the temperature cannot be constant, but must rise with the contraction.
We thus have the somewhat astonishing result that a gaseous globe in space radiating heat, and thereby growing smaller, is all the time actually increasing in temperature. But, it may be said, surely this cannot go on for ever. Are we to suppose that the gaseous mass will go on contracting and contracting with a temperature ever fiercer and fiercer, and actually radiating out more and more heat the more it loses? Where lies the limit to such a prospect? As the body contracts, its density must increase, until it either becomes a liquid, or a solid, or, at any rate, until it ceases to obey the laws of a purely gaseous body which we have supposed. Once these laws cease to be observed the argument disappears; the loss of heat may then really be attended with a loss of temperature, until in the course of time the body has sunk to the temperature of space itself.
It is not assumed that this reasoning can be applied in all its completeness to the present state of the sun. The sun's density is now so great that the laws of gases cannot be there strictly followed. There is, however, good reason to believe that the sun was once more gaseous than at present; possibly at one time he may have been quite gaseous enough to admit of this reasoning in all its fulness. At present the sun appears to be in some intermediate stage of its progress from the gaseous condition to the solid condition. We cannot,[Pg 524] therefore, say that the temperature of the sun is now increasing in correspondence with the process of contraction. This may be true or it may not be true; we have no means of deciding the point. We may, however, feel certain that the sun is still sufficiently gaseous to experience in some degree the rise of temperature associated with the contraction. That rise in temperature may be partly or wholly obscured by the fall in temperature which would be the more obvious consequence of the radiation of heat from the partially solid body. It will, however, be manifest that the cooling of the sun may be enormously protracted if the fall of temperature from the one cause be nearly compensated by the rise of temperature from the other. It can hardly be doubted that in this we find the real explanation of the fact that we have no historical evidence of any appreciable alteration in the radiation of heat from the sun.
This question is one of such interest that it may be worth while to look at it from a slightly different point of view. The sun contains a certain store of energy, part of which is continually disappearing in the form of radiant heat. The energy remaining in the sun is partly transformed in character; some of it is transformed into heat, which goes wholly or partly to supply the loss by radiation. The total energy of the sun must, however, be decreasing; and hence it would seem the sun must at some time or other have its energy exhausted, and cease to be a source of light and of heat. It is true that the rate at which the sun contracts is very slow. We are, indeed, not able to measure with certainty the decrease in the sun's bulk. It is a quantity so minute, that the contraction since the birth of accurate astronomy is not large enough to be perceptible in our telescopes. It is, however, possible to compute what the contraction of the sun's bulk must be, on the supposition that the energy lost by that contraction just suffices to supply the daily radiation of heat. The change is very small when we consider the present size of the sun. At the present time the sun's diameter is about 860,000 miles. If each year this diameter decreases by about 300 feet, sufficient energy will be yielded to account[Pg 525] for the entire radiation. This gradual decrease is always in progress.
These considerations are of considerable interest when we apply them retrospectively. If it be true that the sun is at this moment shrinking, then in past times his globe must have been greater than it is at present. Assuming the figures already given, it follows that one hundred years ago the diameter of the sun must have been nearly six miles greater than it is now; one thousand years ago the diameter was fifty-seven miles greater; ten thousand years ago the diameter of the sun was five hundred and seventy miles greater than it is to-day. When man first trod this earth it would seem that the sun must have been many hundreds, perhaps many thousands, of miles greater than it is at this time.
We must not, however, over-estimate the significance of this statement. The diameter of the sun is so great, that a diminution of 10,000 miles would be but little more than the hundredth part of its diameter. If it were suddenly to shrink to the extent of 10,000 miles, the change would not be appreciable to ordinary observation, though a much smaller change would not elude delicate astronomical measurement. It does not necessarily follow that the climates on our earth in these early times must have been very different from those which we find at this day, for the question of climate depends upon other matters besides sunbeams.
Yet we need not abruptly stop our retrospect at any epoch, however remote. We may go back earlier and earlier, through the long ages which geologists claim for the deposition of the stratified rocks; and back again still further, to those very earliest epochs when life began to dawn on the earth. Still we can find no reason to suppose that the law of the sun's decreasing heat is not maintained; and thus we would seem bound by our present knowledge to suppose that the sun grows larger and larger the further our retrospect extends. We cannot assume that the rate of that growth is always the same. No such assumption is required; it is sufficient for our purpose that we find the sun growing[Pg 526] larger and larger the further we peer back into the remote abyss of time past. If the present order of things in our universe has lasted long enough, then it would seem that there was a time when the sun must have been twice as large as it is at present; it must once have been ten times as large. How long ago that was no one can venture to say. But we cannot stop at the stage when the sun was even ten times as large as it is at present; the arguments will still apply in earlier ages. We see the sun swelling and swelling, with a corresponding decrease in its density, until at length we find, instead of our sun as we know it, a mighty nebula filling a gigantic region of space.
Such is, in fact, the doctrine of the origin of our system which has been advanced in that celebrated speculation known as the nebular theory of Laplace. Nor can it be ever more than a speculation; it cannot be established by observation, nor can it be proved by calculation. It is merely a conjecture, more or less plausible, but perhaps in some degree necessarily true, if our present laws of heat, as we understand them, admit of the extreme application here required, and if also the present order of things has reigned for sufficient time without the intervention of any influence at present unknown to us. This nebular theory is not confined to the history of our sun. Precisely similar reasoning may be extended to the individual planets: the farther we look back, the hotter and the hotter does the whole system become. It has been thought that if we could look far enough back, we should see the earth too hot for life; back further still, we should find the earth and all the planets red-hot; and back further still, to an exceedingly remote epoch, when the planets would be heated just as much as our sun is now. In a still earlier stage the whole solar system is thought to have been one vast mass of glowing gas, from which the present forms of the sun, with the planets and their satellites, have been gradually evolved. We cannot be sure that the course of events has been what is here indicated; but there are sufficient grounds for thinking that this doctrine substantially represents what has actually occurred.
Many of the features in the solar system harmonise with the supposition that the origin of the system has been that suggested by the nebular theory. We have already had occasion in an earlier chapter to allude to the fact that all the planets perform their revolutions around the sun in the same direction. It is also to be observed that the rotation of the planets on their axes, as well as the movements of the satellites around their primaries, all follow the same law, with two slight exceptions in the case of the Uranian and Neptunian systems. A coincidence so remarkable naturally suggests the necessity for some physical explanation. Such an explanation is offered by the nebular theory. Suppose that countless ages ago a mighty nebula was slowly rotating and slowly contracting. In the process of contraction, portions of the condensed matter of the nebula would be left behind. These portions would still revolve around the central mass, and each portion would rotate on its axis in the same direction. As the process of contraction proceeded, it would follow from dynamical principles that the velocity of rotation would increase; and thus at length these portions would consolidate into planets, while the central mass would gradually contract to form the sun. By a similar process on a smaller scale the systems of satellites were evolved from the contracting primary. These satellites would also revolve in the same direction, and thus the characteristic features of the solar system could be accounted for.
The nebular origin of the solar system receives considerable countenance from the study of the sidereal heavens. We have already dwelt upon the resemblance between the sun and the stars. If, then, our sun has passed through such changes as the nebular theory requires, may we not anticipate that similar phenomena should be met with in other stars? If this be so, it is reasonable to suppose that the evolution of some of the stars may not have progressed so far as has that of the sun, and thus we may be able actually to witness stars in the earlier phases of their development. Let us see how far the telescope responds to these anticipations.
The field of view of a large telescope usually discloses a number of stars scattered over a black background of sky;[Pg 528] but the blackness of the background is not uniform: the practised eye of the skilled observer will detect in some parts of the heavens a faint luminosity. This will sometimes be visible over the whole extent of the field, or it may even occupy several fields. Years may pass on, and still there is no perceptible change. There can be no illusion, and the conclusion is irresistible that the object is a stupendous mass of faintly luminous glowing gas or vapour. This is the simplest type of nebula; it is characterised by extreme faintness, and seems composed of matter of the utmost tenuity. On the other hand we are occasionally presented with the beautiful and striking phenomenon of a definite and brilliant star surrounded by a luminous atmosphere. Between these two extreme types of a faint diffused mass on the one hand, and a bright star with a nebula surrounding it on the other, a graduated series of various other nebulæ can be arranged. We thus have a series of links passing by imperceptible gradations from the most faintly diffused nebulæ on the one side, into stars on the other.
The nebulæ seemed to Herschel to be vast masses of phosphorescent vapour. This vapour gradually cools down, and ultimately condenses into a star, or a cluster of stars. When the varied forms of nebulæ were classified, it almost seemed as if the different links in the process could be actually witnessed. In the vast faint nebulæ the process of condensation had just begun; in the smaller and brighter nebulæ the condensation had advanced farther; while in others, the star, or stars, arising from the condensation had already become visible.
But, it may be asked, how did Herschel know this? what is his evidence? Let us answer this question by an illustration. Go into a forest, and look at a noble old oak which has weathered the storm for centuries; have we any doubt that the oak-tree was once a young small plant, and that it grew stage by stage until it reached maturity? Yet no one has ever followed an oak-tree through its various stages; the brief span of human life has not been long enough to do so. The reason why we believe the oak-tree to have passed through all these stages is, because we are familiar with oak-trees[Pg 529] of every gradation in size, from the seedling up to the noble veteran. Having seen this gradation in a vast multitude of trees, we are convinced that each individual passes through all these stages.
It was by a similar train of reasoning that Herschel was led to adopt the view of the origin of the stars which we have endeavoured to describe. The astronomer's life is not long enough, the life of the human race might not be long enough, to watch the process by which a nebula condenses down so as to form a solid body. But by looking at one nebula after another, the astronomer thinks he is able to detect the various stages which connect the nebula in its original form with the final form. He is thus led to believe that each of the nebulæ passes, in the course of ages, through these stages. And thus Herschel adopted the opinion that stars—some, many, or all—have each originated from what was once a glowing nebula.
Such a speculation may captivate the imagination, but it must be carefully distinguished from the truths of astronomy, properly so called. Remote posterity may perhaps obtain evidence on the subject which to us is inaccessible: our knowledge of nebulæ is too recent. There has not yet been time enough to detect any appreciable changes: for the study of nebulæ can only be said to date from Messier's Catalogue in 1771.
Since Herschel's time, no doubt, many careful drawings and observations of the nebulæ have been obtained; but still the interval has been much too short, and the earlier observations are too imperfect, to enable any changes in the nebulæ to be investigated with sufficient accuracy. If the human race lasts for very many centuries, and if our present observations are preserved during that time for comparison, then Herschel's theory may perhaps be satisfactorily tested.
A hundred years have passed since Laplace, with some diffidence, set forth his hypothesis as to the mode of formation of the solar system. On the whole it must be said that this "nebular hypothesis" has stood the test of advancing science well, though some slight modifications have become[Pg 530] necessary in the light of more recent discoveries. Laplace (and Herschel also) seems to have considered a primitive nebula to consist of a "fiery mist" or glowing gas at a very high temperature. But this is by no means necessary, as we have seen that the gradual contraction of the vast mass supplies energy which may be converted into heat, and the spectroscopic evidence seems also to point to the existence of a moderate temperature in the gaseous nebulæ, which must be considered to be representatives of the hypothetical primitive chaos out of which our sun and planets have been evolved. Another point which has been reconsidered is the formation of the various planets. It was formerly thought that the rotation of the original mass had by degrees caused a number of rings of different dimensions to be separated from the central part, the material of which rings in time collected into single planets. The ring of Saturn was held to be a proof of this process, since we here have a ring, the condensation of which into one or more satellites has somehow been arrested. But while it is not impossible that matter in the shape of rings may have been left behind during the contraction of the nebulous mass (indeed, the minor planets between Mars and Jupiter have perhaps originated in this way), it seems likely that the larger planets were formed from the agglomeration of matter at a point on the equator of the rotating nebula.
The actual steps of the process by which the primeval nebula became transformed into the solar system seem to lie beyond reach of discovery.
Mathematical Astronomy—Lagrange's Theories: how far they are really True—The Solar System not Made of Rigid Bodies—Kepler's Laws True to Observation, but not Absolutely True when the Bodies are not Rigid—The Errors of Observation—The Tides—How the Tides were Observed—Discovery of the Connection between the Tides and the Moon—Solar and Lunar Tides—Work done by the Tides—Whence do the Tides obtain the Power to do the Work?—Tides are Increasing the Length of the Day—Limit to the Shortness of the Day—Early History of the Earth-Moon System—Unstable Equilibrium—Ratio of the Month to the Day—The Future Course of the System—Equality of the Month and the Day—The Future Critical Epoch—The Constant Face of the Moon accounted for—The other Side of the Moon—The Satellites of Mars—Their Remarkable Motions—Have the Tides Possessed Influence in Moulding the Solar System generally?—Moment of Momentum—Tides have had little or no Appreciable Effect on the Orbit of Jupiter—Conclusion.
That the great discoveries of Lagrange on the stability of the planetary system are correct is in one sense strictly true. No one has ever ventured to impugn the mathematics of Lagrange. Given the planetary system in the form which Lagrange assumed and the stability of that system is assured for all time. There is, however, one assumption which Lagrange makes, and on which his whole theory was founded: his assumption is that the planets are rigid bodies.
No doubt our earth seems a rigid body. What can be more solid and unyielding than the mass of rocks and metals which form the earth, so far as it is accessible to us? In the wide realms of space the earth is but as a[Pg 532] particle; it surely was a natural and a legitimate assumption to suppose that that particle was a rigid body. If the earth were absolutely rigid—if every particle of the earth were absolutely at a fixed distance from every other particle—if under no stress of forces, and in no conceivable circumstance, the earth experienced even the minutest change of form—if the same could be said of the sun and of all the other planets—then Lagrange's prediction of the eternal duration of our system must be fulfilled.
But what are the facts of the case? Is the earth really rigid? We know from experiment that a rigid body in the mathematical sense of the word does not exist. Rocks are not rigid; steel is not rigid; even a diamond is not perfectly rigid. The whole earth is far from being rigid even on the surface, while part of the interior is still, perhaps, more or less fluid. The earth cannot be called a perfectly rigid body; still less can the larger bodies of our system be called rigid. Jupiter and Saturn are perhaps hardly even what could be called solid bodies. The solar system of Lagrange consisted of a rigid sun and a number of minute rigid planets; the actual solar system consists of a sun which is in no sense rigid, and planets which are only partially so.
The question then arises as to whether the discoveries of the great mathematicians of the last century will apply, not only to the ideal solar system which they conceived, but to the actual solar system in which our lot has been cast. There can be no doubt that these discoveries are approximately true: they are, indeed, so near the absolute truth, that observation has not yet satisfactorily shown any departure from them.
But in the present state of science we can no longer overlook the important questions which arise when we deal with bodies not rigid in the mathematical sense of the word. Let us, for instance, take the simplest of the laws to which we have referred, the great law of Kepler, which asserts that a planet will revolve for ever in an elliptic path of which the sun is one focus. This is seen to be verified by actual observation; indeed, it was established by observation before any[Pg 533] theoretical explanation of that movement was propounded. If, however, we state the matter with a little more precision, we shall find that what Newton really demonstrated was, that if two rigid particles attract each other by a law of force which varies with the inverse square of the distance between the particles, then each of the particles will describe an ellipse with the common centre of gravity in the focus. The earth is, to some extent, rigid, and hence it was natural to suppose that the relative behaviour of the earth and the sun would, to a corresponding extent, observe the simple elliptic law of Kepler; as a matter of fact, they do observe it with such fidelity that, if we make allowance for other causes of disturbance, we cannot, even by most careful observation, detect the slightest variation in the motion of the earth arising from its want of rigidity.
There is, however, a subtlety in the investigations of mathematics which, in this instance at all events, transcends the most delicate observations which our instruments enable us to make. The principles of mathematics tell us that though Kepler's laws may be true for bodies which are absolutely and mathematically rigid, yet that if the sun or the planets be either wholly, or even in their minutest part, devoid of perfect rigidity, then Kepler's laws can be no longer true. Do we not seem here to be in the presence of a contradiction? Observation tells us that Kepler's laws are true in the planetary system; theory tells us that these laws cannot be true in the planetary system, because the bodies in that system are not perfectly rigid. How is this discrepancy to be removed? Or is there really a discrepancy at all? There is not. When we say that Kepler's laws have been proved to be true by observation, we must reflect on the nature of the proofs which are attainable. We observe the places of the planets with the instruments in our observatories; these places are measured by the help of our clocks and of the graduated circles on the instruments. These observations are no doubt wonderfully accurate; but they do not, they cannot, possess absolute accuracy in the mathematical sense of the word. We can, for instance, determine the place of a planet[Pg 534] with such precision that it is certainly not one second of arc wrong; and one second is an extremely small quantity. A foot-rule placed at a distance of about forty miles subtends an angle of a second, and it is surely a delicate achievement to measure the place of a planet, and feel confident that no error greater than this can have intruded into our result.
When we compare the results of observation with the calculations conducted on the assumption of the truth of Kepler's laws, and when we pronounce on the agreement of the observations with the calculations, there is always a reference, more or less explicit, to the inevitable errors of the observations. If the calculations and observations agree so closely that the differences between the two are minute enough to have arisen in the errors inseparable from the observations, then we are satisfied with the accordance; for, in fact, no closer agreement is attainable, or even conceivable. The influence which the want of rigidity exercises on the fulfilment of the laws of Kepler can be estimated by calculation; it is found, as might be expected, to be extremely small—so small, in fact, as to be contained within that slender margin of error by which observations are liable to be affected. We are thus not able to discriminate by actual measurement the effects due to the absence of rigidity; they are inextricably hid among the small errors of observation.
The argument on which we are to base our researches is really founded on a very familiar phenomenon. There is no one who has ever visited the sea-side who is not familiar with that rise and fall of the sea which we call the tide. Twice every twenty-four hours the sea advances on the beach to produce high tide; twice every day the sea again retreats to produce low tide. These tides are not merely confined to the coasts; they penetrate for miles up the courses of rivers; they periodically inundate great estuaries. In a maritime country the tides are of the most profound practical importance; they also possess a significance of a far less obvious character, which it is our object now to investigate.
These daily pulses of the ocean have long ceased to be a mystery. It was in the earliest times perceived that there was a connection between the tides and the moon. Ancient writers, such as Pliny and Aristotle, have referred to the alliance between the times of high water and the age of the moon. I think we sometimes do not give the ancient astronomers as much credit as their shrewdness really entitles them to. We have all read—we have all been taught—that the moon and the tides are connected together; but how many of us are in a position to say that we have actually noticed that connection by direct personal observation? The first man who studied this matter with sufficient attention to convince himself and to convince others of its reality must have been a great philosopher. We know not his name, we know not his nation, we know not the age in which he lived; but our admiration of his discovery must be increased by the reflection that he had not the theory of gravitation to guide him. A philosopher of the present day who had never seen the sea could still predict the necessity of tides as a consequence of the law of universal gravitation; but the primitive astronomer, who knew not of the invisible bond by which all bodies in the universe are drawn together, made a splendid—indeed, a typical—inductive discovery, when he ascertained the relation between the moon and the tides.
We can surmise that this discovery, in all probability, first arose from the observations of experienced navigators. In all matters of entering port or of leaving port, the state of the tide is of the utmost concern to the sailor. Even in the open sea he has sometimes to shape his course in accordance with the currents produced by the tides; or, in guiding his course by taking soundings, he has always to bear in mind that the depth varies with the tide. All matters relating to the tide would thus come under his daily observation. His daily work, the success of his occupation, the security of his life, depend often on the tides; and hence he would be solicitous to learn from his observation all that would be useful to him in the future. To the coasting sailor the question of the day is the time of high water. That time[Pg 536] varies from day to day; it is an hour or more later to-morrow than to-day, and there is no very simple rule which can be enunciated. The sailor would therefore welcome gladly any rule which would guide him in a matter of such importance. We can make a conjecture as to the manner in which such a rule was first discovered. Let us suppose that a sailor at Calais, for example, is making for harbour. He has a beautiful night—the moon is full; it guides him on his way; he gets safely into harbour; and the next morning he finds the tide high between 11 and 12.[45] He often repeats the same voyage, but he finds sometimes a low and inconvenient tide in the morning. At length, however, it occurs to him that when he has a moonlight night he has a high tide at 11. This occurs once or twice: he thinks it but a chance coincidence. It occurs again and again. At length he finds it always occurs. He tells the rule to other sailors; they try it too. It is invariably found that when the moon is full, the high tide always recurs at the same hour at the same place. The connection between the moon and the tide is thus established, and the intelligent sailor will naturally compare other phases of the moon with the times of high water. He finds, for example, that the moon at the first quarter always gives high water at the same hour of the day; and finally, he obtains a practical rule, by which, from the state of the moon, he can at once tell the time when the tide will be high at the port where his occupation lies. A diligent observer will trace a still further connection between the moon and the tides; he will observe that some high tides rise higher than others, that some low tides fall lower than others. This is a matter of much practical importance. When a dangerous bar has to be crossed, the sailor will feel much additional security in knowing that he is carried over it on the top of a spring tide; or if he has to contend against tidal currents, which in some places have enormous force, he will naturally prefer for his voyage the neap tides, in which the strength of these currents is less[Pg 537] than usual. The spring tides and the neap tides will become familiar to him, and he will perceive that the spring tides occur when the moon is full or new—or, at all events, that the spring tides are within a certain constant number of days of the full or new moon. It was, no doubt, by reasoning such as this, that in primitive times the connection between the moon and the tides came to be perceived.
It was not, however, until the great discovery of Newton had disclosed the law of universal gravitation that it became possible to give a physical explanation of the tides. It was then seen how the moon attracts the whole earth and every particle of the earth. It was seen how the fluid particles which form the oceans on the earth were enabled to obey the attraction in a way that the solid parts could not. When the moon is overhead it tends to draw the water up, as it were, into a heap underneath, and thus to give rise to the high tide. The water on the opposite side of the earth is also affected in a way that might not be at first anticipated. The moon attracts the solid body of the earth with greater intensity than it attracts the water at the other side which lies more distant from it. The earth is thus drawn away from the water, and there is therefore a tendency to a high tide as well on the side of the earth away from the moon as on that towards the moon. The low tides occupy the intermediate positions.
The sun also excites tides on the earth; but owing to the great distance of the sun, the difference between its attraction on the sea and on the solid interior of the earth is not so appreciable. The solar tides are thus smaller than the lunar tides. When the two conspire, they cause a spring tide; when the solar and lunar tides are opposed, we have the neap tide.
There are, however, a multitude of circumstances to be taken into account when we attempt to apply this general reasoning to the conditions of a particular case. Owing to local peculiarities the tides vary enormously at the different parts of the coast. In a confined area like the Mediterranean Sea, the tides have only a comparatively small range, varying[Pg 538] at different places from one foot to a few feet. In mid-ocean also the tidal rise and fall is not large, amounting, for instance, to a range of three feet at St. Helena. Near the great continental masses the tides become very much modified by the coasts. We find at London a tide of eighteen or nineteen feet; but the most remarkable tides in the British Islands are those in the Bristol Channel, where, at Chepstow or Cardiff, there is a rise and fall during spring tides to the height of thirty-seven or thirty-eight feet, and at neap tides to a height of twenty-eight or twenty-nine. These tides are surpassed in magnitude at other parts of the world. The greatest of all tides are those in the Bay of Fundy, at some parts of which the rise and fall at spring tides is not less than fifty feet.
The rising and falling of the tide is necessarily attended with the formation of currents. Such currents are, indeed, well known, and in some of our great rivers they are of the utmost consequence. These currents of water can, like water-streams of any other kind, be made to do useful work. We can, for instance, impound the rising water in a reservoir, and as the tide falls we can compel the enclosed water to work a water-wheel before it returns to the sea. We have, indeed, here a source of actual power; but it is only in very unusual circumstances that it is found to be economical to use the tides for this purpose. The question can be submitted to calculation, and the area of the reservoir can be computed which would retain sufficient water to work a water-wheel of given horse-power. It can be shown that the area of the reservoir necessary to impound water enough to produce 100 horse-power would be 40 acres. The whole question is then reduced to the simple one of expense: would the construction and the maintenance of this reservoir be more or less costly than the erection and the maintenance of a steam-engine of equivalent power? In most cases it would seem that the latter would be by far the cheaper; at all events, we do not practically find tidal engines in use, so that the power of the tides is now running to waste. The economical aspects of the case may, however, be very profoundly altered at some[Pg 539] remote epoch, when our stores of fuel, now so lavishly expended, give appreciable signs of approaching exhaustion.
The tides are, however, doing work of one kind or another. A tide in a river estuary will sometimes scour away a bank and carry its materials elsewhere. We have here work done and energy consumed, just as much as if the same task had been accomplished by engineers directing the powerful arms of navvies. We know that work cannot be done without the consumption of energy in some of its forms; whence, then, comes the energy which supplies the power of the tides? At a first glance the answer to this question seems a very obvious one. Have we not said that the tides are caused by the moon? and must not the energy, therefore, be derived from the moon? This seems plain enough, but, unfortunately, it is not true. It is one of those cases by no means infrequent in Dynamics, where the truth is widely different from that which seems to be the case. An illustration will perhaps make the matter clearer. When a rifle is fired, it is the finger of the rifleman that pulls the trigger; but are we, then, to say that the energy by which the bullet has been driven off has been supplied by the rifleman? Certainly not; the energy is, of course, due to the gunpowder, and all the rifleman did was to provide the means by which the energy stored up in the powder could be liberated. To a certain extent we may compare this with the tidal problem; the tides raised by the moon are the originating cause whereby a certain store of energy is drawn upon and applied to do such work as the tides are competent to perform. This store of energy, strange to say, does not lie in the moon; it is in the earth itself. Indeed, it is extremely remarkable that the moon actually gains energy from the tides by itself absorbing some of the store which exists in the earth. This is not put forward as an obvious result; it depends upon a refined dynamical theorem.
We must clearly understand the nature of this mighty store of energy from which the tides draw their power, and on which the moon is permitted to make large and incessant drafts. Let us see in what sense the earth is said to possess a store of energy. We know that the earth rotates on its axis once[Pg 540] every day. It is this rotation which is the source of the energy. Let us compare the rotation of the earth with the rotation of the fly-wheel belonging to a steam-engine. The rotation of the fly-wheel is really a reservoir, into which the engine pours energy at each stroke of the piston. The various machines in the mill worked by the engine merely draw upon the store of energy accumulated in the fly-wheel. The earth may be likened to a gigantic fly-wheel detached from the engine, though still connected with the machines in the mill. From its stupendous dimensions and from its rapid velocity, that great fly-wheel possesses an enormous store of energy, which must be expended before the fly-wheel comes to rest. Hence it is that, though the tides are caused by the moon, yet the energy they require is obtained by simply appropriating some of the vast supply available from the rotation of the earth.
There is, however, a distinction of a very fundamental character between the earth and the fly-wheel of an engine. As the energy is withdrawn from the fly-wheel and consumed by the various machines in the mill, it is continually replaced by fresh energy, which flows in from the exertions of the steam-engine, and thus the velocity of the fly-wheel is maintained. But the earth is a fly-wheel without the engine. When the tides draw upon the store of energy and expend it in doing work, that energy is not replaced. The consequence is irresistible: the energy in the rotation of the earth must be decreasing. This leads to a consequence of the utmost significance. If the engine be cut off from the fly-wheel, then, as everyone knows, the massive fly-wheel may still give a few rotations, but it will speedily come to rest. A similar inference must be made with regard to the earth; but its store of energy is so enormous, in comparison with the demands which are made upon it, that the earth is able to hold out. Ages of countless duration must elapse before the energy of the earth's rotation can be completely exhausted by such drafts as the tides are capable of making. Nevertheless, it is necessarily true that the energy is decreasing; and if it be decreasing, then the speed of the earth's rotation[Pg 541] must be surely, if slowly, abating. Now we have arrived at a consequence of the tides which admits of being stated in the simplest language. If the speed of rotation be abating, then the length of the day must be increasing; and hence we are conducted to the following most important statement: that the tides are increasing the length of the day.
To-day is longer than yesterday—to-morrow will be longer than to-day. The difference is so small that even in the course of ages it can hardly be said to have been distinctly established by observation. We do not pretend to say how many centuries have elapsed since the day was even one second shorter than it is at present; but centuries are not the units which we employ in tidal evolution. A million years ago it is quite probable that the divergence of the length of the day from its present value may have been very considerable. Let us take a glance back into the profound depths of times past, and see what the tides have to tell us. If the present order of things has lasted, the day must have been shorter and shorter the farther we look back into the dim past. The day is now twenty-four hours; it was once twenty hours, once ten hours; it was once six hours. How much farther can we go? Once the six hours is past, we begin to approach a limit which must at some point bound our retrospect. The shorter the day the more is the earth bulged at the equator; the more the earth is bulged at the equator the greater is the strain put upon the materials of the earth by the centrifugal force of its rotation. If the earth were to go too fast it would be unable to cohere together; it would separate into pieces, just as a grindstone driven too rapidly is rent asunder with violence. Here, therefore, we discern in the remote past a barrier which stops the present argument. There is a certain critical velocity which is the greatest that the earth could bear without risk of rupture, but the exact amount of that velocity is a question not very easy to answer. It depends upon the nature of the materials of the earth; it depends upon the temperature; it depends upon the effect of pressure, and on other details not accurately known to us. An estimate of the critical velocity has, however, been made,[Pg 542] and it has been shown mathematically that the shortest period of rotation which the earth could have, without flying into pieces, is about three or four hours. The doctrine of tidal evolution has thus conducted us to the conclusion that, at some inconceivably remote epoch, the earth was spinning round its axis in a period approximating to three or four hours.
We thus learn that we are indebted to the moon for the gradual elongation of the day from its primitive value up to twenty-four hours. In obedience to one of the most profound laws of nature, the earth has reacted on the moon, and the reaction of the earth has taken a tangible form. It has simply consisted in gradually driving the moon away from the earth. You may observe that this driving away of the moon resembles a piece of retaliation on the part of the earth. The consequence of the retreat of the moon is sufficiently remarkable. The path in which the moon is revolving has at the present time a radius of 240,000 miles. This radius must be constantly growing larger, in consequence of the tides. Provided with this fact, let us now glance back into the past history of the moon. As the moon's distance is increasing when we look forwards, so we find it decreasing when we look backwards. The moon must have been nearer the earth yesterday than it is to-day; the difference is no doubt inappreciable in years, in centuries, or in thousands of years; but when we come to millions of years, the moon must have been significantly closer than it is at present, until at length we find that its distance, instead of 240,000 miles, has dwindled down to 40,000, to 20,000, to 10,000 miles. Nor need we stop—nor can we stop—until we find the moon actually close to the earth's surface. If the present laws of nature have operated long enough, and if there has been no external interference, then it cannot be doubted that the moon and the earth were once in immediate proximity. We can, indeed, calculate the period in which the moon must have been revolving round the earth. The nearer the moon is to the earth the quicker it must revolve; and at the critical epoch when the satellite was[Pg 543] in immediate proximity to our earth it must have completed each revolution in about three or four hours.
This has led to one of the most daring speculations which has ever been made in astronomy. We cannot refrain from enunciating it; but it must be remembered that it is only a speculation, and to be received with corresponding reserve. The speculation is intended to answer the question, What brought the moon into that position, close to the surface of the earth? We will only say that there is the gravest reason to believe that the moon was, at some very early period, fractured off from the earth when the earth was in a soft or plastic condition.
At the beginning of the history we found the earth and the moon close together. We found that the rate of rotation of the earth was only a few hours, instead of twenty-four hours. We found that the moon completed its journey round the primitive earth in exactly the same time as the primitive earth rotated on its axis, so that the two bodies were then constantly face to face. Such a state of things formed what a mathematician would describe as a case of unstable dynamical equilibrium. It could not last. It may be compared to the case of a needle balanced on its point; the needle must fall to one side or the other. In the same way, the moon could not continue to preserve this position. There were two courses open: the moon must either have fallen back on the earth, and been reabsorbed into the mass of the earth, or it must have commenced its outward journey. Which of these courses was the moon to adopt? We have no means, perhaps, of knowing exactly what it was which determined the moon to one course rather than to another, but as to the course which was actually taken there can be no doubt. The fact that the moon exists shows that it did not return to the earth, but commenced its outward journey. As the moon recedes from the earth it must, in conformity with Kepler's laws, require a longer time to complete its revolution. It has thus happened that, from the original period of only a few hours, the duration has increased until it has reached the present number of 656[Pg 544] hours. The rotation of the earth has, of course, also been modified, in accordance with the retreat of the moon. Once the moon had commenced to recede, the earth was released from the obligation which required it constantly to direct the same face to the moon. When the moon had receded to a certain distance, the earth would complete the rotation in less time than that required by the moon for one revolution. Still the moon gets further and further away, and the duration of the revolution increases to a corresponding extent, until three, four, or more days (or rotations of the earth) are identical with the month (or revolution of the moon). Although the number of days in the month increases, yet we are not to suppose that the rate of the earth's rotation is increasing; indeed, the contrary is the fact. The earth's rotation is getting slower, and so is the revolution of the moon, but the retardation of the moon is greater than that of the earth. Even though the period of rotation of the earth has greatly increased from its primitive value, yet the period of the moon has increased still more, so that it is several times as large as that of the rotation of the earth. As ages roll on the moon recedes further and further, its orbit increases, the duration of the revolution augments, until at length a very noticeable epoch is attained, which is, in one sense, a culminating point in the career of the moon. At this epoch the revolution periods of the moon, when measured in rotation periods of the earth, attain their greatest value. It would seem that the month was then twenty-nine days. It is not, of course, meant that the month and the day at that epoch were the month and the day as our clocks now measure time. Both were shorter then than now. But what we mean is, that at this epoch the earth rotated twenty-nine times on its axis while the moon completed one circuit.
This epoch has now been passed. No attempt can be made at present to evaluate the date of that epoch in our ordinary units of measurement. At the same time, however, no doubt can be entertained as to the immeasurable antiquity of the event, in comparison with all historic records; but whether it is to be reckoned in hundreds of[Pg 545] thousands of years, in millions of years, or in tens of millions of years, must be left in great degree to conjecture.
This remarkable epoch once passed, we find that the course of events in the earth-moon system begins to shape itself towards that remarkable final stage which has points of resemblance to the initial stage. The moon still continues to revolve in an orbit with a diameter steadily, though very slowly, growing. The length of the month is accordingly increasing, and the rotation of the earth being still constantly retarded, the length of the day is also continually growing. But the ratio of the length of the month to the length of the day now exhibits a change. That ratio had gradually increased, from unity at the commencement, up to the maximum value of somewhere about twenty-nine at the epoch just referred to. The ratio now begins again to decline, until we find the earth makes only twenty-eight rotations, instead of twenty-nine, in one revolution of the moon. The decrease in the ratio continues until the number twenty-seven expresses the days in the month. Here, again, we have an epoch which it is impossible for us to pass without special comment. In all that has hitherto been said we have been dealing with events in the distant past; and we have at length arrived at the present state of the earth-moon system. The days at this epoch are our well-known days, the month is the well-known period of the revolution of our moon. At the present time the month is about twenty-seven of our days, and this relation has remained sensibly true for thousands of years past. It will continue to remain sensibly true for thousands of years to come, but it will not remain true indefinitely. It is merely a stage in this grand transformation; it may possess the attributes of permanence to our ephemeral view, just as the wings of a gnat seem at rest when illuminated by the electric spark; but when we contemplate the history with time conceptions sufficiently ample for astronomy we realise how the present condition of the earth-moon system can have no greater permanence than any other stage in the history.
Our narrative must, however, now assume a different form. We have been speaking of the past; we have been conducted to the present; can we say anything of the future? Here, again, the tides come to our assistance. If we have rightly comprehended the truth of dynamics (and who is there now that can doubt them?), we shall be enabled to make a forecast of the further changes of the earth-moon system. If there be no interruption from any external source at present unknown to us, we can predict—in outline, at all events—the subsequent career of the moon. We can see how the moon will still follow its outward course. The path in which it revolves will grow with extreme slowness, but yet it will always grow; the progress will not be reversed, at all events, before the final stage of our history has been attained. We shall not now delay to dwell on the intervening stages; we will rather attempt to sketch the ultimate type to which our system tends. In the dim future—countless millions of years to come—this final stage will be approached. The ratio of the month to the day, whose decline we have already referred to, will continue to decline. The period of revolution of the moon will grow longer and longer, but the length of the day will increase much more rapidly than the increase in the duration of the moon's period. From the month of twenty-seven days we shall pass to a month of twenty-six days, and so on, until we shall reach a month of ten days, and, finally, a month of one day.
Let us clearly understand what we mean by a month of one day. We mean that the time in which the moon revolves around the earth will be equal to the time in which the earth rotates around its axis. The length of this day will, of course, be vastly greater than our day. The only element of uncertainty in these enquiries arises when we attempt to give numerical accuracy to the statements. It seems to be as true as the laws of dynamics that a state of the earth-moon system in which the day and the month are equal must be ultimately attained; but when we attempt to state the length of that day we introduce a hazardous[Pg 547] element into the enquiry. In giving any estimate of its length, it must be understood that the magnitude is stated with great reserve. It may be erroneous to some extent, though, perhaps, not to any considerable amount. The length of this great day would seem to be about equal to fifty-seven of our days. In other words, at some critical time in the excessively distant future, the earth will take something like 1,400 hours to perform a rotation, while the moon will complete its journey precisely in the same time.
We thus see how, in some respects, the first stage of the earth-moon system and the last stage resemble each other. In each case we have the day equal to the month. In the first case the day and the month were only a small fraction of our day; in the last stage the day and the month are each a large multiple of our day. There is, however, a profound contrast between the first critical epoch and the last. We have already mentioned that the first epoch was one of unstability—it could not last; but this second state is one of dynamical stability. Once that state has been acquired, it would be permanent, and would endure for ever if the earth and the moon could be isolated from all external interference.
There is one special feature which characterises the movement when the month is equal to the day. A little reflection will show that when this is the case the earth must constantly direct the same face towards the moon. If the day be equal to the month, then the earth and moon must revolve together, as if bound by invisible bands; and whatever hemisphere of the earth be directed to the moon when this state of things commences will remain there so long as the day remains equal to the month.
At this point it is hardly possible to escape being reminded of that characteristic feature of the moon's motion which has been observed from all antiquity. We refer, of course, to the fact that the moon at the present time constantly turns the same face to the earth.
It is incumbent upon astronomers to provide a physical explanation of this remarkable fact. The moon revolves[Pg 548] around our earth once in a definite number of seconds. If the moon always turns the same face to the earth, then it is demonstrated that the moon rotates on its axis once in the same number of seconds also. Now, this would be a coincidence wildly improbable unless there were some physical cause to account for it. We have not far to seek for a cause: the tides on the moon have produced the phenomenon. We now find the moon has a rugged surface, which testifies to the existence of intense volcanic activity in former times. Those volcanoes are now silent—the internal fires in the moon seem to have become exhausted; but there was a time when the moon must have been a heated and semi-molten mass. There was a time when the materials of the moon were so hot as to be soft and yielding, and in that soft and yielding mass the attraction of our earth excited great tides. We have no historical record of these tides (they were long anterior to the existence of telescopes, they were probably long anterior to the existence of the human race), but we know that these tides once existed by the work they have accomplished, and that work is seen to-day in the constant face which the moon turns towards the earth. The gentle rise and fall of the oceans which form our tides present a picture widely different from the tides by which the moon was once agitated. The tides on the moon were vastly greater than those of the earth. They were greater because the weight of the earth is greater than that of the moon, so that the earth was able to produce much more powerful tides in the moon than the moon has ever been able to raise on the earth.
That the moon should bend the same face to the earth depends immediately upon the condition that the moon shall rotate on its axis in precisely the same period as that which it requires to revolve around the earth. The tides are a regulating power of unremitting efficiency to ensure that this condition shall be observed. If the moon rotated more slowly than it ought, then the great lava tides would drag the moon round faster and faster until it attained the desired velocity; and then, but not till then, they would give the moon peace.[Pg 549] Or if the moon were to rotate faster on its axis than in its orbit, again the tides would come furiously into play; but this time they would be engaged in retarding the moon's rotation, until they had reduced the speed of the moon to one rotation for each revolution.
Can the moon ever escape from the thraldom of the tides? This is not very easy to answer, but it seems perhaps not impossible that the moon may, at some future time, be freed from tidal control. It is, indeed, obvious that the tides, even at present, have not the extremely stringent control over the moon which they once exercised. We now see no ocean on the moon, nor do the volcanoes show any trace of molten lava. There can hardly be tides on the moon, but there may be tides in the moon. It may be that the interior of the moon is still hot enough to retain an appreciable degree of fluidity, and if so, the tidal control would still retain the moon in its grip; but the time will probably come, if it have not come already, when the moon will be cold to the centre—cold as the temperature of space. If the materials of the moon were what a mathematician would call absolutely rigid, there can be no doubt that the tides could no longer exist, and the moon would be emancipated from tidal control. It seems impossible to predicate how far the moon can ever conform to the circumstances of an actual rigid body, but it may be conceivable that at some future time the tidal control shall have practically ceased. There would then be no longer any necessary identity between the period of rotation and that of revolution. A gleam of hope is thus projected over the astronomy of the distant future. We know that the time of revolution of the moon is increasing, and so long as the tidal governor could act, the time of rotation must increase sympathetically. We have now surmised a state of things in which the control is absent. There will then be nothing to prevent the rotation remaining as at present, while the period of revolution is increasing. The privilege of seeing the other side of the moon, which has been withheld from all previous astronomers, may thus in the distant future be granted to their successors.
The tides which the moon raises in the earth act as a brake on the rotation of the earth. They now constantly tend to bring the period of rotation of the earth to coincide with the period of revolution of the moon. As the moon revolves once in twenty-seven days, the earth is at present going too fast, and consequently the tidal control at the present moment endeavours to retard the rotation of the earth. The rotation of the moon long since succumbed to tidal control, but that was because the moon was comparatively small and the tidal power of the earth was enormous. But this is the opposite case. The earth is large and more massive than the moon, the tides raised by the moon are but small and weak, and the earth has not yet completely succumbed to the tidal action. But the tides are constant, they never for an instant relax the effort to control, and they are gradually tending to render the day and the month coincident, though the progress is a very slow one.
The theory of the tides leads us to look forward to a remote state of things, in which the moon revolves around the earth in a period equal to the day, so that the two bodies shall constantly bend the same face to each other, provided the tidal control be still able to guide the moon's rotation. So far as the mutual action of the earth and the moon is concerned, such an arrangement possesses all the attributes of permanence. If, however, we venture to project our view to a still more remote future, we can discern an external cause which must prevent this mutual accommodation between the earth and the moon from being eternal. The tides raised by the moon on the earth are so much greater than those raised by the sun, that we have, in the course of our previous reasoning, held little account of the sun-raised tides. This is obviously only an approximate method of dealing with the question. The influence of the solar tide is appreciable, and its importance relatively to the lunar tide will gradually increase as the earth and moon approach the final critical stage. The solar tides will have the effect of constantly applying a further brake to the rotation of the earth. It will therefore follow that, after the day and the month have become equal, a still further[Pg 551] retardation awaits the length of the day. We thus see that in the remote future we shall find the moon revolving around the earth in a shorter time than that in which the earth rotates on its axis.
A most instructive corroboration of these views is afforded by the discovery of the satellites of Mars. The planet Mars is one of the smaller members of our system. It has a mass which is only the eighth part of the mass of the earth. A small planet like Mars has much less energy of rotation to be destroyed than a larger one like the earth. It may therefore be expected that the small planet will proceed much more rapidly in its evolution than the large one; we might, therefore, anticipate that Mars and his satellites have attained a more advanced stage of their history than is the case with the earth and her satellite.
When the discovery of the satellites of Mars startled the world, in 1877, there was no feature which created so much amazement as the periodic time of the interior satellite. We have already pointed out in Chapter X. how Phobos revolves around Mars in a period of 7 hours 39 minutes. The period of rotation of Mars himself is 24 hours 37 minutes, and hence we have the fact, unparalleled in the solar system, that the satellite is actually revolving three times as rapidly as the planet is rotating. There can hardly be a doubt that the solar tides on Mars have abated its velocity of rotation in the manner just suggested.
It has always seemed to me that the matter just referred to is one of the most interesting and instructive in the whole history of astronomy. We have, first, a very beautiful telescopic discovery of the minute satellites of Mars, and we have a determination of the anomalous movement of one of them. We have then found a satisfactory physical explanation of the cause of this phenomenon, and we have shown it to be a striking instance of tidal evolution. Finally, we have seen that the system of Mars and his satellite is really a forecast of the destiny which, after the lapse of ages, awaits the earth-moon system.
It seems natural to enquire how far the influence of tides[Pg 552] can have contributed towards moulding the planetary orbits. The circumstances are here very different from those we have encountered in the earth-moon system. Let us first enunciate the problem in a definite shape. The solar system consists of the sun in the centre, and of the planets revolving around the sun. These planets rotate on their axes; and circulating round some of the planets we have their systems of satellites. For simplicity, we may suppose all the planets and their satellites to revolve in the same plane, and the planets to rotate about axes which are perpendicular to that plane. In the study of the theory of tidal evolution we must be mainly guided by a profound dynamical principle known as the conservation of the "moment of momentum." The proof of this great principle is not here attempted; suffice it to say that it can be strictly deduced from the laws of motion, and is thus only second in certainty to the fundamental truths of ordinary geometry or of algebra. Take, for instance, the giant planet, Jupiter. In one second he moves around the sun through a certain angle. If we multiply the mass of Jupiter by that angle, and if we then multiply the product by the square of the distance from Jupiter to the sun, we obtain a certain definite amount. A mathematician calls this quantity the "orbital" moment of momentum of Jupiter.[46] In the same way, if we multiply the mass of Saturn by the angle through which the planet moves in one second, and this product by the square of the distance between the planet and the sun, then we have the orbital moment of momentum of Saturn. In a similar manner we ascertain the moment of momentum for each of the other planets due to revolution around the sun. We have also to define the moment of momentum of the planets around their axes. In one second Jupiter rotates[Pg 553] through a certain angle; we multiply that angle by the mass of Jupiter, and by the square of a certain line which depends on his internal constitution: the product forms the "rotational" moment of momentum. In a similar manner we find the rotational moment of momentum for each of the other planets. Each satellite revolves through a certain angle around its primary in one second; we obtain the moment of momentum of each satellite by multiplying its mass into the angle described in one second, and then multiplying the product into the square of the distance of the satellite from its primary. Finally, we compute the moment of momentum of the sun due to its rotation. This we obtain by multiplying the angle through which the sun turns in one second by the whole mass of the sun, and then multiplying the product by the square of a certain line of prodigious length, which depends upon the details of the sun's internal structure.
If we have succeeded in explaining what is meant by the moment of momentum, then the statement of the great law is comparatively simple. We are, in the first place, to observe that the moment of momentum of any planet may alter. It would alter if the distance of the planet from the sun changed, or if the velocity with which the planet rotates upon its axis changed; so, too, the moment of momentum of the sun may change, and so may those of the satellites. In the beginning a certain total quantity of moment of momentum was communicated to our system, and not one particle of that total can the solar system, as a whole, squander or alienate. No matter what be the mutual actions of the various bodies of the system, no matter what perturbations they may undergo—what tides may be produced, or even what mutual collisions may occur—the great law of the conservation of moment of momentum must be obeyed. If some bodies in the solar system be losing moment of momentum, then other bodies in the system must be gaining, so that the total quantity shall remain unaltered. This consideration is one of supreme importance in connection with the tides. The distribution of moment[Pg 554] of momentum in the system is being continually altered by the tides; but, however the tides may ebb or flow, the total moment of momentum can never alter so long as influences external to the system are absent.
We must here point out the contrast between the endowment of our system with energy and with moment of momentum. The mutual actions of our system, in so far as they produce heat, tend to squander the energy, a considerable part of which can be thus dissipated and lost; but the mutual actions have no power of dissipating the moment of momentum.
The total moment of momentum of the solar system being taken to be 100, this is at present distributed as follows:—
| Orbital moment of momentum of Jupiter | 60 |
| Orbital moment of momentum of Saturn | 24 |
| Orbital moment of momentum of Uranus | 6 |
| Orbital moment of momentum of Neptune | 8 |
| Rotational moment of momentum of Sun | 2 |
| — | |
| 100 | |
The contributions of the other items are excessively minute. The orbital moments of momentum of the few interior planets contain but little more than one thousandth part of the total amount. The rotational contributions of all the planets and of their satellites is very much less, being not more than one sixty-thousandth part of the whole. When, therefore, we are studying the general effects of tides on the planetary orbits these trifling matters may be overlooked. We shall, however, find it desirable to narrow the question still more, and concentrate our attention on one splendid illustration. Let us take the sun and the planet Jupiter, and, supposing all other bodies of our system to be absent, let us discuss the influence of tides produced in Jupiter by the sun, and of tides in the sun by Jupiter.
It might be hastily thought that, just as the moon was born of the earth, so the planets were born of the sun, and have gradually receded by tides into their present condition.[Pg 555] We have the means of enquiry into this question by the figures just given, and we shall show that it is impossible that Jupiter, or any of the other planets, can ever have been very much closer to the sun than they are at present. In the case of Jupiter and the sun we have the moment of momentum made up of three items. By far the largest of these items is due to the orbital revolution of Jupiter, the next is due to the sun, the third is due to the rotation of Jupiter on its axis. We may put them in round numbers as follows:—
| Orbital moment of momentum of Jupiter | 600,000 |
| Rotational moment of momentum of Sun | 20,000 |
| Rotational moment of momentum of Jupiter | 12 |
The sun produces tides in Jupiter, those tides retard the rotation of Jupiter. They make Jupiter rotate more and more slowly, therefore the moment of momentum of Jupiter is decreasing, therefore its present value of 12 must be decreasing. Even the mighty sun himself may be distracted by tides. Jupiter raises tides in the sun, those tides retard the motion of the sun, and therefore the moment of momentum of the sun is decreasing, and it follows from both causes that the item of 600,000 must be increasing; in other words, the orbital motion of Jupiter must be increasing, or Jupiter must be receding from the sun. To this extent, therefore, the sun-Jupiter system is analogous to the earth-moon system. As the tides on the earth are driving away the moon, so the tides in Jupiter and the sun are gradually driving the two bodies apart. But there is a profound difference between the two cases. It can be proved that the tides produced in Jupiter by the sun are more effective than those produced in the sun by Jupiter. The contribution of the sun may, therefore, be at present omitted; so that, practically, the augmentations of the orbital moment of momentum of Jupiter are now achieved at the expense of that stored up by Jupiter's rotation. But what is 12 compared with 600,000. Even when the whole of Jupiter's rotational moment of momentum and that of his satellites[Pg 556] has become absorbed into the orbital motion, there will hardly be an appreciable difference in the latter. In ancient days we may indeed suppose that Jupiter being hotter was larger than at present, and that he had considerably more rotational moment of momentum. But it is hardly credible that Jupiter can ever have had one hundred times the moment of momentum that he has at present. Yet even if 1,200 units of rotational momentum had been transferred to the orbital motion it would only correspond with the most trivial difference in the distance of Jupiter from the sun. We are hence assured that the tides have not appreciably altered the dimensions of the orbit of Jupiter, or of the other great planets.
The time will, however, come when the rotation of Jupiter on his axis will be gradually abated by the influence of the tides. It will then be found that the moment of momentum of the sun's rotation will be gradually expended in increasing the orbits of the planets, but as this reserve only holds about two per cent. of the whole amount in our system it cannot produce any considerable effect.
The theory of tidal evolution, which in the hands of Professor Darwin has taught us so much with regard to the past history of the systems of satellites in the solar system, will doubtless also, as pointed out by Dr. See, be found to account for the highly eccentric orbits of double star systems. In the earth-moon system we have two bodies exceedingly different in bulk, the mass of the earth being about eighty times as great as that of the moon. But in the case of most double stars we have to do with two bodies not very different as regards mass. It can be demonstrated that the orbit must have been originally of slight eccentricity, but that tidal friction is capable not only of extending, but also of elongating it. The accelerating force is vastly greater at periastron (when the two bodies are nearest each other) than at apastron (when their distance is greatest). At periastron the disturbing force will, therefore, increase the apastron distance by an enormous amount, while at apastron it increases the periastron distance by a very small amount.[Pg 557] Thus, while the ellipse is being gradually expanded, the orbit grows more and more eccentric, until the axial rotations have been sufficiently reduced by the transfer of axial to orbital moment of momentum.
And now we must draw this chapter to a close, though there are many other subjects that might be included. The theory of tidal evolution is, indeed, one of quite exceptional interest. The earlier mathematicians expended their labour on the determination of the dynamics of a system which consisted of rigid bodies. We are indebted to contemporary mathematicians for opening up celestial mechanics upon the more real supposition that the bodies are not rigid; in other words, that they are subject to tides. The mathematical difficulties are enormously enhanced, but the problem is more true to nature, and has already led to some of the most remarkable astronomical discoveries made in modern times.
Our Story of the Heavens has now been told. We commenced this work with some account of the mechanical and optical aids to astronomy; we have ended it with a brief description of an intellectual method of research which reveals some of the celestial phenomena that occurred ages before the human race existed. We have spoken of those objects which are comparatively near to us, and then, step by step, we have advanced to the distant nebulæ and clusters which seem to lie on the confines of the visible universe. Yet how little can we see with even our greatest telescopes, when compared with the whole extent of infinite space! No matter how vast may be the depth which our instruments have sounded, there is yet a beyond of infinite extent. Imagine a mighty globe described in space, a globe of such stupendous dimensions that it shall include the sun and his system, all the stars and nebulæ, and even all the objects which our finite capacities can imagine. Yet, what ratio must the volume of this great globe bear to the whole extent of infinite space? The ratio is infinitely less than that which the water in a single drop of dew bears to the water in the whole Atlantic Ocean.
The Sun.
The sun's mean distance from the earth is 92,900,000 miles; his diameter is 866,000 miles; his mean density, as compared with water, is 1·4; his ellipticity is insensible; he rotates on his axis in a period between 25 and 26 days.
The Moon.
The moon's mean distance from the earth is 239,000 miles. The diameter of the moon is 2,160 miles; and her mean density, as compared with water, is 3·5. The time of a revolution around the earth is 27·322 days.
The Planets.
| Distance from the Sun in Millions of Miles. |
Periodic Time in Days. |
Mean Diameter in Miles. |
Axial Rotation. | Density compared with Water. |
|||
| Mean. | Least. | Greatest. | |||||
| Mercury | 36·0 | 28·6 | 43·3 | 87·969 | 3,030 | (?) | 6·85(?) |
| Venus | 67·2 | 66·6 | 67·5 | 224·70 | 7,700 | (?) | 4·85 |
| Earth | 92·9 | 91·1 | 94·6 | 365·26 | 7,918 | 23 56 4·09 | 5·58 |
| Mars | 141 | 128 | 155 | 686·98 | 4,230 | 24 37 22·7 | 4·01 |
| Jupiter | 483 | 459 | 505 | 4,332·6 | 86,500 | 9 55 — | 1·38 |
| Saturn | 886 | 834 | 936 | 10,759 | 71,000 | 10 14 — | 0·72 |
| Uranus | 1,782 | 1,700 | 1,860 | 30,687 | 31,900 | Unknown | 1·22 |
| Neptune | 2,792 | 2,760 | 2,810 | 60,127 | 34,800 | Unknown | 1·11 |
The Satellites of Mars.
| Mean Distance from Centre of Mars. |
Periodic Time. | |||
| hrs. | mins. | secs. | ||
| Phobos | 5,800 miles | 7 | 39 | 14 |
| Deimos | 14,500 miles | 30 | 17 | 54 |
The Satellites of Jupiter.
| Mean Distance from Centre of Jupiter. |
Periodic Time. | ||||
| days. | hrs. | mins. | secs. | ||
| New Inner Sattellite Barnard | 112,500 miles | 0 | 11 | 57 | 22 |
| I. | 261,000 miles | 1 | 18 | 27 | 34 |
| II. | 415,000 miles | 3 | 13 | 13 | 42 |
| III. | 664,000 miles | 7 | 3 | 42 | 33 |
| IV. | 1,167,000 miles | 16 | 16 | 32 | 11 |
The Satellites of Saturn.
| Mean Distance from Centre of Saturn. |
Periodic Time. | ||||
| days. | hrs. | mins. | secs. | ||
| Mimas | 115,000 miles | 0 | 22 | 37 | 6 |
| Enceladus | 148,000 miles | 1 | 8 | 53 | 7 |
| Tethys | 183,000 miles | 1 | 21 | 18 | 26 |
| Dione | 235,000 miles | 2 | 17 | 41 | 9 |
| Rhea | 329,000 miles | 4 | 12 | 25 | 12 |
| Titan | 760,000 miles | 15 | 22 | 41 | 27 |
| Hyperion | 921,000 miles | 21 | 6 | 38 | 31 |
| Iapetus | 2,215,000 miles | 79 | 7 | 56 | 40 |
The Satellites of Uranus.
| Mean Distance from Centre of Uranus. |
Periodic Time. | ||||
| days. | hrs. | mins. | secs. | ||
| Ariel | 119,000 miles | 2 | 12 | 29 | 21 |
| Umbriel | 166,000 miles | 4 | 3 | 27 | 37 |
| Titania | 272,000 miles | 8 | 16 | 56 | 30 |
| Oberon | 364,000 miles | 13 | 11 | 7 | 6 |
The Satellite of Neptune.
| Mean Distance from Centre of Neptune. |
Periodic Time. | ||||
| days. | hrs. | mins. | secs. | ||
| Satellite | 220,000 miles | 5 | 21 | 2 | 44 |
A
Aberration of light, 503–512;
and the apparent movements of stars, 504, 507;
Bradley's discoveries, 503;
causes, 507–511;
circles of stars, 505–507;
dependent upon the velocity of light, 511;
effect on Draco, 505;
telescopic investigation, 510
Achromatic combination of glasses, 11
Adams, Professor J.C., and the discovery of Neptune, 324–327, 330–332;
and the Ellipse of the Leonids, 386
Aërolite, the Chaco, 398;
the Orgueil, 399
Airy, Sir George, 325
Alban Mount Meteorites, the, 393
Alcor, 438
Aldebaran, 209, 418, 419;
spectrum of, 480;
value of velocity of, 484
Algol, 485, 487
Almagest, the, 7
Alphonsus, 92
Alps, the great valley of the (lunar), 88
Altair, 424
Aluminium in the Sun, 50
Ancients, astronomy of the, 2–7
Andrews, Professor, and basaltic formation at Giant's Causeway, 407
Andromeda, 414;
nebula in, 469, 489
Andromedes, The, shooting star shower, and Biela's comet, 390
Antares, 423
Apennines (lunar), 83
Aphelion, 163
Aquarius, 215, 413
Aquila, or the Eagle, 424
Arago, 326
Archimedes, 88
Arcturus, 358, 480;
value of velocity of, 484
Argelander's Catalogue of Stars, 431, 476
Argus, 481
Ariel, 309, 559
Aristarchus, 90
Aristillus, 88
Aristotle, lunar crater named after him, 88;
credulity respecting his writings, 267;
the Moon and the tides and, 535
Asteroids, 229–244
Astrea, 328
Astronomers of Nineveh, 156
Astronomical quantities, 558
Astronomy, ancient, 2–7;
Galileo's achievements in, 10;
the first phenomenon of, 2
Athenæum, the, and Sir John Herschel's letter on Adams's share in the discovery of Neptune, 330
Atmosphere, height of the Earth's, 100
Attraction, between the Moon and the Earth, 75;
between the planets, 148;
between the Sun and the planets, 144, 148;
of Jupiter, 248, 249;
producing precession, 498
Auriga, 414, 489
Aurora borealis, 42
Autolycus, 88
Auwers and star distances, 449;
and the irregularity in movement of Sirius, 427
Axis, Polar, 196, 497;
precession and nutation of the Earth's, 492–502
B
Backlund, and Encke's comet, 349, 351
Barnard, Professor E.E., and Saturn, 271, 278, 282;
and Titan, 294;
and the comet of 1892, 355;
and the Milky Way, 475
Beehive, the, 422
Belopolsky, M., and Binaries, 487, 488
Benares meteorite, the, 392
Bessel, and Bradley, 501;
and the distance of 61 Cygni, 446, 448, 449;
and the distances of stars, 442;
and the irregular movements of Sirius, 426;
receives gold medal of Royal Astronomical Society, 442
Betelgeuze, 209, 418, 419, 482;
value of velocity of, 484
Biela's comet, and Sir John
Herschel, 357;
and the Andromedes, 390
Binaries, spectroscopic, 487
Binocular glass, 27
Biot and the L'Aigle meteorites, 392
Bode's law, 230;
list of double stars, 435
Bond, Professor, and Saturn's satellites, 296;
and the nebula in Orion, 469;
and the third ring of Saturn, 280
Boötes, 422
Bradley, and nutation, 501;
and the aberration of light, 503;
his observations of Uranus, 312
Bredichin, Professor, and the tails of comets, 365, 366, 367
Breitenbach iron, the, 397
Bristol Channel, tides in the, 538
Brünnow, Dr., observations on the parallax of 61 Cygni, 449
Burial of Sir John Moore, 72
Burnham, Mr., and the orbit of Sirius, 427;
his additions to the known number of double stars, 439
Butler, Bishop, and probability, 460
Butsura meteorite, 397
C
Cadmium in the Sun, 50
Calais, tides at, 536
Calcium in the Sun, 50
Campbell, Mr., and Argus, 481;
and Mars, 223
Canals on Mars, 220
Cancri 20, 154
Cancri, ζ, 154
Cancri, θ, 154
Canis major, 419
Canopus, 422
Cape Observatory, 27
Capella, 414, 480, 487
Carboniferous period, 518
Cardiff, tides at, 538
Cassini, J.D., and double stars, 434;
and Saturn's satellites, 294;
and the rings of Saturn, 278
Cassiopeia, 412
Castor, 420, 487;
a binary star, 437;
revolution of, 437
[Pg 562]Catalogues of stars, 310, 311;
Messier's, 529
Catharina, 92
Centauri, α, 422;
Dr. Gill's observations of, 451;
Henderson's measurement of distance of, 442, 451
Ceres, 231, 232, 238;
and meteorites, 404, 405
Chaco meteorite, the, 398
Chacornac, and the lunar crater Schickard, 90
Challenger, the cruise of the, and magnetic particles in the Atlantic, 408
Challis, Professor, 326;
his search for Neptune, 327, 328, 331, 332
Chandler, Mr., and Algol, 485
Charles's Wain, 28
Chepstow, tides at, 538
Chéseaux, discoverer of comet of 1744, 367
Chicago, telescope at Yerkes Observatory, 16
Chladni and the meteorite of Siberia, 392
Chromium in the Sun, 50
Chromosphere, the, 54
Chronometers tested by the Moon, 80
Clairaut and the attraction of planets on comets, 342, 343
Clavius, 91;
and Jupiter's satellites, 267
Clock, astronomical, 23
Clusters, star, 461–464
Cobalt in the Sun, 50
Coggia's comet, 1874, 337
Colour of light and indication of its source, 46
Colours, the seven primary, 45
Columbiad, the, 401
Columbus, 7
Comets, 112, 149, 250, 336;
and the spectroscope, 355;
attraction from planets, 342, 360;
Biela's, 357;
Biela's and the Andromedes, 390;
Clairaut's investigations, 342, 343;
Coggia's, 337;
Common's (1882), 354;
connection of, with shooting star showers, 388;
constitution of, 336;
containing sodium and iron, 356;
Donati's (1858), 353, 358, 366;
eccentricity of, 360;
Encke's, 344–352;
existence of carbon in, 356, 367;
gravitation and, 343, 348;
Halley's investigations about, 341–344;
head or nucleus of, 337;
Lexell's, 370;
mass of, 359;
movements of, 336;
Newton's explanations of, 338;
non-periodic, 353–356;
of 1531, 341;
of 1607, 341;
of 1681, 338, 339;
of 1682, 341;
of 1744 (Chéseaux's), 367;
of 1818, 345;
of 1843, 352;
of 1866, 388;
of 1874, 337;
of 1892, 355;
origin of, 369;
parabolic orbits of, 338–340, 360;
periodic return of, 338–341;
shape of, 336;
size of, 337;
tailless, 370;
tails of, 337, 361;
Bredichin's researches, 365;
Chéseaux's, 367;
composition of, 365, 369;
condensation of, 369;
electricity and, 368;
gradual growth of, 363;
law of direction of, 362;
repelled by the Sun, 364;
repulsive force of, 364, 368;
various types of, 365;
Tebbutt's (1881), 353;
tenuity of, 357
Common, Dr., constructor of reflectors, 21;
and the comet of 1882, 354;
and the nebula in Orion, 469
Cook, Captain, and the transit of Venus, 184
Copeland, Dr., and Schmidt's star, 489;
and the lunar crater, Tycho, 92;
and the spectra of nebula, 473;
and the transit of Venus, 189
Copernicus and Mercury, 156;
confirmation of his theory by the discovery of Jupiter's satellites, 267;
his theory of astronomy, 7;
lunar crater called after him, 89
Copper in the Sun, 50
Cor scorpionis, 423
Corona Borealis, 423, 488
Corona of Sun, during an eclipse, 62–64, 151
Coronium, 64
Cotopaxi and meteorites, 401
Crab, the, 422
Crabtree, and the transit of Venus, 180
Crape ring of Saturn, 281
Craters in the Moon, 83–85, 87–98
Critical velocity, 103, 104, 237
Crown, the, 423
Cryptograph of Huyghens, the, 277
Cygni, β, 439
Cygni 61, annual parallax of, 450;
Bessel's measurement of distance of, 442, 446, 447;
Brünnow's observations of, 449;
distance from the Sun of, 452;
disturbing influence of, 452;
double, 446;
Professor A. Hall's measurement of, 449;
Professor Pritchard's photographic researches concerning, 449;
proper motion of, 446;
Struve's observations of, 448, 449;
velocity of, 452
Cygnus, 424
Cyrillus, 92
Cysat, and the Belt of Orion, 467
D
D line in solar spectrum, 48
Darwin, Professor G.H., and tidal evolution, 531
Dawes, Professor, and Saturn's third ring, 281
Day, length of, and the Moon, 542;
and the tides, 541
Deimos, 226, 558
Denebola, 423
Diffraction, 56
Dione, 559
Dispersion of colours, 47
Distances, astronomical, 558, 559
Doerfel, and comets, 339
Dog star (see Sirius)
Dog, the Little, 420
Donati's comet, 353, 358;
tails, 366
Double stars, 434–440
D Q, 236
Draco, nebula in, 470
Dragon, the, 415
Draper, Professor, and the nebula in Orion, 469
Dunsink Observatory, 12, 184, 447, 449
Dynamical stability, 547;
theory of Newton, 214
Dynamics and the Earth-Moon system, 546
Dynamics, Galileo the founder of, 10
E
Eagle, the, 424
Earth, The, ancient ideas respecting, 3;
annual movement of, and the apparent movement of the stars, 507, 512;
attraction of Jupiter, 319;
attraction of on Encke's comet, 350;
attraction of, on the Leonids, 386;
attraction of Saturn, 319;
attraction of the Moon, 75, 497;
attraction of the Sun, 496;
axial rotation of, 558;
carboniferous period on, 518;
change of climate on, 518;
composition of, 496;
contact of atmosphere of, with meteors, 377–379;
density of, 558;
diameter of, 558;
distance of, from Mars, 213;
distance of, from the Moon, 73, 558;
distance of, from the Sun, 31, 114, 184, 240, 265, 351, 512, 558;
energy from rotation of, 540;
formerly a molten globe, 200, 201;
geological records and, 517;
glacial period on, 518;
gravitation and, 204, 206, 207, 497;
heat in the interior of, 94, 197, 198, 251, 514;
how it is measured, 193–196;
its mass increasing owing to the fall of meteoric matter, 408;
its oceans once vapour, 251;
once in immediate proximity to the Moon, 542;
orbit of, 114;
orbit of, its elliptic form, 139;
path of deranged by Venus and Mars, 319;
periodic time of, 558;
plane of orbit of, 309;
polar axis of, 196, 492–502;
position of, relatively to the Sun and the Moon, 76, 77;
precession and nutation of axis of, 492–502;
radius of, 193, 512;
rotation of, 75, 196, 200, 494, 496;
shape of, 192, 195, 197, 201, 207;
size of, compared with Jupiter, 119,
and with other planets, 119;
size and weight of, compared with those of the Sun, 30,
and Moon, 74, 75;
[Pg 563]velocity of, 115, 139, 146, 512,
and periodic time, 143;
volcanic outbreaks on, 197,
and the origin of meteorites, 405;
weight of, 202, 248,
as compared with Saturn, 271, 272
Earthquakes, astronomical instruments disturbed by, 24
Eccentricity of planetary ellipses, 136, 211
Eclipse of Jupiter's satellites, 261, 262, 265–267
Ellipse of the Moon, 77–80;
of the Sun, 53
Eclipses, ancient explanations of, 6;
calculations of the recurrence of, 79, 80
Ecliptic, the, 5, 233;
Pole of the, 493, 500, 505
Electric Light, the, 44
Ellipse, the, 136;
eccentricity of, 137;
focus of, 137;
Kepler's discoveries respecting, 136, 138, 142–144, 505;
the form which the orbit of a planet takes, 136;
the parallactic, 444;
variety of form of, 139
Enceladus, 559
Encke, and the distance of the Sun from the Earth, 147, 184;
his comet, 344–352
Encke's comet, 344–352;
approach to Jupiter of, 349;
and Mercury, 349;
and the Sun, 346;
diminution in periodic time of, 351;
distance from Mercury of, 347;
disturbed by the Earth, 350,
and by Mercury, 348;
irregularities of, 347, 351;
orbit of, 346;
periodical return of, 351;
Von Asten's calculations concerning, 349–350
Energy supplying the tides, 539
Ensisheim meteorite, the, 393
Equatorial diameter, 196, 497;
telescope, 14
Eratosthenes, 89
Eros, 236
Eruptions, 197
Evening star, 109, 169
Eye, structure of the, 10
F
Faculæ of the Sun, 37
Fire ball of 1869, 375
Fire balls, 374
"Fixed" stars, 503
Flamsteed, first Astronomer-Royal, 311;
his Historia Cœlestis, 311
Focus of planetary ellipse, 137–139
Fomalhaut, 413
Fraunhofer, 478
Fraunhofer lines, 48
Fundy, Bay of, tides in, 538
G
Galileo, achievements of, 10;
and Jupiter's satellites, 267;
and Saturn's rings, 273, 274;
and the Pleiades, 418
Galle, Dr., and Neptune, 328–330
Gassendi, and the transit of Mercury, 164;
and the transit of Venus, 178;
lunar crater named after him, 90
Gauss, and the minor planet Ceres, 232
Gemini, constellation of, 303, 420
Geminids, the, 400
Geologists and the lapse of time, 453
Geometers, Oriental, 5
Geometry, cultivation by the ancients of, 6
George III. and Sir W. Herschel, 299, 306
Giant's Causeway, 407
Gill, Dr. D., 27;
and Juno, 243;
and the minor planets, 242;
and the parallax of α Centauri, 451;
and the parallax of Mars, 214
Glacial period, 518
Gravitation, law of, 122–149;
and binary stars, 437;
and precession, 497;
and the Earth's axis, 495, 497, 499;
and the parabolic path of comets, 340;
and the periodical return of comets, 343;
and the weight of the Earth, 203, 204;
illustrated by experiments, 123, 124, 127, 129–132;
its discovery aided by lunar observations, 108, 125;
its influence on the satellites, 149;
its influence on stars, 149;
its influence on tides, 149;
Le Verrier's triumphant proof of, 330;
Newton's discoveries, 125, 126, 147;
on the Moon, 96;
universality amongst the heavenly bodies, 128, 373
Great Bear, 27, 28, 241;
configuration, 410;
double star in the, 438;
positions of, 409, 411
Green, Mr., and Mars, 220
Greenwich Observatory, 26, 311
Griffiths, Mr., and Jupiter, 252
Grimaldi, 90
Grubb, Sir Howard, 14
"Guards," the, 412
Gulliver's Travels and the satellites of Mars, 228
H
Hadley's observations of Saturn, 282
Hall, Professor Asaph, and the satellites of Mars, 225
Halley, and the periodicity of comets, 341–343;
and the transit of Venus, 180
Heat, bearings on astronomy, 513;
in the interior of the Earth, 197–199, 514;
of the Sun, 515–526
Heliometer, the, 243
Helium, 55
Henderson, and the distance of α Centauri, 442, 451
Hercules, star cluster in, 269, 462
Herodotus (lunar crater), 90
Herschel, Caroline, 299, 465
Herschel, Sir John, address to British Association, 328;
address on the presentation of gold medal to Bessel, 443;
and Biela's comet, 357;
and nebulæ, 464;
letter to Athenœum on Adams's share in the discovery of Neptune, 330
Herschel, Sir W., and double stars, 435, 436;
and Saturn, 279;
and Saturn's satellites, 295;
and the Empress Catherine, 301;
and the movement of solar system towards Lyra, 457;
discovery of satellite of Uranus by, 308, 309;
discovery of Uranus by, 305, 308;
early life of, 299;
friendship with Sir W. Watson of 302;
he makes his own telescopes, 301;
"King's Astronomer," 307;
method of making his telescopes, 302;
musical talent of, 299;
organist of Octagon Chapel, Bath, 300;
pardon for desertion from George III., 299;
passion for astronomy of, 300, 301;
relinquishes musical profession, 307;
sidereal aggregation theory of, 529;
study of the nebulæ by, 464–465, 529
Herschelian telescope, 19
Historia Cœlestis, 311
Hœdi, the, 414
Holmes's, Mr., comet (1892), 355
Horrocks, and the transit of Venus, 179
Howard, Mr., and the Benares meteorite, 392
Huggins, Sir W., 479, 483;
and nebulæ, 472
Huyghens, and Saturn's rings, 275–278;
discovers first satellite of Saturn, 293
Hyades, the, 419
Hydrogen in Sirius and Vega, 479;
in the Sun, 50
Hyginus, 93
Hyperion, 559
I
Iapetus, 559
Iberians, the, 3
Inquisition, the, and Galileo, 10
Iris, 242
Iron, dust in the Arctic regions, 408;
in the Sun, 50;
of meteorites, the, 396;
spectrum of, 50
J
Janssen, M., 34, 53;
and the transit of Venus, 177
Juno, 233, 238
Jupiter, ancient study of, 6;
and the Leonids, 386;
attraction of, 248;
axial rotation of, 558;
belts of, 252;
brilliancy of, 257;
composition of, 250;
covered with an atmosphere of clouds, 253, 254;
density of, 558;
[Pg 564]diameter of, 247, 558;
distance from the Earth of, 110, 111;
distance from the Sun of, 246, 558;
habitability of, 257;
heat received from the Sun by, 256;
internal heat of, 252, 256, 515;
lack of permanent features of, 253;
lack of solidity of, 248, 253, 254;
moment of momentum of, 554, 555;
occultation of, 255;
orbit of, 114, 115, 246;
path of, perturbed by the attraction of Saturn, 316;
periodic time of, 558;
a planet, or "wanderer," 111;
red spot in 1878, 253;
revolution of, 246;
rotation of, 201, 202;
satellites of, 247, 249, 257–261, 265, 559;
satellites of, and gravitation, 266;
satellites of, and the Copernican theory, 267;
shadow from satellites of, 257;
shape of, 201, 202, 247, 252;
size of, compared with the Earth, 19, 246, 248,
and other planets, 114;
and the Sun, 114;
storms on, 256;
tides on, 555;
weight of, 248, 250,
and Encke's comet, 350
K
Keeler, Professor, and Saturn's ring, 288
Kempf, Dr., and the Sun's velocity, 484
Kepler, and comets, 360;
and laws of planetary motion, 10;
and meteors, 386;
and the orbit of Mars, 209;
explanation of his laws, 147, 148, 533;
his discovery of the shape of the planetary orbits, 136, 138;
his first planetary law, 138;
lunar crater called after him, 90;
prediction of the transit of Venus and Mercury, 163, 178;
second law, 141;
third law, 142
Kids, the, 414
Kirchhoff, and spectrum analysis, 478
Kirkwood, Professor, and the movements of Saturn's satellites, 296
Klinkerfues, Professor, 390
L
Lagrange, and the theory of planetary perturbation, 320–322;
his assumption of planetary rigidity, 531
L'Aigle meteorites, the, 392
Lalande, and Neptune, 332, 333
Landscapes, lunar, 98
Lane, Mr. J. Homer, 522
Laplace, and the nebular theory, 526;
and the satellites of Jupiter, 266;
and the theory of planetary perturbation, 320
Lassell, Mr., and Saturn's eighth satellite, 296;
discovers Neptune's satellite, 334
Law of gravitation (see Gravitation)
Laws of Planetary Motion (see Planetary Motion)
Lead in the Sun, 50
Ledger, Mr., and Mercury, 163
Leibnitz, lunar mountains named after him, 93
Lemonnier, and Uranus, 312
Leo, and shooting stars, 380, 420
Leonids, attractions of planets on, 386;
breadth of stream of, 387;
change of shape of, 383;
decrease of, 385;
enormous number of, 382;
historical records, 383;
length of stream of, 387;
Le Verrier, and the cause of their introduction into the solar system, 388;
meteor shoal of, 382;
periodic return of, 382;
their connection with comets and Professor, Schiaparelli, 388
Leonis γ, value of velocity of, 484
Leverage by equatorial protuberance, 498
Le Verrier, and Mars, 214;
and the discovery of Neptune, 324–332;
and the introduction of the Leonids into the solar system, 388;
and the weight of Mercury, 349
Lexell's comet, 370
Libration, 84
Lick Observatory, 16
Light, aberration of, 503–512;
velocity of, 261, 262, 265, 505, 512
Linné, 87, 94
Lion, the, 420, 421
Little Bear, the, 412
Little Dog, the, 420
Livy, and meteorites, 393
Lloyd, Provost, 407
Lockyer, Sir Norman, and Betelgeuze, 482;
and solar light, 52
London, tides at, 538
Louvain, F. Terby, and Titan, 295
Lowell, Mr., and Mercury, 165
Lunar tides, 548, 549
Lyra, motion of solar system towards, 459
Lyre, the, 424;
Nebula in, 469
Lyrids, the, 400
M
Mädler, and the lunar craters, 88, 90, 91
Magellanic clouds, 463
Magnesium, colour of flame from, 46;
in the Sun, 50
Magnetism, connection with Sun spots, 42
Manganese in the Sun, 50
Maraldi, and the rings of Saturn, 279
Mare crisium, 83;
fœcunditatis, 83;
humorum, 83;
imbrium, 83, 98;
nectaris 83;
nubium, 83;
serenitatis, 83;
tranquillitatis, 83;
vaporum, 83
Mars, ancient study of, 6;
appearance of, through the telescope, 218;
atmosphere of, 222;
axial rotation of, 558;
canals on, 220;
density of, 558;
diameter of, 558;
distance, from the Earth of, 213;
distance from the Sun of, 213, 558;
gravitation on, 225;
Le Verrier's discovery of, 214;
life improbable on, 224;
marking on, 218;
movements of, 211–213;
opposition of, 209–211;
orbit of, 116, 209, 210, 213;
orbit of, and the laws of Kepler, 209;
parallax (1877), and Dr. D. Gill, 214;
periodic time of, 558;
a planet or "wanderer," 111;
"Polar Caps" on, 218, 219;
proximity to the Earth of, 110;
rising and setting of, 209;
rotation of, 218;
satellites of, 225–228, 558;
size of compared with other planets, 116, 216;
tides on, 551;
water and ice on, 219, 224
Maximilian, Emperor, 393
Mayer, Tobias, and Uranus, 312
Measurement of the Earth, 193–196
Mediterranean, tides in the, 537
Mercury, ancient study of, 6;
antiquity of its discovery, 155–157;
atmosphere of, 166;
attraction on comets of, 347;
climate of, 163;
comparative proximity to the Earth of, 111;
composition of, 160;
crescent-shaped, 160;
density of, 558;
diameter of, 558;
distance from the Sun of, 151, 558;
habitability of, 163;
movement of, 160, 161;
its elliptic form, 139, 161;
orbit of, 114;
period of revolution of, 161;
periodic appearances of, 158;
periodic time of, 558;
perturbations of, 350;
a planet or "wanderer," 111;
revolution of, 165;
rotation of, and Professor Schiaparelli, 165;
size of, compared with other planets, 116;
surface of, 162;
transit of, 152;
transit of, and Gassendi's observations, 164;
transit of, predicted by Kepler, 163;
velocity of, 162;
weight of, 166, 349
Meridian circle, 22, 24
Messier's Catalogue of Stars, 529
Meteors (see Stars, shooting)
Meteorites, 391;
Alban Mount, 393;
ancient accounts, 392, 393;
Benares, 392;
Butsura, 397;
Chaco, 398;
characteristics of, 397;
Chladni's account of discovery in Siberia, 392;
composition of, 397–399;
Ensisheim (1492), 393;
Hindoo account of, 391;
L'Aigle, 392;
not connected with comets, 400;
not connected with star showers, 400;
Orgueil, 399;
origin, 400–408;
Ovifak, 407;
Rowton, 395–396;
Wold Cottage, 392
[Pg 565]Micrometer, 86
Milky Way, 462–3, 474–6
Mimas, 559
Minor planets, 229–244
Mira Ceti, 430, 482
Mizar, 438, 486
Moment of momentum, the, 552–554
Month of one day, 547
Moon, The, absence of air on, 85, 99;
absence of heat on, 95;
agent in causing the tides, 70, 535–537;
ancient discoveries respecting, 5;
apparent size of, 73;
attraction to the Earth of, 75;
brightness of, as compared with that of the Sun, 71;
changes during the month of, 71, 74;
chart of surface of, 81;
craters on, 83, 84, 87–98, 514;
density of, 558;
diameter of, 558;
distance from the Earth of, 73, 75, 568;
eclipses of, 6, 77–80;
illustration of the law of gravitation, 96, 131, 133;
landscapes on, 98;
life impossible on, 99;
measuring heights of mountains, etc., of, 85, 86;
micrometer, 86; motion of, 75;
mountains on, 83, 85, 88, 89, 91, 93;
phases of, 71, 76;
plane of orbit of, 310, 500, 501;
poets and artists and, 72;
pole, 500;
possibility of ejecting meteorites, 402;
possibly fractured off from the earth, 543;
prehistoric tides on, 548, 549;
produces precession, 497–499;
proximity to the Earth of, 73, 75;
receding from the Earth, 545;
relative position of with regard to the Earth and the Sun, 76, 77;
revolution of, round the Earth, 75, 76, 558;
"seas" on, 82, 83;
shadows of, 85;
size of, compared with that of the Earth, 74;
test for chronometers, a, 80;
thraldom of terrestrial tides, 549;
waterless, 100;
weather not a affected by the phases of, 82;
weight of, 74
Motion, laws of planetary, 138, 141, 142, 147, 148
Mountains of the Moon, 83, 85, 93
N
Nasmyth, Mr., and the formation of lunar craters, 95
Natural History Museum, meteorites, 394
Nautical Almanack, 189
Neap Tides, 538
Nebula, in Andromeda, 469;
annular, in Lyra, 469;
in Orion, 269, 461, 466–469;
colour of, 468;
magnitude of, 468;
nature of, 467;
planetary, in Draco, 470;
simplest type of a, 528;
various grades of, 528
Nebulæ, 464–472;
condensation, 528;
distances of, 464;
double, 470;
Herschel's labours respecting, 464–465, 528, 529;
number of, 466;
planetary, 470;
self-luminous, 464;
smallest greater than the Sun, 464;
spiral, 470
Nebular theory, the, 526
Neptune, 112;
Adams's researches, 324–326, 332;
Challis's observations of, 326–328;
density of, 558;
diameter of, 333, 558;
disc of, 332;
discovery (1846) of, 315;
distance from the Sun of, 334, 558;
Lalande's observations of, 332, 333;
Le Verrier's calculations, 324–332;
moment of momentum of, 554;
orbit of, 117;
periodic time of, 558;
revolution of, 334;
rotation of uncertain, 333;
satellite of, discovered by Mr. Lassell, 559;
size of, compared with other planets, 119;
vaporous atmosphere of, 333;
weight of, 333
Newall, Mr. H.F., and Capella, 487;
and the values of velocity of stars, 483
Newcomb, Professor, 9, 264, 267, 522
Newton, Professor, and meteoric showers, 377, 384
Newton, Sir Isaac, discovery of gravitation verified Kepler's laws, 144;
dynamical theory, 214;
illustrations of his teaching, 144–147;
law of gravitation and, 125, 126, 537;
parabolic path of comets and, 338–340;
reflecting telescope, 19;
weight of the Earth and, 203
Nickel in the Sun, 50
Nineveh, astronomers of, 156
Nordenskjöld, and the Ovifak meteorite, 407
Nova Cygni, 431;
brilliancy of, 454;
decline of, 455;
distance of, 456;
parallax of, 455
November meteors, 376, 377, 379
Nutation, and Bradley, 501
O
Oberon, 309, 559
Object-glasses, 11, 12, 14, 16, 19
Observatories, 9–28
Observatory, Cape of Good Hope, 27;
Dunsink, 12, 184;
Greenwich, 26, 314;
Lick, 16;
Paris, 22;
Uraniborg, 10;
Vienna, 14;
Washington, 226;
Yerkes, 16
Occultation, 102, 215
Oceanus Procellarum, 83
Opera-glass, 27, 28
Opposition of Mars, 209
Orbital moment of momentum, 552
Orbits of planets, 114, 115, 117;
dimensions, 139–143;
elliptical form, 138–140;
minor planets, 232, 234, 239;
not exactly circles, 135;
of satellites of Uranus, 310;
Sun the common focus, 139
Orgueil meteorite, the, 399
Orion, 4, 418
Orion, belt of, 418, 467;
brilliancy of, 418;
nebula in, 269, 461, 466–469
Orionis, α, 418, 482
Orionis, θ, a multiple star, 318, 467
Ovifak meteorite, the, 407
P
Palisa and the minor planets, 234
Pallas, 233, 238
Parabolic path of comets, 338–340
Parallactic ellipse, 444
Parallax, 181, 182, 214, 443;
of stars, 507
Paris telescope, 22, 23
Pegasus, great square of, 413, 414
Peg-top, the, and the rotation of the Earth, 494
Pendulum for determining the force of the Earth's attraction, 205
Penumbra of Sun-spot, 51
Perihelion, 163
Periodic times of planets, 139–143, 558
Periodicity of Sun-spots, 41
Perseids, 400
Perseus, 415, 416, 429;
sword-handle, 462
Perturbation, planetary, 317–324, 346
Perturbations, theory of, 296
Petavius, 93
Peters, Professor, and charts of minor planets, 234;
and the derangement of Sirius, 427
Phases of the Moon, 71, 76
Phobos, 226, 551, 558
Photography, and practical astronomy, 25;
and the distance of 61 Cygni, 449;
Dr. Roberts and the nebula in Andromeda, 469;
Mr. Common and the nebula in Orion, 469;
Sir W. Huggins and the spectra of nebulæ, 473
Photosphere, the, 37, 54
Physical nature of the stars, 477
Piazzi, discoverer of the first known minor planet, 203
Pickering, Professor, 218, 220, 255, 265;
and Betelgeuze, 482;
and planetary nebulæ, 474;
and Saturn's satellites, 296;
and spectroscopic binaries, 486, 487
Pico, 89
Planetary motion, Kepler's laws of, 138, 141, 142, 147, 148
Planetary nebulæ, 470
Planetary perturbation, 317–324
Planets, ancient ideas respecting, 2, 6;
approximate number of, 112;
attract each other, 148, 317;
[Pg 566]attracted by comets,360;
Bode's law, 230;
comparative sizes of, 118, 119;
distance of, from the Earth, 109–111;
distance of, from the Sun, 558;
how distinguished from stars, 111;
irregularity of motions of, 317–324;
Lagrange's theory of rigidity of, 531;
light of, derived from the Sun, 113;
minor, 229–244;
orbits of the four giant, 117;
orbits of the four interior, 114;
orbits have their focus in the centre of the Sun, 139;
orbits not exactly circles, 135;
orbits take the form of an ellipse, 136–138;
origin of, as suggested by the nebular theory, 526;
periodic times of, 139–143, 558;
relative distances of, 229;
uniformity of direction in their revolution, 120, 322;
velocity of, 139–142, 144, 146, 237
Plato (lunar crater), 89
Pleiades, 241, 416;
invisible in the summer, 416
Pliny, the tides and the Moon, 535
Plough, the, 28
Pogson, Mr., 390
Pointers in the Great Bear, 28, 411
Polar axis, 196
Polar caps on Mars, 218, 219
Pole, the, distance of from Pole Star lessening, 494;
elevation of, 195;
movement of, 492;
near α Draconis, 494;
near Vega or α Lyra, 494
Pole Star, 194;
belongs to the Little Bear, 412;
distance of, from the pole of the heavens, 412, 492, 494;
position of, 411;
slow motion of, 412
Pollux, 420, 480;
value of velocity of, 484
Pons, and the comet of 1818, 345
Posidonius, 87
Potassium in the Sun, 50
Præsepe, 422
Precession and nutation of the Earth's axis, 492–502
Proctor, and the stars in Argelander's atlas, 476
Prism, the, 45;
its analysing power, 46
Pritchard, Professor, stellar photographic researches of, 449
Procyon, 420;
value of velocity of, 484
Prominences on the Sun, 53–59
Ptolemy, his theory of astronomy, 6;
lunar crater named after him, 92
Q
Quarantids, the, 400
R
Radius of the Earth, 193, 512
Rainbow, the, 45
Ram, the, 420
Reflectors, 19, 21, 25
Refraction by the prism, 45
Refractors, 11, 14, 16
Regulus, 421, 479
Reservoir formed from tidal water, 538
Retina, the, and the telescope, 10, 11
Rhea, 559
Rigel, 418, 420, 480
Rigidity of the planets, 532, 533
Roberts, Dr. Isaac, and the nebula in Andromeda, 469;
and the nebula in Orion, 469
Roemer, and the velocity of light, 261
Romance, planet of, 151–154
Rosse telescope, the, 19, 20, 468, 470
Rotational moment of momentum, 553
Rowland, Professor, and spectral lines, 491
Rowton Siderite, 395
Royal Astronomical Society and Bessel, 442
S
Sappho, 242
Satellites of Jupiter, 249, 250, 257–261, 266, 559;
confirmation of the Copernican theory, 267
Satellites of Mars, 209, 225–228, 551, 558
Satellites of Neptune, 334, 559
Satellites of Saturn, 559;
Bond's discoveries, 296;
Cassini's discoveries, 294;
distances, 559;
Herschel's discoveries, 295;
Huyghens' discovery, 293;
Kirkwood's deduction, 296;
Lassell's deduction, 296;
movements, 296;
origin as suggested by the nebular theory, 526
Satellites of Uranus, 308, 309, 310, 559
Saturn, ancient study of, 6;
attraction on Uranus, 322;
axial rotation of, 558;
beauty of, 209;
comparative proximity to the Earth of, 110;
density of, 558;
diameter of, 271, 558;
distance of, from the Sun, 268, 271, 558;
elliptic path of, 271;
gravitation paramount, 283;
internal heat of, 272, 515;
Leonids and, 386;
low density of, 272;
moment of momentum of, 554;
motion of, 271;
orbit of, 117, 118;
path of, perturbed by the attraction of Jupiter, 316;
periodic time of, 558;
period of revolution of, 269;
picturesqueness of, 291;
position of, in the solar system, 269;
rings of, 269;
rings, Bonds discovery, 280;
rings, Cassini's discovery, 278;
rings, consistency, 286;
rings, Dawes's discovery, 281;
rings, Galileo's discovery, 273, 274;
rings, Hadley's observations, 282;
rings, Herschel's researches, 279;
rings, Huyghens' discovery, 275–278;
rings, Keeler's measurement of the rotation, 288;
rings, Maraldi's researches, 279;
rings, rotation of, 285, 288;
rings, spectrum of, 291;
rings, Trouvelot's drawing, 278;
satellites of, 293, 294, 295, 296, 559;
size of, compared with other planets, 119, 269, 272;
spectrum of, 291;
unequal in appearance to Mars and Venus, 269;
velocity of, 271;
weight of, compared with the Earth, 272
Savary and binary stars, 436
Schaeberle, Mr., and Mars, 224
Scheiner, and the values of velocity of stars, 483;
observations on Sun-spots, 36
Schiaparelli, Professor, and Mars, 220;
and the connection between shooting-star showers and comets, 388;
and the rotation of Mercury, 165
Schickard, 90
Schmidt, and Nova Cygni, 454, 489;
and the crater Linné, 87;
and the Leibnitz Mountains, 93
Schröter, and the crater Posidonius, 87
Schwabe, and Sun-spots, 40
Seas in the Moon, 82
Secchi, and stellar spectra, 479
Shoal of shooting stars, 377;
dimensions, 377
Shooting stars (see Stars, shooting)
Sickle, the, 421
Sidereal aggregation theory of Sir W. Herschel, 529
Siderite, Rowton, 395
Sinus Iridum, 83
Sirius, change in position of, 425;
companion of, 427, 428;
exceptional lustre of, 110;
irregularities of movement of, 426;
larger than the Sun, 110;
most brilliant star, 419;
periodical appearances of, 157;
proper motion of, 425;
spectrum of, 479;
velocity of, 426;
weight of, 427
Smyth, Professor C.P., 493
Sodium, colour of flame from, 49;
in the Sun, 50
Solar corona, prominences etc. (see under Sun)
Solar system, 107–121;
Copernican exposition of the, 7;
influence of gravitation on, 149;
information respecting, obtained by observing the transit of Venus, 174;
island in the universe, 121;
minor planets, 229–244;
moment of momentum, 554;
movement of, towards Lyra, 457;
origin of, as suggested by the nebular theory, 526;
position of Saturn and Uranus in, 297, 305
[Pg 567]South, Sir James, 12
Spectra of stars, 479
Spectro-heliograph, 58
Spectroscope, 43–56;
detection of iron in the Sun by the, 50
Spectroscopic binaries, 487
Spectrum analysis, 47;
dark lines, 49, 50;
gaseous nebulæ, 474;
line D, 48, 49
Speculum, the Rosse, 20
Spica, 423, 487
Spider-threads for adjusting the micrometer, 86;
for sighting telescopes, 22
Spots on the Sun, 36–43;
connection with magnetism, 42;
cycles, 41;
duration, 41;
epochs of maximum, 42;
motion, 36;
period of revolution, 40;
Scheiner's observations, 36;
zones in which they occur, 39
Star clusters, 461–464;
in Hercules, 462;
in Perseus, 462
Stars, apparent movements due to precession, nutation, and aberration, 504;
approximate number of, 28;
attraction inappreciable, 316;
catalogues of, 310, 311, 409, 431;
charts of, 325, 328;
circular movement of, 505–507
Stars, distances of, 441;
Bessel's labours, 442–449;
Henderson's labours, 442;
method of measuring, 443–445;
Struve's work, 442, 448, 449;
parallactic ellipse, 444–449
Stars, double, 434;
Bode's list, 435;
Burnham's additions, 439;
Cassini, 434;
Herschel, 435, 436;
measurement, 435, 436;
revolution, 436;
Savary, 436;
shape of orbit, 436;
variation in colour, 438
Stars, elliptic movement of, 506;
gravitation and, 149;
how distinguished from planets, 111;
physical nature of, 477;
probability of their possessing a planetary system, 121;
real and apparent movements of, 504;
really suns, 32, 121
Stars, shooting, attractions of the planets, 386;
connection with comets, 388–390;
countless in number, 372;
dimensions of shoal, 377;
features of, 373;
length of orbit, 387;
orbit, 378;
orbit, gradual change, 386;
period of revolution, 384;
periodic return, 378, 379;
shower of November, 1866, 377, 379–380;
shower of November, 1866, and Professor Adams, 384, 386;
shower of November, 1866, radiation of tracks from Leo, 380;
shower of November, 1872, 389;
showers, 376;
showers and Professor Newton, 377;
track, 377;
transformed into vapour by friction with the Earth's atmosphere, 374, 376;
velocity, 373, 386
Stars, spectra of, 479;
teaching of ancients respecting, 3;
temperature of, 515;
temporary, 430, 488;
values of velocity of, 484;
variable, 429
Stoney, Dr. G.J., 387
Strontium, flame from, 46;
in the Sun, 50
Struve, Otto, and the distance of Vega, 442, 447;
and the distance of 61 Cygni, 448, 449
Sun, The, and the velocity of light, 265;
apparent size of, as seen from the planets, 117, 118;
as a star, 32;
axial rotation of, 558;
compared with the Earth, 29;
connection of, with the seasons, 4;
corona of, during eclipse, 62–64;
density of, 65, 558;
diameter of, 558;
distance of, from Mars, 213;
distance of, from Saturn, 271;
distance of, from the Earth, 31, 114, 184, 240, 558;
eclipse of, 6, 53;
ellipticity of, 558;
faculæ on surface of, 37;
focus of planets' orbits, 138;
gradually parting with its heat, 95;
granules on surface of, 34;
heat of, and its sources, 515–526;
heat of, thrown on Jupiter, 256;
minor planets and, 240;
movement of, towards Lyra, 457;
nebular theory of its heat, 526;
photographed, 34;
precession of the Earth's axis, 497;
prominences of, 53–59;
relation of, to the Moon, 71;
rising and setting of, 2;
rotation of, 40, 201;
size of, 29;
spectrum of, 48;
spots on, 36–43;
spots, connection with magnetism, 42;
storms and convulsions on, 42, 43;
surface of, gaseous matter, 34;
surface of, mottled, 34;
teaching of early astronomers concerning, 3–7;
temperature of, 30, 31, 516;
texture of, 34;
tides on, 530;
velocity of, 484;
weight of, compared with Jupiter, 250, 350;
zodiacal light and, 67;
zones on the surface of, 39
Sunbeam, revelations of a, 44
Swan, the, 424, 439, 445
Sword-handle of Perseus, 462
Syrtis major, 222
T
Taurus, constellation of, 231, 419
Tebbutt's comet, 353
Telescope, construction of the first, 10;
equatorial (Dunsink), 12–14, 185;
Greenwich, 26;
Herschelian, 19;
Lick, 16, 19;
Paris, 22, 23;
reflecting, 19, 21;
refracting, 11, 14;
Rosse, 19, 20, 468, 470;
sighting of a, 23;
structure of the eye illustrates the principle of the, 10;
Vienna, 14–16;
Washington, 226;
Yerkes, 16
Temporary stars, 430, 488
Tethys, 559
Theophilus, 92
Tides, The, actual energy derived from the Earth, 539;
affected by the law of gravitation, 149, 535;
affected by the Moon, 70, 535–537;
at Bay of Fundy, 538;
at Cardiff, 538;
at Chepstow, 538;
at London, 538;
at St. Helena, 538;
excited by the Sun, 537;
formation of currents, 538;
in Bristol Channel, 538;
in Mediterranean, 537;
in mid-ocean, 538;
Jupiter and, 552;
length of the day and, 541;
lunar, 548, 549;
moment of momentum and, 552;
neap, 537;
rotation of the Earth, and revolution of the Moon, 549;
satellites of Mars, 551;
solar, 550;
spring, 537;
variations in, 538;
waste of water power, 538;
work effected, 539
Tin in the Sun, 50
Titan, 294, 295, 559
Titania, 309, 559
Transit of Mercury, 152, 163, 164
Transit of Venus, 152;
Captain Cook, 184;
Copeland's observations of, 189;
Crabtree's observations of, 180;
Gassendi's observations of, 178;
Halley's method, 180, 181;
Horrocks' observations of, 179, 180;
importance of, 173;
Kepler's prediction of, 163;
observations of, at Dunsink, 184–188
Transit of Vulcan, 152–153
Triesnecker, 84, 93
Trouvelot, Mr. L., and Saturn's rings, 278
Tschermak, and the origin of meteorites, 400, 401
Tycho (lunar crater), 91
Tycho Brahe, and the Observatory of Uraniborg, 9, 10, 430
U
Umbra of Sun-spot, 51
Umbriel, 309, 559
Unstable dynamical equilibrium, 543
Uraniborg, Observatory of, 10
Uranus, 112;
attraction of Saturn, 322;
Bradley's observations of, 312;
composition of, 308;
density of, 558;
diameter of, 308, 558;
diameter of orbit of, 305;
disc of, 308;
discovery of, by Herschel, 305, 308;
distance from Sun of, 558;
ellipse of, 313;
first taken for a comet, 304;
Flamsteed's observations of, 311, 312;
formerly regarded as a star, 311, 312;
[Pg 568]investigations to discover a planet outside the orbit, 323–324;
irregular motion of, 314, 323;
Lemonnier's observations of, 312;
Leonids and, 386;
Mayer's observations of, 312;
moment of momentum of, 554;
orbit of, 117, 310;
periodic time of, 558;
period of revolution of, 312;
rotation of, 308;
satellites of, 559;
satellites, discovery by Herschel, 308;
satellites, movement nearly circular, 309;
satellites, periodical movements, 309;
satellites, plane of orbits, 309, 310;
size of compared with the Earth, 308;
and with other planets, 119;
subject to another attraction besides the Sun, 314
Ursa major (see Great Bear)
V
Variable Stars, 429
Vega, 414, 423, 424, 479;
Struve's measurement of, 442
Velocity, of light, 261, 262, 265;
of light, laws dependent upon, 511;
of planets, 140–143, 146, 237;
of stars, values of, 483–4
Venus, ancient study of, 6;
aspects of, 171;
atmosphere of, 189;
brilliancy of, 168;
density of, 558;
diameter of, 191, 558;
distance of, from the Sun, 191, 558;
habitability of, 173;
movement of, 168;
neighbour to the Earth, 109;
orbit of, 114, 135;
orbit form of, 139, 191;
periodic time of, 558;
a planet or "wanderer," 111;
rotation of, 191;
shape of, 169;
size of, compared with other planets, 116, 169;
surface of, 171;
transit of, 152, 176–190;
transit, importance of, 173;
transit predicted by Kepler, 163;
velocity and periodic time of, 142, 143, 191;
view of the ancients about, 157
Vesta, 233, 238
Victoria, 242
Vienna telescope, 14–16
Virgo, 423
Vogel and Algol, 485;
and Spica, 486, 487;
and the spectra of the stars, 479, 483
Volcanic origin of meteorites, 400;
outbreaks on the Earth, 197
Von Asten and Encke's comet, 349, 350;
and the distance of the Sun, 351;
and the weight of Mercury, 166
Vortex rings, 469
Vulcan, 152, 153;
and the Sun, 3
W
Wargentin, 90
Watson, Professor, and Mercury, 154
Watson, Sir William, friendship with Herschel, 302
Wave-lengths, 60
Weather, not affected by the Moon, 82
Wilson, Mr. W.E., and the nebula in Orion, 469
Witt, Herr G., and Eros, 236
Wold Cottage meteorite, the, 392
Wright, Thomas, and the Milky Way, 474
Y
"Year of Stars," the, 377
Yerkes Observatory, Chicago, 16
Young, Professor, account of a marvellous Sun-prominence, 42;
and Sun-spots, 38;
observations on magnetic storms, 39
Z
Zeeman, Dr., and spectral lines, 491
Zinc in the Sun, 50
Zodiac, the, 5
Zodiacal light, 67
Zone of minor planets, 234
Printed by Cassell & Company, Limited, la Belle Sauvage, London, E.C.
[1] It may, however, be remarked that a star is never seen to set, as, owing to our atmosphere, it ceases to be visible before it reaches the horizon.
[2] "Popular Astronomy," p. 66.
[3] Limb is the word used by astronomers to denote the edge or circumference of the apparent disc of a heavenly body.
[4] "The Sun," p. 119.
[5] It has been frequently stated that the outburst in 1859, witnessed by Carrington and Hodgson, was immediately followed by an unusually intense magnetic storm, but the records at Kew and Greenwich show that the magnetic disturbances on that day were of a very trivial character.
[6] Some ungainly critic has observed that the poet himself seems to have felt a doubt on the matter, because he has supplemented the dubious moonbeams by the "lantern dimly burning." The more generous, if somewhat a sanguine remark has been also made, that "the time will come when the evidence of this poem will prevail over any astronomical calculations."
[7] This sketch has been copied by permission from the very beautiful view in Messrs. Nasmyth and Carpenter's book, of which it forms Plate XI. So have also the other illustrations of lunar scenery in Plates VIII., IX. The photographs were obtained by Mr. Nasmyth from models carefully constructed from his drawings to illustrate the features on the moon. During the last twenty years photography has completely superseded drawing by eye in the delineation of lunar objects. Long series of magnificent photographs of lunar scenery have been published by the Paris and Lick Observatories.
[8] At the British Association's meeting at Cardiff in 1892, Prof. Copeland exhibited a model of the moon, on which the appearance of the streaks near full moon was perfectly shown by means of small spheres of transparent glass attached to the surface.
[9] The duration of an occultation, or, in other words, the length of time during which the moon hides the star, would be slightly shorter than the computed time, if the moon had an atmosphere capable of sensibly refracting the light from the star. But, so far, our observations do not indicate this with certainty.
[10] I owe my knowledge of this subject to Dr. G. Johnstone Stoney, F.R.S. There has been some controversy as to who originated the ingenious and instructive doctrine here sketched.
[11] The space described by a falling body is proportional to the product of the force and the square of the time. The force varies inversely as the square of the distance from the earth, so that the space will vary as the square of the time, and inversely as the square of the distance. If, therefore, the distance be increased sixty-fold, the time must also be increased sixty-fold, if the space fallen through is to remain the same.
[12] See Newcomb's "Popular Astronomy," p. 78.
[13] Recent investigation by Newcomb on the motion of Mercury have led to the result that the hypothesis of a planet or a ring of very small planets between the orbit of Mercury and the sun cannot account for the difference between theory and observation in the movements of Mercury. Harzer has come to the same result, and has shown that the disturbing element may possibly be the material of the Solar Corona.
[14] "The Sun: its Planets, and their Satellites." London: 1882 (page 147).
[15] James Gregory, in a book on optics written in 1667, had already suggested the use of the transit of Venus for this purpose.
[16] See "Astronomy and Astrophysics," No. 128.
[17] See "Astronomy and Astrophysics," No. 128.
[18] This is the curved marking which on Plate XVIII. appears in longitude 290° and north of (that is, below) the equator. Here, as in all astronomical drawings, north is at the foot and south at the top. See above, p. 82 (Chapter III.).
[19] Now Director of the Lick Observatory.
[20] The heliometer is a telescope with its object-glass cut in half along a diameter. One or both of these halves is movable transversely by a screw. Each half gives a complete image of the object. The measures are effected by observing how many turns of the screw convey the image of the star formed by one half of the object-glass to coincide with the image of the planet formed by the other.
[21] See "Astronomy and Astrophysics," No. 109.
[22] It is only right to add that some observers believe that, in exceptional circumstances, points of Jupiter have shown some slight degree of intrinsic light.
[23] Professor Pickering, of Cambridge, Mass., has, however, effected the important improvement of measuring the decline of light of the satellite undergoing eclipse by the photometer. Much additional precision may be anticipated in the results of such observations.
[24] "Newcomb's Popular Astronomy," p. 336.
[25] See Grant, "History of Physical Astronomy," page 255.
[26] Now Director of the Lick Observatory.
[27] We are here neglecting the orbital motion of Saturn, by which the whole system is moved towards or from the earth, but as this motion is common to the ball and the ring, it will not disturb the relative positions of the three spectra.
[28] According to Prof. Barnard's recent measures, the diameter of Titan is 2,700 miles. This is the satellite discovered by Huyghens; it is the sixth in order from the planet.
[29] Extract from "Three Cities of Russia," by C. Piazzi Smyth, vol. ii., p. 164: "In the year 1796. It then chanced that George III., of Great Britain, was pleased to send as a present to the Empress Catharine of Russia a ten-foot reflecting telescope constructed by Sir William Herschel. Her Majesty immediately desired to try its powers, and Roumovsky was sent for from the Academy to repair to Tsarskoe-Selo, where the Court was at the time residing. The telescope was accordingly unpacked, and for eight long consecutive evenings the Empress employed herself ardently in observing the moon, planets, and stars; and more than this, in inquiring into the state of astronomy in her dominions. Then it was that Roumovsky set before the Imperial view the Academy's idea of removing their observatory, detailing the necessity for, and the advantages of, such a proceeding. Graciously did the 'Semiramis of the North,' the 'Polar Star,' enter into all these particulars, and warmly approve of the project; but death closed her career within a few weeks after, and prevented her execution of the design."
[30] See Professor Holden's "Sir William Herschel, his Life and Works."
[31] Arago says that "Lemonnier's records were the image of chaos." Bouvard showed to Arago one of the observations of Uranus which was written on a paper bag that in its time had contained hair-powder.
[32] The first comet of 1884 also suddenly increased in brightness, while a distinct disc, which hitherto had formed the nucleus, became transformed into a fine point of light.
[33] The three numbers 12, 1, and 1⁄4 are nearly inversely proportional to the atomic weights of hydrogen, hydrocarbon gas, and iron vapour, and it is for this reason that Bredichin suggested the above-mentioned composition of the various types of tail. Spectroscopic evidence of the presence of hydrogen is yet wanting.
[34] This illustration, as well as the figure of the path of the meteors, has been derived from Dr. G.J. Stoney's interesting lecture on "The Story of the November Meteors," at the Royal Institution, in 1879.
[35] On the 27th November, 1885, a piece of meteoric iron fell at Mazapil, in Mexico, during the shower of Andromedes, but whether it formed part of the swarm is not known. It is, however, to be noticed that meteorites are said to have fallen on several other occasions at the end of November.
[36] Hooke had noticed, in 1664, that the star Gamma Arietis was double.
[37] Perhaps if we could view the stars without the intervention of the atmosphere, blue stars would be more common. The absorption of the atmosphere specially affects the greenish and bluish colours. Professor Langley gives us good reason for believing that the sun itself would be blue if it were not for the effect of the air.
[38] The declination of a star is the arc drawn from the star to the equator at right angles to the latter.
[39] The distance of 61 Cygni has, however, again been investigated by Professor Asaph Hall, of Washington, who has obtained a result considerably less than had been previously supposed; on the other hand, Professor Pritchard's photographic researches are in confirmation of Struve's and those obtained at Dunsink.
[40] I am indebted for this drawing to the kindness of Messrs. De la Rue.
[41] See Chapter XIX., on the mass of Sirius and his satellite.
[42] As the earth carries on the telescope at the rate of 18 miles a second, and as light moves with the velocity of 180,000 miles a second very nearly, it follows that the velocity of the telescope is about one ten-thousandth part of that of light. While the light moves down the tube 20 feet long, the telescope will therefore have moved the ten-thousandth part of 20 feet—i.e., the fortieth of an inch.
[43] See Newcomb's "Popular Astronomy," p. 508, where the discovery of this law is attributed to Mr. J. Homer Lane, of Washington. The contraction theory is due to Helmholtz.
[44] The theory of Tidal Evolution sketched in this chapter is mainly due to the researches of Professor G.H. Darwin, F.R.S.
[45] The hour varies with the locality: it would be 11.49 at Calais; at Liverpool, 11.23; at Swansea Bay, 5.56, etc.
[46] Having decided upon the units of mass, of angle, and of distance which we intend to use for measuring these quantities, then any mass, or angle, or distance is expressed by a certain definite number. Thus if we take the mass of the earth as the unit of mass, the angle through which it moves in a second as the unit of angle, and its distance from the sun as the unit of distance, we shall find that the similar quantities for Jupiter are expressed by the numbers 316, 0·0843, and 5·2 respectively. Hence its orbital moment of momentum is 316 × 0·0843 × (5·2)2.