|
Transcriber’s note:
|
A few typographical errors have been corrected. They
appear in the text like this, and the
explanation will appear when the mouse pointer is moved over the marked
passage. Sections in Greek will yield a transliteration
when the pointer is moved over them, and words using diacritic characters in the
Latin Extended Additional block, which may not display in some fonts or browsers, will
display an unaccented version.
Links to other EB articles: Links to articles residing in other EB volumes will
be made available when the respective volumes are introduced online.
|
THE ENCYCLOPÆDIA BRITANNICA
A DICTIONARY OF ARTS, SCIENCES, LITERATURE AND GENERAL INFORMATION
ELEVENTH EDITION
VOLUME IX SLICE II
Ehud to Electroscope
Articles in This Slice
| EHUD | ELBERFELD |
| EIBENSTOCK | ELBEUF |
| EICHBERG, JULIUS | ELBING |
| EICHENDORFF, JOSEPH, FREIHERR VON | ELBOW |
| EICHHORN, JOHANN GOTTFRIED | ELBURZ |
| EICHHORN, KARL FRIEDRICH | ELCHE |
| EICHSTÄTT | ELCHINGEN |
| EICHWALD, KARL EDUARD VON | ELDAD BEN MAḤLI |
| EIDER (river of Prussia) | ELDER (ruler or officer) |
| EIDER (duck) | ELDER (shrubs and trees) |
| EIFEL | ELDON, JOHN SCOTT |
| EIFFEL TOWER | EL DORADO |
| EILDON HILLS | ELDUAYEN, JOSÉ DE |
| EILENBURG | ELEANOR OF AQUITAINE |
| EINBECK | ELEATIC SCHOOL |
| EINDHOVEN | ELECAMPANE |
| EINHARD | ELECTION (politics) |
| EINHORN, DAVID | ELECTION (English law choice) |
| EINSIEDELN | ELECTORAL COMMISSION |
| EISENACH | ELECTORS |
| EISENBERG | ELECTRA |
| EISENERZ | ELECTRICAL MACHINE |
| EISLEBEN | ELECTRIC EEL |
| EISTEDDFOD | ELECTRICITY |
| EJECTMENT | ELECTRICITY SUPPLY |
| EKATERINBURG | ELECTRIC WAVES |
| EKATERINODAR | ELECTROCHEMISTRY |
| EKATERINOSLAV (government of Russia) | ELECTROCUTION |
| EKATERINOSLAV (town of Russia) | ELECTROKINETICS |
| EKHOF, KONRAD | ELECTROLIER |
| EKRON | ELECTROLYSIS |
| ELABUGA | ELECTROMAGNETISM |
| ELAM | ELECTROMETALLURGY |
| ELAND | ELECTROMETER |
| ELASTICITY | ELECTRON |
| ELATERITE | ELECTROPHORUS |
| ELATERIUM | ELECTROPLATING |
| ELBA | ELECTROSCOPE |
| ELBE | |
131
EHUD, in the Bible, a “judge” who delivered Israel from
the Moabites (Judg. iii. 12-30). He was sent from Ephraim to
bear tribute to Eglon king of Moab, who had crossed over the
Jordan and seized the district around Jericho. Being, like the
Benjamites, left-handed (cf. xx. 16), he was able to conceal a
dagger and strike down the king before his intentions were suspected.
He locked Eglon in his chamber and escaped. The
men from Mt Ephraim collected under his leadership and by
seizing the fords of the Jordan were able to cut off the Moabites.
He is called the son of Gera a Benjamite, but since both Ehud
and Gera are tribal names (2 Sam. xvi. 5, 1 Chron. viii. 3, 5 sq.)
it has been thought that this notice is not genuine. The tribe
of Benjamin rarely appears in the old history of the Hebrews
before the time of Saul. See further Benjamin; Judges.
EIBENSTOCK, a town of Germany, in the kingdom of Saxony,
near the Mulde, on the borders of Bohemia, 17 m. by rail S.S.E.
of Zwickau. Pop. (1905) 7460. It is a principal seat of the
tambour embroidery which was introduced in 1775 by Clara
Angermann. It possesses chemical and tobacco manufactories,
and tin and iron works. It has also a large cattle market. Eibenstock,
together with Schwarzenberg, was acquired by purchase
in 1533 by Saxony and was granted municipal rights in the
following year.
EICHBERG, JULIUS (1824-1893), German musical composer,
was born at Düsseldorf on the 13th of June 1824. When he was
nineteen he entered the Brussels Conservatoire, where he took
first prizes for violin-playing and composition. For eleven years
he occupied the post of professor in the Conservatoire of Geneva.
In 1857 he went to the United States, staying two years in New
York and then proceeding to Boston, where he became director
of the orchestra at the Boston Museum. In 1867 he founded the
Boston Conservatory of Music. Eichberg published several
educational works on music; and his four operettas, The Doctor
of Alcantara, The Rose of Tyrol, The Two Cadis and A Night in
Rome, were highly popular. He died in Boston on the 18th of
January 1893.
EICHENDORFF, JOSEPH, FREIHERR VON (1788-1857),
German poet and romance-writer, was born at Lubowitz, near
Ratibor, in Silesia, on the 10th of March 1788. He studied law
at Halle and Heidelberg from 1805 to 1808. After a visit to
Paris he went to Vienna, where he resided until 1813, when he
joined the Prussian army as a volunteer in the famous Lützow
corps. When peace was concluded in 1815, he left the army,
and in the following year he was appointed to a judicial office
at Breslau. He subsequently held similar offices at Danzig,
Königsberg and Berlin. Retiring from public service in 1844,
he lived successively in Danzig, Vienna, Dresden and Berlin.
He died at Neisse on the 26th of November 1857. Eichendorff
was one of the most distinguished of the later members of the
German romantic school. His genius was essentially lyrical.
Thus he is most successful in his shorter romances and dramas,
where constructive power is least called for. His first work,
written in 1811, was a romance, Ahnung und Gegenwart (1815).
This was followed at short intervals by several others, among
which the foremost place is by general consent assigned to Aus
dem Leben eines Taugenichts (1826), which has often been reprinted.
Of his dramas may be mentioned Ezzelin von Romano
(1828); and Der letzte Held von Marienburg (1830), both tragedies;
and a comedy, Die Freier (1833). He also translated several
of Calderon’s religious dramas (Geistliche Schauspiele, 1846).
It is, however, through his lyrics (Gedichte, first collected 1837)
that Eichendorff is best known; he is the greatest lyric poet of
the romantic movement. No one has given more beautiful
expression than he to the poetry of a wandering life; often, again,
his lyrics are exquisite word pictures interpreting the mystic
meaning of the moods of nature, as in Nachts, or the old-time
mystery which yet haunts the twilight forests and feudal castles
of Germany, as in the dramatic lyric Waldesgespräch or Auf
einer Burg. Their language is simple and musical, which makes
them very suitable for singing, and they have been often set,
notably by Schubert and Schumann.
In the later years of his life Eichendorff published several
works on subjects in literary history and criticism such as Über
die ethische und religiöse Bedeutung der neuen romantischen
Poesie in Deutschland (1847), Der deutsche Roman des 18.
Jahrhunderts in seinem Verhältniss zum Christenthum (1851),
and Geschichte der poetischen Litteratur Deutschlands (1856),
but the value of these works is impaired by the author’s reactionary
standpoint. An edition of his collected works in six
volumes, appeared at Leipzig in 1870.
Eichendorff’s Sämtliche Werke appeared in 6 vols., 1864 (reprinted
1869-1870); his Sämtliche poetische Werke in 4 vols. (1883). The
latest edition is that edited by R. von Gottschall in 4 vols. (1901).
A good selection edited by M. Kaoch will be found in vol. 145 of
Kürschner’s Deutsche Nationalliteratur (1893). Eichendorff’s critical
writings were collected in 1866 under the title Vermischte Schriften
(5 vols.). Cp. H. von Eichendorff’s biographical introduction to the
Sämtliche Werke; also H. Keiter, Joseph von Eichendorff (Cologne,
1887); H.A. Krüger, Der junge Eichendorff (Oppeln, 1898).
EICHHORN, JOHANN GOTTFRIED (1752-1827), German
theologian, was born at Dörrenzimmern, in the principality of
Hohenlohe-Oehringen, on the 16th of October 1752. He was
educated at the state school in Weikersheim, where his father
was superintendent, at the gymnasium at Heilbronn and at the
university of Göttingen (1770-1774), studying under J.D.
Michaelis. In 1774 he received the rectorship of the gymnasium
at Ohrdruf, in the duchy of Gotha, and in the following year was
made professor of Oriental languages at Jena. On the death
of Michaelis in 1788 he was elected professor ordinarius at
Göttingen, where he lectured not only on Oriental languages and
on the exegesis of the Old and New Testaments, but also on political
history. His health was shattered in 1825, but he continued
his lectures until attacked by fever on the 14th of June 1827.
He died on the 27th of that month. Eichhorn has been called
“the founder of modern Old Testament criticism.” He first
properly recognized its scope and problems, and began many of
its most important discussions. “My greatest trouble,” he
says in the preface to the second edition of his Einleitung, “I had
to bestow on a hitherto unworked field—on the investigation of
the inner nature of the Old Testament with the help of the Higher
Criticism (not a new name to any humanist).” His investigations
led him to the conclusion that “most of the writings of the
Hebrews have passed through several hands.” He took for
granted that all the so-called supernatural facts relating to the
Old and New Testaments were explicable on natural principles.
He sought to judge them from the standpoint of the ancient
world, and to account for them by the superstitious beliefs which
were then generally in vogue. He did not perceive in the biblical
books any religious ideas of much importance for modern times;
they interested him merely historically and for the light they
cast upon antiquity. He regarded many books of the Old
Testament as spurious, questioned the genuineness of 2 Peter
and Jude, denied the Pauline authorship of Timothy and Titus,
132
and suggested that the canonical gospels were based upon various
translations and editions of a primary Aramaic gospel. He did
not appreciate as sufficiently as David Strauss and the Tübingen
critics the difficulties which a natural theory has to surmount,
nor did he support his conclusions by such elaborate discussions
as they deemed necessary.
His principal works were—Geschichte des Ostindischen Handels vor
Mohammed (Gotha, 1775); Allgemeine Bibliothek der biblischen
Literatur (10 vols., Leipzig, 1787-1801); Einleitung in das Alte Testament
(3 vols., Leipzig, 1780-1783); Einleitung in das Neue Testament
(1804-1812); Einleitung in die apokryphischen Bücher des Alten
Testaments (Gött., 1795); Commentarius in apocalypsin Joannis
(2 vols., Gött., 1791); Die Hebr. Propheten (3 vols., Gött., 1816-1819);
Allgemeine Geschichte der Cultur und Literatur des neuern
Europa (2 vols., Gött., 1796-1799); Literärgeschichte (1st vol., Gött.,
1799, 2nd ed. 1813, 2nd vol. 1814); Geschichte der Literatur von
ihrem Anfange bis auf die neuesten Zeiten (5 vols., Gött., 1805-1812);
Übersicht der Französischen Revolution (2 vols., Gött., 1797); Weltgeschichte
(3rd ed., 5 vols., Gött., 1819-1820); Geschichte der drei
letzten Jahrhunderte (3rd ed., 6 vols., Hanover, 1817-1818); Urgeschichte
des erlauchten Hauses der Welfen (Hanover, 1817).
See R.W. Mackay, The Tübingen School and its Antecedents (1863),
pp. 103 ff.; Otto Pfleiderer, Development of Theology (1890), p. 209;
T.K. Cheyne, Founders of Old Testament Criticism (1893), pp. 13 ff.
EICHHORN, KARL FRIEDRICH (1781-1854), German jurist,
son of the preceding, was born at Jena on the 20th of November
1781. He entered the university of Göttingen in 1797. In 1805
he obtained the professorship of law at Frankfort-on-Oder,
holding it till 1811, when he accepted the same chair at Berlin.
On the call to arms in 1813 he became a captain of horse, and
received at the end of the war the decoration of the Iron Cross.
In 1817 he was offered the chair of law at Göttingen, and, preferring
it to the Berlin professorship, taught there with great
success till ill-health compelled him to resign in 1828. His
successor in the Berlin chair having died in 1832, he again entered
on its duties, but resigned two years afterwards. In 1832 he also
received an appointment in the ministry of foreign affairs, which,
with his labours on many state committees and his legal researches
and writings, occupied him till his death at Cologne
on the 4th of July 1854. Eichhorn is regarded as one of the
principal authorities on German constitutional law. His chief
work is Deutsche Staats- und Rechtsgeschichte (Göttingen, 1808-1823,
5th ed. 1843-1844). In company with Savigny and
J.F.L. Göschen he founded the Zeitschrift für geschichtliche
Rechtswissenschaft. He was the author besides of Einleitung
in das deutsche Privatrecht mit Einschluss des Lehnrechts (Gött.,
1823) and the Grundsätze des Kirchenrechts der Katholischen und
der Evangelischen Religionspartei in Deutschland, 2 Bde. (ib., 1831-1833).
See Schulte, Karl Friedrich Eichhorn, sein Leben und Wirken
(1884).
EICHSTÄTT, a town and episcopal see of Germany, in the
kingdom of Bavaria, in the deep and romantic valley of the
Altmühl, 35 m. S. of Nuremberg, on the railway to Ingolstadt
and Munich. Pop. (1905) 7701. The town, with its numerous
spires and remains of medieval fortifications, is very picturesque.
It has an Evangelical and seven Roman Catholic churches,
among the latter the cathedral of St Wilibald (first bishop of
Eichstätt),—with the tomb of the saint and numerous pictures
and relics,—the church of St Walpurgis, sister of Wilibald,
whose remains rest in the choir, and the Capuchin church, a copy
of the Holy Sepulchre. Of its secular buildings the most noticeable
are the town hall and the Leuchtenberg palace, once the
residence of the prince bishops and later of the dukes of Leuchtenberg
(now occupied by the court of justice of the district), with
beautiful grounds. The Wilibaldsburg, built on a neighbouring
hill in the 14th century by Bishop Bertold of Hohenzollern, was
long the residence of the prince bishops of Eichstätt, and now
contains an historical museum. There are an episcopal lyceum,
a clerical seminary, a classical and a modern school, and numerous
religious houses. The industries of the town include bootmaking,
brewing and the production of lithographic stones.
Eichstätt (Lat. Aureatum or Rubilocus) was originally a Roman
station which, after the foundation of the bishopric by Boniface
in 745, developed into a considerable town, which was surrounded
with walls in 908. The bishops of Eichstätt were princes of the
Empire, subject to the spiritual jurisdiction of the archbishops
of Mainz, and ruled over considerable territories in the Circle of
Franconia. In 1802 the see was secularized and incorporated
in Bavaria. In 1817 it was given, with the duchy of Leuchtenberg,
as a mediatized domain under the Bavarian crown, by the
king of Bavaria to his son-in-law Eugène de Beauharnais,
ex-viceroy of Italy, henceforth styled duke of Leuchtenberg.
In 1855 it reverted to the Bavarian crown.
EICHWALD, KARL EDUARD VON (1795-1876), Russian
geologist and physician, was born at Mitau in Courland on the
4th of July 1795. He became doctor of medicine and professor
of zoology in Kazañ in 1823; four years later professor of zoology
and comparative anatomy at Vilna; in 1838 professor of
zoology, mineralogy and medicine at St Petersburg; and finally
professor of palaeontology in the institute of mines in that city.
He travelled much in the Russian empire, and was a keen
observer of its natural history and geology. He died at St
Petersburg on the 10th of November 1876. His published works
include Reise auf dem Caspischen Meere und in den Caucasus,
2 vols. (Stuttgart and Tübingen, 1834-1838); Die Urwelt Russlands
(St Petersburg, 1840-1845); Lethaea Rossica, ou paléontologie
de la Russie, 3 vols. (Stuttgart, 1852-1868), with Atlases.
EIDER, a river of Prussia, in the province of Schleswig-Holstein.
It rises to the south of Kiel, in Lake Redder, flows
first north, then west (with wide-sweeping curves), and after a
course of 117 m. enters the North Sea at Tönning. It is navigable
up to Rendsburg, and is embanked through the marshes across
which it runs in its lower course. Since the reign of Charlemagne,
the Eider (originally Ägyr Dör—Neptune’s gate) was known
as Romani terminus imperii and was recognized as the boundary
of the Empire in 1027 by the emperor Conrad II., the founder
of the Salian dynasty. In the controversy arising out of the
Schleswig-Holstein Question, which culminated in the war of
Austria and Prussia against Denmark in 1864, the Eider gave
its name to the “Eider Danes,” the intransigeant Danish party
which maintained that Schleswig (Sonderjylland, South Jutland)
was by nature and historical tradition an integral part of Denmark.
The Eider Canal (Eider-Kanal), which was constructed
between 1777 and 1784, leaves the Eider at the point where the
river turns to the west and enters the Bay of Kiel at Holtenau. It
was hampered by six sluices, but was used annually by some
4000 vessels, and until its conversion in 1887-1895 into the
Kaiser Wilhelm Canal afforded the only direct connexion between
the North Sea and the Baltic.
EIDER (Icelandic, Ædur), a large marine duck, the Somateria
mollissima of ornithologists, famous for its down, which, from
its extreme lightness and elasticity, is in great request for filling
bed-coverlets. This bird generally frequents low rocky islets
near the coast, and in Iceland and Norway has long been afforded
every encouragement and protection, a fine being inflicted for
killing it during the breeding-season, or even for firing a gun near
its haunts, while artificial nesting-places are in many localities
contrived for its further accommodation. From the care thus
taken of it in those countries it has become exceedingly tame at
its chief resorts, which are strictly regarded as property, and the
taking of eggs or down from them, except by authorized persons,
is severely punished by law. In appearance the eider is somewhat
clumsy, though it flies fast and dives admirably. The
female is of a dark reddish-brown colour barred with brownish-black.
The adult male in spring is conspicuous by his pied
plumage of velvet-black beneath, and white above: a patch
of shining sea-green on his head is only seen on close inspection.
This plumage he is considered not to acquire until his third
year, being when young almost exactly like the female, and
it is certain that the birds which have not attained their full
dress remain in flocks by themselves without going to the
breeding-stations. The nest is generally in some convenient
corner among large stones, hollowed in the soil, and furnished
with a few bits of dry grass, seaweed or heather. By the time
that the full number of eggs (which rarely if ever exceeds five)
is laid the down is added. Generally the eggs and down are
133
taken at intervals of a few days by the owners of the “eider-fold,”
and the birds are thus kept depositing both during the
whole season; but some experience is needed to ensure the
greatest profit from each commodity. Every duck is ultimately
allowed to hatch an egg or two to keep up the stock, and the
down of the last nest is gathered after the birds have left the spot.
The story of the drake’s furnishing down, after the duck’s
supply is exhausted is a fiction. He never goes near the nest.
The eggs have a strong flavour, but are much relished by both
Icelanders and Norwegians. In the Old World the eider breeds
in suitable localities from Spitsbergen to the Farne Islands off
the coast of Northumberland—where it is known as St Cuthbert’s
duck. Its food consists of marine animals (molluscs and crustaceans),
and hence the young are not easily reared in captivity.
The eider of the New World differs somewhat, and has been
described as a distinct species (S. dresseri). Though much
diminished in numbers by persecution, it is still abundant on
the coast of Newfoundland and thence northward. In Greenland
also eiders are very plentiful, and it is supposed that three-fourths
of the supply of down sent to Copenhagen comes from
that country. The limits of the eider’s northern range are not
known, but the Arctic expedition of 1875 did not meet with it
after leaving the Danish settlements, and its place was taken
by an allied species, the king-duck (S. spectabilis), a very beautiful
bird which sometimes appears on the British coast. The female
greatly resembles that of the eider, but the male has a black
chevron on his chin and a bright orange prominence on his
forehead, which last seems to have given the species its English
name. On the west coast of North America the eider is represented
by a species (S. v-nigrum) with a like chevron, but otherwise
resembling the Atlantic bird. In the same waters two
other fine species are also found (S. fischeri and S. stelleri), one
of which (the latter) also inhabits the Arctic coast of Russia
and East Finmark and has twice reached England. The Labrador
duck (S. labradoria), now extinct, also belongs to this
group.
(A. N.)
EIFEL, a district of Germany, in the Prussian Rhine Province,
between the Rhine, the Moselle and the frontier of the grand
duchy of Luxemburg. It is a hilly region, most elevated in the
eastern part (Hohe Eifel), where there are several points from
2000 up to 2410 ft. above sea-level. In the west is the Schneifels
or Schnee-Eifel; and the southern part, where the most picturesque
scenery and chief geological interest is found, is called
the Vorder Eifel.
The Eifel is an ancient massif of folded Devonian rocks
upon the margins of which, near Hillesheim and towards Bitburg
and Trier, rest unconformably the nearly undisturbed sandstones,
marls and limestones of the Trias. On the southern border,
at Wittlich, the terrestrial deposits of the Permian Rothliegende
are also met with. The slates and sandstones of the Lower
Devonian form by far the greater part of the region; but folded
amongst these, in a series of troughs running from south-west
to north-east lie the fossiliferous limestones of the Middle
Devonian, and occasionally, as for example near Büdesheim,
a few small patches of the Upper Devonian. Upon the ancient
floor of folded Devonian strata stand numerous small volcanic
cones, many of which, though long extinct, are still very perfect
in form. The precise age of the eruptions is uncertain. The
only sign of any remaining volcanic activity is the emission in
many places of carbon dioxide and of heated waters. There is no
historic or legendary record of any eruption, but nevertheless the
eruptions must have continued to a very recent geological period.
The lavas of Papenkaule are clearly posterior to the excavation
of the valley of the Kyll, and an outflow of basalt has forced
the Uess to seek a new course. The volcanic rocks occur both
as tuffs and as lava-flows. They are chiefly leucite and nepheline
rocks, such as leucitite, leucitophyre and nephelinite, but basalt
and trachyte also occur. The leucite lavas of Niedermendig contain
haüyne in abundance. The most extensive and continuous
area of volcanic rocks is that surrounding the Laacher See and
extending eastwards to Neuwied and Coblenz and even beyond
the Rhine.
The numerous so-called crater-lakes or maare of the Eifel
present several features of interest. They do not, as a rule,
lie in true craters at the summit of volcanic cones, but rather
in hollows which have been formed by explosions. The most
remarkable group is that of Daun, where the three depressions
of Gemünd, Weinfeld and Schalkenmehren have been hollowed
out in the Lower Devonian strata. The first of these shows no
sign of either lavas or scoriae, but volcanic rocks occur on the
margins of the other two. The two largest lakes in the Eifel
region, however, are the Laacher See in the hills west of Andernach
on the Rhine, and the Pulvermaar S.E. of the Daun group,
with its shores of peculiar volcanic sand, which also appears in
its waters as a black powder (pulver).
EIFFEL TOWER. Erected for the exposition of 1889, the
Eiffel Tower, in the Champ de Mars, Paris, is by far the highest
artificial structure in the world, and its height of 300 metres
(984 ft.) surpasses that of the obelisk at Washington by 429 ft.,
and that of St Paul’s cathedral by 580 ft. Its framework is
composed essentially of four uprights, which rise from the
corners of a square measuring 100 metres on the side; thus the
area it covers at its base is nearly 2½ acres. These uprights
are supported on huge piers of masonry and concrete, the
foundations for which were carried down, by the aid of iron
caissons and compressed air, to a depth of about 15 metres on
the side next the Seine, and about 9 metres on the other side.
At first they curve upwards at an angle of 54°; then they
gradually become straighter, until they unite in a single shaft
rather more than half-way up. The first platform, at a height
of 57 metres, has an area of 5860 sq. yds., and is reached either
by staircases or lifts. The next, accessible by lifts only, is 115
metres up, and has an area of 32 sq. yds; while the third, at
276, supports a pavilion capable of holding 800 persons. Nearly
25 metres higher up still is the lantern, with a gallery 5 metres
in diameter. The work of building this structure, which is
mainly composed of iron lattice-work, was begun on the 28th
of January 1887, and the full height was reached on the 13th of
March 1889. Besides being one of the sights of Paris, to which
visitors resort in order to enjoy the extensive view that can be
had from its higher galleries on a clear day, the tower is used to
some extent for scientific and semi-scientific purposes; thus
meteorological observations are carried on. The engineer under
whose direction the tower was constructed was Alexandre
Gustave Eiffel (born at Dijon on the 15th of December 1832),
who had already had a wide experience in the construction of
large metal bridges, and who designed the huge sluices for the
Panama Canal, when it was under the French company.
EILDON HILLS, a group of three conical hills, of volcanic
origin, in Roxburghshire, Scotland, 1 m. S. by E. of Melrose,
about equidistant from Melrose and St Boswells stations on the
North British railway. They were once known as Eldune—the
Eldunum of Simeon of Durham (fl. 1130)—probably derived from
the Gaelic aill, “rock,” and dun, “hill”; but the name is also
said to be a corruption of the Cymric moeldun, “bald hill.”
The northern peak is 1327 ft. high, the central 1385 ft. and the
southern 1216 ft. Whether or not the Roman station of Trimontium
was situated here is matter of controversy. According
to General William Roy (1726-1790) Trimontium—so called,
according to this theory, from the triple Eildon heights—was
Old Melrose; other authorities incline to place the station on the
northern shore of the Solway Firth. The Eildons have been the
subject of much legendary lore. Michael Scot (1175-1234),
acting as a confederate of the Evil One (so the fable runs) cleft
Eildon Hill, then a single cone, into the three existing peaks.
Another legend states that Arthur and his knights sleep in a
vault beneath the Eildons. A third legend centres in Thomas
of Erceldoune. The Eildon Tree Stone, a large moss-covered
boulder, lying on the high road as it bends towards the west
within 2 m. of Melrose, marks the spot where the Fairy Queen
led him into her realms in the heart of the hills. Other places
associated with this legend may still be identified. Huntly
Banks, where “true Thomas” lay and watched the queen’s
approach, is half a mile west of the Eildon Tree Stone, and on the
134
west side of the hills is Bogle Burn, a streamlet that feeds the
Tweed and probably derives its name from his ghostly visitor.
Here, too, is Rhymer’s glen, although the name was invented
by Sir Walter Scott, who added the dell to his Abbotsford estate.
Bowden, to the south of the hills, was the birthplace of the poets
Thomas Aird (1802-1876) and James Thomson, and its parish
church contains the burial-place of the dukes of Roxburghe.
Eildon Hall is a seat of the duke of Buccleuch.
EILENBURG, a town of Germany, in the Prussian province
of Saxony, on an island formed by the Mulde, 31 m. E. from
Halle, at the junction of the railways Halle-Cottbus and Leipzig-Eilenburg.
Pop. (1905) 15,145. There are three churches, two
Evangelical and one Roman Catholic. The industries of the
town include the manufacture of chemicals, cloth, quilting,
calico, cigars and agricultural implements, bleaching, dyeing,
basket-making, carriage-building and trade in cattle. In the
neighbourhood is the iron foundry of Erwinhof. Opposite the
town, on the steep left bank of the Mulde, is the castle from
which it derives its name, the original seat of the noble family
of Eulenburg. This castle (Ilburg) is mentioned in records of
the reigns of Henry the Fowler as an important outpost against
the Sorbs and Wends. The town itself, originally called
Mildenau, is of great antiquity. It is first mentioned as a town
in 981, when it belonged to the house of Wettin and was the
chief town of the East Mark. In 1386 it was incorporated in
the margraviate of Meissen. In 1815 it passed to Prussia.
See Gundermann, Chronik der Stadt Eilenburg (Eilenburg, 1879).
EINBECK, or Eimbeck, a town of Germany, in the Prussian
province of Hanover, on the Ilm, 50 m. by rail S. of Hanover.
Pop. (1905) 8709. It is an old-fashioned town with many quaint
wooden houses, notable among them the “Northeimhaus,” a
beautiful specimen of medieval architecture. There are several
churches, among them the Alexanderkirche, containing the
tombs of the princes of Grubenhagen, and a synagogue. The
schools include a Realgymnasium (i.e. predominantly for
“modern” subjects), technical schools for the advanced study
of machine-making, for weaving and for the textile industries,
a preparatory training-college and a police school. The industries
include brewing, weaving and the manufacture of
cloth, carpets, tobacco, sugar, leather-grease, toys and roofing-felt.
Einbeck grew up originally round the monastery of St
Alexander (founded 1080), famous for its relic of the True Blood.
It is first recorded as a town in 1274, and in the 14th century
was the seat of the princes of Grubenhagen, a branch of the
ducal house of Brunswick. The town subsequently joined the
Hanseatic League. In the 15th century it became famous for
its beer (“Eimbecker,” whence the familiar “Bock”). In 1540
the Reformation was introduced by Duke Philip of Brunswick-Saltzderhelden
(d. 1551), with the death of whose son Philip II.
(1596) the Grubenhagen line became extinct. In 1626, during
the Thirty Years’ War, Einbeck was taken by Pappenheim and
in October 1641 by Piccolomini. In 1643 it was evacuated by the
Imperialists. In 1761 its walls were razed by the French.
See H.L. Harland, Gesch. der Stadt Einbeck, 2 Bde. (Einbeck,
1854-1859; abridgment, ib. 1881).
EINDHOVEN, a town in the province of North Brabant,
Holland, and a railway junction 8 m. by rail W. by S. of
Helmond. Pop. (1900) 4730. Like Tilburg and Helmond it
has developed in modern times into a flourishing industrial
centre, having linen, woollen, cotton, tobacco and cigar,
matches, &c., factories and several breweries.
EINHARD (c. 770-840), the friend and biographer of Charlemagne;
he is also called Einhartus, Ainhardus or Heinhardus,
in some of the early manuscripts. About the 10th century
the name was altered into Agenardus, and then to Eginhardus,
or Eginhartus, but, although these variations were largely used
in the English and French languages, the form Einhardus, or
Einhartus, is unquestionably the right one.
According to the statement of Walafrid Strabo, Einhard was
born in the district which is watered by the river Main, and his
birth has been fixed at about 770. His parents were of noble
birth, and were probably named Einhart and Engilfrit; and
their son was educated in the monastery of Fulda, where he
was certainly residing in 788 and in 791. Owing to his intelligence
and ability he was transferred, not later than 796, from Fulda
to the palace of Charlemagne by abbot Baugulf; and he soon
became very intimate with the king and his family, and undertook
various important duties, one writer calling him domesticus
palatii regalis. He was a member of the group of scholars who
gathered around Charlemagne and was entrusted with the
charge of the public buildings, receiving, according to a fashion
then prevalent, the scriptural name of Bezaleel (Exodus xxxi. 2
and xxxv. 30-35) owing to his artistic skill. It has been supposed
that he was responsible for the erection of the basilica at Aix-la-Chapelle,
where he resided with the emperor, and the other
buildings mentioned in chapter xvii. of his Vita Karoli Magni,
but there is no express statement to this effect. In 806 Charlemagne
sent him to Rome to obtain the signature of Pope Leo III.
to a will which he had made concerning the division of his
empire; and it was possibly owing to Einhard’s influence that
in 813, after the death of his two elder sons, the emperor made
his remaining son, Louis, a partner with himself in the imperial
dignity. When Louis became sole emperor in 814 he retained
his father’s minister in his former position; then in 817 made
him tutor to his son, Lothair, afterwards the emperor Lothair I.;
and showed him many other marks of favour. Einhard married
Emma, or Imma, a sister of Bernharius, bishop of Worms, and
a tradition of the 12th century represented this lady as a daughter
of Charlemagne, and invented a romantic story with regard to
the courtship which deserves to be noticed as it frequently
appears in literature. Einhard is said to have visited the
emperor’s daughter regularly and secretly, and on one occasion
a fall of snow made it impossible for him to walk away without
leaving footprints, which would lead to his detection. This risk,
however, was obviated by the foresight of Emma, who carried
her lover across the courtyard of the palace; a scene which was
witnessed by Charlemagne, who next morning narrated the
occurrence to his counsellors, and asked for their advice. Very
severe punishments were suggested for the clandestine lover,
but the emperor rewarded the devotion of the pair by consenting
to their marriage. This story is, of course, improbable, and is
further discredited by the fact that Einhard does not mention
Emma among the number of Charlemagne’s children. Moreover,
a similar story has been told of a daughter of the emperor
Henry III. It is uncertain whether Einhard had any children.
He addressed a letter to a person named Vussin, whom he calls
fili and mi nate, but, as Vussin is not mentioned in documents
in which his interests as Einhard’s son would have been
concerned, it is possible that he was only a young man in whom
he took a special interest. In January 815 the emperor Louis I.
bestowed on Einhard and his wife the domains of Michelstadt
and Mulinheim in the Odenwald, and in the charter conveying
these lands he is called simply Einhardus, but, in a document
dated the 2nd of June of the same year, he is referred to as abbot.
After this time he is mentioned as head of several monasteries:
St Peter, Mount Blandin and St Bavon at Ghent, St Servais
at Maastricht, St Cloud near Paris, and Fontenelle near Rouen,
and he also had charge of the church of St John the Baptist
at Pavia.
During the quarrels which took place between Louis I. and
his sons, in consequence of the emperor’s second marriage,
Einhard’s efforts were directed to making peace, but after a time
he grew tired of the troubles and intrigues of court life. In 818
he had given his estate at Michelstadt to the abbey of Lorsch,
but he retained Mulinheim, where about 827 he founded an
abbey and erected a church, to which he transported some relics
of St Peter and St Marcellinus, which he had procured from
Rome. To Mulinheim, which was afterwards called Seligenstadt,
he finally retired in 830. His wife, who had been his constant
helper, and whom he had not put away on becoming an abbot,
died in 836, and after receiving a visit from the emperor, Einhard
died on the 14th of March 840. He was buried at Seligenstadt,
and his epitaph was written by Hrabanus Maurus. Einhard
135
was a man of very short stature, a feature on which Alcuin wrote
an epigram. Consequently he was called Nardulus, a diminutive
form of Einhardus, and his great industry and activity caused
him to be likened to an ant. He was also a man of learning and
culture. Reaping the benefits of the revival of learning brought
about by Charlemagne, he was on intimate terms with Alcuin,
was well versed in Latin literature, and knew some Greek. His
most famous work is his Vita Karoli Magni, to which a prologue
was added by Walafrid Strabo. Written in imitation of the
De vitis Caesarum of Suetonius, this is the best contemporary
account of the life of Charlemagne, and could only have been
written by one who was very intimate with the emperor and his
court. It is, moreover, a work of some artistic merit, although
not free from inaccuracies. It was written before 821, and having
been very popular during the middle ages, was first printed
at Cologne in 1521. G.H. Pertz collated more than sixty
manuscripts for his edition of 1829, and others have since come
to light. Other works by Einhard are: Epistolae, which are of
considerable importance for the history of the times; Historia
translationis beatorum Christi martyrum Marcellini et Petri,
which gives a curious account of how the bones of these martyrs
were stolen and conveyed to Seligenstadt, and what miracles
they wrought; and De adoranda cruce, a treatise which has only
recently come to light, and which has been published by E.
Dümmler in the Neues Archiv der Gesellschaft für ältere deutsche
Geschichtskunde, Band xi. (Hanover, 1886). It has been asserted
that Einhard was the author of some of the Frankish annals,
and especially of part of the annals of Lorsch (Annales Laurissenses
majores), and part of the annals of Fulda (Annales
Fuldenses). Much discussion has taken place on this question,
and several of the most eminent of German historians, Ranke
among them, have taken part therein, but no certain decision
has been reached.
The literature on Einhard is very extensive, as nearly all those
who deal with Charlemagne, early German and early French literature,
treat of him. Editions of his works are by A. Teulet, Einhardi
omnia quae extant opera (Paris, 1840-1843), with a French translation;
P. Jaffé, in the Bibliotheca rerum Germanicarum, Band iv. (Berlin,
1867); G.H. Pertz in the Monumenta Germaniae historica, Bände
i. and ii. (Hanover, 1826-1829), and J.P. Migne in the Patrologia
Latina, tomes 97 and 104 (Paris, 1866). The Vita Karoli Magni,
edited by G.H. Pertz and G. Waitz, has been published separately
(Hanover, 1880). Among the various translations of the Vita may
be mentioned an English one by W. Glaister (London, 1877) and a
German one by O. Abel (Leipzig, 1893). For a complete bibliography
of Einhard, see A. Potthast, Bibliotheca historica, pp. 394-397
(Berlin, 1896), and W. Wattenbach, Deutschlands Geschichtsquellen,
Band i. (Berlin, 1904).
(A. W. H.*)
EINHORN, DAVID (1809-1879), leader of the Jewish reform
movement in the United States of America, was born in Bavaria.
He was a supporter of the principles of Abraham Geiger (q.v.),
and while still in Germany advocated the introduction of prayers
in the vernacular, the exclusion of nationalistic hopes from the
synagogue service, and other ritual modifications. In 1855 he
migrated to America, where he became the acknowledged leader
of reform, and laid the foundation of the régime under which the
mass of American Jews (excepting the newly arrived Russians)
now worship. In 1858 he published his revised prayer book,
which has formed the model for all subsequent revisions. In 1861
he strongly supported the anti-slavery party, and was forced
to leave Baltimore where he then ministered. He continued his
work first in Philadelphia and later in New York.
(I. A.)
EINSIEDELN, the most populous town in the Swiss canton of
Schwyz. It is built on the right bank of the Alpbach (an affluent
of the Sihl), at a height of 2908 ft. above the sea-level on a rather
bare moorland, and by rail is 25 m. S.E. of Zürich, or by a round-about
railway route about 38 m. north of Schwyz, with which
it communicates directly over the Hacken Pass (4649 ft.) or the
Holzegg Pass (4616 ft.). In 1900 the population was 8496, all
(save 75) Romanists and all (save 111) German-speaking. The
town is entirely dependent on the great Benedictine abbey that
rises slightly above it to the east. Close to its present site
Meinrad, a hermit, was murdered in 861 by two robbers, whose
crime was made known by Meinrad’s two pet ravens. Early
in the 10th century Benno, a hermit, rebuilt the holy man’s cell,
but the abbey proper was not founded till about 934, the church
having been consecrated (it is said by Christ Himself) in 948.
In 1274 the dignity of a prince of the Holy Roman Empire was
confirmed by the emperor to the reigning abbot. Originally
under the protection of the counts of Rapperswil (to which town
on the lake of Zürich the old pilgrims’ way still leads over the
Etzel Pass, 3146 ft., with its chapel and inn), this position passed
by marriage with their heiress in 1295 to the Laufenburg or
cadet line of the Habsburgs, but from 1386 was permanently
occupied by Schwyz. A black wooden image of the Virgin and
the fame of St Meinrad caused the throngs of pilgrims to resort
to Einsiedeln in the middle ages, and even now it is much
frequented, particularly about the 14th of September. The
existing buildings date from the 18th century only, while the
treasury and the library still contain many precious objects,
despite the sack by the French in 1798. There are now about
100 fully professed monks, who direct several educational
institutions. The Black Virgin has a special chapel in the stately
church. Zwingli was the parish priest of Einsiedeln 1516-1518
(before he became a Protestant), while near the town Paracelsus
(1493-1541), the celebrated philosopher, was born.
See Father O. Ringholz, Geschichte d. fürstl. Benediktinerstiftes
Einsiedeln, vol. i. (to 1526), (Einsiedeln, 1904).
(W. A. B. C.)
EISENACH, a town of Germany, second capital of the grand-duchy
of Saxe-Weimar-Eisenach, lies at the north-west foot
of the Thuringian forest, at the confluence of the Nesse and
Hörsel, 32 m. by rail W. from Erfurt. Pop. (1905) 35,123.
The town mainly consists of a long street, running from east to
west. Off this are the market square, containing the grand-ducal
palace, built in 1742, where the duchess Hélène of Orleans
long resided, the town-hall, and the late Gothic St Georgenkirche;
and the square on which stands the Nikolaikirche, a
fine Romanesque building, built about 1150 and restored in 1887.
Noteworthy are also the Klemda, a small castle dating from
1260; the Lutherhaus, in which the reformer stayed with the
Cotta family in 1498; the house in which Sebastian Bach was
born, and that (now a museum) in which Fritz Reuter lived
(1863-1874). There are monuments to the two former in the
town, while the resting-place of the latter in the cemetery is
marked by a less pretentious memorial. Eisenach has a school
of forestry, a school of design, a classical school (Gymnasium)
and modern school (Realgymnasium), a deaf and dumb school, a
teachers’ seminary, a theatre and a Wagner museum. The
most important industries of the town are worsted-spinning,
carriage and wagon building, and the making of colours and
pottery. Among others are the manufacture of cigars, cement
pipes, iron-ware and machines, alabaster ware, shoes, leather,
&c., cabinet-making, brewing, granite quarrying and working,
tile-making, and saw- and corn-milling.
The natural beauty of its surroundings and the extensive
forests of the district have of late years attracted many summer
residents. Magnificently situated on a precipitous hill, 600 ft.
above the town to the south, is the historic Wartburg (q.v.), the
ancient castle of the landgraves of Thuringia, famous as the
scene of the contest of Minnesingers immortalized in Wagner’s
Tannhäuser, and as the place where Luther, on his return from
the diet of Worms in 1521, was kept in hiding and made his
translation of the Bible. On a high rock adjacent to the Wartburg
are the ruins of the castle of Mädelstein.
Eisenach (Isenacum) was founded in 1070 by Louis II. the
Springer, landgrave of Thuringia, and its history during the
middle ages was closely bound up with that of the Wartburg,
the seat of the landgraves. The Klemda, mentioned above,
was built by Sophia (d. 1284), daughter of the landgrave Louis
IV., and wife of Duke Henry II. of Brabant, to defend the town
against Henry III., margrave of Meissen, during the succession
contest that followed the extinction of the male line of the
Thuringian landgraves in 1247. The principality of Eisenach
fell to the Saxon house of Wettin in 1440, and in the partition of
1485 formed part of the territories given to the Ernestine line.
It was a separate Saxon duchy from 1596 to 1638, from 1640
136
to 1644, and again from 1662 to 1741, when it finally fell to Saxe-Weimar.
The town of Eisenach, by reason of its associations,
has been a favourite centre for the religious propaganda of
Evangelical Germany, and since 1852 it has been the scene of
the annual conference of the German Evangelical Church, known
as the Eisenach conference.
See Trinius, Eisenach und Umgebung (Minden, 1900); and H.A.
Daniel, Deutschland (Leipzig, 1895), and further references in U.
Chevalier, “Répertoire des sources,” &c., Topo-bibliogr. (Montbéliard,
1894-1899), s.v.
EISENBERG (Isenberg), a town of Germany, in the duchy of
Saxe-Altenburg, on a plateau between the rivers Saale and
Elster, 20 m. S.W. from Zeitz, and connected with the railway
Leipzig-Gera by a branch to Crossen. Pop. (1905) 8824. It
possesses an old castle, several churches and monuments to
Duke Christian of Saxe-Eisenberg (d. 1707), Bismarck, and the
philosopher Karl Christian Friedrich Krause (q.v.). Its principal
industries are weaving, and the manufacture of machines,
ovens, furniture, pianos, porcelain and sausages.
See Back, Chronik der Sladt und des Amtes Eisenberg (Eisenb., 1843).
EISENERZ (“Iron ore”), a market-place and old mining
town in Styria, Austria, 68 m. N.W. of Graz by rail. Pop.
(1900) 6494. It is situated in a deep valley, dominated on the
east by the Pfaffenstein (6140 ft.), on the west by the Kaiserschild
(6830 ft.), and on the south by the Erzberg (5030 ft.). It
has an interesting example of a medieval fortified church, a
Gothic edifice founded by Rudolph of Habsburg in the 13th
century and rebuilt in the 16th. The Erzberg or Ore Mountain
furnishes such rich ore that it is quarried in the open air like
stone, in the summer months. There is documentary evidence
of the mines having been worked as far back as the 12th century.
They afford employment to two or three thousand hands in
summer and about half as many in winter, and yield some
800,000 tons of iron per annum. Eisenerz is connected with the
mines by the Erzberg railway, a bold piece of engineering work,
14 m. long, constructed on the Abt’s rack-and-pinion system.
It passes through some beautiful scenery, and descends to
Vordernberg (pop. 3111), an important centre of the iron trade
situated on the south side of the Erzberg. Eisenerz possesses,
in addition, twenty-five furnaces, which produce iron, and
particularly steel, of exceptional excellence. A few miles to the
N.W. of Eisenerz lies the castle of Leopoldstein, and near it the
beautiful Leopoldsteiner Lake. This lake, with its dark-green
water, situated at an altitude of 2028 ft., and surrounded on all
sides by high peaks, is not big, but is very deep, having a depth
of 520 ft.
EISLEBEN (Lat. Islebia), a town of Germany, in the Prussian
province of Saxony, 24 m. W. by N. from Halle, on the railway
to Nordhausen and Cassel. Pop. (1905) 23,898. It is divided
into an old and a new town (Altstadt and Neustadt). Among
its principal buildings are the church of St Andrew (Andreaskirche),
which contains numerous monuments of the counts of
Mansfeld; the church of St Peter and St Paul (Peter-Paulkirche),
containing the font in which Luther was baptized; the royal
gymnasium (classical school), founded by Luther shortly before
his death in 1546; and the hospital. Eisleben is celebrated
as the place where Luther was born and died. The house in
which he was born was burned in 1689, but was rebuilt in 1693
as a free school for orphans. This school fell into decay under
the régime of the kingdom of Westphalia, but was restored in
1817 by King Frederick William III. of Prussia, who, in 1819,
transferred it to a new building behind the old house. The
house in which Luther died was restored towards the end of the
19th century, and his death chamber is still preserved. A
bronze statue of Luther by Rudolf Siemering (1835-1905) was
unveiled in 1883. Eisleben has long been the centre of an
important mining district (Luther was a miner’s son), the
principal products being silver and copper. It possesses smelting
works and a school of mining.
The earliest record of Eisleben is dated 974. In 1045, at
which time it belonged to the counts of Mansfeld, it received
the right to hold markets, coin money, and levy tolls. From
1531 to 1710 it was the seat of the cadet line of the counts of
Mansfeld-Eisleben. After the extinction of the main line of
the counts of Mansfeld, Eisleben fell to Saxony, and, in the
partition of Saxony by the congress of Vienna in 1815, was
assigned to Prussia.
See G. Grössler, Urkundliche Gesch. Eislebens bis zum Ende des 12.
Jahrhunderts (Halle, 1875); Chronicon Islebiense; Eisleben Stadtchronik
aus den Jahren 1520-1738, edited from the original, with
notes by Grössler and Sommer (Eisleben, 1882).
EISTEDDFOD (plural Eisteddfodau), the national bardic congress
of Wales, the objects of which are to encourage bardism
and music and the general literature of the Welsh, to maintain
the Welsh language and customs of the country, and to foster and
cultivate a patriotic spirit amongst the people. This institution,
so peculiar to Wales, is of very ancient origin.1 The term
Eisteddfod, however, which means “a session” or “sitting,”
was probably not applied to bardic congresses before the 12th
century.
The Eisteddfod in its present character appears to have
originated in the time of Owain ap Maxen Wledig, who at the
close of the 4th century was elected to the chief sovereignty
of the Britons on the departure of the Romans. It was at this
time, or soon afterwards, that the laws and usages of the Gorsedd
were codified and remodelled, and its motto of “Y gwir yn erbyn
y byd” (The truth against the world) given to it. “Chairs”
(with which the Eisteddfod as a national institution is now
inseparably connected) were also established, or rather perhaps
resuscitated, about the same time. The chair was a kind of
convention where disciples were trained, and bardic matters
discussed preparatory to the great Gorsedd, each chair having a
distinctive motto. There are now existing four chairs in Wales,—namely,
the “royal” chair of Powys, whose motto is “A laddo
a leddir” (He that slayeth shall be slain); that of Gwent and
Glamorgan, whose motto is “Duw a phob daioni” (God and all
goodness); that of Dyfed, whose motto is “Calon wrth galon”
(Heart with heart); and that of Gwynedd, or North Wales, whose
motto is “Iesu,” or “O Iesu! na’d gamwaith” (Jesus, or Oh
Jesus! suffer not iniquity).
The first Eisteddfod of which any account seems to have
descended to us was one held on the banks of the Conway in
the 6th century, under the auspices of Maelgwn Gwynedd, prince
of North Wales. Maelgwn on this occasion, in order to prove
the superiority of vocal song over instrumental music, is recorded
to have offered a reward to such bards and minstrels as should
swim over the Conway. There were several competitors, but on
their arrival on the opposite shore the harpers found themselves
unable to play owing to the injury their harps had sustained
from the water, while the bards were in as good tune as ever.
King Cadwaladr also presided at an Eisteddfod about the
middle of the 7th century.
Griffith ap Cynan, prince of North Wales, who had been born
in Ireland, brought with him from that country many Irish
musicians, who greatly improved the music of Wales. During
his long reign of 56 years he offered great encouragement to
bards, harpers and minstrels, and framed a code of laws for their
better regulation. He held an Eisteddfod about the beginning
of the 12th century at Caerwys in Flintshire, “to which there
repaired all the musicians of Wales, and some also from England
and Scotland.” For many years afterwards the Eisteddfod
appears to have been held triennially, and to have enforced the
rigid observance of the enactments of Griffith ap Cynan. The
places at which it was generally held were Aberffraw, formerly
the royal seat of the princes of North Wales; Dynevor, the
royal castle of the princes of South Wales; and Mathrafal,
the royal palace of the princes of Powys: and in later times
137
Caerwys in Flintshire received that honourable distinction, it
having been the princely residence of Llewelyn the Last. Some
of these Eisteddfodau were conducted in a style of great magnificence,
under the patronage of the native princes. At Christmas
1107 Cadwgan, the son of Bleddyn ap Cynfyn, prince of Powys,
held an Eisteddfod in Cardigan Castle, to which he invited the
bards, harpers and minstrels, “the best to be found in all Wales”;
and “he gave them chairs and subjects of emulation according
to the custom of the feasts of King Arthur.” In 1176 Rhys ab
Gruffydd, prince of South Wales, held an Eisteddfod in the same
castle on a scale of still greater magnificence, it having been
proclaimed, we are told, a year before it took place, “over Wales,
England, Scotland, Ireland and many other countries.”
On the annexation of Wales to England, Edward I. deemed it
politic to sanction the bardic Eisteddfod by his famous statute of
Rhuddlan. In the reign of Edward III. Ifor Hael, a South Wales
chieftain, held one at his mansion. Another was held in 1451,
with the permission of the king, by Griffith ab Nicholas at
Carmarthen, in princely style, where Dafydd ab Edmund, an
eminent poet, signalized himself by his wonderful powers of
versification in the Welsh metres, and whence “he carried home
on his shoulders the silver chair” which he had fairly won.
Several Eisteddfodau, were held, one at least by royal mandate,
in the reign of Henry VII. In 1523 one was held at Caerwys
before the chamberlain of North Wales and others, by virtue of
a commission issued by Henry VIII. In the course of time,
through relaxation of bardic discipline, the profession was
assumed by unqualified persons, to the great detriment of the
regular bards. Accordingly in 1567 Queen Elizabeth issued
a commission for holding an Eisteddfod at Caerwys in the
following year, which was duly held, when degrees were conferred
on 55 candidates, including 20 harpers. From the terms of the
royal proclamation we find that it was then customary to bestow
“a silver harp” on the chief of the faculty of musicians, as it had
been usual to reward the chief bard with “a silver chair.” This
was the last Eisteddfod appointed by royal commission, but
several others of some importance were held during the 16th
and 17th centuries, under the patronage of the earl of Pembroke,
Sir Richard Neville, and other influential persons. Amongst
these the last of any particular note was one held in Bewper
Castle, Glamorgan, by Sir Richard Basset in 1681.
During the succeeding 130 years Welsh nationality was at its
lowest ebb, and no general Eisteddfod on a large scale appears
to have been held until 1819, though several small ones were
held under the auspices of the Gwyneddigion Society, established
in 1771,—the most important being those at Corwen (1789),
St Asaph (1790) and Caerwys (1798).
At the close of the Napoleonic wars, however, there was a
general revival of Welsh nationality, and numerous Welsh
literary societies were established throughout Wales, and in
the principal English towns. A large Eisteddfod was held under
distinguished patronage at Carmarthen in 1819, and from that
time to the present they have been held (together with numerous
local Eisteddfodau), almost without intermission, annually.
The Eisteddfod at Llangollen in 1858 is memorable for its archaic
character, and the attempts then made to revive the ancient
ceremonies, and restore the ancient vestments of druids, bards
and ovates.
To constitute a provincial Eisteddfod it is necessary that
it should be proclaimed by a graduated bard of a Gorsedd a
year and a day before it takes place. A local one may be held
without such a proclamation. A provincial Eisteddfod generally
lasts three, sometimes four days. A president and a conductor
are appointed for each day. The proceedings commence with a
Gorsedd meeting, opened with sound of trumpet and other
ceremonies, at which candidates come forward and receive
bardic degrees after satisfying the presiding bard as to their
fitness. At the subsequent meetings the president gives a brief
address; the bards follow with poetical addresses; adjudications
are made, and prizes and medals with suitable devices are given
to the successful competitors for poetical, musical and prose
compositions, for the best choral and solo singing, and singing with
the harp or “Pennillion singing”2 as it is called, for the best playing
on the harp or stringed or wind instruments, as well as
occasionally for the best specimens of handicraft and art. In the
evening of each day a concert is given, generally attended by very
large numbers. The great day of the Eisteddfod is the “chair” day—usually
the third or last day—the grand event of the Eisteddfod
being the adjudication on the chair subject, and the chairing and
investiture of the fortunate winner. This is the highest object
of a Welsh bard’s ambition. The ceremony is an imposing one,
and is performed with sound of trumpet. (See also the articles
Bard, Celt: Celtic Literature, and Wales.)
(R. W.*)
1 According to the Welsh Triads and other historical records, the
Gorsedd or assembly (an essential part of the modern Eisteddfod,
from which indeed the latter sprung) is as old at least as the time of
Prydain the son of Ædd the Great, who lived many centuries before
the Christian era. Upon the destruction of the political ascendancy
of the Druids, the Gorsedd lost its political importance, though it
seems to have long afterwards retained its institutional character as
the medium for preserving the laws, doctrines and traditions of
bardism.
2 According to Jones’s Bardic Remains, “To sing ‘Pennillion’
with a Welsh harp is not so easily accomplished as may be imagined.
The singer is obliged to follow the harper, who may change the tune,
or perform variations ad libitum, whilst the vocalist must keep time,
and end precisely with the strain. The singer does not commence
with the harper, but takes the strain up at the second, third or
fourth bar, as best suits the ‘pennill’ he intends to sing....
Those are considered the best singers who can adapt stanzas of various
metres to one melody, and who are acquainted with the twenty-four
measures according to the bardic laws and rules of composition.”
EJECTMENT (Lat. e, out, and jacere, to throw), in English law,
an action for the recovery of the possession of land, together
with damages for the wrongful withholding thereof. In the old
classifications of actions, as real or personal, this was known
as a mixed action, because its object was twofold, viz. to recover
both the realty and personal damages. It should be noted that
the term “ejectment” applies in law to distinct classes of
proceedings—ejectments as between rival claimants to land,
and ejectments as between those who hold, or have held, the
relation of landlord and tenant. Under the Rules of the Supreme
Court, actions in England for the recovery of land are commenced
and proceed in the same manner as ordinary actions. But the
historical interest attaching to the action of ejectment is so
great as to render some account of it necessary.
The form of the action as it prevailed in the English courts
down to the Common Law Procedure Act 1852 was a series of
fictions, among the most remarkable to be found in the entire
body of English law. A, the person claiming title to land,
delivered to B, the person in possession, a declaration in ejectment
in which C and D, fictitious persons, were plaintiff and
defendant. C stated that A had devised the land to him for a
term of years, and that he had been ousted by D. A notice
signed by D informed B of the proceedings, and advised him to
apply to be made defendant in D’s place, as he, D, having no
title, did not intend to defend the suit. If B did not so apply,
judgment was given against D, and possession of the lands was
given to A. But if B did apply, the Court allowed him to
defend the action only on condition that he admitted the three
fictitious averments—the lease, the entry and the ouster—which,
together with title, were the four things necessary to maintain
an action of ejectment. This having been arranged the action
proceeded, B being made defendant instead of D. The names
used for the fictitious parties were John Doe, plaintiff, and
Richard Roe, defendant, who was called “the casual ejector.”
The explanation of these mysterious fictions is this. The writ
de ejectione firmae was invented about the beginning of the reign
of Edward III. as a remedy to a lessee for years who had been
ousted of his term. It was a writ of trespass, and carried damages,
but in the time of Henry VII., if not before that date, the courts
of common law added thereto a species of remedy neither
warranted by the original writ nor demanded by the declaration,
viz. a judgment to recover so much of the term as was still to
run, and a writ of possession thereupon. The next step was to
extend the remedy—limited originally to leaseholds—to cases
of disputed title to freeholds. This was done indirectly by the
claimant entering on the land and there making a lease for a
term of years to another person; for it was only a term that
could be recovered by the action, and to create a term required
actual possession in the granter. The lessee remained on the land,
and the next person who entered even by chance was accounted
an ejector of the lessee, who then served upon him a writ of
trespass and ejectment. The case then went to trial as on a
138
common action of trespass; and the claimant’s title, being the
real foundation of the lessee’s right, was thus indirectly determined.
These proceedings might take place without the knowledge
of the person really in possession; and to prevent the
abuse of the action a rule was laid down that the plaintiff in
ejectment must give notice to the party in possession, who
might then come in and defend the action. When the action
came into general use as a mode of trying the title to freeholds,
the actual entry, lease and ouster which were necessary to found
the action were attended with much inconvenience, and accordingly
Lord Chief Justice Rolle during the Protectorate (c. 1657)
substituted for them the fictitious averments already described.
The action of ejectment is now only a curiosity of legal history.
Its fictitious suitors were swept away by the Common Law
Procedure Act of 1852. A form of writ was prescribed, in which
the person in possession of the disputed premises by name and
all persons entitled to defend the possession were informed that
the plaintiff claimed to be entitled to possession, and required
to appear in court to defend the possession of the property or
such part of it as they should think fit. In the form of the writ
and in some other respects ejectment still differed from other
actions. But, as already mentioned, it has now been assimilated
(under the name of action for the recovery of lands) to ordinary
actions by the Rules of the Supreme Court. It is commenced
by writ of summons, and—subject to the rules as to summary
judgments (v. inf.)—proceeds along the usual course of pleadings
and trial to judgment; but is subject to one special rule, viz:
that except by leave of the Court or a judge the only claims
which may be joined with one for recovery of land are claims
in respect of arrears of rent or double value for holding over,
or mesne profits (i.e. the value of the land during the period
of illegal possession), or damages for breach of a contract under
which the premises are held or for any wrong or injury to the
premises claimed (R.S.C., O. xviii. r. 2). These claims were
formerly recoverable by an independent action.
With regard to actions for the recovery of land—apart from
the relationship of landlord and tenant—the only point that
need be noted is the presumption of law in favour of the actual
possessor of the land in dispute. Where the action is brought
by a landlord against his tenant, there is of course no presumption
against the landlord’s title arising from the tenant’s possession.
By the Common Law Procedure Act 1852 (ss. 210-212) special
provision was made for the prompt recovery of demised premises
where half a year’s rent was in arrear and the landlord was
entitled to re-enter for non-payment. These provisions are
still in force, but advantage is now more generally taken of the
summary judgment procedure introduced by the Rules of the
Supreme Court (Order 3, r. 6.). This procedure may be adopted
when (a) the tenant’s term has expired, (b) or has been duly
determined by notice to quit, or (c) has become liable to forfeiture
for non-payment of rent, and applies not only to the tenant
but to persons claiming under him. The writ is specially endorsed
with the plaintiff’s claim to recover the land with or
without rent or mesne profits, and summary judgment obtained
if no substantial defence is disclosed. Where an action to
recover land is brought against the tenant by a person claiming
adversely to the landlord, the tenant is bound, under penalty
of forfeiting the value of three years’ improved or rack rent of the
premises, to give notice to the landlord in order that he may
appear and defend his title. Actions for the recovery of land,
other than land belonging to spiritual corporations and to the
crown, are barred in 12 years (Real Property Limitation Acts
1833 (s. 29) and 1874 (s. 1). A landlord can recover possession
in the county court (i.) by an action for the recovery of possession,
where neither the value of the premises nor the rent exceeds
£100 a year, and the tenant is holding over (County Courts Acts
of 1888, s. 138, and 1903, s. 3); (ii.) by “an action of ejectment,”
where (a) the value or rent of the premises does not exceed
£100, (b) half a year’s rent is in arrear, and (c) no sufficient
distress (see Rent) is to be found on the premises (Act of 1888,
s. 139; Act of 1903, s. 3; County Court Rules 1903, Ord. v. rule 3).
Where a tenant at a rent not exceeding £20 a year of premises
at will, or for a term not exceeding 7 years, refuses nor neglects,
on the determination or expiration of his interest, to deliver up
possession, such possession may be recovered by proceedings
before justices under the Small Tenements Recovery Act 1838,
an enactment which has been extended to the recovery of allotments.
Under the Distress for Rent Act 1737, and the Deserted
Tenements Act 1817, a landlord can have himself put by the order
of two justices into premises deserted by the tenant where half
a year’s rent is owing and no sufficient distress can be found.
In Ireland, the practice with regard to the recovery of land is
regulated by the Rules of the Supreme Court 1891, made under
the Judicature (Ireland) Act 1877; and resembles that of
England. Possession may be recovered summarily by a special
indorsement of the writ, as in England; and there are analogous
provisions with regard to the recovery of small tenements
(see Land Act, 1860 ss. 84 and 89). The law with regard to
the ejectment or eviction of tenants is consolidated by the Land
Act 1860. (See ss. 52-66, 68-71, and further under Landlord
and Tenant.)
In Scotland, the recovery of land is effected by an action of
“removing” or summary ejection. In the case of a tenant
“warning” is necessary unless he is bound by his lease to
remove without warning. In the case of possessors without
title, or a title merely precarious, no warning is needed. A
summary process of removing from small holdings is provided
for by Sheriff Courts (Scotland) Acts of 1838 and 1851.
In the United States, the old English action of ejectment was
adopted to a very limited extent, and where it was so adopted
has often been superseded, as in Connecticut, by a single action
for all cases of ouster, disseisin or ejectment. In this action,
known as an action of disseisin or ejectment, both possession of
the land and damages may be recovered. In some of the states
a tenant against whom an action of ejectment is brought by a
stranger is bound under a penalty, as in England, to give notice
of the claim to the landlord in order that he may appear and
defend his title.
In French law the landlord’s claim for rent is fairly secured
by the hypothec, and by summary powers which exist for the
seizure of the effects of defaulting tenants. Eviction or annulment
of a lease can only be obtained through the judicial
tribunals. The Civil Code deals with the position of a tenant
in case of the sale of the property leased. If the lease is by
authentic act (acte authentique) or has an ascertained date, the
purchaser cannot evict the tenant unless a right to do so was
reserved on the lease (art. 1743), and then only on payment of an
indemnity (arts. 1744-1747). If the lease is not by authentic
act, or has not an ascertained date, the purchaser is not liable
for indemnity (art. 1750). The tenant of rural lands is bound
to give the landlord notice of acts of usurpation (art. 1768).
There are analogous provisions in the Civil Codes of Belgium
(arts. 1743 et seq.), Holland (arts. 1613, 1614), Portugal (art.
1572); and see the German Civil Code (arts. 535 et seq.). In
many of the colonies there are statutory provisions for the
recovery of land or premises on the lines of English law (cf.
Ontario, Rev. Stats. 1897, c. 170. ss. 19 et seq.; Manitoba, Rev.
Stats. 1902, c. 1903). In others (e.g. New Zealand, Act. No. 55
of 1893, ss. 175-187; British Columbia, Revised Statutes, 1897,
c. 182: Cyprus, Ord. 15 of 1895) there has been legislation similar
to the Small Tenements Recovery Act 1838.
Authorities.—English Law: Cole on Ejectment; Digby, History
of Real Property (3rd ed., London, 1884); Pollock and Maitland,
History of English Law (Cambridge, 1895); Foa, Landlord and
Tenant (4th ed., London, 1907); Fawcett, Landlord and Tenant
(London, 1905). Irish Law: Nolan and Kane’s Statutes relating
to the Law of Landlord and Tenant (5th ed., Dublin, 1898); Wylie’s
Judicature Acts (Dublin, 1900). Scots Law: Hunter on Landlord
and Tenant (4th ed., Edin., 1878); Erskine’s Principles (20th ed.,
Edin., 1903). American Law: Two Centuries’ Growth of American
Law (New York and London, 1901); Bouvier’s Law Dictionary
(Boston and London, 1897); Stimson, American Statute Law
(Boston, 1886).
(A. W. R.)
EKATERINBURG, a town of Russia, in the government of
Perm, 311 m. by rail S.E. of the town of Perm, on the Iset river,
near the E. foot of the Ural Mountains, in 56° 49′ N. and
139
60° 35′ E., at an altitude of 870 ft. above sea-level. It is the
most important town of the Urals. Pop. (1860) 19,830; (1897)
55,488. The streets are broad and regular, and several of the
houses of palatial proportions. In 1834 Ekaterinburg was made
the see of a suffragan bishop of the Orthodox Greek Church.
There are two cathedrals—St Catherine’s, founded in 1758, and
that of the Epiphany, in 1774—and a museum of natural history,
opened in 1853. Ekaterinburg is the seat of the central mining
administration of the Ural region, and has a chemical laboratory
for the assay of gold, a mining school, the Ural Society of
Naturalists, and a magnetic and meteorological observatory.
Besides the government mint for copper coinage, which dates
from 1735, the government engineering works, and the
imperial factory for the cutting and polishing of malachite,
jasper, marble, porphyry and other ornamental stones, the
industrial establishments comprise candle, paper, soap and
machinery works, flour and woollen mills, and tanneries. There is
a lively trade in cattle, cereals, iron, woollen and silk goods,
and colonial products; and two important fairs are held annually.
Nearly forty gold and platinum mines, over thirty iron-works,
and numerous other factories are scattered over the district,
while wheels, travelling boxes, hardware, boots and so forth
are extensively made in the villages. Ekaterinburg took its
origin from the mining establishments founded by Peter the
Great in 1721, and received its name in honour of his wife,
Catherine I. Its development was greatly promoted in 1763
by the diversion of the Siberian highway from Verkhoturye to
this place.
EKATERINODAR, a town of South Russia, chief town of the
province of Kubañ, on the right bank of the river Kubañ, 85 m.
E.N.E. of Novo-rossiysk on the railway to Rostov-on-Don,
and in 45° 3′ N. and 38° 50′ E. It is badly built, on a swampy
site exposed to the inundations of the river; and its houses,
with few exceptions, are slight structures of wood and plaster.
Founded by Catherine II. in 1794 on the site of an old town
called Tmutarakan, as a small fort and Cossack settlement, its
population grew from 9620 in 1860 to 65,697 in 1897. It has
various technical schools, an experimental fruit-farm, a military
hospital, and a natural history museum. A considerable trade is
carried on, especially in cereals.
EKATERINOSLAV, a government of south Russia, having the
governments of Poltava and Kharkov on the N., the territory
of the Don Cossacks on the E., the Sea of Azov and Taurida on
the S., and Kherson on the W. Area, 24,478 sq. m. Its surface
is undulating steppe, sloping gently south and north, with a few
hills reaching 1200 ft. in the N.E., where a slight swelling (the
Don Hills) compels the Don to make a great curve eastwards.
Another chain of hills, to which the eastward bend of the Dnieper
is due, rises in the west. These hills have a crystalline core
(granites, syenites and diorites), while the surface strata belong
to the Carboniferous, Permian, Cretaceous and Tertiary formations.
The government is rich in minerals, especially in coal—the
mines lie in the middle of the Donets coalfield—iron ores,
fireclay and rock-salt, and every year the mining output increases
in quantity, especially of coal and iron. Granite, limestone,
grindstone, slate, with graphite, manganese and mercury are
found. The government is drained by the Dnieper, the Don and
their tributaries (e.g. the Donets and Volchya) and by several
affluents (e.g. the Kalmius) of the Sea of Azov. The soil is the
fertile black earth, but the crops occasionally suffer from drought,
the average annual rainfall being only 15 in. Forests are scarce.
Pop. (1860) 1,138,750; (1897) 2,118,946, chiefly Little Russians,
with Great Russians, Greeks (48,740), Germans (80,979),
Rumanians and a few gypsies. Jews constitute 4.7% of the
population. The estimated population in 1906 was 2,708,700.
Wheat and other cereals are extensively grown; other noteworthy
crops are potatoes, tobacco and grapes. Nearly 40,000
persons find occupation in factories, the most important being
iron-works and agricultural machinery works, though there are
also tobacco, glass, soap and candle factories, potteries, tanneries
and breweries. In the districts of Mariupol the making of
agricultural implements and machinery is carried on extensively
as a domestic industry in the villages. Bees are kept in very considerable
numbers. Fishing employs many persons in the Don
and the Dnieper. Cereals are exported in large quantities via
the Dnieper, the Sevastopol railway, and the port of Mariupol.
The chief towns of the eight districts, with their populations in
1897, are Ekaterinoslav (135,552 inhabitants in 1900), Alexandrovsk
(28,434), Bakhmut (30,585), Mariupol (31,772),
Novomoskovsk (12,862), Pavlograd (17,188), Slavyanoserbsk
(3120), and Verkhne-dnyeprovsk (11,607).
EKATERINOSLAV, a town of Russia, capital of the government
of the same name, on the right bank of the Dnieper above
the rapids, 673 m. by rail S.S.W. of Moscow, in 48° 21′ N. and
35° 4′ E., at an altitude of 210 ft. Pop. (1861) 18,881, without
suburbs; (1900) 135,552. If the suburb of Novyikoindak be
included, the town extends for upwards of 4 m. along the river.
The oldest part lies very low and is much exposed to floods. Contiguous
to the towns on the N.W. is the royal village of Novyimaidani
or the New Factories. The bishop’s palace, mining
academy, archaeological museum and library are the principal
public buildings. The house now occupied by the Nobles Club
was formerly inhabited by the author and statesman Potemkin.
Ekaterinoslav is a rapidly growing city, with a number of technical
schools, and is an important depot for timber floated down the
Dnieper, and also for cereals. Its iron-works, flour-mills and
agricultural machinery works give occupation to over 5000
persons. In fact since 1895 the city has become the centre of
numerous Franco-Belgian industrial undertakings. In addition
to the branches just mentioned, there are tobacco factories and
breweries. Considerable trade is carried on in cattle, cereals,
horses and wool, there being three annual fairs. On the site of
the city there formerly stood the Polish castle of Koindak, built
in 1635, and destroyed by the Cossacks. The existing city was
founded by Potemkin in 1786, and in the following year Catherine
II. laid the foundation-stone of the cathedral, though it was not
actually built until 1830-1835. On the south side of it is a bronze
statue of the empress, put up in 1846. Paul I. changed the name
of the city to Novo-rossiysk, but the original name was restored
in 1802.
EKHOF, KONRAD (1720-1778), German actor, was born in
Hamburg on the 12th of August 1720. In 1739 he became a
member of Johann Friedrich Schönemann’s (1704-1782) company
in Lüneburg, and made his first appearance there on the 15th
of January 1740 as Xiphares in Racine’s Mithridate. From
1751 the Schönemann company performed mainly in Hamburg
and at Schwerin, where Duke Christian Louis II. of Mecklenburg-Schwerin
made them comedians to the court. During this
period Ekhof founded a theatrical academy, which, though
short-lived, was of great importance in helping to raise the
standard of German acting and the status of German actors.
In 1757 Ekhof left Schönemann to join Franz Schuch’s company
at Danzig; but he soon returned to Hamburg, where, in conjunction
with two other actors, he succeeded Schönemann in
the direction of the company. He resigned this position, however,
in favour of H.G. Koch, with whom he acted until 1764, when
he joined K.E. Ackermann’s company. In 1767 was founded
the National Theatre at Hamburg, made famous by Lessing’s
Hamburgische Dramaturgie, and Ekhof was the leading member
of the company. After the failure of the enterprise Ekhof was
for a time in Weimar, and ultimately became co-director of the
new court theatre at Gotha. This, the first permanently established
theatre in Germany, was opened on the 2nd of October
1775. Ekhof’s reputation was now at its height; Goethe called
him the only German tragic actor; and in 1777 he acted with
Goethe and Duke Charles Augustus at a private performance
at Weimar, dining afterwards with the poet at the ducal table.
He died on the 16th of June 1778. His versatility may be
judged from the fact that in the comedies of Goldoni and Molière
he was no less successful than in the tragedies of Lessing and
Shakespeare. He was regarded by his contemporaries as an
unsurpassed exponent of naturalness on the stage; and in this
respect he has been not unfairly compared with Garrick. His
fame, however, was rapidly eclipsed by that of Friedrich U.L.
140
Schröder. His literary efforts were chiefly confined to translations
from French authors.
See H. Uhde, biography of Ekhof in vol. iv. of Der neue Plutarch
(1876), and J. Rüschner, K. Ekhofs Leben und Wirken (1872). Also
H. Devrient, J.F. Schönemann und seine Schauspielergesellschaft
(1895).
EKRON (better, as in the Septuagint and Josephus, Accaron,
Ἀκκαρών), a royal city of the Philistines commonly identified
with the modern Syrian village of ‘Aḳir, 5 m. from Ramleh,
on the southern slope of a low ridge separating the plain of
Philistia from Sharon. It lay inland and off the main line of
traffic. Though included by the Israelites within the limits of
the tribe of Judah, and mentioned in Judges xix. as one of the
cities of Dan, it was in Philistine possession in the days of
Samuel, and apparently maintained its independence. According
to the narrative of the Hebrew text, here differing from the
Greek text and Josephus (which read Askelon), it was the last
town to which the ark was transferred before its restoration to
the Israelites. Its maintenance of a sanctuary of Baal Zebub
is mentioned in 2 Kings i. From Assyrian inscriptions it has
been gathered that Padi, king of Ekron, was for a time the
vassal of Hezekiah of Judah, but regained his independence
when the latter was hard pressed by Sennacherib. A notice of
its history in 147 B.C. is found in 1 Macc. x. 89; after the fall of
Jerusalem A.D. 70 it was settled by Jews. At the time of the
crusades it was still a large village. Recently a Jewish agricultural
colony has been settled there. The houses are built of
mud, and in the absence of visible remains of antiquity, the
identification of the site is questionable. The neighbourhood
is fertile.
(R. A. S. M.)
ELABUGA, a town of Russia, in the government of Vyatka,
on the Kama river, 201 m. by steamboat down the Volga from
Kazan and then up the Kama. It has flour-mills, and carries
on a brisk trade in exporting corn. Pop. (1897) 9776.
The famous Ananiynskiy Mogilnik (burial-place) is on the
right bank of the Kama, 3 m. above the town. It was discovered
in 1858, was excavated by Alabin, Lerch and Nevostruyev,
and has since supplied extremely valuable collections belonging
to the Stone, Bronze and Iron Ages. It consisted of a mound,
about 500 ft. in circumference, adorned with decorated stones
(which have disappeared), and contained an inner wall, 65 ft.
in circumference, made of uncemented stone flags. Nearly
fifty skeletons were discovered, mostly lying upon charred logs,
surrounded with cinerary urns filled with partially burned
bones. A great variety of bronze decorations and glazed clay
pearls were strewn round the skeletons. The knives, daggers
and arrowpoints are of slate, bronze and iron, the last two being
very rough imitations of stone implements. One of the flags
bore the image of a man, without moustaches or beard, dressed
in a costume and helmet recalling those of the Circassians.
ELAM, the name given in the Bible to the province of Persia
called Susiana by the classical geographers, from Susa or Shushan
its capital. In one passage, however (Ezra iv. 9), it is confined
to Elymais, the north-western part of the province, and its
inhabitants distinguished from those of Shushan, which elsewhere
(Dan. viii. 2) is placed in Elam. Strabo (xv. 3. 12, &c.)
makes Susiana a part of Persia proper, but a comparison of his
account with those of Ptolemy (vi. 3. 1, &c.) and other writers
would limit it to the mountainous district to the east of Babylonia,
lying between the Oroatis and the Tigris, and stretching
from India to the Persian Gulf. Along with this mountainous
district went a fertile low tract of country on the western side,
which also included the marshes at the mouths of the Euphrates
and Tigris and the north-eastern coast land of the Gulf. This low
tract, though producing large quantities of grain, was intensely
hot in summer; the high regions, however, were cool and well
watered.
The whole country was occupied by a variety of tribes, speaking
agglutinative dialects for the most part, though the western
districts were occupied by Semites. Strabo (xi. 13. 3, 6), quoting
from Nearchus, seems to include the Susians under the Elymaeans,
whom he associates with the Uxii, and places on the frontiers
of Persia and Susa; but Pliny more correctly makes the Eulaeus
the boundary between Susiana and Elymais (N.H. vi. 29-31).
The Uxii are described as a robber tribe in the mountains
adjacent to Media, and their name is apparently to be identified
with the title given to the whole of Susiana in the Persian
cuneiform inscriptions, Uwaja, i.e. “Aborigines.” Uwaja is
probably the origin of the modern Khuzistan, though Mordtmann
would derive the latter from  “a sugar-reed.” Immediately
bordering on the Persians were the Amardians or Mardians,
as well as the people of Khapirti (Khatamti, according to Scheil),
the name given to Susiana in the Neo-Susian texts. Khapirti
appears as Apir in the inscriptions of Mal-Amir, which fix the
locality of the district. Passing over the Messabatae, who
inhabited a valley which may perhaps be the modern Māh-Sabadan,
as well as the level district of Yamutbal or Yatbur
which separated Elam from Babylonia, and the smaller districts
of Characene, Cabandene, Corbiana and Gabiene mentioned
by classical authors, we come to the fourth principal tribe of
Susiana, the Cissii (Aesch. Pers. 16; Strabo xv. 3. 2) or Cossaei
(Strabo xi. 5. 6, xvi. 11. 17; Arr. Ind. 40; Polyb. v. 54, &c.),
the Kassi of the cuneiform inscriptions. So important were they,
that the whole of Susiana was sometimes called Cissia after
them, as by Herodotus (iii. 91, v. 49, &c.). In fact Susiana
was only a late name for the country, dating from the time
when Susa had been made a capital of the Persian empire. In
the Sumerian texts of Babylonia it was called Numma, “the
Highlands,” of which Elamtu or Elamu, “Elam,” was the
Semitic translation. Apart from Susa, the most important
part of the country was Anzan (Anshan, contracted Assan),
where the native population maintained itself unaffected by
Semitic intrusion. The exact position of Anzan is still disputed,
but it probably included originally the site of Susa and was
distinguished from it only when Susa became the seat of a
Semitic government. In the lexical tablets Anzan is given
as the equivalent of Elamtu, and the native kings entitle themselves
kings of “Anzan and Susa,” as well as “princes of the
Khapirti.”
“a sugar-reed.” Immediately
bordering on the Persians were the Amardians or Mardians,
as well as the people of Khapirti (Khatamti, according to Scheil),
the name given to Susiana in the Neo-Susian texts. Khapirti
appears as Apir in the inscriptions of Mal-Amir, which fix the
locality of the district. Passing over the Messabatae, who
inhabited a valley which may perhaps be the modern Māh-Sabadan,
as well as the level district of Yamutbal or Yatbur
which separated Elam from Babylonia, and the smaller districts
of Characene, Cabandene, Corbiana and Gabiene mentioned
by classical authors, we come to the fourth principal tribe of
Susiana, the Cissii (Aesch. Pers. 16; Strabo xv. 3. 2) or Cossaei
(Strabo xi. 5. 6, xvi. 11. 17; Arr. Ind. 40; Polyb. v. 54, &c.),
the Kassi of the cuneiform inscriptions. So important were they,
that the whole of Susiana was sometimes called Cissia after
them, as by Herodotus (iii. 91, v. 49, &c.). In fact Susiana
was only a late name for the country, dating from the time
when Susa had been made a capital of the Persian empire. In
the Sumerian texts of Babylonia it was called Numma, “the
Highlands,” of which Elamtu or Elamu, “Elam,” was the
Semitic translation. Apart from Susa, the most important
part of the country was Anzan (Anshan, contracted Assan),
where the native population maintained itself unaffected by
Semitic intrusion. The exact position of Anzan is still disputed,
but it probably included originally the site of Susa and was
distinguished from it only when Susa became the seat of a
Semitic government. In the lexical tablets Anzan is given
as the equivalent of Elamtu, and the native kings entitle themselves
kings of “Anzan and Susa,” as well as “princes of the
Khapirti.”
The principal mountains of Elam were on the north, called
Charbanus and Cambalidus by Pliny (vi. 27, 31), and belonging
to the Parachoathras chain. There were numerous rivers
flowing into either the Tigris or the Persian Gulf. The most
important were the Ulai or Eulaeus (Kūran) with its tributary
the Pasitigris, the Choaspes (Kerkhah), the Coprates (river of
Diz called Ititē in the inscriptions), the Hedyphon or Hedypnus
(Jerrāhi), and the Croatis (Hindyan), besides the monumental
Surappi and Ukni, perhaps to be identified with the Hedyphon
and Oroatis, which fell into the sea in the marshy region at the
mouth of the Tigris. Shushan or Susa, the capital now marked
by the mounds of Shush, stood near the junction of the Choaspes
and Eulaeus (see Susa); and Badaca, Madaktu in the inscriptions,
lay between the Shapur and the river of Diz. Among the
other chief cities mentioned in the inscriptions may be named
Naditu, Khaltemas, Din-sar, Bubilu, Bit-imbi, Khidalu and
Nagitu on the sea-coast. Here, in fact, lay some of the oldest
and wealthiest towns, the sites of which have, however, been
removed inland by the silting up of the shore. J. de Morgan’s
excavations at Susa have thrown a flood of light on the early
history of Elam and its relations to Babylon. The earliest settlement
there goes back to neolithic times, but it was already a
fortified city when Elam was conquered by Sargon of Akkad
(3800 B.C.) and Susa became the seat of a Babylonian viceroy.
From this time onward for many centuries it continued under
Semitic suzerainty, its high-priests, also called “Chief Envoys
of Elam, Sippara and Susa,” bearing sometimes Semitic, sometimes
native “Anzanite” names. One of the kings of the dynasty
of Ur built at Susa. Before the rise of the First Dynasty of
Babylon, however, Elam had recovered its independence, and
in 2280 B.C. the Elamite king Kutur-Nakhkhunte made a raid
in Babylonia and carried away from Erech the image of the
goddess Nanā. The monuments of many of his successors have
been discovered by de Morgan and their inscriptions deciphered
by v. Scheil. One of them was defeated by Ammi-zadoq
141
of Babylonia (c. 2100 B.C.); another would have been the
Chedor-laomer (Kutur-Lagamar) of Genesis xiv. One of the
greatest builders among them was Untas-Gal (the pronunciation
of the second element in the name is uncertain). About 1330
B.C. Khurba-tila was captured by Kuri-galzu III., the Kassite
king of Babylonia, but a later prince Kidin-Khutrutas avenged
his defeat, and Sutruk-Nakhkhunte (1220 B.C.) carried fire and
sword through Babylonia, slew its king Zamama-sum-iddin and
carried away a stela of Naram-Sin and the famous code of laws
of Khammurabi from Sippara, as well as a stela of Manistusu
from Akkuttum or Akkad. He also conquered the land of
Asnunnak and carried off from Padan a stela belonging to a
refugee from Malatia. He was succeeded by his son who was
followed on the throne by his brother, one of the great builders of
Elam. In 750 B.C. Umbadara was king of Elam; Khumban-igas
was his successor in 742 B.C. In 720 B.C. the latter prince
met the Assyrians under Sargon at Dur-ili in Yamutbal, and
though Sargon claims a victory the result was that Babylonia
recovered its independence under Merodach-baladan and the
Assyrian forces were driven north. From this time forward it
was against Assyria instead of Babylonia that Elam found
itself compelled to exert its strength, and Elamite policy was
directed towards fomenting revolt in Babylonia and assisting the
Babylonians in their struggle with Assyria. In 716 B.C. Khumban-igas
died and was followed by his nephew, Sutruk-Nakhkhunte.
He failed to make head against the Assyrians; the frontier cities
were taken by Sargon and Merodach-baladan was left to his
fate. A few years later (704 B.C.) the combined forces of Elam
and Babylonia were overthrown at Kis, and in the following
year the Kassites were reduced to subjection. The Elamite king
was dethroned and imprisoned in 700 B.C. by his brother Khallusu,
who six years later marched into Babylonia, captured the son of
Sennacherib, whom his father had placed there as king, and raised
a nominee of his own, Nergal-yusezib, to the throne. Khallusu
was murdered in 694 B.C., after seeing the maritime part of his
dominions invaded by the Assyrians. His successor Kudur-Nakhkhunte
invaded Babylonia; he was repulsed, however,
by Sennacherib, 34 of his cities were destroyed, and he himself
fled from Madaktu to Khidalu. The result was a revolt in which
he was killed after a reign of ten months. His brother Umman-menan
at once collected allies and prepared for resistance to the
Assyrians. But the terrible defeat at Khalulē broke his power;
he was attacked by paralysis shortly afterwards, and Khumba-Khaldas
II. followed him on the throne (689 B.C.). The new king
endeavoured to gain Assyrian favour by putting to death the
son of Merodach-baladan, but was himself murdered by his
brothers Urtaki and Teumman (681 B.C.), the first of whom
seized the crown. On his death Teumman succeeded and almost
immediately provoked a quarrel with Assur-bani-pal by demanding
the surrender of his nephews who had taken refuge at the
Assyrian court. The Assyrians pursued the Elamite army to
Susa, where a battle was fought on the banks of the Eulaeus, in
which the Elamites were defeated, Teumman captured and slain,
and Umman-igas, the son of Urtaki, made king, his younger
brother Tammaritu being given the district of Khidalu. Umman-igas
afterwards assisted in the revolt of Babylonia under Samas-sum-yukin,
but his nephew, a second Tammaritu, raised a
rebellion against him, defeated him in battle, cut off his head
and seized the crown. Tammaritu marched to Babylonia;
while there, his officer Inda-bigas made himself master of Susa
and drove Tammaritu to the coast whence he fled to Assur-bani-pal.
Inda-bigas was himself overthrown and slain by a new
pretender, Khumba-Khaldas III., who was opposed, however,
by three other rivals, two of whom maintained themselves in
the mountains until the Assyrian conquest of the country, when
Tammaritu was first restored and then imprisoned, Elam being
utterly devastated. The return of Khumba-Khaldas led to a
fresh Assyrian invasion; the Elamite king fled from Madaktu
to Dur-undasi; Susa and other cities were taken, and the
Elamite army almost exterminated on the banks of the Ititē.
The whole country was reduced to a desert, Susa was plundered
and razed to the ground, the royal sepulchres were desecrated,
and the images of the gods and of 32 kings “in silver, gold,
bronze and alabaster,” were carried away. All this must have
happened about 640 B.C. After the fall of the Assyrian empire
Elam was occupied by the Persian Teispes, the forefather of
Cyrus, who, accordingly, like his immediate successors, is called
in the inscriptions “king of Anzan.” Susa once more became
a capital, and on the establishment of the Persian empire remained
one of the three seats of government, its language,
the Neo-Susian, ranking with the Persian of Persepolis and the
Semitic of Babylon as an official tongue. In the reign of Darius,
however, the Susianians attempted to revolt, first under Assina
or Atrina, the son of Umbadara, and later under Martiya, the son
of Issainsakria, who called himself Immanes; but they gradually
became completely Aryanized, and their agglutinative dialects
were supplanted by the Aryan Persian from the south-east.
Elam, “the land of the cedar-forest,” with its enchanted
trees, figured largely in Babylonian mythology, and one of the
adventures of the hero Gilgamesh was the destruction of the
tyrant Khumbaba who dwelt in the midst of it. A list of the
Elamite deities is given by Assur-bani-pal; at the head of them
was In-Susinak, “the lord of the Susians,”—a title which went
back to the age of Babylonian suzerainty,—whose image and
oracle were hidden from the eyes of the profane. Nakhkhunte,
according to Scheil, was the Sun-goddess, and Lagamar, whose
name enters into that of Chedor-laomer, was borrowed from
Semitic Babylonia.
See W.K. Loftus, Chaldaea and Susiana (1857); A. Billerbeck,
Susa (1893); J. de Morgan, Mémoires de la Délégation en Perse
(9 vols., 1899-1906).
(A. H. S.)
ELAND (= elk), the Dutch name for the largest of the South
African antelopes (Taurotragus oryx), a species near akin to the
kudu, but with horns present in both sexes, and their spiral
much closer, being in fact screw-like instead of corkscrew-like.
There is also a large dewlap, while old bulls have a thick forelock.
In the typical southern form the body-colour is wholly pale
fawn, but north of the Orange river the body is marked by
narrow vertical white lines, this race being known as T. oryx
livingstonei. In Senegambia the genus is represented by T.
derbianus, a much larger animal, with a dark neck; while in the
Bahr-el-Ghazal district there is a gigantic local race of this species
(T. derbianus giganteus).
(R. L.*)
ELASTICITY. 1. Elasticity is the property of recovery of
an original size or shape. A body of which the size, or shape,
or both size and shape, have been altered by the application of
forces may, and generally does, tend to return to its previous
size and shape when the forces cease to act. Bodies which
exhibit this tendency are said to be elastic (from Greek, ἐλαύνειν,
to drive). All bodies are more or less elastic as regards size;
and all solid bodies are more or less elastic as regards shape.
For example: gas contained in a vessel, which is closed by a
piston, can be compressed by additional pressure applied to the
piston; but, when the additional pressure is removed, the gas
expands and drives the piston outwards. For a second example:
a steel bar hanging vertically, and loaded with one ton for each
square inch of its sectional area, will have its length increased by
about seven one-hundred-thousandths of itself, and its sectional
area diminished by about half as much; and it will spring back
to its original length and sectional area when the load is gradually
removed. Such changes of size and shape in bodies subjected
to forces, and the recovery of the original size and shape when
the forces cease to act, become conspicuous when the bodies
have the forms of thin wires or planks; and these properties
of bodies in such forms are utilized in the construction of spring
balances, carriage springs, buffers and so on.
It is a familiar fact that the hair-spring of a watch can be
coiled and uncoiled millions of times a year for several years
without losing its elasticity; yet the same spring can have its
shape permanently altered by forces which are much greater
than those to which it is subjected in the motion of the watch.
The incompleteness of the recovery from the effects of great
forces is as important a fact as the practical completeness of
the recovery from the effects of comparatively small forces.
142
The fact is referred to in the distinction between “perfect”
and “imperfect” elasticity; and the limitation which must
be imposed upon the forces in order that the elasticity may be
perfect leads to the investigation of “limits of elasticity”
(see §§ 31, 32 below). Steel pianoforte wire is perfectly elastic
within rather wide limits, glass within rather narrow limits;
building stone, cement and cast iron appear not to be perfectly
elastic within any limits, however narrow. When the limits of
elasticity are not exceeded no injury is done to a material or
structure by the action of the forces. The strength or weakness
of a material, and the safety or insecurity of a structure, are thus
closely related to the elasticity of the material and to the change
of size or shape of the structure when subjected to forces. The
“science of elasticity” is occupied with the more abstract side
of this relation, viz. with the effects that are produced in a body
of definite size, shape and constitution by definite forces; the
“science of the strength of materials” is occupied with the
more concrete side, viz. with the application of the results
obtained in the science of elasticity to practical questions of
strength and safety (see Strength of Materials).
2. Stress.—Every body that we know anything about is
always under the action of forces. Every body upon which
we can experiment is subject to the force of gravity, and must,
for the purpose of experiment, be supported by other forces.
Such forces are usually applied by way of pressure upon a
portion of the surface of the body; and such pressure is exerted
by another body in contact with the first. The supported body
exerts an equal and opposite pressure upon the supporting body
across the portion of surface which is common to the two. The
same thing is true of two portions of the same body. If, for
example, we consider the two portions into which a body is
divided by a (geometrical) horizontal plane, we conclude that
the lower portion supports the upper portion by pressure across
the plane, and the upper portion presses downwards upon the
lower portion with an equal pressure. The pressure is still
exerted when the plane is not horizontal, and its direction may
be obliquely inclined to, or tangential to, the plane. A more
precise meaning is given to “pressure” below. It is important
to distinguish between the two classes of forces: forces such as
the force of gravity, which act all through a body, and forces
such as pressure applied over a surface. The former are named
“body forces” or “volume forces,” and the latter “surface
tractions.” The action between two portions of a body separated
by a geometrical surface is of the nature of surface traction.
Body forces are ultimately, when the volumes upon which they
act are small enough, proportional to the volumes; surface
tractions, on the other hand, are ultimately, when the surfaces
across which they act are small enough, proportional to these
surfaces. Surface tractions are always exerted by one body
upon another, or by one part of a body upon another part,
across a surface of contact; and a surface traction is always
to be regarded as one aspect of a “stress,” that is to say of a
pair of equal and opposite forces; for an equal traction is always
exerted by the second body, or part, upon the first across the
surface.
3. The proper method of estimating and specifying stress is
a matter of importance, and its character is necessarily mathematical.
The magnitudes of the surface tractions which compose
a stress are estimated as so much force (in dynes or tons) per
unit of area (per sq. cm. or per sq. in.). The traction across an
assigned plane at an assigned point is measured by the mathematical
limit of the fraction F/S, where F denotes the numerical
measure of the force exerted across a small portion of the plane
containing the point, and S denotes the numerical measure
of the area of this portion, and the limit is taken by diminishing
S indefinitely. The traction may act as “tension,” as it does
in the case of a horizontal section of a bar supported at its
upper end and hanging vertically, or as “pressure,” as it
does in the case of a horizontal section of a block resting on
a horizontal plane, or again it may act obliquely or even
tangentially to the separating plane. Normal tractions are
reckoned as positive when they are tensions, negative when
they are pressures. Tangential tractions are often called
“shears” (see § 7 below). Oblique tractions can always
be resolved, by the vector law, into normal and tangential
tractions. In a fluid at rest the traction across any plane at
any point is normal to the plane, and acts as pressure. For the
complete specification of the “state of stress” at any point of a
body, we should require to know the normal and tangential
components of the traction across every plane drawn through
the point. Fortunately this requirement can be very much
simplified (see §§ 6, 7 below).
4. In general let ν denote the direction of the normal drawn in a
specified sense to a plane drawn through a point O of a body; and
let Tν denote the traction exerted across the plane, at the point O,
by the portion of the body towards which ν is drawn upon the
remaining portion. Then Tν is a vector quantity, which has a definite
magnitude (estimated as above by the limit of a fraction of the form
F/S) and a definite direction. It can be specified completely by its
components Xν, Yν, Zν, referred to fixed rectangular axes of x, y, z.
When the direction of ν is that of the axis of x, in the positive sense,
the components are denoted by Xx, Yx, Zx; and a similar notation
is used when the direction of ν is that of y or z, the suffix x being
replaced by y or z.
5. Every body about which we know anything is always in a
state of stress, that is to say there are always internal forces
acting between the parts of the body, and these forces are
exerted as surface tractions across geometrical surfaces drawn in
the body. The body, and each part of the body, moves under
the action of all the forces (body forces and surface tractions)
which are exerted upon it; or remains at rest if these forces are
in equilibrium. This result is expressed analytically by means
of certain equations—the “equations of motion” or “equations
of equilibrium” of the body.
Let ρ denote the density of the body at any point, X, Y, Z, the
components parallel to the axes of x, y, z of the body forces, estimated
as so much force per unit of mass; further let ƒx, ƒy, ƒz denote
the components, parallel to the same axes, of the acceleration of the
particle which is momentarily at the point (x, y, z). The equations
of motion express the result that the rates of change of the momentum,
and of the moment of momentum, of any portion of the body are
those due to the action of all the forces exerted upon the portion
by other bodies, or by other portions of the same body. For the
changes of momentum, we have three equations of the type
∫ ∫ ∫ ρ Xdx dy dz + ∫ ∫ XνdS = ∫ ∫ ∫ ρ ƒxdx dy dz,
(1)
in which the volume integrations are taken through the volume
of the portion of the body, the surface integration is taken over its
surface, and the notation Xν is that of § 4, the direction of ν being
that of the normal to this surface drawn outwards. For the changes
of moment of momentum, we have three equations of the type
∫ ∫ ∫ ρ (yZ − zY) dx dy dz + ∫ ∫ (yZν − zYν) dS =
∫ ∫ ∫ ρ (yƒz − zƒy) dx dy dz.
(2)
The equations (1) and (2) are the equations of motion of any kind of
body. The equations of equilibrium are obtained by replacing the
right-hand members of these equations by zero.
6. These equations can be used to obtain relations between the
values of Xν, Yν, ... for different directions ν. When the equations
are applied to a very small volume, it appears that the terms expressed
by surface integrals would, unless they tend to zero limits
in a higher order than the areas of the surfaces, be very great compared
with the terms expressed by volume integrals. We conclude
that the surface tractions on the portion of the body which is bounded
by any very small closed surface, are ultimately in equilibrium.
When this result is interpreted for a small portion in the shape of a
tetrahedron, having three of its faces at right angles to the co-ordinate
axes, it leads to three equations of the type
Xν = Xx cos(x, ν) + Xy cos(y, ν) + Xz cos(z, ν),
(1)
where ν is the direction of the normal (drawn outwards) to the
remaining face of the tetrahedron, and (x, ν) ... denote the angles
which this normal makes with the axes. Hence Xν, ... for any
direction ν are expressed in terms of Xx,.... When the above
result is interpreted for a very small portion in the shape of a cube,
having its edges parallel to the co-ordinate axes, it leads to the
equations
Yz = Zy, Zx = Xz, Xy = Yx.
(2)
When we substitute in the general equations the particular results
which are thus obtained, we find that the equations of motion take
such forms as
| ρX + | ∂Xx |
+ | ∂Xy |
+ | ∂Zx |
= ρƒx, |
| ∂x | ∂y | ∂z |
(3)
and the equations of moments are satisfied identically. The equations
of equilibrium are obtained by replacing the right-hand
members by zero.
143
 |
| Fig. 1. |
 |
| Fig. 2. |
7. A state of stress in which the traction across any plane of
a set of parallel planes is normal to the plane, and that across
any perpendicular plane vanishes, is described as a state of
“simple tension” (“simple pressure” if the traction is negative).
A state of stress in which the traction across any plane is normal
to the plane, and the traction is the same for all planes passing
through any point, is described
as a state of “uniform
tension” (“uniform
pressure” if the traction
is negative). Sometimes
the phrases “isotropic
tension” and “hydrostatic
pressure” are used
instead of “uniform”
tension or pressure. The
distinction between the two states, simple tension and uniform
tension, is illustrated in fig. 1.
A state of stress in which there is purely tangential traction
on a plane, and no normal traction on any perpendicular plane,
is described as a state of “shearing stress.” The result (2) of
§ 6 shows that tangential tractions occur in pairs. If, at any
point, there is tangential traction, in any direction, on a plane
parallel to this direction,
and if we draw through
the point a plane at right
angles to the direction of
this traction, and therefore
containing the normal to
the first plane, then there
is equal tangential traction
on this second plane in the
direction of the normal to
the first plane. The result
is illustrated in fig. 2, where
a rectangular block is subjected
on two opposite faces
to opposing tangential tractions,
and is held in equilibrium by equal tangential tractions
applied to two other faces.
Through any point there always pass three planes, at
right angles to each other, across which there is no tangential
traction. These planes are called the “principal planes of
stress,” and the (normal) tractions across them the “principal
stresses.” Lines, usually curved, which have at every point the
direction of a principal stress at the point, are called “lines of
stress.”
8. It appears that the stress at any point of a body is completely
specified by six quantities, which can be taken to be the
Xx, Yy, Zz and Yz, Zx, Xy of § 6. The first three are tensions
(pressures if they are negative) across three planes parallel to
fixed rectangular directions, and the remaining three are tangential
tractions across the same three planes. These six quantities
are called the “components of stress.” It appears also that the
components of stress are connected with each other, and with the
body forces and accelerations, by the three partial differential
equations of the type (3) of § 6. These equations are available
for the purpose of determining the state of stress which exists
in a body of definite form subjected to definite forces, but they
are not sufficient for the purpose (see § 38 below). In order
to effect the determination it is necessary to have information
concerning the constitution of the body, and to introduce subsidiary
relations founded upon this information.
9. The definite mathematical relations which have been found
to connect the components of stress with each other, and with
other quantities, result necessarily from the formation of a clear
conception of the nature of stress. They do not admit of experimental
verification, because the stress within a body does not
admit of direct measurement. Results which are deduced by
the aid of these relations can be compared with experimental
results. If any discrepancy were observed it would not be interpreted
as requiring a modification of the concept of stress, but
as affecting some one or other of the subsidiary relations which
must be introduced for the purpose of obtaining the theoretical
result.
10. Strain.—For the specification of the changes of size and
shape which are produced in a body by any forces, we begin by
defining the “average extension” of any linear element or
“filament” of the body. Let l0 be the length of the filament
before the forces are applied, l its length when the body is subjected
to the forces. The average extension of the filament is measured
by the fraction (l − l0)/l0. If this fraction is negative there is
“contraction.” The “extension at a point” of a body in any
assigned direction is the mathematical limit of this fraction when
one end of the filament is at the point, the filament has the
assigned direction, and its length is diminished indefinitely. It
is clear that all the changes of size and shape of the body are
known when the extension at every point in every direction
is known.
The relations between the extensions in different directions
around the same point are most simply expressed by introducing the
extensions in the directions of the co-ordinate axes and the angles
between filaments of the body which are initially parallel to these
axes. Let exx, eyy, ezz denote the extensions parallel to the axes of
x, y, z, and let eyz, ezx, exy denote the cosines of the angles between
the pairs of filaments which are initially parallel to the axes of y
and z, z and x, x and y. Also let e denote the extension in the
direction of a line the direction cosines of which are l, m, n. Then,
if the changes of size and shape are slight, we have the relation
e = exxl² + eyym² + ezzn² + eyzmn + ezxnl + exylm.
The body which undergoes the change of size or shape is said
to be “strained,” and the “strain” is determined when the
quantities exx, eyy, ezz and eyz, ezx, exy defined above are known
at every point of it. These quantities are called “components
of strain.” The three of the type exx are extensions, and the
three of the type eyz are called “shearing strains” (see § 12
below).
11. All the changes of relative position of particles of the body
are known when the strain is known, and conversely the strain
can be determined when the changes of relative position are
given. These changes can be expressed most simply by the
introduction of a vector quantity to represent the displacement
of any particle.
When the body is deformed by the action of any forces its particles
pass from the positions which they occupied before the action of the
forces into new positions. If x, y, z are the co-ordinates of the
position of a particle in the first state, its co-ordinates in the second
state may be denoted by x + u, y + v, z + w. The quantities, u, v, w
are the “components of displacement.” When these quantities are
small, the strain is connected with them by the equations
exx = ∂u / ∂x, eyy = ∂v / ∂y, ezz = ∂w / ∂z,
(1)
| eyz = | ∂w |
+ | ∂v |
, ezx = | ∂u |
+ | ∂w |
, exy = | ∂v |
+ | ∂u |
. |
| ∂y | ∂z |
∂z | ∂x |
∂x | ∂y |
12. These equations enable us to determine more exactly the
nature of the “shearing strains” such as exy. Let u, for example,
be of the form sy, where s is constant, and let v and w vanish.
Then exy = s, and the remaining components of strain vanish.
The nature of the strain (called “simple shear”) is simply
appreciated by imagining the body to consist of a series of thin
sheets, like the leaves of a book, which lie one over another and
are all parallel to a plane (that of x, z); and the displacement
is seen to consist in the shifting of each sheet relative to the sheet
below in a direction (that of x) which is the same for all the
sheets. The displacement of any sheet is proportional to its
distance y from a particular sheet, which remains undisplaced.
The shearing strain has the effect of distorting the shape of any
portion of the body without altering its volume. This is shown
in fig. 3, where a square ABCD is distorted by simple shear
(each point moving parallel to the line marked xx) into a rhombus
A′B′C′D′, as if by an extension of the diagonal BD and a contraction
of the diagonal AC, which extension and contraction
are adjusted so as to leave the area unaltered. In the general
case, where u is not of the form sy and v and w do not vanish,
the shearing strains such as exy result from the composition
of pairs of simple shears of the type which has just been
explained.
144
13. Besides enabling us to express the extension in any direction
and the changes of relative direction of any filaments of the body,
the components of strain also express the changes of size of volumes
and areas. In particular, the “cubical dilatation,” that is to say,
the increase of volume per unit of volume, is expressed by the
quantity exx + eyy + ezz or
∂u / ∂x + ∂v / ∂y + ∂w / ∂z. When this quantity is negative
there is “compression.”
 |
| Fig. 3. |
14. It is important to distinguish between two types of
strain: the “rotational” type and the “irrotational” type.
The distinction is illustrated in fig. 3, where the figure
A″B″C″D″ is obtained from the figure ABCD by contraction
parallel to AC and extension parallel to BD, and the figure
A′B′C′D′ can be obtained from ABCD by the same contraction
and extension followed by a rotation through the
angle A″OA′. In strains of the irrotational type there are at
any point three filaments at right angles to each other, which are
such that the particles which lie in them before strain continue
to lie in them after strain. A small spherical element of the body
with its centre at the point becomes a small ellipsoid with its
axes in the directions of these three filaments. In the case
illustrated in the figure, the lines of the filaments in question,
when the figure ABCD is strained into the figure A″B″C″D″,
are OA, OB and a line through O at right angles to their plane. In
strains of the rotational type, on the other hand, the single existing
set of three filaments (issuing from a point) which cut each other
at right angles both before and after strain do not retain their
directions after strain, though one of them may do so in certain
cases. In the figure, the lines of the filaments in question, when
the figure ABCD is strained into A′B′C′D′, are OA, OB and a
line at right angles to their plane before strain, and after strain
they are OA′, OB′, and the same third line. A rotational
strain can always be analysed into an irrotational strain (or
“pure” strain) followed by a rotation.
Analytically, a strain is irrotational if the three quantities
| ∂w | − | ∂v |
, | ∂u |
− | ∂w |
, | ∂v |
− | ∂u |
| ∂y | ∂z |
∂z | ∂x |
∂x | ∂y |
vanish, rotational if any one of them is different from zero. The
halves of these three quantities are the components of a vector
quantity called the “rotation.”
15. Whether the strain is rotational or not, there is always one
set of three linear elements issuing from any point which cut each
other at right angles both before and after strain. If these directions
are chosen as axes of x, y, z, the shearing strains eyz, ezx, exy vanish
at this point. These directions are called the “principal axes of
strain,” and the extensions in the directions of these axes the
“principal extensions.”
16. It is very important to observe that the relations between
components of strain and components of displacement imply
relations between the components of strain themselves. If
by any process of reasoning we arrive at the conclusion that
the state of strain in a body is such and such a state, we have a
test of the possibility or impossibility of our conclusion. The
test is that, if the state of strain is a possible one, then there
must be a displacement which can be associated with it in accordance
with the equations (1) of § 11.
We may eliminate u, v, w from these equations. When this is
done we find that the quantities exx, ... eyz are connected by the
two sets of equations
| ∂²eyy |
+ | ∂²ezz |
= | ∂²eyz |
| ∂z² | ∂y² |
∂y∂z |
(1)
| ∂²ezz |
+ | ∂²exx |
= | ∂²ezx |
| ∂x² | ∂z² |
∂z∂x |
| ∂²exx |
+ | ∂²eyy |
= | ∂²exy |
| ∂y² | ∂x² |
∂x∂y |
and
| 2 | ∂²exx |
= | ∂ |
( − | ∂eyz |
+ | ∂ezx |
+ | ∂exy |
) |
| ∂y∂z | ∂x |
∂x | ∂y |
∂z |
(2)
| 2 | ∂²eyy |
= | ∂ |
( | ∂eyz |
− | ∂ezx |
+ | ∂exy |
) |
| ∂z∂x | ∂y |
∂x | ∂y |
∂z |
| 2 | ∂²ezz |
= | ∂ |
( | ∂eyz |
+ | ∂ezx |
− | ∂exy |
) |
| ∂x∂y | ∂z |
∂x | ∂y |
∂z |
These equations are known as the conditions of compatibility
of strain-components. The components of strain which specify
any possible strain satisfy them. Quantities arrived at in any
way, and intended to be components of strain, if they fail to
satisfy these equations, are not the components of any possible
strain; and the theory or speculation by which they are reached
must be modified or abandoned.
When the components of strain have been found in accordance
with these and other necessary equations, the displacement is
to be found by solving the equations (1) of § 11, considered as
differential equations to determine u, v, w. The most general
possible solution will differ from any other solution by terms which
contain arbitrary constants, and these terms represent a possible
displacement. This “complementary displacement” involves no
strain, and would be a possible displacement of an ideal perfectly
rigid body.
17. The relations which connect the strains with each other
and with the displacement are geometrical relations resulting
from the definitions of the quantities and not requiring any
experimental verification. They do not admit of such verification,
because the strain within a body cannot be measured.
The quantities (belonging to the same category) which can be
measured are displacements of points on the surface of a body.
For example, on the surface of a bar subjected to tension we may
make two fine transverse scratches, and measure the distance
between them before and after the bar is stretched. For such
measurements very refined instruments are required. Instruments
for this purpose are called barbarously “extensometers,”
and many different kinds have been devised. From measurements
of displacement by an extensometer we may deduce the
average extension of a filament of the bar terminated by the
two scratches. In general, when we attempt to measure a
strain, we really measure some displacements, and deduce the
values, not of the strain at a point, but of the average extensions
of some particular linear filaments of a body containing the point;
and these filaments are, from the nature of the case, nearly
always superficial filaments.
18. In the case of transparent materials such as glass there is
available a method of studying experimentally the state of strain
within a body. This method is founded upon the result that a
piece of glass when strained becomes doubly refracting, with its
optical principal axes at any point in the directions of the
principal axes of strain (§ 15) at the point. When the piece has
two parallel plane faces, and two of the principal axes of strain
at any point are parallel to these faces, polarized light transmitted
through the piece in a direction normal to the faces can be used
to determine the directions of the principal axes of the strain
at any point. If the directions of these axes are known theoretically
the comparison of the experimental and theoretical results
yields a test of the theory.
19. Relations between Stresses and Strains.—The problem
of the extension of a bar subjected to tension is the one which
has been most studied experimentally, and as a result of this
study it is found that for most materials, including all metals
except cast metals, the measurable extension is proportional
145
to the applied tension, provided that this tension is not too great.
In interpreting this result it is assumed that the tension is uniform
over the cross-section of the bar, and that the extension
of longitudinal filaments is uniform throughout the bar; and
then the result takes the form of a law of proportionality connecting
stress and strain: The tension is proportional to the extension.
Similar results are found for the same materials when other
methods of experimenting are adopted, for example, when a
bar is supported at the ends and bent by an attached load and the
deflexion is measured, or when a bar is twisted by an axial couple
and the relative angular displacement of two sections is measured.
We have thus very numerous experimental verifications of the
famous law first enunciated by Robert Hooke in 1678 in the words
“Ut Tensio sic vis”; that is, “the Power of any spring is in the
same proportion as the Tension (—stretching) thereof.” The
most general statement of Hooke’s Law in modern language
would be:—Each of the six components of stress at any point of
a body is a linear function of the six components of strain at the
point. It is evident from what has been said above as to the
nature of the measurement of stresses and strains that this law
in all its generality does not admit of complete experimental
verification, and that the evidence for it consists largely in the
agreement of the results which are deduced from it in a theoretical
fashion with the results of experiments. Of such results one of
a general character may be noted here. If the law is assumed
to be true, and the equations of motion of the body (§ 5) are
transformed by means of it into differential equations for
determining the components of displacement, these differential
equations admit of solutions which represent periodic vibratory
displacements (see § 85 below). The fact that solid bodies can
be thrown into states of isochronous vibration has been
emphasized by G.G. Stokes as a peremptory proof of the truth
of Hooke’s Law.
20. According to the statement of the generalized Hooke’s
Law the stress-components vanish when the strain-components
vanish. The strain-components contemplated in experiments
upon which the law is founded are measured from a zero of
reckoning which corresponds to the state of the body subjected
to experiment before the experiment is made, and the stress-components
referred to in the statement of the law are those
which are called into action by the forces applied to the body
in the course of the experiment. No account is taken of the stress
which must already exist in the body owing to the force of gravity
and the forces by which the body is supported. When it is
desired to take account of this stress it is usual to suppose that the
strains which would be produced in the body if it could be freed
from the action of gravity and from the pressures of supports are
so small that the strains produced by the forces which are
applied in the course of the experiment can be compounded with
them by simple superposition. This supposition comes to the
same thing as measuring the strain in the body, not from the
state in which it was before the experiment, but from an ideal
state (the “unstressed” state) in which it would be entirely free
from internal stress, and allowing for the strain which would
be produced by gravity and the supporting forces if these forces
were applied to the body when free from stress. In most practical
cases the initial strain to be allowed for is unimportant
(see §§ 91-93 below).
21. Hooke’s law of proportionality of stress and strain leads
to the introduction of important physical constants: the
moduluses of elasticity of a body. Let a bar of uniform section
(of area ω) be stretched with tension T, which is distributed
uniformly over the section, so that the stretching force is Twω,
and let the bar be unsupported at the sides. The bar will undergo
a longitudinal extension of magnitude T/E, where E is a constant
quantity depending upon the material. This constant is called
Young’s modulus after Thomas Young, who introduced it into
the science in 1807. The quantity E is of the same nature as a
traction, that is to say, it is measured as a force estimated per
unit of area. For steel it is about 2.04 × 1012 dynes per square
centimetre, or about 13,000 tons per sq. in.
22. The longitudinal extension of the bar under tension is
not the only strain in the bar. It is accompanied by a lateral
contraction by which all the transverse filaments of the bar
are shortened. The amount of this contraction is σT/E, where
σ is a certain number called Poisson’s ratio, because its importance
was at first noted by S.D. Poisson in 1828. Poisson arrived
at the existence of this contraction, and the corresponding
number σ, from theoretical considerations, and his theory led
him to assign to σ the value ¼. Many experiments have been
made with the view of determining σ, with the result that it
has been found to be different for different materials, although
for very many it does not differ much from ¼. For steel the
best value (Amagat’s) is 0.268. Poisson’s theory admits of
being modified so as to agree with the results of experiment.
23. The behaviour of an elastic solid body, strained within
the limits of its elasticity, is entirely determined by the constants
E and σ if the body is isotropic, that is to say, if it has the same
quality in all directions around any point. Nevertheless it is
convenient to introduce other constants which are related to the
action of particular sorts of forces. The most important of these
are the “modulus of compression” (or “bulk modulus”) and
the “rigidity” (or “modulus of shear”). To define the modulus
of compression, we suppose that a solid body of any form is
subjected to uniform hydrostatic pressure of amount p. The
state of stress within it will be one of uniform pressure, the same
at all points, and the same in all directions round any point.
There will be compression, the same at all points, and proportional
to the pressure; and the amount of the compression can
be expressed as p/k. The quantity k is the modulus of compression.
In this case the linear contraction in any direction
is p/3k; but in general the linear extension (or contraction)
is not one-third of the cubical dilatation (or compression).
24. To define the rigidity, we suppose that a solid body is
subjected to forces in such a way that there is shearing stress
within it. For example, a cubical block may be subjected to
opposing tractions on opposite faces acting in directions which
are parallel to an edge of the cube and to both the faces. Let
S be the amount of the traction, and let it be uniformly distributed
over the faces. As we have seen (§ 7), equal tractions
must act upon two other faces in suitable directions in order
to maintain equilibrium (see fig. 2 of § 7). The two directions
involved may be chosen as axes of x, y as in that figure. Then
the state of stress will be one in which the stress-component
denoted by Xy is equal to S, and the remaining stress-components
vanish; and the strain produced in the body is shearing strain of
the type denoted by exy. The amount of the shearing strain
is S/μ, and the quantity μ is the “rigidity.”
25. The modulus of compression and the rigidity are quantities
of the same kind as Young’s modulus. The modulus of compression
of steel is about 1.43 × 1012 dynes per square centimetre,
the rigidity is about 8.19 × 1011 dynes per square centimetre.
It must be understood that the values for different
specimens of nominally the same material may differ considerably.
The modulus of compression k and the rigidity μ of an isotropic
material are connected with the Young’s modulus E and Poisson’s
ratio σ of the material by the equations
k = E / 3(1 − 2σ), μ = E / 2(1 + σ).
26. Whatever the forces acting upon an isotropic solid body may
be, provided that the body is strained within its limits of elasticity,
the strain-components are expressed in terms of the stress-components
by the equations
exx = (Xx − σYy − σZz) / E, eyz = Yz / μ,
eyy = (Yy − σZz − σXx) / E, ezx = Zx / μ,
ezz = (Zz − σXx − σYy) / E, exy = Xy / μ.
(1)
If we introduce a quantity λ, of the same nature as E or μ, by the
equation
λ = Eσ / (1 + σ)(1 − 2σ),
(2)
we may express the stress-components in terms of the strain-components
by the equations
Xx = λ(exx + eyy + ezz) + 2μexx, Yz = μeyz,
Yy = λ(exx + eyy + ezz) + 2μeyy, Zx = μezx,
Zz = λ(exx + eyy + ezz) + 2μezz, Xy = μexy;
(3)
and then the behaviour of the body under the action of any forces
146
depends upon the two constants λ and μ. These two constants were
introduced by G. Lamé in his treatise of 1852. The importance of
the quantity μ had been previously emphasized by L.J. Vicat and
G.G. Stokes.
27. The potential energy per unit of volume (often called the
“resilience”) stored up in the body by the strain is equal to
½ (λ + 2μ) (exx + eyy + ezz)² + ½μ (e²yz + e²zx + e²xy − 4eyyezz − 4ezzexx − 4exxeyy),
or the equivalent expression
½ [(X²x + Y²y + Z²z) − 2σ (YyZz + ZzXx + XxYy) + 2 (1 + σ) (Y²z + Z²x + X²y)] / E.
The former of these expressions is called the “strain-energy-function.”
28. The Young’s modulus E of a material is often determined
experimentally by the direct method of the extensometer
(§ 17), but more frequently it is determined indirectly by means
of a result obtained in the theory of the flexure of a bar (see
§§ 47, 53 below). The rigidity μ is usually determined indirectly
by means of results obtained in the theory of the torsion of a
bar (see §§ 41, 42 below). The modulus of compression k may
be determined directly by means of the piezometer, as was
done by E.H. Amagat, or it may be determined indirectly by
means of a result obtained in the theory of a tube under pressure,
as was done by A. Mallock (see § 78 below). The value of
Poisson’s ratio σ is generally inferred from the relation connecting
it with E and μ or with E and k, but it may also be determined
indirectly by means of a result obtained in the theory of the
flexure of a bar (§ 47 below), as was done by M.A. Cornu and
A. Mallock, or directly by a modification of the extensometer
method, as has been done recently by J. Morrow.
29. The elasticity of a fluid is always expressed by means of a
single quantity of the same kind as the modulus of compression
of a solid body. To any increment of pressure, which is not too
great, there corresponds a proportional cubical compression,
and the amount of this compression for an increment δp of
pressure can be expressed as δp/k. The quantity that is usually
tabulated is the reciprocal of k, and it is called the coefficient
of compressibility. It is the amount of compression per unit
increase of pressure. As a physical quantity it is of the same
dimensions as the reciprocal of a pressure (or of a force per unit
of area). The pressures concerned are usually measured in
atmospheres (1 atmosphere = 1.014 × 106 dynes per sq. cm.).
For water the coefficient of compressibility, or the compression
per atmosphere, is about 4.5 × 10-5. This gives for k the value
2.22 × 1010 dynes per sq. cm. The Young’s modulus and the
rigidity of a fluid are always zero.
30. The relations between stress and strain in a material
which is not isotropic are much more complicated. In such a
material the Young’s modulus depends upon the direction of
the tension, and its variations about a point are expressed
by means of a surface of the fourth degree. The Poisson’s
ratio depends upon the direction of the contracted lateral
filaments as well as upon that of the longitudinal extended
ones. The rigidity depends upon both the directions involved
in the specification of the shearing stress. In general there is
no simple relation between the Young’s moduluses and Poisson’s
ratios and rigidities for assigned directions and the modulus
of compression. Many materials in common use, all fibrous
woods for example, are actually aeolotropic (that is to say, are not
isotropic), but the materials which are aeolotropic in the most
regular fashion are natural crystals. The elastic behaviour
of crystals has been studied exhaustively by many physicists,
and in particular by W. Voigt. The strain-energy-function is a
homogeneous quadratic function of the six strain-components,
and this function may have as many as 21 independent coefficients,
taking the place in the general case of the 2 coefficients
λ, μ which occur when the material is isotropic—a result first
obtained by George Green in 1837. The best experimental
determinations of the coefficients have been made indirectly
by Voigt by means of results obtained in the theories of the
torsion and flexure of aeolotropic bars.
31. Limits of Elasticity.—A solid body which has been strained
by considerable forces does not in general recover its original
size and shape completely after the forces cease to act. The
strain that is left is called set. If set occurs the elasticity is
said to be “imperfect,” and the greatest strain (or the greatest
load) of any specified type, for which no set occurs, defines the
“limit of perfect elasticity” corresponding to the specified
type of strain, or of stress. All fluids and many solid bodies,
such as glasses and crystals, as well as some metals (copper,
lead, silver) appear to be perfectly elastic as regards change of
volume within wide limits; but malleable metals and alloys
can have their densities permanently increased by considerable
pressures. The limits of perfect elasticity as regards change
of shape, on the other hand, are very low, if they exist at all,
for glasses and other hard, brittle solids; but a class of metals
including copper, brass, steel, and platinum are very perfectly
elastic as regards distortion, provided that the distortion is not
too great. The question can be tested by observation of the
torsional elasticity of thin fibres or wires. The limits of perfect
elasticity are somewhat ill-defined, because an experiment
cannot warrant us in asserting that there is no set, but only
that, if there is any set, it is too small to be observed.
32. A different meaning may be, and often is, attached to
the phrase “limits of elasticity” in consequence of the following
experimental result:—Let a bar be held stretched under a
moderate tension, and let the extension be measured; let the
tension be slightly increased and the extension again measured;
let this process be continued, the tension being increased by
equal increments. It is found that when the tension is not too
great the extension increases by equal increments (as nearly as
experiment can decide), but that, as the tension increases, a
stage is reached in which the extension increases faster than
it would do if it continued to be proportional to the tension.
The beginning of this stage is tolerably well marked. Some
time before this stage is reached the limit of perfect elasticity
is passed; that is to say, if the load is removed it is found that
there is some permanent set. The limiting tension beyond
which the above law of proportionality fails is often called the
“limit of linear elasticity.” It is higher than the limit of perfect
elasticity. For steel bars of various qualities J. Bauschinger
found for this limit values varying from 10 to 17 tons per square
inch. The result indicates that, when forces which produce
any kind of strain are applied to a solid body and are gradually
increased, the strain at any instant increases proportionally
to the forces up to a stage beyond that at which, if the forces
were removed, the body would completely recover its original
size and shape, but that the increase of strain ceases to be
proportional to the increase of load when the load surpasses
a certain limit. There would thus be, for any type of strain, a
limit of linear elasticity, which exceeds the limit of perfect
elasticity.
33. A body which has been strained beyond the limit of
linear elasticity is often said to have suffered an “over-strain.”
When the load is removed, the set which can be observed is not
entirely permanent; but it gradually diminishes with lapse of
time. This phenomenon is named “elastic after-working.”
If, on the other hand, the load is maintained constant, the
strain is gradually increased. This effect indicates a gradual
flowing of solid bodies under great stress; and a similar effect
was observed in the experiments of H. Tresca on the punching
and crushing of metals. It appears that all solid bodies under
sufficiently great loads become “plastic,” that is to say, they
take a set which gradually increases with the lapse of time.
No plasticity is observed when the limit of linear elasticity is
not exceeded.
34. The values of the elastic limits are affected by overstrain.
If the load is maintained for some time, and then removed,
the limit of linear elasticity is found to be higher than before.
If the load is not maintained, but is removed and then reapplied,
the limit is found to be lower than before. During a period of
rest a test piece recovers its elasticity after overstrain.
35. The effects of repeated loading have been studied by
A. Wöhler, J. Bauschinger, O. Reynolds and others. It has
been found that, after many repetitions of rather rapidly alternating
stress, pieces are fractured by loads which they have
many times withstood. It is not certain whether the fracture
147
is in every case caused by the gradual growth of minute flaws
from the beginning of the series of tests, or whether the elastic
quality of the material suffers deterioration apart from such
flaws. It appears, however, to be an ascertained result that,
so long as the limit of linear elasticity is not exceeded, repeated
loads and rapidly alternating loads do not produce failure of
the material.
36. The question of the conditions of safety, or of the conditions
in which rupture is produced, is one upon which there has
been much speculation, but no completely satisfactory result
has been obtained. It has been variously held that rupture
occurs when the numerically greatest principal stress exceeds
a certain limit, or when this stress is tension and exceeds a
certain limit, or when the greatest difference of two principal
stresses (called the “stress-difference”) exceeds a certain
limit, or when the greatest extension or the greatest shearing
strain or the greatest strain of any type exceeds a certain limit.
Some of these hypotheses appear to have been disproved. It
was held by G.F. Fitzgerald (Nature, Nov. 5, 1896) that rupture
is not produced by pressure symmetrically applied all round a
body, and this opinion has been confirmed by the recent experiments
of A. Föppl. This result disposes of the greatest stress
hypothesis and also of the greatest strain hypothesis. The
fact that short pillars can be crushed by longitudinal pressure
disposes of the greatest tension hypothesis, for there is no
tension in the pillar. The greatest extension hypothesis failed
to satisfy some tests imposed by H. Wehage, who experimented
with blocks of wrought iron subjected to equal pressures in two
directions at right angles to each other. The greatest stress-difference
hypothesis and the greatest shearing strain hypothesis
would lead to practically identical results, and these results
have been held by J.J. Guest to accord well with his experiments
on metal tubes subjected to various systems of combined
stress; but these experiments and Guest’s conclusion have been
criticized adversely by O. Mohr, and the question cannot be
regarded as settled. The fact seems to be that the conditions
of rupture depend largely upon the nature of the test (tensional,
torsional, flexural, or whatever it may be) that is applied to
a specimen, and that no general formula holds for all kinds
of tests. The best modern technical writings emphasize the
importance of the limits of linear elasticity and of tests of
dynamical resistance (§ 87 below) as well as of statical resistance.
37. The question of the conditions of rupture belongs rather
to the science of the strength of materials than to the science
of elasticity (§ 1); but it has been necessary to refer to it briefly
here, because there is no method except the methods of the
theory of elasticity for determining the state of stress or strain
in a body subjected to forces. Whatever view may ultimately
be adopted as to the relation between the conditions of safety
of a structure and the state of stress or strain in it, the calculation
of this state by means of the theory or by experimental means
(as in § 18) cannot be dispensed with.
38. Methods of determining the Stress in a Body subjected to given
Forces.—To determine the state of stress, or the state of strain,
in an isotropic solid body strained within its limits of elasticity by
given forces, we have to use (i.) the equations of equilibrium, (ii.)
the conditions which hold at the bounding surface, (iii.) the relations
between stress-components and strain-components, (iv.) the relations
between strain-components and displacement. The equations
of equilibrium are (with notation already used) three partial differential
equations of the type
| ∂Xx | + | ∂Xy |
+ | ∂Zz |
+ ρX = 0. |
| ∂x | ∂y | ∂z |
(1)
The conditions which hold at the bounding surface are three equations
of the type
Xx cos (x, ν) + Xy cos (y, ν) + Zx cos (z, ν) = Xν,
(2)
where ν denotes the direction of the outward-drawn normal to the
bounding surface, and Xν denotes the x-component of the applied
surface traction. The relations between stress-components and
strain-components are expressed by either of the sets of equations
(1) or (3) of § 26. The relations between strain-components and
displacement are the equations (1) of § 11, or the equivalent conditions
of compatibility expressed in equations (1) and (2) of § 16.
39. We may proceed by either of two methods. In one method
we eliminate the stress-components and the strain-components and
retain only the components of displacement. This method leads
(with notation already used) to three partial differential equations
of the type
| (λ + μ) | ∂ |
( | ∂u |
+ | ∂v |
+ | ∂w |
) + μ ( | ∂²u |
+ | ∂²u |
+ | ∂²u |
) + ρX = 0, |
| ∂x | ∂x |
∂y | ∂z |
∂x² | ∂y² |
∂z² |
(3)
and three boundary conditions of the type
| λ cos (x, ν) ( | ∂u |
+ | ∂v |
+ | ∂w |
) + μ { 2 cos (x, ν) | ∂u |
+ cos (y, ν) ( | ∂v |
+ | ∂u |
) |
| ∂x | ∂y |
∂z | ∂x |
∂x | ∂y |
| + cos (z, ν) ( | ∂u |
+ | ∂w |
) } = Xν. |
| ∂z | ∂x |
(4)
In the alternative method we eliminate the strain-components and
the displacements. This method leads to a system of partial differential
equations to be satisfied by the stress-components. In this
system there are three equations of the type
| ∂Xx | + | ∂Xy |
+ | ∂Xz |
+ ρX = 0, |
| ∂x | ∂y |
∂z |
(1 bis)
three of the type
| ∂²Xx |
+ | ∂²Xx |
+ | ∂²Xx |
+ | 1 |
| ∂² |
(Xx + Yy + Zz) = |
| ∂x² | ∂y² |
∂z² | 1 + σ |
∂x² |
| − | σ |
ρ ( | ∂X |
+ | ∂Y |
+ | ∂Z |
) − 2ρ | ∂X |
, |
| 1 − σ | ∂x |
∂y | ∂z |
∂x |
(5)
and three of the type
| ∂²Yz |
+ | ∂²Yz |
+ | ∂²Yz |
+ | 1 |
| ∂² |
(Xx + Yy + Zz) = − ρ ( | ∂Z |
+ | ∂Y |
), |
| ∂x² | ∂y² |
∂z² | 1 + σ |
∂y∂z | ∂y |
∂z |
(6)
the equations of the two latter types being necessitated by the
conditions of compatibility of strain-components. The solutions of
these equations have to be adjusted so that the boundary conditions
of the type (2) may be satisfied.
40. It is evident that whichever method is adopted the mathematical
problem is in general very complicated. It is also evident
that, if we attempt to proceed by help of some intuition as to the
nature of the stress or strain, our intuition ought to satisfy the
tests provided by the above systems of equations. Neglect of this
precaution has led to many errors. Another source of frequent error
lies in the neglect of the conditions in which the above systems of
equations are correct. They are obtained by help of the supposition
that the relative displacements of the parts of the strained body
are small. The solutions of them must therefore satisfy the test of
smallness of the relative displacements.
41. Torsion.—As a first example of the application of the
theory we take the problem of the torsion of prisms. This
problem, considered first by C.A. Coulomb in 1784, was finally
solved by B. de Saint-Venant in 1855. The problem is this:—A
cylindrical or prismatic bar is held twisted by terminal
couples; it is required to determine the state of stress and
strain in the interior. When the bar is a circular cylinder
the problem is easy. Any section is displaced by rotation about
the central-line through a small angle, which is proportional
to the distance z of the section from a fixed plane at right angles
to this line. This plane is a terminal section if one of the two
terminal sections is not displaced. The angle through which
the section z rotates is τz, where τ is a constant, called the
amount of the twist; and this constant τ is equal to G/μI,
where G is the twisting couple, and I is the moment of inertia
of the cross-section about the central-line. This result is often
called “Coulomb’s law.” The stress within the bar is shearing
stress, consisting, as it must, of two sets of equal tangential
tractions on two sets of planes which are at right angles to each
other. These planes are the cross-sections and the axial planes
of the bar. The tangential traction at any point of the cross-section
is directed at right angles to the axial plane through
the point, and the tangential traction on the axial plane is
directed parallel to the length of the bar. The amount of
either at a distance r from the axis is μτr or Gr/I. The result
that G = μτI can be used to determine μ experimentally, for τ
may be measured and G and I are known.
42. When the cross-section of the bar is not circular it is
clear that this solution fails; for the existence of tangential
traction, near the prismatic bounding surface, on any plane
which does not cut this surface at right angles, implies the
existence of traction applied to this surface. We may attempt
to modify the theory by retaining the supposition that the
stress consists of shearing stress, involving tangential traction
distributed in some way over the cross-sections. Such traction
is obviously a necessary constituent of any stress-system
which could be produced by terminal couples around the axis.
148
We should then know that there must be equal tangential
traction directed along the length of the bar, and exerted across
some planes or other which are parallel to this direction. We
should also know that, at the bounding surface, these planes
must cut this surface at right angles. The corresponding strain
would be shearing strain which could involve (i.) a sliding
of elements of one cross-section relative to another, (ii.) a relative
sliding of elements of the above mentioned planes in the direction
of the length of the bar. We could conclude that there may
be a longitudinal displacement of the elements of the cross-sections.
We should then attempt to satisfy the conditions
of the problem by supposing that this is the character of the
strain, and that the corresponding displacement consists of
(i.) a rotation of the cross-sections in their planes such as we
found in the case of the circle, (ii.) a distortion of the cross-sections
into curved surfaces by a displacement (w) which is
directed normally to their planes and varies in some manner
from point to point of these planes. We could show that all
the conditions of the problem are satisfied by this assumption,
provided that the longitudinal displacement (w), considered as
a function of the position of a point (x, y) in the cross-section,
satisfies the equation
(1)
and the boundary condition
| ( | ∂w |
− τy ) cos(x, ν) + ( | ∂w |
+ τx ) cos(y, ν) = 0, |
| ∂x | ∂y |
(2)
where τ denotes the amount of the twist, and ν the direction
of the normal to the boundary. The solution is known for a
great many forms of section. (In the particular case of a circular
section w vanishes.) The tangential traction at any point of
the cross-section is directed along the tangent to that curve
of the family ψ = const. which passes through the point, ψ being
the function determined by the equations
| ∂w |
= τ ( | ∂ψ |
+ y ), | ∂w |
= − τ ( | ∂ψ |
+ x ). |
| ∂x | ∂y |
∂y | ∂x |
The amount of the twist τ produced by terminal couples of
magnitude G is G/C, where C is a constant, called the “torsional
rigidity” of the prism, and expressed by the formula
| C = μ ∫∫ {( | ∂ψ |
) | ² |
+ ( | ∂ψ |
) | ² |
} dxdy, |
| ∂x | | ∂y | |
the integration being taken over the cross-section. When
the coefficient of μ in the expression for C is known for any
section, μ can be determined by experiment with a bar of that
form of section.
 |
| Fig. 4. |
 |
| Fig. 5. |
43. The distortion of the cross-sections into curved surfaces
is shown graphically by drawing the contour lines (w = const.).
In general the section is divided into a number of compartments,
and the portions that lie within two adjacent compartments
are respectively concave
and convex. This result
is illustrated in the
accompanying figures
(fig. 4 for the ellipse,
given by x²/b² + y²/c² = 1;
fig. 5 for the equilateral
triangle, given by (x + 1⁄3a)
(x² − 3y² − 4⁄3ax + 4⁄9a²) = 0;
fig. 6 for the square).
44. The distribution of
the shearing stress over
the cross-section is determined
by the function ψ, already introduced. If we
draw the curves ψ = const., corresponding to any form of
section, for equidifferent values of the constant, the tangential
traction at any point on the cross-section is directed along the
tangent to that curve of the family which passes through the
point, and the magnitude of it is inversely proportional to the
distance between consecutive curves of the family. Fig. 7
illustrates the result in the case of the equilateral triangle. The
boundary is, of course, one of the lines. The “lines of shearing
stress” which can thus be drawn are in every case identical
with the lines of flow of frictionless liquid filling a cylindrical
vessel of the same cross-section as the bar, when the liquid
circulates in the plane of the section with uniform spin. They
are also the same as the contour lines of a flexible and slightly
extensible membrane, of
which the edge has the
same form as the bounding
curve of the cross-section
of the bar, when the membrane
is fixed at the edge
and slightly deformed by
uniform pressure.
 |
| Fig. 6. |
 |
| Fig. 7. |
45. Saint-Venant’s theory
shows that the true torsional
rigidity is in general
less than that which would
be obtained by extending
Coulomb’s law (G = μτI)
to sections which are not
circular. For an elliptic
cylinder of sectional area ω and moment of inertia I about
its central-line the torsional rigidity is μω4 / 4π²I, and this
formula is not far from being correct for a very large
number of sections. For a bar of square section of side a
centimetres, the torsional rigidity in C.G.S. units is (0.1406) μa4
approximately, μ being expressed in dynes per square centimetre.
How great the defect of the true value from that
given by extending Coulomb’s law may be in the case of
sections with projecting corners is shown by the diagrams (fig. 8
especially no. 4). In these diagrams the upper of the two
numbers under each figure indicates the fraction which the true
torsional rigidity corresponding to the section is of that value
which would be obtained by extending Coulomb’s law; and the
lower of the two numbers indicates the
ratio which the torsional rigidity for a
bar of the corresponding section bears
to that of a bar of circular section of
the same material and of equal sectional
area. These results have an
important practical application, inasmuch
as they show that strengthening
ribs and projections, such as are introduced
in engineering to give stiffness
to beams, have the reverse of
a good effect when torsional stiffness is an object, although
they are of great value in increasing the resistance to
bending. The theory shows further that the resistance to
torsion is very seriously diminished when there is in the
surface any dent approaching to a re-entrant angle. At such
a place the shearing strain tends to become infinite, and some
149
permanent set is produced by torsion. In the case of a section
of any form, the strain and stress are greatest at points on the
contour, and these points are in many cases the points of the
contour which are nearest to the centroid of the section. The
theory has also been applied to show that a longitudinal flaw
near the axis of a shaft transmitting a torsional couple has
little influence on the strength of the shaft, but that in the
neighbourhood of a similar flaw which is much nearer to the
surface than to the axis the shearing strain may be nearly
doubled, and thus the possibility of such flaws is a source of
weakness against which special provision ought to be made.
 |
| Fig. 8.—Diagrams showing Torsional Rigidities. |
 |
| Fig. 9. |
46. Bending of Beams.—As a second example of the application
of the general theory we take the problem of the flexure
of a beam. In this case also we begin by forming a simple
intuition as to the nature of the strain and the stress. On the
side of the beam towards the centre of curvature the longitudinal
filaments must be contracted, and on the other side
they must be extended. If we assume that the cross-sections
remain plane, and that the central-line is unaltered in length,
we see (at once from fig. 9) that the extensions (or contractions)
are given by the formula y/R, where y
denotes the distance of a longitudinal
filament from the plane drawn through
the unstrained central-line at right-angles
to the plane of bending, and
R is the radius of curvature of the
curve into which this line is bent
(shown by the dotted line in the figure).
Corresponding to this strain there must
be traction acting across the cross-sections.
If we assume that there is no other stress, then the
magnitude of the traction in question is Ey/R, where E is Young’s
modulus, and it is tension on the side where the filaments are
extended and pressure on the side where they are contracted.
If the plane of bending contains a set of principal axes of the
cross-sections at their centroids, these tractions for the whole
cross-section are equivalent to a couple of moment EI/R, where
I now denotes the moment of inertia of the cross-section about
an axis through its centroid at right angles to the plane of
bending, and the plane of the couple is the plane of bending.
Thus a beam of any form of section can be held bent in a
“principal plane” by terminal couples of moment M, that is
to say by a “bending moment” M; the central-line will take
a curvature M/EI, so that it becomes an arc of a circle of radius
EI/M; and the stress at any point will be tension of amount
My/I, where y denotes distance (reckoned positive towards the
side remote from the centre of curvature) from that plane which
initially contains the central-line and is at right angles to the
plane of the couple. This plane is called the “neutral plane.”
The restriction that the beam is bent in a principal plane means
that the plane of bending contains one set of principal axes of the
cross-sections at their centroids; in the case of a beam of rectangular
section the plane would bisect two opposite edges at
right angles. In order that the theory may hold good the
radius of curvature must be very large.
 |
| Fig. 10. |
 |
| Fig. 11. |
47. In this problem of the bending of a beam by terminal
couples the stress is tension, determined as above, and the
corresponding strain consists therefore of longitudinal extension
of amount My/EI or y/R (contraction if y is negative), accompanied
by lateral contraction of amount σMy/EI or σy/R (extension
if y is negative), σ being Poisson’s ratio for the material.
Our intuition of the nature of the strain was imperfect, inasmuch
as it took no account of these lateral strains. The necessity
for introducing them was pointed out by Saint-Venant. The
effect of them is a change
of shape of the cross-sections
in their own
planes. This is shown in
an exaggerated way in fig.
10, where the rectangle
ABCD represents the
cross-section of the unstrained
beam, or a rectangular
portion of this
cross-section, and the curvilinear figure A′B′C′D′ represents in an
exaggerated fashion the cross-section (or the corresponding portion
of the cross-section) of the same beam, when bent so that the
centre of curvature of the central-line (which is at right angles
to the plane of the figure) is on the line EF produced beyond F.
The lines A′B′ and C′D′ are approximately circles of radii R/σ,
when the central-line is a circle of radius R, and their centres
are on the line FE produced beyond E. Thus the neutral plane,
and each of the faces that is parallel to it, becomes strained
into an anticlastic surface, whose principal curvatures are in the
ratio σ : 1. The general appearance of the bent beam is shown
in an exaggerated fashion in fig. 11, where the traces of the surface
into which the neutral plane is bent are dotted. The result
that the ratio of the
principal curvatures of
the anticlastic surfaces,
into which the top and
bottom planes of the
beam (of rectangular
section) are bent, is
Poisson’s ratio σ, has
been used for the experimental
determination
of σ. The result that the radius of curvature of the bent
central-line is EI/M is used in the experimental determination
of E. The quantity EI is often called the “flexural rigidity”
of the beam. There are two principal flexural rigidities corresponding
to bending in the two principal planes (cf. § 62 below).
 |
| Fig. 12. |
48. That this theory requires modification, when the load
does not consist simply of terminal couples, can be seen most
easily by considering the problem of a beam loaded at one end
with a weight W, and supported in a horizontal position at its
other end. The forces that are exerted at any section p, to
balance the weight W, must reduce statically to a vertical
force W and a couple, and these forces arise from the action of
the part Ap on the part Bp (see fig. 12), i.e. from the stresses
across the section at p. The couple is equal to the moment of
the applied load W
about an axis drawn
through the centroid
of the section
p at right angles to
the plane of bending.
This moment
is called the “bending
moment” at
the section, it is the
product of the load
W and the distance
of the section from
the loaded end, so
that it varies uniformly
along the
length of the beam. The stress that suffices in the simpler problem
gives rise to no vertical force, and it is clear that in addition to
longitudinal tensions and pressures there must be tangential
tractions on the cross-sections. The resultant of these tangential
tractions must be a force equal to W, and directed vertically;
150
but the direction of the traction at a point of the cross-section
need not in general be vertical. The existence of tangential
traction on the cross-sections implies the existence of equal
tangential traction, directed parallel to the central-line, on
some planes or other which are parallel to this line, the two sets
of tractions forming a shearing stress. We conclude that such
shearing stress is a necessary constituent of the stress-system
in the beam bent by terminal transverse load. We can develop
a theory of this stress-system from the assumptions (i.) that the
tension at any point of the cross-section is related to the bending
moment at the section by the same law as in the case of uniform
bending by terminal couples; (ii.) that, in addition to this
tension, there is at any point shearing stress, involving tangential
tractions acting in appropriate directions upon the elements
of the cross-sections. When these assumptions are made it
appears that there is one and only one distribution of shearing
stress by which the conditions of the problem can be satisfied.
The determination of the amount and direction of this shearing
stress, and of the corresponding strains and displacements, was
effected by Saint-Venant and R.F.A. Clebsch for a number of
forms of section by means of an analysis of the same kind as that
employed in the solution of the torsion problem.
 |
| Fig. 13. |
49. Let l be the length of the beam, x the distance of the section
p from the fixed end A, y the distance of any point below the horizontal
plane through the centroid of the
section at A, then the bending moment at
p is W (l − x), and the longitudinal tension P
or Xx at any point on the cross-section is
−W (l − x)y/I, and this is related to the
bending moment exactly as in the
simpler problem.
50. The expressions for the
shearing stresses depend on the
shape of the cross-section. Taking
the beam to be of isotropic
material and the cross-section to
be an ellipse of semiaxes a and b
(fig. 13), the a axis being vertical
in the unstrained state, and drawing the axis
z at right angles to the plane of flexure, we
find that the vertical shearing stress U or Xy
at any point (y, z) on any cross-section is
| 2W [(a² − y²) {2a² (1 + σ) + b²} − z²a² (1 − 2σ)] | . |
| πa³b (1 + σ) (3a² + b²) |
The resultant of these stresses is W, but the
amount at the centroid, which is the maximum
amount, exceeds the average amount,
W/πab, in the ratio
{4a² (1 + σ) + 2b²} / (3a² + b²) (1 + σ).
If σ = ¼, this ratio is 7⁄5 for a circle, nearly 4⁄3 for a flat elliptic bar
with the longest diameter vertical, nearly 8⁄5 for a flat elliptic bar with
the longest diameter horizontal.
In the same problem the horizontal shearing stress T or Zx at any
point on any cross-section is of amount
| − | 4Wyz {a² (1 + σ) + b²σ} |
. |
| πa³b (1 + σ) (3a² + b²) |
The resultant of these stresses vanishes; but, taking as before σ = ¼,
and putting for the three cases above a = b, a = 10b, b = 10a, we find
that the ratio of the maximum of this stress to the average vertical
shearing stress has the values 3⁄5, nearly 1⁄15, and nearly 4. Thus the
stress T is of considerable importance when the beam is a plank.
As another example we may consider a circular tube of external
radius r0 and internal radius r1. Writing P, U, T for Xx, Xy, Zx, we find
| P = − | 4W |
(l − x)y, |
| π (r04 − r14) |
| U = | W |
[ (3 + 2σ) { r0² + r1² − y² − | r0² r1² |
(y² − z²) } − (1 − 2σ) z² ] |
| 2(1 + σ) π (r04 − r14) |
(y² + z²)² |
| T = − | W |
{ 1 + 2σ + (3 + 2σ) | r0² r1² |
} yz; |
| (1 + σ) π (r04 − r14) |
(y² + z²)² |
and for a tube of radius r and small thickness t the value of P and
the maximum values of U and T reduce approximately to
P = − W (l − x)y / πr³t
Umax. = W / πrt, Tmax. = W / 2πrt.
The greatest value of U is in this case approximately twice its
average value, but it is possible that these results for the bending
of very thin tubes may be seriously at fault if the tube is not plugged,
and if the load is not applied in the manner contemplated in the
theory (cf. § 55). In such cases the extensions and contractions of
the longitudinal filaments may be practically confined to a small
part of the material near the ends of the tube, while the rest of the
tube is deformed without stretching.
51. The tangential tractions U, T on the cross-sections are
necessarily accompanied by tangential tractions on the longitudinal
sections, and on each such section the tangential traction
is parallel to the central line; on a vertical section z = const.
its amount at any point is T, and on a horizontal section y =
const. its amount at any point is U.
The internal stress at any point is completely determined
by the components P, U, T, but these are not principal stresses
(§ 7). Clebsch has given an elegant geometrical construction
for determining the principal stresses at any point when the
values of P, U, T are known.
 |
| Fig. 14. |
From the point O (fig. 14) draw lines OP, OU, OT, to represent
the stresses P, U, T at O, on the cross-section through O, in magnitude,
direction and sense, and
compound U and T into a
resultant represented by OE;
the plane EOP is a principal
plane of stress at O, and the
principal stress at right angles
to this plane vanishes. Take
M the middle point of OP, and
with centre M and radius ME
describe a circle cutting the
line OP in A and B; then OA
and OB represent the magnitudes
of the two remaining
principal stresses. On AB
describe a rectangle ABDC so
that DC passes through E; then OC is the direction of the principal
stress represented in magnitude by OA, and OD is the direction
of the principal stress represented in magnitude by OB.
 |
| Fig. 15. |
52. As regards the strain in the beam, the longitudinal and
lateral extensions and contractions depend on the bending
moment in the same way as in the simpler problem; but, the
bending moment being variable, the anticlastic curvature
produced is also variable. In addition to these extensions
and contractions there are shearing strains corresponding to the
shearing stresses T, U. The shearing strain corresponding to
T consists of a relative sliding parallel to the central-line of
different longitudinal linear elements combined with a relative
sliding in a transverse horizontal direction of elements of different
cross-sections; the latter of these is concerned in the production
of those displacements by which the variable anticlastic curvature
is brought about; to see the effect of the former we may most
suitably consider, for the case of an elliptic cross-section, the
distortion of the shape of a rectangular portion of a plane of the
material which in the natural state
was horizontal; all the boundaries
of such a portion become parabolas of
small curvature, which is variable along
the length of the beam, and the particular
effect under consideration is
the change of the transverse horizontal
linear elements from straight lines
such as HK to parabolas such as H’K’
(fig. 15); the lines HL and KM are
parallel to the central-line, and the
figure is drawn for a plane above the neutral plane. When the
cross-section is not an ellipse the character of the strain is the
same, but the curves are only approximately parabolic.
The shearing strain corresponding to U is a distortion which
has the effect that the straight vertical filaments become curved
lines which cut the longitudinal filaments obliquely, and thus
the cross-sections do not remain plane, but become curved
surfaces, and the tangent plane to any one of these surfaces
at the centroid cuts the central line obliquely (fig. 16). The
angle between these tangent planes and the central-line is the
same at all points of the line; and, if it is denoted by ½π + s0,
the value of s0 is expressible as
| shearing stress at centroid |
, |
| rigidity of material |
151
and it thus depends on the shape of the cross-section; for the
elliptic section of § 50 its value is
| 4W | | 2a² (1 + σ) + b² |
; |
| Eπab | 3a² + b² |
for a circle (with σ = ¼) this becomes 7W / 2Eπa². The vertical
filament through the centroid of any cross-section becomes
a cubical parabola, as shown in fig. 16, and the contour lines
of the curved surface into which any cross-section is distorted
are shown in fig. 17 for a circular section.
 |
| Fig. 16. |
 |
| Fig. 17. |
53. The deflection of the beam is determined from the equation
curvature of central line = bending moment ÷ flexural rigidity,
and the special conditions at the supported end; there is no
alteration of this statement on account of the shears. As regards
the special condition at
an end which is encastrée,
or built in, Saint-Venant
proposed to assume that
the central tangent plane
of the cross-section at
the end is vertical; with
this assumption the tangent
to the central line
at the end is inclined
downwards and makes an
angle s0 with the horizontal
(see fig. 18); it is,
however, improbable that
this condition is exactly
realized in practice. In the application of the theory to the
experimental determination of Young’s modulus, the small
angle which the central-line at the support makes with the
horizontal is an unknown quantity, to be eliminated by observation
of the deflection at two or more points.
54. We may suppose the displacement in a bent beam to be
produced by the following operations: (1) the central-line is
deflected into its curved form, (2) the cross-sections are rotated
about axes through their centroids at right angles to the plane
of flexure so as to make angles equal to ½π + s0 with the central-line,
(3) each cross-section is distorted in its own plane in such
a way that the appropriate variable anticlastic curvature is
produced, (4) the cross-sections are further distorted into curved
surfaces. The contour lines of fig. 17 show the disturbance
from the central tangent plane, not from the original vertical
plane.
55. Practical Application of Saint-Venant’s Theory.—The
theory above described is exact provided the forces applied to
the loaded end, which
have W for resultant,
are distributed over the
terminal section in a particular
way, not likely to
be realized in practice;
and the application to
practical problems depends
on a principle due
to Saint-Venant, to the
effect that, except for
comparatively small portions
of the beam near
to the loaded and fixed
ends, the resultant only
is effective, and its mode
of distribution does not
seriously affect the internal
strain and stress. In fact, the actual stress is that due
to forces with the required resultant distributed in the manner
contemplated in the theory, superposed upon that due to a
certain distribution of forces on each terminal section which, if
applied to a rigid body, would keep it in equilibrium; according
to Saint-Venant’s principle, the stresses and strains due to such
distributions of force are unimportant except near the ends. For
this principle to be exactly applicable it is necessary that the
length of the beam should be very great compared with any
linear dimension of its cross-section; for the practical application
it is sufficient that the length should be about ten times the
greatest diameter.
56. In recent years the problem of the bending of a beam by
loads distributed along its length has been much advanced.
It is now practically solved for the case of a load distributed
uniformly, or according to any rational algebraic law, and it is
also solved for the case where the thickness is small compared
with the length and depth, as in a plate girder, and the load is
distributed in any way. These solutions are rather complicated
and difficult to interpret. The case which has been worked
out most fully is that of a transverse load distributed uniformly
along the length of the beam. In this case two noteworthy
results have been obtained. The first of these is that the central-line
in general suffers extension. This result had been found
experimentally many years before. In the case of the plate
girder loaded uniformly along the top, this extension is just
half as great as the extension of the central-line of the same
girder when free at the ends, supported along the base, and
carrying the same load along the top. The second noteworthy
result is that the curvature of the strained central-line
is not proportional to the bending moment. Over and
above the curvature which would be found from the ordinary
relation—
curvature of central-line = bending moment ÷ flexural rigidity,
 |
| Fig. 18. |
there is an additional curvature which is the same at all the
cross-sections. In ordinary cases, provided the length is large
compared with any linear dimension of the cross-section, this
additional curvature is small compared with that calculated
from the ordinary formula, but it may become important in
cases like that of suspension
bridges, where a load carried
along the middle of the roadway
is supported by tensions in rods
attached at the sides.
57. When the ordinary relation
between the curvature and the
bending moment is applied to the
calculation of the deflection of continuous
beams it must not be
forgotten that a correction of the
kind just mentioned may possibly
be requisite. In the usual method
of treating the problem such corrections
are not considered, and the ordinary relation is made
the basis of the theory. In order to apply this relation to the
calculation of the deflection, it is necessary to know the bending
moment at every point; and, since the pressures of the supports
are not among the data of the problem, we require a method
of determining the bending moments at the supports either
by calculation or in some other way. The calculation of the
bending moment can be replaced by a method of graphical
construction, due to Mohr, and depending on the two following
theorems:—
(i.) The curve of the central-line of each span of a beam, when
the bending moment M is given,1 is identical with the catenary
or funicular curve passing through the ends of the span under a
(fictitious) load per unit length of the span equal to M/EI, the
horizontal tension in the funicular being unity.
(ii.) The directions of the tangents to this funicular curve
at the ends of the span are the same for all statically equivalent
systems of (fictitious) load.
When M is known, the magnitude of the resultant shearing
stress at any section is dM/dx, where x is measured along the
beam.
152
 |
| Fig. 20. |
58. Let l be the length of a span of a loaded beam (fig. 19), M1
and M2 the bending moments at the ends, M the bending moment
at a section distant x from the end (M1), M′ the bending moment at
the same section when the same span with the same load is simply
supported; then M is given by the formula
| M = M′ + M1 | l − x |
+ M2 | x |
, |
| l | l |
 |
| Fig. 19. |
and thus a fictitious load statically equivalent to M/EI can be
easily found when M′ has been found. If we draw a curve (fig. 20)
to pass through the ends of the span, so that its ordinate represents
the value of M′/EI, the corresponding fictitious loads are statically
equivalent to a single load, of amount represented by the area of the
curve, placed at the point of the span vertically above the centre of
gravity of this area. If PN is the ordinate of this curve, and if at
the ends of the span we erect ordinates in the proper sense to represent
M1/EI and M2/EI, the bending moment at any point is represented
by the length PQ.2 For
a uniformly distributed
load the curve of M’ is a
parabola M′ = ½wx (l − x),
where w is the load per
unit of length; and the
statically equivalent fictitious
load is 1⁄12wl³ / EI
placed at the middle point
G of the span; also the
loads statically equivalent
to the fictitious loads
M1 (l − x) / lEI and M2x / lEI
are ½M1l / EI and ½M2l / EI
placed at the points g, g′ of trisection of the span. The funicular
polygon for the fictitious loads can thus be drawn, and the
direction of the central-line at the supports is determined when the
bending moments at the supports are known.
 |
| Fig. 21. |
 |
| Fig. 22. |
 |
| Fig. 23. |
59. When there is more than one span the funiculars in question
may be drawn for each of the spans, and, if the bending moments
at the ends of the extreme spans are known, the intermediate ones
can be determined. This determination depends on two considerations:
(1) the fictitious loads corresponding to the bending moment
at any support are proportional to the lengths of the spans which
abut on that support; (2) the sides of two funiculars that end at
any support coincide in direction. Fig. 21 illustrates the method
for the case of a uniform beam on three supports A, B, C, the ends
A and C being freely supported. There will be an unknown bending
moment M0 at B, and the system3 of fictitious loads is 1⁄12wAB³/EI
at G the middle point of AB, 1⁄12wBC³ / EI at G′ the middle point of
BC, −½M0AB / EI at g and −½M0BC / EI at g′, where g and g′ are the
points of trisection nearer to B of the spans AB, BC. The centre of
gravity of the two latter is a fixed point independent of M0, and the
line VK of the figure is the vertical through this point. We draw
AD and CE to represent the loads at G and G’ in magnitude; then
D and E are fixed points. We construct any triangle UVW whose
sides UV, UW pass through D, B, and whose vertices lie on the
verticals gU, VK, g′W; the point F where VW meets DB is a fixed
point, and the lines EF, DK are the two sides (2, 4) of the required
funiculars which do not pass through A, B or C. The remaining
sides (1, 3, 5) can then be drawn, and the side 3 necessarily passes
through B; for the triangle UVW
and the triangle whose sides are
2, 3, 4 are in perspective.
The bending moment M0 is represented
in the figure by the vertical
line BH where H is on the continuation
of the side 4, the scale
being given by
this appears from the diagrams of
forces, fig. 22, in which the oblique
lines are marked to correspond to the sides of the funiculars to
which they are parallel.
In the application of the method to more complicated cases there
are two systems of fixed points corresponding to F, by means of
which the sides of the funiculars are drawn.
60. Finite Bending of Thin Rod.—The equation
curvature = bending moment ÷ flexural rigidity
may also be applied to the problem of the flexure in a principal
plane of a very thin rod or wire, for which the curvature need
not be small. When the forces that produce
the flexure are applied at the ends
only, the curve into which the central-line
is bent is one of a definite family of curves,
to which the name elastica has been given,
and there is a division of the family into two
species according as the external forces are
applied directly to the ends or are applied
to rigid arms attached to the ends; the
curves of the former species are characterized
by the presence of inflections at all the points
at which they cut the line of action of the
applied forces.
We select this case for consideration. The
problem of determining the form of the curve
(cf. fig. 23) is mathematically identical with
the problem of determining the motion of a
simple circular pendulum oscillating through a
finite angle, as is seen by comparing the differential equation of the
curve
with the equation of motion of the pendulum
The length L of the curve between two inflections corresponds to the
time of oscillation of the pendulum from rest to rest, and we thus
have
L √(W / EI) = 2K,
 |
| Fig. 24. |
where K is the real quarter period of elliptic functions of modulus
sin ½α, and α is the angle at which the curve cuts the line of action
of the applied forces. Unless
the length of the rod exceeds
π√(EI / W) it will not bend under
the force, but when the length is
great enough there may be more
than two points of inflection and
more than one bay of the curve;
for n bays (n + 1 inflections) the
length must exceed nπ √(EI / W).
Some of the forms of the curve
are shown in fig. 24.
For the form d, in which two
bays make a figure of eight, we
have
L√(W / EI) = 4.6, α = 130°
approximately. It is noteworthy
that whenever the length and force
admit of a sinuous form, such as
α or b, with more than two inflections,
there is also possible a
crossed form, like e, with two inflections only; the latter form is
stable and the former unstable.
 |
| Fig. 25. |
61. The particular case of the above for which α is very
small is a curve of sines of small amplitude, and the result
in this case has been applied to the problem of the buckling
of struts under thrust. When the strut, of length L′, is
153
maintained upright at its lower end, and loaded at its upper
end, it is simply contracted, unless L′²W > ¼π²EI, for the
lower end corresponds to a point at which the tangent is
vertical on an elastica for which the line of inflections is also
vertical, and thus the length must be half of one bay (fig. 25, a).
For greater lengths or loads
the strut tends to bend or
buckle under the load. For
a very slight excess of L′²W
above ¼π²EI, the theory on
which the above discussion
is founded, is not quite
adequate, as it assumes the
central-line of the strut to be
free from extension or contraction,
and it is probable
that bending without extension
does not take place
when the length or the force
exceeds the critical value but
slightly. It should be noted
also that the formula has no application to short struts, as the
theory from which it is derived is founded on the assumption
that the length is great compared with the diameter
(cf. § 56).
The condition of buckling, corresponding to the above, for a
long strut, of length L′, when both ends are free to turn is
L′²W > π²EI; for the central-line forms a complete bay (fig. 25,
b); if both ends are maintained in the same vertical line, the
condition is L′²W > 4π²EI, the central-line forming a complete
bay and two half bays (fig. 25, c).
62. In our consideration of flexure it has so far been supposed
that the bending takes place in a principal plane. We may remove
this restriction by resolving the forces that tend to produce
bending into systems of forces acting in the two principal planes.
To each plane there corresponds a particular flexural rigidity,
and the systems of forces in the two planes give rise to independent
systems of stress, strain and displacement, which
must be superposed in order to obtain the actual state. Applying
this process to the problem of §§ 48-54, and supposing that
one principal axis of a cross-section at its centroid makes an
angle θ with the vertical, then for any shape of section the
neutral surface or locus of unextended fibres cuts the section
in a line DD′, which is conjugate to the vertical diameter CP
with respect to any ellipse of inertia of the section. The central-line
is bent into a plane curve which is not in a vertical plane,
but is in a plane through the line CY which is perpendicular
to DD′ (fig. 26).
 |
| Fig. 26. |
63. Bending and Twisting of Thin Rods.—When a very thin
rod or wire is bent and twisted by applied forces, the forces on
any part of it limited by a normal section are balanced by the
tractions across the section, and these tractions are statically
equivalent to certain forces and couples at the centroid of the
section; we shall call them the stress-resultants and the stress-couples.
The stress-couples consist of two flexural couples in
the two principal planes, and the torsional couple about the
tangent to the central-line. The torsional couple is the product
of the torsional rigidity and the twist produced; the torsional
rigidity is exactly the same as for a straight rod of the same
material and section twisted without bending, as in Saint-Venant’s
torsion problem (§ 42). The twist τ is connected with
the deformation of the wire in this way: if we suppose a very
small ring which fits the cross-section of the wire to be provided
with a pointer in the direction of one principal axis of the section
at its centroid, and to move along the wire with velocity v, the
pointer will rotate about the central-line with angular velocity τv.
The amount of the flexural couple for either principal plane at
any section is the product of the flexural rigidity for that plane,
and the resolved part in that plane of the curvature of the central
line at the centroid of the section; the resolved part of the
curvature along the normal to any plane is obtained by treating
the curvature as a vector directed along the normal to the osculating
plane and projecting this vector. The flexural couples
reduce to a single couple in the osculating plane proportional
to the curvature when the two flexural rigidities are equal, and
in this case only.
The stress-resultants across any section are tangential forces
in the two principal planes, and a tension or thrust along the
central-line; when the stress-couples and the applied forces are
known these stress-resultants are determinate. The existence,
in particular, of the resultant tension or thrust parallel to the
central-line does not imply sensible extension or contraction of
the central filament, and the tension per unit area of the cross-section
to which it would be equivalent is small compared
with the tensions and pressures in longitudinal filaments not
passing through the centroid of the section; the moments
of the latter tensions and pressures constitute the flexural
couples.
 |
| Fig. 27. |
64. We consider, in particular, the case of a naturally straight
spring or rod of circular section, radius c, and of homogeneous
isotropic material. The torsional rigidity is ¼Eπc4 / (1 + σ);
and the flexural rigidity, which is the same for all planes through
the central-line, is ¼Eπc4; we shall denote these by C and A
respectively. The rod may be held bent by suitable forces into
a curve of double curvature with an amount of twist τ, and then
the torsional couple is Cτ, and the flexural couple in the osculating
plane is A/ρ, where ρ is the radius of circular
curvature. Among the curves in which
the rod can be held by forces and couples
applied at its ends only, one is a circular
helix; and then the applied forces and
couples are equivalent to a wrench about
the axis of the helix.
Let α be the angle and r the radius of the
helix, so that ρ is r sec²α; and let R and K be
the force and couple of the wrench (fig. 27).
Then the couple formed by R and an equal
and opposite force at any section and the
couple K are equivalent to the torsional and
flexural couples at the section, and this gives
the equations for R and K
| R = A | sin α cos³ α |
− | cos α |
, |
| r² | r |
| K = A | cos³ α |
+ Cτ sin α. |
| r |
The thrust across any section is R sin α
parallel to the tangent to the helix, and
the shearing stress-resultant is R cos α at right angles to the
osculating plane.
When the twist is such that, if the rod were simply unbent, it
154
would also be untwisted, τ is (sin α cos α) / r, and then, restoring the
values of A and C, we have
| R = | Eπc4 |
| σ |
sin α cos² α, |
| 4r² | 1 + σ |
| K = | Eπc4 |
| 1 + σ cos² α |
cos α. |
| 4r | 1 + σ |
65. The theory of spiral springs affords an application of these
results. The stress-couples called into play when a naturally helical
spring (α, r) is held in the form of a helix (α′, r′), are equal to the
differences between those called into play when a straight rod of the
same material and section is held in the first form, and those called
into play when it is held in the second form.
Thus the torsional couple is
| C ( | sin α′ cos α′ |
− | sin α cos α |
). |
| r′ | r |
and the flexural couple is
| A ( | cos² α′ |
− | cos² α |
). |
| r′ | r |
The wrench (R, K) along the axis by which the spring can be held
in the form (α′, r′) is given by the equations
| R = A | sin α′ |
( | cos² α′ |
− | cos² α |
) − C | cos α′ |
( | sin α′ cos α′ |
− | sin α cos α |
), |
| r′ | r′ |
r | r′ |
r′ | r |
| K = A cos α′ ( | cos² α′ |
− | cos² α |
) + sin α′ ( | sin α′ cos α′ |
− | sin α cos α |
). |
| r′ | r |
r′ | r |
When the spring is slightly extended by an axial force F, = −R,
and there is no couple, so that K vanishes, and α′, r′ differ very
little from α, r, it follows from these equations that the axial elongation,
δx, is connected with the axial length x and the force F by the
equation
| F = | Eπc4 |
| sin α |
| δx |
, |
| 4r² | 1 + σ cos² α |
x |
and that the loaded end is rotated about the axis of the helix through
a small angle
the sense of the rotation being such that the spring becomes more
tightly coiled.
66. A horizontal pointer attached to a vertical spiral spring
would be made to rotate by loading the spring, and the angle
through which it turns might be used to measure the load, at
any rate, when the load is not too great; but a much more
sensitive contrivance is the twisted strip devised by W.E.
Ayrton and J. Perry. A very thin, narrow rectangular strip
of metal is given a permanent twist about its longitudinal
middle line, and a pointer is attached to it at right angles to
this line. When the strip is subjected to longitudinal tension
the pointer rotates through a considerable angle. G.H. Bryan
(Phil. Mag., December 1890) has succeeded in constructing a
theory of the action of the strip, according to which it is regarded
as a strip of plating in the form of a right helicoid, which,
after extension of the middle line, becomes a portion of a slightly
different helicoid; on account of the thinness of the strip, the
change of curvature of the surface is considerable, even when
the extension is small, and the pointer turns with the generators
of the helicoid.
If b stands for the breadth and t for the thickness of the strip,
and τ for the permanent twist, the approximate formula for the
angle θ through which the strip is untwisted on the application of
a load W was found to be
| θ = | Wbτ (1 + σ) | . |
| 2Et3 ( 1 + |
(1 + σ) | |
b4τ2 |
) |
| |
30 | t² |
The quantity bτ which occurs in the formula is the total twist in a
length of the strip equal to its breadth, and this will generally be
very small; if it is small of the same order as t/b, or a higher order,
the formula becomes ½Wbτ (1+σ) / Et3, with sufficient approximation,
and this result appears to be in agreement with observations of the
behaviour of such strips.
67. Thin Plate under Pressure.—The theory of the deformation
of plates, whether plane or curved, is very intricate, partly
because of the complexity of the kinematical relations involved.
We shall here indicate the nature of the effects produced in a
thin plane plate, of isotropic material, which is slightly bent by
pressure. This theory should have an application to the stress
produced in a ship’s plates. In the problem of the cylinder
under internal pressure (§ 77 below) the most important stress
is the circumferential tension, counteracting the tendency of
the circular filaments to expand under the pressure; but in the
problem of a plane plate some of the filaments parallel to the
plane of the plate are extended and others are contracted,
so that the tensions and pressures along them give rise to resultant
couples but not always to resultant forces. Whatever
forces are applied to bend the plate, these couples are always
expressible, at least approximately in terms of the principal
curvatures produced in the surface which, before strain, was the
middle plane of the plate. The simplest case is that of a rectangular
plate, bent by a distribution of couples applied to its
edges, so that the middle surface becomes a cylinder of large
radius R; the requisite couple per unit of length of the straight
edges is of amount C/R, where C is a certain constant; and the
requisite couple per unit of length of the circular edges is of
amount Cσ/R, the latter being required to resist the tendency
to anticlastic curvature (cf. § 47). If normal sections of the
plate are supposed drawn through the generators and circular
sections of the cylinder, the action of the neighbouring portions
on any portion so bounded involves flexural couples of the
above amounts. When the plate is bent in any manner, the
curvature produced at each section of the middle surface may
be regarded as arising from the superposition of two cylindrical
curvatures; and the flexural couples across normal sections
through the lines of curvature, estimated per unit of length
of those lines, are C (1/R1 + σ/R2) and C (1/R2 + σ/R1), where
R1 and R2 are the principal radii of curvature. The value of
C for a plate of small thickness 2h is 2⁄3Eh3 / (1 − σ²). Exactly as
in the problem of the beam (§§ 48, 56), the action between
neighbouring portions of the plate generally involves shearing
stresses across normal sections as well as flexural couples; and
the resultants of these stresses are determined by the conditions
that, with the flexural couples, they balance the forces applied
to bend the plate.
 |
| Fig. 28. |
68. To express this theory analytically, let the middle plane of
the plate in the unstrained position be taken as the plane of (x, y),
and let normal sections at right angles to the axes of x and y be
drawn through any point. After strain let w be the displacement
of this point in the direction perpendicular to the plane, marked
p in fig. 28. If the axes of x and y were parallel to the lines of
curvature at the point, the flexural couple acting across the section
normal to x (or y) would have the axis of y (or x) for its axis; but
when the lines of curvature are inclined to the axes of co-ordinates,
the flexural couple across a section normal to either axis has a
component about that axis as well as a component about the perpendicular
axis. Consider an element ABCD of the section at
right angles to the axis of x, contained between two lines near
together and perpendicular to the middle plane. The action of the
portion of the plate to the right upon the portion to the left,
across the element, gives rise to a couple about the middle line
(y) of amount, estimated per unit of length of that line, equal
to C [∂²w/∂x² + σ (∂²w/∂y²)], = G1, say, and to a couple, similarly estimated,
about the normal (x) of amount −C (1 − σ) (∂²w/∂x∂y), H, say. The
155
corresponding couples on an element of a section at right angles
to the axis of y, estimated per unit of length of the axis of x, are
of amounts −C [∂²w/∂y² + σ (∂²w/∂x²)], = G2 say, and −H. The resultant
S1 of the shearing stresses on the element ABCD, estimated as
before, is given by the equation S1 = ∂G1/∂x − ∂H/∂y (cf. § 57), and the
corresponding resultant S2 for an element perpendicular to the
axis of y is given by the equation S2= −∂H/∂x − ∂G2/∂y. If the plate
is bent by a pressure p per unit of area, the equation of equilibrium
is ∂S1/∂x + ∂S2/∂y = p, or, in terms of w,
| ∂4w |
+ | ∂4w |
+ 2 | ∂4w |
= | p |
. |
| ∂x4 | ∂y4 |
∂x2∂y2 | C |
This equation, together with the special conditions at the rim,
suffices for the determination of w, and then all the quantities
here introduced are determined. Further, the most important
of the stress-components are those which act across elements of
normal sections: the tension in direction x, at a distance z from
the middle plane measured in the direction of p, is of amount
−3Cz/2h3 [∂²w/∂x² + σ (∂²w/∂y²)], and there is a corresponding tension in direction
y; the shearing stress consisting of traction parallel to y on
planes x = const., and traction parallel to x on planes y = const., is of
amount [3C(1 − σ)z/2h3] · (∂²w/∂x∂y); these tensions and shearing stresses are
equivalent to two principal tensions, in the directions of the lines of
curvature of the surface into which the middle plane is bent, and
they give rise to the flexural couples.
69. In the special example of a circular plate, of radius a, supported
at the rim, and held bent by a uniform pressure p, the value
of w at a point distant r from the axis is
| 1 |
| p |
(a² − r²) ( | 5 + σ |
a² − r² ), |
| 64 | C |
1 + σ |
and the most important of the stress components is the radial
tension, of which the amount at any point is 3⁄32(3 + σ) pz (a² − r)/h³;
the maximum radial tension is about 1⁄3(a/h)²p, and, when the thickness
is small compared with the diameter, this is a large multiple of p.
70. General Theorems.—Passing now from these questions
of flexure and torsion, we consider some results that can be
deduced from the general equations of equilibrium of an elastic
solid body.
 |
| Fig. 29. |
The form of the general expression for the potential energy
(§ 27) stored up in the strained body leads, by a general property
of quadratic functions, to a reciprocal theorem relating to the
effects produced in the body by two different systems of forces,
viz.: The whole work done by the forces of the first system,
acting over the displacements produced by the forces of the
second system, is equal to the whole work done by the forces
of the second system, acting over the displacements produced
by the forces of the first system. By a suitable choice of the
second system of forces, the average values of the component
stresses and strains produced by given forces, considered as
constituting the first system, can
be obtained, even when the distribution
of the stress and strain
cannot be determined.
Taking for example the problem
presented by an isotropic body of
any form4 pressed between two
parallel planes distant l apart (fig.
29), and denoting the resultant pressure
by p, we find that the diminution
of volume -δv is given by the
equation
−δv = lp / 3k,
where k is the modulus of compression,
equal to 1⁄3E / (1 − 2σ). Again,
take the problem of the changes
produced in a heavy body by different
ways of supporting it; when the body is suspended from
one or more points in a horizontal plane its volume is increased by
δv = Wh / 3k,
where W is the weight of the body, and h the depth of its centre
of gravity below the plane; when the body is supported by upward
vertical pressures at one or more points in a horizontal plane the
volume is diminished by
−δv = Wh′ / 3k,
where h′ is the height of the centre of gravity above the plane; if
the body is a cylinder, of length l and section A, standing with
its base on a smooth horizontal plane, its length is shortened by
an amount
−δl = Wl / 2EA;
if the same cylinder lies on the plane with its generators horizontal,
its length is increased by an amount
δl = σWh′ / EA.
71. In recent years important results have been found by
considering the effects produced in an elastic solid by forces
applied at isolated points.
Taking the case of a single force F applied at a point in the interior,
we may show that the stress at a distance r from the point consists of
(1) a radial pressure of amount
| 2 − σ |
| F |
| cos θ |
, |
| 1 − σ | 4π |
r² |
(2) tension in all directions at right angles to the radius of amount
| 1 − 2σ |
| F |
| cos θ |
, |
| 2(1 − σ) | 4π |
r² |
(3) shearing stress consisting of traction acting along the radius dr
on the surface of the cone θ = const. and traction acting along the
meridian dθ on the surface of the sphere r = const. of amount
| 1 − 2σ |
| F |
| sin θ |
, |
| 2(1 − σ) | 4π |
r² |
where θ is the angle between the radius vector r and the line of
action of F. The line marked T in fig. 30 shows the direction of
the tangential traction on the spherical surface.
 |
| Fig. 30. |
 |
| Fig. 31. |
Thus the lines of stress are in and perpendicular to the
meridian plane, and the direction
of one of those in the
meridian plane is inclined to
the radius vector r at an angle
| ½ tan−1 ( | 2 − 4σ |
tan θ ). |
| 5 − 4σ |
The corresponding displacement
at any point is compounded
of a radial displacement
of amount
| 1 + σ |
| F |
| cos θ |
| 2(1 − σ) | 4πE |
r |
and a displacement parallel to
the line of action of F of
amount
| (3 − 4σ) (1 + σ) |
| F |
| 1 |
. |
| 2(1 − σ) | 4πE |
r |
The effects of forces applied
at different points and in different directions can be obtained by
summation, and the effect of continuously distributed forces can
be obtained by integration.
72. The stress system considered in § 71 is equivalent, on the
plane through the origin at right angles to the line of action of
F, to a resultant pressure of magnitude ½F at the origin and a
[1 − 2σ/2(1 − σ)] · F/4πr², and, by the application
of this system of tractions to a solid bounded by a plane, the
displacement just described would be produced. There is also
another stress system for a solid so bounded which is equivalent,
on the same plane, to a resultant pressure at the origin, and a
radial traction proportional to
1/r², but these are in the ratio
2π : r−2, instead of being in
the ratio 4π(1 − σ) : (1 − 2σ)r−2.
The second stress system (see
fig. 31) consists of:
(1) radial pressure F′r−2,
(2) tension in the meridian
plane across the radius vector
of amount
F′r−2 cos θ / (1 + cos θ),
(3) tension across the meridian
plane of amount
F′r−2 / (l + cos θ),
(4) shearing stress as in § 71 of amount
F′r−2 sin θ / (1 + cos θ),
and the stress across the plane boundary consists of a resultant
pressure of magnitude 2πF′ and a radial traction of amount F′r−2. If
156
then we superpose the component stresses of the last section multiplied
by 4(1 − σ)W/F, and the component stresses here written down
multiplied by −(1 − 2σ)W/2πF′, the stress on the plane boundary
will reduce to a single pressure W at the origin. We shall thus
obtain the stress system at any point due to such a force applied
at one point of the boundary.
In the stress system thus arrived at the traction across any plane
parallel to the boundary is directed away from the place where W
is supported, and its amount is 3W cos²θ / 2πr². The corresponding
displacement consists of
(1) a horizontal displacement radially outwards from the vertical
through the origin of amount
| W (1 + σ) sin θ |
( cos θ − | 1 − 2σ |
), |
| 2πEr | 1 + cos θ |
(2) a vertical displacement downwards of amount
| W (1 + σ) |
{2 (1 − σ) + cos²θ }. |
| 2πEr |
The effects produced by a system of loads on a solid bounded by a
plane can be deduced.
The results for a solid body bounded by an infinite plane
may be interpreted as giving the local effects of forces applied
to a small part of the surface of a body. The results show
that pressure is transmitted into a body from the boundary
in such a way that the traction at a point on a section parallel
to the boundary is the same at all points of any sphere which
touches the boundary at the point of pressure, and that its
amount at any point is inversely proportional to the square of
the radius of this sphere, while its direction is that of a line
drawn from the point of pressure to the point at which the
traction is estimated. The transmission of force through a
solid body indicated by this result was strikingly demonstrated
in an attempt that was made to measure the lunar deflexion
of gravity; it was found that the weight of the observer on the
floor of the laboratory produced a disturbance of the instrument
sufficient to disguise completely the effect which the instrument
had been designed to measure (see G.H. Darwin, The Tides
and Kindred Phenomena in the Solar System, London, 1898).
73. There is a corresponding theory of two-dimensional
systems, that is to say, systems in which either the displacement
is parallel to a fixed plane, or there is no traction across any
plane of a system of parallel planes. This theory shows that,
when pressure is applied at a point of the edge of a plate in any
direction in the plane of the plate, the stress developed in the
plate consists exclusively of radial pressure across any circle
having the point of pressure as centre, and the magnitude of
this pressure is the same at all points of any circle which touches
the edge at the point of pressure, and its amount at any point
is inversely proportional to the radius of this circle. This result
leads to a number of interesting solutions of problems relating
to plane systems; among these may be mentioned the problem
of a circular plate strained by any forces applied at its edge.
74. The results stated in § 72 have been applied to give an
account of the nature of the actions concerned in the impact
of two solid bodies. The dissipation of energy involved in the
impact is neglected, and the resultant pressure between the
bodies at any instant during the impact is equal to the rate of
destruction of momentum of either along the normal to the
plane of contact drawn towards the interior of the other. It
has been shown that in general the bodies come into contact
over a small area bounded by an ellipse, and remain in contact
for a time which varies inversely as the fifth root of the initial
relative velocity.
For equal spheres of the same material, with σ = ¼, impinging
directly with relative velocity v, the patches that come into contact
are circles of radius
| ( | 45π |
) | 1⁄5 |
( | v |
) | 2⁄5 |
r, |
| 256 | |
V | |
where r is the radius of either, and V the velocity of longitudinal
waves in a thin bar of the material. The duration of the impact is
approximately
| (2.9432) ( | 2025π² |
) | 1⁄5 |
r |
. |
| 512 | |
v1/5V4/5 |
For two steel spheres of the size of the earth impinging with a
velocity of 1 cm. per second the duration of the impact would be
about twenty-seven hours. The fact that the duration of impact
is, for moderate velocities, a considerable multiple of the time
taken by a wave of compression to travel through either of two
impinging bodies has been ascertained experimentally, and constitutes
the reason for the adequacy of the statical theory here
described.
75. Spheres and Cylinders.—Simple results can be found for
spherical and cylindrical bodies strained by radial forces.
For a sphere of radius a, and of homogeneous isotropic material
of density ρ, strained by the mutual gravitation of its parts, the
stress at a distance r from the centre consists of
(1) uniform hydrostatic pressure of amount 1⁄10 gρa (3 − σ) / (1 − σ),
(2) radial tension of amount 1⁄10 gρ (r²/a) (3 − σ) / (1 − σ),
(3) uniform tension at right angles to the radius vector of amount
1⁄10 gρ (r²/a) (1 + 3σ) / (1 − σ),
where g is the value of gravity at the surface. The corresponding
strains consist of
(1) uniform contraction of all lines of the body of amount
1⁄30 k−1gρa (3 − σ) / (1 − σ),
(2) radial extension of amount 1⁄10 k−1gρ (r²/a) (1 + σ) / (1 − σ),
(3) extension in any direction at right angles to the radius vector
of amount
1⁄30 k−1gρ (r²/a) (1 + σ) / (1 − σ),
where k is the modulus of compression. The volume is diminished
by the fraction gρa/5k of itself. The parts of the radii vectors within
the sphere r = a {(3 − σ) / (3 + 3σ)}1/2 are contracted, and the parts
without this sphere are extended. The application of the above
results to the state of the interior of the earth involves a neglect of
the caution emphasized in § 40, viz. that the strain determined by
the solution must be small if the solution is to be accepted. In a
body of the size and mass of the earth, and having a resistance to
compression and a rigidity equal to those of steel, the radial contraction
at the centre, as given by the above solution, would be
nearly 1⁄3, and the radial extension at the surface nearly 1⁄6, and these
fractions can by no means be regarded as “small.”
76. In a spherical shell of homogeneous isotropic material, of
internal radius r1 and external radius r0, subjected to pressure p0
on the outer surface, and p1 on the inner surface, the stress at any
point distant r from the centre consists of
(1) uniform tension in all directions of amount
| p1r1³ − p0r0³ | , |
| r0³ − r1³ |
(2) radial pressure of amount
| p1 − p0 |
| r0³r1³ |
, |
| r0³ − r1³ | r³ |
(3) tension in all directions at right angles to the radius vector
of amount
| ½ | p1 − p0 |
| r0³r1³ |
. |
| r0³ − r1³ | r³ |
The corresponding strains consist of
(1) uniform extension of all lines of the body of amount
| 1 |
| p1r1³ − p0r0³ |
, |
| 3k | r0³ − r1³ |
(2) radial contraction of amount
| 1 |
| p1 − p0 |
| r0³r1³ |
, |
| 2μ | r0³ − r1³ |
r³ |
(3) extension in all directions at right angles to the radius vector
of amount
| 1 |
| p1 − p0 |
| r0³r1³ |
, |
| 4μ | r0³ − r1³ |
r³ |
where μ is the modulus of rigidity of the material, = ½E / (1 + σ).
The volume included between the two surfaces of the body is increased
by the fraction (p1r1³ − p0r0³) / k(r0³ − r1³) of itself, and the volume within
the inner surface is increased by the fraction
| 3 (p1 − p0) |
| r0³ |
+ | p1r1³ − p0r0³ |
| 4μ | r0³ − r1³ |
k (r0³ − r1³) |
of itself. For a shell subject only to internal pressure p the greatest
extension is the extension at right angles to the radius at the inner
surface, and its amount is
| pr1³ |
( | 1 |
+ | 1 |
| r0³ |
); |
| r0³ − r1³ | 3k |
4μ | r1³ |
the greatest tension is the transverse tension at the inner surface,
and its amount is p (½ r0³ + r1³) / (r0³ − r1³).
77. In the problem of a cylindrical shell under pressure a complication
may arise from the effects of the ends; but when the
ends are free from stress the solution is very simple. With notation
similar to that in § 76 it can be shown that the stress at a distance r
from the axis consists of
(1) uniform tension in all directions at right angles to the axis
of amount
| p1r1² − p0r0² | , |
| r0² − r1² |
(2) radial pressure of amount
| p1 − p0 |
| r0²r1² |
, |
| r0² − r1² | r² |
(3) hoop tension numerically equal to this radial pressure.
157
The corresponding strains consist of
(1) uniform extension of all lines of the material at right angles
to the axis of amount
| 1 − σ |
| p1r1² − p0r0² |
, |
| E | r0² − r1² |
(2) radial contraction of amount
| 1 + σ |
| p1 − p0 |
| r0²r1² |
, |
| E | r0² − r1² |
r² |
(3) extension along the circular filaments numerically equal to
this radial contraction,
(4) uniform contraction of the longitudinal filaments of amount
| 2σ |
| p1r1² − p0r0² |
. |
| E | r0² − r1² |
For a shell subject only to internal pressure p the greatest extension
is the circumferential extension at the inner surface, and its amount is
| p |
( | r0² + r1² |
+ σ ); |
| E | r0² − r1² |
the greatest tension is the hoop tension at the inner surface, and
its amount is p (r0² + r1²) / (r0² − r1²).
78. When the ends of the tube, instead of being free, are closed by
disks, so that the tube becomes a closed cylindrical vessel, the
longitudinal extension is determined by the condition that the
resultant longitudinal tension in the walls balances the resultant
normal pressure on either end. This condition gives the value of the
extension of the longitudinal filaments as
(p1r1² − p0r0²) / 3k (r0² − r1²),
where k is the modulus of compression of the material. The result
may be applied to the experimental determination of k, by measuring
the increase of length of a tube subjected to internal pressure
(A. Mallock, Proc. R. Soc. London, lxxiv., 1904, and C. Chree, ibid.).
79. The results obtained in § 77 have been applied to gun
construction; we may consider that one cylinder is heated
so as to slip over another upon which it shrinks by cooling,
so that the two form a single body in a condition of initial stress.
We take P as the measure of the pressure between the two, and
p for the pressure within the inner cylinder by which the system
is afterwards strained, and denote by r′ the radius of the common
surface. To obtain the stress at any point we superpose the
system consisting of radial pressure p (r1²/r²) · (r0² − r²) / (r0² − r1²) and hoop tension
p (r1²/r²) · (r0² + r²) / (r0² − r1²) upon a system which, for the outer cylinder, consists
of radial pressure P (r′²/r²) · (r0² − r²) / (r0² − r′²)
and hoop tension P (r′²/r²) · (r0² + r²) / (r0² − r′²), and
for the inner cylinder consists of radial pressure
P (r′²/r²) · (r² − r1²) / (r′² − r1²) and
hoop tension P (r′²/r²) · (r² + r1²) / (r′² − r1²). The hoop tension at the inner surface
is less than it would be for a tube of equal thickness without initial
stress in the ratio
| 1 − | P |
| 2r′² |
| r0² + r1² |
: 1. |
| p | r0² + r1² |
r′² − r1² |
This shows how the strength of the tube is increased by the initial
stress. When the initial stress is produced by tightly wound wire,
a similar gain of strength accrues.
80. In the problem of determining the distribution of stress
and strain in a circular cylinder, rotating about its axis, simple
solutions have been obtained which are sufficiently exact for
the two special cases of a thin disk and a long shaft.
Suppose that a circular disk of radius a and thickness 2l, and of
density ρ, rotates about its axis with angular velocity ω, and consider
the following systems of superposed stresses at any point distant r
from the axis and z from the middle plane:
(1) uniform tension in all directions at right angles to the axis
of amount 1⁄8 ω²ρa² (3 + σ),
(2) radial pressure of amount 1⁄8 ω²ρr² (3 + σ),
(3) pressure along the circular filaments of amount 1⁄8 ω²ρr² (1 + 3σ),
(4) uniform tension in all directions at right angles to the axis
of amount 1⁄6 ω²ρ (l² − 3z²) σ (1 + σ) / (1 − σ).
The corresponding strains may be expressed as
(1) uniform extension of all filaments at right angles to the axis
of amount
| 1 − σ | 1⁄8 ω²ρa² (3 + σ), |
| E |
(2) radial contraction of amount
(3) contraction along the circular filaments of amount
(4) extension of all filaments at right angles to the axis of amount
| 1 | 1⁄6 ω²ρ (l² − 3z²) σ (1 + σ), |
| E |
(5) contraction of the filaments normal to the plane of the disk
of amount
| 2σ |
1⁄8 ω²ρa² (3 + σ) − | σ |
1⁄2 ω²ρr² (1 + σ) + | 2σ |
1⁄6 ω²ρ (l² − 3z²) σ | (1 + σ) |
. |
| E | E |
E | (1 − σ) |
The greatest extension is the circumferential extension near the
centre, and its amount is
| (3 + σ) (1 − σ) |
ω²ρa² + | σ (1 + σ) |
ω²ρl². |
| 8E | 6E |
 |
| Fig. 32. |
The longitudinal contraction is required to make the plane faces
of the disk free from pressure, and the terms in l and z enable
us to avoid tangential traction on any cylindrical surface. The
system of stresses and strains thus expressed satisfies all the conditions,
except that there is a small
radial tension on the bounding
surface of amount per unit area
1⁄6 ω²ρ (l² − 3z²) σ (1 + σ) / (1 − σ). The resultant
of these tensions on any
part of the edge of the disk
vanishes, and the stress in question
is very small in comparison with
the other stresses involved when
the disk is thin; we may conclude
that, for a thin disk, the expressions
given represent the actual
condition at all points which are
not very close to the edge (cf. § 55).
The effect to the longitudinal contraction
is that the plane faces
become slightly concave (fig. 32).
81. The corresponding solution
for a disk with a circular axle-hole
(radius b) will be obtained from that given in the last section by
superposing the following system of additional stresses:
(1) radial tension of amount 1⁄8 ω²ρb² (1 − a²/r²) (3 + σ),
(2) tension along the circular filaments of amount
1⁄8 ω²ρb² (1 + a²/r²) (3 + σ).
The corresponding additional strains are
(1) radial contraction of amount
| 3 + σ |
{ (1 + σ) | a² |
− (1 − σ) } ω²ρb², |
| 8E | r² |
(2) extension along the circular filaments of amount
| 3 + σ |
{ (1 + σ) | a² |
+ (1 − σ) } ω²ρb². |
| 8E | r² |
(3) contraction of the filaments parallel to the axis of amount
Again, the greatest extension is the circumferential extension at
the inner surface, and, when the hole is very small, its amount is
nearly double what it would be for a complete disk.
82. In the problem of the rotating shaft we have the following
stress-system:
(1) radial tension of amount 1⁄8 ω²ρ (a² − r²) (3 − 2σ) / (1 − σ),
(2) circumferential tension of amount
1⁄8 ω²ρ {a² (3 − 2σ) / (1 − σ) − r² (1 + 2σ) / (1 − σ)},
(3) longitudinal tension of amount ¼ ω²ρ (a² − 2r²) σ / (1 − σ).
The resultant longitudinal tension at any normal section vanishes,
and the radial tension vanishes at the bounding surface; and
thus the expressions here given may be taken to represent the
actual condition at all points which are not very close to the ends
of the shaft. The contraction of the longitudinal filaments is
uniform and equal to ½ ω²ρa²σ / E. The greatest extension in the
rotating shaft is the circumferential extension close to the axis,
and its amount is 1⁄8 ω²ρa² (3 − 5σ) / E (1 − σ).
The value of any theory of the strength of long rotating shafts
founded on these formulae is diminished by the circumstance that
at sufficiently high speeds the shaft may tend to take up a curved
form, the straight form being unstable. The shaft is then said to
whirl. This occurs when the period of rotation of the shaft is very
nearly coincident with one of its periods of lateral vibration. The
lowest speed at which whirling can take place in a shaft of length l,
freely supported at its ends, is given by the formula
ω²ρ = ¼ Ea² (π/l)4.
As in § 61, this formula should not be applied unless the length of
the shaft is a considerable multiple of its diameter. It implies that
whirling is to be expected whenever ω approaches this critical value.
83. When the forces acting upon a spherical or cylindrical body
are not radial, the problem becomes more complicated. In the
case of the sphere deformed by any forces it has been completely
solved, and the solution has been applied by Lord Kelvin and
158
Sir G.H. Darwin to many interesting questions of cosmical
physics. The nature of the stress produced in the interior of
the earth by the weight of continents and mountains, the spheroidal
figure of a rotating solid planet, the rigidity of the earth,
are among the questions which have in this way been attacked.
Darwin concluded from his investigation that, to support the
weight of the existing continents and mountain ranges, the
materials of which the earth is composed must, at great depths
(1600 kilometres), have at least the strength of granite. Kelvin
concluded from his investigation that the actual heights of the
tides in the existing oceans can be accounted for only on the
supposition that the interior of the earth is solid, and of rigidity
nearly as great as, if not greater than, that of steel.
84. Some interesting problems relating to the strains produced in a
cylinder of finite length by forces distributed symmetrically round
the axis have been solved. The most important is that of a cylinder
crushed between parallel planes in contact with its plane ends.
The solution was applied to explain the discrepancies that have been
observed in different tests of crushing strength according as the
ends of the test specimen are or are not prevented from spreading.
It was applied also to explain the fact that in such tests small conical
pieces are sometimes cut out at the ends subjected to pressure.
85. Vibrations and Waves.—When a solid body is struck, or
otherwise suddenly disturbed, it is thrown into a state of vibration.
There always exist dissipative forces which tend to
destroy the vibratory motion, one cause of the subsidence of the
motion being the communication of energy to surrounding
bodies. When these dissipative forces are disregarded, it is
found that an elastic solid body is capable of vibrating in such
a way that the motion of any particle is simple harmonic motion,
all the particles completing their oscillations in the same period
and being at any instant in the same phase, and the displacement
of any selected one in any particular direction bearing a definite
ratio to the displacement of an assigned one in an assigned
direction. When a body is moving in this way it is said to be
vibrating in a normal mode. For example, when a tightly
stretched string of negligible flexural rigidity, such as a violin
string may be taken to be, is fixed at the ends, and vibrates
transversely in a normal mode, the displacements of all the
particles have the same direction, and their magnitudes are
proportional at any instant to the ordinates of a curve of sines.
Every body possesses an infinite number of normal modes of
vibration, and the frequencies (or numbers of vibrations per
second) that belong to the different modes form a sequence
of increasing numbers. For the string, above referred to, the
fundamental tone and the various overtones form an harmonic
scale, that is to say, the frequencies of the normal modes of
vibration are proportional to the integers 1, 2, 3, .... In all
these modes except the first the string vibrates as if it were
divided into a number of equal pieces, each having fixed ends;
this number is in each case the integer defining the frequency.
In general the normal modes of vibration of a body are distinguished
one from another by the number and situation of the
surfaces (or other loci) at which some characteristic displacement
or traction vanishes. The problem of determining the normal
modes and frequencies of free vibration of a body of definite
size, shape and constitution, is a mathematical problem of a
similar character to the problem of determining the state of
stress in the body when subjected to given forces. The bodies
which have been most studied are strings and thin bars, membranes,
thin plates and shells, including bells, spheres and
cylinders. Most of the results are of special importance in their
bearing upon the theory of sound.
86. The most complete success has attended the efforts of mathematicians
to solve the problem of free vibrations for an isotropic
sphere. It appears that the modes of vibration fall into two classes:
one characterized by the absence of a radial component of displacement,
and the other by the absence of a radial component of rotation
(§ 14). In each class there is a doubly infinite number of modes.
The displacement in any mode is determined in terms of a single
spherical harmonic function, so that there are modes of each class
corresponding to spherical harmonics of every integral degree;
and for each degree there is an infinite number of modes, differing
from one another in the number and position of the concentric
spherical surfaces at which some characteristic displacement vanishes.
The most interesting modes are those in which the sphere becomes
slightly spheroidal, being alternately prolate and oblate during the
course of a vibration; for these vibrations tend to be set up in a
spherical planet by tide-generating forces. In a sphere of the size
of the earth, supposed to be incompressible and as rigid as steel,
the period of these vibrations is 66 minutes.
87. The theory of free vibrations has an important bearing
upon the question of the strength of structures subjected to
sudden blows or shocks. The stress and strain developed in a
body by sudden applications of force may exceed considerably
those which would be produced by a gradual application of the
same forces. Hence there arises the general question of dynamical
resistance, or of the resistance of a body to forces applied
so quickly that the inertia of the body comes sensibly into play.
In regard to this question we have two chief theoretical results.
The first is that the strain produced by a force suddenly applied
may be as much as twice the statical strain, that is to say, as the
strain which would be produced by the same force when the
body is held in equilibrium under its action; the second is that
the sudden reversal of the force may produce a strain three
times as great as the statical strain. These results point to the
importance of specially strengthening the parts of any machine
(e.g. screw propeller shafts) which are subject to sudden applications
or reversals of load. The theoretical limits of twice, or
three times, the statical strain are not in general attained. For
example, if a thin bar hanging vertically from its upper end is
suddenly loaded at its lower end with a weight equal to its own
weight, the greatest dynamical strain bears to the greatest
statical strain the ratio 1.63 : 1; when the attached weight is
four times the weight of the bar the ratio becomes 1.84 : 1. The
method by which the result just mentioned is reached has
recently been applied to the question of the breaking of winding
ropes used in mines. It appeared that, in order to bring the
results into harmony with the observed facts, the strain in the
supports must be taken into account as well as the strain in the
rope (J. Perry, Phil. Mag., 1906 (vi.), vol. ii.).
88. The immediate effect of a blow or shock, locally applied
to a body, is the generation of a wave which travels through
the body from the locality first affected. The question of the
propagation of waves through an elastic solid body is historically
of very great importance; for the first really successful efforts
to construct a theory of elasticity (those of S.D. Poisson, A.L.
Cauchy and G. Green) were prompted, at least in part, by
Fresnel’s theory of the propagation of light by transverse
vibrations. For many years the luminiferous medium was
identified with the isotropic solid of the theory of elasticity.
Poisson showed that a disturbance communicated to the body
gives rise to two waves which are propagated through it with
different velocities; and Sir G.G. Stokes afterwards showed
that the quicker wave is a wave of irrotational dilatation, and
the slower wave is a wave of rotational distortion accompanied
by no change of volume. The velocities of the two waves in a
solid of density ρ are √ {(λ + 2μ)/ρ} and √ (μ/ρ), λ and μ being
the constants so denoted in § 26. When the surface of the body
is free from traction, the waves on reaching the surface are
reflected; and thus after a little time the body would, if there
were no dissipative forces, be in a very complex state of motion
due to multitudes of waves passing to and fro through it. This
state can be expressed as a state of vibration, in which the motions
belonging to the various normal modes (§ 85) are superposed,
each with an appropriate amplitude and phase. The waves of
dilatation and distortion do not, however, give rise to different
modes of vibration, as was at one time supposed, but any mode
of vibration in general involves both dilatation and rotation.
There are exceptional results for solids of revolution; such
solids possess normal modes of vibration which involve no
dilatation. The existence of a boundary to the solid body
has another effect, besides reflexion, upon the propagation of
waves. Lord Rayleigh has shown that any disturbance originating
at the surface gives rise to waves which travel away over
the surface as well as to waves which travel through the interior;
and any internal disturbance, on reaching the surface, also
gives rise to such superficial waves. The velocity of the superficial
waves is a little less than that of the waves of distortion:
159
0.9554 √ (μ/ρ) when the material is incompressible 0.9194 √ (μ/ρ)
when the Poisson’s ratio belonging to the material is ¼.
89. These results have an application to the propagation of
earthquake shocks (see also Earthquake). An internal disturbance
should, if the earth can be regarded as solid, give rise
to three wave-motions: two propagated through the interior
of the earth with different velocities, and a third propagated
over the surface. The results of seismographic observations
have independently led to the recognition of three phases of
the recorded vibrations: a set of “preliminary tremors”
which are received at different stations at such times as to show
that they are transmitted directly through the interior of the
earth with a velocity of about 10 km. per second, a second
set of preliminary tremors which are received at different
stations at such times as to show that they are transmitted
directly through the earth with a velocity of about 5 km. per
second, and a “main shock,” or set of large vibrations, which
becomes sensible at different stations at such times as to show
that a wave is transmitted over the surface of the earth with
a velocity of about 3 km. per second. These results can be
interpreted if we assume that the earth is a solid body the
greater part of which is practically homogeneous, with high
values for the rigidity and the resistance to compression, while
the superficial portions have lower values for these quantities.
The rigidity of the central portion would be about (1.4)1012
dynes per square cm., which is considerably greater than that
of steel, and the resistance to compression would be about
(3.8)1012 dynes per square cm. which is much greater than that
of any known material. The high value of the resistance to
compression is not surprising when account is taken of the great
pressures, due to gravitation, which must exist in the interior
of the earth. The high value of the rigidity can be regarded as
a confirmation of Lord Kelvin’s estimate founded on tidal
observations (§ 83).
90. Strain produced by Heat.—The mathematical theory
of elasticity as at present developed takes no account of the
strain which is produced in a body by unequal heating. It
appears to be impossible in the present state of knowledge
to form as in § 39 a system of differential equations to determine
both the stress and the temperature at any point of a solid body
the temperature of which is liable to variation. In the cases
of isothermal and adiabatic changes, that is to say, when the
body is slowly strained without variation of temperature, and
also when the changes are effected so rapidly that there is no
gain or loss of heat by any element, the internal energy of the
body is sufficiently expressed by the strain-energy-function
(§§ 27, 30). Thus states of equilibrium and of rapid vibration
can be determined by the theory that has been explained above.
In regard to thermal effects we can obtain some indications
from general thermodynamic theory. The following passages
extracted from the article “Elasticity” contributed to the 9th
edition of the Encyclopaedia Britannica by Sir W. Thomson
(Lord Kelvin) illustrate the nature of these indications:—“From
thermodynamic theory it is concluded that cold is produced
whenever a solid is strained by opposing, and heat when
it is strained by yielding to, any elastic force of its own, the
strength of which would diminish if the temperature were raised;
but that, on the contrary, heat is produced when a solid is
strained against, and cold when it is strained by yielding to, any
elastic force of its own, the strength of which would increase
if the temperature were raised. When the strain is a condensation
or dilatation, uniform in all directions, a fluid may be
included in the statement. Hence the following propositions:—
“(1) A cubical compression of any elastic fluid or solid in an
ordinary condition causes an evolution of heat; but, on the
contrary, a cubical compression produces cold in any substance,
solid or fluid, in such an abnormal state that it would contract
if heated while kept under constant pressure. Water below its
temperature (3.9° Cent.) of maximum density is a familiar instance.
“(2) If a wire already twisted be suddenly twisted further,
always, however, within its limits of elasticity, cold will be
produced; and if it be allowed suddenly to untwist, heat will
be evolved from itself (besides heat generated externally by any
work allowed to be wasted, which it does in untwisting). It is
assumed that the torsional rigidity of the wire is diminished
by an elevation of temperature, as the writer of this article
had found it to be for copper, iron, platinum and other metals.
“(3) A spiral spring suddenly drawn out will become lower
in temperature, and will rise in temperature when suddenly
allowed to draw in. [This result has been experimentally
verified by Joule (’Thermodynamic Properties of Solids,’
Phil. Trans., 1858) and the amount of the effect found to agree
with that calculated, according to the preceding thermodynamic
theory, from the amount of the weakening of the spring which
he found by experiment.]
“(4) A bar or rod or wire of any substance with or without
a weight hung on it, or experiencing any degree of end thrust,
to begin with, becomes cooled if suddenly elongated by end pull
or by diminution of end thrust, and warmed if suddenly shortened
by end thrust or by diminution of end pull; except abnormal
cases in which with constant end pull or end thrust elevation
of temperature produces shortening; in every such case pull
or diminished thrust produces elevation of temperature, thrust
or diminished pull lowering of temperature.
“(5) An india-rubber band suddenly drawn out (within its
limits of elasticity) becomes warmer; and when allowed to
contract, it becomes colder. Any one may easily verify this
curious property by placing an india-rubber band in slight
contact with the edges of the lips, then suddenly extending it—it
becomes very perceptibly warmer: hold it for some time
stretched nearly to breaking, and then suddenly allow it to
shrink—it becomes quite startlingly colder, the cooling effect
being sensible not merely to the lips but to the fingers holding
the band. The first published statement of this curious observation
is due to J. Gough (Mem. Lit. Phil. Soc. Manchester, 2nd
series, vol. i. p. 288), quoted by Joule in his paper on ‘Thermodynamic
Properties of Solids’ (cited above). The thermodynamic
conclusion from it is that an india-rubber band, stretched
by a constant weight of sufficient amount hung on it, must,
when heated, pull up the weight, and, when cooled, allow the
weight to descend: this Gough, independently of thermodynamic
theory, had found to be actually the case. The experiment
any one can make with the greatest ease by hanging
a few pounds weight on a common india-rubber band, and
taking a red-hot coal in a pair of tongs, or a red-hot poker, and
moving it up and down close to the band. The way in which
the weight rises when the red-hot body is near, and falls when
it is removed, is quite startling. Joule experimented on the
amount of shrinking per degree of elevation of temperature,
with different weights hung on a band of vulcanized india-rubber,
and found that they closely agreed with the amounts calculated
by Thomson’s theory from the heating effects of pull, and cooling
effects of ceasing to pull, which he had observed in the same
piece of india-rubber.”
91. Initial Stress.—It has been pointed out above (§ 20)
that the “unstressed” state, which serves as a zero of reckoning
for strains and stresses is never actually attained, although
the strain (measured from this state), which exists in a body
to be subjected to experiment, may be very slight. This is the
case when the “initial stress,” or the stress existing before the
experiment, is small in comparison with the stress developed
during the experiment, and the limit of linear elasticity (§ 32)
is not exceeded. The existence of initial stress has been correlated
above with the existence of body forces such as the force
of gravity, but it is not necessarily dependent upon such forces.
A sheet of metal rolled into a cylinder, and soldered to maintain
the tubular shape, must be in a state of considerable initial
stress quite apart from the action of gravity. Initial stress is
utilized in many manufacturing processes, as, for example, in
the construction of ordnance, referred to in § 79, in the winding
of golf balls by means of india-rubber in a state of high tension
(see the report of the case The Haskell Golf Ball Company v.
Hutchinson & Main in The Times of March 1, 1906). In the
case of a body of ordinary dimensions it is such internal stress
160
as this which is especially meant by the phrase “initial stress.”
Such a body, when in such a state of internal stress, is sometimes
described as “self-strained.” It would be better described as
“self-stressed.” The somewhat anomalous behaviour of cast
iron has been supposed to be due to the existence within the
metal of initial stress. As the metal cools, the outer layers cool
more rapidly than the inner, and thus the state of initial stress
is produced. When cast iron is tested for tensile strength, it
shows at first no sensible range either of perfect elasticity or of
linear elasticity; but after it has been loaded and unloaded
several times its behaviour begins to be more nearly like that
of wrought iron or steel. The first tests probably diminish the
initial stress.
92. From a mathematical point of view the existence of initial
stress in a body which is “self-stressed” arises from the fact that
the equations of equilibrium of a body free from body forces or surface
tractions, viz. the equations of the type
| ∂Xx |
+ | ∂Xy |
+ | ∂Zx |
= 0, |
| ∂x | ∂y | ∂z |
possess solutions which differ from zero. If, in fact, φ1, φ2, φ3 denote
any arbitrary functions of x, y, z, the equations are satisfied by
putting
| Xx = | ∂²φ3 |
+ | ∂²φ2 |
, ..., Yz = − | ∂²φ1 |
, ... ; |
| ∂y² | ∂z |
∂y∂z |
and it is clear that the functions φ1, φ2, φ3 can be adjusted in an
infinite number of ways so that the bounding surface of the body
may be free from traction.
93. Initial stress due to body forces becomes most important
in the case of a gravitating planet. Within the earth the stress
that arises from the mutual gravitation of the parts is very great.
If we assumed the earth to be an elastic solid body with moduluses
of elasticity no greater than those of steel, the strain (measured
from the unstressed state) which would correspond to the stress
would be much too great to be calculated by the ordinary methods
of the theory of elasticity (§ 75). We require therefore some
other method of taking account of the initial stress. In many
investigations, for example those of Lord Kelvin and Sir G.H.
Darwin referred to in § 83, the difficulty is turned by assuming
that the material may be treated as practically incompressible;
but such investigations are to some extent incomplete, so long
as the corrections due to a finite, even though high, resistance to
compression remain unknown. In other investigations, such as
those relating to the propagation of earthquake shocks and to
gravitational instability, the possibility of compression is an
essential element of the problem. By gravitational instability
is meant the tendency of gravitating matter to condense into
nuclei when slightly disturbed from a state of uniform diffusion;
this tendency has been shown by J.H. Jeans (Phil. Trans.
A. 201, 1903) to have exerted an important influence upon the
course of evolution of the solar system. For the treatment of
such questions Lord Rayleigh (Proc. R. Soc. London, A. 77,
1906) has advocated a method which amounts to assuming that
the initial stress is hydrostatic pressure, and that the actual
state of stress is to be obtained by superposing upon this initial
stress a stress related to the state of strain (measured from the
initial state) by the same formulae as hold for an elastic solid
body free from initial stress. The development of this method
is likely to lead to results of great interest.
Authorities.—In regard to the analysis requisite to prove the
results set forth above, reference may be made to A.E.H. Love,
Treatise on the Mathematical Theory of Elasticity (2nd ed., Cambridge,
1906), where citations of the original authorities will also be found.
The following treatises may be mentioned: Navier, Résumé des
leçons sur l’application de la mécanique (3rd ed., with notes by Saint-Venant,
Paris, 1864); G. Lamé, Leçons sur la théorie mathématique
de l’élasticité des corps solides (Paris, 1852); A. Clebsch, Theorie der
Elasticität fester Körper (Leipzig, 1862; French translation with
notes by Saint-Venant, Paris, 1883); F. Neumann, Vorlesungen
über die Theorie der Elasticität (Leipzig, 1885); Thomson and Tait,
Natural Philosophy (Cambridge, 1879, 1883); Todhunter and
Pearson, History of the Elasticity and Strength of Materials (Cambridge,
1886-1893). The article “Elasticity” by Sir W. Thomson (Lord
Kelvin) in 9th ed. of Encyc. Brit. (reprinted in his Mathematical
and Physical Papers, iii., Cambridge, 1890) is especially valuable,
not only for the exposition of the theory and its practical
applications, but also for the tables of physical constants which
are there given.
(A. E. H. L.)
1 The sign of M is shown by the arrow-heads in fig. 19, for which,
with y downwards,
2 The figure is drawn for a case where the bending moment has the
same sign throughout.
3 M0 is taken to have, as it obviously has, the opposite sense to that
shown in fig. 19.
4 The line joining the points of contact must be normal to the
planes.
ELATERITE, also termed Elastic Bitumen and Mineral
Caoutchouc, a mineral hydrocarbon, which occurs at Castleton
in Derbyshire, in the lead mines of Odin and elsewhere. It
varies somewhat in consistency, being sometimes soft, elastic
and sticky; often closely resembling india-rubber; and occasionally
hard and brittle. It is usually dark brown in colour and
slightly translucent. A substance of similar physical character
is found in the Coorong district of South Australia, and is hence
termed coorongite, but Prof. Ralph Tate considers this to be a
vegetable product.
ELATERIUM, a drug consisting of a sediment deposited
by the juice of the fruit of Ecballium Elaterium, the squirting
cucumber, a native of the Mediterranean region. The plant,
which is a member of the natural order Cucurbitaceae, resembles
the vegetable marrow in its growth. The fruit resembles a
small cucumber, and when ripe is highly turgid, and separates
almost at a touch from the fruit stalk. The end of the stalk
forms a stopper, on the removal of which the fluid contents of
the fruit, together with the seeds, are squirted through the
aperture by the sudden contraction of the wall of the fruit.
To prepare the drug the fruit is sliced lengthwise and slightly
pressed; the greenish and slightly turbid juice thus obtained
is strained and set aside; and the deposit of elaterium formed
after a few hours is collected on a linen filter, rapidly drained,
and dried on porous tiles at a gentle heat. Elaterium is met
with in commerce in light, thin, friable, flat or slightly incurved
opaque cakes, of a greyish-green colour, bitter taste and tea-like
smell.
The drug is soluble in alcohol, but insoluble in water and ether.
The official dose is 1⁄10-1⁄2 grain, and the British pharmacopeia
directs that the drug is to contain from 20 to 25% of the active
principle elaterinum or elaterin. A resin in the natural product
aids its action. Elaterin is extracted from elaterium by chloroform
and then precipitated by ether. It has the formula
C20H28O5. It forms colourless scales which have a bitter taste,
but it is highly inadvisable to taste either this substance or
elaterium. Its dose is 1⁄40-1⁄10 grain, and the British pharmacopeia
contains a useful preparation, the Pulvis Elaterini Compositus,
which contains one part of the active principle in forty.
The action of this drug resembles that of the saline aperients,
but is much more powerful. It is the most active hydragogue
purgative known, causing also much depression and violent
griping. When injected subcutaneously it is inert, as its action
is entirely dependent upon its admixture with the bile. The
drug is undoubtedly valuable in cases of dropsy and Bright’s
disease, and also in cases of cerebral haemorrhage, threatened or
present. It must not be used except in urgent cases, and must
invariably be employed with the utmost care, especially if the
state of the heart be unsatisfactory.
ELBA (Gr. Αἰθαλία; Lat. Ilva), an island off the W. coast
of Italy, belonging to the province of Leghorn, from which
it is 45 m. S., and 7 m. S.W. of Piombino, the nearest point of
the mainland. Pop. (1901) 25,043 (including Pianosa). It is
about 19 m. long, 6½ m. broad, and 140 sq. m. in area; and its
highest point is 3340 ft. (Monte Capanne). It forms, like Giglio
and Monte Cristo, part of a sunken mountain range extending
towards Corsica and Sardinia.
The oldest rocks of Elba consist of schist and serpentine which
in the eastern part of the island are overlaid by beds containing
Silurian and Devonian fossils. The Permian may be represented,
but the Trias is absent, and in general the older Palaeozoic rocks
are overlaid directly by the Rhaetic and Lias. The Liassic beds
are often metamorphosed and the limestones contain garnet
and wollastonite. The next geological formation which is
represented is the Eocene, consisting of nummulitic limestone,
sandstone and schist. The Miocene and Pliocene are absent.
The most remarkable feature in the geology of Elba is the extent
of the granitic and ophiolitic eruptions of the Tertiary period.
Serpentines, peridotites and diabases are interstratified with the
Eocene deposits. The granite, which is intruded through the
Eocene beds, is associated with a pegmatite containing tourmaline
and cassiterite. The celebrated iron ore of Elba is of
161
Tertiary age and occurs indifferently in all the older rocks. The
deposits are superficial, resulting from the opening out of veins
at the surface, and consist chiefly of haematite. These ores were
worked by the ancients, but so inefficiently that their spoil-heaps
can be smelted again with profit. This process is now
gone through on the island itself. The granite was also quarried
by the Romans, but is not now much worked.
Parts of the island are fertile, and the cultivation of vines,
and the tunny and sardine fishery, also give employment to a part
of the population. The capital of the island is Portoferraio—pop.
(1901) 5987—in the centre of the N. coast, enclosed by an
amphitheatre of lofty mountains, the slopes of which are covered
with villas and gardens. This is the best harbour, the ancient
Portus Argous. The town was built and fortified by Cosimo I.
in 1548, who called it Cosmopolis. Above the harbour, between
the forts Stella and Falcone, is the palace of Napoleon I., and
4 m. to the S.W. is his villa; while on the N. slope of Monte
Capanne is another of his country houses. The other villages
in the island are Campo nell’ Elba, on the S. near the W. end,
Marciana and Marciana Marina on the N. of the island near the
W. extremity, Porto Longone, on the E. coast, with picturesque
Spanish fortifications, constructed in 1602 by Philip III.; Rio
dell’ Elba and Rio Marina, both on the E. side of the island, in
the mining district. At Le Grotte, between Portoferraio and Rio
dell’ Elba, and at Capo Castello, on the N.E. of the island, are
ruins of Roman date.
Elba was famous for its mines in early times, and the smelting
furnaces gave it its Greek name of Α᾽ θαλία (“soot island”).
In Roman times, and until 1900, however, owing to lack of fuel,
the smelting was done on the mainland. In 453 B.C. Elba was
devastated by a Syracusan squadron. From the 11th to the
14th century it belonged to Pisa, and in 1399 came under the
dukes of Piombino. In 1548 it was ceded by them to Cosimo I.
of Florence. In 1596 Porto Longone was taken by Philip III.
of Spain, and retained until 1709, when it was ceded to Naples.
In 1802 the island was given to France by the peace of Amiens.
On Napoleon’s deposition, the island was ceded to him with full
sovereign rights, and he resided there from the 5th of May 1814
to the 26th of February 1815. After his fall it was restored
to Tuscany, and passed with it to Italy in 1860.
See Sir R. Colt Hoare, A Tour through the Island of Elba (London,
1814).
ELBE (the Albis of the Romans and the Labe of the Czechs),
a river of Germany, which rises in Bohemia not far from the
frontiers of Silesia, on the southern side of the Riesengebirge,
at an altitude of about 4600 ft. Of the numerous small streams
(Seifen or Flessen as they are named in the district) whose confluent
waters compose the infant river, the most important are
the Weisswasser, or White Water, and the Elbseifen, which is
formed in the same neighbourhood, but at a little lower elevation.
After plunging down the 140 ft. of the Elbfall, the latter stream
unites with the steep torrential Weisswasser at Mädelstegbaude,
at an altitude of 2230 ft., and thereafter the united stream of
the Elbe pursues a southerly course, emerging from the mountain
glens at Hohenelbe (1495 ft.), and continuing on at a soberer pace
to Pardubitz, where it turns sharply to the west, and at Kolin
(730 ft.), some 27 m. farther on, bends gradually towards the
north-west. A little above Brandeis it picks up the Iser, which,
like itself, comes down from the Riesengebirge, and at Melnik
it has its stream more than doubled in volume by the Moldau,
a river which winds northwards through the heart of Bohemia
in a sinuous, trough-like channel carved through the plateaux.
Some miles lower down, at Leitmeritz (433 ft.), the waters of
the Elbe are tinted by the reddish Eger, a stream which drains
the southern slopes of the Erzgebirge. Thus augmented, and
swollen into a stream 140 yds. wide, the Elbe carves a path
through the basaltic mass of the Mittelgebirge, churning its
way through a deep, narrow rocky gorge. Then the river winds
through the fantastically sculptured sandstone mountains of the
“Saxon Switzerland,” washing successively the feet of the lofty
Lilienstein (932 ft. above the Elbe), the scene of one of Frederick
the Great’s military exploits in the Seven Years’ War, Königstein
(797 ft. above the Elbe), where in times of war Saxony has more
than once stored her national purse for security, and the pinnacled
rocky wall of the Bastei, towering 650 ft. above the surface of
the stream. Shortly after crossing the Bohemian-Saxon frontier,
and whilst still struggling through the sandstone defiles, the
stream assumes a north-westerly direction, which on the whole
it preserves right away to the North Sea. At Pirna the Elbe
leaves behind it the stress and turmoil of the Saxon Switzerland,
rolls through Dresden, with its noble river terraces, and finally,
beyond Meissen, enters on its long journey across the North
German plain, touching Torgau, Wittenberg, Magdeburg,
Wittenberge, Hamburg, Harburg and Altona on the way, and
gathering into itself the waters of the Mulde and Saale from the
left, and those of the Schwarze Elster, Havel and Elde from the
right. Eight miles above Hamburg the stream divides into the
Norder (or Hamburg) Elbe and the Süder (or Harburg) Elbe,
which are linked together by several cross-channels, and embrace
in their arms the large island of Wilhelmsburg and some smaller
ones. But by the time the river reaches Blankenese, 7 m. below
Hamburg, all these anastomosing branches have been reunited,
and the Elbe, with a width of 4 to 9 m. between bank and bank,
travels on between the green marshes of Holstein and Hanover
until it becomes merged in the North Sea off Cuxhaven. At
Kolin the width is about 100 ft., at the mouth of the Moldau
about 300, at Dresden 960, and at Magdeburg over 1000. From
Dresden to the sea the river has a total fall of only 280 ft., although
the distance is about 430 m. For the 75 m. between Hamburg
and the sea the fall is only 3¼ ft. One consequence of this is that
the bed of the river just below Hamburg is obstructed by a bar,
and still lower down is choked with sandbanks, so that navigation
is confined to a relatively narrow channel down the middle of
the stream. But unremitting efforts have been made to maintain
a sufficient fairway up to Hamburg (q.v.). The tide advances
as far as Geesthacht, a little more than 100 m. from the sea.
The river is navigable as far as Melnik, that is, the confluence of
the Moldau, a distance of 525 m., of which 67 are in Bohemia.
Its total length is 725 m., of which 190 are in Bohemia, 77 in the
kingdom of Saxony, and 350 in Prussia, the remaining 108 being
in Hamburg and other states of Germany. The area of the drainage
basin is estimated at 56,000 sq. m.
Navigation.—Since 1842, but more especially since 1871, improvements
have been made in the navigability of the Elbe by
all the states which border upon its banks. As a result of these
labours there is now in the Bohemian portion of the river a
minimum depth of 2 ft. 8 in., whilst from the Bohemian frontier
down to Magdeburg the minimum depth is 3 ft., and from
Magdeburg to Hamburg, 3 ft. 10 in. In 1896 and 1897 Prussia
and Hamburg signed covenants whereby two channels are to be
kept open to a depth of 9¾ ft., a width of 656 ft., and a length
of 550 yds. between Bunthaus and Ortkathen, just above the
bifurcation of the Norder Elbe and the Süder Elbe. In 1869 the
maximum burden of the vessels which were able to ply on the
upper Elbe was 250 tons; but in 1899 it was increased to 800 tons.
The large towns through which the river flows have vied with one
another in building harbours, providing shipping accommodation,
and furnishing other facilities for the efficient navigation of the
Elbe. In this respect the greatest efforts have naturally been
made by Hamburg; but Magdeburg, Dresden, Meissen, Riesa,
Tetschen, Aussig and other places have all done their relative
shares, Magdeburg, for instance, providing a commercial
harbour and a winter harbour. In spite, however, of all that has
been done, the Elbe remains subject to serious inundations at
periodic intervals. Among the worst floods were those of the
years 1774, 1799, 1815, 1830, 1845, 1862, 1890 and 1909. The
growth of traffic up and down the Elbe has of late years become
very considerable. A towing chain, laid in the bed of the river,
extends from Hamburg to Aussig, and by this means, as by
paddle-tug haulage, large barges are brought from the port of
Hamburg into the heart of Bohemia. The fleet of steamers and
barges navigating the Elbe is in point of fact greater than on
any other German river. In addition to goods thus conveyed,
enormous quantities of timber are floated down the Elbe; the
162
weight of the rafts passing the station of Schandau on the Saxon
Bohemian frontier amounting in 1901 to 333,000 tons.
A vast amount of traffic is directed to Berlin, by means of the
Havel-Spree system of canals, to the Thuringian states and the
Prussian province of Saxony, to the kingdom of Saxony and
Bohemia, and to the various riverine states and provinces of the
lower and middle Elbe. The passenger traffic, which is in the
hands of the Sächsisch-Böhmische Dampfschifffahrtsgesellschaft
is limited to Bohemia and Saxony, steamers plying up and down
the stream from Dresden to Melnik, occasionally continuing the
journey up the Moldau to Prague, and down the river as far as
Riesa, near the northern frontier of Saxony, and on the average
1½ million passengers are conveyed.
In 1877-1879, and again in 1888-1895, some 100 m. of canal
were dug, 5 to 6½ ft. deep and of various widths, for the purpose of
connecting the Elbe, through the Havel and the Spree, with the
system of the Oder. The most noteworthy of these connexions
are the Elbe Canal (14¼ m. long), the Reek Canal (9½ m.), the
Rüdersdorfer Gewässer (11½ m.), the Rheinsberger Canal (11¼ m.),
and the Sacrow-Paretzer Canal (10 m.), besides which the Spree
has been canalized for a distance of 28 m., and the Elbe for a
distance of 70 m. Since 1896 great improvements have been
made in the Moldau and the Bohemian Elbe, with the view of
facilitating communication between Prague and the middle of
Bohemia generally on the one hand, and the middle and lower
reaches of the Elbe on the other. In the year named a special
commission was appointed for the regulation of the Moldau and
Elbe between Prague and Aussig, at a cost estimated at about
£1,000,000, of which sum two-thirds were to be borne by the
Austrian empire and one-third by the kingdom of Bohemia.
The regulation is effected by locks and movable dams, the latter
so designed that in times of flood or frost they can be dropped flat
on the bottom of the river. In 1901 the Austrian government laid
before the Reichsrat a canal bill, with proposals for works
estimated to take twenty years to complete, and including the
construction of a canal between the Oder, starting at Prerau, and
the upper Elbe at Pardubitz, and for the canalization of the Elbe
from Pardubitz to Melnik (see Austria: Waterways). In 1900
Lübeck was put into direct communication with the Elbe at
Lauenburg by the opening of the Elbe-Trave Canal, 42 m. in
length, and constructed at a cost of £1,177,700, of which the state
of Lübeck contributed £802,700, and the kingdom of Prussia
£375,000. The canal has been made 72 ft. wide at the bottom,
105 to 126 ft. wide at the top, has a minimum depth of 81⁄6 ft., and
is equipped with seven locks, each 262½ ft. long and 39¼ ft. wide.
It is thus able to accommodate vessels up to 800 tons burden;
and the passage from Lübeck to Lauenburg occupies 18 to 21
hours. In the first year of its being open (June 1900 to June
1901) a total of 115,000 tons passed through the canal.1 A
gigantic project has also been put forward for providing water
communication between the Rhine and the Elbe, and so with the
Oder, through the heart of Germany. This scheme is known as
the Midland Canal. Another canal has been projected for connecting
Kiel with the Elbe by means of a canal trained through
the Plön Lakes.
Bridges.—The Elbe is crossed by numerous bridges, as at
Königgrätz, Pardubitz, Kolin, Leitmeritz, Tetschen, Schandau,
Pirna, Dresden, Meissen, Torgau, Wittenberg, Rosslau, Barby,
Magdeburg, Rathenow, Wittenberge, Dömitz, Lauenburg, and
Hamburg and Harburg. At all these places there are railway
bridges, and nearly all, but more especially those in Bohemia,
Saxony and the middle course of the river—these last on the main
lines between Berlin and the west and south-west of the empire—possess
a greater or less strategic value. At Leitmeritz there is an
iron trellis bridge, 600 yds long. Dresden has four bridges, and
there is a fifth bridge at Loschwitz, about 3 m. above the city.
Meissen has a railway bridge, in addition to an old road bridge.
Magdeburg is one of the most important railway centres in
northern Germany; and the Elbe, besides being bridged—it
divides there into three arms—several times for vehicular traffic,
is also spanned by two fine railway bridges. At both Hamburg
and Harburg, again, there are handsome railway bridges, the one
(1868-1873 and 1894) crossing the northern Elbe, and the other
(1900) the southern Elbe; and the former arm is also crossed by a
fine triple-arched bridge (1888) for vehicular traffic.
Fish.—The river is well stocked with fish, both salt-water and
fresh-water species being found in its waters, and several varieties
of fresh-water fish in its tributaries. The kinds of greatest
economic value are sturgeon, shad, salmon, lampreys, eels, pike
and whiting.
Tolls.—In the days of the old German empire no fewer than
thirty-five different tolls were levied between Melnik and Hamburg,
to say nothing of the special dues and privileged exactions of
various riparian owners and political authorities. After these had
been de facto, though not de jure, in abeyance during the period of
the Napoleonic wars, a commission of the various Elbe states met
and drew up a scheme for their regulation, and the scheme,
embodied in the Elbe Navigation Acts, came into force in 1822.
By this a definite number of tolls, at fixed rates, was substituted
for the often arbitrary tolls which had been exacted previously.
Still further relief was afforded in 1844 and in 1850, on the latter
occasion by the abolition of all tolls between Melnik and the
Saxon frontier. But the number of tolls was only reduced to one,
levied at Wittenberge, in 1863, about one year after Hanover was
induced to give up the Stade or Brunsbüttel toll in return for a
compensation of 2,857,340 thalers. Finally, in 1870, 1,000,000
thalers were paid to Mecklenburg and 85,000 thalers to Anhalt,
which thereupon abandoned all claims to levy tolls upon the
Elbe shipping, and thus navigation on the river became at last
entirely free.
History.—The Elbe cannot rival the Rhine in the picturesqueness
of the scenery it travels through, nor in the glamour which
its romantic and legendary associations exercise over the imagination.
But it possesses much to charm the eye in the deep
glens of the Riesengebirge, amid which its sources spring, and
in the bizarre rock-carving of the Saxon Switzerland. It has
been indirectly or directly associated with many stirring events
in the history of the German peoples. In its lower course, whatever
is worthy of record clusters round the historical vicissitudes
of Hamburg—its early prominence as a missionary centre
(Ansgar) and as a bulwark against Slav and marauding Northman,
its commercial prosperity as a leading member of the Hanseatic
League, and its sufferings during the Napoleonic wars, especially
at the hands of the ruthless Davoût. The bridge over the river
at Dessau recalls the hot assaults of the condottiere Ernst von
Mansfeld in April 1626, and his repulse by the crafty generalship
of Wallenstein. But three years later this imperious leader was
checked by the heroic resistance of the “Maiden” fortress of
Magdeburg; though two years later still she lost her reputation,
and suffered unspeakable horrors at the hands of Tilly’s lawless
and unlicensed soldiery. Mühlberg, just outside the Saxon
frontier, is the place where Charles V. asserted his imperial
authority over the Protestant elector of Saxony, John Frederick,
the Magnanimous or Unfortunate, in 1547. Dresden, Aussig
and Leitmeritz are all reminiscent of the fierce battles of the
Hussite wars, and the last named of the Thirty Years’ War.
But the chief historical associations of the upper (i.e. the Saxon
and Bohemian) Elbe are those which belong to the Seven Years’
War, and the struggle of the great Frederick of Prussia against
the power of Austria and her allies. At Pirna (and Lilienstein) in
1756 he caught the entire Saxon army in his fowler’s net, after
driving back at Lobositz the Austrian forces which were hastening
to their assistance; but only nine months later he lost his
reputation for “invincibility” by his crushing defeat at Kolin,
where the great highway from Vienna to Dresden crosses the
Elbe. Not many miles distant, higher up the stream, another
decisive battle was fought between the same national antagonists,
but with a contrary result, on the memorable 3rd of July
1866.
See M. Buchheister, “Die Elbe u. der Hafen von Hamburg,”
in Mitteil. d. Geog. Gesellsch. in Hamburg (1899), vol. xv. pp. 131-188;
V. Kurs, “Die künstlichen Wasserstrassen des deutschen
163
Reichs,” in Geog. Zeitschrift (1898), pp. 601-617; and (the official)
Der Elbstrom (1900); B. Weissenborn, Die Elbzölle und Elbstapelplätze
im Mittelalter (Halle, 1900); Daniel, Deutschland; and A.
Supan, Wasserstrassen und Binnenschifffahrt (Berlin, 1902).
1 See Der Bau des Elbe-Trave Canals und seine Vorgeschichte
(Lübeck, 1900).
ELBERFELD, a manufacturing town of Germany, in the
Prussian Rhine province, on the Wupper, and immediately west
of and contiguous to Barmen (q.v.). Pop. (1816) 21,710; (1840)
31,514; (1885) 109,218; (1905) 167,382. Elberfeld-Barmen,
although administratively separate, practically form a single
whole. It winds, a continuous strip of houses and factories,
for 9 m. along the deep valley, on both banks of the Wupper,
which is crossed by numerous bridges, the engirdling hills
crowned with woods. Local intercommunication is provided
by an electric tramway line and a novel hanging railway—on
the Langen mono-rail system—suspended over the bed of the
river, with frequent stations. In the centre of the town are a
number of irregular and narrow streets, and the river, polluted
by the refuse of dye-works and factories, constitutes a constant
eyesore. Yet within recent years great alterations have been
effected; in the newer quarters are several handsome streets
and public buildings; in the centre many insanitary dwellings
have been swept away, and their place occupied by imposing
blocks of shops and business premises, and a magnificent new
town-hall, erected in a dominant position. Among the most
recent improvements must be mentioned the Brausenwerther
Platz, flanked by the theatre, the public baths, and the railway
station and administrative offices. There are eleven Evangelical
and five Roman Catholic churches (noticeable among the latter
the Suitbertuskirche), a synagogue, and chapels of various other
sects. Among other public buildings may be enumerated the
civic hall, the law courts and the old town-hall.
The town is particularly rich in educational, industrial, philanthropic
and religious institutions. The schools include the
Gymnasium (founded in 1592 by the Protestant community
as a Latin school), the Realgymnasium (founded in 1830, for
“modern” subjects and Latin), the Oberrealschule and Realschule
(founded 1893, the latter wholly “modern”), two girls’
high schools, a girls’ middle-class school, a large number of
popular schools, a mechanics’ and polytechnic school, a school
of mechanics, an industrial drawing school, a commercial school,
and a school for the deaf and dumb. There are also a theatre,
an institute of music, a library, a museum, a zoological garden,
and numerous scientific societies. The town is the seat of the
Berg Bible Society. The majority of the inhabitants are
Protestant, with a strong tendency towards Pietism; but the
Roman Catholics number upwards of 40,000, forming about
one-fourth of the total population. The industries of Elberfeld
are on a scale of great magnitude. It is the chief centre in
Germany of the cotton, wool, silk and velvet manufactures, and
of upholstery, drapery and haberdashery of all descriptions, of
printed calicoes, of Turkey-red and other dyes, and of fine
chemicals. Leather and rubber goods, gold, silver and aluminium
wares, machinery, wall-paper, and stained glass are also among
other of its staple products. Commerce is lively and the exports
to foreign countries are very considerable. The railway system
is well devised to meet the requirements of its rapidly increasing
trade. Two main lines of railway traverse the valley; that on
the south is the main line from Aix-la-Chapelle, Cologne and
Düsseldorf to central Germany and Berlin, that on the north
feeds the important towns of the Ruhr valley.
The surroundings of Elberfeld are attractive, and public
grounds and walks have been recently opened on the hills around
with results eminently beneficial to the health of the population.
In the 12th century the site of Elberfeld was occupied by the
castle of the lords of Elverfeld, feudatories of the archbishops of
Cologne. The fief passed later into the possession of the counts
of Berg. The industrial development of the place started with
a colony of bleachers, attracted by the clear waters of the Wupper,
who in 1532 were granted the exclusive privilege of bleaching
yarn. It was not, however, until 1610 that Elberfeld was raised
to the status of a town, and in 1640 was surrounded with walls.
In 1760 the manufacture of silk was introduced, and dyeing with
Turkey-red in 1780; but it was not till the end of the century
that its industries developed into importance under the influence
of Napoleon’s continental system, which barred out British
competition. In 1815 Elberfeld was assigned by the congress
of Vienna, with the grand-duchy of Berg, to Prussia, and its
prosperity rapidly developed under the Prussian Zollverein.
See Coutelle, Elberfeld, topographisch-statistische Darstellung (Elberfeld,
1853); Schell, Geschichte der Stadt Elberfeld (1900); A. Shadwell,
Industrial Efficiency (London, 1906); and Jorde, Führer durch Elberfeld
und seine Umgebung (1902).
ELBEUF, a town of northern France in the department of
Seine-Inférieure, 14 m. S.S.W. of Rouen by the western railway.
Pop. (1906) 17,800. Elbeuf, a town of wide, clean streets, with
handsome houses and factories, stands on the left bank of the
Seine at the foot of hills over which extends the forest of Elbeuf.
A tribunal and chamber of commerce, a board of trade-arbitrators,
a lycée, a branch of the Bank of France, a school of industry,
a school of cloth manufacture and a museum of natural history
are among its institutions. The churches of St Étienne and St
Jean, both of the Renaissance period with later additions,
preserve stained glass of the 16th century. The hôtel-de-ville
and the Cercle du Commerce are the chief modern buildings.
The town with its suburbs, Orival, Caudebec-lès-Elbeuf,
St Aubin and St Pierre, is one of the principal and most ancient
seats of the woollen manufacture in France; more than half the
inhabitants are directly maintained by the staple industry and
numbers more by the auxiliary crafts. As a river-port it has a
brisk trade in the produce of the surrounding district as well as in
the raw materials of its manufactures, especially in wool from
La Plata, Australia and Germany. Two bridges, one of them a
suspension-bridge, communicate with St Aubin on the opposite
bank of the Seine, and steamboats ply regularly to Rouen.
Elbeuf was, in the 13th century, the centre of an important
fief held by the house of Harcourt, but its previous
history goes back at least to the early years of the Norman
occupation, when it appears under the name of Hollebof. It
passed into the hands of the houses of Rieux and Lorraine, and
was raised to the rank of a duchy in the peerage of France by
Henry III. in favour of Charles of Lorraine (d. 1605), grandson
of Claude, duke of Guise, master of the hounds and master of
the horse of France. The last duke of Elbeuf was Charles Eugène
of Lorraine, prince de Lambesc, who distinguished himself in
1789 by his energy in repressing risings of the people at Paris.
He fought in the army of the Bourbons, and later in the service
of Austria, and died in 1825.
ELBING, a seaport town of Germany, in the kingdom of
Prussia, 49 m. by rail E.S.E. of Danzig, on the Elbing, a small
river which flows into the Frische Haff about 5 m. from the
town, and is united with the Nogat or eastern arm of the Vistula
by means of the Kraffohl canal. Pop. (1905) 55,627. By the
Elbing-Oberländischer canal, 110 m. long, constructed in 1845-1860,
Lakes Geserich and Drewenz are connected with Lake
Drausen, and consequently with the port of Elbing. The old
town was formerly surrounded by fortifications, but of these only
a few fragments remain. There are several churches, among
them the Marienkirche (dating from the 15th century and restored
in 1887), a classical school (Gymnasium) founded in 1536, a
modern school (Realschule), a public library of over 28,000
volumes, and several charitable institutions. The town-hall
(1894) contains a historical museum.
Elbing is a place of rapidly growing industries. At the great
Schichau iron-works, which employ thousands of workmen, are
built most of the torpedo-boats and destroyers for the German
navy, as well as larger craft, locomotives and machinery. In
addition to this there are at Elbing important iron foundries, and
manufactories of machinery, cigars, lacquer and metal ware, flax
and hemp yarn, cotton, linen, organs, &c. There is a considerable
trade also in agricultural produce.
The origin of Elbing was a colony of traders from Lübeck and
Bremen, which established itself under the protection of a castle
of the Teutonic Knights, built in 1237. In 1246 the town acquired
“Lübeck rights,” i.e. the full autonomy conceded by the charter
164
of the emperor Frederick II. in 1226 (see Lübeck), and it was
early admitted to the Hanseatic League. In 1454 the town
repudiated the overlordship of the Teutonic Order, and placed
itself under the protection of the king of Poland, becoming the
seat of a Polish voivode. From this event dates a decline in its
prosperity, a decline hastened by the wars of the early 18th
century. In 1698, and again in 1703, it was seized by the elector
of Brandenburg as security for a debt due to him by the
Polish king. It was taken and held to ransom by Charles XII. of
Sweden, and in 1710 was captured by the Russians. In 1772,
when it fell to Prussia through the first partition of Poland, it was
utterly decayed.
See Fuchs, Gesch. der Stadt Elbing (Elbing, 1818-1852); Rhode,
Der Elbinger Kreis in topographischer, historischer, und statistischer
Hinsicht (Danzig, 1871); Wernick, Elbing (Elbing, 1888).
ELBOW, in anatomy, the articulation of the humerus, the bone
of the upper arm, and the ulna and radius, the bones of the forearm
(see Joints). The word is thus applied to things which are
like this joint in shape, such as a sharp bend of a stream or river,
an angle in a tube, &c. The word is derived from the O. Eng.
elnboga, a combination of eln, the forearm, and boga, a bow or
bend. This combination is common to many Teutonic languages,
cf. Ger. Ellbogen. Eln still survives in the name of a linear
measure, the “ell,” and is derived from the O. Teut. alina,
cognate with Lat. ulna and Gr. ὠλένη, the forearm. The use of
the arm as a measure of length is illustrated by the uses of ulna,
in Latin, cubit, and fathom.
ELBURZ, or Alburz (from O. Pers. Hara-bere-zaiti, the
“High Mountain”), a great chain of mountains in northern
Persia, separating the Caspian depression from the Persian
highlands, and extending without any break for 650 m. from the
western shore of the Caspian Sea to north-eastern Khorasan.
According to the direction, or strike, of its principal ranges the
Elburz may be divided into three sections: the first 120 m. in
length with a direction nearly N. to S., the second 240 m. in length
with a direction N.W. to S.E., and the third 290 m. in length striking
S.W. to N.E. The first section, which is connected with the
system of the Caucasus, and begins west of Lenkoran in 39° N. and
45° E., is known as the Talish range and has several peaks 9000 to
10,000 ft. in height. It runs almost parallel to the western shore
of the Caspian, and west of Astara is only 10 or 12 m. distant from
the sea. At the point west of Resht, where the direction of the
principal range changes to one of N.W. to S.E., the second section
of the Elburz begins, and extends from there to beyond Mount
Demavend, east of Teheran. South of Resht this section is broken
through at almost a right angle by the Safid Rud (White river), and
along it runs the principal commercial road between the Caspian
and inner Persia, Resht-Kazvin-Teheran. The Elburz then
splits into three principal ranges running parallel to one another
and connected at many places by secondary ranges and spurs.
Many peaks of the ranges in this section have an altitude of
11,000 to 13,000 ft., and the elevation of the passes leading over
the ranges varies between 7000 and 10,000 ft. The highest peaks
are situated in the still unexplored district of Talikan, N.W. of
Teheran, and thence eastwards to beyond Mount Demavend.
The part of the Elburz immediately north of Teheran is known as
the Kuh i Shimran (mountain of Shimran, from the name of the
Shimran district on its southern slopes) and culminates in the
Sar i Tochal (12,600 ft.). Beyond it, and between the border of
Talikan in the N.W. and Mount Demavend in the N.E., are the
ranges Azadbur, Kasil, Kachang, Kendevan, Shahzad, Varzeh,
Derbend i Sar and others, with elevations of 12,000 to 13,500 ft.,
while Demavend towers above them all with its altitude of
19,400 ft. The eastern foot of Demavend is washed by the river
Herhaz (called Lar river in its upper course), which there breaks
through the Elburz in a S.-N. direction in its course to the Caspian,
past the city of Amol. The third section of the Elburz, with its
principal ranges striking S.W. to N.E., has a length of about 290
m., and ends some distance beyond Bujnurd in northern Khorasan,
where it joins the Ala Dagh range, which has a direction to
the S.E., and, continuing with various appellations to northern
Afghanistan, unites with the Paropamisus. For about two-thirds
of its length—from its beginning to Khush Yailak—the
third section consists of three principal ranges connected by
lateral ranges and spurs. It also has many peaks over 10,000 ft.
in height, and the Nizva mountain on the southern border of the
unexplored district of Hazarjirib, north of Semnan, and the
Shahkuh, between Shahrud and Astarabad, have an elevation
exceeding 13,000 ft. Beyond Khush Yailak (meaning “pleasant
summer quarters”), with an elevation of 10,000 ft., are the
Kuh i Buhar (8000) and Kuh i Suluk (8000), which latter joins
the Ala Dagh (11,000).
The northern slopes of the Elburz and the lowlands which lie
between them and the Caspian, and together form the provinces of
Gilan, Mazandaran and Astarabad, are covered with dense forest
and traversed by hundreds (Persian writers say 1362) of perennial
rivers and streams. The breadth of the lowlands between the
foot of the hills and the sea is from 2 to 25 m., the greatest breadth
being in the meridian of Resht in Gilan, and in the districts of
Amol, Sari and Barfurush in Mazandaran. The inner slopes and
ranges of the Elburz south of the principal watershed, generally
the central one of the three principal ranges which are outside of
the fertilizing influence of the moisture brought from the sea,
have little or no natural vegetation, and those farthest south are,
excepting a few stunted cypresses, completely arid and bare.
“North of the principal watershed forest trees and general
verdure refresh the eye. Gurgling water, strips of sward and tall
forest trees, backed by green hills, make a scene completely unlike
the usual monotony of Persian landscape. The forest scenery
much resembles that of England, with fine oaks and greensward.
South of the watershed the whole aspect of the landscape is as
hideous and disappointing as scenery in Afghanistan. Ridge after
ridge of bare hill and curtain behind curtain of serrated mountain,
certainly sometimes of charming greys and blues, but still all bare
and naked, rugged and arid” (“Beresford Lovett, Proc. R.G.S.,
Feb. 1883).
The higher ranges of the Elburz are snow-capped for the
greater part of the year, and some, which are not exposed to the
refracted heat from the arid districts of inner Persia, are rarely
without snow. Water is plentiful in the Elburz, and situated in
well-watered valleys and gorges are innumerable flourishing
villages, embosomed in gardens and orchards, with extensive
cultivated fields and meadows, and at higher altitudes small
plateaus, under snow until March or April, afford cool camping
grounds to the nomads of the plains, and luxuriant grazing to
their sheep and cattle during the summer.
(A. H.-S.)
ELCHE, a town of eastern Spain, in the province of Alicante,
on the river Vinalapo. Pop. (1900) 27,308. Elche is the meeting-place
of three railways, from Novelda, Alicante and Murcia.
It contains no building of high architectural merit, except,
perhaps, the collegiate church of Santa Maria, with its lofty
blue-tiled dome and fine west doorway. But the costume and
physiognomy of the inhabitants, the narrow streets and flat-roofed,
whitewashed houses, and more than all, the thousands
of palm-trees in its gardens and fields, give the place a strikingly
Oriental aspect, and render it unique among the cities of Spain.
The cultivation of the palm is indeed the principal occupation;
and though the dates are inferior to those of the Barbary States,
upwards of 22,500 tons are annually exported. The blanched
fronds are also sold in large quantities for the processions of
Palm Sunday, and after they have received the blessing of the
priest they are regarded throughout Spain as certain defences
against lightning. Other thriving local industries include the
manufacture of oil, soap, flour, leather, alcohol and esparto
grass rugs. The harbour of Elche is Santa Pola (pop. 4100),
situated 6 m. E.S.E., where the Vinalapo enters the Mediterranean,
after forming the wide lagoon known as the Albufera de Elche.
Elche is usually identified with the Iberian Helike, afterwards
the Roman colony of Ilici or Illici. From the 8th century to
the 13th it was held by the Moors, who finally failed to recapture
it from the Spaniards in 1332.
ELCHINGEN, a village of Germany, in the kingdom of Bavaria,
not far from the Danube, 5 m. N.E. from Ulm. Here, on the
14th of October 1805, the Austrians under Laudon were
165
defeated by the French under Ney, who by taking the bridge
decided the day and gained for himself the title of duke of
Elchingen.
ELDAD BEN MAḤLI, also surnamed had-Dani, Abu-Dani,
David-had-Dani, or the Danite, Jewish traveller, was the supposed
author of a Jewish travel-narrative of the 9th century
A.D., which enjoyed great authority in the middle ages, especially
on the question of the Lost Ten Tribes. Eldad first set out to
visit his Hebrew brethren in Africa and Asia. His vessel was
wrecked, and he fell into the hands of cannibals; but he was
saved by his leanness, and by the opportune invasion of a neighbouring
tribe. After spending four years with his new captors,
he was ransomed by a fellow-countryman, a merchant of the
tribe of Issachar. He then (according to his highly fabulous
narrative) visited the territory of Issachar, in the mountains
of Media and Persia; he also describes the abodes of Zabulon,
on the “other side” of the Paran Mountains, extending to
Armenia and the Euphrates; of Reuben, on another side of the
same mountains; of Ephraim and Half Manasseh, in Arabia,
not far from Mecca; and of Simeon and the other Half of
Manasseh, in Chorazin, six months’ journey from Jerusalem.
Dan, he declares, sooner than join in Jeroboam’s scheme of an
Israelite war against Judah, had migrated to Cush, and finally,
with the help of Naphthali, Asher and Gad, had founded an
independent Jewish kingdom in the Gold Land of Havila, beyond
Abyssinia. The tribe of Levi had also been miraculously guided,
from near Babylon, to Havila, where they were enclosed and
protected by the mystic river Sambation or Sabbation, which
on the Sabbath, though calm, was veiled in impenetrable mist,
while on other days it ran with a fierce untraversable current of
stones and sand.
Apart from these tales, we have the genuine Eldad, a celebrated
Jewish traveller and philologist; who flourished c. A.D. 830-890;
to whom the work above noticed is ascribed; who was a native
either of S. Arabia, Palestine or Media; who journeyed in Egypt,
Mesopotamia, North Africa, and Spain; who spent several
years at Kairawan in Tunis; who died on a visit to Cordova,
and whose authority, as to the lost tribes, is supported by a
great Hebrew doctor of his own time, Ẓemaḥ Gaon, the rector
of the Academy at Sura (A.D. 889-898). It is possible that a
certain relationship exists (as suggested by Epstein and supported
by D.H. Müller) between the famous apocryphal Letter of
Prester John (of c. A.D. 1165) and the narrative of Eldad; but
the affinity is not close. Eldad is quoted as an authority on
linguistic difficulties by the leading medieval Jewish grammarians
and lexicographers.
The work ascribed to Eldad is in Hebrew, divided into six chapters,
probably abbreviated from the original text. The first edition
appeared at Mantua about 1480; the second at Constantinople in
1516; this was reprinted at Venice in 1544 and 1605, and at Jessnitz
in 1722. A Latin version by Gilb. Génébrard was published at Paris
in 1563, under the title of Eldad Danius ... de Judaeis clausis
eorumque in Aethiopia ... imperio, and was afterwards incorporated
in the translator’s Chronologia Hebraeorum of 1584; a German version
appeared at Prague in 1695, and another at Jessnitz in 1723.
In 1838 E. Carmoly edited and translated a fuller recension which
he had found in a MS. from the library of Eliezer Ben Hasan, forwarded
to him by David Zabach of Morocco (see Relation d’Eldad le
Danite, Paris, 1838). Both forms are printed by Dr Jellinek in his
Bet-ha-Midrasch, vols. ii. p. 102, &c., and iii. p. 6, &c. (Leipzig, 1853-1855).
See also Bartolocci, Bibliotheca magna Rabbinica, i. 101-130;
Fürst, Bibliotheca Judaica, i. 30, &c.; Hirsch Graetz, Geschichte der
Juden (3rd ed., Leipzig, 1895), v. 239-244; Rossi, Dizionario degli
Ebrei; Steinschneider, Cat. librorum Hebraeorum in bibliotheca
Bodleiana, cols. 923-925; Kitto’s Biblical Cyclopaedia (3rd edition,
sub nomine); Abr. Epstein, Eldad ha-Dani (Pressburg, 1891);
D.H. Müller, “Die Recensionen und Versionen des Eldad had-Dani,”
in Denkschriften d. Wiener Akad. (Phil.-Hist. Cl.), vol. xli. (1892),
pp. 1-80.
ELDER (Gr. πρεσβύτερος), the name given at different times
to a ruler or officer in certain political and ecclesiastical systems
of government.
1. The office of elder is in its origin political and is a relic of
the old patriarchal system. The unit of primitive society is
always the family; the only tie that binds men together is that
of kinship. “The eldest male parent,” to quote Sir Henry
Maine,1 “is absolutely supreme in his household. His dominion
extends to life and death and is as unqualified over his children
and their houses as over his slaves.” The tribe, which is a later
development, is always an aggregate of families or clans, not a
collection of individuals. “The union of several clans for common
political action,” as Robertson Smith says, “was produced by
the pressure of practical necessity, and always tended towards
dissolution when this practical pressure was withdrawn. The
only organization for common action was that the leading men
of the clans consulted together in time of need, and their influence
led the masses with them. Out of these conferences arose the
senates of elders found in the ancient states of Semitic and Aryan
antiquity alike.”2 With the development of civilization there
came a time when age ceased to be an indispensable condition
of leadership. The old title was, however, generally retained,
e.g. the γέροντες so often mentioned in Homer, the γερουσία of
the Dorian states, the senatus and the patres conscripti of Rome,
the sheikh or elder of Arabia, the alderman of an English borough,
the seigneur (Lat. senior) of feudal France.
2. It was through the influence of Judaism that the originally
political office of elder passed over into the Christian Church
and became ecclesiastical. The Israelites inherited the office
from their Semitic ancestors (just as did the Moabites and the
Midianites, of whose elders we read in Numbers xxii. 7), and traces
of it are found throughout their history. Mention is made in
Judges viii. 14 of the elders of Succoth whom “Gideon taught
with thorns of the wilderness and with briers.” It was to the
elders of Israel in Egypt that Moses communicated the plan of
Yahweh for the redemption of the people (Exodus iii. 16).
During the sojourn in the wilderness the elders were the intermediaries
between Moses and the people, and it was out of the
ranks of these elders that Moses chose a council of seventy “to
bear with him the burden of the people” (Numbers xi. 16).
The elders were the governors of the people and the administrators
of justice. There are frequent references to their work in the
latter capacity in the book of Deuteronomy, especially in
relation to the following crimes—the disobedience of sons;
slander against a wife; the refusal of levirate marriage; manslaughter;
and blood-revenge. Their powers were gradually
curtailed by (a) the development of the monarchy, to which of
course they were in subjection, and which became the court of
appeal in questions of law;3 (b) the appointment of special
judges, probably chosen from amongst the elders themselves,
though their appointment meant the loss of privilege to the
general body; (c) the rise of the priestly orders, which usurped
many of the prerogatives that originally belonged to the elders.
But in spite of the rise of new authorities, the elders still retained
a large amount of influence. We hear of them frequently in the
Persian, Greek and Roman periods. In the New Testament
the members of the Sanhedrin in Jerusalem are very frequently
termed “elders” or πρεσβύτεροι, and from them the name was
taken over by the Church.
3. The name “elder” was probably the first title bestowed
upon the officers of the Christian Church—since the word deacon
does not occur in connexion with the appointment of the Seven
in Acts vi. Its universal adoption is due not only to its currency
amongst the Jews, but also to the fact that it was frequently
used as the title of magistrates in the cities and villages of Asia
Minor. For the history of the office of elder in the early Church
and the relation between elders and bishops see Presbyter.
4. In modern times the use of the term is almost entirely
confined to the Presbyterian church, the officers of which are
always called elders. According to the Presbyterian theory of
church government there are two classes of elders—“teaching
elders,” or those specially set apart to the pastoral office, and
“ruling elders,” who are laymen, chosen generally by the congregation
and set apart by ordination to be associated with the
pastor in the oversight and government of the church. When
166
the word is used without any qualification it is understood to
apply to the latter class alone. For an account of the duties,
qualifications and powers of elders in the Presbyterian Church
see Presbyterianism.
See W.R. Smith, History of the Semites; H. Maine, Ancient Law;
E. Schürer, The Jewish People in the Time of Christ; J. Wellhausen,
History of Israel and Judah; G.A. Deissmann, Bible Studies, p. 154.
1 Ancient Law, p. 126.
2 Religion of the Semites, p. 34.
3 There is a hint at this even in the Pentateuch, “every great
matter they shall bring unto thee, but every small matter they shall
judge themselves.”
ELDER (O. Eng. ellarn; Ger. Holunder; Fr. sureau), the
popular designation of the deciduous shrubs and trees constituting
the genus Sambucus of the natural order Caprifoliaceae.
The Common Elder, S. nigra, the bourtree of Scotland, is found
in Europe, the north of Africa, Western Asia, the Caucasus, and
Southern Siberia; in sheltered spots it attains a height of over
20 ft. The bark is smooth; the shoots are stout and angular,
and the leaves glabrous, pinnate, with oval or elliptical leaflets.
The flowers, which form dense flat-topped clusters (corymbose
cymes), with five main branches, have a cream-coloured, gamopetalous,
five-lobed corolla, five stamens, and three sessile
stigmas; the berries are purplish-black, globular and three- or
four-seeded, and ripen about September. The elder thrives best
in moist, well-drained situations, but can be grown in a great
diversity of soils. It grows readily from young shoots, which
after a year are fit for transplantation. It is found useful for
making screen-fences in bleak, exposed situations, and also as
a shelter for other shrubs in the outskirts of plantations. By
clipping two or three times a year, it may be made close and
compact in growth. The young trees furnish a brittle wood,
containing much pith; the wood of old trees is white, hard and
close-grained, polishes well, and is employed for shoemakers’ pegs,
combs, skewers, mathematical instruments and turned articles.
Young elder twigs deprived of pith have from very early times
been in request for making whistles, popguns and other toys.
The elder was known to the ancients for its medicinal properties,
and in England the inner bark was formerly administered as a
cathartic. The flowers (sambuci flores) contain a volatile oil, and
serve for the distillation of elder-flower water (aqua sambuci),
used in confectionery, perfumes and lotions. The leaves of the
elder are employed to impart a green colour to fat and oil (unguentum
sambuci foliorum and oleum viride), and the berries for
making wine, a common adulterant of port. The leaves and
bark emit a sickly odour, believed to be repugnant to insects.
Christopher Gullet (Phil. Trans., 1772, lxii. p. 348) recommends
that cabbages, turnips, wheat and fruit trees, to preserve them
from caterpillars, flies and blight, should be whipped with twigs
of young elder. According to German folklore, the hat must be
doffed in the presence of the elder-tree; and in certain of the
English midland counties a belief was once prevalent that the
cross of Christ was made from its wood, which should therefore
never be used as fuel, or treated with disrespect (see Quart. Rev.
cxiv. 233). It was, however, a common medieval tradition,
alluded to by Ben Jonson, Shakespeare and other writers, that the
elder was the tree on which Judas hanged himself; and on this
account, probably, to be crowned with elder was in olden times
accounted a disgrace. In Cymbeline (act iv. s. 2) “the stinking
elder” is mentioned as a symbol of grief. In Denmark the tree is
supposed by the superstitious to be under the protection of the
“Elder-mother”: its flowers may not be gathered without her
leave; its wood must not be employed for any household
furniture; and a child sleeping in an elder-wood cradle would
certainly be strangled by the Elder-mother.
Several varieties are known in cultivation: aurea, golden elder,
has golden-yellow leaves; laciniata, parsley-leaved elder, has the
leaflets cut into fine segments; rotundifolia has rounded leaflets;
forms also occur with variegated white and yellow leaves, and
virescens is a variety having white bark and green-coloured berries.
The scarlet-berried elder, S. racemosa, is the handsomest species
of the genus. It is a native of various parts of Europe, growing in
Britain to a height of over 15 ft., but often producing no fruit.
The dwarf elder or Danewort (supposed to have been introduced
into Britain by the Danes), S. Ebulus, a common European
species, reaches a height of about 6 ft. Its cyme is hairy, has
three principal branches, and is smaller than that of S. nigra; the
flowers are white tipped with pink. All parts of the plant are
cathartic and emetic.
ELDON, JOHN SCOTT, 1st Earl of (1751-1838), lord high
chancellor of England, was born at Newcastle on the 4th of June
1751. His grandfather, William Scott of Sandgate, a suburb of
Newcastle, was clerk to a “fitter”—a sort of water-carrier and
broker of coals. His father, whose name also was William,
began life as an apprentice to a fitter, in which service he obtained
the freedom of Newcastle, becoming a member of the gild of
Hoastmen (coal-fitters); later in life he became a principal in the
business, and attained a respectable position as a merchant in
Newcastle, accumulating property worth nearly £20,000.
John Scott was educated at the grammar school of his native
town. He was not remarkable at school for application to his
studies, though his wonderful memory enabled him to make good
progress in them; he frequently played truant and was whipped
for it, robbed orchards, and indulged in other questionable schoolboy
freaks; nor did he always come out of his scrapes with
honour and a character for truthfulness. When he had finished
his education at the grammar school, his father thought of
apprenticing him to his own business, to which an elder brother
Henry had already devoted himself; and it was only through
the interference of his elder brother William (afterwards Lord
Stowell, q.v.), who had already obtained a fellowship at University
College, Oxford, that it was ultimately resolved that he should
continue the prosecution of his studies. Accordingly, in 1766,
John Scott entered University College with the view of taking
holy orders and obtaining a college living. In the year following
he obtained a fellowship, graduated B.A. in 1770, and in 1771 won
the prize for the English essay, the only university prize open in
his time for general competition.
His wife was the eldest daughter of Aubone Surtees, a Newcastle
banker. The Surtees family objected to the match, and
attempted to prevent it; but a strong attachment had sprung
up between them. On the 18th November 1772 Scott, with the
aid of a ladder and an old friend, carried off the lady from her
father’s house in the Sandhill, across the border to Blackshiels,
in Scotland, where they were married. The father of the bridegroom
objected not to his son’s choice, but to the time he chose to
marry; for it was a blight on his son’s prospects, depriving him
of his fellowship and his chance of church preferment. But
while the bride’s family refused to hold intercourse with the pair,
Mr Scott, like a prudent man and an affectionate father, set
himself to make the best of a bad matter, and received them
kindly, settling on his son £2000. John returned with his wife
to Oxford, and continued to hold his fellowship for what is called
the year of grace given after marriage, and added to his income
by acting as a private tutor. After a time Mr Surtees was
reconciled with his daughter, and made a liberal settlement
on her.
John Scott’s year of grace closed without any college living
falling vacant; and with his fellowship he gave up the church
and turned to the study of law. He became a student at the
Middle Temple in January 1773. In 1776 he was called to the
bar, intending at first to establish himself as an advocate in his
native town, a scheme which his early success led him to abandon,
and he soon settled to the practice of his profession in London,
and on the northern circuit. In the autumn of the year in which
he was called to the bar his father died, leaving him a legacy of
£1000 over and above the £2000 previously settled on him.
In his second year at the bar his prospects began to brighten.
His brother William, who by this time held the Camden professorship
of ancient history, and enjoyed an extensive acquaintance
with men of eminence in London, was in a position materially
to advance his interests. Among his friends was the notorious
Andrew Bowes of Gibside, to the patronage of whose house
the rise of the Scott family was largely owing. Bowes having
contested Newcastle and lost it, presented an election petition
against the return of his opponent. Young Scott was retained as
junior counsel in the case, and though he lost the petition he did
not fail to improve the opportunity which it afforded for displaying
his talents. This engagement, in the commencement of his
167
second year at the bar, and the dropping in of occasional fees,
must have raised his hopes; and he now abandoned the scheme
of becoming a provincial barrister. A year or two of dull drudgery
and few fees followed, and he began to be much depressed. But
in 1780 we find his prospects suddenly improved, by his appearance
in the case of Ackroyd v. Smithson, which became a leading
case settling a rule of law; and young Scott, having lost his
point in the inferior court, insisted on arguing it, on appeal,
against the opinion of his clients, and carried it before Lord
Thurlow, whose favourable consideration he won by his able
argument. The same year Bowes again retained him in an
election petition; and in the year following Scott greatly
increased his reputation by his appearance as leading counsel in
the Clitheroe election petition. From this time his success was
certain. In 1782 he obtained a silk gown, and was so far cured
of his early modesty that he declined accepting the king’s
counselship if precedence over him were given to his junior,
Thomas (afterwards Lord) Erskine, though the latter was the son
of a peer and a most accomplished orator. He was now on the
high way to fortune. His health, which had hitherto been but
indifferent, strengthened with the demands made upon it; his
talents, his power of endurance, and his ambition all expanded
together. He enjoyed a considerable practice in the northern
part of his circuit, before parliamentary committees and at the
chancery bar. By 1787 his practice at the equity bar had so far
increased that he was obliged to give up the eastern half of his
circuit (which embraced six counties) and attend it only at
Lancaster.
In 1782 he entered parliament for Lord Weymouth’s close
borough of Weobley, which Lord Thurlow obtained for him
without solicitation. In parliament he gave a general and
independent support to Pitt. His first parliamentary speeches
were directed against Fox’s India Bill. They were unsuccessful.
In one he aimed at being brilliant; and becoming merely
laboured and pedantic, he was covered with ridicule by Sheridan,
from whom he received a lesson which he did not fail to turn
to account. In 1788 he was appointed solicitor-general, and
was knighted, and at the close of this year he attracted attention
by his speeches in support of Pitt’s resolutions on the state of
the king (George III., who then laboured under a mental malady)
and the delegation of his authority. It is said that he drew the
Regency Bill, which was introduced in 1789. In 1793 Sir John
Scott was promoted to the office of attorney-general, in which
it fell to him to conduct the memorable prosecutions for high
treason against British sympathizers with French republicanism,—amongst
others, against the celebrated Horne Tooke. These
prosecutions, in most cases, were no doubt instigated by Sir
John Scott, and were the most important proceedings in which
he was ever professionally engaged. He has left on record, in
his Anecdote Book, a defence of his conduct in regard to them.
A full account of the principal trials, and of the various legislative
measures for repressing the expressions of popular opinion for
which he was more or less responsible, will be found in Twiss’s
Public and Private Life of the Lord Chancellor Eldon, and in the
Lives of the Lord Chancellors, by Lord Campbell.
In 1799 the office of chief justice of the Court of Common
Pleas falling vacant, Sir John Scott’s claim to it was not overlooked;
and after seventeen years’ service in the Lower House,
he entered the House of Peers as Baron Eldon. In February
1801 the ministry of Pitt was succeeded by that of Addington,
and the chief justice now ascended the woolsack. The chancellorship
was given to him professedly on account of his notorious
anti-Catholic zeal. From the peace of Amiens (1802) till 1804
Lord Eldon appears to have interfered little in politics. In the
latter year we find him conducting the negotiations which
resulted in the dismissal of Addington and the recall of Pitt to
office as prime minister. Lord Eldon was continued in office
as chancellor under Pitt; but the new administration was of
short duration, for on the 23rd of January 1806 Pitt died, worn
out with the anxieties of office, and his ministry was succeeded
by a coalition, under Lord Grenville. The death of Fox, who
became foreign secretary and leader of the House of Commons,
soon, however, broke up the Grenville administration; and in
the spring of 1807 Lord Eldon once more, under Lord Liverpool’s
administration, returned to the woolsack, which, from that
time, he continued to occupy for about twenty years, swaying
the cabinet, and being in all but name prime minister of England.
It was not till April 1827, when the premiership, vacant through
the paralysis of Lord Liverpool, fell to Canning, the chief advocate
of Roman Catholic emancipation, that Lord Eldon, in the
seventy-sixth year of his age, finally resigned the chancellorship.
When, after the two short administrations of Canning and
Goderich, it fell to the duke of Wellington to construct a cabinet,
Lord Eldon expected to be included, if not as chancellor, at least
in some important office, but he was overlooked, at which he
was much chagrined. Notwithstanding his frequent protests
that he did not covet power, but longed for retirement, we find
him again, so late as 1835, within three years of his death, in
hopes of office under Peel. He spoke in parliament for the last
time in July 1834.
In 1821 Lord Eldon had been created Viscount Encombe and
earl of Eldon by George IV., whom he managed to conciliate,
partly, no doubt, by espousing his cause against his wife, whose
advocate he had formerly been, and partly through his reputation
for zeal against the Roman Catholics. In the same year his
brother William, who from 1798 had filled the office of judge
of the High Court of Admiralty, was raised to the peerage under
the title of Lord Stowell.
Lord Eldon’s wife, his dear “Bessy,” his love for whom is a
beautiful feature in his life, died before him, on the 28th of June
1831. By nature she was of simple character, and by habits
acquired during the early portion of her husband’s career almost
a recluse. Two of their sons reached maturity—John, who
died in 1805, and William Henry John, who died unmarried
in 1832. Lord Eldon himself survived almost all his immediate
relations. His brother William died in 1836. He himself died
in London on the 13th of January 1838, leaving behind him two
daughters, Lady Frances Bankes and Lady Elizabeth Repton,
and a grandson John (1805-1854), who succeeded him as second
earl, the title subsequently passing to the latter’s son John
(b. 1846).
Lord Eldon was no legislator—his one aim in politics was to
keep in office, and maintain things as he found them; and almost
the only laws he helped to pass were laws for popular coercion.
For nearly forty years he fought against every improvement in
law, or in the constitution—calling God to witness, on the smallest
proposal of reform, that he foresaw from it the downfall of his
country. Without any political principles, properly so called,
and without interest in or knowledge of foreign affairs, he maintained
himself and his party in power for an unprecedented
period by his great tact, and in virtue of his two great political
properties—of zeal against every species of reform, and zeal
against the Roman Catholics. To pass from his political to his
judicial character is to shift to ground on which his greatness
is universally acknowledged. His judgments, which have
received as much praise for their accuracy as abuse for their
clumsiness and uncouthness, fill a small library. But though
intimately acquainted with every nook and cranny of the English
law, he never carried his studies into foreign fields, from which
to enrich our legal literature; and it must be added that against
the excellence of his judgments, in too many cases, must be set
off the hardships, worse than injustice, that arose from his
protracted delays in pronouncing them. A consummate judge
and the narrowest of politicians, he was doubt on the bench,
and promptness itself in the political arena. For literature, as
for art, he had no feeling. What intervals of leisure he enjoyed
from the cares of office he filled up with newspapers and the
gossip of old cronies. Nor were his intimate associates men of
refinement and taste; they were rather good fellows who quietly
enjoyed a good bottle and a joke; he uniformly avoided encounters
of wit with his equals. He is said to have been
parsimonious, and certainly he was quicker to receive than to
reciprocate hospitalities; but his mean establishment and mode
of life are explained by the retired habits of his wife, and her
168
dislike of company. His manners were very winning and courtly,
and in the circle of his immediate relatives he is said to have
always been lovable and beloved.
“In his person,” says Lord Campbell, “Lord Eldon was about
the middle size, his figure light and athletic, his features regular
and handsome, his eye bright and full, his smile remarkably
benevolent, and his whole appearance prepossessing. The
advance of years rather increased than detracted from these
personal advantages. As he sat on the judgment-seat, ‘the deep
thought betrayed in his furrowed brow—the large eyebrows,
overhanging eyes that seemed to regard more what was taking
place within than around him—his calmness, that would have
assumed a character of sternness but for its perfect placidity—his
dignity, repose and venerable age, tended at once to win
confidence and to inspire respect’ (Townsend). He had a voice
both sweet and deep-toned, and its effect was not injured by his
Northumbrian burr, which, though strong, was entirely free from
harshness and vulgarity.”
Authorities.—Horace Twiss, Life of Lord Chancellor Eldon
(1844); W.E. Surtees, Sketch of the Lives of Lords Stowell and
Eldon (1846); Lord Campbell, Lives of the Chancellors; W.C.
Townsend, Lives of Twelve Eminent Judges (1846); Greville Memoirs.
EL DORADO (Span. “the gilded one”), a name applied, first,
to the king or chief priest of a South American tribe who was said
to cover himself with gold dust at a yearly religious festival held
near Santa Fé de Bogotá; next, to a legendary city called Manoa
or Omoa; and lastly, to a mythical country in which gold and
precious stones were found in fabulous abundance. The legend,
which has never been traced to its ultimate source, had many
variants, especially as regards the situation attributed to Manoa.
It induced many Spanish explorers to lead expeditions in search
of treasure, but all failed. Among the most famous were the
expedition undertaken by Diego de Ordaz, whose lieutenant
Martinez claimed to have been rescued from shipwreck, conveyed
inland, and entertained at Omoa by “El Dorado” himself (1531);
and the journeys of Orellana (1540-1541), who passed down the
Rio Napo to the valley of the Amazon; that of Philip von Hutten
(1541-1545), who led an exploring party from Coro on the coast of
Caracas; and of Gonzalo Ximenes de Quesada (1569), who started
from Santa Fé de Bogotá. Sir Walter Raleigh, who resumed the
search in 1595, described Manoa as a city on Lake Parimá in
Guiana. This lake was marked on English and other maps until
its existence was disproved by A. von Humboldt (1769-1859).
Meanwhile the name of El Dorado came to be used metaphorically
of any place where wealth could be rapidly acquired. It was
given to a county in California, and to towns and cities in various
states. In literature frequent allusion is made to the legend,
perhaps the best-known references being those in Milton’s
Paradise Lost (vi. 411) and Voltaire’s Candide (chs. 18, 19).
See A.F.A. Bandelier, The Gilded Man, El Dorado (New York,
1893).
ELDUAYEN, JOSÉ DE, 1st Marquis del Pazo de la Merced
(1823-1898), Spanish politician, was born in Madrid on the
22nd of June 1823. He was educated in the capital, took the
degree of civil engineer, and as such directed important works
in Asturias and Galicia, entered the Cortes in 1856 as deputy
for Vigo, and sat in all the parliaments until 1867 as member of
the Union Liberal with Marshal O’Donnell. He attacked the
Miraflores cabinet in 1864, and became under-secretary of the
home office when Canovas was minister in 1865. He was made a
councillor of state in 1866, and in 1868 assisted the other members
of the Union Liberal in preparing the revolution. In the Cortes
of 1872 he took much part in financial debates. He accepted
office as member of the last Sagasta cabinet under King Amadeus.
On the proclamation of the republic Elduayen very earnestly
co-operated in the Alphonsist conspiracy, and endeavoured to
induce the military and politicians to work together. He went
abroad to meet and accompany the prince after the pronunciamiento
of Marshal Campos, landed with him at Valencia, was made
governor of Madrid, a marquis, grand cross of Charles III., and
minister for the colonies in 1878. He accepted the portfolio of
foreign affairs in the Canovas cabinet from 1883 to 1885, and was
made a life senator. He always prided himself on having been
one of the five members of the Cortes of 1870 who voted for
Alphonso XII. when that parliament elected Amadeus of Savoy.
He died at Madrid on the 24th of June 1898.
ELEANOR OF AQUITAINE (c. 1122-1204), wife of the English
king Henry II., was the daughter and heiress of Duke William X.
of Aquitaine, whom she succeeded in April 1137. In accordance
with arrangements made by her father, she at once married
Prince Louis, the heir to the French crown, and a month later her
husband became king of France under the title of Louis VII.
Eleanor bore Louis two daughters but no sons. This was probably
the reason why their marriage was annulled by mutual consent
in 1151, but contemporary scandal-mongers attributed the
separation to the king’s jealousy. It was alleged that, while
accompanying her husband on the Second Crusade (1146-1149),
Eleanor had been unduly familiar with her uncle, Raymond of
Antioch. Chronology is against this hypothesis, since Louis and
she lived on good terms together for two years after the Crusade.
There is still less ground for the supposition that Henry of Anjou,
whom she married immediately after the divorce, had been her
lover before it. This second marriage, with a youth some years
her junior, was purely political. The duchy of Aquitaine required
a strong ruler, and the union with Anjou was eminently desirable.
Louis, who had hoped that Aquitaine would descend to his
daughters, was mortified and alarmed by the Angevin marriage;
all the more so when Henry of Anjou succeeded to the English
crown in 1154. From this event dates the beginning of the
secular strife between England and France which runs like a red
thread through medieval history.
Eleanor bore to her second husband five sons and three
daughters; John, the youngest of their children, was born in
1167. But her relations with Henry passed gradually through
indifference to hatred. Henry was an unfaithful husband, and
Eleanor supported her sons in their great rebellion of 1173.
Throughout the latter years of the reign she was kept in a sort of
honourable confinement. It was during her captivity that Henry
formed his connexion with Rosamond Clifford, the Fair Rosamond
of romance. Eleanor, therefore, can hardly have been
responsible for the death of this rival, and the romance of the
poisoned bowl appears to be an invention of the next century.
Under the rule of Richard and John the queen became a
political personage of the highest importance. To both her sons
the popularity which she enjoyed in Aquitaine was most valuable.
But in other directions also she did good service. She helped to
frustrate the conspiracy with France which John concocted
during Richard’s captivity. She afterwards reconciled the king
and the prince, thus saving for John the succession which he had
forfeited by his misconduct. In 1199 she crushed an Angevin
rising in favour of John’s nephew, Arthur of Brittany. In 1201
she negotiated a marriage between her grand-daughter, Blanche
of Castile, and Louis of France, the grandson of her first husband.
It was through her staunch defence of Mirabeau in Poitou that
John got possession of his nephew’s person. She died on the 1st
of April 1204, and was buried at Fontevrault. Although a woman
of strong passions and great abilities she is, historically, less
important as an individual than as the heiress of Aquitaine, a part
of which was, through her second marriage, united to England for
some four hundred years.
See the chronicles cited for the reigns of Henry II., Richard I.
and John. Also Sir J.H. Ramsay, Angevin Empire (London, 1903);
K. Norgate, England under the Angevin Kings (London, 1887);
and A. Strickland, Lives of the Queens of England, vol. i. (1841).
(H. W. C. D.)
ELEATIC SCHOOL, a Greek school of philosophy which came
into existence towards the end of the 6th century B.C., and
ended with Melissus of Samos (fl. c. 450 B.C.). It took its
name from Elea, a Greek city of lower Italy, the home of its
chief exponents, Parmenides and Zeno. Its foundation is often
attributed to Xenophanes of Colophon, but, although there is
much in his speculations which formed part of the later Eleatic
doctrine, it is probably more correct to regard Parmenides as
the founder of the school. At all events, it was Parmenides who
gave it its fullest development. The main doctrines of the
Eleatics were evolved in opposition, on the one hand, to the
169
physical theories of the early physical philosophers who explained
all existence in terms of primary matter (see Ionian School),
and, on the other hand, to the theory of Heraclitus that all
existence may be summed up as perpetual change. As against
these theories the Eleatics maintained that the true explanation
of things lies in the conception of a universal unity of being.
The senses with their changing and inconsistent reports cannot
cognize this unity; it is by thought alone that we can pass
beyond the false appearances of sense and arrive at the knowledge
of being, at the fundamental truth that “the All is One.” There
can be no creation, for being cannot come from not-being; a
thing cannot arise from that which is different from it. The
errors of common opinion arise to a great extent from the
ambiguous use of the verb “to be,” which may imply existence
or be merely the copula which connects subject and predicate.
In these main contentions the Eleatic school achieved a real
advance, and paved the way to the modern conception of metaphysics.
Xenophanes in the middle of the 6th century had
made the first great attack on the crude mythology of early Greece,
including in his onslaught the whole anthropomorphic system
enshrined in the poems of Homer and Hesiod. In the hands of
Parmenides this spirit of free thought developed on metaphysical
lines. Subsequently, whether from the fact that such bold
speculations were obnoxious to the general sense of propriety
in Elea, or from the inferiority of its leaders, the school degenerated
into verbal disputes as to the possibility of motion,
and similar academic trifling. The best work of the school was
absorbed in the Platonic metaphysic (see E. Caird, Evolution
of Theology in the Greek Philosophers, 1904).
See further the articles on Xenophanes; Parmenides; Zeno
(of Elea); Melissus, with the works there quoted; also the histories
of philosophy by Zeller, Gomperz, Windelband, &c.
ELECAMPANE (Med. Lat. Enula Campana), a perennial
composite plant, the Inula Helenium of botanists, which is
common in many parts of Britain, and ranges throughout
central and southern Europe, and in Asia as far eastwards as
the Himalayas. It is a rather rigid herb, the stem of which
attains a height of from 3 to 5 ft.; the leaves are large and
toothed, the lower ones stalked, the rest embracing the stem; the
flowers are yellow, 2 in. broad, and have many rays, each three-notched
at the extremity. The root is thick, branching and
mucilaginous, and has a warm, bitter taste and a camphoraceous
odour. For medicinal purposes it should be procured from
plants not more than two or three years old. Besides inulin,
C12H20O10, a body isomeric with starch, the root contains helenin,
C6H8O, a stearoptene, which may be prepared in white acicular
crystals, insoluble in water, but freely soluble in alcohol. When
freed from the accompanying inula-camphor by repeated
crystallization from alcohol, helenin melts at 110° C. By the
ancients the root was employed both as a medicine and as a
condiment, and in England it was formerly in great repute as
an aromatic tonic and stimulant of the secretory organs. “The
fresh roots of elecampane preserved with sugar, or made into a
syrup or conserve,” are recommended by John Parkinson in
his Theatrum Botanicum as “very effectual to warm a cold and
windy stomack, and the pricking and stitches therein or in the
sides caused by the Spleene, and to helpe the cough, shortnesse
of breath, and wheesing in the Lungs.” As a drug, however,
the root is now seldom resorted to except in veterinary practice,
though it is undoubtedly possessed of antiseptic properties. In
France and Switzerland it is used in the manufacture of absinthe.
ELECTION (from Lat. eligere, to pick out), the method by
which a choice or selection is made by a constituent body (the
electors or electorate) of some person to fill a certain office or
dignity. The procedure itself is called an election. Election,
as a special form of selection, is naturally a loose term covering
many subjects; but except in the theological sense (the doctrine
of election), as employed by Calvin and others, for the choice
by God of His “elect,” the legal sense (see Election, in law,
below), and occasionally as a synonym for personal choice (one’s
own “election”), it is confined to the selection by the preponderating
vote of some properly constituted body of electors
of one of two or more candidates, sometimes for admission only
to some private social position (as in a club), but more particularly
in connexion with public representative positions in political
government. It is thus distinguished from arbitrary methods
of appointment, either where the right of nominating rests in an
individual, or where pure chance (such as selection by lot)
dictates the result. The part played by different forms of
election in history is alluded to in numerous articles in this work,
dealing with various countries and various subjects. It is only
necessary here to consider certain important features in the
elections, as ordinarily understood, namely, the exercise of the
right of voting for political and municipal offices in the United
Kingdom and America. See also the articles Parliament;
Representation; Voting; Ballot, &c., and United
States: Political Institutions. For practical details as to the
conduct of political elections in England reference must be made
to the various text-books on the subject; the candidate and his
election agent require to be on their guard against any false
step which might invalidate his return.
Law in the United Kingdom.—Considerable alterations have
been made in recent years in the law of Great Britain and Ireland
relating to the procedure at parliamentary and municipal
elections, and to election petitions.
As regards parliamentary elections (which may be either the
“general election,” after a dissolution of parliament, or “by-elections,”
when casual vacancies occur during its continuance),
the most important of the amending statutes is the Corrupt
and Illegal Practices Act 1883. This act, and the Parliamentary
Elections Act 1868, as amended by it, and other enactments
dealing with corrupt practices, are temporary acts requiring
annual renewal. As regards municipal elections, the Corrupt
Practices (Municipal Elections) Act 1872 has been repealed by
the Municipal Corporations Act 1882 for England, and by the
Local Government (Ireland) Act 1898 for Ireland. The governing
enactments for England are now the Municipal Corporations
Act 1882, part iv., and the Municipal Elections (Corrupt and
Illegal Practices) Act 1884, the latter annually renewable. The
provisions of these enactments have been applied with necessary
modifications to municipal and other local government elections
in Ireland by orders of the Irish Local Government Board made
under powers conferred by the Local Government (Ireland) Act
1898. In Scotland the law regulating municipal and other
local government elections is now to be found in the Elections
(Scotland) (Corrupt and Illegal Practices) Act 1890.
The alterations in the law have been in the direction of
greater strictness in regard to the conduct of elections, and
increased control in the public interest over the proceedings
on election petitions. Various acts and payments which were
previously lawful in the absence of any corrupt bargain or
motive are now altogether forbidden under the name of “illegal
practices” as distinguished from “corrupt practices.” Failure
on the part of a parliamentary candidate or his election agent
to comply with the requirements of the law in any particular
is sufficient to invalidate the return (see the articles Bribery
and Corrupt Practices). Certain relaxations are, however,
allowed in consideration of the difficulty of absolutely avoiding
all deviation from the strict rules laid down. Thus, where the
judges who try an election petition report that there has been
treating, undue influence, or any illegal practice by the candidate
or his election agent, but that it was trivial, unimportant and
of a limited character, and contrary to the orders and without
the sanction or connivance of the candidate or his election agent,
and that the candidate and his election agent took all reasonable
means for preventing corrupt and illegal practices, and that the
election was otherwise free from such practices on their part,
the election will not be avoided. The court has also the power
to relieve from the consequences of certain innocent contraventions
of the law caused by inadvertence or miscalculation.
The inquiry into a disputed parliamentary election was
formerly conducted before a committee of the House of Commons,
chosen as nearly as possible from both sides of the House for that
particular business. The decisions of these tribunals laboured
170
under the suspicion of being prompted by party feeling, and by an
act of 1868 the jurisdiction was finally transferred to judges of
the High Court, notwithstanding the general unwillingness of the
bench to accept a class of business which they feared might bring
their integrity into dispute. Section 11 of the act ordered, inter
alia, that the trial of every election petition shall be conducted
before a puisne judge of one of the common law courts at Westminster
and Dublin; that the said courts shall each select a
judge to be placed on the rota for the trial of election petitions;
that the said judges shall try petitions standing for trial according
to seniority or otherwise, as they may agree; that the trial shall
take place in the county or borough to which the petition refers,
unless the court should think it desirable to hold it elsewhere.
The judge shall determine “whether the member whose return
is complained of, or any and what other person, was duly returned
and elected, or whether the election was void,” and shall certify
his determination to the speaker. When corrupt practices have
been charged the judge shall also report (1) whether any such
practice has been committed by or with the knowledge or consent
of any candidate, and the nature thereof; (2) the names of persons
proved to have been guilty of any corrupt practice; and (3)
whether corrupt practices have extensively prevailed at the
election. Questions of law were to be referred to the decision of
the court of common pleas. On the abolition of that court by the
Judicature Act 1873, the jurisdiction was transferred to the
common pleas division, and again on the abolition of that
Election petitions.
division was transferred to the king’s bench division,
in whom it is now vested. The rota of judges for
the trial of election petitions is also supplied by the
king’s bench division. The trial now takes place before two
judges instead of one; and, when necessary, the number of
judges on the rota may be increased. Both the judges who try a
petition are to sign the certificates to be made to the speaker. If
they differ as to the validity of a return, they are to state such
difference in their certificate, and the return is to be held good;
if they differ as to a report on any other matter, they are to
certify their difference and make no report on such matter.
The director of public prosecutions attends the trial personally or
by representative. It is his duty to watch the proceedings in the
public interest, to issue summonses to witnesses whose evidence
is desired by the court, and to prosecute before the election court
or elsewhere those persons whom he thinks to have been guilty of
corrupt or illegal practices at the election in question. If an
application is made for leave to withdraw a petition, copies of the
affidavits in support are to be delivered to him; and he is
entitled to be heard and to call evidence in opposition to such
application. Witnesses are not excused from answering criminating
questions; but their evidence cannot be used against them in
any proceedings except criminal proceedings for perjury in
respect of that evidence. If a witness answers truly all questions
which he is required by the court to answer, he is entitled to
receive a certificate of indemnity, which will save him from all
proceedings for any offence under the Corrupt Practices Acts
committed by him before the date of the certificate at or in
relation to the election, except proceedings to enforce any
incapacity incurred by such offence. An application for leave to
withdraw a petition must be supported by affidavits from all the
parties to the petition and their solicitors, and by the election
agents of all of the parties who were candidates at the election.
Each of these affidavits is to state that to the best of the deponent’s
knowledge and belief there has been no agreement and
no terms or undertaking made or entered into as to the withdrawal,
or, if any agreement has been made, shall state its terms.
The applicant and his solicitor are also to state in their affidavits
the grounds on which the petition is sought to be withdrawn. If
any person makes an agreement for the withdrawal of a petition
in consideration of a money payment, or of the promise that the
seat shall be vacated or another petition withdrawn, or omits to
state in his affidavit that he has made an agreement, lawful or
unlawful, for the withdrawal, he is guilty of an indictable
misdemeanour. The report of the judges to the speaker is to
contain particulars as to illegal practices similar to those
previously required as to corrupt practices; and they are to
report further whether any candidate has been guilty by his
agents of an illegal practice, and whether certificates of indemnity
have been given to persons reported guilty of corrupt or illegal
practices.
The Corrupt Practices Acts apply, with necessary variations
in details, to parliamentary elections in Scotland and Ireland.
The amendments in the law as to municipal elections are
generally similar to those which have been made in parliamentary
election law. The procedure on trial of petitions is substantially
the same, and wherever no other provision is made by the acts or
rules the procedure on the trial of parliamentary election petitions
is to be followed. Petitions against municipal elections were
dealt with in 35 & 36 Vict. c. 60. The election judges appoint
a number of barristers, not exceeding five, as commissioners to
try such petitions. No barrister can be appointed who is of less
than fifteen years’ standing, or a member of parliament, or holder
of any office of profit (other than that of recorder) under the
crown; nor can any barrister try a petition in any borough in
which he is recorder or in which he resides, or which is included in
his circuit. The barrister sits without a jury. The provisions are
generally similar to those relating to parliamentary elections. The
petition may allege that the election was avoided as to the
borough or ward on the ground of general bribery, &c., or that the
election of the person petitioned against was avoided by corrupt
practices, or by personal disqualification, or that he had not the
majority of lawful votes. The commissioner who tries a petition
sends to the High Court a certificate of the result, together with
reports as to corrupt and illegal practices, &c., similar to those
made to the speaker by the judges who try a parliamentary
election petition. The Municipal Elections (Corrupt and Illegal
Practices) Act 1884 applied to school board elections subject to
certain variations, and has been extended by the Local Government
Act 1888 to county council elections, and by the Local
Government Act 1894 to elections by parochial electors. The
law in Scotland is on the same lines, and extends to all non-parliamentary
elections, and, as has been stated, the English
statutes have been applied with adaptations to all municipal
and local government elections in Ireland.
United States.—Elections are much more frequent in the United
States than they are in Great Britain, and they are also more
complicated. The terms of elective officers are shorter; and as
there are also more offices to be filled, the number of persons to
be voted for is necessarily much greater. In the year of a
presidential election the citizen may be called upon to vote at one
time for all of the following: (1) National candidates—president
and vice-president (indirectly through the electoral college) and
members of the House of Representatives; (2) state candidates—governor,
members of the state legislature, attorney-general,
treasurer, &c.; (3) county candidates—sheriff, county judges,
district attorney, &c.; (4) municipal or town candidates—mayor,
aldermen, selectmen, &c. The number of persons actually voted
for may therefore be ten or a dozen, or it may be many more.
In addition, the citizen is often called upon to vote yea or nay on
questions such as amendments to the state constitutions, granting
of licences, and approval or disapproval of new municipal
undertakings. As there may be, and generally is, more than one
candidate for each office, and as all elections are now, and have
been for many years, conducted by ballot, the total number of
names to appear on the ballot may be one hundred or may be
several hundred. These names are arranged in different ways,
according to the laws of the different states. Under the Massachusetts
law, which is considered the best by reformers, the names
of candidates for each office are arranged alphabetically on a
“blanket” ballot, as it is called from its size, and the elector
places a mark opposite the names of such candidates as he may
wish to vote for. Other states, New York for example, have the
blanket system, but the names of the candidates are arranged in
party columns. Still other states allow the grouping on one
ballot of all the candidates of a single party, and there would be
therefore as many separate ballots in such states as there were
parties in the field.
171
The qualifications for voting, while varying in the different
states in details, are in their main features the same throughout
the Union. A residence in the state is required of from three
months to two years. Residence is also necessary, but for a
shorter period, in the county, city or town, or voting precinct.
A few states require the payment of a poll tax. Some require
that the voter shall be able to read and understand the Constitution.
This latter qualification has been introduced into several
of the Southern states, partly at least to disqualify the ignorant
coloured voters. In all, or practically all, the states idiots,
convicts and the insane are disqualified; in some states paupers;
in some of the Western states the Chinese. In some states
women are allowed to vote on certain questions, or for the
candidates for certain offices, especially school officials; and in
four of the Western states women have the same rights of
suffrage as men. The number of those who are qualified to vote,
but do not avail themselves of the right, varies greatly in the
different states and according to the interest taken in the election.
As a general rule, but subject to exceptions, the national elections
call out the largest number, the state elections next, and the local
elections the smallest number of voters. In an exciting national
election between 80 and 90% of the qualified voters actually
vote, a proportion considerably greater than in Great Britain or
Germany.
The tendency of recent years has been towards a decrease both
in the number and in the frequency of elections. A president and
vice-president are voted for every fourth year, in the years
divisible by four, on the first Tuesday following the first Monday
of November. Members of the national House of Representatives
are chosen for two years on the even-numbered years.
State and local elections take place in accordance with state laws,
and may or may not be on the same day as the national elections.
Originally the rule was for the states to hold annual elections; in
fact, so strongly did the feeling prevail of the need in a democratic
country for frequent elections, that the maxim “where annual
elections end, tyranny begins,” became a political proverb. But
opinion gradually changed even in the older or Eastern states,
and in 1909 Massachusetts and Rhode Island were the only states
in the Union holding annual elections for governor and both
houses of the state legislature. In the Western states especially
state officers are chosen for longer terms—in the case of the
governor often for four years—and the number of elections has
correspondingly decreased. Another cause of the decrease in the
number of elections is the growing practice of holding all the
elections of any year on one and the same day. Before the Civil
War Pennsylvania held its state elections several months before
the national elections. Ohio and Indiana, until 1885 and 1881
respectively, held their state elections early in October. Maine,
Vermont and Arkansas keep to September. The selection of one
day in the year for all elections held in that year has resulted
in a considerable decrease in the total number.
Another tendency of recent years, but not so pronounced, is to
hold local elections in what is known as the “off” year; that is,
on the odd-numbered year, when no national election is held.
The object of this reform is to encourage independent voting.
The average American citizen is only too prone to carry his
national political predilections into local elections, and to vote for
the local nominees of his party, without regard to the question of
fitness of candidates and the fundamental difference of issues
involved. This tendency to vote the entire party ticket is the
more pronounced because under the system of voting in use in
many of the states all the candidates of the party are arranged on
one ticket, and it is much easier to vote a straight or unaltered
ticket than to change or “scratch” it. Again, the voter,
especially the ignorant one, refrains from scratching his ticket,
lest in some way he should fail to comply with the technicalities
of the law and his vote be lost. On the other hand, if local
elections are held on the “off” or odd year, and there be no
national or state candidates, the voter feels much more free to
select only those candidates whom he considers best qualified for
the various offices.
On the important question of the purity of elections it is
difficult to speak with precision. In many of the states, especially
those with an enlightened public spirit, such as most of the
New England states and many of the North-Western, the elections
are fairly conducted, there being no intimidation at all, little or no
bribery, and an honest count. It can safely be said that through
the Union as a whole the tendency of recent years has been
decidedly towards greater honesty of elections. This is owing to
a number of causes: (1) The selection of a single day for all
elections, and the consequent immense number voting on that
day. Some years ago, when for instance the Ohio and Indiana
elections were held a few weeks before the general election, each
party strained every nerve to carry them, for the sake of prestige
and the influence on other states. In fact, presidential elections
were often felt to turn on the result in these early voting states,
and the party managers were none too scrupulous in the means
employed to carry them. Bribery has decreased in such states
since the change of election day to that of the rest of the country.
(2) The enactment in most of the states of the Australian or
secret ballot (q.v.) laws. These have led to the secrecy of the
ballot, and hence to a greater or less extent have prevented
intimidation and bribery. (3) Educational or other such test,
more particularly in the Southern states, the object of which is to
exclude the coloured, and especially the ignorant coloured, voters
from the polls. In those southern states in which the coloured
vote was large, and still more in those in which it was the majority,
it was felt among the whites that intimidation or ballot-box
stuffing was justified by the necessity of white supremacy. With
the elimination of the coloured vote by educational or other tests
the honesty of elections has increased. (4) The enactment of new
and more stringent registration laws. Under these laws only
those persons are allowed to vote whose names have been placed
on the rolls a certain number of days or months before election.
These rolls are open to public inspection, and the names may be
challenged at the polls, and “colonization” or repeating is
therefore almost impossible. (5) The reform of the civil service
and the gradual elimination of the vicious principle of “to the
victors belong the spoils.” With the reform of the civil service
elections become less a scramble for office and more a contest of
political or economic principle. They bring into the field,
therefore, a better class of candidates. (6) The enactment in a
number of states of various other laws for the prevention of corrupt
practices, for the publication of campaign expenses, and for the
prohibition of party workers from coming within a certain
specified distance of the polls. In the state of Massachusetts, for
instance, an act passed in 1892, and subsequently amended,
provides that political committees shall file a full statement, duly
sworn to, of all campaign expenditures made by them. The act
applies to all public elections except that of town officers, and also
covers nominations by caucuses and conventions as well. Apart
from his personal expenses such as postage, travelling expenses,
&c., a candidate is prohibited from spending anything himself to
promote either his nomination or his election, but he is allowed
to contribute to the treasury of the political committee. The law
places no limit on the amount that these committees may spend.
The reform sought by the law is thorough publicity, and not only
are details of receipts and expenditures to be published, but the
names of contributors and the amount of their contributions. In
the state of New York the act which seeks to prevent corrupt
practices relies in like manner on the efficacy of publicity, but
it is less effective than the Massachusetts law in that it provides
simply for the filing by the candidates themselves of sworn
statements of their own expenses. There is nothing to prevent
their contributing to political committees, and the financial
methods and the amounts expended by such committees are not
made public. But behind all these causes that have led to more
honest elections lies the still greater one of a healthier public
spirit. In the reaction following the Civil War all reforms halted.
In recent years, however, a new and healthier interest has sprung
up in things political; and one result of this improved civic
spirit is seen in the various laws for purification of elections. It
may now be safely affirmed that in the majority of states the
elections are honestly conducted; that intimidation, bribery,
172
stuffing of the ballot boxes or other forms of corruption, when
they exist, are owing in large measure to temporary or local
causes; and that the tendency of recent years has been towards
a decrease in all forms of corruption.
The expenses connected with elections, such as the renting and
preparing of the polling-places, the payment of the clerks and
other officers who conduct the elections and count the vote, are
borne by the community. A candidate therefore is not, as far
as the law is concerned, liable to any expense whatever. As a
matter of fact he does commonly contribute to the party treasury,
though in the case of certain candidates, particularly those for the
presidency and for judicial offices, financial contributions are not
general. The amount of a candidate’s contribution varies
greatly, according to the office sought, the state in which he lives,
and his private wealth. On one occasion, in a district in New
York, a candidate for Congress is credibly believed to have spent
at one election $50,000. On the other hand, in a Congressional
election in a certain district in Massachusetts, the only expenditure
of one of the candidates was for the two-cent stamp
placed on his letter of acceptance. No estimate of the average
amount expended can be made. It is, however, the conclusion of
Mr Bryce, in his American Commonwealth, that as a rule a seat in
Congress costs the candidate less than a seat for a county
division in the House of Commons. (See also Ballot.)
ELECTION, in English law, the obligation imposed upon a
party by courts of equity to choose between two inconsistent
or alternative rights or claims in cases where there is a clear
intention of the person from whom he derives one that he should
not enjoy both. Thus a testator died seized of property in fee
simple and in fee tail—he had two daughters, and devised the
fee simple property to one and the entailed property to the other;
the first one claimed to have her share of the entailed property
as coparcener and also to retain the benefit she took under the
will. It was held that she was put to her election whether she
would take under the will and renounce her claim to the entailed
property or take against the will, in which case she must renounce
the benefits she took under the will in so far as was necessary
to compensate her sister. As the essence of the doctrine is
compensation, a person electing against a document does not
lose all his rights under it, but the court will sequester so much
only of the benefit intended for him as will compensate the persons
disappointed by his election. For the same reason it is necessary
that there should be a free and disposable fund passing by the
instrument from which compensation can be made in the event
of election against the will. If, therefore, a man having a special
power of appointment appoint the fund equally between two
persons, one being an object of the power and the other not an
object, no question of election arises, but the appointment to
the person not an object is bad.
Election, though generally arising in cases of wills, may also
arise in the case of a deed. There is, however, a distinction to
be observed. In the case of a will a clear intention on the part
of the testator that he meant to dispose of property not his own
must be shown, and parol evidence is not admissible as to this.
In the case of a deed, however, no such intention need be shown,
for if a deed confers a benefit and imposes a liability on the same
person he cannot be allowed to accept the one and reject the other,
but this must be distinguished from cases where two separate
gifts are given to a person, one beneficial and the other onerous.
In such a case no question of election arises and he may take
the one and reject the other, unless, indeed, there are words
used which make the one conditional on the acceptance of the
other.
Election is either express, e.g. by deed, or implied; in the
latter case it is often a question of considerable difficulty
whether there has in fact been an election or not; each case
must depend upon the particular circumstances, but quite
generally it may be said that the person who has elected must
have been capable of electing, aware of the existence of the
doctrine of election, and have had the opportunity of satisfying
himself of the relative value of the properties between which
he has elected. In the case of infants the court will sometimes
elect after an inquiry as to which course is the most advantageous,
or if there is no immediate urgency, will allow the matter to stand
over till the infant attains his majority. In the cases of married
women and lunatics the courts will exercise the right for them.
It sometimes happens that the parties have so dealt with
the property that it would be inequitable to disturb it; in
such cases the court will not interfere in order to allow of
election.
ELECTORAL COMMISSION, in United States history, a
commission created to settle the disputed presidential election
of 1876. In this election Samuel J. Tilden, the Democratic
candidate, received 184 uncontested electoral votes, and Rutherford
B. Hayes, the Republican candidate, 163.1 The states of
Florida, Louisiana, Oregon and South Carolina, with a total
of 22 votes, each sent in two sets of electoral ballots,2 and from
each of these states except Oregon one set gave the whole vote
to Tilden and the other gave the whole vote to Hayes. From
Oregon one set of ballots gave the three electoral votes of the
state to Hayes; the other gave two votes to Hayes and one to
Tilden.
The election of a president is a complex proceeding, the method
being indicated partly in the Constitution, and being partly left
to Congress and partly to the states. The manner of selecting
the electors is left to state law; the electoral ballots are sent
to the president of the Senate, who “shall, in the presence of
the Senate and House of Representatives, open all certificates,
and the votes shall then be counted.” Concerning this provision
many questions of vital importance arose in 1876: Did the president
of the Senate count the votes, the houses being mere
witnesses; or did the houses count them, the president’s duties
being merely ministerial? Did counting imply the determination
of what should be counted, or was it a mere arithmetical process;
that is, did the Constitution itself afford a method of settling
disputed returns, or was this left to legislation by Congress?
Might Congress or an officer of the Senate go behind a state’s
certificate and review the acts of its certifying officials? Might
it go further and examine into the choice of electors? And if
it had such powers, might it delegate them to a commission?
As regards the procedure of Congress, it seems that, although
in early years the president of the Senate not only performed or
overlooked the electoral count but also exercised discretion in
some matters very important in 1876, Congress early began to
assert power, and, at least from 1821 onward, controlled the
count, claiming complete power. The fact, however, that the
Senate in 1876 was controlled by the Republicans and the House
by the Democrats, lessened the chances of any harmonious
settlement of these questions by Congress. The country seemed
on the verge of civil war. Hence it was that by an act of the
29th of January 1877, Congress created the Electoral Commission
to pass upon the contested returns, giving it “the same powers,
if any” possessed by itself in the premises, the decisions to stand
unless rejected by the two houses separately. The commission
was composed of five Democratic and five Republican Congressmen,
two justices of the Supreme Court of either party, and a
fifth justice chosen by these four. As its members of the commission
the Senate chose G.F. Edmunds of Vermont, O.P.
Morton of Indiana, and F.T. Frelinghuysen of New Jersey
(Republicans); and A.G. Thurman of Ohio and T.F. Bayard
of Delaware (Democrats). The House chose Henry B. Payne
of Ohio, Eppa Hunton of Virginia, and Josiah G. Abbott of
Massachusetts (Democrats); and George F. Hoar of Massachusetts
and James A. Garfield of Ohio (Republicans). The
Republican judges were William Strong and Samuel F. Miller;
the Democratic, Nathan Clifford and Stephen J. Field. These
four chose as the fifteenth member Justice Joseph P. Bradley,
173
a Republican but the only member not selected avowedly as a
partisan. As counsel for the Democratic candidate there appeared
before the commission at different times Charles O’Conor
of New York, Jeremiah S. Black of Pennsylvania, Lyman
Trumbull of Illinois, R.T. Merrick of the District of Columbia,
Ashbel Green of New Jersey, Matthew H. Carpenter of Wisconsin,
George Hoadley of Ohio, and W.C. Whitney of New York.
W.M. Evarts and E.W. Stoughton of New York and Samuel
Shellabarger and Stanley Matthews of Ohio appeared regularly
in behalf of Mr Hayes.
The popular vote seemed to indicate that Hayes had carried
South Carolina and Oregon, and Tilden Florida and Louisiana.
It was evident, however, that Hayes could secure the 185 votes
necessary to elect only by gaining every disputed ballot. As
the choice of Republican electors in Louisiana had been accomplished
by the rejection of several thousand Democratic votes
by a Republican returning board, the Democrats insisted that
the commission should go behind the returns and correct injustice;
the Republicans declared that the state’s action was
final, and that to go behind the returns would be invading its
sovereignty. When this matter came before the commission
it virtually accepted the Republican contention, ruling that it
could not go behind the returns except on the superficial issues
of manifest fraud therein or the eligibility of electors to their
office under the Constitution; that is, it could not investigate
antecedents of fraud or misconduct of state officials in the results
certified. All vital questions were settled by the votes of eight
Republicans and seven Democrats; and as the Republican
Senate would never concur with the Democratic House in overriding
the decisions, all the disputed votes were awarded to Mr
Hayes, who therefore was declared elected.
The strictly partisan votes of the commission and the adoption
by prominent Democrats and Republicans, both within and
without the commission, of an attitude toward states-rights
principles quite inconsistent with party tenets and tendencies,
have given rise to much severe criticism. The Democrats and
the country, however, quietly accepted the decision. The
judgments underlying it were two: (1) That Congress rightly
claimed the power to settle such contests within the limits set;
(2) that, as Justice Miller said regarding these limits, the people
had never at any time intended to give to Congress the power,
by naming the electors, to “decide who are to be the president
and vice-president of the United States.”
There is no doubt that Mr Tilden was morally entitled to the
presidency, and the correction of the Louisiana frauds would
certainly have given satisfaction then and increasing satisfaction
later, in the retrospect, to the country. The commission might
probably have corrected the frauds without exceeding its Congressional
precedents. Nevertheless, the principles of its
decisions must be recognized by all save ultra-nationalists as
truer to the spirit of the Constitution and promising more for
the good of the country than would have been the principles
necessary to a contrary decision.
By an act of the 3rd of February 1887 the electoral procedure
is regulated in great detail. Under this act determination by a
state of electoral disputes is conclusive, subject to certain
formalities that guarantee definite action and accurate certification.
These formalities constitute “regularity,” and are in all
cases judgable by Congress. When Congress is forced by the
lack or evident inconclusiveness of state action, or by conflicting
state action, to decide disputes, votes are lost unless both
houses concur.
Authorities.—J.F. Rhodes, History of the United States, vol. 7,
covering 1872-1877 (New York, 1906); P.L. Haworth, The Hayes-Tilden
disputed Presidential Election of 1876 (Cleveland, 1906);
J.W. Burgess, Political Science Quarterly, vol. 3 (1888), pp. 633-653,
“The Law of the Electoral Count”; and for the sources. Senate
Miscellaneous Document No. 5 (vol. 1), and House Miscel. Doc.
No. 13 (vol. 2), 44 Congress, 2 Session,—Count of the Electoral Vote.
Proceedings of Congress and Electoral Commission,—the latter
identical with Congressional Record, vol. 5, pt. 4, 44 Cong., 2 Session;
also about twenty volumes of evidence on the state elections involved.
The volume called The Presidential Counts (New York,
1877) was compiled by Mr. Tilden and his secretary.
1 The election of a vice-president was, of course, involved also.
William A. Wheeler was the Republican candidate, and Thomas A.
Hendricks the Democratic.
2 A second set of electoral ballots had also been sent in from
Vermont, where Hayes had received a popular majority vote of
24,000. As these ballots had been transmitted in an irregular
manner, the president of the Senate refused to receive them, and
was sustained in this action by the upper House.
ELECTORS (Ger. Kurfürsten, from Küren, O.H.G. kiosan,
choose, elect, and Fürst, prince), a body of German princes,
originally seven in number, with whom rested the election of
the German king, from the 13th until the beginning of the 19th
century. The German kings, from the time of Henry the
Fowler (919-936) till the middle of the 13th century, succeeded
to their position partly by heredity, and partly by election.
Primitive Germanic practice had emphasized the element of
heredity. Reges ex nobilitate sumunt: the man whom a German
tribe recognized as its king must be in the line of hereditary
descent from Woden; and therefore the genealogical trees of
early Teutonic kings (as, for instance, in England those of the
Kentish and West Saxon sovereigns) are carefully constructed
to prove that descent from the god which alone will constitute
a proper title for his descendants. Even from the first, however,
there had been some opening for election; for the principle of
primogeniture was not observed, and there might be several
competing candidates, all of the true Woden stock. One of
these competing candidates would have to be recognized (as
the Anglo-Saxons said, geceosan); and to this limited extent
Teutonic kings may be termed elective from the very first. In
the other nations of western Europe this element of election
dwindled, and the principle of heredity alone received legal
recognition; in medieval Germany, on the contrary, the principle
of heredity, while still exercising an inevitable natural force,
sank formally into the background, and legal recognition was
finally given to the elective principle. De facto, therefore, the
principle of heredity exercises in Germany a great influence,
an influence never more striking than in the period which follows
on the formal recognition of the elective principle, when the
Habsburgs (like the Metelli at Rome) fato imperatores fiunt:
de jure, each monarch owes his accession simply and solely to
the vote of an electoral college.
This difference between the German monarchy and the other
monarchies of western Europe may be explained by various
considerations. Not the least important of these is what seems
a pure accident. Whereas the Capetian monarchs, during the
three hundred years that followed on the election of Hugh Capet
in 987, always left an heir male, and an heir male of full age,
the German kings again and again, during the same period,
either left a minor to succeed to their throne, or left no issue
at all. The principle of heredity began to fail because there
were no heirs. Again the strength of tribal feeling in Germany
made the monarchy into a prize, which must not be the apanage
of any single tribe, but must circulate, as it were, from Franconian
to Saxon, from Saxon to Bavarian, from Bavarian to Franconian,
from Franconian to Swabian; while the growing power of the
baronage, and its habit of erecting anti-kings to emphasize its
opposition to the crown (as, for instance, in the reign of Henry
IV.), coalesced with and gave new force to the action of tribal
feeling. Lastly, the fact that the German kings were also
Roman emperors finally and irretrievably consolidated the growing
tendency towards the elective principle. The principle of
heredity had never held any great sway under the ancient Roman
Empire (see under Emperor); and the medieval Empire,
instituted as it was by the papacy, came definitely under the
influence of ecclesiastical prepossessions in favour of election.
The church had substituted for that descent from Woden, which
had elevated the old pagan kings to their thrones, the conception
that the monarch derived his crown from the choice of God,
after the manner of Saul; and the theoretical choice of God
was readily turned into the actual choice of the church, or, at
any rate, of the general body of churchmen. If an ordinary
king is thus regarded by the church as essentially elected, much
more will the emperor, connected as he is with the church as
one of its officers, be held to be also elected; and as a bishop
is chosen by the chapter of his diocese, so, it will be thought,
must the emperor be chosen by some corresponding body in his
empire. Heredity might be tolerated in a mere matter of kingship:
the precious trust of imperial power could not be allowed
to descend according to the accidents of family succession. To
Otto of Freising (Gesta Frid. ii. 1) it is already a point of right
174
vindicated for itself by the excellency of the Roman Empire,
as a matter of singular prerogative, that it should not descend
per sanguinis propaginem, sed per principum electionem.
The accessions of Conrad II. (see Wipo, Vita Cuonradi, c. 1-2),
of Lothair II. (see Narratio de electione Lotharii, M.G.H. Scriptt.
xii. p. 510), of Conrad III. (see Otto of Freising, Chronicon, vii.
22) and of Frederick I. (see Otto of Freising, Gesta Frid. ii. 1)
had all been marked by an element, more or less pronounced,
of election. That element is perhaps most considerable in the
case of Lothair, who had no rights of heredity to urge. Here
we read of ten princes being selected from the princes of the
various duchies, to whose choice the rest promise to assent, and
of these ten selecting three candidates, one of whom, Lothair,
is finally chosen (apparently by the whole assembly) in a somewhat
tumultuary fashion. In this case the electoral assembly
would seem to be, in the last resort, the whole diet of all the
princes. But a de facto pre-eminence in the act of election is
already, during the 12th century, enjoyed by the three Rhenish
archbishops, probably because of the part they afterwards
played at the coronation, and also by the dukes of the great
duchies—possibly because of the part they too played, as vested
for the time with the great offices of the household, at the coronation
feast.1 Thus at the election of Lothair it is the archbishop
of Mainz who conducts the proceedings; and the election is
not held to be final until the duke of Bavaria has given his assent.
The fact is that, votes being weighed by quality as well as by
quantity (see Diet), the votes of the archbishops and dukes,
which would first be taken, would of themselves, if unanimous,
decide the election. To prevent tumultuary elections, it was
well that the election should be left exclusively with these great
dignitaries; and this is what, by the middle of the 13th century,
had eventually been done.
The chaos of the interregnum from 1198 to 1212 showed the
way for the new departure; the chaos of the great interregnum
(1250-1273) led to its being finally taken. The decay of the great
duchies, and the narrowing of the class of princes into a close
corporation, some of whose members were the equals of the old
dukes in power, introduced difficulties and doubts into the
practice of election which had been used in the 12th century.
The contested election of the interregnum of 1198-1212 brought
these difficulties and doubts into strong relief. The famous
bull of Innocent III. (Venerabilem), in which he decided for
Otto IV. against Philip of Swabia, on the ground that, though
he had fewer votes than Philip, he had a majority of the votes
of those ad quos principaliter spectat electio, made it almost
imperative that there should be some definition of these principal
electors. The most famous attempt at such a definition is that
of the Sachsenspiegel, which was followed, or combated, by
many other writers in the first half of the 13th century.
Eventually the contested election of 1257 brought light and
definition. Here we find seven potentates acting—the same
seven whom the Golden Bull recognizes in 1356; and we find
these seven described in an official letter to the pope, as principes
vocem in hujusmodi electione habentes, qui sunt septem numero.
The doctrine thus enunciated was at once received. The pope
acknowledged it in two bulls (1263); a cardinal, in a commentary
on the bull Venerabilem of Innocent III., recognized it about
the same time; and the erection of statues of the seven electors
at Aix-la-Chapelle gave the doctrine a visible and outward
expression.
By the date of the election of Rudolph of Habsburg (1273)
the seven electors may be regarded as a definite body, with an
acknowledged right. But the definition and the acknowledgment
were still imperfect. (1) The composition of the electoral body
was uncertain in two respects. The duke of Bavaria claimed
as his right the electoral vote of the king of Bohemia; and the
practice of partitio in electoral families tended to raise further
difficulties about the exercise of the vote. The Golden Bull of
1356 settled both these questions. Bohemia (of which Charles
IV., the author of the Golden Bull, was himself the king) was
assigned the electoral vote in preference to Bavaria; and a
provision annexing the electoral vote to a definite territory,
declaring that territory indivisible, and regulating its descent
by the rule of primogeniture instead of partition, swept away the
old difficulties which the custom of partition had raised. After
1356 the seven electors are regularly the three Rhenish archbishops,
Mainz, Cologne and Trier, and four lay magnates, the
palatine of the Rhine, the duke of Saxony, the margrave of
Brandenburg, and the king of Bohemia; the three former
being vested with the three archchancellorships, and the four
latter with the four offices of the royal household (see Household).
(2) The rights of the seven electors, in their collective
capacity as an electoral college, were a matter of dispute with the
papacy. The result of the election, whether made, as at first,
by the princes generally or, as after 1257, by the seven electors
exclusively, was in itself simply the creation of a German king—an
electio in regem. But since 962 the German king was also,
after coronation by the pope, Roman emperor. Therefore the
election had a double result: the man elected was not only
electus in regem, but also promovendus ad imperium. The
difficulty was to define the meaning of the term promovendus.
Was the king elect inevitably to become emperor? or did the
promotio only follow at the discretion of the pope, if he thought
the king elect fit for promotion? and if so, to what extent, and
according to what standard, did the pope judge of such fitness?
Innocent III. had already claimed, in the bull Venerabilem,
(1) that the electors derived their power of election, so far as it
made an emperor, from the Holy See (which had originally “translated”
the Empire from the East to the West), and (2) that the
papacy had a jus et auctoritas examinandi personam electam in
regem et promovendam ad imperium. The latter claim he had
based on the fact that he anointed, consecrated and crowned
the emperor—in other words, that he gave a spiritual office
according to spiritual methods, which entitled him to inquire
into the fitness of the recipient of that office, as a bishop inquires
into the fitness of a candidate for ordination. Innocent had put
forward this claim as a ground for deciding between competing
candidates: Boniface VIII. pressed the claim against Albert I.
in 1298, even though his election was unanimous; while John
XXII. exercised it in its harshest form, when in 1324 he ex-communicated
Louis IV. for using the title and exerting the
rights even of king without previous papal confirmation. This
action ultimately led to a protest from the electors themselves,
whose right of election would have become practically meaningless,
if such assumptions had been tolerated. A meeting of the
electors (Kurverein) at Rense in 1338 declared (and the declaration
was reaffirmed by a diet at Frankfort in the same year)
that postquam aliquis eligitur in Imperatorem sive Regem ab
Electoribus Imperii concorditer, vel majori parte eorundem, statim
ex sola electione est Rex verus et Imperator Romanus censendus
... nec Papae sive Sedis Apostolicae ... approbatione ...
indiget. The doctrine thus positively affirmed at Rense is
negatively reaffirmed in the Golden Bull, in which a significant
silence is maintained in regard to papal rights. But the doctrine
was not in practice followed: Sigismund himself did not venture
to dispense with papal approbation.
By the end of the 14th century the position of the electors,
both individually and as a corporate body, had become definite
and precise. Individually, they were distinguished from all
other princes, as we have seen, by the indivisibility of their
territories and by the custom of primogeniture which secured
that indivisibility; and they were still further distinguished by
the fact that their person, like that of the emperor himself, was
protected by the law of treason, while their territories were only
subject to the jurisdiction of their own courts. They were
independent territorial sovereigns; and their position was at
once the envy and the ideal of the other princes of Germany.
Such had been the policy of Charles IV.; and thus had he, in the
Golden Bull, sought to magnify the seven electors, and himself
175
as one of the seven, in his capacity of king of Bohemia, even at
the expense of the Empire, and of himself in his capacity of
emperor. Powerful as they were, however, in their individual
capacity, the electors showed themselves no less powerful as a
corporate body. As such a corporate body, they may be considered
from three different points of view, and as acting in
three different capacities. They are an electoral body, choosing
each successive emperor; they are one of the three colleges of
the imperial diet (see Diet); and they are also an electoral
union (Kurfürstenverein), acting as a separate and independent
political organ even after the election, and during the reign, of
the monarch. It was in this last capacity that they had met at
Rense in 1338; and in the same capacity they acted repeatedly
during the 15th century. According to the Golden Bull, such
meetings were to be annual, and their deliberations were to
concern “the safety of the Empire and the world.” Annual
they never were; but occasionally they became of great importance.
In 1424, during the attempt at reform occasioned by
the failure of German arms against the Hussites, the Kurfürstenverein
acted, or at least it claimed to act, as the predominant
partner in a duumvirate, in which the unsuccessful Sigismund
was relegated to a secondary position. During the long reign
of Frederick III.—a reign in which the interests of Austria
were cherished, and the welfare of the Empire neglected, by
that apathetic yet tenacious emperor—the electors once more
attempted, in the year 1453, to erect a new central government
in place of the emperor, a government which, if not conducted
by themselves directly in their capacity of a Kurfürstenverein,
should at any rate be under their influence and control. So,
they hoped, Germany might be able to make head against that
papal aggression, to which Frederick had yielded, and to take
a leading part in that crusade against the Turks, which he had
neglected. Like the previous attempt at reform during the
Hussite wars, the scheme came to nothing; the forces of disunion
in Germany were too strong for any central government, whether
monarchical and controlled by the emperor, or oligarchical and
controlled by the electors. But a final attempt, the most
strenuous of all, was made in the reign of Maximilian I., and
under the influence of Bertold, elector and archbishop of Mainz.
The council of 1500, in which the electors (with the exception
of the king of Bohemia) were to have sat, and which would have
been under their control, represents the last effective attempt
at a real Reichsregiment. Inevitably, however, it shipwrecked
on the opposition of Maximilian; and though the attempt was
again made between 1521 and 1530, the idea of a real central
government under the control of the electors perished, and the
development of local administration by the circle took its place.
In the course of the 16th century a new right came to be
exercised by the electors. As an electoral body (that is to say,
in the first of the three capacities distinguished above), they
claimed, at the election of Charles V. in 1519 and at subsequent
elections, to impose conditions on the elected monarch, and to
determine the terms on which he should exercise his office in
the course of his reign. This Wahlcapitulation, similar to the
Pacta Conventa which limited the elected kings of Poland, was
left by the diet to the discretion of the electors, though after
the treaty of Westphalia an attempt was made, with some little
success,2 to turn the capitulation into a matter of legislative
enactment by the diet. From this time onwards the only fact of
importance in the history of the electors is the change which
took place in the composition of their body during the 17th
and 18th centuries. From the Golden Bull to the treaty of
Westphalia (1356-1648) the composition of the electoral body
had remained unchanged. In 1623, however, in the course
of the Thirty Years’ War, the vote of the count palatine of the
Rhine had been transferred to the duke of Bavaria; and at the
treaty of Westphalia the vote, with the office of imperial butler
which it carried, was left to Bavaria, while an eighth vote, along
with the new office of imperial treasurer, was created for the
count palatine. In 1708 a ninth vote, along with the office of
imperial standard-bearer, was created for Hanover; while
finally, in 1778, the vote of Bavaria and the office of imperial
butler returned to the counts palatine, as heirs of the duchy,
on the extinction of the ducal line, while the new vote created
for the Palatinate in 1648, with the office of imperial treasurer,
was transferred to Brunswick-Lüneburg (Hanover) in lieu of the
one which this house already held. In 1806, on the dissolution
of the Holy Roman Empire, the electors ceased to exist.
Literature.—T. Lindner, Die deutschen Königswahlen und die
Entstehung des Kurfürstentums (1893), and Der Hergang bei den
deutschen Königswahlen (1899); R. Kirchhöfer, Zur Entstehung des
Kurkollegiums (1893); W. Maurenbrecher, Geschichte der deutschen
Königswahlen (1889); and G. Blondel, Étude sur Frédéric II,
p. 27 sqq. See also J. Bryce, Holy Roman Empire (edition of 1904),
c. ix.; and R. Schröder, Lehrbuch der deutschen Rechtsgeschichte,
pp. 471-481 and 819-820.
(E. Br.)
1 This is the view of the Sachsenspiegel, and also of Albert of Stade
(quoted in Schröder, p. 476, n. 27): “Palatinus eligit, quia dapifer est;
dux Saxoniae, quia marescalcus,” &c. Schröder points out (p. 479,
n. 45) that “participation in the coronation feast is an express
recognition of the king”; and those who are to discharge their office
in the one must have had a prominent voice in the other.
2 See Schröder’s Lehrbuch der deutschen Rechtsgeschichte, p. 820.
ELECTRA (Ἠλέκτρα), “the bright one,” in Greek mythology.
(1) One of the seven Pleiades, daughter of Atlas and Pleïone.
She is closely connected with the old constellation worship and
the religion of Samothrace, the chief seat of the Cabeiri (q.v.),
where she was generally supposed to dwell. By Zeus she was the
mother of Dardanus, Iasion (or Eëtion), and Harmonia; but in
the Italian tradition, which represented Italy as the original
home of the Trojans, Dardanus was her son by a king of Italy
named Corythus. After her amour with Zeus, Electra fled to the
Palladium as a suppliant, but Athena, enraged that it had been
touched by one who was no longer a maiden, flung Electra and
the image from heaven to earth, where it was found by Ilus, and
taken by him to Ilium; according to another tradition, Electra
herself took it to Ilium, and gave it to her son Dardanus (Schol.
Eurip. Phoen. 1136). In her grief at the destruction of the city
she plucked out her hair and was changed into a comet; in
another version Electra and her six sisters had been placed among
the stars as the Pleiades, and the star which she represented lost
its brilliancy after the fall of Troy. Electra’s connexion with
Samothrace (where she was also called Electryone and Strategis)
is shown by the localization of the carrying off of her reputed
daughter Harmonia by Cadmus, and by the fact that, according
to Athenicon (the author of a work on Samothrace quoted by the
scholiast on Apollonius Rhodius i. 917), the Cabeiri were
Dardanus and Iasion. The gate Electra at Thebes and the
fabulous island Electris were said to have been called after her
(Apollodorus iii. 10. 12; Servius on Aen. iii. 167, vii. 207, x. 272,
Georg. i. 138).
(2) Daughter of Agamemnon and Clytaemnestra, sister of
Orestes and Iphigeneia. She does not appear in Homer, although
according to Xanthus (regarded by some as a fictitious personage),
to whom Stesichorus was indebted for much in his Oresteia, she
was identical with the Homeric Laodice, and was called Electra
because she remained so long unmarried (Ἀ-λέκτρα). She was
said to have played an important part in the poem of Stesichorus,
and subsequently became a favourite figure in tragedy. After
the murder of her father on his return from Troy by her mother
and Aegisthus, she saved the life of her brother Orestes by
sending him out of the country to Strophius, king of Phanote in
Phocis, who had him brought up with his own son Pylades.
Electra, cruelly ill-treated by Clytaemnestra and her paramour,
never loses hope that her brother will return to avenge his father.
When grown up, Orestes, in response to frequent messages from
his sister, secretly repairs with Pylades to Argos, where he
pretends to be a messenger from Strophius bringing the news
of the death of Orestes. Being admitted to the palace, he slays
both Aegisthus and Clytaemnestra. According to another story
(Hyginus, Fab. 122), Electra, having received a false report that
Orestes and Pylades had been sacrificed to Artemis in Tauris,
went to consult the oracle at Delphi. In the meantime Aletes,
the son of Aegisthus, seized the throne of Mycenae. Her arrival
at Delphi coincided with that of Orestes and Iphigeneia. The
same messenger, who had already communicated the false report
of the death of Orestes, informed her that he had been slain by
Iphigeneia. Electra in her rage seized a burning brand from
the altar, intending to blind her sister; but at the critical
moment Orestes appeared, recognition took place, and the brother
and sister returned to Mycenae. Aletes was slain by Orestes, and
176
Electra became the wife of Pylades. The story of Electra is the
subject of the Choëphori of Aeschylus, the Electra of Sophocles
and the Electra of Euripides. It is in the Sophoclean play that
Electra is most prominent.
There are many variations in the treatment of the legend, for
which, as also for a discussion of the modern plays on the subject
by Voltaire and Alfieri, see Jebb’s Introduction to his edition of the
Electra of Sophocles.
ELECTRICAL (or Electrostatic) MACHINE, a machine
operating by manual or other power for transforming mechanical
work into electric energy in the form of electrostatic charges of
opposite sign delivered to separate conductors. Electrostatic
machines are of two kinds: (1) Frictional, and (2) Influence
machines.
 |
| Fig. 1.—Ramsden’s electrical machine. |
Frictional Machines.—A primitive form of frictional electrical
machine was constructed about 1663 by Otto von Guericke
(1602-1686). It consisted of a globe of sulphur fixed on an axis
and rotated by a winch, and it was electrically excited by the
friction of warm hands held against it. Sir Isaac Newton
appears to have been the first to use a glass globe instead of
sulphur (Optics, 8th Query). F. Hawksbee in 1709 also used a
revolving glass globe. A metal chain resting on the globe served
to collect the charge. Later G.M. Bose (1710-1761), of Wittenberg,
added the prime conductor, an insulated tube or cylinder
supported on silk strings, and J.H. Winkler (1703-1770),
professor of physics at Leipzig, substituted a leather cushion for
the hand. Andreas Gordon (1712-1751) of Erfurt, a Scotch
Benedictine monk, first used a glass cylinder in place of a sphere.
Jesse Ramsden (1735-1800) in 1768 constructed his well-known
form of plate electrical machine (fig. 1). A glass plate fixed to a
wooden or metal shaft is rotated by a winch. It passes between
two rubbers made of leather, and is partly covered with two silk
aprons which extend over quadrants of its surface. Just below
the places where the aprons terminate, the glass is embraced by
two insulated metal forks having the sharp points projecting
towards the glass, but not quite touching it. The glass is
excited positively by friction with the rubbers, and the charge is
drawn off by the action of the points which, when acted upon
inductively, discharge negative electricity against it. The
insulated conductor to which the points are connected therefore
becomes positively electrified.
The cushions must
be connected to earth to
remove the negative electricity
which accumulates
on them. It was found
that the machine acted
better if the rubbers were
covered with bisulphide of
tin or with F. von Kienmayer’s
amalgam, consisting
of one part of zinc, one
of tin and two of mercury.
The cushions were
greased and the amalgam
in a state of powder
spread over them. Edward
Nairne’s electrical machine
(1787) consisted of a glass
cylinder with two insulated
conductors, called
prime conductors, on glass
legs placed near it. One
of these carried the leather
exacting cushions and the
other the collecting metal points, a silk apron extending over the
cylinder from the cushion almost to the points. The rubber was
smeared with amalgam. The function of the apron is to prevent
the escape of electrification from the glass during its passage
from the rubber to the collecting points. Nairne’s machine could
give either positive or negative electricity, the first named being
collected from the prime conductor carrying the collecting
points and the second from the prime conductor carrying the
cushion.
 |
| Fig. 2. |
Influence Machines.—Frictional machines are, however, now
quite superseded by the second class of instrument mentioned
above, namely, influence machines. These operate by electrostatic
induction and convert mechanical work into electrostatic
energy by the aid of a small initial charge which is continually
being replenished
or reinforced. The
general principle of
all the machines described
below will be
best understood by
considering a simple
ideal case. Imagine
two Leyden jars with
large brass knobs, A
and B, to stand on the
ground (fig. 2). Let
one jar be initially
charged with positive electricity on its inner coating and
the other with negative, and let both have their outsides
connected to earth. Imagine two insulated balls A′ and B′
so held that A′ is near A and B′ is near B. Then the positive
charge on A induces two charges on A′, viz.: a negative
on the side nearest and a positive on the side most removed.
Likewise the negative charge on B induces a positive charge
on the side of B′ nearest to it and repels negative electricity to
the far side. Next let the balls A′ and B′ be connected together
for a moment by a wire N called a neutralizing conductor which
is subsequently removed. Then A′ will be left negatively
electrified and B′ will be left positively electrified. Suppose
that A′ and B′ are then made to change places. To do this we
shall have to exert energy to remove A′ against the attraction
of A and B′ against the attraction of B. Finally let A′ be
brought in contact with B and B′ with A. The ball A′ will give
up its charge of negative electricity to the Leyden jar B, and the
ball B′ will give up its positive charge to the Leyden jar A.
This transfer will take place because the inner coatings of the
Leyden jars have greater capacity with respect to the earth than
the balls. Hence the charges of the jars will be increased. The
balls A′ and B′ are then practically discharged, and the above
cycle of operations may be repeated. Hence, however small
may be the initial charges of the Leyden jars, by a principle of
accumulation resembling that of compound interest, they can
be increased as above shown to any degree. If this series of
operations be made to depend upon the continuous rotation of
a winch or handle, the arrangement constitutes an electrostatic
influence machine. The principle therefore somewhat resembles
that of the self-exciting dynamo.
The first suggestion for a machine of the above kind seems
to have grown out of the invention of Volta’s electrophorus.
Bennet’s Doubler.
Abraham Bennet, the inventor of the gold leaf electroscope,
described a doubler or machine for multiplying
electric charges (Phil. Trans., 1787).
The principle of this apparatus may be explained thus. Let A and
C be two fixed disks, and B a disk which can be brought at will within
a very short distance of either A or C. Let us suppose all the plates
to be equal, and let the capacities of A and C in presence of B be
each equal to p, and the coefficient of induction between A and B,
or C and B, be q. Let us also suppose that the plates A and C are so
distant from each other that there is no mutual influence, and that p’
is the capacity of one of the disks when it stands alone. A small
charge Q is communicated to A, and A is insulated, and B, uninsulated,
is brought up to it; the charge on B will be—(q/p)Q.
B is now uninsulated and brought to face C, which is uninsulated;
the charge on C will be (q/p)²Q. C is now insulated and connected
with A, which is always insulated. B is then brought to face A and
uninsulated, so that the charge on A becomes rQ, where
| r = | p |
( 1 + | q² |
). |
| p + p′ | p² |
A is now disconnected from C, and here the first operation ends.
It is obvious that at the end of n such operations the charge on
A will be rnQ, so that the charge goes on increasing in geometrical
progression. If the distance between the disks could be made
177
infinitely small each time, then the multiplier r would be 2, and
the charge would be doubled each time. Hence the name of the
apparatus.
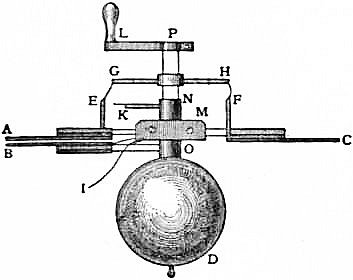 |
| Fig. 3.—Nicholson’s Revolving Doubler. |
Erasmus Darwin, B. Wilson, G.C. Bohnenberger and J.C.E.
Peclet devised various modifications of Bennet’s instrument
(see S.P. Thompson, “The Influence Machine from
1788 to 1888,” Journ. Soc. Tel. Eng., 1888, 17, p. 569).
Nicholson’s doubler.
Bennet’s doubler appears to have given a suggestion
to William Nicholson (Phil. Trans., 1788, p. 403) of
“an instrument which by turning a winch produced the two
states of electricity without friction or communication with the
earth.” This “revolving doubler,” according to the description
of Professor S.P. Thompson (loc. cit.), consists of two fixed
plates of brass A and C (fig. 3), each two inches in diameter and
separately supported on insulating arms in the same plane, so
that a third revolving plate B may pass very near them without
touching. A brass ball D two inches in diameter is fixed on
the end of the axis that carries the plate B, and is loaded within
at one side, so as to act as a counterpoise to the revolving plate
B. The axis P N is made of varnished glass, and so are the axes
that join the three plates with the brass axis N O. The axis N O
passes through the brass piece M, which stands on an insulating
pillar of glass, and supports the plates A and C. At one extremity
of this axis is the ball D, and the other is connected with a rod
of glass, N P, upon which is fixed the handle L, and also the piece
G H, which is separately insulated. The pins E, F rise out of the
back of the fixed plates A and C, at unequal distances from the
axis. The piece K is parallel to G H, and both of them are
furnished at their ends with small pieces of flexible wire that they
may touch the pins E, F in certain points of their revolution.
From the brass
piece M there
stands out a pin
I, to touch against
a small flexible
wire or spring
which projects
sideways from the
rotating plate B
when it comes opposite
A. The
wires are so adjusted
by bending
that B, at the
moment when it
is opposite A, communicates
with the ball D, and A communicates with C
through GH; and half a revolution later C, when B comes
opposite to it, communicates with the ball D through the contact
of K with F. In all other positions A, B, C and D are completely
disconnected from each other. Nicholson thus described the
operation of his machine:—
“When the plates A and B are opposite each other, the two fixed
plates A and C may be considered as one mass, and the revolving
plate B, together with the ball D, will constitute another mass.
All the experiments yet made concur to prove that these two masses
will not possess the same electric state.... The redundant electricities
in the masses under consideration will be unequally distributed;
the plate A will have about ninety-nine parts, and the plate
C one; and, for the same reason, the revolving plate B will have
ninety-nine parts of the opposite electricity, and the ball D one.
The rotation, by destroying the contacts, preserves this unequal
distribution, and carries B from A to C at the same time that the tail
K connects the ball with the plate C. In this situation, the electricity
in B acts upon that in C, and produces the contrary state,
by virtue of the communication between C and the ball; which
last must therefore acquire an electricity of the same kind with that
of the revolving plate. But the rotation again destroys the contact
and restores B to its first situation opposite A. Here, if we attend
to the effect of the whole revolution, we shall find that the electric
states of the respective masses have been greatly increased; for the
ninety-nine parts in A and B remain, and the one part of electricity
in C has been increased so as nearly to compensate ninety-nine parts
of the opposite electricity in the revolving plate B, while the communication
produced an opposite mutation in the electricity of the
ball. A second rotation will, of course, produce a proportional
augmentation of these increased quantities; and a continuance of
turning will soon bring the intensities to their maximum, which is
limited by an explosion between the plates” (Phil. Trans., 1788, p. 405).
 |
| Fig. 4.—Belli’s Doubler. |
Nicholson described also another apparatus, the “spinning
condenser,” which worked on the same principle. Bennet and
Nicholson were followed by T. Cavallo, John Read,
Bohnenberger, C.B. Désormes and J.N.P. Hachette
Belli’s doubler.
and others in the invention of various forms of rotating
doubler. A simple and typical form of doubler, devised in 1831
by G. Belli (fig. 4), consisted of two curved metal plates between
which revolved a pair of
balls carried on an insulating
stem. Following the
nomenclature usual in connexion
with dynamos we
may speak of the conductors
which carry the initial
charges as the field plates,
and of the moving conductors
on which are induced
the charges which are subsequently
added to those on
the field plates, as the
carriers. The wire which
connects two armature
plates for a moment is the neutralizing conductor. The
two curved metal plates constitute the field plates and must
have original charges imparted to them of opposite sign. The
rotating balls are the carriers, and are connected together for a
moment by a wire when in a position to be acted upon inductively
by the field plates, thus acquiring charges of opposite sign. The
moment after they are separated again. The rotation continuing
the ball thus negatively charged is made to give up this
charge to that negatively electrified field plate, and the ball
positively charged its charge to the positively electrified field
plate, by touching little contact springs. In this manner the
field plates accumulate charges of opposite sign.
 |
| Fig. 5.—Varley’s Machine. |
Modern types of influence machine may be said to date from
1860 when C.F. Varley patented a type of influence machine
which has been the parent of numerous subsequent
forms (Brit. Pat. Spec. No. 206 of 1860). In it the
Varley’s machine.
field plates were sheets of tin-foil attached to a glass
plate (fig. 5). In front of them a disk of ebonite or glass, having
carriers of metal fixed to its edge, was rotated by a winch. In
the course of their rotation two diametrically opposite carriers
touched against the ends of a neutralizing conductor so as to form
for a moment one conductor, and the moment afterwards these
two carriers were insulated, one carrying away a positive charge
and the other a negative. Continuing their rotation, the positively
charged carrier gave up its positive charge by touching a little
knob attached to the positive field plate, and similarly for the
negative charge carrier. In this way the charges on the field
plates were continually replenished
and reinforced. Varley also constructed
a multiple form of influence
machine having six rotating disks,
each having a number of carriers
and rotating between field plates.
With this apparatus he obtained
sparks 6 in. long, the initial source
of electrification being a single
Daniell cell.
Varley was followed by A.J.I.
Toepler, who in 1865 constructed
an influence machine consisting of
two disks fixed on the same shaft and rotating in the same
direction. Each disk carried two strips of tin-foil extending
Toepler machine.
nearly over a semi-circle, and there were two field
plates, one behind each disk; one of the plates was
positively and the other negatively electrified. The
carriers which were touched under the influence of the positive
field plate passed on and gave up a portion of their negative
charge to increase that of the negative field plate; in the same
178
way the carriers which were touched under the influence of the
negative field plate sent a part of their charge to augment that
of the positive field plate. In this apparatus one of the charging
rods communicated with one of the field plates, but the other
with the neutralizing brush opposite to the other field plate.
Hence one of the field plates would always remain charged
when a spark was taken at the transmitting terminals.
 |
| Fig. 6.—Holtz’s Machine. |
Between 1864 and 1880, W.T.B. Holtz constructed and
described a large number of influence machines which were for a
long time considered the most advanced development
of this type of electrostatic machine. In one form the
Holtz machine.
Holtz machine consisted of a glass disk mounted on a
horizontal axis F (fig. 6) which could be made to rotate at a
considerable speed by a multiplying gear, part of which is seen at
X. Close behind this disk was fixed another vertical disk of glass
in which were cut two windows B, B. On the side of the fixed
disk next the rotating disk were pasted two sectors of paper A, A,
with short blunt points attached to them which projected out
into the windows on the side away from the rotating disk. On
the other side of the rotating disk were placed two metal combs
C, C, which consisted of sharp points set in metal rods and were
each connected to one of a pair of discharge balls E, D, the
distance between which could be varied. To start the machine the
balls were brought in contact, one of the paper armatures
electrified, say, with positive electricity, and the disk set in
motion. Thereupon very shortly a hissing sound was heard
and the machine became harder to turn as if the disk were moving
through a resisting medium. After that the discharge balls
might be separated a little and a continuous series of sparks or
brush discharges would take place between them. If two Leyden
jars L, L were hung upon the conductors which supported the
combs, with their outer coatings put in connexion with one
another by M, a series of strong spark discharges passed between
the discharge balls. The action of the machine is as follows:
Suppose one paper armature to be charged positively, it acts by
induction on the right hand comb, causing negative electricity to
issue from the comb points upon the glass revolving disk; at the
same time the positive electricity passes through the closed
discharge circuit to the left comb and issues from its teeth upon
the part of the glass disk at the opposite end of the diameter.
This positive electricity electrifies the left paper armature by
induction, positive electricity issuing from the blunt point upon
the side farthest from the rotating disk. The charges thus
deposited on the glass disk are carried round so that the upper
half is electrified negatively on both sides and the lower half
positively on both sides, the sign of the electrification being
reversed as the disk passes between the combs and the armature
by discharges issuing from them respectively. If it were not for
leakage in various ways, the electrification would go on everywhere
increasing, but in practice a stationary state is soon
attained. Holtz’s machine is very uncertain in its action in a
moist climate, and has generally to be enclosed in a chamber in
which the air is kept artificially dry.
Robert Voss, a Berlin instrument maker, in 1880 devised a form
of machine in which he claimed that the principles of Toepler and
Holtz were combined. On a rotating glass or ebonite
disk were placed carriers of tin-foil or metal buttons
Voss’s machine.
against which neutralizing brushes touched. This
armature plate revolved in front of a field plate carrying two
pieces of tin-foil backed up by larger pieces of varnished paper.
The studs on the armature plate were charged inductively by
being connected for a moment by a neutralizing wire as they
passed in front of the field plates, and then gave up their charges
partly to renew the field charges and partly to collecting combs
connected to discharge balls. In general design and construction,
the manner of moving the rotating plate and in the use of the two
Leyden jars in connexion with the discharge balls, Voss borrowed
his ideas from Holtz.
All the above described machines, however, have been thrown
into the shade by the invention of a greatly improved type of influence
machine first constructed by James Wimshurst
about 1878. Two glass disks are mounted on two shafts
Wimshurst machine.
in such a manner that, by means of two belts and pulleys
worked from a winch shaft, the disks can be rotated
rapidly in opposite directions close to each other (fig. 7). These
glass disks carry on them a certain number (not less than 16 or
20) tin-foil carriers which may or may not have brass buttons
upon them. The glass plates are well varnished, and the carriers
are placed on the outer sides of the two glass plates. As therefore
the disks revolve, these carriers travel in opposite directions,
coming at intervals in opposition to each other. Each upright
bearing carrying the shafts of the revolving disks also carries a
neutralizing conductor or wire ending in a little brush of gilt
thread. The neutralizing conductors for each disk are placed at
right angles to each other. In addition there are collecting
combs which occupy an intermediate position and have sharp
points projecting inwards, and coming near to but not touching
the carriers. These combs on opposite sides are connected
respectively to the inner coatings of two Leyden jars whose outer
coatings are in connexion with one another.
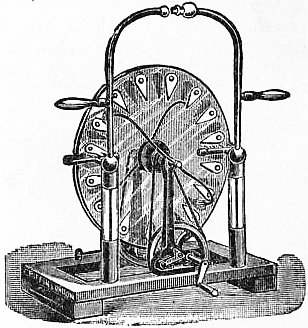 |
| Fig. 7.—Wimshurst’s Machine. |
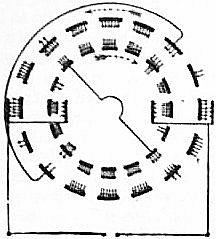 |
| Fig. 8.—Action of the
Wimshurst Machine. |
The operation of the machine is as follows: Let us suppose
that one of the studs on the back plate is positively electrified
and one at the opposite end of a diameter is negatively electrified,
and that at that moment two corresponding studs on the front
plate passing opposite to these back studs are momentarily
connected together by
the neutralizing wire
belonging to the front
plate. The positive stud
on the back plate will
act inductively on the
front stud and charge it
negatively, and similarly
for the other stud, and
as the rotation continues
these charged studs will
pass round and give up
most of their charge
through the combs to
the Leyden jars. The
moment, however, a pair
of studs on the front
plate are charged, they
act as field plates to
studs on the back plate which are passing at the moment,
provided these last are connected by the back neutralizing wire.
After a few revolutions of the disks half the studs on the front
plate at any moment are charged negatively and half positively
and the same on the back plate, the neutralizing wires forming the
boundary between the positively and negatively charged studs.
The diagram in fig. 8, taken by permission from S.P. Thompson’s
paper (loc. cit.), represents a view of the distribution of these
charges on the front and back plates respectively. It will be
179
seen that each stud is in turn both a field plate and a carrier
having a charge induced on it, and then passing on in turn
induces further charges on other studs. Wimshurst constructed
numerous very powerful machines
of this type, some of them with
multiple plates, which operate in
almost any climate, and rarely fail
to charge themselves and deliver a
torrent of sparks between the discharge
balls whenever the winch is
turned. He also devised an alternating
current electrical machine
in which the discharge balls were
alternately positive and negative.
Large Wimshurst multiple plate
influence machines are often used
instead of induction coils for exciting
Röntgen ray tubes in medical
work. They give very steady illumination on fluorescent
screens.
In 1900 it was found by F. Tudsbury that if an influence
machine is enclosed in a metallic chamber containing compressed
air, or better, carbon dioxide, the insulating properties of compressed
gases enable a greatly improved effect to be obtained
owing to the diminution of the leakage across the plates and from
the supports. Hence sparks can be obtained of more than
double the length at ordinary atmospheric pressure. In one
case a machine with plates 8 in. in diameter which could give
sparks 2.5 in. at ordinary pressure gave sparks of 5, 7, and 8 in.
as the pressure was raised to 15, 30 and 45 ℔ above the normal
atmosphere.
The action of Lord Kelvin’s replenisher (fig. 9) used by him
in connexion with his electrometers for maintaining their
charge, closely resembles that of Belli’s doubler and will be
understood from fig. 9. Lord Kelvin also devised an influence
machine, commonly called a “mouse mill,” for electrifying the
ink in connexion with his siphon recorder. It was an electrostatic
and electromagnetic machine combined, driven by an electric
current and producing in turn electrostatic charges of electricity.
In connexion with this subject mention must also be made of the
water dropping influence machine of the same inventor.1
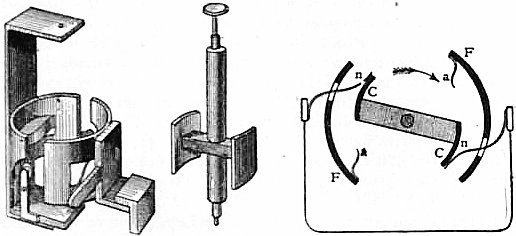 |
| Fig. 9.—Lord Kelvin’s Replenisher. |
C, C, Metal carriers fixed to ebonite cross-arm.
F, F, Brass field-plates or conductors. |
a, a, Receiving springs.
n, n, Connecting springs or neutralizing brushes. |
The action and efficiency of influence machines have been
investigated by F. Rossetti, A. Righi and F.W.G. Kohlrausch.
The electromotive force is practically constant no matter what the
velocity of the disks, but according to some observers the internal
resistance decreases as the velocity increases. Kohlrausch,
using a Holtz machine with a plate 16 in. in diameter, found
that the current given by it could only electrolyse acidulated
water in 40 hours sufficient to liberate one cubic centimetre of
mixed gases. E.E.N. Mascart, A. Roiti, and E. Bouchotte have
also examined the efficiency and current producing power of
influence machines.
Bibliography.—In addition to S.P. Thompson’s valuable paper
on influence machines (to which this article is much indebted) and
other references given, see J. Clerk Maxwell, Treatise on Electricity
and Magnetism (2nd ed., Oxford, 1881), vol. i. p. 294; J.D. Everett,
Electricity (expansion of part iii. of Deschanel’s Natural Philosophy)
(London, 1901), ch. iv. p. 20; A. Winkelmann, Handbuch der Physik
(Breslau, 1905), vol. iv. pp. 50-58 (contains a large number of
references to original papers); J. Gray, Electrical Influence Machines,
their Development and Modern Forms (London, 1903).
(J. A. F.)
1 See Lord Kelvin, Reprint of Papers on Electrostatics and Magnetism
(1872); “Electrophoric Apparatus and Illustrations of Voltaic
Theory,” p. 319; “On Electric Machines Founded on Induction
and Convection,” p. 330; “The Reciprocal Electrophorus,”
p. 337.
ELECTRIC EEL (Gymnotus electricus), a member of the
family of fishes known as Gymnotidae. In spite of their external
similarity the Gymnotidae have nothing to do with the eels
(Anguilla). They resemble the latter in the elongation of the
body, the large number of vertebrae (240 in Gymnotus), and the
absence of pelvic fins; but they differ in all the more important
characters of internal structure. They are in fact allied to the
carps or Cyprinidae and the cat-fishes or Siluridae. In common
with these two families and the Characinidae of Africa and South
America, the Gymnotidae possess the peculiar structures called
ossicula auditus or Weberian ossicles. These are a chain of
small bones belonging to the first four vertebrae, which are
much modified, and connecting the air-bladder with the auditory
organs. Such an agreement in the structure of so complicated
and specialized an apparatus can only be the result of a community
of descent of the families possessing it. Accordingly
these families are now placed together in a distinct sub-order,
the Ostariophysi. The Gymnotidae are strongly modified and
degraded Characinidae. In them the dorsal and caudal fins are
very rudimentary or absent, and the anal is very long, extending
from the anus, which is under the head or throat, to the end of
the body.
Gymnotus is the only genus of the family which possesses
electric organs. These extend the whole length of the tail, which
is four-fifths of the body. They are modifications of the lateral
muscles and are supplied with numerous branches of the spinal
nerves. They consist of longitudinal columns, each composed
of an immense number of “electric plates.” The posterior end
of the organ is positive, the anterior negative, and the current
passes from the tail to the head. The maximum shock is given
when the head and tail of the Gymnotus are in contact with
different points in the surface of some other animal. Gymnotus
electricus attains a length of 3 ft. and the thickness of a man’s
thigh, and frequents the marshes of Brazil and the Guianas,
where it is regarded with terror, owing to the formidable electrical
apparatus with which it is provided. When this natural battery
is discharged in a favourable position, it is sufficiently powerful
to stun the largest animal; and according to A. von Humboldt,
it has been found necessary to change the line of certain roads
passing through the pools frequented by the electric eels. These
fish are eaten by the Indians, who, before attempting to capture
them, seek to exhaust their electrical power by driving horses
into the ponds. By repeated discharges upon these they
gradually expend this marvellous force; after which, being
defenceless, they become timid, and approach the edge for
shelter, when they fall an easy prey to the harpoon. It is only
after long rest and abundance of food that the fish is able to
resume the use of its subtle weapon. Humboldt’s description of
this method of capturing the fish has not, however, been verified
by recent travellers.
ELECTRICITY. This article is devoted to a general sketch of
the history of the development of electrical knowledge on both
the theoretical and the practical sides. The two great branches
of electrical theory which concern the phenomena of electricity
at rest, or “frictional” or “static” electricity, and of electricity
in motion, or electric currents, are treated in two separate
articles, Electrostatics and Electrokinetics. The phenomena
attendant on the passage of electricity through solids,
through liquids and through gases, are described in the article
Conduction, Electric, and also Electrolysis, and the propagation
of electrical vibrations in Electric Waves. The interconnexion
of magnetism (which has an article to itself) and
180
electricity is discussed in Electromagnetism, and these manifestations
in nature in Atmospheric Electricity; Aurora
Polaris and Magnetism, Terrestrial. The general principles
of electrical engineering will be found in Electricity Supply,
and further details respecting the generation and use of electrical
power are given in such articles as Dynamo; Motors, Electric;
Transformers; Accumulator; Power Transmission:
Electric; Traction; Lighting: Electric; Electrochemistry
and Electrometallurgy. The principles of telegraphy (land,
submarine and wireless) and of telephony are discussed in the
articles Telegraph and Telephone, and various electrical
instruments are treated in separate articles such as Amperemeter;
Electrometer; Galvanometer; Voltmeter;
Wheatstone’s Bridge; Potentiometer; Meter, Electric;
Electrophorus; Leyden Jar; &c.
The term “electricity” is applied to denote the physical
agency which exhibits itself by effects of attraction and repulsion
when particular substances are rubbed or heated, also in certain
chemical and physiological actions and in connexion with moving
magnets and metallic circuits. The name is derived from the
word electrica, first used by William Gilbert (1544-1603) in his
epoch-making treatise De magnete, magneticisque corporibus,
et de magno magnete tellure, published in 1600,1 to denote
substances which possess a similar property to amber (= electrum,
from ἤλεκτρον) of attracting light objects when rubbed. Hence
the phenomena came to be collectively called electrical, a term
first used by William Barlowe, archdeacon of Salisbury, in 1618,
and the study of them, electrical science.
Historical Sketch.
Gilbert was the first to conduct systematic scientific experiments
on electrical phenomena. Prior to his date the scanty
knowledge possessed by the ancients and enjoyed in the middle
ages began and ended with facts said to have been familiar to
Thales of Miletus (600 B.C.) and mentioned by Theophrastus
(321 B.C.) and Pliny (A.D. 70), namely, that amber, jet and one
or two other substances possessed the power, when rubbed, of
attracting fragments of straw, leaves or feathers. Starting with
careful and accurate observations on facts concerning the
mysterious properties of amber and the lodestone, Gilbert laid
the foundations of modern electric and magnetic science on the
true experimental and inductive basis. The subsequent history
of electricity may be divided into four well-marked periods.
The first extends from the date of publication of Gilbert’s great
treatise in 1600 to the invention by Volta of the voltaic pile and
the first production of the electric current in 1799. The second
dates from Volta’s discovery to the discovery by Faraday in
1831 of the induction of electric currents and the creation of
currents by the motion of conductors in magnetic fields, which
initiated the era of modern electrotechnics. The third covers
the period between 1831 and Clerk Maxwell’s enunciation of the
electromagnetic theory of light in 1865 and the invention of the
self-exciting dynamo, which marks another great epoch in the
development of the subject; and the fourth comprises the modern
development of electric theory and of absolute quantitative
measurements, and above all, of the applications of this knowledge
in electrical engineering. We shall sketch briefly the historical
progress during these various stages, and also the growth of
electrical theories of electricity during that time.
First Period.—Gilbert was probably led to study the
phenomena of the attraction of iron by the lodestone in consequence
of his conversion to the Copernican theory of the earth’s
motion, and thence proceeded to study the attractions produced
by amber. An account of his electrical discoveries is given in
the De magnete, lib. ii. cap. 2.2 He invented the versorium or
electrical needle and proved that innumerable bodies he called
electrica, when rubbed, can attract the needle of the versorium
(see Electroscope). Robert Boyle added many new facts and
gave an account of them in his book, The Origin of Electricity.
He showed that the attraction between the rubbed body and
the test object is mutual. Otto von Guericke (1602-1686) constructed
the first electrical machine with a revolving ball of
sulphur (see Electrical Machine), and noticed that light
objects were repelled after being attracted by excited electrics.
Sir Isaac Newton substituted a ball of glass for sulphur in the
electrical machine and made other not unimportant additions
to electrical knowledge. Francis Hawksbee (d. 1713) published
in his book Physico-Mechanical Experiments (1709), and in several
Memoirs in the Phil. Trans. about 1707, the results of his electrical
inquiries. He showed that light was produced when mercury
was shaken up in a glass tube exhausted of its air. Dr Wall
observed the spark and crackling sound when warm amber was
rubbed, and compared them with thunder and lightning (Phil.
Trans., 1708, 26, p. 69). Stephen Gray (1696-1736) noticed in
1720 that electricity could be excited by the friction of hair, silk,
wool, paper and other bodies. In 1729 Gray made the important
discovery that some bodies were conductors and others non-conductors
of electricity. In conjunction with his friend
Granville Wheeler (d. 1770), he conveyed the electricity from
rubbed glass, a distance of 886 ft., along a string supported on
silk threads (Phil. Trans., 1735-1736, 39, pp. 16, 166 and 400).
Jean Théophile Desaguliers (1683-1744) announced soon after
that electrics were non-conductors, and conductors were non-electrics.
C.F. de C. du Fay (1699-1739) made the great discovery
that electricity is of two kinds, vitreous and resinous
(Phil. Trans., 1733, 38, p. 263), the first being produced when
glass, crystal, &c. are rubbed with silk, and the second when
resin, amber, silk or paper, &c. are excited by friction with
flannel. He also discovered that a body charged with positive
or negative electricity repels a body free to move when the
latter is charged with electricity of like sign, but attracts it if
it is charged with electricity of opposite sign, i.e. positive repels
positive and negative repels negative, but positive attracts
negative. It is to du Fay also that we owe the abolition of the
distinction between electrics and non-electrics. He showed
that all substances could be electrified by friction, but that
to electrify conductors they must be insulated or supported
on non-conductors. Various improvements were made in the
electrical machine, and thereby experimentalists were provided
with the means of generating strong electrification; C.F.
Ludolff (1707-1763) of Berlin in 1744 succeeded in igniting ether
with the electric spark (Phil. Trans., 1744, 43, p. 167).
For a very full list of the papers and works of these early electrical
philosophers, the reader is referred to the bibliography on Electricity
in Dr Thomas Young’s Natural Philosophy, vol. ii. p. 415.
In 1745 the important invention of the Leyden jar or condenser
was made by E.G. von Kleist of Kammin, and almost simultaneously
by Cunaeus and Pieter van Musschenbroek (1692-1761)
of Leiden (see Leyden Jar). Sir William Watson (1715-1787)
in England first observed the flash of light when a Leyden jar
is discharged, and he and Dr John Bevis (1695-1771) suggested
coating the jar inside and outside with tinfoil. Watson carried
out elaborate experiments to discover how far the electric
discharge of the jar could be conveyed along metallic wires and
was able to accomplish it for a distance of 2 m., making
the important observation that the electricity appeared to be
transmitted instantaneously.
Franklin’s Researches.—Benjamin Franklin (1706-1790) was
one of the great pioneers of electrical science, and made the ever-memorable
experimental identification of lightning and electric
spark. He argued that electricity is not created by friction, but
merely collected from its state of diffusion through other matter
by which it is attracted. He asserted that the glass globe, when
rubbed, attracted the electrical fire, and took it from the rubber,
the same globe being disposed, when the friction ceases, to give
out its electricity to any body which has less. In the case of the
charged Leyden jar, he asserted that the inner coating of tinfoil
181
had received more than its ordinary quantity of electricity, and
was therefore electrified positively, or plus, while the outer
coating of tinfoil having had its ordinary quantity of electricity
diminished, was electrified negatively, or minus. Hence the
cause of the shock and spark when the jar is discharged, or
when the superabundant or plus electricity of the inside is
transferred by a conducting body to the defective or minus
electricity of the outside. This theory of the Leyden phial
Franklin supported very ingeniously by showing that the outside
and the inside coating possessed electricities of opposite sign, and
that, in charging it, exactly as much electricity is added on one
side as is subtracted from the other. The abundant discharge of
electricity by points was observed by Franklin is his earliest
experiments, and also the power of points to conduct it copiously
from an electrified body. Hence he was furnished with a simple
method of collecting electricity from other bodies, and he was
enabled to perform those remarkable experiments which are
chiefly connected with his name. Hawksbee, Wall and J.A.
Nollet (1700-1770) had successively suggested the identity of
lightning and the electric spark, and of thunder and the snap
of the spark. Previously to the year 1750, Franklin drew up a
statement, in which he showed that all the general phenomena
and effects which were produced by electricity had their counterparts
in lightning. After waiting some time for the erection of
a spire at Philadelphia, by means of which he hoped to bring
down the electricity of a thunderstorm, he conceived the idea
of sending up a kite among thunder-clouds. With this view he
made a small cross of two small light strips of cedar, the arms
being sufficiently long to reach to the four corners of a large
thin silk handkerchief when extended. The corners of the
handkerchief were tied to the extremities of the cross, and when
the body of the kite was thus formed, a tail, loop and string were
added to it. The body was made of silk to enable it to bear the
violence and wet of a thunderstorm. A very sharp pointed wire
was fixed at the top of the upright stick of the cross, so as to rise a
foot or more above the wood. A silk ribbon was tied to the end
of the twine next the hand, and a key suspended at the junction
of the twine and silk. In company with his son, Franklin raised
the kite like a common one, in the first thunderstorm, which
happened in the month of June 1752. To keep the silk ribbon
dry, he stood within a door, taking care that the twine did not
touch the frame of the door; and when the thunder-clouds came
over the kite he watched the state of the string. A cloud passed
without any electrical indications, and he began to despair of
success. At last, however, he saw the loose filaments of the twine
standing out every way, and he found them to be attracted by
the approach of his finger. The suspended key gave a spark on
the application of his knuckle, and when the string had become
wet with the rain the electricity became abundant. A Leyden
jar was charged at the key, and by the electric fire thus obtained
spirits were inflamed, and many other experiments performed
which had been formerly made by excited electrics. In subsequent
trials with another apparatus, he found that the clouds
were sometimes positively and sometimes negatively electrified,
and so demonstrated the perfect identity of lightning and
electricity. Having thus succeeded in drawing the electric fire
from the clouds, Franklin conceived the idea of protecting
buildings from lightning by erecting on their highest parts pointed
iron wires or conductors communicating with the ground. The
electricity of a hovering or a passing cloud would thus be carried
off slowly and silently; and if the cloud was highly charged, the
lightning would strike in preference the elevated conductors.3
The most important of Franklin’s electrical writings are his
Experiments and Observations on Electricity made at Philadelphia,
1751-1754; his Letters on Electricity; and various memoirs and
letters in the Phil. Trans. from 1756 to 1760.
About the same time that Franklin was making his kite
experiment in America, T.F. Dalibard (1703-1779) and others in
France had erected a long iron rod at Marli, and obtained results
agreeing with those of Franklin. Similar investigations were
pursued by many others, among whom Father G.B. Beccaria
(1716-1781) deserves especial mention. John Canton (1718-1772)
made the important contribution to knowledge that
electricity of either sign could be produced on nearly any body by
friction with appropriate substances, and that a rod of glass
roughened on one half was excited negatively in the rough part
and positively in the smooth part by friction with the same rubber.
Canton first suggested the use of an amalgam of mercury and tin
for use with glass cylinder electrical machines to improve their
action. His most important discovery, however, was that of
electrostatic induction, the fact that one electrified body can
produce charges of electricity upon another insulated body, and
that when this last is touched it is left electrified with a charge of
opposite sign to that of the inducing charge (Phil. Trans., 1753-1754).
We shall make mention lower down of Canton’s contributions
to electrical theory. Robert Symmer (d. 1763) showed that
quite small differences determined the sign of the electrification
that was generated by the friction of two bodies one against the
other. Thus wearing a black and a white silk stocking one over the
other, he found they were electrified oppositely when rubbed and
drawn off, and that such a rubbed silk stocking when deposited in
a Leyden jar gave up its electrification to the jar (Phil. Trans.,
1759). Ebenezer Kinnersley (1711-1778) of Philadelphia made
useful observations on the elongation and fusion of iron wires
by electrical discharges (Phil. Trans., 1763). A contemporary of
Canton and co-discoverer with him of the facts of electrostatic
induction was the Swede, Johann Karl Wilcke (1732-1796), then
resident in Germany, who in 1762 published an account of
experiments in which a metal plate held above the upper surface
of a glass table was subjected to the action of a charge on an
electrified metal plate held below the glass (Kon. Schwedische
Akad. Abhandl., 1762, 24, p. 213).
Pyro-electricity.—The subject of pyro-electricity, or the power
possessed by some minerals of becoming electrified when merely
heated, and of exhibiting positive and negative electricity, now
began to attract notice. It is possible that the lyncurium of
the ancients, which according to Theophrastus attracted light
bodies, was tourmaline, a mineral found in Ceylon, which had
been christened by the Dutch with the name of aschentrikker, or
the attractor of ashes. In 1717 Louis Lémery exhibited to the
Paris Academy of Sciences a stone from Ceylon which attracted
light bodies; and Linnaeus in mentioning his experiments
gives the stone the name of lapis electricus. Giovanni Caraffa,
duca di Noja (1715-1768), was led in 1758 to purchase some of
the stones called tourmaline in Holland, and, assisted by L.J.M.
Daubenton and Michel Adanson, he made a series of experiments
with them, a description of which he gave in a letter to G.L.L.
Buffon in 1759. The subject, however, had already engaged the
attention of the German philosopher, F.U.T. Aepinus, who
published an account of them in 1756. Hitherto nothing had
been said respecting the necessity of heat to excite the tourmaline;
but it was shown by Aepinus that a temperature between 99½°
and 212° Fahr. was requisite for the development of its attractive
powers. Benjamin Wilson (Phil. Trans., 1763, &c.), J. Priestley,
and Canton continued the investigation, but it was reserved for
the Abbé Haüy to throw a clear light on this curious branch
of the science (Traité de minéralogie, 1801). He found that the
electricity of the tourmaline decreased rapidly from the summits
or poles towards the middle of the crystal, where it was imperceptible;
and he discovered that if a tourmaline is broken into
any number of fragments, each fragment, when excited, has
two opposite poles. Haüy discovered the same property in the
Siberian and Brazilian topaz, borate of magnesia, mesotype,
prehnite, sphene and calamine. He also found that the polarity
which minerals receive from heat has a relation to the secondary
forms of their crystals—the tourmaline, for example, having
its resinous pole at the summit of the crystal which has three
faces. In the other pyro-electric crystals above mentioned,
Haüy detected the same deviation from the rules of symmetry
182
in their secondary crystals which occurs in tourmaline. C.P.
Brard (1788-1838) discovered that pyro-electricity was a
property of axinite; and it was afterwards detected in other
minerals. In repeating and extending the experiments of Haüy
much later, Sir David Brewster discovered that various artificial
salts were pyro-electric, and he mentions the tartrates of potash
and soda and tartaric acid as exhibiting this property in a very
strong degree. He also made many experiments with the
tourmaline when cut into thin slices, and reduced to the finest
powder, in which state each particle preserved its pyro-electricity;
and he showed that scolezite and mesolite, even when deprived
of their water of crystallization and reduced to powder, retain
their property of becoming electrical by heat. When this white
powder is heated and stirred about by any substance whatever,
it collects in masses like new-fallen snow, and adheres to the
body with which it is stirred.
For Sir David Brewster’s work on pyro-electricity, see Trans. Roy.
Soc. Edin., 1845, also Phil. Mag., Dec. 1847. The reader will also
find a full discussion on the subject in the Treatise on Electricity, by
A. de la Rive, translated by C.V. Walker (London, 1856), vol. ii.
part v. ch. i.
Animal electricity.—The observation that certain animals
could give shocks resembling the shock of a Leyden jar induced
a closer examination of these powers. The ancients were
acquainted with the benumbing power of the torpedo-fish, but
it was not till 1676 that modern naturalists had their attention
again drawn to the fact. E. Bancroft was the first person who
distinctly suspected that the effects of the torpedo were electrical.
In 1773 John Walsh (d. 1795) and Jan Ingenhousz (1730-1799)
proved by many curious experiments that the shock of the
torpedo was an electrical one (Phil. Trans., 1773-1775); and
John Hunter (id. 1773, 1775) examined and described the
anatomical structure of its electrical organs. A. von Humboldt
and Gay-Lussac (Ann. Chim., 1805), and Etienne Geoffroy Saint-Hilaire
(Gilb. Ann., 1803) pursued the subject with success;
and Henry Cavendish (Phil. Trans., 1776) constructed an
artificial torpedo, by which he imitated the actions of the living
animal. The subject was also investigated (Phil. Trans., 1812,
1817) by Dr T.J. Todd (1789-1840), Sir Humphry Davy
(id. 1829), John Davy (id. 1832, 1834, 1841) and Faraday
(Exp. Res., vol. ii.). The power of giving electric shocks has
been discovered also in the Gymnotus electricus (electric eel),
the Malapterurus electricus, the Trichiurus electricus, and the
Tetraodon electricus. The most interesting and the best known
of these singular fishes is the Gymnotus or Surinam eel. Humboldt
gives a very graphic account of the combats which are
carried on in South America between the gymnoti and the wild
horses in the vicinity of Calabozo.
Cavendish’s Researches.—The work of Henry Cavendish (1731-1810)
entitles him to a high place in the list of electrical investigators.
A considerable part of Cavendish’s work was rescued
from oblivion in 1879 and placed in an easily accessible form
by Professor Clerk Maxwell, who edited the original manuscripts
in the possession of the duke of Devonshire.4 Amongst Cavendish’s
important contributions were his exact measurements of
electrical capacity. The leading idea which distinguishes his
work from that of his predecessors was his use of the phrase
“degree of electrification” with a clear scientific definition
which shows it to be equivalent in meaning to the modern term
“electric potential.” Cavendish compared the capacity of
different bodies with those of conducting spheres of known
diameter and states these capacities in “globular inches,” a
globular inch being the capacity of a sphere 1 in. in diameter.
Hence his measurements are all directly comparable with modern
electrostatic measurements in which the unit of capacity is that
of a sphere 1 centimetre in radius. Cavendish measured the
capacity of disks and condensers of various forms, and proved
that the capacity of a Leyden pane is proportional to the surface
of the tinfoil and inversely as the thickness of the glass. In
connexion with this subject he anticipated one of Faraday’s
greatest discoveries, namely, the effect of the dielectric or insulator
upon the capacity of a condenser formed with it, in other
words, made the discovery of specific inductive capacity (see
Electrical Researches, p. 183). He made many measurements
of the electric conductivity of different solids and liquids, by
comparing the intensity of the electric shock taken through his
body and various conductors. He seems in this way to have
educated in himself a very precise “electrical sense,” making
use of his own nervous system as a kind of physiological galvanometer.
One of the most important investigations he made in
this way was to find out, as he expressed it, “what power of the
velocity the resistance is proportional to.” Cavendish meant
by the term “velocity” what we now call the current, and
by “resistance” the electromotive force which maintains the
current. By various experiments with liquids in tubes he found
this power was nearly unity. This result thus obtained by
Cavendish in January 1781, that the current varies in direct
proportion to the electromotive force, was really an anticipation
of the fundamental law of electric flow, discovered independently
by G.S. Ohm in 1827, and since known as Ohm’s Law. Cavendish
also enunciated in 1776 all the laws of division of electric current
between circuits in parallel, although they are generally supposed
to have been first given by Sir C. Wheatstone. Another of his
great investigations was the determination of the law according
to which electric force varies with the distance. Starting from
the fact that if an electrified globe, placed within two hemispheres
which fit over it without touching, is brought in contact
with these hemispheres, it gives up the whole of its charge to
them—in other words, that the charge on an electrified body is
wholly on the surface—he was able to deduce by most ingenious
reasoning the law that electric force varies inversely as the
square of the distance. The accuracy of his measurement, by
which he established within 2% the above law, was only limited
by the sensibility, or rather insensibility, of the pith ball electrometer,
which was his only means of detecting the electric charge.5
In the accuracy of his quantitative measurements and the range
of his researches and his combination of mathematical and
physical knowledge, Cavendish may not inaptly be described
as the Kelvin of the 18th century. Nothing but his curious indifference
to the publication of his work prevented him from
securing earlier recognition for it.
Coulomb’s Work.—Contemporary with Cavendish was C.A.
Coulomb (1736-1806), who in France addressed himself to the
same kind of exact quantitative work as Cavendish in England.
Coulomb has made his name for ever famous by his invention
and application of his torsion balance to the experimental
verification of the fundamental law of electric attraction, in
which, however, he was anticipated by Cavendish, namely,
that the force of attraction between two small electrified spherical
bodies varies as the product of their charges and inversely as the
square of the distance of their centres. Coulomb’s work received
better publication than Cavendish’s at the time of its accomplishment,
and provided a basis on which mathematicians could
operate. Accordingly the close of the 18th century drew into
the arena of electrical investigation on its mathematical side
P.S. Laplace, J.B. Biot, and above all, S.D. Poisson. Adopting
the hypothesis of two fluids, Coulomb investigated experimentally
and theoretically the distribution of electricity on the surface
of bodies by means of his proof plane. He determined the law
of distribution between two conducting bodies in contact; and
measured with his proof plane the density of the electricity
at different points of two spheres in contact, and enunciated
an important law. He ascertained the distribution of electricity
among several spheres (whether equal or unequal) placed in
contact in a straight line; and he measured the distribution of
183
electricity on the surface of a cylinder, and its distribution
between a sphere and cylinder of different lengths but of the
same diameter. His experiments on the dissipation of electricity
possess also a high value. He found that the momentary
dissipation was proportional to the degree of electrification at
the time, and that, when the charge was moderate, its dissipation
was not altered in bodies of different kinds or shapes. The
temperature and pressure of the atmosphere did not produce
any sensible change; but he concluded that the dissipation was
nearly proportional to the cube of the quantity of moisture in
the air.6 In examining the dissipation which takes place along
imperfectly insulating substances, he found that a thread of
gum-lac was the most perfect of all insulators; that it insulated
ten times as well as a dry silk thread; and that a silk thread
covered with fine sealing-wax insulated as powerfully as gum-lac
when it had four times its length. He found also that the
dissipation of electricity along insulators was chiefly owing to
adhering moisture, but in some measure also to a slight conducting
power. For his memoirs see Mém. de math. et phys. de
l’acad. de sc., 1785, &c.
Second Period.—We now enter upon the second period of
electrical research inaugurated by the epoch-making discovery
of Alessandro Volta (1745-1827). L. Galvani had made in
1790 his historic observations on the muscular contraction
produced in the bodies of recently killed frogs when an electrical
machine was being worked in the same room, and described
them in 1791 (De viribus electricitatis in motu musculari commentarius,
Bologna, 1791). Volta followed up these observations
with rare philosophic insight and experimental skill. He showed
that all conductors liquid and solid might be divided into two
classes which he called respectively conductors of the first and
of the second class, the first embracing metals and carbon in its
conducting form, and the second class, water, aqueous solutions
of various kinds, and generally those now called electrolytes.
In the case of conductors of the first class he proved by the use
of the condensing electroscope, aided probably by some form
of multiplier or doubler, that a difference of potential (see
Electrostatics) was created by the mere contact of two such
conductors, one of them being positively electrified and the other
negatively. Volta showed, however, that if a series of bodies of
the first class, such as disks of various metals, are placed in
contact, the potential difference between the first and the last
is just the same as if they are immediately in contact. There
is no accumulation of potential. If, however, pairs of metallic
disks, made, say, of zinc and copper, are alternated with disks
of cloth wetted with a conductor of the second class, such, for
instance, as dilute acid or any electrolyte, then the effect of the
feeble potential difference between one pair of copper and zinc
disks is added to that of the potential difference between the
next pair, and thus by a sufficiently long series of pairs any
required difference of potential can be accumulated.
The Voltaic Pile.—This led him about 1799 to devise his famous
voltaic pile consisting of disks of copper and zinc or other metals
with wet cloth placed between the pairs. Numerous examples
of Volta’s original piles at one time existed in Italy, and were
collected together for an exhibition held at Como in 1899, but
were unfortunately destroyed by a disastrous fire on the 8th of
July 1899. Volta’s description of his pile was communicated
in a letter to Sir Joseph Banks, president of the Royal Society
of London, on the 20th of March 1800, and was printed in the
Phil. Trans., vol. 90, pt. 1, p. 405. It was then found that when
the end plates of Volta’s pile were connected to an electroscope
the leaves diverged either with positive or negative electricity.
Volta also gave his pile another form, the couronne des tasses
(crown of cups), in which connected strips of copper and zinc
were used to bridge between cups of water or dilute acid. Volta
then proved that all metals could be arranged in an electromotive
series such that each became positive when placed in contact
with the one next below it in the series. The origin of the
electromotive force in the pile has been much discussed, and
Volta’s discoveries gave rise to one of the historic controversies
of science. Volta maintained that the mere contact
of metals was sufficient to produce the electrical difference
of the end plates of the pile. The discovery that chemical
action was involved in the process led to the advancement of
the chemical theory of the pile and this was strengthened by the
growing insight into the principle of the conservation of energy.
In 1851 Lord Kelvin (Sir W. Thomson), by the use of his then
newly-invented electrometer, was able to confirm Volta’s observations
on contact electricity by irrefutable evidence, but the
contact theory of the voltaic pile was then placed on a basis
consistent with the principle of the conservation of energy.
A.A. de la Rive and Faraday were ardent supporters of the
chemical theory of the pile, and even at the present time opinions
of physicists can hardly be said to be in entire accordance as to
the source of the electromotive force in a voltaic couple or pile.7
Improvements in the form of the voltaic pile were almost
immediately made by W. Cruickshank (1745-1800), Dr W.H.
Wollaston and Sir H. Davy, and these, together with other
eminent continental chemists, such as A.F. de Fourcroy, L.J.
Thénard and J.W. Ritter (1776-1810), ardently prosecuted
research with the new instrument. One of the first discoveries
made with it was its power to electrolyse or chemically decompose
certain solutions. William Nicholson (1753-1815) and Sir
Anthony Carlisle (1768-1840) in 1800 constructed a pile of
silver and zinc plates, and placing the terminal wires in water
noticed the evolution from these wires of bubbles of gas, which
they proved to be oxygen and hydrogen. These two gases, as
Cavendish and James Watt had shown in 1784, were actually
the constituents of water. From that date it was clearly recognized
that a fresh implement of great power had been given
to the chemist. Large voltaic piles were then constructed by
Andrew Crosse (1784-1855) and Sir H. Davy, and improvements
initiated by Wollaston and Robert Hare (1781-1858) of Philadelphia.
In 1806 Davy communicated to the Royal Society
of London a celebrated paper on some “Chemical Agencies of
Electricity,” and after providing himself at the Royal Institution
of London with a battery of several hundred cells, he announced
in 1807 his great discovery of the electrolytic decomposition of
the alkalis, potash and soda, obtaining therefrom the metals
potassium and sodium. In July 1808 Davy laid a request
before the managers of the Royal Institution that they would
set on foot a subscription for the purchase of a specially large
voltaic battery; as a result he was provided with one of 2000
pairs of plates, and the first experiment performed with it was
the production of the electric arc light between carbon poles.
Davy followed up his initial work with a long and brilliant
series of electrochemical investigations described for the most
part in the Phil. Trans. of the Royal Society.
Magnetic Action of Electric Current.—Noticing an analogy
between the polarity of the voltaic pile and that of the magnet,
philosophers had long been anxious to discover a relation between
the two, but twenty years elapsed after the invention of the pile
before Hans Christian Oersted (1777-1851), professor of natural
philosophy in the university of Copenhagen, made in 1819 the
discovery which has immortalized his name. In the Annals of
Philosophy (1820, 16, p. 273) is to be found an English translation
of Oersted’s original Latin essay (entitled “Experiments on the
Effect of a Current of Electricity on the Magnetic Needle”),
dated the 21st of July 1820, describing his discovery. In it
Oersted describes the action he considers is taking place around
184
the conductor joining the extremities of the pile; he speaks of
it as the electric conflict, and says: “It is sufficiently evident
that the electric conflict is not confined to the conductor, but is
dispersed pretty widely in the circumjacent space. We may
likewise conclude that this conflict performs circles round the
wire, for without this condition it seems impossible that one part
of the wire when placed below the magnetic needle should drive
its pole to the east, and when placed above it, to the west.”
Oersted’s important discovery was the fact that when a wire
joining the end plates of a voltaic pile is held near a pivoted
magnet or compass needle, the latter is deflected and places itself
more or less transversely to the wire, the direction depending
upon whether the wire is above or below the needle, and on the
manner in which the copper or zinc ends of the pile are connected
to it. It is clear, moreover, that Oersted clearly recognized the
existence of what is now called the magnetic field round the
conductor. This discovery of Oersted, like that of Volta, stimulated
philosophical investigation in a high degree.
Electrodynamics.—On the 2nd of October 1820, A.M. Ampère
presented to the French Academy of Sciences an important
memoir,8 in which he summed up the results of his own and
D.F.J. Arago’s previous investigations in the new science of
electromagnetism, and crowned that labour by the announcement
of his great discovery of the dynamical action between conductors
conveying the electric currents. Ampère in this paper gave an
account of his discovery that conductors conveying electric
currents exercise a mutual attraction or repulsion on one another,
currents flowing in the same direction in parallel conductors
attracting, and those in opposite directions repelling. Respecting
this achievement when developed in its experimental and
mathematical completeness, Clerk Maxwell says that it was
“perfect in form and unassailable in accuracy.” By a series
of well-chosen experiments Ampère established the laws of this
mutual action, and not only explained observed facts by a
brilliant train of mathematical analysis, but predicted others
subsequently experimentally realized. These investigations led
him to the announcement of the fundamental law of action
between elements of current, or currents in infinitely short
lengths of linear conductors, upon one another at a distance;
summed up in compact expression this law states that the action
is proportional to the product of the current strengths of the two
elements, and the lengths of the two elements, and inversely
proportional to the square of the distance between the two
elements, and also directly proportional to a function of the angles
which the line joining the elements makes with the directions
of the two elements respectively. Nothing is more remarkable
in the history of discovery than the manner in which Ampère
seized upon the right clue which enabled him to disentangle the
complicated phenomena of electrodynamics and to deduce them
all as a consequence of one simple fundamental law, which
occupies in electrodynamics the position of the Newtonian law
of gravitation in physical astronomy.
In 1821 Michael Faraday (1791-1867), who was destined
later on to do so much for the science of electricity, discovered
electromagnetic rotation, having succeeded in causing a wire
conveying a voltaic current to rotate continuously round the pole
of a permanent magnet.9 This experiment was repeated in a
variety of forms by A.A. De la Rive, Peter Barlow (1776-1862),
William Ritchie (1790-1837), William Sturgeon (1783-1850),
and others; and Davy (Phil. Trans., 1823) showed that when two
wires connected with the pole of a battery were dipped into a
cup of mercury placed on the pole of a powerful magnet, the
fluid rotated in opposite directions about the two electrodes.
Electromagnetism.—In 1820 Arago (Ann. Chim. Phys., 1820,
15, p. 94) and Davy (Annals of Philosophy, 1821) discovered
independently the power of the electric current to magnetize
iron and steel. Félix Savary (1797-1841) made some very
curious observations in 1827 on the magnetization of steel
needles placed at different distances from a wire conveying the
discharge of a Leyden jar (Ann. Chim. Phys., 1827, 34). W.
Sturgeon in 1824 wound a copper wire round a bar of iron bent
in the shape of a horseshoe, and passing a voltaic current through
the wire showed that the iron became powerfully magnetized
as long as the connexion with the pile was maintained (Trans.
Soc. Arts, 1825). These researches gave us the electromagnet,
almost as potent an instrument of research and invention as the
pile itself (see Electromagnetism).
Ampère had already previously shown that a spiral conductor
or solenoid when traversed by an electric current possesses
magnetic polarity, and that two such solenoids act upon one
another when traversed by electric currents as if they were
magnets. Joseph Henry, in the United States, first suggested
the construction of what were then called intensity electromagnets,
by winding upon a horseshoe-shaped piece of soft
iron many superimposed windings of copper wire, insulated by
covering it with silk or cotton, and then sending through the
coils the current from a voltaic battery. The dependence of
the intensity of magnetization on the strength of the current was
subsequently investigated (Pogg. Ann. Phys., 1839, 47) by
H.F.E. Lenz (1804-1865) and M.H. von Jacobi (1801-1874).
J.P. Joule found that magnetization did not increase proportionately
with the current, but reached a maximum (Sturgeon’s
Annals of Electricity, 1839, 4). Further investigations on this
subject were carried on subsequently by W.E. Weber (1804-1891),
J.H.J. Müller (1809-1875), C.J. Dub (1817-1873),
G.H. Wiedemann (1826-1899), and others, and in modern times
by H.A. Rowland (1848-1901), Shelford Bidwell (b. 1848),
John Hopkinson (1849-1898), J.A. Ewing (b. 1855) and many
others. Electric magnets of great power were soon constructed
in this manner by Sturgeon, Joule, Henry, Faraday and Brewster.
Oersted’s discovery in 1819 was indeed epoch-making in the
degree to which it stimulated other research. It led at once to
the construction of the galvanometer as a means of detecting
and measuring the electric current in a conductor. In 1820
J.S.C. Schweigger (1779-1857) with his “multiplier” made
an advance upon Oersted’s discovery, by winding the wire
conveying the electric current many times round the pivoted
magnetic needle and thus increasing the deflection; and L.
Nobili (1784-1835) in 1825 conceived the ingenious idea of
neutralizing the directive effect of the earth’s magnetism by
employing a pair of magnetized steel needles fixed to one axis,
but with their magnetic poles pointing in opposite directions.
Hence followed the astatic multiplying galvanometer.
Electrodynamic Rotation.—The study of the relation between
the magnet and the circuit conveying an electric current then
led Arago to the discovery of the “magnetism of rotation.”
He found that a vibrating magnetic compass needle came to
rest sooner when placed over a plate of copper than otherwise,
and also that a plate of copper rotating under a suspended
magnet tended to drag the magnet in the same direction. The
matter was investigated by Charles Babbage, Sir J.F.W.
Herschel, Peter Barlow and others, but did not receive a final
explanation until after the discovery of electromagnetic induction
by Faraday in 1831. Ampère’s investigations had led electricians
to see that the force acting upon a magnetic pole due to a current
in a neighbouring conductor was such as to tend to cause the
pole to travel round the conductor. Much ingenuity had,
however, to be expended before a method was found of exhibiting
such a rotation. Faraday first succeeded by the simple but
ingenious device of using a light magnetic needle tethered
flexibly to the bottom of a cup containing mercury so that one
pole of the magnet was just above the surface of the mercury.
On bringing down on to the mercury surface a wire conveying
an electric current, and allowing the current to pass through the
mercury and out at the bottom, the magnetic pole at once began
to rotate round the wire (Exper. Res., 1822, 2, p. 148). Faraday
and others then discovered, as already mentioned, means to
make the conductor conveying the current rotate round a
185
magnetic pole, and Ampère showed that a magnet could be made
to rotate on its own axis when a current was passed through it.
The difficulty in this case consisted in discovering means by
which the current could be passed through one half of the magnet
without passing it through the other half. This, however, was
overcome by sending the current out at the centre of the magnet
by means of a short length of wire dipping into an annular groove
containing mercury. Barlow, Sturgeon and others then showed
that a copper disk could be made to rotate between the poles
of a horseshoe magnet when a current was passed through the
disk from the centre to the circumference, the disk being rendered
at the same time freely movable by making a contact with the
circumference by means of a mercury trough. These experiments
furnished the first elementary forms of electric motor, since it
was then seen that rotatory motion could be produced in masses
of metal by the mutual action of conductors conveying electric
current and magnetic fields. By his discovery of thermo-electricity
in 1822 (Pogg. Ann. Phys., 6), T.J. Seebeck (1770-1831)
opened up a new region of research (see Thermo-electricity).
James Cumming (1777-1861) in 1823 (Annals of
Philosophy, 1823) found that the thermo-electric series varied
with the temperature, and J.C.A. Peltier (1785-1845) in 1834
discovered that a current passed across the junction of two
metals either generated or absorbed heat.
Ohm’s Law.—In 1827 Dr G.S. Ohm (1787-1854) rendered a
great service to electrical science by his mathematical investigation
of the voltaic circuit, and publication of his paper, Die
galvanische Kette mathematisch bearbeitet. Before his time,
ideas on the measurable quantities with which we are concerned
in an electric circuit were extremely vague. Ohm introduced
the clear idea of current strength as an effect produced by
electromotive force acting as a cause in a circuit having resistance
as its quality, and showed that the current was directly proportional
to the electromotive force and inversely as the resistance.
Ohm’s law, as it is called, was based upon an analogy with the
flow of heat in a circuit, discussed by Fourier. Ohm introduced
the definite conception of the distribution along the circuit of
“electroscopic force” or tension (Spannung), corresponding to
the modern term potential. Ohm verified his law by the aid of
thermo-electric piles as sources of electromotive force, and Davy,
C.S.M. Pouillet (1791-1868), A.C. Becquerel (1788-1878),
G.T. Fechner (1801-1887), R.H.A. Kohlrausch (1809-1858)
and others laboured at its confirmation. In more recent times,
1876, it was rigorously tested by G. Chrystal (b. 1851) at Clerk
Maxwell’s instigation (see Brit. Assoc. Report, 1876, p. 36), and
although at its original enunciation its meaning was not at first
fully apprehended, it soon took its place as the expression of the
fundamental law of electrokinetics.
Induction of Electric Currents.—In 1831 Faraday began the
investigations on electromagnetic induction which proved more
fertile in far-reaching practical consequences than any of those
which even his genius gave to the world. These advances all
centre round his supreme discovery of the induction of electric
currents. Fully familiar with the fact that an electric charge
upon one conductor could produce a charge of opposite sign
upon a neighbouring conductor, Faraday asked himself whether
an electric current passing through a conductor could not in any
like manner induce an electric current in some neighbouring
conductor. His first experiments on this subject were made in
the month of November 1825, but it was not until the 29th of
August 1831 that he attained success. On that date he had
provided himself with an iron ring, over which he had wound
two coils of insulated copper wire. One of these coils was connected
with the voltaic battery and the other with the galvanometer.
He found that at the moment the current in the battery
circuit was started or stopped, transitory currents appeared
in the galvanometer circuit in opposite directions. In ten days
of brilliant investigation, guided by clear insight from the very
first into the meaning of the phenomena concerned, he established
experimentally the fact that a current may be induced in a
conducting circuit simply by the variation in a magnetic field,
the lines of force of which are linked with that circuit. The
whole of Faraday’s investigations on this subject can be summed
up in the single statement that if a conducting circuit is placed
in a magnetic field, and if either by variation of the field or by
movement or variation of the form of the circuit the total
magnetic flux linked with the circuit is varied, an electromotive
force is set up in that circuit which at any instant is measured
by the rate at which the total flux linked with the circuit is
changing.
Amongst the memorable achievements of the ten days which
Faraday devoted to this investigation was the discovery that
a current could be induced in a conducting wire simply by moving
it in the neighbourhood of a magnet. One form which this
experiment took was that of rotating a copper disk between the
poles of a powerful electric magnet. He then found that a conductor,
the ends of which were connected respectively with the
centre and edge of the disk, was traversed by an electric current.
This important fact laid the foundation for all subsequent
inventions which finally led to the production of electromagnetic
or dynamo-electric machines.
Third Period.—With this supremely important discovery
of Faraday’s we enter upon the third period of electrical research,
in which that philosopher himself was the leading figure. He
not only collected the facts concerning electromagnetic induction
so industriously that nothing of importance remained for future
discovery, and embraced them all in one law of exquisite simplicity,
but he introduced his famous conception of lines of
force which changed entirely the mode of regarding electrical
phenomena. The French mathematicians, Coulomb, Biot,
Poisson and Ampère, had been content to accept the fact that
electric charges or currents in conductors could exert forces on
other charges or conductors at a distance without inquiring
into the means by which this action at a distance was produced.
Faraday’s mind, however, revolted against this notion; he felt
intuitively that these distance actions must be the result of
unseen operations in the interposed medium. Accordingly
when he sprinkled iron filings on a card held over a magnet and
revealed the curvilinear system of lines of force (see Magnetism),
he regarded these fragments of iron as simple indicators of a
physical state in the space already in existence round the magnet.
To him a magnet was not simply a bar of steel; it was the
core and origin of a system of lines of magnetic force attached
to it and moving with it. Similarly he came to see an electrified
body as a centre of a system of lines of electrostatic force. All
the space round magnets, currents and electric charges was
therefore to Faraday the seat of corresponding lines of magnetic
or electric force. He proved by systematic experiments that the
electromotive forces set up in conductors by their motions in
magnetic fields or by the induction of other currents in the
field were due to the secondary conductor cutting lines of magnetic
force. He invented the term “electrotonic state” to signify
the total magnetic flux due to a conductor conveying a current,
which was linked with any secondary circuit in the field or even
with itself.
Faraday’s Researches.—Space compels us to limit our account
of the scientific work done by Faraday in the succeeding twenty
years, in elucidating electrical phenomena and adding to the
knowledge thereon, to the very briefest mention. We must
refer the reader for further information to his monumental work
entitled Experimental Researches on Electricity, in three volumes,
reprinted from the Phil. Trans. between 1831 and 1851. Faraday
divided these researches into various series. The 1st and 2nd
concern the discovery of magneto-electric induction already
mentioned. The 3rd series (1833) he devoted to discussion of
the identity of electricity derived from various sources, frictional,
voltaic, animal and thermal, and he proved by rigorous experiments
the identity and similarity in properties of the electricity
generated by these various methods. The 5th series (1833) is
occupied with his electrochemical researches. In the 7th series
(1834) he defines a number of new terms, such as electrolyte,
electrolysis, anode and cathode, &c., in connexion with electrolytic
phenomena, which were immediately adopted into the
vocabulary of science. His most important contribution at
186
this date was the invention of the voltameter and his enunciation
of the laws of electrolysis. The voltameter provided a means
of measuring quantity of electricity, and in the hands of Faraday
and his successors became an appliance of fundamental importance.
The 8th series is occupied with a discussion of the
theory of the voltaic pile, in which Faraday accumulates evidence
to prove that the source of the energy of the pile must be chemical.
He returns also to this subject in the 16th series. In the 9th
series (1834) he announced the discovery of the important
property of electric conductors, since called their self-induction
or inductance, a discovery in which, however, he was anticipated
by Joseph Henry in the United States. The 11th series (1837)
deals with electrostatic induction and the statement of the
important fact of the specific inductive capacity of insulators
or dielectrics. This discovery was made in November 1837
when Faraday had no knowledge of Cavendish’s previous
researches into this matter. The 19th series (1845) contains
an account of his brilliant discovery of the rotation of the plane
of polarized light by transparent dielectrics placed in a magnetic
field, a relation which established for the first time a practical
connexion between the phenomena of electricity and light. The
20th series (1845) contains an account of his researches on the
universal action of magnetism and diamagnetic bodies. The
22nd series (1848) is occupied with the discussion of magneto-crystallic
force and the abnormal behaviour of various crystals
in a magnetic field. In the 25th series (1850) he made known
his discovery of the magnetic character of oxygen gas, and the
important principle that the terms paramagnetic and diamagnetic
are relative. In the 26th series (1850) he returned
to a discussion of magnetic lines of force, and illuminated the
whole subject of the magnetic circuit by his transcendent insight
into the intricate phenomena concerned. In 1855 he brought
these researches to a conclusion by a general article on magnetic
philosophy, having placed the whole subject of magnetism and
electromagnetism on an entirely novel and solid basis. In
addition to this he provided the means for studying the phenomena
not only qualitatively, but also quantitatively, by the profoundly
ingenious instruments he invented for that purpose.
Electrical Measurement.—Faraday’s ideas thus pressed upon
electricians the necessity for the quantitative measurement of
electrical phenomena.10 It has been already mentioned that
Schweigger invented in 1820 the “multiplier,” and Nobili in
1825 the astatic galvanometer. C.S.M. Pouillet in 1837 contributed
the sine and tangent compass, and W.E. Weber effected
great improvements in them and in the construction and use
of galvanometers. In 1849 H. von Helmholtz devised a tangent
galvanometer with two coils. The measurement of electric
resistance then engaged the attention of electricians. By his
Memoirs in the Phil. Trans. in 1843, Sir Charles Wheatstone gave
a great impulse to this study. He invented the rheostat and
improved the resistance balance, invented by S.H. Christie
(1784-1865) in 1833, and subsequently called the Wheatstone
Bridge. (See his Scientific Papers, published by the Physical
Society of London, p. 129.) Weber about this date invented
the electrodynamometer, and applied the mirror and scale
method of reading deflections, and in co-operation with C.F.
Gauss introduced a system of absolute measurement of electric
and magnetic phenomena. In 1846 Weber proceeded with
improved apparatus to test Ampère’s laws of electrodynamics.
In 1845 H.G. Grassmann (1809-1877) published (Pogg. Ann.
vol. 64) his “Neue Theorie der Electrodynamik,” in which he
gave an elementary law differing from that of Ampère but leading
to the same results for closed circuits. In the same year F.E.
Neumann published another law. In 1846 Weber announced
his famous hypothesis concerning the connexion of electrostatic
and electrodynamic phenomena. The work of Neumann and
Weber had been stimulated by that of H.F.E. Lenz (1804-1865),
whose researches (Pogg. Ann., 1834, 31; 1835, 34) among other
results led him to the statement of the law by means of which
the direction of the induced current can be predicted from the
theory of Ampère, the rule being that the direction of the induced
current is always such that its electrodynamic action tends to
oppose the motion which produces it.
Neumann in 1845 did for electromagnetic induction what
Ampère did for electrodynamics, basing his researches upon the
experimental laws of Lenz. He discovered a function, which
has been called the potential of one circuit on another, from
which he deduced a theory of induction completely in accordance
with experiment. Weber at the same time deduced the mathematical
laws of induction from his elementary law of electrical
action, and with his improved instruments arrived at accurate
verifications of the law of induction, which by this time had been
developed mathematically by Neumann and himself. In 1849
G.R. Kirchhoff determined experimentally in a certain case
the absolute value of the current induced by one circuit in
another, and in the same year Erik Edland (1819-1888) made
a series of careful experiments on the induction of electric
currents which further established received theories. These
labours laid the foundation on which was subsequently erected
a complete system for the absolute measurement of electric
and magnetic quantities, referring them all to the fundamental
units of mass, length and time. Helmholtz gave at the same
time a mathematical theory of induced currents and a valuable
series of experiments in support of them (Pogg. Ann., 1851).
This great investigator and luminous expositor just before that
time had published his celebrated essay, Die Erhaltung der
Kraft (“The Conservation of Energy”), which brought to a
focus ideas which had been accumulating in consequence of the
work of J.P. Joule, J.R. von Mayer and others, on the transformation
of various forms of physical energy, and in particular
the mechanical equivalent of heat. Helmholtz brought to bear
upon the subject not only the most profound mathematical
attainments, but immense experimental skill, and his work in
connexion with this subject is classical.
Lord Kelvin’s Work.—About 1842 Lord Kelvin (then William
Thomson) began that long career of theoretical and practical
discovery and invention in electrical science which revolutionized
every department of pure and applied electricity. His early
contributions to electrostatics and electrometry are to be found
described in his Reprint of Papers on Electrostatics and Magnetism
(1872), and his later work in his collected Mathematical and
Physical Papers. By his studies in electrostatics, his elegant
method of electrical images, his development of the theory of
potential and application of the principle of conservation of
energy, as well as by his inventions in connexion with electrometry,
he laid the foundations of our modern knowledge of
electrostatics. His work on the electrodynamic qualities of
metals, thermo-electricity, and his contributions to galvanometry,
were not less massive and profound. From 1842 onwards to the
end of the 19th century, he was one of the great master workers
in the field of electrical discovery and research.11 In 1853 he
published a paper “On Transient Electric Currents” (Phil.
Mag., 1853 [4], 5, p. 393), in which he applied the principle of
the conservation of energy to the discharge of a Leyden jar.
He added definiteness to the idea of the self-induction or inductance
of an electric circuit, and gave a mathematical expression
for the current flowing out of a Leyden jar during its discharge.
He confirmed an opinion already previously expressed by
Helmholtz and by Henry, that in some circumstances this discharge
is oscillatory in nature, consisting of an alternating electric
current of high frequency. These theoretical predictions were
confirmed and others, subsequently, by the work of B.W.
Feddersen (b. 1832), C.A. Paalzow (b. 1823), and it was then
seen that the familiar phenomena of the discharge of a Leyden
187
jar provided the means of generating electric oscillations of very
high frequency.
Telegraphy.—Turning to practical applications of electricity,
we may note that electric telegraphy took its rise in 1820,
beginning with a suggestion of Ampère immediately after
Oersted’s discovery. It was established by the work of Weber
and Gauss at Göttingen in 1836, and that of C.A. Steinheil
(1801-1870) of Munich, Sir W.F. Cooke (1806-1879) and Sir
C. Wheatstone in England, Joseph Henry and S.F.B. Morse
(1791-1872) in the United States in 1837. In 1845 submarine
telegraphy was inaugurated by the laying of an insulated conductor
across the English Channel by the brothers Brett, and
their temporary success was followed by the laying in 1851
of a permanent Dover-Calais cable by T.R. Crampton. In
1856 the project for an Atlantic submarine cable took shape
and the Atlantic Telegraph Company was formed with a capital
of £350,000, with Sir Charles Bright as engineer-in-chief and
E.O.W. Whitehouse as electrician. The phenomena connected
with the propagation of electric signals by underground insulated
wires had already engaged the attention of Faraday in 1854,
who pointed out the Leyden-jar-like action of an insulated
subterranean wire. Scientific and practical questions connected
with the possibility of laying an Atlantic submarine cable then
began to be discussed, and Lord Kelvin was foremost in developing
true scientific knowledge on this subject, and in the invention
of appliances for utilizing it. One of his earliest and most useful
contributions (in 1858) was the invention of the mirror galvanometer.
Abandoning the long and somewhat heavy magnetic
needles that had been used up to that date in galvanometers,
he attached to the back of a very small mirror made of microscopic
glass a fragment of magnetized watch-spring, and suspended
the mirror and needle by means of a cocoon fibre in the
centre of a coil of insulated wire. By this simple device he
provided a means of measuring small electric currents far in
advance of anything yet accomplished, and this instrument
proved not only most useful in pure scientific researches, but at
the same time was of the utmost value in connexion with submarine
telegraphy. The history of the initial failures and final
success in laying the Atlantic cable has been well told by Mr.
Charles Bright (see The Story of the Atlantic Cable, London, 1903).12
The first cable laid in 1857 broke on the 11th of August during
laying. The second attempt in 1858 was successful, but the
cable completed on the 5th of August 1858 broke down on the
20th of October 1858, after 732 messages had passed through it.
The third cable laid in 1865 was lost on the 2nd of August 1865,
but in 1866 a final success was attained and the 1865 cable also
recovered and completed. Lord Kelvin’s mirror galvanometer
was first used in receiving signals through the short-lived 1858
cable. In 1867 he invented his beautiful siphon-recorder for
receiving and recording the signals through long cables. Later,
in conjunction with Prof. Fleeming Jenkin, he devised his automatic
curb sender, an appliance for sending signals by means
of punched telegraphic paper tape. Lord Kelvin’s contributions
to the science of exact electric measurement13 were enormous.
His ampere-balances, voltmeters and electrometers, and double
bridge, are elsewhere described in detail (see Amperemeter;
Electrometer, and Wheatstone’s Bridge).
Dynamo.—The work of Faraday from 1831 to 1851 stimulated
and originated an immense mass of scientific research, but at
the same time practical inventors had not been slow to perceive
that it was capable of purely technical application. Faraday’s
copper disk rotated between the poles of a magnet, and producing
thereby an electric current, became the parent of
innumerable machines in which mechanical energy was directly
converted into the energy of electric currents. Of these
machines, originally called magneto-electric machines, one of
the first was devised in 1832 by H. Pixii. It consisted of a fixed
horseshoe armature wound over with insulated copper wire in
front of which revolved about a vertical axis a horseshoe magnet.
Pixii, who invented the split tube commutator for converting
the alternating current so produced into a continuous current
in the external circuit, was followed by J. Saxton, E.M. Clarke,
and many others in the development of the above-described
magneto-electric machine. In 1857 E.W. Siemens effected a
great improvement by inventing a shuttle armature and improving
the shape of the field magnet. Subsequently similar machines
with electromagnets were introduced by Henry Wilde (b. 1833),
Siemens, Wheatstone, W. Ladd and others, and the principle
of self-excitation was suggested by Wilde, C.F. Varley (1828-1883),
Siemens and Wheatstone (see Dynamo). These machines
about 1866 and 1867 began to be constructed on a commercial
scale and were employed in the production of the electric light.
The discovery of electric-current induction also led to the production
of the induction coil (q.v.), improved and brought to its
present perfection by W. Sturgeon, E.R. Ritchie, N.J. Callan,
H.D. Rühmkorff (1803-1877), A.H.L. Fizeau, and more recently
by A. Apps and modern inventors. About the same time
Fizeau and J.B.L. Foucault devoted attention to the invention
of automatic apparatus for the production of Davy’s electric
arc (see Lighting: Electric), and these appliances in conjunction
with magneto-electric machines were soon employed in lighthouse
work. With the advent of large magneto-electric machines the
era of electrotechnics was fairly entered, and this period, which
may be said to terminate about 1867 to 1869, was consummated
by the theoretical work of Clerk Maxwell.
Maxwell’s Researches.—James Clerk Maxwell (1831-1879)
entered on his electrical studies with a desire to ascertain if the
ideas of Faraday, so different from those of Poisson and the
French mathematicians, could be made the foundation of a
mathematical method and brought under the power of analysis.14
Maxwell started with the conception that all electric and magnetic
phenomena are due to effects taking place in the dielectric or in
the ether if the space be vacuous. The phenomena of light had
compelled physicists to postulate a space-filling medium, to which
the name ether had been given, and Henry and Faraday had long
previously suggested the idea of an electromagnetic medium.
The vibrations of this medium constitute the agency called
light. Maxwell saw that it was unphilosophical to assume a
multiplicity of ethers or media until it had been proved that one
would not fulfil all the requirements. He formulated the conception,
therefore, of electric charge as consisting in a displacement
taking place in the dielectric or electromagnetic medium
(see Electrostatics). Maxwell never committed himself to a
precise definition of the physical nature of electric displacement,
but considered it as defining that which Faraday had called the
polarization in the insulator, or, what is equivalent, the number
of lines of electrostatic force passing normally through a unit of
area in the dielectric. A second fundamental conception of
Maxwell was that the electric displacement whilst it is changing
is in effect an electric current, and creates, therefore, magnetic
force. The total current at any point in a dielectric must be
considered as made up of two parts: first, the true conduction
current, if it exists; and second, the rate of change of dielectric
displacement. The fundamental fact connecting electric currents
and magnetic fields is that the line integral of magnetic
force taken once round a conductor conveying an electric current
is equal to 4 π-times the surface integral of the current density,
or to 4 π-times the total current flowing through the closed
line round which the integral is taken (see Electrokinetics).
A second relation connecting magnetic and electric force is
188
based upon Faraday’s fundamental law of induction, that the
rate of change of the total magnetic flux linked with a conductor
is a measure of the electromotive force created in it (see Electrokinetics).
Maxwell also introduced in this connexion the
notion of the vector potential. Coupling together these ideas
he was finally enabled to prove that the propagation of electric
and magnetic force takes place through space with a certain
velocity determined by the dielectric constant and the magnetic
permeability of the medium. To take a simple instance, if we
consider an electric current as flowing in a conductor it is, as
Oersted discovered, surrounded by closed lines of magnetic
force. If we imagine the current in the conductor to be instantaneously
reversed in direction, the magnetic force surrounding
it would not be instantly reversed everywhere in direction,
but the reversal would be propagated outwards through space
with a certain velocity which Maxwell showed was inversely
as the square root of the product of the magnetic permeability
and the dielectric constant or specific inductive capacity of the
medium.
These great results were announced by him for the first time
in a paper presented in 1864 to the Royal Society of London
and printed in the Phil. Trans. for 1865, entitled “A Dynamical
Theory of the Electromagnetic Field.” Maxwell showed in this
paper that the velocity of propagation of an electromagnetic
impulse through space could also be determined by certain experimental
methods which consisted in measuring the same electric
quantity, capacity, resistance or potential in two ways. W.E.
Weber had already laid the foundations of the absolute system
of electric and magnetic measurement, and proved that a
quantity of electricity could be measured either by the force
it exercises upon another static or stationary quantity of electricity,
or magnetically by the force this quantity of electricity
exercises upon a magnetic pole when flowing through a neighbouring
conductor. The two systems of measurement were called
respectively the electrostatic and the electromagnetic systems
(see Units, Physical). Maxwell suggested new methods for
the determination of this ratio of the electrostatic to the electromagnetic
units, and by experiments of great ingenuity was able
to show that this ratio, which is also that of the velocity of the
propagation of an electromagnetic impulse through space, is
identical with that of light. This great fact once ascertained,
it became clear that the notion that electric phenomena are
affections of the luminiferous ether was no longer a mere speculation
but a scientific theory capable of verification. An immediate
deduction from Maxwell’s theory was that in transparent dielectrics,
the dielectric constant or specific inductive capacity should
be numerically equal to the square of the refractive index for very
long electric waves. At the time when Maxwell developed his
theory the dielectric constants of only a few transparent insulators
were known and these were for the most part measured with
steady or unidirectional electromotive force. The only refractive
indices which had been measured were the optical refractive
indices of a number of transparent substances. Maxwell made
a comparison between the optical refractive index and the
dielectric constant of paraffin wax, and the approximation
between the numerical values of the square of the first and that
of the last was sufficient to show that there was a basis for further
work. Maxwell’s electric and magnetic ideas were gathered
together in a great mathematical treatise on electricity and
magnetism which was published in 1873.15 This book stimulated
in a most remarkable degree theoretical and practical research
into the phenomena of electricity and magnetism. Experimental
methods were devised for the further exact measurements
of the electromagnetic velocity and numerous determinations
of the dielectric constants of various solids, liquids and gases,
and comparisons of these with the corresponding optical refractive
indices were conducted. This early work indicated
that whilst there were a number of cases in which the square
of optical refractive index for long waves and the dielectric
constant of the same substance were sufficiently close to afford
an apparent confirmation of Maxwell’s theory, yet in other
cases there were considerable divergencies. L. Boltzmann
(1844-1907) made a large number of determinations for solids
and for gases, and the dielectric constants of many solid and
liquid substances were determined by N.N. Schiller (b. 1848),
P.A. Silow (b. 1850), J. Hopkinson and others. The accumulating
determinations of the numerical value of the electromagnetic
velocity (v) from the earliest made by Lord Kelvin
(Sir W. Thomson) with the aid of King and McKichan, or those
of Clerk Maxwell, W.E. Ayrton and J. Perry, to more recent
ones by J.J. Thomson, F. Himstedt, H.A. Rowland, E.B. Rosa,
J.S.H. Pellat and H.A. Abraham, showed it to be very close
to the best determinations of the velocity of light (see Units,
Physical). On the other hand, the divergence in some cases
between the square of the optical refractive index and the
dielectric constant was very marked. Hence although Maxwell’s
theory of electrical action when first propounded found many
adherents in Great Britain, it did not so much dominate opinion
on the continent of Europe.
Fourth Period.—With the publication of Clerk Maxwell’s
treatise in 1873, we enter fully upon the fourth and modern
period of electrical research. On the technical side the invention
of a new form of armature for dynamo electric machines by
Z.T. Gramme (1826-1901) inaugurated a departure from which
we may date modern electrical engineering. It will be convenient
to deal with technical development first.
Technical Development.—As far back as 1841 large magneto-electric
machines driven by steam power had been constructed,
and in 1856 F.H. Holmes had made a magneto machine with
multiple permanent magnets which was installed in 1862 in
Dungeness lighthouse. Further progress was made in 1867
when H. Wilde introduced the use of electromagnets for the field
magnets. In 1860 Dr Antonio Pacinotti invented what is now
called the toothed ring winding for armatures and described it
in an Italian journal, but it attracted little notice until reinvented
in 1870 by Gramme. In this new form of bobbin, the armature
consisted of a ring of iron wire wound over with an endless coil
of wire and connected to a commutator consisting of copper bars
insulated from one another. Gramme dynamos were then soon
made on the self-exciting principle. In 1873 at Vienna the fact
was discovered that a dynamo machine of the Gramme type
could also act as an electric motor and was set in rotation when
a current was passed into it from another similar machine.
Henceforth the electric transmission of power came within the
possibilities of engineering.
Electric Lighting.—In 1876, Paul Jablochkov (1847-1894),
a Russian officer, passing through Paris, invented his famous
electric candle, consisting of two rods of carbon placed side by
side and separated from one another by an insulating material.
This invention in conjunction with an alternating current
dynamo provided a new and simple form of electric arc lighting.
Two years afterwards C.F. Brush, in the United States, produced
another efficient form of dynamo and electric arc lamp suitable
for working in series (see Lighting: Electric), and these inventions
of Brush and Jablochkov inaugurated commercial arc
lighting. The so-called subdivision of electric light by incandescent
lighting lamps then engaged attention. E.A. King in
1845 and W.E. Staite in 1848 had made incandescent electric
lamps of an elementary form, and T.A. Edison in 1878 again
attacked the problem of producing light by the incandescence of
platinum. It had by that time become clear that the most
suitable material for an incandescent lamp was carbon contained
in a good vacuum, and St G. Lane Fox and Sir J.W. Swan in
England, and T.A. Edison in the United States, were engaged
in struggling with the difficulties of producing a suitable carbon
incandescence electric lamp. Edison constructed in 1879 a
successful lamp of this type consisting of a vessel wholly of glass
containing a carbon filament made by carbonizing paper or
some other carbonizable material, the vessel being exhausted
and the current led into the filament through platinum wires.
189
In 1879 and 1880, Edison in the United States, and Swan in
conjunction with C.H. Stearn in England, succeeded in completely
solving the practical problems. From and after that date
incandescent electric lighting became commercially possible,
and was brought to public notice chiefly by an electrical exhibition
held at the Crystal Palace, near London, in 1882. Edison,
moreover, as well as Lane-Fox, had realized the idea of a public
electric supply station, and the former proceeded to establish
in Pearl Street, New York, in 1881, the first public electric supply
station. A similar station in England was opened in the basement
of a house in Holborn Viaduct, London, in March 1882. Edison,
with copious ingenuity, devised electric meters, electric mains,
lamp fittings and generators complete for the purpose. In 1881
C.A. Faure made an important improvement in the lead
secondary battery which G. Planté (1834-1889) had invented
in 1859, and storage batteries then began to be developed as
commercial appliances by Faure, Swan, J.S. Sellon and many
others (see Accumulator). In 1882, numerous electric lighting
companies were formed for the conduct of public and private
lighting, but an electric lighting act passed in that year greatly
hindered commercial progress in Great Britain. Nevertheless
the delay was utilized in the completion of inventions necessary
for the safe and economical distribution of electric current for
the purpose of electric lighting.
Telephone.—Going back a few years we find the technical
applications of electrical invention had developed themselves
in other directions. Alexander Graham Bell in 1876 invented
the speaking telephone (q.v.), and Edison and Elisha Gray in
the United States followed almost immediately with other
telephonic inventions for electrically transmitting speech.
About the same time D.E. Hughes in England invented the
microphone. In 1879 telephone exchanges began to be developed
in the United States, Great Britain and other countries.
Electric Power.—Following on the discovery in 1873 of the
reversible action of the dynamo and its use as a motor, efforts
began to be made to apply this knowledge to transmission of
power, and S.D. Field, T.A. Edison, Leo Daft, E.M. Bentley
and W.H. Knight, F.J. Sprague, C.J. Van Depoele and others
between 1880 and 1884 were the pioneers of electric traction. One
of the earliest electric tram cars was exhibited by E.W. and W.
Siemens in Paris in 1881. In 1883 Lucien Gaulard, following a
line of thought opened by Jablochkov, proposed to employ high
pressure alternating currents for electric distributions over wide
areas by means of transformers. His ideas were improved by
Carl Zipernowsky and O.T. Bláthy in Hungary and by S.Z.
de Ferranti in England, and the alternating current transformer
(see Transformers) came into existence. Polyphase alternators
were first exhibited at the Frankfort electrical exhibition in 1891,
developed as a consequence of scientific researches by Galileo
Ferraris (1847-1897), Nikola Tesla, M.O. von Dolivo-Dobrowolsky
and C.E.L. Brown, and long distance transmission of electrical
power by polyphase electrical currents (see Power Transmission:
Electric) was exhibited in operation at Frankfort in
1891. Meanwhile the early continuous current dynamos devised
by Gramme, Siemens and others had been vastly improved in
scientific principle and practical construction by the labours of
Siemens, J. Hopkinson, R.E.B. Crompton, Elihu Thomson,
Rudolf Eickemeyer, Thomas Parker and others, and the theory
of the action of the dynamo had been closely studied by J. and
E. Hopkinson, G. Kapp, S.P. Thompson, C.P. Steinmetz and
J. Swinburne, and great improvements made in the alternating
current dynamo by W.M. Mordey, S.Z. de Ferranti and Messrs
Ganz of Budapest. Thus in twenty years from the invention of
the Gramme dynamo, electrical engineering had developed from
small beginnings into a vast industry. The amendment, in 1888,
of the Electric Lighting Act of 1882, before long caused a huge
development of public electric lighting in Great Britain. By
the end of the 19th century every large city in Europe and in
North and South America was provided with a public electric
supply for the purposes of electric lighting. The various improvements
in electric illuminants, such as the Nernst oxide lamp, the
tantalum and osmium incandescent lamps, and improved forms
of arc lamp, enclosed, inverted and flame arcs, are described
under Lighting: Electric.
Between 1890 and 1900, electric traction advanced rapidly
in the United States of America but more slowly in England.
In 1902 the success of deep tube electric railways in Great
Britain was assured, and in 1904 main line railways began to
abandon, at least experimentally, the steam locomotive and substitute
for it the electric transmission of power. Long distance
electrical transmission had been before that time exemplified
in the great scheme of utilizing the falls of Niagara. The first
projects were discussed in 1891 and 1892 and completed practically
some ten years later. In this scheme large turbines were
placed at the bottom of hydraulic fall tubes 150 ft. deep, the
turbines being coupled by long shafts with 5000 H.P. alternating
current dynamos on the surface. By these electric current was
generated and transmitted to towns and factories around, being
sent overhead as far as Buffalo, a distance of 18 m. At the end
of the 19th century electrochemical industries began to be
developed which depended on the possession of cheap electric
energy. The production of aluminium in Switzerland and
Scotland, carborundum and calcium carbide in the United
States, and soda by the Castner-Kellner process, began to be
conducted on an immense scale. The early work of Sir W.
Siemens on the electric furnace was continued and greatly
extended by Henri Moissan and others on its scientific side, and
electrochemistry took its place as one of the most promising
departments of technical research and invention. It was
stimulated and assisted by improvements in the construction
of large dynamos and increased knowledge concerning the
control of powerful electric currents.
In the early part of the 20th century the distribution in bulk
of electric energy for power purposes in Great Britain began to
assume important proportions. It was seen to be uneconomical
for each city and town to manufacture its own supply since,
owing to the intermittent nature of the demand for current for
lighting, the price had to be kept up to 4d. and 6d. per unit.
It was found that by the manufacture in bulk, even by steam
engines, at primary centres the cost could be considerably
reduced, and in numerous districts in England large power
stations began to be erected between 1903 and 1905 for the
supply of current for power purposes. This involved almost a
revolution in the nature of the tools used, and in the methods
of working, and may ultimately even greatly affect the factory
system and the concentration of population in large towns
which was brought about in the early part of the 19th century
by the invention of the steam engine.
Development of Electric Theory.
Turning now to the theory of electricity, we may note the
equally remarkable progress made in 300 years in scientific
insight into the nature of the agency which has so recast the
face of human society. There is no need to dwell upon the
early crude theories of the action of amber and lodestone. In
a true scientific sense no hypothesis was possible, because few
facts had been accumulated. The discoveries of Stephen Gray
and C.F. de C. du Fay on the conductivity of some bodies for
the electric agency and the dual character of electrification gave
rise to the first notions of electricity as an imponderable fluid,
or non-gravitative subtile matter, of a more refined and penetrating
kind than ordinary liquids and gases. Its duplex character,
and the fact that the electricity produced by rubbing
glass and vitreous substances was different from that produced
by rubbing sealing-wax and resinous substances, seemed to
necessitate the assumption of two kinds of electric fluid; hence
there arose the conception of positive and negative electricity,
and the two-fluid theory came into existence.
Single-fluid Theory.—The study of the phenomena of the
Leyden jar and of the fact that the inside and outside coatings
possessed opposite electricities, so that in charging the jar as
much positive electricity is added to one side as negative to the
other, led Franklin about 1750 to suggest a modification called
the single fluid theory, in which the two states of electrification
190
were regarded as not the results of two entirely different fluids
but of the addition or subtraction of one electric fluid from
matter, so that positive electrification was to be looked upon
as the result of increase or addition of something to ordinary
matter and negative as a subtraction. The positive and negative
electrifications of the two coatings of the Leyden jar were
therefore to be regarded as the result of a transformation of
something called electricity from one coating to the other, by
which process a certain measurable quantity became so much
less on one side by the same amount by which it became more
on the other. A modification of this single fluid theory was put
forward by F.U.T. Aepinus which was explained and illustrated
in his Tentamen theoriae electricitatis et magnetismi, published
in St Petersburg in 1759. This theory was founded on the
following principles:—(1) the particles of the electric fluid
repel each other with a force decreasing as the distance increases;
(2) the particles of the electric fluid attract the atoms of all
bodies and are attracted by them with a force obeying the same
law; (3) the electric fluid exists in the pores of all bodies, and
while it moves without any obstruction in conductors such as
metals, water, &c., it moves with extreme difficulty in so-called
non-conductors such as glass, resin, &c.; (4) electrical phenomena
are produced either by the transference of the electric fluid of a
body containing more to one containing less, or from its attraction
and repulsion when no transference takes place. Electric
attractions and repulsions were, however, regarded as differential
actions in which the mutual repulsion of the particles of electricity
operated, so to speak, in antagonism to the mutual attraction
of particles of matter for one another and of particles of electricity
for matter. Independently of Aepinus, Henry Cavendish
put forward a single-fluid theory of electricity (Phil. Trans.,
1771, 61, p. 584), in which he considered it in more precise
detail.
Two-fluid Theory.—In the elucidation of electrical phenomena,
however, towards the end of the 18th century, a modification of
the two-fluid theory seems to have been generally preferred.
The notion then formed of the nature of electrification was
something as follows:—All bodies were assumed to contain a
certain quantity of a so-called neutral fluid made up of equal
quantities of positive and negative electricity, which when in
this state of combination neutralized one another’s properties.
The neutral fluid could, however, be divided up or separated
into its two constituents, and these could be accumulated on
separate conductors or non-conductors. This view followed
from the discovery of the facts of electric induction of J. Canton
(1753, 1754). When, for instance, a positively electrified body
was found to induce upon another insulated conductor a charge
of negative electricity on the side nearest to it, and a charge of
positive electricity on the side farthest from it, this was explained
by saying that the particles of each of the two electric fluids
repelled one another but attracted those of the positive fluid.
Hence the operation of the positive charge upon the neutral
fluid was to draw towards the positive the negative constituent
of the neutral charge and repel to the distant parts of the conductor
the positive constituent.
C.A. Coulomb experimentally proved that the law of attraction
and repulsion of simple electrified bodies was that the force
between them varied inversely as the square of the distance
and thus gave mathematical definiteness to the two-fluid hypothesis.
It was then assumed that each of the two constituents
of the neutral fluid had an atomic structure and that the so-called
particles of one of the electric fluids, say positive, repelled
similar particles with a force varying inversely as a square of the
distance and attracted those of the opposite fluid according to
the same law. This fact and hypothesis brought electrical
phenomena within the domain of mathematical analysis and,
as already mentioned, Laplace, Biot, Poisson, G.A.A. Plana
(1781-1846), and later Robert Murphy (1806-1843), made them
the subject of their investigations on the mode in which electricity
distributes itself on conductors when in equilibrium.
Faraday’s Views.—The two-fluid theory may be said to have
held the field until the time when Faraday began his researches
on electricity. After he had educated himself by the study of
the phenomena of lines of magnetic force in his discoveries on
electromagnetic induction, he applied the same conception to
electrostatic phenomena, and thus created the notion of lines
of electrostatic force and of the important function of the dielectric
or non-conductor in sustaining them. Faraday’s notion
as to the nature of electrification, therefore, about the middle
of the 19th century came to be something as follows:—He
considered that the so-called charge of electricity on a conductor
was in reality nothing on the conductor or in the conductor
itself, but consisted in a state of strain or polarization, or a
physical change of some kind in the particles of the dielectric
surrounding the conductor, and that it was this physical state
in the dielectric which constituted electrification. Since Faraday
was well aware that even a good vacuum can act as a dielectric,
he recognized that the state he called dielectric polarization
could not be wholly dependent upon the presence of gravitative
matter, but that there must be an electromagnetic medium of a
supermaterial nature. In the 13th series of his Experimental
Researches on Electricity he discussed the relation of a vacuum
to electricity. Furthermore his electrochemical investigations,
and particularly his discovery of the important law of electrolysis,
that the movement of a certain quantity of electricity through an
electrolyte is always accompanied by the transfer of a certain
definite quantity of matter from one electrode to another and the
liberation at these electrodes of an equivalent weight of the ions,
gave foundation for the idea of a definite atomic charge of electricity.
In fact, long previously to Faraday’s electrochemical
researches, Sir H. Davy and J.J. Berzelius early in the 19th
century had advanced the hypothesis that chemical combination
was due to electric attractions between the electric charges
carried by chemical atoms. The notion, however, that electricity
is atomic in structure was definitely put forward by Hermann
von Helmholtz in a well-known Faraday lecture. Helmholtz
says: “If we accept the hypothesis that elementary substances
are composed of atoms, we cannot well avoid concluding that
electricity also is divided into elementary portions which behave
like atoms of electricity.”16 Clerk Maxwell had already used in
1873 the phrase, “a molecule of electricity.”17 Towards the
end of the third quarter of the 19th century it therefore became
clear that electricity, whatever be its nature, was associated
with atoms of matter in the form of exact multiples of an indivisible
minimum electric charge which may be considered to be
“Nature’s unit of electricity.” This ultimate unit of electric
quantity Professor Johnstone Stoney called an electron.18 The
formulation of electrical theory as far as regards operations in
space free from matter was immensely assisted by Maxwell’s
mathematical theory. Oliver Heaviside after 1880 rendered
much assistance by reducing Maxwell’s mathematical analysis
to more compact form and by introducing greater precision into
terminology (see his Electrical Papers, 1892). This is perhaps
the place to refer also to the great services of Lord Rayleigh
to electrical science. Succeeding Maxwell as Cavendish professor
of physics at Cambridge in 1880, he soon devoted himself especially
to the exact redetermination of the practical electrical
units in absolute measure. He followed up the early work of the
British Association Committee on electrical units by a fresh
determination of the ohm in absolute measure, and in conjunction
with other work on the electrochemical equivalent of silver and
the absolute electromotive force of the Clark cell may be said
to have placed exact electrical measurement on a new basis.
He also made great additions to the theory of alternating electric
currents, and provided fresh appliances for other electrical
measurements (see his Collected Scientific Papers, Cambridge,
1900).
Electro-optics.—For a long time Faraday’s observation on the
rotation of the plane of polarized light by heavy glass in a
191
magnetic field remained an isolated fact in electro-optics. Then
M.E. Verdet (1824-1860) made a study of the subject and
discovered that a solution of ferric perchloride in methyl alcohol
rotated the plane of polarization in an opposite direction to heavy
glass (Ann. Chim. Phys., 1854, 41, p. 370; 1855, 43, p. 37;
Com. Rend., 1854, 39, p. 548). Later A.A.E.E. Kundt prepared
metallic films of iron, nickel and cobalt, and obtained powerful
negative optical rotation with them (Wied. Ann., 1884, 23,
p. 228; 1886, 27, p. 191). John Kerr (1824-1907) discovered
that a similar effect was produced when plane polarized light was
reflected from the pole of a powerful magnet (Phil. Mag., 1877,
[5], 3, p. 321, and 1878, 5, p. 161). Lord Kelvin showed that
Faraday’s discovery demonstrated that some form of rotation
was taking place along lines of magnetic force when passing
through a medium.19 Many observers have given attention to
the exact determination of Verdet’s constant of rotation for
standard substances, e.g. Lord Rayleigh for carbon bisulphide,20
and Sir W.H. Perkin for an immense range of inorganic and
organic bodies.21 Kerr also discovered that when certain homogeneous
dielectrics were submitted to electric strain, they
became birefringent (Phil. Mag., 1875, 50, pp. 337 and 446).
The theory of electro-optics received great attention from
Kelvin, Maxwell, Rayleigh, G.F. Fitzgerald, A. Righi and
P.K.L. Drude, and experimental contributions from innumerable
workers, such as F.T. Trouton, O.J. Lodge and J.L. Howard,
and many others.
Electric Waves.—In the decade 1880-1890, the most important
advance in electrical physics was, however, that which originated
with the astonishing researches of Heinrich Rudolf Hertz (1857-1894).
This illustrious investigator was stimulated, by a certain
problem brought to his notice by H. von Helmholtz, to undertake
investigations which had for their object a demonstration of the
truth of Maxwell’s principle that a variation in electric displacement
was in fact an electric current and had magnetic effects.
It is impossible to describe here the details of these elaborate
experiments; the reader must be referred to Hertz’s own papers,
or the English translation of them by Prof. D.E. Jones. Hertz’s
great discovery was an experimental realization of a suggestion
made by G.F. Fitzgerald (1851-1901) in 1883 as to a method of
producing electric waves in space. He invented for this purpose
a radiator consisting of two metal rods placed in one line, their
inner ends being provided with poles nearly touching and their
outer ends with metal plates. Such an arrangement constitutes
in effect a condenser, and when the two plates respectively are
connected to the secondary terminals of an induction coil in
operation, the plates are rapidly and alternately charged, and
discharged across the spark gap with electrical oscillations (see
Electrokinetics). Hertz then devised a wave detecting
apparatus called a resonator. This in its simplest form consisted
of a ring of wire nearly closed terminating in spark balls very
close together, adjustable as to distance by a micrometer screw.
He found that when the resonator was placed in certain positions
with regard to the oscillator, small sparks were seen between the
micrometer balls, and when the oscillator was placed at one end
of a room having a sheet of zinc fixed against the wall at the
other end, symmetrical positions could be found in the room at
which, when the resonator was there placed, either no sparks
or else very bright sparks occurred at the poles. These effects, as
Hertz showed, indicated the establishment of stationary electric
waves in space and the propagation of electric and magnetic
force through space with a finite velocity. The other additional
phenomena he observed finally contributed an all but conclusive
proof of the truth of Maxwell’s views. By profoundly ingenious
methods Hertz showed that these invisible electric waves could
be reflected and refracted like waves of light by mirrors and
prisms, and that familiar experiments in optics could be repeated
with electric waves which could not affect the eye. Hence
there arose a new science of electro-optics, and in all parts of
Europe and the United States innumerable investigators took
possession of the novel field of research with the greatest delight.
O.J. Lodge,22 A. Righi,23 J.H. Poincaré,24 V.F.K. Bjerknes,
P.K.L. Drude, J.J. Thomson,25 John Trowbridge, Max Abraham,
and many others, contributed to its elucidation.
In 1892, E. Branly of Paris devised an appliance for detecting
these waves which subsequently proved to be of immense
importance. He discovered that they had the power of affecting
the electric conductivity of materials when in a state of powder,
the majority of metallic filings increasing in conductivity.
Lodge devised a similar arrangement called a coherer, and E.
Rutherford invented a magnetic detector depending on the
power of electric oscillations to demagnetize iron or steel. The
sum total of all these contributions to electrical knowledge
had the effect of establishing Maxwell’s principles on a firm basis,
but they also led to technical inventions of the very greatest
utility. In 1896 G. Marconi applied a modified and improved
form of Branly’s wave detector in conjunction with a novel
form of radiator for the telegraphic transmission of intelligence
through space without wires, and he and others developed this
new form of telegraphy with the greatest rapidity and success
into a startling and most useful means of communicating through
space electrically without connecting wires.
Electrolysis.—The study of the transfer of electricity through
liquids had meanwhile received much attention. The general
facts and laws of electrolysis (q.v.) were determined experimentally
by Davy and Faraday and confirmed by the researches of
J.F. Daniell, R.W. Bunsen and Helmholtz. The modern
theory of electrolysis grew up under the hands of R.J.E. Clausius,
A.W. Williamson and F.W.G. Kohlrausch, and received a
great impetus from the work of Svante Arrhenius, J.H. Van’t
Hoff, W. Ostwald, H.W. Nernst and many others. The theory
of the ionization of salts in solution has raised much discussion
amongst chemists, but the general fact is certain that electricity
only moves through liquids in association with matter, and
simultaneously involves chemical dissociation of molecular
groups.
Discharge through Gases.—Many eminent physicists had an
instinctive feeling that the study of the passage of electricity
through gases would shed much light on the intrinsic nature
of electricity. Faraday devoted to a careful examination of the
phenomena the XIIIth series of his Experimental Researches,
and among the older workers in this field must be particularly
mentioned J. Plücker, J.W. Hittorf, A.A. de la Rive, J.P.
Gassiot, C.F. Varley, and W. Spottiswoode and J. Fletcher
Moulton. It has long been known that air and other gases at
the pressure of the atmosphere were very perfect insulators,
but that when they were rarefied and contained in glass tubes
with platinum electrodes sealed through the glass, electricity
could be passed through them under sufficient electromotive
force and produced a luminous appearance known as the electric
glow discharge. The so-called vacuum tubes constructed by
H. Geissler (1815-1879) containing air, carbonic acid, hydrogen,
&c., under a pressure of one or two millimetres, exhibit beautiful
appearances when traversed by the high tension current produced
by the secondary circuit of an induction coil. Faraday discovered
the existence of a dark space round the negative electrode which
is usually known as the “Faraday dark space.” De la Rive
added much to our knowledge of the subject, and J. Plücker
and his disciple J.W. Hittorf examined the phenomena exhibited
in so-called high vacua, that is, in exceedingly rarefied gases.
C.F. Varley discovered the interesting fact that no current
could be sent through the rarefied gas unless a certain minimum
potential difference of the electrodes was excited. Sir William
Crookes took up in 1872 the study of electric discharge through
192
high vacua, having been led to it by his researches on the radiometer.
The particular details of the phenomena observed will
be found described in the article Conduction, Electric (§ III.).
The main fact discovered by researches of Plücker, Hittorf and
Crookes was that in a vacuum tube containing extremely rarefied
air or other gas, a luminous discharge takes place from the
negative electrode which proceeds in lines normal to the surface
of the negative electrode and renders phosphorescent both the
glass envelope and other objects placed in the vacuum tube
when it falls upon them. Hittorf made in 1869 the discovery
that solid objects could cast shadows or intercept this cathode
discharge. The cathode discharge henceforth engaged the
attention of many physicists. Varley had advanced tentatively
the hypothesis that it consisted in an actual projection of electrified
matter from the cathode, and Crookes was led by his researches
in 1870, 1871 and 1872 to embrace and confirm this
hypothesis in a modified form and announce the existence of a
fourth state of matter, which he called radiant matter, demonstrating
by many beautiful and convincing experiments that
there was an actual projection of material substance of some
kind possessing inertia from the surface of the cathode. German
physicists such as E. Goldstein were inclined to take another
view. Sir J.J. Thomson, the successor of Maxwell and Lord
Rayleigh in the Cavendish chair of physics in the university of
Cambridge, began about the year 1899 a remarkable series of
investigations on the cathode discharge, which finally enabled
him to make a measurement of the ratio of the electric charge
to the mass of the particles of matter projected from the cathode,
and to show that this electric charge was identical with the
atomic electric charge carried by a hydrogen ion in the act of
electrolysis, but that the mass of the cathode particles, or
“corpuscles” as he called them, was far less, viz. about 1⁄2000th
part of the mass of a hydrogen atom.26 The subject was pursued
by Thomson and the Cambridge physicists with great mathematical
and experimental ability, and finally the conclusion
was reached that in a high vacuum tube the electric charge is
carried by particles which have a mass only a fraction, as above
mentioned, of that of the hydrogen atom, but which carry a
charge equal to the unit electric charge of the hydrogen ion as
found by electrochemical researches.27 P.E.A. Lenard made
in 1894 (Wied. Ann. Phys., 51, p. 225) the discovery that these
cathode particles or corpuscles could pass through a window
of thin sheet aluminium placed in the wall of the vacuum tube
and give rise to a class of radiation called the Lenard rays.
W.C. Röntgen of Munich made in 1896 his remarkable discovery
of the so-called X or Röntgen rays, a class of radiation produced
by the impact of the cathode particles against an impervious
metallic screen or anticathode placed in the vacuum tube.
The study of Röntgen rays was ardently pursued by the principal
physicists in Europe during the years 1897 and 1898 and subsequently.
The principal property of these Röntgen rays which
attracted public attention was their power of passing through
many solid bodies and affecting a photographic plate. Hence
some substances were opaque to them and others transparent.
The astonishing feat of photographing the bones of the living
animal within the tissues soon rendered the Röntgen rays
indispensable in surgery and directed an army of investigators
to their study.
Radioactivity.—One outcome of all this was the discovery
by H. Becquerel in 1896 that minerals containing uranium, and
particularly the mineral known as pitchblende, had the power
of affecting sensitive photographic plates enclosed in a black
paper envelope when the mineral was placed on the outside, as
well as of discharging a charged electroscope (Com. Rend., 1896,
122, p. 420). This research opened a way of approach to the
phenomena of radioactivity, and the history of the steps by which
P. Curie and Madame Curie were finally led to the discovery of
radium is one of the most fascinating chapters in the history of
science. The study of radium and radioactivity (see Radioactivity)
led before long to the further remarkable knowledge
that these so-called radioactive materials project into surrounding
space particles or corpuscles, some of which are identical
with those projected from the cathode in a high vacuum tube,
together with others of a different nature. The study of radioactivity
was pursued with great ability not only by the Curies
and A. Debierne, who associated himself with them, in France,
but by E. Rutherford and F. Soddy in Canada, and by J.J.
Thomson, Sir William Crookes, Sir William Ramsay and others
in England.
Electronic Theory.—The final outcome of these investigations
was the hypothesis that Thomson’s corpuscles or particles
composing the cathode discharge in a high vacuum tube must
be looked upon as the ultimate constituent of what we call
negative electricity; in other words, they are atoms of negative
electricity, possessing, however, inertia, and these negative
electrons are components at any rate of the chemical atom.
Each electron is a point-charge of negative electricity equal to
3.9 × 10−10 of an electrostatic unit or to 1.3 × 10−20 of an electromagnetic
unit, and the ratio of its charge to its mass is nearly
2 × 107 using E.M. units. For the hydrogen atom the ratio of
charge to mass as deduced from electrolysis is about 104. Hence
the mass of an electron is 1⁄2000th of that of a hydrogen atom.
No one has yet been able to isolate positive electrons, or to give
a complete demonstration that the whole inertia of matter is
only electric inertia due to what may be called the inductance
of the electrons. Prof. Sir J. Larmor developed in a series of
very able papers (Phil. Trans., 1894, 185; 1895, 186; 1897,
190), and subsequently in his book Aether and Matter (1900), a
remarkable hypothesis of the structure of the electron or corpuscle,
which he regards as simply a strain centre in the aether
or electromagnetic medium, a chemical atom being a collection
of positive and negative electrons or strain centres in stable
orbital motion round their common centre of mass (see Aether).
J.J. Thomson also developed this hypothesis in a profoundly
interesting manner, and we may therefore summarize very
briefly the views held on the nature of electricity and matter
at the beginning of the 20th century by saying that the term
electricity had come to be regarded, in part at least, as a collective
name for electrons, which in turn must be considered as constituents
of the chemical atom, furthermore as centres of certain
lines of self-locked and permanent strain existing in the universal
aether or electromagnetic medium. Atoms of matter are composed
of congeries of electrons and the inertia of matter is probably
therefore only the inertia of the electromagnetic medium.28
Electric waves are produced wherever electrons are accelerated
or retarded, that is, whenever the velocity of an electron is
changed or accelerated positively or negatively. In every solid
body there is a continual atomic dissociation, the result of which
is that mixed up with the atoms of chemical matter composing
them we have a greater or less percentage of free electrons.
The operation called an electric current consists in a diffusion
or movement of these electrons through matter, and this is
controlled by laws of diffusion which are similar to those of the
diffusion of liquids or gases. Electromotive force is due to a
difference in the density of the electronic population in different
or identical conducting bodies, and whilst the electrons can
move freely through so-called conductors their motion is much
more hindered or restricted in non-conductors. Electric charge
consists, therefore, in an excess or deficit of negative electrons
in a body. In the hands of H.A. Lorentz, P.K.L. Drude, J. J,
Thomson, J. Larmor and many others, the electronic hypothesis
of matter and of electricity has been developed in great detail
and may be said to represent the outcome of modern researches
upon electrical phenomena.
193
The reader may be referred for an admirable summary of the
theories of electricity prior to the advent of the electronic
hypothesis to J.J. Thomson’s “Report on Electrical Theories”
(Brit. Assoc. Report, 1885), in which he divides electrical
theories enunciated during the 19th century into four classes,
and summarizes the opinions and theories of A.M. Ampère,
H.G. Grassman, C.F. Gauss, W.E. Weber, G.F.B. Riemann,
R.J.E. Clausius, F.E. Neumann and H. von Helmholtz.
Bibliography.—M. Faraday, Experimental Researches in Electricity
(3 vols., London, 1839, 1844, 1855); A.A. De la Rive, Treatise
on Electricity (3 vols., London, 1853, 1858); J. Clerk Maxwell, A
Treatise on Electricity and Magnetism (2 vols., 3rd ed., 1892); id.,
Scientific Papers (2 vols., edited by Sir W.J. Niven, Cambridge,
1890); H.M. Noad, A Manual of Electricity (2 vols., London, 1855,
1857); J.J. Thomson, Recent Researches in Electricity and Magnetism
(Oxford, 1893); id., Conduction of Electricity through Gases (Cambridge,
1903); id., Electricity and Matter (London, 1904); O.
Heaviside, Electromagnetic Theory (London, 1893); O.J. Lodge,
Modern Views of Electricity (London, 1889); E. Mascart and J.
Joubert, A Treatise on Electricity and Magnetism, English trans. by
E. Atkinson (2 vols., London, 1883); Park Benjamin, The Intellectual
Rise in Electricity (London, 1895); G.C. Foster and A.W. Porter,
Electricity and Magnetism (London, 1903); A. Gray, A Treatise on
Magnetism and Electricity (London, 1898); H.W. Watson and S.H.
Burbury, The Mathematical Theory of Electricity and Magnetism
(2 vols., 1885); Lord Kelvin (Sir William Thomson), Mathematical
and Physical Papers (3 vols., Cambridge, 1882); Lord Rayleigh,
Scientific Papers (4 vols., Cambridge, 1903); A. Winkelmann,
Handbuch der Physik, vols. iii. and iv. (Breslau, 1903 and 1905;
a mine of wealth for references to original papers on electricity and
magnetism from the earliest date up to modern times). For
particular information on the modern Electronic theory the reader
may consult W. Kaufmann, “The Developments of the Electron
Idea.” Physikalische Zeitschrift (1st of Oct. 1901), or The Electrician
(1901), 48, p. 95; H.A. Lorentz, The Theory of Electrons (1909);
E.E. Fournier d’Albe, The Electron Theory (London, 1906); H.
Abraham and P. Langevin, Ions, Electrons, Corpuscles (Paris, 1905);
J.A. Fleming, “The Electronic Theory of Electricity,” Popular
Science Monthly (May 1902); Sir Oliver J. Lodge, Electrons, or the
Nature and Properties of Negative Electricity (London, 1907).
(J. A. F.)
1 Gilbert’s work, On the Magnet, Magnetic Bodies and the Great
Magnet, the Earth, has been translated from the rare folio Latin
edition of 1600, but otherwise reproduced in its original form by the
chief members of the Gilbert Club of England, with a series of valuable
notes by Prof. S.P. Thompson (London, 1900). See also The
Electrician, February 21, 1902.
2 See The Intellectual Rise in Electricity, ch. x., by Park Benjamin
(London, 1895).
3 See Sir Oliver Lodge, “Lightning, Lightning Conductors and
Lightning Protectors,” Journ. Inst. Elec. Eng. (1889), 18, p. 386, and
the discussion on the subject in the same volume; also the book
by the same author on Lightning Conductors and Lightning Guards
(London, 1892).
4 The Electrical Researches of the Hon. Henry Cavendish 1771-1781,
edited from the original manuscripts by J. Clerk Maxwell,
F.R.S. (Cambridge, 1879).
5 In 1878 Clerk Maxwell repeated Cavendish’s experiments with
improved apparatus and the employment of a Kelvin quadrant
electrometer as a means of detecting the absence of charge on the
inner conductor after it had been connected to the outer case, and
was thus able to show that if the law of electric attraction varies
inversely as the nth power of the distance, then the exponent n
must have a value of 2±1⁄21600. See Cavendish’s Electrical Researches,
p. 419.
6 Modern researches have shown that the loss of charge is in fact
dependent upon the ionization of the air, and that, provided the
atmospheric moisture is prevented from condensing on the insulating
supports, water vapour in the air does not per se bestow on it conductance
for electricity.
7 Faraday discussed the chemical theory of the pile and arguments
in support of it in the 8th and 16th series of his Experimental Researches
on Electricity. De la Rive reviews the subject in his large
Treatise on Electricity and Magnetism, vol. ii. ch. iii. The writer
made a contribution to the discussion in 1874 in a paper on “The
Contact Theory of the Galvanic Cell,” Phil. Mag., 1874, 47, p. 401.
Sir Oliver Lodge reviewed the whole position in a paper in 1885,
“On the Seat of the Electromotive Force in a Voltaic Cell,” Journ.
Inst. Elec. Eng., 1885, 14, p. 186.
8 “Mémoire sur la théorie mathématique des phénomènes électrodynamiques,”
Mémoires de l’institut, 1820, 6; see also Ann. de
Chim., 1820, 15.
9 See M. Faraday, “On some new Electro-Magnetical Motions
and on the Theory of Magnetism,” Quarterly Journal of Science,
1822, 12, p. 74; or Experimental Researches on Electricity, vol. ii.
p. 127.
10 Amongst the most important of Faraday’s quantitative researches
must be included the ingenious and convincing proofs he
provided that the production of any quantity of electricity of one
sign is always accompanied by the production of an equal quantity
of electricity of the opposite sign. See Experimental Researches on
Electricity, vol. i. § 1177.
11 In this connexion the work of George Green (1793-1841) must
not be forgotten. Green’s Essay on the Application of Mathematical
Analysis to the Theories of Electricity and Magnetism, published in
1828, contains the first exposition of the theory of potential. An
important theorem contained in it is known as Green’s theorem,
and is of great value.
12 See also his Submarine Telegraphs (London, 1898).
13 The quantitative study of electrical phenomena has been
enormously assisted by the establishment of the absolute system of
electrical measurement due originally to Gauss and Weber. The
British Association for the advancement of science appointed in
1861 a committee on electrical units, which made its first report in
1862 and has existed ever since. In this work Lord Kelvin took a
leading part. The popularization of the system was greatly assisted
by the publication by Prof. J.D. Everett of The C.G.S. System of
Units (London, 1891).
14 The first paper in which Maxwell began to translate Faraday’s
conceptions into mathematical language was “On Faraday’s Lines
of Force,” read to the Cambridge Philosophical Society on the 10th
of December 1855 and the 11th of February 1856. See Maxwell’s
Collected Scientific Papers, i. 155.
15 A Treatise on Electricity and Magnetism (2 vols.), by James
Clerk Maxwell, sometime professor of experimental physics in the
university of Cambridge. A second edition was edited by Sir W.D.
Niven in 1881 and a third by Prof. Sir J.J. Thomson in 1891.
16 H. von Helmholtz, “On the Modern Development of Faraday’s
Conception of Electricity,” Journ. Chem. Soc., 1881, 39, p. 277.
17 See Maxwell’s Electricity and Magnetism, vol. i. p. 350 (2nd ed.,
1881).
18 “On the Physical Units of Nature,” Phil. Mag., 1881, [5], 11,
p. 381. Also Trans. Roy. Soc. (Dublin, 1891), 4, p. 583.
19 See Sir W. Thomson, Proc. Roy. Soc. Lond., 1856, 8, p. 152; or
Maxwell, Elect. and Mag., vol. ii. p. 831.
20 See Lord Rayleigh, Proc. Roy. Soc. Lond., 1884, 37, p. 146;
Gordon, Phil. Trans., 1877, 167, p. 1; H. Becquerel, Ann. Chim.
Phys., 1882, [3], 27, p. 312.
21 Perkin’s Papers are to be found in the Journ. Chem. Soc. Lond.,
1884, p. 421; 1886, p. 177; 1888, p. 561; 1889, p. 680; 1891,
p. 981; 1892, p. 800; 1893, p. 75.
22 The Work of Hertz (London, 1894).
23 L’Ottica delle oscillazioni elettriche (Bologna, 1897).
24 Les Oscillations électriques (Paris, 1894).
25 Recent Researches in Electricity and Magnetism (Oxford, 1892).
26 See J.J. Thomson, Proc. Roy. Inst. Lond., 1897, 15, p. 419;
also Phil. Mag., 1899, [5], 48, p. 547.
27 Later results show that the mass of a hydrogen atom is not far
from 1.3×10-24 gramme and that the unit atomic charge or natural
unit of electricity is 1.3 × 10−20 of an electromagnetic C.G.S. unit.
The mass of the electron or corpuscle is 7.0 × 10−28 gramme and its
diameter is 3 × 10−13 centimetre. The diameter of a chemical atom is
of the order of 10−7 centimetre.
See H.A. Lorentz, “The Electron Theory,” Elektrotechnische
Zeitschrift, 1905, 26, p. 584; or Science Abstracts, 1905, 8, A, p. 603.
28 See J.J. Thomson, Electricity and Matter (London, 1904).
ELECTRICITY SUPPLY. I. General Principles.—The improvements
made in the dynamo and electric motor between
1870 and 1880 and also in the details of the arc and incandescent
electric lamp towards the close of that decade, induced engineers
to turn their attention to the question of the private and public
supply of electric current for the purpose of lighting and power.
T.A. Edison1 and St G. Lane Fox2 were among the first to see
the possibilities and advantages of public electric supply, and
to devise plans for its practical establishment. If a supply
of electric current has to be furnished to a building the option
exists in many cases of drawing from a public supply or of
generating it by a private plant.
Private Plants.—In spite of a great amount of ingenuity
devoted to the development of the primary battery and the
thermopile, no means of generation of large currents can compete
in economy with the dynamo. Hence a private electric generating
plant involves the erection of a dynamo which may be driven
either by a steam, gas or oil engine, or by power obtained by
means of a turbine from a low or high fall of water. It may be
either directly coupled to the motor, or driven by a belt; and
it may be either a continuous-current machine or an alternator,
and if the latter, either single-phase or polyphase. The convenience
of being able to employ storage batteries in connexion
with a private-supply system is so great that unless power has
to be transmitted long distances, the invariable rule is to employ
a continuous-current dynamo. Where space is valuable this
is always coupled direct to the motor; and if a steam-engine
is employed, an enclosed engine is most cleanly and compact.
Where coal or heating gas is available, a gas-engine is exceedingly
convenient, since it requires little attention. Where coal gas
is not available, a Dowson gas-producer can be employed. The
oil-engine has been so improved that it is extensively used in
combination with a direct-coupled or belt-driven dynamo and
thus forms a favourite and easily-managed plant for private
electric lighting. Lead storage cells, however, as at present
made, when charged by a steam-driven dynamo deteriorate less
rapidly than when an oil-engine is employed, the reason being
that the charging current is more irregular in the latter case,
since the single cylinder oil-engine only makes an impulse every
other revolution. In connexion with the generator, it is almost
the invariable custom to put down a secondary battery of storage
cells, to enable the supply to be given after the engine has stopped.
This is necessary, not only as a security for the continuity of
supply, but because otherwise the costs of labour in running
the engine night and day become excessive. The storage battery
gives its supply automatically, but the dynamo and engine
require incessant skilled attendance. If the building to be
lighted is at some distance from the engine-house the battery
should be placed in the basement of the building, and underground
or overhead conductors, to convey the charging current,
brought to it from the dynamo.
It is usual, in the case of electric lighting installations, to reckon
all lamps in their equivalent number of 8 candle power (c.p.)
incandescent lamps. In lighting a private house or building,
the first thing to be done is to settle the total number of incandescent
lamps and their size, whether 32 c.p., 16 c.p. or 8 c.p.
Lamps of 5 c.p. can be used with advantage in small bedrooms
and passages. Each candle-power in the case of a carbon filament
lamp can be taken as equivalent to 3.5 watts, or the 8 c.p. lamp
as equal to 30 watts, the 16 c.p. lamp to 60 watts, and so on.
In the case of metallic filament lamps about 1.0 or 1.25 watts.
Hence if the equivalent of 100 carbon filament 8 c.p. lamps is
required in a building the maximum electric power-supply available
must be 3000 watts or 3 kilowatts. The next matter to
consider is the pressure of supply. If the battery can be in a
position near the building to be lighted, it is best to use 100-volt
incandescent lamps and enclosed arc lamps, which can be
worked singly off the 100-volt circuit. If, however, the lamps
are scattered over a wide area, or in separate buildings somewhat
far apart, as in a college or hospital, it may be better to select 200
volts as the supply pressure. Arc lamps can then be worked three
in series with added resistance. The third step is to select the size
of the dynamo unit and the amount of spare plant. It is desirable
that there should be at least three dynamos, two of which
are capable of taking the whole of the full load, the third being
reserved to replace either of the others when required. The
total power to be absorbed by the lamps and motors (if any)
being given, together with an allowance for extensions, the size
of the dynamos can be settled, and the power of the engines
required to drive them determined. A good rule to follow is
that the indicated horse-power (I.H.P.) of the engine should be
double the dynamo full-load output in kilowatts; that is to
say, for a 10-kilowatt dynamo an engine should be capable of
giving 20 indicated (not nominal) H.P. From the I.H.P. of the
engine, if a steam engine, the size of the boiler required for steam
production becomes known. For small plants it is safe to reckon
that, including water waste, boiler capacity should be provided
equal to evaporating 40 ℔ of water per hour for every
I.H.P. of the engine. The locomotive boiler is a convenient
form; but where large amounts of steam are required, some
modification of the Lancashire boiler or the water-tube boiler
is generally adopted. In settling the electromotive force of
the dynamo to be employed, attention must be paid to the
question of charging secondary cells, if these are used. If a
secondary battery is employed in connexion with 100-volt lamps,
it is usual to put in 53 or 54 cells. The electromotive force of
these cells varies between 2.2 and 1.8 volts as they discharge;
hence the above number of cells is sufficient for maintaining the
necessary electromotive force. For charging, however, it is
necessary to provide 2.5 volts per cell, and the dynamo must
therefore have an electromotive force of 135 volts, plus any
voltage required to overcome the fall of potential in the cable
connecting the dynamo with the secondary battery. Supposing
this to be 10 volts, it is safe to install dynamos having an electromotive
force of 150 volts, since by means of resistance in the
field circuits this electromotive force can be lowered to 110 or
115 if it is required at any time to dispense with the battery.
The size of the secondary cell will be determined by the nature
194
of the supply to be given after the dynamos have been stopped.
It is usual to provide sufficient storage capacity to run all the
lamps for three or four hours without assistance from the dynamo.
As an example taken from actual practice, the following figures
give the capacity of the plant put down to supply 500 8 c.p. lamps
in a hospital. The dynamos were 15-unit machines, having a full-load
capacity of 100 amperes at 150 volts, each coupled direct to an
engine of 25 H.P.; and a double plant of this description was supplied
from two steel locomotive boilers, each capable of evaporating 800 ℔
of water per hour. One dynamo during the day was used for charging
the storage battery of 54 cells; and at night the discharge from the
cells, together with the current from one of the dynamos, supplied
the lamps until the heaviest part of the load had been taken; after
that the current was drawn from the batteries alone. In working
such a plant it is necessary to have the means of varying the electromotive
force of the dynamo as the charging of the cells proceeds.
When they are nearly exhausted, their electromotive force is less
than 2 volts; but as the charging proceeds, a counter-electromotive
force is gradually built up, and the engineer-in-charge has to raise
the voltage of the dynamo in order to maintain a constant charging
current. This is effected by having the dynamos designed to give
normally the highest E.M.F. required, and then inserting resistance
in their field circuits to reduce it as may be necessary. The space
and attendance required for an oil-engine plant are much less than
for a steam-engine.
Public Supply.—The methods at present in successful operation
for public electric supply fall into two broad divisions:—(1)
continuous-current systems and (2) alternating-current systems.
Continuous-current systems are either low- or high-pressure.
In the former the current is generated by dynamos at some
pressure less than 500 volts, generally about 460 volts, and is
supplied to users at half this pressure by means of a three-wire
system (see below) of distribution, with or without the addition
of storage batteries.
The general arrangements of a low-pressure continuous-current
town supply station are as follows:—If steam is the motive
power selected, it is generated under all the best
conditions of economy by a battery of boilers, and
Low-pressure continuous supply.
supplied to engines which are now almost invariably
coupled direct, each to its own dynamo, on one
common bedplate; a multipolar dynamo is most
usually employed, coupled direct to an enclosed engine. Parsons
or Curtis steam turbines (see Steam-Engine) are frequently
selected, since experience has shown that the costs of oil and
attendance are far less for this type than for the reciprocating
engine, whilst the floor space and, therefore, the building cost
are greatly reduced. In choosing the size of unit to be adopted,
the engineer has need of considerable experience and discretion,
and also a full knowledge of the nature of the public demand
for electric current. The rule is to choose as large units as possible,
consistent with security, because they are proportionately
more economical than small ones. The over-all efficiency of a
steam dynamo—that is, the ratio between the electrical power
output, reckoned say in kilowatts, and the I.H.P. of the
engine, reckoned in the same units—is a number which falls
rapidly as the load decreases, but at full load may reach some
such value as 80 or 85%. It is common to specify the efficiency,
as above defined, which must be attained by the plant at full-load,
and also the efficiencies at quarter- and half-load which
must be reached or exceeded. Hence in the selection of the size
of the units the engineer is guided by the consideration that
whatever units are in use shall be as nearly as possible fully
loaded. If the demand on the station is chiefly for electric
lighting, it varies during the hours of the day and night with
tolerable regularity. If the output of the station, either in
amperes or watts, is represented by the ordinates of a curve,
the abscissae of which represent the hours of the day, this load
diagram for a supply station with lighting load only, is a curve
such as is shown in fig. 1, having a high peak somewhere between
6 and 8 P.M. The area enclosed by this load-diagram compared
with the area of the circumscribing rectangle is called the load-factor
of the station. This varies from day to day during the
year, but on the average for a simple lighting load is not generally
above 10 or 12%, and may be lower. Thus the total output
from the station is only some 10% on an average of that which
it would be if the supply were at all times equal to the maximum
demand. Roughly speaking, therefore, the total output of an
electric supply station, furnishing current chiefly for electric
lighting, is at best equal to about two hours’ supply during the
day at full load. Hence during the greater part of the twenty-four
hours a large part of the plant is lying idle. It is usual to
provide certain small sets of steam dynamos, called the daylight
machines, for supplying the demand during the day and later
part of the evening, the remainder of the machines being called
into requisition only for a short time. Provision must be made
for sufficient reserve of plant, so that the breakdown of one or
more sets will not cripple the output of the station.
 |
| Fig. 1. |
 |
| Fig. 2. |
Assuming current to be supplied at about 460 volts by different
and separate steam dynamos, Dy1, Dy2 (fig. 2), the machines are
connected through proper amperemeters and voltmeters
with omnibus bars, O1, O2, O3, on a main switchboard,
Three-wire system.
so that any dynamo can be put in connexion
or removed. The switchboard is generally divided
into three parts—one panel for the connexions of the positive
feeders, F1, with the positive terminals of the generators; one for
the negative feeders, F3, and negative generator terminals;
while from the third (or middle-wire panel) proceed an equal
number of middle-wire feeders, F2. These sets of conductors
are led out into the district to be supplied with current, and are
there connected into a distributing system, consisting of three
separate insulated conductors, D1, D2, D3, respectively called the
positive, middle and negative distributing mains. The lamps
in the houses, H1, H2, &c., are connected between the middle and
negative, and the middle and positive, mains by smaller supply
and service wires. As far as possible the numbers of lamps
installed on the two sides of the system are kept equal; but since
it is not possible to control the consumption of current, it becomes
necessary to provide at the station two small dynamos called
the balancing machines, B1, B2, connected respectively between
the middle and positive and the middle and negative omnibus
bars. These machines may have their shafts connected together,
or they may be driven by separate steam dynamos; their
function is to supply the difference in the total current circulating
through the whole of the lamps respectively on the two opposite
sides of the middle wire. If storage batteries are employed in
the station, it is usual to install two complete batteries, S1, S2,
195
which are placed in a separate battery room and connected
between the middle omnibus bar and the two outer omnibus
bars. The extra electromotive force required to charge these
batteries is supplied by two small dynamos b1, b2, called boosters.
It is not unusual to join together the two balancing dynamos
and the two boosters on one common bedplate, the shafts being
coupled and in line, and to employ the balancing machines as
electromotors to drive the boosters as required. By the use of
reversible boosters, such as those made by the Lancashire Dynamo
& Motor Company under the patents of Turnbull & McLeod,
having four field windings on the booster magnets (see The
Electrician, 1904, p. 303), it is possible to adjust the relative duty
of the dynamos and battery so that the load on the supply
dynamos is always constant. Under these conditions the main
engines can be worked all the time at their maximum steam
economy and a smaller engine plant employed. If the load in
the station rises above the fixed amount, the batteries discharge
in parallel with the station dynamos; if it falls below, the
batteries are charged and the station dynamos take the external
load.
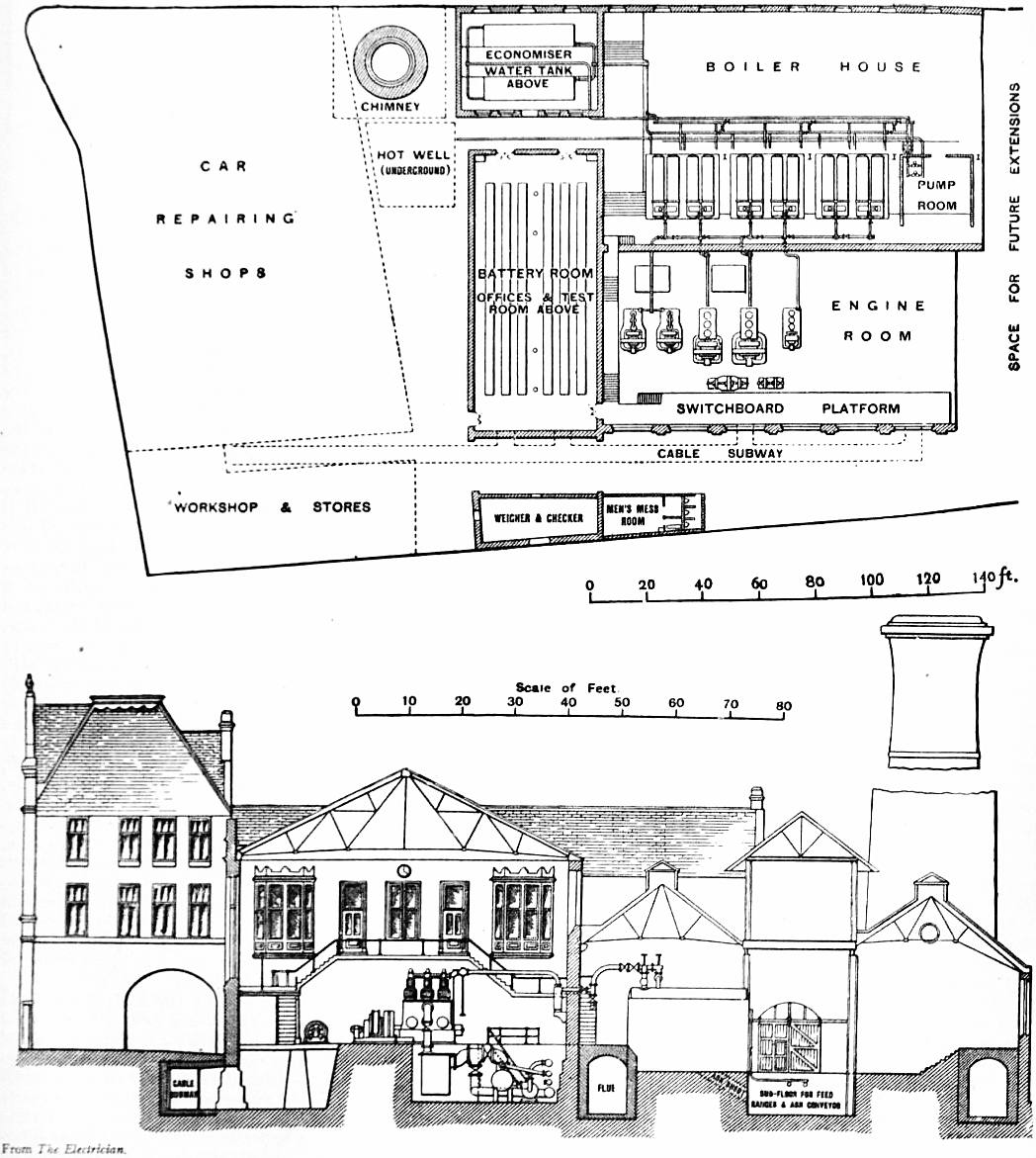 |
| Figs. 3 and 4.—Low-pressure Supply Station. |
The general arrangements of a low-pressure supply station
are shown in figs. 3 and 4. It consists of a boiler-house containing
a bank of boilers, either Lancashire or Babcock & Wilcox being
generally used (see Boiler), which furnish steam to the engines
Generating stations.
196
and dynamos, provision being made by duplicate steam-pipes
or a ring main so that the failure of a single engine or dynamo
does not cripple the whole supply. The furnace
gases are taken through an economizer (generally
Green’s) so that they give up their heat to the cold
feed water. If condensing water is available the engines
are worked condensing, and this is an essential condition of
economy when steam turbines are employed. Hence, either
a condensing water pond or a cooling tower has to be provided
to cool the condensing water and enable it to be used over and
over again. Preferably the station should be situated near a
river or canal and a railway siding. The steam dynamos are
generally arranged in an engine-room so as to be overlooked
from a switchboard gallery (fig. 3), from which all the control
is carried out. The boiler furnaces are usually stoked by automatic
stokers. Owing to the relatively small load factor (say
8 or 10%) of a station giving electric supply for lighting only,
the object of every station engineer is to cultivate a demand for
electric current for power during the day-time by encouraging
the use of electric motors for lifts and other purposes, but above
all to create a demand for traction purposes. Hence most urban
stations now supply current not only for electric lighting but
for running the town tramway system, and this traction load
being chiefly a daylight load serves to keep the plant employed
and remunerative. It is usual to furnish a continuous current
supply for traction at 500 or 600 volts, although some station
engineers are advocating the use of higher voltages. In those
stations which supply current for traction, but which have a
widely scattered lighting load, double current dynamos are often
employed, furnishing from one and the same armature a
continuous current for traction purposes, and an alternating
current for lighting purposes.
In some places a high voltage system of electric supply by
continuous current is adopted. In this case the current is
generated at a pressure of 1000 or 2000 volts, and
transmitted from the generating station by conductors,
High-pressure continuous supply.
called high-pressure feeders, to certain sub-centres
or transformer centres, which are either buildings
above ground or cellars or excavations under the ground. In
these transformer centres are placed machines, called continuous-current
transformers, which transform the electric energy and
create a secondary electric current at a lower pressure, perhaps
100 or 150 volts, to be supplied by distributing mains to users
(see Transformers). From these sub-centres insulated conductors
are run back to the generating station, by which the
engineer can start or stop the continuous-current rotatory
transformers, and at the same time inform himself as to their
proper action and the electromotive force at the secondary
terminals. This system was first put in practice in Oxford,
England, and hence has been sometimes called by British
engineers “the Oxford system.” It is now in operation in a
number of places in England, such as Wolverhampton, Walsall,
and Shoreditch in London. It has the advantage that in connexion
with the low-pressure distributing system secondary
batteries can be employed, so that a storage of electric energy
is effected. Further, continuous-current arc lamps can be worked
in series off the high-pressure mains, that is to say, sets of 20
to 40 arc lamps can be operated for the purpose of street lighting
by means of the high-pressure continuous current.
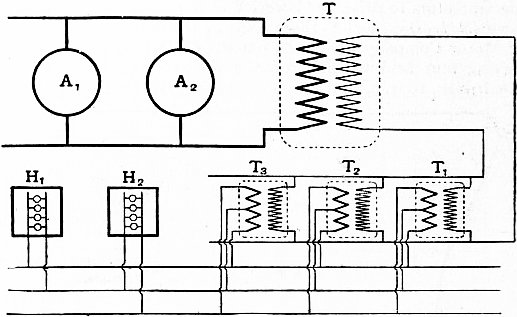 |
| Fig. 5. |
The alternating current systems in operation at the present
time are the single-phase system, with distributing transformers
or transformer sub-centres, and the polyphase systems,
in which the alternating current is transformed down
Alternating supply.
into an alternating current of low pressure, or, by means
of rotatory transformers, into a continuous current.
The general arrangement of a single-phase alternating-current
system is as follows: The generating station contains a number
of alternators, A1 A2 (fig. 5), producing single-phase alternating
current, either at 1000, 2000, or sometimes, as at Deptford and
other places, 10,000 volts. This current is distributed from the
station either at the pressure at which it is generated, or after
being transformed up to a higher pressure by the transformer T.
The alternators are sometimes worked in parallel, that is to
say, all furnish their current to two common omnibus bars on a
high-pressure switchboard, and each is switched into circuit at
the moment when it is brought into step with the other machines,
as shown by some form of phase-indicator. In some cases,
instead of the high-pressure feeders starting from omnibus bars,
each alternator works independently and the feeders are grouped
together on the various alternators as required. A number of
high-pressure feeders are carried from the main switchboard to
various transformer sub-centres or else run throughout the
district to which current is to be furnished. If the system laid
down is the transformer sub-centre system, then at each of these
sub-centres is placed a battery of alternating-current transformers,
T1 T2 T3, having their primary circuits all joined in parallel to
the terminals of the high-pressure feeders, and their secondary
circuits all joined in parallel on a distributing main, suitable
switches and cut-outs being interposed. The pressure of the
current is then transformed down by these transformers to the
required supply pressure. The secondary circuits of these
transformers are generally provided with three terminals, so as
to supply the low-pressure side on a three-wire system. It is
not advisable to connect together directly the secondary circuits
of all the different sub-centres, because then a fault or short
circuit on one secondary system affects all the others. In banking
together transformers in this manner in a sub-station it is
necessary to take care that the transformation ratio and
secondary drop (see Transformers) are exactly the same,
otherwise one transformer will take more than its full share of
the load and will become overheated. The transformer sub-station
system can only be adopted where the area of supply
is tolerably compact. Where the consumers lie scattered over
a large area, it is necessary to carry the high-pressure mains
throughout the area, and to place a separate transformer or
transformers in each building. From a financial point of view,
this “house-to-house system” of alternating-current supply,
generally speaking, is less satisfactory in results than the transformer
sub-centre system. In the latter some of the transformers
can be switched off, either by hand or by automatic apparatus,
during the time when the load is light, and then no power is
expended in magnetizing their cores. But with the house-to-house
system the whole of the transformers continually remain
connected with the high-pressure circuits; hence in the case of
supply stations which have only an ordinary electric lighting
load, and therefore a load-factor not above 10%, the efficiency
of distribution is considerably diminished.
The single-phase alternating-current system is defective in
that it cannot be readily combined with secondary batteries for
the storage of electric energy. Hence in many places preference
is now given to the polyphase system. In such a system a polyphase
alternating current, either two- or three-phase, is transmitted
from the generating station at a pressure of 5000 to
10,000 volts, or sometimes higher, and at various sub-stations
is transformed down, first by static transformers into an alternating
current of lower pressure, say 500 volts, and then by
197
means of rotatory transformers into a continuous current of
500 volts or lower for use for lighting or traction.
In the case of large cities such as London, New York, Chicago,
Berlin and Paris the use of small supply stations situated in the
interior of the city has gradually given way to the establishment
of large supply stations outside the area; in these alternating
current is generated on the single or polyphase system at a high
voltage and transmitted by underground cables to sub-stations
in the city, at which it is transformed down for distribution
for private and public electric lighting and for urban electric
traction.
Owing to the high relative cost of electric power when generated
in small amounts and the great advantages of generating it in
proximity to coal mines and waterfalls, the supply of electric
power in bulk to small towns and manufacturing districts has
become a great feature in modern electrical engineering. In
Great Britain, where there is little useful water power but
abundance of coal, electric supply stations for supply in bulk
have been built in the coal-producing districts of South Wales,
the Midlands, the Clyde valley and Yorkshire. In these cases
the current is a polyphase current generated at a high voltage,
5000 to 10,000 volts, and sometimes raised again in pressure to
20,000 or 40,000 volts and transmitted by overhead lines to the
districts to be supplied. It is there reduced in voltage by transformers
and employed as an alternating current, or is used to
drive polyphase motors coupled to direct current generators to
reproduce the power in continuous current form. It is then
distributed for local lighting, street or railway traction, driving
motors, and metallurgical or electrochemical applications.
Experience has shown that it is quite feasible to distribute in all
directions for 25 miles round a high-pressure generating station,
which thus supplies an area of nearly 2000 sq. m. At such
stations, employing large turbine engines and alternators,
electric power may be generated at a works cost of 0.375d. per
kilowatt (K.W.), the coal cost being less than 0.125d. per K.W.,
and the selling price to large load-factor users not more than
0.5d. per K.W. The average price of supply from the local
generating stations in towns and cities is from 3d. to 4d. per unit,
electric energy for power and heating being charged at a lower
rate than that for lighting only.
We have next to consider the structure and the arrangement
of the conductors employed to convey the currents from their
place of creation to that of utilization. The conductors
themselves for the most part consist of copper having
Conductors.
a conductivity of not less than 98% according to
Matthiessen’s standard. They are distinguished as (1) External
conductors, which are a part of the public supply and belong
to the corporation or company supplying the electricity; (2)
Internal conductors, or house wiring, forming a part of the structure
of the house or building supplied and usually the property of its
owner.
The external conductors may be overhead or underground.
Overhead conductors may consist of bare stranded copper cables
carried on porcelain insulators mounted on stout iron
or wooden poles. If the current is a high-pressure
External conductors.
one, these insulators must be carefully tested, and are
preferably of the pattern known as oil insulators.
In and near towns it is necessary to employ insulated overhead
conductors, generally india-rubber-covered stranded copper
cables, suspended by leather loops from steel bearer wires which
take the weight. The British Board of Trade have issued
elaborate rules for the construction of overhead lines to transmit
large electric currents. Where telephone and telegraph wires
pass over such overhead electric lighting wires, they have to be
protected from falling on the latter by means of guard wires.
By far the largest part, however, of the external electric
distribution is now carried out by underground conductors, which
are either bare or insulated. Bare copper conductors may be
carried underground in culverts or chases, air being in this case
the insulating material, as in the overhead system. A culvert
and covered chase is constructed under the road or side-walk,
and properly shaped oak crossbars are placed in it carrying
glass or porcelain insulators, on which stranded copper cables,
or, preferably, copper strips placed edgeways, are stretched
and supported. The advantages of this method of construction
are cheapness and the ease with which connexions can be made
with service-lines for house supply; the disadvantages are the
somewhat large space in which coal-gas leaking out of gas-pipes
can accumulate, and the difficulty of keeping the culverts at all
times free from rain-water. Moisture has a tendency to collect
on the negative insulators, and hence to make a dead earth on
the negative side of the main; while unless the culverts are
well ventilated, explosions from mixtures of coal-gas and air
are liable to occur. Insulated cables are insulated either with
a material which is in itself waterproof, or with one which is
only waterproof in so far as it is enclosed in a waterproof tube,
e.g. of lead. Gutta-percha and india-rubber are examples of
materials of the former kind. Gutta-percha, although practically
everlasting when in darkness and laid under water, as in the
case of submarine cables, has not been found satisfactory for
use with large systems of electric distribution, although much
employed for telephone and telegraph work. Insulated underground
external conductors are of three types:—(a) Insulated
Cables drawn into Pipes.—In this system of distribution cast-iron
or stoneware pipes, or special stoneware conduits, or conduits
made of a material called bitumen concrete, are first laid underground
in the street. These contain a number of holes or “ways,”
and at intervals drawing-in boxes are placed which consist of a
brick or cast-iron box having a water-tight lid, by means of which
access is gained to a certain section of the conduit. Wires are
used to draw in the cables, which are covered with either india-rubber
or lead, the copper being insulated by means of paper,
impregnated jute, or other similar material. The advantages
of a drawing-in system are that spare ways can be left when
the conduits are put in, so that at a future time fresh cables can
be added without breaking up the roadway. (b) Cables in Bitumen.—One
of the earliest systems of distribution employed by T.A.
Edison consisted in fixing two segment-shaped copper conductors
in a steel tube, the interspace between the conductors and the
tube being filled in with a bitumen compound. A later plan is
to lay down an iron trough, in which the cables are supported by
wooden bearers at proper distances, and fill in the whole with
natural bitumen. This system has been carried out extensively
by the Callendar Cable Company. Occasionally concentric lead-covered
and armoured cables are laid in this way, and then
form an expensive but highly efficient form of insulated conductor.
In selecting a system of distribution regard must be paid to the
nature of the soil in which the cables are laid. Lead is easily
attacked by soft water, although under some conditions it is
apparently exceedingly durable, and an atmosphere containing
coal-gas is injurious to india-rubber. (c) Armoured Cables.—In
a very extensively used system of distribution armoured cables
are employed. In this case the copper conductors, two, three
or more in number, may be twisted together or arranged concentrically,
and insulated by means of specially prepared jute or
paper insulation, overlaid with a continuous tube of lead. Over
the lead, but separated by a hemp covering, is put a steel armour
consisting of two layers of steel strip, wound in opposite directions
and kept in place by an external covering. Such a cable can
be laid directly in the ground without any preparation other
than the excavation of a simple trench, junction-boxes being
inserted at intervals to allow of branch cables being taken off.
The armoured cable used is generally of the concentric pattern
(fig. 6). It consists of a stranded copper cable composed of a
number of wires twisted together and overlaid with an insulating
material. Outside this a tubular arrangement of copper wires
and a second layer of insulation, and finally a protective covering
of lead and steel wires or armour are placed. In some cases
three concentric cylindrical conductors are formed by twisting
wires or copper strips with insulating material between. In
others two or three cables of stranded copper are embedded in
insulating material and included in a lead sheath. This last
type of cable is usually called a two- or three-core pattern cable
(fig. 7).
198
 |
| Fig. 6.—Armoured Concentric
Cable (Section). |
Fig. 7.—Triple Conductor
Armoured Cable (Section). |
IC, Inner conductor.
OC, Outer conductor.
I, Insulation.
L, Lead sheath.
S, Steel armour.
H, Hemp covering. |
C, Copper conductor.
I, Insulation.
L, Lead sheath.
H, Hemp covering.
S, Steel armour. |
The arrangement and nature of the external conductors
depends on the system of electric supply in which they are used.
In the case of continuous-current supply for incandescent
electric lighting and motive power in small units, when the
external conductors are laid down on the three-wire system,
each main or branch cable in the street consists of a set of three
conductors called the positive, middle and negative. Of these
triple conductors some run from the supply station to various
points in the area of supply without being tapped, and are called
the feeders; others, called the distributing mains, are used for
making connexions with the service lines of the consumers, one
service line, as already explained, being connected to the middle
conductor, and the other to either the positive or the negative
one. Since the middle conductor serves to convey only the
difference between the currents being used on the two sides of
the system, it is smaller in section than the positive and negative
ones. In laying out the system great judgment has to be exercised
as to the selection of the points of attachment of the feeders
to the distributing mains, the object being to keep a constant
electric pressure or voltage between the two service-lines in all
the houses independently of the varying demand for current.
Legally the suppliers are under regulations to keep the supply
voltage constant within 4% either way above or below the
standard pressure. As a matter of fact very few stations do
maintain such good regulation. Hence a considerable variation
in the light given by the incandescent lamps is observed, since
the candle-power of carbon glow lamps varies as the fifth or
sixth power of the voltage of supply, i.e. a variation of only
2% in the supply pressure affects the resulting candle-power
of the lamps to the extent of 10 or 12%. This variation is, however,
less in the case of metallic filament lamps (see Lighting:
Electric). In the service-lines are inserted the meters for measuring
the electric energy supplied to the customer (see Meter,
Electric).
In the interior of houses and buildings the conductors generally
consist of india-rubber-covered cables laid in wood casing.
The copper wire must be tinned and then covered,
first with a layer of unvulcanized pure india-rubber,
Interior wiring.
then with a layer of vulcanized rubber, and lastly
with one or more layers of protective cotton twist or tape. No
conductor of this character employed for interior house-wiring
should have a smaller insulation resistance than 300 megohms
per mile when tested with a pressure of 600 volts after soaking
24 hours in water. The wood casing should, if placed in damp
positions or under plaster, be well varnished with waterproof
varnish. As far as possible all joints in the run of the cable
should be avoided by the use of the so-called looping-in system,
and after the wiring is complete, careful tests for insulation
should be made. The Institution of Electrical Engineers of
Great Britain have drawn up rules to be followed in interior
house-wiring, and the principal Fire Insurance offices, following
the lead of the Phoenix Fire Office, of London, have made
regulations which, if followed, are a safeguard against bad
workmanship and resulting possibility of damage by fire. Where
fires having an electric origin have taken place, they have invariably
been traced to some breach of these rules. Opinions
differ, however, as to the value and security of this method of
laying interior conductors in buildings, and two or three alternative
systems have been much employed. In one of these,
called the interior conduit system, highly insulating waterproof
and practically fireproof tubes or conduits replace the wooden
casing; these, being either of plain insulating material, or
covered with brass or steel armour, may be placed under plaster
or against walls. They are connected by bends or joint-boxes.
The insulated wires being drawn into them, any short circuit or
heating of the wire cannot give rise to a fire, as it can only take
place in the interior of a non-inflammable tube. A third system
of electric light wiring is the safety concentric system, in which
concentric conductors are used. The inner one, which is well
insulated, consists of a copper-stranded cable. The outer may
be a galvanized iron strand, a copper tape or braid, or a brass
tube, and is therefore necessarily connected with the earth. A
fourth system consists in the employment of twin insulated
wires twisted together and sheathed with a lead tube; the
conductor thus formed can be fastened by staples against walls,
or laid under plaster or floors.
The general arrangement for distributing current to the
different portions of a building for the purpose of electric lighting
is to run up one or more rising mains, from which branches are
taken off to distributing boxes on each floor, and from these
boxes to carry various branch circuits to the lamps. At the
distributing boxes are collected the cut-outs and switches
controlling the various circuits. When alternating currents
are employed, it is usual to select as a type of conductor either
twin-twisted conductor or concentric; and the employment
of these types of cable, rather than two separate cables, is
essential in any case where there are telephone or telegraph
wires in proximity, for otherwise the alternating current would
create inductive disturbances in the telephone circuit. The
house-wiring also comprises the details of switches for controlling
the lamps, cut-outs or fuses for preventing an excess of current
passing, and fixtures or supports for lamps often of an ornamental
character. For the details of these, special treatises on electric
interior wiring must be consulted.
For further information the reader may be referred to the following
books:—C.H. Wordingham, Central Electrical Stations (London,
1901); A. Gay and C.Y. Yeaman, Central Station Electricity Supply
(London, 1906); S.P. Thompson, Dynamo Electric Machinery (2
vols., London, 1905); E. Tremlett Carter and T. Davies, Motive
Power and Gearing (London, 1906); W.C. Clinton, Electric Wiring
(2nd ed., London, 1906); W. Perren Maycock, Electric Wiring,
Fitting, Switches and Lamps (London, 1899); D. Salomons, Electric
Light Installations (London, 1894); Stuart A. Russell, Electric Light
Cables (London, 1901); F.A.C. Perrine, Conductors for Electrical
Distribution (London, 1903); E. Rosenberg, W.W. Haldane Gee
and C. Kinzbrunner, Electrical Engineering (London, 1903); E.C.
Metcalfe, Practical Electric Wiring for Lighting Installations (London,
1905); F.C. Raphael, The Wireman’s Pocket Book (London,
1903).
(J. A. F.)
II. Commercial Aspects.—To enable the public supply enterprises
referred to in the foregoing section to be carried out in
England, statutory powers became necessary to break
up the streets. In the early days a few small stations
History.
were established for the supply of electricity within “block”
buildings, or by means of overhead wires within restricted areas,
but the limitations proved uneconomical and the installations
were for the most part merged into larger undertakings sanctioned
by parliamentary powers. In the year 1879 the British
government had its attention directed for the first time to electric
lighting as a possible subject for legislation, and the consideration
of the then existing state of electric lighting was referred to a
select committee of the House of Commons. No legislative
action, however, was taken at that time. In fact the invention
of the incandescent lamp was incomplete—Edison’s British
master-patent was only filed in Great Britain in November
1879. In 1881 and 1882 electrical exhibitions were held in Paris
and at the Crystal Palace, London, where the improved electric
199
incandescent lamp was brought before the general public. In
1882 parliament passed the first Electric Lighting Act, and
considerable speculation ensued. The aggregate capital of the
companies registered in 1882-1883 to carry out the public
supply of electricity in the United Kingdom amounted to
£15,000,000, but the onerous conditions of the act deterred
investors from proceeding with the enterprise. Not one of the
sixty-two provisional orders granted to companies in 1883 under
the act was carried out. In 1884 the Board of Trade received
only four applications for provisional orders, and during the
subsequent four years only one order was granted. Capitalists
declined to go on with a business which if successful could be
taken away from them by local authorities at the end of twenty-one
years upon terms of paying only the then value of the plant,
lands and buildings, without regard to past or future profits,
goodwill or other considerations. The electrical industry in
Great Britain ripened at a time when public opinion was averse
to the creation of further monopolies, the general belief being
that railway, water and gas companies had in the past received
valuable concessions on terms which did not sufficiently safeguard
the interests of the community. The great development
of industries by means of private enterprise in the early part
of the 19th century produced a reaction which in the latter part
of the century had the effect of discouraging the creation by
private enterprise of undertakings partaking of the nature of
monopolies; and at the same time efforts were made to strengthen
local and municipal institutions by investing them with wider
functions. There were no fixed principles governing the relations
between the state or municipal authorities and commercial
companies rendering monopoly services. The new conditions
imposed on private enterprise for the purpose of safeguarding
the interests of the public were very tentative, and a former
permanent secretary of the Board of Trade has stated that the
efforts made by parliament in these directions have sometimes
proved injurious alike to the public and to investors. One of
these tentative measures was the Tramways Act 1870, and
twelve years later it was followed by the first Electric Lighting
Act.
It was several years before parliament recognized the harm
that had been done by the passing of the Electric Lighting Act
1882. A select committee of the House of Lords sat in 1886
to consider the question of reform, and as a result the Electric
Lighting Act 1888 was passed. This amending act altered the
period of purchase from twenty-one to forty-two years, but
the terms of purchase were not materially altered in favour of
investors. The act, while stipulating for the consent of local
authorities to the granting of provisional orders, gives the
Board of Trade power in exceptional cases to dispense with the
consent, but this power has been used very sparingly. The
right of vetoing an undertaking, conferred on local authorities
by the Electric Lighting Acts and also by the Tramways Act
1870, has frequently been made use of to exact unduly onerous
conditions from promoters, and has been the subject of complaint
for years. Although, in the opinion of ministers of the Crown,
the exercise of the veto by local authorities has on several
occasions led to considerable scandals, no government has so
far been able, owing to the very great power possessed by local
authorities, to modify the law in this respect. After 1888
electric lighting went ahead in Great Britain for the first time,
although other countries where legislation was different had
long previously enjoyed its benefits. The developments proceeded
along three well-defined lines. In London, where none
of the gas undertakings was in the hands of local authorities,
many of the districts were allotted to companies, and competition
was permitted between two and sometimes three companies.
In the provinces the cities and larger towns were held by the
municipalities, while the smaller towns, in cases where consents
could be obtained, were left to the enterprise of companies.
Where consents could not be obtained these towns were for
some time left without supply.
Some statistics showing the position of the electricity supply
business respectively in 1896 and 1906 are interesting as indicating
the progress made and as a means of comparison between these two
periods of the state of the industry as a whole. In 1896 thirty-eight
companies were at work with an aggregate capital of about £6,000,000,
and thirty-three municipalities with electric lighting loans of nearly
£2,000,000. The figures for 1906, ten years later, show that 187
electricity supply companies were in operation with a total investment
of close on £32,000,000, and 277 municipalities with loans
amounting to close on £36,000,000. The average return on the
capital invested in the companies at the later period was 5.1% per
annum. In 1896 the average capital expenditure was about £100
per kilowatt of plant installed; and £50 per kilowatt was regarded
as a very low record. For 1906 the average capital expenditure per
kilowatt installed was about £81. The main divisions of the average
expenditure are:—
| | 1896. | 1906. |
| Land and buildings | 22.3% | 17.8% |
| Plant and machinery | 36.7 | 36.5 |
| Mains | 32.2 | 35.5 |
| Meters and instruments | 4.6 | 5.7 |
| Provisional orders, &c. | 3.2 | 2.8 |
The load connected, expressed in equivalents of eight candle-power
lamps, was 2,000,000 in 1896 and 24,000,000 in 1906. About one-third
of this load would be for power purposes and about two-thirds
for lighting. The Board of Trade units sold were 30,200,000 in 1896
and 533,600,000 in 1906, and the average prices per unit obtained
were 5.7d. and 2.7d. respectively, or a revenue of £717,250 in 1896
and over £6,000,000 in 1906. The working expenses per Board of
Trade unit sold, excluding depreciation, sinking fund and interest
were as follows:—
| | 1896. | 1906. |
| Generation and distribution | 2.81d. | .99d. |
| Rent, rates and taxes | .35 | .14 |
| Management | .81 | .18 |
| Sundries | .10 | .02 |
| | ——— | ——— |
| Total | 4.07d. | 1.33d. |
In 1896 the greatest output at one station was about 5½ million
units, while in 1906 the station at Manchester had the largest output
of over 40 million units.
The capacity of the plants installed in the United Kingdom in
1906 was:—
| | K.W. | | |
| Continuous current | 417,000 | Provinces | 333,000 |
| London | 84,000 |
| Alternating current | 132,000 | Provinces | 83,000 |
| London | 49,000 |
Continuous current and
alternating current combined
| 480,000 | Provinces | 366,000 |
| London | 114,000 |
| | ———— | | |
| | 1,029,000 | k.w. | |
The economics of electric lighting were at first assumed to be
similar to those of gas lighting. Experience, however, soon
proved that there were important differences, one
being that gas may be stored in gasometers without
Economics.
appreciable loss and the work of production carried
on steadily without reference to fluctuations of demand. Electricity
cannot be economically stored to the same extent, and for
the most part it has to be used as it is generated. The demand
for electric light is practically confined to the hours between
sunset and midnight, and it rises sharply to a “peak” during
this period. Consequently the generating station has to be
equipped with plant of sufficient capacity to cope with the
maximum load, although the peak does not persist for many
minutes—a condition which is very uneconomical both as regards
capital expenditure and working costs (see Lighting:
Electric). In order to obviate the unproductiveness of the
generating plant during the greater part of the day, electricity
supply undertakings sought to develop the “daylight” load.
This they did by supplying electricity for traction purposes, but
more particularly for industrial power purposes. The difficulties
in the way of this line of development, however, were that
electric power could not be supplied cheaply enough to compete
with steam, hydraulic, gas and other forms of power, unless
it was generated on a very large scale, and this large demand
could not be developed within the restricted areas for which
provisional orders were granted and under the restrictive
conditions of these orders in regard to situation of power-house
and other matters.
The leading factors which make for economy in electricity
supply are the magnitude of the output, the load factor, and
200
the diversity factor, also the situation of the power house, the
means of distribution, and the provision of suitable, trustworthy
and efficient plant. These factors become more favourable the
larger the area and the greater and more varied the demand
to be supplied. Generally speaking, as the output increases so
the cost per unit diminishes, but the ratio (called the load factor)
which the output during any given period bears to the maximum
possible output during the same period has a very important
influence on costs. The ideal condition would be when a power
station is working at its normal maximum output continuously
night and day. This would give a load-factor of 100%, and
represents the ultimate ideal towards which the electrical
engineer strives by increasing the area of his operations and
consequently also the load and the variety of the overlapping
demands. It is only by combining a large number of demands
which fluctuate at different times—that is by achieving a high
diversity factor—that the supplier of electricity can hope to
approach the ideal of continuous and steady output. Owing
to the dovetailing of miscellaneous demands the actual demand
on a power station at any moment is never anything like the
aggregate of all the maximum demands. One large station
would require a plant of 36,000 k.w. capacity if all the demands
came upon the station simultaneously, but the maximum demand
on the generating plant is only 15,000 kilowatts. The difference
between these two figures may be taken to represent the economy
effected by combining a large number of demands on one station.
In short, the keynote of progress in cheap electricity is increased
and diversified demand combined with concentration of load.
The average load-factor of all the British electricity stations in
1907 was 14.5%—a figure which tends to improve.
Several electric power supply companies have been established
in the United Kingdom to give practical effect to these principles.
The Electric Lighting Acts, however, do not provide
for the establishment of large power companies, and
Power companies.
special acts of parliament have had to be promoted
to authorize these undertakings. In 1898 several
bills were introduced in parliament for these purposes. They
were referred to a joint committee of both Houses of Parliament
presided over by Lord Cross. The committee concluded that,
where sufficient public advantages are shown, powers should be
given for the supply of electricity over areas including the districts
of several local authorities and involving the use of exceptional
plant; that the usual conditions of purchase of the undertakings
by the local authorities did not apply to such undertakings;
that the period of forty-two years was “none too long” a
tenure; and that the terms of purchase should be reconsidered.
With regard to the provision of the Electric Lighting Acts which
requires that the consent of the local authority should be obtained
as a condition precedent to the granting of a provisional order,
the committee was of opinion that the local authority should
be entitled to be heard by the Board of Trade, but should not
have the power of veto. No general legislation took place as a
result of these recommendations, but the undermentioned special
acts constituting power supply companies were passed.
In 1902 the president of the Board of Trade stated that a bill
had been drafted which he thought “would go far to meet all
the reasonable objections that had been urged against the present
powers by the local authorities.” In 1904 the government
introduced the Supply of Electricity Bill, which provided for
the removal of some of the minor anomalies in the law relating
to electricity. The bill passed through all its stages in the
House of Lords but was not proceeded with in the House of
Commons. In 1905 the bill was again presented to parliament
but allowed to lie on the table. In the words of the president
of the Board of Trade, there was “difficulty of dealing with this
question so long as local authorities took so strong a view as to
the power which ought to be reserved to them in connexion with
this enterprise.” In the official language of the council of the
Institution of Electrical Engineers, the development of electrical
science in the United Kingdom is in a backward condition as
compared with other countries in respect of the practical application
to the industrial and social requirements of the nation,
notwithstanding that Englishmen have been among the first in
inventive genius. The cause of such backwardness is largely
due to the conditions under which the electrical industry has been
carried on in the country, and especially to the restrictive
character of the legislation governing the initiation and development
of electrical power and traction undertakings, and to the
powers of obstruction granted to local authorities. Eventually
The Electric Lighting Act 1909 was passed. This Act provides:—(1)
for the granting of provisional orders authorizing any local
authority or company to supply electricity in bulk; (2) for the
exercise of electric lighting powers by local authorities jointly
under provisional order; (3) for the supply of electricity to
railways, canals and tramways outside the area of supply with
the consent of the Board of Trade; (4) for the compulsory
acquisition of land for generating stations by provisional order;
(5) for the exemption of agreements for the supply of electricity
from stamp duty; and (6) for the amendment of regulations
relating to July notices, revision of maximum price, certification
of meters, transfer of powers of undertakers, auditors’ reports,
and other matters.
The first of the Power Bills was promoted in 1898, under which
it was proposed to erect a large generating station in the Midlands
from which an area of about two thousand square miles would
be supplied. Vigorous opposition was organized against the
bill by the local authorities and it did not pass. The bill was
revived in 1899, but was finally crushed. In 1900 and following
years several power bills were successfully promoted, and the
following are the areas over which the powers of these acts extend:
In Scotland, (1) the Clyde Valley, (2) the county of Fife,
(3) the districts described as “Scottish Central,” comprising
Linlithgow, Clackmannan, and portions of Dumbarton and
Stirling, and (4) the Lothians, which include portions of Midlothian,
East Lothian, Peebles and Lanark.
In England there are companies operating in (1) Northumberland,
(2) Durham county, (3) Lancashire, (4) South Wales and
Carmarthenshire, (5) Derbyshire and Nottinghamshire, (6)
Leicestershire and Warwickshire, (7) Yorkshire, (8) Shropshire,
Worcestershire and Staffordshire, (9) Somerset, (10) Kent, (11)
Cornwall, (12) portions of Gloucestershire, (13) North Wales,
(14) North Staffordshire, Derbyshire, Denbighshire and Flintshire,
(15) West Cumberland, (16) the Cleveland district,
(17) the North Metropolitan district, and (18) the West Metropolitan
area. An undertaking which may be included in this
category, although it is not a Power Act company, is the Midland
Electric Corporation in South Staffordshire. The systems of
generation and distribution are generally 10,000 or 11,000 volts
three-phase alternating current.
The powers conferred by these acts were much restricted as a
result of opposition offered to them. In many cases the larger
towns were cut out of the areas of supply altogether, but the
general rule was that the power company was prohibited from
supplying direct to a power consumer in the area of an authorized
distributor without the consent of the latter, subject to appeal
to the Board of Trade. Even this restricted power of direct
supply was not embodied in all the acts, the power of taking
supply in bulk being left only to certain authorized distributors
and to authorized users such as railways and tramways. Owing
chiefly to the exclusion of large towns and industrial centres from
their areas, these power supply companies did not all prove as
successful as was expected.
In the case of one of the power companies which has been in a
favourable position for the development of its business, the
theoretical conclusions in regard to the economy of large production
above stated have been amply demonstrated in practice.
In 1901, when this company was emerging from the stage of a
simple electric lighting company, the total costs per unit were
1.05d. with an output of about 2½ million units per annum.
In 1905 the output rose to over 30 million units mostly for power
and traction purposes, and the costs fell to 0.56d. per unit.
An interesting phase of the power supply question has arisen
in London. Under the general acts it was stipulated that the
power-house should be erected within the area of supply, and
201
amalgamation of undertakings was prohibited. After less than
a decade of development several of the companies in London
found themselves obliged to make considerable additions to their
generating plants. But their existing buildings were full to their
utmost capacity, and the difficulties of generating cheaply on
crowded sites had increased instead of diminished during the
interval. Several of the companies had to promote special acts
of parliament to obtain relief, but the idea of a general combination
was not considered to be within the range of practical
politics until 1905, when the Administrative County of London
Electric Power Bill was introduced. Compared with other
large cities, the consumption of electricity in London is small.
The output of electricity in New York for all purposes is 971
million units per annum or 282 units per head of population.
The output of electricity in London is only 42 units per head
per annum. There are in London twelve local authorities and
fourteen companies carrying on electricity supply undertakings.
The capital expenditure is £3,127,000 by the local authorities
and £12,530,000 by the companies, and their aggregate capacity
of plant is 165,000 k.w. The total output is about 160,000,000
units per annum, the total revenue is over £2,000,000, and the
gross profit before providing for interest and sinking fund
charges is £1,158,000. The general average cost of production
is 1.55d. per unit, and the average price per unit sold is 3.16d.,
but some of the undertakers have already supplied electricity
to large power consumers at below 1d. per unit. By generating
on a large scale for a wide variety of demands the promoters of
the new scheme calculated to be able to offer electrical energy
in bulk to electricity supply companies and local authorities
at prices substantially below their costs of production at separate
stations, and also to provide them and power users with electricity
at rates which would compete with other forms of power. The
authorized capital was fixed at £6,666,000, and the initial outlay
on the first plant of 90,000 k.w., mains, &c., was estimated at
£2,000,000. The costs of generation were estimated at 0.15d.
per unit, and the total cost at 0.52d. per unit sold. The output
by the year 1911 was estimated at 133,500,000 units at an
average selling price of 0.7d. per unit, to be reduced to 0.55d. by
1916 when the output was estimated at 600,000,000 units. The
bill underwent a searching examination before the House of
Lords committee and was passed in an amended form. At the
second reading in the House of Commons a strong effort was made
to throw it out, but it was allowed to go to committee on the
condition—contrary to the general recommendations of the
parliamentary committee of 1898—that a purchase clause
would be inserted; but amendments were proposed to such an
extent that the bill was not reported for third reading until the
eve of the prorogation of parliament. In the following year
(1906) the Administrative Company’s bill was again introduced
in parliament, but the London County Council, which had
previously adopted an attitude both hostile and negative, also
brought forward a similar bill. Among other schemes, one known
as the Additional Electric Power Supply Bill was to authorize
the transmission of current from St Neots in Hunts. This bill
was rejected by the House of Commons because the promoters
declined to give precedence to the bill of the London County
Council. The latter bill was referred to a hybrid committee with
instructions to consider the whole question of London power
supply, but it was ultimately rejected. The same result attended
a second bill which was promoted by the London County Council
in 1907. The question was settled by the London Electric
Supply Act 1908, which constitutes the London County Council
the purchasing authority (in the place of the local authorities)
for the electric supply companies in London. This Act also
enabled the Companies and other authorized undertakers to
enter into agreements for the exchange of current and the
linking-up of stations.
The general supply of electricity is governed primarily by
the two acts of parliament passed in 1882 and 1888, which apply
to the whole of the United Kingdom. Until 1899 the other
statutory provisions relating to electricity supply were incorporated
Legislation and regulations.
in provisional orders granted by the Board of Trade
and confirmed by parliament in respect of each undertaking, but
in that year an Electric Lighting Clauses Act was passed by
which the clauses previously inserted in each order
were standardized. Under these acts the Board of
Trade made rules with respect to applications for
licences and provisional orders, and regulations for
the protection of the public, and of the electric lines and works
of the post office, and others, and also drew up a model form
for provisional orders.
Until the passing of the Electric Lighting Acts, wires could be
placed wherever permission for doing so could be obtained, but
persons breaking up streets even with the consent of the local
authority were liable to indictment for nuisance. With regard
to overhead wires crossing the streets, the local authorities had
no greater power than any member of the public, but a road
authority having power to make a contract for lighting the road
could authorize others to erect poles and wires for the purpose.
A property owner, however, was able to prevent wires from being
taken over his property. The act of 1888 made all electric lines
or other works for the supply of electricity, not entirely enclosed
within buildings or premises in the same occupation, subject to
regulations of the Board of Trade. The postmaster-general
may also impose conditions for the protection of the post office.
Urban authorities, the London County Council, and some other
corporations have now powers to make by-laws for prevention
of obstruction from posts and overhead wires for telegraph,
telephone, lighting or signalling purposes; and electric lighting
stations are now subject to the provisions of the Factory Acts.
Parliamentary powers to supply electricity can now be obtained
by (A) Special Act, (B) Licence, or (C) Provisional order.
A. Special Act.—Prior to the report of Lord Cross’s joint
committee of 1898 (referred to above), only one special act was
passed. The provisions of the Electric Power Acts passed
subsequently are not uniform, but the following are some of the
usual provisions:—
The company shall not supply electricity for lighting purposes
except to authorized undertakers, provided that the energy
supplied to any person for power may be used for lighting any
premises on which the power is utilized. The company shall not
supply energy (except to authorized undertakers) in any area
which forms part of the area of supply of any authorized distributors
without their consent, such consent not to be unreasonably
withheld. The company is bound to supply authorized
undertakers upon receiving notice and upon the applicants
agreeing to pay for at least seven years an amount sufficient to
yield 20% on the outlay (excluding generating plant or wires
already installed). Other persons to whom the company is
authorized to supply may require it upon terms to be settled,
if not agreed, by the Board of Trade. Dividends are usually
restricted to 8%, with a provision that the rate may be increased
upon the average price charged being reduced. The maximum
charges are usually limited to 3d. per unit for any quantity up
to 400 hours’ supply, and 2d. per unit beyond. No preference is
to be shown between consumers in like circumstances. Many provisions
of the general Electric Lighting Acts are excluded from
these special acts, in particular the clause giving the local
authority the right to purchase the undertaking compulsorily.
B. Licence.—The only advantages of proceeding by licence
are that it can be expeditiously obtained and does not require
confirmation by parliament; but some of the provisions usually
inserted in provisional orders would be ultra vires in a licence,
and the Electric Lighting Clauses Act 1899 does not extend to
licences. The term of a licence does not exceed seven years,
but is renewable. The consent of the local authority is necessary
even to an application for a licence. None of the licences that
have been granted is now in force.
C. Provisional Order.—An intending applicant for a provisional
order must serve notice of his intention on every local
authority within the proposed area of supply on or before the 1st
of July prior to the session in which application is to be made to
the Board of Trade. This provision has given rise to much complaint,
as it gives the local authorities a long time for bargaining
202
and enables them to supersede the company’s application by
themselves applying for provisional orders. The Board of Trade
generally give preference to the applications of local authorities.
In 1905 the Board of Trade issued a memorandum stating
that, in view of the revocation of a large number of provisional
orders which had been obtained by local authorities, or in regard
to which local authorities had entered into agreements with
companies for carrying the orders into effect (which agreements
were in many cases ultra vires or at least of doubtful validity), it
appeared undesirable that a local authority should apply for a
provisional order without having a definite intention of exercising
the powers, and that in future the Board of Trade would not
grant an order to a local authority unless the board were satisfied
that the powers would be exercised within a specified period.
Every undertaking authorized by provisional order is subject
to the provision of the general act entitling the local authority
to purchase compulsorily at the end of forty-two years (or
shorter period), or after the expiration of every subsequent
period of ten years (unless varied by agreement between the
parties with the consent of the Board of Trade), so much of the
undertaking as is within the jurisdiction of the purchasing
authority upon the terms of paying the then value of all lands,
buildings, works, materials and plant, suitable to and used for
the purposes of the undertaking; provided that the value of
such lands, &c., shall be deemed to be their fair market value
at the time of purchase, due regard being had to the nature and
then condition and state of repair thereof, and to the circumstance
that they are in such positions as to be ready for immediate
working, and to the suitability of the same to the purposes of
the undertaking, and where a part only of the undertaking is
purchased, to any loss occasioned by severance, but without
any addition in respect of compulsory purchase or of goodwill,
or of any profits which may or might have been or be made from
the undertaking or any similar consideration. Subject to this
right of purchase by the local authority, a provisional order
(but not a licence) may be for such period as the Board of Trade
may think proper, but so far no limit has been imposed, and
unless purchased by a local authority the powers are held in
perpetuity. No monopoly is granted to undertakers, and since
1889 the policy of the Board of Trade has been to sanction two
undertakings in the same metropolitan area, preferably using
different systems, but to discourage competing schemes within
the same area in the provinces. Undertakers must within two
years lay mains in certain specified streets. After the first
eighteen months they may be required to lay mains in other
streets upon conditions specified in the order, and any owner
or occupier of premises within 50 yds. of a distributing main
may require the undertakers to give a supply to his premises;
but the consumer must pay the cost of the lines laid upon his
property and of so much outside as exceeds 60 ft. from the
main, and he must also contract for two and in some cases for
three years’ supply. But undertakers are prohibited in making
agreements for supply from showing any undue preference.
The maximum price in London is 13s. 4d. per quarter for any
quantity up to 20 units, and beyond that 8d. per unit, but 11s. 8d.
per quarter up to 20 units and 7d. per unit beyond is the more
general maximum. The “Bermondsey clause” requires the
undertakers (local authority) so to fix their charges (not exceeding
the specified maximum) that the revenue shall not be less than
the expenditure.
There is no statutory obligation on municipalities to provide
for depreciation of electricity supply undertakings, but after
providing for all expenses, interest on loans, and sinking fund
instalments, the local authority may create a reserve fund until
it amounts, with interest, to one-tenth of the aggregate capital
expenditure. Any deficiency when not met out of reserve is
payable out of the local rates.
The principle on which the Local Government Board sanctions
municipal loans for electric lighting undertakings is that the
period of the loan shall not exceed the life of the works, and that
future ratepayers shall not be unduly burdened. The periods
of the loans vary from ten years for accumulators and arc lamps
to sixty years for lands. Within the county of London the
loans raised by the metropolitan borough councils for electrical
purposes are sanctioned by the London County Council, and that
body allows a minimum period of twenty years for repayment.
Up to 1904-1905, 245 loans had been granted by the council
amounting in the aggregate to £4,045,067.
In 1901 the Institution of Civil Engineers appointed a committee
to consider the advisability of standardizing various
kinds of iron and steel sections. Subsequently the
original reference was enlarged, and in 1902 the
Standardization.
Institution of Electrical Engineers was invited to
co-operate. The treasury, as well as railway companies, manufacturers
and others, have made grants to defray the expenses.
The committee on electrical plant has ten sub-committees. In
August 1904 an interim report was issued by the sub-committee
on generators, motors and transformers, dealing with pressures
and frequencies, rating of generators and motors, direct-current
generators, alternating-current generators, and motors.
In 1903 the specification for British standard tramway rails
and fish-plates was issued, and in 1904 a standard specification
for tubular tramway poles was issued. A sectional committee
was formed in 1904 to correspond with foreign countries with
regard to the formation of an electrical international commission
to study the question of an international standardization of
nomenclature and ratings of electrical apparatus and machinery.
The electrical manufacturing branch, which is closely related
to the electricity supply and other operating departments of the
electrical industry, only dates from about 1880. Since
that time it has undergone many vicissitudes. It
The electrical industry.
began with the manufacture of small arc lighting
equipments for railway stations, streets and public
buildings. When the incandescent lamp became a commercial
article, ship-lighting sets and installations for theatres and
mansions constituted the major portion of the electrical work.
The next step was the organization of house-to-house distribution
of electricity from small “central stations,” ultimately
leading to the comprehensive public supply in large towns,
which involved the manufacture of generating and distributing
plants of considerable magnitude and complexity. With the
advent of electric traction about 1896, special machinery had
to be produced, and at a later stage the manufacturer had to
solve problems in connexion with bulk supply in large areas and
for power purposes. Each of these main departments involved
changes in ancillary manufactures, such as cables, switches,
transformers, meters, &c., so that the electrical manufacturing
industry has been in a constant state of transition. At the
beginning of the period referred to Germany and America were
following the lead of England in theoretical developments, and
for some time Germany obtained electrical machinery from
England. Now scarcely any electrical apparatus is exported
to Germany, and considerable imports are received by England
from that country and America. The explanation is to be found
mainly in the fact that the adverse legislation of 1882 had the
effect of restricting enterprise, and while British manufacturers
were compulsorily inert during periods of impeded growth of
the two most important branches of the industry—electric
lighting and traction—manufacturers in America and on the
continent of Europe, who were in many ways encouraged by
their governments, devoted their resources to the establishment
of factories and electrical undertakings, and to the development
of efficient selling organizations at home and abroad. When
after the amendment of the adverse legislation in 1888 a demand
for electrical machinery arose in England, the foreign manufacturers
were fully organized for trade on a large scale, and
were further aided by fiscal conditions to undersell English
manufacturers, not only in neutral markets, but even in their
own country. Successful manufacture on a large scale is possible
only by standardizing the methods of production. English
manufacturers were not able to standardize because they had
not the necessary output. There had been no repetitive demand,
and there was no production on a large scale. Foreign manufacturers,
however, were able to standardize by reason of the
203
large uniform demand which existed for their manufactures.
Statistics are available showing the extent to which the growth
of the electrical manufacturing industry in Great Britain was
delayed. Nearly twenty years after the inception of the industry
there were only twenty-four manufacturing companies registered
in the United Kingdom, having an aggregate subscribed capital
of under £7,000,000. But in 1907 there were 292 companies
with over £42,000,000 subscribed capital. The cable and incandescent
lamp sections show that when the British manufacturers
are allowed opportunities they are not slow to take
advantage of them. The cable-making branch was established
under the more encouraging conditions of the telegraph industry,
and the lamp industry was in the early days protected by patents.
Other departments not susceptible to foreign competition on
account of freightage, such as the manufacture of storage
batteries and rolling stock, are also fairly prosperous. In
departments where special circumstances offer a prospect of
success, the technical skill, commercial enterprise and general
efficiency of British manufacturers manifest themselves by
positive progress and not merely by the continuance of a struggle
against adverse conditions. The normal posture of the British
manufacturer of electrical machinery has been described as one
of desperate defence of his home trade; that of the foreign
manufacturer as one of vigorous attack upon British and other
open markets. In considering the position of English manufacturers
as compared with their foreign rivals, some regard
should be had to the patent laws. One condition of a grant
of a patent in most foreign countries is that the patent shall
be worked in those countries within a specified period. But a
foreign inventor was until 1907 able to secure patent protection
in Great Britain without any obligation to manufacture there.
The effect of this was to encourage the manufacture of patented
apparatus in foreign countries, and to stimulate their exportation
to Great Britain in competition with British products. With
regard to the electrochemical industry the progress which has
been achieved by other nations, notably Germany, is very
marvellous by comparison with the advance made by England,
but to state the reasons why this industry has had such extraordinary
development in Germany, notwithstanding that many
of the fundamental inventions were made in England, would
require a statement of the marked differences in the methods
by which industrial progress is promoted in the two countries.
There has been very little solidarity among those interested
in the commercial development of electricity, and except for
the discussion of scientific subjects there has been very little
organization with the object of protecting and promoting common
interests.
(E. Ga.)
1 British Patent Specification, No. 5306 of 1878, and No. 602 of
1880.
2 Ibid. No. 3988 of 1878.
ELECTRIC WAVES. § 1. Clerk Maxwell proved that on his
theory electromagnetic disturbances are propagated as a wave
motion through the dielectric, while Lord Kelvin in 1853 (Phil.
Mag. [4] 5, p. 393) proved from electromagnetic theory that the
discharge of a condenser is oscillatory, a result which Feddersen
(Pogg. Ann. 103, p. 69, &c.) verified by a beautiful series of
experiments. The oscillating discharge of a condenser had been
inferred by Henry as long ago as 1842 from his experiments on
the magnetization produced in needles by the discharge of a
condenser. From these two results it follows that electric waves
must be passing through the dielectric surrounding a condenser
in the act of discharging, but it was not until 1887 that the
existence of such waves was demonstrated by direct experiment.
This great step was made by Hertz (Wied. Ann. 34, pp. 155,
551, 609; Ausbreitung der elektrischen Kraft, Leipzig, 1892),
whose experiments on this subject form one of the greatest
contributions ever made to experimental physics. The difficulty
which had stood in the way of the observations of these waves
was the absence of any method of detecting electrical and
magnetic forces, reversed some millions of times per second, and
only lasting for an exceedingly short time. This was removed
by Hertz, who showed that such forces would produce small
sparks between pieces of metal very nearly in contact, and that
these sparks were sufficiently regular to be used to detect electric
waves and to investigate their properties. Other and more
delicate methods have subsequently been discovered, but the
results obtained by Hertz with his detector were of such signal
importance, that we shall begin our account of experiments on
these waves by a description of some of Hertz’s more fundamental
experiments.
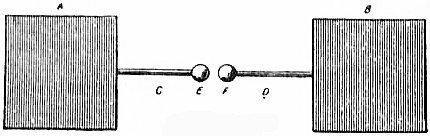 |
| Fig. 1. |
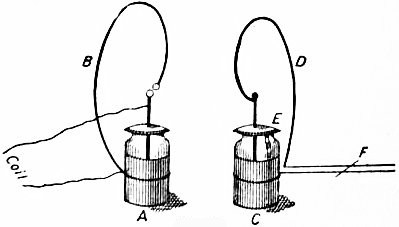 |
| Fig. 2. |
To produce the waves Hertz used two forms of vibrator. The
first is represented in fig. 1. A and B are two zinc plates about
40 cm. square; to these brass rods, C, D, each about 30 cm. long,
are soldered, terminating in brass balls E and F. To get good
results it is necessary that these balls should be very brightly
polished, and as they get roughened by the sparks which pass
between them it is necessary to repolish them at short intervals;
they should be shaded from light and from sparks, or other
source of ultra-violet light. In order to excite the waves, C and
D are connected to the two poles of an induction coil; sparks
cross the air-gap which becomes a conductor, and the charges on
the plates oscillate backwards and forwards like the charges on
the coatings of a Leyden jar when it is short-circuited. The
object of polishing the balls and screening off light is to get a
sudden and sharp discharge; if the balls are rough there will
be sharp points from which the charge will gradually leak, and
the discharge will not be abrupt enough to start electrical
vibrations, as these have an exceedingly short period. From
the open form of this vibrator we should expect the radiation
to be very large and the rate of decay of the amplitude very
rapid. Bjerknes (Wied. Ann. 44, p. 74) found that the amplitude
fell to 1/e of the original value, after a time 4T where T was the
period of the electrical vibrations. Thus after a few vibrations
the amplitude becomes inappreciable. To detect the waves
produced by this vibrator Hertz used a piece of copper wire bent
into a circle, the ends being furnished with two balls, or a ball
and a point connected by a screw, so that the distance between
them admitted of very fine adjustment. The radius of the
circle for use with the vibrator just described was 35 cm., and
was so chosen that the free period of the detector might be the
same as that of the vibrator, and the effects in it increased by
resonance. It is evident, however, that with a primary system
as greatly damped as the vibrator used by Hertz, we could not
expect very marked resonance effects, and as a matter of fact
the accurate timing of vibrator and detector in this case is not
very important. With electrical vibrators which can maintain
a large number of vibrations, resonance effects are very striking,
as is beautifully shown by the following experiment due to
Lodge (Nature, 41, p. 368), whose researches have greatly
advanced our knowledge of electric waves. A and C (fig. 2) are
two Leyden jars, whose inner and outer coatings are connected
by wires, B and D, bent so as to include a considerable area.
There is an air-break in the circuit connecting the inside and
outside of one of the jars, A, and electrical oscillations are started
in A by joining the inside and outside with the terminals of a
coil or electrical machine. The circuit in the jar C is provided
204
with a sliding piece, F, by means of which the self-induction of
the discharging circuit, and, therefore, the time of an electrical
oscillation of the jar, can be adjusted. The inside and outside
of this jar are put almost, but not quite, into electrical contact
by means of a piece of tin-foil, E, bent over the lip of the jar.
The jars are placed face to face so that the circuits B and D
are parallel to each other, and approximately at right angles to
the line joining their centres. When the electrical machine is
in action sparks pass across the air-break in the circuit in A,
and by moving the slider F it is possible to find one position for
it in which sparks pass from the inside to the outside of C across
the tin-foil, while when the slider is moved a short distance on
either side of this position the sparks cease.
Hertz found that when he held his detector in the neighbourhood
of the vibrator minute sparks passed between the balls.
These sparks were not stopped when a large plate of non-conducting
substance, such as the wall of a room, was interposed between
the vibrator and detector, but a large plate of very thin metal
stopped them completely.
To illustrate the analogy between electric waves and waves
of light Hertz found another form of apparatus more convenient.
The vibrator consisted of two equal brass cylinders, 12 cm. long
and 3 cm. in diameter, placed with their axes coincident, and in
the focal line of a large zinc parabolic mirror about 2 m. high,
with a focal length of 12.5 cm. The ends of the cylinders nearest
each other, between which the sparks passed, were carefully
polished. The detector, which was placed in the focal line of
an equal parabolic mirror, consisted of two lengths of wire,
each having a straight piece about 50 cm. long and a curved
piece about 15 cm. long bent round at right angles so as to pass
through the back of the mirror. The ends which came through
the mirror were connected with a spark micrometer, the sparks
being observed from behind the mirror. The mirrors are shown,
in fig. 3.
 |
| Fig. 3. |
§ 2. Reflection and Refraction.—To show the reflection of the
waves Hertz placed the mirrors side by side, so that their openings
looked in the same direction, and their axes converged at a point
about 3 m. from the mirrors. No sparks were then observed
in the detector when the vibrator was in action. When, however,
a large zinc plate about 2 m. square was placed at right angles
to the line bisecting the angle between the axes of the mirrors
sparks became visible, but disappeared again when the metal
plate was twisted through an angle of about 15° to either side.
This experiment showed that electric waves are reflected, and
that, approximately at any rate, the angle of incidence is equal
to the angle of reflection. To show refraction Hertz used a large
prism made of hard pitch, about 1.5 m. high, with a slant side
of 1.2 m. and an angle of 30°. When the waves from the vibrator
passed through this the sparks in the detector were not excited
when the axes of the two mirrors were parallel, but appeared
when the axis of the mirror containing the detector made a
certain angle with the axis of that containing the vibrator. When
the system was adjusted for minimum deviation the sparks were
most vigorous when the angle between the axes of the mirrors
was 22°. This corresponds to an index of refraction of 1.69.
§ 3. Analogy to a Plate of Tourmaline.—If a screen be made
by winding wire round a large rectangular framework, so that
the turns of the wire are parallel to one pair of sides of the frame,
and if this screen be interposed between the parabolic mirrors
when placed so as to face each other, there will be no sparks in
the detector when the turns of the wire are parallel to the focal
lines of the mirror; but if the frame is turned through a right
angle so that the wires are perpendicular to the focal lines of the
mirror the sparks will recommence. If the framework is substituted
for the metal plate in the experiment on the reflection
of electric waves, sparks will appear in the detector when the
wires are parallel to the focal lines of the mirrors, and will disappear
when the wires are at right angles to these lines. Thus
the framework reflects but does not transmit the waves when the
electric force in them is parallel to the wires, while it transmits
but does not reflect waves in which the electric force is at right
angles to the wires. The wire framework behaves towards the
electric waves exactly as a plate of tourmaline does to waves
of light. Du Bois and Rubens (Wied. Ann. 49, p. 593), by using
a framework wound with very fine wire placed very close together,
have succeeded in polarizing waves of radiant heat, whose wave
length, although longer than that of ordinary light, is very small
compared with that of electric waves.
§ 4. Angle of Polarization.—When light polarized at right
angles to the plane of incidence falls on a refracting substance
at an angle tan−1μ, where μ is the refractive index of the substance,
all the light is refracted and none reflected; whereas
when light is polarized in the plane of incidence, some of the
light is always reflected whatever the angle of incidence.
Trouton (Nature, 39, p. 391) showed that similar effects take
place with electric waves. From a paraffin wall 3 ft. thick,
reflection always took place when the electric force in the incident
wave was at right angles to the plane of incidence, whereas
at a certain angle of incidence there was no reflection when
the vibrator was turned, so that the electric force was in the
plane of incidence. This shows that on the electromagnetic
theory of light the electric force is at right angles to the plane of
polarization.
 |
| Fig. 4. |
§ 5. Stationary Electrical Vibrations.—Hertz (Wied. Ann.
34, p. 609) made his experiments on these in a large room about
15 m. long. The vibrator, which was of the type first described,
was placed at one end of the room, its plates being parallel to
the wall, at the other end a piece of sheet zinc about 4 m. by
2 m. was placed vertically against the wall. The detector—the
circular ring previously described—was held so that its plane
was parallel to the metal plates of the vibrator, its centre on the
line at right angles to the metal plate bisecting at right angles
the spark gap of the vibrator, and with the spark gap of the
detector parallel to that of the vibrator. The following effects
were observed when the detector was moved about. When it
was close up to the zinc plate there were no sparks, but they
began to pass feebly as soon as it was moved forward a little
way from the plate, and increased rapidly in brightness until it
was about 1.8 m. from the plate, when they attained their
maximum. When its distance was still further increased they
diminished in brightness, and vanished again at a distance of
about 4 m. from the plate. When the distance was still further
increased they reappeared, attained another maximum, and so
on. They thus exhibited a remarkable
periodicity similar to that which occurs
when stationary vibrations are produced
by the interference of direct waves with
those reflected from a surface placed at
right angles to the direction of propagation.
Similar periodic alterations in the
spark were observed by Hertz when the
waves, instead of passing freely through
the air and being reflected by a metal
plate at the end of the room, were led
along wires, as in the arrangement shown
in fig. 4. L and K are metal plates
placed parallel to the plates of the vibrator, long parallel
wires being attached to act as guides to the waves which
were reflected from the isolated end. (Hertz used only one
205
plate and one wire, but the double set of plates and wires
introduced by Sarasin and De la Rive make the results more
definite.) In this case the detector is best placed so that its
plane is at right angles to the wires, while the air space is parallel
to the plane containing the wires. The sparks instead of vanishing
when the detector is at the far end of the wire are a maximum
in this position, but wax and wane periodically as the detector is
moved along the wires. The most obvious interpretation of
these experiments was the one given by Hertz—that there was
interference between the direct waves given out by the vibrator
and those reflected either from the plate or from the ends of the
wire, this interference giving rise to stationary waves. The
places where the electric force was a maximum were the
places where the sparks were brightest, and the places
where the electric force was zero were the places where
the sparks vanished. On this explanation the distance between
two consecutive places where the sparks vanished
would be half the wave length of the waves given out by the
vibrator.
Some very interesting experiments made by Sarasin and De
la Rive (Comptes rendus, 115, p. 489) showed that this explanation
could not be the true one, since by using detectors of different
sizes they found that the distance between two consecutive places
where the sparks vanished depended mainly upon the size of
the detector, and very little upon that of the vibrator. With
small detectors they found the distance small, with large detectors,
large; in fact it is directly proportional to the diameter
of the detector. We can see that this result is a consequence
of the large damping of the oscillations of the vibrator and the
very small damping of those of the detector. Bjerknes showed
that the time taken for the amplitude of the vibrations of the
vibrator to sink to 1/e of their original value was only 4T, while
for the detector it was 500T′, when T and T′ are respectively
the times of vibration of the vibrator and the detector. The
rapid decay of the oscillations of the vibrator will stifle the
interference between the direct and the reflected wave, as the
amplitude of the direct wave will, since it is emitted later, be
much smaller than that of the reflected one, and not able to
annul its effects completely; while the well-maintained vibrations
of the detector will interfere and produce the effects observed
by Sarasin and De la Rive. To see this let us consider the extreme
case in which the oscillations of the vibrator are absolutely dead-beat.
Here an impulse, starting from the vibrator on its way
to the reflector, strikes against the detector and sets it in vibration;
it then travels up to the plate and is reflected, the electric
force in the impulse being reversed by reflection. After reflection
the impulse again strikes the detector, which is still vibrating
from the effects of the first impact; if the phase of this vibration
is such that the reflected impulse tends to produce a current
round the detector in the same direction as that which is circulating
from the effects of the first impact, the sparks will be increased,
but if the reflected impulse tends to produce a current in the
opposite direction the sparks will be diminished. Since the
electric force is reversed by reflection, the greatest increase in the
sparks will take place when the impulse finds, on its return, the
detector in the opposite phase to that in which it left it; that
is, if the time which has elapsed between the departure and return
of the impulse is equal to an odd multiple of half the time of
vibration of the detector. If d is the distance of the detector
from the reflector when the sparks are brightest, and V the
velocity of propagation of electromagnetic disturbance, then
2d/V = (2n + 1) (T′/2); where n is an integer and T′ the time of
vibration of the detector, the distance between two spark
maxima will be VT′/2, and the places where the sparks are a
minimum will be midway between the maxima. Sarasin and
De la Rive found that when the same detector was used the
distance between two spark maxima was the same with the
waves through air reflected from a metal plate and with those
guided by wires and reflected from the free ends of the wire, the
inference being that the velocity of waves along wires is the
same as that through the air. This result, which follows from
Maxwell’s theory, when the wires are not too fine, had been
questioned by Hertz on account of some of his experiments on
wires.
§ 6. Detectors.—The use of a detector with a period of vibration
of its own thus tends to make the experiments more complicated,
and many other forms of detector have been employed by
subsequent experimenters. For example, in place of the sparks
in air the luminous discharge through a rarefied gas has been
used by Dragoumis, Lecher (who used tubes without electrodes
laid across the wires in an arrangement resembling that shown
in fig. 7) and Arons. A tube containing neon at a low pressure
is especially suitable for this purpose. Zehnder (Wied. Ann.
47, p. 777) used an exhausted tube to which an external electromotive
force almost but not quite sufficient of itself to produce
a discharge was applied; here the additional electromotive
force due to the waves was sufficient to start the discharge.
Detectors depending on the heat produced by the rapidly
alternating currents have been used by Paalzow and Rubens,
Rubens and Ritter, and I. Klemenčič. Rubens measured the
heat produced by a bolometer arrangement, and Klemenčič
used a thermo-electric method for the same purpose; in consequence
of the great increase in the sensitiveness of galvanometers
these methods are now very frequently resorted to. Boltzmann
used an electroscope as a detector. The spark gap consisted
of a ball and a point, the ball being connected with the electroscope
and the point with a battery of 200 dry cells. When the
spark passed the cells charged up the electroscope. Ritter
utilized the contraction of a frog’s leg as a detector, Lucas and
Garrett the explosion produced by the sparks in an explosive
mixture of hydrogen and oxygen; while Bjerknes and Franke
used the mechanical attraction between oppositely charged
conductors. If the two sides of the spark gap are connected with
the two pairs of quadrants of a very delicate electrometer, the
needle of which is connected with one pair of quadrants, there
will be a deflection of the electrometer when the detector is
struck by electric waves. A very efficient detector is that invented
by E. Rutherford (Trans. Roy. Soc. A. 1897, 189, p. 1);
it consists of a bundle of fine iron wires magnetized to saturation
and placed inside a small magnetizing coil, through which the
electric waves cause rapidly alternating currents to pass which
demagnetize the soft iron. If the instrument is used to detect
waves in air, long straight wires are attached to the ends of the
demagnetizing coil to collect the energy from the field; to
investigate waves in wires it is sufficient to make a loop or two
in the wire and place the magnetized piece of iron inside it.
The amount of demagnetization which can be observed by the
change in the deflection of a magnetometer placed near the iron,
measures the intensity of the electric waves, and very accurate
determinations can be made with ease with this apparatus.
It is also very delicate, though in this respect it does not equal
the detector to be next described, the coherer; Rutherford got
indications in 1895 when the vibrator was ¾ of a mile away from
the detector, and where the waves had to traverse a thickly
populated part of Cambridge. It can also be used to measure
the coefficient of damping of the electric waves, for since the
wire is initially magnetized to saturation, if the direction of the
current when it first begins to flow in the magnetizing coil is
such as to tend to increase the magnetization of the wire, it will
produce no effect, and it will not be until the current is
reversed that the wire will lose some of its magnetization.
The effect then gives the measure of the intensity half a period
after the commencement of the waves. If the wire is put in the
coil the opposite way, i.e. so that the magnetic force due to the
current begins at once to demagnetize the wire, the demagnetization
gives a measure of the initial intensity of the waves. Comparing
this result with that obtained when the wires were
reversed, we get the coefficient of damping. A very convenient
detector of electric waves is the one discovered almost simultaneously
by Fessenden (Electrotech. Zeits., 1903, 24, p. 586) and
Schlömilch (ibid. p. 959). This consists of an electrolytic cell in
which one of the electrodes is an exceedingly fine point. The
electromotive force in the circuit is small, and there is large
polarization in the circuit with only a small current. When the
206
circuit is struck by electric waves there is an increase in the
currents due to the depolarization of the circuit. If a galvanometer
is in the circuit, the increased deflection of the instrument
will indicate the presence of the waves.
§ 7. Coherers.—The most sensitive detector of electric waves
is the “coherer,” although for metrical work it is not so suitable
as that just described. It depends upon the fact discovered by
Branly (Comptes rendus, 111, p. 785; 112, p. 90) that the resistance
between loose metallic contacts, such as a pile of iron turnings,
diminishes when they are struck by an electric wave. One of
the forms made by Lodge (The Work of Hertz and some of his
Successors, 1894) on this principle consists simply of a glass tube
containing iron turnings, in contact with which are wires led
into opposite ends of the tube. The arrangement is placed in
series with a galvanometer (one of the simplest kind will do)
and a battery; when the iron turnings are struck by electric
waves their resistance is diminished and the deflection of the
galvanometer is increased. Thus the deflection of the galvanometer
can be used to indicate the arrival of electric waves. The
tube must be tapped between each experiment, and the deflection
of the galvanometer brought back to about its original value.
This detector is marvellously delicate, but not metrical, the
change produced in the resistance depending upon so many
things besides the intensity of the waves that the magnitude of
the galvanometer deflection is to some extent a matter of chance.
Instead of the iron turnings we may use two iron wires, one
resting on the other; the resistance of this contact will be altered
by the incidence of the waves. To get greater regularity Bose
uses, instead of the iron turnings, spiral springs, which are pushed
against each other by means of a screw until the most sensitive
state is attained. The sensitiveness of the coherer depends on
the electromotive force put in the galvanometer circuit. Very
sensitive ones can be made by using springs of very fine silver
wire coated electrolytically with nickel. Though the impact
of electric waves generally produces a diminution of resistance
with these loose contacts, yet there are exceptions to the rule.
Thus Branly showed that with lead peroxide, PbO2, there is an
increase in resistance. Aschkinass proved the same to be true
with copper sulphide, CuS; and Bose showed that with potassium
there is an increase of resistance and great power of self-recovery
of the original resistance after the waves have ceased. Several
theories of this action have been proposed. Branly (Lumière
électrique, 40, p. 511) thought that the small sparks which
certainly pass between adjacent portions of metal clear away
layers of oxide or some other kind of non-conducting film, and
in this way improve the contact. It would seem that if this
theory is true the films must be of a much more refined kind than
layers of oxide or dirt, for the coherer effect has been observed
with clean non-oxidizable metals. Lodge explains the effect by
supposing that the heat produced by the sparks fuses adjacent
portions of metal into contact and hence diminishes the resistance;
it is from this view of the action that the name coherer
is applied to the detector. Auerbeck thought that the effect was
a mechanical one due to the electrostatic attractions between
the various small pieces of metal. It is probable that some
or all of these causes are at work in some cases, but the
effects of potassium make us hesitate to accept any of them
as the complete explanation. Blanc (Ann. chim. phys., 1905,
[8] 6, p. 5), as the result of a long series of experiments,
came to the conclusion that coherence is due to pressure. He
regarded the outer layers as different from the mass of the metal
and having a much greater specific resistance. He supposed
that when two pieces of metal are pressed together the molecules
diffuse across the surface, modifying the surface layers and increasing
their conductivity.
§ 8. Generators of Electric Waves.—Bose (Phil. Mag. 43, p. 55)
designed an instrument which generates electric waves with a length
of not more than a centimetre or so, and therefore allows their
properties to be demonstrated with apparatus of moderate dimensions.
The waves are excited by sparking between two platinum
beads carried by jointed electrodes; a platinum sphere is placed
between the beads, and the distance between the beads and the
sphere can be adjusted by bending the electrodes. The diameter of
the sphere is 8 mm., and the wave length of the shortest electrical
waves generated is said to be about 6 mm. The beads are connected
with the terminals of a small induction coil, which, with the battery
to work it and the sparking arrangement, are enclosed in a metal
box, the radiation passing out through a metal tube opposite to
the spark gap. The ordinary vibrating break of the coil is not used,
a single spark made by making and breaking the circuit by means of
a button outside the box being employed instead. The detector is
one of the spiral spring coherers previously described; it is shielded
from external disturbance by being enclosed in a metal box provided
with a funnel-shaped opening to admit the radiation. The wires
leading from the coherers to the galvanometer are also surrounded
by metal tubes to protect them from stray radiation. The radiating
apparatus and the receiver are mounted on stands sliding in an
optical bench. If a parallel beam of radiation is required, a cylindrical
lens of ebonite or sulphur is mounted in a tube fitting on to
the radiator tube and stopped by a guide when the spark is at the
principal focal line of the lens. For experiments requiring angular
measurements a spectrometer circle is mounted on one of the sliding
stands, the receiver being carried on a radial arm and pointing to the
centre of the circle. The arrangement is represented in fig. 5.
 |
| Fig. 5. |
With this apparatus the laws of reflection, refraction and polarization
can readily be verified, and also the double refraction of crystals,
and of bodies possessing a fibrous or laminated structure such as
jute or books. (The double refraction of electric waves seems first
to have been observed by Righi, and other researches on this subject
have been made by Garbasso and Mack.) Bose showed the rotation
of the plane of polarization by means of pieces of twisted jute rope;
if the pieces were arranged so that their twists were all in one direction
and placed in the path of the radiation, they rotated the plane of
polarization in a direction depending upon the direction of twist;
if they were mixed so that there were as many twisted in one direction
as the other, there was no rotation.
 |
| Fig. 6. |
A series of experiments showing the complete analogy between
electric and light waves is described by Righi in his book L’Ottica
delle oscillazioni elettriche. Righi’s exciter, which is especially
convenient when large statical electric machines are used instead
of induction coils, is shown in fig. 6. E and F are balls connected
with the terminals of the machine, and AB and CD are conductors
insulated from each other, the ends B, C, between which the sparks
pass, being immersed in vaseline oil. The period of the vibrations
given out by the system is adjusted by means of metal plates M and
N attached to AB and CD. When the waves are produced by induction
coils or by electrical machines the intervals between the
emission of different sets of waves occupy by far the largest part
of the time. Simon (Wied. Ann., 1898, 64, p. 293; Phys. Zeit.,
1901, 2, p. 253), Duddell (Electrician, 1900, 46, p. 269) and Poulsen
(Electrotech. Zeits., 1906, 27, p. 1070) reduced these intervals very
considerably by using the electric arc to excite the waves, and in this
way produced electrical waves possessing great energy. In these
methods the terminals between which the arc is passing are connected
through coils with self-induction L to the plates of a condenser of
capacity C. The arc is not steady, but is continually varying. This
is especially the case when it passes through hydrogen. These
variations excite vibrations with a period 2π√(LC) in the circuit
containing the capacity of the self-induction. By this method
Duddell produced waves with a frequency of 40,000. Poulsen, who
cooled the terminals of the arc, produced waves with a frequency of
1,000,000, while Stechodro (Ann. der Phys. 27, p. 225) claims to
have produced waves with three hundred times this frequency, i.e.
having a wave length of about a metre. When the self-induction
207
and capacity are large so that the frequency comes within the limits
of the frequency of audible notes, the system gives out a musical
note, and the arrangement is often referred to as the singing arc.
 |
| Fig. 7. |
 |
| Fig. 8. |
§ 9. Waves in Wires.—Many problems on electric waves along
wires can readily be investigated by a method due to Lecher (Wied.
Ann. 41, p. 850), and known as Lecher’s bridge, which furnishes us
with a means of dealing with waves of a definite and determinable
wave-length. In this arrangement (fig. 7) two large plates A and
B are, as in Hertz’s exciter, connected with the terminals of an
induction coil; opposite these and insulated from them are two
smaller plates D, E, to which long parallel wires DFH, EGJ are
attached. These wires are bridged across by a wire LM, and their
farther ends H, J, may be insulated, or connected together, or with
the plates of a condenser. To detect the waves in the circuit beyond
the bridge, Lecher used an exhausted tube placed across the wires,
and Rubens a bolometer, but Rutherford’s detector is the most
convenient and accurate. If this detector is placed in a fixed position
at the end of the circuit, it is found that the deflections of this detector
depend greatly upon the position of the bridge LM, rising rapidly
to a maximum for some positions, and falling rapidly away when the
bridge is displaced. As the bridge is moved from the coil end towards
the detector the deflections show periodic variations, such as are
represented in fig. 8 when the ordinates represent the deflections of
the detector and the abscissae the distance of the bridge from the
ends D, E. The maximum deflections of the detector correspond to
the positions in which the two circuits DFLMGE, HLMJ (in which
the vibrations are but slightly damped) are in resonance. For since
the self-induction and resistance of the bridge LM is very small
compared with that of the circuit beyond, it follows from the theory
of circuits in parallel that only a small part of the current will in
general flow round the longer circuit; it is only when the two circuits
DFLMGE, HLMJ are in resonance that a considerable current will
flow round the latter. Hence when we get a maximum effect in
the detector we know that the waves we are dealing with are those
corresponding to the free periods of the system HLMJ, so that if
we know the free periods of this circuit we know the wave length
of the electric waves under consideration. Thus if the ends of
the wires H, J are free and have no capacity, the current along them
must vanish at H and J, which must be in opposite electric condition.
Hence half the wave length must be an odd submultiple of the length
of the circuit HLMJ. If H and J are connected together the wave
length must be a submultiple of the length of this circuit. When the
capacity at the ends is appreciable the wave length of the circuit is
determined by a somewhat complex expression. To facilitate the
determination of the wave length in such cases, Lecher introduced a
second bridge L′M′, and moved this about until the deflection of the
detector was a maximum; when this occurs the wave length is one
of those corresponding to the closed circuit LMM′L′, and must therefore
be a submultiple of the length of the circuit. Lecher showed
that if instead of using a single wire LM to form the bridge, he used
two parallel wires PQ, LM, placed close together, the currents in the
further circuit were hardly appreciably diminished when the main
wires were cut between PL and QM. Blondlot used a modification of
this apparatus better suited for the production of short waves. In his
form (fig. 9) the exciter consists of two semicircular arms connected
with the terminals of an induction coil, and the long wires, instead
of being connected with the small plates, form a circuit round the
exciter.
 |
| Fig. 9. |
As an example of the use of Lecher’s arrangement, we may quote
Drude’s application of the method to find the specific induction
capacity of dielectrics under electric oscillations of varying frequency.
In this application the ends of the wire are connected to the plates
of a condenser, the space between whose plates can be filled
with the liquid whose specific inductive capacity is required, and
the bridge is moved until
the detector at the end of
the circuit gives the maximum
deflection. Then if
λ is the wave length of
the waves, λ is the wave
length of one of the free
vibrations of the system
HLMJ; hence if C is the
capacity of the condenser
at the end in electrostatic
measure we have
where l is the distance of
the condenser from the
bridge and C′ is the capacity of unit length of the wire. In the
condenser part of the lines of force will pass through air and part
through the dielectric; hence C will be of the form C0 + KC1 where
K is the specific inductive capacity of the dielectric. Hence if l is
the distance of maximum deflection when the dielectric is replaced
by air, l′ when filled with a dielectric whose specific inductive
capacity is known to be K′, and l″ the distance when filled with
the dielectric whose specific inductive capacity is required, we easily
see that—
| cot | 2πl | − cot | 2πl′ | | |
| λ | λ | = | 1 − K′ |
| cot | 2πl | − cot | 2πl″ | 1 − K |
| λ | λ | | |
an equation by means of which K can be determined. It was in
this way that Drude investigated the specific inductive capacity
with varying frequency, and found a falling off in the specific inductive
capacity with increase of frequency when the dielectrics
contained the radicle OH. In another method used by him the
wires were led through long tanks filled with the liquid whose specific
inductive capacity was required; the velocity of propagation of the
electric waves along the wires in the tank being the same as the
velocity of propagation of an electromagnetic disturbance through
the liquid filling the tank, if we find the wave length of the waves
along the wires in the tank, due to a vibration of a given frequency,
and compare this with the wave lengths corresponding to the same
frequency when the wires are surrounded by air, we obtain the
velocity of propagation of electromagnetic disturbance through the
fluid, and hence the specific inductive capacity of the fluid.
 |
| Fig. 10. |
§ 10. Velocity of Propagation of Electromagnetic Effects through Air.—The
experiments of Sarasin and De la Rive already described
(see § 5) have shown that, as theory requires, the velocity of propagation
of electric effects through air is the same as along wires.
The same result had been arrived at by J.J. Thomson, although
from the method he used greater differences between the velocities
might have escaped detection than was possible by Sarasin and De
la Rive’s method. The velocity of waves along wires has been
directly determined by Blondlot by two different methods. In the
first the detector consisted of two parallel plates about 6 cm. in
diameter placed a fraction of a millimetre apart, and forming a
condenser whose capacity C was determined in electromagnetic
measure by Maxwell’s method. The plates were connected by a
rectangular circuit whose self-induction L was calculated from the
dimensions of the rectangle and the size of the wire. The time of
vibration T is equal to 2π√(LC). (The wave length corresponding
to this time is long compared with the length of the circuit, so that
the use of this formula is legitimate.) This detector is placed
between two parallel wires, and the waves produced by the exciter
are reflected from a movable bridge. When this bridge is placed just
beyond the detector vigorous sparks are observed, but as the bridge
is pushed away a place is reached where the sparks disappear; this
place is distance 2/λ from the detector, when λ is the wave length
of the vibration given out by the detector. The sparks again disappear
when the distance of the bridge from the detector is 3λ/4.
Thus by measuring the distance between two consecutive positions
of the bridge at which the sparks disappear λ can be determined,
208
and v, the velocity of propagation, is equal to λ/T. As the means
of a number of experiments Blondlot found v to be 3.02 × 1010
cm./sec., which, within the errors of experiment, is equal to 3 × 1010
cm./sec., the velocity of light. A second method used by Blondlot,
and one which does not involve
the calculation of the
period, is as follows:—A and
A′ (fig. 10) are two equal
Leyden jars coated inside
and outside with tin-foil.
The outer coatings form two
separate rings a, a1; a′, a′1,
and the inner coatings are
connected with the poles of
the induction coil by means
of the metal pieces b, b′. The
sharply pointed conductors p
and p′, the points of which
are about ½ mm. apart, are
connected with the rings of
the tin-foil a and a′, and two
long copper wires pca1, p′c′a′1,
1029 cm. long, connect these
points with the other rings
a1, a1′. The rings aa′, a1a1′,
are connected by wet strings
so as to charge up the jars.
When a spark passes between
b and b′, a spark at once
passes between pp′, and this
is followed by another spark
when the waves travelling by
the paths a1cp, a′1c′p′ reach
p and p′. The time between
the passage of these sparks,
which is the time taken by
the waves to travel 1029 cm.,
was observed by means of
a rotating mirror, and the
velocity measured in 15 experiments varied between 2.92 × 1010 and
3.03 × 1010 cm./sec., thus agreeing well with that deduced by the
preceding method. Other determinations of the velocity of electromagnetic
propagation have been made by Lodge and Glazebrook,
and by Saunders.
On Maxwell’s electromagnetic theory the velocity of propagation
of electromagnetic disturbances should equal the velocity of light,
and also the ratio of the electromagnetic unit of electricity to the
electrostatic unit. A large number of determinations of this ratio
have been made:—
| Observer. | Date. | Ratio 1010 ×. |
| Klemenčič | 1884 | 3.019 cm./sec. |
| Himstedt | 1888 | 3.009 cm./sec. |
| Rowland | 1889 | 2.9815 cm./sec. |
| Rosa | 1889 | 2.9993 cm./sec. |
| J.J. Thomson and Searle | 1890 | 2.9955 cm./sec. |
| Webster | 1891 | 2.987 cm./sec. |
| Pellat | 1891 | 3.009 cm./sec. |
| Abraham | 1892 | 2.992 cm./sec. |
| Hurmuzescu | 1895 | 3.002 cm./sec. |
| Rosa | 1908 | 2.9963 cm./sec. |
The mean of these determinations is 3.001 × 1010 cm./sec., while
the mean of the last five determinations of the velocity of light in
air is given by Himstedt as 3.002 × 1010 cm./sec. From these experiments
we conclude that the velocity of propagation of an electromagnetic
disturbance is equal to the velocity of light, and to the
velocity required by Maxwell’s theory.
In experimenting with electromagnetic waves it is in general
more difficult to measure the period of the oscillations than their
wave length. Rutherford used a method by which the period of
the vibration can easily be determined; it is based upon the theory
of the distribution of alternating currents in two circuits ACB, ADB
in parallel. If A and B are respectively the maximum currents in
the circuits ACB, ADB, then
| A |
= √ | S² + (N − M)²p² |
| B | R² + (L − M)²p² |
when R and S are the resistances, L and N the coefficients of self-induction
of the circuits ACB, ADB respectively, M the coefficient
of mutual induction between the circuits, and p the frequency of the
currents. Rutherford detectors were placed in the two circuits, and
the circuits adjusted until they showed that A = B; when this is
the case
| p² = | R² − S² |
. |
| N² − L² − 2M (N − L) |
If we make one of the circuits, ADB, consist of a short length
of a high liquid resistance, so that S is large and N small, and
the other circuit ACB of a low metallic resistance bent to have
considerable self-induction, the preceding equation becomes approximately
p = S/L, so that when S and L are known p is readily
determined.
(J. J. T.)
ELECTROCHEMISTRY. The present article deals with
processes that involve the electrolysis of aqueous solutions,
whilst those in which electricity is used in the manufacture of
chemical products at furnace temperatures are treated under
Electrometallurgy, although, strictly speaking, in some
cases (e.g. calcium carbide and phosphorus manufacture) they
are not truly metallurgical in character. For the theory and
elemental laws of electro-deposition see Electrolysis; and
for the construction and use of electric generators see Dynamo
and Battery: Electric. The importance of the subject may
be gauged by the fact that all the aluminium, magnesium,
sodium, potassium, calcium carbide, carborundum and artificial
graphite, now placed on the market, is made by electrical processes,
and that the use of such processes for the refining of copper
and silver, and in the manufacture of phosphorus, potassium
chlorate and bleach, already pressing very heavily on the older
non-electrical systems, is every year extending. The convenience
also with which the energy of waterfalls can be converted into
electric energy has led to the introduction of chemical industries
into countries and districts where, owing to the absence of coal,
they were previously unknown. Norway and Switzerland have
become important producers of chemicals, and pastoral districts
such as those in which Niagara or Foyers are situated manufacturing
centres. In this way the development of the electrochemical
industry is in a marked degree altering the distribution
of trade throughout the world.
Electrolytic Refining of Metals.—The principle usually followed
in the electrolytic refining of metals is to cast the impure metal
into plates, which are exposed as anodes in a suitable solvent,
commonly a salt of the metal under treatment. On passing a
current of electricity, of which the volume and pressure are
adjusted to the conditions of the electrolyte and electrodes,
the anode slowly dissolves, leaving the insoluble impurities in
the form of a sponge, if the proportion be considerable, but
otherwise as a mud or slime which becomes detached from the
anode surface and must be prevented from coming into contact
with the cathode. The metal to be refined passing into solution
is concurrently deposited at the cathode. Soluble impurities
which are more electro-negative than the metal under treatment
must, if present, be removed by a preliminary process, and the
voltage and other conditions must be so selected that none of
the more electro-positive metals are co-deposited with the metal
to be refined. From these and other considerations it is obvious
that (1) the electrolyte must be such as will freely dissolve the
metal to be refined; (2) the electrolyte must be able to dissolve
the major portion of the anode, otherwise the mass of insoluble
matter on the outer layer will prevent access of electrolyte to
the core, which will thus escape refining; (3) the electrolyte
should, if possible, be incapable of dissolving metals more
electro-negative than that to be refined; (4) the proportion of
soluble electro-positive impurities must not be excessive, or these
substances will accumulate too rapidly in the solution and
necessitate its frequent purification; (5) the current density
must be so adjusted to the strength of the solution and to other
conditions that no relatively electro-positive metal is deposited,
and that the cathode deposit is physically suitable for subsequent
treatment; (6) the current density should be as high as
is consistent with the production of a pure and sound deposit,
without undue expense of voltage, so that the operation may be
rapid and the “turnover” large; (7) the electrolyte should
be as good a conductor of electricity as possible, and should not,
ordinarily, be altered chemically by exposure to air; and (8) the
use of porous partitions should be avoided, as they increase the
resistance and usually require frequent renewal. For details
of the practical methods see Gold; Silver; Copper and headings
for other metals.
Electrolytic Manufacture of Chemical Products.—When an
aqueous solution of the salt of an alkali metal is electrolysed, the
209
metal reacts with the water, as is well known, forming caustic
alkali, which dissolves in the solution, and hydrogen, which comes
off as a gas. So early as 1851 a patent was taken out by Cooke
for the production of caustic alkali without the use of a separate
current, by immersing iron and copper plates on opposite sides
of a porous (biscuit-ware) partition in a suitable cell, containing
a solution of the salt to be electrolysed, at 21°-65° C. (70°-150° F.).
The solution of the iron anode was intended to afford the
necessary energy. In the same year another patent was granted
to C. Watt for a similar process, involving the employment of an
externally generated current. When an alkaline chloride, say
sodium chloride, is electrolysed with one electrode immersed
in a porous cell, while caustic soda is formed at the cathode,
chlorine is deposited at the anode. If the latter be insoluble,
the gas diffuses into the solution and, when this becomes
saturated, escapes into the air. If, however, no porous division
be used to prevent the intermingling by diffusion of the anode
and cathode solutions, a complicated set of subsidiary reactions
takes place. The chlorine reacts with the caustic soda, forming
sodium hypochlorite, and this in turn, with an excess of chlorine
and at higher temperatures, becomes for the most part converted
into chlorate, whilst any simultaneous electrolysis of a hydroxide
or water and a chloride (so that hydroxyl and chlorine are simultaneously
liberated at the anode) also produces oxygen-chlorine
compounds direct. At the same time, the diffusion of these
compounds into contact with the cathode leads to a partial
reduction to chloride, by the removal of combined oxygen by the
instrumentality of the hydrogen there evolved. In proportion as
the original chloride is thus reproduced, the efficiency of the
process is of course diminished. It is obvious that, with suitable
methods and apparatus, the electrolysis of alkaline chlorides
may be made to yield chlorine, hypochlorites (bleaching liquors),
chlorates or caustic alkali, but that great care must be exercised
if any of these products is to be obtained pure and with economy.
Many patents have been taken out in this branch of electrochemistry,
but it is to be remarked that that granted to C. Watt
traversed the whole of the ground. In his process a current
was passed through a tank divided into two or three cells by
porous partitions, hoods and tubes were arranged to carry off
chlorine and hydrogen respectively, and the whole was heated
to 120° F. by a steam jacket when caustic alkali was being made.
Hypochlorites were made, at ordinary temperatures, and
chlorates at higher temperatures, in a cell without a partition in
which the cathode was placed horizontally immediately above the
anode, to favour the mixing of the ascending chlorine with the
descending caustic solution.
The relation between the composition of the electrolyte and the
various conditions of current-density, temperature and the like
has been studied by F. Oettel (Zeitschrift f. Elektrochem., 1894, vol. i.
pp. 354 and 474) in connexion with the production of hypochlorites
and chlorates in tanks without diaphragms, by C. Häussermann and
W. Naschold (Chemiker Zeitung, 1894, vol. xviii. p. 857) for their
production in cells with porous diaphragms, and by F. Haber and
S. Grinberg (Zeitschrift f. anorgan. Chem., 1898, vol. xvi. pp. 198, 329,
438) in connexion with the electrolysis of hydrochloric acid. Oettel,
using a 20% solution of potassium chloride, obtained the best
yield of hypochlorite with a high current-density, but as soon
as 1¼% of bleaching chlorine (as hypochlorite) was present, the
formation of chlorate commenced. The yield was at best very
low as compared with that theoretically possible. The best yield
of chlorate was obtained when from 1 to 4% of caustic potash
was present. With high current-density, heating the solution tended
to increase the proportion of chlorate to hypochlorite, but as the
proportion of water decomposed is then higher, the amount of
chlorine produced must be less and the total chlorine efficiency
lower. He also traced a connexion between alkalinity, temperature
and current-density, and showed that these conditions should be
mutually adjusted. With a current-density of 130 to 140 amperes
per sq. ft., at 3 volts, passing between platinum electrodes, he
attained to a current-efficiency of 52%, and each (British) electrical
horse-power hour was equivalent to a production of 1378.5 grains of
potassium chlorate. In other words, each pound of chlorate would
require an expenditure of nearly 5.1 e.h.p. hours. One of the
earliest of the more modern processes was that of E. Hermite,
which consisted in the production of bleach-liquors by the electrolysis
(according to the 1st edition of the 1884 patent) of magnesium
or calcium chloride between platinum anodes carried in wooden
frames, and zinc cathodes. The solution, containing hypochlorites
and chlorates, was then applied to the bleaching of linen, paper-pulp
or the like, the solution being used over and over again. Many
modifications have been patented by Hermite, that of 1895 specifying
the use of platinum gauze anodes, held in ebonite or other
frames. Rotating zinc cathodes were used, with scrapers to prevent
the accumulation of a layer of insoluble magnesium compounds,
which would otherwise increase the electrical resistance beyond
reasonable limits. The same inventor has patented the application
of electrolysed chlorides to the purification of starch by the oxidation
of less stable organic bodies, to the bleaching of oils, and to the
purification of coal gas, spirit and other substances. His system for
the disinfection of sewage and similar matter by the electrolysis of
chlorides, or of sea-water, has been tried, but for the most part abandoned
on the score of expense. Reference may be made to papers
written in the early days of the process by C.F. Cross and E.J. Bevan
(Journ. Soc. Chem. Industry, 1887, vol. vi. p. 170, and 1888, vol. vii.
p. 292), and to later papers by P. Schoop (Zeitschrift f. Elektrochem.,
1895, vol. ii. pp. 68, 88, 107, 209, 289).
E. Kellner, who in 1886 patented the use of cathode (caustic soda)
and anode (chlorine) liquors in the manufacture of cellulose from
wood-fibre, and has since evolved many similar processes, has produced
an apparatus that has been largely used. It consists of a
stoneware tank with a thin sheet of platinum-iridium alloy at
either end forming the primary electrodes, and between them a
number of glass plates reaching nearly to the bottom, each having
a platinum gauze sheet on either side; the two sheets belonging to
each plate are in metallic connexion, but insulated from all the
others, and form intermediary or bi-polar electrodes. A 10-12%
solution of sodium chloride is caused to flow upwards through the
apparatus and to overflow into troughs, by which it is conveyed
(if necessary through a cooling apparatus) back to the circulating
pump. Such a plant has been reported as giving 0.229 gallon of a
liquor containing 1% of available chlorine per kilowatt hour, or
0.171 gallon per e.h.p. hour. Kellner has also patented a “bleaching-block,”
as he terms it, consisting of a frame carrying parallel
plates similar in principle to those last described. The block is
immersed in the solution to be bleached, and may be lifted in or out
as required. O. Knöfler and Gebauer have also a system of bi-polar
electrodes, mounted in a frame in appearance resembling a filter-press.
Other Electrochemical Processes.—It is obvious that electrolytic
iodine and bromine, and oxygen compounds of these elements,
may be produced by methods similar to those applied to chlorides
(see Alkali Manufacture and Chlorates), and Kellner and
others have patented processes with this end in view. Hydrogen
and oxygen may also be produced electrolytically as gases, and
their respective reducing and oxidizing powers at the moment
of deposition on the electrode are frequently used in the
laboratory, and to some extent industrially, chiefly in the field
of organic chemistry. Similarly, the formation of organic
halogen products may be effected by electrolytic chlorine, as,
for example, in the production of chloral by the gradual introduction
of alcohol into an anode cell in which the electrolyte is a
strong solution of potassium chloride. Again, anode reactions,
such as are observed in the electrolysis of the fatty acids, may be
utilized, as, for example, when the radical CH3CO2—deposited
at the anode in the electrolysis of acetic acid—is dissociated,
two of the groups react to give one molecule of ethane, C2H6, and
two of carbon dioxide. This, which has long been recognized
as a class-reaction, is obviously capable of endless variation.
Many electrolytic methods have been proposed for the purification
of sugar; in some of them soluble anodes are used for a few
minutes in weak alkaline solutions, so that the caustic alkali
from the cathode reaction may precipitate chemically the
hydroxide of the anode metal dissolved in the liquid, the precipitate
carrying with it mechanically some of the impurities
present, and thus clarifying the solution. In others the current
is applied for a longer time to the original sugar-solution with
insoluble (e.g. carbon) anodes. F. Peters has found that with
these methods the best results are obtained when ozone is employed
in addition to electrolytic oxygen. Use has been made
of electrolysis in tanning operations, the current being passed
through the tan-liquors containing the hides. The current,
by endosmosis, favours the passage of the solution into the
hide-substance, and at the same time appears to assist the chemical
combinations there occurring; hence a great reduction in
the time required for the completion of the process. Many
patents have been taken out in this direction, one of the best
known being that of Groth, experimented upon by S. Rideal
and A.P. Trotter (Journ. Soc. Chem. Indust., 1891, vol. x. p. 425),
210
who employed copper anodes, 4 sq. ft. in area, with current-densities
of 0.375 to 1 (ranging in some cases to 7.5) ampere per
sq. ft., the best results being obtained with the smaller current-densities.
Electrochemical processes are often indirectly used,
as for example in the Villon process (Elec. Rev., New York,
1899, vol. xxxv. p. 375) applied in Russia to the manufacture of
alcohol, by a series of chemical reactions starting from the production
of acetylene by the action of water upon calcium carbide.
The production of ozone in small quantities during electrolysis,
and by the so-called silent discharge, has long been known, and
the Siemens induction tube has been developed for use industrially.
The Siemens and Halske ozonizer, in form somewhat
resembling the old laboratory instrument, is largely used in
Germany; working with an alternating current transformed
up to 6500 volts, it has been found to give 280 grains or more
of ozone per e.h.p. hour. E. Andreoli (whose first British
ozone patent was No. 17,426 of 1891) uses flat aluminium plates
and points, and working with an alternating current of 3000
volts is said to have obtained 1440 grains per e.h.p. hour.
Yarnold’s process, using corrugated glass plates coated on one
side with gold or other metal leaf, is stated to have yielded as
much as 2700 grains per e.h.p. hour. The ozone so prepared
has numerous uses, as, for example, in bleaching oils, waxes,
fabrics, &c., sterilizing drinking-water, maturing wines, cleansing
foul beer-casks, oxidizing oil, and in the manufacture of vanillin.
For further information the following books, among others, may
be consulted:—Haber, Grundriss der technischen Elektrochemie
(München, 1898); Borchers and M’Millan, Electric Smelting and
Refining (London, 1904); E.D. Peters, Principles of Copper Smelting
(New York, 1907); F. Peters, Angewandte Elektrochemie, vols. ii.
and iii. (Leipzig, 1900); Gore, The Art of Electrolytic Separation of
Metals (London, 1890); Blount, Practical Electro-Chemistry (London,
1906); G. Langbein, Vollständiges Handbuch der galvanischen
Metall-Niederschläge (Leipzig, 1903), Eng. trans. by W.T. Brannt
(1909); A. Watt, Electro-Plating and Electro-Refining of Metals
(London, 1902); W.H. Wahl, Practical Guide to the Gold and Silver
Electroplater, &c. (Philadelphia, 1883); Wilson, Stereotyping and
Electrotyping (London); Lunge, Sulphuric Acid and Alkali, vol. iii.
(London, 1909). Also papers in various technical periodicals.
The industrial aspect is treated in a Gartside Report, Some Electro-Chemical
Centres (Manchester, 1908), by J.N. Pring.
(W. G. M.)
ELECTROCUTION (an anomalous derivative from “electro-execution”;
syn. “electrothanasia”), the popular name, invented
in America, for the infliction of the death penalty on
criminals (see Capital Punishment) by passing through the body
of the condemned a sufficient current of electricity to cause
death. The method was first adopted by the state of New York,
a law making this method obligatory having been passed and
approved by the governor on the 4th of June 1888. The law
provides that there shall be present, in addition to the warden,
two physicians, twelve reputable citizens of full age, seven deputy
sheriffs, and such ministers, priests or clergymen, not exceeding
two, as the criminal may request. A post-mortem examination
of the body of the convict is required, and the body, unless
claimed by relatives, is interred in the prison cemetery with a
sufficient quantity of quicklime to consume it. The law became
effective in New York on the 1st of January 1889. The first
criminal to be executed by electricity was William Kemmler,
on the 6th of August 1890, at Auburn prison. The validity of
the New York law had previously been attacked in regard to
this case (Re Kemmler, 1889; 136 U.S. 436), as providing “a
cruel and unusual punishment” and therefore being contrary
to the Constitution; but it was sustained in the state courts and
finally in the Federal courts. By 1906 about one hundred and
fifteen murderers had been successfully executed by electricity in
New York state in Sing Sing, Auburn and Dannemora prisons.
The method has also been adopted by the states of Ohio
(1896), Massachusetts (1898), New Jersey (1906), Virginia
(1908) and North Carolina (1910).
The apparatus consists of a stationary engine, an alternating
dynamo capable of generating a current at a pressure of 2000
volts, a “death-chair” with adjustable head-rest, binding
straps and adjustable electrodes devised by E.F. Davis, the
state electrician of New York. The voltmeter, ammeter and
switch-board controlling the current are located in the execution-room;
the dynamo-room is communicated with by electric
signals. Before each execution the entire apparatus is thoroughly
tested. When everything is in readiness the criminal is brought
in and seats himself in the death-chair. His head, chest, arms
and legs are secured by broad straps; one electrode thoroughly
moistened with salt-solution is affixed to the head, and another to
the calf of one leg, both electrodes being moulded so as to secure
good contact. The application of the current is usually as
follows: the contact is made with a high voltage (1700-1800
volts) for 5 to 7 seconds, reduced to 200 volts until a half-minute
has elapsed; raised to high voltage for 3 to 5 seconds, again reduced
to low voltage for 3 to 5 seconds, again reduced to a low
voltage until one minute has elapsed, when it is again raised to
the high voltage for a few seconds and the contact broken. The
ammeter usually shows that from 7 to 10 amperes pass through
the criminal’s body. A second or even a third brief contact is
sometimes made, partly as a precautionary measure, but rather
the more completely to abolish reflexes in the dead body. Calculations
have shown that by this method of execution from 7 to
10 h. p. of energy are liberated in the criminal’s body. The
time consumed by the strapping-in process is usually about 45
seconds, and the first contact is made about 70 seconds after the
criminal has entered the death-chamber.
When properly performed the effect is painless and instantaneous
death. The mechanism of life, circulation and respiration
cease with the first contact. Consciousness is blotted out
instantly, and the prolonged application of the current ensures
permanent derangement of the vital functions beyond recovery.
Occasionally the drying of the sponges through undue generation
of heat causes desquamation or superficial blistering of the skin
at the site of the electrodes. Post-mortem discoloration, or
post-mortem lividity, often appears during the first contact.
The pupils of the eyes dilate instantly and remain dilated after
death.
The post-mortem examination of “electrocuted” criminals
reveals a number of interesting phenomena. The temperature
of the body rises promptly after death to a very high point.
At the site of the leg electrode a temperature of over 128° F. was
registered within fifteen minutes in many cases. After the removal
of the brain the temperature recorded in the spinal canal was
often over 120° F. The development of this high temperature is
to be regarded as resulting from the active metabolism of tissues
not (somatically) dead within a body where all vital mechanisms
have been abolished, there being no circulation to carry off the
generated heat. The heart, at first flaccid when exposed soon
after death, gradually contracts and assumes a tetanized condition;
it empties itself of all blood and takes the form of a heart
in systole. The lungs are usually devoid of blood and weigh
only 7 or 8 ounces (avoird.) each. The blood is profoundly
altered biochemically; it is of a very dark colour and it rarely
coagulates.
(E. A. S.*)
ELECTROKINETICS, that part of electrical science which is
concerned with the properties of electric currents.
Classification of Electric Currents.—Electric currents are
classified into (a) conduction currents, (b) convection currents,
(c) displacement or dielectric currents. In the case of conduction
currents electricity flows or moves through a stationary
material body called the conductor. In convection currents
electricity is carried from place to place with and on moving
material bodies or particles. In dielectric currents there is no
continued movement of electricity, but merely a limited displacement
through or in the mass of an insulator or dielectric. The
path in which an electric current exists is called an electric
circuit, and may consist wholly of a conducting body, or partly
of a conductor and insulator or dielectric, or wholly of a dielectric.
In cases in which the three classes of currents are present together
the true current is the sum of each separately. In the case of
conduction currents the circuit consists of a conductor immersed
in a non-conductor, and may take the form of a thin wire or
cylinder, a sheet, surface or solid. Electric conduction currents
may take place in space of one, two or three dimensions, but for
211
the most part the circuits we have to consider consist of thin
cylindrical wires or tubes of conducting material surrounded
with an insulator; hence the case which generally presents itself
is that of electric flow in space of one dimension. Self-closed
electric currents taking place in a sheet of conductor are called
“eddy currents.”
Although in ordinary language the current is said to flow in
the conductor, yet according to modern views the real pathway
of the energy transmitted is the surrounding dielectric, and the
so-called conductor or wire merely guides the transmission of
energy in a certain direction. The presence of an electric
current is recognized by three qualities or powers: (1) by the
production of a magnetic field, (2) in the case of conduction
currents, by the production of heat in the conductor, and (3) if
the conductor is an electrolyte and the current unidirectional,
by the occurrence of chemical decomposition in it. An electric
current may also be regarded as the result of a movement of
electricity across each section of the circuit, and is then measured
by the quantity conveyed per unit of time. Hence if dq is the
quantity of electricity which flows across any section of the
conductor in the element of time dt, the current i = dq/dt.
Electric currents may be also classified as constant or variable
and as unidirectional or “direct,” that is flowing always in the
same direction, or “alternating,” that is reversing their direction
at regular intervals. In the last case the variation of current
may follow any particular law. It is called a “periodic current”
if the cycle of current values is repeated during a certain time
called the periodic time, during which the current reaches a
certain maximum value, first in one direction and then in the
opposite, and in the intervals between has a zero value at certain
instants. The frequency of the periodic current is the number
of periods or cycles in one second, and alternating currents are
described as low frequency or high frequency, in the latter case
having some thousands of periods per second. A periodic current
may be represented either by a wave diagram, or by a polar
diagram.1 In the first case we take a straight line to represent
the uniform flow of time, and at small equidistant intervals
set up perpendiculars above or below the time axis, representing
to scale the current at that instant in one direction or the other;
the extremities of these ordinates then define a wavy curve
which is called the wave form of the current (fig. 1). It is obvious
that this curve can only be a single valued curve. In one particular
and important case the form of the current curve is a
simple harmonic curve or simple sine curve. If T represents
the periodic time in which the cycle of current values takes
place, whilst n is the frequency or number of periods per second
and p stands for 2πn, and i is the value of the current at any
instant t, and I its maximum value, then in this case we have
i = I sin pt. Such a current is called a “sine current” or simple
periodic current.
 |
| Fig. 1. |
Fig. 2. |
In a polar diagram (fig. 2) a number of radial lines are drawn
from a point at small equiangular intervals, and on these lines
are set off lengths proportional to the current value of a periodic
current at corresponding intervals during one complete period
represented by four right angles. The extremities of these
radii delineate a polar curve. The polar form of a simple sine
current is obviously a circle drawn through the origin. As a
consequence of Fourier’s theorem it follows that any periodic
curve having any wave form can be imitated by the superposition
of simple sine currents differing in maximum value and
in phase.
Definitions of Unit Electric Current.—In electrokinetic investigations
we are most commonly limited to the cases of unidirectional
continuous and constant currents (C.C. or D.C.), or of simple
periodic currents, or alternating currents of sine form (A.C.).
A continuous electric current is measured either by the magnetic
effect it produces at some point outside its circuit, or by the
amount of electrochemical decomposition it can perform in a
given time on a selected standard electrolyte. Limiting our
consideration to the case of linear currents or currents flowing
in thin cylindrical wires, a definition may be given in the first
place of the unit electric current in the centimetre, gramme,
second (C.G.S.) of electromagnetic measurement (see Units,
Physical). H.C. Oersted discovered in 1820 that a straight
wire conveying an electric current is surrounded by a magnetic
field the lines of which are self-closed lines embracing the electric
circuit (see Electricity and Electromagnetism). The unit
current in the electromagnetic system of measurement is defined
as the current which, flowing in a thin wire bent into the form
of a circle of one centimetre in radius, creates a magnetic field
having a strength of 2π units at the centre of the circle, and
therefore would exert a mechanical force of 2π dynes on a unit
magnetic pole placed at that point (see Magnetism). Since
the length of the circumference of the circle of unit radius is
2π units, this is equivalent to stating that the unit current on
the electromagnetic C.G.S. system is a current such that unit
length acts on unit magnetic pole with a unit force at a unit
of distance. Another definition, called the electrostatic unit
of current, is as follows: Let any conductor be charged with
electricity and discharged through a thin wire at such a rate
that one electrostatic unit of quantity (see Electrostatics)
flows past any section of the wire in one unit of time. The
electromagnetic unit of current defined as above is 3 × 1010 times
larger than the electrostatic unit.
In the selection of a practical unit of current it was considered
that the electromagnetic unit was too large for most purposes,
whilst the electrostatic unit was too small; hence a practical
unit of current called 1 ampere was selected, intended originally
to be 1⁄10 of the absolute electromagnetic C.G.S. unit of current
as above defined. The practical unit of current, called the
international ampere, is, however, legally defined at the present
time as the continuous unidirectional current which when
flowing through a neutral solution of silver nitrate deposits in
one second on the cathode or negative pole 0.001118 of a gramme
of silver. There is reason to believe that the international unit
is smaller by about one part in a thousand, or perhaps by one
part in 800, than the theoretical ampere defined as 1⁄10 part of
the absolute electromagnetic unit. A periodic or alternating
current is said to have a value of 1 ampere if when passed through
a fine wire it produces in the same time the same heat as a
unidirectional continuous current of 1 ampere as above electrochemically
defined. In the case of a simple periodic alternating
current having a simple sine wave form, the maximum value
is equal to that of the equiheating continuous current multiplied
by √2. This equiheating continuous current is called the effective
or root-mean-square (R.M.S.) value of the alternating one.
Resistance.—A current flows in a circuit in virtue of an electromotive
force (E.M.F.), and the numerical relation between the
current and E.M.F. is determined by three qualities of the
circuit called respectively, its resistance (R), inductance (L), and
capacity (C). If we limit our consideration to the case of continuous
unidirectional conduction currents, then the relation
between current and E.M.F. is defined by Ohm’s law, which states
that the numerical value of the current is obtained as the quotient
of the electromotive force by a certain constant of the circuit
called its resistance, which is a function of the geometrical form
of the circuit, of its nature, i.e. material, and of its temperature,
but is independent of the electromotive force or current. The
resistance (R) is measured in units called ohms and the electromotive
force in volts (V); hence for a continuous current the
value of the current in amperes (A) is obtained as the quotient
212
of the electromotive force acting in the circuit reckoned in volts
by the resistance in ohms, or A = V/R. Ohm established his law
by a course of reasoning which was similar to that on which
J.B.J. Fourier based his investigations on the uniform motion
of heat in a conductor. As a matter of fact, however, Ohm’s
law merely states the direct proportionality of steady current
to steady electromotive force in a circuit, and asserts that this
ratio is governed by the numerical value of a quality of the conductor,
called its resistance, which is independent of the current,
provided that a correction is made for the change of temperature
produced by the current. Our belief, however, in its universality
and accuracy rests upon the close agreement between deductions
made from it and observational results, and although it is not
derivable from any more fundamental principle, it is yet one of
the most certainly ascertained laws of electrokinetics.
Ohm’s law not only applies to the circuit as a whole but to any
part of it, and provided the part selected does not contain a
source of electromotive force it may be expressed as follows:—The
difference of potential (P.D.) between any two points of a
circuit including a resistance R, but not including any source of
electromotive force, is proportional to the product of the resistance
and the current i in the element, provided the conductor
remains at the same temperature and the current is constant and
unidirectional. If the current is varying we have, however, to take
into account the electromotive force (E.M.F.) produced by this
variation, and the product Ri is then equal to the difference
between the observed P.D. and induced E.M.F.
We may otherwise define the resistance of a circuit by saying
that it is that physical quality of it in virtue of which energy is
dissipated as heat in the circuit when a current flows through it.
The power communicated to any electric circuit when a current
i is created in it by a continuous unidirectional electromotive
force E is equal to Ei, and the energy dissipated as heat in that
circuit by the conductor in a small interval of time dt is measured
by Ei dt. Since by Ohm’s law E = Ri, where R is the resistance
of the circuit, it follows that the energy dissipated as heat per
unit of time in any circuit is numerically represented by Ri², and
therefore the resistance is measured by the heat produced per
unit of current, provided the current is unvarying.
Inductance.—As soon as we turn our attention, however, to
alternating or periodic currents we find ourselves compelled to take
into account another quality of the circuit, called its “inductance.”
This may be defined as that quality in virtue of which energy is
stored up in connexion with the circuit in a magnetic form.
It can be experimentally shown that a current cannot be created
instantaneously in a circuit by any finite electromotive force,
and that when once created it cannot be annihilated instantaneously.
The circuit possesses a quality analogous to the inertia
of matter. If a current i is flowing in a circuit at any moment,
the energy stored up in connexion with the circuit is measured
by ½Li², where L, the inductance of the circuit, is related to the
current in the same manner as the quantity called the mass of
a body is related to its velocity in the expression for the ordinary
kinetic energy, viz. ½Mv². The rate at which this conserved
energy varies with the current is called the “electrokinetic
momentum” of this circuit (= Li). Physically interpreted this
quantity signifies the number of lines of magnetic flux due to
the current itself which are self-linked with its own circuit.
Magnetic Force and Electric Currents.—In the case of every
circuit conveying a current there is a certain magnetic force (see
Magnetism) at external points which can in some instances be
calculated. Laplace proved that the magnetic force due to an
element of length dS of a circuit conveying a current I at a point
P at a distance r from the element is expressed by IdS sin θ/r²,
where θ is the angle between the direction of the current element
and that drawn between the element and the point. This force
is in a direction perpendicular to the radius vector and to the
plane containing it and the element of current. Hence the
determination of the magnetic force due to any circuit is reduced
to a summation of the effects due to all the elements of length.
For instance, the magnetic force at the centre of a circular
circuit of radius r carrying a steady current I is 2πI/r, since all
elements are at the same distance from the centre. In the same
manner, if we take a point in a line at right angles to the plane
of the circle through its centre and at a distance d, the magnetic
force along this line is expressed by 2πr²I / (r² + d²)3⁄2. Another
important case is that of an infinitely long straight current.
By summing up the magnetic force due to each element at
any point P outside the continuous straight current I, and at a
distance d from it, we can show that it is equal to 2I/d or is
inversely proportional to the distance of the point from the wire.
In the above formula the current I is measured in absolute
electromagnetic units. If we reckon the current in amperes
A, then I = A/10.
It is possible to make use of this last formula, coupled with an
experimental fact, to prove that the magnetic force due to an
element of current varies inversely as the square of the distance.
If a flat circular disk is suspended so as to be free to rotate round
a straight current which passes through its centre, and two
bar magnets are placed on it with their axes in line with the
current, it is found that the disk has no tendency to rotate round
the current. This proves that the force on each magnetic pole
is inversely as its distance from the current. But it can be shown
that this law of action of the whole infinitely long straight current
is a mathematical consequence of the fact that each element of
the current exerts a magnetic force which varies inversely as
the square of the distance. If the current flows N times round
the circuit instead of once, we have to insert NA/10 in place of
I in all the above formulae. The quantity NA is called the
“ampere-turns” on the circuit, and it is seen that the magnetic
field at any point outside a circuit is proportional to the ampere-turns
on it and to a function of its geometrical form and the
distance of the point.
 |
| Fig. 3. |
Fig. 4. |
There is therefore a distribution of magnetic force in the field
of every current-carrying conductor which can be delineated by
lines of magnetic force and rendered visible to the eye by iron
filings (see Magnetism). If a copper wire is passed vertically
through a hole in a card on which iron filings are sprinkled, and
a strong electric current is sent through the circuit, the filings
arrange themselves in concentric circular lines making visible
the paths of the lines of magnetic force (fig. 3). In the same
manner, by passing a circular wire through a card and sending
a strong current through the wire we can employ iron filings to
delineate for us the form of the lines of magnetic force (fig. 4).
In all cases a magnetic pole of strength M, placed in the field of an
electric current, is urged along the lines of force with a mechanical
force equal to MH, where H is the magnetic force. If then we
carry a unit magnetic pole against the direction in which it would
naturally move we do work. The lines of magnetic force embracing
a current-carrying conductor are always loops or endless
lines.
The work done in carrying a unit magnetic pole once round a
circuit conveying a current is called the “line integral of magnetic
force” along that path. If, for instance, we carry a unit pole in a
circular path of radius r once round an infinitely long straight
filamentary current I, the line integral is 4πI. It is easy to prove
that this is a general law, and that if we have any currents flowing
in a conductor the line integral of magnetic force taken once round
a path linked with the current circuit is 4π times the total current
flowing through the circuit. Let us apply this to the case of an
endless solenoid. If a copper wire insulated or covered with cotton
or silk is twisted round a thin rod so as to make a close spiral, this
213
forms a “solenoid,” and if the solenoid is bent round so that its two
ends come together we have an endless solenoid. Consider such a
solenoid of mean length l and N turns of wire. If it is made endless,
the magnetic force H is the same everywhere along the central axis
and the line integral along the axis is Hl. If the current is denoted
by I, then NI is the total current, and accordingly 4πNI = Hl, or
H = 4πNI/l. For a thin endless solenoid the axial magnetic force is
therefore 4π times the current-turns per unit of length. This holds
good also for a long straight solenoid provided its length is large
compared with its diameter. It can be shown that if insulated wire
is wound round a sphere, the turns being all parallel to lines of
latitude, the magnetic force in the interior is constant and the lines
of force therefore parallel. The magnetic force at a point outside a
conductor conveying a current can by various means be measured
or compared with some other standard magnetic forces, and it
becomes then a means of measuring the current. Instruments called
galvanometers and ammeters for the most part operate on this
principle.
Thermal Effects of Currents.—J.P. Joule proved that the heat
produced by a constant current in a given time in a wire having
a constant resistance is proportional to the square of the strength
of the current. This is known as Joule’s law, and it follows,
as already shown, as an immediate consequence of Ohm’s law
and the fact that the power dissipated electrically in a conductor,
when an electromotive force E is applied to its extremities,
producing thereby a current I in it, is equal to EI.
If the current is alternating or periodic, the heat produced in
any time T is obtained by taking the sum at equidistant intervals of
time of all the values of the quantities Ri²dt, where dt represents a
small interval of time and i is the current at that instant. The
quantity T−1 ∫
T0 i²dt is called the mean-square-value of the variable
current, i being the instantaneous value of the current, that is, its
value at a particular instant or during a very small interval of time
dt. The square root of the above quantity, or
[ T−1
∫ T0 i²dt
]1/2,
is called the root-mean-square-value, or the effective value of the
current, and is denoted by the letters R.M.S.
Currents have equal heat-producing power in conductors of
identical resistance when they have the same R.M.S. values.
Hence periodic or alternating currents can be measured as regards
their R.M.S. value by ascertaining the continuous current which
produces in the same time the same heat in the same conductor
as the periodic current considered. Current measuring instruments
depending on this fact, called hot-wire ammeters, are
in common use, especially for measuring alternating currents.
The maximum value of the periodic current can only be determined
from the R.M.S. value when we know the wave form of
the current. The thermal effects of electric currents in conductors
are dependent upon the production of a state of equilibrium
between the heat produced electrically in the wire and the
causes operative in removing it. If an ordinary round wire is
heated by a current it loses heat, (1) by radiation, (2) by air
convection or cooling, and (3) by conduction of heat out of the
ends of the wire. Generally speaking, the greater part of the
heat removal is effected by radiation and convection.
If a round sectioned metallic wire of uniform diameter d and
length l made of a material of resistivity ρ has a current of A amperes
passed through it, the heat in watts produced in any time t seconds
is represented by the value of 4A²ρlt / 109πd², where d and l must be
measured in centimetres and ρ in absolute C.G.S. electromagnetic
units. The factor 109 enters because one ohm is 109 absolute electromagnetic
C.G.S. units (see Units, Physical). If the wire has an
emissivity e, by which is meant that e units of heat reckoned in
joules or watt-seconds are radiated per second from unit of surface,
then the power removed by radiation in the time t is expressed
by πdlet. Hence when thermal equilibrium is established we have
4A²ρlt / 109πd² = πdlet, or A² =
109π²ed³ / 4ρ. If the diameter of the
wire is reckoned in mils (1 mil = .001 in.), and if we take e to have
a value 0.1, an emissivity which will generally bring the wire to
about 60° C., we can put the above formula in the following forms
for circular sectioned copper, iron or platinoid wires, viz.
A = √d³ / 500 for copper wires
A = √d³ / 4000 for iron wires
A = √d³ / 5000 for platinoid wires.
|
These expressions give the ampere value of the current which
will bring bare, straight or loosely coiled wires of d mils in diameter
to about 60° C. when the steady state of temperature is reached.
Thus, for instance, a bare straight copper wire 50 mils in diameter
(= 0.05 in.) will be brought to a steady temperature of about 60° C.
if a current of √50³/500 = √250 = 16 amperes (nearly) is passed
through it, whilst a current of √25 = 5 amperes would bring a
platinoid wire to about the same temperature.
A wire has therefore a certain safe current-carrying capacity
which is determined by its specific resistance and emissivity,
the latter being fixed by its form, surface and surroundings.
The emissivity increases with the temperature, else no state of
thermal equilibrium could be reached. It has been found
experimentally that whilst for fairly thick wires from 8 to 60
mils in diameter the safe current varies approximately as the
1.5th power of the diameter, for fine wires of 1 to 3 mils it varies
more nearly as the diameter.
 |
| Fig. 5. |
Action of one Current on Another.—The investigations of Ampère
in connexion with electric currents are of fundamental importance
in electrokinetics. Starting from the discovery of Oersted,
Ampère made known the correlative fact that not only is there
a mechanical action between a current and a magnet, but that
two conductors conveying electric currents exert mechanical
forces on each other. Ampère devised ingenious methods of
making one portion of a circuit movable so that he might observe
effects of attraction or repulsion between this circuit and some
other fixed current. He employed for this purpose an astatic
circuit B, consisting of a wire bent into a double rectangle
round which a current flowed first in one and then in the opposite
direction (fig. 5). In
this way the circuit
was removed from
the action of the
earth’s magnetic
field, and yet one
portion of it could
be submitted to the
action of any other
circuit C. The
astatic circuit was
pivoted by suspending
it in mercury
cups q, p, one of
which was in electrical
connexion
with the tubular support A, and the other with a strong insulated
wire passing up it.
Ampère devised certain crucial experiments, and the theory
deduced from them is based upon four facts and one assumption.2
He showed (1) that wire conveying a current bent back on itself
produced no action upon a proximate portion of a movable
astatic circuit; (2) that if the return wire was bent zig-zag but
close to the outgoing straight wire the circuit produced no action
on the movable one, showing that the effect of an element of the
circuit was proportional to its projected length; (3) that a closed
circuit cannot cause motion in an element of another circuit free
to move in the direction of its length; and (4) that the action
of two circuits on one and the same movable circuit was null if
one of the two fixed circuits was n times greater than the other
but n times further removed from the movable circuit. From
this last experiment by an ingenious line of reasoning he proved
that the action of an element of current on another element of
current varies inversely as a square of their distance. These
experiments enabled him to construct a mathematical expression
of the law of action between two elements of conductors conveying
currents. They also enabled him to prove that an element of
current may be resolved like a force into components in different
directions, also that the force produced by any element of the
circuit on an element of any other circuit was perpendicular
to the line joining the elements and inversely as the square of
their distance. Also he showed that this force was an attraction
if the currents in the elements were in the same direction, but
a repulsion if they were in opposite directions. From these
experiments and deductions from them he built up a complete
formula for the action of one element of a current of length dS
214
of one conductor conveying a current I upon another element
dS′ of another circuit conveying another current I′ the elements
being at a distance apart equal to r.
If θ and θ’ are the angles the elements make with the line joining
them, and φ the angle they make with one another, then Ampère’s
expression for the mechanical force f the elements exert on one
another is
f = 2II′r−2 {cos φ − 3⁄2 cos θ cos θ′} dSdS′.
This law, together with that of Laplace already mentioned, viz. that
the magnetic force due to an element of length dS of a current I at a
distance r, the element making an angle θ with the radius vector o is
IdS sin θ/r², constitute the fundamental laws of electrokinetics.
Ampère applied these with great mathematical skill to elucidate
the mechanical actions of currents on each other, and experimentally
confirmed the following deductions: (1) Currents in
parallel circuits flowing in the same direction attract each
other, but if in opposite directions repel each other. (2) Currents
in wires meeting at an angle attract each other more into
parallelism if both flow either to or from the angle, but repel
each other more widely apart if they are in opposite directions.
(3) A current in a small circular conductor exerts a magnetic
force in its centre perpendicular to its plane and is in all respects
equivalent to a magnetic shell or a thin circular disk of steel
so magnetized that one face is a north pole and the other a south
pole, the product of the area of the circuit and the current flowing
in it determining the magnetic moment of the element. (4) A
closely wound spiral current is equivalent as regards external
magnetic force to a polar magnet, such a circuit being called a
finite solenoid. (5) Two finite solenoid circuits act on each other
like two polar magnets, exhibiting actions of attraction or
repulsion between their ends.
Ampère’s theory was wholly built up on the assumption of
action at a distance between elements of conductors conveying
the electric currents. Faraday’s researches and the discovery
of the fact that the insulating medium is the real seat of the
operations necessitates a change in the point of view from which
we regard the facts discovered by Ampère. Maxwell showed
that in any field of magnetic force there is a tension along the
lines of force and a pressure at right angles to them; in other
words, lines of magnetic force are like stretched elastic threads
which tend to contract.3 If, therefore, two conductors lie parallel
and have currents in them in the same direction they are impressed
by a certain number of lines of magnetic force which
pass round the two conductors, and it is the tendency of these
to contract which draws the circuits together. If, however, the
currents are in opposite directions then the lateral pressure of the
similarly contracted lines of force between them pushes the
conductors apart. Practical application of Ampère’s discoveries
was made by W.E. Weber in inventing the electrodynamometer,
and later Lord Kelvin devised ampere balances for the measurement
of electric currents based on the attraction between coils
conveying electric currents.
Induction of Electric Currents.—Faraday4 in 1831 made the
important discovery of the induction of electric currents (see
Electricity). If two conductors are placed parallel to each
other, and a current in one of them, called the primary, started
or stopped or changed in strength, every such alteration causes
a transitory current to appear in the other circuit, called the
secondary. This is due to the fact that as the primary current
increases or decreases, its own embracing magnetic field alters,
and lines of magnetic force are added to or subtracted from its
fields. These lines do not appear instantly in their place at a
distance, but are propagated out from the wire with a velocity
equal to that of light; hence in their outward progress they
cut through the secondary circuit, just as ripples made on the
surface of water in a lake by throwing a stone on to it expand
and cut through a stick held vertically in the water at a distance
from the place of origin of the ripples. Faraday confirmed this
view of the phenomena by proving that the mere motion of a
wire transversely to the lines of magnetic force of a permanent
magnet gave rise to an induced electromotive force in the wire.
He embraced all the facts in the single statement that if there
be any circuit which by movement in a magnetic field, or by the
creation or change in magnetic fields round it, experiences a
change in the number of lines of force linked with it, then an
electromotive force is set up in that circuit which is proportional
at any instant to the rate at which the total magnetic flux linked
with it is changing. Hence if Z represents the total number of
lines of magnetic force linked with a circuit of N turns, then
−N (dZ/dt) represents the electromotive force set up in that
circuit. The operation of the induction coil (q.v.) and the
transformer (q.v.) are based on this discovery. Faraday also
found that if a copper disk A (fig. 6) is rotated between the poles
of a magnet NO so that the disk moves with its plane perpendicular
to the lines of magnetic force of the field, it has created in
it an electromotive force directed from the centre to the edge
or vice versa. The action of the dynamo (q.v.) depends on
similar processes, viz. the cutting of the lines of magnetic force
of a constant field produced by certain magnets by certain moving
conductors called armature bars or coils in which an electromotive
force is thereby created.
 |
| Fig 6. |
In 1834 H.F.E. Lenz enunciated a law which connects together
the mechanical actions between electric circuits discovered by
Ampère and the induction of electric currents discovered by Faraday.
It is as follows: If a constant current flows in a primary circuit P,
and if by motion of P a secondary current is created in a neighbouring
circuit S, the direction of the secondary current will be such as to
oppose the relative motion of the circuits. Starting from this, F.E.
Neumann founded a mathematical theory of induced currents,
discovering a quantity M, called the “potential of one circuit on
another,” or generally their “coefficient of mutual inductance.”
Mathematically M is obtained by taking the sum of all such quantities
as ƒƒ dSdS′ cos φ/r, where dS and dS′ are the elements of length of the
two circuits, r is their distance, and φ is the angle which they make
with one another; the summation or integration must be extended
over every possible pair of elements. If we take pairs of elements in
the same circuit, then Neumann’s formula gives us the coefficient
of self-induction of the circuit or the potential of the circuit on itself.
For the results of such calculations on various forms of circuit the
reader must be referred to special treatises.
H. von Helmholtz, and later on Lord Kelvin, showed that the
facts of induction of electric currents discovered by Faraday could
have been predicted from the electrodynamic actions discovered by
Ampère assuming the principle of the conservation of energy.
Helmholtz takes the case of a circuit of resistance R in which acts
an electromotive force due to a battery or thermopile. Let a magnet
be in the neighbourhood, and the potential of the magnet on the
circuit be V, so that if a current I existed in the circuit the work done
on the magnet in the time dt is I (dV/dt)dt. The source of electromotive
force supplies in the time dt work equal to EIdt, and according
to Joule’s law energy is dissipated equal to RI²dt. Hence, by the
conservation of energy,
EIdt = RI²dt + I (dV/dt) dt.
If then E = 0, we have I = −(dV/dt) / R, or there will be a current
due to an induced electromotive force expressed by −dV/dt. Hence
if the magnet moves, it will create a current in the wire provided
that such motion changes the potential of the magnet with respect
to the circuit. This is the effect discovered by Faraday.5
Oscillatory Currents.—In considering the motion of electricity
in conductors we find interesting phenomena connected with the
discharge of a condenser or Leyden jar (q.v.). This problem was
first mathematically treated by Lord Kelvin in 1853 (Phil. Mag.,
1853, 5, p. 292).
If a conductor of capacity C has its terminals connected by a wire
of resistance R and inductance L, it becomes important to consider
215
the subsequent motion of electricity in the wire. If Q is the quantity
of electricity in the condenser initially, and q that at any time t
after completing the circuit, then the energy stored up in the condenser
at that instant is ½q² / C, and the energy associated with the
circuit is ½L (dq/dt)², and the rate of dissipation of energy by resistance
is R (dq/dt)², since dq/dt = i is the discharge current. Hence we can
construct an equation of energy which expresses the fact that at
any instant the power given out by the condenser is partly stored
in the circuit and partly dissipated as heat in it. Mathematically
this is expressed as follows:—
| − | d |
[ ½ | q² |
] = | d |
[ ½L ( | dq |
) | ² |
] + R ( | dq |
) | ² |
| dt | C |
dt | dt |
| dt | |
or
| d²q |
+ | R |
| dq |
+ | 1 |
q = 0. |
| dt² | L |
dt | LC |
The above equation has two solutions according as R² / 4L² is greater
or less than 1/LC. In the first case the current i in the circuit can
be expressed by the equation
| i = Q | α² + β² |
e−αt (eβt − e−βt), |
| 2β |
where α = R/2L, β = √(R²/4L² − 1/LC), Q is the value of q when t = 0,
and e is the base of Napierian logarithms; and in the second case
by the equation
| i = Q | α²+β² |
e−αt sin βt |
| β |
where
| α = R/2L, and β = √ | 1 |
− | R² |
. |
| LC | 4L² |
These expressions show that in the first case the discharge current
of the jar is always in the same direction and is a transient unidirectional
current. In the second case, however, the current is an
oscillatory current gradually decreasing in amplitude, the frequency
n of the oscillation being given by the expression
| n = | 1 |
√ | 1 |
− | R² |
. |
| 2π | LC |
4L² |
In those cases in which the resistance of the discharge circuit is
very small, the expression for the frequency n and for the time
period of oscillation R take the simple forms n = 1, 2π √LC, or
T = 1/n = 2π √LC.
The above investigation shows that if we construct a circuit
consisting of a condenser and inductance placed in series with
one another, such circuit has a natural electrical time period of
its own in which the electrical charge in it oscillates if disturbed.
It may therefore be compared with a pendulum of any kind
which when displaced oscillates with a time period depending
on its inertia and on its restoring force.
The study of these electrical oscillations received a great
impetus after H.R. Hertz showed that when taking place in
electric circuits of a certain kind they create electromagnetic
waves (see Electric Waves) in the dielectric surrounding the
oscillator, and an additional interest was given to them by their
application to telegraphy. If a Leyden jar and a circuit of low
resistance but some inductance in series with it are connected
across the secondary spark gap of an induction coil, then when
the coil is set in action we have a series of bright noisy sparks,
each of which consists of a train of oscillatory electric discharges
from the jar. The condenser becomes charged as the secondary
electromotive force of the coil is created at each break of the
primary current, and when the potential difference of the
condenser coatings reaches a certain value determined by the
spark-ball distance a discharge happens. This discharge, however,
is not a single movement of electricity in one direction but
an oscillatory motion with gradually decreasing amplitude.
If the oscillatory spark is photographed on a revolving plate or
a rapidly moving film, we have evidence in the photograph that
such a spark consists of numerous intermittent sparks gradually
becoming feebler. As the coil continues to operate, these trains
of electric discharges take place at regular intervals. We can
cause a train of electric oscillations in one circuit to induce
similar oscillations in a neighbouring circuit, and thus construct
an oscillation transformer or high frequency induction coil.
Alternating Currents.—The study of alternating currents of
electricity began to attract great attention towards the end of
the 19th century by reason of their application in electrotechnics
and especially to the transmission of power. A circuit in which
a simple periodic alternating current flows is called a single phase
circuit. The important difference between such a form of current
flow and steady current flow arises from the fact that if the circuit
has inductance then the periodic electric current in it is not in
step with the terminal potential difference or electromotive force
acting in the circuit, but the current lags behind the electromotive
force by a certain fraction of the periodic time called the
“phase difference.” If two alternating currents having a fixed
difference in phase flow in two connected separate but related
circuits, the two are called a two-phase current. If three or more
single-phase currents preserving a fixed difference of phase flow
in various parts of a connected circuit, the whole taken together
is called a polyphase current. Since an electric current is a
vector quantity, that is, has direction as well as magnitude,
it can most conveniently be represented by a line denoting its
maximum value, and if the alternating current is a simple
periodic current then the root-mean-square or effective value
of the current is obtained by dividing the maximum value by
√2. Accordingly when we have an electric circuit or circuits
in which there are simple periodic currents we can draw a vector
diagram, the lines of which represent the relative magnitudes and
phase differences of these currents.
A vector can most conveniently be represented by a symbol such
as a + ib, where a stands for any length of a units measured horizontally
and b for a length b units measured vertically, and the symbol ι
is a sign of perpendicularity, and equivalent analytically6 to √−1.
Accordingly if E represents the periodic electromotive force (maximum
value) acting in a circuit of resistance R and inductance L and
frequency n, and if the current considered as a vector is represented
by I, it is easy to show that a vector equation exists between these
quantities as follows:—
E = RI + ι2πnLI.
Since the absolute magnitude of a vector a + ιb is √(a² + b²), it follows
that considering merely magnitudes of current and electromotive
force and denoting them by symbols (E) (I), we have the following
equation connecting (I) and (E):—
(I) = (E) / √R² + p²L²,
where p stands for 2πn. If the above equation is compared with the
symbolic expression of Ohm’s law, it will be seen that the quantity
√(R² + p²L²) takes the place of resistance R in the expression of
Ohm. This quantity √(R² + p²L²) is called the “impedance” of the
alternating circuit. The quantity pL is called the “reactance” of
the alternating circuit, and it is therefore obvious that the current
in such a circuit lags behind the electromotive force by an angle,
called the angle of lag, the tangent of which is pL/R.
 |
| Fig. 7. |
Currents in Networks of Conductors.—In dealing with problems
connected with electric currents we have to consider the laws which
govern the flow of currents in linear conductors (wires), in plane
conductors (sheets), and throughout the mass of a material conductor.7
In the first case consider the collocation of a number of
linear conductors, such as rods or wires of metal, joined at their ends
to form a network of conductors. The network consists of a number
of conductors joining certain points and forming meshes. In each
conductor a current may exist, and along each conductor there is a
fall of potential, or an active electromotive force may be acting in it.
Each conductor has a certain resistance. To find the current in each
conductor when the individual resistances and electromotive forces
are given, proceed as follows:—Consider any one mesh. The sum
of all the electromotive forces which exist in the branches bounding
that mesh must be equal to the sum of all the products of the resistances
into the currents flowing along them, or Σ(E) = Σ(C.R.).
Hence if we consider each mesh as traversed by imaginary currents
all circulating in the same direction, the real currents are the sums
or differences of these imaginary cyclic currents in each branch.
Hence we may assign to each mesh a cycle symbol x, y, z, &c., and
form a cycle equation. Write down the cycle symbol for a mesh
and prefix as coefficient the sum of all the resistances which bound
that cycle, then subtract the cycle symbols of each adjacent cycle,
each multiplied by the value of the bounding or common resistances,
and equate this sum to the total electromotive force acting round the
cycle. Thus if x y z are the cycle currents, and a b c the resistances
bounding the mesh x, and b and c those separating it from the
meshes y and z, and E an electromotive force in the branch a, then
216
we have formed the cycle equation x(a + b + c) − by − cz = E. For
each mesh a similar equation may be formed. Hence we have as
many linear equations as there are meshes, and we can obtain the
solution for each cycle symbol, and therefore for the current in
each branch. The solution giving the current in such branch of
the network is therefore always in the
form of the quotient of two determinants.
The solution of the well-known
problem of finding the current
in the galvanometer circuit of the
arrangement of linear conductors called
Wheatstone’s Bridge is thus easily obtained.
For if we call the cycles (see
fig. 7) (x + y), y and z, and the resistances
P, Q, R, S, G and B, and if E be
the electromotive force in the battery
circuit, we have the cycle equations
(P + G + R) (x + y) − Gy − Rz = 0,
(Q + G + S)y − G (x + y) − Sz = 0,
(R + S + B)z − R (x + y) − Sy = E.
|
From these we can easily obtain the
solution for (x + y) − y = x, which is the current through the galvanometer
circuit in the form
x = E (PS − RQ) Δ.
where Δ is a certain function of P, Q, R, S, B and G.
Currents in Sheets.—In the case of current flow in plane sheets,
we have to consider certain points called sources at which the current
flows into the sheet, and certain points called sinks at which it leaves.
We may investigate, first, the simple case of one source and one sink
in an infinite plane sheet of thickness δ and conductivity k. Take
any point P in the plane at distances R and r from the source and
sink respectively. The potential V at P is obviously given by
where Q is the quantity of electricity supplied by the source per
second. Hence the equation to the equipotential curve is r1r2 = a
constant.
If we take a point half-way between the sink and the source as
the origin of a system of rectangular co-ordinates, and if the distance
between sink and source is equal to p, and the line joining them is
taken as the axis of x, then the equation to the equipotential line is
| y² + (x + p)² | = a constant. |
| y² + (x − p)² |
This is the equation of a family of circles having the axis of y for
a common radical axis, one set of circles surrounding the sink and
another set of circles surrounding the source. In order to discover
the form of the stream of current lines we have to determine the
orthogonal trajectories to this family of coaxial circles. It is easy
to show that the orthogonal trajectory of the system of circles is
another system of circles all passing through the sink and the source,
and as a corollary of this fact, that the electric resistance of a circular
disk of uniform thickness is the same between any two points taken
anywhere on its circumference as sink and source. These equipotential
lines may be delineated experimentally by attaching the
terminals of a battery or batteries to small wires which touch at
various places a sheet of tinfoil. Two wires attached to a galvanometer
may then be placed on the tinfoil, and one may be kept
stationary and the other may be moved about, so that the galvanometer
is not traversed by any current. The moving terminal then
traces out an equipotential curve. If there are n sinks and sources
in a plane conducting sheet, and if r, r′, r″ be the distances of any
point from the sinks, and t, t′, t″ the distances of the sources, then
| r r′ r″ ... | = a constant, |
| t t′ t″ ... |
is the equation to the equipotential lines. The orthogonal trajectories
or stream lines have the equation
Σ (θ − θ′) = a constant,
where θ and θ′ are the angles which the lines drawn from any point
in the plane to the sink and corresponding source make with the line
joining that sink and source. Generally it may be shown that if
there are any number of sinks and sources in an infinite plane-conducting
sheet, and if r, θ are the polar co-ordinates of any one,
then the equation to the equipotential surfaces is given by the
equation
Σ (A log e r) = a constant,
where A is a constant; and the equation to the stream of current
lines is
Σ (θ) = a constant.
In the case of electric flow in three dimensions the electric potential
must satisfy Laplace’s equation, and a solution is therefore found
in the form Σ (A/r) = a constant, as the equation to an equipotential
surface, where r is the distance of any point on that surface from a
source or sink.
Convection Currents.—The subject of convection electric
currents has risen to great importance in connexion with modern
electrical investigations. The question whether a statically
electrified body in motion creates a magnetic field is of fundamental
importance. Experiments to settle it were first undertaken
in the year 1876 by H.A. Rowland, at a suggestion of
H. von Helmholtz.8 After preliminary experiments, Rowland’s
first apparatus for testing this hypothesis was constructed, as
follows:—An ebonite disk was covered with radial strips of gold-leaf
and placed between two other metal plates which acted as
screens. The disk was then charged with electricity and set in
rapid rotation. It was found to affect a delicately suspended
pair of astatic magnetic needles hung in proximity to the disk
just as would, by Oersted’s rule, a circular electric current
coincident with the periphery of the disk. Hence the statically-charged
but rotating disk becomes in effect a circular electric
current.
The experiments were repeated and confirmed by W.C.
Röntgen (Wied. Ann., 1888, 35, p. 264; 1890, 40, p. 93) and by
F. Himstedt (Wied. Ann., 1889, 38, p. 560). Later V. Crémieu
again repeated them and obtained negative results (Com. rend.,
1900, 130, p. 1544, and 131, pp. 578 and 797; 1901, 132, pp. 327 and
1108). They were again very carefully reconducted by H. Pender
(Phil. Mag., 1901, 2, p. 179) and by E.P. Adams (id. ib., 285).
Pender’s work showed beyond any doubt that electric convection
does produce a magnetic effect. Adams employed charged
copper spheres rotating at a high speed in place of a disk, and
was able to prove that the rotation of such spheres produced a
magnetic field similar to that due to a circular current and agreeing
numerically with the theoretical value. It has been shown
by J.J. Thomson (Phil. Mag., 1881, 2, p. 236) and O. Heaviside
(Electrical Papers, vol. ii. p. 205) that an electrified sphere,
moving with a velocity v and carrying a quantity of electricity
q, should produce a magnetic force H, at a point at a distance
ρ from the centre of the sphere, equal to qv sin θ/ρ², where θ
is the angle between the direction of ρ and the motion of the
sphere. Adams found the field produced by a known electric
charge rotating at a known speed had a strength not very
different from that predetermined by the above formula. An
observation recorded by R.W. Wood (Phil. Mag., 1902, 2, p. 659)
provides a confirmatory fact. He noticed that if carbon-dioxide
strongly compressed in a steel bottle is allowed to escape suddenly
the cold produced solidifies some part of the gas, and the issuing
jet is full of particles of carbon-dioxide snow. These by friction
against the nozzle are electrified positively. Wood caused the
jet of gas to pass through a glass tube 2.5 mm. in diameter,
and found that these particles of electrified snow were blown
through it with a velocity of 2000 ft. a second. Moreover, he
found that a magnetic needle hung near the tube was deflected
as if held near an electric current. Hence the positively electrified
particles in motion in the tube create a magnetic field round it.
Nature of an Electric Current.—The question, What is an
electric current? is involved in the larger question of the nature
of electricity. Modern investigations have shown that negative
electricity is identical with the electrons or corpuscles which are
components of the chemical atom (see Matter and Electricity).
Certain lines of argument lead to the conclusion that a solid
conductor is not only composed of chemical atoms, but that there
is a certain proportion of free electrons present in it, the electronic
density or number per unit of volume being determined by
the material, its temperature and other physical conditions. If
any cause operates to add or remove electrons at one point there
is an immediate diffusion of electrons to re-establish equilibrium,
and this electronic movement constitutes an electric current.
This hypothesis explains the reason for the identity between the
laws of diffusion of matter, of heat and of electricity. Electromotive
force is then any cause making or tending to make an
inequality of electronic density in conductors, and may arise
from differences of temperature, i.e. thermoelectromotive force
217
(see Thermoelectricity), or from chemical action when part
of the circuit is an electrolytic conductor, or from the movement
of lines of magnetic force across the conductor.
Bibliography.—For additional information the reader may be
referred to the following books: M. Faraday, Experimental Researches
in Electricity (3 vols., London, 1839, 1844, 1855); J. Clerk Maxwell,
Electricity and Magnetism (2 vols., Oxford, 1892); W. Watson and
S.H. Burbury, Mathematical Theory of Electricity and Magnetism,
vol. ii. (Oxford, 1889); E. Mascart and J. Joubert, A Treatise on
Electricity and Magnetism (2 vols., London, 1883); A. Hay, Alternating
Currents (London, 1905); W.G. Rhodes, An Elementary Treatise
on Alternating Currents (London, 1902); D.C. Jackson and J.P.
Jackson, Alternating Currents and Alternating Current Machinery
(1896, new ed. 1903); S.P. Thompson, Polyphase Electric Currents
(London, 1900); Dynamo-Electric Machinery, vol. ii., “Alternating
Currents” (London, 1905); E.E. Fournier d’Albe, The Electron
Theory (London, 1906).
(J. A. F.)
1 See J.A. Fleming, The Alternate Current Transformer, vol. i.
p. 519.
2 See Maxwell, Electricity and Magnetism, vol. ii. chap. ii.
3 See Maxwell, Electricity and Magnetism, vol. ii. 642.
4 Experimental Researches, vol. i. ser. 1.
5 See Maxwell, Electricity and Magnetism, vol. ii. § 542, p. 178.
6 See W.G. Rhodes, An Elementary Treatise on Alternating Currents
(London, 1902), chap. vii.
7 See J.A. Fleming, “Problems on the Distribution of Electric
Currents in Networks of Conductors,” Phil. Mag. (1885), or Proc.
Phys. Soc. Lond. (1885), 7; also Maxwell, Electricity and Magnetism
(2nd ed.), vol. i. p. 374, § 280, 282b.
8 See Berl. Acad. Ber., 1876, p. 211; also H.A. Rowland and C.T.
Hutchinson, “On the Electromagnetic Effect of Convection Currents,”
Phil. Mag., 1889, 27, p. 445.
ELECTROLIER, a fixture, usually pendent from the ceiling,
for holding electric lamps. The word is analogous to chandelier,
from which indeed it was formed.
ELECTROLYSIS (formed from Gr. λύειν, to loosen). When
the passage of an electric current through a substance is accompanied
by definite chemical changes which are independent
of the heating effects of the current, the process is known as
electrolysis, and the substance is called an electrolyte. As an
example we may take the case of a solution of a salt such as
copper sulphate in water, through which an electric current is
passed between copper plates. We shall then observe the following
phenomena. (1) The bulk of the solution is unaltered,
except that its temperature may be raised owing to the usual
heating effect which is proportional to the square of the strength
of the current. (2) The copper plate by which the current is
said to enter the solution, i.e. the plate attached to the so-called
positive terminal of the battery or other source of current, dissolves
away, the copper going into solution as copper sulphate.
(3) Copper is deposited on the surface of the other plate, being
obtained from the solution. (4) Changes in concentration are
produced in the neighbourhood of the two plates or electrodes.
In the case we have chosen, the solution becomes stronger near
the anode, or electrode at which the current enters, and weaker
near the cathode, or electrode at which it leaves the solution.
If, instead of using copper electrodes, we take plates of platinum,
copper is still deposited on the cathode; but, instead of the
anode dissolving, free sulphuric acid appears in the neighbouring
solution, and oxygen gas is evolved at the surface of the platinum
plate.
With other electrolytes similar phenomena appear, though
the primary chemical changes may be masked by secondary
actions. Thus, with a dilute solution of sulphuric acid and
platinum electrodes, hydrogen gas is evolved at the cathode,
while, as the result of a secondary action on the anode, sulphuric
acid is there re-formed, and oxygen gas evolved. Again, with
the solution of a salt such as sodium chloride, the sodium, which
is primarily liberated at the cathode, decomposes the water and
evolves hydrogen, while the chlorine may be evolved as such,
may dissolve the anode, or may liberate oxygen from the water,
according to the nature of the plate and the concentration of
the solution.
Early History of Electrolysis.—Alessandro Volta of Pavia
discovered the electric battery in the year 1800, and thus placed
the means of maintaining a steady electric current in the hands
of investigators, who, before that date, had been restricted to
the study of the isolated electric charges given by frictional
electric machines. Volta’s cell consists essentially of two plates
of different metals, such as zinc and copper, connected by an
electrolyte such as a solution of salt or acid. Immediately on
its discovery intense interest was aroused in the new invention,
and the chemical effects of electric currents were speedily
detected. W. Nicholson and Sir A. Carlisle found that hydrogen
and oxygen were evolved at the surfaces of gold and platinum
wires connected with the terminals of a battery and dipped in
water. The volume of the hydrogen was about double that of
the oxygen, and, since this is the ratio in which these elements
are combined in water, it was concluded that the process consisted
essentially in the decomposition of water. They also
noticed that a similar kind of chemical action went on in the
battery itself. Soon afterwards, William Cruickshank decomposed
the magnesium, sodium and ammonium chlorides, and
precipitated silver and copper from their solutions—an observation
which led to the process of electroplating. He also found
that the liquid round the anode became acid, and that round
the cathode alkaline. In 1804 W. Hisinger and J.J. Berzelius
stated that neutral salt solutions could be decomposed by
electricity, the acid appearing at one pole and the metal at the
other. This observation showed that nascent hydrogen was
not, as had been supposed, the primary cause of the separation
of metals from their solutions, but that the action consisted
in a direct decomposition into metal and acid. During the
earliest investigation of the subject it was thought that, since
hydrogen and oxygen were usually evolved, the electrolysis of
solutions of acids and alkalis was to be regarded as a direct
decomposition of water. In 1806 Sir Humphry Davy proved
that the formation of acid and alkali when water was electrolysed
was due to saline impurities in the water. He had shown
previously that decomposition of water could be effected although
the two poles were placed in separate vessels connected by
moistened threads. In 1807 he decomposed potash and soda,
previously considered to be elements, by passing the current
from a powerful battery through the moistened solids, and thus
isolated the metals potassium and sodium.
The electromotive force of Volta’s simple cell falls off rapidly
when the cell is used, and this phenomenon was shown to be
due to the accumulation at the metal plates of the products of
chemical changes in the cell itself. This reverse electromotive
force of polarization is produced in all electrolytes when the
passage of the current changes the nature of the electrodes.
In batteries which use acids as the electrolyte, a film of
hydrogen tends to be deposited on the copper or platinum
electrode; but, to obtain a constant electromotive force, several
means were soon devised of preventing the formation of the film.
Constant cells may be divided into two groups, according as
their action is chemical (as in the bichromate cell, where the
hydrogen is converted into water by an oxidizing agent placed
in a porous pot round the carbon plate) or electrochemical (as
in Daniell’s cell, where a copper plate is surrounded by a solution
of copper sulphate, and the hydrogen, instead of being liberated,
replaces copper, which is deposited on the plate from the solution).
 |
| Fig. 1. |
Faraday’s Laws.—The first exact quantitative study of electrolytic
phenomena was made about 1830 by Michael Faraday
(Experimental Researches, 1833). When an electric current flows
round a circuit, there is no accumulation of electricity anywhere
in the circuit, hence the current strength is everywhere
the same, and we may picture the current as analogous
to the flow of an incompressible fluid. Acting on this view,
Faraday set himself to examine the relation between the flow
of electricity round the circuit and the amount of chemical
decomposition. He passed the current driven by a voltaic
battery ZnPt (fig. 1) through two branches containing the two
electrolytic cells A and
B. The reunited current
was then led
through another cell C,
in which the strength of
the current must be the
sum of those in the
arms A and B. Faraday
found that the mass of
substance liberated at
the electrodes in the cell
C was equal to the sum
of the masses liberated
in the cells A and B. He also found that, for the same current,
the amount of chemical action was independent of the size of
the electrodes and proportional to the time that the current
flowed. Regarding the current as the passage of a certain
amount of electricity per second, it will be seen that the results
218
of all these experiments may be summed up in the statement
that the amount of chemical action is proportional to the
quantity of electricity which passes through the cell.
Faraday’s next step was to pass the same current through
different electrolytes in series. He found that the amounts of
the substances liberated in each cell were proportional to the
chemical equivalent weights of those substances. Thus, if the
current be passed through dilute sulphuric acid between hydrogen
electrodes, and through a solution of copper sulphate, it will
be found that the mass of hydrogen evolved in the first cell is
to the mass of copper deposited in the second as 1 is to 31.8.
Now this ratio is the same as that which gives the relative
chemical equivalents of hydrogen and copper, for 1 gramme of
hydrogen and 31.8 grammes of copper unite chemically with
the same weight of any acid radicle such as chlorine or the
sulphuric group, SO4. Faraday examined also the electrolysis
of certain fused salts such as lead chloride and silver chloride.
Similar relations were found to hold and the amounts of chemical
change to be the same for the same electric transfer as in the
case of solutions.
We may sum up the chief results of Faraday’s work in the
statements known as Faraday’s laws: The mass of substance
liberated from an electrolyte by the passage of a current is
proportional (1) to the total quantity of electricity which passes
through the electrolyte, and (2) to the chemical equivalent
weight of the substance liberated.
Since Faraday’s time his laws have been confirmed by modern
research, and in favourable cases have been shown to hold good
with an accuracy of at least one part in a thousand. The principal
object of this more recent research has been the determination
of the quantitative amount of chemical change associated with
the passage for a given time of a current of strength known in
electromagnetic units. It is found that the most accurate and
convenient apparatus to use is a platinum bowl filled with a
solution of silver nitrate containing about fifteen parts of the
salt to one hundred of water. Into the solution dips a silver
plate wrapped in filter paper, and the current is passed from the
silver plate as anode to the bowl as cathode. The bowl is
weighed before and after the passage of the current, and the
increase gives the mass of silver deposited. The mean result
of the best determinations shows that when a current of one
ampere is passed for one second, a mass of silver is deposited
equal to 0.001118 gramme. So accurate and convenient is
this determination that it is now used conversely as a practical
definition of the ampere, which (defined theoretically in terms
of magnetic force) is defined practically as the current which in
one second deposits 1.118 milligramme of silver.
Taking the chemical equivalent weight of silver, as determined
by chemical experiments, to be 107.92, the result described gives
as the electrochemical equivalent of an ion of unit chemical
equivalent the value 1.036 × 10−5. If, as is now usual, we take
the equivalent weight of oxygen as our standard and call it 16,
the equivalent weight of hydrogen is 1.008, and its electrochemical
equivalent is 1.044 × 10−5. The electrochemical equivalent
of any other substance, whether element or compound, may
be found by multiplying its chemical equivalent by 1.036 × 10−5.
If, instead of the ampere, we take the C.G.S. electromagnetic
unit of current, this number becomes 1.036 × 10−4.
Chemical Nature of the Ions.—A study of the products of
decomposition does not necessarily lead directly to a knowledge
of the ions actually employed in carrying the current through
the electrolyte. Since the electric forces are active throughout
the whole solution, all the ions must come under its influence
and therefore move, but their separation from the electrodes
is determined by the electromotive force needed to liberate them.
Thus, as long as every ion of the solution is present in the layer
of liquid next the electrode, the one which responds to the least
electromotive force will alone be set free. When the amount of
this ion in the surface layer becomes too small to carry all the
current across the junction, other ions must also be used, and
either they or their secondary products will appear also at the
electrode. In aqueous solutions, for instance, a few hydrogen
(H) and hydroxyl (OH) ions derived from the water are always
present, and will be liberated if the other ions require a higher
decomposition voltage and the current be kept so small that
hydrogen and hydroxyl ions can be formed fast enough to carry
all the current across the junction between solution and electrode.
The issue is also obscured in another way. When the ions are
set free at the electrodes, they may unite with the substance
of the electrode or with some constituent of the solution to
form secondary products. Thus the hydroxyl mentioned above
decomposes into water and oxygen, and the chlorine produced
by the electrolysis of a chloride may attack the metal of the
anode. This leads us to examine more closely the part played
by water in the electrolysis of aqueous solutions. Distilled
water is a very bad conductor, though, even when great care is
taken to remove all dissolved bodies, there is evidence to show
that some part of the trace of conductivity remaining is due to
the water itself. By careful redistillation F. Kohlrausch has
prepared water of which the conductivity compared with that
of mercury was only 0.40 × 10−11 at 18° C. Even here some
little impurity was present, and the conductivity of chemically
pure water was estimated by thermodynamic reasoning as
0.36 × 10−11 at 18° C. As we shall see later, the conductivity of
very dilute salt solutions is proportional to the concentration, so
that it is probable that, in most cases, practically all the current
is carried by the salt. At the electrodes, however, the small
quantity of hydrogen and hydroxyl ions from the water are
liberated first in cases where the ions of the salt have a higher
decomposition voltage. The water being present in excess, the
hydrogen and hydroxyl are re-formed at once and therefore are
set free continuously. If the current be so strong that new
hydrogen and hydroxyl ions cannot be formed in time, other
substances are liberated; in a solution of sulphuric acid a strong
current will evolve sulphur dioxide, the more readily as the
concentration of the solution is increased. Similar phenomena
are seen in the case of a solution of hydrochloric acid. When
the solution is weak, hydrogen and oxygen are evolved; but,
as the concentration is increased, and the current raised, more
and more chlorine is liberated.
An interesting example of secondary action is shown by the
common technical process of electroplating with silver from a bath
of potassium silver cyanide. Here the ions are potassium and the
group Ag(CN)2.1 Each potassium ion as it reaches the cathode
precipitates silver by reacting with the solution in accordance with
the chemical equation
K + KAg(CN)2 = 2KCN + Ag,
while the anion Ag(CN)2 dissolves an atom of silver from the anode,
and re-forms the complex cyanide KAg(CN)2 by combining with the
2KCN produced in the reaction described in the equation. If the
anode consist of platinum, cyanogen gas is evolved thereat from the
anion Ag(CN)2, and the platinum becomes covered with the insoluble
silver cyanide, AgCN, which soon stops the current. The coating of
silver obtained by this process is coherent and homogeneous, while
that deposited from a solution of silver nitrate, as the result of the
primary action of the current, is crystalline and easily detached.
In the electrolysis of a concentrated solution of sodium acetate,
hydrogen is evolved at the cathode and a mixture of ethane and
carbon dioxide at the anode. According to H. Jahn,2 the processes
at the anode can be represented by the equations
2CH3·COO + H2O = 2CH3·COOH + O
2CH3·COOH + O = C2H6 + 2CO2 + H2O.
|
The hydrogen at the cathode is developed by the secondary action
2Na + 2H2O = 2NaOH + H2.
Many organic compounds can be prepared by taking advantage of
secondary actions at the electrodes, such as reduction by the cathodic
hydrogen, or oxidation at the anode (see Electrochemistry).
It is possible to distinguish between double salts and salts of
compound acids. Thus J.W. Hittorf showed that when a current
was passed through a solution of sodium platino-chloride, the
platinum appeared at the anode. The salt must therefore be derived
from an acid, chloroplatinic acid, H2PtCl6, and have the formula
Na2PtCl6, the ions being Na and PtCl6”, for if it were a double salt
it would decompose as a mixture of sodium chloride and platinum
chloride and both metals would go to the cathode.
219
Early Theories of Electrolysis.—The obvious phenomena to be
explained by any theory of electrolysis are the liberation of the
products of chemical decomposition at the two electrodes while
the intervening liquid is unaltered. To explain these facts,
Theodor Grotthus (1785-1822) in 1806 put forward an hypothesis
which supposed that the opposite chemical constituents of an
electrolyte interchanged partners all along the line between the
electrodes when a current passed. Thus, if the molecule of a
substance in solution is represented by AB, Grotthus considered
a chain of AB molecules to exist from one electrode to the other.
Under the influence of an applied electric force, he imagined that
the B part of the first molecule was liberated at the anode, and
that the A part thus isolated united with the B part of the second
molecule, which, in its turn, passed on its A to the B of the
third molecule. In this manner, the B part of the last molecule
of the chain was seized by the A of the last molecule but one, and
the A part of the last molecule liberated at the surface of the
cathode.
Chemical phenomena throw further light on this question.
If two solutions containing the salts AB and CD be mixed,
double decomposition is found to occur, the salts AD and CB
being formed till a certain part of the first pair of substances
is transformed into an equivalent amount of the second pair.
The proportions between the four salts AB, CD, AD and CB,
which exist finally in solution, are found to be the same whether
we begin with the pair AB and CD or with the pair AD and CB.
To explain this result, chemists suppose that both changes can
occur simultaneously, and that equilibrium results when the rate
at which AB and CD are transformed into AD and CB is the same
as the rate at which the reverse change goes on. A freedom of
interchange is thus indicated between the opposite parts of the
molecules of salts in solution, and it follows reasonably that with
the solution of a single salt, say sodium chloride, continual
interchanges go on between the sodium and chlorine parts of the
different molecules.
These views were applied to the theory of electrolysis by
R.J.E. Clausius. He pointed out that it followed that the
electric forces did not cause the interchanges between the opposite
parts of the dissolved molecules but only controlled their direction.
Interchanges must be supposed to go on whether a current
passes or not, the function of the electric forces in electrolysis
being merely to determine in what direction the parts of the
molecules shall work their way through the liquid and to effect
actual separation of these parts (or their secondary products)
at the electrodes. This conclusion is supported also by the
evidence supplied by the phenomena of electrolytic conduction
(see Conduction, Electric, § II.). If we eliminate the reverse
electromotive forces of polarization at the two electrodes, the conduction
of electricity through electrolytes is found to conform
to Ohm’s law; that is, once the polarization is overcome, the
current is proportional to the electromotive force applied to
the bulk of the liquid. Hence there can be no reverse forces of
polarization inside the liquid itself, such forces being confined
to the surface of the electrodes. No work is done in separating
the parts of the molecules from each other. This result again
indicates that the parts of the molecules are effectively separate
from each other, the function of the electric forces being merely
directive.
 |
| Fig. 2. |
Migration of the Ions.—The opposite parts of an electrolyte,
which work their way through the liquid under the action of the
electric forces, were named by Faraday the ions—the travellers.
The changes of concentration which occur in the solution near
the two electrodes were referred by W. Hittorf (1853) to the
unequal speeds with which he supposed the two opposite ions
to travel. It is clear that, when two opposite streams of ions
move past each other, equivalent quantities are liberated at the
two ends of the system. If the ions move at equal rates, the salt
which is decomposed to supply the ions liberated must be taken
equally from the neighbourhood of the two electrodes. But if
one ion, say the anion, travels faster through the liquid than
the other, the end of the solution from which it comes will be
more exhausted of salt than the end towards which it goes.
If we assume that no other cause is at work, it is easy to prove
that, with non-dissolvable electrodes, the ratio of salt lost at
the anode to the salt lost at the cathode must be equal to the
ratio of the velocity of the cation to the velocity of the anion.
This result may be illustrated by fig. 2. The black circles represent
one ion and the white
circles the other. If the black
ions move twice as fast as the
white ones, the state of things
after the passage of a current
will be represented by the
lower part of the figure. Here the middle part of the solution is
unaltered and the number of ions liberated is the same at either
end, but the amount of salt left at one end is less than that at
the other. On the right, towards which the faster ion travels,
five molecules of salt are left, being a loss of two from the original
seven. On the left, towards which the slower ion moves, only
three molecules remain—a loss of four. Thus, the ratio of the
losses at the two ends is two to one—the same as the ratio of
the assumed ionic velocities. It should be noted, however, that
another cause would be competent to explain the unequal
dilution of the two solutions. If either ion carried with it some
of the unaltered salt or some of the solvent, concentration or
dilution of the liquid would be produced where the ion was
liberated. There is reason to believe that in certain cases such
complex ions do exist, and interfere with the results of the
differing ionic velocities.
Hittorf and many other observers have made experiments
to determine the unequal dilution of a solution round the two
electrodes when a current passes. Various forms of apparatus
have been used, the principle of them all being to secure efficient
separation of the two volumes of solution in which the changes
occur. In some cases porous diaphragms have been employed;
but such diaphragms introduce a new complication, for the liquid
as a whole is pushed through them by the action of the current,
the phenomenon being known as electric endosmose. Hence
experiments without separating diaphragms are to be preferred,
and the apparatus may be considered effective when a considerable
bulk of intervening solution is left unaltered in composition.
It is usual to express the results in terms of what is called the
migration constant of the anion, that is, the ratio of the amount
of salt lost by the anode vessel to the whole amount lost by both
vessels. Thus the statement that the migration constant or
transport number for a decinormal solution of copper sulphate
is 0.632 implies that of every gramme of copper sulphate lost
by a solution containing originally one-tenth of a gramme
equivalent per litre when a current is passed through it between
platinum electrodes, 0.632 gramme is taken from the cathode
vessel and 0.368 gramme from the anode vessel. For certain
concentrated solutions the transport number is found to be greater
than unity; thus for a normal solution of cadmium iodide its
value is 1.12. On the theory that the phenomena are wholly
due to unequal ionic velocities this result would mean that the
cation like the anion moved against the conventional direction
of the current. That a body carrying a positive electric charge
should move against the direction of the electric intensity is contrary
to all our notions of electric forces, and we are compelled
to seek some other explanation. An alternative hypothesis is
given by the idea of complex ions. If some of the anions, instead
of being simple iodine ions represented chemically by the symbol I,
are complex structures formed by the union of iodine with unaltered
cadmium iodide—structures represented by some such
chemical formula as I(CdI2), the concentration of the solution
round the anode would be increased by the passage of an electric
current, and the phenomena observed would be explained. It
is found that, in such cases as this, where it seems necessary to
imagine the existence of complex ions, the transport number
changes rapidly as the concentration of the original solution is
changed. Thus, diminishing the concentration of the cadmium
iodine solution from normal to one-twentieth normal changes
the transport number from 1.12 to 0.64. Hence it is probable
that in cases where the transport number keeps constant with
220
changing concentration the hypothesis of complex ions is unnecessary,
and we may suppose that the transport number is a
true migration constant from which the relative velocities of
the two ions may be calculated in the matter suggested by
Hittorf and illustrated in fig. 2. This conclusion is confirmed
by the results of the direct visual determination of ionic velocities
(see Conduction, Electric, § II.), which, in cases where the
transport number remains constant, agree with the values
calculated from those numbers. Many solutions in which the
transport numbers vary at high concentration often become
simple at greater dilution. For instance, to take the two solutions
to which we have already referred, we have—
| Concentration | 2.0 | 1.5 | 1.0 | 0.5 | 0.2 | 0.1 | 0.05 | 0.02 | 0.01 normal |
| Copper sulphate transport numbers | 0.72 | 0.714 | 0.696 | 0.668 | 0.643 | 0.632 | 0.626 | 0.62 | · · |
| Cadmium iodide ” ” | 1.22 | 1.18 | 1.12 | 1.00 | 0.83 | 0.71 | 0.64 | 0.59 | 0.56 |
It is probable that in both these solutions complex ions exist at
fairly high concentrations, but gradually gets less in number and
finally disappear as the dilution is increased. In such salts as
potassium chloride the ions seem to be simple throughout a wide
range of concentration since the transport numbers for the same
series of concentrations as those used above run—
Potassium chloride—
0.515, 0.515, 0.514, 0.513, 0.509, 0.508, 0.507, 0.507, 0.506.
The next important step in the theory of the subject was made
by F. Kohlrausch in 1879. Kohlrausch formulated a theory
of electrolytic conduction based on the idea that, under the action
of the electric forces, the oppositely charged ions moved in
opposite directions through the liquid, carrying their charges
with them. If we eliminate the polarization at the electrodes,
it can be shown that an electrolyte possesses a definite electric
resistance and therefore a definite conductivity. The conductivity
gives us the amount of electricity conveyed per second
under a definite electromotive force. On the view of the process
of conduction described above, the amount of electricity conveyed
per second is measured by the product of the number of ions,
known from the concentration of the solution, the charge carried
by each of them, and the velocity with which, on the average,
they move through the liquid. The concentration is known,
and the conductivity can be measured experimentally; thus
the average velocity with which the ions move past each other
under the existent electromotive force can be estimated. The
velocity with which the ions move past each other is equal to
the sum of their individual velocities, which can therefore be
calculated. Now Hittorf’s transport number, in the case of
simple salts in moderately dilute solution, gives us the ratio
between the two ionic velocities. Hence the absolute velocities
of the two ions can be determined, and we can calculate the
actual speed with which a certain ion moves through a given
liquid under the action of a given potential gradient or electromotive
force. The details of the calculation are given in the
article Conduction, Electric, § II., where also will be found
an account of the methods which have been used to measure
the velocities of many ions by direct visual observation. The
results go to show that, where the existence of complex ions is
not indicated by varying transport numbers, the observed
velocities agree with those calculated on Kohlrausch’s theory.
Dissociation Theory.—The verification of Kohlrausch’s theory
of ionic velocity verifies also the view of electrolysis which regards
the electric current as due to streams of ions moving in opposite
directions through the liquid and carrying their opposite electric
charges with them. There remains the question how the
necessary migratory freedom of the ions is secured. As we have
seen, Grotthus imagined that it was the electric forces which
sheared the ions past each other and loosened the chemical
bonds holding the opposite parts of each dissolved molecule
together. Clausius extended to electrolysis the chemical ideas
which looked on the opposite parts of the molecule as always
changing partners independently of any electric force, and regarded
the function of the current as merely directive. Still, the
necessary freedom was supposed to be secured by interchanges
of ions between molecules at the instants of molecular collision
only; during the rest of the life of the ions they were regarded
as linked to each other to form electrically neutral molecules.
In 1887 Svante Arrhenius, professor of physics at Stockholm,
put forward a new theory which supposed that the freedom
of the opposite ions from each other was not a mere momentary
freedom at the instants of molecular collision, but a more or less
permanent freedom, the ions moving independently of each other
through the liquid. The evidence which led Arrhenius to this
conclusion was based on van ‘t Hoff’s work on the osmotic
pressure of solutions (see Solution). If a solution, let us say
of sugar, be confined in a closed vessel through the walls of
which the solvent can pass but the solution cannot, the solvent
will enter till a certain equilibrium pressure is reached. This
equilibrium pressure is called the osmotic pressure of the solution,
and thermodynamic theory shows that, in an ideal case of
perfect separation between solvent and solute, it should have the
same value as the pressure which a number of molecules equal
to the number of solute molecules in the solution would exert if
they could exist as a gas in a space equal to the volume of the solution,
provided that the space was large enough (i.e. the solution
dilute enough) for the intermolecular forces between the dissolved
particles to be inappreciable. Van ‘t Hoff pointed out that
measurements of osmotic pressure confirmed this value in the
case of dilute solutions of cane sugar.
Thermodynamic theory also indicates a connexion between
the osmotic pressure of a solution and the depression of its
freezing point and its vapour pressure compared with those of the
pure solvent. The freezing points and vapour pressures of solutions
of sugar are also in conformity with the theoretical numbers.
But when we pass to solutions of mineral salts and acids—to
solutions of electrolytes in fact—we find that the observed values
of the osmotic pressures and of the allied phenomena are greater
than the normal values. Arrhenius pointed out that these
exceptions would be brought into line if the ions of electrolytes
were imagined to be separate entities each capable of producing
its own pressure effects just as would an ordinary dissolved
molecule.
Two relations are suggested by Arrhenius’ theory. (1) In
very dilute solutions of simple substances, where only one kind of
dissociation is possible and the dissociation of the ions is complete,
the number of pressure-producing particles necessary to produce
the observed osmotic effects should be equal to the number of
ions given by a molecule of the salt as shown by its electrical
properties. Thus the osmotic pressure, or the depression of the
freezing point of a solution of potassium chloride should, at
extreme dilution, be twice the normal value, but of a solution
of sulphuric acid three times that value, since the potassium
salt contains two ions and the acid three. (2) As the concentration
of the solutions increases, the ionization as measured
electrically and the dissociation as measured osmotically might
decrease more or less together, though, since the thermodynamic
theory only holds when the solution is so dilute that the dissolved
particles are beyond each other’s sphere of action, there is much
doubt whether this second relation is valid through any appreciable
range of concentration.
At present, measurements of freezing point are more convenient
and accurate than those of osmotic pressure, and we may
test the validity of Arrhenius’ relations by their means. The
theoretical value for the depression of the freezing point of a
dilute solution per gramme-equivalent of solute per litre is
1.857° C. Completely ionized solutions of salts with two ions
should give double this number or 3.714°, while electrolytes
with three ions should have a value of 5.57°.
The following results are given by H.B. Loomis for the
concentration of 0.01 gramme-molecule of salt to one thousand
grammes of water. The salts tabulated are those of which the
221
equivalent conductivity reaches a limiting value indicating that
complete ionization is reached as dilution is increased. With
such salts alone is a valid comparison possible.
| Molecular Depressions of the Freezing Point. |
| Electrolytes with two Ions. |
| Potassium chloride | 3.60 | Nitric acid | 3.73 |
| Sodium chloride | 3.67 | Potassium nitrate | 3.46 |
| Potassium hydrate | 3.71 | Sodium nitrate | 3.55 |
| Hydrochloric acid | 3.61 | Ammonium nitrate | 3.58 |
| Electrolytes with three Ions. |
| Sulphuric acid | 4.49 | Calcium chloride | 5.04 |
| Sodium sulphate | 5.09 | Magnesium chloride | 5.08 |
At the concentration used by Loomis the electrical conductivity
indicates that the ionization is not complete, particularly
in the case of the salts with divalent ions in the second list.
Allowing for incomplete ionization the general concordance
of these numbers with the theoretical ones is very striking.
The measurements of freezing points of solutions at the extreme
dilution necessary to secure complete ionization is a matter of
great difficulty, and has been overcome only in a research
initiated by E.H. Griffiths.3 Results have been obtained for
solutions of sugar, where the experimental number is 1.858,
and for potassium chloride, which gives a depression of 3.720.
These numbers agree with those indicated by theory, viz. 1.857
and 3.714, with astonishing exactitude. We may take Arrhenius’
first relation as established for the case of potassium chloride.
The second relation, as we have seen, is not a strict consequence
of theory, and experiments to examine it must be treated as
an investigation of the limits within which solutions are dilute
within the thermodynamic sense of the word, rather than as a
test of the soundness of the theory. It is found that divergence
has begun before the concentration has become great enough
to enable freezing points to be measured with any ordinary
apparatus. The freezing point curve usually lies below the
electrical one, but approaches it as dilution is increased.4
Returning once more to the consideration of the first relation,
which deals with the comparison between the number of ions and
the number of pressure-producing particles in dilute solution,
one caution is necessary. In simple substances like potassium
chloride it seems evident that one kind of dissociation only
is possible. The electrical phenomena show that there are two
ions to the molecule, and that these ions are electrically charged.
Corresponding with this result we find that the freezing point of
dilute solutions indicates that two pressure-producing particles
per molecule are present. But the converse relation does not
necessarily follow. It would be possible for a body in solution
to be dissociated into non-electrical parts, which would give
osmotic pressure effects twice or three times the normal value,
but, being uncharged, would not act as ions and impart electrical
conductivity to the solution. L. Kahlenberg (Jour. Phys. Chem.,
1901, v. 344, 1902, vi. 43) has found that solutions of diphenylamine
in methyl cyanide possess an excess of pressure-producing
particles and yet are non-conductors of electricity. It is possible
that in complicated organic substances we might have two
kinds of dissociation, electrical and non-electrical, occurring
simultaneously, while the possibility of the association of molecules
accompanied by the electrical dissociation of some of them
into new parts should not be overlooked. It should be pointed
out that no measurements on osmotic pressures or freezing points
can do more than tell us that an excess of particles is present;
such experiments can throw no light on the question whether
or not those particles are electrically charged. That question
can only be answered by examining whether or not the particles
move in an electric field.
The dissociation theory was originally suggested by the
osmotic pressure relations. But not only has it explained
satisfactorily the electrical properties of solutions, but it seems
to be the only known hypothesis which is consistent with the
experimental relation between the concentration of a solution
and its electrical conductivity (see Conduction, Electric,
§ II., “Nature of Electrolytes”). It is probable that the
electrical effects constitute the strongest arguments in favour
of the theory. It is necessary to point out that the dissociated
ions of such a body as potassium chloride are not in the same
condition as potassium and chlorine in the free state. The ions
are associated with very large electric charges, and, whatever
their exact relations with those charges may be, it is certain that
the energy of a system in such a state must be different from
its energy when unelectrified. It is not unlikely, therefore,
that even a compound as stable in the solid form as potassium
chloride should be thus dissociated when dissolved. Again,
water, the best electrolytic solvent known, is also the body of
the highest specific inductive capacity (dielectric constant),
and this property, to whatever cause it may be due, will reduce
the forces between electric charges in the neighbourhood, and
may therefore enable two ions to separate.
This view of the nature of electrolytic solutions at once explains
many well-known phenomena. Other physical properties of
these solutions, such as density, colour, optical rotatory power,
&c., like the conductivities, are additive, i.e. can be calculated
by adding together the corresponding properties of the parts.
This again suggests that these parts are independent of each other.
For instance, the colour of a salt solution is the colour obtained
by the superposition of the colours of the ions and the colour
of any undissociated salt that may be present. All copper salts
in dilute solution are blue, which is therefore the colour of the
copper ion. Solid copper chloride is brown or yellow, so that its
concentrated solution, which contains both ions and undissociated
molecules, is green, but changes to blue as water is added and
the ionization becomes complete. A series of equivalent solutions
all containing the same coloured ion have absorption spectra
which, when photographed, show identical absorption bands
of equal intensity.5 The colour changes shown by many substances
which are used as indicators (q.v.) of acids or alkalis can
be explained in a similar way. Thus para-nitrophenol has colourless
molecules, but an intensely yellow negative ion. In neutral,
and still more in acid solutions, the dissociation of the indicator
is practically nothing, and the liquid is colourless. If an alkali
is added, however, a highly dissociated salt of para-nitrophenol
is formed, and the yellow colour is at once evident. In other
cases, such as that of litmus, both the ion and the undissociated
molecule are coloured, but in different ways.
Electrolytes possess the power of coagulating solutions of
colloids such as albumen and arsenious sulphide. The mean
values of the relative coagulative powers of sulphates of mono-,
di-, and tri-valent metals have been shown experimentally to
be approximately in the ratios 1 : 35 : 1023. The dissociation
theory refers this to the action of electric charges carried by the
free ions. If a certain minimum charge must be collected in
order to start coagulation, it will need the conjunction of 6n
monovalent, or 3n divalent, to equal the effect of 2n tri-valent
ions. The ratios of the coagulative powers can thus be calculated
to be 1 : x : x², and putting x = 32 we get 1 : 32 : 1024, a satisfactory
agreement with the numbers observed.6
The question of the application of the dissociation theory to
the case of fused salts remains. While it seems clear that the
conduction in this case is carried on by ions similar to those of
solutions, since Faraday’s laws apply equally to both, it does
not follow necessarily that semi-permanent dissociation is the
only way to explain the phenomena. The evidence in favour
of dissociation in the case of solutions does not apply to fused
salts, and it is possible that, in their case, a series of molecular
interchanges, somewhat like Grotthus’s chain, may represent
the mechanism of conduction.
An interesting relation appears when the electrolytic conductivity
of solutions is compared with their chemical activity.
The readiness and speed with which electrolytes react are in
222
sharp contrast with the difficulty experienced in the case of
non-electrolytes. Moreover, a study of the chemical relations
of electrolytes indicates that it is always the electrolytic ions
that are concerned in their reactions. The tests for a salt,
potassium nitrate, for example, are the tests not for KNO3, but
for its ions K and NO3, and in cases of double decomposition
it is always these ions that are exchanged for those of other
substances. If an element be present in a compound otherwise
than as an ion, it is not interchangeable, and cannot be recognized
by the usual tests. Thus neither a chlorate, which contains the
ion ClO3, nor monochloracetic acid, shows the reactions of
chlorine, though it is, of course, present in both substances;
again, the sulphates do not answer to the usual tests which
indicate the presence of sulphur as sulphide. The chemical
activity of a substance is a quantity which may be measured
by different methods. For some substances it has been shown
to be independent of the particular reaction used. It is then
possible to assign to each body a specific coefficient of affinity.
Arrhenius has pointed out that the coefficient of affinity of an
acid is proportional to its electrolytic ionization.
The affinities of acids have been compared in several ways.
W. Ostwald (Lehrbuch der allg. Chemie, vol. ii., Leipzig, 1893) investigated
the relative affinities of acids for potash, soda and ammonia,
and proved them to be independent of the base used. The method
employed was to measure the changes in volume caused by the action.
His results are given in column I. of the following table, the affinity
of hydrochloric acid being taken as one hundred. Another method
is to allow an acid to act on an insoluble salt, and to measure the
quantity which goes into solution. Determinations have been made
with calcium oxalate, CaC2O4 + H2O, which is easily decomposed by
acids, oxalic acid and a soluble calcium salt being formed. The
affinities of acids relative to that of oxalic acid are thus found, so
that the acids can be compared among themselves (column II.).
If an aqueous solution of methyl acetate be allowed to stand, a slow
decomposition goes on. This is much quickened by the presence
of a little dilute acid, though the acid itself remains unchanged. It
is found that the influence of different acids on this action is proportional
to their specific coefficients of affinity. The results of this
method are given in column III. Finally, in column IV. the electrical
conductivities of normal solutions of the acids have been tabulated.
A better basis of comparison would be the ratio of the actual to the
limiting conductivity, but since the conductivity of acids is chiefly
due to the mobility of the hydrogen ions, its limiting value is nearly
the same for all, and the general result of the comparison would be
unchanged.
| Acid. | I. | II. | III. | IV. |
| Hydrochloric | 100 | 100 | 100 | 100 |
| Nitric | 102 | 110 | 92 | 99.6 |
| Sulphuric | 68 | 67 | 74 | 65.1 |
| Formic | 4.0 | 2.5 | 1.3 | 1.7 |
| Acetic | 1.2 | 1.0 | 0.3 | 0.4 |
| Propionic | 1.1 | · · | 0.3 | 0.3 |
| Monochloracetic | 7.2 | 5.1 | 4.3 | 4.9 |
| Dichloracetic | 34 | 18 | 23.0 | 25.3 |
| Trichloracetic | 82 | 63 | 68.2 | 62.3 |
| Malic | 3.0 | 5.0 | 1.2 | 1.3 |
| Tartaric | 5.3 | 6.3 | 2.3 | 2.3 |
| Succinic | 0.1 | 0.2 | 0.5 | 0.6 |
It must be remembered that, the solutions not being of quite the
same strength, these numbers are not strictly comparable, and that
the experimental difficulties involved in the chemical measurements
are considerable. Nevertheless, the remarkable general agreement
of the numbers in the four columns is quite enough to show the
intimate connexion between chemical activity and electrical conductivity.
We may take it, then, that only that portion of these
bodies is chemically active which is electrolytically active—that
ionization is necessary for such chemical activity as we are dealing
with here, just as it is necessary for electrolytic conductivity.
The ordinary laws of chemical equilibrium have been applied to
the case of the dissociation of a substance into its ions. Let x be
the number of molecules which dissociate per second when the
number of undissociated molecules in unit volume is unity, then
in a dilute solution where the molecules do not interfere with each
other, xp is the number when the concentration is p. Recombination
can only occur when two ions meet, and since the frequency with
which this will happen is, in dilute solution, proportional to the
square of the ionic concentration, we shall get for the number of
molecules re-formed in one second yq² where q is the number of dissociated
molecules in one cubic centimetre. When there is equilibrium,
xp = yq². If μ be the molecular conductivity, and μ ∞ its value
at infinite dilution, the fractional number of molecules dissociated is
μ / μ ∞, which we may write as α. The number of undissociated molecules
is then 1 − α, so that if V be the volume of the solution containing
1 gramme-molecule of the dissolved substance, we get
q = α / V and p = (1 − α) / V,
hence
x (1 − α) V = ya² / V²,
and
| α² |
= | x |
= constant = k. |
| V (1 − α) | y |
This constant k gives a numerical value for the chemical affinity,
and the equation should represent the effect of dilution on the
molecular conductivity of binary electrolytes.
In the case of substances like ammonia and acetic acid, where the
dissociation is very small, 1 − α is nearly equal to unity, and only
varies slowly with dilution. The equation then becomes α²/V = k, or
α = √(Vk), so that the molecular conductivity is proportional to the
square root of the dilution. Ostwald has confirmed the equation
by observation on an enormous number of weak acids (Zeits.
physikal. Chemie, 1888, ii. p. 278; 1889, iii. pp. 170, 241, 369).
Thus in the case of cyanacetic acid, while the volume V changed by
doubling from 16 to 1024 litres, the values of k were 0.00 (376, 373,
374, 361, 362, 361, 368). The mean values of k for other common
acids were—formic, 0.0000214; acetic, 0.0000180; monochloracetic,
0.00155; dichloracetic, 0.051; trichloracetic, 1.21; propionic,
0.0000134. From these numbers we can, by help of the
equation, calculate the conductivity of the acids for any dilution.
The value of k, however, does not keep constant so satisfactorily in the
case of highly dissociated substances, and empirical formulae have
been constructed to represent the effect of dilution on them. Thus
the values of the expressions α² / (1 − α√V) (Rudolphi, Zeits. physikal.
Chemie, 1895, vol. xvii. p. 385) and α³ / (1 − α)²V (van ’t Hoff, ibid.,
1895, vol. xviii. p. 300) are found to keep constant as V changes.
Van ’t Hoff’s formula is equivalent to taking the frequency of dissociation
as proportional to the square of the concentration of the
molecules, and the frequency of recombination as proportional to
the cube of the concentration of the ions. An explanation of the
failure of the usual dilution law in these cases may be given if we
remember that, while the electric forces between bodies like undissociated
molecules, each associated with equal and opposite
charges, will vary inversely as the fourth power of the distance, the
forces between dissociated ions, each carrying one charge only, will
be inversely proportional to the square of the distance. The forces
between the ions of a strongly dissociated solution will thus be considerable
at a dilution which makes forces between undissociated
molecules quite insensible, and at the concentrations necessary to
test Ostwald’s formula an electrolyte will be far from dilute in the
thermodynamic sense of the term, which implies no appreciable
intermolecular or interionic forces.
When the solutions of two substances are mixed, similar considerations
to those given above enable us to calculate the resultant
changes in dissociation. (See Arrhenius, loc. cit.) The simplest
and most important case is that of two electrolytes having one
ion in common, such as two acids. It is evident that the undissociated
part of each acid must eventually be in equilibrium with
the free hydrogen ions, and, if the concentrations are not such as
to secure this condition, readjustment must occur. In order that
there should be no change in the states of dissociation on mixing,
it is necessary, therefore, that the concentration of the hydrogen
ions should be the same in each separate solution. Such solutions
were called by Arrhenius “isohydric.” The two solutions, then,
will so act on each other when mixed that they become isohydric.
Let us suppose that we have one very active acid like hydrochloric,
in which dissociation is nearly complete, another like acetic, in
which it is very small. In order that the solutions of these should be
isohydric and the concentrations of the hydrogen ions the same,
we must have a very large quantity of the feebly dissociated acetic
acid, and a very small quantity of the strongly dissociated hydrochloric,
and in such proportions alone will equilibrium be possible.
This explains the action of a strong acid on the salt of a weak acid.
Let us allow dilute sodium acetate to react with dilute hydrochloric
acid. Some acetic acid is formed, and this process will go on till
the solutions of the two acids are isohydric: that is, till the dissociated
hydrogen ions are in equilibrium with both. In order
that this should hold, we have seen that a considerable quantity
of acetic acid must be present, so that a corresponding amount of
the salt will be decomposed, the quantity being greater the less
the acid is dissociated. This “replacement” of a “weak” acid
by a “strong” one is a matter of common observation in the chemical
laboratory. Similar investigations applied to the general case of
chemical equilibrium lead to an expression of exactly the same form
as that given by C.M. Guldberg and P. Waage, which is universally
accepted as an accurate representation of the facts.
The temperature coefficient of conductivity has approximately
the same value for most aqueous salt solutions. It decreases
both as the temperature is raised and as the concentration is
increased, ranging from about 3.5% per degree for extremely
dilute solutions (i.e. practically pure water) at 0° to about 1.5
223
for concentrated solutions at 18°. For acids its value is usually
rather less than for salts at equivalent concentrations. The
influence of temperature on the conductivity of solutions depends
on (1) the ionization, and (2) the frictional resistance of the
liquid to the passage of the ions, the reciprocal of which is called
the ionic fluidity. At extreme dilution, when the ionization is
complete, a variation in temperature cannot change its amount.
The rise of conductivity with temperature, therefore, shows
that the fluidity becomes greater when the solution is heated.
As the concentration is increased and un-ionized molecules are
formed, a change in temperature begins to affect the ionization
as well as the fluidity. But the temperature coefficient of
conductivity is now generally less than before; thus the effect
of temperature on ionization must be of opposite sign to its
effect on fluidity. The ionization of a solution, then, is usually
diminished by raising the temperature, the rise in conductivity
being due to the greater increase in fluidity. Nevertheless, in
certain cases, the temperature coefficient of conductivity becomes
negative at high temperatures, a solution of phosphoric acid,
for example, reaching a maximum conductivity at 75° C.
The dissociation theory gives an immediate explanation of the
fact that, in general, no heat-change occurs when two neutral
salt solutions are mixed. Since the salts, both before and after
mixture, exist mainly as dissociated ions, it is obvious that large
thermal effects can only appear when the state of dissociation
of the products is very different from that of the reagents. Let
us consider the case of the neutralization of a base by an acid
in the light of the dissociation theory. In dilute solution such
substances as hydrochloric acid and potash are almost completely
dissociated, so that, instead of representing the reaction as
HCl + KOH = KCl + H2O,
we must write
+ − + − + −
H + Cl + K + OH = K + Cl + H2O.
|
The ions K and Cl suffer no change, but the hydrogen of the acid
and the hydroxyl (OH) of the potash unite to form water, which
is only very slightly dissociated. The heat liberated, then, is
almost exclusively that produced by the formation of water
from its ions. An exactly similar process occurs when any
strongly dissociated acid acts on any strongly dissociated base,
so that in all such cases the heat evolution should be approximately
the same. This is fully borne out by the experiments of
Julius Thomsen, who found that the heat of neutralization of one
gramme-molecule of a strong base by an equivalent quantity of a
strong acid was nearly constant, and equal to 13,700 or 13,800
calories. In the case of weaker acids, the dissociation of which
is less complete, divergences from this constant value will occur,
for some of the molecules have to be separated into their ions.
For instance, sulphuric acid, which in the fairly strong solutions
used by Thomsen is only about half dissociated, gives a higher
value for the heat of neutralization, so that heat must be evolved
when it is ionized. The heat of formation of a substance from
its ions is, of course, very different from that evolved when it is
formed from its elements in the usual way, since the energy
associated with an ion is different from that possessed by the
atoms of the element in their normal state. We can calculate
the heat of formation from its ions for any substance dissolved
in a given liquid, from a knowledge of the temperature coefficient
of ionization, by means of an application of the well-known
thermodynamical process, which also gives the latent heat of
evaporation of a liquid when the temperature coefficient of its
vapour pressure is known. The heats of formation thus obtained
may be either positive or negative, and by using them to supplement
the heat of formation of water, Arrhenius calculated the
total heats of neutralization of soda by different acids, some of
them only slightly dissociated, and found values agreeing well
with observation (Zeits. physikal. Chemie, 1889, 4, p. 96; and
1892, 9, p. 339).
Voltaic Cells.—When two metallic conductors are placed in
an electrolyte, a current will flow through a wire connecting
them provided that a difference of any kind exists between the
two conductors in the nature either of the metals or of the
portions of the electrolyte which surround them. A current
can be obtained by the combination of two metals in the same
electrolyte, of two metals in different electrolytes, of the same
metal in different electrolytes, or of the same metal in solutions
of the same electrolyte at different concentrations. In accordance
with the principles of energetics (q.v.), any change which
involves a decrease in the total available energy of the system
will tend to occur, and thus the necessary and sufficient condition
for the production of electromotive force is that the available
energy of the system should decrease when the current flows.
In order that the current should be maintained, and the
electromotive force of the cell remain constant during action, it
is necessary to ensure that the changes in the cell, chemical or
other, which produce the current, should neither destroy the
difference between the electrodes, nor coat either electrode
with a non-conducting layer through which the current cannot
pass. As an example of a fairly constant cell we may take that
of Daniell, which consists of the electrical arrangement—zinc |
zinc sulphate solution | copper sulphate solution | copper,—the
two solutions being usually separated by a pot of porous earthenware.
When the zinc and copper plates are connected through
a wire, a current flows, the conventionally positive electricity
passing from copper to zinc in the wire and from zinc to copper
in the cell. Zinc dissolves at the anode, an equal amount of
zinc replaces an equivalent amount of copper on the other side
of the porous partition, and the same amount of copper is
deposited on the cathode. This process involves a decrease in
the available energy of the system, for the dissolution of zinc
gives out more energy than the separation of copper absorbs.
But the internal rearrangements which accompany the production
of a current do not cause any change in the original nature
of the electrodes, fresh zinc being exposed at the anode, and
copper being deposited on copper at the cathode. Thus as long
as a moderate current flows, the only variation in the cell is the
appearance of zinc sulphate in the liquid on the copper side of the
porous wall. In spite of this appearance, however, while the
supply of copper is maintained, copper, being more easily
separated from the solution than zinc, is deposited alone at the
cathode, and the cell remains constant.
It is necessary to observe that the condition for change in
a system is that the total available energy of the whole system
should be decreased by the change. We must consider what
change is allowed by the mechanism of the system, and deal with
the sum of all the alterations in energy. Thus in the Daniell cell
the dissolution of copper as well as of zinc would increase the
loss in available energy. But when zinc dissolves, the zinc
ions carry their electric charges with them, and the liquid tends
to become positively electrified. The electric forces then soon
stop further action unless an equivalent quantity of positive
ions are removed from the solution. Hence zinc can only dissolve
when some more easily separable substance is present in solution
to be removed pari passu with the dissolution of zinc. The
mechanism of such systems is well illustrated by an experiment
devised by W. Ostwald. Plates of platinum and pure or amalgamated
zinc are separated by a porous pot, and each surrounded
by some of the same solution of a salt of a metal
more oxidizable than zinc, such as potassium. When the plates
are connected together by means of a wire, no current flows,
and no appreciable amount of zinc dissolves, for the dissolution
of zinc would involve the separation of potassium and a gain
in available energy. If sulphuric acid be added to the vessel
containing the zinc, these conditions are unaltered and still no
zinc is dissolved. But, on the other hand, if a few drops of acid
be placed in the vessel with the platinum, bubbles of hydrogen
appear, and a current flows, zinc dissolving at the anode, and
hydrogen being liberated at the cathode. In order that positively
electrified ions may enter a solution, an equivalent amount of
other positive ions must be removed or negative ions be added,
and, for the process to occur spontaneously, the possible action
at the two electrodes must involve a decrease in the total available
energy of the system.
Considered thermodynamically, voltaic cells must be divided
224
into reversible and non-reversible systems. If the slow processes
of diffusion be ignored, the Daniell cell already described
may be taken as a type of a reversible cell. Let an electromotive
force exactly equal to that of the cell be applied to it in the reverse
direction. When the applied electromotive force is diminished
by an infinitesimal amount, the cell produces a current in the
usual direction, and the ordinary chemical changes occur. If
the external electromotive force exceed that of the cell by ever
so little, a current flows in the opposite direction, and all the
former chemical changes are reversed, copper dissolving from
the copper plate, while zinc is deposited on the zinc plate. The
cell, together with this balancing electromotive force, is thus
a reversible system in true equilibrium, and the thermodynamical
reasoning applicable to such systems can be used to examine its
properties.
Now a well-known relation connects the available energy of
a reversible system with the corresponding change in its total
internal energy.
The available energy A is the amount of external work obtainable
by an infinitesimal, reversible change in the system which occurs
at a constant temperature T. If I be the change in the internal
energy, the relation referred to gives us the equation
A = I + T (dA/dT),
where dA/dT denotes the rate of change of the available energy
of the system per degree change in temperature. During a small
electric transfer through the cell, the external work done is Ee,
where E is the electromotive force. If the chemical changes which
occur in the cell were allowed to take place in a closed vessel without
the performance of electrical or other work, the change in energy
would be measured by the heat evolved. Since the final state of the
system would be the same as in the actual processes of the cell,
the same amount of heat must give a measure of the change in
internal energy when the cell is in action. Thus, if L denote the heat
corresponding with the chemical changes associated with unit
electric transfer, Le will be the heat corresponding with an electric
transfer e, and will also be equal to the change in internal energy
of the cell. Hence we get the equation
Ee = Le + Te (dE/dT) or E = L + T (dE/dT),
as a particular case of the general thermodynamic equation of
available energy. This equation was obtained in different ways by
J. Willard Gibbs and H. von Helmholtz.
It will be noticed that when dE/dT is zero, that is, when the
electromotive force of the cell does not change with temperature,
the electromotive force is measured by the heat of reaction per unit of
electrochemical change. The earliest formulation of the subject,
due to Lord Kelvin, assumed that this relation was true in all cases,
and, calculated in this way, the electromotive force of Daniell’s
cell, which happens to possess a very small temperature coefficient,
was found to agree with observation.
When one gramme of zinc is dissolved in dilute sulphuric acid,
1670 thermal units or calories are evolved. Hence for the electrochemical
unit of zinc or 0.003388 gramme, the thermal evolution is
5.66 calories. Similarly, the heat which accompanies the dissolution
of one electrochemical unit of copper is 3.00 calories. Thus, the
thermal equivalent of the unit of resultant electrochemical change in
Daniell’s cell is 5.66 − 3.00 = 2.66 calories. The dynamical equivalent
of the calorie is 4.18 × 107 ergs or C.G.S. units of work, and therefore
the electromotive force of the cell should be 1.112 × 108 C.G.S. units
or 1.112 volts—a close agreement with the experimental result of
about 1.08 volts. For cells in which the electromotive force varies
with temperature, the full equation given by Gibbs and Helmholtz
has also been confirmed experimentally.
As stated above, an electromotive force is set up whenever
there is a difference of any kind at two electrodes immersed
in electrolytes. In ordinary cells the difference is secured by
using two dissimilar metals, but an electromotive force exists
if two plates of the same metal are placed in solutions of different
substances, or of the same substance at different concentrations.
In the latter case, the tendency of the metal to dissolve in the
more dilute solution is greater than its tendency to dissolve in
the more concentrated solution, and thus there is a decrease in
available energy when metal dissolves in the dilute solution and
separates in equivalent quantity from the concentrated solution.
An electromotive force is therefore set up in this direction, and,
if we can calculate the change in available energy due to the
processes of the cell, we can foretell the value of the electromotive
force. Now the effective change produced by the action
of the current is the concentration of the more dilute solution by
the dissolution of metal in it, and the dilution of the originally
stronger solution by the separation of metal from it. We may
imagine these changes reversed in two ways. We may evaporate
some of the solvent from the solution which has become weaker
and thus reconcentrate it, condensing the vapour on the solution
which had become stronger. By this reasoning Helmholtz
showed how to obtain an expression for the work done. On the
other hand, we may imagine the processes due to the electrical
transfer to be reversed by an osmotic operation. Solvent may
be supposed to be squeezed out from the solution which has
become more dilute through a semi-permeable wall, and through
another such wall allowed to mix with the solution which in
the electrical operation had become more concentrated. Again,
we may calculate the osmotic work done, and, if the whole cycle
of operations be supposed to occur at the same temperature,
the osmotic work must be equal and opposite to the electrical
work of the first operation.
The result of the investigation shows that the electrical work Ee
is given by the equation
Ee = ∫p2p1 vdp,
where v is the volume of the solution used and p its osmotic pressure.
When the solutions may be taken as effectively dilute, so that the
gas laws apply to the osmotic pressure, this relation reduces to
where n is the number of ions given by one molecule of the salt, r the
transport ratio of the anion, R the gas constant, T the absolute
temperature, y the total valency of the anions obtained from one
molecule, and c1 and c2 the concentrations of the two solutions.
If we take as an example a concentration cell in which silver plates
are placed in solutions of silver nitrate, one of which is ten times as
strong as the other, this equation gives
E = 0.060 × 108 C.G.S. units
= 0.060 volts.
|
W. Nernst, to whom this theory is due, determined the electromotive
force of this cell experimentally, and found the value 0.055 volt.
The logarithmic formulae for these concentration cells indicate
that theoretically their electromotive force can be increased
to any extent by diminishing without limit the concentration
of the more dilute solution, log c1/c2 then becoming very great.
This condition may be realized to some extent in a manner that
throws light on the general theory of the voltaic cell. Let us
consider the arrangement—silver | silver chloride with potassium
chloride solution | potassium nitrate solution | silver nitrate
solution | silver. Silver chloride is a very insoluble substance,
and here the amount in solution is still further reduced by the
presence of excess of chlorine ions of the potassium salt. Thus
silver, at one end of the cell in contact with many silver ions of the
silver nitrate solution, at the other end is in contact with a
liquid in which the concentration of those ions is very small
indeed. The result is that a high electromotive force is set up,
which has been calculated as 0.52 volt, and observed as 0.51 volt.
Again, Hittorf has shown that the effect of a cyanide round a
copper electrode is to combine with the copper ions. The concentration
of the simple copper ions is then so much diminished
that the copper plate becomes an anode with regard to zinc.
Thus the cell—copper | potassium cyanide solution | potassium
sulphate solution—zinc sulphate solution | zinc—gives a current
which carries copper into solution and deposits zinc. In a similar
way silver could be made to act as anode with respect to cadmium.
It is now evident that the electromotive force of an ordinary
chemical cell such as that of Daniell depends on the concentration
of the solutions as well as on the nature of the metals. In
ordinary cases possible changes in the concentrations only affect
the electromotive force by a few parts in a hundred, but, by
means such as those indicated above, it is possible to produce
such immense differences in the concentrations that the electromotive
force of the cell is not only changed appreciably but even
reversed in direction. Once more we see that it is the total
impending change in the available energy of the system which
controls the electromotive force.
Any reversible cell can theoretically be employed as an
accumulator, though, in practice, conditions of general convenience
are more sought after than thermodynamic efficiency.
225
The effective electromotive force of the common lead accumulator
(q.v.) is less than that required to charge it. This drop in
the electromotive force has led to the belief that the cell is not
reversible. F. Dolezalek, however, has attributed the difference
to mechanical hindrances, which prevent the equalization of
acid concentration in the neighbourhood of the electrodes,
rather than to any essentially irreversible chemical action. The
fact that the Gibbs-Helmholtz equation is found to apply also
indicates that the lead accumulator is approximately reversible
in the thermodynamic sense of the term.
Polarization and Contact Difference of Potential.—If we connect
together in series a single Daniell’s cell, a galvanometer, and two
platinum electrodes dipping into acidulated water, no visible
chemical decomposition ensues. At first a considerable current
is indicated by the galvanometer; the deflexion soon diminishes,
however, and finally becomes very small. If, instead of using
a single Daniell’s cell, we employ some source of electromotive
force which can be varied as we please, and gradually raise its
intensity, we shall find that, when it exceeds a certain value,
about 1.7 volt, a permanent current of considerable strength
flows through the solution, and, after the initial period, shows
no signs of decrease. This current is accompanied by chemical
decomposition. Now let us disconnect the platinum plates
from the battery and join them directly with the galvanometer.
A current will flow for a while in the reverse direction; the system
of plates and acidulated water through which a current has been
passed, acts as an accumulator, and will itself yield a current in
return. These phenomena are explained by the existence of a
reverse electromotive force at the surface of the platinum plates.
Only when the applied electromotive force exceeds this reverse
force of polarization, will a permanent steady current pass
through the liquid, and visible chemical decomposition proceed.
It seems that this reverse electromotive force of polarization is
due to the deposit on the electrodes of minute quantities of the
products of chemical decomposition. Differences between the
two electrodes are thus set up, and, as we have seen above, an
electromotive force will therefore exist between them. To pass
a steady current in the direction opposite to this electromotive
force of polarization, the applied electromotive force E must
exceed that of polarization E′, and the excess E − E′ is the
effective electromotive force of the circuit, the current being,
in accordance with Ohm’s law, proportional to the applied
electromotive force and represented by (E − E′) / R, where R is
a constant called the resistance of the circuit.
When we use platinum electrodes in acidulated water, hydrogen
and oxygen are evolved. The opposing force of polarization is
about 1.7 volt, but, when the plates are disconnected and used
as a source of current, the electromotive force they give is only
about 1.07 volt. This irreversibility is due to the work required
to evolve bubbles of gas at the surface of bright platinum
plates. If the plates be covered with a deposit of platinum
black, in which the gases are absorbed as fast as they are produced,
the minimum decomposition point is 1.07 volt, and the
process is reversible. If secondary effects are eliminated, the
deposition of metals also is a reversible process; the decomposition
voltage is equal to the electromotive force which the metal
itself gives when going into solution. The phenomena of polarization
are thus seen to be due to the changes of surface produced,
and are correlated with the differences of potential which exist
at any surface of separation between a metal and an electrolyte.
Many experiments have been made with a view of separating
the two potential-differences which must exist in any cell made
of two metals and a liquid, and of determining each one individually.
If we regard the thermal effect at each junction
as a measure of the potential-difference there, as the total
thermal effect in the cell undoubtedly is of the sum of its potential-differences,
in cases where the temperature coefficient is negligible,
the heat evolved on solution of a metal should give the electrical
potential-difference at its surface. Hence, if we assume that,
in the Daniell’s cell, the temperature coefficients are negligible
at the individual contacts as well as in the cell as a whole, the
sign of the potential-difference ought to be the same at the surface
of the zinc as it is at the surface of the copper. Since zinc goes
into solution and copper comes out, the electromotive force of
the cell will be the difference between the two effects. On the
other hand, it is commonly thought that the single potential-differences
at the surface of metals and electrolytes have been
determined by methods based on the use of the capillary electrometer
and on others depending on what is called a dropping
electrode, that is, mercury dropping rapidly into an electrolyte
and forming a cell with the mercury at rest in the bottom of
the vessel. By both these methods the single potential-differences
found at the surfaces of the zinc and copper have opposite signs,
and the effective electromotive force of a Daniell’s cell is the
sum of the two effects. Which of these conflicting views represents
the truth still remains uncertain.
Diffusion of Electrolytes and Contact Difference of Potential
between Liquids.—An application of the theory of ionic velocity
due to W. Nernst7 and M. Planck8 enables us to calculate the
diffusion constant of dissolved electrolytes. According to the
molecular theory, diffusion is due to the motion of the molecules
of the dissolved substance through the liquid. When the dissolved
molecules are uniformly distributed, the osmotic pressure will
be the same everywhere throughout the solution, but, if the
concentration vary from point to point, the pressure will vary
also. There must, then, be a relation between the rate of change
of the concentration and the osmotic pressure gradient, and thus
we may consider the osmotic pressure gradient as a force driving
the solute through a viscous medium. In the case of non-electrolytes
and of all non-ionized molecules this analogy completely
represents the facts, and the phenomena of diffusion can
be deduced from it alone. But the ions of an electrolytic solution
can move independently through the liquid, even when no current
flows, as the consequences of Ohm’s law indicate. The ions
will therefore diffuse independently, and the faster ion will
travel quicker into pure water in contact with a solution. The
ions carry their charges with them, and, as a matter of fact, it is
found that water in contact with a solution takes with respect
to it a positive or negative potential, according as the positive
or negative ion travels the faster. This process will go on until
the simultaneous separation of electric charges produces an
electrostatic force strong enough to prevent further separation
of ions. We can therefore calculate the rate at which the salt
as a whole will diffuse by examining the conditions for a steady
transfer, in which the ions diffuse at an equal rate, the faster
one being restrained and the slower one urged forward by the
electric forces. In this manner the diffusion constant can
be calculated in absolute units (HCl = 2.49, HNO3 = 2.27,
NaCl = 1.12), the unit of time being the day. By experiments
on diffusion this constant has been found by Scheffer, and the
numbers observed agree with those calculated (HCl = 2.30,
HNO3 = 2.22, NaCl = 1.11).
As we have seen above, when a solution is placed in contact
with water the water will take a positive or negative potential
with regard to the solution, according as the cation or anion has
the greater specific velocity, and therefore the greater initial
rate of diffusion. The difference of potential between two
solutions of a substance at different concentrations can be calculated
from the equations used to give the diffusion constants.
The results give equations of the same logarithmic form as those
obtained in a somewhat different manner in the theory of concentration
cells described above, and have been verified by
experiment.
The contact differences of potential at the interfaces of metals
and electrolytes have been co-ordinated by Nernst with those
at the surfaces of separation between different liquids. In
contact with a solvent a metal is supposed to possess a definite
solution pressure, analogous to the vapour pressure of a liquid.
Metal goes into solution in the form of electrified ions. The
liquid thus acquires a positive charge, and the metal a negative
charge. The electric forces set up tend to prevent further
separation, and finally a state of equilibrium is reached, when no
226
more ions can go into solution unless an equivalent number are
removed by voltaic action. On the analogy between this case
and that of the interface between two solutions, Nernst has
arrived at similar logarithmic expressions for the difference of
potential, which becomes proportional to log (P1/P2) where P2
is taken to mean the osmotic pressure of the cations in the
solution, and P1 the osmotic pressure of the cations in the substance
of the metal itself. On these lines the equations of concentration
cells, deduced above on less hypothetical grounds,
may be regained.
Theory of Electrons.—Our views of the nature of the ions of
electrolytes have been extended by the application of the ideas
of the relations between matter and electricity obtained by the
study of electric conduction through gases. The interpretation
of the phenomena of gaseous conduction was rendered possible
by the knowledge previously acquired of conduction through
liquids; the newer subject is now reaching a position whence
it can repay its debt to the older.
Sir J.J. Thomson has shown (see Conduction, Electric,
§ III.) that the negative ions in certain cases of gaseous conduction
are much more mobile than the corresponding positive
ions, and possess a mass of about the one-thousandth part of
that of a hydrogen atom. These negative particles or corpuscles
seem to be the ultimate units of negative electricity, and may be
identified with the electrons required by the theories of H.A.
Lorentz and Sir J. Larmor. A body containing an excess of these
particles is negatively electrified, and is positively electrified if
it has parted with some of its normal number. An electric
current consists of a moving stream of electrons. In gases the
electrons sometimes travel alone, but in liquids they are always
attached to matter, and their motion involves the movement of
chemical atoms or groups of atoms. An atom with an extra
corpuscle is a univalent negative ion, an atom with one corpuscle
detached is a univalent positive ion. In metals the electrons
can slip from one atom to the next, since a current can pass
without chemical action. When a current passes from an
electrolyte to a metal, the electron must be detached from the
atom it was accompanying and chemical action be manifested
at the electrode.
Bibliography.—Michael Faraday, Experimental Researches in
Electricity (London, 1844 and 1855); W. Ostwald, Lehrbuch der
allgemeinen Chemie, 2te Aufl. (Leipzig, 1891); Elektrochemie (Leipzig,
1896); W Nernst, Theoretische Chemie, 3te Aufl. (Stuttgart, 1900;
English translation, London, 1904); F. Kohlrausch and L. Holborn,
Das Leitvermögen der Elektrolyte (Leipzig, 1898); W.C.D. Whetham,
The Theory of Solution and Electrolysis (Cambridge, 1902); M. Le
Blanc, Elements of Electrochemistry (Eng. trans., London, 1896);
S. Arrhenius, Text-Book of Electrochemistry (Eng. trans., London,
1902); H.C. Jones, The Theory of Electrolytic Dissociation (New
York, 1900); N. Munroe Hopkins, Experimental Electrochemistry
(London, 1905); Lüphe, Grundzüge der Elektrochemie (Berlin, 1896).
Some of the more important papers on the subject have been
reprinted for Harper’s Series of Scientific Memoirs in Electrolytic
Conduction (1899) and the Modern Theory of Solution (1899). Several
journals are published specially to deal with physical chemistry, of
which electrochemistry forms an important part. Among them may
be mentioned the Zeitschrift für physikalische Chemie (Leipzig);
and the Journal of Physical Chemistry (Cornell University). In
these periodicals will be found new work on the subject and
abstracts of papers which appear in other physical and chemical
publications.
(W. C. D. W.)
1 See Hittorf, Pogg. Ann. cvi. 517 (1859).
2 Grundriss der Elektrochemie (1895), p. 292; see also F. Kaufler
and C. Herzog, Ber., 1909, 42, p. 3858.
3 Brit. Ass. Rep., 1906, Section A, Presidential Address.
4 See Theory of Solution, by W.C.D. Whetham (1902), p. 328.
5 W. Ostwald, Zeits. physikal. Chemie, 1892, vol. IX. p. 579;
T. Ewan, Phil. Mag. (5), 1892, vol. xxxiii. p. 317; G.D. Liveing,
Cambridge Phil. Trans., 1900, vol. xviii. p. 298.
6 See W.B. Hardy, Journal of Physiology, 1899, vol. xxiv. p. 288;
and W.C.D. Whetham, Phil. Mag., November 1899.
7 Zeits. physikal. Chem. 2, p. 613.
8 Wied. Ann., 1890, 40, p. 561.
ELECTROMAGNETISM, that branch of physical science
which is concerned with the interconnexion of electricity and
magnetism, and with the production of magnetism by means of
electric currents by devices called electromagnets.
History.—The foundation was laid by the observation first
made by Hans Christian Oersted (1777-1851), professor of
natural philosophy in Copenhagen, who discovered in 1820 that
a wire uniting the poles or terminal plates of a voltaic pile has the
property of affecting a magnetic needle1 (see Electricity).
Oersted carefully ascertained that the nature of the wire itself
did not influence the result but saw that it was due to the electric
conflict, as he called it, round the wire; or in modern language,
to the magnetic force or magnetic flux round the conductor.
If a straight wire through which an electric current is flowing is
placed above and parallel to a magnetic compass needle, it is
found that if the current is flowing in the conductor in a direction
from south to north, the north pole of the needle under the conductor
deviates to the left hand, whereas if the conductor is
placed under the needle, the north pole deviates to the right hand;
if the conductor is doubled back over the needle, the effects of
the two sides of the loop are added together and the deflection is
increased. These results are summed up in the mnemonic rule:
Imagine yourself swimming in the conductor with the current, that
is, moving in the direction of the positive electricity, with your face
towards the magnetic needle; the north pole will then deviate to
your left hand. The deflection of the magnetic needle can therefore
reveal the existence of an electric current in a neighbouring
circuit, and this fact was soon utilized in the construction of
instruments called galvanometers (q.v.).
Immediately after Oersted’s discovery was announced,
D.F.J. Arago and A.M. Ampère began investigations on the
subject of electromagnetism. On the 18th of September 1820,
Ampère read a paper before the Academy of Sciences in Paris,
in which he announced that the voltaic pile itself affected a
magnetic needle as did the uniting wire, and he showed that the
effects in both cases were consistent with the theory that electric
current was a circulation round a circuit, and equivalent in
magnetic effect to a very short magnet with axis placed at right
angles to the plane of the circuit. He then propounded his
brilliant hypothesis that the magnetization of iron was due to
molecular electric currents. This suggested to Arago that wire
wound into a helix carrying electric current should magnetize
a steel needle placed in the interior. In the Ann. Chim. (1820,
15, p. 94), Arago published a paper entitled “Expériences relatives
à l’aimantation du fer et de l’acier par l’action du courant
voltaïque,” announcing that the wire conveying the current,
even though of copper, could magnetize steel needles placed
across it, and if plunged into iron filings it attracted them. About
the same time Sir Humphry Davy sent a communication to Dr
W.H. Wollaston, read at the Royal Society on the 16th of
November 1820 (reproduced in the Annals of Philosophy for
August 1821, p. 81), “On the Magnetic Phenomena produced by
Electricity,” in which he announced his independent discovery
of the same fact. With a large battery of 100 pairs of plates at
the Royal Institution, he found in October 1820 that the uniting
wire became strongly magnetic and that iron filings clung to it;
also that steel needles placed across the wire were permanently
magnetized. He placed a sheet of glass over the wire and
sprinkling iron filings on it saw that they arranged themselves
in straight lines at right angles to the wire. He then proved that
Leyden jar discharges could produce the same effects. Ampère
and Arago then seem to have experimented together and magnetized
a steel needle wrapped in paper which was enclosed in a
helical wire conveying a current. All these facts were rendered
intelligible when it was seen that a wire when conveying an
electric current becomes surrounded by a magnetic field. If
the wire is a long straight one, the lines of magnetic force are
circular and concentric with centres on the wire axis, and if the
wire is bent into a circle the lines of magnetic force are endless
loops surrounding and linked with the electric circuit. Since
a magnetic pole tends to move along a line of magnetic force it
was obvious that it should revolve round a wire conveying a
current. To exhibit this fact involved, however, much ingenuity.
It was first accomplished by Faraday in October 1821 (Exper.
Res. ii. p. 127). Since the action is reciprocal a current free to
move tends to revolve round a magnetic pole. The fact is most
easily shown by a small piece of apparatus made as follows:
In a glass cylinder (see fig. 1) like a lamp chimney are fitted two
corks. Through the bottom one is passed the north end of a bar
magnet which projects up above a little mercury lying in the
cork. Through the top cork is passed one end of a wire from a
227
battery, and a piece of wire in the cylinder is flexibly connected
to it, the lower end of this last piece just touching the mercury.
When a current is passed in at the top wire and out at the lower
end of the bar magnet, the loose wire revolves round the magnet
pole. All text-books on physics contain in their
chapters on electromagnetism full accounts of
various forms of this experiment.
 |
| Fig. 1. |
In 1825 another important step forward was
taken when William Sturgeon (1783-1850) of
London produced the electromagnet. It consisted
of a horseshoe-shaped bar of soft iron,
coated with varnish, on which was wrapped a
spiral coil of bare copper wire, the turns not
touching each other. When a voltaic current
was passed through the wire the iron became a
powerful magnet, but on severing the connexion
with the battery, the soft iron lost
immediately nearly all its magnetism.2
At that date Ohm had not announced his
law of the electric circuit, and it was a matter
of some surprise to investigators to find that
Sturgeon’s electromagnet could not be operated
at a distance through a long circuit of wire
with such good results as when close to the
battery. Peter Barlow, in January 1825, published in the
Edinburgh Philosophical Journal, a description of such an
experiment made with a view of applying Sturgeon’s electromagnet
to telegraphy, with results which were unfavourable.
Sturgeon’s experiments, however, stimulated Joseph Henry
(q.v.) in the United States, and in 1831 he gave a description
of a method of winding electromagnets which at once put a new
face upon matters (Silliman’s Journal, 1831, 19, p. 400). Instead
of insulating the iron core, he wrapped the copper wire round
with silk and wound in numerous turns and many layers upon
the iron horseshoe in such fashion that the current went round
the iron always in the same direction. He then found that such
an electromagnet wound with a long fine wire, if worked with a
battery consisting of a large number of cells in series, could be
operated at a considerable distance, and he thus produced what
were called at that time intensity electromagnets, and which
subsequently rendered the electric telegraph a possibility. In
fact, Henry established in 1831, in Albany, U.S.A., an electromagnetic
telegraph, and in 1835 at Princeton even used an
earth return, thereby anticipating the discovery (1838) of C.A.
Steinheil (1801-1870) of Munich.
 |
| Fig. 2. |
Inventors were then incited to construct powerful electromagnets
as tested by the weight they could carry from their
armatures. Joseph Henry made a magnet for Yale College,
U.S.A., which lifted 3000 ℔ (Silliman’s Journal, 1831, 20, p. 201),
and one for Princeton which lifted 3000 with a very small
battery. Amongst others J.P. Joule, ever memorable for his
investigations on the mechanical equivalent of heat, gave much
attention about 1838-1840 to the construction of electromagnets
and succeeded in devising some forms remarkable for their
lifting power. One form was constructed by cutting a thick
soft iron tube longitudinally
into two equal parts. Insulated
copper wire was then
wound longitudinally over
one of both parts (see fig. 2)
and a current sent through
the wire. In another form
two iron disks with teeth at
right angles to the disk had
insulated wire wound zigzag between the teeth; when a current
was sent through the wire, the teeth were so magnetized that
they were alternately N. and S. poles. If two such similar disks
were placed with teeth of opposite polarity in contact, a very
large force was required to detach them, and with a magnet and
armature weighing in all 11.575 ℔ Joule found that a weight
of 2718 was supported. Joule’s papers on this subject will be
found in his Collected Papers published by the Physical Society
of London, and in Sturgeon’s Annals of Electricity, 1838-1841,
vols. 2-6.
The Magnetic Circuit.—The phenomena presented by the electromagnet
are interpreted by the aid of the notion of the magnetic
circuit. Let us consider a thin circular sectioned ring of iron wire
wound over with a solenoid or spiral of insulated copper wire through
which a current of electricity can be passed. If the solenoid or wire
windings existed alone, a current having a strength A amperes
passed through it would create in the interior of the solenoid a
magnetic force H, numerically equal to 4π/10 multiplied by the
number of windings N on the solenoid, and by the current in amperes
A, and divided by the mean length of the solenoid l, or H = 4πAN/10l.
The product AN is called the “ampere-turns” on the solenoid.
The product Hl of the magnetic force H and the length l of the
magnetic circuit is called the “magnetomotive force” in the magnetic
circuit, and from the above formula it is seen that the magnetomotive
force denoted by (M.M.F.) is equal to 4π/10 (= 1.25 nearly) times
the ampere-turns (A.N.) on the exciting coil or solenoid. Otherwise
(A.N.) = 0.8(M.M.F.). The magnetomotive force is regarded as
creating an effect called magnetic flux (Z) in the magnetic circuit,
just as electromotive force E.M.F. produces electric current (A) in
the electric circuit, and as by Ohm’s law (see Electrokinetics) the
current varies as the E.M.F. and inversely as a quality of the electric
circuit called its “resistance,” so in the magnetic circuit the magnetic
flux varies as the magnetomotive force and inversely as a
quality of the magnetic circuit called its “reluctance.” The great
difference between the electric circuit and the magnetic circuit lies
in the fact that whereas the electric resistance of a solid or liquid
conductor is independent of the current and affected only by the
temperature, the magnetic reluctance varies with the magnetic
flux and cannot be defined except by means of a curve which shows
its value for different flux densities. The quotient of the total
magnetic flux, Z, in a circuit by the cross section, S, of the circuit is
called the mean “flux density,” and the reluctance of a magnetic
circuit one centimetre long and one square centimetre in cross
section is called the “reluctivity” of the material. The relation
between reluctivity ρ = 1/μ magnetic force H, and flux density B,
is defined by the equation H = ρB, from which we have Hl = Z (ρl/S) =
M.M.F. acting on the circuit. Again, since the ampere-turns (AN)
on the circuit are equal to 0.8 times the M.M.F., we have finally
AN/l = 0.8(Z/μS). This equation tells us the exciting force reckoned
in ampere-turns, AN, which must be put on the ring core to create
a total magnetic flux Z in it, the ring core having a mean perimeter l
and cross section S and reluctivity ρ = 1/μ corresponding to a flux
density Z/S. Hence before we can make use of the equation for
practical purposes we need to possess a curve for the particular
material showing us the value of the reluctivity corresponding to
various values of the possible flux density. The reciprocal of ρ is
usually called the “permeability” of the material and denoted by μ.
Curves showing the relation of 1/ρ and ZS or μ and B, are called
“permeability curves.” For air and all other non-magnetic matter
the permeability has the same value, taken arbitrarily as unity.
On the other hand, for iron, nickel and cobalt the permeability may
in some cases reach a value of 2000 or 2500 for a value of B = 5000 in
C.G.S. measure (see Units, Physical). The process of taking these
curves consists in sending a current of known strength through a
solenoid of known number of turns wound on a circular iron ring of
known dimensions, and observing the time-integral of the secondary
current produced in a secondary circuit of known turns and resistance
R wound over the iron core N times. The secondary electromotive
force is by Faraday’s law (see Electrokinetics) equal to the time
rate of change of the total flux, or E = NdZ/dt. But by Ohm’s
law E = Rdq/dt, where q is the quantity of electricity set flowing in
the secondary circuit by a change dZ in the co-linked total flux.
Hence if 2Q represents this total quantity of electricity set flowing
in the secondary circuit by suddenly reversing the direction of the
magnetic flux Z in the iron core we must have
RQ = NZ or Z = RQ/N.
The measurement of the total quantity of electricity Q can be
made by means of a ballistic galvanometer (q.v.), and the resistance
R of the secondary circuit includes that of the coil wound on the
iron core and the galvanometer as well. In this manner the value
of the total flux Z and therefore of Z/S = B or the flux density, can be
found for a given magnetizing force H, and this last quantity is
determined when we know the magnetizing current in the solenoid
and its turns and dimensions. The curve which delineates the relation
of H and B is called the magnetization curve for the material in
question. For examples of these curves see Magnetism.
The fundamental law of the non-homogeneous magnetic circuit
traversed by one and the same total magnetic flux Z is that the sum
of all the magnetomotive forces acting in the circuit is numerically
equal to the product of the factor 0.8, the total flux in the circuit,
and the sum of all the reluctances of the various parts of the circuit.
If then the circuit consists of materials of different permeability
228
and it is desired to know the ampere-turns required to produce a given
total of flux round the circuit, we have to calculate from the magnetization
curves of the material of each part the necessary magnetomotive
forces and add these forces together. The practical application
of this principle to the predetermination of the field windings of
dynamo magnets was first made by Drs J. and E. Hopkinson (Phil.
Trans., 1886, 177, p. 331).
We may illustrate the principles of this predetermination by a
simple example. Suppose a ring of iron has a mean diameter of
10 cms. and a cross section of 2 sq. cms., and a transverse cut on air
gap made in it 1 mm. wide. Let us inquire the ampere-turns to
be put upon the ring to create in it a total flux of 24,000 C.G.S. units.
The total length of the iron part of the circuit is (10π − 0.1) cms.,
and its section is 2 sq. cms., and the flux density in it is to be 12,000.
From Table II. below we see that the permeability of pure iron
corresponding to a flux density of 12,000 is 2760. Hence the reluctance
of the iron circuits is equal to
| 10π − 0.1 |
= | 220 |
C.G.S. units. |
| 2760 × 2 | 38640 |
The length of the air gap is 0.1 cm., its section 2 sq. cms., and its
permeability is unity. Hence the reluctance of the air gap is
| 0.1 |
= | 1 |
C.G.S. unit. |
| 1 × 2 | 20 |
Accordingly the magnetomotive force in ampere-turns required to
produce the required flux is equal to
| 0.8 (24,000) ( | 1 |
+ | 220 |
) = 1070 nearly. |
| 20 | 38640 |
It follows that the part of the magnetomotive force required to
overcome the reluctance of the narrow air gap is about nine times
that required for the iron alone.
In the above example we have for simplicity assumed that the
flux in passing across the air gap does not spread out at all. In
dealing with electromagnet design in dynamo construction we have,
however, to take into consideration the spreading as well as the
leakage of flux across the circuit (see Dynamo). It will be seen,
therefore, that in order that we may predict the effect of a certain
kind of iron or steel when used as the core of an electromagnet,
we must be provided with tables or curves showing the reluctivity
or permeability corresponding to various flux densities or—which
comes to the same thing—with (B, H) curves for the sample.
Iron and Steel for Electromagnetic Machinery.—In connexion
with the technical application of electromagnets such as those
used in the field magnets of dynamos (q.v.), the testing of different
kinds of iron and steel for magnetic permeability has therefore
become very important. Various instruments called permeameters
and hysteresis meters have been designed for this purpose,
but much of the work has been done by means of a ballistic
galvanometer and test ring as above described. The “hysteresis”
of an iron or steel is that quality of it in virtue of which energy
is dissipated as heat when the magnetization is reversed or
carried through a cycle (see Magnetism), and it is generally
measured either in ergs per cubic centimetre of metal per cycle
of magnetization, or in watts per ℔ per 50 or 100 cycles
per second at or corresponding to a certain maximum flux
density, say 2500 or 600 C.G.S. units. For the details of various
forms of permeameter and hysteresis meter technical books
must be consulted.3
An immense number of observations have been carried out
on the magnetic permeability of different kinds of iron and
steel, and in the following tables are given some typical results,
mostly from experiments made by J.A. Ewing (see Proc. Inst.
C.E., 1896, 126, p. 185) in which the ballistic method was
employed to determine the flux density corresponding to various
magnetizing forces acting upon samples of iron and steel in the
form of rings.
The figures under heading I. are values given in a paper by A.W.S.
Pocklington and F. Lydall (Proc. Roy. Soc., 1892-1893, 52, pp. 164
and 228) as the results of a magnetic test of an exceptionally pure
iron supplied for the purpose of experiment by Colonel Dyer, of the
Elswick Works. The substances other than iron in this sample
were stated to be: carbon, trace; silicon, trace; phosphorus,
none; sulphur, 0.013%; manganese, 0.1%. The other five
specimens, II. to VI., are samples of commercial iron or steel. No.
II. is a sample of Low Moor bar iron forged into a ring, annealed and
turned. No. III. is a steel forging furnished by Mr R. Jenkins as a
sample of forged ingot-metal for dynamo magnets. No. IV. is a steel
casting for dynamo magnets, unforged, made by Messrs Edgar Allen
& Company by a special pneumatic process under the patents of
Mr A. Tropenas. No. V. is also an unforged steel casting for dynamo
magnets, made by Messrs Samuel Osborne & Company by the
Siemens process. No. VI. is also an unforged steel casting for
dynamo magnets, made by Messrs Fried. Krupp, of Essen.
Table I.—Magnetic Flux Density corresponding to various Magnetizing
Forces in the case of certain Samples of Iron and Steel
(Ewing).
Magnetizing
Force
H (C.G.S.
Units). |
Magnetic Flux Density B (C.G.S. Units). |
| | I. | II. | III. | IV. | V. | VI. |
| 5 | 12,700 | 10,900 | 12,300 | 4,700 | 9,600 | 10,900 |
| 10 | 14,980 | 13,120 | 14,920 | 12,250 | 13,050 | 13,320 |
| 15 | 15,800 | 14,010 | 15,800 | 14,000 | 14,600 | 14,350 |
| 20 | 16,300 | 14,580 | 16,280 | 15,050 | 15,310 | 14,950 |
| 30 | 16,950 | 15,280 | 16,810 | 16,200 | 16,000 | 15,660 |
| 40 | 17,350 | 15,760 | 17,190 | 16,800 | 16,510 | 16,150 |
| 50 | · · | 16,060 | 17,500 | 17,140 | 16,900 | 16,480 |
| 60 | · · | 16,340 | 17,750 | 17,450 | 17,180 | 16,780 |
| 70 | · · | 16,580 | 17,970 | 17,750 | 17,400 | 17,000 |
| 80 | · · | 16,800 | 18,180 | 18,040 | 17,620 | 17,200 |
| 90 | · · | 17,000 | 18,390 | 18,230 | 17,830 | 17,400 |
| 100 | · · | 17,200 | 18,600 | 18,420 | 18,030 | 17,600 |
It will be seen from the figures and the description of the materials
that the steel forgings and castings have a remarkably high permeability
under small magnetizing force.
Table II. shows the magnetic qualities of some of these
materials as found by Ewing when tested with small magnetizing
forces.
Table II.—Magnetic Permeability of Samples of Iron and Steel under
Weak Magnetizing Forces.
Magnetic Flux
Density B
(C.G.S. Units). |
I.
Pure Iron. | III.
Steel Forging. | VI.
Steel Casting. |
| | H | μ | H | μ | H | μ |
| 2,000 | 0.90 | 2220 | 1.38 | 1450 | 1.18 | 1690 |
| 4,000 | 1.40 | 2850 | 1.91 | 2090 | 1.66 | 2410 |
| 6,000 | 1.85 | 3240 | 2.38 | 2520 | 2.15 | 2790 |
| 8,000 | 2.30 | 3480 | 2.92 | 2740 | 2.83 | 2830 |
| 10,000 | 3.10 | 3220 | 3.62 | 2760 | 4.05 | 2470 |
| 12,000 | 4.40 | 2760 | 4.80 | 2500 | 6.65 | 1810 |
The numbers I., III. and VI. in the above table refer to the samples
mentioned in connexion with Table I.
It is a remarkable fact that certain varieties of low carbon
steel (commonly called mild steel) have a higher permeability
than even annealed Swedish wrought iron under large magnetizing
forces. The term steel, however, here used has reference
rather to the mode of production than the final chemical nature
of the material. In some of the mild-steel castings used for
dynamo electromagnets it appears that the total foreign matter,
including carbon, manganese and silicon, is not more than 0.3%
of the whole, the material being 99.7% pure iron. This valuable
magnetic property of steel capable of being cast is, however,
of great utility in modern dynamo building, as it enables field
magnets of very high permeability to be constructed, which can
be fashioned into shape by casting instead of being built up as
formerly out of masses of forged wrought iron. The curves in
fig. 3 illustrate the manner in which the flux density or, as it is
usually called, the magnetization curve of this mild cast steel
crosses that of Swedish wrought iron, and enables us to obtain a
higher flux density corresponding to a given magnetizing force
with the steel than with the iron.
From the same paper by Ewing we extract a number of results
relating to permeability tests of thin sheet iron and sheet steel,
such as is used in the construction of dynamo armatures and
transformer cores.
No. VII. is a specimen of good transformer-plate, 0.301 millimetre
thick, rolled from Swedish iron by Messrs Sankey of Bilston. No.
VIII. is a specimen of specially thin transformer-plate rolled from
scrap iron. No. IX. is a specimen of transformer-plate rolled from
229
ingot-steel. No. X. is a specimen of the wire which was used by
J. Swinburne to form the core of his “hedgehog” transformers. Its
diameter was 0.602 millimetre. All these samples were tested in the
form of rings by the ballistic method, the rings of sheet-metal
being stamped or turned in the flat. The wire ring No. X. was
coiled and annealed after coiling.
 |
| Fig. 3. |
Table III.—Permeability Tests of Transformer Plate and Wire.
Magnetic
Flux
Density B
(C.G.S.
Units). | VII.
Transformer-
plate of
Swedish Iron. |
VIII.
Transformer-
plate of
Scrap Iron. | IX.
Transformer-
plate of
of Steel. |
X.
Transformer-
wire. |
| | H | μ | H | μ | H | μ | H | μ |
| 1,000 | 0.81 | 1230 | 1.08 | 920 | 0.60 | 1470 | 1.71 | 590 |
| 2,000 | 1.05 | 1900 | 1.46 | 1370 | 0.90 | 2230 | 2.10 | 950 |
| 3,000 | 1.26 | 2320 | 1.77 | 1690 | 1.04 | 2880 | 2.30 | 1300 |
| 4,000 | 1.54 | 2600 | 2.10 | 1900 | 1.19 | 3360 | 2.50 | 1600 |
| 5,000 | 1.82 | 2750 | 2.53 | 1980 | 1.38 | 3620 | 2.70 | 1850 |
| 6,000 | 2.14 | 2800 | 3.04 | 1970 | 1.59 | 3770 | 2.92 | 2070 |
| 7,000 | 2.54 | 2760 | 3.62 | 1930 | 1.89 | 3700 | 3.16 | 2210 |
| 8,000 | 3.09 | 2590 | 4.37 | 1830 | 2.25 | 3600 | 3.43 | 2330 |
| 9,000 | 3.77 | 2390 | 5.3 | 1700 | 2.72 | 3310 | 3.77 | 2390 |
| 10,000 | 4.6 | 2170 | 6.5 | 1540 | 3.33 | 3000 | 4.17 | 2400 |
| 11,000 | 5.7 | 1930 | 7.9 | 1390 | 4.15 | 2650 | 4.70 | 2340 |
| 12,000 | 7.0 | 1710 | 9.8 | 1220 | 5.40 | 2220 | 5.45 | 2200 |
| 13,000 | 8.5 | 1530 | 11.9 | 1190 | 7.1 | 1830 | 6.5 | 2000 |
| 14,000 | 11.0 | 1270 | 15.0 | 930 | 10.0 | 1400 | 8.4 | 1670 |
| 15,000 | 15.1 | 990 | 19.5 | 770 | · · | · · | 11.9 | 1260 |
| 16,000 | 21.4 | 750 | 27.5 | 580 | · · | · · | 21.0 | 760 |
Some typical flux-density curves of iron and steel as used in
dynamo and transformer building are given in fig. 4.
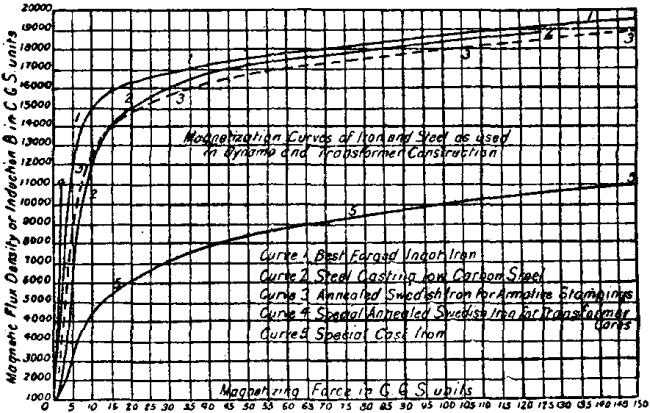 |
| Fig. 4. |
The numbers in Table III. well illustrate the fact that the
permeability, μ = B/H has a maximum value corresponding to a
certain flux density. The tables are also explanatory of the fact
that mild steel has gradually replaced iron in the manufacture
of dynamo electromagnets and transformer-cores.
Broadly speaking, the materials which are now employed
in the manufacture of the cores of electromagnets for technical
purposes of various kinds may be said to fall into three classes,
namely, forgings, castings and stampings. In some cases the
iron or steel core which is to be magnetized is simply a mass of
iron hammered or pressed into shape by hydraulic pressure;
in other cases it has to be fused and cast; and for certain other
purposes it must be rolled first into thin sheets, which are subsequently
stamped out into the required forms.
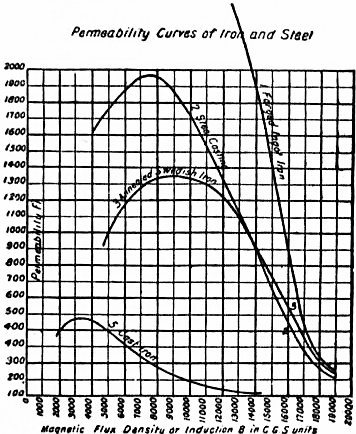 |
| Fig. 5. |
For particular purposes it is necessary to obtain the highest
possible magnetic permeability corresponding to a high, or the
highest attainable flux density. This is generally the case in
the electromagnets which are employed as the field magnets in
dynamo machines. It may generally be said that whilst the best
wrought iron, such as annealed Low Moor or Swedish iron, is
more permeable for low flux densities than steel castings, the
cast steel may surpass the wrought metal for high flux density.
For most electro-technical purposes the best magnetic results
are given by the employment of forged ingot-iron. This material
is probably the most permeable throughout the whole scale of
attainable flux densities. It is slightly superior to wrought iron,
and it only becomes inferior to the highest class of cast steel
when the flux density is pressed above 18,000 C.G.S. units (see
fig. 5). For flux densities above 13,000 the forged ingot-iron
has now practically replaced for electric engineering purposes
the Low Moor or Swedish iron. Owing to the method of its
production, it might in truth be called a soft steel with a very
small percentage of combined carbon. The best description of
this material is conveyed by the German term “Flusseisen,”
but its nearest British equivalent is “ingot-iron.” Chemically
speaking, the material is for all practical purposes very nearly
pure iron. The same may be said of the cast steels now much
employed for the production of dynamo magnet cores. The
cast steel which is in demand for this purpose has a slightly
lower permeability than the ingot-iron for low flux densities,
but for flux densities above 16,000 the required result may be
more cheaply obtained with a steel casting than with a forging.
When high tensile strength is required in addition to considerable
magnetic permeability, it has been found advantageous to employ
a steel containing 5% of nickel. The rolled sheet iron and sheet
steel which is in request for the construction of magnet cores,
especially those in which the exciting current is an alternating
current, are, generally speaking, produced from Swedish iron.
Owing to the mechanical treatment necessary to reduce the
material to a thin sheet, the permeability at low flux densities
is rather higher than, although at high flux densities it is inferior
230
to, the same iron and steel when tested in bulk. For most
purposes, however, where a laminated iron magnet core is
required, the flux density is not pressed up above 6000 units,
and it is then more important to secure small hysteresis loss than
high permeability. The magnetic permeability of cast iron is
much inferior to that of wrought or ingot-iron, or the mild steels
taken at the same flux densities.
The following Table IV. gives the flux density and permeability
of a typical cast iron taken by J.A. Fleming by the
ballistic method:—
Table IV.—Magnetic Permeability and Magnetization Curve of
Cast Iron.
| H | B | μ | H | B | μ | H | B | μ |
| .19 | 27 | 139 | 8.84 | 4030 | 456 | 44.65 | 8,071 | 181 |
| .41 | 62 | 150 | 10.60 | 4491 | 424 | 56.57 | 8,548 | 151 |
| 1.11 | 206 | 176 | 12.33 | 4884 | 396 | 71.98 | 9,097 | 126 |
| 2.53 | 768 | 303 | 13.95 | 5276 | 378 | 88.99 | 9,600 | 108 |
| 3.41 | 1251 | 367 | 15.61 | 5504 | 353 | 106.35 | 10,066 | 95 |
| 4.45 | 1898 | 427 | 18.21 | 5829 | 320 | 120.60 | 10,375 | 86 |
| 5.67 | 2589 | 456 | 26.37 | 6814 | 258 | 140.37 | 10,725 | 76 |
| 7.16 | 3350 | 468 | 36.54 | 7580 | 207 | 152.73 | 10,985 | 72 |
The metal of which the tests are given in Table IV. contained
2% of silicon, 2.85% of total carbon, and 0.5% of manganese.
It will be seen that a magnetizing force of about 5 C.G.S. units is
sufficient to impart to a wrought-iron ring a flux density of
18,000 C.G.S. units, but the same force hardly produces more
than one-tenth of this flux density in cast iron.
The testing of sheet iron and steel for magnetic hysteresis
loss has developed into an important factory process, giving
as it does a means of ascertaining the suitability of the metal
for use in the manufacture of transformers and cores of alternating-current
electromagnets.
In Table V. are given the results of hysteresis tests by Ewing on
samples of commercial sheet iron and steel. The numbers VII.,
VIII., IX. and X. refer to the same samples as those for which
permeability results are given in Table III.
Table V.—Hysteresis Loss in Transformer-iron.
Maximum
Flux
Density
B. | Ergs per Cubic Centimetre
per Cycle. | Watts per ℔ at a Frequency
of 100. |
VII.
Swedish
Iron. | VIII.
Forged
Scrap-
iron. |
IX.
Ingot-
steel. | X.
Soft
Iron
Wire. |
VII. | VIII. | IX. | X. |
| 2000 | 240 | 400 | 215 | 600 | 0.141 | 0.236 | 0.127 | 0.356 |
| 3000 | 520 | 790 | 430 | 1150 | 0.306 | 0.465 | 0.253 | 0.630 |
| 4000 | 830 | 1220 | 700 | 1780 | 0.490 | 0.720 | 0.410 | 1.050 |
| 5000 | 1190 | 1710 | 1000 | 2640 | 0.700 | 1.010 | 0.590 | 1.550 |
| 6000 | 1600 | 2260 | 1350 | 3360 | 0.940 | 1.330 | 0.790 | 1.980 |
| 7000 | 2020 | 2940 | 1730 | 4300 | 1.200 | 1.730 | 1.020 | 2.530 |
| 8000 | 2510 | 3710 | 2150 | 5300 | 1.480 | 2.180 | 1.270 | 3.120 |
| 9000 | 3050 | 4560 | 2620 | 6380 | 1.800 | 2.680 | 1.540 | 3.750 |
In Table VI. are given the results of a magnetic test of
some exceedingly good transformer-sheet rolled from Swedish
iron.
Table VI.—Hysteresis Loss in Strip of Transformer-plate rolled
Swedish Iron.
Maximum Flux
Density B. | Ergs per Cubic Centimetre
per Cycle. | Watts per ℔ at a
Frequency of 100. |
| 2000 | 220 | 0.129 |
| 3000 | 410 | 0.242 |
| 4000 | 640 | 0.376 |
| 5000 | 910 | 0.535 |
| 6000 | 1200 | 0.710 |
| 7000 | 1520 | 0.890 |
| 8000 | 1900 | 1.120 |
| 9000 | 2310 | 1.360 |
In Table VII. are given some values obtained by Fleming for
the hysteresis loss in the sample of cast iron, the permeability test
of which is recorded in Table IV.
Table VII.—Observations on the Magnetic Hysteresis of Cast Iron.
| Loop. | B (max.) | Hysteresis Loss. |
Ergs per cc.
per Cycle. | Watts per ℔ per.
100 Cycles per sec. |
| I. | 1475 | 466 | .300 |
| II. | 2545 | 1,288 | .829 |
| III. | 3865 | 2,997 | 1.934 |
| IV. | 5972 | 7,397 | 4.765 |
| V. | 8930 | 13,423 | 8.658 |
For most practical purposes the constructor of electromagnetic
machinery requires his iron or steel to have some one of the following
characteristics. If for dynamo or magnet making, it should
have the highest possible permeability at a flux density corresponding
to practically maximum magnetization. If for transformer
or alternating-current magnet building, it should have
the smallest possible hysteresis loss at a maximum flux density
of 2500 C.G.S. units during the cycle. If required for permanent
magnet making, it should have the highest possible coercivity
combined with a high retentivity. Manufacturers of iron and
steel are now able to meet these demands in a very remarkable
manner by the commercial production of material of a quality
which at one time would have been considered a scientific
curiosity.
It is usual to specify iron and steel for the first purpose by
naming the minimum permeability it should possess corresponding
to a flux density of 18,000 C.G.S. units; for the second,
by stating the hysteresis loss in watts per ℔ per 100 cycles
per second, corresponding to a maximum flux density of 2500
C.G.S. units during the cycle; and for the third, by mentioning
the coercive force required to reduce to zero magnetization a
sample of the metal in the form of a long bar magnetized to a
stated magnetization. In the cyclical reversal of magnetization
of iron we have two modes to consider. In the first case, which is
that of the core of the alternating transformer, the magnetic
force passes through a cycle of values, the iron remaining
stationary, and the direction of the
magnetic force being always the same.
In the other case, that of the dynamo
armature core, the direction of the
magnetic force in the iron is constantly
changing, and at the same time
undergoing a change in magnitude.
It has been shown by F.G. Baily
(Proc. Roy. Soc., 1896) that if a mass
of laminated iron is rotating in a
magnetic field which remains constant
in direction and magnitude in any
one experiment, the hysteresis loss
rises to a maximum as the magnitude
of the flux density in the iron is
increased and then falls away again to
nearly zero value. These observations have been confirmed
by other observers. The question has been much debated
whether the values of the hysteresis loss obtained by these
two different methods are identical for magnetic cycles in which
the flux density reaches the same maximum value. This question
is also connected with another one, namely, whether the hysteresis
loss per cycle is or is not a function of the speed with which the
cycle is traversed. Early experiments by C.P. Steinmetz and
others seemed to show that there was a difference between slow-speed
and high-speed hysteresis cycles, but later experiments
by J. Hopkinson and by A. Tanakadaté, though not absolutely
exhaustive, tend to prove that up to 400 cycles per second the
hysteresis loss per cycle is practically unchanged.
Experiments made in 1896 by R. Beattie and R.C. Clinker on
magnetic hysteresis in rotating fields were partly directed to
determine whether the hysteresis loss at moderate flux densities,
such as are employed in transformer work, was the same as that
found by measurements made with alternating-current fields
on the same iron and steel specimens (see The Electrician, 1896,
231
37, p. 723). These experiments showed that over moderate ranges
of induction, such as may be expected in electro-technical work,
the hysteresis loss per cycle per cubic centimetre was practically
the same when the iron was tested in an alternating field with a
periodicity of 100, the field remaining constant in direction,
and when the iron was tested in a rotating field giving the same
maximum flux density.
With respect to the variation of hysteresis loss in magnetic
cycles having different maximum values for the flux density,
Steinmetz found that the hysteresis loss (W), as measured by
the area of the complete (B, H) cycle and expressed in ergs per
centimetre-cube per cycle, varies proportionately to a constant
called the hysteretic constant, and to the 1.6th power of the
maximum flux density (B), or W = ηB1.6.
The hysteretic constants (η) for various kinds of iron and steel
are given in the table below:—
| Metal. | Hysteretic Constant. |
| Swedish wrought iron, well annealed | .0010 to .0017 |
| Annealed cast steel of good quality; small | |
| percentage of carbon | .0017 to .0029 |
| Cast Siemens-Martin steel | .0019 to .0028 |
| Cast ingot-iron | .0021 to .0026 |
| Cast steel, with higher percentages of carbon, | |
| or inferior qualities of wrought iron | .0031 to .0054 |
Steinmetz’s law, though not strictly true for very low or very
high maximum flux densities, is yet a convenient empirical rule
for obtaining approximately the hysteresis loss at any one
maximum flux density and knowing it at another, provided
these values fall within a range varying say from 1 to 9000
C.G.S. units. (See Magnetism.)
The standard maximum flux density which is adopted in
electro-technical work is 2500, hence in the construction of the
cores of alternating-current electromagnets and transformers
iron has to be employed having a known hysteretic constant
at the standard flux density. It is generally expressed by stating
the number of watts per ℔ of metal which would be dissipated
for a frequency of 100 cycles, and a maximum flux density
(B max.) during the cycle of 2500. In the case of good iron or
steel for transformer-core making, it should not exceed 1.25 watt
per ℔ per 100 cycles per 2500 B (maximum value).
It has been found that if the sheet iron employed for cores
of alternating electromagnets or transformers is heated to a
temperature somewhere in the neighbourhood of 200° C. the
hysteresis loss is very greatly increased. It was noticed in 1894
by G.W. Partridge that alternating-current transformers which
had been in use some time had a very considerably augmented
core loss when compared with their initial condition. O.T.
Bláthy and W.M. Mordey in 1895 showed that this augmentation
in hysteresis loss in iron was due to heating. H.F. Parshall
investigated the effect up to moderate temperatures, such as
140° C., and an extensive series of experiments was made in
1898 by S.R. Roget (Proc. Roy. Soc., 1898, 63, p. 258, and 64,
p. 150). Roget found that below 40° C. a rise in temperature
did not produce any augmentation in the hysteresis loss in iron,
but if it is heated to between 40° C. and 135° C. the hysteresis
loss increases continuously with time, and this increase is now
called “ageing” of the iron. It proceeds more slowly as the
temperature is higher. If heated to above 135° C., the hysteresis
loss soon attains a maximum, but then begins to decrease.
Certain specimens heated to 160° C. were found to have their
hysteresis loss doubled in a few days. The effect seems to come
to a maximum at about 180° C. or 200° C. Mere lapse of time
does not remove the increase, but if the iron is reannealed the
augmentation in hysteresis disappears. If the iron is heated
to a higher temperature, say between 300° C. and 700° C.,
Roget found the initial rise of hysteresis happens more quickly,
but that the metal soon settles down into a state in which the
hysteresis loss has a small but still augmented constant value.
The augmentation in value, however, becomes more nearly zero
as the temperature approaches 700° C. Brands of steel are now
obtainable which do not age in this manner, but these non-ageing
varieties of steel have not generally such low initial hysteresis
values as the “Swedish Iron,” commonly considered best for
the cores of transformers and alternating-current magnets.
The following conclusions have been reached in the matter:—(1)
Iron and mild steel in the annealed state are more liable to
change their hysteresis value by heating than when in the
harder condition; (2) all changes are removed by re-annealing;
(3) the changes thus produced by heating affect not only the
amount of the hysteresis loss, but also the form of the lower part
of the (B, H) curve.
Forms of Electromagnet.—The form which an electromagnet
must take will greatly depend upon the purposes for which it is
to be used. A design or form of electromagnet which will be
very suitable for some purposes will be useless for others.
Supposing it is desired to make an electromagnet which shall
be capable of undergoing very rapid changes of strength, it
must have such a form that the coercivity of the material is
overcome by a self-demagnetizing force. This can be achieved
by making the magnet in the form of a short and stout bar rather
than a long thin one. It has already been explained that the
ends or poles of a polar magnet exert a demagnetizing power
upon the mass of the metal in the interior of the bar. If then
the electromagnet has the form of a long thin bar, the length of
which is several hundred times its diameter, the poles are very
far removed from the centre of the bar, and the demagnetizing
action will be very feeble; such a long thin electromagnet,
although made of very soft iron, retains a considerable amount
of magnetism after the magnetizing force is withdrawn. On the
other hand, a very thick bar very quickly demagnetizes itself,
because no part of the metal is far removed from the action of the
free poles. Hence when, as in many telegraphic instruments, a
piece of soft iron, called an armature, has to be attracted to the
poles of a horseshoe-shaped electromagnet, this armature should
be prevented from quite touching the polar surfaces of the magnet.
If a soft iron mass does quite touch the poles, then it completes
the magnetic circuit and abolishes the free poles, and the magnet
is to a very large extent deprived of its self-demagnetizing power.
This is the explanation of the well-known fact that after exciting
the electromagnet and then stopping the current, it still requires
a good pull to detach the “keeper”; but when once the keeper
has been detached, the magnetism is found to have nearly
disappeared. An excellent form of electromagnet for the production
of very powerful fields has been designed by H. du
Bois (fig. 6).
 |
| Fig. 6.—Du Bois’s Electromagnet. |
Various forms of electromagnets used in connexion with
232
dynamo machines are considered in the article Dynamo, and there
is, therefore, no necessity to refer particularly to the numerous
different shapes and types employed in electrotechnics.
Bibliography.—For additional information on the above subject
the reader may be referred to the following works and original
papers:—
H. du Bois, The Magnetic Circuit in Theory and Practice; S.P.
Thompson, The Electromagnet; J.A. Fleming, Magnets and Electric
Currents; J.A. Ewing, Magnetic Induction in Iron and other Metals;
J.A. Fleming, “The Ferromagnetic Properties of Iron and Steel,”
Proceedings of Sheffield Society of Engineers and Metallurgists (Oct.
1897); J.A. Ewing, “The Magnetic Testing of Iron and Steel,”
Proc. Inst. Civ. Eng., 1896, 126, p. 185; H.F. Parshall, “The
Magnetic Data of Iron and Steel,” Proc. Inst. Civ. Eng., 1896,
126, p. 220; J.A. Ewing, “The Molecular Theory of Induced
Magnetism,” Phil. Mag., Sept. 1890; W.M. Mordey, “Slow Changes
in the Permeability of Iron,” Proc. Roy. Soc. 57, p. 224; J.A.
Ewing, “Magnetism,” James Forrest Lecture, Proc. Inst. Civ. Eng.
138; S.P. Thompson, “Electromagnetic Mechanism,” Electrician,
26, pp. 238, 269, 293; J.A. Ewing, “Experimental Researches in
Magnetism,” Phil. Trans., 1885, part ii.; Ewing and Klassen,
“Magnetic Qualities of Iron,” Proc. Roy. Soc., 1893.
(J. A. F.)
1 In the Annals of Philosophy for November 1821 is a long article
entitled “Electromagnetism” by Oersted, in which he gives a
detailed account of his discovery. He had his thoughts turned to
it as far back as 1813, but not until the 20th of July 1820 had he
actually made his discovery. He seems to have been arranging a
compass needle to observe any deflections during a storm, and placed
near it a platinum wire through which a galvanic current was passed.
2 See Trans. Soc. Arts, 1825, 43, p. 38, in which a figure of Sturgeon’s
electromagnet is given as well as of other pieces of apparatus for
which the Society granted him a premium and a silver medal.
3 See S.P. Thompson, The Electromagnet (London, 1891); J.A.
Fleming, A Handbook for the Electrical Laboratory and Testing Room,
vol. 2 (London, 1903); J.A. Ewing, Magnetic Induction in Iron and
other Metals (London, 1903, 3rd ed.).
ELECTROMETALLURGY. The present article, as explained
under Electrochemistry, treats only of those processes in
which electricity is applied to the production of chemical reactions
or molecular changes at furnace temperatures. In
many of these the application of heat is necessary to bring
the substances used into the liquid state for the purpose of
electrolysis, aqueous solutions being unsuitable. Among the
earliest experiments in this branch of the subject were
those of Sir H. Davy, who in 1807 (Phil. Trans., 1808,
p. 1), produced the alkali metals by passing an intense current
of electricity from a platinum wire to a platinum dish,
through a mass of fused caustic alkali. The action was started
in the cold, the alkali being slightly moistened to render it a
conductor; then, as the current passed, heat was produced
and the alkali fused, the metal being deposited in the liquid
condition. Later, A. Matthiessen (Quarterly Journ. Chem. Soc.
viii. 30) obtained potassium by the electrolysis of a mixture
of potassium and calcium chlorides fused over a lamp. There
are here foreshadowed two types of electrolytic furnace-operations:
(a) those in which external heating maintains the
electrolyte in the fused condition, and (b) those in which a current-density
is applied sufficiently high to develop the heat necessary
to effect this object unaided. Much of the earlier electro-metallurgical
work was done with furnaces of the (a) type, while
nearly all the later developments have been with those of class
(b). There is a third class of operations, exemplified by the
manufacture of calcium carbide, in which electricity is employed
solely as a heating agent; these are termed electrothermal, as
distinguished from electrolytic. In certain electrothermal
processes (e.g. calcium carbide production) the heat from the
current is employed in raising mixtures of substances to the
temperature at which a desired chemical reaction will take
place between them, while in others (e.g. the production of
graphite from coke or gas-carbon) the heat is applied solely to
the production of molecular or physical changes. In ordinary
electrolytic work only the continuous current may of course
be used, but in electrothermal work an alternating current is
equally available.
Electric Furnaces.—Independently of the question of the
application of external heating, the furnaces used in electrometallurgy
may be broadly classified into (i.) arc furnaces, in
which the intense heat of the electric arc is utilized, and (ii.)
resistance and incandescence furnaces, in which the heat is
generated by an electric current overcoming the resistance
of an inferior conductor.
Excepting such experimental arrangements as that of C.M.
Despretz (C.R., 1849, 29) for use on a small scale in the laboratory,
Pichou in France and J.H. Johnson in England
appear, in 1853, to have introduced the earliest
Arc furnaces.
practical form of furnace. In these arrangements,
which were similar if not identical, the furnace charge was
crushed to a fine powder and passed through two or more electric
arcs in succession. When used for ore smelting, the reduced
metal and the accompanying slag were to be caught, after leaving
the arc and while still liquid, in a hearth fired with ordinary
fuel. Although this primitive furnace could be made to act, its
efficiency was low, and the use of a separate fire was disadvantageous.
In 1878 Sir William Siemens patented a form of furnace1
which is the type of a very large number of those designed by
later inventors.
In the best-known form a plumbago crucible was used with a
hole cut in the bottom to receive a carbon rod, which was ground
in so as to make a tight joint. This rod was connected with the
positive pole of the dynamo or electric generator. The crucible
was fitted with a cover in which were two holes; one at the side to
serve at once as sight-hole and charging door, the other in the
centre to allow a second carbon rod to pass freely (without touching)
into the interior. This rod was connected with the negative pole of
the generator, and was suspended from one arm of a balance-beam,
while from the other end of the beam was suspended a vertical hollow
iron cylinder, which could be moved into or out of a wire coil or
solenoid joined as a shunt across the two carbon rods of the furnace.
The solenoid was above the iron cylinder, the supporting rod of which
passed through it as a core. When the furnace with this well-known
regulating device was to be used, say, for the melting of metals or
other conductors of electricity, the fragments of metal were placed
in the crucible and the positive electrode was brought near them.
Immediately the current passed through the solenoid it caused the
iron cylinder to rise, and, by means of its supporting rod, forced the
end of the balance beam upwards, so depressing the other end that
the negative carbon rod was forced downwards into contact with the
metal in the crucible. This action completed the furnace-circuit,
and current passed freely from the positive carbon through the
fragments of metal to the negative carbon, thereby reducing the
current through the shunt. At once the attractive force of the
solenoid on the iron cylinder was automatically reduced, and the
falling of the latter caused the negative carbon to rise, starting an
arc between it and the metal in the crucible. A counterpoise was
placed on the solenoid end of the balance beam to act against the
attraction of the solenoid, the position of the counterpoise determining
the length of the arc in the crucible. Any change in the resistance
of the arc, either by lengthening, due to the sinking of the charge
in the crucible, or by the burning of the carbon, affected the proportion
of current flowing in the two shunt circuits, and so altered
the position of the iron cylinder in the solenoid that the length of
arc was, within limits, automatically regulated. Were it not for the
use of some such device the arc would be liable to constant fluctuation
and to frequent extinction. The crucible was surrounded with a
bad conductor of heat to minimize loss by radiation. The positive
carbon was in some cases replaced by a water-cooled metal tube, or
ferrule, closed, of course, at the end inserted in the crucible. Several
modifications were proposed, in one of which, intended for the heating
of non-conducting substances, the electrodes were passed horizontally
through perforations in the upper part of the crucible walls, and the
charge in the lower part of the crucible was heated by radiation.
The furnace used by Henri Moissan in his experiments on
reactions at high temperatures, on the fusion and volatilization
of refractory materials, and on the formation of carbides, silicides
and borides of various metals, consisted, in its simplest form,
of two superposed blocks of lime or of limestone with a central
cavity cut in the lower block, and with a corresponding but much
shallower inverted cavity in the upper block, which thus formed
the lid of the furnace. Horizontal channels were cut on opposite
walls, through which the carbon poles or electrodes were passed
into the upper part of the cavity. Such a furnace, to take a
current of 4 H.P. (say, of 60 amperes and 50 volts), measured
externally about 6 by 6 by 7 in., and the electrodes were about
0.4 in. in diameter, while for a current of 100 H.P. (say, of 746
amperes and 100 volts) it measured about 14 by 12 by 14 in.,
and the electrodes were about 1.5 in. in diameter. In the latter
case the crucible, which was placed in the cavity immediately
beneath the arc, was about 3 in. in diameter (internally), and
about 3½ in. in height. The fact that energy is being used at
so high a rate as 100 H.P. on so small a charge of material
sufficiently indicates that the furnace is only used for experimental
work, or for the fusion of metals which, like tungsten
or chromium, can only be melted at temperatures attainable
by electrical means. Moissan succeeded in fusing about ¾ ℔ of
either of these metals in 5 or 6 minutes in a furnace similar to
that last described. He also arranged an experimental tube-furnace
by passing a carbon tube horizontally beneath the arc
233
in the cavity of the lime blocks. When prolonged heating is
required at very high temperatures it is found necessary to line
the furnace-cavity with alternate layers of magnesia and carbon,
taking care that the lamina next to the lime is of magnesia;
if this were not done the lime in contact with the carbon crucible
would form calcium carbide and would slag down, but magnesia
does not yield a carbide in this way. Chaplet has patented
a muffle or tube furnace, similar in principle, for use on a larger
scale, with a number of electrodes placed above and below the
muffle-tube. The arc furnaces now widely used in the manufacture
of calcium carbide on a large scale are chiefly developments
of the Siemens furnace. But whereas, from its construction,
the Siemens furnace was intermittent in operation,
necessitating stoppage of the current while the contents of the
crucible were poured out, many of the newer forms are specially
designed either to minimize the time required in effecting the
withdrawal of one charge and the introduction of the next, or
to ensure absolute continuity of action, raw material being
constantly charged in at the top and the finished substance
and by-products (slag, &c.) withdrawn either continuously or
at intervals, as sufficient quantity shall have accumulated. In
the King furnace, for example, the crucible, or lowest part of the
furnace, is made detachable, so that when full it may be removed
and an empty crucible substituted. In the United States a
revolving furnace is used which is quite continuous in action.
The class of furnaces heated by electrically incandescent
materials has been divided by Borchers into two groups: (1)
those in which the substance is heated by contact
with a substance offering a high resistance to the
Incandescence furnaces.
current passing through it, and (2) those in which the
substance to be heated itself affords the resistance to
the passage of the current whereby electric energy is converted
into heat. Practically the first of these furnaces was that of
Despretz, in which the mixture to be heated was placed in a
carbon tube rendered incandescent by the passage of a current
through its substance from end to end. In 1880 W. Borchers
introduced his resistance-furnace, which, in one sense, is the
converse of the Despretz apparatus. A thin carbon pencil,
forming a bridge between two stout carbon rods, is set in the
midst of the mixture to be heated. On passing a current through
the carbon the small rod is heated to incandescence, and imparts
heat to the surrounding mass. On a larger scale several pencils
are used to make the connexions between carbon blocks which
form the end walls of the furnace, while the side walls are of
fire-brick laid upon one another without mortar. Many of the
furnaces now in constant use depend mainly on this principle,
a core of granular carbon fragments stamped together in the
direct line between the electrodes, as in Acheson’s carborundum
furnace, being substituted for the carbon pencils. In other
cases carbon fragments are mixed throughout the charge, as
in E.H. and A.H. Cowles’s zinc-smelting retort. In practice, in
these furnaces, it is possible for small local arcs to be temporarily
set up by the shifting of the charge, and these would contribute
to the heating of the mass. In the remaining class of furnace,
in which the electrical resistance of the charge itself is utilized,
are the continuous-current furnaces, such as are used for the
smelting of aluminium, and those alternating-current furnaces,
(e.g. for the production of calcium carbide) in which a portion
of the charge is first actually fused, and then maintained in the
molten condition by the current passing through it, while the
reaction between further portions of the charge is proceeding.
For ordinary metallurgical work the electric furnace, requiring
as it does (excepting where waterfalls or other cheap sources
of power are available) the intervention of the boiler
and steam-engine, or of the gas or oil engine, with a
Uses and advantages.
consequent loss of energy, has not usually proved so
economical as an ordinary direct fired furnace. But in
some cases in which the current is used for electrolysis and for
the production of extremely high temperatures, for which the
calorific intensity of ordinary fuel is insufficient, the electric
furnace is employed with advantage. The temperature of the
electric furnace, whether of the arc or incandescence type, is
practically limited to that at which the least easily vaporized
material available for electrodes is converted into vapour. This
material is carbon, and as its vaporizing point is (estimated at)
over 3500° C., and less than 4000° C., the temperature of the
electric furnace cannot rise much above 3500° C. (6330° F.);
but H. Moissan showed that at this temperature the most stable
of mineral combinations are dissociated, and the most refractory
elements are converted into vapour, only certain borides, silicides
and metallic carbides having been found to resist the action of
the heat. It is not necessary that all electric furnaces shall be
run at these high temperatures; obviously, those of the incandescence
or resistance type may be worked at any convenient
temperature below the maximum. The electric furnace has
several advantages as compared with some of the ordinary types
of furnace, arising from the fact that the heat is generated from
within the mass of material operated upon, and (unlike the blast-furnace,
which presents the same advantage) without a large
volume of gaseous products of combustion and atmospheric
nitrogen being passed through it. In ordinary reverberatory
and other heating furnaces the burning fuel is without the mass,
so that the vessel containing the charge, and other parts of the
plant, are raised to a higher temperature than would otherwise
be necessary, in order to compensate for losses by radiation,
convection and conduction. This advantage is especially
observed in some cases in which the charge of the furnace is
liable to attack the containing vessel at high temperatures,
as it is often possible to maintain the outer walls of the electric
furnace relatively cool, and even to keep them lined with a
protecting crust of unfused charge. Again, the construction
of electric furnaces may often be exceedingly crude and simple;
in the carborundum furnace, for example, the outer walls are
of loosely piled bricks, and in one type of furnace the charge is
simply heaped on the ground around the carbon resistance used
for heating, without containing-walls of any kind. There is,
however, one (not insuperable) drawback in the use of the electric
furnace for the smelting of pure metals. Ordinarily carbon is
used as the electrode material, but when carbon comes in contact
at high temperatures with any metal that is capable of forming
a carbide a certain amount of combination between them is inevitable,
and the carbon thus introduced impairs the mechanical
properties of the ultimate metallic product. Aluminium, iron,
platinum and many other metals may thus take up so much
carbon as to become brittle and unforgeable. It is for this reason
that Siemens, Borchers and others substituted a hollow water-cooled
metal block for the carbon cathode upon which the melted
metal rests while in the furnace. Liquid metal coming in contact
with such a surface forms a crust of solidified metal over it, and
this crust thickens up to a certain point, namely, until the heat
from within the furnace just overbalances that lost by conduction
through the solidified crust and the cathode material to the flowing
water. In such an arrangement, after the first instant, the
melted metal in the furnace does not come in contact with the
cathode material.
Electrothermal Processes.—In these processes the electric
current is used solely to generate heat, either to induce chemical
reactions between admixed substances, or to produce a physical
(allotropic) modification of a given substance. Borchers predicted
that, at the high temperatures available with the electric
furnace, every oxide would prove to be reducible by the action
of carbon, and this prediction has in most instances been justified.
Alumina and lime, for example, which cannot be reduced at
ordinary furnace temperatures, readily give up their oxygen
to carbon in the electric furnace, and then combine with an
excess of carbon to form metallic carbides. In 1885 the brothers
Cowles patented a process for the electrothermal reduction of
oxidized ores by exposure to an intense current of electricity
when admixed with carbon in a retort. Later in that year they
patented a process for the reduction of aluminium by carbon,
and in 1886 an electric furnace with sliding carbon rods passed
through the end walls to the centre of a rectangular furnace.
The impossibility of working with just sufficient carbon to reduce
the alumina, without using any excess which would be free to
234
form at least so much carbide as would suffice, when diffused
through the metal, to render it brittle, practically restricts the
Aluminium alloys.
use of such processes to the production of aluminium
alloys. Aluminium bronze (aluminium and copper)
and ferro-aluminium (aluminium and iron) have
been made in this way; the latter is the more satisfactory
product, because a certain proportion of carbon is
expected in an alloy of this character, as in ferromanganese and
cast iron, and its presence is not objectionable. The furnace is
built of fire-brick, and may measure (internally) 5 ft. in length
by 1 ft. 8 in. in width, and 3 ft. in height. Into each end wall
is built a short iron tube sloping downwards towards the centre,
and through this is passed a bundle of five 3-in. carbon rods,
bound together at the outer end by being cast into a head of
cast iron for use with iron alloys, or of cast copper for aluminium
bronze. This head slides freely in the cast iron tubes, and is
connected by a copper rod with one of the terminals of the
dynamo supplying the current. The carbons can thus, by the
application of suitable mechanism, be withdrawn from or plunged
into the furnace at will. In starting the furnace, the bottom
is prepared by ramming it with charcoal-powder that has been
soaked in milk of lime and dried, so that each particle is coated
with a film of lime, which serves to reduce the loss of current
by conduction through the lining when the furnace becomes
hot. A sheet iron case is then placed within the furnace, and
the space between it and the walls rammed with limed charcoal;
the interior is filled with fragments of the iron or copper to be
alloyed, mixed with alumina and coarse charcoal, broken pieces
of carbon being placed in position to connect the electrodes.
The iron case is then removed, the whole is covered with charcoal,
and a cast iron cover with a central flue is placed above all.
The current, either continuous or alternating, is then started,
and continued for about 1 to 1½ hours, until the operation is
complete, the carbon rods being gradually withdrawn as the
action proceeds. In such a furnace a continuous current, for
example, of 3000 amperes, at 50 to 60 volts, may be used at first,
increasing to 5000 amperes in about half an hour. The reduction
is not due to electrolysis, but to the action of carbon on alumina,
a part of the carbon in the charge being consumed and evolved
as carbon monoxide gas, which burns at the orifice in the cover
so long as reduction is taking place. The reduced aluminium
alloys itself immediately with the fused globules of metal in
its midst, and as the charge becomes reduced the globules of
alloy unite until, in the end, they are run out of the tap-hole
after the current has been diverted to another furnace. It was
found in practice (in 1889) that the expenditure of energy per
pound of reduced aluminium was about 23 H.P.-hours, a
number considerably in excess of that required at the present
time for the production of pure aluminium by the electrolytic
process described in the article Aluminium. Calcium carbide,
graphite (q.v.), phosphorus (q.v.) and carborundum (q.v.) are now
extensively manufactured by the operations outlined above.
Electrolytic Processes.—The isolation of the metals sodium
and potassium by Sir Humphry Davy in 1807 by the electrolysis
of the fused hydroxides was one of the earliest applications of
the electric current to the extraction of metals. This pioneering
work showed little development until about the middle of the
19th century. In 1852 magnesium was isolated electrolytically
by R. Bunsen, and this process subsequently received much
attention at the hands of Moissan and Borchers. Two years
later Bunsen and H.E. Sainte Claire Deville working independently
obtained aluminium (q.v.) by the electrolysis of the fused
double sodium aluminium chloride. Since that date other
processes have been devised and the electrolytic processes have
entirely replaced the older methods of reduction with sodium.
Methods have also been discovered for the electrolytic manufacture
of calcium (q.v.), which have had the effect of converting
a laboratory curiosity into a product of commercial importance.
Barium and strontium have also been produced by electro-metallurgical
methods, but the processes have only a laboratory
interest at present. Lead, zinc and other metals have also been
reduced in this manner.
For further information the following books, in addition to those
mentioned at the end of the article Electrochemistry, may be
consulted: Borchers, Handbuch der Elektrochemie; Electric Furnaces
(Eng. trans. by H.G. Solomon, 1908); Moissan, The Electric Furnace
(1904); J. Escard, Fours électriques (1905); Les Industries électrochimiques
(1907).
(W. G. M.)
1 Cf. Siemens’s account of the use of this furnace for experimental
purposes in British Association Report for 1882.
ELECTROMETER, an instrument for measuring difference
of potential, which operates by means of electrostatic force
and gives the measurement either in arbitrary or in absolute
units (see Units, Physical). In the last case the instrument
is called an absolute electrometer. Lord Kelvin has classified
electrometers into (1) Repulsion, (2) Attracted disk, and (3)
Symmetrical electrometers (see W. Thomson, Brit. Assoc. Report,
1867, or Reprinted Papers on Electrostatics and Magnetization,
p. 261).
Repulsion Electrometers.—The simplest form of repulsion
electrometer is W. Henley’s pith ball electrometer (Phil. Trans.,
1772, 63, p. 359) in which the repulsion of a straw ending in a
pith ball from a fixed stem is indicated on a graduated arc (see
Electroscope). A double pith ball repulsion electrometer
was employed by T. Cavallo in 1777.
It may be pointed out that such an arrangement is not merely an
arbitrary electrometer, but may become an absolute electrometer
within certain rough limits. Let two spherical pith balls of radius r
and weight W, covered with gold-leaf so as to be conducting, be
suspended by parallel silk threads of length l so as just to touch each
other. If then the balls are both charged to a potential V they will
repel each other, and the threads will stand out at an angle 2θ,
which can be observed on a protractor. Since the electrical repulsion
of the balls is equal to C²V²4l² sin² θ dynes, where C = r is the capacity
of either ball, and this force is balanced by the restoring force due
to their weight, Wg dynes, where g is the acceleration of gravity, it
is easy to show that we have
as an expression for their common potential V, provided that the
balls are small and their distance sufficiently great not sensibly to
disturb the uniformity of electric charge upon them. Observation of
θ with measurement of the value of l and r reckoned in centimetres
and W in grammes gives us the potential difference of the balls in
absolute C.G.S. or electrostatic units. The gold-leaf electroscope
invented by Abraham Bennet (see Electroscope) can in like
manner, by the addition of a scale to observe the divergence of the
gold-leaves, be made a repulsion electrometer.
 |
| Fig. 1.—Snow-Harris’s Disk Electrometer. |
Attracted Disk Electrometers.—A form of attracted disk
absolute electrometer was devised by A. Volta. It consisted
of a plane conducting plate forming one pan of a balance which
was suspended over another insulated plate which could be
electrified. The attraction between the two plates was balanced
by a weight put in
the opposite pan.
A similar electric
balance was subsequently
devised by
Sir W. Snow-Harris,1
one of whose instruments
is shown in
fig. 1. C is an insulated
disk over
which is suspended
another disk attached
to the arm
of a balance. A
weight is put in the
opposite scale pan
and a measured
charge of electricity
is given to the disk
C just sufficient to
tip over the balance.
Snow-Harris found that this charge varied as the square root
of the weight in the opposite pan, thus showing that the
235
attraction between the disks at given distance apart varies as
the square of their difference of potential.
The most important improvements in connexion with electrometers
are due, however, to Lord Kelvin, who introduced the
guard plate and used gravity or the torsion of a wire as a means
for evaluating the electrical forces.
 |
Fig. 2.—Kelvin’s Portable
Electrometer. |
Fig. 3. |
His portable electrometer is shown in fig. 2. H H (see fig. 3) is a
plane disk of metal called the guard plate, fixed to the inner coating
of a small Leyden jar (see fig. 2). At F a square hole is cut out of
H H, and into this fits loosely without touching, like a trap door,
a square piece of aluminium foil having a projecting tail, which carries
at its end a stirrup L, crossed by a fine hair (see fig. 3). The square
piece of aluminium is pivoted round a horizontal stretched wire.
If then another horizontal disk G is placed over the disk H H and a
difference of potential made between G and H H, the movable
aluminium trap door F will be attracted by the fixed plate G.
Matters are so arranged by giving a torsion to the wire carrying the
aluminium disk F that for a certain potential difference between the
plates H and G, the movable part F comes into a definite sighted
position, which is observed by means of a small lens. The plate G
(see fig. 2) is moved up and down, parallel to itself, by means of a
screw. In using the instrument the conductor, whose potential is
to be tested, is connected to the plate G. Let this potential be
denoted by V, and let v be the potential of the guard plate and the
aluminium flap. This last potential is maintained constant by
guard plate and flap being part of the interior coating of a charged
Leyden jar. Since the distribution of electricity may be considered
to be constant over the surface S of the attracted disk, the mechanical
force f on it is given by the expression,2
 |
| Fig. 4.—Kelvin’s Absolute
Electrometer. |
where d is the distance between the two plates. If this distance is
varied until the attracted disk comes into a definite sighted position
as seen by observing the end of the
index through the lens, then since the
force f is constant, being due to the
torque applied by the wire for a definite
angle of twist, it follows that the difference
of potential of the two plates
varies as their distance. If then two
experiments are made, first with the
upper plate connected to earth, and
secondly, connected to the object being
tested, we get an expression for the
potential V of this conductor in the
form
V = A (d′ − d),
where d and d′ are the distances of the
fixed and movable plates from one
another in the two cases, and A is some
constant. We thus find V in terms of
the constant and the difference of the
two screw readings.
Lord Kelvin’s absolute electrometer
(fig. 4) involves the same principle.
There is a certain fixed guard disk B
having a hole in it which is loosely occupied
by an aluminium trap door plate,
shielded by D and suspended on springs, so that its surface is parallel
with that of the guard plate. Parallel to this is a second movable plate
A, the distances between the two being measurable by means of a
screw. The movable plate can be drawn down into a definite sighted
position when a difference of potential is made between the two
plates. This sighted position is such that the surface of the trap
door plate is level with that of the guard plate, and is determined
by observations made with the lenses H and L. The movable plate
can be thus depressed by placing on it a certain standard weight W
grammes.
Suppose it is required to measure the difference of potentials V
and V′ of two conductors. First one and then the other conductor
is connected with the electrode of the lower or movable plate, which
is moved by the screw until the index attached to the attracted disk
shows it to be in the sighted position. Let the screw readings in
the two cases be d and d′. If W is the weight required to depress the
attracted disk into the same sighted position when the plates are
unelectrified and g is the acceleration of gravity, then the difference
of potentials of the conductors tested is expressed by the formula
| V − V′ = (d − d′) √ | 8πgW |
, |
| S |
where S denotes the area of the attracted disk.
The difference of potentials is thus determined in terms of a
weight, an area and a distance, in absolute C.G.S. measure or electrostatic
units.
 |
| Fig. 5. |
Symmetrical Electrometers include the dry pile electrometer
and Kelvin’s quadrant electrometer. The principle underlying
these instruments is that we can
measure differences of potential by means
of the motion of an electrified body in a
symmetrical field of electric force. In the
dry pile electrometer a single gold-leaf is
hung up between two plates which are
connected to the opposite terminals of a
dry pile so that a certain constant difference
of potential exists between these
plates. The original inventor of this
instrument was T.G.B. Behrens (Gilb.
Ann., 1806, 23), but it generally bears the name of J.G.F.
von Bohnenberger, who slightly modified its form. G.T. Fechner
introduced the important improvement of using only one pile,
which he removed from the immediate neighbourhood of the
suspended leaf. W.G. Hankel still further improved the dry
pile electrometer by giving a slow motion movement to the two
plates, and substituted a galvanic battery with a large number of
cells for the dry pile, and also employed a divided scale to measure
the movements of the gold-leaf (Pogg. Ann., 1858, 103). If the
gold-leaf is unelectrified, it is not acted upon by the two plates
placed at equal distances on either side of it, but if its potential
is raised or lowered it is attracted by one disk and repelled by
the other, and the displacement becomes a measure of its
potential.
 |
| Fig. 6.—Kelvin’s Quadrant Electrometer. |
A vast improvement in this instrument was made by the
invention of the quadrant electrometer by Lord Kelvin, which is
the most sensitive form
of electrometer yet devised.
In this instrument
(see fig. 5) a flat paddle-shaped
needle of aluminium
foil U is supported
by a bifilar suspension
consisting of two cocoon
fibres. This needle is suspended
in the interior
of a glass vessel partly
coated with tin-foil on
the outside and inside,
forming therefore a Leyden
jar (see fig. 6). In
the bottom of the vessel
is placed some sulphuric
acid, and a platinum wire
attached to the suspended
needle dips into this acid.
By giving a charge to
this Leyden jar the needle can thus be maintained at a certain
constant high potential. The needle is enclosed by a sort of
flat box divided into four insulated quadrants A, B, C, D (fig. 5),
whence the name. The opposite quadrants are connected together
by thin platinum wires. These quadrants are insulated
236
from the needle and from the case, and the two pairs are connected
to two electrodes. When the instrument is to be used to determine
the potential difference between two conductors, they are
connected to the two opposite pairs of quadrants. The needle
in its normal position is symmetrically placed with regard to
the quadrants, and carries a mirror by means of which its displacement
can be observed in the usual manner by reflecting
the ray of light from it. If the two quadrants are at different
potentials, the needle moves from one quadrant towards the
other, and the image of a spot of light on the scale is therefore
displaced. Lord Kelvin provided the instrument with two
necessary adjuncts, viz. a replenisher or rotating electrophorus
(q.v.), by means of which the charge of the Leyden jar which forms
the enclosing vessel can be increased or diminished, and also a
small aluminium balance plate or gauge, which is in principle the
same as the attracted disk portable electrometer by means of
which the potential of the inner coating of the Leyden jar is
preserved at a known value.
According to the mathematical theory of the instrument,3 if V
and V′ are the potentials of the quadrants and v is the potential of
the needle, then the torque acting upon the needle to cause rotation
is given by the expression,
C (V − V′) {v − ½ (V + V′)},
where C is some constant. If v is very large compared with the
mean value of the potentials of the two quadrants, as it usually is,
then the above expression indicates that the couple varies as the
difference of the potentials between the quadrants.
Dr J. Hopkinson found, however, before 1885, that the above
formula does not agree with observed facts (Proc. Phys. Soc. Lond.,
1885, 7, p. 7). The formula indicates that the sensibility of the instrument
should increase with the charge of the Leyden jar or needle,
whereas Hopkinson found that as the potential of the needle was
increased by working the replenisher of the jar, the deflection due
to three volts difference between the quadrants first increased and
then diminished. He found that when the potential of the needle
exceeded a certain value, of about 200 volts, for the particular
instrument he was using (made by White of Glasgow), the above
formula did not hold good. W.E. Ayrton, J. Perry and W.E.
Sumpner, who in 1886 had noticed the same fact as Hopkinson,
investigated the matter in 1891 (Proc. Roy. Soc., 1891, 50, p. 52;
Phil. Trans., 1891, 182, p. 519). Hopkinson had been inclined to
attribute the anomaly to an increase in the tension of the bifilar
threads, owing to a downward pull on the needle, but they showed
that this theory would not account for the discrepancy. They
found from observations that the particular quadrant electrometer
they used might be made to follow one or other of three distinct laws.
If the quadrants were near together there were certain limits between
which the potential of the needle might vary without producing more
than a small change in the deflection corresponding with the fixed
potential difference of the quadrants. For example, when the
quadrants were about 2.5 mm. apart and the suspended fibres near
together at the top, the deflection produced by a P.D. of 1.45 volts
between the quadrants only varied about 11% when the potential
of the needle varied from 896 to 3586 volts. When the fibres were
far apart at the top a similar flatness was obtained in the curve
with the quadrants about 1 mm. apart. In this case the deflection
of the needle was practically quite constant when its potential varied
from 2152 to 3227 volts. When the quadrants were about 3.9 mm.
apart, the deflection for a given P.D. between the quadrants was
almost directly proportional to the potential of the needle. In other
words, the electrometer nearly obeyed the theoretical law. Lastly,
when the quadrants were 4 mm. or more apart, the deflection increased
much more rapidly than the potential, so that a maximum
sensibility bordering on instability was obtained. Finally, these observers
traced the variation to the fact that the wire supporting the
aluminium needle as well as the wire which connects the needle with
the sulphuric acid in the Leyden jar in the White pattern of Leyden
jar is enclosed in a metallic guard tube to screen the wire from
external action. In order that the needle may project outside
the guard tube, openings are made in its two sides; hence the moment
the needle is deflected each half of it becomes unsymmetrically
placed relatively to the two metallic pieces which join the upper and
lower half of the guard tube. Guided by these experiments, Ayrton,
Perry and Sumpner constructed an improved unifilar quadrant
electrometer which was not only more sensitive than the White
pattern, but fulfilled the theoretical law of working. The bifilar
suspension was abandoned, and instead a new form of adjustable
magnetic control was adopted. All the working parts of the instrument
were supported on the base, so that on removing a glass shade
which serves as a Leyden jar they can be got at and adjusted in
position. The conclusion to which the above observers came was
that any quadrant electrometer made in any manner does not
necessarily obey a law of deflection making the deflections proportional
to the potential difference of the quadrants, but that an
electrometer can be constructed which does fulfil the above law.
The importance of this investigation resides in the fact that an
electrometer of the above pattern can be used as a wattmeter (q.v.),
provided that the deflection of the needle is proportional to the
potential difference of the quadrants. This use of the instrument
was proposed simultaneously in 1881 by Professors Ayrton and G.F.
Fitzgerald and M.A. Potier. Suppose we have an inductive and a
non-inductive circuit in series, which is traversed by a periodic
current, and that we desire to know the power being absorbed to the
inductive circuit. Let v1, v2, v3 be the instantaneous potentials of
the two ends and middle of the circuit; let a quadrant electrometer
be connected first with the quadrants to the two ends of the inductive
circuit and the needle to the far end of the non-inductive circuit,
and then secondly with the needle connected to one of the quadrants
(see fig. 5). Assuming the electrometer to obey the above-mentioned
theoretical law, the first reading is proportional to
| v1 − v2
{ v3 − | v1 + v2 |
} |
| 2 |
and the second to
| v1 − v2
{ v2 − | v1 + v2 |
}. |
| 2 |
The difference of the readings is then proportional to
(v1 − v2) (v2 − v3).
But this last expression is proportional to the instantaneous power
taken up in the inductive circuit, and hence the difference of the
two readings of the electrometer is proportional to the mean power
taken up in the circuit (Phil. Mag., 1891, 32, p. 206). Ayrton and
Perry and also P.R. Blondlot and P. Curie afterwards suggested
that a single electrometer could be constructed with two pairs of
quadrants and a duplicate needle on one stem, so as to make two
readings simultaneously and produce a deflection proportional at
once to the power being taken up in the inductive circuit.
 |
| Fig. 7.—Quadrant Electrometer. Dolezalek Pattern. |
Quadrant electrometers have also been designed especially
for measuring extremely small potential differences. An instrument
of this kind has been constructed by Dr. F. Dolezalek
(fig. 7). The needle and quadrants are of small size, and the
electrostatic capacity is correspondingly small. The quadrants
are mounted on pillars of amber which afford a very high
insulation. The needle, a piece of paddle-shaped paper thinly
coated with silver foil, is suspended by a quartz fibre, its extreme
lightness making it possible to use a very feeble controlling force
without rendering the period of oscillation unduly great. The
resistance offered by the air to a needle of such light construction
suffices to render the motion nearly dead-beat. Throughout a
wide range the deflections are proportional to the potential
difference producing them. The needle is charged to a potential
237
of 50 to 200 volts by means of a dry pile or voltaic battery, or
from a lighting circuit. To facilitate the communication of
the charge to the needle, the quartz fibre and its attachments
are rendered conductive by a thin film of solution of hygroscopic
salt such as calcium chloride. The lightness of the needle enables
the instrument to be moved without fear of damaging the suspension.
The upper end of the quartz fibre is rotated by a torsion
head, and a metal cover serves to screen the instrument from stray
electrostatic fields. With a quartz fibre 0.009 mm. thick and
60 mm. long, the needle being charged to 110 volts, the period
and swing of the needle was 18 seconds. With the scale at a
distance of two metres, a deflection of 130 mm. was produced by
an electromotive force of 0.1 volt. By using a quartz fibre of
about half the above diameter the sensitiveness was much
increased. An instrument of this form is valuable in measuring
small alternating currents by the fall of potential produced
down a known resistance. In the same way it may be employed
to measure high potentials by measuring the fall of potential
down a fraction of a known non-inductive resistance. In this
last case, however, the capacity of the electrometer used must be
small, otherwise an error is introduced.4
See, in addition to references already given, A. Gray, Absolute
Measurements in Electricity and Magnetism (London, 1888), vol. i.
p. 254; A. Winkelmann, Handbuch der Physik (Breslau, 1905),
pp. 58-70, which contains a large number of references to original
papers on electrometers.
(J. A. F.)
1 It is probable that an experiment of this kind had been made as
far back as 1746 by Daniel Gralath, of Danzig, who has some claims
to have suggested the word “electrometer” in connexion with it.
See Park Benjamin, The Intellectual Rise in Electricity (London, 1895),
p. 542.
2 See Maxwell, Treatise on Electricity and Magnetism (2nd ed.),
i. 308.
3 See Maxwell, Electricity and Magnetism (2nd ed., Oxford, 1881),
vol. i. p. 311.
4 See J.A. Fleming, Handbook for the Electrical Laboratory and
Testing Room, vol. i. p. 448 (London, 1901).
ELECTRON, the name suggested by Dr G. Johnstone Stoney
in 1891 for the natural unit of electricity to which he had drawn
attention in 1874, and subsequently applied to the ultra-atomic
particles carrying negative charges of electricity, of which
Professor Sir J.J. Thomson proved in 1897 that the cathode
rays consisted. The electrons, which Thomson at first called
corpuscles, are point charges of negative electricity, their inertia
showing them to have a mass equal to about 1⁄2000 that of
the hydrogen atom. They are apparently derivable from all
kinds of matter, and are believed to be components at any rate
of the chemical atom. The electronic theory of the chemical
atom supposes, in fact, that atoms are congeries of electrons
in rapid orbital motion. The size of the electron is to that of an
atom roughly in the ratio of a pin’s head to the dome of St
Paul’s cathedral. The electron is always associated with the unit
charge of negative electricity, and it has been suggested that
its inertia is wholly electrical. For further details see the
articles on Electricity; Magnetism; Matter; Radioactivity;
Conduction, Electric; The Electron Theory, E.
Fournier d’Albe (London, 1907); and the original papers of
Dr G. Johnstone Stoney, Proc. Brit. Ass. (Belfast, August 1874),
“On the Physical Units of Nature,” and Trans. Royal Dublin
Society (1891), 4, p. 583.
ELECTROPHORUS, an instrument invented by Alessandro
Volta in 1775, by which mechanical work is transformed into
electrostatic charge by the aid of a small initial charge of electricity.
The operation depends on the facts of electrostatic induction
discovered by John Canton in 1753, and, independently,
by J.K. Wilcke in 1762 (see Electricity). Volta, in a letter
to J. Priestley on the 10th of June 1775 (see Collezione dell’ opere,
ed. 1816, vol. i. p. 118), described the invention of a device
he called an elettroforo perpetuo, based on the fact that a conductor
held near an electrified body and touched by the finger
was found, when withdrawn, to possess an electric charge of
opposite sign to that of the electrified body. His electrophorus
in one form consisted of a disk of non-conducting material, such
as pitch or resin, placed between two metal sheets, one being
provided with an insulating handle. For the pitch or resin
may be substituted a sheet of glass, ebonite, india-rubber or
any other good dielectric placed upon a metallic sheet, called
the sole-plate. To use the apparatus the surface of the dielectric
is rubbed with a piece of warm flannel, silk or catskin, so as to
electrify it, and the upper metal plate is then placed upon it.
Owing to the irregularities in the surfaces of the dielectric and
upper plate the two are only in contact at a few points, and owing
to the insulating quality of the dielectric its surface electrical
charge cannot move over it. It therefore acts inductively upon
the upper plate and induces on the adjacent surface an electric
charge of opposite sign. Suppose, for instance, that the dielectric
is a plate of resin rubbed with catskin, it will then be negatively
electrified and will act by induction on the upper plate across
the film of air separating the upper resin surface and lower
surface of the upper metal plate. If the upper plate is touched
with the finger or connected to earth for a moment, a negative
charge will escape from the metal plate to earth at that moment.
The arrangement thus constitutes a condenser; the upper plate
on its under surface carries a charge of positive electricity and
the resin plate a charge of negative electricity on its upper
surface, the air film between them being the dielectric of the
condenser. If, therefore, the upper plate is elevated, mechanical
work has to be done to separate the two electric charges. Accordingly
on raising the upper plate, the charge on it, in old-fashioned
nomenclature, becomes free and can be communicated
to any other insulated conductor at a lower potential, the upper
plate thereby becoming more or less discharged. On placing
the upper plate again on the resin and touching it for a moment,
the process can be repeated, and so at the expense of mechanical
work done in lifting the upper plate against the mutual attraction
of two electric charges of opposite sign, an indefinitely large
electric charge can be accumulated and given to any other
suitable conductor. In course of time, however, the surface charge
of the resin becomes dissipated and it then has to be again excited.
To avoid the necessity for touching the upper plate every time
it is put down on the resin, a metal pin may be brought through
the insulator from the sole-plate so that each time that the
upper plate is put down on the resin it is automatically connected
to earth. We are thus able by a process of merely lifting the
upper plate repeatedly to convey a large electrical charge to
some conductor starting from the small charge produced by
friction on the resin. The above explanation does not take into
account the function of the sole-plate, which is important. The
sole-plate serves to increase the electrical capacity of the upper
plate when placed down upon the resin or excited insulator.
Hence when so placed it takes a larger charge. When touched
by the finger the upper plate is brought to zero potential. If
then the upper plate is lifted by its insulating handle its capacity
becomes diminished. Since, however, it carries with it the charge
it had when resting on the resin, its potential becomes increased
as its capacity becomes less, and it therefore rises to a high
potential, and will give a spark if the knuckle is approached to
it when it is lifted after having been touched and raised.
The study of Volta’s electrophorus at once suggested the
performance of these cyclical operations by some form of rotation
instead of elevation, and led to the invention of various
forms of doubler or multiplier. The instrument was thus the
first of a long series of machines for converting mechanical work
into electrostatic energy, and the predecessor of the modern
type of influence machine (see Electrical Machine). Volta
himself devised a double and reciprocal electrophorus and also
made mention of the subject of multiplying condensers in a paper
published in the Phil. Trans. for 1782 (p. 237, and appendix,
p. vii.). He states, however, that the use of a condenser in
connexion with an electrophorus to make evident and multiply
weak charges was due to T. Cavallo (Phil. Trans., 1788).
For further information see S.P. Thompson, “The Influence
Machine from 1788 to 1888,” Journ. Inst. Tel. Eng., 1888, 17, p. 569.
Many references to original papers connected with the electrophorus
will be found in A. Winkelmann’s Handbuch der Physik (Breslau,
1905), vol. iv. p. 48.
(J. A. F.)
ELECTROPLATING, the art of depositing metals by the
electric current. In the article Electrolysis it is shown how
the passage of an electric current through a solution containing
metallic ions involves the deposition of the metal on the cathode.
Sometimes the metal is deposited in a pulverulent form, at others
as a firm tenacious film, the nature of the deposit being dependent
upon the particular metal, the concentration of the solution, the
difference of potential between the electrodes, and other experimental
conditions. As the durability of the electro-deposited
238
coat on plated wares of all kinds is of the utmost importance,
the greatest care must be taken to ensure its complete adhesion.
This can only be effected if the surface of the metal on which
the deposit is to be made is chemically clean. Grease must
be removed by potash, whiting or other means, and tarnish
by an acid or potassium cyanide, washing in plenty of water
being resorted to after each operation. The vats for depositing
may be of enamelled iron, slate, glazed earthenware, glass,
lead-lined wood, &c. The current densities and potential
differences frequently used for some of the commoner metals
are given in the following table, taken from M’Millan’s Treatise
on Electrometallurgy. It must be remembered, however, that
variations in conditions modify the electromotive force required
for any given process. For example, a rise in temperature of
the bath causes an increase in its conductivity, so that a lower
E.M.F. will suffice to give the required current density; on the
other hand, an abnormally great distance between the electrodes,
or a diminution in acidity of an acid bath, or in the strength of
the solution used, will increase the resistance, and so require
the application of a higher E.M.F.
| Metal. | Amperes. | Volts between
Anode and
Cathode. |
Per sq. decimetre
of Cathode
Surface. | Per sq. in. of
Cathode
Surface. |
| Antimony | 0.4-0.5 | 0.02-0.03 | 1.0-1.2 |
| Brass | 0.5-0.8 | 0.03-0.05 | 3.0-4.0 |
| Copper, acid bath | 1.0-1.5 | 0.065-0.10 | 0.5-1.5 |
| Copper, alkaline bath | 0.3-0.5 | 0.02-0.03 | 3.0-5.0 |
| Gold | 0.1 | 0.006 | 0.5-4.0 |
| Iron | 0.5 | 0.03 | 1.0 |
| Nickel, at first | 1.4-1.5 | 0.09-0.10 | 5.0 |
| Nickel, after | 0.2-0.3 | 0.015-0.02 | 1.5-2.0 |
| Nickel, on zinc | 0.4 | 0.025 | 4.0-5.0 |
| Silver | 0.2-0.5 | 0.015-0.03 | 0.75-1.0 |
| Zinc | 0.3-0.6 | 0.02-0.04 | 2.5-3.0 |
Large objects are suspended in the tanks by hooks or wires,
care being taken to shift their position and so avoid wire-marks.
Small objects are often heaped together in perforated trays or
ladles, the cathode connecting-rod being buried in the midst of
them. These require constant shifting because the objects are
in contact at many points, and because the top ones shield those
below from the depositing action of the current. Hence processes
have been patented in which the objects to be plated are suspended
in revolving drums between the anodes, the rotation of the drum
causing the constant renewal of surfaces and affording a burnishing
action at the same time. Care must be taken not to expose goods
in the plating-bath to too high a current density, else they may
be “burnt”; they must never be exposed one at a time to the
full anode surface, with the current flowing in an empty bath,
but either one piece at a time should be replaced, or some of the
anodes should be transferred temporarily to the place of the
cathodes, in order to distribute the current over a sufficient
cathode-area. Burnt deposits are dark-coloured, or even pulverulent
and useless. The strength of the current may also
be regulated by introducing lengths of German silver or iron
wire, carbon rod, or other inferior conductors in the path of the
current, and a series of such resistances should always be provided
close to the tanks. Ammeters to measure the volume, and voltmeters
to determine the pressure of current supplied to the baths,
should also be provided. Very irregular surfaces may require
the use of specially shaped anodes in order that the distance
between the electrodes may be fairly uniform, otherwise the
portion of the cathode lying nearest to the anode may receive
an undue share of the current, and therefore a greater thickness
of coat. Supplementary anodes are sometimes used in difficult
cases of this kind. Large metallic surfaces (especially external
surfaces) are sometimes plated by means of a “doctor,” which,
in its simplest form, is a brush constantly wetted with the
electrolyte, with a wire anode buried amid the hairs or bristles;
this brush is painted slowly over the surface of the metal to be
coated, which must be connected to the negative terminal of the
electrical generator. Under these conditions electrolysis of the
solution in the brush takes place. Iron ships’ plates have recently
been coated with copper in sections (to prevent the adhesion of
barnacles), by building up a temporary trough against the side
of the ship, making the thoroughly cleansed plate act both as
cathode and as one side of the trough. Decorative plating-work
in several colours (e.g. “parcel-gilding”) is effected by painting
a portion of an object with a stopping-out (i.e. a non-conducting)
varnish, such as copal varnish, so that this portion is not coated.
The varnish is then removed, a different design stopped out, and
another metal deposited. By varying this process, designs in
metals of different colours may readily be obtained.
Reference must be made to the textbooks (see Electrochemistry)
for a fuller account of the very varied solutions and
methods employed for electroplating with silver, gold, copper,
iron and nickel. It should be mentioned here, however, that
solutions which would deposit their metal on any object by simple
immersion should not be generally used for electroplating that
object, as the resulting deposit is usually non-adhesive. For
this reason the acid copper-bath is not used for iron or zinc
objects, a bath containing copper cyanide or
oxide dissolved in potassium cyanide being
substituted. This solution, being an inferior
conductor of electricity, requires a much higher
electromotive force to drive the current through
it, and is therefore more costly in use. It is,
however, commonly employed hot, whereby its
resistance is reduced. Zinc is commonly deposited
by electrolysis on iron or steel goods
which would ordinarily be “galvanized,” but
which for any reason may not conveniently be
treated by the method of immersion in fused
zinc. The zinc cyanide bath may be used
for small objects, but for heavy goods the
sulphate bath is employed. Sherard Cowper-Coles
patented a process in which, working
with a high current density, a lead anode is used, and
powdered zinc is kept suspended in the solution to maintain
the proportion of zinc in the electrolyte, and so to
guard against the gradual acidification of the bath. Cobalt
is deposited by a method analogous to that used for its sister-metal
nickel. Platinum, palladium and tin are occasionally
deposited for special purposes. In the deposition of gold the
colour of the deposit is influenced by the presence of impurities
in the solution; when copper is present, some is deposited with
the gold, imparting to it a reddish colour, whilst a little silver
gives it a greenish shade. Thus so-called coloured-gold deposits
may be produced by the judicious introduction of suitable
impurities. Even pure gold, it may be noted, is darker or lighter
in colour according as a stronger or a weaker current is used.
The electro-deposition of brass—mainly on iron ware, such as
bedstead tubes—is now very widely practised, the bath employed
being a mixture of copper, zinc and potassium cyanides, the
proportions of which vary according to the character of the brass
required, and to the mode of treatment. The colour depends
in part upon the proportion of copper and zinc, and in part upon
the current density, weaker currents tending to produce a redder
or yellower metal. Other alloys may be produced, such as bronze,
or German silver, by selecting solutions (usually cyanides) from
which the current is able to deposit the constituent metals
simultaneously.
Electrolysis has in a few instances been applied to processes
of manufacture. For example, Wilde produced copper printing
surfaces for calico printing-rollers and the like by immersing
rotating iron cylinders as cathodes in a copper bath. Elmore,
Dumoulin, Cowper-Coles and others have prepared copper
cylinders and plates by depositing copper on rotating mandrels
with special arrangements. Others have arranged a means of
obtaining high conductivity wire from cathode-copper without
fusion, by depositing the metal in the form of a spiral strip on
a cylinder, the strip being subsequently drawn down in the
usual way; at present, however, the ordinary methods of wire
239
production are found to be cheaper. J.W. Swan (Journ. Inst.
Elec. Eng., 1898, vol. xxvii. p. 16) also worked out, but did not
proceed with, a process in which a copper wire whilst receiving
a deposit of copper was continuously passed through the draw-plate,
and thus indefinitely extended in length. Cowper-Coles
(Journ. Inst. Elec. Eng., 1898, 27, p. 99) very successfully
produced true parabolic reflectors for projectors, by depositing
copper upon carefully ground and polished glass surfaces rendered
conductive by a film of deposited silver.
 |
| Fig. 1.—Henley’s
Electroscope. |
ELECTROSCOPE, an instrument for detecting differences of
electric potential and hence electrification. The earliest form
of scientific electroscope was the versorium
or electrical needle of William Gilbert (1544-1603),
the celebrated author of the treatise
De magnete (see Electricity). It consisted
simply of a light metallic needle balanced on
a pivot like a compass needle. Gilbert employed
it to prove that numerous other
bodies besides amber are susceptible of being
electrified by friction.1 In this case the
visible indication consisted in the attraction
exerted between the electrified body and the
light pivoted needle which was acted upon
and electrified by induction. The next improvement
was the invention of simple forms
of repulsion electroscope. Two similarly
electrified bodies repel each other. Benjamin
Franklin employed the repulsion of two linen
threads, C.F. de C. du Fay, J. Canton, W.
Henley and others devised the pith ball, or
double straw electroscope (fig. 1). T. Cavallo
about 1770 employed two fine silver wires
terminating in pith balls suspended in a glass
vessel having strips of tin-foil pasted down
the sides (fig. 2). The object of the thimble-shaped
dome was to keep moisture from the
stem from which the pith balls were supported, so that the
apparatus could be used in the open air even in the rainy
weather. Abraham Bennet (Phil. Trans., 1787, 77, p. 26)
invented the modern form of gold-leaf electroscope. Inside
a glass shade he fixed to an insulated wire a pair of strips
of gold-leaf (fig. 3). The wire terminated in a plate or
knob outside the vessel. When an electrified body was held
near or in contact with the knob, repulsion of the gold leaves
ensued. Volta added the condenser (Phil. Trans., 1782),
which greatly increased the power of the instrument. M.
Faraday, however, showed long subsequently that to bestow
upon the indications of such an electroscope definite meaning
it was necessary to place a cylinder of metallic gauze connected
to the earth inside the vessel, or better still, to line the glass
shade with tin-foil connected to the earth and observe through
a hole the indications of the gold leaves (fig. 4). Leaves of
aluminium foil may with advantage be substituted for gold-leaf,
and a scale is sometimes added to indicate the angular divergence
of the leaves.
 |
| Fig. 2.—Cavallo’s Electroscope. |
Fig. 3.—Bennet’s
Electroscope. |
The uses of an electroscope are, first, to ascertain if any body
is in a state of electrification, and secondly, to indicate the sign
of that charge. In connexion with the modern study of radioactivity,
the electroscope has become an instrument of great
usefulness, far outrivalling the spectroscope in sensibility.
Radio-active bodies are chiefly recognized by the power they
possess of rendering the air in their neighbourhood conductive;
hence the electroscope detects the presence of a radioactive body
by losing an electric charge given to it more quickly than it
would otherwise do. A third great use of the electroscope is
therefore to detect electric conductivity either in the air or in
any other body.
 |
| Fig. 4.—Gold-Leaf
Electroscope. |
To detect electrification it is best to charge the electroscope
by induction. If an electrified body is held near the gold-leaf
electroscope the leaves diverge with electricity of the same sign
as that of the body being tested. If, without removing the
electrified body, the plate or knob of the electroscope is touched,
the leaves collapse. If the electroscope is insulated once more and
the electrified body removed, the leaves
again diverge with electricity of the
opposite sign to that of the body being
tested. The sign of charge is then determined
by holding near the electroscope a
glass rod rubbed with silk or a sealing-wax
rod rubbed with flannel. If the
approach of the glass rod causes the
leaves in their final state to collapse,
then the charge in the rod was positive,
but if it causes them to expand still
more the charge was negative, and vice
versa for the sealing-wax rod. When
employing a Volta condensing electroscope,
the following is the method of
procedure:—The top of the electroscope
consists of a flat, smooth plate
of lacquered brass on which another plate of brass rests,
separated from it by three minute fragments of glass or
shellac, or a film of shellac varnish. If the electrified body
is touched against the upper plate whilst at the same time the
lower plate is put to earth, the condenser formed of the two plates
and the film of air or varnish becomes charged with positive
electricity on the one plate and negative on the other. On insulating
the lower plate and raising the upper plate by the glass
handle, the capacity of the condenser formed by the plates is
vastly decreased, but since the charge on the lower plate including
the gold leaves attached to it remains the same, as the capacity
of the system is reduced the potential is raised and therefore the
gold leaves diverge widely. Volta made use of such an electroscope
in his celebrated experiments (1790-1800) to prove that
metals placed in contact with one another are brought to different
potentials, in other words to prove the existence of so-called
contact electricity. He was assisted to detect the small potential
differences then in question by the use of a multiplying condenser
or revolving doubler (see Electrical Machine). To employ the
electroscope as a means of detecting radioactivity, we have first
to test the leakage quality of the electroscope itself. Formerly
it was usual to insulate the rod of the electroscope by passing it
through a hole in a cork or mass of sulphur fixed in the top of
the glass vessel within which the gold leaves were suspended.
A further improvement consisted in passing the metal wire to
which the gold leaves were attached through a glass tube much
wider than the rod, the latter being fixed concentrically in the
glass tube by means of solid shellac melted and run in. This
insulation, however, is not sufficiently good for an electroscope
intended for the detection of radioactivity; for this purpose
240
it must be such that the leaves will remain for hours or days in
a state of steady divergence when an electrical charge has been
given to them.
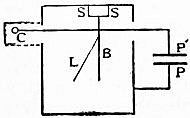 |
| Fig. 5.—Curie’s Electroscope. |
In their researches on radioactivity M. and Mme P. Curie
employed an electroscope made as follows:—A metal case
(fig. 5), having two holes in its sides, has a vertical brass strip B
attached to the inside of the lid by a block of sulphur SS or any
other good insulator. Joined to the strip is a transverse wire
terminating at one end in a knob C,
and at the other end in a condenser
plate P′. The strip B carries also a
strip of gold-leaf L, and the metal case
is connected to earth. If a charge is
given to the electroscope, and if any
radioactive material is placed on a
condenser plate P attached to the
outer case, then this substance bestows
conductivity on the air between the plates P and P′,
and the charge of the electroscope begins to leak away. The
collapse of the gold-leaf is observed through an aperture in
the case by a microscope, and the time taken by the gold-leaf
to fall over a certain distance is proportional to the
ionizing current, that is, to the intensity of the radioactivity
of the substance.
A very similar form of electroscope was employed by J.P.L.J.
Elster and H.F.K. Geitel (fig. 6), and also by C.T.R. Wilson
(see Proc. Roy. Soc., 1901, 68, p. 152). A metal box has a metal
strip B suspended from a block or insulator by means of a bit of
sulphur or amber S, and to it is fastened a strip of gold-leaf L.
The electroscope is provided with a charging rod C. In a dry
atmosphere sulphur or amber is an early perfect insulator,
and hence if the air in the interior of the box is kept dry by
calcium chloride, the electroscope will hold its charge for a
long time. Any divergence or collapse of the gold-leaf can be
viewed by a microscope through an aperture in the side of the
case.
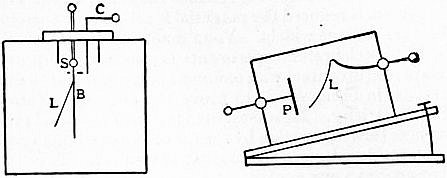 |
Fig. 6.—Elster and
Geitel Electroscope. |
Fig. 7.—Wilson’s Electroscope. |
Another type of sensitive electroscope is one devised by
C.T.R. Wilson (Proc. Cam. Phil. Soc., 1903, 12, part 2). It consists
of a metal box placed on a tilting stand (fig. 7). At one end
is an insulated plate P kept at a potential of 200 volts or so above
the earth by a battery. At the other end is an insulated metal
wire having attached to it a thin strip of gold-leaf L. If the plate
P is electrified it attracts the strip which stretches out towards it.
Before use the strip is for one moment connected to the case, and
the arrangement is then tilted until the strip extends at a certain
angle. If then the strip of gold-leaf is raised or lowered in potential
it moves to or from the plate P, and its movement can be observed
by a microscope through a hole in the side of the box. There is
a particular angle of tilt of the case which gives a maximum
sensitiveness. Wilson found that with the plate electrified to
207 volts and with a tilt of the case of 30°, if the gold-leaf was
raised one volt in potential above the case, it moved over 200
divisions of the micrometer scale in the eye-piece of the microscope,
54 divisions being equal to one millimetre. In using the
instrument the insulated rod to which the gold-leaf is attached
is connected to the conductor, the potential of which is being
examined. In the use of all these electroscopic instruments it
is essential to bear in mind (as first pointed out by Lord Kelvin)
that what a gold-leaf electroscope really indicates is the difference
of potential between the gold-leaf and the solid walls enclosing
the air space in which they move.1 If these enclosing walls are
made of anything else than perfectly conducting material, then
the indications of the instrument may be uncertain and meaningless.
As already mentioned, Faraday remedied this defect by
coating the inside of the glass vessel in which the gold-leaves were
suspended to form an electroscope with tinfoil (see fig. 4).
In spite of these admonitions all but a few instrument makers
have continued to make the vicious type of instrument consisting
of a pair of gold-leaves suspended within a glass shade or bottle,
no means being provided for keeping the walls of the vessel
continually at zero potential.
See J. Clerk Maxwell, Treatise on Electricity and Magnetism, vol. i.
p. 300 (2nd ed., Oxford, 1881); H.M. Noad, A Manual of Electricity,
vol. i. p. 25 (London, 1855); E. Rutherford, Radioactivity.
(J. A. F.)
1 See the English translation by the Gilbert Club of Gilbert’s De
magnete, p. 49 (London, 1900).
1 See Lord Kelvin, "Report on Electrometers and Electrostatic
Measurements," Brit. Assoc. Report for 1867, or Lord Kelvin's
Reprint of Papers on Electrostatics and Magnetism, p. 260.
 “a sugar-reed.” Immediately
bordering on the Persians were the Amardians or Mardians,
as well as the people of Khapirti (Khatamti, according to Scheil),
the name given to Susiana in the Neo-Susian texts. Khapirti
appears as Apir in the inscriptions of Mal-Amir, which fix the
locality of the district. Passing over the Messabatae, who
inhabited a valley which may perhaps be the modern Māh-Sabadan,
as well as the level district of Yamutbal or Yatbur
which separated Elam from Babylonia, and the smaller districts
of Characene, Cabandene, Corbiana and Gabiene mentioned
by classical authors, we come to the fourth principal tribe of
Susiana, the Cissii (Aesch. Pers. 16; Strabo xv. 3. 2) or Cossaei
(Strabo xi. 5. 6, xvi. 11. 17; Arr. Ind. 40; Polyb. v. 54, &c.),
the Kassi of the cuneiform inscriptions. So important were they,
that the whole of Susiana was sometimes called Cissia after
them, as by Herodotus (iii. 91, v. 49, &c.). In fact Susiana
was only a late name for the country, dating from the time
when Susa had been made a capital of the Persian empire. In
the Sumerian texts of Babylonia it was called Numma, “the
Highlands,” of which Elamtu or Elamu, “Elam,” was the
Semitic translation. Apart from Susa, the most important
part of the country was Anzan (Anshan, contracted Assan),
where the native population maintained itself unaffected by
Semitic intrusion. The exact position of Anzan is still disputed,
but it probably included originally the site of Susa and was
distinguished from it only when Susa became the seat of a
Semitic government. In the lexical tablets Anzan is given
as the equivalent of Elamtu, and the native kings entitle themselves
kings of “Anzan and Susa,” as well as “princes of the
Khapirti.”
“a sugar-reed.” Immediately
bordering on the Persians were the Amardians or Mardians,
as well as the people of Khapirti (Khatamti, according to Scheil),
the name given to Susiana in the Neo-Susian texts. Khapirti
appears as Apir in the inscriptions of Mal-Amir, which fix the
locality of the district. Passing over the Messabatae, who
inhabited a valley which may perhaps be the modern Māh-Sabadan,
as well as the level district of Yamutbal or Yatbur
which separated Elam from Babylonia, and the smaller districts
of Characene, Cabandene, Corbiana and Gabiene mentioned
by classical authors, we come to the fourth principal tribe of
Susiana, the Cissii (Aesch. Pers. 16; Strabo xv. 3. 2) or Cossaei
(Strabo xi. 5. 6, xvi. 11. 17; Arr. Ind. 40; Polyb. v. 54, &c.),
the Kassi of the cuneiform inscriptions. So important were they,
that the whole of Susiana was sometimes called Cissia after
them, as by Herodotus (iii. 91, v. 49, &c.). In fact Susiana
was only a late name for the country, dating from the time
when Susa had been made a capital of the Persian empire. In
the Sumerian texts of Babylonia it was called Numma, “the
Highlands,” of which Elamtu or Elamu, “Elam,” was the
Semitic translation. Apart from Susa, the most important
part of the country was Anzan (Anshan, contracted Assan),
where the native population maintained itself unaffected by
Semitic intrusion. The exact position of Anzan is still disputed,
but it probably included originally the site of Susa and was
distinguished from it only when Susa became the seat of a
Semitic government. In the lexical tablets Anzan is given
as the equivalent of Elamtu, and the native kings entitle themselves
kings of “Anzan and Susa,” as well as “princes of the
Khapirti.”














































































