
Title: Encyclopaedia Britannica, 11th Edition, "Cube" to "Daguerre, Louis Jacques Mandé"
Author: Various
Release date: January 29, 2012 [eBook #38709]
Most recently updated: January 8, 2021
Language: English
Credits: Produced by Marius Masi, Don Kretz and the Online
Distributed Proofreading Team at https://www.pgdp.net
| Transcriber’s note: |
A few typographical errors have been corrected. They
appear in the text like this, and the
explanation will appear when the mouse pointer is moved over the marked
passage. Sections in Greek will yield a transliteration
when the pointer is moved over them, and words using diacritic characters in the
Latin Extended Additional block, which may not display in some fonts or browsers, will
display an unaccented version. Links to other EB articles: Links to articles residing in other EB volumes will be made available when the respective volumes are introduced online. |
Articles in This Slice
CUBE (Gr. κύβος, a cube), in geometry, a solid bounded by six equal squares, so placed that the angle between any pair of adjacent faces is a right angle. This solid played an all-important part in the geometry and cosmology of the Greeks. Plato (Timaeus) described the figure in the following terms:—“The isosceles triangle which has its vertical angle a right angle ... combined in sets of four, with the right angles meeting at the centre, form a single square. Six of these squares joined together formed eight solid angles, each produced by three plane right angles: and the shape of the body thus formed was cubical, having six square planes for its surfaces.” In his cosmology Plato assigned this solid to “earth,” for “‘earth’ is the least mobile of the four (elements—‘fire,’ ‘water,’ ‘air’ and ‘earth’) and most plastic of bodies: and that substance must possess this nature in the highest degree which has its bases most stable.” The mensuration of the cube, and its relations to other geometrical solids are treated in the article Polyhedron; in the same article are treated the Archimedean solids, the truncated and snub-cube; reference should be made to the article Crystallography for its significance as a crystal form.
A famous problem concerning the cube, namely, to construct a cube of twice the volume of a given cube, was attacked with great vigour by the Pythagoreans, Sophists and Platonists. It became known as the “Delian problem” or the “problem of the duplication of the cube,” and ranks in historical importance with the problems of “trisecting an angle” and “squaring the circle.” The origin of the problem is open to conjecture. The Pythagorean discovery of “squaring a square,” i.e. constructing a square of twice the area of a given square (which follows as a corollary to the Pythagorean property of a right-angled triangle, viz. the square of the hypotenuse equals the sum of the squares on the sides), may have suggested the strictly analogous problem of doubling a cube. Eratosthenes (c. 200 B.C.), however, gives a picturesque origin to the problem. In a letter to Ptolemy Euergetes he narrates the history of the problem. The Delians, suffering a dire pestilence, consulted their oracles, and were ordered to double the volume of the altar to their tutelary god, Apollo. An altar was built having an edge double the length of the original; but the plague was unabated, the oracles not having been obeyed. The error was discovered, and the Delians applied to Plato for his advice, and Plato referred them to Eudoxus. This story is mere fable, for the problem is far older than Plato.
Hippocrates of Chios (c. 430 B.C.), the discoverer of the square of a lune, showed that the problem reduced to the determination of two mean proportionals between two given lines, one of them being twice the length of the other. Algebraically expressed, if x and y be the required mean proportionals and a, 2a, the lines, we have a : x :: x : y :: y : 2a, from which it follows that x³ = 2a³. Although Hippocrates could not determine the proportionals, his statement of the problem in this form was a great advance, for it was perceived that the problem of trisecting an angle was reducible to a similar form which, in the language of algebraic geometry, is to solve geometrically a cubic equation. According to Proclus, a man named Hippias, probably Hippias of Elis (c. 460 B.C.), trisected an angle with a mechanical curve, named the quadratrix (q.v.). Archytas of Tarentum (c. 430 B.C.) solved the problems by means of sections of a half cylinder; according to Eutocius, Menaechmus solved them by means of the intersections of conic sections; and Eudoxus also gave a solution.
All these solutions were condemned by Plato on the ground that they were mechanical and not geometrical, i.e. they were not effected by means of circles and lines. However, no proper geometrical solution, in Plato’s sense, was obtained; in fact it is now generally agreed that, with such a restriction, the problem is insoluble. The pursuit of mechanical methods furnished a stimulus to the study of mechanical loci, for example, the locus of a point carried on a rod which is caused to move according to a definite rule. Thus Nicomedes invented the conchoid (q.v.); Diocles the cissoid (q.v.); Dinostratus studied the quadratrix invented by Hippias; all these curves furnished solutions, as is also the case with the trisectrix, a special form of Pascal’s limaçon (q.v.). These problems were also attacked by the Arabian mathematicians; Tobit ben Korra (836-901) is credited with a solution, while Abul Gud solved it by means of a parabola and an equilateral hyperbola.
In algebra, the “cube” of a quantity is the quantity multiplied by itself twice, i.e. if a be the quantity a × a × a (= a³) is its cube. Similarly the “cube root” of a quantity is another quantity which when multiplied by itself twice gives the original quantity; thus a1/3 is the cube root of a (see Arithmetic and Algebra). A “cubic equation” is one in which the highest power of the unknown is the cube (see Equation); similarly, a “cubic curve” has an equation containing no term of a power higher than the third, the powers of a compound term being added together.
In mensuration, “cubature” is sometimes used to denote the volume of a solid; the word is parallel with “quadrature,” to determine the area of a surface (see Mensuration; Infinitesimal Calculus).
CUBEBS (Arab. kabábah), the fruit of several species of pepper (Piper), belonging to the natural order Piperaceae. The cubebs of pharmacy are produced by Piper Cubeba, a climbing woody shrub indigenous to south Borneo, Sumatra, Prince of Wales Island and Java. It has round, ash-coloured, smooth branches; lanceolate, or ovate-oblong, somewhat leathery, shining leaves, 4 to 6½ in. long and 1½ to 2 in. broad. Male and female flowers are borne on distinct plants. The fruits are small, globose, about 1⁄5 in. in diameter, and not so large as white pepper; their contracted stalk-like bases are between 1⁄3 and ½ in. in length; and from forty to fifty of them are borne upon a common stem. The cubeb is cultivated in Java and Sumatra, the fruits are gathered before they are ripe, and carefully dried. Commercial cubebs consist of the dried berries, usually with their stalks attached; the pericarp is greyish-brown, or blackish and wrinkled; and the seed, when present, is hard, white and oily. The odour of cubebs is agreeable and aromatic; the taste, pungent, acrid, slightly bitter and persistent. About 15% of a volatile oil is obtained by distilling cubebs with water; after rectification with water, or on keeping, this deposits rhombic crystals of camphor of cubebs, C15H26O; cubebene, the liquid portion, has the formula C15H24. Cubebin, CH2[O]2C6H3·CH:CH·CH2OH, is a crystalline substance existing in cubebs, discovered by Eugène Soubeiran and Capitaine in 1839; it may be prepared from cubebene, or from the pulp left after the distillation of the oil. The drug, along with gum, fatty oils, and malates of magnesium and calcium, contains also about 1% of cubebic acid, and about 6% of a resin.
The dose of the fruit is 30 to 60 grains, and the British Pharmacopoeia contains a tincture with a dose of ½ to 1 drachm. The volatile oil—oleum cubebae—is also official, and is the form in which this drug is most commonly used, the dose being 5 to 20 minims, which may be suspended in mucilage or given after meals in a cachet. The drug has the typical actions of a volatile oil, but exerts some of them in an exceptional degree. Thus it is liable to cause a cutaneous erythema in the course of its excretion by the skin; it has a marked diuretic action; and it is a fairly efficient disinfectant of the urinary passages. Its administration causes the appearance in the urine of a salt of cubebic acid which is precipitated by heat or nitric acid, and is therefore liable to be mistaken for albumin, when these two most common tests for the occurrence of albuminuria are applied. Cubebs is frequently used in the form of cigarettes for asthma, chronic pharyngitis and hay-fever. A small percentage of cubebs is also commonly included in lozenges designed for use in bronchitis, in which the antiseptic and expectoral properties of the drug are useful. But the most important therapeutic application of this drug is in gonorrhoea, where its antiseptic action is of much value. As compared with copaiba in this connexion cubebs has the advantages of being less disagreeable to take and somewhat less likely to disturb the digestive apparatus in prolonged administration. The introduction of the drug into medicine is supposed to have been due to the Arabian physicians in the middle ages. Cubebs were formerly candied and eaten whole, or used ground as a seasoning for meat. Their modern employment in England as a drug dates from 1815. “Cubebae” were purchased in 1284 and 1285 by Lord Clare at 2s. 3d. and 2s. 9d. per ℔ respectively; and in 1307 1 ℔ for the king’s wardrobe cost 9s., a sum representing about £3, 12s. in present value (Rogers, Hist. of Agriculture and Prices, i. 627-628, ii. 544).
A closely allied species, Piper Clusii, produces the African cubebs or West African black-pepper, the berry of which is smoother than that of common cubebs and usually has a curved pedicel. In the 14th century it was imported into Europe from the Grain Coast, under the name of pepper, by merchants of Rouen and Lippe.
CUBICLE (Lat. cubiculum), a small chamber containing a couch or a bed. The small rooms opening into the atrium of a Pompeian house are known as cubicula. In modern English schools “cubicle” is the term given to the separate small bedrooms into which the dormitories are divided, as opposed to the system of large open dormitories.
CUBITT, THOMAS (1788-1855), English builder, was born at Buxton, near Norwich, on the 25th of February 1788. Few men have exhibited greater self-reliance in early life in the pursuit of a successful career. In his nineteenth year, when he was working as a journeyman carpenter, his father died, and he tried to better his position by going on a voyage to India, as captain’s joiner. He returned to London, two years after, in the possession of a small capital, and began business as a carpenter. The growth of his establishment was steady and rapid. He was one of the first to combine several trades in a “builder’s” business; and this very much increased his success. One of the earlier works which gave him reputation was the London Institution in Finsbury Circus; but it is from 1824 that the vast building operations date which identify his name with many splendid ranges of London houses, such as Tavistock, Gordon, Belgrave and Lowndes Squares, and the district of South Belgravia. While these and similar extensive operations were in progress, a financial panic, which proved ruinous to many, was surmounted in his case by a determined spirit and his integrity of character. He took great interest in sanitary measures, and published, for private circulation, a pamphlet on the general drainage of London, the substance of which was afterwards embodied in a letter to The Times; the plan he advocated was subsequently adopted by the conveyance of the sewage matter some distance below London. He advocated the provision of open spaces in the environs of London as places of public recreation, and was one of the originators of Battersea Park, the first of the people’s parks. At a late period he received professionally the recognition of royalty, the palace at Osborne being erected after his designs, and under his superintendence; and in the Life of the Prince Consort he is described by Queen Victoria as one “than whom a better and kinder man did not exist.” In 1851, although he was not identified with the management of the Great Exhibition, he showed the warmest sympathy with its objects, and aided its projectors in many ways, especially in the profitable investment of their surplus funds. Cubitt, when he rose to be a capitalist, never forgot the interests and well-being of his workpeople. He was elected president of the Builders’ Society some time before his death, which took place at his seat Denbies, near Dorking, on the 20th of December 1855.
His son, George Cubitt (1828- ), who had a long and useful parliamentary career, as Conservative member for West Surrey (1860-1865) and Mid-Surrey (1885-1892), was in 1892 raised to the peerage as Baron Ashcombe.
CUBITT, SIR WILLIAM (1785-1861), English engineer, was born in 1785 at Dilham in Norfolk, where his father was a miller. After serving an apprenticeship of four years (1800-1804) as a joiner and cabinetmaker at Stalham, he became associated with an agricultural-machine maker, named Cook, who resided at Swanton. In 1807 he patented self-regulating sails for windmills, and in 1812 he entered the works of Messrs Ransome of Ipswich, where he soon became chief engineer, and ultimately a partner. Meanwhile, the subject of the employment of criminals had been much in his thoughts; and the result was his introduction of the treadmill about 1818. In 1826 he removed to London, where he gained a very large practice as a civil engineer. Among his works were the Oxford canal, the Birmingham & Liverpool Junction Canal, the improvement of the river Severn, the Bute docks at Cardiff, the Black Sluice drainage and its outfall sluice at Boston harbour, the Middlesborough docks and coal drops in the Tees, and the South-Eastern railway, of which he was chief engineer. The Hanoverian government consulted him about the harbour and docks at Harburg; the water-works of the city of Berlin were constructed under his immediate superintendence; he was asked to report on the construction of the Paris & Lyons railway; and he was consulting engineer for the line from Boulogne to Amiens. Among his later works were two floating landing stages at Liverpool, and the bridge for carrying the London turnpike across the Medway at Rochester. In 1851, when he was president of the Institution of Civil Engineers, he was knighted for his services in connexion with the buildings erected in Hyde Park for the exhibition of that year. 608 He retired from active work in 1858, and died on the 13th of October 1861 at his house on Clapham Common, London. His son, Joseph Cubitt (1811-1872), was trained under him, and was engineer of various railways, including the Great Northern, London, Chatham & Dover, and part of the London & South-Western.
CUCHULINN (Cūchúlinn; pronounced “Coohoollin”), the chief warrior in the Conchobar-Cuchulinn or older heroic (Ulster) cycle of Ireland. The story of his origin is very obscure. The god Lug is represented as having been swallowed in a draught of wine by his mother Dechtire, sister of Conchobar, who was king of Ulster. But it is not unlikely that this story was invented to supersede the account of the incestuous union of Conchobar with his sister, which seems to be hinted at on various occasions. Usually, however, he is styled son of Sualdam, an Ulster warrior who plays a very inferior part in the cycle. His earliest name was Setanta, and he was brought up at Dun Imbrith (Louth). When he was six years of age he announced his intention of going to Conchobar’s court at Emain Macha (Navan Rath near Armagh) to play with the boys there. He defeats all the boys in marvellous fashion and is received as one of their number. Shortly after he kills Culann, the smith’s hound, a huge watch-dog. The smith laments that all his property is of no value now that his watchman is slain, whereupon the young hero offers to guard his domains until a whelp of the hound’s has grown. From this the boy received the name of Cū Chulinn or Culann’s Hound. The next year Cuchulinn receives arms, makes his first foray, and slays the three sons of Necht, redoubtable hereditary foes of the Ulstermen, in the plain of Meath. The men of Ulster decide that Cuchulinn must marry, as all the women of Ireland are in love with him. Chosen envoys fail to find a bride worthy of him after a year’s search, but the hero goes straight to Emer, the daughter of Forgall the Wily, at Lusk (county Dublin). The lady is promised to him if he will go to learn chivalry of Domnall the Soldierly and the amazon Scathach in Alba. After enduring great hardships he goes through the course and leaves a son Connlaech behind in Scotland by another amazon, Aife. On his return he carries off and weds Emer. He is represented as living at Dun Delgan (Dundalk). The greatest of all the hero’s achievements was the defence of the frontier of Ulster against the forces of Medb, queen of Connaught, who had come to carry off the famous Brown Bull of Cualnge (Cooley). The men of Ulster were all suffering from a strange debility, and Cuchulinn had to undertake the defence single-handed from November to February. This was when he was seventeen years of age. The cycle contains a large number of episodes, such as the gaining of the champion’s portion and the tragical death by the warrior’s hand of his own son Connlaech. When he was twenty-seven he met with his end at the hands of Lugaid, son of Cūrōi MacDaire, the famous Munster warrior, and the children of Calatīn Dāna, in revenge for their father’s death (see Celt: Irish Literature).
Medieval Christian synchronists make Cuchulinn’s death take place about the beginning of the Christian era. It is not necessary to regard Cuchulinn as a form of the solar hero, as some writers have done. Most, if not all, of his wonderful attributes may be ascribed to the Irish predilection for the grotesque. It is true that Cuchulinn seems to stand in a special relation to the Tuatha De Danann leader, the god Lug, but in primitive societies there is always a tendency to ascribe a divine parentage to men who stand out pre-eminently in prowess beyond their fellows.
See A. Nutt, Cuchulainn, the Irish Achilles (London, 1900); E. Hull, The Cuchullin Saga (London, 1898).
CUCKOO, or Cuckow, as the word was formerly spelt, the common name of a well-known and often-heard bird, the Cuculus canorus of Linnaeus. In some parts of the United Kingdom it is more frequently called gowk, and it is the Gr. κόκκυξ, the Ital. cuculo or cucco, the Fr. coucou, the Ger. Kuckuk, the Dutch koekkoek, the Dan. kukker or gjög, and the Swed. gök. The oldest English spelling of the name seems to have been cuccu.
No single bird has perhaps so much occupied the attention both of naturalists and of those who are not naturalists, or has had so much written about it, as the common cuckoo, and of no bird perhaps have more idle tales been told. Its strange and, according to the experience of most people, its singular habit of entrusting its offspring to foster-parents is enough to account for much of the interest which has been so long felt in its history; but this habit is shared probably by many of its Old World relatives, as well as in the New World by birds which are not in any degree related to it. The cuckoo is a summer visitant to the whole of Europe, reaching even far within the Arctic circle, and crossing the Mediterranean from its winter quarters in Africa at the end of March or beginning of April. Its arrival is at once proclaimed by the peculiar and in nearly all languages onomatopoeic cry of the cock—a true song in the technical sense of the word, since it is confined to the male sex and to the season of love. In a few days the cock is followed by the hen, and amorous contests between keen and loud-voiced suitors are to be commonly noticed, until the respective pretensions of the rivals are decided. Even by night they are not silent; but as the season advances the song is less frequently heard, and the cuckoo seems rather to avoid observation as much as possible, the more so since whenever it shows itself it is a signal for all the small birds of the neighbourhood to be up in its pursuit, just as though it were a hawk, to which indeed its mode of flight and general appearance give it an undoubted resemblance—a resemblance that misleads some into confounding it with the birds of prey, instead of recognizing it as a harmless if not a beneficial destroyer of hairy caterpillars. Thus pass away some weeks. Towards the middle or end of June its “plain-song” cry alters; it becomes rather hoarser in tone, and its first syllable or note is doubled. Soon after it is no longer heard at all, and by the middle of July an old cuckoo is seldom to be found in the British Islands, though a stray example, or even, but very rarely, two or three in company, may occasionally be seen for a month longer. Of its breeding comparatively few have any personal experience. Yet a diligent search for and peering into the nests of several of the commonest little birds—more especially the pied wagtail (Motacilla lugubris), the titlark (Anthus pratensis), the reed-wren (Acrocephalus streperus), and the hedge-sparrow (Accentor modularis)—will be rewarded by the discovery of the egg of the mysterious stranger which has been surreptitiously introduced, and those who wait till this egg is hatched may be witnesses (as was Edward Jenner in the 18th century) of the murderous eviction of the rightful tenants of the nest by the intruder, who, hoisting them one after another on his broad back, heaves them over to die neglected by their own parents, of whose solicitous care he thus becomes the only object. In this manner he thrives, and, so long as he remains in the country of his birth his wants are anxiously supplied by the victims of his mother’s dupery. The actions of his foster-parents become, when he is full grown, almost ludicrous, for they often have to perch between his shoulders to place in his gaping mouth the delicate morsels he is too indolent or too stupid to take from their bills. Early in September he begins to shift for himself, and then follows the seniors of his kin to more southern climes.
So much caution is used by the hen cuckoo in choosing a nest in which to deposit her egg that the act of insertion has been but seldom witnessed. The nest selected is moreover often so situated, or so built, that it would be an absolute impossibility for a bird of her size to lay her egg therein by sitting upon the fabric as birds commonly do; and there have been a few fortunate observers who have actually seen the deposition of the egg upon the ground by the cuckoo, who, then taking it in her bill, introduces it into the nest. Of these, the earliest in Great Britain seem to have been two Scottish lads, sons of Mr Tripeny, a farmer in Coxmuir, who, as recorded by Macgillivray (Brit. Birds, iii. 130, 131) from information communicated to him by Mr Durham Weir, saw most part of the operation performed, June 24, 1838. But perhaps the most satisfactory evidence on the point is that of Adolf Müller, a forester at Gladenbach in Darmstadt, who says (Zoolog. Garten, 1866, pp. 374, 375) that through a telescope he watched a cuckoo as she laid her egg on a 609 bank, and then conveyed the egg in her bill to a wagtail’s nest. Cuckoos, too, have been not unfrequently shot as they were carrying a cuckoo’s egg, presumably their own, in their bill, and this has probably given rise to the vulgar, but seemingly groundless, belief that they suck the eggs of other kinds of birds. More than this, Mr G. D. Rowley, who had much experience of cuckoos, declares (Ibis, 1865, p. 186) his opinion to be that traces of violence and of a scuffle between the intruder and the owners of the nest at the time of introducing the egg often appear, whence we are led to suppose that the cuckoo ordinarily, when inserting her egg, excites the fury (already stimulated by her hawk-like appearance) of the owners of the nest by turning out one or more of the eggs that may be already laid therein, and thus induces the dupe to brood all the more readily and more strongly what is left to her. Of the assertion that the cuckoo herself takes any interest in the future welfare of the egg she has foisted on her victim, or of its product, there is no good evidence.
But a much more curious assertion has also been made, and one that at first sight appears so incomprehensible as to cause little surprise at the neglect it long encountered. To this currency was first given by Salerne (L’Hist. nat. &c., Paris, 1767, p. 42), who was, however, hardly a believer in it, and it is to the effect, as he was told by an inhabitant of Sologne, that the egg of a cuckoo resembles in colour that of the eggs normally laid by the kind of bird in whose nest it is placed. In 1853 the same notion was prominently and independently brought forward by Dr A. C. E. Baldamus (Naumannia, 1853, pp. 307-325), and in time became known to English ornithologists, most of whom were naturally sceptical as to its truth, since no likeness whatever is ordinarily apparent in the very familiar case of the blue-green egg of the hedge-sparrow and that of the cuckoo, which is so often found beside it.1 Dr Baldamus based his notion on a series of eggs in his cabinet,2 a selection from which he figured in illustration of his paper, and, however the thing may be accounted for, it seems impossible to resist, save on one supposition, the force of the testimony these specimens afford. This one supposition is that the eggs have been wrongly ascribed to the cuckoo, and that they are only exceptionally large examples of the eggs of the birds in the nests of which they were found, for it cannot be gainsaid that some such abnormal examples are occasionally to be met with. But it is well known that abnormally large eggs are not only often deficient in depth of colour, but still more often in stoutness of shell. Applying these rough criteria to Dr Baldamus’s series, most of the specimens stood the test very well.
There are some other considerations to be urged. For instance, Herr Braune, a forester at Greiz in the principality of Reuss (Naumannia, tom. cit. pp. 307, 313), shot a hen cuckoo as she was leaving the nest of an icterine warbler (Hypolais icterina). In the oviduct of this cuckoo he found an egg coloured very like that of the warbler, and on looking into the nest he found there an exactly similar egg, which there can be no reasonable doubt had just been laid by that very cuckoo. Moreover, Herr Grunack (Journ. für Orn., 1873, p. 454) afterwards found one of the most abnormally coloured specimens, quite unlike the ordinary egg of the cuckoo, to contain an embryo so fully formed as to show the characteristic zygodactyl feet of the bird, thus proving unquestionably its parentage.
On the other hand, we must bear in mind the numerous instances in which not the least similarity can be traced—as in the not uncommon case of the hedge-sparrow already mentioned, and if we attempt any explanatory hypothesis it must be one that will fit all round. Such an explanation seems to be this. We know that certain kinds of birds resent interference with their nests much less than others, and among them it may be asserted that the hedge-sparrow will patiently submit to various experiments. She will brood with complacency the egg of a redbreast (Erithacus rubecula), so unlike her own, and for aught we know to the contrary may even be colour-blind. In the case of such a species there would be no need of anything further to ensure success—the terror of the nest-owner at seeing her home invaded by a hawk-like giant, and some of her treasures tossed out, would be enough to stir her motherly feelings so deeply that she would without misgiving, if not with joy that something had been spared to her, resume the duty of incubation so soon as the danger was past. But with other species it may be, and doubtless is, different. Here assimilation of the introduced egg to those of the rightful owner may be necessary, for there can hardly be a doubt as to the truth of Dr Baldamus’s theory as to the object of the assimilation being to render the cuckoo’s egg “less easily recognized by the foster-parents as a substituted one.” It is especially desirable to point out that there is not the slightest ground for imagining that the cuckoo, or any other bird, can voluntarily influence the colour of the egg she is about to lay. Over that she can have no control, but its destination she can determine. It would seem also impossible that a cuckoo, having laid an egg, should look at it, and then decide from its appearance in what bird’s nest she should put it. That the colour of an egg-shell can be in some mysterious way affected by the action of external objects on the perceptive faculties of the mother is a notion too wild to be seriously entertained. Consequently, only one explanation of the facts can here be suggested. Every one who has sufficiently studied the habits of animals will admit the influence of heredity. That there is a reasonable probability of each cuckoo most commonly putting her eggs in the nest of the same species of bird, and of this habit being transmitted to her posterity, does not seem to be a very violent supposition. Without attributing any wonderful sagacity to her, it does not seem unlikely that the cuckoo which had once successfully foisted her egg on a reed-wren or a titlark should again seek for another reed-wren’s or another titlark’s nest (as the case may be), when she had another egg to dispose of, and that she should continue her practice from one season to another. It stands on record (Zoologist, 1873, p. 3648) that a pair of wagtails built their nest for eight or nine years running in almost exactly the same spot, and that in each of those years they fostered a young cuckoo, while many other cases of like kind, though not perhaps established on so good authority, are believed to have happened. Such a habit could hardly fail to become hereditary, so that the daughter of a cuckoo which always put her egg into a reed-wren’s, titlark’s or wagtail’s nest would do as did her mother. Furthermore it is unquestionable that, whatever variation there may be among the eggs laid by different individuals of the same species, there is a strong family likeness between the eggs laid by the same individual, even at the interval of many years, and it can hardly be questioned that the eggs of the daughter would more or less resemble those of her mother. Hence the supposition may be fairly credited that the habit of laying a particular style of egg is also likely to become hereditary. Combining this supposition with that as to the cuckoo’s habit of using the nest of the same species becoming hereditary, it will be seen that it requires only an application of the principle of natural selection to show the probability of this principle operating in the course of time to produce the facts asserted by the anonymous Solognot of the 18th century, and by Dr Baldamus and others since. The particular gens of cuckoo which inherited and transmitted the habit of depositing in the nest of any particular species of bird eggs having more or less resemblance to the eggs of that species would prosper most in those members of the gens where the likeness was strongest, and the other members would (ceteris paribus) in time be eliminated. As already shown, it is not to be supposed that all species, or even all individuals of a species, are duped with equal ease. The operation of this kind of natural selection would be most needed in those cases where the species are not easily duped—that is, in those cases which occur the least frequently. Here it is we find it, for observation shows that eggs of the cuckoo deposited in nests of the red-backed shrike (Lanius collurio), of the bunting (Emberiza miliaria), and of the icterine warbler approximate in their colouring to eggs of those species—species in whose nests the cuckoo rarely (in comparison with others) deposits eggs. 610 Of species which are more easily duped, such as the hedge-sparrow, mention has already been made.
More or less nearly allied to the British cuckoo are many other forms of the genus from various parts of Africa, Asia and their islands, while one even reaches Australia. In some cases the chief difference is said to lie in the diversity of voice—a character only to be appreciated by those acquainted with the living birds, and though of course some regard should be paid to this distinction, the possibility of birds using different “dialects” according to the locality they inhabit must make it a slender specific diagnostic. All these forms are believed to have essentially the same habits as the British cuckoo, and, as regards parasitism the same is to be said of the large cuckoo of southern Europe and North Africa (Coccystes glandarius), which victimizes pies (Pica mauritanica and Cyanopica cooki) and crows (Corvus cornix). True it is that an instance of this species, commonly known as the great spotted cuckoo, having built a nest and hatched its young, is on record, but the later observations of others tend to cast doubt on the credibility of the ancient report. It is worthy of remark that the eggs of this bird so closely resemble those of one of the pies in whose nest they have been found, that even expert zoologists have been deceived by them, only to discover the truth when the cuckoo’s embryo had been extracted from the supposed pie’s egg. This species of cuckoo, easily distinguishable by its large size and long crest, has more than once made its appearance as a straggler in the British Isles. Equally parasitic are many other cuckoos, belonging chiefly to genera which have been more or less clearly defined as Cacomantis, Chrysococcyx, Eudynamis, Oxylophus, Polyphasia and Surniculus, and inhabiting parts of the Ethiopian, Indian and Australian regions;3 but there are certain aberrant forms of Old World cuckoos which unquestionably do not shirk parental responsibilities. Among these especially are the birds placed in or allied to the genera Centropus and Coua—the former having a wide distribution from Egypt to New South Wales, living much on the ground and commonly called lark-heeled cuckoos; the latter bearing no English name, and limited to the island of Madagascar. These build a nest, not perhaps in a highly finished style of architecture, but one that serves its end.
Respecting the cuckoos of America, the evidence, though it has been impugned, is certainly enough to clear them from the charge which attaches to so many of their brethren of the Old World. There are two species very well known in parts of the United States and some of the West Indian Islands (Coccyzus Americanus and C. erythrophthalmus), and each of them has occasionally visited Europe. They both build nests—remarkably small structures when compared with those of other birds of their size—and faithfully incubate their delicate sea-green eggs. In the south-western states of the Union and thence into Central America is found another curious form of cuckoo (Geococcyx)—the chaparral-cock of northern and paisano of southern settlers. The first of these names it takes from the low brushwood (chaparral) in which it chiefly dwells, and the second is said to be due to its pheasant-like (faisan corrupted into paisano, properly a countryman) appearance as it runs on the ground. Indeed, one of the two species of the genus was formerly described as a Phasianus. They both have short wings, and seem never to fly, but run with great rapidity. Returning to arboreal forms, the genera Neomorphus, Diplopterus, Saurothera and Piaya (the last two commonly called rain-birds, from the belief that their cry portends rain) may be noticed—all of them belonging to the Neotropical region; but perhaps the most curious form of American cuckoos is the ani (Crotophaga), of which three species inhabit the same region. The best-known species (C. ani) is found throughout the Antilles and on the opposite continent. In most of the British colonies it is known as the black witch, and is accused of various malpractices—it being, in truth, a perfectly harmless if not a beneficial bird. As regards its propagation this aberrant form of cuckoo departs in one direction from the normal habit of birds, for several females, unite to lay their eggs in one nest. It is evident that incubation is carried on socially, since an intruder on approaching the rude nest will disturb perhaps half a dozen of its sable proprietors, who, loudly complaining, seek safety either in the leafy branches of the tree that holds it, or in the nearest available covert, with all the speed that their feeble powers of flight permit.
1 An instance to the contrary has been recorded by Mr A. C. Smith (Zoologist, 1873, p. 3516) on Mr Brine’s authority.
2 This series was seen in 1861 by the writer.
3 Evidence tends to show that the same is to be said of the curious channel-bill (Scythrops novae-hollandiae), though absolute proof seems to be wanting.
CUCKOO-SPIT, a frothy secretion found upon plants, and produced by the immature nymphal stage of various plant-lice of the familiar Cercopidae and Jassidae, belonging to the homopterous division of the Hemiptera, which in the adult condition are sometimes called frog-hoppers.
CUCUMBER (Cucumis sativus, Fr. concombre, O. Fr. coucombre, whence the older English spelling and pronunciation “cowcumber,” the standard in England up to the beginning of the 18th century), a creeping plant of the natural order Cucurbitaceae. It is widely cultivated, and originated probably in northern India, where Alphonse de Candolle affirms (Origin of Cultivated Plants) that it has been cultivated for at least three thousand years. It spread westward to Europe and was cultivated by the ancient Greeks under the name σίκυος; it did not reach China until two hundred years before the Christian era. It is an annual with a rough succulent trailing stem and stalked hairy leaves with three to five pointed lobes; the stem bears branched tendrils by means of which the plant can be trained to supports. The short-stalked, bell-shaped flowers are unisexual, but staminate and pistillate are borne on the same plant; the latter are recognized by the swollen warty green ovary below the rest of the flower. The ovary develops into the “cucumber” without fertilization, and unless seeds are wanted, it is advisable to pinch off the male flowers.
There are a great many varieties of cucumber in cultivation, which may be grouped under the two headings (1) forcing, (2) field varieties.
1. The former are large-leaved strong-growing plants, not suited to outdoor culture, with long smooth-rinded fruit; there are many excellent varieties such as Telegraph, Sion House, duke of Edinburgh, &c. The plants are grown in a hot-bed which is prepared towards the end of February from rich stable manure, leaves, &c. A rich turfy loam with a little well-decomposed stable manure forms a good soil. The seeds are sown singly in rich, sandy soil in small pots early in February and plunged in a bottom heat. After they have made one or two foliage-leaves the seedlings are transferred to larger pots, and ultimately about the middle of March to the hot-bed. Each plant is placed in the centre of a mound of soil about a foot deep and well watered with tepid water. The plants should be well watered during their growing period, and the foliage sprinkled or syringed two or three times a day. In bright sunshine the plants are lightly shaded. When grown in frames the tops of the main stems are pinched off when the stems are about 2 ft. long; this causes the development of side shoots on which fruits are borne. When these have produced one or two fruits, they are also stopped at the joint beyond the fruit. When grown in greenhouses the vines may be allowed to reach the full length of the house before they are stopped. To keep the fruits straight they may be grown in cylindrical glass tubes about a foot long, or along narrow wooden troughs. If seeds are required one or more female flowers should be selected and pollen from male flower placed on their stigmas.
2. The outdoor varieties are known as hill or ridge cucumbers. They may be grown in any good soil. A warm, sheltered spot with a south aspect and a mound of rich, sandy loam with a little leaf-mould placed over a hot-bed of dung and leaves is recommended. The mounds or ridges should be 4 to 5 ft. apart, and one plant is placed in the centre of each. The seeds are sown in March in light, rich soil in small pots with gentle heat. The seedlings are repotted and well hardened for planting out in June. The plants must be well watered in and, until established, shaded by a hand-light from bright sunshine. When the leading shoots are from 1½ to 2 ft. long the tips are pinched off to induce the formation of fruit-bearing side-shoots. If seed is required a pistillate 611 flower is selected and pollinated. There are numerous varieties distinguished by size and the smooth or prickly rind. King of the Ridge has smooth fruits a foot or more long; gherkin, a short, prickly form, is much used for pickling.
Cucumber is subject to the attacks of green fly, red spider and thrips; for the two latter, infected leaves should be sponged with soapy water; for green fly careful fumigating is necessary.
The Sikkim cucumber, C. sativus var. sikkimensis, is a large fruited form, reaching 15 in. long by 6 in. thick, grown in the Himalayas of Sikkim and Nepal. It was discovered by Sir Joseph Hooker in the eastern Himalayas in 1848. He says “so abundant were the fruits, that for days together I saw gnawed fruits lying by the natives’ paths by thousands, and every man, woman and child seemed engaged throughout the day in devouring them.” The fruit is reddish-brown, marked with yellow, and is eaten both raw and cooked.
The West India gherkin is Cucumis Anguria, a plant with small, slender vines, and very abundant small ellipsoid green fruit covered with warts and spines. It is used for pickling.
Cucumbers were much esteemed by the ancients. According to Pliny, the emperor Tiberius was supplied with them daily, both in summer and winter. The kishuim or cucumbers of the scriptures (Num. xi. 5; Isa. i. 8) were probably a wild form of C. Melo, the melon, a plant common in Egypt, where a drink is prepared from the ripe fruit. Peter Forskäl, one of the early botanical writers on the country, describes its preparation. The pulp is broken and stirred by means of a stick thrust through a hole cut at the umbilicus of the fruit; the hole is then closed with wax, and the fruit, without removing it from its stem, is buried in a little pit; after some days the pulp is found to be converted into an agreeable liquor (see Flora aegyptiaco-arabica, p. 168, 1775). The squirting cucumber, Ecballium Elaterium, the Σίκυος ἄγριος of Theophrastus, furnishes the drug elaterium (q.v.).
See Naudin in Annal. des sci. nat. ser. 4 (Botany), t. xi. (1859); G. Nicholson, Dictionary of Gardening (1885); L. H. Bailey, Cyclopaedia of American Horticulture (1900).
CUCURBITACEAE, a botanical order of dicotyledons, containing 87 genera and about 650 species, found in the temperate and warmer parts of the earth but especially developed in the tropics. The plants are generally annual herbs, climbing by means of tendrils and having a rapid growth. The long-stalked leaves are arranged alternately, and are generally palmately lobed and veined. The flowers or inflorescences are borne in the leaf-axils, in which a vegetative bud is also found, and at the side of the leaf-stalk is a simple or branched tendril. There has been much difference of opinion as to what member or members the tendril represents; the one which seems most in accordance with facts regards the tendril as a shoot, the lower portion representing the stem, the upper twining portion a leaf. The flowers are unisexual, and strikingly epigynous, the perianth and stamens being attached to a bell-shaped prolongation of the receptacle above the ovary. The five narrow pointed sepals are followed by five petals which are generally united to form a more or less bell-shaped corolla. There are five stamens in the male flowers; the anthers open towards the outside, are one-celled, with the pollen-sacs generally curved and variously united. The carpels, normally three in number, form an ovary with three thick, fleshy, bifid placentas bearing a large number of ovules on each side, and generally filling the interior of the ovary with a juicy mass. The short thick style has generally three branches each bearing a fleshy, usually forked stigma. The fruit is a fleshy many-seeded berry with a tough rind (known as a pepo), and often attains considerable size. The embryo completely fills the seed.
 |
| Fig. 1.—Bryonia dioica, Bryony. 1, part of corolla of male flower with attached stamens; 2, female flower after removal of calyx and corolla; 3, berries; 1, 2, 3 about nat. size. |
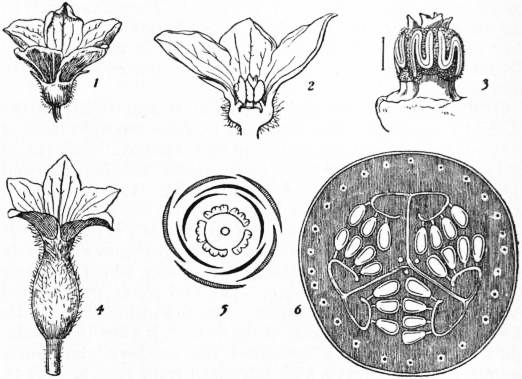 | |
| Fig. 2. | |
|
1, Male flower of cucumber (Cucumis). 2, Same, in vertical section, slightly enlarged. 3, Stamens, after removal of calyx and corolla. |
4, Female flower. 5, Horizontal plan of male flower. 6, Transverse section of fruit.
|
The order is represented in Britain by bryony (Bryonia dioica), (fig. 1) a hedge-climber, perennial by means of large fleshy tubers which send up each year a number of slender angular stems. The leaves are heart-shaped with wavy margined lobes. The flowers are greenish, ½ to ¾ in. in diameter; the fruit, a red several-seeded berry, is about ¼ in. in diameter.
Many genera are of economic importance; Cucumis (fig. 2) affords cucumber (q.v.) and melon (q.v.) Cucurbita, pumpkin and marrow; Citrullus vulgaris is water-melon, and C. Colocynthis, colocynth; Ecballium Elaterium (squirting cucumber) is medicinal; Sechium edule (chocho), a tropical American species, is largely cultivated for its edible fruit; it contains one large seed which germinates in situ. Lagenaria is the gourd (q.v.). The fruits of Luffa aegyptiaca have a number of closely netted vascular bundles in the pericarp, forming a kind of loose felt which supplies the well-known loofah or bath-sponge.
CUDDALORE, a town of British India, in the South Arcot district of Madras, on the coast 125 m. S. of Madras by rail. Pop. (1901) 52,216, showing an increase of 10% in the decade. It lies low, but is regarded as exceptionally healthy, and serves as a kind of sanatorium for the surrounding district. The principal exports are sugar, oil-seeds and indigo. There are two colleges and two high schools. In the neighbourhood are the ruins of Fort St David situated on the river Gadilam, which has 612 as stirring a history as any spot in the Presidency. As a small fort built by a Hindu merchant it fell into the hands of the Mahrattas after the capture of Gingi by Sivaji in 1677. From them it was purchased by the English in 1690, the purchase including not only the fort but the adjacent towns and villages “within ye randome shott of a piece of ordnance.” A great gun was fired to different points of the compass and all the country within its range, including the town of Cuddalore, passed into the possession of the English. The villages thus obtained are still spoken of as “cannon ball villages.” From 1725 onwards the fortifications were greatly strengthened. In 1746 Fort St David became the British headquarters for the south of India, and Dupleix’ attack was successfully repulsed. Clive was appointed its governor in 1756; in 1758 the French captured it, but abandoned it two years later to Sir Eyre Coote. In 1782 they again took it and restored it sufficiently to withstand a British attack in 1783. In 1785 it finally passed into British possession.
CUDDAPAH, a town and district of British India, in the Madras Presidency. The town is 6 m. from the right bank of the river Pennar, and 161 m. by rail from Madras. Pop. (1901) 16,432. It is now a poor place, but has some trade in cotton and indigo, and manufactures of cotton cloth. Hills surround it on three sides, and it has a bad reputation for unhealthiness.
The District of Cuddapah has an area of 8723 sq. m. It is in shape an irregular parallelogram, divided into two nearly equal parts by the range of the Eastern Ghats, which intersects it throughout its entire length. The two tracts thus formed possess totally different features. The first, which constitutes the north, east and south-east of the district, is a low-lying plain; while the other, which comprises the southern and south-western portion, forms a high table-land from 1500 to 2500 ft. above sea-level. The chief river is the Pennar, which enters the district from Bellary on the west, and flows eastwards into Nellore. Though a large and broad river, and in the rains containing a great volume of water, in the hot weather months it dwindles down to an inconsiderable stream. Its principal tributaries are the Kundaur, Saglair, Cheyair, and Papagni rivers. One of the most interesting antiquities in the district is the ancient fort of Gurramkonda. The fort is supposed to have been built by the Golconda sultans; it stands on a hill 500 ft. high, three sides of which consist of almost perpendicular precipices. According to a local legend the name Gurramkonda, meaning “horse hill,” was derived from the fact that a horse was supposed to be guardian of the fort and that the place was impregnable so long as the horse remained there. The story goes that a Mahratta chief at length succeeded in scaling the precipice and in carrying off the horse, and although the thief was captured before reaching the base of the hill, the spell was broken and the fort, when next attacked, fell. The population of the district in 1901 was 1,291,267. The principal crops are millet, rice, other food grains, pulse, oil-seeds, cotton and indigo. The two last are largely exported. There are several steam factories for pressing cotton, and indigo vats. The district is served by lines of the Madras and the South Indian railways.
CUDWORTH, RALPH (1617-1688), English philosopher, was born at Aller, Somersetshire, the son of Dr Ralph Cudworth (d. 1624), rector of Aller, formerly fellow of Emmanuel College, Cambridge. His father died in 1624, and his mother then married the Rev. Dr Stoughton, who gave the boy a good home education. Cudworth was sent to his father’s college, was elected fellow in 1639, and became a successful tutor. In 1642 he published A Discourse concerning the true Notion of the Lord’s Supper, and a tract entitled The Union of Christ and the Church. In 1645 he was appointed master of Clare Hall and the same year was elected Regius professor of Hebrew. He was now recognized as a leader among the remarkable group known as the Cambridge Platonists (q.v.). The whole party were more or less in sympathy with the Commonwealth, and Cudworth was consulted by John Thurloe, Cromwell’s secretary of state, in regard to university and government appointments. His sermons, such as that preached before the House of Commons, on the 31st of March 1647, advocate principles of religious toleration and charity. In 1650 he was presented to the college living of North Cadbury, Somerset. From the diary of his friend John Worthington we learn that Cudworth was nearly compelled, through poverty, to leave the university, but in 1654 he was elected master of Christ’s College, whereupon he married. On the Restoration he contributed some Hebrew verses to the Academiae Cantabrigiensis Σῶστρα, a congratulatory volume addressed to the king. In 1662 he was presented to the rectory of Ashwell, Herts. In 1665 he almost quarrelled with his fellow-Platonist, Henry More, because the latter had written an ethical work which Cudworth feared would interfere with his own long-contemplated treatise on the same subject. To avoid clashing, More brought out his book, the Enchiridion ethicum, in Latin; Cudworth’s never appeared. In 1678 he published The True Intellectual System of the Universe: the first part, wherein all the reason and philosophy of atheism is confuted and its impossibility demonstrated (imprimatur dated 1671). No more was published, perhaps because of the theological clamour raised against this first part. Cudworth was installed prebendary of Gloucester in 1678. He died on the 26th of June 1688, and was buried in the chapel of Christ’s. His only surviving child, Damaris, a devout and talented woman, became the second wife of Sir Francis Masham, and was distinguished as the friend of John Locke. Much of Cudworth’s work still remains in manuscript; A Treatise concerning eternal and immutable Morality was published in 1731; and A Treatise of Freewill, edited by John Allen, in 1838; both are connected with the design of his magnum opus, the Intellectual System.
The Intellectual System arose, so its author tells us, out of a discourse refuting “fatal necessity,” or determinism. Enlarging his plan, he proposed to prove three matters: (a) the existence of God; (b) the naturalness of moral distinctions; and (c) the reality of human freedom. These three together make up the intellectual (as opposed to the physical) system of the universe; and they are opposed respectively by three false principles, atheism, religious fatalism which refers all moral distinctions to the will of God, and thirdly the fatalism of the ancient Stoics, who recognized God and yet identified Him with nature. The immense fragment dealing with atheism is all that was published by its author. Cudworth criticizes two main forms of materialistic atheism, the atomic, adopted by Democritus, Epicurus and Hobbes; and the hylozoic, attributed to Strato, which explains everything by the supposition of an inward self-organizing life in matter. Atomic atheism is by far the more important, if only because Hobbes, the great antagonist whom Cudworth always has in view, is supposed to have held it. It arises out of the combination of two principles, neither of which is atheistic taken separately, i.e. atomism and corporealism, or the doctrine that nothing exists but body. The example of Stoicism, as Cudworth points out, shows that corporealism may be theistic. Into the history of atomism Cudworth plunges with vast erudition. It is, in its purely physical application, a theory that he fully accepts; he holds that it was taught by Pythagoras, Empedocles, and in fact, nearly all the ancient philosophers, and was only perverted to atheism by Democritus. It was first invented, he believes, before the Trojan war, by a Sidonian thinker named Moschus or Mochus, who is identical with the Moses of the Old Testament. In dealing with atheism Cudworth’s method is to marshal the atheistic arguments elaborately, so elaborately that Dryden remarked “he has raised such objections against the being of a God and Providence that many think he has not answered them”; then in his last chapter, which by itself is as long as an ordinary treatise, he confutes them with all the reasons that his reading could supply. A subordinate matter in the book that attracted much attention at the time is the conception of the “Plastic Medium,” which is a mere revival of Plato’s “World-Soul,” and is meant to explain the existence and laws of nature without referring all to the direct operation of God. It occasioned a long-drawn controversy between Pierre Bayle and Le Clerc, the former 613 maintaining, the latter denying, that the Plastic Medium is really favourable to atheism.
No modern reader can endure to toil through the Intellectual System; its only interest is the light it throws upon the state of religious thought after the Restoration, when, as Birch puts it, “irreligion began to lift up its head.” It is immensely diffuse and pretentious, loaded with digressions, its argument buried under masses of fantastic, uncritical learning, the work of a vigorous but quite unoriginal mind. As Bolingbroke said, Cudworth “read too much to think enough, and admired too much to think freely.” It is no calamity that natural procrastination, or the clamour caused by his candid treatment of atheism and by certain heretical tendencies detected by orthodox criticism in his view of the Trinity, made Cudworth leave the work unfinished.
A much more favourable judgment must be given upon the short Treatise on eternal and immutable Morality, which deserves to be read by those who are interested in the historical development of British moral philosophy. It is an answer to Hobbes’s famous doctrine that moral distinctions are created by the state, an answer from the standpoint of Platonism. Just as knowledge contains a permanent intelligible element over and above the flux of sense-impressions, so there exist eternal and immutable ideas of morality. Cudworth’s ideas, like Plato’s, have “a constant and never-failing entity of their own,” such as we see in geometrical figures; but, unlike Plato’s, they exist in the mind of God, whence they are communicated to finite understandings. Hence “it is evident that wisdom, knowledge and understanding are eternal and self-subsistent things, superior to matter and all sensible beings, and independent upon them”; and so also are moral good and evil. At this point Cudworth stops; he does not attempt to give any list of Moral Ideas. It is, indeed, the cardinal weakness of this form of intuitionism that no satisfactory list can be given and that no moral principles have the “constant and never-failing entity,” or the definiteness, of the concepts of geometry. Henry More, in his Enchiridion ethicum, attempts to enumerate the “noemata moralia”; but, so far from being self-evident, most of his moral axioms are open to serious controversy.
The Intellectual System was translated into Latin by J. L. Mosheim and furnished with notes and dissertations which were translated into English in J. Harrison’s edition (1845). Our chief biographical authority is T. Birch’s “Account,” which appears in editions of the Works. There is a good chapter on Cudworth in J. Tulloch’s Rational Theology, vol. ii. Consult also P. Janet’s Essai sur le médiateur plastique (1860), W. R. Scott’s Introduction to Cudworth’s “Treatise,” and J. Martineau’s Types of Ethical Theory, vol. ii.
CUENCA, a city and the capital of the province of Azuay, Ecuador, about 190 m. S. of Quito and 70 m. S.E. of Guayaquil. Pop. (1908 estimate) 30,000 (largely Indians), including the suburb of Ejido. Cuenca stands at the northern end of a broad valley, or basin, of the Andes, lying between the transverse ridges of Azuay and Loja, and is about 8640 ft. above sea-level. Near by is the hill of Tarqui which the French astronomers chose for their meridian in 1742. Communication with the coast is difficult. Cuenca is the third most important city of Ecuador, being the seat of a bishopric, and having a college, a university faculty, a cathedral, and several churches, and a considerable industrial and commercial development. It manufactures sugar, woollen goods and pottery, and exports Peruvian bark (cinchona), hats, cereals, cheese, hides, &c. It was founded in 1557 on the site of a native town called Tumibamba, and was made an episcopal see in 1786.
CUENCA, a province of central Spain bounded on the N. by Guadalajara, N.E. by Teruel, E. by Valencia, S. by Albacete, S.W. by Ciudad Real, W. by Toledo and N.W. by Madrid. Pop. (1900) 249,696; area, 6636 sq. m. Cuenca occupies the eastern part of the ancient kingdom of New Castile, and slopes from the Serrania de Cuenca (highest point the Cerro de San Felipe, on the north-eastern border of the province, 5905 ft.), down into the great southern Castilian plain watered by the upper streams of the Guadiana. The lowlands bordering on Ciudad Real belong to the wide plain of La Mancha (q.v.). The rocky and bare highland of Cuenca on the north and east includes the upper valley of the Jucar and its tributary streams, but in the north-west the province is watered by tributaries of the Tagus. The forests are proverbial for their pine timber, and rival those of Soria; considerable quantities of timber are floated down the Tagus to Aranjuez and thence taken to Madrid for building purposes. Excessive droughts prevail; the climate of the hills and of the high plateaus is harsh and cold, but the valleys are excessively hot in summer. The soil, where well watered, is fertile, but little attention is paid to agriculture, and three-fourths of the area is left under pasture. The rearing of cattle, asses, mules and sheep is the principal employment of the people; olive oil, nuts, wine, wheat, silk, wax and honey are the chief products. Iron, copper, alum, saltpetre, jasper and agates are found, but in 1903 all the workings had been abandoned except three salt mines; and there are few manufactures except the weaving of coarse cloth. The roads are in such a backward condition that they cripple not only the mining interests but also the exports of timber, and at the beginning of the 20th century there was no railway except a branch line which passed westwards from Aranjuez through Tarancon to Cuenca, the capital (pop. 1900, 10,756). No other town has as many as 6000 inhabitants, and no other Spanish province is so thinly populated as Cuenca. In 1900 there were only 37.6 inhabitants per sq. m. Education is backward, and extreme poverty almost universal among the peasantry. See also Castile.
CUENCA, the capital of the Spanish province of Cuenca; 125 m. by rail E. by S. of Madrid. Pop. (1900) 10,756. Cuenca occupies a height of the well-wooded Serrania de Cuenca, at an elevation of 2960 ft., overlooking the confluence of the rivers Jucar and Huecar. A fine bridge, built in 1523, crosses the Jucar to the convent of San Pablo. Among several interesting churches in the city, the most noteworthy is the 13th-century Gothic cathedral, celebrated for the beautiful carved woodwork of its 16th-century doorway, and containing some admirable examples of Spanish sculpture. The city has a considerable trade in timber, and was long the headquarters of the provincial wool industry; the loss of which, in modern times, has partly been compensated by the development of soap, paper, chocolate, match and leather manufactures. Cuenca was captured from the Moors by Alphonso VIII. of Castile in 1177, and shortly afterwards became an episcopal see. In 1874 it offered a prolonged and gallant resistance to the Carlist rebels.
CUESTA, a name of Spanish origin used in New Mexico for low ridges of steep descent on one side and gentle slope on the other. It has been proposed as a term for the land form which consists of the two elements of a steep scarp or “strike” face, and an inclined plain or gentle “dip” slope.
CUEVAS DE VERA, a town of south-eastern Spain, in the province of Almería; on the right bank of the river Almanzora, 8 m. W. of the Mediterranean Sea. Pop. (1900) 20,562. Cuevas de Vera is built at the eastern extremity of the Sierra de los Filabres (6823 ft.), which isolate it from the railway system of Almería. It is, however, the chief market for the rich agricultural districts towards the south and for the argentiferous lead and other mines among the mountains. In appearance it is modern, with wide streets, two fine squares, and a parish church in Doric style, dating from 1758. But in reality the town is of considerable antiquity. One of the towers in the Moorish palace owned by the marquesses of Villafranca is probably of Roman origin.
CUFF. (1) (Of uncertain origin), the lower edge of a sleeve turned back to show an ornamental border, or with an addition of lace or trimming; now used chiefly of the stiff bands of linen worn under the coat-sleeve either loose or attached to the shirt. (2) Also uncertain in origin, but with no connexion, probably, with (1), a blow with the hand either open or closed, as opposed to the use of weapons.
CUIRASS (Fr. cuirasse, Lat. coriaceus, made of leather, from corium, the original breastplate being of leather), the plate armour, whether formed of a single piece of metal or other rigid material or composed of two or more pieces, which covers the 614 front of the wearer’s person. In a suit of armour, however, since this important piece was generally worn in connexion with a corresponding defence for the back, the term cuirass commonly is understood to imply the complete body-armour, including both the breast and the back plates. Thus this complete body-armour appears in the middle ages frequently to have been described as a “pair of plates.” The corslet (Fr. corselet, diminutive of the O. Fr. cors, body), a comparatively light cuirass, is more strictly a breast-plate only. As parts of the military equipment of classic antiquity, cuirasses and corslets of bronze, and at later periods also of iron or some other rigid substance, were habitually in use; but while some special kind of secondary protection for the breast had been worn in earlier times by the men-at-arms in addition to their mail hauberks and their “cotes” armed with splints and studs, it was not till the 14th century that a regular body-defence of plate can be said to have become an established component of medieval armour. As this century continued to advance, the cuirass is found gradually to have come into general use, in connexion with plate defences for the limbs, until, at the close of the century, the long familiar interlinked chain-mail is no longer visible in knightly figures, except in the camail of the bassinet and at the edge of the hauberk. The prevailing, and indeed almost the universal, usage throughout this century was that the cuirass was worn covered. Thus, the globose form of the breast-armour of the Black Prince, in his effigy in Canterbury cathedral, 1376, intimates that a cuirass as well as a hauberk is to be considered to have been covered by the royalty-emblazoned jupon of the prince. The cuirass, thus worn in the 14th century, was always made of sufficient length to rest on the hips; otherwise, if not thus supported, it must have been suspended from the shoulders, in which case it would have effectually interfered with the free and vigorous action of the wearer. Early in the 15th century, the entire panoply of plate, including the cuirass, began to be worn without any surcoat; but in the concluding quarter of the century the short surcoat, with full short sleeves, known as the tabard, was in general use over the armour. At the same time that the disuse of the surcoat became general, small plates of various forms and sizes (and not always made in pairs, the plate for the right or sword-arm often being smaller and lighter than its companion), were attached to the armour in front of the shoulders, to defend the otherwise vulnerable points where the plate defences of the upper-arms and the cuirass left a gap on each side. About the middle of the century, instead of being formed of a single plate, the breast-plate of the cuirass was made in two parts, the lower adjusted to overlap the upper, and contrived by means of a strap or sliding rivet to give flexibility to this defence. In the second half of the 15th century the cuirass occasionally was superseded by the “brigandine jacket,” a defence formed of some textile fabric, generally of rich material, lined throughout with overlapping scales (resembling the earlier “imbricated” form) of metal, which were attached to the jacket by rivets, having their heads, like studs, visible on the outside. In the 16th century, when occasionally, and by personages of exalted rank, splendid surcoats were worn over the armour, the cuirass—its breast-piece during the first half of the century, globular in form—was constantly reinforced by strong additional plates attached to it by rivets or screws. About 1550 the breast-piece of the cuirass was characterized by a vertical central ridge, called the “tapul” having near its centre a projecting point; this projection, somewhat later, was brought lower down, and eventually the profile of the plate, the projection having been carried to its base, assumed the singular form which led to this fashion of the cuirass being distinguished as the “peascod cuirass.”
Corslets provided with both breast and back pieces were worn by foot-soldiers in the 17th century, while their mounted comrades were equipped in heavier and stronger cuirasses; and these defences continued in use after the other pieces of armour, one by one, had gradually been laid aside. Their use, however, never altogether ceased, and in modern armies mounted cuirassiers, armed as in earlier days with breast and back plates, have in some degree emulated the martial splendour of the body-armour of the era of medieval chivalry. Some years after Waterloo certain historical cuirasses were taken from their repose in the Tower of London, and adapted for service by the Life Guards and the Horse Guards. For parade purposes, the Prussian Gardes du Corps and other corps wear cuirasses of richly decorated leather.
CUIRASSIERS, a kind of heavy cavalry, originally developed out of the men-at-arms or gendarmerie forming the heavy cavalry of feudal armies. Their special characteristic was the wearing of full armour, which they retained long after other troops had abandoned it. Hence they became distinguished as cuirassiers. The first Austrian corps of kyrissers was formed in 1484 by the emperor Maximilian and was 100 strong. In 1705 Austria possessed twenty regiments of cuirassiers. After the war of 1866, however, the existing regiments were converted into dragoons. Russia has likewise in modern times abolished all but a few guard regiments of cuirassiers. The Prussian cuirassiers were first so called under Frederick William I., and in the wars of his successor Frederick the Great they bore a conspicuous part. After the Seven Years’ War they ceased to wear the cuirass on service, but after 1814 these were reintroduced, the spoils taken from the French cuirassiers being used to equip the troops. The cuirass is now worn only on ceremonial parades. In France the cuirassiers date from 1666, when a regiment, subsequently numbered 8th of the line, was formed. During the first Empire many regiments were created, until in 1812 there were fourteen. The number was reduced after the fall of Napoleon, but in modern times it has been again increased. The French regiments alone in Europe wear the cuirass on all parades and at manœuvres.
CUJAS (or Cujacius), JACQUES (or as he called himself, Jacques de Cujas) (1520-1590), French jurisconsult, was born at Toulouse, where his father, whose name was Cujaus, was a fuller. Having taught himself Latin and Greek, he studied law under Arnoul Ferrier, then professor at Toulouse, and rapidly gained a great reputation as a lecturer on Justinian. In 1554 he was appointed professor of law at Cahors, and about a year after L’Hôpital called him to Bourges. Duaren, however, who also held a professorship at Bourges, stirred up the students against the new professor, and such was the disorder produced in consequence that Cujas was glad to yield to the storm, and accept an invitation he had received to the university of Valence. Recalled to Bourges at the death of Duaren in 1559, he remained there till 1567, when he returned to Valence. There he gained a European reputation, and collected students from all parts of the continent, among whom were Joseph Scaliger and de Thou. In 1573 Charles IX. appointed Cujas counsellor to the parlement of Grenoble, and in the following year a pension was bestowed on him by Henry III. Margaret of Savoy induced him to remove to Turin; but after a few months (1575) he once more took his old place at Bourges. But the religious wars drove him thence. He was called by the king to Paris, and permission was granted him by the parlement to lecture on civil law in the university of the capital. A year after, however, he finally took up his residence at Bourges, where he remained till his death in 1590, in spite of a handsome offer made him by Gregory XIII. in 1584 to attract him to Bologna.
The life of Cujas was altogether that of a scholar and teacher. In the religious wars which filled all the thoughts of his contemporaries he steadily refused to take any part. Nihil hoc ad edictum praetoris, “this has nothing to do with the edict of the praetor,” was his usual answer to those who spoke to him on the subject. His surpassing merit as a jurisconsult consisted in the fact that he turned from the ignorant commentators on Roman law to the Roman law itself. He consulted a very large number of manuscripts, of which he had collected more than 500 in his own library; but, unfortunately, he left orders in his will that his library should be divided among a number of purchasers, and his collection was thus scattered, and in great part lost. His emendations, of which a large number were published under the title of Animadversiones et observationes, were not confined to lawbooks, but extended to many of the Latin and Greek classical 615 authors. In jurisprudence his study was far from being devoted solely to Justinian; he recovered and gave to the world a part of the Theodosian Code, with explanations; and he procured the manuscript of the Basilica, a Greek abridgment of Justinian, afterwards published by Fabrot (see Basilica). He also composed a commentary on the Consueludines Feudorum, and on some books of the Decretals. In the Paratitla, or summaries which he made of the Digest, and particularly of the Code of Justinian, he condensed into short axioms the elementary principles of law, and gave definitions remarkable for their admirable clearness and precision. His lessons, which he never dictated, were continuous discourses, for which he made no other preparation than that of profound meditation on the subjects to be discussed. He was impatient of interruption, and upon the least noise he would instantly quit the chair and retire. He was strongly attached to his pupils, and Scaliger affirms that he lost more than 4000 livres by lending money to such of them as were in want.
In his lifetime Cujas published an edition of his works (Neville, 1577). It is beautiful and exact, but incomplete; it is now very scarce. The edition of Colombet (1634) is also incomplete. Fabrot, however, collected the whole in the edition which he published at Paris (1658), in 10 vols. folio, and which was reprinted at Naples (1722, 1727), in 11 vols. folio, and at Naples and at Venice (1758), in 10 vols. folio, with an index forming an eleventh volume. In the editions of Naples and Venice there are some additions not to be found in that of Fabrot, particularly a general table, which will be found very useful, and interpretations of all the Greek words used by Cujas.
See Papire-Masson, Vie de Cujas (Paris, 1590); Terrasson, Histoire de la jurisprudence romaine, and Mélanges d’histoire, de littérature, et de jurisprudence; Bernardi, Éloge de Cujas (Lyons, 1775); Hugo, Civilistisches Magazin; Berriat Saint Prix, Mémoires de Cujas, appended to his Histoire du droit romain; Biographie universelle; Gravina, De ortu et progressu juris civilis; Spangenberg, Cujacius und seine Zeitgenossen (Leipzig, 1882).
CULDEES, an ancient monastic order with settlements in Ireland and Scotland. It was long fondly imagined by Protestant and especially by Presbyterian writers that they had preserved primitive Christianity free from Roman corruptions in one remote corner of western Europe, a view enshrined in Thomas Campbell’s Reullura:
| “Peace to their shades. The pure Culdees Were Albyn’s earliest priests of God, Ere yet an island of her seas By foot of Saxon monk was trod.” |
Another view, promulgated like the above by Hector Boece in his Latin history of Scotland (1516), makes them the direct successors in the 9th to the 12th century of the organized Irish and Iona monasticism of the 6th to the 8th century. Both these views were disproved by William Reeves (1815-1892), bishop of Down, Connor and Dromore.
As found in the Irish MSS. the name is Céle Dé, i.e. God’s comrade or sworn ally. It was latinized as Coli dei, whence Boece’s culdei. The term seems, like the Latin vir dei, to have been applied generally to monks and hermits. There are very few trustworthy ancient sources of information, but it seems probable that the Rule of Chrodegang,1 archbishop of Metz (d. 766), was brought by Irish monks to their native land from the monasteries of north-eastern Gaul, and that Irish anchorites originally unfettered by the rules of the cloister bound themselves by it. In the course of the 9th century we find mention of nine places in Ireland (including Armagh, Clonmacnoise, Clones, Devenish and Sligo) where communities of these Culdees were established as a kind of annexe to the regular monastic institutions. They seem especially to have had the care of the poor and the sick, and were interested in the musical part of worship. Meanwhile in Scotland the Iona monks had been expelled by the Pictish king Nechtan in 717, and the vacancies thus caused were by no means filled by the Roman monks who thronged into the north from Northumbria. Into the gap, towards the end of the 8th century, came the Culdees from Ireland. The features of their life in Scotland, which is the most important epoch in the history of the order, seem to resemble closely those of the secular canons of England and the continent. From the outset they were more or less isolated, and, having no fixed forms or common head, tended to decay. In the 12th century the Celtic Church was completely metamorphosed on the Roman pattern, and in the process the Culdees also lost any distinctiveness they may formerly have had, being brought, like the secular clergy, under canonical rule. The pictures that we have of Culdee life in the 12th century vary considerably. The chief houses in Scotland were at St Andrews, Dunkeld, Lochleven, Monymusk in Aberdeenshire, Abernethy and Brechin. Each was an independent establishment controlled entirely by its own abbot and apparently divided into two sections, one priestly and the other lay and even married. At St Andrews about the year 1100 there were thirteen Culdees holding office by hereditary tenure and paying more regard to their own prosperity and aggrandizement than to the services of the church or the needs of the populace. A much-needed measure of reform, inaugurated by Queen Margaret, was carried through by her sons Alexander I. and David I.; gradually the whole position passed into the hands of Turgot and his successors in the bishopric. Canons Regular were instituted and some of the Culdees joined the new order. Those who declined were allowed a life-rent of their revenues and lingered on as a separate but ever-dwindling body till the beginning of the 14th century, when, excluded from voting at the election of the bishop, they disappear from history. At Dunkeld, Crinan, the grandfather of Malcolm Canmore, was a lay abbot, and tradition says that even the clerical members were married, though like the priests of the Eastern Church, they lived apart from their wives during their term of sacerdotal service. The Culdees of Lochleven lived on St Serf’s Inch, which had been given them by a Pictish prince, Brude, about 850. In 1093 they surrendered their island to the bishop of St Andrews in return for perpetual food and clothing, but Robert, who was bishop in 1144, handed over all their vestments, books,2 and other property, with the island, to the newly founded Canons Regular, in which probably the Culdees were incorporated. There is no trace of such partial independence as was experienced at St Andrews itself, possibly because the bishop’s grant was backed up by a royal charter. In the same fashion the Culdees of Monymusk, originally perhaps a colony from St Andrews, became Canons Regular of the Augustinian order early in the 13th century, and those of Abernethy in 1273. At Brechin, famous like Abernethy for its round tower, the Culdee prior and his monks helped to form the chapter of the diocese founded by David I. in 1145, though the name persisted for a generation or two. Similar absorptions no doubt account for the disappearance of the Culdees of York, a name borne by the canons of St Peter’s about 925, and of Snowdon and Bardsey Island in north Wales mentioned by Giraldus Cambrensis (c. 1190) in his Speculum Ecclesiae and Itinerarium respectively. The former community was, he says, sorely oppressed by the covetous Cistercians. These seem to be the only cases where the Culdees are found in England and Wales. In Ireland the Culdees of Armagh endured until the dissolution in 1541, and enjoyed a fleeting resurrection in 1627, soon after which their ancient property passed to the vicars choral of the cathedral.
See W. Reeves, The Culdees of the British Islands (Dublin, 1864); W. F. Skene, Celtic Scotland (1876-1880), especially vol. ii.; W. Beveridge, Makers of the Scottish Church (1908). The older view will be found in J. Jamieson’s Historical Account of the Ancient Culdees (1811).
1 Devised originally for the clergy of Chrodegang’s cathedral, it was largely an adaptation of St Benedict’s rule to secular clergy living in common. In 816 it was confirmed, with certain modifications, by the synod of Aix-la-Chapelle, and became the law for collegiate and cathedral churches in the Frankish empire. See Canon.
2 The list of these in the deed of transfer is the oldest Scottish library catalogue.
CULEBRA, the smaller of two islands lying in the Virgin Passage immediately E. of Porto Rico and known as the Islas de Passaje. It is about 18 m. distant from Cape San Juan and rises from the same submerged plateau with the larger islands of the Antilles. Its extreme dimensions are 3 by 6 m., and its surface is low and comparatively uniform, which gives the 616 prevailing winds an unbroken sweep across it. For this reason the rainfall is limited to a short season, and the population is compelled to store rainwater in cisterns for drinking purposes. Its soil is fertile, and cattle, poultry, vegetables and small fruits are produced. The island has been a dependency of Porto Rico since 1879, when its colonization was formally undertaken, and it is now described as a ward of the Vieques district of the department of Humacao. In 1902 the American naval authorities selected the Playa Sardinas harbour on the S. side of Culebra as a rendezvous of the fleet and marine encampments were located on shore. The strategic position of the island, its healthiness and its continued use as a naval station have given it considerable importance. Its population was 704 in 1899, which had increased to nearly 1200 in 1903.
CULLEN, PAUL (1803-1878), cardinal and archbishop of Dublin, was born near Ballytore, Co. Kildare, and educated first at the Quaker school at Carlow and afterwards at Rome, where he joined the Urban College of the Propaganda and, after passing a brilliant course, was ordained in 1829. He then became vice-rector, and afterwards rector, of the Irish National College in Rome; and during the Mazzini revolution of 1848 he was rector of the Urban College, saving the property under the protection of the American flag. In 1849, on the strong recommendation of Archbishop John MacHale of Tuam, Cullen was nominated as successor to the primatial see of Armagh; and, on his return to Ireland, presided as papal delegate at the national council of Thurles in the August of 1850. Taking a strong line on the educational question which was then agitating Ireland, he took a leading part in the national movement of 1850-1852, and at first supported the Tenant Rights League. In May 1852 he was translated to Dublin, and soon a divergence of opinion broke out between him and the more ardent Nationalists under Archbishop MacHale. When the Irish university was started, with Newman, appointed by Cullen, at its head, the scheme was wrecked by the personal opposition to the archbishop of Dublin. As time went on, his distrust of the national movement grew deeper; and in 1853 he sternly forbade his clergy to take part publicly in politics, and for this he was denounced by the Tablet newspaper. His own political opinion had best be told in his own words. “For thirty years I have studied the revolution on the continent, and for nearly thirty years I have watched the Nationalist movement in Ireland. It is tainted at its sources with the revolutionary spirit. If any attempt is made to abridge the rights and liberties of the Catholic Church in Ireland, it will not be by the English government nor by a ‘No Popery’ cry in England, but by the revolutionary and irreligious Nationalists of Ireland” (Purcell’s Life of Manning, ii. 610). Cullen, therefore, while an ardent patriot, was consistently an opponent of Fenianism. He was made cardinal in 1866, being the first Irish cardinal. Energetic as an administrator, churches and schools rose throughout his diocese; and the excellent Mater Misericordiae Hospital and the seminary at Clonlife are lasting memorials of his zeal. He took part in the Vatican Council as an ardent infallibilist. In 1873 he was defendant in a libel action brought against him by the Rev. R. O’Keeffe, parish priest of Callan, on account of two sentences of ecclesiastical censure pronounced by the cardinal as papal delegate. The damages were laid at £10,000. Three of the four judges allowed the defence of the cardinal to be valid; but it was held that the papal rescript upon which he relied for his extraordinary powers as delegate was illegal under statute; and the lord chief justice decided that the plaintiff could not renounce his natural and civil liberty. After several days’ trial, during which Cullen was submitted to a very close examination, the verdict was given for the plaintiff with ¼d. damages. The cardinal died in Dublin on the 24th of October 1878.
CULLEN, WILLIAM (1710-1790), Scottish physician and medical teacher, was born at Hamilton, Lanarkshire, on the 15th of April 1710. He received his early education at the grammar-school of Hamilton, and he appears to have subsequently attended some classes at the university of Glasgow. He began his medical career as apprentice to John Paisley, a Glasgow surgeon, and after completing his apprenticeship he became surgeon to a merchant vessel trading between London and the West Indies. On his return to Scotland in 1732 he settled as a practitioner in the parish of Shotts, Lanarkshire, and in 1734-1736 studied medicine at Edinburgh, where he was one of the founders of the Royal Medical Society. In 1736 he began to practise in Hamilton, where he rapidly acquired a high reputation. From 1737 to 1740 William Hunter was his resident pupil, and at one time they proposed to enter into partnership. In 1740 Cullen took the degree of M.D. at Glasgow, whither he removed in 1744. During his residence at Hamilton, besides the arduous duties of medical practice, he found time to devote to the study of the natural sciences, and especially of chemistry. On coming to Glasgow he appears to have begun to lecture in connexion with the university, the medical school of which was as yet imperfectly organized. Besides the subjects of theory and practice of medicine, he lectured systematically on botany, materia medica and chemistry. His great abilities, enthusiasm and power of conveying instruction made him a successful and highly popular teacher, and his classes increased largely in numbers. At the same time he diligently pursued the practice of his profession. Chemistry was the subject which at this time seems to have engaged the greatest share of his attention. He was himself a diligent investigator and experimenter, and he did much to encourage original research among his pupils, one of whom was Dr Joseph Black. In 1751 he was appointed professor of medicine, but continued to lecture on chemistry, and in 1756 he was elected joint professor of chemistry at Edinburgh along with Andrew Plummer, on whose death in the following year the sole appointment was conferred on Cullen. This chair he held for ten years—his classes always increasing in numbers. He also practised his profession as a physician with eminent success. From 1757 he delivered lectures on clinical medicine in the Royal Infirmary. This was a work for which his experience, habits of observation, and scientific training peculiarly fitted him, and in which his popularity as a teacher, no less than his power as a practical physician, became more than ever conspicuous. On the death of Charles Alston in 1760, Cullen at the request of the students undertook to finish his course of lectures on materia medica; he delivered an entirely new course, which were published in an unauthorized edition in 1771, but which he re-wrote and issued as A Treatise on Materia Medica in 1789.
On the death of Robert Whytt (1714-1766), the professor of the institutes of medicine, Cullen accepted the chair, at the same time resigning that of chemistry. In the same year he had been an unsuccessful candidate for the professorship of the practice of physic, but subsequently an arrangement was made between him and John Gregory, who had gained the appointment, by which they agreed to deliver alternate courses on the theory and practice of physic. This arrangement proved eminently satisfactory, but it was brought to a close by the sudden death of Gregory in 1773. Cullen was then appointed sole professor of the practice of physic, and he continued in this office till a few months before his death, which took place on the 5th of February 1790.
As a lecturer Cullen appears to have stood unrivalled in his day. His clearness of statement and power of imparting interest to the most abstruse topics were the conspicuous features of his teaching, and in his various capacities as a scientific lecturer, a physiologist, and a practical physician, he was ever surrounded with large and increasing classes of intelligent pupils, to whom his eminently suggestive mode of instruction was specially attractive. Living at the time he did, when the doctrines of the humoral pathologists were carried to an extreme extent, and witnessing the ravages which disease made on the solid structures of the body, it was not surprising that he should oppose a doctrine which appeared to him to lead to a false practice and to fatal results, and adopt one which attributed more to the agency of the solids and very little to that of the fluids of the body. His chief works were First Lines of the Practice of Physic (1774); Institutions of Medicine (1770); and Synopsis 617 Nosologicae Medicae (1785), which contained his classification of diseases into four great classes—(1) Pyrexiae, or febrile diseases, as typhus fever; (2) Neuroses, or nervous diseases, as epilepsy; (3) Cachexiae, or diseases resulting from bad habit of body, as scurvy; and (4) Locales, or local diseases, as cancer.
Cullen’s eldest son Robert became a Scottish judge in 1796 under the title of Lord Cullen, and was known for his powers of mimicry.
The first volume of an account of Cullen’s Life, Lectures and Writings was published by Dr John Thomson in 1832, and was reissued with the second volume (completing the work) by Drs W. Thomson and D. Craigie in 1859.
CULLEN, a royal, municipal and police burgh of Banffshire, Scotland. Pop. (1901) 1936. It is situated on Cullen Bay, 11½ m. W. by N. of Banff and 66½ m. N.W. of Aberdeen by the Great North of Scotland railway. Deskford Burn, after a course of 7½ m., enters the sea at Cullen, which it divides into two parts, Seatown, the older, and Newtown, dating only from 1822. St Mary’s, the parish church, a cruciform structure, was founded by Robert Bruce, whose second wife died at Cullen. The industries include rope and sail making, boat-building, brewing and fishing. The harbour, constructed between 1817 and 1834, though artificial, is one of the best on this coast. About 1 m. to the S. is Cullen House, a seat of the earl of Seafield, which contains some fine works of art. A mile and a half to the W. is the picturesque fishing village of Port Knockie with a deep-sea harbour, built in 1891. On the cliffs, 2 m. to the E., stand the ruins of Findlater Castle, fortified in 1455. From 1638 to 1811, when the title expired, it gave the title of earl to the Ogilvies, whose name was adopted in addition to his own by Sir Lewis Alexander Grant, when he succeeded, as 5th earl of Seafield, to the surviving dignities. Five miles to the E. of Cullen is the thriving fishing town of Portsoy, with a small, safe harbour and a station on the Great North of Scotland railway. Besides the fisheries there is fish-curing and a distillery; and the quarrying of a pink-coloured variety of granite and of Portsoy marble is carried on. Good limestone is also found in the district. Pop. (1901) 2061.
CULLERA, a seaport of eastern Spain, in the province of Valencia; on the Mediterranean Sea, at the mouth of the river Jucar, and at the southern terminus of the Valencia-Silla-Cullera railway. Pop. (1900) 11,947. Cullera is a walled town, containing a ruined Moorish citadel, large barracks, several churches and convents and a hospital. It occupies the Jucar valley, south of the Sierra de Zorras, a low range of hills which terminates eastward in Cape Cullera, a conspicuous headland surmounted by a lighthouse. To the south and west extends a rich agricultural district, noted for its rice. Besides farming and fishing, the inhabitants carry on a coasting trade with various Mediterranean ports. In 1903 the harbour was entered by 66 vessels of about 25,000 tons, engaged in the exportation of grain, rice and fruit, and the importation of guano. The town of Sueca (q.v.) is 4 m. W.N.W. by rail.
CULLINAN, a town of the Transvaal, 36 m. by rail E. by N. of Pretoria. It grew up round the Premier diamond mine and dates from 1903, being named after T. Cullinan, the purchaser of the ground on which the mine is situated. Here was discovered in January 1905 a diamond—the largest on record—weighing 3025¾ carats. This diamond was in 1907 presented by the Transvaal government to Edward VII. and was subsequently cut into two stones, one of 516½ carats, the other of 309 carats, intended to ornament the sceptre and crown of England. The “chippings” yielded several smaller diamonds (see Diamond).
CULLODEN, a desolate tract of moorland, Inverness-shire, Scotland. It forms part of the north-east of Drummossie Muir, and is situated about 6 m. by road E. of Inverness, and ½ m. from Culloden Muir station on the Highland railway from Aviemore to Inverness via Daviot. It is celebrated as the scene of the battle of the 16th of April 1746 (see Cumberland, William Augustus, Duke of, and Murray, Lord George), by which the fate of the house of Stuart was decided. By Highlanders the battle is more generally described as the battle of Drummossie. Memorial stones bearing the names of the clans engaged in the conflict were erected in 1881 at the head of each trench where the clansmen—about 1000 in number—were buried. A monumental cairn, 20 ft. high, marks the chief scene of the fight, and the Cumberland Stone, a huge boulder, indicates the spot where the English commander took up his position. A mile to the north is Culloden House, which belonged to Duncan Forbes, the president of the Court of Session. The Culloden Papers, a number of historical documents ranging from 1625 to 1748, were discovered in this mansion in 1812 and published in 1815 by Duncan George Forbes. On the death of the 10th laird, the collection of Jacobite relics and works of art was sold by auction in 1897. About 1 m. to the south of the field, on the right bank of the Nairn, is the plain of Clava, containing several stone circles, monoliths, cairns and other prehistoric remains. The circles, some apparently never completed, vary in circumference from 12 yds. to 140 yds.
CULM, in geology, the name applied to a peculiar local phase of the Carboniferous system. In 1837 A. Sedgwick and R. I. Murchison classified into two divisions the dark shales, grits and impure limestones which occupy a large area in Devonshire and extend into the neighbouring counties of Somerset and Cornwall. These two divisions were the Upper and Lower Culm Measures, so named from certain impure coals, locally called “culm,”1 contained within the shales near Bideford. Subsequently, these two geologists, when prosecuting their researches in Germany and Austria, applied the same name to similar rocks which contained, amongst others, Posidonomya Becheri, common to the phase of sedimentation in both areas.
The Culm measures of the Devonshire district are folded into a broad syncline with its axis running east and west; but within this major fold the rocks have been subjected to much compression accompanied by minor folding. This circumstance, together with the apparent barrenness of the strata, has always made a correct interpretation of their position and relationships a matter of difficulty; and for long they were regarded as an abnormal expression of the Lower Carboniferous, with the uppermost beds as doubtful equivalents of the Millstone Grit of other parts of Britain. The labours of W. A. E. Ussher and of G. J. Hinde and H. Fox have resulted in the differentiation of the following subdivisions in the Devonshire Culm:—(1) Upper Culm Measures or Eggesford grits; (2) Middle Culm Measures, comprising the Morchard, Tiverton and Ugbrooke lithological types overlying the Exeter type; (3) Lower Culm, the Posidonomya limestone and shale overlying the Coddon Hill beds with radiolaria. Ussher’s subdivisions were introduced to satisfy the exigencies of geological mapping, but, as he pointed out, while they are necessary in some parts of the district and convenient in others, the lithological characters upon which they are founded are variable and inconstant. More recently E. A. N. Arber (1904-1907) clearly demonstrated that no palaeontological subdivision of the Upper Culm (Middle and Upper) is possible, and that these strata, on the evidence of the fossil plants, represent the Middle Coal Measures of other parts of the country. Wheelton Hind has called attention to the probability that the Posidonomya limestone and shale may represent the Pendleside group of Lancashire, Derbyshire, &c. The Coddon Hill beds may belong to this or to a lower horizon. Thus the English Culm measures comprise an Upper Carboniferous and a Lower Carboniferous group, while in Germany, Austria and elsewhere, as it is important to bear in mind, the Culm, or “Kulm,” stage is shown by its contained fossils to belong to the lower division alone.
The typical Carboniferous limestone of the Franco-Belgian area changes as it is traced towards the east and south into the sandy, shaly Culm phase, with the characteristic “Posidonia” (Posidonomya) schists. This aspect of the Culm is found in Saxony, where there are workable coals, in Bohemia, Thuringia, the Fichtelgebirge, the Harz, where the beds are traversed by mineral veins, and in Moravia and Silesia. In the last-mentioned region the thickness of the Culm formation has been estimated 618 by D. Stur at over 45,000 ft. In the east and south of the Schiefergebirge (a general term for the slaty mountains of the Hundsrück and Taunus range, the Westerwald and part of the Eifel district), the Culm shales pass upwards into a coarser deposit, the “Culm-grauwacke,” which attains a considerable thickness and superficial extent. Culm fossils appear in the Carnic Alps, in the Balkans and parts of Spain, also in Spitzbergen and part of New Guinea.
The most characteristic fossil is of course Posidonomya Becheri; others are Glyphioceras sphaericum, Rhodea patentissima, Asterocalamites scrobiculatus (Schloth), Lepidodendron veltheimianum, Gastrioceras carbonarium.
See E. A. N. Arber, “On the Upper Carboniferous Rocks of West Devon and North Cornwall,” Q.J.G.S. lxiii. (1907), which contains a bibliography of the English Culm; E. Holzapfel, Paläont. Abhandl. Bd. v. Heft i. (1889); H. Potonié, Abhandl. preuss. geol. Landesanst., Neue Folge, 36 (1901); D. Stur, “Die Culm Flora,” Abhandl. k.k. geol. Reichsanst. viii. (Vienna, 1875).
1 This word is possibly connected with col, coal; distinguish “culm,” the stem of a plant, Lat. culmus.
CULMINATION (from Lat. culmen, summit), the attainment of the highest point. In astronomy the term is given to the passage of a heavenly body over the meridian of a place. Two culminations take place in the course of the day, one above and the other below the pole. The first is called the upper, the second the lower. Either or both may occur below the horizon and therefore be invisible.
CULPRIT, properly the prisoner at the bar, one accused of a crime; so used, generally, of one guilty of an offence. In origin the word is a combination of two Anglo-French legal words, culpable, guilty, and prit or prist, i.e. prest, Old French for prêt, ready. On the prisoner at the bar pleading “not guilty,” the clerk of the crown answered “culpable,” and stated that he was ready (prest) to join issue. The words cul. prist (or prit) were then entered on the roll as showing that issue had been joined. When French law terms were discontinued the words were taken as forming one word addressed to the prisoner. The formula “Culprit, how will you be tried?” in answer to a plea of “not guilty,” is first found in the trial for murder of the 7th earl of Pembroke in 1678.
CULROSS (locally pronounced Coo-rus), a royal and police burgh, Fifeshire, Scotland, 6½ m. W. by S. of Dunfermline and 2½ m. from East Grange station on the North British railway company’s line from Dunfermline to Stirling. Pop. 348. Until 1890 it belonged to the detached portion of Perthshire. Attractively situated on a hillside sloping gently to the Forth, its placid old-world aspect is in keeping with its great antiquity. Here St Serf carried on his missionary labours, and founded a church and cemetery, and here he died and was buried. For centuries the townsfolk used to celebrate his day (July 1st) by walking in procession bearing green boughs. Kentigern, the apostle to Cumbria and first bishop of Glasgow, was born at Culross, his mother having been driven ashore during a tempest, and was adopted by St Serf as his son. These religious associations, coupled with the fertility of the soil, led to the founding of a Cistercian abbey in 1217. Of this structure the only remains are the western tower and the choir, which, greatly altered as well as repaired early in the 19th century, now forms the parish church. It is supposed that a chapel of which some traces exist in the east end of the town was dedicated to Kentigern. James VI. made Culross a royal burgh in 1588. In 1808 there was discovered in the abbey church, embalmed in a silver casket, still preserved there, bearing his name and arms, the heart of Edward, Lord Bruce of Kinloss, who was killed in August 1613 near Bergen-op-Zoom in a duel with Sir Edward Sackville, afterwards earl of Dorset. Robert Pont (1524-1606), the Reformer, was born at Shirresmiln, or Shiresmill, a hamlet in Culross parish. Nearly all its old industries—the coal mines, salt works, linen manufacture, and even the making of iron girdles for the baking of scones—have dwindled, but its pleasant climate and picturesqueness make it a holiday resort. Dunimarle Castle, a handsome structure on the sea-shore, adjoins the site of the castle where, according to tradition, Macbeth slew the wife and children of Macduff. Culross belongs to the Stirling district group of parliamentary burghs.
 |
| Ransome’s Spring Tine Cultivator. |
CULTIVATOR,1 also called Scuffler, Scarifier or Grubber, an agricultural implement employed in breaking up land or in stirring it after ploughing. The first all-iron cultivator, known as Finlayson’s grubber, was a large harrow with curved teeth carried on wheels, and was brought out about 1820. It was designed to meet the need for some implement of intermediate character between the plough and harrow, which should stir the soil deeply and expeditiously without reversing it, and bring the weeds unbroken to the surface. The chief modern improvement has been the imparting of vibratory movement and hence greater stirring capacity to the tines, either by making them of spring steel or by fitting springs to the point of attachment of the tine to the framework of the machine. In its modern form the implement consists of a framework fitted with rows of curved stems or tines, which may be raised clear of the ground or lowered into work by means of a lever, and differs from the harrow in that it is provided with two wheels, which prevent the tines from embedding themselves too deeply in the soil. The stems may be fitted either with chisel-points or with broad shares, according as it is required to merely stir the soil or to bring up weeds and clean the surface. In the disk cultivator revolving disks take the place of tines. The implement is usually provided with a seat for the driver and is drawn by horses, but steam power is also commonly applied to it, the speed of the operation in that case increasing its effectiveness. The method is the same as that of steam-ploughing (see Plough).
1 From Late Lat. cultivare, through cultivus, from colere, to till, cultivate; whence cultus, worship, form of religion, cult.
CUMAE (Gr. Κύμη), an ancient city of Campania, Italy, about 12 m. W. of Neapolis, on the W. coast of Campania, on a volcanic eminence, overlooking the plain traversed by the Volturno.
There are many legends as to its foundation, but even the actual period of its colonization by the Greeks is so early (ancient authorities give it as 1050 B.C.) that there is some doubt as to who established it, whether Chalcidians from Euboea or Aeolians from Κύμη (Cyme), and it should probably be regarded as a joint settlement. It was certainly, as Strabo says, the oldest of the Greek colonies on the mainland of Italy or in Sicily. Livy tells us (viii. 22) that the settlers first landed on Pithecusae (Ischia) and thence transferred their position to the mainland, which seems a probable story. We find it in 721 B.C. founding Zancle (Messina) in Sicily jointly with Chalcis, and it extended its power gradually over the coast of the Gulf of Puteoli and the harbours of the promontory of Misenum. Puteoli itself under the name Dicaearchia was probably founded by Cumae. In the 7th century, according to the legends, Parthenope, whither the demos of Cumae had taken refuge after an unsuccessful rising against the aristocracy, was attacked by the latter and destroyed, but soon rebuilt under the name of Neapolis (New City, the present Naples).1 The most fertile portion of the Campanian plain was also under its dominion; the name “fossa Graeca” still lingered on in 205 B.C. to testify to its ancient limits. Cumae was now at the height of its power, and many fine coins testify to its prosperity. In 524 B.C. it was the object of a joint attack by the Etruscans of Capua, the Daunians of the district of Nola, and the Aurunci of the Mons Massicus. A brilliant victory was, however, won in the hilly district outside the town, largely owing 619 to the bravery of Aristodemus, who then led a force to the relief of Aricia, which was being attacked by the Etruscans, and, returning at the head of his victorious army, overturned the aristocracy and made himself tyrant, but was ultimately murdered by the aristocrats. These were unable to repel a renewed Etruscan attack without the help of Hiero of Syracuse, who in the battle of Cumae of 474 B.C. drove the Etruscan fleet from the sea, and broke their power in Campania.
The Samnites finally destroyed the Etruscan supremacy by the capture of Capua in the latter half of the 5th century (see Capua; Campania), and the Greeks of Cumae were overwhelmed by the same invasion, either in 420 B.C. (Livy iv. 44) or in 421 (Diodor. Sic. xii. 76), if his statement is drawn from Greek sources, 428 if it is to be dated by the Roman consuls to whose year he ascribes it. This catastrophe brought to an end the beautiful series of Greek coins from the town (B. V. Head, Historia Numorum, p. 31), and Oscan became its language, though in many respects the Greek character of the town survived (Strabo v. 4. 3, and the other references given by R. S. Conway, Italic Dialects, p. 84). One or two inscriptions in Oscan survive (id. ib. 88-92), one of which is a Iovila or heraldic dedication. The date of the general disuse of Oscan in the town appears to be fixed about 180 B.C. by the request (Livy xl. 44) which the Cumaeans addressed to Rome that they might be allowed to use Latin for public purposes. Cumae now ceased to have any independent history. It came under the supremacy of Rome in 343 (or 340) as Capua did, obtained the civitas sine suffragio and was governed after 318 by the praefecti Capuam Cumas.
In the Hannibalic wars it remained faithful to Rome. It probably acquired civic rights in the Social War and remained a municipium until Augustus established a colony here. Under the empire it is spoken of as a quiet country town, in contrast to the gay and fashionable Baiae, which, however, with the lacus Avernus and lacus Lucrinus, formed a part of its territory. Cicero’s villa on the east bank of the latter, for example, which he called the Academia, was also known as Cumanum. In the Gothic wars the acropolis of Cumae was, except Naples, the only fortified town in Campania, and it retained its military importance until it was destroyed by the Neapolitans in 1205, since, which time it has been deserted.
The acropolis hill (269 ft. above sea-level), a mass of trachyte which has broken through the surrounding tufa, lies hardly 100 yds. from the low sandy shore. It is traversed by caves, which are at three different levels with many branches. Some of them may belong to a remote date, while others may be quarries, but they have not been thoroughly investigated. They are famous in legend as the seat of the oracle of the Cumaean Sibyl.
The acropolis has only one approach, on the south-east; on all other sides it falls away steeply. Remains of fortifications of all ages run round the edge of the hill; some of the original Greek work, in finely hewn rectangular tufa blocks, exists on the east. The medieval line follows the ancient, except on the N.E., where it takes in a larger area.
Within the acropolis stood the temple of Apollo, erected, according to tradition, by Daedalus himself, the remains of which, restored in Roman times, were discovered in 1817, on the eastern and lower summit. On the higher western summit stood another temple, excavated in 1792, but now covered up again. This may be that of the Olympian Zeus (Liv. xxvii. 23).
There are also various remains of buildings of the imperial period, and these are far more frequent on the site of the lower town (now occupied by vineyards) which lies below the acropolis to the south. The line of the city walls can be traced both on the E. and on the W., though the remains on the E. are insignificant, and on the W. (the seaward side) only the scarping of the hill remains. To the S. of the town, just outside the wall, is the amphitheatre. To the N. of it is the point where the roads from Liternum (the Via Domitiana running along the sandy coast), Capua (a branch of the Via Campana), Misenum and Puteoli meet. The last passes through the Arco Felice, an arch of brick-faced concrete 63 ft. high which spans a cutting through the Monte Grillo, made by Domitian to shorten the course of the road, which had hitherto run farther north. The Grotto della Pace leads to the shores of Avernus. On the E. side of Cumae are considerable remains of the Roman period, among them those of the temple of Demeter, as restored by the family of the Lucceii.
The cemeteries of Cumae extended on all sides of the ancient city, except towards the sea, but the most important lay on the north, between this temple and the Lago di Licola. Excavations during the 19th century in Greek, Samnite and Roman graves have produced many important objects, now in the various museums of Europe, but especially at Naples. Recent discoveries in this necropolis (including that of a circular archaic tomb with a conical roof) have led to considerable discussion as to the true date of the foundation of Cumae, and have made it clear that, in any case, a pre-Hellenic indigenous settlement existed here—a result of great importance.
See J. Beloch, Campanien (Breslau, 1890), 145 seq.; G. Pellegrini, Monumenti dei Lincei, xiii. (1903); G. Patroni, Atti del Congresso di Scienze Storiche (1904), vol. v. p. 215 seq.
1 Mommsen, however (Corpus Inscrip. Latin. x., Berlin, 1883, p. 170), rightly throws considerable doubt on the existence of Parthenope and even of Palaeopolis, of which there is some mention in Roman annals; under both he is inclined to trace Cumae itself.
CUMANÁ, a city and port of Venezuela, capital of the state of Bermudez, situated on the Manzanares river about 1 m. above its mouth, 52 ft. above sea-level and 180 m. E. of Caracas. It is the oldest existing European settlement on the South American continent, having been founded by Diego Castellon in 1523 under the name of Nueva Toledo. The city was almost totally destroyed by an earthquake in 1766, and again in 1797. Slight shocks are very frequent, some of them severe enough to cause considerable damage to the buildings. The mean annual temperature is 83° F. and the climate is enervating. In colonial times the city was rich and prosperous and enjoyed a lucrative trade with the mother country, its population at that time being estimated at 30,000, but much of its prosperity has disappeared and its population is now estimated at 10,000. Excellent fruits are produced in its vicinity, and its exports include cacáo, coffee, sugar, hides, tobacco and sundry products in small quantities. A tramway connects the city with its port at the mouth of the Manzanares.
CUMBERLAND, DUKES AND EARLS OF. The earldom of Cumberland was held by the family of Clifford (q.v.) from 1525 to 1643, when it became extinct by the death of Henry, the 5th earl. The 1st earl of Cumberland was Henry, 11th Lord Clifford (1493-1542), a son of Henry, 10th Lord Clifford (c. 1454-1523). Created an earl by Henry VIII. in 1525, Henry remained loyal during the great rising in the north of England in 1536, and died on the 22nd of April 1542. His son and successor, Henry, the 2nd earl (c. 1517-1570), married Eleanor (d. 1547), a daughter of Charles Brandon, duke of Suffolk, and Mary, daughter of King Henry VII.; he had the tastes of a scholar rather than a soldier, and died early in 1570. By his first wife, Eleanor, he left an only daughter Margaret (1540-1596), who married Henry Stanley, 4th earl of Derby, and who in 1557 was regarded by many as the rightful heiress to the English throne. By his second wife he left two sons and a daughter; his elder son George succeeding to the earldom in 1570, and his younger son Francis succeeding his brother in 1605. George, 3rd earl of Cumberland (1558-1605), was born on the 8th of August 1558, and married Margaret (c. 1560-1616), daughter of his guardian, Francis, 2nd earl of Bedford. Although interested in mathematics and geography he passed his early years in dissipation and extravagance; then he took to the sea, commanded the “Bonaventure” against the Spanish Armada, and from this time until his death on the 30th of October 1605 was mainly engaged in fitting out and leading plundering expeditions, some of which, especially the one undertaken in 1589, gained a large amount of booty. The earl left no sons, and his barony was claimed by his only daughter Anne (1590-1676), the wife successively of Richard Sackville, 3rd earl of Dorset, and of Philip Herbert, 4th earl of Pembroke and Montgomery; while his earldom was inherited by his brother Francis (1559-1641). A long law-suit between the new earl and the countess Anne over the possession of the 620 family estates was settled in 1617. The 5th earl was Francis’s only son Henry (1591-1643), who was born on the 28th of February 1591, and was educated at Christ Church, Oxford. He was a supporter of Charles I. during his two short wars with the Scots, and also during the Civil War until his death on the 11th of December 1643. He left no sons; his earldom became extinct; his new barony of Clifford, created in 1628, passed to his daughter Elizabeth (1618-1691), wife of Richard Boyle, earl of Cork and Burlington; and the Cumberland estates to his cousin Anne, countess of Dorset and Pembroke.
In 1644 the English title of duke of Cumberland was created in favour of Rupert, son of Frederick V., elector palatine of the Rhine, and nephew of Charles I. Having lapsed on Rupert’s death without legitimate issue in 1682, it was created again in 1689 to give an English title to George, prince of Denmark, who had married the lady who afterwards became Queen Anne. It again became extinct when George died in 1708, but was revived in 1726 in favour of William Augustus, third son of George II. As this duke was never married the title lapsed on his death in 1765, but was revived in the following year in favour of Henry Frederick (1745-1790), son of Frederick, prince of Wales, and brother of George III. Having again become extinct on Henry Frederick’s death, the title of duke of Cumberland was created for the fifth time in favour of Ernest Augustus, who was made duke of Cumberland and Teviotdale in 1799. In 1837 Ernest (q.v.) became king of Hanover, and on his death in 1851 the title descended with the kingdom of Hanover to his son King George V. (q.v.), and on George’s death in 1878 to his grandson Ernest Augustus (b. 1845). In 1866 Hanover was annexed by Prussia, but King George died without renouncing his rights. His son Ernest, while maintaining his claim to the kingdom of Hanover, is generally known by his title of duke of Cumberland.
CUMBERLAND, RICHARD (1632-1718), English philosopher and bishop of Peterborough, the son of a citizen of London, was born in the parish of St Ann, near Aldersgate. He was educated in St Paul’s school, and at Magdalene College, Cambridge, where he obtained a fellowship. He took the degree of B.A. in 1653; and, having proceeded M.A. in 1656, was next year incorporated to the same degree in the university of Oxford. For some time he studied medicine; and although he did not adhere to this profession, he retained his knowledge of anatomy and medicine. He took the degree of B.D. in 1663 and that of D.D. in 1680. Among his contemporaries and intimate friends were Dr Hezekiah Burton, Sir Samuel Morland, who was distinguished as a mathematician, Sir Orlando Bridgeman, who became keeper of the great seal, and Samuel Pepys. To this academical connexion he appears to have been in a great measure indebted for his advancement in the Church. When Bridgeman was appointed lord keeper, he nominated Cumberland and Burton as his chaplains, nor did he afterwards neglect the interest of either. Cumberland’s first preferment, bestowed upon him in 1658 by Sir John Norwich, was the rectory of Brampton in Northamptonshire. In 1661 he was appointed one of the twelve preachers of the university. The lord keeper, who obtained his office in 1667, invited him to London, and soon afterwards bestowed upon him the rectory of Allhallows at Stamford, where he acquired new credit by the fidelity with which he discharged his duties. In addition to his ordinary work he undertook the weekly lecture. This labour he constantly performed, and in the meantime found leisure to prosecute his scientific and philological studies.
At the age of forty he published his earliest work, entitled De legibus naturae disquisitio philosophica, in qua earum forma, summa capita, ordo, promulgatio, el obligatio e rerum natura investigantur; quin etiam elementa philosophiae Hobbianae, cum moralis tum civilis, considerantur et refutantur (London, 1672). It is dedicated to Sir Orlando Bridgeman, and is prefaced by an “Alloquium ad Lectorem,” contributed by Dr Burton. It appeared during the same year as Pufendorf’s De jure naturae et gentium, and was highly commended in a subsequent publication by Pufendorf, whose approbation must have had the effect of making it known on the continent. Having thus established a solid reputation, Cumberland next prepared a work on a very different subject—An Essay towards the Recovery of the Jewish Measures and Weights, comprehending their Monies; by help of ancient standards, compared with ours of England: useful also to state many of those of the Greeks and Romans, and the Eastern Nations (London, 1686). This work, dedicated to Pepys, obtained a copious notice from Leclerc, and was translated into French.
About this period he was depressed by apprehensions respecting the growth of Popery; but his fears were dispelled by the Revolution, which brought along with it another material change in his circumstances. One day in 1691 he went, according to his custom on a post-day, to read the newspaper at a coffee-house in Stamford, and there, to his surprise, he read that the king had nominated him to the bishopric of Peterborough. The bishop elect was scarcely known at court, and he had resorted to none of the usual methods of advancing his temporal interest.
“Being then sixty years old,” says his great-grandson, “he was with difficulty persuaded to accept the offer, when it came to him from authority. The persuasion of his friends, particularly Sir Orlando Bridgeman, at length overcame his repugnance; and to that see, though very moderately endowed, he for ever after devoted himself, and resisted every offer of translation, though repeatedly made and earnestly recommended. To such of his friends as pressed an exchange upon him he was accustomed to reply, that Peterborough was his first espoused, and should be his only one.”
He discharged his new duties with energy and kept up his episcopal visitations till his eightieth year. His charges to the clergy are described as plain and unambitious, the earnest breathings of a pious mind. When Dr Wilkins (David Wilke) published the New Testament in Coptic he presented a copy to the bishop, who began to study the language at the age of eighty-three. “At this age,” says his chaplain, “he mastered the language, and went through great part of this version, and would often give me excellent hints and remarks, as he proceeded in reading of it.” He died in 1718, in the eighty-seventh year of his age; he was found sitting in his library, in the attitude of one asleep, and with a book in his hand.1 His great-grandson was Richard Cumberland, the dramatist.
Bishop Cumberland was distinguished by his gentleness and humility. He could not be roused to anger, and spent his days in unbroken serenity. The basis of his ethical theory is Benevolence, and is the natural outcome of his temperament. He was a man of a sound understanding, improved by extensive learning, and left behind him several monuments of his talents and industry. His favourite motto was that a man had better “wear out than rust out.”
The philosophy of Cumberland is expounded in the treatise De legibus naturae. The merits of the work are almost confined to its speculative theories; its style is destitute of strength and grace, and its reasoning is diffuse and unmethodical. Its main design is to combat the principles which Hobbes had promulgated as to the constitution of man, the nature of morality, and the origin of society, and to prove that self-advantage is not the chief end of man, that force is not the source of personal obligation to moral conduct nor the foundation of social rights, and that the state of nature is not a state of war. The views of Hobbes seem 621 to Cumberland utterly subversive of religion, morality and civil society, and he endeavours, as a rule, to establish directly antagonistic propositions. He refrains, however, from denunciation, and is a fair opponent up to the measure of his insight.
Laws of nature are defined by him as “immutably true propositions regulative of voluntary actions as to the choice of good and the avoidance of evil, and which carry with them an obligation to outward acts of obedience, even apart from civil laws and from any considerations of compacts constituting government.” This definition, he says, will be admitted by all parties. Some deny that such laws exist, but they will grant that this is what ought to be understood by them. There is thus common ground for the two opposing schools of moralists to join issue. The question between them is, Do such laws exist or do they not? In reasoning thus Cumberland obviously forgot what the position maintained by his principal antagonist really was. Hobbes must have refused to accept the definition proposed. He did not deny that there were laws of nature, laws antecedent to government, laws even in a sense eternal and immutable. The virtues as means to happiness seemed to him to be such laws. They precede civil constitution, which merely perfects the obligation to practise them. He expressly denied, however, that “they carry with them an obligation to outward acts of obedience, even apart from civil laws and from any consideration of compacts constituting governments.” And many besides Hobbes must have felt dissatisfied with the definition. It is ambiguous and obscure. In what sense is a law of nature a “proposition”? Is it as the expression of a constant relation among facts, or is it as the expression of a divine commandment? A proposition is never in itself an ultimate fact although it may be the statement of such a fact. And in what sense is a law of nature an “immutably true” proposition? Is it so because men always and everywhere accept and act on it, or merely because they always and everywhere ought to accept and act on it? The definition, in fact, explains nothing.
The existence of such laws may, according to Cumberland, be established in two ways. The inquirer may start either from effects or from causes. The former method had been taken by Grotius, Robert Sharrock (1630-1684) and John Selden. They had sought to prove that there were universal truths, entitled to be called laws of nature, from the concurrence of the testimonies of many men, peoples and ages, and through generalizing the operations of certain active principles. Cumberland admits this method to be valid, but he prefers the other, that from causes to effects, as showing more convincingly that the laws of nature carry with them a divine obligation. It shows not only that these laws are universal, but that they were intended as such; that man has been constituted as he is in order that they might be. In the prosecution of this method he expressly declines to have recourse to what he calls “the short and easy expedient of the Platonists,” the assumption of innate ideas of the laws of nature. He thinks it ill-advised to build the doctrines of natural religion and morality on a hypothesis which many philosophers, both Gentile and Christian, had rejected, and which could not be proved against Epicureans, the principal impugners of the existence of laws of nature. He cannot assume, he says, that such ideas existed from eternity in the divine mind, but must start from the data of sense and experience, and thence by search into the nature of things discover their laws. It is only through nature that we can rise to nature’s God. His attributes are not to be known by direct intuition. He, therefore, held that the ground taken up by the Cambridge Platonists could not be maintained against Hobbes. His sympathies, however, were all on their side, and he would do nothing to diminish their chances of success. He would not even oppose the doctrine of innate ideas, because it looked with a friendly eye upon piety and morality. He granted that it might, perhaps, be the case that ideas were both born with us and afterwards impressed upon us from without.
Cumberland’s ethical theory (see Ethics) is summed up in his principle of universal Benevolence, the one source of moral good. “No action can be morally good which does not in its own nature contribute somewhat to the happiness of men.” The theory is important in comparison (1) with that of Hobbes, and (2) with modern utilitarianism.
1. Cumberland’s Benevolence is, deliberately, the precise antithesis to the Egoism of Hobbes. To this fact it owes its existence and also its extravagance. Feeling that the most forcible method of attacking Hobbes was to assert the opposite in the same form, he maintained that the whole-hearted pursuit of the good of all contributes to the good of each and brings personal happiness; that the opposite process involves misery to individuals including the self. If, then, Hobbes went to the one extreme of postulating selfishness as the sole motive of human action, Cumberland was equally extravagant as regards Benevolence. The testimony of history shows, prima facie at least, that both motives have operated throughout, and just as self-interest has been increasingly modified by conscious benevolence, so benevolence alone does not explain all personal virtue nor love to God. But it is essential to notice that Cumberland never appealed to the evidence of history, although he believed that the law of universal benevolence had been accepted by all nations and generations; and he carefully abstains from arguments founded on revelation, feeling that it was indispensable to establish the principles of moral right on nature as a basis. His method was the deduction of the propriety of certain actions from the consideration of the character and position of rational agents in the universe. He argues that all that we see in nature is framed so as to avoid and reject what is dangerous to the integrity of its constitution; that the human race would be an anomaly in the world had it not for end its conservation in its best estate; that benevolence of all to all is what in a rational view of the creation is alone accordant with its general plan; that various peculiarities of man’s body indicate that he has been made to co-operate with his fellow men and to maintain society; and that certain faculties of his mind show the common good to be more essentially connected with his perfection than any pursuit of private advantage. The whole course of his reasoning proceeds on, and is pervaded by, the principle of final causes.
2. To the question, What is the foundation of rectitude?, he replies, the greatest good of the universe of rational beings. He may be regarded as the founder of English utilitarianism, but his utilitarianism is distinct from what is known as the selfish system; it goes to the contrary extreme, by almost absorbing individual in universal good. Nor does it look merely to the lower pleasures, the pleasures of sense, for the constituents of good, but rises above them to include especially what tends to perfect, strengthen and expand our true nature. Existence and the extension of our powers of body and mind are held to be good for their own sakes without respect to enjoyment. Cumberland’s views on this point were long abandoned by utilitarians as destroying the homogeneity and self-consistency of their theory; but J. S. Mill and some recent writers have reproduced them as necessary to its defence against charges not less serious than even inconsistency.
The answer which Cumberland gives to the question, Whence comes our obligation to observe the laws of nature?, is that happiness flows from obedience, and misery from disobedience to them, not as the mere results of a blind necessity, but as the expressions of the divine will. Reward and punishment, supplemented by future retribution, are, in his view, the sanctions of the laws of nature, the sources of our obligation to obey them. To the other great ethical question, How are moral distinctions apprehended?, he replies that it is by means of right reason. But by right reason he means merely the power of rising to general laws of nature from particular facts of experience. It is no peculiar faculty or distinctive function of mind; it involves no original element of cognition; it begins with sense and experience; it is gradually generated and wholly derivative. This doctrine lies only in germ in Cumberland, but will be found in full flower in Hartley, Mackintosh and later associationists.
Bibliography.—Editions of the De legibus naturae (Lübeck, 1683 and 1694); English versions by John Maxwell, prebendary of 622 Connor, A Treatise of the Laws of Nature (London, 1727), and John Towers (Dublin, 1750); French translation by Jean Barbeyrac (Amsterdam, 1744); James Tyrrell (1642-1718), grandson of Archbishop Ussher, published an abridgment of Cumberland’s views in A Brief Disquisition of the Laws of Nature according to the Principles laid down in the Rev. Dr Cumberland’s Latin Treatise (London, 1692; ed. 1701). For biographical details see Squier Payne, Account of the Life and Writings of R. Cumberland (London, 1720); Cumberland’s Memoirs (1807), i. 3-6; Pepys’s Diary. For his philosophy, see E. Albee, Philosophical Review, iv. 3 (1895), pp. 264 and 371; F. E. Spaulding, R. Cumberland als Begründer der englischen Ethik (Leipzig, 1894); and text-books on ethics.
1 The care of his posthumous publications devolved upon his domestic chaplain and son-in-law, Squier Payne, who soon after the bishop’s death edited “Sanchoniato’s Phoenician History, translated from the first book of Eusebius, De praeparatione evangelica: with a continuation of Sanchoniato’s history of Eratosthenes Cyrenaeus’s Canon, which Dicaearchus connects with the first Olympiad. These authors are illustrated with many historical and chronological remarks, proving them to contain a series of Phoenician and Egyptian chronology, from the first man to the first Olympiad, agreeable to the Scripture accounts” (London, 1720). The preface contains an account of the life, character and writings of the author, which was likewise published in a separate form, and exhibits a pleasing picture of his happy old age. A German translation appeared under the title of Cumberlands phönizische Historie des Sanchoniathons, übersetzt von Joh. Phil. Cassel (Magdeburg, 1755). The sequel to the work was likewise published by Payne—Origines gentium antiquissimae; or Attempts for discovering the Times of the First Planting of Nations: in several Tracts (London, 1724).
CUMBERLAND, RICHARD (1732-1811), English dramatist, was born in the master’s lodge of Trinity College, Cambridge, on the 19th of February 1732. He was the great-grandson of the bishop of Peterborough; and his father, Dr Denison Cumberland, became successively bishop of Clonfert and of Kilmore. His mother was Joanna, the youngest daughter of the great scholar Richard Bentley, and the heroine of John Byrom’s once popular little eclogue, Colin and Phoebe. Of the great master of Trinity his grandson has left a kindly account; he afterwards collected all the pamphlets bearing on the Letters of Phalaris controversy, and piously defended the reputation of his ancestor in his Letter to Bishop Lowth, who had called Bentley “aut caprimulgus aut fossor.” Cumberland was in his seventh year sent to the grammar-school at Bury St Edmunds, and he relates how, on the head-master Arthur Kinsman undertaking, in conversation with Bentley, to make the grandson as good a scholar as the grandfather himself, the latter retorted: “Pshaw, Arthur, how can that be, when I have forgot more than thou ever knewest?” Bentley died during his grandson’s Bury schooldays; and in 1744 the boy, who, while rising to the head of his school, had already begun to “try his strength in several slight attempts towards the drama,” was removed to Westminster, then at the height of its reputation under Dr Nicholls. Among his schoolfellows here were Warren Hastings, George Colman (the elder), Lloyd, and (though he does not mention them as such) Churchill and Cowper. From Westminster Cumberland passed, in his fourteenth year, to Trinity College, Cambridge, where in 1750 he took his degree as tenth wrangler. His account of his degree examination, as well as that for a fellowship at his college, part of which he underwent in the “judges’ chamber,” where he was born, is curious; he was by virtue of an alteration in the statutes elected to his fellowship in the second year of his degree.
Meanwhile his projects of work as a classical scholar had been interspersed with attempts at imitating Spenser—whom, by his mother’s advice, he “laid upon the shelf”—and a dramatic effort (unprinted) on the model of Mason’s Elfrida, called Caractacus. He had just begun to read for his fellowship, when he was offered the post of private secretary by the earl of Halifax, first lord of trade and plantations in the duke of Newcastle’s ministry. His family persuaded him to accept the office, to which he returned after his election as fellow. It left him abundant leisure for literary pursuits, which included the design of a poem in blank verse on India. He resigned his Trinity fellowship on his marriage—in 1759—to his cousin Elizabeth Ridge, to whom he had paid his addresses on receiving through Lord Halifax “a small establishment as crown-agent for Nova Scotia.” In 1761 he accompanied his patron (who had been appointed lord-lieutenant) to Ireland as Ulster secretary; and in acknowledgment of his services was afterwards offered a baronetcy. By declining this he thinks he gave offence; at all events, when in 1762 Halifax became secretary of state, Cumberland in vain applied for the post of under-secretary, and could only obtain the clerkship of reports at the Board of Trade under Lord Hillsborough. While he takes some credit to himself for his incorruptibility when in Ireland, he showed zeal for his friend and secured a bishopric for his father. On the accession to office of Lord George Germaine (Sackville) in 1775, Cumberland was appointed secretary to the Board of Trade and Plantations, which post he held till the abolition of that board in 1782 by Burke’s economical reform. Before this event he had, in 1780, been sent on a confidential mission to Spain, to negotiate a separate treaty of peace with that power; but though he was well received by King Charles III. and his minister Floridablanca, the question of Gibraltar proved a stumbling-block, and the Gordon riots at home a most untoward occurrence. He was recalled in 1781, and was refused repayment of the expenses he had incurred, towards which only £1000 had been advanced to him. He thus found himself £4500 out of pocket: in vain, he says, “I wearied the door of Lord North till his very servants drove me from it”; his memorial remained unread or unnoticed either by the prime minister or by secretary Robinson, through whom the original promise had been made. Soon after this experience he lost his office, and had to retire on a compensation allowance of less than half-pay. He now took up his residence at Tunbridge Wells; but during his last years he mostly lived in London, where he died on the 7th of May 1811. He was buried in Westminster Abbey, a short oration being pronounced on this occasion by his friend Dean Vincent.
Cumberland’s numerous literary productions are spread over the whole of his long life; but it is only by his contributions to the drama, and perhaps by his Memoirs, that he is likely to be remembered. The collection of essays and other pieces entitled The Observer (1785), afterwards republished together with a translation of The Clouds, found a place among The British Essayists. For the accounts given in The Observer of the Greek writers, especially the comic poets, Cumberland availed himself of Bentley’s MSS. and annotated books in his possession; his translations from the Greek fragments, which are not inelegant but lack closeness, are republished in James Bailey’s Comicorum Graecorum (part i., 1840) and Hermesianactis, Archilochi, et Pratinae fragmenta. Cumberland further produced Anecdotes of Eminent Painters in Spain (1782 and 1787); a Catalogue of the King of Spain’s Paintings (1787); two novels—Arundel (1789), a story in letters, and Henry (1795), a “diluted comedy” on the construction and polishing of which he seems to have expended great care; a religious epic, Calvary, or the Death of Christ (1792); his last publication was a poem entitled Retrospection. He is also supposed to have joined Sir James Bland Burges in an epic, the Exodiad (1807), and in John de Lancaster, a novel. Besides these he wrote the Letter to the Bishop of O[xfor]d in vindication of Bentley (1767); another to the Bishop of Llandaff (Richard Watson) on his proposal for equalizing the revenues of the Established Church (1783); a Character of the late Lord Sackville (1785), whom in his Memoirs he vindicates from the stigma of cowardice; and an anonymous pamphlet, Curtius rescued from the Gulf, against the redoubtable Dr Parr. He was also the author of a version of fifty of the Psalms of David; of a tract on the evidences of Christianity; and of other religious exercises in prose and verse, the former including “as many sermons as would make a large volume, some of which have been delivered from the pulpits.” Lastly, he edited, in 1809, a short-lived critical journal called The London Review, intended to be a rival to the Quarterly, with signed articles.
Cumberland’s Memoirs, which he began at the close of 1804, and concluded in September 1805, were published in 1806, and a supplement was added in 1807. This narrative, which includes a long account of his Spanish mission, contains some interesting reminiscences of several persons of note—more especially Bubb Dodington, Single-Speech Hamilton, and Lord George Sackville among politicians, and of Garrick, Foote and Goldsmith; but the accuracy of some of the anecdotes concerning the last-named is not beyond suspicion. The book exhibits its author as an amiable egotist, careful of his own reputation, given to prolixity and undistinguished by wit, but a good observer of men and manners. The uneasy self-absorption which Sheridan immortalized in the character of Sir Fretful Plagiary in The Critic is apparent enough in this autobiography, but presents itself there in no offensive form. The incidental criticisms of actors have been justly praised.
Cumberland was hardly warranted in the conjecture that no English author had yet equalled his list of dramas in point of number; but his plays, published and unpublished, have been 623 computed to amount to fifty-four. About 35 of these are regular plays, to which have been added 4 operas and a farce; and about half of the whole list are comedies. The best known of them belong to what he was pleased to term “legitimate comedy,” and to that species of it known as “sentimental.” The essential characteristic of these plays is the combination of plots of domestic interest with the rhetorical enforcement of moral precepts, and with such small comic humour as the author possesses. These comedies are primarily, to borrow Cumberland’s own phraseology, designed as “attempts upon the heart.” He takes great credit to himself for weaving his plays out of “homely stuff, right British drugget,” and for eschewing “the vile refuse of the Gallic stage”; on the other hand, he borrowed from the sentimental fiction of his own country, including Richardson, Fielding and Sterne. The favourite theme of his plays is virtue in distress or danger, but safe of its reward in the fifth act; their most constant characters are men of feeling and young ladies who are either prudes or coquettes. Cumberland’s comic power—such as it was—lay in the invention of comic characters taken from the “outskirts of the empire,” and professedly intended to vindicate from English prejudice the good elements in the Scotch, the Irish and the colonial character. For the rest, patriotic sentiment liberally asserts itself by the side of general morality. If Cumberland’s dialogue lacks brilliance and his characters reality, the construction of the plots is as a rule, skilful, and the situations are contrived with what Cumberland indisputably possessed—a thorough insight into the secrets of theatrical effect. It should be added that, though Cumberland’s sentimentality is often wearisome, his morality is generally sound; that if he was without the genius requisite for elevating the national drama, he did his best to keep it pure and sweet; and that if he borrowed much, as he undoubtedly did, it was not the vicious attractions of other dramatists of which he was the plagiary.
His début as a dramatic author was made with a tragedy, The Banishment of Cicero, published in 1761 after its rejection by Garrick; this was followed in 1765 by a musical drama, The Summer’s Tale, subsequently compressed into an afterpiece Amelia (1768). Cumberland first essayed sentimental comedy in The Brothers (1769). The theme of this comedy is inspired by Fielding’s Tom Jones; its comic characters are the jolly old tar Captain Ironsides, and the henpecked husband Sir Benjamin Dove, whose progress to self-assertion is genuinely comic, though not altogether original. Horace Walpole said that it acted well, but read ill, though he could distinguish in it “strokes of Mr Bentley.” The epilogue paid a compliment to Garrick, who helped the production of Cumberland’s second comedy The West-Indian (1771). The hero of this comedy, which probably owes much to the suggestion of Garrick, is a young scapegrace fresh from the tropics, “with rum and sugar enough belonging to him to make all the water in the Thames into punch,”—a libertine with generous instincts, which in the end prevail. This early example of the modern drame was received with the utmost favour; it was afterwards translated into German by Boden, and Goethe acted in it at the Weimar court. The Fashionable Lover (1772) is a sentimental comedy of the most pronounced type. The Choleric Man (1774), founded on the Adelphi of Terence, is of a similar type, the comic element rather predominating, but philanthropy being duly represented by a virtuous lawyer called Manlove. Among his later comedies may be mentioned The Natural Son (1785), in which Major O’Flaherty who had already figured in The West-Indian, makes his reappearance; The Impostors (1789), a comedy of intrigue; The Box Lobby Challenge (1794), a protracted farce; The Jew (1794), a serious play, highly effective when the character of Sheva was played by the great German actor Theodor Döring; The Wheel of Fortune (1795), in which John Kemble found a celebrated part in the misanthropist Penruddock, who cannot forget but learns to forgive (a character declared by Kotzebue to have been stolen from his Menschenhass und Reue), while the lawyer Timothy Weasel was made comic by Richard Suett; First Love (1795); The Last of the Family (1795); False Impressions (1797); The Sailor’s Daughter (1804); and a Hint to Husbands (1806), which, unlike the rest, is in blank verse. The other works printed during his lifetime include The Note of Hand (1774), a farce; the songs of his musical comedy, The Widow of Delphi (1780); his tragedies of The Battle of Hastings (1778); and The Carmelite (1784), a romantic domestic drama in blank verse, in the style of Home’s Douglas, furnishing some effective scenes for Mrs Siddons and John Kemble as mother and son; and the domestic drama (in prose) of The Mysterious Husband (1783). His posthumously printed plays (published in 2 vols. in 1813) include the comedies of The Walloons (acted in 1782); The Passive Husband (acted as A Word for Nature, 1798); The Eccentric Lover (acted 1798); and Lovers’ Resolutions (once acted in 1802); the serious quasi-historic drama Confession; the drama Don Pedro (acted 1796); and the tragedies of Alcanor (acted as The Arab, 1785); Torrendal; The Sibyl, or The Elder Brutus (afterwards amalgamated with other plays on the subject into a very successful tragedy for Edmund Kean by Payne); Tiberius in Capreae; and The False Demetrius (on a theme which attracted Schiller). Cumberland translated the Clouds of Aristophanes (1797), and altered for the stage Shakespeare’s Timon of Athens (1771), Massinger’s The Bondman and The Duke of Milan (both 1779).
In 1806-1807 appeared Memoirs of R. Cumberland, written by himself. Cumberland’s novel, Henry, was printed in Ballantyne’s Novelists’ Library (1821), with a prefatory notice of the author by Sir Walter Scott. A so-called Critical Examination of Cumberland’s works and a memoir of the author based oh his autobiography, with the addition of some more or less feeble criticisms, by William Madford, appeared in 1812. An excellent account of Cumberland is included in “George Paston’s” Little Memoirs of the Eighteenth Century (1901). Hettner well characterizes Cumberland’s position in the history of the English drama in Litteraturgesch. d. 18. Jahrhunderts (2nd ed., 1865), i. 520. Cumberland’s portrait by Romney (whose talent he was one of the first to encourage) is in the National Portrait Gallery.
CUMBERLAND, WILLIAM AUGUSTUS, Duke of (1721-1765), son of King George II. and Queen Caroline, was born on the 15th of April 1721, and when five years of age was created duke of Cumberland. His education was well attended to, and his courage and capacity in outdoor exercises were notable from his early years. He was intended by the king and queen for the office of lord high admiral, and in 1740 he sailed as a volunteer in the fleet under the command of Sir John Norris; but he quickly became dissatisfied with the navy, and early in 1742 he began a military career. In December 1742 he was made a major-general, and in the following year he first saw active service in Germany. George II. and the “martial boy” shared in the glory of Dettingen (June 27), and Cumberland, who was wounded in the action, displayed an energy and valour, the report of which in England founded his military popularity. After the battle he was made lieutenant-general. In 1745, having been made captain-general of the British land forces at home and in the field, the duke was again in Flanders as commander-in-chief of the allied British, Hanoverian, Austrian and Dutch troops. Advancing to the relief of Tournay, which was besieged by Marshal Saxe, he engaged that great general in the battle of Fontenoy (q v.) on the 11th of May. It cannot now be doubted that, had the duke been supported by the allies in his marvellously courageous attack on the superior positions of the French army, Fontenoy would not have been recorded as a defeat to the British arms. He himself was in the midst of the heroic column which penetrated the French centre, and his conduct of the inevitable retreat was unusually cool and skilful.
Notwithstanding the severity of his discipline, the young duke had the power to inspire his men with a strong attachment to his person and a very lively esprit de corps. As a general his courage and resolution were not sufficiently tempered with sagacity and tact; but he displayed an energy and power in military affairs which pointed him out to the British people as the one commander upon whom they could rely to put a decisive stop to the successful career of Prince Charles Edward in the rebellion of 1745-1746. John (Earl) Ligonier wrote of him at this time: “Ou je suis fort trompé ou il se forme là un grand capitaine.”
He was recalled from Flanders, and immediately proceeded with his preparations for quelling the insurrection. He joined the midland army under Sir John Ligonier, and was at once in pursuit of his swift-footed foe. But the retreat of Charles Edward from Derby disconcerted his plans; and it was not till they had reached Penrith, and the advanced portion of his army had been repulsed on Clifton Moor, that he became aware how hopeless an attempt to overtake the retreating Highlanders would then be. Carlisle having been retaken, he retired to London, till the news of the defeat of Hawley at Falkirk roused again the fears of the English people, and centred the hopes of Britain on the royal duke. He was appointed commander of the forces in Scotland.
Having arrived in Edinburgh on the 30th of January 1746, he at once proceeded in search of the young Pretender. He diverged, however, to Aberdeen, where he employed his time in training the well-equipped forces now under his command for the peculiar nature of the warfare in which they were about to engage. What the old and experienced generals of his time had failed to accomplish or even to understand, the young duke of Cumberland, as yet only twenty-four years of age, effected with simplicity and ease. He prepared to dispose his army so as to withstand with firmness that onslaught on which all Highland successes depended; and he reorganized the forces and restored their discipline and self-confidence in a few weeks.
On the 8th of April 1746 he set out from Aberdeen towards Inverness, and on the 15th he fought the decisive battle of Culloden, in which, and in the pursuit which followed, the forces of the Pretender were completely destroyed. He had become convinced that the sternest measures were needed to break down the Jacobitism of the Highlanders. He told his troops to take notice that the enemy’s orders were to give no quarter to the “troops of the elector,” and they took the hint. No trace of such orders remains (see Murray, Lord George), and it is probable that Cumberland had merely received word of wild talk in the enemy’s camp, which he credited the more easily as he thought that those who were capable of rebellion were capable of any crime. On account of the merciless severity with which the fugitives were treated, Cumberland received the nickname of the “Butcher.” That the implied taunt was unjust need not be laboured. It was used for political purposes in England, and his own brother, the prince of Wales, encouraged, it appears, the virulent attacks which were made upon the duke. In any case there is a marked similarity between Cumberland’s conduct in Scotland and that of Cromwell in Ireland. Both dared to do acts which they knew would be cast against them for the rest of their lives, and terrorized an obstinate and unyielding enemy into submission. How real was the danger of a protracted guerrilla warfare in the Highlands may be judged from the explicit declarations of Jacobite leaders that they intended to continue the struggle. As it was, the war came to an end almost at once. Here, as always, Cumberland preserved the strictest discipline in his camp. He was inflexible in the execution of what he deemed to be his duty, without favour to any man. At the same time he exercised his influence in favour of clemency in special cases that were brought to his notice. Some years later James Wolfe spoke of the duke as “for ever doing noble and generous actions.”
The relief occasioned to Britain by the duke’s victorious efforts was acknowledged by his being voted an income of £40,000 per annum in addition to his revenue as a prince of the royal house. The duke took no part in the Flanders campaign of 1746, but in 1747 he again opposed the still victorious Marshal Saxe; and received a heavy defeat at the battle of Lauffeld, or Val, near Maestricht (2nd of July 1747). During the ten years of peace Cumberland occupied himself chiefly with his duties as captain-general, and the result of his work was clearly shown in the conduct of the army in the Seven Years’ War. His unpopularity, which had steadily increased since Culloden, interfered greatly with his success in politics, and when the death of the prince of Wales brought a minor next in succession to the throne the duke was not able to secure for himself the contingent regency, which was vested in the princess-dowager of Wales. In 1757, the Seven Years’ War having broken out, Cumberland was placed at the head of a motley army of allies to defend Hanover. At Hastenbeck, near Hameln, on the 26th of July 1757, he was defeated by the superior forces of D’Estrées (see Seven Years’ War). In September of the same year his defeat had almost become disgrace. Driven from point to point, and at last hemmed in by the French under Richelieu, he capitulated at Klosterzeven on the 8th of the month, agreeing to disband his army and to evacuate Hanover. His disgrace was completed on his return to England by the king’s refusal to be bound by the terms of the duke’s agreement. In chagrin and disappointment he retired into private life, after having formally resigned the public offices he held. In his retirement he made no attempt to justify his conduct, applying in his own case the discipline he had enforced in others. For a few years he lived quietly at Windsor, and subsequently in London, taking but little part in politics. He did much, however, to displace the Bute ministry and that of Grenville, and endeavoured to restore Pitt to office. Public opinion had now set in his favour, and he became almost as popular as he had been in his youth. Shortly before his death the duke was requested to open negotiations with Pitt for a return to power. This was, however, unsuccessful. On the 31st of October 1765 the duke died.
A Life of the duke of Cumberland by Andrew Henderson was published in 1766, and anonymous (Richard Rolt) Historical Memoirs appeared in 1767. See especially A. N. Campbell Maclachlan, William Augustus, Duke of Cumberland (1876).
CUMBERLAND, the north-westernmost county of England, bounded N. by the Scottish counties of Dumfries and Roxburgh, E. by Northumberland, S. by Westmorland and Lancashire, and W. by the Irish Sea. Its area is 1520.4 sq m. In the south the county includes about one-half of the celebrated Lake District (q.v.), with the highest mountain in England, Scafell Pike (3210 ft.), and the majority of the principal lakes, among which are Derwentwater and Bassenthwaite, Buttermere and Crummock Water, Ennerdale, Wastwater, and, on the boundary with Westmorland, Ullswater. From this district valleys radiate north, west and south to a flat coastal belt, the widest part of which (about 8 m.) is found in the north in the Solway Plain, bordering Solway Firth, which here intervenes between England and Scotland. The valley of the Eden, opening upon this plain from the south-east, separates the mountainous Lake District from the straight westward face of a portion of the Pennine Chain (q.v.), which, though little of it lies within this county, reaches its highest point within it in Cross Fell (2930 ft.). A well-marked pass, called the Tyne Gap, at the water-parting between the rivers Irthing and South Tyne, traversed by the Newcastle & Carlisle railway, intervenes between these hills and their northward continuation in the hills of the Scottish border. Besides the waters of the Eden, Solway Firth receives those of the Esk, which enter Cumberland from Scotland. Liddel Water, joining this river from the north east from Liddisdale, forms a large part of the boundary with Scotland. The Eden receives the Irthing from the east, and from the Lake District the Caldew, rising beneath Skiddaw and joining the main river at Carlisle, and the Eamont, draining Ullswater and forming part of the boundary with Westmorland. The principal streams flowing east and south from the Lake District are the Derwent, from Borrowdale and Derwentwater, the Eden from Ennerdale, the Esk from Eskdale, and the Duddon, forming the greater part of the boundary with Lancashire. There are valuable salmon fisheries in the Eden, and trout are taken in many of the streams and lakes.
Geology.—The mountainous portion of Cumberland is built up of two different types of rock. The older, a sedimentary slaty series of Ordovician age, the Skiddaw slates, surrounds Bassenthwaite, Saddleback, Crummock Water, Keswick and Cockermouth and the western end of Ennerdale Water. The same formation is found in the northern flanks of Ullswater also north and east of Whitbeck. The other type of rock is volcanic; it gives a more rugged aspect to the scenery, as may be seen in comparing the rough outlines of Scafell and Honister Crags or Helvellyn with the smoother form of Saddleback or Skiddaw. These volcanic rocks, owing to much 625 alteration, are often slaty; they have been called the “green slates and porphyries” or the Borrowdale Series. The Skiddaw slates are usually separated from the newer green slates above them by a plane of differential movement, for both have been thrust by earth-pressures from south to north, but the former rocks have travelled farther than the latter which have lagged behind; hence Messrs Marr and Harker describe the plane of separation as a “lag-fault.” Much general faulting and folding have resulted from the movement; the thrusting took place in Devonian times. About the same period great masses of granitic rock were intruded into the slates in the form of laccolites, which often lie along the lag planes. Such rocks are the granophyre hills of Buttermere and Ennerdale, the microgranite patches on either side of the Vale of St John, and the great mass of Eskdale granite which reaches from Wastwater to the flanks of Black Combe. At Carrock Fell, N.E. of Skiddaw, is an extremely interesting complex of volcanic rocks, and in many other places are diabase and other forms, e.g. the well-known rock at Castle Head, Keswick.
From Pooley Bridge, Ullswater, on the east, by Udale round to Egremont on the west, the mountainous region just described, is surrounded by the Carboniferous Limestone series, with a conglomerate at the base. Upon these rocks the coalfield of Whitehaven rests and extends as far as Maryport. The coal seams are worked for some distance beneath the sea. The vale of Eden between Penrith, Hornsby and Wreay is occupied by Permian sandstone, usually bright red in colour. Red Triassic rocks form a strip about 4 m. broad east of the Permian outcrop; a similar strip forms a coastal fringe from St Bees Head to Duddon Sands. The same formations are spread out round Carlisle, Brampton, Longtown, Wigton and Aspatria. East of Carlisle they are covered by an outlier of Lias. A great dislocation, the Pennine Fault, runs along the eastern side of the vale of Eden; it throws up the Lower Carboniferous limestones with their associated shales and sandstones to form the elevated ground in the north and north-east of the county. Several basic intrusions penetrate the limestone series, the best known being the Whin Sill, which may be traced for a number of miles northward from Crossfell. Evidences of glacial action are abundant; till with sands and gravel lie on the lower ground; striated rocks and roches moutonnées are common; perched blocks are found on the plateau by Sprinkling Tarn and elsewhere. Moraine mounds are quite numerous in the valleys, and have frequently been the cause of small lakes.
Climate and Agriculture.—The climate is generally temperate, but in the higher parts bleak, snow sometimes lying fully six months of the year on Cross Fell and the mountains of the Lake District. As regards rainfall, the physical configuration makes for contrast. At Carlisle, on the Solway plain, the mean annual fall is 30.6 in. At Penrith, on the north-eastern flank of the Lake District, it is 31.67; on the western flank 42.3 in. are recorded at Ravenglass, close to the coast, and 51.78 at Cockermouth, some miles inland. In the heart of the district, however, the fall is as a rule much heavier, in fact, the heaviest recorded in the British Isles (see Lake District). Somewhat less than three-fifths of the total area of the county is under cultivation, the proportion being higher than that of the neighbouring counties of Northumberland and Westmorland, but still much below the average of the English counties. Black peaty earth is the most prevalent soil in the mountainous districts; but dry loams occur in the lowlands, and are well adapted to green crops, grain and pasture. Wheat and barley are practically neglected, but large crops of oats are grown. Turnips and swedes form the bulk of the green crops. Hill pasture amounts to nearly 270,000 acres, and a good number of cattle are reared, but the principal resource of the farmer is sheep-breeding. The sheep on the lowland farms are generally of the Leicester class or cross-bred between the Leicester and Herdwick, with a few Southdowns. Throughout the mountainous districts the Herdwicks have taken the place of the smaller black-faced heath variety of sheep once so commonly met with on the sheep farms. They are peculiar to this part of England; the ewes and wethers and many of the rams are polled, the faces and legs are speckled, and the wool is finer and heavier in fleece than that of the heath breed. They originally came from the neighbourhood of Muncaster in the Duddon and Esk district, and tradition ascribes their origin variously to introduction by Scandinavian settlers, or to parents that escaped from a wrecked ship of the Spanish Armada. In general they belong to the proprietors of the sheep-walks, and have been farmed out with them from time immemorial, from which circumstance it is said they obtained the name of “Herdwicks.” Long after the Norman Conquest Cumberland remained one of the most densely forested regions of England, and much of the low-lying land is still well wooded, the Lake District in particular displaying beautiful contrasts between bare mountain and tree-clad valley. The oak, ash and birch are the principal natural trees, while sycamores have been planted for shelter round many farmsteads. Plantations of larch are also numerous, and the holly, yew, thorn and juniper flourish locally.
Landed property was formerly much divided in this county, and the smaller holdings were generally occupied by their owners, who were known as “statesmen,” i.e. “estatesmen,” a class of men long noted for their sturdy independence and attachment to routine husbandry. Most of these estates were held of the lords of manors under customary tenure, which subjected them to the payments of fines and heriots on alienation as well as on the death of the lord or tenant. According to the Agricultural Survey printed in 1794, about two-thirds of the county was held by this tenure, in parcels worth from £15 to £30 rental. On large estates, also, the farms were in general rather small, few then reaching £200 a year, held on verbal contracts, or very short leases, and burdened like the small estates with payments or services over and above a money rent. In modern times these conditions have changed, the “statesmen” gradually becoming extinct as a class, and many of the small holdings falling into the hands of the larger landed proprietors.
Other Industries.—Carlisle is the seat of a variety of manufactures; there are also in the county cotton and woollen industries, pencil mills at Keswick, and iron shipbuilding yards at Whitehaven. But the mining industry is the most important, coal being raised principally in the district about Whitehaven, Workington and Maryport. Side by side with this industry much iron ore is raised, and there is a large output of pig-iron, and ore is also found in the south, in the neighbourhood of Millom. Gypsum, zinc and some lead are mined. Copper was formerly worked near Keswick, and there was a rich deposit of black lead at the head of Borrowdale. Granite and limestone are extensively quarried. Stone is very largely used even for housebuilding, a fine green slate being often employed. Shap and other granites are worked for building and roadstones.
Communications.—The chief ports of Cumberland are Whitehaven, Workington, Maryport, Harrington and Silloth. The London & North-Western railway enters the county near Penrith, and terminates at Carlisle, which is also served by the Midland. The Caledonian, North British and Glasgow & South-Western lines further serve this city, which is thus an important junction in through communications between England and Scotland. The North-Eastern railway connects Carlisle with Newcastle. The Maryport & Carlisle, the Cockermouth, Keswick & Penrith, and the Cleator & Workington Junction lines serve the districts indicated by their names, while the Furness railway passes along the west coast from the district of Furness in Lancashire as far north as Whitehaven, also serving Cleator and Egremont. The Ravenglass & Eskdale light railway gives access from this system to Boot in Eskdale. Coaches and motor cars maintain passenger communications in the Lake District where the railways do not penetrate.
Population and Administration.—The area of the ancient and the administrative county is 973,086 acres, with a population in 1891 of 266,549 and in 1901 of 266,933. The county contains five wards, divisions which in this and neighbouring counties correspond to hundreds, and also appear in Lanarkshire and Renfrewshire in Scotland. The municipal boroughs are Carlisle (pop. 45,480), a city and the county town, Whitehaven (19,324), and Workington (26,143). The other urban districts are Arlecdon and Frizington (5341), Aspatria (2885), Cleator Moor (8120), Cockermouth (5355), Egremont (5761), Harrington (3679), Holme Cultram (4275), Keswick (4451), Maryport (11,897), Millom (10,426), Penrith (9182), Wigton (3692). Of these all except Keswick, Millom and Penrith are in the industrial district of the west and north-west. The urban district of Holme Cultram includes the port of Silloth. Among lesser towns may be mentioned St Bees (1236), on the coast south of Whitehaven, 626 until 1897 the seat of a Church of England theological college. The grammar school here, founded in 1533, is liberally endowed, with scholarships and exhibitions. Cumberland is in the northern circuit, and assizes are held at Carlisle. It has one court of quarter sessions and 12 petty sessional divisions. The city of Carlisle has a separate commission of the peace and court of quarter sessions. There are 213 civil parishes. Cumberland is in the diocese of Carlisle, with a small portion in that of Newcastle. There are 167 ecclesiastical parishes or districts within the county. There are four parliamentary divisions, the Northern or Eskdale, Mid or Penrith, Cockermouth and Western or Egremont, each returning one member; while the parliamentary boroughs of Carlisle and Whitehaven each return one member.
History.—After the withdrawal of the Romans (of whose occupation there are various important relics in the county) little is known of the region which is now Cumberland, until the great battle of Ardderyd in 573 resulted in its consolidation with the kingdom of Strathclyde. About 670-680 the western district between the Solway and the Mersey was conquered by the Angles of Northumbria and remained an integral portion of that kingdom until the Danish invasion of the 9th century. In 878 the kingdom of the Cumbri is referred to, but without any indication of its extent, and the first mention of Cumberland to denote a geographical area occurs in 945 when it was ceded by Edmund to Malcolm of Scotland. At this date it included the territory north and south of the Solway from the Firth of Forth to the river Duddon. The Scottish supremacy was not uninterrupted, for the district at the time of its invasion by Ethelred in 1000 was once more a stronghold of the Danes, whose influence is clearly traceable in the nomenclature of the Lake District. At the time of the Norman invasion Cumberland was a dependency of the earldom of Northumbria, but its history at this period is very obscure, and no notice of it occurs in the Domesday Survey of 1086; Kirksanton, Bootle and Whicham, however, are entered under the possessions of the earl of Northumbria in the West Riding of Yorkshire. The real Norman conquest of Cumberland took place in 1092, when William Rufus captured Carlisle, repaired the city, built the castle, and after sending a number of English husbandmen to till the land, placed the district under the lordship of Ranulf Meschines. The fief of Ranulf was called the Power or Honour of Carlisle, and a sheriff of Carlisle is mentioned in 1106. The district was again captured by the Scots in the reign of Stephen, and on its recovery in 1157 the boundaries were readjusted to include the great barony of Coupland. At this date the district was described as the county of Carlisle, and the designation county of Cumberland is not adopted in the sheriff’s accounts until 1177. The five present wards existed as administrative areas in 1278, when they were termed bailiwicks, the designation ward not appearing until the 16th century, though the bailiwicks of the Forest of Cumberland are termed wards in the 14th century. In the 17th and 18th centuries each of the five wards was under the administration of a chief constable.
Owing to its position on the Border Cumberland was the scene of constant warfare from the time of its foundation until the union of England and Scotland, and families like the Tilliols, the Lucies, the Greystokes, and the Dacres were famous for their exploits in checking or avenging the depredations of the Scots. During the War of Independence in the reign of Edward I. Carlisle was the headquarters of the English army. In the Wars of the Roses the prevailing sympathy was with the Lancastrian cause, which was actively supported by the representatives of the families of Egremont, Dacre and Greystoke. In 1542 the Scottish army under James V. suffered a disastrous defeat at Solway Moss. After the union of the crowns of England and Scotland in 1603, the countries hitherto known as “the Borders” were called “the Middle Shires,” and a period of comparative peace ensued. On the outbreak of the Civil War of the 17th century the northern counties associated in raising forces for the king, and the families of Howard, Dalston, Dacre and Musgrave rendered valuable service to the royalist cause. In 1645 Carlisle was captured by the parliamentary forces, but in April 1648 it was retaken by Sir Philip Musgrave and Sir Thomas Glenham, and did not finally surrender until the autumn of 1648. Cumberland continued, however, to support the Stuarts; it was one of the first counties to welcome back Charles II.; in 1715 it was associated with the rising on behalf of the Pretender, and Carlisle was the chief seat of operations in the 1745 rebellion.
In 685 Carlisle and the surrounding district was annexed by Ecgfrith king of Northumbria to the diocese of Lindisfarne, to which it continued subject, at least until the Danish invasion of the 9th century. In 1133 Henry I. created Carlisle (q.v.) a bishopric. The diocese included the whole of modern Cumberland (except the barony of Coupland and the parishes of Alston, Over-Denton and Kirkandrews), and also the barony of Appleby in Westmorland. The archdeaconry of Carlisle, co-extensive with the diocese, comprised four deaneries. Coupland was a deanery in the archdeaconry of Richmond and diocese of York until 1541, when it was annexed to the newly created diocese of Chester. In 1856 the area of the diocese of Carlisle was extended, so as to include the whole of Cumberland except the parish of Alston, the whole of Westmorland, and the Furness district of Lancashire. In 1858 the deaneries were made to number eighteen, and in 1870 were increased to twenty.
The principal industries of Cumberland have been from earliest times connected with its valuable fisheries and abundant mineral wealth. The mines of Alston and the iron mines about Egremont were worked in the 12th century. The Keswick copper mines were worked in the reign of Henry III., but the black-lead mine was not worked to any purpose until the 18th century. Coal-mining is referred to in the 15th century, and after the revival of the mining industries in the 16th century, rose to great importance. The saltpans about the estuaries of the Esk and the Eden were a source of revenue in the 12th century.
Cumberland returned three members for the county to the parliament of 1290, and in 1295 returned in addition two members for the city of Carlisle and two members each for the boroughs of Cockermouth and Egremont. The boroughs did not again return members until in 1640 Cockermouth regained representation. Under the Reform Act of 1832, Cumberland returned four members for two divisions, and Whitehaven returned one member. The county now returns six members to parliament; one each for the four divisions of the county, Egremont, Cockermouth, Eskdale and Penrith, one for the city of Carlisle and one for the borough of Whitehaven.
Antiquities.—Very early crosses, having Celtic or Scandinavian characteristics, are seen at Gosforth, Bewcastle and elsewhere. In ecclesiastical architecture Cumberland is not rich as a whole, but it possesses Carlisle cathedral, with its beautiful choir, and certain monastic remains of importance. Among these are the fine remnants of Lanercost priory (see Brampton). Calder Abbey, near Egremont, a Cistercian abbey founded in 1134, has ruins of the church and cloisters, of Norman and Early English character, and is very beautifully situated on the Calder. The parish Church of St Bees, with good Norman and Early English work, belonged to a Benedictine priory of 1120; but according to tradition the first religious house here was a nunnery founded c. 650 by St Bega, who became its abbess. Among the parish churches there are a few instances of towers strongly fortified for purposes of defence; that at Burgh-on-the-Sands, near Carlisle, being a good illustration. Castles, in some cases ruined, in others modernized, are fairly numerous, both near the Scottish border and elsewhere. Naworth Castle near Brampton is the finest example; others are at Bewcastle, Carlisle, Kirkoswald, Egremont, Cockermouth and Millom. Among many notable country seats, Rose Castle, the palace of the bishops of Carlisle; Greystoke Castle and Armathwaite Hall may be mentioned.
See J. Nicolson and R. Burn, History and Antiquities of the Counties of Westmorland and Cumberland (London, 1777); W. Hutchinson, History of Cumberland (Carlisle, 1794); S. Jefferson, History and Antiquities of Cumberland (Carlisle, 1840-1842); S. Gilpin, Songs and Ballads of Cumberland (London, 1866); W. Dickinson, Glossary of Words and Phrases of Cumberland (London, English Dialect 627 Society, 1878, with a supplement, 1881); Sir G. F. Duckett, Early Sheriffs of Cumberland (Kendal, 1879); J. Denton, “Account of Estates and Families in the County of Cumberland, 1066-1603,” in Antiquarian Society’s Transactions (1887); R. S. Ferguson, History of Cumberland (London, 1890); “Archaeological Survey of Cumberland,” in Archaeologia, vol. liii. (London, 1893); W. Jackson, Papers and Pedigrees relating to Cumberland (2 vols., London, 1892); T. Ellwood, The Landnama Book of Iceland as it illustrates the Dialect and Antiquities of Cumberland (Kendal, 1894); Victoria County History, Cumberland; and Transactions of the Cumberland and Westmorland Antiquarian and Archaeological Society.
CUMBERLAND, a city and the county-seat of Allegany county, Maryland, U.S.A., on the Potomac river, about 178 m. W. by N. of Baltimore and about 153 m. S. by E. of Pittsburg. Pop. (1890) 12,729; (1900) 17,128, of whom 1113 were foreign-born and 1100 were of negro descent; (1910) 21,839. Cumberland is served by the Baltimore & Ohio, the Western Maryland, the Pennsylvania, the Cumberland & Pennsylvania (from Cumberland to Piedmont, Virginia), and the George’s Creek & Cumberland railways, the last a short line extending to Lonaconing (19 m.); by an electric line extending to Western Port, Maryland; and by the Chesapeake & Ohio Canal, of which it is a terminus. The city is about 635 ft. above sea-level, and from a distance appears to be completely shut in by lofty ranges of hills, which are cut through to the westward by a deep gorge called “The Narrows,” making a natural gateway of great beauty. Cumberland has a large trade in coal, which is mined in the vicinity. As a manufacturing centre it ranked in 1905 second in the state, the chief products being iron, steel, bricks, flour, cement, silk and leather; there is also a large dyeing and cleaning establishment. The value of the city’s factory products increased from $2,900,267 in 1900 to $4,595,023 in 1905, or 58.4%. Cumberland is an important jobbing centre also. The municipality owns and operates its water-works and electric lighting plant. The first settlement of the place was made in 1750; in 1754 Fort Cumberland was erected within what are now the city limits, and in the year following this fort was occupied by General Edward Braddock. Cumberland was laid out in 1763, but there was little growth until 1787, and it was not incorporated as a town until 1815; it was chartered as a city in 1850.
CUMBERLAND, a township of Providence county, Rhode Island, U.S.A., in the N.E. part of the state, about 6 m. N. of Providence and having the Blackstone river for most of its W. boundary. Pop. (1890) 8090; (1900) 8925, of whom 3473 were foreign-born; (1910) 10,107; area, 27.5 sq. m. It is served by the New York, New Haven & Hartford railway. Within its borders are the villages of Cumberland Hill, Diamond Hill, Arnold Mills, Abbott Run, Berkeley, Robin Hollow, Happy Hollow, East Cumberland, and parts of Manville, Ashton, Lonsdale and Valley Falls. The surface of the township is generally hilly and rocky. In the N. part is a valuable granite quarry; and limestone, and some coal, iron and gold are also found. Cumberland has been called the “mineral pocket of New England.” The Blackstone and its tributaries provide considerable water power; and there are various manufactures, including cotton goods, silk goods, and horse-shoes and other iron ware. The value of the township’s factory product in 1905 was $3,171,318, an increase of 80.6% since 1900, this ratio of increase being greater than that shown by any other “municipality” in the state having a population in 1900 of 8000 or more. At Lonsdale, William Blackstone (c. 1595-1675), the first permanent white settler within the present limits of Rhode Island, built his residence, “Study Hall,” about 1635. Cumberland was originally a part of Rehoboth, and then of Attleborough, Massachusetts, and for many years was called, like other sparse settlements, the Gore, or Attleborough Gore. In 1747, by the royal decree establishing the boundary between Massachusetts and Rhode Island, Attleborough Gore, with other territory formerly under the jurisdiction of Massachusetts, was annexed to Rhode Island, and the township of Cumberland was incorporated, the name being adopted in honour of William Augustus, duke of Cumberland. In 1867 a part of Cumberland was set off to form the township of Woonsocket.
CUMBERLAND MOUNTAINS (or more correctly the Cumberland Plateau or Highlands), the westernmost of the three great divisions of the Appalachian uplift in the United States, composed of many small ranges of mountains (of which Cumberland Mountain in eastern Kentucky is one). It extends from Pennsylvania to Alabama, attaining its greatest height (about 4000 ft.) in Virginia. The plateau is rich in a variety of mineral products, of which special mention may be made of coal, which occurs in many places, and of the beautiful marbles quarried in that portion of the plateau which lies between Virginia and Kentucky and crosses Tennessee. The plateau has an abrupt descent, almost an escarpment, into the great Appalachian Valley on its E., while the W. slope is deeply and roughly broken. The whole mass is eroded in Virginia into a maze of ridges. Cumberland Mountain parts the waters of the Cumberland and Tennessee rivers. This range and the other ranges about it are perhaps the loveliest portion of the whole plateau. The peaks here and in the Blue Ridge to the E. are the highest of the Appalachian system. Forest-filled valleys, rounded hills and rugged gorges afford in every part scenery of surpassing beauty. The Cumberland Valley between the Cumberland range and the Pine range is one of special fame. In the former range there are immense caverns and subterranean streams. Cumberland Gap, crossing the ridge at about 167 ft. above the sea, where Kentucky, Virginia and Tennessee meet, is a gorge about 500 ft. deep, with steep sides that barely give room in places for a roadway. The mountains, river and gap were all discovered by a party of Virginians in 1748, and named in honour of the victor of Culloden, William, duke of Cumberland. Afterwards the gap gained a place in American history as one of the main pathways by which emigrants crossed the mountains to Kentucky and Tennessee. During the Civil War it was a position of great strategic importance, as it afforded an entrance to eastern and central Tennessee from Kentucky, which was held by the Union arms; and it was repeatedly occupied in alternation by the opposing forces.
The mountaineers of Kentucky and Tennessee are a strange stock, who retain in their customs and habits the primitive conditions of a life that has elsewhere long since disappeared. They have been pictured in the novels of Miss Murfree and John Fox, Junr. They are a tall, straight, angular folk, of fine physical development; the volunteers for the Union army from Kentucky and Tennessee during the Civil War—most of whom came from the non-slave-holding mountain region—exceeded in physical development the volunteers from all other states. For the education of these mountaineers Major-General Oliver Otis Howard founded in 1895 at Cumberland Gap, Tennessee, the Lincoln Memorial University (co-educational; non-sectarian; opened in 1897), which has collegiate, normal training and industrial courses, and an affiliated school of medicine, Tennessee Medical College, at Knoxville. The university had in 1907-1908 14 instructors and 570 students. Berea College in Kentucky was a pioneer institution for the education of mountaineers.
CUMBERLAND RIVER, a large southern branch of the Ohio river, U.S.A., rising in the highest part of the Cumberland plateau in south-east Kentucky, and emptying into the Ohio in Kentucky (near Smithland) after a devious course of 688 m. through that state and Tennessee. It drains a basin of somewhat more than 18,000 sq. m., and is navigable for light-draught steamers through about 500 m. under favourable conditions—Burnside, Pulaski county, 518 m. from the mouth, is the head of navigation—and through 193 m.—to Nashville—all the year round; for boats drawing not more than 3 ft. the river is navigable to Nashville for 6 to 8 months. At the Great Falls, in Whitley county, Kentucky, it drops precipitously 63 ft. Above the falls it is a mountain stream, of little volume in the dry months. It descends rapidly at its head to the highland bench below the mountains and traverses this to the falls, then flows in rapids (the Great Shoals) for some 10 m. through a fine gorge with cliffs 300-400 ft. high, and descends between bluffs of decreasing height and beauty into its lower level. Save in the mountains its gradient is slight, and below the falls, except for a number of small rapids, the 628 flow of the stream is equable. Timbered ravines lend charm to much of its shores, and in the mountains the scenery is most beautiful. Below Nashville the stream is some 400 to 500 ft. wide, and its high banks are for the most part of alluvium, with rocky bluffs at intervals. At the mouth of the river lies Cumberland Island, in the Ohio. During low water of the latter stream the Cumberland discharges around both ends of the island, but in high water of the Ohio the gradient of the Cumberland is so slight that its waters are held back, forming a deep quiet pool that extends some 20 m. up the river. A system of locks and dams below Nashville was planned in 1846 by a private company, which accomplished practically nothing. Congress appropriated $155,000 in 1832-1838; in the years immediately after 1888 $305,000 was expended, notably for deepening the shoals at the junction of the Cumberland and the Ohio; in 1892 a project was undertaken for 7 locks and dams 52 ft. wide and 280 ft. long below Nashville. Above Nashville $346,000 was expended on the open channel project (of 1871-1872) from Nashville to Cumberland Ford (at Pineville); in 1886 a canalization project was undertaken and 22 locks and dams below Burnside and 6 above Burnside were planned, but by the act of 1907 the project was modified—$2,319,000 had been appropriated up to 1908 for the work of canalization. During the Civil War Fort Donelson on the Cumberland, and Fort Henry near by on the Tennessee were erected by the Confederates, and their capture by Flag-officer A. H. Foote and General Grant (Feb. 1862) was one of the decisive events of the war, opening the rivers as it did for the advance of the Union forces far into Confederate Territory.
CUMBRAES, THE, two islands forming part of the county of Bute, Scotland, lying in the Firth of Clyde, between the southern shores of Bute and the coast of Ayrshire. Great Cumbrae Island, about 1½ m. W.S.W. of Largs, is 3¾ m. long and 2 m. broad, and has a circumference of 10 m. and an area of 3200 acres or 5 sq. m. Its highest point is 417 ft. above the sea. There is some fishing and a little farming, but the mainstay of the inhabitants is the custom of the visitors who crowd every summer to Millport, which is reached by railway steamer from Largs. This town (pop. 1901, 1663) is well situated at the head of a fine bay and has a climate that is both warm and bracing. Its chief public buildings include the cathedral, erected in Gothic style on rising ground behind the town, the college connected with it, the garrison, a picturesque seat belonging to the marquess of Bute, who owns the island, the town hall, a public hall, library and reading room, the Lady Margaret fever hospital, and a marine biological station. The cathedral, originally the collegiate church, was founded in 1849 by the earl of Glasgow and opened in 1851. In 1876 it was constituted the cathedral of Argyll and the Isles. Millport enjoys exceptional facilities for boating and bathing, and there is also a good golf-course. Pop. (1901) 1754, of whom 1028 were females, and 59 spoke both English and Gaelic. Little Cumbrae Island lies to the south, separated by the Tan, a strait half a mile wide. It is 1¾ m. long, barely 1 m. broad, and has an area of almost a square mile. Its highest point is 409 ft. above sea-level. On the bold cliffs of the west coast stands a lighthouse. Robert II. is said to have built a castle on the island which was demolished by Cromwell’s soldiers in 1653.
The strata met with in the Great and Little Cumbrae belong to the Upper Old Red Sandstone and Carboniferous systems. The former, consisting of false-bedded sandstones and conglomerates, are confined to the larger island. The Carboniferous rocks of the Cumbrae belong to the lower part of the Calciferous Sandstone series with the accompanying volcanic zone. In the larger island these sediments, comprising sandstones, red, purple and mottled clays with occasional bands of nodular limestone or cornstone, occupy a considerable area on the north side of Millport Bay. In the Little Cumbrae they appear on the east side, where they underlie and are interbedded with the lavas. The interesting geological feature of these islands is the development of Lower Carboniferous volcanic rocks. They cover nearly the whole of the Little Cumbrae, where they give rise to marked terraced features and are arranged in a gentle synclinal fold. The flows are often scoriaceous at the top and sometimes display columnar structure, as in the crags at the lighthouse. Those rocks examined microscopically consist of basalts which are often porphyritic. In Great Cumbrae the intrusive rocks mark four periods of eruption, three of which may be of Carboniferous age. The oldest, consisting of trachytes, occur as sheets and dikes trending generally E.N.E., and are confined chiefly to the Upper Old Red Sandstone. They seem to be of older date than the Carboniferous lavas of Little Cumbrae and south Bute. Next come dikes of olivine basalt of the type of the Lion’s Haunch on Arthur’s Seat, which, though possessing the same general trend as the trachytes, are seen to cut them. The members of the third group comprise dikes of dolerite or basalt with or without olivine, which have a general east and west trend, and as they intersect the two previous groups they must be of later date. They probably belong to the east and west quartz dolerite dikes which are now referred to late Carboniferous time. Lastly there are representatives of the basalt dikes of Tertiary age with a north-west trend.
CUMIN, or Cummin (Cuminum Cyminum), an annual herbaceous plant, a member of the natural order Umbelliferae and probably a native of some part of western Asia, but scarcely known at the present time in a wild state. It was early cultivated in Arabia, India and China, and in the countries bordering the Mediterranean. Its stem is slender and branching, and about a foot in height; the leaves are deeply cut, with filiform segments; the flowers are small and white. The fruits, the so-called seeds, which constitute the cumin of pharmacy, are fusiform or ovoid in shape and compressed laterally; they are two lines long, are hotter to the taste, lighter in colour, and larger than caraway seeds, and have on each half nine fine ridges, overlying as many oil-channels or vittae. Their strong aromatic smell and warm bitterish taste are due to the presence of about 3% of an essential oil. The tissue of the seeds contains a fatty oil, with resin, mucilage and gum, malates and albuminous matter; and in the pericarp there is much tannin. The volatile oil of cumin, which may be separated by distillation of the seed with water, is mainly a mixture of cymol or cymene, C10H14, and cumic aldehyde, C6H4(C3H7)COH. Cumin is mentioned in Isaiah xxviii. 25, 27, and Matthew xxiii. 23, and in the works of Hippocrates and Dioscorides. From Pliny we learn that the ancients took the ground seed medicinally with bread, water or wine, and that it was accounted the best of condiments as a remedy for squeamishness. It was found to occasion pallor of the face, whence the expression of Horace, exsangue cuminum (Epist. i. 19), and that of Persius, pallentis grana cumini (Sat. v. 55). Pliny relates the story that it was employed by the followers of Porcius Latro, the celebrated rhetorician, in order to produce a complexion such as bespeaks application to study (xx. 57). In the middle ages cumin was one of the commonest spices of European growth. Its average price per pound in England in the 13th and 14th centuries was 2d. or, at present value, about 1s. 4d. (Rogers, Hist. of Agric. and Prices, i. 631). It is stimulant and carminative, and is employed in the manufacture of curry powder. The medicinal use of the drug is now confined to veterinary practice. Cumin is exported from India, Mogador, Malta and Sicily.
CUMMERBUND, a girdle or waistbelt (Hindostani kamar-band, a loin-band). In the East the principle of health is to keep the head cool and the stomach warm; the turban protects the one from the sun, and the cummerbund ensures the other against changes of temperature. In India the cummerbund consists of many folds of muslin or bright-coloured cloth.
CUMMING, JOSEPH GEORGE (1812-1868), English geologist and archaeologist, was born at Matlock in Derbyshire on the 15th of February 1812. He was educated at Oakham grammar school, and Emmanuel College, Cambridge, taking the degree of M.A., and entering holy orders in 1835. In 1841 he was appointed vice-principal of King William’s College, Castletown, in the Isle of Man, and this position he held until 1856. During this period his leisure time was devoted to a study of the geology and archaeology of the island. The results were published in a classic volume The Isle of Man; its History, Physical, Ecclesiastical, Civil and Legendary (1848). In 1856 he became master of King Edward’s grammar school at Lichfield, in 1858 warden and professor of classical literature and geology in Queen’s College, Birmingham, in 1862 rector of Mellis, in Suffolk, and in 1867 vicar of St John’s, Bethnal Green, London. He died in London on the 21st of September 1868.
CUMNOCK AND HOLMHEAD, a police burgh of Ayrshire, Scotland, on the Lugar, 33¾ m. S. of Glasgow by road, with two stations (Cumnock and Old Cumnock) on the Glasgow & South-Western railway. Pop. (1901) 3088. It lies in the parish of Old Cumnock (pop. 5144), and is a thriving town, with a town hall, cottage hospital, public library and an athenaeum. Coal and ironstone are extensively mined in the neighbourhood, and the manufactures include woollens, tweeds, agricultural implements and pottery. When Alexander Peden (1626-1686), the persecuted Covenanter, died, he was buried in the Boswell aisle of Auchinleck church; but his corpse was borne thence with every indignity by a company of dragoons to the foot of the gallows at Cumnock, where they intended to hang it in chains. This proving to be impracticable they buried it at the gallows-foot. After the Revolution the inhabitants out of respect for the “Prophet’s” memory abandoned their then burying-ground and turned the old place of execution into the present cemetery. Five miles S.E. lies the parish of New Cumnock (pop. 5367) at the confluence of Afton Water and the Nith. It is rich in minerals, iron, coal, limestone and freestone, and has a station on the Glasgow & South-Western railway. Two miles N.W. of Cumnock is Auchinleck (pronounced Affleck), with a station on the Glasgow & South-Western railway. Coal and iron mining and farming are important industries. It is the seat of the Boswell family, three generations of which abbreviated greatness—Lord Auchinleck, the judge (who dubbed Dr Johnson “Ursa Major”), his son James, the biographer, and his grandson Sir Alexander, the author of “Gude nicht and joy be wi’ you a’,” “Jenny’s Bawbee,” “Jenny dang the weaver,” and other songs and poems, who perished miserably in a duel. Pop. of Auchinleck parish (1901) 6605.
CUNARD, SIR SAMUEL, Bart. (1787-1865), British civil engineer, founder of the Cunard line of steam-ships, was born at Halifax, Nova Scotia, on the 21st of November 1787. He was the son of a merchant, and was himself trained for the pursuits of commerce, in which, by his abilities and enterprising spirit, he attained a conspicuous position. When, in the early years of steam navigation, the English government made known its desire to substitute steam vessels for the sailing ships then employed in the mail service between England and America, Cunard heartily entered into the scheme, came to England, and accepted the government tender for carrying it out. In conjunction with Messrs Burns of Glasgow and Messrs MacIver of Liverpool, proprietors of rival lines of coasting steamers between Glasgow and Liverpool, he formed a company, and the first voyage of a Cunard steamship was successfully made by the “Britannia” from Liverpool to Boston, U.S.A., between July 4 and 19, 1840 (see Steamship Lines). In acknowledgment of his energetic and successful services Cunard was, in 1859, created a baronet. He died in London on the 28th of April 1865.
CUNAS, a tribe of Central American Indians. Their home is the Isthmus of Panama, from the Chagres to the Atrato. They are sometimes called Darien or San Blas Indians. They are a small active people, with remarkably light complexions.
CUNDINAMARCA, till 1909 a department of the eastern plateau of Colombia, South America, having the departments of Quesada and Tundama on the N., Tolima on the W. and S., and the Meta territory on the S.E. and E. The territorial redistribution of 1905 deprived Cundinamarca of its territories on the eastern plains, and a part of its territory in the Eastern Cordillera out of which Quesada and the Federal district were created—its area being reduced from 79,691 to 5060 sq. m., and its estimated population from 500,000 to 225,000. A considerable part of its area consists of plateaus enjoying a temperate climate and producing the fruits and cereals of the temperate zone, and another important part lies in the valley of the Magdalena and is tropical in character. The district of Fusagasuga in the southern part of this region is celebrated for the excellence of its coffee. The capital of the department was Facatativá (est. population, 7500), situated on the western margin of the sabana of Bogotá, 25 m. N.W. from that capital by rail. Other important towns are Caqueza, Sibaté, La Meza and Tocaima.
CUNEIFORM (from Lat. cuneus, a wedge), a form of writing,
extensively used in the ancient world, especially by the Babylonians
and Assyrians. The word “cuneiform” was first
applied in 1700 by Thomas Hyde, professor of Hebrew in the
university of Oxford, in the expression “dactuli pyramidales
seu cuneiformes,” and it has found general acceptance, though
efforts have been made to introduce the expression “arrow-headed”
writing. The name “cuneiform” is fitting, for each
character or sign is composed of a wedge ( or
or  ), or a combination
of wedges (
), or a combination
of wedges ( ), written from left to right. The wedge
is always pointed towards the right (
), written from left to right. The wedge
is always pointed towards the right ( ) or downwards (
) or downwards ( ) or
aslant (
) or
aslant ( ), or two may be so combined as to form an angle (
), or two may be so combined as to form an angle ( )
called by German Assyriologists a Winkelhaken, a word now
sometimes adopted by English writers on the subject. The
word cuneiform has passed into most modern languages, but
the Germans use Keilschrift (i.e. wedge-script) and the Arabs
mismārī (
)
called by German Assyriologists a Winkelhaken, a word now
sometimes adopted by English writers on the subject. The
word cuneiform has passed into most modern languages, but
the Germans use Keilschrift (i.e. wedge-script) and the Arabs
mismārī ( ) or nail-writing.
) or nail-writing.

In Persia, 40 m. N.E. of Shiraz, is a range of hills, Mount Rachmet, in front of which, in a semicircular form, rises a vast terrace-like platform. It is partly natural, but was walled up in front, levelled off and used as the base Discovery and decipherment. of great temples and palaces. The earliest European, at present known to us, who visited the site was a wandering friar Odoricus (about A.D. 1320), who does not seem to have noticed the inscriptions cut in the stone. These were first observed by Josaphat Barbaro, a Venetian traveller, about 1472. In 1621 the ruins were visited by Pietro della Valle, who was the first to copy a few of the signs, which he sent in a letter to a friend in Naples. His copy was not well made, but it served the useful purpose of directing attention to an unknown script which was certain to attract scholars to the problem of its decipherment. To this end it was necessary that complete inscriptions and not merely separate signs should be made accessible to European scholars. The first man to attempt to satisfy this need was Sir John Chardin, in whose volumes of travels published at Amsterdam in 1711 one of the small inscriptions found at the ruins of Persepolis was carefully and accurately reproduced. It was now plainly to be seen, as indeed others had surmised, that these inscriptions at Persepolis had been written in three languages, distinguished each from other by an increasing complexity in the signs with which they were written. The three languages have since been determined as Persian, Susian and Babylonian. But before the decipherment could begin it was necessary that all the available material should be copied and published. The honour of performing this great task fell to Carsten Niebuhr, who visited Persepolis in March 1765, and in three weeks and a half copied all the texts, so well that little improvement has been made in them since. When Niebuhr returned to Denmark he studied carefully the little inscriptions and convinced himself that the guesses of some of his predecessors were correct, and that the inscriptions were to be read from left to right. He observed that three systems of writing were discernible, and that these were always kept distinct in the inscriptions. He did not, however, draw the natural conclusion that they represented three languages, but supposed that the proud builders of Persepolis had written their inscriptions in threefold form. He divided the little inscriptions into three classes, according to the manner of their writing, calling them classes I., II. and III. He then arranged all those he had copied that belonged to class I., and by careful comparison decided that in them there were employed altogether but forty-two signs. These he copied out and set in order in one of his plates. This list of signs was so nearly complete and accurate that later study has made but slight changes in it. When 630 Niebuhr had made his list of signs he naturally enough decided that this language, whatever it might be, was written in alphabetic characters, a conclusion which later investigation has not overthrown. Beyond this Niebuhr was not able to go, and not even one sign revealed its secret to his inquiry. When, however, he had published his copies (in 1777) there were other scholars ready to take up the difficult task. Two scholars independently, Olav Tychsen of Rostock and Friedrich Münter of Copenhagen, began work upon the problem. Tychsen first observed that there occurred at irregular intervals in the inscriptions of the first class a wedge that pointed neither directly to the right nor downward, but inclined diagonally. This he suggested was the dividing sign used to separate words. This very simple discovery later became of great importance in the hands of Münter. Tychsen also correctly identified the alphabetic signs for “a,” “d,” “u” and “s,” but he failed to decipher an entire inscription, chiefly perhaps because, through an error in history, he supposed that they were written during the Parthian dynasty (246 B.C.-A.D. 227). Münter was more fortunate than Tychsen in his historical researches, and this made him also more successful in linguistic attempts. He rightly identified the builders of Persepolis with the Achaemenian dynasty, and so located in time the authors of the inscriptions (538-465 B.C.). Independently of Tychsen he identified the oblique wedge as a divider between words, and found the meaning of the sign for “b.” These may appear to be small matters, but it must be remembered that they were made without the assistance of any bilingual text, and were indeed taken bodily out of the gloom which had settled upon these languages centuries before. They did not, however, bring us much nearer to the desired goal of a reading of any portion of the inscriptions. The whole case indeed seemed now perilously near a stalemate. New methods must be found, and a new worker, with patience, persistence, power of combination, insight, the historical sense and the feeling for archaeological indications.
In 1802 Georg Friedrich Grotefend (q.v.) was persuaded by the librarian of Göttingen University to essay the task. He began with the assumption that there were three languages, and that of these the first was ancient Persian, the language of the Achaemenians, who had erected these palaces and caused these inscriptions to be written. For his first attempts at decipherment he chose two of these old Persian inscriptions and laid them side by side. They were of moderate length, and the frequent recurrence of the same signs in them seemed to indicate that their contents were similar. The method which he now pursued was so simple, yet so sure, as he advanced step by step, that there seemed scarcely a chance of error. Münter had observed in all the Persian texts a word which occurred in two forms, a short and a longer form. This word appeared in Grotefend’s two texts in both long and short forms. Münter had suggested that it meant “king” in the short form and “kings” in the longer, and that when the two words occurred together the expression meant “king of kings.” But further, this word occurred in both inscriptions in the first line, and in both cases was followed by the same word. This second word Grotefend supposed to mean “great,” the combined expression being “king great,” that is, “great king.” All this found support in the phraseology of the lately deciphered Sassanian inscriptions, and it was plausible in itself. It must, however, be supported by definite facts, and furthermore each word must be separated into its alphabetic parts, every one of them identified, and the words themselves be shown to be philologically possible by the production of similar words in related languages. In other words, the archaeological method must find support in a philological method. To this Grotefend now devoted himself with equal energy. His method was as simple as before. He had made out to his own satisfaction the titles “great king, king of kings.” Now, in the Sassanian inscriptions, the first word was always the king’s name, followed immediately by “great king, king of kings,” and Grotefend reasoned that this was probably true in his texts. But if true, then these two texts were set up by two different kings, for the names were not the same at the beginning. Furthermore the name with which his text No. I. began appears in the third line of text No. II., but in a somewhat longer form, which Grotefend thought was a genitive and meant “of N.” It followed the word previously supposed to be “king” and another which might mean son (N king son), so that the whole expression would be “son of N king.” From these facts Grotefend surmised that in these two inscriptions he had the names of three rulers, grandfather, father and son. It was now easy to search the list of the Achaemenian dynasty and to find three names which would suit the conditions, and the three which he ventured to select were Hystaspes, Darius, Xerxes. According to his hypothesis the name at the beginning of inscription I. was Darius, and he was ready to translate his texts in part as follows:—
| I. | Darius, great king, king of kings ... son of Hystaspes.... |
| II. | Xerxes, great king, king of kings ... son of Darius king. |
The form which he provisionally adopted for Darius was Darheush; later investigation has shown that it ought really to be read as Daryavush, but the error was not serious, and he had safely secured at least the letters D, A, R, SH. It was a most wonderful achievement, the importance of which he did not realize, for in it was the key to the decipherment of three ancient languages. To very few men has it been given to make discoveries so important both for history and for philology.
To Grotefend it was, however, not given to translate a whole text, or even to work out all the words whose meaning he had surmised. Rasmus Christian Rask (1787-1832), who followed him, found the plural ending in Persian, which had baffled him; and Eugène Burnouf (1801-1852), by the study of a list of Persian geographical names found at Naksh-i-Rustam, discovered at a single stroke almost all the characters of the Persian alphabet, and incidentally confirmed the values already determined by his predecessors.
At the same time as Burnouf, the eminent Sanskrit scholar Professor Christian Lassen (1800-1876), of Bonn, was studying the same list of names; and his results were published at the same time. The controversy which resulted as to priority of discovery may be here passed over while we sum up the results in general conclusions. Lassen may certainly claim in the final court of history that he discovered independently of Burnouf the values of at least six and possibly of eight signs. But in another respect he made very definite progress over Burnouf. He discovered that, if the system of Grotefend were rigidly followed, and to every sign were given the value Grotefend had assigned, some words would be left wholly or almost wholly without vowels; and therefore unpronounceable. As instances of such words he mentioned ÇPRD, THTGUS, KTPTUK, FRAISJM. This situation led Lassen to a very important discovery, towards which his knowledge of the Sanskrit alphabet did much to bring him. He came, in short, to the conclusion that the ancient Persian signs were not entirely alphabetic, but were at least partially syllabic, that is, that certain signs were used to represent not merely an alphabetic character like “b,” but also a syllable such as “ba,” “bi” or “bu.” He claimed that he had successfully demonstrated that the sign for “a” was only used at the beginning of a word, or before a consonant, or before another vowel, and that in every other case it was included in the consonant sign. Thus in the inscription No I. in the second line the signs should be read VA-ZA-RA-KA. This was a most important discovery, and may be said to have revolutionized the study of these long puzzling texts.
During the entire time of this slow process of decipherment, from the first essays of Grotefend in 1802 until the publication of Lassen’s book in 1836, there were more sceptics than believers in the results of the deciphering process. Indeed the history of all forms of decipherment of unknown languages shows that scepticism concerning them is far more prevalent than credulity or even a too ready acceptance. There was need for a man of another people, of different training and a fresh and unbiased mind, to put the capstone upon the decipherment, and he was already at work when Lassen’s important researches appeared.
Major (afterward Sir) Henry Rawlinson had gone out to India, in the service of the East India Company, while still a boy. There he had learned Persian and several of the Indian vernaculars. That was not the sort of training that had prepared Grotefend, Burnouf or Lassen, but it was the kind that the early travellers and copyists had enjoyed. In 1833 young Rawlinson went to Persia, to work with other British officers in the reorganization of the Persian army. While engaged in this service his attention was drawn to the ancient Persian cuneiform inscriptions. In 1835 he copied with great care the texts at Hamadan, and began their decipherment. Of all the eager work which had been going on in Europe he knew little. It is no longer possible to ascertain when he gained his first information of Grotefend’s work, for Norris, the secretary of the Royal Asiatic Society, has left us no record of when he began to send notices of the German’s work. Whenever it was, there seems to be no doubt that Rawlinson worked independently for a time. His method was strikingly like Grotefend’s. He had copied two trilingual inscriptions, and recognized at once that he had three languages before him. In 1839 (Journal of the Royal Asiatic Society, x. pp. 5, 6) he thus wrote of his method: “When I proceeded ... to compare and interline the two inscriptions (or rather the Persian columns of the two inscriptions, for, as the compartments exhibiting the inscription in the Persian language occupied the principal place in the tablets, and were engraved in the least complicated of the three classes of cuneiform writing, they were naturally first submitted to examination) I found that the characters coincided throughout, except in certain particular groups, and it was only reasonable to suppose that the grounds which were thus brought out and individualized must represent proper names. I further remarked that there were but three of these distinct groups in the two inscriptions; for the group which occupied the second place in one inscription, and which, from its position, suggested the idea of its representing the name of the father of the king who was there commemorated, corresponded with the group which occupied the first place in the other inscription, and thus not only served determinately to connect the two inscriptions together, but, assuming the groups to represent proper names, appeared also to indicate a genealogical succession. The natural inference was that in these three groups of characters I had obtained the proper names belonging to three consecutive generations of the Persian monarchy; and it so happened that the first three names of Hystaspes, Darius and Xerxes, which I applied at hazard to the three groups, according to the succession, proved to answer in all respects satisfactorily and were, in fact, the true identification.”
Rawlinson’s next work was the copying of the great inscription of Darius on the rocks at Behistun (q.v.). He had first seen it in 1835, and as it was high up on the rocky face, and apparently inaccessible, he had studied it by means of a field-glass. He was not able to copy the whole of the Persian text, but in 1837, when he was more skilled in the script, he secured more of it. In the next year he forwarded to the Royal Asiatic Society of London his translation of the first two paragraphs of the Persian text, containing the name, titles and genealogy of Darius. This was little less than a tour de force, for it must be remembered that this had been accomplished without the knowledge of other ancient languages which his European competitors had enjoyed. The translation, received in London on the 14th of March, made a sensation, and a transcript sent in April to the Asiatic Society of Paris secured him an honorary membership in that distinguished body. He was now known, and many made haste to send him copies of everything important which had been published in Europe. The works of Burnouf, Niebuhr, le Brun and Porter came to his hands, and with such assistance he made rapid progress, and in the winter of 1838-1839 his alphabet of ancient Persian was almost complete. In 1839 he was in Bagdad, his work written out and almost ready for publication. But he delayed, hoping for more light, and revising sign by sign with exhaustless patience. He expected to publish his preliminary memoir in the spring of 1840, when he was suddenly sent to Afghanistan as political agent at Kandahar. Here he was too busily engaged in war administration to attend to his favourite studies, which were not renewed until 1843 when he returned to Bagdad. There he received fresh copies and corrections of the Persepolis inscriptions which had been made by Westergaard, and later made a journey to Behistun to perfect his own copies of the texts which had formed the basis of his own first study. At last, after many delays and discouragements, he published, in 1846, in the Journal of the Royal Asiatic Society, his memoir, or series of memoirs, on the ancient Persian inscriptions, in which for the first time he gave a nearly complete translation of the Persian text of Behistun. In this one publication Rawlinson attained imperishable fame in Oriental research. His work had been carried on under greater difficulties than those in the path of his European colleagues, but he had surpassed them all in the making of an intelligible and connected translation of a long inscription. He had indeed not done it without assistance from the work of Burnouf, Grotefend and Lassen, but when all allowance is made for these influences his fame is not diminished nor the extent of his services curtailed. His method was adopted before he knew of Lassen’s work. That two men of such different training and of such opposite types of mind should have lighted upon the same method, and by it have attained the same results, confirmed in the eyes of many the truth of the decipherment.
The work of the decipherment of the old Persian texts was now complete for all practical purposes. But in 1846 there appeared a paper read before the Royal Irish Academy by the Rev. Edward Hincks of Killyleagh, County Down, Ireland, whose keen criticisms of Lassen’s work, and original contributions to the definite settlement of syllabic values, may be regarded as closing the period of decipherment of Persian cuneiform writing.
The next problem in the study of cuneiform was the decipherment of the second language in each of the trilingual groups. The first essay in this difficult task was made in 1844 by Niels Louis Westergaard. His method was very similar to that used by Grotefend in the decipherment of Persian. He selected the names of Darius, Hystaspes, Persians and others, and compared them with their equivalents in the Persian texts. By this means he learned a number of signs, and sought by their use in other words to spell out syllables or words whose meanings were then ascertained by conjecture or by comparison. He estimated the number of characters at eighty-two or eighty-seven, and judged the writing to be partly alphabetic and partly syllabic. The language he called Median, and classified it in “the Scythian, rather than in the Japhetic family.” The results of Westergaard were subjected to incisive criticism by Hincks, who made a distinct gain in the problem. It next passed to the hands of de Saulcy, who was able to see further than either. But the matter moved with difficulty because the copied texts were not accurate. By the generosity of Sir Henry Rawlinson his superb copies of the Behistun text, second column, were placed in the hands of Mr Edwin Norris, who was able in 1852 to present a paper to the Royal Asiatic Society deciphering nearly all of it. Mordtmann followed him, naming the language Susian, which was met with general acceptance and was not displaced by the name Amardian, suggested by A. H. Sayce in two papers which otherwise made important contributions to the subject. With his contributions the problem of decipherment of Susian may be considered as closed. The latter workers could only be builders on foundations already laid.
The decipherment of the third of the three languages found at Persepolis and Behistun followed quickly on the success with Susian. The first worker was Isadore Löwenstern, who made out the words for “king” and “great” and the sign for the plural, but little more. The first really great advance was made by Hincks in 1846 and 1847. In these he determined successfully the values of several signs, settled the numerals, and was apparently on the high-road toward the translation of an entire Assyrian text. He was, however, too cautious to proceed so far, and the credit of first translating a short Assyrian text belongs to Longpérier, who in 1847 published the following as the translation of an entire text: “Glorious is Sargon, the great king, the (...) king, king of kings, king of the land of Assyria.” 632 It was nearly all correct, but it advanced our knowledge but slightly because it did not give the forms of the words—because (to put it in another way) he was not able to transliterate the Assyrian words. This was the great problem. In the Persian texts there were but forty-four signs, but in the third column of the Persepolis texts Grotefend had counted one hundred and thirty different characters, and estimated that in all the Babylonian texts known to him there were about three hundred different signs, while Botta discovered six hundred and forty-two in the texts found by him at Khorsabad. That was enough to make the stoutest heart quail, for a meaning must be found for every one of these signs. There could not be so many syllables, and it was, therefore, quite plain that the Babylonian language must have been written in part at least in ideograms. But in 1851 Rawlinson published one hundred and twelve lines of the Babylonian column from Behistun, accompanied by an interlinear transcription into Roman characters, and a translation into Latin. That paper, added to Hinck’s still more acute detail studies, brought to an end the preliminary decipherment of Babylonian. There were still enormous difficulties to be surmounted in the full appreciation of the complicated script, but these would be solved by the combined labours of many workers.
The cuneiform script had its origin in Babylonia and its inventors were a people whom we call the Sumerians. Before the Semitic Babylonians conquered the land it was inhabited by a people of unknown origin variously Origin. classified, by different scholars, with the Ural-altaic or even with the Indo-European family, or as having blood relationship with both. This people is known to us from thousands of cuneiform inscriptions written entirely in their language, though our chief knowledge of them was for a long time derived from Sumerian inscriptions with interlinear translations in Assyrian. Their language is called Sumerian (li-ša-an Su-me-ri) by the Assyrians (Br. Mus. 81-7-27, 130), and its characteristics are being slowly developed by the elaborate study of the immense literature which has come down to us. In 1884 Halévy denied the existence of the Sumerian language, and claimed that it was merely a cabalistic script invented by the priests of the Semites. His early success has not been sustained, and the vast majority of scholars have ceased to doubt the existence of the language.
The Sumerians developed their script from a rude picture-writing,
some early forms of which have come down to us. In
course of time they used the pictures to represent sounds, apart
from ideas. They wrote first on stone, and when clay was
adopted soon found that straight lines in soft clay when made
by a single pressure of the stylus tend to become wedges, and the
pictures therefore lost their character and came to be mere
conventional groups of wedges. Some of these wedge-shaped
signs are of such character that we are still able to recognize
or re-construct the original picture from which they came. The
Assyrian sign 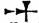 , which means heaven, appears in early texts
in the form
, which means heaven, appears in early texts
in the form  in which its star-like form is quite evident
(star = heaven) and from which the linear form
in which its star-like form is quite evident
(star = heaven) and from which the linear form  may be not
improbably pre-supposed. A number of other cases were
enumerated by the Assyrians themselves (see Cuneiform Texts
from Bab. Tab. in Brit. Museum, vol. v., 1898), and there can be
no reasonable doubt that this is the origin of the script.
may be not
improbably pre-supposed. A number of other cases were
enumerated by the Assyrians themselves (see Cuneiform Texts
from Bab. Tab. in Brit. Museum, vol. v., 1898), and there can be
no reasonable doubt that this is the origin of the script.
The number of the original picture-signs cannot have been
great, but the development of new signs never ceased till the
cuneiform script passed wholly from use. The simplest
form of development was doubling, to express plurality
Development and characteristics.
or intensity. After this came the working of two
signs into one; thus  “water,” when placed in
“water,” when placed in  “mouth” gave the new sign
“mouth” gave the new sign 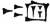 “to drink,” and many others.
Other signs were formed by the addition of four lines, either
vertically or horizontally, to intensify the original meaning.
Thus, for instance, the old linear sign
“to drink,” and many others.
Other signs were formed by the addition of four lines, either
vertically or horizontally, to intensify the original meaning.
Thus, for instance, the old linear sign 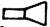 means dwelling, but
with four additional signs, thus
means dwelling, but
with four additional signs, thus  , it means “great house.”
This sign gradually changed in form until it came to be
, it means “great house.”
This sign gradually changed in form until it came to be 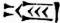 .
This method of development was called by the Sumerians gunu,
and signs thus formed are now commonly called by us, gunu
signs. They number hundreds and must be reckoned with in
our study of the script development, though perhaps recent
scholars have somewhat exaggerated their importance. The
process of development is obscure and must always remain so.
.
This method of development was called by the Sumerians gunu,
and signs thus formed are now commonly called by us, gunu
signs. They number hundreds and must be reckoned with in
our study of the script development, though perhaps recent
scholars have somewhat exaggerated their importance. The
process of development is obscure and must always remain so.
The script as finally developed and used by the Assyrians is
cumbrous and complicated, and very ill adapted to the sounds
of the Semitic alphabet. It has (1) simple syllables, consisting
of one vowel and a consonant, or a vowel by itself, thus  “a,”
“a,”
 ab,
ab,  ib,
ib,  ub,
ub,  ba,
ba,  bi,
bi,  bu. In addition to
these the Assyrian had also (2) compound syllables, such as
bu. In addition to
these the Assyrian had also (2) compound syllables, such as  bit,
bit,  bal, and (3) ideograms, or signs which express an
entire word, such as
bal, and (3) ideograms, or signs which express an
entire word, such as  beltu, lady,
beltu, lady,  abu, father. The
difficulty of reading this script is enormously increased by the
fact that many signs are polyphonous, i.e. they may have more
than one syllabic value and also be used as an ideogram. Thus
the sign
abu, father. The
difficulty of reading this script is enormously increased by the
fact that many signs are polyphonous, i.e. they may have more
than one syllabic value and also be used as an ideogram. Thus
the sign  has the ideographic values of matu, land, shadu,
mountain, kashadu, to conquer, napachu, to arise (of the sun),
and also the syllabic values kur, mad, mat, shad, shat, lat, nad,
nat, kin and gin. This method of writing must lead to ambiguity,
and this difficulty is helped somewhat by (4) determinatives,
which are signs intended to indicate the class to which the word
belongs. Thus, the
has the ideographic values of matu, land, shadu,
mountain, kashadu, to conquer, napachu, to arise (of the sun),
and also the syllabic values kur, mad, mat, shad, shat, lat, nad,
nat, kin and gin. This method of writing must lead to ambiguity,
and this difficulty is helped somewhat by (4) determinatives,
which are signs intended to indicate the class to which the word
belongs. Thus, the  is placed before names of persons, and
is placed before names of persons, and  (the ideogram for matu, country, and shadu, mountain) is
placed before names of countries and mountains, and
(the ideogram for matu, country, and shadu, mountain) is
placed before names of countries and mountains, and  (ilu,
god) before the names of gods.
(ilu,
god) before the names of gods.
The cuneiform writing, begun by the Sumerians in a period so remote that it is idle to speculate concerning it, had a long and very extensive history. It was first adopted by the Semitic Babylonians, and as we have seen was History. modified, developed, nay almost made over. Their inscriptions are written in it from circa 4500 B.C. to the 1st century B.C. From their hands it passed to the Assyrians, who simplified some characters and conventionalized many more, and used the script during the entire period of their national existence from 1500 B.C. to 607 B.C. From the Babylonian by a slow process of evolution the much simplified Persian script was developed, and with the Babylonian is also to be connected the Susian, less complicated than the Babylonian, but less simple than the Persian. The Chaldians (not Chaldaeans), who lived about Lake Van, also adopted the cuneiform script with values of their own, and expressed a considerable literature in it. The discovery in 1887 of the Tell-el-Amarna tablets in upper Egypt showed that the same script was in use in the 15th century B.C., from Elam to the Mediterranean and from Armenia to the Persian Gulf for purposes of correspondence. There is good reason to expect the discovery of its use by yet other peoples. It was one of the most widely used of all the forms of ancient writing.
Bibliography.—The history of the decipherment may be further studied in R. W. Rogers, History of Babylonia and Assyria, vol. i. (N.Y. and London, 1900); and in A. J. Booth, The Discovery and Decipherment of the Trilingual Cuneiform Inscriptions (London, 1902), which is very exhaustive and accurate. The Sumerian question may best be studied in F. H. Weissbach, Die Sumerische Frage (Leipzig, 1898), and Charles Fossey, Manuel d’Assyriologie, tome i. (Paris, 1904). For development and characteristics, see Friedrich Delitzsch, Die Entstehung des ältesten Schriftsystems (Leipzig, 1897); Paul Toscanne, Les Signes sumériens dérivés (Paris, 1905).
CUNEO (Fr. Coni), a town and episcopal see of Piedmont, Italy, the capital of the province of Cuneo, 55 m. by rail S. of Turin, 1722 ft. above sea-level. Cuneo lies on the railway from Turin to Ventimiglia, which farther on passes under the Col di Tenda (tunnel 5 m. long). It is also a junction for Mondovi and Saluzzo, and has steam tramways to Borgo S. Dalmazzo, Boves, Saluzzo and Dronero. Pop. (1901) 15,412 (town), 26,879 (commune). Its name (“wedge”) is due to its position on a hill between two streams, the Stura and the Gesso, with fine views of the mountains. The Franciscan church, now converted into a military storehouse, belongs to the 12th century, but there are no other buildings of special interest. The fortifications have 633 been converted into promenades. Cuneo was founded about 1120 by refugees from local baronial tyranny, who, after the destruction of Milan by Barbarossa, were joined by Lombards. In 1382 it swore fealty to Amedeus VI., duke of Savoy. It was an important fortress, and was ceded by the treaty of Cherasco (1796), with Ceva and Tortona, to the French. In 1799 it was taken after ten days’ bombardment by the Austrian and Russian armies, and, in 1800, after the victory of Marengo, the French demolished the fortifications.
CUNEUS (Latin for “wedge”; plural, cunei), the architectural term applied to the wedge-shaped divisions of the Roman theatre separated by the scalae or stairways; see Vitruvius v. 4.
CUNITZ, MARIA (c. 1610-1664), Silesian astronomer, was the eldest daughter of Dr Heinrich Cunitz of Schweinitz, and the wife (1630) of Dr Elias von Löven, of Pitschen in Silesia—both of them men of learning and distinction. From her universal accomplishments she was called the “Silesian Pallas,” and the publication of her work, Urania propitia (Oels, 1650), a simplification of the Rudolphine Tables, gained her a European reputation. It was composed at the village of Lugnitz, close by the convent of Olobok (Posen), where, with her husband, she had taken refuge at the outbreak of the Thirty Years’ War, and was dedicated to the emperor Frederick III. The author became a widow in 1661, and died at Pitschen on the 24th of August 1664.
See A. G. Kästner, Geschichte der Mathematik, iv. 430 (1800); N. Henelii, Silesiographia renovata, cap. vi. p. 684; J. C. Eberti’s Schlesiens wohlgelehrtes Frauenzimmer, p. 25 (Breslau, 1727); Allgemeine deutsche Biographie (Schimmelpfenning); &c.
CUNNINGHAM, ALEXANDER (c. 1655-1730), Scottish classical scholar and critic, was born in Ayrshire. Very little is known of his uneventful life. It is probable that he completed his education at Leiden or Utrecht. He was tutor to the son of the first duke of Queensberry, through whose influence he was appointed professor of civil law in the university of Edinburgh. In 1710, the Edinburgh magistrates, regarding the university patronage as their privilege, appointed another professor, ignoring the appointment of Cunningham, who had been installed in the office for at least ten years. Cunningham thereupon left England for the Hague, where he resided until his death. He is chiefly known for his edition of Horace (1721) with notes, mostly critical, which included a volume of Animadversiones upon Richard Bentley’s notes and emendations. They marked him as one of the most able critics of Bentley’s (in many cases) rash and tasteless conjectural alterations of the text. Cunningham also edited the works of Virgil and Phaedrus (together with the Sententiae of Publilius Syrus and others). He had also been engaged for some years in the preparation of an edition of the Pandects and of a work on Christian evidences.
Life by D. Irving in Lives of Scottish Writers (1839).
The above must not be confused with Alexander Cunningham, British minister to Venice (1715-1720), a learned historian and author of The History of Great Britain (from 1688 to the accession of George I.), originally written in Latin and published in an English translation after his death.
CUNNINGHAM, ALLAN (1784-1842), Scottish poet and man of letters, was born at Keir, Dumfriesshire, on the 7th of December 1784, and began life as a stone mason’s apprentice. His father was a neighbour of Burns at Ellisland, and Allan with his brother James visited James Hogg, the Ettrick shepherd, who became a friend to both. Cunningham contributed some songs to Roche’s Literary Recreations in 1807, and in 1809 he collected old ballads for Robert Hartley Cromek’s Remains of Nithsdale and Galloway Song; he sent in, however, poems of his own, which the editor inserted, even though he may have suspected their real authorship. In 1810 Cunningham went to London, where he supported himself chiefly by newspaper reporting till 1814, when he became clerk of the works in the studio of Francis Chantrey, retaining this employment till the sculptor’s death in 1841. He meanwhile continued to be busily engaged in literary work. Cunningham’s prose is often spoiled by its misplaced and too ambitious rhetoric; his verse also is often over-ornate, and both are full of mannerisms. Some of his songs, however, hold a high place among British lyrics. “A Wet Sheet and a Flowing Sea” is one of the best of our sea-songs, although written by a landsman; and many other of Cunningham’s songs will bear comparison with it. He died on the 30th of October 1842.
He was married to Jean Walker, who had been servant in a house where he lived, and had five sons and one daughter. Joseph Davey Cunningham (1812-1851) entered the Bengal Engineers, and is known by his History of the Sikhs (1849). Sir Alexander Cunningham (1814-1893) also entered the Bengal Engineers, attaining the rank of major-general; he was director general of the Indian Archaeological Survey (1870-1885), and wrote an Ancient Geography of India (1871) and Coins of Medieval India (1894). Peter Cunningham (1816-1869) published several topographical and biographical studies, of which the most important are his Handbook of London (1849) and The Life of Drummond of Hawthornden (1833). Francis Cunningham (1820-1875) joined the Indian army, and published editions of Ben Jonson (1871), Marlowe (1870) and Massinger (1871).
The works of Allan Cunningham include Lives of the Most Eminent British Painters, Sculptors and Architects (1829-1833); Sir Marmaduke Maxwell (1820), a dramatic poem; Traditionary Tales of the Peasantry (1822), several novels (Paul Jones, Sir Michael Scott, Lord Roldan); the Maid of Elwar, a sort of epic romance; the Songs of Scotland (1825); Biographical and Critical History of the Literature of the Last Fifty Years (1833); an edition of The Works of Robert Burns, with notes and a life containing a good deal of new material (1834); Biographical and Critical Dissertations affixed to Major’s Cabinet Gallery of Pictures; and Life, Journals and Correspondence of Sir David Wilkie, published in 1843. An edition of his Poems and Songs was issued by his son, Peter Cunningham, in 1847.
CUNNINGHAM, WILLIAM (1805-1861), Scottish theologian and ecclesiastic, was born at Hamilton, in Lanarkshire, on the 2nd of October 1805, and educated at the university of Edinburgh. He was licensed to preach in 1828, and in 1830 was ordained to a collegiate charge in Greenock, where he remained for three years. In 1834 he was transferred to the charge of Trinity College parish, Edinburgh. His removal coincided with the commencement of the period known in Scottish ecclesiastical history as the Ten Years’ Conflict, in which he was destined to take a leading share. In the stormy discussions and controversies which preceded the Disruption the weight and force of his intellect, the keenness of his logic, and his firm grasp of principle made him one of the most powerful advocates of the cause of spiritual independence; and he has been generally recognized as one of three to whom mainly the existence of the Free Church is due, the others being Chalmers and Candlish. On the formation of the Free Church in 1843, Cunningham was appointed professor of church history and divinity in the New College, Edinburgh, of which he became principal in 1847 in succession to Thomas Chalmers. His career was very successful, his controversial sympathies combined with his evident desire to be rigidly impartial qualifying him to be an interesting delineator of the more stirring periods of church history, and a skilful disentangler of the knotty points in theological polemics. In 1859 he was appointed moderator of the General Assembly. He had received the degree of D.D. from the university of Princeton in 1842. He died on the 14th of December 1861. He was one of the founders of the Evangelical Alliance. A theological lectureship at the New College, Edinburgh, was endowed in 1862, to be known as the Cunningham lectureship.
A Life of Cunningham, by Rainy and Mackenzie, appeared in 1871.
CUNNINGHAM, WILLIAM (1849- ), English economist, was born at Edinburgh on the 29th of December 1849. Educated at Edinburgh Academy and University and Trinity College, Cambridge, he graduated 1st class in the Moral Science tripos in 1873, and in the same year took holy orders. He was university lecturer in history from 1884 to 1891, in which year he was appointed professor of economics at King’s College, London, a post which he held until 1897. He was lecturer in economic history at Harvard University (1899), and Hulsean lecturer at Cambridge (1885). He became vicar of Great St Mary’s, Cambridge, in 1887, and was made a fellow of the British Academy. In 1906 he was appointed archdeacon of Ely. Dr Cunningham’s 634 Growth of English Industry and Commerce during the Early and Middle Ages (1890; 4th ed., 1905) and Growth of English Industry and Commerce in Modern Times (1882; 3rd ed., 1903) are the standard works of reference on the industrial history of England. He also wrote The Use and Abuse of Money (1891); Alien Immigration (1897); Western Civilization in its Economic Aspect in Ancient Times (1898), and in Modern Times (1900), and The Rise and Decline of Free Trade (1905). Dr Cunningham’s eminence as an economic historian gave special importance to his attitude as one of the leading supporters of Mr Chamberlain from 1903 onwards in criticizing the English free-trade policy and advocating tariff reform.
CUP (in O.E. cuppe; generally taken to be from Late Lat. cuppa, a variant of Lat. cupa, a cask, cf. Gr. κύπελλον), a drinking vessel, usually in the form of a half a sphere, with or without a foot or handles. The footless type with a single handle is preserved in the ordinary tea-cup. The cup on a stem with a base is the usual form taken by the cup as used in the celebration of the eucharist, to which the name “chalice” (Lat. calix, Gr. κύλιξ, a goblet) is generally given. (See Drinking Vessels and Plate.)
CUPAR, a royal, municipal and police burgh, and capital of the county of Fifeshire, Scotland, 11 m. W. by S. of St Andrews by the North British railway. Pop. (1901) 4511. It is situated on the left bank of the Eden, in the east of the Howe (Hollow) of Fife, and is sometimes written Cupar-Fife to distinguish it from Coupar-Angus in Perthshire. Among the chief buildings are the town hall, county buildings, corn exchange, Duncan Institute, cottage hospital, Union Street Hall and the Bell-Baxter school. The school, formerly called the Madras Academy, was originally endowed (1832) by Dr Bell, founder of the Madras system of education, but, having been enriched at a later date by a bequest of Sir David Baxter (1873), it was afterwards called the Bell-Baxter school. The Mercat Cross stands at “the Cross” in the main street, where it was set up in 1897, having been removed from Hilltarvit, an eminence in the neighbourhood of Cupar, on the western slope of which, at Garliebank, the truce was signed between Mary of Guise and the lords of the Congregation. In the parish, but at a distance from the town, are the Fife and Kinross asylum and the Adamson institute, a holiday home for poor children from Leith. The town received its charter in 1356 from David II., and, being situated between Falkland and St Andrews, was constantly visited by Scottish sovereigns, James VI. holding his court there for some time in 1583. The site of the 12th-century castle, one of the strongholds of the Macduffs, thanes or earls of Fife, is occupied by a public school. On the esplanade in front of Macduff Castle, still called the Playfield, took place in 1552 one of the first recorded performances of Sir David Lindsay’s Ane Satyre of the Three Estaits (1540); his Tragedy of the Cardinal (1547), referring to the murder of Beaton, being also performed there. Sir David sat in the Scottish parliament as commissioner for Cupar, his place, the Mount, being within 3 m. north-west of the town. Lord Chancellor Campbell (1799-1861) was a native of Cupar.
Cupar is an agricultural and legal centre. Its chief industry is the manufacture of linen, and tanning is carried on. At Cupar Muir, 1½ m. to the west, there are a sandstone quarry and brick works. The town has also some repute for the quality of its printing, both in black and colour. This was largely due to the Tullis press, which produced about the beginning of the 19th century editions of Virgil, Horace and other classical writers, under the recension of Professor John Hunter of St Andrews, which were highly esteemed for the accuracy of their typography. Cupar belongs to the St Andrews district group of burghs for returning one member to parliament, the other constituents being Crail, the two Anstruthers, Kilrenny, Pittenweem and St Andrews.
There are several interesting places within a few miles. To the north-east is the parish of Dairsie, where one of the few parliaments that ever met in Fife assembled in 1335. The castle in which the senate sat was also the residence for a period of Archbishop Spottiswood, who founded the parish church in 1621. Two miles and a half north of Dairsie is situated Kilmany, which was the first charge of Thomas Chalmers. He was ordained to it in May 1803 and held it for twelve years. David Hackston, the Covenanter, who was a passive assister at the assassination of Archbishop Sharp, belonged to this parish, his place being named Rathillet. After his execution at Edinburgh (1680) one of his hands was buried at Cupar, where a monument inscription records the circumstances of his death. To the west of Kilmany lies Creich, where Alexander Henderson (1583-1646), the Covenanting divine and diplomatist, and John Sage (1652-1711), the non-juring archbishop of Glasgow, were born. Henderson took a keen interest in education and gave the school at Creich a small endowment. Some 3 m. to the south-west of Cupar is Cults, where Sir David Wilkie, the painter, was born. His father was minister of the parish, and Pitlessie, the fair of which provided the artist with the subject of the first picture in which he showed distinct promise, lies within a mile of the manse. In the sandstone of Dura Den, a ravine on Ceres Burn, 2½ m. E. of Cupar, have been found great quantities of fossils of ganoid fishes. The rocks belong to the Upper Old Red Sandstone.
CUPBOARD, a fixed or movable closet usually with shelves. As the name suggests, it is a descendant of the credence or buffet, the characteristic of which was a series of open shelves for the reception of drinking vessels and table requisites. After the word lost its original meaning—and down to the end of the 16th century we still find the expression “on the cupboard”—this piece of furniture was, as it to some extent remains, movable, but it is now most frequently a fixture designed to fill a corner or recess. Throughout the 18th century the cupboard was a distinguished domestic institution, and the housewife found her chief joy in accumulating cupboards full of china, glass and preserves. With the exception of a very few examples of fine ecclesiastical cupboards which partook chiefly of the nature of the armoire in that they were intended for the storage of vestments, the so-called court-cupboard is perhaps the oldest form of the contrivance. The derivation of the expression is somewhat obscure, but it is generally taken to refer to the French word court, short. This particular type was much used from the Elizabethan to the end of the Carolinian period. It was really a sideboard with small square doors below, and a recessed superstructure supported upon balusters. Of these many examples remain. Less frequent is the livery cupboard, the meaning of which may be best explained by the following quotation from Spenser’s Account of the State of Ireland:—“What livery is we by common use in England know well enough, namely, that it is an allowance of horse-meat, as they commonly use the word stabling, as to keep horses at livery; the which word I guess is derived of livering or delivering forth their nightly food; so in great houses the livery is said to be served up for all night—that is, their evening allowance for drink.” The livery cupboard appears usually to have been placed in bedrooms, so that a supply of food and drink was readily available when a very long interval separated the last meal of the evening from the first in the morning. The livery cupboard was often small enough to stand upon a sideboard or cabinet, and had an open front with a series of turned balusters. It was often used in churches to contain the loaves of bread doled out to poor persons under the terms of ancient charities. They were then called dole cupboards; there are two large and excellent examples in St Alban’s Abbey. The butter, or bread and cheese cupboard, was a more ordinary form, with the back and sides bored with holes, sometimes in a geometrical pattern, for the admission of air to the food within. The corner cupboard, which is in many ways the most pleasing and artistic form of this piece of furniture, originated in the 18th century, which as we have seen was the golden age of the cupboard. It was often of oak, but more frequently of mahogany, and had either a solid or a glass front. The older solid-fronted pieces are fixed to the wall half-way up, but those of the somewhat more modern type, in which there is much glass, usually have a wooden base with glazed superstructure. Most corner cupboards are attractive 635 in form and treatment, and many of them, inlaid with satinwood, ebony, holly or box, are extremely elegant.
CUPID (Cupido, “desire”), the Latin name for the god of love, Eros (q.v.). Cupid is generally identical with Amor. The idea of the god of love in Roman poetry is due to the influence of Alexandrian poets and artists, in whose hands he degenerated into a mischievous boy with essentially human characteristics. His usual attribute is the bow. For the story of Cupid and Psyche, see under Psyche.
CUPOLA (Ital., from Lat. cupula, small cask or vault, cupa, tub), a term, in architecture, for a spherical or spheroidal covering to a building, or to any part of it. In fortification the word is used of a form of armoured structure, in which guns or howitzers are mounted. It is a low flat turret resembling an overturned saucer and showing little above the ground except the muzzles of the guns. See for details and illustrations Fortification and Siegecraft; also Ordnance.
CUPPING. The operation of cupping is one of the methods that have been adopted by surgeons to draw blood from an inflamed part in order to relieve the inflammation. The skin is washed and dried; a glass cup with a rounded edge is then firmly applied, after the air in it has been heated; the cooling of the air causes the formation of a partial vacuum, and the blood is thus drawn from the neighbouring parts to the skin under the cup. Either the blood is drawn from the patient’s body through a number of small wounds which are made in the skin, with a special instrument, before the cup is applied; or the cup is simply applied to the unbroken skin and the blood drawn into the subcutaneous tissue within the circumference of the cup. The result of both methods is the same,—namely, a withdrawal of blood locally from the inflamed part. The former is called moist cupping, the latter dry cupping. This operation has naturally declined in vogue with the obsolescence of blood-letting as a remedy.
CUPRA, the name of two ancient Italian municipia in Picenum.
1. Cupra Maritima (Civita di Marano near the modern Cupra Marittima), on the Adriatic coast, 48 m. S.S.E. of Ancona, erected in the neighbourhood of an ancient temple of the Sabine goddess Cupra, which was restored by Hadrian in A.D. 127, and probably (though there is some controversy on the point) occupied the site of the church of S. Martino, some way to the south, in which the inscription of Hadrian exists. At Civita the remains of what was believed to be the temple were more probably those of the forum of the town, as is indicated by the discovery of fragments of a calendar and of a statue of Hadrian. Some statuettes of Juno were also among the finds. An inscription of a water reservoir erected in 7 B.C. is also recorded. But the more ancient Picene town appears to have been situated near the hill of S. Andrea, a little way to the south, where pre-Roman tombs have been discovered.
See C. Hülsen in Pauly-Wissowa, Realencyclopädie (Stuttgart, 1901), iv. 1760; G. Speranza, Il Piceno (Ascoli Piceno, 1900), i. 119 seq.
2. Cupra Montana, 10 m. S.W. of Aesis (mod. Jesi) by road. The village, formerly called Massaccio, has resumed the ancient name. Its site is fixed by inscriptions—cf. Th. Mommsen in Corp. Inscrip. Lat. ix. (Berlin, 1883), p. 543; and various ruins, perhaps of baths, and remains of subterranean aqueducts have been discovered near the church of S. Eleuterio.
See F. Menicucci in G. Colucci, Antichità Picene, xx. (1793).
 |
CUPRITE, a mineral consisting of cuprous oxide, Cu2O, crystallizing in the cubic system, and forming an important ore of copper, of which element cuprite contains 88.8%. The name cuprite (from Lat. cuprum, copper) was given by W. Haidinger in 1845; earlier names are red copper ore and ruby copper, which at once distinguish this mineral from the other native copper oxide—cupric oxide—known as black copper ore or melaconite. Well-developed crystals are of common occurrence; they usually have the form of the regular octahedron, sometimes in combination with the cube and the rhombic dodecahedron. A few Cornish crystals have been observed with faces of a form {hkl} known as the pentagonal icositetrahedron, since it is bounded by twenty-four irregular pentagons. In this class of cubic crystals there are no planes or centre of symmetry, but the full number (thirteen) of axes of symmetry; it is known as the trapezohedral hemihedral class, and cuprite affords the best example of this type of symmetry. The etching figures do not, however, conform to this lower degree of symmetry, nor do crystals of cuprite rotate the plane of polarization of plane-polarized light. The colour of the mineral is cochineal-red, and the lustre brilliant and adamantine to sub-metallic in character; crystals are often translucent, and show a crimson-red colour by transmitted light. On prolonged exposure to light the crystals become dull and opaque. The streak is brownish-red. Hardness 3½; specific gravity 6.0; refractive index 2.85.
Compact to granular masses also occur, and there are two curious varieties—chalcotrichite and tile-ore—which require special mention. Chalcotrichite (from Gr. χαλκός, copper, and θρίξ, τριχός, hair) or “plush copper ore” is a capillary form with a rich carmine colour and silky lustre; the delicate hairs are loosely matted together, and each one is an individual crystal enormously elongated in the direction of the diagonal or the edge of the cube. Tile-ore (Ger. Ziegelerz) is a soft earthy variety of a brick-red to brownish-red colour; it contains admixed limonite, and has been formed by the alteration of chalcopyrite (copper and iron sulphide).
Cuprite occurs in the upper part of copper-bearing lodes, and is of secondary origin, having been produced by the alteration of copper sulphides. Beautifully crystallized specimens were formerly found in Wheal Gorland and Wheal Unity at Gwennap, and in Wheal Phoenix near Liskeard in Cornwall; they also occur in the copper mines of the Urals, and in Arizona. Isolated crystals bounded by faces on all sides, and an inch or more in diameter, are found embedded in a soft white clay at Chessy near Lyons; they are usually altered on the surface, or throughout, to malachite. Chalcotrichite comes from Wheal Phoenix and Fowey Consols mine in Cornwall, and from Morenci in Arizona; tile-ore from Bogoslovsk in the Urals, Atacama in South America, and other localities. Small crystals of cuprite, together with malachite, azurite and cerussite, are sometimes found encrusting ancient objects of copper and bronze, such as celts and Roman coins, which have for long periods remained buried in the soil. Artificially formed crystals have been observed in furnace products.
CUPULIFERAE, a botanical order, or, in recent arrangements, group of orders, containing several familiar trees. The plants are trees or shrubs with simple leaves alternately arranged and small unisexual flowers generally arranged in catkins and pollinated by wind-agency. The generally one-seeded nut-like fruit is associated with the persistent often hardened or greatly enlarged bracts forming the so-called cupule which gives the name to the group. The group is subdivided as follows, and these subdivisions are now generally regarded either as distinct natural orders or the first two as sub-orders of one natural order.
Betuleae or Betulaceae. Female flowers arranged, two to three together on scale-like structures formed by the union of bracts, in catkins; ovary two-celled; fruit small, flattened, protected between the ripened scales of the catkin. Includes Betula (birch) and Alnus (alder).
Coryleae or Corylaceae. Female flowers in pairs, the bracts enlarging in the fruit to form a membranous cup (hazel), or a flat three-lobed structure (hornbeam). Ovary two-celled. Includes Corylus (hazel) and Carpinus (hornbeam).
Fagaceae (Cupuliferae in a restricted sense). Bracts forming a fleshy or hard cupule which envelops the one to several fruits. Ovary three-celled. Includes Quercus (oak), Fagus (beech), Castanea (sweet-chestnut).
Detailed accounts of the trees will be found under separate headings.
CURAÇAO, or Curaçoa, an island in the Dutch West Indies. It lies 40 m. from the north coast of Venezuela, in 12° N. and 69° W., being 40 m. long from N.W. to S.E., with an average width of 10 m. and an area of 212 sq. m. The surface is generally flat, but in the south-west there are hills attaining an elevation of 1200 ft. The shores are in places deeply indented, forming several natural harbours, the chief of which is that of St Anna on the south-west coast. Curaçao consists of eruptive rocks, chiefly diorite and diabase, and is surrounded by coral reefs. Streams are few and the rainfall is scanty, averaging only 16 in. per annum. Although the plains are for the most part arid wastes, sugar, aloes, tobacco and divi-divi are produced with much toil in the more fertile glens. Salt, phosphates and cattle are exported. The commerce is mainly with the United States, and there is a large carrying trade with Venezuela. The famous Curaçoa liqueur (see below) was originally made on the island from a peculiar variety of orange, the Citrus Aurantium curassuviensis. Willemstad (pop. about 8000), on the harbour of St. Anna, is the principal town. It bears a strong resemblance to a Dutch town, for the houses are built in the style of those of Amsterdam, and the narrow channel separating it from its western suburb of Overzijde and the waters of the Waigat, which intersect it, recall the canals. The narrow entrance leading to the Schottegat or Inner Harbour is protected by forts. The negroes of the island speak a curious dialect called Papaimento, composed of Spanish, Dutch, English and native words. Curaçao gives name to the government of the Dutch West Indies, which consists of Aruba, an island lying W. of Curaçao, with an area of 69 sq. m. and a population of 9591; Buen Ayre, lying 20 m. N.E., with an area of 95 sq. m. and a population of 4926; together with St Eustatius, Saba and part of St Martin. The governor is assisted by a council of four members and a colonial council of eight members nominated by the crown. The island of Curaçao has a population of 30,119; and altogether the Dutch West Indies have a population of 51,693.
Curaçao was discovered by Hojeda about 1499 and occupied by the Spaniards in 1527. In 1634 it fell into the hands of the Dutch, who have held it ever since, except during the year 1798 and from 1806 to 1814 when it passed into the possession of Great Britain.
See Wynmalen, “Les Colonies néerlandaises dans les Antilles,” Revue colon. internat. (1887), ii. p. 391; K. Martin, West-Indische Skizzen (Leiden, 1887); De Veer, La Colonie de Curaçoa (Les Pays Bas, 1898). Also several articles on all the islands in Tijdschrift v. h. Ned. Aardr. Genootschap (1883-1886).
CURAÇOA, a liqueur, chiefly manufactured in Holland. It is relatively simple in composition, the predominating flavour being obtained from the dried peel of the Curaçoa orange. The method of preparation is in principle as follows. The peel is first softened by maceration; then a part of the softened peel is distilled with spirit and water, and the remainder is macerated in a portion of the distillate so obtained. After two or three days the infusion is strained and added to the remainder of the original distillate. This simple method is subject to variations in manufacture, and the addition of a small quantity of Jamaica rum, in particular, is said to much improve the flavour. Dry Curaçoa contains about 39%, the sweet variety about 36% of alcohol. A lighter variety of Curaçoa, made with fine brandy, is known as “Grand Marnier.”
CURASSOW (Cracinae), a group of gallinaceous birds forming one of the subfamilies of Cracidae, the species of which are among the largest and most splendid of the game birds of South America, where they may be said to represent the pheasants of the Old World. They are large, heavy birds, many of them rivalling the turkey in size, with short wings, long and broad tail, and strong bill. In common with the family to which they belong, they have the hind toe of the foot placed on a level with the others, thus resembling the pigeons, and unlike the majority of gallinaceous birds. With the exception of a single species found north of Panama, the curassows are confined to the tropical forests of South America, east of the Andes, and not extending south of Paraguay. They live in small flocks, and are arboreal in their habits, only occasionally descending to the ground, while always roosting and building their nests on the branches of trees. Their nests are neat structures, made of slender branches interlaced with stems of grass, and lined internally with leaves. They feed on fruits, seeds and insects. They are often tamed in several parts of South America, but have never been thoroughly domesticated anywhere. Large numbers of these birds were, according to K. J. Temminck, brought to Holland from Dutch Guiana towards the end of the 18th century, and got so completely acclimatized and domesticated as to breed in confinement like ordinary poultry; but the establishments in which these were kept were broken up during the troubles that followed on the French Revolution. Their flesh is said to be exceedingly white and delicate, and this, together with their size and the beauty of their plumage, would make the curassows an important gain to the poultry yards of Europe, if they were not such bad breeders. The subfamily of curassows contains four genera and twelve species, all confined to South America, with the exception of Crax globicera—a Central American species, which extends northward into Mexico. This bird is about 3 ft. in length, of a glossy black colour over the whole body, excepting the abdomen and tail coverts, which are white. In common with the other species of this genus its head bears a crest of feathers curled forward at the tips, which can be raised or depressed at will. The female is of a reddish-brown colour, although varying greatly in this respect, and was formerly described as a separate species—the red curassow. In another species, Crax incommoda, the greater part of the black plumage is beautifully varied with narrow transverse bars of white. The galeated curassow (Pauxi galeata) is peculiar in having a large blue tubercle, hard and stony externally, but cellular within, and resembling a hen’s egg in size and shape, situated at the base of the hill. It only appears after the first moulting, and is much larger in the male than in the female.
CURATE (from the Lat. curare, to take care of), properly a presbyter who has the cure of souls within a parish. The term is used in this general sense in certain rubrics of the English Book of Common Prayer, in which it is applied equally to rectors and vicars as to perpetual curates. So, on the continent of Europe, it is applied in this sense to parish priests, as the Fr. curé, Ital. curato, Span. cura, &c. In a more limited sense it is applied in the Church of England to the incumbent of a parish who has no endowment of tithes, as distinguished from a perpetual vicar, who has an endowment of small tithes, which are for that reason sometimes styled vicarial tithes. The origin of such unendowed curacies is traceable to the fact that benefices were sometimes granted to religious houses pleno jure, and with liberty for them to provide for the cure; and when such appropriations were transferred to lay persons, being unable to serve themselves, the impropriators were required to nominate a clerk in full orders to the ordinary for his licence to serve the cure. Such curates, being not removable at the pleasure of the impropriators, but only on due revocation of the licence of the ordinary, came to be entitled perpetual curates. The term “curate” in the present day is almost exclusively used to signify a clergyman who is assistant to a rector or vicar, by whom he is employed and paid; and a clerk in deacon’s orders is competent to be licensed by a bishop to the office of such assistant curate. The consequence of this misuse of the term “curate” was that the title of “perpetual curate” fell into desuetude in the Anglican Church, and an act of parliament (1868) was passed to authorize perpetual curates to style themselves vicars (see Vicar). The term is in use in the Roman Catholic Church in Ireland to designate an assistant clergyman, and also to a certain extent in the American Episcopal Church, though “assistant minister” is usually preferred.
CURATOR (Lat. for “one who takes care,” curare, to take care of), in Roman law the “caretaker” or guardian of a spendthrift (prodigus) or of a person of unsound mind (furiosus), and, more particularly, one who takes charge of the estate of an adolescens, i.e. of a person sui juris, above the age of a pupillus, fourteen or twelve years, according to sex, and below the full age of twenty-five. Such persons were known as “minors,” 637 i.e. minores viginti quinque annis. While the tutor, the guardian of the pupillus, was said to be appointed for the care of the person, the curator took charge of the property. The term survives in Scots law for the guardian of one in the second stage of minority, i.e. below twenty-one, and above fourteen, if a male, and twelve, if a female. Under the Roman empire the title of curator was given to several officials who were in charge of departments of public administration, such as the curatores annonae, of the public supplies of corn and oil, or the curatores regionum, who were responsible for order in the fourteen regiones or districts into which the city of Rome was divided, and who protected the citizen from exaction in the collection of taxes; the curatores aquarum had the charge of the aqueducts. Many of these curatorships were instituted by Augustus. In modern usage “curator” is applied chiefly to the keeper of a museum, art collection, public gallery, &c., but in many universities to an official or member of a board having a general control over the university, or with the power of electing to professorships. In the university of Oxford “curators” are nominated to administer certain departments, such as the University Chest.
CURCI, CARLO MARIA (1810-1891), Italian theologian, was born at Naples. He joined the Jesuits in 1826, and for some time was devoted to educational work and the care of the poor and prisoners. He became one of the first editors of the Jesuit organ, the Civiltà Cattolica; but then came under the influence of Gioberti, Rosmini and other advocates for reform. He wrote a preface to Gioberti’s Primato (1843), but dissented from his Prolegomena. After the events of 1870, Curci, at Florence, delivered a course on Christian philosophy; and in 1874 began to publish several Scriptural works. In his edition of the New Testament (1879-1880) he makes some severe remarks on the neglect of the study of Scripture amongst the Italian clergy. In the meantime he began to attack the political action of the Vatican, and in his Il Moderno Dissidio tra la Chiesa e l’Italia (1878) he advocated an understanding between the church and state. This was followed by La Nuova Italia ed i Vecchi Zelanti (1881), another attack on the Vatican policy; and by his Vaticano Regio (1883), in which he accuses the Vatican of trafficking in holy things and declares that the taint of worldliness came from the false principles accepted by the Curia. His former work at Naples drew him also in the direction of Christian Socialism. He was condemned at Rome, and in a letter to The Times (10th of September 1884) declares that it was on account of his disobedience to the decrees of the Roman Congregation: “I am a dutiful son of the Church who hesitates to obey an order of his mother because he does not see clear enough the maternal authority in it.” He was cast out of the Society of Jesus and suspended, and during this time Cardinal Manning put his purse at Curci’s disposal. Finally he accepted the decrees against him and retracted “all that he said contrary to the faith, morals and discipline of the Church.” He passed the remainder of his life in retirement at Florence, and, a few months before his death, was readmitted to the Jesuit Society. He died on the 8th of June 1891.
CUREL, FRANÇOIS, Vicomte de (1854- ), French dramatist, was born at Metz on the 10th of June 1854. He was educated at the École Centrale as a civil engineer, the family wealth being derived from smelting works. He began his literary career with two novels, L’Été des fruits secs (1885) and Le Sauvetage du grand duc (1889). In 1891 three pieces were accepted by the Théâtre Libre. The list of his plays includes L’Envers d’une sainte (1892); Les Fossiles (1892), a picture of the prejudices of the provincial nobility; L’Invitée (1893), the story of a mother who returns to her children after twenty years’ separation; L’Amour brode (1893), which was withdrawn by the author from the Théâtre Français after the second representation; La Figurante (1896); Le Repas du lion (1898), dealing with the relations between capital and labour; La Fille sauvage (1902), the history of the development of the religious idea; La Nouvelle Idole (1899), dealing with the worship of science; and Le Coup d’aile (1906).
See also Contemporary Review for August 1903.
CURÉLY, JEAN NICOLAS (1774-1827), French cavalry leader, was the son of a poor peasant of Lorraine. Joining, in 1793, a regiment of hussars, he served with great distinction as private and as sous-officier in the Rhine campaigns from 1794 to 1800. He was, however, still a non-commissioned officer of twelve years’ service, when at Afflenz (12th of November 1805) he attacked and defeated, with twenty-five men, a whole regiment of Austrian cavalry. This brilliant feat of arms won him the grade of sous-lieutenant, and the reputation of being one of the men of the future. The next two campaigns of the Grande Armée gained him two more promotions, and as a captain of hussars he performed, in the campaign of Wagram, a feat of even greater daring than the affair of Afflenz. Entrusted with despatches for the viceroy of Italy, Curély, with forty troopers, made his way through the Austrian lines, reconnoitred everywhere, even in the very headquarters-camp of the archduke John, and finally accomplished his mission in safety. This exploit, only to be compared to the famous raids of the American Civil War, and almost unparalleled in European war, gained him the grade of chef d’escadrons, in which for some years he served in the Peninsular War. Under Gouvion St Cyr he took part in the Russian War of 1812, and in 1813 was promoted colonel. In the campaign of France (1814) Curély, now general of brigade, commanded a brigade of “improvised” cavalry, and succeeded in infusing into this unpromising material some of his own daring spirit. His regiments distinguished themselves in several combats, especially at the battle of Arcis-sur-Aube. The Restoration government looked with suspicion on the most dashing cavalry leader of the younger generation, and in 1815 Curély, who during the Hundred Days had rallied to his old leader, was placed on the retired list. Withdrawing to the little estate of Jaulny (near Thiaucourt), which was his sole property, he lived in mournful retirement, which was saddened still further when in 1824 he was suddenly deprived of his rank. This last blow hastened his death. Curély, had he arrived at high command earlier, would have been ranked with Lasalle and Montbrun, but his career, later than theirs in beginning, was ended by the fall of Napoleon. His devoted friend, De Brack, in his celebrated work Light Cavalry Outposts, considers Curély incomparable as a leader of light cavalry, and the portrait of Curély to be found in its pages is justly ranked as one of the masterpieces of military literature. The general himself left but a modest manuscript, which was left for a subsequent generation to publish.
See also Thoumas, Le Général Curély: itinéraires d’un Cavalier léger, 1793-1815 (Paris, 1887).
CURES, a Sabine town between the left bank of the Tiber and the Via Salaria, about 26 m. from Rome. According to the legend, it was from Cures that Titus Tatius led to the Quirinal the Sabine settlers, from whom, after their union with the settlers on the Palatine, the whole Roman people took the name Quirites. It was also renowned as the birthplace of Numa, and its importance among the Sabines at an early period is indicated by the fact that its territory is often called simply ager Sabinus. At the beginning of the imperial period it is spoken of as an unimportant place, but seems to have risen to greater prosperity in the 2nd century. It appears as the seat of a bishop in the 5th century, but seems to have been destroyed by the Lombards in A.D. 589. The site consists of a hill with two summits, round the base of which runs the Fosso Corese: the western summit was occupied by the necropolis, the eastern by the citadel, and the lower ground between the two by the city itself. A temple, the forum, the baths, &c., were excavated in 1874-1877.
See T. Ashby in Papers of the British School at Rome, iii. 34.
CURETES (Gr. Κούρητες and Κουρῆτες). (1) A legendary people mentioned by Homer (Il. ix. 529 ff.) as taking part in the quarrel over the Calydonian boar. They were identified in antiquity as either Aetolians or Acarnanians (Strabo 462, 26), and were also represented by a stock in Chalcis in Euboea. (2) In mythology (unconnected with the above), the attendants of Rhea. The story went that they saved the infant Zeus from his father Cronus in Crete by surrounding his cradle and with 638 clashing of sword and shield preventing his cries from being heard, and thus became the body-guard of the god and the first priests of Zeus and Rhea. In historic times the cult of the Curetes was widely known in Greece in connexion with that of Rhea (q.v.). Its ceremonies consisted principally in the performance of the Pyrrhic dance to the accompaniment of hymns and flute music, by the priests, who represented and thus commemorated the original act of the Curetes themselves. The dance was originally distinguished from that of the Corybantes by its comparative moderation, and took on the full character of the latter only after the cult of the Great Mother, Cybele, to which it belonged, spread to Greek soil. The origin of the dance may have lain in the supposed efficacy of noise in averting evil.
The Curetes are represented in art with shield and sword performing the sacred dance about the infant Zeus, sometimes in the presence of a female figure which may be Rhea. Their number in art is usually two or three, but in literature is sometimes as high as ten. Of their names the following have survived: Kures, Kres, Biennos, Eleuther, Itanos, Labrandos, Panamoros, Palaxos; but no complete list of names is possible because of their confusion with the names of the Corybantes and other like deities. Their origin is variously related: they were earth-born, sprung of the rain, sons of Zeus and Hera, sons of Apollo and Danais, sons of Rhea, of the Dactyli, contemporary with the Titans (Diod. Sic. v. 66). Rationalism made them the mortal sons of a mortal Zeus, or originators of the Pyrrhic dance, inventors of weapons, fosterers of agriculture, regulators of social life, &c. A plausible theory is that of Georg Kaibel (Göttinger Nachrichten, 1901, pp. 512-514), who sees in them, together with the Corybantes, Cabeiri, Dactyli, Telchines, Titans, &c., only the same beings under different names at different times and in different places. Kaibel holds that they all had a phallic significance, having once been great primitive deities of procreation, and that having fallen to an indistinct, subordinate position in the course of the development and formalization of Greek religion, they survive in historic times only as half divine, half demonic beings, worshipped in connexion with the various forms of the great nature goddess. The resemblances, especially between Rhea and her Curetes and the Great Mother and her Corybantes (q.v.), were so striking that their origins were inextricably confused even in the minds of the ancients: e.g. Demetrius of Scepsis (Strabo 469, 12) derives the Curetes and Rhea from the cult of the Great Mother in Asia, while Virgil (Aen. iii. 111) looks upon the latter and the Corybantes as derivations from the former. The worship of both was akin in nature to that of the Dactyli, the Cabeiri, and even of Dionysus, the special visible bond being the orgiastic character of their rites.
Consult Immisch in Roscher’s Lexicon, s.v. “Kureten.”
CURETON, WILLIAM (1808-1864), English Orientalist, was born at Westbury, in Shropshire. After being educated at the free grammar school of Newport, and at Christ Church, Oxford, he took orders in 1832, became chaplain of Christ Church, sub-librarian of the Bodleian, and, in 1837, assistant keeper of MSS. in the British Museum. He was afterwards appointed select preacher to the university of Oxford, chaplain in ordinary to the queen, rector of St Margaret’s, Westminster, and canon of Westminster. He was elected a fellow of the Royal Society and a trustee of the British Museum, and was also honoured by several continental societies. He died on the 17th of June 1864.
Cureton’s most remarkable work was the edition with notes and an English translation of the Epistles of Ignatius to Polycarp, the Ephesians and the Romans, from a Syriac MS. that had been found in the monastery of St Mary Deipara, in the desert of Nitria, near Cairo. He held that the MS. he used gave the truest text, that all other texts were inaccurate, and that the epistles contained in the MS. were the only genuine epistles of Ignatius that we possess—a view which received the support of F. C. Baur, Bunsen, and many others, but which was opposed by Charles Wordsworth and by several German scholars, and is now generally abandoned (see Ignatius). Cureton supported his view by his Vindiciae Ignatianae and his Corpus Ignatianum,—a Complete Collection of the Ignatian Epistles, genuine, interpolated and spurious. He also edited a partial Syriac text of the Festal Letters of St Athanasius, which was translated into English by Henry Burgess (1854), and published in the Library of Fathers of the Holy Catholic Church; Remains of a very Ancient Recension of the Four Gospels in Syriac, hitherto unknown in Europe; Spicilegium Syriacum, containing Remains of Bardesan, Meliton, Ambrose, Mara Bar Serapion; The third Part of the Ecclesiastical History of John, Bishop of Ephesus, which was translated by Payne Smith; Fragments of the Iliad of Homer from a Syriac Palimpsest; an Arabic work known as the Thirty-first Chapter of the Book entitled The Lamp that guides to Salvation, written by a Christian of Tekrit; The Book of Religious and Philosophical Sects, by Muhammed al Sharastani; a Commentary on the Book of Lamentations, by Rabbi Tanchum; and the Pillar of the Creed of the Sunnites. Cureton also published several sermons, among which was one entitled The Doctrine of the Trinity not Speculative but Practical. After his death Dr W. Wright edited with a preface the Ancient Syriac Documents relative to the earliest Establishment of Christianity in Edessa and the neighbouring Countries, from the Year of our Lord’s Ascension to the beginning of the Fourth Century; discovered, edited and annotated by the late W. Cureton.
CURETUS, a tribe of South American Indians, inhabiting the country between the rivers of Japura and Uaupés, north-western Brazil. They are short but sturdy, wear their hair long, and paint their bodies. Their houses are circular, with walls of thatch and a high conical roof. They are a peaceable people, living in small villages, each of which is governed by a chief.
CURFEW, Curfeu or Couvre-feu, a signal, as by tolling a bell, to warn the inhabitants of a town to extinguish their fires or cover them up (hence the name) and retire to rest. This was a common practice throughout Europe during the middle ages, especially in cities taken in war. In the law Latin of those times it was termed ignitegium or pyritegium. In medieval Venice it was a regulation from which only the Barbers’ Quarter was exempt, doubtless because they were also surgeons and their services might be needed during the night. The curfew originated in the fear of fire when most cities were built of timber. That it was a most useful and practical measure is obvious when it is remembered that the household fire was usually made in a hole in the middle of the floor, under an opening in the roof through which the smoke escaped. The custom is commonly said to have been introduced into England by William the Conqueror, who ordained, under severe penalties, that at the ringing of the curfew-bell at eight o’clock in the evening all lights and fires should be extinguished. But as there is good reason to believe that the curfew-bell was rung each night at Carfax, Oxford (see Peshall, Hist. of Oxford), in the reign of Alfred the Great, it would seem that all William did was to enforce more strictly an existing regulation. The absolute prohibition of lights after the ringing of the curfew-bell was abolished by Henry I. in 1100. The practice of tolling a bell at a fixed hour in the evening, still extant in many places, is a survival of the ancient curfew. The common hour was at first seven, and it was gradually advanced to eight, and in some places to nine o’clock. In Scotland ten was not an unusual hour. In early Roman times curfew may possibly have served a political purpose by obliging people to keep within doors, thus preventing treasonable nocturnal assemblies, and generally assisting in the preservation of law and order. The ringing of the “prayer-bell,” as it is called, which is still practised in some Protestant countries, originated in that of the curfew-bell. In 1848 the curfew was still rung at Hastings, Sussex, from Michaelmas to Lady-Day, and this was the custom too at Wrexham, N. Wales.
CURIA, in ancient Rome, a section of the Roman people, according to an ancient division traditionally ascribed to Romulus. He is said to have divided the people into three tribes, and to have subdivided each of these into ten curiae, each of which contained a number of families (gentes). It is more probable that the curiae were not purely artificial creations, but represent natural associations of families, artificially regulated and distributed to serve a political purpose. The local names of curiae which have come down to us suggest a local origin for the groups; but as membership was hereditary, the local tie doubtless grew weak with successive generations. Each curia was organized as a political and religious unit. As a political corporation it had no recognized activities beyond the command of a vote in the Comitia Curiata (see Comitia), a vote whose nature was determined by a majority in the votes of the individual members 639 (curiales). But as a religious unit the curia had more individual activity. There were, it is true, ceremonies (sacra) performed by all the curiae to Juno Curis in which each curia offered its part in a collective rite of the whole people; but each curia had also its peculiar sacra and its own special place of worship. The religious affairs of each were conducted by a priest called curio assisted by a flamen curialis. The thirty curiae must always have comprised the whole Roman people; for citizenship depended on membership of a gens (gentilitas) and every member of a gens was ipso facto attached to a curia. They therefore included plebeians as well as patricians (q.v.) from the date at which plebeians were recognized as free members of the body politic. But, just as enjoyment of the full rights of gentilitas was only very gradually granted to plebeians, so it is probable that a plebeian did not, when admitted through a gens into a curia, immediately exercise all the rights of a curialis. It is unlikely, for instance, that plebeians voted in the Comitia Curiata at the early date implied by the authorities; but it is probable that they acquired the right early in the republican period, and certain that they enjoyed it in Cicero’s time. A plebeian was for the first time elected curio maximus in 209 B.C. The curia ceased to have any importance as a political organization some time before the close of the republican period. But its religious importance survived during the principate; for the two festivals of the Fornacalia and the Fordicidia were celebrated by the Curiales (Ovid, Fasti, ii. 527, iv. 635).
The term curia seems often to have been applied to the common shrine of the curiales, and thus to other places of assembly. Hence the ancient senate house at Rome was known as the Curia Hostilia. The curia was also adopted as a state division in a large number of municipal towns; and the term was often applied to the senate in municipal towns (see Decurio), probably from the name of the old senate house at Rome.
Authorities.—Mommsen, Römisches Staatsrecht, iii. p. 89 ff. (Leipzig, 1887); Römische Forschungen i. p. 140 ff. (Berlin, 1864, &c.); Clason, “Die Zusammensetzung der Curien und ihrer Comitien” (Kritische Erörterungen i., Rostock, 1871); Karlowa, Römische Rechtsgeschichte, i. p. 382 ff. (Leipzig, 1885); E. Hofmann, Patricische und plebeische Curien (Wien, 1879); for the Fornacalia, &c., Marquardt, Staatsverwaltung, iii. p. 197 (Leipzig, 1885); for local names of curiae, Pauly-Wissowa, Realencyclopädie, iv. p. 1822 (new edition, 1893, &c.); O. Gilbert, Geschichte und Topographie der Stadt Rom (Leipzig, 1883); for municipal curiae, Mommsen, in Ephemeris epigraphica, ii. p. 125; Schmidt, in Rheinisches Museum, xlv. (1890) p. 599 ff. On the Roman comitia in general see also G. W. Botsford, Roman Assemblies (1909).
In medieval Latin the word curia was used in the general sense of “court.” It was thus used of “the court,” meaning the royal household (aula); of “courts” in the sense of solemn assemblies of the great nobles summoned by the king (curiae solennes, &c.); of courts of law generally, whether developed out of the imperial or royal curia (see Curia Regis) or not (e.g. curia baronis, Court Baron, curia christianitatis, Court Christian). Sometimes curia means jurisdiction, or the territory over which jurisdiction is exercised; whence possibly its use, instead of cortis, for an enclosed space, the court-yard of a house, or for the house itself (cf. the English “court,” e.g. Hampton Court, and the Ger. Hof). The word Curia is now only used of the court of Rome, as a convenient term to express the sum of the organs that make up the papal government (see Curia Romana).
See Du Cange, Gloss. med. et inf. Lat. (1883), s.v. “Curia.”
CURIA REGIS, or Aula Regis, a term used in England from the time of the Norman Conquest to about the end of the 13th century to describe a council and a court of justice, the composition and functions of which varied considerably from time to time. Meaning in general the “king’s court,” it is difficult to define the curia regis with precision, but it is important and interesting because it is the germ from which the higher courts of law, the privy council and the cabinet, have sprung. It was, at first the general council of the king, or the commune concilium, i.e. the feudal assembly of the tenants-in-chief; but it assumed a more definite character during the reign of Henry I., when its members, fewer in number, were the officials of the royal household and other friends and attendants of the king. It was thus practically a committee of the larger council, and assisted the king in his judicial work, its authority being as undefined as his own. About the same time the curia undertook financial duties, and in this way was the parent of the court of exchequer (curia regis ad scaccarium). The members were called “justices,” and in the king’s absence the chief justiciar presided over the court. A further step was taken by Henry II. In 1178 he appointed five members of the curia to form a special court of justice, and these justices, unlike the other members of the curia, were not to follow the king’s court from place to place, but were to remain in one place. Thus the court of king’s bench (curia regis de banco) was founded, and the foundation of the court of common pleas was provided for in one of the articles of Magna Carta. The court of chancery is also an offshoot of the curia regis. About the time of Edward I. the executive and advising duties of the curia regis were discharged by the king’s secret council, the later privy council, which is thus connected with the curia regis, and from the privy council has sprung the cabinet.
In his work Tractatus de legibus Angliae, Ranulf de Glanvill treats of the procedure of the curia regis as a court of law. See W. Stubbs, Constitutional History, vol. i. (Oxford, 1883); R. Gneist, Englische Verfassungsgeschichte, English translation by P. A. Ashworth (London, 1891); A. V. Dicey, The Privy Council (London, 1887); and the article Privy Council.
CURIA ROMANA, the name given to the whole body of administrative and judicial institutions, by means of which the pope carries on the general government of the Church; the name is also applied by an extension of meaning to the persons who form part of it, and sometimes to the Holy See itself. Rome is almost the only place where the word curia has preserved its ancient form; elsewhere it has been almost always replaced by the word court (cour, corte), which is etymologically the same. Even at Rome, however, the expression “papal court” (corte romana) has acquired by usage a sense different from that of the word curia; as in the case of royal courts it denotes the whole body of dignitaries and officials who surround and attend on the pope; the pope, however, has two establishments: the civil establishment, in which he is surrounded by what is termed his “family” (familia); and the religious establishment, the members of which form his “chapel” (capella). The word curia is more particularly reserved to the tribunals and departments which actually deal with the general business of the Church.
I. In order to understand the organization of the various constituent parts of the Roman Curia, we must remember that the modern principle of the separation of powers is unknown to the Church; the functions of each department General remarks. are limited solely by the extent of the powers delegated to it and the nature of the business entrusted to it; but each of them may have a share at the same time in the legislative, judicial and administrative power. Similarly, the necessity for referring matters to the pope in person, for his approval or ratification of the decisions arrived at, varies greatly according to the department and the nature of the business. But on the whole, all sections of the Curia hold their powers direct from the pope, and exercise them in his name. Each of them, then, has supreme authority within its own sphere, while the official responsibility belongs to the pope, just as in all governments it is the government that is responsible for the acts of its departments. Of these official acts, however, it is possible to distinguish two categories: those emanating directly from the heads of departments are generally called Acts of the Holy See (and in this sense the Holy See is equivalent to the Curia); those which emanate direct from the pope are called Pontifical Acts. The latter are actually the Apostolic Letters, i.e. those documents in which the pope speaks in his own name (bulls, briefs, encyclicals, &c.) even when he does not sign them, as we shall see. The Apostolic Letters alone may be ex cathedra documents, and may have the privilege of infallibility, if the matter admit of it. There are also certain differences between the two sorts of documents with regard to their penal consequences. But in all cases the disciplinary authority is evidently the same; we need only note that acts concerning individuals 640 do not claim the force of general law; the legal decisions serve at most to settle matters of jurisprudence, like the judgments of all sovereign courts.
The constituent parts of the Roman Curia fall essentially into two classes: (1) the tribunals and offices, which for centuries served for the transaction of business and which continue their activity; (2) the permanent commissions Division. of cardinals, known by the name of the Roman Congregations. These, though more recent, have taken precedence of the former, the work of which they have, moreover, greatly relieved; they are indeed composed of the highest dignitaries of the church, the cardinals (q.v.), and are, as it were, subdivisions of the consistory (q.v.), a council in which the whole of the Sacred College takes part.
II. The Roman Congregations.—The constitution of all of these is the same; a council varying in numbers, the members of which are cardinals, who alone take part in the deliberations. One of the cardinals acts as president, Roman Congregations. or prefect, as he is called; the congregation is assisted by a secretary and a certain number of inferior officials, for secretarial and office work. They have also consultors, whose duty it is to study the subjects for consideration. Their deliberations are secret and are based on prepared documents bearing on the case, written, or more often printed, which are distributed to all the cardinals about ten days in advance. The deliberations follow a simplified procedure, which is founded more on equity than on the more strictly legal forms, and decisions are given in the shortest possible form, in answer to carefully formulated questions or dubia. The cardinal prefect, aided by the secretariate, deals with the ordinary business, only important matters being submitted for the consideration of the general meeting. To have the force of law the acts of the congregations must be signed by the cardinal prefect and secretary, and sealed with his seal. Practically the only exception is in the cases of the Holy Office, and of the Consistorial Congregation of which the pope himself is prefect; the acts of the first are signed by the “notary,” and the acts of the second by the assessor.
We may pass over those temporary congregations of cardinals known also as “special,” the authority and existence of which extend only to the consideration of one particular question; and also those which had as their object various aspects of the temporal administration of the papal states, which have ceased to exist since 1870. We deal here only with the permanent ecclesiastical congregations, the real machinery of the papal administration. Some of them go quite far back into the 16th century; but it was Sixtus V. who was their great organizer; by his bull Immensa of the 22nd of January 1587, he apportioned all the business of the Church (including that of the papal states) among fifteen Congregations of cardinals, some of which were already in existence, but most of which were established by him; and these commissions, or those of them at least which are concerned with spiritual matters, are still working. A few others have been added by his successors. Pius X., by the constitution Sapienti Consilio of the 29th of June 1908, proceeded to a general reorganization of the Roman Curia: Congregations, tribunals and offices. In this constitution he declared that the competency of these various organs was not always clear, and that their functions were badly arranged; that certain of them had only a small amount of business to deal with, while others were overworked; that strictly judicial affairs, with which the Congregations had not to deal originally, had developed to an excessive extent, while the tribunals, the Rota and the Signatura, had nothing to do. He consequently withdrew all judicial affairs from the Congregations, and handed them over to the two tribunals, now revived, of the Rota and the papal Signatura; all affairs concerning the discipline of the sacraments were entrusted to a new Congregation of that name; the competency of the remaining Congregations was modified, according to the nature of the affairs with which they deal, and certain of them were amalgamated with others; general rules were laid down for the expedition of business and regarding personnel; in short, the work of Sixtus V. was repeated and adapted to later conditions. We will now give the nomenclature of the Roman Congregations, as they were until 1908, and mentioning the modifications made by Pius X.
(1) The Holy Inquisition, Roman and universal, or Holy Office (Sacra Congregatio Romanae et universalis Inquisitionis seu Sancti Officii), the first of the Congregations, hence called the supreme. It is composed of twelve cardinals, The Holy Office. assisted by a certain number of officials: the assessor, who practically fulfils the functions of the secretary, the commissary general, some consultors and the qualificators, whose duty it is to determine the degree of theological condemnation deserved by erroneous doctrinal propositions (haeretica, erronea, temeraria, &c.). The presidency is reserved to the pope, and the cardinal of longest standing takes the title of secretary. This Congregation, established in 1542 by Paul III., constitutes the tribunal of the Inquisition (q.v.), of which the origins are much older, since it was instituted in the 13th century against the Albigenses. It deals with all questions of doctrine and with the repression of heresy, together with those crimes which are more or less of the character of heresy. Its procedure is subject to the strictest secrecy. Pius X. attached to it all matters concerning indulgences; on the other hand, he transferred to the Congregation of the Council matters concerning the precepts of the Church such as fasting, abstinence and festivals. The choosing of bishops, which had in recent times been entrusted to the Holy Office, was given to the Consistorial Congregation, and dispensations from religious vows to the Congregation of the Religious Orders. The Holy Office continues, however, to deal with mixed marriages and marriages with infidels.
(2) The Consistorial Congregation (Sacra Congregatio Consistorialis), established by Sixtus V., has as its object the preparation of business to be dealt with and decided in secret consistory (q.v.); notably promotions to cathedral Consistorial. churches and consistorial benefices, the erection of dioceses, &c. To this congregation is also subject the administration of the common property of the college of cardinals. Pius X. restored this Congregation to a position of great importance; in the first place he gave it the effective control of all matters concerning the erection of dioceses and chapters and the appointment of bishops, except in the case of countries subject to the Propaganda, and save that for countries outside Italy it has to act upon information furnished by the papal secretary of state. He further entrusted to this Congregation everything relating to the supervision of bishops and of the condition of the dioceses, and business connected with the seminaries. It has also the duty of deciding disputes as to the competency of the other Congregations. The pope continues to be its prefect, and the cardinal secretary of the Holy Office and the secretary of state are ex officio members of it; the cardinal who occupies the highest rank in it, with the title of secretary, is chosen by the pope; he is assisted by a prelate with the title of assessor, who is ex officio secretary of the Sacred College. The assessor of the Holy Office and the secretary for extraordinary ecclesiastical affairs are ex officio consultors.
(3) The Pontifical Commission for the reunion of the dissident Churches, established by Leo XIII. in 1895 after his constitution Orientalium. The pope reserved the presidency for himself; its activity is merely nominal. It was attached by Pius X. to the Congregation of the Propaganda.
(4) The Congregation of the Apostolic Visitation (Sacra Congregatio Visitationis apostolicae). The Visitation is the personal inspection of institutions, churches, religious establishments and their personnel, to correct abuses The Visitation. and enforce the observation of rules. Through this Congregation the pope, as bishop of Rome, made the inspection of his diocese; it is for this reason that he was president of this commission, the most important member of which was the cardinal vicar. He takes the place of the pope in the administration of the diocese of Rome; he has his own offices and diocesan assistants as in other bishoprics. The Congregation of the Visitation was suppressed by Pius X. as a separate Congregation, 641 and was reduced to a mere commission which is attached, as before, to the Vicariate.
(5) The Congregation on the discipline of the sacraments (Sacra Congregatio de Disciplina Sacramentorum), established by Pius X., thus comes to occupy the third rank. With the reservation of those questions, especially of a dogmatic character, which belong to the Holy Office, and of purely ritual questions, which come under the Congregation of Rites, this Congregation brings under one authority all disciplinary questions concerning the sacraments, which were formerly distributed among several Congregations and offices. It deals with dispensations for marriages, ordinations, &c., concessions with regard to the mass, the communion, &c.
(6) The Congregation of the Bishops and Regulars, of which the full official title was, Congregation for the Affairs and Consultations of the Bishops and Regulars (Sacra Congregatio super negotiis Episcoporum et Regularium; now Sacra Congregatio negotiis religiosorum sodalium praeposita). Bishops and Regulars. It is the result of the fusion of two previous commissions; that for the affairs of bishops, established by Gregory XIII., and that for the affairs of the regular clergy, founded by Sixtus V.; the fusion dates from Clement VIII. (1601). This congregation was very much occupied, being empowered to deal with all disciplinary matters concerning both the secular and regular clergy, whether in the form of consultations or of contentious suits; it had further the exclusive right to regulate the discipline of the religious orders and congregations bound by the simple vows, the statutes of which it examined, corrected and approved; finally it judged disputes and controversies between the secular and regular clergy. On the 26th of May 1906, Pius X. incorporated in this Congregation two others having a similar object: that on the discipline of the regular clergy (Congregatio super Disciplina Regularium), founded by Innocent XII. in 1695, and that on the condition of the regular clergy (Congregatio super Statu Regularium), established by Pius IX. in 1846. In 1908 Pius X. withdrew from this Congregation all disciplinary matters affecting the secular clergy, and limited its competency to matters concerning the religious orders, both as regards their internal affairs and their relations with the bishops.
(7) The Congregation of the Council (Sacra Congregatio Cardinalium Concilii Tridentini interpretum), i.e. a number of cardinals whose duty it is to interpret the disciplinary decrees of the council of Trent, was instituted by Pius Council. IV. in 1563, and reorganized by Sixtus V.; its mission is to promote the observation of these disciplinary decrees, to give authoritative interpretations of them, and to reconcile disputes arising out of them. Pius X. in 1908 entrusted to this Congregation the supervision of the general discipline of the secular clergy and the faithful laity, empowering it to deal with matters concerning the precepts of the Church, festivals, foundations, church property, benefices, provincial councils and episcopal assemblies. Proceedings for annulling marriages, which used to be reserved to it, were transferred to the tribunal of the Rota; reports on the condition of the dioceses were henceforth to be addressed to the Consistorial Congregation, which involved the suppression of the commission which had hitherto dealt with them. The other commission, formerly charged with the revision of the decrees of provincial councils, was merged in the Congregation itself. The Congregation of Immunity (Sacra Congregatio Jurisdictionis et Immunitatis ecclesiasticae) was created by Urban VIII. (1626) to watch over the immunities of the clergy in respect of person or property, whether local or general. This, having no longer any object, was also attached to the Congregation of the Council, and is now amalgamated with it.
(8) The Congregation of the Propaganda (Sacra Congregatio de Propaganda Fide) was established by Gregory XV. in 1622, and added to by Urban VIII., who founded the celebrated College of the Propaganda for the education Propaganda. of missionaries, and his polyglot press for printing the liturgical books of the East. It had charge of the administration of the Catholic churches in all non-Catholic countries, for which it discharged the functions of all the Congregations, except in doctrinal and strictly legislative matters. Its sphere was very wide; it administered all non-European countries, except Latin America and the old colonies of the Catholic countries of Europe; in Europe it had also charge of the United Kingdom and the Balkan States. But the constitution “Sapienti” of 1908 withdrew from the Propaganda and put under the common law of the Church most of those parts in which the episcopal hierarchy had been re-established, i.e. in Europe, the United Kingdom, Holland and Luxemburg; in America, Canada, Newfoundland and the United States. Further, even for those countries which it continues to administer, the Propaganda has to submit to the various Congregations all questions affecting the Faith, marriage and rites. The missions begin by establishing apostolic prefectures under the charge of priests; the prefecture is later transformed into an apostolic vicariate, having at its head a bishop; finally, the hierarchy, i.e. the diocesan episcopate, is established in the country, with residential sees. Thus the hierarchy was re-established in England in 1850 by Pius IX., in 1878 by Leo XIII. in Scotland, in 1886 in India, in 1891 in Japan. It is also the work of the Propaganda to appoint the bishops for the countries it administers. Under the same cardinal prefect is found that section of the Propaganda which deals with matters concerning oriental rites (Congregatio specialis pro negotiis ritus Orientalis), the object of which is indicated by its name. To the former were attached two commissions, one for the approbation of those religious congregations which devote themselves to missions, which is now transferred to the Congregation of the Religious Orders; the other for the examination of the reports sent in by the bishops and vicars apostolic on their dioceses or missions. With the latter is connected the commission for the examination of the liturgical books of the East (Commissio pro corrigendis libris ecclesiae Orientalis). Finally, the popes have devoted to the missions the income arising from the Chamber of Spoils (Camera Spoliorum), i.e. that portion of the revenue from church property which cannot be bequeathed by the holders of benefices as their own property; this source of income, however, has decreased greatly.
(9) The Congregation of the Index (Congregatio indicis librorum prohibitorum), founded by St Pius V. in 1571 and reorganized by Sixtus V., has as its object the examination Index. and the condemnation or interdiction of bad or dangerous books which are submitted to it, or, since the constitution “Sapienti,” of those which it thinks fit to examine on its own initiative (see Index).
(10) The Congregation of Rites (Congregatio sacrorum Rituum), founded by Sixtus V., has exclusive charge of the liturgy and liturgical books; it also deals with the proceedings Rites. in the beatification and canonization of saints. Of late years there have been added to it a Liturgical Commission, a Historico-liturgical Commission, and a Commission for church song, the functions of which are sufficiently indicated by their names.
(11) The Ceremonial Congregation (Sacra Congregatio caeremonialis), the prefect of which is the cardinal dean, Ceremonial. was instituted by Sixtus V.; its mission is to settle questions of precedence and etiquette, especially at the papal court; it is nowadays but little occupied.
(12) The Congregation of Indulgences and Relics (Sacra Congregatio Indulgentiarum et Sacrarum Reliquiarum), founded in 1669 by Clement IX., devoted itself to eradicating any abuses which might creep into the practice of indulgences and the cult of relics. It had also the Indulgences. duty of considering applications for the concession of indulgences and of interpreting the rules with regard to them. In 1904 Pius X. attached this Congregation to that of Rites, making the personnel of both the same, without suppressing it. In 1908, however, it was suppressed, as stated above, and its functions as to indulgences were transferred to the Holy Office, and those as to relics to the Congregation of Rites.
(13) The Congregation of the Fabric of St Peter’s (Sacra Congregatio reverendae Fabricae S. Petri) is charged with the upkeep, repairs and temporal administration of the great basilica; 642 in this capacity it controls the famous manufacture of the Fabric of St Peter’s. Vatican mosaics. It also formerly enjoyed certain spiritual powers for the reduction of the obligations imposed by pious legacies and foundations, the objects of which, for want of funds or any other reason, could not be fully carried out, and for the condonation of past omission of such obligations, e.g. of priests to celebrate the foundation masses of their benefices. In 1908 these powers were taken away from it by Pius X., and transferred to the Congregation of the Council, which already exercised some of them.
(14) The Congregation of Loretto (Congregatio Lauretana) discharged the same functions for the sanctuary of that name; its temporal administration was latterly very much reduced, and in 1908 it was united by Pius X. with the Congregation of the Council.
(15) The Congregation for extraordinary ecclesiastical affairs (Sacra Congregatio super negotiis ecclesiasticis extraordinariis), established by Pius VI. at the end of the 18th century to study the difficult questions relative to France, Extraordinary affairs. was afterwards definitively continued by Pius VII.; and there has been no lack of fresh extraordinary matters. It also dealt with the administration of the churches of Latin America, not to mention certain European countries, such as Russia, under the same conditions as the Propaganda in countries under missions. Since the constitution Sapienti, its competency has been confined to the examination, at the request of the secretary of state, of questions which are submitted to it, and especially those arising from civil laws and concordats.
(16) The Congregation of Studies (Congregatio pro Universitate studii Romani, Congregazione degli Studi), founded by Sixtus V. to act as a higher council for the Roman university of La Sapienza, had ceased to have any functions Studies. when in 1824 it was re-established by Leo XII. to supervise education in Rome and the Papal States; since 1870 it has been exclusively concerned with the Catholic universities, so far as the sacred sciences are concerned. With this should be connected the commission for historical studies, instituted in 1883 by Leo XIII., at the same time as he threw the Vatican archives freely open to scholars.
III. The Tribunals and Offices.—Though it has been relieved of the functions allotted to the Congregations of cardinals, the old machinery of the ecclesiastical administration has not been abolished; and the process of centralization Tribunals and offices. which has been accentuated in the course of the last few centuries, together with the facility of communication, ensured for them a fresh activity, new offices having even been added. The chief thing to be observed is that the prelates who were formerly at the head of these departments have almost all been replaced by cardinals. The following is the list of the tribunals and offices, including the changes introduced by the reorganization of the Curia by Pius X. in 1908. The tribunals are three in number: one for the forum internum, the Penitentiary; the other two for judicial matters in foro externo, the Rota and the papal Signatura.
(1) The Penitentiary (Sacra poenitentiaria Apostolica) is the tribunal having exclusive jurisdiction in matters of conscience (in foro interno), e.g. dispensations from secret impediments and private vows, the absolution of reserved Penitentiary. cases. These concessions are applied for anonymously. It also had, previously to the constitution Sapienti, a certain jurisdiction in foro externo, such as over matrimonial dispensations for poor people. Its concessions are absolutely gratuitous. Since the 12th century, the papal court had already had officials known as penitentiaries (poenitentiarii) for matters of conscience; the organization of the Penitentiary, after several modifications, was renewed by Benedict XIV. in 1748. At the head of it is the cardinal grand penitentiary (major poenitentiarius), assisted by the regens (It. regente) and various other functionaries and officials.
(2) The court of the Rota (Sacra Rota Romana) used to be the supreme ecclesiastical tribunal for civil affairs, and its decisions had great authority. This tribunal goes back at least as far as the 14th century, but its activity had been reduced as Rota. a result of the more expeditious and summary, and less costly, procedure of the Congregations. The constitution Sapienti restored the Rota to existence and activity: it is now once more the ecclesiastical court of appeal for both civil and criminal cases. Pius X. also made special regulations for it, by which its ancient usages are adapted to modern circumstances. The tribunal of the Rota consists of ten judges called auditors (uditori), of whom the most senior is president with the title of dean. Each judge has an auxiliary; to the tribunal are attached a promotor fiscalis, charged with the duty of securing the due application of the law, and an official charged with the defence of marriage and ordination; there is also a clerical staff (notaries, scribes) attached to the court. Cases are judged by three auditors, who succeed each other periodically (per turnum) according to the order in which the cases are entered, and in exceptional cases by all the auditors (videntibus omnibus). Under the jurisdiction of the Rota, in addition to cases of first instance submitted to it by the pope, are such judgments of episcopal courts as are strictly speaking subject to appeal; for petitions against non-judicial decisions are referred to the Congregations. Appeal is sometimes allowed from one “turn” to another; if the second sentence of the Rota confirms the first, it is definitive; if not, a third may be obtained.
(3) The supreme tribunal of the papal Signatura (Signatura Apostolica). There were formerly two sections: the Signatura Justitiae and the Signatura Gratiae; by the constitution Sapientis they were suppressed and amalgamated Signatura. into one body, the Signatura Apostolica, which is the exact equivalent of other modern courts of cassation. This tribunal is composed of six cardinals, one of whom is the prefect, assisted by a prelate secretary, consultors and the necessary inferior officials. It judges cases in which auditors of the Rota are concerned, such as personal objections, but especially objections (querelae) lodged against sentences of the Rota, with a view to their being annulled or revised (restitutio in integrum).
Next come the offices, now reduced to six in number.
(1) The Chancery (Cancellaria Apostolica), the department
from which are sent out the papal letters, has for a long time
drawn up only those letters written in solemn form
known as bulls. The bull, so called from the leaden
Chancery.1
Bull.
seal (bulla), is written on thick parchment; the special writing
known as Lombard, which used to be used for bulls, was abolished
by Leo XIII., and the leaden seal reserved for the
more important letters; on the others it has been
replaced by a red ink stamp bearing both the emblems represented
on the leaden seal: the two heads, face to face, of St
Peter and St Paul, and the name of the reigning pope. Bulls
are written in the name of the pope, who styles himself “(Pius)
Episcopus servus servorum Dei; (Pius), bishop, servant of
the servants of God.” They were formerly dated by kalends
and from the era of the Incarnation, which begins on the 25th
of March, but in 1908 Pius X. ordered them to be dated according
to the common era. It is practically only bulls of canonization
which are signed by the pope and all the cardinals present in
Rome; the signature of the pope is then “(Pius) Episcopus
Ecclesiae catholicae,” while his ordinary signature bears only his
name and number, “Pius PP. X.” Ordinary bulls are signed
by several officials of the chancery, and a certain number only
by the cardinal at its head, who until 1908 was styled vice-chancellor,
because the chancellor used formerly to be a prelate,
not a cardinal; but since the constitution Sapienti has been
entitled chancellor. He is assisted by several officials, beginning
with the regens of the chancery. To the chancery were attached
the abbreviatores de parco majori vel minori (see Abbreviators),
formerly charged with the drawing up or “extension” of bulls;
they were suppressed by Pius X., and their functions transferred
to the Protonotarii apostolici participantes (i.e. active).
Further, Pope Pius confined the functions of the chancery
to the sending out of bulls under the leaden seal (sub plumbo),
for the erection of dioceses, the provision of bishoprics and
643
consistorial benefices, and other affairs of importance, these
bulls being sent out by order of the Consistorial Congregation.
(2) The Apostolic Dataria is the department dealing with matters of grace, e.g. the concession of privileges, nominations to benefices and dispensations in foro externo, especially matrimonial ones; but its functions have been greatly Dataria Apostolica. reduced by the reforms of Pius X.; the matrimonial section has been suppressed, dispensations for marriages now belonging to the Congregation for the discipline of the sacraments; the section dealing with benefices, which is the only one preserved, deals with non-consistorial benefices reserved to the Holy See; it examines the claims of the candidates, draws up and sends out the letters of collation, gives dispensations, when necessary, in matters concerning the benefices, and manages the charges (i.e. pensions to incumbents who have resigned, &c.) imposed on the benefices by the pope. It has at its head a cardinal formerly called the pro-datarius, the datarius having formerly been a prelate; and now datarius, since the reform by Pius X. The cardinal is assisted by a prelate called the sub-datarius, and other officials.
(3) The Apostolic Chamber (Reverenda Camera Apostolica) was before the abolition of the temporal power of the papacy the ministry of finance, at once treasury and exchequer, of the popes as heads of the Catholic Church as well as Apostolic chamber. sovereigns of the papal states. Although it is necessarily diminished in importance, it has retained the administration of the property of the Holy See, especially during a vacancy. At its head is the cardinal camerlengo (Sanctae Romanae Ecclesiae Cardinalis Camerarius), who, as we know, exercises the external authority during the vacancy of the Holy See.
(4) Next come the palatine secretariates, the first and principal of which is the secretariate of state (Secretaria status). The cardinal secretary of state is as it were the pope’s prime minister, gathering into one centre the internal Secretaryship of State. administration and foreign affairs, by means of the nunciatures and delegations depending on his department. The secretary of state is the successor of what was called in the 17th century the cardinal nephew; his functions and importance have increased more and more. The secretariate of state is the department dealing with the political affairs of the Church. To it belongs the internal administration of the apostolic palaces, with the library, archives, museums, &c. In 1908 Pius X. divided the departments of the secretariate of state into three sections, under the authority of the cardinal secretary. The first is the department of extraordinary ecclesiastical affairs, having at its head the secretary of the Congregation of the same name; the second, that of ordinary affairs, directed by a substitute, is the department dealing, among other things, with the concession of honorary distinctions, both for ecclesiastics and laymen; the third is that of the briefs, which hitherto Briefs. formed a separate secretariate. It is this department which sends out, at the command of the secretary of state or the various Congregations, those papal letters which are written in less solemn form, brevi manu, hence the word “brief.” They are written in the pope’s name, but he only takes the less solemn style of: “Pius PP. X.” The brief is written on thin parchment, and dated by the ordinary era and the day of the month; they were formerly signed only by the cardinal secretary of briefs or his substitute, but now by the cardinal secretary of state or the head of the office, called the chancellor of Briefs (cancellarius Brevium). The seal is that of the fisherman’s ring, hence the formula of conclusion, “Datum Romae, sub annulo Piscatoris.” The “Fisherman’s ring” is a red ink stamp representing St Peter on a boat casting out his nets, with the name of the reigning pope.
The reform of Pius X. maintained untouched the two offices called the secretariate of briefs to princes, and the secretariate of Latin Letters, the names of which are sufficient indication of their functions. The secretariate of memorials Other offices. (Secretaria Memorialium), through which pass requests addressed to the pope for the purpose of obtaining certain favours, was formerly of great importance; it is now suppressed and the requests are addressed to the proper departments. Finally, the pope has his special secretary, his auditor, with his offices, as well as the papal almonry, the officials of which administer the papal charities.
IV. The pontifical “family” (familia) forms the pope’s civil court. First come the palatine cardinals, i.e. those who, on account of their office, have the right of living in the papal palaces. These were formerly four in number: The pontifical “family.” the pro-datarius (now datarius), the secretary of state, the secretary of briefs, and the secretary of the memorials; the two last of these were suppressed in 1908. Next come the four palatine prelates, the majordomo, the superintendent of the household and its staff, and successor of the ancient vicedominus; the master of the chamber, who presides over the arrangement of audiences; the auditor, or private secretary; and finally the master of the sacred palace (magister sacri palatii), a kind of theological adviser, always a Dominican, whose special duty is nowadays the revision of books published at Rome. Other prelates rank with the above, but in a lower degree, notably the almoner and the various secretaries. All ecclesiastics admitted, by virtue of their office or by a gracious concession of the pope, to form part of the “family,” are called domestic prelates, prelates of the household; this is an honorary title conferred on many priests not resident in Rome. The external service of the palace is performed by the Swiss Guard and the gendarmerie; the service of the ante-chamber by the lay and ecclesiastical chamberlains; this service has also given rise to certain honorary titles both for ecclesiastics, e.g. honorary chamberlain, and for laymen, e.g. secret chamberlain (cameriere segreto). (See Chamberlain.)
V. The pontifical “chapel” (capella) is the papal court for purposes of religious worship. In it the pope is surrounded by the cardinals according to their order; by the patriarchs, archbishops and bishops attending at the Pontifical chapel. throne, and others; by the prelates of the Curia, and by all the clergy both secular and regular. Among the prelates we should mention the protonotaries, the successors of the old notaries or officials of the papal chancery in the earliest centuries; the seven protonotarii participantes were restored by Pope Pius X. to the chancery, as noted above, but they have kept important honorary privileges; this is yet another source of distinctions conferred upon a great number of priests outside of Rome, the protonotaries of different classes. In a lower degree there are also the chaplains of honour. Since 1870 the great pontifical ceremonies have lost much of their splendour.
Bibliography.—La Gerarchia cattolica, an annual directory published at Rome; Lunadoro, Relazione della corte di Roma (Rome, 1765); Moroni, Dizionario di erudizione, under the various headings; Card. De Luca, Relatio curiae romanae (Cologne, 1683); Bouix, De curia romana (Paris, 1859); Ferraris, Prompta bibliotheca (addit. Cassinenses), s.v. Congregatio; Grimaldi, Les Congrégations romaines (Sienna, 1891); Dictionnaire de théologie catholique, s.v. Cour romaine (Paris, 1907); Publications of the acts of the Roman Congregations: Bishops and regulars—Bizzarri, Collectanea in usum Secretariae (Rome, 1866, 1885). Council: the Thesaurus resolutionum has published all business since 1700; a volume is issued every year, and the contents have been published in alphabetical order by Zamboni (4 vols., Rome, 1812; Arras, 1860) and by Pallottini (18 vols., Rome, 1868, &c.). Immunity: Ricci, Synopsis, decreta et resolutiones (Palestrina, 1708). Propaganda: De Martinis, Juris pontificii de Propaganda Fide, &c. (Rome, 1888, &c.); Collectanea S. C. de Prop. Fide (2nd ed., Rome, 1907). Index: Index librorum prohibitorum (Rome, 1900). Rites: Decreta authentica (Rome, 1898). Indulgences: Decreta authentica (Regensburg, 1882); Rescripta authentica (ib., 1885).
CURICÓ, a province of central Chile, lying between the provinces of Colchagua and Talca and extending from the Pacific to the Argentine frontier; area, 2978 sq. m.; pop. (1895) 103,242. The eastern and western sections are mountainous, and are separated by the fertile valley of central Chile. The mineral resources are undeveloped, but are said to include copper, gold and silver. Cattle, wheat and wine are the principal products, but Indian corn and fruit also are produced. On the coast are important salt-producing industries. The climate is mild and the rainfall more abundant than at the northern part of the valley, and the effects of this are to be seen in the better 644 pasturage. Irrigation is used to a large extent. The province was created in 1865 by a division of Colchagua. The capital is Curicó, on the Mataquito river, in lat. 34° 58′ S. long. 71° 19′ W., 114 m. S. of Santiago by the Chilean Central railway, which crosses the province. The city stands on the great central plain, 748 ft. above sea-level, and in the midst of a comparatively well-cultivated district. It was founded in 1742 by José de Manso, and is one of the more cultured and progressive provincial towns of Chile. Pop. (1895) 12,669. Vichiquen, on a tide-water lake on the coast, is a prosperous town, the centre of the salt trade.
CURIE, PIERRE (1859-1906), French physicist, was born in Paris on the 15th of May 1859, and was educated at the Sorbonne, where he subsequently became professor of physics. Although he had previously published meritorious researches on piezoelectricity, the magnetic properties of bodies at different temperatures, and other topics, he was chiefly known for his work on radium carried out jointly with his wife, Marie Sklodowska, who was born at Warsaw on the 7th of November 1867. After the discovery of the radioactive properties of uranium by Henri Becquerel in 1896, it was noticed that some minerals of uranium, such as pitchblende, were more active than the element itself, and this circumstance suggested that such minerals contained small quantities of some unknown substance or substances possessing radioactive properties in a very high degree. Acting on this surmise M. and Mme Curie subjected a large amount of pitchblende to a laborious process of fractionation, with the result that in 1898 they announced the existence in it of two highly radioactive substances, polonium and radium. In subsequent years they did much to elucidate the remarkable properties of these two substances, one of which, polonium, came to be regarded as one of the transformation-products of the other (see Radioactivity). In 1903 they were awarded the Davy medal of the Royal Society in recognition of this work, and in the same year the Nobel prize for physics was divided between them and Henri Becquerel. Professor Curie, who was elected to the Academy of Sciences in 1905, was run over by a dray and killed instantly in Paris on the 19th of April 1906.
His elder brother, Paul Jacques Curie, born at Paris on the 29th of October 1856, published an elaborate memoir on the specific inductive capacities of crystalline bodies (Ann. Chim. Phys. 1889, 17 and 18).
CURIO, GAIUS SCRIBONIUS, Roman statesman and orator, son of a distinguished orator of the same name, flourished during the 1st century B.C. He was tribune of the people in 90 B.C., and afterwards served in Sulla’s army in Greece against Archelaus, general of Mithradates, and as his legate in Asia, where he was commissioned to restore order in the kingdoms abandoned by Mithradates. In 76 he was consul, and as governor of Macedonia carried on war successfully against the Thracians and Dardanians, and was the first Roman general who penetrated as far as the Danube. On his return he was granted the honour of a triumph. During the discussion as to the punishment of the Catilinarian conspirators he supported Cicero, but he spoke in favour of P. Clodius (q.v.) when the latter was being tried for the Bona Dea affair. This led to a violent attack on the part of Cicero, but it does not appear to have interfered with their friendship. Curio was a vehement opponent of Caesar, against whom he wrote a political pamphlet in the form of a dialogue. He was pontifex maximus in 57, and died in 53. His reputation as an orator was considerable, but according to Cicero he was very illiterate, and his only qualifications were brilliancy of style and the purity of his Latin. He was nicknamed Burbuleius (after an actor) from the way in which he moved his body while speaking.
Orelli, Onomasticon to Cicero; Florus iii. 4; Eutropius vi. 2; Val. Max. ix. 14, 5; Quintilian, Instit., vi. 3, 76; Dio Cassius xxxviii. 16.
His son, Gaius Scribonius Curio, was first a supporter of Pompey, but after his tribuneship (50 B.C.) went over to Caesar, by whom he was said to have been bribed. But, while breaking off relations with Pompey, Curio desired to keep up the appearance of impartiality. When it was demanded that Caesar should lay down his imperium before entering Rome, Curio proposed that Pompey should do the same, adding that, if the rivals refused to do so, they ought both to be declared public enemies. His proposal was carried by a large majority, but a report having spread that Caesar was on the way to attack Rome, the consuls called upon Pompey to undertake the command of all the troops stationed in Italy. Curio’s appeal to the people to prevent the levying of an army by Pompey was disregarded; whereupon, feeling himself in danger, he fled to Ravenna to Caesar. He was commissioned by Caesar, who was still unwilling to proceed to extremities, to take a message to the senate. But Curio’s reception was so hostile that he hurriedly returned during the night to Caesar. It was now obvious that civil war would break out. Curio collected troops in Umbria and Etruria for Caesar, who sent him to Sicily as propraetor in 49. After having fought with considerable success there against the Pompeians, Curio crossed over to Africa, where he was defeated and slain by Juba, king of Numidia. Curio, although a man of profligate character, possessed conspicuous ability, and was a distinguished orator. In spite of his faults, Cicero, as an old friend of his father, took a great interest in him and did his utmost to reform him. Seven of Cicero’s letters (Ad. Fam. ii. 1-7) are addressed to him. There can be no doubt that Curio’s behaviour in regard to the laying down of the imperium by Caesar and Pompey in great measure contributed to the outbreak of civil war. The first amphitheatre in Rome was erected by him (50), for the celebration of the funeral games in honour of his father.
Orelli, Onomasticon to Cicero; Livy, Epit. 109, 110; Caesar, Bell. Civ., ii. 23, for Curio’s African campaign; Appian, Bell. Civ., ii. 26-44; Vell. Pat. ii. 48.
CURITYBA (also Corityba and Curitiba), capital of the state of Paraná, Brazil, situated on an elevated plateau (2916 ft. above sea-level) 68 m. W. of its seaport Paranaguá, with which it is connected by a railway remarkable for the engineering difficulties overcome and for the beautiful scenery through which it passes. Pop. (1890) 22,694; of the municipality, 24,553. There is a large foreign element in the population, the Germans preponderating. The city has a temperate, healthy climate, and is surrounded by a charming campo country, which, however, is less fertile than the forested river valleys. Maté is the principal export.
CURLEW (Fr. Courlis or Corlieu), a name given to two birds, of whose cry it is an imitation, both belonging to the group Limicolae, but possessing very different habits and features.
1. The long-billed curlew, or simply curlew of most British writers, the Numenius arquata of ornithologists, is one of the largest of the family Scolopacidae, or snipes and allied forms. It is common on the shores of the United Kingdom and most parts of Europe, seeking the heaths and moors of the interior and more northern countries in the breeding-season, where it lays its four brownish-green eggs, suffused with cinnamon markings, in an artless nest on the ground. In England it has been ascertained to breed in Cornwall and in the counties of Devon, Dorset, Salop, and Derby—though sparingly. In Yorkshire it is more numerous, and thence to the extreme north of Scotland, as well as throughout Ireland, it is, under the name of whaup, familiar to those who have occasion to traverse the wild and desolate tracts that best suit its habits. So soon as the young are able to shift for themselves, both they and their parents resort to the sea-shore or mouths of rivers, from the muddy flats of which they at low tide obtain their living, and, though almost beyond any other birds wary of approach, form an object of pursuit to numerous gunners. While leading this littoral life the food of the curlew seems to consist of almost anything edible that presents itself. It industriously probes the mud or sand in quest of the worms that lurk therein, and is also active in seeking for such crustaceans and molluscs as can be picked up on the surface, while vegetable matter as well has been found in its stomach. During its summer-sojourn on the moorlands insects and berries, when they are ripe, enter largely into its diet. In bulk the curlew is not less than a crow, but it looks larger still from its long legs, wings and neck. Its bill, from 5 to 7 in. in length, and terminating in the delicate nervous apparatus 645 common to all birds of its family, is especially its most remarkable feature. Its plumage above is of a drab colour, streaked and mottled with very dark brown; beneath it is white, while the flight-quills are of a brownish black.
Nearly allied to the curlew, but smaller and with a more northern range, is the whimbrel (N. phaeopus), called in some parts jack-curlew, from its small size; May-fowl, from the month in which it usually arrives; and titterel, from one of its cries.1 This so much resembles the former in habit and appearance that no further details need be given of it. In the countries bordering on the Mediterranean occurs a third species (N. tenuirostris). Some fifteen other species, or more, have been described, but it is probable that this number is too great. The genus Numenius is almost cosmopolitan. In North America three very easily recognized species are found—the first (N. longirostris) closely agreeing with the European curlew, but larger and with a longer bill; the second (N. hudsonicus) representing the British whimbrel; and the third (N. borealis), which has several times found its way to Britain, very much less in size—indeed the smallest of the genus. All these essentially agree with the species of the Old World in habit; but it is remarkable that the American birds can be easily distinguished by the rufous colouring of their axillary feathers—a feature which is also presented by the American godwits (Limosa).
2. The curlew of inlanders, or stone-curlew—called also, by some writers, from its stronghold in England, the Norfolk plover, and sometimes the thick-knee—is usually classed among the Charadriidae, but it offers several remarkable differences from the more normal plovers. It is the Charadrius oedicnemus of Linnaeus, the C. scolopax of Sam. Gottl. Gmelin, and the Oedicnemus crepitans of K. J. Temminck. With much the same cry as that of the Numenii, only uttered in a far sweeter tone, it is as fully entitled to the name of curlew as the bird most commonly so called. In England it is almost solely a summer visitor, though an example will occasionally linger throughout a mild winter; and is one of the few birds whose distribution is affected by geological formation, since it is nearly limited to the chalk-country—the open spaces of which it haunts, and its numbers have of late years been sensibly diminished by their inclosure. The most barren spots in these districts, even where but a superficial coating of light sand and a thin growth of turf scarcely hide the chalk below, supply its needs; though at night (and it chiefly feeds by night) it resorts to moister and more fertile places. Its food consists of snails, coleopterous insects, and earth-worms, but larger prey, as a mouse or a frog, is not rejected. Without making the slightest attempt at a nest, it lays its two eggs on a level spot, a bare fallow being often chosen. These are not very large, and in colour so closely resemble the sandy, flint-strewn surface that their detection except by a practised eye is difficult. The bird, too, trusts much to its own drab colouring to elude observation, and, on being disturbed, will frequently run for a considerable distance and then squat with outstretched neck so as to become almost invisible. In such a case it may be closely approached, and its large golden eye, if it do not pass for a tuft of yellow lichen, is perhaps the first thing that strikes the searcher. As autumn advances the stone-curlew gathers in large flocks, and then is as wary as its namesake. Towards October these take their departure, and their survivors return, often with wonderful constancy, to their beloved haunts. In size this species exceeds any other European plover, and looks even still larger than it is. The bill is short, blunt, and stout; the head large, broad, and flat at the top; the wings and legs long—the latter presenting the peculiarity of a singular enlargement of the upper part of the tarsus, whence the names Oedicnemus and Thick-knee have been conferred. The toes are short and fleshy, and the hind-toe is wanting. This bird seems to have been an especial favourite with Gilbert White, in whose classical writings mention of it is often made. Its range extends to North Africa and India. Five other species of Oedicnemus from Africa have also been described as distinct. Australia possesses a very distinct species (O. grallarius), and the genus has two members in the Neotropical Region (O. bistriatus and O. superciliaris). An exaggerated form of Oedicnemus is found in Aesacus, of which two species have been described, one (A. recurvirostris) from the Indian, and the other (A. magnirostris) from the northern parts of the Australian region.
1 The name spowe (cf. Icelandic Spói) also seems to have been anciently given to this bird (see Stevenson’s Birds of Norfolk, ii. 201).
CURLING, THOMAS BLIZARD (1811-1888), British surgeon, was born in London in 1811. Through his uncle, Sir William Blizard, he became assistant-surgeon to the London hospital in 1833, becoming full surgeon in 1849. After filling other important posts in the College of Surgeons, he was appointed president in 1873. In 1843 he won the Jacksonian prize for his investigations on tetanus; and he became famous for his skill in treating diseases of the testes and rectum, his published works on which went through many editions. He died on the 4th of March 1888.
CURLING, a game in which the players throw large rounded stones upon a rink or channel of ice, towards a mark called the tee. Where the game originated is not precisely known; but it has been popular in Scotland for three centuries at least. Some writers, looking to the name and technical terms of the game, trace its invention to the Netherlands; thus “curl” may have been derived from the Ger. kurzweil, a game; “tee” from the Teutonic tighen, to point out; “bonspiel,” a district curling competition, from the Belgic bonne, a district, and spel, play; the further supposition that “rink” is merely a modification of the Saxon hrink, a strong man, seems scarcely tenable. Curling is called “kuting” in some parts of Lanarkshire and Ayrshire, and very much resembles quoiting on the ice, so that the name may have some connexion with the Dutch coete, a quoit; while Cornelis Kiliaan (1528-1607) in his Teutonic Dictionary gives the term khuyten as meaning a pastime in which large globes of stone like the quoit or discus are thrown upon ice. Possibly some of the Flemish merchants who settled in Scotland towards the close of the 16th century may have brought the game to the country. Unfortunately, however, for the theory that assigns to it a far-away origin, we find no early mention of it in the literature of the continent; while Camden, when describing the Orkney Islands in 1607, tells us that one of them supplies “plenty of excellent stones for the game called curling”; and incidental references to it as a game played in Scotland are made by several authors during the first half of the same century.
If the game be not indigenous to Scotland it certainly owes its development to that country, and in the course of time it has come to be the national sport. It was played at first with very rude engines—random whin boulders fashioned by nature alone, or misshapen granite blocks, bored through to let in the thumb of the player, having been the primitive channel stones. In course of years the rough block was superseded by a symmetrical object usually made of whinstone or granite, beautifully rounded, brilliantly polished, and supplied with a convenient handle.
Although curling boasts a literature of its own and songs innumerable, yet it has received but the scantiest notice from such important Scottish writers as Scott and Burns, or from contemporary literature in general. In 1834 an “Amateur Curling Club of Scotland” was formed, but this “mutual admiration amateur society came to nothing, as might be expected.” Far more businesslike were the methods of the men who set afoot the “Grand Caledonian Curling Club,” which began its existence on the 15th of November 1838, and which, under its present title of “The Royal Caledonian Curling Club,” is regarded in all parts of the world as the mother-club and legislative body, even in Canada, where, however, curling conditions differ widely from those of Scotland; devotion to the mother-club does not by any means imply submission. Starting with 28 allied clubs the Royal Club grew so rapidly that there were 500 such in 1880 and 720 in 1903. It was under the auspices of the Royal Caledonian that a body of Scottish curlers visited Canada and the United States in the winter of 1902-1903, and, while a slight margin of victory remained with the home players under their own climatic conditions, 646 the visit did much to bring together the lovers of the game on both sides of the Atlantic. The assumption of the title “Royal” in place of “Grand” was due to the visit of Queen Victoria and the prince consort to Scotland in 1842, on which occasion they were initiated into the mysteries of the game on the polished floor of the drawing-room in the Palace of Scone; and the prince consort, who was presented with a pair of curling-stones, consented to become patron of the club. On his death he was succeeded by the prince of Wales, who, as Edward VII., still continued his patronage. The Club’s main duties are to further the interests of the game, to revise the laws and to arrange the important matches, especially the grand match, played annually between the Scottish clubs north of the Forth & Clyde Canal and those south of it. In the first of these matches (1847) only twelve “rinks” were played; in 1903 there were no fewer than 286. During this time the southern clubs were usually victorious. Curlers claim to be a united brotherhood within which peer and peasant are equal “on the ice.” To the same end the laws of the club are framed with a due regard to economy, not forgetting conviviality in the matter of “beef and greens,” the curler’s traditional dish, washed down with whisky. A formal freemasonry exists among curlers, who must be initiated into the mysteries and instructed in the grip, password and ceremony, being liable at any moment to be examined in these essentials and fined for lapses of memory. Betting, excepting for the smallest stakes, is discountenanced.
Glossary.—As curling has a language which contains many curious terms, puzzling to the uninitiated, the English equivalents of some of them are here given. Baugh ice, rough or soft ice. Bias, a slope on the ice. Boardhead (also house or parish), the large circle round the tee. Bonspiel, a match between two clubs. Break an egg on a stone, touch it very slightly. Broughs, the small circles round the tee. Chipping, striking a stone of which a small part can be seen. Core, old name for rink. Cowe or kowe, a besom made of broom-twigs. Draw, to play gently. Drive, to play hard. Drug ice, soft bad ice. Fill the port, to block the interval between two stones. Gogsee, tee. Guard, a stone that covers and protects another. Hack, a hollow cut in the ice for the player’s foot, used in place of a crampit. Hands up! stop sweeping. Hog, a stone that stops short of the hog-score, a line drawn one-sixth of the length of the rink from the tee. Head, an innings, both sides delivering all their stones once. Howe, the middle of the rink, gradually hollowed by stones. In-ringing, gaining a good position by rebounding off another stone. In-wick, the same. Lie shot, the stone resting nearest the tee. Mar, to interfere with a stone while running. Out-Turn, to make the stone twist to the left. In-Turn, to make one turn to the right. Out-wick, to strike a stone on the edge so as to drive it towards the tee. Pat-lid, a stone that lies on the tee. Pittycock, the oldest form of curling-stone. Raise, to drive a “friendly” stone nearer the tee. Rebut, to deliver the stone with great force, so as to scatter the stones on the boardhead. Red the ice, clear away the opponents’ stones. Rink, the space in which the game is played; also the members of a side. Sole, the under part of the stone; also to deliver the stone. Soop, to sweep. Souter, to win without allowing the opponents to score at all; a term derived from a famous team of cobblers (souters) of Lochmaben, whose opponents seldom or never scored a point. Spiel, a match between members of the same club. Spend the stone, to waste a shot by playing wide intentionally. Stug, a fluke. Tee, the mark in the centre of the boardhead, against which it is the curler’s object to lay the stone. The tee may be any kind of a mark; a small iron plate with a spike in it is often used. Tozee, tee. Tramp, crampit, trigger or tricker, an iron plate fitted with spikes which the player stands upon to deliver the stone. Wittyr, tee.
The Rink and Implements.—The rink is marked out in the ice, which should be very hard and smooth, in curling language “keen and clear.” To keep it swept every curler carries a broom, sometimes a mere bundle of broom-twigs, more often an ordinary housemaid’s broom. Good “sooping,” or sweeping, is part of the curler’s art, and is performed subject to strict rules and under the direction of the skip, or captain; its importance lying in the fact that the progress of a stone is retarded by the ice-dust caused by the play, the sweeping of which in front of a running stone consequently prolongs its course. Apart from the broom and the crampit, the “roarin’ game,” as curlers love to call it, requires no further implement than the stone, a flattened, polished disk, fitted with a handle. In weight it must not exceed 44 ℔, 35 to 40 ℔ being usual. It must not exceed 36 in. in circumference or be less in height than one-eighth of the circumference. The two flat sides, or soles, are so shaped that one is serviceable for keen ice and the other for ice that is soft, rough or “baugh.” The handle can be fitted to either side, as the case demands. The cost of a pair of stones is not less than £2, generally more. In the intense cold of Canada and the United States iron is found more serviceable than stone, and the irons weigh from 60 to 70 ℔. Even these are light compared with the earlier rough boulder-stones, some of which weighed over 115 ℔, although the very early ones were much lighter. The modern stone took shape at the beginning of the 19th century. The ancient stones had no handles, but notches were hewn in them for finger and thumb, and, as their weight varied from 5 to 25 ℔, it is probable that they were thrown after the manner of quoits. Channel-stones, stones rounded by the action of water in a river-bed, were the favourites, while the shape was a matter of individual taste, oblong and triangular stones having been common. The soles were artificially flattened. During the next period we find the heavy boulder-stones, unhewn blocks fitted with handles and probably used at shorter distances, 70 or 80 ℔ being no uncommon weight. The rounded stone, made on scientific principles, did not appear until about 1800. Even then it was of all shapes and sizes, with and without handles, and not uncommonly made of wood. The stones of to-day are named after the places in which they are quarried, Ailsa Craigs, Burnocks, Carsphairn Reds and Crawfordjohns being some of the best-known varieties. The stones are quarried and never blasted, as the shock of the explosion is apt to strain or split the rock.
The Game.—Curling is practically bowls played on the ice, the place of the “jack” being taken by a fixed mark, as at quoits, called the tee, to which the curler aims his stone; every stone that finally lies nearer than any of the opposing stones counting a point or “shot.” As each side has four players, each playing two stones, it is possible for one side to score eight points at a “head” or innings; but in practice it is found wiser, when a good shot has been made, to play some or all following stones to such positions as will prevent opposing stones from disturbing the stone lying near the tee. Stones thus placed are called “guards.” Strategic matters like this are decided by the skip, or captain, of the rink, who plays last, and who is an autocrat whose will is law. The “lead,” or first player, is expected to play quietly up the rink, leaving his stone as close to the tee as possible, but on no account beyond it. He is followed by the “lead” of the other side, who, instructed by his skip, will either try to drive away the first stone, if well placed, or put his own stone in a better position. When the skip’s turn comes he is “skipped,” or directed, by another player, appointed by himself, usually the third player. When all sixteen stones have been delivered the players cross over, the scores are counted, and the game proceeds from the other end of the rink. If a stone fails to cross the “hog-score” it is a “hog” and is removed from the rink, unless it has struck another stone in position. Stones that pass the back-score or touch the swept snow on either side are also removed. By a cleverly imparted twist a stone may be made to curve round a guard and either drive away an opposing winner or find a favourable lie for itself. This, the equivalent of “bias” in the game of bowls, is the height of scientific play. If the situation seems desperate a very hard throw, a “thunderin’ cast,” may succeed in clearing away the opponents’ stones from the neighbourhood of the tee. Different methods are adopted in delivering the stone, but in all of them a firm stand should be taken on the crampit, and the stone swung, either quietly, or, if the skip calls for a “thunderin’ cast,” vigorously; but care must be taken to avoid striking the ice with the stone so as to crack or “star” the ice. All matches are for a certain number of “heads” or of points, or for all that can be made within a certain time limit, as may be agreed.
Abridged Rules.—Tees shall be 38 yds. apart, and with the tee as centre a circle having a radius of 7 ft. shall be drawn. In alignment with the tees, lines, to be called Central Lines, are drawn from the tees to points 4 yds. behind each tee, and at these points Foot Scores 18 in. long shall be drawn at right angles, on which, at 6 in. from Central Line, the heel of the Crampit shall be placed. All matches shall be of a certain number of heads, or shots, or by time, as agreed. 647 Every rink of players shall be composed of four a side. No shoes likely to break the ice may be worn.
The skips opposing each other shall settle by lot, or in any other way they may agree upon, which party shall lead at the first head, after which the winning party shall do so.
All curling stones shall be of a circular shape. No stone shall be of a greater weight than 44 ℔ imperial, or of greater circumference than 36 in., or of less height than one-eighth part of its greatest circumference.
No stone, or side of a stone, shall be changed after a match has been begun, or during its continuance, unless by consent.
Should a stone happen to be broken, the largest fragment shall be considered in the game for that end—the player being entitled afterwards to use another stone or another pair.
If a played stone rolls over, or stops, on its side or top, it shall be put off the ice. Should the handle quit the stone in delivery, the player must keep hold of it, otherwise he shall not be entitled to replay the shot.
Players, during the course of each end, to be arranged along the sides of the rink, anywhere skips may direct; and no party, except when sweeping according to rule, shall go upon the middle of the rink, or cross it, under any pretence whatever. Skips alone to stand at or about the tee—that of the playing party having the choice of place, and not to be obstructed by the other.
If a player should play out of turn, the stone so played may be stopped in its progress, and returned to the player. Should the mistake not be discovered till the stone be at rest, or has struck another stone, the opposite skip shall have the option of adding one to his score, allowing the game to proceed, or declaring the end null and void. But if a stone be played before the mistake has been discovered, the head must be finished as if it had been properly played from the beginning.
The sweeping shall be under the direction and control of the skips. The player’s party may sweep the ice anywhere from the centre line to the tee, and behind it,—the adverse party having liberty to sweep behind the tee, and in front of any of their own stones when moved by another, and till at rest. Skips to have full liberty to clean and sweep the ice behind the tee at any time, except when a player is being directed by his skip.
If in sweeping or otherwise, a running stone be marred by any of the party to which it belongs, it may, at the option of the opposite skip, be put off the ice; if by any of the adverse party, it may be placed where the skip of the party to which it belongs shall direct. If otherwise marred, it shall be replayed.
Every player to be ready to play when his turn comes, and not to take more than a reasonable time to play. Should he play a wrong stone, any of the players may stop it while running; but if not stopped till at rest, the one which ought to have been played shall be placed instead, to the satisfaction of the opposing skip.
No measuring of shots allowable previous to the termination of the end. Disputed shots to be determined by the skips, or, if they disagree, by the umpire, or, when there is no umpire, by some neutral person chosen by the skips. All measurements to be taken from the centre of the tee, to that part of the stone which is nearest it. No stone shall be considered without a circle, or over a line, unless it clear it;—and in every case, this is to be determined by placing a square on the ice, at the circle or line.
Skips shall have the exclusive regulation and direction of the game for their respective parties, and may play last stone, or in what part of it they please; and, when their turn to play comes, they may name one of their party to take charge for them.
If any player shall speak to, taunt or interrupt another, not being of his own party, while in the act of delivering his stone, one shot shall be added to the score of the party so interrupted.
If from any change of weather after a match has been begun, or from any other reasonable cause, one party shall desire to shorten the rink, or to change to another one, and, if the two skips cannot agree, the umpire shall, after seeing one end played, determine whether the rink shall be shortened, and how much or whether it shall be changed, and his decision shall be final.
See Annual of the Royal Caledonian Curling Club, Edinburgh.
CURLL, EDMUND (1675-1747), English bookseller, was born in 1675 in the west of England. His parents were in humble circumstances. After being apprenticed to an Exeter bookseller he came to London and started business on his own account, advertising himself by a system of newspaper quarrels. His connexion with the anonymously-published Court Poems in 1716 led to the long quarrel with Pope, who took his revenge by immortalizing Curll in the Dunciad. Curll became notorious for his indecent publications, so much so that “Curlicism” was regarded as a synonym for literary indecency. In 1716 and again in 1721 he had to appear at the bar of the House of Lords for publishing matter concerning its members. In 1725 he was convicted of publishing obscene books, and fined in 1728 for publishing The Nun in her Smock and De Usu Flagrorum, while his Memories of John Ker of Kersland cost him an hour in the pillory. When Curll in 1735 announced the forthcoming publication of “Mr Pope’s Literary Correspondence,” his stock, at Pope’s instigation, was seized. It has since been proved that the publication was really instigated by Pope, who wanted an excuse to print his letters, as he actually did (1737-1741). In his forty years of business Curll published a great variety of books, of which a very large number, fortunately, were quite free from “Curlicisms.” A list of his publications contains, indeed, 167 standard works. He died on the 11th of December 1747.
For Curll’s relations with Pope, see the Life of Pope, by Sir Leslie Stephen in the English Men of Letters series.
CURRAGH, a level stretch of open ground in Co. Kildare, Ireland, famous for its race-course and its military camp. It has an area of upwards of 4800 acres; and its soft natural sward, which has never been broken by the plough, affords excellent pasture for sheep. From the peculiarity of its herbage, the district is known in the neighbourhood as “the short grass”; and the young men of Kildare are jocularly distinguished as the “boys of the short grass.” The land is the property of the crown, which appoints a special officer as the ranger of the Curragh; but the right of pasturage is possessed by the landowners of the vicinity. The oldest mention of the Curragh occurs in the Liber Hymnorum (the manuscript of which probably dates from the 10th century) in connexion with St Bridget, who is said to have received a grant of the district from the king of Leinster, and is popularly credited with the honour of having turned it into a common. It is evident, however, that long before the days of the saint the downs of Kildare had afforded a regular place of assembly for the people of the south of Ireland. The word cuirrech, cognate with the Lat. cursus, signifies a race-course, and chariot-races are spoken of as taking place on the Curragh as early as the 1st century A.D. The Aenach Colmain (Curragh fair), also called Aenach Lifè (the fair on the plain of the Liffey), is frequently mentioned in the Irish annals, and both racing and other sports were carried on at this, the principal meeting of its kind in southern Ireland, and the plain appears from time to time as the scene of hostile encounters between the kings of Meath, Leinster and Offaly. In 1234 the earl of Pembroke was defeated here by the viceroy of Ireland, Lord Geoffrey de Monte Marisco; and in 1406 the Irish under the prior of Connell were routed by the English. In 1789 the Curragh was the great rendezvous for the volunteers, and in 1804 it saw the gathering of 30,000 United Irishmen. The camp was established at the time of the Crimean War, and is capable of accommodating 12,000 men. The races are held in April, June, September and October.
See W. M. Hennessy, in Proceedings of Royal Irish Acad., 1866.
CURRAN, JOHN PHILPOT (1750-1817), Irish politician and judge, was born on the 24th of July 1750, at Newmarket, Cork, where his father, a descendant of one of Cromwell’s soldiers, was seneschal to the manor-court. He was educated at Middleton, through the kind help of a friend, the Rev. Nathaniel Boyse, and at Trinity College, Dublin; and in 1773, having taken his M.A. degree, he entered the Middle Temple. In 1774 he married a lady who brought him a small dowry; but the marriage proved unhappy, and Mrs Curran finally eloped from her husband.
In 1775 Curran was called to the Irish bar, where he very soon obtained a practice. On his first rising in court excessive nervousness prevented him from even reading distinctly the few words of a legal form, and when requested by the judge to read more clearly he became so agitated as to be totally unable to proceed. But, his feelings once roused, all nervousness disappeared. His effective and witty attack upon a judge who had sneered at his poverty, the success with which he prosecuted a nobleman for a disgraceful assault upon a priest, the duel which he fought with one of the witnesses for this nobleman, and other similar exploits, gained him such a reputation that he was soon the most popular advocate in Ireland.
In 1783 Curran was appointed king’s counsel; and in the same year he was presented to a seat in the Irish House of Commons. His conduct in connexion with this affair displays his conduct 648 in a most honourable light; finding that he differed radically in politics from the gentleman from whom he had received his seat, he expended £1500 in buying another to replace that which he occupied. In his parliamentary career Curran was throughout sincere and consistent. He spoke vigorously on behalf of Catholic emancipation, and strenuously attacked the ministerial bribery which prevailed. His declamations against the government party led him into two duels—the first with John Fitzgibbon, then attorney-general, afterwards Lord Clare; the second with the secretary of state, Major Hobart, afterwards earl of Buckinghamshire. The Union caused him the bitterest disappointment; he even talked of leaving Ireland, either for America or for England.
Curran’s fame rests most of all upon his speeches on behalf of the accused in the state trials that were so numerous between 1794 and 1803; and among them may be mentioned those in defence of Hamilton Rowan, the Rev. William Jackson, the brothers John and Henry Sheares, Peter Finnerty, Lord Edward Fitzgerald, Wolfe Tone and Owen Kirwan. Another of his most famous and characteristic speeches is that against the marquis of Headfort, who had eloped with the wife of a clergyman named Massey. On the arrest of Robert Emmet, who had formed an attachment to his daughter, Curran was himself under suspicion; but, on examination before the privy council, nothing was brought forward to implicate him in the intended rebellion.
In 1806, on the death of Pitt and the formation of the Fox ministry, Curran received the post of master of the rolls, with a seat in the privy council, much to his disappointment, for he had desired a position of greater political influence. For eight years, however, he held this office. He then retired on a pension of £3000; and the three remaining years of his life were spent in London, where he became one of the most brilliant members of the society which included Sheridan, Erskine, Thomas Moore, and William Godwin. He died at his house in Brompton on the 14th of October 1817.
Curran’s legal erudition was never profound; and though he was capable of the most ingenious pleading, his appeal was always to the emotions of his audience. His best speeches are one fiery torrent of invective, pathos, national feeling and wit. His diction was lofty and sonorous. He was, too, a most brilliant wit and of wonderful quickness in repartee. To his personal presence he owed nothing; for he was short, slim and boyish-looking, and his voice was thin and shrill.
See Curran and his Contemporaries, a most entertaining work, by Charles Phillips, a personal friend of Curran’s (1818), and the Life of Curran, by his son, W. H. Curran (1819), and with additions by Dr Shelton Mackenzie, New York, (1855), both of which contain numerous samples of Curran’s eloquence. See also Curran’s Speeches (1805, 1808, 1845); Memoirs of Curran, by Wm. O’Regan (1817); Letters to Rev. H. Weston (1819); T. Moore’s Memoirs (1853).
CURRANT. (1) The dried seedless fruit of a variety of the grape-vine, Vitis vinifera, cultivated principally in Zante, Cephalonia and Ithaca, and near Patras, in the Morea (see Greece). Currants were brought originally from Corinth, whence their name; in the 13th and 14th centuries they were known as raisins de Corauntz. In the Ionian Islands the currant-vine is grown on the sides of the lower hills, or in the valleys, the grape-vine occupying the higher and less open and rich ground. Gypseous marls, or calcareous marls containing a little gypsum, are preferred to limestone soils, as they allow of deep penetration of the roots of the vines. The most favourable situations are those where a good supply of water can be obtained for the irrigation of the plantations. This is carried on from the end of October to the close of the year, after which all that is necessary is to keep the ground moist. The vines are planted in rows 3 or 4 ft. apart. Propagation is effected by grafting on stocks of the grape-vine, or by planting out in spring the young, vigorous shoots obtained at the end of the previous year from old currant-vines that have been cut away below the ground. The grafts bear fruit in three years, the slips in about double that time. The vine stock for grafting is cut down to the depth of a foot below the surface of the soil; two or three perpendicular incisions are made near the bark with a chisel; and into these are inserted shoots of the last year’s growth. The engrafted part then receives an application of moist marls, is wrapped in leaves and bound with rushes, and is covered with earth, two or three eyes of the shoots being left projecting above ground. In December the currant plantations are cleared of dead and weak wood. In February the branches are cut back, and pruned of median shoots, which are said to prevent the lateral ones proceeding from the same bud from bearing fruit. In order effectually to water the trees, the earth round about them is in February and March hoed up so as to leave them in a kind of basin, or is piled up against their stems. In March, when the leaves begin to show, the ground is thoroughly turned, and if requisite manured, and is then re-levelled. By the middle of April the leaves are fully out, and in June it is necessary to break back the newly-formed shoots. The fruit begins to ripen in July, and in the next month the vintage takes place. At this season rain is greatly dreaded, as it always damages and may even destroy the ripe fruit. The plantations, which are commonly much exposed, are watched by dogs and armed men. In Cephalonia the currant-grape is said to ripen at least a week earlier than in Zante. To destroy the oïdium, a fungal pest that severely injures the plantations, the vines are dusted, at the time the fruit is maturing, with finely-ground brimstone. The currants when sufficiently ripe are gathered and placed on a drying ground, where they are exposed to the sun in layers half an inch thick; from time to time they are turned and swept into heaps, until they become entirely detached from stalk. They are then packed in large butts for exportation. The wine made from the currant-grape is inferior in quality, but is said to be capable of much improvement. The fresh fruit is luscious and highly flavoured, but soon cloys the palate.
(2) The currants of British kitchen-gardens—so called from a resemblance to the foregoing—are the produce of Ribes nigrum and R. rubrum, deciduous shrubs of the natural order Ribesiaceae, indigenous to Britain, northern and central Europe, Siberia and Canada. The former species bears the black, the latter the red currant. White currants are the fruit of a cultivated variety of R. rubrum. Both red and black currants are used for making tarts and pies, jams, jellies and wine; the latter are also employed in lozenges, popularly supposed to be of value in relieving a sore throat, are occasionally preserved in spirits, and in Russia are fermented with honey to produce a strong liquor.
Currants will flourish in any fairly good soil, but to obtain large crops and fine fruit a good rich loam is desirable; with an annual dressing of farmyard manure or cowdung, after the winter pruning, for established trees. The plants are best propagated by cuttings, which should consist of strong well-ripened young shoots taken off close to the old wood. These should be planted as soon as possible after the wood is matured in autumn about 6 in. apart. The plants are grown with the best results as bushes, but may also be trained against a wall or trellis. In the matter of pruning it must be borne in mind that red and white currants form their fruit buds on wood two to three years old, and the main shoots and side branches may therefore be cut back. Black currants on the other hand form fruit buds on the new wood of the previous year, hence the old wood should be cut away and the young left.
The black currant is subject to the attacks of a mite, Phytoptus ribis, which destroys the unopened buds. The buds, when attacked, recognized by their swollen appearance, should be picked off and burned. The attacks of the caterpillars of the gooseberry and other moths may be met by dusting the bushes with lime and soot when the plants are moist with dew or after syringing.
The following forms are recommended for cultivation:—Black: Lee’s Prolific, Baldwin’s or Carter’s Champion and Black Naples; Red: Cherry, Raby Castle, Red Dutch and Comet; White: White Dutch. A kind of black currant (Ribes magellanicum), bearing poor and acid fruit, is indigenous to Tierra del Fuego.
CURRICLE (Lat. curriculum, a small car), a light two-wheeled vehicle, generally for driving with two horses.
CURRIE, SIR DONALD (1825-1909), British shipowner, was born at Greenock on the 17th of September 1825. At a very early age he was employed in the office of a shipowner in that port, but at the age of eighteen left Scotland for Liverpool, where shipping business offered more scope. By a fortunate chance he attracted the notice of the chief partner in the newly started Cunard steamship line, who found him a post in that company. In 1849 the Cunard Company started a service between Havre and Liverpool to connect with their transatlantic service. Currie was appointed Cunard agent at Havre and Paris, and secured for his firm a large share of the freight traffic between France and the United States. About 1856 he returned to Liverpool, where till 1862 he held an important position at the Cunard Company’s headquarters. In 1862 he determined to strike out for himself, and leaving the Cunard established the “Castle” line of sailing-ships between Liverpool and Calcutta. Business prospered, but in 1864 Currie found it profitable to substitute London for Liverpool as the home port of his vessels, and himself settled in London. In 1872 he came to the conclusion, after a careful study of all the circumstances, that the development of Cape Colony justified the starting of a new line of steamers between England and South Africa. The result of this decision was the founding of the successful Castle line of steamers (see under Steamship Lines), which after 1876 divided the South African mail contract with the older Union line, and was finally amalgamated with the latter under the title Union Castle line in 1900. Currie’s intimate knowledge of South African conditions and persons was on several occasions of material service to the British government. His acquaintance with Sir John Brand, the president of what was then the Orange Free State, caused him to be entrusted by the home government with the negotiations in the dispute concerning the ownership of the Kimberley diamond-fields, which were brought to a successful conclusion. He introduced the two Transvaal deputations which came to England in 1877 and 1878 to protest against annexation, and though his suggestions for a settlement were disregarded by the government of the day, the terms on which the Transvaal was subsequently restored to the Boers agreed, in essentials, with those he had advised. The first news of the disaster of Isandhlwana in the Zulu War was given to the home government through his agency. At that time there was no cable between England and South Africa, and the news was sent by a Castle liner to St Vincent, and telegraphed thence to Currie. At the same time by diverting his outward mail-boat then at sea from its ordinary course to St Vincent, he enabled the government to telegraph immediate instructions to that island for conveyance thence by the mail, thus saving serious delay, and preventing the annihilation of the British garrison at Eshowe. The present arrangement under which the British admiralty is enabled to utilize certain fast steamers of the mercantile marine as armed cruisers in war-time was suggested and strongly urged by Currie in 1880. In the same year he was returned to parliament as Liberal member for Perthshire, but, though a strong personal friend of W. E. Gladstone, he was unable to follow that statesman on the Home Rule question, and from 1885 to 1900 he represented West Perthshire as a Unionist. In 1881 his services in connexion with the Zulu War were rewarded with knighthood, and in 1897 he was created G.C.M.G. He died at Sidmouth on the 13th of April 1909.
CURRIE, JAMES (1756-1805), Scottish physician and editor of Burns, son of the minister of Kirkpatrick-Fleming, in Dumfriesshire, was born there on the 31st of May 1756. Attracted by the stories of prosperity in America he went in 1771 to Virginia, where he spent five hard years, much of the time ill and always in unprofitable commercial business. The outbreak of war between the Colonies and England ended any further chance of success, and sailing for home in the spring of 1776 after many delays he reached England a year later. He then proceeded to study medicine at Edinburgh, and after taking his degree at Glasgow he settled at Liverpool in 1780, where three years later he became physician to the infirmary. He died at Sidmouth on the 31st of August 1805. Among other pamphlets Currie was the author of Medical Reports on the Effects of Water, Cold and Warm, as a Remedy in Fevers and Febrile Diseases (1797), which had some influence in promoting the use of cold water affusion, and contains the first systematic record in English of clinical observations with the thermometer. But he is best known for his edition (1800), long regarded as the standard, of Robert Burns, which he undertook in behalf of the family of the poet. It contained an introductory criticism and an essay on the character and condition of the Scottish peasantry.
See the Memoir by W. W. Currie, his son (1831).
CURRY. (1) (Through the O. Fr. correier, from Late Lat. conredare, to make ready, prepare; a later form of the French is courroyer, and modern French is corroyer), to dress a horse by rubbing down and grooming with a comb; to dress and prepare leather already tanned. The currier pares off roughnesses and inequalities, makes the leather soft and pliable, and gives it the necessary surface and colour (see Leather). The word “currier,” though early confused in origin with “to curry,” is derived from the Late Lat. coriarius, a leather dresser, from corium, hide. The phrase “to curry favour,” to flatter or cajole, is a 16th century corruption of “to curry favel,” i.e. a chestnut horse. This older phrase is an adaptation of an Old French proverbial expression estriller fauvel, and is paralleled in German by the similar den fahlen Hengst streichen. A chestnut or fallow horse seems to have been taken as typical of deceit and trickery, at least since the appearance of a French satirical beast romance the Roman de fauvel (1310), the hero of which is a counterpart of Reynard the Fox (q.v.).
(2) A name applied to a great variety of seasoned dishes, especially those of Indian origin. The word is derived from the Tamil kari, a sauce or relish for rice. In the East, where the staple food of the people consists of a dish of rice, wheaten cakes, or some other cereal, some kind of relish is required to lend attraction to this insipid food; and that is the special office of curry. In India the following are employed as ingredients in curries: anise, coriander, cumin, mustard and poppy seeds; allspice, almonds, assafoetida, butter or ghee, cardamoms, chillies, cinnamon, cloves, cocoa-nut and cocoanut milk and oil, cream and curds, fenugreek, the tender unripe fruit of Buchanania lancifolia, cheroonjie nuts (the produce of another species, B. latifolia), garlic and onions, ginger, lime-juice, vinegar, the leaves of Bergera Koenigii (the curry-leaf tree), mace, mangoes, nutmeg, pepper, saffron, salt, tamarinds and turmeric.
The cumin and coriander seeds are generally used roasted. The various materials are cleaned, dried, ground, sifted, thoroughly mixed and bottled. In the East the spices are ground freshly every day, which gives the Indian curry its superiority in flavour over dishes prepared with the curry-powders of the European market.
CURSOR, LUCIUS PAPIRIUS, Roman general, five times consul and twice dictator. In 325 he was appointed dictator to carry on the second Samnite War. His quarrel with Q. Fabius Maximus Rullianus, his magister equitum, is well known. The latter had engaged the enemy against the orders of Cursor, by whom he was condemned to death, and only the intercession of his father, the senate and the people, saved his life. Cursor treated his soldiers with such harshness that they allowed themselves to be defeated; but after he had regained their good-will by more lenient treatment and lavish promises of booty, they fought with enthusiasm and gained a complete victory. After the disaster of the Caudine Forks, Cursor to some extent wiped out the disgrace by compelling Luceria (which had revolted) to surrender. He delivered the Roman hostages who were held in captivity in the town, recovered the standards lost at Caudium, and made 7000 of the enemy pass under the yoke. In 309, when the Samnites again rose, Cursor was appointed dictator for the second time, and gained a decisive victory at Longula, in honour of which he celebrated a magnificent triumph. Cursor’s strictness was proverbial; he was a man of immense bodily strength, while his bravery was 650 beyond dispute. He was surnamed Cursor from his swiftness of foot.
Livy viii., ix.; Aurelius Victor, De viris illustribus, 31; Eutropius ii. 8. 9.
His son of the same name, also a distinguished general, completed the subjection of Samnium (272). He set up a sun-dial, the first of its kind in Rome, in the temple of Quirinus.
Livy x. 39-47; Pliny, Nat. Hist., vii. 60.
CURSOR MUNDI, an English poem in the Northern dialect dating from the 13th century. It is a religious epic of 24,000 lines “over-running” the history of the world as related in the Old and New Testaments. “Cursur o werld man aght it call, For almast it over-rennes all.” The author explains in his prologue his reasons for undertaking the work. Men desire to read old romances of Alexander, Julius Caesar, Greece, Troy, Brut, Arthur, of Tristram, Sweet Ysoude and others. But better than tales of love is the story of the Virgin who is man’s best lover, therefore in her honour he will write this book, founded on the steadfast ground of the Holy Trinity. He writes in English for the love of English people of merry England, so that those who know no French may understand. The history is treated under seven ages. The first four include the period from the creation of the world to the successors of Solomon, the fifth deals with Mary and the birth and childhood of Jesus, the sixth with the lives of Christ and the chief apostles, and with the finding of the holy cross, and the seventh with Doomsday. Four short poems follow, more in some MSS. The bulk of the poem is written in rhyming couplets of short lines of four accents, and maintains a fair level throughout. The narrative is enlivened by many legends and much entertaining matter drawn from various sources; and the numerous transcripts of it prove that it was able to hold its own against profane romance.
The chief sources of the compilation have been identified by Dr Haenisch. For the Old Testament history the author draws largely from the Historia scholastica of Peter Comestor; for the history of the Virgin he often translates literally from Wace’s Établissement de la fête de la conception Notre Dame; the parables of the king and four daughters, and of the castle of Love and Grace, are taken from “Sent Robert bok” (1.9516), that is, from the Chasteau d’Amour of Robert Grosseteste, bishop of Lincoln; other sources are the apocryphal gospels of Matthew and Nicodemus, a southern English poem on the Assumption of Our Lady, attributed by the writer of Cursor mundi to Edmund Rich of Pontigny, the Vulgate, the Legenda aurea of Jacobus de Voragine, and the De vita et morte sanctorum of Isidore of Seville. The original of the section on the invention of the holy cross is still to seek. In its general plan the work is similar to the Livre de sapience of Herman de Valenciennes.
Of the author nothing is known. In the Cotton MS. Vespasian (A III.) the name of the owner William Cosyn is given (for particulars of this family, which is mentioned in Lincolnshire records as early as 1276, see Dr H. Hupe in the E.E.T.S. ed. of Cursor mundi, vol. i. p. 124 *). The date of the book was placed by Dr J. A. H. Murray (The Dialect of the Southern Counties of Scotland, 1873, p. 30) in the last quarter of the 13th century, and the place of writing near Durham. Dr Hupe (loc. cit. p. 186 *) gives good reasons for believing that the author was a Lincolnshire man, who wrote between 1260 and 1290, although the Cotton MS. probably belongs to the late 14th century. In the Göttingen MS. there are lines (17099-17110) desiring the reader to pray for John of Lindbergh, “that this bock gart dight,” and cursing anybody who shall steal it. Lindberg is probably Limber Magna, near Ulceby, in north Lincolnshire. Dr Hupe hazards an identification of the author with this John of Lindberg, who may have been a member of the Cistercian Abbey of Lindberg; but this is improbable.
Cursor mundi was edited for the Early English Text Society in 1874-1893 by Dr Richard Morris in parallel columns from four MSS.:—Cotton Vespasian A III., British Museum; Fairfax MS. 14, in the Bodleian library, Oxford; MS. theol. 107 at Göttingen; and MS. R. 3.8 in Trinity College, Cambridge. The edition includes a “Preface” by the editor, “An Inquiry into the Sources of the Cursor mundi” (1885), by Dr Haenisch, an essay “On the Filiation and the Text of the MSS. of Cursor mundi” (1885), by Dr H. Hupe, “Cursor Studies and Criticisms on the Dialects of its MSS.” (1888), by Dr Hupe and a glossary by Dr Max Kaluza.
CURTAIN, a screen of any textile material, running by means of rings fixed to a rod or pole. Curtains are now used chiefly to cover windows and doors, but for many centuries every bed of importance was surrounded by them, and sometimes, as in France, the space thus screened off was much larger than the actual bed and was called the ruelle. The curtain is very ancient—indeed the absence of glass and ill-fitting windows long made it a necessity. Originally single curtains were used; it would appear that it was not until the 17th century that they were employed in pairs. Curtains are made in an infinite variety of materials and styles; when placed over a door they are usually called portières. In fortification the “curtain” is that part of the enceinte which lies between two bastions, towers, gates, &c.
The word comes into English through the O. Fr. cortine or courtine from the Late Lat. cortina. According to Du Cange (Glossarium, s.v. “Cortis”) this is a diminutive of cortis, an enclosed space, a court. It is used in the various senses of the English “curtain.” Classical Latin had also a word cortina, meaning a caldron or round kettle. It was very rarely applied to round objects generally. In the Vulgate cortina is used of the curtains of the tabernacle (Exodus xxvi). There is some difficulty in connecting the classical and the Late Latin words. The earliest use in English is, according to the New English Dictionary, for the hangings of a bed.
CURTANA (a latinized form of the A.-Fr. curtein, from Lat. curtus, shortened), the pointless sword of mercy, known also as Edward the Confessor’s sword, borne at the coronation of the kings of England between the two pointed swords of temporal and spiritual justice (see Regalia).
CURTEA DE ARGESH (Rumanian, Curtea de Arges; also written Curtea d’Argesh, Curtea d’Ardges, Argish and Ardjish), the capital of the department of Argesh, Rumania; situated on the right bank of the river Argesh, where it flows through a valley of the lower Carpathians; and on the railway from Pitesci to the Rothenthurm Pass. Pop. (1900) 4210. The city is one of the oldest in Rumania. According to tradition it was founded early in the 14th century by Prince Radu Negru, succeeding Câmpulung as capital of Walachia. Hence its name Curtea, “the court.” It contains a few antique churches, and was created a bishopric at the close of the 18th century.
The cathedral of Curtea de Argesh, by far the most famous building in Rumania, stands in the grounds of a monastery, 1½ m. N. of the city. It resembles a very large and elaborate mausoleum, built in Byzantine style, with Moorish arabesques. In shape it is oblong, with a many-sided annexe at the back. In the centre rises a dome, fronted by two smaller cupolas; while a secondary dome, broader and loftier than the central one, springs from the annexe. Each summit is crowned by an inverted pear-shaped stone, bearing a triple cross, emblematic of the Trinity. The windows are mere slits; those of the tambours, or cylinders, on which the cupolas rest, are curved, and slant at an angle of 70°, as though the tambours were leaning to one side. Between the pediment and the cornice a thick corded moulding is carried round the main building. Above this comes a row of circular shields, adorned with intricate arabesques, while bands and wreaths of lilies are everywhere sculptured on the windows, balconies, tambours and cornices, adding lightness to the fabric. The whole is raised on a platform 7 ft. high, and encircled by a stone balustrade. Facing the main entrance is a small open shrine, consisting of a cornice and dome upheld by four pillars. The cathedral is faced with pale grey limestone, easily chiselled, but hardening on exposure. The interior is of brick, plastered and decorated with frescoes. Close by stands a large royal palace, Moorish in style. The archives of the cathedral were plundered by Magyars and Moslems, but several inscriptions, Greek, Slav and Ruman, are left. One tablet records that the founder was Prince Neagoe Bassarab (1512-1521); another that Prince John Radu 651 completed the work in 1526. A third describes the repairs executed in 1681 by Prince Sherban Cantacuzino; a fourth, the restoration, in 1804, by Joseph, the first bishop. Between 1875 and 1885 the cathedral was reconstructed; and in 1886 it was reconsecrated. Its legends have inspired many Rumanian poets, among them the celebrated V. Alexandri (1821-1890). One tradition describes how Neagoe Bassarab, while a hostage in Constantinople, designed a splendid mosque for the sultan, returning to build the cathedral out of the surplus materials. Another version makes him employ one Manole or Manoli as architect. Manole, being unable to finish the walls, the prince threatened him and his assistant with death. At last Manole suggested that they should follow the ancient custom of building a living woman into the foundations; and that she who first appeared on the following morning should be the victim. The other masons warned their families, and Manole was forced to sacrifice his own wife. Thus the cathedral was built except the roof. So arrogant, however, did the masons become, that the prince bade remove the scaffolding, and all, save Manole, perished of hunger. He fell to the ground, and a spring of clear water, which issued from the spot, is still called after him.
CURTESY (a variant of “courtesy,” q.v.), in law, the life interest which a husband has in certain events in the lands of which his wife was in her lifetime actually seised for an estate of inheritance. As to the historical origin of the custom and the meaning of the word there is considerable doubt. It has been said to be an interest peculiar to England and to Scotland, hence called the “curtesy of England” and the “curtesy of Scotland”; but this is erroneous, for it is found also in Germany and France. The Mirroir des Justices ascribes it to Henry I. K. E. Digby (Hist. Real Prop. chap. iii.) says that it is connected with curia, and has reference either to the attendance of the husband as tenant of the lands at the lord’s court, or to mean simply that the husband is acknowledged tenant by the courts of England (tenens per legem Angliae). The requisites necessary to make tenancy by the curtesy are: (1) a legal marriage; (2) an estate in possession of which the wife must have been actually seised; (3) issue born alive and during the mother’s existence, though it is immaterial whether the issue live or die, or whether it is born before or after the wife’s seisin; in the case of gavelkind lands the husband has a right to curtesy, whether there is issue born or not; but the curtesy extends only to a moiety of the wife’s lands and ceases if the husband marries again. The issue must have been capable of inheriting as heir to the wife, e.g. if a wife were seised of lands in tail male the birth of a daughter would not entitle the husband to a tenancy by curtesy; (4) the title to the tenancy vests only on the death of the wife. The Married Women’s Property Act 1882 has not affected the right of curtesy so far as relates to the wife’s undisposed-of realty (Hope v. Hope, 1892, 2 Ch. 336), and the Settled Land Act 1884, s. 8, provides that for the purposes of the Settled Land Act 1882 the estate of a tenant by curtesy is to be deemed an estate arising under a settlement made by the wife.
See Pollock and Maitland, Hist. Eng. Law; K. E. Digby, Hist. Real Prop.; Goodeve, Real Property.
CURTILAGE (Med. Lat. curtilagium, from curtile or cortile, a court or yard, cf. “court”), the area of land which immediately surrounds a dwelling-house and its yard and outbuildings. In feudal times every castle with its dependent buildings was protected by a surrounding wall, and all the land within the wall was termed the curtilage; but the modern legal interpretation of the word, i.e. what area is enclosed by the curtilage, depends upon the circumstances of each individual case, such as the terms of the grant or deed which passes the property, or upon what is held to be a convenient amount of land for the occupation of the house, &c. The importance of the word in modern law depends on the fact that the curtilage marks the limit of the premises in which housebreaking can be committed.
CURTIN ANDREW GREGG (1817-1894), American political leader, was born at Bellefonte, Centre county, Pennsylvania, on the 22nd of April 1817, the son of a native of Ireland who was a pioneer iron manufacturer in Pennsylvania. He graduated from the law department of Dickinson College in 1837, was admitted to the bar in 1839, and successfully practised his profession. Entering politics as a Whig, he was chairman of the Whig state central committee in 1854, and from 1855 to 1858 was secretary of the commonwealth. In this capacity he was also ex officio the superintendent of common schools, and rendered valuable services to his state in perfecting and expanding the free public school system, and in establishing state normal schools. Upon the organization of the Republican party he became one of its leaders in Pennsylvania, and in October 1860 was chosen governor of the state on its ticket, defeating Henry D. Foster, the candidate upon whom the Douglas and Breckinridge Democrats and the Constitutional Unionists had united, by 32,000 votes, after a spirited campaign which was watched with intense interest by the entire country as an index of the result of the ensuing presidential election. During the Civil War he was one of the closest and most constant advisers of President Lincoln, and one of the most efficient, most energetic and most patriotic of the “war governors” of the North. Pennsylvania troops were the first to reach Washington after the president’s call, and from first to last the state, under Governor Curtin’s guidance, furnished 387,284 officers and men to the Northern armies. One of his wisest and most praiseworthy acts Was the organization of the famous “Pennsylvania Reserves,” by means of which the state was always able to fill at once its required quota after each successive call. In raising funds and equipping and supplying troops the governor showed great energy and resourcefulness, and his plans and organizations for caring for the needy widows and children of Pennsylvania soldiers killed in battle, and for aiding and removing to their homes the sick and wounded were widely copied throughout the North. He was re-elected governor in 1863 and served until January 1867. He was United States minister to Russia from 1869 until 1872, when he returned to America and took part in the Liberal Republican revolt against President U. S. Grant. In 1872-1873 he was a member of the state constitutional convention. Subsequently he joined the Democratic party and was a representative in Congress from 1881 to 1887. He died at his birthplace, Bellefonte, Pennsylvania, on the 7th of October 1894.
See William H. Egle’s Life and Times of Andrew Gregg Curtin (Philadelphia, 1896), which contains chapters written by A. K. McClure, Jno. Russell Young, Wayne McVeagh, Fitz John Porter and others.
CURTIS, GEORGE TICKNOR (1812-1894), American lawyer, legal writer and constitutional historian, was born in Watertown, Massachusetts, on the 28th of November 1812. He graduated at Harvard in 1832, was admitted to the bar in 1836, and practised in Worcester, Boston, New York and Washington, appearing before the United States Supreme Court in many important cases, including the Dred Scott case, in which he argued the constitutional question for Scott, and the “legal tender” cases. In Boston he was for many years the United States commissioner, and in this capacity, despite the vigorous protests of the abolitionists and his own opposition to slavery, ordered the return to his owner of the famous fugitive slave, Themas Sims, in 1852. He was the nephew and close friend of George Ticknor, the historian of Spanish literature, and his association with his uncle was influential in developing his scholarly tastes; while his other personal friendships with eminent Bostonians during the period of conservative Whig ascendancy in Massachusetts politics were of direct influence upon his political opinions and published estimates. He is best known as the author of A History of the Origin, Formation and Adoption of the Constitution of the United States, with Notices of its principal Framers (1854), republished, with many additions, as The Constitutional History of the United States from their Declaration of Independence to the Close of their Civil War (2 vols., 1889-1896). This history, which had been watched in its earlier progress by Daniel Webster, may be said to present the old Federalist or “Webster-Whig” view of the formation and powers of the Constitution; and it was natural that Curtis should follow it with 652 a voluminous Life of Daniel Webster (2 vols., 1870), the most valuable biography of that statesman. Both these works are characterized by solidity and comprehensiveness rather than by rhetorical attractiveness or literary perspective. In his later years Mr Curtis, like so many of the followers of Webster, turned towards the Democratic party; and he wrote, among other works of minor importance, an exculpatory life of President James Buchanan (2 vols., 1883) and two vindications of General George B. McClellan’s career (1886 and 1887). He died in New York on the 28th of March 1894.
In addition to the works above mentioned he published: Digest of the English and American Admiralty Decisions (1839); Rights and Duties of Merchant Seamen (1841), which elicited the hearty praise of Justice Joseph Story; Law of Patents (1849); Equity Precedents (1850); Commentaries on the Jurisprudence, Practice and Peculiar Jurisdiction of the Courts of the United States (1854-1858); Creation or Evolution: A Philosophical Inquiry (1887); and a novel, John Chambers: A Tale of the Civil War in America (1889).
His brother, Benjamin Robbins Curtis (1809-1874), also an eminent jurist, was born on the 4th of November 1809, in Watertown, Massachusetts, graduated at Harvard in 1829, studied law at Cambridge and at Northfield, Mass., where, after his admission to the bar in 1832, he practised law for two years, and then in Boston in 1834-1851. In 1851, being then a member of the lower house of the Massachusetts legislature, he was on the 22nd of September appointed to the Supreme Court of the United States, where he gained his greatest fame in 1857 by his dissenting opinion in the Dred Scott case, in which he argued that the Missouri Compromise was constitutional, and that negroes could become citizens. His argument was immediately published as an anti-slavery document. On the 1st of September 1857 he resigned from the Supreme Court and resumed his private practice. In 1868 he was one of the counsel for President Andrew Johnson in his impeachment trial, and opened for the defence in a remarkable two-days’ speech. He died at Newport, Rhode Island, on the 15th of September 1874. He prepared Decisions of the Supreme Court (22 vols.) and a Digest of its decisions down to 1854.
A Memoir of Benjamin Robbins Curtis, with Some of his Professional and Miscellaneous Papers, edited by his son Benjamin R. Curtis, was published at Boston in 1879, the Memoir being by George Ticknor Curtis.
CURTIS, GEORGE WILLIAM (1824-1892), American man of letters, was born in Providence, Rhode Island, on the 24th of February 1824, of old New England stock. His mother died when he was two years old. At six he was sent with his elder brother to school in Jamaica Plain, Massachusetts, where he remained for five years. Then, his father having again married happily, the boys were brought home to Providence, where they stayed till, in 1839, their father removed to New York. Three years later, Curtis, being allowed to determine for himself his course of life, and being in sympathy with the spirit of the so-called Transcendental movement, became a boarder at the community of Brook Farm. He was accompanied by his brother, James Burrill Curtis, whose influence upon him was strong and helpful. He remained there for two years, brought into stimulating and serviceable relations with many interesting men and women. Then came two years, passed partly in New York, partly in Concord in order mainly to be in the friendly neighbourhood of Emerson, and then followed four years spent in Europe, Egypt and Syria.
Curtis returned from Europe in 1850, handsome, attractive, accomplished, ambitious of literary distinction. He instantly plunged into the whirl of life in New York, obtained a place on the staff of the Tribune, entered the field as a popular lecturer, set himself to work on a volume published in the spring of 1851, under the title of Nile Notes of a Howadji, and became a favourite in society. He wrote much for Putnam’s Magazine, of which he was associate editor; and a number of volumes, composed of essays written for that publication and for Harper’s Monthly, came in rapid succession from his pen. The chief of these were the Potiphar Papers (1853), a satire on the fashionable society of the day; and Prue and I (1856), a pleasantly sentimental, fancifully tender and humorous study of life. In 1855 he married Miss Anna Shaw. Not long after his marriage he became, through no fault of his own, deeply involved in debt owing to the failure of Putnam’s Magazine; and his high sense of honour compelled him to devote the greater part of his earnings for many years to the discharge of obligations for which he had become only by accident responsible, and from which he might have freed himself by legal process. In the period just preceding the Civil War other interests became subordinate to those of national concern. Curtis made his first important speech on the questions of the day at Wesleyan University in 1856; he engaged actively in the presidential campaign of that year, and was soon recognized not only as an effective public speaker, but also as one of the ablest, most high-minded, and most trustworthy leaders of public opinion. In 1863 he became the political editor of Harper’s Weekly, and no other journal exercised during the war and after it a more important part in shaping public opinion. His writing was always clear, direct, forcible; his fairness of mind and sweetness of temper were invincible. He never became a mere partisan, and never failed to apply the test of moral principle to political measures. From month to month he contributed to Harper’s Monthly, under the title of “The Easy Chair,” brief essays on topics of social and literary interest, charming in style, touched with delicate humour and instinct with generous spirit. His service to the Republican party was such, that more than once he was offered nominations to office of high distinction, and might have been sent as minister to England; but he refused all offers of the kind, feeling that he could render more essential service to the country as editor and public speaker.
In 1871 he was appointed by President Grant chairman of the commission to report on the reform of the civil service. The report which he wrote was the foundation of every effort since made for the purification and regulation of the service and for the destruction of political patronage. From that time till his death Curtis was the leader in this reform, and to his sound judgment, his vigorous presentation of the evils of the corrupt prevailing system, and his untiring efforts, the progress of the reform is mainly due. He was president of the National Civil Service Reform League and of the New York Civil Service Reform Association. In 1884 he refused to support the nomination of James G. Blaine as candidate for the presidency, and thus broke with the Republican party, of which he had been one of the founders and leaders. From that time he stood as the typical independent in politics. In April 1892 he delivered at Baltimore his eleventh annual address as president of the National Civil Service Reform League, and in May he appeared for the last time in public, to repeat in New York an admirable address on James Russell Lowell, which he had first delivered in Brooklyn on the 22nd of the preceding February, the anniversary of Lowell’s birth. On the 31st of the following August he died. He was a man of consistent virtue, whose face and figure corresponded with the traits and stature of his soul. The grace and charm of his manner were the expression of his nature. Of the Americans of his time few were more widely beloved, and the respect in which he was held was universal.
See George William Curtis, by Edward Cary, in the “American Men of Letters” series (Boston, 1894), an excellent biography; “An Epistle to George William Curtis,” by James Russell Lowell (1874-1887), in Lowell’s Poems; George William Curtis, a Commemorative Address delivered before The Century Association, 17th December 1892, by Parke Godwin (New York, 1893); Orations and Addresses by George William Curtis, edited by Charles Eliot Norton (3 vols. New York, 1894).
CURTIUS, ERNST (1814-1896), German archaeologist and historian, was born at Lübeck on the 2nd of September 1814. On completing his university studies he was chosen by C. A. Brandis to accompany him on a journey to Greece for the prosecution of archaeological researches. Curtius then became Otfried Müller’s companion in his exploration of the Peloponnese, and on Müller’s death in 1840 returned to Germany. In 1844 he became an extraordinary professor at the university of Berlin, and in the same year was appointed tutor to Prince Frederick William (afterwards the Emperor Frederick III.)—a post which he held till 1850. After holding a professorship at Göttingen and 653 undertaking a further journey to Greece in 1862, Curtius was appointed (in 1863) ordinary professor at Berlin. In 1874 he was sent to Athens by the German government, and concluded an agreement by which the excavations at Olympia (q.v.) were entrusted exclusively to Germany. Curtius died at Berlin on the 11th of July 1896. His best-known work is his History of Greece (1857-1867, 6th ed. 1887-1888; Eng. trans. by A. W. Ward, 1868-1873). It presented in an attractive style what were then the latest results of scholarly research, but was criticized as wanting in erudition. It is now superseded (see Greece: History, Ancient, § Bibliography). His other writings are chiefly archaeological. The most important are: Die Akropolis von Athen (1844); Naxos (1846); Peloponnesos, eine historisch-geographische Beschreibung der Halbinsel (1851); Olympia (1852); Die Ionier vor der ionischen Wanderung (1855); Attische Studien (1862-1865); Ephesos (1874); Die Ausgrabungen zu Olympia (1877, &c.); Olympia und Umgegend (edited by Curtius and F. Adler, 1882); Olympia; Die Ergebnisse der von dem deutschen Reich veranstalteten Ausgrabung (with F. Adler, 1890-1898); Die Stadtgeschichte von Athen (1891); Gesammelte Abhandlungen (1894). His collected speeches and lectures were published under the title of Altertum und Gegenwart (5th ed., 1903 foll.), to which a third volume was added under the title of Unter drei Kaisern (2nd ed., 1895).
A full list of his writings will be found in L. Gurlitt, Erinnerungen an Ernst Curtius (Berlin, 1902); see also article by O. Kern in Allgemeine deutsche Biographie, xlvii. (1903), to which may be added Ernst Curtius. Ein Lebensbild in Briefen, by F. Curtius (1903); T. Hodgkin, Ernest Curtius (1905).
His brother, Georg Curtius (1820-1885), philologist, was born at Lübeck on the 16th of April 1820. After an education at Bonn and Berlin he was for three years a schoolmaster in Dresden, until (in 1845) he returned to Berlin University as privat-docent. In 1849 he was placed in charge of the Philological Seminary at Prague, and two years later was appointed professor of classical philology in Prague University. In 1854 he removed from Prague to a similar appointment at Kiel, and again in 1862 from Kiel to Leipzig. He died at Hermsdorf on the 12th of August 1885. His philological theories exercised a widespread influence. The more important of his publications are: Die Sprachvergleichung in ihrem Verhältniss zur classischen Philologie (1845; Eng. trans. by F. H. Trithen, 1851); Sprachvergleichende Beiträge zur griechischen und lateinischen Grammatik (1846); Grundzüge der griechischen Etymologie (1858-1862, 5th ed. 1879); Das Verbum der griechischen Sprache (1873). The last two works have been translated into English by A. S. Wilkins and E. B. England. From 1878 till his death Curtius was general editor of the Leipziger Studien zur classischen Philologie. His Griechische Schulgrammatik, first published in 1852, has passed through more than twenty editions, and has been edited in English. In his last work, Zur Kritik der neuesten Sprachforschung (1885), he attacks the views of the “new” school of philology.
Opuscula of Georg Curtius were edited after his death by E. Windisch (Kleine Schriften von E. C., 1886-1887). For further information consult articles by R. Meister in Allgemeine deutsche Biographie, xlvii. (1903), and by E. Windisch in C. Bursian’s Biographisches Jahrbuch für Alterthumskunde (1886).
CURTIUS, MARCUS, a legendary hero of ancient Rome. It is said that in 362 B.C. a deep gulf opened in the forum, which the seers declared would never close until Rome’s most valuable possession was thrown into it. Then Curtius, a youth of noble family, recognizing that nothing was more precious than a brave citizen, leaped, fully armed and on horseback, into the chasm, which immediately closed again. The spot was afterwards covered by a marsh called the Lacus Curtius. Two other explanations of the name Lacus Curtius are given: (1) a Sabine general, Mettius (or Mettus) Curtius, hard pressed by the Romans under Romulus, leaped into a swamp which covered the valley afterwards occupied by the forum, and barely escaped with his life; (2) in 445 B.C. the spot was struck by lightning, and enclosed as sacred by the consul, Gaius Curtius. It was marked by an altar which was removed to make room for the games in celebration of Caesar’s funeral (Pliny, Nat. Hist. xv. 77), but restored by Augustus (cf. Ovid, Fasti, vi. 403), in whose time there was apparently nothing but a dry well. The altar seems to have been restored early in the 4th century A.D. In April 1904, on the N. side of the Via Sacra and 20 ft. N.W. of the Equus Domitiani, remains of the buildings were discovered.
See Livy i. 12, vii. 6; Dion Halic. ii. 42; Varro, De lingua Latina, v. 148; Ch. Hülsen, The Roman Forum (Eng. trans. of 2nd ed., J. B. Carter, 1906); O. Gilbert, Geschichte und Topographie der Stadt Rom im Altertum, i. (1883), 334-338.
CURTIUS RUFUS, QUINTUS, biographer of Alexander the Great. Of his personal history nothing is known, nor can his date be fixed with certainty. Modern authorities regard him as a rhetorician who flourished during the reign of Claudius (A.D. 41-54). His work (De Rebus gestis Alexandri Magni) originally consisted of ten books, of which the first two are entirely lost, and the remaining eight are incomplete. Although the work is uncritical, and shows the author’s ignorance of geography, chronology and military matters, it is written in a picturesque style.
There are numerous editions: (text) T. Vogel (1889), P. H. Damste (1897), E. Hedicke (1908); (with notes), T. Vogel (1885 and later), M. Croiset (1885), H. W. Reich (1895), C. Lebaigue (1900), T. Stangl (1902). There is an English translation by P. Pratt (1821). See S. Dosson, Étude sur Quinte-Curce, sa vie, et ses œuvres (1887) a valuable work; F. von Schwarz, Alexander des Grossen Feldzüge in Turkestan (1893), a commentary on Arrian and Curtius based upon the author’s personal knowledge of the topography; C. Wachsmuth, Einleitung in das Studium der alten Geschichte (1895), p. 574, cf. p. 567, note 2; Schwarz, “Curtius Rufus” No. 31 in Pauly-Wissowa (1901).
CURULE (Lat. currus, “chariot”), in Roman antiquities, the epithet applied to the chair of office, sella curulis, used by the “curule” or highest magistrates and also by the emperors. This chair seems to have been originally placed in the magistrate’s chariot (hence the name). It was inlaid with ivory or in some cases made of it, had curved legs but no back, and could be folded up like a camp-stool. In English the word is used in the general sense of “official.” (See Consul, Praetor and Aedile.)
CURVE (Lat. curvus, bent), a word commonly meaning a shape represented by a line bending continuously out of the straight without making an angle, but only properly to be defined in its geometrical sense in the terms set out below. This subject is treated here from an historical point of view, for the purpose of showing how the different leading ideas were successively arrived at and developed.
1. A curve is a line, or continuous singly infinite system of points. We consider in the first instance, and chiefly, a plane curve described according to a law. Such a curve may be regarded geometrically as actually described, or kinematically as in the course of description by the motion of a point; in the former point of view, it is the locus of all the points which satisfy a given condition; in the latter, it is the locus of a point moving subject to a given condition. Thus the most simple and earliest known curve, the circle, is the locus of all the points at a given distance from a fixed centre, or else the locus of a point moving so as to be always at a given distance from a fixed centre. (The straight line and the point are not for the moment regarded as curves.)
Next to the circle we have the conic sections, the invention of them attributed to Plato (who lived 430-347 B.C.); the original definition of them as the sections of a cone was by the Greek geometers who studied them soon replaced by a proper definition in plano like that for the circle, viz. a conic section (or as we now say a “conic”) is the locus of a point such that its distance from a given point, the focus, is in a given ratio to its (perpendicular) distance from a given line, the directrix; or it is the locus of a point which moves so as always to satisfy the foregoing condition. Similarly any other property might be used as a definition; an ellipse is the locus of a point such that the sum of its distances from two fixed points (the foci) is constant, &c., &c.
The Greek geometers invented other curves; in particular, the conchoid (q.v.), which is the locus of a point such that its distance from a given line, measured along the line drawn through 654 it to a fixed point, is constant; and the cissoid (q.v.), which is the locus of a point such that its distance from a fixed point is always equal to the intercept (on the line through the fixed point) between a circle passing through the fixed point and the tangent to the circle at the point opposite to the fixed point. Obviously the number of such geometrical or kinematical definitions is infinite. In a machine of any kind, each point describes a curve; a simple but important instance is the “three-bar curve,” or locus of a point in or rigidly connected with a bar pivoted on to two other bars which rotate about fixed centres respectively. Every curve thus arbitrarily defined has its own properties; and there was not any principle of classification.
2. Cartesian Co-ordinates.—The principle of classification first presented itself in the Géometrie of Descartes (1637). The idea was to represent any curve whatever by means of a relation between the co-ordinates (x, y) of a point of the curve, or say to represent the curve by means of its equation. (See Geometry: Analytical.)
Any relation whatever between (x, y) determines a curve, and conversely every curve whatever is determined by a relation between (x, y).
Observe that the distinctive feature is in the exclusive use of such determination of a curve by means of its equation. The Greek geometers were perfectly familiar with the property of an ellipse which in the Cartesian notation is x²/a² + y²/b² = 1, the equation of the curve; but it was as one of a number of properties, and in no wise selected out of the others for the characteristic property of the curve.
3. Order of a Curve.—We obtain from the equation the notion of an algebraical as opposed to a transcendental curve, viz. an algebraical curve is a curve having an equation F(x, y) = 0 where F(x, y) is a rational and integral function of the co-ordinates (x, y); and in what follows we attend throughout (unless the contrary is stated) only to such curves. The equation is sometimes given, and may conveniently be used, in an irrational form, but we always imagine it reduced to the foregoing rational and integral form, and regard this as the equation of the curve. And we have hence the notion of a curve of a given order, viz. the order of the curve is equal to that of the term or terms of highest order in the co-ordinates (x, y) conjointly in the equation of the curve; for instance, xy − 1 = 0 is a curve of the second order.
It is to be noticed here that the axes of co-ordinates may be any two lines at right angles to each other whatever; and that the equation of a curve will be different according to the selection of the axes of co-ordinates; but the order is independent of the axes, and has a determinate value for any given curve.
We hence divide curves according to their order, viz. a curve
is of the first order, second order, third order, &c., according as
it is represented by an equation of the first order, ax + by + c = 0,
or say (* x, y, 1) = 0; or by an equation of the second order,
ax² + 2hxy + by² + 2fy + 2gx + c = 0, say (*
x, y, 1) = 0; or by an equation of the second order,
ax² + 2hxy + by² + 2fy + 2gx + c = 0, say (* x, y, 1)² = 0; or by an
equation of the third order, &c.; or what is the same thing,
according as the equation is linear, quadric, cubic, &c.
x, y, 1)² = 0; or by an
equation of the third order, &c.; or what is the same thing,
according as the equation is linear, quadric, cubic, &c.
A curve of the first order is a right line; and conversely every right line is a curve of the first order. A curve of the second order is a conic, and is also called a quadric curve; and conversely every conic is a curve of the second order or quadric curve. A curve of the third order is called a cubic; one of the fourth order a quartic; and so on.
A curve of the order m has for its equation (* x, y, 1)m = 0;
and when the coefficients of the function are arbitrary, the curve
is said to be the general curve of the order m. The number of
coefficients is ½(m + 1)(m + 2); but there is no loss of generality
if the equation be divided by one coefficient so as to reduce the
coefficient of the corresponding term to unity, hence the number
of coefficients may be reckoned as ½(m + 1)(m + 2) − 1, that is,
½m(m + 3); and a curve of the order m may be made to satisfy
this number of conditions; for example, to pass through ½m(m + 3)
points.
x, y, 1)m = 0;
and when the coefficients of the function are arbitrary, the curve
is said to be the general curve of the order m. The number of
coefficients is ½(m + 1)(m + 2); but there is no loss of generality
if the equation be divided by one coefficient so as to reduce the
coefficient of the corresponding term to unity, hence the number
of coefficients may be reckoned as ½(m + 1)(m + 2) − 1, that is,
½m(m + 3); and a curve of the order m may be made to satisfy
this number of conditions; for example, to pass through ½m(m + 3)
points.
It is to be remarked that an equation may break up; thus a quadric equation may be (ax + by + c)(a′x + b′y + c′) = 0, breaking up into the two equations ax + by + c = 0, a′x + b′y + c′ = 0, viz. the original equation is satisfied if either of these is satisfied. Each of these last equations represents a curve of the first order, or right line; and the original equation represents this pair of lines, viz. the pair of lines is considered as a quadric curve. But it is an improper quadric curve; and in speaking of curves of the second or any other given order, we frequently imply that the curve is a proper curve represented by an equation which does not break up.
4. Intersections of Curves.—The intersections of two curves are obtained by combining their equations; viz. the elimination from the two equations of y (or x) gives for x (or y) an equation of a certain order, say the resultant equation; and then to each value of x (or y) satisfying this equation there corresponds in general a single value of y (or x), and consequently a single point of intersection; the number of intersections is thus equal to the order of the resultant equation in x (or y).
Supposing that the two curves are of the orders m, n, respectively, then the order of the resultant equation is in general and at most = mn; in particular, if the curve of the order n is an arbitrary line (n = 1), then the order of the resultant equation is = m; and the curve of the order m meets therefore the line in m points. But the resultant equation may have all or any of its roots imaginary, and it is thus not always that there are m real intersections.
The notion of imaginary intersections, thus presenting itself, through algebra, in geometry, must be accepted in geometry—and it in fact plays an all-important part in modern geometry. As in algebra we say that an equation of the mth order has m roots, viz. we state this generally without in the first instance, or it may be without ever, distinguishing whether these are real or imaginary; so in geometry we say that a curve of the mth order is met by an arbitrary line in m points, or rather we thus, through algebra, obtain the proper geometrical definition of a curve of the mth order, as a curve which is met by an arbitrary line in m points (that is, of course, in m, and not more than m, points).
The theorem of the m intersections has been stated in regard to an arbitrary line; in fact, for particular lines the resultant equation may be or appear to be of an order less than m; for instance, taking m = 2, if the hyperbola xy − 1 = 0 be cut by the line y = β, the resultant equation in x is βx − 1 = 0, and there is apparently only the intersection (x = 1/β, y = β); but the theorem is, in fact, true for every line whatever: a curve of the order m meets every line whatever in precisely m points. We have, in the case just referred to, to take account of a point at infinity on the line y = β; the two intersections are the point (x = 1/β, y = β), and the point at infinity on the line y = β.
It is, moreover, to be noticed that the points at infinity may be all or any of them imaginary, and that the points of intersection, whether finite or at infinity, real or imaginary, may coincide two or more of them together, and have to be counted accordingly; to support the theorem in its universality, it is necessary to take account of these various circumstances.
5. Line at Infinity.—The foregoing notion of a point at infinity is a very important one in modern geometry; and we have also to consider the paradoxical statement that in plane geometry, or say as regards the plane, infinity is a right line. This admits of an easy illustration in solid geometry. If with a given centre of projection, by drawing from it lines to every point of a given line, we project the given line on a given plane, the projection is a line, i.e. this projection is the intersection of the given plane with the plane through the centre and the given line. Say the projection is always a line, then if the figure is such that the two planes are parallel, the projection is the intersection of the given plane by a parallel plane, or it is the system of points at infinity on the given plane, that is, these points at infinity are regarded as situate on a given line, the line infinity of the given plane.1
Reverting to the purely plane theory, infinity is a line, related like any other right line to the curve, and thus intersecting it in m points, real or imaginary, distinct or coincident.
Descartes in the Géométrie defined and considered the remarkable curves called after him the ovals of Descartes, or simply Cartesians, which will be again referred to. The next important work, founded on the Géométrie, was Sir Isaac Newton’s Enumeratio linearum tertii ordinis (1706), establishing a classification of cubic curves founded chiefly on the nature of their infinite branches, which was in some details completed by James Stirling (1692-1770), Patrick Murdoch (d. 1774) and Gabriel Cramer; the work also contains the remarkable theorem (to be again referred to), that there are five kinds of cubic curves giving by their projections every cubic curve whatever. Various properties of curves in general, and of cubic curves, are established in Colin Maclaurin’s memoir, “De linearum geometricarum proprietatibus generalibus Tractatus” (posthumous, say 1746, published in the 6th edition of his Algebra). We have in it a particular kind of correspondence of two points on a cubic curve, viz. two points correspond to each other when the tangents at the two points again meet the cubic in the same point.
6. Reciprocal Polars. Intersections of Circles. Duality. Trilinear and Tangential Co-ordinates.—The Géométrie descriptive, by Gaspard Monge, was written in the year 1794 or 1795 (7th edition, Paris, 1847), and in it we have stated, in plano with regard to the circle, and in three dimensions with regard to a surface of the second order, the fundamental theorem of reciprocal polars, viz. “Given a surface of the second order and a circumscribed conic surface which touches it ... then if the conic surface moves so that its summit is always in the same plane, the plane of the curve of contact passes always through the same point.” The theorem is here referred to partly on account of its bearing on the theory of imaginaries in geometry. It is in Charles Julian Brianchon’s memoir “Sur les surfaces du second degré” (Jour. Polyt. t. vi. 1806) shown how for any given position of the summit the plane of contact is determined, or reciprocally; say the plane XY is determined when the point P is given, or reciprocally; and it is noticed that when P is situate in the interior of the surface the plane XY does not cut the surface; that is, we have a real plane XY intersecting the surface in the imaginary curve of contact of the imaginary circumscribed cone having for its summit a given real point P inside the surface.
Stating the theorem in regard to a conic, we have a real point P (called the pole) and a real line XY (called the polar), the line joining the two (real or imaginary) points of contact of the (real or imaginary) tangents drawn from the point to the conic; and the theorem is that when the point describes a line the line passes through a point, this line and point being polar and pole to each other. The term “pole” was first used by François Joseph Servois, and “polar” by Joseph Diez Gergonne (Gerg. t. i. and iii., 1810-1813); and from the theorem we have the method of reciprocal polars for the transformation of geometrical theorems, used already by Brianchon (in the memoir above referred to) for the demonstration of the theorem called by his name, and in a similar manner by various writers in the earlier volumes of Gergonne. We are here concerned with the method less in itself than as leading to the general notion of duality.
Bearing in a somewhat similar manner also on the theory of imaginaries in geometry (but the notion presents itself in a more explicit form), there is the memoir by L. Gaultier, on the graphical construction of circles and spheres (Jour. Polyt. t. ix., 1813). The well-known theorem as to radical axes may be stated as follows. Consider two circles partially drawn so that it does not appear whether the circles, if completed, would or would not intersect in real points, say two arcs of circles; then we can, by means of a third circle drawn so as to intersect in two real points each of the two arcs, determine a right line, which, if the complete circles intersect in two real points, passes through the points, and which is on this account regarded as a line passing through two (real or imaginary) points of intersection of the two circles. The construction in fact is, join the two points in which the third circle meets the first arc, and join also the two points in which the third circle meets the second arc, and from the point of intersection of the two joining lines, let fall a perpendicular on the line joining the centre of the two circles; this perpendicular (considered as an indefinite line) is what Gaultier terms the “radical axis of the two circles”; it is a line determined by a real construction and itself always real; and by what precedes it is the line joining two (real or imaginary, as the case may be) intersections of the given circles.
The intersections which lie on the radical axis are two out of the four intersections of the two circles. The question as to the remaining two intersections did not present itself to Gaultier, but it is answered in Jean Victor Poncelet’s Traité des propriétés projectives (1822), where we find (p. 49) the statement, “deux circles placés arbitrairement sur un plan ... ont idéalement deux points imaginaires communs à l’infini”; that is, a circle qua curve of the second order is met by the line infinity in two points; but, more than this, they are the same two points for any circle whatever. The points in question have since been called (it is believed first by Dr George Salmon) the circular points at infinity, or they may be called the circular points; these are also frequently spoken of as the points I, J; and we have thus the circle characterized as a conic which passes through the two circular points at infinity; the number of conditions thus imposed upon the conic is = 2, and there remain three arbitrary constants, which is the right number for the circle. Poncelet throughout his work makes continual use of the foregoing theories of imaginaries and infinity, and also of the before-mentioned theory of reciprocal polars.
Poncelet’s two memoirs Sur les centres des moyennes harmoniques and Sur la théorie générale des polaires réciproques, although presented to the Paris Academy in 1824, were only published (Crelle, t. iii. and iv., 1828, 1829) subsequent to the memoir by Gergonne, Considérations philosophiques sur les élémens de la science de l’étendue (Gerg. t. xvi., 1825-1826). In this memoir by Gergonne, the theory of duality is very clearly and explicitly stated; for instance, we find “dans la géométrie plane, à chaque théorème il en répond nécessairement un autre qui s’en déduit en échangeant simplement entre eux les deux mots points et droites; tandis que dans la géométrie de l’espace ce sont les mots points et plans qu’il faut échanger entre eux pour passer d’un théorème à son corrélatif”; and the plan is introduced of printing correlative theorems, opposite to each other, in two columns. There was a reclamation as to priority by Poncelet in the Bulletin universel reprinted with remarks by Gergonne (Gerg. t. xix., 1827), and followed by a short paper by Gergonne, Rectifications de quelques théorèmes, &c., which is important as first introducing the word class. We find in it explicitly the two correlative definitions: “a plane curve is said to be of the mth degree (order) when it has with a line m real or ideal intersections,” and “a plane curve is said to be of the mth class when from any point of its plane there can be drawn to it m real or ideal tangents.”
It may be remarked that in Poncelet’s memoir on reciprocal polars, above referred to, we have the theorem that the number of tangents from a point to a curve of the order m, or say the class of the curve, is in general and at most = m(m − 1), and that he mentions that this number is subject to reduction when the curve has double points or cusps.
The theorem of duality as regards plane figures may be thus stated: two figures may correspond to each other in such manner that to each point and line in either figure there correspond in the other figure a line and point respectively. It is to be understood that the theorem extends to all points or lines, drawn or not drawn; thus if in the first figure there are any number of points on a line drawn or not drawn, the corresponding lines in the second figure, produced if necessary, must meet in a point. And we thus see how the theorem extends to curves, their points and tangents; if there is in the first figure a curve of the order m, any line meets it in m points; and hence from the corresponding point in the second figure there must be to the corresponding curve m tangents; that is, the corresponding curve must be of the class m.
Trilinear co-ordinates (see Geometry: Analytical) were first
used by E. E. Bobillier in the memoir Essai sur un nouveau mode
de recherche des propriétés de l’étendue (Gerg. t. xviii., 1827-1828).
It is convenient to use these rather than Cartesian co-ordinates.
We represent a curve of the order m by an equation (* x, y, z)m = 0,
the function on the left hand being a homogeneous rational and
integral function of the order m of the three co-ordinates (x, y, z);
clearly the number of constants is the same as for the equation
(*
x, y, z)m = 0,
the function on the left hand being a homogeneous rational and
integral function of the order m of the three co-ordinates (x, y, z);
clearly the number of constants is the same as for the equation
(* x, y, 1)m = 0 in Cartesian co-ordinates.
x, y, 1)m = 0 in Cartesian co-ordinates.
The theorem of duality is considered and developed, but chiefly in regard to its metrical applications, by Michel Chasles in the Mémoire de géométrie sur deux principes généraux de la science, la dualité et l’homographie, which forms a sequel to the Aperçu historique sur l’origine et le développement des méthodes en géométrie (Mém. de Brux. t. xi., 1837).
We now come to Julius Plücker; his “six equations” were given in a short memoir in Crelle (1842) preceding his great work, the Theorie der algebraischen Curven (1844). Plücker first gave a scientific dual definition of a curve, viz.; “A curve is a locus generated by a point, and enveloped by a line—the point moving continuously along the line, while the line rotates continuously about the point”; the point is a point (ineunt.) of the curve, the line is a tangent of the curve. And, assuming the above theory of geometrical imaginaries, a curve such that m of its points are situate in an arbitrary line is said to be of the order m; a curve such that n of its tangents pass through an arbitrary point is said to be of the class n; as already appearing, this notion of the order and class of a curve is, however, due to Gergonne. Thus the line is a curve of the order 1 and class 0; and corresponding dually thereto, we have the point as a curve of the order 0 and class 1.
Plücker, moreover, imagined a system of line-co-ordinates (tangential co-ordinates). (See Geometry: Analytical.) The Cartesian co-ordinates (x, y) and trilinear co-ordinates (x, y, z) are point-co-ordinates for determining the position of a point; the new co-ordinates, say (ξ, η, ζ) are line-co-ordinates for determining the position of a line. It is possible, and (not so much for any application thereof as in order to more fully establish the analogy between the two kinds of co-ordinates) important, to give independent quantitative definitions of the two kinds of co-ordinates; but we may also derive the notion of line-co-ordinates from that of point-co-ordinates; viz. taking ξx + ηy + ζz = 0 to be the equation of a line, we say that (ξ, η, ζ) are the line-co-ordinates of this line. A linear relation aξ + bη + cζ = 0 between these co-ordinate determines a point, viz. the point whose point-co-ordinates are (a, b, c); in fact, the equation in question aξ + bη + cζ = 0 expresses that the equation ξx + ηy + ζz = 0, where (x, y, z) are current point-co-ordinates, is satisfied on writing therein x, y, z = a, b, c; or that the line in question passes through the point (a, b, c). Thus (ξ, η, ζ) are the line-co-ordinates of any line whatever; but when these, instead of being absolutely arbitrary, are subject to the restriction aξ + bη + cζ = 0, this obliges the line to pass through a point (a, b, c); and the last-mentioned equation aξ + bη + cζ = 0 is considered as the line-equation of this point.
A line has only a point-equation, and a point has only a line-equation;
but any other curve has a point-equation and also a
line-equation; the point-equation (* x, y, z)m = 0 is the relation
which is satisfied by the point-co-ordinates (x, y, z) of each point
of the curve; and similarly the line-equation (*
x, y, z)m = 0 is the relation
which is satisfied by the point-co-ordinates (x, y, z) of each point
of the curve; and similarly the line-equation (* ξ, η, ζ)n = 0 is
the relation which is satisfied by the line-co-ordinates (ξ, η, ζ)
of each line (tangent) of the curve.
ξ, η, ζ)n = 0 is
the relation which is satisfied by the line-co-ordinates (ξ, η, ζ)
of each line (tangent) of the curve.
There is in analytical geometry little occasion for any explicit use of line-co-ordinates; but the theory is very important; it serves to show that in demonstrating by point-co-ordinates any purely descriptive theorem whatever, we demonstrate the correlative theorem; that is, we do not demonstrate the one theorem, and then (as by the method of reciprocal polars) deduce from it the other, but we do at one and the same time demonstrate the two theorems; our (x, y, z.) instead of meaning point-co-ordinates may mean line-co-ordinates, and the demonstration is then in every step of it a demonstration of the correlative theorem.
7. Singularities of a Curve. Plücker’s Equations.—The above dual generation explains the nature of the singularities of a plane curve. The ordinary singularities, arranged according to a cross division, are
| Proper. | Improper. | |
| Point-singularities— | 1. The stationary point, cusp or spinode; | 2. The double point or node; |
| Line-singularities— | 3. The stationary tangent or inflection; | 4. The double tangent; |
arising as follows:—
1. The cusp: the point as it travels along the line may come to rest, and then reverse the direction of its motion.
3. The stationary tangent: the line may in the course of its rotation come to rest, and then reverse the direction of its rotation.
2. The node: the point may in the course of its motion come to coincide with a former position of the point, the two positions of the line not in general coinciding.
4. The double tangent: the line may in the course of its motion come to coincide with a former position of the line, the two positions of the point not in general coinciding.
It may be remarked that we cannot with a real point and line obtain the node with two imaginary tangents (conjugate or isolated point or acnode), nor again the real double tangent with two imaginary points of contact; but this is of little consequence, since in the general theory the distinction between real and imaginary is not attended to.
The singularities (1) and (3) have been termed proper singularities, and (2) and (4) improper; in each of the first-mentioned cases there is a real singularity, or peculiarity in the motion; in the other two cases there is not; in (2) there is not when the point is first at the node, or when it is secondly at the node, any peculiarity in the motion; the singularity consists in the point coming twice into the same position; and so in (4) the singularity is in the line coming twice into the same position. Moreover (1) and (2) are, the former a proper singularity, and the latter an improper singularity, as regards the motion of the point; and similarly (3) and (4) are, the former a proper singularity, and the latter an improper singularity, as regards the motion of the line.
But as regards the representation of a curve by an equation, the case is very different.
First, if the equation be in point-co-ordinates, (3) and (4) are
in a sense not singularities at all. The curve (* x, y, z)m = 0,
or general curve of the order m, has double tangents and inflections;
(2) presents itself as a singularity, for the equations
dx(*
x, y, z)m = 0,
or general curve of the order m, has double tangents and inflections;
(2) presents itself as a singularity, for the equations
dx(* x, y, z)m = 0, dy(*
x, y, z)m = 0, dy(* x, y, z)m = 0, dz(*
x, y, z)m = 0, dz(* x, y, z)m = 0, implying
(*
x, y, z)m = 0, implying
(* x, y, z)m = 0, are not in general satisfied by any values (a, b, c)
whatever of (x, y, z), but if such values exist, then the point
(a, b, c) is a node or double point; and (1) presents itself as a
further singularity or sub-case of (2), a cusp being a double point
for which the two tangents becomes coincident.
x, y, z)m = 0, are not in general satisfied by any values (a, b, c)
whatever of (x, y, z), but if such values exist, then the point
(a, b, c) is a node or double point; and (1) presents itself as a
further singularity or sub-case of (2), a cusp being a double point
for which the two tangents becomes coincident.
In line-co-ordinates all is reversed:—(1) and (2) are not singularities; (3) presents itself as a sub-case of (4).
The theory of compound singularities will be referred to farther on.
In regard to the ordinary singularities, we have
| m, | the | order, |
| n | ” | class, |
| δ | ” | number of double points, |
| κ | ” | ” cusps, |
| τ | ” | ” double tangents, |
| ι | ” | ” inflections; |
and this being so, Plücker’s “six equations” are
| (1) | n = m (m − 1) − 2 δ − 3κ, |
| (2) | ι = 3m (m − 2) − 6δ − 8κ, |
| (3) | τ = ½m (m − 2) (m² − 9) − (m² − m − 6) (2δ + 3κ) + 2δ (δ − 1) + 6δκ + 9⁄2κ (κ − 1), |
| (4) | m = n (n − 1) − 2τ − 3ι, |
| (5) | κ = 3n (n − 2) − 6τ − 8ι, |
| (6) | δ = ½n (n − 2) (n² − 9) − (n² − n − 6) (2τ + 3ι) + 2τ (τ − 1) + 6τι + 9⁄2ι (ι − i). |
It is easy to derive the further forms—
| (7) | ι − κ | = 3 (n − m), |
| (8) | 2 (τ − δ) | = (n − m) (n + m − 9), |
| (9) | ½m (m + 3) − δ − 2κ | = ½n (n + 3) − τ − 2ι, |
| (10) | ½ (m − 1) (m − 2) − δ − κ | = ½ (n − 1) (n − 2) − τ − ι, |
| (11, 12) | m² − 2δ − 3κ | = n² − 2τ − 3ι, = m + n,— |
the whole system being equivalent to three equations only; and it may be added that using a to denote the equal quantities 3m + ι and 3n + κ everything may be expressed in terms of m, n, a. We have
| κ = a − 3n, ι = a − 3m, 2δ = m² − m + 8n − 3a. 2τ = n² − n + 8m − 3a. |
It is implied in Plücker’s theorem that, m, n, δ, κ, τ, ι signifying as above in regard to any curve, then in regard to the reciprocal curve, n, m, τ, ι, δ, κ will have the same significations, viz. for the reciprocal curve these letters denote respectively the order, class, number of nodes, cusps, double tangent and inflections.
The expression ½m(m + 3) − δ − 2κ is that of the number of the disposable constants in a curve of the order m with δ nodes and κ cusps (in fact that there shall be a node is 1 condition, a cusp 2 conditions) and the equation (9) thus expresses that the curve and its reciprocal contain each of them the same number of disposable constants.
For a curve of the order m, the expression ½m(m − 1) − δ − κ is termed the “deficiency” (as to this more hereafter); the equation (10) expresses therefore that the curve and its reciprocal have each of them the same deficiency.
The relations m² − 2δ − 3κ = n² − 2τ − 3ι = m + n, present themselves in the theory of envelopes, as will appear farther on.
With regard to the demonstration of Plücker’s equations it
is to be remarked that we are not able to write down the equation
in point-co-ordinates of a curve of the order m, having the given
numbers δ and κ of nodes and cusps. We can only use the general
equation (* x, y, z)m = 0, say for shortness u = 0, of a curve of the
mth order, which equation, so long as the coefficients remain
arbitrary, represents a curve without nodes or cusps. Seeking
then, for this curve, the values, n, ι, τ of the class, number of
inflections, and number of double tangents,—first, as regards
the class, this is equal to the number of tangents which can be
drawn to the curve from an arbitrary point, or what is the same
thing, it is equal to the number of the points of contact of these
tangents. The points of contact are found as the intersections
of the curve u = 0 by a curve depending on the position of the
arbitrary point, and called the “first polar” of this point;
the order of the first polar is = m − 1, and the number of intersections
is thus = m(m − 1). But it can be shown, analytically
or geometrically, that if the given curve has a node, the first
polar passes through this node, which therefore counts as two
intersections, and that if the curve has a cusp, the first polar
passes through the cusp, touching the curve there, and hence
the cusp counts as three intersections. But, as is evident, the
node or cusp is not a point of contact of a proper tangent from the
arbitrary point; we have, therefore, for a node a diminution 2,
and for a cusp a diminution 3, in the number of the intersections;
and thus, for a curve with δ nodes and κ cusps, there is a diminution
2δ + 3κ, and the value of n is n = m(m − 1) − 2δ −
3κ.
x, y, z)m = 0, say for shortness u = 0, of a curve of the
mth order, which equation, so long as the coefficients remain
arbitrary, represents a curve without nodes or cusps. Seeking
then, for this curve, the values, n, ι, τ of the class, number of
inflections, and number of double tangents,—first, as regards
the class, this is equal to the number of tangents which can be
drawn to the curve from an arbitrary point, or what is the same
thing, it is equal to the number of the points of contact of these
tangents. The points of contact are found as the intersections
of the curve u = 0 by a curve depending on the position of the
arbitrary point, and called the “first polar” of this point;
the order of the first polar is = m − 1, and the number of intersections
is thus = m(m − 1). But it can be shown, analytically
or geometrically, that if the given curve has a node, the first
polar passes through this node, which therefore counts as two
intersections, and that if the curve has a cusp, the first polar
passes through the cusp, touching the curve there, and hence
the cusp counts as three intersections. But, as is evident, the
node or cusp is not a point of contact of a proper tangent from the
arbitrary point; we have, therefore, for a node a diminution 2,
and for a cusp a diminution 3, in the number of the intersections;
and thus, for a curve with δ nodes and κ cusps, there is a diminution
2δ + 3κ, and the value of n is n = m(m − 1) − 2δ −
3κ.
Secondly, as to the inflections, the process is a similar one; it can be shown that the inflections are the intersections of the curve by a derivative curve called (after Ludwig Otto Hesse who first considered it) the Hessian, defined geometrically as the locus of a point such that its conic polar (§8 below) in regard to the curve breaks up into a pair of lines, and which has an equation H = 0, where H is the determinant formed with the second differential coefficients of u in regard to the variables (x, y, z); H = 0 is thus a curve of the order 3(m − 2), and the number of inflections is = 3m(m − 2). But if the given curve has a node, then not only the Hessian passes through the node, but it has there a node the two branches at which touch respectively the two branches of the curve; and the node thus counts as six intersections; so if the curve has a cusp, then the Hessian not only passes through the cusp, but it has there a cusp through which it again passes, that is, there is a cuspidal branch touching the cuspidal branch of the curve, and besides a simple branch passing through the cusp, and hence the cusp counts as eight intersections. The node or cusp is not an inflection, and we have thus for a node a diminution 6, and for a cusp a diminution 8, in the number of the intersections; hence for a curve with δ nodes and κ cusps, the diminution is = 6δ + 8κ, and the number of inflections is ι = 3m(m − 2) − 6δ − 8κ.
Thirdly, for the double tangents; the points of contact of these are obtained as the intersections of the curve by a curve Π = 0, which has not as yet been geometrically defined, but which is found analytically to be of the order (m − 2)(m² − 9); the number of intersections is thus = m(m − 2)(m² − 9); but if the given curve has a node then there is a diminution = 4(m² − m − 6), and if it has a cusp then there is a diminution = 6(m² − m − 6), where, however, it is to be noticed that the factor (m² − m − 6) is in the case of a curve having only a node or only a cusp the number of the tangents which can be drawn from the node or cusp to the curve, and is used as denoting the number of these tangents, and ceases to be the correct expression if the number of nodes and cusps is greater than unity. Hence, in the case of a curve which has δ nodes and κ cusps, the apparent diminution 2(m² − m − 6)(2δ + 3κ) is too great, and it has in fact to be diminished by 2{2δ(δ − 1) + 6δκ + 9⁄2κ(κ − 1)}, or the half thereof is 4 for each pair of nodes, 6 for each combination of a node and cusp, and 9 for each pair of cusps. We have thus finally an expression for 2τ, = m(m − 2)(m² − 9) − &c.; or dividing the whole by 2, we have the expression for τ given by the third of Plücker’s equations.
It is obvious that we cannot by consideration of the equation u = 0 in point-co-ordinates obtain the remaining three of Plücker’s equations; they might be obtained in a precisely analogous manner by means of the equation v = 0 in line-co-ordinates, but they follow at once from the principle of duality, viz. they are obtained by the mere interchange of m, δ, κ, with n, τ, ι respectively.

To complete Plücker’s theory it is necessary to take account of compound singularities; it might be possible, but it is at any rate difficult, to effect this by considering the curve as in course of description by the point moving along the rotating line; and it seems easier to consider the compound singularity as arising from the variation of an actually described curve with ordinary singularities. The most simple case is when three double points come into coincidence, thereby giving rise to a triple point; and a somewhat more complicated one is when we have a cusp of the second kind, or node-cusp arising from the coincidence of a node, a cusp, an inflection, and a double tangent, as shown in the annexed figure, which represents the singularities as on the point of coalescing. The general conclusion (see Cayley, Quart. Math. Jour. t. vii., 1866, “On the higher singularities of plane curves”; Collected Works, v. 520) is that every singularity whatever may be considered as compounded of ordinary singularities, say we have a singularity = δ′ nodes, κ′ cusps, τ′ double tangents and ι′ inflections. So that, in fact, Plücker’s equations properly understood apply to a curve with any singularities whatever.
By means of Plücker’s equations we may form a table—
| m | n | δ | κ | τ | ι |
| 0 | 1 | − | − | 0 | 0 |
| 1 | 0 | 0 | 0 | − | − |
| 2 | 2 | 0 | 0 | 0 | 0 |
| 3 | 6 | 0 | 0 | 0 | 9 |
| ” | 4 | 1 | 0 | 0 | 3 |
| ” | 3 | 0 | 1 | 0 | 1 |
| 4 | 12 | 0 | 0 | 28 | 24 |
| ” | 10 | 1 | 0 | 16 | 18 |
| ” | 9 | 0 | 1 | 10 | 16 |
| ” | 8 | 2 | 0 | 8 | 12 |
| ” | 7 | 1 | 1 | 4 | 10 |
| ” | 6 | 0 | 2 | 1 | 8 |
| ” | 6 | 3 | 0 | 4 | 6 |
| ” | 5 | 2 | 1 | 2 | 4 |
| ” | 4 | 1 | 2 | 1 | 2 |
| ” | 3 | 0 | 3 | 1 | 0 |
The table is arranged according to the value of m; and we have m = 0, n = 1, the point; m = 1, n = 0, the line; m = 2, n = 2, the conic; of m = 3, the cubic, there are three cases, the class being 6, 4 or 3, according as the curve is without singularities, or as it has 1 node or 1 cusp; and so of m = 4, the quartic, there are ten cases, where observe that in two of them the class is = 6,—the reduction of class arising from two cusps or else from three nodes. The ten cases may be also grouped together into four, according as the number of nodes and cusps (δ + κ) is = 0, 1, 2 or 3.
The cases may be divided into sub-cases, by the consideration of compound singularities; thus when m = 4, n = 6, δ = 3, the three nodes may be all distinct, which is the general case, or two of them may unite together into the singularity called a tacnode, or all three may unite together into a triple point or else into an oscnode.
We may further consider the inflections and double tangents, as well in general as in regard to cubic and quartic curves.
The expression for the number of inflections 3m(m − 2) for a curve of the order m was obtained analytically by Plücker, but the theory was first given in a complete form by Hesse in the two papers “Über die Elimination, u.s.w.,” and “Über die Wendepuncte der Curven dritter Ordnung” (Crelle, t. xxviii., 1844); in the latter of these the points of inflection are obtained as the intersections of the curve u = 0 with the Hessian, or curve Δ = 0, where Δ is the determinant formed with the second derived functions of u. We have in the Hessian the first instance of a covariant of a ternary form. The whole theory of the inflections of a cubic curve is discussed in a very interesting manner by means of the canonical form of the equation x³ + y³ + z³ + 6lxyz = 0; and in particular a proof is given of Plücker’s theorem that the nine points of inflection of a cubic curve lie by threes in twelve lines.
It may be noticed that the nine inflections of a cubic curve represented by an equation with real coefficients are three real, six imaginary; the three real inflections lie in a line, as was known to Newton and Maclaurin. For an acnodal cubic the six imaginary inflections disappear, and there remain three real inflections lying in a line. For a crunodal cubic the six inflections which disappear are two of them real, the other four imaginary, and there remain two imaginary inflections and one real inflection. For a cuspidal cubic the six imaginary inflections and two of the real inflections disappear, and there remains one real inflection.
A quartic curve has 24 inflections; it was conjectured by George Salmon, and has been verified by H. G. Zeuthen that at most eight of these are real.
The expression ½m(m − 2)(m² − 9) for the number of double tangents of a curve of the order m was obtained by Plücker only as a consequence of his first, second, fourth and fifth equations. An investigation by means of the curve Π = 0, which by its intersections with the given curve determines the points of contact of the double tangents, is indicated by Cayley, “Recherches sur l’élimination et la théorie des courbes” (Crelle, t. xxxiv., 1847; Collected Works, vol. i. p. 337), and in part carried out by Hesse in the memoir “Über Curven dritter Ordnung” (Crelle, t. xxxvi., 1848). A better process was indicated by Salmon in the “Note on the Double Tangents to Plane Curves,” Phil. Mag., 1858; considering the m − 2 points in which any tangent to the curve again meets the curve, he showed how to form the equation of a curve of the order (m − 2), giving by its intersection with the tangent the points in question; making the tangent touch this curve of the order (m − 2), it will be a double tangent of the original curve. See Cayley, “On the Double Tangents of a Plane Curve” (Phil. Trans. t. cxlviii., 1859; Collected Works, iv. 186), and O. Dersch (Math. Ann. t. vii., 1874). The solution is still in so far incomplete that we have no properties of the curve Π = 0, to distinguish one such curve from the several other curves which pass through the points of contact of the double tangents.
A quartic curve has 28 double tangents, their points of contact determined as the intersections of the curve by a curve Π = 0 of the order 14, the equation of which in a very elegant form was first obtained by Hesse (1849). Investigations in regard to them are given by Plücker in the Theorie der algebraischen Curven, and in two memoirs by Hesse and Jacob Steiner (Crelle, t. xlv., 1855), in respect to the triads of double tangents which have their points of contact on a conic and other like relations. It was assumed by Plücker that the number of real double tangents might be 28, 16, 8, 4 or 0, but Zeuthen has found that the last case does not exist.
8. Invariants and Covariants. Polar Curves.—The Hessian Δ has just been spoken of as a covariant of the form u; the notion of invariants and covariants belongs rather to the form u than to the curve u = 0 represented by means of this form; and the theory may be very briefly referred to. A curve u = 0 may have some invariantive property, viz. a property independent of the particular axes of co-ordinates used in the representation of the curve by its equation; for instance, the curve may have a node, and in order to this, a relation, say A = 0, must exist between the coefficients of the equation; supposing the axes of co-ordinates altered, so that the equation becomes u′ = 0, and writing A′ = 0 for the relation between the new coefficients, then the relations A = 0, A′ = 0, as two different expressions of the same geometrical property, must each of them imply the other; this can only be the case when A, A′ are functions differing only by a constant factor, or say, when A is an invariant of u. If, however, the geometrical property requires two or more relations between the coefficients, say A = 0, B = 0, &c., then we must have between the new coefficients the like relations, A′ = 0, B′ = 0, &c., and the two systems of equations must each of them imply the other; when this is so, the system of equations, A = 0, B = 0, &c., is said to be invariantive, but it does not follow that A, B, &c., are of necessity invariants of u. Similarly, if we have a curve U = 0 derived from the curve u = 0 in a manner independent of the particular axes of co-ordinates, then from the transformed equation u’ = 0 deriving in like manner the curve U′ = 0, the two equations U = 0, U′ = 0 must each of them imply the other; and when this is so, U will be a covariant of u. The case is less frequent, but it may arise, that there are covariant systems U = 0, V = 0, &c., and U′ = 0, V′ = 0, &c., each implying the other, but where the functions U, V, &c., are not of necessity covariants of u.
If we take a fixed point (x′, y′, z′) and a curve u = 0 of order m, and suppose the axes of reference altered, so that x′, y′, z′ are linearly transformed in the same way as the current x, y, z, the curves [x′(∂/∂x) + y′(∂/∂y) + z′(∂/∂z)]ru = 0, (r = 1, 2, ... m − 1) have the covariant property. They are the polar curves of the point with regard to u = 0.
The theory of the invariants and covariants of a ternary cubic function u has been studied in detail, and brought into connexion with the cubic curve u = 0; but the theory of the invariants and covariants for the next succeeding case, the ternary quartic function, is still very incomplete.
9. Envelope of a Curve.—In further illustration of the Plückerian dual generation of a curve, we may consider the question of the envelope of a variable curve. The notion is very probably older, but it is at any rate to be found in Lagrange’s Théorie des fonctions analytiques (1798); it is there remarked that the equation obtained by the elimination of the parameter a from an equation ƒ(x, y, a) = 0 and the derived equation in respect to a is a curve, the envelope of the series of curves represented by the equation ƒ(x, y, a) = 0 in question. To develop the theory, consider the curve corresponding to any particular value of the parameter; this has with the consecutive curve (or curve belonging to the consecutive value of the parameter) a certain number of intersections and of common tangents, which may be considered as the tangents at the intersections; and the so-called envelope is the curve which is at the same time generated by the points of intersection and enveloped by the common tangents; we have thus a dual generation. But the question needs to be further examined. Suppose that in general the variable curve is of the order m with δ nodes and κ cusps, and therefore of the class n with τ double tangents and ι inflections, m, n, δ, κ, τ, ι being connected by the Plückerian equations,—the number of nodes or cusps may be 659 greater for particular values of the parameter, but this is a speciality which may be here disregarded. Considering the variable curve corresponding to a given value of the parameter, or say simply the variable curve, the consecutive curve has then also δ and κ nodes and cusps, consecutive to those of the variable curve; and it is easy to see that among the intersections of the two curves we have the nodes each counting twice, and the cusps each counting three times; the number of the remaining intersections is = m² − 2δ − 3κ. Similarly among the common tangents of the two curves we have the double tangents each counting twice, and the stationary tangents each counting three times, and the number of the remaining common tangents is = n² − 2τ − 3ι (= m² − 2δ − 3κ, inasmuch as each of these numbers is as was seen = m + n). At any one of the m² − 2δ − 3κ points the variable curve and the consecutive curve have tangents distinct from yet infinitesimally near to each other, and each of these two tangents is also infinitesimally near to one of the n² − 2τ − 3ι common tangents of the two curves; whence, attending only to the variable curve, and considering the consecutive curve as coming into actual coincidence with it, the n² − 2τ − 3ι common tangents are the tangents to the variable curve at the m² − 2δ − 3κ points respectively, and the envelope is at the same time generated by the m² − 2δ − 3κ points, and enveloped by the n² − 2τ − 3ι tangents; we have thus a dual generation of the envelope, which only differs from Plücker’s dual generation, in that in place of a single point and tangent we have the group of m² − 2δ − 3κ points and n² − 2τ − 3ι tangents.
The parameter which determines the variable curve may be given as a point upon a given curve, or say as a parametric point; that is, to the different positions of the parametric point on the given curve correspond the different variable curves, and the nature of the envelope will thus depend on that of the given curve; we have thus the envelope as a derivative curve of the given curve. Many well-known derivative curves present themselves in this manner; thus the variable curve may be the normal (or line at right angles to the tangent) at any point of the given curve; the intersection of the consecutive normals is the centre of curvature; and we have the evolute as at once the locus of the centre of curvature and the envelope of the normal. It may be added that the given curve is one of a series of curves, each cutting the several normals at right angles. Any one of these is a “parallel” of the given curve; and it can be obtained as the envelope of a circle of constant radius having its centre on the given curve. We have in like manner, as derivatives of a given curve, the caustic, catacaustic or diacaustic as the case may be, and the secondary caustic, or curve cutting at right angles the reflected or refracted rays.
10. Forms of Real Curves.—We have in much that precedes disregarded, or at least been indifferent to, reality; it is only thus that the conception of a curve of the m-th order, as one which is met by every right line in m points, is arrived at; and the curve itself, and the line which cuts it, although both are tacitly assumed to be real, may perfectly well be imaginary. For real figures we have the general theorem that imaginary intersections, &c., present themselves in conjugate pairs; hence, in particular, that a curve of an even order is met by a line in an even number (which may be = 0) of points; a curve of an odd order in an odd number of points, hence in one point at least; it will be seen further on that the theorem may be generalized in a remarkable manner. Again, when there is in question only one pair of points or lines, these, if coincident, must be real; thus, a line meets a cubic curve in three points, one of them real, and other two real or imaginary; but if two of the intersections coincide they must be real, and we have a line cutting a cubic in one real point and touching it in another real point. It may be remarked that this is a limit separating the two cases where the intersections are all real, and where they are one real, two imaginary.
Considering always real curves, we obtain the notion of a branch; any portion capable of description by the continuous motion of a point is a branch; and a curve consists of one or more branches. Thus the curve of the first order or right line consists of one branch; but in curves of the second order, or conics, the ellipse and the parabola consist each of one branch, the hyperbola of two branches. A branch is either re-entrant, or it extends both ways to infinity, and in this case, we may regard it as consisting of two legs (crura, Newton), each extending one way to infinity, but without any definite separation. The branch, whether re-entrant or infinite, may have a cusp or cusps, or it may cut itself or another branch, thus having or giving rise to crunodes or double points with distinct real tangents; an acnode, or double point with imaginary tangents, is a branch by itself,—it may be considered as an indefinitely small re-entrant branch. a branch may have inflections and double tangents, or there may be double tangents which touch two distinct branches; there are also double tangents with imaginary points of contact, which are thus lines having no visible connexion with the curve. A re-entrant branch not cutting itself may be everywhere convex, and it is then properly said to be an oval; but the term oval may be used more generally for any re-entrant branch not cutting itself; and we may thus speak of a once indented, twice indented oval, &c., or even of a cuspidate oval. Other descriptive names for ovals and re-entrant branches cutting themselves may be used when required; thus, in the last-mentioned case a simple form is that of a figure of eight; such a form may break up into two ovals or into a doubly indented oval or hour-glass. A form which presents itself is when two ovals, one inside the other, unite, so as to give rise to a crunode—in default of a better name this may be called, after the curve of that name, a limaçon (q.v.). Names may also be used for the different forms of infinite branches, but we have first to consider the distinction of hyperbolic and parabolic. The leg of an infinite branch may have at the extremity a tangent; this is an asymptote of the curve, and the leg is then hyperbolic; or the leg may tend to a fixed direction, but so that the tangent goes further and further off to infinity, and the leg is then parabolic; a branch may thus be hyperbolic or parabolic as to its two legs; or it may be hyperbolic as to one leg and parabolic as to the other. The epithets hyperbolic and parabolic are of course derived from the conic hyperbola and parabola respectively. The nature of the two kinds of branches is best understood by considering them as projections, in the same way as we in effect consider the hyperbola and the parabola as projections of the ellipse. If a line Ω cut an arc aa′ at b, so that the two segments ab, ba′ lie on opposite sides of the line, then projecting the figure so that the line Ω goes off to infinity, the tangent at b is projected into the asymptote, and the arc ab is projected into a hyperbolic leg touching the asymptote at one extremity; the arc ba′ will at the same time be projected into a hyperbolic leg touching the same asymptote at the other extremity (and on the opposite side), but so that the two hyperbolic legs may or may not belong to one and the same branch. And we thus see that the two hyperbolic legs belong to a simple intersection of the curve by the line infinity. Next, if the line Ω touch at b the arc aa’ so that the two portions ab, ba’ lie on the same side of the line Ω, then projecting the figure as before, the tangent at b, that is, the line Ω itself, is projected to infinity; the arc ab is projected into a parabolic leg, and at the same time the arc ba′ is projected into a parabolic leg, having at infinity the same direction as the other leg, but so that the two legs may or may not belong to the same branch. And we thus see that the two parabolic legs represent a contact of the line infinity with the curve,—the point of contact being of course the point at infinity determined by the common direction of the two legs. It will readily be understood how the like considerations apply to other cases,—for instance, if the line Ω is a tangent at an inflection, passes through a crunode, or touches one of the branches of a crunode, &c.; thus, if the line Ω passes through a crunode we have pairs of hyperbolic legs belonging to two parallel asymptotes. The foregoing considerations also show (what is very important) how different branches are connected together at infinity, and lead to the notion of a complete branch or circuit.
The two legs of a hyperbolic branch may belong to different asymptotes, and in this case we have the forms which Newton 660 calls inscribed, circumscribed, ambigene, &c.; or they may belong to the same asymptote, and in this case we have the serpentine form, where the branch cuts the asymptote, so as to touch it at its two extremities on opposite sides, or the conchoidal form, where it touches the asymptote on the same side. The two legs of a parabolic branch may converge to ultimate parallelism, as in the conic parabola, or diverge to ultimate parallelism, as in the semi-cubical parabola y² = x³, and the branch is said to be convergent, or divergent, accordingly; or they may tend to parallelism in opposite senses, as in the cubical parabola y = x³. As mentioned with regard to a branch generally, an infinite branch of any kind may have cusps, or, by cutting itself or another branch, may have or give rise to a crunode, &c.
11. Classification of Cubic Curves.—We may now consider the various forms of cubic curves as appearing by Newton’s Enumeratio, and by the figures belonging thereto. The species are reckoned as 72, which are numbered accordingly 1 to 72; but to these should be added 10a, 13a, 22a and 22b. It is not intended here to consider the division into species, nor even completely that into genera, but only to explain the principle of classification. It may be remarked generally that there are at most three infinite branches, and that there may besides be a re-entrant branch or oval.
The genera may be arranged as follows:—
| 1,2,3,4 | redundant hyperbolas |
| 5,6 | defective hyperbolas |
| 7,8 | parabolic hyperbolas |
| 9 | hyperbolisms of hyperbola |
| 10 | hyperbolisms of ellipse |
| 11 | hyperbolisms of parabola |
| 12 | trident curve |
| 13 | divergent parabolas |
| 14 | cubic parabola; |
and thus arranged they correspond to the different relations of the line infinity to the curve. First, if the three intersections by the line infinity are all distinct, we have the hyperbolas; if the points are real, the redundant hyperbolas, with three hyperbolic branches; but if only one of them is real, the defective hyperbolas, with one hyperbolic branch. Secondly, if two of the intersections coincide, say if the line infinity meets the curve in a onefold point and a twofold point, both of them real, then there is always one asymptote: the line infinity may at the twofold point touch the curve, and we have the parabolic hyperbolas; or the twofold point may be a singular point,—viz., a crunode giving the hyperbolisms of the hyperbola; an acnode, giving the hyperbolisms of the ellipse; or a cusp, giving the hyperbolisms of the parabola. As regards the so-called hyperbolisms, observe that (besides the single asymptote) we have in the case of those of the hyperbola two parallel asymptotes; in the case of those of the ellipse the two parallel asymptotes become imaginary, that is, they disappear; and in the case of those of the parabola they become coincident, that is, there is here an ordinary asymptote, and a special asymptote answering to a cusp at infinity. Thirdly, the three intersections by the line infinity may be coincident and real; or say we have a threefold point: this may be an inflection, a crunode or a cusp, that is, the line infinity may be a tangent at an inflection, and we have the divergent parabolas; a tangent at a crunode to one branch, and we have the trident curve; or lastly, a tangent at a cusp, and we have the cubical parabola.
It is to be remarked that the classification mixes together non-singular and singular curves, in fact, the five kinds presently referred to: thus the hyperbolas and the divergent parabolas include curves of every kind, the separation being made in the species; the hyperbolisms of the hyperbola and ellipse, and the trident curve, are nodal; the hyperbolisms of the parabola, and the cubical parabola, are cuspidal. The divergent parabolas are of five species which respectively belong to and determine the five kinds of cubic curves; Newton gives (in two short paragraphs without any development) the remarkable theorem that the five divergent parabolas by their shadows generate and exhibit all the cubic curves.
The five divergent parabolas are curves each of them symmetrical with regard to an axis. There are two non-singular kinds, the one with, the other without, an oval, but each of them has an infinite (as Newton describes it) campaniform branch; this cuts the axis at right angles, being at first concave, but ultimately convex, towards the axis, the two legs continually tending to become at right angles to the axis. The oval may unite itself with the infinite branch, or it may dwindle into a point, and we have the crunodal and the acnodal forms respectively; or if simultaneously the oval dwindles into a point and unites itself to the infinite branch, we have the cuspidal form. (See Parabola.) Drawing a line to cut any one of these curves and projecting the line to infinity, it would not be difficult to show how the line should be drawn in order to obtain a curve of any given species. We have herein a better principle of classification; considering cubic curves, in the first instance, according to singularities, the curves are non-singular, nodal (viz. crunodal or acnodal), or cuspidal; and we see further that there are two kinds of non-singular curves, the complex and the simplex. There is thus a complete division into the five kinds, the complex, simplex, crunodal, acnodal and cuspidal. Each singular kind presents itself as a limit separating two kinds of inferior singularity; the cuspidal separates the crunodal and the acnodal, and these last separate from each other the complex and the simplex.
The whole question is discussed very fully and ably by A. F. Möbius in the memoir “Ueber die Grundformen der Linien dritter Ordnung” (Abh. der K. Sachs. Ges. zu Leipzig, t. i., 1852). The author considers not only plane curves, but also cones, or, what is almost the same thing, the spherical curves which are their sections by a concentric sphere. Stated in regard to the cone, we have there the fundamental theorem that there are two different kinds of sheets; viz., the single sheet, not separated into two parts by the vertex (an instance is afforded by the plane considered as a cone of the first order generated by the motion of a line about a point), and the double or twin-pair sheet, separated into two parts by the vertex (as in the cone of the second order). And it then appears that there are two kinds of non-singular cubic cones, viz. the simplex, consisting of a single sheet, and the complex, consisting of a single sheet and a twin-pair sheet; and we thence obtain (as for cubic curves) the crunodal, the acnodal and the cuspidal kinds of cubic cones. It may be mentioned that the single sheet is a sort of wavy form, having upon it three lines of inflection, and which is met by any plane through the vertex in one or in three lines; the twin-pair sheet has no lines of inflection, and resembles in its form a cone on an oval base.
In general a cone consists of one or more single or twin-pair sheets, and if we consider the section of the cone by a plane, the curve consists of one or more complete branches, or say circuits, each of them the section of one sheet of the cone; thus, a cone of the second order is one twin-pair sheet, and any section of it is one circuit composed, it may be, of two branches. But although we thus arrive by projection at the notion of a circuit, it is not necessary to go out of the plane, and we may (with Zeuthen, using the shorter term circuit for his complete branch) define a circuit as any portion (of a curve) capable of description by the continuous motion of a point, it being understood that a passage through infinity is permitted. And we then say that a curve consists of one or more circuits; thus the right line, or curve of the first order, consists of one circuit; a curve of the second order consists of one circuit; a cubic curve consists of one circuit or else of two circuits.
A circuit is met by any right line always in an even number, or always in an odd number, of points, and it is said to be an even circuit or an odd circuit accordingly; the right line is an odd circuit, the conic an even circuit. And we have then the theorem, two odd circuits intersect in an odd number of points; an odd and an even circuit, or two even circuits, in an even number of points. An even circuit not cutting itself divides the plane into two parts, the one called the internal part, incapable of containing any odd circuit, the other called the external part, capable of containing an odd circuit.
We may now state in a more convenient form the fundamental distinction of the kinds of cubic curve. A non-singular cubic is simplex, consisting of one odd circuit, or it is complex, consisting of one odd circuit and one even circuit. It may be added that there are on the odd circuit three inflections, but on the even circuit no inflection; it hence also appears that from any point of the odd circuit there can be drawn to the odd circuit two tangents, and to the even circuit (if any) two tangents, but that from a point of the even circuit there cannot be drawn (either to the odd or the even circuit) any real tangent; consequently, in a simplex curve the number of tangents from any point is two; but in a complex curve the number is four, or none,—four if the point is on the odd circuit, none if it is on the even circuit. It at once appears from inspection of the figure of a non-singular cubic curve, which is the odd and which the even circuit. The singular kinds arise as before; in the crunodal and the cuspidal kinds the whole curve is an odd circuit, but in an acnodal kind the acnode must be regarded as an even circuit.
12. Quartic Curves.—The analogous question of the classification of quartics (in particular non-singular quartics and nodal quartics) is considered in Zeuthen’s memoir “Sur les différentes formes des courbes planes du quatrième ordre” (Math. Ann. t. vii., 1874). A non-singular quartic has only even circuits; it has at most four circuits external to each other, or two circuits one internal to the other, and in this last case the internal circuit has no double tangents or inflections. A very remarkable theorem is established as to the double tangents of such a quartic: distinguishing as a double tangent of the first kind a real double tangent which either twice touches the same circuit, or else touches the curve in two imaginary points, the number of the double tangents of the first kind of a non-singular quartic is = 4; it follows that the quartic has at most 8 real inflections. The forms of the non-singular quartics are very numerous, but it is not necessary to go further into the question.
We may consider in relation to a curve, not only the line infinity, but also the circular points at infinity; assuming the curve to be real, these present themselves always conjointly; thus a circle is a conic passing through the two circular points, and is thereby distinguished from other conics. Similarly a cubic through the two circular points is termed a circular cubic; a quartic through the two points is termed a circular quartic, and if it passes twice through each of them, that is, has each of them for a node, it is termed a bicircular quartic. Such a quartic is of course binodal (m = 4, δ = 2, κ = 0); it has not in general, but it may have, a third node or a cusp. Or again, we may have a quartic curve having a cusp at each of the circular points: such a curve is a “Cartesian,” it being a complete definition of the Cartesian to say that it is a bicuspidal quartic curve (m = 4, δ = 0, κ = 2), having a cusp at each of the circular points. The circular cubic and the bicircular quartic, together with the Cartesian (being in one point of view a particular case thereof), are interesting curves which have been much studied, generally, and in reference to their focal properties.
13. Foci.—The points called foci presented themselves in the theory of the conic, and were well known to the Greek geometers, but the general notion of a focus was first established by Plücker (in the memoir “Über solche Puncte die bei Curven einer höheren Ordnung den Brennpuncten der Kegelschnitte entsprechen” (Crelle, t. x., 1833). We may from each of the circular points draw tangents to a given curve; the intersection of two such tangents (belonging of course to the two circular points respectively) is a focus. There will be from each circular point λ tangents (λ, a number depending on the class of the curve and its relation to the line infinity and the circular points, = 2 for the general conic, 1 for the parabola, 2 for a circular cubic, or bicircular quartic, &c.); the λ tangents from the one circular point and those from the other circular point intersect in λ real foci (viz. each of these is the only real point on each of the tangents through it), and in λ² − λ imaginary foci; each pair of real foci determines a pair of imaginary foci (the so-called antipoints of the two real foci), and the ½λ(λ − 1) pairs of real foci thus determine the λ² − λ imaginary foci. There are in some cases points termed centres, or singular or multiple foci (the nomenclature is unsettled), which are the intersections of improper tangents from the two circular points respectively; thus, in the circular cubic, the tangents to the curve at the two circular points respectively (or two imaginary asymptotes of the curve) meet in a centre.
14. Distance and Angle. Curves described mechanically.—The notions of distance and of lines at right angles are connected with the circular points; and almost every construction of a curve by means of lines of a determinate length, or at right angles to each other, and (as such) mechanical constructions by means of linkwork, give rise to curves passing the same definite number of times through the two circular points respectively, or say to circular curves, and in which the fixed centres of the construction present themselves as ordinary, or as singular, foci. Thus the general curve of three bar-motion (or locus of the vertex of a triangle, the other two vertices whereof move on fixed circles) is a tricircular sextic, having besides three nodes (m = 6, δ = 3 + 3 + 3 = 9), and having the centres of the fixed circles each for a singular focus; there is a third singular focus, and we have thus the remarkable theorem (due to S. Roberts) of the triple generation of the curve by means of the three several pairs of singular foci.
Again, the normal, qua line at right angles to the tangent, is connected with the circular points, and these accordingly present themselves in the before-mentioned theories of evolutes and parallel curves.
15. Theories of Correspondence.—We have several recent theories which depend on the notion of correspondence: two points whether in the same plane or in different planes, or on the same curve or in different curves, may determine each other in such wise that to any given position of the first point there correspond α′ positions of the second point, and to any given position of the second point a positions of the first point; the two points have then an (α, α) correspondence; and if α, α are each = 1, then the two points have α (1, 1) or rational correspondence. Connecting with each theory the author’s name, the theories in question are G. F. B. Riemann, the rational transformation of a plane curve; Luigi Cremona, the rational transformation of a plane; and Chasles, correspondence of points on the same curve, and united points. The theory first referred to, with the resulting notion of “Geschlecht,” or deficiency, is more than the other two an essential part of the theory of curves, but they will all be considered.
Riemann’s results are contained in the memoirs on “Abelian Integrals,” &c. (Crelle, t. liv., 1857), and we have next R. F. A. Clebsch, “Über die Singularitäten algebraischer Curven” (Crelle, t. lxv., 1865), and Cayley, “On the Transformation of Plane Curves” (Proc. Lond. Math. Soc. t. i., 1865; Collected Works, vol. vi. p. 1). The fundamental notion of the rational transformation is as follows:—
Taking u, X, Y, Z to be rational and integral functions (X, Y, Z all of the same order) of the co-ordinates (x, y, z), and u′, X′, Y′, Z′ rational and integral functions (X′, Y′, Z′, all of the same order) of the co-ordinates (x′, y′, z′), we transform a given curve u = 0, by the equations of x′ : y′ : z′ = X : Y : Z, thereby obtaining a transformed curve u′ = 0, and a converse set of equations x : y : z = X′ : Y′ : Z′; viz. assuming that this is so, the point (x, y, z) on the curve u = 0 and the point (x′, y′, z′) on the curve u′ = 0 will be points having a (1, 1) correspondence. To show how this is, observe that to a given point (x, y, z) on the curve u = 0 there corresponds a single point (x′, y′, z′) determined by the equations x′ : y′ : z′ = X : Y : Z; from these equations and the equation u = 0 eliminating x, y, z, we obtain the equation u′ = 0 of the transformed curve. To a given point (x′, y′, z′) not on the curve u’ = 0 there corresponds, not a single point, but the system of points (x, y, z) given by the equations x′ : y′ : z′ = X : Y : Z, viz., regarding x′, y′, z′ as constants (and to fix the ideas, assuming that the curves X = 0, Y = 0, Z = 0, have no common intersections), these are the points of intersection of the curves X : Y : Z, = x′ : y′ : z′, but no one of these points is situate on the curve u = 0. If, however, the point (x′, y′, z′) is situate on the curve u′ = 0, then one point of the system of points in question is situate on the curve u = 0, that is, to a given point of the curve u′ = 0 there corresponds a single point of the curve u = 0; and hence also this point must be given by a system of equations such as x : y : z = X′ : Y′ : Z′.
It is an old and easily proved theorem that, for a curve of 662 the order m, the number δ + κ of nodes and cusps is at most = ½(m − 1)(m − 2); for a given curve the deficiency of the actual number of nodes and cusps below this maximum number, viz. ½(m − 1)(m − 2) − δ − κ, is the “Geschlecht” or “deficiency,” of the curve, say this is = D. When D = 0, the curve is said to be unicursal, when = 1, bicursal, and so on.
The general theorem is that two curves corresponding rationally to each other have the same deficiency. [In particular a curve and its reciprocal have this rational or (1, 1) correspondence, and it has been already seen that a curve and its reciprocal have the same deficiency.]
A curve of a given order can in general be rationally transformed into a curve of a lower order; thus a curve of any order for which D = 0, that is, a unicursal curve, can be transformed into a line; a curve of any order having the deficiency 1 or 2 can be rationally transformed into a curve of the order D + 2, deficiency D; and a curve of any order deficiency = or > 3 can be rationally transformed into a curve of the order D + 3, deficiency D.
Taking x′, y′, z′ as co-ordinates of a point of the transformed curve, and in its equation writing x′ : y′ : z′ = 1 : θ : φ we have φ a certain irrational function of θ, and the theorem is that the co-ordinates x, y, z of any point of the given curve can be expressed as proportional to rational and integral functions of θ, φ, that is, of θ and a certain irrational function of θ.
In particular if D = 0, that is, if the given curve be unicursal, the transformed curve is a line, φ is a mere linear function of θ, and the theorem is that the co-ordinates x, y, z of a point of the unicursal curve can be expressed as proportional to rational and integral functions of θ; it is easy to see that for a given curve of the order m, these functions of θ must be of the same order m.
If D = 1, then the transformed curve is a cubic; it can be shown that in a cubic, the axes of co-ordinates being properly chosen, φ can be expressed as the square root of a quartic function of θ; and the theorem is that the co-ordinates x, y, z of a point of the bicursal curve can be expressed as proportional to rational and integral functions of θ, and of the square root of a quartic function of θ.
And so if D = 2, then the transformed curve is a nodal quartic; φ can be expressed as the square root of a sextic function of θ and the theorem is, that the co-ordinates x, y, z of a point of the tricursal curve can be expressed as proportional to rational and integral functions of θ, and of the square root of a sextic function of θ. But D = 3, we have no longer the like law, viz. φ is not expressible as the square root of an octic function of θ.
Observe that the radical, square root of a quartic function, is connected with the theory of elliptic functions, and the radical, square root of a sextic function, with that of the first kind of Abelian functions, but that the next kind of Abelian functions does not depend on the radical, square root of an octic function.
It is a form of the theorem for the case D = 1, that the co-ordinates x, y, z of a point of the bicursal curve, or in particular the co-ordinates of a point of the cubic, can be expressed as proportional to rational and integral functions of the elliptic functions snu, cnu, dnu; in fact, taking the radical to be √1 − θ²·1 − k²θ², and writing θ = snu, the radical becomes = cnu, dnu; and we have expressions of the form in question.
It will be observed that the equations x′ : y′ : z′ = X : Y : Z before mentioned do not of themselves lead to the other system of equations x : y : z = X′ : Y′ : Z′, and thus that the theory does not in anywise establish a (1, 1) correspondence between the points (x, y, z) and (x′, y′, z′) of two planes or of the same plane; this is the correspondence of Cremona’s theory.
In this theory, given in the memoirs “Sulle trasformazioni geometriche delle figure piani,” Mem. di Bologna, t. ii. (1863) and t. v. (1865), we have a system of equations x′ : y′ : z′ = X : Y : Z which does lead to a system x : y : z = X′ : Y′ : Z′, where, as before, X, Y, Z denote rational and integral functions, all of the same order, of the co-ordinates x, y, z, and X′, Y′, Z′ rational and integral functions, all of the same order, of the co-ordinates x′, y′, z′, and there is thus a (1, 1) correspondence given by these equations between the two points (x, y, z) and (x′, y′, z′). To explain this, observe that starting from the equations of x′ : y′ : z′ = X : Y : Z, to a given point (x, y, z) there corresponds one point (x′, y′, z′), but that if n be the order of the functions X, Y, Z, then to a given point x′, y′, z′ there would, if the curves X = 0, Y = 0, Z = 0 had no common intersections, correspond n² points (x, y, z). If, however, the functions are such that the curves X = 0, Y = 0, Z = 0 have k common intersections, then among the n² points are included these k points, which are fixed points independent of the point (x′, y′, z′); so that, disregarding these fixed points, the number of points (x, y, z) corresponding to the given point (x′, y′, z′) is = n² − k; and in particular if k = n² − 1, then we have one corresponding point; and hence the original system of equations x′ : y′ : z′ = X : Y : Z must lead to the equivalent system x : y : z = X′ : Y′ : Z′; and in this system by the like reasoning the functions must be such that the curves X′ = 0, Y′ = 0, Z′ = 0 have n′² − 1 common intersections. The most simple example is in the two systems of equations x′ : y′ : z′ = yz : zx : xy and x : y : z = y′z′ : z′x′ : x′y′; where yz = 0, zx = 0, xy = 0 are conics (pairs of lines) having three common intersections, and where obviously either system of equations leads to the other system. In the case where X, Y, Z are of an order exceeding 2 the required number n² − 1 of common intersections can only occur by reason of common multiple points on the three curves; and assuming that the curves X = 0, Y = 0, Z = 0 have α1 + α2 + α3 ... + αn−1 common intersections, where the α1 points are ordinary points, the α2 points are double points, the α3 points are triple points, &c., on each curve, we have the condition
α1 + 4α2 + 9α3 + ... (n − 1)² αn−1 = n² − 1;
but to this must be joined the condition
α1 + 3α2 + 6α3 ... + ½n(n − 1) αn−1 = ½n (n + 3) − 2
(without which the transformation would be illusory); and the conclusion is that α1, α2, ... αn−1 may be any numbers satisfying these two equations. It may be added that the two equations together give
α2 + 3α3 ... + ½ (n − 1) (n − 2) αn−1 = ½ (n − 1) (n − 2),
which expresses that the curves X = 0, Y = 0, Z = 0 are unicursal. The transformation may be applied to any curve u = 0, which is thus rationally transformed into a curve u′ = 0, by a rational transformation such as is considered in Riemann’s theory: hence the two curves have the same deficiency.
Coming next to Chasles, the principle of correspondence is established and used by him in a series of memoirs relating to the conics which satisfy given conditions, and to other geometrical questions, contained in the Comptes rendus, t. lviii. (1864) et seq. The theorem of united points in regard to points in a right line was given in a paper, June-July 1864, and it was extended to unicursal curves in a paper of the same series (March 1866), “Sur les courbes planes ou à double courbure dont les points peuvent se déterminer individuellement—application du principe de correspondance dans la théorie de ces courbes.”
The theorem is as follows: if in a unicursal curve two points
have an (α, β) correspondence, then the number of united points
(or points each corresponding to itself) is = α + β. In fact in a
unicursal curve the co-ordinates of a point are given as proportional
to rational and integral functions of a parameter, so that any point
of the curve is determined uniquely by means of this parameter;
that is, to each point of the curve corresponds one value of the
parameter, and to each value of the parameter one point on the
curve; and the (α, β) correspondence between the two points is given
by an equation of the form (* θ,
1)α(φ, 1)β = 0 between their parameters
θ and φ; at a united point φ = θ, and the value of θ is given by
an equation of the order α + β. The extension to curves of any given
deficiency D was made in the memoir of Cayley, “On the correspondence
of two points on a curve,”—Proc. Lond. Math. Soc. t. i.
(1866; Collected Works, vol. vi. p. 9),—viz. taking P, P′ as the corresponding
points in an (α, α′) correspondence on a curve of deficiency
D, and supposing that when P is given the corresponding points P′
are found as the intersections of the curve by a curve Θ containing
the co-ordinates of P as parameters, and having with the given curve
k intersections at the point P, then the number of united points is
a = α + α′ + 2kD; and more generally, if the curve Θ intersect the
given curve in a set of points P′ each p times, a set of points Q′ each
g times, &c., in such manner that the points (P, P′) the points (P, Q′)
&c., are pairs of points corresponding to each other according to
distinct laws; then if (P, P′) are points having an (α, α′) correspondence
with a number = a of united points, (P, Q′) points having a (β, β′)
correspondence with a number = b of united points, and so on, the
theorem is that we have
θ,
1)α(φ, 1)β = 0 between their parameters
θ and φ; at a united point φ = θ, and the value of θ is given by
an equation of the order α + β. The extension to curves of any given
deficiency D was made in the memoir of Cayley, “On the correspondence
of two points on a curve,”—Proc. Lond. Math. Soc. t. i.
(1866; Collected Works, vol. vi. p. 9),—viz. taking P, P′ as the corresponding
points in an (α, α′) correspondence on a curve of deficiency
D, and supposing that when P is given the corresponding points P′
are found as the intersections of the curve by a curve Θ containing
the co-ordinates of P as parameters, and having with the given curve
k intersections at the point P, then the number of united points is
a = α + α′ + 2kD; and more generally, if the curve Θ intersect the
given curve in a set of points P′ each p times, a set of points Q′ each
g times, &c., in such manner that the points (P, P′) the points (P, Q′)
&c., are pairs of points corresponding to each other according to
distinct laws; then if (P, P′) are points having an (α, α′) correspondence
with a number = a of united points, (P, Q′) points having a (β, β′)
correspondence with a number = b of united points, and so on, the
theorem is that we have
p (a − α − α′) + q (b − β − β′) + ... = 2kD.
The principle of correspondence, or say rather the theorem of united points, is a most powerful instrument of investigation, which may be used in place of analysis for the determination of the number of solutions of almost every geometrical problem. We can by means of it investigate the class of a curve, number of inflections, &c.—in fact, Plücker’s equations; but it is necessary to take account of special solutions: thus, in one of the most simple instances, in finding the class of a curve, the cusps present themselves as special solutions.
Imagine a curve of order m, deficiency D, and let the corresponding points P, P′ be such that the line joining them passes through a given 663 point O; this is an (m − 1, m − 1) correspondence, and the value of k is = 1, hence the number of united points is = 2m − 2 + 2D; the united points are the points of contact of the tangents from O and (as special solutions) the cusps, and we have thus the relation n + κ = 2m − 2 + 2D; or, writing D = ½(m − 1)(m − 2) − δ − κ, this is n = m(m − 1) − 2δ − 3κ, which is right.
The principle in its original form as applying to a right line was used throughout by Chasles in the investigations on the number of the conics which satisfy given conditions, and on the number of solutions of very many other geometrical problems.
There is one application of the theory of the (α, α′) correspondence between two planes which it is proper to notice.
Imagine a curve, real or imaginary, represented by an equation (involving, it may be, imaginary coefficients) between the Cartesian co-ordinates u, u′; then, writing u = x + iy, u′ = x′ + iy′, the equation determines real values of (x, y), and of (x′, y′), corresponding to any given real values of (x′, y′) and (x, y) respectively; that is, it establishes a real correspondence (not of course a rational one) between the points (x, y) and (x′, y′); for example in the imaginary circle u² + u′² = (a + bi)², the correspondence is given by the two equations x² − y² + x′² − y′² = a² − b², xy + x′y′ = ab. We have thus a means of geometrical representation for the portions, as well imaginary as real, of any real or imaginary curve. Considerations such as these have been used for determining the series of values of the independent variable, and the irrational functions thereof in the theory of Abelian integrals, but the theory seems to be worthy of further investigation.
16. Systems of Curves satisfying Conditions.—The researches of Chasles (Comptes Rendus, t. lviii., 1864, et seq.) refer to the conics which satisfy given conditions. There is an earlier paper by J. P. E. Fauque de Jonquières, “Théorèmes généraux concernant les courbes géométriques planes d’un ordre quelconque,” Liouv. t. vi. (1861), which establishes the notion of a system of curves (of any order) of the index N, viz. considering the curves of the order n which satisfy ½n(n + 3) − 1 conditions, then the index N is the number of these curves which pass through a given arbitrary point. But Chasles in the first of his papers (February 1864), considering the conics which satisfy four conditions, establishes the notion of the two characteristics (μ, ν) of such a system of conics, viz. μ is the number of the conics which pass through a given arbitrary point, and ν is the number of the conics which touch a given arbitrary line. And he gives the theorem, a system of conics satisfying four conditions, and having the characteristics (μ, ν) contains 2ν − μ line-pairs (that is, conics, each of them a pair of lines), and 2μ − ν point-pairs (that is, conics, each of them a pair of points,—coniques infiniment aplaties), which is a fundamental one in the theory. The characteristics of the system can be determined when it is known how many there are of these two kinds of degenerate conics in the system, and how often each is to be counted. It was thus that Zeuthen (in the paper Nyt Bydrag, “Contribution to the Theory of Systems of Conics which satisfy four Conditions” (Copenhagen, 1865), translated with an addition in the Nouvelles Annales) solved the question of finding the characteristics of the systems of conics which satisfy four conditions of contact with a given curve or curves; and this led to the solution of the further problem of finding the number of the conics which satisfy five conditions of contact with a given curve or curves (Cayley, Comptes Rendus, t. lxiii., 1866; Collected Works, vol. v. p. 542), and “On the Curves which satisfy given Conditions” (Phil. Trans. t. clviii., 1868; Collected Works, vol. vi. p. 191).
It may be remarked that although, as a process of investigation, it is very convenient to seek for the characteristics of a system of conics satisfying 4 conditions, yet what is really determined is in every case the number of the conics which satisfy 5 conditions; the characteristics of the system (4p) of the conics which pass through 4p points are (5p), (4p, 1l), the number of the conics which pass through 5 points, and which pass through 4 points and touch 1 line: and so in other cases. Similarly as regards cubics, or curves of any other order: a cubic depends on 9 constants, and the elementary problems are to find the number of the cubics (9p), (8p, 1l), &c., which pass through 9 points, pass through 8 points and touch 1 line, &c.; but it is in the investigation convenient to seek for the characteristics of the systems of cubics (8p), &c., which satisfy 8 instead of 9 conditions.
The elementary problems in regard to cubics are solved very completely by S. Maillard in his Thèse, Recherche des caractéristiques des systèmes élémentaires des courbes planes du troisième ordre (Paris, 1871). Thus, considering the several cases of a cubic
| No. of consts. | |
| 1. With a given cusp | 5 |
| 2. ” cusp on a given line | 6 |
| 3. ” cusp | 7 |
| 4. ” a given node | 6 |
| 5. ” node on given line | 7 |
| 6. ” node | 8 |
| 7. non-singular | 9 |
he determines in every case the characteristics (μ, ν) of the corresponding systems of cubics (4p), (3p, 1l), &c. The same problems, or most of them, and also the elementary problems in regard to quartics are solved by Zeuthen, who in the elaborate memoir “Almindelige Egenskaber, &c.,” Danish Academy, t. x. (1873), considers the problem in reference to curves of any order, and applies his results to cubic and quartic curves.
The methods of Maillard and Zeuthen are substantially identical; in each case the question considered is that of finding the characteristics (μ, ν) of a system of curves by consideration of the special or degenerate forms of the curves included in the system. The quantities which have to be considered are very numerous. Zeuthen in the case of curves of any given order establishes between the characteristics μ, ν, and 18 other quantities, in all 20 quantities, a set of 24 equations (equivalent to 23 independent equations), involving (besides the 20 quantities) other quantities relating to the various forms of the degenerate curves, which supplementary terms he determines, partially for curves of any order, but completely only for quartic curves. It is the discussion and complete enumeration of the special or degenerate forms of the curves, and of the supplementary terms to which they give rise, that the great difficulty of the question seems to consist; it would appear that the 24 equations are a complete system, and that (subject to a proper determination of the supplementary terms) they contain the solution of the general problem.
17. Degeneration of Curves.—The remarks which follow have reference to the analytical theory of the degenerate curves which present themselves in the foregoing problem of the curves which satisfy given conditions.
A curve represented by an equation in point-co-ordinates may break up: thus if P1, P2, ... be rational and integral functions of the co-ordinates (x, y, z) of the orders m1, m2 ... respectively, we have the curve P1α1P2α2 ... = 0, of the order m, = α1m1 + α2m2 + ..., composed of the curve P1 = 0 taken α1 times, the curve P2 = 0 taken α2 times, &c.
Instead of the equation P1α1P2α2 ... = 0, we may start with an equation u = 0, where u is a function of the order m containing a parameter θ, and for a particular value say θ = 0, of the parameter reducing itself to P1α1P2α2.... Supposing θ indefinitely small, we have what may be called the penultimate curve, and when θ = 0 the ultimate curve. Regarding the ultimate curve as derived from a given penultimate curve, we connect with the ultimate curve, and consider as belonging to it, certain points called “summits” on the component curves P1 = 0, P2 = 0 respectively; a summit Σ is a point such that, drawing from an arbitrary point O the tangents to the penultimate curve, we have OΣ as the limit of one of these tangents. The ultimate curve together with its summits may be regarded as a degenerate form of the curve u = 0. Observe that the positions of the summits depend on the penultimate curve u = 0, viz. on the values of the coefficients in the terms multiplied by θ, θ², ...; they are thus in some measure arbitrary points as regards the ultimate curve P1α1P2α2 ... = 0.
It may be added that we have summits only on the component curves P1 = 0, of a multiplicity α1 > 1; the number of summits on such a curve is in general = (α1² − α1)m1². Thus assuming that the penultimate curve is without nodes or cusps, the number of the tangents to it is = m² − m, = (α1m1 + α2m2 + ...)² − (α1m1 + α2m2 + ...). Taking P1 = 0 to have δ1 nodes and κ1 cusps, and therefore its class n1 to be = m1² − m1 − 2δ1 − 3κ1, &c., the expression for the number of tangents to the penultimate curve is
= (α1² − α1) m1² + (α2² − α2) m2² + ... + 2α1α2m1m2 +
+ α1 (n1 + 2δ1 + 3κ1) + α2 (n2 + 2δ2 + 3κ2) + ...
where a term 2α1α2m1m2 indicates tangents which are in the limit the lines drawn to the intersections of the curves P1 = 0, P2 = 0 each line 2α1α2 times; a term α1(n1 + 2δ1 + 3κ1) tangents which are in the 664 limit the proper tangents to P1 = 0 each α1 times, the lines to its nodes each 2α1 times, and the lines to its cusps each 3α1, times; the remaining terms (α1² − α1)m1² + (α2² − α2)m2² + ... indicate tangents which are in the limit the lines drawn to the several summits, that is, we have (α1² − α1)m1² summits on the curve P1 = 0, &c.
There is, of course, a precisely similar theory as regards line-co-ordinates; taking Π1, Π2, &c., to be rational and integral functions of the co-ordinates (ξ, η, ζ) we connect with the ultimate curve Π1α1Π2α2 ... = 0, and consider as belonging to it, certain lines, which for the moment may be called “axes” tangents to the component curves Π1 = 01, Π2 = 0 respectively. Considering an equation in point-co-ordinates, we may have among the component curves right lines, and if in order to put these in evidence we take the equation to be L1γ1 .. P1α1 ... = 0, where L1 = 0 is a right line, P1 = 0 a curve of the second or any higher order, then the curve will contain as part of itself summits not exhibited in this equation, but the corresponding line-equation will be 1Λδ1 ... Π1α1 = 0, where Λ1 = 0,... are the equations of the summits in question, Π1 = 0, &c., are the line-equations corresponding to the several point-equations P1 = 0, &c.; and this curve will contain as part of itself axes not exhibited by this equation, but which are the lines L1 = 0,... of the equation in point-co-ordinates.
18. Twisted Curves.—In conclusion a little may be said as to curves of double curvature, otherwise twisted curves or curves in space. The analytical theory by Cartesian co-ordinates was first considered by Alexis Claude Clairaut, Recherches sur les courbes à double courbure (Paris, 1731). Such a curve may be considered as described by a point, moving in a line which at the same time rotates about the point in a plane which at the same time rotates about the line; the point is a point, the line a tangent, and the plane an osculating plane, of the curve; moreover the line is a generating line, and the plane a tangent plane, of a developable surface or torse, having the curve for its edge of regression. Analogous to the order and class of a plane curve we have the order, rank and class of the system (assumed to be a geometrical one), viz. if an arbitrary plane contains m points, an arbitrary line meets r lines, and an arbitrary point lies in n planes, of the system, then m, r, n are the order, rank and class respectively. The system has singularities, and there exist between m, r, n and the numbers of the several singularities equations analogous to Plücker’s equations for a plane curve.
It is a leading point in the theory that a curve in space cannot in general be represented by means of two equations U = 0, V = 0; the two equations represent surfaces, intersecting in a curve; but there are curves which are not the complete intersection of any two surfaces; thus we have the cubic in space, or skew cubic, which is the residual intersection of two quadric surfaces which have a line in common; the equations U = 0, V = 0 of the two quadric surfaces represent the cubic curve, not by itself, but together with the line.
Authorities.—In addition to the copious authorities mentioned in the text above, see Gabriel Cramer, Introduction à l’analyse des lignes courbes algébriques (Geneva, 1750). Bibliographical articles are given in the Ency. der math. Wiss. Bd. iii. 2, 3 (Leipzig, 1902-1906); H. C. F. von Mangoldt, “Anwendung der Differential- und Integralrechnung auf Kurven und Flächen,” Bd. iii. 3 (1902); F. R. v. Lilienthal, “Die auf einer Fläche gezogenen Kurven,” Bd. iii. 3 (1902); G. W. Scheffers, “Besondere transcendente Kurven,” Bd. iii. 3 (1903); H. G. Zeuthen, “Abzahlende Methoden,” Bd. iii. 2 (1906); L. Berzolari, “Allgemeine Theorie der höheren ebenen algebraischen Kurven,” Bd. iii. 2 (1906). Also A. Brill and M. Noether, “Die Entwicklung der Theorie der algebraischen Funktionen in älterer und neuerer Zeit” (Jahresb. der deutschen math. ver., 1894); E. Kötter, “Die Entwickelung der synthetischen Geometrie” (Jahresb. der deutschen math. ver., 1898-1901); E. Pascal, Repertorio di matematiche superiori, ii. “Geometrìa” (Milan, 1900); H. Wieleitner, Bibliographie der höheren algebraischen Kurven für den Zeitabschnitt von 1890-1894 (Leipzig, 1905).
Text-books:—G. Salmon, A Treatise on the Higher Plane Curves (Dublin, 1852, 3rd ed., 1879); translated into German by O. W. Fiedler, Analytische Geometrie der höheren ebenen Kurven (Leipzig, 2te Aufl., 1882); L. Cremona, Introduzione ad una teoria geometrica delle curve piane (Bologna, 1861); J. H. K. Durège, Die ebenen Kurven dritter Ordnung (Leipzig, 1871); R. F. A. Clebsch and C. L. F. Lindemann, Vorlesungen über Geometrie, Band i. and i2 (Leipzig, 1875-1876); H. Schroeter, Die Theorie der ebenen Kurven dritter Ordnung (Leipzig, 1888); H. Andoyer, Leçons sur la théorie des formes et la géométrie analytique supérieure (Paris, 1900); Wieleitner, Theorie der ebenen algebraischen Kurven höherer Ordnung (Leipzig, 1905).
1 In solid geometry infinity is a plane—its intersection with any given plane being the right line which is the infinity of this given plane.
CURVILINEAR, in architecture, that which is formed by curved or flowing lines; the roofs over the domes and vaults of the Byzantine churches were generally curvilinear. The term is also given to the flowing tracery of the Decorated and the Flamboyant styles.
CURWEN, HUGH (d. 1568), English ecclesiastic and statesman, was a native of Westmorland, and was educated at Cambridge, afterwards taking orders in the church. In May 1533 he expressed approval of Henry VIII.’s marriage with Anne Boleyn in a sermon preached before the king. In 1541 he became dean of Hereford, and in 1555 Queen Mary nominated him to the archbishopric of Dublin, and in the same year he was appointed lord chancellor of Ireland. He acted as one of the lords justices during the absence from Ireland of the lord deputy, the earl of Sussex, in 1557. On the accession of Elizabeth, Curwen at once accommodated himself to the new conditions by declaring himself a Protestant, and was continued in the office of lord chancellor. He was accused by the archbishop of Armagh of serious moral delinquency, and his recall was demanded both by the primate and the bishop of Meath. In 1567 Curwen resigned the see of Dublin and the office of lord chancellor, and was appointed bishop of Oxford. He died on the 1st of November 1568.
See John Strype, Life and Acts of Archbishop Parker (3 vols., Oxford, 1824), and Memorials of Thomas Cranmer (2 vols., Oxford, 1840); John D’Alton. Memoirs of the Archbishops of Dublin (Dublin, 1838).
CURWEN, JOHN (1816-1880), English Nonconformist minister and founder of the Tonic Sol-Fa system of musical teaching, was born at Heckmondwike, Yorkshire, of an old Cumberland family. His father was a Nonconformist minister, and he himself adopted this profession, which he practised till 1864, when he gave it up in order to devote himself to his new method of musical nomenclature, designed to avoid the use of the stave with its lines and spaces. He adapted it from that of Miss Sarah Ann Glover (1785-1867) of Norwich, whose Sol-Fa system was based on the ancient gamut; but she omitted the constant recital of the alphabetical names of each note and the arbitrary syllable indicating key relationship, and also the recital of two or more such syllables when the same note was common to as many keys (e.g. “C, Fa, Ut,” meaning that C is the subdominant of G and the tonic of C). The notes were represented by the initials of the seven syllables, still in use in Italy and France as their names but in the “Tonic Sol-Fa” the seven letters refer to key relationship and not to pitch. Curwen was led to feel the importance of a simple way of teaching how to sing by note by his experiences among Sunday-school teachers. Apart from Miss Glover, the same idea had been elaborated in France since J. J. Rousseau’s time, by Pierre Galin (1786-1821), Aimé Paris (1798-1866) and Emile Chevé (1804-1864), whose method of teaching how to read at sight also depended on the principle of “tonic relationship” being inculcated by the reference of every sound to its tonic, by the use of a numeral notation. Curwen brought out his Grammar of Vocal Music in 1843, and in 1853 started the Tonic Sol-Fa Association; and in 1879, after some difficulties with the education department, the Tonic Sol-Fa College was opened. Curwen also took to publishing, and brought out a periodical called the Tonic Sol-fa Reporter, and in his later life was occupied in directing the spreading organization of his system. He died at Manchester on the 26th of May 1880. His son John Spencer Curwen (b. 1847), who became principal of the Tonic Sol-Fa College, published Memorials of J. Curwen in 1882. The Sol-Fa system has been widely adopted for use in education, as an easily teachable method in the reading of music at sight, but its more ambitious aims, which are strenuously pushed, for providing a superior method of musical notation generally, have not recommended themselves to musicians at large.
CURZOLA (Serbo-Croatian Korčula or Karkar), an island in the Adriatic Sea, forming part of Dalmatia, Austria; and lying west of the Sabionicello promontory, from which it is divided by a strait less than 2 m. wide. Its length is about 25 m.; its average breadth, 4 m. Curzola (Korčula), the capital and 665 principal port, is a fortified town on the east coast, and occupies a rocky foreland almost surrounded by the sea. Besides the interesting church (formerly a cathedral), dating from the 12th or 13th century, the loggia or council chambers, and the palace of its former Venetian governors, it possesses the noble mansion of the Arnieri, and other specimens of the domestic architecture of the 15th and 16th centuries, together with the massive walls and towers, erected in 1420, and the 15th-century Franciscan monastery, with its beautiful Venetian Gothic cloister. The main resources of the islanders are boat-building (for which they are celebrated throughout the Adriatic), fishing and sea-faring, the cultivation of the vine, corn and olives, and breeding of mules. Pop. (1900) of island, 17,377; of capital (town and commune), 6486. Prehistoric grave-mounds are common on the hills of the interior, and in later times Curzola may have been a Phoenician settlement. Its early history is very obscure, but it was certainly colonized by Greeks from Cnidus. The present name is a corruption of the Gr. Κέρκυρα Μέλαινα, or Lat. Corcyra Nigra, “Black Corcyra”; and is perhaps due to the dark pines which still partly cover the island. In 998 Curzola first came under Venetian suzerainty. During the 12th century it was ruled by Hungary and Genoa in turn, and enjoyed a brief period of independence; but after 1255 its hereditary counts again submitted to Venice. The Roman Catholic see of Curzola, created in 1301, was only suppressed in 1806. Curzola surrendered to the Hungarians in 1358, was purchased by Ragusa (1413-1417), and finally declared itself subject to Venice in 1420. In 1571 it defended itself so gallantly against the Turks that it obtained the designation fidelissima. From 1776 to 1797 it succeeded Lesina as the main Venetian arsenal in this region. During the Napoleonic wars it was ruled successively by Russians, French and British, ultimately passing to Austria in 1815.
CURZON OF KEDLESTON, GEORGE NATHANIEL, 1st Baron (1859- ), English statesman, eldest son of the 4th baron Scarsdale, rector of Kedleston, Derbyshire, was born on the 11th of January 1859, and was educated at Eton and Balliol College, Oxford. At Oxford he was president of the Union, and after a brilliant university career was elected a fellow of All Souls College in 1883. He became assistant private secretary to Lord Salisbury in 1885, and in 1886 entered parliament as member for the Southport division of S.W. Lancashire. He was appointed under secretary for India in 1891-1892 and for foreign affairs in 1895-1898. In the meantime he had travelled in Central Asia, Persia, Afghanistan, the Pamirs, Siam, Indo-China and Korea, and published several books describing central and eastern Asia and the political problems connected with those regions. In 1895 he married Mary Victoria Leiter (d. 1906), daughter of a Chicago millionaire. In January 1899 he was appointed governor-general of India, where his extensive knowledge of Asiatic affairs showed itself in the inception of a strong foreign policy, while he took in hand the reform of every department of Indian administration. He was created an Irish peer on his appointment, the creation taking this form, it was understood, in order that he might remain free during his father’s lifetime to re-enter the House of Commons. Reaching India shortly after the suppression of the frontier risings of 1897-98, he paid special attention to the independent tribes of the north-west frontier, inaugurated a new province called the North West Frontier Province, and carried out a policy of conciliation mingled with firmness of control. The only trouble on this frontier during the period of his administration was the Mahsud Waziri campaign of 1901. Being mistrustful of Russian methods he exerted himself to encourage British trade in Persia, paying a visit to the Persian Gulf in 1903; while on the north-east frontier he anticipated a possible Russian advance by the Tibet Mission of 1903, which rendered necessary the employment of military force for the protection of the British envoys. The mission, which had the ostensible support of China as suzerain of Tibet, penetrated to Lhasa, where a treaty was signed in September 1904. In pursuance of his reforming policy Lord Curzon appointed a number of commissions to inquire into Indian education, irrigation, police and other branches of administration, on whose reports legislation was based during his second term of office as viceroy. With a view to improving British relations with the native chiefs and raising the character of their rule, he established the Imperial Cadet corps, settled the question of Berar with the nizam of Hyderabad, reduced the salt tax, and gave relief to the smaller income-tax payers. Lord Curzon exhibited much interest in the art and antiquities of India, and during his viceroyalty took steps for the preservation and restoration of many important monuments and buildings of historic interest. In January 1903 he presided at the durbar held at Delhi in honour of the coronation of King Edward VII. It was attended by all the leading native princes and by large numbers of visitors from Europe and America; and the magnificence of the spectacle surpassed anything that had previously been witnessed even in the gorgeous ceremonial of the East. On the expiration of his first term of office, Lord Curzon was reappointed governor-general. His second term of office was marked by the passing of several acts founded on the recommendations of his previous commissions, and by the partition of Bengal (1905), which roused bitter opposition amongst the natives of that province. A difference of opinion with the commander-in-chief, Lord Kitchener, regarding the position of the military member of council in India, led to a controversy in which Lord Curzon failed to obtain support from the home government. He resigned (1904) and returned to England. In 1904 he was appointed lord warden of the Cinque Ports; in the same year he was given the honorary degree of D.C.L. by Oxford University, and in 1908 he was elected chancellor of the university. In the latter year he was elected a representative peer for Ireland, and thus relinquished any idea of returning to the House of Commons. In 1909-1910 he took an active part in defending the House of Lords against the Liberals. Lord Curzon’s publications include Russia in Central Asia (1889); Persia and the Persian Question (1892); Problems of the Far East (1894; new ed., 1896).
See Caldwell Lipsett, Lord Curzon in India, 1898-1903 (1906); and C. J. O’Donnell, The Failure of Lord Curzon (1903).
CUSANUS, NICOLAUS (Nicholas of Cusa) (1401-1464), cardinal, theologian and scholar, was the son of a poor fisherman named Krypffs or Krebs, and derived the name by which he is known from the place of his birth, Kues or Cusa, on the Moselle, in the archbishopric of Trier (Treves). In his youth he was employed in the service of Count Ulrich of Manderscheid, who, seeing in him evidence of exceptional ability, sent him to study at the school of the Brothers of the Common Life at Deventer, and afterwards at the university of Padua, where he took his doctor’s degree in law in his twenty-third year. Failing in his first case he abandoned the legal profession, and resolved to take holy orders. After filling several subordinate offices he became archdeacon of Liége. He was a member of the council of Basel, and dedicated to the assembled fathers a work entitled De concordantia Catholica, in which he maintained the superiority of councils over popes, and assailed the genuineness of the False Decretals and the Donation of Constantine. A few years later, however, he had reversed his position, and zealously defended the supremacy of the pope. He was entrusted with various missions in the interests of Catholic unity, the most important being to Constantinople, to endeavour to bring about a union of the Eastern and Western churches. From 1440 to 1447 he was in Germany, acting as papal legate at the diets of 1441, 1442, 1445 and 1446. In 1448, in recognition of his services, Nicholas V. raised him to the cardinalate; and in 1450 he was appointed bishop of Brixen against the wish of Sigismund, archduke of Austria, who opposed the reforms the new bishop sought to introduce into the diocese. In 1451 he was sent to Germany and the Netherlands to check ecclesiastical abuses and bring back the monastic life to the original rule of poverty, chastity and obedience—a mission which he discharged with well-tempered firmness. Soon afterwards his dispute with the archduke Sigismund in his own diocese was brought to a point by his claiming certain dues of the bishopric, which the temporal prince had appropriated. Upon this the bishop was imprisoned by the archduke, who, in his turn, was excommunicated by the pope. 666 These extreme measures were not persisted in; but the dispute remained unsettled at the time of the bishop’s death, which occurred at Lodi in Umbria on the 11th of August 1464. In 1459 he had acted as governor of Rome during the absence of his friend Pope Pius II. at the assembly of princes at Milan; and he wrote his Crebratio Alcorani, a treatise against Mahommedanism, in support of the expedition against the Turks proposed at that assembly. Some time before his death he had founded a hospital in his native place for thirty-three poor persons, the number being that of the years of the earthly life of Christ. To this institution he left his valuable library.
Although one of the great leaders in the reform movement of the 15th century, Nicholas of Cusa’s interest for later times lies in his philosophical much more than in his political or ecclesiastical activity. As in religion he is entitled to be called one of the “Reformers before the Reformation,” so in philosophy he was one of those who broke with scholasticism while it was still the orthodox system. In his principal work, De docta ignorantia (1440), supplemented by De conjecturis libri duo published in the same year, he maintains that all human knowledge is mere conjecture, and that man’s wisdom is to recognize his ignorance. From scepticism he escapes by accepting the doctrine of the mystics that God can be apprehended by intuition (intuitio, speculatio), an exalted state of the intellect in which all limitations disappear. God is the absolute maximum and also the absolute minimum, who can be neither greater nor less than He is, and who comprehends all that is or that can be (“deum esse omnia, ut non possit esse aliud quam est”). Cusanus thus laid himself open to the charge of pantheism, which did not fail to be brought against him in his own day. His chief philosophical doctrine was taken up and developed more than a hundred years later by Giordano Bruno, who calls him the divine Cusanus. In mathematical and physical science Cusanus was much in advance of his age. In a tract, Reparatio Calendarii, presented to the council of Basel, he proposed the reform of the calendar after a method resembling that adopted by Gregory. In his De Quadratura Circuli he professed to have solved the problem; and in his Conjectura de novissimis diebus he prophesied that the world would come to an end in 1734. Most noteworthy, however, in this connexion is the fact that he anticipated Copernicus by maintaining the theory of the rotation of the earth.
The works of Cusanus were published in a complete form by Henri Petrie (1 vol. fol., Basel, 1565). See F. A. Scharpff’s Der Kardinal und Bischof Nikolaus von Cusa als Reformator in Kirche, Reich, und Philos. des 15. Jahrhund. (Tübingen, 1871); J. M. Düx, Der deutsche Kard. Nicolaus von Cusa und die Kirche seiner Zeit (Regensburg, 1848); R. Falckenberg, Grundzüge d. Philos. d. Nikolaus Cusanus (Breslau, 1880) and Aufgabe und Wesen d. Erkenntniss bei Nikolaus von Kues (Breslau, 1880); T. Stumpf, Die politischen Ideen des Nikolaus von Cues (Cologne, 1865); M. Glossner, Nikolaus von Cusa und Marius Nizolius als Vorläufer der neueren Philosophie (Münster, 1891); F. Fiorentino, Il Risorgimento filosofico nel quattro cento (Naples, 1885); Axel Herrlin, Studier i Nicolaus af Cues’ Filosofi (Lund, 1892); H. Höffding, Hist. of Mod. Phil. (Eng. trans., 1900), bk. i. chap. x.; F. J. Clemens, Giordano Bruno und Nikolaus Cusanus (Bonn, 1847); R. Zimmermann, Der Card. Nikolaus Cusanus als Vorläufer Leibnitzens (Vienna, 1852); J. Übinger, Philosophie des Nikolaus Cusanus (Würzburg, 1881); art. by R. Schmid in Herzog-Hauck, Realencyk. s.v. “Cusanus”; see also Mysticism.
CUSH, the eldest son of Ham, in the Bible, from whom seems to have been derived the name of the “Land of Cush,” commonly rendered “Ethiopia” by the Septuagint and by the Vulgate. The locality of the land of Cush has long been a much-vexed question. Bochart maintained that it was exclusively in Arabia; Schulthess and Gesenius held that it should be sought for nowhere but in Africa (see Ethiopia). Others again, like Michaelis and Rosenmüller, have supposed that the name Cush was applied to tracts of country both in Arabia and in Africa, but the defective condition of the ancient knowledge of countries and peoples, as also the probability of early migrations of “Cushite” tribes (carrying with them their name), will account for the main facts. The existence of an African Cush cannot reasonably be questioned, though the term is employed in the Old Testament with some latitude. The African Cush covers Upper Egypt, and extends southwards from the first cataract (Syene, Ezek. xxix. 10). That the term was also applied to parts of Arabia is evident from Gen. x. 7, where Cush is the “father” of certain tribal and ethnical designations, all of which point very clearly to Arabia, with the very doubtful exception of Seba, which Josephus (Ant. ii. 10. 2) identifies with Meroë.1 Even in the 5th century A.D. the Himyarites, in the south of Arabia, were styled by Syrian writers Cushaeans and Ethiopians. Moreover, the Babylonian inscriptions mention the Kashshi, an Elamite race, whose name has been equated with the classical Κοσσαῖοι, Κίσσιοι, and it has been held that this affords a more appropriate explanation of Cush (perhaps rather Kash), the ancestor of (the Babylonian) Nimrod in Gen. x. 8. Although decisive evidence is lacking, it seems extremely probable that several references to Cush in the Old Testament cannot refer to Ethiopia, despite the likelihood that considerable confusion existed in the minds of early writers. The Cushite invasion in 2 Chron. xiv. (see Asa) is intelligible if the historical foundation for the story be a raid by Arabians, but in xvi. 8 the inclusion of Libyans shows that the enemy was subsequently supposed to be African. In several passages the interpretation is bound up with that of Mizraim (q.v.), and depends in general upon the question whether Ethiopia at a given time enjoyed the prominence given to it.
On Num. xii. I see Jethro; and consult H. Winckler, Keil. u. das alte Test., 3rd ed., p. 144 sq., and Im Kampfe um den alten Orient, ii. pp. 36 seq., and the literature cited under Mizraim.
1 For Seba, see Sabaeans, and cf. generally the commentaries on Gen. x. 7. In Hab. iii. 7 Cushan (obviously a related form) is parallel to Midian.
CUSHING, CALEB (1800-1879), American political leader and lawyer, was born in Salisbury, Massachusetts, on the 17th of January 1800. He graduated at Harvard in 1817, was tutor in mathematics there in 1820-1821, was admitted to practice in the court of common pleas in December 1821, and began the practice of law in Newburyport, Mass., in 1824. After serving, as a Democratic-Republican, in the state house of representatives in 1825, in the state senate in 1826, and in the house again in 1828, he spent two years, from 1829 to 1831, in Europe, again served in the state house of representatives in 1833 and 1834, and in the latter year was elected by the Whigs a representative in Congress. He served in this body from 1835 until 1843, and here the marked inconsistency which characterized his public life became manifest; for when John Tyler had become president, had been “read out” of the Whig party, and had vetoed Whig measures (including a tariff bill), for which Cushing had voted, Cushing first defended the vetoes and then voted again for the bills. In 1843 President Tyler nominated him for secretary of the treasury, but the senate refused to confirm him for this office. He was, however, appointed later in the same year commissioner of the United States to China, holding this position until 1845, and in 1844 negotiating the first treaty between China and the United States. In 1847, while again a representative in the state legislature, he introduced a bill appropriating money for the equipment of a regiment to serve in the Mexican War; although the bill was defeated, he raised the necessary funds privately, and served in Mexico first as colonel and afterwards as brigadier-general of volunteers. In 1847 and again in 1848 the Democrats nominated him for governor of Massachusetts, but on each occasion he was defeated at the polls. He was again a representative in the state legislature in 1851, became an associate justice of the supreme court of Massachusetts in 1852, and during the administration (1853-1857) of President Pierce, was attorney-general of the United States. In 1858, 1859, 1862 and 1863 he again served in the state house of representatives. In 1860 he presided over the National Democratic Convention which met first at Charleston and later at Baltimore, until he joined those who seceded from the regular convention; he then presided also over the convention of the seceding delegates, who nominated John C. Breckinridge for the presidency. During the Civil War, however, he supported the National Administration. At the Geneva conference for the settlement of the “Alabama” claims in 1871-1872 he was one of the counsel for the United States. 667 In 1873 President Grant nominated him for chief justice of the United States, but in spite of his great learning and eminence at the bar, his ante-war record and the feeling of distrust experienced by many members of the senate on account of his inconsistency, aroused such vigorous opposition that his nomination was soon withdrawn. From 1874 to 1877 Cushing was United States minister to Spain. He died at Newburyport, Mass., on the 2nd of January 1879. He published History and Present State of the Town of Newburyport, Mass. (1826); Review of the late Revolution in France (1833); Reminiscences of Spain (1833); Oration on the Growth and Territorial Progress of the United States (1839); Life and Public Services of William H. Harrison (1840); and The Treaty of Washington (1873).
CUSHING, WILLIAM BARKER (1842-1874), American naval officer, was born in Delafield, Wisconsin, on the 4th of November 1842. He entered the Naval Academy from New York in 1857, but resigned in March 1861. When, however, the Civil War began, he volunteered into the navy, was rated acting master’s mate, and became a midshipman in October 1861, and a lieutenant in July 1862, serving in the North Atlantic blockading squadron. The work of blockade, and of harassing the Confederates on the coast and the rivers of the Atlantic seaboard, called for much service in boats, and entailed a great deal of exposure. Cushing was distinguished by his readiness to volunteer, his indefatigability, and by his good fortune, the reward of vigilance and intelligence. The feat by which he will be remembered was the destruction of the Confederate ironclad “Albemarle” in the Roanoke river on the 27th of October in 1864. The vessel had done much damage to the Federal naval forces, and her destruction was greatly desired. She was at anchor surrounded by baulks of timber, and a cordon of boats had been stationed to row guard against an expected Federal attack. Lieutenant Cushing undertook the attack on her with a steam launch carrying a spar-torpedo and towing an armed cutter. He eluded the Confederate lookout and reached the “Albemarle” unseen. When close to he was detected, but he had time to drive the steam launch over the baulks and to explode the torpedo against the “Albemarle” with such success that a hole was made in her and she sank. Cushing’s own launch was destroyed. He and the few men with him were compelled to take to the water; one was killed, another was drowned, Cushing and one other escaped, and the rest were captured. Cushing himself swam to the swamps on the river bank, and after wading among them for hours reached a Federal picket boat. For destroying the “Albemarle” he was thanked by Congress and was promoted to be lieutenant-commander. On the 15th of January 1865 he took a conspicuous part in the land attack on the sea-front wall of Fort Fisher. After the war he commanded the “Lancaster” (1866-1867) and the “Maumee” (1868-1869) in the Asiatic Squadron. In 1872 he was promoted commander at what was an exceptionally early age, but he died on the 17th of December 1874 of brain fever. He had suffered extreme pain for years before his death, and in fact broke down altogether under disease contracted in the discharge of his duty.
CUSHION (from O. Fr. coisson, coussin; according to the New English Dict., from Lat. coxa, a hip; others say from Lat. culcita, a quilt), a soft bag of some ornamental material, stuffed with wool, hair, feathers, or even paper torn into fragments. It may be used for sitting or kneeling upon, or to soften the hardness or angularity of a chair or couch. It is a very ancient article of furniture, the inventories of the contents of palaces and great houses in the early middle ages constantly making mention of it. It was then often of great size, covered with leather, and firm enough to serve as a seat, but the steady tendency of all furniture has been to grow smaller. It was, indeed, used as a seat, at all events in France and Spain, at a very much later period, and in Saint-Simon’s time we find that at the Spanish court it was still regarded as a peculiarly honourable substitute for a chair. In France the right to kneel upon a cushion in church behind the king was jealously guarded and strictly regulated, as we may learn again from Saint-Simon. This type of cushion was called a carreau or square. When seats were rude and hard the cushion may have been a necessity; it is now one of the minor luxuries of life.
The term “cushion” is given in architecture to the sides of the Ionic capital. It is also applied to an early and simple form of the Romanesque capitals of Germany and England, which consist of cubical masses, square at the top and rounded off at the four corners, so as to reduce the lower diameter to a circle of the same size as the shaft.
CUSHMAN, CHARLOTTE SAUNDERS (1816-1876), American actress, was born in Boston, Massachusetts, on the 23rd of July 1816. Her father, a West India merchant, left his family in straitened circumstances, and Charlotte, who had a fine contralto voice, went on the operatic stage. In 1835 she successfully appeared at the Tremont theatre as the countess Almaviva in The Marriage of Figaro. But her singing voice failing her she entered the drama, and played Lady Macbeth in the same year. She then engaged herself as a stock actress, but was soon given leading parts. In 1842 she managed and played in the Walnut Street theatre in Philadelphia. She accompanied Macready on an American tour, winning a great reputation in tragedy, and in 1845 and in 1854-1855 she fulfilled successful engagements in London. She was a keen student, and acquired a large range of classic rôles. Her best parts were perhaps Lady Macbeth and Queen Katherine, her most popular Meg Merrilies, in a dramatization of Scott’s Guy Mannering. Her figure was commanding and her face expressive, and she was animated by a temperament full of vigour and fire. These qualities enabled her to play with success such male parts as Romeo and Cardinal Wolsey. During her later years Miss Cushman worked hard as a dramatic reader, in which capacity she was much appreciated. Her last appearance on the stage took place on the 15th of May 1875, at the Globe theatre, Boston, in which city she died on the 18th of February 1876.
See Emma Stebbins’s Charlotte Cushman, her Letters and Memories of her Life (Boston, 1878); H. A. Clapp’s Reminiscences of a Dramatic Critic (Boston, 1902); and W. T. Price, A Life of Charlotte Cushman (New York, 1894).
CUSP (Lat. cuspis, a spear, point), a projecting point, or pointed end. In architecture (Fr. feuille, Ital. cuspide, Ger. Knöpfe), a cusp is the point where the foliations of tracery intersect. The earliest example of a plain cusp is probably that at Pythagoras school, at Cambridge,—of an ornamented cusp at Ely cathedral, where a small roll, with a rosette at the end, is formed at the termination of a cusp. In the later styles the terminations of the cusps were more richly decorated; they also sometimes terminate not only in leaves or foliages, but in rosettes, heads and other fanciful ornaments. The term “feathering” is used of the junction of the foliated cusps in window tracery, but is usually restricted to those cases where it is ornamented with foliage, &c.
CUSTARD1 APPLE, a name applied to the fruit of various species of the genus Anona, natural order Anonaceae. The members of this genus are shrubs or small trees having alternate, exstipulate leaves, and flowers with three small sepals, six petals arranged in a double row and numerous stamens. The fruit of A. reticulata, the common custard apple, or “bullock’s heart” of the West Indies, is dark brown in colour, and marked with depressions, which give it a quilted appearance; its pulp is reddish-yellow, sweetish and very soft (whence the name); the kernels of the seeds are said to be poisonous. The sour-sop is the fruit of A. muricata, native of the West Indies. The plant, which is a small tree, has become naturalized in some parts of India where it is extensively cultivated, as elsewhere in the tropics. It is covered with soft prickles, is of a light-greenish hue, and has a peculiar but agreeable sour taste, and a scent resembling that of black currants. The sweet-sop is produced by A. squamosa, also a native of the West Indies and widely cultivated 668 in the tropics. It is known as the custard apple by Europeans in India. It is an egg-shaped fruit, with a thick rind and luscious pulp. An acrid principle, fatal to insects, is contained in its seeds, leaves and unripe fruits, which, powdered and mixed with the flour of gram (Cicer arietinum), are used to destroy vermin. A. Cherimolia yield the Peruvian cherimoyer, which is held to be a fruit of very superior flavour, and is much esteemed by the creoles. A. palustris, alligator apple, or cork-wood, a native of South America and the West Indies, is valued for its wood, which serves the same purposes as cork; the fruit, commonly known as the alligator-apple, is not eaten, being reputed to contain a dangerous narcotic principle.
1 The term “custard,” now given to a dish made with eggs beaten up with milk, &c., and either served in liquid form or baked to a stiff consistency, originally denoted a kind of open pie. It represents the older form “crustade,” Fr. croustade, Ital. crostata, from crostare, to encrust.
CUSTER, GEORGE ARMSTRONG (1839-1876), American cavalry soldier, was born in New Rumley, Harrison county, Ohio, on the 5th of December 1839. He graduated from West Point in 1861, and was at once sent to the theatre of war in Virginia, joining his regiment on the battlefield of Bull Run. Afterwards he served on the staff of General Kearny, and on that of General W. F. Smith in the Peninsular Campaign. His daring and energy, and in particular a spirited reconnaissance on the Chickahominy river, brought him to the notice of General McClellan, who made him an aide-de-camp on his own staff, with the rank of captain. A few hours afterwards Custer attacked a Confederate picket post and drove back the enemy. He continued to serve with McClellan until the general was relieved of his command, when Custer returned to duty with his regiment as a lieutenant. Early in 1863 General Pleasonton selected him as his aide-de-camp, and in June 1863 Custer was promoted to the rank of brigadier-general of volunteers. He distinguished himself at the head of the Michigan cavalry brigade in the battle of Gettysburg, and frequently did good service in the remaining operations of the campaign of 1863. When the cavalry corps of the Army of the Potomac was reorganized under Sheridan in 1864, Custer retained his command, and took part in the various actions of the cavalry in the Wilderness and Shenandoah campaigns. At the end of September 1864, he was appointed to command a division, and on the 9th of October fought, along with General Merritt, the brilliant cavalry action called the battle of Woodstock. Soon afterwards he was made brevet-major-general, U.S.V., having already won the brevets of major, lieutenant-colonel and colonel U.S.A., for his services at Gettysburg, Yellow Tavern and Winchester. His part in the decisive battle of Cedar Creek (q.v.) was most conspicuous. He served with Sheridan in the last great cavalry raid, won the action of Waynesboro, and in the final campaign added to his laurels by his conduct at Dinwiddie and Five Forks, and in other operations. At the close of the war he received the brevets of brigadier and major-general in the regular army, and was promoted major-general of volunteers. In 1866 Custer was made lieutenant-colonel of the 7th U.S. Cavalry, and took part under General Hancock in the expedition against the Cheyenne Indians, upon whom he inflicted a crushing defeat at Washita river on the 27th of November 1868. In 1873 he was sent to Dakota Territory to serve against the Sioux.
In 1876 an expedition, of which Custer and his regiment formed part, was made against the Sioux and their allies. As the advanced guard of the troops under General Terry, Custer’s force arrived at the junction of Big Horn and Little Big Horn rivers, in what is now the state of Montana, on the night of June 24; the main body was due to join him on the 26th. Unfortunately, the presence of what was judged to be a small isolated force of Indians was reported to the general. On the 25th, dividing his regiment into three parties, he moved forward to surround this force. But instead of meeting only a small force of Indians, the 7th were promptly attacked by the full forces of the enemy. The flanking columns maintained themselves with difficulty until Terry came up. Custer and 264 men of the centre column rode into the midst of the enemy and were slaughtered to a man.
The general’s wife, Elizabeth Bacon Custer, who accompanied him in many of his frontier expeditions, wrote Boots and Saddles, Life with General Custer in Dakota (1885), Tenting on the Plains (1887) and Following the Guidon (1891). General Custer himself wrote My Life on the Plains (1874).
See F. Whittaker, Life of General George A. Custer (1876).
His brother Thomas Ward Custer (1845-1876), in spite of his youth, fought in the early campaigns of the Civil War. Becoming aide-de-camp to General Custer, he accompanied him throughout the latter part of the war, distinguishing himself by his daring on all occasions, and winning successively the brevets of captain, major and lieutenant-colonel, though he was barely twenty years of age when the war ended. He was first lieutenant in the 7th cavalry when he fell with his brother at the Little Big Horn.
CUSTINE, ADAM PHILIPPE, Comte de (1740-1793), French general, began his military career in the Seven Years’ War. He next served with distinction against the English in the War of American Independence. In 1789 he was elected to the states-general by the bailliage of Metz. In October 1791 he again joined the army, with the rank of lieutenant-general and became popular with the soldiers, amongst whom he was known as “général moustache.” General-in-chief of the army of the Vosges, he took Spires, Worms, Mainz and Frankfort in September and October 1792. He carried on the revolutionary propaganda by proclamations, and levied heavy taxes on the nobility and clergy. During the winter a Prussian army forced him to evacuate Frankfort, re-cross the Rhine and fall back upon Landau. He was accused of treason, defended by Robespierre, and sent back to the army of the north. But he dared not take the offensive, and did nothing to save Condé, which the Austrians were besieging. Sent to Paris to justify himself, he was found guilty by the Revolutionary Tribunal of having intrigued with the enemies of the republic, and guillotined on the 28th of August 1793. (See French Revolutionary Wars.)
See A. Rambaud, Les Français sur le Rhin (Paris, 1880); A. Chuquet, Les Guerres de la Révolution (1886-1895; vol. vi. “L’Expédition de Custine”).
CUSTOM (from O. Fr. custume, costume or coustume; Low Lat. costuma, a shortened form of consuetudo), in general, a habit or practice. Thus a tradesman calls those who deal with him his “customers,” and the trade resulting as their “custom.” The word is also used for a toll or tax levied upon goods; there was at one time a distinction between the tax on goods exported or imported, termed magna custuma (the great custom), and that on goods taken to market within the realm, termed parva custuma (the little custom), but the word is now used in this sense only in the plural, to signify the duties levied upon imported goods. It is also used as a name for that department of the public service which is employed in levying the duty.
In law, such long-continued usage as has by common consent become a rule of conduct is termed custom. Jessel, M. R. (Hammerton v. Honey, 24 W. R. 603), has defined it as “local common law. It is common law because it is not statute law; it is local law because it is the law of a particular place, as distinguished from the general common law. Local common law is the law of the country (i.e. particular place) as it existed before the time of legal memory.” There has been much discussion among jurists as to whether custom can properly be reckoned a source of law (see Jurisprudence). As to the distinction between prescription (which is a personal claim) and custom, see Prescription. The adoption of local customs by the judiciary has undoubtedly been the origin of a great portion of the English common law. Blackstone divides custom into (1) general, which is the common law properly so called, and (2) particular, which affects only the inhabitants of particular districts. The requisites necessary to make a particular custom good are: (1) it must have been used so long that the memory of man runneth not to the contrary; (2) it must have been continued, and (3) enjoyed peaceably; (4) it must be reasonable, and (5) certain; (6) it must be compulsory, and not left to the option of every man whether he will use it or no; (7) it must be consistent with other customs, for one custom cannot be set up in opposition to another. Customs may be of various kinds, for example, customs of merchants, customs of a certain district 669 (such as gavelkind and borough English), customs of a particular manor, &c. The word custom is also generally employed for the usage of a particular trade or market; for a trade custom to be established to the satisfaction of the law it must be a uniform and universal practice so well defined and recognized that contracting parties must be assumed to have had it in their minds when they contracted (Russell, C. J., Fox-Bourne v. Vernon, 10 Times Rep. 649).
In the history of France the term “custom” was given to those special usages of different districts which had grown up into a body of local law, as the “custom of Paris,” the “custom of Normandy” (see France: Law and Institutions).
CUSTOMARY FREEHOLD, in English law, a species of tenure which may be described as a variety of copyhold. It is also termed privileged copyhold or copyhold of frank tenure. It is a tenure by copy of court roll, but not expressed to be at the will of the lord. It is, in fact, only a superior kind of copyhold, and the freehold is in the lord. It is subject to the general law of copyholds, except where the law may be varied by the custom of the particular manor. (See Copyhold.)
CUSTOM-HOUSE, the house or office appointed by a government where the taxes or duties (if any) are collected upon the importation and exportation of commodities; where duties, bounties or drawbacks payable or receivable upon exportation or importation are paid or received, and where vessels are entered and cleared. In the United Kingdom there is usually a custom-house established at every port or harbour to which any considerable amount of shipping resorts, the officer in charge being called “collector of customs”; in the minor ports the officer is usually termed “superintendent of customs” or “principal coast officer.”
CUSTOM DUTIES, the name given to taxes on the import and export of commodities. They rank among the most ancient, as they continue to prevail as one of the most common modes, in all countries, of levying revenue for public purposes. In an insular country like the United Kingdom customs duties came in process of time to be levied only or chiefly in the seaports, and thus applied only to the foreign commerce, where they may be brought under the control of fair and reasonable principles of taxation. But this simplification of customs duties was only reached by degrees; and during a long period special customs were levied on goods passing between England and Scotland; and the trade of Ireland with Great Britain and with foreign countries was subjected to fiscal regulations which could not now stand in the light of public reason. The taxes levied, on warrant of some ancient grant or privilege, upon cattle or goods at a bridge or a ferry or other point of passage from one county or province to another, of which there are some lingering remains even in the United Kingdom, and those levied at the gates of cities on the produce of the immediate country—a not uncommon form of municipal taxation on the European continent—are all of the nature of customs dues. It is from the universality of this practice that the English term “customs” appears to have been derived.
See Taxation; Protection; Tariff.
CUSTOS ROTULORUM, the keeper of the English county records, and by virtue of that office the highest civil officer in the county. The appointment until 1545 lay with the lord chancellor, but is now exercised by the crown under the royal sign-manual, and is usually held by a person of rank, most frequently the lord-lieutenant of the county. He is one of the justices of the peace. In practice the records are in the custody of the clerk of the peace. This latter official was, until 1888, appointed by the custos rotulorum, but since the passing of the Local Government Act of that year, the appointment is made by the standing joint-committee of the county council. Lambarde described the custos rotulorum as a “man for the most part especially picked out either for wisdom, countenance or credit.”
CUSTOZZA, a village of Italy, in the province of Verona, 11 m. S.W. of Verona, famous as the scene of two battles between the Austrians and the Italians in the struggle for Italian unity. The first battle of Custozza was fought on the 23rd-25th of July 1848, the Austrians commanded by Field-Marshal Radetzky being victorious over the Piedmontese army under King Charles Albert. The second battle was fought on the 24th of June 1866, and resulted in the complete victory of the Austrians under the archduke Albert, over the Italian army of King Victor Emmanuel I. (See Italian Wars, 1848-1870.)
CÜSTRIN, or Küstrin, a town of Germany, in the kingdom of Prussia, a fortress of the first rank, at the confluence of the Oder and Warthe, 18 m. N.E. from Frankfort-on-Oder and 51 m. N.E. of Berlin by rail. Pop. (1900) 16,473 (including the garrison). It consists of the town proper within the strong fortifications, a suburb on the left bank of the Oder, and one on the right bank of the Warthe. There are three Evangelical churches and one Roman Catholic, and a handsome town hall. There are bridges over both rivers. Cüstrin has some manufactories of potato-meal, machinery, pianos, furniture, cigars, &c., and there is a considerable river trade.
About 1250 a town was erected on the site of Cüstrin, where a fishing village originally stood. From 1535 till 1571 it was the residence of John, margrave of Brandenburg-Cüstrin, who died without male heirs in 1571. Cüstrin was the prison of Frederick the Great when crown-prince, and the scene of the execution of his friend Hans Hermann von Katte on the 6th of November 1730.
CUTCH, or Kach, a native state of India within the Gujarat division of Bombay, with an area of 7616 sq. m. It is a peninsular tract of land, enclosed towards the W. by the eastern branch of the Indus, on the S. by the Indian Ocean and the Gulf of Cutch, and on the N. and E. towards the interior, by the great northern Runn, a salt morass or lake. The interior of Cutch is studded with hills of considerable elevation, and a range of mountains runs through it from east to west, many of them of the most fantastic shapes, with large isolated masses of rock scattered in all directions. The general appearance of Cutch is barren and uninteresting. The greater part is a rock destitute of soil, and presenting the wildest aspect; the ground is cold, poor and sterile; and the whole face of the country bears marks of volcanic action. From the violence of tyranny, and the rapine of a disorderly banditti, by which this district long suffered, as well as from shocks of earthquakes, the villages have a ruinous and dilapidated appearance; and, with the exception of a few fields in their neighbourhood, the country presents a rocky and sandy waste, with in many places scarcely a show of vegetation. Water is scarce and brackish, and is chiefly found at the bottom of low ranges of hills, which abound in some parts; and the inhabitants of the extensive sandy tracts suffer greatly from the want of it. Owing to the uncertainty of the periodical rains in Cutch, the country is liable to severe famines, and it has suffered greatly from plague.
The temperature of Cutch during the hot season is high, the thermometer frequently rising to 100° or 105° F.; and in the months of April and May clouds of dust and sand, blown about by hurricanes, envelop the houses, the glass windows scarcely affording any protection. The influence of the monsoon is greatly moderated before it reaches this region, and the rains sometimes fail altogether. Bhuj, the capital of the state, is situated inland, and is surrounded by an amphitheatre of hills, some of which approach within 3 or 4 m. of the city. The hill of Bhuja, on which the fort is situated, rises to the height of 500 ft. in the middle of the plain, and is detached from other high ground. The residency is 4 m. distant in a westerly direction. There are many mountain streams, but no navigable rivers. They contain scarcely any water except in the rainy season, when they are very full and rapid, and discharge themselves into the Runn, all along the coast of which the wells and springs are more or less impregnated with common salt and other saline ingredients.
Various causes have contributed to thin the population of this country. In 1813 it was ravaged by a famine and pestilence, which destroyed a great proportion of its inhabitants,—according to some accounts, nearly one-half. This, joined to the tyranny and violence of the government until the year 1819, and subsequently to a succession of unfavourable seasons, forced many 670 of the cultivators to remove to Sind and other countries. The inhabitants numbered 488,022 in 1901, being a decrease of 13% during the decade, due to the famines of 1899-1900. One-third are Mahommedans and the remainder Hindus of various castes. The Jareja Rajputs form a particular class, being the aristocracy of the country; and all are more or less connected with the family of the rao or prince. There are in Cutch about 200 of these Jareja chiefs, who all claim their descent from a prince who reigned in Sind about 1000 years ago. From him also the reigning sovereign is lineally descended, and he is the liege lord of whom all the chiefs or nobles hold their lands in feu, for services which they or their ancestors had performed, or in virtue of their relationship to the family. They are all termed the brotherhood of the rao or Bhayad, and supposed to be his hereditary advisers, and their possessions are divided among their male children. To prevent the breaking down of their properties, the necessary consequence of this law of inheritance, there is no doubt that infanticide was common among them, and that it extended to the male as well as the female progeny, but it has been put down by the Infanticide Rules, which provide for the registration of Jareja children. The Jarejas have a tradition that when they entered Cutch they were Mahommedans, but that they afterward adopted the customs and religion of the Hindus. It is certain, indeed, that they still retain many Mahommedan customs. They take oaths equally on the Koran or on the Shastras; they employ Mussulman books; they eat from their hands; the rao, when he appears in public, alternately worships God in a Hindu pagoda and a Mahommedan mosque; and he fits out annually at Mandvi a ship for the conveyance of pilgrims to Mecca, who are maintained during the voyage chiefly by the liberality of the prince. The Mahommedans in Cutch are of the same degenerate class as those usually found in the western parts of India. The natives are in general of a stronger and stouter make, and even handsomer, than those of western India; and the women of the higher classes are also handsome. The peasants are described as intelligent, and the artizans are justly celebrated for their ingenuity and mechanical skill. The palace at Mandvi, and a tomb of one of their princes at Bhuj, are fair specimens of their architectural skill. The estimated gross revenue is £126,322. There are special manufactures of silver filigree-work and embroidery. The maritime population supplies the best sailors in India. There are cotton presses and ginning factories.
The country of Cutch was invaded about the 13th century by a body of Mahommedans of the Summa tribe, who under the guidance of five brothers emigrated from Sind, and who gradually subdued or expelled the original inhabitants, consisting of three distinct races. Cutch continued tranquil under their sway for many years, until some family quarrel arose, in which the chief of an elder branch of the tribe was murdered by a rival brother. His son Khengayi fled to Ahmedabad to seek the assistance of the viceroy, who reinstated him in the sovereignty of Cutch, and Morvi in Káthiáwár, and in the title of rao, about the year 1540. The succession continued in the same line from the time of this prince until 1697, when a younger brother, Pragji, murdered his elder brother and usurped the sovereignty. This line of princes continued till 1760 without any remarkable event, when, in the reign of Rao Ghodji, the country was invaded four times by the Sinds, who wasted it with fire and sword. The reign of this prince, as well as that of his son Rao Rayadan, by whom he was succeeded in 1778, was marked by cruelty and blood. The latter prince was dethroned, and, being in a state of mental derangement, was during his lifetime confined by Fateh Mahommed, a native of Sind, who continued, with a short interval (in which the party of the legal heir, Bhaiji Bawa, gained the ascendancy), to rule the country until his death in 1813. It was in the reign of Fateh Mahommed that a communication first took place with the British government. During the contests for the sovereignty between the usurper and the legal heir, the leader of the royal party, Hansraj, the governor of Mandvi, sought the aid of the British. But no closer connexion followed at that time than an agreement for the suppression of piracy, or of inroads of troops to the eastward of the Runn or Gulf of Cutch. But the gulf continued notwithstanding to swarm with pirates, who were openly encouraged or connived at by the son of Hansraj, who had succeeded his father, as well as by Fateh Mahommed. The latter left several sons by different wives, who were competitors for the vacant throne. Husain Miyan succeeded to a considerable portion of his father’s property and power. Jugjevan, a Brahman, the late minister of Fateh Mahommed, also received a considerable share of influence; and the hatred of these two factions was embittered by religious animosities, the one being Hindu and the other Mahommedan. The deceased rao had declared himself a Mahommedan, and his adherents were preparing to inter his body in a magnificent tomb, when the Jarejas and other Hindus seized the corpse and consigned it to the flames, according to Hindu custom.
The administration of affairs was nominally in the hands of Husain Miyan and his brother Ibrahim Miyan. Many sanguinary broils now ensued, in the course of which Jugjevan was murdered, and the executive authority was much weakened by the usurpations of the Arabs and other chiefs. In the meantime Ibrahim Miyan was assassinated; and after various other scenes of anarchy, the rao Bharmulji, son of Rao Rayadan, by general consent, assumed the chief power. But his reign was one continued series of the grossest enormities; his hostility to the British became evident, and accordingly a force of 10,500 men crossed the Runn in November 1815, and were within five miles of Bhuj, the capital of the country, when a treaty was concluded, by which the rao Bharmulji was confirmed in his title to the throne, on agreeing, among other stipulations, to cede Anjar and its dependencies in perpetuity to the British. He was, however, so far from fulfilling the terms of this treaty that it was determined to depose him; and an army being sent against him, he surrendered to the British, who made a provision for his maintenance, and elevated his infant son Desalji II. to the throne (1819).
In 1822 the relations subsisting between the ruler of Cutch and the British were modified by a new treaty, under which the territorial cessions made by the rao in 1816 were restored in consideration of an annual payment. The sum fixed was subsequently thought too large, and in 1832 the arrears, amounting to a considerable sum, were remitted, and all future payments on this account relinquished. From that time the rao has paid a subsidy of £13,000 per annum to the British for the maintenance of the military force stationed within his dominions.
Rao Desalji II. did much to suppress infanticide, suttee and the slave trade in his state. His successor Maharao Pragmalji in recognition of his excellent administration was in 1871 honoured with the title of knight grand commander of the Star of India. During his rule harbour works were built at Mandvi, an immense reservoir for rain water in the Chadwa hills was constructed, and many schools and colleges were endowed. In 1876 he was succeeded by Maharaja Rao Khengarji III., who was also a keen advocate for education and especially the education of women. He founded museums, libraries and schools, and inaugurated scholarships and a fund from which deserving scholars desirous of studying in England and America could obtain their expenses.
CUTCH, GULF OF, an inlet of the sea on the coast of western India. It lies between the peninsula of Kathiawar and that of Cutch, leading into the Runn of Cutch.
CUTCH, RUNN OF, or Rann of Kach, a salt morass on the western coast of India in the native state of Cutch. From May to October it is flooded with salt water and communicates, at its greatest extent, with the Gulf of Cutch on the west and the Gulf of Cambay on the east, these two gulfs being united during the monsoon. It varies in breadth from five to eighty miles across, and during the rains is nearly impassable for horsemen. The total area of this immense morass is estimated at about 8000 sq. m., without including any portion of the Gulf of Cutch, which is in parts so shallow as to resemble a marshy fen rather than an arm of the sea. The Runn is said to be formed by the overflow of the rivers Pharan, Luni, Banas and others, during the monsoon; but in December it is quite dry, and in most places hard, but in some moist and muddy. The soil is impregnated 671 with salt, and the Runn is an important source for the supply of salt. The present condition of the Runn is probably the result of some natural convulsion, but the exact method of its formation is disputed. The wild ass is very common on the borders of this lake, being seen in herds of 60 or 70 together.
CUTHBERT, SAINT (d. 687), bishop of Lindisfarne, was probably a Northumbrian by birth. According to the extant Lives he was led to take the monastic vows by a vision at the death of bishop Aidan, and the date of his entry at Melrose would be 651. At this time Eata was abbot there, and Boisel, who is mentioned as his instructor, prior, in which office Cuthbert succeeded him about 661, having previously spent some time at the monastery of Ripon with Eata. Bede gives a glowing picture of his missionary zeal at Melrose, but in 664 he was transferred to act as prior at Lindisfarne. In 676 he became an anchorite on the island of Farne, and it is said that he performed miracles there. In 684 at the council of Twyford in Northumberland, Ecgfrith, king of Northumbria, prevailed upon him to give up his solitary life and become a bishop. He was consecrated at York in the following year as bishop of Hexham, but afterwards he exchanged his see with Eata for that of Lindisfarne. In 687 he retired to Farne, and died on the island on the 20th of March 687, the same day as his friend Hereberht, the anchorite of Derwentwater. He was buried in the island of Lindisfarne, but his remains were afterwards deposited at Chester-le-Street, and then at Durham.
Another Cuthbert was bishop of Hereford from 736 to about 740, and archbishop of Canterbury from the latter date until his death in October 758.
There are several lives of St Cuthbert, the best of which is the prose life by Bede, which is published in Bede’s Opera, edited by J. Stevenson (1841). See also C. Eyre, The History of St Cuthbert (1887); and J. Raine, St Cuthbert (1828).
CUTLASS, the naval side-arm, a short cutting sword with a slightly curved blade, and a solid basket-shaped guard (see Sword). The word is derived from the Fr. coutelas, or coutelace, a form of coutel, modern couteau, a knife, from Lat. cultellus, diminutive of culter, a ploughshare, or cutting instrument. Two variations appear in English: “curtelace,” where the r represents probably the l of the original Latin word, or is a further variant of the second variation; and “curtelaxe,” often spelled as two words, “curtal axe,” where the prefix curtal is confused with various English words such as “curtan,” “curtal” and “curtail,” which all mean “shortened,” and are derived from the Lat. curtus; the word thus wrongly derived has been supposed to refer to some non-existent form of battle-axe. In every case the weapon to which these various forms apply is a broad cutting or slashing sword.
CUTLER, MANASSEH (1742-1823), American clergyman, was born in Killingly, Connecticut, on the 13th of May 1742. He graduated at Yale College in 1765, and after being a school teacher and a merchant, and occasionally appearing in the courts as a lawyer, he decided to enter the ministry, and from 1771 until his death was pastor of the Congregational church at what is now Hamilton, but until 1793 was a parish of Ipswich, Massachusetts. During the War of Independence he was for several months in 1776 chaplain to the regiment of Colonel Ebenezer Francis, raised for the defence of Boston; and in 1778, as chaplain to the brigade of General Jonathan Titcomb (1728-1817), he took part in General John Sullivan’s expedition to Rhode Island. Soon after his return from this expedition he fitted himself for the practice of medicine, in order to supplement the scanty income of a minister, and in 1782 he established a private boarding school, which he conducted for about a quarter of a century. In 1786 he became interested in the settlement of western lands, and in the following year, as agent of the Ohio Company (q.v.), which he had taken a prominent part in organizing, he made a contract with Congress, whereby his associates, former soldiers in the War of Independence, might purchase, with the certificates of indebtedness issued to them by the government for their services, 1,500,000 acres of land in the region north of the Ohio at the mouth of the Muskingum river. He also took a leading part in drafting the famous Ordinance of 1787 for the government of the Northwest Territory, the instrument as it was finally presented to Congress by Nathan Dane (1752-1835), a Massachusetts delegate, probably being largely Cutler’s work. From 1801 to 1805 he was a Federalist representative in Congress. He died at Hamilton, Massachusetts, on the 28th of July 1823. A versatile man, Cutler was one of the early members of the American Academy of Arts and Sciences, and besides being proficient in the theology, law and medicine of his day, conducted painstaking astronomical and meteorological investigations, and was one of the first Americans to make researches of a real scientific value in botany. In 1789 the degree of doctor of laws was conferred upon him by Yale.
See William P. and Julia P. Cutler, The Life, Journals, and Correspondence of Manasseh Cutler (2 vols., Cincinnati, 1888); and an article, “The Ordinance of 1787 and Dr Manasseh Cutler,” by W. F. Poole, in vol. 122 of the North American Review.
CUTLERY (Fr. coutellerie, from the Lat. cultellus, a little knife), a branch of industry which originally embraced the manufacture of all cutting instruments of whatever form or material. The progress of manufacturing industry has, however, detached from it the fabrication of several kinds of edge-tools, saws and similar implements, the manufacture of which is now regarded as forming distinct branches of trade. On the other hand modern cutlery includes a great number of articles which are not strictly cutting instruments, but which, owing to their more or less intimate relation to table or pocket cutlery, are classed with such articles for convenience’ sake. A steel table or carving fork, for example, is an important article of cutlery, although it is not a cutting tool.
The original cutting instruments used by the human race consisted of fragments of flint, obsidian, or similar stones, rudely flaked or chipped to a cutting edge; and of these tools numerous remains yet exist. Stone knives and other tools must have been employed for a long period by the prehistoric races of mankind, as their later productions show great perfection of form and finish. In the Bronze period, which succeeded the Stone Age, the cutlery of our ancestors was fabricated of that alloy. The use of iron was introduced at a later but still remote period; and it now, in the form of steel, is the staple article from which cutlery is manufactured.
From the earliest period in English history the manufacture of cutlery has been peculiarly associated with the town of Sheffield, the prominence of which in this manufacture in his own age is attested by Chaucer, who says of the miller of Trumpington—
“A Sheffeld thwitel baar he in his hose.”
That town still retains a practical monopoly of the ordinary cutlery trade of Great Britain, and remains the chief centre of the industry for the whole world. Its influence on methods of production has also been widely extended; for instance, many Sheffield workmen emigrated to the United States of America to take part in the manufacture of pocket-knives when it was started in Connecticut towards the middle of the 19th century.
The thwitel or whittle of Chaucer’s time was a very poor rude implement, consisting of a blade of bar steel fastened into a wooden or horn handle. It was used for cutting food as well as for the numerous miscellaneous duties which now fall to the pocket-knife. To the whittle succeeded the Jack knife,—the Jacques-de-Liége, or Jock-te-leg of the Scottish James VI.,—which formed the prototype of the modern clasp-knife, inasmuch as the blade closed into a groove in the handle. About the beginning of the 17th century, the pocket-knife with spring back was introduced, and no marked improvement thereafter took place till the early part of the 19th century. In 1624, two centuries after the incorporation of the Cutlers’ Company of London, the cutlers of Hallamshire—the name of the district of which Sheffield is the centre—were formed into a body corporate for the protection of the “industry, labour, and reputation” of the trade, which was being disgraced by the “deceitful and unworkmanlike wares of various persons.” The act of incorporation specifies the manufacture of “knives, scissors, shears, sickles and 672 other cutlery,” and provides that all persons engaged in the business shall “make the edge of all steel implements manufactured by them of steel, and steel only, and shall strike on their wares such mark, and such only, as should be assigned to them by the officers of the said company.” Notwithstanding these regulations, and the pains and penalties attached to their infringement, the corporation was not very successful in maintaining the high character of Sheffield wares. Most manufacturers made cutlery to the order of their customers, on which the name of the retailer was stamped, and very inferior malleable or cast iron blades went forth to the public with “London made,” “best steel,” and other falsehoods stamped on them to order. The corporate mark and name of a few firms, among which Joseph Rodgers & Sons stand foremost, are a guarantee of the very highest excellence of material and finish; and such firms decline to stamp any name or mark other than their own on their manufactures. In foreign markets, however, the reputation of such firms is much injured by impudent forgeries; and so far was this system of fraud carried that inferior foreign work was forwarded to London to be transhipped and sent abroad ostensibly as English cutlery. To protect the trade against frauds of this class the Trades Mark Act of 1862 was passed chiefly at the instigation of the Sheffield chamber of commerce.
The variety of materials which go to complete any single article of cutlery is very considerable; and as the stock list of a cutler embraces a vast number of articles different in form, properties and uses, the cutlery manufacturer must have a practical knowledge of a wide range of substances. The leading articles of the trade include carving and table knives and forks, pocket or clasp knives, razors, scissors, daggers, hunting knives and similar articles, surgical knives and lancets, butchers’ and shoemakers’ knives, gardeners’ pruning-knives, &c. The blades or cutting portions of a certain number of these articles are made of shear steel, and for others crucible cast steel is employed. Sometimes the cutting edge alone is of steel, backed or strengthened with iron, to which it is welded. The tang, or part of the blade by which it is fastened to the handles, and other non-cutting portions, are also very often of iron. Brass, German silver, silver, horn, tortoise-shell, ivory, bone, mother-of-pearl, and numerous fancy woods are all brought into requisition for handles and other parts of cutlery, each demanding special treatment according to its nature. The essential processes in making a piece of steel cutlery are (1) forging, (2) hardening and tempering, (3) grinding, (4) polishing, and (5) putting together the various pieces and finishing the knife, the workmen who perform these last operations being the only ones known in the trade as “cutlers.”
The following outline of the stages in the manufacture of a razor will serve to indicate the sequence of operations in making an article which, though simple in form, demands the highest care and skill. The first essential of a good razor is that it be made of the finest quality of cast steel. The steel for razors is obtained in bars the thickness of the back of the instrument. Taking such a bar, the forger heats one end of it to the proper forging temperature, and then dexterously fashions it upon his anvil, giving it roughly the required form, edge and concavity. It is then separated from the remainder of the bar, leaving only sufficient metal to form the tang, if that is to be made of steel. The tang of the “mould,” as the blade in this condition is termed, is next drawn out, and the whole “smithed” or beaten on the anvil to compact the metal and improve the form and edge of the razor. At this stage the razor is said to be “forged in the rough,” and so neatly can some workmen finish off this operation that a shaving edge may be given to the blade by simple whetting. The forged blade is next “shaped” by grinding on the dry stone; this operation considerably reduces its weight, and removes the oxidized scale, thereby allowing the hardening and tempering to be done with certainty and proper effect. The shaped razor is now returned to the forge, where the tang is file-cut and pierced with the joint-hole, and into the blade is stamped either the name and corporate mark of the maker, or any mark and name ordered by the tradesman for whom the goods are being manufactured. The hardening is accomplished by heating the blade to a cherry-red heat and suddenly quenching it in cold water, which leaves the metal excessively hard and brittle. To bring it to the proper temper for a razor, it is again heated till the metallic surface assumes a straw colour, and after being plunged into water, it is ready for the process of wet grinding. The wet grinding is done on stones which vary in diameter from 1½ to 12 in. according to the concavity of surface desired (“hollow-ground,” “half hollow-ground,” &c.). “Lapping,” which is the first stage in polishing, is performed on a wheel of the same diameter as the wet-grinding stone. The lap is built up of segments of wood having the fibres towards the periphery, and covered with a metallic alloy of tin and lead. The lap is fed with a mixture of emery powder and oil. “Glazing” and “polishing,” which follow, are for perfecting the polish on the surface of the razor, leather-covered wheels with fine emery being used; and the work is finished off with crocus. The finished blade is then riveted into the scales or handle, which may be of ivory, bone, horn or other material; and when thereafter the razor is set on a hone it is ready for use.
The processes employed in making a table-knife do not differ essentially from those required for a razor. Table-knife blades are forged from shear and other steels, and, if they are not in one piece, a bit of malleable iron sufficient for the bolster or shoulder and tang is welded to each, often by machinery, especially in the case of the cheaper qualities. The bolster is formed with the aid of a die and swage called “prints,” and the tang is drawn out. The tang is variously formed, according to the method by which it is to be secured in the haft, and the various processes of tempering, wet grinding and polishing are pursued as described above. Steel forks of an inferior quality are cast and subsequently cleaned and polished; but the best quality are forged from bar steel, and the prongs are cut or stamped out of an extended flattened extremity called the mould or “mood.” In the United States of America machinery has been extensively adopted for performing the various mechanical operations in forging and fitting table cutlery, and in Sheffield it is employed to a great extent in the manufacture of table and pocket knife blades, scissors and razors. The cutler of the 18th century was an artisan who forged and ground the blades and fitted them in the hafts ready for sale; to-day the division of labour is carried to an extreme degree. In the making of a common pocket-knife with three blades not fewer than one hundred separate operations are involved, and these may be performed by as many workmen composed of five distinct classes—the scale and spring makers (the scale being the metal lining which is covered by the handle proper), the blade forgers, the grinders, the cutters of the coverings of ivory, horn, &c., that form the handles, and the hafters or cutlers proper. Grinders are divided into three classes—dry, wet and mixed grinders, according as they work at dry or wet stones. This branch of trade is, in Sheffield, conducted in distinct establishments called “wheels,” which are divided up into separate apartments or “hulls,” the dry grinding being as much as possible separated from the wet grinding. Dry grinding, such as is practised in the shaping of razors described above, the “humping” or rounding of scissors, and other operations, used to be a process especially dangerous to health, lung diseases being induced by the fine dust of silica and steel with which the atmosphere was loaded; but a great improvement has been effected by resorting to wet grinding as much as possible, by arranging fans to remove the dust by suction, and by general attention to sanitary conditions.
CUTTACK, a city and district of British India in the Orissa division of Bengal. The city is situated at the head of the delta of the Mahanadi. Pop. (1901) 51,364. It is the centre of the Orissa canal system, and an important station on the East Coast railway from Madras to Calcutta. It contains the government college, named after Mr Ravenshaw, a former commissioner; a high school, a training school, a survey school, a medical school and a law school. The city formed one of the five royal strongholds of ancient Orissa and was founded by a warlike Hindu prince, Makar Kesari, who reigned from 953 to 961. Native kings protected it from the rivers by a masonry embankment several miles long, built of enormous blocks of hewn stone, and 673 in some places 25 ft. high. A fortress defended the north-west corner of the town, and was captured by the English from the Mahrattas in October 1803. It is now abandoned as a place of defence.
The District of Cuttack lies in the centre of Orissa, occupying the deltas of the Mahanadi and Brahmani, together with a hilly tract inland. Its area is 3654 sq. m. It consists of three physical divisions: first, a marshy woodland strip along the coast, from 3 to 30 m. in breadth; second, an intermediate stretch of rice plains; third, a broken hilly region, which forms the western boundary of the district. The marshy strip along the coast is covered with swamps and malaria-breeding jungles. Towards the sea the solid land gives place to a vast network of streams and creeks, whose sluggish waters are constantly depositing silt, and forming morasses or quicksands. Cultivation does not begin till the limits of this dismal region are passed. The intermediate rice plains stretch inland for about 40 m. and occupy the older part of the delta between the sea-coast strip and the hilly frontier. They are intersected by three large rivers, the Baitarani, Brahmani and Mahanadi. These issue in magnificent streams through three gorges in the frontier hills. The Cuttack delta is divided into two great valleys, one of them lying between the Baitarani and the Brahmani, the other between the Brahmani and the Mahanadi. The rivers having, by the silt of ages, gradually raised their beds, now run along high levels. During floods they pour over their banks upon the surrounding valleys, by a thousand channels which interlace and establish communication between the main streams. After numerous bifurcations they find their way into the sea by three principal mouths. Silt-banks and surf-washed bars render the entrance to these rivers perilous. The best harbour in Cuttack district is at False Point, on the north of the Mahanadi estuary. It consists of an anchorage, land-locked by islands or sand-banks, and with two fair channels navigable towards the land. The famine commissioners in 1867 reported it to be the best harbour on the coast of India from the Hugli to Bombay.
The intermediate tract is a region of rich cultivation, dotted with great banyan trees, thickets of bamboos, exquisite palm foliage and mango groves. The hilly frontier separates the delta of British Orissa from the semi-independent tributary states. It consists of a series of ranges, 10 to 15 m. in length, running nearly due east and west, with densely-wooded slopes and lovely valleys between. The timber, however, is small, and is of little value except as fuel. The political character of these three tracts is as distinct as are their natural features. The first and third are still occupied by feudal chiefs, and have never been subjected to a regular land-settlement, by either the Mussulman or the British government. They pay a light fixed tribute. The intermediate rice plains, known as the Mogholbandi, from their having been regularly settled by the Mahommedans, have yielded to the successive dynasties and conquerors of Orissa almost the whole of the revenues derived from the province. The deltaic portions are of course a dead level; and the highest hills within the district in the western or frontier tract do not exceed 2500 ft. They are steep, and covered with jungle, but can be climbed by men. The most interesting of them are the Assa range, with its sandal trees and Buddhist remains; Udayagiri (Sunrise-hill), with its colossal image of Buddha, sacred reservoir, and ruins; and Assagiri, with its mosque of 1719. The Mahavinayaka peak, visible from Cuttack, has been consecrated for ages to Siva-worship by ascetics and pilgrims.
The population of the district in 1901 was 2,062,758, showing an increase of 6% in the preceding decade. The aboriginal tribes here, as elsewhere, cling to their mountains and jungles. They chiefly consist of the Bhumij, Tala, Kol and Savara peoples, the Savaras being by far the most numerous, numbering 14,775. They are regarded by the orthodox Hindus as little better than the beasts of the wildernesses which they inhabit. Miserably poor, they subsist for the most part by selling firewood or other products of their jungle; but a few of them have patches of cultivated land, and many earn wages as day labourers to the Hindus. They occupy, in fact, an intermediate stage of degradation between the comparatively well-to-do tribes in the tributary states (the stronghold and home of the race), and the Pans, Bauris, Kandras and other semi-aboriginal peoples on the lowlands, who rank as the basest castes of the Hindu community. The great bulk of the Indo-Aryan or Hindu population consists of Uriyas, with a residue of immigrant Bengalis, Lala Kayets from Behar and northern India, Telingas from the Madras coast, Mahrattas from central and western India, a few Sikhs from the Punjab and Marwaris from Rajputana. The Mahommedans are chiefly the descendants of the Pathans who took refuge in Orissa after the subversion of their kingdom in Bengal by the Moguls in the 16th century.
Rice forms the staple product of the district; its three chief varieties are biali or early rice, sarad or winter rice, and dalua or spring rice. The other cereal crops consist of mandua (a grass-like plant producing a coarse grain resembling rice), wheat, barley, and china, a rice-like cereal. Suan, another rice-like cereal, not cultivated, grows spontaneously in the paddy fields. Pulses of different sorts, oilseeds, fibres, sugar-cane, tobacco, spices and vegetables also form crops of the district. The cultivators consist of two classes—the resident husbandmen (thani) and the non-resident or migratory husbandmen (pahe).
The Orissa canal system, which lies mainly within Cuttack district, is used both for irrigation and transport purposes. The railway across the district towards Calcutta, a branch of the Bengal-Nagpur system, was opened in 1899. Considerable trade is carried on at the mouth of the rivers along the coast.
CUTTLE-FISH. The more familiar and conspicuous types of the molluscan class Cephalopoda (q.v.) are popularly known in English as cuttle-fish, squid, octopus and nautilus. The first of these names (from the A.S. cudele) is applied more particularly to the common Sepia (fig. 1), characterized by its internal calcareous shell, sometimes known as cuttle-bone, and its ink-sac, the contents of which have been long in use as a pigment (sepia). The term squid is employed among fishermen for the ten-armed Cephalopods in which the shell is represented by an uncalcified flexible structure somewhat resembling a pen. Hence in Italian a squid is called calamaio, from calamus a reed or pen, and in English the similar term calamary is sometimes used. Like the Sepia, squids also possess the ink-sac, whence they have sometimes been called pen and ink fish, and in German both Sepia and squid and their allies are known as Tinten-fische. The squids have generally softer and more watery tissues than the Sepia, but the former term is not in general use, and the distinction not generally understood. The term cuttle-fishes is sometimes extended to include all the Cephalopoda, but as the peculiarities of the remarkable shell of the true nautilus, and those of the shell-less Octopoda are widely known, we shall consider the name here as applying only to those forms which have ten arms, an ink-sac, an internal shell-rudiment, and only one pair of gills in the mantle cavity. Technically these form the sub-order Decapoda, of the order Dibranchia.
The cuttle-fishes are characteristically swimming animals, in contrast with the octopods, which creep about by means of their suckers among the rocks, and lurk in holes. In Sepia the integument is produced laterally into two muscular fins, rather narrow and of uniform breadth running the whole length of the body, but separated by a notch behind. There are four pairs of short non-retractile arms surrounding the mouth, and furnished with suckers on their oral surface, and between the third and fourth of these arms on each side is a much longer tentacular arm, which is usually kept entirely withdrawn into a pocket of the skin. The mantle cavity is on the posterior side of the body, which is the lower side in the swimming position, and the funnel is a tube open at both ends and connected with the body within the mouth of the mantle cavity. The mantle during life performs regular respiratory movements by which water is drawn into the cavity, passing between mantle and funnel, and is expelled through the funnel. In swimming the short arms are directed forwards, the fins undulate, and the motion is slow and deliberate; but if the animal is threatened or alarmed it swims suddenly and rapidly backwards by expelling water 674 forcibly from the mantle cavity through the funnel, at the same time expelling a cloud of ink from its ink-sac.
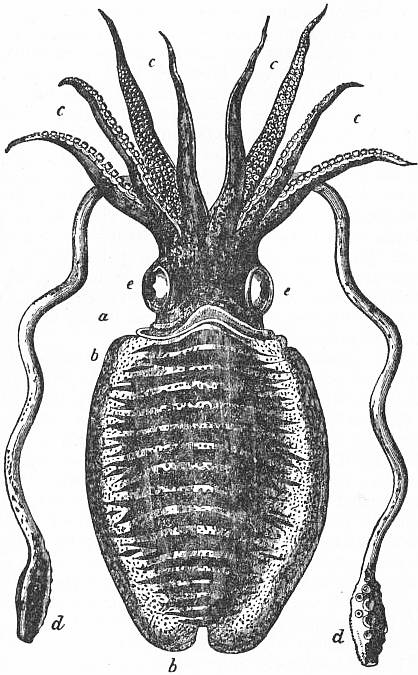 |
| Fig. 1.—Sepia officinalis, L., about ½ natural size, as seen when dead, the long prehensile arms being withdrawn from the pouches at the side of the head, in which they are carried during life when not actually in use. a, Neck; b, lateral fin of the mantle-sac; c, the eight shorter arms of the fore-foot; d, the two long prehensile arms; e, the eyes. |
The Sepia feeds principally on Crustacea, and in aquaria has been observed to pursue and capture prawns. The method in which it secures its prey has been carefully observed and described by the present writer, who studied the living animal in the aquarium of the biological laboratory at Plymouth. The prawns support themselves on their long slender legs on convenient points of the rockwork, and the Sepia stalks them with great caution and determination, the rapid play of its chromatophores giving evidence of its excitement. When it has arrived within striking distance, the two tentacular arms are shot out with great rapidity, and the prawn is seized between the two expanded ends, drawn within the circle of short arms, and devoured; unless, as sometimes happens, the prawn springs away and the Sepia misses its aim.
Two species of Sepia occur in British and European waters, including the Mediterranean, namely, S. elegans and S. officinalis. The usual length of the body is about 9 or 10 in. They live mostly between ten and forty fathoms, coming into shallower water in July and August to deposit their eggs, which are about as large as black currants and of somewhat similar colour, and are connected by elongated stalks into a cluster attached to the sea-bottom. Other species occur in various parts of the world, e.g. S. cultrata, which is common on the coasts of Australia. The Sepiidae form the only family of cuttle-fishes in which the shell is calcified. They belong to the tribe Myopsida, characterized by the complete closure of the external corneal covering of the eye outside the iris and the lens.
Sepiola and Rossia belong to another family of the Myopsida. Both are British genera living in shallow water, and entering estuaries. The animals of both genera are small, not more than 2 or 3 in. in length, with the body rounded at the aboral end, and the fins short and rounded, inserted in the middle of the body length, instead of extending from end to end. Sepiola, although it swims by means of its fins and funnel when active, spends much of its time buried in the sand for concealment. Rossia has similar habits. The shell is chitinous and shorter than the body. In other genera of the Sepiolidae the shell is entirely absent. Idiosepius is the smallest of the Cephalopoda, only 1.5 in. in length. It inhabits the Indian Ocean. The body is elongated and the fins rudimentary. In the Sepiadariidae also the shell is absent. The body is short and the mantle united with the head dorsally. The two genera Sepiadarium and Sepioloidea occur in the Pacific Ocean. The common squid Loligo is the type of the only remaining family of the Myopsida. In this species the shell is a well-developed chitinous pen or gladius with a thickened axis narrowing to a point behind, but bearing posteriorly a wide thin plate on each side. The shape closely resembles that of a quill pen with the quill in front. The fins are large and triangular, extending over rather more than half of the length of the body aborally. The tentacular arms are only partly retractile. The body is elongated and conical, and reaches about a foot in length. The squid is gregarious, and forms a favourite food of the larger fishes, especially of conger. All the Myopsida are more or less littoral in habit, and the British forms are familiar in consequence of their frequent capture in the nets of fishermen. The shell, or “bone” as it is commonly called, of the common Sepia frequently occurs in abundance on the shore among the sea-weed and other refuse left by the tide.
 |
| Fig. 2.—A, Loligo vulgaris; a, arms; t, tentacles. B, Pen of the same reduced in size. C, Side-view of one of the suckers, showing the horny hooks surrounding the margin. D, View of the head from in front, showing the arms (a), the tentacles (t), the mouth (m), and the funnel (f). |
The Oigopsida, or cuttle-fishes in which the corneal covering of the eye is perforated, are on the whole more oceanic than littoral, and many of the species are abyssal. Ommatostrephes sagittatus is one of the forms that occurs off the British coasts, especially the more northern, e.g. in the Firth of Forth. In general appearance it resembles the common squid, but the fins are broader and shorter, not extending to the middle of the body. 675 The shell is similar to that of Loligo, but ends aborally in a little hollow cone. The suckers bear chitinous rings which are toothed along the outer edge. The tentacular arms are rather short and thick. Two specimens of allied species have been taken on British coasts, one of which, captured off Salcombe in Devonshire in 1892, had a body 66 cm. (22 in.) long, and tentacular arms 64 cm. long, or nearly the same length as the body. Most of the species of Ommatostrephes are naturally gregarious and oceanic, and occur in the open seas in all latitudes, swimming near the surface and often leaping out of the water. They are largely devoured by albatrosses and other marine birds, and by Cetacea. They are used as bait in the Newfoundland cod fishery.
Some of the oceanic cuttle-fishes reach a very large size, and the stories of these ocean monsters which are narrated by the older writers, though to some extent exaggerated, are now known to be founded on fact. The figure given by one author of a gigantic Cephalopod rising from the surface of the ocean and embracing with its arms a full-rigged ship does not accurately represent an actual occurrence, but on the other hand there are authentic instances on record of fishermen in small boats on the banks of Newfoundland being in great peril in consequence of large squids throwing their arms across their boats. In November 1874 a specimen was brought ashore at St John’s, Newfoundland, which had been caught in herring nets. Its body was 7 ft. long, its fins 22 in. broad, and its tentacular arms 24 ft. long. Several others have been recorded, taken in the same region, which were as large or larger, the total length of the body and tentacles together varying from 30 to 52 ft., and the estimated weight of one of them being 1000 ℔.
In April 1875 one of these large squids occurred off Boffin’s Island on the Irish coast. The crew of a curragh rowed out to it and attacked it, cutting off two of its arms and its head. The shorter arms measured 8 ft. in length and 15 in. in circumference; the tentacular arms are said to have been 30 ft. long. In the Natural History Museum in London there is one of the shorter arms of a specimen; this arm is 9 ft. in length and 11 in. in circumference, and the total length of the specimen, including body and tentacles, is stated to have been 40 ft. The maximum known length of these giant squids is stated to be 18 metres or about 58½ ft. All these gigantic specimens belong, so far as at present known, to one genus called Architeuthis, referred to the same family as Ommatostrephes. They are the largest known invertebrates.
These huge cuttle-fishes as well as those of various other oceanic species form the food of the cachalot or sperm whale, and F. T. Bullen, in his Cruise of the Cachalot and other writings, has graphically described contests which came under his own observation between the cachalot and its prey. The prince of Monaco in his yacht the “Princess Alice” was fortunate enough to be able to make a very complete scientific investigation in the case of one specimen of the cachalot, which not only confirmed the most important of Mr Bullen’s statements, but added considerably to our knowledge of oceanic cuttle-fishes. Off the Azores in July 1895 the prince in his yacht witnessed the killing of a cachalot 13.70 metres long (about 45 ft. 8 in.) by the crew of a whaler. The animal in its death-agony vomited the contents of its stomach, most of which were carefully collected and preserved, and afterwards examined by Professor Joubin. On the lips of the whale were found impressions several centimetres wide which corresponded exactly to the toothed suckers of the largest cuttle-fish arms obtained from its stomach. The contents of the stomach consisted entirely of cuttle-fish or parts of cuttle-fish, including the giant Architeuthis, and among them was the body, without the head, of a form new to science, distinguished by a condition of the external surface which occurs in no other species of the group. The surface of the skin was divided into small angular flat projections like scales, arranged in a regular spiral like the scales of a pine cone. From this character the new genus was called Lepidoteuthis. The body, without the head, of the specimen obtained was 86 cm. (nearly 3 ft.) in length.
The family Onychoteuthidae is remarkable for the formidable chitinous hooks borne on the arms. These hooks are special modifications of the toothed chitinous ring which covers the sucker-rim in the Decapoda generally. The teeth of the ring are often unequal in size, and in the Onychoteuthidae one tooth is enormously developed. The maximum development occurs in Veranya, found in the Mediterranean, where the suckers have lost their function and are merely fleshy projections bearing the hooks at their extremities. Onychoteuthis reaches a large size, the length of the body without the arms being in one specimen from the Pacific coast of America 8 ft. Figures of this and several of the following genera are given in the article Cephalopoda.
In the family Cheiroteuthidae many of the species occur at abyssal depths of the ocean, and exhibit curious modifications of structure. In Cheiroteuthis itself the tentacular arms are very long and slender, and are not capable of retraction into pockets. In several species of this genus the suckers are no longer organs of adhesion, but are simple cups containing a network of filaments resembling a fishing net. In Histioteuthis and Histiopsis, as in some Octopods, the six dorsal arms are more or less completely united by a web, which also probably serves for capturing fish. In these two genera and in Calliteuthis the skin bears luminous organs. Cheiroteuthis has been taken at 2600 fms., Calliteuthis at 2200, Histiopsis at nearly 2000. Bathyteuthis, placed in the same family as Ommatostrephes, has been taken at 1700 fms.
The Cranchiidae are remarkable for their small size, the shortness of the ordinary arms, and the protuberance of the eyes, which in Taonius are actually on the ends of stalk-like outgrowths of the body. Cranchia is a deep-sea form taken at 1700 fms. Its body is pear-shaped, swollen posteriorly and quite narrow at the neck.
Spirula is distinguished from all other existing Cephalopods by the structure of its coiled shell, which in many respects resembles those of the extinct Ammonites, and is not completely internal. In the structure of the body the animal is a true cuttle-fish in the sense in which the term is here used, having ten arms and a perforated cornea. Three species are distinguished, and their empty shells occur abundantly on the shores of the tropical regions of the Atlantic, Pacific and Indian Oceans. In German the shells are known from their shape as Posthörnchen. They are common on the shores of the Azores. But the animal has very rarely been obtained; only a few specimens occur in museum collections. One specimen was taken by the “Challenger” in a deep-sea trawl, at a depth between 300 and 400 fathoms off Banda Neira in the Molluccas. Dr Willemoes Suhm, in describing the capture, stated that the specimen seemed to have been in the stomach of a fish, as its surface was slightly digested, and he thought it must have habits of concealment which usually prevent its capture, and that it was secured on this occasion only by the capture of the fish which had swallowed it. The fact that the shells are washed ashore in such large numbers is not fully explained. Possibly when freed from the animal the air in the chambers of the shell causes it to float, and in that case it would naturally be sooner or later washed ashore.
CUTTS OF GOWRAN, JOHN CUTTS, Baron (1661-1707), British soldier and author, came of an Essex family. After a short university career at Catherine Hall, Cambridge, he came into the enjoyment of the family estates, but evinced a decided preference for the life of court and camp. The double ambition for military and literary fame inspired his first work, which appeared in 1685 under the name La Muse de cavalier, or An Apology for such Gentlemen as make Poetry their Diversion not their Business. The next year saw Cutts serving as a volunteer under Charles of Lorraine in Hungary, and it is said that he was the first to plant the imperialist standard on the walls at the storm of Buda (July 1686). In 1687 he published a book of verse entitled Poetical Exercises, and the following year we find him serving as lieutenant-colonel in Holland. General Hugh Mackay describes Cutts about this time as “pretty tall, lusty and well shaped, an agreeable companion with abundance of wit, affable and familiar, but too much seized with vanity and self-conceit.”
Lieutenant-Colonel Cutts was one of William’s companions in the English revolution of 1688, and in 1690 he went in command of a regiment of foot to the Irish war. He served with distinction 676 at the battle of the Boyne, and at the siege of Limerick (where he was wounded), and King William created him Baron Cutts of Gowran in the kingdom of Ireland. In 1691 he succeeded to the command of the brigade of the prince of Hesse (wounded at Aughrim), and on the surrender of Limerick was appointed commandant of the town. Next year he served again in Flanders as a brigadier, his brigade of Mackay’s division being one of those almost destroyed at Steinkirk. At this battle Cutts himself was wounded. For some time after this, Lord Cutts was lieutenant-governor of the Isle of Wight, but he returned to active service in 1694, holding a command in the disastrous Brest expedition. He was one of Carmarthen’s companions in the daring reconnaissance of Camaret Bay, and was soon afterwards again wounded. He succeeded Talmash, the commander of the expedition (who died of his wounds), as colonel of the Coldstream Guards. Next year, after serving as a commissioner for settling the bank of Antwerp, he distinguished himself once more at the famous siege of Namur, winning for himself the name of “Salamander” by his indifference to the heaviest fire. Henceforward court service and war service alternated. He was deep in the confidence of William III., and acted as a diplomatic agent in the negotiations which ended in the peace of Ryswick. On the occasion of the great fire in Whitehall (1698) Cutts, at the head of the Coldstreams, earned afresh the honourable nickname of “the Salamander.” A little later we find Captain Richard Steele acting as his private secretary. In 1702, now a major-general, Cutts was serving under Marlborough in the opening campaign of the War of the Spanish Succession, and at the siege of Venloo, conspicuous as usual for romantic bravery, he led the stormers at Fort Saint Michael. His enemies, and even the survivors of the assault, were amazed at the success of a seemingly hare-brained enterprise. Probably, however, Cutts, who was now a veteran of great and varied experience, measured the factors of success and failure better than his critics. It was on this occasion that Swift lampooned the lieutenant-general in his Ode to a Salamander. He made the campaign of 1703 in Flanders, and in 1704, after a visit to England, he rejoined Marlborough on the banks of the Danube. At Blenheim he was third in command, and it was his division that bore the brunt of the desperate fighting at the village which gave its name to the battle.
Blenheim was Cutts’s last battle. His remaining years were spent at home, and, at the time of his death, he was the holder of eight distinct political and military offices. He sat in five parliaments for the county of Cambridge, and in Queen Anne’s first Parliament he was returned for Newport in the Isle of Wight, for which he sat until the time of his death. He was twice married, but left no issue.
CUVIER, GEORGES LÉOPOLD CHRÉTIEN FRÉDÉRIC DAGOBERT, Baron (1769-1832), French naturalist, was born on the 23rd of August 1769 at Montbéliard, and was the son of a retired officer on half-pay belonging to a Protestant family which had emigrated from the Jura in consequence of religious persecution. He early showed a bent towards the investigation of natural phenomena, and was noted for his studious habits and marvellous memory. After spending four years at the Academy of Stuttgart, he accepted the position of tutor in the family of the Comte d’Héricy, who was in the habit of spending the summer near Fécamp. It thus came about that he made the acquaintance of the agriculturist, A. H. Tessier, who was then living at Fécamp, and who wrote strongly in favour of his protégé to his friends in Paris—with the result that Cuvier, after corresponding with the well-known naturalist E. Geoffroy Saint-Hilaire, was appointed in 1795 assistant to the professor of comparative anatomy at the Muséum d’Histoire Naturelle. The National Institute was founded in the same year and he was elected a member. In 1796 he began to lecture at the École Centrale du Panthéon, and at the opening of the National Institute in April, he read his first palaeontological paper, which was subsequently published in 1800 under the title Mémoires sur les espèces d’éléphants vivants et fossiles. In 1798 was published his first separate work, the Tableau élémentaire de l’histoire naturelle des animaux, which was an abridgment of his course of lectures at the École du Panthéon, and may be regarded as the foundation and first and general statement of his natural classification of the animal kingdom.
In 1799 he succeeded L. J. M. Daubenton as professor of natural history in the Collège de France, and in the following year he published the Leçons d’anatomie comparée, a classical work, in the production of which he was assisted by A. M. C. Dumeril in the first two volumes, and by G. L. Duvernoy in three later ones. In 1802 Cuvier became titular professor at the Jardin des Plantes; and in the same year he was appointed commissary of the Institute to accompany the inspectors-general of public instruction. In this latter capacity he visited the south of France; but he was in the early part of 1803 chosen perpetual secretary of the National Institute in the department of the physical and natural sciences, and he consequently abandoned the appointment just mentioned and returned to Paris.
He now devoted himself more especially to three lines of inquiry—one dealing with the structure and classification of the mollusca, the second with the comparative anatomy and systematic arrangement of the fishes, and the third with fossil mammals and reptiles primarily, and secondarily with the osteology of living forms belonging to the same groups. His papers on the mollusca began as early as 1792, but most of his memoirs on this branch were published in the Annales du muséum between 1802 and 1815; they were subsequently collected as Mémoires pour servir à l’histoire et à l’anatomie des mollusques, published in one volume at Paris in 1817. In the department of fishes, Cuvier’s researches, begun in 1801, finally culminated in the publication of the Histoire naturelle des poissons, which contained descriptions of 5000 species of fishes, and was the joint production of Cuvier and A. Valenciennes, its publication (so far as the former was concerned) extending over the years 1828-1831. The department of palaeontology dealing with the Mammalia may be said to have been essentially created and established by Cuvier. In this region of investigation he published a long list of memoirs, partly relating to the bones of extinct animals, and partly detailing the results of observations on the skeletons of living animals specially examined with a view of throwing light upon the structure and affinities of the fossil forms. In the second category must be placed a number of papers relating to the osteology of the Rhinoceros Indicus, the tapir, Hyrax Capensis, the hippopotamus, the sloths, the manatee, &c. In the former category must be classed an even greater number of memoirs, dealing with the extinct mammals of the Eocene beds of Montmartre, the fossil species of hippopotamus, the Didelphys gypsorum, the Megalonyx, the Megatherium, the cave-hyaena, the extinct species of rhinoceros, the cave-bear, the mastodon, the extinct species of elephant, fossil species of manatee and seals, fossil forms of crocodilians, chelonians, fishes, birds, &c. The results of Cuvier’s principal palaeontological and geological investigations were ultimately given to the world in the form of two separate works. One of these is the celebrated Recherches sur les ossements fossiles de quadrupèdes, published in Paris in 1812, with subsequent editions in 1821 and 1825; and the other is his Discours sur les révolutions de la surface du globe, published in Paris in 1825.
But none of his works attained a higher reputation than his Règne animal distribué d’après son organisation, the first edition of which appeared in four octavo volumes in 1817, and the second in five volumes in 1829-1830. In this classical work Cuvier embodied the results of the whole of his previous researches on the structure of living and fossil animals. The whole of the work was his own, with the exception of the Insecta, in which he was assisted by his friend P. A. Latreille.
Apart from his own original investigations in zoology and palaeontology Cuvier carried out a vast amount of work as perpetual secretary of the National Institute, and as an official connected with public education generally; and much of this work appeared ultimately in a published form. Thus, in 1808 he was placed by Napoleon upon the council of the Imperial University, and in this capacity he presided (in the years 1809, 677 1811 and 1813) over commissions charged to examine the state of the higher educational establishments in the districts beyond the Alps and the Rhine which had been annexed to France, and to report upon the means by which these could be affiliated with the central university. Three separate reports on this subject were published by him. In his capacity, again, of perpetual secretary of the Institute, he not only prepared a number of éloges historiques on deceased members of the Academy of Sciences, but he was the author of a number of reports on the history of the physical and natural sciences, the most important of these being the Rapport historique sur le progrès des sciences physiques depuis 1789, published in 1810. Prior to the fall of Napoleon (1814) he had been admitted to the council of state, and his position remained unaffected by the restoration of the Bourbons. He was elected chancellor of the university, in which capacity he acted as interim president of the council of public instruction, whilst he also, as a Lutheran, superintended the faculty of Protestant theology. In 1819 he was appointed president of the committee of the interior, and retained the office until his death. In 1826 he was made grand officer of the Legion of Honour; and in 1831 he was raised by Louis Philippe to the rank of peer of France, and was subsequently appointed president of the council of state. In the beginning of 1832 he was nominated to the ministry of the interior, but on the 13th of May he died in Paris after a brief illness.
See P. J. M. Flourens, Éloge historique de G. Cuvier, published as an introduction to the Éloges historiques of Cuvier; Histoire des travaux de Georges Cuvier (3rd ed., Paris, 1858); A. P. de Candolle, “Mort de G. Cuvier,” Bibliothèque universelle (1832, 59, p. 442); C. L. Laurillard, “Cuvier,” Biographie universelle, supp. vol. 61 (1836); Sarah Lee, Memoirs of Cuvier, translated into French by T. Lacordaire (1833).
CUVILLES, FRANÇOIS DE (1698-c. 1767), French architect and engraver. He helped to carry the French rococo taste to Germany—he was summoned about 1720 to Cologne by the elector James Clement; in 1738 he became architect to the elector of Bavaria, and afterwards occupied the same position towards the emperor Charles VII. His style, while essentially thin, is often painfully elaborate and bizarre. He designed mirrors and consoles, balustrades for staircases, ceilings and fireplaces, and in furniture, beds and commodes especially. He also laid out parks and gardens. He wrote several treatises on artistic and decorative subjects, which were edited by his son, François de Cuvilles the younger, who succeeded his father at the court of Munich.
CUXHAVEN, or Kuxhaven, a seaport town of Germany, belonging to the state of Hamburg, and situated at the extremity of the west side of the mouth of the Elbe, 71 m. by rail N.W. from Hamburg. Pop. (1900) 6898. The harbour is good and secure, and is much frequented by vessels delayed in the Elbe by unfavourable weather. A new harbour was made in 1891-1896, having a depth of 26¼ ft., with a fore port 1000 ft. long by 800 ft. wide; and it is now the place of departure and arrival of the mail steamers of the Hamburg-American Steamship Company, who in 1901 transferred here a part of their permanent staff. The port is free, i.e. outside the customs union (Zollverein), the imports being principally coals, bricks and timber, and the exports fish. There is a fishing fleet, for which a new harbour was opened in 1892. Though lying on a bare strand, the town is much frequented as a bathing place by Hamburgers. It is strongly fortified, and there are a lighthouse, and lifeboat and pilot stations. The town only dates from 1873, having been formed by uniting the villages of Ritzebüttel and Cuxhaven, which had belonged to Hamburg since 1394.
CUYABÁ, or Cuiabá, capital of the inland state of Matto Grosso, Brazil, about 972 m. N.W. of Rio de Janeiro, on the Cuyabá river near its discharge into the São Lourenço, the principal Brazilian tributary of the Paraguay. Pop. (1890) 14,507; of the municipality, 17,815. The surrounding country is thickly populated. Cuyabá has uninterrupted steamer communication with Montevideo, about 2500 m. distant, but has no land communication with the national capital, except by telegraph. The climate is hot and malaria is prevalent. Cuyabá was founded in 1719 by Paulista gold hunters, and its gold-washings, now apparently exhausted, yielded rich results in the 18th century. It is the see of a bishopric and headquarters of an important military district, having an arsenal and military barracks.
CUYAPO, a town of the province of Nueva Ecija, Luzon, Philippine Islands, 28 m. N.N.W. of San Isidro, the capital. Pop. (1903) 16,292. Rice is grown here. In 1907 the town of Nampicuan was formed from part of Cuyapo.
CUYP, the name of a Dutch family which produced two generations of painters. The Cuyps were long settled at Dordrecht, in the neighbourhood of which they had a country house, where Albert Cuyp (the most famous) was born and bred.
The eldest member of the family who acquired fame was Jacob Gerritsz Cuyp, born it is said at Dordrecht in 1575, and taught by Abraham Bloemaert of Utrecht. He is known to have been alive in 1649, and the date of his death is obscure. J. G. Cuyp’s pictures are little known. But he produced portraits in various forms, as busts and half-lengths thrown upon plain backgrounds, or groups in rooms, landscapes and gardens. Solid and clever as an imitator of nature in its ordinary garb, he is always spirited, sometimes rough, but generally plain, and quite as unconscious of the sparkle conspicuous in Frans Hals as incapable of the concentrated light-effects peculiar to Rembrandt. In portrait busts, of which there are signed examples dated 1624, 1644, 1646 and 1649, in the museums of Berlin, Rotterdam, Marseilles, Vienna and Metz, his treatment is honest, homely and true; his touch and tone firm and natural. In portraying children he is fond of introducing playthings and pets—a lamb, a goat or a roedeer; and he reproduces animal life with realistic care. In a family scene at the Amsterdam Museum we have likenesses of men, women, boys and girls with a cottage and park. In the background is a coach with a pair of horses. These examples alone give us a clue to the influences under which Albert Cuyp grew up, and explain to some extent the direction which his art took as he rose to manhood.
Albert Cuyp (1620-1691), the son of Jacob Gerritsz by Grietche Dierichsdochter (Dierich’s daughter), was born at Dordrecht. He married in 1658 Cornelia Bosman, a rich widow, by whom he had an only daughter. By right of his possessions at Dordwyck, Cuyp was a vassal of the county of Holland, and privileged to sit in the high court of the province. As a citizen he was sufficiently well known to be placed on the list of those from whom William III., stadtholder of the Netherlands, chose the regency of Dordrecht in 1672. His death, and his burial on the 7th of November 1691 in the church of the Augustines of Dordrecht, are historically proved. But otherwise the known facts concerning his life are few. He seldom dates his pictures, but it appears probable that he ceased to paint about 1675. It has been said that Albert was the pupil of his father. The scanty evidence of Dutch annalists to this effect seems confirmed by a certain coincidence in the style and treatment of father and son. That he was a pupil of van Goyen has been surmised on the strength of the style of his early works. It has been likewise stated that Albert was skilled, not only in the production of portraits, landscapes and herds, but in the representation of still life. His works are supposed to be divisible into such as bear the distinctive marks C. or A. C. in cursive characters, the letters A. C. in Roman capitals, and the name “A. Cuyp” in full. A man of Cuyp’s acknowledged talent may have been versatile enough to paint in many different styles. But whether he was as versatile as some critics have thought is a question not quite easy to answer. It is to be observed that pieces assigned to Cuyp representing game, shell-fish and fruit, and inscribed A. C. in Roman capitals (Rotterdam, Amsterdam and Berlin museums), though cleverly executed, are not in touch or treatment like other pictures of less dubious authenticity, signed either with C. or A. C. or “A. Cuyp” in cursive letters. The panels marked C. and A. C. in cursive are portraits or landscapes, with herds, and interiors of stables or sheds, in which there are cows, horses and poultry. The subjects and their handling are akin to those which strike us in panels bearing the master’s full 678 signature, though characterized, as productions of an artist in the first phase of his progress would naturally be, by tones more uniform, touch more flat, and colour more deep than we find in the delicate and subtle compositions of the painter’s later time. Generally speaking, the finished examples of Cuyp’s middle and final period all bear his full signature. They are all remarkable for harmonies attained by certain combinations of shade in gradations with colours in contraposition.
Albert Cuyp, a true child of the Netherlands, does not seem to have wandered much beyond Rotterdam on the one hand or Nijmwegen on the other. His scenery is that of the Meuse or Rhine exclusively; and there is little variety to notice in his views of water and meadows at Dordrecht, or the bolder undulations of the Rhine banks east of it, except such as results from diversity of effect due to change of weather or season or hour. Cuyp is to the river and its banks what Willem Vandevelde is to calm seas and Hobbema to woods. There is a poetry of effect, an eternity of distance in his pictures, which no Dutchman ever expressed in a similar way. His landscapes sparkle with silvery sheen at early morning, they are bathed in warm or sultry haze at noon, or glow with heat at eventide. Under all circumstances they have a peculiar tinge of auburn which is Cuyp’s and Cuyp’s alone. Bürger truly says van Goyen is gray, Ruysdael is brown, Hobbema olive, but Cuyp “is blond.” The utmost delicacy may be observed in Cuyp’s manner of defining reflections of objects in water, or of sight from water on ship’s sides. He shows great cleverness in throwing pale-yellow clouds against clear blue skies, and merging yellow mists into olive-green vegetation. He is also very artful in varying light and shade according to distance, either by interchange of cloud-shadow and sun-gleam or by gradation of tints. His horses and cattle are admirably drawn, and they relieve each other quite as well if contrasted in black and white and black and red, or varied in subtler shades of red and brown. Rich weed-growth is expressed by light but marrowy touch, suggestive of detail as well as of general form. The human figure is given with homely realism in most cases, but frequently with a charming elevation, when, as often occurs, the persons represented are meant to be portraits. Whatever the theme may be it remains impressed with the character and individuality of Cuyp. Familiar subjects of the master’s earlier period are stables with cattle and horses (Rotterdam, Amsterdam, Petersburg and Brussels museums). Occasionally he painted portraits in the bust form familiar to his father, one of which is dated 1649, and exhibited in the National Gallery, London. More frequently he produced likenesses of ladies and gentlemen on horseback, in which the life and dress of the period and the forms of horses are most vividly represented (Buckingham Palace, Bridgewater Gallery, Louvre and Dresden Museum). Later on we find him fondest of expansive scenery with meadows and cattle and flocks, or rivers and barges in the foreground and distances showing the towers and steeples of Dordrecht. Cuyp was more partial to summer than to winter, to noon than to night, to calm than to storm. But some of his best groups are occasionally relieved on dark and gusty cloud (Louvre and Robarts’s collection). A few capital pieces show us people sledging and skating or netting ice-holes (Yarborough, Neeld and Bedford collections). A lovely “Night on the Banks of a River,” in the Grosvenor collection, reminds us that Cuyp’s friend and contemporary was the painter of moonlights, Aart van der Neer, to whom he was equal in the production of these peculiar effects and superior in the throw of figures. Sometimes Cuyp composed fancy subjects. His “Orpheus charming the Beasts,” in the Bute collection, is judiciously arranged with the familiar domestic animals in the foreground, and the wild ones, to which he is a comparative stranger, thrown back into the distance. One of his rare gospel subjects is “Philip baptizing the Eunuch” (Marchmont House, Berwickshire), described as a fine work by Waagen. The best and most attractive of Cuyp’s pieces are his Meuse and Rhine landscapes, with meadows, cattle, flocks and horsemen, and occasionally with boats and barges. In these he brought together and displayed—during his middle and final period—all the skill of one who is at once a poet and a finished artist; grouping, tinting, touch, harmony of light and shade, and true chords of colours are all combined. Masterpieces of acknowledged beauty are the “Riders with the Boy and Herdsman” in the National Gallery; the Meuse, with Dordrecht in the distance, in three or four varieties, in the Bridgewater, Grosvenor, Holford and Brownlow collections; the “Huntsman” (Ashburton); “Herdsmen with Cattle,” belonging to the marquess of Bute; and the “Piper with Cows,” in the Louvre. The prices paid for Cuyp’s pictures in his own time were comparatively low. In 1750, 30 florins was considered to be the highest sum to which any one of his panels was entitled. But in more recent times the value of the pictures has naturally risen very largely. At the sale of the Clewer collection at Christie’s in 1876 a small “Hilly Landscape in Morning Light” was sold for £5040, and a view on the Rhine, with cows on a bank, for £3150.
John Smith’s Catalogue raisonné of the Dutch and Flemish painters, in 9 vols. (1840), enumerated 335 of Albert Cuyp’s works, of which in 1877 Sir J. A. Crowe wrote in this encyclopaedia that “it would be difficult now to find more than a third of them.” In C. Hofstede de Groot’s Catalogue raisonné, vol. ii. (1909), revising Smith’s, the number is extended to nearly 850, but he accepts too readily the attributions of sale catalogues; the work is, however, the best modern authority on the painter.
CUZA (or Couza), ALEXANDER JOHN [Alexandru Joan] (1820-1873), first prince of Rumania, was born on the 20th of March 1820, at Galatz in Moldavia, and belonged to an ancient boiar, or noble, family. He was educated at Jassy, Pavia, Bologna and Athens; and, after a brief period of military service, visited Paris from 1837 to 1840 for a further course of study. In 1845 he married the daughter of another boiar, Elena Rosetti, who in 1862 founded the Princess Elena refuge for orphans, at Bucharest. Cuza was imprisoned by the Russian authorities for taking part in the Rumanian revolution of 1848, but escaped to Vienna. On his return, in 1850, he was appointed prefect of Galatz. In 1857 he rejoined the army, and within a few months rose to the rank of colonel. He became minister of war in 1858, and represented Galatz in the Assembly which was elected in the same year to nominate a prince for Moldavia. Cuza was a prominent speaker in the critical debates which ensued when the assembly met at Jassy, and strongly advocated the union of the two Danubian principalities, Moldavia and Walachia. In default of a foreign prince, he was himself elected prince of Moldavia by the assembly at Jassy (17th Jan. 1859), and prince of Walachia by the assembly at Bucharest (5th Feb.). He thus became ruler of the united principalities, with the title Prince Alexander John I.; but as this union was forbidden by the congress of Paris (18th Oct. 1858), his authority was not recognized by his suzerain, the sultan of Turkey, until the 23rd of December 1861, when the union of the principalities under the name of Rumania was formally proclaimed. For a full account of Cuza’s reign see Rumania. The personal vices of the prince, and the drastic and unconstitutional reforms which he imposed on all classes, alienated his subjects, although many of these reforms proved to be of lasting excellence. Financial distress supervened, and the popular discontent culminated in revolution. At four o’clock on the morning of the 22nd of February 1866, a band of military conspirators broke into the palace, and compelled the prince to sign his abdication. On the following day they conducted him safely across the frontier. Prince Alexander spent the remainder of his life chiefly in Paris, Vienna and Wiesbaden. He died at Heidelberg on the 15th of May 1873.
CUZCO, an inland city of southern Peru, capital of an Andean department of the same name, about 360 m. E.S.E. of Lima, in lat. 13° 31′ S., long. 73° 03′ W. The population, largely composed of Indians and mestizos, was estimated at 30,000 in 1896, but according to the official estimate of 1906, it was then about 25% less. The city stands at the head of a small valley, 11,380 ft. above sea-level, and is nearly enclosed by mountains of considerable elevation. The valley itself is 9 m. in length and extends S.E. to the valley of Vilcamayu. Overlooking the city from the N. is the famous hill of Sacsahuaman, crowned by ruins of the cyclopean fortress of the Incas and their predecessors, and separated from adjacent heights by the deep ravines of two 679 streams, called the Huatenay and Rodadero. The principal part of the city lies between these two streams, with its great plaza in the centre. On the W. side of the Huatenay are two more fine squares, called the Cabildo and San Francisco. The houses of the city are built of stone, their walls commonly showing the massive masonry of the Incas at the bottom, crowned with a light modern superstructure roofed with red tiles. The streets cross each other at right angles and afford fine vistas on every side. The principal public buildings are the cathedral, which is classed among the best in South America, the convent of San Domingo, which partly occupies the site of the great Temple of the Sun of the Incas, the cabildo or government-house, a university founded in 1598, a college of science and arts, a public library, hospital, mint and museum of Incarial antiquities. Cuzco was made the see of a bishopric soon after it was occupied by the Spaniards. The Church has always exercised a dominating influence in this region, and the city has many churches and religious establishments. There are a number of small manufacturing industries in Cuzco, including the manufacture of cotton and woollen fabrics, leather, beer, embroidery and articles of gold and silver. Its trade is not large, however, owing to the costs of transportation. The climate is cool and bracing, and the products of the vicinity include many of the temperate zone. A railway from Juliaca (a station on the line from Mollendo to Puno) to Cuzco was virtually completed early in 1908. This railway gives Cuzco an outlet to the coast, and also direct connexion with La Paz, the Bolivian capital. A branch of the Callao & Oroya railway is also projected southward to Cuzco, and reached Huancayo in 1908. Cuzco was the capital of a remarkable empire ruled by the Incas previous to the discovery of Peru, and it was one of the largest and most civilized of the native cities of the New World. It was captured by Pizarro in 1533, and it is said that its size and the magnificence of its principal edifices filled the Spaniards with surprise. It was for many years an object of contention among the Spanish factions, but ultimately the greater attractions of Lima and its own isolation diminished its importance.
The department of Cuzco is the second largest in Peru, having an area of 156,317 sq. m., and a population, according to a reduced official estimate of 1906, of only 328,980. It occupies an extremely mountainous region on the frontier of Bolivia, E. of the departments of Junin, Ayacucho and Apurimac, and extends from Loreto on the N. to Puno and Arequipa on the S. Its area, however, includes a large district E. of the Andes which is claimed by Bolivia, and the settlement of the dispute may materially diminish its size. The elevation of a large part of the department gives it a temperate climate and permits the cultivation of cereals and other products of the temperate zone. Cattle and sheep are produced in large numbers in some of the provinces, while in others mining forms the chief industry. On the eastern forested slopes and in the lower valleys tropical conditions prevail. The population is chiefly composed of Indians who form a sturdy, docile labouring class, but are in great part strongly disinclined to accept the civilization of the dominant white race.
CYANAMIDE, NC·NH2, the amide of normal cyanic acid, obtained by the action of ammonia on cyanogen chloride, bromide or iodide, or by the desulphurization of thio-urea with mercuric oxide; it is generally prepared by the latter process. It forms white crystals, which melt at 40° C., and are readily soluble in water, alcohol and ether. Heated above its melting point it polymerizes to di-cyandiamide (CN2H2)2, which at 150° C. is transformed into the polymer n-tri-cyantriamide or melamine (CN2H2)3, the mass solidifying. Nascent hydrogen reduces cyanamide to ammonia and methylamine. It gives mono-metallic salts of the type NC·NHM when treated with aqueous or alcoholic solutions of alkalis. Di-metallic salts are obtained by heating cyanates alone, e.g. calcium, or cyanides in a current of nitrogen, e.g. barium.
Calcium cyanamide has assumed importance in agriculture since the discovery of its economic production in the electric furnace, wherein calcium carbide takes up nitrogen from the atmosphere to form the cyanamide with the simultaneous liberation of carbon. It may also be produced by heating lime or chalk with charcoal to 2000° in a current of air. The commercial product (which is known in Germany as “Kalkstickstoff”) contains from 14 to 22% of nitrogen, which is liberated as ammonia when the substance is treated with water; to this decomposition it owes its agricultural value. It appears that with soils which are not rich in humus or not deficient in lime, calcium cyanamide is almost as good, nitrogen for nitrogen, as ammonium sulphate or sodium nitrate; but it is of doubtful value with peaty soils or soils containing little lime, nor is it usefully available as a top-dressing or for storing.
CYANIC ACID AND CYANATES. Cyanic acid, CN·OH, was discovered by F. Wöhler in 1824, and may be obtained by distilling its polymeride, cyanuric acid, in a current of carbon dioxide (F. Wöhler and J. v. Liebig, Berzelius Jahresberichte, 1827, 11, p. 84), the vapours which distil over being condensed in a freezing mixture. It is a very volatile liquid of strong acid reaction, and is only stable below 0° C. It has a smell resembling that of acetic acid. At 0° C. it is rapidly converted into a mixture of cyanuric acid, C3N3O3H3, and another polymer, cyamelide (CNOH)x; this latter substance is a white amorphous powder, insoluble in water. An aqueous solution of cyanic acid is rapidly hydrolysed (above 0° C.) into a mixture of carbon dioxide and ammonia. Cyanogen chloride, CNCl, may be regarded as the chloride of cyanic acid. It may be prepared by the action of chlorine on hydrocyanic acid or on mercury cyanide. It is a very poisonous volatile liquid, which boils at 15.5° C. It polymerizes readily to cyanuric chloride, C3N3Cl3. Caustic alkalis hydrolyse it readily to the alkaline chloride and cyanate.
The salts of cyanic acid are known as the cyanates, the two most important being potassium cyanate (KOCN) and ammonium cyanate (NH4OCN). Potassium cyanate may be prepared by heating potassium cyanide with an oxidizing agent, or by heating potassium ferrocyanide with manganese dioxide, potassium carbonate or potassium dichromate (J. v. Liebig, Ann., 1841, 38, p. 108; C. Lea, Jahresb., 1861, p. 789; L. Gattermann, Ber., 1890, 23, p. 1224), the fused mass being extracted with boiling alcohol. It crystallizes in flat plates and is readily soluble in cold water. It is a somewhat important reagent, and has been used by Emil Fischer in various syntheses in the uric acid group (see Purin). Ammonium cyanate possesses considerable theoretical importance since the first synthetical production of an organic from inorganic compounds was accomplished by warming its aqueous solution for some time, urea being formed (F. Wöhler, Berzelius Jahresberichte, 1828, 12, p. 266). J. Walker and J. K. Wood (Jour. Chem. Soc., 1900, 77, p. 24) prepared pure ammonium cyanate by the union of gaseous ammonia and cyanic acid, special precautions being taken to keep the temperature below the point at which the salt is transformed into urea. It crystallizes in fine needles, which melt suddenly at about 80° C., then resolidify, and melt again at about 128° to 130° C. (this temperature being that of the melting point of urea). Substituted ammonias were also made to combine with cyanic acid, and it was found that the substituted ammonium cyanates produced pass much more readily into the corresponding ureas than ammonium cyanate itself. (On the constitution of cyanic acid see F. D. Chattaway and J. M. Wadmore, Jour. Chem. Soc., 1902, 81, p. 191.)
Esters of normal cyanic acid are not known, but those of isocyanic acid (HN·CO) may be prepared by the action of alkyl halides on silver cyanate, or by oxidizing the isonitriles with mercuric oxide. They are volatile liquids which boil without decomposition, and possess a nauseating smell. When hydrolysed with caustic alkalis, they yield primary amines (this reaction determines their constitution). C2H5NCO + H2O = C2H5NH2 + CO2. When heated with water they yield carbon dioxide and symmetrical dialkyl ureas; with ammonia and amines they form alkyl ureas; and with acid anhydrides they yield tertiary amides.
Ethyl isocyanate, C2H5NCO, was first prepared by A. Wurtz (Ann. chim., 1854 (3), 42, p. 43) by distilling a mixture of potassium 680 ethyl sulphate and potassium cyanate. It is a colourless liquid which boils at 60° C.
Cyanuric acid, H3C3N3O3, was obtained by Wöhler and Liebig by heating urea, and by A. Wurtz by passing chlorine into melting urea. It forms white efflorescent crystals. Treatment with phosphorus pentachloride gives cyanuric chloride, C3N3Cl3, which is also formed by the combination of anhydrous chlorine and prussic acid in the presence of sunlight. These substances contain a ring of three carbon and three nitrogen atoms, i.e. they are symmetrical triazines.
CYANIDE, in chemistry, a salt of prussic of hydrocyanic acid, the name being more usually restricted to inorganic salts, i.e. the salts of the metals, the organic salts (or esters) being termed nitriles. The preparation, properties, &c., of cyanides are treated in the article Prussic Acid; reference should also be made to the articles on the particular metals. The most important cyanide commercially is potassium cyanide, which receives application in the “cyanide process” of gold extraction (see Gold).
 |
CYANITE, a native aluminium silicate, Al2SiO5, crystallizing in the anorthic system. It has the same percentage chemical composition as andalusite and sillimanite, but differs from these in its crystallographic and physical characters. P. Groth writes the formula as a metasilicate (AlO)2SiO3. The name cyanite was given by A. G. Werner in 1789, from κύανος, blue, in allusion to the characteristic colour of the mineral; the form kyanite is also in common use, and the name disthène, proposed by R. J. Haüy in 1801, is used by French writers.
Distinctly developed crystals with terminal planes are rare, the mineral being commonly found as lamellar cleavage masses or long blade-shaped crystals embedded in crystalline rocks. The colour is usually a pale sky-blue, but may be white, greenish or yellowish; it varies in intensity in different bands, so that the crystals usually present a more or less striped appearance. There is a perfect cleavage parallel to the broad face m (100), and a less perfect one parallel to t (010): the basal plane p (001), oblique to the prism zone, is a gliding plane on which secondary twinning is produced by pressure, giving rise to characteristic horizontal striations on the cleavage face m. The accompanying figure represents a crystal twinned on the plane m (100). A negative biaxial optic figure is seen in convergent polarized light through the cleavage plane m, the axial plane being inclined at about 30° to the edge between m and t. A remarkable feature of cyanite is the great difference in hardness on different faces of the same crystal and in different directions on the same face: on the face m in a direction parallel to the edge between m and p the hardness is 7, whilst in a direction parallel to the edge between m and t it is 4½. The name disthène, from δίς, two, and σθένος, strong, has reference to these differences in hardness.
Analyses of cyanite often show the presence of a small amount (usually less than 1%) of ferric oxide and sometimes traces of copper, and to these constituents the blue or green colour of the mineral is doubtless due. The mineral is infusible before the blowpipe, and is not decomposed by acids. At a high temperature, about 1350° C., it becomes transformed into sillimanite, changing in specific gravity from 3.6 to 3.2.
Cyanite is a characteristic mineral of the metamorphic crystalline rocks—gneiss, schist, granulite and eclogite—and is often associated with garnet and staurolite. A typical occurrence is in the white, fine-scaled paragonite-schist of Monte Campione, near St Gotthard in Switzerland, where long transparent crystals of a fine blue colour are abundant. In the gneiss of the Pfitscher Tal near Sterzing in Tirol a white variety known as rhaetizite is found. It occurs at several places in Scotland, for instance, at Botriphnie in Banffshire, with muscovite in a quartz-vein. Fine specimens are found in mica-schist at Chesterfield in Massachusetts, and at several other localities in the United States. It is found in the gold-washings of the southern Urals and in the diamond-washings of Brazil. As minute crystal fragments it is met with in many sands and sandstones.
When of sufficient transparency and depth of colour (deep cornflower-blue) the mineral has a limited application as a gem-stone; it is usually cut en cabochon.
CYANOGEN (Gr. κύανος, blue γεννᾶν, to produce), C2N2, in chemistry, a gas composed of carbon and nitrogen. The name was suggested by Prussian blue, the earliest known compound of cyanogen. It was first isolated in 1815 by J. Gay-Lussac, who obtained it by heating mercury or silver cyanide; this discovery is of considerable historical importance, since it recorded the isolation of a “compound radical.” It may also be prepared by heating ammonium oxalate; by passing induction sparks between carbon points in an atmosphere of nitrogen (see H. von Wartenburg, Abs. J.C.S., 1907, i. p. 299), or by the addition of a concentrated solution of potassium cyanide to one of copper sulphate, the mixed solutions being then heated. It also occurs in blast-furnace gases. When cyanogen is prepared by heating mercuric cyanide, a residue known as para-cyanogen, (CN)x, is left; this is to be regarded as a polymer of cyanogen. It is a brownish amorphous solid, which is insoluble in water. Cyanogen is a colourless gas, possessing a peculiar characteristic smell, and is very poisonous. It burns with a purple flame, forming carbon dioxide and nitrogen; and may be condensed (by cooling to −25° C.) to a colourless liquid, and further to a solid, which melts at −34.4° C. (M. Faraday, Ann., 1845, 56, p. 158). It dissolves readily in water and the aqueous solution decomposes on standing; a dark-brown flocculent precipitate of azulmic acid, C4H5N5O, separating whilst ammonium oxalate, urea and hydrocyanic acid are found in the solution. In many respects it resembles chlorine in its chemical behaviour, a circumstance noted by Gay-Lussac; it combines directly with hydrogen (at 500° to 550° C.) to form hydrocyanic acid, and with chlorine, bromine, iodine and sulphur, to form cyanogen chloride, &c.; it also combines directly with zinc, cadmium and iron to form cyanides of these metals. It combines with sulphuretted hydrogen, in the presence of water, to form the compound C2N2·H2S, and in the presence of alcohol, to form the compound C2N2·2H2S. Concentrated hydrochloric acid converts it into oxamide. Potash solution converts it into a mixture of potassium cyanide and cyanate. When heated with hydriodic acid (specific gravity 1.96) it forms amino-acetic acid, and with tin and hydrochloric acid it yields ethylene diamine.
CYAXARES (Pers. Uvakhshatra), king of Media, reigned according to Herodotus (i. 107) forty years, about 624-584 B.C. That he was the real founder of the Median empire is proved by the fact that in Darius’s time a Median usurper, Fravartish, pretended to be his offspring (Behistun inscr. 2. 43); but about his history we know very little. Herodotus narrates (i. 103 ff.) that he renewed the war against the Assyrians, in which his father Phraortes had perished, but was, while he besieged Nineveh, attacked by a great Scythian army under Madyas, son of Protothyes, which had come from the northern shores of the Black Sea in pursuit of the Cimmerians. After their victory over Cyaxares, the Scythians conquered and wasted the whole of western Asia, and ruled twenty-eight years, till at last they were made drunk and slain by Cyaxares at a banquet (cf. another story about Cyaxares and a Scythian host in Herod, i. 73). As we possess scarcely any contemporary documents it is impossible to find out the real facts. But we know from the prophecies of Jeremiah and Zephaniah that Syria and Palestine were really invaded by northern barbarians in 626 B.C., and it is probable that this invasion was the principal cause of the downfall of the Assyrian empire (see Media and Persia: Ancient History).
After the destruction of the Scythians Cyaxares regained the supremacy, renewed his attack on Assyria, and in 606 B.C. destroyed Nineveh and the other capitals of the empire (Herod. i. 106; Berossus ap. Euseb. Chron. i. 29, 37, confirmed by a stele of Nabonidus found in Babylon: Scheil in Recueil de 681 travaux, xviii.; Messerschmidt, “Die Inschrift der Stele Nabonaids,” in Mitteilungen der vorderasiatischen Gesellschaft, i., 1896). According to Berossus he was allied with Nabopolassar of Babylon, whose son Nebuchadrezzar married Amyitis, the daughter of the Median king (who is wrongly called Astyages). The countries north and east of the Tigris and the northern part of Mesopotamia with the city of Harran (Carrhae) became subject to the Medes. Armenia and Cappadocia were likewise subdued; the attempt to advance farther into Asia Minor led to a war with Alyattes of Lydia. The decisive battle, in the sixth year, was interrupted by the famous solar eclipse on the 28th of May 585 predicted by Thales. Syennesis of Cilicia and Nebuchadrezzar (in Herodotus named Labynetus) of Babylon interceded and effected a peace, by which the Halys was fixed as frontier between the two empires, and Alyattes’s daughter married to Cyaxares’s son Astyages (Herod. i. 74). If Herodotus’s dates are correct, Cyaxares died shortly afterwards.
In a fragmentary letter from an Assyrian governor to King Sargon (about 715 B.C.) about rebellions of Median chieftains, a dynast Uvakshatar (i.e. Cyaxares) is mentioned as attacking an Assyrian fortress (Kharkhar, in the chains of the Zagros). Possibly he was an ancestor of the Median king.
CYBELE, or Cybebe (Gr. Κυβέλη, Κυβήβη), a goddess native to Asia Minor and worshipped by most of the peoples of the peninsula, was known to the Romans most commonly as the Great Mother or the Gods (q.v.), or the Great Idaean Mother of the Gods—Magna Deum Mater, Mater Deum Magna Idaea. She was known by many other names, such as Mater Idaea, Dindymene, Sipylene, derived from famous seats of worship, and Mountain Mother, &c., in token of her character, but Cybele is the name by which she is most frequently known in literature. Her cult became centralized in Phrygia, had found its way into Greece, where it never flourished greatly, as early as the latter 6th century B.C., and was introduced at Rome in 204 B.C. Under the Empire it attained to great importance, and was one of the last pagan cults to die. Cybele was usually worshipped in connexion with Attis (q.v.), as Aphrodite with Adonis, the two being a duality interpreted by the philosophers as symbolic of Mother Earth and her vegetation.
CYCLADES, a compact group of islands in the Greek Archipelago, forming a cluster around the island of Syra (Syros), the principal town of which, now officially known as Hermoupolis, is the capital of a department. Population of the group (1907) 130,378. The islands, though seldom visited by foreigners, are for the most part highly interesting and picturesque, notwithstanding their somewhat barren appearance when viewed from the sea; many of them bear traces of the feudal rule of Venetian families in the middle ages, and their inhabitants in general may be regarded as presenting the best type of the Greek race. To the student of antiquity the most interesting are: Delos (q.v.), one of the greatest centres of ancient religious, political and commercial life, where an important series of researches has been carried out by French archaeologists; Melos (q.v.), where, in addition to various buildings of the Hellenic and Roman periods, the large prehistoric stronghold of Phylakopi has been excavated by members of the British school at Athens; and Thera (see Santorin), the ancient capital of which has been explored by Baron Hiller von Gaertringen. Thera is also of special interest to geologists owing to its remarkable volcanic phenomena. Naxos, the largest and most fertile island of the group, contains the highest mountain in the Cyclades (Zia, 3290 ft.); the island annually exports upwards of 2000 tons of emery, a state monopoly the proceeds of which are now hypothecated to the foreign debt. The oak woods of Ceos (Zeá) and Ios furnish considerable supplies of valonia. Kimolos, which is absolutely treeless, produces fuller’s-earth. The famous marble quarries of Paros have been practically abandoned in modern times; the marble of Tenos is now worked by a British syndicate. The mineral wealth of the Cyclades has hitherto been much neglected; iron ore is exported from Seriphos, manganese and sulphur from Melos, and volcanic cement (pozzolana) from Santorin. Other articles of export are wine, brandy, hides and tobacco. Cythnos, Melos and other islands possess hot springs with therapeutic qualities. The prosperity of Syra, formerly an important distributing centre for the whole Levant, has been declining for several years.
Population (1907):—Syra 31,939 (communes, Hermoupolis 18,132, Mykonos 4589, Syra 9218); Andros 18,035 (Andros 8536, Arni 2166, Gaurio 2897, Corthion 4436); Thera 19,597 (Thera 4226, Egiale 1513, Amorgos 2627, Anaphe 579, Emporium 2172, Therasia 679, Ios 2090, Kalliste 3519, Oea 2192); Ceos 11,032 (Ceos 3817, Dryopis 1628, Cythnos 1563, Seriphos 4024); Melos, 12,774 (Melos 4864, Adamas 529, Siphnos 3777, Kimolos 2015, Pholegandros 962, Sikinos 627); Naxos 25,185 (Naxos 2064, Apiranthe 2421, Vivlos 4343, Coronis 3205, Marpessa 1313, Naoussa 1670, Paros 3586, Tragea 4661, Hyrie 1922); Tenos 11,816 (Tenos 4697, Panorme 2658, Peree 2801, Sosthenion 1660).
CYCLAMEN, in botany, a genus belonging to the natural order Primulaceae, containing about ten species native in the mountains of central Europe and the Mediterranean region. C. europaeum (Sow-bread) is found as an introduced plant in copses in Kent and Sussex. The plants are low-growing herbs with large tuberous rootstocks, from the surface of which spring a number of broad, generally heart-shaped or kidney-shaped, long-stalked leaves, which in cultivated forms are often beautifully marbled, ribbed or splashed. The flowers are nodding, and white, pink, lilac or crimson in colour. The corolla has a short tube and five large reflexed lobes. After flowering the stalk becomes spirally coiled, drawing the fruit down to the soil. Cyclamen is a favourite winter and spring flowering plant. C. persicum is probably the best known. It is a small-growing kind bearing medium-sized leaves and numerous flowers. C. giganteum is a large, strong-growing species; not quite so free flowering as C. persicum, but in all other respects superior to it when well grown. C. papilio differs in the fringed character of the petals. It has been obtained by selection from C. persicum. There is also a very beautiful crested race, probably derived from C. giganteum.
The plants are raised from seed, and, with good cultivation, flower in fifteen to eighteen months from date of sowing. Seed should be sown as soon as ripe, in July or August, in pots or pans, filled up to 2½ in. of the rim with broken crocks for drainage. The soil should consist of fibrous yellow loam, leaf-mould in flakes, and coarse silver-sand, in equal parts. Sow the seed thinly—¼ in. to ½ in. apart—and cover with a very thin sprinkling of the soil. Protect with a square of glass covered with a piece of brown paper for shade, and place on a shelf in a warm greenhouse. The soil should never be allowed to get dry.
When the seedlings appear, remove the covering, care being taken that they do not suffer for want of shade, water or a moist atmosphere. As soon as the third leaf appears, repot singly into thumb-pots in slightly coarser soil, so that the crowns of the little plants are just above the level of the soil. In December transfer into a little richer soil, consisting of two parts fibrous loam broken into small bits by hand and the fine particles rejected, one part flaked leaf-mould, passed through a half-inch sieve, half a part of plant ash from the burnt refuse heap and half a part of coarse silver-sand. Keep through the winter in a moist atmosphere at a temperature not below 50° Fahr., and as near the glass as possible. In March they should be ready for their next shift into 5-in. pots. The potting compost should be the same as for the last shift, with the addition of half a part of well-sweetened manure, such as a spent mushroom bed. Keep in a warm moist atmosphere and shade from strong sunlight. In June remove to cold frames and stand them on inverted pots well clear of one another. Slugs show a marked partiality for the succulent young leaves and should be excluded by dusting round the frames occasionally with newly slaked lime. The inverted pots serve as traps. The frames may thus be frequently syringed without keeping the plants unduly wet. Shade heavily from direct sunlight, but afford as much diffused light as practicable. Ventilate on all favourable occasions, and close the frames early after copious syringing.
By the end of the month they will be ready for the final shift into 7-in. pots. Much care must be used in handling them, the leaves being large, tender and numerous. The soil is as for the last potting. The frames should be kept close and heavily shaded 682 for a few days after potting; then gradually reduce shade and increase ventilation. By the end of July the elegance of the foliage alone should well repay the care bestowed on them. From this time onwards very little shading will be needed, the object of the cultivator being to harden the growth already made. With the advent of cool weather in September, remove to flowering quarters in a warm greenhouse. Flowering will begin in November and will continue through the winter and spring. The damping off of the flower-buds may occasionally prove troublesome during winter. This may generally be traced to checks, such as sudden changes in temperature, too low a temperature, careless watering, &c. During spring plants that are flowering freely will require weak manure water about twice a week.
Plants selected to bear seed should be set aside for that purpose, and as soon as the capsules are found to be developing properly they should be reduced to six or seven per plant, and all flower-buds picked off as soon as they are large enough to handle. The production of strong seeds is of the utmost importance.
Plants grown for market purposes, either for decoration or for seed, are sown later than the above, are kept cooler, and during summer receive more ventilation and less shade. This results in the production of plants with much smaller and more erect leaves, which travel well. They are flowered in spring and early summer. The species grown for this purpose is C. persicum.
A few species are hardy in dry sheltered positions, such as rockeries, under walls and old trees, provided the positions are well drained. Such are C. europaeum, with reddish-purple flowers in summer; C. hederifolium in autumn; and C. neapolitanum, with large leaves marbled with silver and rosy-pink flowers.
CYCLE (Gr. κύκλος, a circle), in astronomy, a period of time at the end of which some aspect or relation of the heavenly bodies recurs. The more important cycles are discussed in the articles Calendar and Eclipse. In physics, the term is applied to a series of operations which, performed upon a system, brings it back to its original state; “Carnot’s Cycle” is an example (see Thermodynamics). From the use of the word for any period at the end of which the same events recur in the same order or for any complete series of phenomena, it is used loosely of any long period of time. The name ὁ ἐπικὸς κύκλος, the epic cycle, was given to the poems which complete the Homeric account of the Trojan War (see below). It is this use which has given rise to the application of the term “cycle” to a series of prose or poetical romances which have for a centre one subject, whether a person, as in the Alexander, Arthurian or Charlemagne cycles, or an object, such as the ring of the Nibelungenlied. In music “Song-cycle” (Ger. Liederkreis) is similarly used of a series of songs written round one subject or set to poems by the same author. Beethoven’s An die ferne Geliebte (Op. 98), published in 1816, is the earliest instance. Schubert’s Die schöne Müllerin, Schumann’s Dichterliebe and Brahms’s Magelone-Lieder are well-known instances.
Epic Cycle.—This is a collection or corpus of lays written about 776-580 B.C. by poets of the Ionian School, introductory or complementary to the Homeric poems, dealing with the legends of the Trojan and Theban wars. At a later date they were arranged so as to form a continuous narrative (the Iliad and the Odyssey included), perhaps after certain alterations had been made, to fill up gaps and remove inconsistencies and repetitions. By whom, and when, they were so arranged, cannot be decided; it is possible that it was the work of Zenodotus of Ephesus, who had the care of the epic section of the Alexandrian library. In order to furnish the general reader with a comprehensive sketch of mythological history, Proclus—according to Welcker and Valesius (Valois), not the neo-Platonist, but an unknown 2nd or 3rd century grammarian, perhaps Eutychius Proclus of Sicca1 in Africa, one of the tutors of Marcus Aurelius (see Proclus)—compiled a prose summary (Γραμματικὴ Χρηστομάθεια) of the contents of the poems, to serve as a sort of primer to Greek literature. Extracts from this are preserved in the Codex Venetus of Homer and Photius (cod. 239), according to which the epic cycle began with the union of Uranus and Ge and ended with the death of Odysseus on his return to Ithaca at the hands of his son Telegonus. The cycle was in existence in his (Proclus’s) time, and was in request not so much for its artistic merit, as for the “sequence of the events described in it.” Further light is thrown on the subject by pictorial representations, intended for school use during the Roman imperial period, the most famous of which is the Tabula Iliaca in the Capitoline museum.
The expression “epic cycle” in the sense of a poetical collection does not occur before the Christian era; the word κύκλος (“cycle,” “circle”) is used of a special kind of short poem and also of a prose abstract of mythological history; the adjective has the general sense of “hackneyed,” “conventional,” and is applied contemptuously (by Callimachus and Horace) to a particular Alexandrian school of poetry.
The most important poems of the Trojan legendary cycle are the Cypria of Stasinus (q.v.); the Aethiopis and Iliou Persis (Sack of Troy) of Arctinus (q.v.); the Little Iliad of Lesches (q.v.); the Nosti of Hagias or Agias; the Telegonia of Eugammon. To the Theban cycle belong: the Thebais or Expedition of Amphiaraus and the Epigoni of Antimachus. The Oechalias Halosis (capture of Oechalia) of Creophylus (q.v.); the Phocais (or Minyas) of Prodicus; and the Danais of Cercops, although belonging to the old Homeric epos, cannot with certainty be included in the epic cycle. The names of the authors are in several cases exceedingly doubtful.
Bibliography.—The standard work on the subject is F. G. Welcker, Der epische Cyclus (1865-1882); see also T. W. Allen, “The Epic Cycle,” in Classical Quarterly, Jan. and April 1908 (summary of sources and authorities); Wilamowitz-Möllendorff, Homerische Untersuchungen (1884), who regards the traditional names and personalities of the poets of the cycle with great scepticism; D. B. Monro, Journal of Hellenic Studies, iv. (1883), appendix to his edition of the Odyssey, xiii.-xxiv. (1900), and on the Codex Venetus fragment of Proclus; J. E. Sandys, Hist. of Class. Schol. (2nd ed., 1906), vol. i. ch. 2; J. B. Bury, Ancient Greek Historians (1909), pp. 2-8 on the epics as history; articles by H. Flach in Ersch and Gruber, Allgemeine Encyklopädie, and by E. Schwartz and others in Pauly-Wissowa, Realencyclopädie.
1 An objection to this view is that according to the Augustan historian Capitolinus (Antoninus, 2) Eutychius of Sicca was a Latin not a Greek grammarian.
CYCLING, the clipped term now given comprehensively to the sport or exercise of riding a bicycle (q.v.) or tricycle (q.v.).
 |
| Fig. 1.—Gentleman’s Hobby Horse. |
 |
| Fig. 2.—Lady’s Hobby Horse. |
 |
| Fig. 3.—The Boneshaker, 1868. |
 |
| Fig. 4.—The “Phantom,” 1869. |
Suggestions of vehicles having two or more wheels and propelled by the muscular effort of the rider or riders are to be found in very early times, even on the bas-reliefs of Egypt and Babylon and the frescoes of Pompeii; but though History. sporadic examples of such contrivances are recorded in the 17th and 18th centuries, it was apparently not till the beginning of the 19th century that they were used to any considerable extent. A “velocipede” invented by Blanchard and Magurier, and described in the Journal de Paris on the 27th of July 1779, differed little from the célérifère proposed by another Frenchman, de Sivrac, in 1690; it consisted of a wooden bar rigidly connecting two wheels placed one in front of the other, and was propelled by the rider, seated astride the bar, pushing against the ground with his feet. The next advance was made in the draisine of Freiherr Karl Drais von Sauerbronn (1785-1851), described in his Abbildung und Beschreibung seiner neu erfundenen Laufmaschine (Nuremberg, 1817). In this the front wheel was pivoted on the frame so that it could be turned sideways by a handle, thus serving to steer the machine (figs. 1 and 2). A similar machine, the “celeripede,” also with a movable front wheel, is said to have been ridden by J. N. Niepce in Paris some years before. In England the draisine achieved a great, though temporary, vogue under various names, such as velocipede, patent accelerator, bivector, bicipedes, pedestrian curricle (patented by Dennis Johnson in 1818), dandy horse, hobby horse, &c., and for a time it was popular in America also. The propulsion of the draisine by pushing with the feet being alleged to give rise to diseases of the legs, arrangements were soon suggested, as by Louis Gompertz in England in 1821, by which the front wheel could be rotated by the hands with the aid of a system 683 of gearing, but the idea of providing mechanical connexions between the feet and the wheels was apparently not thought of till later. Pedals with connecting rods working on the rear axle are said to have been applied to a tricycle in 1834 by Kirkpatrick McMillan, a Scottish blacksmith of Keir, Dumfriesshire, and to a draisine by him in 1840, and by a Scottish cooper, Gavin Dalzell, of Lesmahagow, Lanarkshire, about 1845. The draisine thus fitted had wooden wheels, with iron tires, the leading one about 30 in. in diameter and the driving one about 40 in., and thus it formed the prototype, though not the ancestor, of the modern rear-driven safety bicycle.
For the next 20 years little was done, and then began the evolution of the high “ordinary” bicycle with a large driving wheel in front and a small trailing one behind. About 1865 Pierre Lallement in Paris constructed a bicycle in which the front wheel was driven by pedals and cranks attached directly to its axle, but it is doubtful whether the origin of this idea must be attributed to him or to Ernest Michaux, the son of his employer, who was a carriage repairer. Lallement took his machine to the United States, and in 1866 was granted a patent which had an important influence on the subsequent course of the cycle industry in that country. This machine, consisting of a wooden frame supported on two wooden wheels (fig. 3), soon became popular in England, as well as in France and America, and came to be called bicycle (or bysicle) by those who took it seriously and “boneshaker” by those who did not. Improvements quickly followed, chiefly in England, for in America the popularity of the machine was short-lived, and in France the industry was checked by the Franco-German war. Rubber tires, in place of iron ones, appeared in 1868, and in two or three years were made very large, 2 in. or more in width. Suspension wheels, with wire spokes in tension, were seen at the Crystal Palace, London, on the “Phantom” (fig. 4) of W. F. Reynolds and J. A. Mays in 1869, and early in the same year the manufacture of bicycles, at first for export to France, was begun in England by the Coventry Sewing Machine Company, till then makers of sewing machines. There was a rapid growth in the size of the front wheel, which in the boneshaker normally measured 36 or 38 in. in diameter, with a corresponding shrinkage in the rear wheel (fig. 5), until by 1874, the date of the invention of the tangent wheel by J. K. Starley 54-in. wheels were being made. The high bicycle was now fairly established in form, and the changes made in the subsequent 10 or 15 years during which it retained its supremacy were chiefly in the details of construction, such as the adoption of steel tubing for the frames, the use of hollow rims in the wheels and the application first of cone and then of ball bearings to points of friction. The weight of a 54-in. bicycle, which in 1874-1875 exceeded 50 or even 60 ℔, was thus reduced to well under 40 ℔ in machines intended for use on ordinary roads, and to not much over 20 ℔ in the case of racers.
 |
| Fig. 5.—Humber’s “Spider,” 1872. |
 |
| Fig. 6.—Rudge Racing Ordinary, 1887. |
 |
| Fig. 7.—Otto Dicycle, 1879. |
The high “ordinary” bicycle (fig. 6) gave unquestionable pleasure to many riders, and very fast times were made with it both on the road and on the racing path. In 1882 H. L. Cortis rode 20 m. 300 yds. in one hour, and in April 1884 Thomas Stevens started from San Francisco to ride round the world, a feat which he accomplished in December 1886. But it had various disadvantages. The vibration set up by the small back wheel was very trying, and in spite of the size of the front one the rider had to move his pedals at an uncomfortably rapid rate if he wished to maintain a good speed. Moreover his seat was placed in such a position that he was liable to be pitched over the handlebar if his wheel encountered a comparatively small obstacle. Attempts were made to remedy these inconveniences in various ways. From the early ’eighties much attention was devoted to tricycles, and these were produced in innumerable designs, whether for a single rider, or for two in the form of “sociables,” in which the riders sat side by side, or of “tandems,” in which one sat behind the other. But their weight, and consequently the exertion of propelling them, was necessarily greater than in the case of the bicycle, and by the end of the decade, the demand for them had fallen off, though they are still made to a certain extent, chiefly for carrying purposes. The two-track dicycle (fig. 7), invented by E. C. F. Otto about 1879, in which the rider balanced himself between two equal wheels placed abreast, also failed to secure lasting success.
The improvement of the high bicycle was attempted in two directions. On the one hand it was modified by placing the rider farther back, his position “over his work” being ensured by arranging the pedals immediately below him and connecting them to the front wheel, which was usually reduced in size, by levers and cranks or by chain-gearing, often with a multiplying action. On the other, the rear wheel was enlarged and made the driving wheel. The “’Xtraordinary” (fig. 8), “Facile” (fig. 9) and “Kangaroo” were examples of the former kind, which were often spoken of as “dwarf-safeties”; but though a good many of them were used about 1880 and following years, both they and the “ordinary” bicycle ultimately disappeared before machines of the second kind, which developed into the modern rear-driven safety. There are numerous claimants for the invention—or rather the reinvention—of this type, 684 but it appears that the credit for its practical and commercial introduction in substantially its present form is due to J. K. Starley in England. His “Rover” (fig. 10), brought out late in 1885, had two nearly equal wheels, the driving wheel 30 in. in diameter and the steering 32 in., and the rider sat so far back that he could not be thrown forward over the handles. The motion imparted by the pedals to a sprocket wheel mounted between the wheels was transmitted by an endless chain to the rear wheel, and by sufficiently increasing the size of this sprocket wheel the machine could be made to travel as far or farther than the “ordinary” for each complete revolution of the pedals. From about 1890 the “safety” monopolized the field. At first it was fitted with the narrow rubber tires customary at the time, but these gave way to pneumatic tires, invented in 1888 by J. B. Dunlop, a veterinary surgeon of Belfast, whose idea, however, had been anticipated in the English patent taken out by R. W. Thomson in 1845. The result was a great gain in comfort, due to reduction of vibration, and a remarkable increase of speed or, alternatively, decrease of exertion. Subsequent progress was mainly in the details of design and manufacture, tending to secure lightness combined with adequate strength, and such was the success attained, by the application of scientific principles and of improved methods and materials to the construction of the frames and other parts, that while the weight of the original “Rover” was about 50 ℔ that of its successors 20 years later with 28-in. wheels was reduced by 35 or 45%, or even 60% in the case of racing machines. The beginning of the 20th century saw the introduction of two innovations: one was the “free-wheel,” a device which allows the driving wheel to rotate independently of the chain and pedals, so that the rider, controlling his speed with powerful brakes, can “coast” down a hill using the stationary pedals as foot-rests; and the other was the motor-cycle, in which a petrol-engine relieves him, except at starting, from all personal exertion, though at the cost of considerable vibration. A third contrivance, which, however, was an idea of considerably older date, also began to find favour about the same period in the shape of two-speed and three-speed gears, enabling the rider at will to alter the ratio between the speed of revolution of his pedals and of his driving wheel, and thereby accommodate himself to the varying gradients of the road he is traversing (see also Bicycle, Tricycle and Tire).
 |
| Fig. 8.—Singers’ “’Xtraordinary,” 1879. |
 |
| Fig. 9.—The “Facile,” 1879. |
 |
| Fig. 10.—Starley’s “Rover,” 1885. |
The safety bicycle, with pneumatic tires, rendered cycling universally popular, not merely as a pastime but as a convenient means of locomotion for everyday use. Made with a drop-frame, it also enabled women to cycle without being confined to a heavy tricycle or compelled to assume “rational dress.” In consequence there was an enormous expansion in the cycle industry. In England the demand for machines had become so great by 1895 that the makers were unable to cope with it. Numbers of new factories were started, small shops grew into large companies, and the capital invested advanced by millions of pounds. The makers who had devoted their mechanical skill to perfecting the methods of cycle-construction were swallowed up by company promoters and adventurers, bent simply upon filling their own pockets. The march of mechanical invention and improvement was arrested, and machines, instead of being built by mechanics proud of their work, in many cases were merely put together in the shortest possible time and in a few standard patterns. For these the world clamoured, and for a year they could not be produced fast enough. Then the demand fell off, the British market became over-stocked, and as the British makers declined to consider the wants of foreign customers, their store-rooms remained crowded with machines that could not be sold. Speculative finance, such as was exemplified in 1896 by the flotation for £5,000,000 of the Dunlop tire company, which had been started in 1889 with a capital of £25,000, had its natural effects. There ensued widespread and continuing disorganization of the trade, which had to be met by extensive reconstructions of over-capitalized companies. English makers too had lost the commanding international position they once enjoyed, when they supplied almost the entire demand for bicycles in many parts of the world, including the United States. In America the manufacture of bicycles was not begun until about 1878, when it was introduced by A. A. Pope (1843-1909), and even by 1890 the value of the products barely exceeded 2½ million dollars, while for several years later much of the steel tubing required for bicycle manufacture continued to be imported from Great Britain. The industry, however, thanks to automatic machinery and perfect organization, grew rapidly, and in 1900 the value of its products was nearly 32 million dollars. In the two years 1897 and 1898 the exports of cycles and cycle parts alone were worth nearly 14 million dollars, though they fell off in subsequent years, and English makers had to contend with an American invasion in addition to their domestic troubles. But the competition was short-lived. The American makers sent over machines with single tube tires and wooden rims which did not secure the approval of the British purchaser, and so they too lost their hold. In the opening years of the 20th century the industry in Great Britain gradually recovered itself. More attention was paid to the production of cheap machines which were sound and trustworthy, and sales were further stimulated by the introduction of systems of deferred payments. In 1905 about 600,000 machines were made in Great Britain, and 47,604 were exported, the total value of the home-market for cycles and their parts being about 3½ millions sterling, and of the export trade about one million. In the same year the number of machines imported was only 2345.
Cycle tours were taken and cycle clubs established almost as soon as the cycle appeared, the Pickwick Bicycle Club in London, founded in 1870, being the oldest in the world. The organization of these clubs is chiefly of Touring clubs. a social character, and a few possess well-appointed club-houses. To a great extent they have been superseded by the large touring organizations. The Cyclists’ Touring Club, organized in 1878 as the Bicycle Touring Club, has members scattered through Europe, America and even the East. Many other countries possess national clubs, as for instance the League of American Wheelmen, founded in 1880, and the Touring Club de France, founded in 1895, of whose objects cycling is only one, though the chief. The aim of these national associations, which have formed an international touring league, is the promotion of cycle touring. To this end they publish roadbooks, maps and journals; they recommend hotels, with fixed tariffs, in their own and other countries; they appoint representatives to aid their members when touring; and they have succeeded in inducing most governments to allow their members to travel freely across frontiers without paying duty on their machines. In all countries they have erected warning-boards at dangerous places; in France the best route is suggested by a sign-post, and cyclists who meet with accidents in lonely places find repair outfits provided for their free use. Another important part of the work of these clubs, either directly or indirectly, is the improvement of the roads. France has done more for the cyclist than any other country, owing to the fact 685 that she possesses the best roads, kept up to a certain extent by the cycle tax, whereby the cyclist acquires a certain official position and right; moreover cycles accompanied by their owners are conveyed without extra charge on the railways, and aid is given to the sport and pastime from public funds. In Belgium the cycle has worked a veritable revolution in the national life. The surface of the greater part of the country being loose and sandy, the roads have been paved, and this paving is so bad as to be impossible for light traffic. The cycle tax has consequently been devoted, first, to the construction of paths on which cyclists have equal rights with pedestrians, and secondly to the replacing of the paving by macadam. In this way alone cycling has proved of inestimable benefit to Belgium and Luxembourg. In the United States measures for securing good roads and side paths have been introduced in various states, mainly at the instigation first of cyclists and then of motorists, and in Great Britain the Roads Improvement Association has worked for the same end.
Each country also possesses an organization for the government of cycle racing; and although these unions, one object of which—usually the main one—is the encouragement of cycle racing and cycle legislation, boast an enormous Racing. membership, their membership is often composed of clubs and not individuals. Among the most important are the National Cyclists’ Union of England and the Union Vélocipédique of France. These bodies are also bound together by the International Cyclists’ Association, which is devoted mainly to the promotion of racing and legislation connected with it all over the world. The National Cyclists’ Union, originally the Bicycle Union, which was the parent body of all, formed in February 1878, was the first to put up danger-boards, and also was early instrumental, alone and with the C.T.C., in framing or suggesting laws for the proper government and regulation of cycle traffic, notably in establishing its position as a vehicle in securing universal rights, in endeavouring, again in conjunction with the C.T.C., to increase facilities for the carriage of cycles on the railways, in securing the opening of parks, and in promoting many other equally praiseworthy objects. For a number of years, however, it has been more prominent as the ruling race-governing body. But cycle racing has fallen upon evil days. At one time cycle racing attracted a large number of spectators, but gradually it lost the public favour, or rather was ignored by the public because it became mainly an advertisement for cycle makers. The presence of the man, directly or indirectly, in the employ of, or aided by a maker, and the consequent mixing up of trade and sport, lowered racing not only in the public estimation, but in that of all genuine amateurs. There have always been a few amateurs who have raced for the love of the sport, but the greater number of prominent racing men have raced for the benefit of a firm, so much so that, at one time, an entire section of racing men were classed as “makers’ amateurs.” They did not confine themselves to the race track, but appropriated the public roads until they became a danger and a nuisance, and road-racing finally was abolished, though record rides, as they are called, are still indulged in, being winked at by the police and by the cycling authorities. The makers’ amateurs at least rode to win and to make the best time possible. But the scandal was so great that a system of licensing riders was adopted by the N.C.U., and if this did not effectively kill the sport, the introduction of waiting races did. There probably is considerable skill in riding two-thirds of a race as slowly as possible, and only hurrying the last part of the last lap, but it does not amuse the public, who want to see a fast race as well as a close finish. The introduction of pacing by multicycles and motors next took from cycle racing what interest was left. A motor race, in which the machines are run at top speed, is more exciting than the spectacle of a motor being driven at a rate which the cyclist can follow with the protection of a wind-shield. In America this system of proving what cyclists can do with racing machines was carried so far that in 1899 a board track was laid down on the Long Island railway for about 2 m. between the metals, and a cyclist named Murphy, followed a train, and protected by enormous wind-shields, succeeded in covering a mile in less than a minute in the autumn of 1900. Other cyclists have devoted themselves, at the instigation of makers, to the riding of 100 m. a day every day for a year. It would be difficult to say what advantage there is in these trials and contests. They are not convincing records, and only prove that some people are willing to take great personal risks for the benefit of their employers. E. Hale, during 1899-1900, covered 32,496 m. in 313 days. For many years also long-distance races, mostly of six days’ duration, have been promoted on covered tracks, and though condemned by all cycling organizations, they find a great deal of pecuniary support.
The cycle has also been taken up for military purposes. For this idea the British army is indebted to Colonel A. R. Savile, who Military. in 1887 organized the first series of cycle manœvres in England. Since then military cycling has undergone a great development, not only in the country of its origin but in most others.
Cycling has produced a literature of its own, both of the pastime and of the trade. Owing to the enormous profits which, for several years, were obtained by cycle makers, a trade press Literature. appeared which simply lived by, and out of, its advertisers; and though each country has one or more genuine trade journals, the large proportion of these sheets have been worth, in a business aspect, as little practically as from a literary standpoint. On the other hand a vast mass of practical and unpractical, scientific and medical, historical and touring treatises and records have appeared, but mostly of a rather ephemeral character.
CYCLOID (from Gr. κύκλος, circle, and εἶδος, form), in geometry, the curve traced out by a point carried on a circle which rolls along a straight line. The name cycloid is now restricted to the curve described when the tracing-point is on the circumference of the circle; if the point is either within or without the circle the curves are generally termed trochoids, but they are also known as the prolate and curtate cycloids respectively. The cycloid is the simplest member of the class of curves known as roulettes.
No mention of the cycloid has been found in writings prior to the 15th century. Francis Schooten (Commentary on Descartes) assigns the invention of the curve to René Descartes and the first publication on this subject after Descartes to Marin Mersenne. Evangelista Torricelli, in the first regular dissertation on the cycloid (De dimensione cycloidis, an appendix to his De dimensione parabolae, 1644), states that his friend and tutor Galileo discovered the curve about 1599. John Wallis discussed both the history and properties of the curve in a tract De cycloide published at Oxford in 1659. He there shows that the cycloid was investigated by Carolus Bovillus about 1500, and by Cardinal Cusanus (Nicolaus de Cusa) as early as 1451. Honoré Fabri (Synopsis geometrica, 1669) treated of the curve and enumerated many theorems concerning it. Many other mathematicians have written on the cycloid—Blaise Pascal, W. G. Leibnitz, the Bernoullis, Roger Cotes and others—and so assiduously was it studied that it was sometimes named the “Helen of Geometers.” The determination of the area was the subject of many investigations and much controversy. Galileo attempted the evaluation by weighing the curve against the generating circle; this rough method gave only an approximate value, viz., a little less than thrice the generating circle. Torricelli, by employing the “method of indivisibles,” deduced that the area was exactly three times that of the generating circle; this result had been previously established in 1640 in France by G. P. de Roberval, but his investigation was unknown in Italy. Blaise Pascal determined the area of the section made by any line parallel to the base and the volumes and centres of gravity of the solids generated by revolving the curve about its axis and base. Before publishing his results he proposed these problems for public competition in 1658 under the assumed name of Amos Dettonville. John Wallis in England, and A. la Louère in France, accepted the challenge, but the former could only submit incorrect solutions, while the latter failed completely. Having established his priority, Pascal published his investigations, which occasioned a great sensation among his contemporaries, and Wallis was enabled to correct his methods. Sir Christopher Wren, the famous architect, determined the length of the arc and 686 its centre of gravity, and Pierre Fermat deduced the surface of the spindle generated by its revolution. A famous period in the history of the cycloid is marked by a bitter controversy which sprang up between Descartes and Roberval. The evaluation of the area of the curve had made Roberval famous in France, but Descartes considered that the value of his investigation had been grossly exaggerated; he declared the problem to be of an elementary nature and submitted a short and simple solution. At the same time he challenged Roberval and Fermat to construct the tangent; Roberval failed but Fermat succeeded. This problem was solved independently by Vicenzo Viviani in Italy. The cartesian equation was first given by Wilhelm Gottfried Leibnitz (Acta eruditorum, 1686) in the form y = (2x − x²)½ + ∫(2x − x²)½dx. Among other early writers on the cycloid were Phillippe de Lahire (1640-1718) and François Nicole (1683-1758).
The mechanical properties of the cycloid were investigated by Christiaan Huygens, who proved the curve to be tautochronous. His enquiries into evolutes enabled him to prove that the evolute of a cycloid was an equal cycloid, and by utilizing this property he constructed the isochronal pendulum generally known as the cycloidal pendulum. In 1697 John Bernoulli proposed the famous problem of the brachistochrone (see Mechanics), and it was proved by Leibnitz, Newton and several others that the cycloid was the required curve.
 |
| Fig. 1. |
 |
| Fig. 2. |
 |
| Fig. 3. |
The method by which the cycloid is generated shows that it consists of an infinite number of cusps placed along the fixed line and separated by a constant distance equal to the circumference of the rolling circle. The name cycloid is usually restricted to the portion between two consecutive cusps (fig. 1, curve a); the fixed line LM is termed the base, and the line PQ which divides the curve symmetrically is the axis. The co-ordinates of any point R on the cycloid are expressible in the form x = a(θ + sin θ); y = a(1 − cos θ), where the co-ordinate axes are the tangent at the vertex O and the axis of the curve, a is the radius of the generating circle, and θ the angle R′CO, where RR′ is parallel to LM and C is the centre of the circle in its symmetric position. Eliminating θ between these two relations the equation is obtained in the form x = (2ay − y²)½ + a vers-¹ y/a. The clumsiness of the relation renders it practically useless, and the two separate relations in terms of a single parameter θ suffice for the deduction of most of the properties of the curve. The length of any arc may be determined by geometrical considerations or by the methods of the integral calculus. When measured from the vertex the results may be expressed in the forms s = 4a sin ½θ and s = √(8ay); the total length of the curve is 8a. The intrinsic equation is s = 4a sin ψ, and the equation to the evolute is s = 4a cos ψ, which proves the evolute to be a similar cycloid placed as in fig. 2, in which the curve QOP is the evolute and QPR the original cycloid. The radius of curvature at any point is readily deduced from the intrinsic equation and has the value ρ = 4 cos ½θ, and is equal to twice the normal which is 2a cos ½θ.
The trochoids were studied by Torricelli and F. van Schooten, and more completely by John Wallis, who showed that they possessed properties similar to those of the common cycloid. The cartesian equation in terms similar to those used above is x = aθ + b sin θ; y = a − b cos θ, where a is the radius of the generating circle and b the distance of the carried point from the centre of the circle. If the point is without the circle, i.e. if a < b, then the curve exhibits a succession of nodes or loops (fig. 1, curve b); if within the circle, i.e. if a > b, the curve has the form shown in fig. 1, curve c.
The companion to the cycloid is a curve so named on account of its similarity of construction, form and equation to the common cycloid. It is generated as follows: Let ABC be a circle having AB for a diameter. Draw any line DE perpendicular to AB and meeting the circle in E, and take a point P on DE such that the line DP = arc BE; then the locus of P is the companion to the cycloid. The curve is shown in fig. 3. The cartesian equation, referred to the fixed diameter and the tangent at B as axes may be expressed in the forms x = aθ, y = a(1 − cos θ) and y − a = a sin (x/a − ½π); the latter form shows that the locus is the harmonic curve.
For epi- and hypo-cycloids and epi- and hypo-trochoids see Epicycloid.
References.—Geometrical constructions relating to the curves above described are to be found in T. H. Eagles, Constructive Geometry of Plane Curves. For the mechanical and analytical investigation, reference may be made to articles Mechanics and Infinitesimal Calculus. A historical bibliography of these curves is given in Brocard, Notes de bibliographie des courbes géométriques (1897). See also Moritz Cantor, Geschichte der Mathematik (1894-1901).
CYCLOMETER (Gr. κύκλος, circle, and μέτρον, measure), an instrument used especially by cyclists to determine the distance they have traversed. In a common form a stud attached to one spoke of the wheel engages with a toothed pinion and moves it on one tooth at each revolution. The pinion is connected with a train of clockwork, the gearing of which bears such a ratio to the circumference of the wheel that the distance corresponding to the number of times it has revolved is shown on a dial in miles or other units.
CYCLONE (Gr. κυκλῶν, whirling, from κύκλος, a circle), an atmospheric system where the pressure is lowest at the centre. The winds in consequence tend to blow towards the centre, but being diverted according to Ferrel’s law they rotate spirally inwards at the surface of the earth in a direction contrary to the movement of the hands of a watch in the northern hemisphere, and the reverse in the southern hemisphere. The whole system has a motion of translation, being usually carried forward with the great wind-drifts like eddies upon a swift stream. Thus their direction of movement over the British Islands is usually from S.W. to N.E., though they may remain stationary or move in other directions. The strength of the winds depends upon the atmospheric gradients. (See Meteorology.)
CYCLOPEAN MASONRY (from the Cyclopes, the supposed builders of the walls of Mycenae), a term in architecture, used, in conjunction with Pelasgic, to define the rude polygonal construction employed by the Greeks and the Etruscans in the walls of their cities. In the earliest examples they consist only of huge masses of rock, of irregular shape, piled one on the other and trusting to their great size and weight for cohesion; sometimes smaller pieces of rock filled up the interstices. The walls and gates of Tiryns and Mycenae were thus constructed. Later, these blocks were rudely shaped to fit one another. It is not always possible to decide the period by the type of construction, as this depended on the material; where stratified rocks could be obtained, horizontal coursing might be adopted; in fact, there are instances in Greece, where a later wall of cyclopean construction has been built over one with horizontal courses.
CYCLOPES (Κύκλωπες, the round-eyed, plural of Cyclops), a type of beings variously described in Greek mythology. In Homer they are gigantic cave-dwellers, cannibals having only one eye, living a pastoral life in the far west (Sicily), ignorant of law and order, fearing neither gods nor men. The most prominent among them was Polyphemus. In Hesiod (Theogony, 264) they are the three sons of Uranus and Gaea—Brontes, Steropes and Arges,—storm-gods belonging to the family of the Titans, who furnished Zeus with thunder and lightning out of gratitude for his having released them from Tartarus. They were slain by Apollo for having forged the thunderbolt with which Zeus slew Asclepius. Later legend transferred their abode to Mt Aetna, the Lipari islands or Lemnos, where they assisted Hephaestus at his forge. A third class of Cyclopes are the builders of the so-called “Cyclopean” walls of Mycenae and Tiryns, giants with arms in their belly, who were said to have been brought by Proetus from Lycia to Argos, his original home (Pausanias ii. 16. 5; 25. 8). Like the Curetes and Telchines they are mythical types of prehistoric workmen and architects, and as such the objects of worship.
The standard work on these and similar mythological characters is M. Mayer, Die Giganten und Titanen (1887); see also A. Boltz, Die Kyklopen (1885), who endeavours to show that they were an historical people; W. Mannhardt, Wald- und Feldkulte (1904); J. E. Harrison, Myths of the Odyssey (1882); and article in Roscher’s Lexikon der Mythologie (bibliography).
CYCLOSTOMATA, or Marsipobranchii, a group of fishes including the ordinary lampreys and hagfish, and so called from the wide permanently gaping mouth which is without the hinged jaws characteristic of other vertebrates (Gnathostomata). 687 The class Cyclostomata consists of two orders, the Myxinoids (or Hyperotreti) and the Petromyzontes (or Hyperoartii), which, while showing sufficient resemblance in structure to warrant their inclusion in the same class, are yet marked off by such deep-seated differences as to indicate that they commenced to diverge from one another far back in evolutionary time. The order Myxinoids includes the hagfish (Myxine), common off the eastern, and occurring also, though less commonly, off the western coasts of the north Atlantic, and the genus Bdellostoma (also known as Homea, Eptatretus, in part—Polistotrema), including the “borers” of the western American coast, New Zealand and the Cape of Good Hope. The order Petromyzontes includes the widely distributed lampreys. The original genus Petromyzon (which it is now customary to subdivide into a number of genera) includes the large sea lamprey (P. marinus) of the north Atlantic coasts and the two fresh-water lampreys of European streams (P. fluviatilis and P. planeri, the latter of which is possibly only a small-sized variety of the former species). In North America nine or ten species of lampreys are known to occur, descriptions of which are given by Jordan and Evermann (1). In the southern hemisphere occur the two genera Mordacia (Chile, Tasmania) and Geotria (Chile, Australia, New Zealand) (2).
The Cyclostomes are remarkable among vertebrates in that they are semiparasitic in habit. The lampreys—except some of the small fresh-water forms—attach themselves to other fishes by their suctorial mouth and proceed to rasp off the flesh by means of the horny teeth carried by the highly-developed tongue. The Myxinoids have gone a step further and actually bore their way right into the body of their prey, devouring all the soft parts and leaving the skin behind as a mere shell, empty but for the bones. Where the hagfish or borers are abundant, as in certain localities off the east coast of Scotland and off the west coast of California, they may do great damage to fisheries from their habit of attacking fishes which are in difficulties through being caught by a hook or in a net; the fish when drawn up being frequently completely deprived of their flesh.
The Myxinoids retain the ancestral marine habitat, but the lampreys have sought refuge from the struggle for existence by taking to fresh water to a less or greater extent. Such a form as Petromyzon marinus or Entosphenus tridentatus of the west coast of America is what is known as anadromous in habit, i.e. it takes refuge in fresh water during the breeding season, ascending rivers like the salmon for the purpose of spawning. Certain species of lampreys, on the other hand, have completely deserted the sea and spend their whole lives in fresh-water streams or lakes. The lake lampreys show a reminiscence of their ancestral migratory habits in leaving lakes and ascending streams in order to deposit their spawn.
Anatomy.—In structural features, the Cyclostomes show a curious mixture of features which must be looked on as primitive with others which are indicative of high specialization for their peculiar mode of life. In general appearance they are “eel-like”: they are elongated in shape and adapted for swimming in eel fashion, i.e. the body is propelled forward by the backward passage along it of waves of lateral flexure. There are, however, certain conspicuous differences which at once serve to distinguish a Cyclostome from any other fishes of eel-like shape:—(1) the circular permanently open mouth, (2) the absence of all trace of paired limbs, (3) the absence of paired external nasal openings, and (4) the presence on the roof or at the tip of the head of a conspicuous median opening—the pituitary opening.
It will be convenient, in describing the structural features of the group, to take as a basis for the description the marine lamprey, Petromyzon marinus. A marine lamprey is an eel-like creature 70 to 75 cm. in length. At the anterior end and situated somewhat ventrally is the circular widely gaping mouth or buccal cavity, its lining studded with sharply pointed thorn-like “teeth” and its edge fringed with numerous sensory papillae. On the dorsal side of the head is the conspicuous circular pituitary opening with prominent lips, while on the sides are seen the eyes, and behind these a row of somewhat rounded branchial openings or gill-clefts. At about the beginning of the posterior fourth of the body, and in the midventral line, is the anal opening, and immediately behind it is the prominent papilla carrying the opening of the urogenital sinus. The hinder portion of the body, in accordance with its function in locomotion, is flattened from side to side, while its surface is increased by the development of a median fin fold, divided, except in early stages of development, into three portions, known as the first and second dorsal fins and the caudal fin. The last mentioned is of the primitive protocercal type. The whole surface of the body—which shows a conspicuous dark marbling, especially dorsally, on a light ground—is covered with highly glandular epidermis. An important feature is the complete absence of all trace of the calcified placoid plates which are so characteristic of the Elasmobranchii.
The Myxinoids differ from the lampreys in regard to several of the above-mentioned characters. The edges of the mouth carry tentacle-like barbels. The pituitary opening is close to the anterior edge of the mouth opening instead of being right up on the dorsal side of the head. The eyes are invisible, being greatly reduced and sunk far below the surface, and in Myxine, though not in Bdellostoma, the row of gill openings is represented by a single opening on each side nearly in the midventral line and situated at about the end of the first quarter of the body length. Ventrally the Myxinoid possesses on each side of the body a row of remarkable epidermal glands which can produce at will enormous quantities of glutinous slime. This secretion, which, no doubt, is of much value as a protection from attack, is composed of very fine threads, formed by the conversion of the protoplasm of certain cells of the epidermal glands (“thread cells”) into an extremely fine, tightly coiled filament, which becomes unwound when discharged to the exterior.
 |
| From D. Starr Jordan, A Guide to the Study of Fishes, by permission of A. Constable & Co., Ltd. |
| Fig. 1.—The Marine Lamprey (Petromyzon marinus, L.). |
Pituitary Tube.—A remarkable peculiarity of the Cyclostomes lies in the fact that the pituitary ingrowth of ectoderm does not, as in other forms, become involved in the inpushing of ectoderm which forms the buccal cavity. On the contrary, it lies outside the edge of the stomodaeum, and in the case of the lampreys active growth takes place in the tissue between the pituitary and stomodaeal ingrowths, so that the two openings come to be widely separated, the pituitary opening being pushed back on to the dorsal side of the head. The pituitary opening remains patent throughout life, as is the case with Crossopterygians alone amongst Gnathostomata. In Myxine a further remarkable peculiarity in regard to the hypophysis, probably adaptive in nature, occurs, inasmuch as the pituitary invagination develops an opening at its posterior end into the pharynx.
Nervous System.—The anterior end of the nervous tube is enlarged and differentiated to form a brain as in other Vertebrates, but this brain in the lampreys at least shows remarkably primitive features. The enlargement as compared with the spinal cord is seen to be comparatively slight: the brain is much elongated, and its various regions lie in a straight line one behind the other: the roof of the brain retains to a great extent the primitive epithelial condition. On each side anteriorly there is present a comparatively large olfactory lobe, and this is continued posteriorly into a small cerebral hemisphere.
The lampreys are amongst those vertebrates in which there is an eye-like apparatus (3) connected with the roof of the thalamencephalon. There grow out from the roof of the thalamencephalon two processes, a posterior (the pineal process), and an anterior (the parapineal process). The pineal process grows forwards so as to overlie the parapineal process. Each of these projections from the roof of the thalamencephalon dilates to form a vesicle, and each vesicle shows certain eye-like characteristics, its deep wall forming a “retina” and its superficial wall being clear and translucent (“pellucida”). The retinal cells are packed in the case of the pineal organ with opaque white pigment: similar pigment occurs in smaller quantity in the parapineal organ. Definite sensory cells are also present with rod-like structures projecting into the lumen of the vesicle. Nerve fibres have been traced—from the pineal organ into the posterior commissure and possibly into the right habenular ganglion. As regards other parts of the brain, the chief point to note is that the cerebellum is in a most rudimentary condition, forming merely a slight transverse thickening of the hind-brain roof at its anterior end. In Myxinoids the brain is much larger as compared with the spinal cord, and it differs from that of the lampreys by being relatively much shorter in an anteroposterior direction. A remarkable negative feature lies in the complete absence of the pineal and parapineal organs so conspicuous in the lampreys. The olfactory organ of Cyclostomes is remarkable for two special characteristics, firstly, that the two olfactory organs of other vertebrates are here represented by a single median structure, and secondly, 688 that the olfactory organ becomes sunk down beneath the surface through becoming involved in the ectodermal ingrowth which forms the pituitary tube. As a further consequence in the case of the lampreys the olfactory organ becomes transported to the roof of the head along with the pituitary opening, which latter functions as an external nostril. That the unpaired olfactory organ of existing Cyclostomes has passed through, in their ancestors, a paired condition such as exists in other vertebrates, is indicated by the fact that it retains a pair of olfactory nerves.
The eyes in adult lampreys are of moderate size, while in the Myxinoids they are greatly reduced—sunk beneath the skin (Bdellostoma) or even in amongst the muscles of the head (Myxine). The lens is completely absent, also the ocular muscles. The otocyst or auditory organ is unique amongst craniate vertebrates in regard to the semicircular canals. In the lampreys there are only two instead of the normal three, while the Myxinoids have only one.
Alimentary Canal.—The widely gaping buccal funnel is morphologically an inpushing of the outer skin, i.e. it is stomodaeal in nature. The thorn-like teeth which stud its lining are formed simply by cornification of the epidermal cells (4) like the provisional horny teeth of a tadpole, and are not homologous with the true teeth of ordinary vertebrates. As to whether they represent the remnant of a once present system of epidermal scales, which may have preceded the coating of placoid elements in the evolution of the vertebrate, there is no evidence.
 | |
| Modified from T. J. Parker, Zootomy, fig. 4, by permission of Macmillan & Co., Ltd. | |
| Fig. 2.—Median longitudinal section through anterior end of Petromyzon. | |
|
a.v.o, Atrio-ventricular opening. br, Brain. br.o, Internal opening of gill sac. d.a, Dorsal aorta. d.c, Ductus cuvieri. h.v, Hepatic vein. i.j.v, Inferior jugular vein. N, Notochord. |
oes, Oesophagus. olf, Olfactory organ. pc, Pericardium. p.c.v, Left posterior cardinal vein. pit, Pituitary tube. V, Ventricle. v, Velum. |
The pharyngeal region, closely associated with the respiratory function, possesses, on each side, a series of gill-sacs (six in Myxine: seven in Petromyzon, besides an anterior one which is laid down in the embryo but disappears later: up to as many as fourteen in Bdellostoma) opening on the one hand to the pharynx and on the other to the exterior. In Bdellostoma and in the larva of Petromyzon the gill-sacs open directly from the pharynx to the exterior, but in the adult lamprey and in Myxine the original relations are modified. In Myxine, the external openings of the gill-sacs have migrated backwards along the side of the body and become coincident at a point slightly posterior to the last sac. It follows from this that each sac is connected with the common aperture by a tube, longest in the case of the first sac, shortest in the case of the last. In the adult lamprey a different modification is found. Here the dorsal portion of the pharynx has become nipped off as a narrow tube which functions as an oesophagus from the larger ventral portion, which forms an elongated saccular structure ending blindly at its hinder end and having in its lateral wall the internal openings of the gill-sacs.
Breathing.—The inspiratory current passes inwards by the mouth opening in the larval lamprey, by the pituitary tube in Myxine, while in the adult lamprey both expiration and inspiration takes place through the external gill-openings. In the case of the lampreys the elastic skeleton of the branchial region (see below) plays an important part in respiration. The branchial region shows rhythmic contraction through the agency of the transverse muscles—and expansion, through the elasticity of the branchial skeleton—in the adult lamprey. These rhythmic movements of the branchial region cause successive inflow and outflow through the branchial openings. In the larva, on the other hand, the respiratory current always passes in one direction—backwards. This is helped by the presence of a velar fold at the front end of the pharynx, which acts as a valve opening only backwards, and to the presence of membranous flaps projecting back from the anterior border of each gill-opening and acting as valves which open only outwards.
Behind the pharynx comes the truly digestive part of the alimentary canal in the form of a straight tube showing little differentiation into special regions. The lining of the intestine is increased in area by an inwardly projecting fold, which is compared by some morphologists with the spiral valve of certain other groups. In the mature river lamprey the digestive tract becomes in great part degenerate.
Coelomic Organs.—The chief point of interest about the splanchnocoele or perivisceral cavity is that in the Myxinoids the adult shows a persistent embryonic condition in that the pericardiac portion never becomes isolated from the main body cavity.
The renal organs are of special interest in the Myxinoids from their very simple character. The kidney duct is seen running along the roof of the coelom on either side. Into the duct open short segmentally arranged tubes, each possessing at its closed rounded extremity a Malpighian body. Each of these short tubes is morphologically a nephric tubule, which, however, in correlation with its shortness, is without the turns and twists so characteristic of such tubules generally. A further consequence of the short simple character of the tubules is that they are quite separate from one another, instead of being massed together to form a compact gland such as the kidney is elsewhere. In Petromyzon the kidney has the ordinary compact form, and here also the Malpighian bodies are shut off from the splanchnocoele.
The ovary or testis is a large unpaired structure hanging from the dorsal wall of the splanchnocoele and shedding its products into it; from the coelomic space the genital products pass into the urogenital sinus—formed by the fusion of the kidney ducts at their hinder ends—through a small opening, one at each side. This opening, which leads directly from coelom into urogenital sinus, is known as the genital pore. Its morphological significance is doubtful.
Skeleton.—The vertebral column of the lamprey is represented by a persistent notochord surrounded by a thick sheath, which shows no signs of invasion by cartilage cells or of segmentation. Resting on the sheath are paired dorsal arch elements, more numerous than the neuromuscular segments. In the tail region these are united into a continuous band of cartilage on each side: similar cartilaginous bands represent the ventral arch elements of the tail region. The skeleton of the head region consists of a cartilaginous cranium, into the formation of which enter typical parachordal and trabecular elements, together with olfactory and auditory capsules. In addition to these, there are a number of other cartilaginous pieces present in the head region, the homologies of which are doubtful.
Branchial Basket.—One of the most characteristic features of the skeleton of the lamprey is the remarkable cartilaginous “branchial basket,” which supports the gill region. In an adult river lamprey the basketwork consists on each side of a series of eight vertical half-hoops of cartilage. The hoops of each side are connected together dorsally by a pair of longitudinal bars, lying ventral to the notochord, and ventrally by a similar pair of rods which are fused in the middle line. Slender cartilaginous projections arise from the anterior and posterior sides of the hoops, and certain of these meeting at their ends form additional longitudinal bars connecting together successive hoops. Connected with the basketwork posteriorly is a remarkable cup-shaped cartilage, which supports the hind wall of the pericardium. The series of cartilaginous half-hoops naturally suggest the half-hoops of cartilage which form the skeleton of the visceral arches in the Gnathostomata. They are, however, more superficial in position, and this has led many to doubt their actual homology with the cartilaginous visceral arches. Taking into account, however, our present knowledge of the development of the two sets of structures, it seems on the whole probable that a true homology exists and that the branchial basket of the lamprey represents merely a set of visceral arches modified in accordance with the peculiar breathing methods of the creature. In the Myxinoids the branchial basket is reduced to a few vestigial masses of cartilage.
Vascular System.—The heart (5) of the lamprey consists of an atrium and a single ventricle, the atrium on the left, the ventricle on the right. Into the atrium, on its right side, and behind the atrio-ventricular opening, there opens a nearly vertical chamber usually termed the sinus venosus (see below), the opening guarded by a pair of vertically placed valves. The ventricle passes anteriorly into what is clearly the homologue of the conus arteriosus of other forms. In its interior are present a pair of laterally placed longitudinal ridges similar to the ridges which occur in other forms in the conus. The opening from ventricle into conus is guarded by a pair of laterally placed pocket valves situated just within the boundary of the ventricle.
The arterial system is of the ordinary piscine type. From the heart there passes forwards a ventral aorta, split into two separate vessels in its anterior half, and giving off on each side a series of efferent vessels to the gill-sacs, one passing between each two gill-sacs and an additional one to the front wall of the front sac and to the posterior wall of the last. The blood is collected from the walls of the gill-sacs by a series of efferent vessels which open into the dorsal aorta. It is to be noted that the dorsal aorta retains the probably primitive unpaired condition, except for a very short extent at its anterior end, where it is split so as to form two short aortic roots.
Venous System.—The main venous channels are like those in other fishes, though their connexion with the heart becomes modified in the adult. The two posterior cardinals—with their continuations forwards, the anterior cardinals—approach the median plane and undergo fusion in the region of their opening into the two ductus Cuvieri. The left ductus Cuvieri then atrophies so that all the blood from the cardinals reaches the heart by way of the originally right 689 ductus Cuvieri. It is this right ductus Cuvieri which forms the dorsal part of what is usually termed the sinus venosus. The inferior jugular veins which return the blood from the ventral side of the head also become replaced in the adult by a median unpaired vein which opens posteriorly into the sinus venosus by what probably represents the hinder end of the original right inferior jugular. It is interesting to note that in Polypterus, one of the Crossopterygian ganoids, there is a somewhat similar asymmetrical condition of inferior jugulars and ductus Cuvieri.
Oviposition of Lamprey (6).—The lamprey chooses as spawning ground a part of the stream with fairly rapid current and where the bottom is composed of sand with scattered stones. By means of the suctorial mouth, stones are removed from more or less circular area so as to form a shallow excavation. The male and female frequently work together at the task of preparing the nest. When oviposition is about to take place, the male may be seen to suddenly attach himself to the dorsal surface of the head of the female which holds on to one of the stones at the upper margin of the nest. The urogenital opening of the male, with its specially prominent papilla, is approximated to that of the female, and with a peculiar quivering movement the eggs and sperms are emitted synchronously amidst clouds of sand stirred up by the movements of the tail. The eggs fertilized thus at the moment of exit are very sticky from their coating of albumen, and become weighted down by adherent grains of sand.
Development.—The development of the lamprey is of much morphological importance from the archaic nature of the creature and from the fact that the egg is comparatively small (about 1 mm. in diameter), so that development is not greatly modified by a large mass of yolk. It has been worked out so far only in the river lamprey (7). Segmentation is complete and unequal. It, as well as the process of gastrulation, agrees in its main features with the same phenomenon in Amia, Dipnoans and Urodele amphibians. The blastopore persists as the anal opening of the adult. The mesoderm arises in a manner closely comparable with that which occurs in Amphioxus, the chief difference being that the mesoderm segments are solid instead of hollow, except in the anterior head region, where they are true hollow enterocoelic pouches. The rudiment of the central nervous system has the form of a solid keel-like ingrowth of ectoderm along the mid-dorsal line, which only secondarily becomes hollowed out—just as happens in Teleostean fishes. The young lamprey, after completing its embryonic development, passes three or four years, in fact its whole life up to the time of sexual maturity, in a prolonged larval condition in which its structure shows important differences from that of the adult. This larval stage of the fresh-water lamprey of Europe was long supposed to be a separate genus of Cyclostomes and was called Ammocoetes. The Ammocoetes lives in the mud and breathes and feeds by means of a current of water produced by ciliary action, which carries Flagellates and other microscopic organisms in through the mouth opening. Correlated with this mode of feeding the buccal cavity is without the teeth so characteristic of the adult. A number of complicated branched sensory processes grow into and nearly occlude the cavity, forming a kind of sieve with only narrow chinks through which the ingoing current passes. The water passes out by the gill openings, which in Ammocoetes open direct from pharynx to exterior. Certain arrangements of the pharyngeal wall of Ammocoetes show a remarkable resemblance to what is found in Amphioxus. The thyroid, which in the adult is a complicated ductless gland, has in the young Ammocoetes the form of a longitudinal groove of the ventral wall of the pharynx. This groove is lined by columnar cells, some carrying cilia, others being glandular and secreting sticky slime. These gland cells are arranged in four longitudinal bands. The thyroid is, in fact, in this stage in a condition corresponding exactly with the endostyle of Amphioxus. The agreement extends to function the secretion, forming sticky threads which entangle food particles. Anteriorly a pair of peripharyngeal bands pass dorsalwards, one on each side, to bend back suprapharyngeal bands which are continued to the hinder end of the pharynx. Here again the resemblance to what occurs in Amphioxus is very close.
The Ammocoetes possesses a functional liver with bileduct, while in the adult river lamprey the alimentary canal is degenerate. It has no arch elements on its notochord. Its eyes are sunk beneath the surface and nonfunctional, and they retain to a great extent an embryonic character (8). There is a rapid process of metamorphosis from the larval to the adult condition, the details of which are by no means sufficiently known. After the metamorphosis the now mature lamprey accomplishes the act of reproduction and then apparently dies almost immediately. The development of the Myxinoids is much less well known than that of the lampreys. As regards the common hagfish (Myxine glutinosa), we are indeed still in complete ignorance in regard to its developmental history in spite of persistent efforts to obtain embryological material. It seems probable that during the breeding period the hagfishes retire into some particularly inaccessible habitat. Within the last few years, however, abundant material illustrating the developmental history of Bdellostoma (9) has been obtained on the Californian coast, and this when fully worked out will give us a good idea of the general lines of Myxinoid development. The egg differs greatly from that of the lampreys. It is—as is that of Myxine—of large size, richly yolked and of a shortened-up sausage shape. It measures about 22 mm. by 8 mm. Surrounding the egg is a protective capsule of a yellow horny appearance. At one end a cap-like portion of this forms a detachable operculum, in the middle of which is a minute opening, the micropyle. Each end of the capsule is prolonged into a group of stiff processes with anchor-like expansions at their tips. Segmentation is, as in other richly yolked eggs, incomplete, confined to the germinal disk at the opercular pole. The central nervous system in Bdellostoma develops by the overarching of medullary folds, not out of a solid keel as is the case with the lampreys.
History in Time.—The softness of the skeletal tissues and the absence of scales in Cyclostomata provide little opportunity for the preservation of fossil remains of this group, and no known fossils can be referred with certainty to the Cyclostomata. The Devonian Palaeospondylus gunni has been regarded as a Cyclostome by some authors, but this relationship is at the least doubtful. Other authors have associated the Ostracoderms, the oldest known vertebrates, with this group.
References.—1. D. S. Jordan and B. W. Evermann, Fishes of North and Middle America (Washington, 1896), part i. p. 8; 2. L. Plate, SB. Ges. Naturf. (Berlin, Jg. 1897), p. 137; 3. F. Studnicka in Oppel’s Lehrbuch der vergleichenden mikroskopischen Anatomie der Wirbeltiere (Jena, 1905), Teil v. s. i.; 4. E. Warren, Q. J. Micr. Sci. xlv. (1902) p. 631; 5. L. Vialleton, Arch. d’anat. micr. T. vi. (1903) p. 283; 6. H. A. Surface in D. S. Jordan’s Fishes (1905), vol. i. p. 494; 7. A. E. Shipley, Q. J. Micr. Sci. xxvii. (1887), W. B. Scott, Journ. Morphol. i. (1887), C. Kupffer, Arch. mikr. Anat. xxxv. (1890), A. Goette, Entwick. des Flussneunauges (Hamburg and Leipzig, 1890); 8. C. Kohl, in Bibliotheca zoologica, Heft 13 (Cassel, 1892); 9. Bashford Dean in Kupffer’s Festschrift (Jena, 1899).
CYCLOSTYLE (Gr. κύκλος, a circle, and στῦλος, a column), a term used in architecture. A structure composed of a circular range of columns without a core is cyclostylar; with a core the range would be peristyle. This is the species of edifice called by Vitruvius monopteral.
CYGNUS (“The Swan”), in astronomy, a constellation of the northern hemisphere, mentioned by Eudoxus (4th century B.C.) and Aratus (3rd century B.C.), and fabled by the Greeks to be the swan in the form of which Zeus seduced Leda. Ptolemy catalogued 19 stars, Tycho Brahe 18, and Hevelius 47. In this constellation β Cygni is a fine coloured double star, consisting of a yellow star, magnitude 3, and a blue star, magnitude 5½. The fine double star, μ Cygni, separated by Sir William Herschel in 1779, has magnitudes 4 and 5; it has a companion, of magnitude 7½, which, however, does not form part of the system. A double star, 61 Cygni, of magnitudes 5.3 and 5.9, was the first star whose distance was determined; its parallax is 0″.39, and it is therefore the nearest star in the northern hemisphere with the exception of σ Centauri. A regular variable, χ Cygni, has extreme magnitudes of 5 to 13.5, and its period is 406 days. Nova Cygni is a “new” star discovered by Johann Schmidt in 1876. There is also an extended nebula in the constellation.
CYLINDER (Gr. κύλινδρος, from κυλίνδειν, to roll). A cylindrical surface, or briefly a cylinder, is the surface traced out by a line, named the generatrix, which moves parallel to itself and always passes through the circumference of a curve, named the directrix; the name cylinder is also given to the solid contained between such a surface and two parallel planes which intersect a generatrix. A “right cylinder” is the solid traced out by a rectangle which revolves about one of its sides, or the curved surface of this solid; the surface may also be defined as the locus of a line which passes through the circumference of a circle, and is always perpendicular to the plane of the circle. If the moving line be not perpendicular to the plane of the circle, but moves parallel to itself, and always passes through the circumference, it traces an “oblique cylinder.” The “axis” of a circular cylinder is the line joining the centres of two circular sections; it is the line through the centre of the directrix parallel to the generators. The characteristic property of all cylindrical surfaces is that the tangent planes are parallel to the axis. They are “developable” surfaces, i.e. they can be applied to a plane surface without crinkling or tearing (see Surface).
Any section of a cylinder which contains the axis is termed a “principal section”; in the case of the solids this section is a rectangle; in the case of the surfaces, two parallel straight lines. A section of the right cylinder parallel to the base is obviously a circle; any other section, excepting those limited by two 690 generators, is an ellipse. This last proposition may be stated in the form:—“The orthogonal projection of a circle is an ellipse”; and it permits the ready deduction of many properties of the ellipse from the circle. The section of an oblique cylinder by a plane perpendicular to the principal section, and inclined to the axis at the same angle as the base, is named the “subcontrary section,” and is always a circle; any other section is an ellipse.
The mensuration of the cylinder was worked out by Archimedes, who showed that the volume of any cylinder was equal to the product of the area of the base into the height of the solid, and that the area of the curved surface was equal to that of a rectangle having its sides equal to the circumference of the base, and to the height of the solid. If the base be a circle of radius r, and the height h, the volume is πr²h and the area of the curved surface 2πrh. Archimedes also deduced relations between the sphere (q.v.) and cone (q.v.) and the circumscribing cylinder.
The name “cylindroid” has been given to two different surfaces. Thus it is a cylinder having equal and parallel elliptical bases; i.e. the surface traced out by an ellipse moving parallel to itself so that every point passes along a straight line, or by a line moving parallel to itself and always passing through the circumference of a fixed ellipse. The name was also given by Arthur Cayley to the conoidal cubic surface which has for its equation z(x² + y²) = 2mxy; every point on this surface lies on the line given by the intersection of the planes y = x tan θ, z = m sin 2θ, for by eliminating θ we obtain the equation to the surface.
CYLLENE (mod. Ziria), a mountain in Greece, in the N.E. of Arcadia (7789 ft.). It was specially sacred to Hermes, who was born in a cave on the mountain, and had a temple and an ancient statue on its summit. The name Cyllene belongs also to an ancient port town in Elis, and, owing to doubtful identification with this, to a modern port at Glarentza, and also to some mineral baths a little to the south of it.
CYMA (Gr. κῦμα, wave), in architecture, a moulding of double curvature, concave at one end, convex at the other. When the concave part is uppermost, it is called a cyma recta; but if the convex portion is at the top, it is called a cyma reversa. When the crowning moulding of an entablature is of the cyma form, it is called a “cymatium.”
CYMBALS (Fr. cymbales; Ger. Becken; Ital. piatti or cinelli),
a modern instrument of percussion of indefinite musical pitch,
whereas the small ancient cup-shaped cymbals sounded a definite
note. Cymbals consist of two thin round plates of an alloy containing
8 parts of copper to two of tin, each having a handle-strap
set in the little knob surmounting the centre of the plate.
The sound is obtained not by clashing them against each other,
but by rubbing their edges together by a sliding movement.
Sometimes a weird effect is obtained by suspending one of the
cymbals by the strap and letting a drummer execute a roll upon
it as it swings; or by holding a cymbal in the left hand and
striking it with the soft stick of the bass drum, which produces
a sound akin to that of the tam-tam. All gradations of piano
and forte can be obtained on the cymbals. The composer
indicates his intention of letting the cymbals vibrate by “Let
them vibrate,” and the contrary effect by “Damp the sound.”
To stop the vibrations the performer presses the cymbals against
his chest, as soon as he has played a note. The duration of the
vibration is indicated by the value of the note placed upon the
staff; the name signifies nothing, since the pitch of the cymbals
is indefinite. The instrument is played from the same part of
the score as the bass drum, unless otherwise indicated by senza
piatti, or piatti soli if the bass drum is to remain silent. Although
cymbals are not often required they form part of every orchestra;
their chief use is for marking the rhythm and for producing
weird, fantastic effects or adding military colour, and their
shrill notes hold their own against a full orchestra playing
fortissimo. Cymbals are specially suited for suggesting frenzy,
fury or bacchanalian revels, as in the Venus music in Wagner’s
Tannhäuser and Grieg’s Peer Gynt suite. Damping gives
a suggestion of impending evil or tragedy. The timbre of the
ancient cymbals is entirely different, more like that of small
hand-bells or of the notes of the keyed harmonica. They are
not struck full against each other, but by one of their edges,
and the note given out by them is higher in proportion as they
are thicker and smaller. Berlioz in Romeo and Juliet scored
for two pairs of cymbals, modelled on some ancient Pompeian
instruments no larger than the hand (some are no larger than
a crown piece), and tuned to  and
and 
The origin of the cymbals must be referred to prehistoric times. The ancient Egyptian cymbals closely resembled our own. The British Museum possesses two pairs, 51⁄3 in. in diameter, one of which was found in the coffin of the mummy of Ankhhapē, a sacred musician; they are shown in the same case as the mummy, and have been reproduced by Carl Engel.1 Those used by the Assyrians were both plate- and cup-shaped. The Greek cymbals were cup- or bell-shaped, and are to be seen in the hands of fauns and satyrs innumerable in sculptures and on painted vases. The word cymbal is derived from κύμβη (Lat. cymba), a hollow vessel, and κύμβαλα = small cymbals. During the middle ages the word cymbal was applied to the Glockenspiel, or peal of small bells, and later to the dulcimer, perhaps on account of the clear bell-like tone produced by the hammers striking the wire strings. After the introduction or invention of the keyed dulcimer or clavichord, and of the spinet, the word clavicymbal was used in the Romance languages to denote the varieties of spinet and harpsichord. Ancient cymbals are among the instruments played by King David and his musicians in the 9th-century illuminated MS. known as the Bible of Charles the Bald in the Bibliothèque Nationale, Paris.
1 The Music of the Most Ancient Nations, fig. 75, p. 227.
CYNEGILS (d. 643), king of the West Saxons, succeeded his uncle King Ceolwulf in 611. With his son Cwichelm (d. 636), he defeated the advancing Britons at Bampton in Oxfordshire in 614, and Cwichelm sought to arrest the growing power of the Northumbrian king Eadwine by procuring his assassination; the attempt, however, failed, and in 626 the West Saxons were defeated in battle and forced to own Eadwine’s supremacy. Cynegils’ next struggle was with Penda of Mercia, and here again he was worsted, the battle being fought in 628 at Cirencester, and was probably compelled to surrender part of his kingdom to Mercia. Cynegils was converted to Christianity through the preaching of Birinus, and was baptized in 635 at Dorchester in Oxfordshire, where he founded a bishopric. He was succeeded as king by his son Cenwalh.
CYNEWULF (d. 785), king of Wessex, succeeded to the throne in 757 on the deposition of Sigeberht. He was constantly at war with the Welsh. In 779 Offa of Mercia defeated him and took Bensington. In 785 he was surprised and killed, with all his thegns present, at Marten, Wilts (Merantune), by Cyneheard, brother of the deposed Sigeberht.
See Earle and Plummer’s edition of the Anglo-Saxon Chronicle, 755, 779 (Oxford, 1892).
CYNEWULF, the only Old-English vernacular poet, known by name, of whom any undisputed writings are extant. He is the author of four poems preserved in two MSS., the Exeter Book and the Vercelli Book, both of the early 11th century. An epilogue to each poem contains the runic characters answering to the letters c, y, n (e), w, u, l, f. The runes are to be read as the words that served as their names; these words enter into the metre of the verse, and (except in one poem) are significant in their context. The poems thus signed are the following. (1) A meditation on The Ascension, which stands in the Exeter Book between two similar poems on the Incarnation and the Last Judgment. The three are commonly known as Cynewulf’s Christ, but the runic signature attests only the second. (2) A version of the legend of the martyr St Juliana, also in the Exeter Book. (3) Elene, in the Vercelli Book, on the story of the empress Helena and the “Invention of the Cross.” (4) A short poem on The Fates of the Apostles, in the same MS. The page containing the signature to this poem was first discovered by Professor A. S. Napier in 1888, so that the piece is not included in earlier enumerations of the poet’s signed works.
In Juliana and Elene the name is spelt Cynewulf; in The Ascension the form is Cynwulf. In The Fates of the Apostles the page is defaced, but the spelling Cynwulf is almost certain. 691 The absence of the E in The Ascension can hardly be due to a scribal omission, for the name of this letter (meaning “horse”) would not suit the context; this, was perhaps the motive for the choice of the shorter form. The orthography (authenticated as the poet’s own by the nature of his device) has chronological significance. If the poems had been written before 740, the spelling would almost certainly have been Cyniwulf. If it were safe to judge from the scanty extant evidence, we should conclude that the form Cynwulf came in about 800; and presumably the poet would not vary his accustomed signature until the new form had become common. In Elene Cynewulf speaks of himself as an old man; and the presence of the runic signature in the four works suggests that they are not far apart in date. They may therefore be referred provisionally to the beginning of the 9th century, any lower date being for linguistic and metrical reasons improbable.
The MSS. of the poems are in the West-Saxon dialect, with occasional peculiarities that indicate transcription from Northumbrian or Mercian. Professor E. Sievers’s arguments for a Northumbrian original have considerable weight; for the Mercian theory no linguistic arguments have been adduced, but it has been advocated on grounds of historical probability which seem to be of little value.
Cynewulf’s unquestioned poems show that he was a scholar, familiar with Latin and with religious literature, and they display much metrical skill and felicity in the use of traditional poetic language; but of the higher qualities of poetry they give little evidence. There are pleasing passages in Elene, but the clumsy and tasteless narration of the Latin original is faithfully reproduced, and the added descriptions of battles and voyages are strings of conventional phrases, with no real imagination. In The Ascension the genuine religious fervour imparts a higher tone to the poetry; the piece has real but not extraordinary merit. Of the other two poems no critic has much to say in praise. If Cynewulf is to be allowed high poetic rank, it must be on the ground of his authorship of other works than those which he has signed. At one time or other nearly the whole body of extant Old English poetry (including Beowulf) has been conjecturally assigned to him. Some of the attributed works show many striking resemblances in style and diction to his authentic writings. But it is impossible to determine with certainty how far the similarities may be due to imitation or to the following of a common tradition.
Until recently, it was commonly thought that Cynewulf’s authorship of the Riddles (q.v.) in the Exeter Book was beyond dispute. The monodramatic lyric Wulf and Eadwacer, imagined to be the first of these Riddles, was in 1857 interpreted by Heinrich Leo as a charade on the name Cynewulf. This absurd fancy was for about thirty years generally accepted as a fact, but is now abandoned. Some of the Riddles have been shown by Professor E. Sievers to be older than Cynewulf’s time; that he may have written some of the rest remains a bare possibility.
The similarity of tone in the three poems known as the Christ affords some presumption of common authorship, which the counter arguments that have been urged seem insufficient to set aside. Both The Incarnation and The Last Judgment contain many passages of remarkable power and beauty. It is unlikely that the author regarded the three as forming one work. The Christ is followed in the MS. by two poems on Saint Guthlac, the second of which is generally, and with much probability, assigned to Cynewulf. The first Guthlac poem is almost universally believed to be by another hand. Cynewulf’s celebration of a midland saint is the strongest of the arguments that have been urged against his Northumbrian origin; but this consideration is insufficient to outweigh the probability derived from the linguistic evidence.
Cynewulf’s reputation can gain little by the attribution to him of Guthlac, which is far inferior even to Juliana. Very different would be the effect of the establishment of his much disputed claim to Andreas, a picturesque version of the legend of the Apostle Andrew. The poem abounds to an astonishing extent in “Cynewulfian” phrases, but it is contended that these are due to imitation. If the author of Andreas imitated Elene and Juliana, he bettered his model. The question whether Cynewulf may not have been the imitator has apparently never been discussed. The poem (so far agreeing with The Fates of the Apostles) copies the style of the old heroic poetry.
Cynewulf’s authorship has been asserted by some scholars for The Dream of the Rood, the noblest example of Old English religious poetry. But an extract from this poem is carved on the Ruthwell Cross; and, notwithstanding the arguments of Prof. A. S. Cook, the language of the inscription seems too early for Cynewulf’s date. The similarities between the Dream and Elene are therefore probably due to Cynewulf’s acquaintance with the older poem.
The only remaining attribution that deserves notice is that of the Phoenix. The author of this fine poem was, like Cynewulf, a scholar, and uses many of his turns of expression, but he was a man of greater genius than is shown in Cynewulf’s signed compositions.
Professor M. Trautmann, following J. Grimm and F. Dietrich, would identify the poet with Cynewulf, bishop of Lindisfarne, who died in 783. This speculation conflicts with the chronology suggested in this article, and is destitute of evidence. Cynewulf was indeed probably a Northumbrian churchman, but it is unlikely that there were not many Northumbrian churchmen bearing this common name; and as the bishop is not recorded to have written anything, the identification is at best an unsupported possibility. Professor A. S. Cook has suggested that our Cynewulf may have been the “Cynulf,” priest of Dunwich, whose name is among those appended to a decree of the council of Clofesho in 803, and of whom nothing else is known. This conjecture suits the probable date of Cynewulf, but otherwise there is nothing in its favour.
For the older literature relating to Cynewulf, see R. Wülker, Grundriss der angelsächsischen Litteratur (1885). References to the most important later discussions will be found in M. Trautmann, Kynewulf, der Bischof und Dichter (1898), and the introductions and notes to the editions of Cynewulf’s Christ, by I. Gollancz (1892) and A. S. Cook (1900). For the arguments for Cynewulf’s authorship of Andreas, see F. Ramhorst, Andreas und Cynewulf (1885).
CYNICS, a small but influential school of ancient philosophers. Their name is variously derived from the building in Athens called Cynosarges, the earliest home of the school, and from the Greek word for a dog (κύων), in contemptuous allusion to the uncouth and aggressive manners adopted by the members of the school. Whichever of these explanations is correct, it is noticeable that the Cynics agreed in taking a dog as their common badge or symbol (see Diogenes). From a popular conception of the intellectual characteristics of the school comes the modern sense of “cynic,” implying a sneering disposition to disbelieve in the goodness of human motives and a contemptuous feeling of superiority.
As regards the members of the school, the separate articles on Antisthenes, Crates, Diogenes and Demetrius contain all biographical information. We are here concerned only to examine the general principles of the school in its internal and external relations as forming a definite philosophic unit. The importance of these principles lies not only in their intrinsic value as an ethical system, but also in the fact that they form the link between Socrates and the Stoics, between the essentially Greek philosophy of the 4th century B.C. and a system of thought which has exercised a profound and far-reaching influence on medieval and modern ethics. From the time of Socrates in unbroken succession up to the reign of Hadrian, the school was represented by men of strong individuality. The leading earlier Cynics were Antisthenes, Diogenes of Sinope, Crates of Thebes, and Zeno; in the later Roman period, the chief names are Demetrius (the friend of Seneca), Oenomaus and Demonax. All these men adhered steadfastly to the principles laid down by Antisthenes.
Antisthenes was a pupil of Socrates, from whom he imbibed the fundamental ethical precept that virtue, not pleasure, is the end of existence. He was, therefore, in the forefront of that intellectual revolution in the course of which speculation ceased 692 to move in the realms of the physical1 and focused itself upon human reason in its application to the practical conduct of life. “Virtue,” says Socrates, “is knowledge”: in the ultimate harmony of morality with reason is to be found the only true existence of man. Antisthenes adopted this principle in its most literal sense, and proceeded to explain “knowledge” in the narrowest terms of practical action and decision, excluding from the conception everything except the problem of individual will realizing itself in the sphere of ordinary existence. Just as in logic the inevitable result was the purest nominalism, so in ethics he was driven to individualism, to the denial of social and national relations, to the exclusion of scientific study and of almost all that the Greeks understood by education. This individualism he and his followers carried to its logical conclusion. The ordinary pleasures of life were for them not merely negligible but positively harmful inasmuch as they interrupted the operation of the will. Wealth, popularity and power tend to dethrone the authority of reason and to pervert the soul from the natural to the artificial. Man exists for and in himself alone; his highest end is self-knowledge and self-realization in conformity with the dictates of his reason, apart altogether from the state and society. For this end, disrepute and poverty are advantageous, in so far as they drive back the man upon himself, increasing his self-control and purifying his intellect from the dross of the external. The good man (i.e. the wise man) wants nothing: like the gods, he is αὐταρκής (self-sufficing); “let men gain wisdom—or buy a rope”; he is a citizen of the world, not of a particular country (cf. Diogenes Laërtius vi. 11 μόνην τε ὀρθὴν πολιτείαν εἶναι τὴν, ἐν κόσμῳ).
It is not surprising that the pioneers of such a system were criticized and ridiculed by their fellows, and this by no means unjustly. We learn that Diogenes and Crates sought to force their principles upon their fellows in an obtrusive, tactless manner. The very essence of their philosophy was the negation of the graces of social courtesy; it was impossible to “return to nature” in the midst of a society clothed in the accumulated artificiality of evolved convention without shocking the ingrained sensibilities of its members. Nor is it unjust to infer that the sense of opposition provoked some of the Cynics to an overweening display of superiority. At the same time, it is absurd to regard the eccentricities of a few as the characteristics of the school, still more as a condemnation of the views which they held.
In logic Antisthenes was troubled by the problem of the One and the Many. A nominalist to the core, he held that definition and predication are either false or tautological. Ideas do not exist save for the consciousness which thinks them. “A horse,” said Antisthenes, “I can see, but horsehood I cannot see.” Definition is merely a circuitous method of stating an identity: “a tree is a vegetable growth” is logically no more than “a tree is a tree.”
Cynicism appears to have had a considerable vogue in Rome in the 1st and 2nd centuries A.D. Demetrius (q.v.) and Demonax are highly eulogized by Seneca and Lucian respectively. It is probable that these later Cynics adapted themselves somewhat to the times in which they lived and avoided the crude extravagance of Diogenes and others. But they undoubtedly maintained the spirit of Antisthenes unimpaired and held an honourable place in Roman thought. This very popularity had the effect of attracting into their ranks charlatans of the worst type. So that in Rome also Cynicism was partly the butt of the satirist and partly the ideal of the thinker.
Disregarding all the accidental excrescences of the doctrine, Cynicism must be regarded as a most valuable development and as a real asset in the sum of ethical speculation. With all its defective psychology, its barren logic, its immature technique, it emphasized two great and necessary truths, firstly, the absolute responsibility of the individual as the moral unit, and, secondly, the autocracy of the will. These two principles are sufficient ground for our gratitude to these “athletes of righteousness” (as Epictetus calls them). Furthermore they are profoundly important as the precursors of Stoicism. The closeness of the connexion is illustrated by Juvenal’s epigram that a Cynic differed from a Stoic only by his cloak. Zeno was a pupil of Crates, from whom he learned the moral worth of self-control and indifference to sensual indulgence (see Stoics).
Finally it is necessary to point out two flaws in the Cynic philosophy. In the first place, the content of the word “knowledge” is never properly developed. “Virtue is knowledge”; knowledge of what? and how is that knowledge related to the will? These questions were never properly answered by them. Secondly they fell into the natural error of emphasizing the purely animal side of the “nature,” which was their ethical criterion. Avoiding the artificial restraints of civilization, they were prone to fall back into animalism pure and simple. Many of them upheld the principle of community of wives (see Diogenes Laërtius vi. 11); some of them are said to have outraged the dictates of public decency. It was left to the Stoics to separate the wheat from the chaff, and to assign to the words “knowledge” and “nature” a saner and more comprehensive meaning.
For relation of Cynicism to contemporary thought, compare Cyrenaics, Megarian School. See also Asceticism.
See F. W. Mullach, Fragmenta philosophorum Graecorum (Paris, 1867), ii. 261-438; H. Ritter and L. Preller, Hist. phil. Graec. et Rom. ch. v.; histories of ancient philosophy, and specially Ed. Zeller, Socrates and the Socratic Schools, Eng. trans., O. J. Reichel (1868, 2nd ed. 1877); Th. Gomperz, Greek Thinkers, Eng. trans., vol. ii., G. G. Berry (1905); E. Caird, Evolution of Theology in the Greek Philosophers (1904), ii. 44 seq., 55 seq., 62 seq.; arts. Stoics and Socrates.
CYNOSURE (Lat. cynosura, Gr. κυνόσουρα, from κυνός, genitive of κύων, a dog, and οὐρά, tail), the name given by the Greeks and Romans to the constellation of the Little Bear, Ursa Minor; the word is applied in English to the pole-star which appears in that constellation, and hence to something bright which, like a “guiding-star,” draws all attention to it, as in Milton’s “cynosure of neighbouring eyes.”
 |
| Fig. 1.—Partial inflorescence of Cyperus longus (Galingale), slightly reduced. 1, Spikelet of same; 2, flower. |
CYPERACEAE, in botany, a natural order of the monocotyledonous group of seed-bearing plants. They are grass-like herbs, sometimes annual, but more often persist by means of an underground stem from which spring erect solitary or clustered, generally three-sided aerial stems, with leaves in three rows. The minute flowers are arranged in spikelets somewhat as in grasses, and these again in larger spike-like or panicled inflorescences. The flower has in rare cases a perianth of six scale-like leaves arranged in two whorls, and thus conforming to the common monocotyledonous type of flower. Generally the perianth is represented by hairs, bristles or similar developments, often indefinite in number; in the two largest genera, Cyperus, (fig. 1) and Carex (fig. 2), the flowers are naked. In a few cases two whorls of stamens are present, with three members in each, but generally only three are present; the pistil consists of three or two carpels, united to form an ovary bearing a corresponding number of styles and containing one ovule. The flowers, which are often unisexual, are wind-pollinated. The fruit is one-seeded, with a tough, leathery or hard wall. There are nearly 70 genera containing about 3000 species and widely distributed throughout the earth, chiefly as marsh-plants. In the arctic zone they form 10% of the flora; they will flourish in soils rich in humus which are too acid to support grasses. The large genus Cyperus contains about 400 species, chiefly in the warmer parts of the earth; C. Papyrus is the Egyptian Papyrus. Carex, 693 the largest genus of the order, the sedges, is widely distributed in the temperate, alpine and arctic regions of both hemispheres, and is represented by 60 species in Britain. Carex arenaria, the sea-bent, grows on sand-dunes and helps to bind the sand with its long cord-like underground stem which branches widely. Scirpus lacustris (fig. 3, 1) the true bulrush, occurs in lakes, ditches and marshes; it has a spongy, green, cylindrical stem, reaching nearly an inch in thickness and 1 to 8 ft. high, which is usually leafless with a terminal branched inflorescence. Eriophorum (fig. 3), cotton grass, is represented in Britain by several species in boggy land; they are small tufted herbs with cottony heads due to the numerous hair-like bristles which take the place of the perianth and become much elongated in the fruiting stage.
 |
| Fig. 2.—Carex riparia, the largest British sedge, from 3 to 5 ft. high. 1, Male flower of Carex; 2, female flower of Carex; 3, seed of Carex, cut lengthwise. |
 |
| Fig. 3.—Inflorescence of Cotton-grass (Eriophorum polystachion), about 2⁄3 nat. size. 1, Flower of true bulrush (Scirpus lacustris). |
CY-PRÈS (A.-Fr. for “so near”), in English law, a principle adopted by the court of chancery in dealing with trusts for charitable purposes. When the charitable purpose intended by a testator cannot be carried into effect, the court will apply the funds to some other purpose, as near the original as possible (whence the name). For instance, a testator having left a fund to be divided into four parts—one-fourth to be used for “the redemption of British slaves in Turkey and Barbary,” and the other three-fourths for various local charities—it was found that there were no British slaves in Turkey or Barbary, and as to that part of the gift therefore the testator’s purpose failed. Instead of allowing the portion of the fund devoted to this impossible purpose to lapse to the next of kin, the court devoted it to the purposes specified for the rest of the estate. This doctrine is only applied where “a general intention of charity is manifest” in the will, and not where one particular object only was present to the mind of the testator. Thus, a testator having left money to be applied in building a church in a particular parish, and that having been found to be impossible, the fund will not be applied cy-près, but will go to the next of kin.
In the United States, charitable trusts have become more frequent as the wealth of the country has progressed, and are regarded with increasing favour by the courts. The cy-près doctrine has been either expressly or virtually applied to uphold them in several of the states, and in some there has been legislation in the same direction. In others the doctrine has been repudiated, e.g. in Michigan, Tennessee, Indiana and Virginia. For many years the New York courts held that this doctrine was not in force there, but in 1893 the legislature repealed the provisions of the revised statutes on which these decisions rested and restored the ancient law. Statutes passed in Pennsylvania have established the doctrine there, and dissolved any doubt as to its being in force in that state.
CYPRESS (Cupressus), in botany, a genus of fifteen species belonging to the tribe Cupressineae, natural order Coniferae, represented by evergreen aromatic trees and shrubs indigenous to the south of Europe, western Asia, the Himalayas, China, Japan, north-western and north-eastern America, California and Mexico. The leaves of the cypresses are scale-like, overlapping and generally in four rows; the female catkins are roundish, and fewer than the male; the cones consist of from six to ten peltate woody scales, which end in a curved point, and open when the seeds are ripe; the seeds are numerous and winged. All the species exude resin, but no turpentine.
C. sempervirens, the common cypress, has been well known throughout the Mediterranean region since classic times; it may have been introduced from western Asia where it is found wild. It is a tapering, flame-shaped tree resembling the Lombardy poplar; its branches are thickly covered with small, imbricated, shining-green leaves; the male catkins are about 3 lines in length; the cones are between 1 and 1½ in. in diameter, sessile, and generally in pairs, and are made up of large angular scales, slightly convex exteriorly, and with a sharp point in the centre. In Britain the tree grows to a height of 40 ft., in its native soil to 70 or 90 ft. It thrives best on a dry, deep, sandy loam, on airy sheltered sites at no great elevation above the sea. It was introduced into Great Britain before the middle of the 16th century. In the climate of the south of England its rate of growth when young is between 1 and 1½ ft. a year. The seeds are sown in April, and come up in three or four weeks; the plants require protection from frost during their first winter.
The timber of the cypress is hard, close-grained, of a fine reddish hue, and very durable. Among the ancients it was in request for poles, rafters, joists, and for the construction of wine-presses, tables and musical instruments; and on that account was so valuable that a plantation of cypresses was considered a sufficient dowry for a daughter. Owing to its durability the wood was employed for mummy cases, and images of the gods; 694 a statue of Jupiter carved out of cypress is stated by Pliny to have existed 600 years without showing signs of decay. The cypress doors of the ancient St Peter’s at Rome, when removed by Eugenius IV., were about 1100 years old, but nevertheless in a state of perfect preservation. Laws were engraved on cypress by the ancients, and objects of value were preserved in receptacles made of it; thus Horace speaks of poems levi servanda cupresso.
The cypress, which grows no more when once cut down, was regarded as a symbol of the dead, and perhaps for that reason was sacred to Pluto; its branches were placed by the Greeks and Romans on the funeral pyres and in the houses of their departed friends. Its supposed ill-boding nature is alluded to in Shakespeare’s Henry VI., where Suffolk desires for his enemies “their sweetest shade, a grove of cypress trees.” The cypress was the tree into which Cyparissus, a beautiful youth beloved by Apollo, was transformed, that he might grieve to all time (Ovid, Met. x. 3). In Turkish cemeteries the cypress—
| “Dark tree, still sad when others’ grief is fled, The only constant mourner o’er the dead”— |
is the most striking feature, the rule being to plant one for each interment. The tree grows straight, or nearly so, and has a gloomy and forbidding, but wonderfully stately aspect. With advancing age its foliage becomes of a dark, almost black hue. William Gilpin calls the cypress an architectural tree: “No Italian scene,” says he, “is perfect without its tall spiral form, appearing as if it were but a part of the picturesquely disposed edifices which rise from the middle ground against the distant landscape.” The cypress of Somma, in Lombardy, is believed to have been in existence in the time of Julius Caesar; it is about 121 ft. in height, and 23 ft. in circumference. Napoleon, in making the road over the Simplon, deviated from the straight line in order to leave it standing. The cypress, as the olive, is found everywhere in the dry hollows and high eastern slopes of Corfu, of the scenery of which it is characteristic. As an ornamental tree in Britain the cypress is useful to break the outline formed by round-headed low shrubs and trees. The berosh, or beroth, of the Hebrew Scriptures, translated “fir” in the authorized version, in 1 Kings v. 8 and vi. 15, 2 Chron. ii. 8 and many other passages, is supposed to signify the cypress.
The common or tall variety of C. sempervirens is known as C. fastigiata; the other variety, C. horizontalis, which is little planted in England, is distinguished by its horizontally spreading branches, and its likeness to the cedar. The species C. torulosa of North India, so called from its twisted bark, attains an altitude of 150 ft.; its branches are erect or ascending, and grow so as to form a perfect cone. In the Kulu and Ladakh country the tree is sacred to the deities of the elements. It has been introduced into England, but does not thrive where the winter is severe. The wood, which in Indian temples is burnt as incense, is yellowish-red, close-grained, tough, hard, readily worked, durable, and equal in quality to that of the deodar. Another species, C. lusitanica or glauca, the “cedar of Goa,” is a handsome tree, 50 ft. in height when full-grown, with spreading branches drooping at their extremities; it has been much planted in Portugal, especially in the neighbourhood of Cintra. Its origin is doubtful. It was well established in Portugal before the middle of the 17th century, and has since been cultivated generally in the south of Europe, but is nowhere believed to be indigenous. The name “cedar of Goa” is misleading, as no cypress is found wild anywhere near Goa. It was cultivated in England in the 17th century, and the name C. lusitanica was given by Philip Miller, the curator of the Chelsea Physick garden, in 1768, in reference to its supposed Portuguese origin. Experience has shown this cypress to be too tender for British climate generally, though good specimens are to be found in the milder climate of the south and west of England and in Ireland.
The species G. Lawsoniana, the Port Orford cedar, a native of south Oregon and north California, where it attains a height of 100 ft., was introduced into Scotland in 1854; it is much grown for ornamental purposes in Britain, a large number of varieties of garden origin being distinguished by differences in habit and by colour of foliage. Other Californian cypresses are C. macrocarpa, the Monterey cypress, which is 60 ft. high when mature, with a habit suggesting that of cedar of Lebanon, and C. Joveniana and C. Macnabiana, smaller trees generally from 20 to 30 ft. in height. C. funebris is a native of the north of China, where it is planted near pagodas. C. nootkaensis, the Nootka Sound cypress or Alaska cedar, was introduced into Britain in 1850. It is a hardy species, reaching a height of from 80 to 100 ft. Several varieties are distinguished by habit and colour of foliage. C. obtusa, a native of Japan, is a tall tree reaching 100 ft. in height, and widely planted by the Japanese for its timber, which is one of the best for interior construction. It is also cultivated by them as a decorative plant, in many forms, including dwarf forms not exceeding a foot in height.
The “deciduous cypress,” “swamp cypress” or “bald cypress,” Taxodium distichum, is another member of the order Coniferae (tribe Taxodineae), a native of the southern United States and Mexico. It is a lofty tree reaching a height of 170 ft. or more, with a massive trunk 10 to 15 ft. or more in diameter, growing in or near water or on low-lying land which is subject to periodical flooding. The lower part of the trunk bears huge buttresses, each of which ends in a long branching far-spreading root, from the branches of which spring the peculiar knees which rise above the level of the water. The knees are of a soft spongy texture and act as breathing organs, supplying the roots with air, which they would otherwise be unable to obtain when submerged. The stout horizontally spreading branches give a cedar-like appearance; the foliage is light and feathery; the leaves and the slender shoots which bear them fall in the autumn. The cones, about the size of a small walnut, bear spirally arranged imbricated scales which subtend the three-angled winged seeds. The wood is light, soft, straight-grained and easily worked; it is very durable in contact with the soil, and is used for railway-ties, posts, fencing and for construction. The deciduous cypress was one of the first American trees introduced into England; it is described by John Parkinson in his Herbal of 1640. It thrives only near water or where the soil is permanently moist.
CYPRIAN, SAINT [Caecilius Cyprianus, called Thascius] (c. 200-258), bishop of Carthage, one of the most illustrious in the early history of the church, and one of the most notable of its early martyrs, was born about the year 200, probably at Carthage. He was of patrician family, wealthy, highly educated, and for some time occupied as a teacher of rhetoric at Carthage. Of an enthusiastic temperament, accomplished in classical literature, he seems while a pagan to have courted discussion with the converts to Christianity. Confident in his own powers, he entered ardently into what was no doubt the great question of the time at Carthage as elsewhere. He sought to vanquish, but was himself vanquished by, the new religious force which was making such rapid inroads on the decaying paganism of the Roman empire. Caecilianus (or Caecilius), a presbyter of Carthage, is supposed to have been the instrument of his conversion, which seems to have taken place about 246.
Cyprian carried all his natural enthusiasm and brilliant powers into his new profession. He devoted his wealth to the relief of the poor and other pious uses; and so, according to his deacon Pontius, who wrote a diffuse and vague account of his “life and passion,” “realized two benefits: the contempt of the world’s ambition, and the observance of that mercy which God has preferred to sacrifice.” The result of his charity and activity as a Christian convert was his unanimous call by the Christian people to the head of the church in Carthage, at the end of 248 or beginning of 249. The time was one of fierce persecution directed against the Christians, and the bishop of Carthage became a prominent object of attack. During the persecution of Decius (250-251) Cyprian was exposed to imminent danger, and was compelled for a time to seek safety in retreat. Under Gallus, the successor of Decius, the persecution was relaxed, and Cyprian returned to Carthage. Here he held several councils for the discussion of the affairs of the church, especially for grave questions as to the rebaptism of heretics, and the readmission into the church of the lapsi, or those who had fallen 695 away through fear during the heat of the persecution. Cyprian, although inspired by lofty notions of the prerogatives of the church, and inclined to severity of opinion towards heretics, and especially heretical dissentients from the belief in the divine authorship of the episcopal order and the unity of Christendom, was leniently disposed towards those who had temporarily fallen from the faith. He set himself in opposition to Novatian, a presbyter of Rome, who advocated their permanent exclusion from the church; and it was his influence which guided the tolerant measures of the Carthaginian synods on the subject. While in this question he went hand in hand with Cornelius, bishop of Rome, his strict attitude in the matter of baptism by heretics brought him into serious conflict with the Roman bishop Stephen. It would almost have come to a rupture, since both parties held firmly to their standpoint, had not a new persecution arisen under the emperor Valerian, which threw all internal quarrels into the background in face of the common danger. Stephen became a martyr in August 257. Cyprian was at first banished to Curubis in Africa Proconsularis. But soon he was recalled, taken into custody, and finally condemned to death. He was beheaded on the 14th of September 258, the first African bishop to obtain the martyr’s crown.
All Cyprian’s literary works were written in connexion with his episcopal office; almost all his treatises and many of his letters have the character of pastoral epistles, and their form occasionally betrays the fact that they were intended as addresses. These writings bear the mark of a clear mind and a moderate and gentle spirit. Cyprian had none of that character which makes the reading of Tertullian, whom he himself called his magister, so interesting and piquant, but he possessed other qualities which Tertullian lacked, especially the art of presenting his thoughts in simple, smooth and clear language, yet in a style which is not wanting in warmth and persuasive power. Like Tertullian, and often in imitation of him, Cyprian took certain apologetic, dogmatic and pastoral themes as subjects of his treatises. By far the best known of these is the treatise De catholicae ecclesiae unitate, called forth in A.D. 251 by the schism at Carthage, but particularly by the Novatian schism at Rome. In this is proclaimed the doctrine of the one church founded upon the apostle Peter, whose “tangible bond is her one united episcopate, an apostleship universal yet only one—the authority of every bishop perfect in itself and independent, yet not forming with all the others a mere agglomeration of powers, but being a tenure upon a totality like that of a shareholder in some joint property.”
Attention must also be called to the treatise Ad Donatum (De gratia dei), in which the new life after regeneration with its moral effects is set forth in a pure and clear light, as contrasted with the night of heathendom and its moral degradation, which were known to the author from personal experience. The numerous Letters of Cyprian are not only an important source for the history of church life and of ecclesiastical law, on account of their rich and manifold contents, but in large part they are important monuments of the literary activity of their author, since, not infrequently, they are in the form of treatises upon the topic in question. Of the eighty-two letters in the present collection, sixty-six were written by Cyprian. In the great majority of cases the chronology of their composition, as far as the year is concerned, presents no difficulties; more precise assignments are mainly conjectural. In the editions of the works of Cyprian a number of treatises are printed which, certainly or probably, were not written by him, and have therefore usually been described as pseudo-Cyprianic. Several of them, e.g. the treatise on dice (De aleatoribus), have attracted the attention of scholars, who are never weary of the attempt to determine the identity of the author, unfortunately hitherto without much success.
The best, though by no means faultless, edition of Cyprian’s works is that of W. von Hartel in the Corpus scriptorum ecclesiasticorum (3 vols., Vienna, 1868-1871). There is an English translation in the Library of the Ante-Nicene Fathers. The most complete monograph is that by Archbishop E. W. Benson, Cyprian, his Life, his Times, his Work (London, 1897). See also J. A. Faulkner, Cyprian the Churchman (Cincinnati and New York, 1906).
CYPRINODONTS. In spite of their name, the small fishes called Cyprinodonts are in no way related to the Cyprinids, or carp family, but are near allies of the pike, characterized by a flat head with protractile mouth beset with cardiform, villiform, or compressed, bi- or tri-cuspid teeth, generally large scales, and the absence of a well-developed lateral line. About two hundred species are known, mostly inhabitants of the fresh and brackish waters of America; only about thirty are known from the old world (south Europe, south Asia, China and Japan, and Africa). Several forms occur in the Oligocene and Miocene beds of Europe. Many species are ovo-viviparous, and from their small size and lively behaviour they are much appreciated as aquarium fishes.
In many species the sexes are dissimilar, the female being larger and less brilliantly coloured, with smaller fins; the anal fin of the male may be modified into an intromittent organ by means of which internal fertilization takes place, the ova developing in a sort of uterus. In the remarkable genus Anableps, from Central and South America, the strongly projecting eyes are divided by a horizontal band of the conjunctiva into an upper part adapted for vision in the air, and a lower for vision in the water, and the pupil is also divided into two parts by a constriction.
The latest monograph of these fishes is by S. Garman in Mem. Mus. Comp. Zool. xix. (1895).
The Amblyopsidae, which include the remarkable blind cave fishes of North America (Mammoth cave and others), are nearly related to the Cyprinodontidae, and like many of them ovo-viviparous. Chologaster, from the lowland streams and swamps of the south Atlantic states, has the eyes well developed and the body is coloured. Amblyopsis and Typhlichthys, which are evidently derived from Chologaster, or from forms closely related to it, but living in complete darkness, have the eyes rudimentary and more or less concealed under the skin, and the body is colourless.
See F. W. Putnam, Amer. Nat. (1872), p. 6, and P. Boston Soc. xvii. (1875), p. 222; and C. H. Eigenmann, Archiv. für Entwickelungsmechanik der Organismen, viii. (1899), p. 545.
CYPRUS, one of the largest islands in the Mediterranean, nominally in the dominion of Turkey, but under British administration, situated in the easternmost basin of that sea, at roughly equal distance from the coasts of Asia Minor to the north and of Syria to the east. The headland of Cape Kormakiti in Cyprus is distant 44 m. from Cape Anamur in Asia Minor, and its north-east point, Cape St Andrea, is 69 m. from Latakieh in Syria. It lies between 34° 33′ and 35° 41′ N., and between 32° 20′ and 34° 35′ E., so that it is situated in almost exactly the same latitude as Crete. Its greatest length is about 141 m., from Cape Drepano in the west to Cape St Andrea in the north-east, and its greatest breadth, from Cape Gata in the south to Cape Kormakiti in the north, reaches 60 m.; while it retains an average width of from 35 to 50 m. through the greater part of its extent, but narrows suddenly to less than 10 m. about 34° E., and from thence sends out a long narrow tongue of land towards the E.N.E. for a distance of 46 m., terminating in Cape St Andrea. The coast-line measures 486 m. Cyprus is the largest island in the Mediterranean after Sicily and Sardinia. In 1885 a trigonometrical survey and a map on the scale of 1 in. to 1 m. were made by Captain (afterwards Lord) Kitchener, R.E., who worked out the area of the island at 3584 sq. m., or a little more than the area of Norfolk and Suffolk.
Mountains.—Great part of the island is occupied by two mountain ranges, both of which have a general direction from west to east. Of these the most extensive, as well as the most lofty, is that which fills up almost the whole southern portion of the island, and is generally designated by modern geographers as Mount Olympus, though that name appears to have been applied by the ancients only to one particular peak. The highest summit is known at the present day as Mount Troödos, and attains an elevation of 6406 ft. It sends down subordinate ranges or spurs, of considerable altitude, on all sides, one of which extends to Cape Arnauti (the ancient Acamas), which forms the 696 north-west extremity of the island, while others descend on both sides quite to the northern and southern coasts. On the south-eastern slope are governmental and military summer quarters. The main range is continued eastward by the lofty summits known as Mount Adelphi (5305 ft.), Papoutsa (5124) and Machaira or Chionia (4674), until it ends in the somewhat isolated peak called Santa Croce (Stavrovouni or Oros Stavro), the Hill of the Holy Cross (2260 ft.). This mountain, designated by Strabo Mount Olympus, is a conspicuous object from Larnaca, from which it is only 12 m. distant, and is well known from being frequented as a place of pilgrimage. The northern range of mountains begins at Cape Kormakiti (the ancient Crommyon) and is continued from thence in an unbroken ridge to the eastern extremity of the island, Cape St Andrea, a distance of more than 100 m. It is not known by any collective name; its western part is called the Kyrenia mountains, while the remainder has the name of Carpas. It is inferior in elevation to the southern range, its highest summit (Buffavento) attaining only 3135 ft., while in the eastern portion the elevation rarely exceeds 2000 ft. But it is remarkable for its continuous and unbroken character—consisting throughout of a narrow but rugged and rocky ridge, descending abruptly to the south into the great plain of Lefkosia, and to the north to a narrow plain bordering the coast.

The Mesaoria.—Between the two mountain ranges lies a broad plain, extending across the island from the bay of Famagusta to that of Morphou on the west, a distance of nearly 60 m., with a breadth varying from 10 to 20 m. It is known by the name of the Mesaoria or Messaria, and is watered by a number of intermittent streams from the mountains on either hand. The chief streams are the Pedias and the Yalias, which follow roughly parallel courses eastward. The greater part of the plain is open and uncultivated, and presents nothing but barren downs; but corn is grown in considerable quantities in the northern portions of it, and there is no doubt that the whole is readily susceptible of cultivation. It is remarkable that Cyprus was celebrated in antiquity for its forests, which not only clothed the whole of its mountain ranges, but covered the entire central plain with a dense mass, so that it was with difficulty that the land could be cleared for cultivation. At the present day the whole plain of the Mesaoria is naturally bare and treeless, and it is only the loftiest and central summits of Mount Olympus that still retain their covering of pine woods. The disappearance of the forests (which has in a measure been artificially remedied) naturally affected the rivers, which are mostly mere torrents, dry in summer. Even the Pedias (ancient Pediaeus) does not reach the sea in summer, and its stagnant waters form unhealthy marshes. In the marshy localities malarial fever occurs but is rarely (in modern times) of a severe type. The mean annual temperature in Cyprus is about 69° F. (mean maximum 78°, and minimum 57°). The mean annual rainfall is about 19 ins. October to March is the cool, wet season. Earthquakes are not uncommon.
Geology.—Cyprus lies in the continuation of the folded belt of the Anti-taurus. The northern coast range is formed by the oldest rocks in the island, consisting chiefly of limestones and marbles with occasional masses of igneous rock. These are supposed to be of Cretaceous age, but no fossils have been found in them. On both sides the range is flanked by sandstones and shales (the Kythraean series), supposed to be of Upper Eocene age; and similar rocks occur around the southern mountain mass. The Oligocene consists of grey and white marls (known as the Idalian series), which are distributed all over the island and attain their greatest development on the south side of the Troödos. All these rocks have been folded, and take part in the formation of the mountains. The great igneous masses of Troödos, &c., consisting of diabase, basalt and serpentine, are of later date. Pliocene and later beds cover the central plain and occur at intervals along the coast. The Pliocene is of marine origin, and rests unconformably upon all the older beds, including the Post-oligocene igneous rocks, thus proving that the final folding and the last volcanic outbursts were approximately of Miocene age. The caves of the Kyrenian range contain a Pleistocene mammalian fauna.
Population.—The population of Cyprus in 1901 was 237,022, an increase of 27,736 since 1891 and of 51,392 since 1881. The people are mainly Greeks and Turks. About 22% of the population are Moslems; nearly all the remainder are Christians of the Orthodox Greek Church. The Moslem religious courts, presided over by cadis, are strictly confined to jurisdiction in religious cases affecting the Mahommedan population. The island is divided into the six districts of Famagusta, Kyrenia, Larnaca, Limasol, Nicosia and Papho. The chief towns are Nicosia (pop. 14,752), the capital, in the north central part of the island, Limasol (8298) and Larnaca (7964) on the south-eastern coast. The other capitals of districts are Famagusta on the east coast, Kyrenia on the north, and Ktima, capital of Papho, on the south-west. Kyrenia, a small port, has a castle built about the beginning of the 13th century, and notable, through the troubled history of the island, as never having been captured.
Agriculture, &c.—The most important species of the few trees that remain in the island are the Aleppo pine, the Pinus laricio, cypress, cedar, carob, olive and Quercus alnifolia. Recent additions are the eucalyptus, casuarina, Pinus pinea and ailanthus. Some protection has been afforded to existing plantations, and some attempt made to extend their area; but the progress in both directions is slow. Agriculture is the chief industry in the island, in spite of various disabilities. The soil is extremely fertile, and, with a fair rainfall, say 13 in., between November and April, yields magnificent crops, but the improvements in agriculture are scarcely satisfactory. The methods and appliances used are extremely primitive, and inveterate prejudice debars the average peasant from the use of new implements, fresh seed, or manure; he generally cares nothing for the rotation of crops, or for the cleanliness of his land. Modern improvements and the use of imported machinery have, however, been adopted by some. A director of agriculture was appointed in 1896, and leaflets are issued pointing out improvements within the means of the villager, and how to deal with plant diseases and insect pests. The products of the soil include grain, fruit, including carob, olive, mulberry, cotton, vegetables and oil seeds. Vineyards occupy a considerable area, and the native wines are pure and strong, but not always palatable. The native practice of conveying wine in tarred skins was deleterious to its flavour, and is now for the most part abolished. A company has exploited and improved the industry. Large sums have been expended on the destruction of locusts; they are now practically harmless, but live locusts are diligently collected every year, a reward being paid by the government for their destruction. Under the superintendence of an officer lent by the government of Madras, two great works of irrigation, from the lack of which agriculture had seriously suffered, were undertaken in 1898 and 1899. The smaller includes a reservoir at Syncrasi (Famagusta), with a catchment of 27 sq. m. and a capacity of 70,000,000 cub. ft. It reclaims 360 acres, and was estimated to irrigate 4320. The larger scheme includes three large reservoirs in the Mesaoria to hold up and temporarily store the flood waters of the Pedias and Yalias rivers. The estimate premised a cost of £50,000, the 697 irrigation of 42,000 acres, and the reclamation of 10,000. These works were completed respectively in 1899 and 1901.
The rearing of live stock is of no little importance. A committee exists “for the improvement of the breeds of Cyprus stock”; stallions of Arab blood have been imported, and prizes are offered for the best donkeys. Cattle, sheep, mules and donkeys are sent in large numbers to Egypt. Cyprus mules have found favour in war in the Crimea, India, Uganda, Eritrea and Egypt. The sea fisheries are not important, with the exception of the sponge fishery, which is under the protection of the administration. The manufactures of the island are insignificant.
Minerals.—Next to its forests, which long supplied the Greek monarchs of Egypt with timber for their fleets, Cyprus was celebrated among the ancients for its mineral wealth, especially for its mines of copper, which were worked from a very early period, and continued to enjoy such reputation among both Greeks and Romans that the modern name for the metal is derived from the term of Aes Cyprium or Cuprium by which it was known to the latter. According to Strabo the most valuable mines were worked at a place called Tamasus, in the centre of the island, on the northern slopes of Mount Olympus, but their exact site has not been identified. An attempt to work copper towards the close of the 19th century was a failure, but some prospecting was subsequently carried on. Besides copper, according to Strabo, the island produced considerable quantities of silver; and Pliny records it as producing various kinds of precious stones, among which he mentions diamonds and emeralds, but these were doubtless nothing more than rock crystal and beryl. Salt, which was in ancient times one of the productions for which the island was noted, is still made in large quantities, and there are extensive salt works in the neighbourhood of Larnaca and Limasol, where there are practically inexhaustible salt lakes. Rock crystal and asbestos are still found in the district of Paphos. Gypsum is exported unburnt from the Carpas, and as plaster of Paris from Limasol and Larnaca. Statuary marble has been found on the slopes of Buffavento in the northern range. Excellent building stone exists throughout the island.
Commerce.—A disability against the trade of Cyprus has been the want of natural harbours, the ports possessing only open roadsteads; though early in the 20th century the construction of a satisfactory commercial harbour was undertaken at Famagusta, and there is a small harbour at Kyrenia. Trade is carried on principally from the ports already indicated among the chief towns. The various agricultural products, cattle and mules, cheese, wines and spirits, silk cocoons and gypsum make up the bulk of the exports. Barley and wheat, carobs and raisins may be specially indicated among the agricultural exports. The annual value of exports and of imports (which are of a general character) may be set down as about £300,000 each. Good roads are maintained connecting the more important towns, and when the harbour at Famagusta was undertaken the construction of a railway from that port to Nicosia was also put in hand. The Eastern Telegraph Co. maintains a cable from Alexandria (Egypt) to Larnaca, and the greater part of the lines on the island. The Imperial Ottoman Telegraph Co. has also some lines. The British sovereign is the current gold coin, the unit of the bronze and silver coinage being the piastre (11⁄3 penny). Turkish weights and measures are used. The oke, equalling 2.8 ℔ avoirdupois, and the donum, about ¼ of an acre, are the chief units.
Constitution and Government.—Under a convention signed at Constantinople on the 4th of June 1878, Great Britain engaged to join the sultan of Turkey in defending his Asiatic possessions (in certain contingencies) against Russia, and the sultan, “in order to enable England to make necessary provision for executing her engagement,” consented to assign the island of Cyprus to be occupied and administered by England. The British flag was hoisted on the 12th of June, and the conditions of the occupation were explained in an annex to the convention, dated the 1st of July. An order in council of the 14th of September, modified so far as related to legislation by another of the 30th of November, regulated the government of the island. The administration was placed in the hands of a high commissioner with the usual powers of a colonial governor. Executive and legislative councils were established; and in each of the six districts into which, for administrative and legal purposes, the island was divided, a commissioner was appointed to represent the government. The executive council consists of the high commissioner, the chief secretary, the king’s advocate, the senior officer in charge of the troops, and the receiver-general, with, as “additional” members, two Christians and one Mussulman. The legislative council consists of six non-elected members, being office-holders, and twelve elected members, three being chosen by the Moslems and nine by the non-Moslem inhabitants. British subjects and foreigners, who have resided five years in Cyprus, can exercise the franchise as well as Ottoman subjects. The qualification otherwise is the payment of any of the taxes classed as Vergi Taxes (see below). The courts in existence at the time of the occupation were superseded by the following, constituted by an order in council dated the 30th of November 1882:—(1) a supreme court of criminal and civil appeal; (2) six assize courts; (3) six district courts; (4) six magistrates’ courts; and (5) village courts. Actions are divided, according to the nationality of the defendant, into “Ottoman” and “Foreign”; in the latter, the president of the court alone exercises jurisdiction as a rule, so also in criminal cases against foreigners. The law administered is that contained in the Ottoman codes, modified by ordinances passed by the legislative council.
Finance.—The principal sources of revenue are:—
(1) Vergi taxes, or taxes on house and land property, and trade profits and incomes (not including salaries); (2) military exemption tax, payable by Moslems and Christians alike, but not by foreigners, of 2s. 6d. a head on males between 18 and 60 years of age; (3) tithes. All tithes have been abolished, except those on cereals, carobs, silk cocoons, and, in the form of 10% ad valorem export duties, those on cotton, linseed, aniseed and raisins (all other export duties and a fishing tax have been abolished); (4) sheep, goat, and pig tax; (5) an excise on wine, spirits and tobacco; (6) import duties; (7) stamps, court fees, royalties, licenses, &c.; (8) salt monopoly. Foreigners are liable to all the above taxes except the military exemption tax. The annual sum of £92,800, payable to Turkey as the average excess (according to the years 1873-1878) of revenue over expenditure, but really appropriated to the interest on the British guaranteed loan of 1855, is a heavy burden. But if not lightened, taxation is at least better apportioned than formerly.
Instruction.—A general system of grants in aid of elementary schools was established in 1882. There are some 300 connected with the Greek Orthodox Church, and 160 elementary Moslem schools. Aid is also given to a few Armenian and Maronite schools. Among other schools are a Moslem high school (maintained entirely by government), a training college at Nicosia for teachers in the Orthodox Church schools, Greek high schools at Larnaca and Limasol, an English school for boys and a girls’ school at Nicosia. By a law of 1895 separate boards of education for Moslem and Greek Christian schools were established, and in each district there are separate committees, presided over by the commissioner. An institution worthy of special notice is the home and farm for lepers near Nicosia, accommodating over a hundred inmates.
History and Archaeology down to the Roman Occupation
The Stone Age has left but few traces in Cyprus; no sites have been found and even single implements are very rare. The “megalithic” monuments of Agia Phaneromeni1 and Halá Sultán Teké near Larnaca may perhaps be early, like the Palestinian cromlechs; but the vaulted chamber of Agia Katrína near Enkomi seems to be Mycenaean or later; and the perforated monoliths at Ktima seem to belong to oil presses of uncertain but probably not prehistoric date.
The Bronze Age, on the other hand, is of peculiar importance in an area which, like Cyprus, was one of the chief early sources of copper. Its remains have been carefully studied both on 698 settlement sites at Leondári Vounò and Kalopsída, and in tombs in more than thirty places, notably at Agia Paraskevì, Psemmatisméno, Alámbra, Episkopì and Enkomi. Throughout this period, which began probably before 3000 B.C. and ended about 1000 B.C., Cyprus evidently maintained a large population, and an art and culture distinct from those of Egypt, Syria and Cilicia. The Cypriote temper, however, lacks originality; at all periods it has accepted foreign innovations slowly, and discarded them even more reluctantly. The island owes its importance, therefore, mainly to its copious supply of a few raw materials, notably copper and timber. Objects of Cypriote manufacture are found but rarely on sites abroad; in the later Bronze Age, however, they occur in Egypt and South Palestine, and as far afield as Thera (Santorin), Athens and Troy (Hissarlik).
The Bronze Age culture of Cyprus falls into three main stages. In the first, the implements are rather of copper than of bronze, tin being absent or in small quantities (2 to 3%); the types are common to Syria and Asia Minor as far as the Hellespont, and resemble also the earliest forms in the Aegean and in central Europe; the pottery is all hand-made, with a red burnished surface, gourd-like and often fantastic forms, and simple geometrical patterns incised; zoomorphic art is very rare, and imported objects are unknown. In the second stage, implements of true bronze (9 to 10% tin) become common; painted pottery of buff clay with dull black geometrical patterns appears alongside the red-ware; and foreign imports occur, such as Egyptian blue-glazed beads (XIIth-XIIIth Dynasty, 2500-2000 B.C.),2 and cylindrical Asiatic seals (one of Sargon I., 2000 B.C.).3
In the third stage, Aegean colonists introduced the Mycenaean (late Minoan) culture and industries; with new types of weapons, wheel-made pottery, and a naturalistic art which rapidly becomes conventional; gold and ivory are abundant, and glass and enamels are known. Extended intercourse with Syria, Palestine and Egypt brought other types of pottery, jewelry, &c. (especially scarabs of XVIIIth and XIXth Dynasties, 1600-1200 B.C.), which were freely copied on the spot. There is, however, nothing in this period which can be ascribed to specifically “Phoenician” influence; the only traces of writing are in a variety of the Aegean script. The magnificent tombs from Enkomi and Episkopì illustrate the wealth and advancement of Cyprus at this time.4
It is in this third stage that Cyprus first appears in history, under the name Asi, as a conquest of Tethmosis (Thothmes) III. of Egypt (XVIIIth Dynasty, c. 1500 B.C.),5 yielding tribute of chariots, horses, copper, blue-stone and other products. It was still in Egyptian hands under Seti I., and under Rameses III. a list of Cypriote towns seems to include among others the names of Salamis, Citium, Soli, Idalium, Cerynia (Kyrenia), and Curium. Another Egyptian dependency, Alašia, has by some been identified with Cyprus or a part of it (but may perhaps be in North Syria). It sent copper, oil, horses and cattle, ivory and timber; under Amenophis (Amenhotep) III. it exported timber and imported silver; it included a town Şiķra, traded with Byblus in North Syria, and was exposed to piratical raids of Lykki (? Lycians).
The decline of Egypt under the XXth Dynasty, and the contemporary fall of the Aegean sea-power, left Cyprus isolated and defenceless, and the Early Iron Age which succeeds is a period of obscurity and relapse. Iron, which occurs rarely, and almost exclusively for ornaments, in a few tombs at Enkomi, suddenly superseded bronze for tools and weapons, and its introduction was accompanied, as in the Aegean, by economic, and probably by political changes, which broke up the high civilization of the Mycenaean colonies, and reduced them to poverty, isolation and comparative barbarism. It is significant that the first iron swords in Cyprus are of a type characteristic of the lands bordering the Adriatic. Gold and even silver become rare;6 foreign imports almost cease; engraved cylinders and scarabs are replaced by conical and pyramidal seals like those of Asia Minor, and dress-pins by brooches (fibulae) like those of south-eastern Europe. Representative art languishes, except a few childish terra-cottas; decorative art becomes once more purely geometrical, but shows only slight affinity with the contemporary geometrical art of the Aegean.
Lingering thus in Cyprus (as also in some islands of the Aegean) Mycenaean traditions came into contact with new oriental influences from the Syrian coast; and these were felt in Cyprus somewhat earlier than in the West. But there is at present no clear proof of Phoenician or other Semitic activity in Cyprus until the last years of the 8th century.
No reference to Cyprus has been found in Babylonian or Assyrian records before the reign of Sargon II. (end of 8th century B.C.), and the occasional discovery of Mesopotamian cylinders of early date in Cyprus is no proof of direct intercourse.7 Isaiah (xxiii. 1, 12), writing about this time, describes Kittim (a name derived from Citium, q.v.) as a port of call for merchantmen homeward bound for Tyre, and as a shelter for Tyrian refugees; but the Hebrew geographers of this and the next century classify Kittim, together with other coast-lands and islands, under the heading Javan, “Ionian” (q.v.), and consequently reckoned it as predominantly Greek.
Sargon’s campaigns in north Syria, Cilicia and south-east Asia Minor (721-711) provoked first attacks, then an embassy and submission in 709, from seven kings of Yatnana (the Assyrian name for Cyprus); and an inscription of Sargon himself, found at Citium, proves an Assyrian protectorate, and records tribute of gold, silver and various timbers. These kings probably represent that “sea-power of Cyprus” which precedes that of Phoenicia in the Greek “List of Thalassocracies” preserved by Eusebius. Under Sennacherib’s rule, Yatnana figures (as in Isaiah) as the refuge of a disloyal Sidonian in 702; but in 668 ten kings of Cypriote cities joined Assur-bani-pal’s expedition to Egypt; most of them bear recognizable Greek names, e.g. Pylagoras of Chytroi, Eteandros of Paphos, Onasagoras of Ledroi. They are gazetted with twelve other “kings of the Hatti” (S.E. Asia Minor). Citium, the principal Phoenician state, does not appear by name; but is usually recognized in the list under its Phoenician title Karṭi-ḥadasti, “new town.”
Thus before the middle of the 7th century Cyprus reappears in history divided among at least ten cities, of which some are certainly Greek, and one at least certainly Phoenician: with this, Greek tradition agrees.8 The Greek colonists traced their descent, at Curium, from Argos; at Lapathus, from Laconia; at Paphos, from Arcadia; at Salamis, from the Attic island of that name; and at Soli, also from Attica. The settlements at Paphos and Salamis, and probably at Curium, were believed to date from the period of the Trojan War, i.e. from the 13th century, and the latter part of the Mycenaean age; the name of Teucer, the legendary founder of Salamis, probably is a reminiscence of the piratical Tikkara who harried the Egyptian coast under Rameses III. (c. 1200 B.C.), and the discovery of late Mycenaean settlements on these sites, and also at Lapathus, suggests that these legends rest upon history. The Greek dialect of Cyprus points in the same direction; it shows marked resemblances with that of Arcadia, and forms with it a “South Achaean” or “South Aeolic” group, related to the “Northern Aeolic” of Thessaly and other parts of north Greece.9 Further 699 evidence of continuity comes from the peculiar Cypriote script, a syllabary related to the linear scripts of Crete and the south Aegean, and traceable in Cyprus to the Mycenaean age.10 It remained in regular use until the 4th century; before that time the Greek alphabet occurs in Cyprus only in a few inscriptions erected for visitors.11 In Citium and Idalium, on the other hand, a Phoenician dialect and alphabet were in use from the time of Sargon onward.12 Sargon’s inscription at Citium is cuneiform.13
The culture and art of Cyprus in this Graeco-Phoenician period are well represented by remains from Citium, Idalium, Tamassus, Amathus and Curium; the earlier phases are best represented round Lapathus, Soli, Paphos and Citium; the later Hellenization, at Amathus and Marion-Arsinoë. Three distinct foreign influences may be distinguished: they originate in Egypt, in Assyria, and in the Aegean. The first two predominate earlier, and gradually recede before the last-named. Their effects are best seen in sculpture and in metal work, though it remains doubtful whether the best examples of the latter were made in Cyprus or on the mainland. Among a great series of engraved silver bowls,14 found mostly in Cyprus, but also as far off as Nineveh, Olympia, Caere and Praeneste, some examples show almost unmixed imitation of Egyptian scenes and devices; in others, Assyrian types are introduced among the Egyptian in senseless confusion; in others, both traditions are merged in a mixed art, which betrays a return to naturalism and a new sense of style, like that of the Idaean bronzes in Crete.15 From its intermediate position between the art of Phoenicia and its western colonies (so far as this is known) and the earliest Hellenic art in the Aegean, this style has been called Graeco-Phoenician. The same sequence of phases is represented in sculpture by the votive statues from the sanctuaries of Aphrodite at Dali and of Apollo at Vóni and Frángissa; and by examples from other sites in the Cesnola collection; in painting by a rare class of naïvely polychromic vases; and in both by the elaborately coloured terra-cotta figures from the “Toumba” site at Salamis. Gem-engraving and jewelry follow similar lines; pottery-painting for the most part remains geometrical throughout, with crude survivals of Mycenaean curvilinear forms. Those Aegean influences, however, which had been predominant in the later Bronze Age, and had never wholly ceased, revived, as Hellenism matured and spread, and slowly repelled the mixed Phoenician orientalism. Imported vases from the Aegean, of the “Dipylon,” “proto-Corinthian” and “Rhodian” fabrics, occur rarely, and were imitated by the native potters; and early in the 6th century appears the specific influence of Ionia, and still more of Naucratis in the Egyptian delta. For the failure of Assyria in Egypt in 668-664, and the revival of Egypt as a phil-Hellene state under the XXVIth Dynasty, admitted strong Graeco-Egyptian influences in industry and art, and led about 560 B.C. to the political conquest of Cyprus by Amasis (Ahmosi) II.;16 once again Cypriote timber maintained a foreign sea-power in the Levant.
The annexation of Egypt by Cambyses of Persia in 525 B.C. was preceded by the voluntary surrender of Cyprus, which formed part of Darius’s “fifth satrapy.”17 The Greek cities, faring ill under Persia, and organized by Onesilaus of Salamis, joined the Ionic revolt in 500 B.C.;18 but the Phoenician states, Citium and Amathus, remained loyal to Persia; the rising was soon put down; in 480 Cyprus furnished no less than 150 ships to the fleet of Xerxes;19 and in spite of the repeated attempts of the Delian League to “liberate” the island, it remained subject to Persia during the 5th century.20 The occasion of the siege of Idalium by Persians (which is commemorated in an important Cypriote inscription) is unknown.21 Throughout this period, however, Athens and other Greek states maintained a brisk trade in copper, sending vases and other manufactures in return, and bringing Cyprus at last into full contact with Hellenism. But the Greek cities retained monarchical government throughout, and both the domestic art and the principal religious cults remained almost unaltered. The coins of the Greek dynasts and autonomous towns are struck on a variable standard with a stater of 170 to 180 grs.22 The principal Greek cities were now Salamis, Curium, Paphos, Marion, Soli, Kyrenia and Khytri. Phoenicians held Citium and Amathus on the south coast between Salamis and Curium, also Tamassus and Idalium in the interior; but the last named was little more than a sanctuary town, like Paphos. At the end of the 5th century a fresh Salaminian League was formed by Evagoras (q.v.), who became king in 410, aided the Athenian Conon after the fall of Athens in 404, and revolted openly from Persia in 386, after the peace of Antalcidas.23 Athens again sent help, but as before the Phoenician states supported Persia; the Greeks were divided by feuds, and in 380 the attempt failed; Evagoras was assassinated in 374, and his son Nicocles died soon after. After the victory of Alexander the Great at Issus in 333 B.C. all the states of Cyprus welcomed him, and sent timber and ships for his siege of Tyre in 332.
After Alexander’s death in 323 B.C. Cyprus, coveted still for its copper and timber, passed, after several rapid changes, to Ptolemy I., king of Egypt. Then in 306 B.C. Demetrius Poliorcetes of Macedon overran the whole island, besieged Salamis, and utterly defeated there the Egyptian fleet. Ptolemy, however, recovered it in 295 B.C. Under Ptolemaic rule Cyprus has little history. Usually it was governed by a viceroy of the royal line, but it gained a brief independence under Ptolemy Lathyrus (107-89 B.C.), and under a brother of Ptolemy Auletes in 58 B.C. The great sanctuaries of Paphos and Idalium, and the public buildings of Salamis, which were wholly remodelled in this period, have produced but few works of art; the sculpture from local shrines at Vóni and Vitsáda, and the frescoed tombstones from Amathus, only show how incapable the Cypriotes still were of utilizing Hellenistic models; a rare and beautiful class of terra-cottas like those of Myrina may be of Cypriote fabric, but their style is wholly of the Aegean. It is in this period that we first hear of Jewish settlements,24 which later become very populous.
In 58 B.C. Rome, which had made large unsecured loans to Ptolemy Auletes, sent M. Porcius Cato to annex the island, nominally because its king had connived at piracy, really because its revenues and the treasures of Paphos were coveted to finance a corn law of P. Clodius.25 Under Rome Cyprus was at first appended to the province of Cilicia; after Actium (31 B.C.) it became a separate province, which remained in the hands of Augustus and was governed by a legatus Caesaris pro praetore as long as danger was feared from the East.26 No monuments 700 remain of this period. In 22 B.C., however, it was transferred to the senate,27 so that Sergius Paulus, who was governor in A.D. 46, is rightly called ἀνθύπατος(proconsul).28 Of Paulus no coins are known, but an inscription exists.29 Other proconsuls are Julius Cordus and L. Annius Bassus who succeeded him in A.D. 52.30 The copper mines, which were still of great importance, were farmed at one time by Herod the Great.31 The persecution of Christians on the mainland after the death of Stephen drove converts as far as Cyprus; and soon after converted Cypriote Jews, such as Mnason (an “original convert” ) and Joses the Levite (better known as Barnabas), were preaching in Antioch. The latter revisited Cyprus twice, first with Paul on his “first journey” in A.D. 46, and later with Mark.32 In 116-117 the Jews of Cyprus, with those of Egypt and Cyrene, revolted, massacred 240,000 persons, and destroyed a large part of Salamis. Hadrian, afterwards emperor, suppressed them, and expelled all Jews from Cyprus.
For the culture of the Roman period there is abundant evidence from Salamis and Paphos, and from tombs everywhere, for the glass vessels which almost wholly supersede pottery are much sought for their (quite accidental) iridescence; not much else is found that is either characteristic or noteworthy; and little attention has been paid to the sequence of style.
The Christian church of Cyprus was divided into thirteen bishoprics. It was made autonomous in the 5th century, in recognition of the supposed discovery of the original of St Matthew’s Gospel in a “tomb of Barnabas” which is still shown at Salamis. The patriarch has therefore the title μακαριώτατος and the right to sign his name in red ink. A council of Cyprus, summoned by Theophilus of Alexandria in A.D. 401, prohibited the reading of the works of Origen (see Cyprus, Church of).
Of the Byzantine period little remains but the ruins of the castles of St Hilarion, Buffavento and Kantára; and a magnificent series of gold ornaments and silver plate, found near Kyrenia in 1883 and 1897 respectively. Christian tombs usually contain nothing of value.
The Frank conquest is represented by the “Crusaders’ Tower” at Kolossi, and the church of St Nicholas at Nicosia; and, later, by masterpieces of a French Gothic style, such as the church (mosque) of St Sophia, and other churches at Nicosia; the cathedral (mosque) and others at Famagusta (q.v.), and the monastery at Bella Pais; as well as by domestic architecture at Nicosia; and by forts at Kyrenia, Limasol and elsewhere.
The Turks and British have added little, and destroyed much, converting churches into mosques and grain-stores, and quarrying walls and buildings at Famagusta.
History of Excavation.—Practically all the archaeological discoveries above detailed have been made since 1877. A few chance finds of vases, inscriptions and coins; of a hoard of silver bowls at Dali (anc. Idalium)33 in 1851; and of a bronze tablet with Phoenician and Cypriote bilingual inscriptions,34 also at Dali, and about the same time, had raised questions of great interest as to the art and the language of the ancient inhabitants. T. B. Sandwith, British consul 1865-1869, had laid the foundations of a sound knowledge of Cypriote pottery;35 his successor R. H. Lang (1870-1872) had excavated a sanctuary of Aphrodite at Dali;36 and at the time of the publication of the 9th ed. of the Ency. Brit.,37 General Louis P. di Cesnola (q.v.), American consul, was already exploring ancient sites, and opening tombs, in all parts of the island, though his results were not published till 1877.38 But though his vast collection, now in the Metropolitan Museum of New York, remains the largest series of Cypriote antiquities in the world, the accounts which have been given of its origin are so inadequate, and have provoked so much controversy,39 that its scientific value is small, and a large part of subsequent excavation has necessarily been directed to solving the problems suggested by its practically isolated specimens. From 1876 to 1878 Major Alexander P. di Cesnola continued his brother’s work, but the large collection which he exhibited in London in 1880 was dispersed soon afterwards.40
On the British occupation of Cyprus in 1878, the Ottoman law of 1874 in regard to antiquities was retained in force. Excavation is permitted under government supervision, and the finds are apportioned in thirds, between the excavator, the landowner (who is usually bought out by the former), and the government. The government thirds lie neglected in a “Cyprus Museum” maintained at Nicosia by voluntary subscription. There is no staff, and no effective supervision of ancient sites or monuments. A catalogue of the collections was published by the Oxford University Press in 1899.41
Since 1878 more than seventy distinct excavations have been made in Cyprus, of which the following are the most important. In 1879 the British government used the acropolis of Citium (Larnaca) to fill up the ancient harbour; and from the destruction a few Phoenician inscriptions and a proto-Ionic capital were saved. In 1882 tombs were opened by G. Hake at Salamis and Curium for the South Kensington Museum, but no scientific record was made. In 1883 the Cyprus Museum was founded by private enterprise, and on its behalf Max Ohnefalsch-Richter, who had already made trial diggings for Sir Charles Newton and the British Museum, excavated sanctuaries at Vóni and Kythréa (Chytri), and opened tombs on some other sites.42
In 1885 Dr F. Dümmler opened tombs at Dali, Alámbra and elsewhere, and laid the foundations of knowledge of the Bronze Age and Early Iron Age;43 and Richter, on behalf of officials and private individuals, excavated parts of Frángissa (Tamassus), Episkopì and Dali.44
In the same year, 1885, and in 1886, a syndicate opened many tombs at Póli-tis-Khrýsochou (Marium, Arsinoë), and sold the contents by auction in Paris. From Richter’s notes of this excavation, Dr P. Herrmann compiled the first scientific account of Graeco-Phoenician and Hellenistic Cyprus.45 In 1886 also M. le vicomte E. de Castillon de St Victor opened rich Graeco-Phoenician tombs at Episkopì, the contents of which are in the Louvre.46
The successes of 1885-1886 led to the foundation of the Cyprus Exploration Fund, on behalf of which (1) in 1888 the sanctuary of Aphrodite at Paphos (Kouklia) was excavated by Messrs E. Gardner, M. R. James, D. G. Hogarth and R. Elsey Smith;47 (2) in 1889-1890 more tombs were opened at Póli by Messrs J. A. R. Munro and H. A. Tubbs;48 (3) in 1890-1891 extensive trials were made at Salamis, by the same;49 (4) minor sites were examined at Leondári Vounò (1888),50 Amargetti (1888),51 and Limniti (1889);52 (5) in 1888 Hogarth made a surface-survey of the Karpass promontory;53 and finally, (6) in 1894 the balance was expended by J. L. Myres in a series of trials, to settle special 701 points, at Agia Paraskevì, Kalopsída and Larnaca.54 In 1894 also Dr Richter excavated round Idalium and Tamassus for the Prussian government: the results, unpublished up to 1902, are in the Berlin Museum.55 Finally, a legacy from Miss Emma T. Turner enabled the British Museum to open numerous tombs, by contract, of the Graeco-Phoenician age, in 1894, at Palaeò-Lemessò (Amathus); and of the Mycenaean age, in 1894-1895 at Episkopì, in 1895-1896 at Enkomi (near Salamis), and in 1897-1899 on small sites between Larnaca and Limasol.56
For ancient Oriental references to Cyprus see E. Oberhummer, Die Insel Cypern, i. (Munich, 1903); for classical references, W. H. Engel, Kypros (2 vols., Berlin, 1841); for culture and art, G. Perrot and C. Chipiez, Histoire de l’art dans l’antiquité, vol. iii. “Phénicie et Cypre” (Paris, 1885); L. P. di Cesnola, A Descriptive Atlas of the Cesnola Collection of Cypr. Antiquities in the Metropolitan Museum of Art, New York (3 vols., Boston, U.S.A., 1884-1886); M. Ohnefalsch-Richter, Kypros, the Bible and Homer (2 vols., London and Berlin, 1893); J. L. Myres and M. Ohnefalsch-Richter, Cyprus Museum Catalogue (Oxford, 1899). The principal publications on special topics are given in the footnotes. For Cypriote coins see also Numismatics. See further the general bibliography below.
Modern History
After the division of the Roman empire Cyprus naturally passed, with all the neighbouring countries, into the hands of the Eastern or Byzantine emperors, to whom it continued subject, with brief intervals, for more than seven centuries. Until 644 the island was exceedingly prosperous, but in that year began the period of Arab invasions, which continued intermittently until 975. At the outset the Arabs under the caliph Othman made themselves masters of the island, and destroyed the city of Salamis, which until that time had continued to be the capital. The island was recovered by the Greek emperors and, though again conquered by the Arabs in the reign of Harun al-Rashid (802), it was finally restored to the Byzantine empire under Nicephorus Phocas. Its princes became practically independent, and tyrannized the island, until in 1191 Isaac Comnenus provoked the wrath of Richard I., king of England, by wantonly ill-treating his crusaders. He thereupon wrested the island from Isaac, whom he took captive. He then sold Cyprus to the Knights Templars, who presently resold it to Guy de Lusignan, titular king of Jerusalem.
Guy ruled from 1192 till his death in 1194; his brother Amaury took the title of king, and from this time Cyprus was governed for nearly three centuries by a succession of kings of the same dynasty, who introduced into the island the feudal system and other institutions of western Europe. During the later part of this period, indeed, the Genoese made themselves masters of Famagusta—which had risen in place of Salamis to be the chief commercial city in the island—and retained possession of it for a considerable time (1376-1464); but it was recovered by King James II., and the whole island was reunited under his rule. His marriage with Caterina Cornaro, a Venetian lady of rank, was designed to secure the support of the powerful republic of Venice, but had the effect after a few years, in consequence of his own death and that of his son James III., of transferring the sovereignty of the island to his new allies. Caterina, feeling herself unable to contend alone with the increasing power of the Turks, was induced to abdicate the sovereign power in favour of the Venetian republic, which at once entered into full possession of the island (1489).
The Venetians retained their acquisition for eighty-two years, notwithstanding the neighbourhood of the Turks. Cyprus was now harshly governed by a lieutenant, and the condition of the natives, who had been much oppressed under the Lusignan dynasty, became worse. In 1570 the Turks, under Selim II., made a serious attempt to conquer the island, in which they landed an army of 60,000 men. The greater part of the island was reduced with little difficulty; Nicosia, the capital, was taken after a siege of 45 days, and 20,000 of its inhabitants put to the sword. Famagusta alone made a gallant and protracted resistance, and did not capitulate till after a siege of nearly a year’s duration (August 1571). The terms of the capitulation were shamefully violated by the Turks, who put to death the governor Marcantonio Bragadino with cruel torments. From that time Cyprus was under Turkish administration until the agreement with Great Britain in 1878. Its history during that period is almost a blank. A serious insurrection broke out in 1764, but was speedily suppressed; and a few similar incidents are the only evidence of the Turkish oppression of the Christian population of the island, and the consequent stagnation of its trade.
Authorities.—An Attempt at a Bibliography of Cyprus, by C. D. Cobham (4th ed., Nicosia, 1900), registers over 700 works which deal with Cyprus. A Handbook of Cyprus, by Sir J. T. Hutchinson and C. D. Cobham (London), treats the island briefly from every standpoint. See also E. Oberhummer, Die Insel Cypern (Munich, 1903 et seq.), a comprehensive work. The most interesting travels may be found under the names of Felix Faber, Evagatorium (Stuttgart, 1843); de Villamont, Voyages (Arras, 1598); van Kootwyck, Cotovici itinerarium (Antwerp, 1619); R. Pococke, Description of the East (London, 1743); A. Drummond, Travels (London, 1754); E. D. Clarke, Travels (London, 1812); Sir S. Baker, Cyprus in 1879 (London, 1879); W. H. Mallock, In an Enchanted Island (London, 1879). The geology of the island has been handled by A. Gaudry, Géologie de l’île de Chypre (Paris, 1862); C. V. Bellamy, Notes on the Geology of Cyprus, to accompany a Geological Map of Cyprus (London, 1905); C. V. Bellamy and A. J. Jukes-Brown, Geology of Cyprus (Plymouth, 1905). Its natural history by F. Unger and T. Kotschy, Die Insel Cypern (Wien, 1865). Numismatics by the Duc de Luynes, Numismatique et inscriptions cypriotes (Paris, 1852); R. H. Lang, Numism. Chronicle, vol. xi. (1871); J. P. Six, Rev. num. pp. 249-374 (Paris, 1883); and E. Babelon, Monnaies grecques (Paris, 1893). The coins of medieval date have been described by P. Lambros, Monnaies inédites (Athens, 1876); and G. Schlumberger, Num. de l’orient latin (Paris, 1878). Inscriptions in the Cypriote character have been collected by M. Schmidt, Sammlung (Jena, 1876); and W. Deecke, Die griechisch-kyprischen Inschriften (Göttingen, 1883); in Phoenician in the C.I.P. (Paris, 1881). J. Meursius, Cyprus (Amsterdam, 1675), marshals the classical authorities; and W. Engel, Kypros (Berlin, 1841), gives a good summary of the ancient history of the island. For the Phoenician element, see F. Movers, Die Phönizier (Bonn and Berlin, 1841-1856). L. Comte de Mas Latrie published between 1852 and 1861 one volume of History (1191-1291), and two of most precious documents in illustration of the reigns of the Lusignan kings. Fra Stefano Lusignano, Chorograffia di Cipro (Bologna, 1573), and Bp. Stubbs, Two Lectures (Oxford, 1878), are useful for the same period; and perhaps a score of contemporary pamphlets—the best of them by N. Martinengo, Relatione di tutto il successo di Famagosta (Venezia, 1572), and A. Calepio (in Lusignan’s Chorograffia)—preserve details of the famous sieges of Nicosia and Famagusta. G. Mariti, Viaggi (Lucca, 1769; Eng. trans. C. D. Cobham, 2nd ed., 1909), and Cyprianos, History (Venice, 1768), are the best authorities of Cyprus under Turkish rule. Medieval tombs and their inscriptions are recorded and illustrated in T. J. Chamberlayne, Lacrimae nicossienses (Paris, 1894); and C. Enlart’s volumes, L’Art gothique et la Renaissance en Chypre (Paris, 1899), deal with medieval architecture. For Cypriote pottery in Athens and Constantinople, see G. Nicole, Bulletin de l’Institut Genevois, xxxvii.
1 M. Ohnefalsch-Richter, Arch. Zeitung (1881), p. 311, pl. xviii. The principal publications respecting this and all sites and phases of culture mentioned in this section are collected in Myres and Ohnefalsch-Richter, Cyprus Museum Catalogue (Oxford, 1899), pp. 1-35.
2 Myres, Journ. Hellenic Studies, xvii. p. 146.
3 Sayce, Trans. Soc. Bibl. Arch. v. pp. 441-444. The exact provenance of these cylinders is not known, but there is every reason to believe that they were found in Cyprus.
4 British Museum, Excavations in Cyprus (London, 1900). The official publication stands alone in referring these tombs to the Hellenic period (800-600 B.C.).
5 E. Oberhummer, Die Insel Cypern (Munich, 1903), i. pp. 1-3 (all the Egyptian evidence).
6 A. J. Evans, Journ. Anthrop. Inst. xxx. p. 199 ff.; J. Naue, Die vorrömischen Schwerter (Munich, 1903), p. 25.
7 E. Oberhummer, l.c. p. 5 ff. (all the Assyrian and biblical evidence).
8 W. H. Engel, Kypros (Berlin, 1841) (all the Greek traditions).
9 Moriz Schmidt, Z. f. vergl. Sprachw. (1860), p. 290 ff., 361 ff.; H. W. Smith, Trans. Amer. Philol. Assoc. xviii. (1887); R. Meister, Zum eleischen, arkadischen u. kyprischen Dialekte (Leipzig, 1890); O. Hoffmann, Die griechischen Dialekte, i. (Göttingen, 1891); C. D. Cobham, Bibliography of Cyprus, pp. 40-45.
10 G. Smith, Tr. Soc. Bibl. Arch. i. 129 ff.; Moritz Schmidt, Monatsb. k. Ak. Wiss. (Berlin, 1874), pp. 614-615; Sammlung kypr. Inschriften (Jena, 1876); W. Deecke, Ursprung der kypr. Sylbenschrift (Strassburg, 1877); cf. Deecke-Collitz, Samml. d. gr. Dialektinschriften, i. (Göttingen, 1884); cf. C. D. Cobham, l.c. On its Aegean origin, A. J. Evans, “Cretan Pictographs” (1895), Journ. Hell. Studies, xiv., cf. xvii.; British Museum, Exc. in Cypr. (London, 1900), p. 27.
11 British Museum, Exc. in Cypr. (London, 1900), p. 95 (Ionic inscriptions of 5th century from Amathus).
12 M. de Voguë, Mélanges d’archéologie orientale (Paris, 1869); J. Euting, Sitzb. k. preuss. Ak. Wiss. (1887), pp. 115 ff.; Ph. Berger, C. R. Acad. Inscr. (1887), pp. 155 ff., 187 ff., 203 ff. Cf. Corpus Inscr. Semit. (Paris, 1881), ii. 35 ff.
13 E. Schrader, Abh. d. k. preuss. Ak. Wiss. (1881).
14 G. Perrot and C. Chipiez, Histoire de l’art dans l’antiquité, iii. (Paris, 1885), interpret these and most other Cypriote materials without reserve as “Phoenician.”
15 F. Halbherr and P. Orsi, Antichità dell’ antro di Zeus Ideo in Creta (Rome, 1888). Cf. H. Brunn, Griechische Kunstgeschichte (Munich, 1893), i. 90 ff.
16 Herod. ii. 182; see also Egypt: History (Dyn. XXVI.).
17 Herod. iii. 19. 91; see also Persia: History.
18 Herod. v. 108, 113, 115.
19 Herod. vii. 90.
20 Thuc. i. 94, 112.
21 M. Schmidt, Die Inschrift von Idalion (Jena, 1874).
22 G. F. Hill, Brit. Mus. Cat. Coins of Cyprus (London, 1904). Earlier literature in Cobham, l.c. p. 39.
23 H. F. Talbot, Tr. Soc. Bibl. Arch. v. 447 ff. (translation). For Evagoras and the place of Cyprus in later Greek history, see G. Grote, History of Greece (Index, s.v.), and W. H. Engel, Kypros (Berlin, 1841).
24 1 Macc. xv. 23.
25 Livy, Epit. 104; Cic. pro Sestio, 26, 57.
26 Dio Cass. liii. 12; Strabo 683, 840.
27 Dio Cass. liv. 4; Strabo 685.
28 Acts xiii. 7.
29 D. G. Hogarth, Devia Cypria, pp. 114 ff. and app.
30 Corp. Inscr. Lat. 2631-2632.
31 Jos. Ant. 16. 4, 5; 19. 26, 28.
32 Acts iv. 36, xi. 19, 20, xiii. 4-13, xv. 39, xxi. 16.
33 De Longpérier, Athenæum français (1853), pp. 413 ff.; Musée Napoléon, pls. x. xi.
34 De Luynes, Numismatique et inscriptions chypriotes (1852).
35 Archaeologia, xlv. (1877), pp. 127-142.
36 Trans. Roy. Soc. Literature, 2nd ser. xi. (1878), pp. 30 ff.
37 Article “Cyprus” ad. fin.
38 Cyprus: its Cities, Tombs and Temples (London, 1877).
39 See Cobham, An Attempt at a Bibliography of Cyprus (4th ed., Nicosia, 1900), Appendix, “Cesnola Controversy,” p. 54.
40 The Lawrence-Cesnola Collection (London, 1881); Salaminia, id. 1882.
41 Myres and Ohnefalsch-Richter, A Catalogue of the Cyprus Museum, with a Chronicle of Excavations since the British Occupation, and Introductory Notes on Cypriote Archaeology (Oxford, 1899).
42 Mitt. d. arch. Inst. ii. (Athens, 1881).
43 Mitt. d. arch. Inst. vi. (Athens, 1886); Bemerkungen z. ält Kunsthandwerk, &c., ii. “Der kypr. geometrische Stil” (Halle, 1888).
44 Summarized in Cyprus, the Bible and Homer (London and Berlin, 1893).
45 Das Gräberfeld von Marion (Berlin, 1888).
46 Archives des missions scientifiques, xvii. (Paris, 1891).
47 Journal of Hellenic Studies, ix. (London, 1888).
48 Id. xi. (1890); xii. (1891).
49 Id. xii. (1891).
50 Id. ix. (1888).
51 Id. ix. (1888).
52 Id. xi. (1890).
53 Devia Cypria (Oxford, 1889).
54 J.H.S. xvii. (1897).
55 Summarized in Cyprus Museum Catalogue (Oxford, 1899).
56 Excavations in Cyprus (London, 1900).
CYPRUS, CHURCH OF. The Church of Cyprus is in communion and in doctrinal agreement with the other Orthodox Churches of the East (see Orthodox Eastern Church), but is independent and subject to no patriarch. This position it has always claimed (see, however, W. Bright, Notes on the Canons, on Ephesus 8). At any rate, its independence “by ancient custom” was recognized, as against the claims of the patriarch of Antioch, by the council of Ephesus, A.D. 431, by an edict of the emperor Zeno (to whom the church had sent a cogent argument on its own behalf, the alleged body of its reputed founder St Barnabas, then just discovered at Salamis), and by the Trullan Council in 692. Attempts have been made subsequently by the patriarchs of Antioch to claim authority over it, the last as recently as 1600; but they came to nothing. And excepting for the period during which Cyprus was in the hands of the Lusignans and the Venetian Republic (1193-1571), the Church has never lost its independence. It receives the holy ointment (μῦρον) from without, till 1860 from Antioch and subsequently from Constantinople, but this is a matter of courtesy and not of right. Of old there were some twenty sees in the island. The bishop of the capital, Salamis or Constantia, was constituted metropolitan by Zeno, with the title “archbishop 702 of all Cyprus,” enlarged subsequently into “archbishop of Justiniana Nova and of all Cyprus,” after an enforced expatriation to Justinianopolis in 688. Zeno also gave him the unique privileges of wearing and signing his name in the imperial purple, &c., which are still preserved. A Latin hierarchy was set up in 1196 (an archbishop at Nicosia with suffragans at Limasol, Paphos and Famagusta), and the Greek bishops were made to minister to their flocks in subjection to it. The sees were forcibly reduced to four, the archbishopric was ostensibly abolished, and the bishops were compelled to do homage and swear fealty to the Latin Church. This bondage ceased at the conquest of the island by the Turks: the Latin hierarchy disappeared (the cathedral at Nicosia is now used as a mosque), and the native church emerged into comparative freedom. In 1821, it is true, all the bishops and many of their flock were put to death by way of discouraging sympathies with the Greeks; but successors were soon consecrated, by bishops sent from Antioch at the request of the patriarch of Constantinople, and on the whole the Church has prospered. The bishops-elect required the berat of the sultan; but having received this, they enjoyed no little civil importance. Since 1878 the berat has not been given, and the bishops are less influential. The suppressed sees have never been restored, but the four which survive (now known as Nicosia, Paphos, Kition and Kyrenia) are of metropolitan rank, so that the archbishop, whose headquarters, first at Salamis, then at Famagusta, are now at Nicosia, is a primate amongst metropolitans. There are several monasteries dating from the 11th century and onwards; also an archiepiscopal school at Nicosia, founded in 1812 and raised to the status of a “gymnasion” in 1893; and a high school for girls.
Authorities.—Ph. Georgiou, Εἰδήσεις Ἱστορικαὶ περὶ τῆς Ἐκκλησίας τῆς Κύπρου (Athens, 1875); K. Kouriokurineos (Archbishop of Cyprus), Ἱστορία χρονολογικὴ τῆς νήσου Κύπρου (Venice, 1788); de Mas Latrie, Histoire de l’île de Chypre sous les princes de la maison de Lusignan (Paris, 1852 f.); H. T. F. Duckworth, The Church of Cyprus(London, 1900); J. Hackett, History of the Orthodox Church of Cyprus (1901).
CYPSELUS, tyrant of Corinth (c. 657-627 B.C.), was the son of Aeëtion and Labda, daughter of Amphion, a member of the ruling family, the Bacchiadae. He is said to have derived his name from the fact that when the Bacchiadae, warned that he would prove their ruin, sent emissaries to kill him in his cradle, his mother saved him by concealing him in a chest (Gr. κυψέλη). The story was, of course, a subsequent invention. When he was grown up, Cypselus, encouraged by an oracle, drove out the Bacchiadae, and made himself master of Corinth. It is stated that he first ingratiated himself with the people by his liberal conduct when Polemarch, in which capacity he had to exact the fines imposed by the law. In the words of Aristotle he made his way through demagogy to tyranny. Herodotus, in the spirit of 5th-century Greeks, which conventionally regarded the tyrants as selfish despots, says he ruled harshly, but he is generally represented as mild, beneficent and so popular as to be able to dispense with a bodyguard, the usual attribute of a tyrannis. He pursued an energetic commercial and colonial policy (see Corinth), and thus laid the foundations of Corinthian prosperity. He may well be compared with the Athenian Peisistratus in these respects. He laid out the large sums thus derived on the construction of buildings and works of art. At the same time he wisely strove to gain the goodwill of the powerful priesthoods of the great sanctuaries of Delphi and Olympia. At Delphi he built a treasure-house for Corinthian votive offerings; at Olympia he dedicated a colossal statue of Zeus and the famous “chest of Cypselus,” supposed to be identical with the chest of the legend, of which Pausanias (v. 17-19) has given an elaborate description. It was of cedar-wood, gold and ivory, and on it were represented the chief incidents in Greek (especially Corinthian) mythology and legend. Cypselus was succeeded by his son Periander.
See Corinth: History; histories of Greece; Herodotus v. 92; Aristotle, Politics, 1310b, 1315b; P. Knapp, Die Kypseliden und die Kypseloslade (Tübingen, 1888); L. Preller, Ausgewahlte Aufsatze (1864); H. Stuart Jones, in Journ. Hell. Stud. (1894), 30 foll.
CYRANO DE BERGERAC, SAVINIEN (1620-1655), French romance-writer and dramatist, son of Abel de Cyrano, seigneur de Mauvières et de Bergerac, was born in Paris on the 6th of March 1619-1620. He received his first education from a country priest, and had for a fellow pupil his friend and future biographer, Henri Lebret. He then proceeded to Paris to the collège de Beauvais, where he had for master Jean Grangier, whom he afterwards ridiculed in his comedy Le Pédant joué (1654). At the age of nineteen he entered a corps of the guards, serving in the campaigns of 1639 and 1640, and began the series of exploits that were to make of him a veritable hero of romance. The story of his adventure single-handed against a hundred enemies is vouched for by Lebret as the simple truth. After two years of this life Cyrano left the service and returned to Paris to pursue literature, producing tragedies cast in the orthodox classical mode. He was, however, as a pupil of Gassendi, suspected of thinking too freely, and in the Mort d’Agrippine (1654) his enemies even found blasphemy. The most interesting section of his work is that which embraces the two romances L’Histoire comique des états du soleil (1662) and L’Histoire comique des états de la lune (1656?). Cyrano’s ingenious mixture of science and romance has furnished a model for many subsequent writers, among them Swift and E. A. Poe. It is impossible to determine whether he adopted his fanciful style in the hope of safely conveying ideas that might be regarded as unorthodox, or whether he simply found in romance writing a relaxation from the serious study of physics. Cyrano spent a stormy existence in Paris and was involved in many duels, and in quarrels with the comedian Montfleury, with Scarron and others. He entered the household of the duc d’Arpajon as secretary in 1653. In the next year he was injured by the fall of a piece of timber, as he entered his patron’s house. Arpajon, perhaps alarmed by his reputation as a free-thinker, desired him to leave, and he found refuge with friends in Paris. During the illness which followed his accident, he is said to have been reconciled with the Church, and he died in September 1655.
M. Edmond Rostand’s romantic play of Cyrano de Bergerac (1897) revived interest in the author of the Histoires comiques. A modern edition of his Œuvres (2 vols.), by P. L. Jacob (Paul Lacroix), appeared in 1858, with the preface by H. Lebret originally prefixed to the Histoire comique des états de la lune (1656?). For an interesting analysis of the romances see Garnet Smith in the Cornhill for July 1898. See also P.A. Brun, Savinien de Cyrano Bergerac (1894). Other studies of Cyrano are those of Charles Nodier (1841), F. Merilhon (Périgueux, 1856), Fourgeaud-Lagrèze (in Le Périgord littéraire, 1875) and of Théophile Gautier, in his Grotesques.
CYRENAICA, in ancient geography, a district of the N. African coast, lying between the Syrtis Major and Marmarica, the western limit being Arae Philaenorum, and the eastern a vague line drawn inland from the head of the gulf of Platea (Bomba). On the south the limit was undefined, but understood to be the margin of the desert, some distance north of the oasis of Augila (Aujila). The northern half of this district, which alone was fertile, was known as Pentapolis from its possession of five considerable cities (1) Hesperides-Berenice (Bengazi), (2) Barca (Merj), (3) Cyrene (Ain Shahat-Grenna), (4) Apollonia (Marsa Susa), (5) Teucheira-Arsinoë (Tocra). In later times two more towns rose to importance, Ptolemais (Tolmeita) and Darnis-Zarine (Derna). These all lay on the coast, with the exception of Barca and Cyrene, which were situated on the highland now called Jebel Akhdar, a few miles inland. Cyrene was the first city to arise, being founded among Libyan barbarians by Aristotle of Thera (later called Battus) in the middle of the 7th century B.C. (see Cyrene). For about 500 years this district enjoyed great prosperity, owing partly to its natural products, but more to its trade with interior Africa.
Under the Ptolemies, the inland cities declined in comparison with the maritime ones, and the Cyrenaica began to feel the commercial competition of Egypt and Carthage, whence easier roads lead into the continent. After all N. Africa had passed to Rome, and Cyrenaica itself, bequeathed by Apion, the last Ptolemaic sovereign, was become (in combination with Crete) a Roman province (after 96 B.C.), this competition told more severely than ever, and the Greek colonists, grown weaker, found 703 themselves less able to hold their own against the Libyan population. A great revolt of the Jewish settlers in the time of Trajan settled the fate of Cyrene and Barca; the former is mentioned by Ammianus Marcellinus in the 4th century A.D. as “urbs deserta,” and Synesius, a native, describes it in the following century as a vast ruin at the mercy of the nomads. Long before this its most famous article of export, the silphium plant, a representation of which was the chief coin-type of Cyrene, had come to an end. This plant, credited with wonderful medicinal and aromatic properties, has not been certainly identified with any existing species. The similar Thapsia garganica (Arab. drias), which now grows freely in Cyrenaica, though it has medicinal properties, has not those ascribed to silphium. Henceforward till the Arab invasion (A.D. 641) Apollonia was the chief city, with Berenice and Ptolemais next in order. After the conquest by Amr ibn el-’Asi, inland Cyrenaica regained some importance, lying as it did on the direct route between Alexandria and Kairawan, and Barca became its chief place. But with the substitution of Ottoman for Arab empire, resulting in the virtual independence of both Egypt and Tripoli, the district lying between them relapsed to anarchy. This state of things continued even after Mahmud II. had resumed direct control over Tripoli (1835), and in the middle of the 19th century Cyrenaica was still so free of the Turks that Sheik Ali bin-Senussi chose it as the headquarters of his nascent dervish order. All over the district were built Senussi convents (zawia), which still exist and have much influence, although the headquarters of the order were withdrawn about the year 1855 to Jarabub, and in 1895 to Kufra, still farther into the heart of Africa. In 1875 the district, till then a sanjak of the vilayet of Tripoli, was made to depend directly on the Ministry of the Interior at Constantinople; and the Senussites soon ceased to be de facto rulers of Cyrenaica. Their preserves have now been still further encroached upon by a number of Cretan Moslem refugees (1901-1902). This is not the first effort made by Turkey to colonize Cyrenaica. In 1869 Ali Riza Pasha of Tripoli tried to induce settlers to go to Bomba and Tobruk; and in 1888 an abortive effort was made to introduce Kurds. To protect the Cretans the Ottoman government has extended the civil administration and created several small garrisoned posts. The district is accordingly safer for Europeans than it was; but these still find themselves ill received. The Ottoman officials discourage travel in the interior, partly from fear of the Senussites, partly from suspicions, excited by the lively interest manifested by Italy in Cyrenaica.
At the present day we understand by Cyrenaica a somewhat larger district than of old, and include ancient Marmarica up to the head of the gulf of Sollum (Catabathmus Magnus). The whole area is about 30,000 sq. m., and has some 250,000 inhabitants, inclusive of nomads. Projecting like a bastion into the Mediterranean at a very central point, Cyrenaica seems intended to play a commercial part; but it does not do so to any extent because of (1) lack of natural harbours, Bengazi and Derna having only open and dangerous roads (this is partly due to coastal subsidence; ancient ports have sunk); (2) the difficulty of the desert routes behind it, wells being singularly deficient in this part of the Sahara. The ivory and feather caravans from Wadai and Borku have latterly deserted it altogether. Consequently Cyrenaica is still in a very backward and barbarous state and largely given up to nomad Arabs. There are only two towns, Bengazi and Derna, and not half a dozen settlements beside, worthy to be called villages. In many districts the Senussi convents supply the only settled element, and the local Bedouins largely belong to the Order. There are no roads in the province, and very little internal communication and trade; but a wireless telegraphic system has been installed in communication with Rhodes: and there is a landline from Bengazi to Tripoli.
Geologically and structurally Cyrenaica is a mass of Miocene limestone tilted up steeply from the Mediterranean and falling inland by a gentle descent to sea-level again at the line of depression, which runs from the gulf of Sidra through Aujila to Siwa. This mass is divided into two blocks, the higher being the western Jebel Akhdar, on which Cyrene was built (about 1800 ft.): the lower, the eastern Jebel el-Akabah, the ancient Marmaric highlands (700 ft.). There is no continuous littoral plain, the longest strip running from the recess of the Syrtis round past Bengazi to Tolmeita. Thereafter, except for deltaic patches at Marsa Susa and Derna, the shore is all precipitous. Jebel Akhdar, being without “faults,” has no deep internal valleys, and presents the appearance of downs: but its seaward face is very deeply eroded, and deep circular sinkings (swallow-holes) are common. There is much forest on its northward slopes, and good red earth on the higher parts, which bears abundant crops of barley, much desired by European maltsters. Plenty of springs issue on the highlands, and wide expanses of grassy country dotted with trees like an English park are met with. Here the Bedouins (mostly Beni Hassa) pasture flocks and herds, amounting to several million head. The climate is temperate and the rainfall usually adequate, but one year in five is expected to be droughty. The southward slopes fall through ever-thinning pasture lands to sheer desert about 80 m. inland. Jebel el-Akabah is much more barren than Jebel Akhdar, and the desert comes right down to the sea in Marmarica, whose few inhabitants are more concerned with salt-collecting and sponge fishing than with agriculture. They have, however, the only good ports on the whole coast, Bomba and Tobruk. Much might be made of Cyrenaica by judicious colonization. All kinds of trees grow well, from the date palm to the oak; and there are over 200,000 wild olives in the country. The conditions in general are very like those of central Italy, and there is ample room for new settlers.
Bibliography.—(1) Ancient Cyrenaica: J. P. Thrige, Historia Cyrenes (1819); C. Ritter, Erdkunde, i. (1822); A. F. Gottschick, Gesch. der Grundung und Blute des hell. Staates in Kyrenaika (1858).
(2) Modern Cyrenaica: Paul Lucas, Voyage (1712); T. Shaw, Travels and Observations (1738); J. Bruce, Travels (1790); P. della Cella, Viaggio da Tripoli, &c. (1819); G. F. Lyon, Narrative of Travels (1821); A. Cervelli, in Recueil de voyages, pub. by Soc. de Géog., ii. (1825); J. R. Pacho, Relation d’un voyage (1827); F. W. Beechey, Proceedings of Expedition to explore N. Coast of Africa (1828); H. Barth, Wanderungen, &c. (1849); V. de Bourville, Rapport (1850); J. Hamilton, Wanderings in N. Africa (1856); R. M. Smith and E. A. Porcher, Hist. of Discoveries (1864); G. Rohlfs, Von Tripoli nach Alexandrien (1871); G. Haimann, La Cirenaica (1882); M. Camperio, Una Gita in Cirenaica (1881); H. Duveyrier, “La Confr. musulmane de Sidi Moh. Ben Ali es-Senousi” (Bull. soc. géog., 1884); H. W. Blundell in Geog. Journ. v. (1895) and Annual Brit. Sch. at Athens, ii. (1895); D. G. Hogarth in Monthly Review (Jan. 1904); G. Hildebrand, Cyrenaïka, &c. (1904); G. de Martino, Cirene e Cartagine (1908).
(3) Maps: The best are that by P. Carlo, to illustrate Camperio and Haimann’s Report, in Petermann’s Mitth. (1881); and Sheet No. 2 of Carte de l’Afrique (Service géog. de l’armée, 1892).
CYRENAICS, a Greek school of philosophy, so called from Cyrene, the birthplace of the founder, Aristippus (q.v.). It was one of the two earliest Socratic schools, and emphasized one side only of the Socratic teaching (cf. Cynics). Socrates, although he held that virtue was the only human good, admitted to a certain extent the importance of its utilitarian side, making happiness at least a subsidiary end of moral action (see Ethics). Aristippus and his followers seized upon this, and made it the prime factor in existence, denying to virtue any intrinsic value. Logic and physical science they held to be useless, for all knowledge is immediate sensation (see Protagoras). These sensations are motions (κινήσεις) which (1) are purely subjective, and (2) are painful, indifferent or pleasant, according as they are violent, tranquil or gentle. Further they are entirely individual, and can in no way be described as constituting absolute objective knowledge. Feeling, therefore, is the only possible criterion alike of knowledge and of conduct. “Our modes of being affected (πάθη) alone are knowable.” Thus Cyrenaicism goes beyond the critical scepticism of the Sophists and deduces a single, universal aim for all men, namely pleasure. Furthermore, all feeling is momentary and homogeneous. It follows (1) that past and future pleasure have no real existence for us, and (2) that among present pleasures there is no distinction of kind, but 704 only of intensity. Socrates had spoken of the higher pleasures of the intellect; the Cyrenaics denied the validity of this distinction and said that bodily pleasures as being more simple and more intense are to be preferred. Momentary pleasure (μονόχρονος ἡδόνη), preferably of a carnal kind, is the only good for man. Yet Aristippus was compelled to admit that some actions which give immediate pleasure entail more than their equivalent of pain. This fact was to him the basis of the conventional distinction of right and wrong, and in this sense he held that regard should be paid to law and custom. It is of the utmost importance that this development of Cyrenaic hedonism should be fully realized. To overlook the Cyrenaic recognition of social obligation and the hedonistic value of altruistic emotion is a very common expedient of those who are opposed to all hedonistic theories of life. Like many of the leading modern utilitarians, they combined with their psychological distrust of popular judgments of right and wrong, and their firm conviction that all such distinctions are based solely on law and convention, the equally unwavering principle that the wise man who would pursue pleasure logically must abstain from that which is usually denominated “wrong” or “unjust.” This idea, which occupies a prominent position in systems like those of Bentham, Volney, and even Paley, was evidently of prime importance at all events to the later Cyrenaics.
Developing from this is a new point of practical importance to the hedonism of the Cyrenaics. Aristippus, both in theory and in practice, insisted that true pleasure belongs only to him who is self-controlled and master of himself. The truly happy man must have φρόνησις (prudence), which alone can save him from falling a prey to mere passion. Thus, in the end, Aristippus, the founder of the purest hedonism in the history of thought, comes very near not only to the Cynics, but to the more cultured hedonism of Epicurus and modern thinkers. Theodorus, held even more strongly that passing pleasure may be a delusion, and that permanent tranquillity is a truer end of conduct. Hegesias denied the possibility of real pleasure and advocated suicide as ensuring at least the absence of pain. Anniceris, in whose thought the school reached its highest perfection, declared that true pleasure consists sometimes in self-sacrifice and that sympathy in enjoyment is a real source of happiness. Other members of the school were Arete, wife of Aristippus, Aristippus the younger (her son), Bio and Euhemerus.
The Cyrenaic ideal was, of course, utterly alien to Christianity, and, in general, subsequent thinkers found it an ideal of hopeless pessimism. Yet in modern times it has found expression in many ethical and literary works, and it is common also in other ancient non-Hellenic literature. There are quatrains in the Rubáiyát of Omar Khayyám and pessimistic verses in Ecclesiastes which might have been uttered by Aristippus. (“Then I commended mirth, because a man hath no better thing than to eat and to drink and to be merry; for that shall abide with him of his labour the days of his life which God giveth him under the sun”). So in Byron and Heine, and, in a sense, in Walter Pater (Marius the Epicurean), there is the same tendency to seek relief from the intellectual cul-de-sac in frankly aesthetic satisfaction. Thus Cyrenaicism did not entirely vanish with its absorption in Epicureanism.
See Hedonism, Epicurus; histories of philosophy by Zeller, Windelband, Ueberweg; H. Sidgwick, Methods of Ethics and Outlines of the History of Ethics; J. Watson, Hedonistic Theories (1895); James Seth, Ethical Principles, c. i. (A), (1898); A. Wendt, De philosophia Cyrenaica (1841); H. von Stein, De philosophia Cyrenaica (1855); T. Gomperz, Greek Thinkers (Eng. trans., vol. ii. bk. iv., ad fin., 1905); Beare, Greek Theories of Elementary Cognition; G. van Lyng, Om den Kyrenaiske skole (Christiania, 1868); and general ethical text-books.
CYRENE [mod. Ain Shahat-Grenna], the original capital of ancient Cyrenaica (q.v.) and one of the greatest of Greek colonies. The Theraean story of its foundation, as told by Herodotus, runs thus. Battus (whose true Greek name seems to have been Aristoteles), a native of Thera (Santorin), itself a Laconian colony, was bidden by the Delphic oracle, if he wished to put an end to domestic dissensions, to lead a portion of the citizens to Libya and build a city in a “place between waters.” (For other stories see Battus.) By this he understood an island, and therefore established his followers on the barren islet of Platea in the gulf of Bomba. The colony being unsuccessful made further application to the oracle and was bidden to transfer itself to the mainland. The Libyan barbarians reported that a fertile and well-watered district lay to the west and were induced to act as guides. They brought the Greeks through forests to high ground from various points of which issued springs, and Battus, recognizing “a place between waters,” began to build. This was in the middle of the 7th century B.C.
The result was Cyrene, so called (it was said) from a local nymph, who has been shown by Studniczka to have been a Nature goddess, like the Greek Artemis. The point first occupied was probably the hill above the “Apollo” fountain on the west; and there was erected the fortress-palace of the Battiadae, who continued to rule the colony for eight generations. The neighbouring Libyans were conciliated and given a position similar to that of Laconian perioeci, and intermarriage between them and Greeks became so frequent that the colony rapidly assumed a somewhat hybrid character, and while being one of the centres of Hellenic culture, showed barbarian characteristics of violence and luxury. Battus I. reigned c. 630 to 590 B.C. and was succeeded by his son Arcesilaus (c. 590-574) of whom nothing is known. The kings henceforth bore alternately the names Battus and Arcesilaus, of which the first is said to be simply the native Libyan word for “king”: the latter is, of course, Greek. This fact suggests that some compromise with the natives had been come to, resulting, perhaps, in an alternation of the supreme office. Under Battus II. (570 B.C.?) a fresh band of settlers was invited from Greece, and the colony tended to become henceforth more maritime and democratic. Its port, Apollonia (Marsa Susa), now rose to importance: and a second (winter) port was created at Naustathmos (Marsa Hilal) about 15 m. E. behind a sheltering cape. Fine roads were cut through the rock connecting these harbours with the capital. Trouble followed, however, with the Libyans, who saw themselves robbed in favour of the new settlers, and they called in Egyptian help; but the force sent by Apries was defeated near the spring Theste, and presently Amasis of Egypt made peace and took a Battiad princess to wife. Under Arcesilaus II. (c. 560-550) domestic dissensions and Libyan revolt led to the founding of a rival inland city, Barca, and a severe defeat and massacre. These misfortunes, coupled with the fact that Battus III. was thought to have disgraced the house by his lameness, prompted the Cyrenaeans to send to Delphi for more advice, and as a result Demonax of Mantinea arrived as arbitrator and framed a constitution limiting the monarchy and dividing the citizens tribally according to the date of their settlement and their place of origin. Further attempts of the Battiadae (e.g. of Pheretima, wife of Battus III., and Arcesilaus his son) to annul this constitution, and bitter family dissensions, brought about a Persian invasion and finally the extinction of the dynasty about 450 B.C. A republic of more or less Spartan type succeeded, but it was often interrupted by tyrannies; and having made submission by embassy to Alexander in 331, Cyrene passed under Ptolemaic domination ten years later. From this epoch dates a decline which was due to economic causes (see Cyrenaica) and to the Ptolemaic policy of favouring easily controlled harbour-towns rather than an inland place like Cyrene, whose ancient factions still continued to give trouble under the earlier Ptolemies. Apollonia and Berenice gradually superseded Cyrene and Barca respectively, being more in touch with Greece and less exposed to the hostile nomad Libyans, who increased in boldness and power: but Cyrene continued to be a great city after it had passed to Rome (96 B.C.), and up to the reign of Trajan, when a Jewish revolt and the repressive measures taken by the imperial government dealt it an irreparable blow. Ere Christianity became the religion of the empire, it was largely a ruin, and henceforward to the epoch of Arab conquest (A.D. 641) its Greek life gradually deserted it for Apollonia. At its 705 acme Cyrene is said to have had over 100,000 inhabitants. It was noted among the ancients for its intellectual life. Its medical school was famous, and it numbered among its celebrities Callimachus the poet, Carneades, the founder of the New Academy at Athens, Aristippus, a pupil of Socrates and the founder of the so-called Cyrenaics (q.v.), Eratosthenes the polyhistor, and Synesius, one of the most elegant of the ancient Christian writers.
The first account of the site in modern times seems to be that of M. le Maire, who was French consul at Tripoli from 1703 to 1708, and twice visited Cyrene. Paul Lucas was there in 1710, and again in 1723, and Dr Thomas Shaw in 1738; an Italian, Dr A. Cervelli, who was there in 1812, furnished some information to the Société de Géographie of Paris; and P. Della Cella published an account of his visit, made in 1817. In 1821-1822 important explorations were made by Lieutenant F. W. Beechey, R.N.; and he was almost immediately followed by a French artist, M. J. R. Pacho, whose pencil preserved a number of interesting monuments that have since disappeared. L. Delaporte, French consul at Tangier, and Vattier de Bourville come next in order of time. H. Barth, the famous African traveller, published an account of his investigations in his Wanderungen durch die Küstenländer des Mittelmeers, 1849, and James Hamilton, who was there in 1851, described the place in his Wanderings in N. Africa. In 1861 excavations were made on behalf of the British Museum by Lieuts. R. Murdoch Smith, R.E., and E. A. Porcher, R.N., the results of which are detailed in their valuable Discoveries in Cyrene (London, 1864). Since that date, owing to the increase of Senussi influence, and the consequent fears of the Ottoman authorities, the site has been very seldom visited. The Italians, M. Camperio and G. Haimann, leading commercial missions, were there in the eighties, and Mr H. W. Blundell succeeded with a special firman and a strong escort in reaching the place in 1895, but had trouble with the local Senussi Arabs. The prohibition of travel became thereafter more stringent, and it has only been overcome by a party from Mr A. V. Armour’s yacht “Utowana,” which marched up from Marsa Susa in April 1904, and stayed one night. They found some fifty families of Cretan refugees established at Ain Shahat and a mudir with a small guard on the spot: but no inhabited houses, except the Senussi convent and the mudiria. Cretans and Arabs live in the ancient rock-tombs. An Italian senator, Chev. G. de Martino, with two Italian residents at Derna, passed through the place in 1907, and found it in Bedouin hands.
The site lies on the crest of the highland of Jebel Akhdar (about 1800 ft.) and 10 m. from the sea. The ground slopes very gradually south, and being entirely denuded of trees, makes good corn land. The northward slope falls more steeply in a succession of shelves, covered here and there with forest. Ravines surround the site on three sides, and there are at least four springs in its area, of which one, having great volume, has been at all times the attraction and focus of the place. This is the so-called “Fount of Apollo,” which issues from a tunnel artificially enlarged, and once faced with a portico. The acropolis was immediately above this on the W., and the main entrance of the city, through which came the sacred processions, passed it. The remains of Cyrene itself are enclosed by a wall having a circuit of about 4 m., of which little remains but the foundations and fragments of two towers; but tombs and isolated structures extend far outside this area. The local Arabs say it takes them six camel-hours to go from one end to the other of the ruins, which they call generally “Grenna” (i.e. Kyrenna). Within the city itself not very much is now to be seen. Below the Apollo fountain on the N. lie a great theatre and the substructures of the main temple of Apollo, both included now in the Senussi convent garden. Above the fountain and by the main road is a smaller theatre. On the E., upon the crown of the plateau, are the sites on which Smith and Porcher placed temples of Bacchus, Venus and Augustus, but they are marked only by rubbish heaps. Remains of a large Byzantine church and a much ruined stadium lie to S.E. On the S. are immense covered tanks of Roman date, with remains of the aqueducts which supplied them. On the W. a fine fragment of a tower, the fortifications of the acropolis, and a pedestal sculptured on four sides in good 3rd century style, are the only things worth seeing. The Cretan occupation is fast obliterating other traces. The great spectacle, however, which distinguishes the site of Cyrene, is provided by its cemeteries, which for extent, variety and preservation are unparalleled in the classic lands. There is one along each of the approaches to the main gates, but the largest and most splendid lies by the Apollonian road which winds by easy curves up the northern buttresses of the plateau. Here the sepulchres rise in tiers one above the other along fully a mile of the way. The most important have pillared façades, Doric, Ionic, and even a hybrid mixture of both orders. Within, they open out either into large halls, leading one out of another with graves in recesses and pits in the floor; or into rock corridors lined with loculi, disposed one above another like pigeon holes. Most of the wall paintings, seen by Beechey and Pacho, have perished or become black with the smoke of troglodytes’ fires; but one tomb below the road at about the middle of the cemetery still retains its decoration comparatively fresh, and seems to be that specially described by Smith and Porcher. The scenes are agonistic, i.e. represent funeral games, in which both white and black persons take part, the latter doubtless Libyan perioeci: but all wear Greek garments. Several tombs are inscribed and on some external paintings are still faintly visible. The commonest type of grave is a simple pit covered by a gabled lid. These occur by hundreds. But not all the sepulchres are rock-cut: altar tombs and other forms of heroa are found built upon plinths of rock. All visible tombs have long ago been violated, but it is probable that there are others still virgin under the talus of the hill side. To discover these and determine the topography of the city, excavation is urgently needed.
Many historical and artistic questions concerning Cyrene remain unsettled, but since the discoveries made in Laconia in 1908, the much disputed “Cyrenaic ware” has been ascribed to Sparta. A good deal of Cyrenaic sculpture, all of comparatively late date, was sent to the British Museum by Smith and Porcher. Nothing has yet been found on the site belonging to the great age of the city’s independence, the fine vases sent to the British Museum in 1864, by Mr G. Dennis, having been discovered not there, but near Berenice (Bengazi). The latter site, with Ptolemais and Apollonia, has supplied most of the antiquities found latterly in Cyrenaica.
See authorities for Cyrenaica, and F. Studniczka, Kyrene, eine alt-griechische Göttin (1890).
CYRIL (c. 315-386), bishop of Jerusalem, where he was probably born, was ordained a presbyter in 345, and had the instruction of the catechumens entrusted to him. In 350 he was elevated to the see of Jerusalem, and became deeply involved in the dogmatic controversies of his time. His metropolitan, Acacius of Caesarea, inclined to Arianism, while Cyril strongly espoused the Nicene creed and was, in consequence, deposed for a time. On the death of the emperor Constantine he was restored; but on the accession of Valens, an Arian emperor, he had once more to resign his post till the accession of Theodosius permitted him to return finally in peace in 379. He attended the second oecumenical council held at Constantinople in 381, where he was received with grateful acclamations for his sufferings in defence of orthodoxy. Cyril was even more conspicuous as a pastor than as a controversialist, and this is seen in his one important work—his twenty-three addresses to catechumens delivered in A.D. 348. The first eighteen of these were meant for candidates for baptism; they deal with general topics like repentance and faith, and then expound in detail the baptismal creed of the Jerusalem church. The remaining five addresses were spoken to the newly-baptized in Easter week and explain the mysteries and ritual of baptism, confirmation and the Eucharist. These lectures are said to be “the first example of a popular compend of religion,” and are particularly interesting for the insight which they give us both into the creed-forms of the early church and the various ceremonies of initiation constituting baptism in the 4th century. The evidence which Cyril supplies as to the 706 Jerusalem use is supplemented by the S. Silviae peregrinatio, dating from about a generation later. Other tracts and homilies have been ascribed to Cyril of Jerusalem, but they are of doubtful genuineness.
Editions.—A. A. Touttée (Paris, 1720); W. C. Reischl and J. Rupp (Munich, 1848-1860); Migne, Patrol. Graeca. xxxiii. Translation: Catecheses (“Oxford Library of Fathers,” vol. ii.). See Herzog-Hauck, Realencyk. (Förster); Delacroix, St C. de Jérus., sa vie et ses œuvres (Paris, 1865).
CYRIL (376-444), bishop of Alexandria, a more distinguished father of the church than his namesake of Jerusalem, was born in 376, and died in 444. Becoming patriarch of Alexandria about 412, he soon made himself known by the violence of his zeal against Jews, pagans and heretics or supposed heretics alike. He had hardly entered upon his office when he closed all the churches of the Novatians and seized their ecclesiastical effects. He assailed the Jewish synagogues with an armed force, drove the Jews in thousands from the city, and exposed their houses and property to pillage. The prefect of Egypt, Orestes, who endeavoured to withstand his furious zeal, was in turn denounced himself, and had difficulty in maintaining his ground against the fury of the Christian multitude. It was during one of the violent commotions kindled by the strifes of these parties in Alexandria that the illustrious Hypatia, famed for her beauty and her eloquent advocacy of the Neo-Platonic philosophy in opposition to Christianity, was murdered. Her murder has been attributed to the direct instigation of the patriarch himself; but this charge is held to be baseless by others, although there can be no doubt that “the perpetrators were officers of his church,” and undoubtedly drew encouragement from his own violent proceedings. Hypatia was a friend of Orestes, and the hostility that existed betwixt the prefect and the patriarch overflowed towards her, and undoubtedly led to her destruction.
But Cyril’s violence was not merely confined to those who might be considered enemies of the church. He inherited from Theophilus, his uncle and predecessor in the see of Alexandria, a strong aversion to John Chrysostom, the noble bishop of Constantinople, and even after his death opposed for a time all attempts to remove the unjust sentence of condemnation which had been passed upon him. Afterwards he so far yielded to remonstrances as to allow the name of Chrysostom to appear in the list of distinguished martyrs and bishops mentioned in the prayers of his church. These names were inserted in what were called “diptychs” (δίπτυχα νεκρῶν), or two-leaved tablets preserved in the churches—a usage which the Greek Church has continued to this day.
Cyril thus represents—though he differs largely from his predecessors—the tendencies dominant at Alexandria in the 5th century, and their antagonism to the Antiochene school. The story of his opposition to Nestorius at the council of Ephesus in 431 is told elsewhere (see Nestorius). He himself incurred the charge of heresy from the oriental bishops. Satisfied, however, with the deprivation and exile of his opponent, he returned to Alexandria in triumph as the great champion of the faith, and thence continued, by the “unscrupulous use of all the means at his command,” the theological strife for years. He was a bitter opponent of the great Antiochene expositor and apologist Theodoret.
Altogether Cyril presents a character not only unamiable, but singularly deficient in the graces of the Christian life. His style of writing is as objectionable as his character and spirit. Yet he takes high rank as a dogmatic theologian, and those who seek precise and rigid definitions of orthodox belief conjoined with tenacity of conviction find him indispensable. In addition to his Twelve Anathematisms and the defence of the same, he wrote five other books against Nestorius, Thesaurus—a treatise in dialogue form on the Trinity, a book On the Right Way and another On the Incarnation. In other fields—mystical, exegetical and apologetical—he was equally prolific and forceful. He wrote a tract “On worshipping in spirit and in truth” to defend a spiritual interpretation of the Mosaic law, several commentaries, festival-orations, and a reply to the emperor Julian’s attack on the church. His letters are valuable sources to the student of the Nestorian controversy.
Literature.—The collected edition of J. Aubert (Paris, 1638) formed the basis of Migne’s reprint in vols. 68-77 of the Patr. Graec. Many of the writings have been edited separately (see bibliography in Herzog-Hauck). For an account of his career and position in the history of dogma, see A. Harnack, vols. iii. and iv. passim; O. Bardenhewer’s Patrologie (Freiburg, 1894), pp. 335-343; R. L. Ottley’s Doctrine of the Incarnation, ii. 80 ff.; A. Largent’s Études d’hist. ecclés.; St Cyrille d’Alexandrie et le concile d’Éphèse (Paris, 1892). See also Charles Kingsley’s romance Hypatia.
CYRIL (827-869), apostle of the Slavs, amongst whom he worked in conjunction with his elder brother Methodius (q.v.). Tradition says that while in the Khazar country (where he combated Jewish and Mahommedan influence) he found at Kherson the remains of Clement of Rome, which he bore with him wherever he went, finally depositing them at Rome in 867. His name is associated with the invention of the modified (Cyrillic) form of the Greek alphabet, which largely superseded the ancient Slavonic characters.
CYRILLIC, the alphabet used by the Orthodox Slavs. It is modelled on the Greek Liturgical Uncial of the 9th century, and its invention is traditionally, though in all probability wrongly, ascribed to the Greek missionary Cyril (d. 869). For an account of its origin and development, with a table of its letters, see Slavs.
CYRILLUS, Greek jurist of the 5th century, was professor in the ancient law college of Berytus, and one of the founders of the oecumenical school of jurists (τῆς οἰκουμένης διδάσκαλοι) which preceded the succession of Anastasius to the Eastern empire (A.D. 491), and paved the way for Justinian’s legislation. His reputation as a teacher of law was very great; and from the fragments of his works which have been preserved it may be inferred that his merit as a teacher consisted in his going direct to the ancient sources of law, and in interpreting the best writers, such as the commentary of Ulpian on the edict and the Responsa Papiniani. He wrote a treatise on definitions (ὑπόμνημα τῶν δεφινίτων), in which, according to a statement of his contemporary Patricius, the subject of contracts was treated with superior precision and great method, and which has supplied the materials for many important scholia appended to the first and second titles of the eleventh book of the Basilica. He is generally styled “the great,” to distinguish him from a more modern jurist of the same name, who lived after the reign of Justinian, and who compiled an epitome of the Digest.
CYRTO-STYLE (Gr. κυρτός, convex, and στῦλος, column), in architecture, a circular projecting portico with columns; like those of the transept entrances of St Paul’s cathedral and the western entrance of St Mary-le-Strand, London.
CYRUS (Gr. Κῦρος; Pers. Kuru-sh; Babyl. Kurash; Hebr. Kōresh), the Latinized form of a Persian name borne by two prominent members of the Achaemenid house.
1. Cyrus the Great, the founder of the Persian empire, was the son of Cambyses I. His family belonged to the clan of the Achaemenidae—in the inscription on the pillars and columns of the palace of Pasargadae (Murghab) he says: “I am Cyrus the king, the Achaemenid”—the principal clan (φρήτρη) of the Persian tribe of the Pasargadae (q.v.). But in his proclamation to the Babylonians (V.R. 35; Sir H. Rawlinson, Journal of the R. Asiat. Soc., n.s., xii., 1880; Schrader, Keilinschriftliche Bibliothek, iii. 2, 120 ff.; Hagen, in Delitzsch and Haupt, Beiträge zur Assyriologie, ii., 1894, where the chronicle of Nabonidus is also published anew with a much improved translation) he calls his ancestors, Teispes, Cyrus I. and Cambyses I., “kings of Anshan,” and the same title is given to him in the inscriptions and in the chronicle of Nabonidus of Babylon before his victory over Astyages. Anshan is a district of Elam or Susiana, the exact position of which is still subject to much discussion. As we know from Jeremiah xlix. 34 ff. (cf. Ezekiel xxxii. 24 ff.) that the Elamites suffered a heavy defeat in 596 B.C., it is very probable that the Pasargadian dynast Teispes conquered Anshan in this year. Modern authors have often supposed that Cyrus and his ancestors were in reality Elamites; but this 707 is contrary to all tradition, and there can be no doubt that Cyrus was a genuine Persian and a true believer in the Zoroastrian religion. In Herodotus vii. 11 the genealogy of Cyrus is given in exactly the same way as in the proclamation of Cyrus himself; Teispes is called here the son of the eponym Achaemenes.
The Pasargadian kings of Anshan were vassals of the Median empire. Their kingdom cannot have been of large extent, as Nabonidus in a contemporary inscription (Cylinder from Abu Habba, VR. 64, Schrader, Keilinschriftl. Bibliothek, iii. 2, 96), where he mentions his rebellion against Astyages, calls Cyrus “king of Anshan, his (i.e. Astyages’) small servant (vassal).” From this inscription we learn that the rebellion of Cyrus (who seems to have become king in 558 B.C., as Herod. i. 214 gives him a reign of 29 years) began in 553 B.C., and from the annals that in 550 Astyages marched against Cyrus, but was defeated; his troops revolted against him, he was taken prisoner, and Cyrus occupied and plundered Ecbatana. The relation of Ctesias (preserved by Nic. Dam. fr. 66; Anaximenes of Lampsacus in Steph. Byz. s.v. Πασαργάδαι, Strabo xv. p. 729; Polyaen. vii. 6. 1, 9, 45. 2) that Cyrus was three times beaten by Astyages and that the decisive battle took place in the mountains of Pasargadae, is certainly in the main historical although Herodotus (i. 127 ff.) only mentions the treason of the Median general Harpagus and the defeat and captivity of Astyages. In the rebellion the Persian tribes of the Maraphians and Maspians joined the Pasargadae (Herod. i. 125), while the other tribes appear not to have acknowledged Cyrus till after his victory (see Persis). From then he calls himself “king of the Persians.”
The history of Cyrus very soon became involved and quite overgrown with legends. Herodotus (i. 95) tells us that he knew four different traditions about him. One makes him the son of Mandane, a daughter of Astyages (originally evidently by a god), who is exposed in the mountains by his grandfather on account of an oracle, but suckled by a dog (a sacred animal of the Iranians) and educated by a shepherd; i.e. the myth which we know from the stories of Oedipus, Perseus, Telephus, Pelias and Neleus, Romulus, Sargon of Agade, Moses, the Indian hero Krishna, and many others, has been transferred to the founder of the Persian empire. At the same time, the rule of Cyrus and the Persians is legitimated by his family connexion with Astyages. This account is partly preserved in Justin i. 4. 10 (probably from Charon of Lampsacus) and in Aelian, Var. Hist. xiv. 42, and alluded to by Herodotus i. 95 and 122. The second account, which Herodotus follows, is a rationalized version of the first, where the dog is changed into a woman (the wife of the shepherd) named Spako (bitch). In the later part of his story Herodotus is dependent on the family traditions of Harpagus, whose treason is justified by the cruelty with which Astyages had treated him (the story of Atreus and Thyestes is transferred to them). Harpagus afterwards stood in high favour with Cyrus, and commanded the army which subdued the coasts of Asia Minor; his family seems to have been settled in Lycia. In a third version, preserved from Ctesias in Nicolaus Damasc. p. 66 (cf. Dinon ap. Athen. xiv. 633 C), Cyrus is the son of a poor Mardian bandit Atradates (the Mardians are a nomadic Persian tribe, Herod. i. 125), who comes as a voluntary slave to the court of Astyages, and finds favour with the king. A Chaldaean sage prophesies to him his future greatness, and another Persian slave, Oebares, becomes his associate. He flies to Persia, evades the pursuers whom Astyages sends after him, and begins the rebellion. After the victory Oebares kills Astyages against the will of Cyrus, and afterwards kills himself to evade the wrath of Cyrus. Parts of this story are preserved also in Strabo xv. p. 729, and Justin i. 6. 1-3; 7. 1; cf. Ctesias ap. Photium 2-7; many traces of it were afterwards transferred to the story of Ardashir I. (q.v.), the founder of the Sassanid empire. With this version Ctesias and Nicolaus have connected another, in which Cyrus is the son of a Persian shepherd who lives at Pasargadae, and fights the decisive battle at this place. The didactic novel of Xenophon, the Cyropaedia, is a free invention adapted to the purposes of the author, based upon the account of Herodotus and occasionally influenced by Ctesias, without any independent traditional element. The account of Aeschylus, Pers. 765 ff., is a mixture of Greek traditions with a few oriental elements; here the first king is Medos (the Median empire); his nameless son is succeeded by Cyrus, a blessed ruler, beloved by the gods, who gave peace to all his friends and conquered Lydia, Phrygia, Ionia. Then comes his nameless son, then Mardos (i.e. Smerdis, to whom the name of the Mardians is transferred) who is killed by Artaphrenes (i.e. Artaphernes, Herod. iii. 78, one of the associates of Darius), then Maraphis (eponym of the Maraphian tribe), then another Artaphrenes, then Darius.
The principal events of the later history of Cyrus are in the main correctly stated by Herodotus, although his account contains many legendary traditions. The short excerpt from Ctesias, which Photius has preserved, contains useful information, although we must always mistrust him. Of great value are a short notice in the fragments of Berossus and another in the Old Testament. The original sources are very scanty, besides the cylinder containing his proclamation to the Babylonians we possess only a great many dated private documents from Babylon. These serve to fix the chronology, which is here as everywhere quite in accordance with the dates of the canon of Ptolemy.
Soon after the conquest of the Median empire, Cyrus was attacked by a coalition of the other powers of the East, Babylon, Egypt and Lydia, joined by Sparta, the greatest military power of Greece. In the spring of 546 Croesus of Lydia began the attack and advanced into Cappadocia, while the other powers were still gathering their troops. But Cyrus anticipated them; he defeated Croesus and followed him to his capital. In the autumn of 546 Sardis was taken and the Lydian kingdom became a province of the Persians. The famous story of Herodotus, that the conqueror condemned Croesus to the stake, from which he was saved by the intervention of the gods, is quite inconsistent with the Persian religion (see Croesus).
During the next years the Persian army under Harpagus suppressed a rebellion of the Lydians under Pactyas, and subjugated the Ionian cities, the Carians and the Lycians (when the town Xanthus resisted to the utmost). The king of Cilicia (Syennesis) voluntarily acknowledged the Persian supremacy. Why the war with Babylon, which had become inevitable, was delayed until 539, we do not know. Here too Cyrus in a single campaign destroyed a mighty state. The army of Nabonidus was defeated; Babylon itself attempted no resistance, but surrendered on the 16th Tishri (10th of October) 539, to the Persian general Gobryas (Gaubaruva, see the chronicle of the reign of Nabonidus; the name Gobryas is preserved also by Xenophon, Cyrop. vii. 4. 24); it is possible that the Chaldaean priests, who were hostile to Nabonidus, betrayed the town. In a proclamation issued after his victory Cyrus guarantees life and property to all the inhabitants and designates himself as the favourite of Marduk, the great local god (Bel, Bel-Merodak) of Babel. It is very odd that modern authors have considered this proclamation as inconsistent with the Zoroastrian creed.
From the beginning of 538 Cyrus dates his years as “king of Babylon and king of the countries” (i.e. of the world). With the capital, the Babylonian provinces in Syria fell to the Persians; in 538 Cyrus granted to the Jews, whom Nebuchadrezzar had transported to Babylonia, the return to Palestine and the rebuilding of Jerusalem and its temple (see Jews, § 19). It is probable that Cyrus had fought more than one war against the peoples of eastern Iran; according to Ctesias he had, before the war with Croesus, defeated the Bactrians and the Sacae (in Ferghana; their king Amorges is the eponym of the Amyrgian Sacae, Herod. vii. 64, called by Darius Haumavarkā); and the historians of Alexander mention a march through Gedrosia, where he lost his whole army but seven men (Arrian vi. 24. 2; Strabo xv. 722), a tribe Ariaspae on the Etymandros (in Sijistan), who, on account of the support which they gave him against the Scythians, were called Euergetae (Arrian iii. 27. 4; Diod. xvii. 81; Curt. vii. 3. 1), and a town Cyropolis, founded by him 708 on the Jaxartes (Arrian iv. 2. 3; Curt. vii. 6. 16; Strabo xi. 517, called Cyreskhata by Ptolem. vi. 12. 5). In 530, having appointed his son Cambyses king of Babel, he set out for a new expedition against the East. In this war he was killed (Herod.) or mortally wounded (Ctesias). According to Herodotus he attacked the Massagetae beyond the Jaxartes; according to Ctesias, the Derbices, a very barbarous tribe (cf. Strabo xi. 520; Aelian, Var. Hist. iv. 1) on the border of the Caspian, near the Hyrcanians (Strabo xi. 514; Steph. Byz.; Curt. vii. 2. 7; Dion. Perieg. 734 ff.; Pomp. Mela iii. 5), or on the Oxus (Plin. vi. 48; Ptolem. vi. 10. 2; Tab. Peuting.). Berossus (ap. Euseb. Chron. i. 29) simply says that he fell against the Dahae, i.e. the nomads of the Turanian desert. His death occurred in 528 B.C., as we have a Babylonian tablet from the Adar of the tenth year of Cyrus, i.e. February 528; for in Babylon the first year of Cyrus began in the spring of 538.
In his native district Cyrus had built a city with a palace, called after his tribe Pasargadae (now Murghab), and here he was buried (see Pasargadae). In a short time he, the petty prince of an almost unknown tribe, had founded a mighty empire, which extended from the Indus and Jaxartes to the Aegaean and the borders of Egypt. This result shows that Cyrus must have been a great warrior and statesman. Nor is his character without nobility. He excels in the humanity with which he treated the vanquished. He destroyed no town nor did he put the captive kings to death; in Babylonia he behaved like a constitutional monarch; by the Persians his memory was cherished as “the father of the people” (Herod. iii. 89), and the Greek tradition preserved by Aeschylus (cf. above) shows that his greatness was acknowledged also by his enemies. He therefore deserves the homage which Xenophon paid to him in choosing him as hero for his didactic novel.
2. Cyrus the Younger, son of Darius II. and Parysatis, was born after the accession of his father in 424. When, after the victories of Alcibiades, Darius II. decided to continue the war against Athens and give strong support to the Spartans, he sent in 408 the young prince into Asia Minor, as satrap of Lydia and Phrygia Major with Cappadocia, and commander of the Persian troops, “which gather into the field of Castolos” (Xen. Hell. i. 4. 3; Anab. i. 9. 7), i.e. of the army of the district of Asia Minor. He gave strenuous support to the Spartans; evidently he had already then formed the design, in which he was supported by his mother, of gaining the throne for himself after the death of his father; he pretended to have stronger claims to it than his elder brother Artaxerxes, who was not born in the purple. For this plan he hoped to gain the assistance of Sparta. In the Spartan general Lysander he found a man who was willing to help him, as Lysander himself hoped to become absolute ruler of Greece by the aid of the Persian prince. So Cyrus put all his means at the disposal of Lysander in the Peloponnesian War, but denied them to his successor Callicratidas; by exerting his influence in Sparta, he brought it about that after the battle of Arginusae Lysander was sent out a second time as the real commander (though under a nominal chief) of the Spartan fleet in 405 (Xen. Hell. ii. 1. 14). At the same time Darius fell ill and called his son to his deathbed; Cyrus handed over all his treasures to Lysander and went to Susa. After the accession of Artaxerxes II. in 404, Tissaphernes denounced the plans of Cyrus against his brother (cf. Plut. Artax. 3); but by the intercession of Parysatis he was pardoned and sent back to his satrapy. Meanwhile Lysander had gained the battle of Aegospotami and Sparta was supreme in the Greek world. Cyrus managed very cleverly to gather a large army by beginning a quarrel with Tissaphernes, satrap of Caria, about the Ionian towns; he also pretended to prepare an expedition against the Pisidians, a mountainous tribe in the Taurus, which was never obedient to the Empire. Although the dominant position of Lysander had been broken in 403 by King Pausanias, the Spartan government gave him all the support which was possible without going into open war against the king; it caused a partisan of Lysander, Clearchus, condemned to death on account of atrocious crimes which he had committed as governor of Byzantium, to gather an army of mercenaries on the Thracian Chersonesus, and in Thessaly Menon of Pharsalus, head of a party which was connected with Sparta, collected another army.
In the spring of 401 Cyrus united all his forces and advanced from Sardis, without announcing the object of his expedition. By dexterous management and large promises he overcame the scruples of the Greek troops against the length and danger of the war; a Spartan fleet of thirty-five triremes sent to Cilicia opened the passes of the Amanus into Syria and conveyed to him a Spartan detachment of 700 men under Cheirisophus. The king had only been warned at the last moment by Tissaphernes and gathered an army in all haste; Cyrus advanced into Babylonia, before he met with an enemy. Here ensued, in October 401, the battle of Cunaxa. Cyrus had 10,400 Greek hoplites and 2500 peltasts, and besides an Asiatic army under the command of Ariaeus, for which Xenophon gives the absurd number of 100,000 men; the army of Artaxerxes he puts down at 900,000. These numbers only show that he, although an eyewitness, has no idea of large numbers; in reality the army of Cyrus may at the very utmost have consisted of 30,000, that of Artaxerxes of 40,000 men. Cyrus saw that the decision depended on the fate of the king; he therefore wanted Clearchus, the commander of the Greeks, to take the centre against Artaxerxes. But Clearchus, a tactician of the old school, disobeyed. The left wing of the Persians under Tissaphernes avoided a serious conflict with the Greeks; Cyrus in the centre threw himself upon Artaxerxes, but was slain in a desperate struggle. Afterwards Artaxerxes pretended to have killed the rebel himself, with the result that Parysatis took cruel vengeance upon the slayer of her favourite son. The Persian troops dared not attack the Greeks, but decoyed them into the interior, beyond the Tigris, and tried to annihilate them by treachery. But after their commanders had been taken prisoners the Greeks forced their way to the Black Sea. By this achievement they had demonstrated the internal weakness of the Persian empire and the absolute superiority of the Greek arms.
The history of Cyrus and of the retreat of the Greeks is told by Xenophon in his Anabasis (where he tries to veil the actual participation of the Spartans). Another account, probably from Sophaenetus of Stymphalus, was used by Ephorus, and is preserved in Diodor. xiv. 19 ff. Further information is contained in the excerpts from Ctesias by Photius; cf. also Plutarch’s life of Artaxerxes. The character of Cyrus is highly praised by the ancients, especially by Xenophon (cf. also his Oeconomics, c. iv.); and certainly he was much superior to his weak brother in energy and as a general and statesman. If he had ascended the throne he might have regenerated the empire for a while, whereas it utterly decayed under the rule of Artaxerxes II. (See also Persia: Ancient History.)
CYSTOFLAGELLATA (so named by E. Haeckel), a group of Mastigophorous Protozoa, distinguished from Flagellata by their large size (0.15-1.5 mm.), and their branched endoplasm, recalling that of Trachelius among Infusoria, within a firm ectosarc bounded by a strong cuticle. Nutrition is holozoic, a deep groove leading down to a mouth and pharynx. A long fine flagellum arises from the pharynx in Noctiluca (E. Suriray) Leptodiscus and (R. Hertwig); and in the former genus, a second flagellum, thick, long and transversely striated, rises farther out, in the groove; this was likened by E. R. Lankester to a proboscis, whence his name of Rhynchoflagellata, which we discard as unnecessary and posterior to Haeckel’s. Noctiluca has thus the form of an apple with a long stalk. Leptodiscus (R. Hertwig) has the form of a medusa without a proboscis—it is menisciform with the thin contractile margin produced inwards like a velum on the concave side, while the mouth is on the convex surface and the single flagellum springs from a blind tube on the same surface. Craspedotella (C. A. Kofoid), the third genus, is still more medusiform, with a broad velum, and the mouth in a convex central protrusion of the roof of the bell; and a thick flagellum springs from a blind tube on the convex surface. All three genera are pelagic and phosphorescent, this property being seated in the ectoplasm; Noctiluca miliaris is indeed the chief source of the phosphorescence of our summer seas. O. Bütschli, like other writers, regards the Cystoflagellates as closely allied to the Dinoflagellates, the small flagellum 709 corresponding to the longitudinal, the large flagellum to the transverse flagellum of that group.
 | |
| After E. Ray Lankester, Ency. Brit., 9th ed. | |
| Cystoflagellate Protozoa. | |
|
1 and 2, Young stages of Noctiluca miliaris. a, the big flagellum; the unlettered filament becomes the oral flagellum of the adult. n, nucleus. s, the so-called spine (superficial ridge of the adult). 3 and 4, Two stages in the fission of Noctiluca miliaris, Suriray. n, nucleus. N, food-particles. t, muscular flagellum. 5. Noctiluca miliaris, viewed from the aboral side (after Allman, Quart. Jour. Mic. Sci., 1872). a, entrance to atrium or flagellar fossa (= longitudinal groove of Dinoflagellata). c, superficial ridge. d, big flagellum (= flagellum of transverse groove of Dinoflagellata). h, nucleus. |
6. Noctiluca miliaris, acted upon by iodine solution, showing the protoplasm shrunk away from the structureless pellicle. a = entrance to atrium. 7. Lateral view of Noctiluca miliaris. a, entrance to atrium. b, atrium. c, superficial ridge. d, big flagellum. e = mouth and gullet, in which is seen Krohn’s oral flagellum (= the chief flagellum, or flagellum of the longitudinal groove of Dinoflagellata). f, broad process of protoplasm extending from the superficial ridge c to the central protoplasm. g, duplicature of pellicle in connexion with superficial ridge. h, nucleus. |
The reproduction of Noctiluca has been fairly made out; in the adult state it divides by fission down the oral groove; as a preliminary the external differentiations disappear, and the nucleus divides by modified mitosis; then the external organs are regenerated. Under circumstances not well made out, conjugation between two adults takes place by their fusion commencing at the oral region; flagella and pharynx disappear and the nuclei fuse, while the cytoplasts condense into a sphere. The nucleus undergoes broad division, the young nuclei pass to the surface, which becomes imperfectly divided by grooves into as many rounded prominences as there are nuclei (up to 128 or 256); and these become constricted off from the residual useless cytoplasm as zoospores with two unequal flagella, which were at first regarded as Dinoflagellates, of which they have the form (figs. 5, 6). The metamorphosis of these has not yet been observed.
Literature.—E. Suriray, Magazin de zoologie, 1836; G. J. Allman, Quarterly Journal of Microscopic Science, n.s. xii., 1872; L. Cienkowsky, “Zoospore formation in Noctiluca,” Archiv f. mikroskopische Anatomie, vii., 1871; R. Hertwig, “Leptodiscus,” Jenaische Zeitschrift, xi., 1877; C. Ischikawa, Journal of the College of Science (Tokyo, 1894), xii., 1899; F. Doflein, “Conjugation of Noctiluca,” Zoologische Jahrbücher, Anatomie, xiv., 1900; C. A. Kofoid, “Craspedotella,” in Bull. Mus. Comp. Zool. Harvard, xlvi., 1905; O. Bütschli, “Mastigophora,” in Protozoa (Braun’s Thierreich, vol. i., Protozoa) (1883-1887).
CYSTOLITH (Gr. κύστις, cavity, and λίθος, stone), a botanical term for the inorganic concretions, usually of calcium carbonate, formed in a cellulose matrix in special cells, generally in the leaf of plants of certain families, e.g. Ficus elastica, the india-rubber plant.
CYTHERA (mod. Cerigo, but still officially known as Cythera), one of the Ionian islands, situated not less than 150 m. from Zante, but only about 8 m. from Cape Malea on the southern coast of Greece. Its length from N. to S. is nearly 20 m., and its greatest breadth about 12; its area is 114 sq. m. The surface is rocky and broken, but streams abound, and there are various parts of considerable fertility. Two caves, of imposing dimensions, and adorned with stalactites of great beauty, are the most notable among its natural peculiarities; one is situated at the seaward end of the glen of the Mylopotamus, and the other, named Santa Sophia, about two hours’ ride from Capsali (Kapsali). Less of the ground is cultivated and more of it is in pasture land than in any other of the seven islands. Some wine and corn are produced, and the quality of the olive oil is good. The honey is still highly prized, as it was in remote antiquity; and a considerable quantity of cheese is manufactured from the milk of the goat. Salt, flax, cotton and currants are also mentioned among the produce. The people are industrious, and many of them seek employment as labourers in the Morea and Asia Minor. Owing to emigration, the population appears to be steadily diminishing, and is now only about 6000, or less than half what it was in 1857. Unfortunately the island has hardly a regular harbour on any part of the coast; from its situation at the meeting, as it were, of seas, the currents in the neighbourhood are strong, and storms are very frequent. The best anchorage is at San Nicolo, at the middle of the eastern side of the island. The principal village is Capsali, a place of about 1500 inhabitants, at the southern extremity, with a bishop, and several convents and churches; the lesser hamlets are Modari, Potamo and San Nicolo.
There are comparatively few traces of antiquity, and the identification of the ancient cities has been disputed. The capital, which bore the same name as the island, was at Paleo-Kastro, about 3 m. from the present port of Avlemona. In the church of St Kosmas are preserved some of the archaic Doric columns of the famous temple of Aphrodite of Cythera, whose worship had been introduced from Syria, and ultimately spread over Greece. According to the accepted story, it was here that the goddess first landed when she emerged from the sea. At a very early date Cythera was the seat of a Phoenician settlement, established in connexion with the purple fishery of the neighbouring coast; it is said that it was therefore called Porphyris (cf. Pliny iv. 18, 19). For a time dependent on Argos, it became afterwards an important possession of the Spartans, who annually despatched a governor named the Cytherodices. In the Peloponnesian war, Nicias occupied the island, but in 421 it was recovered by Sparta. Its modern history has been very much the same as that of the other Ionian islands; but it was subject to Venice for a much shorter period—from 1717 to 1797.
See the works referred to under Cephalonia, and also Weil, in Mittheil. d. deutsch. Inst. zu Athen (1880), pp. 224-243.
CYTISINE (Ulexin, Sophorin), C11H14N2O, an alkaloid discovered in 1818 by J. B. Chevreul in the seeds of laburnum (Cytisus Laburnum) and isolated by A. Husemann and W. Marmé in 1865 (Zeit. f. Chemie, 1865, i. p. 161). It is also found in the seeds of furze (Ulex europaeus), Sophora tormentosa, and Euchresta horsfieldii. It is extracted from the seeds by an 710 alcoholic solution of acetic acid, and forms large crystals which melt at 153° C., and are easily soluble in water, alcohol and chloroform. It is a secondary and tertiary di-acid base, and is strongly alkaline in its reaction. Hydrogen peroxide oxidizes it to oxycytisine, C11H14N2O2, chromic acid to an acid, C11H9NO3, and potassium permanganate to oxalic acid and ammonia. It acts as a violent poison.
See further, P. C. Plugge, Arch. der Pharm. (1891), 229, p. 48 et seq.; A. Partheil, Ber. (1890), 23, p. 3201, Arch. der Pharm. (1892), 230, p. 448; M. Freund and A. Friedmann, Ber. (1901), 34, p. 615; and J, Herzig and H. Meyer, Monats. f. Chem. (1897), 18, p. 379.
CYTOLOGY (from κύτος, a hollow vessel, and λόγος, science), the scientific study of the “cells” or living units of protoplasm (q.v.), of which plants and animals are composed. All the higher, and the great majority of the lower, plants and animals are composed of a vast number of these vital units or “cells.” In the case of many microscopic forms, however, the entire organism, plant or animal, consists throughout life of a single cell. Familiar examples of these “unicellular” forms are Bacteria and Diatoms among the plants, and Foraminifera and Infusoria among the animals. In all cases, however, whether the cell-unit lives freely as a unicellular organism or forms an integral part of a multicellular individual, it exhibits in itself all the phenomena characteristic of living things. Each cell assimilates food material, whether this is obtained by its own activity, as in the majority of the protozoa, or is brought, as it were, to its own door by the blood stream, as in the higher Metazoa, and builds this food material into its own substance, a process accompanied by respiration and excretion and resulting in growth. Each cell exhibits in greater or less degree “irritability,” or the power of responding to stimuli; and finally each cell, at some time in its life, is capable of reproduction. It is evident therefore that in the multicellular forms all the complex manifestations of life are but the outcome of the co-ordinated activities of the constituent cells. The latter are indeed, as Virchow has termed them, “vital units.” It is therefore in these vital units that the explanation of vital phenomena must be sought (see Physiology). As Verworn1 said, “It is to the cell that the study of every bodily function sooner or later drives us. In the muscle cell lies the problem of the heart beat and that of muscular contraction; in the gland cell reside the causes of secretion; in the epithelial cell, in the white blood corpuscle, lies the problem of the absorption of food, and the secrets of the mind are hidden in the ganglion cell.” So also the problems of development and inheritance have shown themselves to be cell problems, while the study of disease has produced a “cellular pathology.” The most important problems awaiting solution in biology are cell problems.
Historical.—The cell-theory ranks with the evolution theory in the far-reaching influence it has exerted on the growth of modern biology; and although almost entirely a product of the 19th century, the history of its development gives place, in point of interest, to that of no other general conception. The cell-theory—in a form, however, very different from that in which we now know it—was originally suggested by the study of plant structure; and the first steps to the formulation, many years later, of a definite cell-theory, were made as early as the later part of the 17th century by Robert Hooke, Marcello Malpighi and Nehemiah Grew. Hooke (1665) noted and described the vesicular nature of cork and similar vegetable substances, and designated the cavities by the term “cells.” A few years later Malpighi (1674) and Grew (1682), still of course working with the low power lenses alone available at that time, gave a more detailed description of the finer structure of plant tissue. They showed that it consisted in part of little cell-like cavities, provided with firm cell-walls and filled with fluid, and in part of long tube-like vessels. A long time passed before the next important step forward was made by C. L. Treviranus,2 who, working on the growing parts of young plants, showed that the tubes and vessels of Malpighi and Grew arose from cells by the latter becoming elongated and attached end to end, the intervening walls breaking down; a conclusion afterwards confirmed by Hugo von Mohl (1830). It was not, however, until the appearance of Matthias Jakob Schleiden’s paper Beiträge zur Phytogenesis (1838) that we have a really comprehensive treatment of the cell, and the formulation of a definite cell-theory for plants. It is to the wealth of correlated observations and to the philosophic breadth of the conclusions in this paper that the subsequent rapid progress in cytology is undoubtedly to be attributed. Schleiden in this paper attempted to solve the problem of the mode of origin of cells. The nucleus (vide infra) of the cell had already been discovered by Robert Brown (1831), who, however, failed to realize its importance. Schleiden utilized Brown’s discovery, and although his theory of phytogenesis is based on erroneous observations, yet the great importance which he rightly attached to the nucleus as a cell-structure made it possible to extend the cell-theory to animal tissues also. We may indeed date the birth of animal cytology from Schleiden’s short but epoch-making paper. Comparisons between plant and animal tissues had already been made by several workers, among others by Johannes Müller (1835), and by F. G. J. Henle and J. E. Purkinje (1837). But the first real step to a comprehensive cell-theory to include animal tissues was made by Theodor Schwann. This author, stimulated by Schleiden’s work, published in 1830 a series of Mikroskopische Untersuchungen über die Übereinstimmung in der Structur und dem Wachstum der Tiere und Pflanzen. This epoch-making work ranks with that of Schleiden in its stimulating influence on biological research, and in spite of the greater technical difficulties in the way, raised animal cytology at one blow to the position already, and so laboriously, acquired by plant cytology. In the animal cell it is the nucleus and not the cell-wall that is most conspicuous, and it is largely to the importance which Schwann, following the example of Schleiden, attached to this structure as a cell constituent, that the success and far-reaching influence of his work is due. Another feature determining the success of Schwann’s work was his selection of embryonic tissue as material for investigation. He showed that in the embryo the cells all closely resemble one another, only becoming later converted into the tissue elements—nerve cells, muscle cells and so forth—as development proceeded; just as a similar mode of investigation had enabled Treviranus to trace the origin from typical cells of the vascular tissue in plants more than 30 years previously. And just as Treviranus showed that there was a union of cells to form the vessels in plants, so Schwann now showed that a union of cells frequently occurred in the formation of animal tissues.
So great was the stimulus given to cytological research by the work of Schleiden and Schwann that these authors are often referred to as the founders of the cell-theory. Their theory, however, differed very greatly from that of the present time. Not only did they suppose new cells to arise by a sort of “crystallization” from a formative “mother liquor” or “cytoblastema” (vide infra), but they both defined the cell as a “vesicle” provided with a firm cell-wall and with fluid contents. The cell-wall was regarded as the essential cell-structure, which by its own peculiar properties controlled the cell-processes. The work of Schleiden and Schwann marks the close of the first period in the history of the cell-theory—the period dominated by the cell-wall. The subsequent history is marked by the gradual recognition of the importance of the cell-contents. Schleiden had noticed in the plant cell a finely granular substance which he termed “plant slime” (Pflanzenschleim). In 1846 Hugo von Mohl applied to this substance the term “protoplasm”; a term already used by Purkinje six years previously for the formative substance of young animal embryos. Mohl showed that the young plant cell was at first completely filled by the protoplasm, and that only later, by the gradual accumulation of vacuoles in the interior, did this substance come to form a thin layer on the inner surface of the cell-wall. Mohl also described the spontaneous movement of the protoplasm, a phenomenon already noted by Schleiden for his plant slime, and originally discovered by Bonaventura Corti in 1772 for the cells of Chara, and rediscovered in 1807 711 by Treviranus. Not only was attention thus gradually directed to the importance of the cell-contents, but observations were not lacking, even in the plant kingdom, tending to weaken the importance hitherto attached to the cell-wall. Among these may be mentioned Cohn’s observation that in the reproduction of Algal forms the protoplasm contracts away from the cell-wall and escapes as a naked “swarm spore.” Similarly in the animal kingdom instances began to be noted in which no membrane appeared to be present (Kolliker, 1845; Bischoff, 1842), and for some time it was hotly debated whether these structures could be regarded as true cells. As a result of the resemblance between the streaming movements in these apparently naked cells (e.g. lymphocytes) and those seen in plant cells, R. Remak was led (1852-1853) to apply Mohl’s term “protoplasm” to the substance of these animal cells also. Similarly Max Schultze (1863) and H. A. de Bary (1859), as a result of the study of unicellular animals, came to the conclusion that the substance of these organisms, originally termed “Sarcode” by F. Dujardin, was identical with that of the plant and animal cell. Numerous workers now began to realize the subordinate position of the cell-wall (e.g. Nägeli, Alexander Braun, Leydig, Kolliker, Cohn, de Bary, &c.), but it is to Max Schultze above all that the credit is due for having laid the foundation of the modern conception of the cell—a conception often referred to as the proto-plasmic-theory in opposition to the cell-theory of Schleiden and Schwann. Max Schultze showed that one and the same substance, protoplasm, occurred in unicellular forms and in the higher plants and animals; that in plants this substance, though usually enclosed within a cell membrane, was sometimes naked (e.g. swarm spores), while in many animal tissues and in many of the unicellular forms the cell-membrane was always absent. He therefore concluded that in all cases the cell-membrane was unessential, and he redefined the “cell” of Schleiden and Schwann as “a small mass of protoplasm endowed with the attributes of life” (1861). In the same year the physiologist Brücke maintained that the complexity of vital phenomena necessitated the assumption for the cell-protoplasm itself of a complex structure, only invisible because of the limitations of our methods of observation. The cell in fact was to be regarded as being itself an “elementary organism.” By this time too it was realized that the formation of cells de novo, postulated by Schleiden’s theory of “phytogenesis,” did not occur. Cells only arose by the division of pre-existing cells,—as Virchow neatly expressed it in his since famous aphorism, omnis cellula e cellula. It was, however, many years before the details of this “cell-division” were laid bare (see Cell-Division below).
General Morphology of the Cell.—In its simplest form the cell is a more or less spherical mass of viscid, translucent and granular protoplasm. In addition to the living protoplasm there is present in the cell food-material in various stages of assimilation, which usually presents the appearance of fine granules or spherules suspended in the more or less alveolar or reticular mesh-work of the living protoplasm. In addition there may be more or less obvious accumulations of waste material, pigment, oil drops, &c.—products of the cell’s metabolic activity. All these relatively passive inclusions3 are distinguished from the living protoplasm by the term “metaplasm” (Hanstein), or “paraplasm” (Kupffer), although in practice no very sharp distinction can be drawn between them. The cell is frequently, but by no means always, bounded by a cell-wall of greater or less thickness. In plants this cell-wall consists of cellulose, a substance closely allied to starch; in animals only very rarely is this the case. Usually the cell-wall, when this is present, is a product of the cell’s secretive activity; sometimes, however, it appears to be formed by an actual conversion of the surface layer of the protoplasm, and retains the power of growth by “intussusception” like the rest of the protoplasm. Even when a limiting membrane is present, however, evidence is steadily accumulating to show that the cell is not an isolated physiological unit, but that, in the vast majority of cases, there is a protoplasmic continuity between the cells of the organism. This continuity, which is effected by fine protoplasmic threads (“cell-bridges”) piercing the cell-wall and bridging the intercellular spaces when these are present, is to be regarded as the morphological expression of the physiological interdependence of the various—often widely separated—tissues of the body.4 It is probable that it is the specialization of this primitive condition which has produced the cell-elements of the nervous system. In many cases the cell-connexions are so extensive as to obliterate cell-boundaries. A good example of such a “syncytial” tissue is provided by the heart muscle of Vertebrates and the intestinal musculature of Insects (Webber).5
In all multicellular, and in the great majority of unicellular, organisms the protoplasm of the cell-unit is differentiated into two very distinct regions,—a more or less central region, the nucleus, and a peripheral region (usually much more extensive), the cell-body or cytoplasm. This universal morphological differentiation of the cell-protoplasm is accompanied by corresponding chemical differences, and is the expression of a physiological division of labour of fundamental importance. In some of the simpler unicellular organisms, e.g. Tetramitus, the differentiated protoplasm is not segregated. Such forms are said to have a “distributed” nucleus, and among the Protozoa correspond to Haeckel’s “Protista.” It is probable that among plants the Bacteria and Cyanophyceae have a similar distributed nucleus. In all the higher forms, however, the segregation is well marked, and a “nuclear membrane” separates the substance of the nucleus, or “karyoplasm”6 from the surrounding “cytoplasm.” Within the nuclear membrane the karyoplasm is differentiated into two very distinct portions, a clear fluid portion, the “karyolymph,” and a firmer portion in the form of a coarser or finer “nuclear reticulum.” This latter is again composed of two parts, the “linin reticulum,”7 and, embedded in the latter and often irregularly aggregated at its nodal points, a granular substance, the “chromatin,”8 the latter being the essential constituent of the nucleus. In addition to the chromatin there may be present in the nucleus one or more, usually spherical, and as yet somewhat enigmatical bodies, the “nucleoli.” In addition to the nucleus and cytoplasm, a third body, the “centrosome,” has often been considered as a constant cell-structure. It is a minute granule, usually lying in the cytoplasm not far from the nucleus, and plays an important part in cell-division and fertilization (see below).
Cell-differentiation.—Both among unicellular and multicellular individuals the cell assumes the most varied forms and performs the most diverse functions. In all cases, however, whether we examine the free-living shapeless and slowly creeping Amoeba, or the striped muscle cell or spermatozoon of the Metazoa (fig. 1, b and c), the constant recurrence of cytoplasm and nucleus show that we have to deal in each case with a cell. The variation in the form and structure of the cell is an expression of that universal economic law of nature, “division of labour,” with its almost invariable accompanying “morphological differentiation”; the earliest and most fundamental example being in the differentiation of the cell-protoplasm into cytoplasm and nucleus. In multicellular individuals the division of labour to which the structural complexity of the organism is due is between the individual cell-units, some cells developing one 712 aspect, some another, of their vital attributes. Thus one cell specializes in, say, secretion, another in contractility, another in receiving and carrying stimuli, and so forth, so that we have the gland cell, the muscle cell, and the nerve cell, each appropriately grouped with its fellows to constitute the particular tissue or organ—gland, muscle or brain—which has for its function that of its constituent cells. In unicellular animals we also find division of labour and its accompanying morphological differentiation, but here there is no subdivision of the protoplasm of the organism into the semi-autonomous units which so greatly facilitate division of labour in the Metazoa; instead, division of labour must be between different regions of protoplasm in the single cell. The sharply defined character of this regional differentiation in the Protozoa, and the surprising structural complexity it may produce, sufficiently clearly show that although multicellular structure has greatly facilitated regional differentiation in the Metazoa, it is by no means essential to this process (see below, Present Position of the Cell-theory).
It is not within the scope of this article to attempt a comprehensive review of the variety in structural complexity to which this division of labour among the cells of the Metazoan and the regional differentiation of the cell-bodies of the Protozoa has given rise. Some indication of the wealth of variety may be best given by taking a general survey of cell-modifications, grouped according to the cell-attributes the expression of which they facilitate.
 |
| a and b from Schäfer’s Essentials of Histology, by permission of Longmans, Green & Co. |
| Fig. 1.—Types of Cells. a, Fat-cell enclosing a huge fat-globule. b, Part of a Mammalian “striated” muscle-cell (diagrammatic). c, Spermatozoa of mouse and bird. |
(a) Structural Complexity facilitating Movement.—One of the most striking, and hence earliest described, of the fundamental attributes of protoplasm is its power of spontaneous movement. This is seen in the walled cell of plant tissue and in the naked cell-body of Amoeba. In the latter case the streaming movements of the naked protoplasm are accompanied by the formation of “pseudopodia,” and result in the highly characteristic “amoeboid” creeping movement of this and similar organisms (e.g. lymph corpuscles of the blood).9 In these examples the whole protoplasm participates in the movement,—there has been no division of labour, and there is, therefore, no visible morphological differentiation. In many cells, movement (either of the entire body or of the surrounding medium) is by means of slender whip-like processes of the protoplasm flagella or cilia. These represent modified pseudopodia, and in the formation of the motile gametes of some of the lower forms, e.g. Myxomycetes (de Bary, 1859), Rhizopods (R. Hertwig, 1874), &c., the actual conversion of a pseudopodium into a flagellum can be witnessed. These vibratile processes may be either one or few in number, and are then large in size and move independently of one another; or they may be very numerous, covering the free surface of the cell (fig. 2, a); they are then very small and move strictly in unison. In the former case they are termed “flagella,” in the latter “cilia.” In some cases the flagellum is accompanied by an undulating membrane (e.g. Trypanosoma among the protozoa and in many spermatozoa), and it may be situated either at the front end (Euglena) or hind end (spermatozoa) of the body during motion. The cilia may form a uniform coating to the free surface of the cell, as in ciliated epithelium (fig. 2, a) and many infusoria, or the cilia may be variously modified and restricted to special regions of the body, e.g. the “undulating membrane” of the peristomial region in many infusoria, the swimming combs of the Ctenophora (q.v.), and the flame cells of the Platyelmia (q.v.). In one group of infusoria (Hypotricha), the cilia, “cirri,” have attained a high degree of differentiation, and reach a considerable size. Both cilia and flagella spring directly from the cell-protoplasm, piercing the cell-membrane, when this is present. At the point where they become continuous with the cell-body there is usually a deeply staining “basal granule.” In some cases the flagella are in direct connexion with the centrosome (see below, Cell-division), e.g. Trypanosoma and spermatozoa, in some cases even while the centrosome is functioning in mitosis (e.g. insect spermatogenesis, Henneguy10 and Meves11 (fig. 3).
 |
| From A. Gurwitsch, Morphologie und Biologie der Zelle, by permission of Gustav Fischer. |
| Fig. 2.—Types of Cells. a, Ciliated epithelial cells. (After Heidenhain.) b, Mucus-secreting “goblet”-cells. (After Gurwitsch.) |
 |
| From O. Hertwig, Allgemeine Biologie, by permission of Gustav Fischer. |
| Fig. 3.—Spermatocytes of Bombyx mori, showing the precocious appearance of the spermatozoon flagellum and its relation to the centrosome. (After Henneguy.) |
In the ability of Amoeba to contract into a spherical mass, and in the presence in its protoplasm of the contractile vacuole, we see another type of spontaneous movement—contractility—of the protoplasm. In the “musculo-epithelial” cells of Hydra, the elongated basal portion of the cell alone possesses this contractility. In the higher Metazoa the whole cell—muscle cell—is specialized for contractility, and shows, as a result of its specialization, a distinct fibrillation. This fibrillation is foreshadowed in the contractile regions of many Protozoa, e.g. 713 in the cirri of hypotrichous Infusoria, the tentacle of Noctiluca, and the myophane layer of Gregarines. In the quickly contracting muscle cell of Vertebrates and insects, further specialization has produced a structure of considerable complexity (fig. 1, b). Here also the cell is fibrillated, but the fibrillae (sarcostyles) are much more distinct, and are segmented in a manner which gives to the entire cell a “cross striated” appearance. Since quick movement is usually (but not always) associated with voluntary control, these striated muscle cells are often termed “voluntary” muscle fibres. The great increase in length of these cells is accompanied by the fragmentation of the originally single nucleus.
(b) Cell-modification in Relation to Secretion.—Just as the complex movements considered above were the result of a great development of the power of spontaneous movement possessed by all protoplasm, so cell-secretion is the result of a development of the metabolic processes underlying all vital phenomena. But whereas specialization of the protoplasm for movement resulted in a very obvious morphological complexity, specialization for secretion results in molecular complexity, and only rarely and indirectly results in morphological differentiation. Usually indeed the specialization is only rendered evident by the appearance of the formed secretion, e.g. mucus-secreting epithelial cells (fig. 2, b), the ovarian ovum and the fat cell (fig. 1, a). In some cases a distinct fibrillation of the cytoplasm accompanies or precedes the appearance of the cell-secretion (Mathews, pancreas cell of Amphibia). In many cases the internal secretion is no mere accumulation, e.g. the internal skeleton of the Radiolaria, and the nematocysts of the Coelentera. Frequently in animal tissues the cell-secretions are accumulated in the intercellular spaces, and result in the formation of the various “connective tissues,” all of which are characterized by the immense amount of intercellular substance, e.g. fibrous tissue, cartilage and bone. Cell-modifications facilitating the general metabolism, but not necessarily indicating specialized secretion, also occur, e.g. the “gullet” of many Protozoa, the suctorial tubules of the Acinetaria, and the “nutritive processes” of the ovarian ova in many Lepidoptera. Mention may be made here of the network or canal system of the cytoplasm, described for many cells by Golgi, Holgren and others. An enigmatical structure, the “yolk-nucleus” of many ova, has been frequently regarded as a structure of considerable metabolic importance, e.g. Bambeke (1898) for Pholcus.12
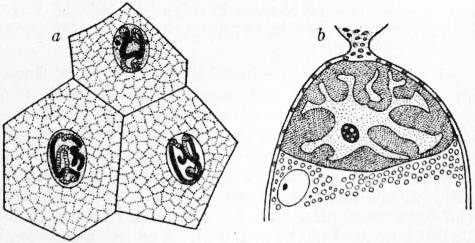 |
| Fig. 4.—Types of Nuclei. |
From Prof. E. B. Wilson’s The Cell in Development and Inheritance, by permission of the author and of the Macmillan Co., New York.
a, Permanent spireme-nuclei in cells from the intestinal epithelium
of a dipterous larva, Ptychoptera. (After van Gehuchten.)
From Korschelt and Heider, Lehrbuch der verg. Entwicklungsgeschichte der wirbellosen Tiere, by permission of Gustav Fischer.
b, Branched nucleus of the “nutritive” cell, from a portion of an ovarial tube of Forficula auricularia.
Striking modifications resulting from specialization in secretion are frequently presented by the nucleus. In many secreting cells this structure is extensively branched, e.g. many gland cells and ovarian nutritive cells of insects (fig. 4, b). In some cases the nucleus of the gland cell contains a persistent spireme thread (fig. 4, a); while almost all actively secreting cells are characterized by the possession of large or numerous nucleoli.
 |
| From Schäfer’s Essentials of Histology, by permission of Longmans, Green & Co. |
| Fig. 5.—Nervous and Sensory Cells. |
A and B, Ganglion cells from the cerebral cortex; in A the only slightly branched axon may extend the whole length of the spinal cord. (After Schäfer.)
C, Body of a ganglion-cell showing “Nissl’s granules.”
D, Sensory cells from olfactory epithelium. (After Schultze.)
E, Diagrammatic representation of the sensory epithelium of retina (rod and cone layer). (After Schwalbe.)
(c) Specialization for the Reception and Conduction of Stimuli.—One of the most striking of the fundamental attributes of living protoplasm is its “irritability,” that is to say, its power of responding to external impressions, “stimuli,” by movement, which, both in kind and intensity, is wholly independent of the amount of energy expended by the stimulus. The stimulus conveyed by the nerve fibre to the muscle is out of all proportion to the amount of work it may cause the muscle to do. Although protoplasmic irritability is thus incapable of a simple mechanical explanation, science has rejected the assumption of a special “vital force,” and interprets protoplasmic response as being a long series of chemico-physical changes,13 initiated, but only initiated, by the original stimulus; the latter thus standing in the same relation to the response it produces as the pull on the trigger to the propulsion of the rifle bullet. The function of receiving stimuli from the outer world, originally possessed to a greater or less extent by all cells, has, in the Metazoa, been relegated to one class of cells, the sensory cells14 (fig. 5, D and E). Another class of cells—the “ganglion cells” or “neurones” (fig. 5, A and B), are concerned with the conduction of the stimuli so received. The contractile elements in the Metazoa are thus dependent for their stimuli on the nervous elements—the sensory cells and neurones.
Origin of Cells.—In the preceding sections we have considered the structure of the cell in relation to the fundamental attributes of cell-metabolism, irritability, and movement. We have now 714 to consider the cell in relation to yet another vital attribute, that of reproduction. Just as we now know that the phenomena of assimilation, respiration, excretion, response, movement and so forth, characteristic of living things, are but the co-ordinated expressions of the corresponding activities of the constituent cells, so we now know that the reproduction of the organism is, in its ultimate analysis, a cell-process. Our knowledge of the essential fact that cells only arise by the division of pre-existing cells, now a fundamental axiom of biology, and of the details of this process, have been acquired during recent years by the strenuous efforts of numerous workers.15 Matthias Jakob Schleiden (1838) supposed that in plants the new cell arose from the parent cell by a sort of “crystallizing” process from the cell fluid or “cytoblastema”; the nucleolus appearing first, then the nucleus, and finally the cell-body. Theodor Schwann (1839) extended Schleiden’s theory to animal tissues, with this yet greater error, that new cells might arise, not only within the mother cell as Schleiden had supposed, but also in the intercellular substance so common in animal tissues (to which he also gave the term “cytoblastema”). By 1846, however, the botanists, thanks mainly to the efforts of Hugo von Mohl and Nägeli, recognized as a general law that cells only arise by the division of a pre-existing cell. But it was long before the universal application of this law was recognized by zoologists; the delay being largely due to pathological phenomena. The work of Kölliker (1844-1845), Karl Bogislaus Reichert (1841-1847), and Remak (1852-1855), however, finally enabled Virchow in 1858 to maintain the law of the genetic continuity of cells in the since famous aphorism omnis cellula e cellula. At this time, however, nothing was known of the details of cell-division,—one school (Reichert, L. Auerbach, and the majority of the botanists) maintaining that the nucleus disappeared prior to cell-division, the other school (von Baer, Remak, Leydig, Haeckel, &c.) maintaining that it took a leading part in the process. It is not until the appearance of Anton Schneider’s work in 1873, followed by those of Fol, Auerbach, Strasburger and many others, that we begin to gain an insight into the process. In 1882 W. Flemming was able to extend Virchow’s aphorism to the nucleus also: omnis nucleus e nucleo.
Outline of Cell-division.—There are two very distinct methods of cell-division. The more general and also more complicated method is accompanied by the formation of a complex fibrillar mechanism, and was on this account termed “mitosis” (μίτος, a thread) by W. Flemming (1882), and “karyokinesis” (κάρυον, nut, nucleus, and κίνησις, change, movement) by W. Schleicher (1878). The other method, “amitosis,” or direct division, is unaccompanied by any visible mechanism and is of relatively exceptional occurrence. In the more usual method of cell-division, or “mitosis,” we can distinguish two distinct but parallel processes, the one undergone by the chromatin and resulting in the “chromatic figure,” the other usually only concerning the cytoplasm and resulting in the “achromatic figure.”16
 |
| a, b and c from Prof. E. B. Wilson’s The Cell in Development and Inheritance, by permission of the author and the Macmillan Co., New York; d from A. Gurwitsch, Morphologie u. Biologie der Zelle, by permission of Gustav Fischer. |
| Fig. 6.—Diagram of Nuclear Division. a, Spireme stage; b, Spindle formed; c, Spindle complete; equatorial plate formed; d, Division completed. |
We will consider the chromatin changes first. The chromatin granules lose their scattered arrangement on the nuclear reticulum, and become instead arranged in a linear series to form a coiled and deeply staining “spireme thread”17 (fig. 6, a). As the thread contracts, its granular origin becomes less evident, and at the same time the coils become fewer in number; the “close” spireme of earlier stages becomes the “loose” spireme of later stages. As the spireme thread contracts, it segments into a number of short, and usually U-shaped, segments—the “chromosomes” (Waldeyer, 1888). The number of these chromosomes is always constant for the cells of any given species of plant or animal, but varies greatly in number in different species. Thus in the parasitic worm Ascaris megalocephala, var. univalens, there are only two. In the crustacean Artemia Bauer found 168, while in the amphibian Salamandra maculata, as also in the lily, the number is 24. While these changes have been proceeding in the nucleus, changes in the cytoplasm have resulted in the formation of the achromatic figure. These cytoplasmic changes are initiated by the division into two of a minute body, the “centrosome,” originally discovered by P. J. van Beneden in 1883,18 and usually lying not far from the nucleus (fig. 6, a). The daughter centrosomes separate from one another, travelling to opposite poles of the nucleus. At the same time radiations extend out into the cytoplasm from the centrosomes, and, as the nuclear membrane disappears, invade the nuclear area (fig. 7, a). Some of the fibrillae in the latter region become attached to the chromosomes and are termed “mantle fibres”; others become continuous from one centrosome to the other and constitute the “spindle fibres.” The remaining radiations at the two poles of the spindle are the “astral rays.” (The details of the formation of the achromatic figure vary considerably, some indication of this is given in the next section in connexion with the question of the origin of the mitotic mechanism.) The chromosomes now arrange themselves in the “equatorial plate” of the spindle and each splits longitudinally into two19 (fig. 6, b and c). The sister chromosomes now pass to opposite poles of the spindle (fig. 6, d), and there, returning to the “resting” condition, constitute the daughter nuclei. Division of the cell follows, usually, in animals, by simple constriction. Both Theodor Boveri and van Beneden, in their papers of 1887, regarded the centrosome as initiating, not only the division of the cell-body but that of the chromatin also; Beneden even suggested that the pull of the mantle fibres caused the division of the chromatin in the equatorial plate. W. Pfitzner in 1882 was the first to show that the splitting of the chromosomes in the equatorial plate was only the reappearance of a split in the spireme thread and was due to a corresponding 715 division into two of each of the chromatin granules. In the spermatogenic cells of Ascaris, A. Brauer has shown that the chromatin granules divide while still scattered over the nuclear reticulum and before either the formation of a spireme thread or the division of the centrosome. In many other cases the reverse of this condition occurs, the centrosome dividing long before there is any indication of division in the nucleus (e.g. salamander spermatogenic cells, Meves, &c.). We must therefore, with Boveri and Brauer, regard the division of the chromatin in mitosis as a distinct reproductive act on the part of the chromatin granules, the chromosomes being merely aggregates (temporary or permanent, vide infra) of these self-propagating units.
For convenience of description it is usual to recognize four periods in mitosis: (i.) Prophase, (ii.) Metaphase, (iii.) Anaphase, and (iv.) Telophase (Strasburger, 1884). The prophase covers all changes up to the completion of the mitotic figure. The metaphase is the parting of the sister chromosomes in the equatorial plate; their passage to opposite poles of the spindle constitutes the anaphase; and their reconstruction to form the resting daughter nuclei, the telophase.
 |
| Fig. 7.—Centrosomes. |
| From Prof. E. B. Wilson’s The Cell in Development and Inheritance, by permission of the author and of The Macmillan Co., New York. |
| a, Leucocyte from a Salamander, showing permanent aster and
centrosome. |
| From A. Gurwitsch, Morphologie u. Biologie der Zelle, by permission of Gustav Fischer. |
| b, Sperm-mother cell of Salamandra maculata, showing Hermann’s “central spindle.” |
The Achromatic Figure.—The mode of origin of the achromatic figure varies greatly. In some cases a distinct and continuous spindle, the “central spindle” of F. Hermann, is visible from the very first separation of the daughter centrosomes (e.g. salamander spermatogenic cell)20 (fig. 7, b). In other cases the rays only invade the nuclear area and become continuous in the equatorial plane after the centrosomes have assumed their definitive positions at the two poles of the nucleus, and may even appear to indent the disappearing nuclear membrane as they invade the nuclear area.21 In the salamander testis cell (fig. 7, b), and in many other cases, the whole of the achromatic figure is obviously of cytoplasmic origin. In many cases, however, it equally obviously arises within the nucleus,22 while in yet other cases23 the spindle fibres are of mixed origin. The question, therefore, of the cytoplasmic or nuclear origin of the achromatic figure, at one time regarded as of considerable importance, is wholly immaterial. Various elaborate theories have been propounded to explain the mechanism of the mitotic figure. H. Fol (1873) regarded the centrosomes as centres of attractive forces, and compared the mitotic figure to the lines of force in the magnetic field, a comparison made by numerous subsequent workers. E. Klein’s hypotheses of two opposing systems of contractile fibrillae, elaborated by van Beneden (1883, 1887) and accepted by Boveri (1888), was still further extended by R. Heidenhain in relation to the leucocytes of the salamander, in which there is a permanent centrosome and astral rays to which the contractile movements of the cell appear to be due24 (fig. 7, a). Hermann on the other hand confined the contractility to the astral and mantle fibres; while L. Druner regarded the spindle as exerting a pushing force, for not only do the interzonal spindle fibres elongate during the anaphase, but they were often at this period contorted, while on the other hand astral rays may be entirely absent (e.g. Infusoria), and in some cases the spindle pole may be caused to project at the surface of the cell. The futility of these attempted mechanical explanations of mitosis is sufficiently clearly shown, not only by the contradictory nature of the explanations themselves, but by the fact that, in amitosis, nuclear and cytoplasmic division occur without any fibrillar mechanism whatever.
Centrosome.25—This minute body was first detected at the spindle poles by Flemming in 1875, and independently by P. J. van Beneden in 1876. The important part played by the centrosome in fertilization,26 first described by van Beneden and Theodor Boveri in their papers of 1887-1888, together with the behaviour of this structure in mitosis, led these authors to regard the centrosome not only as the dynamic centre of the cell but as a permanent cell-organ, which, like the nucleus, passed by division from one cell-generation to the next. This conclusion appeared to receive considerable support from the recognition of the centrosome in various kinds of resting cells,27 and especially from the relation this structure frequently shows to the locomotor apparatus of the cell (e.g. its position in the centre of the radiating fibrillae in the contractile lymph and pigment cells, and its relation to the vibratile flagellum in spermatozoa and some protozoa, e.g. Trypanosoma).28 In almost all cases the centrosome of the resting cell, when this can be detected, lies in the cytoplasm, and is often already divided in preparation for the next mitotic division (e.g. spermatogenic cells of the salamander; Meves). In some cases, however, it resides in, or arises from, the nucleus (Brauer; spermatogenesis of Ascaris, var. univalens). This indifferent nuclear or cytoplasmic position for the centrosome is paralleled by the attraction sphere or homologue of the centrosome in many Protozoa. Thus in many forms, e.g. Euglena (Keuten), it lies within the nucleus, while in other forms, e.g. Noctiluca (Ishikawa, 1894, 1898; Calkins, 1898) and Paramoeba (F. Schaudinn, 1896), it lies in the cytoplasm, while in Tetramitus it coexists with a “distributed” nucleus. In the Heliozoa conditions are exceptionally interesting; not only is the centrosome—here resembling in appearance that of the higher forms—permanently visible and extranuclear, lying at the centre of the radiations characteristic of these forms, but there is the strongest possible evidence for its formation de novo. For Schaudinn has shown in Acanthocystis that, in the formation of the swarm spores, the nucleus divides amitotically, the centrosome remaining visible and unchanged at the centre of the radiating processes. Yet a centrosome appears later in the nucleus of the swarm spores and migrates into the cytoplasm. The experiments of T. H. Morgan and E. B. Wilson, in which numerous centrosomes and asters (“cytasters”) are caused to appear in unfertilized sea-urchin eggs by a brief immersion in a 13% solution of magnesium 716 chloride in sea-water,29 as also the possibility in many cases that even in normal fertilization the cleavage centrosomes may arise de novo,30 make it no longer possible to regard the centrosome as a permanent cell-structure.
Significance of Mitosis.—Whatever may be the nature of the chemico-physical changes occurring during cell-division, of which the achromatic spindle and astral rays are the visible expression, it is certain that the whole of this complicated process has for its function, not the division of the chromatin, for that has already occurred on the spireme thread or even earlier, but the distribution of the divided chromatin granules to the two daughter nuclei. It is indeed usually assumed that the mitotic mechanism is not merely for the distribution, but for the equal distribution, of the sister granules to the two daughter nuclei. The conspicuous part the chromatin is seen to play in the whole mechanism of heredity—in maturation, fertilization and development—indicating as it does that the chromatin is the chief, if not the only, bearer of the specific qualities of the organism, sufficiently clearly emphasizes the importance of the equal distribution of this substance between the daughter cells at successive cell-divisions. There are, however, serious objections to the interpretation of mitosis as an adaptation to ensure this equal distribution of the chromatin. Not only does the occurrence of amitosis show that the mitotic mechanism is not essential for either nuclear or cytoplasmic division, but direct division may occur31 in the life-history of the germ cells, the very point at which it should not occur had mitosis the significance usually attached to it. On the other hand, the most elaborate mitosis occurs in cell-tissues (e.g. skin of salamander larva) which can take no possible share in the reproduction of the species. Moreover, we have no reason for supposing that the division of the chromatin in amitosis is not as meristic, and its subsequent distribution as equal, as is so visibly the case in mitosis.32 It is necessary, therefore, to seek for some other explanation of the elaborate mechanism of mitosis than that which assumes it necessary for the equal distribution of the divided chromatin granules. The present writer believes the true explanation to be found in that great economic law of nature, “division of labour.” The same economy which, working under the control of natural selection, has produced the complexly differentiated tissues of the higher metazoa, which has led to the sexual differentiation between the conjugating gametes and thus to the sexual differentiation of the parents, has resulted in the production of mitosis. Only here the economy finds expression in division of labour, not in space, but in time. The work of the self-propagating chromatin granules is so ordered that periods of undisturbed metabolic activity alternate with periods of reproductive activity. The brief space of time occupied by the latter process has necessitated a more elaborate specialization of the forces—whatever their nature—controlling cell-division; a specialization which has resulted, just as a similar specialization in so many other cases has resulted, in a visible differentiation of the cell-protoplasm. This explanation is in harmony with the occurrence of typical mitosis in active tissue cells on the one hand, and of amitosis in the relatively quiescent primary germ cells on the other.
Individuality of the Chromosomes.—The most striking feature in the behaviour of the chromatin in mitosis is its resolution, at each division, into a—for any particular species—constant number of chromosomes. This constant recurrence of the specific number of chromosomes at every cell-division is capable of explanation in two radically different ways. One explanation assumes for the organism a specific peculiarity determining the segmentation of the spireme thread into a definite number of segments (Delage, 1899 and 1901).33 The other regards chromosomes as independent units of the cell, retaining their identity between successive cell-divisions. The latter “Individualitäts Hypothese” was originally put forward by Theodor Boveri in 1887 as a result of C. Rabl’s observation (1885) that in epidermal cells of the salamander larva the chromosomes reappear in the mitosis of the daughter cells with the same arrangement as they possessed in the prophase of the mother cell—the angles of the U-shaped chromosomes being all directed towards one pole (Rabl’s “Poleseite”) of the nucleus. In the formation of the “resting” nucleus, the chromatin, becoming metabolically active, flows out on to the linin reticulum, all trace of the chromosomes being for the time lost. In Ascaris, Boveri (1888) obtained similar but still more striking results. The thickened ends of the four elongated chromosomes cause projections on the nuclear surface throughout the resting period, and the ends of the reappearing chromosomes always coincided with these protuberances; cf. also Sutton (1902) on locust spermatagonia. Moreover, the arrangement of the chromosomes must follow one of three well-marked groupings, and this is determined for each individual in the cleavage spindle of the egg and maintained throughout later development (fig. 8).
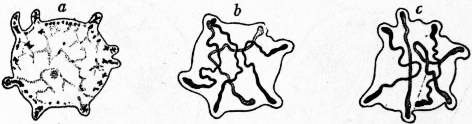 |
| From Boveri’s Ergebnisse ü. d. Konstitution der chromatischen Substanz des Zellkerns, by permission of Gustav Fischer. |
| Fig. 8.—Preparation for Mitosis. a, Nucleus of “½ blastomere” of Ascaris megalocephala bivalens in resting condition; b and c, nuclei from sister ½ blastomeres in preparation for mitosis. |
In the same worm (var. univalens) Boveri (1888 and 1899) found that occasional abnormalities in maturation resulted in the suppression of the first polar body and the inclusion of its chromosomes in the second maturation spindle; the egg-nucleus at the time of fertilization thus having two chromosomes instead of one, while the spermatozoon nucleus has only one. Three chromosomes instead of two reappear in subsequent divisions. Boveri’s “Individualitäts Hypothese” received striking support from the work of Herla (1893), L. R. Zoja (1895) and O. zur Strassen (1898). Herla and Zoja showed that if the egg of Ascaris megalocephala (var. bivalens), which possesses two chromosomes, be fertilized with the spermatozoon of var. univalens, in which the germ cell has only one chromosome and that smaller than either of the two in the other variety, three chromosomes reappear, two large and one small, in the cleavage divisions of the resulting hybrid embryo. Zur Strassen’s observations on the giant embryos of Ascaris also support Boveri’s theory. These embryos arise by the fusion of eggs, either before or after fertilization. The number of chromosomes in the subsequent cleavage-figures is proportional to the number of nuclei that have fused together. Similar results are given by Boveri’s (1893-1895) and T. H. Morgan’s (1895) experiments on the fertilization of enucleated sea-urchin egg-fragments; all the nuclei of the resulting embryo having only half the number of chromosomes characteristic of the species (e.g. in Echinus 9 instead of 18). All the above facts point to the conclusion that, as Boveri expressed it in his Grundgesetz der Zahlenkonstanz (1888), “the number of chromosomes arising from a resting nucleus is solely dependent on the number which originally entered into its composition.”34
Boveri’s Law of Proportional Nuclear Growth.—The chromatin in the nucleus is exactly halved at every cell-division. As the bulk of the chromatin remains constant from one cell-generation to another, it must double its bulk between successive divisions. That this proportional growth of the chromatin is dependent solely on the chromatin mass, and not on that of the cell, is very clearly indicated by cases where the normal chromatin mass has been artificially increased or reduced,35 the chromatin in either case doubling its bulk between successive cell-divisions, and neither the mass of the chromatin nor the number of the chromosomes undergoing any readjustment. By double or partial fertilization, different regions in the same embryo may show nuclei of different sizes (Boveri). We must therefore distinguish in the cell between “young” and “adult” chromatin. In other words the chromatin must be regarded as being composed of individual units, each with a definite constant structure and maximum growth (Boveri, 1904). This conclusion is strongly suggested, not only by the evidence in favour of the individuality of the chromosomes considered above, but also by the independent reproductive activity of the chromatin granules in the prophase of mitosis.
 |
| From Boveri’s Ergebnisse ü. d. Konstitution der chromatischen Substanz des Zellkerns, by permission of Gustav Fischer. |
| Fig. 9.—Preparation for Mitosis. a, Spermatogonium of Brachystola magna with resting nucleus; b, Same with prophase for mitosis. (After Sutton.) |
Differentiation among the Chromosomes.—If we grant the assumption of a persistent individuality for the chromosomes, then it becomes possible to consider whether in one and the same nucleus these structures may not take varying parts in controlling the cell’s activity in development and in inheritance. Such a differentiation among the chromosomes would be due to independent ancestry rather than to the economy resulting from a division of labour; nevertheless a division of labour of a sort would be the result of this gradual divergence of the chromosomes from one another, and we might therefore expect that, in some cases at least, a morphological would accompany the physiological differentiation. Examples of such a morphological differentiation do indeed occur in the “accessory” chromosomes first described by H. Henking (1891) for the spermatogonia of Pyrrhocoris, and since described for numerous other insects, Arachnids and Myriapods. W. Sutton’s work on the spermatogenesis of Brachystola magna is of especial interest in this connexion. Not only does the “accessory chromosome” in this insect form a resting nucleus independent, and obviously physiologically differentiated from that formed from the remaining chromosomes (fig. 9, a), but the latter are themselves differentiated by size, there being one pair of chromosomes of each size (fig. 9, b), a point of considerable interest when we remember that half the chromosomes in each cell are necessarily derived from each parent.36
Although this morphological differentiation among the chromosomes is undoubtedly to be regarded as indicating a corresponding physiological differentiation, it by no means follows that the latter need always, or even generally, be accompanied by the former. Since, however, the specific characters of the organism must be due to the combined activity of all the chromosomes, any physiological differentiation among the latter should result in abnormal development if the full complement of chromosomes be not present.37 Boveri,38 utilizing Herbst’s method39 for separating echinoderm blastomeres, has interpreted in this manner the abnormal development which H. Driesch40 found almost invariably to follow the double fertilization of the sea-urchin egg. In such eggs the first cleavage spindle is four-poled. The chromosomes are half again as numerous as in normally fertilized eggs (54 instead of 36), but each is only divided once, so that in the distribution of the resulting 108 chromosomes the four daughter nuclei receive each only 27 instead of 36 (assuming the distribution to be fairly equal, which is by no means usually the case in four-poled mitosis). Driesch had already (1900) shown that any one of the first four blastomeres of a normally fertilized egg will, if isolated, develop normally. Boveri found that in the case of the doubly fertilized egg the isolated “¼” blastomeres develop very variously, a variability only to be accounted for by their varying chromosome equipment. Occasionally a three-poled instead of a four-poled figure resulted from double fertilization. In such cases Driesch found, as we should expect from Boveri’s interpretation, that the percentage of approximately normal larvae was considerably greater; for not only would the chances of an equal distribution of the chromosomes be much greater, but the number received by each of the three daughter cells would approximate to, or even equal, the normal.
Reduction.—In all the Metazoa the prevailing, and in the higher forms the only, method of reproduction is by the union (conjugation) of two “sexually” differentiated germ-cells or “gametes”; a small motile “microgamete” or spermatozoon and a large yolk-laden “macrogamete” or ovum (see Reproduction). This differentiation between the germ-cells is another example of the advantages of division of labour; for while the onus of bringing about the union of the germ-cells is thrown entirely on the spermatozoon, the egg devotes itself to the accumulation of food-material (yolk) for the subsequent use of the developing embryo. Far more yolk is thus secreted than would be possible by the combined efforts of both the germ-cells had each of these at the same time to preserve its motility. The fundamental physiological difference which this division of labour has produced in the germ-cells is reflected on to the general metabolism of the parents and underlies the sexual differentiation of the latter.41 Beyond this, however, sexual differentiation does not go. The two germ nuclei which enter into the formation of the first mitotic figure of the developing egg are not only physiologically equivalent, but, at the time of their union in the egg, are usually morphologically identical.42 The essence of fertilization is, therefore, the union of two germ nuclei only differing from one another in that they are derived from separate individuals.43 Since the number of chromosomes appearing in mitosis is solely dependent on the number which 718 originally entered into the composition of the nucleus (Boveri’s Law of Chromosome-Constancy), it follows that, in the mitotic figures of the developing embryo, the chromosomes will be half maternal, half paternal in origin;44 the germ nuclei thus necessarily possessing only half the number of chromosomes characteristic of the ordinary tissue cells of species, i.e. the somatic number.45 The manner in which this “reduction” in the number of chromosomes in the germ-cells is brought about, and the significance to be attached to the process, constitute the most hotly debated questions in cytology. In all the metazoa the phenomenon of reduction is associated with the two last and, usually, rapidly succeeding “maturation” divisions by which the definitive germ-cells—ova or spermatozoa—are produced.46
Assuming the persistent individuality of the chromosomes, then there are only three conceivable methods by which this numerical reduction can be brought about (Boveri, 1904, p. 60). (1) One-half the chromosomes degenerate. (2) The chromosomes are distributed entire, half to one daughter cell, half to the other (reducing division of Weismann, 1887). (3) The chromosomes fuse in pairs (Conjugation of the Chromosomes, Boveri, 1892). The first possibility—that of an actual degeneration of a part of the chromatin originally suggested by van Beneden and adopted by August Weismann, Boveri and others, has been long abandoned, and a steadily increasing bulk of evidence is tending to prove the general, if not universal, occurrence of the second method—the distribution between the daughter cells of undivided chromosomes. The occurrence of such a “reducing division” was postulated on theoretical grounds by Weismann (1887)47 and by Boveri (1888); by the former as a result of his adoption of de Vries’s hypothesis of self-propagating and qualitatively varying units for the chromatin; by the latter in relation to his theory of chromosome individuality. The actual occurrence of this reducing division was first demonstrated by Henking (1891) for Pyrrhocoris, and afterwards by Häcker, vom Rath and many others, but especially by Rückert (1894) for Cyclops (fig. 10). In this latter type the chromatin of the oocyte, as this prepares for the first maturation division, resolves itself into 12 (instead of 24) longitudinally split chromosomes (fig. 10, a). As these continue to thicken and contract a transverse fission appears (fig. 10, c). This is to be regarded as a belated segmentation of the spireme thread, and shows that the reduction so far is only a “pseudo-reduction” (Rückert), the chromosomes being really all present but temporally united in pairs, i.e. “bivalent” (Häcker). A striking confirmation of this interpretation is provided by Korschelt’s description of reduction in the annelid Ophryotrocha. In this type the full somatic number of split chromosomes (here only four) appears, and these secondarily associate end to end in pairs, thus forming split “diads” (i.e. tetrads), in every way similar to those described by Rückert for Cyclops. In the latter type, at the first maturation division, the sister diads are separated from one another, an “equating” division thus taking place. At the second division the diads are resolved into their constituent parts, and the “univalent” chromosomes are distributed to the daughter cells (reducing division). A similar process has since been described for numerous other types (e.g. various arthropods, Häcker, 1895-1898; vom Rath, 1895; and by Sutton for Brachystola, 1902-1903). In Ophryotrocha, as in Pyrrhocoris (Henking), Anasa (Paulmeir), Peripatus (Montgomery), &c., reduction occurs at the first maturation division (“pre-reduction” of Korschelt and Heider, 1900), instead of at the second division (post-reduction) as in most Copepods and Orthoptera. In many cases the tetrads (i.e. split chromosomes associated in pairs) have the form of rings, the genesis of which was first clearly determined by vom Rath (1892) in the mole cricket Gryllotalpa (fig. 11). In this form the sister diads remain united by their ends but widely separate in the middle (fig. 11, b). As in Cyclops, the belated transverse segmentation appears as the condensation of the chromatin proceeds (fig. 11, d), but the symmetrical tetrads which this process here produces make it impossible to determine at which of the two divisions reduction is effected. An essentially similar ring formation occurs in 719 Enchaeta and Calanus (vom Rath), and in the Copepods Heterocope and Diaptomus (Rückert), and in other types.48
 |
| From Korschelt and Heider’s Lehrbuch d. vergl. Entwicklungsgeschichte d. wirbellosen Tiere, by permission of Gustav Fischer. |
| Fig. 10.—Maturation Divisions. a-d, Formation of the tetrads in
Cyclops. (After Rückert.) e, 1st maturation division; separation
of the bivalent sister chromosomes. f, 2nd maturation division;
distribution of the univalent chromosomes. |
 |
| From Prof. E. B. Wilson’s The Cell in Development and Inheritance, by permission of the author and of the Macmillan Co., N. Y. |
| Fig. 11.—Maturation Divisions. Origin of the tetrads by ring
formation in the spermatogenesis of the mole-cricket (Gryllotalpa)
(vom Rath). a, Primary spermatocyte with six split, bivalent
chromosomes. b and c, Split has opened out. d, Concentration of
the chromatin has made visible the belated transverse division.
e and f, Grouping of the completed tetrads in the equatorial plate
of the first maturation division. |
 |
| From O. Hertwig, Allgemeine Biologie, by permission of Gustav Fischer. |
| Fig. 12.—Heterotypical Mitosis. (Schematic, after Flemming.) |
All the above cases, in which the reduction is effected by the distribution of entire chromosomes at one or other of the maturation divisions, may be grouped together as “pseudomitotic” (Häcker, and Korschelt & Heider). In sharp contrast to the pseudomitotic method is the “Eumitotic” method, in which the chromosomes are longitudinally divided at both divisions. Such a method not only robs the process of any “reducing” value in Weismann’s sense, but is in serious conflict with the chromosome-individuality hypothesis. Nevertheless it is in this sense that Boveri (1881) and van Beneden (1883-1887) described the maturation of the egg, and at a later period Brauer (1893) that of the spermatozoon, in Ascaris. In each case the tetrads are formed by the double longitudinal splitting of the chromosomes, the latter appearing in the prophase in the reduced number. Not only was the eumitotic method of Ascaris the first method to be described, but the descriptions are fully equal in point of clearness to that of Hertwig for the pseudomitotic maturation of Cyclops.49 A similar eumitotic maturation has been described for other types also, e.g. Sagitta and the Heteropods, but nowhere more frequently than in the Vertebrates among animals and the Phanerogams among plants. In these two latter groups the chromosomes of the reducing division only rarely have a ring form comparable to that seen in Gryllotalpa, &c. When such rings do occur their genesis is very obscure, and at no time do they present the appearance of “tetrads.” It is the characteristic appearance these looped chromosomes give to the first maturation division in many Vertebrates, and especially in the Amphibia (fig. 12), that originally led Flemming (1887) to term this type of mitosis “heterotypical”; the second division, lacking this peculiar appearance, being distinguished as “homotypical.” Until quite recently these looped chromosomes of the heterotypical mitosis of Vertebrates (and plants) were described as arising by the opening out of longitudinally split chromosomes, exactly as this occurs in the early prophase of the maturation divisions in such types as Gryllotalpa, Diaptomus, &c. In the heterotype mitosis, however, no transverse segmentation appears, and the halves of the rings, as they separate in the first division, show an obvious longitudinal split in preparation for the second division.50 Both divisions were thus interpreted as equating divisions.51 The more recent works of Farmer and Moore (1903-1905), Montgomery (1903, Amphibia), and (for plants) Strasburger (1903-1904) have shown, however, that even for the higher plants and animals, a reducing division in Weismann’s sense occurs in an essentially similar manner to that so convincingly described by Rückert, vom Rath and others, for Invertebrate types. For the chromosomes of the heterotype mitosis arise by the looping round, not opening out, of the bivalent chromosomes. The first division is thus a reducing division, while the split appearing in the anaphase of the heterotype and presumably reappearing in the prophase of the homotype is the original split of the spireme thread.
The widespread, if not universal, formation of tetrads, i.e. the temporary union in pairs of split chromosomes, in reduction, and the relation this latter process always bears to two rapidly succeeding maturation divisions—those completing the gametogenic cycle in animals and terminating the sporophytic generation in plants,—has received a suggestive explanation at the hands of Boveri (1904). The growth of the chromatin is an indispensable prelude to its reproduction (Boveri’s Law of Proportional Growth). The chromatin is therefore incapable of undergoing reproductive fission in two successive mitotic divisions when these are not separated by a resting (i.e. growth) period. In addition to this, the “bipolar” condition of the adult chromosomes, which determines its mode of attachment to mantle fibres from both poles of the spindle, is not possessed by the unripe chromatin. The undivided, i.e. unripe, chromosomes are therefore incapable of utilizing the mitotic mechanism for such a transverse fission as Weismann originally postulated. The difficulty is, however, at once overcome if the unripe chromosomes are associated in pairs in the equatorial plate, for the bivalent chromosomes so produced are bipolar just as are the adult (i.e. split) chromosomes in the ordinary and homotype mitosis.52
Synopsis (συνάπτειν, to fuse together).—During the prophase of the reducing or heterotype divisions the whole of the chromatin becomes temporarily massed together at one pole of the nucleus (Moore, 1896, for Elasmobranchs). Montgomery (1901) has suggested that this is to facilitate the temporary union in pairs, or “conjugation” of homologous paternal and maternal chromosomes. In Ascaris megalocephala var. univalens, where the somatic number is only two, the association must necessarily be between homologous chromosomes. The assumption that this “selective pairing” of equivalent chromosomes is universal is supported by the behaviour of the “Heterochromosomes” (Montgomery) of the Hemiptera. These chromosomes, distinguished by their size, are paired before, and single after, the “pseudo-reduction” has taken place. Even more convincing is Sutton’s account of reduction in Brachystola already referred to.53 Boveri (1904) has suggested that this temporary association of the chromosomes—presumably facilitated by the synapsis—has a much deeper meaning than to ensure their correct distribution between the daughter nuclei in the heterotype mitosis; the associated chromosomes exchanging material in a manner analogous to conjugation in Paramoecium.54
Present Position of the Cell-theory.—Since the time of Schleiden and Schwann a wealth of evidence has accumulated in support of the “cell-theory”—the theory which regards the cell as the unit of organic structure. “The organism consists 720 morphologically, of cells, and subsists, physiologically, by means of the ‘reciprocal action’ of the cells,”—this was the cell standpoint of Schleiden and Schwann, and it is no exaggeration to say that this same conception has dominated the cell-theory almost to the present day.55 The frequently striking correlation between cell-division and cell-differentiation in development has caused this process to be regarded as dependent on cell-division, while a wholly exaggerated importance has been attached to the distinction between “unicellular” and “multicellular” organisms—between “intercellular” and “intracellular” organs. The influence of the “cells” upon one another, the subordination of the cell’s growth, division and differentiation, to the requirements of the whole organism—seen in normal growth, but nowhere more strikingly than in development and regeneration,—is, however, very difficult of explanation in terms of the cell-theory as this was, until quite recently, generally understood. The very elaborate regional differentiation of the protoplasm often seen in the Protozoa sufficiently indicate that multicellular structure is no essential condition for complex regional differentiation. That the regional differentiation of the protoplasm in the Metazoa should usually correspond with cell-limits is scarcely surprising. Nor is it to be wondered at that, with so convenient a mechanism for segregation to hand as cell-division, the progressive differentiation seen during development should often appear to go hand in hand with this process. In recent years, however, evidence has been steadily accumulating to show that this association between cell-division and regional differentiation of the protoplasm in development is a casual one—as casual, and as natural, as the correspondence between cell limits and regional differentiation in the formed tissues. The fact that the regional differentiation may be foreshadowed in the egg before cleavage begins,56—that as Driesch has shown, the mode of cleavage may be artificially altered without affecting the ultimate organization of the embryo,—and many other similar observations, tend to emphasize the importance of the “organism” standpoint (C. O. Whitman, 1903, p. 642) in contradistinction to the widely prevalent “cell” standpoint. The occurrence of syncytial organs and organisms, and the increasing frequency with which protoplasmic continuity is being demonstrated between all kinds of cells, are facts tending in the same direction. In the plant kingdom the growth of the mass has been recognized as the primary factor in development;57 die Pflanze bildet Zellen, nicht die Zelle bildet Pflanzen (de Bary). For the animal kingdom this “Inadequacy of the Cell-Theory of Development” has been maintained amongst others by Whitman,58 and by Adam Sedgwick.59 The latter author, mainly as the result of work on the development of Peripatus and of Elasmobranch embryos, regards the developing embryo as a continuous protoplasmic reticulum, for the nuclei of which the limiting epithelial layers constitute as it were a breeding ground. Differentiation is a regional specialization of this nucleated meshwork, and is not to be regarded as the result of the proliferation and subsequent specialization of cells predestined by cleavage for this end.
It is possible to suggest a mechanico-physical explanation of multicellular structure which will deprive the cell of much of its assumed significance as a unit of organization. The fact that surface area becomes relatively less extensive as bulk increases would alone set a limit to the size of “unicellular” organisms; for not only is there a constant reaction between nucleus and cytoplasm through the nuclear membrane, but the surface of the cell serves both for the intake of food and the elimination of waste material. In addition to the limit thus imposed upon the cytoplasmic area which can be effectually controlled by the nucleus, and the necessity for a minimum surface area to the protoplasmic mass, the advantages of the more or less complete subdivision of the living substance into—as far as their metabolism is concerned—semi-autonomous units, is indicated by the mechanical support derived from the specialized cell walls and turgescent cells of the plant, and the intercellular secretions of the animal tissues. It is more than possible that these two conditions—i.e. surface area for diffusion, and mechanical support—are alone responsible for the origin of multicellular structure, and that the sharply defined character this now so generally possesses has been secondarily acquired as a result of the facilities it undoubtedly offers for regional specialization in the protoplasmic mass.
Bibliography.—The special literature of cytology has grown to large dimensions. The following are the more important text-books and papers of general interest: E. B. Wilson, The Cell in Development and Inheritance (2nd ed., 1900); A. Gurwitsch, Morphologie und Biologie der Zelle (Jena, 1904); O. Hertwig, Allgemeine Biologie (Jena, 1906); Korschelt and Heider, Lehrbuch der vergl. Entwicklungsgeschichte der wirbellosen Tiere, Allgem. Teil, “The Germ Cells and Experimental Embryology” (Jena, 1903); Whitman, “The Inadequacy of the Cell Theory of Development,” Journ. Morph. viii., 1893; Adam Sedgwick, “On the Inadequacy of the Cellular Theory of Development,” Quart. Journ. Micro. Science, xxxvii.; G. C. Bourne, “A Criticism of the Cell Theory” (an answer to Sedgwick’s paper), Quart. Journ. Micro. Science, xxxviii.; Th. Boveri, “Befruchtung,” Merkel-Bonnets Ergebnisse der Anat. u. Entwicklungsgesch. Bd. i. (1892), Das Problem der Befruchtung (Jena, 1902), Ergebnisse über die Konstitution der chromatischen Substanz des Zellkerns (Jena, 1904); J. Rückert, “Die Chromatinreduktion bei der Reifung der Sexualzellen,” Merkel-Bonnets Ergebnisse, Bd. iii. (1894); V. Häcker, “Die Reifungserscheinungen,” Ergebn. Anat. u. Entwicklungsgesch. Bd. viii. (1898); F. Meves, “Zellteilung,” Merkel-Bonnets Ergebnisse, Bd. viii. (1898, 1899); W. Waldeyer, “Die Geschlechtszellen,” in O. Hertwig’s Handbuch der vergleich. u. experiment. Entwicklungslehre d. Wirbeltiere (1901, 1903).
1 Allgemeine Physiologie, p. 53 (1895).
2 Vom inwendigen Bau der Gewachse (1806).
3 The Chromoplastids of the vegetable cell come under a different category of cell-inclusions; see Plants: Cytology.
4 Cf. Pfeffer’s classical experiments on the physiological significance of cell-continuity in plant tissues (Über den Einfluss des Zellkerns auf die Bildung der Zellhaut, 1896). The recent work in physiology on the influence substances secreted by certain tissues and circulating in the blood-stream exert upon other and widely different tissues, should not be lost sight of in this connexion.
5 The influence this protoplasmic continuity may have upon our conception of the cell as a unit of organization is referred to below (Present Position of the Cell-theory).
6 A term (from κάρυον, kernel) suggested by Flemming to replace Strasburger’s hybrid term “nucleoplasm” (1882). The earlier workers, e.g. Leydig, Schultze, Brücke, de Bary, &c., restricted the term protoplasm to the cell-body—the “Cytoplasm” of Strasburger, an example still followed by O. Hertwig.
7 From linum, a thread, Schwarz, 1887.
8 From χρῶμα, colour, Flemming, 1879.
9 The formation of pseudopodia and accompanying changes in form of Amoeba were observed as early as 1755 by Raesel von Rosenhof, who named it on this account the “little Proteus.”
10 “Sur les rapports des cils vibratiles avec les centrosomes,” Archives d’anatomie microscopique (1898).
11 “Über Zentralkörper in männlichen Geschlechtszellen von Schmetterlingen” (Anat. Anz. Bd. xiv., 1897). Cf. also the papers of Lenhossek (Über Flimmerzellen, 1898), Karl Peter (Das Zentrum für die Flimm- und Giesselbewegung, 1899) and Verworn (Studien zur Physiologie der Flimmerbewegung, 1899).
12 Cf., however, the present writer’s interpretation of this structure in the oocyte of Antedon. Phil. Trans. Royal Soc. (1906), B. 249.
13 Claude Bernard expressed the same conclusion in 1885. Rejecting both the view that vital phenomena were identical with chemico-physical phenomena, and that which regarded them as totally distinct, he suggested a third point of view: “l’élément ultime du phénomène est physique; l’arrangement est vital.”
14 Many forms of response to stimulus involve no visible specialization, e.g. positive and negative heliotropism, chemiotropism, geotropism, &c., seen more especially in plants, but occurring also in the animal kingdom.
15 Prominent among these are: Schleiden (1873), Fol (1873-1877), Auerbach (1874), Bütschli (1876), Strasburger (1875-1888), O. Hertwig (1875-1890), R. Hertwig (1875-1877); Flemming (1879-1891), van Beneden (1883-1887), Rabl (1889), Boveri (1887-1903).
16 This distinction between the chromatic and achromatic portions of the mitotic figure is due to Flemming.
17 The genesis of the spireme thread was first described by E. G. Balbiani in 1876.
18 “Recherches sur la maturation de l’œuf, la fécondation et la division cellulaire” (Archives de biologie, vol. iv.).
19 First discovered by Flemming in 1879 and confirmed by Retzius in 1881.
20 The discovery by Hermann of the central spindle first clearly showed that two kinds of fibres must be recognized in the mitotic figure. Those of the central spindle correspond to the continuous spindle fibres of Flemming (1891) and Strasburger (1884), and the mantle fibres, i.e. half-spindle or Polstrahlen, of van Beneden (1887) and Boveri (1889-1890).
21 Planter, Watasé, Griffen and others.
22 e.g. Euglypha (Schewiakoff, 1888), Infusoria (R. Hertwig, 1898). So also Korschelt for Ophryotrocha, and many other cases.
23 e.g. Bauer, spermatogenic cells of Ascaris univalens.
24 Cf. also Watasé, Solger and Zimmermann.
25 This term is due to Boveri (Zellenstudien, ii., 1888, p. 68; Jen. Zeit. xxii.), but it was intended by him to include the region of modified cytoplasm or “centrosphere” often enclosing the centrosome proper, i.e. “centriole” of Boveri.
26 For outline of fertilization see article Reproduction.
27 e.g. lymph and various epithelial and connective tissue cells of salamander larva (Flemming, 1891; Heidenhain, 1892); pigment cells of fishes (Solger, 1891); red blood corpuscles (Heidenhain, Eisen, 1897); and numerous other cases.
28 For an interesting development of this subject see Watasé (1894). This author not only identifies the centrosome with the structures seen in lymph cells, &c., but compares it to the basal granules of ciliated cells and to the varicose swellings on the sarcostyles of striped muscle cells!
29 The force of this evidence is admitted by Boveri himself. Meves, however, maintains the possibility that the numerous centrosomes appearing in the egg arise by the rapid fragmentation of a centrosome already present.
30 Cf. especially the behaviour of the centrosomes in the fertilization of the egg of Pleurophyllidia (MacFarland, 1897) and that of Cerebratulus (Coe, 1901). Not only may the sperm centrosomes totally disappear before reaching the egg-nucleus, but in the latter type the definitive centrosomes appear while the last traces of the sperm asters are still visible.
31 e.g. Meves; Spermatagonia of Salamandra.
32 Cf. especially the artificial production of amitosis in Spirogyra; W. Pfeffer, 1899.
33 Cf. Boveri, 1904, p. 13. (For Boveri’s criticism of Delage’s views, cf. Boveri, 1901 and 1902.)
34 It should, however, be noted that the assumption that a particular group of characters remains always associated in a particular chromosome is one that is very difficult to reconcile with the mode of inheritance of Mendelian pairs of characters in the case of organisms with a relatively small chromosome number.
35 Boveri (1902), “Fertilization of enucleated Echinus-egg fragments,” and M. Boveri (1903); by shaking the egg shortly after fertilization the sperm centrosome is prevented from dividing, and a monaster instead of a diaster results, the divided chromosomes remaining in the one nucleus.
36 Cf. especially in this connexion Häcker’s paper Über die Schicksale der elterlichen und grosselterlichen Kernanteile (1902).
37 Each nucleus contains a duplicate set of chromosomes, the one of maternal, the other of paternal origin, and either of these sets alone suffices for development. This is clearly shown by the experiments of Loeb (1899) and Wilson (1901) on the artificial parthenogenesis of the sea-urchin egg; and those of O. Hertwig (1889 and 1895), Delage (1899) and Winkler (1901), on the fertilization of enucleated Echinoderm eggs (Merogony, Delage). The fact that in some forms, e.g. Ascaris megalocephala var. univalens, only one chromosome is derived from each parent, originally led Boveri to conclude that all chromosomes must necessarily be physiologically equivalent.
38 Über mehrpolige Mitosen als Mittel zur Analyse des Zellkerns (1902).
39 Über das Auseinandergehen von Furchungs- und Gewebezellen in kalkfreien Medium (1900).
40 “Entwicklungsmechanische Studien V.” (Zeit. für wiss. Zool., Bd. lv., 1892).
41 See Geddes and Thomson, Sex, esp. pp. 127, 137 and 139.
42 The equivalence of the germ nuclei in development is shown by the experiments on the fertilization of enucleated eggs and artificial parthenogenesis already referred to.
43 O. Hertwig, 1873; but esp. van Beneden, 1883.
44 Häcker, “Über die Selbstständigkeit der väterlichen und mütterlichen Kernbestandteile,” Arch. f. mikr. Anat. Bd. xlvi. (1896).
45 First discovered by van Beneden (1883, 1887) for the egg of Ascaris.
46 In the case of the egg the whole of the yolk stored by the “oocyte” (cell-generation immediately preceding the maturation divisions) is handed on to only one of the four resulting cells—an obvious economy. The three yolkless cells are necessarily functionless—abortive ova—and are known as the “polar bodies” (Hertwig). In spermatogenesis the maturation divisions, though bearing the same relation to reduction as in oogenesis (Platner, 1889; O. Hertwig, 1890), give rise to four functional germ-cells. The explanation of sexual differentiation given above, and that of polar body formation given here, render it needless to do more than mention the theories of Mimot (1877), van Beneden (1883) and others, by which “maturation” was regarded as removing the “male” element from the otherwise “hermaphrodite” egg.
47 Weismann postulated a transverse division of the chromosomes, not a distribution of entire chromosomes; but the result as far as the reduction in the number of hereditary qualities goes is the same. The inability of the mitotic mechanism to effect the transverse division of unsplit chromosomes is pointed out by Boveri (1904).
48 For an exhaustive account of reduction in Invertebrates see Korschelt and Heider, Entwicklungsgeschichte, Allgem. Teil ii. (Jena, 1903).
49 Nevertheless the possibility of a pseudomitotic interpretation of maturation in Ascaris also has been maintained by O. Hertwig (1890), p. 277, Carnoy and Boveri (1904).
50 The partial or even complete reconstruction of the nucleus between the heterotype and homotype division in Vertebrates makes it difficult to determine the identity of the split seen in the anaphase of the heterotype with that reappearing in the prophase of the homotype.
51 e.g. Moore, 1895 (Scyllium); Flemming, 1897; Carnoy and Lebrun, 1899 (Amphibia); McGregor, 1899; Lenhossek, 1898 (mammals), and many others. So also for plants: Strasburger and Mottier, 1897; Dixon, 1896; Sargant, 1896-1897; Farmer and Moore, 1895; Gregoire, 1899; Guignard, 1899, &c.
52 H. Henking (1899), T. Montgomery (1898) and F. C. Paulmeir (1899) describe the diverging bivalent halves of the tetrad as being united each by two fibres with the corresponding spindle pole. At the next division, at which the diad is resolved into its constituent univalent chromosomes, the daughter chromosomes are attached to the spindle pole each by only one fibre; the two fibres now passing to opposite poles of the spindle being the same fibres which, in the preceding mitosis, were attached to one and the same pole.
53 Reference may be here made to Rosenberg’s description (1904) of the heterotype mitosis in Drosera hybrids. In the one parent (D. rotundifolia) the somatic number is 20, in the other (D. longifolia) 10; while the hybrid itself has a somatic number of 30. The reduced number in the hybrid, however, is not 15 but 20. Of these 10 are large and 10 small, the latter presumably representing the supernumerary, and hence unpaired, chromosomes of the D. rotundifolia parent.
54 In their 1905 paper J. B. Farmer and J. E. S. Moore describe two successive synaptic stages (e.g. Elasmobranchs), the first during the contraction of the spireme thread, the second during the looping up of the bivalent segments. (In this paper the authors suggest the term “Meiosis” or “Meiotic phase” for the nuclear changes accompanying the two maturation divisions in plants and animals (μείωσις, reduction).
55 Whitman, Jour. Morph., 1903.
56 This “Precocious segregation” (Lankester, 1877) is well seen in the eggs of many Ctenophorae, Annelids, Gastropods and Nematodes. See the papers by Lillie (1901), Conklin (1902), &c., and especially Wilson on “Dentalium,” Journ. of Exp. Zool., No. 1, 1904.
57 Hofmeister, de Bary, Sachs, &c.
58 Loc. cit.
59 Quart. Journ. Micro. Science, 1894, vol. xxxvii.
CYZICENUS, the architectural term given by Vitruvius to the large hall, used by the Greeks, which faced the north, with a prospect towards the gardens; the windows of this hall opened down to the ground, so that the green verdure could be seen by those lying on the couches.
CYZICUS, an ancient town of Mysia in Asia Minor, situated on the shoreward side of the present peninsula of Kapu-Dagh (Arctonnesus), which is said to have been originally an island in the Sea of Marmora, and to have been artificially connected with the mainland in historic times. It was, according to tradition, occupied by Thessalian settlers at the coming of the Argonauts, and in 756 B.C. the town was founded by Greeks from Miletus. Owing to its advantageous position it speedily acquired commercial importance, and the gold staters of Cyzicus were a staple currency in the ancient world till they were superseded by those of Philip of Macedon. During the Peloponnesian War (431-404 B.C.) Cyzicus was subject to the Athenians and Lacedaemonians alternately, and at the peace of Antalcidas (387 B.C.), like the other Greek cities in Asia, it was made over to Persia. The history of the town in Hellenistic times is closely connected with that of the dynasts of Pergamum, with whose extinction it came into direct relations with Rome. Cyzicus was held for the Romans against Mithradates in 74 B.C. till the siege was raised by Lucullus: the loyalty of the city was rewarded by an extension of territory and other privileges. Still a nourishing centre in Imperial times, the place appears to have been ruined by a series of earthquakes—the last in A.D. 1063—and the population was transferred to Artaki at least as early as the 13th century, when the peninsula was occupied by the Crusaders. The site is now known as Bal-Kiz (Παλαία Κύζικος?) and entirely uninhabited, though under cultivation. The principal extant ruins are:—the walls, which are traceable for nearly their whole extent, a picturesque amphitheatre intersected by a stream, and the substructures of the temple of Hadrian. Of this magnificent building, sometimes ranked among the seven wonders of the ancient world, thirty-one immense columns still stood erect in 1444. These have since been carried away piecemeal for building purposes by the Turks.
See J. Marquardt, Cyzicus (Berlin, 1830); G. Perrot, Exploration de la Galatie (Paris, 1862); F. W. Hasluck and A. E. Henderson in Journal of Hellenic Studies (1904), 135-143.
CZARNIECKI, STEPHEN (1590-1665), Polish general, learnt the science of war under Stanislaw Koniecpolski in the Prussian campaigns against Gustavus Adolphus (1626-1629), and under Wladislaus IV. in the Muscovite campaign of 1633. On the 15th of April 1648 he was one of the many noble Polish prisoners who fell into the hands of Chmielnicki at the battle of “Yellow Waters,” and was sent in chains to the Crimea, whence he was ransomed in 1649. He took an active part in all the subsequent wars with the Cossacks and received more disfiguring wounds than any other commander. When Charles X. of Sweden invaded Poland in 1655, Czarniecki distinguished himself by his heroic defence of Cracow, which he only surrendered under the most honourable conditions. His energy and ability as a leader of guerillas hampered Charles X. at every step, and though frequently worsted he from time to time inflicted serious defeats upon the Swedes, notably at Jaroslaw and at Kozienice in 1656. Under his direction the popular rising against the invader ultimately proved triumphant. It was he who brought King John Casimir back from exile and enabled him to regain his lost kingdom. It was against his advice that the great battle of Warsaw was fought, and his subsequent strategy neutralized the ill effects of that national disaster. On the retirement of the Swedes from Cracow and Warsaw, and the conclusion of the treaty of Copenhagen with the Danes, he commanded the army corps sent to drive the troops of Charles X. out of Jutland and greatly contributed to the ultimate success of the Allies. On the conclusion of the Peace of Oliva, which adjusted the long outstanding differences between Poland and Sweden, Czarniecki was transferred to the eastern frontier where the war with Muscovy was still raging. In the campaign of 1660 he won the victories of Polonka and Lachowicza and penetrated to the heart of the enemy’s country. The diet of 1661 publicly thanked him for his services; the king heaped honours and riches upon him, and in 1665 he was appointed acting commander-in-chief of Poland, but died a few days after receiving this supreme distinction. By his wife Sophia Kobierzycka he left two daughters. Czarniecki is rightly regarded as one of the most famous of heroic Poland’s great captains, and to him belongs the chief merit of extricating her from the difficulties which threatened to overwhelm her during the disastrous reign of John Casimir. Czarniecki raised partisan-warfare to the dignity of a science, and by his ubiquity and tenacity demoralized and exhausted the regular armies to which he was generally opposed.
See Ludwik Jenike, Stephen Czarniecki (Pol.) (Warsaw, 1891); Michal Dymitr Krajewski, History of Stephen Czarniecki (Pol.), (Cracow, 1859).
CZARTORYSKI, ADAM GEORGE, Prince (1770-1861), Polish statesman, was the son of Prince Adam Casimir Czartoryski and Isabella Fleming. After a careful education at home by eminent specialists, mostly Frenchmen,1 he first went abroad in 1786. At Gotha he heard Goethe read his Iphigenie auf Tauris, and made the acquaintance of the dignified Herder and “fat little Wieland.” In 1789 he visited England with his mother, and was present at the trial of Warren Hastings. On a second visit in 1793 he made many acquaintances among the English aristocracy and studied the English constitution. In the interval between these visits he fought for his country during the war of the second partition, and would subsequently have served under Kosciuszko also had he not been arrested on his way to Poland at Brussels by the Austrian government. After the third partition the estates of the Czartoryskis were confiscated, and in May 1795 Adam and his younger brother Constantine were summoned to St Petersburg; later in the year they were commanded to enter the Russian service, Adam becoming an officer in the horse, and Constantine in the foot guards. Catherine was so favourably impressed by the youths that she restored them part of their estates, and in the beginning of 1796 made them gentlemen in waiting. Adam had already met the grand duke Alexander at a ball at the princess Golitsuin’s, and the youths at once conceived a strong “intellectual friendship” for each other. On the accession of the emperor Paul, Czartoryski was appointed adjutant to Alexander, now Cesarevich, and was permitted to revisit his Polish estates for three months. At this time the tone of the Russian court was extremely liberal, humanitarian enthusiasts like Peter Volkonsky and Nikolai Novosiltsov possessing great influence.
Throughout the reign of Paul, Czartoryski was in high favour and on terms of the closest intimacy with the emperor, who in December 1798 appointed him ambassador to the court of Sardinia. On reaching Italy Czartoryski found that the monarch to whom he was accredited was a king without a kingdom, so that the outcome of his first diplomatic mission was a pleasant tour through Italy to Naples, the acquisition of the Italian language, and a careful exploration of the antiquities of Rome. In the spring of 1801 the new emperor Alexander summoned his friend back to St Petersburg. Czartoryski found the tsar still suffering from remorse at his father’s assassination, and incapable of doing anything but talk religion and politics to a small circle of private friends. To all remonstrances he only replied “There’s plenty of time.” The senate did most of the current business; Peter Vasilevich Zavadovsky, a pupil of the Jesuits, was minister of education. Alexander appointed Czartoryski curator of the academy of Vilna (April 3, 1803) that he might give full play to his advanced ideas. He was unable, however, to give much attention to education, for from the beginning of 1804, as adjunct of foreign affairs, he had the practical control of Russian diplomacy. His first act was to protest energetically against the murder of the due d’Enghien (March 20, 1804), and insist on an immediate rupture with France. On the 7th of June the French minister Hédouville quitted St Petersburg; and on the 11th of August a note dictated by Czartoryski to Alexander was sent to the Russian minister in London, urging the formation of an anti-French coalition. It was Czartoryski also who framed the Convention of the 6th of November 1804, whereby Russia agreed to put 115,000 and Austria 235,000 men in the field against Napoleon. Finally, on the 11th of April 1805 he signed an offensive-defensive alliance with England. But his most striking ministerial act was a memorial written in 1805, but otherwise undated, which aimed at transforming the whole map of Europe. In brief it amounted to this. Austria and Prussia were to divide Germany between them. Russia was to acquire the Dardanelles, the Sea of Marmora, the Bosphorus with Constantinople, and Corfu. Austria was to have Bosnia, Wallachia and Ragusa. Montenegro, enlarged by Mostar and the Ionian Islands, was to form a separate state. England and Russia together were to maintain the equilibrium of the world. In return for their acquisitions in Germany, Austria and Prussia were to consent to the erection of an autonomous Polish state extending from Danzig to the sources of the Vistula, under the protection of Russia. Fantastic as it was in some particulars, this project was partly realized2 in more recent times, and it presented the best guarantee for the independent existence of Poland which had never been able to govern itself. But in the meantime Austria had come to an understanding with England as to subsidies, and war had begun.
In 1805 Czartoryski accompanied Alexander both to Berlin and Olmütz as chief minister. He regarded the Berlin visit as a blunder, chiefly owing to his profound distrust of Prussia; but Alexander ignored his representations, and in February 1807 he lost favour and was superseded by Andrei Eberhard Budberg. But though no longer a minister Czartoryski continued to enjoy Alexander’s confidence in private, and in 1810 the emperor candidly admitted to Czartoryski that his policy in 1805 had been erroneous and he had not made a proper use of his opportunities. The same year Czartoryski quitted St Petersburg for ever; but the personal relations between him and Alexander were never better. The friends met again at Kalisch shortly before the signature of the Russo-Prussian alliance of the 20th of February 1813, and Czartoryski was in the emperor’s suite at Paris in 1814, and rendered his sovereign material services at the congress of Vienna.
On the erection of the congressional kingdom of Poland 722 every one thought that Czartoryski, who more than any other man had prepared the way for it, would be its first governor-general, but he was content with the title of senator-palatine and a share in the administration. In 1817 the prince married Anna Sapiezanko, the wedding leading to a duel with his rival Pac. On the death of his father in 1823 he retired to his ancestral castle at Pulawy; but the Revolution of 1830 brought him back to public life. As president of the provisional government he summoned (Dec. 18th, 1830) the Diet of 1831, and after the termination of Chlopicki’s dictatorship was elected chief of the supreme council by 121 out of 138 votes (January 30th). On the 16th of September his disapproval of the popular excesses at Warsaw caused him to quit the government after sacrificing half his fortune to the national cause; but it must be admitted that throughout the insurrection he did not act up to his great reputation. Yet the energy of the sexagenarian statesman was wonderful. On the 23rd of August he joined Girolano Ramorino’s army-corps as a volunteer, and subsequently formed a confederation of the three southern provinces of Kalisch, Sandomir and Cracow. At the end of the war he emigrated to France, where he resided during the last thirty years of his life. He died at his country residence at Montfermeil, near Meaux, on the 15th of July 1861. He left two sons, Witold (1824-1865), and Wladyslaus (1828-1894), and a daughter Isabella, who married Jan Dzialynski in 1857. The principal works of Czartoryski are Essai sur la diplomatie (Marseilles, 1830); Life of J. U. Niemcewiez (Pol). (Paris, 1860); Alexander I. et Czartoryski: correspondance ... et conversations (1801-1823) (Paris, 1865); Mémoires et correspondance avec Alex. I., with preface by C. de Mazade, 2 vols. (Paris, 1887); an English translation Memoirs of Czartoryski, &c., edited by A. Gielguch, with documents relating to his negotiations with Pitt, and conversations with Palmerston in 1832 (2 vols., London, 1888).
See Bronislaw Zaleski, Life of Adam Czartoryski (Pol.) (Paris, 1881); Lubomir Gadon, Prince Adam Czartoryski (Pol.) (Cracow, 1892); Ludovik Debicki, Pulawy, vol. iv.; Lubomir Gadon, Prince Adam Czartoryski during the Insurrection of November (Pol.) (Cracow, 1900).
1 Among them was the famous democrat Dupont de Nemours.
2 e.g. Austria obtained Bosnia, and Montenegro has been enlarged.
CZARTORYSKI, FRYDERYK MICHAL, Prince (1696-1775), Polish statesman, was born in 1696. Of small means and no position, he owed his elevation in the world to extraordinary ability, directed by an energetic but patriotic ambition. After a careful education on the best French models, which he completed at Paris, Florence and Rome, he attached himself to the court of Dresden, and through the influence of Count Fleming, the leading minister there, obtained the vice-chancellorship of Lithuania and many other dignities. Czartoryski was one of the many Polish nobles who, when Augustus II. was seriously ill at Bialyvostok in 1727, signed the secret declaration guaranteeing the Polish succession to his son; but this did not prevent him from repudiating his obligations when Stanislaus Leszczynski was placed upon the throne by the influence of France in 1733. When Stanislaus abdicated in 1735 Czartoryski voted for Augustus III. (of Saxony), who gladly employed him and his family to counteract the influence of the irreconcilable Potokis. For the next forty years Czartoryski was certainly the leading Polish statesman. In foreign affairs he was the first to favour an alliance with Russia, Austria and England, as opposed to France and Prussia—a system difficult to sustain and not always beneficial to Poland or Saxony. In Poland Czartoryski was at the head of the party of reform. His palace was the place where the most promising young gentlemen of the day were educated and sent abroad that they might return as his coadjutors in the great work. His plan aimed at the restoration of the royal prerogative and the abolition of the liberum veto, an abuse that made any durable improvement impossible. These patriotic endeavours made the Czartoryskis very unpopular with the ignorant szlachta, but for many years they had the firm and constant support of the Saxon court, especially after Brühl succeeded Fleming.
Czartoryski reached the height of his power in 1752 when he was entrusted with the great seal of Lithuania; but after that date the influence of his rival Mniszek began to prevail at Dresden, whereupon Czartoryski sought a reconciliation with his political opponents at home and foreign support both in England and Russia. In 1755 he sent his nephew Stanislaus Poniatowski to St Petersburg as Saxon minister, a mission which failed completely. Czartoryski’s philo-Russian policy had by this time estranged Brühl, but he frustrated all the plans of the Saxon court by dissolving the diets of 1760, 1761 and 1762. In 1763 he went a step farther and proposed the dethronement of Augustus III., who died the same year. During the ensuing interregnum the prince chancellor laboured night and day at the convocation diet of 1764 to reform the constitution, and it was with displeasure that he saw his incompetent nephew Stanislaus finally elected king in 1765. But though disgusted with the weakness of the king and obliged to abandon at last all hope of the amelioration of his country, Czartoryski continued to hold office till the last; and as chancellor of Lithuania he sealed all the partition treaties. He died in the full possession of his faculties and was considered by the Russian minister Repnin “the soundest head in the kingdom.” It is a mistake, however, to regard Czartoryski as the sole reforming statesman of his day, and despite his great services there were occasions when the partisan in him got the better of the statesman. His foreign policy, moreover, was very vacillating, and he changed his “system” more frequently perhaps than any contemporary diplomatist. But when all is said he must remain one of the noblest names in Polish history.
See the Correspondence of Czartoryski in the Collections of the Russian Historical Society, vols. 7, 10, 13, 48, 51, 67 (St Petersburg, 1890, &c.); Wladyslaw Tadeusz Kisielewski, Reforms of the Czartorysccy (Pol.) (Sambor, 1880); Adalbert Roepell, Polen um die Mitte des XVIII. Jahrhunderts (Gotha, 1876); Jacques Victor Albert de Broglie, Le Secret du roi (Paris, 1878); Antoni Waliszewki, The Potoccy and the Czartorysccy (Pol.); Carl Heinrich Heyking, Aus Polens und Kurlands letzten Tagen (Berlin, 1897); Ludwik Denbicki, Pulawy (Pol.) (Lemberg, 1887-1888).
CZECH (in Bohemian, Čech), a name which signifies an inhabitant of Čechy, the native designation of Bohemia. The Czechs belong to the Slavic race, and according to the usually accepted division they form, together with the Poles and the almost extinct Lusatians, the group of the Western Slavs. Speaking generally, it can be said that the Czechs inhabit a large part of Bohemia, a yet larger part of Moravia, parts of Silesia—both Austrian and Prussian—and extensive districts in northern Hungary. In the 19th century the Czechs of Hungary—much to their own detriment—developed a written language that differs slightly from that used in Bohemia, but as regards their race they are identical with the Bohemians and Moravians. Beyond the borders of this continuous territory there are many Czechs in Lower Austria. Vienna in particular has a large and increasing Czech population. There are also numerous Czechs in Russia, particularly Volhynia, in the United States—where a large number of newspapers and periodicals are published in the Czech language—and in London. Though the statistics are very uncertain and untrustworthy, it can be stated that the Czechs number about eight millions.
The period at which the Czechs settled in Bohemia is very uncertain; all theories, indeed, with regard to the advent of the Slavs in northern and eastern Europe are merely conjectural. It was formerly generally accepted as a fact that all Bohemia was originally inhabited by Celtic tribes, who were succeeded by the Germanic Marcomanni, and later by the Slavic Czechs. According to a very ancient tradition reproduced in the book of Cosmas, the earliest Bohemian chronicler, the Czechs arrived in Bohemia led by their eponymous chief Čechus, and first settled on the Řip Hill (Georgberg) near Roudnice. It is a strange proof of the intense obscurity of the earliest Bohemian history that Cosmas, writing at the beginning of the 12th century, is already unaware of the existence of pre-Slavic inhabitants of Bohemia. It is historically certain that the Czechs inhabited parts of Bohemia as early as the 6th century. In the absence of all historical evidence, modern Czech scholars have endeavoured by other means to throw some light on the earliest period of the 723 Czechs. By craniological studies and a thorough examination of the fields where the dead were burnt (in Czech žárove pole), still found in some parts of Bohemia, they have arrived at the conclusion that parts of the country were inhabited by Czechs, or at least by Slavs, long before the Christian era, perhaps about the year 500 B.C.
It is certain that the Slavs at the time when they first appeared in history had a common language, known as the ancient Slavic (praslovanský) language. When in the course of time the Slavs occupied various countries, which were often widely apart, different dialects arose among them, many of which were influenced by the language of the neighbouring non-Slavic populations. Thus the Czech language from an early period absorbed many German words. It is probable that the development of the Czech language as an independent one, was very gradual. Existent documents, such as the hymn to St Wenceslas, which belongs to the second half of the 10th century, are written partly in old-Slavic, partly in Czech. When the Slavs first occupied Bohemia, they were probably divided into several tribes, of which the Czechs, who inhabited Prague and the country surrounding it, were the most powerful. It is probable that these smaller tribes were only gradually subdued by the Czechs and that some of them had previously to their absorption adopted special dialects. The Netolice, Lučane, Pšovane, Sedlčane appear to have been among the more important tribes who were forced to acknowledge the supremacy of the Czechs, and it may be conjectured that their language for a time differed slightly from that of their conquerors. The Czech language has, like all Slavic ones, a strong tendency to develop dialects; this was the case at the time of its first appearance as an independent language, and has to a certain extent continued up to the present day. The dialects of Moravia and the northern districts of Hungary still show variations from the generally accepted forms of the Czech language, though since the foundation of the Czech university of Prague this—at least among the educated classes—is no longer true to the same extent as it formerly was. The Czech language at the time of its formation naturally remained closest to those other Slav-speaking countries which were geographically its neighbours, the Poles and the Lusatians, and it may be said that this is still the case. The Czech language at the time when in the 12th and 13th centuries it first appears as a separate and distinct one, differed considerably from that of the present day. Ancient Czech had several diphthongs, such as: ia, ie, iu, uo and au, that are unknown to the present language. The letter “l” had a threefold sound, and besides the letters b, p, m, v, the softer forms b′, p′, m′, v′, were also in existence. The letter g (as in other Slavic languages) was often used where modern Czechs employ the letter h. Ancient Bohemian had three numbers, the singular, plural and dual; of the dual only scant vestiges remain in modern Czech.
Once it had obtained its independence, the Czech language developed rapidly, and the philosophical and theological writings of Thomas of Štitný (1331-1401) proved that it could already be used even for dealing with the most abstract subjects, though Štitný was blamed by the monks for not writing in Latin, as was then customary. The Czech language is greatly indebted also to John Hus, whose best and most original works were written in the language of his country. Hus showed great interest in the orthography and grammar of his language, and has devoted an interesting treatise entitled “Orthographia bohemica” to it. As already mentioned, the Czech language had sprung from diverse dialects, and Hus endeavoured to establish uniformity. To the Bohemian reformer is also due the system of so-called diacritic marks—such as č, ů, ý—which with some modifications are still in use.1 The Latin characters which were in the earliest times, as again at the present day, used when writing Czech, are quite unable to reproduce some sounds peculiar to Slavic languages. This was remedied by the introduction of these marks, and Hus’s system of orthography became known as the diacritic one. The Bohemian reformer, zealous for the purity of the language of his country, often in his sermons inveighed quaintly and vehemently against those who defiled the Czech language by introducing numerous “Germanisms.” A century later the Czech language was largely indebted to the then recently founded community of the Bohemian (or as they were also often called, Moravian) brethren. A member of the community, Brother John Blakoslav, wrote in 1571 a Grammatika Česká, that still has considerable philological interest. It contains a full account of the construction of the Czech language, based on Latin grammar, with which the writer was thoroughly acquainted. Divines belonging to the same community also at the end of the 16th century published at Kralice in Moravia a complete Czech version of the Old and New Testaments. Together with the Labyrint Světa (Labyrinth of the World) of Komensky (Comenius), who was also a member of the brotherhood, it can be considered a model of the Czech language in the period immediately preceding its downfall.
The Czechs have always enthusiastically upheld the language of their country. In ancient Czech, indeed, the same word jazyk denotes both “nation” and “language.” As late as in 1608 a decree of the estates of Bohemia declared that Czech was the only official and recognized state-language, and that all who wished to acquire citizenship in the country should be obliged to acquire the knowledge of it. While all patriots thus supported the national language, it was greatly disliked by the absolutists who were opposed to the ancient free constitution of Bohemia, as well as by all who favoured the Church of Rome. The overthrow of Bohemian independence at the battle of the White Mountain (1620) was therefore shortly followed by the decline of the Czech language. All Czech writings which could be found were destroyed by the Austrian authorities as being tainted with heresy, while no new books written in Czech appeared, except occasional prayer-books and almanacs. For these scanty writings the German so-called “Schwabach” characters were used, and this custom only ceased in the middle of the 19th century. The Czech language, for some time entirely excluded from the schools, all but ceased to be written, and its revival at the beginning of the 19th century was almost a resurrection.
The first originator of the movement, Joseph Dobrovský or Doubravský (1753-1829) seems himself, at least at the beginning of his life, to have considered it impossible that Czech should again become a widely-spoken language, and one whose literature could successfully compete with that of larger countries. Yet it was the works of this “patriarch of Slavic philology” which first drew the public attention to the half-forgotten Czech language. Dobrovský’s work was afterwards continued by Kolar, Jungmann, Palacký, Šafařek, and many others, and Czech literature has, both as regards its value and its extension, reached a height that in the middle of the 19th century would have appeared incredible.
Though met by constant opposition on the part of the Austrian authorities, the Czechs have succeeded in re-establishing the use of their language in many of the lower and middle schools of Bohemia and Moravia, and the foundation of a Czech university at Prague (1882-1884) has of course contributed very largely to the ever-increasing expansion of the Czech language. The national language has at all times appeared to the Bohemians as the palladium of their nationality and independence, and the movement in favour of the revival of the Czech language necessarily became a political one, as soon as circumstances permitted. The friends of the national language at the beginning of the 19th century were generally known as the vlastenci (patriots), but when in 1848 representatives of many parts of Austria met at Vienna, the deputies of Bohemia—with the exception of the Germans—formed what was called the national or Czech party. Parliamentary government did not at that period long survive, and at the end of the year 1851 absolutism had been re-established. In 1860 a new attempt to establish constitutional government in Austria was made, and representatives of the Czech party appeared at the provincial diet of Prague and the central parliament at Vienna. The Czech party endeavoured to obtain the re-establishment of the ancient 724 Bohemian constitution, but, allied as they were with a large part of the Bohemian nobility, it was their policy to maintain a somewhat conservative attitude. After having absented themselves for a considerable time from the parliament of Vienna, the legality of which they denied, the Czech deputies reappeared in Vienna in 1879, and, together with the representatives of the Bohemian nobility, formed there what was known as the Česky Klub.
While the Czechs for a time continued united at Vienna, a schism among them had some time previously occurred at Prague. Dissatisfied with the policy of the Czechs, a new party had been formed in Bohemia which affected more advanced views and became known as the “Young Czech” party. The more conservative Czechs were henceforth known as the “Old Czechs.” The “Young Czechs,” when the party first became independent in 1872, had thirty-five representatives in the diet of Prague, but at the elections of 1874 their number was reduced to seven. They continued, however, to gain in strength, and obtained for a long time a large majority in the diet, while the Old Czech party for a considerable period almost disappeared. In Vienna also the Old Czech party gradually lost ground. Its leader Dr Rieger, indeed, obtained for the Czechs certain concessions which, underrated at the time, have since proved by no means valueless. The decision of the Old Czech party to take part at a conference in Vienna under the presidency of Count Taafe—then Austrian prime-minister—which was to settle the national differences in Bohemia, caused its complete downfall. The proposals of the Vienna conference were rejected with indignation, and the Old Czechs, having become very unpopular, for a time ceased to contest the elections for the legislative assemblies of Prague and Vienna. The victorious Young Czechs, however, soon proved themselves very unskilful politicians. After very unsuccessfully assuming for a short time an attitude of intransigeant opposition, they soon became subservient to the government of Vienna to an extent which the Old Czechs had never ventured. Dr Kramář, in particular, as leader of the Young Czech party, supported the foreign policy of Austria even when its tendency was most hostile to the interests of Bohemia. The Vienna government has, in recent years, as regards internal affairs, also adopted a policy very unfavourable to the Czech race. Even the continuance of some of the concessions formerly obtained by the Old Czechs has become doubtful. At the elections to the diet of Prague which took place in March 1908, the Young Czechs lost many seats to the Old Czechs, while the Agrarians, Clericals and Radicals were also successful.
See J. Dobrovský, Geschichte der böhmischen Sprache (1818), and Lehrgebäude der böhmischen Sprache (1819); J. Blahoslav, Grammatika Česká, printed from MS. (1867); Lippert, Social-Geschichte Böhmens (1896); Gebauer, Slovník Staročesky (Dictionary of the ancient Czech language, 1903); I. Herzer, Böhmisch-deutsches Wörterbuch (Prague, 1901, &c.); Coufal and Zába, Slovník Česko-latinský a Latinsko-český (Prague, 1904, &c.), and Historicka Uluonice Jazyka českéha (Historical grammar of the Czech language, 1904); Morfill, Grammar of the Bohemian or Čech Language (1899); Bourlier, Les Tchèques (1897).
CZENSTOCHOWA, or Chenstokhov, a town of Russian Poland, in the government of Piotrkow, on the left bank of the Warta (Warthe), 143 m. S.W. of Warsaw, on the railway between that city and Cracow. Pop. (1900) 53,650. Here is a celebrated monastery crowning the steep eminence called Yaznagora or Klarenberg. It was founded by King Vladislaus of the house of Jagiello and was at one time fabulously wealthy. In 1430 it was attacked and plundered by the Hussites; in 1655, and again in 1705, it bravely resisted the Swedes; but in 1772 it was forced to capitulate to the Russians, and in 1793 to the Prussians. The fortifications, which had been built from 1500 onwards, were razed in 1813. This monastery, which is occupied by monks of the order of Paul the Hermit, contains over the altar in its church a painted image of the Virgin, traditionally believed to have been painted by St Luke, and visited annually by throngs (400,000) of pilgrims from all over Russia, eastern Prussia and other neighbouring regions. The inhabitants of the town manufacture cotton, cloth and paper, and do a lively business in rosaries, images, scapularies and so forth.
CZERNOWITZ (Rum. Cernautzi), the capital of the Austrian duchy of Bukovina, 420 m. E. of Vienna and 164 m. S.E. of Lemberg by rail. Pop. (1900) 69,619. It is picturesquely situated on a height above the right bank of the river Pruth, which is crossed here by two bridges, of which one is a railway bridge. Czernowitz is a clean, pleasant town of recent date, and is the seat of the Greek Orthodox archbishop or metropolitan of Bukovina. The principal buildings include the Greek Orthodox cathedral, finished in 1864 after the model of the church of St Isaac at St Petersburg; the Armenian church, in a mixed Gothic and Renaissance style, consecrated in 1875; a handsome new Jesuit church, and a new synagogue in Moorish style, built in 1877. The most conspicuous building of the town is the Episcopal palace, in Byzantine style, built in 1864-1875, which is adorned with a high tower and possesses a magnificent reception hall. In one of the public squares stands the Austrian monument, executed by Pekary and erected in 1875 to commemorate the centenary of Austria’s possession of Bukovina. It consists of a marble statue of Austria erected on a pedestal of green Carpathian sandstone. The Francis Joseph University, also opened in 1875, had 50 lecturers and over 500 students in 1901. The language of instruction is German, and it possesses three faculties: theology, law and philosophy. The industry is not very developed and consists chiefly in corn-milling and brewing. An active trade is carried on in agricultural produce, wood, wool, cattle and spirits. Czernowitz has a mixed population, which consists of Germans, Ruthenians, Rumanians, Poles, Jews, Armenians and Gypsies. The town presents, therefore, a cosmopolitan and on market days a very varied appearance, when side by side with people turned out in the latest fashions from Paris or Vienna, we meet peasants of various nationalities, attired in their national costume, intermingled with very scantily-clad Gypsies.
On the opposite bank of the Pruth, at a very little distance to the N., is situated the town of Sadagora (pop. 4512, mostly Jews), where a famous cattle fair takes place every year.
Czernowitz was at the time of the Austrian occupation (1775) an unimportant village. It was created a town in 1786, and at the beginning of the 19th century it numbered only 5000 inhabitants.
CZERNY, KARL (1791-1857), Austrian pianist and composer, was born at Vienna on the 21st of February 1791. His father, who was a teacher of the piano, trained him for that instrument from an early age with such success that he performed in public at the age of nine, and commenced his own career as a teacher at fourteen. He was brought under the notice of Beethoven, and was his pupil in the sense in which the great master had pupils. It is perhaps his greatest claim to distinction as a performer that he was selected to be the first to play Beethoven’s celebrated Emperor concerto in public. He soon became the most popular teacher of his instrument in a capital which abounded in pianists of the first rank. Among his pupils he numbered Liszt, Theodor Döhler (1814-1843) and many others who afterwards became famous. As a composer he was prolific to an astonishing degree, considering the other demands on his time. His works, which included every class of composition, numbered 849 at the time of his death. Comparatively few of them possess high merit, and none is the production of genius. He had considerable skill in devising variations for the piano of the display type, and in this and other ways helped to develop the executive power which in the modern school of pianoforte playing seems to have reached the limits of the possible. His various books of exercises, elementary and advanced, of which the best known are the Études de la vélocité, have probably had a wider circulation than any other works of their class. To the theory of music he contributed a translation of Reicha’s Traité de composition, and a work entitled Umriss der ganzen Musikgeschichte. Czerny died on the 15th of July 1857 at Vienna. Having no family, he left his fortune, which was considerable, to the Vienna Conservatorium and various benevolent institutions.
D The fourth letter in the English alphabet occupies the
same position in the Latin, Greek and Phoenician
alphabets, which represent the preceding stages in its
history. The Phoenician name Daleth is represented
by the Greek Delta. In form D has varied throughout its career
comparatively little. In the earliest Phoenician it is  with
slight variations; in most Greek dialects
with
slight variations; in most Greek dialects  which has been
adopted as the Greek literary form, but in others as e.g. the
earliest Attic
which has been
adopted as the Greek literary form, but in others as e.g. the
earliest Attic  or
or  . The form with the rounded back, which
has passed from Latin into the languages of western Europe,
was borrowed from the Greeks of S.W. Italy, but is widely
spread also amongst the peoples of the Peloponnese and of
northern Greece. It arises from a form like
. The form with the rounded back, which
has passed from Latin into the languages of western Europe,
was borrowed from the Greeks of S.W. Italy, but is widely
spread also amongst the peoples of the Peloponnese and of
northern Greece. It arises from a form like  when the sides
which meet to the right are written or engraved at one stroke.
From a very early period one side of the triangle was often
prolonged, thus producing a form
when the sides
which meet to the right are written or engraved at one stroke.
From a very early period one side of the triangle was often
prolonged, thus producing a form  which is characteristic of
Aramaic from 800 B.C. In Greek this was avoided because of
the likelihood of its confusion with
which is characteristic of
Aramaic from 800 B.C. In Greek this was avoided because of
the likelihood of its confusion with  , the oldest form of the
symbol for r, but in the alphabets of Italy—which were borrowed
from Etruscan—this confusion actually takes place. Etruscan
had no sound corresponding to the symbol D (in inscriptions
written from right to left,
, the oldest form of the
symbol for r, but in the alphabets of Italy—which were borrowed
from Etruscan—this confusion actually takes place. Etruscan
had no sound corresponding to the symbol D (in inscriptions
written from right to left,  ), and hence used it as a by-form
for
), and hence used it as a by-form
for  , the symbol for r. The Oscans and Umbrians took it over
in this value, but having the sound d they used for it the symbol
for r (
, the symbol for r. The Oscans and Umbrians took it over
in this value, but having the sound d they used for it the symbol
for r ( in Umbrian,
in Umbrian,  in Oscan).
in Oscan).
The sound which D represents is the voiced dental corresponding
to the unvoiced t. The English d, however, is not a true
dental, but is really pronounced by placing the tongue against
the sockets of the teeth, not the teeth themselves. It thus
differs from the d of French and German, and in phonetic terminology
is called an alveolar. In the languages of India where
both true dentals and alveolars are found, the English d is
represented by the alveolar symbol (transliterated ḍ). Etymologically
in genuine English words d represents in most cases
dh of the original Indo-European language, but in some cases
an original t. In many languages d develops an aspirate after it,
and this dh becomes then a voiced spirant (ð), the initial sound
of there and that. This has occurred widely in Semitic, and is
found also in languages like modern Greek, where δ, except after
ν, is always spirant, δέν (= not) being pronounced like English
then. As the mouth position for l differs from that for d only by
the breath being allowed to escape past one or both sides of
the tongue, confusion has arisen in many languages between
d and l, the best-known being cases like the Latin lacrima as
compared with the Greek δάκ-ρυ. The English tear and the
forms of other languages show that d and not l is the more
original sound. Between vowels in the ancient Umbrian d
passed into a sound which was transliterated in the Latin
alphabet by rs; this was probably a sibilant r, like the Bohemian
ř. In many languages it is unvoiced at the end of words, thus
becoming almost or altogether identical with t. As an abbreviation
it is used in Latin for the praenomen Decimus, and under
the empire for the title Divus of certain deceased emperors.
As a Roman numeral (= 500) it is only the half of the old symbol
 (= 1000); this was itself the old form of the Greek φ, which
was useless in Latin as that language had no sound identical
with the Greek φ.
(= 1000); this was itself the old form of the Greek φ, which
was useless in Latin as that language had no sound identical
with the Greek φ.
DACCA, a city of British India, giving its name to a district and division of Eastern Bengal and Assam. It was made the capital of that province on its creation in October 1905. The city is 254 m. N.E. by E. of Calcutta, on an old channel of the Ganges. Railway station, 10 m. from the terminus of the river steamers at Narayanganj. The area is about 8 sq. m. The population in 1901 was 90,542. The ruins of the English factory, St Thomas’s church, and the houses of the European residents lie along the river banks. Of the old fort erected by Islam Khan, who in 1608 was appointed nawab of Bengal, and removed his capital from Rajmahal to Dacca, no vestige remains; but the jail is built on a portion of its site. The principal Mahommedan public buildings, erected by subsequent governors and now in ruins, are the Katra and the Lal-bagh palace—the former built by Sultan Mahommed Shuja in 1645, in front of the chauk or market place. Its extensive front faced the river, and had a lofty central gateway, flanked by smaller entrances, and by two octagonal towers rising to some height above the body of the building. The Lal-bagh palace was commenced by Azam Shah, the third son of the emperor Aurangzeb. It originally stood close to the Buriganga river; but the channel has shifted its course, and there is now an intervening space covered with trees between it and the river. The walls on the western side, and the terrace and battlement towards the river, are of a considerable height, and present a commanding aspect from the water. These outworks, with a few gateways, the audience hall and the baths, were the only parts of the building that survived in 1840. Since then their dilapidation has rapidly advanced; but even in ruin they show the extensive and magnificent scale on which this princely residence was originally designed. It appears never to have been completed; and when Jean Baptiste Tavernier visited Dacca (c. 1666), the nawab was residing in a temporary wooden building in its court. The English factory was built about that year. The central part of the old factory continued to be used as a court-house till the 19th century, but owing to its ruinous state it was pulled down in 1829 or 1830; in 1840 the only portion that remained was the outward wall. The French and Dutch factories were taken possession of by the English in the years 1778 and 1781 respectively. In the mutiny of 1857 two companies of the 73rd Native Infantry which were stationed in the town joined in the revolt, but were overpowered by a small European force and dispersed. The city still shows some signs of its former magnificence. The famous manufacture of fine muslins is almost extinct, but the carving of shells, carried on from ancient times, is an important industry in the city. There are a Government college, a collegiate school and an unaided Hindu college. There is a large settlement of mixed Portuguese descent, known as Feringhis. Many of the public buildings, including the college, suffered severely from the earthquake of the 12th of June 1897; and great damage was done by tornadoes in April of 1888 and 1902.
The district of Dacca comprises an area of 2782 sq. m. In 1901 the population was 2,649,522, showing an increase of 11% in the decade. The district consists of a vast level plain, divided into two sections by the Dhaleswari river. The northern part, again intersected by the Lakshmia river, contains the city of Dacca, and as a rule lies well above flood-level.
Dacca is watered by a network of rivers and streams, ten of which are navigable throughout the year by native cargo boats of four tons burthen. Among them are the Meghna, the Ganges or Padma, the Lakshmia, a branch of the Brahmaputra, the Jamuna, or main stream of the Brahmaputra, the Mendi-Khali, a large branch of the Meghna, the Dhaleswari, an offshoot of the Jamuna, the Ghazi-khali and the Buriganga. The soil is composed of red ferruginous kankar, with a stratum of clay in the more elevated parts, covered by a thin layer of vegetable mould, or by recent alluvial deposits. The scenery along the Lakshmia is very beautiful, the banks being high and wooded. About 20 m. north of Dacca city, small ridges are met with in the Madhupur jungle, stretching into Mymensingh district. These hills, however, are mere mounds of from 20 to 40 ft. high, composed of red soil containing a considerable quantity of iron ore; and the whole tract is for the most part unproductive. Towards the city the red soil is intersected by creeks and morasses, whose margins yield crops of rice, mustard and til seed; while to the east of the town, a broad, alluvial, well-cultivated plain reaches as far as the junction of the Dhaleswari and Lakshmia rivers. The country lying to the south of the Dhaleswari is the most 726 fertile part of the district. It consists entirely of rich alluvial soil, annually inundated to a depth varying from 2 to 14 ft. of water. The villages are built on artificial mounds of earth, so as to raise them above the flood-level.
The wild animals found in the district comprise a few tigers, leopards and wild elephants, deer, wild pig, porcupines, jackals, foxes, hares, otters, &c. The green monkey is very common; porpoises abound in the large rivers. The manufactures consist of weaving, embroidery, gold and silver work, shell-carving and pottery. The weaving industry and the manufacture of fine Dacca muslins have greatly fallen off, owing to the competition of European piece goods. Forty different kinds of cloth were formerly manufactured in this district, the bulk of which during many years was made from English twist, country thread being used only for the finest muslins. It is said that, in the time of the emperor Jahangir, a piece of muslin, 15 ft. by 3, could be manufactured, weighing only 900 grains, its value being £40. In 1840 the finest cloth that could be made of the above dimensions weighed about 1600 grains, and was worth £10. Since then the manufacture has still further decayed, and the finer kinds are not now made at all except to order. The district is traversed by a line of the Eastern Bengal railway, but most of the traffic is still conducted by water. It is a centre of the jute trade.
The division of Dacca occupies the delta of the Brahmaputra, where it joins the main stream of the Ganges. It consists of the four districts of Dacca, Mymensingh, Faridpur and Backergunge. Its area is 15,837 sq. m. Its population in 1901 was 10,793,988.
DACE, Dare, or Dart (Leuciscus vulgaris, or L. dobula), a fresh-water fish belonging to the family Cyprinidae. It is an inhabitant of the rivers and streams of Europe north of the Alps, but it is most abundant in those of France and Germany. It prefers clear streams flowing over a gravelly bottom, and deep, still water, keeping close to the bottom in winter but disporting itself near the surface in the sunshine of summer. It is preyed upon by the larger predaceous fishes of fresh waters, and owing to its silvery appearance is a favourite bait in pike-fishing. The dace is a lively, active fish, of gregarious habits, and exceedingly prolific, depositing its eggs in May and June at the roots of aquatic plants or in the gravelly beds of the streams it frequents. Its flesh is wholesome, but is not held in much estimation. In appearance it closely resembles the roach, usually attaining a length of 8 or 9 in., with the head and back of a dusky blue colour and the sides of a shining silvery aspect, with numerous dark lines running along the course of the scales. The ventral and anal fins are white, tinged with pale red; and the dorsal, pectoral and caudal tipped with black. The dace feeds on worms, insects, insect-larvae, and also on vegetable matter. It is abundant in many of the streams of the south of England, but is unknown in Scotland and Ireland. In America the name of dace is also applied to members of other genera of the family; the “horned dace” (Semnotilus atromaculatus) is a well-known variety.
DACH, SIMON (1605-1659), German lyrical poet, was born at Memel in East Prussia on the 29th of July 1605. Although brought up in humble circumstances, he received a careful education in the classical schools of Königsberg, Wittenberg and Magdeburg, and entered the university of Königsberg in 1626 as a student of theology and philosophy. After taking his degree, he was appointed in 1633 Kollaborator (teacher) and in 1636 co-rector of the Domschule (cathedral school) in that city. In 1639 he received the chair of poetry at the university of Königsberg, which he occupied until his death on the 15th of April 1659. In Königsberg he entered into close relations with Heinrich Albert (1604-1651), Robert Roberthin (1600-1648) and Sibylla Schwarz (1621-1638), and with them formed the so-called Königsberger Dictergruppe. He sang the praises of the house of the electors of Brandenburg in a collection of poems entitled Kurbrandenburgische Rose, Adler, Löwe und Scepter (1661), and also produced many occasional poems, several of which became popular; the most famous of them is Anke von Tharaw öss, de my geföllt (rendered by Herder into modern German as Ännchen von Tharau), composed in 1637 in honour of the marriage of a friend. Among his hymns, many of which are of great beauty, are the following: Ich bin ja, Herr, in deiner Macht, Ich bin bei Gott in Gnaden durch Christi Blut und Tod, and O, wie selig seid ihr boch, ihr Frommen.
Editions of Dach’s poems have been published by W. Müller (1823), by H. Österley (for the Stuttgart Literarischer Verein, 1876); also selections by the same editor (1876), and in Kürschner’s Deutsche Nationalliteratur (1883). See especially the introductions to Österley’s editions; also H. Stiehler, Simon Dach, sein Leben und seine ausgewählte Dichtungen (1896).
DACIA, in ancient geography, the land of the Daci, a large district of central Europe, bounded on the N. by the Carpathians, on the S. by the Danube, on the W. by the Pathissus (Theiss), on the E. by the Tyras (Dniester), thus corresponding in the main to the modern Rumania and Transylvania. Towards the west it may originally have extended as far as the Danube where it runs from north to south at Waitzen (Vacz), while on the other hand Ptolemy puts its eastern boundary as far back as the Hierasus (Sereth). The inhabitants of this district were a Thracian stock, originally called Δᾶοι, a name which after the 4th century B.C. gave place to Δακοί. Of the other Thracian tribes the Getae (q.v.) were most akin to them in language and manners; by the Greeks the Dacians were usually called Getae, by the Romans Daci. Δᾶος and Γέτα (Davus, Geta) were common as names of slaves in Attic comedy and in the adaptations of Plautus and Terence.
The Dacians had attained a considerable degree of civilization when they first became known to the Romans. They believed in the immortality of the soul, and regarded death as merely a change of country (μετοικίζεσθαι). Their chief priest held a prominent position as the representative of the deity upon earth; he was the king’s chief adviser and his decisions were accepted as final. They were divided into two classes—an aristocracy and a proletariate. The first alone had the right to cover their heads and wore a felt hat (hence tarabostesei = πιλοφόροι, pileati); they formed a privileged class, and were the predecessors of the Rumanian boyars. The second class, who comprised the rank and file of the army, the peasants and artisans, wore their hair long (κομηταί, capillati). They dwelt in wooden huts surrounded by palisades, but in later times, aided by Roman architects, built walled strongholds and conical stone towers. Their chief occupations were agriculture and cattle breeding; horses were mainly used as draught animals. They also worked the gold and silver mines of Transylvania, and carried on a considerable outside trade, as is shown by the number of foreign coins found in the country.
A kingdom of Dacia was in existence at least as early as the beginning of the 2nd century B.C. under a king Oroles. Conflicts with the Bastarnae and the Romans (112-109, 74), against whom they had assisted the Scordisci and Dardani, had greatly weakened the resources of the Dacians. Under Burbista (Boerebista), a contemporary of Caesar, who thoroughly reorganized the army and raised the moral standard of the people, the limits of the kingdom were extended; the Bastarnae and Boii were conquered, and even Greek towns (Olbia, Apollonia) on the Euxine fell into his hands. Indeed the Dacians appeared so formidable that Caesar contemplated an expedition against them, which was prevented by his death. About the same time Burbista was murdered, and the kingdom was divided into four (or five) parts under separate rulers. One of these was Cotiso, whose daughter Augustus is said to have desired to marry and to whom he betrothed his own five-year-old daughter Julia. He is well known from the line in Horace (“Occidit Daci Cotisonis agmen,” Odes, iii. 8. 18), which, as the ode was written on the 1st of March 29, probably refers to the campaign of Marcus Crassus (30-28), not to that of Cornelius Lentulus, who was not consul till 18. The Dacians are often mentioned under Augustus, according to whom they were compelled to recognize the Roman supremacy. But they were by no means subdued, and in later times seized every opportunity of crossing the frozen Danube and ravaging the province of Moesia. From A.D. 85 to 89 the Dacians were engaged in two wars with the Romans, under Duras or Diurpaneus, and the great Decebalus, who ruled from 86-87 727 to 107. After two severe reverses, the Romans, under Tettius Julianus, gained a signal advantage, but were obliged to make peace owing to the defeat of Domitian by the Marcomanni. Decebalus restored the arms he had taken and some of the prisoners and received the crown from Domitian’s hands, an apparent acknowledgment of Roman suzerainty. But the Dacians were really left independent, as is shown by the fact that Domitian agreed to purchase immunity from further Dacian inroads by the payment of an annual tribute.
To put an end to this disgraceful arrangement, Trajan resolved to crush the Dacians once and for all. The result of his first campaign (101-102) was the occupation of the Dacian capital Sarmizegethusa (Várhely) and the surrounding country; of the second (105-107), the suicide of Decebalus, the conquest of the whole kingdom and its conversion into a Roman province. The history of the war is given in Dio Cassius, but the best commentary upon it is the famous column of Trajan. According to Marquardt, the boundaries of the province were the Tibiscus (Temes) on the W., the Carpathians on the N., the Tyras on the E., and the Danube on the S., but Brandis (in Pauly-Wissowa’s Realencyclopädie) maintains that it did not extend farther eastwards than the river Olt (Aluta)—the country beyond belonging to lower Moesia—and not so far as the Theiss westwards, being thus limited to Transylvania and Little Walachia. It was under a governor of praetorian rank, and the legio xiii. gemina with numerous auxiliaries had their fixed quarters in the province. To make up for the ravages caused by the recent wars colonists were imported to cultivate the land and work the mines, and the old inhabitants gradually returned. Forts were built as a protection against the incursions of the surrounding barbarians, and three great military roads were constructed to unite the chief towns, while a fourth, named after Trajan, traversed the Carpathians and entered Transylvania by the Roteturm pass. The two chief towns were Sarmizegethusa (afterwards Ulpia Trajana) and Apulum (Karlsburg). With the religion the Dacians also adopted the language of the conquerors, and modern Rumanian is full of Latin words easily recognizable.
In 129, under Hadrian, Dacia was divided into Dacia Superior and Inferior, the former comprising Transylvania, the latter Little Walachia, with procurators, probably both under the same praetorian legate (according to Brandis, the procurator of Dacia inferior was independent, but see A. Domaszewski in Rheinisches Museum, xlviii., 1893). Marcus Aurelius redivided it into three (tres Daciae): Porolissensis, from the chief town Porolissum (near Mojrad), Apulensis from Apulum and Maluensis (site unknown). The tres Daciae formed a commune in so far that they had a common capital, Sarmizegethusa, and a common diet, which discussed provincial affairs, formulated complaints and adjusted the incidence of taxation; but in other respects they were practically independent provinces, each under an ordinary procurator, subordinate to a governor of consular rank.
The Roman hold on the country was, however, still precarious. Indeed it is said that Hadrian, conscious of the difficulty of retaining it, had contemplated its abandonment and was only deterred by consideration for the safety of the numerous Roman settlers. Under Gallienus (256), the Goths crossed the Carpathians and drove the Romans from Dacia, with the exception of a few fortified places between the Temes and the Danube. No details of the event are recorded, and the chief argument in support of the statement in Ruf(i)us Festus that “under the Emperor Gallienus Dacia was lost” is the sudden cessation of Roman inscriptions and coins in the country after 256. Aurelian (270-275) withdrew the troops altogether and settled the Roman colonists on the south of the Danube, in Moesia, where he created the province Dacia Aureliani. This was subsequently divided into Dacia Ripensis on the Danube, with capital Ratiaria (Arcar in Bosnia), and Dacia Mediterranea, with capital Sardica (Sofia, the capital of Bulgaria), the latter again being subdivided into Dardania and Dacia Mediterranea.
See J. D. F. Neigebaur, Dacien aus den Überresten des klassischen Alterthums. (Kronstadt, 1851); C. Gooss, Studien zur Geographie und Geschichte des trajanischen Daciens (Hermannstadt, 1874); E. R. Rösler, Dacier und Romanen (Vienna, 1866), and Romänische Studien (Leipzig, 1871); J. Jung, Römer und Romanen in den Donauländern (Innsbruck, 1877), Die römanischen Landschaften des römischen Reiches (1881), and Fasten der Provinz Dacien (1894); W. Tomaschek, “Die alten Thraker,” in Sitzungsberichte der k. Akad. der Wissenschaften, cxxviii. (Vienna, 1893); J. Marquardt, Römische Staatsverwaltung, i. (1881), p. 308; T. Mommsen in Corpus Inscriptionum Latinarum, iii. 160, and Provinces of Roman Empire (Eng. trans., 1886); C. G. Brandis in Pauly-Wissowa’s Realencyclopädie, iv. pt. 2 (1901); W. Miller, The Balkans in “The Story of the Nations,” vol. 44; on the boundaries of the Roman province of Dacia, see T. Hodgkin and F. Haverfield in English Historical Review, ii. 100, 734. (See also Vlachs.)
DACIER, ANDRÉ (1651-1722), French classical scholar, was born at Castres in upper Languedoc, on the 6th of April 1651. His father, a Protestant advocate, sent him first to the academy of Puy Laurens, and afterwards to Saumur to study under Tanneguy Lefèvre. On the death of Lefèvre in 1672, Dacier removed to Paris, and was appointed one of the editors of the Delphin series of the classics. In 1683 he married Anne Lefèvre, the daughter of his old tutor (see below). In 1695 he was elected member of the Academy of Inscriptions, and also of the French Academy; not long after, as payment for his share in the “medallic” history of the king’s reign, he was appointed keeper of the library of the Louvre. He died two years after his wife, on the 18th of September 1722. The most important of his works were his editions of Pompeius Festus and Verrius Flaccus, and his translations of Horace (with notes), Aristotle’s Poetics, the Electra and Oedipus Coloneus of Sophocles, Epictetus, Hippocrates and Plutarch’s Lives.
His wife, Anne Lefèvre (1654-1720), French scholar and translator from the classics, was born at Saumur, probably in March 1654. On her father’s death in 1672 she removed to Paris, carrying with her part of an edition of Callimachus, which she afterwards published. This was so well received that she was engaged as one of the editors of the Delphin series of classical authors, in which she edited Florus, Dictys Cretensis, Aurelius Victor and Eutropius. In 1681 appeared her prose version of Anacreon and Sappho, and in the next few years she published prose versions of Terence and some of the plays of Plautus and Aristophanes. In 1684 she and her husband retired to Castres, with the object of devoting themselves to theological studies. In 1685 the result was announced in the conversion to Roman Catholicism of both M. and Mme Dacier, who were rewarded with a pension by the king. In 1699 appeared the prose translation of the Iliad (followed nine years later by a similar translation of the Odyssey), which gained for her the position she occupies in French literature. The appearance of this version, which made Homer known for the first time to many French men of letters, and among others to A. Houdart de la Motte, gave rise to a famous literary controversy. In 1714 la Motte published a poetical version of the Iliad, abridged and altered to suit his own taste, together with a Discours sur Homère, stating the reasons why Homer failed to satisfy his critical taste. Mme Dacier replied in the same year in her work, Des causes de la corruption du goût. La Motte carried on the discussion with light gaiety and badinage, and had the happiness of seeing his views supported by the abbé Jean Terrasson, who in 1715 produced two volumes entitled Dissertation critique sur l’Iliade, in which he maintained that science and philosophy, and especially the science and philosophy of Descartes, had so developed the human mind that the poets of the 18th century were immeasurably superior to those of ancient Greece. In the same year Père C. Buffier published Homère en arbitrage, in which he concluded that both parties were really agreed on the essential point—that Homer was one of the greatest geniuses the world had seen, and that, as a whole, no other poem could be preferred to his; and, soon after (on the 5th of April 1716), in the house of M. de Valincourt, Mme Dacier and la Motte met at supper, and drank together to the health of Homer. Nothing of importance marks the rest of Mme Dacier’s life. She died at the Louvre, on the 17th of August 1720.
See C. A. Sainte-Beuve, Causeries du lundi, vol ix.; J. F. Bodin, Recherches historiques sur la ville de Saumur (1812-1814); P. J. Burette, Éloge de Mme Dacier (1721); Mémoires de Mme de Staël 728 (1755); E. Egger, L’Hellénisme en France, ii. (1869); Mémoires de Saint-Simon, iii.; R. Rigault, Histoire de la querelle des anciens et des modernes (1856).
DACITE (from Dacia, mod. Transylvania), in petrology, volcanic rocks which may be considered a quartz-bearing variety of andesite. Like the latter they consist for the most part of plagioclase felspar with biotite, hornblende, augite or enstatite, and have generally a porphyritic structure, but they contain also quartz as rounded, corroded phenocrysts, or as an element of the ground-mass. Their felspar ranges from oligoclase to andesite and labradorite, and is often very zonal; sanidine occurs also in some dacites, and when abundant gives rise to rocks which form transitions to the rhyolites. The biotite is brown; the hornblende brown or greenish brown; the augite usually green. The ground-mass of these rocks is often micro-crystalline, with a web of minute felspars mixed with interstitial grains of quartz; but in many dacites it is largely vitreous, while in others it is felsitic or cryptocrystalline. In the hand specimen many of the hornblende and biotite dacites are grey or pale brown and yellow rocks with white felspars, and black crystals of biotite and hornblende. Other dacites, especially augite- and enstatite-dacites, are darker coloured. The rocks of this group occur in Hungary, Almería (Spain), Argyllshire and other parts of Scotland, New Zealand, the Andes, Martinique, Nevada and other districts of western North America, Greece, &c. They are mostly associated with andesites and trachytes, and form lava flows, dikes, and in some cases massive intrusions in the centres of old volcanoes. Among continental petrographers the older dacites (Carboniferous, &c.) are often known as “porphyrites.”
DACOIT, a term used in India for a robber belonging to an armed gang. The word is derived from the Hindustani dakait, and being current in Bengal got into the Indian penal code. By law, to constitute dacoity, there must be five or more in the gang committing the crime. In the time of the Thugs (q.v.) a special police department was created in India to deal with thuggy and dacoity (thagi and dakaiti), which exists down to the present day. In Burma also the word dacoit came to be applied in a special sense to the armed gangs, which maintained a state of guerilla warfare for several years after the defeat of the king and his army. (See Burmese Wars.)
DA COSTA, ISAAK (1798-1860), Dutch poet and theologian, was born at Amsterdam on the 14th of January 1798. His father was a Jew of Portuguese descent, and claimed kindred with the celebrated Uriel D’Acosta. An early acquaintance with Bilderdijk had a strong influence over the boy both in poetry and in theology. He studied at Amsterdam, and afterwards at Leiden, where he took his doctor’s degree in law in 1818, and in literature in 1821. In 1814 he wrote De Verlossing van Nederland, a patriotic poem, which placed him in line with the contemporary national romantic poets in Germany and in France. His Poëzy (2 vols., 1821-1822) revealed his emancipation from the Bilderdijk tradition, and the oriental colouring of his poems, his hymn to Lamartine, and his translation of part of Byron’s Cain, establish his claim to be considered as the earliest of the Dutch romantic poets. In 1822 he became a convert to Christianity, and immediately afterwards asserted himself as a champion of orthodoxy and an assailant of latitudinarianism in his Bezwaren tegen den Geest der Eeuw (1823). He took a lively interest in missions to the Jews, and towards the close of his life was a director of the seminary established in Amsterdam in connexion with the mission of the Free Church of Scotland. He died at Amsterdam on the 28th of April 1860. Da Costa ranked first among the poets of Holland after the death of Bilderdijk. His principal poetical works were: Alphonsus I. (1818), a tragedy; Poëzy (Leiden, 1821); God metons (1826); Festliedern (1828); Vijf-en-twintig jaren (1840); Hagar (1852); De Slag bij Nieupoort (1857). He also translated The Persians (1816) and the Prometheus (1818) of Aeschylus, and edited the poetical works of Bilderdijk in sixteen volumes, the last volume being an account of the poet. He was the author of a number of theological works, chiefly in connexion with the criticism of the gospels.
His complete poetical works were edited by J. P. Hasebroek (3 vols., Haarlem, 1861-1862). See G. Groen van Prinsterer, Brieven van, Mr I. da Costa, 1830-1849 (1872), and J. ten Brink, Geschiedenis der Noord-Nederlandsche Letteren in de XIXe Eeuw (vol. i., 1888), which contains a complete bibliography of his works.
DACTYL (from Gr. δάκτυλος, a finger), in prosody, a long syllable followed by two short (see Verse).
DAEDALUS, a mythical Greek architect and sculptor, who figures largely in the early legends of Crete and of Athens. He was said to have built the labyrinth for Minos, to have made a wooden cow for Pasiphaë and to have fashioned a bronze man who repelled the Argonauts. Falling under the displeasure of Minos, he fashioned wings for himself and his son Icarus, and escaped to Sicily. These legends seem primarily to belong to Crete; and the Athenian element in them which connected Daedalus with the royal house of Erechtheus is a later fabrication. To Daedalus the Greeks of the historic age were in the habit of attributing buildings, and statues the origin of which was lost in the past, and which had no inscription belonging to them. In a later verse in the Iliad (date, 7th or 6th century), Daedalus is mentioned as the maker of a dancing-place for Ariadne in Crete; and such a dancing-place has been discovered by A. J. Evans, in the Minoan palace of Cnossus. Diodorus Siculus says that he executed various works in Sicily for King Cocalus. In many cities of Greece there were rude wooden statues, said to be by him. Later critics, judging from their own notions of the natural course of development in art, ascribed to Daedalus such improvements as separating the legs of statues and opening their eyes. In fact the name Daedalus is a mere symbol, standing for a particular phase of early Greek art, when wood was the chief material, and other substances were let into it for variety.
This Daedalus must not be confused with Daedalus of Sicyon, a great sculptor of the early part of the 4th century B.C., none of whose works is extant.
DAFFODIL, the common name of a group of plants of the genus Narcissus, and natural order Amaryllidaceae. (See generally under Narcissus.) The common daffodil, N. Pseudo-narcissus, is common in woods and thickets in most parts of the N. of Europe, but is rare in Scotland. Its leaves are five or six in number, are about a foot in length and an inch in breadth, and have a blunt keel and flat edges. The stem is about 18 in. long, and the spathe single-flowered. The flowers are large, yellow, scented and a little drooping, with a corolla deeply cleft into six lobes, and a central bell-shaped nectary, which is crisped at the margin. They appear early in the year, or, as Shakespeare says, “come before the swallow dares, and take the winds of March with beauty.” The stamens are shorter than the cup, the anthers oblong and converging; the ovary is globose, and has three furrows; the seeds are roundish and black. Many new varieties of the flower have recently been cultivated in gardens. The bulbs are large and orbicular, and have a blackish coat; they, as well as the flowers, are reputed to be emetic in properties. The Peruvian daffodil and the sea daffodil are species of the genus Ismene. (For derivation see Asphodel.)
DAFYDD AB GWILYM (c. 1340-c. 1400), son of Gwilym Gam and Ardudful Fychan, greatest of the medieval Welsh poets, was born at Bro Gynin, Cardiganshire, about the year 1340. Educated by a scholarly uncle, Llewelyn ab Gwilym Fychan of Emlyn, he became steward to his kinsman, Ivor Hael of Maesaleg, Monmouthshire, who also appointed him instructor to his daughter. The latter arrangement leading to an attachment between tutor and pupil, the girl was banished to a convent in Anglesey, whither the poet followed her, taking service in an adjacent monastery, but on returning to Maesaleg he was permitted to retain his stewardship. He was elected chief bard of Glamorgan and became household bard to Ivor Hael. At Rhosyr in North Wales he met Morfudd Lawgam, to whom he addressed 147 amatory odes. In consequence of attempting to elope with this lady, Dafydd ab Gwilym, being unable to pay the fine demanded by her husband, was imprisoned. Liberated by the goodwill of his friends, he went back to Maesaleg, and after the death of his patron, retired to his birthplace, Bro Gynin. 729 Tradition states that he was a man of noble appearance, and his poems bear evidence of high mental culture. He was acquainted with the works of Homer, Virgil, Ovid and Horace, and was also a student of Italian literature. Especially remarkable as a poet of nature in an age when more warlike themes were chosen by his contemporaries, his poems entitled “The Lark,” “The Wind” and “The Mist” are amongst his finest efforts. He has been called the Petrarch, the Ovid, and (by George Borrow) the Horace of Wales. His poems were almost all written in the cywydd form: a short ode not divided into stanzas, each line having the same number of syllables. The poet died about the year 1400, and according to tradition was buried in the graveyard of the monastery of Strata Florida, in Cardiganshire.
See also under Celt; Celtic Literature, iv. Welsh.
DAGGER, a hand weapon with a short blade. The derivation is obscure (cf. Fr. dague and Ger. Degen), but the word is related to dag, a long pointed jag such as would be made in deeply nicking the edge of a garment. The war knife in various forms and under many names has of course been in use in all ages and amongst all races. But the dagger as generally understood was not a short sword, but a special stabbing weapon which could be used along with the sword. The distinction is often difficult to establish in a given case owing to the variations in the length of the weapon. The principal medieval dagger was the miséricorde, which from the end of the 12th century was used, in all countries in which chivalry flourished, to penetrate the joints of the armour of an unhorsed adversary (hence Ger. Panzerbrecher, armour-breaker). It was so called either because the threat of it caused the vanquished to surrender “at mercy,” or from its use in giving what was called the coup de grâce. From about 1330 till the end of the succeeding century, in many knightly effigies it is often represented as attached on the right side by a cord or a chain to the sword-belt. This weapon and its sheath were often elaborately adorned. It was customary to secure it from accidental loss by a guard-chain fastened to the breast-armour. Occasionally the miséricorde was fixed to the body-armour by a staple; or, more rarely, it was connected with a gypcière or pouch. The miséricorde may be called a poniard. The distinction between the dagger and the poniard is arbitrary, and in ordinary language the latter is taken as being the shorter and as having less resemblance to a short sword or cutlass. A weapon, with a longer blade than the miséricorde, was habitually worn by civilians, including judges, during the middle ages; such weapons bore the name of anlace (from annulus, as it was fastened by a ring), basilarde or langue de bœuf, the last from the broad ox-tongue shape of the blade. This had often a small knife fixed on the scabbard, like a Highland officer’s dirk of the present day. By nobles and knights the dagger or poniard was worn when they had exchanged their armour for the costume of peace. It is recorded besides that when they appeared at a tournament and on some other occasions, ladies at that time wore daggers depending, with their gypcieres, from their girdles. Thus, writing of the year 1348, Knighton speaks of certain ladies who were present at jousts as “habentes cultellos, quos daggerios vulgariter dicunt, in powchiis desuper impositis.” A longer and heavier dagger with a broad blade (Italian) is called cinquedea. The Scottish “dirk” was a long dagger, and survives in name in the dirk worn by midshipmen of the royal navy, and in fact in that worn by officers of Highland regiments. In the 15th and 16th centuries the infantry soldiers (Swiss or landsknecht) carried a heavy poniard or dagger. This and the earlier Spanish dagger with a thumb-ring were distinctively the weapons of professional soldiers. The rise of duelling produced another type, called the main gauche, which was a parrying weapon and often had a toothed edge on which the adversary’s sword was caught and broken. One form of this dagger had a blade which expanded into a triple fork on pressing a spring; this served the same purpose. The satellites of the Vehmgericht had a similar weapon, in order, it is suggested, that their acts should be done in the name of the Trinity. The smaller poniards are generally called “stilettos.” Much ingenuity and skill have been lavished on the adornment of daggers, and in rendering the blades more capable of inflicting severe wounds. Daggers also were sometimes made to poison as well as to wound. Of oriental daggers may be mentioned the Malay “crease” or “kris,” which has a long waxed blade; the Gurkha “kukri,” a short curved knife, broadest and heaviest towards the point; and the Hindu “khuttar,” which has a flat triangular-shaped blade, and a hilt of H-shape, the cross-bar forming the grip and the sides the guard.
DAGHESTAN, a province of Russia, Transcaucasia, occupying the triangular space between the Andi ridge, the south-east division of the main Caucasus range, and the Caspian Sea. It has the province of Terek on the N.W., the government of Tiflis on the S.W., and that of Baku on the S.E. With the exception of a narrow strip along the sea-coast and a small district in the N., it is entirely mountainous. Area, 11,332 sq. m. The snow-clad Andi ridge, belonging to the system of transverse upheavals which cross the Caucasus, branches off the latter at Borbalo Peak (10,175 ft.), and reaches its highest altitudes in Tebulos-mta (14,775 ft.) and Diklos-mta (13,740 ft.). It is encircled on the N. by a lower outer ridge, the Karadagh, through which the rivers cut their way. This ridge is thickly clothed with forests, chiefly beech. The Boz-dagh and another ridge run between the four Koisu rivers, the head-streams of the Sulak, which flows into the Caspian. The next most important stream, out of the great number which course down the flanks of the Caucasus and terminate in the Caspian, is the Samur. The most notable feature of the province is, however, according to O. W. H. Abich (Sur la structure et la géologie du Daghestan, 1862), the successive folds of Jurassic limestones and slates, all nearly parallel to the Caucasus, which form lofty, narrow plateaus. Many of the peaks upon them rise higher than 12,000 ft., and the passes lie at altitudes of 11,000 ft. in the interior and 9000 ft. towards the Caspian. Towards the Caspian, especially between Petrovsk and the river Sulak, the Cretaceous system is well represented, and upon its rocks rest marls, shales, and sandstones of the Eocene period. The country is altogether difficult of access, and only one military route leads up from the river Terek, while every one of the eleven passes known across the Caucasus is a mere bridle-path. The climate is severe on the plateaus, hot towards the Caspian, and dry everywhere. The average temperatures are—year 51°, January 26°, July 73° at Temir-khan-shura (42° 49′ N.; alt. 1510 ft.). The annual rainfall varies from 17 to 21 in. The population, estimated at 605,100 in 1906, numbered 587,326 in 1897, of whom only 5000 were Russians. They consist chiefly of mountaineers known as Lesghians (i.e. 158,550 Avars, 121,375 Darghis, 94,506 Kurins), a race closely akin to the Circassians, intermingled towards the Caspian Sea with Tatars and Georgians. There are also sprinklings of Jews and Persians. The highlands of Daghestan were for many years the stronghold of the Circassians in their struggle against Russia, especially under the leadership of Shamyl, whose last stand was made on the steep mountain fastness of Gunib, 74 m. S. of Temir-khan-shura, in 1859. The difficulty of communication between the valleys has resulted in the growth of a great number of dialects. Avarian is a sort of inter-tribal tongue, while Lakh or Kazi-kumukh, Kurin, Darghi-kaitakh, Andi, and Tabasaran are some of the more important dialects, each subdivided into sub-dialects. The mountaineers breed some cattle and sheep, and cultivate small fields on the mountain-sides. In the littoral districts excellent crops of cereals, cotton, fruit, wine and tobacco are obtained with the aid of irrigation. Silkworms are bred. The mountaineers excel also in a variety of petty trades. Sulphur, salt and copper are the most important of the minerals. A railway line to connect the North Caucasian line (Rostov to Petrovsk) with the Transcaucasian line (Batum to Baku) has been built along the Caspian shore from Petrovsk, through the “gate” or pass of Derbent, to Baku. The province is divided into nine districts—Temir-khan-shura, Avar, Andi, Gunib, Dargo, Kazi-kumukh, Kaitago-Tabasaran, Kurin, and Samur. The only towns are Temir-khan-shura (pop. 9208 in 1897), the capital of the government, Derbent (14,821) and Petrovsk (9806), the last two both on the Caspian.
See G. Radde, “Aus den Daghestanischen Hochalpen,” in Petermanns Mitteilungen, Erganzungsheft, No. 85, 1887, and, with E. König, “Der Nordfuss des Daghestan,” in Petermanns Mitteil., Erganzungsheft, No. 117, 1895.
DAGO, a name given somewhat contemptuously to Spanish, Portuguese and Italian sailors, as “Dutchman” is similarly applied to Germans and Scandinavians as well as to natives of Holland. In America the word is generally confined to the poorer class of Italian immigrants. In the South Wales mining districts the casual labourers, who are only engaged when work is plentiful, are so called. The word is apparently a corruption of the common Spanish and Portuguese Christian name “Diego.”
DAGOBERT I. (d. 639), king of the Franks, was the son of Clotaire II. In 623 his father established him as king of the region east of the Ardennes, and in 626 revived for him the ancient kingdom of Austrasia, minus Aquitaine and Provence. As Dagobert was yet but a child, he was placed under the authority of the mayor of the palace, Pippin, and Arnulf, bishop of Metz. At the death of Clotaire II. in 629, Dagobert wished to re-establish unity in the Frankish realm, and in 629 and 630 made expeditions into Neustria and Burgundy, where he succeeded in securing the recognition of his authority. In Aquitaine he gave his brother Charibert the administration of the counties of Toulouse, Cahors, Agen, Périgueux, and Saintes; but at Charibert’s death in 632 Dagobert became sole ruler of the whole of the Frankish territories south of the Loire. Under him the Merovingian monarchy attained its culminating point. He restored to the royal domain the lands that had been usurped by the great nobles and by the church; he maintained at Paris a luxurious, though, from the example he himself set, a disorderly court; he was a patron of the arts, and delighted in the exquisite craftsmanship of his treasurer, the goldsmith St Eloi. His authority was recognized through the length and breadth of the realm. The duke of the Basques came to his court to swear fidelity, and at his villa at Clichy the chief of the Bretons of Domnoné promised obedience. He intervened in the affairs of the Visigoths of Spain and the Lombards of Italy, and was heard with deference. Indeed, as a sovereign, Dagobert was reckoned superior to the other barbarian kings. He entered into relations with the eastern empire, and swore a “perpetual peace” with the emperor Heraclius; and it is probable that the two sovereigns took common measures against the Slav and Bulgarian tribes, which ravaged in turn the Byzantine state and the German territories subject to the Franks. Dagobert protected the church and placed illustrious prelates at the head of the bishoprics—Eloi (Eligius) at Noyon, Ouen (Audoenus) at Rouen, and Didier (Desiderius) at Cahors. His reign is also marked by the creation of numerous monasteries and by renewed missionary activity in Flanders and among the Basques. He died on the 19th of January 639, and was buried at St Denis. After his death the Frankish monarchy was again divided. In 634 he had been obliged to give the Austrasians a special king in the person of his eldest son Sigebert, and at the birth of a second son, Clovis, in 635, the Neustrians had immediately claimed him as king. Thus the unification of the realm, which Dagobert had re-established with so much pains, was annulled.
See the Chronicon of Fredegarius; “Gesta Dagoberti I. regis Francorum” in Mon. Germ. hist. Script. rer. Meroving. vol. ii. edited by B. Krusch; J. H. Albers, Konig Dagobert in Gesch., Legende, und Sage (2nd ed., Kaiserslautern, 1884); E. Vacandard, Vie de Saint Ouen, évêque de Rouen (Paris, 1901); and H. E. Bonnell, Die Anfange des karoling. Hauses (Berlin, 1866).
DAGON, a god of the Philistines who had temples at Ashdod (1 Sam. v. 1), and Gaza (Judg. xvi. 21, 23); the former was destroyed by Jonathan, the brother of Judas the Maccabee (1 Macc. x. 84; 148 B.C.). But Dagon was more than a mere local deity; there was a place called Beth-Dagon in Judah (Josh. xv. 41), another on the borders of Asher (ib. xix. 27), and a third underlies the modern Bēt Dejān, south-east of Nāblus. Dagon was in all probability an old Canaanite deity; it appears in the name of the Canaanite Dagantakala as early as the 15th century, and is possibly to be identified with the Babylonian god Dagan. Little is known of his cult (Judg. xvi. 23 seq.), although as the male counterpart of Ashtoreth (see Astarte) his worship would scarcely differ from that of the Baalim (see Baal). The name Dāgōn seems to come from dāg “fish,” and that his idol was half-man half-fish is possible from the ichthyomorphic representations found upon coins of Ascalon and Arvad, and from the fact that Berossus speaks of an Assyrian merman-god.
The true meaning of the name is doubtful. In 1 Sam. v. 4, Thenius and Wellhausen, followed by Robertson Smith and others, read “only his fish-part (dāgō) was left to him”; against this, see the comm. of H. P. Smith and Budde. The identification of Dagon with the Babylonian Dagan is doubted by G. F. Moore (Encyc. Bib., col. 985), and that of the latter with Odacon and Ea-Oannes is questionable. Philo Byblius (Müller, Fr. Hist. Graec. iii. 567 seq.) makes Dagon the inventor of corn and the plough, whence he was called Ζεὺς Ἀρότριος. This points to a natural though possibly late etymology from the Hebrew and Phœnician dagan “corn.” It is not improbable that, at least in later times, Dagon had in place of, or in addition to, his old character, that of the god who presided over agriculture; for in the last days of paganism, as we learn from Marcus Diaconus in the Life of Porphyry of Gaza (§ 19), the great god of Gaza, now known as Marna (our Lord), was regarded as the god of rains and invoked against famine. That Marna was lineally descended from Dagon is probable in every way, and it is therefore interesting to note that he gave oracles, that he had a circular temple, where he was sometimes worshipped by human sacrifices, that there were wells in the sacred circuit, and that there was also a place of adoration to him situated, as was usual, outside the town. Certain “marmora” in the temple, which might not be approached, especially by women, may perhaps be connected with the threshold which the priests of Dagon would not touch with their feet (1 Sam. v. 5, Zeph. i. 9). See further, the comm. on the Old Testament passages, Moore (loc. cit.), and Lagrange, Relig. sémit. p. 131 seq.
DAGUERRE, LOUIS JACQUES MANDÉ (1789-1851), French, painter and physicist, inventor of the daguerreotype, was born at Cormeilles, in the department of Seine-et-Oise, and died on the 12th of July 1851 at Petit-Brie-sur-Marne, near Paris. He was at first occupied as an inland revenue officer, but soon took to scene-painting for the opera. He assisted Pierre Prévost (1764-1823) in the execution of panoramic views of Rome, Naples, London, Jerusalem, and Athens, and subsequently (July 11, 1822), in conjunction with Bouton, he opened at Paris the Diorama (δίς, double; ὅραμα, view), an exhibition of pictorial views, the effect of which was heightened by changes in the light thrown upon them. An establishment similar to that at Paris was opened by Daguerre in Regent’s Park, London. On the 3rd of March 1839 the Diorama, together with the work on which Daguerre was then engaged, was destroyed by fire. This reverse of fortune was soon, however, more than compensated for by the distinction he achieved as the inventor of the daguerreotype photographic process. J. Nicéphore Niepce, who since 1814 had been seeking a means of obtaining permanent pictures by the action of sunlight, learned in 1826 that Daguerre was similarly occupied. In 1829 he communicated to Daguerre particulars of his method of fixing the images produced in the camera lucida by making use of metallic plates coated with a composition of asphalt and oil of lavender; this, where acted on by the light, remained undissolved when the plate was plunged into a mixture of petroleum and oil of lavender, and the development of the image was effected by the action of acids and other chemical reagents on the exposed surface of the plate. The two investigators laboured together in the production of their “heliographic pictures” from 1829 until the death of Niepce in 1833. Daguerre, continuing his experiments, discovered eventually the process connected with his name. This, as he described it, consists of five operations:—the polishing of the silver plate; the coating of the plate with iodide of silver by submitting it for about 20 minutes to the action of iodine vapour; the projection of the image of the object upon the golden-coloured iodized surface, the development of the latent image by means of the vapour of mercury; and, lastly, the fixing of the picture by immersing the plate in a solution of sodium “hyposulphite” (sodium thiosulphate). On the 9th of January 1839, at a meeting of the Academy of Sciences, Arago dwelt on the importance of the discovery of the daguerreotype; and, in consequence of the representations made by him and Gay Lussac to the French government, Daguerre was on the 15th of June appointed an officer of the Legion of Honour. On the same day a bill was presented to the chambers, according to the provisions of which 731 Daguerre and the heir of Niepce were to receive annuities of 6000 and 4000 francs respectively, on the condition that their process should be made known to the Academy. The bill having been approved at the meetings of the two chambers on the 9th of July and on the 2nd of August, Daguerre’s process, together with his system of transparent and opaque painting, was published by the government, and soon became generally known (see Photography).
Daguerre’s Historique et description des procédés du daguerréotype et du diorama (Paris, 1839) passed through several editions, and was translated into English. Besides this he wrote an octavo work, entitled Nouveau moyen de préparer la couche sensible des plaques destinées à recevoir les images photographiques (Paris, 1844).