PHYSICS
TOWER, SMITH, TURTON,
AND
COPE
 (See p.441)
(See p.441)
Three-color Printing
Y. Yellow impression; negative made through a blue-violet filter. R. Crimson
impression; negative made through a green filter. RY. Crimson on yellow.
B. Blue impression; negative made through a red filter. YRB. Yellow, crimson,
and blue combined; the final product. (Courtesy of Phototype Engraving
Co., Philadelphia.)
[Pg i]
[Pg ii]
[Pg iii]
PHYSICS
BY
WILLIS E. TOWER, M. SCI. (Univ. of Illinois)
HEAD OF THE DEPARTMENT OF PHYSICS, ENGLEWOOD
HIGH SCHOOL, CHICAGO
CHARLES H. SMITH, M. E. (Cornell)
HEAD OF THE DEPARTMENT OF PHYSICS AND ASSISTANT
PRINCIPAL, HYDE PARK SCHOOL, CHICAGO
CHARLES M. TURTON, A. M. (Syracuse)
HEAD OF THE DEPARTMENT OF PHYSICS, BOWEN
HIGH SCHOOL, CHICAGO
IN COLLABORATION WITH
THOMAS D. COPE, Ph.D. (Pennsylvania)
ASSISTANT PROFESSOR OF PHYSICS, UNIVERSITY
OF PENNSYLVANIA
BASED UPON
PRINCIPLES OF PHYSICS
BY
TOWER, SMITH and TURTON
WITH 7 PLATES AND 448 OTHER ILLUSTRATIONS
PHILADELPHIA
P. BLAKISTON'S SON & CO.
1012 WALNUT STREET
[Pg iv][Pg v]
Copyright, 1920, by P. Blakiston's Son & Co.
In the preparation of this text, the pupil, his experience,
needs, and interests have been constantly kept in mind.
The order of topics, illustrations, and problems have
been selected with the purpose of leading the pupil into
a clear understanding of the physical phenomena continually
taking place about him.
The recommendations and conclusions reached by the
"New Movement in the Teaching of Physics" have been
incorporated into the book as a whole. These conclusions
indicate that the most efficient teaching in physics involves
a departure from the quantitative, mathematical methods
of presentation that were in general use a dozen or more
years ago, toward a method better adapted to the capabilities,
interests, and requirements of the young people in
our physics classes.
The older methods are effective with a portion of the
student body which has the greater mathematical ability
and training, but they discourage a large majority of the
pupils who are not gifted or prepared for severe mathematical
analysis. For this reason, many of the more difficult
mathematical demonstrations often given in physics
texts are omitted. Most of the problems involve only the
units employed in practical every-day measurements.
The portions of Mechanics that are ordinarily so difficult
for the average pupil are not taken up until he has
covered considerable ground with which he is more or less
familiar and not until he has become somewhat accustomed[Pg vi]
to the methods of study and the technical terms of the
subject.
The pupil comes to the study of physics with a great
number of experiences and impressions of physical phenomena
continually occurring about him. In recognition
of this fact, it has been thought best to consider first the
explanation of common things well known to all pupils,
such as the diffusion of gases, evaporation of liquids,
expansion of bodies when heated, and capillary action.
Since the molecular theory of matter is now supported by
so many conclusive evidences, we have not hesitated to
make free use of it in the early chapters. The applications
of this theory are extremely helpful in explaining every-day
phenomena. Our experience shows that beginners in physics
understand and apply this theory without difficulty.
The illustrations and drawings have been selected from
a pedagogical rather than a spectacular point of view.
Practically all of them are new. The problems and exercises
have been selected for the distinct purpose of illustrating
the principles taught in the text and for their
practical applications.
Many direct applications to common every-day experiences
are given in order to connect the subject matter with
the home environment and daily observation of physical
phenomena. Some phenomena are mentioned without
detailed explanation as it is felt that the presentation of
these subjects in this manner is better for this grade of
student than a complete analysis.
Some of the special features of the text may be briefly
summarized as follows:
(A) Simplicity of presentation is emphasized. The
methods of attack, the illustrations and examples employed
in developing the subjects are particularly adapted
to beginners in physics.
[Pg vii]
(B) The text is divided into some seventy-seven sections,
each containing material enough for one recitation.
(C) Each of these sections is summarized by a list of
important topics which point out to the pupil the principles
and subject matter requiring most careful attention.
The lists of important topics are also of assistance to the
teacher in assigning recitations.
(D) The problems and practical exercises emphasize
physical principles as distinguished from mathematical
training. A list of exercises is placed at the end of the
several sections. They are in sufficient number to permit
testing at many points and of a choice of problems by
teachers.
The authors wish to express their appreciation for suggestions
and helpful criticisms to many who have read the
text in manuscript or proof. Especially to Professor A. P.
Carman of the University of Illinois and his associate,
Professor F. R. Watson, who have gone carefully over the
whole text; and to Mr. Chas. M. Brunson, Scott High
School, Toledo, Ohio, Mr. Frank E. Goodell, North High
School, Des Moines, Iowa, and to Mr. Walter R. Ahrens,
Englewood High School, Chicago, for assistance in reading
the proofs. Also to Mr. W. H. Collins, Jr., Bowen
High School, Chicago, who supervised the preparation of
drawings for the diagrams and figures; and to many firms
and individuals that have courteously furnished material
for illustrations.
Willis E. Tower.
Charles H. Smith.
Charles M. Turton.
[Pg viii]
[Pg ix]
When a pupil begins the study of Physics he has in his
possession many bits of knowledge which are fundamental
in the science. He has learned to throw a ball and can tell
how a thrown ball moves. He has drawn out nails with a
claw hammer. He has seen wood float and iron sink. He
has sucked liquids up through straws. In his mother's
kitchen, he sees water as ice, liquid, and steam. On a
wintry day he reads the temperature on a thermometer.
He sees sparks fly from car wheels when the brakes are
applied. He has played with a horseshoe magnet, and has
found the north by means of a compass. The telephone,
the electric light and the motor he sees, and perhaps uses,
many times a day. He dresses before a mirror, focuses
his camera, watches the images at a moving picture
show, and admires the colors of the rainbow. He has
cast stones into water to watch the ripples spread, has
shouted to hear the echo, and perhaps plays some musical
instrument. These, and a thousand other things, are
known to the intelligent and normal boy or girl who has
reached the age at which the study of Physics is properly
begun.
To a great extent even the terms used in the science are
familiar to the beginner. He speaks of the horse-power
of an engine, reads kilowatt-hours from the meter in the
cellar, and may know that illuminating gas costs one
dollar per thousand "cubic feet." "Ampere" and "volt"
are words he frequently hears and sees.
When he takes up the study of Physics, the attitude of[Pg x]
the student toward these familiar things and words must
undergo a change. Casual information about them must
be changed to sound knowledge, purposely acquired.
Hazy notions about the meanings of words must be
replaced by exact definitions. Bits of knowledge must
be built into a structure in which each fact finds its proper
place in relation to the others.
The only agent which can accomplish these changes is
the student himself. He must consciously and purposely
seek the truth and must reflect upon it until he
sees it in its relation to other truth. Upon him, and upon
him alone, rests the final responsibility for the success or
failure of his study.
But the student is not without assistance. In his
teacher he finds a guide to stimulate, to direct, and to aid
his efforts, and a critic to point out wherein his efforts
have failed and wherein they have succeeded. Weights,
measures, and other apparatus are furnished to enable
him to answer for himself questions which have arisen in
his studies.
In addition to these the student has his text book, his
teacher for his hours of private study. A good text book
is an inspiring teacher in print. It directs attention to
things familiar to the student through long experience, and
inspires him to make a closer scrutiny of them. It invites
him to observe, to analyze, to compare, to discover likenesses
and differences in behavior. It questions him at
every turn. Its ever repeated challenge reads, "Weigh
and consider." It furnishes him needed information that
he cannot otherwise acquire. It satisfies his desire to
know, "By whom, where, when, and how was this first
discovered?"
The student of Physics must never forget that he is
studying not pages of text but the behavior and properties[Pg xi]
of iron, water, mica, moving balls, pumps, boiling liquids,
compressed air, mirrors, steam engines, magnets, dynamos,
violins, flutes, and a host of other things. His studies
should, whenever possible, be made first hand upon the
things themselves. The text is an aid to study, never a
substitute for the thing studied.
It is an excellent plan for each student to select some
one thing for special study, the telephone for example.
By observation, experiment, and reading, he may acquire
a large amount of valuable information about such a
subject while pursuing his course in Physics. Every part
of the science will be found to bear some relation to it.
The student who takes up the study of Physics in the
way suggested will find himself at the end of a year of
study in possession of much new and valuable knowledge
about the physical world in which he lives. By virtue
of this knowledge he will be better able to enjoy the world,
to control it, and to use it.
Thomas D. Cope.
Philadelphia.
[Pg xiii]
[Pg xii]
Chapter I. Introduction And Measurement. Page
- (1) Introduction 1
- (2) States of Matter 4
- (3) The Metric System 8
Chapter II. Molecular Forces And Motions.
- (1) Molecular Motions in Gases 13
- (2) Molecular Motions in Liquids 18
- (3) Molecular Forces in Liquids 21
- (4) Molecular Forces in Liquids and Solids 27
- (5) Molecular Forces in Solids 31
Chapter III. Mechanics or Liquids.
- (1) Liquid Pressure 36
- (2) Transmission of Liquid Pressure 41
- (3) Archimedes' Principle 47
- (4) Density and Specific Gravity 52
Chapter IV. Mechanics Of Gases.
- (1) Weight and Pressure of the Air 55
- (2) Compressibility and Expansibility of the Air 62
- (3) Pneumatic Appliances 66
Chapter V. Force And Motion.
- (1) Force, how Measured and Represented 79
- (2) Motion. Newton's Laws 85
- (3) Resolution of Forces 96
- (4) Moment of Force and Parallel Forces 99
- (5) Gravitation and Gravity 103
- (6) Falling Bodies 109
- (7) The Pendulum 115
Chapter VI. Work And Energy.
- (1) Work and Energy 119
- (2) Power and Energy 123
- (3) The Lever and Simple Machines 129
- (4) Wheel and Axle and Pulley 136
- (5) Efficiency and the Inclined Plane 142
- (6) Friction and its Uses 147
- (7) Water Power 152
Chapter VII. Heat, Its Production And Transmission.[Pg xiv]
- (1) Sources and Effects of Heat 159
- (2) Temperature and Expansion 162
- (3) Expansion of Gases, Liquids and Solids 167
- (4) Modes of Transmitting Heat 173
- (5) Convection, Heating and Ventilation 179
- (6) The Moisture in the Air, Hygrometry 191
- (7) Evaporation 196
Chapter VIII. Heat And Work.
- (1) Heat Measurement and Specific Heat 200
- (2) Heat and Changes of State 205
- (3) Heat and Work 212
- (4) Heat Engines 222
Chapter IX. Magnetism.
- (1) General Properties of Magnets 228
- (2) Theory of Magnetism, Magnetic Fields 232
- (3) The Earth's Magnetism 238
Chapter XI. Static Electricity.
- (1) Electrification and Electrical Charges 243
- (2) Electric Fields and Electrostatic Induction 247
- (3) Electric Theories, Distribution and Electric Charges 252
- (4) Potential, Capacity, and the Electric Condenser 257
- (5) Electrostatic Generators 262
Chapter XI. Electric Currents Produced By Voltaic
Cells.
- (1) Electrical Currents and Circuits 267
- (2) The Simple Voltaic Cell and its Action 270
- (3) Practical Voltaic Cells 274
Chapter XII. Magnetic Effects Of Electric Currents,
And Electrical Measurements.
- (1) The Magnetic Effect of Electric Currents 279
- (2) Electrical Measurements 289
- (3) Ohm's Law and Electrical Circuits 298
- (4) Grouping of Cells and Measuring Resistance 302
Chapter XIII. Chemical And Heat Effects Of Electric
Currents.
- (1) The Chemical Effect of Electric Currents 307
- (2) The Storage Battery and Electric Power 312
- (3) The Heat Effect of Electric Currents 318
Chapter XIV. Induced Currents.
- (1) Electromagnetic Induction 326
- (2) The Dynamo and the Motor 335
- (3) The Induction Coil and the Transformer 343
- (4) The Telephone 349
[Pg xv]
Chapter XV. Sound.
- (1) Sound, Source, Speed, Media 354
- (2) Waves and Wave Motion 357
- (3) Intensity and Pitch of Sound 363
- (4) Musical Scales and Resonance 368
- (5) Interference, Beats, Vibration of Strings 374
- (6) Tone Quality, Vibrating Plates and Air Columns 384
Chapter XVI. Light.
- (1) Rectilinear Propagation of Light 388
- (2) Photometry and Law of Reflection 393
- (3) Mirrors and Formation of Images 400
- (4) Refraction of Light 410
- (5) The Formation of Images by Lenses 416
- (6) Optical Instruments 423
- (7) Color and Spectra 430
- (8) Nature of Light 442
Chapter XVII. Invisible Radiations.
- (1) Electric waves and Radioactivity 448
Chapter XVIII. Wireless Telephony And Alternating
Currents.
- (1) Wireless Telephony 460
- (2) Alternating Currents 466
- Index 487
[Pg xvi]
[Pg 1]
PHYSICS
INTRODUCTION AND MEASUREMENT
(1) Introduction
1. Physics, an Explanation of Common Things.—Many
students take up the study of physics expecting to see
wonderful experiments with the "X" rays, wireless telegraphy,
dynamos, and other interesting devices. Others
are dreading to begin a study that to them seems strange
and difficult, because they fear it deals with ideas and
principles that are beyond their experience and hard to
comprehend.
Each of these classes is surprised to learn that physics
is mainly an explanation of common things. It is a study
that systematizes our knowledge of the forces and changes
about us; such as the pull of the earth, the formation of
dew, rain and frost, water pressure and pumps, echoes
and music, thermometers and engines, and many other
things about us with which people are more or less familiar.
Physics is like other school subjects, such as mathematics
and language, in having its own peculiar vocabulary and
methods of study; these will be acquired as progress is
made in the course.
The most useful habit that the student of physics can[Pg 2]
form is that of connecting or relating each new idea or
fact that is presented to him to some observation or experience
that will illustrate the new idea. This relating
or connecting of the new ideas to one's own personal
experience is not only one of the best known means of
cultivating the memory and power of association, but it
is of especial help in a subject such as physics, which deals
with the systematic study and explanation of the facts
of our every-day experience.
2. Knowledge—Common and Scientific.—This leads
to the distinction between common knowledge and scientific
knowledge. We all possess common knowledge of the
things about us, gained from the impressions received by
our senses, from reading, and from the remarks of others.
Scientific knowledge is attained when the bits of common
knowledge are connected and explained by other information
gained through study or experience. That is, common
knowledge becomes scientific, when it is organized.
This leads to the definition: Science is organized knowledge.
Common knowledge of the forces and objects about
us becomes scientific only as we are able to make accurate
measurements of these. That is, science is concerned
not only in how things work, but even more in how much
is involved or results from a given activity. For example,
a scientific farmer must be able to compute his costs and
results in order to determine accurately his net profits.
The business man who is conducting his business with
efficiency knows accurately his costs of production and
distribution.
This book is written in the hope that it will make more
scientific the student's common knowledge of the forces
and changes in the world about him and will give him many
ideas and principles that will help him to acquire the
habit of looking from effects to their natural causes and[Pg 3]
thus tend to develop what is called the scientific habit of
thought.
3. Hypothesis, Theory, and Law.—Three words that
are frequently used in science may be mentioned here:
hypothesis, theory, and law. An hypothesis is a supposition
advanced to explain some effect, change, or condition that
has been observed. For example, the Nebular Hypothesis
of which many high-school students have heard, is an
attempt to explain the origin of the sun, the earth, the
planets, and other solar systems.
A theory is an hypothesis which has been tested in a
variety of ways and which seems to fit the conditions and
results so that it is generally accepted as giving a satisfactory
explanation of the matter in question. The
Molecular Theory of Matter which states that matter of
all kinds is composed of very small particles called molecules
(see Art. 6), is a familiar example of a theory.
A theory becomes a law when it may be definitely proved.
Many laws are expressed in mathematical language,
e.g., the law of gravitation. (See Art. 88.) Many of
the laws of physics are illustrated by laboratory experiments,
which show in a simple way just what the law
means.
Exercises
Explain what is meant by the following terms and expressions:
1. Common knowledge.
2. Scientific knowledge.
3. Science.
4. Topics in physics.
5. Scientific habit of thought.
6. Value of relating new ideas to former experiences.
7. Hypothesis.
8. Theory.
9. Law.
[Pg 4]
(2) The States of Matter
4. Physics Defined.—In the study of any science or
field of knowledge, it is helpful to have a basis for grouping
or classifying the facts studied. In physics we are to
study the objects, forces, and changes about us, to understand
them and their relations to one another. Accordingly,
physics, dealing with the material world about us,
is often defined as the science of matter and energy, matter
being anything that occupies space and energy the capacity
for doing work. This definition of physics while not
strictly accurate is sufficiently comprehensive for our
present purpose.
5. The Three States of Matter.—Our bodies are matter
since they occupy space. Further, they possess energy
since they are able to do work. In beginning the study
of physics it will simplify our work if we study one of
these topics before the other. We will therefore begin
with matter and consider first its three states.
Some bodies are solid; as ice, iron, wax. Others are
liquid; as water, mercury, oil. Still others are in the state
of gas; as steam, air, and illuminating gas. Further we
notice that the same substance may be found in any one
of the three states. For example water may be either ice,
water or steam; that is, either a solid, a liquid, or a gas.
Most persons have heard of liquid air and possibly some
know of ice air, i.e., air cooled until it not only liquefies,
but is solidified. On the other hand, iron may be melted
and, if heated hot enough, may be turned into iron vapor.
In fact most substances by heating or cooling sufficiently
may be changed into any one of the three states.
Before defining the three states, let us consider the
structure of matter. This may help us to answer the
question: How is it possible to change a hard solid, such[Pg 5]
as ice, into a liquid, water, and then into an invisible gas
like steam? This is explained by the molecular theory
of matter.
6. The Molecular Theory of Matter.—It is believed
that all bodies are made up of very small particles called
molecules, and that these instead of being packed tightly
together like square packages in a box, are, strange as it
may seem, very loosely packed even in solids and do not
permanently touch their neighbors. The size of these
molecules is so minute that it has been estimated that if
a drop of water could be magnified to the size of the earth,
the molecules magnified in the same proportion would be in
size between a baseball and a football. The air and all
other gases are believed to be made up of molecules in
rapid motion, striking and rebounding continually from
one another and from any objects in contact with the
gas.
7. States of Matter Defined.—These ideas of the structure
of matter assist us in understanding the following
definitions: A solid is that state of matter in which the
molecules strongly cling together and tend to keep the same
relative positions. (This of course follows from the tendency
of a solid to retain a definite form.) A liquid is
that state of matter in which the molecules tend to cling
together, yet move about freely. Hence a liquid takes the
form of any vessel in which it is placed. A gas is that
state of matter in which the molecules move about freely
and tend to separate indefinitely. Hence a gas will fill
any space in which it is placed.
8. Effect of Heat on Matter.—It is further believed that
when a body is heated, that the action really consists in
making its molecules move or vibrate faster and faster
as the heating progresses. This increase of motion causes
the molecules to push apart from one another and this[Pg 6]
separation of the molecules causes an expansion of the
body whether it be solid, liquid, or gas. Fig. 1 shows
the expansion of air in an air thermometer.
Fig. 2 shows the expansion of a solid on
heating.
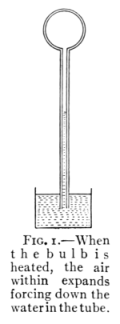 Fig. 1.—When
the bulb is
heated, the air
within expands
forcing down the
water in the tube.
Fig. 1.—When
the bulb is
heated, the air
within expands
forcing down the
water in the tube.
9. Physical and Chemical Changes.
A change of state such as the freezing
or boiling of water is called a physical
change, for this change has not affected
the identity of the substance. It is water
even though it has become solid or
gaseous. Heating a platinum wire red
hot is also a physical change for the wire
when on cooling is found to be the same substance
as before. Further if salt or sugar
be dissolved in water the act of solution
is also a physical change since the identical
substance (salt or sugar) is in the solution
and may be obtained by evaporating the water.
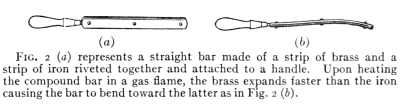 Fig. 2 (a) represents a straight bar made of a strip of brass and a
strip of iron riveted together and attached to a handle. Upon heating
the compound bar in a gas flame, the brass expands faster than the iron
causing the bar to bend toward the latter as in Fig. 2 (b).
Fig. 2 (a) represents a straight bar made of a strip of brass and a
strip of iron riveted together and attached to a handle. Upon heating
the compound bar in a gas flame, the brass expands faster than the iron
causing the bar to bend toward the latter as in Fig. 2 (b).
If some sugar, however, is heated strongly, say in a
test-tube, it is found to blacken, some water is driven off
and on cooling some black charcoal is found in the tube
instead of the sugar. This action which has resulted in a
change in the nature of the substance treated is called a
chemical change. To illustrate further, if some magnesium
wire is heated strongly in a flame, it burns, giving off an
intense light and when it cools one finds it changed to a
light powdery substance like ashes. Chemical changes,[Pg 7]
or those that change the nature of the substance affected,
are studied in chemistry. In physics we have to do only
with physical changes, that is, with those changes that
do not affect the nature of the substance.
Important Topics
1. Physics defined.
2. The three states of matter; solid, liquid, gas.
3. Molecular theory of matter.
4. Physical and chemical changes.
Exercises
Write out in your own words your understanding of:
1. The structure of matter.
2. Some of the differences between solids, liquids, and gases.
3. How to change solids to liquids and gases and vice versa.
4. The reason for the changes of size of a body on heating.
5. Why cooling a gas tends to change it to a liquid or a solid.
6. The actual size of molecules.
Which of the following changes are chemical and which
physical?
Give reasons.
1. Melting of ice.
2. Burning of a candle.
3. Production of steam.
4. Falling of a weight.
5. Drying of clothes.
6. Making an iron casting.
7. Decay of vegetables.
8. Sprouting of seeds.
9. Flying an aeroplane.
10. Growth of a plant.
11. Grinding of grain.
12. Sawing a board.
13. Pulverizing stone.
14. Making toast.
15. Sweetening tea or coffee with sugar.
16. Burning wood or gas.
[Pg 8]
(3) The Metric System
10. The Metric System.—In order to study the three
states of matter with sufficient exactness it is necessary
to employ a system of measurement. The system universally
employed by scientists is called The Metric System.
In many respects it is the most convenient for all purposes.
Every student should therefore become familiar with it
and learn to use it. At the present time, not only do scientists
everywhere use it, but many countries have adopted
it and use it in common measurements. It was legalized
in the United States in 1866. The metric system was
originated by the French Academy of Sciences during the
latter part of the 18th century. There were so many
different systems of weights and measures in use, each
country having a system of its own, that commerce was
much hindered. It was therefore decided to make a system
based upon scientific principles. The length of the
earth's quadrant passing from the equator to the pole
was determined by surveying and computation. One-ten-millionth
of this distance was selected as the unit of
length and called a meter. Accurate copies of this meter
were made and preserved as standards.
Later surveys have shown that the original determination
of the earth's quadrant was not strictly accurate; so
that after all the meter is not exactly one-ten-millionth of
the earth's quadrant.
11. The Standard Meter.—The standard unit of length
in the metric system is the meter. It is the distance, at
the temperature of melting ice, between two transverse
parallel lines ruled on a bar of platinum (see Fig. 3), which[Pg 9]
is kept in the Palace of the Archives in Paris. Accurate
copies of this and other metric standards are also kept at
the Bureau of Standards at Washington,
D. C. Fig. 4 shows the relation between
the inch and the centimeter (one-hundredth
of a meter).
12. Units and Tables in the Metric
System.—The metric unit of area commonly
used in physics is the square centimeter.
 Fig. 3—The
standard meter.
Fig. 3—The
standard meter.
The standard unit of volume or capacity
is the liter. It is a cube one-tenth of a
meter on each edge. It is equal to 1.057
quarts. It corresponds, therefore, to the quart in English
measure.
 Fig. 4.—Centimeter and inch scales.
Fig. 4.—Centimeter and inch scales.
The standard unit of mass is the kilogram. It is the
mass of 1 liter of pure water at the temperature of its
greatest density, 4°C. or 39.2°F.
The three principal units of the metric system, the
meter, the liter, and the kilogram, are related to one another
in a simple manner, since the liter is a cube one-tenth of
a meter in each dimension and the kilogram is the mass
of a liter of water. (See Fig. 5.)
The metric system is a decimal system that is, one unit
is related to another unit in the ratio of ten or of some
power of ten. This is indicated by the following
tables:
[Pg 10]
| Metric Table of Length |
| 10 millimeters (mm.) | equal 1 centimeter. |
| 10 centimeters (cm.) | equal 1 decimeter. |
| 10 decimeters (dm.) | equal 1 meter. |
| 10 meters (m.) | equal 1 dekameter. |
| 10 dekameters (Dm.) | equal 1 hectometer. |
| 10 hectometers (hm.) | equal 1 kilometer. |
| 10 kilometers (km.) | equal 1 myriameter. |
The measures commonly used are the centimeter, meter and kilometer.
| Metric Table of Mass (or Weight) |
| 10 milligrams (mg.) | equal 1 centigram. |
| 10 centigrams (cg.) | equal 1 decigram. |
| 10 decigrams (dg.) | equal 1 gram. |
| 10 grams (g.) | equal 1 dekagram. |
| 10 dekagrams (Dg.) | equal 1 hectogram. |
| 10 hectograms (hg.) | equal 1 kilogram. |
| 10 kilograms (kg.) | equal 1 myriagram. |
The masses commonly used are the milligram, gram and kilogram.
Notice in these tables the similarity to 10 mills equal 1 cent, 10
cents equal 1 dime, 10 dimes equal 1 dollar, in the table of United
States money.
Other tables in the metric system are built upon the same plan.
Learn the prefixes in order thus: milli, centi, deci, deka, hecto, kilo,
myria. The first three prefixes are Latin numerals and represent
divisions of the unit. The last four are Greek numerals and represent
multiples. In these tables, milli means 1/1000, centi means
1/100, deci means 1/10, deka means 10, hecto, 100, kilo, 1000, myria,
10,000. Two other prefixes are sometimes used, micro which means
1/1,000,000; as microfarad or microvolt, and meg which means
1,000,000, as megohm meaning 1,000,000 ohms.
13. Advantages of the Metric System.—First, it is a
decimal system; second, the same form and prefixes are
used in every table; third, the standards of length (meter),
volume (liter), and mass (kilogram) bear a simple relation[Pg 11]
to one another. This simple relation between the three
standard units may be given thus: first, the liter is a cubic
decimeter, and second, the kilogram is the mass of a liter
of water. (See Fig. 5) Since the liter is a cubic decimeter,
the length of one side is 10 cm. The liter therefore
holds 1000 ccm. (10 × 10 × 10). Therefore, 1 liter
= 1 cu. dm. = 1000 ccm. and since 1 liter of water has a
mass of 1 kg. or 1000 g., then 1000 ccm. of water has a mass
of 1000 g., or 1 ccm. of water has a mass of 1 g.
 Fig. 5.—One liter of the water has a mass of one kilogram.
Fig. 5.—One liter of the water has a mass of one kilogram.
The following table of equivalents gives the relation
between the most common English and metric units.
Those marked (*) should be memorized.
| (*) 1 meter | = 39.37 inches. | 1 cu, in. | = 16.387 ccm. |
| (*) 1 inch | = 2.54 cm. | 1 cu. ft. | = 28315 cm. |
| 1 foot | = 30.48 cm. | 1 cu. m. | = 1.308 cu. yd. |
| 1 mile | = 1.609 km. | (*) 1 liter | = 1.057 qt. |
| 1 sq. in. | = 6.45 sq. cm. | (*) 1 kg. | = 2.204 lbs. |
| 1 sq. cm. | = 0.155 sq. in. | 1 g. | = 15.44 grains. |
| 1 sq. m. | = 1.196 sq. yd. | 1 lb. | = 0.4536 kg. |
| 1 acre | = 0.405 ha. | 1 oz. | = 28.35 g. |
| 1 hectare | = 2.45 acres. | 1 g. | = 0.0353 oz. |
The c. g. s. system. Scientists have devised a plan for expressing
any measurement in terms of what are called the three fundamental units of length,[Pg 12]
mass, and time. The units used are the centimeter,
the gram and the second. Whenever a measurement has been
reduced to its equivalent in terms of these units, it is said to be
expressed in C.G.S. units.
Important Topics
1. The metric system; how originated.
2. Units; meter, liter, kilogram.
3. Metric tables.
4. Advantages of the metric system.
5. Equivalents.
6. The C.G.S. system.
Exercises
1. Which is cheaper, milk at 8 cents a quart or 8 cents a liter?
Why?
2. Which is more expensive, cloth at $1.00 a yard or at $1.00 a
meter? Why?
3. Which is a better bargain, sugar at 5 cents a pound or 11 cents
a kilogram? Why?
4. Express in centimeters the height of a boy 5 ft. 6 in. tall.
5. What is the length of this page in centimeters? In inches?
6. What is the mass of a liter of water? Of 500 ccm.? Of 1 ccm.?
7. From Chicago to New York is 940 miles. Express in kilometers.
8. A 10-gallon can of milk contains how many liters?
9. What will 100 meters of cloth cost at 10 cents a yard?
10. What will 4 kg. of beef cost at 15 cents a pound?
11. What will 5-1/2 lbs. of mutton cost at 40 cents a kilogram?
12. How can you change the state of a body? Give three methods.
13. Correct the statement 1 ccm. = 1 g.
14. How many liters in 32 quarts?
[Pg 13]
MOLECULAR FORCES AND MOTIONS
(1) Evidences of Molecular Motion in Gases
14. Size of Molecules.—The difference between solids,
liquids, and gases has been explained as due to the different
behavior of molecules in the three states of matter.
That is, in solids they cling together, in liquids they move
freely, and in gases they separate. At this time we are
to consider the evidences of molecular motion in gases.
It must be kept in mind that molecules are exceedingly
small. It has been said that if a bottle containing about
1 ccm. of ordinary air has pierced in it a minute opening
so that 100,000,000 molecules (a number nearly equal to
the population of the United States) pass out every second,
it would take, not minutes or hours, but nearly 9000
years for all of the molecules to escape. The number of
molecules in 1 ccm. of air at 0°C. and 76 cm. pressure has
been calculated by Professor Rutherford to be 2.7 × 1019.
It is evident that such minute particles cannot be seen
or handled as individuals. We must judge of their size
and action by the results obtained from experiments.
15. Diffusion of Gases.—One line of evidence which
indicates that a gas consists of moving particles is the
rapidity with which a gas having a strong odor penetrates
to all parts of a room. For example, if illuminating gas
is escaping it soon diffuses and is noticed throughout the
room. In fact, the common experience of the diffusion
of gases having a strong odor is such that we promptly[Pg 14]
recognize that it is due to motion of some kind. The gas
having the odor consists of little particles that are continually
hitting their neighbors and are being struck and
buffeted in turn until the individual molecules are widely
scattered. When cabbage is boiled in the kitchen soon
all in the house know it. Other illustrations of the diffusion
of gases will occur to anyone from personal experience,
such for instance as the pleasing
odor from a field of clover
in bloom.
The following experiment
illustrates the rapid diffusion
of gases.
 Fig. 6a.—Diffusion of gases. Fig. 6b.—Effusion of gases.
Fig. 6a.—Diffusion of gases. Fig. 6b.—Effusion of gases.
Take two tumblers (see Fig. 6a), wet the inside of one with a few
drops of strong ammonia water and the other with a little hydrochloric
acid. Cover each with a sheet of clean paper. Nothing can
now be seen in either tumbler. Invert the second one over the first
with the paper between, placing them so that the edges will match.
On removing the paper it is noticed that both tumblers are quickly
filled with a cloud of finely divided particles, the two substances having
united chemically to form a new substance, ammonium chloride.
On account of their small size, molecules of air readily
pass through porous solids, cloth, unglazed earthenware,
etc. The following experiment shows this fact strikingly.
(See Fig. 6b.)
[Pg 15]
A flask containing water is closed by a rubber stopper through
which pass the stem of a glass funnel and a bent glass tube that has
been drawn out to a small opening (J). The funnel has cemented
in its top an inverted porous clay jar (C), over the top of the
latter is placed a beaker (B). A piece of flexible rubber tubing
(H) leading from a hydrogen generator is brought up to the top of
the space between the jar and the beaker. When hydrogen gas
is allowed to flow into the space between C and B, the level of the
water in W is seen to lower and a stream of water runs out at J
spurting up into the air.
On stopping the flow of hydrogen and removing B, the water
falls rapidly in J and bubbles of air are seen to enter the water
from the tube. (The foregoing steps may be repeated as often as
desired).
This experiment illustrates the fact that the molecules of some
gases move faster than those of some other gases. Hydrogen molecules
are found to move about four times as fast as air molecules.
Hence, while both air and hydrogen molecules are at first going in
opposite directions through the walls of C, the hydrogen goes in
much faster than the air comes out. In consequence it accumulates,
creates pressure, and drives down the water in W and out at J. On
removing B, the hydrogen within the porous cup comes out much
faster than the air reënters. This lessens the pressure within, so
that air rushes in through J. This experiment demonstrates not
only the fact of molecular motion in gases but also that molecules
of hydrogen move much faster than those of air. (This experiment
will work with illuminating gas but not so strikingly.)
Careful experiments have shown that the speed of
ordinary air molecules is 445 meters or 1460 ft. per second;
while hydrogen molecules move at the rate of 1700 meters
or 5575 ft. or more than a mile per second.
16. Expansion of Gases.—Gases also possess the property
of indefinite expansion, that is, if a small quantity of
gas is placed in a vacuum, the gas will expand immediately
to fill the entire space uniformly. This is shown by an
experiment with the air pump. On raising the piston the
air follows instantly to fill up the space under it. As[Pg 16]
the air is removed from the receiver of an air pump the air
remaining is uniformly distributed within.
17. How Gases Exert Pressure.—It is further found
that air under ordinary conditions exerts a pressure of
about 15 lbs. to the square inch. In an automobile tire
the pressure may be 90 lbs. and in a steam boiler it may
be 200 lbs. or more to the square inch.
How is the pressure produced? The molecules are not
packed together solidly in a gas, for when steam changes to
water it shrinks to about 1/1600 of its former volume.
Air diminishes to about 1/800 of its volume on changing to
liquid air. The pressure of a gas is not due then to the
gas filling all of the space in which it acts, but is due rather
to the motion of the molecules. The blow of a single molecule
is imperceptible, but when multitudes of molecules
strike against a surface their combined effect is considerable.
In fact, this action is known to produce the
pressure that a gas exerts against the walls of a containing
vessel. Naturally if we compress twice as much
gas into a given space there will be twice as many
molecules striking in a given time, which will give twice
as much pressure.
If gas is heated, it is found that the heat will cause a
swifter motion of the molecules. This will also make the
molecules strike harder and hence cause the gas to expand
or exert more pressure.
17a. Brownian Movements.—Direct photographic
evidence of the motion of molecules in gases has been
obtained by studying the behavior of minute drops of
oil suspended in stagnant air. Such drops instead of
being at rest are constantly dancing about as if they
were continually receiving blows from many directions.
These motions have been called Brownian Movements
(see Fig. 7).
[Pg 17]
It has been proved that these movements are due to
the blows that these small drops receive from the swiftly
moving molecules of the gas about them. If the drops
are made smaller or the gas more dense, the movements
increase in intensity. These effects are especially marked
at a pressure of 0.01 of an atmosphere.
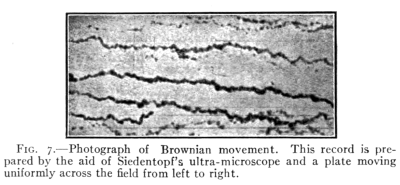 Fig. 7.—Photograph of Brownian movement. This record is prepared
by the aid of Siedentopf's ultra-microscope and a plate moving
uniformly across the field from left to right.
Fig. 7.—Photograph of Brownian movement. This record is prepared
by the aid of Siedentopf's ultra-microscope and a plate moving
uniformly across the field from left to right.
Important Topics
It is assumed that air and all gases are made up of molecules in
rapid motion; that this motion is dependent upon temperature and
pressure. Evidence of this is shown by (a) diffusion, (b) expansion,
(c) pressure. Brownian Movements.
Questions
1. What is the molecular (kinetic) theory of gases?
2. What three kinds of evidence help to confirm the theory?
3. What have you seen that seems to show that a gas consists of
molecules in motion?
4. How many meters long is a 10-ft. pole?
5. A 50-kg. boy weighs how many pounds?
6. What are three advantages of the metric system?
7. What will 12 qts. of milk cost at 8 cents a liter?
8. A cube 1 meter each way will contain how many cubic centimeters?
How many liters? What will a cubic meter of water
weigh?
[Pg 18]
(2) Molecular Motion in Liquids
18. Diffusion of Liquids.—From the evidence given in
Arts. 14-17, (a) of diffusion of odors, (b) of the continued
expansion of air in the air pump, and (c) of the pressure
exerted by a gas in all directions, one may realize without
difficulty that a gas consists of small particles in rapid
motion. Let us now consider some of the evidence of
molecular motion in liquids. If a little vinegar is placed
in a pail of water, all of the water will soon taste sour.
A lump of sugar in a cup of tea will sweeten the entire
contents. This action is somewhat similar to the diffusion
of gases but it takes place much more slowly. It is therefore
believed that the motion of liquid molecules is
much slower than that of gas molecules.
Again, if a dish of water is left standing in the open air
in fine weather, within a few days the dish will become
dry though no one has taken anything from it. We say
the water has evaporated. What was liquid is now vapor.
If we were to observe carefully any dish of water we would
find that it continually loses weight on dry days. That is,
there is a constant movement of the molecules of water
into the air. This movement of the molecules is explained
as follows. There appear to be in the dish of water some
molecules that by moving back and forth acquire a greater
velocity than their neighbors; when these reach the surface
of the liquid, some vibration or movement sends them
flying into the air above. They are now vapor or gas
molecules, flying, striking, and rebounding like the air
molecules. Sometimes on rebounding, the water molecules
get back into the water again. This is especially
apt to happen when the air is damp, i.e., when it contains
many water molecules. Sometimes the air over a dish
becomes saturated, as in the upper part of a corked bottle[Pg 19]
containing water. Although molecules are continually
leaving the surface of the water they cannot escape from
the bottle, so in time as many molecules must return
to the water from the space above as leave the water in
the same time. When this condition exists, the air above
the water is said to be saturated. On
very damp days the air is often saturated.
The explanation above shows
why wet clothes dry so slowly on such
a day (See Arts. 166-7 on Saturation.)
19. Cooling Effect of Evaporation.
We have seen that warming a gas
increases its volume. This expansion
is due to the increased motion of the
warmed molecules. Now the molecules
that escape from a liquid when it
evaporates are naturally the fastest
moving ones, i.e., the hottest ones. The
molecules remaining are the slower
moving ones or colder molecules. The
liquid therefore becomes colder as it
evaporates, unless it is heated. This
explains why water evaporating on
the surface of our bodies cools us. In
evaporating, the water is continually
losing its warm, fast moving molecules.
The cooling effect of evaporation is,
therefore an evidence of molecular
motion in liquids.
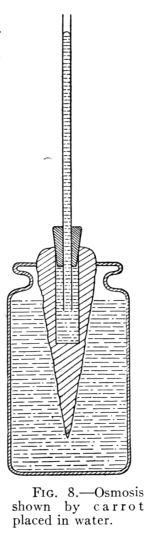 Fig. 8.—Osmosis
Shown by carrot
placed in water.
Fig. 8.—Osmosis
Shown by carrot
placed in water.
20. Osmosis.—If two liquids are separated by a membrane
or porous partition, they tend to pass through and
mix. This action is called osmose, or osmosis.
Such a movement of liquid molecules in osmosis may be illustrated
by filling a beet or carrot that has had its interior cut out[Pg 20]
to form a circular opening (see Fig. 8) with a thick syrup. The
opening is then closed at the top with a rubber stopper through
which passes a long glass tube.
If the carrot is immersed in water, as in Fig. 8, a movement of
water through the porous wall to the interior begins at once. Here,
as in the experiment of the hydrogen and air passing through the
porous cup, the lighter fluid moves faster. The water collecting in
the carrot rises in the tube. This action of liquids passing through
porous partitions and mingling is called osmosis.
Gases and liquids are alike in that each will flow. Each
is therefore called a fluid. Sometimes there is much resistance
to the flow of a liquid as in molasses. This
resistance is called viscosity. Alcohol and gasoline have
little viscosity. They are limpid or mobile. Air also has
some viscosity. For instance, a stream of air always drags
some of the surrounding air along with it.
Important Topics
1. Liquids behave as if they were composed of small particles in
motion.
2. This is shown by (1) Diffusion, (2) Solution, (3) Evaporation,
(4) Expansion, (5) Osmosis.
Exercises
1. Give an example or illustration of each of the five evidences of
molecular motion in liquids.
2. When is air saturated? What is the explanation?
3. Why does warming a liquid increase its rate of evaporation?
4. Air molecules are in rapid motion in all directions. Do they
enter a liquid with a surface exposed to the air? Give reason.
5. What are some of the inconveniences of living in a saturated
atmosphere?
6. Fish require oxygen. How is it obtained?
[Pg 21]
(3) Molecular Forces in Liquids
21. Cohesion and Adhesion.—In liquids "the molecules
move about freely yet tend to cling together." This
tendency of molecules to cling together which is not
noticeable in gases is characteristic of liquids and especially
of solids. It is the cause of the viscosity mentioned in
the previous section and is readily detected in a variety
of ways. For instance, not only do liquid molecules
cling together to form drops and streams, but they cling
to the molecules of solids as well, as is shown by the wet
surface of an object that has been dipped in water. The
attraction of like molecules for one another is called
cohesion, while the attraction of unlike molecules is called
adhesion, although the force is the same whether the molecules
are alike or unlike. It is the former that causes
drops of water to form and that holds iron, copper, and
other solids so rigidly together. The adhesion of glue to
other objects is well known. Paint also "sticks" well.
Sometimes the "joint" where two boards are glued together
is stronger than the board itself. The force of attraction
between molecules has been studied
carefully. The attraction acts
only through very short distances.
The attraction even in liquids is
considerable and may be measured.
The cohesion of water may be
shown by an experiment where
the force required to pull a glass
plate from the surface of water
is measured.
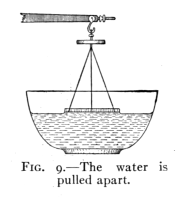 Fig. 9.—The water
is pulled apart.
Fig. 9.—The water
is pulled apart.
Take a beam balance and suspend from one arm a circular glass
plate, Fig. 9. Weigh the plate and its support. Adjust the glass
plate so that it hangs horizontally and just touches the surface of
clean water, the under side being completely wet. Now find what
additional weight is required to raise the glass plate from the water.
[Pg 22]
Just as the plate comes from the water its under side
is found to be wet. That is, the water was pulled apart,
and the plate was not pulled from the water. The cohesion
of the water to itself is not so strong as its adhesion
to the glass.
The cohesion of liquids is further shown by the form a
drop of liquid tends to take when left to itself. This is
readily seen in small drops of liquids. The spherical
shape of drops of water or mercury is an example. A
mixture of alcohol and water in proper proportions will
just support olive oil within it. By carefully dropping
olive oil from a pipette into such a mixture, a drop of the
oil, an inch or more in diameter suspended in the liquid,
may be formed. It is best to use a bottle with plane or
flat sides, for if a round bottle is used, the sphere of oil will
appear flattened.
 Figs. 10 a and b.—Surface tension of a liquid film.
Figs. 10 a and b.—Surface tension of a liquid film.
22. Surface Tension.—The cohesion of liquids is also
indicated by the tendency of films to assume the smallest
possible surface. Soap bubble films show this readily.
Fig. 10 a represents a circular wire form holding a film
in which floats a loop of thread. The tension of the[Pg 23]
film is shown in Fig. 10 b by the circular form of the loop
after the film within it has been pierced by a hot wire,
Fig. 11 shows a rectangular wire form with a "rider."
The tension in the film draws the rider forward.
 Fig. 11.—The rider is drawn forward.
Fig. 11.—The rider is drawn forward.
Fig. 12.—Surface tension causes the pointed shape.
A soap bubble takes its
spherical shape because
this form holds the confined
air within the
smallest possible surface. A drop of liquid is spherical
for the same reason. Many illustrations of the tension
in films may be given. Users of water colors notice that
a dry camel's-hair brush is bushy. (Fig. 12 A). When
in water it is still bushy. (Fig. 12 B.)
But when it is taken from the water
and the excess is shaken from it, it is
pointed as in Fig. 12 C. It is held to
the pointed shape by the tension of
the liquid film about the brush.
 Fig. 13.—A needle depresses the surface when floating.
Fig. 13.—A needle depresses the surface when floating.
The surface of water acts as if covered by a film which
coheres more strongly than the water beneath it. This is
shown by the fact that a steel needle or a thin strip of
metal may be floated upon the surface of water. It is supported
by the surface film. (See Fig. 13.) If the film
breaks the needle sinks. This film also supports the little
water bugs seen running over the surface of a quiet pond in[Pg 24]
summer. The surface film is stronger in some liquids than
in others. This may be shown by taking water, colored
so that it can be seen, placing a thin layer of it on a white
surface and dropping alcohol upon it. Wherever the
alcohol drops, the water is seen to pull away from it,
leaving a bare space over which the alcohol has been spread.
This indicates that the alcohol has the weaker film. The
film of greasy benzine is stronger than the film of the pure
material. If one wishes to remove a grease spot and
places pure benzine at the center of the spot, the stronger
film of the greasy liquid will pull away from the pure
benzine, and spread out, making a larger spot than before,
while if pure benzine is placed around the grease spot, the
greasy liquid at the center pulls away from the pure benzine,
drawing more and more to the center, where it may
be wiped up and the grease entirely removed.
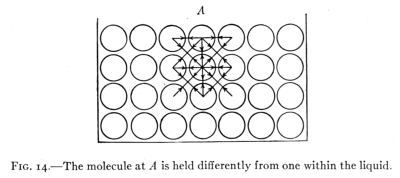 Fig. 14.—The molecule at A is held differently from one within the liquid.
Fig. 14.—The molecule at A is held differently from one within the liquid.
23. Explanation of the Surface Film.—Beneath the surface
of a liquid each molecule is attracted by all the other
molecules around it. It is attracted equally in all directions.
Consequently the interior molecules move very
easily over each other in any direction. A molecule at the
surface, as at A, Fig. 14, is not attracted upward by other
liquid molecules. Its freedom of motion is thereby
hindered with the result that a molecule at the surface[Pg 25]
behaves differently from one beneath the surface. The
surface molecules act as if they form an elastic skin or
membrane upon the liquid surface.
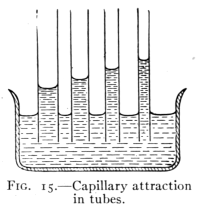 Fig. 15.—Capillary attraction
in tubes.
Fig. 15.—Capillary attraction
in tubes.
24. Capillarity.—A striking action of the surface film
of a liquid is seen in the rise of liquids in tubes of small
bore when the liquid wets them. If the liquid does not wet
the tube, as when mercury is placed in glass, the liquid is
depressed. It is found in general
that: Liquids rise in capillary
tubes when they wet them
and are depressed in tubes
which they do not wet; the
smaller the diameter of the tube
the greater the change of level.
(See Fig. 15.) This action is
explained as follows: The molecules
of a liquid have an attraction
for each other and also
for the sides of a tube. The former is called "cohesion
for itself," the latter is called "adhesion for the sides
of the containing vessel." If the cohesion for itself is
greater than the adhesion for the side of the containing
vessel, the liquid is pulled away from the side and is
depressed. If the adhesion is greater, the liquid is elevated.
This action is called "capillary action" from
the Latin word (capillus) signifying hair, since it shows
best in fine hairlike tubes.
There are many common illustrations of capillary action:
oil rising in a wick; water rising in a towel or through
clothes; ink in a blotter, etc. The minute spaces between
the fibers composing these objects act as fine
tubes. If cloth is treated with a preparation which prevents
water from adhering to its fibers, the material
will not be wet when water is poured upon it, because[Pg 26]
the water will not run in between the fibers; a surface
film spreads over the cloth so that no water enters it.
Cravenette cloth has been treated in this way and hence is
waterproof.
The action of this film may be shown by the following experiment.
Dip a sieve of fine copper gauze in melted paraffin, thus coating
each wire so that water will not adhere to it. Water may now be
poured into the sieve, if a piece of paper is first laid in it to break
the force of the water. On carefully removing the paper the surface
film of the water will prevent the passage of the water through
the sieve.
25. Capillary Action in Soils.—The distribution of
moisture in the soil depends largely upon capillary action.
When the soil is compact the minute spaces between the
soil particles act as capillary tubes, thus aiding the water
to rise to the surface. As the water evaporates from the
surface more of it rises by capillary action from the damper
soil below. Keeping the soil loose by cultivation, makes
the spaces between the particles too large for much capillary
action, thus the moisture is largely prevented from
rising to the surface.
In the semi-arid regions of the West "dry farming"
is successfully practised. This consists in keeping the surface
covered with a "dust mulch" produced by frequent
cultivation. In this way the moisture is kept below the
surface, where it can be utilized during the hot dry summer
by the roots of growing plants.
Important Topics
1. Attractive forces between liquid molecules.
2. Cohesion (like molecules); adhesion (unlike molecules).
3. Special effects of this force are classified as (a) capillary action,
and (b) surface tension.
[Pg 27]
Exercises
1. What evidence of capillary action have you seen outside of the
laboratory?
2. What is the explanation for capillary action?
3. Where are surface films found?
4. What are three common effects of surface films?
5. Explain why cravenette cloth sheds water.
6. If a circular glass disc 10 cm. in diameter requires 50 grams of
force to draw it from the water, what is the cohesion of water
per square centimeter?
7. What is the weight in grams of 1 ccm. of water? of a liter of
water?
8. Name five examples of adhesion to be found in your home.
9. Under what conditions will a liquid wet a solid and spread over
it?
10. When will it form in drops on the surface?
11. Explain the proper procedure for removing a grease spot with
benzine.
12. What difference is there between a liquid and a fluid?
13. Why cannot a "soap bubble" be blown from pure water?
14. Which are larger, the molecules of steam or those of water?
Why?
15. Why is the ground likely to be damp under a stone or board
when it is dry all around?
16. Why does any liquid in falling through the air assume the
globule form?
17. Give three examples of capillary attraction found in the home.
Three out of doors.
18. Why does cultivation of the soil prevent rapid evaporation
of water from the ground?
(4) Evidences of Molecular Forces in Liquids and
Solids
26. Solutions.—A crystal of potassium permanganate
is placed in a liter of water. It soon dissolves and on shaking
the flask each portion of the liquid is seen to be colored
red. The dissolving of the permanganate is an illustration[Pg 28]
of the attraction of the molecules of water for the
molecules of the permanganate. We are familiar with this
action in the seasoning of food with salt and sweetening
with sugar.
Water will dissolve many substances, but in varying
degrees, i.e., of some it will dissolve much, of others, little,
and some not at all. Further, different liquids have different
solvent powers. Alcohol will dissolve resin and shellac,
but it will not dissolve gum arabic, which is soluble in
water. Benzine dissolves grease. Beeswax is not dissolved
by water, alcohol or benzine, but is soluble in
turpentine.
It is found that the temperature of the liquid has a
marked effect upon the amount of substance that will
dissolve. This is an indication that the motions of the
molecules are effective in solution. It appears that dissolving
a solid is in some respects similar to evaporation,
and just as at higher temperatures more of the liquid
evaporates, because more of the molecules will escape from
the liquid into the air above, so at higher temperatures,
more molecules of a solid will detach themselves through
greater vibration and will move into the liquid.
Further, just as an evaporating liquid may saturate
the space above it so that any escape of molecules is
balanced by those returning, so with a dissolving solid, the
liquid may become saturated so that the solution of more
of the solid is balanced by the return of the molecules
from the liquid to the solid condition.
27. Crystals and Crystallization.—This return from
the liquid to the solid state, of molecules that are in solution,
is especially noticeable when the solution is cooling
or evaporating and hence is losing its capacity to hold so
much of the solid. On returning to the solid, the molecules
attach themselves in a definite manner to the solid[Pg 29]
portion, building up regular solid forms. These regular
forms are crystals. The action that forms them is called
crystallization.
Each substance seems to have its own peculiar form of
crystal due to the manner in which the molecules attach
themselves to those previously in place. The largest
and most symmetrical crystals are those in which the
molecules are deposited slowly with no disturbance of
the liquid. Beautiful crystals of alum may be obtained
by dissolving 25 g. of alum in 50 ccm. of hot water, hanging
two or three threads in the solution and letting it
stand over night. The thread fibers provide a foundation
upon which crystals grow.
When a solution of a solid evaporates, the molecules of
the liquid escape as a gas, the molecules of the solid remain
accumulating as crystals. This principle has many uses:
(a) sea water is purified by evaporating the water and
condensing the vapor, which of course forms pure water.
(b) water is forced down to salt beds where it dissolves
the salt. The brine is then raised and evaporated, leaving
the salt in the evaporating pans.
28. Absorption of Gases by Solids and Liquids.—If a piece of
heated charcoal is placed in a test-tube containing ammonia gas,
inverted in mercury, the ammonia is seen to disappear, the mercury
rising to take its place. The ammonia has been absorbed by the
charcoal, the gas molecules clinging closely to the solid. The
charcoal being very porous presents a large surface to the action of
the gas.
This experiment indicates that attraction exists between
gas molecules and other molecules. Many porous substances
have this power of absorbing gases. We have all
noticed that butter has its flavor affected by substances
placed near it.
That liquids absorb gases is shown by slowly heating[Pg 30]
cold water in a beaker. Small bubbles of air form on the
sides and rise before the boiling point is reached. Ammonia
gas is readily absorbed in water, the bubbles disappearing
almost as soon as they escape into the water
from the end of the delivery tube. Household ammonia is
simply a solution of ammonia gas in water. On warming
the solution of ammonia the gas begins to pass off; thus,
warming a liquid tends to drive off any gas dissolved in it.
Soda water is made by forcing carbon dioxide gas into
water under strong pressure. When placed in a vessel
open to the air the pressure is lessened and part of the
gas escapes. The dissolved gas gives the characteristic
taste to the beverage.
Important Topics
1. The solution of solids is increased by heating.
2. The solution of gases is decreased by heating.
3. Pressure increases the quantity of gas that can be dissolved in a
liquid.
4. The attraction (cohesion) of molecules of a dissolved solid for
each other is shown by crystallization.
Exercises
1. How do fish obtain oxygen for breathing?
2. Why does warming water enable it to dissolve more of a salt?
3. Why does warming water lessen the amount of a gas that will
stay in solution?
4. Will water absorb gases of strong odor? How do you know?
5. Name three solvents. Give a use for each.
6. What liquids usually contain gases in solution? Name some
uses for these dissolved gases.
7. What is the weight of a cubic meter of water?
8. Name three substances obtained by crystallization.
9. How is maple sugar obtained?
10. Name five crystalline substances.
[Pg 31]
(5) Evidence of Molecular Forces in Solids
29. Differences between Solids and Gases.—In studying
gases, it is seen that they behave as if they were
composed of small particles in rapid motion, continually
striking and rebounding, and separating to fill any space
into which they are released. This action indicates that
there is practically no attractive force between such
molecules.
Between the molecules of a solid, however, the forces
of attraction are strong, as is shown by the fact that a
solid often requires a great force to pull it apart; some, as
steel and iron, show this property in a superlative degree,
a high-grade steel rod 1 cm. in diameter requiring nearly
9 tons to pull it apart. Tests show that the breaking
strengths of such rods are directly proportional to their
areas of cross-section.
That is, twice the area
has twice the breaking
strength.
 Fig. 16.—Elasticity of bending.
Fig. 16.—Elasticity of bending.
30. Elasticity.—Fully
as important as
a knowledge of the
breaking strengths of
solids, is the knowledge of what happens when the forces
used are not great enough to break the rods or wires.
Take a wooden rod (as a meter stick) and clamp one end to the
table top, as in Fig. 16. At the other end hang a weight. Fasten a
wire to this end so that it projects out in front of a scale. Add successively
several equal weights and note the position of the wire each
time. Remove the weights in order, noting the positions as before.
The rod will probably return to the first position.
This simple experiment illustrates a characteristic of
solids: that of changing shape when force is applied and of[Pg 32]
returning to the original shape when the force is removed.
This property is called elasticity.
Tests of elasticity are made by subjecting wire of different
materials but of the same dimensions to the same
tension. The one changing least is said to have the greatest
elastic force or elasticity. If greater forces are applied
to the wire and then removed, one will finally be found
that will permanently stretch the wire so that it will not
return exactly to the former length. The wire has now
passed its elastic limit and has been permanently stretched.
Just as there are great differences between the elastic
forces of different substances, so there are great differences
in the limits of elasticity. In some substances the limit
is reached with slight distortion, while others are perfectly
elastic even when greatly stretched. India rubber is an
example of a body having perfect elasticity through wide
limits. Glass has great elastic force but its limit of elasticity
is soon reached. Substances like India rubber may
be said to have great "stretchability," but little elastic
force. In physics, elasticity refers to the elastic force
rather than to ability to endure stretching.
31. Kinds of Elasticity.—Elasticity may be shown in
four ways: compression, bending or flexure, extension or
stretching, twisting or torsion. The first is illustrated by
squeezing a rubber eraser, the second by an automobile
spring, the third by the stretching of a rubber band, the
fourth by the twisting and untwisting of a string by which
a weight is suspended.
There are two kinds of elasticity: (1) elasticity of form
or shape; (2) elasticity of volume. Gases and liquids
possess elasticity of volume, but not of shape, while solids
may have both kinds. Gases and liquids are perfectly
elastic because no matter how great pressure may be
applied, as soon as the pressure is removed they regain[Pg 33]
their former volume. No solid possesses perfect elasticity,
because sooner or later the limit of elasticity will be
reached.
32. Hooke's Law.[A]—On examining the successive movements
of the end of the rod in Art. 30, we find that they
are approximately equal. Carefully conducted experiments
upon the elasticity of bodies have shown that the
changes in shape are directly proportional to the forces
applied, provided that the limit of elasticity is not reached.
This relation, discovered by Robert Hooke, is sometimes
expressed as follows: "Within the limits of perfect elasticity,
all changes of size or shape are directly proportional to the
forces producing them."
33. Molecular Forces and Molecular Motions.—If a
solid is compressed, on releasing the pressure the body
regains its former shape if it has not been compressed too
far. This indicates that at a given temperature the
"molecules of a solid tend to remain at a fixed distance
from each other, and resist any attempt to decrease or
increase this distance." This raises the question, Why
does not the cohesion pull the molecules tightly together
so that compression would be impossible? The reason
is that heat affects the size of solid bodies. On lowering
the temperature, bodies do contract, for as soon as the
temperature is lowered the vibration of the molecule is
lessened. On raising the temperature the molecules are
pushed farther apart.
The size of a body, then, is the result of a balance of
opposing forces. The attractive force between the molecules
pulling them together is cohesion, while the force
which pushes them apart is due to the motions of the
molecules. Raising the temperature and thus increasing[Pg 34]
the motion causes expansion; lowering the temperature
decreases the molecular motion and so causes contraction.
If an outside force tries to pull the body apart or to compress
it this change of size is resisted by either cohesion or
molecular motion.
34. Properties of Matter.—Many differences in the
physical properties of solids are due to differences between
the cohesive force of different kinds of molecules. In
some substances, the attraction is such that they may be
rolled out in very thin sheets. Gold is the best example of
this, sheets being formed 1/300,000 of an inch thick. This
property is called malleability. In other substances the
cohesion permits it to be drawn out into fine threads or
wire. Glass and quartz are examples of this. This
property is called ductility. In some, the cohesion makes
the substance excessively hard, so that it is difficult to
work or scratch its surface. The diamond is the hardest
substance known. Some substances are tough, others
brittle. These are tested by the ability to withstand
sudden shocks as the blow of a hammer.
Important Topics
1. Molecular forces in solids; (a) adhesion, (b) cohesion.
2. Elasticity, Hooke's Law.
3. Contraction on cooling.
4. Malleability, ductility, hardness, brittleness, etc.
Exercises
1. Give an illustration of Hooke's Law from your own experience.
2. What devices make use of it?
3. Do solids evaporate. Give reasons.
4. When iron is welded, is cohesion or adhesion acting?
5. When a tin basin is soldered, is cohesion or adhesion acting?
6. Sometimes a spring is made more elastic by tempering and made
soft by annealing. Look up the two terms. How is each
accomplished?
[Pg 35]
7. Review the definitions: solid, liquid, and gas. Why do these
definitions mean more to you now than formerly?
8. If a wire is stretched 0.3 cm. on applying 4 kg. of force, what
force will stretch it 0.75 cm? Explain.
9. How long will it take under ordinary conditions for a gas molecule
to cross a room? Give reasons for your answer.
10. What is meant by the elastic limit of a body?
11. Without reaching the elastic limit, if a beam is depressed 4 mm.
under a load of 60 kg., what will be the depression under a load
of 400 kg.? Of 600 kg.?
12. Name three substances that possess elasticity of volume.
13. Give three examples of each; elasticity of (1) compression, (2)
stretching, (3) torsion, (4) flexure.
Review Outline: Introduction and Molecules
Physics; definition, topics considered, physical and chemical
changes.
Science; hypothesis, theory, law. Knowledge; common, scientific.
Matter; three states, molecular theory. Mass, weight, volume.
Metric system; units, tables, equivalents, advantages.
Evidences of molecular motions; gases (3), liquids (5), solids (3).
Evidences of molecular forces; liquids (3), solids (many) special
properties such as: elasticity, tenacity, ductility, hardness, etc.
Hooke's law; applications.
[Pg 36]
MECHANICS OF LIQUIDS
(1) The Gravity Pressure of Liquids
35. Pressure of Liquids against Surfaces.—The sight
of a great ship, perhaps built of iron and floating on
water, causes one to wonder at the force that supports
it. This same force is noticed when one pushes a light
body, as a cork, under water. It is quite evident in
such a case that a force exists
sufficient to overcome the
weight of the cork so that it
tends to rise to the surface.
Even the weight of our bodies
is so far supported by water
that many persons can float.
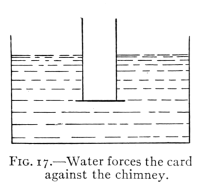 Fig. 17.—Water forces the card
against the chimney.
Fig. 17.—Water forces the card
against the chimney.
The following experiment
provides a means of testing
this force:
If an empty can is pushed down into water, we feel at once the
force of the liquid acting against the object and tending to push
it upward. It may be noticed also that so long as the can is not
completely submerged the deeper the can is pushed into the water
the greater is the upward force exerted by the liquid.
We may test this action in various ways: a simple way is to take
a cylindrical lamp chimney, press a card against its lower end and
place it in the water in a vertical position. The force of the water
will hold the card firmly against the end of the chimney. (See Fig.
17.) The amount of force may be tested by dropping shot into the
tube until the card drops off. At greater depths more shot will be
required, showing that the force of the water increases with the
depth. Or one may pour water into the chimney. It will then be[Pg 37]
found that the card does not drop until the level of the water inside
the chimney is the same as on the outside. That is, before the card
will fall off, the water must stand as high within the chimney as
without no matter to what depth the lower end of the chimney is
thrust below the surface of the water.
36. Law of Liquid Pressure.—As there is twice as
much water or shot in the chimney when it is filled to a
depth of 10 cm. as there is when it is filled to a depth of
5 cm. the force of the water upward on the bottom must
be twice as great at a depth of 10 cm. as at a depth of
5 cm. Since this reasoning will hold good for a comparison
of forces at any two depths, we have the law: "The pressure
exerted by a liquid is directly proportional to the depth."
The amount of this force may be computed as follows:
First, the card stays on the end of the tube until the
weight of water from above equals the force of the water
from below, and second, the card remains until the water is
at the same height inside the tube as it is outside. Now
if we find the weight of water at a given depth in the tube,
we can determine the force of the water from below. If
for instance the chimney has an area of cross-section of
12 sq. cm. and is filled with water to a depth of 10 cm.,
the volume of the water contained will be 120 ccm. This
volume of water will weigh 120 g. This represents then,
not only the weight of the water in the tube, but also the
force of the water against the bottom. In a similar way
one may measure the force of water against any horizontal
surface.
37. Force and Pressure.—We should now distinguish
between force and pressure. Pressure refers to the force
acting against unit area, while force refers to the action
against the whole surface. Thus for example, the atmospheric
pressure is often given as 15 pounds to the square
inch or as one kilogram to the square centimeter. On[Pg 38]
the other hand, the air may exert a force of more than 300
pounds upon each side of the hand of a man; or a large
ship may be supported by the force of thousands of tons
exerted by water against the bottom of the ship.
In the illustration, given in Art. 36, the upward force
of the water against the end of the tube at a depth of 10
cm. is computed as 120 grams. The pressure at the same
depth will be 10 grams per sq. cm. What will be the pressure
at a depth of 20 cm.? at a depth of 50 cm.? of 100
cm.? Compare these answers with the law of liquid pressure
in Art. 36.
38. Density.—If other liquids, as alcohol, mercury, etc.,
were in the jar, the chimney would need filling to the
same level outside, with the same liquid, before the card
would fall off. This brings in a factor that was not considered
before, that of the mass[B] of a cubic centimeter of
the liquid. This is called the density of the liquid. Alcohol
has a density of 0.8 g. per cubic centimeter, mercury of
13.6 g. per cubic centimeter, while water has a density of
1 g. per cubic centimeter.
39. Liquid Force against Any Surface.—To find the
force exerted by a liquid against a surface we must take
into consideration the area of the surface, and the height
and the density of the liquid above the surface. The following
law, and the formula representing it, which concisely
expresses the principle by which the force exerted
by a liquid against any surface may be computed, should
be memorized:
The force which a liquid exerts against any surface, equals
the area of the surface, times its average depth below the surface
of the liquid, times the weight of unit volume of the liquid.
Or, expressed by a formula, F = Ahd. In this formula,[Pg 39]
"F" stands for the force which a liquid exerts against any
surface, "A" the area of the surface, "h," for the average
depth (or height) of the liquid pressing on the surface, and
"d", for the weight of unit volume of the liquid. This is
the first illustration in this text, of the use of a formula to
represent a law. Observe how accurately and concisely
the law is expressed by the formula. When the formula
is employed, however, we should keep in mind the law
expressed by it.
We must remember that a liquid presses not only downward
and upward but sideways as well, as we see when
water spurts out of a hole in the side of a vessel. Experiments
have shown that at a point the pressure in a fluid
is the same in all directions, hence the rule given above
may be applied to the pressure of a liquid against the
side of a tank, or boat, or other object, provided we are
accurate in determining the average depth of the liquid;
The following example illustrates the use of the law.
For Example: If the English system is used, the area of the surface
should be expressed in square feet, the depth in feet and the
weight of the liquid in pounds per cubic foot. One cubic foot of
water weighs 62.4 lbs.
Suppose that a box 3 ft. square and 4 ft. deep is full of water.
What force will be exerted by the water against the bottom and a
side?
From the law given above, the force of a liquid against a surface
equals the product of the area of the surface, the depth of the liquid
and its weight per unit volume, or using the formula, F = Ahd.
To compute the downward force against the bottom we have the
area, 9, depth, 4, and the weight 62.4 lbs. per cubic foot. 9 ×
4 × 62.4 lbs. = 2246.4 lbs. To compute the force against a side, the
area is 12, the average depth of water on the side is 2, the weight
62.4, 12 × 2 × 62.4 lbs. = 1497.6 lbs.
Important Topics
1. Liquids exert pressure; the greater the depth the greater the
pressure.
[Pg 40]
2. Difference between force and pressure.
3. Rules for finding upward and horizontal force exerted by a
liquid. F = Ahd.
4. Weight, mass, density.
Exercises
1. What is the density of water?
2. What force is pressing upward against the bottom of a flat boat,
if it is 60 ft. long, 15 ft. wide and sinks to a depth of 2 ft. in the
water? What is the weight of the boat?
3. If a loaded ship sinks in the water to an average depth of 20 ft.,
the area of the bottom being 6000 sq. ft., what is the upward
force of the water? What is the weight of the ship?
4. If this ship sinks only 10 ft. when empty, what is the weight of
the ship alone? What was the weight of the cargo in Problem
3?
5. What is the liquid force against one side of an aquarium 10 ft.
long, 4 ft. deep and full of water?
6. What is the liquid force on one side of a liter cube full of water?
Full of alcohol? Full of mercury? What force is pressing on
the bottom in each case?
7. What depth of water will produce a pressure of 1 g. per square
centimeter? 10 g. per square centimeter? 1000 g. per square
centimeter?
8. What depth of water will produce a pressure of 1 lb. per square
inch? 10 lbs. per square inch? 100 lbs. per square inch?
9. What will be the force against a vertical dam-breast 30 meters
long, the depth of the water being 10 meters?
10. A trap door with an area of 100 sq. dcm. is set in the bottom
of a tank containing water 5 meters deep. What force does
the water exert against the trap door?
11. What is the force on the bottom of a conical tank, filled with
water, the bottom of which is 3 meters in diameter, the depth
1.5 meters?
12. If alcohol, density 0.8 were used in problem 11, what would be
the force? What would be the depth of alcohol to have the
same force on the bottom as in problem 11?
13. What is the pressure in pounds per square inch at a depth of
1 mile in sea water, density 1.026 grams per cc.?
[Pg 41]
14. Find the force on the sides and bottom of a rectangular cistern
filled with water, 20 ft. long, 10 ft. wide, and 10 ft. deep?
15. Find the force on the bottom of a water tank 14 ft. in diameter
when the water is 15 ft. deep, when full of water.
16. Find the force on one side of a cistern 8 ft. deep and 10 ft.
square, when full of water.
17. Find the force on a vertical dam 300 ft. long and 10 ft. high,
when full of water.
18. Find the pressure at the bottom of the dam in question 17.
19. Why are dams made thicker at the bottom than at the top?
20. A ship draws 26 ft. of water, i.e., its keel is 26 ft. under water.
What is the liquid force against a square foot surface of the
keel? Find the pressure on the bottom.
(2) Transmission of Liquid Pressure
40. Pascal's Principle.—Liquids exert pressure not only
due to their own weight, but when confined, may be made
to transmit pressure to considerable distances. This is a
matter of common knowledge wherever a system of waterworks
with connections to houses is found, as in cities.
The transmission of liquid pressure
has a number of important applications.
The principle underlying each
of these was first discovered by Pascal,
a French scientist of the seventeenth
century. Pascal's Principle, as it is
called, may be illustrated as follows:
Suppose a vessel of the shape shown in Fig.
18, the upper part of which we may assume
has an area of 1 sq. cm., is filled with water
up to the level AB. A pressure will be
exerted upon each square centimeter of area
depending upon the depth. Suppose that the
height of AB above CD is 10 cm., then the force upon 1 sq. cm.
of CD is 10 g., or if the area of CD is 16 sq. cm., it receives a force
of 160 g.
 Fig. 18.—The force
increases with the
depth.
Fig. 18.—The force
increases with the
depth.
[Pg 42]
If now a cubic centimeter of water be poured upon AB it will raise
the level 1 cm., or the head of water exerting pressure upon CD becomes
11 cm., or the total force in CD is 16×11 g., i.e., each square
centimeter of CD receives an additional force of 1 g. Hence the
force exerted on a unit area at AB is transmitted to every unit area
within the vessel.
The usual form in which this law is expressed is as
follows: Pressure applied to any part of a confined liquid
is transmitted unchanged, in all directions, and adds the same
force to all equal surfaces in contact with the liquid.
 Fig. 19.—The force is proportional to the area.
Fig. 19.—The force is proportional to the area.
The importance of this principle, as Pascal himself
pointed out, lies in the fact that by its aid we are able to
exert a great force upon a large area by applying a small
force upon a small area of a confined liquid, both areas
being in contact with the same liquid. Thus in Fig. 19
if the area of the surface CD is 2000 times the area of the
surface AB, then 1 lb. applied to the liquid on AB will
exert or sustain a force of 2000 lbs. on CD.
41. Hydraulic Press.—An important application of
Pascal's principle is the hydraulic press. See Fig. 20.
It is used for many purposes where great force is required,
as in pressing paper or cloth, extracting oil from seeds,
lifting heavy objects, etc. Many high school pupils
have been seated in a hydraulic chair used by a dentist or
barber. This chair is a modified hydraulic press.
[Pg 43]
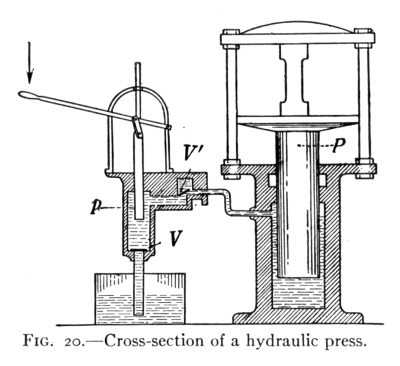 Fig. 20.—Cross-section of a hydraulic press.
Fig. 20.—Cross-section of a hydraulic press.
The hydraulic press contains two movable pistons, P
and p (see Fig. 20). The larger of these, P, has a cross-sectional
area that may be 100 or 1000 times that of the
smaller. The smaller one is moved up and down by a
lever; on each upstroke, liquid is drawn in from a reservoir,
while each down-stroke forces some of the liquid into the
space about the large piston. Valves at V and V´ prevent
the return of the liquid. If the area of P is 1,000 times
that of p, then the force exerted by P is 1000 times the
force employed in moving p. On the other hand, since
the liquid moved by the small piston is distributed over
the area of the large one, the latter will move only 1/1000
as far as does the small piston. The relation between the
motions of the two pistons and the forces exerted by them
may be stated concisely as follows: The motions of the
two pistons of the hydraulic press are inversely proportional
to the forces exerted by them. The cross-sectional
areas of the two pistons are, on the other hand, directly
proportional to the forces exerted by them.
An application of Pascal's principle often employed in[Pg 44]
cities is the hydraulic elevator. In this device a long
plunger or piston extends downward from the elevator car
into a cylinder sunk into the
earth, sometimes to a depth
of 300 ft. Water forced
into this cylinder pushes
the piston upward and
when the water is released
from the cylinder the piston
descends.
Fig. 21 represents another form
of hydraulic elevator, where the
cylinder and piston are at one
side of the elevator shaft. In
this type, to raise the elevator,
water is admitted to the cylinder
pushing the piston downward.
42. Artesian Wells.—Sometimes
a porous stratum
containing water in the
earth's crust is inclined.
Then if there are impervious
strata (see Fig. 22), both
above and below the water-bearing
one, and the latter
comes to the surface so that
rain may fill it, a well sunk
to the water-bearing stratum
at a point where it is below
the surface will usually give
an artesian well, that is, one
in which the water rises to or above the surface. Many
are found in the United States.
 Fig. 21.—A hydraulic freight elevator.
Fig. 21.—A hydraulic freight elevator.
 Fig. 22.—Conditions producing an artesian well.
Fig. 22.—Conditions producing an artesian well.
 Fig. 23.—A standpipe.
Fig. 23.—A standpipe.
43. Standpipes and Air Cushions.—Many who have[Pg 45]
lived in cities where water is pumped into houses under
pressure know that the water pressure is changed when
several faucets are opened at the same time. Again, if
several persons are using a hose for sprinkling, the pressure
may be lessened so as to be insufficient to force the water
above the first floor. In order to allow for these changes
some flexibility or spring must be introduced somewhere[Pg 46]
into the water-pipe system. Water is nearly incompressible
and if no means were employed to take care of the
pressure changes, the sudden stopping and starting of
the flow would cause serious jars and start leaks in the
pipes. Two common devices for controlling sudden
changes in the water pressure are the standpipe and the
air cushion.
The standpipe is simply a large vertical tube connected to the
water mains from which and into which water readily flows. When
many faucets are opened the water lowers; when most faucets are
closed the water rises, giving a simple automatic control of the
surplus water and a supply of water for a short time during a shut-down
of the pumps. Standpipes are often used in towns and small
cities. Fig. 23 represents the standpipe at Jerome, Idaho.
The air cushion (Fig. 24) is a
metal pipe or dome filled with air
attached to a water pipe where sudden
changes in pressure are to be
controlled. At many faucets in a
city water system such an air
cushion is employed. It contains
air; this, unlike water, is easily compressible
and the confined air when
the tap is suddenly closed receives
and checks gradually the rush of
water in the pipe. Even with an air
cushion, the "pound" of the water
in the pipe when a tap is suddenly closed is often heard. If air
cushions were not provided, the "water hammer" would frequently
crack or break the pipes.
 Fig. 24.—The short pipe
above the faucet contains air
forming an air cushion.
Fig. 24.—The short pipe
above the faucet contains air
forming an air cushion.
Important Topics
1. Pascal's law.
2. Hydraulic press.
3. Artesian wells.
4. Standpipes and air cushions.
[Pg 47]
Exercises
1. Where have you seen an air cushion? Describe it and its use.
2. Where have you seen an hydraulic press? Why and how used?
3. Where have you seen hydraulic elevators? What moves them?
4. Where do you know of liquids under pressure? Three examples.
5. What is the pressure in water at a depth of 1500 cm. Express
in grams per square centimeter and in kilograms per square
centimeter.
6. What head[C] of water is required to give a pressure of 200 g. per
square centimeter? 2 kg. per square centimeter?
7. What pressure will be produced by a "head" of water of 20
meters?
8. If 1728 cu. in. of water are placed in a vertical tube 1 sq. in.
in cross section to what height would the water rise? It would
give how many feet of head?
9. What would the water in problem 8 weigh? What pressure
would it produce at the bottom, in pounds per square inch?
From this, compute how many feet of "head" of water will
produce a pressure of 1 lb. per square inch.
10. Using the result in problem 9, what "head" of water will produce
a pressure of 10 lbs. per square inch? 100 lbs. per square
inch?
11. From the result in 9, 100 ft. of "head" of water will produce
what pressure? 1000 ft. of "head?"
12. If the diameter of the pump piston in a hydraulic press is 2 cm.
and that of the press piston 50 cm. what will be the force
against the latter if the former is pushed down with a force of
40 kg.?
(3) Archimedes' Principle
44. A Body Supported by a Liquid.—Among the
applications of the force exerted by a liquid upon a surface,
Archimedes' Principle is one of the most important.
Most persons have noted that a body placed in water is
partly or wholly supported by the force of the water upon
it. A stone held by a cord and lowered into water is felt[Pg 48]
to have a part of its weight supported, while a piece of
cork or wood is wholly supported and floats.
The human body is almost entirely supported in water,
in fact, many people can easily float in water. It was the
consideration of this fact that led the Greek philosopher
Archimedes to discover and state the principle that describes
the supporting of a body in a liquid.
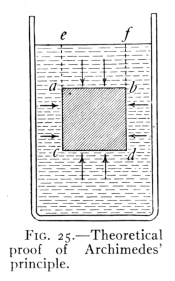 Fig. 25.—Theoretical
proof of Archimedes'
principle.
Fig. 25.—Theoretical
proof of Archimedes'
principle.
45. Archimedes' Principle.—"A body immersed in a
liquid is pushed up by a force equal to the weight of the
liquid that it displaces." The proof
for this law is simply demonstrated.
Suppose a cube, abcd, is immersed in
water (Fig. 25). The upward force
on cd is equal to the weight of a
column of water equal to cdef. (See
Art. 39.) The downward force
upon the top of the cube is equal
to the weight of the column of water
abef. Then the net upward force
upon the cube, that is, the upward
force upon the bottom less the downward
force upon the top, or the
buoyant force exerted by the liquid is exactly equal to
the weight of the displaced water abcd.
46. Law of Floating Bodies.—This same reasoning
may be applied to any liquid and to any body immersed
to any depth below the surface of the liquid. If the body
weighs more than the displaced liquid it will sink. If it
weighs less than the displaced liquid it will float or rise
in the water. A block of wood rises out of the water in
which it floats until its own weight just equals the weight
of the water it displaces. From this we have the law of
floating bodies.
[Pg 49]
A floating body displaces its own weight of the liquid in
which it floats.
 Fig. 26.—A
floating body
displaces its
own weight of
water.
Fig. 26.—A
floating body
displaces its
own weight of
water.
To test the law of floating bodies, take a rod of light
wood 1 cm. square and 30 cm. long (Fig.
26). Bore out one end and fill the opening
with lead and seal with paraffin so that the
rod will float vertically when placed in water.
Mark upon one side of the rod a centimeter
scale, and dip the rod in hot paraffin to
make it waterproof. Now find the weight
of the stick in grams and note the depth to
which it sinks in water in centimeters.
Compute the weight of the displaced water.
It will equal the weight of the rod.
47. Applications of Archimedes' Principle.
There are numerous applications of Archimedes'
Principle and the law of floating bodies.
(a) To Find the Weight of a Floating Body: Problem.—A boat
20 ft. long and with an average width of 6 ft. sinks to an average
depth of 3 ft. in the water. Find the weight of the boat. What
weight of cargo will sink it to an average depth of 5 ft.?
Solution.—The volume of the water displaced is 20 × 6 × 3 cu.
ft. = 360 cu. ft. Since 1 cu. ft. of water weighs 62.4 lbs., 360 ×
62.4 lbs. = 22,464 lbs., the weight of water displaced. By the law of
floating bodies this is equal to the weight of the boat. When loaded
the volume of water displaced is 20 ft. × 6 × 5 ft. which equal 600
cu. ft. 600 × 62.4 lbs. = 37,440 lbs. This is the weight of the water
displaced when loaded. 37,440 lbs. - 22,464 lbs. = 14,976 lbs., the
weight of the cargo.
(b) To Find the Volume of an Immersed Solid: Problem.—A
stone weighs 187.2 lbs. in air and appears to weigh 124.8 lbs. in
water. What is its volume?
Solution.—187.2 lbs. - 124.8 lbs. = 62.4 lbs., the buoyant force of
the water. By Archimedes' Principle, this equals the weight of the
displaced water which has a volume of 1 cu. ft. which is therefore the
volume of the stone.
[Pg 50]
(c) To Find the Density of a Body: The density of a body is
defined as the mass of unit volume.
We can easily find the mass of a body by weighing it, but the
volume is often impossible to obtain by measurements, especially
of irregular solids.
Archimedes' Principle, however,
provides a method of
finding the volume of a body
accurately by weighing it first
in air and then in water (Fig.
27), the apparent loss in weight
being equal to the weight of the
displaced water. One needs
only to find the volume of
water having the same weight
as the loss of weight to find
the volume of the body.
If the metric system is used,
1 ccm. of water weighs 1 g.,
and the volume is numerically the same as the loss of
weight.
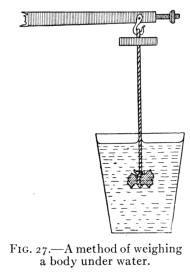 Fig. 27.—A method of weighing
a body under water.
Fig. 27.—A method of weighing
a body under water.
Important Topics
1. Archimedes' Principle.
2. Law of floating bodies.
3. The applications of Archimedes' Principle are to determine (a)
the weight of a floating body; (b) the volume of an immersed
solid, and (c) the density of a body.
Exercises
1. Look up the story of Archimedes and the crown. Write a
brief account of it.
2. Why is it easier for a fat man to float in water than for a lean
one?
[Pg 51]
3. A fish weighing 1 lb. is placed in a pail full of water. Will the
pail and contents weigh more than before adding the fish?
Why?
4. Why can a large stone be lifted more easily while under water
than when on the land?
5. Why does the air bubble in a spirit level move as one end of the
instrument is raised or lowered?
6. Why does a dead fish always float?
7. A ship is built for use in fresh water. What will be the effect
on its water line when passing into the ocean?
8. Why can small bugs walk on water while large animals cannot?
9. If an object weighing 62.4 lbs. just floats in water, what weight
of water does it displace? What volume of water is displaced?
What is the volume of the body?
10. What is the volume of a man who just floats in water if he
weighs 124.8 lbs.? If he weighs 187.2 lbs.?
11. An object weighing 500 g. just floats in water. What is its
volume? How much water does a floating block of wood
displace if it weighs 125 lbs.? 125 g.? 2 kg.? 2000 kg.?
12. A flat boat 10 × 40 ft. in size will sink how much in the
water when 10 horses each weighing 1250 lbs. are placed on
board?
13. A ship 900 ft. long and 80 ft. average width sinks to an average
depth of 25 ft. when empty and 40 ft. when loaded. What is
the weight of the ship and of its load?
14. Will a 1000 cc. block sink or float in water if it weighs 800 g.?
If it weighs 1200 g.? Explain.
15. If a 1000 cc. block of metal weighing 1200 g. is placed in the
water in mid ocean what will become of it?
16. Prove Archimedes' Principle by use of the principles of liquid
pressure.
17. An irregular stone, density 2.5 g. per ccm. displaces 2 cu. ft. of
water. What is its weight? Its apparent weight in water?
18. Will the depth to which a vessel sinks in water change as she
sails from Lake Ontario into the Atlantic Ocean? Why?
19. If the density of sea water is 1.0269 g. per cubic centimeter and
that of ice 0.918 g. per ccm., what portion of an iceberg is above
water?
20. In drawing water from a well by means of a bucket, why is
less force used when it is under water than when entirely above?
[Pg 52]
21. A stone which weighs 300 lbs. can be lifted under water with a
force of 150 lbs. What is the volume of the stone?
22. The average density of the human body is 1.07 grams per c.c.
How much water will a man who weighs 150 lbs. displace when
diving? How much when floating?
(4) Density and Specific Gravity
48. Density.—The density of a substance is often used
as a test of its purity. Archimedes in testing King Hiero's
crown to find out if it were made of pure gold determined
first its density. It is by such tests that the purity of
milk, of alcohol, of gold, and a great variety of substances
is often determined.
Knowledge of methods of finding density is of value to
everyone and should be included in the education of every
student. The density of a substance is the mass of unit
volume of the substance. In the metric system, for example,
the density of a substance is the mass in grams per 1 ccm.
Taking water, 1 ccm. weighs 1 gr. or its density is therefore
1 g. to the cubic centimeter. A cubic centimeter
of aluminium weighs 2.7 g. Its density therefore is 2.7 g.
per ccm.
49. Specific Gravity.—Specific gravity is the ratio of the
weight of any volume of a substance to the weight of an
equal volume of water. Its meaning is not quite the same
as that of density, since specific gravity is always a ratio,
i.e., an abstract number, as 2.7. Density of a substance
is a concrete number, as 2.7 grams per ccm. In the
metric system the density of water is one gram per cubic
centimeter, therefore we have:
Density (g. per ccm.) = (numerically) specific gravity.
In the English system, the density of water is 62.4
pounds per cubic foot, therefore in this system we have:
Density (lbs. per cu. ft.) = (numerically) 62.4 × sp. gr.
[Pg 53]
50. Methods for Finding Density and Specific Gravity
(a) Regular Solids.—Solids of regular shapes such as cubes,
spheres, etc., whose volumes may be readily found by
measurement, may be weighed. The mass divided by the
volume gives the density, or D = Mμ/v.
(b) Irregular Solids.—with these the volume cannot be
found by measurement but may be obtained by Archimedes'
Principle. Weigh the solid first in the air and
then in water. The apparent loss of weight equals the
weight of the equal volume of water displaced. From
this the volume may be found. And then the
density equals mass/volume; the specific gravity =
wt. in air / wt. of equal volume of water = wt. in air / ((wt. in air) - (wt. in water))
(c) Solids Lighter than Water.—This will require a
sinker to hold the body under water. Weigh the solid
in air (w). Weigh the sinker in water (s). Attach
the sinker to the solid and weigh both in water (w´).
The specific gravity equals
(wt. of solid in air)/(loss in wt. of solid in water) or w/((w + s) - w´)
The apparent loss of weight of the solid is equal to the sum
of its weight in air plus the weight of the sinker in water,
less the combined weight of both in water.
(d) The Density of a Liquid by a Hydrometer.—One
may also easily find the density of any liquid by Archimedes'
Principle. If one takes the rod described in Art.
46, and places it in water, the number of cubic centimeters
of water it displaces indicates its weight in grams. On
placing the rod in another liquid in which it floats, it will
of course displace its own weight and the height to which
the liquid rises on the scale gives the volume. By dividing[Pg 54]
the weight of the rod as shown by its position in water
by the volume of the liquid displaced we obtain the density
of the liquid. Commercial hydrometers
for testing the density of milk, alcohol
and other liquids are made of glass of the
form shown in Fig. 28. The long narrow
stem permits small differences in volume
to be noticed, hence they are more
accurate than the rod described in the
preceding paragraph. For convenience
this rod contains a paper scale, so that
when the height of the liquid on the stem
is noted, the density is read at once.
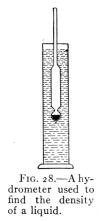 Fig. 28.—A hydrometer
used to
find the density
of a liquid.
Fig. 28.—A hydrometer
used to
find the density
of a liquid.
Density of Liquids by Loss of Weight.
Weigh a piece of glass in air (Wa), in
water (Ww), and in the liquid to be
tested (Wl).
Then (Wa - Ww)gives the weight of the water displaced.
And (Wa - Wl) gives the weight of the liquid displaced.
Hence, (Wa - Wl)/(Wa - Ww) equals the specific gravity of the liquid.
Important Topics
1. Definitions of density and specific gravity.
2. Methods of finding density: (a) regular solids; (b) irregular
solids; (c) solids lighter than water; (d) liquids by hydrometer;
(e) liquids by loss of weight.
Exercises
Note.—Consider that 1 cu. ft. of water weighs 62.4 lbs. Consider
that 1 ccm. of water weighs 1 g.
1. What is meant by the statement that a block of wood has a
specific gravity of 0.6?
2. Considering that the density of the human body is the same as
that of water, what is the volume of a 125-lb. boy? Of a 250-lb.
man? Of a 62.4-lb. boy? What is the volume of your body?
3. How is the weight of large ships found? Give an example.
[Pg 55]
4. Mention three cases where determinations of density are important.
5. A body weighs 40 g. in air, 15 g. in water, 5 g. in an acid. Find
(a) the density of the body; (b) its volume; (c) density of the
acid.
6. If the specific gravity of a horse is 1, what is the volume of a
horse weighing 500 kg.? Of one weighing 1248 lbs.?
7. A weighted wooden box sinks to a depth of 20 cm. in water and
24 cm. in alcohol, and to a depth of 18 cm. in brine. What is
the density of the alcohol and of the brine?
8. A glass stopper weighs in the air 25 g., in water 15 g., in oil 18 g.
Find the density and volume of the stopper. Find the density
of the oil.
9. What would a cubic foot of wood weigh if the specific gravity
were 0.5.?
10. The specific gravity of aluminum is 2.7. Find the weight of
a cubic foot of it.
11. A block of wood weighs 40 g. A piece of lead appears to weigh
70 g. in water. Both together appear to weigh 60 g. in water.
Find the density of the wood.
12. A stone weighs 30 g. in air, 22 g. in water, and 20 g. in salt
water. Find the density of the salt water.
13. Will iron sink in mercury? Why?
14. A submarine boat weighing 200 tons must have what volume
in order to float?
15. Find the weight of 2 cu. ft. of copper from its density.
16. What is the weight in water of a mass whose specific gravity is
3.3 and whose weight is 50 kg.?
17. A block of granite weighs 1656 lbs.; its volume is 10 cu. ft.,
what is its density?
18. If the specific gravity of hard coal is 1.75 how would you
determine how many tons of coal a bin would hold?
19. A hollow copper ball weighs 2 kg. What must be its volume to
enable it to just float in water?
20. A mass having a volume of 100 ccm. and a specific gravity
of 2.67 is fastened to 200 ccm. of wood, specific gravity 0.55.
What will the combination weigh in water?
21. A block weighing 4 oz. in air is tied to a sinker which appears to
weigh 14 oz. in water. Both together appear to weigh 6 oz.
in water. What is the specific gravity of the block?
[Pg 56]
MECHANICS OF GASES
(1) Weight and Pressure of the Air
51. Weight of Air.—It is said that savages are unaware
of the presence of air. They feel the wind and hear and
see it moving the leaves and branches of the trees, but of
air itself they have little conception.
To ordinary observers, it seems to have no weight, and
to offer little resistance to bodies passing through it.
That it has weight may be readily shown as follows:
(See Fig. 29.) If a hollow metal
sphere, or a glass flask, provided
with tube and stopcock, be
weighed when the stopcock is
open, and then after the air has
been exhausted from it by an air
pump, a definite loss of weight is
noticeable.
 Fig. 29.—Proof that air has
weight.
Fig. 29.—Proof that air has
weight.
If the volume of the sphere is
known and it is well exhausted
of air, a fair approximation of
the weight of air may be obtained. Under "standard
conditions," which means at the freezing temperature and
a barometric pressure of 76 cm., a liter of air weighs
1.293 g. while 12 cu. ft. of air weigh approximately 1 lb.
52. Pressure of Air.—Since air has weight it may
be supposed to exert pressure like a liquid. That it
does so may be shown in a variety of ways.
[Pg 57]
If a plunger fitting tightly in a glass cylinder be drawn
upward, while the lower end of the tube is under water,
the water will rise in the tube (Fig. 30). The common
explanation of this is that the water rises because of
"suction." The philosophers of the ancient Greeks explained
it by saying that "nature abhors
a vacuum," and therefore the water rises.
Neither explanation is correct. It was
found in 1640 that water would not rise
in a pump more than 32 ft. despite the fact
that a vacuum was maintained above the
water. Galileo was applied to for an
explanation. He said, "evidently nature's
horror of a vacuum does not extend above
32 ft." Galileo began tests upon "the
power of a vacuum" but dying left his
pupil Torricelli to continue the experiment.
Torricelli reasoned that if water
would rise 32 ft., then mercury, which is
13.6 times as dense as water, would rise
about 1/13 as much. To test this, he performed the following
famous experiment.
 Fig. 30.—Air
pressure forces
the liquid up the
tube.
Fig. 30.—Air
pressure forces
the liquid up the
tube.
53. Torricelli's Experiment (1643).—Take a glass tube
about 3 ft. long, sealed at one end, and fill it with mercury.
Close the end with the finger and invert, placing the end
closed by the finger under mercury in a dish (Fig. 31).
Remove the finger and the mercury sinks until the top
of the mercury is about 30 in. above the level of the mercury
in the dish. Torricelli concluded that the rise of
liquids in exhausted tubes is due to the pressure of the
atmosphere acting on the surface of the mercury in the
dish.
To test this, place the tube with its mercury upon the
plate of an air pump and place a tubulated bell jar over[Pg 58]
the apparatus so that the tube projects through a tightly
fitting stopper. (See Fig. 32.) If the air pressure is the
cause of the rise of mercury in the tube, on removing the
air from the bell jar the mercury should fall in the tube.
This is seen to happen as soon as the pump is started. It
is difficult to remove all the air from the receiver so the
mercury rarely falls to the same level in the tube as in
the dish. A small tube containing mercury is often attached
to air pumps to indicate the degree of exhaustion.
Such tubes are called manometers.
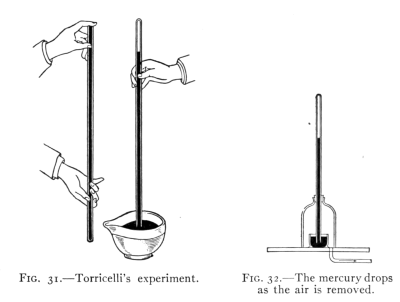 Fig. 31.—Torricelli's experiment.
Fig. 31.—Torricelli's experiment.
Fig. 32.—The mercury drops as the air is removed.
54. The Amount of Atmospheric Pressure.—Torricelli's
experiment enables us to compute readily the
pressure of the atmosphere, since it is the atmospheric
pressure that balances the column of mercury in the
tube. By Pascal's Law, the pressure of the atmosphere
on the surface of the mercury in the dish is transmitted
as an exactly equal pressure on the mercury[Pg 59]
column in the tube at the same level as the mercury
outside.
This pressure, due to the air, must balance
the weight of the column of mercury
in the tube. It therefore equals the weight
of the column of mercury of unit cross-section.
The average height of the column
of mercury at sea-level is 76 cm. Since the
weight of 1 cc. of mercury is 13.6 grams,
the pressure inside the tube at the level of
the surface of the mercury in the dish is
equal to 1 × 76 × 13.6 or 1033.6 g. per
square centimeter. Therefore the atmospheric
pressure on the surface of the mercury
in the dish is 1033.6 g. per square centimeter,
approximately 1 kg. per square centimeter or
15 lbs. per square inch.
55. Pascal's Experiment.—Pascal tested
in another way the action of atmospheric
pressure upon the column of mercury by
requesting his brother-in-law, Perrier, who
lived near a mountain, to try the experiment
on its top. Perrier found that on ascending
1000 meters the mercury fell 8 cm. in the
tube. Travelers, surveyors, and aviators
frequently determine the altitude above
sea-level by reading the barometer, an
ascent of 11 meters giving a fall of about
1 mm. in the mercury column, or 0.1 in. for
every 90 ft. of ascent.
 Fig. 33.—A
standard
barometer.
Fig. 33.—A
standard
barometer.
56. The Barometer.—The modern barometer
(Fig. 33), consists of a Torricellian
tube properly mounted. Reading a barometer consists
in accurately reading the height of the mercury column.[Pg 60]
This height varies from 75 to 76.5 cm. or 29 to 30 in.
in localities not far from the sea-level. The atmospheric
pressure varies because of disturbances in the atmosphere.
It is found that these disturbances of the atmosphere
pass across the country from west to east in a
somewhat regular manner, hence a series of readings of
the barometer may give reliable information of the movement
of these disturbances and so assist in forecasting the
weather. The weather Bureau has observations taken
at the same moment at various stations over the country.
These observations form the basis for the daily forecast
of the weather.
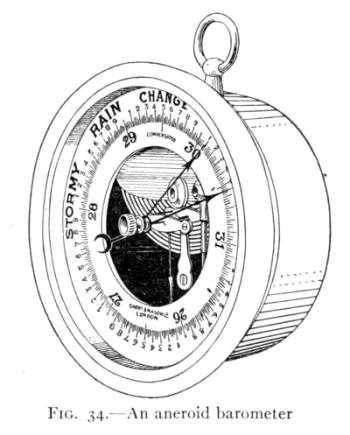 Fig. 34.—An aneroid barometer
Fig. 34.—An aneroid barometer
Another form of barometer in common use is the Aneroid Barometer
(Fig. 34). Its essential parts are a cylindrical air-tight box
with an elastic corrugated cover. Inside the box is a partial vacuum.
This makes the cover very sensitive to slight changes of
pressure. The motion of the top of the box is conveyed by a series
of levers to an indicating hand which moves over a dial. This[Pg 61]
barometer can be made so sensitive as to indicate the change of
air pressure from a table top to the floor. It is much used by
travelers, explorers, surveying parties and aviators, since the mercurial
barometer is inconvenient to carry.
Important Topics
1. Weight and Pressure of air in English and metric units. How
shown. Evidences.
2. Work of Galileo, Torricelli, and Perrier.
3. Barometer: construction, action, mercurial, aneroid.
 Fig. 35.—Air pressure keeps the
water In the tumbler.
Fig. 35.—Air pressure keeps the
water In the tumbler.
Fig. 36.—Cross-section of a
modern drinking fountain.
Exercises
1. Do you think Archimedes' Principle applies to the air? Does
Pascal's Law? Why?
2. Find the downward pressure of the mercury in a barometer
tube if the cross-section is 1 sq. cm. and the height 75 cm. at
the level of the mercury surface in contact with the air.
(The density of mercury is 13.6 grams per cc.)
[Pg 62]
3. What is the weight of the air in a room if it is 10 × 8 × 4 meters?
4. What weight of air is in a room 10 × 15 × 10 ft.?
5. When smoke rises in a straight line from chimneys, is it an
indication of a high or low barometric pressure? Why?
6. Why does a tumbler filled with water and inverted in a dish
with its rim under water remain full?
7. If the barometer tube is inclined the mercury remains at the
same horizontal level. How can this be explained?
8. When the mercurial barometer stands at 76 cm., how high would
a water barometer stand? Explain.
9. Explain why it is possible for one to suck soda water through a
tube?
10. Fill a tumbler with water. Place a sheet of paper over the top
and invert. The paper clings to the tumbler and prevents the
water from escaping. Explain. (See Fig. 35.)
11. Why must a kerosene oil can have two openings in order to
allow the oil to flow freely?
12. Explain the action of the modern drinking fountain (Fig. 36).
(2) Compressibility and Expansibility of the air
57. Effect of Pressure on Liquids and Gases.—Both
classes of fluids, liquids and gases, have many characteristics
in common. Both are composed of molecules that
move freely; hence both flow. At any point within a fluid
the pressure is the same in all directions. Archimedes'
Principle applies, therefore, to both liquids and gases.
We now come to an important difference between liquids
and gases. Liquids are practically incompressible. "So
much so, that if water is subjected to a pressure of 3000
kg. per sq. cm., its volume is reduced only about one-tenth."
Gases show a very different behavior from liquids
on being subjected to pressure. They may readily be
compressed to a small fraction of their volume as is noticed
on inflating a pneumatic tire. A gas has also the ability to
spring back to a larger volume as soon as the pressure is
released, as when a cork is driven from a pop gun. Not[Pg 63]
only is compressed air able to expand, but air under ordinary
conditions will expand if it is released in a space
where the pressure is less.
Hollow bodies, animals and plants, are not crushed by
atmospheric pressure, because the air and gases contained
within exert as much
force outward as the air exerts
inward.
58. Boyle's Law.—The relation
between the volume and
pressure of a gas was first investigated
by Robert Boyle in
the seventeenth century. The
experiment by which he first
discovered the law or the relation
between the volume and
the pressure of a gas is briefly
described as follows:
 Figs. 37 a and 37 b.—Boyle's
law apparatus.
Figs. 37 a and 37 b.—Boyle's
law apparatus.
A glass tube is bent in the form of
the capital letter J, the short arm
being closed. A little mercury is
poured in to cover the bend. (See
Fig. 37 a.) Since the mercury is at
the same level in both arms, the pressure
in (A) is the same as in (B).
Mercury is now poured into (A)
until it stands in the long tube at a height above that in (B)
which is equal to the height of the mercury column of the barometer.
(See Fig. 37 b.) The air in (BC) is now under a pressure of
two atmospheres (one atmosphere is due to the mercury column).
On measurement the air in (BC) will be found to have just one-half
of its original volume.
Thus doubling the pressure to which a gas is subjected
reduces its volume to one-half. Tripling the pressure, reduces
the volume to one-third and so on.
[Pg 64]
Careful experiments reveal the following law: The
volume of a given mass of gas at constant temperature is
inversely proportional to the pressure to which it is subjected.
This law is often expressed mathematically. P/P´ = V´/V, or
PV = P´V´. Since doubling the pressure reduces the
volume one-half, it doubles the density. Tripling the
pressure triples the density. We therefore have P/P´ = D/D´
or the density of a gas directly proportional to its pressure.
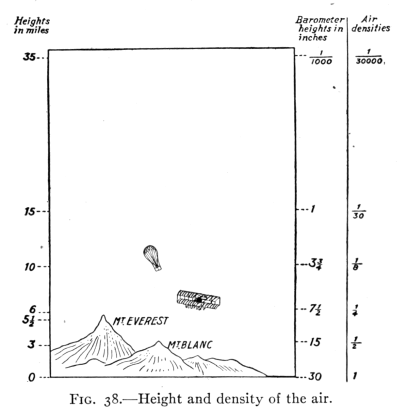 Fig. 38.—Height and density of the air.
Fig. 38.—Height and density of the air.
59. Height of the Atmosphere.—From its properties
of compression and expansion, the air varies in density
and pressure as one ascends in it. At a height of 3 miles
the pressure is reduced to about one-half. This is an
indication that one-half of the air is below this level.
Balloonists have gone to a height of 7 miles, Glaser and[Pg 65]
Coxwell in England in 1862 and Berson in France in 1901.
The atmosphere has been explored to a height of 30,500
meters (18.95 miles) by sending up self-registering barometers
in small balloons which burst at great altitudes.
A parachute protects the instruments from breakage
from too rapid fall. This height of 30,500 meters was
reached by a balloon sent up by William R. Blair, at
Huron, South Dakota, September 1, 1910.
At a height of 35 miles, the density is estimated at
1/30,000 of its value at sea-level. (See Fig. 38.) It is
believed that some rarefied air exists for a considerable
distance above this point, some estimates placing the extent
at 100 miles, and others from 200 to 500 miles. Evidences
of some air at such heights are shown by: (a)
the height at which meteors first appear, (b) the height of
the Aurora Borealis, and (c), the distance that the sun
is below the horizon when the last traces of color disappear
from the sky in the evening.
Although the exact limits of the atmosphere are unknown,
the weight of a column of air 1 sq. cm. in cross-section,
and extending upward as high as the atmosphere,
may be accurately computed. For this column of air
exactly balances the column of mercury in the tube of
the barometer.
Below sea-level, the air increases rapidly in density and
it is estimated that at a depth of 35 miles, the density of
the air would be a thousand times that at the earth's
surface, or more than that of water.
Important Topics
1. Evidence of compressibility of gases and incompressibility of
liquids.
2. Boyle's Law. Proof, applications.
3. Extent of the atmosphere—three evidences.
[Pg 66]
Exercises
1. Mention three illustrations of the compressibility and
expansibility of air that you know from your own experience.
2. Increasing the pressure increases the amount of a gas that will
be absorbed by a liquid? Explain this. Have you ever observed
this fact? Where?
3. If a toy balloon containing 2000 ccm. of gas at the earth's surface
where the barometer reading is 76 cm., rises to an elevation where
the barometer reads 54 cm., the balloon will tend to expand to
what volume? Explain. Will it attain this volume?
4. If a gas is compressed, it changes in temperature. How do
you explain this?
5. What change in temperature will occur when compressed air
is allowed to expand? Explain.
6. Air blowing up a mountain side has its pressure lessened as
it approaches the top. How will this affect the temperature?
Why? What may result from this change in temperature?
Explain.
7. To what pressure must 500 ccm. of air be subjected to compress
it to 300 ccm. the barometer reading at first being 75 cm.
Explain.
 Fig. 39.—The air pump.
Fig. 39.—The air pump.
(3) Pneumatic Appliances
60. The Air Pump.—The air pump is used to remove air
or other gases from a closed vessel. It was invented
about 1650 by Otto Von Guericke, burgomaster of Magdeburg,[Pg 67]
Germany. One form of air pump is shown in Fig.
39. C is a cylinder within which slides a tightly fitting
piston. R is the vessel from which the air is to be exhausted.
r and u are valves opening upward. The action
of the pump is as follows:
On pushing the piston down, the air in C is compressed.
This opens valve r allowing the confined air to escape
above the piston. The piston is then raised making the
space in C a partial vacuum. The pressure in R now being
greater than in C, u is pushed up and the air from R
rushes into C, until the pressure is equalized. On pushing
down the piston again, valve u closes and the process is
repeated until the pressure in R is no longer able to raise
the valve u. Some air pumps are so constructed that the
valves are opened and closed automatically by the movement
of the piston. With these pumps a higher degree of
rarefaction can be obtained.
Air is often partially exhausted from receivers
or vessels by the use of a filter
pump or aspirator. A stream of water
flowing through a constriction causes a
reduced pressure, draws in air and carries
it away, and thus produces a partial
vacuum. See Fig. 40 for a section of the
device.
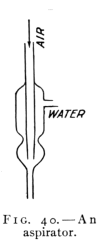 Fig. 40.—An
aspirator.
Fig. 40.—An
aspirator.
61. The Condensing Pump.—This is
like the exhaust pump except that its
valves are reversed. It is used in compressing
illuminating gases into cylinders
for use in lighting vehicles, stereopticons, Pintsch lights,
gas light buoys, etc., and also for compressing air to
operate air brakes, pneumatic hammers and drills, and
for other uses.
The common condensing pump is the kind used for[Pg 68]
inflating tires. (See Fig. 41.) In this, a loosely fitting
metal piston is attached to a disc of leather somewhat
larger than the cylinder. This device is called a cup valve.
On raising the piston, air rushes in from the top past the
valve, but on pushing the piston down, the valve is pressed
tightly against the sides of the cylinder and prevents
the escape of any air. The compressed air
pushes open a valve on the tire and
enters it. This valve closes as soon as the
pressure is lessened from outside. It is
well to notice in all of these pumps that
two valves are used. One holds the air
already secured while the other opens for
a new supply. Both valves are never
open at the same time.
 Fig. 41.—Condensing pump used in inflating tires.
Fig. 41.—Condensing pump used in inflating tires.
62. Water Pumps.—The Common Lift
Pump. This, the simplest pump for raising water, consists
of a cylinder C (Fig. 42) connected by a pipe R to a
supply of water as a cistern or well. A valve opening
upward is placed at the bottom of the cylinder over the
entrance to the pipe. In the cylinder is a tightly fitting
piston connected by a rod to a lever for ease in action.
The piston contains a valve opening upward. In operating
this pump water is usually first poured into the
cylinder to "prime" it. This helps to close the valves
and prevents air leaking past them. When the piston is
lowered the lower valve closes, the air in the cylinder
being compressed pushes the upper valve open and
passes above the piston. On raising the piston the
upper valve closes. This forms a partial vacuum in the
cylinder.
The air pressing on the surface of the water below forces
the water and air that may be in the tube upward through
the lower valve to fill this partial vacuum.
[Pg 69]
When the cylinder becomes filled with water, this is
lifted out on the up-stroke, whence its name, "lift pump."
Since the atmospheric pressure at sea-level can only
support a column of water about 34 ft. high, the lower
valve must be within this distance of the water surface.
In actual practice the limit is about 27 ft. In deeper
wells, the cylinder and valves are placed so that they are
within 25 or 27 ft. of the surface of the water in the well,
a long piston rod reaching above the surface of the ground
and connected to a pump handle operates the piston. A
discharge pipe extends from the cylinder to the surface of
the ground above.
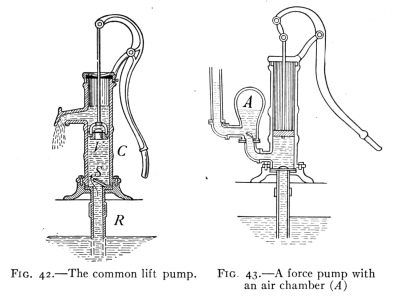 Fig. 42.—The common lift pump.
Fig. 42.—The common lift pump.
Fig. 43.—A force pump with
an air chamber (A).
63. The Force Pump.—The force pump is used to
deliver water under pressure either for spraying or to
an elevated reservoir. The piston is solid, the second
valve being placed at the entrance of the discharge pipe.
(See Fig. 43.) The action is the same as that of the
lift pump, with this exception; the piston in its down[Pg 70]
stroke forces the water out through the discharge pipe,
the velocity depending upon the pressure exerted.
A force pump is usually provided with an air chamber
which is connected with the discharge pipe. On the down
stroke of the piston, water is forced into the air chamber.
This compresses the air it contains. The compressed
air reacts and exerts pressure on the water forcing it out in
a steady stream.
Force pumps are used in deep wells, being placed at the
bottom.
The pumps used in city water works, fire engines, and
all steam pumps, are force pumps. (See Fig. 44.)
 Fig. 44.—A steam pump used on a fire engine.
Fig. 44.—A steam pump used on a fire engine.
64. The Siphon.—The siphon is a tube used to convey a
liquid from one level over an elevation to a lower level by
atmospheric pressure. It is used to remove liquids from
tanks or vessels that have no opening at the bottom.
The siphon cannot be completely understood until
one has mastered the laws of the flow of liquids. The
following is offered as an incomplete explanation of its
behavior. Consider the siphon to be full of water and[Pg 71]
closed at d (Fig. 45). Atmospheric pressure on a will
hold the siphon full if ab does not exceed 34 feet. If
d is opened the water falls out with a speed equal to
that acquired in falling from the
level of a to that of d. This speed
is acquired by all the water in the
siphon and results in a drop in
pressure throughout it. The pressure
at a inside the siphon becomes
less than the pressure at
the same level outside as soon as
the water starts flowing. The water
in the vessel then flows into the
siphon and out at d. This flow continues
as long as there is a fall from
the free surface of the water in the
vessel to the outlet at d.
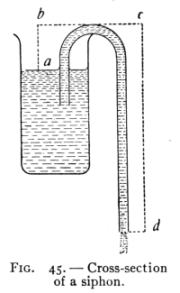 Fig. 45.—Cross-section of a siphon.
Fig. 45.—Cross-section of a siphon.
 Fig. 46.—The Cartesian diver.
Fig. 46.—The Cartesian diver.
65. The Cartesian Diver.—This is a device which illustrates
at the same time transmission of pressure by liquids,
Archimedes' principle, and compressibility of gases.
It was invented by Des Cartes (1596-1650).
As ordinarily made, it is a
hollow glass image with a small opening
in the foot. It contains air and water
in such amounts that the average density
of image and contents is slightly less
than that of water. It is placed in a tall
glass jar filled with water and covered
with tightly stretched rubber tissue. (See
Fig. 46.) By pressing on the rubber cover
the diver may be made to sink, since
the air and water transmit the pressure
on the cover which compresses the air inside the figure
admitting some water to it, thus making the diver more[Pg 72]
dense than water. By varying the pressure it can be
made to sink, rise, or remain stationary at will.[D] A small
vial can be used instead of the image.
66. Hydraulic Ram.—The hydraulic ram (see Fig. 47)
is an automatic device that is much used for raising water
from springs to houses located on higher ground. Water
flows through the pipe A through the opening at B. The
pressure closes the valve at B. The increased pressure
in the pipe due to the
closing of B opens the
valve C and some of the
water flows into the air
chamber D. This reduces
the pressure
against the valve B so
that it drops and allows
a little water to escape. Just as this happens, valve C
closes. The pressure in the pipe then closes B and forces
water past C. This action being continually repeated,
the air in D becomes so compressed that it has elastic
force enough to raise the water in a steady stream to a
height of many feet.
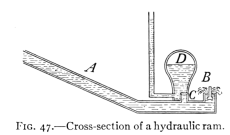 Fig. 47.—Cross-section of a hydraulic ram.
Fig. 47.—Cross-section of a hydraulic ram.
67. The Balloon.—Since air is a fluid, Archimedes'
principle applies to it as well as to liquids. Therefore
any object in the air is lifted up by a force equal to the
weight of the air it displaces. The object will rise, if it
weighs less than this displaced air and will continue to
rise until both weights are equal.
The Balloon (Fig. 48) rises because it weighs less than
the air it displaces, and therefore it is pushed up by the
heavier air, the "lifting power" being the difference between
its weight and that of the air displaced. The[Pg 73]
neck at the bottom is left open to allow for expansion
of the gas. When the aeronaut wishes to descend,
he opens a valve at the top allowing some of the gas to
escape.
 Fig. 48.—Winner of international championship race, Paris, 1913.
Fig. 48.—Winner of international championship race, Paris, 1913.
Hydrogen is the lightest gas, weighing 0.09 kg. per cubic
meter, and so gives the greatest lifting power, but as it is
expensive to make, coal gas, density 0.75 kg. per cubic
meter, is ordinarily employed. Helium has recently been
used to fill military balloons because it cannot be set on fire.
[Pg 74]
The Parachute (Fig. 49) is an umbrella-shaped device
for use in descending from a balloon. After falling a few
seconds it opens, the large surface exposed to the air causing
it to descend slowly. The hole
in the top keeps the parachute upright
by allowing the air to escape
through it, thus relieving the pressure.
 Fig. 49.—A parachute.
Fig. 49.—A parachute.
 Fig. 50.—Cross-section of a Westinghouse
air brake.
Fig. 50.—Cross-section of a Westinghouse
air brake.
68. The Air Brake.—Compressed
air is used to do work in many
machines, such as pneumatic drills,
hammers, and air brakes. The
Westinghouse air brake (Fig. 50)
uses air at a pressure of about 70
lbs. to the square inch. The essential
parts as shown are a reservoir R,
the brake cylinder C and a triple valve V, placed under
each car with an air pipe P, leading to the engine. This
is connected to R by the triple valve V. When the pressure
in P is reduced by the engineer or by accident, the
triple valve operates so
as to admit air from R
into the cylinder C
pushing the piston H
to the left. H is connected
to the brakes
by levers which press
the brake shoes
strongly against the
wheels. When the air
pressure in P is restored
the triple valve acts
so as to permit the air in C to escape while R is filled
again from P. The hissing sound heard when a train
stops is caused by air escaping from cylinder C. The[Pg 75]
spring in C keeps the brakes from the wheels except
when the "air is on."
 Fig. 51.—Cross-section of a gas meter showing
its construction and action.
Fig. 51.—Cross-section of a gas meter showing
its construction and action.
69. The Gas Meter.—The gas meter consists of a
box divided into two parts by a vertical partition (Fig.
51). Two bellows are attached
to this partition, one
on each side. The valves
that regulate the flow of gas
to and from the bellows and
the chambers A and D are
opened and closed by levers
connected with the bellows.
These levers also operate the
hands upon the dials. When
the inlet to the bellows B
is opened, the outlet of A is
also opened. Gas entering B
opens the bellows and forces
the gas in A out into the
house-pipe E. When B is
full its inlet valve closes and
its outlet valve opens. The
inlet of A also opens and its
outlet closes. Gas now flows
into A, compressing the bellows
and B, and forcing the
gas from it into the house-pipe.
At each filling of the bellows B there will be displaced
from A and forced into the house-pipe as much
gas as enters B. It is evident that at each emptying of
B an equal amount of gas enters A. Thus we have A
and B alternately filling and emptying as long as the
gas burner is open. To have a continuous flow of gas
in the house-pipes two pipes and two chambers are[Pg 76]
necessary, one being filled while the other is being
emptied.
Fig. 52 represents the
dials upon a gas meter
showing a reading of
54,600 cu. ft.
 Fig. 52.—Dials of a gas meter.
Fig. 52.—Dials of a gas meter.
70. Centrifugal Pumps.
Fluids, such as water and
air, are often put in motion
by devices called centrifugal pumps (see Art. 78). These
pumps contain a revolving part, like a wheel without a
rim, whose spokes are replaced by thin blades. This revolving
part resembles the paddle wheel of some steam
boats and is enclosed in a case or cover having one
opening at the rim and another opening on one side
about the axle.
 Fig. 53.—A vacuum sweeper. (Courtesy of the Hoover Suction
Sweeper Co.)
Fig. 53.—A vacuum sweeper. (Courtesy of the Hoover Suction
Sweeper Co.)
When the wheel is rapidly revolved, the fluid is driven
out with considerable force through the opening at the
rim, while a partial vacuum is produced at the axle
causing a rapid flow into the device at this point.
This is the principle of the action of the vacuum cleaner.[Pg 77]
Fig. 53 is a section of a vacuum sweeper showing the
revolving wheel and the current of air passing into the
wheel at the lower side and out of the rim of the case at
the rear.
Centrifugal water pumps work on the same principle
and furnish a continuous flow of water, often large in
volume and at considerable pressure.
Important Topics
1. Air pump.
2. Condensing pump.
3. Lift and force pumps.
4. Siphon.
5. Cartesian diver.
6. Hydraulic ram.
7. Balloon.
8. Air brake.
9. Gas meter.
10. Vacuum cleaner.
Exercises
1. Explain why smoke settles to the ground before storms.
2. Why does the water rise in the suction pipe of a pump?
3. Why is it easier to float in water when the lungs are filled with
air than when they are not filled?
4. Why is it easier to swim in salt water than in fresh water?
5. How are submarines made to sink? to rise to the surface?
6. How can a fish rise or sink in water?
7. Explain why a life preserver made of cork will enable a person
to float.
8. Hold the open hand out flat with the fingers together. Place
underneath the fingers a piece of paper. Blow between the
first and second fingers against the paper. As long as you blow
hard the paper will not fall but will stick to the hand. Explain.
9. Why does pressing the bulb of an atomizer force out the liquid
in a fine spray?
10. Why is air that contains a large amount of water vapor lighter
than air that only contains a small amount?
11. How are heights above sea-level ascertained by a barometer?
12. Oil floats on water but sinks in alcohol. Explain.
13. In a balloon the lower end is often open to the air. Why does
not the gas escape and prevent the balloon from rising?
14. How long will a balloon continue to rise?
[Pg 78]
15. If the pressure against the 8-in. piston of an air brake is 70 lbs.
per square inch, how much force does the piston exert?
16. The capacity of a balloon is 40,000 cu. ft. The weight of the
balloon, car, etc., is 600 lbs.; specific gravity of the gas used is
0.46 that of the air. Find how much weight the balloon can
carry.
17. The so-called Magdeburg hemispheres were invented by Otto
von Guericke of Magdeburg, Germany. When the hemispheres
(see Fig. 54) are placed in contact and the air exhausted it is
found very difficult to pull them apart. Explain.
18. Von Guericke's hemispheres had an inside diameter of 22 in.
What force would be required to pull them apart if all the air
were exhausted from them? (Find the atmospheric
force on a circle, 22 in. in diameter.)
19. Von Guericke made a water barometer whose
top extended through the roof of his house.
On the top of the water in the tube was
placed a wooden image. In fair weather the
image appeared above the roof, but it descended
before a storm. Explain.
20. The balloon "Goodyear" (Fig. 48), which won
the International championship race at Paris
in 1913, has a capacity of 80,000 cu. ft. The
gas bag weighs 653 lbs., the net 240 lbs. and
the basket 92 lbs. How large a load can it
carry when filled with hydrogen specific gravity
0.069 (compared with air).
 Fig. 54.—Magdeburg
hemispheres.
Fig. 54.—Magdeburg
hemispheres.
Review Outline: Liquids and Gases
Liquids: Force, pressure, and density. Floating and immersed
bodies.
Laws: Liquid force, F = A.h.d, Pascal's, Archimedes.
Illustrations and Applications:
Specific gravity, W_{a}/(W_{a} - W_{w}), (W_{a} - W_{l})/(W_{a} - W_{w}), Boyle's, PV = P´V´
Devices: Hydraulic press, air cushion, barometer—mercurial and
aneroid. Pumps, lift, force, vacuum, compression, centrifugal,
balloon, siphon, etc. Construction and action of each.
[Pg 79]
FORCE AND MOTION
(1) Force, How Measured and Represented
71. Force.—We have been studying various forces,
such as air pressure, pressure in liquids, and the force of
elasticity in solids, and have considered them simply as
pushes or pulls. A more formal study of forces in general
and of devices for representing and measuring them will
be helpful at this point of the course.
A force is that which tends to cause a change in the size
or shape of a body or in its state of motion. In other words a
force is a push or a pull. That is, force tends to produce
distortion or change of motion in a body. Force itself
is invisible. We measure it by the effect it produces.
Forces are usually associated with the objects exerting
them. Thus we speak of muscular force, air pressure,
liquid pressure, the force of a spring, the force of the earth's
attraction and so on.
Forces are classified in various ways.
I. With respect to the duration and steadiness of the
force.
(a) Constant, as the earth's attraction. (b) Impulsive,
as the stroke of a bat on a ball. (c) Variable, as the force
of the wind.
II. With respect to the direction of the force.
(a) Attractive, as the earth's attraction. (b) Repulsive,
as air pressure, liquid pressure, etc.
72. Methods of Measuring Force.—Since forces are
measured by their effects which are either distortion or
change of motion, either of these effects may be used to[Pg 80]
measure them. For example, the force exerted by a
locomotive is sometimes computed by the speed it can
develop in a train of cars in a given time, or the force of
the blow of a baseball bat is estimated by the distance the
ball goes before it strikes the ground.
The more common method of measuring
force, however, is by distortion, that is, by
measuring the change of shape of a body
caused by the force. In doing this, use
is made of Hooke's Law (Art. 32), in which
it is stated that "within the limits of perfect
elasticity," changes of size or shape
are directly proportional to the forces employed.
That is, twice as great a force will
produce twice as great a change of shape
and so on.
 Fig. 55.—A
spring balance.
Fig. 55.—A
spring balance.
A common contrivance using this principle
is the spring balance (Fig. 55), with
which all are familiar, as ice scales, meat
scales, postal scales, etc. The object
which changes shape in this device is a
coiled spring contained in the case of the
instrument. The balance is so constructed
that when the spring is pulled out as far as
possible it has not reached its limit of
elasticity, since, if the spring were stretched so as to exceed
its elastic limit, the index would not return to its first
position on removing the load. (See Arts. 30-32.)
73. Graphic Representation of Forces.—A force is
said to have three elements. These are (a) its point of
application, (b) its direction, and (c) its magnitude. For
example, if there is hung upon the hook of a spring balance
a weight of 5 lbs., then we have: (a) its point of application
on the hook of the balance, (b) its downward direction[Pg 81]
and (c) its magnitude, or 5 lbs. These three elements
may be represented by a line. Thus in Fig. 56a, a line
AB is drawn as shown, five units long; A represents the
point of application; B, the arrow head, shows the direction;
and the length of the line (five units) shows the magnitude
of the force.
This is called a graphic representation since it represents
by a line the quantity in question. If another weight of
5 lbs. were hung from the
first one, the graphic representation
of both forces
would be as in Fig. 56b.
Here the first force is represented
by AB as before, BC
representing the second
force applied. The whole
line represents the resultant
of the two forces or the result
of their combination. If the
two weights were hung one
at each end of a short stick
AC (Fig. 56c), and the latter
suspended at its center
their combined weight or resultant would of course be
applied at the center. The direction would be the same
as that of the two weights. The resultant therefore is
represented by ON. In order to exactly balance this
resultant ON, a force of equal magnitude but opposite in
direction must be applied at the point of application of
ON, or O. OM then represents a force that will just
balance or hold in equilibrium the resultant of the two
forces AB and CD. This line OM therefore represents the
equilibrant of the weights AB and CD. The resultant
of two forces at an angle with each other is formed differently,[Pg 82]
as in Fig. 57 a. Here two forces AB and AC act
at an angle with each other. Lay off at the designated
angle the lines AB and AC of such length as will accurately
represent the forces. Lay off BD equal to AC and CD
equal to AB. The figure ABCD is then a parallelogram.
Its diagonal AD represents the resultant of the forces
AB and AC acting at the angle BAC. If BAC equals 90
degrees or is a right angle, AD may be computed thus:
AB2 + BD2 = AD2. Why?
and AD = √([line]AB2 + [line]BD2).
 Fig. 56.—Graphic representation
of forces acting along the same or
parallel lines.
Fig. 56.—Graphic representation
of forces acting along the same or
parallel lines.
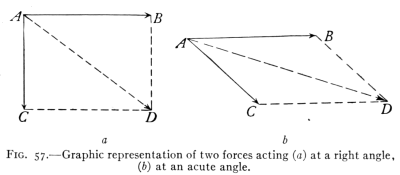 Fig. 57.—Graphic representation of two forces acting (a) at a right angle,
(b) at an acute angle.
Fig. 57.—Graphic representation of two forces acting (a) at a right angle,
(b) at an acute angle.
This method of determining the resultant by computation
may be used when the two forces are at right angles.
(In any case, AD may be measured using the same scale
that is laid off upon AB and AC, as shown in Fig. 57 b.)
The three cases of combining forces just given may be
classified as follows: The first is that of two forces acting
along the same line in the same or opposite direction, as
when two horses are hitched tandem, or in a tug of war.
The second is that of two forces acting along parallel lines, in
the same direction, as when two horses are hitched side by
side or abreast. The third is that of two forces acting at
the same point at an angle. It may be represented by the
device shown in Fig. 58, consisting of two spring balances[Pg 83]
suspended from nails at the top of the blackboard at A
and B. A cord is attached to both hooks and is passed
through a small ring at O from which is suspended a
known weight, W. Lines are drawn on the blackboard
under the stretched cords, from O toward OA, OB, and OW
and distances measured on each from O to correspond to
the three forces as read on balance A and B and the
weight W. Let a parallelogram be constructed on the
lines measured off on OA and OB. Its diagonal drawn
from O will be found to
be vertical and of the
same length as the line
measured on OW. The
diagonal is the resultant
of the two forces and
OW is the equilibrant
which is equal and opposite
to the resultant.
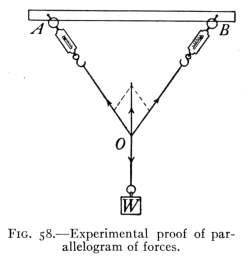 Fig. 58.—Experimental proof of parallelogram
of forces.
Fig. 58.—Experimental proof of parallelogram
of forces.
Again, the first case
may be represented by a
boat moving up or down
a stream; the resultant
motion being the combined effect of the boat's motion
and that of the stream. The second, may be represented
by two horses attached side by side to the same evener.
The resultant force equals the sum of the two component
forces. The third, may be represented by a boat going
across a stream, the resultant motion being represented
by the diagonal of the parallelogram formed by using the
lines that represent the motion of the stream and of the
boat.
74. Units for Measuring Force.—Force is commonly
measured in units of weight: in pounds, kilograms, and
grams. For example, we speak of 15 lbs. pressure per[Pg 84]
square inch and 1033.6 g. pressure per square centimeter
as representing the air pressure. It should be noted here
that the words pound, kilogram, and gram are used not
only to represent weight or force but also the masses of the
objects considered. Thus, one may speak of a pound-mass
meaning the amount of material in the object.
It will help to avoid confusion if we reserve the simple
terms "gram" and "pound" to denote exclusively an
amount of matter, that is, a mass, and to use the full
expression "gram of force" or "pound of force" whenever
we have in mind the pull of the earth upon these masses.
Or, one may speak of a pound-weight meaning the amount
of attraction exerted by the earth upon the object. The
same is true of gram-mass and gram-weight. The mass of
a body does not change when the body is transferred to
another place. The weight, however, may vary, for on
moving a body from the equator toward the poles of the
earth the weight is known to increase.
Important Topics
1. Definition of force.
2. Classification of forces. (a) Duration: constant, impulsive,
variable. (b) Direction: attractive, repulsive.
3. Methods of measuring force. (a) By distortion. (b) By change
of motion.
4. Graphic representation of forces: component, resultant, equilibrant.
5. Three cases of combining forces. (1) Two forces acting on the
same line. (2) Two forces acting in parallel lines. (3) Two
forces acting at the same point at an angle.
6. Units for measuring force, pound, gram.
Exercises
1. Name five natural forces. Which produce a tension? Which a
pressure?
2. How much can you lift? Express in pounds and kilograms.
[Pg 85]
3. Show graphically the resultant of two forces at right angles, one
of 12 lbs., the other of 16 lbs. What is the magnitude of this
resultant? Then determine the answer, first by measurement
and then by computation. Which answer is more accurate?
Why?
4. Represent by a parallelogram the two forces that support a person
sitting in a hammock and draw the line representing the resultant.
5. Find graphically the resultant of the pull of two forces, one of
500 lbs. east and one of 600 lbs. northwest.
6. Determine the equilibrant of two forces, one of 800 lbs. south and
one of 600 lbs. west.
7. Would the fact that weight varies on going from the equator
to either pole be shown by a spring balance or a beam balance?
Explain.
(2) Motion. Newton's Laws of Motion
75. Motion a Change of Position.—Motion is defined
as a continuous change in the position of a body. The position
of a body is usually described as its distance and direction
from some fixed point. Thus a man on a boat may be
at rest with respect to the boat and moving with respect
to the earth. Or, if he walks toward the stern as fast
as the boat moves forward, he may keep directly over a
rock on the bottom of the lake and hence not be moving
with reference to the rock and yet be in motion with
respect to the boat. Motion and rest, therefore, are
relative terms. The earth itself is in motion in turning
on its axis, in moving along its orbit, and in following
the sun in its motion through space. Motions are classified
in several ways:
(A) Modes of Motion
1. Translation.—A body is said to have motion of
translation when every line in it keeps the same direction.
2. Rotation.—A body has motion of rotation when it[Pg 86]
turns upon a fixed axis within the body, as a wheel upon
its axle or the earth upon its axis.
3. Vibration or Oscillation.—A body is said to have
vibratory or oscillatory motion when it returns to the
same point at regular intervals by reversals of motion
along a given path, e.g., a pendulum.
(B) Direction of Motion
1. Rectilinear.—A body has rectilinear motion when its
path is a straight line. Absolute rectilinear motion does
not exist, although the motion of a train on a straight
stretch of track is nearly rectilinear.
2. Curvilinear.—A body has curvilinear motion when
its path is a curved line, e.g., the path of a thrown ball.
(C) Uniformity of Motion
1. Uniform.—A body has uniform motion when its
speed and direction of motion do not change. Uniform
motion for extended periods is rarely observed. A train
may cover, on an average, 40 miles per hour but during
each hour its speed may rise and fall.
2. Variable.—A body has variable motion when its
speed or direction of motion is continually changing. Most
bodies have variable motion.
3. Accelerated.—A body has accelerated motion when
its speed or direction of motion continually changes.
If the speed changes by the same amount each second,
and the direction of motion does not change the motion is
said to be uniformly accelerated, e.g., a falling body.
Uniformly accelerated motion will be studied further
under the topic of falling bodies.
Velocity is the rate of motion of a body in a given direction.
For example, a bullet may have a velocity of 1300 ft. a[Pg 87]
second upwards. Acceleration is the rate of change of
velocity in a given direction, or the change of velocity in a
unit of time. A train starting from a station gradually
increases its speed. The gain in velocity during one
second is its acceleration. When the velocity is decreasing,
as when a train is slowing down, the acceleration is
opposite in direction to the velocity. A falling body falls
faster and faster. It has downward acceleration. A ball
thrown upward goes more and more slowly. It also has
downward acceleration.
76. Momentum.—It is a matter of common observation
that a heavy body is set in motion with more difficulty
than a light one, or if the same force is used for the same
length of time upon a light and a heavy body,[E] the light
body will be given a greater velocity. This observation
has led to the calculation of what is called the "quantity
of motion" of a body, or its momentum. It is computed
by multiplying the mass by the velocity. If the C.G.S.
system is used we shall have as the momentum of a 12 g.
body moving 25 cm. a second a momentum of 12 × 25
or 300 C.G.S. units of momentum. This unit has no
name and is therefore expressed as indicated above. The
formula for computing momentum is: M = mv.
Newton's Laws of Motion
77. Inertia, First Law of Motion.—One often observes
when riding in a train that if the train moves forward
suddenly the passengers do not get into motion as soon
as the train, and apparently are jerked backward. While
if the train is stopped suddenly, the passengers tend to
keep in motion. This tendency of matter to keep moving
when in motion and to remain at rest when at rest is[Pg 88]
often referred to as the property of inertia. Newton's
first law of motion, often called the law of inertia, describes
this property of matter as follows:
Every body continues in a state of rest or of uniform
motion in a straight line unless it is compelled to change
that state by some external force. This means that if an
object like a book is lying on a table it will remain there
until removed by some outside force. No inanimate
object can move itself or stop itself. If a ball is thrown
into the air it would move on forever if it were not for
the force of attraction of the earth
and the resistance of the air.
It takes time to put a mass into
motion, a heavy object requiring
more time for a change than a light
object. As an example of this, note
the movements of passengers in a
street car when it starts or stops
suddenly. Another illustration of
the law of inertia is the so-called
"penny and card" experiment. Balance a card on the end
of a finger. Place on it a coin directly over the finger,
snap the card quickly so as to drive the card from beneath
the coin. The coin will remain on the finger. (See Fig.
59.)
 Fig. 59.—The ball remains
when the card is
driven away.
Fig. 59.—The ball remains
when the card is
driven away.
According to Newton's first law of motion a moving
body which could be entirely freed from the action of all
external forces would have uniform motion, and would
describe a perfectly straight course. The curved path
taken by a baseball when thrown shows that it is acted
upon by an outside force. This force, the attraction of
the earth, is called gravity.
 Sir Isaac Newton
"By Permission of the Berlin Photographic
Co., New York."
Sir Isaac Newton
"By Permission of the Berlin Photographic
Co., New York."
Sir Isaac Newton (1642-1727)
Professor of mathematics at
Cambridge university; discovered
gravitation; invented calculus;
announced the laws of motion;
wrote the Principia; made many
discoveries in light.
 Galileo Galilei
"By Permission of the Berlin Photographic
Co., New York."
Galileo Galilei
"By Permission of the Berlin Photographic
Co., New York."
Galileo Galilei (1564-1642).
Italian. "Founder of experimental
science"; "Originator of
modern physics"; made the first
thermometer; discovered the laws
of falling bodies and the laws of
the pendulum; invented Galilean
telescope.
78. Curvilinear Motion.—Curvilinear motion occurs
when a moving body is pulled or pushed away from a[Pg 89]
[Pg 90]
[Pg 91]
straight path. The pull or push is called centripetal
(center-seeking) force. A moving stone on the end of a
string when pulled toward the hand moves in a curve.
If the string is released the stone moves in a tangent to the
curve. The string pulls the hand. This phase of the pull
is called centrifugal force. The centripetal force is the
pull on the stone. Centripetal and centrifugal force[Pg 92]
together cause a tension in the string. Examples of curvilinear
motion are very common. The rider and horse
in a circus ring lean inward in order to move in a curve.
The curve on a running track in a gymnasium is "banked"
for the same reason. Mud flying from the wheel of a
carriage, the skidding of an automobile when passing
rapidly around a corner, and sparks flying from an emery
wheel, are illustrations of the First Law of Motion.
Cream is separated from milk by placing the whole
milk in a rapidly revolving bowl, the cream being lighter
collects in the center and is thrown off at the top. (See
Fig. 60.) Clothes in steam laundries are dried by a
centrifugal drier. In amusement parks many devices
use this principle. (See centrifugal pumps, Art. 70.)
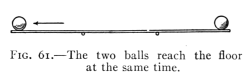 Fig. 61.—The two balls reach the floor
at the same time.
Fig. 61.—The two balls reach the floor
at the same time.
79. The Second Law of Motion, sometimes called the
law of momentum, leads to the measurement of force,
by the momentum or the quantity of motion, produced
by it. The law is stated as follows:
Change of motion,
or momentum, is proportional
to the acting
force and takes place in
the direction in which
the force acts. In other words, if two or more forces act at
the same instant upon a body each produces the same
effect that it would if acting alone. If a card be supported
on two nails driven horizontally close together into an
upright board (see Fig. 61), and two marbles be so placed
on the ends as to balance each other, when one marble is
snapped horizontally by a blow, the other will fall. Both
reach the floor at the same time. The two balls are
equally pulled down by the earth's attraction and strike
the ground at the same time, though one is shot sidewise,
and the other is dropped vertically.
[Pg 93]
As gravity is a constant force, while the blow was only a
momentary force, the actual path or resultant motion
will be a curved line.
The constant relation, between the acting force and the
change of momentum it produces in a body, has led to
the adoption of a convenient C.G.S. unit of force called
the dyne. The dyne is that force which can impart to a
mass of one gram a change of velocity at the rate of one centimeter
per second every second. This definition assumes
that the body acted upon is free to move without hindrance
of any kind, so that the acting force has to overcome only
the inertia of the body. However, the law applies in every
case of application of force, so that each force produces
its full effect independently of other forces that may be
acting at the same time upon the body.
80. Newton's Third Law.—This law has been experienced
by everyone who has jumped from a rowboat near
the shore. The muscular action that pushes the body
forward from the boat also pushes the boat backward,
often with awkward results. The law is stated: To
every action, there is always an opposite and equal reaction,
or the mutual actions of any two bodies are always equal
and opposite in direction. Many illustrations of this law
are in every one's mind: a stretched rope pulls with
the same force in one direction as it does in the opposite
direction. If a bat hits a ball, the ball hits the bat with an
equal and opposite force. The third law is therefore sometimes
called the law of reaction. When a weight is hung
upon a spring balance the action of the weight pulls down
the spring until it has stretched sufficiently (Hooke's
Law) to produce an elastic reaction that equals and hence
supports the weight. When a man stands at the center
of a plank supported at its ends, the action of the man's
weight bends the plank until the elastic force developed[Pg 94]
in the plank equals the weight applied. Further, when a
train or a wagon is on a bridge the bridge yields until it
has developed an elastic reaction equal to the weight
applied. If a person stands in the center of a room, the
floor beams yield until the third law is satisfied. In fact,
whenever a force acts, a contrary equal force always acts.
81. Stress and Strain.—A pair of forces that constitute
an action and a reaction is called a stress. The two forces
are two parts of one stress. If the two forces act away
from each other, as in the breaking of a string, the stress
is called a tension, but if they act toward each other as
in crushing anything, the stress is called a pressure. In
order for a body to exert force it must meet with resistance.
The force exerted is never greater than the resistance encountered.
Thus one can exert but little force upon a
feather floating in the air or upon other light objects. A
fast moving shot exerts no force unless it encounters some
resistance.
Forces, then, are always found in pairs. Thus to break
a string, to stretch an elastic band, to squeeze a lemon, one
must exert two equal and opposite forces. Such a thing
as a single force acting alone is unknown. Usually, however,
we give our attention mainly to one of the forces and
ignore the other. When a force acts upon a body the
change of shape or size resulting is called a strain.
Hooke's law (Art. 32) is often expressed as follows: "The
strain is proportional to the stress," e.g., the stretch of the
spring of a spring balance is proportional to the load placed
upon it.
Important Topics
1. Motion a change of position. Kinds of motion.
2. Newton's laws of motion.
3. Momentum.
4. Inertia. First law of motion. Curvilinear motion.
[Pg 95]
5. Second law of motion.
6. Third law of motion. Action and reaction, stress and strain.
Exercises
1. Mention three illustrations of the third law, different from those
given.
2. A rifle bullet thrown against a board standing upon edge will
knock it down; the same bullet fired at the board will pass
through it without disturbing its position. Explain.
3. A hammer is often driven on to its handle by striking the end
of the latter. Explain.
4. Consider a train moving 60 miles an hour, with a gun on the
rear platform pointing straight backward. If a ball is fired from
the gun with a speed of 60 miles an hour, what will happen to
the ball?
5. Could one play ball on the deck of an ocean steamer going 25
miles an hour without making allowance for the motion of the
ship? Explain.
6. On a railroad curve, one rail is always higher. Which? Why?
7. Why can a small boy when chased by a big boy often escape by
dodging?
8. Will a stone dropped from a moving train fall in a straight line?
Explain.
9. A blast of fine sand driven against a sheet of glass soon gives it
a rough surface. Explain.
10. Explain the use of fly-wheels in steadying the motion of machinery
(for example, the sewing machine).
11. Is it easier to walk to the front or rear of a passenger train
when it is stopping? Why?
12. Why does lowering the handles of a wheel-barrow on the instant
of striking make it easier to go over a bump?
13. Why should a strong side wind interfere with a game of tennis?
How can it be allowed for?
14. On which side of a railroad track at a curve is it the safer to
walk while a train is passing? Why?
15. Why does a bullet when fired through a window make a clean
round hole in the glass, while a small stone thrown against the
window shatters the glass?
16. A tallow candle can be fired through a pine board. Why?
[Pg 96]
17. In cyclones, straws are frequently found driven a little distance
into trees; why are the straws not broken and crushed instead
of being driven into the tree unbroken?
18. A bullet weighing one-half oz. is fired from a gun weighing
8 lb. The bullet has a velocity of 1800 ft. per second. Find
the velocity of the "kick" or recoil of the gun.
18. When football players run into each other which one is thrown
the harder? Why?
20. A railroad train weighing 400 tons has a velocity of 60 miles
per hour. An ocean steamer weighing 20,000 tons has a velocity
of one half mile per hour. How do their momenta compare?
21. Why is a heavy boy preferable to a lighter weight boy for a
football team?
22. Why does a blacksmith when he desires to strike a heavy blow,
select a heavy sledge hammer and swing it over his head?
23. Why does the catcher on a baseball team wear a padded glove?
(3) Resolution of Forces
82. Resolution of Forces.—We have been studying the
effect of forces in producing motion and the results of combining
forces in many ways; in the same line, in parallel lines,
and in diverging lines. Another case of much interest and
importance is the determination of the effectiveness of a force
in a direction different from the one in which it acts. This
case which is called resolution of forces is frequently used.
To illustrate: one needs but to recall that a sailor uses this
principle in a practical way whenever he sails his boat in
any other direction than the one in which the wind is
blowing, e.g., when the wind is blowing, say from the north,
the boat may be driven east, west, or to any point south
between the east and west and it is even possible to beat
back against the wind toward the northeast or northwest.
Take a sled drawn by a short rope with the force applied
along the line AB (see Fig. 62); part of this force tends to
lift the front of the sled as AC and a part to draw it forward
as AD. Hence not all of the force applied along[Pg 97]
AB is used in drawing the sled forward. Its effectiveness
is indicated by the relative size of the component AD
compared to AB.
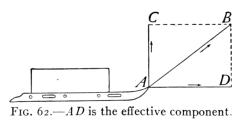 Fig. 62.—AD is the effective component.
Fig. 62.—AD is the effective component.
The force of gravity acting upon a sphere that is resting
on an inclined plane may be readily resolved into two components,
one, the
effective component,
as OR, and the other,
the non-effective as
OS. (See Fig. 63.)
If the angle ACB is
30 degrees, AB equals
1/2 of AC and OR equals 1/2 of OG, so that the speed of the
sphere down the plane developed in 1 second is less than
(about one-half of) the speed of a freely falling body developed
in the same time. Why is OS non-effective?
 Fig. 63.—The effective component is OR.
Fig. 63.—The effective component is OR.
Fig. 64.—Resolution
of the forces acting on an
aeroplane.
83. The Aeroplane.—The aeroplane consists of one or
two frames ABCD (see Fig. 64), over which is stretched
cloth or thin sheet metal. It is driven through the air by
a propeller turned by a powerful gasoline motor. This
has the effect of creating a strong breeze coming toward
the front of the aeroplane. As in the case of the sailboat
a pressure is created at right angles to the plane
along GF and this may be resolved into two components[Pg 98]
as GC and GE, GC acting to lift the aeroplane vertically
and GE opposing the action of the propeller. Fig. 65
represents the Curtis Flying Boat passing over the Detroit
river.
 Fig. 65.—The Curtis hydroplane.
Fig. 65.—The Curtis hydroplane.
Exercises.
1. If a wagon weighing 4000 lbs. is upon a hill which rises 1 ft. in 6,
what force parallel to the hill will just support the load? (Find
the effective component of the weight down the hill.)
2. If a barrel is being rolled up a 16-ft. ladder into a wagon box 3 ft.
from the ground, what force will hold the barrel in place on the
ladder, if the barrel weighs 240 lbs. Show by diagram.
3. Show graphically the components into which a man's push upon
the handle of a lawn mower is resolved.
4. Does a man shooting a flying duck aim at the bird? Explain.
5. What are the three forces that act on a kite when it is "standing"
in the air?
6. What relation does the resultant of any two of the forces in problem
five have to the third?
[Pg 99]
7. Into what two forces is the weight of a wagon descending a hill
resolved? Explain by use of a diagram.
8. A wind strikes the sail of a boat at an angle of 60 degrees to the
perpendicular with a pressure of 3 lbs. per square foot. What is
the effective pressure, perpendicular to the sail? What would
be the effective pressure when it strikes at 30 degrees?
9. How is the vertical component of the force acting on an aeroplane
affected when the front edge of the plane is elevated?
Show by diagram.
(4) Moment of Force and Parallel Forces
84. Moment of Force.—In the study of motion we found
that the quantity of motion is called momentum and is
measured by the product of the mass times the velocity. In
the study of parallel forces,
especially such as tend to produce
rotation, we consider a
similar quantity. It is called
a moment of force, which is the
term applied to the effectiveness
of a force in producing
change of rotation.
It also measured by the product of two quantities; One,
the magnitude of the force itself, and the other, the perpendicular
distance from the axis about which the rotation
takes place to the line representing the direction of the force.
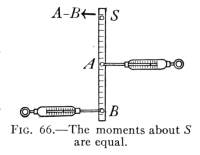 Fig. 66.—The moments about S
are equal.
Fig. 66.—The moments about S
are equal.
To illustrate: Take a rod, as a meter stick, drill a hole
at S and place through it a screw fastened at the top of
the blackboard. Attach by cords two spring balances
and draw to the right and left, A and B as in Fig. 66.
Draw out the balance B about half way, hold it steadily,
or fasten the cord at the side of the blackboard, and read
both balances. Note also the distance AS and BS. Since
the rod is at rest, the tendency to rotate to the right and
left must be equal. That is, the moments of the forces[Pg 100]
at A and B about S are equal. Since these are computed
by the product of the force times the force arm, multiply
B by BS and A by AS and see if the computed moments
are equal. Hence a force that tends to turn or rotate a body to
the right can be balanced by another of equal moment that
acts toward the left.
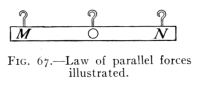 Fig. 67.—Law of parallel forces
illustrated.
Fig. 67.—Law of parallel forces
illustrated.
85. Parallel Forces.—Objects are frequently supported
by two or more upward forces acting at different points
and forming in this way a system of parallel forces; as
when two boys carry a string of fish on a rod between
them or when a bridge is
supported at its ends. The
principle of moments just described
aids in determining
the magnitude of such forces
and of their resultant. To illustrate this take a
wooden board 4 in. wide and 4 ft. long of uniform
dimensions. (See Fig. 67.) Place several screw hooks
on one edge with one set at O where the board will
hang horizontally when the board is suspended there.
Weigh the board by a spring balance hung at O. This
will be the resultant in the following tests. Now hang
the board from two spring balances at M and N and read
both balances. Call readings f and f´. To test the forces
consider M as a fixed point (see Fig. 67) and the weight
of the board to act at O. Then the moment of the weight
of the board should be equal the moment of the force at
N since the board does not move, or w times OM equals
f´ times NM. If N is considered the fixed point then the
moment of the weight of the board and of f with reference
to the point N should be equal, or w times ON = f times NM.
Keeping this illustration in mind, the law of parallel forces
may be stated at follows: 1. The resultant of two parallel
forces acting in the same direction at different points in a body is equal to their sum and has the same direction as the
components.
[Pg 101]
The moment of one of the components about the point of
application of the other is equal and opposite to the moment
of the supported weight about the other.
Problem.—If two boys carry a string of fish weighing 40 lbs. on
a rod 8 ft. long between them, what force must each boy exert if
the string is 5 ft. from the rear boy?
Solution.—The moment of the
force F exerted about the opposite
end by the rear boy is F × 8. The
moment of the weight about the
same point is 40 × (8 - 5) = 120.
Therefore F × 8 = 120, or F = 15,
the force exerted by the rear boy.
The front boy exerts a force of F
whose moment about the other end of the rod is F × 8. The
moment of the weight about the same point is 40 × 5 = 200.
Since the moment of F equals this, 200 = F × 8, or F = 25. Hence
the front boy exerts 25 lbs. and the rear boy 15 lbs.
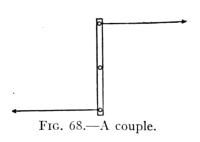 Fig. 68.—A couple.
Fig. 68.—A couple.
86. The Couple.—If two equal parallel forces act upon
a body along different lines in opposite directions, as in Fig.
68, they have no single resultant or there is no one force
that will have the same effect as the two components
acting together. A combination of forces of this kind is
called a couple. Its tendency is to produce change of rotation
in a body. An example is the action upon a compass
needle which is rotated by a force which urges one end
toward the north and by an equal force which urges the
other end toward the south.
Important Topics
1. Moment of force, how measured.
2. Parallel forces.
3. The two laws of parallel forces.
4. The couple.
[Pg 102]
Exercises
1. Show by diagram how to arrange a three-horse evener so that
each horse must take one-third of the load.
2. Two boys support a 10-ft. pole on their shoulders with a 40-lb.
string of fish supported from it 4 ft. from the front boy. What
load does each boy carry? Work by principle of moments.
3. If two horses draw a load exerting a combined pull of 300 lbs.,
what force must each exert if one is 28 in. and the other is 32
in. from the point of attachment of the evener to the load?
 Fig. 69.—Forces acting upon
a stretched rope.
Fig. 69.—Forces acting upon
a stretched rope.
Fig. 70.—A crane with horizontal
tie.
4. A weight of 100 lbs. is suspended
at the middle of a rope
ACB 20 ft. long. (See Fig. 69.)
The ends of the rope are fastened
at points A and B at the
same height. Consider D as the center of the line AB.
What is the tension of the rope when CD is 3 ft.? When
CD is 1 ft.? When CD is 1 in.?
5. A crane is set up with the tie horizontal. (See Fig. 70.) If 1000
lbs. is to be lifted, find the tie stress and the boom stress if the
boom angle is 30 degrees? If 45 degrees? 60 degrees?
6. A ball is placed on a plane inclined at an angle of 30 degrees
to the horizontal. What fraction of its weight tends to cause
motion down the plane? What effect does the other component
of the weight have? Why?
7. A person weighing 150 lbs. is lying in a hammock. The distance
between the supports is 15 ft. The hammock sags 4 ft. What
is the tension in the supports at each end? What is the tension
when the sag is only 1 ft.?
[Pg 103]
8. A ladder 30 ft. long and weighing 80 lbs. leans against the side
of a building so that it makes an angle of 30 degrees with the
building. Find the direction and magnitude of the component
forces on the ground and at the building.
9. A traveling crane 50 ft. long weighing 10 tons moves from
one end of a shop to the other, at the same time a load of 4000
lbs. moves from end to end
of the crane. Find the pressure
of the trucks of the
crane on the track when the
load is at a distance of 5, 10,
15, and 25 ft. from either end.
 Fig. 71—A truss.
Fig. 71—A truss.
10. Resolve a force of 500 lbs.
into two components at right
angles to each other, one of which shall be four times the
other.
11. A truss (see Fig. 71), carries a load of 1000 lbs. at C. Find the
forces acting along AC, BC, and AB. If AC and BC are each
12 ft. and AB 20 ft., which of these forces are tensions and
which are pressures?
(5) Gravitation and Gravity
87. Gravitation.—Gravitation is the force of attraction
that exists between all bodies of matter at all distances.
This attraction exists not only between the heavenly
bodies, the stars and planets, etc., but is also found between
bodies on the earth. A book attracts all objects
in a room and outside of a room as well, since its weight
shows that it is attracted by the earth itself. The gravitational
attraction between ordinary bodies is so slight
that it requires careful experiments to detect it. In fact,
it is only when one of the attracting bodies is large, as
for example the earth, that the force becomes considerable.
Careful studies of the motions of the heavenly bodies,
especially of that of the moon in its orbit about the earth,
led Sir Isaac Newton to the statement of the law of gravitation
which is well expressed in the following statement:
[Pg 104]
88. Law of Gravitation.—Every particle of matter in the
universe attracts every other particle with a force that is
directly proportional to the product of their masses and
inversely proportional to the square of the distance between
them.
The law may be separated into two parts, one referring
to the masses of the bodies concerned, the other to the
effect of the distance between them. The first part is
easily understood since we all know that two quarts of
milk will weigh just twice as much as one quart. To
illustrate the second part of the law, suppose that the moon
were removed to twice its present distance from the earth,
then the attraction between the earth and the moon would
be one-fourth its present attraction. If removed to three
times its present distance, the attraction would be one-ninth,
etc.
The attraction of the earth for other bodies on or near
it is called gravity. The weight of a body is the measure
of the earth's attraction for it; or it is the force of gravity
acting upon it. Newton's third law of motion states
that every action is accompanied by an equal and opposite
reaction (Art. 80). Hence, the attraction of the earth
for a book or any other object is accompanied by an equal
attraction of the book for the earth.
89. Weight.—In advanced physics it is proved that a
sphere attracts as if it were concentrated at its center.
Thus if the earth's radius be considered as 4000 miles,
then a body 4000 miles above the earth's surface would
be 8000 miles above the earth's center, or twice as far from
the center of the earth as is a body upon the earth's surface.
A body then 4000 miles above the earth's surface will
weigh then but one-fourth as much as it will at the surface
of the earth.
Since the earth is flattened at the poles, the surface at[Pg 105]
the equator is farther from the center of the earth than
at points north or south. Thus a body weighing 1 lb.
at the equator weighs 1.002 lb. at Chicago, or about
1/500 more. The rotation of the earth also affects the
weight of a body upon it so that at the equator the weight
of a body is 1/289 less than at the pole. Both effects,
that of flattening and of rotation, tend to diminish the
weight of bodies at the equator, so that a body at the
latter place weighs about 1/192 less than at the poles.
In studying the effect of the earth's gravity, the following illustration
will be helpful: Imagine an open shaft a mile square extending
through the earth. What would happen to a stone thrown into
the shaft? At first it would have the attraction of the whole earth
drawing it and continually increasing its speed downward. As it
descends from the surface, the pull toward the center grows less and
less. Halfway to the center the body has lost half its weight.
When the stone reaches the center, the pull in all directions is the
same, or in other words, it has no weight. It would, however, continue
moving rapidly on account of its inertia, and as it continues
on from the center, the greater part of the earth being left behind,
the attraction pulling toward the center will gradually stop it. It
will then fall again toward the center and be stopped again after
passing it, and after repeatedly moving up and down will finally come
to rest at the center of the earth. At this point it will be found to be
a body without weight since it is pulled equally in all directions by
the material of the earth. What force brings the body to rest?
90. Center of Gravity.—A body is composed of a great
many particles each of which is pulled toward the center
of the earth by the force of gravity. A single force that
would exactly equal the combined effect of the pull of the
earth for all the particles of a body would be their resultant.
The magnitude of this resultant is the weight of the body.
The direction of this resultant is in a line passing toward
the earth's center, while the point of application of this[Pg 106]
resultant is called the center of gravity of the body. The
center of gravity of a body may also be briefly defined as
the point about which it may be balanced. As the location
of this point depends upon the distribution of matter in
the body, the center of gravity is also sometimes called
the center of mass of the body.
The earth's attraction for a body is considered for the
sake of simplicity, not as a multitude
of little forces, but as a single force
applied at its center of gravity. To
find the center of gravity of a body
find two intersecting lines along which
it balances, see Fig. 72, and the center
of gravity will be at the intersection. A
vertical line through this point is sometimes
called the line of direction of the
weight.
 Fig. 72.—The center
of gravity is at the
intersection of the
lines of direction.
Fig. 72.—The center
of gravity is at the
intersection of the
lines of direction.
91. Equilibrium of Bodies.—Equilibrium means equally
balanced. A body at rest or in uniform motion is then in
equilibrium. An object is in equilibrium under gravity
when a vertical line through its center of gravity passes
through the point of support. A trunk is an example of a
body in equilibrium since a vertical line from its center of
gravity falls within the base formed by the area upon
which it rests. Work will be necessary to tip the trunk
from its position. The amount of work required will
depend upon the weight of the body and the location of
the center of gravity.
92. Kinds of Equilibrium.—(a) Stable.—A body is in
stable equilibrium under gravity if its center of gravity
is raised whenever the body is displaced. It will return to
its first position if allowed to fall after being slightly displaced.
In Fig. 73, a and b if slightly tipped will return
to their first position. They are in stable equilibrium.[Pg 107]
Other examples are a rocking chair, and the combination
shown in Fig. 74.
 Fig. 73.—Stable equilibrium.
Fig. 73.—Stable equilibrium.
(b) Unstable.—A body is in unstable equilibrium under
gravity if its center of gravity is lowered whenever the
body is slightly displaced. It will fall farther from its first
position. A pencil balanced
on its point or a broom
balanced on the end of the
handle are in unstable equilibrium.
The slightest disturbance
will make the line
of direction of the weight fall
outside of (away from) the
point of support (Fig. 75 a).
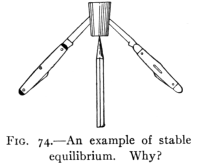 Fig. 74—An example of stable
equilibrium. Why?
Fig. 74—An example of stable
equilibrium. Why?
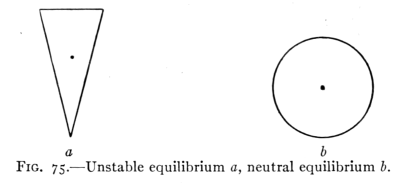 Fig. 75.—Unstable equilibrium a, neutral equilibrium b.
Fig. 75.—Unstable equilibrium a, neutral equilibrium b.
(c) Neutral.—A body is in neutral equilibrium if its
center of gravity is neither raised nor lowered whenever
the body is moved. Familiar examples are a ball lying
on a table (Fig. 75 b) and a wagon moving on a level street
(referring to its forward motion).
[Pg 108]
 Fig. 76.—B is more stable than A.
Fig. 76.—B is more stable than A.
93. Stability.—When a body is in stable equilibrium,
effort must be exerted to overturn it, and the degree of
stability is measured by the effort required to overturn it.
To overturn a body, it must be moved so that the vertical
line through its center
of gravity will pass outside
of its supporting
base. This movement
in stable bodies necessitates
a raising of the
center of gravity. The
higher this center of
gravity must be raised
in overturning the body,
the more stable it is, e.g., see Fig. 76. Thus a wagon on a
hillside will not overturn until its weight falls outside of
its base, as in Fig. 77 B. The stability of a body depends
upon the position of its center of gravity and the area of
its base. The lower the
center of gravity and the
larger the base, the more
stable the body. What
means are employed to
give stability to bodies,
in every-day use (such
as clocks, ink-stands,
pitchers, vases, chairs,
lamps, etc.)?
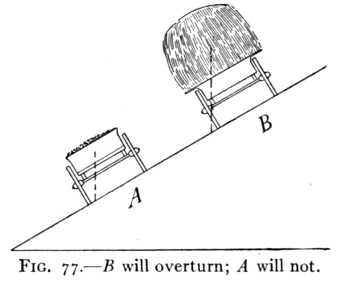 Fig. 77.—B will overturn; A will not.
Fig. 77.—B will overturn; A will not.
Important Topics
1. Gravitation; law of gravitation, gravity, weight.
2. Center of gravity.
3. The three states of equilibrium. Stability.
[Pg 109]
Exercises
1. Why is a plumb-line useful in building houses?
2. What is the center of gravity of a body?
3. Explain the action of a rocking chair that has been tipped
forward.
4. Is the stability of a box greater when empty or when filled with
sand? Explain.
5. How can you start yourself swinging, in a swing, without touching
the ground?
6. Is the center of gravity of the beam of a balance above, below, or
at the point of a support? How did you find it out?
7. Why are some ink bottles cone shaped with thick bottoms?
8. Would an electric fan in motion on the rear of a light boat move
it? Would it move the boat if revolving under water? Explain.
9. What turns a rotary lawn sprinkler?
10. Why, when you are standing erect against a wall and a coin is
placed between your feet, can you not stoop and pick it up
unless you shift your feet or fall over?
11. What would become of a ball dropped into a large hole bored
through the center of the earth?
12. When an apple falls to the ground, does the earth rise to meet it?
13. How far from the earth does the force of gravity extend?
14. Why in walking up a flight of stairs does the body bend forward?
15. In walking down a steep hill why do people frequently bend
backward?
16. Why is it so difficult for a child to learn to walk, while a kitten
or a puppy has no such difficulty?
17. Explain why the use of a cane by old people makes it easier
for them to walk?
(6) Falling Bodies
94. Falling Bodies.—One of the earliest physical facts
learned by a child is that a body unsupported falls toward
the earth. When a child lets go of a toy, he soon learns to
look for it on the floor. It is also of common observation
that light objects, as feathers and paper, fall much slower
than a stone. The information, therefore, that all bodies[Pg 110]
actually fall at the same rate in a vacuum or when removed
from the retarding influence of the air is received with
surprise.
This fact may be shown by using what is called a coin
and feather tube. On exhausting the air from this tube,
the feather and coin within are seen
to fall at the same rate. (See Fig. 78.)
when air is again admitted, the feather
flutters along behind.
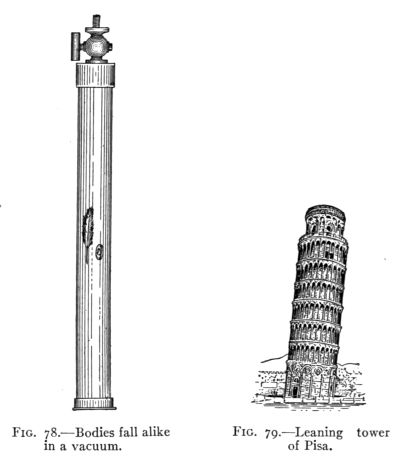 Fig. 78.—Bodies fall alike
in a vacuum.
Fig. 78.—Bodies fall alike
in a vacuum.
Fig. 79.—Leaning tower
of Pisa.
95. Galileo's Experiment.—The fact
that bodies of different weight tend
to fall at the same rate was first experimentally
shown by Galileo by dropping
a 1-lb. and a 100-lb. ball from the
top of the leaning tower of Pisa in Italy (represented
in Fig. 79). Both starting at the same time struck the
ground together. Galileo inferred from this that feathers
and other light objects would fall at the same rate as
iron or lead were it not for the resistance of the air. After
the invention of the air pump this supposition was verified
as just explained.
[Pg 111]
96. Acceleration Due to Gravity.—If a body falls freely,
that is without meeting a resistance or a retarding influence,
its motion will continually increase. The increase
in motion is found to be constant or uniform during each
second. This uniform increase in motion or in velocity
of a falling body gives one of the best illustrations that
we have of uniformly accelerated motion. (Art. 75.) On
the other hand, a body thrown upward has uniformly
retarded motion, that is, its acceleration is downward.
The velocity acquired by a falling body in unit time is
called its acceleration, or the acceleration due to gravity,
and is equal to 32.16 ft. (980 cm.) per second, downward,
each second of time. In one second, therefore, a falling
body gains a velocity of 32.16 ft. (980 cm.) per second,
downward. In two seconds it gains twice this, and so on.
In formulas, the acceleration of gravity is represented
by "g" and the number of seconds by t, therefore the
formula for finding the velocity, V,[F] of a falling body
starting from rest is V = gt. In studying gravity (Art.
89) we learned that its force varies as one moves toward
or away from the equator. (How?) In latitude 38° the
acceleration of gravity is 980 cm. per second each second
of time.
97. Experimental Study of Falling Bodies.—To study
falling bodies experimentally by observing the fall of
unobstructed bodies is a difficult matter. Many devices
have been used to reduce the motion so that the action of
a falling body may be observed within the limits of a
laboratory or lecture room. The simplest of these, and in
some respects the most satisfactory, was used by Galileo.
It consists of an inclined plane which reduces the
effective component of the force of gravity so that the
motion of a body rolling down the plane may be observed[Pg 112]
for several seconds. For illustrating this principle a steel
piano wire has been selected as being the simplest and the
most easily understood. This wire is stretched taut across
a room by a turn-buckle so that its slope is about one in
sixteen. (See Fig. 80.) Down this wire a weighted pulley
is allowed to run and the distance it travels in 1, 2, 3,
and 4 seconds is observed. From these observations we
can compute the distance covered each second and the
velocity at the end of each second.
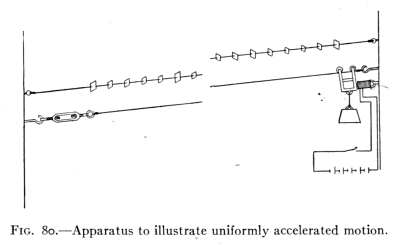 Fig. 80.—Apparatus to illustrate uniformly accelerated motion.
Fig. 80.—Apparatus to illustrate uniformly accelerated motion.
In Fig. 63, if OG represents the weight of the body or
the pull of gravity, then the line OR will represent the
effective component along the wire, and OS the non-effective
component against the wire. Since the ratio of the
height of the plane to its length is as one to sixteen, then
the motion along the wire in Fig. 80 will be one-sixteenth
that of a falling body.
98. Summary of Results.—The following table gives
the results that have been obtained with an apparatus
arranged as shown above.
In this table, column 2 is the one which contains the
results directly observed by the use of the apparatus. Columns,
3, 4, and 5 are computed from preceding columns.
[Pg 113]
| (1) No. of seconds | (2) Total distance moved | (3) Distance each second | (4) Velocity at end of second | (5) Acceleration each second |
| | | | Per second | Per second |
| 1 | 30 cm. | 30 cm. | 60 cm. | 60 cm. |
| 2 | 120 cm. | 90 cm. | 120 cm. | 60 cm. |
| 3 | 270 cm. | 150 cm. | 180 cm. | 60 cm. |
| 4 | 480 cm. | 210 cm. | 240 cm. | 60 cm. |
Column 5 shows that the acceleration is uniform, or the
same each second. Column 4 shows that the velocity
increases with the number of seconds or that V = at. Column
3 shows that the increase in motion from 1 second
to the next is just equal to the acceleration or 60 cm. This
is represented by the following formula: s = 1/2 a(2t - 1).
The results of the second column, it may be seen, increase
as 1:4:9:16, while the number of seconds vary as
1:2:3:4. That is, the total distance covered is proportional
to the square of the number of seconds.
This fact expressed as a formula gives: S = 1/2at2.
Substituting g, the symbol for the acceleration of
gravity, for a in the above formulas, we have:
(1) V = gt, (2) S = 1/2gt2, (3) s = 1/2g(2t - 1).
99. Laws of Falling Bodies.—These formulas may be
stated as follows for a body which falls from rest:
1. The velocity of a freely falling body at the end of any
second is equal to 32.16 ft. per sec. or 980 cm. per second
multiplied by the number of the second.
2. The distance passed through by a freely falling body
during any number of seconds is equal to the square of the
number of seconds multiplied by 16.08 ft. or 490 cm.
3. The distance passed through by a freely falling body
during any second is equal to 16.08 feet or 490 cm. multiplied
by one less than twice the number of the second.
[Pg 114]
Important Topics
1. Falling bodies.
2. Galileo's experiment.
3. Acceleration due to gravity.
4. Laws of falling bodies.
Exercises
1. How far does a body fall during the first second? Account for
the fact that this distance is numerically equal to half the
acceleration.
2. (a) What is the velocity of a falling body at the end of the first
second? (b) How far does it fall during the second second?
(c) Account for the difference between these numbers.
3. What is the velocity of a falling body at the end of the fifth
second?
4. How far does a body fall (a) in 5 seconds (b) in 6 seconds (c)
during the sixth second?
5. (a) What is the difference between the average velocity during
the sixth second and the velocity at the beginning of that
second?
(b) Is this difference equal to that found in the second problem?
Why?
6. A stone dropped from a cliff strikes the foot of it in 5 seconds.
What is the height of the cliff?
7. Why is it that the increased weight of a body when taken
to higher latitudes causes it to fall faster, while at the same
place a heavy body falls no faster than a light one?
8. When a train is leaving a station its acceleration gradually
decreases to zero, although the engine continues to pull.
Explain.
9. Would you expect the motion of equally smooth and perfect
spheres of different weight and material to be equally accelerated
on the same inclined plane? Give reason for your answer.
Try the experiment.
10. A body is thrown upward with the velocity of 64.32 ft. per sec.
How many seconds will it rise? How far will it rise? How
many seconds will it stay in the air before striking the ground?
11. 32.16 feet = how many centimeters?
12. The acceleration of a freely falling body is constant at any
one place. What does this show about the pull which the
earth exerts on the body?
[Pg 115]
(7) The Pendulum
100. The Simple Pendulum.—Any body suspended so
as to swing freely to and fro is a pendulum, as in Fig. 81.
A simple pendulum is defined as a single particle of matter
suspended by a cord without weight. It is of course impossible
to construct such a pendulum. A small metal
ball suspended by a thread
is approximately a simple
pendulum. When allowed to
swing its vibrations are made
in equal times. This feature
of the motion of a pendulum
was first noticed by Galileo
while watching the slow
oscillations of a bronze
chandelier suspended in the
Cathedral in Pisa.
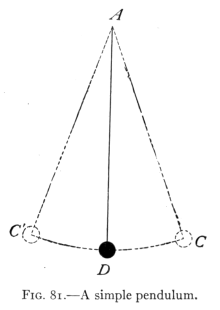 Fig. 81—A simple pendulum.
Fig. 81—A simple pendulum.
101. Definition of Terms.
The center of suspension is
the point about which the
pendulum swings. A single
vibration is one swing across the arc. A complete or double
vibration is the swing across the arc and back again. The
time required for a double vibration is called the period.
The length of a simple pendulum is approximately the distance
from the point of support to the center of the bob.
A seconds pendulum is one making a single vibration
per second. Its length at sea-level, at New York is
99.31 cm. or 39.1 in., at the equator 39.01 in., at the poles
39.22 in.
A compound pendulum is one having an appreciable portion
of its mass elsewhere than in the small compact
body or sphere called a bob. The ordinary clock pendulum[Pg 116]
or a meter stick suspended by one end are examples
of compound pendulums.
The amplitude of a vibration is one-half the arc through
which it swings, for example, the arc DC or the angle DAC
in Fig. 81.
102. Laws of the Pendulum.—The following laws may
be stated:
1. The period of a pendulum is not affected by its
mass or the material of which the pendulum is made.
2. For small amplitudes, the period is not affected by
the length of the arc through which it swings.
3. The period is directly proportional to the square root
of the length. Expressed mathematically, t/t´ = √l/√l´.
103. Uses of the Pendulum.—The chief use of the pendulum
is to regulate motion in clocks. The wheels are
kept in motion by a spring or a weight and the regulation
is effected by an escapement (Fig. 82). At each vibration
of the pendulum one tooth of the wheel D slips past the
prong at one end of the escapement C, at the same time
giving a slight push to the escapement. This push transmitted
to the pendulum keeps it in motion. In this way,
the motion of the wheel work and the hands is controlled.
Another use of the pendulum is in finding the acceleration
of gravity, by using the formula, t = π√(l/g), in which t is
the time in seconds of a single vibration and l the length
of the pendulum. If, for example, the length of the
seconds pendulum is 99.31 cm., then 1 = π√(99.31/g); squaring
both sides of the equation, we have 12 = π2(99.31/g), or g =
[Pg 117]π2 × 99.31/12 = 980.1 cm. per sec., per sec. From this it follows
that, since the force of gravity depends upon the
distance from the center of the earth, the pendulum may
be used to determine the elevation of a place above sea
level and also the shape of the earth.
Important Topics
1. Simple pendulum.
2. Definitions of terms used.
3. Laws of the pendulum.
4. Uses of the pendulum.
Exercises
1. What is the usual shape of the bob of a
clock pendulum? Why is this shape used
instead of a sphere?
2. Removing the bob from a clock pendulum
has what effect on its motion? Also on
the motion of the hands?
3. How does the expansion of the rod of a
pendulum in summer and its contraction
in winter affect the keeping of time by a
clock? How can this be corrected?
4. Master clocks that control the time of a
railway system have a cup of mercury for
a bob. This automatically keeps the
same rate of vibration through any
changes of temperature. How?
5. How will the length of a seconds pendulum
at Denver, 1 mile above sea-level,
compare with one at New York? Why?
 Fig. 82—Escapement
and pendulum
of a clock.
Fig. 82—Escapement
and pendulum
of a clock.
6. What is the period of a pendulum 9 in. long? Note. In
problems involving the use of the third law, use the length of a
seconds pendulum for l, and call its period 1.
7. A swing is 20 ft. high, find the time required for one swing across
the arc.
8. A pendulum is 60 cm. long. What is its period?
9. If in a gymnasium a pupil takes 3 sec. to swing once across
while hanging from a ring, how long a pendulum is formed?
10. A clock pendulum makes four vibrations a second, what is its
length?
[Pg 118]
Review Outline: Force and Motion
Force; definition, elements, how measured, units, dyne.
Graphic Representation; typical examples of finding a component,
a resultant, or an equilibrant.
Motion; Laws of motion (3), inertia, curvilinear motion, centrifugal
force, momentum, (M = mv), reaction, stress and strain.
Moment of Force; parallel forces, couple, effective and non-effective
component.
Gravitation; law; gravity, center of; weight. Equilibrium 3 forms;
stability, how increased.
Falling Bodies; velocity, acceleration, "g," Laws; V = gt, S = (1/2)gt2
- s = (1/2)g(2t - 1).
Pendulum; simple, seconds, laws (3), t = π√(l/g).
[Pg 119]
WORK AND ENERGY
104. Work.—"Whenever a force moves a body upon
which it acts, it is said to do work upon that body." For
example, if a man pushes a wheelbarrow along a path, he
is doing work on it as long as the wheelbarrow moves, but
if the wheelbarrow strikes a stone and the man continues
to push and no motion results, from a scientific point of
view he is then doing no work on it.
"Work signifies the overcoming of resistance," and
unless the resistance is overcome no work is done. Lifting
a weight is doing work on it, supporting a weight is not, although
the latter may be nearly as tiresome as the former.
Work as used in science is a technical term. Do not
attach to it meanings which it has in every-day speech.
105. Measurement of Work.—Work is measured by the
product of the force by the displacement caused in the
direction of the force, that is W = fs. Therefore if a
unit of force acts through a unit of space, a unit of work
will be done. There are naturally several units of work
depending upon the units of force and space employed.
English Work Unit.—If the force of one pound acts
through the distance of one foot, a foot-pound of work is
done. A foot-pound is defined as the work done when 1
lb. is lifted 1 ft. against the force of gravity.
Metric Work Unit.—If the force is one kilogram and
the distance one meter, one kilogram-meter of work is done.
Absolute Work Unit.—If the force of one dyne acts
through the distance of one centimeter a dyne-centimeter[Pg 120]
of work is done. This usually is called an i. Other
work units are sometimes used depending upon the force
and distance units employed. One, the i, is equal to
10,000,000 ergs or 107 ergs.
Problem.—If a load is drawn 2 miles by a team exerting 500
lbs. force, how much work is done?
Solution.—Since the force employed is 500 lbs., and the distance
is 2 × 5280 ft., the work done is 500 × 2 × 5280 or 5,280,000
ft.-lbs.
106. Energy.—In the various cases suggested in the
paragraphs upon work, an agent, a man, an animal or a
machine, was mentioned as putting forth an effort in order
to do the work. It is also true that in order to perform
work an agent must employ energy, or the energy of a body
is its capacity for doing work. Where an agent does work
upon a body, as in winding up a spring or in lifting a weight,
the body upon which the work has been done may acquire
energy by having work done upon it. That is, it may
become able to do work itself upon some other body.
For instance, a lifted weight in falling back to its first
position may turn wheels, or drive a post into the ground
against resistance; a coiled spring may run clock work,
strike a blow, or close a door. Hence the energy, or the
capacity for doing work, is often acquired by a body
because work has first been done upon that body.
107. Potential Energy.—The wound up spring may do
work because work has first been done upon it. The lifted
weight may also do work because work has first been done
in raising it to its elevated position since in falling it may
grind an object to powder, lift another weight or do some
other kind of work. The energy that a body possesses on
account of its position or shape and a stress to which it is
subjected is called potential energy. The potential energy
of a body is measured by the work done in lifting it,[Pg 121]
changing its shape, or by bringing about the conditions
by which it can do work. Thus if a block of iron weighing
2000 lbs. is lifted 20 ft., it possesses 40,000 ft.-lbs. of
potential energy. It is therefore able to do 40,000 ft.-lbs.
of work in falling back to its first position. If the block
just mentioned should fall from its elevated position upon
a post, it could drive the post into the ground because its
motion at the instant of striking enables it to do work. To
compute potential energy you compute the work done upon
the body. That is, P.E. = w × h or f × s.
108. Kinetic Energy.—The energy due to the motion
of a body is called kinetic energy. The amount of kinetic
energy in a body may be measured by the amount of work
done to put it in motion. It is usually computed, however,
by using its mass and velocity on striking. To illustrate,
a 100-lb. ball is lifted 16 ft. The work done upon
it, and hence its potential energy, is 1600 ft.-lbs. On falling
to the ground again, this will be changed into kinetic
energy, or there will be 1600 ft.-lbs. of kinetic energy on
striking. It will be noted that since energy is measured
by the work it can do, work units are always used in measuring
energy. To compute the kinetic energy of a falling
body by simply using its mass and velocity one proceeds
as follows, in solving the above problem:
First, find the velocity of the falling body which has fallen 16
ft. A body falls 16 ft. in one second. In this time it gains a velocity
of 32 ft. per second. Now using the formula for kinetic energy
K.E. = wv2/(2g), we have K.E. = 100 × 32 × 32/(2 × 32) = 1600 ft.-lbs. as before.
The formula, K.E. = wv2/(2g), may be derived in the following
manner:
The kinetic energy of a falling body equals the work done in giving
it its motion, that is, K.E. = w × S, in which, w = the weight
of the body and S = the distance the body must fall freely in order
[Pg 122]to acquire its velocity. The distance fallen by a freely falling body,
S, = 1/2gt2 = g2t2/(2g) (Art. 98, p. 111). Now, v = gt and v2 = g2t2.
Substituting for g2t2, its equal v2, we have S = v2/(2g). Substituting
this value of S in the equation K.E. = w × S, we have K.E.
= wv2/(2g).
Since the kinetic energy of a moving body depends upon its mass
and velocity and not upon the direction of motion, this formula may
be used to find the kinetic energy of any moving body. Mass and
weight in such problems may be considered numerically equal.
Important Topics
1. Work defined.
2. Work units, foot-pound, kilogram-meter, erg.
3. Energy defined.
4. Kinds of energy, potential and kinetic.
Problems
1. How much work will a 120-lb. boy do climbing a mountain 3000
ft. high? Should the vertical or slant height be used? Why?
2. In a mine 4000 kg. of coal are lifted 223 meters: how much work
is done upon the coal? What is the kind and amount of energy
possessed by the coal?
3. A pile driver weighs 450 lbs. It is lifted 16 ft. How much work
has been done upon it? What kind and amount of energy will
it have after falling 16 ft. to the pile?
4. A train weighing 400 tons is moving 30 miles per hour. Compute
its kinetic energy. (Change its weight to pounds and
velocity to feet per second.)
5. What would be the kinetic energy of the train in problem 4 if it
were going 60 miles per hour? If it were going 90 miles per
hour? How does doubling or trebling the speed of an object
affect its kinetic energy? How does it affect its momentum?
6. What is the kinetic energy of a 1600-lb. cannon ball moving
2000 ft. per second?
7. Mention as many kinds of mechanical work as you can and show
how each satisfies the definition of work.
8. A pile driver weighing 3000 lbs. is lifted 10 ft. How much work
is done upon it?
[Pg 123]
9. If the pile driver in problem 8 is dropped upon the head of a
pile which meets an average resistance of 30,000 lbs., how far
will one blow drive it?
10. A 40 kg. stone is placed upon the top of a chimney 50 meters
high. Compute the work done in kilogram-meters and foot-pounds.
(2) Power and Energy
109. Horse-power.—In computing work, no account
is taken of the time required to accomplish it. But since
the time needed to perform an undertaking is of much
importance, the rate of work, or the power or activity of
an agent is an important factor. Thus if one machine
can do a piece of work in one-fifth the time required by
another machine, it is said to have five times the power of
the other. Therefore the power of a machine is the rate
at which it can do work. James Watt (1736-1819), the
inventor of the steam-engine, in expressing the power of
his engine, used as a unit a horse-power. He considered
that a horse could do 33,000 ft.-lbs. of work a minute.
This is equal to 550 ft.-lbs. per second or 76.05 kg.-m. per
second. This is too high a value but it has been used ever
since his time. Steam engines usually have their power
rated in horse-power. That is, locomotives produce from
500 to 1500 horse-power. Some stationary and marine
engines develop as high as 25,000 horse-power. The
power of an average horse is about 3/4 horse-power and of a
man about 1/7 horse-power when working continuously
for several hours.
110. The Watt.—In the metric system, the erg as a
unit of work would give as a unit of power 1 erg per second.
This amount is so small, however, that a larger unit is
usually employed, the practical unit being 10,000,000 ergs
a second, that is, one joule per second. (See Art. 105.)
This practical unit is called a Watt after James Watt.[Pg 124]
The power of dynamos is usually expressed in kilowatts,
a kilowatt representing 1000 watts. Steam-engines in
modern practice are often rated in kilowatts instead of
horse-power. A horse-power is equivalent to 746 watts,
or is nearly 3/4 of a kilowatt.
111. Energy. Its Transference and Transformation.
We have considered energy as the capacity for doing work,
and noted the two kinds, potential and kinetic, and the
facility with which one may change into another. In
fact, the transference of energy from one body to another,
and its transformation from one form to another is one
of the most common processes in nature. Take a pendulum
in motion, at the end of a swing, its energy being
entirely due to its elevated position is all potential; at the
lowest point in its path its energy being entirely due to its
motion is all kinetic. The change goes on automatically
as long as the pendulum swings. A motor attached by a
belt to a washing machine is started running. The energy
of the motor is transferred by the belt to the washer where
it is used in rubbing and moving the clothes.
The heat used in warming a house is usually obtained
by burning coal or wood. Coal is believed to be formed
from the remains of plants that grew in former geologic
times. These plants grew through the help of the radiant
energy of the sun. The following are transformations
of energy that have occurred: The radiant energy of
sunlight was transformed into the chemical energy of the
plants. This remained as chemical energy while the
plants were being converted into coal, was mined, brought
to the stove or furnace and burned. The burning transformed
the chemical energy into heat energy in which form
we use it for warming rooms. Take the energy used in
running a street car whose electrical energy comes from a
waterfall. The energy of the car itself is mechanical.[Pg 125]
Its motor, however, receives electrical energy and transforms
it into mechanical. This electrical energy comes
along a wire from a dynamo at the waterfall, where water-wheels
and generators transform into electrical energy the
mechanical energy of the falling water. The water
obtained its energy of position by being evaporated by
the heat of the radiant energy of the sun. The vapor
rising into the air is condensed into clouds and rain, and
falling on the mountain side, has, from its elevated position,
potential energy. The order of transformation,
therefore, is in this case, radiant, heat, mechanical, electrical,
and mechanical. Can you trace the energy from
the sun step by step to the energy you are using in reading
this page?
112. Forms of Energy.—A steam-engine attached to a
train of cars employs its energy in setting the cars in
motion, i.e., in giving them kinetic energy and in overcoming
resistance to motion. But what is the source of
the energy of the engine? It is found in the coal which it
carries in its tender. But of what kind? Surely not
kinetic, as no motion is seen. It is therefore potential.
What is the source of the energy of the coal? This question
leads us back to the time of the formation of coal beds,
when plants grew in the sunlight and stored up the energy
of the sun's heat and light as chemical energy. The
sun's light brings to the earth the energy of the sun,
that central storehouse of energy, which has supplied
nearly all the available energy upon the earth. Five
forms of energy are known, viz., mechanical, heat, electrical,
radiant, and chemical.
113. Energy Recognized by its Effects.—Like force,
energy is invisible and we are aware of the forms only by
the effects produced by it.
We recognize heat by warming, by expansion, by
pressure.
[Pg 126]
We recognize light by warming, by its affecting
vision.
We recognize electrical energy by its heat, light, motion,
or magnetic effect. We recognize mechanical energy by
the motion that it produces. We recognize chemical energy
by knowing that the source of energy does not belong to
any of the foregoing.
A boy or girl is able to do considerable work. They
therefore possess energy. In what form does the energy
of the body mainly occur? One can determine this for
himself by applying questions to each form of energy in
turn as in Art. 114.
114. Source of the Energy of the Human Body.—Is
the energy of the human body mostly heat? No, since we
are not very warm. Is it light or electrical? Evidently
not since we are neither luminous nor electrical. Is it
mechanical? No, since we have our energy even when
at rest. Is it chemical? It must be since it is none
of the others. Chemical energy is contained within the
molecule.
It is a form of potential energy and it is believed to be
due to the position of the atoms within the molecule. As a
tightly coiled watch spring may have much energy within
it, which is set free on allowing the spring to uncoil, so
the chemical energy is released on starting the chemical
reaction. Gunpowder and dynamite are examples of
substances containing chemical energy. On exploding
these, heat, light, and motion are produced. Gasoline,
kerosene, and illuminating gas are purchased because of
the potential energy they contain. This energy is set
free by burning or exploding them.
The source of the energy of our bodies is of course the
food we eat. The energy contained in the food is also
chemical. Vegetables obtain their energy from the sunlight[Pg 127]
(radiant energy). This is why plants will not grow
in the dark. The available energy is mostly contained in
the form of starch, sugar and oil. Digestion is employed
principally to dissolve these substances so that the blood
may absorb them and carry them to the tissues of the body
where they are needed. The energy is set free by oxidation
(burning), the oxygen needed for this being supplied
by breathing. Breathing also removes the carbon dioxide,
which results from the combustion. It is for its
energy that our food is mostly required.
115. Conservation of Energy.—In the study of matter
we learned that it is indestructible. Energy is also
believed to be indestructible. This principle stated concisely
teaches that despite the innumerable changes which
energy undergoes the amount in the universe is unchangeable,
and while energy may leave the earth and be lost
as far as we are concerned, that it exists somewhere in
some form. The principle which teaches this is called the
"Conservation of Energy." The form into which energy
is finally transformed is believed to be heat.
Important Topics
1. Power defined. Units. Horse-power. Watt.
2. Transference and transformations of energy.
3. Forms of energy; heat, electrical, mechanical, radiant, chemical.
4. Effects of the several forms of energy.
5. Energy of the human body.
6. Conservation of energy.
Exercises
1. A boy weighing 110 lbs. ran up a stairs 10 ft. high, in 4 seconds.
How much work was done? What was his rate of
work (foot-pounds per second)? Express also in horse-power.
2. A locomotive drawing a train exerts a draw bar pull of 11,000
lbs. How much work does it do in moving 3 miles? What[Pg 128]
is its rate of work if it moves 3 miles in 5 minutes? Express in
horse-power.[G]
3. If 400 kg. are lifted 35 meters in 5 seconds what work is done?
What is the rate of work? Express in horse-power, watts and
kilowatts.
4. Trace the energy of a moving railway train back to its source in
the sun.
5. Why does turning the propeller of a motor boat cause the boat
to move?
6. Does it require more power to go up a flight of stairs in 5
seconds than in 10 seconds? Explain. Is more work done in
one case than in the other? Why?
7. Can 1 man carrying bricks up to a certain elevation for 120
days do as much work as 120 men carrying up bricks for 1 day?
8. If the 1 man and 120 men of problem 7 do the same amount of
work have they the same power? Explain.
9. If 160 cu. ft. of water flow each second over a dam 15ft. high
what is the available power?
10. What power must an engine have to fill a tank 11 × 8 × 5 ft.
with water 120 ft. above the supply, in 5 minutes?
11. A hod carrier weighing 150 lbs. carries a load of bricks weighing
100 lbs. up a ladder 30 ft. high. How much work does he do?
12. How much work can a 4-horse-power engine do in 5 minutes?
13. Find the horse-power of a windmill that pumps 6 tons of water
from a well 90 ft. deep in 30 minutes.
14. How many horse-power are there in a waterfall 20 ft. high over
which 500 cu. ft. of water pass in a minute?
15. The Chicago drainage canal has a flow of about 6000 cu. ft. a
second. If at the controlling works there is an available fall of
34 ft. how many horse-power can be developed?
16. How long will it take a 10-horse-power pump to fill a tank
of 4000 gallons capacity, standing 300 ft. above the pump?
17. A boy weighing 162 lbs. climbs a stairway a vertical height of
14 ft. in 14.6 seconds. How much power does he exert?
18. The same boy does the same work a second time in 4.2 seconds.
How much power does he exert this time? What causes the
difference?
19. What is a horse-power-hour? a kilowatt-hour?
[Pg 129]
(3) Simple Machines and the Lever
116. Machines and Their Uses.—A man, while standing
on the ground, can draw a flag to the top of a pole,
by using a rope passing over a pulley.
A boy can unscrew a tightly fitting nut that he cannot
move with his fingers, by using a wrench.
A woman can sew a long seam by using a sewing machine
in much less time than by hand.
A girl can button her shoes much quicker and easier
with a button-hook than with her fingers.
These illustrations show some of the reasons why
machines are used. In fact it is almost impossible to do
any kind of work efficiently without using one or more
machines.
117. Advantages of Machines.—(a) Many machines
make possible an increased speed as in a sewing machine
or a bicycle.
(b) Other machines exert an increased force. A rope
and a set of pulleys may enable a
man to lift a heavy object such as
a safe or a piano. By the use of
a bar a man can more easily move
a large rock. (See Fig. 83.)
 Fig. 83.—The rock is easily
moved.
Fig. 83.—The rock is easily
moved.
(c) The direction of a force
may be changed thus enabling work to be done that
could not be readily accomplished otherwise. As, e.g.,
the use of a pulley in raising a flag to the top of a flag pole,
or in raising a bucket of ore from a mine by using a horse
attached to a rope passing over two or more pulleys.
(See Fig. 84.)
(d) Other agents than man or animals can be used such as
electricity, water power, the wind, steam, etc. Fig. 85
represents a windmill often used in pumping water.
[Pg 130]
A machine is a device for transferring or transforming energy.
It is usually therefore an instrument for doing work.
An electric motor is a machine since it transforms the
energy of the electric current into motion or mechanical
energy, and transfers the energy from the wire to the
driving pulley.
 Fig. 84.—The horse lifts the bucket of ore.
Fig. 84.—The horse lifts the bucket of ore.
118. A Machine Cannot Create Energy.—Whatever
does work upon a machine (a man, moving water, wind,
etc.) loses energy which is employed in doing the work of the
machine. A pair of shears is a machine since it transfers
energy from the hand to the edges that do the cutting.
Our own bodies are often considered as machines since
they both transfer and transform energy.
We must keep in mind that a machine cannot create
energy. The principle of "Conservation of Energy"
is just as explicit on one side as the other. Just as energy,
cannot be destroyed, so energy cannot be created. A
machine can give out no more energy than is given to it.
It acts simply as an agent in transferring energy from one[Pg 131]
body to another. Many efforts have been made to construct
machines that when once started will run themselves,
giving out more energy than they receive. Such efforts,
called seeking for perpetual motion, have never succeeded.
This fact is strong evidence in
favor of the principle of the conservation
of energy.
 Fig. 85.—A windmill.
Fig. 85.—A windmill.
119. Law of Machines.—When
a body receives energy,
work is done upon it. Therefore
work is done upon a
machine when it receives energy
and the machine does
work upon the body to which it
gives the energy. In the operation
of a machine, therefore,
two quantities of work are to
be considered and by the principle
of the conservation of
energy, these two must be
equal. The work done by a
machine equals the work done
upon it, or the energy given out
by a machine equals the energy
received by it. These two
quantities of work must each be composed of a force
factor and a space factor. Therefore two forces and
two spaces are to be considered in the operation of a
machine. The force factor of the work done on the
machine is called the force or effort. It is the force applied
to the machine. The force factor of the work done by a
machine is called the weight or resistance. It is the force
exerted by the machine in overcoming the resistance and
equals the resistance overcome.
[Pg 132]
If f represents the force or effort, and Df the space it acts
through, and w represents the weight or resistance, and
Dw the space it acts through, then the law of machines
may be expressed by an equation, f × Df = w × Dw.
That is, the effort times the distance the effort acts equals the
resistance times the distance the resistance is moved or overcome.
When the product of two numbers equals the
product of two other numbers either pair may be made
the means and the other the extremes of a proportion.
The equation given above may therefore be expressed
w: f = Df: Dw. Or the resistance is to the effort as the
effort distance is to the resistance distance. The law of
machines may therefore be expressed in several ways.
One should keep in mind, however, that the same law of
machines is expressed even though the form be different.
What two ways of expressing the law are given?
120. The Simple Machines.—There are but six simple
machines. All the varieties of machines known are
simply modifications and combinations of the six simple
machines. The six simple machines are more easily
remembered if we separate them into two groups of three
each. The first or lever group consists of those machines
in which a part revolves about a fixed axis. It contains
the lever, pulley and wheel and axle. The second or inclined
plane group includes those having a sloping surface.
It contains the inclined plane, the wedge, and the screw.
121. The Lever.—The lever is one of the simple machines
most frequently used, being seen in scissors, broom,
coal shovel, whip, wheelbarrow, tongs, etc. The lever
consists of a rigid bar capable of turning about a fixed axis
called the fulcrum. In studying a lever, one wishes to
know what weight or resistance it can overcome when a
certain force is applied to it. Diagrams of levers, therefore,
contain the letters w and f. In addition to these, O[Pg 133]
stands for the fulcrum on which it turns. By referring
to Fig. 86, a, b, c, one may notice that each of these may
occupy the middle position between the other two. The
two forces (other than the one exerted by the fulcrum)
acting on a lever always oppose each other in the matter
of changing rotation. They may be considered as a
pair of parallel forces acting on a body, each tending to
produce rotation.
 Fig. 86.—The three classes of levers.
Fig. 86.—The three classes of levers.
122. Moment of Force.—The effectiveness of each force
may therefore be determined by computing its moment
about the fixed axis (see Art. 84), that is, by multiplying
each force by its distance to the fulcrum or axis of rotation.
Let a meter stick have a small hole bored through
it at the 50 cm. mark near one edge, and let it be mounted
on a nail driven into a vertical support and balanced by
sliding a bent wire along it. Suspend by a fine wire or
thread a 100 g. weight, 15 cm. from the nail and a 50 g.
weight 30 cm. from the nail, on the other side of the support.
These two weights will be found to balance. When
viewed from this side A (Fig. 87) tends to turn the lever
in a clockwise direction (down at right), B in the counter-clockwise
direction (down at left). Since the lever balances,
the forces have equal and opposite effects in changing
its rotation as may also be computed by determining the[Pg 134]
moment of each force by multiplying each by its distance
from the fulcrum. Therefore the effectiveness of a
force in changing rotation depends upon the distance from
it to the axis as well as upon the magnitude of the force.
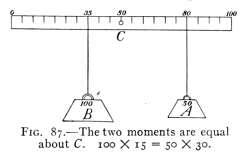 Fig. 87.—The two moments are equal
about C. 100 × 15 = 50 × 30
Fig. 87.—The two moments are equal
about C. 100 × 15 = 50 × 30
From the experiment
just described,
the moment of the
acting force equals
the moment of the
weight or f × Df =
w × Dw, or the effort
times the effort arm
equals the weight times the weight arm. This equation is
called the law of the lever. It corresponds to the general
law of machines and may also be written w: f = Df: Dw.
123. Mechanical Advantage.—A lever often gives an
advantage because by its use one may lift a stone or weight
which the unaided strength of man could not move. If
the lever is used in lifting a stone weighing 500 lbs., the
force available being only 100 lbs., then its mechanical
advantage would be 5, the ratio of w:f. In a similar way,
the mechanical advantage of any machine is found by
finding the ratio of the resistance or weight to the effort.
What must be the relative lengths of the effort arm and
resistance or weight arm in the example just mentioned?
Since the effort times the effort arm equals the weight
times the weight arm, if f × Df = w × Dw, then Df is
five times Dw. Hence the mechanical advantage of a lever
is easily found by finding the ratio of the effort arm to
the weight arm.
Important Topics
1. Advantage of machines.
2. Machines cannot create energy.
3. Law of machines.
[Pg 135]
4. Six simple machines.
5. Lever and principle of moments.
6. Mechanical advantage of a machine.
Exercises
1. Give six examples of levers you use.
2. Fig. 88a represents a pair of paper shears, 88b a pair of tinner's
shears. Which has the greater mechanical advantage? Why?
Explain why each has the most effective shape for its particular
work.
 Fig. 88.—(a) Paper shears. (b) Tinner's shears.
Fig. 88.—(a) Paper shears. (b) Tinner's shears.
3. Find examples of levers in a sewing machine.
4. What would result if, in Art. 122, the 100 g. weight were put
25 cm. from O and the 50 g. weight 45
cm. from O? Why? Explain using
principle of moments.
5. How is the lever principle applied in
rowing a boat?
6. When you cut cardboard with shears,
why do you open them wide and cut
near the pivot?
7. In carrying a load on a stick over the
shoulder should the pack be carried near
the shoulder or out on the stick? Why?
8. How can two boys on a see-saw start it
without touching the ground?
9. In lifting a shovel full of sand do you
lift up with one hand as hard as you
push down with the other? Why?
 Fig. 89.—The hammer
is a bent lever.
What is its mechanical
advantage?
Fig. 89.—The hammer
is a bent lever.
What is its mechanical
advantage?
10. Why must the hinges of a gate 3 ft.
high and 16 ft. wide be stronger than the hinges of a gate 16
ft. high and 3 ft. wide?
11. When one sweeps with a broom do the hands do equal amounts
of work? Explain.
[Pg 136]
12. A bar 6 ft. long is used as a lever to lift a weight of 500 lbs.
If the fulcrum is placed 6 in. from the weight, what will be
the effort required? Note: two arrangements of weight, fulcrum
and effort are possible.
13. The handle of a hammer is 12 in. long and the claw that is used
in drawing a nail is 2.5 in. long. (See Fig. 89.) A force of 25
lbs. is required to draw the nail. What is the resistance of the
nail?
14. The effective length of the head of a hammer is 2 in. The
handle is 15 in. long and the nail holds in the wood with a force
of 500 lbs. Only 60 lbs. of force is available at the end of the
handle. What will be the result?
15. If an effort of 50 lbs. acting on a machine moves 10 ft., how far
can it lift a weight of 1000 lbs.?
16. A bar 10 ft. long is to be used as a lever. The weight is kept
2 ft. from the fulcrum. What different levers can it represent?
17. The effort arm of a lever is 6 ft., the weight arm 6 in. How long
will the lever be? Give all possible answers.
18. Two boys carry a weight of 100 lbs. on a pole 5 ft. long between
them. Where should the weight be placed in order that one boy
may carry one and one-fourth times as much as the other?
(4) The Wheel and Axle and the Pulley
124. The Wheel and Axle.—1. One of the simple machines
most commonly applied in compound machines is
the wheel and axle. It consists of a wheel H mounted
on a cylinder Y so fastened together that both turn on
the same axis. In Fig. 90, ropes are shown attached to
the circumferences of the wheel and axle. Sometimes a
hand wheel is used as on the brake of a freight or street
car, or simply a crank and handle is used, as in Fig. 91.
The capstan is used in moving buildings. Sometimes
two or three wheels and axles are geared together as on a
derrick or crane as in Fig. 92.
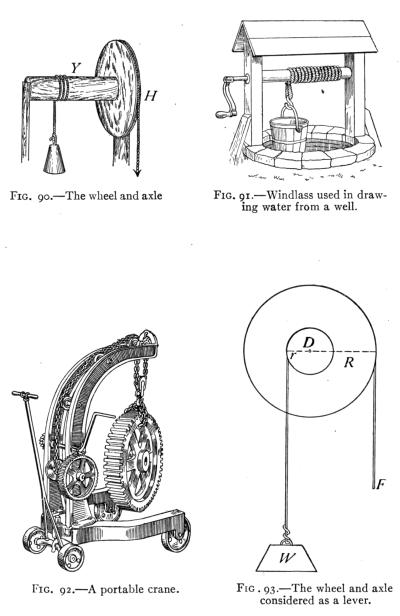 Fig. 90.—The wheel and axle.
Fig. 90.—The wheel and axle.
Fig. 91.—Windlass used in drawing
water from a well.
Fig. 92.—A portable crane.
Fig. 93.—The wheel and axle
considered as a lever.
 Fig. 94.—View of transmission gears in an automobile. 1, Drive gear;
2, High and intermediate gear; 3, Low and reverse gear; 4, 8, Reverse
idler gears; 5, 6, 7, Countershaft gears. (Courtesy of the Automobile
Journal.)
Fig. 94.—View of transmission gears in an automobile. 1, Drive gear;
2, High and intermediate gear; 3, Low and reverse gear; 4, 8, Reverse
idler gears; 5, 6, 7, Countershaft gears. (Courtesy of the Automobile
Journal.)
Fig. 95.—Reducing gear of a steam turbine.
Fig. 93 is a diagram showing that the wheel and axle
acts like a lever. The axis D is the fulcrum, the effort
is applied at F, at the extremity of a radius of the wheel[Pg 137]
[Pg 138]
and the resisting weight W at the extremity of a radius
of the axle. Hence, if Df, the effort distance, is three
times Dw, the weight distance, the weight that can be
supported is three times the effort. Here as in the lever,[Pg 139]
f × Df = w × Dw, or w:f = Df:Dw, or the ratio of the
weight to the effort equals the ratio of the radius of the wheel
to the radius of the axle. This is therefore the mechanical
advantage of the wheel and axle. Since the diameters
or circumferences are in the same ratio as the radii these
can be used instead of the radii. Sometimes, when
increased speed instead of increased force is desired, the
radius of the wheel or part to which power is applied is
less than that of the axle. This is seen in the bicycle,
buzzsaw, and blower. Sometimes geared wheels using the
principle of the wheel and axle are used to reduce speed,
as in the transmission of an automobile (see Fig. 94), or the
reducing gear of a steam turbine. (See Figs. 95 and 293.)
A bevel gear is frequently used to change the direction
of the force. (See Fig. 94.)
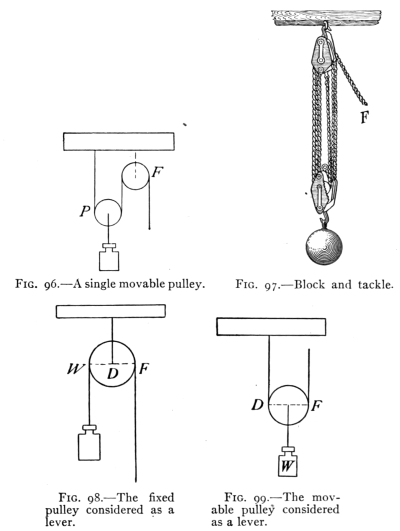 Fig. 96.—A single movable pulley.
Fig. 96.—A single movable pulley.
Fig. 97.—Block and tackle.
Fig. 98.—The fixed
pulley considered as a
lever.
Fig. 99.—The movable
pulley considered
as a lever.
125. The Pulley.—The pulley consists of a wheel turning
on an axis in a frame. The wheel is called a sheave and
the frame a block. The rim may be smooth or grooved.
The grooved rim is used to hold a cord or rope. One use of
the pulley is to change the direction of the acting force as
in Fig. 84, where pulley B changes a horizontal pull at H
to a downward force and pulley A changes this into an
upward force lifting the weight W. These pulleys are fixed
and simply change the direction. Without considering
the loss by friction, the pull at W will equal that at F.
Sometimes, a pulley is attached to the weight and is lifted
with it. It is then called a movable pulley. In Fig. 96
the movable pulley is at P, a fixed pulley is at F. When
fixed pulleys are used, a single cord runs through from the
weight to the effort, so that if a force of 100 lbs. is applied
by the effort the same force is received at the weight. But
with movable pulleys several sections of cord may extend
upward from the weight each with the force of the effort
upon it. By this arrangement, a weight several times
larger than the effort can be lifted. Fig. 97 represents[Pg 140]
what is called a block and tackle. If a force of 50 lbs.
is exerted at F, each section of the rope will have the same
tension and hence the six sections of the rope will support
300 lbs. weight. The mechanical advantage of the pulley
or the ratio of the weight to the effort,
therefore, equals the number of sections
of cord supporting the weight. The
fixed pulley represents a lever, see
Fig. 98, where the effort and weight
are equal. In the movable pulley,
the fulcrum (see Fig. 99) is at D; the weight, W, is applied
at the center of the pulley and the effort at F. The weight
[Pg 141]distance, Dw, is the radius, and the effort distance, Df, is
the diameter of the pulley. Since W/F = Df / Dw = 2
in a movable pulley, the weight is twice the effort, or its
mechanical advantage is 2.
Important Topics
1. Wheel and Axle, Law of Wheel and Axle.
2. Pulley, Fixed and Movable, Block and Tackle, Law of Pulley.
Exercises
1. Why do door knobs make it easier to unlatch doors? What
simple machine do they represent? Explain.
2. What combination of pulleys will enable a 160-lb. man to raise
a 900-lb. piano?
3. When you pull a nail with an ordinary claw hammer, what is
the effort arm? the resistance arm?
4. How much work is done by the machine in problem 2 in lifting
the piano 20 ft.? How much
work must be done upon the
machine to do this work?
5. The pilot wheel of a boat has
a diameter of 60 in.; the
diameter of the axle is 6 in.
If the resistance is 175 lbs.,
what force must be applied
to the wheel?
6. Four men raise an anchor
weighing {1 1/2} tons, with a
capstan (see Fig. 110) having
a barrel 9 in. in diameter.
The circle described by the
hand-spikes is {13 1/2} ft. in diameter. How much force must
each man exert?
 Fig. 100.—The Capstan.
Fig. 100.—The Capstan.
7. A bicycle has a 28-in. wheel. The rear sprocket is 3 in. in
diameter,[H] the radius of the pedal crank is 7 in.; 24 lbs. applied
to the pedal gives what force on the rim of the wheel? What
will be the speed of the rim when the pedal makes one revolution
a second?
8. Measure the diameters of the large and small pulleys on the
sewing-machine at your home. What mechanical advantage[Pg 142]
in number of revolutions does it give? Verify your computation
by turning the wheel and counting the revolutions.
9. What force is required with a single fixed pulley to raise a
weight of 200 lbs.? How far will the effort move in raising the
weight 10 ft.? What is the mechanical advantage?
10. In the above problem substitute a single movable pulley for
the fixed pulley and answer the same questions.
11. What is the smallest number of pulleys required to lift a weight
of 600 lbs. with a force of 120 lbs.? How should they be
arranged?
12. A derrick in lifting a safe weighing 2 tons uses a system of pulleys
employing 3 sections of rope. What is the force required?
13. Name three instances where pulleys are used to do work that
otherwise would be difficult to do.
14. Draw a diagram for a set of pulleys by means of which 100 lbs.
can lift 400 lbs.
(5) The Inclined Plane. Efficiency
126. Efficiency.—The general law of machines which
states that the work done by a machine equals the work
put into it requires a modification, when we apply the law
in a practical way, for the reason that in using any machine
there is developed more or less friction due to parts of the
machine rubbing on each other and to the resistance of the
air as the parts move through it. Hence the statement of
the law that accords with actual working conditions runs
somewhat as follows: The work put into a machine equals
the useful work done by the machine plus the wasted work
done by it. The efficiency of a machine is the ratio of the
useful work done by it to the total work done on the
machine. If there were no friction or wasted work, the
efficiency would be perfect, or, as it is usually expressed,
would be 100 per cent. Consider a system of pulleys into
which are put 600 ft.-lbs. of work. With 450 ft.-lbs. of
useful work resulting, the efficiency would be 450 ÷
600 = {3/4}, or 75 per cent. In this case 25 per cent. of the[Pg 143]
work done on the machine is wasted. In a simple lever
the friction is slight so that nearly 100 per cent. efficiency
is often secured.
Some forms of the wheel and axle have high efficiencies
as in bicycles with gear wheels. Other forms in which
ropes are employed have more friction. Pulleys have
sometimes efficiencies as low as 40 per cent. when heavy
ropes are used.
127. Inclined Plane.—We now come to a type of simple
machine of lower efficiency than those previously mentioned.
These belong to the inclined plane group, which
includes the inclined plane (see Fig. 101), the wedge and
the screw. They are extensively used, however, notwithstanding
their low efficiency, on account of often giving a
high mechanical advantage. The relation between these
machines may be easily shown, as the wedge is obviously
a double inclined plane. In Art. 82 it is shown that the
effort required to hold a weight upon an inclined plane is
to the weight supported as the height of the plane is to its
length.
 Fig. 101.—An inclined plane.
Fig. 101.—An inclined plane.
Or while the weight is being lifted the vertical height
BC, the effort has to move the length of the plane AC.
Since by the law of machines the effort times its distance
equals the weight times its distance, or the weight is to[Pg 144]
the effort as the effort distance is to the weight distance,
therefore the mechanical advantage of the inclined plane
is the ratio of the length to the height of the inclined plane.
Inclined planes are used to raise heavy objects short
distances, as barrels into a wagon, and iron safes into a
building. Stairways are inclined planes with steps cut
into them.
128. The Wedge.—Wedges are used to separate objects,
as in splitting wood (see Fig. 102), cutting wood, and where
great force is to be exerted for short distances. An axe is
a wedge, so is a knife. A fork consists of several round
wedges set in a handle. The edge of
any cutting tool is either an inclined
plane or a wedge. Our front teeth are
wedges. Numerous examples of inclined
planes may be seen about us.
No definite statement as to the
mechanical advantage of the wedge can
be given as the work done depends
largely on friction. The force used is
generally applied by blows on the thick
end. In general, the longer the wedge for a given thickness
the greater the mechanical advantage.
 Fig. 102.—One use
of the wedge.
Fig. 102.—One use
of the wedge.
129. The Screw.—The screw is a cylinder around whose
circumference winds a spiral groove. (See Fig. 103.)
The raised part between the two adjacent grooves is the
thread of the screw. The screw turns in a block called a
nut, within which is a spiral groove and thread exactly
corresponding to those of the screw. The distance between
two consecutive threads measured parallel to the
axis is called the pitch of the screw. (See Fig. 104.) If
the thread winds around the cylinder ten times in the
space of 1 in., the screw is said to have ten threads to the
inch, the pitch being {1/10} in. The screw usually is turned[Pg 145]
by a lever or wheel with the effort applied at the end of
the lever, or at the circumference of the wheel. While the
effort moves once about the circumference of the wheel the
weight is pushed forward a distance equal to the distance
between two threads (the pitch of the screw). The work
done by the effort therefore equals F × 2πr, r being the
radius of the wheel, and the work done on the weight
equals W × s, s being the pitch of the screw. By the law
of machines F × 2πr = W × s or W / F
= (2πr) / s. Therefore the mechanical
advantage of the screw equals (2πr) / s.
Since the distance the weight moves is
small compared to that the power travels,
there is a great gain in force. The
screw is usually employed where great force is to be exerted
through small distances as in the vise (Fig. 105) the jack
screw (Fig. 106), screw clamps, to accurately measure
small distances as in the micrometer (Fig. 107) and spherometer,
and to lessen the motion in speed-reducing devices.
The worm gear (Fig. 108) is a modification of the screw
that is sometimes used where a considerable amount of
speed reduction is required.
 Fig. 103.—The screw
is a spiral inclined
plane.
Fig. 103.—The screw
is a spiral inclined
plane.
Fig. 104.—The pitch is S.
[Pg 146]
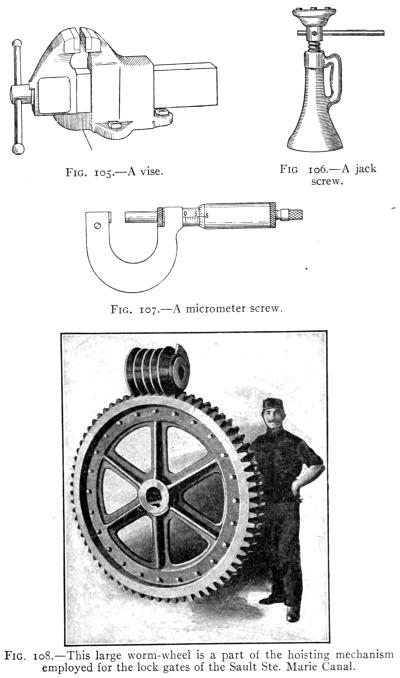 Fig. 105.—A vise.
Fig. 105.—A vise.
Fig. 106.—A jack screw.
Fig. 107.—A micrometer screw.
Fig. 108.—This large worm-wheel is a part of the hoisting mechanism
employed for the lock gates of the Sault Ste. Marie Canal.
[Pg 147]
Important Topics
1. Efficiency of machines.
2. The inclined plane, wedge and screw. Applications.
Exercises
1. A plank 12 ft. long is used to roll a barrel weighing 200 lbs. into
a wagon 3 ft. high. Find the force required parallel to the
incline.
2. How long a plank will be needed to roll an iron safe weighing 1-1/2
tons into a wagon 3 ft. high using a pull of 600 lbs. parallel to the
incline.
3. An effort of 50 lbs. acting parallel to the plane prevents a 200-lb.
barrel from rolling down an inclined plane. What is the ratio
of the length to the height of the plane?
4. A man can push with a force of 150 lbs. and wishes to raise a box
weighing 1200 lbs. into a cart 3 ft. high. How long a plank must
he use?
5. The radius of the wheel of a letter press is 6 in., the pitch of its
screw is 1/4 in. What pressure is produced by a force of 40 lbs.?
6. The pitch of a screw of a vice is 1/4 in., the handle is 1 ft. long.
what pressure can be expected if the force used is 100 lbs.?
7. A jackscrew is used to raise a weight of 2 tons. The bar of the
jackscrew extends 2 ft. from the center of the screw. There
are two threads to the inch. Find the force required.
(6) Friction, Its Uses and Laws
130. Friction.—Although often inconvenient and expensive,
requiring persistent and elaborate efforts to reduce
it to a minimum, friction has its uses, and advantages.
Were it not for friction between our shoes and the floor or
sidewalk, we could not keep our footing. Friction is the
resistance that must be overcome when one body moves over
another. It is of two kinds, sliding and rolling. If one
draws a block and then a car of equal weight along a
board, the force employed in each case being measured[Pg 148]
by a spring balance, a large difference in the force required
will be noticed, showing how much less rolling friction is
than sliding friction.
131. Ways of Reducing Friction.—(a) Friction is often
caused by the minute projections of one surface sinking
into the depressions of the other surface as one moves over
the other. It follows, therefore, that if these projections
could be made as small as possible that friction would be
lessened. Consequently polishing is one of the best
means for reducing friction. In machines all moving
surfaces are made as smooth as possible. In different
kinds of materials
these little ridges
and depressions are
differently arranged.
(b) In Fig. 109 the
friction between R
and S would be greater than between R and T. In
R and S the surfaces will fit closer together than in R and
T. The use of different materials will reduce friction.
The iron axles of car wheels revolve in bearings of brass.
Jewels are used in watches for the same reason. (c)
Another very common method of reducing friction is by
the use of lubricants. The oil or grease used fills up the
irregularities of the bearing surfaces and separates them.
Rolling friction is frequently substituted for sliding friction
by the use of ball and roller bearings. These are used
in many machines as in bicycles, automobiles, sewing
machines, etc. (See Fig. 110.)
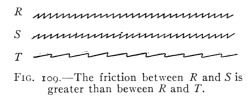 Fig. 109.—The friction between R and S is
greater than between R and T.
Fig. 109.—The friction between R and S is
greater than between R and T.
132. Value of Friction.—Friction always hinders motion
and whenever one body moves over or through another
the energy used in overcoming the friction is transformed
into heat which is taken up by surrounding bodies and
usually lost. Friction is therefore the great obstacle to[Pg 149]
perfect efficiency in machines. Friction, however, like
most afflictions has its uses. We would find it hard to get
along without it. Without friction we could neither walk
nor run; no machines could be run by belts; railroad trains,
street cars, in fact all ordinary means of travel would be
impossible, since these depend upon friction between the
moving power and the road for propulsion.
 Fig. 110.—Timken roller bearings. As used in the front wheel of an
automobile.
Fig. 110.—Timken roller bearings. As used in the front wheel of an
automobile.
133. Coefficient of Friction.—The ratio between the
friction when motion is just starting and the force pushing
the surfaces together is called the coefficient of friction.
If the block in Fig. 111 is drawn along the board with
uniform motion, the reading of the spring balances indicates
the amount of friction. Suppose the friction is
found to be 500 g., and the weight of the block to be 2000 g.[Pg 150]
Then the coefficient of friction for these two substances
will be {500/2000} = {1/4}, or 25 per cent.
134. Laws of Friction, Law I.—The friction when motion
is occurring between two surfaces is proportional to the force
holding them together. Thus if one measures the friction
when a brick is drawn along a board, he will find that it is
doubled if a second brick is placed on the first. On
brakes greater pressure causes greater friction. If a rope is
drawn through the hands more pressure makes more
friction.
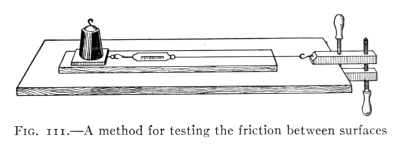 Fig. 111.—A method for testing the friction between surfaces.
Fig. 111.—A method for testing the friction between surfaces.
Law II.—Friction is independent of the extent of surface
in contact. Thus a brick has the same friction drawn on
its side as on its edge, since, although the surface is increased,
the weight is unchanged.
Law III.—Friction is greatest at starting, but after
starting is practically the same for all speeds.
135. Fluid Friction.—When a solid moves through a
fluid, as when a ship moves through the water or railroad
trains through the air, the resistance encountered is not the
same as with solids but increases with the square of the
velocity for slow speeds and for high speeds at a higher
rate. This is the reason why it costs so much to increase
the speed of a fast train, since the resistance of the
air becomes the prominent factor at high speeds. The
resistance to the motion of a ship at high speed is usually[Pg 151]
considered to increase as the cube of the velocity so that
to double the speed of a boat its driving force must be eight
times as great.
Important Topics
1. Friction: two kinds; sliding and rolling.
2. Four ways of reducing friction.
3. Uses of friction.
4. Coefficient of friction. Three laws of friction.
5. Fluid friction.
Exercises
1. How long must an inclined plane be which is 10 meters high
to enable a car weighing 2000 kg. to be pushed up its length
by a force of 100 kg. parallel to the incline?
2. State how and where friction is of use in the operation of the
inclined plane, the wedge, the screw, the wheel and axle.
3. A wheelbarrow has handles 6 ft. long. If a load of 300 lbs. is
placed 18 in. from the axis of the wheel, what force placed at
the end of the handles will be required to lift it?
4. A jackscrew has 3 threads to the inch, and the lever used to
turn it is 4 ft. long. If the efficiency of the screw is 60 per cent.,
what force must be applied to raise a load of 5 tons?
5. In problem 4 how far must the force move in raising the weight
3 in. Compute the work done upon the weight, the work done
by the power and the efficiency of the machine from these two
amounts of work.
6. What simple machines are represented in a jackknife, a sewing-machine,
a screw-driver, a plane, a saw, a table fork?
7. A laborer carries 1500 lbs. of brick to a platform 40 ft. high.
How much useful work does he do?
8. If he weighs 150 lbs. and his hod weighs 10 lbs., how much useless
work does he do in taking 30 trips to carry up the bricks
of problem 7? What is his efficiency?
9. If the laborer hoists the brick of problem 7 in a bucket weighing
50 lbs., using a fixed pulley and rope, what is the useless work
done if it takes 12 trips to carry up the brick? What is the
efficiency of the device?
10. The efficiency of a set of pulleys is 70 per cent. How much
force should be applied if acting through 100 ft. it is to raise
a load of 400 lbs. 20 ft.?
[Pg 152]
11. The spokes of the pilot wheel of a motor-boat are 1 ft. long, the
axle around which the rudder ropes are wound is 3 in. in diameter.
What effort must be applied if the tension in the ropes is 50 lbs.?
12. Why are the elevated railway stations frequently placed at the
top of an incline, the tracks sloping gently away in both
directions?
13. The screw of a press has 4 threads to the inch and is worked by
a lever of such length that an effort of 25 lbs. produces a force
of 2 tons. What is the length of the lever?
14. It takes a horizontal force of 10 lbs. to draw a sled weighing
50 lbs. along a horizontal surface. What is the coefficient of
friction?
15. The coefficient of rolling friction of a railroad train on a track
is 0.009. What pull would an engine have to exert to haul a
train weighing 1000 tons along a level track?
16. How heavy a cake of ice can be dragged over a floor by a horizontal
force of 20 lbs., if the coefficient of friction is 0.06?
17. The coefficient of friction of iron on iron is 0.2. What force
can a switch engine weighing 20 tons exert before slipping?
18. Using a system of pulleys with a double movable block a man
weighing 200 lbs. is just able to lift 600 lbs. What is the efficiency
of the system?
19. What is the horse-power of a pump that can pump out a cellar
full of water 40 ft. × 20 ft. by 10 ft. deep, in 30 minutes?
20. How many tons of coal can a 5 horse-power hoisting engine
raise in 30 minutes from a barge to the coal pockets, a height
of 50 ft.?
(7) Water Power
136. Energy of Falling Water.—The energy of falling
and running water has been used from the earliest times
for developing power and running machinery. The
energy is derived from the action of the moving water in
striking and turning some form of water-wheel, several
varieties of which are described below.
The Overshot Wheel.—The overshot wheel (Fig. 112)
is turned by the weight of the water in the buckets. It
was formerly much used in the hilly and mountainous[Pg 153]
sections of this country for running sawmills and grist
mills as it is very easily made and requires only a small
amount of water. Its efficiency is high, being from 80
to 90 per cent., the loss being due to friction and spilling
of water from the buckets. To secure this high efficiency
the overshot wheel must have
a diameter equal to the height
of the fall which may be as
much as 80 or 90 ft.
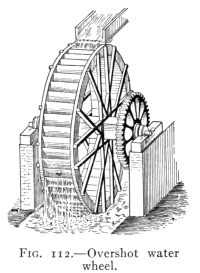 Fig. 112.—Overshot water
wheel.
Fig. 112.—Overshot water
wheel.
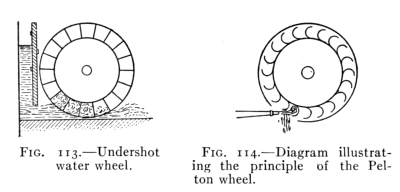 Fig. 113.—Undershot
water wheel.
Fig. 113.—Undershot
water wheel.
Fig. 114.—Diagram illustrating
the principle of the Pelton
wheel.
The Undershot Wheel.—The
old style undershot
wheel (Fig. 113) is used in
level countries, where there is
little fall, often to raise water
for irrigation. Its efficiency is
very low, seldom rising more
than 25 per cent. The principle
of the undershot wheel,
however, is extensively used
in the water motor and the Pelton wheel (Fig. 114).
In these the water is delivered from a nozzle in a jet
against the lower buckets of the wheel. They have
an efficiency of about 80 per cent. and are much used in
cities for running small machines, washing machines, pipe[Pg 154]
organ blowers, etc., and in mountainous districts where
the head is great.
 Fig. 115.—Diagram of a hydro-electric power house showing a vertical
turbine A with penstock B and tail race C.
Fig. 115.—Diagram of a hydro-electric power house showing a vertical
turbine A with penstock B and tail race C.
 Fig. 116.—The outer case of a turbine showing the mechanism for controlling
the gates.
Fig. 116.—The outer case of a turbine showing the mechanism for controlling
the gates.
Fig. 117.—Inner case of a turbine showing the gates and the lower end
of the runner within.
 Fig. 118.—The runner of a turbine.
Fig. 118.—The runner of a turbine.
Fig. 119.—Turbine and generator of the Tacoma hydro-electric power
plant.
137. The Turbine.—The turbine is now used more than
any other form of water-wheel. It was invented in 1827
by De Fourneyron in France. It can be used with a
small or large amount of water, the power depending on
the head (the height of the water, in the reservoir above
the wheel). It is the most efficient type of water-wheel,
efficiencies of 90 per cent. often being obtained. The
wheel is entirely under water (Fig. 115). It is enclosed
in an outer case (Fig. 116) which is connected with the
reservoir by a penstock or pipe and is always kept full of
water. The wheel itself is made in two parts, a rotating
part called the runner (see Fig. 118) and an inner case[Pg 155]
[Pg 156]
(Fig. 117) with gates that regulate the amount of water
entering the wheel. This case has blades curved so
that the water can strike the curved blades of the rotating
part (Fig. 118) at the angle that is best adapted to use
the energy of the water. The water then drops through
the central opening into the tail race below (see Fig. 115).[Pg 157]
The energy available is the product of the weight of the
water and the head. The turbine is extensively used to
furnish power for generating electricity at places where
there is a sufficient fall of water. The electrical energy
thus developed is transmitted from 50 to 200 miles to
cities where it is used in running street cars, electric lighting,
etc. Turbines can be made to revolve about either
vertical or horizontal axes. Fig. 119 represents a horizontal
water turbine connected to a dynamo. Compare this
with the vertical turbine in Fig. 115.
Exercises
1. Does a person do more work when he goes up a flight of stairs
in 5 seconds than when he goes up in 15 seconds? Explain.
2. A motorcycle has a 4 horse-power motor and can go at a rate
of 50 miles per hour. Why cannot 4 horses draw it as fast?
3. What is the efficiency of a motor that is running fast but doing
no useful work?
4. What horse-power can be had from a waterfall, 12 ft. high, if
20 cu. ft. of water pass over it each second?
5. What is the horse-power of a fire engine if it can throw 600
gallons of water a minute to a height of 100 ft.?
6. Why are undershot wheels less efficient than the overshot
wheel or turbine?
7. A revolving electric fan is placed on the stern of a boat. Does
the boat move? Why? Place the fan under water. Does
the boat now move? Why?
8. Why does an electric fan produce a breeze?
9. Explain the action of the bellows in an organ.
10. At Niagara Falls the turbines are 136 ft. below the surface of
the river. Their average horse-power is 5000 each. 430 cu.
ft. of water each second pass through each turbine. Find
the efficiency.
11. At Laxey on the Isle of Man is the largest overshot wheel now
in use. It has a horse-power of 150, a diameter of 72.5 ft., a
width of 10 ft., and an efficiency of 85 per cent. How many
cubic feet of water pass over it each second?
[Pg 158]
12. The power plant at the Pikes Peak Hydro-electric Company
utilizes a head of 2150 ft., which is equal to a pressure of 935
lbs. per square inch, to run a Pelton wheel. If the area of the
nozzle is 1 sq. in. and the jet has a velocity of 22,300 ft. per
minute, what is the horse-power developed if the efficiency is
80 per cent.?
13. A test made in 1909 of the turbines at the Centerville power
house of the California Gas and Electric Corporation showed a
maximum horse-power of 9700, speed 400 r.p.m. under a head
of 550 ft. The efficiency was 86.25 per cent. How many
cubic feet of water passed through the turbines each second?
14. The turbine in the City of Tacoma Power Plant (see Fig. 120)
uses a head of 415 ft. 145 cu. ft. a second pass through the
turbine. Calculate the horse-power.
15. In problem 14, what is the water pressure per square inch at
the turbine?
16. The power plant mentioned in problem 13 develops 6000 kw.
What is the efficiency?
Review Outline: Work and Energy
Work; how measured, units, foot-pound, kilogram meter, erg.
Energy; how measured, units, potential, P.E. = w × h, or f × s.
Kinetic = (wv2)/(2g).
Power; how measured, units, horse power, watt, 5 forms of energy,
conservation. H.p. = (lbs. × ft.)/(550 × sec.).
Machines; 6 simple forms, 2 groups, advantages, uses, Law: W × Dw
= F × Df.
Lever; moments, mechanical advantage, uses and applications.
Wheel and Axle and Pulley; common applications, mechanical
advantage.
Inclined Plane, Wedge, and Screw; mechanical advantage and
efficiency.
Friction; uses, how reduced, coefficient of, laws (3).
Water Wheels; types, efficiency, uses.
[Pg 159]
HEAT, ITS PRODUCTION AND TRANSMISSION
(1) Sources and Effects of Heat
138. Importance of the Study of Heat.—Heat is brought
to our attention through the sensations of heat and cold.
In winter, we warm our houses and prevent the escape of
heat from them as much as possible. In summer we
endeavor to keep our living rooms cool and our bodies from
being overheated.
A clear understanding of the several sources, effects, and
modes of transferring heat is of importance to everyone
living in our complex civilization, especially when we consider
the multitudes of objects that have as their principal
use the production, transfer or utilization of heat.
139. Principal Sources of Heat.—First and most important
is the Sun, which is continually sending to us
radiant energy in the form of light and heat waves. These
warm the earth, make plants grow, evaporate water,
besides producing many other important effects.
Second, chemical energy is often transformed into heat.
One has but to think of the heat produced by burning
coal, wood, oil, and gas, to recognize the importance of
this source. Chemical energy is also the source of the
heat produced within our bodies. The action of quicklime
and water upon each other produces much heat. This
action is sometimes employed during balloon trips as a
means of warming things.
Third, Electrical Energy.—In many cities electric cars
are heated by the electric current. We have all heard of[Pg 160]
electric toasters and other devices for heating by electricity.
Electric light is produced
by the heating of some
material to incandescence by
an electric current. The
electric furnace has a wide
application in the preparation
and refining of metals.
 Fig. 120.—Boy-scout method of
making fire by friction.
Fig. 120.—Boy-scout method of
making fire by friction.
Fourth, heat is also produced
whenever mechanical
energy of motion is overcome,
whether it be by friction, concussion, or compression.
Friction always results in the production of heat, as
when we warm our hands by rubbing them together.
When friction is excessive, such as in the
case of a heavy bearing not properly oiled, the
bearing may get very hot. This is the cause of
the "hot box" on a railway car. Friction may
produce heat enough to set wood on fire. Some
fires in mills are believed to be due to this cause.
Every boy scout must learn how to produce fire by
friction. (See Fig. 120.) Concussion may be
illustrated by the heating of a piece of metal by
hammering it, while the compression of a gas
always makes it warmer, as those who have used
a bicycle pump have observed. The production
of heat by compressing a gas is illustrated by
the "fire syringe" (Fig. 121). This consists of a
glass tube with a tightly fitted piston. A sudden
compression of the air contained may ignite a
trace of carbon bisulfid vapor.
 Fig.
121.—A
fire
syringe.
Fig.
121.—A
fire
syringe.
The interior of the earth is hot, but its heat
seldom gets to the surface except at hot springs and
volcanoes.
[Pg 161]
140. The Effects of Heat.—There are five important
changes produced by heat: (a) change of size, (b) change
of temperature, (c) change of state, as the melting of ice or
evaporating of water, (d) chemical change, as the charring
of sugar when it is overheated, and (e) electrical change.
This is illustrated by the production of an electric current,
by the heating of the junction of two different metals. A
thermo-electric generator (see Fig. 122) has been constructed
upon this principle and works successfully.
 Fig. 122.—A thermo-electric generator.
Fig. 122.—A thermo-electric generator.
Important Topics
1. Importance of a study of heat.
2. Four sources of heat.
3. Five effects of heat.
4. Examples of each.
5. Illustrations of transformation of energy which involve heat.
Exercises
1. Write a list of the sources of heat in the order of their importance
to you. State why each is important to you.
2. Which three of the effects of heat do you make most use of? Explain
what use you make of each of these effects.
3. Which of the forms of energy can be transformed into heat?
How in each case?
[Pg 162]
4. Into what other forms of energy may heat be transformed?
Name the device or process used in each case.
5. What five different commodities are purchased by people in
your neighborhood for the production of heat? Which of these
costs least for the amount of heat furnished? Which is most
expensive? How do you determine these answers?
6. Why do many people buy heat in an expensive form, as in using
an electric toaster, when they can obtain it in a cheaper form by
burning gas or coal?
7. How many of the five effects of heat have you observed outside
of school?
(2) Temperature and Expansion
141. Heat and Temperature.—We should now clearly
distinguish between the terms, heat and temperature.
Heat is a form of energy consisting of molecular motion.
The temperature of a body is its degree of hotness. The
amount of heat present in a body and its temperature are
very different things. The temperature refers to the
intensity of the heat in the body. A quart of water and a
red hot iron ball may contain equal amounts of heat,
although the ball has a much higher temperature than the
water. A cup of boiling water will have the same temperature
as a tank full of boiling water, but the tank will contain
more heat. Every one knows that it will take longer
to boil a kettle full of water than a cupful. A hot-water
bag, holding 2 quarts of water will give off heat longer than
a 1-quart bag, both being filled with water at the same
temperature. To put it in another way, more work is done
in heating a large amount of water, than a small amount
through the same change of temperature.
142. Units of Heat and Temperature.—There are two
common units for measuring heat: the Calorie and the
British thermal unit. The calorie is the amount of heat
required to raise the temperature of a gram of water one
centigrade degree. The British thermal unit is[Pg 163]
the amount of heat required to raise the temperature of one pound
of water one Fahrenheit degree. One of the units plainly
belongs to the metric system, the other to the English.
An instrument for measuring temperature is called a
thermometer. Various scales are placed upon thermometers.
The two thermometer scales most commonly used
in this country are the Centigrade
and the Fahrenheit. The Fahrenheit
thermometer scale has the
temperature of melting ice marked
32°. The boiling point or steam
temperature of pure water under
standard conditions of atmospheric
pressure is marked 212°
and the space between these two
fixed points is divided into 180
parts.
The centigrade thermometer
scale has the same fixed points
marked 0 and 100 and the space
between divided into 100 parts.
(See Fig. 123.) The centigrade
scale is the one used by scientists
everywhere.
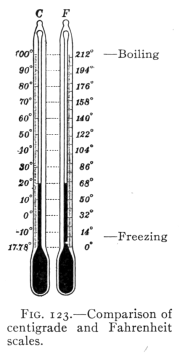 Fig. 123.—Comparison of
centigrade and Fahrenheit
scales.
Fig. 123.—Comparison of
centigrade and Fahrenheit
scales.
143. Comparison of Thermometer Scales.—It is often
necessary to express in centigrade degrees a temperature
for which the Fahrenheit reading is given or vice versa.
Since there are 180 Fahrenheit degrees between the
"fixed points" and 100 centigrade degrees, the Fahrenheit
degrees are smaller than the centigrade, or 1°F. =
5/9°C. and 1°C. = 9/5°F. One must also take into account
the fact that the melting point of ice on the Fahrenheit
scale is marked 32°. Hence the following rule: To
change a Fahrenheit reading to centigrade subtract 32[Pg 164]
and take 5/9 of the remainder, while to change centigrade
to Fahrenheit multiply the centigrade by 9/5 and add 32
to the product. These two rules are expressed by the
following formulas.
(F.° - 32)5/9 = C.°, 9C.°/5 + 32° = F.°
Another method of changing from one thermometric scale
to another is as follows:
A temperature of -40°F. is also represented by -40°C., therefore
to change a Fahrenheit reading into centigrade, we add 40
to the given reading, then divide by 1.8 after which subtract 40.
To change from a centigrade to Fahrenheit reading the only difference
in this method is to multiply by 1.8 or
C. = (F. + 40)/1.8 - 40 and F. = 1.8(C. + 40) - 40.
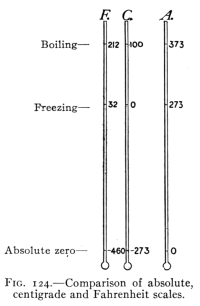 Fig. 124—Comparison of absolute,
centigrade and Fahrenheit scales.
Fig. 124—Comparison of absolute,
centigrade and Fahrenheit scales.
144. The Absolute Scale
of Temperature.—One
often hears the statement
"as cold as ice." This expresses
the incorrect idea
that ice cannot become
colder than its freezing
temperature. The fact is
that ice may be cooled below
freezing down to the
temperature of its surroundings.
If a piece of
ice is placed where the temperature
is below the melting
point, the ice, like any
other solid, cools to the
temperature of the surrounding
space. For example, a piece of ice out of doors
is at 10°F. when the air is at this temperature. It follows
then, that when ice has been cooled below the freezing[Pg 165]
temperature that heat is required to warm the ice up to its
melting point; or in other words that ice at its melting
temperature possesses some heat. The temperature at
which absolutely no heat exists is called absolute zero. There
has been devised an absolute scale of temperature. This
scale is based upon the centigrade scale, i.e., with 100°
between the two fixed points; the scale, however, extends
down, below the centigrade zero, 273°, to what is called
absolute zero. It follows therefore that upon the absolute
scale, the melting point of ice, and the boiling point of
water are 273° and 373° respectively. (See Fig. 124.)
The means employed to find the location of absolute
zero are of much interest. It has been observed that
when heated a gas tends to expand. If a measured volume
of air at 0°C. is cooled or heated 1°C., it changes its
volume 1/273, the pressure remaining the same. If it is
cooled 10° it loses 10/273, if cooled 100° it loses 100/273 and
so on. No matter how far it is cooled the same rate of
reduction continues as long as it remains in the gaseous
state. From these facts it is concluded that if the cooling
could be carried down 273° that the volume would be reduced
273/273 or that the volume of the gas would be
reduced to nothing. This is believed to mean that the
molecular motion constituting heat would cease rather
than that the matter composing the gas would disappear.
Scientists have been able to obtain temperatures of extreme
cold far down on the absolute scale. Liquid air
has a temperature of -292°F., or -180°C. or 93°A.
The lowest temperature thus far reported is 1.7°A.
or -271.3°C., obtained in 1911, by evaporating liquid
helium.
145. The Law of Charles.—The facts given in the last
paragraph mean that if 273 ccm. of a gas at 0°C. or 273°
A. are cooled 100°, or to -100°C., or 173°A., then it[Pg 166]
will lose 100/273 of its volume or have a volume of 173
ccm. If warmed 100°, or up to 100°C., or 373°A., it
will have a volume of 373 ccm. It follows then that in
every case the volume will correspond to its absolute
temperature, providing the pressure remains unchanged.
The expression of this fact in scientific language is called
the law of Charles. At a constant pressure the volume of a
given mass of gas is proportional to its absolute temperature.
Expressed mathematically, we have V1/V2 = T1/T2. Compare
the statement and mathematical expression of the laws of
Charles and Boyle.
The formulas for the laws of Boyle and Charles are
sometimes combined into one expression as follows:
or the product of the volume and pressure of a constant
mass of gas is proportional to its absolute temperature.
Important Topics
1. Heat units; calorie, British thermal unit.
2. Three thermometer scales, fixed points on each.
3. Absolute zero, how determined. Its value on each scale.
4. Law of Charles, its meaning. Combination of laws of Boyle
and Charles.
Exercises
1. Does ice melt at the same temperature at which water freezes?
Express the temperature of freezing water on the three thermometer
scales.
2. A comfortable room temperature is 68°F. What is this temperature
on the centigrade and absolute scales?
3. Change a temperature of 15°C. to F.; 15°F. to C.; -4°C. to F.;
-20°F. to C.
[Pg 167]
4. The temperature of the human body is 98.6°F. What is this
temperature on the absolute and centigrade scales?
5. The temperature of liquid air is -180°C. What is it on the
Fahrenheit scale?
6. Mercury is a solid at -40°F. What is this on the centigrade
scale?
7. How much heat will be required to raise the temperature of
8 lbs. of water 32°F.; 5 lbs. 10°F.?
 Fig. 125.—A clinical thermometer used to take the temperature of the
body.
Fig. 125.—A clinical thermometer used to take the temperature of the
body.
8. How much heat will be required to raise the temperature of
30 g. of water 43°C.; 20 g., 50°C.?
9. Compute the temperature of absolute zero on the Fahrenheit
scale.
10. Take three basins of water, one hot, one cold, and one lukewarm.
If one hand be placed in the hot water while the other is placed in
the cold and after a few minutes both are placed in the lukewarm
water, this water will feel cool to one hand and warm to
the other. Explain.
11. If 200 ccm. of air at 200° absolute is heated to 300°A. under
constant pressure, what volume will the air occupy at the latter
temperature?
12. How does one change a reading on the centigrade scale to a
corresponding reading on the absolute scale?
(3) Expansion of Liquids and Solids
146. Expansion of Gases.—The law of Charles is found
to apply to all gases. That is, all gases change in volume
in proportion to the change of temperature provided the
pressure remains constant. It is for this reason that we
have the gas thermometer (see Fig. 126) which gives in
skillful hands more accurate temperature readings than
the best mercurial thermometer. Galileo devised and
used the first air thermometer which consisted of a hollow[Pg 168]
bulb blown on a glass tube and inverted in a dish of water.
(See Fig. 1.) The water thermometer consists of a glass
bulb filled with water which rises into a tube attached to
the bulb. One disadvantage of the water thermometer
is its limited range since it cannot be used below 0° or
above 100°. Why?
147. Expansion of Liquids.—The expansion
of liquids differs from that of gases
in several important respects:
(a) Liquids have a smaller rate of expansion
than gases. The rate of expansion
per degree is called the Coefficient of Expansion.
For example, the coefficient of
expansion of a gas under constant pressure
at 0°C. is {1/273} of its volume per degree
centigrade.
(b) Different liquids expand at wholly
different rates, that is, their coefficients of
expansion differ widely. For example, the
coefficient of expansion of mercury is 0.00018
per degree centigrade, of glycerine 0.0005 per
degree centigrade, of petroleum 0.0009 per
degree centigrade.
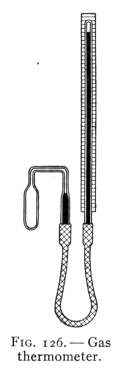 Fig. 126.—Gas
thermometer.
Fig. 126.—Gas
thermometer.
(c) The same liquid often has different coefficients of
expansion at different temperatures. Water between
5°C. and 6°C. has a coefficient expansion of 0.00002 per
degree centigrade, between 8° and 50° of 0.0006, between
99° and 100° of 0.00076. The coefficient of expansion of
mercury, however, is constant for a wide range of temperature
and, therefore, it is well adapted for use in
thermometers.
148. Peculiarity in the Expansion of Water.—Water
has a peculiar rate of expansion. This is illustrated by
the following experiment:
[Pg 169]
A test-tube filled with cold water is closed by a stopper containing
a small glass tube, the water extending up into the
small tube. (See Fig. 127.) The test-tube is placed in a freezing
mixture of salt and ice contained in a tumbler. As the water
cools, the level of the water in the small tube at first sinks. But
before the water freezes it rises again, showing that
after the water cools to a certain temperature that
expansion of the water occurs with further cooling.
Careful tests show that the water on cooling
contracts until it reaches 4°C. On cooling
below this temperature it expands. For this
reason, when the water of a lake or river
freezes, the coldest water is at the surface. On
account of this the ice forms at the top instead
of at the bottom. If water contracted as it
cooled to the freezing temperature the coldest
water would be at the bottom. Freezing
would begin at the bottom instead of at the
surface. Lakes and rivers would freeze solid.
In the summer only in shallow waters would all
the ice melt. The result would be that fish
and other aquatic life would be killed. Climate
would be so changed that the earth might
become uninhabitable. Since water is densest
at 4°C. all the water in a lake or river, when
it is covered with ice, is at 4°C. except that
near the surface.
 Fig. 127.—Apparatus
used in
testing the
expansion
of water.
Fig. 127.—Apparatus
used in
testing the
expansion
of water.
149. The Expansion Of Solids.—Most solids when
heated expand less than liquids and gases. Careful experiments
show that expansion is:
(a) Proportional to the change in temperature.
(b) Different in different solids.
Here are a few coefficients of linear (length)
expansion.
[Pg 170]
| Brass | 0.000018 per degree C. |
| Glass | 0.000009 per degree C. |
| Ice | 0.000052 per degree C. |
| Iron | 0.000012 per degree C. |
| Platinum | 0.000009 per degree C. |
| Zinc | 0.000027 per degree C. |
The coefficient of linear expansion is the fraction of its
length that a body expands when heated one degree.
The coefficient of cubical expansion is the fraction of its
volume that a body expands when heated one degree.
The expansion of solids is used or allowed for in many
cases:
a. Joints between the rails on a railroad allow for the
expansion of the rails in summer.
b. One end of a steel truss bridge is usually supported
on rollers so that it can expand and contract with changing
temperatures. (See Fig. 128.)
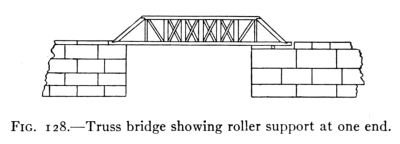 Fig. 128.—Truss bridge showing roller support at one end.
Fig. 128.—Truss bridge showing roller support at one end.
c. Suspension bridges have expansion joints where the
ends of the iron girders can move in or out of an expansion
joint thus making the bridge longer or shorter according
to the temperature.
d. Iron tires are heated, slipped on to wagon wheels
and then cooled, the contraction on cooling setting them
tightly in place.
e. Metallic thermometers depend upon the movement
due to the expansion of a coiled strip of metal which turns
a pointer on the dial of the instrument. (See Fig. 129.)
[Pg 171]
f. The wires that are fused into glass in incandescent
light bulbs must have the same coefficient of expansion
as the glass. Platinum has therefore been used for this
purpose. (See table above.)
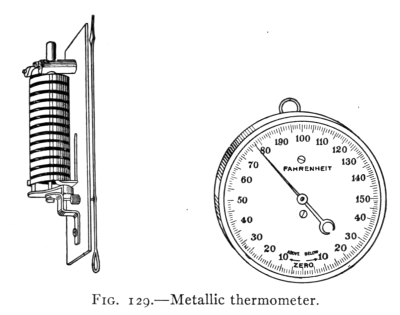 Fig. 129.—Metallic thermometer.
Fig. 129.—Metallic thermometer.
Important Topics
1. Expansion of Liquids; peculiarities. Anomalous expansion of
water and its results.
2. Expansion of solids; peculiarities, applications.
3. Coefficient of linear expansion.
4. Coefficient of cubical expansion.
Exercises
1. The gas within a partly inflated balloon has a volume of 1000
cu. ft. at a pressure of 74 cm., and a temperature of 15°C.
What will be the volume of the gas when its pressure is 37 cm.
and the temperature is -17°C.?
2. A man taking a full breath on the top of a mountain fourteen
thousand feet high inhales 4 liters of air, the pressure being 40
cm. What volume would this same mass of air have in a
place 600 ft. above sea-level when the barometer reads 75 cm.
and the temperature is the same as on the mountain top?
3. If the coefficient of linear expansion of iron is 0.000012 per[Pg 172]
degree C., how much will an iron bridge 1000 ft. long change
in length in warming from -20°C. on a winter day to 30°C.
upon a summer day.
4. What are some of the results that would follow in freezing
weather if water continually contracted on being cooled to
zero instead of beginning to expand when cooled below 4°C.?
5. Mention two instances that you have noticed of expansion
occurring when a body is heated?
6. Compare the density of air at 30°C. with that at 10°C. at the
same pressure. If both are present in a room, where will each
be found? Why?
7. Compare the density of water at 40°C. with that at 10°C. If
water at the two temperatures are in a tank, where will each be
found? Why?
8. If water at 0°C. and at 4°C. are both in a tank, where will
each be found? Why?
9. How much heat will be required to raise the temperature of a
cubic foot of water 10°F.?
10. How much heat will be required to raise the temperature of
4 liters of water 25°C.?
11. How much longer would the cables of the Brooklyn suspension
bridge be on a summer's day when the temperature is 30°C.
than in winter at -20°C., the length of cable between the supports
being about 1600 ft.
12. If 25 liters of air at -23°C. is warmed to 77°C. under constant
pressure, what will be the resulting volume of air? Explain.
13. White pig iron melts at about 2000°F. Express this temperature
upon the centigrade and absolute scales.
14. If 200 ccm. of air at 76 cm. pressure and 27°C. temperature be
heated to 127°C. at a pressure of 38 cm. what will be the resulting
volume?
15. A balloon contains 10,000 cu. ft. of gas at 75.2 cm. pressure and
24°C. It ascends until the pressure is 18 cm. and the temperature
is -10°C. What is the volume of gas it then contains.
16. A gas holder contains 50 "cu. ft." of gas at a pressure of one
atmosphere and 62°F. How much gas will it hold at 10 atmospheres
and 32°F.
17. One thousand "cubic feet" of illuminating gas has what volume
with 75 lbs. pressure and temperature of 10°C.
18. Define a "cubic foot" of illuminating gas.
[Pg 173]
150. Methods of Transmitting Heat.—One of the most
practical benefits of the study of heat is clearer understanding
of the different methods by which heat is transferred
from one place to another and an intelligent idea
of the means employed to prevent the transfer of
heat.
It should be definitely understood at the beginning that
cold signifies the absence of heat, just as darkness implies the
absence of light, so when one speaks of cold getting into a
house what is really meant is either the entrance of cold
air by some opening or else the escape of the heat.
There are three distinct methods by which heat energy
is transferred from one place to another, depending upon
the medium or substance that transfers the heat.
a. A solid transmits heat by the method called conduction.
b. A fluid, either a liquid or a gas, transmits heat
mainly by the method called convection.
c. Space transmits the energy of hot objects by the
method called radiation.
 Fig. 130.—Solids conduct heat.
Fig. 130.—Solids conduct heat.
151. Conduction.—To illustrate
conduction, place in a gas flame the
ends of same metal wires supported
as in Fig. 130. In a short time the
other ends of the wires become hot
enough to burn one's hand. This
may be explained as follows: The
hot gas flame contains molecules in
violent vibration and those striking
the wire set its molecules rapidly
vibrating. Since, in a solid, the molecules are held in the
same relative positions, when one end of a wire is heated the
rapidly vibrating molecules at the hot end set their neighbors
vibrating and these the next in turn and so on until the[Pg 174]
whole wire is hot. It is a fortunate circumstance that
different substances have different rates of conductivity
for heat. To realize this, suppose that our clothing were
as good a conductor as iron, clothing would then be very
uncomfortable both in hot and in
cold weather. The best conductors
for heat are metals. It is
interesting to note that, as a rule
good conductors of heat are also
good conductors of electricity,
while poor conductors of heat are
also poor electric conductors.
Careful experiments in testing the
rate that heat will be conducted
through different substances show
the following rates of conductivity.
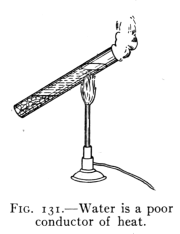 Fig. 131.—Water is a poor
conductor of heat.
Fig. 131.—Water is a poor
conductor of heat.
These figures are averages taken mainly from the
Smithsonian Physical Tables:
| Silver | 100 |
| Copper | 74 |
| Aluminum | 35 |
| Brass | 27 |
| Zinc | 26 |
| Iron | 15 |
| Tin | 14.7 |
| German silver | 8.4 |
| Mercury | 1.7 |
| Granite | 0.53 |
| Limestone | 0.52 |
| Ice | 0.5 |
| Glass | 0.2 |
| Water | 0.124 |
| Pine, with grain | 0.03 |
| Pine, across grain | 0.01 |
| Felt | 0.008 |
| Air | 0.005 |
To test the conductivity of liquids, take a test-tube
nearly full of cold water, hold the lower end in the hand
while the tube is inclined so that the upper end is heated
by a gas flame until the water boils. The lower end will
be found to remain cold. (See Fig. 131.) Careful measurements
of the conductivity of water show that heat is
transmitted through it only {1/800} as rapidly as in silver,
while air conducts but {1/25} as rapidly as water.
[Pg 175]
 Fig. 132.—Wall construction of a refrigerator. 1, Porcelain enamel
lining lock joint; 2, inside wood lining; 3, 3-ply red rope waterproof paper;
4, wool felt deafening paper; 5, flaxlinum insulation; 6, dead air space;
7, flaxlinum insulation; 8, wool felt deafening paper; 9, 3-ply red rope
waterproof paper; 10, outside wood case.
Fig. 132.—Wall construction of a refrigerator. 1, Porcelain enamel
lining lock joint; 2, inside wood lining; 3, 3-ply red rope waterproof paper;
4, wool felt deafening paper; 5, flaxlinum insulation; 6, dead air space;
7, flaxlinum insulation; 8, wool felt deafening paper; 9, 3-ply red rope
waterproof paper; 10, outside wood case.
Fig. 133.—Sectional view of a Thermos bottle.
152. Non-conductors and Their Uses.—Many solids,
however, are poor conductors, as leather, fur, felt, and
woolen cloth. These substances owe their non-conductivity
mainly to the fact that
they are porous. The air
which fills the minute spaces
of these substances is one of
the poorest conductors known
and hinders the transfer of
heat through these solids. For the same reason loosely
packed snow is a protection to vegetation covered by it
during a period of severe cold in winter. The efficiency[Pg 176]
of storm sash or double windows, and of the double and
triple walls of ice-houses and refrigerators (see Fig. 132)
in preventing the conduction of heat is also largely due
to the poor conductivity of the air confined in the spaces
between the walls. To prevent the circulation of the air,
sawdust, charcoal, and other porous material is often
loosely packed into the space between the walls of such
structure.
Other illustrations of effective non-conductors will occur
to every one; such as woolen clothing, wooden handles for
hot objects, and the packing used in fireless cookers. A
Thermos bottle is effective as a non-conductor of heat because
the space between the double walls has the air exhausted
from it (Figs. 133 and 134).
Of several objects in a cold room, some feel much colder
to the touch than others, thus iron, marble, oil cloth, and
earthenware will feel colder than woolen
cloth, carpet, feathers, or paper. The first
four objects feel cold because they are conductors,
and conduct the heat away from the
hand rapidly. The other substances named
are non-conductors and hence remove heat
from the hand less rapidly, and therefore
do not feel so cold. In a similar way, if
several hot objects are touched by the hand,
the good conductors are the ones which will
burn one most quickly by conducting heat
rapidly to the hand. The non-conductors,
however, will rarely burn one. Why are
the handles of hot utensils often made of non-conducting
materials such as wood, cloth, asbestos, etc.?
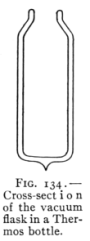 Fig. 134.—Cross-section
of the vacuum
flask in a Thermos
bottle.
Fig. 134.—Cross-section
of the vacuum
flask in a Thermos
bottle.
153. Radiation is the method by which heat comes to
us from the sun across space containing no tangible matter.
It is also the method by which heat gets to us when we[Pg 177]
stand near a fire. Everyone has noticed that this heat is
cut off by holding an object between the person and the
fire. This fact indicates that radiant heat travels in
straight lines.
The radiation of heat is believed to be accomplished by
means of waves in a medium called ether, which is invisible
and yet pervades everything. Three of the most important
characteristics of radiation are first, heat is transferred
by radiation with the speed of light, or 186,000 miles per
second. This fact is shown by the cutting off of both
the sun's heat and light at the same instant during an
eclipse of the sun. Second, radiant heat[I] travels in straight
lines, while other modes of transferring heat may follow
irregular paths. The straight line motion of radiant heat
is shown by its being cut off where a screen is placed between
the source of heat and the object sheltered. Third,
radiant heat may pass through an object without heating it.
This is shown by the coldness of the upper layers of the
atmosphere and also by the fact that a pane of glass may
not be heated appreciably by the heat and light from the
sun which passes through it.
When radiant energy falls upon any object it may be
(a) reflected at the surface of the object, (b) transmitted
through the substance, (c), absorbed. All three of these
effects occur in different degrees with different portions
of the radiation. Well-polished surfaces are good reflectors.
Rough and blackened surfaces are good absorbers. Transparent
objects are those which transmit light well, but
even they absorb some of the energy.
154. The Radiometer.—Radiant heat may be detected
by means of the radiometer (Fig. 135). This consists of
a glass bulb from which the air has been nearly exhausted.[Pg 178]
Within it is a wheel with four vanes of mica or of aluminum
mounted on a vertical axis. One side of each vane is
covered with lampblack, the other being highly polished.
when exposed to radiant heat from any source the vanes
revolve with the bright side in advance.
The bulb is so nearly exhausted of air
that a single molecule remaining may travel
from the walls of the bulb to the vanes
without coming in contact with another
molecule.
The blackened sides absorb more heat
than the highly polished sides. The air
molecules striking these blackened sides receive
more heat and so rebound with
greater velocity than from the other side,
thus exerting greater pressure. The blackened
sides therefore are driven backward.
If the air were not so rarified the air
molecules would hit each other so frequently
as to equalize the pressure and there would be no
motion.
 Fig. 135.—A
radiometer.
Fig. 135.—A
radiometer.
Sun's Radiation.—Accurate tests of the amount of the
sun's radiation received upon a square centimeter of the
earth's surface perpendicular to the sun's rays were made
at Mt. Wilson in 1913. The average of 690 observations
gave a value of 1.933 calories per minute. These results
indicate that the sun's radiation per square centimeter is
sufficient to warm 1 g. of water 1.933°C. each minute.
Although the nature of radiation is not discussed until
Art. 408-411 in light, it should be said here that all bodies
are radiating heat waves at all temperatures, the heat
waves from cool bodies being much longer than those from
hot bodies. Glass allows the short luminous waves to
pass through freely but the longer heat waves from objects[Pg 179]
at the room temperature pass through with difficulty.
This is the reason why glass is used in the covering of
greenhouses and hot beds. Water also absorbs many of
the longer heat waves. It is therefore used in stereopticons
to prevent delicate lantern slides from being injured
by overheating.
Important Topics
1. Conduction in solids, liquids, gases.
2. Non-conductors; uses, best non-conductors.
3. Radiation, three characteristics.
4. The sun's radiation, amount. The radiometer.
Exercises
1. Does clothing ever afford us heat in winter? How then does
it keep us warm?
2. Why are plants often covered with paper on a night when
frost is expected?
3. Will frost form in the fall of the year sooner on a wooden or
a cement sidewalk? Why? On which does ice remain longer?
Why?
4. Why in freezing ice-cream do we put the ice in a wooden pail
and the cream in a tin one?
5. Is iron better than brick or porcelain as a material for stoves?
Explain.
6. Which is better, a good or a poor conductor for keeping a
body warm? for keeping a body cool?
7. Should the bottom of a teakettle be polished? Explain.
8. How are safes made fireproof?
9. Explain the principle of the Thermos bottle.
10. Explain why the coiled wire handles of some objects as stove-lid
lifters, oven doors, etc., do not get hot.
(5) Transmission of Heat in Fluids. Heating
and Ventilation
155. Convection.—While fluids are poor conductors,
they may transmit heat more effectively than solids by
the mode called convection. To illustrate: if heat is[Pg 180]
applied at the top of a test-tube of water, the hot water
being lighter is found at the top, while at the bottom the
water remains cold. On the other hand, if heat is applied
at the bottom of the vessel, as soon as the water at the bottom
is warmed (above 4°C.) it expands, becomes lighter
and is pushed up to the top by the colder, denser water
about it. This circulation of
water continues as long as heat
is applied below, until all of the
water is brought to the boiling
temperature. (See Fig. 136.)
When a liquid or a gas is
heated in the manner just
described, the heat is said to
be transferred by convection.
Thus the air in the lower part
of a room may receive heat by
conduction from a stove or
radiator. As it expands on
being warmed, it is pushed up
by the colder denser air about
it, which takes its place, thus
creating a circulation of the air
in the room. (See Fig. 137.)
The heated currents of air give
up their heat to the objects in the room as the circulation
continues. These air currents may be observed readily
by using the smoke from burning "touch paper" (unglazed
paper that has been dipped into a solution of potassium
nitrate ["saltpeter"] and dried).
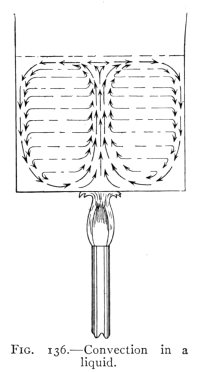 Fig. 136.—Convection in a
liquid.
Fig. 136.—Convection in a
liquid.
156. Draft of a Chimney.—When a fire is started in a
stove or a furnace the air above the fire becomes heated,
expands, and therefore is less dense than it was before.
This warm air and the heated gases which are the products[Pg 181]
of the combustion of the fuel weigh less than an equal
volume of the colder air outside. Therefore they are
pushed upward by a force equal to the difference between
their weight and the weight of an equal volume of the
colder air.
The chimney soon becomes filled with these heated
gases. (See Fig. 138.) These are pushed upward by the
pressure of the colder, denser air, because this colder air
is pulled downward more strongly by the force of gravity
than are the heated gases in the chimney.
Other things being equal, the taller the chimney, the
greater the draft, because there is a greater difference
between the weight of the gases inside and the weight of
an equal volume of outside air.
 Fig. 137.—Convection currents in a room.
Fig. 137.—Convection currents in a room.
Fig. 138.—Fire place
showing draft of a
chimney.
157. Convection Currents in Nature.—Winds are produced
by differences in the pressure or density of the air,
the movement being from places of high toward places of
low pressure. One of the causes of a difference in density[Pg 182]
of the air is a difference in temperature. This is illustrated
by what are called the land and sea breezes along the
sea shore or large lakes. During the day, the temperature
of the land becomes higher than that of the sea. The air
over the land expands and being lighter is moved back and
upward by the colder, denser air from the sea or lake.
This constitutes the sea breezes (Fig. 139). At night the
land becomes cooler much sooner than the sea and the
current is reversed causing the land breeze. (See Fig. 140.)
 Fig. 139.—Sea breeze.
Fig. 139.—Sea breeze.
Fig. 140.—Land breeze.
The trade winds are convection currents moving toward
the hot equatorial belt from both the north and the south.
In the hot belt the air rises and the upper air flows back
to the north and the south. This region of ascending
currents of air is a region of heavy rainfall, since the saturated
air rises to cool altitudes where its moisture is condensed.
The ocean currents are also convection currents.
Their motion is due to prevailing winds, differences in
density due to evaporation and freezing, and to the rotation
of the earth, as well as to changes in temperature.
158. The heating and ventilation of buildings and the
problems connected therewith are matters of serious concern
to all who live in winter in the temperate zone. Not
only should the air in living rooms be comfortably heated,
but it should be continually changed especially in the
crowded rooms of public buildings, as those of schools,
churches, and assembly halls, so that each person may be
supplied with 30 or more cubic feet of fresh air per minute.
In the colonial days, the open fire place afforded the ordinary[Pg 183]
means for heating rooms. This heated the room
mainly by radiation. It was wasteful as most of the heat
passed up the chimney. This mode of heating secured
ample ventilation. Fire places are sometimes built in
modern homes as an aid to ventilation.
Benjamin Franklin seeing the waste of heat in the open
fire places devised an iron box to contain the fire. This
was placed in the room and provided heat by conduction,
convection, and radiation. It was called Franklin's
stove and in many forms is still commonly used. It saves
a large part of the heat produced by burning the fuel and
some ventilation is provided by its draft.
 Fig. 141.—Heating and ventilating by means of a hot-air furnace.
Fig. 141.—Heating and ventilating by means of a hot-air furnace.
159. Heating by Hot Air.—The presence of stoves in
living rooms of homes is accompanied by the annoyance of
scattered fuel, dust, ashes, smoke, etc. One attempt to
remove this inconvenience led to placing a large stove or
fire box in the basement or cellar, surrounding this with a
jacket to provide a space for heating air which is then
conducted by pipes to the rooms above. This device is
called the hot-air furnace. (See Fig. 141.) The heated[Pg 184]
air rises because it is pushed up by colder, denser air which
enters through the cold-air pipes. The hot-air furnace
provides a good circulation of warm air and also ventilation,
provided some cold air is admitted to the furnace from
the outside. One objection to its use is that it may not
heat a building evenly, one part being very hot while
another may be cool. To provide even and sufficient
heat throughout a large building, use is made of hot water
or steam heating.
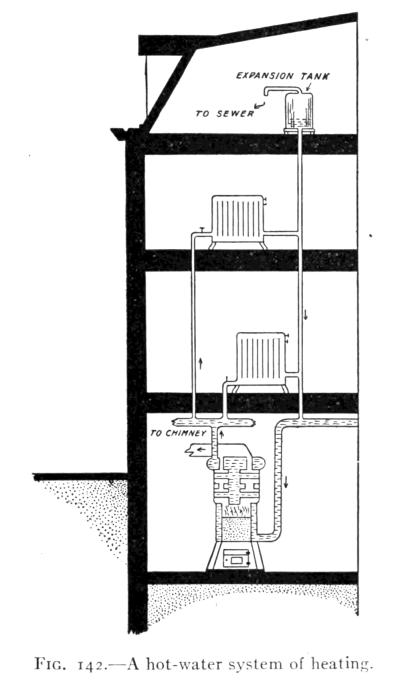 Fig. 142.—A hot-water system of heating.
Fig. 142.—A hot-water system of heating.
[Pg 185]
[Pg 186]
160. Hot-water Heating.—In hot-water heating a furnace
arranged for heating water is placed in the basement.
(See Fig. 142.) Attached to the top of the heater are pipes
leading to the radiators in the various rooms; other pipes
connect the radiators to the bottom of the boiler. The
heater, pipes, and radiators are all filled with water before
the fire is started. When the water is warmed, it expands
and is pushed up through the pipes by the colder water in
the return pipe. The circulation continuing brings hot
water to the radiator while the cooled water returns to the
heater, the hot radiators heating the several rooms.
161. Steam Heating.—In steam heating a steam boiler
is connected to radiators by pipes. (See Fig. 143.) The
steam drives the air out of the pipes and radiators and
serves as an efficient source of heat. Heating by steam is
quicker than heating with hot water. It is therefore preferred
where quick, efficient heating is required. Hot
water is less intense
and more economical
in mild weather and
is often used in private
homes.
 Fig. 144.—Heating by an indirect radiator
with side-wall register.
Fig. 144.—Heating by an indirect radiator
with side-wall register.
162. Direct and
Indirect Heating.—In
heating by direct
radiation (Figs. 142,
143), the steam or
hot-water radiators
are placed in the rooms to be heated. With direct
radiation, ventilation must be provided by special means,
such as opening windows, doors, and ventilators. Sometimes
radiators are placed in a box or room in the basement.
Air from out of doors is then driven by a fan
over and about the hot radiators. The air thus heated[Pg 187]
is conducted by pipes to the several rooms. This arrangement
is called indirect
heating. (See Fig. 144.) The
latter method, it may be observed,
provides both heat and
ventilation, and hence is often
used in schools, churches, court
houses, and stores. Since heated
air, especially in cold weather,
has a low relative humidity some
means of moistening the air of
living rooms should be provided.
Air when too dry is
injurious to the health and
also to furniture and wood
work. The excessive drying of wood and glue in a piece
of furniture often causes it to fall apart.
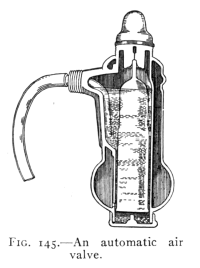 Fig. 145.—An automatic air
valve.
Fig. 145.—An automatic air
valve.
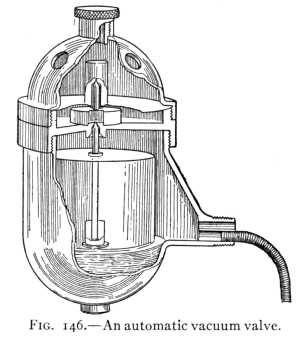 Fig. 146.—An automatic vacuum valve.
Fig. 146.—An automatic vacuum valve.
163. Vacuum Steam Heating.—In steam heating, air
valves (Fig. 145) are
placed on the radiators
to allow the
air they contain to
escape when the
steam is turned on.
When all the air is
driven out the valve
closes. Automatic
vacuum valves (Fig.
146) are sometimes
used. When the fire
is low and there is no
steam pressure in the
radiators the pressure
of the air closes the valve, making a partial vacuum[Pg 188]
inside. The boiling point of water falls as the pressure
upon it is reduced. As water will not boil under ordinary
atmospheric pressure until its temperature is 100°C.
(212°F.), it follows that by the use of vacuum systems,
often called vapor systems, of steam heating, water will be
giving off hot vapor even after the fire has been banked for
hours. This results in a considerable saving of fuel.
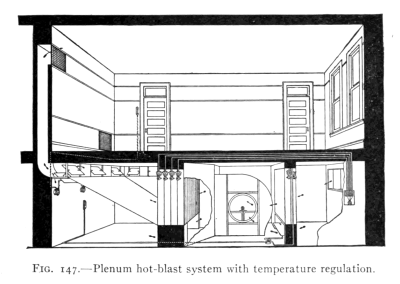 Fig. 147.—Plenum hot-blast system with temperature regulation.
Fig. 147.—Plenum hot-blast system with temperature regulation.
164. The Plenum System of Heating.—In the plenum
system of heating (see Fig. 147) fresh air is drawn through
a window from outdoors and goes first through tempering
coils where the temperature is raised to about 70°. The
fan then forces some of the air through heating coils,
where it is reheated and raised to a much higher temperature,
depending upon the weather conditions. Both
the hot and tempered air are kept under pressure by the
fan in the plenum room and are forced from this room
through galvanized iron ducts to the various rooms to be[Pg 189]
heated. The foul air is forced out of the room through
vent ducts which lead to the attic where it escapes through
ventilators in the roof.
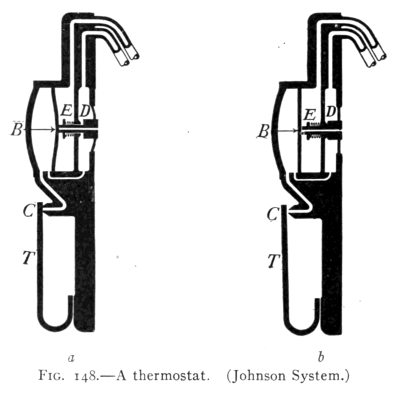 Fig. 148.—A thermostat. (Johnson System.)
Fig. 148.—A thermostat. (Johnson System.)
A thermostat is placed in the tempered-air part of the
plenum room to maintain the proper temperature of the
tempered air. This thermostat operates the by-pass
damper under the tempering coils, and sometimes the
valves on the coils. The mixing dampers at the base
of the galvanized-iron ducts are controlled by their respective
room thermostats. Attic-vent, fresh-air, and
return-air dampers are under pneumatic switch control.
A humidifier can be provided readily for this system.
This system of heating is designed particularly for school
houses where adequate ventilation is a necessity.
165. The Thermostat.—One of the many examples of
the expansion of metals is shown in one form of the thermostat
(Fig. 148) in which two pieces of different metals[Pg 190]
and of unequal rates of expansion, as brass and iron, are
securely fastened together.
The thermostatic strip T moving inward and outward,
as affected by the room temperature, varies the amount of
air which can escape through the small port C. When the
port C is completely closed (Fig. 148a) the full air pressure
collects on the diaphragm B which forces down the main
valve, letting the compressed air from the main pass
through the chamber D into chamber E as the valve is
forced off its seat. The air from chamber E then passes
into the branch to operate the damper.
When port C is fully open (Fig. 148b) the air pressure
on diaphragm B is relieved, the back pressure in E lifts
up the diaphragm and the air from the branch escapes out
through the hollow stem of the main valve, operating the
damper in the opposite direction from that when C is
closed.
Important Topics
1. Transmission of heat in fluids.
2. Convection. Drafts of a chimney. Land and sea breezes.
3. Heating and ventilation of buildings.
(a) By hot air.
(b) Hot-water heating.
(c) Steam heating.
(d) Direct and indirect heating.
(e) Vacuum steam heating.
(f) The plenum system.
(g) The thermostat.
Exercises
1. Is a room heated mainly by conduction, convection, or radiation,
from (a) a stove, (b) a hot-air furnace, (c) a steam radiator?
2. Name three natural convection currents.
3. Explain the draft of a chimney. What is it? Why does it
occur?
[Pg 191]
4. Make a cross-section sketch of your living room and indicate
the convection currents by which the room is heated. Explain
the heating of the room.
5. Make a sketch showing how the water in the hot-water tank
in the kitchen or laundry is heated. Explain your sketch,
indicating convection currents.
6. Is it economical to keep stoves and radiators highly polished?
Explain.
7. If you open the door between a warm and a cool room what will
be the direction of the air currents at the top and at the bottom
of the door? Explain.
8. If a hot-water heating system contains 100 cu. ft. of water
how much heat will be required to raise its temperature 150°F.?
9. Why does a tall chimney give a better draft than a short one?
10. Explain how your school room is heated and ventilated.
11. Should a steam or hot-water radiator be placed near the floor
or near the ceiling of a room? Why?
12. In a hot-water heating system an open tank connected with the
pipes is placed in the attic or above the highest radiator.
Explain its use.
(6) The Moisture in the Atmosphere,
Hygrometry
166. Water Vapor in the Air.—The amount of water
vapor present in the air has a marked effect upon the
weather and the climate of a locality. The study of the
moisture conditions of the atmosphere, or hygrometry,
is therefore a matter of general interest and importance.
The water vapor in the atmosphere is entirely due to
evaporation from bodies of water, or snow, or ice. In the
discussion of evaporation, it is described as due to the
gradual escape of molecules into the air from the surface
of a liquid. This description fits exactly the conditions
found by all careful observers. Since the air molecules
are continually striking the surface of the liquid, many of
them penetrate it and become absorbed. In the same
manner many vapor molecules reenter the liquid, and if[Pg 192]
enough vapor molecules are present in the air so that as
many vapor molecules reenter the liquid each second as
leave it, the space above the liquid is said to be saturated
as previously described. (See Art. 18.)
167. Conditions for Saturation.—If a liquid is evaporating
into a vacuum, the molecules on leaving find no
opposition until they reach the limits of the vessel containing
the vacuum. Evaporation under these conditions
goes on with great rapidity and the space becomes saturated
almost instantly. If, however, air be present at
ordinary pressure, many of the ordinary water vapor
molecules on leaving are struck and returned to the water
by the air molecules directly above. Those escaping
gradually work their way upward through the air. This
explains why it is that our atmosphere is not often saturated
even near large bodies of water, the retarding
effect of the air upon the evaporation preventing more
than the layers of air near the water surface becoming
saturated.
Just as the amount of salt that can be held in solution
in a liquid is lessened by cooling the solution (Art. 26), so
the amount of water vapor that can be held in the air is
lessened by lowering its temperature. If air not moist
enough to be saturated with water vapor is cooled, it will,
as the cooling continues, finally reach a temperature at
which it will be saturated or will contain all the water
vapor it can hold at this temperature. If the air be still
further cooled some of the water vapor will condense and
may form fog, dew, rain, snow, etc., the form it takes
depending upon where and how the cooling takes place.
168. The Formation of Dew.—If the cooling of the
atmosphere is at the surface of some cold object which
lowers the temperature of the air below its saturation
point, some of its moisture condenses and collects upon the[Pg 193]
cold surface as dew. This may be noticed upon the surface
of a pitcher of ice-water in summer. At night, the temperature
of grass and other objects near or on the ground
may fall much faster than that of the atmosphere owing to
the radiation of heat from these objects. If the temperature
falls below the saturation point, dew will be formed.
This natural radiation is hindered when it is cloudy, therefore
little dew forms on cloudy nights. Clear nights help
radiation, therefore we have the most dew on nights when
the sky is clear. If the temperature is below freezing,
frost forms instead of dew.
169. Formation of Fog.—If the cooling at night is great
enough to cool the body of air near the earth below the
saturation temperature, then not only may dew be formed,
but some moisture is condensed in the air itself, usually
upon fine dust particles suspended in it. This constitutes
a fog. If the cooling of the body of air takes place above
the earth's surface as when a warm moist current of air
enters a colder region, e.g., moves over the top of a cold
mountain, or into the upper air, then as this air is cooled
below its saturation point, condensation upon fine suspended
dust particles takes place, and a cloud is formed.
If much moisture is present in the cloud, the drops of
water grow in size until they begin to fall and rain results;
or if it is cold enough, instead of rain, snowflakes will be
formed and fall. Sometimes whirling winds in severe
thunderstorms carry the raindrops into colder and then
warmer regions, alternately freezing and moistening the
drops or bits of ice. It is in this way that hail is said to be
formed.
170. The Dew Point.—The temperature to which air
must be cooled to saturate it or the temperature at which
condensation begins is called the dew point. This is often
determined in the laboratory by partly filling a polished[Pg 194]
metal vessel with water and cooling the water by adding
ice until a thin film of moisture is formed upon the outer
surface. The temperature of the surface when the moisture
first forms is the dew point.
171. The Humidity of the Atmosphere.—After the dew
point has been obtained, one may compute the relative
humidity or degree of saturation of the atmosphere, from the
table given below. This is defined as the ratio of the
amount of water vapor present in the air to the amount that
would be present if the air were saturated at the same
temperature.
For example, if the dew point is 5°C. and the temperature of
the air is 22°C., we find the densities of the water vapor at the two
temperatures, and find their ratio: 6.8/19.3 = 35 per cent. nearly.
Determinations of humidity may give indication of rain or frost and
are regularly made at weather bureau stations. They are also
made in buildings such as greenhouses, hospitals, and schoolhouses
to see if the air is moist enough. For the most healthful conditions
the relative humidity should be from 40 per cent. to 50 per cent.
Weight of Water (w) in Grams Contained in 1 Cubic Meter of
Saturated Air at Various Temperatures (t°)C.
| t°C. | w |
| -10 | 2.1 |
| - 9 | 2.4 |
| - 8 | 2.7 |
| - 7 | 3.0 |
| - 6 | 3.2 |
| - 5 | 3.5 |
| - 4 | 3.8 |
| - 3 | 4.1 |
| - 2 | 4.4 |
| - 1 | 4.6 |
| 0 | 4.9 |
| 1 | 5.2 |
| 2 | 5.6 |
| 3 | 6.0 |
| 4 | 6.4 |
| 5 | 6.8 |
| 6 | 7.3 |
| 7 | 7.7 |
| 8 | 8.1 |
| 9 | 8.8 |
| 10 | 9.4 |
| 11 | 10.0 |
| 12 | 10.6 |
| 13 | 11.3 |
| 14 | 12.0 |
| 15 | 12.8 |
| 16 | 13.6 |
| 17 | 14.5 |
| 18 | 15.1 |
| 19 | 16.2 |
| 20 | 17.2 |
| 21 | 18.2 |
| 22 | 19.3 |
| 23 | 20.4 |
| 24 | 21.5 |
| 25 | 22.9 |
| 26 | 24.2 |
| 27 | 25.6 |
| 28 | 27.0 |
| 29 | 28.6 |
| 30 | 30.1 |
172. Wet and Dry Bulb Hygrometer.—A device for
indicating the relative humidity of the air is called an[Pg 195]
hygrometer. There are various forms. The wet and dry
bulb hygrometer is shown in Fig. 149. This device consists
of two thermometers, one with its bulb dry and exposed
to the air, the other bulb being kept continually
moist by a wick dipping into a vessel of water. An
application of the principle of cooling by evaporation is
made in this instrument. Unless the air is saturated so
that evaporation is prevented,
the wet-bulb thermometer
shows a lower temperature, the
difference depending upon the
amount of moisture in the air,
or upon the relative humidity.
Most determinations of relative
humidity are made with this kind of instrument. It is
necessary in order to make an accurate determination,
to fan or set the air in motion about the thermometers
for some time before reading them. The relative humidity
is then found by using tables giving the relative humidity
that corresponds to any reading of the thermometers.
 Fig. 149.—Wet and dry bulb
hygrometer.
Fig. 149.—Wet and dry bulb
hygrometer.
Fig. 150.—A dial hygrometer.
A form of hygrometer in common use is shown in Fig. 150. In
this device, a thin strip of hygroscopic material (as a piece of goose
quill) is formed into a spiral coil. One end of this is fastened to a
post. The other end carried a hand or pointer. The latter moves[Pg 196]
over a printed scale and indicates directly the relative humidity.
Its indications should be tested by comparing its readings with the
results of dew-point determinations. The position of the pointer
may be adjusted by turning the post.
Important Topics
1. Water vapor in the air. Cause and effect.
2. Formation of dew, fog, rain, and snow.
3. Dew point, relative humidity.
4. Use of the dry- and wet-bulb hygrometer. Goose-quill
hygrometer.
Exercises
1. How is the relative humidity of the air affected by warming it?
Explain.
2. How does the white cloud of steam seen about a locomotive in
cold weather differ from fog? Explain.
3. In cold weather is the relative humidity of air out of doors
and indoors the same? Explain.
4. Compare the relative humidity of air in a desert and near the
ocean.
5. Look up the derivation of the term "hygrometer." Give the
use of the instrument.
6. Find the relative humidity of air at 20°C. if its dew point is
at 10°C.
7. How may the relative humidity of the air in a home be increased?
8. What is the effect of high humidity in the summer upon human
beings? How do you explain this?
9. Does dew fall? Explain how dew is formed?
10. In what respects is a cloud similar to a fog? In what respects
different?
11. Why are icebergs frequently enveloped in fog?
12. Does dew form in the day time? Explain.
(7) Evaporation
173. Effects of Evaporation.—In Art. 19 the cooling
effect of evaporation is mentioned and some explanation
is made of the cooling effect observed. Since evaporation
is employed in so many ways, and since its action is simply
explained by the study we have made of molecular motions[Pg 197]
and molecular forces, it may be well to consider this
subject further.
Take three shallow dishes, and place in one a little water, in
another some alcohol, and some ether in the third, the liquids being
taken from bottles that have stood several hours in the room so
that all are at the same temperature. After a short time take the
temperature of the three liquids. Each will be at a lower temperature
than at first, but of the three the ether will be found to be
the coolest, alcohol next, and the water nearest its first temperature.
It will be noticed also that the ether has evaporated most in the
same time. Similar effects may be observed by placing a few drops
of each of these three liquids upon the back of one's hand, or by
placing a few drops in turn upon the bulb of a simple air thermometer.
174. Cooling Effect of Evaporation.—The molecules
that leave an evaporating liquid are naturally the swiftest
moving ones, that is, the ones having the highest temperature,
so their escape leaves the liquids cooler than before,
and the one whose molecules leave fastest is naturally the
one that becomes coldest, that is, the ether, in the experiment
of Art. 173. If no air pressure were exerted upon
the surface of the liquid, the escape of the molecules would
be much increased and the temperature of the liquid
would be lowered rapidly.
To test this, fill a thin watch glass with ether and place it over a
thin slip of glass with a drop of cold water between the two. Now
place this apparatus under the receiver of an air pump and exhaust
the air. The rapid evaporation of the ether so lowers its temperature,
that often the drop of water is frozen. The lowest temperatures
are obtained by evaporating liquids at reduced pressure.
Onnes by evaporating liquid helium at a pressure of
about 1.2 mm. reached the lowest temperature yet attained, -456°F.,
or -271.3°C.
If four thermometers are taken, the bulbs of three being wetted
respectively with ether, alcohol, and water the fourth being dry, on
vigorously fanning these, the moistened thermometers show that
they have been cooled while the dry one is unaffected.
[Pg 198]
This indicates that fanning a dry body at the temperature
of the air does not change its temperature. Fanning
does increase evaporation by removing the air containing
the evaporated molecules near the surface of the liquid
so that unsaturated air is continually over the liquid. If
a pint of water is placed in a bottle and another pint in a
wide pan the latter will become dry much sooner because
of the greater surface over which evaporation can take
place. Application of this is made at salt works where
the brine is spread out in shallow pans.
175. Rate of Evaporation.—The rate of evaporation is
affected by several factors. These have been illustrated
in the preceding paragraphs. To briefly summarize:
The rate of evaporation of a liquid is affected by—
(a) The nature of the liquid.
(b) The temperature of the liquid.
(c) The pressure upon its evaporating surface.
(d) The degree of saturation of the space into which
the liquid is evaporating.
(e) The rate of circulation of air over its surface.
(f) The extent of surface exposed to evaporation.
176. Molecular Motion in Solids.—Evidence of molecular
motion in liquids is given by expansion on heating,
evaporation, and diffusion. Do any of these lines of
evidence apply to solids? It is a fact of common experience
that solids do become larger on heating. Spaces
are left between the ends of rails on railroads so that
when they expand in summer they will not distort the
track. Iron tires are placed on wheels by heating them
until they slip on easily. Then on cooling, the iron shrinks
and presses the wheel tightly. Many common demonstrations
of expansion are found in lecture rooms. The
fact of the evaporation of a solid is often detected by noticing
the odor of a substance. The odor of moth balls is[Pg 199]
one example. Camphor also evaporates. Heated tin has
a characteristic odor noted by many. Ice and snow
disappear in winter even though the temperature is below
freezing. Wet clothes, "freeze dry," that is, dry after
freezing, by evaporation. A few crystals of iodine placed
in a test-tube and gently heated form a vapor easily seen,
even though none of the iodine melts. Where the vapor
strikes the side of the tube, it condenses back to dark gray
crystals of iodine. This change from solid directly to gas
and back again without becoming liquid is called sublimation.
A number of solids are purified by this process.
Important Topics
1. Cooling effect of evaporation, rate of evaporation affected by
six conditions.
2. Effects of molecular motion in solids: (a) Expansion, (b) Evaporation,
(c) Sublimation.
Exercises
1. Does sprinkling the streets or sidewalks cool the air? Why?
2. Give an illustration for each of the factors affecting evaporation.
3. Give an illustration for each of the three evidences of molecular
motions in solids.
4. Since three-quarters of the earth's surface is covered with water,
why is not the air constantly saturated?
5. If the air has the temperature of the body, will fanning the
perfectly dry face cool one? Explain. Will the effect be the
same if the face is moist? Explain.
6. What is the cause of "Cloud Capped" mountains?
7. Why does the exhaust steam from an engine appear to have so
much greater volume on a cold day in winter than on a warm one
in summer?
8. What causes an unfrozen pond or lake to "steam" on a very
cold day in winter, or on a very cool morning in summer?
9. As the air on a mountain top settles down the sides to places
of greater pressure, how will its temperature be affected? its
relative humidity? Explain.
10. On our Pacific coast, moist winds blow from the west over the
mountains. Where will it rain? Where be dry? Explain.
[Pg 200]
HEAT AND WORK
(1) Heat Measurement and Specific Heat
177. Specific Heat.—In the study of density and specific
gravity it is made clear that different substances differ
widely in the amount of matter contained in equal volumes,
e.g., lead is much denser than water. The study of
the relative densities of substance is usually considered
under the subject of specific gravity.
Specific heat as distinguished from specific gravity is
concerned with the capacity for heat possessed by different
substances. The definition for specific heat is: The
ratio of the amount of heat required to change the temperature
of a given mass of a substance 1 C. degree to the amount
of heat required to change the temperature of the same mass
of water 1 C. degree. By definition, it requires 1 calorie to
raise the temperature of the gram of water 1°C. The
specific heat therefore of water is taken as one. The
specific heat of most substances except hydrogen, is less
than that of water, and as a rule, the denser the body the
less its specific heat, as may be observed in the following
table:
| | Specific gravity | Specific heat |
| Gold | 19.3 | 0.032 |
| Mercury | 13.6 | 0.033 |
| Copper | 8.9 | 0.093 |
| Brass | 8.4-8.9 | 0.094 |
| Nickel | 8.57 | 0.11 |
| Iron | 7.5+ | 0.1125 |
| Aluminum | 2.67 | 0.218 |
| Glass | 2.5-3.6 | 0.19 |
| Ice | 0.918 | 0.504 |
| Air | 0.00129 | 0.237 |
| Steam | 0.00061 | 0.480 |
| Hydrogen | 0.00009 | 3.409 |
[Pg 201]
178. Method of Determining Specific Heat.—The
specific heat of a body is usually determined by what is
called the method of mixtures.
For example, a definite weight of a substance, say a 200-g. iron
ball, is placed in boiling water until it has the temperature of the
hot water, 100°C. Suppose that 300 g. of water at 18°C. be placed
in a calorimeter, and that the hot iron ball on being placed in the
water raises its temperature to 23.5°C. The heat received by the
water equals 5.5 × 300 = 1650 calories. This must have come
from the heated iron ball. 200 g. of iron then in cooling 76.5°C.
(100°-23.5°) gave out 1650 calories. Then 1 g. of iron in cooling
76.5°C. Would give out 8.25 calories or 1 g. of iron cooling 1°C.
would yield about 0.11 calorie. The specific heat of the iron is
then 0.11. For accurate determination the heat received by the
calorimeter must be considered.
179. Heat Capacity of Water.—The large capacity for
heat shown by water is useful in regulating the temperature
of the air near lakes and the ocean. In hot weather the
water rises slowly in temperature absorbing heat from the
warm winds blowing over it. In winter the large amount
of heat stored in the water is slowly given out to the air
above. Thus the climate near the ocean is made more
moderate both in winter and summer by the large capacity
of water for heat. This large heat capacity of water may
seem to be a disadvantage when one is warming it for
domestic purposes since it requires so much heat to warm
water to boiling. However, it is this capacity that makes
hot-water bottles and hot-water heating effective.
If one takes a pound of ice at 0°C. in one dish and a pound of
water at 0°C. in another, and warms the dish of ice by a Bunsen
flame until the ice is just melted, and then warms the water in the
other dish for the same time, the water will be found to be hot and
at a temperature 80°C., or 176°F.
180. The Heat of Fusion of Ice.—This experiment indicates
the large amount of heat required to change the ice
to water without changing its temperature. As indicated[Pg 202]
by the experiment, it requires 80 calories to melt 1 g. of
ice without changing its temperature or, in other words,
if one placed 1 g. of ice at 0°C. in 1 g. of water at 80°C.,
the ice would be melted and the water would be cooled to
0°C.
181. Heat Given out by Freezing water.—Just as 80
calories of heat are required to melt 1 g. of ice, so in freezing
1 g. of water, 80 calories of heat are given out.
The fact that heat is set free or given out when a liquid solidifies
may be strikingly shown by making a strong solution of sodium
acetate. On allowing this to cool quietly it will come to the room
temperature and remain liquid. If now a small crystal of sodium
acetate is dropped into the liquid the latter quickly becomes a solid
mass of crystals, at the same time rising markedly in temperature.
The amount of heat now liberated must enter the sodium acetate
when the mass of crystals is melted again.
The large amount of heat that must be liberated before
water freezes accounts for the slowness of the formation
of ice. It is also the reason why the temperature never
falls so low in the vicinity of large lakes as it does far
inland, the heat given out by the freezing water warming
the surrounding air.
The heat that disappears on melting and reappears on
solidifying is called the heat of fusion. It is sometimes
called latent heat since the heat seems to become hidden
or latent. It is now believed that the heat energy that disappears
when a body melts has been transformed into the
potential energy of partially separated molecules. The
heat of fusion therefore represents the work done in changing
a solid to a liquid without a change of temperature.
182. Melting of Crystalline and Amorphous Substances.—If
a piece of ice is placed in boiling hot water and then
removed, the temperature of the unmelted ice is still
0°C. There is no known means of warming ice under[Pg 203]
atmospheric pressure above its melting point and maintaining
its solid state. Ice being composed of ice crystals is
called a crystalline body. All crystalline substances have
fixed melting points. For example, ice always melts at
0°C. The melting points of some common crystalline
substances are given below:
Melting Points of Some Crystalline Substances
| 1. Aluminum | 658 C. |
| 2. Cast iron | 1200 C. |
| 3. Copper | 1083 C. |
| 4. Ice | 0 C. |
| 5. Lead | 327 C. |
| 6. Mercury | -39 C. |
| 7. Phenol (carbolic acid) | 43 C. |
| 8. Platinum | 1755 C. |
| 9. Salt (sodium chloride) | 795 C. |
| 10. Saltpeter (potassium nitrate) | 340 C. |
| 11. Silver | 961 C. |
| 12. Sodium hyposulphite (hypo) | 47 C. |
| 13. Zinc | 419 C. |
Non-crystalline or amorphous substances such as glass,
tar, glue, etc., do not have well defined melting points
as do crystalline bodies. When heated they gradually
soften and become fluid. For this reason glass can be
pressed and molded.
183. Change of Volume During Solidification.—The
fact that ice floats and that it breaks bottles and pipes in
which it freezes shows that water expands on freezing.
How a substance may occupy more space when solid than
when liquid may be understood when we learn that ice
consists of masses of star-shaped crystals. (See Fig. 151.)
The formation of these crystals must leave unoccupied
spaces between them in the ice. When liquefied, however,
no spaces are left and the substance occupies less volume.[Pg 204]
Most substances contract upon solidifying. Antimony
and bismuth, however, expand on solidifying while iron
changes little in volume. Only those bodies that expand,
or else show little change of volume on solidifying, can
make sharp castings, for if they contract they will not
completely fill the mold. For this reason gold and silver
coins must be stamped and not cast. Type metal, an
alloy of antimony and lead, expands on solidifying to form
the sharp outlines of good type. Several important
effects of the expansion
of water when freezing
should be noted. (a)
Ice floats, (b) if it sank
as soon as formed, lakes
and rivers would freeze
solid, (c) freezing water
is one of the active
agents in the disintegration
of rocks.
 Fig. 151.—Ice crystals.
Fig. 151.—Ice crystals.
 Fig. 152.—Melting ice by pressure.
Fig. 152.—Melting ice by pressure.
Since water expands on freezing, pressure would on compressing
ice at 0°C., tend to turn it into water. Pressure
does lower the melting point of ice, so that a little ice may
melt when it is subjected to pressure. On removing the
pressure the water freezes. This may be shown by placing
a loop of fine piano wire (see Fig. 152) over a piece of ice[Pg 205]
supported so that a weight may be hung upon the wire.
The wire will be found to gradually cut through the ice, the
melted ice refreezing above the wire.
Important Topics
1. Specific heat.
2. Heat of fusion of ice.
3. Crystalline substances have fixed melting points.
4. Expansion on freezing, importance.
Exercises
1. What are two advantages in the high heat of fusion of ice?
2. What are two advantages in the expansion of water while freezing?
3. How much heat will be required to melt 1000 g. of ice and warm
the water to 20°C.?
4. How many grams of ice at 0°C. can be melted by 400 g. of water
at 55°C.?
5. What are two advantages of the high specific heat of water?
Two disadvantages?
6. If the specific heat of iron is 0.1125, how much ice at 0°C. can
be melted by a 200-g. ball of iron heated to 300°C?
7. What is the temperature of a hot ball of iron weighing 80 g.,
if when placed on a piece of ice at 0°C. it melts 90 g. of ice?
8. If 500 g. of copper at 400°C. are placed into 3000 g. of water
at 10°C. what will be the resulting temperature?
9. What weight of water at 90°C. will just melt 10 kg. of ice at
0°C.?
10. If the smooth dry surface of two pieces of ice are pressed together
for a short time the two pieces will be frozen into one
piece. Explain.
11. Tubs of hot water are sometimes placed in vegetable cellars to
prevent the vegetables from freezing. Explain.
12. How many B.t.u. are given out when 2 lbs. of water freeze?
(2) Heat and Change of State
 Fig. 153.—The black cube in the upper corner represents one cubic
inch of water. The entire cube represents the space occupied by the cubic
inch of water in the form of steam. The reduced spaces at the bottom
and sides show how much short the cube is of being one cubic foot.
(American Radiator Co.)
Fig. 153.—The black cube in the upper corner represents one cubic
inch of water. The entire cube represents the space occupied by the cubic
inch of water in the form of steam. The reduced spaces at the bottom
and sides show how much short the cube is of being one cubic foot.
(American Radiator Co.)
184. Heat of Vaporization.—In our study of evaporation
in Art. 174 we considered the more rapidly moving or
vibrating molecules in the liquid escaping to the air above[Pg 206]
and the slower moving molecules being left behind in the
liquid; this means that a loss of heat will result upon
evaporation, the liquid remaining becoming cooler as the
process continues. Now just as a ball thrown up in the
air loses its kinetic energy as it rises, and acquires energy
of position or potential energy, so molecules escaping from
a liquid lose a certain amount of kinetic energy or heat and
acquire a corresponding amount of energy of position or
potential energy. Conversely, as the ball returns to the
ground its potential energy is changed to kinetic energy.
Similarly when vapor molecules return to the liquid condition
they lose their energy of position and acquire kinetic
energy. In other words, when a liquid evaporates a certain
amount of heat disappears, or becomes latent and
when the vapor condenses the heat reappears, or becomes
sensible heat. The amount of heat that disappears when
1 g. of a substance is vaporized is called the heat of vaporization.[Pg 207]
In the case of water at its boiling point, 536 calories
of heat disappear when 1 g. of water turns to vapor, and
this same amount of heat reappears when the vapor
condenses.
The change of volume of water on turning to steam is
shown in Fig. 153.
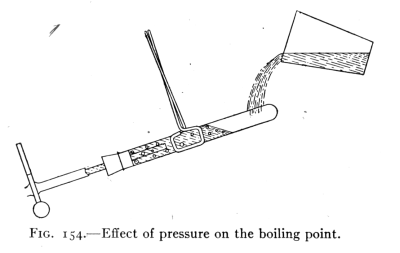 Fig. 154.—Effect of pressure on the boiling point.
Fig. 154.—Effect of pressure on the boiling point.
185. The Boiling Point.—The boiling temperature
depends upon the pressure. The boiling point may be
defined as the temperature at which bubbles of vapor are
formed within the liquid. These bubbles increase the
surface at which evaporation can take place in the liquid,
and the principal reason why rapid application of heat to
a liquid does not raise its temperature above the boiling
point is that as more heat is applied more bubbles form
so that the increase of evaporating surface supplies a
correspondingly greater surface for cooling. The variation
of the boiling temperature with changing pressure may
be shown by partly filling a strong 7/8-in. test-tube with
water. Close the neck with a one-hole rubber stopper
through which passes a glass tube to which is attached a
soft rubber tube. (See Fig. 154.) Support the tube by
a holder, heat the water and boil until all the air is driven[Pg 208]
from the tube, then close the soft rubber tube with a
pinch cock and hold the tube in an inverted position. On
cooling the end of the tube above the water with cold water
or snow, the vapor within is condensed and the pressure
upon the water is reduced. Vigorous boiling begins at
once. By condensing the vapor repeatedly the water may
be made to boil at the room temperature. At the top of
Mt. Blanc water boils at 84°C. While in steam boilers at
225 lbs. pressure to the square inch the boiling point is
nearly 200°C.
186. Laws of Boiling.—The following statements have
been found by experiments to be true.
1. Every liquid has its own boiling point which under
the same conditions of pressure is always the same.
2. The temperature of the boiling liquid remains at the
boiling point until all the liquid is changed into vapor.
3. The boiling point
rises with increased
pressure and falls if the
pressure is diminished.
4. A boiling liquid
and the vapor formed
from it have the same
temperature. On cooling,
a vapor will liquefy
at the boiling point.
 Fig. 155.—Distilling apparatus.
Fig. 155.—Distilling apparatus.
5. The solution of
solid substances in a liquid raises its boiling point, additional
energy being needed to overcome the adhesion
involved in the solution. The boiling point is also affected
by the character of the vessel containing the liquid. In
glass the boiling point is 101°.
 Fig. 156.—A vacuum pan.
Fig. 156.—A vacuum pan.
187. Distillation of Water.—Usually when solids are
dissolved in liquids the vapor coming from the liquid contains[Pg 209]
none of the dissolved solid. Thus by evaporating
salt sea water, and collecting and condensing the vapor,
pure water is obtained. Distillation is the process of
boiling a liquid and condensing the vapor formed back
again into a liquid. (See Fig. 155.) The liquid to be
distilled is placed in vessel F and boiled. The vapor is
conducted into the tube J which is surrounded by a larger
tube containing cold
water. The vapor is
condensed on the cold
walls of the tube.
The resulting liquid
is collected in the
vessel R. Distillation
is employed for two
purposes: (a) To remove
impurities from
a liquid (water is purified
in this way). (b)
Mixtures of different
liquids having different
boiling points may
be separated by distillation.
The one
having the lower boiling point will be vaporized first.
Thus a mixture of alcohol and water, on distillation
yields a distillate having a much larger percentage of
alcohol than at first. Repeating this process which is
called fractional distillation yields alcohol of increasing
strength of purity. Distilled liquor such as alcohol,
brandy, and whisky are made by distilling fermented
liquor, alcohol being made from fermented grains.
Gasoline and kerosene are distilled from crude petroleum.
Sometimes as in the production of sugar or evaporated[Pg 210]
milk the object is to remove the water by evaporation in
order to obtain the solid material. Since the two substances
named are injured by heating, the syrup, or milk
is evaporated under reduced pressure in a vacuum pan,
that is in a boiler from which air and vapor are removed
by an air pump. (See Fig. 156.)
188. Artificial Cooling.—The fact has been brought out
that when a solid is melted, a certain amount of heat,
called the heat of fusion, is absorbed or disappears. This
absorption of heat is also noticed when a solid is liquefied
by dissolving it in a liquid as well as when it is liquefied
by simply applying heat. Thus if some table salt is
placed in a tumbler of water the temperature of the solution
is lowered several degrees below that of the salt and
water used. The liquefaction or solution of the salt has
been accompanied by an absorption or disappearance of
heat. This heat has been taken from the salt and from
the water, resulting in a lowered temperature. Sal ammoniac
or ammonium nitrate when dissolved in water
produce a much more marked cooling effect than does
table salt. The dissolving of a crystal in a liquid is something
like evaporation, except that the molecules of the
liquid attract the molecules of the solid and thus assist
the change of state.
189. Freezing Mixtures.—If one attempts to freeze a
solution of salt and water, ice will not form at 0°C. but
several degrees lower. The ice formed however is pure.
Evidently the attraction of the molecules of salt for the
water molecules prevented the formation of ice until the
motions of the water molecules had been reduced more
than is necessary in pure water. As the temperature of
freezing water is that of melting ice, ice in a salt solution
melts at lower temperature than in pure water. In a
saturated salt solution this temperature is -22°C. It[Pg 211]
is for this reason that the mixture of ice and salt used in
freezing cream is so effective, the salt water in melting
the ice, being cooled to a temperature many degrees below
the freezing point of the cream. The best proportion
for a freezing mixture of salt and ice is one part salt to
three parts of finely powdered or shaved ice.
190. Refrigeration by Evaporation.—Intense cold is
also produced by permitting the rapid evaporation of
liquids under pressure. Carbon dioxide under high pressure
is a liquid, but when allowed to escape into the air
evaporates so rapidly that a portion of the liquid is frozen
into solid carbon dioxide which has a temperature of -80°
C. The evaporation of liquid ammonia by permitting
it to escape into a pipe, under reduced pressure, is used on
a large scale as a means of producing cold in cold storage
and refrigeration plants. (See Fig. 157.)
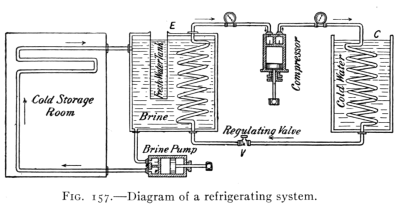 Fig. 157.—Diagram of a refrigerating system.
Fig. 157.—Diagram of a refrigerating system.
The essential parts of the refrigerating system employing
ammonia is represented in Fig. 157. The compressor
exhausts ammonia gas from the coiled pipe in
"E" and compresses the gas in "C," where under 150
pounds pressure and the cooling effect of water it condenses
to liquid ammonia. This is allowed to pass
slowly through the regulating valve, whereupon it[Pg 212]
evaporates and expands in the long coiled pipe in "E"
on its way back to the compressor. This evaporation
and expansion causes a large amount of heat to be
absorbed from the brine, cooling the latter below the
freezing point of pure water and thus permitting
the freezing of cans of water suspended in the brine.
The chilled brine may also be sent through pipes in
order to cool storage rooms containing meat or other
food products. The ammonia absorbs heat when it
vaporizes and gives up heat when it is compressed and
liquified.
Important Topics
1. Heat of vaporization, of water 536 calories per gram.
2. Boiling point, effect of pressure upon boiling point, laws of
boiling.
3. Distillation, artificial cooling, freezing mixtures, refrigeration by
evaporation.
Exercises
1. How much heat is required (a) to melt 1 g. of ice at 0°C., (b)
to raise the temperature of the water resulting to 100°C., (c)
to change this water to steam?
2. If the water leaving a steam radiator is as hot as the steam
how is the room warmed?
3. What is the effect of placing salt upon icy sidewalks in cold
weather?
4. Is rain water distilled water? Is it perfectly pure?
5. What are two advantages of the high heat of vaporization of
water?
6. If the heat from 1 g. of steam at 100°C. in changing to water
and cooling to 0°C. could be used in melting ice at 0°C. how
much ice would be melted?
(3) Heat and Work
191. Necessity for Heat Energy.—From early times
man has been able to transform motion into heat, and has
used this ability in many directions as in starting fires and[Pg 213]
warming himself by friction. It took man many centuries,
however, to devise an effective machine for transforming
heat into mechanical energy or to use it in doing
work.
The power of a man is small and as long as the work of
the world had to be done by man power, progress was
retarded. When man began the use of beasts of burden,
he took a long step in advance since one man could then
employ and direct the power of many men in the animals
he controlled. Man also built water-wheels and windmills
thus gaining power directly from the forces of nature and
these added much to his working ability. But he took
the greatest step in gaining control over his surroundings
when he learned to use heat energy and to make it drive
his machines.
192. Heat Engines.—At the present time there is a
great variety of heat engines in use such as steam, hot air,
gas, and gasoline engines, all using heat energy to produce
motion. The expansive power of steam when confined
has been observed for hundreds of years and many different
machines have been invented to use it in doing work.
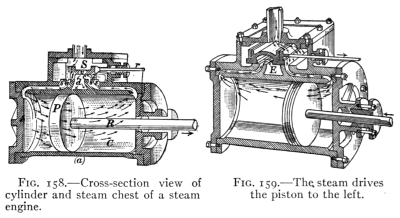 Fig. 158.—Cross-section view of
cylinder and steam chest of a steam
engine.
Fig. 158.—Cross-section view of
cylinder and steam chest of a steam
engine.
Fig. 159.—The steam drives
the piston to the left.
 Fig. 160.—External view of steam engine.
Fig. 160.—External view of steam engine.
193. The Steam-engine.—The man who perfected the
steam-engine, and devised its modern form was James
Watt (1736-1819). The essential parts and the action
of the steam engine may be readily understood by studying
a diagram. In Fig. 158, S stands for steam chest, C for
cylinder, P for piston and v for slide valve. The first two
are hollow iron boxes, the latter are parts that slide back
and forth within them. The action of the steam engine is
as follows: Steam under pressure enters the steam chest,
passes into the cylinder and pushes the piston to the other
end. The slide valve is moved to its position in Fig. 159.
Steam now enters the right end of the cylinder, driving
the piston to the left, the "dead" steam in the left end of[Pg 214]
the cylinder escaping at E to the air. The slide valve is
now shifted to its first position and the process is repeated.
It will assist the student to understand this action if he
makes a cardboard model of these parts, the piston and
slide valve being movable. In practical steam-engines,
the piston rod is attached to a crank rod fastened to a crank
which turns a wheel. (See Fig. 160.) The back and
forth, or reciprocating motion of the piston is by this means
transformed into rotary motion, just as in the sewing-machine
the back-and-forth motion of the treadle produces
rotary motion of the large wheel. Upon the shaft of the
steam engine is fastened an eccentric (see Fig. 163) which[Pg 215]
moves the slide valve. The steam engine acts continuously
as long as steam is supplied to it. Since it shifts the
position of the slide
valve automatically,
it is called an automatic
steam engine.
And because the
team drives the piston
both ways, it is
called a double-acting
steam engine. See
Fig. 161 for a length-section
of a modern
locomotive.
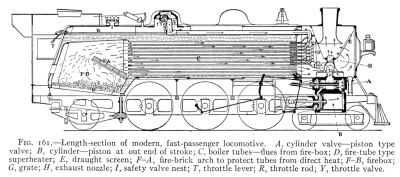 Fig. 161.—Length-section of modern, fast-passenger locomotive. A, cylinder valve—piston type
valve; B, cylinder—piston at out end of stroke; C, boiler tubes—flues from fire-box; D, fire-tube type
superheater; E, draught screen; F-A, fire-brick arch to protect tubes from direct heat; F-B, firebox;
G, grate; H, exhaust nozzle; I, safety valve nest; T, throttle lever; R, throttle rod; Y, throttle valve.
Fig. 161.—Length-section of modern, fast-passenger locomotive. A, cylinder valve—piston type
valve; B, cylinder—piston at out end of stroke; C, boiler tubes—flues from fire-box; D, fire-tube type
superheater; E, draught screen; F-A, fire-brick arch to protect tubes from direct heat; F-B, firebox;
G, grate; H, exhaust nozzle; I, safety valve nest; T, throttle lever; R, throttle rod; Y, throttle valve.
194. The Mechanical
Equivalent
of Heat.—While
watching workmen
bore holes in cannon,
Count Rumford,
1753-1814, noticed
with much interest
the large amount of
heat produced in the
process. He observed
that the heat
developed seemed to
have some relation to
the work done upon
the drill in boring the
holes. Later experiments
performed by
many men indicated that a definite relation exists between
the heat produced by friction and the amount[Pg 216]
of work done in overcoming the friction. This discovery
indicates that in some way heat is related to energy
and that heat is probably a form of energy. Later
experiments have confirmed this idea, and it is now considered
well established that heat is a form of energy.
Many attempts have been made to discover the relation
between the units of heat energy and the units of mechanical
energy. To illustrate one method employed, suppose
one measures a given
length in inches and in
centimeters; on dividing
one result by the
other, it will be found
that a certain relation
exists between the two
sets of measurements,
and that in every case
that 1 in. equals 2.54
cm. Similarly, when
the same amount of energy is measured both in heat
units and in work units a constant relation is always
found between the units employed. One B.T.U. is found
equivalent to 778 ft.-lbs. 1 calorie being equivalent to 42,700
g. cm. (427 g. m.). This relation is called the mechanical
equivalent of heat, or in other words it represents the
number of work units equivalent to one heat unit.
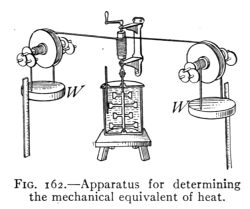 Fig. 162.—Apparatus for determining
the mechanical equivalent of heat.
Fig. 162.—Apparatus for determining
the mechanical equivalent of heat.
 William Gilbert (1540-1603),
"Father of magnetic philosophy."
Especially noted for his experiments
and discoveries in magnetism;
first to use the word "electricity."
First man to practically
emphasize experimental science.
William Gilbert (1540-1603),
"Father of magnetic philosophy."
Especially noted for his experiments
and discoveries in magnetism;
first to use the word "electricity."
First man to practically
emphasize experimental science.
Dr. William Gilbert
(Popular Science Monthly)
 James Prescott Joule (1818-1889),
England, determined the
mechanical equivalent of heat; discovered
the relation between an
electric current and the heat produced;
first proved experimentally
the identity of various forms of
energy.
James Prescott Joule (1818-1889),
England, determined the
mechanical equivalent of heat; discovered
the relation between an
electric current and the heat produced;
first proved experimentally
the identity of various forms of
energy.
James Prescott Joule
(Popular Science Monthly)
One of the first successful experiments in determining the
relation between work units and heat units was devised
by Joule in England. (See portrait p. 217.) The experiment
consisted in taking a can of metal containing water
(Fig. 162) in which was placed a thermometer, and a rod
carrying paddles. The rod was turned by a cord connected
through suitable apparatus to heavy weights,
W and W. The energy represented by the downward[Pg 217]
[Pg 218]
[Pg 219]
motion of the weights through a given distance was compared
with the heat energy developed in the water as
shown by its rise in temperature. Careful experiments
showed that when 778 ft.-lbs. of work had been done
by the moving weights the heat produced at the same
time would warm one pound of water 1 Fahrenheit
degree. If the experiment was performed using metric
units, it was found that the expenditure of 42,700 gram
centimeters (427 gram meters) would result in producing
enough heat to warm one gram of water one centigrade
degree. The facts just given may be summarized as
follows: 778 foot-pounds of energy are equivalent to 1 British
thermal unit and 42,700 gram centimeters, or 427 gram meters,
of energy are equivalent to 1 calorie. This relation of work
units to heat units is called the mechanical equivalent of
heat.
195. The Heat Equivalent of Fuels and Efficiency
Tests of Engines.—To determine the efficiency of a steam
engine it is necessary to know not only the mechanical
equivalent of heat but also the heat produced by burning
coal or gas; 1 lb. of average soft coal should produce about
12,600 B.t.u. Now since 778 ft.-lbs. are equivalent to
one B.t.u. the energy produced when 2 lbs. of average soft
coal is burned is 778 × 12,600 × 2 = 19,605,600 ft.-lbs.
In actual practice 2 lbs. of average soft coal burned will
develop about 1 horse-power for 1 hour. 1 horse-power-hour
= 33,000 ft.-lbs. × 60 = 1,980,000 ft.-lbs. Now efficiency
equals (work out)/(work in) 1,980,000/19,605,600 = 1/10 or 10 per cent..
This is the efficiency of a good steam engine. Ordinary
ones require 3 lbs. of coal burned to each horse-power-hour
produced or they are but 2/3 as efficient or have but about
7 per cent. efficiency.
[Pg 220]
Heat of Combustion of Various Fuels
Data in this table are taken from U. S. Geological Survey, Bulletin
No. 332, and U. S. Bureau of Mines, Bulletin No. 23.
| B.T.U. | Calories |
| per lb. | per gram |
| Alcohol, denatured | 11,600 | 6,450 |
| Coal, anthracite, average | 12,600 | 7,500 |
| Coal, bituminous, average | 19,000 | 7,000 |
| Gasoline | 19,000 | 10,550 |
| Illuminating gas | 18,000 | 10,000 |
| Kerosene | 19,990 | 11,050 |
Constants for Heat Transmission
Data from "Ideal Fitter," American Radiator Co.
B.t.u. transmitted per square foot per hour per degree
(Fahrenheit) difference in temperature between inside
and outside air.
Brick work
4 in. thick = 0.68
8 in. thick = 0.46
12 in. thick = 0.33
concrete cement 50 per cent. more than brick.
stone 33-1/3 per cent. more than brick.
Window = 1.090
Wood as wall = 0.220
Double window = 0.560
concrete reinforced 20 per cent. more than brick.
Important Topics
1. Heat a manifestation of energy.
2. Steam-engine and its action.
3. Mechanical equivalent of heat and heat equivalent of fuels
and efficiency of engines.
Exercises
1. Construct a working model of the cylinder and steam chest of
a steam engine and be prepared to explain its action.
2. At $5.00 per ton how many B.T.U.'s should be produced from
1 cent's worth of bituminous coal?
[Pg 221]
3. Try the following experiment: Place a quart of water in a teakettle
and place it over the fire for 5 minutes, and note the rise
in temperature and compute the number of B.T.U.'s entering
the water. Place another quart of water at the same temperature
in an aluminum or tin dish and heat for 5 minutes, note
the rise in temperature and compute the heat used before.
Which of the dishes shows the greater efficiency? How do
the efficiencies of the two dishes compare? How do you account
for any differences in the efficiencies found?
4. How high would 8 cu. ft. of water be lifted if all of the energy
produced by burning 1 lb. of coal were used in raising it?
5. What is the mechanical equivalent of a pound of coal expressed
in horse-power hours?
6. If a furnace burns 100 lbs. of coal a day and its efficiency is
50 per cent. how many B.T.U.'s are used in warming the house?
7. How many B.T.U.'s can be obtained by burning 1/2 ton of
bituminous coal?
8. when a pound of water is heated from 40°F. to 212°F., how many
foot-pounds of energy are absorbed by the water?
9. How many loads of coal each weighing 2 tons, could be lifted
12 ft. by the energy put into the water in problem 8?
 Fig. 163.—An eccentric.
Fig. 163.—An eccentric.
10. When 3 cu. ft. of water are used for a hot bath and the water
has been heated from 50°F. to 112°F., how many B.T.U.'s
have been absorbed by the water?
11. If the average temperature of water at the surface of Lake
Michigan is 50°F., how many B.T.U.'s would be given off
by each cubic foot of water at the surface, if the temperature
of the water should drop 5°F.?
12. In a cold storage plant carbon dioxide gas is used. The pipe[Pg 222]
leading from the compression pump to the expansion valve passes
through a condensing tank of cold water. Why?
13. When the gas is compressed in a cold storage plant, what becomes
of the energy used by the compression pump?
14. An eccentric (Fig. 163), is a round disc mounted a little to one
side of its center, A, on the engine shaft B. A band, C, on the
circumference of the disc is connected by a rod, D, with the
slide valve in the steam chest. How is the rotary motion of
the shaft changed into a backward and forward motion of the
slide valve?
(4) Heat Engines
196. The Gas Engine.—One of the heat engines in
common use to-day is the gasoline engine. It is used to
propel automobiles and motor boats, to drive machinery,
etc. The construction and action of a gasoline engine
may be understood by studying a working model, or by
proper diagrams.
The common gasoline or gas engine is called a four-cycle
(better four-part cycle) engine (see Fig. 164), since it requires[Pg 223]
four movements of the piston to complete one cycle
or series of changes. This is illustrated in Fig. 165 1, which
represents a cross-section of the cylinder of the gasoline
engine with the piston moving downward. At the upper
end of the cylinder are two ports or openings. One, the
exhaust port, is closed, the
inlet port is open and a mixture
of gas and air is entering.
Fig. 165 2 shows the
piston returning; both ports
are closed and the "charge"
of air and gas is being compressed.
As the piston
reaches the end of its stroke
in compressing the charge, an
electric spark explodes or
"fires" the charge of gas and
air. The hot burning gas
expands suddenly driving the
piston downward with great
force (Fig. 165 3). The piston
rod is attached to the
crank of a heavy fly-wheel
and this is given sufficient
energy or momentum to keep
it going through the next three strokes. Fig. 165 4 represents
the returning piston pushing out the burnt
"charge" through the open exhaust valve e. On the next
downward motion of the piston the valve e closes. It
opens, and new charges of gas and air enter and the
"cycle" is repeated.
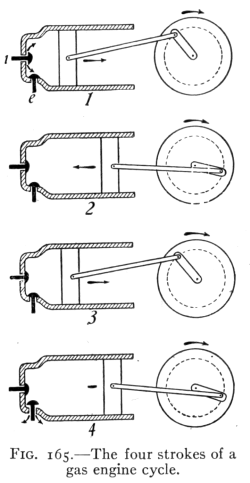 Fig. 165.—The four strokes of a
gas engine cycle.
Fig. 165.—The four strokes of a
gas engine cycle.
In order to make the motion more even and continuous
and also to secure more power, more than one cylinder is
attached to the same shaft and fly-wheel. Two, three,[Pg 224]
four, six, eight and even more cylinders have been attached
to one shaft. Four or six cylinders are commonly used in
automobile gasoline motors. To lessen the sound of the
"exhaust," the latter is sent through a "muffler" which
often reduces the noise to a low throbbing. (See Fig. 166.)
The gasoline engine is more efficient than the steam-engine,
since the fuel, gas, is burned in the cylinder and not in a
separate furnace. The combustion of the fuel in the cylinders
makes some special cooling device necessary to prevent
their overheating. This usually consists of a casing
about the cylinders. Between the cylinder and this
casing is water which on being heated passes to a tank or
radiator. In the radiator the water cools and then returns
to the space between the cylinders and casing thus
keeping up the circulation.
 Fig. 166.—An efficient automobile muffler. (Courtesy Popular Science
Monthly.)
Fig. 166.—An efficient automobile muffler. (Courtesy Popular Science
Monthly.)
197. Efficiency of Gas Engines.—One may test the
efficiency of a gas engine by determining the amount of
power developed and comparing it with the mechanical
equivalent of the fuel burned. Illuminating gas is sometimes
employed to drive gas engines. One cubic foot of
illuminating gas should produce 600 B.T.U. when burned.
The efficiency of the gas or gasoline engines is sometimes
as high as 25 per cent. This engine is free from smoke
and is also compact and quickly started. While the fuel,
gas or gasoline, is somewhat expensive it is light and easily[Pg 225]
carried. Suppose a gas engine produces 1 horse-power
and uses 20 cu. ft. of
gas an hour, what is its
efficiency? 1 horse-power-hour
= 550 × 60
× 60 = 1,980,000 ft.-lbs.
20 cu. ft. of gas = 20
× 600 × 778 = 9,336,000
ft.-lbs.
Efficiency = work out/work in =
1,980,000/9,336,000 = 21.2 per cent.
 Fig. 167.—The principle of the steam
turbine.
Fig. 167.—The principle of the steam
turbine.
 Fig. 168.—Path of steam in DeLaval
steam turbine. (a) and (c) movable
blades, (b) stationary.
Fig. 168.—Path of steam in DeLaval
steam turbine. (a) and (c) movable
blades, (b) stationary.
198. The Steam Turbine.
One form of the steam-engine
that is coming
into general use
is the turbine. (See
Fig. 167.) This consists
of a shaft to which
are attached blades, the
shaft and blades being
contained in a closed
case. Steam is admitted
by nozzles and strikes
the blades so as to set
them and the shaft in
motion. There are also
stationary blades (see
Fig. 168), which assist
in directing the steam
effectively against the
rotating parts. The[Pg 226]
steam turbine is used for large power plants. (See Fig.
293.) It is very efficient, makes very little vibration, and
occupies about one-tenth the floor space that a reciprocating
engine of equal power uses. Some large ocean
steamers are now driven by steam turbines.
Important Topics
1. The gas engine, its construction, action and efficiency.
2. The steam turbine.
Exercises
1. If coal costs $4.00 a ton, and gas, $0.80 per 1000 cu. ft. what
amounts of heat can be secured from 1 cent's worth of each?
2. What will it cost to heat 30 gallons of water (1 gal. of water
weighs about 8-1/3 lbs.) from 40°F. to 190°F. with coal costing
$4.00 per ton and yielding 12,000 B.T U. per lb. if the heater
has an efficiency of 50 per cent.
3. What will it cost to heat 30 gallons of water from 40°F. to
190°F. with gas at $0.80 per 1000 cu. ft. if the heating device
has an efficiency of 75 per cent.
4. Construct a cardboard working-model showing the action of the
gas engine and be prepared to explain the action of the various
parts.
5. If 500 lbs. of iron should fall 2000 ft. and all of the resulting
mechanical kinetic energy should be transformed into heat,
what would be the amount of heat produced?
6. What are the special advantages of (a) the gasoline engine?
(b) the turbine? (c) the reciprocating steam engine?
7. Do you burn coal or gas in your kitchen stove at home? Which
is for you the more economical? Why?
8. What are the advantages of using a fireless cooker?
9. What is the efficiency of a locomotive that burns 3.2 lbs. of coal
per horse-power-hour?
10. A gas engine developed in a test 0.34 horse-power for 1 minute.
and 50 seconds, 0.5 cu. ft. of gas being used. The heat of combustion
of the gas was 600 B.T.U. per cu. ft. Find the
efficiency of the engine.
11. Find the horse-power of an engine, the diameter of the piston
being 19 in., stroke 26 in.; it uses steam at an average pressure
of 200 lbs. per square. inch and makes 100 strokes a minute.
[Pg 227]
12. What is the efficiency of an engine and boiler that develops
200 horse-power, while burning 390 lbs. of soft coal per hour?
13. If a locomotive has an efficiency of 6 per cent. and develops
1700 horse-power how much coal is burned in an hour?
14. If an automobile engine burns 1 gallon of gasoline in an hour and
develops 10 horse-power, what is its efficiency?
15. The A.L.A.M.[J] formula for horse-power is (N B2)/2.5 when the piston
speed is 1000 ft. per minute, N being the number of cylinders
and B, their diameter. Find the horse-power of a 4-cylinder
engine, the cylinders having a diameter of 4 in.
16. Find the horse-power of a 6-cylinder automobile engine, if the
cylinder diameter is 4.5 in.
17. A 4-cylinder automobile having 4-in. cylinders, uses 1 gallon of
gasoline in 1 hour. Find its efficiency, if its average horse-power
developed is 6.
18. The motor boat Disturber III, has 24 cylinders each with diameter
3.5 in. If the piston speed is 1000 ft. per minute, what is
the horse-power? (See problem 15.)
Review Outline: Heat
Heat; sources (4), effects (5), units (2).
Temperature; thermometer scales (3), absolute temperature,
9C°/5 + 32° = F°.
Expansion; gases, Law of Charles (V1/V2 = T1/T2), liquids,
peculiarity of water, solids, coefficient of expansion, uses, results.
Heat Transference; conduction, uses of good and poor conductors,
convection, in nature, heating and ventilating systems,
radiation, 3 peculiarities, value of sun's radiation.
Heat and Moisture; relative humidity, dew point, formation of
dew, fog, rain, snow, etc., evaporation, effects, conditions.
Heat Measurement; specific heat, heat of fusion, of vaporization,
combustion.
Vaporization; Boiling point, laws of boiling, distillation, artificial
cooling.
Heat Engines; steam, gas.—construction, action, efficiency, mechanical
equivalent of heat. Heat equivalent of fuels.
[Pg 228]
MAGNETISM
(1) General Properties of Magnets
199. Magnets.—Since the times of the early Greek
philosophers men have known of certain stones that have
the property of attracting to themselves objects of iron
and steel. Such stones are called natural magnets. It is
thought by many that the name magnet is derived from
Magnesia in Asia Minor, where these stones are abundant,
though this is but tradition.
It was also learned long ago that iron and steel objects
when rubbed with natural magnets become
magnetized, that is, acquire the
properties of magnets. These are said to
be artificial magnets.
 Fig. 169.—A bar magnet.
Fig. 169.—A bar magnet.
Fig. 170.—A horseshoe
magnet.
Some 800 years ago it was discovered
that magnets, natural or artificial, when
suspended so as to turn freely, always come to rest in a
definite position pointing approximately north or south.
This is especially noticeable when the magnet is long
and narrow. Because of this property of indicating
direction, natural magnets were given the name of lodestone
(lode-leading).
Artificial magnets are made by rubbing steel bars with a[Pg 229]
magnet or by placing the steel bar in a coil of wire through
which a current of electricity is flowing. The magnetized
steel bars may have any form, usually they are either
straight or bent into a "U" shape. These forms are
known as bar and horseshoe magnets. (See Figs. 169 and
170.) Magnets retain their strength best
when provided with soft-iron "keepers,"
as in Fig. 171.
 Fig. 170.—A horseshoe
magnet.Fig. 171.—Bar
magnets with
keepers.
Fig. 170.—A horseshoe
magnet.Fig. 171.—Bar
magnets with
keepers.
200. Magnetic Poles.—If a magnet
is placed in iron filings and removed,
the filings will be found to cling strongly
at places near the ends of the magnet,
but for a portion of its length near the
middle no attraction is found. (See
Fig. 172.) These places of greatest
attraction on a magnet are called poles.
If a bar magnet is suspended so as to
swing freely about a vertical axis the
magnetic pole at the end pointing north is called the
north-seeking pole; at the other end, is the south-seeking
pole. In most places the needle does not point to the true
north, but somewhat to the east or west of north. The
direction taken by a magnetic needle is parallel to the
magnetic meridian.
 Fig. 172.—Iron filings attracted to
the poles of a magnet.
Fig. 172.—Iron filings attracted to
the poles of a magnet.
201. Law of Magnetic Action.—The
north pole of a
magnet is usually marked.
If a marked bar magnet be
held in the hand and its north-seeking pole be brought near
the north-seeking pole of a freely suspended bar magnet,
the two poles will be found to repel each other, as will also
two south-seeking poles, while a north-seeking and a south-seeking
pole attract each other. (See Fig. 173.) This
action leads to the statement of the Law of Magnetic Action:[Pg 230]
Like poles repel, while unlike poles attract each
other. The force of attraction or repulsion lessens as the
distance increases. The force of the action between magnetic
poles is inversely proportional to the square of the distance
between them. Compare this with the law of gravitation
(Art. 88).
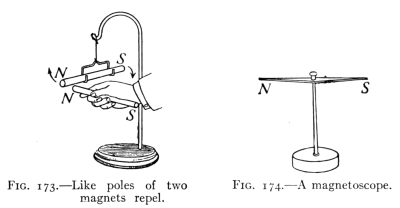 Fig. 173.—Like poles of two
magnets repel.
Fig. 173.—Like poles of two
magnets repel.
Fig. 174.—A magnetoscope.
202. Magnetic Substances and Properties.—It is found
that if an iron or steel magnet is heated red hot that its
magnetic properties disappear. Accordingly one method
of demagnetizing a magnet is to raise it to a red heat. If
a magnet that has been heated red hot and then cooled is
brought near a suspended bar magnet, it is found to
attract either end, showing that it has regained magnetic
properties even though it has lost its magnetic polarity.
A suspended bar magnet used to test the magnetic properties
of a body is called a magnetoscope. (See Fig. 174.)
The needle of a magnetic compass serves very well as a
magnetoscope. Magnetic properties are most strongly
exhibited by iron and steel, though nickel and cobalt show
some magnetic effects. There is a peculiar alloy of copper,
aluminum, and manganese, known as Heusler's Alloy, that
is also magnetic. However, of all substances, iron and
steel show the strongest magnetic effects.
[Pg 231]
203. Magnetic Induction.—Let the north-seeking pole of
a bar magnet support an iron nail by its head. (See Fig.
175.) Test the point of the nail for polarity. See whether
a second nail can be attached by its head to the point of the
first. Test the polarity of the point of this nail. Find by
trial how many nails can be suspended in succession from
the magnet. Test in each case for polarity. Withdraw
carefully the magnet from the first nail—the string of
nails will fall apart. Repeat the test with a thickness of
paper between the magnet and the first nail.
Results similar to those secured at first will
be found, though probably fewer nails will
be supported. The presence of paper between
the magnet and nails simply weakens
the action. Test the action of the magnet
upon the nail when there is between them a
piece of glass, one's thumb, thin pieces of
wood, copper, zinc, etc. The magnetizing
of a piece of iron or steel by a magnet near or
touching it is called magnetic induction. This
action takes place through all substances
except large bodies of iron or steel hence
these substances are often used as magnetic
screens. The pole of the new induced magnet
adjacent to the bar magnet is just opposite to the pole
used. Thus the N.-pole of the magnet used will produce
a S.-pole at the near end of the nail and a N.-pole at
the end farther away. (See Fig. 175.) On removing the
magnet, the nails are found to retain a part of their induced
magnetism.
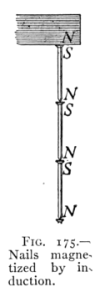 Fig. 175.—Nails
magnetized
by induction.
Fig. 175.—Nails
magnetized
by induction.
204. Retentivity.—In several of the foregoing paragraphs
it has been seen that a piece of iron or steel when
once magnetized does not entirely lose its magnetism when
the magnetizing force is removed. Different pieces of[Pg 232]
iron and steel vary greatly in this respect, some remaining
strongly magnetized, others losing much of their magnetism.
This property of retaining magnetism is called retentivity.
Hardened steel has a high degree of retentivity,
while soft iron retains but little magnetism.
Important Topics
1. Magnet; natural, artificial, bar, horseshoe.
2. Magnetic poles; north seeking, south seeking.
3. Law of action, magnetoscope, retentivity, induced magnet.
Exercises
1. Make a summary of the facts of magnetism presented in this
lesson.
2. Is magnetism matter, force, or energy? How do you decide?
To what other phenomenon that we have studied is it similar?
How?
3. Make a simple magnetoscope for yourself by suspending a thin
steel needle or rod 5 to 10 cm. long, with a light thread or silk
fiber at its center, so that it will hang level. Then magnetize
the needle, and keep the magnetoscope in your book.
4. Name three uses for magnets or magnetism.
5. Mention three uses for a magnetoscope.
6. Are all magnets produced by induction? Explain.
7. In what magnetic devices is a high retentivity desirable?
(2) The Theory of Magnetism and Magnetic Fields
205. The Theory of Magnetism.—If a magnetized
watch spring is broken in two, each part is found to be a
magnet. If one of these parts be broken and this process
of breaking be continued as far as possible, the smallest
part obtained has two poles and is in fact a complete
magnet. (See Fig. 176.) It is supposed that if the division
could be continued far enough that each of the molecules
of the steel spring would be found to have two poles[Pg 233]
and to be a magnet. In other words, magnetism is believed
to be molecular. Other evidence supporting this
idea is found in the fact that when a magnet is heated red
hot, to a temperature of violent molecular motion, its
magnetism disappears.
Also if a
long, fine soft iron
wire be strongly
magnetized, a
light jar causes its
magnetism to disappear.
This would lead us to believe that magnetism
is not a property of the surface of the body, but that it
depends upon molecular structure or the arrangement
of the molecules.
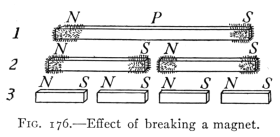 Fig. 176.—Effect of breaking a magnet.
Fig. 176.—Effect of breaking a magnet.
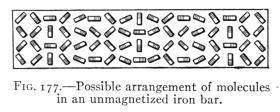 Fig. 177.—Possible arrangement of molecules
in an unmagnetized iron bar.
Fig. 177.—Possible arrangement of molecules
in an unmagnetized iron bar.
It is believed
also that the molecules
of a magnetic substance are
magnets at all
times; that before
the body is magnetized the molecules are arranged
haphazard (see Fig. 177) but that when a magnet is
brought near, the molecules tend to arrange themselves
in line, with their
north-seeking
poles pointing in
the same direction.
(See Fig. 178.) If
the magnet is
jarred some of the molecules tend to get out of line, perhaps
to form little closed chains of molecules. (See Fig. 177.)
 Fig. 178.—Arrangement of molecules in a
saturated magnet.
Fig. 178.—Arrangement of molecules in a
saturated magnet.
206. Magnetic Fields and Lines of Force.—The behavior
of magnets is better understood after observing and[Pg 234]
studying the lines of force of a magnet. The earliest
descriptions of these are by William Gilbert, the first
Englishman to appreciate fully the value of making
experimental observations. He wrote a book in 1600
called De Magnete in which he published his experiments
and discoveries in magnetism. (See p. 217.)
Magnetic lines of force may be observed by placing a
magnet upon the table, then laying upon it a sheet of paper
and sprinkling over the latter fine iron filings. On gently
tapping the paper, the filings arrange themselves along
curved lines extending from one end of the magnet to
the other. These are called the magnetic lines of force.
(See Fig. 179.) The space about a magnet in which the
magnetic lines are found is called the magnetic field. (See
Fig. 180.)
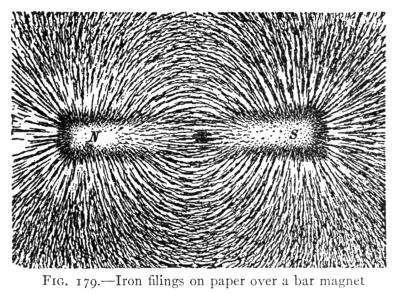 Fig. 179.—Iron filings on paper over a bar magnet.
Fig. 179.—Iron filings on paper over a bar magnet.
Many interesting things have been discovered concerning
the lines of force. Some of the facts of magnetic action
are given a simple explanation if we think of them as due
to the magnetic lines of force. A summary of several
discoveries concerning magnetic fields follows:
[Pg 235]
(A) Magnetic lines of force run side by side and do not
cross one another. (See magnetic fields.)
(B) Magnetic lines of force are believed to form "closed
curves" or to be continuous. The part outside of the magnet
is a continuation of the
part within the magnet. (See
Fig. 180.)
 Fig. 180.—Diagram of the field of a bar magnet.
Fig. 180.—Diagram of the field of a bar magnet.
(C) The attraction of a
magnet is strongest where the
magnetic lines are thickest,
hence they are believed to be
the means by which a magnet
attracts.
(D) Since like poles repel and unlike poles attract, it
is known that the action along a line of force is not the
same in both directions. It has therefore been agreed by
physicists to indicate by an arrow head (Fig. 180), the
direction that a north-seeking pole tends to move along a
line of force. The lines of force are considered as leaving
the north-seeking pole of a magnet and entering the south-seeking
pole. (See Figs. 181 and 182.)
 Fig. 181.—Magnetic field between like poles showing repulsion.
Fig. 181.—Magnetic field between like poles showing repulsion.
[Pg 236]
(E) A freely suspended small magnet in a magnetic field
places itself parallel to the lines of force. (Test this by
holding a magnetic compass in different portions of a
magnetic field). Note the position of the needle and the
lines of force. This fact indicates that the compass needle
points north on account of its tendency to turn so as to be
parallel to the earth's magnetic held.
 Fig. 182.—Magnetic field between unlike poles showing attraction.
Fig. 182.—Magnetic field between unlike poles showing attraction.
(F) Each magnet is accompanied by its own magnetic
field. When a piece of iron is brought within the field
of a magnet the lines of force passing through the iron
tend to arrange the iron molecules in line or to magnetize
the iron.
207. Magnetic Induction.—The action of magnetic
lines of force in magnetizing iron when they pass through
it, is called Magnetic Induction. This may now be defined
as the production of magnetism in a body by placing it
within a magnetic field. Freely suspended magnets place
themselves parallel to the lines of force in a magnetic
field, therefore when an iron rod is placed in a weak field,
or one with few lines of force, the iron is but slightly
magnetized; that is, but few molecules are brought into[Pg 237]
line. Increasing the strength of the magnetizing field,
gives stronger magnetization to the iron up to a certain
point. After this, stronger fields give no increase in
magnetizing effect. When iron exhibits its greatest
magnetization it is said to be saturated.
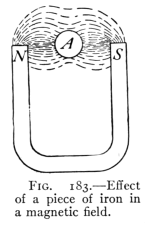 Fig. 183.—Effect
of a piece of iron in
a magnetic field.
Fig. 183.—Effect
of a piece of iron in
a magnetic field.
208. Permeability.—If a piece of iron is placed between
the poles of a horseshoe magnet, the "field" obtained by
sprinkling iron filings upon a sheet of paper over the
magnet resembles that shown in Fig.
183. The lines in the space between
the poles of the magnet seem to
crowd in to the piece of iron. The
property of the iron by which it tends
to concentrate and increase the number
of lines of force of a magnetic
field is called permeability. Soft iron
shows high permeability. Marked
differences in behavior are shown
by different kinds of iron and steel
when placed in a magnetic field. Very pure iron, or soft
iron, is strongly magnetized by a magnetic field of medium
strength. Its magnetism, however, is quickly lost when
the magnetizing field is removed. This indicates that
soft-iron molecules are easily swung into line, but also
disarrange themselves as easily when removed from a
magnetizing force. Soft-iron magnets having high permeability
quickly lose their magnetism. They are therefore
called temporary magnets. On the other hand a
hardened steel bar is difficult to magnetize, but when once
magnetized retains its magnetism permanently, unless
some action weakens the magnet. Such magnets are
called permanent magnets.
Note.—The term "line of force" as used in this text means the
same as "line of induction" as used in more advanced texts.
[Pg 238]
Important Topics
1. Molecular theory of magnetism, saturation, permeability.
2. Magnetic fields and lines of force.
3. Six facts concerning magnetic fields.
Exercises
1. Name an object whose usefulness depends upon its retentivity.
Explain.
2. How do you explain the retentivity of hard steel?
3. Are the molecules of a piece of iron magnetized at all times?
Explain.
4. When a piece of iron is magnetized by induction does any
magnetism enter the iron from the magnet? Does the magnet
lose as the iron gains magnetism? Explain.
5. Have all magnets been produced by induction? Explain.
6. Why will tapping a piece of iron when in a magnetic field increase
the amount it will be magnetized?
7. Express in your own words the theory of magnetism.
8. Place two bar magnets in a line 5 cm. apart, unlike poles adjacent;
obtain the magnetic field with iron filings. Sketch it.
9. Repeat Exercise No. 8 using like poles. Describe the appearance
of a field that gives attraction; of a field that gives repulsion.
(3) The Earth's Magnetism
209. The Earth's Magnetic Field.—Dr. William Gilbert's
famous book, De Magnete, contains many helpful
and suggestive ideas, none perhaps more important than
his explanation of the behavior of the compass needle. He
assumed that the earth is a magnet, with a south-seeking
pole near the geographical north pole, and with a north-seeking
pole near the geographical south pole. This idea
has since been shown to be correct. The north magnetic
(or south-seeking) pole was found in 1831, by Sir James
Ross in Boothia Felix, Canada. Its approximate present
location as determined by Captain Amundsen in 1905 is[Pg 239]
[Pg 240]
latitude 70° 5´ N. and longitude 96° 46´ W. The south
magnetic pole is in latitude 72° S., longitude 155° 16´ E.
The north magnetic pole is continually changing its position.
At present it is moving slowly westward.
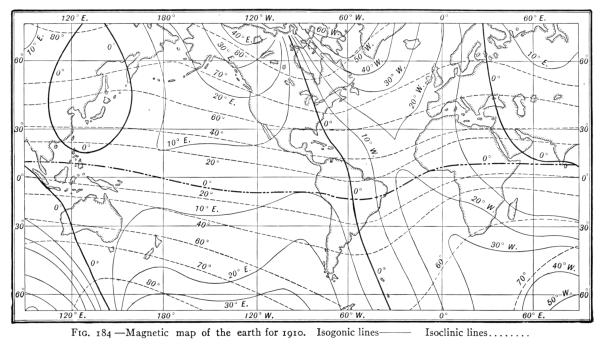 Fig. 184.—Magnetic map of the earth for 1910. Isogonic lines ——— Isoclinic lines - - - -
Fig. 184.—Magnetic map of the earth for 1910. Isogonic lines ——— Isoclinic lines - - - -
210. Direction of the Earth's Magnetic Field.—Reference
has been made to the fact that the compass does
not always point exactly north. This indicates that the
earth's magnetic field varies in its direction. Columbus
discovered this fact upon his first voyage. The discovery
alarmed the sailors since they feared they might come to
a place where the compass would be unreliable. This
variation is called declination. It is defined as the angle
between the direction of the needle and the geographical
meridian. Declination is due to the fact that the geographical
and magnetic poles do not coincide. What is
meant by a declination of 90°? Lines drawn upon a map
so as to pass through places of the same declination are
called isogonic lines. The line passing through points
where the needle points north, without declination, is
the agonic line. The agonic line is slowly moving westward.
It now passes near Lansing, Michigan; Cincinnati,
Ohio; and Charleston, S. Carolina. (See Fig. 184.) At
all points in the United States and Canada east of the
agonic line the declination is west, at points west of the
agonic line the declination is east.
211. The Dipping Needle.—Mount an unmagnetized
steel needle on a horizontal axis so as to be in neutral
equilibrium, that is, so as to remain balanced in any position
in which it is left. Upon being magnetized and
placed so that it can swing in a north and south plane,
the north-seeking pole will now be found to be depressed,
the needle forming an angle of nearly 70° with the horizontal.
(See Fig. 185.) The position assumed by the
needle indicates that the earth's magnetic field instead of[Pg 241]
being horizontal in the United States dips down at an angle
of about 70°. Over the magnetic pole, the dipping needle
as it is called, is vertical. At the earth's equator it is
nearly horizontal. The angle between a horizontal plane
and the earth's magnetic lines of force
is called the inclination or dip.
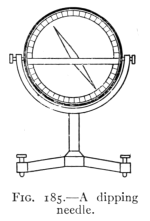 Fig. 185.—A dipping
needle.
Fig. 185.—A dipping
needle.
212. Inductive Effect of the
Earth's Magnetic Field.—The
earth's magnetic lines of force are
to be considered as filling the space
above the earth, passing through
all objects on the surface and into
and through the earth's interior.
The direction of the earth's field is
shown by the compass and the
dipping needle. Magnetic lines of
force tend to crowd into and follow iron and steel objects
on account of their permeability. Therefore, iron or
steel objects, such as posts, columns, etc., are permeated
by the earth's lines of force, which in the United States
enter at the top of these objects and leave at the bottom.
The lines of force passing through these bodies arrange
their molecules in line or magnetize the bodies. The
inductive effect of the earth's magnetism indicates how
lodestones or natural magnets acquire their magnetized
condition. So far as is known, magnetism produces no
effect upon the human body. It can therefore be studied
only by observing its effects upon magnets or bodies
affected by it.
Important Topics
The earth's magnetic field, dip, declination, agonic line, induction
by the earth's field.
[Pg 242]
Exercises
1. How would a dipping needle be of assistance in locating the
magnetic poles of the earth?
2. Will a dipping needle weigh more before or after it is magnetized?
Explain.
3. It is said that induction precedes attraction. Using this idea,
explain how a magnet attracts a piece of soft iron.
4. Devise an experiment to show that a piece of iron attracts a
magnet just as a magnet attracts a piece of iron.
5. Give two methods for determining the poles of a magnet.
6. State three of the most important points in the theory of magnetism.
What evidence supports each?
7. Why is a permanent magnet injured when it is dropped?
8. Name two important uses of the earth's magnetic field.
9. What magnetic pole would you find at the top of an iron post
that has stood for some time in the ground? What pole at the
bottom? How would you test this?
[Pg 243]
STATIC ELECTRICITY
(1) Electrification and Electrical Charges
213. Electrical Charges.—The ideas gained in the study
of magnetism are of assistance in the study of electricity
in giving some fundamental ideas and principles that will
often be referred to as a basis for comparing the actions
of magnetized and electrified bodies. The process of
electrifying a body is very different from that of magnetizing
it. Thus if a rubber comb or rod be rubbed with a
woolen cloth the object rubbed is able to attract to itself
light bits of paper, thread, etc. This peculiar attraction
was noticed and recorded by the ancient Greeks, 600 B.C.,
when it was found that amber when rubbed would attract
light objects to itself. For a long time it was supposed
that amber was the only substance showing this property.
Dr. William Gilbert, however, discovered that the electrified
condition could be produced by rubbing a great
variety of substances. He named the result produced,
electrification, after the Greek name for amber (elektron).
A body like hard rubber or amber which will attract light
objects when rubbed is said to be electrified, or to have
been given a charge of electricity.
214. Law of Electric Action.—Let a vulcanite rod be
electrified by rubbing with a woolen cloth until it will
attract light objects; then place it in a wire stirrup
suspended by a silk thread. If a second vulcanite rod is
similarly electrified and brought near the first, the two[Pg 244]
will be found to repel. (See Fig. 186.) If now a glass rod
be rubbed with silk and brought near the suspended rod,
the two will attract. This difference in behavior indicates
a difference in the electrification or charge upon the rods.
The two charged vulcanite rods repelling and the charged
glass and vulcanite attracting indicate
the law of electric action. Like charges
repel each other and unlike charges attract
each other. Extensive experiments with
all kinds of substances indicate that
there are but two kinds of electrical
charges. The electrical charge upon
glass when rubbed with silk or wool is
called positive, and that upon hard rubber or vulcanite
when rubbed with wool is called negative.
 Fig. 186.—Repulsion
of like charges.
Fig. 186.—Repulsion
of like charges.
 Fig. 187.—An aluminum
foil electroscope.
Fig. 187.—An aluminum
foil electroscope.
Fig. 188.—A proof plane.
215. The Electroscope and its Uses.—An electroscope
is a device employed to test the presence
of an electrical charge. The
aluminum foil electroscope consists of a
flask closed by a rubber stopper
through which passes a rod which ends
at the top in a ball or plate and below
is attached two narrow leaves of thin
aluminum-foil. Ordinarily the two
leaves hang close together and parallel but if a charged
body is brought near the electroscope the leaves
spread apart at the bottom. (See Fig. 187.) The
kind of charge upon a body may be determined with an
electroscope as follows: Make a proof-plane by sealing a[Pg 245]
small metal disc on the end of a hard rubber rod. (See
Fig. 188.) Touch the disc of the proof-plane first to a
charged rubber rod and then to the top of the electroscope.
The leaves of the latter will separate showing that the
electroscope is charged. This charge remains after the
proof-plane is removed. If the charged vulcanite rod is
brought near the electroscope, the leaves separate further
That is, a charge like that on the electroscope makes the
leaves separate further. But if an unlike charge, as that
on a positively charged glass rod, is cautiously brought
near, the leaves will be seen to move together.
 Fig. 189.—Rod with woolen cap.
Fig. 189.—Rod with woolen cap.
216. Two Charges are Produced at the Same Time.—A
closely fitting woolen cover or cap some 3 in. long is
made for the end of a vulcanite rod. A silk thread attached
to the cap enables one
to hold the latter while the
rod is turned within it. (See
Fig. 189.) If the rod bearing
the cap is held near a
charged electroscope little or no effect is noticed. If
now the cap is removed by the silk thread and held near
the electroscope, it will be found to be positively charged
while the rod is negatively charged. The fact that no
result is seen when the cap and rod are together, indicates
that one charge neutralizes the other. In other words,
the charges must be equal. This illustrates the truth that
when electrification is produced by friction, the two objects
rubbed together acquire equal and opposite charges.
217. Charging by Contact and Conduction.—If a small
pith ball is suspended by a silk thread, a charged rod
brought near is at first attracted, but after contact is
repelled (see Fig. 190) showing that the ball has become
charged with the same kind of electrification that is upon
the rod. That is, a charge given to an object by contact[Pg 246]
with a charged body is of the same kind as that upon the
charged one. The proof-plane in Art. 215 carries the
same kind of charge that is upon the rod it is charged from.
Some substances have the ability to transfer charges of
electrification. These are called conductors, those that
do not conduct electrification are insulators. The conducting
power of a body is readily
tested by placing one end of a rod
of the material upon the top of an
electroscope and the other end upon
an insulated support, as in Fig. 191.
If now a charge be put in contact
with the body of a, the electroscope will show by its leaves
whether the rod tested conducts or not. The leaves separate
instantly when conducting substances are tested,
while no action results with insulators. In testing some
materials for conductivity the leaves are found to diverge
gradually. Such bodies are said to be poor conductors.
All degrees of conductivity are found. The metals are
the best conductors. The best insulators are rubber,
mica, shellac, glass, silk, porcelain, paraffin, and oils.
 Fig. 190.—The pith ball
charged by contact is repelled.
Fig. 190.—The pith ball
charged by contact is repelled.
Fig. 191.—Testing for conductivity.
Important Topics
1. Positive and negative changes. Law of electric action.
2. Electroscope and its uses.
3. Conductors and insulators.
[Pg 247]
Exercises
1. Is air a conductor? Give reasons for your answer.
2. Mention two points of likeness and two points of difference
between magnetism and electrification.
3. If you were testing the electrification of a body with a charged
pith ball suspended by a silk thread, would attraction or repulsion
be the better test? Give reasons.
4. Have you ever produced electrification by friction outside of a
laboratory? Explain.
5. Are the rods upon which we produce electrification by friction,
conductors or insulators? How do you explain this?
6. Are conductors or insulators of the greater importance in practical
electricity? Explain.
(2) Electric Fields and Electrostatic Induction
 Fig. 192.—An electric field about
a positively charged shell.
Fig. 192.—An electric field about
a positively charged shell.
Fig. 193.—A "detector."
218. Electrical Fields.—In our study of magnetism we
learned that a magnet affects objects about it by its magnetic
lines of force. In a similar
way it is assumed that a charged
body produces electrical effects
upon its surroundings by electric
lines of force. For example,
the attraction that a charged body exerts upon light objects
through short distances or the influence of a charge upon an
electroscope several feet away, is said to be due to the electric
field about the charged body. (See Fig. 192.) The presence
of the electric lines of force may be shown by placing
a perforated, slender, diamond-shaped piece of tissue
paper upon a light glass pointer (Fig. 193). When placed[Pg 248]
in an electric field the tissue paper "detector" places itself
parallel to the lines of force. Electric lines of force are
said to extend from a positive to a negative charge. (See
Fig. 194.) The direction shown by the arrow upon the
lines is that along which
a small positive charge
tends to move. Electric
lines of force unlike
those from magnets are
not continuous. They
extend from a positive
charge to a negative
charge. Therefore each
positive charge is connected by lines of force to a negative
charge somewhere. These ideas of electric fields are of
much assistance in explaining many electrical effects.
Electrical fields between oppositely charged shells will be
found similar to Fig. 194, while between shells with like
charges, fields are found as in Fig. 195.
 Fig. 194.—Electric field between unlike
charges.
Fig. 194.—Electric field between unlike
charges.
 Fig. 195.—Electric field between like
charges.
Fig. 195.—Electric field between like
charges.
219. Electrostatic Induction.—If
a charged
body is brought near
an aluminum-foil electroscope,
the leaves
separate. (See Fig.
198.) The nearer the
charge is brought the
wider the leaves spread,
but when the charge is removed, the leaves collapse showing
that nothing was given to the electroscope. It was
simply affected by the charge in its vicinity. This production
of an electrified condition in a body by the influence
of a charge near it is called electrostatic induction. Placing
insulators, such as a sheet of glass, between the charge[Pg 249]
and the electroscope does not affect the result, which is
apparently brought about by the action of the electric
lines of force. These lines of force extend without difficulty
through uncharged insulators and terminate often at
the surface of a conductor, where their influence causes
a charge to accumulate. Charged insulators, however, do
affect inductive action. This may be noticed by using a
sensitive electroscope.
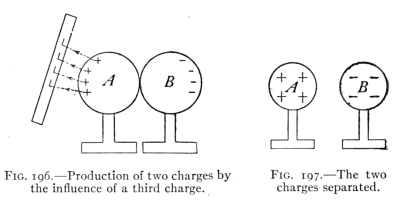 Fig. 196.—Production of two charges by
the influence of a third charge.
Fig. 196.—Production of two charges by
the influence of a third charge.
Fig. 197.—The two
charges separated.
220. Electrical Separation by Induction.—The action
just described may be illustrated further by taking two
insulated, uncharged brass shells, A and B. (See Fig.
196.) Bring a charged vulcanite rod near shell "A"
while the shells are touching each other. Then remove
shell B (Fig. 197) while the rod remains near A. On
testing the shells for electrification, A is found to possess
a positive charge. This action is in some respects similar
to magnetic induction, for if one places a north-seeking
pole near a piece of iron, the iron develops by induction a
south-seeking pole at the end nearest the magnet and a
north-seeking at the other end. There is, however, one
striking difference. If the magnetized iron be separated
into two parts, each part is a complete magnet possessing
two unlike poles; while if the object affected by electrostatic[Pg 250]
induction is separated into two parts one part
has a positive charge and the other a negative charge.
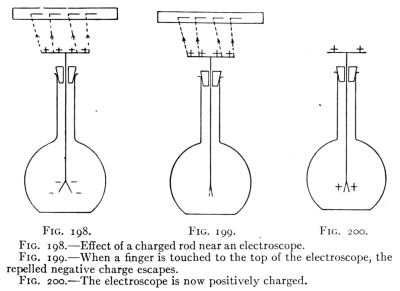 Fig. 198.—Effect of a charged rod near an electroscope.
Fig. 198.—Effect of a charged rod near an electroscope.
Fig. 199.—When a finger is touched to the top of the electroscope, the
repelled negative charge escapes.
Fig. 200.—The electroscope is now positively charged.
221. Charging a body by induction is easily accomplished.
To charge an aluminum-foil electroscope by
induction bring near (say 10 cm.) from the top of the
electroscope a charged rubber rod. (See Fig. 198.)
The separated leaves show the presence of the repelled
or negative charge, the positive charge being on the disc at
the top. If while the charged rod is held near, the
metal top of the electroscope is touched by the finger the
leaves at once fall together showing that the repelled
negative charge has escaped from the electroscope (Fig.
199). On removing first the finger and next the charged
rod, the positive charge spreads over the metal parts of
the electroscope, as is shown by the separation of the
leaves (Fig. 200). The electroscope is now charged positively
by induction. If the charged rubber rod is brought
to about 30 cm. from the electroscope, its leaves tend to[Pg 251]
move together. If a body charged similarly to the electroscope
or positively, is moved toward the electroscope the
leaves separate further. This behavior of the electroscope
enables one to determine the kind of charge upon a
body.
Two principles of electrostatic induction may now be
stated: (1) Two equal, unlike charges are always produced
by electrostatic induction.
(2) If the body affected by induction is connected to
the earth by a conductor, the repelled or "free" charge
is conducted away from the body while the "bound"
charge is held by the inducing charge.
These principles apply in every case of induction.
Important Topics
1. Electric lines of force. Characteristics (3).
2. Electrostatic induction. Principles (2).
3. Charging by induction. Explanation.
Exercises
1. What are electric lines of force? Where are they found? What
does the arrow mean upon the lines?
2. Name three effects produced by electric fields.
3. Does electrostatic induction occur outside of laboratories?
Where? When?
4. Given a charged rubber rod, how may one charge from it by
induction, insulated brass shells, giving some a positive and
some a negative charge?
5. How may the charges upon the shells be tested?
6. In charging an electroscope by induction, why must the finger
be removed before the glass rod?
7. Why is it best to have the rubber and glass rods, used in electrification,
warmer than the air of the room in which the experiments
are being performed?
8. When a sharp metallic point is held near the knob of a charged
electroscope the leaves quickly come together. Explain.
[Pg 252]
9. Might one of the members of your class in physics be charged
with electricity, if he should stand on a board supported by dry
glass insulators? Explain.
10. If a metal can is charged strongly while standing on an insulator,
tests made by means of the proof-plane and electroscope show
no charge on the inside. Explain.
(3) Electrical Theories and Distribution of Charges
222. Franklin's Theory of Electricity.—We have studied
the production of electrification by friction and induction.
It will be helpful now to consider some of the theories of
electricity. From the ease with which electrification
moves, along a conductor, many have imagined that electricity
is a fluid. Benjamin Franklin's One Fluid Theory
held that a positive charge consisted in an accumulation
or an excess of electricity while a negative charge implies
a deficiency or less than the usual amount. This theory
led to representing positive electrification by a plus (+)
sign and negative, by a minus (-) sign. These signs are
in general use to-day. The use and significance of these
signs should be clearly fixed in mind.
223. The Electron Theory.—Various discoveries and
experiments made in recent years indicate, however,
that negative electricity consists of little corpuscles or
electrons which may pass readily from one molecule
of a conductor to another while their movement through
an insulator is much retarded if not entirely prevented.
This theory, sometimes called the Electron Theory, holds
that each atom of a substance has as a nucleus a corpuscle
of positive electricity, and surrounding it, minute negative
corpuscles or electrons. It is thought that the electrons
in the atom are very much smaller than the positive
charges and are revolving about the latter with great
rapidity. Ordinarily, the positive and negative charges
are equal so that the atom is in a neutral or uncharged[Pg 253]
condition. By the action of various forces some of the
negative corpuscles within a conductor may be moved from
molecule to molecule. Thus if a negatively charged rod
is brought near a conductor, many electrons stream away
to the far end charging it negatively, while the nearer end
of the conductor is left with fewer electrons than usual
along with the fixed positive corpuscles. Hence the near
end is positively charged. (See Fig. 198.) On the other
hand, if a positive charge is used, it attracts the electrons
from the far end, leaving the immovable positive corpuscles
there, and that end becomes positively electrified,
while the nearer end with its surplus of electrons is, of
course, negatively electrified.
The Electron Theory is considered well founded since
the electrons have (a) had their mass determined, (b)
their speed measured, (c) their electric charge determined,
(d) and their behavior while passing through magnetic
and electric fields observed. These facts and other
experimental evidence have demonstrated the existence of
electrons. The positive corpuscle has not been directly
observed but is assumed to exist to account for the
effects observed in induction, charging by friction, etc.
224. Distribution of an Electric Charge upon a Conductor.—We
have applied the electron theory in explaining
the phenomenon of electrostatic induction. Let us
now use it in studying the distribution of an electric charge
upon a conductor. Let a cylindrical metal vessel open
at the top and insulated by being placed upon pieces of
sealing wax have a charge of negative electricity given
it. (See Fig. 201.) On now taking a proof plane and
attempting to obtain a charge from the interior of the
vessel no result is found, while a charge is readily obtained
from the outside of the dish. This result is explained by
considering that the electrons are mutually self-repellent[Pg 254]
and in their attempt to separate as widely as possible pass
to the outer surface of the vessel. This same condition
is also true of a dish made of woven wire. If the charged
conductor is not spherical in outline, an uneven distribution
of the charge is observed. Thus if an egg-shaped conductor
is insulated and charged (see Fig. 202),
a proof plane touched to the broad end
of the body and then to an electroscope
causes a certain divergence of the leaves
of the latter. If now a charge be taken
from the pointed end by the proof plane
to the uncharged electroscope, a greater
spreading of the leaves than before will
be noticed. This indicates that the
electricity may be unevenly distributed
over the surface of a body. It is found
that the electric density, as it is called, is greatest where the
surface curves most sharply. At a very sharp curve, as at
a point, the electric density may be so great that a part
of the charge escapes into the air. (See Fig. 203.) For
this reason electric conductors on which it is desired to
keep an electric charge have round surfaces
and all sharp points and corners are avoided.
While conductors, such as lightning rods,
which are designed to facilitate the escape
of electric charges, are provided with a number
of sharp points at the end or elsewhere.
At such points, air particles are drawn
forcibly against the point and after being
charged are driven away strongly, creating
the so-called electrical wind which carries away the charge
at a rapid rate. (See Fig. 203.)
 Fig. 201.—No
charge is found inside
a hollow vessel.
Fig. 201.—No
charge is found inside
a hollow vessel.
 Fig. 202.—More
charge at
the pointed
end.
Fig. 202.—More
charge at
the pointed
end.
225. Lightning and Electricity.—The fact that lightning
is an electrical discharge was first shown in 1752 by[Pg 255]
Benjamin Franklin, who drew electric charges from a cloud
by flying a kite in a thunderstorm. With the electricity
which passed down the kite string he performed a number
of electrical experiments. This discovery made Franklin
famous among scientific men everywhere. Franklin then
suggested the use of lightning rods to protect buildings
from lightning. These rods act as conductors for the
electric discharge and thus prevent it from passing through
the building, with the risk of overheating some part and
setting the latter on fire. The
points provided at the top of
lightning rods are believed to aid
in preventing strokes of lightning
by the silent discharge of the so-called
electric wind which tends
to quietly unite the charges in the
clouds and on the earth beneath.
 Fig. 203.—Electrical wind produced
by a pointed conductor.
Fig. 203.—Electrical wind produced
by a pointed conductor.
Fig. 204.—Electrical whirl.
The reaction from the electrical
wind causes it to revolve.
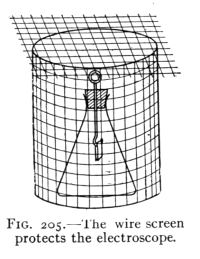 Fig 205. The wire screen
protects the electroscope.
Fig 205. The wire screen
protects the electroscope.
The charge in an electrified cloud
acts inductively upon the earth
beneath, attracting an opposite
charge to the objects below. The
discharge from the cloud often passes to the objects
beneath, such as trees or buildings. Thunder is believed
to be due to the sudden expansion of the air when intensely[Pg 256]
heated by the electric discharge and its sudden contraction,
like a slap, as the track instantly cools. Thunder at a
distance is usually followed by rumblings due to changes
in the intensity of the sound mainly due to reflections of
sound waves from clouds and other reflecting surfaces.
226. An electric screen is a device for cutting off the
influence of an electric charge. Faraday found that if a
sensitive electroscope is surrounded by a wire mesh screen
(see Fig. 205), no evidence of electrification could be found
inside. In other words, a network of conductors on a
building makes the best protection against lightning,
provided it is connected to the earth by good conductors
at several places.
Important Topics
1. Electrical theories. Evidences for electron theory.
2. How is the theory used in explaining induction?
3. Charges, and distribution on conductors (effect of shape).
4. Lightning: cause, effects, lightning rods.
Exercises
1. In what respects is Franklin's one-fluid theory like the electron
theory? In what respects different?
2. Consider two shells charged by induction from an electrified
rubber rod, one positively and one negatively. Explain the
process, using the ideas of the electron theory.
3. Should the metal top of an electroscope have sharp corners?
Explain.
4. Would a tall steel tower have the same need of a lightning rod
as a brick chimney of the same height? Explain.
5. Will a solid sphere hold a greater charge of electricity than a
hollow one of the same diameter? Explain.
6. If a positively charged cloud floats over a tree which is a good
conductor of electricity will the tree be charged? Show diagram.
Explain.
[Pg 257]
(4) Potential, Capacity and the Electric
Condenser
227. Conditions Causing a Movement of Electricity.—In
the study of conductors and insulators it was observed
that an electric charge moved along the conducting rod
to the electroscope. This movement of electricity along a
conductor is a result of great practical importance. We
will now consider the conditions that produce the "flow"
or "current" of electricity.
Let two electroscopes stand
near each other. Charge
one, C´ (Fig. 206), strongly
and charge the other
slightly. If now a light
stiff wire attached to a
stick of sealing wax be
placed so as to connect the
tops of the electroscopes,
the leaves of C will partly
close while those of D will
open slightly, thus indicating a movement of electricity
from C to D along the wire. The movement was from
a place of greater degree of electrification to one of less.
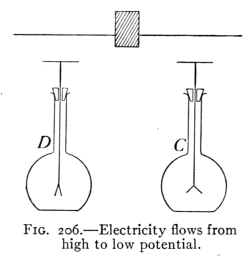 Fig. 206.—Electricity flows from
high to low potential.
Fig. 206.—Electricity flows from
high to low potential.
228. Potential.—The potential of an electrified body is
its degree of electrification. Therefore, it is said that
electroscope C mentioned above has a greater potential
than electroscope D. The movement of electricity is from
a place of greater or high potential to one of lesser or low
potential. If two bodies are at the same potential there
will be found no movement of electricity between them.
A difference of potential between two points connected by
a conductor is therefore the necessary condition for an
electric current. Just as heat is transmitted along a conductor[Pg 258]
from a place of high to one of lower temperature, so
electricity is transmitted along a conductor from a place
of high to one of low potential. Thus potential in electricity
corresponds to temperature in heat. One is the
"degree of electrification," the other, "the degree of
hotness."
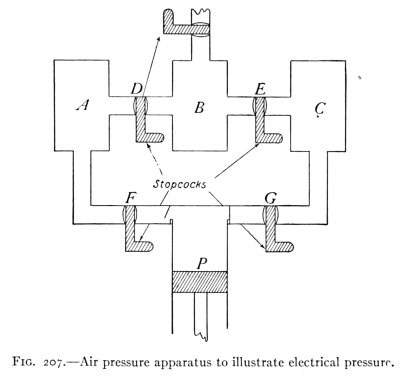 Fig. 207.—Air pressure apparatus to illustrate electrical pressure.
Fig. 207.—Air pressure apparatus to illustrate electrical pressure.
229. Electrical pressure is a term sometimes used for
difference of potential. To better understand electrical
pressure consider three round tanks (Fig. 207) containing
air. A is a tank holding air at 10 lbs. pressure per square
inch, above atmospheric pressure, B is open to the air
and hence is at atmospheric pressure while C has a partial
vacuum, with 10 lbs. less pressure than that of the atmosphere.
If the valve at D or E is opened a flow of air sets
up until the pressures are equalized. While if the pump[Pg 259]
at P is working a difference in pressure is easily maintained.
Tank A corresponds to an insulated body charged to a high
positive potential; tank B, open to the air, a body connected
to the earth; while tank C represents a body having a
negative potential. The earth is said to have zero potential.
Now just as compressed air will be pushed into the
atmosphere (as from A to B) while air
at atmospheric pressure will if possible be
forced itself into a partial vacuum (as from
B to C), so electricity at a positive potential
will tend to move to a place at zero
potential, while that at zero potential
tends to move to a place of negative
potential. Bodies at the same potential
as the earth, or at zero potential, are also
said to be neutral. Those positively
electrified have a positive potential,
those negatively electrified have a negative
potential. As in gases, movement
always tends from higher pressure (potential)
to lower pressure (potential).
 Fig. 208.—The
metal plate gives
the electroscope a
greater surface
and hence greater
capacity.
Fig. 208.—The
metal plate gives
the electroscope a
greater surface
and hence greater
capacity.
230. Capacity.—If we have a 100-gallon
tank and a 10-gallon tank connected by
a pipe both filled with compressed air,
the larger tank will contain ten times as much air as the
smaller at the same pressure since it has ten times the
capacity, or, if the two tanks are separated and the same
amount of air is contained in each, the pressure of the
air contained in the small tank will be ten times that in
the large one.
The electrical capacity of a conductor is in some respects
similar to the capacity of a tank for air. Since, however,
electrical charges are upon the surface of a body, its capacity
depends in part upon the extent of surface. For[Pg 260]
example, if a charge is taken from a charged rubber rod by a
proof plane to an electroscope a certain divergence of the
leaves will be noticed. If a circular metal plate several
times the diameter of the top of the electroscope is laid
upon the latter (see Fig. 208), and a charge equal to that
used before is brought to the electroscope, the leaves show
less divergence than before, showing that the same charge
gives a lower potential
when placed upon a body
of greater capacity.
 Fig. 209.—A plate condenser.
Fig. 209.—A plate condenser.
 Fig. 210.—A condenser of several
plates.
Fig. 210.—A condenser of several
plates.
231. The electric
condenser is a device
having a large electrical capacity consisting of parallel
conductors separated by good insulators. It has been
devised to enable one to obtain a large electrical charge
upon a body of convenient size. Such an apparatus is
of great practical value in many experiments and operations.
Its construction involves the principle of electrostatic
induction in which a charge of one kind attracts
and "holds" strongly a
charge of opposite kind
near it. In its simplest
form it consists of two
parallel conductors separated
from each other
(Fig. 209). The upper
plate has been charged negatively. This has given the
lower plate a positive charge by induction, since the
latter is connected to the earth. These positive and negative
charges hold or "bind" each other so that a
large quantity may be accumulated. To increase the
capacity of a condenser, several plates are used connected
as in Fig. 210.
It is a curious fact that the kind of insulator between the[Pg 261]
charged conductors of a condenser affects its capacity.
Thus if glass, paraffine, or beeswax is between the plates
instead of air, the plates will "hold" more electricity at
the same potential. For this reason condenser plates
are often separated by sheets of glass, paraffined paper,
or mica.
 Fig. 211.—A Leyden jar
and a discharger.
Fig. 211.—A Leyden jar
and a discharger.
232. The Leyden Jar.—A convenient form of condenser,
used as long ago as 1745, is the Leyden jar. It
consists of a glass jar (Fig. 211) coated part way up,
inside and out, with tinfoil. The inner coating is connected
by a chain to a knob at the
top. The Leyden jar is charged by
connecting the outer coating to the
earth while to the inner coating is
given a charge of either kind of
electricity. The other kind of charge
is developed by induction upon the
outer coating, and each charge binds
the other. To discharge a jar, a
conductor, as a wire, is connected first to the outer coating
and held there while the other end is brought to the
knob at the top. A bright spark is produced when the
two charges combine. It is best not to let the discharge
from the jar pass through the body unless one is certain
that only a very small charge is present.
233. Oscillatory Discharge.—The discharge from a
Leyden jar is an interesting phenomenon. The rush of
electricity from one coat to the other does not stop when
the two coats are exactly neutralized but continues until
the two plates are charged just oppositely to their condition
at first, then a rush of electricity in the opposite
direction occurs. This alternation continues several
times and constitutes what is called the oscillatory discharge.
(See Fig. 414.) This oscillatory discharge sets[Pg 262]
up waves in the ether. These are called Hertzian waves
in honor of their discoverer, Heinrich Hertz. They are
the ether waves used in wireless telegraphy. A lightning
flash has been shown by photographs and by other
means to be oscillatory. This fact supports the idea
that the electrical conditions just preceding the stroke
of lightning reproduce a condenser on a large scale.
The charged cloud is the upper charged plate, the earth
beneath, charged by induction from the cloud, is the lower
charged plate, while the air between is the insulator or
dielectric as it is sometimes called.
Important Topics
1. Potential: high, low, zero, positive, negative, similar to temperature
and air pressure.
2. Capacity affected by (1) area, (2) induction.
3. Condensers, Leyden jar, parallel plate.
4. Oscillatory discharge, conditions, results.
Exercises
1. Is the air a conductor? Explain.
2. Can the Leyden jar be strongly charged if the outer coat is
insulated? Explain.
3. Upon what two conditions does the capacity of a body depend?
How in each case?
4. Would a lightning discharge produce wireless waves? Explain.
5. If a sharp tack be dropped point up on the plate of an electroscope
the latter is quickly discharged. Explain.
(5) Electrostatic Generators
234. Static Electric Machines.—Many machines have
been invented to produce larger quantities of static electricity
than we have used in the experiments previously
described. One of the earlier of these was the plate friction
machine in which a large circular glass plate was
rotated while a pad of some material was held against it.
This machine was capable of producing powerful effects,[Pg 263]
but it took much work to turn it, and it has been abandoned
for a more efficient device, the static induction
machine.
235. The electrophorus is the simplest static induction
generator, consisting
simply of a flat circular
plate of some insulating
material, as
paraffine, shellac, or
rosin contained in a metal pan, and a flat circular metal
disc having an insulating handle.
 Fig. 212.—An electrophorus.
Fig. 212.—An electrophorus.
The electrophorus is used as follows: The plate is first
electrified by rubbing or beating with fur or a woolen
cloth. The plate will be found to be charged negatively.
The metal disc is placed upon the plate by holding the
insulating handle. The upper surface of the charged body
is slightly uneven so that the disc touches but a few high
points. The greater part of the charged surface is separated
from the metal
disc by air, a good insulator.
The charge
therefore acts inductively
upon the disc
repelling negative electricity
to the upper
surface of the disc,
leaving the lower surface charged positively (Fig. 212).
If now the finger is touched to the disc the repelled negative
charge escapes and the whole disc is left positively
charged. The disc is now removed (Fig. 213) and the
charge upon it may be tested or used in any desired manner.
The disc may be recharged many times without
rubbing the plate again.
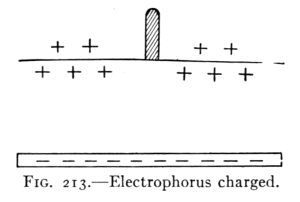 Fig. 213.—Electrophorus charged.
Fig. 213.—Electrophorus charged.
These electrical charges possess energy. What is the[Pg 264]
source of this energy? The answer may be determined
by the following experiment. Place the disc upon the
charged plate. Touch the disc with the finger to remove
the repelled charge. Connect an electroscope to the disc
by a fine wire. Nothing appears on the electroscope,
since the disc has been connected to the earth, and is
therefore at zero potential. If now the disc is lifted
slowly, the leaves of the electroscope gradually separate,
showing that a charge of electricity appears when the
disc is being lifted against the force of attraction between
the two charges. Just as potential energy is developed in
a weight when it is lifted against the earth's attraction
so electrical energy appears in the disc while it is being
separated from the plate. The electrical energy of the
charge is therefore due to the work done in separating the
two charges. This electrical energy appears as heat and
light, when the disc is discharged. It may be employed
to ignite gas, gunpowder, etc.
236. The Toepler-Holtz Induction Machine.—This
is a type of induction or influence machine that is often used
for producing a continuous supply of electricity as in the
operation of "X" ray machines, in lecture demonstrations,
etc. This machine (Fig. 214) consists of two discs: one
fixed, the other mounted so as to revolve. Upon the
back of the fixed plate are two sectors of tinfoil which
become charged oppositely. Upon the revolving plate
are six metallic discs. These discs act like the discs of
the electrophorus. They become charged by induction
from the charges upon the sectors fastened to the fixed
plate. The brushes held by a rod touch the discs at just
the right time to take off the repelled charge. The charges
induced upon the discs are taken off by two metal combs
whose points are held close to the revolving disc. The
Leyden jars assist in accumulating a good strong charge[Pg 265]
before a spark passes between the terminal knobs. Some
machines are built up of several pairs of plates and give
correspondingly large amounts of electricity.
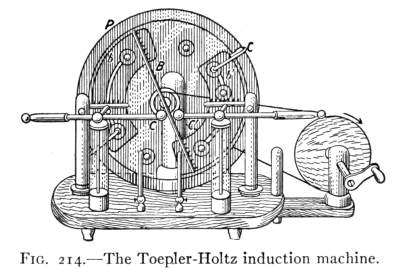 Fig. 214.—The Toepler-Holtz induction machine.
Fig. 214.—The Toepler-Holtz induction machine.
Important Topics
Static Electric Generators.—(a) plate friction machine, (b) electrophorus,
(c) induction or influence machine.
Exercises
1. Potential is similar to what other terms that we have studied?
2. What three electrical phenomena are better understood from a
study of the lines of force?
3. How many charges may be produced by an electrophorus before
the plate needs to be electrified again? Explain.
4. The static induction machine is often called a "continuous
electrophorous." Why?
5. The Leyden jars used with the induction machine cause much
brighter sparks to be produced than without them. Explain.
6. With the Leyden jars removed, would the frequency with which
the sparks pass between the knobs be increased or decreased?
Explain.
7. Mention three likenesses and three differences between magnetism
and static electricity.
8. Will you receive a greater shock by touching a knob of a charged
Leyden jar when it is held in the hand or when it is standing on
a sheet of glass? Explain.
9. In what way may an electric charge be divided into three
equal parts?
[Pg 266]
Review Outline: Magnetism and Static Electricity
Comparison between Magnetism and Static Electricity.
| Substances are: | magnetic, non-magnetic. | conductors, insulators. |
| Produced by: | induction. | friction, or induction. |
| Theory: | molecular. | electron. (fluid) |
| Fields of Force Explain: | attraction, repulsion, induction, action of compass. | attraction, repulsion, induction. |
| Terms: | magnetoscope, dip, declination, pole, retentivity, permeability, lodestone, magnetic meridian. | electroscope, electron, positive, negative, potential, capacity, condenser, electrophorus, oscillatory discharge, lightning. |
| Likeness: both are: | a—produced by induction, b—attract and repel, c—have fields of force. |
| Differences: | a—electricity can be conducted, magnetism cannot. b—electricity in all substances, magnetism in few. c—magnetism with the compass indicates direction. |
[Pg 267]
CURRENT ELECTRICITY
(1) Electrical Currents and Circuits
237. Sources of Electric Currents.—In studying the
production and distribution of static electricity it was
seen that if two bodies at different potentials are connected
by a copper wire a movement of electricity to the body having
the lower potential occurred along the conducting wire.
This movement of electricity is called an electric current
(Art. 227). A difference of potential is therefore often
called an electromotive force (E.M.F.), since it produces the
movement of electricity in a conductor. The current
between two oppositely charged bodies lasts for so short a
time as to be of little or no practical value unless some
means are found for continually recharging the bodies.
That is, some device must be used to restore the difference
in potential as fast as the conducting wire equalizes it.
The continual charging of the bodies takes work. In
other words, it requires a continual expenditure of some
form of energy (which is converted into electrical energy)
to produce the electric current. Two forms of energy are
commonly used for this purpose.
(A) Chemical energy is employed in voltaic cells for producing
electric currents. (B) Mechanical energy is used
for the same purpose in the dynamo and similar devices.
238. The voltaic cell is named after Volta, an Italian
physicist, who in 1800 invented it. In its simplest form
it consists of a strip of copper and a strip of zinc placed in
dilute sulphuric acid (one part acid to fifteen or twenty[Pg 268]
of water) (Fig. 215). By the use of sensitive apparatus,
it can be shown that the copper plate of the voltaic cell
has a positive charge and the zinc plate a negative charge.
For example, let a flat plate 10 cm. in diameter be placed
upon the knob of an electroscope and a similar plate,
coated with shellac and provided with an insulating handle,
be set upon it to form a condenser. (See Fig. 216.) If
now wires from the two plates of a simple voltaic cell be
respectively connected to the plates of the condenser,
charges from the copper and zinc plates will accumulate
upon the two condenser plates. Now remove the wires
and lift the upper plate. The "bound" charge upon
the lower plate will spread over the leaves and cause them
to separate. Upon testing, the charge from the zinc plate
will be found to be negative and that from the copper plate,
positive. Since a positive charge is found upon the
copper plate it is called the positive electrode; the zinc
plate is called the negative electrode.
 Fig. 215.—Cross-section
of a simple voltaic
cell.
Fig. 215.—Cross-section
of a simple voltaic
cell.
Fig. 216.—Testing the charges upon
the plates of a simple voltaic cell.
239. Test for an Electric Current.—If the copper and
zinc plates of a voltaic cell are connected by a wire, a[Pg 269]
current of electricity is set up in the conductor. Evidence
of the current may be obtained by holding the conducting
wire over and parallel to the needle of a magnetoscope.
The needle is deflected by the action of the current parallel
to it (Fig. 217). This magnetic effect of a current is the
means usually employed for the detection and measurement
of an electric current. Such
a device which detects an
electric current by its magnetic
effect is called a galvanoscope,
in honor of Galvani,
who in 1786 was the first to
discover how to produce an
electric current.
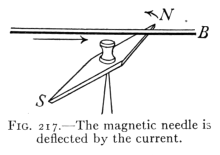 Fig. 217.—The magnetic needle is
deflected by the current.
Fig. 217.—The magnetic needle is
deflected by the current.
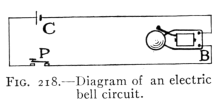 Fig. 218.—Diagram of an electric
bell circuit.
Fig. 218.—Diagram of an electric
bell circuit.
240. The Electric Circuit.—The entire conducting path
along which a current of electricity flows is called an electric
circuit. In the case of a voltaic cell, the circuit includes
not only the wires connecting the plates but also the plates
themselves and the liquid between them. When some
device or apparatus is to receive current from the cell,
it is attached to the plates and wires so that the device
is a part of the electric circuit. Separating the circuit
at any point is called breaking
or opening the circuit,
while connecting the ends of
an open circuit is called making
or closing the circuit. A
device for opening and closing
a circuit is called a key or switch. The electric circuit used
in ringing a door bell is familiar to most boys and girls.
This circuit is open most of the time. It is closed by
pressing the push-button at the door, and the flow of
current through the electric bell causes the latter to ring.
Such a circuit is represented in Fig. 218. Here C is the[Pg 270]
voltaic cell, the two lines representing the plates of the
cell. A cross-section view of the push-button (P), shows
how the circuit is closed, (B) is the bell. Wherever current
electricity is used the device in which it is employed
forms a part of an electric circuit extending back to some
electric generator. This generator must be able to
continually produce an E.M.F., or a difference of potential
between its terminals, in order that the movement of
electricity may be continuous.
Important Topics
(a) Electric generators: (1) voltaic cell uses chemical energy; (2)
dynamo uses mechanical energy.
(b) Electric circuits: (1) open, (2) closed, (3) key and switch.
(c) Voltaic and galvanic electricity (names).
(d) Galvanoscope, uses.
Exercises
1. In what two ways are static and current electricity alike? In
what two different?
2. Draw a diagram of an electric bell circuit at your home. Give
the location of the electric bell, the electric generator and the
push-button. Show the connecting wires, and explain briefly
how the circuit is operated.
3. Represent some other electric circuit, naming the generator and
other devices in the circuit.
4. Look up the work of Volta and Galvani and write a statement of
the electrical discoveries and inventions made by them.
(2) The Voltaic Cell and its Action
241. The simple voltaic cell consists of a strip of copper
and a strip of zinc placed in dilute sulphuric acid. (See
Fig. 219.) A short time after placing the plates in the
acid, bubbles of a gas (hydrogen) appear on the surface
of the zinc. These bubbles increase in size and some rise
to the surface of the liquid. Nothing appears upon the[Pg 271]
copper plate. If the tops of the plates are connected by a
wire, an electric current is set up through the wire and the
cell, and bubbles of gas also appear upon the copper as
well as on the zinc. In a short time the surface of the
copper becomes coated with bubbles and the current becomes
much weaker. If the plates are left in the acid for
some time the zinc is found to be eaten away, having been
dissolved in the acid through
chemical action. The copper,
however, remains practically
unaffected.
 Fig. 219.—A simple voltaic cell.
Fig. 219.—A simple voltaic cell.
242. How the Current is
Produced.—To maintain the
electric current a continual
supply of energy is required.
This is furnished by the chemical
action of the acid upon the
zinc. The chemical action
is in several respects like combustion
or burning, by means
of which chemical energy is
transformed into heat energy. In the voltaic cell the
chemical action of the acid upon the zinc transforms
chemical energy into electrical energy. The E.M.F.
or difference of potential may be considered as originating
at the surface of the zinc where the chemical action takes
place. At this point the zinc has the lower and the liquid
in contact with it the higher potential. The molecules
of the acid are believed to be separated or broken up into
two parts called ions; one ion, the SO4 or sulphion, combines
with the zinc forming zinc sulphate, the other, or
hydrogen (H) ion, passes over to the copper plate, and
accumulates on the surface of this plate giving it a positive
charge. It is therefore called the positive ion.[Pg 272]
The sulphion ion, or SO4 ion, carries a negative charge to
the zinc. It is therefore called the negative ion.
243. The Direction of the Current.[K]—Beginning at the
surface of the zinc the direction of the movement of positive
electricity may be traced through the liquid to the
copper plate, to the wire, to the zinc plate, to the starting
point, thus completing the electric circuit. When the
circuit is closed it is found that the movement of electricity
starts in all parts of the circuit at practically the same instant.
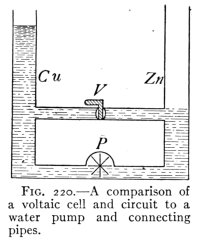 Fig. 220.—A comparison of
a voltaic cell and circuit to a
water pump and connecting pipes.
Fig. 220.—A comparison of
a voltaic cell and circuit to a
water pump and connecting pipes.
244. The production of the current may be illustrated
by describing a device for producing a continuous circulation
of water. Thus let Cu
and Zn represent two pipes
connected by two horizontal
tubes, one at V provided
with a valve and one at P
with a rotary Pump. (See
Fig. 220.) Suppose the pipes
filled to the level of V and the
pump started. The pump
will force water from Zn to
Cu, through P, the level falling
in Zn and rising in Cu.
If the valve V is open the water will flow back through
V as long as the pump is working. If V is closed, the level
in Cu will rise as high as the driving force of the pump can
send it. If now V is opened, the pump will maintain the
water in circulation from Cu to Zn through V. In the
illustration, the tubes Cu and Zn correspond to the conducting
plates of copper and zinc of a voltaic cell. The
pump P represents the chemical action which produces[Pg 273]
the electrical pressure. The upper pipe represents the
part of the circuit outside of the cell, the valve V corresponds
to an electric key or switch which is used to open
and close the electric circuit.
245. Polarization.—In the simple voltaic cell, after the
circuit is closed, bubbles of hydrogen collect upon the
copper plate. This accumulation of hydrogen gas is
called polarization. It acts as a non-conducting layer
upon the surface of the plate and seriously interferes
with the movement of electricity from the liquid to the
copper plate not only in the simple voltaic cell but in
many others as well. Some voltaic cells are made entirely
free from this defect, either (a) by the removal of
the hydrogen as fast as it is formed, or (b) by the use of
such chemicals that no hydrogen is produced.
246. Local Action.—It is noticed that when a strip of
zinc is placed in dilute acid that bubbles appear upon the
surface of the zinc. The appearance of these
bubbles indicates that some of the hydrogen ions
carrying positive electricity have moved to the
zinc plate. Careful examination of the plate after
it has been in acid shows numerous black spots
upon it. These are bits of carbon. They are
always found in ordinary zinc. Small electric currents
are set up which run from molecules of pure
zinc into the liquid and back to the carbon particles,
thus forming small closed circuits. (See Fig. 221.) The
formation of these circuits from and to the zinc is called
local action. This action is a defect in voltaic cells since
a part of the current is thus kept from passing through
the main outside circuit, and the zinc may be consumed
even when no outside current is flowing.
 Fig. 221.—Local
action.
Fig. 221.—Local
action.
247. Amalgamation.—Local action is prevented by coating
the zinc with mercury. This process is called amalgamation.
The mercury covers the entire surface of the[Pg 274]
plate in the acid. Its action is to dissolve pure zinc and
bring it to the outer surface where it is acted upon by the
acid. The carbon particles are kept covered so that no
local currents can be formed as long as the bits of carbon
are below the surface. Amalgamation therefore prevents
local action.
Important Topics
The Simple Voltaic Cell
1. Two plates: zinc, copper; electrolyte, dilute sulphuric acid.
2. Ions: hydrogen, positive: sulphion, negative.
3. Current, where and how produced, direction, illustration.
4. Polarization: cure, local action, cure.
Exercises
1. Write in your own words an account of the production of an
electric current by the simple voltaic cell. Use sketches.
2. Which plate has the higher potential? How is it produced?
3. Would you expect to get an E.M.F. by forming a cell of two
copper plates? Why?
(3) Practical Voltaic Cells
248. Advantages of Voltaic Cells.—Many forms of voltaic
cells have been devised. Several of the more common
of these will be described and their electro-chemical
action explained.
At the present time voltaic cells are employed only where
small currents are needed, such as for electric bells and
induction coils. Where more than a small amount of
current is required, the dynamo and the storage battery
have generally taken their place as sources of electric
current.
The advantages of voltaic cells as electric generators are:
(a) they are inexpensive, (b) they are easily taken from
place to place, (c) they may be ready for instant use.
The most desirable voltaic cell would be one having the[Pg 275]
following qualities: (a) High electromotive force, (b) no
polarization or local action, (c) very low internal resistance,
(d) small expense, both as to first cost and upkeep.
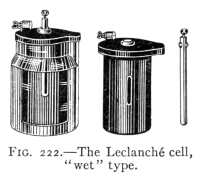 Fig. 222.—The Leclanché cell,
"wet" type.
Fig. 222.—The Leclanché cell,
"wet" type.
249. The Leclanché cell is the one commonly used for
ringing door bells. It has two plates: one of zinc and the
other of carbon. These are placed in a solution of sal
ammoniac (Fig. 222). Take up the desirable qualities
mentioned at the end of the preceding paragraph. (a)
It may be shown that this cell has a good E.M.F. about
1.5 volts. (b) It polarizes easily yet it recovers well when
left upon open circuit. Usually
a substance called manganese
dioxide is mixed with the carbon.
This acts as a depolarizer, that
is, it combines with the hydrogen
to form water. (c) Its
resistance varies and is often
considerable. (d) The expense
for upkeep is small, since a
5-cent rod of zinc, and a 5-cent charge of sal ammoniac
will keep the cell in action on a bell circuit from six
months to a year or more. It is well suited for use on
open circuits that is, where the circuit is open the greater
part of the time and is closed only occasionally; as in
ringing door bells, operating telephones, and other devices
whose circuits are usually open.
250. The Dry Cell.—Many forms of Leclanché cells
are made. One of these is called the dry cell (See Fig.
223.) In this cell the zinc plate is made into a jar or can
and contains the other materials. At the center of the
cell is a rod of carbon and manganese dioxide. The
space between the carbon and zinc is filled with a porous
material such as sawdust or plaster of Paris. A strong
solution of sal ammoniac fills the porous material. The[Pg 276]
top of the cell is sealed with pitch or wax to prevent
evaporation. The great advantage of this cell is that it
may be used or carried in any position without danger
of spilling its contents. Dry cells are often used to
operate the spark coils of gas and
gasoline engines. The Leclanché
cell described in Art. 249 is commonly
known as the "wet cell."
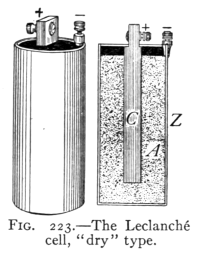 Fig. 223.—The Leclanché
cell, "dry" type.
Fig. 223.—The Leclanché
cell, "dry" type.
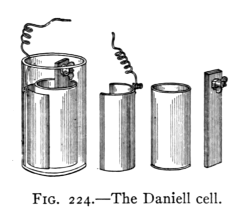 Fig. 224.—The Daniell cell.
Fig. 224.—The Daniell cell.
251. The Daniell Cell.—This
cell is often used in laboratories,
and on closed circuits such as those
connected with fire and burglar
alarms and telegraph lines. It
has two plates of zinc and copper
placed in two different liquids
which are kept separated by a porous clay cup (Fig. 224).
The zinc rod is kept in a solution of zinc sulphate contained
in the porous cup. The copper plate is in a solution
of copper sulphate filling the rest of the glass jar. Unlike
the Leclanché cell, this one must be kept upon a closed
circuit to do its best work, as
the two liquids mix when the
circuit is open. Taking its
qualities in order, (a) its
E.M.F. is about one volt, (b)
it has no polarization since
copper instead of hydrogen
is deposited upon the copper
plate. Therefore a uniform
E.M.F. may be obtained
from it, making it especially useful in laboratory experiments
and tests. (c) Its resistance is considerable and (d)
it is more expensive to operate than the Leclanché. It is
sometimes used upon closed circuits outside of laboratories[Pg 277]
as in burglar and fire alarms, although in recent years, the
storage battery is taking its place for these purposes.
252. The Gravity Cell.—Fig. 225 is like the Daniell cell
in most respects, except that in this cell, the zinc plate is
held at the top of the jar in a solution
of zinc sulphate while the copper
plate is at the bottom, surrounded
by a solution of copper
sulphate. The solutions mix but
slowly as the copper sulphate
solution is denser and remains at
the bottom. This cell like the
Daniell must also be kept upon
closed circuit. On account of its
simplicity and economy it is often
used to operate telegraph instruments.
Its qualities are similar
to those of the Daniell cell.
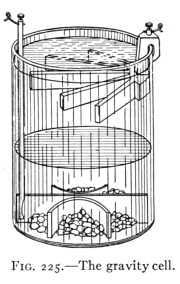 Fig. 225.—The gravity cell.
Fig. 225.—The gravity cell.
253. Symbol for Voltaic Cells.—In electrical diagrams,
the symbol employed to represent a voltaic cell is a short
thick line near to and parallel to a longer thin one. As
in Fig. 226. If several cells are to be represented the
conventional symbol of the combination is represented as
in Fig. 227. A single cell and a group of cells are each
frequently called a battery.
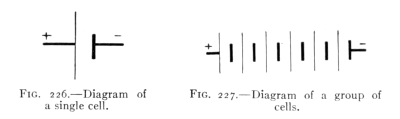 Fig. 226.—Diagram of
a single cell.
Fig. 226.—Diagram of
a single cell.
Fig. 227.—Diagram of a group of
cells.
254. Effects of Electric Currents.—Having studied
some of the devices for producing an electric current, let[Pg 278]
us now consider some of the effects caused by it. These
effects will be studied under three heads: (a) Magnetic,
(b) Chemical, and (c) Heat effects. Devices or articles
showing these effects known to most high school students
are respectively: (a) the electromagnet (b) electro-plated
silver ware and (c) electric heaters, such as electric flat
irons, electric toasters, etc. The magnetic
effect of an electric current was
first detected by Oersted at the University
of Copenhagen in 1819. It may
be observed by holding a wire carrying
a current from a voltaic cell above and
parallel to the needle of a magnetoscope. The needle
is at once deflected (Fig. 228). If the current is reversed
in direction the magnetoscope needle is deflected in the
reverse direction. This simple device is the most common
means for detecting an electric current. It therefore
constitutes a galvanoscope. (See Art. 239.)
 Fig. 227.—Diagram of a group of
cells.Fig. 228.—A galvanoscope.
Fig. 227.—Diagram of a group of
cells.Fig. 228.—A galvanoscope.
Important Topics
1. Leclanché cells, (a), wet, (b), dry, construction, advantages, uses.
2. Daniell and gravity cells, construction, advantages, uses.
3. Three effects of electric currents, illustrations.
4. The galvanoscope, uses.
Exercises
1. Explain how the direction of current in a wire can be determined
by a compass.
2. Would you expect to obtain a current from a zinc and copper cell
containing a solution of common salt? Perform the experiment.
3. What conditions in a voltaic cell will give a steady electromotive
force.
4. What conditions in a voltaic cell will give a strong electromotive
force.
5. Name three different electric circuits that you know exist.
Which are open and which are closed circuits?
6. Are voltaic cells used in your home? If so, for what purpose are
they used? On open or closed circuits? Have you seen them?
what kind are they?
[Pg 279]
THE MAGNETIC EFFECT OF ELECTRIC CURRENTS.
ELECTRICAL MEASUREMENTS
(1) The Magnetic Effect of Electric Currents
255. The Magnetic Effect.—Of all the effects of electric
currents, it is generally conceded that the magnetic effect
is the one of greatest practical importance, and it is also the
one most extensively used. An experiment illustrating
this effect has been described in Art. 239. This experiment
shows that an electric current, if parallel to a magnetic
needle, and near it will deflect the north-seeking pole
of the needle to the right or left depending upon the direction
of the current flow. This deflection of the magnetic
needle is due to the fact that surrounding every electric
current are magnetic lines of force. It is this magnetic
field of the current that causes the needle to turn. The
position taken by the needle is the resultant of the forces
of two magnetic fields; one, the earth's field, the other,
that of the current.
256. Right-hand Rule for a Conductor.—To show the
presence of the magnetic field about a current, pass a thick
copper wire vertically through a sheet of paper, and connect
the ends of the wire to a source of current. While
the current (this should be as much as 10 amperes if
possible) is flowing, sprinkle iron filings upon the paper and
tap gently. The filings will arrange themselves in circles
about the wire showing the magnetic field. (See Fig. 229.)
The needle of a magnetoscope tends to place itself parallel
to the lines of force of this field and from this action or[Pg 280]
tendency the direction of the magnetic lines about a
current may be determined. The following rule is helpful
and should be memorized: Grasp the conductor with the
right hand with the outstretched thumb in the direction that
the current is flowing. The fingers will then encircle the
wire in the direction of the lines of force. This rule may be
reversed, for, if the fingers of the right hand grasp the
wire so as to point with the magnetic field, then the
current flows in the direction in which the thumb points.
(See Fig. 230.)
 Fig. 229.—Magnetic field
about a wire carrying an
electric current.
Fig. 229.—Magnetic field
about a wire carrying an
electric current.
Fig. 230.—Right-hand rule for the magnetic
field of a current.
257. Magnetic Field of a Helix.—If a wire be wound
about a cylinder to form a cylindrical coil with parallel
turns, it forms a helix or solenoid. The shape of the
magnetic field about a current depends upon the form
of the conductor. If the latter is in the form of a helix its
magnetic field resembles that of a straight bar magnet.
(See Fig. 231). In fact the helix has the properties of a
magnet with north- and south-seeking poles while a current
is flowing through it. If such a coil is suspended so as to
turn freely, it tends to turn until the field within it is
parallel to the earth's magnetic field. Such a suspended
helix may therefore be used as a compass. In order to
strengthen the magnetic field of a helix or solenoid, the
space within its turns is filled with iron, often in the form[Pg 281]
of small soft-iron wires. This bundle of iron wire is called
the core of the helix. The core becomes strongly magnetized
by the field of the helix while the current is flowing
and quickly loses its magnetic force when the current is
stopped. The direction of the current in a helix (Fig. 232)
or the polarity of its core may be determined by another
right-hand rule. If the helix is grasped with the right hand
so that the fingers point in the direction in which the current
is flowing, the extended thumb will point in the direction of
the north pole of the helix. On the other hand, if the
poles of the helix are known, then, when the helix is
grasped with the right hand so that the thumb points to
the north-seeking pole, the current is flowing in the wires
in the direction that the fingers point.
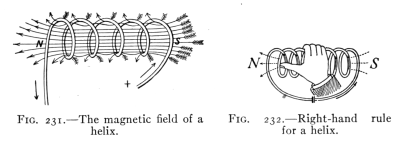 Fig. 231.—The magnetic field of a
helix.
Fig. 231.—The magnetic field of a
helix.
Fig. 232.—Right-hand rule
for a helix.
258. The Electromagnet.—These "right-hand" rules
are applied in many different devices. Among these,
perhaps the most important is the electromagnet, which
is used in the electric bell, the telegraph, the telephone,
the dynamo, the motor, and many other electric
contrivances.
The electromagnet is defined as a mass of iron around
which is placed a helix for conducting an electric current.
On account of its large permeability, the iron core of the
helix adds greatly to the effectiveness of the electromagnet,
since the magnetism of the iron is added to that
of the current in the helix. The magnetism remaining[Pg 282]
in the iron after the current stops is called the residual
magnetism. The residual magnetism is small when the
core is made of small wires or thin plates, but is larger
when the iron core is solid. Like artificial steel magnets,
electromagnets are usually of two forms, bar and horseshoe.
(See Figs. 233 and 234.) For most purposes the horseshoe
form is the more effective since it permits a complete
iron circuit for the magnetic lines of force. (See Fig. 235.)
This is the form used in the electric bell, in the telegraph
sounder, and in lifting magnets. (See Fig. 236.)
 Fig. 233.—A bar electromagnet.
Fig. 233.—A bar electromagnet.
Fig. 234.—A horseshoe electromagnet.
 Fig. 235.—A horseshoe electromagnet
may have a complete
iron circuit for its lines of force.
Fig. 235.—A horseshoe electromagnet
may have a complete
iron circuit for its lines of force.
Fig. 236.—A lifting
magnet.
259. Effective Electromagnets.—The magnetic effect
of a current in a helix is small, hence the force usually is
increased by inserting a core of iron. When at first man[Pg 283]
tried to signal with electromagnets at a distance it was
found that the current would not work the electromagnet.
An American by the name of Joseph Henry discovered
the remedy for this condition. He found that if the copper
wire was insulated by wrapping silk thread about it, and
then many layers of the silk insulated wire were wound upon
a spool with an iron core, that the magnet would work at
a great distance from the source of current. If the current
is increased, the magnet is stronger than at first.
Thus an electromagnet may be made stronger by (a) increasing
the number of turns of wire in its coils and by (b)
sending a stronger current through it.
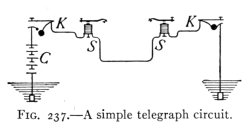 Fig. 237.—A simple telegraph circuit.
Fig. 237.—A simple telegraph circuit.
260. The Telegraph.—The invention of an effective
electromagnet by Henry made possible the electric telegraph.
In its simplest form it consists of a battery, C, a
key, K, and a sounder,
S, with connecting
wires. (See Fig. 237.)
The sounder (Fig. 238)
contains a horseshoe
electromagnet and a bar
of soft iron across its
poles called an armature, A, attached to a lever L. When
the key is closed, the electromagnet draws down the armature
and lever until the latter hits a stop O, making a
click. When the key is raised, the magnet releases the
armature which is raised by the action of a spring at S
until the lever hits a stop at T making another click.
Closing and opening the circuit at K will start and stop
the current which operates S which may be 100 miles or
more from K. One voltaic cell will work a sounder in
the same room. But if many miles of wire are in the circuit,
the E.M.F. of a single cell will not force sufficient
current through the long wire to operate the sounder.
[Pg 284]
 Fig. 238.—A telegraph sounder.
Fig. 238.—A telegraph sounder.
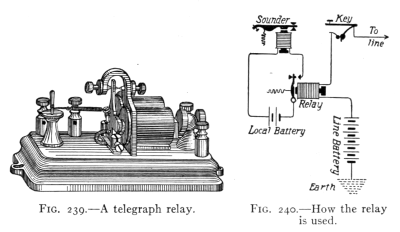 Fig. 239.—A telegraph relay.
Fig. 239.—A telegraph relay.
Fig. 240.—How the relay
is used.
 Samuel F. B. Morse (1791-1872).
Inventor of the electromagnetic recording telegraph and
of the dot and dash alphabet.
Samuel F. B. Morse (1791-1872).
Inventor of the electromagnetic recording telegraph and
of the dot and dash alphabet.
Samuel F. B. Morse
"From Appleton's Cyclopedia of
American Biography, Copyright
1888 by D. Appleton & Co."
 Thomas A. Edison, Orange, New
Jersey. Invented the incandescent
lamp; phonograph; moving picture;
most noted inventor of electrical
appliances of the present day.
Thomas A. Edison, Orange, New
Jersey. Invented the incandescent
lamp; phonograph; moving picture;
most noted inventor of electrical
appliances of the present day.
Thomas A. Edison
"Copyright, Photographische
Gessellschaft," and "By Permission
of the Berlin Photographic Co., New
York."
A battery of several cells is then required. Even a
large battery is insufficient to operate a long line containing
many sounders in circuit. Recourse is therefore usually
made to a more sensitive
device called a
relay. (See Fig. 239.)
In the relay a very
small current will magnetize
its electromagnet
enough to draw
toward it the delicately
hung armature
thereby closing a second
circuit which contains a sounder and a battery. (See
Fig. 240.) when the current in the main circuit is
stopped, the armature of the relay is drawn back by a light
spring. This opens the local circuit. Thus the local circuit
is closed and opened by the relay just in time with
the starting and stopping of the current in the main line.
It is thus possible for a small current in the main line by
the use of a relay, to close and open a second local circuit[Pg 285]
[Pg 286]
[Pg 287]
containing a local battery and sounder. Modern telegraph
lines are operated in this manner.
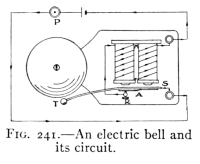 Fig. 241.—An electric bell and
its circuit.
Fig. 241.—An electric bell and
its circuit.
261. The electric bell (see Fig. 241), consists of an
electromagnet, M, a soft iron armature, A, attached to
the tapper, T, and a post, R. When no current is flowing
a spring at S holds the armature against the post R.
When current flows through the helix, its core becomes
magnetized and attracts the
armature, drawing it away from
the post, R, and causing the
tapper to hit the bell. Drawing
A away from the post,
however, breaks the circuit at
R and the current stops. The
magnetism in the core disappears
releasing the armature, which is then pulled back by
the spring S against the post R. This completes the circuit
and the process repeats itself several times a second as
long as the current flows.
 Fig. 242.—Magnetizing by the
discharge of a Leyden jar.
Fig. 242.—Magnetizing by the
discharge of a Leyden jar.
262. Static and Current
Electricity Compared.—The
likeness between a discharge
of static electricity and an
electric current may be shown
by winding a coil of insulated
wire about a glass tube which
contains a steel needle. If
a Leyden jar (see Fig. 242) is
discharged through the coil
the steel needle is usually found to be magnetized,
showing that the discharge of the static electricity has
a magnetic effect similar to that of an electric current.
Sometimes a given end of the needle has a north pole
and at other times a south pole. This is believed to indicate[Pg 288]
that the charge of the Leyden jar is oscillatory, and
that in different discharges sometimes a surge in one direction
and at other times a surge in the reverse direction
has been most effective in magnetizing the needle. Compare
this action with that described in Art. 233.
Important Topics
1. Right-hand rules, for conductor, for helix.
2. The electromagnet, two forms, where used?
3. Likeness between static and current electricity.
4. The electric bell, parts, action.
5. The telegraph, key, sounder, relay.
Exercises
1. What is the difference between an electric charge and a current?
2. How can a magnetic effect be produced from an electric charge?
3. What is a magnetic field? Give two evidences of a magnetic
field about a current in a wire?
4. A current is flowing north in trolley wire, what is the direction
of the magnetic field under the wire? Explain.
5. What would be the result if a hard steel core were placed in the
electromagnet? Explain.
6. If the north-seeking pole of a helix is facing you, does the current
in the coils before you move in a clockwise or in a counter-clockwise
direction? Explain.
7. A helix is placed horizontally with its north-seeking pole toward
the north. Does the current in the wire at the top of the helix
move east or west? Explain.
8. State at least six conditions any one of which will put an electric
bell circuit out of commission.
9. If one desires to insert a battery into a telegraph circuit already
in operation, how will he determine the direction of the current
in the wire?
10. If a boy who had magnetized his knife blade in a physics laboratory,
pointed end south-seeking, should lose his way in the woods
on a cloudy day, how could he determine his way out?
11. At a certain point the earth's field acts north, that of an electric
current, east. The magnetoscope needle points exactly northeast
when placed at that point. How do the two magnetic
fields compare?
[Pg 289]
(2) Electrical Measurements
263. Galvanometers.—In using electric currents it is
often necessary or desirable to be able to know not only
that a given current is weak or strong, but precisely what
its strength is. We can determine the relative strengths
of two currents by the use of a galvanometer.
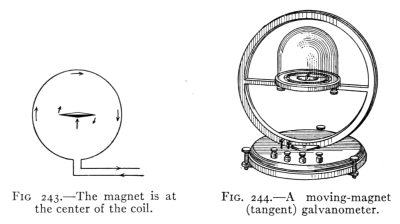 Fig. 243.—The magnet is at
the center of the coil.
Fig. 243.—The magnet is at
the center of the coil.
Fig. 244.—A moving-magnet
(tangent) galvanometer.
The older or moving-magnet type of galvanometer is
similar to the galvanoscope mentioned in Art. 239. It
consists of a magnetic needle mounted at the center of a
coil of wire. The coil is placed facing east and west, so
that the needle will be held by the earth's magnetic field
parallel to the plane of the coil. When a current is sent
through the coil a magnetic field is produced within it.
This deflects the needle, its north end turning east or
west depending upon the direction of the current. (See
Fig. 243.) The coils of a moving-magnet or tangent galvanometer
(see Fig. 244) are large and firmly fastened to the
base, while the magnet is small.
The moving-coil type of galvanometer (see Fig. 245)
consists of a large magnet fastened to the frame of the
device. The magnet usually has a horseshoe form to[Pg 290]
produce as strong a field as possible. The coil is wound
on a light rectangular frame and is suspended between the
two poles of the magnet. To concentrate the magnetic
field, a cylinder of soft iron is usually placed within the
coil. Fig. 246 represents a common form of moving-coil
galvanometer.
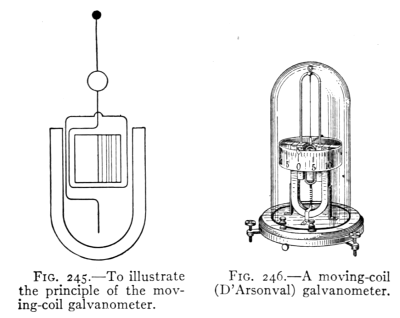 Fig. 245.—To illustrate
the principle of the moving-coil
galvanometer.
Fig. 245.—To illustrate
the principle of the moving-coil
galvanometer.
Fig. 246.—A moving-coil
(D'Arsonval) galvanometer.
264. Measurement of Electric Currents.—A galvanometer
enables one to compare electric currents. To
measure electric currents it is necessary to employ a unit
of electrical quantity, just as in measuring the quantity of
water delivered by a pipe, a unit of liquid measure is
employed; thus, e.g., the current delivered by a given pipe
may be 2 gallons of water per second, so in measuring
the flow of an electric current one may speak of two
coulombs per second. The coulomb is the unit quantity
of electricity just as the unit of quantity of water is the
gallon.
For most practical purposes, however, we are more
interested in the rate or intensity of flow of current than in[Pg 291]
the actual quantity delivered. The unit of rate of flow
or current is called the ampere.
In determining the exact quantity of an electric current,
physicists make use of a device called a coulomb meter.
(See Fig. 247.) This contains a solution of silver nitrate
in which are placed two silver plates. The current to
be measured is sent through the solution, in at one plate
and out at the other. The
plate where the current goes
in, the anode, A (Fig. 247),
loses in weight since some of
the silver is dissolved. The
plate where the current goes
out, the cathode, C, increases
in weight since some of the
silver is deposited. By an
international agreement, the
intensity of the current which
deposits silver at the rate of
0.001118 g. per second is 1
ampere. This is equal to
4.025 g. per hour.
 Fig. 247.—A coulomb meter, the
anode A is separated from the
cathode C by a porous cup.
Fig. 247.—A coulomb meter, the
anode A is separated from the
cathode C by a porous cup.
The coulomb is defined as
the quantity of electricity
delivered by a current of one ampere during one
second.
A 40-watt-incandescent lamp takes about 0.4 ampere of
current. An arc lamp takes from 6 to 15 amperes. A
new dry cell may send 20 amperes through a testing meter.
A street car may take from 50 to 100 amperes.
265. The Ammeter.—The method described above is
not used ordinarily for measuring current strengths on
account of its inconvenience. The usual device employed
is an ammeter. This instrument is a moving-coil galvanometer.[Pg 292]
It contains, wound on a light form, a coil of fine
copper wire. The form is mounted on jewel bearings
between the poles of a strong permanent horseshoe magnet.
(See Fig. 248.) As in other moving-coil galvanometers, a
soft iron cylinder within the form concentrates the field
of the magnet. The form and its coil is held in balance
by two spiral springs which also conduct current into and
out of the coil.
Only a small part
of the whole current
measured, in some
cases only 0.0001
passes through the
coil, the larger part
of the current passing
through a metal
wire or strip called a
shunt[L] (see Fig. 248)
connecting the binding
posts of the instrument.
A fixed
fraction of the whole
current flows through
the coil. Its field crossing the field of the horseshoe
magnet, tends to turn until its turning force is balanced
by the spiral springs. As the coil turns it moves a
pointer attached to it across a scale graduated to indicate
the number of amperes in the whole current.
 Fig. 248.—Diagram of a commercial ammeter.
S is the shunt.
Fig. 248.—Diagram of a commercial ammeter.
S is the shunt.
It should be noted that while all of the current measured
passed through the ammeter, but a small part goes through
the coil.
[Pg 293]
266. Resistance of Conductors.—With an ammeter
one may study the change produced in the amount of
current flowing in a wire when a change is made in the
wire conducting the current. For example, if one measures
with an ammeter the current flowing from a dry
cell through a long and then through a short piece of fine
copper wire, it will be seen that less current flows when the
long piece is used. That is, the long wire seems to hinder
or to resist the passing of the current more than the short
piece. In other words, the long wire is said to have more
resistance.
The resistance of a conducting body is affected by
several conditions.
(a) It is directly proportional to the length of the conductor,
one hundred feet of wire having twice the resistance
of fifty feet.
(b) It is inversely proportional to the square of the
diameter; a wire 0.1 inch in diameter has four times the
resistance of a wire 0.2 inch in diameter.
(c) It differs with different substances, iron having
about six times as much as copper.
(d) It varies with the temperature, metals having
greater resistance at a higher temperature.
Since silver is the best conductor known, the resistances
of other substances are compared with it as a
standard.
The ratio of the resistance of a wire of any substance
as compared to the resistance of a silver wire of exactly
the same diameter and length is called its relative
resistance.
Purified substances arranged in order of increasing
resistance for the same length and sectional area (Ayrton-Mather)
are given on p. 294.
[Pg 294]
| Silver annealed | 1.00 |
| Copper annealed from | 1.04 |
| (Copper annealed) to | 1.09 |
| Aluminum annealed | 1.64 |
| Nickel annealed | 4.69 |
| Platinum annealed | 6.09 |
| Iron annealed | 6.56 |
| German Silver from | 12.80 |
| (German Silver) to | 20.20 |
| Mercury | 63.30 |
| Nichrome | 67.50 |
| Carbon from | 2700.00 |
| (Carbon) to | 6700.00 |
267. The ohm, the unit of resistance, is defined by international
agreement as follows: An ohm is the resistance
of a column of pure mercury, 106.3 cm. long with a cross-section
of a square millimeter and at a temperature of 0°C.
It should be noted that each of the four conditions
affecting resistance is mentioned in the definition, viz.,
length, cross-section, material, and temperature. Since it
is inconvenient to handle mercury, standard resistance
coils, made of an alloy of high resistance are used in comparing
and measuring resistances.
A piece of copper wire No. 22 (diameter 0.644 mm.)
60. 5 ft. long has a resistance of 1 ohm. See table
p. 296.
The resistance of some telephone receivers is 75 ohms,
of a telegraph sounder, 4 ohms, of a relay 200 ohms.
268. Resistance of Circuits.—Every part of an electrical
circuit possesses resistance. In an electric-bell circuit,
for instance, the wires, the bell, the push-button, and
the cell itself, each offers a definite resistance to the passage
of the current. The resistance within the cell is termed
internal resistance, while the resistance of the parts outside
of the electric generator is called external resistance.
[Pg 295]
269. Electromotive Force.—In order to set in motion
anything, some force must be applied. This is as true of
electricity as of solids, liquids, or gases. By analogy
that which is exerted by a battery or by a dynamo in
causing current to flow is called an electromotive force.
The unit of electromotive force, the volt, may be defined
as the electromotive force that will drive a current
of 1 ampere through the resistance of 1 ohm. The electromotive
force of a dry
cell is about 1.5
volts, of a Daniell
cell 1.08 volts. Most
electric light circuits
in buildings carry
current at 110 or
220 volts pressure.
Currents for street
cars have an electromotive
force of
from 550 to 660
volts.
 Fig. 249.—Diagram of a commercial voltmeter.
Fig. 249.—Diagram of a commercial voltmeter.
270. The Voltmeter.—An
instrument
for measuring
the electromotive force of electric currents is called a
voltmeter (Fig. 249). It is usually a moving-coil galvanometer,
and is always of high resistance. It is like an
ammeter in construction and appearance. In fact, a voltmeter
is an ammeter which has had its shunt removed or
disconnected. In place of a shunt, the voltmeter uses a
coil of wire of high resistance (see R, Fig. 249) in series with
the galvanometer coil. The high resistance of the voltmeter
permits but a very small current to flow through it.
Hence a voltmeter must be placed across a circuit and[Pg 296]
not in it. In other words a voltmeter is connected in
shunt, while an ammeter is in series with the circuit as is
shown in Fig. 250.
Dimensions and Functions of Copper Wires
| B. & S. gauge number | Diameter | Circular mils | Sectional area in square millimeters | Weight and length, Density = 8.9, feet per pound | Resistance at 24°C., feet per ohm | Capacity in amperes |
| Mils | Millimeters |
| 0000 | 460.000 | 11.684 | 211,600.00 | 107.219 | 1.56 | 19,929.700 | 312.0 |
| 000 | 409.640 | 10.405 | 167,805.00 | 85.028 | 1.97 | 15,804.900 | 262.0 |
| 00 | 364.800 | 9.266 | 133,079.40 | 67.431 | 2.49 | 12,534.200 | 220.0 |
| 0 | 324.950 | 8.254 | 105,592.50 | 53.470 | 3.13 | 9,945.300 | 185.0 |
| 2 | 257.630 | 6.544 | 66,373.00 | 33.631 | 4.99 | 6,251.400 | 131.0 |
| 4 | 204.310 | 5.189 | 41,742.00 | 21.151 | 7.93 | 3,931.600 | 92.3 |
| 6 | 162.020 | 4.115 | 26,250.50 | 13.301 | 12.61 | 2,472.400 | 65.2 |
| 8 | 128.490 | 3.264 | 16,509.00 | 8.366 | 20.05 | 1,555.000 | 46.1 |
| 10 | 101.890 | 2.588 | 10,381.00 | 5.260 | 31.38 | 977.800 | 32.5 |
| 12 | 80.808 | 2.053 | 6,529.90 | 3.309 | 50.69 | 615.020 | 23.0 |
| 14 | 64.084 | 1.628 | 4,106.80 | 2.081 | 80.59 | 386.800 | 16.2 |
| 16 | 50.820 | 1.291 | 2,582.90 | 1.309 | 128.14 | 243.250 | 11.5 |
| 18 | 40.303 | 1.024 | 1,624.30 | 0.823 | 203.76 | 152.990 | 8.1 |
| 20 | 31.961 | 0.812 | 1,021.50 | 0.5176 | 324.00 | 96.210 | 5.7 |
| 22 | 25.347 | 0.644 | 642.70 | 0.3255 | 515.15 | 60.510 | 4.0 |
| 24 | 20.100 | 0.511 | 504.01 | 0.2047 | 819.21 | 38.050 | 2.8 |
| 26 | 15.940 | 0.405 | 254.01 | 0.1288 | 1,302.61 | 23.930 | 2.0 |
| 28 | 12.641 | 0.321 | 159.79 | 0.08097 | 2,071.22 | 15.050 | 1.4 |
| 30 | 10.025 | 0.255 | 100.50 | 0.05092 | 3,293.97 | 9.466 | 1.0 |
| 32 | 7.950 | 0.202 | 63.20 | 0.03203 | 5,236.66 | 5.952 | 0.70 |
| 34 | 6.304 | 0.160 | 39.74 | 0.02014 | 8,328.30 | 3.743 | 0.50 |
| 36 | 5.000 | 0.127 | 25.00 | 0.01267 | 13,238.83 | 2.355 | 0.35 |
| 38 | 3.965 | 0.101 | 15.72 | 0.00797 | 20,854.65 | 1.481 | 0.25 |
| 40 | 3.144 | 0.080 | 9.89 | 0.00501 | 33,175.94 | 0.931 | 0.17 |
Important Topics
(1) Galvanometers: (1) moving magnet, fixed coil; (2) moving coil,
fixed magnet, ammeter, voltmeter.
(2) Unit of quantity, coulomb.
(3) Unit of current, ampere.
(4) Unit of resistance, ohm.
(5) Unit of electromotive force, volt.
[Pg 297]
Exercises
1. How will the resistance of 20 ft. of No. 22 German silver wire
compare with that of 10 ft. of No. 22 copper wire? Explain.
2. Where in a circuit is copper wire desirable? Where should
German silver wire be used?
3. Explain the action of the ammeter. Why does not the needle
or coil swing the full distance with a small current?
4. Why is a telegraph sounder more apt to work on a short line
than upon a long one?
 Fig. 250.—The ammeter is connected in series and the voltmeter in shunt.
Fig. 250.—The ammeter is connected in series and the voltmeter in shunt.
5. Find the resistance of 15 miles of copper telephone wire No. 12.
(See table p. 296.)
6. What will be the weight and resistance of 1,000 feet of No. 20
copper wire?
7. A storage battery sends 4 amperes of current through a plating
solution. How much silver will it deposit in 2 hours?
8. (a) Compare the diameters of No. 22 and No. 16 copper wire.
(b) Compare the lengths of the same wires giving 1 ohm resistance.
(c) What relation exists between (a) and (b)?
9. Why is an electric bell circuit usually open while a telegraph
line circuit is usually closed?
10. A copper wire and an iron wire of the same length are found to
have the same resistance. Which is thicker? Why?
11. Why are electric bells usually arranged in parallel instead of in
series?
12. What would happen if a voltmeter were put in series in a line?
[Pg 298]
(3) Ohm's Law and Electrical Circuits
271. Conditions Affecting Current Flow.—Sometimes
over a long circuit one cell will not work a telegraph
sounder. In such a case, two, three, or more cells are
connected so that the zinc of one is joined to the
copper plate of the other. When connected in this way
the cells are said to be in series (Fig. 251). In the
figure A represents a voltmeter. It is found that when
cells are in series the E.M.F. of the battery is the sum
of the electromotive forces of the cells.
An ammeter in the circuit shows increased
current as the cells are added.
Hence if the resistance of the circuit
remains unchanged, the greater the
E.M.F. the greater is the current
strength. In this respect, the movement
of electricity in a circuit is similar
to the flow of water in a small pipe under pressure,
as in the latter the flow of water increases as the pressure
becomes greater. The current in a circuit may also be
increased by lessening the resistance, since the current
through a long wire is less than that through a short one,
just as the flow of water will be greater through a short
pipe than through a long one. To increase the current
flowing in an electric circuit, one may therefore either
increase the E.M.F. or decrease the resistance.
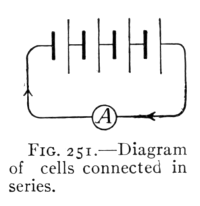 Fig. 251.—Diagram
of cells connected in
series.
Fig. 251.—Diagram
of cells connected in
series.
272. Ohm's Law.—The relation between the electromotive
force applied to a circuit, its resistance, and the
current produced was discovered in 1827 by George Ohm.
Ohm's law, one of the most important laws of electricity,
states that, in any circuit, the current in amperes equals
the electromotive force in volts divided by the resistance in
ohms.
[Pg 299]
This principle is usually expressed thus:
Current intensity = electromotive force/resistance or
Amperes = volts/ohms or I = E/R
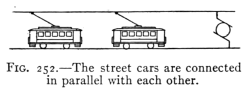 Fig. 252.—The street cars are connected
in parallel with each other.
Fig. 252.—The street cars are connected
in parallel with each other.
273. Resistance of Conductors in Series.—A study of
the resistance of conductors when alone and when grouped
in various ways is of importance since, the current flow
through any circuit is dependent upon its resistance. The
two most common methods of combining several conductors
in a circuit are in series and in parallel. Conductors
are in series when all of the current passes through each of
the conductors in turn
(Fig. 218), thus the cell,
push-button, wires, and
electric bell in an electric-bell
circuit are in
series. Conductors are in parallel when they are so
connected that they are side by side and a part of
the whole current goes through each. None of the current
that passes through one conductor can go through
the conductors in parallel with it. Thus the electric
street cars are in parallel with each other. (See Fig. 252.)
It is easily seen that none of the current passing through
one car can go through any of the others. When the conductors
are in series the combined resistance is the sum
of the several resistances. Thus in an electric-bell circuit
if the battery has a resistance of 1 ohm, the bell of
2 ohms, and the wire 1 ohm, the total resistance in the
circuit is 4 ohms. When conductors are in parallel the
combined resistance is always less than the separate resistances.
Just as a crowd of people meets less resistance
in leaving a building through several exits, so electricity[Pg 300]
finds less resistance in moving from one point to another
along several parallel lines, than along one of the lines.
274. Resistance of Conductors in Parallel.—If three
conductors of equal resistance are in parallel, the combined
resistance is just one-third the resistance of each
separately (Fig. 253). The rule that states the relation
between the combined resistance of conductors in parallel
and the separate resistances is as follows:The combined
resistance of conductors in parallel
is the reciprocal of the sum
of the reciprocals of the several
resistances. For example, find
the combined resistance of
three unequal resistances in
parallel; the first being 4 ohms,
the second, 6 ohms, and third
3 ohms. The reciprocals of the three resistances are 1/4,
1/6, and 1/3. Their sum equals 6/24 + 4/24 + 8/24 = 18/24.
The reciprocal of this is 24/18 which equals 1-1/3 ohms, the
combined resistance.
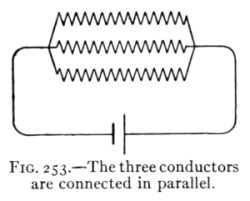 Fig. 253.—The three conductors
are connected in parallel.
Fig. 253.—The three conductors
are connected in parallel.
This rule may be understood better if we consider the conductance
of the conductors in parallel. Since the conductance of a two ohm
wire is just one-half that of a one-ohm wire, we say that the conductance
of a body is inversely as the resistance, or that it is the reciprocal
of the resistance. The conductance of the 4-, 6-, and 3-ohm coils
will therefore be respectively 1/4, 1/6, and 1/3, and since the combined
conductance is the sum of the several conductances, the total
conductance is 18/24. Also since this is the reciprocal of the total
resistance, the latter is 24/18 or 1-1/3 ohms.
When two or more conductors are connected in parallel
each one is said to be a shunt of the others. Many circuits
are connected in shunt or in parallel. Fig. 254 represents
four lamps in parallel. Incandescent lamps in buildings
are usually connected in parallel, while arc lamps are[Pg 301]
usually connected in series. Fig. 255 represents four
lamps in series.
Important Topics
1. Conditions affecting current flow, (a) E.M.F., (b) resistance.
2. Ohm's law, three forms for formula.
3. Resistance of conductors: (a) in series, (b) in parallel; how computed,
illustrations.
 Fig. 255.—The four lamps are
connected in series.
Fig. 255.—The four lamps are
connected in series.
Fig. 254.—The four lamps are
connected in parallel.
Exercises
1. What current flows through a circuit if its E.M.F. is 110 volts
and the resistance is 220 ohms?
2. A circuit contains four conductors in series with resistances of
10, 15, 6, and 9 ohms respectively. What current will flow
through this circuit at 110 volts pressure? What will be the
resistance of these four conductors in parallel?
3. What is the combined resistance of 8 conductors in parallel
if each is 220 ohms? What current will flow through these
8 conductors at 110 volts pressure?
4. What is the resistance of a circuit carrying 22 amperes, if the
E.M.F. is 20 volts?
5. What E.M.F. will send 8 amperes of current through a circuit
of 75 ohms resistance?
6. How does the voltmeter differ from the ammeter?
7. How can one determine the resistance of a conductor?
8. The resistance of a hot incandescent lamp is 100 ohms. The
current used is 1.1 amperes. Find the E.M.F. applied.
9. What is the resistance of the wires in an electric heater if the
current used is 10 amperes, the voltage being 110?
10. The resistance of 1000 ft. of No. 36 copper wire is 424 ohms.
How many feet should be used in winding a 200 ohms relay?
11. The resistance of No. 00 trolley wire is 0.80 ohm per 1000 ft.
What is the resistance of a line 1 mile long?
12. A wire has a resistance of 20 ohms. It is joined in parallel with
another wire of 6 ohms, find their combined resistance.
[Pg 302]
13. The separate resistances of two incandescent lamps are 200 ohms
and 70 ohms. What is their combined resistance when joined
in parallel? When joined in series?
(4) Methods of Grouping Cells and Measuring
Resistance
275. Internal Resistance of a Voltaic Cell.—The current
produced by a voltaic cell is affected by the resistance
that the current meets in passing from
one plate to another through the liquid
of the cell. This is called the internal
resistance of the cell. A Daniell cell
has several (1-5) ohms internal resistance.
The resistance of dry cells varies
from less than 0.1 of an ohm when new
to several ohms when old. If cells are
joined together their combined internal
resistance depends upon the method of
grouping the cells.
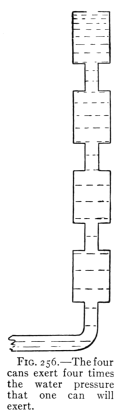 Fig. 256.—The four
cans exert four times
the water pressure
that one can will
exert.
Fig. 256.—The four
cans exert four times
the water pressure
that one can will
exert.
276. Cells Grouped in Series and
in Parallel.—When in series the copper
or carbon plate of one cell is joined to
the zinc of another and so on. (See
Fig. 251.) The effect of connecting,
say four cells, in series may be illustrated
by taking four cans of water,
placed one above another. (See Fig.
256.) The combined water pressure of
the series is the sum of the several
pressures of the cans of water, while
the opposition offered to the movement
of a quantity of water through the group
of cans is the sum of the several resistances of the cans.
In applying this illustration to the voltaic cell, we make[Pg 303]
use of Ohm's law. Let E represent the e.m.f. of a single
cell, r the internal resistance of the cell, and R the external
resistance or the resistance of the rest of the circuit.
Consider a group of cells in series. If n represents the
number of cells in series, then Ohm's law becomes
I = nE/(nr + R).
Cells are grouped in series when large E.M.F. is required
to force a current through a large external resistance such
as through a long telegraph line. Cells
are connected in parallel when it is desired
to send a large current through a small
external resistance. To connect cells in
parallel all the copper plates are joined
and also all the zinc plates. (See Fig. 257.) To illustrate
the effect of this mode of grouping cells, suppose several
cans of water are placed side by side (Fig. 258). It is
easily seen that the pressure of the group is the same as
that of a single cell, while the resistance to the flow is less
than that of a single cell. Applying this reasoning to
the electric circuit we have by Ohm's law the formula for
the current flow of a group of
n cells arranged in parallel I = E/((r/n) + R).
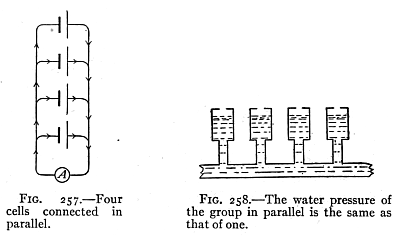 Fig. 257.—Four
cells connected in
parallel.
Fig. 257.—Four
cells connected in
parallel.
Fig. 258.—The water pressure of
the group in parallel is the same as
that of one.
[Pg 304]
277. Illustrative Problems.—Suppose that four cells
are grouped in parallel, each with an E.M.F. of 1.5 volts
and an internal resistance of 2 ohms. What current will
flow in the circuit if the external resistance is 2.5 ohms?
Substitute in the formula for cells in parallel the values
given above, and we have I = 1.5/(0.5 + 2.5) = 1.5/3 = 0.5
ampere. Suppose again that these four cells were grouped
in series with the same external resistance, substituting
the values in the formula for cells in series we have I
= 4(1.5)/(4 × 2 + 2.5) = 6/10.5 = 0.57 ampere.
278. Volt-ammeter Method for Finding Resistance.—Measurements
of the resistance of conductors are often
made. One of these methods depends upon an application
of Ohm's law. It is called the volt-ammeter method
since it employs both a voltmeter and an ammeter. If
the conductor whose resistance is to be measured is made
a part of an electric circuit, being connected in series with
the ammeter and in shunt with the voltmeter, the resistance
may easily be determined, since R = E/I. (See Fig. 250.)
If, for example, the difference in E.M.F., or as it is often
called, the fall of potential between the ends of the wire
as read on the voltmeter is 2 volts, and the current is
0.5 ampere, then the resistance of the wire is 4 ohms.
This method may be readily applied to find the resistance
of any wire that is a part of an electric circuit.
279. The Wheatstone Bridge.—To find the resistance
of a separate wire or of an electrical device another method
devised by an Englishman named Wheatstone is commonly
employed. This method requires that three known
resistances, a, b, c, in addition to the unknown resistance[Pg 305]
x be taken. These four resistances are arranged in the
form of a parallelogram. (See Fig. 259.) A voltaic cell is
joined to the parallelogram at the extremities of one diagonal
while a moving-coil galvanometer is connected across
the extremities of the other diagonal. The known resistances
are changed until when on pressing the keys
at E and K no current flows through the galvanometer.
when this condition is
reached, the four resistances
form a true proportion, thus
a: b = c: x.
Since the values of a, b,
and c are known, x is readily
computed. Thus if a = 10,
b = 100, and c = 1.8 ohms,
then x, the unknown resistance,
equals 18 ohms, since
10: 100 = 1.8: 18. This
method devised by Wheatstone
may be employed to find the resistance of a great
variety of objects. It is the one most commonly employed
by scientists and practical electricians.
 Fig. 259.—Diagram of a Wheatstone
bridge.
Fig. 259.—Diagram of a Wheatstone
bridge.
Important Topics
1. The internal resistance of voltaic cells.
2. Ohm's law applied to groups of cells. (a) Cells in series, (b)
cells in parallel.
3. Measurement of resistance: (a) volt-ammeter method, (b)
Wheatstone bridge method.
Exercises
1. What is the resistance of an electric bell circuit where the E.M.F.
is 3 volts and the current is 0.6 ampere?
2. A telegraph wire is broken somewhere, the ends lying upon damp
ground. If an E.M.F. of 30 volts is applied from the ground[Pg 306]
to the wire and a current of 0.1 of an ampere flows, what is the
resistance of the part connected to the ammeter. (The earth
which completes the circuit from the end of the wire has very
small resistance.) Why?
3. How far away is the break in the wire if the latter has a resistance
of 80 ohms to the mile? Diagram.
4. What current will flow through a bell circuit of 8 ohms resistance
if it contains three cells in series each with an E.M.F. of 1.5
volts and an internal resistance of 1/3 ohm?
5. If the same three cells are connected in parallel on the same circuit
what current flows? Is the current in problem 4 or 5 the
larger? Why?
6. If four cells each with 1.5 volts E.M.F. and an internal resistance
of 0.4 ohm are connected with a circuit having an external
resistance of 0.8 ohm, what current will the parallel connection
give? The series connection? Which gives the larger current?
Why?
7. Four Daniell cells each having 1 volt E.M.F. and 3 ohms internal
resistance are connected in series with 2 telegraph sounders of
4 ohms each. The connecting wires have 6 ohms resistance.
Find the current intensity.
8. A battery of 2 cells arranged in series is used to ring a door bell.
The E.M.F. of each cell is 1.5 volts, internal resistance 0.3 ohm,
and the resistance of the bell is 4 ohms. What is the current
in amperes?
9. In the above problem find the current if the cells are connected
in parallel.
[Pg 307]
THE CHEMICAL AND HEAT EFFECTS OF
ELECTRIC CURRENTS
(1) The Chemical Effect of an Electric Current
280. Electroplating.—If two carbon rods (electric light
carbons answer very well) are placed in a solution of
copper sulphate (Fig. 260) and then connected by wires to
the binding posts of an electric battery, one of the rods
soon becomes covered with a coating of metallic copper
while bubbles of gas may be seen upon
the other carbon. If a solution of lead
acetate is used in the same way a deposit
of metallic lead is secured, while a
solution of silver nitrate gives silver.
 Fig. 260.—Two carbons
placed in a solution
of copper sulphate.
Fig. 260.—Two carbons
placed in a solution
of copper sulphate.
Fig. 261.—An electroplating bath.
This process of depositing metals upon the surface of
solids by an electric current is called electroplating.
Everyone has seen electroplated articles such as silver
plated knives, forks, and spoons, and nickel-plated rods,
handles, etc. Copper electrotype plates such as are used
in printing school books are made by this process. In[Pg 308]
practical electroplating a solution of the metal to be deposited
is placed in a tank; across the top of this tank are
placed copper rods to act as conducting supports. From
one of these rods, the cathode, objects to be plated are
hung so as to be immersed in the liquid. From other rods,
the anodes, are hung plates of the metal to be deposited.
These are dissolved as the current deposits a coating upon
the articles, thus keeping the
solution up to its proper
strength. (See Fig. 261.)
 Fig. 262.—The current is carried
through the solution by ions.
Fig. 262.—The current is carried
through the solution by ions.
281. Electrolysis.—A solution
from which a deposit is
made by an electric current is
called an electrolyte. The
plates or other objects by
which the current enters or
leaves the electrolyte are called
the electrodes. The electrode
by which the current enters
is called the anode (an = in)
while the electrode by which
it leaves is the cathode (cath = away).
The process by which
an electric current decomposes
a solution and deposits a substance
upon an electrode is called electrolysis. The current
always flows within the cell from anode to the cathode.
(See Fig. 262.) The metal goes with the current and is
found deposited upon the cathode.
282. Theory of Electrolysis.—The action going on in
an electrolytic cell has been carefully studied. The theory
of electrolysis, which is supported by much experimental
evidence, supposes that many of the molecules in a dilute
solution of a substance "split up" into two parts called[Pg 309]
"ions," one ion having a positive, the other a negative
charge. In a dilute solution of sulphuric acid, the positive
ion is of hydrogen, while the negative ion is the (SO4) or
sulphion. These ions bearing electric charges are believed
to be the carriers of the electric current through the
electrolyte.
The positive ions move with the current from the anode
to the cathode, while the negative ions apparently are
repelled by the cathode and appear upon the anode.
Evidence of the accumulation of
the two kinds of ions at the two
electrodes is furnished by the electrolysis
of water, described below.
283. Electrolysis of Water.—Two
glass tubes (Fig. 263), H and O, are
attached at the bottom to a horizontal
glass tube. To the latter is
also connected an upright tube T.
At the lower ends of H and O are
inserted, fused in the glass, platinum
wires, A and C. The tubes are filled
with a weak solution of sulphuric
acid. The tops of H and O are
closed with stopcocks, T being
open; a current of electricity is
sent in at A and out at C. A
movement of the ions at once begins,
the positive hydrogen ions appearing at C. These
accumulate as bubbles of hydrogen which rise to the
top of H and displace the liquid. At the same time
bubbles of oxygen appear at A. These rise in O and also
displace the liquid which rises in T. After the action has
continued some time it may be noticed that the volume
of hydrogen is just twice that of the oxygen. This was[Pg 310]
to have been expected since the formula for water is H2O.
The nature of the gas in H or O may be tested by opening
the stopcock and allowing the gas to escape slowly. The
hydrogen gas can be lighted by a flame while the oxygen
gas will cause a spark upon a piece of wood to glow brightly,
but does not burn itself.
 Fig. 263.-Electrolysis
of water; oxygen collects
in O, hydrogen in H.
Fig. 263.-Electrolysis
of water; oxygen collects
in O, hydrogen in H.
284. Evidence that ions are necessary to conduct a
current in a liquid is furnished by the following experiment.
A quart jar is carefully cleaned, and half filled with
distilled water. Two pieces of zinc 5 cm. square are
soldered to pieces of rubber-insulated No. 14 copper wire.
The zincs are placed in the
distilled water (Fig. 264) and
the wires are connected to a
110 volt circuit with a 16
candle-power incandescent
lamp in series with the cell, as
in the figure. If the zincs have
been carefully cleansed and the
water is pure, no current flows
as is shown by the lamp remaining
dark. If a minute quantity of sulphuric acid
or of common salt is placed in the water the lamp at
once begins to glow. Ions are now present in the liquid
and conduct the current. That some substances in solution
do not form ions may be shown by adding to another
jar of pure water some glycerine and some cane sugar, substances
resembling the acid and salt in external appearance
but which do not ionize when dissolved as is shown
by the lamp remaining dark after adding the glycerine
and sugar. The acid and salt are of mineral origin while
the glycerine and sugar are vegetable products. This
experiment illustrates the principle that the water will
conduct only when it contains ions.
 Fig. 264.—The current passes
only when ions are present in the
liquid.
Fig. 264.—The current passes
only when ions are present in the
liquid.
[Pg 311]
285. Laws of Electrolysis.—These were discovered by
Faraday in 1833, and may be stated as follows: I. The
mass of a substance deposited by an electric current from
an electrolyte is proportional to the intensity of current
which passes through it.
II. The mass of any substance deposited by a current of
uniform intensity is directly proportional to the time the
current flows.
These laws have been used as a basis for defining and
measuring the unit of current flow, the ampere. (See
Art. 264.)
286. Instances of Electrolysis.—(a) Medicines, especially
those containing a mineral substance, are sometimes
introduced into the human body by electrolysis. (b)
Water and gas pipes are sometimes much weakened by
the effects of electric currents in the earth, especially
return currents from street railways. Such currents use
the metal pipes as a conductor. At the place where the
current leaves the metal and enters the ground, it removes
metallic ions from the pipe. This process continuing,
the pipe becomes weakened and at length breaks. (c)
Copper is purified by the use of electric currents that
remove the copper from ore or from other metals and deposit
it upon electrodes. Electrolytic copper is the purest
known. (d) Aluminum is obtained by the use of large
currents of electricity that first heat the material used until
it melts and then deposit the metal from the fluid material
by electrolysis. These results are called chemical effects
of the current since by the use of electric currents substances
are changed chemically, that is, they are separated
into different chemical substances.
[Pg 312]
Important Topics
1. Electrolysis, electroplating, anode, cathode, ion.
2. Theory of electrolysis—evidence: (a) electrolysis of water; (b)
conductivity of acid and water.
3. Laws of electrolysis.
4. Practical use of electrolysis.
Exercises
1. A dynamo has an E.M.F. of 10 volts. What is the resistance in
the circuit when 20 amperes are flowing?
2. How much silver will be deposited in an hour by this current?
3. Name five objects outside of the laboratory that have been acted
upon by electrolysis. How in each case?
4. Why is table ware silver plated? Why are many iron objects
nickel plated?
5. How is the electrolysis of water pipes prevented?
6. Two grams of silver are to be deposited on a spoon by a current
of 1 ampere. Find the time required.
7. How long will it take to deposit 20 g. of silver in an electroplating
bath if a current of 20 amperes is used?
8. If 1000 g. of silver are deposited on the cathode of an electrolytic
reduction plant in 10 minutes, what is the current intensity
employed?
(2) The Storage Battery and Electric Power
287. Differences Between Voltaic and Storage Cells.
Voltaic cells in which electric currents are produced by
the chemical action between metal plates and an electrolyte
are often called primary batteries. In voltaic
cells one or both plates and the electrolyte are used up
or lose their chemical energy in producing the current
and after a time need to be replaced by new material, the
chemical energy of the electrolyte and of one of the plates
having been transformed into electrical energy.
A different proceeding obtains with another type of[Pg 313]
cell. This is called a storage battery, or an accumulator.
In these cells, the same plates and electrolyte are used
without change for extended periods, sometimes for a
number of years. For this reason storage batteries have
displaced many other types of cells, and they are now
used (a) to operate many telephone, telegraph, and fire-alarm
circuits, (b) to work the spark coils of gas and
gasoline engines, (c) to help carry the "peak" load upon
lighting and power circuits and (d) to furnish power for
electric automobiles. Since a storage battery can deliver
an electric current only after an electric current from an
outside source has first been sent through it, they are
often called secondary batteries.
288. Construction and Action of a Storage Cell.—The
common type of storage cells consists of a number of
perforated plates made of an alloy of lead and a little
antimony. (See Figs. 265, 266, 267.) Into the perforations
is pressed a paste of red lead and litharge mixed
with sulphuric acid. The plates are placed in a strong
solution (20 to 25 per cent.) of sulphuric acid. The plates
are now ready to be charged. This is accomplished by
sending a direct current from an electric generator through
the cell. The hydrogen ions are moved by the current
to one set of plates and change the paste to spongy metallic
lead. The sulphions move to the other set of plates
and change the paste to lead oxide. This electrolytic
action causes the two plates to become quite different
chemically so that when the cell is fully charged it is
like a voltaic cell, in having plates that are different
chemically. It has, when fully charged, an E.M.F. of
about 2.2 volts. The several plates of a cell being in
parallel and close together, the cell has but small internal
resistance. Consequently a large current is available.
 Fig. 265.—The positive plate
of a storage cell.
Fig. 265.—The positive plate
of a storage cell.
Fig. 266.—The negative plate
of a storage cell.
 Fig. 267.—A complete storage
cell.
Fig. 267.—A complete storage
cell.
Fig. 268.
About 75 per cent. of the energy put into the storage cell[Pg 314]
in charging can be obtained upon discharging. Therefore
the efficiency of a good storage cell is about 75 per cent.
Fig. 268 represents a storage battery connected to charging
and discharging circuits. The lower is the charging
circuit. It contains a dynamo and a resistance (neither
of which are shown in the figure) to control the current
sent into the cell. The charging
current enters the positive pole
and leaves by the negative pole.
The current produced by the
cell, however, flows in the opposite
direction through it, that is,
out from the positive and in at
the negative pole. This current may be controlled by
a suitable resistance and measured by an ammeter.
Storage cells have several advantages: (a) They can be
charged and discharged a great many times before the
material placed in the perforations in the plates falls out.[Pg 315]
(b) The electrical energy used in charging the plates
costs less than the plates and electrolyte of voltaic cells.
(c) Charging storage cells takes much less labor than
replacing the electrolyte and plates of voltaic cells. (d)
Storage cells produce larger currents than voltaic cells.
The two principal disadvantages of storage cells are that
(a) they are very heavy, and (b) their initial cost is
considerable.
 Fig. 269.—The Edison
storage cell.
Fig. 269.—The Edison
storage cell.
Fig. 270.—The plates of the Edison storage
cell.
289. The Edison storage cell (Figs. 269 and 270) has
plates of iron and nickel oxide. The electrolyte is a
strong solution of potassium hydroxide. These cells[Pg 316]
are lighter than lead cells of the same capacity and they
are claimed to have a longer life.
290. Energy and Power of a Storage Cell.—In a
storage cell, the electrical energy of the charging current
is transformed into chemical energy by the action of
electrolysis. It is this chemical energy that is transformed
into the energy of the electric current when the
cell is discharged. The capacity of storage cells is rated
in "ampere hours," a 40 ampere hour cell being capable
of producing a current of 1 ampere for 40 hours, or 5 amperes
for 8 hours, etc. The production and extensive
use of electric currents have made necessary accurate
methods for measuring the energy and power of these
currents. To illustrate how this is accomplished, let
us imagine an electric circuit as represented in Fig. 268.
Here four storage cells in series have an E.M.F. of 8 volts
and in accordance with Ohm's law produce a current of 2
amperes through a resistance in the circuit of 4 ohms.
Now the work done or energy expended by the current in
passing through the resistance between the points M and
N depends upon three factors (1) the E.M.F. or potential
difference; (2) the current intensity and (3) the time. The
energy is measured by their product. That is, electrical
energy = potential difference × current intensity × time.
This represents the electrical energy in joules, or
Joules = volts × amperes × seconds, or
j = E × I × t.
In the circuit represented in Fig. 268 the energy expended
between the points M and N in 1 minute (60 seconds) is
8 × 2 × 60 = 960 joules.
291. Electric Power.—Since power refers to the time
rate at which work is done or energy expended, it may be
computed by dividing the electrical energy by the time,[Pg 317]
or the electrical power = volts × amperes. The power
of 1 joule per second is called a watt. Therefore,
Watts = volts × amperes, or
Watts = E × I.
Other units of power are the kilowatt = 1000 watts
and the horse-power = 746 watts. In the example given
in Art. 290 the power of the current is 8 × 2 = 16 watts,
or if the energy of the current expended between the
joints M and N were converted into mechanical horse-power
it would equal 16/746 of a horse-power. Electrical
energy is usually sold by the kilowatt-hour, or the amount
of electrical energy that would exert a power of 1000 watts
for one hour, or of 100 watts for 10 hours, or of 50 watts
for 20 hours, etc.
Important Topics
1. The storage battery, its construction, electrolyte, action, uses,
advantages, disadvantages.
2. Electric energy, unit value, how computed?
3. Electric power, three units, value, how computed, how sold?
Exercises
1. In what three respects are voltaic and storage cells alike? In
what two ways different?
2. Name the four advantages of storage cells in the order of their
importance. Give your reasons for choosing this order.
3. Why are dry cells more suitable for operating a door-bell circuit,
than a storage battery? Give two reasons.
4. The current for a city telephone system is provided by a storage
battery. Why is this better than dry cells at each telephone?
5. An incandescent lamp takes 0.5 ampere at 110 volts. What
power is required to operate it? How much energy will it
transform in 1 minute?
6. How long would it take for this lamp to use a kilowatt hour of
energy?
7. A street car used 100 amperes at 600 volts pressure. What[Pg 318]
power was delivered to it? Express also in kilowatts and
horse-power.
8. An electric toaster takes 5 amperes at 110 volts. If it toasts
a slice of bread in 2 minutes, what is the cost at 10 cents a
kilowatt hour?
9. An electric flat iron takes 5 amperes at 110 volts. Find the
cost of using it for 2 hours at 12 cents a kilowatt hour.
10. A 1/4 kilowatt motor is used to run a washing-machine for 5
hours. What is the expense for this power at 10 cents a kilowatt
hour?
11. What is the efficiency of a motor that takes 7390 watts and
develops 9 horse-power?
12. How many horse-power are there in a water-fall 212 ft. high
over which flows 800 cu. ft. of water per second? Express
this power in kilowatts.
13. What horse-power must be applied to a dynamo having an
efficiency of go per cent. if it is to light 20 arc lamps in series,
each taking 10 amperes at 60 volts?
(3) The Heat Effect of Electric Currents
292. The Production of Heat by an Electric Current.—When
no chemical or mechanical work is done by an electric
current its energy is employed in overcoming the resistance
of the conducting circuit and is transformed into
heat. This effect has many practical applications and some
disadvantages. Many devices employ the heating effect
of electric currents, (a) the electric furnace, (b) electric
lights, (c) heating coils for street cars, (d) devices about
the home, as flat irons, toasters, etc. Sometimes the
heat produced by an electric current in the wires of a
device such as a transformer is so large in amount that
especial means of cooling are employed. Unusually
heavy currents have been known to melt the conducting
wires of circuits and electrical devices. Hence all circuits
for electric power as well as many others that ordinarily
carry small currents are protected by fuses. An electric fuse[Pg 319]
is a short piece of wire that will melt and break the circuit
if the current exceeds a determined value. The
fuse wire is usually enclosed in an incombustible holder.
Fuse wire is frequently made of lead or of an alloy of lead
and other easily fusible metals. (See Figs. 271 and 272.)
 Fig. 271.—A type of enclosed fuse.
Fig. 271.—A type of enclosed fuse.
Fig. 272.—A link fuse (above);
plug fuses (below).
293. Heat Developed in a Conductor.—A rule for computing
the amount of heat produced in an electric circuit
by a given current has been
accurately determined by
experiment. It has been
found that 1 calorie of heat
(Art. 142), is produced by
an expenditure of 4.2 joules of electrical (or other) energy.
In other words, 1 joule will produce 1/4.2 or 0.24 calorie.
Now the number of joules of electrical energy in an
electric circuit is expressed by the following formula:
Joules = volts × amperes × seconds, or since 1 joule
= 0.24 calorie,
Calories = volts × amperes × seconds × 0.24 or
H = EI × t × 0.24 (1)
By Ohm's law, I = E/R or E = I × R, substituting in equation
(1) IR for its equal E we have
H = I2R × t × 0.24 (2)
Also since I = E/R substitute E/R for I in equation (1) and we
have
H = E2/R t × 0.24 (3)
[Pg 320]
To illustrate the use of these formulas by a problem suppose
that a current of 10 amperes is flowing in a circuit
having a resistance of 11 ohms, for 1 minute. The heat
produced will be by formula (2) = (10)2 × 11 × 60 × 0.24
equals 15,840 calories.
 Fig. 273.—A carbon filament
incandescent lamp.
Fig. 273.—A carbon filament
incandescent lamp.
Fig. 274.—A tungsten
lamp.
294. The Incandescent Lamp.—One of the most common
devices employing the heat effect of an electric current
is the incandescent lamp. (See Fig. 273.) In this
lamp the current is sent through a carbon filament,
which is heated to incandescence. In order to keep the
filament from burning as well as to prevent loss of heat
by convection, it is placed in a glass bulb from which the
air is exhausted. Two platinum wires fused in the glass
connect the carbon filament with the grooved rim and the
end piece of the base. The end piece and rim connect with
the socket so that an electric current may flow through the
filament of the lamp. The carbon incandescent lamp has
a low efficiency. It takes 0.5 ampere of current at 110
volts or in other words it requires 55 watts to cause a 16-candle-power[Pg 321]
lamp to glow brightly, hence 1 candle
power in this lamp takes 55/16 = 3.43 watts.
The efficiency of electric lamps is measured by the number
of watts per candle power. This is a peculiar use of the
term efficiency, as the larger the number the less efficient
is the lamp. More efficient lamps have been devised with
filaments of the metals tantalum and tungsten (Fig. 274).
These give a whiter light than do carbon lamps, and consume
but about 1.25 watts per candle power.
Comparative "Efficiency" of Electric Lamps
| Name of lamp | Watts per candle power | Name of lamp | Watts per candle power |
| Carbon filament | 3 to 4 | Arc lamp | 0.5 to 0.8 |
| Metallized carbon | 2.5 | Mercury arc | 0.6 |
| Tantalum | 2.0 | Flaming arc | 0.4 |
| Tungsten | 1.0 to 1.5 | Nitrogen-filled tungsten | 0.6 to 0.7 |
Incandescent lamps are connected in parallel (see Fig.
254) to wires that are kept at a constant difference of
potential of 110 or 115 volts. It is customary to place
not more than twelve lamps upon one circuit, each circuit
being protected by a fuse and controlled by one or more
switches.
295. The Arc Light.—The electric arc light (see Fig.
275) is extensively used for lighting large rooms, also in
stereopticons and motion picture machines. The light is
intense, varying from 500 to 1700 candle power. The so-called
mean spherical candle power of the arc light is about
510. The candle power in the direction of greatest intensity
is about 1200. It is produced at an expenditure of[Pg 322]
about 500 watts. It is therefore more efficient than the
incandescent lamp, often taking less than 0.5 watt per
candle power produced. The arc light was first devised by
Sir Humphrey Davy in 1809, who used two pieces of charcoal
connected to 2000 voltaic cells. The arc light requires
so much power that its production by voltaic cells is
very expensive. Consequently it did not come into common
use until the dynamo had been perfected. Fig. 276
shows the appearance of the two carbons in an arc light.
If a direct current is used the positive carbon is heated
more intensely, and gives out the greater part of the light.
The positive carbon is consumed about twice as fast as the
negative and its end is concave, the negative remaining
pointed.
 Fig. 275.—An electric arc light.
Fig. 275.—An electric arc light.
Fig. 276.—The appearance
of a pair of
used carbons.
With alternating currents, the rods are equally consumed
and produce equal amounts of light. In the stereopticon,
the carbons are usually placed at right angles as[Pg 323]
in Fig. 277. In the stereopticon as well as in outdoor
lighting the direct current is more effective, although the
alternating current is often used, since the latter can be
produced and distributed more cheaply than can direct
currents. In arc lamps, placing an inner glass globe
(Fig. 278) about the carbons, decreases the consumption
of the carbons materially. The carbon rods of enclosed
arc lamps often last 60 to 100 hours.
 Fig. 277.—A right-angle electric
arc lamp for a stereopticon.
Fig. 277.—A right-angle electric
arc lamp for a stereopticon.
Fig. 278.—An enclosed
arc lamp.
The reason why an open arc lamp needs to be "retrimmed" oftener
than the enclosed lamp, that is, have new carbons placed in it,
is because the carbons "burn" freely, that is unite with the oxygen
of the air. In the enclosed arc lamp, the supply of oxygen in the
inner globe is limited and is soon consumed, therefore the carbons
last many times longer in such lamps.
Some carbon rods have soft cores containing calcium
salts. These vaporize in the arc producing the flaming arc
light of a bright yellow color, and give more light than
the ordinary lamp.
Important Topics
1. Heat effects of electric currents, uses and applications.
2. Computation of the heat developed in a circuit. Three formulas.
3. Electric lamps; incandescent and arc; construction, uses, efficiency.
[Pg 324]
Exercises
1. Sketch a circuit containing 10 incandescent lamps in parallel.
If each lamp when hot has a resistance of 220 ohms, and the
E.M.F. is 100 volts, what current will flow?
2. What will it cost to use these lights for 3 hours a day for 30
days at 10 cents a kilowatt hour?
3. How much heat will these lamps produce per minute?
4. How could you connect 110-volt lamps to a street car circuit
of 660 volts? Explain this arrangement and draw a diagram.
5. A certain arc lamp required 10 amperes of current at 45 volts
pressure. What would it cost at 10 cents per kilowatt hour
if used 3 hours a day for 30 days?
6. Show a diagram of 3 arc lamps in series. If each takes 45 volts
and 10 amperes, how much E.M.F. and current will they
require?
7. If an electric toaster uses 5 amperes at 115 volts, how much
heat will this develop in half an hour?
9. How much heat is developed in an electric toaster in 2 minutes,
if it uses 5 amperes at 100 volts?
10. How many B.t.u.'s are given off in an electric oven that takes
10 amperes at 110 volts for 1 hour? (1 B.t.u. equals 252
calories.)
11. An electric heater supplies heat at the rate of 700 B.t.u.'s an
hour. How much power does it require?
12. How many watts are required to operate 120 incandescent
lamps in parallel if each takes 0.5 amperes at 110 volts?
13. An electric lamp takes 12 amperes at a P.D. of 110 volts.
How many B.t.u.'s are radiated from it each second? How
many calories?
14. If a 110-volt incandescent lamp is submerged for 10 minutes in
400 gr. of cold water while a current of 0.5 amperes is flowing,
how many degrees centigrade will the water be warmed?
15. In an electric furnace a current of 3000 amperes is used at
a P.D. of 10 volts. Find the heat developed in 1 minute.
16. How many candle power should a 20-watt tungsten lamp give
if its efficiency is one watt per candle power?
17. What is the "efficiency" of a 40-watt tungsten lamp if it gives
34 candle power?
[Pg 325]
Review Outline: Current Electricity
Produced by—Chemical action; voltaic and storage cells.
| Three Principal Effects: | Magnetic, electromagnet, uses and applications. |
| Chemical, electrolysis, applications. |
| Heat, lighting and heating devices. |
Theories: (a) of voltaic cells, (b) of electrolysis.
Units: Ampere, ohm, volt, watt, joule, kilowatt, horse power.
Measurement:
- (a) magnetic effect; galvanometer, ammeter, voltmeter, wattmeter, Wheatstone bridge, construction and use.
- (b) chemical effect; voltameter.
Laws:
- (a) Right hand rules, for conductor and helix.
- (b) Resistance, Conductors in series and parallel.
- (c) Ohm's law, heat law, power law, 3 forms for each.
- (d) Cells in parallel and series.
Problems: Upon applications of the laws and formulas studied.
| Devices and Instruments: | Voltaic cells; wet, dry, and Daniell. |
| Electrolysis and the storage battery. |
| Measuring instruments, electric bell, sounder, |
| Heating and lighting devices. |
Terms: Anode, cathode, electrolyte, ion, circuit switch, current,
e.m.f., resistance, potential.
[Pg 326]
INDUCED CURRENTS
(1) Electromagnetic Induction
296. Current Induced by a Magnet.—The discovery
in 1819 that a current in a conductor can deflect a magnetic
needle or that it has a magnetic effect, led to many attempts
to produce an electric current by means of a magnet.
It was not until about 1831, however, that Joseph Henry
in America and Michael Faraday in England, independently
discovered how to accomplish this important result.
At the present time, voltaic cells produce but a very
small part of the current electricity used. Practically all
that is employed for power, light, heat, and electrolysis is
produced by the use of magnetic fields, or by electromagnetic
induction.
297. Laws of Induced Currents.[M]—To illustrate how a
current can be produced by electromagnetic induction:
Connect a coil of 400 or more turns of No. 22 insulated copper
wire to a sensitive galvanometer. (See Fig. 279.) Now insert a
bar magnet in the coil. A sudden movement of the galvanometer
will be noticed, indicating the production of a current. When the
magnet stops moving, however, the current stops, and the coil of
the galvanometer returns to its first position. If now the magnet
is removed, a movement of the galvanometer coil in the opposite
direction is noticed. This action may be repeated as often as desired
with similar results.
Careful experiments have shown that it is the magnetic
field of the magnet that produces the action, and that[Pg 327]
only when the number of lines of force in the coil is changing
do we find a current produced in the coil. These facts
lead to Law I. Any change in the number of magnetic
lines of force passing through or cut by a coil will produce an
electromotive force in the coil. In the account of the experiment
just given, electric currents are produced, while in
Law I, electromotive forces are mentioned. This difference
is due to the fact that an E.M.F. is always produced in a
coil when the magnetic field within it is changed, while a
current is found only when the coil is part of a closed
circuit. The inductive action of the earth's magnetic field
(see Fig. 280), may be shown by means of a coil of 400 to
500 turns a foot in diameter.
 Fig. 279.—The moving magnet
induces a current in the
coil.
Fig. 279.—The moving magnet
induces a current in the
coil.
Fig. 280.—A current may be induced
by turning the coil in the
earth's magnetic field.
Connect its ends to a sensitive galvanometer and hold it at right
angles to the earth's field. Then quickly revolve the coil through
180 degrees and note the movement of the galvanometer. Reverse
the coil and the galvanometer swings in the opposite direction.
If the magnet in Fig. 279 is moved in and out of the
coil at first slowly and later swiftly, small and large deflections
of the galvanometer coil are noticed. The quicker
the movement of the magnetic field the greater are the
galvanometer deflections produced. This leads to Law II.[Pg 328]
The electromotive forces produced are proportional to the
number of lines of force cut per second.
298. The magneto is a device that illustrates the laws
of induced currents stated in Art. 297. The magneto
(see Fig. 281), consists of several permanent, "U"-shaped
magnets placed side by side. Between the poles of these
magnets is placed a slotted iron cylinder having a coil of
many turns of fine insulated copper wire wound in the
slot as in Fig. 282. The cylinder and coil form what is
called an armature. The armature is mounted so as to
be revolved between the poles of the "U"-shaped magnets
by means of a handle. As the armature revolves, the
lines of force from the magnets pass through the coil first
in one direction and then in the other. This repeated
change in the lines of force passing through the coil produces
an E.M.F. which may be felt by holding in the hands
the two wires leading from the armature coil. On turning
the armature faster the current is felt much stronger,
showing that the E.M.F. in the coil increases as the rate
of cutting the magnetic lines of force by the coils increases.
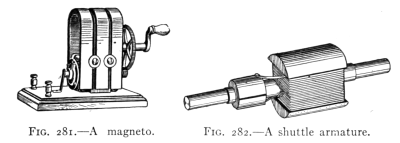 Fig. 281.—A magneto.
Fig. 281.—A magneto.
Fig. 282.—A shuttle armature.
 Fig. 283.—The induced current has a field which opposes the motion of
the magnet. The heavy line represents the direction of the induced
current.
Fig. 283.—The induced current has a field which opposes the motion of
the magnet. The heavy line represents the direction of the induced
current.
299. Lenz's Law.—While one is turning the armature
of a magneto if the two wires leading from its coil are
connected, forming what is called a "short circuit," the
difficulty of turning the armature is at once increased.
If now the circuit is broken, the armature turns as easily[Pg 329]
as at first. The increased difficulty in turning the armature
is due to the current produced in the coil. This current
sets up a magnetic field of its own that opposes
the field from the steel magnets. This opposition makes
it necessary for work to be done to keep up the motion
of the coil when a current is passing through it. This
fact is called Lenz's Law. It may be expressed as follows:
Whenever a current is induced by the relative motion of a
magnetic field and a conductor, the direction of the induced
current is always such as to set up a magnetic field that
opposes the motion. Lenz's Law follows from the principle
of conservation of energy, that energy can be produced
only from an expenditure of other energy. Now since an
electric current possesses energy, such a current can be
produced only by doing mechanical work or by expending
some other form of energy. To illustrate Lenz's Law,
suppose that the north-seeking pole of a bar magnet be
inserted in a closed coil of wire. (See Fig. 283.) The
current induced in the coil has a direction such that its lines[Pg 330]
of force will pass within the coil so as to oppose the field
of the bar magnet, when the north pole of the magnet is
inserted so as to point to the left. That is, the north pole
of the helix is at the right. Applying the right-hand rule
to the coil, its current will then be counter clockwise. On
withdrawing the magnet, the current reverses, becoming
clockwise with its field passing to the left within the coil.
A striking illustration of the opposition offered by the
field of the induced current to that of the inducing field
is afforded by taking a strong electromagnet (see Fig.
284) and suspending a sheet of copper so
as to swing freely between the poles.
When no current flows through the magnet
the sheet swings easily for some
time. When, however, the coils are
magnetized, the copper sheet has induced
within it, currents that set up magnetic
fields strongly opposing the motion, the
swinging being stopped almost instantly.
The principle is applied in good ammeters
and voltmeters to prevent the swinging
of the needle when deflected. The
current induced in the metal form on
which is wound the galvanometer coil is sufficient to make
the needle practically "dead beat."
 Fig. 284.—The
magnetic field
stops the swinging
of the sheet of
copper.
Fig. 284.—The
magnetic field
stops the swinging
of the sheet of
copper.
300. The Magneto and the Dynamo.—Magnetos are
used to develop small currents, such as are used for telephone
signals, and for operating the sparking devices of
gasoline engines. They are therefore found in automobiles
containing gasoline motors. The most important
device for producing electric currents by electromagnetic
induction, however, is the dynamo. It is employed whenever
large currents are desired. The principle of this
device is similar to that of the magneto except that it contains[Pg 331]
[Pg 332]
[Pg 333]
an electromagnet for producing the magnetic field.
Since the electromagnet can develop a much stronger field
than a permanent magnet, the dynamo can produce
a higher E.M.F. and a much larger current than the
magneto.
 Lord Kelvin
Lord Kelvin
"By Permission of the Berlin Photographic
Co., New York."
Lord Kelvin (Sir William Thomson),
(1824-1907). Professor of
Physics, Glasgow University. Invented
the absolute scale of temperature:
also many practical
electrical measuring instruments.
The foremost physicist of the latter
part of the nineteenth century.
 Michael Faraday
Michael Faraday
"By Permission of the Berlin Photographic
Co., New York."
Michael Faraday (1791-1867).
Famous English Physicist. Made
many discoveries in electricity
and magnetism; "Greatest experimentalist
of the nineteenth
century."
301. The Magnetic Fields of Generators.—In the
magneto, the magnetic field is produced by permanent steel
magnets. In dynamos powerful electromagnets are used.
The latter are sometimes excited by currents from some
other source, but usually current from the armature is
sent around the field coils to produce the magnetic fields.
Dynamos are classified according to the manner in which
the current is sent to their field coils.
 Fig. 285.—A series-wound
dynamo.
Fig. 285.—A series-wound
dynamo.
Fig. 286.—A shunt-wound
dynamo.
Fig. 287.—A compound-wound
dynamo.
A. The series wound dynamo (see Fig. 285) is arranged
so that all of the current produced by the armature is sent
through coils of coarse wire upon the fields, after flowing
through the external circuit.
B. The shunt wound dynamo (see Fig. 286) sends a
part only of the current produced through the field coils.
The latter are of many turns of fine wire so as to use as
little current as possible. The greater part of the current
goes to the main circuit. If the number of lamps or motors[Pg 334]
connected to the main circuit is increased, the voltage is
lessened which weakens the current in the field coils,
causing a weaker field and still lower voltage, producing a
fluctuating E.M.F. which is unsatisfactory for many
purposes. This fault is overcome by
C. the compound wound dynamo. This dynamo has
both shunt and series coils upon its fields. (See Fig. 287.)
If more current is drawn into the main circuit with this
dynamo, the series coils produce a stronger field compensating
for the weaker field of the shunt coils, so that
uniform voltage is maintained. The compound wound
generator is therefore the one most commonly employed.
Important Topics
1. Laws of electromagnetic induction (a) conditions, (b) E.M.F.,
(c) direction.
2. Devices, (a) magneto, (b) dynamo: series, shunt, compound.
3. Illustrations of the laws.
Exercises
1. Under what conditions may an electric current be produced
by a magnet?
2. Show how Lenz's Law, follows from the principle of conservation
of energy.
3. A bar magnet is fixed upright with its north-seeking pole upward.
A coil is thrust down over the magnet. What is the
direction of the current induced in the coil? Explain.
4. In what two ways may a current be induced in a closed coil?
5. What method is employed in the magneto? In the dynamo?
6. What is the nature of the current produced in the armature
coil of a magneto, that is, is it direct or alternating? Why?
7. What is the resistance of a 20-watt tungsten lamp if the E.M.F.
is 115 volts?
8. Find the resistance of a 40-watt tungsten lamp when the
voltage is 115? How much heat will it produce per minute?
9. An Edison storage battery cell on a test gave a discharge of
30 amperes. The average voltage was 1.19. What was the
resistance of the cell?
[Pg 335]
10. Eight storage cells are connected in series. Each has an E.M.F.
of 1.2 volts and an internal resistance of 0.03 ohms. What will
be the current flowing through a voltmeter having 500 ohms
resistance in circuit with them?
(2) The Dynamo and the Motor
302. The Dynamo may be defined as a machine for
transforming mechanical energy into the energy of electric
currents by electromagnetic induction. Although electromagnetic
induction was discovered in 1821, practical
dynamos were not built for about 40 years or until between
1860 and 1870. The great development in the production
and use of electric currents has come since the latter date.
The principle parts of the dynamo are (a) the field magnet,
(b) the armature, (c) the
commutator or collecting
rings, (d) the brushes.
Fig. 288 shows several
common methods of
arranging the field coils
and the armature.
 Fig. 288.—Several methods of arranging the field coils and the armature
of a dynamo.
Fig. 288.—Several methods of arranging the field coils and the armature
of a dynamo.
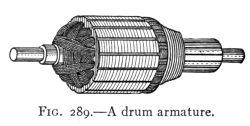 Fig. 289.—A drum armature.
Fig. 289.—A drum armature.
The field coils vary in number and position. The
purpose of their construction is always to send the largest
possible number of lines of force through the armature.
Some dynamos are bipolar, or have two poles, others are
multipolar or have more than two. In Fig. 288 No. 4
has four poles. The armature of a dynamo differs from a
magneto armature in that it consists of a series of coils of[Pg 336]
insulated copper wire wound in numerous slots cut in the
surface of a cylindrical piece of iron. Fig. 289 shows a
side view of the iron core of such an armature. Iron is
used to form the body of the armature since the magnetic
lines of force flow easily through the iron. The iron by its
permeability also concentrates and increases the magnetic
flux. The best armatures are made of many thin sheets
of soft iron. These are called laminated armatures. An
armature made of a solid piece of iron becomes hot when
revolving in a magnetic field. This is due to electric
currents induced in the iron itself. This heating is
largely reduced by laminating the armature. Why?
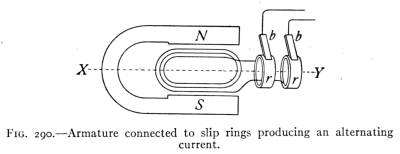 Fig. 290.—Armature connected to slip rings producing an alternating
current.
Fig. 290.—Armature connected to slip rings producing an alternating
current.
303. Methods of Collecting Current from the Armature.—The
electric currents produced in the armature are
conducted away by special sliding contacts. The stationary
part of the sliding contact is called a brush. The
moving part is a slip ring or a commutator. Fig. 290 shows
an armature coil connected to slip rings. As the armature
revolves, the coils and slip rings revolve with it. The two
ends of the armature coils are connected to the two rings
respectively. Now as the armature revolves it cuts the
lines of force first in one direction and then in the other.
This produces in the coils an E.M.F. first one way and then
the other. This E.M.F. sets up a current which is conducted
to the outside circuits through the slip rings and[Pg 337]
brushes. Such a current which repeatedly reverses its
direction is called an alternating current. Fig. 291 (1) indicates
graphically how the current moves alternately
one way and then the other. Alternating currents are
extensively used for electric light, heat, and power. Direct
currents or those going continuously in one direction are
however in much demand especially for street car service,
for electrolysis, and for charging storage batteries.
304. The Commutator.—For a dynamo to deliver a
direct current it must carry upon the shaft of the armature
a commutator. The
commutator is used
to reverse the connections
of the ends
of the armature coils
at the instant that
the current changes
its direction in the
armature. This reversal of connection when the direction
of current changes, keeps the current in the outside
circuit flowing in the same direction. Fig. 291 is a diagram
of an armature with a commutator. The commutator
is a split ring, having as many parts or segments as
there are coils upon the armature. The brushes touch
opposite points upon the commutator as they slide over
the surface of the latter. Suppose that the armature
viewed from the commutator end rotates in a counter-clockwise
direction, also that the currents from the upper
part move toward the commutator and out the top brush.
 Fig. 291.—The armature coils are connected
to a commutator producing a direct current.
Fig. 291.—The armature coils are connected
to a commutator producing a direct current.
As the armature revolves, its coils soon begin to cut
the force lines in the opposite direction. This change in
the direction of cutting the lines of force causes the current
to reverse in the coils of the armature. At the instant the
current changes in direction, what was the upper segment[Pg 338]
of the commutator slips over into contact with the lower
brush, and the other segment swings over to touch the
upper brush. Since the current has reversed in the coils
it continues to flow out of the
upper brush. This change in
connection at the brushes takes
place at each half turn of the
armature, just as the current
changes in direction in the coils.
This is the manner in which
the commutator of a dynamo
changes the alternating current
produced in the armature coils,
into a direct current in the external circuit. Fig. 292 (1)
represents graphically an alternating current, (2) of the
same figure shows current taken from the brushes
of the commutator of a dynamo with one coil on the
armature.
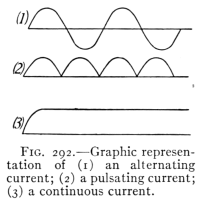 Fig. 292.—Graphic representation
of (1) an alternating
current; (2) a pulsating current;
(3) a continuous current.
Fig. 292.—Graphic representation
of (1) an alternating
current; (2) a pulsating current;
(3) a continuous current.
 Fig. 293.—DeLaval multi-stage turbine and gear driving 750-kw., 750-r.p.m.,
600-volt direct-current generator.
Fig. 293.—DeLaval multi-stage turbine and gear driving 750-kw., 750-r.p.m.,
600-volt direct-current generator.
A practical dynamo, however, has many coils upon its[Pg 339]
armature with a corresponding number of segments upon
the commutator. (See Figs. 289 and 293.) As each coil
and commutator segment passes a brush, it contributes
an impulse to the current with the result that armatures
with many coils produce currents that flow quite evenly.
(See Fig. 292, 3.)
The current represented in Fig. 292 (2) is called a pulsating
current.
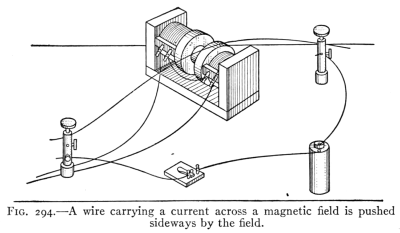 Fig. 294.—A wire carrying a current across a magnetic field is pushed
sideways by the field.
Fig. 294.—A wire carrying a current across a magnetic field is pushed
sideways by the field.
305. The electric motor is a machine which transforms
the energy of an electric current into mechanical energy
or motion. The direct current motor consists of the same
essential parts as a direct current dynamo, viz., the field
magnet, armature, commutator and brushes. Its operation
is readily comprehended after one understands the
following experiment:
Set up two bar electromagnets with unlike poles facing
each other about an inch apart. A wire connected to a
source of current is hung loosely between the poles as in
Fig. 294. The circuit through the wire should contain a
key or switch. If a current is sent through the electromagnets
and then another is sent through the wire, the[Pg 340]
latter will be found to be pushed either up or down, while
if the current is reversed through the wire it is pushed in
the opposite direction. These results may be explained
as follows:
Consider the magnetic field about a wire carrying a current
(See Fig. 295.) If such a wire is placed in the magnetic
field between two opposite poles of an electromagnet
(Fig. 296), the wire will be moved either up or down.
The reason for this is shown by the diagram in Fig. 297.
Here a wire carrying a current and therefore surrounded
by a magnetic field passes
across another magnetic
field. The two fields
affect each other causing
a crowding of the force
lines either above or below
the wire. The wire at
once tends to move sideways
across the field away
from the crowded side. In the figure, the wire tends to
move downward.
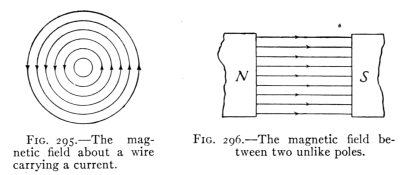 Fig. 295.—The magnetic
field about a wire
carrying a current.
Fig. 295.—The magnetic
field about a wire
carrying a current.
Fig. 296.—The magnetic field between
two unlike poles.
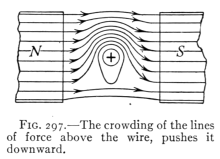 Fig. 297.—The crowding of the lines
of force above the wire, pushes it
downward.
Fig. 297.—The crowding of the lines
of force above the wire, pushes it
downward.
In a practical motor, the wires upon the armature are
so connected that those upon one side (see Fig. 298), carry
currents that pass in, while on the other side they pass out.
To represent the direction of the current in the wires, the[Pg 341]
following device is employed; a circle with a cross (to
represent the feather in the tail of an arrow) indicates a
current going away from the observer, while a circle with
a dot at its center (to
represent the tip of an
arrow) indicates a current
coming toward the
observer.
 Fig. 298.—The crowding of the lines
of force causes the armature to revolve
in a clockwise direction.
Fig. 298.—The crowding of the lines
of force causes the armature to revolve
in a clockwise direction.
In Fig. 298 the north
pole is at the left and
the south pole at the
right. The field of the magnets therefore passes from
left to right as indicated in the figure. Now in the armature
the currents in the wires on the left half of the armature
are coming toward the observer while those on the
right move away.
Applying the right-hand
rule, the magnetic
lines will crowd
under the wires on
the left side of the
armature while they
will crowd over the
wires on the right
side. This will cause
a rotation up on the
left side and down
on the right, or in
a clockwise direction.
 Fig. 299.—View of a one-half horse-power
motor.
Fig. 299.—View of a one-half horse-power
motor.
If the current in
the armature is reversed
(in on the left and out on the right), the lines of
force will crowd the armature around in the opposite
direction or counter clockwise. The rotation of the[Pg 342]
armature will also be reversed if, while the current in the
armature is unchanged in direction, the poles of the
magnet are changed thus reversing the magnetic field.
The motorman of a street car reverses the motion of
his car by reversing the direction of the current in the
armature of the motor.
 Fig. 300.—The frame and electromagnet (at left), front bracket and
brush holder (at right) of the motor shown in Fig. 299.
Fig. 300.—The frame and electromagnet (at left), front bracket and
brush holder (at right) of the motor shown in Fig. 299.
Fig. 301.—The armature of a motor.
306. Practical motors have many coils upon the armature
with a corresponding number of segments upon the
commutator. A large number of coils and commutator
segments enables some one of the coils to exert its greatest
efficiency at each instant, hence a steady force is provided
for turning the armature which causes it to run smoothly.[Pg 343]
Fig. 299 represents a 1/2 horse-power motor ready for use
while Fig. 300 shows the frame and poles and the front
bracket and brush holder, and Fig. 301 represents the
armature.
Important Topics
1. The dynamo, four essential parts, action (a) for alternating
currents, (b) for direct currents.
2. The electric motor: (a) essential parts, (b) action.
Exercises
1. Why is an alternating current produced in the armature of a
dynamo?
2. How is this current produced? Give careful explanations.
3. What is the result of Lenz's law as applied to the dynamo?
4. Apply the first two laws of electromagnetic induction to the
dynamo.
5. What is the power of a dynamo if it produces 40 amperes of current
at 110 volts?
6. How much power must be applied to this dynamo if its efficiency
is 90 per cent.?
7. A motor takes 10 amperes of current at 220 volts; what is the
power of the current in watts? If this motor has an efficiency
of 95 per cent., how many horse-power of mechanical energy
can it develop?
8. Explain why reversing the current in the armature of a motor
reverses the direction of rotation.
9. Find the cost of running a washing machine using a 1/2-horsepower
motor 2 hours if the cost of the electricity is 10 cents
a kilowatt hour.
10. A 1/8-horse-power motor is used to run a sewing machine.
If used for 3 hours what will be the cost at 11 cents a kilowatt
hour?
(3) The Induction Coil and the Transformer
307. The Induction Coil.—Practically all electric currents
are produced either by voltaic cells or by dynamos.
It is frequently found, however, that it is desirable to[Pg 344]
change the E.M.F. of the current used, either for purposes
of effectiveness, convenience, or economy. The induction
coil and the transformer, devices for changing the E.M.F.
of electric currents, are therefore in common use. The
induction coil (see Fig. 302) consists of a primary coil of
coarse wire P (Fig. 303) wound upon a core of soft iron
wire, and a secondary coil,
S, of several thousand
turns of fine wire. In
circuit with the primary
coil is a battery, B, and a
current interrupter, K,
which works like the interrupter
upon an electric
bell. The ends of the secondary coil are brought to
binding posts or spark points as at D.
 Fig. 302.—An induction coil.
Fig. 302.—An induction coil.
The current from the battery flows through the primary
coil magnetizing the iron core. The magnetism in the
core attracts the soft-iron end of the interrupter, drawing
the latter over and breaking the circuit at the screw contact,
K. This abruptly
stops the current and at
once the core loses its
magnetism. The spring
support of the interrupter
now draws the
latter back to the contact,
T, again completing
the circuit. The
whole operation is repeated,
the interrupter vibrating rapidly continually opening
and closing the circuit.
 Fig. 303.—Diagram showing the parts of
an induction coil.
Fig. 303.—Diagram showing the parts of
an induction coil.
308. The Production of Induced Currents in the
Secondary Coil.—When the current flows through the[Pg 345]
primary it sets up a magnetic field in the core. When
the current is interrupted, the field disappears. The increase
and decrease in the field of the core induces an
E.M.F. in the secondary coil, in accordance with the first
law of electromagnetic induction. The E.M.F. produced
depends upon (a) the number of turns in the secondary,
(b) the strength of the magnetic field and (c) the rate of
change of the field. The rate of change in the field is
more rapid at the break than at the make. When the
circuit is closed it takes perhaps 1/10 of a second for the
current to build up to its full strength while at a break
the current stops in perhaps 0.00001 of a second, so that
the induced E.M.F. is perhaps 10,000 times as great at
"break" as at make. To increase the suddenness of the
"make" and "break," a condenser is often connected in
the primary circuit, in parallel, with the interrupter. (See
Fig. 303, C.) This condenser provides a place to hold the
rush of current at the instant that the interrupter breaks
the circuit. This stored up charge reinforces the current
at the make producing a much more sudden change in the
magnetic field with a corresponding increase in the E.M.F.
The induced currents from induction coils are sometimes
called faradic currents in honor of Faraday who discovered
electromagnetic induction. They are used to operate
sparking devices upon gas and gasoline engines and in
many devices and experiments in which high-tension
electricity is employed.
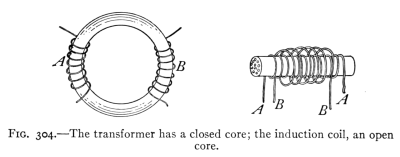 Fig. 304.—The transformer has a closed core; the induction coil, an open
core.
Fig. 304.—The transformer has a closed core; the induction coil, an open
core.
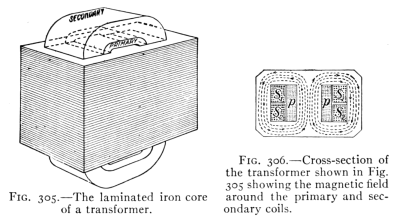 Fig. 305.—The laminated iron core
of a transformer.
Fig. 305.—The laminated iron core
of a transformer.
Fig. 306.—Cross-section of
the transformer shown in Fig.
305 showing the magnetic field
around the primary and secondary
coils.
309. The Transformer.—This is like the induction coil
in that it uses a primary and a secondary coil, and an iron
core to carry the magnetic field. (See Fig. 304.) They
differ in that the transformer has a closed core or one forming
a continuous iron circuit, while the induction coil has
an open core, or one in which the magnetic field must travel
in air from the north to the south poles of the core. The[Pg 346]
transformer must always be used with an alternating current
while the induction coil may use either a direct or an
alternating current. Further, the induction coil always
produces a higher E.M.F. while the transformer may produce
an E.M.F. in its secondary coil that is either higher or
lower than the one in the primary. The former is called
"step-up" while the latter is a "step-down" transformer.
The alternating current in the primary coil of the transformer
produces an alternating magnetic flux in the iron
core. This iron core is laminated (see Fig. 305) to prevent
the heating that would result if a solid core were used.
The alternating magnetic flux induces in the secondary
coil an E.M.F. in accordance with the following rule. The[Pg 347]
ratio of the number of turns in the primary to the number
of the turns in the secondary coil equals the ratio of the
electromotive forces in these respective coils. If the
secondary coil has 8 turns while the primary has 4, the
E.M.F. of the secondary will be just twice that of the primary.
Or, if in the primary coil of the transformer Fig.
306 is an E.M.F. of 110 volts, in the secondary will be
found an E.M.F. of 220 volts.
 Fig. 307.—A
commercial transformer.
Fig. 307.—A
commercial transformer.
310. Uses of Transformers.—In electric lighting systems,
dynamos often produce alternating currents at
1000 to 12,000 volts pressure. It is very
dangerous to admit currents at this pressure
into dwellings and business houses,
so that transformers are installed just
outside of buildings to "step-down" the
high voltage currents to 110 or 220 volts.
The lighting current that enters a house
does not come directly from a dynamo.
It is an induced current produced by a
transformer placed near the house. (See Fig. 307.) In
a perfect transformer the efficiency would be 100 per
cent. This signifies that the energy that is sent into the
primary coil of the transformer exactly equals the energy
in the secondary coil. The best transformers actually
show efficiencies better than 97 per cent. The lost energy
appears as heat in the transformer. "The transfer of
great power in a large transformer from one circuit to
another circuit entirely separate and distinct, without any
motion or noise and almost without loss, is one of the
most wonderful phenomena under the control of man."
311. The mercury arc rectifier is a device for changing
an alternating current into a direct current. It is frequently
used for charging storage batteries where only
alternating current is supplied by the electric power company.[Pg 348]
It consists of an exhausted bulb containing two
carbon or graphite electrodes marked G in Fig. 308 and a
mercury electrode marked M. It is found that current
will pass through such a
bulb only from the graphite
to the mercury but not
in the reverse direction.
In operating the device,
the secondary terminals of
an alternating current
transformer T are connected
to the graphite
terminals of the rectifier.
A wire connected to the
center of the secondary
of the transformer at C is
attached to the negative
terminal of the storage
battery SB. The positive
terminal of the battery is
connected to the mercury electrode of the rectifier tube
through a reactance or choke coil R. This coil serves to
sustain the arc between the alternations. Sw is a starting
switch, used only in striking the arc. It is opened immediately
after the tube begins to glow.
 Fig. 308.—Diagram of a mercury
arc rectifier.
Fig. 308.—Diagram of a mercury
arc rectifier.
Important Topics
Transformer, induction coil, mercury arc rectifier, construction,
action; uses of each.
Exercises
1. Does the spark of an induction coil occur at "make" or at
"break?" Why?
2. What must be the relative number of turns upon the primary
and secondary coils of a transformer if it receives current at[Pg 349]
220 volts and delivers current at 110? Also show by diagram.
3. Would the transformer work upon a direct current? Why?
4. Explain why the interrupter is a necessary part of the induction
coil and not of the transformer.
5. If a building used eighty 110-volt incandescent lamps, what
would be necessary to light them if they were joined
in series? Why would this not be practical?
6. If a 16-candle-power lamp requires 0.5 ampere upon a 110-volt
circuit what current and voltage will be needed to operate 12
such lamps in parallel?
7. What will it cost to run these lamps 4 hours a night for 30 days
at 10 cents per kilowatt hour?
8. If a mercury arc rectifier uses 5 amperes of current at 110 volts
alternating current to produce 5 amperes of direct current at 70
volts, what is the efficiency of the rectifier?
9. Compute the heat produced in a 40 watt tungsten lamp in
1 minute.
10. Compute the heat produced in a 60 watt carbon incandescent
lamp in 1 hour.
(4) The Telephone
312. The Electric Telephone.—This is an instrument
for reproducing the human voice at a distance by an electric
current. The modern electric telephone consists of
at least four distinct parts (see Fig. 312); viz., a transmitter,
an induction coil, an electric battery, and a receiver. The
first three of these are concerned in sending, or transmitting
over the connecting wires a fluctuating electric current,
which has been modified by the waves of a human voice.
The receiver, is affected by the fluctuating current and
reproduces the voice. It will be considered first, in our
study.
313. The telephone receiver was invented in 1876 by
Alexander Graham Bell. It consists of a permanent steel
magnet, U shaped, with a coil of fine insulated copper wire
about each pole. (See Fig. 310.) A disc of thin sheet
iron is supported so that its center does not quite touch the[Pg 350]
poles of the magnet. A hard rubber cap or ear piece with
an opening at its center is screwed on so as to hold the
iron disc firmly in place.
 Fig. 309.—The simplest telephone
system. It consists of two telephone
receivers connected in series on a circuit.
It will work, but not satisfactorily.
Fig. 309.—The simplest telephone
system. It consists of two telephone
receivers connected in series on a circuit.
It will work, but not satisfactorily.
The action of the receiver may be understood from the
following explanation: The electric current sent to the
receiver, comes from the
secondary coil of the induction
coil; it is an
alternating current, fluctuating
back and forth
just in time with the
waves of the voice affecting
it at the transmitter.
This alternating current flows around the coils on the
poles of the permanent magnet. When this current
flows in one direction, its magnetic field assists the
field of the permanent magnet, strengthening it. This
stronger magnetic field draws the thin iron disc in front
of the poles of the magnet a little closer to them. When
the current in the coils flows the other way, its magnetic
field weakens the field of the steel magnet, and the disc is
drawn back by the force of its own elasticity. Thus the
disc of the receiver vibrates with the alternations of the
current, and reproduces the same
sounds that were spoken into the
transmitter.
 Fig. 310.—A telephone
receiver. This receiver has
a permanent horseshoe magnet
with a coil about each
pole.
Fig. 310.—A telephone
receiver. This receiver has
a permanent horseshoe magnet
with a coil about each
pole.
314. The Telephone Transmitter.—The
telephone receiver
just described has great sensitiveness
in reproducing sound, but it
is not satisfactory as a transmitter
or sending apparatus. The transmitter commonly used is
represented in cross-section in Fig. 311. In this figure, back
of the mouthpiece, is a thin carbon disc, D. Back of this[Pg 351]
disc is a circular compartment containing granular carbon,
g. The wires of the circuit are connected to the carbon
disc and to the back of the case containing granular carbon.
The circuit through the transmitter also includes
a voltaic or storage cell and the primary coil of an induction
coil. (See Fig. 312.)
 Fig. 311.—A telephone
transmitter.
Fig. 311.—A telephone
transmitter.
Fig. 312.—Telephone instruments at one
end of a talking circuit.
315. The action of the transmitter is explained as follows:
When the sound waves of the voice strike upon the
carbon disc, the latter vibrates, alternately increasing and
decreasing the pressure upon the granular carbon. When
the pressure increases, the electrical resistance of the
granular carbon is lessened, and when the pressure upon
it is decreased, its resistance increases. This changing resistance
causes fluctuations in the electric current that
correspond exactly with the sound waves of the voice
affecting it.
316. A complete telephone system operating with a
local battery is shown in Fig. 312. A person speaking
into the transmitter causes a fluctuation in the electric
current in the transmitter as described in Art. 315. This
fluctuating current passes through the primary coil of
the induction coil Ic. This fluctuating current produces a
fluctuating magnetic field in its core. This fluctuating
field induces an alternating current in the secondary coil
which alternates just as the primary current fluctuates,[Pg 352]
but with a much higher E.M.F. than the latter. The
alternating current passes to the receiver which reproduces
the speech as described in Art. 313. The line circuit includes
the secondary of the induction coil, the receiving
instrument and the receiver of the sending instrument so
that the voice is reproduced in both receivers. An electric
bell is placed at each station to call the attention of
parties wanted. The movement of the receiver hook
when the receiver is lifted, disconnects the bell and closes
the talking circuit. The latter is opened and the bell
connected when the receiver is hung up again.
 Fig. 313.—Diagram of a telephone system as used in a large exchange.
Fig. 313.—Diagram of a telephone system as used in a large exchange.
In cities and towns, the telephone system in use differs
from the one described in usually having one large battery
placed in the central exchange, instead of dry cells at
each instrument. (See Fig. 313.) Also the operator at
central is called by simply taking the receiver from the
hook instead of being "rung up" by the subscriber. The
operations of the transmitter, induction coil and receiver,
however, are the same in all telephones.
Important Topics
1. Receiver: parts, action.
2. Transmitter: parts, action.
3. Induction coil, bell, line wires, etc.
4. Action of the whole device.
Exercises
1. State three important electrical laws or principles that are
employed in the operation of the telephone. What is the application
of each?
[Pg 353]
2. Connect the binding posts of a telephone receiver with a sensitive
galvanometer and press on the diaphragm of the receiver; a
deflection of the galvanometer will be noticed. Release the
diaphragm and a reflection in the opposite direction is seen.
Explain.
3. Is the current passing through the transmitter the one going to
the receiver of the instrument? Explain.
4. Does the receiver at the telephone used by a person repeat the
speech of the person? Explain.
5. How many 0.5 ampere lamps can be used with a 6 ampere fuse?
6. Why is it necessary to have a rheostat connected in series with
a stereopticon or moving picture machine while a rheostat is
not used with arc lights out doors?
7. How many candle power should a 60 watt carbon incandescent
lamp give, if its efficiency is 3.4 watts per candle power?
8. Three incandescent lamps having resistances of 100, 150, and
240 ohms, respectively, are connected in parallel. What is
their combined resistance?
Review Outline: Induced Currents
Induced currents; 3 laws, illustrations.
Construction, action, and uses of—magneto, dynamo, induction
coil, transformer, motor, telephone. Mercury arc rectifier.
Terms—primary, secondary, for coils and currents, armature, commutator,
slip ring, brush, rectifier, open core, series, shunt, and
compound connections for dynamos.
[Pg 354]
SOUND
(1) Sound and Wave Motion
317. What is a Sound?—This question has two answers,
which may be illustrated as follows: Suppose that an
alarm clock is set so that it will strike in one week and that
it is placed upon a barren rock in the Pacific Ocean by
sailors who immediately sail away. If
when the tapper strikes the bell at the
end of the week no ear is within a hundred
miles, is any sound produced? The two
view-points are now made evident, for
some will answer "no" others "yes."
Those answering "no" hold that sound is
a sensation which would not be produced
if no ear were at hand to be affected.
Those answering "yes" understand, by
the term sound, a mode of motion capable
of affecting the auditory nerves, and that
sound exists wherever such motions are
present. This latter point of view is
called the physical and is the one we are
to use in this study.
 Fig. 314.—The
tuning fork is vibrating.
Fig. 314.—The
tuning fork is vibrating.
318. Source of Sound.—If we trace any sound to its
source, it will be found to originate in a body in rapid
motion usually in what is called a state of vibration. To
illustrate, take a tuning fork, strike it to set it in vibration
and place its stem firmly against a thin piece of wood;
the sound will be strengthened materially by the vibration[Pg 355]
of the wood. If now the vibrating fork is placed with
the tips of the prongs in water, the vibration is plainly
shown by the spattering of the water (Fig. 314). When
one speaks, the vibrating body is in the larynx at the top
of the windpipe. Its vibration may be plainly felt by
the hand placed upon the throat while speaking.
319. Sound Media.—Usually sounds reach the ear
through the air. The air is then said to be a medium for
sound. Other substances may serve as a sound medium,
for if the head is under water and two
stones, also under water, are struck together
a sharp sound is heard. Also if
one end of a wooden rod is held at the ear
and the other end of the rod is scratched
by a pin, the sound is more plainly perceived
through the wood than through
the air. Think of some illustration from
your own experience of a solid acting as
medium for sound. If an electric bell is
placed in a bell jar attached to an air pump, as in Fig.
315, on exhausting the air the loudness of the sound is
found to diminish, indicating that in a perfect vacuum no
sound would be transmitted. This effect of a vacuum
upon the transmission of sound is very different from its
effect upon radiation of heat and light. Both heat and
light are known to pass through a vacuum since both
come to the earth from the sun through space that so far
as we know contains no air or other matter. Sound
differs from this in that it is always transmitted by some
material body and cannot exist in a vacuum.
 Fig. 315.—Sound
does not
travel in a vacuum.
Fig. 315.—Sound
does not
travel in a vacuum.
320. Speed of Sound.—Everyone has noticed that it
takes time for sound to travel from one place to another.
If we see a gun fired at a distance, the report is heard a
few seconds after the smoke or flash is seen. The time[Pg 356]
elapsing between a flash of lightning and the thunder
shows that sound takes time to move from one place to
another. Careful experiments to determine the speed
of sound have been made. One method measures accurately
the time required for the sound of a gun to pass
between two stations several miles apart. A gun or
cannon is placed at each station. These are fired alternately,
first the one at one station and then the one at the
other so as to avoid an error in computation due to the
motion of wind. This mode of determining the speed
of sound is not accurate. Other methods, more refined
than the one just described have given accurate values for
the speed of sound. The results of a number of experiments
show that, at the freezing temperature, 0°C., the
speed of sound in air is 332 meters or 1090 ft. a second.
The speed of sound in air is affected by the temperature,
increasing 2 ft. or 0.6 meter per second for each degree
that the temperature rises above 0°C. The speed decreases
the same amount for each degree C. that the air is cooled
below the freezing point. The speed of sound in various
substances has been carefully determined. It is greater
in most of them than in air. In water the speed is about
1400 meters a second; in wood, while its speed varies with
different kinds, it averages about 4000 meters a second;
in brass the speed is about 3500 meters; while in iron it is
about 5100 meters a second.
321. The Nature of Sound.—We have observed that
sound originates at a vibrating body, that it requires a
medium in order to be transmitted from one place to another,
and that it travels at a definite speed in a given substance.
Nothing has been said, however, of the mode of
transmission, or of the nature of sound. Sounds continue
to come from an alarm clock even though it is placed under
a bell jar. It is certain that nothing material can pass[Pg 357]
through the glass of the jar. If, however, we consider
that sound is transmitted by waves through substances the
whole matter can be given a simple explanation. In order
to better understand the nature of sound a study of waves
and wave motion will be taken up in the next section.
Important Topics
Sound: two definitions, source, medium, speed, nature.
Exercises
1. Give two illustrations from outside the laboratory of the fact
that sound is transmitted by other materials than air.
2. Name the vibrating part that is the source of the sound in three
different musical instruments.
3. Is sound transmitted more strongly in solids, liquids or gases?
How do you explain this?
4. How far away is a steamboat if the sound of its whistle is heard
10 seconds after the steam is seen, the temperature being 20°C.?
Compute in feet and in meters.
5. How many miles away is lightning if the thunder is heard 12
seconds after the flash in seen, the temperature being 25°C.?
6. Four seconds after a flash of lightning is seen the thunder clap
is heard. The temperature is 90°F. How far away was the
discharge?
7. The report of a gun is heard 3 seconds after the puff of smoke
is seen. How far away is the gun if the temperature is 20°C.?
8. An explosion takes place 10 miles away. How long will it
take the sound to reach you, the temperature being 80°F?.
How long at 0°F.?
9. How long after a whistle is sounded will it be heard if the distance
away is 1/4 mile, the temperature being 90°F.?
10. The report of an explosion of dynamite is heard 2 minutes
after the puff of smoke is seen. How far away is the explosion
the temperature being 77°F.?
(2) Waves[N] and Wave Motion
322. Visible Waves.—It is best to begin the study of
wave motion by considering some waves which are familiar[Pg 358]
to most persons. Take for example the waves that move
over the surface of water (Fig. 316). These have an
onward motion, yet boards or chips upon the surface
simply rise and fall as the waves pass them. They are
not carried onward by the waves. The water surface
simply rises and falls as the waves pass by. Consider also
the waves that may be seen to move across a field of tall
grass or grain. Such waves are
produced by the bending and
rising of the stalks as the wind
passes over them. Again, waves
may be produced in a rope fastened at one end, by
suddenly moving the other end up and down. These
waves move to the end of the rope where they are
reflected and return. The three types of waves just mentioned
are illustrations of transverse waves, the ideal case
being that in which the particles move at right angles to
the path or course of the wave. Such waves are therefore
called transverse waves.
 Fig. 316.—Water waves.
Fig. 316.—Water waves.
323. Longitudinal waves.—Another kind of wave is
found in bodies that are elastic and compressible and have
inertia, such as gases and
coiled wire springs. Such
waves may be studied by
considering a wire spring
as the medium through which the waves pass. (See
Fig. 318.)
 Fig. 317.—The compression wave
travels through the spring.
Fig. 317.—The compression wave
travels through the spring.
If the end of the wire spring shown in Fig. 317 is struck
the first few turns of the spring will be compressed. Since
the spring possesses elasticity, the turns will move forward
a little and compress those ahead, these will press the
next in turn and so on. Thus a compression wave will
move to the end of the spring, where it will be reflected
and return. Consider the turns of the spring as they[Pg 359]
move toward the end. On account of their inertia they
will continue moving until they have separated from
each other more than at first, before returning to their
usual position. This condition of a greater separation of
the turns of the spring than usual is called a rarefaction.
It moves along the spring following the wave of compression.
The condensation and rarefaction are considered
as together forming a complete wave. Since the turns
of wire move back and forth in a direction parallel to that
in which the wave is traveling, these waves are called
longitudinal.
 Fig. 318.—Longitudinal waves (1) in a spring, (2) in air, and (3) graphic
representation showing wave length, condensations, and rarefactions.
Fig. 318.—Longitudinal waves (1) in a spring, (2) in air, and (3) graphic
representation showing wave length, condensations, and rarefactions.
324. The transmission of a sound by the air may be
understood by comparing it with the process by which a
wave is transmitted by a wire spring. Consider a light
spring (Fig. 318, 1) attached at the end of a vibrating
tuning fork, K, and also to a diaphragm, D. Each
vibration of the fork will first compress and then separate
the coils of the spring. These impulses will be transmitted
by the spring as described in Art. 315, and cause the
diaphragm to vibrate at the same rate as the tuning fork.
The diaphragm will then give out a sound similar to that
of the tuning fork. Suppose that the spring is replaced
by air, and the diaphragm, by the ear of a person, E, (Fig.[Pg 360]
318, 2.) when the prong of the fork moves toward the
ear it starts a compression and when it moves back a
rarefaction. The fork continues vibrating and these
impulses move onward like those in the spring at a speed
of about 1120 ft. in a second. They strike the diaphragm
of the ear causing it to move back and forth or to
vibrate at the same rate as the tuning fork, just as in the
case of the diaphragm attached to the spring.
325. Graphic Representation of Sound waves.—It is
frequently desirable to represent sound waves graphically.
The usual method is to use a curve like that in (Fig. 318, 3).
This curve is considered as representing a train of waves
moving in the same direction as those in Fig. 318 1 and 2,
and also having the same length. The part of the wave
A-B represents a condensation of the sound wave and the
part B-C represents a rarefaction. A complete wave
consisting of a condensation and a rarefaction is represented
by that portion of the curve A-C. The portion
of the curve B-D also represents a full wave length as the
latter is defined as the distance between two corresponding
parts of the adjacent waves. The curve, Fig. (318, 3) represents
not only the wave length, but also the height of the
wave or the amount of movement of the particles along the
wave. This is called the amplitude and is indicated by
the distance A-b. Since the loudness or intensity of a
sound is found to depend upon the amount of movement of
the particles along the wave, the amplitude of the curve is
used to indicate the loudness of the sound represented.
All of the characteristics of a sound wave may be graphically
represented by curves. Such curves will be used
frequently as an aid in explaining the phenomena of
wave motion both in sound and in light.
326. Reflections of Sound.—It is found that a wave
moving along a wire spring is reflected when it reaches the[Pg 361]
end and returns along the spring. Similarly a sound wave
in air is reflected upon striking the surface of a body.
If the wave strikes perpendicularly it returns along the
line from which it comes, if, however, it strikes at some
other angle it does not return along the same line, but as in
other cases of reflected motion, the direction of the reflected
wave is described by the Law of Reflected Motion
as follows: The angle of reflection is always equal to the
angle of incidence. This law is illustrated in Fig. 319.
Suppose that a series of waves coming from a source of
sound move from H to O. After striking the surface IJ
the waves are reflected and move toward L along the
line OL. Let PO be perpendicular to the surface IJ at O.
Then HOP is the angle of incidence and LOP is the angle
of reflection. By the law of reflected motion these angles
are equal. In an ordinary room when a person speaks
the sound waves reflected from the smooth walls reinforce
the sound waves moving directly to the hearers. It is
for this reason that it is usually easier to speak in at room
than in the open air. Other illustrations of the reinforcement
of sound by reflection are often seen. Thus an
ear trumpet (Fig. 320), uses the principle of reflection
and concentration of sound. So-called sounding boards
are sometimes placed back of speakers in large halls to
reflect sound waves to the audience.
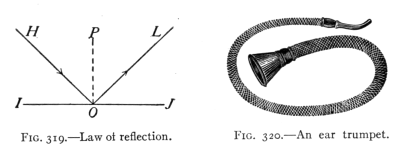 Fig. 319.—Law of reflection.
Fig. 319.—Law of reflection.
Fig. 320.—An ear trumpet.
[Pg 362]
327. Echoes.—An echo is the repetition of a sound
caused by its reflection from some distant surface such as
that of a building, cliff, clouds, trees, etc. The interval of
time between the production of a sound and the perception
of its echo is the time that the sound takes to travel from
its source to the reflecting body and back to the listener.
Experiments have shown that the sensation of a sound
persists about one-tenth of a second. Since the velocity
of sound at 20°C. is about 1130 ft. per second, during one-tenth
of a second the sound wave will travel some 113 ft. If the
reflecting surface is about 56 ft. distant a short sound will
be followed immediately by its echo as it is heard one-tenth
of a second after the original sound. The reflected
sound tends to strengthen the original one if the reflecting
surface is less than 56 ft. away. If the distance of the
reflecting surface is much more than 56 ft. however, the
reflected sound does not blend with the original one but
forms a distinct echo. The echoes in large halls especially
those with large smooth walls may very seriously affect
the clear perception of the sound. Such rooms are said
to have poor acoustic properties. Furniture, drapery,
and carpets help to deaden the echo because of diffused
reflection. The Mormon Tabernacle at Salt Lake City,
Utah, is a fine example of a building in which the reflecting
surfaces of the walls and ceiling are of such shape and
material that its acoustic properties are remarkable, a pin
dropped at one end being plainly heard at the other end
about 200 ft. away.
Important Topics
1. Waves: transverse, longitudinal; wave length, condensation,
rarefaction.
2. Wave motion: in coiled spring, in air, on water.
3. Reflection of waves: law, echoes.
[Pg 363]
Exercises
1. A hunter hears an echo in 8 seconds after firing his gun. How
far is the reflecting surface if the temperature is 20°C.?
2. How far is the reflecting surface of a building if the echo of
one's footsteps returns in 1 second at 10°C.?
3. Why is it easier to speak or sing in a room than out of doors?
4. Draw a curve that represents wave motion. Make it exactly
three full wave lengths, and state why your curve shows this
length. Indicate the parts of the curve that correspond to a
condensation and to a rarefaction.
5. How long does it take the sound of the "pin drop" to reach
a person at the farther end of the building mentioned at the
end of Art. 327?
6. An echo is heard after 6 seconds. How far away is the reflecting
surface, the temperature being 70°F.?
7. Why are outdoor band-stands generally made with the back
curving over the band?
8. A man near a forest calls to a friend. In 4 seconds the echo
comes back. How far away is he from the forest?
9. Would it be possible for us ever to hear a great explosion upon
the moon? Explain.
10. If a sunset gun was fired exactly at 6:00 P.M. at a fort, at what
time was the report heard by a man 25 miles away, if the temperature
was 10°C.?
(3) Intensity and Pitch of Sounds
 Fig. 321.—Graphic representations of (a) a noise, (b) a musical sound.
Fig. 321.—Graphic representations of (a) a noise, (b) a musical sound.
328. Musical Sounds and Noises Distinguished.—The
question is sometimes raised, what is the difference
between a noise and a musical sound? The latter
has been found to be produced by an even and regular[Pg 364]
vibration such as that of a tuning fork or of a piano string.
A noise on the other hand is characterized by sudden or
irregular vibrations such as those produced by a wagon
bumping over a stony street. These differences may be
represented graphically as in Fig. 321, (a) represents a
noise, (b) a musical tone.
 Fig. 322.—Curve b represents a tone
of greater intensity.
Fig. 322.—Curve b represents a tone
of greater intensity.
329. Characteristics of Musical Sounds.—Musical tones
differ from one another in three ways or are said to have
three characteristics, viz., intensity, pitch, and quality.
Thus two sounds may differ only in intensity or loudness,
that is, be alike in all other respects except this one, as when
a string of a piano is struck at first gently, and again
harder. The second
sound is recognized as
being louder. The difference
is due to the
greater amplitude of vibration
caused by more energy being used. Fig. 322 shows
these differences graphically. Curve b represents the tone
of greater intensity or loudness, since its amplitude of
vibration is represented as being greater.
330. Conditions Affecting the Intensity of Sound.—The
intensity of sounds is also affected by the area of the
vibrating body. This is shown by setting a tuning fork
in vibration. The area of the vibrating part being small,
the sound is heard but a short distance from the fork. If,
however, the stem of the vibrating fork is pressed against
the panel of a door or the top of a box, the sound may be
heard throughout a room. The stem of the fork has
communicated its vibrations to the wood. The vibrating
area, being greater, the sound is thereby much increased in
intensity, producing a wave of greater amplitude. The
same principle is employed in the sounding boards of
musical instruments as in the piano, violin, etc. It is a[Pg 365]
common observation that sounds decrease in loudness as
the distance from the source increases. This is due to
the increase of the surface of the spherical sound waves
spreading in all directions from the source. Careful
experiments have shown that in a uniform medium the
intensity of a sound is inversely proportional to the square of
the distance from its source. If a sound is confined so that
it cannot spread, such as the sound moving through a
speaking tube, it maintains its intensity for a considerable
distance. An ear trumpet (see Fig. 320) also applies this
principle. It is constructed so
that sound from a given area
is concentrated by reflection to
a much smaller area with a
corresponding increase in intensity.
The megaphone (Fig.
323), and the speaking trumpet start the sound waves
of the voice in one direction so that they are kept from
spreading widely, consequently by its use the voice
may be heard several times the usual distance. The intensity
of a sound is also affected by the density of the
transmitting medium. Thus a sound produced on a mountain
top is fainter and thinner than one produced in a
valley. The sound of a bell in the receiver of an air
pump becomes weaker as the air is exhausted from the
latter. Four factors thus influence the intensity of a
sound, the area of the vibrating body, its amplitude of
vibration, the distance of the source and the density of the
transmitting medium. It is well to fix in mind the precise
effect of each of these factors.
 Fig. 323.—The megaphone.
Fig. 323.—The megaphone.
331. Pitch.—The most characteristic difference between
musical sounds is that of pitch. Some sounds have a
high pitch, such as those produced by many insects and
birds. Others have a low pitch as the notes of a bass[Pg 366]
drum or the sound of thunder. How notes of different
pitch are produced may be shown by the siren (Fig. 324).
This is a disc mounted so as to be rotated on an axis.
Several rows of holes are drilled in it in concentric circles.
The number of holes in successive rows increases from
within outward. If when the siren is rapidly rotated air
is blown through a tube against a row of holes a clear
musical tone is heard. The tone is due to the succession
of pulses in the air produced by the row of holes in the
rotating disc alternately cutting off and permitting the
air blast to pass through at very short intervals. If the
blast is directed against a row of
holes nearer the circumference the
pitch is higher, if against a row
nearer the center the pitch is
lower. Or if the blast is sent
against the same row of holes the
pitch rises when the speed increases
and lowers when the speed
lessens. These facts indicate that
the pitch of a tone is due to the
number of pulses or vibrations that strike the ear each
second; also that the greater the rate of vibration, the higher
the pitch.
 Fig. 324.—A siren.
Fig. 324.—A siren.
332. The Major Scale.—If a siren is made with eight
rows of holes, it may indicate the relation between the
notes of a major scale. To accomplish this, the number
of holes in the successive rows should be 24, 27, 30, 32,
36, 40, 45, 48. If a disc so constructed is rapidly rotated at
a uniform rate, a blast of air sent against all of the rows
in succession produces the tones of the scale. These facts
indicate that the relative vibration numbers of the notes
of any major scale have the same relation as the numbers
24, 27, 30, 32, 36, 40, 45, 48.
[Pg 367]
The note called middle C is considered by physicists as
having 256 vibrations a second. This would give the
following actual vibration numbers to the remaining notes
of the major scale that begins with "Middle C" D.-288,
E.-320, F.-341.3, G.-384, A.-426.6, B.-480, C'.-512.
Musicians, however, usually make use of a scale of slightly
higher pitch. The international standard of pitch in this
country and in Europe is that in which "A" has 435 vibrations
per second. This corresponds to 261 vibrations
for middle C.
333. The Relation between Speed, Wave Length, and
Number of Vibrations per Second.—Since the notes from
the various musical instruments of an orchestra are
noticed to harmonize as well at a distance as at the place
produced, it is evident that notes of all pitches travel at
the same rate, or have the same speed. Notes of high
pitch, having a high vibration rate produce more waves in a
second than notes of low pitch, consequently the former
are shorter than the latter. The following formula gives
the relation between the speed (v), wave length (l),
and number of vibrations per sec. (n):
v = l × n, or l = v/n
that is, the speed of a sound wave is equal to the number
of vibrations per second times the wave length, or the wave
length is equal to the speed divided by the number of vibrations
per second. This formula may also be employed to
find the number of vibrations when the wave length and
speed are given.
Important Topics
1. Difference between noise and music.
2. Factors affecting intensity: area, amplitude, density, distance.
3. Pitch, major scale, relative vibration numbers.
4. Relation between speed, wave length and vibration rate.
[Pg 368]
Exercises
1. Give an illustration from your own experience of each of the
factors affecting intensity.
2. Write the relative vibration numbers of a major scale in which
do has 120 vibrations.
3. What is the wave length of the "A" of international concert
pitch at 25°C.? Compute in feet and centimeters.
4. At what temperature will sound waves in air in unison with
"Middle C" be exactly 4 ft. long?
5. Explain the use of a megaphone.
6. What tone has waves 3 ft. long at 25°C.?
7. What is the purpose of the "sounding board" of a piano?
8. Two men are distant 1000 and 3000 ft. respectively from a
fog horn. What is the relative intensity of the sounds heard by
the two men?
9. The speaking tone of the average man's voice has 160 vibrations
per second. How long are the waves produced by him
at 20°C.?
(4) Musical Scales and Resonance
334. A musical interval refers to the ratio between the
pitches[O] of two notes as indicated by the results of the siren
experiment. The simplest interval, or ratio between two
notes is the octave, C':C, or 2:1 (48:24). Other important
intervals with the corresponding ratios are the fifth, G:C,
or 3:2 (36:24); the sixth, A:C, or 5:3 (40:24); the fourth,
F:C, 4:3 (32:24); the major third, E:C, or 5:4 (30:24); and
the minor third, G:E, 6:5. The interval between any two
notes may be determined by finding the ratio between the
vibration numbers of the two notes. Thus, if one note
is produced by 600 vibrations a second and another by 400,
the interval is 3:2, or a fifth, and this would be recognized
by a musician who heard the notes sounded together or
one after the other. Below is a table of musical nomenclatures,
showing various relations between the notes of the
major scale.
[Pg 369]
Table of Musical Nomenclatures
| Name of note | C | D | E | F | G | A | B | C´ |
| Frequency in terms of "do" | n | 9/8n | 5/4n | 4/3n | 3/2n | 5/3n | 15/8n | 2n |
| Intervals | 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 |
| Name of note in vocal music | do | re | mi | fa | sol | la | ti | do |
| Treble clef. |
| [Music] |
| Bass clef. |
| [Music] |
| International pitch of treble clef | 261 | 293.6 | 326.3 | 348. | 391.5 | 435 | 489.4 | 522 |
| Scientific scale | 256 | 288 | 320 | 341.3 | 384 | 426.6 | 480 | 512 |
| Relative vibration numbers | 24 | 27 | 30 | 32 | 36 | 40 | 45 | 48 |
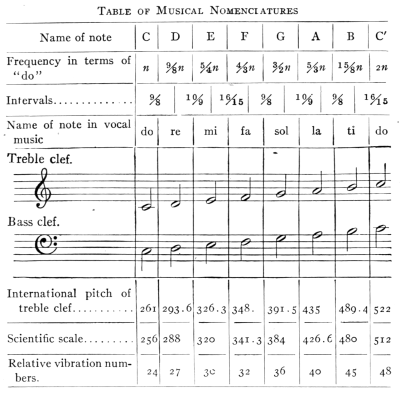
335. Major and Minor Triads.—The notes C, E, G (do,
mi, sol) form what is called a major triad. The relative
vibration numbers corresponding are 24, 30, 36. These in
simplest terms have ratios of 4:5:6. Any three other tones
with vibration ratios of 4:5:6 will also form a major triad.
If the octave of the lower tone is added, the four make a
major chord. Thus: F, A, C´ (fa, la, do), 32:40:48, or 4:5:6,
also form a major triad as do G, B, D´ (sol, ti, re), 36:45:54,
or 4:5:6. Inspection will show that these three major
triads comprise all of the tones of the major scale D´
being the octave of D. It is, therefore, said that the
major scale is based, or built, upon these three major
triads. The examples just given indicate the mathematical[Pg 370]
basis for harmony in music. Three notes having
vibration ratios of 10:12:15 are called minor triads. These
produce a less pleasing effect than those having ratios
of 4:5:6.
336. The Need for Sharps and Flats.—We have considered
the key of C. This is represented upon the piano or
organ by white keys only (Fig. 325). Now in order (a)
to give variety to instrumental selections, and (b) to accommodate
instruments to the range of the human voice,
it has been necessary to introduce other notes in musical
instruments. These are represented by the black keys
upon the piano and organ and are known as sharps and
flats. To illustrate the necessity for these additional
notes take the major scale starting with B. This will give
vibration frequencies of 240, 270, 300, 320, 360, 400, 450,
and 480. The only white keys that may be used with this
scale are E 320 and B 480 vibrations. Since the second
note on this scale requires 270 vibrations about halfway
between C and D the black key C sharp is inserted. Other
notes must be inserted between D and E (D sharp),
between F and G (F sharp), also G and A sharps.
 Fig. 325.—Section of a piano keyboard.
Fig. 325.—Section of a piano keyboard.
337. Tempered Scales.—In musical instruments with
fixed notes, such as the harp, organ, or piano, complications
were early recognized when an attempt was made to adapt
these instruments so that they could be played in all keys.
For the vibration numbers that would give a perfect major
scale starting at C are not the same as will give a perfect[Pg 371]
major scale beginning with any other key. In using the
various notes as the keynote for a major scale, 72 different
notes in the octave would be required. This would make
it more difficult for such instruments as the piano
to be played. To avoid these complications as much as
possible, it has been found necessary to abandon the simple
ratios between successive notes and to substitute another
ratio in order that the vibration ratio between any two
successive notes will be equal in every case. The differences
between semitones are abolished so that, for example,
C sharp and D flat become the same tone instead of two
different tones. Such a scale is called a tempered scale.
The tempered scale has 13 notes to the octave, with 12
equal intervals, the ratio between two successive notes
being the ¹²√2 or 1.059. That is, any vibration rate
on the tempered scale may be computed by multiplying
the vibration rate of the preceding note by 1.059. While
this is a necessary arrangement, there is some loss in perfect
harmony. It is for this reason that a quartette or chorus
of voices singing without accompaniment is often more
harmonious and satisfactory than when accompanied with
an instrument of fixed notes as the piano, since the simple
harmonious ratios may be employed when the voices are
alone. The imperfection introduced by equal temperament
tuning is illustrated by the following table:
| | C | D | E | F | G | A | B | C |
| Perfect Scale of C | 256.0 | 288.0 | 320.0 | 341.3 | 384.0 | 426.6 | 480.0 | 512.0 |
| Tempered Scale | 256.0 | 287.3 | 322.5 | 341.7 | 383.6 | 430.5 | 483.3 | 512.0 |
338. Resonance.—If two tuning forks of the same pitch
are placed near each other, and one is set vibrating, the
other will soon be found to be in vibration. This result
is said to be due to sympathetic vibration, and is an example
of resonance (Fig. 326). If water is poured into a glass[Pg 372]
tube while a vibrating tuning fork is held over its top,
when the air column has a certain length it will start
vibrating, reinforcing strongly the sound of the tuning
fork. (See Fig. 327.) This is also an example of resonance.
These and other similar facts indicate that sound waves
started by a vibrating body will cause another
body near it to start vibrating if the two have
the same rate of vibration. Most persons
will recall illustrations of this effect from
their own experience.
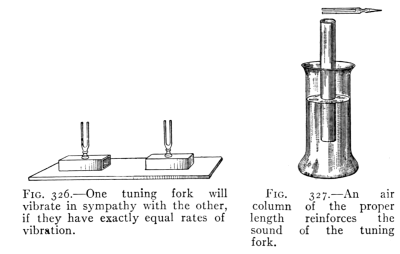 Fig. 326.—One tuning fork will
vibrate in sympathy with the other,
if they have exactly equal rates of
vibration.
Fig. 326.—One tuning fork will
vibrate in sympathy with the other,
if they have exactly equal rates of
vibration.
Fig. 327.—An air
column of the proper
length reinforces the
sound of the tuning
fork.
339. Sympathetic vibration is explained as follows:
Sound waves produce very slight motions in objects
affected by them; if the vibration of a given body is exactly
in time with the vibrations of a given sound each impulse
of the sound wave will strike the body so as to increase
the vibratory motion of the latter. This action continuing,
the body soon acquires a motion sufficient to produce
audible waves. A good illustration of sympathetic vibration
is furnished by the bell ringer, who times his pulls
upon the bell rope with the vibration rate of the swing of
the bell. In the case of the resonant air column over
which is held a vibrating tuning fork (see Fig. 328),
when the prong of the fork starts downward from 1 to
2, a condensation wave moves down to the water surface
and back just in time to join the condensation wave above
the fork as the prong begins to move from 2 to 1; also[Pg 373]
when the prong starts upward from 2 to 1, the rarefaction
produced under it moves to the bottom of the air column
and back so as to join the rarefaction above the fork as the
prong returns. While the prong is making a single
movement, up or down, it is plain that the air wave moves
twice the length of the open tube. During a complete
vibration of the fork, therefore, the sound wave moves
four times the length of the air column. In free air, the
sound progresses a wave length during a complete vibration,
hence the resonant air column
is one-fourth the length of the sound
wave to which it responds. Experiments
with tubes cf different lengths
show that the diameter of the air
column has some effect upon the
length giving best resonance.
About 25 per cent. of the diameter
of the tube must be added to the
length of the air column to make
it just one-fourth the wave length.
The sound heard in seashells and
in other hollow bodies is due to resonance. Vibrations
in the air too feeble to affect the ear are intensified by
sympathetic vibration until they can be heard. A tuning
fork is often mounted upon a box called a resonator, which
contains an air column of such dimensions that it reinforces
the sound of the fork's sympathetic vibration.
 Fig. 328.—Explanation of
resonance.
Fig. 328.—Explanation of
resonance.
Important Topics
1. Musical intervals: octave, sixth, fifth, fourth, third.
2. Major chord, 4:5:6.
3. Use of sharps and flats. Tempered scale.
4. Resonance, sympathetic vibration, explanation, examples.
[Pg 374]
Exercises
1. What is a major scale? Why is a major scale said to be built
upon three triads?
2. Why are sharps and flats necessary in music?
3. What is the tempered scale and why is it used? What instruments
need not use it? Why?
4. Mention two examples of resonance or sympathetic vibration
from your own experience out of school.
5. An air column 2 ft. long closed at one end is resonant to what
wave length? What number of vibrations will this sound have
per second at 25°C.?
6. At 24°C. What length of air column closed at one end will be
resonant to a sound having 27 vibrations a second?
7. A given note has 300 vibrations a second. What will be the
number of vibrations of its (a) octave, (b) fifth, (c) sixth, (d)
major third?
8. In the violin or guitar what takes the place of the sounding
board of the piano?
9. Can you explain why the pitch of the bell on a locomotive rises
as you rapidly approach it and falls as you recede from it?
10. Do notes of high or low pitch travel faster? Explain.
11. An "A" tuning fork on the "international" scale makes 435
vibrations per second. What is the length of the sound waves
produced?
(5) Wave Interference, Beats, Vibration of Strings
340. Interference of waves.—The possibility of two
trains of waves combining so as to produce a reduced motion
or a complete destruction of motion may be shown graphically.
Suppose two trains of waves of equal wave length
and amplitude as in Fig. 329 meet in opposite phases. That
is, the parts corresponding to the crests of A coincide with
the troughs of B, also the troughs of A with the crests
of B; when this condition obtains, the result is that shown
at C, the union of the two waves resulting in complete
destruction of motion. The more or less complete destruction
of one train of waves by another similar train is an
illustration of[Pg 375]
interference. If two sets of water waves
so unite as to entirely destroy each other the result is a
level water surface. If two trains of sound waves combine
they may so interfere that silence results. The conditions
for securing interference of sound waves may
readily be secured by using a tuning fork and a resonating
air column. If the tuning fork is set vibrating and placed
over the open end of the resonating air column (see Fig.
328), an increase in the sound through resonance may be
heard. If the fork is rotated about its axis, in some positions
no sound is heard while in other positions the sound
is strongly reinforced. Similar effects may be perceived
by holding a vibrating fork near the ear and slowly rotating
as before. In some positions interference results
while in other positions the sound is plainly heard. The
explanation of interference may be made clear by the
use of a diagram. (See Fig. 330.) Let us imagine that[Pg 376]
we are looking at the two square ends of a tuning fork.
When the fork is vibrating the two prongs approach
each other and then recede. As they approach, a
condensation is produced at 2 and rarefactions at 1
and 3. As they separate, a rarefaction is produced at 2
and condensations at 1 and 3. Now along the lines at
which the simultaneously produced rarefactions and condensations
meet there is more or less complete interference.
(See Fig. 331.) These positions have been indicated by
dotted lines extending through the ends of the prongs.
As indicated above, these positions may be easily found
by rotating a vibrating fork over a resonant air column,
or near the ear.
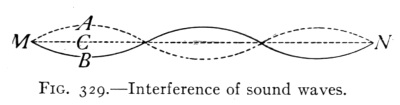 Fig. 329.—Interference of sound waves.
Fig. 329.—Interference of sound waves.
 Fig. 330.—At 2 is a condensation;
at 1 and 3 are rarefactions.
Fig. 330.—At 2 is a condensation;
at 1 and 3 are rarefactions.
Fig. 331.—The condensations
and rarefactions meet along the
dotted lines producing silence.
 Fig. 332.—Diagram illustrating the formations of beats.
Fig. 332.—Diagram illustrating the formations of beats.
341. Beats.—If two tuning forks of slightly different
pitch are set vibrating and placed over resonating air
columns or with the stem of each fork upon a sounding
board, so that the sounds may be intensified, a peculiar
pulsation of the sound may be noticed. This phenomenon
is known as beats. Its production may be easily understood
by considering a diagram (Fig. 332). Let the curve
A represent the sound wave sent out by one tuning fork
and B, that sent out by the other. C represents the effect
produced by the combination of these waves. At R the
two sound waves meet in the same phase and reinforce
each other. This results in a louder sound than either
produces alone. Now since the sounds are of slightly[Pg 377]
different pitch, one fork sends out a few more vibrations
per second than the other. The waves from the first
fork are therefore a little shorter than those from the other.
Consequently, although the two waves are at one time in
the same phase, they must soon be in opposite phases as at
I. Here interference occurs, and silence results. Immediately
the waves reinforce, producing a louder sound and
so on alternately. The resulting rise and fall of the sound
are known as beats. The number of beats per second
must, of course, be the same as the difference between the
numbers of vibrations per second of the two sounds. One
effect of beats is discord. This is especially noticeable
when the number of beats per second is between 30 and
120. Strike the two lowest notes on a piano at the same
time. The beats are very noticeable.
 Fig. 333.—Turkish
cymbals.
Fig. 333.—Turkish
cymbals.
Fig. 334.—The cornet.
342. Three Classes of Musical Instruments.—There
are three classes or groups of musical instruments, if
we consider the vibrating body that produces the sound
in each: (A) Those in which the sound is produced by a
vibrating plate or membrane, as the drum, cymbals (Fig.
333), etc.; (B) those with vibrating air columns, as the
flute, pipe organ, and cornet (Fig. 334), and (C) with
vibrating wires or strings, as the piano, violin, and guitar.
It is worth while to consider some of these carefully.[Pg 378]
We will begin with a consideration of vibrating wires
and strings, these often producing tones of rich quality.
Let us consider the strings of a piano. (If possible, look
at the strings in some instrument.) The range of the
piano is 7-1/3 octaves. Its lowest note, A4, has about 27
vibrations per second. Its highest, C4, about 4176.
This great range in vibration rate is secured by varying
the length, the tension, and the diameter of the strings.
343. The Laws of Vibrating Strings.—The relations
between the vibration rate, the length, the tension and the
diameter, of vibrating strings have been carefully studied
with an instrument called a sonometer (Fig. 335). By
this device it is found that the pitch of a vibrating string
is raised one octave when its vibrating length is reduced
to one-half. By determining the vibration rate of many
lengths, the following law has been derived:
(Law I) The rate of vibration of a string is inversely proportional
to its length.
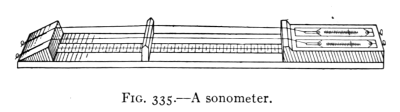 Fig. 335.—A sonometer.
Fig. 335.—A sonometer.
Careful tests upon the change of vibration rate produced
by a change of tension or pull upon the strings show that
if the pull is increased four times its vibrations rate is
doubled, and if it is increased nine times its rate is tripled,
that is: (Law II) The vibration rates of strings are directly
proportional to the square roots of their tensions.
Tests of the effects of diameter are made by taking wires
of equal length and tension and of the same material but
of different diameter. Suppose one is twice as thick as[Pg 379]
the other. This string has a tone an octave lower or vibrates
one-half as fast as the first. Therefore:
(Law III) The vibration rates of strings are inversely proportional
to the diameters. These laws may be expressed
by a formula n ∝√(t)/dl.
The vibration of a string is rarely a simple matter. It
usually vibrates in parts at the same time that it is vibrating
as a whole. The tone produced by a string vibrating
as a whole is called its fundamental. The vibrating parts
of a string are called loops or segments (see Fig. 336), while
the points of least or no vibration are nodes. Segments
are often called antinodes.
 Fig. 336.—A string yielding its fundamental and its first overtone.
Fig. 336.—A string yielding its fundamental and its first overtone.
344. Overtones.—The quality of the tone produced by a
vibrating string is affected by its vibration in parts when
it is also vibrating as a whole. (See Fig. 336.) The tones
produced by the vibration in parts are called overtones or
partial tones. The presence of these overtones may
often be detected by the sympathetic vibration of other
wires near-by. What is called the first overtone is produced
by a string vibrating in two parts, the second overtone
by a string vibrating in three parts, the third overtone
by its vibration in four parts and so on. In any overtone,
the number of the parts or vibrating segments of
the string is one more than the number of the overtone.
For example, gently press down the key of middle C of a
piano. This will leave the string free to vibrate. Now
strongly strike the C an octave lower and then remove
the finger from this key. The middle C string will be[Pg 380]
heard giving its tone. In like manner try E1 and G1, with
C. This experiment shows that the sound of the C string
contains these tones as overtones. It also illustrates
sympathetic vibration.
Important Topics
1. Interference, beats, production, effects.
2. Vibration of strings, three laws.
3. Three classes of musical instruments.
4. Fundamental and overtones, nodes, segments, how produced?
Results.
Exercises
1. What different means are employed to produce variation of
the pitch of piano strings? For violin strings?
2. How many beats per second will be produced by two tuning
forks having 512 and 509 vibrations per second respectively?
3. A wire 180 cm. long produces middle C. Show by a diagram,
using numbers, where a bridge would have to be placed to cause
the string to emit each tone of the major scale.
4. How can a violinist play a tune on a single string?
5. What are the frequencies of the first 5 overtones of a string
whose fundamental gives 256 vibrations per second?
6. One person takes 112 steps a minute and another 116. How
many times a minute will the two walkers be in step? How
many times a minute will one be advancing the left foot just
when the other advances the right?
7. Why is it necessary to have a standard pitch?
8. How can the pitch of the sounds given by a phonograph be
lowered?
9. How many beats per second will occur when two tuning forks
having frequencies of 512 and 515 respectively, are sounded
together?
10. Which wires of a piano give the highest pitch? Why?
(6) Tone Quality, Vibrating Air Columns, Plates
345. Quality.—The reason for the differences in tone
quality between notes of the same pitch and intensity as[Pg 381]
produced, e.g., by a violin and a piano, was long a matter of
conjecture. Helmholtz, a German physicist (see p. 397)
first definitely proved that tone quality is due to the various
overtones present along with the fundamental and their
relative intensities. If a tuning fork is first set vibrating by
drawing a bow across it and then
by striking it with a hard object,
a difference in the quality of the
tones produced is noticeable. It
is thus evident that the manner
of setting a body in vibration
affects the overtones produced
and thus the quality. Piano
strings are struck by felt hammers
at a point about one-seventh
of the length of the
string from one end. This point
has been selected by experiment,
it having been found to yield the
best combination of overtones as shown by the quality
of the tone resulting.
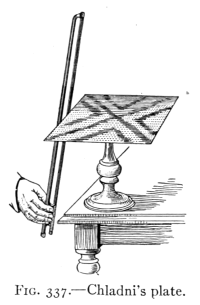 Fig. 337.—Chladni's plate.
Fig. 337.—Chladni's plate.
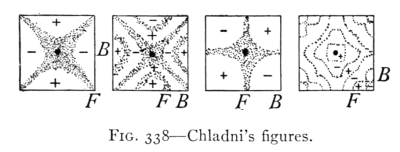 Fig. 338.—Chladni's figures.
Fig. 338.—Chladni's figures.
346. Chladni's Plate.—The fact that vibrating bodies
are capable of many modes of vibration is well illustrated
by what is known as Chladni's plate. This consists of a
circular or square sheet of brass attached to a stand at its
center so as to be held horizontally. (See Fig. 337.) Fine
sand is sprinkled over its surface and the disc is set vibrating[Pg 382]
by drawing a violin bow across its edge. The mode of
vibration of the disc is indicated by the sand accumulating
along the lines of least vibration, called nodal lines.
A variety of nodal lines each accompanied by its characteristic
tone may be obtained by changing the position
of the bow and by touching the fingers at different
points at the edge of the disc. They are known as
Chladni's figures. (See Fig. 338.)
 Fig. 339.—Manometric flame apparatus.
Fig. 339.—Manometric flame apparatus.
347. Manometric Flames.—The actual presence of
overtones along with the fundamental may be made visible
by the manometric flame apparatus. This consists of a
wooden box, C, mounted upon a stand. (See Fig. 339.)
The box is divided vertically by a flexible partition or
diaphragm. Two outlets are provided on one side of
the partition, one, C, leads to a gas pipe, the other is a
glass tube, D. On the other side of the partition a tube,
E, leads to a mouthpiece. A mirror, M, is mounted so
as to be rotated upon a vertical axis in front of F and near
it. Gas is now turned on and lighted at F. The sound
of the voice produced at the mouthpiece sends sound
waves through the tube and against the diaphragm which
vibrates back and forth as the sound waves strike it.[Pg 383]
This action affects the flame which rises and falls. If
now the mirror is rotated, the image of the flame seen in
the mirror rises and falls, showing not only the fundamental
or principal vibrations but also the overtones. If
the different vowel sounds are uttered in succession in the
mouthpiece, each is found to be accompanied by its
characteristic wave form (Fig. 340). In some, the fundamental
is strongly prominent,
while in others, the overtones
produce marked modifications.
Other devices have been invented
which make possible the accurate
analysis of sounds into their component
vibrations, while still
others unite simple tones to produce
any complex tone desired.
348. The Phonograph.—The
graphophone or phonograph provides
a mechanism for cutting
upon a disc or cylinder a groove
that reproduces, in the varying
form or depth of the tracing,
every peculiarity of the sound waves affecting it. The
reproducer consists of a sensitive diaphragm to which is
attached a needle. The disc or cylinder is rotated under
the reproducing needle. The irregularities of the bottom
of the tracing cause corresponding movements of the
needle and the attached diaphragm, which start waves
that reproduce the sounds that previously affected the
recorder. The construction of the phonograph has reached
such perfection that very accurate reproduction of a great
variety of sounds is secured.
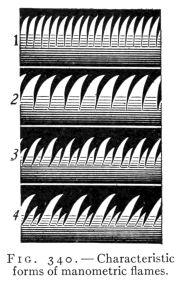 Fig. 340.—Characteristic
forms of manometric flames.
Fig. 340.—Characteristic
forms of manometric flames.
349. Wind Instruments.—In many musical instruments
as the cornet, pipe-organ, flute, etc., and also in whistles,[Pg 384]
the vibrating body that serves as a source of sound is a
column of air, usually enclosed in a tube. Unlike vibrating
strings, this vibrating source of sound changes but little
in tension or density, hence changes in the pitch of air
columns is secured by changing their length. The law
being similar to that with strings, the vibration rates of
air columns are inversely proportional to their lengths.
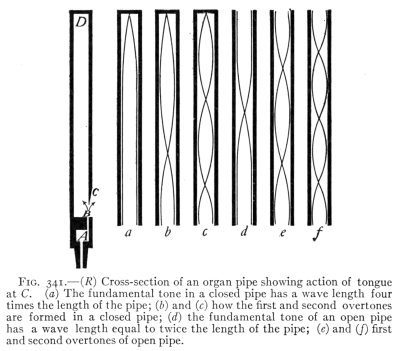 Fig. 341.—(R) Cross-section of an organ pipe showing action of tongue
at C. (a) The fundamental tone in a closed pipe has a wave length four
times the length of the pipe; (b) and (c) how the first and second overtones
are formed in a closed pipe; (d) the fundamental tone of an open pipe
has a wave length equal to twice the length of the pipe; (e) and (f) first
and second overtones of open pipe.
Fig. 341.—(R) Cross-section of an organ pipe showing action of tongue
at C. (a) The fundamental tone in a closed pipe has a wave length four
times the length of the pipe; (b) and (c) how the first and second overtones
are formed in a closed pipe; (d) the fundamental tone of an open pipe
has a wave length equal to twice the length of the pipe; (e) and (f) first
and second overtones of open pipe.
If an open organ pipe be sounded by blowing gently
through it, a tone of definite pitch is heard. Now if one
end is closed, on being sounded again the pitch is found
to be an octave lower. Therefore, the pitch of a closed pipe
is an octave lower than that of an open one of the same length.
350. Nodes in Organ Pipes.—Fig. 341, R represents a
cross-section of a wooden organ pipe. Air is blown through
A, and strikes against a thin tongue of wood C. This[Pg 385]
starts the jet of air vibrating thus setting the column of
air in vibration so that the sound is kept up as long as air
is blown through A. To understand the mode of vibration
of the air column a study of the curve that represents
wave motion (Fig. 342) is helpful Let AB represent such
a curve, in this 2, 4 and 6 represent nodes or points of
least vibration, while 1, 3 and
5 are antinodes or places of
greatest motion. A full wave
length extends from 1-5, or
2-6. Now in the open organ
pipe (Fig. 341d), the end of
the air column d is a place of great vibration or is an antinode.
At the other end also occurs another place of
great vibration or an antinode; between these two antinodes
must be a place of least vibration or a node. The
open air column therefore extends from antinode to antinode
(or from 1-3) or is one-half a wave length. The
closed air column (Fig. 341a) extends from a place of great
vibration at a to a place of no vibration at the closed end.
The distance from an antinode to a node is that from 1-2
on the curve and is one-fourth a wave length.
 Fig. 342.—Graphic representation
of sound waves.
Fig. 342.—Graphic representation
of sound waves.
 Fig. 343.—A clarinet.
Fig. 343.—A clarinet.
When a pipe is blown strongly it yields overtones.
The bugle is a musical instrument in which notes of different
pitch are produced by differences in blowing. (See
Fig. 341.) (d), (e), (f). In playing the cornet different
pitches are produced by differences in blowing, and by
valves which change the length of the vibrating air column.
(See Fig. 334.) The clarinet has a mouthpiece containing[Pg 386]
a reed similar to that made by cutting a tongue on a
straw or quill. The length of the vibrating air column
in the clarinet is changed by opening holes in the sides of
the tube. (See Fig. 343.)
351. How we Hear.—Our hearing apparatus is arranged
in three parts. (See Fig. 344.) The external ear
leads to the tympanum. The middle ear contains three
bones that convey the vibrations
of the tympanum to the internal
ear. The latter is filled with a
liquid which conveys the vibrations
to a part having a coiled
shell-like structure called the Cochlea.
Stretched across within the
cochlea are some 3000 fibers or
strings. It is believed that each is
sensitive to a particular vibration
rate and that each is also attached to a nerve fiber. The
sound waves of the air transmitted by the tympanum, the
ear bones and the liquid of the internal ear start sympathetic
vibrations in the strings of the cochlea which affect the
auditory nerve and we hear. The highest tones perceptible
by the human ear are produced by from 24,000 to
40,000 vibrations per second. The average person cannot
hear sounds produced by more than about 28,000 vibrations.
The usual range of hearing is about 11 octaves.
The tones produced by higher vibrations than about 4100
per second are shrill and displeasing. In music the range
is 7-1/3 octaves, the lowest tone being produced by 27.5
vibrations, the highest by about 4100 per second.
 Fig. 344.—The human ear.
Fig. 344.—The human ear.
The tones produced by men are lower than those of
women and boys. In men the vocal cords are about 18
mm. long; in women they are 12 mm. long.
The compass of the human voice is about two octaves,[Pg 387]
although some noted singers have a range of two and one-half
octaves. In ordinary conversation the wave length
of sounds produced by a man's voice is from 8 to 12 ft.
and that of a woman's voice is from 2 to 4 ft.
Important Topics
1. Tone quality. Fundamental and overtones. Chladni's plate.
2. Manometric flame apparatus.
3. Phonograph recorder and reproducer.
4. Air columns and wind instruments.
5. How we hear.
Exercises
1. What determines the pitch of the note of a toy whistle?
2. The lowest note of the organ has a wave length of about 64 ft.
What is the length of a closed pipe giving this note? Of an
open pipe?
3. What is the first overtone of C? What are the second and third
overtones? Give vibration numbers and pitch names or letters.
4. Why is the music of a band just as harmonious at a distance of
400 ft. as at 100 ft.?
5. A resonant air column 60 cm. long closed at one end will respond
to what rate of vibration at 10°C.?
6. Can you find out how the valves on a cornet operate to change
the pitch of the tone?
7. How is the trombone operated to produce tones of different
pitch?
8. The lowest note on an organ has a wave length of about 64 ft.
What must be the length of a closed pipe giving this note?
9. What is the approximate length of an open organ pipe which
sends out waves 4 ft. long?
Review Outline: Sound
Sound—definition, source, medium, speed, nature.
Waves—longitudinal, transverse, illustrations.
| Characteristics of Musical Sounds: | intensity—area, amplitude, density, distance. |
| pitch—scales; major, tempered, triads, N = V/L quality—fundamental and overtones. |
Sympathetic Vibrations—resonance, interference, beats, discord.
Musical Instruments—string, air column, membrane or plate.
Laws of; (a) vibrating strings (3), (b) vibrating air columns (2).
[Pg 388]
LIGHT
(1) Light, Its Rectilinear Propagation, Shadows
352. A Comparison of Sound and Light.—Light from
the standpoint of physics is considered much as is sound,
as a mode of motion; one affecting the ear, the other producing
the result called vision. There are other differences
also worth considering. (a) While sound travels
as vibrations of some material medium, light travels only
as vibrations of the ether; solids, liquids, and gases act so
as to hinder rather than to assist in its movement. That
is, light travels best in a vacuum or in a space devoid of
ordinary matter. (b) The speed of light is so great that
at ordinary distances on the earth its motion is practically
instantaneous. Experiments have shown that its speed
is about 186,000 miles to 300,000 kilometers a second.
353. Luminous and Illuminated Bodies.—If we consider
the objects within a room, some of them, as books and
furniture, would be invisible if all light from external
sources were excluded. On the other hand, some other
objects, such as a lighted lamp, a burning coal, or a red
hot iron, would be seen if no outside light were present.
Such bodies are said to be luminous. Most luminous
bodies are hot and become non-luminous on cooling.
There are, however, some bodies that are luminous at
ordinary room temperatures, as the firefly and some phosphorescent
paints. When light emitted by a luminous
body strikes an object, a portion of it is always reflected.[Pg 389]
It is this reflected light that makes the illuminated object
visible. If the object is a sheet of glass, some of the light
is transmitted. If a substance is so clear that objects can
be seen through it, the substance is transparent, but if objects
cannot be seen through it, the substance is said to be
translucent. Objects transmitting no light are opaque.
Some of the light falling upon a body is neither reflected
nor transmitted, but is absorbed and tends to warm
the body. The light falling upon
a body is therefore either reflected,
transmitted, or absorbed. Thus Fig.
345 represents light coming from
S to a piece of glass GL. A portion
of the light represented by R
is reflected. Another part A is
absorbed and disappears, while
still another part T is transmitted
and passes on.
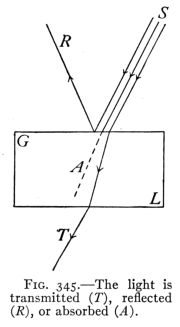 Fig. 345.—The light is
transmitted (T), reflected
(R), or absorbed (A).
Fig. 345.—The light is
transmitted (T), reflected
(R), or absorbed (A).
There is no sharply drawn line
between transparent and opaque
bodies. Very thin sheets of gold
transmit a greenish light, and experiments
have shown that substances
as transparent as clear
water absorb enough light so that at considerable depths
in an ocean or lake little or no light is ever found. All
light whether from luminous bodies or reflected from non-luminous
objects shows certain properties which will now
be considered.
354. The Rectilinear Propagation of Light.—If a beam
of light passes through a hole in a window shade into a
darkened room, it is seen to follow a perfectly straight
course. If a person while coughing holds a book before
the face, the sound passes around the book and is heard[Pg 390]
at any point in the room while the face is hidden by the
book. In other words, light ordinarily does not pass
around corners as sound does, but travels in straight lines.
This fact is made use of when one aims a gun or merely
looks at an object. So well established in our minds is the
idea that an object is in the direction from which we see the
light coming to us from it, that we are sometimes deceived
as to the real position of an object, when the course of the
light from it has been changed by a mirror or some other
reflecting surface. Many illusions are produced in this
way, of which the mirage of the desert is one example.
(See Art. 381.)
 Fig. 346.—Shadow from a small source of light.
Fig. 346.—Shadow from a small source of light.
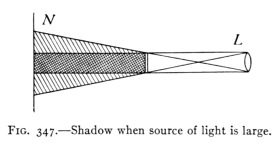 Fig. 347.—Shadow when source of light is large.
Fig. 347.—Shadow when source of light is large.
355. Shadows.—A shadow is the space from which light
is cut off by an opaque body. Thus if a book (see Fig. 346)
is held between a screen, N, and a small source of light, L,
a shadow is produced which extends from the book to the
screen. Notice that the shadow is a space and not an
area. If a large gas flame (see Fig. 347) is used as the
source of light, the shadow of the book is no longer clear[Pg 391]
cut at the edges as before, but has a darker central part
with a lighter fringe of partial shadow at the edges. The
dark portion within the shadow has all the light excluded
from it and is called the umbra. The lighter portion of
the shadow at the edges has only a part of the light from
the flame cut off. This portion is called the penumbra.
when one stands in sunlight his shadow extends from his
body to the ground or object on which the shadow falls.
At night we are in the earth's shadow, which extends out
into space beyond the earth.
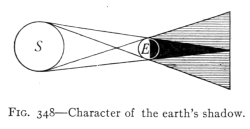 Fig. 348.—Character of the earth's shadow.
Fig. 348.—Character of the earth's shadow.
356. Eclipses.—Since the sun is a very large object the
shadow cast by the earth contains both umbra and penumbra.
(See Fig. 348.) When the moon passes into the
shadow of the earth, there is said to be an eclipse of the
moon, while if the moon's shadow falls upon the earth,
the portion of the earth cut off from the sun's light has
an eclipse of the sun.
357. Images by Small Apertures.—The straight line
movement of light makes possible the pin-hole camera,
by which satisfactory photographs have been made.
The action of this device may be illustrated by placing
a luminous body, a lighted candle, an incandescent lamp,
or a gas flame, in front of a piece of cardboard, S, which
has a small opening in it. Light from the object (see Fig.
349) falls upon a screen, S2, so as to produce an inverted
image. Other applications of this principle will be given
later.
[Pg 392]
In Fig. 349 let PQ represent a gas flame, then light from point
P at the top of the flame will pass in a straight line through the opening
or aperture of the cardboard and strike at P2 at the bottom of
the illuminated spot upon the screen. Light from Q passing in
straight lines through the aperture will strike at Q2 at the top of
the lighted space. This spot of light will have the same outlines
as the luminous body PQ and being formed as just described will
be inverted.
 Fig. 349.—Image formed by a small aperture is inverted.
Fig. 349.—Image formed by a small aperture is inverted.
This spot of light, resembling in its outlines the flame,
is called an image. An image is defined as an optical
counterpart of an object. Images are formed in a variety
of devices, such as apertures, mirrors, and lenses. The pin-hole
camera is simply a light-tight box with a small aperture
in one side. Light passing through this aperture
forms an image upon the opposite side of the interior of
the box, of whatever object is in front of the camera.
Light entering a room through a large aperture such as a
window produces a multitude of overlapping images which
blend to form a somewhat evenly illuminated surface.
Important Topics
1. Light contrasted with sound (three differences).
2. Bodies: transparent, translucent, opaque.
3. Light: reflected, transmitted, absorbed.
[Pg 393]
4. Light travels in straight lines, evidence, shadows, umbra,
penumbra.
5. Formation of images by small apertures.
Exercises
1. Consider the circumference of the earth as 25,000 miles. How
many times would the speed of light cover this distance in a
second?
2. How soon after any great disturbance takes place on the sun,
93,000,000 miles distant, can it be seen upon the earth?
3. Construct a diagram of the moon's shadow. How much of the
sun can one see when in the moon's umbra? When in its
penumbra? Have you ever been in either? When? Have
you ever been in the earth's umbra? In its penumbra?
4. Explain, using a diagram, the formation of an inverted image by
a small aperture.
5. If the sun is 45 degrees above the horizon, what is the height
of a pole casting a shadow 60 ft. long?
6. If a shadow 6 ft. long is cast by a 10-ft. pole standing vertically
upon a walk, how tall is the tree whose shadow is 42 ft. long,
both measurements being made at the same time?
7. Why are the shadows caused by an electric arc lamp so sharply
defined?
8. Why should schoolroom windows be all on one side and reach
to the ceiling?
9. What is the relation between the size of an image and its distance
from the aperture forming it? Can you prove this by
geometry?
10. What are silhouettes and how are they produced?
(2) Photometry and the Law of Reflection
358. Photometry.—It is desirable at times to compare
the intensities of illumination produced by light from
different sources. This is done to determine the relative
cost or effectiveness of various illuminants such as candles,
kerosene and gas lamps, and electric lights The process
of determining the relative intensity of lights or lamps is
called photometry. (Photos = light.)
[Pg 394]
The unit for measuring the power of light is called a
candle power. It is the light produced by a sperm candle
burning 120 grains per hour. An ordinary gas light burns
5 or more cubic feet of gas per hour and yields from 15
to 25 candle power. A Welsbach gas lamp, consuming
3 cu. ft. per hour, produces 50 to 100 candle power.
Instead of using candles, for practical photometry,
incandescent lamps standardized by the Bureau of Standards
are used for testing or calibration purposes.
It is necessary to distinguish between the intensity of a
luminous body, i.e., as a source of light, and the intensity
of illumination upon some surface produced by a light. It
is considered that two sources of light are of equal intensity
if they produce equal illumination at equal distances.
359. Law of Intensity of Light.—A device for measuring
the candle power of a light is called a photometer. Its use
is based upon the law of intensity of light. The intensity of
illumination of a surface is inversely proportional to the
square of its distance from the source of light. This relation
is similar to that existing between the intensity of a sound
and the distance from its source. The following device
illustrates the truth of this law in a simple manner.
 Fig. 350.—The light spreads over four times the area at twice the
distance.
Fig. 350.—The light spreads over four times the area at twice the
distance.
Cut a hole 1 in. square in a large sheet of cardboard (K) and place
the card in an upright position 1 meter from an arc light or other
point source of light (L). Now rule inch squares upon another card
(M) and place it parallel to the first card and 2 meters from it.
(See Fig. 350.) The light that passed through the hole of 1 sq. in.[Pg 395]
at a distance of 1 meter is spread over 4 sq. in. at a distance of 2
meters. Therefore, the intensity of illumination on each square inch
of M is one-fourth that upon the surface of K. If M is placed 3
meters from the light, 9 sq. in. are illuminated, or the intensity is
one-ninth that at 1 meter distance.
 Fig. 351.—The Bunsen photometer.
Fig. 351.—The Bunsen photometer.
These relations show that the intensity of illumination
is inversely proportional to the square of the distance from
the source of light. An application of the law of intensity
is made in using a simple (Bunsen) photometer. This
consists of a card containing a spot soaked with oil or
melted wax. (See Fig. 351.) The lights whose intensities
are to be compared are placed upon opposite sides of the
card. The card is then adjusted so that the spot appears
the same on both sides. The illumination is now equal on
both sides of the card and the candle powers of the two lights
are proportional to the squares of their distances from the
card. The simple device just described will give approximate
results only. For accurate results more elaborate
apparatus is required.
360. Measurement of the Intensity of Illumination.—A
standard candle (Art. 358) produces when lighted 1
candle power. The illumination caused by this upon a
surface 1 ft. away and at right angles to the light rays[Pg 396]
is called a foot-candle. It is the unit of intensity of
illumination. A 4-candle-power lamp, at a distance of
1 ft., produces 4 foot-candles. A 16-candle-power lamp
at a distance of 2 ft. also produces 4 foot-candles—(16 ÷ 22).
The intensity of illumination required for a good light
for seeing varies with the conditions. Thus, for stage and
store lighting about 4 foot-candles are needed, while homes
and churches may require but 1 foot-candle.
Too great an intensity of illumination is as harmful as
not enough. Exposed lights having an intensity of more
than 5 candle power per square inch are often a cause
of eye trouble. Such lights should be protected by frosted
globes.
A pleasing form of lighting for large halls and public
buildings is the indirect system. In this, the lamps are
hidden by reflectors which throw the light upon the ceiling
from which it is diffused over the room. This form of
lighting is more expensive than other systems since but
a part of the light is reflected. Its cost therefore is an
important factor when considering its use.
361. The Reflection of Light.—The
light reflected from the surfaces
of bodies about us gives us information
concerning our surroundings.
A knowledge of the behavior of
light undergoing reflection is not
usually gained from ordinary observation.
The law of reflection of light
may be shown, however, by an experiment.
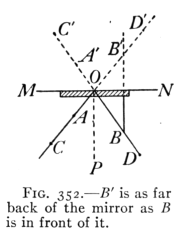 Fig. 352.—B´ is as far
back of the mirror as B
is in front of it.
Fig. 352.—B´ is as far
back of the mirror as B
is in front of it.
 Christian Huygens
Christian Huygens
(Popular Science Monthly)
Christian Huygens (1629-1695).
Dutch physicist; invented the pendulum
clock (1656); developed the
wave theory of light; discovered
polarization of light (1690).
 H. V. Helmholtz
H. V. Helmholtz
"By Permission of the Berlin Photographic
Co., New York."
Hermann von Helmholtz (1821-1894)
Germany. Established the
doctrine of conservation of energy;
made many discoveries in sound;
invented the ophthalmoscope;
established the physical basis of
tone quality.
[Pg 397]
[Pg 398]
[Pg 399]
A plane mirror, M, is held in a vertical position resting upon a
sheet of paper. (See Fig. 352.) Pins are set upright in the paper
at A and B. On placing the eye along the line AC and looking
toward the mirror an image of B may be seen in the mirror due to
the light reflected from its surface. Pins C and D are now set in
the paper so that when one looks along the line BD toward the
mirror one may see all four pins apparently in one line. This
indicates that the light from A and C passing along CA toward
O is reflected back along the light CBD. By means of a ruler,
draw lines through BD and AC till they intersect at O. Also draw
PO perpendicular to the mirror at O.
Then the angles AOP and BOP will be found equal.
These are called the angles of incidence and reflection
respectively. The law of reflection is therefore stated:
The angle of reflection is equal to the angle of incidence.
These angles are in the same plane, that of the paper.
This law applies in all cases of reflection of light. It is
similar to the law of reflection of sound (Art. 326.)
Important Topics
1. Photometry, law of intensity, candle power, foot-candle.
2. Intensity of illumination.
3. Reflected light and law of reflection.
Exercises
1. Both sides of a card are equally illuminated when two lights are
on opposite sides of it and 10 and 30 cm. respectively from it.
what are their relative intensities?
2. What are the relative intensities of illumination from a gas light
upon a book 6 ft. and 2 ft. respectively from the light?
3. Which is more expensive per candle power? How many times
as expensive? A 50-watt 16-candle-power incandescent lamp
at 10 cents per kilowatt-hour or a 100-candle-power Welsbach
light burning 5 cu. ft. of gas per hour at 80 cents per 1000 cu. ft.
of gas. (Find cost of each per hour, and then the cost of 1
candle power hour for each.)
4. Why are not ordinary shadows perfectly dark?
5. At what distance will a 16-candle-power lamp give the same
illumination as a single candle at 10 in.?
6. If the sun is at an elevation of 30 degrees what is the angle of
incidence at which it strikes the surface of water? What is the
angle between the incident and the reflected rays?
[Pg 400]
7. What is the difference between the phenomena of reflection of
light from a white sheet of writing paper and from a piece of
clear window glass?
8. A horizontal ray of light, traveling due east, strikes a vertical
mirror so that after reflection it is traveling due north. If the
mirror be now turned 10 degrees about a vertical axis, the north
edge moving east, what will be the direction of the reflected ray?
9. The necessary illumination for reading is about 2 foot-candles.
How far away may an 8-candle-power lamp be placed?
10. What is the illumination in foot-candles upon a surface 20 ft.
from an arc lamp having an intensity of 1000 candle power?
11. How far from a 100-candle-power Welsbach light would the
illumination be 2 foot-candles?
(3) Mirrors and the Formation of Images
 Fig. 353.—Reflection of light, (a) diffused, (b) regular.
Fig. 353.—Reflection of light, (a) diffused, (b) regular.
362. Mirrors.—The many purposes served by mirrors
in our every-day life has made their use familiar to everyone.
Yet without study and experiment few understand
their properties and action. Any smooth surface may
serve as a mirror, as that of glass, water, polished wood,
or metal. Most objects, unlike mirrors, have irregular
surfaces; these scatter or diffuse the light that falls upon
them. (See Fig. 353a.) This is called diffused or irregular
reflection. The reflection of light from the smooth surface
of a mirror is regular. (See Fig. 353b.) In every case of
reflected light, however, the angle of reflection equals the
angle of incidence, diffusion being due to the irregularity[Pg 401]
of the surface. It is by means of the light "diffused"
from the surface of illuminated bodies, such as plants,
animals, food, and manufactured articles, that we "see"
the various objects about us, and it is this light that
enables us to judge of their distance, size, form, color, etc.
The moon is seen by the sunlight reflected from its surface.
Moonlight is therefore sunlight diffused by reflection.
The new moon is that phase or condition of the moon when
only a narrow strip of the moon's illuminated surface
is turned toward the earth. At the time of the full
moon the whole illuminated surface is seen.
363. Images Formed by a Plane Mirror.—The most
common use of mirrors is in the formation of images. The
way in which images are formed
by a plane mirror may be illustrated
by diagrams. Thus in
Fig. 354, let L represent a
luminous body and E and E´
two positions of the observer's
eye. Take any line or ray as
LO along which the light from
L strikes the mirror O-O´. It
will be reflected so that angle
LOP equals angle POE. Similarly
with any other ray, as
LO´, the reflected ray O´E´ has
a direction such as that angle L´O´E´ equals angle P´O´E´.
Any other rays will be reflected in a similar manner,
each of the reflected rays appearing to the eye to come
from a point L´ behind the mirror.
 Fig. 354.—The virtual image
of a fixed object as seen in a
plane mirror, has the same
location from every position of
the observer's eye.
Fig. 354.—The virtual image
of a fixed object as seen in a
plane mirror, has the same
location from every position of
the observer's eye.
364. Light Waves and Wave Diagrams.—Just as a
stick continually moved at the surface of a body of water
sets up a series of waves spreading in all directions, so one
may imagine a train of waves sent out by a luminous[Pg 402]
body L (as in Fig. 355) to the mirror MN. These waves
will be reflected from the mirror as if the source of light
were at L´. It is much simpler and more convenient to
locate the position of the image of a point by the use of
lines or "rays" (as in Fig. 354) than by the wave diagram
(as in Fig. 355). In all ray diagrams, however, it should be
kept in mind that the so-called ray is a symbol used to
represent the direction taken by a part of a light wave.
Thus in Fig. 354, the light from L moving toward O is
reflected to E along the line OE, the heavy lines representing
rays.
 Fig. 355.—Wave diagram of image formed in a plane mirror.
Fig. 355.—Wave diagram of image formed in a plane mirror.
365. To locate the image of an object formed by a
plane mirror requires simply an application of the law
of reflection. Thus in Fig. 356 let AB represent an object
and MN a plane mirror. Let AA´ be a ray from A striking
the mirror perpendicularly. It is therefore reflected back
along the same line toward A. Let AO represent any other
ray from A. It will be reflected along OE so that angle
r equals i. The intersection of AC and OE at A´ behind
the mirror locates the image of the point A, as seen by
reflection from the mirror. The triangles ACO and
A´CO may be proved equal by geometry. Therefore[Pg 403]
A´C equals AC. This indicates that the image of a point
formed by a plane mirror is the same distance back of the
mirror as the point itself is in front of it. This principle
may be used in locating the image of point B at B´. Locating
the position of the end points of an image determines
the position of the whole image as A´B´.
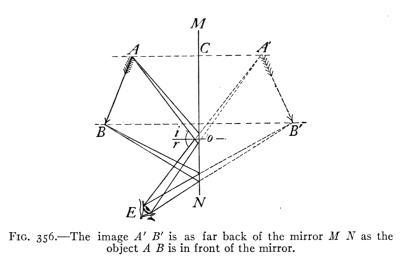 Fig. 356.—The image A´B´ is as far back of the mirror M N as the
object A B is in front of the mirror.
Fig. 356.—The image A´B´ is as far back of the mirror M N as the
object A B is in front of the mirror.
366. How the Image is Seen.—Suppose the eye to be
placed at E. It will receive light from A by reflection
as if it came from A´. Similarly light starting from B
reaches the eye from the direction of B´. There is nothing
back of the mirror in reality that affects our sight, the light
traveling only in the space in front of the mirror. Yet
the action of the reflected light is such that it produces
the same effect as if it came from behind the mirror.
Images such as are seen in plane mirrors are called virtual
to distinguish them from real images, in which light
actually comes to the eye from the various parts of the
visible image, as from the real image formed by a projecting
lantern upon a screen, or by an aperture as in the pin-hole[Pg 404]
camera. Real images therefore are those that can
be obtained upon a screen while virtual images cannot.
367. Multiple Reflection.—If the light from an object
is reflected by two or more mirrors various effects may be
produced, as may be illustrated by the kaleidoscope. This
consists of three plane mirrors so arranged that a cross-section
of the three forms an equilateral triangle. The
mirrors are placed in a tube across the end of which is a
compartment with a translucent cover containing pieces
of colored glass. On looking through the tube, the reflections
from the several surfaces produce beautiful hexagonal
designs.
 Fig. 357.—Perspective view
of "Pepper's ghost."
Fig. 357.—Perspective view
of "Pepper's ghost."
Fig. 358.—Diagram of the "Pepper
Ghost" illusion.
368. Optical Illusions by a Plane Mirror.—The illusion
called Pepper's Ghost is typical of many illusions produced
by reflection. It may be illustrated by taking a piece of
plate glass, M-N, a tumbler of water, W, and a lighted
candle, C, placed in a box, B, having one side open and
arranged as shown in perspective in Fig. 357, and in
section in Fig. 358. If the effect is produced in a darkened
room, the observer at E sees a virtual image of the
lighted candle as if it were in the glass of water, the water
being seen by transmitted light through the plate glass, the[Pg 405]
latter forming a virtual image of the candle by reflection.
Some of the illusions produced by this means are: (a)
the figure suspended in mid air; (b) the bust of a person
without a trunk; (c) the stage ghost; (d) the disappearing
bouquet.
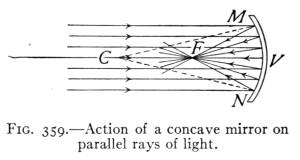 Fig. 359.—Action of a concave mirror on
parallel rays of light.
Fig. 359.—Action of a concave mirror on
parallel rays of light.
 Fig. 360.—Real image formed by a
concave mirror.
Fig. 360.—Real image formed by a
concave mirror.
369. Concave Mirrors.—Another useful piece of physical
apparatus is the
concave spherical mirror.
It is frequently
made from plano-convex
lenses by silvering
the convex surface of
the lens, thus making a
concave reflecting surface from the inner surface of the
silvered part; they are also made by polishing the inner
surfaces of metallic spherical shells. The concave mirror
is represented in section in Fig. 359 by the curve MN;
C is the center of curvature or the center of the surface of
which this mirror MN is a part; the line VC through the
center V of the mirror is
called the principal axis;
while any other line passing
through C is called
a secondary axis. The
point midway between
the vertex V and center
of curvature C is called
the principal focus, F. It is the point through which
parallel incident rays pass after reflection. The angle
MCN which the curve of the mirror subtends at the
center is called the aperture of the mirror. We learned in
Art. 361, the angle of reflection of a ray of light is always
equal to the angle of incidence no matter what the nature
of the reflecting surface may be. If the reflecting surface[Pg 406]
is a regular concave surface, like the inner surface of a
sphere, the rays of light coming from a point source may
after reflection come to a focus, forming a real image.
The two extreme points of an object should be selected
for locating its image; Fig. 360 shows the construction.
The real images formed by concave mirrors are always
inverted. The principal focus of a concave mirror may
be observed by holding the mirror in a beam of sunlight
entering a darkened room. The sun's rays after reflection
converge to form a small, round, intense spot of light,
which is a real image of the sun, located at the principal
focus of the mirror. The distance of the principal focus
from the mirror is the least distance that a real image
can be formed in front of a concave mirror.
370. Virtual Images by Concave Mirrors.—When light
comes from a small point situated between a concave mirror
and its principal focus, the
reflected rays are divergent and
hence no real image of the object
can be found in front of the
mirror. But if the rays are extended
behind the mirror they
will meet in a point called the
virtual focus. This is the point
from which they appear to come.
Any image of an object situated
between the principal focus and a concave mirror is
therefore a virtual image, erect and larger than the
object. (See Fig. 361.)
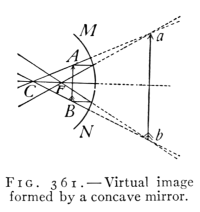 Fig. 361.—Virtual image
formed by a concave mirror.
Fig. 361.—Virtual image
formed by a concave mirror.
371. Construction of Real Images.—There are five
positions at which an object may be situated in front of a
concave mirror, namely: (1) beyond C; (2) at C; (3) between
C and F; (4) at F and (5) between F and V. There
are two ways by means of which the image formed at each[Pg 407]
of these positions may be located, namely; (1) experimentally,
by allowing the rays of light from a luminous
body to focus on a screen and (2) diagrammatically. By
the latter method the two rays of light are considered the
course of each of which may easily be determined; first, the
ray which strikes the mirror parallel to its principal axis
and which after reflection passes through the principal
focus; second, the ray which passing through the center
of curvature strikes the mirror at right angles and therefore
after reflection must pass directly back along its
incident path. Where these two reflected rays intersect
is located the real image of the object. Whenever these
two rays of light do actually intersect, as in Fig. 360, a
real image (ab) is formed of the object AB.
The points A and a, B and b and others similarly
situated on an axis extending through the center of curvature
C are called conjugate foci, for they are so related that
an object being at either one, its image will be found at the
other.
 Fig. 362.—Action of a convex
mirror upon parallel rays of
light.
Fig. 362.—Action of a convex
mirror upon parallel rays of
light.
372. The Convex Mirror.—There are few practical
uses to which convex mirrors can be put. They are sometimes
used to give the chauffeur
of an automobile a view
of the road behind him. It is
then attached to the wind
shield by a short rod. The
reflected rays coming from
a Convex mirror are always
divergent (see Fig. 362), hence
the image is always virtual and
located behind the reflecting surface. The method of
construction for images formed by a convex mirror is
similar to that for concave mirrors. (See Fig. 363.)
The center of curvature and principal focus are behind[Pg 408]
the mirror and consequently the reflected rays have to
be produced backward until
they meet. The images are
always virtual, erect and smaller
than the object.
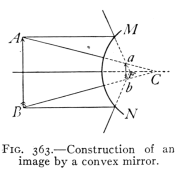 Fig. 363.—Construction of an
image by a convex mirror.
Fig. 363.—Construction of an
image by a convex mirror.
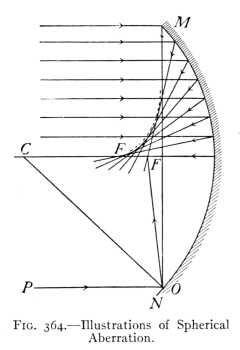 Fig 364.—Illustrations of Spherical
Aberration.
Fig 364.—Illustrations of Spherical
Aberration.
373. Spherical Aberration.
Sometimes in a concave
mirror when the aperture
MCN (Fig. 364) is large the
images are blurred or indistinct.
This is due to the fact
that the incident rays near the outer edge of the mirror
do not focus after reflection at the same point as those
which pass into the mirror near the vertex, but cross
the principal axis at points
between the mirror and
principal focus as is shown
in Fig. 364; this result is
called spherical aberration.
The larger the aperture of
the mirror the more the
image is blurred. Concave
mirrors in practical
use do not have an aperture
much greater than 10
degrees. This non-focusing
of the rays of light by
curved reflecting surfaces
may be noticed in many
places, as when light is
reflected from the inside
of a cup that contains
milk or from the inside of a wide gold ring placed on top
of a piece of white paper. The pupil will note other[Pg 409]
instances. This curve of light observed is called the
caustic by reflection.
374. Parabolic Mirrors.—The best possible surface to
give to concave mirrors is parabolic. This is a curve which
may be generated by moving a point
so that its distance from a fixed point
and a fixed line are always equal.
If a source of light is placed at F
the rays after reflection are rendered
parallel. See Fig. 365. This reflector
is used in automobile lamps, headlights
of locomotives, search-lights,
etc. It is also used in large reflecting
astronomical telescopes to collect as
large an amount of light as possible from distant stars
and bring it to a focus. Such mirrors may be made
exceedingly accurate.
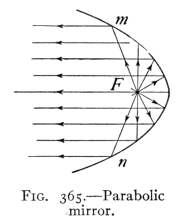 Fig. 365.—Parabolic
mirror.
Fig. 365.—Parabolic
mirror.
Important Topics
1. Reflection: regular, diffused; plane mirrors; laws of reflection.
2. Formation and location of images by plane mirrors. Wave and
ray diagrams.
3. Multiple reflection, illusions.
4. Curved mirrors, uses; concave, convex, parabolic.
Exercises
1. Distinguish between regular and diffused reflection. By means
of which do we see non-luminous bodies?
2. Could a perfect reflecting surface be seen? Explain.
3. A pencil is stood upright in front of a plane mirror set at an
angle of 45 degrees to the vertical. Shown by a diagram the
location and position of the image.
4. Show by diagrams the position and location of the images of a
pencil (a) when standing erect and in front of a vertical mirror.
(b) when standing upon a horizontal mirror.
5. What is the difference between a real and a virtual image?
[Pg 410]
6. A standard candle and a lamp give equal illuminations to a
screen that is 1 ft. from the candle and 6 ft. from the lamp.
What is the candle power of the lamp? Explain.
7. Why are walls finished in rough plaster or painted with soft
tones without gloss better for schoolrooms than glossy paints
or smooth white plaster?
8. Try to read a printed page by looking at its image in a mirror.
write your name backward on a sheet of paper, and then look
at the image of the writing in a mirror. What effect is produced
by the mirror in each case?
9. If the point of a pencil is held to the surface of a piece of plate-glass
mirror two or more images may be seen in the mirror.
Explain.
10. Given a small lighted candle, a concave mirror, a meter stick,
and a white screen, how would you prove the statements made
in Arts. 369 and 370 concerning the location of images formed
by concave mirrors? Make the diagram in each case.
11. Why do images seen in a quiet pond of water appear inverted?
Explain by a diagram.
(4) Refraction of Light
375. Common Examples of Refraction.—Everyone has
noticed the apparent bending of an oar, of a stick, or of a
spoon when placed in water (see
Fig. 366), while many have observed
that the bottom of a pond or stream
looks nearer to the surface than it
really is. These and similar illusions
are due to the refraction or bending
of light rays as they pass from one
medium to another. The principles
of refraction are among the most useful
found in the study of light since application is made of
them in the construction and use of important optical
instruments, such as the camera, microscope, telescope,
and the eye.
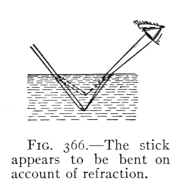 Fig. 366.—The stick
appears to be bent on
account of refraction.
Fig. 366.—The stick
appears to be bent on
account of refraction.
[Pg 411]
376. Action of Light Undergoing Refraction.—If a
beam of sunlight be admitted to a darkened room and reflected
by a mirror so that it strikes the surface of water
in a glass jar, a part of the beam may be seen to be reflected
while another portion is transmitted through the water
(Fig. 367). The reflected
beam follows
the law of reflection
while the transmitted
beam is seen to be
refracted, or to have
its courses slightly
changed in direction
upon entering the
water. If the mirror
is turned so that the
angle at which the
light strikes the water
is changed, the amount
of refraction or change of course of the light is varied.
When the light strikes the water perpendicularly there
is no refraction. On the other hand, the greater the
angle at which the light strikes
the water the greater the
bending.
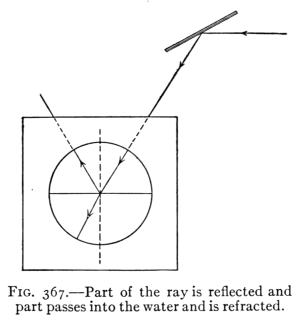 Fig. 367.—Part of the ray is reflected and
part passes into the water and is refracted.
Fig. 367.—Part of the ray is reflected and
part passes into the water and is refracted.
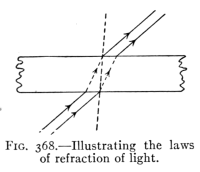 Fig. 368.—Illustrating the laws
of refraction of light.
Fig. 368.—Illustrating the laws
of refraction of light.
377. Laws of Refraction.
The action of light on entering,
passing through, and
leaving a great variety of
substances has been carefully
studied. A summary of
the results of these observations is given in the following
laws of refraction: I. When light enters a transparent body,
perpendicularly, it passes on without changing its direction.[Pg 412]
II. When light enters a denser transparent body obliquely, it
is bent toward the perpendicular; when light enters a less dense
body obliquely, it is bent away from the perpendicular.
(See Fig. 368.)
378. The cause of refraction may be illustrated by
considering a line of men moving across a field and occupying
at equal time intervals the
successive positions 1, 2, 3, etc.,
indicated in Fig. 369. Suppose
that the upper and lower
parts of the field have a smooth
hard surface, while at the center
is a strip of newly ploughed
ground. The line will move
more slowly over the ploughed
field than over the hard field.
This will result in a retardation
of the end of the line first striking
the soft ground with a
resulting change of direction of the line, toward the
perpendicular to the edge of the field (on entering the
place of more difficult travel), and away from the perpendicular
on moving into a place where increased speed
results.
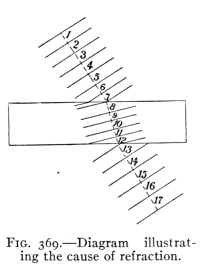 Fig. 369.—Diagram illustrating
the cause of refraction.
Fig. 369.—Diagram illustrating
the cause of refraction.
379. Index of Refraction.—By studying the change of
direction of the marching men as shown in Fig. 369 it is
evident first that it is due to a difference in speed in the
two media. It is not easy to measure the speed of light
in a medium. However, the amount of refraction may be
determined easily and from this the relative speed may be
computed. The number that expresses the ratio of the speed
of light in air to its speed in another medium is called the
index of refraction of that medium. The relative speeds of
light, or the indices of refraction for some substances, are:[Pg 413]
water, 1.33, crown glass, 1.51, flint glass, 1.61, diamond,
2.47, carbon bisulphide, 1.64.
 Fig. 370.—The incident ray and
the emergent rays are parallel.
Fig. 370.—The incident ray and
the emergent rays are parallel.
380. Plates, Prisms, Lenses.—The refraction of light
is usually observed when it is passing through a plate, a
prism, or a lens. The important
differences between
the effects of each in refracting
light are illustrated in
Figs. 370, 371 and 372. In
Fig. 370 it is seen that the
refraction of the ray on entering
the glass is counteracted
by the refraction away from
the perpendicular upon leaving
it. So that the entering
and emergent rays are parallel.
In Fig. 371 the refraction at the two surfaces of
the prism results in a change of direction of the ray, the
course being bent toward the thicker part of the prism. In
Fig. 372 it may be noticed that the convex lens resembles
two prisms with their bases together. Since all parts of
the lens refract light toward the thicker part, the center,
the effect of the convex lens is to bring the rays of light to
a focus, at F.
 Fig. 371.—Effect of a prism upon
a ray of light.
Fig. 371.—Effect of a prism upon
a ray of light.
Fig. 372.—The convex lens brings
the rays of light to a focus.
381. Total Reflection.—It has been shown that when
light passes from a denser to a lighter medium, as from glass[Pg 414]
or water to air, that the beam is refracted away from the
perpendicular. This is illustrated in Fig. 373. The
diagram represents the change in the course of a ray of
light that passes through water to a surface with air above
it. A ray striking perpendicularly passes through without
refraction. Other rays show increasing refraction
with increasing angle of incidence. For one ray the angle
of refraction is so large that the refracted ray is parallel
to the surface. When this condition is reached, the
angle of incidence is called the critical angle. Any increase
in the angle of incidence causes all of the light to be reflected
as is the beam E. This action is called total
reflection, the course of the reflected ray being according
to the law of reflection. A right-angle prism (see Fig. 374)
is often used where a mirror would ordinarily be employed,
the total reflection occurring within the prism giving more
satisfactory results than a mirror. See Art. 398 for a
description of the Zeiss binocular field-glass for an example
of this use of total reflection.
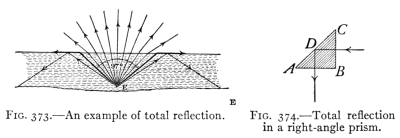 Fig. 373.—An example of total reflection.
Fig. 373.—An example of total reflection.
Fig. 374.—Total reflection
in a right-angle prism.
The mirage (see Fig. 375) is an optical illusion by which distant
objects, below the horizon, are sometimes plainly seen. This phenomenon
is most frequently observed in hot, desert regions, when
the air conditions are such that the lower strata near the ground are
very much hotter than those above. These lower strata, having expanded
the most, are less dense than the cooler ones above. Hence
a ray of light traveling obliquely downward is refracted more and
more until total reflection takes place. The images seen are inverted[Pg 415]
giving a representation of trees or other objects reflected on the surface
of still water. The mirage is also frequently seen at sea, ships
being observed, sometimes erect, sometimes inverted, apparently sailing in
the clouds near the horizon. Over the Great Lakes, trees, boats,
and towns on the opposite shore, sixty or seventy miles away,
can sometimes be plainly seen, apparently but a few miles out. In
this case the images are erect, the total reflection being from warm,
still layers of air over colder layers near the water.
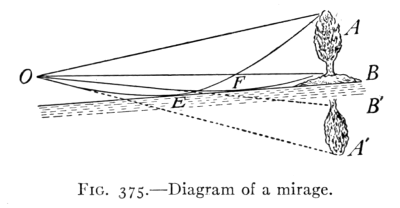 Fig. 375.—Diagram of a mirage.
Fig. 375.—Diagram of a mirage.
Important Topics
(A) Refraction: cause, illustration, two principles.
(B) Index of refraction, meaning.
(C) Plates, prisms, lenses, action of each.
(D) Total reflection, uses.
Exercises
1. Compute the speed of light in water, the index of refraction
being 1.33.
2. If one wished to shoot a fish under water, should he aim at the
apparent location of the fish as viewed from the air? Explain,
using a diagram.
3. Define refraction. Mention two illustrations of this action
that you have observed out of school.
4. Why does the moon look larger near the horizon?
5. Is your reflection seen in a pool of water upside down? Why?
6. Why does it whiten molasses candy to pull it?
7. When looking at a building through the ordinary glass of a
window why do straight lines of the building appear to be so
distorted? What makes them appear to move as you move
your head slightly?
[Pg 416]
8. Explain the phenomenon which one observes when looking at
an object through the air arising from a hot stove or radiator.
9. Frequently the horizontal diameter of the setting sun appears
to be greater than the vertical. Explain.
10. Explain why one observes several images of a luminous body
like a lighted candle when the reflected light from a thick glass
mirror enters the eye, the angle of reflection being large.
(5) The Formation of Images by Lenses
382. Uses of Lenses in Optical Instruments.—The use
of instruments that employ lenses in their operation, such
as spectacles, reading and opera glasses, and the camera,
microscope, and telescope, is familiar to most students of
physics. The part played by the lenses, however, is not
generally understood. Consequently the study of the
formation of images by lenses is of general interest and
importance.
383. Forms of Lenses.—While a lens may be formed
from any transparent solid it is commonly made of glass.
It may have two curved surfaces or
one curved and one plane surface.
Most lenses are spherical lenses, since
their curved surfaces form a part of
the surface of a sphere. Fig. 376
represents a spherical lens with a
curved surface coinciding with that of
a sphere whose center is at C. This
center is called the center of curvature, while the radius of
the sphere R, is the radius of curvature.
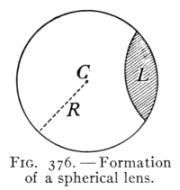 Fig. 376.—Formation
of a spherical lens.
Fig. 376.—Formation
of a spherical lens.
There are two classes of lenses: those thick in the middle
are called convex, while those thick at the edges are concave.
The mode of constructing the six forms of spherical lenses
is shown in Fig. 377. These are named as follows: (1)
double convex, (2) plano convex, (3) concavo-convex,
(4) double concave, (5) plano concave, (6) convexo-concave.
[Pg 417]
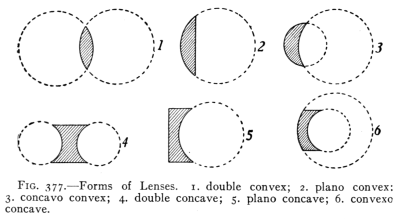 Fig. 377.—Forms of Lenses. 1. double convex; 2. plano convex;
3. concavo convex; 4. double concave; 5. plano concave; 6. convexo
concave.
Fig. 377.—Forms of Lenses. 1. double convex; 2. plano convex;
3. concavo convex; 4. double concave; 5. plano concave; 6. convexo
concave.
 Fig. 378.—The action of a burning glass.
Fig. 378.—The action of a burning glass.
384. Effect of Lenses upon Light.—The most important
characteristic of a lens is its effect upon a beam of light.
Most persons have seen a "burning glass," a double convex
lens, used to bring to a point, or focus, a beam of sunlight.
To show the action of a burning glass send a beam of
light into a darkened room, and place in its path a double
convex lens. (See Fig. 378.) If two blackboard erasers
are struck together near the lens, the chalk particles in the
path of the light are strongly illuminated, showing that the
light after passing through the lens it brought to a focus
and that it spreads out beyond this point. This point
to which the cone of light rays converges after passing
through the convex lens is called the principal focus of
the lens. The distance from the principal focus to the
center of the lens is the focal length or principal focal
distance of the lens. The focal length of double convex lenses of crown glass is about the same as the radius of
curvature of either surface.[Pg 418]
The action of a convex or
converging lens upon light may be better understood by
studying Fig. 379 in which light is passing from S to F.
The successive positions and
shape of the advancing light
waves are indicated by lines
drawn across the beam. The
light being retarded more in
the thicker part of the lens,
the light waves on leaving
the lens have a concave front.
Since light waves tend to move at right angles to the front
of the wave, the light is brought to a focus. After passing
the focus the waves have a convex front, forming a
diverging cone.
 Fig. 379.—Wave diagram of
light passing through a convex
lens.
Fig. 379.—Wave diagram of
light passing through a convex
lens.
385. Concave Lenses.—When sunlight passes through
a concave lens a diverging cone of light is formed. (See
Fig. 380.) This is caused by the edges of the wave being
retarded more than the center, producing a convex wave
front. This diverging cone of light acts as if it had proceeded
from a luminous point at F.
This point is called a virtual focus and is nearly at the
center of the curvature of the nearer surface.
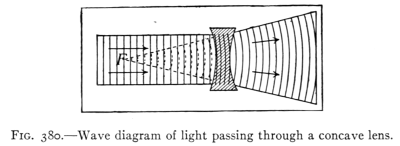 Fig. 380.—Wave diagram of light passing through a concave lens.
Fig. 380.—Wave diagram of light passing through a concave lens.
386. The Formation of Images by Lenses.—If a beam
composed of parallel rays of light, as sunlight, is sent in[Pg 419]
turn through three convex lenses of the same diameter but
of different thickness, it is
found that the thicker the
lens the greater is its converging
power, or the shorter is its
focal length. (See Fig. 381.)
Now if a luminous body,
such as a lighted candle, be
placed near the convex lens
but beyond its focal length,
the light will be brought to a
focus upon the other side of
the lens and an image of the
candle may be clearly seen
upon the screen placed at
this point. (See Fig. 382.)
The two points so situated on
opposite sides of a lens that
an object at one will form an image at the other are called
conjugate foci.
 Fig. 381.—The thicker the lens,
the shorter is its focal length.
Fig. 381.—The thicker the lens,
the shorter is its focal length.
 Fig. 382.—C and S are at conjugate foci.
Fig. 382.—C and S are at conjugate foci.
It will be helpful to compare the images formed of a
candle by an aperture and by a convex lens. Rays of
light from each point of the luminous body pass through[Pg 420]
the aperture in straight lines and produce upon the screen
a lighted space of the same shape as the candle. This
image is rather hazy in outline. Each cone of rays from
luminous points of the flame is brought by the lens to a
focus on the screen, producing a sharp image. It is the
converging power of convex lenses that enables them to
produce clear images.
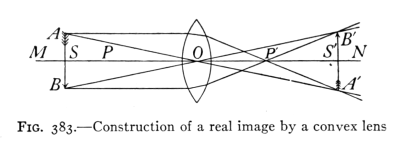 Fig. 383.—Construction of a real image by a convex lens.
Fig. 383.—Construction of a real image by a convex lens.
387. The Construction of Diagrams to Represent the
Formation of Images by Lenses.—Just as the earth has
an axis at right angles to its equator to which are referred
positions and distances, so a lens has a principal axis at
right angles to its greatest diameter and along this axis
are certain definite positions as shown in Fig. 383. Let
MN be the principal axis of a convex lens, P and P´ are
principal foci on either side of the lens, S and S´ are
secondary foci. These are at points on the principal axis
that are twice as far from O, the center of the lens, as are
the principal foci. In the formation of images by a convex
lens, several distinct cases may be noticed:
(A) If a luminous body is at a great distance at the left,
its light is brought to a focus at P, or its image is formed
at P. (B) As the object approaches the lens the image
gradually recedes until the object and image are at S and
S´, equally distant from O and of equal size (as in Fig. 383).
The object and image are now said to be at the secondary
foci of the lens. (C) As the object moves from S to P the
image recedes, rapidly increasing in size until (D) when[Pg 421]
the object is at P the rays become parallel and no image
is formed. (E) When the object is between P and the
lens, the rays appear to proceed from points back of the
object, thus forming an erect, larger, virtual image of the
object. (See Fig. 384.) This last arrangement illustrates
the simple microscope.
With a concave lens but one case is possible, that corresponding
to the one last mentioned with convex lenses;
since the rays from a body are divergent after passing
through a concave lens they appear to proceed from points
nearer the lens than the object and hence a virtual, erect,
smaller image of the object is formed. This virtual image
may be seen by looking through the lens toward the object.
(See Fig. 385.)
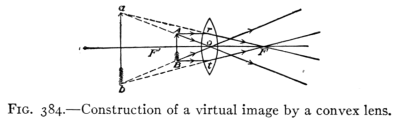 Fig. 384.—Construction of a virtual image by a convex lens.
Fig. 384.—Construction of a virtual image by a convex lens.
 Fig. 385.—Construction of a virtual image by a concave lens.
Fig. 385.—Construction of a virtual image by a concave lens.
388. The Lens Equation.—The location of either the
object or of the image upon the principal axis of the lens
may be calculated if the position of one of these and the[Pg 422]
focal length are known. This is accomplished by the use
of a formula 1/F = 1/D0 + 1/D1 in which F represents the focal
length and D0 and D1 the distance from the lens of the
object and the image respectively. Thus if an object is
placed 30 cm. from a lens of 10 cm. focal length, where will
the image be formed? Thus: 1/10 = 1/30 + 1/D and 3D1 =
D1 + 30, or 2D1 = 30 D1 = 15. This result indicates
that a real image will be 15 cm. from the lens. A minus
value would indicate a virtual image.
Important Topics
(A) Lenses: convex, concave, six forms, center and radius of
curvature.
(B) Principal focus, focal length, virtual focus, conjugate foci.
(C) Principal axis, images formed when object is in various locations.
(D) Computation of location of images.
Exercises
1. Why is an image of a candle formed by an aperture, not sharply
defined?
2. When a photographer takes your picture and moves the camera
nearer you, must he move the ground glass screen toward
the lens or away from it? Explain.
3. How can you find the principal focal length of a lens.
4. How can you test a spectacle lens to see whether it is convex
concave?
5. When will a convex lens produce a virtual image? Have you
ever seen one? Where?
6. When a photographer wishes to obtain a full length view of a
person, where does he place the camera?
7. The focal length of the lens is 24 cm. How far from the lens
must an object be placed in order that a real image may be
three times as long as the object?
8. There is a perfect image of an object on the ground glass of a
camera. The center of the lens is 20 cm. in front of the image[Pg 423]
and the object 75 cm. from the lens. What is the focal length of
the lens?
9. An object is 60 cm. from the lens, the image 120 cm. from it.
Find the focal length.
10. How can you find experimentally the principal focal length
of a lens?
11. A lens is used to project an enlarged image of a candle upon a
screen. Which is farther from the lens, the candle or the image?
Explain.
(6) Optical Instruments
389. The Eye.—The most common optical instrument
is the eye. While the structure of the eye is complicated,
the principle of it is simple, involving the formation of an
image by a double convex lens.
(See Fig. 386, in which is shown
a front to back, vertical cross-section
of the eye.) The eye
appears to be made of portions
of two spheres, one of which,
smaller than the other, is
placed in front. This projecting
part is transparent,
but refracts the light which
strikes it obliquely, so as to turn it into the eye. This
enables us to see objects at the side when looking
straight ahead. Test this by looking directly in front of
you and see how far back on each side of the head you can
notice a movement of the forefinger of each hand.
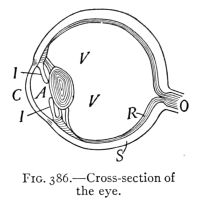 Fig. 386.—Cross-section of
the eye.
Fig. 386.—Cross-section of
the eye.
390. Action of the Eye in Vision.—When we look at an
object, a small, real, inverted image is formed upon the
retina at the back of the interior of the eye. The retina is
an expansion of the optic nerve and covers the inner surface
at the back of the eyeball. Seeing is due to the action
of light in forming images upon the retina. Our eyes are
so constructed that when they are relaxed the lens is adjusted[Pg 424]
to form clear images of distant objects upon the
retina. If we look from distant to near objects without
changing the shape of the eye lens, a sharp image of the
latter cannot be formed and we get a blurred impression.
It is difficult, however, to look at objects without automatically
adjusting the eye lens so that it will make a sharp
image. Test this by looking out of a window at a distant
object, then without moving the head or eyes look at the
glass of the window; you will notice a slight change of some
sort in the eye itself as the vision is adjusted. This adjustment
is made by muscles that pull or compress the eye lens
so as to make it thicker for near objects and thinner for
distant ones. The eye ordinarily does not see objects
nearer than 10 in. clearly. This means that the greatest
possible thickening of lens will not form clear images upon
the retina if the object is nearer than 10 in. (25 cm.).
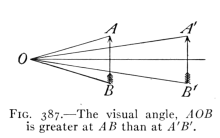 Fig. 387.—The visual angle, AOB
is greater at AB than at A´B´.
Fig. 387.—The visual angle, AOB
is greater at AB than at A´B´.
391. The Visual Angle.—To examine objects carefully
we usually bring them as close to the eye as possible, for
the nearer to the eye the
object is brought, the larger
is the visual angle formed
by it (see Fig. 387), and the
larger is its image upon the
retina. The visual angle of
an object is the angle at the
eye lens between the rays that
have come from the ends of the object. Consequently the more
distant the object, the smaller is its visual angle. Now if we
wish to examine small objects with great care, we frequently
find that it is necessary to bring them close to the eye so
that they have a visual angle of adequate size. If they
must be brought closer than 10 in. a double convex lens
is placed in front of the eye. This assists the eye lens in
converging the light so that a clear image may be formed[Pg 425]
when the object is close, say an inch or so from the eye.
This is the principle of the magnifying glass used by watch-makers
and of the simple microscope. The action of the
latter is illustrated by Fig. 388. The convex lens forms
a virtual, enlarged image
"A´-B´" of the object
"A-B" which it
observed instead of the
object itself.
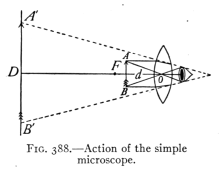 Fig. 388.—Action of the simple
microscope.
Fig. 388.—Action of the simple
microscope.
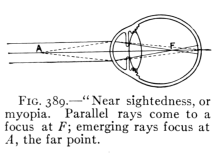 Fig. 389.—"Near sightedness", or
myopia. Parallel rays come to a
focus at F; emerging rays focus at
A, the far point.
Fig. 389.—"Near sightedness", or
myopia. Parallel rays come to a
focus at F; emerging rays focus at
A, the far point.
392. Defects of Vision.—There
are several
defects of vision that
may be corrected by
spectacles or eye-glasses.
One of these is "near-sightedness." It is due
either to an eyeball that is elongated, or to an eye lens that
is too convex, or to both conditions. This condition brings
light from distant objects to a focus too soon (as shown in
Fig. 389). Only light from near objects will focus upon
the retina in such cases. With normal vision light from
distant or near objects may be focused without unusual
effort upon the retina, see
Fig. 390. The remedy for
near-sightedness is to use
concave lenses which will
assist in properly refracting
the light so the focus will be
formed on the retina (Fig.
391). "Far-sightedness" is
the reverse of near-sightedness; the eyeball is either too
short, or the lens too flat, or both conditions obtain, so
that the light entering the eye is brought to a focus behind
the eyeball (Fig. 392). The remedy is convex lenses which
will assist in properly converging the light, see Fig. 393. A[Pg 426]
third defect is called astigmatism. This is caused by some
irregularity or lack of symmetry in the eye. It is corrected
by a cylindrical lens that compensates for this defect of
the eye. A diagram similar to Fig. 394 is used as a test
for astigmatism. If the lines
appear with unequal distinctness,
some irregularity of refraction
(astigmatism) is indicated.
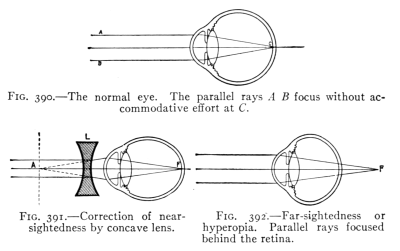 Fig. 390.—The normal eye. The parallel rays A B focus without accommodative
effort at C.
Fig. 390.—The normal eye. The parallel rays A B focus without accommodative
effort at C.
Fig. 391.—Correction of near-sightedness
by concave lens.
Fig. 392.—Far-sightedness or
hyperopia. Parallel rays focused
behind the retina.
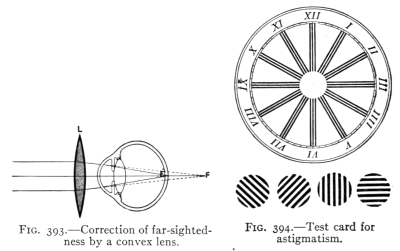 Fig. 393.—Correction of far-sightedness
by a convex lens.
Fig. 393.—Correction of far-sightedness
by a convex lens.
Fig. 394.—Test card for
astigmatism.
393. The Photographic Camera.—This
is a light-tight box, provided with a convex
lens in front, covering an aperture and a ground glass[Pg 427]
screen at the back. The distance between the lens and
the screen is adjusted until a sharp image is obtained
upon the latter, which is then replaced by a sensitive
plate or film. The sensitized surface of the plate or film
contains a salt of silver which is changed by the action of
light. After the plate has been "exposed" to the action
of light, it is "developed" by the use of chemicals producing
a negative image. From "negative," by the use
of sensitized paper, "positive" prints may be secured
which resemble the object photographed.
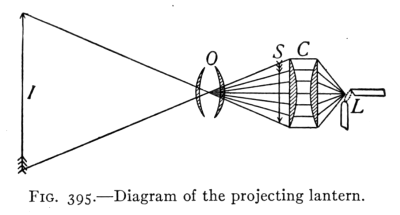 Fig. 395.—Diagram of the projecting lantern.
Fig. 395.—Diagram of the projecting lantern.
394. The projecting lantern (see Fig. 395) employs a
strong source of light, as an electric arc lamp L, to strongly
illuminate a transparent picture, or lantern slide, S, a real
image (I) of which is formed upon a large screen. Two
large plano-convex lenses (C), called condensing lenses,
are placed near the lamp to concentrate the light upon the
"slide" S. The convex lens forming the image is called
the "objective" (O).
395. The compound microscope consists of two lenses.
One called the objective is placed near the object to be
viewed. This lens has a short focal length usually less
than a centimeter. It forms a real image of the object.
A´-B´. The other lens, the eyepiece forms a virtual image
of this real image. A´´-B´´. (See Fig. 396.)
[Pg 428]
396. The telescope consists of two lenses, the eyepiece
and the objective. As in the compound microscope, the
objective of the telescope forms a real image of the distant
object, the eyepiece forming an enlarged virtual image of
the real image. It is the virtual image that is viewed by
the observer. (See Fig. 397.) In order to collect sufficient
light from distant stars the objective is made large, sometimes
50 in. in diameter.
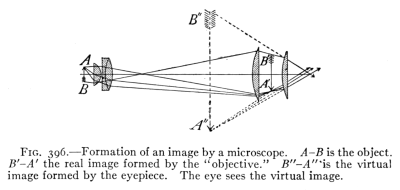 Fig. 396.—Formation of an image by a microscope. A-B is the object.
B´-A´ the real image formed by the "objective." B´´-A´´ is the virtual
image formed by the eyepiece. The eye sees the virtual image.
Fig. 396.—Formation of an image by a microscope. A-B is the object.
B´-A´ the real image formed by the "objective." B´´-A´´ is the virtual
image formed by the eyepiece. The eye sees the virtual image.
The length of the telescope tube depends upon the
focal length of the objective, since the distance between
the two lenses must equal the sum of their focal lengths.
 Fig. 397.—Formation of an image by a telescope. b-a is the real image;
d-c is the virtual image seen by the observer.
Fig. 397.—Formation of an image by a telescope. b-a is the real image;
d-c is the virtual image seen by the observer.
397. The opera glass consists of a convex lens as objective
and a concave lens as an eyepiece. The former tends
to form a real image but the latter diverges the rays before
a real image can be formed, the action of the two lenses
producing an enlarged virtual image (as in Fig. 398) which[Pg 429]
is viewed by the one using the glass. The compact size
of the opera glass is due to the fact that the distance
between the two lenses is the difference of the focal lengths.
 Fig. 398.—Formation of an image by an opera-glass. a-b is the virtual
image.
Fig. 398.—Formation of an image by an opera-glass. a-b is the virtual
image.
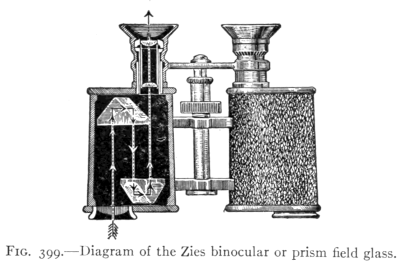 Fig. 399.—Diagram of the Zeiss binocular or prism field glass.
Fig. 399.—Diagram of the Zeiss binocular or prism field glass.
398. The Prism Field Glass or Binocular.—This instrument.
has come into use in recent years. It possesses the
wide field of view of the spy glass but is as compact as the
opera glass. This compact form is secured by causing the
light to pass back and forth between two right-angle
prisms (as shown in Fig. 399). This device permits the
use of an objective lens with a focal length three times
that of the tube, securing much greater magnifying power
than the short instrument would otherwise possess. A
further advantage is secured by the total reflection from[Pg 430][Pg 431]
the two prisms, one of which is placed so as to reverse the
image right for left and the other inverts it, so that when
viewed in the eyepiece it is in its proper position.
Important Topics
1. The eye: parts, formation of image, kind, how, where.
2. Eye defects, how remedied. Visual angle.
3. Simple microscope, camera; images, kind, how formed.
4. Compound microscope, telescope and opera glass; images, action
of each lens.
Exercises
1. Name three instruments in which lenses form virtual images
and three in which real images are formed.
2. In what direction is an oar in water apparently bent? Explain
by a diagram.
3. What optical instruments have you used? Is the visible image
formed by each of these real or virtual?
4. The focal length of a copying camera lens is 14 in. Where must
a drawing be placed so that an image of the same size may be
formed upon the ground glass screen? What must be the distance
of the screen from the lens?
5. What are two methods by which you can determine the focal
lengths of the lens of a photographic camera?
6. The critical angle for water is 48-1/2 degrees. Show by a diagram
how much of the sky can be seen by a diver who looks
upward through the water.
7. How is near-sightedness caused? How is it corrected? Illustrate
by a diagram.
8. How is the eye accommodated (focused) as an object gradually
approaches it?
9. Explain why a simple microscope assists in looking at the parts
of a flower or insect.
10. Why do people who have good eyesight when young require
glasses as they grow old?
(7) Color and Spectra
 Guglielmo Marconi
Guglielmo Marconi
"Copyright by Underwood & Underwood,
N. Y."
Guglielmo Marconi (Italy). Inventor
of wireless telegraphy.
 Alexander Graham Bell
Alexander Graham Bell
"Copyright by Underwood &
Underwood, N. Y."
Alexander Graham Bell, Washington,
D. C. Inventor of the telephone.
[Pg 432]
[Pg 433]
399. Color.—Much of the pleasure experienced in gazing
at beautiful objects is due to the color shown by them.
The blue sky, the green grass, and the varied tints of flowers,
and of the rainbow all excite our admiration The study
of color begins naturally with the production of the spectrum,
the many-colored image upon a screen produced by
passing a beam of light through a prism. The spectrum
is best shown when the light enters by a narrow slit (Fig.
400). The spectrum was first produced by Sir Isaac
Newton in 1675 by the means just described. The names
usually given to the more prominent colors of the spectrum
are violet, indigo, blue, green, yellow, orange, and red.
The initials of these names, combined, spell vibgyor, a
word without meaning except to assist in remembering the
order of the colors in a spectrum.
If the light that has
passed through a prism is sent
through a second prism placed
in reverse position (see Fig.
401), the light passing through
both prisms is found to be
white. This experiment
indicates that white light is composed of light of all colors.
 Fig. 400.—Formation of the spectrum by a prism.
Fig. 400.—Formation of the spectrum by a prism.
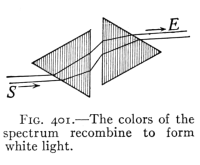 Fig. 401.—The colors of the
spectrum recombine to form
white light.
Fig. 401.—The colors of the
spectrum recombine to form
white light.
400. Dispersion.—The separation of the colors by a
prism is called dispersion. In experimenting to find a[Pg 434]
reason for dispersion, it has been learned that lights of
different colors are of different wave lengths. Color in
light is therefore analogous to pitch in sound. We hear
through many octaves, but we see through about one
octave. That is, the shortest visible waves of violet
light are about 0.000038 cm. in length while the longest
visible red rays are 0.000076 cm., or the longest visible
light waves are about twice the length of the shortest
visible ones. It appears from the evidence of experiments
upon dispersion that light
waves of different lengths
are refracted differently.
This causes the images
formed by refraction
through simple glass lenses
to be fringed with color
and to lose some of their
sharpness and definiteness
of outline, since the violet
light is brought to a focus
sooner than the red. (See Fig. 402.) This seriously affects
the value of such lenses for optical purposes. Fortunately
it is found that different kinds of glass have a different rate
of dispersion for the same amount of refraction.
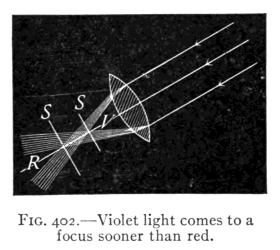 Fig. 402.—Violet light comes to a
focus sooner than red.
Fig. 402.—Violet light comes to a
focus sooner than red.
401. The Achromatic Lens.—The existence of these
different kinds of glass makes possible a combination of
lenses in which dispersion is entirely overcome with the
loss of only about one-half of the refraction. Such a combination
is shown in Fig. 403. It is called an achromatic
lens, since images formed by it are not colored
but white (a = without, chroma = color). The achromatic
lens consists of a double convex lens of crown glass combined
with a plano-concave lens of flint glass. Achromatic lenses
are used in all high-grade optical instruments such as[Pg 435]
telescopes and microscopes. The colored images that are
sometimes seen in cheap opera glasses show the result of
not using achromatic lenses.
 Fig. 403.—An achromatic lens. C is of crown glass; F, of flint glass.
Fig. 403.—An achromatic lens. C is of crown glass; F, of flint glass.
402. The Color of Bodies.—Project the spectrum of
sunlight upon a white surface in a darkened room.
Now place in different parts of the spectrum objects of various
colors. Red objects will show brilliant red when at the red end of
the spectrum but look black at the blue end, while blue objects
appear blue only at the blue end.
These facts indicate that the color of an object depends
upon two things: (a) the light that falls upon it and (b) the
light which it sends to the eye. A black surface absorbs all
color while a white one reflects all wave lengths to the eye
in the same proportion that they come to it. A white
object will appear red in red light, and blue in blue light
since it reflects both of these. A colored object reflects
light of its own color but absorbs all others. The color
then of a body is due to the light which it does not absorb,
but which comes from it to the eye.
403. The color of transparent bodies, such as colored
glass, is due to the presence of a dye or pigment contained in
the body. This pigment absorbs a part of the light, the
part transmitted giving the color. This may be shown by
holding a sheet of colored glass in a beam of light either
before or after it has passed through a prism. Some
colors, as red, may be found to be nearly pure, only the
red passing through, while green glass often transmits in
addition to the green some yellow and some red light.
[Pg 436]
404. Complementary Colors.—If two prisms are placed
in reversed position near each other (see Fig. 401), a beam
of light dispersed by one is recombined into white light
by the other. If now a card is held between the two prisms
so as to cut off some of the colored light, say the red, the
remaining light will be found to form a greenish blue. If
the card is removed, the light becomes white again. That
is, red and peacock blue light together form white. Any
two colors that together form white light are called complementary.
Other complementary colors are light yellow
and blue, green and crimson, orange and greenish blue,
violet and greenish yellow. We must not confuse the
combining of colors (light) and the combining of pigments,
the latter consisting of bodies that absorb light. Yellow
pigment absorbs all but yellow and some green, while
blue pigment absorbs all but blue and some green. Mixing
these two pigments causes the absorption of all
colors but green. Blue and yellow paint mixed produce
green, while blue and yellow light give white.
405. The solar spectrum, as the spectrum of sunlight
is called, may be observed in the rainbow. The
latter is produced through the dispersion of light by spherical
raindrops. Its formation may be imitated by sending
a small circular beam of light through a screen against a
round glass flask filled with water. (See Fig. 404.) The
light passes through the water and is dispersed when
it enters and when it leaves, producing a color upon the
screen at R-V. The course of the light within the drop
is indicated in Fig. 405. The violet ray comes to the
eye more nearly horizontal and is therefore below red, as
we look at the rainbow.
406. Fraunhofer Lines.—Some of the most important
features of the solar spectrum are not seen in the rainbow
or in the band of light usually observed upon a screen.[Pg 437]
By the use of a narrow slit and a convex lens to carefully
focus the slit upon a white screen it is seen that the solar
spectrum is crossed by many dark lines. These are called
Fraunhofer lines, to honor the German scientist who
in 1814 first accurately determined their position. Two
experiments with a spectroscope will help to make clear the
meaning of the Fraunhofer lines.
 Fig. 404.—A rainbow formed by a beam of light striking a flask of water.
Fig. 404.—A rainbow formed by a beam of light striking a flask of water.
Fig. 405.—The course of a beam of light within a drop of water.
[Pg 438]
407. The Spectroscope and Its Uses.—The spectroscope
(Fig. 406) is an instrument for observing spectra. It
consists of a prism, a slit, and a convex lens T for focusing
an image of the slit accurately upon a screen (Fig. 407)
where the spectrum is observed through the eyepiece E.
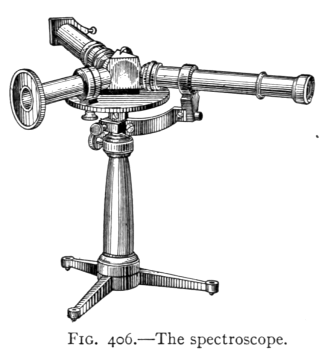 Fig. 406.—The spectroscope.
Fig. 406.—The spectroscope.
(A) A Bunsen flame is placed in front of the slit and a
heated platinum wire which has been dipped in common
salt or some sodium compound placed in the Bunsen flame;
the latter becomes yellow and a vivid yellow line is observed
on the screen in the spectroscope. Other substances,
as barium and strontium salts, when heated to
incandescence in the Bunsen flame, give characteristic
bright lines. In fact each element has been found to have
its own characteristic set of colored lines. This fact is
made use of in spectrum analysis, by which the presence
of certain elements in a substance can be definitely proved
upon the appearance of its particular lines in the spectrum.
 Fig. 407.—Diagram of a spectroscope.
Fig. 407.—Diagram of a spectroscope.
 Fig. 408.—The bright line spectrum of iron and its coincidences with
some of the dark lines of the solar spectrum.
Fig. 408.—The bright line spectrum of iron and its coincidences with
some of the dark lines of the solar spectrum.
(B) If light from, for example, an arc light is sent over a
gas flame containing sodium vapor, a dark line appears in[Pg 439]
the spectrum—in the exact position in which the yellow
sodium line appeared. It seems that the sodium vapor
removes from white light the same wave lengths that it itself
produces. This absorption is supposed to be due to
sympathetic vibration; just as a tuning fork is set in vibration
by the waves of another fork in unison with it, at
the same time absorbing the wave energy, so in the gas
flame the sodium particles absorb the wave motion of the same
vibration rate as that emitted by them. The fact
that the spectrum of sunlight contains a great many dark
lines is believed to indicate that the sun is surrounded
by clouds formed by the vaporization of the various substances
in the sun itself. By comparing the dark lines of[Pg 440]
the solar spectrum with the bright-line spectra of various
substances found in the earth, such an exact correspondence
of the lines is found that the presence of the vapor
of these substances about the sun is considered proved.
(See Fig. 408 which shows the exact correspondence
between the bright-line spectrum of iron vapor and the
dark lines appearing in a portion of the sun's spectrum.)
The spectra of the stars also contain certain dark lines.
Thus the presence of the corresponding substances in distant
stars is considered as determined.
408. Theory of Color Vision.—By combining light of
the three colors red, green and blue-violet in proper proportions,
it has been found possible to produce any color
effect, even white. This leads to the conclusion that in
the retina of the eye are three different kinds or sets of
sensitive nerve endings, sensitive respectively to red, to
green, and to blue light. This idea is given corroboration
by some facts of color blindness. Thus some persons have
no sensation of red, this color not being distinguished
from green. Others are color blind to green or blue. It
is supposed that in color blind persons one of the sets of
nerve endings sensitive to one of these three colors is
lacking.
409. Three-color Printing.—Since all colors may be
produced by mixing the three colors, light red, green, and
blue-violet, these are called the three primary colors. The
so-called primary pigments or paints are simply the complements
of the three primary colors. They are, in order,
peacock blue, crimson, and light yellow. The three
pigments when mixed yield black, since combined they
absorb all kinds of visible light. The process of three-color
printing, now so generally employed in printing
colored pictures for books, calendars, etc., consists in
combining upon white paper three colored impressions,[Pg 441]
using successively the three primary pigments (yellow,
crimson and blue) from plates prepared as follows:
Three photographs of a given colored object are taken,
each through a different sheet of gelatine called a filter,
stained the color of one of the primary colors. From these
photographs half-tone blocks are made in the usual way.
The colored picture is made by carefully superposing impressions
from these blocks, using in each case an ink
whose color is the complement of the "filter" through
which the original picture was taken. An illustration of
the process is given upon the plate in the frontispiece of
this book.
Important Topics
1. Color, due to wave length; dispersion by prism, sphere in rainbow,
complementary colors, color of opaque and transparent
bodies.
2. Spectra, solar; formation of rainbow; bright-line spectra, how
formed, how used; dark-line, how formed, used.
3. Theory of color vision. Three color printing.
Exercises
1. How does a white flower look when viewed through a blue glass?
Through a red glass? Through a red and blue glass at the same
time?
2. Why does a red ribbon appear black when seen by blue light and
red when seen by red light?
3. In what part of the sky must you look to see a rainbow in the
morning? In the afternoon? Explain.
4. How would you arrange two similar prisms so as to produce
double the deviation produced by one?
5. The color of an object depends upon what two things?
6. What kind of a spectrum should moonlight give? Why?
7. A mixture of green and red lights gives a sensation of yellow.
Can you suggest why a mixture of blue and yellow lights gives
the sensation of white?
[Pg 442]
(8) Nature of Light, Interference, Polarization
410. The Corpuscular Theory.—The theory of the
nature of light that was most generally accepted until
about the year 1800, held that light consists of streams of
minute particles, called corpuscles, moving at enormous
velocities. This corpuscular theory was in accord with the
facts of reflection and the rectilinear motion of light, but
was abandoned after the discovery of the interference of
light, as it could not account for the latter phenomenon.
411. The Wave Theory of Light.—The theory that
light is a form of wave motion was first advanced by Huygens,
a Dutch physicist, in the seventeenth century. This
theory was opposed at the start since (A) no medium was
known to exist which would convey wave motion through
space, as from the sun to the earth, and (B) the rectilinear
motion of light was unlike that of any other form of known
wave motions, such as that of water or of sound waves
which are able to bend around corners. In answer to the
first objection, Huygens assumed the presence of a medium
which he named ether, while the second objection has been
completely overcome during the past century by the discovery
that light may deviate from a straight line. It is
now known that the excessive shortness of light waves is
the reason for its straight-line motion. Further, long ether
waves, as those of wireless telegraphy, are found to bend
around obstacles in a manner similar to those of water or
sound.
 Fig. 409.—Two plates pressed
together by a screw clamp.
Fig. 409.—Two plates pressed
together by a screw clamp.
Fig. 410.—Illustrating the interference
of light by a thin film of air.
412. The interference of light is one of the phenomena
for which the wave theory offers the only satisfactory
explanation. Interference of light may be shown by taking
two pieces of plate glass and forcibly pressing them
together by a screw clamp, as shown in Fig. 409. After a
certain pressure has been reached, colored rings will appear[Pg 443]
about the compressed spot when viewed by light reflected
from the upper surface of the glass. If light of one color,
such as that transmitted by red glass, falls upon the apparatus,
the rings are seen to be alternately red and dark
bands. The explanation of this phenomenon according
to the wave theory is as follows: The two sheets of glass,
although tightly pressed together, are separated in most
places by a thin wedge of air (see Fig. 410), which represents
in an exaggerated form the bending of the plates
when pressed by the clamp. Several waves are represented
as coming from the right and entering the glass. Now the
wave moving from R to the plates has some of its light reflected
from each glass surface. Consider the two portions
of the wave reflected at each of the surfaces between the
plates, i.e., from the two surfaces of the wedge of air.
If the portion of the wave reflected from the second surface
of the air wedge combines with that reflected from the
first surface, in the same phase as at C, the two reflected
waves strengthen each other. While if the two reflected
portions of the wave meet in opposite phases as at A and B,
a decrease or a complete extinction of the light results.[Pg 444]
This is called interference. If light of one wave length
is used, as red light, the regions of reinforcement and interference
are shown by red and dark rings, while if white
light is used, the ring where red light interferes, yields its
complementary color, greenish blue. Where interference
of greenish blue occurs, red is found, etc. Many phenomena
are due to interference, such as (A) the color of thin
films of oil on water, where the portions of light reflected
from the two surfaces of the oil film interfere resulting in
the production of color; (B) the color of soap bubbles.
When first formed, soap-bubble films are not thin enough
to show interference well, but as the bubbles increase in
size or become thinner on standing, the conditions for
interference are reached and, as the film becomes thinner,
a regular succession of colors is noticed.
413. Differences Between Light and Sound.—Among
the important differences between light and sound that
have been considered are the following: the former are
(a) waves in the ether, (b) of very short wave length, and
(c) their motion is in straight lines. Another difference (d)
is in the mode of vibration.
Sound waves are longitudinal, while light waves are transverse.
Light waves consist of vibrations of the ether at
right angles to the line of motion. To illustrate the reasoning
that has led to this conclusion, suppose a rope to be
passed through two vertical gratings. (See Fig. 411, 1.)
If the rope be set in transverse vibration by a hand, the
waves produced will readily pass through to the gratings
P and Q and continue in the part extending beyond Q.
If, however, Q is at right angles to P, no motion will
be found beyond Q. Now if a stretched coiled spring with
longitudinal vibrations should take the place of the rope,
it is evident that the crossed position of the two gratings
would offer no obstacles to the movement of the vibration.[Pg 445]
In other words, crossed gratings offer no obstruction to
longitudinal vibrations, while they may completely stop
transverse vibrations.
 Fig. 411.—Transverse waves will pass through both gratings in (1)
where the openings in the two gratings are at right angles. The waves
passing P are stopped by Q (2).Fig. 411.—Transverse waves will pass through both gratings in (1)
where the openings in the two gratings are at right angles. The waves
passing P are stopped by Q (2).
Fig. 411.—Transverse waves will pass through both gratings in (1)
where the openings in the two gratings are at right angles. The waves
passing P are stopped by Q (2).Fig. 411.—Transverse waves will pass through both gratings in (1)
where the openings in the two gratings are at right angles. The waves
passing P are stopped by Q (2).
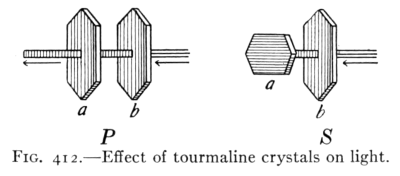 Fig. 412.—Effect of tourmaline crystals on light.
Fig. 412.—Effect of tourmaline crystals on light.
414. Polarization of Light.—It is found that two crystals
of tourmaline behave toward light just as the two gratings
behave with respect to the transverse waves of the rope.
Thus, if a small opening in a screen is covered with a
tourmaline crystal, light comes through but slightly
diminished in intensity. If a second crystal is placed over
the first one so that the two axes are in the same direction
as in Fig. 412P, light is as freely transmitted through the
second crystal as through the first, but if the crystals are
crossed (Fig. 412S) no light passes the second crystal.
This experiment shows that the light which has passed
through one tourmaline crystal will pass through another
only when the latter is held in a certain position, hence it
is believed that a tourmaline crystal is capable of transmitting[Pg 446]
light that is vibrating in one particular plane. The
direct conclusion from this is that light waves are transverse
rather than longitudinal. The experiment just described
illustrates what is called polarization of light. The beam
that after passing through a (Fig. 412) is unable to pass
through b, if the two axes are crossed, is called a polarized
beam. The conclusion that light waves are transverse is
therefore based upon the phenomenon of the polarization
of light. This was first discovered by Huygens in
1690.
Important Topics
1. Interference of light: evidence, reasoning involved, illustration.
2. Polarization of light: evidence, reasoning involved.
3. Nature of light, differences between sound and light.
Exercises
1. Make a list of the differences between sound and light and state
briefly the evidence upon which the knowledge of these differences
is based.
2. Why will a thickness of film that will produce interference of
red light be different from that producing interference for green
or blue?
3. Using the formula n = v/l compute the vibration rate for violet
light if its wave length is considered as 0.00004 cm.
4. Explain how the fact of polarization affects the wave theory of
light.
5. Show how it is possible by comparing the spectrum of the sun
with that of a star to tell whether the star is approaching or
receding from the earth.
Review Outline: Light
Light; speed, source, medium.
Straight Line Motion; shadow, umbra, penumbra, eclipse, image.
Photometry; Law of intensity, candle power, foot-candle.
Mirrors; Law of reflection; image—real, virtual; plane, curved, parabolic,
mirrors.
[Pg 447]
Refraction; cause and effects; plate, prism, lens; total reflection.
Lenses; six forms, principal focus, center, lens equation, 1/F = 1/Do
+ 1/Di.
Optical instruments; eye, defects and correction, camera, microscope,
etc.
Spectra; 3 kinds, dispersion, production of color effects, spectroscope,
uses.
Nature of Light; wave theory, interference, polarization,
significance.
[Pg 448]
INVISIBLE RADIATIONS
(1) Electric Waves and Radio-activity
415. Oscillatory Nature of the Spark from a Leyden
Jar.—In studying sound (Art. 339), the sympathetic
vibration of two tuning forks having the same rate of
vibration was given as an illustration of resonance. The
conditions for obtaining electrical resonance by the use of
two Leyden jars are given in the following experiment.
Join the two coats of a Leyden jar (Fig. 413) to a loop of wire L,
the sliding crosspiece M
being arranged so that the
length of the loop may be
changed as desired. Also
place a strip of tinfoil in
contact with the inner coating
and bring it over to
within about a millimeter
of the outer coating as indicated
at G. Now join the
outer coating of another
exactly similar jar A to a
wire loop of fixed length, the end of the loop being separated from
the knob connected to the inner coating, a short distance at P.
Place the jars near each other with the wire loops parallel and connect
coatings of A to the terminals of a static machine or an
induction coil. At each discharge between the knobs at P, a spark
will appear in the other jar at G, if the crosspiece M is so adjusted
that the areas of the two loops are exactly equal. When the wire
M is moved so as to make the areas of the two loops quite unequal,
the spark at G disappears.
 Fig. 413.
Fig. 413.
The experiment just described shows that two electrical
circuits can be tuned by adjusting their lengths, just as[Pg 449]
two tuning forks may be made sympathetic by adjusting
their lengths. This fact indicates that the discharge of
the Leyden jar is oscillatory, since resonance can plainly
not be secured except between bodies having natural
periods of vibration. This same fact is also shown by
examining the discharge of a Leyden jar as it appears when
viewed in a rapidly revolving mirror. (See Fig. 414.)
The appearance in the
mirror shows that the discharge
is made up of a
number of sparks, often a
dozen or more, vibrating
back and forth until they
finally come to rest. The
time of one vibration varies from one millionth to one
hundred millionth of a second, depending on the space
between the discharging balls and the size of the jars.
 Fig. 414.—Photograph of the oscillatory
discharge of a Leyden jar.
Fig. 414.—Photograph of the oscillatory
discharge of a Leyden jar.
The discharge of a Leyden jar or of another condenser
sets up ether waves that have the speed of light. Heinrich
Hertz in Germany first proved this in 1888. These
waves are now known as Hertzian waves. The length of
these varies from 3 cm. to several miles, depending upon the
size and conditions of
the discharging circuit.
 Fig. 415.—A coherer.
Fig. 415.—A coherer.
416. The Coherer.—The
coherer is a device
for detecting electric
waves. It consists of a glass tube with metal filings
loosely packed between two metal plugs that fit
the tube closely. (See Fig. 415.) These filings offer a
high resistance to the passage of an electric current, but
when electric waves pass through the filings these cohere
and allow a weak current to pass through. This current[Pg 450]
may be strong enough to operate a relay connected
with a sounder or bell that gives audible signals. If the
tube be tapped the filings will be disturbed and the resistance
again made so high that no current can pass through.
417. Wireless Telegraphy.—In 1894 Marconi, then a
young man of twenty, while making some experiments
with electrical discharges discovered that the coherer
would detect electrical waves at a considerable distance
from their source and that by the use of a telegraph key
the "dots and dashes" of the telegraph code could be
reproduced by a sounder attached to a relay. At present
the coherer is used principally in laboratory apparatus,
as much more sensitive detectors are now available for
commercial work. The essential parts of a modern wireless
telegraph apparatus as used in many commercial
stations are shown in Fig. 416.
Alternating current at 110 volts is sent into the primary, P, of
a transformer, the secondary, S, of which produces a potential of
5000 to 20,000 volts. The secondary charges a condenser until
its potential becomes high enough to produce a discharge across a
spark gap, SG. This discharge is oscillatory, the frequency being
at the rate of about one million a second, depending upon the
capacity of the condenser and the induction of the circuit.
These oscillations pass through the primary of the oscillation
transformer, inducing in the secondary, electric oscillations which
surge back and forth through the antennæ, or aerial wires, A. These
oscillations set up the "wireless waves." The production of these
waves is explained as follows: An electric current in a wire sets up
a magnetic field spreading out about the conductor; when the current
stops the field returns to the conductor and disappears. The
oscillations in the antennæ, however, have such a high frequency,
of the order of a million a second, that when one surge of electricity
sets up a magnetic field, the reverse surge immediately following
sets up an opposite magnetic field before the first field can return to
the wire. Under these conditions a succession of oppositely directed
magnetic fields are produced which move out from the antennæ[Pg 451]
with the speed of light and induce electric oscillations in any conductors
cut by them.
While the electric waves are radiated in all directions from the
aerial, the length of the waves set up is approximately four times the
combined length of the aerial wires and the "lead in" connection
to the oscillation transformer.
[Pg 452]
The electric waves induce effective electrical oscillations in the
aerial of the receiving station, even at distances of hundreds of miles,
provided the receiving transformer, RT, is "tuned" in resonance with
the transmitting apparatus by adjustments of the variable condenser,
VC, and the loading coil, L. The detector of these oscillations
in the receiving transformer is simply a crystal of silicon or
carborundum, D, in series with two telephone receivers, Ph. The
crystal detector permits the electric oscillations to pass through it
in one direction only. If the crystal did not possess this property,
the telephone could not be used as a receiver as it cannot respond
to high frequency oscillations. While one spark passes at SG, an
intermittent current passes through the receiver in one direction.
Since some 300 to 1200 sparks pass each second at SG while the key,
K, is closed, the operator at Ph hears a musical note of this frequency
as long as K is depressed. Short and long tones then correspond
to the dots and dashes of ordinary telegraphy. In order to
maintain a uniform tone a rotary spark gap, as shown, is often used.
This insures a tone of fixed pitch by making uniform the rate of
producing sparks.
The Continental instead of the Morse code of signals is
generally employed in wireless telegraphy, since the former
employs only dots and dashes. The latter code employs,
in addition to dots and dashes, spaces which have sometimes
caused confusion in receiving wireless messages.
The United States government has adopted the regulations
of the International Radio Congress which directs that
commercial companies shall use wave lengths between
300 and 600 or above 1600 meters. Amateurs may use
wave lengths less than 200 meters and no others, while the
government reserves the right to wave lengths of 600 to
1600 meters. See p. 459 for Continental telegraph code.
418. Discharges in Rarefied Air.—Fig. 417 represents
a glass tube 60 or more centimeters long, attached to an
air pump. Connect the ends of the tube to the terminals
of a static machine or of an induction coil, a-b. At first
no sparks will pass between a and f, because of the high[Pg 453]
resistance of the air in the tube. Upon exhausting the air
in the tube, however, the discharge begins to pass through
it instead of between a and b. This shows that an electrical
discharge will pass more readily through a partial
vacuum than through air at ordinary pressure. As the
air becomes more and
more exhausted, the
character of the discharge
changes. At first it is a
faint spark, gradually
changing until it becomes
a glow extending
from one terminal to the other and nearly filling the
tube.
 Fig. 417.—An Aurora tube.
Fig. 417.—An Aurora tube.
Geissler tubes are tubes like the above. They are
usually made of different kinds of glass twisted into various
shapes to produce beautiful color effects. The aurora
borealis or northern light is supposed to be electric discharges
through rarefied air at the height of from 60 to
100 miles above the earth's magnetic poles. (See Fig. 418.)
 Fig. 418.—Aurora Borealis.
Fig. 418.—Aurora Borealis.
419. Cathode Rays.—When the tube in Art. 420 is
exhausted to a pressure of 0.001 mm., or a little less than
one millionth of an atmosphere, the character of the discharge[Pg 454]
is entirely changed. The tube becomes filled with
a yellowish green phosphorescent light. This is produced
by what are called cathode rays striking the glass walls of
the tube. These rays are called
cathode rays because they come
from the cathode of the tube.
They are invisible and that they
travel in straight lines is shown
by the shadow obtained by using
a tube with a screen (Fig. 419).
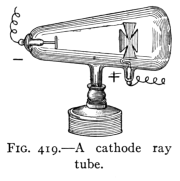 Fig. 419.—A cathode ray
tube.
Fig. 419.—A cathode ray
tube.
420. "X" Rays.—In 1895, Professor
Röntgen of Wurtzburg,
Germany, discovered that when the cathode rays strike
the walls of the tube or any solid within it they excite
a form of invisible radiation. This radiation is called
Röntgen rays, or more commonly, "X" rays. Careful
experiments show that they travel in straight lines, and
that they can not be reflected or refracted as light waves
are. They pass through glass and opaque objects such
as flesh, cardboard, cloth, leather, etc., but not through
metallic substances. The tube in Fig. 420 has a screen
covered with crystals which become luminous when struck
by the cathode rays. On bringing a magnet near the
tube the luminous line is raised or lowered showing that
the magnetic field affects the stream of cathode rays,
attracting it when in one position but repelling it when in
the reverse direction. The cathode rays which cause the
bright line possess a negative charge of electricity. They
are now believed to be electrons shot off from the surface
of the cathode with speeds that may reach 100,000 miles
a second. "X" rays possess no electrical charge whatever
and cannot be deflected by a magnet. They produce the
same effect on a photograph plate as light does, only more
slowly. Hence, they can be used in taking "X" ray[Pg 455]
photographs. Certain crystals, like barium platinum
cyanide, fluoresce when struck by the "X" rays. The
fluoroscope is the name given to a light-tight box closed at
one end by a cardboard covered with these crystals (Fig.[Pg 456]
421). On looking into the fluoroscope with an opaque
object such as the hand placed between the screen and
the "X" ray tube, a shadow of the bones of the hand can
be seen upon the screen of the fluoroscope. (See Fig. 422.)
 Fig. 420.—The stream of cathode
rays is deflected by a magnet.
Fig. 420.—The stream of cathode
rays is deflected by a magnet.
Fig. 421.—A fluoroscope.
Fig. 422.—A view of the "shadow" of a hand as seen in a fluoroscope.
A special form of the tube is used. (See Fig. 423.) In
this tube a platinum disc is placed at the focus of the concave
cathode. This concentrates the "X" rays in one
direction. It is now generally
believed that "X" rays are
waves in the ether set up by
the sudden stoppage of the
cathode rays at the platinum
anode.
 Fig. 423.—An "X" ray tube.
Fig. 423.—An "X" ray tube.
421. The Electromagnetic
Theory of Light.—The study
of electric waves has shown
that they are similar to light
waves in many respects: (a) they have the same velocity;
(b) they can be reflected and refracted. The main difference
is in their length, light waves being very much shorter.
In 1864 James Clerk Maxwell, an English physicist, proposed
the theory that ether waves could be produced by
electrical means and that light waves are electromagnetic.
In 1888 Hertz proved by his experiments that ether waves
having the same velocity as light could be produced in
this way. It is now the general belief that light waves
are ether waves produced by the vibrations of the electrons
within the atoms and that they consist of electromagnetic
waves in the ether.
422. Radio-activity.—In 1896 Henri Becquerel of Paris
discovered that uranium and its compounds emit a form
of radiation that produces an effect upon a photographic
plate that is similar to that resulting from the action of
"X" rays. These rays are often called Becquerel rays in[Pg 457]
honor of their discoverer. The property of emitting such
rays is called radio-activity, and the substances producing
them are called radio-active.
In 1898, Professor and Mme. Curie after an investigation
of all the elements found that thorium, one of the chief
constituents of incandescent gas mantles, together with its
compounds, was also radio-active. This may be shown
by the following experiment:
Place a flattened gas mantle upon a photographic plate and leave
in a light tight-box for several days. Upon developing the plate in
the usual way a distinct image of the mantle will be found upon the
plate.
423. Radium.—Mme. Curie discovered also that pitch-blende
possessed much greater radio-active power than
either thorium or uranium. After prolonged chemical
experiments she obtained from several tons of the ore a
few milligrams of a substance more than a million times
as active as thorium or uranium. She called this new
substance radium. Radium is continually being decomposed,
this decomposition being accompanied by the
production of a great deal of heat. It has been calculated
that it will take about 300 years for a particle of radium
to be entirely decomposed and separated into other substances.
It is also believed that radium itself is the
product of the decomposition of uranium, atomic weight
238, and that the final product of successive decompositions
may be some inert metal, like lead, atomic weight
207.
The radiation given off by radio-active substances consists
of three kinds: (A) Positively charged particles of
helium called alpha rays: (B) negatively charged particles
called beta rays: (C) gamma rays.
The alpha rays have little penetrating power, a sheet[Pg 458]
of paper or a sheet of aluminum 0.05 mm. stopping them.
Upon losing their charges they become atoms of helium.
Their velocity is about 1/10 of that of light or 18,000 miles
a second. The spinthariscope is a little instrument devised
by Sir Williams Crookes in 1903 to show direct evidence
that particles are continually being shot off from radium.
In this instrument (Fig. 424), a speck of radium R is
placed on the under side of a wire placed a
few millimeters above a screen S covered
with crystals of zinc sulphide. Looking in
the dark at this screen through the lens L,
a continuous succession of sparks is seen
like a swarm of fireflies on a warm summer
night. Each flash is due to an alpha particle
striking the screen. The beta rays are
supposed to be cathode rays or electrons
with velocities of from 40,000 to 170,000 miles a second.
The gamma rays are supposed to be "X" rays produced
by the beta rays striking solid objects.
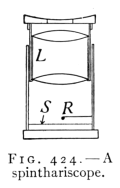 Fig. 424.—A
spinthariscope.
Fig. 424.—A
spinthariscope.
424. The discovery of radio-activity has revolutionized
the ideas of the constitution of matter. Further, the
results of experiments upon radio-active materials reveals
the presence of immense quantities of sub-atomic energy.
If man ever discovers a means of utilizing this, he will
enter a storehouse of energy of far greater extent and
value than any of which he has as yet made use. A
consideration of this unexplored region gives zest to the
work of those who day by day are striving to understand
and control forces of nature.
Important Topics
1. Oscillatory nature of discharge of Leyden jar. Proofs.
2. Wireless telegraphy and telephony.
3. Electrical discharges in rarefied gases.
[Pg 459]
4. Cathode and "X" rays.
5. Electromagnetic theory of light.
6. Radio activity and radium.
 CONTINENTAL TELEGRAPH CODE
CONTINENTAL TELEGRAPH CODE
A . - J . - - - S . . .
B - . . . K - . - T -
C - . - . L . - . . U . . -
D - . . M - - V . . . -
E . N - . W . - -
F . . - . O - - - X - . . -
G - - . P .- - . Y - . - -
H . . . . Q - - . - Z - - . .
I . . R . - .
Period Interrogation Exclamation
. . . . . . . . - - . . - - . . - -
1 . - - - - 2 . . - - - 3 . . . - -
4 . . . . - 5 . . . . . 6 - . . . . 7 - - . . .
8 - - - . . 9 - - - - . 0 - - - - -
[Pg 460]
WIRELESS TELEPHONY AND ALTERNATING
CURRENTS
The developments in wireless communication have been so rapid
during recent years that a more extended account, than that given
in Art. 417 of the apparatus and methods used at the present time,
seems desirable. The study of Alternating Currents is also included
with the idea that it will make the text more complete and of
wider usefulness.
Wireless Telephony
425. The Wireless Telephone.—One of the most
important developments in wireless communication in
recent years has been in wireless telephony. We realize
its possibilities, when we hear of the achievements
of talking across an ocean or between airplanes and the
ground.
The wireless telephone can be best understood by
comparing it with the common telephone. When the
latter is in use, a direct current flows continually through
the instrument. (See Arts. 312-316.) When a person
speaks into the transmitter, the sound waves of the voice
cause the diaphragm to vibrate, this action causes rapid
changes in the resistance of the transmitter, which in turn
causes the direct current to fluctuate just in step with the
pulses of the voice waves. This fluctuating direct current
passes through the primary of an induction coil, producing
in the secondary an intensified alternating current. This
passes over the line wires to the receiver where it produces[Pg 461]
variations in the magnetic field affecting the receiver
diaphragm, causing the latter to reproduce the voice of
the person speaking in the transmitter. Now to make
the comparison clear, two facts must be noted with regard
to the wire telephone: first, there must be an action
in the transmitter which causes variations in a current
through the instrument; second, this fluctuating current
produces a more intense alternating current which flows
over the line and affects the receiver diaphragm, producing
there sound vibrations of greater intensity than those
used at the transmitter. This added energy comes from
the current flowing through the transmitter. The case is
analogous to that of an electric bell. The armature of
the bell vibrates with greater energy than is required
to push the button, the extra energy being derived from
the battery.
426. The Action of the Wireless Telephone.—In the
wireless telephone we have a continuous stream of electric
waves of high frequency. (See Fig. 425A.) This stream
of electric waves corresponds to the current that flows
through the transmitter in the wire telephone. These
waves are of such high frequency that even though we
had a receiver diaphragm vibrating in step with the
waves, we could not hear the sound because the
human ear cannot hear a sound which consists of more
than about 40,000 vibrations per second. The sound
waves act upon this stream of waves very much, as in
the wire telephone, the transmitter acts to modify the
line current. The impulses caused by the voice are
much slower than the electric waves first mentioned
and these slower impulses are reproduced in the receiver.
Not only are these slower impulses reproduced but they
are amplified, that is, produced with greater energy than
the impulses impressed on the stream of waves. Fig.[Pg 462]
425A represents as nearly as is possible in a diagram the
continuous stream of electric waves. Fig. 426B, represents
the impulses produced by the sound alone, and Fig.[Pg 463]
426C, shows how these voice impulses are impressed on
the stream of waves.
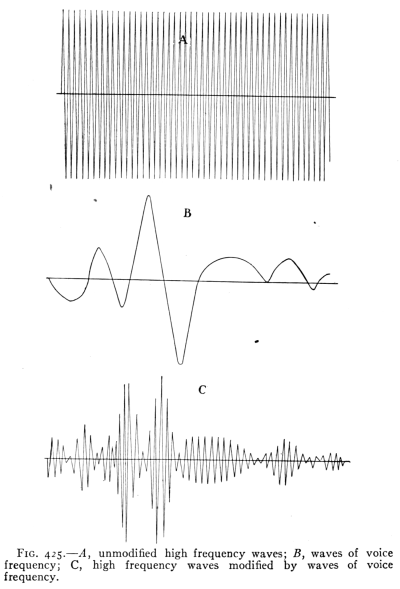 Fig. 425.—A, unmodified high frequency waves; B, waves of voice
frequency; C, high frequency waves modified by waves of voice
frequency.
Fig. 425.—A, unmodified high frequency waves; B, waves of voice
frequency; C, high frequency waves modified by waves of voice
frequency.
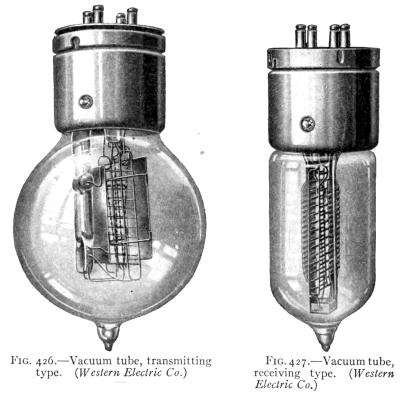 Fig. 426.—Vacuum tube, transmitting
type. (Western Electric Co.)
Fig. 426.—Vacuum tube, transmitting
type. (Western Electric Co.)
Fig. 427.—Vacuum tube,
receiving type. (Western
Electric Co.)
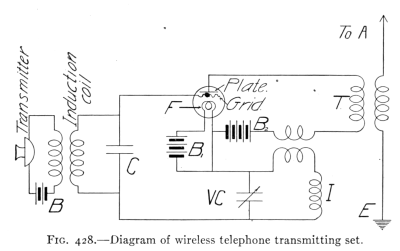 Fig. 428.—Diagram of wireless telephone transmitting set.
Fig. 428.—Diagram of wireless telephone transmitting set.
427. The Vacuum Tube or Audion.—The device by
which all of this is accomplished is the vacuum tube.
(See Fig. 426.) This tube contains three electrodes.
First, a filament (F, in Fig. 428) which is heated by a
current from a battery (B1, Fig. 428) and because it
is heated, sends out a stream of electrons. Second,
the plate which forms the anode of the circuit from
battery, B2. This plate receives the electrons which are
thrown off by the heated filament, hence a current flows
through the circuit of B2; the discharge through the tube
depending on the e.m.f. between the filament and the[Pg 464]
plate. Third, a grid is placed between the filament and
the plate and is connected to the secondary of the induction
coil, the primary of which is connected to the transmitter.
When the transmitter diaphragm is vibrating, the e.m.f.
induced in the secondary of the induction coil causes a
variation in the potential of the grid. This means a
variation in the electric field between the filament and
the plate. (See Fig. 428.) The changing electric field
causes a variation in the discharge of electrons through
the tube; the variation corresponds to the vibrations
of the transmitter diaphragm. This produces a surging
current of the frequency of the sound waves in the primary
of the transformer (T, Fig. 428). The secondary of this
transformer is connected to the antennæ (A) and the earth
(E). By means of the transformer, rapid surgings are set
up in the antennæ and these surgings produce a continuous
stream of electromagnetic waves which goes out in space.
(Like Fig. 426C.) These electromagnetic waves produce oscillations
in the antennæ of a receiving station. The antennæ
transmit the impulses to a tube (Fig. 427) which acts[Pg 465]
as a detector, and makes possible the reproduction of the
sound by an ordinary telephone receiver.
 Fig. 429.—View of wireless telephone set.
Fig. 429.—View of wireless telephone set.
The vacuum tube in the transmitting circuit also amplifies
the impulses, that is, the energy of the waves given out is
greater than that of the impulses which produce them,
the additional energy being derived from the battery
sending current through the plate and filament. In
operation, the filament and the plate are connected to a
battery with a condenser (VC) and an inductance coil
(I) in the circuit, as shown in Fig. 428. Photograph
of a complete modern wireless telephone set is shown in
Fig. 429.
[Pg 466]
Alternating Currents
428. Alternating currents are of interest to us because
of their general commercial use. To understand the
reason for the extensive application of alternating currents
it is necessary to learn the fundamental principles which
pertain to them. The production of such currents has
already been explained in Arts. 300-304. It should be
remembered that the current developed in the armature
of a dynamo is alternating. A dynamo may deliver a
direct or an alternating current, depending on the method
of collecting the current from the armature. If a commutator
is used, the machine delivers direct current,
if slip rings are employed, an alternating current is
delivered.
429. The Magnetic Field of an Alternating Current.—The
magnetic field of a direct current has been considered
in Arts. 255-256. It has been shown to be arranged in
circles about the conductor, according to the Right Hand
Rule. (See Figs. 229 and 230.) These facts will help
one to understand the following experiment:
If a number of magnetic compasses be arranged in a circle about a
straight vertical wire carrying a direct current, the compass needles will
point out a circle about the wire. (See Fig. 430, A.) If now the current be
reversed the compass needles will reverse themselves and point in a direction
just opposite to that taken at first. (See Fig. 430, B.) This will be clear
if you imagine yourself walking around the wire in the direction the compass
needles pointed at first, and then walking around the wire in the
reverse direction. This illustrates what happens in the field of an alternating
current. The field reverses each time the current reverses.
The magnetic field of an alternating current not only
rapidly reverses itself, but also continually changes in intensity.
At the instant when the current reverses, the force of
the magnetic field is zero since the current at that instant
is zero. As the current begins flowing and increases[Pg 467]
to its maximum intensity, the magnetic field appears and
increases in intensity; and as the current decreases to zero,
the magnetic field changes in a similar manner. The
field as it grows in strength extends farther and farther
from the wire, as it decreases in strength it contracts
or draws closer to the wire. Thus the magnetic field may
be said to expand and contract. We may picture the
lines of force as continually moving. In a typical a.-c.
circuit, the complete series of changes takes place in a
small fraction of a second, and is repeated many times
over in a second. Contrast this with the magnetic field
of a constant direct current. Here the magnetic field
has the same direction as long as the current flows and
does not change in strength. This comparison is important
because most of the differences between direct
and alternating currents depend on differences in the
action of their magnetic fields.
 Fig. 430.—Arrangement of compasses about a wire carrying an alternating
current.
Fig. 430.—Arrangement of compasses about a wire carrying an alternating
current.
430. Transformers.—The transformer has been described
in Arts. 309-310. The principle of the transformer
may be illustrated by the following experiment:
A coil having several hundred turns of No. 18 d.c.c. copper wire is
placed over one arm of a "U" shaped iron core (see Fig. 431) and then[Pg 468]
connected to a 110 volt a.-c. lighting circuit. Another coil (S) having about
50 turns of No. 22 d.c.c. copper wire is connected to an electric bell or
buzzer, or a low voltage electric light bulb. When the small coil is held
over the other arm of the "U" shaped iron core, the bell rings or the
bulb glows. It is evident that the electromotive force developed in the
small coil (S) is due to the alternating magnetic field surging back and
forth through the iron core. In Fig. 431 the core is "open" since the
magnetic field must pass through the air from one end of the core to the
other. A typical transformer has a closed core to provide a closed magnetic
circuit. To secure this, take a suitable bar of iron and lay across
the end of the "U" shaped core, and notice any change in the induced
current produced in the small coil, due to increased movement of magnetism
through the closed iron core.
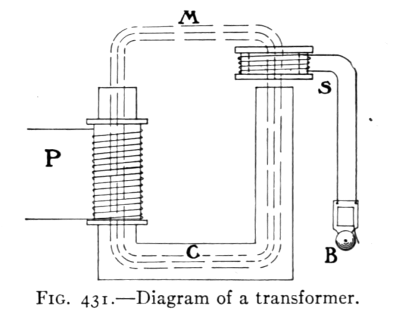 Fig. 431.—Diagram of a transformer.
Fig. 431.—Diagram of a transformer.
This experiment illustrates the construction and action
of a transformer. In a commercial transformer, the two
windings are on a closed magnetic circuit. (See Figs.
304 and 305, p. 346.) To keep the coils insulated, the
transformer is placed in an iron "housing" and covered
with oil. These "housings," or transformer cases are
generally attached to poles near buildings in which alternating
current is used.
431. Voltage Relation in a Transformer.—In the
experiment described above, a bell was rung by an induced
current produced in the secondary coil. The induced
e.m.f. was less than the voltage of the primary coil partly
because there was some magnetic leakage, but mainly[Pg 469]
because there were fewer turns of wire on the secondary.
In a commercial transformer the magnetic leakage is
practically zero. In such a case, the ratio of the number
of turns on the primary coil to the number on the secondary
equals the ratio of the e.m.f. induced in the primary to the
e.m.f. induced in the secondary. Suppose, for example,
we wish to make a bell ringing transformer to use on a
110 volt lighting circuit, 10 volts being required for the
bell; the secondary will then need one-eleventh of the
number of turns of the primary. So that if 550 turns
are on the primary, then 50 turns will be needed for the
secondary. This will be a "step-down" transformer.
On the other hand, suppose we wish to "step-up" the
voltage as is done in a certain power station where the
voltage of the generators is 6000 volts, the voltage being
stepped up to 44,000 by means of large transformers.
This means that the secondary coils have approximately
7-1/3 times as many turns as the primary.
432. Power Loss in a Transformer.—When the voltage
is "stepped up" in a transformer, do we gain power?
To answer this question we must remember that electric
power does not depend on voltage alone but on the product
of e.m.f. and current intensity. (See Art. 291.) By
tests with a.-c. voltmeters and ammeters, we find that
when the secondary e.m.f. is greater than the primary
e.m.f., the secondary current intensity is less than
that in the primary. It is also found that the power
developed is less than the power received by the transformer,
i.e., the "output" is less than the "input" as
we would expect from the law of machines. The power
loss is mainly due to the work required to reverse the
magnetism, that is, to continually reverse the position
of the iron molecules. (See Art. 205.) The energy lost
in this manner is known as "core loss" since it occurs in the[Pg 470]
iron core. The lost energy appears as heat. So much
heat is developed in large transformers that special means
of cooling are provided. In order to make the heat
developed as small as possible, the cores are "laminated"
(see Fig. 305, p. 346), that is, built up of thin sheets of
iron, because if the iron cores were solid, the changing
magnetic fields would induce electric currents in the
iron cores, which would produce an excessive amount of
heat with a correspondingly large power loss.
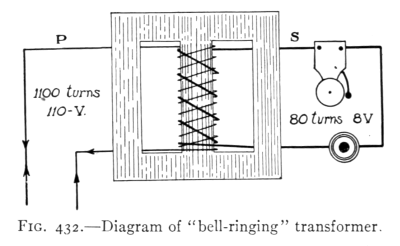 Fig. 432.—Diagram of "bell-ringing" transformer.
Fig. 432.—Diagram of "bell-ringing" transformer.
433. Choke Coils and Inductance.—If we refer to Fig.
432 we see that the primary winding of the bell ringing
transformer is connected across the line. This winding
forms a closed circuit whether the bell is ringing or not.
The resistance of this winding is small. Let us assume
it to be one ohm. With a one ohm resistance connected
across a 110 volt line we might expect a current of 110
amperes. This is certainly what we should get if we were
to connect a one ohm resistance across a line having 110
volts direct. The primary would form a short circuit
if the current were direct. But the fact is that practically
no current flows through the primary winding when the
bell is not ringing. Herein lies one of the important differences
between alternating and direct currents. With
an alternating current the primary winding of our transformer[Pg 471]
acts as a choke coil and "chokes" down the current
almost to zero. Let us see how this is done.
 Fig. 433.—A circuit containing a choke coil.
Fig. 433.—A circuit containing a choke coil.
Let Fig. 433 represent a choke coil. Since alternating
current is used, the magnetic field is continually changing.
Each turn of wire has its own magnetic field. The lines
of force of turn number 1 expand and contract and as
they do so they move across turns 2, 3 and so on. In
like manner the lines of force from each turn of wire move
across the other turns. In other words the coil is cutting
its own lines of force. Now whenever an electric conductor
cuts magnetic lines of force an electromotive
force is induced in the conductor. There is then an e.m.f.
induced in the coil by its own magnetic field. This induced
e.m.f. on the whole opposes the applied e.m.f.;
in the primary of our bell ringing transformer the induced
e.m.f. opposes the e.m.f. of the line to such an
extent as to reduce the current almost to zero. Inductance
is the action of an alternating current in inducing
an opposing e.m.f. in the coil in which the current is flowing.
Since this opposing e.m.f. is induced in the coil by
its own magnetic field this action is also called self-induction.
In a transformer the action of the field of the primary upon
the secondary is mutual induction; while the action of the
field of the primary in choking the current in the primary
itself is self-induction or inductance. A coil having a
single winding and used to introduce inductance in a[Pg 472]
circuit is called a choke coil. A choke coil inserted in a
lamp circuit in series with the lamps dims the lamps
because it reduces the intensity of the current.
 Fig. 434.—Diagram showing graphically an alternating current with a
"lag" of 30° behind its electromotive force.
Fig. 434.—Diagram showing graphically an alternating current with a
"lag" of 30° behind its electromotive force.
Self-induction causes the current to lag, that is, the current
does not quite reach its maximum at the instant the
voltage reaches its maximum. Fig. 434 shows graphically
an e.m.f. and a lagging current. In this figure the maximum
current is shown following the maximum voltage at
an interval of 30 degrees. In other words the armature in
a two-pole field must turn 30 degrees from the position of
maximum voltage before the current in the coil, where the
self-induction occurs, reaches its maximum.
434. Reactance and Impedance.—A choke coil has resistance
as well as inductance. Its resistance can be found
by the voltmeter-ammeter method, using a direct current.
(See Art. 278.) Let us take for example the primary winding
of a bell ringing transformer. Using a direct current
and testing the coil with a voltmeter and ammeter we find
its resistance to be, let us say, one ohm. If we connect the
same coil across a 110 volt a.-c. line we find the current[Pg 473]
to be very small, say 0.05 ampere. The coil now has
resistance and reactance. Reactance is the effect of
self-induction in hindering the flow of current. It is
measured in ohms. The combined effect of resistance
and reactance is called impedance. In the example
above, the coil has 110 (volts)/0.05 (ampere) = 2200 ohms of impedance.
In applying Ohm's law to an alternating current
circuit, impedance must be substituted for resistance.
Ohm's law as applied to an a-c. circuit should be stated:
"Current intensity equals e.m.f. divided by impedance",
or I = E/Z. (Z = impedance.)
 Fig. 435.—The relation between resistance, reactance and impedance.
Fig. 435.—The relation between resistance, reactance and impedance.
Impedance, however, does not equal the sum of resistance
and reactance. The relation between these three
quantities is similar to that between the three sides
of a right triangle, in which the impedance represents
the hypotenuse, and the resistance and reactance the
other two sides. See Fig. 435 which indicates that
Resistance2 + Reactance2 = Impedance2, or (R2 + X2 =
Z2). (X = reactance.) To illustrate this relation; suppose
the primary of a transformer has 10 ohms impedance
and 8 ohms resistance, then the reactance equals 102 - 82
[Pg 474]= 62, or the reactance is 6 ohms.
Exercises
1. Find the reactance of a choke coil having a resistance of 10
ohms, when its impedance is 50 ohms. How great a current flows
through this coil if the terminal voltage is 110 volts?
2. When the bell is ringing, the primary of a bell ringing transformer
has an appreciable current. Suppose this current is 0.2
ampere. What is the impedance if the voltage of the line is 115
volts? What is the reactance if the resistance is 1 ohm?
3. The primary of a large transformer has a terminal voltage
of 6000 volts and a current of 600 amperes. What is the impedance?
If the resistance is 6 ohms, what is the reactance?
 Fig. 436.—A telephone set showing a condenser used in the circuit of the
"ringer."
Fig. 436.—A telephone set showing a condenser used in the circuit of the
"ringer."
435.—The electric condenser (see Art. 231) is a
very useful device in a.-c. circuits; e.g., in telephone sets
used in cities, a condenser is used in the ringing circuit,
as shown in Fig. 436. Alternating current is required to
ring such a bell and a condenser permits an a.-c. current
to act through it, although it entirely prevents the flow of a
direct current. This peculiar action will now be explained.
436. The action of a condenser in an alternating current
circuit may be illustrated by the following experiment.
Connect twelve, 1 m.f. (microfarad) condensers, in parallel,
and then attach them to a 110 volt a.-c. line so that an[Pg 475]
incandescent lamp is in circuit as shown in Fig. 437.
The lamp will be found to glow brightly, although there
is no electrical connection between the two sets of condenser
plates. If the same arrangement is connected to a
110 volt direct current circuit, the lamp does not
glow because it is really an open circuit. The lamp glows
on an a.-c. circuit because, although no electricity flows
through the condenser, it does flow into and out of the
condenser, surging back and forth through the lamp with
sufficient intensity to cause it to glow brightly. When
the a.-c. current moves one way in the circuit, one set
of plates of the condensers becomes charged positively,
the other, negatively. When the a.-c. current reverses,
the charges on the condenser plates reverse. In the
ordinary lighting circuit 120 reversals take place each
second, so that electricity rapidly flows into and out of the
condensers. On removing one condenser after another
from the circuit, the lamp is found to glow less and less,
till when but one condenser is left, no glowing is observed,
since one small condenser does not have sufficient capacity.
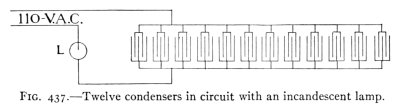 Fig. 437.—Twelve condensers in circuit with an incandescent lamp.
Fig. 437.—Twelve condensers in circuit with an incandescent lamp.
The unit of capacity is the Farad. Capacity is defined
as the quantity of electricity per second that flows into a
condenser when the voltage at the terminals changes at
the rate of one volt per second. If a change of one volt
per second causes one coulomb to flow per second, that
is, a current of one ampere, the capacity is one farad.
The condensers used in the above experiment have a
capacity of one microfarad, or one millionth of a farad.
[Pg 476]
A condenser, on account of its capacity, causes an a.-c.
current to lead the voltage, that is the current reaches
its maximum value before the voltage does. In this
respect a condenser has an effect opposite to that of the
self-induction of a choke coil (the latter causing the
current to "lag"). (See Fig. 435.)
437. Transmission of Electric Power.—A field of
peculiar usefulness for a.-c. currents is in the economical
transmission of electric power. This fact is due to the
following reasons: (a) The loss of electrical power in a
transmission line is due to the production of heat; the
heat produced being proportional to I2R, or to the square
of the current intensity. Any lessening of the current
flow required to transmit a given power will therefore
increase the efficiency of transmission. (b) In order
to employ a small current in transmitting a large amount
of power, we must use a very high e.m.f. Such high
electromotive forces, say from 60,000 to 100,000 volts,
can be obtained only by the use of a.-c. transformers,
since it is not practicable to build a direct current generator
capable of producing 60,000 volts. In large power
transmission systems, a.-c. generators are used to produce
powerful alternating currents. The e.m.f. is then stepped
up to a suitable voltage (2300-100,000) by transformers
and sent over transmission lines to the various places
where the power is to be used; at these places suitable
transformers "step-down" the e.m.f. to a convenient or
safe voltage for use. (See Fig. 442 of a transmission
line and Fig. 438 of a large power transmission system,
and Fig. 439 of an a.-c. generator and power plant.)
 Fig. 438.—Diagram of an alternating current high tension power system. (A) Alternator, (Tu) water turbine,
direct connected to alternator, (E) exciter, (T1) step-up transformers in power station, (T2) step-down
transformers in substation, (M) motor, (L) lamps, single-phase, three-wire system, (T3) step-down transformers
delivering three-phase current to rotary converter (R) which delivers direct current to the trolley line.
Fig. 438.—Diagram of an alternating current high tension power system. (A) Alternator, (Tu) water turbine,
direct connected to alternator, (E) exciter, (T1) step-up transformers in power station, (T2) step-down
transformers in substation, (M) motor, (L) lamps, single-phase, three-wire system, (T3) step-down transformers
delivering three-phase current to rotary converter (R) which delivers direct current to the trolley line.
438. Power Factor.—The power factor is a matter of
interest and importance in the use of a.-c. machines.
Its meaning and use may be learned from the following
explanation: In a direct current circuit, watts equals[Pg 477]
[Pg 478]
volts times amperes. In an alternating current circuit,
this equation is true only when the current is "in step"
with the voltage, that is, only when there is no inductance
or capacity in the circuit. If current and
voltage are out of step, i.e., if there is lag or lead (see
Fig. 434), the product of volts and amperes gives only
the apparent power, the ratio between true and apparent
power depending on the amount of lag or lead. This ratio
is called the power factor. In an a.-c. circuit, then, the
power equation is: watts = volts × amperes × power
factor, or power factor = true power/apparent power.
The product of volts and amperes is the apparent power
and is called volt-amperes in distinction from the true
power or watts. Therefore the following is true: power
factor = true watts/volt-amperes.
 Fig. 439.—Power house showing alternators, direct connected to
horizontal hydraulic turbines. Note the direct current "exciter" on
end of shaft of alternator. (Courtesy of General Electric Co.)
Fig. 439.—Power house showing alternators, direct connected to
horizontal hydraulic turbines. Note the direct current "exciter" on
end of shaft of alternator. (Courtesy of General Electric Co.)
[Pg 479]
439. Single-phase Currents.—There are several kinds
of a.-c. currents. One of the most common is the single-phase.
It is simply the common a.-c. current used for
light and power in the average home, and uses a two-wire
circuit around which the current is rapidly alternating.
Fig. 440 illustrates the changes of e.m.f. in an a.-c. single-phase
current. It may be produced by a single coil
rotating in a magnetic field. The curve of Fig. 440 represents
one cycle, that is, one complete series of changes in
the electromotive forces. At the end of the cycle the armature
is in the same condition as at the beginning so far as
the magnetic field is concerned. It then begins a new
cycle. The ordinary commercial alternating current has a
frequency of 60, that is 60 cycles per second. One rotation
produces as many cycles as there are pairs of poles.
For example, if there are 48 poles in the generator field,
one rotation produces 24 cycles.
 Fig. 440.—Graph showing the e.m.f. changes of a single-phase current
for one "cycle."
Fig. 440.—Graph showing the e.m.f. changes of a single-phase current
for one "cycle."
440. Three-phase Currents.—Now suppose we have
three coils as in Fig. 441, the coils being evenly spaced,
or 120 degrees apart, at A, B, and C. If the coils are
rotated in a magnetic field, each will produce an electromotive[Pg 480]
force. The result produced by three such coils
is called a three-phase current. Ordinarily six wires, or
three circuits, would be required to carry the current produced
by three separate coils; for when coil "C" is in the
90 degree position, where its e.m.f. is a maximum, coil "B"
is 120 degrees past its maximum, and coil "A" is 240 degrees
past its maximum. The graph (Fig. 441) shows the
maximum points of the three e.m.f's. separated by intervals
of 120 degrees. In practice, however, it is found
possible to use three wires instead of six, as explained in
Art. 441.
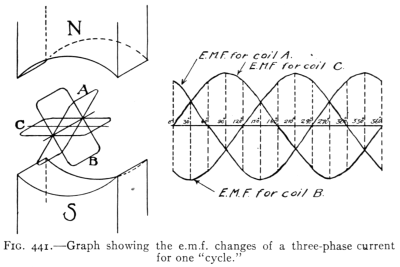 Fig. 441.—Graph showing the e.m.f. changes of a three-phase current
for one "cycle."
Fig. 441.—Graph showing the e.m.f. changes of a three-phase current
for one "cycle."
441. Three-wire Transmission.—The currents produced
in the three coils just described undergo precisely the
same changes as those represented in the graph (Fig. 441)
for the three electromotive forces. Careful examination
of the graph will show that at any point the sum of the
plus e.m.f's. equals the sum of the minus e.m.f's. In
other words the algebraic sum of the three e.m.f's. is
zero. Therefore if we properly connect a transmission
line of three wires to the generator, the sum of the currents[Pg 481]
leaving the generator will equal the sum of the currents
returning to it. Since the algebraic sum of the currents
produced by the three coil combination described in Art.
440 is always zero, it is possible to use three wires on
three-phase transmission lines. Fig. 442 shows a "tower"
carrying three, three-wire transmission lines. Long
distance, high tension transmission lines are generally
three-wire lines carrying three-phase a.-c. currents.
 Fig. 442.—A "tower" supporting three, three-phase circuits of a high
tension transmission line.
Fig. 442.—A "tower" supporting three, three-phase circuits of a high
tension transmission line.
442. Alternators.—A dynamo which delivers alternating
current is known as an alternator. Commercial alternators
have many pairs of poles in the field and as a rule the
field rotates while the armature is stationary. The field
must be supplied with direct current for the polarity of
each coil in the field must remain unchanged. Usually[Pg 482]
a separate "exciter" is used, which is a small direct
current generator. The current from this exciter is fed
into the rotating field by means of slip rings. Fig. 439
shows a d.-c. (direct current) exciter on the end of the
armature shaft of the large alternator.
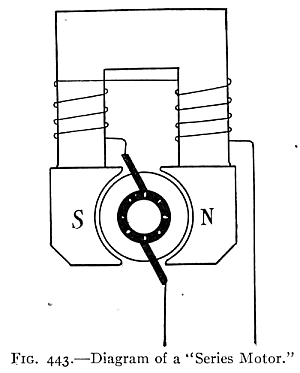 Fig. 443.—Diagram of a "Series Motor."
Fig. 443.—Diagram of a "Series Motor."
443. The A.-C. Series Motors.—The only type of
motor that will run on either alternating or direct current
is the series motor. The "universal" motor used in
household appliances such as electric fans, vacuum
cleaners, etc., is a series motor. The reason a series motor
will run on either direct or alternating current is because
the direction of rotation of the armature of a motor
depends on (a) the direction of the current in the armature,
and (b) the polarity of the field. Reversing either of
these alone, reverses the direction of rotation of the armature,
while reversing both at the same instant leaves
the direction of rotation unchanged. Fig. 443 is a
diagram of a series motor since the field coils and armature[Pg 483]
are connected in series. On an a.-c. line, both field and
armature current must therefore reverse at the same
instant. In a shunt motor (similar to Fig. 286) we have
a divided circuit, and the greater self-induction of the
field coils causes an a.-c. current through these coils to lag
behind that flowing in the armature so that the two
currents do not reverse at the same instant.
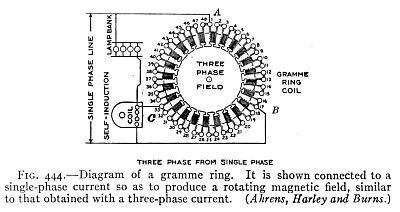 Fig. 444.—Diagram of a gramme ring. It is shown connected to a
single-phase current so as to produce a rotating magnetic field, similar
to that obtained with a three-phase current. (Ahrens, Harley and Burns.)
Fig. 444.—Diagram of a gramme ring. It is shown connected to a
single-phase current so as to produce a rotating magnetic field, similar
to that obtained with a three-phase current. (Ahrens, Harley and Burns.)
 Fig. 445.—The "stator" of an induction motor.
Fig. 445.—The "stator" of an induction motor.
444. The Induction Motor.—Another common type of
a.-c. motor is the induction motor. Its advantage lies in
its simplicity. It has neither commutator nor brushes,
the armature having no connection with an external circuit.
If the wires of a three-phase line be connected
to a coil wound in the form of a gramme ring, the connections
being 120 degrees apart as in Fig. 444, the magnetic
field within this coil will change in the same manner as if a
magnet were spinning upon a pivot at the center of the
coil. Suppose the N pole at one instant is at A, in one-third
of a cycle it moves to B, in another third to C,
and in one cycle it makes a complete revolution. Thus
we have a rotating magnetic field. If a cup of some non-magnetic
metal such as aluminium or copper be placed
on a pivot in the center of this coil, the cup is cut by the[Pg 484]
moving lines of force and currents are induced in it.
Because of these currents, the cup has a magnetic field
of its own, and the action of the two magnetic fields is
such as to pull the cup around and cause it to rotate in the
same direction as that in which the field of the coil rotates.
The coil represents the stationary part, the stator (Fig. 445)
and the cup the rotating part, the rotor, of an induction
motor. While the cup rotates in the same direction, it does
not rotate so rapidly as the magnetic field. If it should it
is plain that it would not cut the lines of force. The difference
between the rate of rotation of the rotor and that
of the magnetic field is called the "slip." The rotating
part in small induction motors is frequently made in a
single casting. In large motors, it is built up of heavy
copper bars. Thus, from its appearance the common form[Pg 485]
of rotor is known as the "squirrel cage" rotor. (See
Fig. 446.)
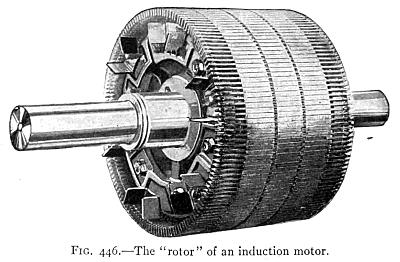 Fig. 446.—The "rotor" of an induction motor.
Fig. 446.—The "rotor" of an induction motor.
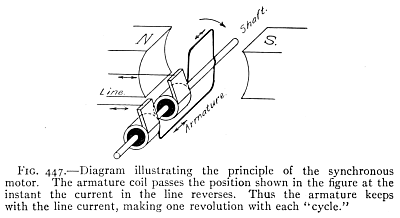 Fig. 447.—Diagram illustrating the principle of the synchronous
motor. The armature coil passes the position shown in the figure at the
instant the current in the line reverses. Thus the armature keeps
with the line current, making one revolution with each "cycle."
Fig. 447.—Diagram illustrating the principle of the synchronous
motor. The armature coil passes the position shown in the figure at the
instant the current in the line reverses. Thus the armature keeps
with the line current, making one revolution with each "cycle."
445. A synchronous motor is one that keeps step with
the alterations of an alternating current. The line current
is fed into the armature by means of two slip rings and
brushes. The principle of the synchronous motor is
illustrated in Fig. 447. This shows a motor having a
two-pole field. The armature current must be reversed[Pg 486]
twice in each revolution. The reversal must take place
when the armature winding is perpendicular to the lines
of force of the field. In a direct current motor this
reversal is brought about by the commutator. In a
synchronous motor the armature reaches the 90 degree
position at the exact instant at which the current reverses
in the line. Thus in the case of a two-pole motor the
armature must make exactly one revolution for each
cycle; it is, therefore, a constant speed motor. Such
motors are frequently employed in converter stations
where alternating current is converted into direct current
by what are called rotary converters.
In practice the synchronous motor has a number of pairs
of field poles. It is essentially an alternating current
generator running as a motor. One of the principal uses
of the synchronous motor is that of a converter, receiving
alternating current and delivering direct current. Synchronous
motors are also used in transmission lines to aid
in maintaining constant voltage.
Important Topics
The wireless telephone, essential parts, action, arrangement.
Alternating currents, alternating fields.
Transformers, voltage relation of coils, power and core losses.
Self-induction, inductance, and coke coils, uses, applications.
Impedance, reactance, and resistance; relation and effects.
Condensers, uses and applications with a-c. circuits.
Alternating current power transmission; uses, advantages.
Power factor, lag, lead, volt-amperes, true watts.
Single- and three-phase currents; uses and nature of each.
Three-wire transmission systems, alternators, construction, and
action.
A-c. motors, series, induction, synchronous.
[Pg 487]
- Aberration, spherical, 408
- Absolute scale of temperature, 164
- Absorptions of gases by solids and liquids, 29
- Accelerated motion, 86
- Acceleration, 87
- Adhesion, 21
- Aeroplane, 97
- Air, aspirator, 67
- brake, 74
- cushion, 46
- height (of atmosphere), 64
- pressure, 56
- pump, 66
- weight, 56
- Alternators, 481
- Alternating current, 337, 466
- Amalgamation, 273
- Ammeter, 291
- Ampere, 291
- Archimedes' principle, 48
- Arc light, 321
- Armature, 335
- Artesian wells, 44
- Audion, 463
- Aurora borealis, 453
- Balloon, 72
- Barometer, 59
- Beats, 376
- Boiling, laws, 208
- Boyle's Law, 63
- Breezes, land and sea, 181
- British thermal unit, 162
- Brownian movements, 16
- Calorie, defined, 162
- Camera, 426
- Candlepower, 394
- Capillary action, 25
- Cartesian diver, 71
- Cathode rays, 453
- Centrifugal force, 91
- Charles' Law, 165
- Chladni's figures, 381
- Choke coils, 470
- Coefficient of expansion, definitions, 170
- Coherer, 449
- Cohesion, 21, 33
- Color, 435
- bodies, 435
- complementary, 436
- primary, 440
- prismatic, 433
- theory of color vision, 440
- three-color printing, 440
- Commutator, 335, 336
- Compass, 230, 240
- Concave lens, 418
- Condenser, 260, 474
- Conductors, 246
- Conservation of energy, 127
- Continental code, 459
- compared with the Morse, 452
- Convection, 179
- currents in nature, 181
- draft of a chimney, 180
- Convex lens, 416
- Cooling, artificial, 210
- Corpuscular theory, 442
- Coulomb, 290
- Couple, 101
- Critical angle, 414
- Crookes' tube, 456
- Crystallization, 28
- melting point of some crystalline substances, 203
[Pg 488]
- Daniel cell, 276
- Declination, 240
- Density, 38, 52
- Dew, 192
- Dew point, 193
- Diffusion of gases, 13
- Dipping needle, 240
- Direct Current, 337
- Dispersion, 433
- Distillation, 208
- Draft of a chimney, 180
- Dry cell, 275
- Dynamo, 330, 333
- Dyne, 93
- Eye, the, 423
- action of, in vision, 423
- defects of, 425
- Ear, the, 386
- Earth's magnetism, 238
- Echoes, 362
- Eclipses, 391
- Efficiency, 142
- engines (tests), 219
- machines, 142
- Elasticity, 31
- Electric bell, 269, 287
- charge, distribution of, upon a conductor, 253
- circuit, 269
- currents, 267
- single phase, 479
- three phase, 479
- discharge in rarefied air, 452
- motor, 339
- screen, 256
- Electrical capacity, 259
- Electrification, 243
- Electrolysis, 308
- Electromagnet, 281
- Electromagnetic theory of light, 456
- Electromotive force, 267
- Electron theory, 252
- Electrophorus, 263
- Electroplating, 307
- Electroscope, 244
- Electrostatic induction, 248
- Energy, 120
- conservation, 127
- falling water, 152
- forms, 125
- human body, 126
- Energy, kinetic, 121
- potential, 120
- transference and transformation, 124
- Engines, 213
- Engines, gas, 222
- Equilibrant, 81
- Equilibrium, 106
- Erg, 119
- Ether, 177
- Evaporation, 18
- Expansion, coefficient, 168
- gases, 167
- liquids, 168
- peculiarity, in water, 168
- solids, 169
- water, on turning to steam, 206
- Falling bodies, 109
- experimental study, 111
- laws, 113
- Floating bodies, 48
- Fluoroscope, 455
- Foot candle, 396
- Force, 79
- dyne, 93
- effectiveness, 134
- graphic representation, 80
- liquid, against any surface, 38
- measuring, 79
- moment, 99
- parallel, 100
- resolution, 96
- units, 83
- Forces, parallel, 100
- Franklin's theory of electricity, 252
- Fraunhofer lines, 439
- Freezing, evaporation, 197, 199
- Friction, 147,
- Friction, laws, 150
[Pg 489]
- Galvanometers, 289
- Galvanoscope, 269
- Gas engine, 222
- Gas meter, 75
- Geissler tubes, 453
- Gravitation, 103
- Gravity, 88, 104
- acceleration due to, 111
- cell, 277
- center of, 105
- Hail, 193
- Hearing, 386
- Heat, capacity for water, 201
- conduction, 173
- constants for transmission, 220
- convection, 179
- effects, 161
- engines, 213, 222
- equivalent of fuels, 219
- fusion, 201
- measurement, 200
- methods of transmitting, 173
- produced by electric current, 318
- radiation, 176
- sources, 159
- units, 162
- vaporization, 205
- work, 212
- Heating of buildings, 182
- direct and indirect radiation, 186
- hot air, 183
- plenum system, 187
- steam, 186
- vacuum steam, 187
- vapor steam, 187
- Hertzian waves, 262, 449
- Hooke's law, 33
- Horse power, 123
- electric equivalent of, 123
- Humidity, 194
- Hydraulic press, 42
- Hygrometers, 194
- Hygrometry, 191
- conditions for saturation, 192
- dew point, 193
- fog, 193
- formation, of dew, 192
- humidity, 194
- hygrometers, 194
- importance, 191
- Hypothesis, 3
- Images, concave mirrors, 405
- construction, 405
- definition, 392
- plain mirror, 401
- small apertures, 391
- Impedance, 472
- Incandescent lamp, 320
- Inclined plane, 143
- Inductance, 471
- Induction coil, 343
- Inertia, 87
- Insulators, 246
- Intensity of sound, 363
- Interference, light, 442
[Pg 490]
- Laws, boiling, 208
- Boyle's 63
- Charles', 165
- electric action, 243
- falling bodies, 113
- floating bodies, 48
- gravitation, 104
- Hooke's, 33
- induced currents, 326
- intensity of light, 394
- Lenz's, 328
- liquid pressure, 37
- machines, 131
- magnetic action, 229
- motion, 87
- Ohm's, 298
- pendulum, 116
- reflection, 399
- refraction of light, 411
- vibration of strings, 378
- Lenses, achromatic, 434
- effect on light, 417
- equation, 421
- formation of images, 418
- forms, 416
- Leclanché cell, 275
- Lever, 132
- Leyden jar, 261
- oscillatory nature of the discharge, 448
- Light, compared with sound, 388, 444
- electromagnetic theory, 456
- intensity, 394
- interference, 442
- polarization, 445
- rectilinear propagation, 389
- reflection, 396
- total reflection, 413
- Lightning, 254
- Lines, of force, 233
- Liquids, pressure, 36
- Local action, 273
- Luminous and illuminated bodies, 388
- Machines, 129
- advantages, 129
- cannot create energy, 130
- efficiency, 142
- law, 131
- mechanical advantage, 134
- the six simple, 132
- uses, 129
- Magnetic action, 229
- fields, 233, 466
- induction, 231, 236
- permeability, 237
- poles, 229
- properties, 230
- retentivity, 231
- substances, 230
- effect of electric current, 279
- Magnetism, 228
- Magnetism, theory, 232
- Major and minor triads, 369
- Magneto, 328
- Magnetoscope, 230
- Magnets, 228
- Major scale, 366
- Manometric flames, 382
- Matter, 4
- effect of heat, 5
- molecular theory, 5
- properties, 34
- states of, 4
- states of, defined, 5
- Mechanical advantage, 134
- Megaphone, 365
- Melting points, 203
- Mercury arc rectifier, 347
- Metric system, 8
- Microscope, 427
- Mirage, 414
- Mirrors, 400
- Molecular motion in liquids, 18
- in gases, 13
- in liquids and solids, 27
- in solids, 31
- Molecules, motion, 16
- Moment of force, 99, 133
- Momentum, 87
- Motion, 85
- accelerated, 86
- curvilinear, 88
- direction, 86
- first law, 87
- modes, 85
- second law, 92
- third law, 93
- uniformity, 86
- Motor (electric), 339
- A. C. series, 482
- induction, 483
- synchronous, 485
- Muffler, 224
- Musical instruments, 377
- interval, 368
- nomenclatures, table, 369
- Musical sounds, characteristics 364
- Newton's Laws of motion, 87
- Nodes, in pipes, 384
- Noise and music, 363
[Pg 491]
- Ohm, 294
- Ohm's Law, 298
- Opera glass, 428
- Optical illusions, 390, 404
- instruments, 423
- camera, 426
- eye, 423
- microscope, 427
- opera glass, 428
- prism field glass, 429
- projecting lantern, 427
- telescope, 428
- Organ pipes, closed, 384
- Oscillatory discharge, 448
- Osmosis, 19
- Outline Review,
- current electricity, 325
- force and motion, 118
- heat, 227
- induced currents, 353
- light, 446
- magnetism and static electricity, 266
- sound, 387
- work and energy, 158
- Overtones, 379
- Pascal's principle, 41
- Pendulum, compound, 115
- Pepper's ghost, 404
- Permeability, 237
- Phonograph, 383
- Physics, definition, 4
- Photometer, 394
- Photometry, 393
- Pitch, 365
- Polarization, of light, 445
- Portraits,
- Bell, 431
- Edison, 285
- Faraday, 331
- Galileo, 89
- Gilbert, 217
- Helmholtz, 397
- Huygens, 397
- Joule, 217
- Kelvin, 331
- Marconi, 431
- Morse, 285
- Newton, 89
- Potential, 257
- Power, 123
- electric, 316
- power factor, 476
- transmission of electric, 476
- water, 152
- Pressure, air, 56
- Pressure, definition, 37
- effect on liquids and gases, 62
- law of liquid, 37
- Prism field glass, 429
- Projecting lantern, 427
- Proof-plane, 244
- Pulley, 139
- Pumps, air, 66
- condensing, 67
- water (lift, 68, force, 69)
- Quality of musical tones, 380
- Radiation, 176
- Radio-activity, 457
- Radiometer, 177
- Radium, 457
- Rainbow, 436
- Reactance, 472
- Reflection, light, 396
- Refraction, 410
- cause, 412
- index, 412
- light, 410
- in plates, prisms, and lenses, 413
- Resolution of forces, 96
- Resistance, cells in series, and parallel, 302
- conductors, 293
- in series and parallel, 299, 300
- unit, 294
- volt-ammeter method for finding, 304
- Resonance, 371
- Resonator, 373
- Resultant, 81
- Retentivity, 231
- Right hand rule, 279
- Rotary converter, 486
[Pg 492]
- Science, definition, 2
- Screw, 144
- Shadows, 390
- Single phase currents, 479
- Siphon, 70
- Siren, 366
- Solidification, change of volume during, 203
- Solutions, 27
- Sound, compared with light, 388
- interference, 374
- media, 355
- nature, 356
- reflection, 360
- rule for finding velocity, 367
- source, 354
- speed, 355
- transmission in air, 359
- Specific heat, 200
- method of determining, 201
- Spectroscope, 438
- Spectrum, 433
- Spherical aberration, 408
- Spinthariscope, 458
- Stability, 108
- Standpipe, 46
- Static and current electricity compared, 287
- Steam engine, 213
- Storage battery, 312
- Stress and strain, 94
- Sublimation, 199
- Surface tension, 22
- Sympathetic vibration, 372
- Telegraph, 283
- Telephone, 349
- Telescope, 428
- Temperature, 162
- Tempered scale, 370
- Theory, 3
- Thermometer, air, 167
- centigrade, Fahrenheit, 163
- gas, 167
- Thermos bottle, 176
- Thermostat, 188
- Three-color printing, 440
- Three-phase currents, 479
- Three wire transmission, 480
- Torricelli's experiment, 57
- Trade winds, 182
- Transformer, 345, 467
- Turbine, steam, 225
- Vacuum cleaner, 76
- Velocity, 86
- Vibration strings, 378
- Visual angle, 424
- Viscosity, 20
- Volt, 295
- Voltaic cell, 270
- advantages, 274
- amalgamation, 273
- local action, 273
- polarization, 273
- simple, 270
- Voltmeter, 295
- Water wheels, 152
- Watt, 123, 317
- Wave theory, of light, 442
- Waves, beats, 376
- interference, 374
- longitudinal, 358
- sound, 358
- transverse, 358
- visible, 357
- Wedge, 144
- Weight, 104
- Wheatstone bridge, 304
- Wheel and axle, 136
- Wind instruments, 383
- Wireless telegraphy, 450
- Work, 119
FOOTNOTES:
Transcriber's note:
This book uses B.T.U. and B.t.u., electrophorous and electrophorus,
e.m.f. and E.M.F. and this has been left as written.
Hyphenation is also left as written, e.g. electro-plated and
electroplated.
On page 324, Exercise number 8 was not used in the original. The
exercises have not been renumbered.
 (See p.441)
(See p.441)