Title: A New Century of Inventions
Author: James White
Release date: June 15, 2013 [eBook #42951]
Most recently updated: October 23, 2024
Language: English
Credits: Produced by Chris Curnow, Harry Lamé and the Online
Distributed Proofreading Team at http://www.pgdp.net (This
file was produced from images generously made available
by The Internet Archive)
Please see Transcriber’s Notes at the end of this text.
Note that all Plates the text refers to may be found at the end of the book (starting here), as in the original work. For ease of reading, (parts of) the plates have been copied to that part of the text where they are described. The Plates at the end of the book provide links to larger scale plates (not available in all formats); many reference letters will only be visible in these larger scale plates.
By JAMES WHITE, Civil Engineer.
Connoissons le principe—
Nourrissons nous des Elemens.
Girard Syn. fr.
Manchester:
PRINTED FOR THE AUTHOR, BY LEECH AND CHEETHAM, WRIGHT’S-COURT, MARKET-STREET.
AND SOLD BY
W. AND W. CLARKE, MARKET-PLACE; E. THOMSON, MARKET-STREET; T. SOWLER, ST. ANN’S-SQUARE, MANCHESTER.
G. WILSON, 49, ESSEX-STREET, STRAND; LONGMAN, HURST, REES, ORME, AND BROWN, PATERNOSTER-ROW, LONDON.
AND BY THE PRINCIPAL BOOKSELLERS IN THE UNITED KINGDOM.
1822.
Entered at Stationers’ Hall.
It has been my lot, during a long and eventful passage through life, to have my attention forcibly drawn to a multitude of Mechanical Subjects; the present review of which permits me to hope, that in making them publicly known, I should render an important service to the Arts and to Society. But the manner of doing this has been so long a question with me, that I have sometimes feared my ability would be extinct before I could do it at all. The reasons, however, that urge me to make the attempt acquire strength with the lapse of time: and whenever my declining health bespeaks the approach of that “night in which no man can work,” I feel deep regret, that this tribute should not have been thrown into the treasury of human knowledge while yet, by the favour of a good Providence, the means of doing it were more fully at my disposal.
I have determined therefore to publish these Inventions. Not because they have been matured into a regular System of Mechanical truth;[iv] but because they consist of many distinct objects of immediate application:—coupled with some ideas of a more comprehensive nature, that may probably extend the usefulness of this admirable study, in the hands of Artists yet unborn.
The form, or rather the title of this work, has but one example, that of the illustrious Marquis of Worcester; whose name may, perhaps, prolong the remembrance of mine: an event the rightful anticipation of which, I confess, would give me pleasure. Not that I either covet or regard what is commonly called popular applause: but the approbation of the wise and good I do regard, and aspire to obtain; since that alone seems to fulfil the adage—“Vox populi vox dei.”
On the subject of our respective Inventions, my views are somewhat different from those of the Noble Marquis; whose description of his labours, as the custom then was, seems chiefly calculated to excite the desire of knowing them better: whereas my wish is to infuse, at once, the knowledge of my subjects into every head capable of receiving it.
This Work then, treats less of Theory than Practice. What are called Principles in Mechanics, are, and must be, founded on numerous suppositions; to present which to “the mind’s eye” requires often a forest of signs, which some readers will not, and others can not penetrate; so that, for many, Theory might as well not exist. This evil is increased when, as it sometimes happens, these suppositions are laid so far from reality, as to leave the result, though correctly deduced, further from the truth than the point to which a sound understanding unassisted by science, would have carried it. To this extreme discrepance of views between theoretical and practical men, may be ascribed their well-known antipathy to each other—in indulging which, they are alike to blame! since no theory inconsistent with fact can be complete; nor any fact be adduced, that a perfect theory will not account for and confirm.
Happily these discussions do not affect my present purpose. For although I shall offer nothing contrary to sound theory, I do not consider that as my subject; but make it my business to[vi] present rational methods of producing useful effects.—In other words to describe these Inventions as connected with immediate Practice. And if, hereafter, it should become desirable to resume the discussion of any principle relating to these subjects, I shall cheerfully enter upon it; but hasten, mean while, to do what seems more important—to place the subjects themselves beyond the danger of being wholly lost, whatever may befall me in the course of those events which are still among the secrets of Heaven.
In the pursuit of knowledge, in general, it is often desirable to trace it from its upper source; and to know all the circumstances that have attended its progress, down to the very moment when it falls under our observation. Nor is it a matter of indifference to examine the minutest form which talent assumed, in the young mind whose subsequent efforts have engaged our attention, or gratified us with more varied and solid productions. In this view I have presumed to think myself justified in commencing this Work, by a succinct reference to those feeble efforts which[vii] marked my first steps in this career. Young I then was, and my musings puerile indeed! But they were original: they were the links of a chain which time has not yet snapt asunder—and of which my honoured Father saw the connection with my subsequent labours, long before I thought, myself, of any thing but working for the purposes of amusement; or, in the childish phraseology, of “playing at work.”

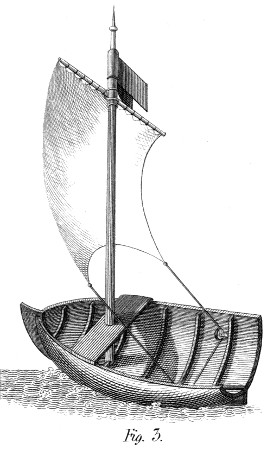
Should any reader then enquire what were my first avocations? the answer would be, I was (in imagination) a Millwright, whose Water-wheels were composed of Matches. Or a Woodman, converting my chairs into Faggots, and presenting them exultingly to my Parents: (who doubtless caressed the workman more cordially than they approved the work.) Or I was a Stone-digger, presuming to direct my friend the Quarry-man, where to bore his Rocks for blasting. Or a Coach-maker, building Phætons with vaneer stripped from the furniture, and hanging them on springs of Whalebone, borrowed from the hoops of my Grandmother. At another time, I was a Ship Builder, constructing[viii] Boats, the sails of which were set to a side-wind by the vane at the mast head; so as to impel the vessel in a given direction, across a given Puddle, without a steersman. (See Plate 2. Fig. 3.) In fine, I was a Joiner, making, with one tool, a plane of most diminutive size, the [relative] perfection of which obtained me from my Father’s Carpenter a profusion of tools, and dubbed me an artist, wherever his influence extended. By means like these I became a tolerable workman in all the mechanical branches, long before the age at which boys are apprenticed to any: not knowing till afterwards, that my good and provident Parent had engaged all his tradesmen to let me work at their respective trades, whenever the more regular engagements of school permitted.
Before I open the list of my intended descriptions, I would crave permission to exhibit two more of the productions of my earliest thought—namely, an Instrument for taking Rats, and a Mouse Trap: subjects with which, fifty years ago, I was vastly taken; but for the appearance of which, here, I would apologize in form, did I not hope the considerations[ix] above adduced would justify this short digression. If more apology were needful.... Emerson himself describes a Rat-trap: and moreover, defies criticism, in a strain I should be sorry to imitate! my chief desire being to instruct at all events, and to please if I can: without, however, daring to attempt the elegant Problem, stated and resolved in the same words—“Omne tulit punctum, qui miscuit utile dulci.”

The town of Cirencester (my native place) is intersected by several branches of the river Churn, whose waters are pure and transparent, and whose banks, formerly, were much perforated by the industry of the Rats that had made them their residence. These holes had generally two openings; one at or near the surface of the ground, and the other near the bottom of the river: so that the rats could range the fields from the former, and dive into the water from the latter—where they were often seen gliding along the bottom, either up or down the stream. The Instrument for taking them in these circumstances, was no other than my Father’s Walking-stick, (represented at A. Fig. 1.[x] Plate 2.) connected with the curve B by the joint C; the curve having a string fastened to it, which, passing through the body of the stick, rose to the hand at D, for the purpose of closing the fork at the proper moment. The Machine, thus constructed, was put over the rat’s back while in the act of diving; and by pulling the string C D, he was sufficiently pinched to be drawn out of the water, where a Dog stood ready to dispatch him.
On the Mouse-trap (Fig. 2. and 4.) more thought was bestowed. It appeared adviseable (I remember) to lay the deceptive plan rather deep: and to lull the little animal into a false security till the snare had taken full effect; and even then to hide from her some of its horrors till she was far enough from this vestibule of misery, not to deposit there any of those tokens of distress that might deter other mice from following her example. The trap then, consisted of a long passage, formed spirally round the surface of a Cone, like the figures we have of the Tower of Babel. This passage is uncovered in Fig. 4 to shew the entrance E, and the subsequent gates F G H, &c. which like the valves of a pump, gave easy entrance to the victim, but forbade her return. At the length[xi] of a mouse from the outer gate E, was placed the first bait N, say a small rind of cheese, well toasted to allure, but nailed down to prevent its removal. Its position was further indicated by a train of meal reaching from it to the outer gate E; which latter was nicely hung on pivots inclined a little to the perpendicular, so as to open with ease but never fail to close itself again. It had besides an horizontal plate O, fixed to its bottom on the inside, so that if the mouse attempted to open it that way, she trode on this plate and destroyed the result of her own efforts.
When, therefore, the little wretch had passed this barrier, she was in reality taken: but unconscious yet of danger, she nibbled the first bait with pleasure, and then skipped forward in search of more substantial food: but to obtain this she must pass more of these faithless gates, F G H, &c. which with progressive effort she opened, and at length found the inner compartments replete with good things, on which she fed to satiety, and then only began to think of her situation. Nor yet, with much alarm: for at the end of this labyrinth, so easy of access, she hoped to find an easy exit. But alas, these[xii] hopes were illusive. Instead of light, she found the dark gallery O; the least evil of which was to be too narrow for two mice abreast, since it overhung a tremendous cavern, Q, that entirely occupied the Cone below, and was filled with water deep enough to drown her, were she to fall, or be jostled into it. And one of these disasters she could hardly escape! for other mice would not fail to be beguiled into this cruel Bastille; to reach the same spot; and finally, to plunge her into this watery grave.
Having endeavoured to recollect the substance of these youthful attempts to unite cause and effect, or to fulfil a given purpose by preconcerted means, I now turn to things of greater importance, and more worthy to be the theme of my readers’ attention. The subjects to be presented will observe a miscellaneous order; since they have not only originated at different periods, but offer likewise different degrees of interest—to equalize which throughout the Work, appears a desirable attempt. As to the manner of treating each subject, it will be, generally, to describe the Machines by a reference to the Figures; and then to add some remarks on their date, construction, properties, and uses.
A NEW CENTURY OF
Inventions.
Dynamics being a science that relates to bodies in motion—comprehending not their weight only, or their velocities only, but the product of the one by the other; so the Dynamometer is a mean of measuring both these circumstances together, and thus of making known the momentum of a power or resistance in motion. As this Machine has a connection more or less intimate with almost every other, it seems entitled to the first place in this collection. Its description follows:
In Plate 3, Fig. 1 and 3, M M, represent two cheeks, standing parallel to each other, and forming a cage or frame by means of the cross bars E and the nuts F G. A P, Fig. 2, is the principal axis of the Dynamometer, fixed to the wheel R N of which it is the centre of motion. It has a square end A, formed to receive the wheels and other supplemental parts, to be mentioned below. After the square A, comes a bearing E, to fit the steps in the frame; and beyond the wheel R N is a cylindrical part O, fitted to the hollow axis T of the wheel or frame I K, (Fig. 4); and in fine the form P of this shaft fits and turns in the cannon of[16] the axis B H, of the wheel C D; so as, when put together and connected with the frame I K, to assume the form C R F G of the third figure. L P, Fig. 3 and 4, are two intermediate wheels (thus placed to balance each other on the common centre T) whose axes turn on proper steps in the frame I K; and which by their teeth connect the motion of this frame with that of both the wheels R N, and C D.
Such are the parts of the Dynamometer properly so called; and they are shewn as in their places in Plate 1, where the parts above described, as far as visible, are marked with the same letters. Moreover, this figure shews a scale-bason P, to receive the weights used to measure equable powers, as will be seen hereafter.

Plate 4 contains some of the auxiliary parts of this Machine. But before we proceed to describe them, it may be proper to observe that the measuring power, by the action of which at K, (Plate 1) the energy of the force is transmitted to the resistance, must, to meet every case, be susceptible of change, according as the resistance or force to be measured is uniform or convulsive. For example, in a mill grinding corn, driven by a fall of water, the whole process is sensibly uniform, and a weight at P is the proper measurer. But if it were desired to measure the effect of a pump driven by water, or of a tilt hammer worked by a Steam Engine, then the measuring power at P must be a spring: for in these cases the vis inertiæ of[17] a weight would add to its force of gravity when suddenly raised, or detract from it when the resistance should suddenly give way. Whenever therefore, the force and resistance are both equable, a weight will best measure them; and when either is convulsive, a spring: but a spring so equalized as to offer the same resistance at every degree of tension it may have to sustain.
In the 6th. and 7th. Figures, (Plate 4) these demands are fulfilled. The first represents a barrel-spring, similar to that of a watch, but surrounded by a fusee, the increasing radii of which compensate for the increased tension of the spring in the barrel G; so that the action of the system on the chain is always the same.
The 7th. Figure exhibits a spring adapted to heavier purposes. It is a cylinder nicely bored and hermetically closed at bottom; in which works a Piston P plunged in oil, which when forcibly drawn up forms a vacuum in the cylinder, into which the atmosphere endeavouring to enter, acts like a spring on the Piston; and preserves the same stress whatever be the height of this Piston in the cylinder.
This then, is also an equalized Spring, such as these experiments require; but it is not my invention. I first saw a vacuum used, as a spring, by my noble Patron, the late Earl Stanhope: to whose mechanical attainments, I owe this tribute of applause on the present occasion.
In the three Figures of this Plate, 8, 9, 10, are shewn two of the means I use for creating those factitious resistances that are sometimes wanted in the process of measuring power. In Fig. 8, E H F, is a gripe or brake, such as millers use to stop their wind-mills with; fixed under L, it surrounds the wheel E H, and is then fastened to the end F of the lever K L. The brake is thus pressed with greater or less force against the wheel, as the weight I is placed more or less distant from the fulcrum L of the lever. By these means a resistance of the equable kind is produced, capable of being adapted to any power it may be wished to measure; which makes this Dynamometer a real tribometer or measurer of friction.
The second kind of resistance brought forward in this Plate, is a Pendulum P (Fig. 9 and 10,) set a vibrating by a pallet-wheel A B, connected with the axis of resistance; and working in the pallets N. It appears besides, in the Figure, that the times of vibration can be changed by the mechanism T N R, which raises or lowers the ball P. This then, is another resistance, such as we sometimes want: but it is also a mean of finding the quantity of resistance that a vibrating body opposes to motion, when oscillating in times not those due to its length as a pendulum. In other words it is a mean of measuring vis inertiæ itself—which an astounding modern writer declares does not exist!
I hasten to give a description of certain other parts relating[19] to the measuring system: and some methods of connecting with the Dynamometer the several kinds of forces it may be desirable to examine.
In Plate 5, Fig. 12, A X represents a Crank or Handle with a variable radius, the intent of which is to adapt a man’s strength to the velocity and intensity of any resistance he may have to overcome. The manner is this: B is a Screw pressing on the quadrant, and fixing the arm C X to any required angle with the part A C: thus determining the virtual radius of the handle.
Fig. 14, shews a method of applying to the Machine the force of a man pumping: for the catch N permits the handle O to rise alone, but carries round the wheel R, at every downward stroke, while the fixed catch C secures all the forward motion thus given. The same Figure shews, at B, the force of a man in the act of rowing: for the catch M permits the lever V M to recede when the man fetches his stroke, and carries the wheel round when he takes it. An operation, by the bye, which I think the best mode of employing human strength, if every possible advantage is taken of the method.
The 13th. Figure shews the last method I shall now offer of adapting power to the Dynamometer. T S represents the Piston of a Steam Engine, the rod of which is formed of two bars, including between them the chains F G and F D, the first of which is single, merely to carry back the acting wheel; and the[20] last double, to draw round the ratchet wheel E, by the catch O, at every stroke of the Piston.
I must obviate here an objection that may strike some readers. This Piston T S, acts only one way, like that of an atmospheric engine, a thing now quite out of date! I answer that this figure is chiefly intended to give the idea; and shew a rotatory Steam Engine that might act without a fly. I will add, that it is my intention some day to bring forward a method of using these suspended actions, better than by a mere ratchet wheel: and especially without incurring danger from the length of the ratchet teeth, or the blow they suffer at the beginning of the strokes. But of this more hereafter.
A short description will suffice for the mechanism of the 18th. figure (Plate 6), which is intended to convert the alternate pressure of a man’s feet into rotatory motion, and then to measure his power. To do this two catches A B, take into the teeth of the same wheel M, and each catch carries an arm, P, embracing somewhat stiffly the boss of the wheel. The treadles have a common centre at E, and are fastened to the same rope going over a pulley, F, so as for the depression of the one to raise the other. Again, the pulling bars C D, are connected with the treadles, and from the form of the catches, it is evident (since the levers move with some stiffness), that the first effect of an ascending motion will be to draw the rising catch out of the teeth, and keep it out until arrived at its greatest height; when[21] the very beginning of its descending motion will bring the catch into the teeth again, and thus carry round the wheel at every downward movement of the treadle;—a method this of making a ratchet work without rattling upon the wheel.
The mechanism shewn in figure 19, is intended to produce another of our factitious resistances; and it serves likewise to make experiments on the resistance of the air. It is a fly, meeting with an equable resistance as does the fly in the striking train of a clock. The wheel W, is put on the axis of resistance of the Dynamometer; and its teeth geer in those of the vertical shaft L H. This latter is perforated from above, and has an open mortice all along its body, which a small bar penetrates, meeting at bottom the ring H, to which it is fastened by a pin going through the mortice. Again, this ring H, is moved, downward, by the rollers of the sliding bracket P, which has its motion from the wheel and rack G: and finally, the leaves I K slide in the horizontal frame; and when the machine turns would obey the centrifugal force and fly outward; but are withheld by the cords N O, which passing over the pulleys N O, and under those L M, are then fixed to the frame above L. When, now, this Machine is used, and the fly made to revolve swiftly, the leaves I K, oppose a certain resistance to the rotatory motion; and if this be too feeble, the key G must be turned backward, which will permit the ring H to rise, and the wings I K to recede from the centre. But if this resistance is already too strong, the key G must be turned forward, and the wings brought nearer: between[22] which extremes, a point will easily be found where the resistance of the air will expend just power enough to balance that brought into the Dynamometer through the power-axis; and thus to keep the measuring weight in the position required for any given experiment.
There remains only one part to be described as belonging to this Machine. It is represented in Plate 5, fig. 15, and is a graduated bar, made to fit in the holes K, of the measuring cylinder I K Plate 1: and to carry one of the arcs A A, which thus serves to extend, virtually, the radius of that cylinder to any required dimension.
It is now time to shew something of the manner of using this Dynamometer in the measurement of forces. Let the object then be to measure the power expended by a Horse in drawing a Carriage.
To do this, we fix a Drum (see fig. 16,) of equal radius with the measuring cylinder, on the power axis A; and a similar Drum to the resisting axis H. After firmly fixing the Machine, we place the Carriage at a distance behind it in the plane of the Drum H; and carry a rope from that Drum to the Carriage: on the other hand, we fill the first Drum A, with a coil of rope, to which the Horse is harnessed; and while he travels in the plane of the Drum A, the scale P (Plate 1,) is loaded with weights, until the Carriage follows the horse’s motion without[23] any (or with little) agitation to the scale P: at which moment the power employed is equal to one half the weight at P, multiplied by the space gone through both by the Horse and the Carriage.
If it were now desired to find the power of a man turning a crank or handle, we should take that given in the figure 12, and fix it to the power-axis A. We should also take the fly-system shewn in fig. 19, and place it on the axis-of-resistance H. Then causing the man to turn the Machine, we should put twice as much weight into the scale P, as his strength was thought able to bear. Then if he thought the work too heavy, we should draw inward the leaves of the fly, and take away part of the weight P, until the man were satisfied he could work with convenience: and when, as before, the weight P should overcome the resistance of the fly I K, without either rising or falling, (sensibly) then the power expended would be one half of the weight P, multiplied by the space described by the man’s hand in the act of turning the handle.
It may occur to some of my readers that in these experiments the whole effect is not actually measured: since the space described by the horse or the man’s hand, must be determined after the experiment. I answer that these quantities, necessarily variable, must bear an inverse proportion to the weight P: and in all cases, this weight multiplied by that space, must give the power or momentum required. Besides, it is most easy to add a piece[24] of mechanism that shall count the number of turns, and express them in space, by the inspection of a graduated scale. Nor need we stop here. The duration, in time, of any experiment, may also be recorded by the Machine itself. These are things so naturally connected with the subject, that I cannot feel it necessary, with so much before me, to attempt exhausting them. But this I engage to do: if any serious difficulty should actually stop any reader in this career of investigation, I will obviate such difficulty at some convenient future period. And mean while those persons who have aptitude for such subjects, will find in this Machine, ample scope for extending their enquiries; and comparing many mechanical realities with the deductions of Theory, thus amending and conciliating the conclusions both of Theory and Practice.
I have said above, that the weight or spring acting on the measuring cylinder at K, must be equalized: but in reference to some applications of this Machine to real use, I would modify that precept a little. I should, indeed, always like the principal action to be of a constant nature: with a supplementary part of less intensity, prepared to add something to the former; and this, for the purpose of meeting spontaneously the case of any unexpected addition of the moving power. Thus in Plate 1, if P be a weight nearly adapted to a given resistance, I would (to prevent accident, from its being overraised by any sudden jerk of the power,) hang one or more heavy chains under the scale, which drawn from the ground to a certain length, would add[25] a known quantity to the measuring power; and transmit with a certain softness to the work, the unequal action of the mover.
One word on the friction of this Machine. All friction must of course be avoided as much as possible; but as it will be nearly the same in every class of experiments, it is not of great importance. The same may be said of the vis inertiæ of the parts, in convulsive motions. The parts would, of course, be made as light as a proper strength would permit. My mechanical readers will easily supply these small items of foresight; to anticipate the whole of which would make this Work interminable.
Although this invention does not properly constitute a new Spring, yet it produces effects both new and important. It protracts almost indefinitely the action of a barrel Spring, and thus reduces considerably the number of wheels in a clock or other spring-driven machine. This effect is produced by setting the two ends of the spring at variance; or making them act one against another: for as these opposite tendencies can be made nearly equal, one end of the spring will be wound up almost as much as the other end runs down: thus prolonging the effect in any desired proportion. It will be making known the principle, to describe the first motion of a clock founded upon it.
In Plate 7, fig. 1, A is the spring barrel, to which is fixed a wheel, B, of 96 teeth, working in C, a pinion of 17. E is another wheel of 92 teeth, working in F, a pinion of 22: both pinions being fixed on the same arbor, I G. The smaller wheel E, turns on a round part of the axis H D; and is connected with its motion in the backward direction only, by a ratchet wheel R, fixed on a square part of the same arbor. As usual, this latter has a cylindrical boss within the barrel A, to which the inner end of the spring is hooked; as its outer end is, to[27] the rim of the barrel; and thus does the wheel B (when the clock is wound up) tend to turn forward as shewn by the arrow B; while the wheel E, tends to turn backward in the direction of E, the second arrow. But these opposite tendencies are not equal; because the wheel B is larger, and acts disadvantageously on C, the smallest pinion; while the wheel E is smaller, and acts to advantage on the larger pinion F: so that there is a decided tendency in the whole to turn backward. Now, to find precisely what is the effect of that tendency, we observe that when the barrel and the larger wheel B, have made one revolution round the common axis H D, the pinions C and F will both have made 96⁄17 of a revolution (being the quotient of the division of the wheel B by the pinion C:) and since the larger pinion of 22 teeth, works in the smaller wheel of 92 teeth; this latter wheel in the same time will have made 96⁄17 of 22⁄92 of a revolution, or 1,350 of a turn very nearly. The difference then between this quantity and unity, namely the decimal 0,350, is what the spring has really gone down during one turn of the barrel. And as the whole number of coils in the spring are 10, the number of turns of the barrel to uncoil it entirely, will be 10⁄0,350 or 10000⁄350 equal to 28,57 nearly: instead of ten revolutions which it would have been on the common principle.
It is almost superfluous to add that this prolongation of the time might have been greater, had I not been confined to the above numbers, for want of others more nearly alike, and having a common difference, on my engine.
An important remark here presents itself, viz. that the best properties of this invention are unattainable by the use of the common geering—the friction of whose teeth would have absorbed the small rotatory tendency thus retained; and in which system, also the working diameters of the wheels could not have been defined with sufficient exactitude. This then, is one of the cases in which (as I have observed in a former work) my late Patent System of Geering has “given rise to machines that could not have existed without it,”—which it does by possessing exclusively the property of realizing (sensibly) the whole calculated effect; and working without commotion or assignable friction. It may please some of my readers to be informed that this System, and the means of executing it in every dimension, will hold a prominent place in some future page of this essay.
Referring again to the figure 1, the teeth X X, Y Y, are there placed to give a first idea of this principle: and they are unaccompanied by others, to avoid the confusion of lines that would have arisen from attempting to shew all the teeth, in their due position, on so small a scale. These things will claim all our attention when the System itself comes under examination.
The above representation of this Machine may leave a technical difficulty on the minds of clock makers relative to the winding up of this spring; which, in the present state of things, will suspend, for the time, it’s action on the pendulum: for in[29] order to effect it, (in a reasonable number of turns) the introduction of the key must, by a proper check-piece, be made to stop the wheel B, and leave it again at liberty when the key is taken out: in which case ten turns of the key will effect the winding, although the Machine should be calculated to give out forty turns in the uncoiling of the spring. But if the wheels B and E had changed places; that is, if E had been fixed to the barrel A, and B been connected with the ratchet wheel R, then the act of winding up would have taken place in the opposite direction; or in that which tends to keep up the motion of the pendulum, in which case, however, the machinery of the clock must have borne the whole stress of the spring during the act of winding, instead of the small portion it sustains when the two ends counteract each other.
But I anticipate another objection to this method of employing a barrel spring: which is the inequality of stress, when the spring is much or little wound. The answer is, that many clocks and watches are made to go well without fusees; either by modifying the thickness of the springs, or employing only a few of the middle coils. My Invention may, perhaps, help to nurse this System to perfection: if not, its influence will be the more confined, but in no wise destroyed.
A B, Plate 7, fig. 2 and 3, is a ring or wheel fixed to the frame C D; and having all round it’s inside, teeth directed to the centre. F is a wheel of half the diameter, and exactly half the number of teeth of the wheel A B. It turns on a Crank-arm, E F, whose radius is equal to one quarter of the diameter of the fixed wheel A B—in the centre of which the axis of this Crank finds it’s due position. The latter, therefore, so conveys the wheel F round the inside of the fixed wheel A B, that the teeth of both are constantly geering to a proper depth: and a stud being fixed on the face of the wheel F, opposite the middle of any tooth, a, directly over the centre of the Crank E, this stud describes the perpendicular diameter of the large wheel: and will either receive motion from the rod R of a Steam Engine Piston, so as to give the fly I K, a rotatory motion; or communicate to a Pump-piston a reciprocating motion, drawn from the rotatory one of the fly, when that is the effect desired to be produced.
This Invention will be remembered, as having procured me a remunerating Medal from the late Napoleon Bonaparte, then first Consul of the French Republic. That period, however,[31] (1801) was not the real date of this production, although then first made public. I have proof, on the contrary, of its existence with me several years before; and it is generally ascribed to me by the publicists. I might quote in particular Doctor Gregory: who likewise mentions its having been executed by Messrs. Murray and Wood, of Leeds, subsequently to it’s exhibition at Paris. The Doctor commits, however, a small error in calling me an Anglo-American; but this is accounted for by my then living in a country where to be an Englishman was itself a crime! and where some kind friends, wishing to hide me from the relentless decrees of the day, felt justified in using this sort of pious fraud in my favour: a resource from which, though I did not authorize it, I reaped no small advantage; and still think of with gratitude, though not with unmixed approbation.
I think it a duty more imperious than agreeable, to expostulate a little with Messrs. Lanz & Betancourt, on their apparent partiality in giving an account of this Machine. In their work on the construction of machines, art. 97, page 37, they make M. de la Hire the inventor of it, by the terms in which they introduce his treatise on Epicycloids: and they leave me the thread-bare merit of having “presented a model of this movement at the last exposition but one,” &c. Now, although I do not attach great importance to this kind of misrepresentation, I cannot but observe, that neither my Machine or their description of it can be called a Theorem! nor especially a theorem relating solely to the Epicycloid, as M. de la Hire’s was. These[32] Gentlemen knew that he insisted principally on the application of this curve to the teeth of wheels, with which my Invention has nothing to do. On the contrary, my Machine is a combination of two curves at least, on which de la Hire says absolutely nothing. Is this then inadvertency? or is it uncandid nationality? I hope, the former.
A further remark on the utility of this System as a first motion, may be of use in this place. It respects the geering of the fixed and moveable wheels A B, and F, on the perfection of which depends the truth of the statement, that the stud, a, describes a diameter of the large wheel. Now, perfection is too much to be expected from common teeth when of the necessary strength; so that my Patent Geering is an indispensable complement to this Invention: as by its use, the principle is made practically true; this line becoming really straight, and this motion, under proper circumstances, being unattended with noise or commotion. In a word, I cannot move a step in this mechanical field, without meeting with instances where the new System shews its superiority to the old: whence it becomes a duty for me to commence the consideration of this subject in the very next part of this publication.
These Pulleys have been frequently described since I first entered my specification at the Patent Office. The Authors of the Encyclopedia Britannica; the Rev. Mr. Joyce, in his juvenile philosophy; and Dr. Gregory in his mechanics, have all adverted to them. In the latter work, I find the following quotation from my own description, thus introduced:
A very considerable improvement in the construction of pulleys has been made by Mr. James White, who obtained a Patent for his Invention, of which he gives the following description: “Fig. 4, Plate 7, of this work, shews the Machine, consisting of two pullies, Q and R; the former fixed, the other moveable. Each of these has six concentric grooves, capable of having a line put round them, and thus of acting like as many different pulleys having diameters equal to those of the grooves. Supposing then, each groove to be a distinct pulley, and that all these diameters were equal, it is evident, that if the weight 144 were to be raised by pulling at S, till the pulleys touched each other, the first pulley must receive the length of line as many times as there are parts of the line hanging between it and the lower pulley.[34] In the present case there are 12 lines, b, d, f, &c. hanging between the two pulleys, formed by its revolution about the six upper and six lower grooves. Hence as much line must pass over the uppermost pulley as is equal to 12 times the distance of the two. But, from an inspection of the figure, it is plain that the second pulley R S, cannot receive the full quantity of line by as much as is equal to the distance betwixt it and the first. In like manner, the third pulley receives less than the first, by as much as is equal to the distance between the first and the third; and so on to the last which receives only 1⁄12 of the whole: for this receives it’s share of line n, from a fixed point in the upper frame which gives it nothing: while all the others in the same frame receive the line partly by moving to meet it, and partly by the line coming to meet them.”
“Supposing now these pulleys to be equal in size, and to move freely as the line determines them, it appears from the nature of the system, that the number of their revolutions, and consequently their velocities, must be in proportion to the number of suspending parts, that are between the fixed point above-mentioned, (n) and each pulley respectively. Thus the outermost pulley would go twelve times round in the time that the pulley under which the part n of the line passes, (if equal to it) would revolve only once; and the intermediate times and velocities would be a series of arithmetical proportionals of which, if the first term were[35] l, the last would always be equal to the whole number of terms. Since then, the revolutions of equal and distinct pulleys are measured by their velocities, and that it is possible to find any proportion of velocity on a single body running on a centre, viz. by finding proportional distances from that centre; it follows, that if the diameters of certain grooves in the same body be exactly adapted to the above series, (the line itself being supposed inelastic and of no magnitude) the necessity of using several pulleys in each frame will be obviated, and with that some of the inconveniences to which the use of the common pulley is liable.”
“In the figure referred to the coils of rope, by which the weight is supported, are represented by the lines a, b, c, &c. a is the line of traction commonly called the fall, which passes over and under the proper grooves, until it is fastened to the upper frame just above n. In practice, however, the grooves are not arithmetical proportionals; nor can they be so, for the diameter of the rope employed must be deducted from each term, without which, the small grooves to which the said diameter bears a greater proportion than to the larger ones, will tend to rise and fall faster than the latter, and thus introduce worse defects than those which they were intended to obviate.”
“The principal advantage of this kind of pulley is, that it destroys lateral friction, and that kind of shaking motion which are so inconvenient in the common pulley; and lest, says[36] Mr. White, (I quote Dr. Gregory) this circumstance (of a long pin) should give the idea of weakness, I would observe, that to have pins for pulleys to run upon, is not the only, nor perhaps the best method: but that I sometimes use centres fixed in the pulleys, and revolving on a short bearing in the side of the frame, by which strength is increased, and friction much diminished: for to the last moment of duration, the motion of the pulley is circular, and this very circumstance is the cause of it’s not wearing out in the centre as soon as it would, assisted by the ever increasing irregularities of a gullied bearing.—These pullies when well executed, apply to Jacks and other Machines of that nature with great advantage: both as to the time of their going and their own durability: and it is possible to produce a System of pulleys of this kind, composed of six or eight parts only, and adapted to the pocket, which by means of a skain of sewing silk, would raise more than a hundred weight.”
There are several real and solid advantages attending the use of this pulley; some of which are only hinted at in this description. I have thought, therefore, it might be useful to introduce here an account of some trials which the System underwent a few years ago at Portsmouth,—at the request of an Officer of the Navy, who had re-invented it with some ingenious additions to my ideas. Not being at present in correspondence with that Gentleman, I hardly think myself at liberty to mention his name; but fully so to give an extract from the report which followed these experiments—in which the superiority of the[37] System in respect of power, is made evident, although some less favourable circumstances prevented its adoption on that occasion.
“With a view to comparison, it was settled with Lieutenant S. that his blocks should be made to correspond with the treble and double 16 inch blocks of a 24 gun ship, which carry a 41⁄2 inch rope. The sheeves in the new blocks are fixed upon the pin, revolving therewith, and are of different diameters proportioned to the velocity of the parts of the rope that pass over them; they are also reeved with a double rope so that there are two grooves of each size, the diameter of the smallest groove in this tackle being 28⁄12, and of the largest 15 inches. The diameter of the sheeves of the common blocks would have been (as usually made) 91⁄8 to the bottom of the grooves, but were reduced at the request of Lieutenant S. in the treble block to 81⁄8, and in the double block to 87⁄8, in order that the sum of the diameters of the sheeves in each tackle should be the same. The Lieutenant intending in the first instance, to have used a roller under the pin, for the purpose of diminishing friction, but afterwards laying aside this idea on account of it’s complication, was the reason that he had not made his sheeves in the same proportion with the common blocks: the weight and length of the respective blocks are as follows:
| Weight. | Length. | ||||
|---|---|---|---|---|---|
| Lieutenant S.’s | treble blocks | 131 | lbs. | 24 | Inches. |
| Common | ditto | 78 | „ | 16 | „ |
| Lieutenant S.’s | double block | 73 | „ | 21 | „ |
| Common | ditto | 60 | „ | 16 | „ |
| Lieutenant S.’s | single block | 22 | „ | 17 | „ |
| Common | ditto | 34 | „ | 16 | „ |
“Lieutenant S.’s blocks were reeved with a 21⁄2 inch double rope, and the common block with a 41⁄2 inch single rope, and both tackles suspended from a beam, and their respective falls let over the single blocks, so as to keep the weight applied as a power, just clear of the weight to be lifted, thus forming a power of six to one; the following experiments were made:
| Weight very slowly lifted. |
Power required with Lieutenant S.’s blocks. |
Power required with the common blocks. |
|---|---|---|
| ℔s. | ℔s. | ℔s. |
| 336 | 88 | 124. |
| 672 | 169 | 252. |
| 1344 | 312 | 448. |
| 2688 | 588 | 808. |
| 5376 | 1101 | 1344. |
“After reeving the common blocks with a 31⁄2 inch rope in lieu of a 41⁄2 inch rope, it was as follows: 5376 1101 1232.
“It must be observed, that the double 21⁄2 inch rope in Lieutenant[39] S.’s blocks, is not of equal strength with the single 41⁄2 inch rope first used in the common blocks; and that his blocks had an undue advantage in the first experiment over the common blocks, in respect to the pliability of the rope. The rope should therefore, be taken larger in the one or smaller in the other case, on this account: The common blocks were reeved in the last experiment, with a 31⁄2 inch rope, which is as near as may be of the same strength as the double 21⁄2 inch rope.
“In these experiments it was observable, that the tar was much more squeezed out of the parts of the rope that passed over the smallest sheeves in Lieutenant S.’s blocks, than out of those passing over the larger sheeves, or out of those passing over the sheeves of the common blocks; by which, as well as by the nature of the thing, we judge that with blocks requiring such small sheeves, the ropes would be more crippled and broken than by the common blocks, especially if any constant strain or weight in motion, as on ship board, should be held by them. In regard to our opinion of the merits of the blocks proposed by Lieutenant S. compared with common blocks, we beg leave to submit, that the mechanical principle of them is very inviting, and it is not to be wondered that an ingenious person should pursue the idea; yet allowing there would be a saving of power, which is attained in so great a degree with the common blocks, but considering the greater complication, weight, and expence of[40] these blocks, and their greater disposition to cripple the ropes, we do not perceive any application of them on ship board, for which we could recommend them in preference to common blocks; neither do we perceive any purposes on shore, for the services of the dock yards in which to recommend their application in preference to the other powers in use.”
To this account of the result of these experiments, I beg leave to add what seems to be a great improvement of this System: namely, a method by which the diameters of the larger pulleys are considerably lessened; and thus the principal, if not the only objection, obviated. It has been before observed, that the larger pulleys, as Q R, are the ultimate terms of an arithmetical progression, beginning at unity; and that consequently they cannot be very small, even though the first terms should be so. If a first pulley were only one inch in diameter, the twelfth pulley would be twelve inches,—where we see a large and inconvenient difference. But this evil I now obviate, by placing at the beginning of the series, one or more loose pulleys, over which to reeve the cord, before the concentric or fixed grooves begin; thus lowering the ratio of the progression, and keeping the larger pulleys within bounds. For example, the smallest fixed pulley (supposed as before, to be one inch in diameter) I now make the second of the series instead of the first: and therefore, the second fixed pulley is to the first as 3 to 2, instead of being as 2 to 1; for the same reason, the third fixed pulley is to the second as 4 to 3; and[41] in a system of 12 pulleys, (with one loose one) the respective terms will be as follows:
| Terms | 1 | — | 2 | — | 3 | — | 4 | — | 5 | — | 6 | — | 7 | — | 8 | — | 9 | — | 10 | — | 11 | — | 12 |
| loose; | 2⁄2; | 3⁄2; | 4⁄2; | 5⁄2; | 6⁄2; | 7⁄2; | 8⁄2; | 9⁄2; | 10⁄2; | 11⁄2; | 12⁄2 |
or 6 inches for the largest pulley, instead of 12 inches given by the last progression.
So likewise, if we take two loose pulleys, (which will not add much to the complication of the Machine) and make the third term 1 inch, the fourth will become 4⁄3, shewing the ratio of the progression to be 1⁄3, so that the series of 12 terms will stand thus:
| Terms, | 1 | — | 2 | — | 3 | — | 4 | — | 5 | — | 6 | — | 7 | — | 8 | — | 9 | — | 10 | — | 11 | — | 12 | |
| loose; | loose; | 1; | 4⁄3; | 5⁄3; | 6⁄3; | 7⁄3; | 8⁄3; | 9⁄3; | 10⁄3; | 11⁄3; | 12⁄3; | or, |
four inches for the largest groove in the concentric part of the System.
Now we saw before, that the first and last pulley were in diameter to each other, as 1 to 12; whereas, here, with only two loose pulleys, these extremes are but as 1 to 4: dimensions much more convenient and manageable. The 5th. figure of the Plate 7, is intended to shew graphically, the effect of this modification of the principle. In that figure, if the line a, be the diameter of the first pulley, that of the sixth pulley will be shewn by the line b c; but if the same line a be made the second pulley, the diameter of the sixth will be shewn by the line e d; only 2⁄3 of the former. And in fine, if the same a, be the third pulley, the sixth will have it’s diameter reduced to the line f g,[42] only one half of what it was in the first case. In a word, the more loose pulleys are put before the fixed ones begin, the nearer to cylindrical will the general form become; and the more conveniently may pulleys be used for general purposes. I might even assert, that if one, or at most two loose pulleys had been used in the above-mentioned experiments, the result would have been as favourable to the System, with respect to the weight of the tackle and stress on the ropes, as it was in respect of power; where it’s advantages were important and undeniable.
This Wheel (see Plate 8, fig. 1,) is technically called a Bucket-wheel. It is plunged almost entirely in water, oil, mercury (or other heavy fluid) contained in the vessel A B. It’s axis carries a waved wheel a b, on which rolls a friction-pulley p, running on a pin in the mortice of the bar c d. This bar works the pump f; which by the descent of it’s loaded Piston, drives cold air (or gas) into the tube g, communicating with several collateral ones placed across the vessel, so as to convey the air to h, below and beyond the centre of the wheel. A fire being made at F under this vessel, the water (or other fluid) is brought to a proper heat; and if then the pump f, be made to give a stroke or two, air will be forced from the tubes at h, which having been heated in the passage, will bubble up into the buckets h, i, k, &c. and turn the wheel so as to perpetuate it’s own supplies from the Pump, and furnish a surplus of power for other purposes. This results from the fact, that air (for example) in rising to the temperature of boiling water, expands, under the pressure of the atmosphere, to about three times the volume it occupied at the mean temperature: so that it resists the entrance into the vessel as unity, and acts (when[44] heated) as 3: leaving a power of two, in the form of a rotatory motion.
It will occur to many readers, that azotic gas or nitrogen, might be used with advantage to turn this wheel: only adding to the Machine a long returning tube, leading from the top of the vessel, through air or water, to the suction valve of the pump f; and that in order to bring down the temperature of the gas from the heat it had acquired in the vessel, to the mean temperature; at which this gas is said to occupy only 1⁄7 of the space it fills when at the heat of boiling water.
I have now to observe that this invention was executed in 1794, of which abundant proof remains. Since then, it has been proposed by other persons, and is I think, patentized either in France or England: but a different method is employed of introducing the cold air, namely an inverted screw of Archimedes, whose manner of working I do not entirely recollect. What I here wish to observe is, that this concurrence of idea between others and myself, gives me no pain; since it would be more strange if it did not happen, while so many active minds are ransacking nature for the very purpose of unveiling her secrets. Only I think it incumbent upon me to use every method, consistent with truth and honour, to avoid being thought unjust enough to purloin other people’s ideas, and call them my own.
This Machine is represented in Plate 8, fig. 2 and 3. It is composed of two barrels A B, both of them forming part of the column of water to be raised; connected together by a crooked tube C, of equal diameter, out of which the lower Piston-rod passes through a stuffing box into the air: as does the upper Piston-rod at D, where the column leaves the Pump to pass upward. The two Pistons fixed to the rods E and F, are of the bucket kind; made as thin and light as possible; their valves opening upwards and their motions being such, generally, that when one of them is drawn up, the water rises through the other, then descending: But here lies both the novelty and utility of this Machine; these upward and downward motions are not reciprocal: Both Pistons fall faster than they rise, and thus leave an interval of time when they both rise together; during which their valves, respectively, close by their own weight before the column of water falls upon them. In such manner, indeed, that the column never falls at all. By this important arrangement, the work is constantly going on, and no commotion occurs to absorb Power uselessly, or to destroy, prematurely, the Machine; circumstances which constantly attend every Pump Machine acting by merely reciprocal motion.
This non-reciprocity then, I produce by several methods; one of which (perhaps the most easily understood) is that shewn in fig. 2: There, A B are two friction-rollers, made as large as possible, rolling on the curves C X, the ascending and descending parts of which are essentially unequal. For example, the rising part of the curve occupies 2⁄3 of the whole circumference; and the falling part 1⁄3 only; so that both curves recede from the centre at the same time, during 1⁄6 of a revolution, at the two opposite positions, A C and X Y. Applying then, these curves and levers to the Pump-barrels represented in fig. 3, we obtain that continuity of uniform motion, which is necessary to doing the greatest quantity of work with the least power; and to securing the greatest durability of the Machine. Having hinted at a minimum of power, I must add here that this Machine appears to promise that result, much more credibly than any reciprocating pump whatever; especially if to this continuity of motion we add a certain largeness of dimension that shall produce the required quantity of water, with the slowest possible motion of each particle; and even here this continuative principle helps us much; since pistons and valves of the largest dimensions may be used without introducing any convulsive, or (what is synonymous) any destructive effects.
One particular remains to be noticed in fig. 2. It relates to the means by which the perpendicularity of the motion in the Piston-rods is secured. The arcs M are portions of cylinders having the bolts Z, for their centres, and which, rolling up[47] and down against the perpendicular plane O N, secure a similar motion to the bolts. The tenons P, are cycloidal, on their upper and lower surfaces; and work in square or oblong holes in the plane N O, being kept in their holes by the action of the two springs on a pin let through these tenons: and thus is the motion of the point Z of the levers M B, a perpendicular one; and that of the friction rollers A B, very nearly so.
My object in this work, is to make known the principles, and some of the forms of these Inventions, but my limits will not permit their being dilated on; else I could give several more useful forms of this Machine: but, to make room for other subjects, I must hasten forward—reserving to some future period, many hints respecting the adaptation of those ideas to particular cases. Those of my readers who love to speculate on the doctrine of permutations, will anticipate how much may be done by the combination of a hundred Machines with each other: and they will give me credit for detached items of knowledge—useful in themselves, though too minute to be severally brought forward. Should, however, the degree of patronage I have already experienced, be proportionably extended as the work advances, I can and will follow it up with many useful hints, tending to shew the extent of some of my present subjects, and the amplitude of the sphere in which they roll.
It should be observed, in concluding this article, that the present Machine was executed in France, in 1793, and also[48] proposed to the Government, as a substitute for the celebrated Machine of Marly. In the report then published, it was preferred to the whole multitude of former projects; but left in equilibrio with one modern Machine,—a competition which prevented it’s adoption for the moment—and indeed till I was glad to escape the notice, instead of courting the favour of the then rapidly succeeding governments.
Let A, Fig. 4 Plate 8, be the barrel-wheel of a Clock, or other Machine, already in use, and driven by a weight; and let the similar barrel B be added to the former; the motion of both being connected by the unequal wheels C D. The rope or chain E F, is then led from the barrel A under the pulley P to the barrel B: By which arrangement, when the weight has occasioned one revolution of the barrel and wheel A C, those B D, will have made a lesser portion of a revolution in the ratio of the wheel C and D; (namely as 22 to 24,) and that motion will have taken up 11⁄12 of the line which the barrel A has given off. By these means, the motion of the whole may be prolonged almost indefinitely. This System may appear to some persons open to the objection that the friction of the wheels C D, will absorb so much of the power, as to leave the rotatory tendency too feeble for it’s intended purpose. But I again take refuge in the well proved property of my patent geering,—of not impeding (sensibly) the motion of any Machine in which it is used.
Should it further be suggested, that this is only an awkward parody on the differential wheel and axle, ascribed by Dr. Gregory[50] (in the introduction to his work, page 4,) to the celebrated George Eckhardt: I would answer, that I made that invention also; though doubtless after Mr. Eckhardt; and especially after the date of the figure given by the Doctor, as coming from China, “among some drawings of nearly a century old;” Of course then, I do not pretend to priority of invention: but truth herself authorises me to say, that I did invent this Machine also, in the night between the 17th. and 18th. of January, 1788, and drew it in bed by moonlight, that it might not escape me! It was the result of a previous fit of close thinking: and of the conclusion I then drew, that in whatever way, slowness of motion is obtained by the connection of two movements, power is invariably gained for the same reason, and in the same proportion. The fact is, that all my ideas respecting differential motions, have flowed from this source; as will be evident to the attentive reader of these pages.
It is a known property of an angle such as g d f (plate 9 fig. 1) when touching two fixed points g f, and gliding from one of these points to the other, to describe a portion of a circle g d f. My object in this instrument is to determine, by inspection, the radius of such circle in all cases.
To do this, I connect with the jointed rule m d n, another rule like itself but shorter g e f, so as that the figure g d e f shall be a perfect parallelogram: and I then say that knowing the distance of the points d and e, (the distance d f being given) I know the radius of the circle of which g d f is a portion. To prove this, a little calculation is necessary: In the circles A B and a b (fig. 6) draw the lines E D; f d, d g, g f, g e, and g D; and bearing in mind the known equation of the circle, let d n = x, g n = y; and g D = a, the absciss, ordinate, and radius respectively. The equation is 2ax - x² = y²: from which we get a = (y² + x²)/2x the denominator of this fraction being the line d e. But further its numerator (y² + x²) is equal to the square of the chord g d of the angle E D g, which chord I call c. This gives a = c²/(line d e); from which equation we derive this proportion[52] a : c ∷ c : line d e; Putting then the chord c = 1 (one foot for instance) this proportion becomes a : 1 ∷ 1 : 1/a; whence we draw this useful conclusion, that, whatever portion of a foot is contained in the line d e, (expressed by a fraction having unity for its numerator) the radius of the circle will be expressed in feet by the denominator of that fraction. Thus if the line d e, be 1 inch or 1⁄12 of a foot (and the line g d or d f be 1 foot) the radius of the circle will be 12 feet; and so for every other fraction. Now in the instrument itself the two points d and e, are connected by a micrometer-screw (not here drawn) of the kind described in a subsequent article, and by which an inch is divided in 40,000 parts, each of which therefore is the 1⁄3333.33, &c. part of a foot: so that if the distance d e, were only one of these parts, we should produce a portion g d f of a circle of 3333.33, &c. feet radius—being more than half a mile.
I had omitted to observe, that the points or studs, against which the rulers m n slide, to trace the curve (by a style in the joint d,) that these studs I say are fixed to a detached ruler o p, laid under the parallelogram on the paper, and having two stump points to hold it steady: one of the studs being moveable in a slide, in order that it may adapt the distance f g, to any required distance of the points d e: We note also that the dotted curve g d f is not the very circle drawn, but one parallel to it and distant one half the width of the rulers. In fact the mortices of these rulers are properly the acting lines, and not their edges. I expect, for several reasons, to resume the subject of this instrument before the work closes.
My principal inducements for giving this Wheel the form represented, by a section, in fig. 3, (see Plate 9) were to save horizontal room; and to gain speed by a Wheel smaller than a common horse-walk,—and yet requiring less obliquity of effort on the part of the horse. With this intention, the horse is placed in a conical Wheel A B, more or less inclined, and not much higher than himself: where, nevertheless, his head is seen to be at perfect liberty out of the cone as at C. The horse then walks in the cone, and is harnessed to a fixed bar introduced from the open side where, by a proper adjustment of the traces, he is made to act partly by his weight, so as to exert his strength in a favourable manner. This Machine applies with advantage where a horse’s power is wanted, in a boat or other confined place: and it is evident, by the relative diameters of the wheel and pinion A B and D, (as well as by the small diameter of the wheel) that a considerable velocity will be obtained at the source of power,—whence, of course, the subsequent geering to obtain the swifter motions, will be proportionately diminished.
In fig. 2, of Plate 9, (which offers an horizontal section of the Machine), A B is an axis, to the cylindrical part of which the wheels C D are fitted, so as to turn with ease in either direction. Each of these wheels, C and D, has two rims of teeth, a b, and c d; and between those b d are placed an intermediate pinion W, connected by it’s centre with the arm x, which forms a part of the axis A B. There is likewise a fourth wheel or pinion Z, working in the outer rims a c of the wheels C and D. It appears from the figure itself, that the action of this Machine depends on the greater or lesser difference between the motion forward of the wheel C, and the motion backward of the wheel D; for if these opposite motions were exactly alike, the wheels would indeed all turn, but produce no effect on the arm x, or the axis A B: whereas this motion is the very thing required. Since then the motion of the bar x, and finger g depends on the difference of action of the wheels C and D on the intermediate pinion W, we now observe, that in the present state of things, the rims a, b, c, d, have respectively 99, 100, 100, and 101 teeth: and that when one revolution has[55] been given to the wheel C, the rim b of this wheel has acted, by 100 of its teeth, on those of the intermediate pinion W; insomuch that if the opposite wheel D had been immoveable, the arm x would have been carried round the common centre a portion equal to 50 teeth, or one half of it’s circumference (which effect takes place because the pinion W rolls against the wheels C and D, it’s centre progressing only half as fast as it’s circumference.) But instead of the wheel D standing still, it has moved in a direction opposite to the former, a space equal to 99⁄100 of a revolution, and brought into the teeth of the pinion W, 99⁄100 of 101 teeth; that is, 99 teeth, and 99 hundredths of one tooth: so that the account between the two motions stands thus:
| The forward motion by the wheel C, is equal to | 100,00 | teeth. | |
| And the backward motion by the wheel D, is | 99,99 | „ | |
| And the difference in favour of the forward motion is | 00,01 | of 1 tooth. | |
Or, dividing the whole circumference into 101 parts (each one equal to a tooth of the rim d,) this difference becomes 1⁄100 part of 1⁄101 = 1⁄10100 of a revolution of the axis A B, for each revolution of the wheel C. But we have observed, that the arm x progresses only half as much, on account of the rolling motion: whence it appears that the wheel C, must make 20200 turns to produce one turn of this axis A B. And if, with 20 teeth in the pinion Z, we suppose the movement to be given by the handle y, this handle must make more than 20200 revolutions, in the proportion of 99 (the teeth in the wheel) to 20, the teeth in the pinion Z. Thus the said 20200 turns must be multiplied by the fraction 99⁄20 which gives 99990 turns of the handle, for one of the axis[56] A B. And finally, if instead of turning this Machine by the handle and pinion y Z, we turned it by an endless screw, taking into the rim c, of 100 teeth; the handle of such screw must revolve 2020000 times to produce one single revolution of the axis A B; or to carry the finger g, once round the common centre.
The above calculations are founded on the very numbers of a Machine of this kind I made in Paris: and of which I handed a model to a public man nearly thirty years ago. I need not add that this kind of movement admits of an almost endless variety: since it depends both on the numbers of the wheels and their differences; nay, on the differences of their differences. I might have gone to some length in these calculations had I not conceived it more important to bring other objects into view, than to touch at present the extensive discussions this subject invites and will doubtless suggest to many. Suffice it now to say, that here is a simple Machine which gains power (or occasions slowness), in the ratio of two millions and twenty thousand to one; giving, (if executed in proper dimensions) to a man of ordinary strength, the power of raising, singly, from three to four hundred millions of pounds. It may be useful to observe that using this Machine for an opposite purpose, that of gaining speed, extreme rapidity may be caused by a power acting very slowly on the axis A B; only in that case, the difference must be enlarged, and the diameters and numbers of the wheels be calculated on the principles of perfect geering—which is as easy in this Machine as in any other.
Doctor Gregory (in his Mechanics 2d. volume page 157,) thus introduces the description of this Crane, and the observations with which he tags that description.
“The several Cranes described in this article, as preferable to the common walking Crane, while they are free from the dangers attending that Machine, lose at the same time one of it’s advantages, that is, they do not avail themselves of that addition to the moving power which the weight of the men employed may furnish: yet this advantage has been long since insured by the mechanists on the continent: who cause the labourers to walk upon an inclined plane, turning upon an axis, after the manner shewn in the figure referred to under the article foot-mill,—where we have described a contrivance of that kind, well known in Germany nearly 150 years ago. The same principle has been lately brought into notice (probably without knowing it had been adopted before) by Mr. Whyte, (White) of Chevening in Kent: His Crane is exhibited,—fig. 2 and 4, Plate 10, as it was described in the Transactions of the Society for the Encouragement of Arts.”
“A, Plate 9, fig. 4, (of this Work) is a circular inclined plane, moving on a pivot under it, and carrying round with it the axis E. A person walking on this plane at A, and pressing against a lever, throws off a gripe or brake, and thus permits the plane to move freely, and raise the weight G by the coiling of the rope F, round the axis E. To shew more clearly the construction and action of the lever and gripe, a plan of the plane connected with them, is added in fig. 5, where B represents the lever, and D the gripe: where it is seen that when the lever B is in the situation in which it now appears, the brake or gripe D, presses against the periphery of the plane; but when the lever B is driven out to the dotted line H, the gripe D is detached, and the whole Machine left at liberty to move: a rope or cord of a proper length, being fastened to B, and to one of the uprights in the frame, to prevent this lever from being pushed too far towards H, by the man working at the Crane.”
“The supposed properties of this Crane, (says Dr. Gregory) for which the premium of forty guineas was adjudged by the society to the Inventor, are as follows:”
“‘1. It is simple, consisting merely of a wheel and axle:
“‘2. It has comparatively little friction, as is obvious from the bare inspection of the figure:
“‘3. It is durable from the two properties above mentioned:
“‘4. It is safe: for it cannot move but during the pleasure[59] of the man, and while he is actually pressing on the gripe lever:
“‘5. This Crane admits of an almost infinite variety of different powers; and this variation is obtained without the least alteration of any part of the Machine. If in unloading a vessel, there should be found goods of every weight, from a few hundreds to a ton and upwards, the workman will be able so to adapt his strength to each, as to raise it in a space of time, (inversely) proportionate to it’s weight, he walking always with the same velocity as nature and his greatest ease may teach him.’”
“‘It is a great disadvantage in some Cranes, that they take as long a time to raise the smallest weight as the largest; unless the man who works them turn or walk with such velocity as must soon tire him. In other Cranes, perhaps, two or three powers may be procured; to obtain which, some pinion must be shifted, or fresh handle applied or resorted to. In this Crane on the contrary, if the labourer find his load so heavy as to permit him to ascend the wheel without turning it, let him only move a step or two towards the circumference, and he will be fully equal to the task. Again, if the load be so light as scarcely to resist the action of his feet, and thus to oblige him to run through so much space as to tire him beyond necessity, let him move laterally towards the centre, and he will soon feel the place where his strength will suffer the least fatigue by raising the load[60] in question. One man’s weight applied to the extremity of the wheel would raise upwards of a ton: and it need not be added that a single sheaved block (at the jib) would double that power. Suffice it to say that the size of the machine may be varied in any required degree, and that this wheel will give as great advantage at any point of its plane as a common walking wheel of equal diameter; as the inclination can be varied at pleasure, as far as expediency may require. It may be well to observe that what in this figure is the frame and seems to form a part of the Crane, must be considered as part of the house in which it is placed; since it would be mostly unnecessary should such cranes be erected in houses already built: and with respect to the horizontal part, by walking on which, the man who attends the jib, occasionally assists in raising the load, it is not an essential part of this invention, when the crane and jib are not contiguous: although, when they are, it would certainly be convenient and economical.’”
The Doctor continues: “Notwithstanding, however, the advantages which have been enumerated, Mr. Whyte’s (White’s) Crane is subject to the theoretical objection, that it derives less use than might be wished from the weight of the man or men: for a great part of that weight (half of it if the inclination be 30 degrees,) lies directly upon the plane, and has no tendency to produce motion. Besides, when this Crane is of small dimensions, the effective power of the men is very[61] unequal; and the barrel too small for winding a thick rope: when large, the weight of the materials, added to that of the men, put it out of shape and give it the appearance of an unwieldy moving floor.”
The Doctor continues: “We know one large Crane of this construction, which has an upright post near the rim on each side, to support it, and keep it in shape; and as much as possible to prevent friction, each post had a vertical wheel at it’s top.” (N. B. I never saw, or heard, before, of this monster.)—“We were informed this Crane was seldom used; and that it was soon put out of order. Nor, moreover, is it every situation that will allow the Crane-rope to form a right angle with the barrel on which it winds; and when this angle is oblique, the friction must be much increased. The friction arising from the wheels at the top of the vertical crutches might indeed be got shut off, by making the inclined wheel very strong; but this would add greatly to the friction of the lower gudgeon of the oblique shaft, and considerably increase the expence of the Machine.”
“There remains then (says Dr. Gregory) another stage of improvement with regard to the construction of Cranes, in which the weight of the labourers shall operate without diminution, at the end of an horizontal lever; and in which the impulsive force thus arising, may be occasionally augmented[62] by the action of the hands, either in pulling or lifting”—and then follows the conclusion. “This step in the progress has been lately effected by Mr. David Hardie, of the East India Company’s Bengal warehouse!”
I cannot follow the author (whoever he be) of the glowing picture next given of Mr. Hardie’s Invention, (to which the obloquy thrown on my poor abortion is clearly the foil) as my readers must already be anxious to “get shut” of such unmitigated Bathos, bestowed on so trivial a theme. With respect to my Crane, I shall only say that it fulfilled the conditions required by the Society, and obtained the Premium: and if on the one hand, the language in which, thirty years ago, I described it, exhibits the impetuosity of youth, untempered with the moderation of age, I will say on the other, that if impartial criticism, mechanical acumen, or comprehensive science are essential components of a mechanical work of high pretensions,—these qualities were seldom more wantonly abandoned or abused, than in the paragraphs above quoted: except, perhaps, in the attack of the same work, on the labours and character of the justly celebrated Watt, whose merits had this author known how to appreciate, he could not thus have attempted to lessen in the public esteem.
But to return, this Diatribe begins by comparing my Crane to a foot mill: and kindly supposes I did not know that its principle existed in Germany 150 years ago. But the fact is,[63] my object was nothing like that of the author of the mill in question: the very figure of which, proves that he had no view to the variation of power by change of place on the wheel: whereas that is the principal use I make of this “unwieldy moving floor,” as the Doctor heavily terms it. Again, this author asserts that by making men walk on an inclined plane, I derive less use than might be wished from their weight; and yet! a page before he told us that “the mechanists on the Continent had long since insured the advantage of availing themselves of that addition to the moving power which the weight of the men may furnish;” so that poor I have the merit of imitating them without knowing it, and yet of not drawing the same advantages as they from the self same principle!
But again, “a great part of the weight of the man (half of it, if the inclination be 30 degrees) lies directly on the plane, and has no tendency to produce motion,” which one sided truism is placed there to give relief to the portentous dictum, which follows:—that “there remains then another stage of improvement with regard to the construction of Cranes, in which the weight of the labourers shall operate without diminution at the end of an horizontal lever: and that stage has been effected by Mr. D. H. of the East India Company’s Bengal warehouse.”
But is this conclusion definitive? are there no countervailing evils? Will Dr. Gregory presume to say there is no disadvantage[64] attending this advantage? Did the Doctor ever ascend an upright ladder? and did he prefer that, to going up an easy flight of stairs? was he ever in the geometrical stairs of St. Paul’s? or in any large winding stair-case? and if so did he prefer ascending close to the nucleus? or did he quickly seek a point where the step was wider than high? most certainly the latter; and why then did he not perceive that if the weight of my man is diminished one half on the plane, for the very same reason, a given elevation of his feet (on which his fatigue depends) will cause a circular motion twice as extensive; yet this is quite as clear as the Doctor’s ex-parte proposition.
But I must wade on a little further, trusting that my readers will exert a little more patience to follow me: for this same dictum of the Doctor’s accuses indirectly, the Society of Arts of being a set of blockheads, for remunerating an Invention with only supposed properties. I really wish these self-constituted judges of other people’s labours would utter their oracles with more regard to truth and propriety! and above all, not mix up their passions (which alas! are not always purified by science) with their judgement on the merits of other men’s inventions. Had the author of this article been wise enough to proceed thus, he would not have supposed me capable of offering suppositions for realities; nor the Society of Arts of rewarding as genuine, suppositious merit; and still less would he have emblazoned the very properties he calls supposed, with reality written in glaring characters[65] on every one of them! These properties are in fact only the transcript of what the society required of the candidates: and I therefore said my Crane is simple: Can this author say it is not? I said it has little friction? will he say it has much? I said it is durable: Is it now possible to contradict this? I said it is safe: and will Dr. G. say it is not, when it is moveable, only during the wish of the workman: since whatever suspends this wish, (whether accident or design) the Crane becomes of itself immoveable. In fine, I observed, that this Crane admits of an indefinite number of powers, without any modification of it’s parts; and can any one say these are supposed properties? If the Doctor or his coadjutors persist in saying so, I must suppose them actuated by improper motives; for truth will never bear them out in these allegations. I take leave to add, that but for the interests of truth, these strictures had never appeared. Even self-defence would not have provoked one line of them: But I felt it incumbent on me to deter, if possible, inadvertency as well as malevolence, from infesting with the thorns of misrepresentation, the paths which genius explores, in search of useful knowledge.
The effects intended to be obtained from this Press, are to introduce two distinct powers; the one to raise and lower the pressing cap with convenient speed; the other to press with very great force. In Plate 10, A B is a frame, the under part of which contains the goods to be pressed. The toothed wheel C D turns the screw S, and that E F turns the nut G H, both the same way. The long pinions I K, turn both these wheels C D, and E F; and occasionally one only, as will be seen presently. L M are two bevil wheels on the axes of the long pinions I K; and N O, are two similar ones, on the power shaft P Q. This latter shaft runs in two boxes R T, the stems of which fit and turn in the gudgeons of the long pinions, or rather suffer these to revolve round them: being pinned on through a circular groove which connects them in the perpendicular direction only. Finally, the rope and pulleys indicated at X Y Z, serve to raise both shaft and pinions; thus disengaging the latter from the wheel E F, when the nut G H, is not to be turned. We may remark, that the parts M T O are doubled in this machinery, at L R N; merely to take away the side tendency from the screw S: as otherwise[67] one half of this mechanism would produce the very same effect, and leave the Machine the more simple. Supposing now, this Press charged with goods in it’s present position,
| The wheel | C D, | having | 69 | teeth; | - | with proportionate diameters. |
|
| The that | E F, | „ | 70 | „ | |||
| The pinions I & K, each | 10 | „ | |||||
| The wheels L N & M O | equal; | ||||||
The thread of the screw S, 1 inch; and in fine, the crank V Q, having a radius of 18 inches.
In this state of things, the motion of the pressing cap W, is to the motion of the handle V, as 1 to 52164; and, the power gained bears the same proportion to the strength exerted: for when the handle has made one revolution, the wheel C D has made 10⁄69 of a revolution, and the screw would have gone down 10⁄69 of a thread, or 10⁄69 of an inch: but in the same time the wheel E F has turned the nut 10⁄70 of a revolution in the same direction; so that the latter has only gone down 10⁄69 less 10⁄70 of an inch; that is, (reducing to a common denominator) 700⁄4830 - 690⁄4830 = 10⁄4830 = 1⁄483 of an inch: Now to do this, the handle Q V has described a circle of three feet in diameter, or in round numbers 9 feet, or 108 inches; and to complete a descent of the screw of one thread, (or one inch) the handle must move through a space 483 times as great; that is, a space of 108 inches multiplied by 483 = 52164 inches: whence we see that the power gained is, as 52164 to 1: and reckoning a man’s strength at 150lbs. (exclusive of friction) that strength[68] exhibits a pressure of five millions two hundred and sixteen thousand four hundred pounds; or upwards of two thousand three hundred tons: a result not unworthy to be mentioned with those of the hydraulic press; to which it might be still further assimilated by other proportions in the screw and nut wheels C D, E F. Adverting now, to the second property of this Machine: namely the simple power intended to act when the press is to be laden or discharged, the handle V should first be turned backward, until the cap W has slackened upon the goods; and the long pinions I K be raised by the mechanism X Y Z, which pinions, then geering only in the wheel C D, will raise the cap 1 inch for every turn of that wheel; or for every 69⁄10 turns of the handle V, say in round numbers for every seven turns: here then is a power of 756 to 1; very different from the former; yet produced by only a few inches motion of the long pinions I K.
We remark further, that the figure shews at G H two of a system of friction rollers, destined to lessen the resistance which the turning-nut would otherwise oppose to the motion of the Machine. As to the friction between the screw itself and the nut—see a future article, in this part, tending to lessen or take away the friction of screws in general.
Physicians will soonest understand the nature of this Machine, from the name I have given it. It is perhaps the most simple of Water-Machines; and certainly not the least efficient where it applies. It’s name is taken from the similarity of its action to the creeping of a worm, and to some of the functions of animal life. Yet it might be explained to the most unlettered housewife, when in the act of converting certain long vessels into chitterlings; or making room for the materials of a sausage or black pudding. To be serious: this Machine, in it’s simplest form, (see Plate 11) consists of a flexible tube C D, fig. 2, nailed to the ground, and connected with a short tube of metal containing two valves, A B, itself affixed to a box D, filled with water, or into which water flows. This water runs through the valve A, and distends the tube C D, on which rolls the body F, similar in form to a land roller. The Machine acts in the following manner: When the roller is drawn to the end D of the tube, the water fills the latter through the valve A; and on the roller’s return, this water is forced into the rising tube through the valve B.
The above is the simplest form of this mechanical trifle: But it has the disadvantage of an inconstant vibratory motion, not only of the water but the roller: which latter being heavy, would absorb considerable power. To remedy this evil, I have given the principle a rotatory form in fig. 1; where A B C is a spiral tube, duly fastened to the bottom of a shallow tub D E. At B is seen a conical roller, having the middle of the bottom of the tub for its summit and centre of gyration. The tube A B C, occupies rather more than one circumference; so that the cone presses during a small part of it’s revolution on both spires at once: by which means the Machine would act without even one valve; though it is better to place one, under the opening A. Now, observe the operation: as the cone rolls over the tube and round the common centre, in the direction of the arrow R the water enters behind it, through the opening A, (for the tub is plunged a few inches into the water) and is forced by it’s pressure into the ascending tube, which is a continuation of that, A B C. It would be superfluous to add, that these tubes are shewn in the figures as cut open, and presenting their inside to view; which representation is adopted in order to shew more completely the valves A and B of the 2d. figure.
An objection may occur to some, at sight of this Machine: namely, that the roller or cone B, would soon destroy the flexible tubes, by pressing too hard on their puckered texture. But to obviate this difficulty I have added, in fig. 3, a form of[71] the tube (supposed of leather) which insures a proper position of the leather under these rollers; accompanied by ledges A B, on which their surplus weight would bear, so as to annul every excess of pressure on the tube.
In many of the subjects I shall have to lay before my readers, the forms are so numerous as to leave some difficulty in judging where the actual descriptions ought to end. This article itself, small as it is, offers an example of this: for I could draw several corollaries from the foregoing, that would offer new degrees of interest: but I am withheld by the apprehended want of room in the plates. I must at least defer my first intention, of multiplying examples and shewing the influence of FORM on mechanical results in general. It will, however, always be open to me, to resume this subject when the principal object has been achieved—that of making known the principles of these inventions, with their most useful forms and properties. I observe, however, what has just occurred to me, that this Machine would be somewhat more durable, if the water-tube was pressed between two rollers, instead of being contracted from one side, by the action of a single one.
This Machine presents a simple method of increasing the power of the inclined plane, as used by carters or draymen for loading their carts; and called by them (in some counties) Canters. It admits of a gentle declivity in those planes: and thus considerably increases their power. The means consist in the transfer of the declivity from one end of the Machine to the other. Thus (plate 11, fig. 4) when the cask is rolled up from A to B, it is wedged in that position by the wedge F; when so much of its weight is supported by the feet C, (for all the feet are in pairs) that the end D of the Canter can be raised with ease to E, so as to re-form the plane, in the direction of C E; at which time the feet D G drop into an upright position, and secure this new state of the plane. The cask is now rolled back from B to E, where it is found twice as high as it was at B; and this manœuvre may be repeated several times according to the number of feet provided, and their length respectively. The power of an inclined plane, is as its length to its height: and that power is doubled when the force is applied at the circumference of a cask or other rolling body. So that, here, the power being as 16 to 1, if a man can exert an energy of 200lb. the cask may weigh 3200lb. and still be raised with[73] ease on this Canter, which therefore is three times as powerful as though the weight was raised directly from A to F in the usual method.
Should it be suggested, or thought, that this Machine applies only to rolling bodies, I would just say that it might apply, cæteris paribus, as well to bodies sliding up the plane; or (using a small truck on the Machine) it might serve in a cotton warehouse, for piling the bags, &c. This System is doubtless susceptible of discussion, and may require to be modified for different purposes: but it is by no means devoid of practical capabilities.
In Plate 12, fig. 5, let A B represent a wheel and axle, of which the wheel A is divided into 100 teeth; (more or less) and let C represent a second wheel with one tooth (or several) less than those of the first wheel A. These two wheels are concentric, for the axis of the wheel A, turns in the hollow centre of the wheel C; which latter wheel is fixed to the frame of the Machine, not here represented. D is a pinion that circulates round the wheel A and C in and along with the frame E as impelled by the hand acting on the handle F. Thus the circulating pinion is constantly occupied by means of its wedge formed teeth (of which one is shewn at D), in bringing the unequal teeth a b of the wheels A and C abreast of each other: whence arises a slow revolution of the wheel A, and of the axis B round the common centre. For if the number of the teeth on these wheels (A and C) differ only by unity or one, then must the handle D revolve one turn about that common centre to occasion 1⁄100 part of a revolution of the wheel A, and of course 100 turns to move the axis B once round that centre. And if further the wheel A be three times the diameter of the axis B, the power gained there would be as 300 to 1,[75] that is a power of 1lb. at a distance from the centre, only equal to the radius of the wheel A, would countervail a weight of 300lb. suspended on the axis B: and supposing a man’s strength to be 100lb. he would raise (exclusive of friction) 30000lb. by this simple machine.
To shew more fully the essential properties of this Machine, I have represented only three teeth in all: one b in the fixed wheel C; one a little smaller a, in the wheel A, (since this wheel has more teeth than the former) and one D in the circulating pinion, whose form and manner of acting justifies in my apprehension, the name I have given to the Machine—a perpetual wedge Machine. I shall only add that there would equally be motion if the teeth of the wheel A instead of being more numerous than those of the wheel C were less numerous: but the manner of action would be different and I think less perfect.
This Machine is among the first inventions I carried into real practice on coming to manhood. It must be about 40 years ago, and was first constructed as a Crane at the request of the late Doctor Bliss, of Paddington. It may offer some difficulty as a Power Engine from the small diameters and the friction thence resulting: but for any Machine where great slowness is desirable, whether to express slow motion, or to count high numbers, &c., it still appears to me a very good Machine.
Suppose A B (plate 12, fig. 4) to be the first wheel of a Clock or other Machine required to go a long time without winding up. This wheel works into the two pinions c d, both of which are connected by ratchets with the axis E F of the wheel G H, in one direction only; insomuch that whether the wheel A B turn forward or backward, the wheel G H will always turn the same way. This process is well known in the mechanical world; and I have merely adapted it to my present invention. F and G are two tubes, or square vessels, of equal size, containing a number of balls—the tubes so balanced against each other, that one of them is always heaviest by the weight of half a ball. Suppose for example that the tube F contains six balls and the tube G five; and that the tube G is so much heavier than F as only to be outweighed by half a ball: That half will then be the moving power; and the vessel F will turn the wheel A B backward, raising the tube G at the same time. But arriving at the bottom the mechanism m will let go the lowest ball in F, and then the tube G which is at the top will preponderate and turn the clock till it also[77] gets to the bottom; when a similar mechanism at n, will disengage one ball from it, by which subtraction the tube F will resume the ascendency and perpetuate the motion. Thus may the going of any clock, jack, &c. be protracted to a period almost indefinite. Nor need it, strictly speaking, be wound up at all. It is only taking care to drop at proper intervals, an equal number of balls into each tube, and this reciprocation of movement will become perpetual. The figure of this little Machine is unfortunately small: and the scapement is but imperfectly shewn; It has however, only one property that it is essential to notice; which is that the detent o, shall suffer the cross m to turn only one quarter round at each discharge: and this is insured by the spiral ledge of the four ratchet teeth m, which by a pin fixed to the side of the detent, draw the latter down into the succeeding tooth as soon as the tube F begins to rise, so that there is only one ball discharged at each descent of that tube.
The vessel containing the liquid to be evaporated, (see Plate 12, fig. 6,) is long and shallow, and the liquid rises nearly to it’s brim. In this vessel is placed a long hollow drum A B, covered with open wire-work, or any kind of cloth of a very loose texture. This drum turns slowly, on the hollow centre C, to which is fitted a stuffing box and tube, connecting the drum A B, with the pump P; the latter worked by any convenient power. The pump then, drives air, either hot or cold into the drum, and thence through the interstices of it’s texture; where it comes in contact with the liquid at an indefinite number of points, breaks the films formed by the liquid, and, saturated thereby, passes into the open air; thus occasioning a rapid evaporation, which might be increased either by heating the liquid or the injected air, or both, ad libitum. The whole idea consists in the multitude of points of contact between the liquid and the drying medium.
This Machine is composed of a perpendicular axis A B, fig. 7, driven with considerable velocity by any proper geering. C D is a vessel formed something like a shoe with the toe cut off: its entrance D is concentric with the shaft A B, and a weight m, fastened to it’s side, equilibrizes the weight of the eccentric part C. Around this vessel, and concentrically with it, is placed a cylindrical rasp or grater E F, consisting, here, of a number of blades so grooved on one surface as that by grinding them obliquely on the edge, each one shall form a line of sharp teeth, which, combined with those of the other blades, constitute a rasp similar to that used for powdering dye-woods; with this difference however, that these blades have interstices between them, through which the pulp escapes outwards, and thus the rasp is kept clean at all times. When this Machine is used the roots are merely thrown into the vessel D as into the hopper of a mill, and they are pressed against the rasp by their own centrifugal force; which is made as strong or weak as desired, by the greater or less velocity of the Machine.
This Machine owes its origin to the decree of the French[80] Emperor, for encouraging the making of sugar from beet-root. With the other mechanicians of Paris I was called upon, by a house engaged in that trade, to try my hand upon it; and this Machine was the result. It acts fast and well; and from being less liable to clog, than most of the others, is I believe superior; though this was never proved by any comparative experiment. If it were desired to cut any substance with this machine, the blades would be sharp knives, instead of being toothed; and they would be placed obliquely to the circumference: but the process of grating is that for which it was exclusively designed.
My readers will perceive, that I have altered the title given in the prospectus to this Invention. It has been done in deference to the opinions of some persons in high reputation in the mechanical world, who hold that there can be no motion whatever without friction. For my own part I am no believer in several sorts of friction: and must therefore, require a new definition of friction, before I can flow with the stream. As the question, however, is not yet before my readers, I shall wave the discussion at present, and describe this invention, as introducing the rolling motion into the threads of a screw; thus taking away the GREATEST PART of the friction on every supposition.
In Plate 12, fig. 8, A is the screw, and B C the nut, bored large enough to receive the screw, bodily, without any penetration of their threads. Nevertheless, these threads are made to occupy the same length, in both screw and nut, as though they did enter each other: so that the two parts running parallel to each other, leave a square interstice b, all along both nut and screw: into which balls of brass, or soft iron are[82] introduced, which at once restore the screw-property without it’s friction: a friction so considerable in the common screw, that it always surpasses the effective power, since it remains closed, (in a vice for example) while holding any object squeezed with all the force a man can apply. I have mentioned the use of soft balls: it is in order that they may all act together, and work themselves to a common bearing. It will appear by fig. 9, that the acting balls might, or perhaps ought to be, separated from each other by a set of smaller ones; since in this case, the surface of the touching balls move the same way, avoiding all friction between them; and leaving the friction only between those surfaces that are exempt from heavy pressure. These circumstances will be understood by consulting the direction of the arrows in fig. 9; and I have added two other sketches, to shew the principle in it’s application to square threaded screws, as at fig. 10; or to oblong threaded screws, whose threads penetrate each other, in fig. 12. I have further, in fig. 8, sketched one of the methods I propose for supporting the weight of the descending balls, and returning them again into the nut. Considering the balls as a fluid, I have provided a rising column of them, which the working of the screw downward will fill: and the weight of the balls themselves will return them into the nut, when the screw is drawn upward.
This interesting Machine, see Plate 12, fig. 11, consists of a screw divided into three parts, a, b, c; the first, a, is a mere cylinder to centre the screw at that end: c is a screw of (suppose) 20 threads to the inch; and b another screw of 21 to the inch. D E represents the frame of the Machine, the part E being the fixed nut of the screw C, while the piece f g, forms the moveable nut of the screw C, carrying a finger g, along the graduated bar, E g D. If now, the screw be turned once round by the button H, it will have moved to the left 1⁄20 of an inch; while the nut and it’s finger g will have progressed on it’s screw 1⁄21 of an inch to the right: and the difference 1⁄20 - 1⁄21 = 1⁄420 of an inch is what the nut f has really moved to the left, along the bar E g D. If therefore, the rim of the button be divided into 100 parts, one of these will represent 1⁄42000 part of an inch by this Micrometer: and I need not add, that this minute portion may be rendered still more minute at pleasure. The means of doing this are evident: It is only making the screws b and c nearer alike in fineness, or number of threads per inch; as 29 and 30, 30 and 31, &c.
I hope it will be understood, that I do not give any of these Machines as the only examples I could furnish of the application of the principles on which they are founded. This very Machine is not a Micrometer only; it might be (if made in proper forms and dimensions) a vice, a press, or other power Machine. It has been already hinted, that change of form must remain to be considered hereafter.
I have chosen to bring forward this Machine at an early stage of the work, because it has, inadvertently perhaps, been ascribed to another person. I refer to an article in the celebrated programme of M. Hachette, of Paris; with which is combined an essay on the composition of Machines, by Messrs. Lanz and Betancourt. In the article D 3, at page 10 of that work, are the following words:
“M. de Prony a trouvé une maniere de transformer le mouvement circulaire, en un autre rectiligne dont la vitesse soit aussi petite que l’on voudra;” and further on—“l’idée en est extremement simple, heureuse; elle est d’ailleurs susceptible de plusieurs applications utiles aux arts.” And in page 11, are these words—“C’est ainsi que M. de Prony est parvenu à une solution aussi simple qu’ingenieuse du probleme qu’il s’etoit proposé.”
For the sake of my English readers, I subjoin a translation of these passages: “Mr. de Prony has found (or invented) a[85] manner of transforming a circular movement into a rectilinear one, of which the velocity shall be as small as may be desired;” and further on “This idea is extremely simple and happy: and is besides, susceptible of several useful applications to the arts.” And in page 11, are these words—“Thus has Mr. de Prony given a solution as simple as it is ingenious, of the problem which he had proposed to himself.”
The above account appears in 1808, and M. de Prony does not prevent or disavow it. Perhaps he had forgotten the circumstance: and perhaps he did not know of this publication: but I solemnly declare that I shewed HIM this Micrometer, executed, fourteen years before! that is, while he and M. Molard were making their report on the Machines proposed for the Water-works at Marly. I certainly wish to accuse no body in this affair: but if I did not state the fact as it is, I should, myself, be stigmatized as a plagiary! I am forced, therefore, to take my stand on the adage—“Fiat justitia ruat cœlum.”
In closing the first Part of this Work, I cannot but express my gratitude for the unexpected degree of support, with which my numerous Subscribers have honoured me. I presume to offer these pages as a fair Specimen of what they may expect in the four succeeding Parts,—namely, as it regards the execution: for the materials of what remains, include objects of greater importance than those preceding. If I have been fortunate[86] enough to raise any favourable expectations in the minds of my present readers, I hope they will express those feelings; and thus induce others to join in bringing to a useful close, a work which is at least intended to produce unmixed public utility. From criticism, I expect candour: and should my intentions, though pure, be misrepresented—should envious tongues or pens assail my labours, or asperse my character, I will defend both, after I can use my Book as my shield—that is, after I have fulfilled my Engagements with my Subscribers: of whom (in expectation of meeting them again within three months) I now respectfully take leave.
J. W.
No. 5, Bedford-street,
Chorlton Row.
Note. The objects with Numbers after them are those contained in the present PART: and the Numbers shew the Pages where they stand.
| A | |
| 1 | Adding Machine; or Machine to cast up correctly large columns of figures. |
| 2 | Air Pump; essay towards completing the vacuum. |
| B | |
| 3 | Barrel Spring, to lengthen the going of Clocks and other spring-driven Machines. 26 |
| 4 | Boats (serpentine) for lessening the expence of traction. |
| 5 | Bobbin or Lace (Machine for making) and for covering Whips, &c. with great rapidity. |
| 6 | Bowking Machine for Calico Printers. |
| 7 | Bucket Wheels (a combination of) to raise water. |
| C | |
| 8 | Canals (open) as Hydraulic Machines of great force. |
| 9 | Canter, or inclined Plane for Draymen. 72 |
| 10 | Chain to act equably on my wheels. |
| 11 | Chocolate Mill (rotatory.) |
| 12 | Cocks (equilibrium) to avoid leakage. |
| 13 | Colour Mill for Calico Printers. |
| 14 | Compasses (bisecting.) |
| 15 | Cotton (Machine for batting.) |
| 16 | Crane, combining variable powers with speed and safety. (rewarded by the Society of Arts.) 57 |
| 17 | Crank (epicycloidal) or parallel motion. Rewarded by Bonaparte. 30 |
| D | |
| 18 | Dash Wheel for Calico Printers, acting with greater rapidity than usual. |
| 19 | Differential Wheels for gaining immense power. 54 |
| 20 | Doffing Machine, of great force for taking Cylinders from their Mandrills. |
| 21 | Draw-bench for my twisted pinions. |
| 22 | Dynamometer, for measuring powers and resistances in motion. 15 |
| 23 | Dynamometer, second kind. |
| E | |
| 24 | Engine for cutting my Patent Wheels in small and middling dimensions. |
| 25 | Engine for cutting my large bevil Wheels and wooden Models, either on my System, or the usual one. |
| N. B. These objects will occupy considerable space in the work. | |
| 26 | Engraving Machine for Calico Printers, being an important application of my Cog or toothed Wheels. |
| 27 | Engraving Machine for large patterns. |
| 28 | Essay to derive power from expanding Solids. |
| 29 | Evaporation (Machine to promote.) 78 |
| 30 | Eyes (Machine for making rapidly.) |
| F | |
| 31 | Fire escape (on a retarding principle.) |
| 32 | —— (by breaking the fall.) |
| 33 | Fires (Portable Engine to extinguish.) |
| 34 | Fires (Watch Engine always ready for.) |
| 35 | Flax (Machine for breaking) with rapidity. |
| 36 | Forging Bar iron and steel (Machine for.) |
| 37 | Friction (to prevent.) |
| 38 | Friction (to prevent) Thoughts on. |
| G | |
| 39 | Geering and ungeering (Machine for). |
| 40 | Do. Do. for swift motions. |
| 41 | Grating or cutting green Roots, Tobacco, &c. (Machine for.) 79 |
| H | |
| 42 | Helico-Centrifugal Machine, for raising water in large quantities. |
| 43 | Horse Wheel for saving room and gaining speed. 53 |
| 44 | Horse Wheel (reciprocating) for Mangles, &c. |
| 45 | Horse Wheel, with means for turning the Horse when he acts in two directions. |
| 46 | Horizontal Pump of large produce, driven by wind. |
| 47 | Hot Air as power, while heating liquids, rooms, &c. |
| L | |
| 48 | Lamp for the Table; suspending the oil by it’s weight. |
| 49 | Lithographic, or Copper-plate Press, with several curious and useful properties. |
| M | |
| 50 | Machine for clearing turbid liquors. |
| 51 | Machine for driving Boats on Canals, under Tunnels, &c. without disturbing the Water. |
| 52 | Machine to assist in taking Medicine, Pills, &c. (Humani nihil alienum.) |
| 53 | Mangle (perpetual or rotatory). |
| 54 | Marine-Level (two essays on a.) |
| 55 | Micrometer for measuring very minute spaces. 83 |
| 56 | Mirrors to collect Solar Heat, (method of forming.) |
| 57 | Mover, by dropping weights. 76 |
| N | |
| 58 | Nails (Machine for moulding.) |
| 59 | Nails (Machine for forging.) |
| P | |
| 60 | Pencyclograph, or Instrument for describing portions of Circles, and finding their centres by inspection. 51 |
| 61 | Peristaltic Machine, for raising much water, to small heights. 69 |
| 62 | Persian Wheel modified, for raising water. |
| 63 | Pitch-fork, for musicians, with variable tones. |
| 64 | Power-wheel by heated Air. 43 |
| 65 | Press, direct and differential. 66 |
| 66 | Press (eccentric Bar.) |
| 67 | Printing Machine (two coloured.) |
| 68 | Protracting Motion (Machine for.) 49 |
| 69 | Pullies (my Patent much improved.) 33 |
| 70 | Pump (my equable.) 45 |
| 71 | Pump, triple, in one column. |
| 72 | Pump (portable) worked by pedals. |
| 73 | Punch Machine for Engravers. |
| 74 | Punch Machine on another principle. |
| 75 | Do. rotatory, for my Engraving Machine. |
| R | |
| 76 | Reciprocating Motion, (long) for Mangles, &c. |
| 77 | Reflector parabolico conical, or plano parabolical for light houses, &c. |
| 78 | Regulator: (not centrifugal) for Wind or Water Mills, Steam Engines, &c. |
| 79 | Retrographic Machine (Machine for Writing backwards) for Engravers. |
| 80 | Rotato-gyratory Churn. |
| S | |
| 81 | Screw, with greatly diminished friction. 81 |
| 82 | Screws, (Machine for forging) &c. |
| 83 | Spinning Machines, (my Patent), Eagles, &c. |
| 84 | Spinning Machinery: another system, adapted chiefly to wool. |
| 85 | Spring, to keep a door strongly closed, yet open easily. |
| 86 | Steel Yard, differential: for weighing vast weights with short levers. |
| 87 | Syphon, (mechanical) to expel part of the water at the highest point. |
| T | |
| 88 | Tallow (Machine for cutting and trying.) |
| 89 | Tea-table (commodious help for the.) |
| V | |
| 90 | Ventilator, rotatory, yet by pressure. |
| 91 | Vessel (expanding) for Pumps, Steam Engines, &c. |
| W | |
| 92 | Washing Apparatus: for Hospitals, &c. confining the offensive matter until cleansed away: thus promoting salubrity. |
| 93 | Water-wheel, (horizontal) probably the best of the impulsive kind. |
| 94 | The same, for high falls. |
| 95 | Water-wheel, (inclined) employing the weight of the fluid. |
| 96 | Water, (Machine for raising large quantities.) |
| 97 | Weaving by Power: manner of driving the Shuttle, (executed A. D. 1780.) |
| 98 | Wedge Machine (perpetual.) |
| 99 | Wheels (my System of cog or toothed.) |
| 100 | Windmill of great power. |
| Page | 16, | line | 17, | for fig. read plate. | ||
| „ | 22, | „ | 4, | for posistion, read position. | ||
| „ | 22, | „ | 7, | for 17, read 15. | ||
| „ | 22, | „ | 9, | for fig. read plate. | ||
| „ | 22, | „ | 23, | for fig. read plate. | ||
| „ | 24, | „ | 16, | for clylinder at P, read cylinder at K. | ||
| „ | 24, | „ | 22, | for fig. read plate. | ||
| „ | 26, | „ | 16, | for E, read C. | ||
| „ | 28, | „ | 5, | for diamenter, read diameters. | ||
| „ | 35, | „ | 10, | for inconvencies, read inconveniences. | ||
| „ | 36, | „ | 8, | for of pulley, read of the pulley. | ||
| „ | 40, | „ | 25, | for as, read of. | ||
| „ | 41, | „ | 4, | for loose 1; read loose — | ||
| „ | 41, | „ | 5, | for pulleys, read pulley. | ||
| „ | 43, | „ | 18, | for furnish surplus, read furnish a surplus. | ||
| „ | 43, | „ | 22, | for occpied, read occupied. | ||
| „ | 46, | „ | 17, | for power, read motion. | ||
| „ | 49, | „ | 22, | for diffential, read differential. | ||
| „ | 55, | „ | 21, | - | for 20,200, read 20200. | |
| „ | 55, | „ | 24, | |||
| „ | 55, | „ | 26, | |||
| „ | 55, | „ | 28, | for 99,990, read ,99990. | ||
| „ | 58, | „ | 23, | for figures, read figure. | ||
| „ | 62, | „ | 2, | end the quotation marks at “lifting.” | ||
| „ | 62, | „ | 8, | for gasping, read anxious. | ||
| „ | 63, | „ | 7, | for wishd, read wished. | ||
| „ | 64, | „ | 2, | for ladders, read ladder. | ||
| „ | 66, | „ | 11, | for occasionaly, read occasionally. | ||
| „ | 67, | „ | 7, | for G N, read L N. | ||
| „ | 68, | „ | 2, | for two hundred, read three hundred. | ||
| „ | 75, | „ | 4, | for 300℔s. read 100℔s. | ||
| „ | 82, | „ | 16, | for fig. 9, read fig. 10. | ||
| „ | 83, | „ | 11, | for an of inch, read of an inch. | ||
A NEW CENTURY OF
Inventions.
In the progress of a work like the present, no competent reason could have been assigned for omitting to bring forward my System of Toothed Wheels, the Patent for which has lately expired:—a System which a few years ago, excited in this town, so much interest, aroused so much animosity, and was treated with so much illiberality:—But which, also, was fostered with so much public spirit, tried with so much candour, and adopted with so much confidence. It was I say, incumbent on me to bring the merits of this System into public view, had it only been to justify myself for proposing, and my friends for adopting it. But stronger reasons point now to the same measure. From the intimate connection the System holds with the subjects of this essay, it must be often adverted to; and I have been already obliged to speak of it in terms which can hardly have been understood by those readers who had not previously considered the general Subject. I should therefore be still in danger of filling these Pages with unintelligible assertions, did I not begin by marking out the foundations on which my statements are built; or by explaining to a certain degree, the Principles of the new System. Without then abandoning the tacit engagement I have taken with my unlearned readers—not to entangle them in too much theory, I think it indispensable to quote the Memoir I read before the Literary and Philosophical Society of Manchester, in[90] December, 1815; which small work will form the basis of the practical remarks I shall have to make on the subject, as this work proceeds. The Memoir is thus introduced in the transactions of that learned body:
By Mr. James White, Engineer.[1]
COMMUNICATED BY T. JARROLD, M. D.
(Read December 29th, 1815.)
[1] N. B. A Patent was taken out for the Invention some years ago.
“The subject of this paper, though merely of a mechanical nature, cannot fail to interest the Philosophical Society of a town like Manchester, so eminently distinguished for the practice of mechanical science; unless as I fear may be the case, my want of sufficient theoretic knowledge or of perspicuity in the explication, should render my communication not completely intelligible. To be convinced of the importance of the subject, we need only reflect on the vast number of toothed[91] wheels that are daily revolving in this active and populous district, and on the share which they take in the quantity and value of its productions; and it is obvious that any invention tending to divest these instruments of their imperfections, whether it be by lessening their expence, prolonging their duration, or diminishing their friction, must have a beneficial influence on the general prosperity. Now I apprehend that all these ends will be obtained in a greater or less degree, by having wheels formed upon the new system.
I shall not content myself by proving the above theoretically, but shall present the society with wheels, the nature of which is to turn each other in perfect silence, while the friction and wear of their teeth, if any exist, are so small as to elude computation, and which communicate the greatest known velocity without shaking, and by a steady and uniform pressure.
Before I proceed to the particular description of my own wheels, I shall point out one striking defect of the system now in use, without reverting to the period when mechanical tools and operations were greatly inferior to those of modern times. Practical mechanics of late, especially in Britain, have accidentally hit upon better forms and proportions for wheels than were formerly used; whilst the theoretic mechanic, from the time of De la Hire, (about a century ago) has uniformly taught that the true form of the teeth of wheels depends upon the curve called an epicycloid, and that of teeth destined to[92] work in a straight rack depends upon the simple cycloid. The cycloid is a curve which may be formed by the trace of a nail in the circumference of a cart wheel, during the period of one revolution of the wheel, or from the nail’s leaving the ground to its return; and the epicycloid is a curve that may be formed by the trace of a nail, in the circumference of a wheel, which wheel rolls (without sliding) along the circumference of another wheel.
Let A B (Plate 13, fig. 1.) be part of the circumference of a wheel A B F to which it is designed to adapt teeth, so formed as to produce equable motion in the wheel C, when that of the wheel A B F is also equable. Also, let the teeth so formed, act upon the indefinitely small pins r, i, t, let into the plane of the wheel C, near its circumference. To give the teeth of the wheel A B F a proper form, (according to the present prevailing system) a style or pencil may be fixed in the circumference of a circle D equal to the wheel C, and a paper may be placed behind both circles, on which by the rolling of the circle D on A B, will be traced the epicycloid d, e, f, g, s, h, of which the circle A B F is called the base, and D the generating circle. Thus then the wheel to which the teeth are to belong is the base of the curve, and the wheel to be acted upon is the generating circle; but it must be understood that those wheels are not estimated in this description at their extreme diameters, but at a distance from their circumferences sufficient to admit of the necessary penetration of the teeth; or, as[93] M. Camus terms it, where the primitive circles of the wheels touch each other, which is in what is called in this country the pitch line.
Now it has been long demonstrated by mathematicians, that teeth constructed as above would impart equable motion to wheels, supposing the pins, r, i, t, &c. indefinitely small. This point therefore need not be farther insisted upon.
So far the theoretic view is clear; but when we come to practice, the pins r, i, t, previously conceived to be indefinitely small, must have strength, and consequently a considerable diameter, as represented at 1, 2; hence we must take away from the area of the curve a breadth as at v and n = to the semidiameter of the pins, and then equable motion will continue to be produced as before. But it is known to mathematicians that the curve so modified will no longer be strictly an epicycloid; and it was on this account that I was careful above, to say that the teeth of wheels producing equable motion, depended upon that curve; for if the curve of the teeth be a true epicycloid in the case of thick pins, the motion of the wheels will not be equable.
I purposely omit other interesting circumstances in the application of this beautiful curve to rotatory motion; a curve by which I acknowledge that equable motions can be produced, when the teeth of the ordinary geering are made in this manner. But here is the misfortune:—besides the difficulty of executing[94] teeth in the true theoretical form, (which indeed is seldom attempted), this form cannot continue to exist; and hence it is that the best, the most silent geering becomes at last imperfect, noisy and destructive of the machinery, and especially injurious to its more delicate operations.
The cause of this progressive deterioration may be thus explained: Referring again to fig. 1, we there see the base of the curve A B divided into the equal parts a b, b c, and c d; and observing the passage of the generating circle D, from the origin of the curve at d, to the first division c on the base, we shall find no more than the small portion d e, of the curve developed, whereas a second equal step of the generating circle c b, will extend the curve forward from e to f, a greater distance than the former; while a third equal step a b, will extend the curve from f to g, a distance greater than the last; and the successive increments of the curve will be still greater, as it approaches its summit; yet all these parts correspond to equal advances of the wheel, namely, to the equal parts a b, b c and c d of the base, and to equal ones of rotation of the generating circle. Surely then the parts s g, g f, of the epicycloidal tooth will be worn out sooner than those f e, e d, which are rubbed with so much less velocity than the other, even though the pressure were the same. But the pressure is not the same. For, the line a g is the direction in which the pressure of the curve acts at the point g, and the line p q, is the length of the lever-arm on which that pressure acts, to turn[95] the generating circle on its axis (now supposed to be fixt;) but, as the turning force or rotatory effort of the wheels, is by hypothesis uniform, the pressure at g must be inversely as p q; that is, inversely as the cosine of half the angle of rotation of the generating circle; hence it would be infinite at s, the summit of the curve, when this circle has made a semi-revolution.
Thus it appears that independently of the effects of percussion, the end of an epicycloidal tooth must wear out sooner than any part nearer its base, (and if so, much more it may be supposed of a tooth of another form;) and that when its form is thus changed, the advantage it gave must cease, since nothing in the working of the wheel can afterwards restore the form, or remedy the growing evil.
Having now shewn one great defect in the common system of wheels, I shall proceed to develope the principles of the new system, which may be understood through the medium of the three following propositions.
1. The action of a wheel of the new kind on another with which it works or geers is the same at every moment of its revolution, so that the least possible motion of the circumference of one, generates an exactly equal and similar motion in that of the other.
2. There are but two points, one in each wheel, that necessarily touch each other at the same time, and their contact will always take place indefinitely near the plane that passes through the two axes of the wheels, if the diameters of the latter, at the useful or pressing points are in the exact ratio of their number of teeth respectively; in which case there will be no sensible friction between the points in contact.
3. In consequence of the properties above-mentioned, the epicycloidal or any other form of the teeth, is no longer indispensable; but many different forms may be used, without disturbing the principle of equable motion.
With regard to the demonstration of the first proposition, I must premise an observation of M. Camus on this subject, in his Mechanics, 3d. part, page 306, viz. “if all wheels could have teeth infinitely fine, their geering, which might then be considered as a simple contact, would have the property required, [that of acting uniformly] since we have seen that a wheel and a pinion have the same tangential force, when the motion of one is communicated to the other, by an infinitely small penetration of the particles of their respective circumferences.”
Now suppose that on the cylindrical surface of a spur-wheel B c, (fig. 3) we cut oblique or rather screw-formed teeth, of which[97] two are shewn at a c, b d, so inclined to the plane of the wheel, as that the end c of the tooth a c may not pass the plane of the axes A B c, until the end b of the other tooth b d has arrived at it, this wheel will virtually be divided into an infinite number of teeth, or at least into a number greater than that of the particles of matter, contained in a circular line of the wheel’s circumference. For suppose the surface of a similar, but longer cylinder, stripped from it and stretched on the plane A B C E (fig. 4) where the former oblique line will become the hypothenuse B C, of the right angled triangle C A B, and will represent all the teeth of the given wheel, according to the sketch E G at the bottom of the diagram. Here the lines A B and C E, are equal to the circumference of the base of the cylinder, and A C and B E to its length; and if between A and B, there exist a number, m, of particles of matter, and between A and C a number, n, the whole surfaced A B C E will contain m n particles, or the product of m and n; and the line B C, will contain a number = √m² + n², from a well known theorem; whence it appears that the line B C is necessarily longer than A B, and hence contains more particles of matter.[2]
[2] It need hardly be observed, that whatever is true of the whole triangle C A B, (fig. 4) is true of every similar part of it, be it ever so small: and in fact, when the hypothenuse B C, is folded again round the cylinder, from which we have supposed it stripped, the acting part will be very small indeed; but it will still act in the way here described, and give tendencies to the wheel it acts on, and to its axis, precisely proportionate to the quantities here mentioned.
It is besides evident, that the difference between the lines B C and A B, depends on the angle A C B; in the choice of which, there is a considerable latitude. For general use however, I have chosen an angle of obliquity of 15°, which I shall now assume as the basis of the following calculations. The tangent of 15°, per tables, is in round numbers 268 to radius 1000; and the object now is to find the number of particles in the oblique line B C, when the line A B, contains any other number, t.
By geometry, B C(x) = √r² + t² = √1000² + 268² = 1035 nearly; and this last number is to 268, as the number of particles in the oblique line B C is to the number contained in the circumference A B, of the base of the cylinder. Hence it appears, that a wheel cut into teeth of this form, contains (virtually) about four times as many teeth, as a wheel of the same diameter, but indefinitely thin, would contain. And the disproportion might be increased, by adopting a smaller angle.
Thus I apprehend it is proved, that the action of a wheel of this kind, on another with which it geers, is perfectly uniform in respect of swiftness; and hence the proof that it is likewise so, as to the force communicated.
Before I proceed to the second proposition, I ought perhaps to anticipate some objections that have been made to this system of geering, and which may have already occurred to some gentlemen present. For example, it has been supposed that the[99] friction of these teeth, is augmented by their inclination to the plane of the wheel; but I dare presume to have already proved, that it is this very obliquity, joined to the total absence of motion in direction of the axes, that destroys the friction, instead of creating it. I acknowledge however, that the pressure on the points of contact, is greater than it would be on teeth, parallel to the axes of the wheels, and I farther concede that this pressure tends to displace the wheels in the direction of the axes, (unless this tendency is destroyed by a tooth, with two opposite inclinations.) But supposing this counteraction neglected, let us ascertain the importance of these objections. First, with regard to the increase of pressure on the point D of the line B C, (representing the oblique tooth in question,) relative to that which would be on the line B E, (which represents a tooth of common geering:) let A D be drawn perpendicular to B C. If the point D can slide freely on the line B C, (and this is the most favourable supposition for the objection,) its pressure will be exerted perpendicularly to this line; and if the point A, moves from A to B, the point D, leaving at the same moment the point A, and moving in direction A D, will only arrive at D in the same time, its motion having been slower than that of A, in the proportion of A B to A D; whence by the principle of virtual velocities, its pressure on B C is to that on A C, as the said lines A B to D A.
To convert these pressures into numbers, according to the above data; we have A C = 1000, A B = 268, B C = 1035;[100] then from the similar triangles B A C, B D A, it will be B C : A C ∷ A B : A D = 268000⁄1035 = 259 nearly. Therefore the pressure on B C, is to that on A C, as 268 to 259, or as 1035 : 1000.
To find what part of the force tends to drive the point B, in the direction B E, (for this is what impels the wheels, in the direction of their axes,) we may consider the triangle B A C as an inclined plane, of which B C is the length, and A B the height; and the total pressure on C B, which may be represented by C B, (1035) may be resolved into two others, namely, A B and A C, which will represent the pressures on those lines respectively, (268 and 1000.) Hence the pressure on B C, is augmented only in the ratio of 1035 to 1000, or about 1⁄29 part by the obliquity; and the tendency of the wheels to move in the direction of their axes, (when this angle is used,) is the 268⁄1000 of the original stress, that is, rather more than one quarter. But since the longitudinal motion of an axis can be prevented by a point almost invisible applied to its centre, it follows that the effect of this tendency can be annulled, without any sensible loss of the active power. It may be added, that in vertical axes, those circumstances lose all their importance, since whatever force tends to depress the one and increase its friction, tends equally to elevate the other, and relieve its step of its load; a case that would be made eminently useful, by throwing a larger portion of pressure on the slow-moving axes, and taking it off from the more rapid ones.
We now proceed to the second proposition. The truth of the assertions, contained in this proposition, must, I should suppose, be evident, from the consideration of two circles touching each other, and at the point of contact, coinciding with their common tangent at that point. Let A and B be two circles, tangent to each other, (fig. 3) in e. A C is the line joining the centres, and D F the common tangent of the circles at e; which is at right angles with A C; and so are the circumferences of the two circles at the point e. For the circles and tangent coincide for the moment. Hence then I conclude, 1st that a motion (evanescently small) of the point common to the three lines, can take place without quitting the tangent D F: and 2d. that if there is an infinite number of teeth in these circles, those which are found in the line of the centres, will geer together in preference to those which are out of it, since the latter have the common tangent, and an interval of space between them.
The truth of this proposition (or an indefinite approximation to truth,) may be deduced from the supposition that the two circles do actually penetrate each other. To this end let A B a b, in fig. 5, be two equal circles, placed parallel to each other in two contiguous planes, so as for one to hide the other, in the indefinitely small curvilinear space d f e g. I say that if the arc d g is indefinitely small, the rotation of the two circles will occasion no more friction between the touching surfaces, g e f and f d g, than there would be between the two[102] circles placed in the same plane, and touching at the point n the same common tangent.
For draw the lines D E, f d, d g, g f, g e and g D; and adverting to the known equation of the circle, let d n = x, g n = y and D g = a, the absciss, ordinate and radius of the circle; we have 2 a x - x² = y². From this equation we obtain a = (y² + x²)/2x, the denominator of this fraction (2x) being the width, d e, of the touching surfaces f d g, and f e g of the two circles. But the numerator (y² + x²) is equal to the square of the chord g d of the angle E D g, which chord I shall call z; then we have a = x²/2x from which equation we derive this proportion, a : z ∷ z : 2x = z²/a. But in very small angles, the sines are taken for the arcs without sensible error; and with greater reason may the chords; if then we suppose the arc d g, or the chord z, indefinitely small, we shall find the line d e = 2x = z²/a, indefinitely smaller; that is, of an order of infinitessimals one degree lower; for it is well known that the square of evanescent quantities are indefinitely smaller than the quantities themselves. And to apply this, if the chord z represent the circular distance of two particles of matter found in the screw-formed tooth a c, of the wheel B c, fig. 3, (referred to the circle a b, fig. 5), that distance z will be a mean proportional between the radius D g of such wheel, and the double versed sine of this inconceivably small angle.[3]
[3] I ought perhaps to have introduced this reasoning on the 5th. figure by observing, that every projection of every part of a screw, on a plane at right angles with the axis of such screw, is a circle; and that therefore the chord z, or the line g d, is the true projection of a proportionate part of any line, B C, fig. 4, when wrapped round a cylinder of equal diameter with the circle a b, fig. 5.
I am aware that some mathematicians maintain, that the smallest portion of a curve cannot strictly coincide with a right line; a doctrine which I am not going to impugn. But however this may be, it appears certain that there is no such mathematical curve exhibited in the material world; but only polygons of a greater or less number of sides, according to the density of the various substances, that fall under our observation. I shall therefore proceed to apply the foregoing theory, not indeed to the ultimate particles of matter, (because I do not know their dimensions,) but to those real particles which have been actually measured. Thus, experimental philosophy shews, that a cube of gold of 1⁄2 inch side, may be drawn upon silver to a length of 1442623 feet, and afterwards flattened to a breadth of 1⁄100 of an inch, the two sides of which form a breadth of 1⁄50 of an inch: so that if we divide the above length by 25, we shall have the length of a similar ribbon of metal of 1⁄2 an inch in breadth, namely, 57704 feet; which cut into lengths of 1⁄2 an inch, (or multiplied by 24, the half inches in a foot) give 1384896 such squares, which must constitute the number of laminæ of a half inch cube of gold, or 2769792 for an inch thickness. Let us suppose then a wheel of gold, of two feet in diameter, the friction of whose teeth it is proposed to determine. We must first seek what number of particles are contained in[104] that part of the tooth or teeth, that are found in one inch of the wheel’s circumference; this we have just seen to be 2769792 thicknesses of the leaves, or diameters of the particles, such as we are now contemplating.
We shall now have this proportion, (see fig. 4) 268 (A B) : 1035 (B C) ∷ 2769792 (no. of particles in one inch of circumference of base) : x = 10696771 particles in that part of the line B C, which corresponds with that inch of the circumference. Thus each of the latter particles measured in the direction A B, is equal to the fraction 1⁄10696771ths of an inch. And if that fraction be taken for the arc g d, (fig. 5) then to find the length of the line d e, (on which the friction of this and all other geering depends) we must use this analogy; 12 inch (rad. of wheel) : 1⁄10696771 of an inch (chord g d) ∷ 1⁄10696771 of an inch (g d) : d e, the line required = 1⁄1273050917917292 of an inch. This result is still beyond the truth, as we do not know how much smaller the ultimate molecules of gold are.
To advert now to some of the practical effects of this system, I would beg leave to present a form of the teeth, the sole working of which would be a sufficient demonstration of the truth of the foregoing theory. A, B, (fig. 6) are two wheels of which the primitive circles or pitch-lines touch each other at o. As all the homologous points of any screw-formed tooth, are at the same distance from the centres of their wheels, I am at liberty to give the teeth a rhomboidal form, o t i; and if the[105] angle o exists all round both wheels, (of which I have attempted graphically to give an idea at D G,) in this case, those particles only which exist in the plane of the tangents f h, &c. and infinitely near that plane passing at right angles to it through the centres A and B, will touch each other; and there, as we have already proved, no sensible motion of the kind producing friction, exists between the points in actual contact. I might add, as the figure evidently indicates, that if any such motion did exist, the angles o would quit each other, and the figure of such teeth become absurd in practice; but on the other hand, if such teeth can exist and work usefully (which I assert they can, nay that all teeth have in this system a tendency to assume that form at the working points;) this circumstance is of itself a practical evidence of the truth of the foregoing theory, and of what I have said concerning it.
It must have been perceived that I have in some degree anticipated the demonstration of my third proposition, namely, that the epicycloidal or any other given form of the teeth, is not essential to this geering. It appears that teeth formed as epicycloids, will become more convex by working; since the base of the curve is the only point where they suffer no diminution by friction; whilst those of every other form, that likewise penetrate beyond the primitive circles of the wheels, will also assume a figure of the same nature, by the rounding off of their points, and the hollowing of the corresponding parts of the teeth they impel; and that operation will continue till an[106] angle similar to that at o, but generally more obtuse, prevails around both wheels; when all sensible change of figure or loss of matter will cease, as the wheels now before you will evince.
On the right of the drawing, (fig. 6) the teeth of the wheel B are angular, (suppose square) and those of the wheel C rounded off by any curve s, within an epicycloid. All that is necessary to remark in this case is, that the teeth of the wheel B must not extend beyond its primitive circle, whilst the round parts of those of the wheel C, do more or less extend beyond its primitive circle; whence it becomes evident, that the contact of such teeth, (if infinite in number) can only take place in the plane of the common tangent at right angles to A B; also that if these teeth are sufficiently hard to withstand ordinary pressure, without indentation in these circumstances, there is no perceptible reason for a sensible change of form; since this contact only takes place where the two motions are alike, both in swiftness and direction. A fact I am going to mention may outweigh this reasoning in the minds of some, but cannot invalidate it. I caused two of these wheels made of brass, to be turned with rapidity under a considerable resistance for several weeks together, keeping them always anointed with oil and emery, one of the most destructive mixtures known for rubbing metals; but after this severe trial, the teeth of the wheels, at their primitive circles were found as entire as before the experiment. And why? Certainly for no other reason than that they worked without sensible friction.
Hitherto nothing has been said of wheels in the conical form, usually denominated mitre and bevel geer. But my models will prove, that they are both comprehended in the system. The only condition of this unity of principle is, that the axes of two wheels, instead of being parallel to each other, be always found in the same plane. With this condition, every property above-mentioned, extends to this class of wheels, which my methods of executing also include, as indeed they do every possible case of geering.
Being afraid of trespassing on the time of the society, I have suppressed a part of this paper, perhaps already too long; but I hope I may be indulged with a few remarks on the application of those wheels to practical purposes. And first, as to what I have myself seen; these wheels have been used in several important machines to which they have given much swiftness, softness or precision of motion as the case required. They have done more; they have given birth to machines of no small importance, that could not have existed without them. In rapid motions they do all that band or cord can perform, with the addition of mathematical exactness, and an important saving of power. In spinning factories these properties must be peculiarly interesting; and in calico-printing, where the various delicate operations require great precision of motion. In clock-making also, this property is of great importance in regulating the action of the weight, and thus giving full scope to the equalizing principle whatever it be. I may add, it almost annuls the cause of[108] anomaly in these machines, since a given clock will go with less than 1⁄4 of the weight usually employed to move it. Another useful application may be mentioned; in flatting mills, where one roller is driven by a pinion from the other, there is a constant combat between the effort of the plate to pass equally through the rollers, and the action of the common geering, which is more or less convulsive. Whence the plate is puckered, and the resistance much increased, both which circumstances these wheels completely obviate; and many similar cases might be adduced.
I shall only add, that my ambition will be highly gratified if, through the approbation of this learned society, I may hope to contribute to the improvement and perfection of the manufactures of this county; and if the invention be found of general utility to my much loved country.”
Subsequently to the reading of the above paper, I had occasion to execute many wheels on this principle; and their appearance, and use, excited on the one hand much interest, and on the other much opposition. I had even to complain of real injury in that contest: against which I defended myself with a warmth that I thought proportionate to the attack.—But all this was local and temporary: and writing now for a more enlarged sphere, and perhaps for a more extended period, I feel inclined to lay aside every consideration, but those immediately connected with the influence of this work on the public prosperity. I shall therefore[109] avoid all reference to the names either of my friends or my opponents. My friends will live in a grateful heart, as long as memory itself shall last; my enemies, if I have any, will be forgiven—or, at worst, forgotten; and my System is henceforward left to wind its way into public notice and usefulness, by its own intrinsic merits.
Certain Observations which I was induced to make on occasion of a re-print of the above Memoir, may assist in introducing what remains to be said on the subject. They commence thus:
The foregoing little work, which first brought this subject into public notice in this town, was not the only method employed to develope its principles, and urge its adoption. A second paper was read, at the next meeting of the society, and some time after, a third, at the Exchange Dining Room; on both which occasions new modes of reasoning were pursued, and new kinds of proof adduced. On the first, a model was exhibited of two screw-formed teeth (connected with proper centres) exactly like those represented in fig. 6; by the action of which on each other, it became manifest that teeth of this angular shape do work together without inconvenience, and therefore, that all sensible friction is, in this case, done away.
On the latter occasion (the lecture at the Exchange) two[110] other methods were brought forward, to corroborate the principles before stated: (see Plate 14, fig. 1.) The first was a kind of transparency, in which a line of light represented the place of contact of two wheels working together; by the partial and variable obscuration of which, the successive action of every portion of the teeth was clearly shewn. The second method consisted of two pair of wheels, made from loaf sugar, the teeth of which were cut one pair in the usual form, and the other on the new principle. Here, the difference in the effects of the two methods was so great, that the common teeth were almost immediately worn or broken down, by the very same kind of impulse that the new wheels sustained without injury: and with a loss of matter almost imperceptible, since many thousand revolutions of the wheels took place without detaching so many grains of sugar!
These Observations include likewise the following remarks:
In adverting to a few of the difficulties we have encountered, it will appear curious that one of them should spring from a most useful property of the system: but the paradox is thus explained. As there is no method more effectual for giving the teeth a perfect form, than working the wheels together, (covering them with an abrasive substance) we have most frequently chosen to depend on that important property; and have therefore set the wheels at work as they came from the foundry, instead of chipping the teeth, as is usual when common[111] wheels are expected to act well in the first instance. But our wheels being then full of asperities, their action would be of course imperfect and noisy, till time had smoothed and equalized the touching surfaces: a state of things that might well stagger the opinion of a candid observer unacquainted with the system. Happily however we can now appeal to the fact of many wheels having become silent, that were once referred to with triumph, as proofs of a radical defect in the principle. It may not be improper to add here, that if highly finished wheels were particularly desired, we would engage to cut them in metal on this principle, with all the perfection of surface given to common wheels by the first masters.
In the use of bevel wheels of this description (with singly inclined teeth) there is doubtless a tendency to approach toward or recede from each other; the extent of which (for cylindrical wheels) has been already determined. This tendency goes, so far, to give a bend to the shaft; and, if this be very weak, to create a degree of friction on the teeth as the wheels revolve. It is therefore desirable that the shafts should be rather too strong than too weak; since the principle can only exist entire, when the wheels in working, are kept in the same planes which they occupy when at rest. This is too evident to be further insisted on.
But a greater, or at least a more frequent cause of friction in the wheels is the motion, endwise, of the shafts, arising[112] from a want of solidity in the bearers, and especially of connection between them; for whenever these are strongly connected, and the shafts well fitted to their steps, all circular commotion is ipso facto destroyed; while the longitudinal tendency produced by the teeth on the shafts is certainly an advantage: because it prevents the shaking that often arises from their vibration, endwise, when lying on unsteady bearers, or on bearers between which they have too much liberty.
A few words will make known the process of reasoning by which I arrived at the idea that forms the basis of this invention. I had been conferring with a well-known mechanical character, (to whom the art is greatly indebted)—and hearing his observations on the advantage derived from having two equal cog wheels connected together, with the teeth of the one placed opposite the spaces of the other; so as to reduce the pitch one half, and the friction still more; (since the latter follows the ratio of the double versed sines of the half-angles between the teeth respectively:)—and no sooner had I left that gentleman, than my imagination thus whispered—“What that gentleman says is both true and important.” “But if two wheels thus placed, produce so good an effect, three wheels (dividing the original pitch into three), would produce a better: and four, a better still: And five a better than that. And for the same reason, an indefinite number of such wheels would be indefinitely better! We must then cut off the corners of all those teeth, and we shall have one screw-formed line, that[113] will represent an indefinite number of teeth, and approach indefinitely near to absolute perfection!” Thus did this Invention originate: and it soon appeared to me, to be the nearest approach of material exactitude to mathematical precision, that is to be found in the whole circle of practical mechanics. For not only is the relative motion of the touching points of two wheels (that is their friction), less than the distance between two of the nearest particles of matter, but it is as many times less than that distance, as that distance is less than the half diameter of any wheel whose teeth are thus formed.
I assert therefore that these teeth, placed in proper circumstances, do work without sensible friction at their pitch lines: as although by means of mathematical abstraction, it may be possible to assign a degree of friction between them, that degree cannot be realized on a material surface: and I fear not the friction on mathematical surfaces, if my material surfaces do not suffer from it. I take leave then to repeat, that no friction can justly be said to arise from a motion, too short to carry a rubbing particle from one particle of a rubbed surface to the next! and this is precisely the case in the present instance.
Continuing to reflect on this important subject, I soon perceived that the screw-formed line would give the teeth a tendency to slide out of each other; and to drive the shafts of the wheels endwise in opposite directions; but even that evil is not great:[114] for, confining the obliquity within 15 degrees, that tendency is only about one quarter of the useful effort; and a stop acting on the central points of the axes, will annul this tendency without any sensible loss of power. We need not even have recourse to this expedient when any good reason opposes it: for this tendency can be destroyed altogether by using two opposite inclinations: giving the teeth the form of a V on the surface of the wheels—a method which I actually followed on the very first pair I ever executed, which I believe are now in the Conservatory of Arts at Paris.
A circumstance somewhat remarkable deserves to be here noticed. In the specification of a Patent which I have seen in a periodical work since my return from Paris, for things respecting steam engines, and dated, if I recollect right, in 1804 or 5, this V formed tooth is introduced—as an article of the specification, yet having no connection whatever with its other subjects; nor being attended with the most distant allusion to the principle of this geering. The fact is that I had these V wheels in my Portique, in 1801, when that exhibition took place in which my Parallel motion appeared and was rewarded by a Medal from Bonaparte: so that two of my countrymen at least, engineers like myself, appear to have taken occasion from that exhibition, to draw my inventions from France to England—a thing by no means wrong in itself nor displeasing to me: who was then totally precluded from holding any communication of that kind with my native country.
It would be repeating the statements contained in the foregoing memoir, to say more on the general principles of this System. I request therefore, my readers to give that paper an attentive perusal; and to accept the following recapitulation of its contents:
1. To cut teeth of this form in any wheel is, virtually, to divide it into a number of teeth as near to infinite, as the smallness of a material point is to that of a mathematical one.
2. By the use of these teeth, and the multitude of contacts succeeding each other thence arising, all perceptible noise or commotion is prevented. (This of course supposes good execution, or long-continued previous working.)
3. For the same reasons, all sensible abrasion is avoided: for we have proved that the passage of any point of one wheel, over the corresponding point of another, is indefinitely less than the distance between the nearest particles of matter. (This supposes the action confined to the pitch line of the wheel; and this it will be in all common cases—since the teeth wear each other in preference, within and without that line; which therefore must remain prominent.)
4. From the foregoing it appears that the teeth of two wheels working together tend constantly to assume a form more and[116] more perfect: as they abrade each other while imperfect, and cannot wear themselves beyond perfection.
5. For a similar reason the division of the teeth cannot remain unequal: for those that are too far distant from a given tooth will be attacked behind, and those that are too near before; so that the division also will finally become perfect.
But it must be remembered that these recoveries of form are in their nature very slow; since the nearer the teeth come to perfection the slower is their approach to it: so that in thus dwelling on these properties, we do not advise the making of bad wheels that they may become good; but only wish to destroy an honest prejudice that has already much impeded the progress of the System; namely, that it requires great nicety to adjust them so as to work together at all: which is—(to say the least) a very great error.
In Plate 14, fig. 1, I have shewn the apparatus presented at the Exchange, as mentioned in page 110 preceding. A B is the stand; C D is a disk turning on the centre E; b a is the transparent line cut through the stand, and representing the place of contact of two wheels geering together. It is there seen, (supposing the disk to turn in the direction of the arrow) that the action of the teeth, is always progressive along the transparent line a b; whether the single or double obliquity[117] G or F be used. In reality, the lower end of any tooth c, does not uncover the line a b, till the upper point of the succeeding tooth d has begun to cover it; whereas, observing a few of the common teeth represented at H, as directed to the centre of the disk, they would be seen to pass the line a b all at once; and thus to represent, with a certain exaggeration, the transient manner of acting of the common geering.
Some knowledge of the nature of this geering may be gathered from its very appearance: see fig. 5 Plate 14. To represent these teeth properly, no light must appear between them. The tops of the teeth offer a continued circular line, similar to what it would be if there were no teeth at all: and the latter are distinguished only by a different shading of their front and lateral surfaces. The reason (as has been already observed) is, that they are necessarily so placed, as that the last end of any tooth shall not quit the plane of the centres, until the first end of the succeeding tooth arrives at it; which principle precludes the possibility of any space remaining between the teeth, that an eye directed parallelly to the axes could penetrate. Such a space indeed would introduce a portion of the properties of the old geering, which it is the object of this System to avoid. As this wheel then appears in fig. 5, so it acts: that is equally and perpetually.
It were well also to observe the appearance of these wheels on their edges; or in the planes which, as wheels they occupy.[118] The 4th. figure of this Plate is outlined with some care, in order to shew the varying, and seemingly anomalous form which the teeth assume as they approach the boundaries of the figure. Although cut as obliquely to the axis there, as any where else, the receding cylindrical surface, thus seen, appears to take this obliquity away; and the very outward teeth seem nearly parallel to the axis of the wheel. But this is only appearance: and we give here one example of it, that we may not be obliged to lose much time hereafter, in drawing correctly, wheels on this principle—a process indeed which in many cases, would be found very difficult, if not impossible.
We have already adverted to the oblique tendencies of these wheels, when used with a single inclination of the teeth; from which, among other things, it follows that, in the act of urging the shafts endwise, they tend also to bend these shafts: for which reason the shafts require to be stronger than those of common wheels—that is, when the effort bears any proportion to their stiffness—a circumstance which, in light rapid movements, is of small moment. And in heavier works, when it is desirable to get rid of these tendencies altogether, we have peremptory means of avoiding the very appearance of this evil.
Suppose then (fig. 2 and 3, plate 14) a b to be a straight rack on this principle; driven by the wheel or pinion c. The motion, backward, of the pinion, tends, clearly, to urge the pinion endwise towards d, and the rack sideways towards a b.[119] But either of these motions is prevented by fixing to the pinion, or the rack, a cheek e f, to support them against this lateral pressure. But then, exclaims a doubting friend, you introduce friction: and it is true: there is now a real rubbing of the ends of the teeth against this cheek; but the pressure there being only one quarter of what it would be on the front of straight teeth, we avoid (on a rough estimate) three quarters of the friction; while preserving all the constancy and smoothness of motion which the system gives; and which after all, is the most important part of the business.
This idea then applies among other things to the racks of slide-lathes; giving a regular motion to the rest and cutting tool, thereby adding to the perfection of the turning process: and many other cases might be adduced.
But instead of using a rack and pinion, as thus described, two wheels, of any desired proportions might have been thus treated, and the result would have been the same. They would have worked with perfect smoothness, under about one quarter of the friction attendant upon common wheels in similar circumstances. There are cases therefore, in which it would be expedient thus to employ the System. I cannot but observe likewise, that this method of using cheeks to prevent any side motion in spur wheels, might also be applied to bevel-wheels, to prevent the angular tendency which the obliquity of their teeth gives them: and that I prefer such a method of obviating this[120] evil (where it is one) to any attempt at using teeth in the V form, on bevel wheels. Still however, as before observed, this counteraction of the oblique tendencies is not always necessary. It may be dispensed with in all light and rapid movements; especially in the use of perpendicular shafts; and where the driven wheels are small and distributed round a central wheel in positions nearly opposite each other: of all which cases we shall see examples in the spinning machinery to be described hereafter.
The figures of this Engine (see Plates 15 and 16,) are drawn to a scale, from the Machine itself, now before me. The scale of the objects on Plate 15, is one inch and three quarters to the foot; and that of the objects on Plate 16, one inch and one third. These were convenient proportions for introducing this object into the present work; but the size itself of the Machine is arbitrary. I did not make it according to my ideas of the best dimensions: but bought it as a common cutting Engine, and gave it those other properties that my System required.
The first remarkable deviation from the usual form is in the shaft or axis of the dividing plate. See fig. 1 and 2 of the Plates 15 and 16. The dividing plate a b, is concentric with, and fixed to an axis A B made as perfectly cylindrical as possible, so as both to slide and turn in the bars C D, and E F composing the frame. These bars are bushed, to fit the axis A B, either with a contracting ring of brass, as usual in some mathematical instruments; or with type metal, cast around the axis into rough holes in those bars:—which metal, closing upon the axis makes a good centre; and will last a long time. My Engine is made in this manner; and has been renewed in[122] this part only twice in several years. This frame C D E F of the Engine, is strongly connected with the feet G G H H, by means of the nuts E F in the plan: and by these feet it is fixed to its bench or table, as will be seen in Plate 16.
Figure 2 of the present Plate, represents the plan of the Machine, but turned upside down; so that the feet G H screwed under the lower plate E F, are wholly visible. In this figure, also, is shewn at c d, the edges (without the bottom) of the horizontal slide which carries the stand for the cutter frame represented in fig. 4. This stand is indicated by the dotted lines of this figure 2, as situated under the arm D of the bar C D; but it is better shewn in fig. 5, where e f marks the slide in which the cutter frame (fig. 4) moves up and down, by means of the screw and handle e f. In general I avoid dwelling much on these smaller parts, because they exist, probably in a more perfect state, in most other machines. In this fig. 5, g h shews the screw that moves this stand nearer to, or further from the axis A B of the Engine, according to the diameter of the wheels: which is also a common process in Machines of this kind, on which therefore much need not be said. But a somewhat greater importance attaches to the cutter frame represented in the 4th. figure: which is a kind of small lathe whose spindle n o, carries the cutter n, outside the frame, for the purpose of changing the former without displacing the latter. The cutter (of any proper section) is placed in or near that line which is a continuation of the centre of the fixing[123] screw o p. It is in that line for wheels whose teeth can be finished with once cutting: but near it for those whose teeth must be cut at twice. In this same figure, i k represent the ends of the standards that form the vertical slide e f of fig. 5; and the separate figure p q, shews the back of the cutter frame l m, the flat part of which, p, presses correctly on these uprights i k, and thus fixes this instrument at any desired height, and to any given angle with the perpendicular: the use of which arrangement we shall soon have occasion to exemplify.
Turning now to fig. 3 of this Plate, we there see the main shaft A B, broken off at B: and the letters a b again shew the dividing plate of figs. 1 and 2: under this Plate is seen an alidade or moveable index, shewn by section only at c, and in elevation at d e; where it clips the plate as far as n and carries a boss between n and e, on which the dividing index e f, turns; and to which it is strongly fixed by a nut o, when the proper number to be cut is determined. Moreover, this boss forms, itself, the nut of a thumb-screw s, which, carrying a circular plate at its lower end, clothed with leather or any soft substance, connects strongly, without injuring the plate, the moveable index with any point of it, as determined by the dividing index e f. This brings us into the midst of things, as it respects the use of this Engine; for the former index c d, is furnished with a small roller, p, the motion of which all the foregoing objects must obey, when they have been fastened together by the thumb-screw s. We turn then to the figures 1 and 2 of Plate 16, in[124] order to shew those parts in action: after remarking only that the form p q r of this fig. 3, is that of the moveable index shewn before at c d; requiring only, to become complete, that the part q should be sufficiently lengthened to make the arc r q a complete semi-circle—for purposes that will shortly be explained.
In the two figures of Plate 16, the Machine is shewn as placed on its bench or table, accompanied by the parts which give it a distinctive character, and in fact embody the System. In addition to the parts already described, we first remark the circular rim c d, fixed to the ends of the bar E F; and made perfectly concentric with the main shaft A B, and the dividing plate a b. This rim is shewn in section only, at v fig. 2. Its section resembles an L, and thus forms a basis for certain plates that will soon appear; and receives the screws by which these plates are fastened to it. This being sufficiently clear, we now proceed to describe the table and the connection of its mechanism with the foregoing.
In Plate 16, K L is the table: to which the Engine is screwed through its feet G H. I, is a square bar of wood, sliding in a mortice through the top of the table; and connected by a joint with the lever M N—itself moving round a pin at O, and carrying a friction roller, P, which pressed by the spiral Q, as turned by the handle R, raises the bar I, and with it the main axis A B of the plate, and of course the wheel to be[125] cut, centered as usual on this axis above B. Finally, p q r, in both figures, is the moveable index first shewn in fig. 3 of Plate 15; prepared to be drawn round by a weight W, hanging to the cord x, passing over the pulley y, and tied to the right end of the arc q r, when this is to move to the left; or to its left end, when the motion is to be toward the right:—these motions depending on the right or left-handed direction of the teeth which it might be wished to cut on the Machine.
Between the two figures 1 and 2 of this Plate, there appears a diagram, the base of which is nothing more than a part of the rim c d supposed straightened, and placed there that its use may be the easier understood. On the rim is seen a right angled triangle e g f, against which the roller p will lean by the action of the weight W on the cord x, and the arc q r of the moving index p q r. So THAT when, by the handle R, the spiral Q depresses the lever M N, by means of its roller P, then the bar I raises the axis A B of the Engine, and the weight W turns it at the same time, as much as the small roller p permits by rolling up the side e f of the plate e g f. And thus may a screw-formed tooth be cut in any wheel centered above B in the usual manner.
Thus then, in describing this Machine, the manner of using it has been also shewn: for the cutter, in this Machine, (to cut spur wheels) is always fixed; and all the motion is composed of the rotatory and longitudinal movements of the principal[126] axis, which carries the wheel along with it. The cutter I say is fixed, at a proper height just above the wheel, and at an angle to the perpendicular, equal to that it is wished the teeth should form at it’s pitch line. This inclination as before observed is 15 degrees; and the tangent of 15° is in round numbers 268, when the radius is 1000. That is, in our present figure, the basis e g of the plate e g f, occupies 268 divisions of a scale, of which the height g f contains 1000. It appears then, that to cut a tooth with 15 degrees inclination, by this Plate, the wheel receiving that tooth, must be just as large as the rim itself; for the surface of the wheel would turn more, with a given elevation, if it were larger than the rim; and would turn less, by the same elevation, if it were smaller. In a word the whole theory of this operation, is now clearly seen. The smaller the wheel to be cut, the longer, horizontally, must be the Plate; or in other words, as the diameter of the wheel is to that of the rim, (c d) so is the length e g of the Plate to the length required. Now this height f g, is always the same; all change therefore, in the plates, takes place on the horizontal length: and this length is most easily found by the foregoing RULE OF THREE. If then, instead of the triangle e f g, I had used the triangle e′ f′ g′ it would have followed at once, that to produce an inclination of 15 degrees, I must have taken a wheel of just half the diameter of the rim; for the plate e′ f′ g′ is just twice as long as that e f g. To prove this, let us suppose the diameter of a wheel wanted, to equal one half that of the rim c d: then the rule will stand thus:
1 is to 2, as 268 is to ...536, the length of the plate according to the theory; which is precisely the length it is drawn to compared with that e f g, namely twice as long. Thus the four triangles, drawn to the right and left in this diagram, represent the plates for the wheels of the following diameters respectively:
| No. | 1 | , a wheel | equal | to | the | plate rim c d; |
| 2 | do. | do. | to | 1⁄2 | do. | |
| 3 | do. | do. | to | 1⁄3 | do. | |
| 4 | do. | do. | to | 1⁄4 | do. |
A small anomaly, of form, may be mentioned here to prevent mistakes. The shaded triangle e f g in the Plate, looks higher than the rest: but if higher, it is also longer in the same proportion; and the roller p never reaches the bottom: so that the effect of this Plate is the same as though it resembled the others in every respect. In general the effect of the Plates depends on their length compared with their height: and indeed they must be made higher than the thickness of the wheel to be cut, that the latter may disengage itself from the (fixed) cutter both above and below.
It is proper to observe, that for every pair of wheels there must be a pair of plates; one leaning to the right and the other to the left, (see the diagram) but, as before said, the degree of obliquity must be different in each pair, except in the case[128] of equal wheels, when the same plate serves for both; only turning it to the right for one wheel, and to the left for the other. Nor does this offer any difficulty, as the plates are made of common tin plate: which is easily brought to fit the rim, whichever way it is applied. I shall now add another example of the process for finding the length of the plates: and to that end repeat that the plate rim c d, is 22 inches in diameter, or 11 inches radius. Supposing then that we wished to cut a pair of wheels, one of them being 1 inch in diameter and the other 12 inches; both to have teeth inclined 15 degrees to the axes; (as without that they could not work together) to do this we must effect these two proportions:
| Both proportions being effected, the first plate is | 5896 | parts. |
| And the second | 491.33 | do. |
The one of course, to be directed toward the right hand,[129] and the other toward the left, on the plate rim; where note, that if the height (1000 parts) is found so numerous as to create confusion, let 100 parts be assumed; when the length of the plate will become 26.8 or 26 and 8⁄10 instead of 268, and the operation will be so much the more simple.
It should be added that this process admits of being further simplified: since the product of 11 inches, radius of the plate rim, multiplied by 268 (tangent of 15 degrees, or length of the plate for a wheel equal in diameter to the plate rim) since this product, I say, is a constant number, namely: 2948—which, divided by the half diameter of any wheel, gives, at once the length of the plate adapted to that operation, in parts of which the height contains 1000; or supposing the height to be 100 only, this constant number becomes (nearly enough for practice) 295. In a word, on a height of plate of 100 parts, when wishing to cut a wheel of 4 inches in diameter, I merely divide 295 by 2, and get for the length of my plate 147.5 parts of which the aforesaid height is 100.
It may possibly be suggested that this method of using plates to determine the obliquity of the teeth is a homely method, giving some trouble in the execution, and leaving a certain degree of roughness in that execution. The fact is allowed; but this method has the advantage of a very general application, which many a better looking apparatus would not present.
Besides, for most uses, these teeth require chiefly that the obliquity should be correct, and not that the surface should be licked like those of a gewgaw. In fine, the principle of this Machine once known, its best form will occur to the reflecting mechanician according to the quality of the work he has in view: And in fact, in the hands of a well known artist, this form has been already varied so as to produce effects much higher wrought than could be drawn from the Machine above described: which latter however in point of generality, still preserves the advantage.
That “necessity is the mother of invention,” is a remark none the less true, for having become a trite proverb; I could mention the time, place, and circumstance which gave birth to this little Invention: but such detail would be superfluous. A certain door was, and is still, most inconvenient, from the stiffness of the spring, and the noise it occasions in a place where silence ought to prevail: which state of things suggested to my mind the Machine represented in fig. 5, of plate 17.
A B C in that Plate, is a horizontal section of the door, door jambs, &c. The door spring now in use, is a barrel-spring, with an arm carrying a small roller which presses in a gutter-formed plate, screwed to the door. My door spring is on a different principle. The roller is fastened in and by a small frame to the door, and the arm is fixed to the axis of the spring, which passes up through the top of the barrel. This spring is much weaker than the former, insomuch as only just to close the door by its elasticity; but when the door is shut, there is a sharp bend in the arm that wedges itself against the roller, and decuples at least the force of the spring, as tending to keep the door closed. When therefore it is desired to open[132] the door, by pressing the door itself, a good push is necessary, but only for an instant: for as soon as the bent part of the arm is forced off the roller, there remains only the small resistance of the spring to be overcome; which latter, when suffered to act in shutting the door, will not shut it with that noise a stronger spring would occasion; and yet, when arrived at its first position, it will keep the door as strongly closed as ever. And should it be wished to avoid the necessity of pushing hard against the door, even at first, there is a sliding button and stem B put through it, which, if pressed from the other side, with the force only of the spring, will raise the latter beyond the roller, and thus open the door with perfect facility: and this same process will take place in pulling the door open by the hook D from the inside: yet still the door when closed will be as firmly so as before; the spring-bar acting in the latter position, as much like an invincible stay as the workman shall have desired—this property depending clearly on the nearness of the bend to a right angle.
This device may appear to some an object too inconsiderable to be justly dignified with the name of an invention. But if I should sometimes fall into such an error as this, I intend to compensate for any thing too trivial by giving in other cases, Inventions of ample size and number. I might even mention the Cutting Engine given in this part, where several Inventions are compressed into one, or rather presented as one, of which several examples will occur.
The pinion wire of clock and watch makers is well known. I am not wholly acquainted with the manner in which it is drawn: but I have made my pinion wire, of brass, in lengths of about a foot, by the Machine described below.
A common Draw-bench (not here represented) is worked in the usual manner: but the instrument which forms the pinion (see Plate 17, fig. 1) is of a peculiar construction. It consists of a plate A B, containing—1st. a guide tube a, (fig. 2) to centre and conduct the blank wire;—2d. a ring b c, with nine grooves cut on one of its surfaces, directed to the centre, and in which are well fitted the cutters 1 2 3 4 5 6 7 8 9; and 3d. a ring d e, formed into nine spirals exactly like each other, answering to the cutters, and destined to urge them equally toward the common centre whenever this circle d e, is turned by the endless screw C D, in the direction of the arrow. In fig. 2, f g is merely a top piece to cover at the same time the cutters and the ring d e; which latter is thus duly centered. The points of the cutters 1, 2, 3, &c. are formed like the spaces of pinion teeth; and in the other direction, are sloped 15 degrees to the common axis, as taken at their pitch line.
The third figure represents the drawing clams, or pinchers, with a piece of blank wire d in them, tapered off to give easy entrance to the cutters. These clams have a cylindrical part of about a foot long, in which is cut a winding groove a b, whose use is to turn the wire in the act of drawing; for which purpose also the swivel e f is provided. The method I employ to trace this groove to the obliquity required, is to measure the circumference of the cylinder, and call that 268; and then, to make its length, in the cylindrical part, equal to 1000 of the same divisions. But this is right, only when the pinion to be drawn is of equal diameter with the clam-cylinder a b: so that if it is wished to draw pinions of a smaller diameter, I further say: diameter of clam-cylinder is to diameter of pinion, at the pitch line; As 1000 (present length of clam-cylinder) is to required length of ditto. Thus, for example, if the diameter of the pinion were only 1⁄4 that of the clam-cylinder, the length of the latter would be only 250 of the 1000 divisions, before found: and so in proportion for smaller diameters.
The figure shews this groove receiving a guide screw or stud a, which, placed in the fixed headstock a c, turns the clams d, with the wire, just enough to give the teeth an inclination of 15 degrees, thus adapting them to the wheels of which the proportions have been already given; where note, that the real dimensions of this pinion Machine are twice as large as those of the figures 1 and 2: but the size of every thing is of course variable, according to the pinions required to be produced.
This Chain is shewn in fig. 4 of Plate 17. The links are formed to an angle, in the middle, similar to that of the wheels at their pitch line; of which the obliquity, for the V wheels, is greater than 15 degrees; since the thickness of the wheel, is necessarily divided between the right and left handed slope. Be this slope what it may, the chain and wheels must of course be alike, measured at the pitch line of the wheels; and then, as the chain geers with a straight line of pinions, they work together without sensible friction on the teeth, and with nearly the same steadiness of motions as wheels would work together. Moreover, if the drum be of a pretty large diameter, its action will likewise be nearly equable. The degree of precision depends, however, on the fineness of the pitch, and the largeness of diameter in the drum; since every chain bending round a cylinder must form a polygon of a greater or less number of sides, dependent on these circumstances. I repeat then, that while the chain works on the pinions in a tangent to them all, there is no necessary friction between them; nor yet on the pins of the chain, but only at the drums which actuate and return the latter:—I shall dismiss the subject, by observing, that I have used the term drum, because of the similarity of this chain-motion[136] to that produced by bands, where drums are generally the movers. But here, this supposed drum is a wheel of proper diameter, cut into teeth similar to those of the pinions; and placed at the same height on its spindle. I have reason to think that this chain, carefully made, would be an useful addition to the bobbin and fly frame, applied both to the bobbins and spindles, instead of the bands now in use; which, though a convenient resource, give a result equally uncertain and imperfect.
The present description of this Machine, will consist, chiefly, of a translation from my own specification, given at Paris with the application for a Brevet, or Patent, obtained in the year 1795, and which is thus introduced.
“It is a well-known fact, that the longer any Boat or Vessel is, in proportion to its width, the less power it requires to convey a given load, from one place to another. But these lengths cannot be extreme, without introducing a degree of weakness, that would offer great danger in the use of such vessels. If then a Boat of a given volume, be divided into several long and narrow ones, the head of each adapted with a certain exactness to the stern of its forerunner, they will (with the trifling difference arising from the asperities of their surfaces) all move through the water with the same ease as any single one; and carry, unitedly, the same weight as did the large Boat before it was divided. This idea constitutes the principle of my Serpentine Vessel.”
“This Invention is not to be considered as an imitation of the well-known manœuvre of towing one vessel in the wake of[138] another: for the resistance of the vessels thus towed, remains nearly, though not quite the same as if drawn along separately. But here, by the adaptation of the prow of one Boat to the poop of another, the first alone suffers resistance from the water—which, although it enters between the joints, strikes only the first—and from this it follows, that the resistance of these vessels, in passing from one place to another, bears no necessary proportion to the weight they carry.”
“Thus then, I obviate the necessity of having broad vessels to carry the heaviest burdens; for I disseminate the load over an indefinite length: by which method also, my vessel rides in shallower water, and depends less for its passage, on the state of the rivers or the seasons. Besides, they require a much less number of horses, or exertion of power, to transport a given quantity of goods; admitting at the same time, a greater swiftness of motion. And finally, if these vessels travel through different towns on the same voyage, the goods of each town may be lodged in the same part, and merely detached in passing, so as to lose no time in unloading them.”
“Fig. 1 of Plate 18, shews the plan of several forms which I give to the articulations or separate parts of these vessels: so as to connect them strongly, yet leave them, as a whole, in some degree flexible. The form A B, is, for the first boat, a straight line across to form the stern, and for the second an obtuse angle terminated by a semi-sphere or vertical semi-cylinder,[139] which enters a hollow and similar figure in the first Boat—which latter, in this case, forms the Head of the whole Serpentine Vessel.”
“These two parts or joints, of which we have been speaking, are held together by a rope c d e f, which, fastened to the second part at c, passes over two pulleys e d, in the head, to the small capstan f, by which, both parts are bound together as tightly as may be judged proper. If it were thought necessary, the spaces A B might be underlined with a piece of leather or metal, not to prevent the water from entering between the Boats, but to prevent its striking those which follow the others through the water—a precaution less urgent in the other kind of joint we are about to describe.”
“C D, in this same figure, presents another form of the head and stern of two contiguous Boats or parts; (which, to save room, are both supposed to be broken off at some point between their ends:) where as in the former case, the Boats are connected so as to remain horizontally flexible. These forms are semi-cylindrical, the stern concave, and the head convex, to the same radius; and the motion takes place around a bolt and pulley p, reeved with a rope coming from one side of the first Boat near C and led again to a small windlass or capstan placed on the other side near D. E F, is another modification of the same kind of joint: the centre of which is a bolt or stud q, (better seen at q in the 2d. figure) over which a triangular[140] frame falls from the preceding Boat, and thus connects them instantaneously; leaving a certain flexibility in the horizontal direction.”
“Finally, G H shews a simple mean of connecting these Boats, on the supposition that both ends of each are formed alike to an obtuse angle in the middle of their breadth. It is a kind of hook r s, mounted in a frame turning on centres in the preceding Boat, and reaching over into the succeeding one; where it finds a hollow step of metal which receives and fits it, so as to hold these neighbouring Boats with sufficient tightness, but still with a certain degree of flexibility. Many other methods might be suggested, by which to form these joints; and almost any might be made to answer the purpose. I shall therefore leave this branch of the subject, observing only, that the second figure of Plate 18, is an elevation of the same things: which, generally, are marked with the same letters as far as they are visible.”
“The third figure presents the same objects in perspective; to which are now added two masts I K, placed obliquely on that Boat which forms the Head of the whole vessel. This obliquity is useful when the boat is drawn from one side only; but is injurious where the traction takes place indifferently on both sides: so that I should not, now, advise the use of this method—which indeed, I have avoided in fig. 4 of this Plate.”
“In every case, each of the masts carries a pulley near I K, over which passes a rope, the ends of which are fastened to the masts by proper brackets, near the deck: and to the middle of this rope is fastened the track rope L, by which the horses draw the Boat along. By these means the vessel is steered either to or from the land: for if the knot of the track rope is brought near the mast I, the Boat (which as before observed is the head of the whole vessel) veers towards the horses; and the contrary when the knot is drawn towards the mast K: both which effects are rendered the more prompt and decisive, by the use of the lee boards K M, the nature and use of which are already fully known.”
“But there are cases in which, from its great length, this Serpentine Boat would require a particular direction, for some intermediate point between its extremities; as although, in theory, every separate part ought to pass through the same water, yet in canals or rivers much bent, this may not invariably take place; and then a rudder would be useful, even in the middle of the vessel. I have therefore placed a pair at P R, fig. 3. Their motion is a vertical revolution, round a horizontal centre; and as they are formed obliquely to the sides of the Boat, when one of them is plunged into the water, it tends to drive the Boat in a sidewise direction: and if at any time it should be desired to stop the whole vessel, both rudders would be plunged at once into the water, when they would greatly contribute to that effect.”
“The fourth figure in this Plate 18, presents a general view of the vessel, comprising five articulations, (or Boats) besides the head and stern—which latter would fit each other without any intermediate parts, and form a Boat alone. Nor do these five parts by any means limit the useful number: but the Plate would not have contained more, unless on a scale too small to be distinctly understood.”
“Returning now to fig. 1, we observe the ropes A D F H and B C E G, which are supposed fixed to the stern Boat, and carried to the capstans represented in the Head. These ropes consolidate the whole fabric, and act, occasionally, as a kind of muscle, to govern the larger evolutions. These ropes pass in the brackets placed near the joints A B and C D, &c. being under the gang ways, of which a portion appears at S fig. 3, hung upon hinges, that they may be turned up when the Boat is used in narrow water.”
To the above specification were added the following remarks, which still apply to this kind of vessel, navigating on canals and inland rivers: “this vessel admits of the use of every kind of mover; such as men, horses, wind, or the steam engine; the latter of which I propose to apply to it in a manner equally simple and effectual; especially so as not to injure the banks of any canal, &c. by acting against and disturbing the water.”
I need not repeat that this Invention dates as high as 1795: as the Brevet was issued in that year. It may be added that four parts of such a Boat were executed about the same time; namely, the head, the stern, and two intermediate pieces: making together a length of 100 feet; and these, loaded to a certain depth with stones, were drawn up the river Seine by a single horse on a trot—which would likewise have taken place had the Boat been ten times as long; since, as before mentioned, the resistance of this kind of vessel bears no given proportion to the Load it carries.
I think it may be assumed that friction is fully expressed by the word rubbing: and that where rubbing cannot be found, friction does not exist; especially that kind of friction which opposes the motion of machinery—in which respect, the subject is chiefly thought interesting to mechanicians. It would be abandoning my intended plan in this work, to treat largely of friction, or any other accident in practical mechanics; but having already declared myself “no believer in several sorts of friction,” I am in a measure bound to introduce my description of the two following articles, by a short reference to the general subject. I offer then the following remarks, more as hints for the consideration of learned experimenters, than as conclusions sufficiently proved to become rules in practice. What I cannot help urging strongly is, that rolling is not rubbing. If it were, I would ask in what direction it takes place? Is it in that of the plane rolled over? or in that of the radii of the rolling body? If in the former, it would indeed glide over that plane, and occasion or suffer real friction; but this, I think, is not pretended. If this motion is in the latter direction, (that of the radii of the rolling body) it is indefinitely short, compared with the progressive motion of the rolling body, so[145] that the power of the latter, to overcome any resistance in that direction, is infinite. Whenever therefore, in experiments of this kind, a finite resistance is perceived, it must, I should think, be ascribed to other causes, and not to friction. In my wheels for example, (see a former article) where there is a real and deep penetration of the surfaces, I have proved that the friction between the teeth is less than the distance between two of the last particles of matter: and surely, when penetratration is purposely made as small as possible (by the use of smooth rollers) the friction thence arising must be still more imperceptible. But I hear it answered, that this friction is both known and measured! and certain celebrated experiments are adduced to prove it. But what I most wonder at is, that a person so truly learned as the author of those experiments, should have adopted so remarkable a misnomer; in which to all appearance, indentation has usurped the name of friction. Nor let this surprise, surprise any body: nor especially, offend this learned author himself; for I am persuaded that the sole act of placing these wooden rollers, on these surfaces of wood, must indent them both sufficiently to account for all the facts observed; and still more so when loaded with weights of 100, 500, or 1000lbs. No friction, therefore, is requisite in accounting for the resistance of these rollers to horizontal motion. Nay, I submit, whether a resistance, arising from indentation alone, would not prove to be “directly as the pressures and inversely as the diameters of the rollers?” To me the subject presents itself under three aspects: either the whole indentation[146] takes place on the rollers, when they are very soft and the rulers very hard; or the latter, when they are very soft and the rollers very hard: or, which is most likely, this indentation takes place on both bodies at once; so as to produce a surface of contact, intermediate between the straight surface of the rulers, and the cylindrical surface of the rollers. But in either case, the place of resistance to horizontal motion, must be out of the line of direction of the roller’s centre of gravity: and thus would the roller present more or less resistance, independently of every thing that can be called friction: and which degree of resistance will continue to exist as long as the place of contact is made to change on the rulers—for thus to change this place of contact is to renew this indentation; which process will elicit a resistance equal to what would be observed were the roller (without indentation) forced up a plane, inclined to the horizon in the same angle as a line, drawn from the centre of the roller to the extreme edge of the surface of contact, makes with the perpendicular.
I cannot possibly enter at length into this subject, as it makes no part of my engagement to the public: but I would observe that this resistance is, a fortiori, something besides friction, since greasing the surfaces “did not cause any sensible diminution of it;” whereas it made a difference of one half! in some others of the experiments alluded to.[4] Were I[147] asked the reason, I should answer, because friction had little or nothing to do with it; and I would say further, that greasing or oiling these surfaces would most likely increase, instead of diminishing, their resistance to horizontal motion: namely by softening them, and making them more susceptible of change of figure: which opinion gathers strength from another fact adduced, viz: that “rollers of elm produced a friction (or resistance) of about 2⁄5 greater than those of lignum vitæ:” but why? because elm is relatively soft and lignum vitæ hard—the only cause that appears sufficient to account for the facts observed.
[4] See Dr. Gregory’s Introduction to his Mechanics. Vol. II.
I must now leave these remarks to persons having more means and leisure than myself, to pursue the subject; wishing only, that useful truth may result from them: and that this unbelief of mine “in several special kinds of friction,” may at least be found to have some reasonable ground to rest upon.
But I may be opposed in some of my statements by the fact, that friction rollers, with centres, have been used with little advantage; and often laid aside. This I acknowledge; and go a step further. Friction is by no means of so much consequence as it was once thought to be: and is not the source of the greatest defalcations that occur in the use of power. Yet, to get rid of it, in some cases, would be of considerable importance; and the subject deserves at least the attention of every intelligent mechanician.
Those who have used friction rollers, know that it is a thing of great difficulty, to place their axes exactly parallel to that which they are intended to support: and even, if rightly placed at first, that a small degree of abrasion, greater on one pivot than another, will soon destroy that parallelism; and thus introduce a growing friction, capable, at length, of rendering the whole completely useless: for although the original friction is lessened by being transferred to a slower-moving axis, yet the latter still resists in some degree, say 1⁄4 of the whole; (its pivots being 1⁄4 of its whole diameter) so that the cohesion, or something else, between the main shaft and the friction roller, (thus resisted) must be sufficient to drag round the latter, against about 1⁄4 of the original friction; which in a word it cannot do without some relative motion between those surfaces, the friction roller lagging behind the main shaft, until its own friction is overcome by another. And thus it is, that a friction roller of this kind, does not make so many revolutions on its pivots, as its diameter compared with that of the main shaft, would imply; for example, if the shaft were 4 inches in diameter and the friction roller 8 inches, the latter would not complete one revolution against two of the former. There would thus remain a difference spent in real friction, in addition to that on the axis of the friction roller. Besides this, we have the want of parallelism above mentioned; which occasions a rubbing, in the direction of the shafts, small indeed in quantity, but for that reason very powerful in bringing on a[149] change of form, and thereby hastening the common destruction. Both these accidents, therefore, make friction rollers, in general, an unsatisfactory and perishable expedient: and it is to make them less so, if not entirely to cure these evils, that the two following articles are designed.
In fig. 6 of Plate 17, A B is an axis which it is desirable to divest of its friction. To do this, as nearly as may be, I connect with it two rings of hard metal C D, formed as truncated cones; and under the shaft, in the same vertical plane, I place two smaller shafts E F, carrying on their tops, other two cones, similar to the former. The summits of each pair of cones meet of course in the points a b of the main shaft; and, on the principle of bevel geer, every contiguous part of the touching cones moves with the same velocity: so that there is no sensible rubbing between them—for, 1st. the pivots c d, are hard and pointed, and run on the hardest steps that can be obtained; and, 2ndly. the tendency of the cones u toward each other, is repelled without friction by the cylinders e f, attached to them, and which lean right and left against each other, turning with the same velocity, without causing any friction, or any creeping, between the two pairs of cones e C, and f D. All the weight therefore, of the shaft A B, (which of course is kept in place in the other direction by proper side cheeks, &c.) rests on the points of the vertical shafts E F, accompanied by no sensible tendency of these points to quit the places assigned to them.
In Plate 17, figs. 7 and 8, offer a mechanism different from the preceding, though intended to produce a similar effect. Referring to that cause of friction which consists in the want of parallelism between a principal shaft and its friction rollers, I here introduce a form for the latter, which admits of this consideration being in a measure neglected. These friction rollers are only portions of cylinders; and they have no shafts. They turn simply on a sharp edge, placed in a prismatic box A B, in a well formed angle of which, they move to and fro, without rubbing. When at rest, these axes D C D, (fig. 7 and 8) are drawn against the right hand side of the box, by small weights E; and the shaft is carried by one or the other of them, according as they are, or are not, within reach of its radius. Thus, in the present position of the shaft, (see fig. 7) the second arc C supports it, the third having fallen behind the first, so as not to be seen: and the first arc D being on the point of taking up the load. In short there are six spaces, either left or cut on the shaft, opposite the three arcs D C D. 1st. one space, of 1⁄3 of the circumference, left concentric with the real centre of the shaft, opposite the first arc D, followed by 2⁄3 of a circumference cut an eighth of an inch lower. 2ndly.[151] another third of a circumference opposite the second arc C, beginning where the first ends, and followed by 2⁄3 of a circumference cut an eighth of an inch lower: and 3rdly, another space of 1⁄3 in circumference, opposite the arc D, followed by a similar space of 2⁄3 cut an eighth of an inch lower. By these means the shaft is never without a concentric bearing: and the better to secure this property these arcs left, may be each of them more than one third of a circumference in length, so as to avoid the least drop at each change of roller; and even to give the shaft a support from two rollers at once, during a good part of its revolution.
In using this mechanism, the vessel A B, would be filled, to a certain level, with oil or water, to prevent any blow from the returning arcs—which latter might be made to fall on a lining of leather, to avoid still further all commotion: and thus, even were these rollers not placed quite parallel to the shaft, this imperfection would be corrected by the frequent renewal of these movements, and the consequent absence of lateral friction between the arcs and the shaft. It may be observed that either of the above methods of destroying friction is not confined to the vertical direction: but may be so used as to receive the pressure caused, in any direction, by the action of a wheel or other agent. And with respect to the best use of each method respectively, I would propose the former for light and swift motions, and the latter for slow-going shafts, heavily laden: it being well understood that the shafts must be kept[152] in their places, in the less essential directions, by proper steps, at the discretion of the person who employs these Machines.
Finally, I consider it as a matter of course, that all the surfaces coming into contact in these operations, should be as hard and impenetrable as possible. For if, by neglecting this precaution, any change of form occurred, what is said above could not be practically true: But these properties can be realized, with only those degrees of hardness that are often employed in the mechanical world. Thus a die of hardened steel, bears almost unimpaired, the strokes and pressure it suffers in the coining-press. A chisel, stands thousands of blows and cuts hard metal, without sensibly giving way. The knife-edges which carry a heavy pendulum, suffer it to vibrate many years without wearing out; and the fulcrums of scale-beams, bear enormous weights, for almost an indefinite period, without any injurious effect. I request therefore, that these facts, may be put into the scale, when my foregoing statements are tried: whether as applied to these anti-attrition machines, or to my late patent wheel work, or both combined: for I foresee the use of these friction rollers, cut into teeth on that principle, to insure the proportionality of their respective motions.
In the common form of this useful instrument, no method seems to have been devised for preventing the plug from being pressed aside, by the weight of the liquid: which provision nevertheless would have diminished the wear and tear of the touching surfaces, and secured much longer the perfection of the instrument. This property would be particularly desirable in cocks which convey a fluid from a great height; and still more so in those used for containing steam or any other fluid under a high pressure. I can hardly persuade myself that I have stood so long alone in my ideas upon this subject; but not having seen any thing published on the subject, under a name implying the above mentioned property, I venture to give this as my invention—which indeed it is, even should other persons have pursued and embodied the same idea.
Fig. 9, 10 and 11 of Plate 17, represents one of the forms of this equilibrium Cock. It consists of a square plug case or chamber a b, with a hole c d bored transversely through it, exactly across its centre: and to this chamber is fixed by the flanches e f, the bifurcated water-passage g h, forming one body at i. The plug of this instrument admits of various forms and[154] proportions; of which I have shewn two in the figures 9 and 11. The first m n, receives the fluid through the two openings c d, which correspond, in one position of the plug, with the double water-passage before mentioned. And further, the plug itself is bored lengthwise in its under end n, so as to form the spout of the cock: or otherwise (see fig. 9) this spout is taken in a double form from the outer surface of the plug at b a, so as to present two streams, thus producing, I think, an instrument of somewhat greater solidity. All that seems important is, that whatever be the pressure of the fluid from without, it be made equal on both sides of the plug, so as to occasion no friction between it and the chamber. The principle is indeed so effectual, that one might distribute steam pressure of the greatest strength or even gunpowder pressure, without much resistance to the operator, and without injuring the mechanism by oft repeated action.
In Plate 19, figs. 3 and 4, shew this mechanism in two directions. It is composed of two wheels C D, cut (or cast) into teeth of a peculiar kind, that both geer with one another, and at the same time, include the chord or round strap A B, by which they are driven. These teeth can be better represented by a figure than in words; and will I suppose be understood from figures 3 and 4: They are divided, on the rim of each wheel by a space too small to admit a tooth of the other wheel: but then, every-other tooth is cut away in a sloping direction on each side of the wheel, from the bottom of the tooth to its top on the opposite side: so that while these teeth are working in each other they offer two grooves, in the form of a V, which coming together surround the chord and press it in four points, either to drive the wheels by the cord, or to pull the chord by the wheels, according to the use it may be wished to make of this mechanism. In fig. 4 the cord is seen at A B, passing among the teeth of the wheels; and in fig. 3 it is shewn at C, as a mere circle, in the centre of a lozenge formed by the teeth whose points now geer together. Fig. 5 is a sketch belonging to this subject, which shews something[156] of the manner of using this round strap as a mover: for by carrying it (either in a horizontal or vertical plane) by a line slightly curved, from one machine to another, it will drive them all and give the means of stopping any one at pleasure. Suppose then, A B C D fig. 5, to be four machines placed as above mentioned. If I wish to stop the machine B, I merely draw back the pressure wheel E, and the cord ceases to lay hold on the machine as shewn by the dotted line: but when I want to set it on again, I do it by bringing back the wheel E to its present position. And thus at a small expence, I could geer a considerable factory, in a way which I think as durable as it appears economical. The principal objection, perhaps, is that this cord is liable to wear out soon, by such incessant action; but then the pressure on it needs not be great; and of friction properly speaking there is very little: Besides which, the cords would be made of a peculiar texture, perhaps of leather, sewed edge to edge and covered like a whip, by one of the machines I shall bring forward hereafter.
It so happens that many of my Inventions are of a generic nature, and thus apply to cases which, appearing different, have nevertheless some common properties. The rule of contraries especially applies to many of them,—of which this is an example. It offers a good method of driving a boat through a tunnel, or other confined space, either by the force of steam or any convenient power. To this end a rope laid along the side[157] of such canal, and fixed at each end, or at several intermediate points, might be led between a pair of wheels like those above described; which duly turned, would drive the boat the distance required with the least possible expence of power, and without the defect of agitating the water.—But I must not anticipate too much on my intended subjects.
This Invention is under the protection of a Patent. It is applied to the spindles of my spinning machinery called Eagles, from their analogy to the machines named Throstles. It is in my opinion an excellent machine; as it secures a mathematical equality of twist to any number of spindles from permitting the use of geering to turn them, which could not have been done without some means of stopping a single spindle. This mechanism (see Plate 19 fig. 1 and 2) consists of a toothed pinion A soldered to the box B C, (partly cut down in the figure to shew its contents) and with it running loose on the lower part of the spindle E D. In this box are placed two weights M N, like that M fig. 2, which both together, fill the box loosely, and, rising above it, are pinned at O P through the spindle. They are moreover kept from quitting the latter by the ring shewn in section at q q, which holds them loosely, yet prevents their flying away or hurting any one. When now the spindle E D, turns swiftly, the centrifugal force of the two weights M N, projects them from the centre as far as possible; and they lay hold, by friction, of the cylindrical surface of the box B C, and thus keep the revolutions of the spindle to the same number of turns per minute, as the pinion A receives from the driving[159] wheel. But when the spindle is stopped and held by the fly as usual, then the centrifugal force ceases to act, and the box B C does not wear out much, by its further revolutions. And when as before, the spindle is again let loose, that friction which takes place on the bottom of the box sets the spindle running again, when the centrifugal force comes to its aid, so as to unite again the box and the spindle, thus renewing that valuable property of all spinning machinery, the mathematical correctness of its movements.
The effect which this Machine is intended to produce, is analogous to several culinary or officinal processes that might be named. It is called rolling: but not in the same sense in which that word is used in manufactories, where rollers form or modify the body acted on. Here this body itself rolls between two surfaces moving different ways and receives from them the desired impressions, and this idea I have extended to screws; proposing to finish them on some metals and in some dimensions; and to rough them out in others. The Machine is represented in figs. 6 and 7 of Plate 19, where fig. 7 shews the faces of the arcs A B of fig. 6. By the form and connection of the arms A C and B D, these arcs move opposite ways: and since they are grooved obliquely as shewn in fig. 7, if a prepared cylinder of soft metal a, be put between them, and the handle C be sharply pressed into the position A E, the cylinder a will be made to roll, and the grooves of fig. 7 be impressed on it so as to meet and form the screw in question. The only conditions are, that the arc B A be at least equal in length to the circumference of the screw, when finished; and that the grooves (fig. 7) be rightly sloped, and have the form intended to be given to the threads of that screw. It will occur[161] of course, that the opening between the arcs at the point where the blank cylinder is introduced, must be larger than the distance between the arcs by the whole depth of the threads to be impressed: which therefore will begin to be formed at two opposite points the moment the screw a begins to roll. This however, might and would be otherwise, if it were thought best to form the arcs A B spirally; and let the deepening process be gradual: in which latter case another consideration would occur, namely; that the grooves themselves (see fig. 7) must diverge a little instead of being parallel, so as to permit the screw to lengthen as the pressure should displace a part of the metal. In all cases the upper surface of the grooves should be milled so as to lay hold of the soft metal, and insure the rolling motion: and should this material be hot-iron, the stroke should be taken in an instant, and the machine be kept cool by every proper method, in the intervals of working.
I need not add that this rolling process would be still easier performed, if the impressions to be made were circular and not oblique: such as beads, balls, &c. but these considerations I leave to my readers.
Plate 19, figs. 8 and 9, offers two representations of this Machine—one intended to shew its manner of acting, and the other one of its practical forms. By means of the first, (fig. 8) we may compare it with the common steel-yard; and even shew the latter as a part of the former. If a weight, or load to be weighed M, were suspended to the arm A B, and the counter-weight W, placed at the point C, of the arm A C, we should have a common steel-yard whose power would be as 5 to 1: for the arm A B is just 1⁄5 of the arm A C, and this is the principle on which steel-yards are commonly made. But instead of this, my steel-yard G E B D C H fig. 8, is now infinitely powerful: so much so indeed, as to be infinitely useless. If millions of pounds were now to be suspended at P, they would not raise the weight W one tittle, for they hang entirely on the point of suspension A. But although the Machine is now useless, it can be altered in a moment and made both useful and commodious; only I thought its principle would be the better understood from being thus shewn in excess. To make it a useful and powerful Instrument, I only move the hanging bar D G, to a b; and the bar E B to c d, the lever b d being similar to that E G. In this state of things, the whole load P is found[163] at the point o of the lever B H, (for the lever-arms c o and d e, and those e b, and a o are equal) and the power of this steel-yard is as the line A C to the line A o; that is as 20 to 1, instead of being as 5 to 1 which it before was. But this is not yet a powerful Machine; being chiefly intended to shew the principle on which it acts—and to prove that however small the distance A o, that distance, dividing the arm A C, gives the real power of the steel-yard. And supposing now the arm A C to be four feet in length, and the distance a D, B c, and A o, to be 1⁄10 of an inch, then the power of the weight w to raise (or weigh) the load P is as 48 inches to 1⁄10 of an inch, or as 480 to 1: so that if the weight w were 10lbs. this steel-yard would weigh 4800lbs. or upwards of two tons; and it is easy to see that this power can be almost indefinitely extended.
Fig. 9 of this Plate shews a real steel-yard made on this principle; the power of which, under its present length, is as 40 to 1. In this Machine all the centres are fixed: and the load is suspended on knife-edges, the distances of which from each other and from the common centres are invariable—as they must be in all instruments of this nature.
This Machine is exhibited in the two figures 10 and 11 of Plate 19. It is composed of a straight ruler A B, having an exactly dove-tailed mortice made along it, to receive the rollers, (or slides) by means of which the parallelogram C D E F slides up and down in this mortice. This parallelogram is composed of four rulers C D, D E, E F, and F C, connected by cannons or tubes fixed to every-other arm: and on which the contiguous rulers turn very correctly. Through which moreover, in two cases, F D the drawing pencils are introduced, and under which in other two cases, C and E, the guide rollers already mentioned are nicely fixed by the screws on which they turn. This is seen by an elevation in fig. 10, where p marks one of these rollers, and o q the end of the ruler supposed fixed to the paper by proper blunt points, &c. At r is seen one of the tubes which form the joints C and E: and r t, are, one the writing pen, and one the retrographic style or pencil. Fig. 11 is a plan of the whole Machine: where if the hand guiding the pen D goes upward, the tracer F rises too. But if the pen or hand D moves to the right, the tracer moves to the left at the same moment. In a word this is to write[165] backward in the sense of engravers, who thus write that their letters may proceed forward after one impression.
If it were desirable to give the engraver the same facility he has in the use of a pen, the tracer t, fig. 10, would be terminated above as a hollow conical cup, into which he would introduce a pointed style held as a pen. In this case the tracer t, would be made as short or low as possible, to bring the style so much the nearer to the paper; and thus to prevent all anomalous movements.
If it were enquired why this Machine is offered to the public without the Hook Machine; the answer would be, this only is finished: and it is wished to present nothing here that admits even a doubt of its utility. The drawings given in Plate 20, figs. 1, 2 and 3, are more intended to be useful in the construction of this Machine than complete in appearance: so that nothing has been done by way of shading, but what it was thought would the better distinguish the parts from each other, and facilitate their assemblage in one effective Machine. The Machine consists first of a slide A B, (worked by a lever-handle, a crank, or any proper first motion.) It glides between two cheeks C D, (see the end view in fig. 1) connected with the several parts about to be mentioned. This slide is marked A B in all the three figures. It carries (by means of the screws a b, coming through the slits c d, in the main Plate E F) a plate g, the chief use of which is to support a tumbler e, whose use is to throw the eye, when made, from the machinery: which tumbler is kept to its work by the spring i, as will be further explained presently. This slide itself has a peculiar form at the end B, (fig. 2) which is shewn by dotted lines at c d in fig. 1. It is a slit, with the corners rounded off for the purpose of working[167] the springs now to be described. These springs m n, (see fig. 2) are fixed to a cock, itself screwed behind the main plate: and they come through the latter to the left-hand-ends of the small curved mortices seen (with the springs) at m n fig. 1. The slide A B then, with its forked end shewn by the dotted lines at c d, is destined to take the springs m n and carry them to r s, where they are now seen surrounded by the eye almost formed: for in this motion these springs take the wire (shewn by the lines dotted across the Machine and previously cut by the sheers u) and meeting with the obstacles t v, being the thicker parts of the clams t v w, they bend it into the form r s—when the screws a b lay hold of the sloping ends of the clams c t w v d, and squeeze them together; by which operation the hooks t v finish the eye, by rolling its two ends round the springs m n now in the position r s. Where note, that the slit c d of the slide A B is so formed as, when it has carried these springs m n to r s, to slide forward without doing any thing more to them, while closing the clams. It performs, however, some other less important operations, to which it is now necessary to allude: among other things this slide works the sheers u that cut the wire, and that, by means of the doubly wedged hook x, which goes back with the plate G, doing nothing: but which by the action of its springs fixed at a, falls under the sloping end of the sheers u; and, when the slide, by the screw b, carries it to the right hand, raises the end x of the sheers u, and cuts the wire near v, to prepare it for the operations already described. The part y in the two figs. 1 and 2, is the[168] other cheek of the sheers fixed by screws to the main plate, and covered by a small plate z, in which a nick is cut to form a passage for the wire, and present it to the sheers, that they may cut it to the proper length, after having directed it right across the springs r s, then placed by their elasticity at m n. It hardly need be added that a stop is placed at o, to determine the length of the wire so as to form the eye complete, and not to admit more wire than is sufficient; all which is regulated between the sheers and the stop, by proper adjusting screws, which it is very easy to suppose or supply.
Fig. 3 is intended chiefly to shew the mechanism by which the eye, when finished, is thrown off the pin round which it is bent by the springs m n. It consists of a tumbler e, placed in a mortice in the end of the plate g, and kept to a given position by the pressure of the spring i. When the slide A B is carried forward, toward E, to perform the operations already noticed, this tumbler e, gives way to the angle G of the doffing lever m G, (this lever being shewn also between c m & d n in fig. 1) and rides towards m without producing any effect either on the plate G or the lever m G: but when it has once passed the said angle G, it cannot go again toward F without depressing smartly the end G of that lever, and thereby raising the end m, thus starting the eye from the stud m, round which it had been bent by the processes above described.
At the right of fig. 1 near F, is an object, the use of which[169] is too evident to need description. It is a double spring for the purpose of keeping the hooks c t w v d pressed against the pins, near t v, which determine the position of the said hooks; and the degree of bend first given to the wire by passing the points t v.
There are some less important parts and operations left undrawn, in order to prevent confusion in the figures: but they are such as would strike any person having the above under his eye. In a word I have done what I thought best to aid the construction of this Instrument:—which is represented at two thirds of its natural size—but whose dimensions, of course, would vary with that of the objects to be produced by it.
By this title I wish to distinguish this Ventilator from all such as act by the mere centrifugal force of the air: and to make this distinction the more palpable, I would add that this Machine acts like a pump, that is by means of a space alternately contracted and expanded, into which the air enters, and from which it is expelled by force as water is from a pump. The means are the following: A B (fig. 4 of Plate 20) is a hollow cylinder, of a diameter proportioned to the effect wanted to be produced. C is a cylinder closed at both ends, which fills that just mentioned as far as the length goes, excepting a play of about 1⁄8 of an inch. This interior cylinder revolves in the former; but not on its own centre. It revolves on an axis E eccentric to itself, but exactly concentric with the outer cylinder A B. The centre therefore, of the inner cylinder C, describes a circle within the outer one, which is always parallel to its circumference. On the axis of motion of this cylinder C, and outside of that A B, are fixed two cranks E F fig. 5, which exactly reach from its centre of motion to its centre of figure: so that whatever circle the latter describes in the large cylinder, the former describe the same line without it. And hence any slide or valve D, driven by these cranks, will always touch,[171] or be equally near, the circumference of that interior cylinder C. The valve D then, worked by the bars G from without, forms a constant separation between the right and left hand parts of the lunular space left between the fixed and moveable cylinders; and if the latter turns from C by B to D, the right hand space C B G is the plenum, and the left hand space C A D is the vacuum of this Instrument; or in other words the air will flow in, through the passage H, and flow out through the passage I: and by a contrary motion of C, it would do the contrary—but I prefer the first process because any pressure within the valve D is not liable, then, to press the valve upon the drum C, and produce contact and friction; which in the second case it might do. Suffice it to add, that the quantity of air displaced at each revolution of C round its centre of motion, is the difference between the area of the drum C and that of the cylinder A B: and that its quantity at each part of the revolution is proportionate to the curvilinear triangle G B, multiplied by the length of either cylinder.
In the prospectus, this Machine was said to be good as “a gas meter,” which I still think it is. For such a purpose however, friction and eccentricity of weight should be obviated, by placing the axis E, in a perpendicular position: when I doubt not it would measure flowing gas better than many of the machines that have been proposed for that purpose.
This mode of raising water in its simplicity, is I think called the Persian wheel. The buckets hang upon centres, dip in the under water, fill themselves there, and by meeting an obstacle above which turns the buckets aside, they empty themselves into the upper back, from which the water is conveyed to the general reservoir prepared for it. This present Machine is such an extension of the above principle as to make it applicable to considerable degrees of elevation, and to many situations where a single wheel would be of no service. Having observed that in every train of wheels, the circumferences of any two wheels, have motions towards each other, as well as from each other; I perceived that, in a vertical train, this circumstance might be laid hold of to compose a machine for raising water. Be therefore, (Plate 21, fig. 1) A B C D four of a set of wheels thus intended: on the left of the lowest wheel the buckets move upward, as indicated by the arrow; while those at B move downward, coming thus to meet the former. The buckets A are full, and those B are empty; and as the latter, by the motions of the equal toothed wheels on which they are hung will infallibly meet the former, and even plunge into them at I K and L, it is only to put a clack of leather or a valve, in[173] the bottom of all the buckets, and we have a machine that will raise water to the top-most wheel, be it ever so high, and there the water will be poured out into the vessel M, as in the common Persian wheel above alluded to. On this principle the first change of buckets will take place at I; where the lower bucket belonging to the wheel B G will take the water from the upper bucket of the wheel A H; when the bucket I will go down, nearly empty, by H and fill itself again in the under water; But the bucket of the wheel B G having now got the water, will rise by G to K, where another bucket belonging to the wheel C F will come empty, and plunging itself into that, take its water and go upward by way of C to L, where a similar change will take place and the water from L will rise by E to M, into which vessel it will be poured by the canting of the bucket as seen in the figure. Thus it appears that any number of toothed wheels geering together, surrounded with buckets valved at bottom, and receiving power from any one of their number, will raise simply and effectually a quantity of water not small in proportion to the power employed, and by means that promise great durability to the Machine.
This press (see Plate 21, fig. 2) is indefinitely powerful. It was invented for the use of my late beloved brother, then contractor with government for cleansing the sea bedding. It is composed of a centre piece A, strongly fixed to a post in the ground, the bars A B A C being suspended above it, so as to remain horizontally moveable, while describing 1⁄4 of a revolution round the general centre A. The blankets (or other goods) are put into the space s, (on a net nailed under the bars) while in the position A B; and the whole is then thrown with force towards B C; the length A C being so calculated as to cease pressing at the desired moment: for such is the power of this Machine, even without this projectile force, that were the stress not moderated, nothing could remain whole under its operation. It is clear however, that, when this operation begins at s, the relative motion of the jaws s and B is assignable, and even visible, as shewn by the dotted circles; but as the whole approaches toward B C that relative motion becomes insensible, the circles parallel, and consequently the power infinite: which is all I shall say on the theory of this Machine.
This Machine is delineated in fig. 3 of Plate 21. It has several properties which I think important in the process of grinding colours, either in a wet state or a dry. It consists of a frame A B, which has a hollow centre, through which the axis of the bevel wheel C D is brought in such manner as to geer with the bevel pinion P, in whatever position the frame A B may be placed. The axis of the pinion P carries a vessel of which E F G is a section, and in which rolls a well turned and heavy ball H, upon the colour to be ground: which it crushes in the line of direction of its centre, and to a greater or lesser width according to the diameter of the ball, as compared with the section of the groove E G, in which it rolls. Now as the motion of the vessel E G F, is oblique to the perpendicular, the contact between it and the ball does not take place in any great circle of the latter: but is constantly varying by a twist in its motion dependent upon the angle of the vessel’s inclination to the horizon. From hence arises the impossibility of any colour remaining on the ball unground: and in order likewise, that none may remain uncrushed in any part of the vessel E F G, the frame A B gives it constantly new positions, one of which is represented by the dotted lines I K:[176] where it is seen that the ball bears on a different line of the vessel’s bottom than it did before. This also adds still greater change of action to the ball itself, and occasions (taking both these properties together) an unbounded variety of effect, which necessarily brings every particle of colour under the ball by the mere continuance of motion: and thus grinds it all without any care on the part of the attendants. It may be added, that this vibrating motion of the frame A B, is easily made to result from an eccentric stud and proper connecting rods behind the frame; all which is too easy to require further description.
In Plate 21 fig. 4, there is a representation of this Instrument. It is composed of a frame A B, containing a strong shaft C D, on which are placed the three following objects. First, a fixed pulley E, working by a strap, the Machine whose resistance is to be measured. 2ndly, a loose pulley F, receiving the power from the mover whatever it be. And 3rdly, a barrel G, which is the acting pulley, when the strap is put on it from F in the common method. But this barrel G acts by means of a barrel-spring within it, which is hooked by one end to the boss of the shaft, and the other to the rim of the barrel, as is usual for barrel-springs in general. Now the power produces the desired motion by coiling this spring to the necessary degree: and to make that degree visible, there is fixed to this barrel G a spiral s, which as the spring bends, drives outward the stud t, and with it the finger v, which, pointing to the graduated scale, shews at once the number of pounds with which the spring acts on the shaft C D to turn it. By these means the stress on the straps and on the Machine turned is known; of which also the velocity is easily determined by counting the number of revolutions performed by either of the pulleys E F G, which are alike in diameter.
In ending the first part of this work, I gave my readers room to expect this part “within three months,” and am happy now to fulfil that engagement. Although these pages contain fewer errors than the former—an apology is due for those that have crept in: to which I add the promise that every thing shall be done to lessen them further in the future parts, and wholly to correct them before the work closes.
| Page | 100, | line | 2, | for | “:”, | read ∷; |
| „ | 126, | „ | 4, | „ | “on its surface” | read at its pitch line. |
| „ | 126, | „ | 17, | „ | “its height f g,” | read the length required. |
| „ | 129, | „ | 16, | „ | “2,” | read 4, |
| „ | „ | „ | 20, | „ | “imperfect,” | read homely. |
| „ | 144, | „ | 7, | take away “alone.” | ||
| „ | „ | „ | 8, | for | “usually” | read chiefly. |
| „ | 146, | „ | 23, | for | “the friction,” | read it. |
| „ | 147, | „ | 1, | for | “nothing,” | read little or nothing. |
| In fig. 7 of Plate 19, slope the groove of both faces the same way. | ||||||
A few words seem wanting to complete the description of the Cutting Engine above given. They relate principally to the cutter-frame and cutters. Although, with a view to celerity, I have shewn the cutter out of the frame (fig. 4) yet a common frame, carrying the arbor on points, may be used with propriety; and would often be an eligible substitute for the frame above described. In cutting bevel wheels however, either on this Machine or that to be described, there is a form of the cutter frame which leaves less freedom of choice, as the cutter itself must have a peculiar form and position. To return to the cutter for spur wheels, their form (or section) depends on the degree of finish which the wheels require. For rough[179] work they may be cylindrical on the face, the sides being under cut, so as to leave them thickest at the circumference—whence a certain coarseness of cut ensues, but without any injury to the spiral form. But, generally speaking, the cutters are best, when made a little tapering towards the edge, and toothed on both sides as well as on the circumference. The teeth should be tolerably fine, but not very so, unless great smoothness of surface were required: and we have seen above that, in this System, great smoothness is very seldom necessary, provided the obliquities be correct. I may add, that those cutters used on common engines, whose great rapidity compensates for the small number of their teeth, would not answer here, on account of the twisting motion in the wheel. But nothing prevents using cutters, so formed on the sides, as to round off the teeth in the act of cutting—only the cutter must be so thin as that its thickness, added to the aforesaid twist, may not make the spaces too wide. A little observation will render these things familiar to an attentive observer: nor shall this work conclude before all that I have gathered from long observation on this subject, be fully known to my readers.
J. W.
5, Bedford-street, Chorlton Row,
20th. November, 1822.
A NEW CENTURY OF
Inventions.
It has been observed and regretted by a well-known writer, that “a periodical work resembles a public carriage—which must depart at the usual hour, whether full or empty;”—and having undertaken to deliver this work at stated periods, I have found myself in a situation not unsimilar: the consequence of which has been a too cursory view of some of the subjects. I feel however, that this is not a sufficient apology for any essential defect: nor would it be more so to say that, although verging to old age, I am still a young author. Yet I may claim the privilege of supplying, in the latter parts of the work, what is most deficient in the former; and thus of proving that I do not intentionally neglect any thing that might make it practically useful.
With these views I commence this third part: intending first to continue the description of the Cutting Engine given at page 121, and here applied to Bevil Wheels; and then to re-consider, shortly, one or two other objects, that were too rapidly passed over in their proper places.
Plate 22, repeats at fig. 1, the first figure of Plate 15; by way of shewing the additions required to extend this method of cutting teeth, to Bevil Wheels. These additions are first, a disk n n, concentrically fixed to the main axis A B of the engine. And, second, an inclined plane o, of variable obliquity,[184] connected by a joint with the forked sliding bar p q, by which the plane o is put in contact with the disk, at whatever distance the cutter-stand e f may be from the common centre, which distance depends, of course, on the diameter of the wheel to be cut; and to secure which is the office of the fixing screw r, in the figure.
It is now evident that for the disk n n, and the shaft A B to rise, the slide p q and the cutter-stand e f must recede: and this more or less according to the degree of obliquity of the inclined plane o, that is according to the slope of the bottom of the teeth in the wheel w: see the dotted line w p.
A circumstance presents itself, that should be here explained: when the bevil of the wheel w, or the cone of which the wheel is a part, is very obtuse, the cutter-stand e f, can not be driven back by the action of the disk n n on the plane o, without too great a stress being applied from below, to the axis A B. (See the apparatus I M O N, Plate 16, fig. 2.) In this case therefore, the handle R is not used: but a weight is suspended to the end N of the lever M N, sufficient to give the whole System A B, a tendency to rise; and the operator now acts on the screw g, so as to draw back the plane o; by which motion the disk m n with it’s axis A B is suffered to move upward, and the wheel is cut, as desired. But on the other hand when the wheels are portions of acute cones,[185] they are cut by means of the aforesaid handle; by which the plane o and the cutter-stand are forced backward as before intimated.
We proceed now to describe the perpendicular part of the cutter stand e f; which is made double, as shewn at i k in fig. 4 of Plate 15; and is also perforated at various heights to receive the bolt which forms the centre of motion of the arm m u, the latter having a cylindrical boss u, fitted into the fork of the stand e f, and so graduated as to determine the angle of it’s obliquity to the horizon, or it’s parallelism to the dotted line w p, which indicates the slope of the bottom of the teeth on the wheel. Finally, the cutter-frame x is fastened to this arm at right angles to it, and thus forms a right angle (or nearly so) with the surface of the wheel: and is, moreover, directed to the centre, produced, of the shaft A B. This latter fact is strictly true, only when the teeth required are of so common a kind as not to require greater exactness: for in theory the sides of the cutter (supposed cylindrical) must alternately direct to that centre—namely, that side which is actually cutting: so that a provision must be made to shift the cutter spindle sideways, a distance equal to it’s diameter; this being no more than what is necessary in every system of wheel cutting.
We may also consider here, the form of the cutter itself, v, fig. 1. It is slightly conical, (more or less so according to it’s use) and of no greater diameter than the smallest width of[186] the spaces between the teeth of the wheel. A common disk-like cutter would not produce perfect, nor even tolerable teeth on a bevil wheel. The reason of this will appear by considering that a spiral line, either on a cone or it’s base, turns more the further it is from the centre, and less the nearer it comes to it. So that a flat cutter placed at any angle, is parallel to the curve at one place only; whence the propriety of using a cutter of the kind represented in this figure. It is however true, that the first opening of the spaces may be made with a common cutter; but it should be very thin comparatively with the spaces required: and it’s cut would serve only as a sketch of such space, serving principally to permit the metal to escape while finishing the teeth with the cutter just described.
I proceed now to the examination of the plates, and the manner of adapting their length to the process of cutting spiral teeth on bevil wheels. But before entering on this subject, I would explain a kind of inadvertency into which I fell at the close of my former description of this Engine (see page 129). In my zeal to be candid in stating the properties of my Machines, I have suffered it to appear that I thought this an “imperfect” one:—an expression which, although modified among the errata, may still cause it to be looked upon as radically defective; than which nothing could be further from the idea I wished to convey. I intended merely to express the want of absolute connection between the two movements of the shaft—the rotatory and longitudinal motions. I meant that the process[187] by this Machine was not theoretically certain, because dependent on the action of a weight (Plate 16, fig. 1 and 2) and an unforced obedience to the direction of the plates. But this small remove from rigourous principle is in my opinion much overballanced by the facility of cutting good wheels of all diameters, by the sole change of a morsel of tin, which leaves untouched every other part of the Engine.
Entering then on this branch of the subject, I first observe that if we chuse for the teeth an inclination of 15 degrees (in imitation of the cylindrical wheels) it can only be for one point of such wheels—as observed above. This point therefore I have placed at r in the middle of the face. And supposing now that at this point the wheel O were 4 inches in diameter and the wheel S two inches, these plates would be found as before by these analogies:
(1) wr, or 2 inches : 11 inches (rad. of plate rim) ∷ 26.8 : 294.8⁄2 = 147.4 plate required.
(2) vr, or 1 inch : 11 inches (rad. of plate rim) ∷ 26.8 : 294.8⁄1 = 294.8 2d. plate required.
But it is plain that the conical face, b C, (common to both wheels) is broader than the supposed cylindrical ones b e and b d: and therefore that the above plates must be made longer (to furnish the said obliquity) in the following proportions, namely: for the wheel O in the ratio of b e to b C; and for the wheel s in that of b d to b C: that is, these plates should be[188] lengthened as the tabular cosines of the angles B A C and D A C to radius (for b e : b C ∷ A B : A C; and b d : b C ∷ A D : A C.) Thus then,
(1) Cos. 63°27′ : radius ∷ 147.4 (present plate) : required plate x, = 147.4 r⁄Cos. 63°27′; and
(2) Cos. 26°33′ : radius ∷ 294.8 (present plate) : required plate y, = 294.8 r⁄Cos. 26°33′.
Now, by the tables, cosine 26°33′ = 894, and cosine 63°27′ (it’s complement) = 447, when radius is 1000: whence dividing the two equations by r, and substituting these values of cosines 63°27′ and 26°33′ we shall find the two quantities x and y, equal. Whence it appears that for every pair of bevil wheels, whose shafts lie at right angles, the same plate serves for both wheels: only turning it once to the right, and once to the left hand on the plate rim.
And if now we measure on a scale of equal parts, the line A r and call it 100, we shall find the line w r (near enough for practice) to be 90, and the line v r to be 45, and these numbers respectively, put for rad. for cos. 26°33′, and for cos. 63°27′, will make the first equation x = 147.4 × 100⁄45 and y = 294.8 × 100⁄90 or x = 327.55 and y = 327.55, &c. confirming the above deduction that the same plate serves for both wheels; and giving, withal, the length of the plate required.
In performing this operation by actual measurement of the lines, I have had in view to trace a path for those of my readers[189] who may not have the tables, or may be unaccustomed to use them. The process, generally, is to take the diameter of any bevil wheel O fig. 4, in the middle of it’s face; and supposing it a spur wheel, to find it’s plate by the method above given: and then to multiply the length of that plate by the line A r and divide the product by the line A w, both measured on the same scale of equal parts.
It may be well to observe, likewise, that the same method of finding the plates, applies to bevil wheels of every description or angle: but that it does not give equal plates for every pair, except in the above case of wheels placed at right angles to each other.
I would just remark that by the figure near B, is shewn a section of the Machine on which I centre the wheels to be cut on this Engine. It is an inverted cup s t, into which the arbor is screwed in a true position; and this cup is fixed on the top of the shaft A B, by the three pressure screws near s t, which enter a triangular neck made round the shaft, against the upper slope of which, the screws press so as to draw the cup downward in the act of centering it. This I say is my present method; but it is in a measure accidental, the shaft not having been perforated to receive arbors of the usual kind. Mine, however, have their utility in the ease with which they are varied in size, and changed on the Machine: but on their[190] comparative usefulness I give no opinion. The other is the most solid method.
In the description of my differential Steel-yard, (see page 163) I stated that the load P was wholly collected in the point o; and that dividing the line A C by the line A o, the power of the Machine was known. But I should have shewn that this line (A o) is equal to one half the difference between the arms A D and A E. To do this, here, (see Plate 23, fig. 4) I take the Machine in the state of infinite power, before mentioned; and observe, that in moving the point of suspension from o towards A, I at once lengthen the arm A E, and shorten the arm A D: by which process, (supposing each arm to have been called a) that which I lengthen by any quantity d becomes a + d, and that which I shorten by the same quantity becomes a - d, and the difference of these quantities, is 2d: so that the line A o is in reality one half the difference between the two arms A D and A E as was required to be shewn.
But we may go a step further: The two arms of the equibrachial lever x y may likewise be made unequal: and the line s a be subdivided in any ratio: which division will augment still more the power of this Machine. If for example, we hang the load on the point v, halfway between a and s, that power will be doubled; for the line c v (representing the space moved[191] through by the load in this case) is only one half of that w s, or o q, and might be still less at pleasure. Thus the whole power of the Machine is now found by dividing the length of the long arm, beyond D, by the line a v, instead of the former line A o, or dividing the motion of it’s extremity upward, by the line c v, the motion downward, of the load P.
It has been further suggested, that the description of my excentric Bar Press was not sufficiently explicit. I have therefore added the figure 2 of Plate 22, to assist in elucidating that description. I had, perhaps made an undue use of the principle of virtual velocities by saying, too concisely, (page 174) that “as the whole approaches toward B C, the relative motion (of the cheeks s and B) becomes insensible, the circles parallel, and consequently, the power infinite.” It is however vulgarly said that power cannot be gained without losing time—which implies that if time is lost, power will be gained: and the principle of virtual velocities says the same thing, though in more appropriate terms—that if a small movement be given to a system of bodies actually counterpoising each other, the quantity of motion with which one body ascends, and the other descends perpendicularly, will be equal: so that, as remarked in page 50, by “whatever means a slow motion is obtained, dependent on that of a moving force, the power is great in the same proportion.” Now, in the eccentric Bar Press, (see fig. 2) this is so in an eminent degree: for when the bars are in the position A B, the distance of the cheeks is equal to[192] B s; and they must move, circularly, as far as A f, to bring them closer to each other by the quantity s a: dividing therefore, the distance B g by the line s a, we find (near enough for practice) the power of the Machine within the limits A g B. It is nearly as 10 to 1. In like manner this power at A e g, is equal to the arc e g divided by the line f b; and at A l n to the arc l n divided by the line d k, namely by the difference of the lines k l and m n. From the above it appears that the nearing motion of the cheeks of the press, becomes slower and slower as the bars A and C come nearer to the point C: insomuch that the difference between the lines m n and o p is nearly imperceptible, and that between the lines o p and C q entirely so. But according to the above process, the distance p C should be divided by this imperceptible line, to find the power of the press at the point C; which therefore is immense. Another proof of this may be drawn from the supposition (see fig. 3) that the small lever a d is turned round the centre o by a bar o C fixed to it, and of equal length with the line A C fig. 2. Fig. 3 shews that the lines or bars C d, and a C are moved endwise by the circular action of the points a and d; and therefore (by statics) their motion is the same as though caused by the perpendiculars b o and o c let down from the centre o, on each of them. Hence the power of this Machine is found by dividing the distance o C by the sum of the lines b o and o c; which sum (when these lines vanish by the union of the bars over the centre) becomes infinitely small: the quotient of which division therefore is infinitely great—as was to be shewn.
The usual method of making Punches for engraving Copper Cylinders, (otherwise than by the milling system) is to cut the desired pattern on a die, and then to transfer that pattern by blows or pressure to the punch, from which it is again transferred to the cylinder. My Machine in this operation, unites motion to the needful pressure; and thus renders the result more easy and complete. This effect I could the better ensure, because the surfaces of my punches are essentially convex, or rather cylindrical; as will appear when my engraving Machine comes to be described. Their convexity however, can be diminished at pleasure—whence this Machine is capable of offering useful assistance to a maker of flat punches.
In Plate 23, A B fig. 1 and 2, is the body of the Machine, with the vibrating bar C D laid upon it; reposing especially on the correct and level parts of the body at a b; this bar contains the die c, with which it vibrates between the cheeks B R, as impelled by the screws E F, it’s centre of motion being the pin P, duly supported by the strong shoulder A. In a line with the bar C D, is placed a second vibrator G, containing the steel d, that is to become a punch, already rounded[194] into the cylindrical shape it must have when finished. This vibrator has it’s centre of motion at e fig. 1, and it need not be added that the curvature of the punch depends on it’s distance e d from that centre: for the centre of the long bar C D is so distant as to have little influence on it’s formation. Further, the cap or bridge H I, which furnishes a centre for the smaller vibrator G, can be brought forward to any useful position by the nuts K L: that cap sliding horizontally between the cheeks M N as directed by the small arms m n. This motion, then, taken from the nuts K L, serves to impress the work of the die on the steel prepared for the punch; and this being done to a first degree, both the handles O Q, are laid hold of: and by turning the screws the same way one of them goes forward and the other recedes, until the punch and die have been in contact over half their surface. At this moment both screws are turned backward, and the motions of the two vibrators reversed: by the repetition of which alternate motions accompanied by the needful pressure, the whole pattern is transferred from the die to the punch—when the latter is taken out of the Machine, and filed up in the usual method.
It should be observed, that the smaller vibrator G can be displaced with ease when the nuts K L are withdrawn: and this should be frequently done to examine the progress of the impression. Nor is there any difficulty in re-entering the figures. In a word, the perfection of this process depends more on[195] much motion than on violent pressure: whence this facility of re-entering is a desirable property. This Machine is usually laid on a bench or tressel, with a long mortice in it, into which the feather x of this Machine enters so as to be firmly fixed.
I was the rather induced to attend a second time to the differential Steel-yard, because I had it in contemplation to apply that principle to the present purpose; since, to make flat punches, is to some engravers a more desirable thing than to make cylindrical ones. I am not fully persuaded that it is even possible to transfer a large pattern, from a flat die to a flat punch, by any pressure acting simultaneously on the whole surface. In those cases, if there is much work, the whole surface goes down; and the parts that form the pattern do not rise. But, all that can be done in this case, is, I believe, feasible by the Machine now to be described.
Plate 23, gives in fig. 3 and 4, a representation of this Machine; A B and C D, are two slides, having wedge-formed ends above A and below D, well made, well steeled, and well tempered. One of these slides contains the die and the other the steel prepared for the punch (see B C). These wedge-ended slides are embraced by two levers E F, G H, which are themselves connected by two stirrups I K and L M, better shewn at fig. 3. These latter are supposed in fig. 4 to be broken at L M, to leave the levers E F and G H more[197] visible. They are formed, at the turning below, into wedge-like edges a b; well hardened, that clip the nicks c d of the lower lever: and at the top of the Machine their arms e f, pass through the caps m n, above which they are nutted like a common bolt, and made to press strongly on the main lever E F. The stirrup placed to the right hand, presses in particular, by it’s cap n, on the moveable step o, exactly in the notch q: this step having a backward and forward motion communicated by the regulating screw p. Before beginning to use this Machine, I make all it’s arms A E, A g, D e, D d, equal, when it’s power (see page 162) is infinite; and to put it in a working state, I turn the screw p backward, say one half round: which motion (if the screw has 20 threads to the inch) makes a difference in the two arms A r and A q of 1⁄40 of an inch, and the virtual centre of the Machine is therefore 1⁄80 of an inch from the former point A, that is from the edge of the slide A in this fig. 3. Supposing now, the whole working lever E F to be 3 feet, and the workman’s force to be 100lbs. in each arm, then by displacing the lever to any proper distance from F towards f, he will produce a pressure between the die and the punch of 200lbs. multiplied by 1440, the number of times that 1⁄80 of an inch is contained in 18 inches.—That is, a pressure of two hundred and eighty-eight thousand pounds!
I have been seduced, by the anticipated brilliancy of this result, from the regular course of description,—and the plate[198] w x, y z, which forms the base or frame of this whole Machine has not yet been spoken of. But that plate is supposed screwed down to a horizontal bench, at or near the height of a man’s breast; the slides or cases are fastened to it, and the man is supposed to work the Machine nearly as he would a die-stock in tapping a screw. This however is not indispensable; the Machine might be placed vertically, and these motions given by any proper mover; or a weight may be suspended to the arm F, so as to add continuity to pressure. It is however important, that the position should comport with the frequent extraction of the punch in order to examine the progress of the work, or cut away any redundant metal. I have before given it as my opinion that much could not be expected from mere pressure: but this is a pressure of a peculiar kind, consisting of immense powers with very short motions. In this respect it is just what was wanted, as it can be renewed and repeated frequently, without loss of time. And the more to facilitate this delicate operation, the hollow slides or cases B C, are made slightly pyramidical, to be furnished with set-screws on the four sides, by which to change the place of bearing; and thus to meet the case of a flat punch with the advantage of impressing it by portions, so as to have only to finish it by brute pressure.
The foregoing application of the principle of the differential Steel-yard, is, I think, important, and founded on unobjectionable principles; for although by changing alone the place[199] of the step o, we disturb a little the parallelism of the stirrups I K, and L M; we do it not enough to produce, any material change in the theoretical result. With respect then to the lesser properties of this Machine, I leave them with confidence in the hands of those whom they most concern—who doubtless, will treat them with greater practical utility than I could myself hope to do.
This Machine offers, I think, a valuable application of a well known Instrument: or rather of the principle on which it is founded. I allude to that parallel ruler which, by means of an additional joint, keeps it’s members not only parallel, but directly opposite each other. In my Machine for moulding Nails, I wanted to give motions to the two plates different, yet dependent on each other. Supposing then, (Plate 24 fig. 1, 2, 3, 4,) the upper plate a b, to be moved up and down by a lever, a screw-press, or any other first mover, I connect the under plate c d, with it by two (or four) strong parallel rulers e f, in such a manner, that when the plate a b is drawn upward it shall extend the arms of the ruler almost to a straight line, as represented in fig. 4; and then carry the under plate with it: and when it comes down again (see fig. 3) it shall not carry down the said under plate, until the same arms are bent into the position f g; that is, till the two plates touch each other: the use of which arrangement I will now explain.
The under side of the upper plate a b, is ground perfectly flat, and bored at proper distances with holes to receive and[201] hold the punches which represent the shanks of the nails that are to be moulded. The lower plate c d is ground true both on it’s upper and under surfaces; the first to fit the under surface of the upper plate, and the under surface to impress a perfect plane on the sand below it. This under surface, shewn in an inverted position at fig. 2, is moreover covered with proper prints 1, 2, 3, &c. to form the heads of the nails in question, and with proper gets (jets?) 3, 5, 6, &c. for conducting the metal to every part of the surface. I mean models in relief of those gets; and the under plate is further pierced with holes, placed exactly like those in the upper plate, bored indeed from that (and through the aforesaid prints of the nail-heads) after the parallel joints e f have been affixed. Now on another level plate with proper ledges, the sand boxes or flasks, fig. 5 and 6, have been prepared; and have received an obtuse pyramidical form at one stroke from a competent press, the construction of which is easily conceived: or this might be done by hand, if preferred. These boxes, in-fine, are successively brought under the before described mechanism while in the state represented in fig. 3, in which all the nail models are protruded through the under plate as at 1, 2, 3. The moulder now gives a stroke under the following circumstances:—Both the plates drop together and the nail models pierce the sand while the under plate makes it’s surface perfectly level: but when that motion is reversed, it is not the under plate which first rises, but the upper—by which the nail models are drawn out of their holes without disturbing[202] the sand, for this is kept to it’s place by the under plate: and when, by the continued motion upward of the upper plate, the parallel joints are duly extended, and the nail models quite extracted; then, and not till then, the under plate leaves the compressed sand, in which are moulded as many scores of nails as the mould has been made for—and that, in a space of time almost imperceptible.
I shall conclude the subject by observing, that the counter flask or box for closing this mould is made in the same way, by a smooth plate prepared in the same manner; and which must fit the former, because they are both perfectly level surfaces.
This Machine, though conceived many years ago, can hardly yet be called an invention—if material existence is necessary to justify that appellation: for I have never seen it in action. It may possibly be one of those fascinating conceptions of which my noble friend the late Earl Stanhope used to say—“’tis a beautiful invention—but ’twill not do;” yet I give it with some confidence, because of the great utility it would present, if it’s chief properties should fulfil my expectations.
The principal idea on which it is founded, is this: to use, as power, the expansion of that air which feeds the fire; and again to employ it’s heat heating liquids or rooms, or any similar purpose. The form I have given to the Machine is by no means the only one it admits; nor perhaps the best: but it was indispensable to give the idea (which I hope is not an “airy nothing”) “a local habitation and a name.”
It consists, then, of two cylinders, lying horizontally, of nearly equal length, but of unequal capacity:—one of which A B, (Plate 24, fig. 7) is an air pump with a valve in it’s end a, and another in it’s piston, both opening to the left.[204] The second cylinder C D, is the working cylinder, as much larger than the former, as may belong to the principle of motion already announced. This cylinder receives the piston E, which fits it nicely, but is not stuffed in the present case. (It may perhaps be made tight by some of the methods, used to close metallic pistons.) At all events, this piston is connected with that c, by a frame F G H I, which embraces the whole Machine, in a horizontal position, though here shewn in a vertical. These two cylinders are cast in one piece, together with an upright cylinder, not bored K; the use of which is to receive the earthen chafing dish L M, with it’s fire, made (according to my present views) with coak or charcoal, and lighted before it is introduced. It is needless to say, that this vessel is let down into the cylinder K, by a kind of bucket handle entering any pair of holes in the dish. The top of this latter cylinder is ground to fit the flanch A N: It swings open on one of the bolts and falls to again in a moment, to prevent loss of time in firing. The means of doing this I do not much insist on, from their extreme facility. Nor do I make it a condition to use this method at all. The coak, (or perhaps the coal, or the wood) might be introduced through an upright tube furnished with two slides, one placed close above the top A N, and the other at a proper distance above; so as for one to be always shut. This is nothing more than the System used for feeding high pressure Steam Engines—only this application is to dry substances, which forms no insuperable obstacle.
When now the Machine is fired, the pistons E, and c, are pushed towards b and B respectively; the valve d having been previously opened, and the valve c opening by this very motion—which thus clears the large cylinder of it’s included air, while the air in the pump A B, is brought into contact with the fire; whence a considerable expansion ensues, and a pressure is created tending at the same time to drive the piston c to the right hand, and that E to the left: but acting in the latter case on a larger area, the whole system moves that way, and all the air in the pump A B is driven through the fire: where, being much heated, it acquires great elasticity and developes considerable power—which, by any of the known methods, may be applied to any of the known purposes.
I hope my readers will conclude here, that I allow for the disappearance of the oxigen in this conflagration: but I expect the expansion of the residue (together with what new vapour may be developed) will more than compensate for that loss of volume. By this motion then, the pump A B is again filled with cold air through the valve a; and the piston E flying out of the cylinder C D, the hot air it contained rushes into the pipe o, and thence goes to perform any heating operation that may be desired. But further, this same recession of the piston E strikes the stem of the valve d against the cover e, and opens that valve; by which means the large piston is at liberty to reach again it’s inner position b: where the bar b closes it’s valve d and prepares the Machine for a new stroke. For, as before, the pump[206] or cylinder A B, is full of cold air, and by the backward motion of it’s piston exposes that air to the fire in K: whence arises the renewal of all the former phenomena.
Many ideas, and doubtless some objections, will present themselves to the readers of these pages; of which I shall probably anticipate some, by noticing a few less important particulars.
And first, is it not to be feared that the vertical cylinder K, and the whole system K C D E will become too hot—nay acquire a red heat, and thus introduce danger? The answer, I think, is that the fire must be lessened, or the Machine enlarged, until this danger disappears: for by heating air to any thing like a red heat (without attaining it) the expansion will be immense: and probably beyond our wants or wishes. The chaffing dish then (if that is used) must be lessened, that the air from A B may partly circulate round it, instead of going wholly through the fire: thus cooling the vertical cylinder K, and diminishing the intensity of the heat in the working cylinder. Further, the two cylinders C D and K, might be inserted in the bottom of a boiler, and surrounded with water; through which also, may be conducted the pipe O, so as to concur in the same effect of heating that water, while the steam thus accruing from the double use of this heat, may be made to drive an engine, heat a room, or fulfil any common purpose.
In a word, all our difficulties on this branch of the subject, seem to lie in excess of action: and we need only mitigate the general effect, to render this Machine useful, safe, and commodious.
There is another objection that must be met, on pain of direct censure, which is this: what will become of the ashes? (for smoke is as yet out of the question) my answer is—a recess, or several, must be found for them beyond o; to do which will not be more difficult than to lodge any other residue. But if this Machine fulfils my views in respect of power, this residue will be no burden. For example, if ever a farmer should hereafter drive his plough by such an engine as this, he will manure his land furrow by furrow with the ashes—an idea which I must not yet indulge, lest I should be thought fanciful beyond the due proportion.
But my mechanical impetus is not to be thus instantly checked. If what I hope, can be realized, there are properties in this invention, for locomotive engines, superior to any the steam engine itself can boast. A light Machine: a light combustible: no water to carry; no steam to condense, &c. &c. As however I have never tried this felicitous creation, I assert nothing.
But again, this seems to be a really good method of distributing heat in any useful direction: for there is an impulsive[208] force which not only requires no draught to make the fire burn, but will drive heat to any distance through pipes of any form, and placed in any position. There is therefore, a certain utility attached to this Machine, whatever may be it’s merits as a power engine. Our present methods—of destroying coals—are excellent! but our methods of making them useful are defective in the extreme. If you have no draught in your chimneys you are stifled with smoke. If you have much draught, you have little heat—for the chimney swallows it, and half your room is in Norway. Use then an impulsive system, (of some kind) and you may send your caloric down into the cellar to be drawn from thence as wanted, for the upper apartments.
But my subject pullulates as I proceed. This idea is by no means exhausted. It is not an indispensable feature of it, to heat rooms with the same air that fed the fire. For instance, if a fire were made under the vertical cylinder K, and led into and through it by a proper pipe, almost filling it—then the cold air of the pump A B would pass round that pipe to the working cylinder C D, and there impel it’s piston E as before. Not perhaps so strongly; but with an air uncontaminated by burning, or by ashes—and therefore more congenial with some uses of the Machine. In fact, air thus introduced might be perfectly fit for breathing, and still get elasticity enough from this passage, to force heat to the bottom of any room we wished to have warmed; whereas, by using only the levity of heated air to give it motion, we scorch the tops of rooms and factories,[209] and unmercifully freeze the bottoms. I must beg leave to be a little severe on this point:—since for a thinking people, as strangers call us, we have been extremely thoughtless in this respect: so that as much seems now to do by way of introducing comfort into our saloons, as was done about the year 1200, when those chimneys were introduced that are now become a kind of nuisance. In a word, and I am serious when I say it, the present arrangement of our chimneys, is in my humble opinion, essentially unphilosophical; and as such ought to be speedily discontinued or greatly modified.
In the above pages I have laid myself open to much animadversion, by a kind of cast for much honest fame. I have let the public into my secret—I have thought aloud: And if the greater part of these cogitations should prove to be imaginary, I shall only plead, that they are drawn from the same source as the many useful Machines I am known to have devoted to public utility.
This title I confess, seems very ambitious, as applied to an utensil for the dairy: but I had to express the combination of it’s own axis, and those of the leaves or wings about their respective axes, while gyrating round the common centre.
The principal shaft A B, fig. 8 and 9 of Plate 24, is the general centre of rotation; and a b are two lighter shafts carried round that centre, and turning at the same time on their own centres by means of the wheels e f geering in the fixed wheel c d, (of which one half only is drawn) and which forms part of the top of the churn. Each of the shafts a b, carries four leaves or wings (better seen in fig. 9) reaching from the top, nearly to the bottom of the vessel; and they run in proper steps in the cross piece m, and also in proper collars in the upper cross piece g h. In fine their wheels e f, and the fixed wheel c d, which turns them, are furnished with teeth on my patent principle; and therefore work without noise or commotion. Now, the principal shaft A B, rests on the step B at the bottom of the vessel; and runs, at top, in a collar formed in the metallic bridge i k, which, fixed to the outside rim of the cover, passes directly over the[211] centre of the Machine. When therefore, the cream is put into the churn, (to do which the above mechanism is taken out) the mechanism is re-placed as now represented; and the main shaft set in motion by any convenient power: when the side shafts a b, turned by the fixed wheel c d, give a backward motion to the wings a b, and create a great agitation of the cream—for, it should be remarked, that this is not a circular motion: but each fly produces a kind of vortex round it’s own centre, while progressing round the common centre. The consequence of which, as above intimated, is, an unceasing agitation of the liquid, and, I believe, the best of churning. This however, I state as a mechanician, not having been initiated into the secrets of the dairy properly so called.
It may finally be observed, that the leaves or partitions l n, fixed to the sides of the churn, (beyond the reach of the moveable wings a b) are destined to prevent still further any general motion of the butyraceous matter; and thus to accelerate the churning process: and further these leaves, both fixed and moveable may be pierced with holes, like the analogous parts of other utensils of this nature.
The screw of Archimedes, is well known. When used to raise water it is placed obliquely, in such a position as that it’s hollow threads become more oblique to the horizon than the axis of the screw itself: observing which practice, some have said of this Machine, that it raises water by letting it run down: But this cannot be true. The threads of the screw merely wedge themselves under the water, and make it rise in a direction parallel to the axis of the screw; at the highest end of which it falls into the upper reservoir.
I once placed a screw of this kind upright, and said (in thought) is it then impossible to raise water by means of this screw thus placed? The answer in a few minutes was—“not at all; there is a force would make it easy: namely, the centrifugal force:” and this mental soliloquy was the origin of this Invention, which, some thirty years ago, I shewed to a public man, whom the lovers of the mechanical arts will long remember.
In Plate 25 fig. 1, A B are two screws, perfectly like those used in exhausting watery foundations; and named of Archimedes.[213] They are placed perpendicularly in the frame C D, so as to turn in the cross bars a b, c d, fixed horizontally on the main shaft E F of the Machine. At the bottom of this shaft, E F, (which turns in a step on the sill G D) is a low cylindrical vessel, shewn by a section only at e f, which dips into the under water nearly to the brim. It is used to carry, in proper steps, the centres of the screws A B, and, being pierced with many holes, to feed them amply, without exposing their motion to any resistance from the stagnant water. These cylinders A B are merely indicated as screws by the threads, dotted between h and d and e and g, and their upper mouths are seen near a b, just under the cross piece marked with these letters. These screws then, are turned by the wheels i k, as actuated by the fixed wheel m n, in the same manner as those of the churn before described; which in fact, is a corollary from this Machine, but of much later date. To return to the Helico-centrifugal Machine—the screws A B are terminated above by circular plates o p (marked with the same letters in fig. 2 and 3) intended to receive the water from the mouths of the screw-threads a b, and carry it on to the plate q q, which insures it’s further progress into the ring canal r s, also shewn by a section only, to prevent confusion in the figure. Now what raises the water in these upright screws, is, it’s own centrifugal force, combined with the revolution of the screws: for while this central force is urging the water outward, the screws are bringing their sloping threads like wedges, against that tendency; and the consequence is, that the water actually[214] rises perpendicularly till it flows over the ledges or rings o p, on the plate q q, and thence into the ring canal r s, from which it is conveyed to any place desired.
If this Machine is well made and proportioned, I think it is one of the best that can be used, to do much work by a given power: It gives no shock to the water; which, when once in motion, continues to rise, and escapes when arrived at it’s proper height: and, being spread over a large surface, no part of it is raised higher than enough. The perfection of the Machine depends on a due relation between the centrifugal force, and the sine of the angle, which the threads of the screw make with the horizon; and this may be modified by the diameter of the wheels i k, as compared with that of the screws A B.
The figures 2 and 3, are two views of the upper part of the Machine. They shew, and mark with the same letters, the cross bar a b, the inside of the screws, and the circular plates o p, together with the circular conducting plate of which q q, fig. 1, is the section. Fig. 3 shews the fixed wheel m n, the two screw-wheels i k, the cross piece a b, and under them the plates o p of the 1st. and 2d. figure.
One other object claims our attention: The threads of the screws (whether more or less numerous) should each be furnished with a valve at bottom: that the water may not run out when the Machine ceases working.
This Machine acts by pressure instead of percussion. But this pressure is so instantaneous as to resemble a blow, and so often repeated as to produce a considerable effect in a short time. The means are represented in fig. 4 of Plate 25.
There, A is a mass of metal answering the purpose of an anvil, but having two surfaces, situated at or nearly at right angles to each other, on which the metal is alternately struck or compressed. The two sides of this mass A, are perforated by two holes, properly bushed, in which turn the crank shafts B, C: the latter furnished with the bevil wheels D, E, which geer into and receive motion from two equal bevil wheels F, G, fixed on the main shaft H I, and to which the power is applied. It is thus evident that the two crank shafts B, C, will make the same number of revolutions; and that if one of the rollers K, L, is placed on the excentric arm of one shaft, and the other roller on the other (their position being as in the figure) that then the rollers K L will impinge alternately on any bar, held in the angle M, and forge or extend it, and finally leave it reduced to the same dimensions, in it’s whole length, if, by hand or proper machinery, the bar has been[216] drawn or pushed along the angle M, in a manner analogous to this motion at the tilt hammer. It is also clear, that the size of the bar will be determined on a given Machine, by the diameters of the rollers K L, compared with the distance of the shafts from the angle M of the anvil.
It may be of use to observe, that the effect of this Machine is not confined to square bars: since with unequal rollers K L, it will produce flat bars; and with rollers properly grooved, (the piece M being formed accordingly) it will produce round iron or steel of better texture (I presume) than when taken from the slitting-mill, and merely passed through grooved rollers. I expect, at all events, a rapid effect, from four or five hundred turns of the cranks per minute.
It will occur to every mechanical reader, that the mass M, which is tempered and adjusted to the principal anvil A, may be still more varied in form, so as to give other results besides those above anticipated. Nor need it be said, that the shafts B C might run in steps capable of being screwed up to their work, even during the process, should any such motion be expedient. These are details I do not wish to dwell on in these descriptions—where I endeavour to make known general and essential properties, leaving particular views and cases to my reflecting readers.
I believe there is no better floor for a working horse to tread on, than a plane of wood—on condition, of the horse being rough shod: I speak however, on recollection of many years’ standing. I then felt persuaded that a horse wastes less effort by travelling on this floor than on any other; which is one of my reasons for the adoption of the present Machine. It consists (Plate 26, fig. 1,) of a wheel A B, on which the horse walks, as indicated by the sketch of him given in the figure. Besides this, he is placed between two shafts C D, affixed to the lever E F, the latter carrying round with it, at intervals, the drum G, whose office it is to raise the weight I, whatever kind of resistance that weight represents. This lever runs by means of it’s cannon L, on a round part of the shaft common to it and to the drum G. Moreover, there is a second drum H, destined to raise the weight K, whatever kind of resistance that represents. Both the drums, G and H, turn on round parts of the main shaft M, but are alternately connected with it—first, the drum G, by the rising of the bolt a into it; and secondly, the drum H, by the falling of the cross piece b c, between the studs e d affixed to it. Now, this cross piece b c, is part of a T-formed bar, that penetrates the centre[218] of the shaft as low as f, where it rests on a transverse lever f g, connected to the right with the bolt a above mentioned, and forming a branch of the bent lever f g h, which works the bolt h i under the wheel. In the present state of things, if the horse steps forward, he draws the shafts C D, round the common centre; for the wheel is immoveable by means of the bolt i, which takes against some fixed object at k: and thus will the weight I be raised. And when this motion is achieved, the handle o is raised a few inches, which brings it into contact with the obstacle p, and puts a stop to that motion of the lever E F. At the same time the bolt a, is drawn out of the drum G, and the cross piece b c is let down between the studs of the drum H, while, by the bent lever f g h, the bolt h i, which held the wheel, is drawn back, and then the horse, instead of progressing round the centre of the wheel, is himself brought locally, to a stand; and without even knowing it, (for he is blinded) he now treads round the wheel in a backward direction, and raises the weight K, while the drum G permits the weight I to descend by the uncoiling of the rope, till this operation has likewise produced the desired effect—when things are again placed in the state first observed. One thing remains to be noticed: It is, that both these motions might have been produced by acting from a fixed point on the central bar b c f, through the upper gudgeon of the shaft, instead of using the handle o, as before directed. It is even easy to conceive how the Machine may itself be made to perform these changes, and thus to produce the whole effect without any personal care or attendance.
It is one of the simplest and most perfect operations of the mechanic art, to form a flat surface: witness the process of grinding looking glasses, and forming one plane from another. Nor is it, necessarily, more difficult to place two surfaces parallel to each other, by means of three or more pillars with proper shoulders, or counternuts against which to screw the plates from behind. It is therefore easy to compose an expanding and contracting vessel, that shall become a mover by the force of any fluid, elastic or not, or shall act as a water or air pump, when driven by a convenient power; or both together, when this combination may be desirable. Thus, in Plate 26, fig. 2 and 3, A B C D is a box with four sides and four jointed angles—which, if one of it’s sides, D A, be fixed to a given position in the cage or frame E F G H, will expand or contract according as the sides A B and D C shall rise toward the perpendicular, or fall toward the horizontal position. The dotted lines A 2, A 4, A 6, &c. shew that the successive capacities included in the vessel, are respectively as the sines of the angles which those sides A B and D C make with the horizon; so that, although this device furnishes an unequable power, yet it is equable enough for many purposes in the first few divisions[220] D 3, D 5, &c. and might be altogether equalized in it’s effect if necessary. Let us suppose then, that the aperture 8, brings steam into this vessel: The lid B C will rise to 6, 7, when, if the pipe 9, communicating with a condenser, be opened, the steam in the vessel will rush thither and be destroyed: when the atmosphere will press on the lid B C, and cause the vessel to collapse with a power proportionate to that area; for the sloping and parallel sides A B and C D counterpoise each other; where note, on occasion of the pressure which I am now speaking of, that the ribs or bars L M, are used to strengthen the sides of the vessel, and thus prevent it’s fracture under this pressure.
From this manner of making these expanding vessels, it follows among other things, that if the frame E F G H were surrounded with wood or any non-conducting substance, and made to communicate with a warm close room, the atmosphere thus acting on the vessel would not cool it, and that therefore, an atmospheric engine, would, in this respect, be as good as a steam-acting one. But steam might be introduced into this outer case, and act as a spring to reciprocate the internal effect of the same agent.
The third figure of Plate 26, offers an end view of this cage or frame, shewing the expanding vessel at B C A D, where the strengthening ribs of fig. 2 are seen endwise at 1, 3, 5, 7,[221] &c. and moreover, F G and H are the pillars or cross bars by which the parallelism of the two end plates is effected and secured.
There remains an important subject to be considered: How to make the corner joints D C, and the end joints steam or water-tight as required. The small figure 4 answers the question as far as water is concerned. A is a strip of leather screwed more or less near to the edges of two contiguous sides of the vessel, so as to cover the joint or hinge, and make it water tight whether the pressure come from within or without. This figure also shews the grooves which receive the stuffing to close the ends of the vessel, by sliding against the plates or cheeks E F, &c. fig. 2. The several members of the corner joints themselves should be well fitted into each other: so indeed as almost to close the vessel without any stuffing. Nor need we in all cases be anxious about this stuffing; for I think it very possible to make this joint close enough for pumping or blowing without any such provision. I observe, however, that the leather A, fig. 4, might give place to a strip of thin metal, bent into the same form, (or nearly so) the elasticity of which would leave play enough for the joints, on the supposition of working only with a moderate degree of motion in the said joints.
I should not have given this idea so much attention, had I merely wished to use it where the cylinder-motion now applies: But my present views go further. I foresee the use of this[222] Machine for very low pressures—and in very large dimensions; and I can conceive a proportion between it’s length and height, that shall as it were annul the effects of friction and leakage, compared with those of the cylinder-formed piston. But I do not undertake, or hardly wish now, to exhaust this subject: being more anxious to deliver the idea to my readers, than to announce all I intend to undertake by it’s means. I shall, therefore, merely finish the description of the other figures 5 and 6 of this Plate. The first, is a small hand pump on this principle, having a suction pipe A, and a rising pipe B, both having proper valves and opening into the expanding vessel, as worked by the handle C, much in the manner of a common pump. It will therefore act by it’s expansive and contractile properties; and have one good quality we should seek in vain elsewhere—It will begin the motion of the water with a softness unknown in the use of pumps in general.
In fine, the sixth figure shews a System of this kind applied to the two objects, of giving power, and using it. The vessel A B, receives the power from steam or any other agent; and the vessel C blows a fire, raises water, or does any analogous work, without requiring any other parts than those here displayed.
This Instrument was first intended to regulate the grinding of a wind-mill; and was used for that purpose in Kent, some time before my departure for France, in 1792. It is founded on the doctrine of opposite qualities—and is a practical combat between equal and unequal motions. In wind-mills, the mechanism is exposed to all the variations of a capricious element: and the common way of preventing these convulsive motions from injuring the flour, was for a man to attend a lever connected with the bridge tree, (which carries the upper stone) and by it to bring the stones nearer together when the wind was strong—and nearer still, when it was violent: and, contrariwise, to lift again the upper stone when the wind assumed a milder movement. A process this, which nearly equalizes the degree of grinding, but not so nearly the quality of the meal—for this is found to be more heated by great, than by moderate velocities. At all events I thought a Machine like the present, would regulate this process, as well as a man; and it was found to do so—except, perhaps, in very extreme cases.
This Governor, is represented in fig. 1 of Plate 27—the[224] ground work of which is the same as that of the third figure in Plate 3: for in reality the present Machine claims the precedence of the Dynamometer; and may therefore, well borrow a figure from it’s description. A is the power-axis, receiving motion from any proper shaft of the mill. It is turned backward by that shaft, and therefore tends to raise the ball B—an operation equivalent to bringing the mill-stones nearer together. At the same time, the axis of resistance C, carries round a pallet-wheel D E, and by the pallet D, sets the pendulum F G a vibrating, which therefore, by every stroke, lets down the ball B, and thus raises the upper mill-stone. A proper position of the latter depends on the similarity of the motion of the power-axis A, which winds up the ball B, and that of the axis C, which lets it down. While these are equal, the weight B remains stationary, and the work goes on well. But if a gust of wind increases the speed of the mover A, (the pendulum F G confining the axis C to it’s usual speed) the ball B is immediately raised and the stones brought closer—which is what the grinding process requires: And should that gust increase in violence and become a hurricane, the intermediate cylinder M, while producing that effect, carries also with it the cord H I, and thereby raises the bob G of the pendulum, and thus fits this movement to the increased speed of the mill: raising, sometimes, the bob to the very centre F of it’s vibration, where it’s oscillations become rapid enough to unwind all the excess of motion which the hurricane had occasioned; until, the wind subsiding, the pendulum acquires a medium length, and things go on moderately as before.
It may be observed, that the present form of this Machine is not quite so simple as it might have been made; nor is it so simple as it first was. The required motions being much shorter than those of a Dynamometer, the cylinder M, among other things, might be dispensed with; and one of the intermediate wheels be likewise suppressed. And if we advert to the retarding principle which resides in the pendulum, the well known conical pendulum might be substituted for the present one; since from it would arise a regular or equable resistance, opposed to an equable effort. Some however, might then consider the conical pendulum as an ordinary centrifugal governor; and, as a mere retarding principle, it may be thought too complex for the occasion: but I think on the contrary, that it’s use in this connection, would make this Machine one of the best of regulators, as well for steam engines as for water and wind-mills of every description: especially if fitted up with my Patent Geering.
There is a strong analogy between this Instrument for forging Nails, and the Machine heretofore given for forging Bar Iron, Steel, &c. The process of kneading the softened metal, by means of a pair of alternating cranks, is the very same: but the acting bars or stampers A, B, are an addition to the former method. Plate 27, at figs. 2 and 3, gives a representation of the present Machine; which forms the nail almost instantaneously, by many contacts of the stampers a b, (fig. 3) on one of which the figure of the nail is engraven—or rather filed across that stamper, for no hollow figure is required by this System.
The second stamper c d fig. 3, whose place is at A fig. 2, is quite plain on it’s face; being destined merely to keep the metal to it’s thickness—as the particular nail here intended, is a floor nail, requiring a head on two sides only. As to the figured stamper b a, fig. 3, it meets a similar form in the anvil, as at e: and it is by the pressure of these half matrices, that the head is formed and the bar separated from the nail. It may be noticed that the stampers a b, c d, are shewn in the figures, as perfectly straight on the face: but the kind of motion resulting[227] from that of the cranks, would require a gentle curve here, which a first experiment will sufficiently indicate.
Some skill would doubtless be necessary in presenting the nail bar to this Machine; but to make this operation the easier, there should be a guage, moving toward the working point e, by a given quantity for each nail: say that this guage comes forward at each time a distance equal to half the length of a nail; and that the thickness of the nail bar is so proportioned as to contain in that length, enough of metal for the nail when finished.
It remains to be observed, that the stampers or bars A, B, fig. 2, are contained, in the direction of their width; by two plates like f, connected with the anvil e, and leaving near e, an opening large enough for the nail-bar to pass easily.
I shall, perhaps, be laughed at by some unfeeling censor, for including the tea table in the field of my mechanical speculations. But, in so doing, I seriously mean to be not only attentive, but useful to the ladies—who, I am old enough to believe, deserve this service at my hands. My object is to obviate for them the necessity of tediously wielding a ponderous tea-pot, until real and painful fatigue ensues: thus emphatically making a toil of that pleasure they had hoped for in administering comfort to others.
This new method of tea-making admits the use of the common tea urn—which is placed on the table near the left hand of the fair distributor. This arrangement is given at figs. 4 and 5 of Plate 27. There, A is the Urn; and B any common tea-pot, for whose spout, the cock a, has been substituted; and the handle of which has been slightly modified, so as to make it a proper centre of rotation. This tea-pot is, of course, opened before it is brought into the position shewn in the figures. At C b c, is placed, first of all, on the table, a stand of metal, terminated upward by the stem C D which forms a vertical centre to the whole apparatus: and which is sufficiently fixed[229] to the table by standing on three feet, b c, &c.; under which are stretched small pieces of Caoutchouc (or India rubber), which, by their adherence to the table, make the whole steady. By these means, the tea-pot can be turned round, by a gentle effort, till it comes under the cock of the urn, from which it receives the boiling water. And, finally, the tea-board, which is itself circular, revolves on the same axle C D, supported by the casters or rollers e f, and bringing successively all the tea-cups m, n, o, &c., to the spout of the tea-pot, where they are filled without the smallest difficulty, as will appear by a further inspection of the figures, and especially by an appeal to experience.
The above, I should presume, is all that need be said upon the subject. It remains for some rationally zealous friend of this social repast, to put these (or other analogous) ideas in practice: in which enterprize, should he succeed in pleasing the ladies, he may depend on the approbation of every lord who deserves the name.
This Machine, as intimated in the Synopsis, was invented expressly for the use of the lithographic art, as an improvement on the roller press used in Paris when that process was first introduced there. I have, however, seen in England the description of a Machine which takes the desired impression without any rolling motion. This Machine, in that description, carries a kind of scraper, or, as the calico printers would say, a Doctor, which, pressing on a line only (while drawn over the paper, or the paper under it), acts successively on every part of the sheet, and, no doubt, gives a good impression. Of the relative perfection of these methods, I do not presume to judge, as it is a technical question; and both Systems are, or have been, used. But, when intense pressure, joined to much precision, and great economy of power, are desirable, this Invention appears to me superior to any thing I have seen used for these purposes.
In fig. 1 and 2, (see Plate 28), A B are two horizontal planes of hard wood or metal, connected, at a proper distance, by the pillars C D, shewn in fig. 1 only. E F are two Sectors of a large cylinder, united at the point a, either by a good hinge or[231] by a joint composed of a hollow prism fixed to the upper sector E, and of a solid one, more acute, fixed to the lower sector F; so that, in the latter case, this joint works with an insensible degree of friction, and thus occasions a great saving of power.
In the working of this Press, the joint just mentioned, however made, describes a straight line, parallel both to the floor B G and the ceiling H A, which have been already shewn to be parallel to each other: and thus are the joint a and the sectors E F suspended to the cap or ceiling A H by a pair of triangular braces I a K, which slide smoothly in two dove-tailed grooves A m. Moreover, to the lower sector F are fixed two working arcs b c, one on each side of the Press, and whose radii are exactly equal to that of the upper sector E (whose circumference, therefore, is invisible in fig. 1.) Further, just above these arcs, and in the middle of the slide I K, are placed, on proper centres, a pair of grooved pulleys P, destined to work the under sector, without disturbing the motion of the upper one, which latter is a rolling motion under the aforesaid ceiling A H. For the said purpose, a metallic cord or chain is fixed at m (fig. 1), which, passing round one of the pulleys P, is led to the end n of the arc b c, n o; and near A is fixed a similar cord, which, carried round the other pulley at P, is led to the angle o of the same arc b c, n o. By these means, the sector F is fixed both in place and position, as long as the slide I K retains it’s present position and state. But, again, a system[232] of similar cords, placed under the ceiling A H, near the edges of the upper sector E, determines the place of that sector, in every case, except a change of position; for a rolling motion can still have place, without occasioning any other change.
When, therefore, a pulling bar, a crank and fly, or any other prime mover, applied at the joint a, carries that joint (say) toward the pillar D, that motion takes place without any rubbing of surface either above or below; for, when the upper section has rolled under the ceiling A H, into the position n p q, the lower section has rolled upon the plate s t, into the position q r s: in such sort that the analogous angles o t, p r of both sectors are always found in the same perpendicular line—or plane—o t, p r; the cause of which I shall now endeavour to unfold.
When a wheel, in general, rolls on or against any fixed plane (and the cords m P, A P, now act the part of a fixed plane), the point of it’s circumference the most distant from that plane, moves, in a direction parallel to it, just twice as fast as the centre of such wheel, because it is twice as far from that plane, the virtual centre of its motion: (an example of which is found in the wheel of a carriage, whose top moves forward just twice as fast as it’s axle-tree.) Supposing, then, in the present case, the frame I a K, with the pulleys P to glide toward the right hand, the cord A o fixed near A, will turn the arc b c to the right, twice as fast as the centre of the pulley P moves in that[233] direction: and if this impulse had acted on the joint a, while fixed in position, the arc b c would have turned too much by half. But it so happens (if this expression may be used), that the joint a itself moves in that direction once as fast as the pulley-pin; so, that the motion remaining to the sector F is a single motion, merely sufficient to keep the two sectors E and F directly under each other, or within the same perpendicular lines p r, n q s, &c.
Thus, it appears, that the turning motion of the two sectors is the same; and that a given point of the lower one will always visit the same point of the corresponding plane s t, independently of contact with any substance lying on it; and that, therefore, the pressure, though successive, is perpendicular, having no tendency to displace or pucker the paper laid on it; besides which, it may be observed, that the power of this Press is immense, from the length of the radii of the sectors E F, and the absence of any rubbing motion.
I observe, further, that racks, made with teeth on my principle, either singly inclined with cheeks, as in Plate 14, or with teeth in the V form, will produce a more certain effect than the cords and pulleys above described, provided the arcs b c, and the upper sector E, be prepared and toothed accordingly.
The object of this Invention is to join economy of light with splendour of effect. The means are the following:—
From the nature of reflecting curves, it follows that the smaller a luminous point is, the more perfectly will its emanations be reflected; for a focus is a point of the smallest magnitude, if, indeed, it has any dimensions. My idea, then, is to make a focus of a line of light very minute in it’s section, but as large, in it’s contents, as may be desired: thus securing a considerable fasces of luminous particles while using them in an economical manner. To this end (see Plate 28, figs. 3 and 4), I form my reflecting surface of two distinct parts, having a section common to both, viz.—1st. a concave-parabolic-spindle, represented at A B C, as cut by a vertical plane passing through it’s centre; and 2ndly, a parabolical bason E D F G (represented in the same manner) surrounding the former, and so placed as that these surfaces have a common focus—namely, the circular line of which a b is the section; the line itself being shewn by an elevation passing behind the aforesaid spindle A B C. This linear focus, therefore, may be two or three feet in diameter; thus imitating the tenuity of a punctual focus, while emitting a large quantity of rays.
This Lamp, then, consists of an oil vessel, which is formed by the outside of the parabolical bowl before-mentioned, surrounded, in it’s turn, by the cylindrical surface P H, I Q, this vessel communicating with the wick-ring a N, b O, by a passage, H I, made as thin as possible, in order to leave the light at greater liberty to pass downward after reflection. (Where it is proper to add that the wick-ring is drawn too thick in the figure.) Now, it is well known that all rays of light issuing from a point, and falling on the concave surface of paraboloid belonging to that point as a focus, are reflected from it in lines parallel to each other; and, therefore, a great part of the particles emanating from the linear (or circular) focus a b, and impinging on the surfaces F G A B, and B C D E, will be reflected perpendicularly downward, as at a, 1 3; b, 2 4, &c. and this being the case all round the common centre B, there will be formed a cylinder of light of the diameter H I, diminished only by the shadows of the wick-ring, the passage H N O I, and the pillar B L, when that is used, which is not indispensable.
If this cylinder of light strikes on the plane mirror K H, placed at an angle of 45° from their direction, these rays will be reflected horizontally, and, preserving their cylindrical form, may serve as a powerful beacon to the benighted mariner; the more useful, because susceptible of those temporary variations of direction and aspect, long since employed to distinguish one station from another.
But, if it were desired to illuminate a large space at sea, or elsewhere, the aforesaid cylinder of rays would be received on a conical surface K L M, which would give it the form of an immense sheet of light, of a thickness (allowing for aberration) equal to the height of P L M, of the same conical surface.
I shall add only one idea—namely, that to light any round space, building, theatre, &c., this system might be made very efficient by throwing the sheet of light M P higher or lower on the walls, &c.; or (altering the angle of the cone K L M) by bringing it down to any position in or below the horizon, as circumstances may direct.
It would be superfluous to say that this Lamp might be furnished with all the advantages of the argand principle; or, the whole wick-apparatus might be superseded by a circle of minute, and very numerous gas lights, forming, sensibly, the same linear focus; or a thin circular slit might produce a real ring of light, strengthened by all the resources of this new and splendid discovery.
In the year 1793 or 4, I received a written problem, desiring me to give a plan of a long Reciprocating Motion, that should be driven by the pit-wheel of a common water-wheel, of given dimensions, and placed in a given position. In a few days, I produced the drawing now represented in Plate 29. Its object, as required, was to move the cylinders L M, figs. 1, 2, 3, backwards and forwards, in the long grooves or gutters N O, for the purpose of crushing or bruising their contents: but what those contents were I never knew. I, however, produced this Machine, considering it as a general thing, and of a nature to perform most operations of a similar kind. The Machine consists—first, of a long rack I K, much like a narrow ladder placed on it’s edge, and in the teeth of which work those of a pinion p, whose axis q is connected with the wheel r, which receives it’s motion from the vertical wheel s t, which is the pit-wheel in question. This communication takes place by means of an universal joint x, being a mean of permitting the pinion p to vibrate from side to side of the rack I K, when arrived at either end of it. For example, the pinion p now turns from left to right, and, being on the other side of the rack, and held by the chain v, it drives the slide P Q in the[238] same right-handed direction, and, with the slide, the two heavy cylinders L M before-mentioned;—for, the said slide P Q carries across it’s middle the axle-tree S T, which is the centre of both these cylinders, and connects their motion with that of the slide now in question. Further, there are rollers placed between the cheeks V V, on which the slide moves horizontally, as guided by other rollers, placed at the points 1, 2, 3, 4, &c. Again, the ends of the axle-tree S T are furnished with two bow-like bridles, which, connected with the pulling bars Y, are again fastened to the slide P Q, at the two ends of the present figure.
When, now, the pinion p turns (see fig. 1 and 3), the rack, slide, and cylinders roll in the grooves, till the end of the rack comes to that pinion; which, finding no more teeth, swings round the last, and taking a new position, reverts the motion, till the other end of the rack comes to it, and occasions another return: ad inf. This will be better seen at the third figure, which is an end elevation of a part of the Machine.—There, P shews the slide and one of the teeth of the rack (which teeth are longer than the rest, as seen near L M, in fig. 1.) In this figure, we see at A, a mass of brick-work, covered by the sleepers 5, 6, 7, &c., on which the long cheeks V V repose. There, also, the chains v z are seen, connected with ring-bolts, which go through the bars a b, and are nutted on the other side of the spring-beams c d, in order to avoid the commotion which would otherwise attend every change of[239] motion in the slide and cylinders. For this purpose, also, and especially to prevent any waste of power at these moments, there are mixti-linear wedges laid in the gutters, such as are shewn at 6, which are formed so as to absorb the momentum of the cylinders, in exact conformity to the time employed by the pinion p, in swinging round the end tooth of the rack; and thus to save all the power and time possible.
An ordinary Syphon acts by the pressure of the air on the upper water, which drives it into the ascending pipe, because there is a (partial) vacuum made there by the weight of the falling water in the descending pipe; this being always longer than the first. Thus, in Plate 29, fig. 5, A B shews the rising pipe of a Syphon, and C D the falling pipe, which is longer, and sinks to a lower level D, than that A of the water, which feeds the machine. E, in this figure, represents the vessel containing the mechanism on which the new effect depends: and which I shall now describe.
B and C, fig. 4, are, one the ascending pipe A B of fig. 5, and the other the descending pipe C D. They are surmounted by two cylinders, of unequal capacities—this inequality bearing a given proportion to the difference in the heights of the rising and falling branches of the Syphon. In each of the cylinders works a piston a, b, which, I think, need not be stuffed, but well fitted. The large piston has proper valves in it, to let the water pass upwards, at all times; and the small piston has a valve i, opening upwards, by means of the mechanism we are now describing; and closing itself merely by the[241] arrival of the piston into it’s present position; for the screw c prevents the valve from rising higher: e, f, are two arcs belonging to the lever E, and being circles round it’s centre of motion. They are cut into teeth, on my Patent principle, and work in the racks similarly toothed, which give motion to the pistons a b, or receive it from them. Further, behind the stand F, common to both levers, vibrates, on a pin, another lever g h, the use of which is to work the aforesaid valve i in the small piston; and this it does, by means of the weight h, in the following manner:—The machine being supposed in the present state, the Syphon will act, as usual, through the valves of the large piston; and the water pressing on the small one, with a power proportionate to the excess of it’s column over that of the other piston (a), will raise the latter as fast as the piston b descends; but the area of the piston a being larger than that of the piston b, there will be a pressure within the vessel b c d a, that must expel (through any prepared aperture at the top) a quantity of water equal to the difference of area between the two pistons, multiplied by the stroke of both: the real quantity of which will ultimately depend on the difference of level between the higher and lower water; or between the lengths of the rising and falling branches of the Syphon, B and C. When, therefore, this stroke is made, the end h of the lever g h, which carries the ball, will touch the screw d, and stop the descent of the valve i, which will thus be opened; when the water will have free egress through the descending pipe C, and the piston b will then rise through that[242] water by the weight of the piston a, the valve i being kept open by the action of the weight h, until the piston b has risen to it’s present position, when a new stroke is prepared, for the same reason as before: and thus may water be carried over a hill of (about) 30 feet above the level of any stream or pond, and dropped into a lower canal on the other side, with the condition of leaving a part of that water upon the hill, proportionate to the difference between the level from which the water is brought, and that to which it is carried.
The two figures, 1 and 2, of Plate 30, are intended to make this Machine known, assisted by the following description:—The first is a front view of it, and the other a partial view from above. In the former, A B is the frame formed of, and firmly connected with the two columns C D, which are fixed strongly to the ground, at such a distance below the ends C D, as to place the aforesaid frame at the height of about two feet, or higher, if convenient.
In the two cheeks of the frame A B, are cast or bored two round holes for receiving the gudgeons of the swivel E, one of which gudgeons is also seen at E, in fig. 2. This swivel turns in these holes; and it is itself perforated with a round hole just large enough to receive freely the body of the mandrel F G. This mandrel has now on it the cylinder, which is to be taken off. I K are, moreover, two ears or studs cast or welded on to the top and bottom of the said frame A B, and at exactly the same distance from the centres of the swivel E before-mentioned. These ears receive the ring-formed ends of the bars L M; see also the bar L, in fig. 2. To these bars is firmly fixed the cross-bar N O, which forms the nut of the screw P,[244] by means of which the operation of the machine is duly prepared; for, now the cup Q (in the centre of which the screw P revolves against a proper shoulder) receives the end G of the mandrel, which it presses forcibly, while the whole is in the position E L, of fig. 2; that is, when the two centres E and R form one right line with the bar L, figs. 1 and 2. To complete, then, the process of driving out the mandrel, the bars, mandrel and cylinder are, at once, strongly made to describe the arcs a M b, a c; the mandrel revolving round the centre E, which is that of the swivel and the bars round the stud R. But, in thus revolving, a given point of the mandrel describes the quadrant a M B, and a contiguous point of the bars L M describes the quadrant a c; insomuch, that the mandrel must have been forced out of the cylinder in direction G F by the distance c b; where we observe that, at the beginning of this motion, the two curves a b and a c coincide in their movements, and only begin greatly to diverge from each other in the latter parts of these motions (see M b c.) The power, then, of this machine, when the cylinder sticks fastest to the mandrel, is infinite: and this power becomes weaker, and the velocity greater toward the end of the operation; that is, when the cylinder has slackened on the mandrel, and no longer requires to be driven with the same force as at the beginning. It may finally be observed, that the bars L M are suspended by an oblique bar or chain S N to the ceiling of the room just over the stud R or I, which is their real centre of motion, in the above-described process.
The wheel A B, Plate 30, fig. 3, was a horse-wheel, but may be a first motion of any given kind. It is placed on the ground-floor; and over it’s centre is another shaft, having on it’s upper end a chopping block C, which revolves with the wheel A B, as turned from below. In this wheel, A B geers a pinion D, driving the lateral shaft D E, which has two functions: the first to work the lying shaft F, and by means of the cams G H, to lift the contiguous stampers; and, by means of the knives I K, to cut the tallow on the revolving block before-mentioned. Over this block is fixed an oblique scraper, which takes the tallow as soon as it is cut, and pushes it down an inclined channel, placed at C x, into the boiler. The second use of the shaft E is to turn the mill M, (better shewn at fig. 4), which is let down into the boiler, in one stage of the process, and drawn out by the tackle N, when not wanted. The use of this mill is to tear the fleshy parts of the substance, while in the act of boiling, and thus to disengage the tallow with so much the less heat, in order that it may be so much the less coloured. Besides this machine, there is a grapple L to be first used, which stirs the tallow in the boiler by the rotatory motion of the arm x. This position of the[246] grapple would alone indicate what I have yet to observe—namely, that the boiler is a kind of ring, the section of which is the line 1, 2, 3, 4, and it’s depth 1, 2, or 3, 4. To prevent, still further, the fat from being burnt or coloured, the flue for the fire is conducted solely under the bottom of the boiler, as shewn by the dotted lines in fig. 5: the smoke or heated air being forced to make two revolutions under it, as indicated by the arrows in this figure, where we see more particularly the fire-place F in close connection with the rising shaft of the chimney at G; and this is so, because, with so great a length of horizontal flue, the fire would not enter the chimney till it had been heated to a first degree. There is, therefore, an opening into the chimney at a, and the fire, in lighting, is suffered to escape directly from the fire-place into the chimney; by which means, continued a few minutes, there is draught enough created to make the fire take its useful course through the flue afore-mentioned. I may just observe, reverting to fig. 3, that O shews the fire-place in elevation, and p the entrance into the flue, which last is double under the boiler, as shewn in fig. 5. Finally, the 4th fig. shews an end view of the tearing-mill, before-mentioned; but here on a larger scale, A B being a part of the side of the boiler.
Doubtless, the salubrity of every place, where many people are collected, would be much increased, if all impure exhalations were expelled as soon as formed; and this is especially true of those awful but sublime receptacles, provided by Philanthropy, for the sick, the wounded, and the dying! To assist in the work of purifying the atmosphere of these doleful abodes, was the object (30 years ago) of the Ventilator, presented in page 170 of this work. But, I conceive, that a share of evil, quite as great, resides in the putrescent qualities contained in or connected with the clothes, the bed-linen, the dressings, &c., of the inmates of an hospital; to whose sacred claims on the efforts of every good citizen, the present article is devoted.
This Washing Machine (see Plate 31, figs. 1 and 2) is a triangular (or square) box A B, furnished with a lid a b, so fitted, as, when screwed down, to be hermetically closed.—And, N. B., to facilitate this operation, I use in it a particular kind of screw (invented for the hose of fire-engines), which I shall now describe. I take a common screw, with it’s nut, and cut away the threads of both, at two opposite quarters of their[248] respective circumferences, so that the screw can enter the nut to the bottom without turning; and the stuffing between the shoulders is so well fitted, in thickness, as to secure the penetration of the threads of the nut and screw the moment the latter begins to turn. There is thus a full quarter of a turn, in which the nut and screw will press as strongly as though the threads had not been cut away; and thus are nine tenths of the time required to use a common screw saved by this simple process: and thus, then, I close the lid afore-mentioned.
This Machine is further composed of a wheel C D, and a pinion E, to turn it with, either by hand, or by any proper application of power. The wheel turns the box A B, and thus agitates the contents in a way not dissimilar to the operation of the dash-wheels of calico printers. But, again, this wheel and vessel turn upon two hollow gudgeons c d; one of which is destined to convey cold water into the wheel from the reservoir F G, to regulate which is the use of the cock f: the stuffing box e being made as good as possible, in order to prevent all leakage, either of air or water. The second hollow axis d serves two purposes: it gives a passage to the fetid matter of which the expulsion is desired, and conveys it through the cock g to the sink or sough below h, without any communication with the surrounding atmosphere.
But we said this hollow gudgeon had a second use: it is to bring steam into the revolving vessel A B, from any proper[249] boiler beyond K, when that part of the process requires it.—There are, moreover, two partitions C D, l m, made near the ends of the vessel, and pierced with many holes, in order to suffer the cold water to flow in, and the dirty water to escape, without choking up the respective passages: and, finally, at the eduction end of the Machine (see n, o, p, fig. 2), there are placed three pipes, reaching from the angles of the box to the hollow centre, and furnished, at those angles, with valves, opening outwards; which thus form a kind of hydraulic machine to raise this matter from those places to the hollow centre, and thus, after a certain number of revolutions, to expel it entirely.
The process, then, for cleansing the objects contained in the vessel A B (including the condition of cutting off all communication with the ambient space,) is as follows:—
1st.—These objects are dropped into the vessel as soon as produced, and the vessel is filled, one half or more, with cold water from the reservoir F G. The things are then left to steep in this bath for a day or two, or what space of time the periodical mutations of the house permit. By which operation alone, the miasmata are already much confined by the water, even though the lid of the vessel should be but partially shut: after which, this steeping operation may be continued, with the accompaniment of a few turns of the handle (E) to fully saturate every part of the mass. In the second place, a small[250] stream of water is let through the cock f, and the wheel C D is kept turning for a few hours, to discharge the cold water and the most offensive matter, through the cock g, into the sink: and, thirdly, the steam-cock K is opened (that g being shut), by which means steam is brought into the vessel A B, and the whole soon raised to the boiling temperature. This state of things is continued, as long as it is found necessary; the motion, of course, being also continued, and even accelerated, that the mass of objects may fall from angle to angle, and be thus well washed—that is, well finished, if plain things; and fully prepared for finishing, by hand, if of a nature to require close attention. And, finally, in many cases, the warm process may now be abandoned, and a new stream of cold water be injected, accompanied by a due motion in the vessel, so as to rince the contents; and thus leave nothing to do for the laundresses, but to dry and mangle, or iron them; where, it is plain, that no inconvenience can have arisen from this process, either to these persons, or to the other inmates of the house.—Hence, then, this Machine has the properties announced—of confining the offensive matter until cleansed away.
The application of steam-power, to the motion of boats on narrow canals, is, I believe, much impeded by the consideration that the agitation of the water injures their banks, and would finally destroy them. On the other hand, it is known, that to drive a vessel, by acting on a fleeting medium, such as water, we must, at once, submit to lose about one half of the whole power employed—that is, the power, armed with energy enough to produce the required velocity, must go through twice the space that constitutes the way or progress of the vessel. This depends, however, on the size of the floats or paddles employed, compared with the section of the boat, as modified by the form of the prow; but it is difficult to employ a paddle so large as to suffer more resistance from the water than the boat itself; and, if they are found just equal, the loss of power is exactly one half of the whole. These, then, are the two difficulties which I hoped to avoid, by the method now to be exhibited.
The idea is this—To have a large and heavy wheel A connected with a long shaft B, reaching from the boat to the shore, and, turning that wheel in the boat, to propel the latter,[252] by means of it’s rolling motion, on the bank or track-way; or, in some cases, on a proper rack, placed there for that purpose.
The Machine itself is represented in figs. 3 and 4, of Plate 31; fig. 3 being a stern-view, and fig. 4 a side-view, both of the machine and the vessel. C is an axis, placed along the vessel, and turned by any convenient power—as a horse, a steam-engine, &c. On this axis, considered as the first motion, are fixed the two bevil wheels b c, from which the long shaft B A of the rolling wheel takes it’s motion. The use of the two wheels b c, is to drive the boat in the same direction on whichever side of the boat the wheel A may be placed; for this, of course, must follow the track-way, which is sometimes to the right and sometimes to the left of the vessel.—Between the two wheels c b, is a sliding block (or catch-box) d, in which the shaft A B of the large wheel has it’s lower pivot, and by which it’s wheel B is almost instantaneously shifted from one to the other of the vertical wheels b c: the catch-box d being itself worked by a lever, of which the end only is seen at e, fig. 4. In fig. 3, there is further shewn a rope or stay f, which, fastened to the socket s, of the rolling wheel A, and fixed in the middle of the boat, at the greatest possible distance from it, serves to keep that shaft at or near an angle of 90 degrees with the boat’s side: so that (the vessel being long) it becomes easy by means of the rudder, assisted, perhaps, by lee-boards to keep the way of the boat in a line parallel to the[253] shore, notwithstanding the tendency to veer outward, given by the wheel A, while acting on a point so far from the body of the vessel.
I further observe, that, in order to shift the apparatus, with a certain facility, from one side of the boat to the other, there is a mast M placed ahead of the mechanism just described, which rises as high as the length of the main-shaft (but can be lowered to pass a bridge, &c.), and to the top of which is fixed the block g, through which a rope passes from the foot of the mast to the above-mentioned socket of the wheel A. By this rope the wheel is hauled up till nearly ready to fall over the centre; when a push from below will complete that passage; and the wheel A, being afterwards lowered by the rope h i, will soon find it’s proper position on the other side of the boat, as before anticipated. Where, it should also be remembered, that this shaft must have a joint and socket, to permit it’s being bent, to pass a bridge, &c.
Hitherto we have supposed this rolling wheel to act on the bank or track-way solely by it’s weight; but this is not our only resource; for this wheel might be made of a moderate weight, and be pressed down by a brace reaching along the boat, toward the head and stern (see k l, fig. 3.), and hauled taught through an eye of the socket s; by which manœuvre (the points k l being lower than the centre A of the wheel) the[254] latter will be pressed forcibly downward, and cause that cohesion there, from which the boat is ultimately to take her motion.
And, as to the wheel A itself, I have not represented it in the very form I should wish it to have, because it can be sufficiently described in words. I should cast this wheel (if made at all in metal) as a shell, the outside of which would be what is really seen in the figure (at A), and the rim would have in it mortices, like those which are made for iron wheels destined to receive wooden cogs, and geer with cogs of iron. In fact, this would become a wooden-toothed-wheel, with its teeth roughly formed and placed, so as to occasion a small expence, and to be easily changed, when worn away by the friction on the track-way. Thus would, I am persuaded, a very moderate weight in the wheel, and as moderate a pressure from the braces k l, connect the wheel with the road enough to produce the desired effect, with a trifling loss of the power employed. And thus might we navigate a narrow canal, with a great saving of expence; not to mention that other advantage of avoiding entirely that injury to the banks, which must attend every system of propelling the boats, founded on the agitation of it’s waters.
The Slide-valve is an excellent substitute for the hand-geering of steam-engines, from the simplicity of form which it introduces, and the certainty of it’s recurring effects. But it is, I believe deservedly, reproached with being too sluggish in it’s operation, at the very moment when activity would be most desirable—namely, at the beginning of the strokes; insomuch, say some, that the power of the engine is materially lessened by it. The fact is, that the excentric (usually placed on the crank-shaft) is almost always moving, and with it the slide-valves also; which thus open by slow degrees, when they should open by rapid ones.
Without discussing the question further, I cannot refrain from introducing this application of the principle of my Parallel Motion, given in page 237; which appears to me greatly calculated to obviate these difficulties; and thus to leave the slide-valve in possession of all it’s own advantages, with the addition of those which have hitherto belonged exclusively to the Hand-geering System.
I have represented this Mechanism in figs. 5 and 6, Plate 31:[256] where A B shew the crank-shaft of a steam-engine, working by means of slide-valves, the place of the excentric being at a b, in a line with the pulling-bar e f. Instead, then, of the usual connecting frame between the excentric at a b, and the valve-lever at g, I use for the above purpose, a lever e f terminated by an arc o, furnished (in the present instance) with five teeth, and connected by the joint e with the valve-lever g, in the usual manner. In the arc, which terminates this lever to the right, are the five teeth above-mentioned; and, they geer in the ten teeth of the wheel c d, which will be seen (in fig. 6) to be on the same shaft with the spur-wheel m, itself driven by the spur-wheel n, of twice the diameter. This wheel c d, therefore, makes two revolutions for one of the crank-shaft: and, supposing it to turn in the direction of the arrow, it will first of all draw upward the arc o, producing no effect on the valve-lever at g; but, when the tooth r is arrived at p (the tooth p being then arrived at the entrance of the curve q), the wheel c d will begin to draw the arc o along with it, round it’s own centre; and, the teeth of the arc being kept in it’s teeth by the similar curve q, the valve-bar will be drawn from g to h, in the course of one quarter of a revolution of the crank-shaft A B. But, now, the tooth r of the arc o will be found at s: and, therefore, the further revolution of the wheel c d will carry the arc o downward toward t, until the tooth r has reached the point t; that is, until the wheel c d has made another half-revolution, and the shaft A B another quarter; when, as before, the arc o, conducted by the curve t r, will[257] again drive back the lever e f, till it comes into it’s present position: after which, their motions will be regularly continued. It is, then, evident, that the slide-valves are thus opened and shut, each during one quarter of a turn of the crank-shaft A B; and thus they remain stationary during another quarter, and that, in two positions of said shaft diametrically opposite to each other. And thus have we a simple mean, adaptable to every engine, of giving it much of the advantage of the hand-geering system, while preserving all that of the slide-valve principle. And, were it desired to lengthen the interregnum of the opening motion, it would be done by making the wheel c d smaller, and the ratio of n to m (see fig. 6) larger in the same proportion.
I observe here, however, that care should be taken not to make the valve motions too rapid, nor the intervals between them too long; for, I consider one of the best properties of this motion to be, that it acts like an excentric; that is, slowly at first, most rapidly afterwards, and finishes as slowly as it began; which is a precious quality in all reciprocating machines.
Finally, I would remark, that the two last rounds in the rack of the arc o might be rather larger than the intermediate ones, and turn, moreover, on pins, so as to suffer less friction when rolling on the conducting curves q and t. There might also be a plate or cap rivetted or screwed over all the teeth, so as to strengthen each one, by the force of the whole, as is shewn in fig. 1, Plate 29; from which, as before observed, this Mechanism is deduced.
The foregoing completes the Third Section of my work: and gives an article beyond the twenty, first intended:—which I thought important enough to claim this distinction. I now beg leave to add a remark or two on the text and plates of this, and the Second Part, by way of clearing up some obscurities, that might otherwise embarrass my readers.
And, first, in fig. 1, of Plate 21, the receiving vessel M, erroneously appears to form part of the wheel D E; but is, in reality, placed before it, as in all similar cases.—And, further, a small deviation of the circular lines, in Plate 22, has set the plate and it’s description, in page 192, at variance; the difference between the lines o p and C q being not “imperceptible,” as there stated. I wish, then, that the dotted radius A o p, in the said fig. 2, may be carried (or supposed) halfway between p and C. Finally, in page 200, line 8, the 24th Plate is incorrectly called the 25th.
I shall conclude this Part, by an observation or two on the reception my System of Toothed Wheels, as described in this work, has met with—not intending to speak of the local difficulties I experienced at a former period. But, here, the interests of truth force me to break silence. The necessity I stood under of bringing out this work in Parts, has, at least, had one advantage: it has given me an opportunity of watching the workings of prejudice—not to say of envy,—and thus of neutralizing, in some degree, the effects of either: from which, however, I claim nothing but the right of making[259] my labours the more extensively useful, by making them better known. I have, then, to say that, among a few other objections to the System, this error has come from so respectable a quarter, that it would be unjust to Science, and injurious to truth, to let it pass unrefuted. It has been said, that “my wheels are a Chinese Invention;” and this proof has been adduced of it—namely, a sugar-mill, from China, having it’s cylinders fluted in a spiral direction. Now, the fact is, it would have been difficult to give a better proof that the wheels are NOT a “Chinese Invention;” for two inventions are then only alike when they produce the same effect, by similar means. But here the effects intended are totally different. A sugar-mill acts in or near the plane of the centres; and one of it’s cylinders is not intended to drive the other independently of pressure between them. This is so true, that the rollers of many sugar-mills are not fluted at all. Besides this, my wheels exert no pressure in that direction; and if they did, they would not be cog-wheels. In a word, their action is at right angles to the former, and has an object of quite a distinct nature. These, then, are by no means the same machine; and, therefore, mine is not a “Chinese Invention.”
Here, however, I beg not to be misunderstood! I should feel no regret at appearing on the mechanical stage, a few hundred years after so ancient and astonishing a nation as the Chinese! But, in this case, truth did not permit me to sanction, by my silence, this flagrant error.
Finally, an opinion exists, somewhere, that these wheels will never be generally used, from the difficulty of making them; and this opinion has been expressed, apparently, with no very amiable feeling. But, amiable or hateful, the opinion is highly erroneous! It is so far from fact, that, in a competent manufactory, they can be made more cheaply than others now are; and many persons are already calling for them from every quarter; nor is any thing wanted to insure their immediate prevalence but a common degree of commercial energy.
A NEW CENTURY OF
Inventions.
One of the most prominent subjects of this essay, if not the most important, is the System of Toothed Wheels, with which the second and third Parts were introduced, and which still claims a share of my readers’ attention. As hinted a few pages backward, it seems not enough for me to exhibit and describe the System, but I must defend it against repeated objections, on pain of seeing it’s utility delayed, and the public deprived of it’s real and solid advantages. I am far from wishing to impeach the motives of those who still nourish or express dissent, when they deign to bring reasons for so doing; but the mere opinion—“it won’t do”—expressed by a man of reputation, may impede, for a time, the progress of an useful discovery, and thus produce a public evil. This, then, is a result I am anxious to avert; as the present System has many points of excellence, against which no insuperable objection can be brought. Had I not declined, already, to name either the friends or enemies of the System, I might here appeal to persons who highly approve of it; and, indeed, who use it daily with manifest advantage. But, I forbear. If, by means of the Engines already given, and that I am going to offer, it is proved, that the difficulty of making these wheels is trifling, compared[264] with their utility, one important point will be gained: I shall not hear it repeated, “that the System cannot succeed, because of the difficulties of it’s execution.”
The present Cutting Engine is shewn in figs. 1, 2, 3, of Plate 32. It’s immediate use is to form the teeth of wooden models, for casting. These are previously built as usual, and lagged with bay-wood, of sufficient thickness to furnish the teeth, and leave a small thickness of that wood behind or under them.—A B, in fig. 2, represents a wheel of this kind, ready for cutting;—mounted correctly on the centre pin C D, which latter is so formed as to be fixable in any position on the table or bench E F. Under the wheel A B, there is a kind of index a b, put upon the said centre pin C D, which, by means of the clamp and screw b c d, can be occasionally connected with the wheel A B so as to turn it, when it is itself turned by the means hereafter to be mentioned. To proceed with the description: G is a slide, moving horizontally on the bench E F, as seen at f e fig. 3; this slide being the basis of the headstock G H, which contains the perpendicular slide H I, itself the support of the cutter-frame K L, so constructed as to turn on it’s bolt above I, and take any proper position over the edge of the wheel or model A B. This slide, then, with it’s appurtenances H I K L, moves along the bench E F, as seen in fig. 3 at f e: and what gives it this motion, is, the screw g, furnished, purposely, with a left-handed thread, working in the half-nut contained in the small frame h, which contains also a jointed[265] cap, that can be lifted off in an instant, and the screw set at liberty. Moreover, the second use of this screw g, is to be thus disengaged from it’s nut, and lifted up to about i, where it serves to push back the slide G towards the wheel, without that loss of time it would occasion if pushed back by the working of the screw. The letters M N, shew another important part of the Machine, applying to the cutting-process. It is an inclined plane, sloped to the same degree as the bottom of the teeth of the wheel. (See the line a k.) This inclined plane, then, is fastened, in any proper place, on the bench E F, by the wedge N, just like the puppet of a common turning lathe; and it passes through an opening in the slide G I, or rather suffers this to pass over it, as better seen at M, fig. 3. Furthermore, the slide I (fig. 2), after gliding down this inclined plane M G, will have to be raised between each cutting: and that is the office of the workman’s hand acting on the lever O P, through the iron frame Q M, which is shewn at fig. 3, in another direction; and marked with the letters Q l m. In fine, the slide G carries on each side of the Machine a pulling bar n, connected with the said slide, and with a smaller sliding piece o, the use of which is to hold a pin (seen in the figure, but leaving no room for a letter of indication), which turns the wheel A B, by the plate p, as the slide G recedes, and the cutter-system I K L descends on the inclined plane before-mentioned. Having thus adverted to all the important parts of the Machine, we turn to fig. 1, for the purpose of shewing[266] what the plate (whose edge is seen at o p) means; and the effect it is intended to produce.
In that figure, let B A c be the section of any wheel it is desired to cut on this principle. The width of the face of such wheel is shewn by the line a b; and a c is called the projection of that face, on the base of the cone of which the wheel A B is a portion; it’s summit being at C. The line e d, shews one of the spiral teeth with which the wheel is to be furnished; and I make it by this uniform process: The pitch of the wheel, whatever it be, is set off from e to f: and that pitch is divided into eight parts, (shewn here as four on account of their smallness) while the width of the face f d, is divided into nine parts, shewn here (for the same reason) by four and a half divisions. This latter division is more numerous than the former, that the principle may be a little overdone; or that the teeth may overlap each other by 1⁄9 of the pitch: To which purpose, beginning the spiral line e d at e, I move in the second circular line from e to the second radial line C i, and draw that diagonal which forms the first part of the curved line e d. From this second point, I go to the third circular line, taking also the third radial line, and drawing the diagonal. This I do until arrived at the fifth circular line, when I find myself likewise at the fifth radial line C d f. These four spaces thus gone over, represent the eight parts into which this part of the face a b would have been divided, had the figure been larger: and there[267] remains a small division near d, equal to one half the others, through which the curve e d is prolonged by a similar process; and this latter portion is what the successive teeth overlap each other, as before stated.
Now, it will be seen below, that the needful circular motion is given to this wheel, by a movement that takes place in a direction parallel to the base a c B of this figure. The curve e d, must, therefore, be transferred from the surface of the cone, to this base a c B. To do this, I place a point of the compasses at A, and trace, with the openings A a, A c, &c., the six quadrants included in the space a c g h, which are now the projections, on the base, of the circular lines a b f d on the surface of the said cone. Here, a slight difficulty should be obviated: strictly speaking, this projection would be horizontal, and, of course, invisible in this position of the wheel. But I have supposed the figure a c g h, turned ninety degrees downward, round the horizontal line a B, so as to make one representation suffice; and also to shew the connection of the lines a b g h, with those f d a b. The curve k l, is thus a copy of that e d, only shortened in the proportion of a b to a c—that is, of the side of the cone a C, to the half-base a A.
To secure, then, the coincidence of the pitch, as set off on the circumferences a f and a g, we must divide a similar portion of both into an equal number of parts, e f; and treat[268] them, on the lines a c g h, as we did on those a b d f; by which means we shall get the curve k l, the projection of that e d. And this curve k l, must be made part of a plate k l m n (about 1⁄10 of an inch in thickness), the use of which is as follows:
This Plate k l m n, is no other than that marked o p in fig. 2; and it is there fixed to the index a b, directed to the central pin C D, as it is in fig. 1 to the centre A—insomuch, that the pin shewn in fig. 2 near o, acting on the sloping curve k l, will turn that index (and with it the wheel) by the very motion which draws back the slide G (fig. 2), and lets down the slide I on it’s inclined plane G M.
We may remark, lastly, that as the present Machine is adapted to large models, it is not, now, provided with a dividing-plate, although the means of so doing are self-evident. On the contrary, the division dots are seen on the edge of the wheel A B, as is likewise one dot, near b, on the clamp b c, from which a given distance is set off to each of the dots on the wheel, so as to give the pitch required. By these means, then, the wheel is divided and cut, in good, if not in exquisite divisions; and all the teeth take their shape from the Plate o p (or k l m n of fig. 1), and are thus good, in that respect also.
To recapitulate the steps of this process—The workman stands behind the Machine, near E; and, working the screw with his right hand, draws back the slide G, (the power then[269] turning the cutter r very swiftly) by which means, the slide I glides down the inclined plane M, and the cutter, impinging on the sloping face of the wheel, cuts it to the depth r a; the shape of the tooth (by the turning of the wheel) being the spiral form e d of fig. 1. It may be added, that the lifting lever O permits this descent of the bar Q M, because it is suffered to fall lower than now represented. Thus, when the slide G is arrived near h, the tooth is finished; and the cutter leaves the wheel at a: after which, the cutter-frame and slide I K L are raised by means of the lever O—the screw g taken out of it’s steps, and the slide G pushed back by it, until the vertical slide I rests again on the inclined plane M, as it at first did. Nothing, now, remains to prepare for cutting a new tooth, but to change the division-dot, by the application of the gauge or compasses, from b to the next point on the wheel; to do which, of course, the clamp b c must be loosened and refastened by the thumb-screw d. I would just notice the 4th figure—to say, it is a sketch of one quarter of a bevil wheel; intended merely to shew the form and position of these teeth, and the general appearance of the System.
Finally, my readers will please to advert to what has been already said on the forms of these teeth, and their uses: and recollect especially what was observed on the epicycloid, as applied to them. It will easily be perceived, that to put that form on one of these teeth would be an almost hopeless attempt!—and, happily, it is not necessary. We can,[270] however, by using the cutter r with various slopes, and going several times through each space, cut facets on the teeth, quite near enough to the theoretical form to make them work well together; and, as before observed, nothing is wanting to make the teeth perfect, but to run them together with the wheels placed in due position.
To form a true estimate of the value of any new machine, it is necessary to examine the nature and operation of those that have been used before for similar purposes. And this is the more needful here, because the present Dash-wheel is essentially good, both in it’s properties and effects. The only room left for improvement, seemed to respect the quantity of work done by it: and this is, the chief point of comparison we shall establish in what follows:—
The third figure, in Plate 33, is a sketch of the common Wash or Dash-wheel. The pieces of calico (or other goods) are put into it through the round holes, dotted in the figure; and, by the revolution of the wheel from right to left, are carried up from a to b, or nearly so; from whence they drop by their weight to about the point c, where they meet the angle formed by the circumference of the wheel and one of the four arms or partitions, by which it is divided. If the wheel go too fast, the line of falling becomes more like the curve b d, and the goods strike the circumference too high, and in an oblique direction;—whence the blow is reduced, and the washing becomes imperfect. If, on the other hand, the wheel move[272] too slowly, the pieces slide down the ascending partition (a) before it comes to the vertex, and thus only fall from the axis to the lowest point of the wheel;—whence, also, an inefficient stroke. Thus, do these wheels require a moderate velocity: and they are reckoned to do their work best when making from 22 to 24 turns, and giving, of course, four times that number of strokes per minute.
The produce of these wheels is thus circumscribed by a natural cause that cannot be altered—namely, by the law of falling bodies; and my Invention has in view to elude the shackles which confine this process, and to produce a much greater effect in the same space,—the same time,—and with the same expence of workmanship.
To this end (see figs. 2 and 4, of the same Plate) I place two, four, or more boxes a, b, c, d, on as many wheels e f, toothed on my Patent principle; the latter, in the present case, being about two feet in diameter, and the boxes, in length, three quarters of that diameter: and of any convenient width, according to the size of the pieces. The wheels e f are mounted on the strong shafts C D, which run, below, in the wheel E; and by which, also, they are turned round the common centre, by means of the vertical wheel F. Further, in the centre, and between the wheels e f, I place the bevil wheel i, of half the diameter, in which the main shaft runs loosely, and which is itself fixed to the upper frame work, so as not to turn at all. The three[273] Patent teeth at e i f shew that these wheels are to geer into each other on that principle: and it is likewise seen that this whole mechanism is included in a set of rails, of an octagonal form, for the purpose of preserving the men from danger, while in the act of charging and discharging the boxes. And here it is worthy of some remark, that this process must be easier, and more quickly performed, with these open boxes, than through holes made in the vertical side of a Dash-wheel, on the usual principle.
To account, now, for the sloping position of the shafts C D, and the consequent slope of the boxes, they are thus placed, in order that the goods may not drag too much on the bottoms of the boxes, when passing from one end of them to the other. Instead of this, they are, in fact, thrown, by the centrifugal force, from the inner angle h (fig. 2) to some point k up that side of the box which is then outwards; where they strike, and then fall into the contiguous angle under k, to be again projected thence, after one revolution round the common centre; for, it should here be remembered, that, by the given proportion of the wheels, the circulating wheels e f turn on their own axes exactly one half round, for every whole revolution round the common centre A B.
To elucidate this still further, I have outlined, at A fig. 1, the central wheel i, of fig. 2, together with one of the excentric wheels B, and the lines a b, a b, &c., representing the boxes,[274] are supposed to be wires with the balls b b, &c. sliding on them, as is usual in some experiments on the Whirling Machine—(See “Ferguson’s Lectures,”) Of these wires, I have given the true directions in 12 positions of the wheel B: the epicycloid b b b, &c., shewing the steps by which the ball b is brought toward the common centre, during three quarters of the revolution; and also the position of the wire on which it slides: where it is evident that the ball b has a tendency to preserve it’s station, at the first end of the wire, until the latter takes the position b b c, when it forms (or nearly) a tangent to the curve, and is, at the same time, at right angles to the radius of motion, A b d. From this moment, then, the ball is free to leave the centre, and to fly off in a tangent with the velocity with which the curve itself is generated at that point. We might, thus, during the rest of it’s flight, seek it somewhere in the line b f g; but, as the wire continues to change it’s position, and must turn half round on it’s own axis, by the time it arrives at B b, or describes a quarter-circle on the common centre, it will again overtake the ball—and, giving it a curvilinear direction, will finally carry it to it’s other extremity, at or near the point B—where it’s motion first began: and thus shall we give as many strokes to the ball, as half turns to the wheel B; or, in other words, as many dashes to the cloth, as we give turns to the boxes, round the common centre.
By this process, then, substituted for that of the common Dash-wheel, we can increase almost indefinitely, the number of[275] passages of the cloth from one end of the boxes to the other; and the force of the dash will be as the squares of those numbers; since (as Ferguson expresses it) “a double centrifugal force balances a quadruple power of gravity.” If, then, with four boxes we turn this machine 60 times in a minute, we shall have 240 strokes in that time, instead of about 90 given by a common Dash-wheel; and this difference might be more than doubled, if so desired: for should, then, the stroke be found too severe, the boxes might be shortened, so as to lessen it’s violence, though preserving all it’s frequency.
There are two other objects that present enough analogy to this Washing process, to be here mentioned. The first is the operation of Fulling, as applied to woollen cloths in general. That process, I fear, is not performed at present in the best manner possible; and I feel persuaded that the centrifugal motion might be applied to it with advantage—whether as to quantity of produce, or perfection of effect: and having thus said, I shall leave the idea to the riper judgment of my manufacturing readers.
The second object I shall just introduce is, that of Kneading Dough, for bread, by the same centrifugal agency. It is well known, that an ingenious baker, of Paris, invented, some time ago, a method of kneading; which consists in letting the lump of dough fall successively from the four sides of a square box, revolving on a horizontal centre. As this idea seems to have[276] succeeded perfectly, I offer the Centrifugal System, as tending to quicken, almost indefinitely, such a process; and I particularly recommend it to the attention of Government, and of all large establishments as a mean of doing well and rapidly, by power, what is frequently done slowly and ineffectually, by the usual methods. Verbum sat.
I call this an Hydraulic Lamp, to distinguish it from the Hydrostatic Lamps, commonly so named: and I think the distinction proper, because this Machine acts in a different manner. It’s principle will be seen in a moment, by turning to the 5th figure, of Plate 33. If, there, we pour oil (or any liquid) into the bent tube A D G at A, the first effect will be to raise it to C, in the rising branch B C; and from C it will trickle down the branch C D, leaving the air, there, to occupy it’s own place. Continuing to pour, slowly, more oil into A the trickling oil in C D will ultimately fill the rising tube E D, expelling the air before it; and, now, the weight to balance the column in A B will be both the columns B C and E D; whence, of course, that column will rise as far above C as C is above B; that is, half-way between C and A. Here, there would be a small deduction to be made, if the height B C were considerable; but, as it is only supposed to be about a foot, the compression of the air in C D, &c., (being about 1⁄3 of a foot or 1⁄90 of an atmosphere) may be neglected. Continuing, then, to pour oil into A, we shall again fill, not the descending tube E F, but the rising tube F G; whose column will thus be to be added to those B C and E D; so that now the column A B[278] will rise to A, and there abide, as long as the mouth G is kept full, or nearly so.
The above is the principle of the Lamp announced in the title; whose effect depends, then, on the number of bends made in the tube A D G, which number (whatever be the form) it would be well to make rather greater than smaller, as the height B C, &c., might be so much the less, compared with the whole height of the column A B; by which means, also, a smaller difference in the level of the column below, would return the oil necessary for the consumption of the wick above.
I have given this idea what I think a better form in fig. 6. Instead of the bent tube A G, of fig. 5, this form supposes a series of air-tight cups, embracing each other; one half of them with their mouths opening upwards, and the other half with theirs opening downwards. They are shewn, by a section only, in this fig. 6; where a b c, c b a, present the under cups, forming one piece with the outer surface of the bottom vessel d a c, c a e: and, while speaking of this part of the Machine, I would just indicate it’s cover d e f g put on like the lid of a snuff-box, and carrying a case or tube f g, the use of which will be mentioned in a moment. To proceed, then, the upper vessel is shewn by the edges of it’s cups seen immediately over the figures 1 2 3, 4 5 6, placed between the letters a b c, &c.—These inverted cups make also one body with the moveable cover shewn between d and e, and to which is soldered the tube h i—which, sliding in the case f g, keeps this inverted[279] vessel steady. Where note: that there is an inner tube soldered into the tube h i, through which alone the oil rises, and which can hardly be made too small, since it has only to supply the consumption of a lamp—namely, a few ounces of oil in a whole evening. We may, finally, take notice of the weight placed under f g, upon the said inverted vessel, and which helps to counterpoise the oil in the rising tube h i; which tube, as before observed, may be as many times higher than the distance a d or e a, as there are rising columns between the cups a b c and those 1 2 3, &c.
I am not wholly prepared to say what portion of the oil it might be best to re-elevate by the pressure of the aforesaid weight f g; but, if it were a considerable part of that contained in the central compartment c c, that column would be shortened in proportion; and the reservoir at i would, doubtless, feel the want of it to preserve it’s level. I think, therefore, it might be well to use, below, a cup or two more than sufficient, so as to raise the main column higher than actually wanted; and to coerce this rising tendency, by a small stop-cock in the rising branch, to be gently opened at the will of the person using the lamp. I cannot say I have exhausted this subject; either in these respects, or as to it’s technical capabilities. But I have fully tried this method of raising oil above it’s level; and used, for some time, a lamp made on this principle, and which is still in my possession: and, at some future time, I intend to bring forward an Hydraulic Machine, founded on the same principles.
It is not supposed that this Essay can lead, immediately, to any result of magnitude; but it is thought to be a subject capable of further extension, and thus, finally, of future usefulness. Were this process only sufficient to supply a single house with water, at a small expence, the labour bestowed on it would not be altogether in vain.
By General Roy’s experiments, cast iron (and steel) expanded by 180° of heat (or, by passing from the freezing to the boiling point of Fahrenheit) 0.013 of an inch per foot.
Supposing, then (Plate 34, fig. 1), the tubes A B C to be 20 feet long, their whole expansion will be 0.26 hundredths of an inch. But, as the tubes are placed in the figure, the half tubes A D B D act together on the sphere D, and, both together, drive it in the direction E D, more than as the above expansion, in the proportion of the line E D to that A D. Taking, then, one half only of the above expansion = 0.13 hundredths of an inch, that must be augmented in the ratio of the sine of 60 degrees to radius, or in that of A D to E D. I, therefore, multiply this decimal 0.13 by the fraction 1000⁄866, which[281] gives 1300 to be divided by 866, or very nearly 0.15 for the expansion, in the direction E D, occasioned by the two half bars A D B D: and the same is true at the other angles F and G.
Again, to find the expansion (and contraction) of the bars a b c, we must compute their length as compared with the half tubes above-mentioned; and that length is to 10 feet (the half tube A D or B D) as 866 is to 1000 = 11.54 nearly: the expansion of which is thus found:—if 10 feet expand 0.13, what will 11.54?—Answer, 0.15. Now, as the machine acts by the heating of the pipes A B C simultaneously with the cooling of the bars a b c, we must add the former expansion to this contraction, which gives us 0.30, or three tenths of an inch for this combined effect at the three angles of the Machine. And, supposing, now, any pair of bars to act directly against each other, as at H I K; and that, further, the bars be stretched until the angle with the horizon be only 2 degrees, then the vertical motion at I will be to the horizontal (arising from the expansion aforesaid) as 1000 to 35, the sine of 2; that will be, in round numbers, 28 times as great, or 28 times three tenths of an inch = 8.4 inches, which is the stroke of this Machine in these dimensions.
In this calculation, I have not forgotten that the vertical and horizontal motions are nearer alike, when the bars are not drawn so tight at K H; that is, when the joint I is lowered.[282] But it is equally true that, when the joint I rises still more, the difference between these motions is still greater; so that, as a medium effect, I think we may reckon on an eight-inch stroke in the present case.
The question now recurs, of what strength are these strokes? Are they sufficiently powerful to produce a useful effect with so short a motion? This I cannot say from experience; but, from the known strength of iron and steel, their power, in these dimensions, must be very great. A few more observations may occur in the course of the enlarged description we shall give of the Machine itself.
A B C are three pipes of cast iron, well turned at the end, and having conical points of iron, well steeled, let into them, so as to have no tendency to bend. a b c are three steel bars, placed in troughs, so as to be heated or cooled by water poured into the latter. Or, these troughs may be exchanged for tubes, to admit heated or cooled air, according to the means used to cause these mutations. In a word, although I have represented these bars as contained in troughs, I intend to finish my description, on the supposition that they are tubes, because I intend to suppose the Machine worked by air instead of water.
To proceed: at d is an opening under the tube B, into which air enters, and C is an opening on the top of the tube which emits the same air, the three pipes being made to communicate[283] by means of a short junction-pipe at each of the angles D and G. Here, then, the fire-place f g, fig. 2, must be noticed: the use of which is both to heat and cool the Machine; and the following are the means:—This little instrument contains fire in it’s middle compartment, and that fire draws air into the part f, and drives it out of the part g. It also turns on a centre-pin, seen in the figure. This chaffing-dish, then, is placed at i d, and there serves a double purpose. When it’s pipe g conveys heated air into the pipes B A C (and out at C), it heats those pipes and expands them; but, at the same time, the pipe f of this instrument draws cold air through the three tubes a b c, in which are the steel bars that require to be contracted: both which operations conduce alike to the above-described effect. By these means, the weight w is raised, and (for example) water sucked into the pump X. But, turning the fire-place half round, we reverse this effect. The hot air is now drawn, out of the pipes A B C, and cold air drawn through them, by which they are cooled; while the hot air, from the fire, is thrown through the pipe g into the tubes a b c, and passing through the chimneys k l, there heat the bars and expand them,—both which operations concur in letting down the weight E, and thus, in forcing the water of the pump to whatever destination was previously assigned it.
Many people, in these parts, have seen a certain machine, said to have been invented by an inmate of that laudable institution the Liverpool Asylum for Blind People; for the purpose of making laces, covering whips, &c. I hope the similarity of name will not induce any reader to suppose that I have had that machine in view, and am endeavouring to cast it into the shade, or purposely to supersede it. If any person should thus think, I have a safe reply at hand. My own invention (somewhat less perfect than it now is) was made, many years ago, on purpose to serve an Asylum for the Blind in Paris!—a reflection with which I shall, at once, close this, perhaps, unnecessary apology.
This Machine is represented in Plate 34, at figs. 3 and 4. It consists of a frame of wood or metal A B, on which are mounted the following objects:—1st, on the traverse B, a fixed tube, having for it’s base the horizontal plate a b, and rising perpendicularly to near c d; where it unites with a conical or trumpet-like vessel c d, f e; the left side of which is shewn in perspective, and the right side in a section only. To this fixture is adjusted the spherical portion g h, h, prepared to[285] receive several cuts or slits 1 2 3 for the bobbin-slides hereafter-mentioned, to slide up and down in. This leads us to observe the upper fixture C, which is a cylinder, terminated downward by a spherical dome i k, k; also receiving the several cuts 4, 5, 6, into which the aforesaid bobbin-slides pass from the former slits 1, 2, 3, &c. Now it will be seen that the two spherical parts thus fixed, are separated from each other by the circular and horizontal slit l m, whose use is to permit the pipes shewn in the section at n o, to circulate all round the machine, while the bobbin-slides and bobbins k p are sometimes above and sometimes under the said slit l m.
Now, then, it becomes necessary to speak of the cause of this passage of the bobbin-slides from the under to the upper parts of the slits 1, 4, 2, 5, and vice versa. That cause is in the second dome q r, which covers, as far as it rises, the inner dome f i, k h; and it consists in a serpentine canal, of which a section is given to the left of q, and at s, in the section of the principal figure.
But to make this important piece of the Machine better known, I have drawn it apart, in figure 4, on the supposition—that it is a portion of a cone instead of a sphere: I say a cone drawn with the radii t q, t r, according to the dotted line t r. The surface then of this cone, is supposed straightened in the lateral figure; and the aforesaid serpentine canal is shewn at a b c d e, having the rollers of the bobbin-slides placed in that canal,[286] at the same points a b c, &c. Here also, certain dotted lines f g, h i, &c. shew the relative positions of the slits 1 4, 2 5, &c. of the principal figure, and also of the horizontal slit l m: whence it appears, that the revolution of the bent canal, a b c, &c. must some times drive the rollers towards g i, &c. and sometimes towards f h, &c. while the pipes n o pass undisturbedly round the Machine, in the horizontal slit l m of both figures.
The question now arises, how is the circular motion given to the outer dome q r of the principal figure? that dome is screwed to the cone r v w r, being itself of one piece with the hollow tube v w, on which the wheel x y is fixed. Now, this wheel x y, is driven by a vertical wheel z, of twice the diameter, for a reason we shall soon disclose.
It remains now, principally, to speak of the drawing-system of this Machine, shewn, in small, at c, and of a natural size in fig. 5 of this Plate. That Machine has also it’s own tube c x′, working inside of the fixed tube a b, &c. and terminated, at bottom, by the wheel x′, which turns it by means of the second vertical wheel x′ z, fixed on the same axis as the wheel z before-mentioned, and of half it’s diameter.
Supposing then, for the moment, that the mechanism c derives from it’s circular motion, the property of drawing downward the threads from the pipe n o, and the bobbin p;[287] (being one of the twelve pair distributed round the Machine) we shall now set the Machine at work, for the purpose of viewing it’s operation a little more narrowly. Looking at the two kinds of texture, indicated in the figure below the traverse B, we see that on the left composed (in weavers’ language) of a straight warp, crossed by an oblique weft; and this I believe, is the common texture of round, small ware, as usually woven: the slope of the weft being less and less as the number of shuttles diminishes, insomuch that with one shuttle that slope, might become almost invisible. But in the work made on this Machine, where, virtually, there are as many shuttles as threads in the chain, the slope would become very perceptible, too much so, perhaps, to give a desirable appearance to the work; although the rapidity of execution, from the multitude of crossings, would compensate for some imperfection of that kind. But, in fact, this Machine is intended to make a diagonal or diamond texture, as in the specimen to the right hand: and that is the object of the two pair of wheels x y, with z; and x′ with x′ z before mentioned. Their effect is this: when the large vertical wheel z, has turned the outer dome and the pins n o, once round the common centre, the smaller vertical wheel x′ z, has turned the drawing-system c, just one half as much round that centre, and thus sloped the threads coming from the fixed slits in which the bobbins move, as much, in one direction, as the whole turn given to the pins n o, has sloped the other half of the threads in the other direction, and the result has been the aforesaid diagonal texture.
There are a few other things to be observed by way of closing this article. As the Lace, or Cord is made on the Machine by a turning motion, it must be received below into a turning vessel, or it will be twisted, and thus injured. The vessel D, is provided for that purpose; and is turned by a cord from a pulley on the axis of the wheel z, coming under two vertical pullies, and acting on an horizontal pulley F E, connected with the said vessel; and if preferred, the draught itself might be placed in, or above, the vessel D, but it would not, I think, produce so perfect an article.
With respect to the drawing Machinery in the Machine at c, there is shewn, a flat surface just under that Machinery. It’s purpose is to serve as a mover for that System: To shew which, in a clearer manner, is the use of the fifth figure. In this figure, the drawing rollers turn in a frame a b b, and carry on one of their shafts a cog-wheel c or d, by which they receive this motion from the pinion e; this pinion being connected with the rowel f g, and running with it on a stud h, more or less removed from the centre, as circumstances may require. This rowel then, (for it’s edge, formed as in the figure, is indented with sharp teeth across it’s face) runs on the flat surface before indicated, at or near e, (fig. 3) and by the rotatory motion received from the wheel x′, gives a drawing motion to the rollers, the use of which has already been explained; namely, to draw down the goods as they are formed. It need hardly be observed further, that any[289] kind of filling may be brought down twisted from C, to the entrance of these rollers at c, and thus be included in the plaited texture; and in fact, the rollers in fig. 5, are shewn (by the dotted lines) as formed to receive an object of considerable diameter, as a whip, &c. that it may be wished to cover. Where I remark, that this lozenge form of the grooves O, is not given without a motive: the grooves are thus formed (the cylinders being supposed capable of opening by a springy movement) in order that, if desired, they may draw the body downward, so much the faster, as it’s diameter increases—and thus keep the covering threads at the same angle in every case. I shall only add, that these movements can be permanently determined by wheels, when the rowel f g, acting on the horizontal surface c, has fixed the real velocities of draught required for a given purpose.
This Machine then, is capable of excellent results, and of a speed almost inconceivable: since at every turn, if there are twelve bobbins p, and twelve pipes n o, it makes twenty-four passages of the threads among each other, answering, in some cases, to an inch in length of the fabricated texture; so that, counting 120 turns per minute, (which is moderate) we have 2880 passages, and 120 inches of work in a minute; equal to 200 yards per hour—a quantity which does not yet limit the produce of this Machine.
This Machine is represented in figs. 1 2 3 of Plate 35. It is composed of a frame A B, on which are placed two sets of rollers a b, c d, round which is stretched an endless feeding cloth, on the upper surface of which the Cotton is laid by the attendant. Across this frame A B, is fixed a strong board C D, having a ledge or bridge at each end, over which are tightened the cat-gut strings 1 2, 3 4, &c. Moreover, across this board, is fixed on proper bearings, (placed either straight or diagonally) the axis e f, furnished with any proper number of iron fingers 7 8, &c. which spring the cords 1 2, 3 4, &c. every time they pass by them: where it may be observed, that by the varied forms of the ends of those fingers, the vibrations are made to be vertical, horizontal, or oblique, at pleasure. In fig. 2, these fingers are seen from one end of their axis e f—and in figs. 1 and 3, they are shewn sideways: and in the latter figure, the strings are shewn as small circles between e and f, with the feeding cloth a c, stretched under them.
The following then, describes the effect of this Machine: The Cotton being laid on this feeding cloth near B, is gently drawn under the vibrating cords at g h: for while this takes[291] place by the action of the handle at e, the pulley f by the cord i, gives a slow motion to the cylinder B, and by it to the feeding cloth B A g h. The Cotton then passes under the strings toward B A, and is greatly agitated in the passage; and when arrived at A, it falls into any proper receptacle—whence it is taken to undergo the succeeding operations of the factory. I would just mention, finally, that the axis e f, though here supposed to be turned by the handle e, would, of course, receive it’s motion from a proper power; set on, or stopped by the usual methods.
This Invention has for it’s object, to make a more abundant use of the wind’s agency, at a given expence, than is usually done: and the means, generally, are to avoid a part of the expence lavished on the foundations or fixtures of wind-mills, and yet to carry more sail than that system admits of. Machines of this nature, are chiefly used in low marshy countries, where there is much water to be raised, and little solid ground to build on. My idea here, is to found the whole on the water, and to make that element the medium, and as it were the centre of every motion.
Let us then suppose already constructed, the long and narrow boat A B, figs. 4 and 5 of Plate 35:—and that there is contained in the middle of it’s width, a cylindrical pipe of iron, (or a square wooden box) of equal length, serving as a pump, by means of a spherical or square piston a or b, drawn from end to end by the means soon to be described. The cost of such a pump-barrel would not be great, though it should be of considerable length—(even 300 feet would not cost so many pounds). Now, at each end of this vessel A B, there would be raised a vertical part of equal size C D, surmounted by a[293] caster, (E F) turning, horizontally, on a hollow centre, through which a rope would pass from the aforesaid piston, (a or b) to the boat or ship S, which is the primum mobile of the System. This boat would further be made to carry as much sail as possible, and to encounter as little resistance as possible from the water. It’s properties of carrying sail, might even be enlarged, by the use of one or more out-riggers, as is done in various eastern countries.
It would be proper, likewise, to give the vessel a rudder at each end, and to reverse her motion by changing the sails, without tacking. This is also represented in the two figures 4 and 5: and, in the present case, the vessel is rigged with three masts, and three large sails nearly square, yet somewhat deeper on the lee side than to windward, to make the sails the more governable, though as large as possible. Supposing now, all these things arranged, and the rope N O fastened to or near the middle of the vessel, and to the aforesaid piston over the pullies of the casters E F; then, if the vessel sails in the long ellipsis 1, 2, 3, 4, the sum of the two portions of rope N, O, will be always the same; and, the wind coming from a, in the direction of the arrow, she will sail advantageously from 1 to 4, or the contrary, carrying the piston from end to end of the pump; and thus exhausting it at every passage; and filling it again from the lower water.
To recapitulate—and bring the several parts again to view; S,[294] in both figures, is the vessel, supposed of the best form for carrying much sail: E F are two casters with their pullies; p q are two pullies at the bottom of the vertical barrels C D, under which the rope passes to the piston at a or b, &c. In fine, q r s are the three sails, and t v the two rudders, by which the vessel is steered in either direction, so as to keep it’s wind without causing too much stress on the rope N O. This consideration involves another, which must now be cleared up: namely, how can this mechanism be made to produce the same effect in every direction of the wind? I answer, the whole System must be moored at one end A, in the strongest manner; while the opposite extremity B, shall have liberty to veer round that point, as a centre, through 90 degrees of a circle; some one position, between which extremes, will suit every wind, on this condition, that the vessel by it’s rudders, keel, &c. be able to keep her ground, although the wind should come from the convex side of the ellipsis; a thing by no means impossible, though less desirable than the state first represented.
Thus it appears, that I expect the favourable result of this System from two sources: the first, (but least) from the length of this pump, which permits much water to be raised without much agitation; and second, from the quantity of sail it is possible to carry by this method, compared with the sails of a wind-mill. My idea is, indeed, that since the power of the wind is so boundless, we ought to use it more liberally than we do: and I[295] am persuaded, that ten times as much work might be done at a given expense, by such means as these, as can be done by the usual methods.
Before I quit this subject, I would just observe, that there are many situations in which this powerful agent might be made useful, in conjunction with water power, as applied, perhaps, to encreasing works, and being itself incapable of proportionate extension. Thus, there are many water mills (used for various purposes) that are obliged to wait the re-filling of the mill pond; and which, therefore, lose much time, although the wheel would be capable of doing even more work than is actually wanted. In fact, it often happens, that the worse the supply of water, the better is the wheel: for this has been sometimes thought a mean of making up the deficiency. In such a case then, a cheap wind apparatus might double or triple the effect of the wheel, and the produce of a given establishment. But it will be objected, that the wind is an uncertain helper! and thus less fit to be resorted to. This I acknowledge; but still say, that could it be used when only a breeze or a zephyr, it’s utility would be much extended; and this is another consequence of a system founded on the application of much sail to a given purpose. Still however, as nothing absolutely conclusive can be said on so variable a subject, I shall not now lengthen this discussion.
It is important, in most machines, to avoid oscillatory motions:—which uniformly protract the time of an operation, or require a greater power to perform it. This consideration has given rise to the form and properties of the Machine I am about to describe.
In Plate 36, figs. 1, 2 and 3, represent this production. The first is an elevation; and the second is a plan, serving to shew the manner of feeding the Machine. To speak first of the second figure—A B is a pulley, (shewn at large in fig. 1, and marked with the same letters;) it’s use is to receive the endless cord C D E, which is composed of three strands, like the apparatus of a peruke-maker; these strands being divided at F, and passing there over three pullies placed at a proper distance on the same shaft F. These pullies are gently turned by that shaft, and carry with them the afore-mentioned triple cord, to which, in the passage toward the Machine, have been woven small handfuls of flax, by the same process as the barber uses to fasten the hair of a wig; one difference however obtains: the flax is knit to the cords at it’s small end, and within a few inches of it, so that the root-ends hang pendent, and when that part of the cord enters beyond the pulley E, those ends hang round the large pulley A B,[297] against the grooved surface of the outer rim: The method of grooving this drum is better shewn in fig. 3: and it should be noted, that the smaller drums C D, are grooved in a similar form, their diameters being such as to divide exactly, in some ratio, the outer cylinder E F. In fig. 1, two portions of these handfulls of flax are represented by the waved lines m n, drawn between the cylinders C D, and the section E F of the said outer cylinder; where it is evident, that if these cylinders had, in that place, teeth like those of fig. 3, these handfulls of flax would appear bent—which is indeed the process by which the wood is broken, and the filament divested of it. It appears also by the figure 1, that the cylinders C D, run on centres, fastened only to the pins of the cross piece o p, (shewn by dotted lines in fig. 2.) These cylinders I say, are thus mounted, that there may be no centres below, to gather up the flax or wood, and thus embarrass the motion of the Machine.
Adverting then, a second time, to the second figure, the flax is fastened in small handfulls, to that part of the endless cord that goes toward the Machine; namely, F E, and taken off from that part which comes from the Machine behind the pulley A B: so that the triple cord before mentioned, there consists of three cords, and passes round the separate pullies at F. The flax being thus taken off at M, is handed to the charger at N, and re-fixed to that cord by it’s other end—so as to be finished by a second passage. It[298] would be superfluous to add, that the waved form of the grooves in the cylinders, is intended to break the flax at every point of it’s passage before those grooves as conducted by the large pulley A B, (in the centre of which the main shaft turns without giving it any of it’s own motion) the said pulley A B, being turned, as before stated, by the triple cord from the slow motion of the pullies F in the figure.
Having heard it observed by some Calico Printers, that there is more or less of inequality in this process as usually performed; and that some parts of the goods are exposed to be more acted on than the inner parts, I have thought the following Machine would be useful, both to equalize and accelerate that operation.
In figs. 4 and 5 of Plate 36, A B is a hollow cylinder, running on two gudgeons C D, with a very slow motion, and thus, requiring very little power. One of these gudgeons C, is hollow, for the purpose of receiving steam from a boiler, like those at present used. The cylinder A B, is double, both around it’s circumference, and at it’s ends, (see a b, c d, figs. 4 and 5). It is also furnished with one or more doors E, through which to introduce the goods; and which doors are afterwards closed with screws, like those mentioned in the article “Washing Machine,” of the third Part. The goods being put in, with the usual doses of alkaline liquor, &c. the steam is introduced through the gudgeon into the interstice a b, and thence through proper openings into the body of the wheel, and between the cylindrical partitions a b, c d, &c. By the[300] steam, the water acquires a boiling heat; and by the motion of the wheel, is carried up in the boxes a b, &c. to the top, whence it falls through proper holes upon the goods; thus keeping them wet, and steaming them at the same time. The figures shew the division of the liquor into several jets 1, 2, 3, &c. which are constantly falling on the goods, as the process requires. The 4th. figure shews further, the effect of the turning motion of the cylinder A B; namely, that of changing the position of the articles; and offering, successively, every part thereof to the steam and flowing liquid: and thus, I presume, must the Bowking process become more rapid and equal, than that which takes place in a Bowking-keer, unaccompanied with such a motion.
This Machine occupies a great part of Plate 37. It is represented in figs. 1 and 2; the first being an inside view of one of the cheeks; and the second, a view endwise—represented as broken in the middle, to gain space in the Plate. As far as possible, both the parts are marked with the same letters.
To begin with fig. 1, A B C is the cheek: being a kind of shallow box with edges to strengthen it and give it thickness for the steps a b, &c. These steps are strongly fixed to the screws that slide in the boxes A B, and the nuts of which, are seen at c d. The screws enter, besides, into the heads of the perpendicular levers D F, E G, against which these nuts press to set the cylinders, by their steps a b, against the bowl H. This pressure of those cylinders a b is a modified effect: for the levers D F, E G, are drawn inward by the pulling bars I K; which, meeting in the centre of the Machine, are pressed downward by the hanging bar L, to which are suspended the scales and weights M, these being more or less heavy according to the wish of the Printer. It were well to mention a circumstance of some importance connected with[302] this subject:—If the bars I K form together an angle very obtuse, the power of pressure is immense; and the weights at M might be the lighter: But, then, the degrees of pressure at different angles of the bars I K would vary too much, if any excentricity of the cylinders a b, occasioned any motion. It is therefore best to use a sensible angle between the bars I K, together with a weight at M, so much the heavier; by which means these motions will be the more mild and manageable. Proceeding with the description: e f are two hooked screws, by which the pulling bars I K are raised, when necessary, so as to increase the nip in any corner of the Machine, without affecting the rest. It should be observed also, that the steps a b, have dove-tailed slides screwed to them from under the rim, and in it’s thickness, to make them move more correctly, when pressed horizontally by the nuts c d. The upper works of this Printing Machine are not greatly different from those of the common one. In one respect, however, I think them superior. The roller, prepared for the returning blanket, is mounted in a frame g, (fig. 2) which moves on a pin in the centre of the Machine, insomuch that one screw and nut h, suffices to regulate this return. This then, is an improvement, as the printer has but one operation to perform instead of two. The use of the piece-roller is the same as usual; and the goods are carried down on stretching bars, &c. exactly in the same manner.
But a more important property of this Machine remains to be noticed, The two cylinders a b, are made to press diametrically[303] across the centre of the bowl H; so that it’s shaft suffers no friction from that pressure. And hence, this two-coloured Machine requires no more power to work it, than a common machine for one colour.
A further property of this Machine deserves attention; but for want of room on the Plate, we are obliged to describe it by means of dotted lines on the face of the present figure. At a b, and at H, we have dotted three toothed wheels, of which one is keyed on each of the mandrels, while the central one is placed in a frame, forming part of a slide N, (fixed on the plate N of fig. 2) and by which this wheel is moved up and down at pleasure. Here it is evident, (see again fig. 1) that if this central wheel rises, it will turn the mandrel a, backward; and the mandrel b, forward: and this is a peremptory method of increasing or lessening the distance between any two points on the cylinders; or in other words, of fitting the colours of one cylinder into those of the other—an operation which is thus performed by a single movement; while in other machines it is necessary to go on both sides of the machine to produce the same effect. In a word, this process is completed in a few moments, by turning backward or forward a nut like that h, applied to the screw placed against the side of the Machine, as at P Q.
But we have another important property to speak of. The colours on the two cylinders must be fitted in, laterally, as well[304] as longitudinally: and the Machine performs this by an easy method. At each side of the Machine (see figs. 1 and 2) is fixed on a centre i, a short lever k l, the bent end of which (l) rises just to the brass step which carries the mandrel of the cylinder a, and is formed so as to push that step inward, when it’s end k is pressed outward; which latter motion is occasioned by the screw m n, which goes all across the Machine, and performs the same office on either side as wanted. This then, is another economy of time and pains; this setting being usually done by passing round the Machine, from one side to the other.
Finally, R S shews one of the cross-bars by which the two cheeks are connected. They are formed as portions of a hollow cylinder, and screwed to the cheeks through flanches, the breadth and form of which give considerable strength to the Machine; which is further strengthened by the bars T V and W X, in it’s upper parts.
In the above description of this Machine, (in which the parts common to other machines are omitted) I have endeavoured to avoid all invidious comparison: and have only said what my additions appear to warrant, and what, I am persuaded they will justify, when this Machine shall be compared with others, placed in the same circumstances for the sake of liberal comparison.
I confess, I again stand on a kind of forbidden ground; and am uncertain to what degree this Invention will justify it’s title. Yet I think myself safe in expecting it will produce an useful effect. But the fact is, I never fully proved it: the apparatus with which, more than twenty years ago, I was trying the System, having broken in the experiment—which I then had no opportunity of resuming.
I had then, as formerly, asked myself a question, viz: “will not the centrifugal force of a heavier body, suspended (without chemical action) in a lighter fluid, increase the subsiding tendency, and quicken the clearing process?”. I then thought “yes,” and do not yet see why it should not. But not having any absolute fact to build my conclusions on, I must leave the whole matter to time and experience; and crave the candour of my readers in favour of my somewhat bold assumption.
This Machine then, which is to purify muddy liquors by motion, is thus composed: a perpendicular axis A, (Plate 37, figs. 3 and 4) turns very swiftly, surmounted by a conical cap B C, so formed, as to receive and lodge in it’s thickness, four or more vessels a b, f e, which hang on pins c d, near that centre[306] and have the liberty of leaving it by the centrifugal force, round the said pins, until lost in the thickness of the cap above mentioned; where they turn on the common centre, without suffering any resistance from the surrounding atmosphere. This conical cap B C, &c. is made as light as possible, by protuberant ledges, but it’s solid form would be restored by lighter substances fixed between the arms, so as to add little to the friction or resistance of the whole mass. Any turbid liquor then, being introduced into any pair of these vessels while in the position g h, fig. 3, and put into swift motion, will have it’s muddy particles thrown from the centre, and (I presume) soon deposited at the greatest possible distance from that centre: since, although the centrifugal force will add, in the same degree, to the tendency outwards of the particles of the liquid, and make them gravitate more towards the circumference; that force will not render the liquid less fluid—which, therefore, will suffer the clearing process to take place sooner with motion than without it; and this is all I dare advance in the present state of my knowledge on this subject. Thus have I again reckoned on the kind forbearance of my readers, and risqued a little more of “the bubble reputation.”
My readers will supply one remark I had omitted—which is, that if bodies heavier than the fluid, recede faster from the centre by this motion, than without it, lighter bodies will approach toward the centre, and be there collected for the same reason—another cause for which, will doubtless be the pressure occasioned by this centrifugal force in the revolving fluid.
I have said, and shall still say, much on the desirableness of making use of a greater portion of that gigantic agent—Wind, than has yet been customary. This article is another attempt to urge it’s propriety. But it will be of no use to those who cannot extend their views beyond the present state of things, to that possible state which every successive mechanical improvement appears to anticipate or promise. These speculations of mine, suppose extensive means and extensive necessities: and they promise results still more extensive. In a neighbouring kingdom, where the country is, as it were, redeemed yearly from the ocean’s grasp, what would not it’s inhabitants give for a security against the encroaching tide? or the means of saving several months to agriculture, by the speedy disembarrassment of it’s fields from the common destroyer of health and produce? It is even said, that in the last winter, some dykes in Holland were broken, and many lives lost by inundation: and in our own country there is many a submerged spot, over which there blows wind enough to drink up, or throw out, it’s last particle. I submit then, the present means, as capable, with proper modifications, of forwarding every analogous purpose;[308] and thus as worthy to occupy the attention of every friend to rational improvement.
If my 38th. Plate were considered as a corner of any inundated country, whose boundary were a dyke contiguous to this chosen spot, I would propose building a long curvilinear canal A B, of which the middle space should receive and contain the lower water; and the two outside spaces the upper: especially the outer circle, which should communicate with a few branches C D, leading to and through the dyke before mentioned. In the two outside canals should float a pair of boats (long and light) E F, joined together by one or more cross-beams G, which would produce the double effect of connecting the boats so as to make them bear much sail, without oversetting; and of carrying along in the middle or lower canal a kind of water-drag H, that should take with it the under water, and raise it’s level nearly to that of the upper canals—into one of which it would enter through it’s lateral valves, and thence flow into the eduction canals C D as before stated. My idea will be better understood by referring to the small figs. 2 and 3, at the bottom of the Plate: for they are, one, the transverse section of the canals with the boats, and the other a longitudinal view of one of the vessels in it’s canal, with the water-drag H in the act of making (what is technically called) a boar, of the lower water; and raising it above the level of the valves I K, which open into the canal.
To recapitulate, E F in fig. 2, are the two vessels seen sternwise, with their sails supposed very large: G the beam that connects them; H the water-drag; and O one of several valves which open from the lower water, and close when the drag is going over them. In fig. 3, H is the same water-drag, whose distance from the bottom is regulated by the brace b: it’s beam or shaft, being fixed to the crossbeam G, of figs. 1, 2, and 3.
Thus then, at one passage of this double vessel along the curved canal A B, all the water in it’s middle compartment will be raised into it’s outer one: and be thrown into the sea through the canals C D, &c. It appears, near E F in this fig. 1, that the vessels E F, have friction pullies or wheels placed horizontally on their decks, to act against the sides of the canal and prevent the lee-way: thus converting the whole effort of the wind to a useful purpose. And here I observe, that if the wind blows in, or nearly in the direction of the diagonal, then, the vessel would go almost from one end to the other of the main canal without tacking, and thus do an abundance of work at each return: for it is a common thing for ships to sail nine or ten knots an hour! And here note, that the present curvilinear form is given to the canal in order to take all winds, (tacking more or less often) whether coming from the inside of the curve or from the outside. I cannot but add that in this Machine—in that I have already given—or in those I may yet give, there is much to be found[310] that promises useful application in many an important position. An example now strikes me. The reservoir at the Manchester Water Works might furnish room for a floating Machine, capable, on windy days, to do all the work of the steam engine, and thus economize a good portion of the fuel it consumes.
This Machine (see Plate 38, fig. 4) is intended to be carried or conveyed in a small cart, to the place where an incipient fire may be preluding to it’s fearful horrors! It is, as to form, a common lifting pump, inclosed in a vessel of air, whose spring perpetuates the jet in the usual manner. When used, it is held on two men’s shoulders, by means of a bar going through the ring A. Further, a rope is fastened to each of the extreme rings B C: and a stick put through each of the second rings b c. Two rows of men are then marshalled along the ropes; one set to hold-on, and the other to pull in regular time, the piston c along it’s pump, thereby sucking water through the pipe D, and forcing it through the valve v into the air vessel: from which it is forcibly expelled through the directing pipe E F. Here it is clear, that this small Machine is capable of an effect almost indefinite: since the rows of men may be very numerous; there being always people enough at a fire. To work the Engine by pulling, is nothing more than to repeat many a nautical manœuvre: and if only one man in the company should have learn’t to sing the sailors’ song, they would soon produce—“a long pull, a strong pull, and a pull altogether.” To be serious, a hundred men may as well work[312] at this Machine, as ten; and the effect will keep pace with the cause. In a word, there is scarcely any limit to the abundance of water, that might be thrown on a fire by such an Engine as this; of which I shall say nothing more, save that the bar of the piston rod at c, is intended to be used for drawing it inward, by the efforts of two men, at each interval in the effort of the working-men. A mere inspection of fig. 4 will fully shew what here remains unsaid.
This Mill produces a double power, merely because it uses two pair of sweeps or sails, both of which (though turning opposite ways) concur in giving the same motion to the vertical shaft of the mill. A B fig. 5, (Plate 38) is the shaft in question. It has on it two bevil wheels or pinions o, b; bearing the same proportion to their respective wheels: one of which (o) works in the wheel C, fixed to the outer shaft a c, and the other (b) in the second wheel D, which takes it’s motion from the inner shaft E D. This latter, then, is turned by the front sweeps F G; which revolve, as usual, “against the sun,” while the other sweeps H I, are braced round the large shaft a c, and turn with the sun—being sloped and clothed for that purpose. Now, lest any doubt should arise, whether these two sets of sails would not injure each other’s motion—I would remark, that one principal effect of the front sail on the wind would only be to turn it aside, and thus make it the more fit to turn the other sails, which require to go the other way; and which, therefore, will rather be favoured than otherwise, by the aforesaid effect on the direction of the airy current. It may be useful to observe, that the two sets of arms can be put, circularly, into any given position, by means[314] of the wheels C D, and will retain that position if the proportions of the wheels to the pinions o b, are the same for each pair—a result which it is easy to insure.
I shall dwell no longer on this subject, convinced as I am that nobody will question the propriety of enlarging the scope of these operations. It is a subject I especially recommend to our Batavian neighbours—the more, as, without presuming to dictate on a subject they may think I have not experience enough to judge of—I have only a hint to give to their Moolen Maakers, to insure their attention to a subject so intimately connected with the welfare of their never-forgotten Vaderland.
It is well known, that many ruinous fires have originated so slowly, that they might have been put out in a minute, had a little water been at hand—especially with the power of throwing it to a short distance. This fact makes it more desirable than it would at first appear, to have small vessels full of water, furnished, in themselves, with the power of forming a jet, without a moment’s delay! and this is the purpose of the Watch Engine, represented in fig. 6 of Plate 39.
In that figure, A B is a cylindrical vessel, with spherical ends, made strong enough to bear (without danger) a pressure of several atmospheres: and into which is introduced, by a condenser, (which might be the very system C p r) a quantity of water sufficient to occasion the aforesaid pressure. The valve C being water-tight, retains entirely this water; and the Machine is placed on it’s three feet, in a corner of the apartment it is wished to secure. It is seen in the figure, that the valve-pipe C p, opens into the ejection pipe p q, while the valve stem p passes through a collar of leather, and comes in contact with the lever p R while in it’s present position. If, now, any part of the house or apartment should be found to be on fire, this[316] Instrument can be carried there instantaneously, by the pipe p q, as a handle; and the jet be levelled at the point desired: when, by taking the lever p R in his hand, with the pipe p q, the bearer will open the valve C, and thus have an immediate supply of water, in a state of impulse sufficient to quell a fire that might else have become so violent as to mock every attempt to extinguish it! This, then, is the object of the present simple tribute to public safety.
The principle of this Machine is as follows: When two equal toothed wheels a b (see Plate 39, fig. 1,) geer together, a given tooth of either wheel visits a given tooth of the other, once every revolution: and will continue to do so as long as the wheels continue to revolve. But, when the wheels are unequal, as A B fig. 2, then different teeth in one wheel, visit the same tooth in the other, until, after a certain number of turns, the revolutions of both wheels have a common divisor. My System of equable Geering (see Part 2d. of this Work,) justified me in applying this principle to Engraving; and is the chief foundation of the Machine now to be described: for this System, as we have seen, communicates the very same kind of motion that two touching cylindrical surfaces would impart to each other by mere contact. The punch, therefore, will not scrape the cylinder, when brought into the desired places of contact by the aforesaid process. Let us suppose then, (fig. 2) that the wheels A B, are to each other in diameter and teeth, as the numbers 2 to 3; and that a given tooth in the wheel A, (which we have pointed out by a dot) now touches a certain spot on the wheel B, marked by a dot like the former. When,[318] now, this spot on the wheel B has made one revolution, the wheel A will have made 3⁄2, or 11⁄2 revolution: and the tooth first mentioned, will be found diametrically opposite to the place where it touched the spot first adverted to. And if, further, we give the wheel B another turn, the wheel A will again have made 11⁄2 turn; and the tooth first mentioned will again visit the spot with which it coincided at the beginning.
| To recapitulate— | The | 1st. | turn of B gave | 1.5 | turns of A, and |
| The | 2d. | turn of B gave | 1.5 | turns of A: | |
| Sum. | 2 | turns of B & | 3.0 | turns of A:— | |
which numbers are thus in the inverse ratio of the number of teeth in the wheels respectively.
Referring again to fig. 3, there we see a cylinder to be engraven, (M) and a porte-outil (or tool-bearer) N, connected by the wheels A B; whose teeth are singly inclined, like those that were considered in Part 2d. It can hardly ever occur, that the circumference of a cylinder can require to be divided into two parts only: but most often into a greater number, as 9, 11, &c. and it so happens, (from these initial diameters 2 and 3) that we must take uneven numbers for our basis, in order to reduce the System to any thing like regularity. And, this admitted, the theory of this division will be as follows:
Let the chosen (uneven) number of figures required round the cylinder be called m: then must the number of teeth in the[319] small wheel A, be likewise m: when the number in the wheel B, will come out uniformly m + (m ± 1)/2; in which formula every case of practice is included. For suppose, any uneven number to be required, say 11: Then will the cylinder-wheel A, have 11 teeth; and that of the porte-outil (B) 11 + 12⁄2 = 17, or 11 + 10⁄2 = 16: either of which numbers, working with the 11 teeth of the cylinder-wheel A, will divide the latter into 11 parts, as was before stated.
It must, however, be observed, that, as expressing a set of teeth actually working, these numbers are fictitious; because the teeth would be too coarse to work well. The numbers thus found, must, therefore, be multiplied by 2, 3, or more, so as to bring the teeth to a reasonable size, say 1⁄8 of an inch thick, according to circumstances.
As another example, take the following: suppose it were required to engrave a cylinder of 4 inches diameter—or 12.56 in circumference, and to put twenty-five figures round it, giving very nearly half an inch for each figure. Then the cylinder wheel (A) must have 25 teeth; and the porte-outil wheel 25 + 26⁄2 = 38: or, doubling both numbers to give the teeth a proper strength, the cylinder-wheel would have 50 teeth, and the porte-outil wheel 76.
To proceed now, in stating the principles of this Machine, it is evident (in this System of geering) that the diameters of the wheels[320] must be in exact proportion with the number of their teeth, taken at the pitch lines; and that these pitch lines must be of the same diameters, respectively, as the cylinder to be engraven, and the porte-outil taken at the surface of the punch: which is saying, in other words, that the length of the punch must be regulated after the diameter of the porte-outil wheel has been determined from it’s number of teeth, compared with those of the cylinder-wheel. But we shall return to this topic after having described more fully the principal parts of the Machine.
In fig. 5, (which is a kind of transparent view of one end of the Machine), A B C is one of the stands or legs on which it rests; a b is a section of the frame or bench, which supports the headstock C D, one of which is bolted down at each end of the frame, (see also C D in fig. 3.) This figure shews the transverse form of the headstock, with the centre (c) of the porte-outil; and e d are the two wedges that go through the headstock to support the step of the cylinder, of which the mandrel appears at f. This mandrel-centre is also covered with a second step, over f, by which it is kept down by means of a regulating screw A, (fig. 3) which finally determines the degree of nearness of the cylinder to the porte-outil, and thus the depth of the engraving:—that is to say, this regulating screw influences this depth as far as the wedges (e d) permit: for by the screw d, these wedges slide on each other so as to raise or let fall the steps f, by small degrees; the position thus given being confirmed by the said regulating screw. It is[321] needless to say that this operation takes place at both ends of the Machine, (C and D) and thus places the surface of the cylinder in a line exactly parallel to the slide n q of the porte-outil.
In fig. 3, all the parts thus adverted to, are given in a front view—where we may observe, that the rope marked by dots at R, is a loaded friction-drag, used to prevent the porte-outil from over-running the cylinder, when the punch is just emerging from between them.
The same figure 3, shews also the position of the frog x, in the triangular slide of the porte-outil; the latter, as well as the cylinder, borne by the headstocks C D. Moreover, the rack w, which gives the end-motion to the punch, is here shewn, as going through the frog, and connected with it in one direction by the catch o: and at n, there is a spring, formed like a horse-shoe, the use of which is to push the frog, by the catch o, to the right, whenever the rack is suffered to go that way, by the mechanism hereafter to be described.
The frog, then, (so called because it seems to leap when the Machine works) must now be adverted to: it consists of an under mass, formed prismatically to fit exactly the slide n q, cut out of the porte-outil N. This mass is capped by a thickness of steel, which completes the passage for the rack n w, and offers, besides, a compartment for the punch-clams[322] o, and another (x) for a wooden or steel bridge, being a portion of a cylinder, so formed, as to support the engraved cylinder after the stress of the impression is passed, and thus to equalize the depth of the engraving. The compartment for the punch-clams at o, is terminated to the right hand by an obtuse angle near x, which serves as a centre, when, by proper fixing screws in the rim near o, it is found necessary to place the punch a little awry. The other properties of this frog will easily be supposed by my mechanical readers.
We come, then, to it’s motion in the slide. p r shews a wheel, running loosely on the axis of the porte-outil; and having fixed to it a concentric rim r, with three or four waves in it’s circumference. Further, above s, is seen a lever, turning on a pin in the stud s, and pressing against the right-hand end of the rack w, when driven to the left by the waves p r, &c. This rack is cut into ratchet teeth as at w, in which enters the catch o, as impelled by a proper spring acting on it, (but not seen in the figure.) As long then, as the waved wheel p r can turn, with the porte-outil N, this last described mechanism does nothing: but when p r is stopped, it begins to work usefully; for the lever s then rides on the waves p r, and presses the rack w against the spring n, so that the catch o, takes into some new tooth; by which means, when the spring n unbends (by the sinking of the lever s into any wave p) the frog is itself carried toward the right hand—which is the effect intended. But, in fine, how is this wheel p r stopped[323] and set agoing a propos? Fig. 5 will shew this, with the aid of a little imagination—since our fig. 5 is a kind of transparency rather than a regular view. The wheel m, is a crown wheel, near which the wheel p r (fig. 3) turns, having a spiral g on it’s hither surface, which runs between the teeth of the wheel m and turns it one tooth, in each of it’s own revolutions: But when, after a given number of these turns, the end of the spiral g meets with a large tooth on m, it lodges on it, and stops the motion of the wheel p, and then the aforesaid waves r perform the task of driving the rack w backward; after which the spring n changes the place of the frog, so as to make another line of impressions round the cylinder. It remains then, only to be explained, how this stoppage is itself stopped; which is thus: to the porte-outil is fastened, near g, a small arm, which turns with it, and which in fig. 5 the dot t represents. This arm, therefore, drives back the beak t, (connected with the spring v) at every revolution of the porte-outil, thereby working the small catch that hangs to that beak. This catch, therefore, slides on the edge of the crown wheel m, but produces no effect, until it finds there, one small notch, so placed as to be acted on by the catch when this disengagement is wanted—and, then, this motion jogs forward the crown wheel m just enough to take the large tooth out of the way—when the spiral g begins to move through the common teeth of m, and thus ceases to act on the rack till the large tooth again comes to stop the wheel p, and recommence the rack’s motions. And thus is the place of action of the punch changed after any[324] number of it’s contacts with the cylinder—that number being doubled or trebled—or more—when necessary, by increasing accordingly the number of common teeth in the crown wheel m, before a large tooth occurs.
A few practical remarks on this mode of engraving may here be added with advantage. Theoretically speaking, the punch should form a portion of a cylinder, of equal radius with the porte-outil wheel, taken at it’s pitch line. But through the relative weakness of some mandrels, a certain spring takes place, which requires the punches to be more curved than that wheel, and even considerably so. This also depends on the size of the punch, and the fullness of the pattern. In a word, it depends likewise on the method of employing the Machine—whether with few passages, and considerable pressure, or with light pressure, and many swift passages:—The latter System is in my opinion much the best; since it brings the practice nearer to the theory of this Machine. If, indeed, the cylinders and mandrels of Calico Printers, had been originally made thicker, and thus strong enough to bear the pressure without sensible deflexion, this would have been, from the first, a perfect process: and the nearer these objects are brought to this state of inflexibility, the nearer will it’s effects approach to perfection; for in all other respects it works with admirable precision.
I may just add, that the facility with which the revolutions[325] of this Machine are counted, has induced some persons to dispense with the rack movement: but for small patterns with numerous impressions, it is doubtless better to use it—especially when employing the rapid and light pressures just alluded to; and these will become additionally interesting when the punches themselves acquire a more exact form—which is the object of the third Punch Machine, still remaining to be described.
It is not superfluous to add, that this Engraving Machine is dangerous to the persons employed—and should therefore be guarded behind, by a fence-bar, to prevent the hands or clothes from being drawn in.
In this title, I have repeated that given in the prospectus: nor do I think I have assumed too much in so doing. It will be seen in the course of this description, on what I found my opinion; which indeed, was substantiated by the fact as soon as formed: the execution having speedily followed the invention. The Machine, in it’s different parts, is represented in figs. 1, 2, 3, and 4 of Plate 40. Fig. 1 is a plan of the floor, on which the upper water flows, to it’s whole depth, when the flood gates are opened: this floor being close over the wheel, as seen in fig. 4, at c d. Further, a b, in both figures, is a circular slit of the whole diameter, through which the water rushes at once on all the floats of the wheel; whose axis goes up into the building through a kind of barrel, that prevents the water from escaping in any other part than the aforesaid circular aperture. The wheel itself is represented at e f, fig. 2; and fig. 4 is an elevation of it, with it’s shaft, and a few of the floats, to shew the manner of their receiving the stroke of the water. A section of the ring-formed slit is also given at a b, with two floats receiving the flowing water: and in that elevation is also shewn two of the swan-necks by which the central part of the[327] floor is supported on the framing, without stopping the watercourse.
Finally, the slit or aperture a b, figs. 1 and 4, is fitted with a set of cast iron curves, of which six are shewn in the Plate, between c and d, and whose use is to turn aside the falling water to any desired inclination; these instruments being moved at will by a proper chain of bars, reaching from one to the other, and connected with eight or more levers at proper intervals on the floor of the water chamber.
Thus then, it appears that this Machine has two or three very important properties: 1st. all the water escapes in the same direction, (relatively to the motion of these wheels) and that direction concurs with that in which the wheel is made to turn. 2d. Every one of those fluid prisms into which the stream is divided, is urged with the same velocity, because impelled by the same head of water. 3d. The velocity of these jets is the greatest possible, because the water is carried as low as possible before it is emitted; and falls as little as possible after it has struck the wheel. 4th. In fine, the inclination of the floats may be made most perfect; and their form, being that of a boat slightly curved, is among the best forms possible for receiving the utmost impulse from flowing water.
Although by these means much is done in favour of the impulsive system, it is allowed, that, in general, a wheel acting[328] by impulse, is less effective than a bucket-wheel acting by the weight of the water. But the higher the fall is made, the more similar these effects become. Hence, a very high fall may be made to produce, by impulse, an effect equal to that of the bucket-wheel. To meet, therefore, such a contingency as this, I have given, in fig. 3, a cover to the water chamber of fig. 4, intended to close it upward, and thus adapt it to a fall of any height; the water entering into this chamber from a large pipe A, of the required length: and being compressed accordingly, the result is forcible in proportion.
A few facts on the above subject will not be uninteresting. When this wheel, fifteen or sixteen years ago, (for I have forgotten it’s exact date) was about to be put in motion at La Ferté in France, several knowing ones took upon them to say “that it would not turn at all.” But who so astonished as they, when, at twelve feet diameter, and with less than five feet fall, they saw it make fifty-four turns in the first minute! I acknowledge, with pleasure, that these men soon expressed their approbation with unsophisticated candour; for although an honest prejudice had beset them, it was un-poisoned by that envy, I have more than once had to deal with in a country we are accustomed to call better! I therefore take leave, on this occasion, to say to my beloved countrymen, “Go and do likewise.”
The Machine commonly used for continued Spinning, in low numbers, is named a Throstle: and as my Invention acts in a similar manner, I have presumed to call it an Eagle. My motive is no mystery. The Machine spins more and better than a throstle: and reaches, especially, to a fineness unknown in throstle spinning. It could not, therefore, justly receive a meaner name, nor even an equal one.
The present Machine then, is a superior kind of throstle, the construction of which will be understood, by spinners, from the annexed figures, 5 and 6 of Plate 40. As the principal difference between the former machines and this, resides in the toothed wheel by which it’s spindles are turned, we shall begin this description by adverting to it: A B is that wheel, cut, at present, into 800 inclined teeth, and working with pinions of 11 teeth, one of which, with it’s spindle, is shewn at a b, fig. 6. The revolutions, therefore, of these spindles to one of the wheel, are 72.7272, &c.; and since the latter, in spinning, makes from 60 to 70 turns per minute, the spindles run at the rate of 5000 turns in that time, and might do more[330] if desired by the spinner. In a word, the useful speed depends on the size and weight of the spindles, the flyers, &c.
Immediately above and below the wheel A B, are two rings of cast iron, to which are screwed rims, either of wood or metal, destined to hold the steps and bolsters of the spindles, as is usual in a throstle, with the difference of the circular form, which the wheel of course requires; and the relation of which, to the rollers, is shewn at a b, fig. 5, being a plan of this Machine. Returning to fig. 6, the next object upward is the roller-beam, (cast hollow for lightness) the form of which is that of an octagon, with two brackets c d, by which it is fastened to the pillars E F: these, in their turn, being connected with the top and bottom cross-pieces (G H, I K) so as to make up the frame, properly so called. All these parts are placed (in section) similarly to those usually composing the throstle; and the copping motion is produced by the curve f, driven by an endless screw on the shaft h f, and acting on the slide f g, and through it on the ring of which the square i is a section: and on whose iron plate, in fine, the bobbins drag, as they do in the throstle. In the Machine before us, the rollers are driven by two side-shafts h f, which take their motion either from a train of spur wheels placed above the traverse G H, or by bevil wheels from two small shafts, coming under that traverse from the central shaft L M, to those h f, and acting on the rollers by means of the bevil wheels f[331] m, seen in the figures. Now, the rollers are contained in eight heads—1, 2, 3, 4, 5, 6, 7, 8, each of which has it’s speed wheels in the angles n o, &c. and receive their motion from six sets of bevil wheels q, &c. which propagate the motion round each half of the Machine, from the points m and p respectively.
Above this roller-beam, is the creel-ring N O, which (either in one or two rows) receives the sixty roving bobbins that supply the sixty spindles, of which the Machine is composed: and whose threads pass under the eight sets of rollers—one thread being suppressed in each of the heads—1, 4, 5, 8, on account of the columns. (This, at least, is the arrangement I prefer; but some of the Machines have been made with eight threads in all the compartments.) Finally, in this frame G H, I K, is placed a ring P Q, (of glass or bright metal) over which the rovings are thrown before they are put in the guides behind the rollers; so that the route of a thread in the act of being spun, is shewn in fig. 5, by the line P R, S b, where it meets the bobbin on the spindle a b, before mentioned.
It may be observed here, to prevent ambiguity, that the guide-boards, with their hooks, are placed below the octagon roller-beam q n o, &c. as they are in the common throstle; being, each, 1⁄8 of the whole circumference, and of a circular form on the outside, reaching, by these hooks, to the point S, so as to hold the thread just over the centre of the[332] spindles as at a b, fig. 6. Considering this as a commonplace subject, I have not attempted to draw these boards, since their form and position would occur to every constructor: and this is the reason also, why I have given only the section of the copping ring i, fig. 6: nor at all shewn the top rollers—nor the detail of the creel—on all which topics, opinions vary considerably, while the things themselves are really of minor importance.
There is, however, in my Patent System, something which I think important, and which, therefore, I have sketched near Q, fig. 6. If w x be there considered as the second communication shaft, a wheel z is put on it, of that kind which is calculated to work in a certain geering chain, called in French chaine de Vaucanson, (from the name of it’s inventor); and further, similar wheels (y) are connected with all the pins on the creel, round which the chain is carried from the wheel z, till it comes to it again. The consequence is, that all the wheels (y) are turned by that chain, so as to untwist the roving while the spinning rollers draw it off the bobbins: and this is so, because, in my Patent System, the rovings are over-twisted, in order to admit their being made very fast, without the danger of breaking. This then, completes my Patent Eagle, formed, on the right hand of the figure so as to use over-twisted roving; and on the left hand, so as to spin common roving in the usual manner. In both cases, the motion of the spindles by geering, ensures a mathematical twist, and thus produces[333] yarn better than common; whence also it’s fineness can be carried much farther than on a common throstle. It need hardly be added, that these spindles are stopped and set in motion by the mechanism described in my second Part, at fig. 1, Plate 19: and there mentioned as “a Machine to set-on and suspend rapid motions.”
This Machine, represented in Plate 41, figures 1 and 2, may be called a Spinning-card: whose use, however, I shall now suppose confined to spinning coarse yarn, or rather rovings, to be re-spun on the common machines, or on machines similar to my Eagle just described. It consists, in reality, of an horizontal card A B, having it’s flyer, &c. adapted to perform, in a perpendicular position, what those several parts do, in an horizontal one, on the common carding engine. All this is so well known, that I have not thought it necessary to draw it in these figures; but merely to say, that in this Machine, those operations are performed on the left hand, as at A, where is introduced a broad flat ribbon of wool, duly made on a preparing card, and laid on edge in a box at C, from whence it is drawn by the feeding rollers, &c. so as to cover the whole of the central card A B. Now, round this central card, are placed, ten or more small fillet cards, 1, 2, 3, 4, &c. being at different heights on the central one; by which arrangement, the whole surface of the latter is stripped by these cards, and as much filament collected on each, as is sufficient to form a thread or roving, as before mentioned. But, further, these small cards have to be stripped in their turn: and that is done[335] by the circular combs a b, which being placed obliquely to the cards, receive motion from them, and gather a regular mass of filament of a size fitted to become the yarn or roving in question. Nor need this roving be re-drawn, by rollers, before it is twisted: for it is the property of the bobbins D E, fig. 2, to draw mathematically: and with any speed that shall have been determined. If we examine how this is done, we shall see at bottom, two wheels F G, (toothed on the patent principle) one of which drives the spindles and flies, and the other the bobbins D E: the wheel that drives the bobbin having a few teeth more than that which drives the spindles—whose pinion is the same in number as that of the bobbin. Thus, therefore, the bobbin goes as much faster than the spindle as is necessary to take up all the wool furnished by the comb, and to the comb by the small card, which receives it from the central card A B; where note—that the draught, by this difference of motion is not variable, but determined: since the heads of the bobbins E D, are a hollow inverted truncated cone, on which the yarn cannot remain—for in winding, it drives downward that which is already wound, so as to fill the whole bobbin from the head—a reason for the conical shape of the latter object.
It will appear by the upper figure, (which is a plan of the central card, and the small cards, 1 2, &c.) that the latter receive their motion from the chain H I, by means of the train of wheels K L, turning on studs in the upper cross-piece. Suffice it[336] to add, that the centres of these cards, of the combs, &c. are fixed to the rings by proper cramps, as will be easily conceived. I have offered to sight, only the essential parts, to avoid confusion: and I presume to hope every thing important will be thus seen without difficulty.
In my present view of this Invention as a preparing Machine, I would observe, that the central card is only considered as a distributor, and that I should, now, add to it a System of machinery to make it a forced distributor. I had, indeed, prepared this very System to be patentized many years ago: but the delays that occurred then, followed by the Restoration, (which gave me an opportunity of coming to England;) made me suspend this intention—respecting a method, perhaps, the only thing wanted to make this Machine in all respects excellent.
In the small figure 5, (Plate 41) x y is supposed to be the section of a central card, such as A B, fig. 2; and the horizontal lines between x and y, shew the height of the card teeth. Of these, I take out a portion in several perpendicular lines round the card—say, at an inch distance from each other: the intervals thus stripped, being about 1⁄16 of an inch in width: and in all these upright slits, I introduce a blade x y, (whose transverse section is like that of a card wire) and whose edge is undulated as at a b. Finally, to these blades is given, (by a proper Machine) a slow up-and-down motion, which makes[337] them push off the filament from the card wires at the highest points of the waves, and suffer the wires to retain these filaments at the lowest points; whence it follows, from the motion just mentioned, that these points of reception and exclusion of filament, are constantly changing on the surface of the whole card, and that, therefore, the card will never be totally clogged with wool—as it is in the common process. It will be seen that the use of this System need not interrupt that of the common flyer, (or stripping card) whose use is to keep the teeth in working order, and to discharge a part of the obtruding filament.
In terminating this article, I cannot resist the desire of recommending this whole subject to any opulent English Manufacturer, whose zeal and public spirit, are commensurate with the scope which these hints embrace, and to which they tend, if duly appreciated.
While this Invention, as described in page 30 of the first Part, is allowed to possess curious properties, and to be a pretty thing, opinions do not all concur in declaring it, essentially and generally, a good thing. Nor could I be unjust enough to insist that it is so, in every kind and magnitude of application. I have, however, convinced myself that it is susceptible of practical excellence, as a first motion to steam engines, whatever be their dimensions; and have, therefore, presumed to re-produce it, with those modifications which are required to make it so. In thus acting, I have again preferred the useful to the agreeable, and in some measure inverted the order of my subjects. But I trust this deviation will be excused, in favour of the motive and the result; on both which I feel a good degree of confidence.
To obviate the point of mechanical weakness in this Parallel Motion, (see Plate 41, fig. 3,) I have doubled it’s parts; and brought the piston rod a b, to act, at once, on two of the circulating wheels c d, placed exactly opposite each other, and rolling, as before, on the inside of the fixed wheels f e, so as to produce the rectilinear motion, by the action of the piston rod on them both. And to make their respective motions one, (as connected with the fly B A) this latter is fixed to a shaft common to the two wheels g h, and by which, therefore,[339] the two other wheels i k, fixed to the crank shafts m n, are kept in due position. Thus, then, is all winding or twisting motion done away: and, therefore, can this System be employed in engines of every required power. Nor need I add, (what will be generally allowed) that much of the expence, and of the retardation, which a given engine suffers from the beam, the connecting rod, &c. will thus be completely obviated.
I must, however, stop every gainsaying mouth, on the circumstance of using geering between the engine and the fly—a system which I acknowledge to have been hitherto an evil; though, perhaps, a necessary evil—as giving (by a simple method) a double speed to the fly from a single motion of the piston. At all events, in this shape, I submit only to a very common difficulty—and might there rest my apology.
But I should have hesitated to go thus far, had I not foreseen that all the evil arising from this use of wheels, can easily be avoided by my geering:—by means of which I am bold to say, every vestige of shake or backlash may be destroyed; and this method of working a steam engine be made as silent as when a beam is used: in which case, considerable advantages must accrue from this method.
To come to the point:—the small figure 4, in Plate 41, relates to this subject. My geering is there seen in three forms or applications—each one intended to bring the above property into play. The part n o, represents the manner in which two wheels with singly-inclined teeth, work together when one of[340] them is furnished with a cheek, as directed in fig. 3 of Plate 14. But here, in addition to that, the teeth of both wheels are sloped more on one side than on the other, so as to assume a wedge-like form: insomuch, that in beginning to work, (if not perfectly formed) the wheels would not occupy the same plane. For, in fact, the cheek screws press home the cheek o against a number of thin washers all round the wheel, and thus only draw the wedge-formed teeth into each other as they become bedded, and successive washers are taken away. Hence, a good degree of precision is obtained—accompanied with little friction, and thus with great durability.
But we stop not here. The part p q of this figure, shews a pair of wheels doubly inclined—one of them only, being made in two halves, which are connected together by screws and washers, like that just described. Here then, another degree of friction is got rid of—namely, that of the cheek o: but still, a small degree remains, (dependent on the double versed sine of the angle formed on the wheel’s circumference, by the thickness of a tooth). This quantity, is indeed, very minute; and brings, perhaps, the whole near enough to perfection. To do, however, completely away with all friction, (see my preceding statement)—as well in the wheel acting backward, as in that acting forward, we must do what is shewn in the parts r or s of fig. 4: we must have a pair of V wheels on the same shaft, with the power of turning one of them in reference to the other; and then connecting them by proper screws, &c. to preserve the position thus given: by which means, in a word, all shake or backlash will be completely annulled.
A NEW CENTURY OF
Inventions.
This Machine is not, generally, an arithmetical Machine. It points lower: and therefore promises more general utility. Though less comprehensive than machines which perform all the rules of arithmetic, it is thought capable of taking a prominent place in the counting-house, and there of effecting two useful purposes—to secure correctness; and thus, in many cases, to banish contention. It is represented in figs. 1, 2, 3, and 4 of Plate 42, and in figs. 3 and 4 of Plate 43.
There are two distinct classes of operations which may be noticed in this Machine: the one that does the addition, properly speaking; and the other that records it by figures, in the very terms of common arithmetic. The first operation is the adding: which is performed by means of an endless geering chain, stretched round the wheels A B C D, (fig. 1) and over the two rows of smaller pulleys a b c d e f g h i; where, observe, that the chain is bent round the pulley A, merely to shorten the Machine, as otherwise the keys 1 2 3, &c. to 9, might have been placed in a straight line, and thus the bending of the chain have been avoided.
The chain, as before observed, geers in the wheels B and D, which both have ratchets to make them turn one way only. Now, the keys 1 2, &c. have pulleys at their lower ends, which press on the aforesaid chain more or less according to the number it is to produce, and the depth to which it is suffered to go by the bed on which the keys rest, when pressed down with the fingers. Thus, if the key 1 be pressed, as low as it can go, it will bend the chain enough to draw the wheel B round one tooth—which the catch E will secure, and which the wheel C will permit it to do by the spring F giving way. But when the key 1 is suffered to rise again, this spring F will tighten the chain by drawing it round the pulleys A and D, thus giving it a circulating motion, more or less rapid, according to the number of the key pressed. Thus, the key 5 would carry five teeth of the wheel B to the left; and the catch E would fix the wheel B in this new position: after which the spring T would tighten the chain in the same direction and manner as before. It is thus evident, that which-ever key is pressed down, a given number of teeth in the wheel B, will be taken and secured by the catch E; and, afterwards, the chain be again stretched by the spring F. It may be remarked, that, in the figure, all the keys are supposed pressed down: so as to turn the wheel B, a number of teeth equal to the sum of the digits 1, 2, 3—to 9. But this is merely supposed to shew the increasing deflexion of the chain, as the digits increase: for the fact can hardly ever occur. We draw from it, however, one piece of knowledge—which is, that should the eye, in computing, catch several numbers at once on the page, the fingers may impress them at[345] once on the keys and chain; when the result will be the same as though performed in due succession.
Thus then, the process of adding, is reduced to that of touching (and pressing as low as possible) a series of keys, which are marked with the names of the several digits, and each of which is sure to affect the result according to it’s real value: And this seems all that need be observed in the description of this process. It remains, however, to describe the 5th. figure, which is an elevation of the edge of the keyboard, intended to shew the manner in which the two rows of keys are combined and brought to a convenient distance, for the purpose of being easily fingered.
We now come to the other part of the subject—that of recording the several effects before-mentioned. The principle feature in this part, is the System of carrying, or transferring to a new place of figures, the results obtained at any given one. This operation depends on the effect we can produce by one wheel on another, placed near it, on the same pin; and on the possibility of affecting the second, much less than the first is affected: Thus, in fig. 3 and 4, (Plate 42,) if A be any tooth of one such wheel, placed out of the plane of the pinion B, it will, in turning, produce no effect upon that pinion: but if we drive a pin (a) into the tooth A, that pin will move the pinion B one tooth (and no more) every time this pin passes from a to b. And if we now place a second wheel (F) similar to A, at a small distance from it, so as to geer in all the teeth of the pinion B, this latter wheel will be[346] turned a space equal to one tooth, every time the pin a passes the line of the centres of the wheel and pinion A B, (say from a to b.) It may be added, likewise, that this motion, of one tooth, is assured by the instrument shewn at E D, which is called in French a tout ou rien, (signifying all or nothing) and which, as soon as the given motion is half performed, is sure to effect the rest: and thus does this part of the process acquire, likewise, a great degree of certainty—if indeed, certainty admits of comparison.
It is then, easy to perceive, how this effect on the different places of figures is produced: and it is clear, that with the chain motion just described, it forms the basis of the whole Machine. There is, however, one other process to be mentioned, and as the 2d. figure is before us, we shall now advert to it. In adding up large sums, we have sometimes to work on the tens, sometimes on the hundreds; which mutations are thus performed: The wheel B, (fig. 2) is the same as that B, fig. 1; and it turns the square shaft B G, on which the wheels k l slide. The wheel l is to our present purpose. It is now opposite the place of shillings; but by the slide m, it can be successively placed opposite pounds, tens, hundreds, &c. at pleasure: on either of which columns, therefore, we can operate by the chain first described—the wheel B being the common mover.
We shall now turn to figs. 3 and 4 of Plate 43, which give another representation of the carrying-mechanism, adapted[347] especially to the anomalous carriages of 4, 12, and 20, in reference to farthings, pence, shillings, and pounds, and then following the decuple ratio.
In fig. 3, k l represent the two acting wheels of the shaft B G, fig. 2; the latter dotted, as being placed behind the former; these wheels, however, are not our present object, but rather the carrying system before alluded to; and described separately, in fig. 3 of Plate 42. A, in figures 3 and 4 (of Plate 43) is the first wheel of this series. It has 12 teeth with three carriage-pins (or plates) a, which jog the carrying-pinion B, at every passage of 4 teeth; thus shewing every penny that is accumulated by the farthings. This is so, because the farthings are marked on the teeth of this first wheel in this order—1, 2, 3, 0; 1, 2, 3, &c. and it is in passing from 3 to 0, that this wheel, by the carriage-pinion B, jogs forward the pence wheel C one tooth: But this pence wheel is divided into 12 numbers, from 0 to 11; and has on it only one carrying-pin (or plate) b; so that, here, there is no effect produced on the third wheel D, until 12 pence have been brought to this second wheel C, by the first, or farthing wheel A. Now, this third wheel D, is marked, on it’s twenty teeth, with the figures 0 to 19, and makes, therefore, one revolution, then only, when there have been twenty shillings impressed upon it by twenty jogs of the carriage-pin b, in the second wheel C. But when this wheel D has made one whole revolution, it’s single carriage-pin c, acting on the small carriage-pinion, like that c d, (but not shewn) jogs forward, by one tooth, the[348] wheel E, which expresses pounds; and having two carriage-pins e f, turns the wheel called tens of pounds, one tooth for every half turn of this wheel E: and as, on all the succeeding wheels, to the left from E—(see fig. 2, Plate 42) there are two sets of digits up to 10, and two carriage-pins; the decuple ratio now continues without any change: and thus can we cast up sums consisting of pounds, shillings, pence, and farthings, expressing the results, in a row of figures, exactly as they would be written by an accountant. The opening, through which they would appear, being shewn in fig. 1, at the point w, corresponding with the line x y of fig. 2 in the same Plate.
I shall only remark, further, that the figures 3 and 4 in Plate 43, are of the natural size, founded, indeed, on the use of a chain that I think too large; being, in a word, the real chain de Vaucanson, mentioned in a former article: and that the figures of Plate 42 are made to half these dimensions, in order to bring them into a convenient compass on the Plate.
I would just repeat, that I have not attempted here an arithmetical machine in general; but a Machine fit for the daily operations of the counting-house; by which to favour the thinking faculty, by easing it of this ungrateful and uncertain labour. Had I been thus minded, I could have gone further, in a road which has been already travelled by my noble friend the late Earl Stanhope, (then Lord Mahon) but I took a lower aim; intending in the words of Bacon—“to come home to men’s business and bosoms.”
It is highly desirable, (not to say indispensable) in the use of my engraving Machine, to have punches not only of the true cylindrical form, but exactly of the proper length. (See the remarks on this subject, in the description of that Machine). It is, therefore, a matter of consequence, to be assured that both these circumstances unite; and to unite them without depending on personal skill, whenever the work can be accomplished without such dependence: and this is the object of the present rotatory Punch Machine. Adverting first to the length of the punch: that is insured by having a kind of slide on the Punch Machine, formed like the frog spoken of in the above article—Engraving Machine. In the 5th. figure of Plate 43, this slide is shewn at a, and it is at exactly the same distance from the centre of motion A, as the bottom of the frog-plate fig. 3 Plate 39 is from it’s centre of motion. Thus, the bottom of the punch is filed straight, once for all, and being fixed in proper clams, as in the figures, the shaft A is set a-turning, by power—from which motion two uses are derived: first, the cylindrical form is given to the punch by presenting to it, in it’s revolution, a file duly wedged on the (now fixed) slide of the Machine B B; against which it is kept[350] turning, till, by a due depression of the centre A, the radius is brought to the length required, and the surface perfectly formed and smoothed. This being achieved, the cams c d, are fixed to the slide B B, and to the turning body A d, so that when the die f is moved toward the left hand by the said cams, the prepared punch gently presses on it, and begins to receive it’s impressions; which are gradually deepened by the set screws g h, fig. 6; till, at once, the proper radius is given, and the engraving sufficiently transferred from the die to the punch—an operation which this process is calculated to perform, rather by means of frequent and gentle contacts, than by slow and heavy pressure. It need not be added, that the motion of the slide B B is reciprocated by the spring C, against that D, after each forward motion given to it—as begun by the cams c d, and continued by the contact of the die and punch, all which a mere inspection of the figures will sufficiently explain. It is likewise evident, that the figs. 5 and 6, shew, both, the same objects, namely:—the regulating wedges i k, the upper set screws g h, and the rollers E, on which the slide vibrates during the operation of the Machine.
It is not solely because, to work with the feet is a good method of employing the strength of men, that this device is presented to the mechanical public; but it is with the view of so employing the feet and hands, that they may occasion a constant and equable flow of water. The means, (see Plate 44, fig. 1) are, to provide the man with two supports a b for his hands, and two pedals c d for his feet, by which the two rods e f are worked; and by them, through the cords or chains g h, the piston rods i and k. Of the latter, the one which answers to the lower pump l, goes through the upper piston, whose rod is i: and the pistons are both constructed in the manner shewn in fig. 2; that is to say, the piston has no body, fitting the pump barrel: but a triangular bar x, going diagonally across the pump barrel, (which is square) and carrying two wings or valves y z; which, both together, fill the barrel when down, and leave it as empty as possible when up, by which motion the chains a e are slackened. Further, these pistons, with their rods, are heavy enough to raise the pedals, the instant the man raises his feet in any degree: so that, by a proper combination of the motions of his hands and feet, he can let down a given piston, and begin again it’s ascending motion before his effort has wholly ceased[352] on the other pedal. A mean this, of producing a constant and equable rising motion in the column of water through the pumps k l; and a mean also, of doing more work with a given fatigue, than would be possible in a pump whose motions were merely reciprocal, and the water of which, in rising, would be subject to any unequable or convulsive motions.
In general, this portable pump was made (many years ago) with a view to being easily carried to any field or garden, bordering on a river, and worked on it’s bank; the flexible suction pipe p being thrown into the river, or a well, as occasion might require. To this end, the whole frame (as is evident from the figure) can be folded up into a kind of faggot: and thus it’s transport from place to place, be made perfectly commodious.
It often happens, that from a central line, (in drawing for example) we want to set off, quickly, many equal distances on each side; or between two given lines we want a central line; to perform either of which operations, is the use of the Instrument just mentioned.
It is represented in Plate 44. figs. 3 and 4, where A B is the central point, being cylindrical in the greatest part of it’s length, and conical at E B. It slides correctly in two cannons or swivels E & A, which also have two short axes or trunnions, on which first, the double compass joints C D turn; and second, the two pairs of arms F G. I have called these cannons, swivels, that I may shew their construction, by referring to figure 1 in Plate 30—which describes the swivel of the forcing Machine; and which will give a complete idea of what is here intended. From this construction it will appear evident, that the point A B, (Plate 44) will be always found in the middle, between the two points, of the outer legs of the compasses; and that whether the question is to take two equal distances from a central point, or to bisect a given line or distance at one operation. The point or style now slides in the two swivels A and E; but the Instrument might be so constructed, as for[354] it to follow the rising motion of the middle joint (E), and thus to keep the three joints in the same horizontal line: but I think a small perpendicular motion of the said style, would be always desirable in the Machine, as a drawing Instrument.
This device is shewn, in two positions, at figs. 1 and 2 of Plate 45. In it’s present application, it is intended to produce a whole octave on the diatonic scale: and therefore, the unsupported ends of the fork are just half as long as they would become if the sliding handle A, were drawn to the bottom end of the branches c d. For, again, the fixing screw C, and it’s box D are fastened to this sliding handle by one or two screws, (s) so as to be always ready to press the branches against the enclosed slide A B, at whatever place the intended tone may be found. Now, the branches a c, b d, spring out of a common trunk c d, which is pierced with a square hole, exactly fitting this sliding handle A B; and the latter is marked, at proper distances, with lines across it, each of which (placed opposite the mark c d) gives such a length to the remaining branches a b, as to make them sound the note desired. Thus, the line l, brought to c d, lengthens the branches a b, to (nearly) 53 parts, from 50 at which they are now fixed; the whole length a c, being 100. This, and the following divisions would, of course, follow any desired temperament, according to the will of the tuner: but I have supposed them founded on the equi-harmonic scale; and thus will[356] the successive intervals to be set off on the slide B A, be as follows: (while the corresponding notes will be those expressed in the table.)
In the state represented by the figures 1 and 2, the line a B, is 5000; being one half of the whole length a b, c d.
| To form the | Sharp | 7th. | it becomes | 5297 | the distance | c d 1, | being | 297. |
| „ | greater | 6th. | „ | 5946 | „ | 1-2, | „ | 649. |
| „ | „ | 5th. | „ | 6674 | „ | 2-3, | „ | 728. |
| „ | „ | 4th. | „ | 7491 | „ | 3-4, | „ | 817. |
| „ | „ | 3rd. | „ | 7937 | „ | 4-5, | „ | 446. |
| „ | „ | 2nd. | „ | 8909 | „ | 5-6, | „ | 972. |
| „ | fundamental note | 10000 | „ | 6-7, | „ | 1091. | ||
The above lengths 1 2, 2 3, &c. have been measured off on the slide A B, as nearly as possible, or at least with precision enough to give the idea: and the rest I must leave the detail of, to those musical readers who may feel interested in the subject.
I have done right in calling these attempts “essays”: and if I had said “immature attempts,” they would have been better designated. Yet, having promised them to my readers, I cannot now withhold them, although, from want of opportunity of trial, I can do little more than talk of their supposed properties.
The first essay, as shewn in fig. 3 of Plate 45, is a mental deduction from a device which I executed in 1801, and brought before the public at the exhibition then given, by the French government, of the produce of national industrie. It was, nothing more than a pendulum, made with a view to lengthen, considerably, the going of a given clock, without altering the wheels. To that end, the weight or bob, was a heavy bar C D, suspended diagonally on two points A B, placed at a distance from each other, exactly equal to the length of the said bar: and that by the double cross-bars B C and A D, of a length sufficient to make the whole assume a form exactly square: where it may be noted—that were this figure longer than high, the curve of vibration would have two points of inflexion, and the bar would not place itself horizontally at last; and that were it narrower and higher, that curve would[358] assume a form more like, though still distant from, the arc of a circle. In the present case, such was the effect of this disposition of things, that the centre of gravity of the bar described, in vibrating, a curve E C D F, the lower form of which, was so near to a horizontal line, that the times of vibration were immensely prolonged; so much indeed, as to represent a common pendulum of several thousand feet in height; and to give a proportionate slowness to any mechanism with which it should have been connected. In fact, this line is so minutely different from such horizontal line, that it is wholly included in the thickness of the drawn-line C D: nor becomes visible but near it’s two ends C D, when it begins to rise, and then rises faster than that described by a short common pendulum.
In fine, this curve itself is formed by continually bisecting the line or bar C D, and drawing lines from it’s centre of gravity, thus found in one of it’s positions, to the same in another position, till the curve E C D, &c. arises from this process.
It follows, then, from the nature of this curve, (or pair of curves) that the time of vibration of this pendulum is the longer, the shorter the arcs are, in which it vibrates; and that, when the vibrations have attained a certain length, compared with the height to which the centre of gravity rises, the time becomes considerably shorter. I shall not now pursue this idea, because it is at once an abstruse question, and at the same time[359] one of uncertain utility—I mean that it’s use is problematical as a pendulum: since the time of a vibration depends on it’s length, which cannot easily be determined by any invariable method. I shall, however, add two things on this subject, by way of land mark; the one, that the balance-wheel of a watch has power enough to drive this pendulum, heavy as it is;—and the other, that I have seen it make (for many hours together) vibrations of half a minute’s duration! In a word, this is one of the subjects, which untoward circumstances have prevented me from bringing to maturity—but which I owe to my subscribers, and the public, in any, or every state, to which I have brought them.
I therefore, say nothing more of this Instrument as a pendulum: but an inspection of the figure will shew, that it will not be useless as an Elipsograph—which it clearly is, since the intersection of the bars A D & B C; describes a true Ellipsis. It may be further shewn, that the ends of the moveable bar C D, are the vibrating foci of a second ellipsis, like the first, which rolls under the other, so that the curve itself is that which the centre of one ellipsis a b c would describe, by rolling on the surface of another e b d. But, into these considerations I cannot now enter, as my “Century of Inventions” is fast becoming due, and time commands dispatch; I beg leave, therefore, to pass to the relation this subject seems to bear to a “Marine Level.”
It must, however, be premised, that I scarcely expect either of these methods to be correct enough for astronomical observations; as among other things, they have the nautical top to contend with: but if I am fortunate enough to have suggested useful methods of procuring relative stability on board a rolling ship, so as to suspend the better, a nice instrument of astronomy; or so to counteract the restless ocean, as to assist the victims of sea-sickness, I shall not entirely have lost my labour.
My first idea on this subject, is the following: If we had on ship-board, a simple pendulum of several thousand feet high, it appears certain that the oscillations of the ship would be begun and ended, before any single vibration could have been given to such a length of pendulum—which therefore, would scarcely vibrate at all: and if the natural time of this compound pendulum (for we are not confined to these small dimensions) were made to be much longer than those of the ship on it’s meta-centre, this pendulum would scarcely vibrate at all: because it’s several tendencies to take motion from the ship, would extinguish each other before they had had time to produce any common effect.
Further, this result would probably be assisted by another property belonging to this mechanism: see fig. 4. This diagonal suspension, as repeated at a b c d, fig. 4, is of such a nature, that when it’s centres a b, are placed in any[361] oblique position e f, (say by the rolling of a ship) the suspended bar c d, immediately takes a position of opposite obliquity g h, pointing upward towards i, just as much as the line e b points downward; while the middle line k l remains level—whether caused by the slides k l, or the single slide m.
I dare not assert any thing respecting the form this principle should assume, in order to produce the most useful effects; but it appears that the principal weight of the apparatus should be placed in the centre of gravity of the under bar c d. It would occur, of course, to every mechanician applying this System to real use, that in this fig. 4, we have only provided for one motion of the ship, the rolling motion: and that, in consequence, this System should be suspended in another similar one, acting longitudinally, so as to provide for the pitching motions of the vessel. In a word, I confess, with regret, that I leave much to do, by way of bringing this idea to maturity—it being at this late hour, more than doubtful, whether I shall myself ever be able to resume the subject at sea, where alone it can be duly tried.
This would seem to be a simpler process than the former: but how far it may go beyond it in effect, I cannot say—having never had it in my power to try either of these ideas on ship-board. I therefore merely present them to my readers, as themes for future thought and experiment.
Plate 45, fig. 5 represents this System—which is founded on the idea of deadening oscillatory motions at sea, by connecting the bodies to be thus guarded, with a stream of flowing liquid, the horizontal motions of which must be subject to laws very different from those which rule vibrating bodies merely suspended.
The fluid used in this Machine (as oil, water, mercury, &c.) is to be pumped up by appropriate mechanism, from the vessel into which it flows at x, into a vessel placed a little above z; and to be let out by the cock y, through a kind of strainer s, of sufficient collective area to supply, with ease, the descending column C. The vessel and tube C D are made as thin and light as possible: and the upper part, which is spherical, is inclosed in and suspended by the universal joint a b c, like[363] those used to suspend other bodies, as a compass, &c. Moreover, the areas, at different heights, of the tube C D, are made in the inverse ratio of the velocities of the spouting fluid, at each given depth—so as to leave it but little tendency to press either outward or inward, while thus obeying the law of gravity. By these means, then, I think no vibrating motion will be excited in the falling column: but that the liquid will continue to flow perpendicularly, so as to preserve (nearly) the quietude of the vessel C D, and of any mirror or instrument it may be wished to keep in a given position, by connecting it with the perpendicular line thus obtained.
I repeat, however, that I know not how far these methods may go towards obtaining an artificial horizon, for astronomical uses. Indeed, I fear they will fall short in this respect—but I think them still worth trying, even for these—but especially for the purposes to which I have already alluded. And, if success crowns this publication, to the degree I am led to anticipate, I will not always leave so rich a question, in this doubtful predicament.
This is a recollection from the specification of a Patent which I took out above thirty years ago, and in which I huddled together as many objects as a child would like to see in a box of play things. I perhaps acted, then, according to the words of a French proverb—“abondance de bien ne nuit pas;” but in so doing, I fell into the charybdis of another French proverb—“qui trop embrasse, mal étreint,” (a wide embrace cannot be a strong one) and in so doing, paved the way to much litigation—which happily did not occur.
The intention of this Machine, as represented in Plate 46, fig. 2, was to retard the fall of any body, or person, suspended to it, so as to prevent any concussion on reaching the ground. The means are brought to view in the perspective sketch given of the Machine. It is a kind of jack, inclosed in a case, and supposed to be laid carefully aside in the house represented in fig. 1 of this Plate. The Machine has a barrel, much like that of the jacks used for roasting; round which a rope is coiled, of sufficient length to reach the ground: and a wheel, connected with this barrel, works in an endless screw, which turns a shaft also like that of a common jack,[365] but somewhat stronger; and finally, to this shaft is fixed a small cross piece, carrying, on pins, two weights y z, inclosed in the fixed barrel x; by the centrifugal force of which enough friction is created, to prevent the acceleration of the falling body—whether a person or weight of any kind.
There is, moreover, a jib a, fig. 1, fixed between some, or all, the windows of the house whose inhabitants it is wished to guard from the danger of fire; this jib having the property, from the form of it’s foot, of taking by the suspension of any weight to it, a position perpendicular to the wall: Insomuch, that by the act of suspending the Machine to the jib—engaging the wrist in the noose n, and perhaps the foot in another loop of the same cord; a person may safely flee those dangers from fire, of which so many persons become the unhappy victims.
Since the 46th. Plate was engraved, it has occurred to me, that a method should have been shewn for raising the cord n, (fig. 2) after each descent. This operation might be performed by a handle put on the axis of the Machine, accompanied by a ratchet on the wheel, just like the similar parts of a jack for roasting. But, lest the inmates of a house on fire, should not have presence of mind enough to perform this operation, it might be better to have a spiral spring in the Machine, to be wound up by the descending body, and of force sufficient to raise again the cord after such descent.
This Machine is also shewn in Plate 46, at fig. 1. It consists of a large truck, A, to be drawn rapidly to any house on fire, by one or more horses. The carriage or frame part B B, is an open square frame subtended by a first sheet of sack cloth, similar to the sacking of a bed: and on this are laid five, or more, air mattrasses made of sack cloth, and varnished on the inside so as to be nearly air-tight; I say nearly so, for it is not intended they should form a spring capable of returning any object thrown on them. On the contrary, each of the mattrasses has, at one or both ends, a valve 1, 2, &c. opening outwards, but kept closed by proper springs, so as to determine the pressure at which the air shall escape; that pressure being carefully graduated, so that the upper mattrass shall give way with ease, the second with greater effort, and the successive ones with progressive difficulty, until the under one remains totally closed, and stops the falling body altogether. By these means, if enough mattrasses are used, and they are duly regulated, a person may jump from a house of three or four stories without incurring any danger. As to the length and breadth of this fire-escape, it should be ample enough to give[367] the sufferers confidence to take the leap, and as small as an easy passage in the principal streets would require.
One thing must be described in words—as the mechanism to which it relates is fixed under the truck; and could not be seen in this perspective figure. These mattrasses are filled with air by an horizontal air pump, worked by a crank, which the axle itself of the hind wheels of the truck forms: whence, by pinning this axle to either of the hind wheels, the very motion of the carriage, as drawn by the horses, would distend the mattrasses—which would thus be ready for use the moment they arrived on the spot; and moreover, when there, this air could be replenished, after using, by turning this axle, through the wheels, by hand cranks slipped on it’s ends at the place of the linch-pins. Or, in fine, this operation might be performed by an air pump prepared for it alone, and placed in any convenient part of the Machine.
Figures 1 & 2 of Plate 47, exhibit this Machine. It is, merely, an attempt to effect, by power and a rotatory motion, what is done by hand and a vibrating one. To understand this latter, my readers (who have not seen chocolate made) will suppose a metallic rolling-pin, but cylindrical held in both hands, and moved parallel to itself, over a slab of marble, to and from the person employed; who holds the instrument fast when pushing it from him, and suffers it to turn a little every time he draws it towards him. He thus presents, sometime or other, every particle of the chocolate to every part of the slab and the roller: and this is also done by the Machine shewn in Plate 47. In figs. 1 and 2, A represents a cylinder of stone or metal, used instead of the aforesaid slab; and B a cylinder answering to the roller in question. The latter is placed, by it’s axis, on two forks a b, so as to lean, by it’s weight, obliquely against the cylinder A, which it does less or more heavily as the forks, or stands a b, are placed nearer or farther off from the general centre. Further, the motions of these two rollers A and B, are connected by two equal (or nearly equal) wheels c d, by which, when A is turned, B turns also; but so as to give the surface of the latter much less velocity than that of A, though in the same direction. By these means, all the matter adhering[369] to both cylinders (for chocolate is made in an unctuous state) is at one time or another, brought into intimate union, and ground together; and thus is the usual problem resolved, on rotatory principles: nor need we mention the several scrapers, &c. that would be applied to gather up the paste to the middle of the rollers, when spread abroad by the grinding process.
It may not be useless, just to say here, that this is likewise a good mill for grinding paint or oil colours.
I have insisted, often, on the propriety, mechanically speaking, of doing every thing by rotatory motion; and thus of avoiding oscillation wherever it is possible. The present Mangle is another attempt to employ that principle. In Plate 47, figs. 3 and 4, is an under cylinder, turned as usual by any convenient power. B is a small cylinder not connected with it, nor touching it, being intended merely to receive the weight of the mangle-cylinder D, with the goods rolled on it. C is an upper cylinder as heavy as necessary, or loaden through it’s journals or centres, with sufficient weights to make it so. Again, the motions of the two cylinders A and C, take place in such a direction, that any round body placed and pressed between them, would receive from them the same motion; and thus, a roller of goods, there introduced, will be mangled. This process is so performed, because the cylinders have toothed wheels a, b, on their axes, but which do not geer together: These wheels being connected by an intermediate wheel c, which makes them concur in producing the rolling effect above mentioned. But, one thing remains to be observed: the wheels a b, though drawn apparently equal, are not equal. The upper one a, has a tooth or two more than the under—so that the motion to the right hand of the under surface of that[371] cylinder, is not equal to the opposite motion of the cylinder A. And hence, the cloth roller D, progresses from D towards x, between the cylinders A C, and finally falls out at x, after as many turns of the whole, as the wheels A C have been calculated to give; and this, is according to the degree of mangling required.
It is too late to bring this Machine into what might almost be called an overstocked market of ingenuity—since many power Looms exist, work, and seem to want nothing to make them perfect. But an idea of forty years standing, founded on a principle worthy of attention then, may perhaps not be altogether vain at present: Besides—I have engaged in my prospectus to present it to the public. I could, indeed, enter into other parts of the Power Loom—which I had then begun to execute; but such is the rapidity with which that Machine is now striding to perfection, that it would be superfluous. I merely then, fulfil my promise.
On the afore-mentioned occasion, I thought it of importance, that the force employed to throw the shuttle, should be capable of being regulated to any and every degree: and especially should be fully prepared to act, before it’s action began: and should, then, act independently of every other impulse.
In fig. 1 of Plate 48, A is a wheel or pulley of about six inches in diameter, from which two cords proceed in opposite[373] directions (B C) to the pickers, which drive the shuttles D E in the usual method. This pulley runs on an axis going through the bottom of the lathe, (or beater) and it might have a crank, behind, of a radius equal to a b: but to shew the whole in one figure, I suppose the following mechanism to be placed in the front of the lathe, and just before the face of this wheel or pulley A. c d is a bar turning on the centre c, and receiving at it’s other end the pressure of a spring e d, which in it’s turn, is susceptible of different degrees of springiness, as regulated by the screw f. On a stud i in the wheel A, is put the small bar i d, which forms also a turning joint in the bar c d: and thus communicates the effort of the spring to the stud i, and thence to the wheel A. Finally, this wheel has either under it, on the front side of the lathe, or on it’s axis, at the back, a pulley, by which it can be turned, by means of one or other of the cords brought from the breast beam of the loom, round the pullies x and y, to this wheel a b i, according to the dotted lines. Supposing then, one of these cords to be tightened by the backward motion of the lathe, it will draw the wheel A about half round: when the stud i will rise to the point b, straining the spring to get over the centre: and as soon as it is over, the spring will act, and drive the picker and the shuttle with the desired speed, independently of any other mover. And it is evident, that now the opposite cord x or y, will be tightened so that when the lathe shall be again pushed backward to form the opening for the shuttle the slide will be carried back over the centre a, and re-produce another impulse in a contrary direction.
The rapidity with which a vacuum is formed by an Air Pump, depends on the ratio between the contents of the receiver and those of the pump barrels. If the latter be just equal to the contents of the former, (which is a very large proportion) the exhaustion will follow this series:—there will remain in the receiver after each stroke, the first contents being 1, 1⁄2, 1⁄4, 1⁄8, 1⁄16, 1⁄32, 1⁄64, 1⁄128, 1⁄256, &c. But if the pump barrel contains twice the volume of the receiver—then the remaining air, after the strokes, will be 1⁄3, 1⁄9, 1⁄27, 1⁄81, 1⁄243, 1⁄729, 1⁄2187, 1⁄6561, &c. being much nearer to a vacuum than on the former supposition.
To meet this case, then, I have thought a water pump might be used: that is, a barrel or vessel, much larger than the receiver; and which by the action of a smaller pump, placed on a lower level, might be alternately filled with water and emptied so as in a few operations to complete the exhaustion, very nearly.
Thus, in fig. 2 of Plate 48, A is a receiver, B is a large vessel that can be filled with water from the tub C below; and D is the pump, worked by the handle E. It is a common water pump, (so much the readier adopted, as requiring little[375] care in the execution.) The question was to make this pump alternately fill and empty the vessel B. Adverting first to the filling, a c are two cocks, having each a side-passage for the water; and these passages are now so placed, as by working the pump we suck water out of the tub C, and throw it into the vessel B, through the valve b;—by which means all its air is driven out through the lateral valve e. When this is done, the cocks c d (which are so made as to be worked by the same mover) are turned into a new position, which opens the pipe p to the pump D, and that q to the returning spout r; by which means the water is drawn from the vessel B, and thrown into the tub C: so that the air is again drawn out of the receiver A, through the inverted valve s, into the vessel B, and another degree of exhaustion occasioned. This being done, the cocks are again put into their present position; the air expelled by the water through the valve e as before, and a new stroke prepared. It is scarcely needful to add, that if the vessel B contained ten times as much volume as the receiver A, the exhaustion of the latter at each emptying of the vessel B would follow this ratio—1⁄11, 1⁄121, 1⁄1331, &c. thus approaching by rapid degrees to a perfect vacuum. The water, or liquid, used for this purpose would of course be as perfectly purged of air, as possible.
The principal mechanical merit I conceive this Machine to possess, lies in the facility it gives of taking a stream of water as high, and discharging it as low as possible: and both nearly in the direction in which it naturally flows. Of the advantage it possesses in keeping the water a long time from falling, I shall not now speak, as it would require more discussion than this work comports; and, moreover, the Plate confines us to a somewhat contracted representation, which I hope my readers will excuse.
Plate 48 fig. 3, A B is the section of the wheel, and C D a small portion of it’s circumference—which shews the form and position of the floats a b c, &c. E is a floor on which the upper water flows, and from which it falls thinly on to the wheel—whose motion is purposely made as slow as possible. The water then, occupies one half of the wheel’s circumference, falls by a gentle slope and finally leaves the wheel at d, whether it there touches the lower water, or not. This wheel is allowed to be incapable of using to advantage a large stream of water—but is doubtless fit to employ a small stream, in the best manner.
I have hesitated a moment to describe this method of helping the weak, in body or mind, to conquer their aversion to medicine—several persons having threatened me with a larger dose of ridicule than I am prepared to swallow. But surely, if we can only conquer a child’s timidity, so as to induce him to take, speedily, what his health requires, we shall not do a thing altogether laughable. We shall, perhaps, preserve a beloved child to the solicitude of a mother! and perhaps—a citizen to his country! If then, some laugh, more will approve; and I therefore continue the promised article.
Fig. 4 of Plate 48, shews this cup, composed of an inner and an outer vessel: the first to hold the medicine, and the latter a little tea, or other proper liquid to wash it down. The cups have a spout common to both; but the outer cup retains it’s contents as long as the small funnel a, is stopped with the thumb or finger. Thus then, the medicine is first taken, while the liquid is retained in the outer vessel—but the thumb being removed, the liquid also flows into the mouth, and in a good measure removes the taste it was wished to disguise.
The art of constructing Mills, or Machines to be driven by the wind, is so well known, that the results are considered as being, very nearly, what a perfect theory would require. It is, therefore, no part of my purpose to discuss either the theory or practice of that art. But I think that a still wider grasp may be taken of this powerful agent, so as to secure a further degree of utility, even while following less closely the abstract principles of mechanical philosophy. I enter then, directly, on the description of another of my wind Machines, in order to give an idea of the means I contemplate for losing the importance of those details in the magnitude of the general effect.
This Machine (see Plate 49, fig. 1,) is capable of great results merely because it employs, at a small expence, a great mass of air in motion; whether ill or well, is not the question: for as this source of power is almost indefinite, methinks we may draw from it without reserve. The present method of so doing, consists in using a very large sail, (A B) both to receive the impulse of the wind, and to raise the water. This figure is a section of the Machine in it’s length:—and it’s[379] width (not represented) is as great as the occasion may require. The sail is here shewn as placed over a lake or other sheet of water which it might be wished to drain, (or which may serve as a mill pond to drive any required Machines, by the water thus raised.) C D is the water in it’s lower bed: and E, is a canal on a higher level, into which a large quantity is thrown at each manœuvre of the Machine, a is the bank of the upper canal, to which is affixed the edge of the canvass, of which a B A d, is a section; and which might be large to immensity. At 1 2 3, &c. is a row of stakes as long as the Machine; and they are capped transversely with round poles, on which the sail rests when in it’s lowest position. In this state, also, the part b of the sail, plunges into the water, which rises above it in the prismatic form, b r s; a row of valves or clacks, (b) permitting it to rise through them, but preventing it from again falling that way. Thus, at every change, this prism of water, is sure to be replenished; and if we suppose the triangle b r s to have an area of ten square feet, and the prism to be one hundred feet long, the water there contained will be a thousand cubic feet—capable, however, of being augmented or diminished at pleasure, by slackening or tightening the sail towards A. At d, is the weather-end of this sail, which is supported when at rest, on the surface of the water, by the posts and caps before mentioned. This end d, of the sail is connected with a row of posts C F, placed more or less closely, as the prevailing strength of the wind and the size of the sail may require. The sail is held to these posts by[380] rolling pulley frames, of which one is seen at g, and is drawn up and down by the rope g h, acting at one end directly on the rolling pulley-frame g, and the other on the sail d, after having passed over a pulley (F) in the post itself: where note, that this effect can be communicated by proper machinery, from any one of these posts (C F) to all collateral ones; so as to make the manœuvres general, across the sail, whatever be it’s magnitude.
The following then, is the operation. The wind blows (by supposition) in the direction of the arrows in the figure: and the rolling pulley-frame g is quickly drawn up to g, where the hook i holds it fast. By a necessary consequence the wind fills the sail d c r, and stretches it into the figure d A B a: in doing which it lifts the water r s, and pours it, in all the width of the sail, into the canal E; thus raising a thousand cubic feet of water at each stroke. As soon as the water is turned into the canal E, the hook i is pulled outward, and the rolling pulley g is forced down, by the wind itself, to the position k, when the wind blowing over the sail, will give it a bent form, (k c a) and soon bring the sail into it’s present position on the posts 1 2, &c.—when water will be again admitted by the valves at b, and another stroke of the Machine be prepared.
The above contains the basis of this idea. I do not expect it will obtain at once universal assent: But if I knew the several grounds of objection, I am persuaded the greatest number[381] of them could be removed. The first I anticipate, is the difficulty of turning this Machine to the several winds that may blow over it. To this objection I would reply, that in such a case, the canal E, should surround an area made large enough for the sail, of some polygonal form, say an octagon, to different sides of which the stretching cords of the sail should be carried, so as to catch the prevailing winds—but the direction of which need not be followed to a nicety; since an obliquity of a few degrees would not prevent the effect.
It might be added, that it is not indispensable that the canal E should be stationary. Made of wood, or metal, it might turn round a fixed centre, and be braced into the necessary positions with ropes—when the posts only (C F) would have to be removed, or quitted for others duly placed. These ideas are connected with immense effects; and cannot, therefore, be lightly disposed of: they both deserve and require serious attention.
This is the last of those conceptions I shall now bring forward, for making more than a common use of the WIND as a first-mover of Machinery. Horizontal windmills are well known; and this is a horizontal windmill—yet not like those already in use: for, here, the sails, very large and numerous, are placed on a boat in the form of a ring, which thus moves through the water without any other resistance than that arising from the asperities of it’s surface.
In Plate 49, fig. 3, B B is a section of the Vessel, placed in a circular canal D, into which the lower water flows through proper arches (C C) in the banks. The vessel is rigged with several narrow horizontal sails, stretched on ropes between the oblique masts a b, c d; and so placed, that the sails (being a little wider than the interval between the ropes) can open in one direction, but not in the other; and they are shewn open at c d, and shut at a b, in the figure. This, therefore, is a mill, that takes all winds; and although it’s uses might be various, we shall finish it’s description as adapted to raise water by the centrifugal force. As before hinted, the canal D D is circular; and has a bank, sloping outward, with a[383] canal (E) on it’s top. When, therefore, the wind blows, the ring boat B (held to the centre by the ropes f g) revolves around it; and by one or more water drags (h) which it carries, collects the water on and up the bank, and finally drives it into the canal E, from which it flows in any destined direction. If for draining watery lands, it will be done rapidly; if for irrigating, it will be done abundantly: if, in fine, for driving any mill with the water thus raised, the machinery will be very efficient, as working with ten or twenty times as much sail, as any other windmill can carry. I add, merely on this occasion, that the sails here mentioned, might be placed obliquely, instead of straight across the ring vessel; (see the plan in fig. 2 of this Plate at E F) from which disposition, nearly all the advantages of the vertical mill might be transferred to the horizontal; and with this remark I leave the present interesting subject to the studious and candid reader.
My fiftieth and last Plate contains this idea: It is not intended to vie with the usual mirror, in correctness of form, or intensity of local effect—but to offer, by the largeness of it’s dimensions, some properties which better mirrors cannot present. It is intended to pave the way for the use of the Sun’s rays in Engines of Power. For this purpose, however, it must probably be transported to some tropical climate, where “a cloudless sun” diffuses it’s rays more constantly, and less obliquely, than in our northern climes.
This is the more necessary here, because this Mirror can only be used in a horizontal position, and is in fact a fluid Mirror. Fig. 1, shews it mounted on a steady frame A B, and having a strong axis on which it can be turned, faster or slower, according to it’s dimensions; and it may or may not be floated on water, to lessen the stress on the axis. The Mirror, properly speaking, is composed of mercury—contained in the revolving vessel C D, whose motion should be given by proper machinery in the most uniform manner possible. The mercury, thus turned, acquires a concave surface, a, b, c; and receiving the parallel rays d c, e b, and, f a, collects them[385] into the focus F; in, or near which, is placed the vessel where the effect is to become useful, and which of course is moveable so as to follow the sun’s motion. Those of my readers who have seen the machines used for fixing the sun’s image in the solar microscope, will be at no loss to conceive how our present focal station must be moved to adapt it to a fixed mirror. I shall only add further, that it is not necessarily an exact movement that is here wanted; since the vessel to be heated would have dimensions somewhat large, and the focus itself be only brought to a moderate degree of precision. In a word, the utmost heat wanted would be, what could be usefully employed in heating water. It remains then to be observed, that the source of power, in this Machine, is magnitude of parts, more than precision of form: yet it may be mentioned, that the form we thus procure in the revolving mercury, is a solid of revolution, having the logarithmic curve (a, b c) for it’s section—a curve, which in fact, comes indefinitely near to the parabolic figure which would be required, if greater precision were attempted. We finish then, by observing, that the bottom itself of the revolving vessel might be made concave, (like the dotted line under that a b c) in order to avoid the necessity of using a large quantity of mercury, to form the reflecting surface.
This Mirror seems superior to the former, as depending on fixed materials. It likewise, produces the desired effect, by offering a very large surface to the sun, and directing the rays to a focus, nearly enough to give the heat required for water, as before mentioned.
To do this, a frame A (Plate 50, fig. 2) holds the Mirror; and this frame has a horizontal motion round the post B, something like a common windmill. In this frame and on two horizontal trunnions, turns the Mirror C D: and one or both these trunnions are hollow, to admit of a process we shall shortly mention. This Mirror itself is composed of an air-tight ring C D, of a width proportionate to the diameter adopted; and on which are fixed two heads, much like those of a tambourine, (or the under head might be made of some metallic substance). The head a b c, is made of a fine texture, duly prepared and varnished till it becomes air tight, and then there are stuck to it, a number of small hexagonal looking-glasses or mirrors of any kind, (see fig. 7) which thus fill up the whole space, and prepare the Mirror for the intended change of form.[387] The method of giving this form, consists in exhausting, more or less, this tambourine of air, when, by the pressure of the atmosphere, the heads will take the form a b c, that is a spherically concave form—fit to reflect the sun’s rays as correctly as this our object requires; and thus may some thousand small images of the sun be brought to fall on the same spot, and an immense heat be occasioned. The accounts we have of the destruction of the Roman fleet by the united mirrors of Archimedes, make this process appear the more feasible—as whatever were the methods of uniting the foci of his mirrors, a similar effect may be expected from this simple process.
My readers will perceive that this Machine has the advantages of the universal joint, by which it can be directed to the sun in every position; and even made to fix his ardours on any immoveable spot for a good length of time. The persons to whom I particularly address these ideas, will require no further details to conceive the less obvious circumstances of this Invention. In general, we want no effect that requires optical precision: but if we did, it could be obtained to a good degree, by methods similar to these.
I shall only add here, that this fig. 2 is given as a section—because intended to represent a parallelogram, as well as a solid of revolution: and thus (with proper mirrors) to make what now appears a spherical focus, a linear one—fit to heat a[388] cylindrical vessel with it’s contents; and thereby draw power from the sun’s heat, without running expense. I am serious when I say, that we can thus, practically, collect the solar rays which fall on many hundred square feet of surface; and produce by them, at any desired distance, effects to which those obtained from modern burning mirrors, are but as sparks to a blaze.
This Machine supposes at once a new kind of engraving, and admits of patterns of very large dimensions. This kind of engraving will be best understood by persons acquainted with figure-weaving; and especially with the manner of mounting the looms for that purpose. In that System, (see Plate 50, fig. 8) the patterns are drawn on ruled paper divided into squares; and each of these squares represents a point in the texture, composed of one or more threads each way; insomuch that whenever that square has any desired colour in it on the pattern, it’s threads are taken by the person who prepares the loom; and they are missed in every case where nothing appears in that square, or a colour not then wanted. Now, whatever be the dimensions of these elementary points on the loom, they may be represented by squares of any convenient size on the pattern: only remembering that the smaller they are, in reality, the better will be the delineation. Thus in carpeting, for example, an element of this kind may be a square of one tenth of an inch and more; while one on a ribbon or a piece of silk, is often not the hundredth part. And therefore, the perfection of this engraving depends on the fineness of the points of which the figures are composed. For, in a word, this System proceeds on the[390] same principle. When any part of a line requires a dot or mark to be made, the Machine strikes a blow there; and when no impression is to be made, the Machine (by means that will be shewn) suffers the cylinder to pass that place without striking. The means of regulating this is committed to workmen who merely know how to read off the pattern in it’s length, as it is now read off in it’s width by the weaver. To describe the construction of the Machine, (as exhibited in figs. 3 and 4 of Plate 50) A is the cylinder to be engraved; and B is a worm-wheel fixed to it’s mandril, and destined to turn it. This it does, slowly, by the endless screw a, as turned by proper straps on the fast and loose pullies b c, (figs. 3 and 4). C shews a second wheel, concentric with that B, but running loose on it’s axis, which is a pin fitted into the end of the mandril. This wheel, when the threads of the screw a are fine, requires a motion more rapid than the wheel B—to give which motion by means of the latter, we use a pair of multiplying wheels d, which geer, one in the larger bevil wheel cut near the edge of the wheel B; and the other in a smaller bevil wheel cut or fixed on the inner face of the wheel C—and whence this latter wheel receives a velocity of about ten times the speed of B. The use of this wheel C, is to carry, across the Machine, certain bars, of wood or metal, shewn in figs. 5 and 6, whose function is to carry short pins or studs 1, 2, 3, 4, &c. for the purpose of determining the places where the punch is to act, and where it is not. To this end, g h is a frame, which is raised by a cam or tappet i, fixed in the[391] endless screw a, once every turn; and that through the medium of the little tumbler i e f, by which is finally determined whether the stroke shall take place or not—for m being a section of the stud bar of figs. 5 and 6, it’s pins, when they occur, raise the end f of the bent lever f e i; and when there is no pin or stud in m, this lever is not raised, and the point i, does not come near enough to the cam to be laid hold of, in which case no stroke is given. This then, is so whenever the studs fail in the bar m; and these fail whenever the pattern-reader has said to the stud-setter, miss: and they occur whenever he has said take—both which cases happen more or less often according to the state of the squares in the pattern.
To be a little more particular: in fig. 5 we see a part of the wheel C of fig. 3, and also a part of the stud bars m m, which geer in the wheel C, and which being conducted by the guides n, follow the motion of that wheel, presenting at f, (fig. 3) a stud to raise the lever f e, whenever the pattern requires it. It may be mentioned, that these studs act obliquely on the wing f of this lever, and thus raise it as they pass under it. And further, these stud bars are made and fitted to each other in the manner shewn at fig. 6. There is a geering tooth under every stud hole, and the last stud hole of a given bar has, fixed in it, a thin tube a, into which the stud enters the same way as in any other place: but this tube whether studded or not serves to lay hold of the succeeding bar b, by it’s first hole—so, in fine,[392] as to make the bars endless; the attendant having nothing else to do than to hook them to each other as the wheel C draws them in.
Thus then, are the strokes of the hammer frame, g h, conformed to the pattern: for these bars have been studded before hand by one or more readers and setters; and it is a merely mechanical process to put them in while the Machine moves: from which, by the bye, they fall out after the passage into a proper box, and the studs out of them, to be composed again from the succeeding figures of the pattern. A dozen or two of these bars might be prepared at any time and place, and to any pattern, which they will thus transfer to a cylinder at any desired moment, without the further preparation of dies, punches, mills, &c.—as used in other Machines. N. B. The strength of the blows thus given by the hammer frame g h, is lessened or augmented by the position of the point i fixed to the bent lever i e f, and which makes that lift higher or lower as required—which is a mean of shading offered by this Machine. But to mention it’s other properties, the endless screw a, (figs. 3 and 4) carries another endless screw o, more or less fine, which turns at the same time the wheel p, and, by that, the long screw s s, whose office it is to shift, slowly, the punch carriers k l, along the Machine, from k by l, towards s. And here an observation occurs: this can only be so, when the pattern permits the action of the punches k or l, to take place spirally on the cylinder; that is, when[393] the sketches are distinct enough not to shew the anomaly that would occur were a straight pattern thus transferred to a set of spiral lines. But should it be desirable to engrave patterns so correct as to require an exact parallel motion round the cylinder, then the motion of this screw must not be continual—but must intermit and be resumed, at every beginning of a new line round the cylinder. I hope, I make myself understood: a pattern drawn on squares, produces lines all parallel to the first; while the spiral motion of the punch causes a slight deviation—which, in a word, can either be suffered or avoided. At all events, this deviation is so much the smaller as the punch motion is slower in both directions; and, in fine patterns, must be very small. One remark will close this part of the subject: although a fine pattern, requires a great number of blows, and thus a certain expence of time, each blow can be so much the lighter and more frequent; so as to compensate, in some degree, for this cause of delay. I add, that the levers shewn above and around fig. 6, are intended to lift the hammer frame g h, equally at both ends: while the screw Z regulates the depth to which it is permitted to fall.
I observe, finally, that, according to the size of the intended pattern, there are more or fewer of the punch bearers k l, connected, by their nuts, with the screw s s; each of which thus engraves it’s sketch, similar to the collateral ones; and that were it wished to make one pattern of the whole length and circumference of the cylinder, a single punch bearer would be required—since nothing else limits the extent of a pattern engraved by this Machine.
Thus have I gone through my proposed “Century of Inventions,” for every imperfection in which I beg the indulgence of my numerous readers. And here I can truly say I have neglected nothing—although the precarious state of my health may have sometimes veiled the evidence of my descriptions. On the other hand, I did not even attempt many of the lesser details of execution; as I wrote for those to whom they would have been superfluous: but as to the objects themselves, I believe there is not one that is without the pale of practical utility. In a word, many of the subjects have been frequently executed, and are in daily use: and as to those which remain to be tried, I engage, if called on, to give them useful existence. And the better to convince candid minds of the serious attention I have paid to these subjects, I shall add the scales on which they have been executed, or to which they are drawn—those scales expressed by a fraction, shewing what proportion the figures bear to the reality. Thus the scale of one inch to a foot will be expressed by the fraction 1⁄12; that of two inches to a foot, by 1⁄6, &c. that is, the figures, in these cases, will be (nearly) 1⁄12 or 1⁄6 of the size of the Machines. This premised—and also that we shall observe the alphabetical order, the following is the
| No. | Scale | Page. | |||
|---|---|---|---|---|---|
| 1 | Adding machine; or Machine to cast up large Sums | 1⁄2 and 1 | 343 | ||
| 2 | Air Pump: Essay to complete the Vacuum | 1⁄10 | 374 | ||
| 3 | Barrel Spring, to lengthen the going of Clocks, &c. | 1 | 26 | ||
| 4 | Boats (serpentine) for lessening the expence of traction, &c. | 1⁄75 | 137 | ||
| 5 | Bobbin or Laces, (Machine for making) covering Whips, &c. | circa. 1⁄5 | 284 | ||
| 6 | Bowking Machine, for Bleachers | 1⁄24 | 299 | ||
| 7 | Bucket or Persian Wheels, (a combination of) to raise Water | 1⁄24 | 172 | ||
| 8 | Canals (open) as hydraulic Machines | circa. 1⁄200 | 307 | ||
| 9 | Canter, or inclined plane for Draymen | 1⁄24 | 72 | ||
| 10 | Chain to act equably on my Wheels | circa. 1 | 135 | ||
| 11 | Chocolate Mill (rotatory) | 1⁄12 | 368 | ||
| 12 | Cocks (equilibrium) to avoid leakage, &c. | ad. lib. | 153 | ||
| 13 | Colour Mill, for Calico Printers | 1⁄12 | 175 | ||
| 14 | Compasses (bisecting) | 1⁄2 | 353 | ||
| 15 | Cotton-Machine for batting or bowing | circa. 1⁄12 | 290 | ||
| 16 | Crane (rewarded by the Society of Arts) | 1⁄60 | 57 | ||
| 17 | Crank, epicycloidal; or parallel motion (rewarded by Bonaparte) | 1⁄8 1⁄12 | 30 | ||
| 18 | Dash, or Wash Wheel, acting with greater rapidity than usual | 1⁄24 | 271 | ||
| 19 | Differential Wheels, for gaining great power | 1⁄4 | 54 | ||
| 20 | Doffing Machine, to take cylinders from their mandrels | 1⁄9 | 243 | ||
| 21 | Draw Bench, for my twisted Pinions | 1⁄2 1⁄6 | 133 | ||
| 22 | Dynamometer, for measuring power in motion | 1⁄4 | 15 | ||
| 23 | —— a second kind for do. | 1⁄3 | 177 | ||
| 24 | Engine, for cutting my Patent Wheels | V. text | - | 121 | |
| 183 | |||||
| 25 | Engine, for cutting large bevil Wheels and Models | 1⁄12 | 263 | ||
| 26 | Engraving Machine, being an important application of my Cog or Toothed Wheels | 1⁄12 and 1⁄14 | 317 | ||
| 27 | Engraving Machine, of a new kind, for large patterns | 1⁄14 | 389 | ||
| 28 | Essay to derive power from expanding solids | 1⁄20 | 280 | ||
| 29 | Evaporation (Machine to promote) | ad. lib. | 78 | ||
| 30 | Eyes (Machine for making rapidly) | 1⁄2 | 166 | ||
| 31 | Fire-Escape, on a retarding principle | 1⁄2 | 364 | ||
| 32 | —— by breaking the fall | ad. lib. | 366 | ||
| 33 | Fires (portable Engine to extinguish) | 1⁄24 | 311 | ||
| 34 | —— (watch Engine always ready for) | 1⁄6 | 315 | ||
| 35 | Flax (Machine for breaking rapidly) | 1⁄24 | 296 | ||
| 36 | Forging bar iron and steel (Machine for) | ad. lib. | 215 | ||
| 37 | Friction (Machine to prevent) | ad. lib. | 144 | ||
| 38 | —— of another kind | ad. lib. | 150 | ||
| 39 | Grating or cutting Green Roots, &c. (Machine for) | circa. 1⁄6 | 79 | ||
| 40 | Helico-centrifugal Machine, for raising water | ad. lib. | 212 | ||
| 41 | Horse Wheel, (inclined) to save room and gain speed | 1⁄60 | 53 | ||
| 42 | —— (reciprocating) for Mangles, &c. | 1⁄30 | 217 | ||
| 43 | Hot Air as power, while heating rooms, &c. | ad. lib. | 203 | ||
| 44 | Lamp (hydraulic) for the table | 1⁄6 | 277 | ||
| 45 | Lithographic, or Copper-plate Press, with curious and useful properties | 1⁄12 | 230 | ||
| 46 | Machine to communicate and suspend Motion | ad. lib. | 155 | ||
| 47 | —— to set-on and suspend rapid Motions | 1⁄2 | 158 | ||
| 48 | —— for clearing turbid Liquors | ad. lib. | 305 | ||
| 49 | —— for driving Boats, without disturbing the Water | ad. lib. | 251 | ||
| 50 | —— to assist in taking Medicine | 1⁄3 | 377 | ||
| 51 | Mangle, perpetual or rotatory | 1⁄16 | 370 | ||
| 52 | Marine Level (essay on a) | circa. 1⁄18 | 357 | ||
| 53 | —— (other essay on a) | ad. lib. | 362 | ||
| 54 | Micrometer, to measure minute spaces | 1 | 83 | ||
| 55 | Mirror, (centrifugal) to collect the Solar rays | ad. lib. | 384 | ||
| 56 | —— of a different kind | ad. lib. | 386 | ||
| 57 | Mover, by dropping weights | ad. lib. | 76 | ||
| 58 | Nails (Machine for moulding) | 1⁄12 | 200 | ||
| 59 | —— (Machine for forging) | 1⁄10 | 226 | ||
| 60 | Parallel Motion (double) for heavy Steam Engines | ad. lib. | 338 | ||
| 61 | Pencyclograph; or instrument for drawing portions of large circles, and finding their centres by inspection | ad. lib. | 51 | ||
| 62 | Peristaltic Machine, for raising water | 69 | |||
| 63 | Pitch Fork for Musicians, with variable tones | circa. 1 | 355 | ||
| 64 | Power Wheel, by heated Air, &c. | ad. lib. | 43 | ||
| 65 | Press, direct and differential (power as 52000 to 1) | ad. lib. | 66 | ||
| 66 | Press (excentric bar)—power indefinite | ad. lib. | 174 | ||
| 67 | Printing Machine (two coloured) | 1⁄12 | 301 | ||
| 68 | Protracting Motion (Machine for) | 1⁄4 | 49 | ||
| 69 | Pullies (my Patent) much improved | 1⁄6 1⁄12 | 33 | ||
| 70 | Pump (equable) proposed 1794, for the Machine of Marly | 1⁄24 | 45 | ||
| 71 | —— portable, worked by the hands and feet | 1⁄24 | 351 | ||
| 72 | Punch Machine, for Engravers | 1⁄4 | 193 | ||
| 73 | —— Machine (differential) for ditto | circa. 1⁄7 | 196 | ||
| 74 | —— rotatory, for my Engraving Machine | 1⁄6 | 349 | ||
| 75 | Reciprocating or long Parallel Motion | ad. lib. | 237 | ||
| 76 | Reflector, for Light Houses, &c. | ad. lib. | 234 | ||
| 77 | Regulator (not centrifugal) for Wind and Water Mills, Steam Engines, &c. | 1⁄4 | 223 | ||
| 78 | Retrographic Machine, for Engravers | ad. lib. | 164 | ||
| 79 | Rotato-gyratory Churn | 1⁄10 | 210 | ||
| 80 | Screw, with greatly diminished friction | ad. lib. | 81 | ||
| 81 | Screws (Machine for forging) | 1⁄3 | 160 | ||
| 82 | Spinning Machines (my Patent) | circa. 1⁄17 | 329 | ||
| 83 | —— adapted chiefly to Wool | 1⁄12 | 334 | ||
| 84 | Spring, to keep a door closed yet open easily | ad. lib. | 131 | ||
| 85 | Steelyard (differential) of great power | 1⁄8 | 162 | ||
| 86 | Syphon (mechanical) to expel part of the Water at the highest point | ad. lib. | 240 | ||
| 87 | Tallow (Machine for cutting and trying) | 1⁄80 | 245 | ||
| 88 | Tea Table (mechanical assistant for) | 1⁄8 | 228 | ||
| 89 | Valves (slide) Machine for working | ad. lib. | 255 | ||
| 90 | Ventilator, rotatory, yet by pressure | 1⁄12 | 170 | ||
| 91 | Vessel (expanding) for Pumps, Steam Engines, &c. | ad. lib. | 219 | ||
| 92 | Washing Apparatus, for Hospitals, &c. | ad. lib. | 247 | ||
| 93 | Water Wheel (horizontal) probably the best of the impulsive kind | 1⁄52 | 326 | ||
| 94 | The same, for high falls | ib. | 326 | ||
| 95 | Water Wheel (inclined) using the weight of the water | ad. lib. | 376 | ||
| 96 | Water (aero-hydraulic Machine for raising) | 1⁄200 or 1⁄300 | 292 | ||
| 97 | Weaving by Power (manner of driving the shuttle, executed A. D. 1780) | 1⁄12 | 372 | ||
| 98 | Wedge Machine (perpetual) | 1⁄12 | 74 | ||
| 99 | Wheels (my System of Cog or Toothed) | all dimensions | 90 | ||
| 100 | Windmill of double power | 1⁄220 | 313 | ||
| Page. | ||
|---|---|---|
| 1, | line | 27, after System, read of. |
| 4, | „ | 27, for them, read it. |
| 10, | „ | 16, for vestuble, read vestibule. |
| 15, | „ | 10, for parralel, read parallel. |
| 15, | „ | 13, after centre, read of. |
| 42, | „ | 7, after was, dele on. |
| 43, | „ | 1, for Plate 2, read Plate 8. |
| 49, | „ | 1, after A, read Fig. 4. |
| 70, | „ | 7, for ionical, read conical. |
| 100, | „ | 2, after A C for :, read ∷. |
| 102, | „ | 16, for z/a, read z2/a. |
| 126, | „ | 4, for on it’s surface, read on it’s pitch line. |
| 126, | „ | 17, for it’s height f g, read the length required. |
| 129, | „ | 16, for 2 inches, read 4 inches. |
| 164, | „ | 10, for other two cases in C & E, read in other two cases C & E. |
| 188, | „ | 17, after b C twice, for :, read ∷. |
| 196, | „ | 20, for fig. 2, read Fig. 4. |
| 200, | „ | 8, for Plate 25, read Plate 24. |
| 203, | „ | 11, after heat, read for. |
| 208, | „ | 6, for is, read are. |
| 209, | „ | 8, for arrangements, read arrangement. |
| 246, | „ | 19, after which, read last. |
| 272, | „ | 23, for wheel, read bevil wheel. |
| 273, | „ | 21, for axis, read axes. |
| 287, | „ | 19, for z´, read z. |
| 289, | „ | 1, after down, read twisted. |
| 294, | „ | 7, for two, read too. |
| 311, | „ | 8, for carried, read used. |
| 335, | „ | 10, for bobbin, read bobbins. |
| 340, | „ | 8, for edged formed, read wedge formed. |
| 350, | „ | 8, for Fig. 3, read Fig. 6. |
| 357, | „ | 18, for light, read double. |
| 374, | „ | 12, after 1/27 read, 1/81, 1/243, 1/729, &c. |
| 375, | „ | 20, for 1/14641 read 1/1331. |
| 387, | „ | 9, for makes, read make. |
⁂ If, in the following List of Names, it has been thought just to mark those of the first promoters of this Work, it has not been to lessen the Author’s obligations to the rest—who, almost uniformly, have given him their Names with the same spontaneous kindness, and thus ensured his lasting gratitude.
Pl. 1.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 1 (260 kB)
Pl. 2.
J. W. inv. (cir. 1770.) & delin. 1899
Engraved by Leech & Cheetham.
Larger image Plate 2 (181 kB)
Pl. 3.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 3 (352 kB)
Pl. 4.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 4 (376 kB)
Pl. 5.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 5 (302 kB)
Pl. 6.
J. White Inv. et del.
Engd by Leech & Cheetham.
Larger image Plate 6 (241 kB)
Pl. 7.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 7 (393 kB)
Pl. 8.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 8 (333 kB)
Pl. 9.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 9 (304 kB)
Pl. 10.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 10 (390 kB)
Pl. 11.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 11 (312 kB)
Pl. 12.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 12 (341 kB)
Pl. 13.
J. White inv. et del.
Eng.d by Leech & Cheetham.
Larger image Plate 13 (300 kB)
Pl. 14.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 14 (332 kB)
Pl. 15.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 15 (377 kB)
Pl. 16.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 16 (401 kB)
Pl. 17.
J. White inv. et del.
Eng.d by Leech & Cheetham.
Larger image Plate 17 (324 kB)
Pl. 18.
J. White inv. et del.
Eng.d by Leech & Cheetham.
Larger image Plate 18 (349 kB)
Pl. 19.
J. White inv. et del.
Eng.d by Leech & Cheetham.
Larger image Plate 19 (260 kB)
Pl. 20.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 20 (353 kB)
Pl. 21.
J. White inv. et del.
Engraved by Leech & Cheetham.
Larger image Plate 21 (300 kB)
Pl. 22.
J. White inv. et del.
Eng.d by Leech & Cheetham.
Larger image Plate 22 (154 kB)
Pl. 23.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 23 (314 kB)
Pl. 24.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 24 (419 kB)
Pl. 25.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 25 (386 kB)
Pl. 26.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 26 (332 kB)
Pl. 27.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 27 (421 kB)
Pl. 28.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 28 (460 kB)
Pl. 29.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 29 (371 kB)
Pl. 30.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 30 (291 kB)
Pl. 31.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 31 (342 kB)
Pl. 32.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 32 (305 kB)
Pl. 33.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 33 (305 kB)
Pl. 34.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 34 (365 kB)
Pl. 35.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 35 (332 kB)
Pl. 36.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 36 (391 kB)
Pl. 37.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 37 (402 kB)
Pl. 38.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 38 (355 kB)
Pl. 39.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 39 (317 kB)
Pl. 40.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 40 (451 kB)
Pl. 41.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 41 (425 kB)
Pl. 42.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 42 (451 kB)
Pl. 43.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 43 (411 kB)
Pl. 44.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 44 (304 kB)
Pl. 45.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 45 (270 kB)
Pl. 46.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 46 (388 kB)
Pl. 47.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 47 (441 kB)
Pl. 48.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 48 (375 kB)
Pl. 49.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 49 (384 kB)
Pl. 50.
J. White inv. et del.
Engr.d by Leech & Cheetham.
Larger image Plate 50 (374 kB)
Depending on the hard- and software used, not all characters and symbols may display properly or at all.
Unusual and inconsistent spellings (including the use of it’s for its) have been retained, except as mentioned under
Changes below.
The author uses both . and , for decimals and for thousands separator; this has not been changed.
The Synopsis does not list all machines described in the text, some machines listed are not described in the book, and some
machines are mentioned more than once. There are several discrepancies between the Synopsis and the Table of Contents.
Page 127, as 268 is to ...536: the reason for the periods is unclear, they have been left as in the original work.
Page 204, horizontal and vertical: the machine in the drawing is horizontal; possibly the words horizontal and vertical should be
interchanged.
Plate 2: the text on the left-hand bottom reads J.W. inv. (cir. 1770.) & delin. 1899. which is unlikely in a book from 1822.
Changes made to the text:
Minor obvious punctuation errors have been corrected silently.
The various Errata have already been included (including the correction to Plate 19 Fig. 7); the given correction ,99990 was changed
to 99990; on page 374, the entire series has been corrected, not only the elements given in the errata; on page 188 the corrections
have been made to line 2, not 17 as given in the errata; some errata repeated on last page of errata; some errors reported in errata
not present in text).
Footnotes have been moved to underneath the text they refer to.
Some tables have been re-arranged.
Page vi: befal changed to befall
Page 21: 18th. figure changed to 18th. figure (Plate 6)
Page 24: dfficulty changed to difficulty; clylinder changed to cylinder; equallized changed to equalized as elsewhere
Page 26: consitute changed to constitute
Page 33: philosohpy changed to philosophy
Page 36: as to the the time changed to as to the time; thepocket changed to the pocket
Page 38: Lieutenat changed to Lieutenant
Page 39: pasing changed to passing
Page 51/52: proporportions changed to proportions
Page 54-55: w changed to W, z changed to Z as in drawing
Page 56: 2,020000 changed to 2020000 (cf. correction of other numbers on page 55, and the written-out number in the next paragraph of the text)
Page 58-59: ’“ changed to “’
Page 61: unweildy changed to unwieldy; shut of changed to shut off
Page 63: difinitive changed to definitive
Page 73: as we llto changed to as well to; theplane changed to the plane
Synopsis: parobolico changed to parabolico; second number 78 changed to 79; some page umbers corrected to conform to text
Page 90: Opening quotes added before The subject of this paper ... to match closing quotes on page 108
Page 96: indispensible changed to indispensable as elsewhere; whould changed to would; circumferencies changed to circumferences
Page 101: circumferencies changed to circumferences
Page 102: arces changed to arcs; quantites changed to quantities
Page 118: side ways changed to sideways as elsewhere
Page 123: once cutting changed to one cutting
Page 133: (Plate 17) changed to (Plate 17, fig. 1)
Page 134: circumferenceof changed to circumference of; inproportion changed to in proportion
Page 137: quote marks added after second and before third paragraph for consistency
Page 138: passsing changed to passing; staight changed to straight
Page 139: beween changed to between
Page 145: penetratration changed to penetration
Page 152: reallized changed to realized
Page 155: representented changed to represented
Page 160: might named changed to might be named
Page 161: intead changed to instead
Page 170: prouced changed to produced
Page 187: opinon changed to opinion; 174.4 changed to 147.4
Page 188: 63 27′ changed to 63°27′; y changed to y =
Page 191: closing quote added after ... same proportion.
Page 200: dependant changed to dependent as elsewhere; Plate 25 changed to Plate 24
Page 203: “tis ... changed to “’tis ...
Page 224: Plate 3d changed to Plate 3
Page 286 some times changed to sometimes
Page 289 (if changed to if
Page 307: analagous changed to analogous; disembarassment changed to disembarrassment
Page 311: mens’ changed to men’s
Page 317: fig. 3 changed to fig. 2
Page 337: cloged changed to clogged
Page 339: ackowledge changed to acknowledge
Page 340: preceeding changed to preceding; a pair of of changed to a pair of
Page 353: contruction changed to construction
Page 357: withold changed to withhold
Page 372: esspecially changed to especially
Page 387: sherical changed to spherical
Table of Contents: some page numbers corrected to conform to text
list of subscribers: De Volvic Comte Chabrol changed to De Volvic, Comte Chabrol
Plate 36, 43: Engraver added as with other plates.