TIME AND ITS
MEASUREMENT
POPULAR MECHANICS MAGAZINE
CONTENTS
| Time as an abstraction. — Ancient divisions of day and night. — Night watches of the Old Testament. — Quarter days and hours of the New Testament. — Shadow, or sun time. — Noon mark dials. — Ancient dials of Herculaneum and Pompeii. — Modern dials. — Equation of time. — Three historic methods of measuring time. — “Time-boy” of India. — Chinese clepsydra. — Ancient weather and time stations. — Tower of the winds, Athens, Greece | Page 13 |
| Chinese and Japanese divisions of the day. — Hours of varying length. — Setting clocks to length of daylight. — Curved line dials. — Numbering hours backwards and strange reasons for same. — Daily names for sixty day period. — Japanese clock movements practically Dutch. — Japanese astronomical clock. — Decimal numbers very old Chinese. — Original vertical dials founded on “bamboo stick” of Chinese clepsydra. — Mathematics and superstition. — Mysterious disappearance of hours 1, 2, 3. — Eastern mental attitude towards time. — Japanese methods of striking hours and half hours | Page 25 |
| De Vick's clock of 1364. — Original “verge” escapement. — “Anchor” and “dead beat” escapements. — “Remontoir” clock. — The pendulum. — Jeweling pallets. — Antique clock with earliest application of pendulum. — Turkish watches. — Correct designs for public clock faces. — Art work on old watches. — 24-hour watch. — Syrian and Hebrew hour numerals. — Correct method of striking hours and quarters. — Design for 24-hour dial and hands. — Curious clocks. — Inventions of the old clock-makers | Page 37 |
| Astronomical motions on which our time is founded. — Reasons for selecting the sidereal day as a basis for our 24-hour day. — Year of the seasons shorter than the zodiacal year. — Precession of the equinoxes. — Earth's rotation most uniform motion known to us. — Time stars and transits. — Local time. — The date line. — Standard time. — Beginning and ending of a day. — Proposed universal time. — Clock dial for universal time and its application to business. — Next great improvement in clocks and watches indicated. — Automatic recording of the earth's rotation. — Year of the seasons as a unit for astronomers. — General conclusions | Page 53 |
ILLUSTRATIONS

Mr. Arthur is an enthusiastic scientist, a successful inventor and extensive traveler, who has for years been making a study of clocks, watches, and time-measuring devices. He is not only a great authority on this subject, but his collection of over 1500 timepieces gathered from all parts of the globe has been pronounced the finest collection in the world. Mr. Arthur is a pleasing exception to the average business man, for he has found time to do a large amount of study and research along various scientific lines in addition to conducting an important manufacturing business in New York City, of which he is president. Mr. Arthur is 67 years of age.—H. H. Windsor.
CHAPTER I
HISTORIC OUTLINE
Time as an abstraction. — Ancient divisions of day and night. — Night watches of the Old Testament. — Quarter days and hours of the New Testament. — Shadow or sun time. — Noon mark dials. — Ancient dials of Herculaneum and Pompeii. — Modern Dials. — Equation of time. — Three historic methods of measuring time. — “Time-boy” of India. — Chinese clepsydra. — Ancient weather and time stations. — Tower of the winds, Athens, Greece.
Time, as a separate entity, has not yet been defined in language. Definitions will be found to be merely explanations of the sense in which we use the word in matters of practical life. No human being can tell how long a minute is; only that it is longer than a second and shorter than an hour. In some sense we can think of a longer or shorter period of time, but this is merely comparative. The difference between 50 and 75 steps a minute in marching is clear to us, but note that we introduce motion and space before we can get a conception of time as a succession of events, but time, in itself, remains elusive.
In time measures we strive for a uniform motion of something and this implies equal spaces in equal times; so we here assume just what we cannot explain, for space is as difficult to define as time. Time cannot be “squared” or used as a multiplier or divisor. Only numbers can be so used; so when we speak of “the square of the time” we mean some number which we have arbitrarily assumed to represent it. This becomes plain when we state that in calculations relating to pendulums, for example, we may use seconds and inches—minutes and feet—or seconds and meters and the answer will come out right in the units which we have assumed. Still more, numbers themselves have no meaning till they are applied to something, and here we are applying them to time, space and motion; so we are trying to explain three abstractions by a fourth! But, happily, the results of these assumptions and calculations are borne out in practical human life, and we are not compelled to settle the deep question as to whether fundamental knowledge is possible to the human mind. Those desiring a few headaches on these questions can easily get them from Kant and Spencer—but that is all they will get on these four necessary assumptions.
Evidently, man began by considering the day as a unit and did not include the night in his time keeping for a long period. “And the evening and the morning were the first day” Gen. 1, 5; “Evening and morning and at noonday,” Ps. LV, 17, divides the day (“sun up”) in two parts. “Fourth part of a day,” Neh. IX, 3, shows another advance. Then comes, “are there not twelve hours in a day,” John XI, 9. The “eleventh hour,” Matt. XX, 1 to 12, shows clearly that sunset was 12 o'clock. A most remarkable feature of this 12-hour day, in the New Testament, is that the writers generally speak of the third, sixth and ninth hours, Acts II, 15; III, 1; X, 9. This is extremely interesting, as it shows that the writers still thought in quarter days (Neh. IX, 3) and had not yet acquired the 12-hour conception given to them by the Romans. They thought in quarter days even when using the 12-hour numerals! Note further that references are to “hours;” so it is evident that in New Testament times they did not need smaller subdivisions. “About the third hour,” shows the mental attitude. That they had no conception of our minutes, seconds and fifth seconds becomes quite plain when we notice that they jumped down from the hour to nowhere, in such expressions as “in an instant—in the twinkling of an eye.”
Before this, the night had been divided into three watches, Judges VII, 19. Poetry to this day uses the “hours” and the “watches” as symbols.
This 12 hours of daylight gave very variable hours in latitudes some distance from the equator, being long in summer and short in winter. The amount of human ingenuity expended on time measures so as to divide the time from sunrise to sunset into 12 equal parts is almost beyond belief. In Constantinople, to-day, this is used, but in a rather imperfect manner, for the clocks are modern and run 24 hours uniformly; so the best they can do is to set them to mark twelve at sunset. This necessitates setting to the varying length of the days, so that the clocks appear to be sometimes more and sometimes less than six hours ahead of ours. A clock on the tower at the Sultan's private mosque gives the impression of being out of order and about six hours ahead, but it is running correctly to their system. Hotels often show two clocks, one of them to our twelve o'clock noon system. Evidently the Jewish method of ending a day at sunset is the same and explains the command, “let not the sun go down upon thy wrath,” which we might read, do not carry your anger over to another day. I venture to say that we still need that advice.
This simple line of steps in dividing the day and night is taken principally from the Bible because everyone can easily look up the passages quoted and many more, while quotations from books not in general use would not be so clear. Further, the neglect of the Bible is such a common complaint in this country that if I induce a few to look into it a little some good may result, quite apart from the matter of religious belief.
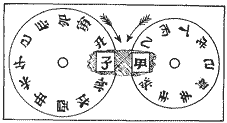
Some Chinese and Japanese methods of dividing the day and night are indicated in Fig. 1. The old Japanese method divides the day into six hours and the night also into six, each hour averaging twice as long as ours. In some cases they did this by changing the rate of the clock, and in others by letting the clock run uniformly and changing the hour marks on the dial, but this will come later when we reach Japanese clocks.
It is remarkable that at the present time in England the “saving daylight” agitation is virtually an attempt to go back to this discarded system. “John Bull,” for a long period the time-keeper of the world with headquarters at Greenwich, and during that time the most pretentious clock-maker, now proposes to move his clocks backward and forward several times a year so as to “fool” his workmen out of their beds in the mornings! Why not commence work a few minutes earlier each fortnight while days are lengthening and the reverse when they are shortening?
This reminds me of a habit which was common in Scotland,—“keeping the clock half an hour forward.” In those days work commenced at six o'clock, so the husband left his house at six and after a good walk arrived at the factory at six! Don't you see that if his clock had been set right he would have found it necessary to leave at half past five? But, you say he was simply deceiving himself and acting in an unreasonable manner. Certainly, but the average man is not a reasonable being, and “John Bull” knows this and is trying to fool the average Englishman.
Now, as to the methods of measuring time, we must use circumstantial evidence for the pre-historic period. The rising and the going down of the sun—the lengthening shadows, etc., must come first, and we are on safe ground here, for savages still use primitive methods like setting up a stick and marking its shadow so that a party trailing behind can estimate the distance the leaders are ahead by the changed position of the shadow. Men notice their shortening and lengthening shadows to this day. When the shadow of a man shortens more and more slowly till it appears to be fixed, the observer knows it is noon, and when it shows the least observable lengthening then it is just past noon. Now, it is a remarkable fact that this crude method of determining noon is just the same as “taking the sun” to determine noon at sea. Noon is the time at which the sun reaches his highest point on any given day. At sea this is determined generally by a sextant, which simply measures the angle between the horizon and the sun. The instrument is applied a little before noon and the observer sees the sun creeping upward slower and slower till a little tremor or hesitation appears indicating that the sun has reached his height,—noon. Oh! you wish to know if the observer is likely to make a mistake? Yes, and when accurate local time is important, several officers on a large ship will take the meridian passage at the same time and average their readings, so as to reduce the “personal error.” All of which is merely a greater degree of accuracy than that of the man who observes his shadow.
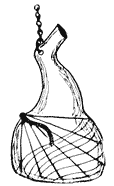
The gradual development of the primitive shadow methods culminated in the modern sundial. The “dial of Ahas,” Isa. XXXVIII, 8, on which the sun went back 10 “degrees” is often referred to, but in one of the revised editions of the unchangeable word the sun went back 10 “steps.” This becomes extremely interesting when we find that in India there still remains an immense dial built with steps instead of hour lines. Figure 2 shows a pocket, or portable sundial taken from the ruins of Herculaneum and now in the Museo National, Naples. It is bronze, was silver plated and is in the form of a ham suspended from the hock joint. From the tail, evidently bent from its original position, which forms the gnomon, lines radiate and across these wavy lines are traced. It is about 5 in. long and 3 in. wide. Being in the corner of a glass case I was unable to get small details, but museum authorities state that names of months are engraved on it, so it would be a good guess that these wavy lines had something to do with the long and short days.
In a restored flower garden, within one of the large houses in the ruins of Pompeii, may be seen a sundial of the Armillary type, presumably in its original position. I could not get close to it, as the restored garden is railed in, but it looks as if the plane of the equator and the position of the earth's axis must have been known to the maker.
Both these dials were in use about the beginning of our era and were covered by the great eruption of Vesuvius in 79 A.D., which destroyed Pompeii and Herculaneum.
Modern sundials differ only in being more accurately made and a few “curiosity” dials added. The necessity for time during the night, as man's life became a little more complicated, necessitated the invention of time machines. The “clepsydra,” or water clock, was probably the first. A French writer has dug up some old records putting it back to Hoang-ti 2679 B.C., but it appears to have been certainly in use in China in 1100 B.C., so we will be satisfied with that date. In presenting a subject to the young student it is sometimes advisable to use round numbers to give a simple comprehension and then leave him to find the overlapping of dates and methods as he advances. Keeping this in mind, the following table may be used to give an elementary hint of the three great steps in time measuring:
- Shadow time, 2000 to 1000 B. C.
- Dials and Water Clocks, 1000 B. C. to 1000 A. D.
- Clocks and watches, 1000 to 2000 A. D.
I have pushed the gear wheel clocks and watches forward to 2000 A.D., as they may last to that time, but I have no doubt we will supersede them. At the present time science is just about ready to say that a time measurer consisting of wheels and pinions—a driving power and a regulator in the form of a pendulum or balance, is a clumsy contrivance and that we ought to do better very soon; but more on this hoped-for, fourth method when we reach the consideration of the motion on which we base all our time keeping.
It is remarkable how few are aware that the simplest form of sundial is the best, and that, as a regulator of our present clocks, it is good within one or two minutes. No one need be without a “noon-mark” sundial; that is, every one may have the best of all dials. Take a post or any straight object standing “plumb,” or best of all the corner of a building as in Fig. 3. In the case of the post, or tree trunk, a stone (shown in solid black) may be set in the ground; but for the building a line may often be cut across a flagstone of the footpath. Many methods may be employed to get this noon mark, which is simply a north and south line. Viewing the pole star, using a compass (if the local variation is known) or the old method of finding the time at which the shadow of a pole is shortest. But the best practical way in this day is to use a watch set to local time and make the mark at 12 o'clock.
On four days of the year the sun is right and your mark may be set at 12 on these days, but you may use an almanac and look in the column marked “mean time at noon” or “sun on meridian.” For example, suppose on the bright day when you are ready to place your noon mark you read in this column 11:50, then when your watch shows 11:50 make your noon mark to the shadow and it will be right for all time to come. Owing to the fact that there are not an even number of days in a year, it follows that on any given yearly date at noon the earth is not at the same place in its elliptical orbit and the correction of this by the leap years causes the equation table to vary in periods of four years. The centennial leap years cause another variation of 400 years, etc., but these variations are less than the error in reading a dial.
| SUN ON NOON MARK, 1909 | |||||
|---|---|---|---|---|---|
| Date | Clock Time |
Date | Clock Time |
Date | Clock Time |
| Jan. 2 | 12:04 | May 1 | 11:57 | Sep. 30 | 11:50 |
| “ 4 | 12:05 | “ 15 | 11:56 | Oct. 3 | 11:49 |
| “ 7 | 12:06 | “ 28 | 11:57 | “ 6 | 11:48 |
| “ 9 | 12:07 | June 4 | 11:58 | “ 10 | 11:47 |
| “ 11 | 12:08 | “ 10 | 11:59 | “ 14 | 11:46 |
| “ 14 | 12:09 | “ 14 | 12:00 | “ 19 | 11:45 |
| “ 17 | 12:10 | “ 19 | 12:01 | “ 26 | 11:44 |
| “ 20 | 12:11 | “ 24 | 12:02 | Nov. 17 | 11:45 |
| “ 23 | 12:12 | “ 29 | 12:03 | “ 22 | 11:46 |
| “ 28 | 12:13 | July 4 | 12:04 | “ 25 | 11:47 |
| Feb. 3 | 12:14 | “ 10 | 12:05 | “ 29 | 11:48 |
| “ 26 | 12:13 | “ 19 | 12:06 | Dec. 1 | 11:49 |
| Mar. 3 | 12:12 | Aug. 11 | 12:05 | “ 4 | 11:50 |
| “ 8 | 12:11 | “ 16 | 12:04 | “ 6 | 11:51 |
| “ 11 | 12:10 | “ 21 | 12:03 | “ 9 | 11:52 |
| “ 15 | 12:09 | “ 25 | 12:02 | “ 11 | 11:53 |
| “ 18 | 12:08 | “ 28 | 12:01 | “ 13 | 11:54 |
| “ 22 | 12:07 | “ 31 | 12:00 | “ 15 | 11:55 |
| “ 25 | 12:06 | Sep. 4 | 11:59 | “ 17 | 11:56 |
| “ 28 | 12:05 | “ 7 | 11:58 | “ 19 | 11:57 |
| Apr. 1 | 12:04 | “ 10 | 11:57 | “ 21 | 11:58 |
| “ 4 | 12:03 | “ 12 | 11:56 | “ 23 | 11:59 |
| “ 7 | 12:02 | “ 15 | 11:55 | “ 25 | 12:00 |
| “ 11 | 12:01 | “ 18 | 11:54 | “ 27 | 12:01 |
| “ 15 | 12:00 | “ 21 | 11:53 | “ 29 | 12:02 |
| “ 19 | 11:59 | “ 24 | 11:52 | “ 31 | 12:03 |
| “ 24 | 11:58 | “ 27 | 11:51 | ||
| The above table shows the variation of the sun from “mean” or clock time, by even minutes. | |||||
The reason that the table given here is convenient for setting clocks to mean time is that a minute is as close as a dial can be read, but if you wish for greater accuracy, then the almanac, which gives the “equation of time” to a second for each day, will be better. The reason that these noon-mark dials are better than ordinary commercial dials is that they are larger, and still further, noon is the only time that any dial is accurate to sun time. This is because the sun's rays are “refracted” in a variable manner by our atmosphere, but at noon this refraction takes place on a north and south line, and as that is our noon-mark line the dial reads correctly. So, for setting clocks, the corner of your house is far ahead of the most pretentious and expensive dial. In Fig. 4 is shown a modern horizontal dial without the usual confusing “ornamentation,” and in Fig. 5 it is shown set up on the latitude of New York City for which it is calculated. This shows clearly why the edge FG of the style which casts the shadow must be parallel to the earth's axis and why a horizontal dial must be made for the latitude of the place where it is set up. Figure 6 is the same dial only the lines are laid out on a square dial plate, and it will give your young scientific readers a hint of how to set up a dial in the garden. In setting up a horizontal dial, consider only noon and set the style, or 12 o'clock line, north and south as described above for noon-mark dials.
A whole issue of Popular Mechanics could be filled on the subject of dials and even then only give a general outline. Astronomy, geography, geometry, mathematics, mechanics, as well as architecture and art, come in to make “dialing” a most charming scientific and intellectual avocation.
During the night and also in cloudy weather the sundial was useless and we read that the priests of the temples and monks of more modern times “went out to observe the stars” to make a guess at the time of night. The most prominent type after the shadow devices was the “water clock” or “clepsydra,” but many other methods were used, such as candles, oil lamps and in comparatively late times, the sand glass. The fundamental principle of all water clocks is the escape of water from a vessel through a small hole. It is evident that such a vessel would empty itself each time it is filled in very nearly the same time. The reverse of this has been used as shown in Fig. 7, which represents the “time-boy” of India. He sits in front of a large vessel of water and floats a bronze cup having a small hole in its bottom in this large vessel, and the leakage gradually lowers this cup till it sinks, after which he fishes it up and strikes one or more blows on it as a gong. This he continues and a rude division of time is obtained,—while he keeps awake!
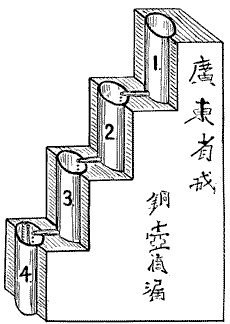
The most interesting of all water clocks is undoubtedly the “copper jars dropping water,” in Canton, China, where I saw it in 1897. Referring to the simple line sketch, which I make from memory, Fig. 8, and reading four Chinese characters downwards the translation is “Canton City.” To the left and still downwards,—“Hon-woo-et-low,” which is,—“Copper jars dropping water.” Educated Chinamen inform me that it is over 3,000 years old and had a weather vane. As they speak of it as “the clock of the street arch” this would look quite probable; since the little open building, or tower in which it stands is higher than surrounding buildings. It is, therefore, reasonably safe to state that the Chinese had a weather and time station over 1,000 years before our era. It consists of four copper jars partially built in masonry forming a stair-like structure. Commencing at the top jar each one drops into the next downward till the water reaches the solid bottom jar. In this lowest one a float, “the bamboo stick,” is placed and indicates the height of the water and thus in a rude way gives the time. It is said to be set morning and evening by dipping the water from jar 4 to jar 1, so it runs 12 hours of our time. What are the uses of jars 2 and 3, since the water simply enters them and drips out again? No information could be obtained, but I venture an explanation and hope the reader can do better, as we are all of a family and there is no jealousy. When the top jar is filled for a 12-hour run it would drip out too fast during the first six hours and too slow during the second six hours, on account of the varying “head” of water. Now, the spigot of jar 2 could be set so that it would gain water during the first six hours, and lose during the second six hours and thus equalize a little by splitting the error of jar 1 in two parts. Similarly, these two errors of jar 2 could be again split by jar 3 making four small variations in lowest jar, instead of one large error in the flow of jar 1. This could be extended to a greater number of jars, another jar making eight smaller errors, etc., etc. But I am inclined to credit our ancient Chinese inventor with the sound reasoning that a human attendant, being very fallible and limited in his capacity, would have all he could properly do to adjust four jars, and that his record would average better than it would with a greater number. Remember, this man lived thousands of years before the modern mathematician who constructed a bell-shaped vessel with a small hole in the bottom, and proportioned the varying diameter in such a manner that in emptying itself the surface of the water sank equal distances in equal times. The sand glass, Fig. 9, poetically called the “hour glass,” belongs to the water-clock class and the sand flows from one bulb into the other, but it gives no subdivisions of its period, so if you are using one running an hour it does not give you the half hour. The sand glass is still in use by chairmen, and when the oldest inhabitant gets on his feet, I always advise setting a 20-minute glass “on him.”
In the “Tower of the Winds” at Athens, Greece (Fig. 10), we have a later “weather bureau” station. It is attributed to the astronomer Andronicos, and was built about 50 B. C. It is octagonal in plan and although 27 ft. in diameter and 44 ft. high, it looks like a sentry box when seen from one of the hills of Athens. It had a bronze weather vane and in later times sundials on its eight sides, but all these are gone and the tower itself is only a dilapidated ruin. In making the drawing for this cut, from a photograph of the tower, I have sharpened the weathered and chipped corners of the stones so as to give a view nearly like the structure as originally built; but nothing is added. Under the eaves it has eight allegorical sculptures, representing wind and weather. Artists state that these sculptures are inferior as compared with Grecian art of an older period. But the most interesting part is inside, and here we find curious passages cut in solid stone, and sockets which look as if they had contained metal bearings for moving machinery. Circumstantial evidence is strong that it contained a complicated water clock which could have been kept running with tolerable accuracy by setting it daily to the dials on the outside. Probably during a few days of cloudy weather the clock would “get off quite a little,” but business was not pressing in those days. Besides, the timekeeper would swear by his little water wheel, anyway, and feel safe, as there was no higher authority wearing an American watch.
Some very interesting engravings of Japanese clocks and a general explanation of them, as well as a presentation of the Japanese mental attitude towards “hours” and their strange method of numbering them may be expected in the next chapter.
CHAPTER II
JAPANESE CLOCKS
Chinese and Japanese divisions of the day. — Hours of varying length. — Setting clocks to length of daylight. — Curved line dials. — Numbering hours backwards and strange reasons for same. — Daily names for sixty day period. — Japanese clock movements practically Dutch. — Japanese astronomical clock. — Decimal numbers very old Chinese. — Original vertical dials founded on “bamboo stick” of Chinese clepsydra. — Mathematics and superstition. — Mysterious disappearance of hours 1, 2, 3. — Eastern mental attitude towards time. — Japanese methods of striking hours and half hours.
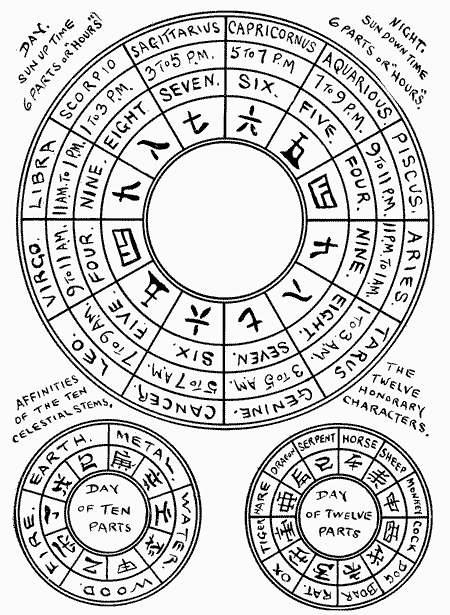
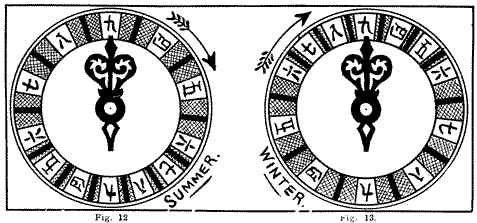
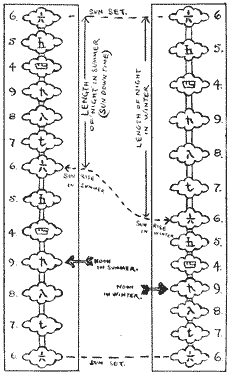
The ancient methods of dividing day and night in China and Japan become more hazy as we go backwards and the complications grow. The three circles in Fig. 1 (Chapter I) are all taken from Japanese clocks, but the interpretation has been obtained from Chinese and Japanese scholars. The Japanese obtained a great deal from the Chinese, in fact nearly everything relating to the ancient methods of time keeping and the compiling of calendars. I have not been able to find any Chinese clocks constructed of wheels and pinions, but have a number of Japanese. These have a distinct resemblance to the earlier Dutch movements, and while made in Japan, they are practically Dutch, so far as the “works” are concerned, but it is easy to see from the illustrations that they are very Japanese in style and ornamentation. The Dutch were the leaders in opening Japan to the European nations and introduced modern mathematics and clocks from about 1590 A. D. The ancient mathematics of Japan came largely from China through Corea. In Fig. 11 are given the Japanese figures beside ours, for the reader's use as a key. The complete day in Japan was divided into twice six hours; that is, six for daylight and six for night, and the clocks are set, as the days vary in length, so that six o'clock is sunrise and sunset. The hour numerals on Fig. 12 are on little plates which are movable, and are shown set for a long day and a short night.
In Fig. 13 they are set for short days and long nights. The narrow plates shown in solid black are the half-hour marks. In this type the hand is stationary and always points straight upward. The dial rotates, as per arrow, once in a full day. This style of dial is shown on complete clocks, Fig. 14 being a weight clock and Fig. 15 a spring clock with chain and fusee. The hours are 9 to 4 and the dials rotate to make them read backwards. The six hours of daylight are 6, 5, 4, 9, 8, 7, 6 and the same for night, so these hours average twice as long as ours. Note that nine is mid-day and mid-night, and as these do not change by long and short days they are stationary on the dial, as you can easily see by comparing Figs. 12 and 13, which are the same dial set for different seasons. Between these extremes the dial hours are set as often as the owner wishes; so if he happens to correspond with our “time crank” he will set them often and dispute with his neighbors about the time. Figure 16 shows a clock with the hour numerals on a vertical series of movable plates and it is set for uniform hours when day and night are equal at the equinox. The ornamental pointer is fastened to the weight through the vertical slit, plainly visible in illustration, and indicates the time as it descends. This clock is wound up at sunset, so the six on the top of the dial is sunset the same as the six on the bottom. Figure 17 shows how this type of dial is set for long and short days and explains itself, but will become plainer as we proceed. This dial is virtually a continuation of the old method of marking time by the downward motion of the water in the clepsydras and will be noticed later.
Figure 18 represents a clock which is a work of art and shows great refinement of design in providing for the varying lengths of days. The bar lying across the dial is fastened to the weight through the two slits running the whole length of the dial. On this cross bar is a small pointer, which is movable by the fingers, and may be set to any one of the thirteen vertical lines. The numerous characters on the top space of dial indicate the dates on which the pointer is to be set. This clock is wound up at sunset, and it is easy to see that as the little pointer is set towards the right, the night hours at the top of the dial become shorter and the day hours longer on the lower part. The left edge of the dial gives the hours, reading downwards, and as the pointer touches any one of the curved lines the hour is read at the left-hand end. The curved lines formed of dots are the half-hours. The right-hand edge of the dial has the “twelve horary characters” which will be explained later. For dividing the varying days into six hours' sunshine it would be difficult to think of a more artistic and beautiful invention than this. It is a fine example of great ingenuity and constant trouble to operate a system which is fundamentally wrong according to our method of uniform hours at all seasons. Clocks having these curved lines for the varying lengths of days—and we shall find them on circular dials as we go on—must be made for a certain latitude, since the days vary more and more as you go farther from the equator. This will become plain when you are reminded that a Japanese clock at the equator would not need any adjustment of hour numerals, because the days and nights are equal there all the year. So after such infinite pains in forming these curved lines the clock is only good in the latitude for which it was made and must not be carried north or south! Our clocks are correct from pole to pole, but all clocks must be set to local time if they are carried east or west. As this is a rather fascinating phase of the subject it might be worth pointing out that if you go north till you have the sun up for a month in the middle of summer—and there are people living as far up as that—the Japanese system would become absurd and break down; so there is no danger of any of our polar expeditions carrying Japanese clocks.
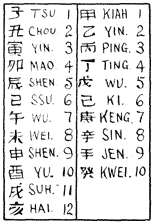
Figure 19 shows a very fine clock in which the dial is stationary and the hand moves just as on our dials. This hour hand corresponds to the single hand of the old Dutch clocks. When the Japanese reached the point of considering the application of minute and second hands to their clocks they found that these refinements would not fit their old method and they were compelled to lay aside their clocks and take ours. On this dial, Fig. 19, nine is noon, as usual, and is on top side of dial. Hand points to three quarters past seven, that is, a quarter to six, near sunset. Between the bell and the top of the clock body two horizontal balances, having small weights hung on them, are plainly shown, and the clock has two verge escapements—one connected with each balance, or “foliot.” Let us suppose a long day coming to a close at sunset, just as the hand indicates. The upper balance, which is the slow one, has been swinging backwards and forwards measuring the long hours of the day. When the clock strikes six, at sunset, the top balance is thrown out of action and the lower one, which is the fast one, is thrown into action and measures the short night hours. At sunrise this is thrown out and the top one in again to measure the next day's long hours. As the days vary in length, the balances, or foliots, can be made to swing faster or slower by moving the weights inwards or outwards a notch or two. The balance with small weights for regulation is the oldest known and was used in connection with the verge escapement, just as in this clock, by the Dutch about 1364. All the evidence I can find indicates that the Japanese clocks are later than this date. In design, ornamentation and methods for marking varying days, however, the Japanese have shown great artistic taste and inventiveness. It is seen that this dial in addition to the usual six hours, twice over, has on the outside circle of dial, the “twelve horary branches” called by the Japanese the “twelve honorary branches,” thus indicating the whole day of twelve Japanese hours, six of them for day and six for night. By this means they avoided repeating the same hours for day and night. When it is pointed out that these “twelve horary branches” are very old Chinese, we are not in a position to boast about our twenty-four hour system, because these branches indicate positively whether any given hour is day or night. When we print a time table in the twenty-four hour system so as to get rid of our clumsy A. M. and P. M., we are thousands of years behind the Chinese. More than that, for they got the matter right without any such pressure as our close running trains have brought to bear on us. These branches have one syllable names and the “ten celestial stems” have also one syllable names, all as shown on Fig. 20. Refer now to Fig. 21 where two disks are shown, one having the “twelve horary branches” and the other the “ten celestial stems.” These disks are usually put behind the dial so that one “branch” and one “stem” can be seen at the same time through two openings. The clock moves these disks one step each night, so that a new pair shows each day. Running in this manner, step by step, you will find that it takes sixty moves, that is sixty days, to bring the same pair around again. Each has a single syllable name, as shown on Fig. 20, and we thus get sixty names of two syllables by reading them together to the left. The two openings may be seen in the dials of Figs. 15 and 19. So the Japanese know exactly what day it is in a period of sixty which they used in their old calendars. These were used by the Chinese over four thousand years ago as the names of a cycle of sixty years, called the “sexagenary.” The present Chinese year 4606 is YU-KI which means the year 46 of the 76th “sexagenary.” That is, 76×60+46 = 4,606. In Fig. 20, we read TSU-KIAH, or the first year. If you will make two disks like Fig. 21 and commence with TSU-KIAH and move the two together you will come to YU-KI on the 46th move. But there is another way which you might like better, thus: Write the twelve “branches,” or syllables, straight downwards, continuously five times; close to the right, write the ten “stems” six times. Now you have sixty words of two syllables and the 46th, counting downwards, will be YU-KI. Besides, this method gives you the whole sixty names of the “sexagenary” at one view. Always read left, that is, pronounce the “stem” syllable first.

Calendars constitute a most interesting and bewildering part of time measuring. We feel that we have settled the matter by determining the length of the year to within a second of time, and keeping the dates correctly to the nearest day by a leap year every fourth and every fourth century, established by Pope Gregory XIII in 1582, and known as the “Gregorian Calendar.” In simple words, our “almanac” is the “Gregorian.” We are in the habit of saying glibly that any year divisible by four is a leap year, but this is far from correct. Any year leaving out the even hundreds, which is divisible by four is a leap year. Even hundreds are leap when divisible by four. This explains why 1900 was a common year, because 19 hundreds is not divisible by four; 2000 will be a leap because 20 hundreds is divisible by four; therefore 2100, 2200 and 2300 will be common years and 2400 a leap, etc., to 4000 which must be made common, to keep things straight, in spite of the fact that it is divisible by four both in its hundreds and thousands. But for practical purposes, during more than two thousand years to come, we may simplify the rule to: Years and even hundreds divisible by four are leaps. But great confusion still exists as a result of several countries holding to their own old methods. The present Chinese year has 384 days, 13 months and 13 full moons. Compared with our 1909 it begins on January 21st and will end on February 8, 1910. Last year the China-Japan calendar had 12 months, or moons, but as that is too short they must put in an extra every thirtieth month. We only allow the error to reach one day and correct it with our leap years, but they are not so particular and let the error grow till they require another “moon.” The Old Testament is full of moons, and even with all our “modernity” our “feasts” and holy days are often “variable” on account of being mixed up with moons. In Japan the present year is the 42nd of Meiji, that is, the 42nd of the present Emperor's reign. The present is the Jewish 5669. These and others of varying lengths overlap our year in different degrees, so that in trade matters great confusion exists. The Chinese and Japanese publish a trade almanac in parallel columns with ours to avoid this. It is easy to say that we ought to have a uniform calendar all over the world, but the same remark applies just as much to money, weights, measures, and even to language itself. Finally, the difficulty consists in the facts that there are not an even number of days in a year—or in a moon—or moons in a year. “These many moons” is a survival in our daily speech of this old method of measuring by moons. Just a little hint as to the amount of superstition still connected with “new moon” will be enough to make clear the fact that we are not yet quite so “enlightened” as we say we are. While our calendar, or almanac, may be considered as final, we must remember that custom and religion are so mixed up with the matter in the older countries of the East that they will change very slowly. Strictly, our “era” is arbitrary and Christian; so we must not expect nations which had some astronomical knowledge and a working calendar, thousands of years before us, to change suddenly to our “upstart” methods.
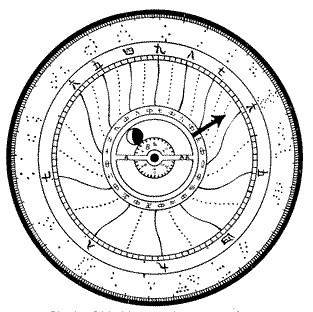
In Fig. 22 we have the dial of a very complicated astronomical clock. This old engraved brass dial did not photograph well, so I made a copy by hand to get clean lines. Commencing at the centre, there is a small disk, B, numbered from 1 to 30, giving days of the moon's age. The moon rises at A and sets at AA, later each day, of course. Her age is shown by the number she touches on disk B, as this disk advances on the moon one number each day. Her phases are shown by the motion of a black disk over her face; so we have here three motions for the moon, so differentiated as to show phase, ascension and age. Still further, as she is represented on the dial when below the horizon, it can be seen when she will rise, and “moonlight” parties may be planned. Just outside the moon's course is an annulus having Japanese numbers 1 to 12, indicating months. Note the recurring character dividing the months in halves, which means “middle,” and is much used. If you will carefully read these numbers you will find a character where one would come; this means “beginning” or “primary” and is often used instead of one. The clock hand is the heavy arrow and sweeps the dial once in a whole day, same direction as our clocks. This circle of the months moves along with the hand, but a little faster, so as to gain one number in a month. As shown on the figure it is about one week into the sixth month. Next outward is the broad band having twelve curved lines for the hours ending outwardly in a ring divided into 100 parts, marked off in tens by dots. These curved lines are numbered with the Japanese numerals for hours which you must now be able to read easily. These hour lines, and the dotted lines for half hours, are really the same as the similar lines on Fig. 18 which you now understand. As the hand sweeps the dial daily it automatically moves outward a little each day, so it shortens the nights and lengthens the days, just as previously explained for Fig. 18. But there is one difference, for you will notice that the last night hour, on which the arrow hand now stands, is longer than the other night hours before it, and that it is divided into three by the dotted lines. The last day hour, on the left of dial, is also long and divided into three. That is, while all the dials previously described have equal hours for any given day, or night, this dial has a last long hour in each case, divided into three instead of the usual half-hours. This is a curious and interesting point having its origin long before clocks. In the early days of the clepsydra in China, a certain time was allowed to dip up the water from the lowest jar, each morning and evening about five o'clock of our time, see Fig. 8 (Chapter 1). During this operation the clepsydra was not marking time, and the oriental mind evidently considered it in some sense outside of the regular hours, and like many other things was retained till it appeared absurdly on the earlier clocks. This wonderful feat of putting an interval between two consecutive hours has always been impossible to modern science; yet President Roosevelt performed it easily in his “constructive” interregnum! Referring to the Canton clepsydra, Fig. 8, we find that the float, or “bamboo stick,” was divided into 100 parts. At one season 60 parts for the day and 40 parts for the night, gradually being changed to the opposite for short days. The day hours were beaten on a drum and the night hours blown on a trumpet.
Later the hour numerals were made movable on the “bamboo stick.” This is virtually a vertical dial with movable hour plates, so their idea of time measuring at that date, was of something moving up or down. This was put on the first clocks by the Japanese; so that the dial of Fig. 16 is substantially the float of the Chinese clepsydra. Further, in this “bamboo stick” of 100 parts, we have our present system of decimal numbers, so we can afford to be a little modest here too. Before leaving Fig. 22 note the band, or annulus, of stars which moves with the month circle. I cannot make these stars match our twelve signs of the Zodiac, but as I have copied them carefully the reader can try and make order out of them. The extreme outer edge of the dial is divided into 360 parts, the tens being emphasized, as in our decimal scales.
As we are getting a little tired of these complicated descriptions, let us branch off for a few remarks on some curiosities of Eastern time keeping. They evidently think of an hour as a period of time more specifically than we do. When we say “6 o'clock” we mean a point of time marked by the striking of the clock. We have no names for the hour periods. We must say “from 5 to 6” or “between 5 and 6” for an hour period. The “twelfth hour” of the New Testament, I understand to mean a whole hour ending at sunset; so we are dealing with an oriental attitude of mind towards time. I think we get that conception nearly correct when we read of the “middle watch” and understand it to mean during the middle third of the night. Secondly, why do the Japanese use no 1, 2, 3 on their dials? These numbers were sacred in the temples and must not be profaned by use on clocks, and they mentally deducted these from the clock hours, but ultimately became accustomed to 9, 8, 7, 6, 5, 4. Thirdly, why this reading of the hours backwards? Let us suppose a toiler commencing at sunrise, or six. When he toiled one hour he felt that there was one less to come and he called it five. This looks quite logical, for the diminishing numbers indicated to him how much of his day's toil was to come. Another explanation which is probably the foundation of “secondly” and “thirdly” above, is the fact that mathematics and superstition were closely allied in the old days of Japan. If you take the numbers 1 to 6, Fig. 23, and multiply them each into the uncanny “yeng number,” or nine, you will find that the last digits, reading downwards, give 9, 8, 7, 6, 5, 4. Stated in other words: When 1 to 6 are multiplied into “three times three” the last figures are 9, 8, 7, 6, 5, 4, and 1, 2, 3, have disappeared; so the common people were filled with fear and awe. Some of the educated, even now, are mystified by the strange results produced by using three and nine as factors, and scientific journals often give space to the matter. We know that these results are produced by the simple fact that nine is one less than the “radix” of our decimal scale of numbers. Nine is sometimes called the “indestructible number,” since adding the digits of any of its powers gives an even number of nines. But in those days it was a mystery and the common people feared the mathematicians, and I have no doubt the shrewd old fellows took full advantage of their power over the plebeians. In Japan, mathematics was not cleared of this rubbish till about 700 A. D.
On the right-hand side of Fig. 23 are given the animal names of the hours, so the day and night hours could not be mistaken. In selecting the rat for night and the horse for day they showed good taste. Their forenoon was “before horse” and their afternoon “after horse.” Japanese clocks are remarkable for variety. It looks as if they were always made to order and that the makers, probably urged by their patrons, made extreme efforts to get in wonderful motions and symbols relating to astronomy and astrology. Anyone examining about fifty of them would be likely to conclude that it was almost hopeless to understand them all. Remember, this is the old Japanese method. Nearly all the clocks and watches I saw in Japan were American. It will now be necessary to close this chapter with a few points on the curious striking of Japanese clocks.
In those like Figs. 14, 15, 19, the bell and hammer can be seen. In the type of Fig. 16, the whole striking mechanism is in the weight. In fact, the striking part of the clock is the weight. On each of the plates, having the hour numerals, Fig. 16, a pin projects inwards and as the weight containing the striking mechanism, descends, a little lever touches these and lets off the striking just when the pointer is on the hour numeral. Keeping this in mind, it is easy to see that the clock will strike correctly when the hour is indicated by the pointer, no matter how the hour plates are set for long or short days. Similar pins project inwards from movable plates on Figs. 12, 13, 14, 15, so they strike correctly as each hour plate comes to the top just under the point of the fixed hand. In Fig. 19, the striking is let off by a star wheel just as in old Dutch clocks. Clocks like Figs. 18-22 do not strike. In all cases the hours are struck backwards, but the half-hours add another strange feature. The odd numbered hours, 9, 7, 5, are followed by one blow at the half hour; and the even hours, 8, 6, 4 by two blows, or stated altogether—
91 82 71 62 51 42.
Here the large figures are the hours and the small ones the half-hours. Only one bell is used, because there being no one and two among the hours, the half-hours cannot be mistaken. This is not all, for you can tell what half hour it is within two hours. For example, suppose you know approximately that it is somewhere between 9 and 7 and you hear the clock strike 2, then you know it is half past 8. See the large and small figures above. This is far superior to our method of one at each half-hour.
By our method the clock strikes one three times consecutively, between 12 and 2 o'clock and thus mixes up the half hours with one o'clock. Some interesting methods of striking will be explained in the third chapter when we deal with modern time keeping.

CHAPTER III
MODERN CLOCKS
DeVick's clock of 1364. — Original “verge” escapement. — “Anchor” and “dead beat” escapements. — “Remontoir” clock. — The pendulum. — Jeweling pallets. — Antique clock with earliest application of pendulum. — Turkish watches. — Correct designs for public clock faces. — Art work on old watches. — Twenty-four hour watch. — Syrian and Hebrew hour numerals. — Correct method of striking hours and quarters. — Design for twenty-four hour dial and hands. — Curious clocks. — Inventions of the old clockmakers.
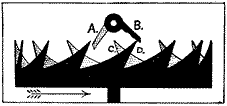
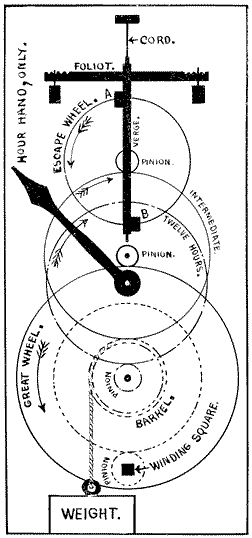
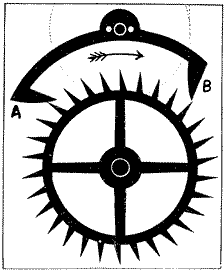
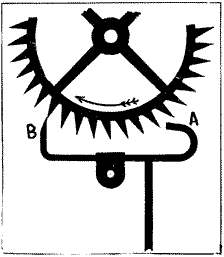
Modern clocks commence with De Vick's of 1364 which is the first unquestioned clock consisting of toothed wheels and containing the fundamental features of our present clocks. References are often quoted back to about 1000 A. D., but the words translated “clocks” were used for bells and dials at that date; so we are forced to consider the De Vick clock as the first till more evidence is obtained. It has been pointed out, however, that this clock could hardly have been invented all at once; and therefore it is probable that many inventions leading up to it have been lost to history. The part of a clock which does the ticking is called the “escapement” and the oldest form known is the “verge,” Fig. 25, the date of which is unknown, but safely 300 years before De Vick. The “foliot” is on the vertical verge, or spindle, which has the pallets A B. As the foliot swings horizontally, from rest to rest, we hear one tick, but it requires two of these single swings, or two ticks, to liberate one tooth of the escape wheel; so there are twice as many ticks in one turn of the escape wheel as it has teeth. We thus see that an escapement is a device in which something moves back and forth and allows the teeth of an “escape wheel” to escape. While this escapement is, in some respects, the simplest one, it has always been difficult to make it plain in a drawing, so I have made an effort to explain it by making the side of the wheel and its pallet B, which is nearest the eye, solid black, and farther side and its pallet A, shaded as in the figure. The wheel moves in the direction of the arrow, and tooth D is very near escaping from pallet B. The tooth C on the farther side of wheel is moving left, so it will fall on pallet A, to be in its turn liberated as the pallets and foliot swing back and forth. It is easy to see that each tooth of the wheel will give a little push to the pallet as it escapes, and thus keep the balance swinging. This escapement is a very poor time-keeper, but it was one of the great inventions and held the field for about 600 years, that is, from the days when it regulated bells up to the “onion” watches of our grandfathers. Scattered references in old writings make it reasonably certain that from about 1,000 to 1,300 bells were struck by machines regulated with this verge escapement, thus showing that the striking part of a clock is older than the clock itself. It seems strange to us to say that many of the earlier clocks were strikers, only, and had no dials or hands, just as if you turned the face of your clock to the wall and depended on the striking for the time. Keeping this action of the verge escapement in mind we can easily understand its application, as made by De Vick, in Fig. 26, where I have marked the same pallets A B. A tooth is just escaping from pallet B and then one on the other side of the wheel will fall on pallet A. Foliot, verge and pallets form one solid piece which is suspended by a cord, so as to enable it to swing with little friction. For the purpose of making the motions very plain I have left out the dial and framework from the drawing. The wheel marked “twelve hours,” and the pinion which drives it, are both outside the frame, just under the dial, and are drawn in dash and dot. The axle of this twelve-hour wheel goes through the dial and carries the hand, which marks hours only. The winding pinion and wheel, in dotted lines, are inside the frame. Now follow the “great wheel”—“intermediate”—“escape wheel” and the two pinions, all in solid lines, and you have the “train” which is the principal part of all clocks. This clock has an escapement, wheels, pinions, dial, hand, weight, and winding square. We have only added the pendulum, a better escapement, the minute and second hands in over 500 years! The “anchor” escapement, Fig. 27, came about 1680 and is attributed to Dr. Hooke, an Englishman. It gets its name from the resemblance of the pallets to the flukes of an anchor. This anchor is connected to the pendulum and as it swings right and left, the teeth of the escape wheel are liberated, one tooth for each two swings from rest to rest, the little push on the pallets A B, as the teeth escape, keeping the pendulum going. It is astonishing how many, even among the educated, think that the pendulum drives the clock! The pendulum must always be driven by some power.
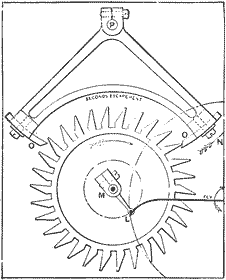
This escapement will be found in nearly all the grandfather clocks in connection with a seconds pendulum. It is a good time-keeper, runs well, wears well, stands some rough handling and will keep going even when pretty well covered with dust and cobwebs; so it is used more than all the numerous types ever invented. Figure 28 gives the general American form of the “anchor” which is made by bending a strip of steel; but it is not the best form, as the acting surfaces of the pallets are straight. It is, therefore, inferior to Fig. 27 where the acting surfaces are curved, since these curves give an easier “recoil.” This recoil is the slight motion backwards which the escape wheel makes at each tick. The “dead beat” escapement is shown in Fig. 29, and is used in clocks of a high grade, generally with a seconds pendulum. It has no recoil as you can easily see that the surfaces O O on which the teeth fall, are portions of a circle around the center P. The beveled ends of these pallets are called the impulse surfaces, and a tooth is just giving the little push on the right-hand pallet. It is found in good railroad clocks, watch-makers' regulators and in many astronomical clocks. These terms are merely comparative, a “regulator” being a good clock and an “astronomical,” an extra good one. Figure 30 gives the movement of a “remontoir” clock in which the dead beat shown is used. The upper one of the three dials indicates seconds, and the lever which crosses its center carries the large wheel on the left.
This wheel makes the left end of the lever heavier than the right, and in sinking it drives the clock for one minute, but at the sixtieth second it “remounts” by the action of the clock weight; hence the name, “remontoir.” Note here that the big weight does not directly drive the clock; it only rewinds it every minute. The minutes are shown on the dial to the right and its hand jumps forward one minute at each sixtieth second as the lever remounts; so if you wish to set your watch to this clock the proper way is to set it to the even minute “on the jump.” The hour hand is on the dial to the left. By this remounting, or rewinding, the clock receives the same amount of driving force each minute. The complete clock is shown in Fig. 31, the large weight which does the rewinding each minute being plainly visible. The pendulum is compensated with steel and aluminum, so that the rate of the clock may not be influenced by hot and cold weather. Was built in 1901 and is the only one I can find room for here. It is fully described in “Machinery,” New York, for Nov., 1901. I have built a considerable number, all for experimental purposes, several of them much more complicated than this one, but all differing from clocks for commercial purposes. Pallets like O O in Fig. 29 are often made of jewels; in one clock I used agates and in another, running thirteen months with one winding, I used pallets jeweled with diamonds. This is done to avoid friction and wear. Those interested in the improvement of clocks are constantly striving after light action and small driving weights. Conversely, the inferior clock has a heavy weight and ticks loud. The “gravity escapement” and others giving a “free” pendulum action would require too much space here, so we must be satisfied with the few successful ones shown out of hundreds of inventions, dozens of them patented. The pendulum stands at the top as a time measurer and was known to the ancients for measuring short periods of time just as musicians now use the metronome to get regular beats. Galileo is credited with noticing its regular beats, but did not apply it to clocks, although his son made a partially successful attempt. The first mathematical investigation of the pendulum was made by Huyghens about 1670, and he is generally credited with applying it to clocks, so there is a “Huyghens” clock with a pendulum instead of the foliot of De Vick's. Mathematically, the longer and heavier the pendulum the better is the time-keeping, but nature does not permit us to carry anything to the extreme; so the difficulty of finding a tower high enough and steady enough, the cumbersomeness of weight, the elasticity of the rod, and many other difficulties render very long and heavy pendulums impracticable beyond about 13 ft. which beats once in two seconds. “Big Ben” of Westminster, London, has one of this length weighing 700 lb. and measuring, over all, 15 ft.
It runs with an error under one second a week. This is surpassed only by some of the astronomical clocks which run sometimes two months within a second. This wonderful timekeeping is done with seconds pendulums of about 39 in., so the theoretical advantage of long pendulums is lost in the difficulties of constructing them. Fractions are left out of these lengths as they would only confuse the explanations. At the Naval observatory in Washington, D. C., the standard clocks have seconds pendulums, the rods of which are nickel steel, called “Invar,” which is little influenced by changes of temperature. These clocks are kept in a special basement, so they stand on the solid earth. The clock room is kept at a nearly uniform temperature and each clock is in a glass cylinder exhausted to about half an atmosphere. They are electric remontoirs, so no winding is necessary and they can be kept sealed up tight in their glass cylinders. Nor is any adjustment of their pendulums necessary, or setting of the hands, as the correction of their small variations is effected by slight changes in the air pressure within the glass cylinders. When a clock runs fast they let a little air into its cylinder to raise the resistance to the pendulum and slow it down, and the reverse for slow. Don't forget that we are now considering variations of less than a second a week.
The clock room has double doors, so the outer one can be shut before the inner one is opened, to avoid air currents. Visitors are not permitted to see these clocks because the less the doors are opened the better; but the Commander will sometimes issue a special permit and detail a responsible assistant to show them, so if you wish to see them you must prove to him that you have a head above your shoulders and are worthy of such a great favor.
The best thing the young student could do at this point would be to grasp the remarkable fact that the clock is not an old machine, since it covers only the comparatively short period from 1364 to the present day. Compared with the period of man's history and inventions it is of yesterday. Strictly speaking, as we use the word clock, its age from De Vick to the modern astronomical is only about 540 years. If we take the year 1660, we find that it represents the center of modern improvements in clocks, a few years before and after that date includes the pendulum, the anchor and dead beat escapements, the minute and second hands, the circular balance and the hair spring, along with minor improvements. Since the end of that period, which we may make 1700, no fundamental invention has been added to clocks and watches. This becomes impressive when we remember that the last 200 years have produced more inventions than all previous known history—but only minor improvements in clocks! The application of electricity for winding, driving, or regulating clocks is not fundamental, for the timekeeping is done by the master clock with its pendulum and wheels, just as by any grandfather's clock 200 years old. This broad survey of time measuring does not permit us to go into minute mechanical details. Those wishing to follow up the subject would require a large “horological library”—and Dr. Eliot's five-foot shelf would be altogether too short to hold the books.
A good idea of the old church clocks may be obtained from Fig. 32 which is one of my valued antiques. Tradition has followed it down as the “English Blacksmith's Clock.” It has the very earliest application of the pendulum. The pendulum, which I have marked by a star to enable the reader to find it, is less than 3 in. long and is hung on the verge, or pallet axle, and beats 222 per minute. This clock may be safely put at 250 years old, and contains nothing invented since that date. Wheels are cast brass and all teeth laboriously filed out by hand. Pinions are solid with the axles, or “staffs,” and also filed out by hand. It is put together, generally by mortise, tenon and cotter, but it has four original screws all made by hand with the file. How did he thread the holes for these screws? Probably made a tap by hand as he made the screws. But the most remarkable feature is the fact that no lathe was used in forming any part—all staffs, pinions and pivots being filed by hand. This is simply extraordinary when it is pointed out that a little dead center lathe is the simplest machine in the world, and he could have made one in less than a day and saved himself weeks of hard labor. It is probable that he had great skill in hand work and that learning to use a lathe would have been a great and tedious effort for him. So we have a complete striking clock made by a man so poor that he had only his anvil, hammer and file. The weights are hung on cords as thick as an ordinary lead pencil and pass over pulleys having spikes set around them to prevent the cords from slipping. The weights descend 7 ft. in 12 hours, so they must be pulled up—not wound up—twice a day. The single hour hand is a work of art and is cut through like lace. Public clocks may still be seen in Europe with only one hand. Many have been puzzled by finding that old, rudely made clocks often have fine dials, but this is not remarkable when we state that art and engraving had reached a high level before the days of clocks. It is worthy of note that clocks in the early days were generally built in the form of a church tower with the bell under the dome and Figs. 32, 33 show a good example. It is highly probable that the maker of this clock had access to some old church clock—a wonderful machine in those days—and that he laboriously copied it. It strikes the hours, only, by the old “count wheel” or “locking plate” method. Between this and our modern clocks appeared a type showing quarter hours on a small dial under the hour dial. No doubt this was at that time a great advance and looked like cutting time up pretty fine. As the hand on the quarter dial made the circuit in an hour the next step was easy, by simply dividing the circle of quarters into sixty minutes. The old fellows who thought in hours must have given it up at this point, so the seconds and fifths seconds came easily.
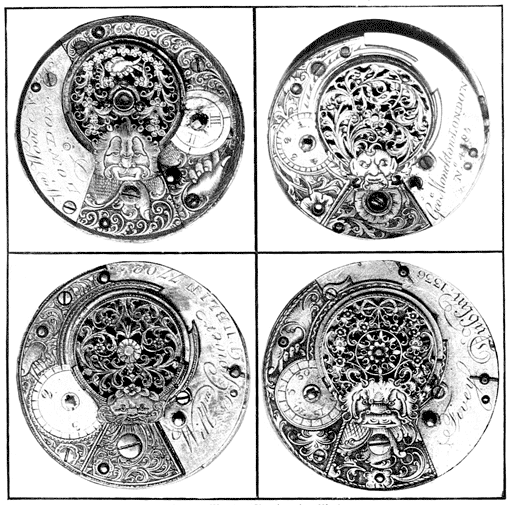
The first watches, about 1500, had the foliot and verge escapement, and in some early attempts to govern the foliot a hog's bristle was used as a spring. By putting a ring around the ends of the foliot and adding the hair spring of Dr. Hooke, about 1640, we have the verge watches of our grandfathers. This balance wheel and hair spring stand today, but the “lever” escapement has taken the place of the verge. It is a modification of the dead beat, Fig. 29, by adding a lever to the anchor, and this lever is acted on by the balance, hence the name “lever watch.” All this you can see by opening your watch, so no detailed explanation is necessary. Figure 34 shows two triple-cased Turkish watches with verge escapements, the one to the left being shown partly opened in Fig. 35. The watch with its inner case, including the glass, is shown to the right. This inner case is complete with two hinges and has a winding hole in the back. The upper case, of “chased” work, goes on next, and then the third, or outer case, covered with tortoise shell fastened with silver rivets, goes on outside the other two. When all three cases are opened and laid on the table, they look like a heap of oyster shells, but they go easily together, forming the grand and dignified watch shown to the left in Fig. 34. Oliver Cromwell wore an immense triple-case watch of this kind, and the poor plebeians who were permitted to examine such a magnificent instrument were favored!
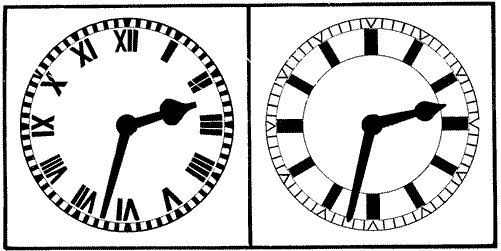
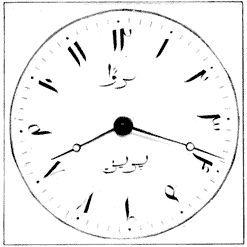
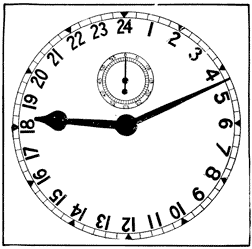
Our boys' watches costing one dollar keep much better time than this type of watch. Comparing the Syrian dial, Fig. 42, with that on Fig. 35, it is evident that the strange hour numerals on both are a variation of the same characters. These, so-called, “Turkish watches” were made in Europe for the Eastern trade. First-class samples of this triple-case type are getting scarce, but I have found four, two of them in Constantinople. Figure 36 shows the double-case style, called “pair cases,” the outer case thin silver, the figures and ornaments being hammered and punched up from the inside and called “repoussé.” Before we leave the old watches, the question of art work deserves notice, for it looks as if ornamentation and time-keeping varied inversely in those days—the more art the worse the watch. I presume, as they could not make a good time-keeper at that date, the watch-maker decided to give the buyer something of great size and style for his money. In Fig. 37 four old movements are shown, and there is no doubt about the art, since the work is purely individual and no dies or templates used. In examining a large number of these watches, I have never found the art work on any two of them alike. Note the grotesque faces in these, and in Fig. 39 which is a fine example of pierced, engraved work. Figure 38 is a fine example of pierced work with animals and flowers carved in relief. Figure 40 is a “Chinese” watch but made in Europe for the Chinese market. In Fig. 41 we have what remains of a quarter repeater with musical attachment. Each of the 24 straight gongs, commencing with the longest one, goes a little nearer the center of the large wheel, so a circle of pins is set in the wheel for each gong, or note, and there is plenty of room for several tunes which the wearer can set off at pleasure. Figure 43 is a modern watch with Hebrew hour numerals. Figure 44 is a modern 24-hour watch used on some railroads and steamship lines. I have a pretty clean-cut recollection of one event in connection with the 24-hour system, as I left Messina between 18 and 19 o'clock on the night of the earthquake! Dials and hands constitute an important branch of the subject. The general fault of hands is that they are too much alike; in many instances they are the same, excepting that the minute hand is a little longer than the hour. The dial shown on the left of Fig. 24 was designed by me for a public clock and can be read twice as far away as the usual dial. Just why we should make the worst dials and hands for public clocks in the United States is more than I can find out, for there is no possible excuse, since the “spade and pointer” hands have been known for generations. Figure 45 is offered as a properly designed dial for watches and domestic clocks, having flat-faced Gothic figures of moderate height, leaving a clear center in the dial, and the heavy “spade” hour hand reaching only to the inner edges of the figures. For public clocks the Arabic numerals are the worst, for at a distance they look like twelve thumb marks on the dial; while the flat-faced Roman remain distinct as twelve clear marks.
Do you know that you do not read a public clock by the figures, but by the position of the hands? This was discovered long ago. Lord Grimthorp had one with twelve solid marks on the dial and also speaks of one at the Athenæum Club, both before 1860. The Philadelphia City Hall clock has dials of this kind as shown on right side of Fig. 24. It has also good hands and can be read at a great distance. Very few persons, even in Philadelphia, know that it has no hour numerals on its dials. Still further, there is no clock in the tower, the great hands being moved every minute by air pressure which is regulated by a master clock set in a clock room down below where the walls are 10 ft. thick. Call and see this clock and you will find that the City Hall officials sustain the good name of Philadelphia for politeness. Generally, we give no attention to the hour numerals, even of our watches, as the following proves. When you have taken out your watch and looked at the time, for yourself, and put it back in your pocket, and when a friend asks the time you take it out again to find the time for him! Why? Because, for yourself, you did not read hours and minutes, but only got a mental impression from the position of the hands; so we only read hours and minutes when we are called on to proclaim the time.
We must find a little space for striking clocks. The simplest is one blow at each hour just to draw attention to the clock. Striking the hours and also one blow at each half hour as well as the quarter double blow, called “ting tong” quarters, are too well known to need description. The next stage after this is “chiming quarters” with three or more musical gongs, or bells. One of the best strikers I have has three trains, three weights and four bells. It strikes the hour on a large bell and two minutes after the hour it strikes it again, so as to give you another chance to count correctly. At the first quarter it repeats the last hour followed by a musical chord of three bells, which we will call one triple blow: at the second quarter the hour again and two triple blows and at the third quarter, the hour again and three triple blows. Suppose a sample hour's striking from four o'clock, this is what you hear, and there can be no mistake. “Four” and in two minutes “four”—“four and one quarter”—“four and two quarters”—“four and three quarters,” and the same for all other hours. This is definite, for the clock proclaims the hour, or the hour and so much past. It can be set silent, but that only stops it from striking automatically, and whether so set or not, it will repeat by pulling a cord. You awake in the night and pull the cord, and then in mellow musical tones, almost as if the clock were speaking, you hear—“four and two quarters.” This I consider a perfect striking clock. It is a large movement of fine workmanship and was made in the department of the Jura, France. When a clock or watch only repeats, I consider the old “five-minute repeater” the best. I used this method in a clock which, on pulling the cord, strikes the hour on a large bell and if that is all it strikes, then it is less than five minutes past. If more than five minutes past it follows the hour by one blow on a small bell for every five minutes. This gives the time within five minutes. It is fully described and illustrated in “Machinery,” New York, for March, 1905. Just one more. An old Dutch clock which I restored strikes the hour on a large bell; at the first quarter it strikes one blow on a small bell; at the half hour it strikes the last hour over again on the small bell; at the third quarter it strikes one blow on the large bell. But this in spite of its great ingenuity, only gives definite information at the hour and half hour.
Of curious clocks there is no end, so I shall just refer to one invented by William Congreve, an Englishman, over one hundred years ago, and often coming up since as something new. A plate about 8 in. long and 4 in. wide has a long zigzag groove crosswise. This plate is pivoted at its center so either end can be tipped up a little. A ball smaller than a boy's marble will roll back and forth across this plate till it reaches the lower end, at which point it strikes a click and the mainspring of the clock tips the plate the other way and the ball comes slowly back again till it strikes the disk at the other end of the plate, etc. Every time the plate tips, the hands are moved a little just like the remontoir clock already described. Clocks of this kind are often used for deceptive purposes and those ignorant of mechanics are deceived into the belief that they see perpetual motion. The extent to which modern machine builders are indebted to the inventions of the ancient clock-maker, I think, has never been appreciated.
In its earlier stages the clock was almost the only machine containing toothed gearing, and the “clock tooth” is still necessary in our delicate machines. It is entirely different from our standard gear tooth as used in heavy machines. The clock-makers led for a long time in working steel for tools, springs and wearing surfaces. They also made investigations in friction, bearings, oils, etc., etc. Any one restoring old clocks for amusement and pleasure will be astonished at the high-class mechanics displayed in them—nearly always by unknown inventors. Here is an example: The old clock-maker found that when he wished to drill a hole in a piece of thick wire so as to make a short tube of it, he could only get the hole central and straight by rotating the piece and holding the drill stationary. By this method the drill tends to follow the center line of rotation; and our great guns as well as our small rifles are bored just that way to get bores which will shoot straight. The fourth and last chapter will deal with the astronomical motions on which our time-keeping is founded, our present hour zones of time, and close with suggestions for a universal time system over the whole world.

CHAPTER IV
ASTRONOMICAL FOUNDATION OF TIME
Astronomical motions on which our time is founded. — Reasons for selecting the sidereal day as a basis for our 24-hour day. — Year of the seasons shorter than the zodiacal year. — Precession of the equinoxes. — Earth's rotation most uniform motion known to us. — Time Stars and Transits. — Local time. — The date line. — Standard time. — Beginning and ending of a day. — Proposed universal time. — Clock dial for universal time and its application to business. — Next great improvement in clocks and watches indicated. — Automatic recording of the earth's rotation. — Year of the seasons as a unit for astronomers. — General conclusions.
The mystery of time encloses all things in its folds, and our grasp of its infinite bearings is measured by our limitations. As there are no isolated facts in the Universe, we can never get to the end of our subject; so we know only what we have capacity to absorb. In considering the foundation on which all our time measuring is based, we are led into the fringe of that Elysian field of science—astronomy. A science more poetical than poetry—more charming than the optimistic phantasies of youth. That science which leaves our imagination helpless; for its facts are more wonderful than our extremest mental flights. The science of vastness and interminable distances which our puny figures fail to express. “The stars sang together for joy,” might almost be placed in the category of facts; while the music of the spheres may now be considered a mathematical reality. Our time keeping is inevitably associated with these motions, and we must select one which has periods not too long. That is, no continuous motion could be used, unless it passed some species of milestones which we could observe. Consequently, our clocks do not—in the strict sense—measure time; but are adjusted to divide periods which they do not determine. We are constantly correcting their errors and never entirely succeed in getting them to run accurately to periods of time which exist entirely outside of such little things as men and clocks. So a clock is better as it approximates or bears a regular relation to some motion in nature. The sidereal clock of the astronomer does run to a regular motion; but our 24-hour clocks do not, as we shall see later. Now consider the year, or the sun's apparent motion in the Zodiac, from any given star around to the same one again. This is altogether too long to be divided by clocks, as we cannot make a clock which could be depended on for anywhere near a year. The next shorter period is that of a “moon.” This is also a little too long, is not easily observed, and requires all sorts of corrections. Observations of the moon at sea are so difficult and subject to error that mariners use them only as a last resort. If a little freedom of language is permissible, I would say that the moon has a bad character all around, largely on account of her long association with superstition, false theology and heathen feasts. She has not purged herself even to this day! The ancients were probably right when they called erratic and ill-balanced persons “luny.” Now we come to the day and find that it is about the right practical length—but what kind of a day? As there are five kinds we ought to be able to select one good enough. They are:—
- 1st. The solar day, or noon to noon by the sun.
- 2nd. An imaginary sun moving uniformly in the ecliptic.
- 3rd. A second imaginary sun moving uniformly parallel to the equator at all seasons of the year.
- 4th. One absolute rotation of the earth.
- 5th. One rotation of the earth measured from the node, or point, of the spring equinox.
The difference between 1st and 2nd is that part of the sun's error due to the elliptical orbit of the earth.
The other part of the sun's error—and the larger—between 2nd and 3rd is that due to the obliquity of the ecliptic to the equator.
The whole error between 1st and 3rd is the “equation of time” as shown for even minutes in the first chapter under the heading, “Sun on Noon Mark 1909.”
Stated simply, for our present purpose, 1st is sundial time, and 3rd our 24-hour clock time.
This 2nd day is therefore a refinement of the astronomers to separate the two principal causes of the sun's error, and I think we ought to handle it cautiously, or my friend, Professor Todd, might rap us over the knuckles for being presumptuous.
This 5th day is the sidereal day of the astronomers and is the basis of our time, so it is entitled to a little attention. I shall confine “sidereal day” to this 5th to avoid confusion with 4th. If you will extend the plane of the equator into the star sphere, you have the celestial equator. When the center of the sun passes through this plane on his journey north, in the Spring, we say, “the sun has crossed the line.” This is a distant point in the Zodiac which can be determined for any given year by reference to the fixed stars. To avoid technicalities as much as possible we will call it the point of the Spring equinox. This is really the point which determines the common year, or year of the seasons. Using popular language, the seasons are marked by four points,—Spring equinox—longest day—; Autumnal equinox—shortest day. This would be very simple if the equinoctial points would stay in the same places in the star sphere; but we find that they creep westward each year to the extent of 50 seconds of arc in the great celestial circle of the Zodiac. This is called the precession of the equinoxes. The year is measured from Spring equinox to Spring equinox again; but each year it comes 50 seconds of arc less than a full revolution of the earth around the sun. Therefore if we measured our year by a full revolution we would displace the months with reference to the seasons till the hot weather would come in January and the cold weather in July in about 13,000 years; or a complete revolution of the seasons back to where we are, in 26,000 years. Leaving out fractions to make the illustration plain, we have:—
| (1) | 360 degrees of Zodiac | = 26,000 years | |
| 50 seconds of arc | |||
| (2) | 1 day of time | = 26,000 years | |
| 31⁄3 seconds | |||
| (3) | 1 year of time | = 26,000 years | |
| 201⁄3 minutes | |||
| (4) | 31⁄3 seconds | = 1⁄110 of a second | |
| days in a year | |||
| all Approximate | |||
In (1) we see that a “precession” of 50 seconds of arc will bring the Spring equinox around in 26,000 years.
In (2) we see, as 50 seconds of arc represents the distance the earth will rotate in 31⁄3 seconds, a difference of one day will result in 26,000 years. That is since the clock regulated by the stars, or absolute rotations of the earth, would get behind 31⁄3 seconds per year, it would be behind a day in 26,000 years, as compared with a sidereal clock regulated by the Spring equinoctial point.
In (3) we see that as 50 seconds of arc is traversed by the earth, in its annual revolution, in 201⁄3 minutes, a complete circle of the Zodiac will be made in 26,000 years.
In (4) we see that as the difference between the year of the seasons and the Zodiacal year is 31⁄3 seconds of the earth's rotation, it follows that if this is divided by the number of days in a year we have the amount which a sidereal day is less than 4th, or an absolute rotation of the earth. That is, any meridian passes the Spring equinoctial point 1⁄110 of a second sooner than the time of one absolute rotation. These four equations are all founded on the precession of the equinoxes, and are simply different methods of stating it. Absolutely and finally, our time is regulated by the earth's rotation; but strange as it may appear, we do not take one rotation as a unit. As shown above, we take a rotation to a movable point which creeps the 1⁄110 of a second daily. But after all, it is the uniform rotation which governs. This is the one “dependable” motion which has not been found variable, and is the most easily observed. When we remember that the earth is not far from being as heavy as a ball of iron, and that its surface velocity at the equator is about 17 miles per minute, it is easy to form a conception of its uniform motion. Against this, however, we may place the friction of the tides, forcing up of mountain ranges, as well as mining and building skyscrapers—all tending to slow it. Mathematicians moving in the ethereal regions of astronomy lead us to conclude that it must become gradually slower, and that it is slowing; but the amount may be considered a vanishing quantity even compared with the smallest errors of our finest clocks; so for uncounted generations past—and to come—we may consider the earth's rotation uniform. Having now found a uniform motion easily observed and of convenient period, why not adopt it as our time unit? The answer has been partially given above in the fact that we are compelled to use a year, measured from the Spring equinoctial point, so as to keep our seasons in order; and therefore as we must have some point where the sidereal clocks and the meantime clocks coincide, we take the same point, and that point is the Spring equinox. Now we have three days:—
- 1st. A sidereal day 1⁄110 of a second less than one rotation of the earth.
- 2nd. One rotation of the earth in 23 hours, 56 minutes and 4 seconds, nearly, of clock time.
- 3rd. One mean time clock day of 24 hours, which has been explained previously.
Now, isn't it remarkable that our 24-hour day is purely artificial, and that nothing in nature corresponds to it? Our real day of 24 hours is a theoretical day. Still more remarkable, this theoretical day is the unit by which we express motions in the solar system. A lunar month is days—hours—minutes—and seconds of this theoretical day, and so for planetary motions. And still more remarkable, the earth's rotation which is itself the foundation is expressed in this imaginary time! This looks like involution involved, yet our 24-hour day is as real as reality; and the man has not yet spoken who can tell whether a mathematical conception, sustained in practical life, is less real than a physical fact. Our legal day of practical life is therefore deduced from the day of a fraction less than one earth rotation. In practice, however, the small difference between this and a rotation is often ignored, because as the tenth of a second is about as near as observations can be made it is evident that for single observations 1⁄110 of a second does not count, but for a whole year it does, and amounts to 31⁄3 seconds. Now as to the setting of our clocks. While the time measured by the point of the Spring equinox is what we must find it is found by noting the transits of fixed stars, because the relation of star time to equinoctial time is known and tabulated. Remember we cannot take a transit of the equinoctial point, because there is nothing to see, and that nothing is moving! But it can be observed yearly and astronomers can tell where it is, at any time of the year, by calculation. The stars which are preferred for observation are called “time stars” and are selected as near the celestial equator as possible. The earth's axis has a little wabbling motion called “nutation” which influences the apparent motion of the stars near the pole; but this motion almost disappears as they come near the equator, because nutation gives the plane of the equator only a little “swashplate” motion. The positions of a number of “time stars” with reference to the equinoctial point, are known, and these are observed and the observations averaged. The distance of any time star from the equinoctial point, in time, is called its “right ascension.” Astronomers claim an accuracy to the twentieth part of a second when such transits are carefully taken, but over a long period, greater exactness is obtained. Really, the time at which any given star passes the meridian is taken, in practical life, from astronomical tables in the Nautical Almanacs. Those tables are the result of the labors of generations of mathematicians, are constantly subject to correction, and cannot be made simple. Remember, the Earth's rotation is the only uniform motion, all the others being subject to variations and even compound variations. This very subject is the best example of the broad fact that science is a constant series of approximations; therefore, nothing is exact, and nothing is permanent but change. But you say that mathematics is an exact science. Yes, but it is a logical abstraction, and is therefore only the universal solvent in physical science.
With our imaginary—but real—time unit of 24 hours we are now ready to consider “local time.” Keeping the above explanation in mind, we may use the usual language and speak of the earth rotating in 24 hours clock time; and since motion is relative, it is permissible to speak of the motion of the sun. In the matter of the sun's apparent motion we are compelled to speak of his “rising,” “setting,” etc., because language to express the motion in terms of the earth's rotation has not been invented yet. For these reasons we will assume that in Fig. 47 the sun is moving as per large arrow and also that the annulus, half black and half white, giving the 24 hours, is fastened to the sun by a rigid bar, as shown, and moves around the earth along with him. In such illustrations the sun must always be made small in proportion, but this rather tends to plainness. For simplicity, we assume that the illustration represents an equinox when the sun is on the celestial equator. Imagine your eye in the center of the sun's face at A, and you would be looking on the meridian of Greenwich at 12 noon; then in one hour you would be looking on 15° west at 12 noon; but this would bring 13 o'clock to Greenwich. Continue till you look down on New York at 12 noon, then it is 17 o'clock at Greenwich (leaving out fractions for simplicity) etc. If you will make a simple drawing like Fig. 47 and cut the earth separate, just around the inside of the annulus, and stick a pin at the North Pole for a center, you may rotate the earth as per small arrow and get the actual motion, but the result will be just the same as if you went by the big arrow. We thus see that every instant of the 24 hours is represented, at some point, on the earth. That is, the earth has an infinity of local times; so it has every conceivable instant of the 24 hours at some place on the circle. Suppose we set up 1,410 clocks at uniform distances on the equator, then they would be about 17 miles apart and differ by minutes. Now make it 86,400 clocks, they would be 1,500 feet apart and differ by seconds. With 864,000 clocks they would be 150 feet apart and vary by tenths of seconds. It is useless to extend this, since you could always imagine more clocks in the circle; thus establishing the fact that there are an infinity of times at an infinity of places always on the earth. It is necessary to ask a little patience here as I shall use this local time and its failure later in our talk. Strictly, local time has never been used, because it has been found impracticable in the affairs of life. This will be plain when we draw attention to the uniform time of London, which is Greenwich time; yet the British Museum is 30 seconds slow of Greenwich, and other places in London even more. This is railroad time for Great Britain; but it is 20 minutes too fast for the west of England. This led to no end of confusion and clocks were often seen with two minute hands, one to local and the other to railroad time. This mixed up method was followed by “standard time,” with which we are all pretty well acquainted. Simply, standard time consists in a uniform time for each 15° of longitude, but this is theoretical to the extreme, and is not even approached in practice. The first zone commences at Greenwich and as that is near the eastern edge of the British Islands, their single zone time is fast at nearly all places, especially the west coast of Ireland. When we follow these zones over to the United States we find an attempt to make the middle of each zone correct to local time, so at the hour jumping points, we pass from half an hour slow to half an hour fast, or the reverse. We thus see that towns about the middle of these four United States zones have sunrise and sunset and their local day correct, but those at the eastern and western edges average half an hour wrong. As a consequence of this disturbance of the working hours depending on the light of the day, many places keep two sets of clocks and great confusion results. Even this is comprehensible; but it is a mere fraction of the trouble and complication, because the hour zones are not separated by meridians in practice, but by zig-zag lines of great irregularity. Look at a time map of the United States and you will see the zones divided by lines of the wildest irregularity. Now question one of the brightest “scientific chaps” you can find in one of the great railroad offices whose lines touch, or enter, Canada and Mexico. Please do not tell me what he said to you! So great is the confusion that no man understands it all. The amount of wealth destroyed in printing time tables, and failing to explain them, is immense. The amount of human life destroyed by premature death, as a result of wear and tear of brain cells is too sad to contemplate. And all by attempting the impossible; for local time, even if it was reduced to hourly periods is not compatible with any continental system of time and matters can only get worse while the attempt continues. For the present, banish this zone system from your mind and let us consider the beginning and ending of a day, using strictly local time.
A civil, or legal, day ends at the instant of 24 o'clock, midnight, and the next day commences. The time is continuous, the last instant of a day touching the first instant of the next. This is true for all parts of the earth; but something in addition to this happens at a certain meridian called the “date line.” Refer again to Fig. 47 which is drawn with 24 meridians representing hours. As we are taking Greenwich for our time, the meridians are numbered from 0°, on which the observatory of Greenwich stands. When you visit Greenwich you can have the pleasure of putting your foot on “the first meridian,” as it is cut plainly across the pavement. Degrees of longitude are numbered east and west, meeting just opposite at 180°, which is the “date line.” Our day begins at this line, so far as dates are concerned; but the local day begins everywhere at midnight. Let us start to go around the world from the date line, westward. When we arrive at 90° we are one quarter around and it takes the sun 6 hours longer to reach us. At 0° (Greenwich) we are half around and 12 hours ahead of the sun motion. At 90° west, three quarters, or 18 hours, and when back to 180° we have added to the length of all days of our journey enough to make one day; therefore our date must be one day behind. Try this example to change the wording:—Let us start from an island B, just west of the date line. These islanders have their 24-hour days, commencing at midnight, like all other places. As we move westward our day commences later and later than theirs, as shown above. Suppose we arrive at the eastern edge of the 180° line on Saturday at 12 o'clock, but before we cross it we call over to the islanders,—what day is it? We would get answer, “Sunday;” because all our days have been longer, totalling one day in the circuit of the globe. So if we step over the line at 12 o clock Saturday, presto, it is 12 o'clock Sunday. It looks like throwing out 24 hours, but this is not so, since we have lived exactly the same number of hours and seconds as the islanders. In this supposition we have all the dates, however, but have jumped half of Saturday and half of Sunday, which equals one day. In practice this would not have been the method, for if the ship was to call at the island, the captain would have changed date on Friday night and thrown Saturday out, all in one piece, and would have arrived on their Sunday; so his log for that week would have contained only 6 days. It is not necessary to go over the same ground for a circuit of the globe eastward, but if you do so you will find that you shorten your days and on arriving at the date line would have a day too much; so in this case you would double a date and have 8 days in that week. In both cases this is caused by compounding your motion with that of the sun; going with him westward and lengthening your days, or eastward meeting him and shortening them. Figure 47 shows Greenwich noon, we will say on Monday, and at that instant, Monday only, exists from 0 to 24 o'clock on the earth; but the next instant, Tuesday begins at 180° B. In one hour it is noon of Monday at 15° West, and midnight at 165° East; so Tuesday is one hour old and there is left 23 hours of Monday. Monday steadily declines to 0 as Tuesday steadily grows to 24 hours; so that, except at the instant of Greenwich noon, there are always two days on the world at once. If we said that there are always two days on the world at once, we could not be contradicted; since there is no conceivable time between Monday and Tuesday; it is an instantaneous change. As we cannot conceive of no time, the statement that there is only one day on the earth at Greenwich noon is not strictly permissible. Since there are always two days on the world at once let us suppose that these two are December 31st and January 1st; then we have two years on the world at once for a period of 24 hours. Nine years ago we had the 19th and 20th centuries on the world at once, etc. As a mental exercise, you may carry this as far as you please. Suppose there was an impassable sea wall built on the 180° meridian, then there would be two days on the world, just as explained above; but, practically, there would be no date line, since in sailing west to this wall we would “lengthen our days,” and then shorten them the same amount coming around east to the other side of the wall, but would never jump or double a date. This explanation is founded, as it ought to be, on uniform local time, and is the simplest I can give. The date line is fundamentally simple, but is difficult to explain. When it is complicated by the standard time—or jumping hour system—and also with the fact that some islands count their dates from the wrong side of the line for their longitudes, scientific paradoxes arise, such as having three dates on the world at once, etc.; but as these things are of no more value than wasting time solving Chinese puzzles, they are left out. Ships change date on the nearest night to the date line; but if they are to call at some island port in the Pacific, they may change either sooner or later to correspond with its date. Here is a little Irish date line wit printed for the first time,—I was telling my bright friend about turning in on Saturday night and getting up for breakfast on Monday morning. “Oh,” said he, “I have known gentlemen to do as good as that without leaving New York City!”
As what is to follow relates to the growing difficulties of local time and a proposed method of overcoming them, let us recapitulate:—
- 1st. Local time has never been kept, and the difficulties of using it have increased as man advanced, reaching a climax of absurdity on the advent of the railroad; so it broke down and became impractical.
- 2nd. To make the irregular disorder of local time an orderly confusion, the “standard time”—jumping by hours—has helped a little, but only because we can tell how much it is wrong at any given place. This is its only advantage over the first method, where we had no means of knowing what to expect on entering any new territory. That is, we have improved things by throwing out local time to the extent of an hour.
My proposal is to throw local time out totally and establish one, invariable, universal time. Greenwich time being most in use now, and meridians numbered from it, may be taken in preference to any other. Still another reason is that the most important timekeepers in modern life—ship's chronometers—are set to Greenwich time. Universal time—no local time—only local day and night. Our 24-hour system is all right, so do not disturb it, as it gets rid of A.M. and P.M. and makes the day our unit of time. Our railroad time now throws out local time to the extent of one hour; but I propose to throw it out entirely and never change the clock hands from Greenwich time. The chronometers do that now, so let us conduct all business to that time.
Now refer to Fig. 46, in which Greenwich is taken as universal time. The annulus, half white and half black, indicates the average day and night, and is a separate ring in the dial which can be set so that “noon” is on the meridian of the place, as shown for four places in the illustration. It is the same dial in all four cases set to local day and night. Strictly, the local time conception is dropped and the local day left for regulating working and sleeping time. All business would have the same time. In traveling east we would not have the short hours; or west, the long hours. All clocks and watches would show the same time as ship's chronometers do now. The only change would be the names of the hours for the parts of the local day. This is just the difficulty, for we are so accustomed to associate a certain number, as seven, with the morning and breakfast time. Suppose breakfast time in London is 7 o'clock, then according to the local day it would be 12 o'clock breakfast time in New York; but in both cases it would be the same time with reference to the local daylight. Let it be distinctly understood that our association of 12 o'clock with noon is not necessary. The Japanese called it “horse” and “nine”—the ancient Romans, the New Testament writers, and the Turks called it the “sixth hour”—the astronomers now call it 24 o'clock, and the Chinese represent it by several characters; but, in all cases, it is simply the middle of the day at any place. By the proposed universal time, morning, noon, and evening would be—at any given place—the same hours. There would be no necessity of establishing legal noon with exactness to the meridian, because that would only regulate labor, meals, etc., and would not touch universal time. This is an important part of the proposal and is worth elaborating a little. Sections in manufacturing districts could make their working hours correspond at pleasure and no confusion would result. That is, local working hours to convenience but by the same universal time. Note how perfectly this would work in traveling,—you arrive in Chicago from the effete east and your watch corresponds all along with the railroad clocks. As you leave the station you glance up at the clock and see that Chicago noon is 17.30, so you set the day and night ring of your watch to match the same ring on the clock, but no disturbance of the hands. As you register at the hotel you ask,—dinner? and get answer, 24.30—then breakfast, 12.30. These questions are necessary now, so I do not add complication here. When you arrive in a strange city you must ask about meals, business hours, theater hours, “doors open” hours, etc., etc.; so all this remains the same. Let us put the matter forcibly,—while we count days, or dates, something must vary with east and west; I propose the fixing of hours for business and sleep to suit each locality, but an invariable time. Get rid of the idea that a certain number, as 7 o'clock, represents the age of the day at all places. See how this would wipe out the silly proposal to “save daylight” by setting the clock back and forward. Suppose workmen commenced at 12.30 in New York; for the long summer days make it 11.30, but no change in universal time. As this is the only difference from our present time system, keep the central conception, firmly,—universal time—local day and night.
Suppose Chicago decided that “early to bed and early to rise” was desirable; then it could establish its legal noon as 17.30, which would be about 20 minutes early for its meridian. You could do business with Chicago for a lifetime and not find this out, unless you looked up the meridian of Chicago and found that it was 17.50 o'clock. None of the railroads or steamship lines of the city would need to know this, except as a matter of scientific curiosity, for the time tables would all be printed in universal time. For hiring labor, receiving and delivering goods, etc., they would only need to know Chicago business hours. To state the matter in different words,—Chicago would only need to decide what portion of the universal 24 hours would suit it best for its day and which for its night, and if it decided, as supposed above, to place its working day forward a little to give some daylight after labor, nothing would be disturbed and only the scientific would ever know. Certainly, “save daylight,” but do not make a fool of the clock! Having shown the great liberty which localities could take without touching the working of the system, the same remarks apply to ultra-scientific localities. A city might establish its noon to the instant; so it is possible—even if a little improbable—that the brilliant and scientific aldermen of New York might appoint a commission with proper campfollowers and instrument bearers to determine the longitude of the city to the Nth of a second and tell us where we “are at.” The glory of this achievement—and especially its total cost—would be all our own and incorruptible time would be untouched! We thus see that great local freedom and great accuracy are alike possible. With our present system, accuracy in local time is impracticable and has never even been attempted, and is confusion confused since we added the railroad hour jumps. Why did we nurse this confusion till it has become almost intolerable? Because man has always been a slave to mental associations, and habits. Primitive man divided the local day into parts and gave them names and this mental attitude sticks to us after it has served its day. The advantages of universal time could hardly be enumerated, yet we can have them all by dropping our childish association of 7 o'clock with breakfast time! Another example,—you visit a friend for a few days and on retiring the first night you ask “what is your breakfast hour”—“8 o'clock.” You have to ask this question and recollect the answer. Now tell me what difference it would make if the answer had been 13 o'clock? None whatever, unless, perhaps, that is, you do not like thirteen! You ask, how about ships? Ships now carry universal time and only change the clock on deck to please the simple minded passengers. How about the date line? No change whatever, so long as we use dates which means numbering local days. It is useless multiplying examples; all difficulties disappear, as if by magic, the moment we can free our minds of local time and the association of the same hour with the same portion of the day at all places. The great interest at present manifested in the attempts to reach the North Pole calls for some consideration of universal time in the extreme north. Commencing at the equator, it is easy to see that the day and night ring, Fig. 46, would represent the days and nights of 12 hours at all seasons. As we go north, however, this ring represents the average day and night. When we reach the Polar Circle, still going north, the daily rising and setting of the sun gradually ceases till we reach the great one-year day at the Pole, consisting of six months darkness and six months light. Let us now assume that an astronomical observatory is established here and the great equatorial placed precisely on the pole. At this point, local time, day and night, and the date line, almost cease to have a meaning. For this very reason universal time would be the only practical method; therefore, it more than stands the test of being carried to the extreme. Universal time would regulate working and sleeping here the same as at all other places. Strictly local time in this observatory would be an absurdity, because in walking around the telescope (pole) you would be in all instants of the 24 hours within five seconds! At the pole the day would commence at the same instant as at some assumed place, and the day and night ring would represent working and sleeping as at that place. Suppose this observatory to be in telegraphic communication with New York, then it would be best for the attendants to set their day and night to New York, so as to correspond with its business hours. Many curious suppositions might be made about this polar observatory with its “great night” and equally “great day.” It is evident that to keep count of itself it would be compelled to note dates and 24-hour days to keep in touch with us; so it would be forced to adopt the local day of some place like New York. This choice would be free, because a polar observatory would stand on all the meridians of the earth at once.
We are now in a position to consider the next possible—and even probable—improvement in our clocks and watches. To minimize the next step it might be well to see what we can do now. Clocks are often regulated by electric impulses over wires. Electricians inform me that they can do this by wireless; but that owing to the rapid attenuation of the impulses it cannot be done commercially, over great distances. In the history of invention the first step was to do something and then find a way of doing it cheaply enough for general use. So far as I know, the watch in the wearer's pocket has not yet been regulated by wireless; but I am willing to risk the statement that the editor of Popular Mechanics can name more than one electrician who can do this. A watch to take these impulses might be larger than our present watches, but it would not stay larger and would ultimately become much smaller. You know what has happened since the days of the big “onions” described in the third chapter. Fig. 34; so get your electric watch and make it smaller at your leisure. We have made many things commercially practicable, which looked more revolutionary than this. Now throw out the mainspring, wheels, pinions, etc., of our watches and reduce the machinery part to little more than dial and hands and do the driving by wireless, say, once every minute. I feel certain that I am restraining the scientific imagination in saying that the man lives among us who can do this. I repeat, that we now possess the elementary knowledge—which if collated and applied—would produce such a watch.
Now I have a big question to ask—the central note of interrogation in this little scientific conversation with you,—does the man live who can make the earth automatically record its rotation? Do not be alarmed, for I am prepared to make a guess as to this possibility. A direct mechanical record of the earth's rotation seems hopeless, but let us see what can be done. You are aware that some of the fixed stars have a distinct spectrum. It is not unreasonable to suppose that an instrument could be made to record the passage of such a star over the meridian. Ah, but you say, there is no mechanical force in this. Do not hurry, for we have long been acquainted with the fact that things which, apparently, have no force can be made to liberate something which manifests mechanical force. We could now start or stop the greatest steam engine by a gleam of sunlight, and some day we might be able to do as much by the lately discovered pressure of light. That is, we can now liberate the greatest forces by the most infinitesimal, by steps; the little force liberating one greater than itself, and that one another still greater. A good example is the stopping of an electric train, from a distance, by wireless. The standard clock in Philadelphia, previously referred to, is a delicate instrument and its most delicate part, having the least force, moves a little valve every minute, and by several steps liberates the air pressure, 200 feet higher in the tower, to move the four sets of great hands. I am not traveling beyond the record when I say that the invisible actinic rays could be used to liberate a great force; therefore what is there unreasonable in the supposition that the displacement of the sodium line in the spectrum of a star might be made to record the earth's rotation? So I say to the electrician—the optician—the photographer—the chemist and the mechanic.—get together and produce this watch. Permit me, with conventional and intentional modesty, to name the new timepiece Chroncosmic. For pocket use, it would be Cosmic watch. In the first chapter I allowed to the year 2,000 for the production of this watch, but it is likely we will not need to wait so long.
Having stated my proposal for universal time as fully as space will permit and given my guess as to the coming cosmic watch, let us in this closing paragraph indulge in a little mental exercise. Suppose we copy the old time lecturer on astronomy and “allow our minds to penetrate into space.” Blessed be his memory, he was a doer of good. How impressive as he repeatedly dropped his wooden pointer, and lo! It always moved straight to the floor; thus triumphantly vindicating universal gravitation!!!
We can think of a time system which would discard months, weeks and days. What is the meaning of the financial almanac in which the days are numbered from 1 to 365 or 366? Simply a step in the right direction, away from the months and weeks, so that the distance between any two dates may be seen at a glance. We would really be better without months and weeks. Now let us consider the year of the seasons as a unit—long since proposed by the astronomers—and divide it into 3,000 chrons. Clocks regulated by star transits, as at present, would divide this decimally, the fourth place being near enough to make the new pendulums of convenient length. This would throw out months, weeks and days, local time and the date line. Each of these chrons would represent the same time in the year, permanently. For example, 464.6731 would mark to a dixmilliemechron (a little more than one second) the point reached in the year; while the date does not, as I have shown in the first chapter. But you still object that this is a great number of figures to use in fixing a point in the year. Let us see what it takes to fix a point in the year now, August 24th, 11-16-32 P. M., New York standard time. A pretty long story, but it does not fix the point of the year even then; for it would require the assistance of an astronomer to fix such a point in any given year, say 1909. But 464.6731 would be eternally right in absolute time of the seasons, and has only one meaning, with no qualifications for any year whatever. I believe the astronomers should use a method something like this. Ah, but there is a difficulty in applying this to the affairs of daily life which looks insurmountable. This is caused by the fact that the day and year are incommeasurable. One of them cannot be exactly expressed in terms of the other. They are like the diagonal and side of a square. The day is now the unit and therefore the year has an interminable fraction; conversely, if we make the year the unit, then the day becomes an endless fraction. This brings us face to face with the local day which we ignored in our scientific year unit. We must regulate our labors, in this world, to day and night and, with the year unit, the chrons would bear no fixed relation to day and night, even for two days in succession. So the year unit and absolute time must be left to the astronomers; but the day unit and the uniform world day of universal time as explained in connection with Fig. 46 I offer as a practical system.
I am satisfied that all attempts to measure the year and the day by the same time yard stick must fail and keep us in our present confusion. Therefore separate them once for all time. Brought down to its lowest terms my final proposal is:—
- 1st. An equinoctial year unit for the astronomers, divided somewhat as suggested, but no attempt to make the divisions even approximate to days and hours. This would fix all astronomical events, absolutely. A variation in the length of the year would not disturb this system, since the year itself would be the unit. In translating this astronomical, or year unit time, into clock time, no difficulties would be added, as compared with our present translation of sidereal time into clock time. Deal with the year unit and day unit separately and convert them mutually when necessary.
- 2nd. A universal mean time day of 24 hours, as now kept at Greenwich, all human business being regulated by this time. Dates and the date line as well as leap years all being retained as at present.
- 3rd. Weight and spring clocks and watches to be superseded by the cosmic clocks and watches regulated by wireless impulses from central time stations, all impulses giving the same invariable time for all places.
- 4th. Automatic recording of the earth's rotations to determine this time.
To avoid any possibility of misunderstanding, I would advise never counting a unit till it is completed. We do this correctly with our hours, as we understand 24 o'clock to be the same as 0 o'clock. But we do not carry this out logically, for we say 24.30. How can this be so, since there is nothing more than 24 o'clock? It ought to be simply 30 minutes, or 0 hour 30 minutes. How can there be any hour when a new day is only 30 minutes old? This brings up the acrimonious controversy, of some years ago, as to whether there was any “year one.” One side insisted that till one year was completed there could only be months and days. The other side argued that the “year one” commenced at 0 and that the month and date showed how much of it had passed. Test yourself,—is this the year 1909, of which only 8 months have passed; or is it 1909 and 8 months more? Regarding the centuries there appears to be no difference of opinion that 1900 is completed, and that we are in the 20th century. But can you tell whether we are 8 years and 8 months into the 20th century or 9 years and 8 months? It ought to be, logically 1909 years complete and 8 months of the next year, which we must not count till it is completed. Take a carpenter's rule, we say 1⁄4 in.—1⁄2 in.—3⁄4 in., but do not count an inch till we complete it. When the ancients are quoted,—“about the middle of the third hour” there is no mistake, because that means 21⁄2 hours since sunrise. If we said the 1909th year that would be definite too, and mean some distance into that year. Popular language states that Greenwich is on the “first meridian”; strictly, it is on the zero meridian, or 0°. These matters are largely academic and I do not look on them as serious subjects of discussion; but they are good thought producers. Bidding you good-bye, for the present, it might be permissible to state that this conversational article on Time was intended to be readable and somewhat instructive; but especially to indicate the infinity of the subject, that thought and investigation might be encouraged.
Original spelling and grammar have mostly been retained. However, on page 31, “clepsydral” was changed to “clepsydra”.
Figures were moved from within paragraphs to between paragraphs. In addition, some figures were originally out of numerical sequence; they are now in sequence (all but Fig. 46, which does need to be the last illustration).
The transcriber created the cover image, and hereby places it into the public domain.