
Title: The Elements of Qualitative Chemical Analysis, vol. 1, parts 1 and 2.
Author: Julius Stieglitz
Release date: February 23, 2014 [eBook #44986]
Most recently updated: October 24, 2024
Language: English
Credits: Produced by Juliet Sutherland, RichardW, and the Online
Distributed Proofreading Team at http://www.pgdp.net


In venturing to add another book on Qualitative Chemical Analysis to the long list of publications on this subject, the author has been moved chiefly by the often expressed wish of students and friends to have his lectures on qualitative analysis rendered available for reference and for a wider circle of instruction. Parts I and II of the present book embody these lectures in the form to which they have developed in the course of the last sixteen years, since, in 1894, the teaching of analytical chemistry, along the lines followed, was first suggested by Ostwald's pioneer "Wissenschaftliche Grundlagen der Analytischen Chemie."
The author believes that instruction in qualitative analysis, besides teaching analysis proper, should demand of the student a very distinct advance in the study of general chemistry, and should also, consciously, pave the way for work in quantitative analysis, if it is not, indeed, accompanied by work in that subject. The professional method of work, whether routine or research work of the academic or the industrial laboratory is involved, inevitably consists in first making an exhaustive study of the general chemical aspects of the subject under examination: it includes a thorough study of books of reference and of the original literature on the subject; and when the experimental work is finally undertaken, it is carried out with a critical, searching mind, which questions every observation made, every process used. The method of instruction in this book aims at developing these habits of the professional, productive chemist. For the reasons given, a rather thorough and somewhat critical study is first made (in Part I) of the fundamental general chemical principles which are most widely involved in analytical work. The applications of these principles to the subject matter of elementary qualitative analysis are then discussed (in Part II), in closest connection with the laboratory work covering the study of analytical reactions (in Part III). The material is presented, not as a finished subject, but as a growing one, with which the present generation of chemists is still busy, and which contains many important, unsolved problems of a fundamental character. Numerous references to standard works and to the current literature are given, of which those suitable for reading by the young student are specially designated. The obvious demand is thereby made on the student to aim to remain in touch with the growth of the science, after he has completed his studies under the guidance of an instructor. Finally, to arouse and develop the critical, questioning attitude of the professional chemist, referred to above, the subject matter of the laboratory work, given in Part III, is put very largely in the form of questions, which demand not only careful observation on the part of the student, but also a thoughtful interpretation of the observations made.
In the experience of the author, although the majority of students attending his lectures had already acquired some knowledge of chemical and physical equilibrium, of the theories of solutions and of ionization and of their applications, the more exhaustive treatment of parts of these subjects and of related topics, to which a course in qualitative analysis lends itself, has been of particular benefit to them, bringing them into closer touch with the method of detailed study of a chemical topic, than the broader, more varied work of general chemistry courses usually does. Throughout the theoretical treatment of the subject, the attempt is made to prepare the student for a more general quantitative expression of chemical relations. For this reason, chemical and physical equilibrium constants are given and used, wherever it is possible. The author is aware that these "constants" have, in part, only a temporary standing; that more exact work will continually modify their numerical values and, probably, limit the field for their rigorous application. The latter facts can be impressed on the student and still the invaluable principle be inculcated in his mind, that chemistry is striving to express its relations, as far as possible, in mathematical terms, exactly as its sister science, physics, has long been doing. At the same time the treatment of physicochemical topics has been kept within the bounds set by the subject matter, and by the chemical maturity of the students addressed: it is elementary in form, and quantitative relations are used, in the main, only to elucidate qualitative facts. The rigorous development of the subjects presented and their elaboration from a purely physicochemical standpoint are left to advanced courses. It has been found that this method interests the better class of students in seeking such advanced courses.
The relations of qualitative to quantitative analysis are touched upon in the theoretical treatment, where it has been feasible to do so. The laboratory methods aim also at beginning the training of students in the habit of accuracy demanded by quantitative analysis, by laying special emphasis on the methods of detecting traces of a number of the common elements and by requiring a report on the relative quantities of components found. The study of reactions is carried out, almost wholly, with solutions of known and uniform molar concentration. However, the actual development of quantitative accuracy is left to the instruction in the courses in quantitative analysis, in which a successful training in this direction is far more readily attained. Simultaneous courses in the two branches of analysis seem to the author to be highly desirable, whenever practicable. The study of quantitative analysis adds neatness of manipulation and accuracy to the work in qualitative analysis; and the latter supplies the opportunity for the further development of a student's knowledge of general chemistry, for which there is a much smaller scope in quantitative analysis courses, and thus relieves a condition where a serious pedagogical defect is likely to exist in the development of our students.
Parts III and IV of this book are published in a separate volume, as a laboratory manual for qualitative analysis. They comprise the instructions for laboratory work introductory to systematic analysis (the study of reactions and of the analysis of groups, in Part III) and an outline for elementary systematic analysis (Part IV). The attempt has been made, in particular, to bring the laboratory work, which otherwise follows the usual lines of instruction in systematic analysis, also into closest relations to the development of the scientific foundations of analytical chemistry, as represented in Parts I and II. It is believed that the subject matter lends itself especially well to such a close interweaving of the two sides of the study, without any special loss of time to the student, and with the result, it is hoped, of a greatly increased interest on his part and an increased stimulus of the habit of scientific thought.
The following plan of work is used by the author with his classes: The first section (lasting eleven weeks) of the course in qualitative analysis is started with some seven to ten (according to the ability of the class) lectures or classroom exercises, given daily, and covering the first seven or the eight chapters of Part I. At the end of the second week the laboratory work is started. During the remainder of this section of the course, two hours of classroom work and eight hours of laboratory work per week are required, and, in this period, Part III, comprising the first half of the laboratory manual, is studied in the laboratory in closest connection with the classroom work on Part II of the book. As far as possible, the laboratory work on a given topic precedes the classroom work. This first course is followed by an eleven weeks' course in systematic analysis, covering Part IV of the book. A third (graduate) course, optional for students specializing in chemistry, is offered, in which very complex commercial and natural products are analyzed and in which special attention is also given to rare elements. During this course, particular care is taken to familiarize students with other works on qualitative analysis, such as the outlines of A. A. Noyes and Bray, and the special parts of Fresenius's manual.
Students who have been prepared in general chemistry along physicochemical lines, as represented, for instance, by Smith's textbooks, make more rapid and more easy progress in the first course than do students otherwise prepared. But the treatment of the subject is intended to make it possible for students, who have not paid particular attention to chemical equilibrium and to the modern theories of solution in their general chemistry course, to complete the course within the time limit indicated. Perhaps one-third of the students in an average class, in the past, have taken the course under these conditions and no special difficulty was encountered by them.
In the theoretical treatment the author is particularly indebted to the original articles and to the larger works of Arrhenius, van 't Hoff, Nernst, A. A. Noyes, Ostwald, and Walker. For the systematic analytical material acknowledgment is due, in particular, to Fresenius's "Qualitative Chemical Analysis," and to the important publications by A. A. Noyes and Bray in the Journal of the American Chemical Society. Some of the excellent methods of the latter authors have been adopted outright, as indicated in the text. For some special matters the author is indebted to the texts of W. A. Noyes and of Böttger. Constant references to his sources of information have been made by the author, partly as a matter of acknowledgment, and more particularly to give students and teachers the opportunity for more extended, first-hand reading on any topic of interest. References suitable for college students are indicated by the addition of (Stud.). In two or three instances, the original source of information has been forgotten and diligent search has failed to trace it. For use in preparing any future edition of the book, the author will be glad to have his attention called to the facts by authors.
The author wishes to express here his particular appreciation of the generous assistance given him by his former colleague, Prof. Alexander Smith of Columbia University, whose suggestions and advice, especially in the editing of the manuscript and proof, have been invaluable. He also wishes to make grateful acknowledgment to his colleagues, Profs. H. N. McCoy, H. Schlesinger, and Dr. Edith Barnard, to Prof. L. W. Jones of the University of Cincinnati, Prof. E. P. Schoch of the University of Texas, Prof. B. B. Freud of Armour Institute, and Prof. W. J. Hale of the University of Michigan, who have assisted him by reading the proofs or the manuscript, or by carrying out experimental studies underlying part of the work, or in other ways. Corrections of his mistakes of omission and commission, and suggestions, will be gratefully received by the author.
JULIUS STIEGLITZ.
Chicago, September, 1911.
| PART I FUNDAMENTAL PRINCIPLES | ||
|---|---|---|
| CHAPTER | PAGE | |
| I. | Introduction | 3 |
| II. | Osmotic Pressure and the Theory of Solution, I | 8 |
| III. | Osmotic Pressure and the Theory of Solution, II | 21 |
| IV. | The Theory of Ionization: Ionization and Electrical Conductivity | 33 |
| V. | The Theory of Ionization, II: Ionization and Osmotic Pressure; Ionization and Chemical Activity | 67 |
| VI. | Chemical Equilibrium. The Law of Mass Action | 90 |
| VII. | Physical or Heterogeneous Equilibrium.—The Colloidal Condition | 118 |
| VIII. | Simultaneous Chemical and Physical Equilibrium.—The Solubility- or Ion-Product | 139 |
| PART II SYSTEMATIC ANALYSIS AND THE APPLICATION OF FUNDAMENTAL PRINCIPLES | ||
| IX. | Systematic Analysis for the Common Metal Ions. The Ions of the Alkalies and of the Alkaline Earths. Order of Precipitation of Difficultly Soluble Salts with a Common Ion | 157 |
| X. | Aluminium; Amphoteric Hydroxides; Hydrolysis of Salts. The Aluminium and Zinc Groups | 171 |
| XI. | The Copper and Silver Groups. Precipitation with Hydrogen Sulphide | 199 |
| XII. | The Copper and Silver Groups (Continued). The Theory of Complex Ions | 216 |
| XIII. | The Arsenic Group. Sulpho-acids and Sulpho-salts | 242 |
| XIV. | Oxidation and Reduction Reactions, I | 251 |
| XV. | Oxidation and Reduction, II. Oxidation by Oxygen, Permanganates, etc.; Oxidation of Organic Compounds | 277 |
| XVI. | Systematic Analysis for Acid Ions | 299 |
Note.—(Stud.) affixed to a reference indicates that the original article is recommended as suitable reading for college students taking their second year of work in chemistry.
Qualitative chemical analysis is concerned with the determination of the kinds of matter present in any given substance. In its broadest sense it includes the determination of all kinds of matter, the elements, rare as well as common, and all their combinations, organic compounds as well as inorganic. The recognition of the presence of rare elements, such as radium, uranium, thorium, tungsten, cerium, etc., is becoming a matter of growing importance with the modern development of the subject of radioactivity and the technical exploitation of the rarer elements, and it is a common experience for an analytical chemist to be called upon to determine the presence or absence of alcohol in beverages, of formalin in milk or other foods, and not a rare experience to be obliged to make tests for the presence of alkaloids like strychnine, morphine, cocaine, or for the presence of numerous other organic compounds. In this book, however, we shall limit our material to the more common elements and their most important inorganic combinations, including only a few typical organic acids. The limitation of our experimental material will make it possible to devote special attention to the scientific principles underlying analysis, to secure a clear and definite grasp of them, and to impart with simple material such experience in the technique and methods of analysis as will train the student to apply both his theoretical and practical knowledge to any field of analysis occasion may require. Accurate qualitative analysis, [p004] in any field, will depend on the care taken in mastering the theoretical significance and the technique of the methods recommended for the specific problem before the analyst; the details of the methods themselves, in any problem involving more than elementary analysis, are sought and found by him as a matter of practice in suitable larger works, in monographs and in the original literature. With the object of suggesting this broader application of the training acquired and of cultivating the invaluable habit of the professional chemist of consulting larger works and the literature, frequent reference will be made to such larger works, and to original papers in which more special subjects of analysis or theory are elaborately treated.
To recognize, in a substance, the presence of any element or compound, one must know its characteristic reactions, which will make it possible to distinguish it from all other elements or compounds. Further, in order to reach conclusions with the greatest possible speed, directness, and conclusiveness, it is usually best to carry out an examination in some systematic way, rather than in a haphazard and irregular fashion. We distinguish, accordingly, two parts in our laboratory work: first, the study of characteristic tests or reactions of the common elements and such of their compounds as are of importance in elementary analysis (Part III), and, secondly, practice in a systematic method of analysis (Part IV). In the study of the reactions, the way will be paved for systematic analysis, by taking the elements in the groups, which form the basis of the system of analysis employed, and by analyses of mixtures of the elements of a group immediately after the group has been studied.
Reliable and intelligent analysis is possible only with a clear knowledge of the chemistry of the reactions used, and the chemistry of the most important typical reactions will therefore be considered (in Part II), simultaneously with the laboratory study of the reactions and of systematic analysis.
The reactions for identifying an element or compound must bring physical evidence which can be recognized by our senses. The sense of touch is scarcely ever appealed to; perhaps the numbness or paralysis of the sense of touch imparted to the tongue or eyelid by the alkaloid cocaine and a few modern substitutes for it, and the tingling sensation produced on the tongue [p005] by aconite and its preparations, are the most important, but rare, instances of an appeal to this sense in analytical work. The sense of taste is also rarely used, and always with the greatest care to prevent poisonous effects. Acids and bases, bitter alkaloids, such as strychnine and brucine, sweet substances, such as cane sugar, glucose, glycerine, are instances of compounds which affect our sense of taste. In all these cases the taste is used rather as a confirmative test than as a conclusive proof of the identity of a suspected substance.
The sense of smell is rather more useful in qualitative analysis than that of taste or of touch. Hydrogen sulphide and ammonia, unless present in traces only, readily reveal themselves by their odor. Every chemist should be familiar with the faint but very characteristic odor of hydrocyanic acid,1 which should instantly and automatically warn him of the presence of this potent poison. Owing to partial decomposition by the moisture and carbonic acid absorbed from the atmosphere, alkali cyanides also give this important warning signal. Tests based on the odors of compounds are particularly valuable in the field of organic chemistry, where the sense of smell is extensively used for qualitative purposes; for instance, the pleasant smell of acetic ester, and the nauseating odor of an organic arsenic derivative, cacodyl oxide, may be used with advantage in identifying acetic acid.
But the evidence of touch, taste, and smell is, on the whole, only occasionally available in chemical analysis—almost all the tests employed are visual ones. A small proportion of these are color tests. The color of iodine vapor or of the solution of iodine in chloroform, the colors of metallic copper or gold, of copper salts in ammoniacal solutions, of sulphides, such as the orange sulphide of antimony (exps.), may be mentioned as instances, in which a test of identity depends on the observation of some characteristic color. But the great majority of analytical tests depend on observations of changes of state; evidence consisting in the solution of solids, the formation of precipitates, the evolution of gases, forms the most important part of the observations, [p006] on which our conclusions are based. In organic chemistry, determinations of melting-points and of boiling-points, which are very commonly used for the qualitative identification of compounds, form further instances of the application, to qualitative purposes, of observations based on changes of state.
In very many cases, where the formation or nonformation of a precipitate is intended to be used as an indication of the presence or absence of a given substance, the precipitating agent may throw down one or more of several different precipitates, which, seen without the aid of a microscope, cannot be identified without further examination. It is, thus, commonly necessary to use a sequence of such tests for the complete identification. For instance, the addition of hydrochloric acid to a solution of lead, mercurous or silver nitrate will produce a white precipitate. The precipitates may be distinguished by a further examination of their solubilities: hot water will dissolve the lead chloride, ammonia readily dissolves the chloride of silver and converts the mercurous chloride into a black insoluble mixture containing finely divided mercury (exps.). By the same means the chlorides, if present together, may be separated from one another and subsequently identified. Systematic analysis consists very largely in the use of a proper, logical sequence of such precipitation and solution reactions, and in the drawing of definite conclusions from the results obtained.
By far the greatest part of the experimental work in qualitative analysis has to do, then, with solution and precipitation. For intelligent and accurate analytical work a clear knowledge of the nature of solution and, in particular, of the simple laws governing chemical action in solution, and of those governing the formation and the solution of precipitates, is indispensable. The discoveries of van 't Hoff, in 1885–8, concerning the nature of solution, and the subsequent discoveries of Arrhenius, Nernst, Ostwald and others, have advanced every branch of chemistry, but perhaps no branch has profited quite so much as the theory of analytical chemistry, which, as a result of these discoveries, for the first time, received a clear, precise and satisfying scientific formulation of its empirical processes.2 [p007]
On account of the fundamental importance of this modern scientific formulation of the principles of analytical chemistry for the proper understanding of our subject, we shall consider first (in Part I) the modern theories of solution, with their experimental foundations, and we shall then develop the simpler fundamental laws governing chemical action and physical changes in solution. The analytical reactions themselves will be utilized as far as possible as the material for developing these general principles, so that this study may lead to the desired grasp of the theory of analysis and yet, at the same time, advance the student's knowledge of the practice of analysis.
[1] On account of the poisonous character of this and other vapors, the vessel containing a substance whose odor one wishes to test is not brought to the nose, but a little of the vapor is carefully wafted towards one by a motion of the hand, the vapor being thus greatly diluted with air.
[2] We owe the first modern scientific treatment of the principles of Analytical Chemistry to Ostwald's Wissenschaftliche Grundlagen der analytischen Chemie, 1894.
If a concentrated solution of a substance like sugar or cupric
nitrate is allowed to flow into a cylinder of water (exp. with
cupric nitrate), we find that the outside forces—gravity—tend
to draw the solution, whose specific gravity is greater than that of
water, to the bottom of the cylinder. In this method of proceeding
there is some inevitable mixing of the solution with the
solvent, as the result of friction, but the main portion of the deep
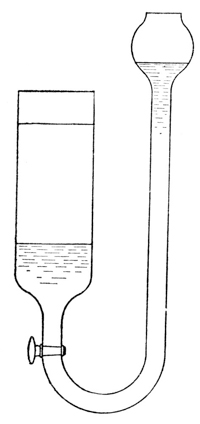 Fig. 1.
blue solution is drawn to the bottom of the
vessel and forms a blue layer under the colorless
water. A much sharper line of separation
may be obtained by allowing the cupric nitrate
solution to enter a cylinder of water from under
the water (see Fig. 1), the great density of the
nitrate solution causing it to displace the
water without perceptible mixing of the two
liquids (exp.). If these vessels are left at rest,
it may be noted, from day to day, that the
copper nitrate diffuses further and further into
the pure solvent, and careful examination would
show that the solvent, in turn, diffuses also into
the copper nitrate solution. The process is a
very slow one, but it will continue until a solution
of uniform concentration is reached, and
this will be the case, whatever the shape of
the vessel may be. If, for the moment, only the copper nitrate be
considered—and what we are developing for the copper nitrate
may be applied equally well, mutatis mutandis, to the diffusion
of water into the copper nitrate solution—it is obvious
then that copper nitrate in solution diffuses in all directions, even
against the force of gravity, and it is plain also, that any object,
resisting or arresting such a motion of material particles, must
have a force or pressure exerted upon it. Whatever the ultimate
[p009] cause of the motion, whether it is the result of inherent molecular
velocities of the dissolved copper nitrate, or of an attraction between
the solute and the solvent, or both, it is inevitable that a
pressure must result from the impact of the moving solute against
the solvent.3
Fig. 1.
blue solution is drawn to the bottom of the
vessel and forms a blue layer under the colorless
water. A much sharper line of separation
may be obtained by allowing the cupric nitrate
solution to enter a cylinder of water from under
the water (see Fig. 1), the great density of the
nitrate solution causing it to displace the
water without perceptible mixing of the two
liquids (exp.). If these vessels are left at rest,
it may be noted, from day to day, that the
copper nitrate diffuses further and further into
the pure solvent, and careful examination would
show that the solvent, in turn, diffuses also into
the copper nitrate solution. The process is a
very slow one, but it will continue until a solution
of uniform concentration is reached, and
this will be the case, whatever the shape of
the vessel may be. If, for the moment, only the copper nitrate be
considered—and what we are developing for the copper nitrate
may be applied equally well, mutatis mutandis, to the diffusion
of water into the copper nitrate solution—it is obvious
then that copper nitrate in solution diffuses in all directions, even
against the force of gravity, and it is plain also, that any object,
resisting or arresting such a motion of material particles, must
have a force or pressure exerted upon it. Whatever the ultimate
[p009] cause of the motion, whether it is the result of inherent molecular
velocities of the dissolved copper nitrate, or of an attraction between
the solute and the solvent, or both, it is inevitable that a
pressure must result from the impact of the moving solute against
the solvent.3

We have thus phenomena of diffusion of solutes through solvents, exactly as we have the well-known diffusion of gases, and the two phenomena are unquestionably very much alike, the solute, like the gas, tending to diffuse from the place of higher, to that of lower concentration.4 Likewise, if a solution of uniform concentration is heated in one part and not in another, the solute,4 like a gas under similar conditions, will move from the warmer to the colder part of the solution, as was demonstrated by Soret.5 Without committing ourselves for the present to any given reason for the diffusion, we note that the tendency to diffusion is a fact, and we must accept the conclusion that every obstacle to such diffusion must have a pressure exerted upon it.
Now, if a solution is separated from the pure solvent by means of a so-called semipermeable membrane, some of the results of this tendency to diffusion may be demonstrated.
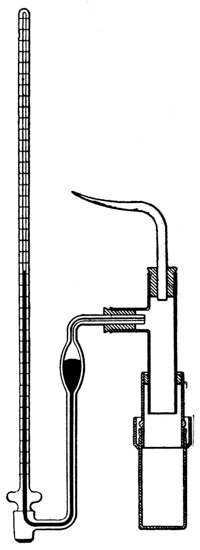
Exp. A concentrated solution of cane sugar in water, colored with some aniline dye, is enclosed in a thimble of parchment paper firmly fastened to a long narrow glass tube (see Fig. 2) and the cell is placed in a vessel of pure water. The parchment is not absolutely semipermeable, but it is approximately so, allowing the solvent, water, to pass, but being practically impervious to the solute sugar. A Schleicher and Schüll diffusion-thimble, No. 579, may be used, with advantage, as the thimble. (Cf. Smith's Introduction to Inorganic Chemistry, p. 284.) [p010]
We observe, presently, that the system is not in a condition of equilibrium; water passes through the thimble into the sugar solution and the latter expands, producing a decided difference of level, and consequently a hydrostatic pressure, between the liquid in the cell and the solvent outside of it. We may note two facts: first, that the change includes an expansion of the solute,6 the sugar, in the solution—that is, the tendency of the solute to expand into larger volumes of the solvent is satisfied exactly as in the experiment (Fig. 1) described above. In the second place, like all natural phenomena which proceed spontaneously, the change is in the direction of equilibrium; for when the hydrostatic pressure on the solution in the cell becomes sufficiently great, or if it is made sufficiently great at once by the application of some outside pressure, a point of equilibrium is reached, at which water will pass neither into the cell nor out of it. At that point, the tendency to expansion, both of the solute and of the solvent in the solution, is just overcome by the pressure on the solution.
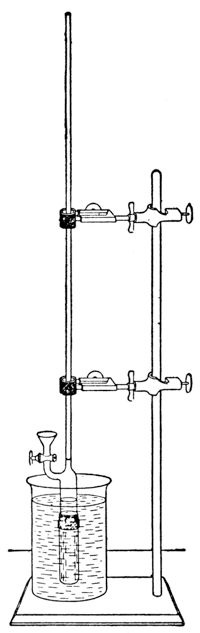
By precipitating these membranes in the pores of unglazed clay cells, especially by the process devised by Morse,7 we may make them sufficiently strong to resist enormous pressures—some used by the Earl of Berkeley were found to withstand a pressure of 130 atmospheres. The hydrostatic pressure required to produce equilibrium may then be measured in either of two ways. The first method, used originally by Pfeffer and more recently by Morse and Frazer8 and their collaborators in a wonderfully conscientious study of osmotic pressures, consists in allowing the hydrostatic pressure to establish itself by the passage of very small quantities of the solvent, through the membrane, into the tightly closed cell containing the solution. When the resulting pressure produces a condition of equilibrium, it is measured9 by a manometer connected with the solution, much as a gas pressure may be measured (Fig. 3).10 This process requires considerable time for exact measurements—weeks, during which the cell must be kept at a constant temperature. The second method, which has been used by Berkeley and Hartley,11 is very much more rapid and requires only a few hours for the measurement. It consists in having the pure solvent within the cell, instead of outside of it, and in [p012] exerting an external pressure on the solution outside of the cell, until a delicate manometer, communicating with the pure solvent, shows that water does not pass through the membrane in either direction—equilibrium having been reached.
Space does not permit the presentation of all the details of the evidence confirming this conclusion, but some of the most direct experimental proofs14 will be considered. [p013]
| Concentration. | Osmotic Pressure. mm. Mercury. |
Pressure/ Concentration. |
|---|---|---|
| 1.00% | 535 | 535 |
| 2.00% | 1016 | 508 |
| 2.74% | 1518 | 554 |
| 4.00% | 2082 | 521 |
| 6.00% | 3075 | 513 |
The ratio of pressure to concentration varies irregularly round a mean value of 526, and is approximately constant. The more recent, exceedingly careful measurements of Morse and Frazer confirm the conclusion, that Boyle's law holds for the osmotic [p014] pressures of dilute solutions; they find that the osmotic pressures of glucose and of cane-sugar solutions vary directly as the concentrations of the solutions, at a constant temperature.15
Expressing the temperature in absolute degrees, we have more simply:
That is, the pressure of a gas varies directly as its absolute temperature, if the volume is kept constant.
Pfeffer's results, on the osmotic pressure of sugar solutions at different temperatures, were not sufficiently accurate to enable van 't Hoff to use them to confirm positively the rigorous thermodynamic proof (footnote 3, p. 12), that the osmotic pressure must increase proportionally to the absolute temperature, as required by Gay-Lussac's law. But the data did show, uniformly, a marked increase of the osmotic pressure with the temperature and, frequently, excellent agreement between theory and experiment. More striking were the results obtained by van 't Hoff in testing the correctness of this extension of Gay-Lussac's law by means of Soret's results on the diffusion of a solute from a warmer to a colder place. It was found that the concentrations, obtained by Soret when equilibrium was reached, agreed closely with the demand that the osmotic pressures in the colder and the warmer parts of the solution should be equal, and that the osmotic pressure of a given weight of solute in a given volume should increase proportionally to the absolute temperature. An elevation of temperature, in a portion of a uniform solution, will increase the osmotic pressure of this part. Diffusion will follow, until the loss in concentration of the solute, and therefore the loss of osmotic pressure (Boyle's law), of the warmer part, and the increased concentration and increased pressure of the colder portion result in all parts of the solution having the same osmotic pressure. [p015] As an example, a concentration of 17.33% copper sulphate at 20° was found to be in equilibrium with a concentration of 14.03% at 80°. Now, if the 17.33% solution had an osmotic pressure of P mm. at 20°, a 14.03% solution at the same temperature would have a pressure of (14.03 / 17.33) × P mm. (Boyle's law), and this would increase to (14.03 / 17.33) × P × (353 / 293) mm. at 80° C., or 0.975 P mm.—a result showing that the osmotic pressure in the hot part was practically the same as that, (P), in the cold part of the solution.17
It is a source of great satisfaction, that the recent very exact and painstaking work of Morse and Frazer,18 in measuring osmotic pressures directly, completely confirms this fundamentally important conclusion, that the osmotic pressure of a solution does increase proportionally to its absolute temperature.
Pfeffer's measurements, with solutions of 1 g. of sugar in 100 c.c. of water (the volume of the solution is 100.6 c.c.), were shown to prove, that the observed osmotic pressures agreed excellently with the gas pressures, calculated for the equimolar weight of hydrogen, in the same volume and at the same temperature:
| Temperature. | Osmotic Pressure | |
|---|---|---|
| Found. Atmosphere. |
Calculated.20 Atmosphere. | |
| 6.8 | 0.664 | 0.665 |
| 13.7 | 0.691 | 0.681 |
| 14.2 | 0.671 | 0.682 |
| 15.5 | 0.684 | 0.686 |
| 22 | 0.721 | 0.701 |
| 32 | 0.716 | 0.725 |
| 36 | 0.746 | 0.735 |
Morse's more recent and more exact results show, that the osmotic pressure of solutions of cane sugar and of glucose (corrected for the volume occupied by the sugar, see footnote, p. 15) agrees within 6% with the values demanded by van 't Hoff's theory, being about 6% larger for concentrations ranging from 0.1 to 1.0 molar. The difference of 6% is noteworthy and is probably due to secondary causes, but suggests extended investigation of its source.
In still other instances, apparently too high osmotic pressures, or too low molecular weights, have been found by the application of the Avogadro-van 't Hoff Hypothesis to solutions: for instance, the molecular weight of sodium, when dissolved in mercury, was found by Ramsay to vary from 21.6, in dilute, to 15.1 in concentrated solutions. But Cady found that the heat of dilution of sodium in mercury solution is considerable, and by taking this properly into account, Bancroft was able to show that the molecular weight, correctly calculated in a given experiment, is 22.7 (agreeing well with the theoretical weight 23), in place of 16.5, as calculated without making the required allowance for the heat of dilution.26 These determinations are most instructive in showing that the sources of some of the most important deviations from the van 't Hoff-Avogadro principle, deviations which have been brought forward as arguments against its assumptions, are due, not to any untrustworthiness of the general principle, but to the error of neglecting to observe the limiting conditions of the formulation, or of neglecting to make corresponding corrections for the non-observance thereof.
The fundamental laws of gases and the Avogadro Hypothesis may be condensed into the following general equation, expressing all of the laws, viz.: P V = n R T. This equation applies equally to the osmotic pressures of dilute solutions, the osmotic pressure being substituted for the gas pressure. In the equation, T is the absolute temperature of the gas or solution, P the gaseous or osmotic pressure, V the free space of the gas volume, i.e. the volume of the gas less the volume occupied by the gas molecules, or the volume of the pure solvent in the solution used, i.e. the volume of the solution less the volume of the solute. R is the so-called gas-constant, and represents the work done against the external pressure when one gram molecule, or mole, of the gas is heated one degree and allowed to expand, say at constant pressure P, against an external pressure P; n represents the number of gram molecules or moles of gas or solute used (the total weight of solute or gas, divided by the average weight of a mole in the gas or solute). If a given weight of a gas or solute is taken, and no dissociation or association occurs (such as would involve appreciable heats of dilution), then n is a given number; and, therefore, at a given temperature T, all the factors on the right side of the general equation being given numbers, P V is a constant (Boyle's law). For a given quantity of gas or solute (n is a given number), kept at constant volume V, the pressure must vary as the absolute temperature (Gay-Lussac's law); P / T = n R / V = a constant. When the pressure, volume and temperature of two gases, or two dilute solutions, are equal, n, the number of gas or solute molecules present, must be the same (Avogadro-van 't Hoff Hypothesis); n = P V / (R T), and all the factors of the right side are the same for the gases and solutions which we are comparing. Finally, if the pressure is expressed in atmospheres, the volume in litres, and the temperature in absolute degrees, the gas-constant R = P V / T = 1 × 22.4 / 273 = 0.082.
[3] Even after a solution of uniform concentration of the solute is formed, the tendency toward diffusion, and the diffusion itself, and the resulting pressure must still persist. But a state of dynamic (or flowing) equilibrium must be considered now to exist, the loss caused by the moving away of the solute, from a given part of the solution, being balanced by the diffusion (into that part) of the solute from the neighboring parts. Whether one ascribes the diffusion to inherent molecular velocities of the solute, or to an attraction between solvent and solute, the discrete particles of the solute in a solution of uniform concentration will continue to have such inherent velocities (Chap. III), and will also continue to be surrounded by pure solvent, exactly as in solutions of unequal concentrations, where the diffusion may be observed, because the net result, in such a case, is a one-sided action.
[4] This again holds equally for the solvent.
[5] See below.
[6] At the same time, the change is also in the direction of an expansion of the solvent in the solution. The two changes are not opposed to each other, but supplementary.
[7] Am. Chem. J., 28, 1 (1902); 40, 266, 325 (1908) (Stud.).
[8] Am. Chem. J., 34, 1 (1905); 36, 39 (1906); 37, 324, 425, 558 (1907); 38, 175 (1907).
[9] The exact concentration of the solution at the point of equilibrium is determined by subsequent analysis.
[10] Cf. Smith's Inorganic Chemistry, p. 287.
[11] Berkeley and Hartley, Phil. Trans. Roy. Soc. A, 206, 481 (1906).
[12] When appreciable heat of dilution is shown by a solution, some chemical change, resulting from dilution, is indicated (such as, dissociation of the solute, hydration, hydrolysis, etc.). In such a case, the Avogadro-van 't Hoff principle holds for each concentration for its actual composition, and the principle may often be used to determine the extent of the chemical change produced by dilution. But then the osmotic pressure will not obey Boyle's and Gay-Lussac's laws. The same exception applies also to gases which undergo chemical changes, as the result of dilution or change of temperature. In the case, for instance, of nitrogen tetroxide, which dissociates according to N2O4 ⇄ 2 NO2, the extent of the dissociation varies with changes of concentration (pressure) and of temperature, and the gas does not obey the laws of Gay-Lussac and of Boyle. In regard to the rôle of heat of dilution in connection with osmotic pressure, see Bancroft, J. Phys. Chem., 10, 319 (1906).
[13] See p. 15 for a more rigorous statement concerning the volume. Cf. Morse and Frazer, Am. Chem. J., 34, 1 (1905).
[14] As a result of numerous vain endeavors, as well as of much direct evidence of a positive character, the scientific world has, for many years, held the opinion that any sort of "perpetual motion machine" is impossible. Every one now admits that a machine which would be able to work continuously, without consuming energy, is an impossibility—that is, that a "perpetuum mobile of the first class," as it is called, is impossible (law of the conservation of energy or first law of thermodynamics). From this law it does not of necessity follow, however, that it would be impossible to make a machine or device that would convert continuously into available energy or work, say, the enormous amounts of heat energy of the earth or of large bodies of water ("dissipated energy") which would thereby be cooled below the temperatures of their surroundings. Such a hypothetical process has been termed a "perpetuum mobile of the second class"; it has never been realized and is universally conceded to be an impossibility; the so-called "second law of thermodynamics" gives expression to this fact.
Now van 't Hoff [Z. phys. Chem., 1, 481 (1887)] showed, first, that a gas like oxygen, nitrogen, hydrogen, etc., which is soluble in proportion to its gas pressure (Henry's law), must exert, in solution, an osmotic pressure equal to the gas pressure, which it would have, if present in the same quantity as a gas in the same volume at the same temperature; for, if such were not the case, the solution and gas could be used to produce a perpetuum mobile of the second class, which, according to the above law, is an impossibility. Similar proofs were given by Rayleigh [Nature, 55, 253 (1897)] and by Larmor [Phil. Trans., 190, 266 (1897), Nature, 55, 545 (1897)] that the principle applies to solutions of other solutes.
Provided, then, that we have (1) perfect semipermeable membranes, (2) sufficiently dilute solutions, and (3) none but negligible heats of dilution (p. 12), van 't Hoff's generalization, concerning the relation of osmotic pressure and the laws of gases, must hold, if the perpetuum mobile of the second class is impossible, as is demanded by the second law of thermodynamics.
[16] The pressure P0 of a given quantity (weight) of a gas at 0° C., in a given constant volume, is also a given number and consequently P0/273 is a constant under these conditions.
[17] The slight differences in the ionization of copper sulphate solutions of 14% and 17% and at 20° and 80° are not included in the calculation, ionization being unknown, when van 't Hoff made his calculations.
[18] Am. Chem. J., 41, 258 (1909).
[19] In the light of recent work, especially by Morse and Frazer, the law would state, more exactly, that a substance in solution produces the osmotic pressure, at a given temperature, which it would exert, if it were contained as a gas, at the same temperature, in the volume occupied by the pure solvent of the solution. For sufficiently dilute solutions, the volume of the solution and the volume of the solvent may be considered identical; for more concentrated solutions, there is a decided difference, and the correct volume to use in calculation is the volume of the solvent alone, i.e. the volume of the solution reduced by the volume of the pure solute. This corresponds to the correction of the volume in the more accurate expression for the behavior of gases, developed by van der Waals; in place of v, the total gas volume, (v − b), the total volume of the gas less the volume of the spheres of action of the gas particles, is used, especially for strongly compressed or concentrated gases. It may be added that van 't Hoff's thermodynamic proof involves the same correct definition of the volume that Morse and Frazer subsequently developed experimentally. Cf. Bancroft, J. Phys. Chem., 10, 319 (1906).
[20] One gram of cane sugar, C12H22O11 (the mol. wt. is 342) corresponds to 1 / 342 gram molecule or mole and, therefore, to 2.02 / 342 gram of hydrogen. The volume containing this quantity of hydrogen is 100.6 c.c.; a liter would contain 2.02 / 342 × 1000 / 100.6 gram of hydrogen. The pressure of a mole or 2.02 grams of hydrogen, contained in a liter at 0°, is 22.4 atmospheres, and the pressure of the quantity of hydrogen given above, in a liter, would be (2.02 × 1000) / (342 × 100.6) × (22.4 / 2.02) at 0°. At 36° C., for instance, the pressure would be 309 / 273 times as great, or Pcalculated = (2.02 × 1000 × 22.4 × 309) / (342 × 100.6 × 2.02 × 273) = 0.735 atmosphere.
[21] The exact relations are discussed in van 't Hoff's Lectures on Physical Chemistry, Part II, pp. 42–59, Nernst's Theoretical Chemistry (1904), pp. 142 and 148, and H. C. Jones's The Elements of Physical Chemistry (1909), pp. 252, 271.
[22] Vide Raoult, Scientific Memoir Series, 4, 71, 127.
[23] I.e. abnormally small depressions of freezing-points or elevations of boiling-points.
[24] Nernst, Theoretical Chemistry, p. 486; Hendrixson, Z. anorg. Chem., 13, 73 (1897).
[25] Cf. Bancroft, J. Phys. Chem., 10, 319 (1906).
[26] For the discussion of other instances, vide Bancroft, loc. cit.
Accepting van 't Hoff's theory of solutions, then, as based on experimental evidence as well as on sound thermodynamic reasoning, we find a number of interesting questions still confronting us. Most insistent is the question as to the source of the remarkable agreement between the osmotic pressure of a solute and the gas pressure, which it would exert in the same volume, as a gas, at the same temperature, and as to the identity of the laws governing the two forms of pressure. Then, we may also ask, what is the mechanism of the process by which osmotic pressure reveals itself, especially in the case of cells with semipermeable membranes. And, finally, we may ask what is the cause of the semipermeability of the membranes.
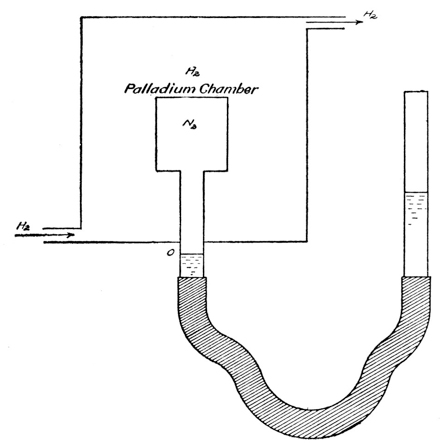
We find the simplest evidence of the cause of semipermeability in the case of gases. Palladium, especially when heated, dissolves hydrogen readily, but not nitrogen or oxygen, and a wall of palladium may be used as a semipermeable membrane to separate a mixture of hydrogen and nitrogen from pure hydrogen, just as copper ferrocyanide membranes are used with aqueous sugar solutions and water. The results with the gases duplicate in every particular the observations made on the solutions (see below, p. 24). Certain gases, such as ammonia and hydrogen chloride, are easily soluble in water, while others, like oxygen, nitrogen and hydrogen, are very difficultly soluble, and a film of [p022] water may be used as a semipermeable membrane for such gases.30
Exp. If the moist membrane of a cell (Fig. 4), containing air, is covered with an atmosphere of hydrogen, there is no increase of pressure produced in the cell, as indicated by the column of colored oil in the manometer in which the cell ends: hydrogen, being very little soluble in water, cannot pass through the film of water in the few minutes it is allowed to act. If now an atmosphere of ammonia is substituted for the hydrogen, the gas passes through the film into the cell. It turns the color of a piece of litmus paper placed in the cell and produces an increased pressure in the cell, the air remaining in the latter, because oxygen and nitrogen are very little soluble in water.
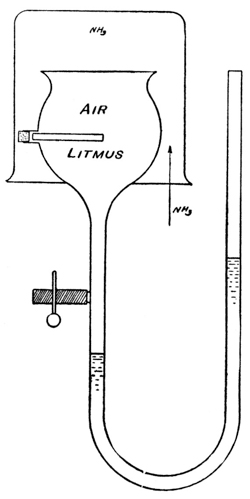
Membranes will be, similarly, semipermeable to solvent or solute, when only one of these is soluble in the membrane, or is capable of forming an unstable compound with it. For instance, salts, holding water of crystallization which is readily lost and recovered, may easily be conceived of as assuming the rôle of semipermeable membranes, allowing the passage of water say from a wet atmosphere to a dry one, or from pure water to a solution; and Tammann31 has realized such membranes by the use of zeolites—silicates, which hold water of crystallization but are insoluble in water. Kahlenberg32 has recently used rubber membranes, that are permeable for solvents like benzene, pyridine, etc., which are soluble in rubber, but not permeable for water, which is insoluble in rubber.

The experiment is particularly instructive, in the first place, because it illustrates with a gas, subject to the laws of gases, why and how osmosis takes place through a semipermeable membrane—namely as a result of the solubility of the diffusing substance in the membrane, and through the flow of the diffusing substance [p026] from higher to lower concentrations. In the second place, while the increase in total pressure in the inner chamber undoubtedly is brought about by the osmosis of hydrogen into the chamber, the excess pressure when equilibrium has been reached, necessarily measures accurately the partial pressure of the nitrogen. In other words, the semipermeable membrane is merely a means or device for measuring the partial pressure of the nitrogen—the membrane is not the cause of the pressure; the latter is a definite one, whether we know what it is or not, and the osmosis of the hydrogen through the palladium merely gives us a means of ascertaining it. Similarly, it would be wrong to consider that the osmotic pressure of a solution is caused, or brought about, by the flow of the solvent through a semipermeable membrane (osmosis); the latter simply is a device which enables us to recognize and measure the pressure that exists in the solution, both in the presence and the absence of such a membrane.
We may consider, then, that the osmosis, or migration of the solvent through a semipermeable membrane into a solution, is the result of the reduced concentration (or partial pressure) of the solvent in the solution, resulting from the presence of the solute.
Inasmuch as the effect of the solute on the solvent can be overcome by a pressure on the surface of the solution, one is led to the conclusion that the solute acts by exerting, in turn, a force or pressure against the surfaces of the solvent, in the directions opposite to the hydrostatic pressure required to overcome it. The significant identity of the value of this pressure, as thus measured, with the gas pressure that would be exerted by a gas of the same number of molecules, in the same volume and at the same temperature, leads us to the last of the three questions which have been raised, namely, the question concerning the theory of the intimate relations between gas and osmotic pressures (p. 21).
The laws of gases, it is known, are in accord with the two simple assumptions of the kinetic theory. The first assumption is that [p027] gases consist of ultimate discrete particles (molecules), which move in all directions through the space filled by the gas and, at ordinary pressures, are so far apart, that the forces of molecular attraction between them are negligible; the pressure of the gas is simply the net result of the impacts of these flying particles upon the walls of the containing vessel. The second assumption of the kinetic theory is that temperature is a function of the mean kinetic energy of the moving molecules, and that the molecules of gases of the same temperature have the same mean kinetic energy. The kinetic energy of particles is a function of their mass m and their velocity u (K.E. = ½ m u2). When a gas is heated, the kinetic energy of its molecules is increased, and, since their masses remain unchanged, their velocity must increase. As a result, the number and the force of their impacts against the walls of a given space increase, and thus the pressure is increased.
We may ask, whether this theory cannot be used to explain the connection between osmotic and gaseous pressure. If temperature is a function of the kinetic energy of the molecules of which a substance consists,—and the whole behavior of gases confirms such a conception,—then one must conclude, that the mean kinetic energy of molecules, at a given temperature, must always be the same, irrespective of whether they are present in gaseous, or liquid, or solid form, or even in solution.39 The tendency of the molecules to move, resulting from the kinetic energy inherent at a given temperature, may be largely balanced (liquids), or overcome (solids), by molecular attractions of surrounding particles, but such conditions are altogether in harmony with the conception of a definite mean molecular kinetic energy, persisting at a given temperature, irrespective of the physical surroundings of the molecule. According to the kinetic theory, then, when we have a dilute solution, say of alcohol in water, the molecules of alcohol, at a given temperature, would have a given mean kinetic energy, [p028] and would be tending to move in all directions with a mass40 and velocity, the same as if the alcohol were present as a gas or vapor at the same temperature. If the solution is sufficiently dilute, the dissolved alcohol molecules are sufficiently far apart, for average time, to make the molecular attractions between them negligible, just as is assumed for gases. As far as the alcohol (solute) molecules alone are concerned, they may, evidently, be assumed to be present in the solution, in the same condition, as to number, mean kinetic energy and mean velocity, as they would be in alcohol vapor of the same concentration and temperature. We may ask, now, whether the osmotic pressure of the solution may not result from the pressure on the solvent, growing out of its bombardment by the solute molecules. And we may ask, further, what numerical relation would subsist between such a pressure and the pressure of the solute, if the latter were present as a gas, under the same conditions of temperature and concentration. In order to be prepared to answer these questions, we must consider, in what way the presence of the solvent must modify the motions and the forces of impact of solute molecules.
One great difference between the dissolved substance and the gas would be, that, in the solution, the solute is in intimate contact with the solvent. A decided attraction must exist between the solute molecules and the solvent molecules, since we could not otherwise understand how a solvent, like water, in dissolving a nonvolatile substance like sugar, could overcome those molecular attractions between the sugar molecules, which make sugar a solid. But we note, that all the solute molecules in a solution, except those at the surface, are surrounded on all sides equally by the solvent. The attractive forces, exerted upon the single molecules of the solute by the solvent molecules, thus sum up to zero, and need not be considered further. Only the small number of solute molecules, which are at the surface of the liquid, would involve a minor correction in the application of the kinetic theory, and this need not be considered here.
A second point of difference between a substance in solution, and the same substance as a gas or vapor at the same temperature [p029] in the same volume, lies in the fact that a gas molecule will go a much greater distance without colliding with some second molecule and changing its path, than would a solute molecule, the latter molecule being closely surrounded by the molecules of the solvent. The mean free path, as it is called, will be very much shorter for a solute molecule than for a gas molecule, and we note, as a matter of fact, how slow is the diffusion through a solvent (see exp. p. 8). But the shortness of the previous path does not affect the force of a blow resulting from the impact of a moving mass, the force of the impact being dependent only on the mass and the change in speed of the striking particle, at the moment of impact. Thus the short free mean path of a dissolved molecule does not affect the mean force of the blow, delivered when it strikes the resisting medium.
The slow diffusion of a dissolved substance represents a difference in degree, not in kind, between gases and dissolved substances. Even in gases, we have such frequent collisions that the mean free path of an oxygen molecule at 0° and atmospheric pressure is only 0.00001 cm., whereas the velocity, the total path covered in one second, is 42,500 cm.
Exp. If a bulb containing a few drops of bromine is broken at the bottom of a tall cylinder, the bromine vapor is seen to diffuse rather slowly into the upper part of the cylinder, the bromine molecules, in their passage upward, rebounding from the air molecules, with which the cylinder is filled. If a second cylinder is first evacuated, and the bromine bulb is broken in vacuo, the vapor is seen to fill the cylinder instantly, the high velocity of the bromine molecules being thus revealed.
But a third question, of fundamental importance in the comparison of the condition of a substance existing as a gas and its condition in a solution of the same concentration and temperature, results from a consideration of the frequency of the impacts of the solute molecules against the solvent, growing out of the reduction of the lengths of the mean free paths of the solute molecules.41 In order to be able to take this fact properly into account, it will be necessary to consider somewhat more precisely the manner in which, according to the kinetic theory, gas pressure is produced.
We may consider that we have in a cube of unit volume (1 c.c.) n molecules of a gas, each of mass m and average velocity u cm. per second. We may assume that one-third of the total number [p030] of molecules moves in each of the three dimensional directions.42 A single molecule of mass m, striking the surface with a velocity u and rebounding with the same velocity in the opposite direction, will exert on the surface a force of 2 m u units. But, with a velocity of u cm. per second, it will reach the opposite wall and return to the surface we are considering, u / 2 times in one second. A single molecule will consequently exert a force 2 m u × u / 2 or m u2 on the surface, and the n / 3 molecules moving in the same direction will exert a force n / 3 × m u2 on the unit surface. This represents, therefore, the pressure of such a gas, as calculated on the basis of the assumptions of the kinetic theory. Now, when a gas is so strongly compressed, that the bulk of the molecules is not negligible in comparison with the total volume of the gas, the number of impacts on unit surface in unit time becomes sensibly greater than n / 3 × u / 2, since the distance to be covered between successive blows on the surface will be sensibly less than 2 cm., in a cube of unit volume. If we imagine, for the sake of a rough illustration, that one-third of the molecules in 1 c.c. are united into one spherical mass (indicated by A in Fig. 7), moving upwards and downwards, it is obvious that the distance covered between two successive blows on a surface is not 2 cm., but that distance diminished by twice the diameter of the sphere. For strongly compressed gases, the total number of impacts on unit surface is therefore sensibly greater than n / 3 × u / 2, and the pressure is proportionately greater. According to van der Waal's correction for this effect, P = n / 3 × m u2 / (1 − b), where b represents the volume actually occupied by the molecules in 1 c.c. of the gas.43
Now, for solute molecules, the "free space" of movement, as we may call it, is, similarly, very considerably reduced by the presence [p031] of the solvent, and the reduction of this free space, as Nernst has shown, will have the same effect on the pressure produced against unit surface of the solvent by the bombardment of the solvent by the solute, as the reduction of the free space has on the gas pressure when a gas is strongly compressed. The resulting pressure on unit surface of the solution must thus be increased, from the pressure Pgas, which would be exerted by the solute against the walls of a vessel, if it were present as a gas of the same concentration, at the same temperature, to Pgas / (1 − v), where v represents the real volume occupied by the solvent and (1 − v) the free space for the solute molecules in unit volume of solution.44 If osmotic pressure is the result of such a bombardment of the solvent by the molecules of the solute, one might, therefore, expect to find the osmotic pressure very much greater than the gas pressure of the same substance in the same volume at the same temperature. However, in all the experimental determinations (by means of semipermeable membrane, vapor pressure, boiling-point and freezing-point measurements) of the osmotic pressure as defined on p. 10, this corrective factor cancels out again.45 According to the kinetic theory, the osmotic pressure of a substance in dilute solution should, consequently, be found by experiment to be equal to the gas pressure which a gas, of the same molecular concentration, would exert at the same temperature.46
We find thus that the significant coincidence between the osmotic pressure of a substance in dilute solution, as defined and measured according to van 't Hoff, and the gas pressure which the substance would exert, if it were present as a gas in the same volume and at the same temperature, is in agreement with the fundamental assumptions of the kinetic theory. This theory, consequently, gives us an adequate theoretical explanation of [p032] osmotic pressure, as it does of gas pressure. As van 't Hoff says,47 "if the osmotic pressure follows Gay-Lussac's law and is proportional to the absolute temperature, then, like gas pressure, it will become zero at 0° absolute temperature and will vanish when molecular movements come to rest. It is therefore natural to look for the cause of osmotic pressure in kinetic phenomena and not in attractions."48
[29] L'Hermite, Compt. rend., 39, 1177 (1854); van 't Hoff, Lectures on Physical Chemistry, Part II, p. 37.
[30] Nernst, Theoretical Chemistry, p. 103.
[31] Van 't Hoff, Lectures on Physical Chemistry, Part II, p. 37.
[32] J. Phys. Chem., 10, 141 (1906).
[33] This term must not be confounded with the term osmotic pressure, which has been defined on p. 10.
[34] See Chapter VII on the law of physical or heterogeneous equilibrium, where the relations are discussed in detail.
[35] Z. phys. Chem., 5, 175 (1890).
[36] Ibid., 3, 119 (1889).
[37] Phil. Mag., 38, 206 (1894).
[38] Cf. van 't Hoff's Lectures on Physical Chemistry, Vol. II, 40 (1899).
[39] The molecules may have different masses in the different conditions, and the principle of the mean kinetic energy would always apply to them as they are, in the condition under observation, and not as they are in some other condition; any change in mass, in solution, for instance, would show itself in the osmotic pressure measurements (see p. 18), just as it is shown in the measurements of gases, when the gas molecules show a change in composition, as is the case with hydrogen fluoride (H2F2 ⇄ 2 HF), nitrogen tetroxide (N2O4 ⇄ 2 NO2), phosphorus pentachloride (PCl5 ⇄ PCl3 + Cl2) and other compounds.
[40] The molecular weight of alcohol in dilute aqueous solution is the same (46) as in vapor form. Raoult, Z. phys. Chem., 27, 656; Loomis, ibid., 32, 592.
[41] Nernst, Theoretical Chemistry, p. 245.
[42] This assumption is not made in the rigorous development of the above relations on the basis of the kinetic theory, but it leads to the same net result.
[43] Even for gases of ordinary concentration, the introduction of the same correction gives an expression for the relation of pressure and volume, which is more exact than Boyle's law and is used in all exact calculations with gases.
[44] One may imagine, first, n molecules of the solute as a gas, with the pressure Pgas, in 1 c.c. Then, one may imagine, crudely, the n molecules of solute, in a free (gas) space of (1 − v) c.c., in the center of 1 c.c. of the solvent, and exerting by their impacts a pressure Posm., against the solvent. According to Boyle's law, we should then have, Pgas × 1 = Posm. × (1 − v), and therefore Posm. = Pgas / (1 − v).
[45] Vide Nernst, Theoretical Chemistry, p. 245, for the detailed discussion of this relation.
[46] This conclusion is reached more rigorously and more simply by thermodynamic analysis.
[47] Lectures on Physical Chemistry, Part II, p. 35.
[48] Rigorous developments of the relations between solute and solvent, for dilute and concentrated solutions, have been made by van der Waals, Z. phys. Chem., 5, 133 (1890); van Laar, ibid., 15, 457 (1894); G. N. Lewis, J. Am. Chem. Soc., 30, 675 (1908), and Washburn, ibid., 32, 653 (1910). An admirable review of the theories of osmotic pressure, by Lovelace, will be found in the Am. Chem. J., 39, 546 (1908) (Stud.).
Of the laws and hypotheses concerning gases, the one that is perhaps of most importance to chemistry is Avogadro's hypothesis. With the aid of this hypothesis, we are able to determine the relative molecular weights49 of such elements and compounds as are gases, or are volatile at higher temperatures. If equal volumes of gases, under the same conditions of temperature and pressure, contain the same number of molecules, then the weights of such equal volumes also represent the relative weights of the molecules composing the gases. As a standard, for expressing the relative molecular weights in definite numbers, the molecular weight of oxygen is taken by convention to be 32, and all other molecular weights are expressed in terms of this standard. The density, or weight of one liter of oxygen at 0° and 760 mm., is 1.429 grams, and the molecular weight expressed in grams (molar weight) of oxygen, 32 grams, occupies, therefore, 32 / 1.429, or 22.4 liters. The weights of this same volume, 22.4 liters, of gases and vapors, calculated for 0° and 760 mm. pressure,50 express then directly, in terms of the oxygen standard, the relative molecular weights of the elements or compounds forming the gases. The weights themselves give us directly their gram-molecular or molar weights.
When molecular weights are determined in this way, with the aid of Avogadro's hypothesis, results are obtained which agree [p034] perfectly with the chemical behavior of the compounds or elements in question. The molecular weights of hydrogen chloride, water, ammonia, and marsh gas, for instance, are found to be 36.5, 18, 17 and 16, respectively, corresponding to the formulæ51 HCl, H2O, NH3 and CH4, and in confirmation of these results we find, by methods used especially in organic chemistry, that these compounds show a chemical behavior agreeing perfectly with the presence of one, two, three and four hydrogen atoms, respectively, in their molecules. Marsh gas, for instance, by treatment with chlorine, yields a monochloride, CH3Cl, a dichloride, CH2Cl2, a trichloride (chloroform), CHCl3, and a tetrachloride, CCl4. Water, by proper treatment, may be converted in successive stages into alcohol, (C2H5)OH, and then into ether, (C2H5)O(C2H5), or into sodium hydroxide, NaOH, and sodium oxide, Na2O.
It is this perfect agreement between the chemical behavior and the formulæ (as based on these molecular weights and on the analysis of compounds), which forms the strongest experimental evidence of the correctness of the fundamental assumption of Avogadro's hypothesis. The agreement has been shown to hold for innumerable compounds, even for those of greatest complexity, and it was such agreement which finally led to the general acceptance of the hypothesis. The experimental evidence of this nature is so strong, so extensive and so completely corroborative of the hypothesis, that many chemists, rather justly, consider the hypothesis to have been established as a law, although the evidence is circumstantial rather than direct.
While the application of Avogadro's hypothesis thus gives results agreeing well with the observed chemical behavior of very many important compounds, observations have been made which, at first sight, do not appear to agree with the requirements of the hypothesis and which seem to raise a doubt as to the universal truth of its fundamental assumption. Thus, if equal volumes of hydrogen chloride and ammonia, of the same temperature and pressure, are brought together, ammonium chloride is formed, both gases being totally consumed. Since, according to the hypothesis, equal volumes, under the conditions obtaining, contain the same numbers of molecules, the formation of ammonium chloride takes place according to the equation NH3 + HCl → NH4Cl, and we should anticipate that the molecular weight of [p035] ammonium chloride would be 17 + 36.5 or 53.5. However, when the molecular weight is determined by obtaining the weight of a measured volume of ammonium chloride vapor, at a temperature sufficiently high to vaporize the salt, and the observations are reduced to standard conditions of temperature and pressure, 26.75 grams is found as the calculated weight of 22.4 liters, and this weight, according to this hypothesis, should be the molecular weight of the chloride. This contradiction in two conclusions, each reached by the application of Avogadro's hypothesis to experimental observations, would, at the first glance, make one hesitate to accept the hypothesis as representing a universal truth; it might seem as if in some gases, such as ammonium chloride vapor, there might be only half as many molecules in a given volume as in the same volume of the majority of gases.
The gaseous dissociation of other ammonium salts, of phosphorus pentachloride and pentabromide (PX5 ⇄ PX3 + X2), and of a number of less common compounds, has been demonstrated in similar ways. As a result of the study of each case, the important conclusion has been reached that, as far as our knowledge goes, there are no exceptions to Avogadro's hypothesis, and this hypothesis seems therefore to represent a universal truth.56
The fact that all solvents and all solutes are included in this hypothesis, with the sole limiting condition that the solution must be dilute, is one of great significance and of greatest practical importance, as we may use any suitable solvent for determinations.
When molecular weights are determined in this way, a very large number of compounds give the same molecular weight by the solution method as by the gas method. For instance we have:
| Substance. | Mol. Wt. Gas Method. |
Mol. Wt. Sol. Method. |
Solvent. |
|---|---|---|---|
| Chloroform, CHCl3 | 119.5 | 119.5 | Benzene |
| Carbon bisulphide, CS2 | 76 | 76 | Benzene |
| Methyl (wood) alcohol, CH4O | 32 | 32 | Water |
| Ethyl (ordinary) alcohol, C2H6O | 46 | 46 | Water |
| Ether, C4H10O | 74 | 74 | Acet. Acid |
Further, the molecular weight of glucose is found in aqueous solutions to be 180, conforming to the formula C6H12O6, and agreeing with the molecular weight as obtained by a chemical study of compounds derived from glucose.
While there are, then, very many agreements in the molecular weights determined by the solution and by the older methods, it was recognized, at the outset,58 that there is also a large number of apparently abnormal cases, in which, in particular, much lower molecular weights are obtained by the solution methods than by the gas method,—lower even than the weights consistent with the accepted atomic weights of the elements in the compounds in question.59 For instance, we find 36.5 to be the molecular weight of hydrogen chloride in the gas form, but in aqueous solution its apparent molecular weight, as determined on the basis of van 't Hoff's hypothesis, is not even a constant; it is found to be less than 36.5 and approaches the limit 18.25, the more dilute the solution, [p038] the lower being the apparent molecular weight.60 For sodium chloride, the formula weight, corresponding to the formula NaCl, is 58.5. This would also represent its smallest molecular weight in gas form, consistent with the accepted atomic weights for sodium and chlorine. In aqueous solution, again, the apparent molecular weight of sodium chloride is found to be less than 58.5, and more than 29.25, the value found depending on the concentration of the solution used. For zinc chloride we have, likewise, in aqueous solution values much less than 136 and tending toward the limit 45, whereas the formula weight for ZnCl2 is 136.
These are instances of a very large class of apparent gross discrepancies between the requirements of the Avogadro-van 't Hoff principle and the generally accepted molecular weights of common compounds. There are three ways, in particular, in which one might be inclined to regard such results: in the first place, one might be tempted to consider that van 't Hoff's extension of Avogadro's hypothesis to solutions is justified in a considerable number of cases, but not as a universal expression, applicable to all dilute solutions. This seems, indeed, to have been van 't Hoff's own attitude originally. Such a view, since it does not throw new light on the matter, but simply shelves the question of the source of the discrepancy, would be tenable only after all other explanations had been found unsatisfactory.
In the second place, we might be inclined to consider whether a molecule like hydrogen chloride is not dissociated in aqueous solution into two smaller molecules, hcl, in which hydrogen and chlorine would appear as atoms with the weights h = 0.5 and cl = 17.75, which are half as large as the atomic weights determined from a study of volatile compounds of hydrogen and chlorine. If we remember that our atomic weights are confessedly maximum weights, and not minimum weights—although they are almost certainly also the true atomic weights—such a view would be, at least, worthy of some consideration. But, in the first place, it would be extraordinary that we should never have found, in the thousands of [p039] hydrogen derivatives that have been investigated, any compound, the molecule of which, in the gaseous condition, contained a single such atom of hydrogen, with the weight 0.5, or an uneven multiple of it: that only even multiples or pairs h2, corresponding to the atom H, should always have been found. In the second place, such an explanation of the results of the molecular weight determinations in aqueous solutions given above, would soon lead to difficulties, which make the view altogether untenable. For instance, the molecule of zinc chloride, according to the data given, would have to break down into three molecules and, if these were of uniform composition, we would have to assume chlorine atoms two-thirds or one-third as large as Cl. Since a moment ago we had to assume chlorine atoms one-half as large as Cl, we would have to conclude that the atomic weight of chlorine could be, at most, Cl / 6, which is the largest common divisor of Cl / 2 and Cl / 3. No chemist would seriously consider an atomic weight for chlorine one-sixth as large as the accepted weight, for that would mean that, in all the chlorine compounds investigated in the condition of gases, we have always at least six such atoms occurring together, and otherwise always multiples of six. Consequently such an interpretation of the so-called "abnormal" behavior of solutions of hydrogen chloride, sodium and zinc chlorides, etc., although at one time advanced by some chemists, must be considered as altogether untenable.
A third explanation of the "abnormally" low molecular weights, which certain substances in aqueous solutions possess, is, that the molecules of these compounds are capable of dissociation into smaller molecules of unlike composition, somewhat like ammonium chloride when it is heated, and that the substances in question are dissociated more or less considerably in this fashion in the solutions under consideration. Hydrogen chloride, for instance, besides existing as such (as HCl), in aqueous solutions, might be capable of dissociating, and actually be dissociated, to a considerable degree into molecules containing either only hydrogen or only chlorine (HCl ⇄ H + Cl); the average of the weights of the molecules in a mixture of molecules, HCl, H, and Cl, would be less than 36.5, and, according to the proportion of dissociated and undissociated molecules of hydrogen chloride, the average would lie between the limits 36.5 and (1 + 35.5) / 2, or 18.25. Such an [p040] explanation,61 made with certain additions and restrictions, was advanced in 1885 by Arrhenius, a Swedish chemist and physicist, when he learned of the exceptional behavior of these solutions, as noted by van 't Hoff. Although at first this interpretation occasioned considerable criticism, it has maintained itself successfully for twenty years, on the basis of a wide range of accumulated facts, and it has been of remarkable value and benefit in the development of all branches of chemistry and the allied sciences.
Exp. The fundamental difference between the two classes of solutions may readily be demonstrated. To water contained in an electrolytic cell, which is connected with a lighting circuit and with an electric lamp, first some alcohol, and later a small quantity of hydrochloric acid are added. The lamp is seen to glow, instantly, when the acid is added.
This simple fact, that the very solutions which give abnormally low molecular weights for the dissolved compounds are also good conductors of electricity, was explained by a theory of electrolytic dissociation or of ionization, which Arrhenius had developed62 from a study of the conductivity of electrolytes. The same fact has aided in establishing this theory which has led to the elucidation of vital problems of electrical conductivity and to a successful [p041] explanation of the problem of the apparently abnormal osmotic pressures (and molecular weights) of electrolyte solutes. It has thus removed the last difficulty in the way of accepting the van 't Hoff-Avogadro Hypothesis (p. 15) as true for all dilute solutions, exactly as the discovery of gaseous dissociation made it possible to recognize in the original Avogadro Hypothesis a universal truth (p. 36) about gases. And to these results was added, chiefly as the fruit of the work of Ostwald, with the aid of the theory of Arrhenius, the most successful and accurate formulation of the problem of the chemical activity of electrolytes, known in the history of chemistry.
When a current is passed through the solution of an ionogen, the electrified particles carry their charges to the electrodes (see [p042] below). They are called the ions64 of the electrolyte; the positively charged ions are distinguished as cations from the negatively charged anions, and the electrode toward which the cations move is called the cathode (negative electrode), and the electrode to which the anions move is called the anode (positive electrode).
The dissociation of hydrogen chloride may be expressed, in the terms of the assumptions made, in the following equation: HCl ⇄ H+ + Cl−; that is, hydrogen chloride is dissociated, to a greater or smaller extent and in reversible fashion, into positively charged hydrogen ions H+, and negatively charged chloride ions Cl−, and the charge on each chloride ion is equal in quantity to the positive charge on each hydrogen ion. Zinc chloride is dissociated according to the equation ZnCl2 ⇄ Zn2+ + 2 Cl−, and, according to (2), the charge on each zinc ion is twice as great in quantity as the charge on each chloride ion, and therefore twice as great also as the charge on each hydrogen ion (see below, p. 58). It is practically certain, according to more recent results, that the ions are combined with water to form hydrates, such as H+(H2O)x and Cl−(H2O)y.65 This does not modify, essentially, the fundamental assumptions of the theory, but contributes rather to a satisfactory explanation of the rôle of water as an ionizing agent, a question to which we shall return later.
One of the most fundamental and most characteristic properties of elements is considered to be the affinity which their atoms show for electrons; thus, the atoms of metals like sodium and potassium, which are generally called "electropositive" elements,68 show an enormous tendency to lose one electron each and to form positively charged particles69 Na-ε (= Na+) and K-ε (= K+).70 The atoms of strongly electronegative elements, like chlorine, have a tremendous tendency for gaining and holding electrons beyond the number originally in such atoms. Thus, chlorine atoms tend to assume an electron each; they thereby become negatively charged particles, Cl+ε ( = Cl−).
On the basis of these views, we have in sodium chloride NaCl a substance, whose molecules contain an atom, Na, with a tremendous tendency to lose an electron, and an atom, Cl, which has a tremendous affinity for an electron. It is natural to suppose, then, that both tendencies will be satisfied by the passage of an electron from the sodium to the chlorine atom, NaCl → Na-εCl+ε. Or, if we use the sign + to designate the positive charge produced on an atom by the loss of an electron and the sign − to indicate the charge gained through the assumption of an electron, we have71: NaCl is Na+Cl−. Similarly we have in hydrogen chloride H-εCl+ε or H+Cl−. It is altogether likely, therefore, that the atoms in a molecule of sodium chloride or of hydrogen chloride already possess electric charges,72 so that, even while combined, [p044] their tendencies to lose or gain electrons are satisfied. It is also possible that the atoms are held together in the molecule by the electrical attraction of the opposite charges.73 The force with which opposite electrical charges attract each other depends, as is well known, on the nature of the surrounding medium. Now, when molecular sodium chloride or hydrogen chloride is dissolved in water (a favorable medium), a decided decrease in the attraction (see p. 62), between the charged atoms within the molecules is brought about, and a process of ionization results: H+Cl− ⇄ H+ + Cl−. The charged particles are called ions only after they have separated from one another and have become independent molecules, capable, for example, of moving in opposite directions.
While the atoms of some metallic elements tend to lose a single electron and form ions Me+ (e.g. Na+, K+), the atoms of other elements tend to lose two or more electrons, forming bivalent ions, Me2+ (e.g. Zn2+, Fe2+, etc.), or trivalent ions, Me3+ (e.g. Bi3+, Fe3+), and so forth. Similarly, atoms of the so-called negative elements may assume two or more electrons, forming bivalent ions, X2− (e.g. S2−), and so forth.
Exp. The migration of the ions throughout the whole solution may be demonstrated by the passage of a current through a large U-tube containing a mixture of a cupric salt and a permanganate,74 placed under some dilute sulphuric acid. The cupric-ion is blue, all ionized solutions of cupric salts, with a colorless negative ion, being blue, while the permanganate-ion is of an intense purple color. In the limb of the U-tube, in which the cathode is placed, a blue zone, containing cupric ions, is soon seen emerging from the purple liquid and rising toward the cathode (see Fig. 8). It will take some time for any cupric ions actually to reach the electrode and be deposited as metallic copper. On the anode side, purple permanganate ions are seen rising toward the positive electrode.
The movement of the electrically charged particles in opposite directions through the solution constitutes an electric current, and such a current has the properties of a current through a [p046] wire—producing, for instance, heat, or being capable of deflecting a magnet placed in its field of action.75
If the conductivity of a given weight of hydrogen chloride, for instance, is measured under comparable conditions, it should be found to be greater, the more completely the acid is ionized. Now, in aqueous solutions, hydrogen chloride ionizes under the influence of the solvent water (pp. 41, 61), and the theory would lead us to anticipate that the greater the proportion of water used, the more extensively will it ionize the acid. Consequently, the addition of water to a given weight of acid should increase the latter's efficiency as a conductor. This conclusion has been fully verified by exact methods of measurement and may be readily demonstrated by the following series of experiments:
Exp.78 An electrolytic cell, having the shape of a parallelopipedon and a capacity of about one liter, is fitted with electrodes of copper, which reach from the bottom to the top of the cell and are connected with a storage cell and an ammeter. The cell is first filled with distilled water: no perceptible current passes through the water and the latter is therefore practically a nonconductor. The cell is then emptied by means of a siphon and 20 c.c. of 4-molar hydrochloric acid is brought into it. The ammeter shows that a definite current passes through the solution (0.17 ampere in an experiment79 with a cell 4.6 cm. wide and 11.5 cm. long, with copper electrodes 4.6 cm. broad and 21 cm. high). (See Fig. 9, p. 48.) [p048]
The conductivity of a solution, like that of a metal conductor, is the reciprocal of its resistance. Since, according to Ohm's law,80 the current for a given potential is inversely proportional to the resistance, the current is also directly proportional to the conductivity. The resistances of the metal connections and of the ammeter in the experiment are very small compared with the resistance of the solution, and they may be considered negligible for our purpose. Thus, the current indicated by the ammeter is a closely approximate measure of the conductivity of the solution. Now, if a volume of water (20 c.c.) equal to the volume of acid, were to be added to the latter, the cross section through which the current flows from plate to plate would be doubled, and, since the conductivity of a liquid conductor, like that of a metal, increases proportionally to the cross section, the current should be doubled by the change in this one factor. On the other hand, the concentration of the conducting acid is now one-half of the original concentration, and this should in turn reduce the conductivity of the solution to one-half. Consequently, if there were no further change in the electrolyte, the original conductivity should be maintained when the acid is thus diluted. But, according to the theory of ionization, as has just been shown, the addition of [p049] water to a given weight of hydrochloric acid should increase the proportion of ionized acid, and since the ions are the carriers of the current, the conductivity of the solution should be increased because of this change in the composition of the electrolyte. Experiment shows that such is the case.
Exp. 20 c.c. of water is added to the 20 c.c. of 4-molar acid in the cell, and the mixture is stirred. The current is decidedly increased (from 0.17 to 0.22 ampere in the experiment under discussion). If 40, 80, 160 and 320 c.c. of water are added in succession to the contents of the cell, the conductivity is increased by every addition of water. But, while each addition dilutes the acid to one-half the previous concentration, the increase grows proportionally smaller and smaller with increasing dilution. In the following table, "Ratios I" are the ratios of the observed conductivities to the original conductivity, "Ratios II" the ratio of each observed conductivity to the preceding one.
| Concentration of Acid. |
Observed Conductivity.A |
Ratios I. | Ratios II. |
|---|---|---|---|
| 4-molar | 0.17 | 1 | 1. |
| 2-molar | 0.22 | 1.30 | 1.30 |
| 1-molar | 0.26 | 1.53 | 1.18 |
| 0.5-molar | 0.30 | 1.76 | 1.15 |
| 0.25-molar | 0.31 | 1.83 | 1.04 |
| 0.125-molar | 0.32 | 1.88B | 1.03 |
[A] This is an artificial scale (see text) of conductivities, and does not represent reciprocal ohms, the standard units of conductivity.
[B] In the exact data on the conductivities of 4-molar and 1/8-molar HCl (Kohlrausch and Holborn, Leitvermögen der Elektrolyte (1898) p. 160), the ratio 348 / 181.5, or 1.92, is found, in place of 1.88 as observed.
We should expect, further, that the increase in conductivity, being dependent on the increased dissociation of a finite quantity of electrolyte, should tend towards a limit, a maximum conductivity being reached when (practically) all the acid is ionized. As a matter of experience, the conductivity of a given quantity of an acid or other ionogen does tend toward a limit. In the experiment just made, the conductivity of the acid increases very rapidly at first, as the 4-molar acid is diluted by water; but the increase in conductivity with the succeeding dilutions grows smaller and smaller and the conductivity is plainly approaching [p050] a limit (see the ratios I and II in the table). For hydrochloric acid at 18°, the limit for one mole81 (36.5 grams HCl) at infinite dilution, as deduced from the curve of conductivities at finite dilutions, is 384 reciprocal ohms.82
The method of calculation of α in a specific case may be illustrated as follows: the resistance of a cube of 1 cm. edge of a solution of hydrochloric acid, which contains 1.825 grams hydrogen chloride in a liter, is found to be 55.55 ohms at 18°. Its conductivity then is 1 / 55.55 reciprocal ohms. Now, 1.825 grams of hydrogen chloride is 1.825 / 36.5 or 1 / 20 gram-equivalent of the acid; a whole gram-equivalent of the acid would be contained in 20 liters or 20,000 c.c. Then Λv = (1 / 55.55) × 20,000, or 360 reciprocal ohms. If we use the value at infinite dilution given above, α = 360 / 384, or 93.75%. That is, 93.75% of the hydrochloric acid is present in the ionized condition in such a solution, and 6.25% is not ionized.
By making the assumption that at infinite dilution electrolytes are completely ionized, and by taking the ratio which the equivalent conductivity of a given solution of an electrolyte bears to the maximum limit-value (calculated for the conductivity at infinite dilution) to be the degree of ionization of the electrolyte, as just explained, the theory of Arrhenius has thus made it appear possible to determine experimentally the proportion of ionized electrolyte present.
It is a significant fact that the equivalent conductivity of hydrochloric acid is close to its limit even at finite dilutions, and that the same relation holds for the strong acids and the strong bases, in general, and for most salts. But the equivalent conductivity of weak acids, like acetic acid, and of weak bases, like ammonium hydroxide, in finite dilutions is still far removed from the limits which may be calculated for infinite dilutions. Arrhenius was led then to the further important conclusion that, in the case of the first electrolytes mentioned, a very large proportion of the electrolyte must exist in the ionized form at finite concentrations, their equivalent conductivities having almost reached the limit characteristic of infinite dilution.
Clausius84 also assumed dissociated molecules or ions to be the real carriers of electricity in the passage of a current through the solution of an electrolyte, but he assumed only a minute quantity of these molecular fragments or ions to be free at any moment, their existence being supposed to be transitory and dependent in particular on exchanges of atoms between molecules. As a result of the oscillations of the atoms composing a molecule, oscillations comparable with the motions of molecules assumed in the kinetic theory of gases, molecules were considered by Clausius occasionally to reach such a condition of instability, that they dissociated into smaller particles; since the atoms were supposed to be held in a molecule by attractions of electrical charges on the atoms (theory of Berzelius), the fragments of the molecule would carry the charges, positive and negative respectively, which they possessed in the molecule. Such a breaking up or dissociation of molecules was, further, supposed to occur with particular ease during the collisions of molecules, the electrical attractions and repulsions of the charged atoms favoring, at such moments, an exchange of atoms. During the exchange, the atoms were considered to be free molecules, charged with electricity—essentially ions,—capable of moving under the influence of electrical forces and of thus carrying a current. Finally, such ions were supposed, in part, to escape recombination, and to remain free, until each ion either collided and combined with an ion of opposite charge, or collided with a molecule and displaced an atom of the same charge from that molecule, a new ion being thus liberated. The theory, as usually interpreted, assumed the existence of only a very small quantity of such free ions, that being all that was supposed to be required to explain the facts known at the time it was advanced.
In what follows, we shall confine the discussion strictly to such contrasts between the two theories as grow out of a consideration of the phenomena of conductivity, and particularly consider some evidence which is directly concerned with the conductivity of solutions.
In the first place, if the formation of ions occurs primarily during the exchange of atoms in collisions of molecules, then, as Whetham85 has shown, the specific conductivity (of 1 cm.3) of an electrolyte, like hydrochloric acid, must increase with the concentration and must increase, approximately, as a function of the third power of the concentration. The more concentrated the solution, the more frequent the collisions between the dissolved molecules must be. As a matter of fact, as shown in the following table, the conductivity [p053] increases a little less than proportionally to the first power of the concentration—which is in conflict with the assumption made in the hypothesis of Clausius, but in perfect agreement with the hypothesis of Arrhenius. The small decrease with increasing concentration, in the simple ratio between conductivity and concentration, is due to the decreasing degree of ionization in the more concentrated solutions, as demanded by the hypothesis of Arrhenius.
The table gives, in the first column, the specific conductivities of hydrochloric acid at 18°, and, in the second column, the concentrations; these concentrations are expressed in moles or gram-equivalents per cubic centimeter; the last column gives the ratio of conductivity to concentration.
| Conductivity of 1 c.c. |
Concentration | Conductivity ───────────── Concentration. |
|---|---|---|
| 0.00370 | 0.00001 | 370 |
| 0.00734 | 0.00002 | 367 |
| 0.01092 | 0.00005 | 364 |
| 0.01800 | 0.00005 | 360 |
| 0.03510 | 0.00010 | 351 |
Furthermore, facts admitted by Clausius to be inexplicable by his own assumptions receive, in the theory of Arrhenius, at least a quantitative formulation borne out by a mass of corroborative evidence. The difference in conductivity between pure water and sulphuric acid is such a fact, mentioned by Clausius. Determinations of the ionization of sulphuric acid and of water, by the conductivity methods which are based on the theory of Arrhenius, show that, while sulphuric acid is very considerably ionized (see p. 104), water is scarcely ionized at all. The ionization of water (see p. 104) has been determined quantitatively by at least four independent methods of examination,86 and, minimal as the ionization is, the results agree so well with each other that van 't Hoff87 was led to write: "If one is not previously convinced of the correctness of the theory of electrolytic dissociation, hardly any result won by means of it is so convincing, as the agreement between the conclusions reached in completely different ways as to the degree of dissociation of water itself. After such an agreement, it is hardly conceivable that the basis on which all these results rest should further be altered."
Such relative speeds of ions may be demonstrated by means of an experiment: the motion of the hydrogen ions, formed by the ionization of hydrochloric and other acids, may be observed by their action on a reddened (alkaline) solution of phenolphthaleïn, which is decolorized by them; and the motion of the hydroxide ions, formed by the ionization of sodium hydroxide and other bases, may be followed by their action on colorless phenolphthaleïn, which turns red in their presence. The hydrogen and the hydroxide ions are the fastest, in aqueous solutions, and their speeds are compared in the next experiment with that of blue cupric ions, which have a speed roughly the same as that of many common ions. In this experiment the hydrogen ions are readily seen to move about twice as fast as the hydroxide ions and five to six times as fast as the cupric ions.
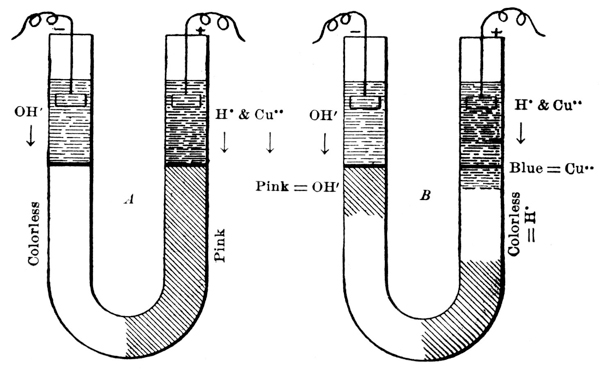
Exp.88 Five grams of agar-agar are dissolved in 250 c.c. of boiling water. To 100 c.c. of the hot solution, 32 c.c. of a saturated solution of potassium chloride and about 1 c.c. of phenolphthaleïn solution are added, together with enough of a solution of potassium hydroxide, added drop by drop, to produce a deep red tint in the phenolphthaleïn. Of this mixture 50 c.c. is treated with dilute hydrochloric acid, added drop by drop, until the red color is just discharged, and then an excess of acid, equal in amount to the quantity used to neutralize the 50 c.c., is added to the mixture. This colorless solution and 50 c.c. of the red solution are poured, while still warm, into the two parts of a wide U-tube, slowly and at equal rates, so that the level on the two sides remains the same. In this way it is possible without difficulty to have the solution on one side red (alkaline) and on the other side colorless (acid). The agar-agar is allowed to congeal, and then a mixture of 0.5 c.c. of hydrochloric acid, (sp. g. 1.12), 6 c.c. of saturated cupric chloride solution and 20 c.c. of water is poured over the red half, and a mixture of 20 c.c. of saturated [p055] potassium chloride solution and 2 c.c. of 10% potassium hydroxide solution is poured over the colorless half. The U-tube is surrounded by ice water during the passage of the current, and the cathode is placed in the solution on the colorless side. In Fig. 10 the ∪-tube is shown when first charged (on the left), and after the current has been running for a short time (on the right).
The conductivity of a solution must be made up, therefore, of the sum of the shares which the positive ions and the negative ions, respectively, take in carrying the current. This principle was first advanced by Kohlrausch. The share of each kind of ion in conducting a current may be determined, for hydrochloric acid for instance, in the following way: A porous diaphragm may be used to divide the solution in an electrolytic cell into two halves, the concentration of the acid being the same in both halves (represented, as indicated in Fig. 11, by 15 molecules89 of ionized acid in each half). A measured current is passed through the solution, say, sufficient to liberate 3 molecules of hydrogen H2, and 3 of chlorine Cl2, corresponding to 6 ions of each, and the concentration of the acid in each half is then again determined by analysis. Say it is found to correspond to 14 molecules of hydrochloric acid in the half of the solution on the side of the cathode and 10 molecules in the half on the side of the anode (see Fig. 12). Then the anode half has lost 5 ions of hydrogen, which must have passed through the diaphragm toward the cathode and taken the place of five of the six hydrogen ions discharged at the cathode. Similarly, the solution around the cathode has lost one chloride ion, which must have passed through the diaphragm toward the anode, and the hydrogen-ion corresponding to it, remaining on the right side without a compensating negative ion, must be the sixth hydrogen-ion discharged at the cathode. In other words, five hydrogen ions passed to the right, while one chloride ion passed to the left. The hydrogen ions then carried five-sixths of the current through the diaphragm, and consequently through the solution, and the chloride ions only one-sixth of the current. Since the solutions were of equal concentration to start with, the hydrogen ions have moved five times as fast toward the cathode as the chloride ions have moved toward the anode.
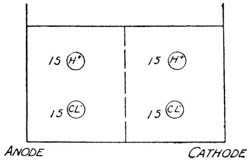
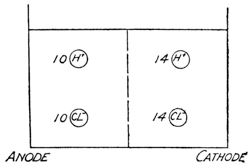
The equivalent conductivity of 0.1-molar hydrochloric acid is 351 at 18°, and experiment shows that the hydrogen-ion carries 84% of the current, the chloride-ion only 16%. The conductivity may then be considered to be the [p056] sum of the share the hydrogen-ion has in carrying the current, i.e. 0.84 × 351, or 295, and of the share of the chloride-ion, 0.16 × 352.5, or 56. These values may be called the equivalent partial conductivities or mobilities of the ions in this solution.
In a similar way, the conductivity of every solution of an electrolyte may be shown to represent the sum of the mobilities of the ions carrying the current (principle of Kohlrausch). The limit of the conductivity of one equivalent of an electrolyte is the sum of the mobilities of the ions composing the electrolyte. The frictional forces being constant for infinitely dilute solutions, at a given temperature, an ion will always show the same mobility, irrespective of the nature of the ion of opposite charge, with which it forms the electrolyte. We may then put Λ∞ = (l+∞ + l−∞), if l+∞ and l−∞ are used to designate the limits of the mobilities of gram-equivalents of the positive and negative ions forming the electrolyte. The following table90 gives the limits of the mobilities for gram equivalents of some of the most important ions at 18°.
| Limits of Mobilities of Common Ions at 18°. | ||
|---|---|---|
| K: 65.3 | ½ Ca: 53.0 | I: 66.7 |
| Na: 44.4 | H: 318.0 | NO3: 60.8 |
| (NH4): 64.2 | OH: 174.0 | C2H3O2: 33.7 |
| Ag: 55.7 | Cl: 65.9 | ½ SO4: 69.7 |
For quite dilute solutions, in which the friction may be assumed to be approximately constant, the conductivity will depend, not only on the mobilities of the ions, which may be taken to be the same as for solutions of extreme dilution, but also on the proportion of electrolyte that is ionized, i.e. on the degree of ionization, α. Then Λv = α (l+∞ + l−∞), which is an elaboration of the original equation given on page 50.
Now, Kohlrausch discovered the principle of the summation of the mobilities of ions a number of years before the theory of Arrhenius was advanced, and the proportion in which the ion is present in a given solution being unknown, the effect of what is here known as the degree of ionization was included empirically in the value of the mobility. It is not surprising, then, that an ion was found to have approximately the same mobility only in solutions of the same concentration of strictly analogous and closely related salts, which, according to present methods of investigation, are now found to have approximately the same degree of ionization. For instance, the mobility of the gram-equivalent of the chloride-ion was found to be approximately the same, 47.3 and 50.5 respectively, in molar solutions of sodium and potassium chloride at 18°, no account being taken of the degrees of ionization. However, the degrees of ionization of the two salts are approximately the same, 66.9% and 74.9% respectively, and might be ignored in a comparison of the conductivities, without affecting the result of the comparison in any marked way. [p057]
When the conductivities of unlike electrolytes are compared, the introduction of the conception of the degree of ionization (by Arrhenius,) into Kohlrausch's principle of the independent conductivities of specific ions, shows most striking results and demonstrates the value of the new conception. For instance, the equivalent conductivity of potassium chloride at 18° in 0.075 molar solution is 113.8 reciprocal ohms and the partial conductivity of the chloride-ion in the solution is 57.4. But the conductivity of an equivalent solution of mercuric chloride at 18° is only 1.51, which is very much less than the conductivity of the chloride-ion alone in the potassium chloride solution. Now, mercuric chloride, according to investigations of its conductivities and of its effect in depressing the freezing-point of water,91 is one of a very few salts that are difficultly ionizable (p. 107); according to the data mentioned, it is ionized, at most, to the extent of 2.5 per cent in the solution in question, whereas 87.5 per cent of the potassium chloride is ionized in such a solution. When the difference in the degree of ionization is taken into account, the conductivity which mercuric chloride should show may be calculated, on the assumption that the chloride-ion has the same mobility in the two solutions, but that there is less of it in the mercuric solutions. We put ΛHgCl2 = α (lHg + lCl) = 0.025 (48 + 65.9) = 2.8. We thus find that the conductivity of the mercuric chloride should be, approximately, only 2.8 reciprocal ohms, which is of the same order as that found (1.51).92
In the same way, when we compare the conductivity of a strong acid, like hydrochloric acid, with that of a weak acid, like acetic acid—the conductivity of 0.1 molar hydrochloric acid is 351, of 0.1 molar acetic acid only 4.6—the principle of the specific, characteristic mobility of the hydrogen-ion, which is present in both solutions, has significance only if we take into account the very different concentrations of the hydrogen-ion in the two solutions, resulting from the different degrees of ionization of the two acids—91% for the hydrochloric and only 1.7% for the acetic acid. The same relations hold in the comparison of the conductivity of a solution of a strong base like sodium hydroxide with that of an equivalent solution of a weak, i.e. much less ionized base like ammonium hydroxide, or in comparing the conductivity of a weak acid or a weak base with the conductivities of their much more highly ionized salts.
In all these cases the use of the conception of the degree of ionization of the electrolytes makes possible a much broader and more general application of the principle of the independent migration or mobility of the ions than was possible before the theory of Arrhenius was proposed, and marks a distinct advance in the theory of conductivity, over what was possible on the basis of the theory of Clausius. [p058]
Exp. The lower plate in an Arrhenius cell is covered with concentrated hydrochloric acid. Very dilute acid is allowed to flow slowly on to the surface of the concentrated acid, from a pipette with a curved, narrow point, until the upper plate is submerged. The two plates are connected with a sensitive galvanometer. The current flows in the direction demanded by the observed mobilities of the ions, the positive current entering the galvanometer from the plate covered by the dilute solution, which is charged positively by the faster moving hydrogen ions coming from the concentrated solution. If the cell is [p061] connected with the electrodes of a very small cell containing copper sulphate, in the course of twenty-four hours quite a deposit of metallic copper is formed on the electrode connected with the concentrated solution of hydrochloric acid.
The existence of the products of the electrolytic dissociation, of hydrochloric acid may therefore be demonstrated,96 by the aid of the individual diffusion of the products of the dissociation, in the same way as was the coëxistence of the products of the gaseous dissociation of ammonium chloride, when the conditions for the experiment are adapted to the nature of the dissociation products. Cells of this type, depending for their current on unequal concentrations of given ions, are called "concentration cells."
If it can be shown that the flow of electricity, resulting from such unequal diffusibility of ions, is a function not only of the difference in the total concentration of the electrolyte in the two solutions brought into contact with each other, but is also a function of the relative degrees of ionization of the electrolyte in the two solutions, as defined by the theory of Arrhenius, then this method of experimentation may be used as a further test of the validity of this theory as against that of Clausius. It is obvious that if such currents are the results of the diffusion of ions from higher to lower concentrations, then the essential concentrations do not embrace all of the electrolyte, but only the ionized part. W. K. Lewis97 has rather recently shown that the degrees of dissociation of electrolytes may be measured by the use of concentration cells, and that the results agree well with the determinations of the degree of dissociation from conductivity measurements (p. 50). From calculations, based on Jahn's accurate measurements of the electromotive forces of concentration cells, A. A. Noyes98 finds that "when the conductivity ratio is assumed to represent the degree of ionization of the salt, the calculated values of the electromotive force of concentration cells exceed the measured ones by only about one per cent, in the case of potassium and sodium chloride between the concentrations of 1 / 600 and 1 / 20 molar."
Solvents which cause ionization only to a minimal extent are benzene (C6H6), carbon bisulphide, ether, chloroform, petroleum ether (gasoline) and similar solvents. Hydrogen chloride dissolved in benzene has an extremely small conductivity, indicating only a trace of ionization.100
The question may be raised, why the first solvents mentioned should have the power to cause ionization, while the second series of solvents named do not have this power, or have it only to a very slight extent. Without attempting to enter into an elaborate discussion of this important question, it may be said that J. J. Thomson101 and Nernst102 suggested that the ionizing powers of solvents must be intimately connected with their dielectric behavior, and this view has now been well established. It may be said, in simple terms, that the so-called dielectric constant of a solvent determines the force with which electrical charges will attract and repel each other; the higher the dielectric coefficient of a medium, the smaller will be the attraction between opposite electrical charges, other conditions being the same. In solvents, then, of high dielectric powers, the coëxistence of oppositely charged particles must be more favored than in solvents of low dielectric powers. The dielectric constants of a number of solvents are given in the following table: [p063]
| Hydrogen cyanide, HNC | 95 |
| Hydrogen peroxide, H2O2 | 93 |
| Water, H2O | 81 |
| Methyl (wood) alcohol, CH4O | 32 |
| Ethyl (ordinary) alcohol, C2H6O | 22 |
| Ammonia, H3N | 22 |
| Chloroform, CHCl3 | 5 |
| Ether, (C2H5)2O | 4 |
| Benzene, C6H6 | 2 |
It is quite apparent that the good ionizing media have, as a matter of fact, the highest constants; those which cause ionization, at most minimally (e.g. benzene), the lowest.
Recent extended and exact investigations by Walden103 have succeeded in bringing the ionizing power of solvents into definite quantitative relations to their dielectric constants, with the result that order has been brought out of a condition of chaos that, for a number of years, existed in this field, as the result of conclusions based on incomplete data. Conductivity being a function both of the proportion of dissociated electrolyte and of the mobility of the ions in a given solution, Walden determined, for a certain salt (an organic derivative of ammonium iodide, namely, tetraethyl ammonium iodide N(C2H5)4I), for all solvents used, not only the conductivities for finite dilutions but also, by extrapolation, the limiting values for infinite dilution. He was thus able to determine the degree of ionization of the salt. Some of his results are particularly interesting; for instance, a poorly conducting solution, such as that of the salt in glycol, a solvent resembling glycerine in general character, may contain the dissolved electrolyte in a highly ionized state, while in a much better conducting solution the degree of ionization may be much smaller—the low conductivity of the first solution being the result of a very high friction and of the slow motion of the ions, while the well-conducting solution might show a very high degree of mobility of the ions. The mobility changes with the nature of the solvent, and the limit, Λ∞, of the equivalent conductivity of the salt, as found by Walden, ranges from 8 in glycol, which is a thick, viscous oil like glycerine, to 200 in acetonitrile, a thin mobile solvent. In the one solution, an observed conductivity of 4 represents 50% ionization of the salt, in the other only 2%.
Now, for solutions of a given electrolyte—tetraethyl ammonium iodide was used—Walden104 found the following exceedingly interesting relation between the ionizations in, and the dielectric constants of, various solvents:
where e1 and e2 represent the dielectric constants of different solvents, and c1 and c2 represent the concentrations of the salt in the solvents when the salt is ionized to the same degree105 in the two solutions.
The bearing of the relation is apparent from the data in the following [p064] table.106 The upper half of the table gives the dielectric constants (column two) of the solvents named in column one; the concentrations which show identical degrees of ionization—47%—are given in the third column, and the last column gives the value of the relation e : ∛c. The lower half of the table presents the same kind of data, for the same salt, when its degree of ionization is 91%, in the different solutions examined. It is clear that the numbers in the third column of each part represent approximately constants.
All solutions, including aqueous solutions, are thus brought into one general relation.
| Solvent. | e | c | e : ∛c |
|---|---|---|---|
| Methyl alcohol | 32.5 | 0.125 | 65 |
| Ethyl alcohol | 21.7 | 0.020 | 80 |
| Acetyl bromide | 16.2 | 0.010 | 75 |
| Benzaldehyde | 16.9 | 0.016 | 78 |
| Acetonitril | 35.8 | 0.100 | 77 |
| Water | 80 | 0.00910 | 383 |
| Furfurol | 39.4 | 0.00125 | 365 |
| Nitromethane | 40 | 0.00125 | 371 |
| Acetonitril | 36 | 0.00100 | 358 |
| Methyl alcohol | 32.5 | 0.00050 | 365 |
In liquid ammonia we might well have, for instance, the action +NH3-NH3− + HCl ⇄ +(NH3-NH3)H + Cl−, or +NH3-NH3− + H+Cl− ⇄ +(NH3-NH3)H + Cl−. Now, in liquid ammonia, the salts NH4Cl, NH4NO3 [or, more probably, (NH3)xHCl, (NH3)x,HNO3] have the functions of the aqueous acids109; that is, the hydrogen-ion of the acids is found combined with the solvent ammonia. The ion +(NH3-NH3)H, and similar ions in liquid ammonia, would correspond then to what is considered the hydrogen-ion in aqueous solutions110 (formed according to HCl ⇄ H+ + Cl−, as ordinarily written), and the polarized charges on molecules like +NH3-NH3− appear thus as possible active agents in this dissociation of the hydrogen chloride molecules. [p066]
Now, it is a significant fact that all the best ionizing solvents are compounds whose simple molecules are unsaturated exactly like those of ammonia; this is true for water H2O, the unsaturated character of whose oxygen atom is now universally recognized. It is now a familiar fact that liquid water is not represented by the formula H2O but consists of more complex molecules (H2O)n. According to the most recent investigations,111 while steam is H2O, or monohydrol, ice is trihydrol (H2O)3, and liquid water, at ordinary temperatures, a mixture consisting chiefly of dihydrol (H2O)2, some trihydrol, and very little monohydrol. The proportion of the last appears to increase with a rise of temperature; the proportion of trihydrol seems to increase with a fall in temperature. One can easily see how such aggregates would result from the saturation of the free charges on oxygen, by further molecules of water. One can also see that such an association of water molecules could leave a positive and a negative charge on the associated molecules, which would be polarized and more effective than the simple molecule would be.
That the molecule of hydrogen cyanide contains a similarly unsaturated atom was demonstrated by Nef.112 He proved that the behavior of hydrocyanic acid agrees with the structure expressed by the formula HN═C═, which we may well write HN═C±. In sulphur dioxide, another good ionizing solvent, we have, similarly, unsaturated sulphur, the sulphur atom being here quadrivalent, whereas its maximum valence is six.
Now, the ionizing power of solvents like water, ammonia, etc., has been ascribed, by various chemists, not only to their dielectric properties, but also to the unsaturated condition of their molecules, and particularly to their powers of association into large molecules. The relations developed suggest that all three properties are most intimately related, the dielectric properties and the powers of association being consequences, possibly, of the fundamental condition of unsaturation, and of the great tendency toward self-saturation,113 of the simple molecules of the best ionizing solvents. From Walden's work it appears that the dielectric constant finally determines the quantitative ionizing effect of a solvent.
[49] From the molecular weights of elements and compounds, the atomic weights of elements may be determined, with the aid of analysis. (Cf. Smith, Inorganic Chemistry (1909), p. 196, or General Chemistry for Colleges (1908), p. 130 (Stud.), or Remsen, Inorganic Chemistry, Advanced Course (1904), pp. 71–80 (Stud.).)
[50] The weight of a small volume of a gas or vapor, at any definite temperature and pressure, is determined. With the aid of Boyle's and Gay-Lussac's laws, this observed volume is then reduced to standard conditions. Finally, the weight of 22.4 liters, under standard conditions, is obtained by calculation.
[51] For the deduction of formulæ see Smith, Inorganic Chemistry, 196, 203; College Chemistry, 40; or Remsen, ibid., p. 79 (Stud.).
[52] Kopp, Liebig's Ann., 105, 390 (1858); Kékulé, ibid., 106, 143 (1858) (Stud.).
[53] Liebig's Ann., 123, 199 (1862) (Stud.).
[54] Wanklyn and Robison, Compt. rend., 52, 549 (1863) (Stud.).
[55] For instance in a test tube held in a horizontal position.
[56] By applying the corrections demanded by the kinetic theory (van der Waals's equation) to gases even under ordinary pressures, Guye and D. Berthollet have obtained, with the aid of Avogadro's hypothesis, values for the molecular weights of gases and for the atomic weights of their components, which compare in accuracy with the best analytical work on solutions and solids.
[57] The usual experimental methods consist in determining the elevation of the boiling-point, or the lowering of the freezing-point, or the lowering of the vapor tension of a solvent by a solute, methods which were discovered by Raoult and used empirically until van 't Hoff developed their relations to the Avogadro principle. The calculation of a molecular weight is much simplified by the use of the different specific constants expressing the lowering or elevation produced by one gram-molecule or mole, dissolved either in one liter or in 100 grams of each specific solvent.
[58] See Arrhenius, Z. phys. Chem., 1, 631 (1887).
[59] Or, on the basis of the accepted molecular weights, abnormally high osmotic pressures, abnormally great lowerings of the freezing-point, raisings of the boiling-point, etc., were obtained. Van 't Hoff, originally, on account of these discrepancies, considered this extension of the Avogadro Hypothesis to hold only for the "majority" of substances in solution, not for all (Arrhenius, loc. cit.). It was considered to have universal application (for dilute solutions) only after Arrhenius had explained the exceptions with the aid of his theory of electrolytic dissociation.
[60] That is, hydrogen chloride, in aqueous solution, depresses the vapor tension and the freezing-point and elevates the boiling-point considerably more than an equimolecular quantity, for instance, of glucose does, and gives a considerably higher osmotic pressure. The differences are relatively greater, the more dilute the solutions used.
[61] A fourth interpretation advanced at one time in opposition to the theory of ionization is that salts like sodium chloride and zinc chloride are hydrolyzed and thereby produce more solute molecules, e.g. NaCl + H2O → NaOH + HCl. Aside from the fact that such hydrolysis of salts, when it does occur (Chapter X.), is easily detected, and that it can be proved not to occur appreciably in the case of sodium chloride (loc. cit.), this interpretation fails utterly to account for the results obtained with acids, e.g. HCl, HNO3, H2SO4, and with bases, e.g. NaOH, Ba(OH)2, which in aqueous solutions show an increase in the number of molecules as great as shown by salts. This explanation is therefore untenable.
[62] Z. phys. Chem., 1, 631, (1887). Previous papers were published in the transactions of the Royal Academy of Sweden (Stockholm). For a history of the theory see Ostwald, Z. phys. Chem., 69, p. 1 (1909), and Arrhenius, The Willard Gibbs Address, J. Am. Chem. Soc., 1911 (Stud.).
[63] In the case of double salts, such as sodium-ammonium phosphate, and similar compounds, the dissociation leads to the formation of more than two products. The molecules of two or more different products may then be charged positively and, conversely, there may be two or more different products of dissociation carrying negative charges. We have, for instance, Na(NH4)HPO4 ⇄ Na+ + NH4+ + H+ + PO43− and Na(NH4)HPO4 ⇄ Na+ + NH4+ + HPO42−. In all cases the rule concerning the sum of all the charges, as expressed in (2), must be fulfilled, the charge on the phosphate ion, PO43−, being three times as great as that on a sodium, ammonium, or hydrogen ion; that on the acid phosphate ion, HPO42−, being twice as great.
[64] Ion = the going or the migrating particle.
[65] See Washburn, J. Am. Chem. Soc., 31, 322 (1909), in regard to the values of x and y, the quantities of water carried by certain ions.
[66] Vide J. J. Thomson, Electricity and Matter (1905) and Corpuscular Theory of Matter (1907) (Stud.). Vide R. A. Millikan, Science, 32, 436 (1910), on the discrete or "granular" nature of electricity (Stud.).
[67] See Millikan, loc. cit., as to the exact value of this "unit charge."
[68] Cf. McCoy, J. Am. Chem. Soc., 33, March, 1911, in regard to electropositive, composite (i.e. nonelementary) "metals."
[69] The symbol ε is used to designate an electron. The loss of one electron by an atom leaves a unit positive charge on the particle.
[70] In Chapter XV (q. v.) the affinity of the elements for electrons and the reactions, of the nature of oxidation and reduction, depending on this affinity, are discussed in detail.
[71] J. J. Thomson, Corpuscular Theory of Matter, p. 120.
[72] A. A. Noyes (Carnegie Institution Publications, No. 63, p. 351 (1907)), believes that we may have two kinds of molecules, HCl and H+Cl−, as well as the ions H+ and Cl−.
[73] Modern theory thus is reverting to the Berzelius theory of chemical affinity [Vide Meyer's History of Chemistry (translated by M'Gowan) 1891, 220–265, or Ladenburg's History of Chemistry (translated by Dobbin) 1900, 86, 88, etc.]
[74] To a saturated solution of cupric nitrate may be added a small amount of a saturated solution of potassium permanganate, sufficient to give a decided purple color to the mixture. Potassium chromate, as recommended by A. A. Noyes, may be used in place of the permanganate. (Cf. Noyes and Blanchard, J. Am. Chem. Soc., 22, 726 (1900).)
[75] Exp.; cf. Eckstein, J. Am. Chem. Soc., 27, 759 (1905) (Stud.).
[76] W. A. Noyes, J. Am. Chem. Soc., 23, 460 (1901); Stieglitz, ibid., 23, 796 (1901); Walden, Z. phys. Chem., 43, 385 (1903).
[77] Corpuscular Theory of Matter, p. 130 (1907).
[78] The experiment is an adaptation of a similar one described by A. A. Noyes and Blanchard, J. Am. Chem. Soc., 22, 726 (1900).
[79] The copper electrodes are polarized by the formation of hydrogen on the cathode, but, in the course of a few seconds, the current becomes rather constant and is then read. The polarization may be considered as simply reducing the potential of the cell, and since, within the range of concentrations of acid used,—4-molar to 1/8-molar—the polarization current does not vary markedly, as compared with the potential of the storage cell, the total potential used through the series of dilutions may be considered sufficiently constant for the purposes of the experiment. Readings are made three or four seconds after each dilution, when the polarization has been fully established. Polarization may be entirely avoided by the use of a silver nitrate solution and silver electrodes or of a cupric salt solution and copper electrodes (Noyes and Blanchard). Hydrochloric acid is used here in order to carry the discussion in the text as far as possible with this typical ionogen. If one takes care to make readings as described, the result is quite satisfactory, as is shown by the comparison of the ratios of the readings with the ratios calculated from the known conductivities of the various dilutions (see table below).
[80] Current = (Potential Difference) / Resistance, or Current = (Potential Difference) × Conductivity. For a constant potential difference, then, Current ~ Conductivity.
[81] The specific conductivity of a solution (commonly designated by κ) is the conductivity of a cube of 1 cm. edge; the molecular conductivity is the conductivity of a mole of the electrolyte; the equivalent conductivity (designated by Λ) is the conductivity of a gram-equivalent of the electrolyte. Λ = κ × v, where v is the volume, expressed in cubic centimeters, containing the gram-equivalent. For instance, the resistance of 0.1 molar hydrochloric acid in a cube of 1 cm. edge is 28.5 ohms and its conductivity (κ) therefore 1 / 28.5 or 0.0351 reciprocal ohms. Since 10 liters or 10,000 c.c. of 0.1-molar hydrochloric acid is the volume (v) containing one mole of the acid (the molar and the equivalent conductivities, for a monobasic acid being the same) Λ = 0.0351 × 10,000, or 351.
[82] Kohlrausch and Holborn, p. 200.
[83] Cf. Kahlenberg, Transactions of the Faraday Society, 1, 42 (1905).
[84] Clausius, Poggendorf's Ann., 101, 347 (1857) (Stud.). His theory replaced the older one of Grotthuss.
[85] Phil. Mag., 5, 729 (1903), and Transactions of the Faraday Society, 1, 55, (1905).
[86] Vide, Hudson, J. Am. Chem. Soc., 31, 1136 (1909), for a recent summary of results.
[87] Lectures on Physical Chemistry, 1, p. 131.
[88] Vide A. A. Noyes and Blanchard, J. Am. Chem. Soc., 22, 726 (1900).
[89] The concentrations are figurative, but may be taken to represent actual concentrations, such as 0.015 molar, etc.
[90] Kohlrausch and Holborn, loc. cit., p. 200.
[91] Raoult, Ann. de Chim. et de Phys. (6), 2, 84 (1884).
[92] The degree of ionization of mercuric chloride is based on Raoult's freezing-point measurements and is subject to revision, and the limit of the mobility of the mercuric-ion (½ Hg) is assumed to be 48, close to the values found for the ions of zinc and cadmium, elements in the same family as mercury.
[93] Lehfeldt's Electrochemistry, 1904, p. 3.
[95] Report of the British Association for the Advancement of Science, 1886, p. 389.
[96] With the aid of more elaborate apparatus rigorous demonstrations and measurements of such diffusion currents of so-called "concentration cells" are made.
[97] Z. phys. Chem., 63, 174 (1908). The work was carried out in Abegg's laboratory.
[98] Report of the St. Louis Congress of Arts and Sciences, IV, 314 (1904).
[99] Am. Chem. J., 20, 21, 23 (1898–1900).
[100] Kablukoff, Z. phys. Chem., 4, 429 (1889).
[101] Phil. Mag. (5), 36, 320 (1893).
[102] Z. phys. Chem., 13, 531 (1893).
[103] Walden, Z. phys. Chem., 54, 129 (1906); McCoy, J. Am. Chem. Soc., 30, 1074 (1908).
[104] Z. phys. Chem., 54, 229 (1906).
[105] The degrees of ionization were always determined from the relation α = Λv / Λ∞ according to the method discussed on page 50.
[106] Walden, loc. cit.
[107] Cf. Arrhenius, Theories of Chemistry, p. 83 (1907).
[108] In hydrogen chloride, the hydrogen and the chlorine atoms may be held in the molecules H+Cl− by the electric attraction of a positive charge on the hydrogen, and a negative charge on the chlorine atom (see p. 43).
[109] Franklin and Kraus, Am. Chem. J., 23, 305 (1900) (Stud.)
[110] It is very likely that in aqueous acids, a large proportion, at least, of the hydrogen-ion is similarly combined with water. (Lapworth, J. Chem. Soc., (London) 93, 2187 (1908). See Chapter XII.)
[111] Vide the discussion on the "Constitution of Water," and the summary by J. Walker, Transactions of the Faraday Society, VI, 71–123 (1910).
[112] Proc. Am. Acad., 1892; Liebig's Ann. 287, 263 (1895).
[113] Cf. Walden, Z. phys. Chem., 55, 683 (1906).
We will turn now to the consideration of evidence bearing on the theory of ionization, found in the data on osmotic pressure. The apparent molecular weight of hydrogen chloride is found to be smaller than 36.5, when determined in aqueous solution (p. 37), and it is found to approach the limit 18.25 as a more and more dilute acid is used.114 The value found represents the average molecular weight of all the molecules in any solution, the osmotic pressure, freezing-point or boiling-point of which has been taken. It is evident that, if there is dissociation of hydrogen chloride into hydrogen and chloride ions, the average values found for the molecular weight must be lower than 36.5, must be variable, and must approach the limit 18.25, as the dissociation into the smaller molecules becomes more and more complete. Such a result is, therefore, what we would anticipate on the basis of the theory of ionization. For a salt like potassium chloride KCl, a similar tendency toward a minimum, average molecular weight of (K+ + Cl−) / 2 or (39.1 + 35.5) / 2 = 37.3 would be anticipated, and, as a matter of fact, molecular weight determinations with potassium chloride in aqueous solution give results agreeing with such a tendency.115 For a salt like calcium chloride, on the other hand, we would expect that its ionization into three ions, according to the equation CaCl2 ⇄ Ca2+ + 2 Cl−, would give a minimum, not of one-half the formula weight, but of one-third, viz., (Ca2+ + 2 Cl−) / 3 or (40 + 71) / 3 = 37, when the molecular weight determination is carried out in aqueous solution. As a matter of fact, with salts of this type, the determinations, by osmotic pressure methods, indicate a dissociation into three smaller components, as required by the theory. It may be added that, for [p068] a salt, sodium mellitate, Na6(C12O12), the salt of a hexabasic acid, Taylor found average molecular weights tending to a minimum of one-seventh of the formula weight, as we should expect from the ionization of the salt into seven smaller molecules, (C12O12)Na6 ⇄ 6 Na+ + (C12O12)6−.
Loomis119 found in a similar way a ratio of 3.61 for HCl, 3.71 [p069] for KOH, 3.60 for KCl, 3.67 for NaCl, 3.73 for HNO3, etc., when 0.01 molar aqueous solutions were used. For similar solutions of calcium chloride CaCl2, magnesium chloride MgCl2, and sodium sulphate Na2SO4, the value 5.07 was found as the ratio between the depressions of the freezing-point and the concentration of the salts in extremely dilute solutions—a result showing, plainly, a dissociation of each salt into three smaller molecules. The limit 5.67 for such a dissociation is not quite reached in these cases, because salts of the types Me″X2 and Me2′Y″ ionize less readily than do the electrolytes Me′X′, a fact also shown by their conductivities.
We thus find that the most exact work on molecular weight determinations in dilute aqueous solutions agrees excellently, as does the conductivity of such solutions, with the demands of the theory of ionization, a fact which is particularly impressive because osmotic pressure and electrical conductivity are in no wise fundamentally related phenomena, and yet each, as a measure of ionization or electrolytic dissociation, leads independently to the same conclusion.120
The compounds which are dissociated into ions, by solvents which cause ionization (p. 62), comprise the salts, the acids and the bases; chemists are, in fact, more inclined now to invert the statement and say that those substances which have long been known as salts, acids and bases, owe the essential characteristics, which led to their classification, to the fact that they are ionizable (see pp. 72–82). The composition of the ions, formed from the simpler of these compounds,121 may be expressed by saying that the metal component or metal-like component (hydrogen, ammonium) forms the positive ion (cation, metal ion) and all the rest of the [p070] molecule forms the negative ion (anion, acid ion122). Thus, sodium chloride, nitrate, sulphate, phosphate yield the sodium-ion, Na+, and the chloride (Cl−), nitrate (NO3−), sulphate (SO42−), or phosphate (PO43−) ions; cupric nitrate Cu(NO3)2 dissociates into the cupric ion (Cu2+) and the nitrate ion, calcium sulphate CaSO4 into the calcium-ion (Ca2+) and the sulphate-ion, aluminium sulphate Al2(SO4)3 into the aluminium-ion (Al3+) and the sulphate-ion.
But the question arises, as to how we know that the salts mentioned produce ions of the given composition; why, for instance, should sodium nitrate be considered to dissociate into sodium, Na+, and nitrate ions, NO3−, the nitrogen atom carrying all of the oxygen atoms with it in the negative ion?
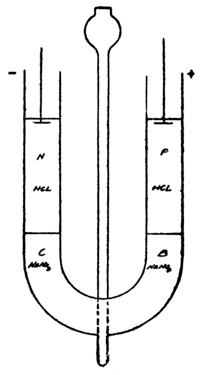
The composition of the ions of a salt can be determined experimentally123 by devices of which the U-tube experiment (p. 45) may be considered to be a simple type. For instance, if we wish to determine the composition of the ions of sodium nitrate, we could cover a solution of sodium nitrate with a solution, say, of hydrochloric acid, pass a current through the liquids, and determine the composition of the components that have moved to the negative and positive poles, respectively. In practice, the device could be elaborated for the sake of convenience. Stopcocks, for instance, might be placed in the U-tube, at the points of separation of the nitrate solution and the hydrochloric acid (see Fig. 13), the stopcocks being opened only during the passage of the current. Or porous plates or cells might be used, in place of stopcocks, at these [p071] points. Now, if we assume sodium nitrate to be dissociated, not into Na+ and NO3−, but let us say into positive ions NaO+ and negative ions NO2−, the changes which would result from the passage of a current would be as follows: starting with the action at the positive pole, we should find chloride ions discharged and chlorine evolved at the pole (the evolution of chlorine could be avoided, if considered desirable, by the use of a silver anode, which would absorb the liberated chloride-ion to form insoluble silver chloride on the electrode). At the same time, hydrogen ions would move out of the space P, being repelled by the positive pole, and attracted by the negative. At the boundary between the sodium nitrate solution and the hydrochloric acid, the negative ions of sodium nitrate, which we are supposing to have the composition NO2−, would move up from B toward the positive pole (cf. exp., p. 45), being attracted by its charge; at any moment we should have in any part of P as many negative ions (Cl− and NO2−), as there are hydrogen ions, the solution showing no excess of free electricity at any point. Now, if NO2− were the ion that moved up into the space P, then we should presently find nitrous acid around the positive pole in space P, H+ and NO2− combining to form nitrous acid, HNO2. But, as a matter of experiment, although the tests for nitrous acid belong to the most sensitive ones in chemistry, no trace of this acid is found there; what we do find is nitric acid, HNO3, resulting obviously from the presence in space P of both hydrogen ions and nitrate ions, NO3−, which have moved up from space B. It is clear, that the presence of nitric acid in the region around the positive pole means that the nitrogen atoms must have carried with them all three of the oxygen atoms of the nitrate—in a word, that the composition of the negative ion of sodium nitrate is NO3− and not, say, NO2−. Similarly, considering what happens in space N, round the negative pole, we have here an evolution of hydrogen, a migration of some chloride ions out of N into the space C, and, at the same time, a migration of the positive ions of space C into the division N. On examining the solution in N, we now find sodium chloride, with unchanged hydrochloric acid, exactly what we should expect from the migration of the ion Na+ toward the negative electrode.124 If the positive ion were, say, [p072] NaO+, we should expect to obtain either some of the hypochlorite NaOCl (NaO+ + Cl−), or, at least, an evolution of oxygen in this place, since sodium chloride is formed. As a matter of experiment, no oxygen is evolved here, and no trace of hypochlorite is found in N round the negative pole, although the tests for hypochlorites are extremely sensitive.
Comparatively simple methods, in principle of the nature outlined, enable us, then, to determine experimentally the composition of the ions into which ionizable compounds, salts, acids and bases, dissociate. Whenever any doubt may exist about the composition of the ions of a given electrolyte, this device may be employed to settle the matter, and there will presently be occasion to employ the U-tube for such a purpose.
Hydrogen chloride, as a perfectly dry gas, is a non-conductor of electricity and, at the same time, it is found to be chemically inactive—it does not combine, for instance, with dry ammonia125 or act upon dry calcium carbonate126 or on dry litmus. Hydrogen chloride, subjected to great pressure at a low temperature, is liquefied. The liquid is also a very poor conductor of [p073] electricity127 and does not show the chemical activity of ordinary, aqueous hydrochloric acid; it does not combine with calcium oxide or attack marble, zinc, iron or even magnesium.127
A solution of hydrogen chloride in a poorly ionizing medium, like benzene or toluene, is an extremely poor conductor. There is an extremely small conductivity indicating only a trace of ionization.128
Exp. A solution of hydrogen chloride, prepared by passing the dried gas into benzene or toluene (thiophene-free benzene will not become discolored), and kept anhydrous by means of fused calcium chloride, is tested for its conductivity, by dipping into it electrodes connected with a lighting circuit and a galvanometer.
Such a solution behaves chemically, also, quite differently from the aqueous solutions of hydrogen chloride with which we are familiar: dry steel nails,129 dropped into it, will remain almost unchanged—there is no marked evolution of hydrogen (exp.). Perfectly dried marble, added to it, will not give rise to the evolution of carbon dioxide129 (exp.). We find thus, in all the cases discussed—the nonconducting dry gas, the anhydrous liquefied hydrogen chloride and the anhydrous benzene solution—an absence of ionization,130 as indicated by the lack of conductivity, and, along with this, a lack of the familiar action of hydrochloric acid as an acid. If we dissolve the gas in water, we obtain a well-conducting solution (exp.), in which, according to molecular weight determinations, the [p074] hydrogen chloride is more or less largely ionized, and this same solution has all the well-known chemical properties of hydrochloric acid—it evolves hydrogen liberally when given an opportunity to act upon zinc or iron (exp.), it evolves carbon dioxide copiously when marble is brought into contact with it (exp.). In such an aqueous solution we have both the ions of the acid and the more or less non-ionized hydrogen chloride, the action (HCl ⇄ H+ + Cl−) being reversible.
Now, since in those cases in which we have admittedly only non-ionized hydrogen chloride, there is no vigorous chemical action, we are bound to conclude that, in the aqueous solution where we have both the non-ionized and the ionized substance, it must be the new components, the ions of the acid, which give this solution its new qualities, the well-known properties of a pronounced acid.131 This conclusion, that the acid properties of hydrogen chloride in aqueous solution are due to the ionized hydrogen chloride, rather than to the hydrogen chloride itself, is one of fundamental importance.
Since there is no interaction when the dry salts, containing only the non-ionized substances, are mixed, and since there is interaction [p075] when the solutions are mixed, in which both the non-ionized and the ionized salts are present, one must conclude again that the formation of silver chromate is the result of the action of the silver ions on the chromate ions in the solution. In point of fact, there could hardly fail to be an action, since the positive silver ions and the negative chromate ions, moving in all directions through the solution, must collide and be discharged, or combine, to form molecular silver chromate. This salt happens to be very difficultly soluble, and to be colored red, as well, so that silver chromate is precipitated and is immediately recognizable.
The two dry powders in the experiment were allowed to be in contact for only a few moments. It is important to note, therefore, that dry sodium acid carbonate and dry potassium acid tartrate are also nonconductors (exp.), and that the intimate mixture of these two powders is kept for years in the well-known form of baking powders without appreciable decomposition—yet best in tin vessels, to exclude moisture. The aqueous solutions, however, are good conductors (exp.), and, when dissolved, these salts are more or less ionized. The addition of water to the mixed salts (exp.) leads at once to the well-known action, carbon dioxide being liberated and sodium-potassium tartrate or Rochelle salt being formed.
Exp. Two platinum wires, fused, one inch apart, into a glass rod, are connected with a sensitive galvanometer and the lighting circuit. When the glass is warmed, a current is found to pass.
The action between barium sulphate and sodium carbonate at a high temperature does not mean, then, that the non-ionized salts interact; on the contrary, we find that, under such conditions, coincident with the evidence of reactivity, we have also decided conductivity—again indicating decided ionization.
Conductivity measurements, and the lowering of freezing-points and the elevation of boiling-points, show that there are very decided differences in the degrees of ionization of different acids and bases in solutions of equivalent concentration. For instance, potassium hydroxide is somewhat more ionized than is barium hydroxide, and decidedly more so than ammonium hydroxide, a fact that can readily be demonstrated by the conductivities of the solutions136:
Exp. Equivalent solutions (1 / 10 normal) of the three bases are introduced into three vertical tubes, containing electrodes connected, in parallel, with a lighting circuit and with small electric lamps. When the two electrodes in each of the three tubes are at equal distances from each other, the lamp connected with the potassium hydroxide solution glows most brightly, that connected with the barium hydroxide solution a little less brightly, and the lamp connected with the ammonium hydroxide solution does not glow at all—not enough current is carried through the ammonium hydroxide solution to heat the filament in the corresponding lamp sufficiently to make it red. Now, the current, for a given fall of potential, is proportional to the conductivity of a solution (p. 48) and, in the equivalent solutions137 the conductivity depends on the proportion of charged particles (the degree of ionization) of the base. It is clear then, that ammonium hydroxide is very much less ionized than are the two other bases. [p078]
The resistance in a tube may be reduced, and the conductivity increased, by reducing the distance through which the current must be carried, i.e. by bringing the electrodes closer together. In the solution of barium hydroxide, we find that we must reduce the distance between the electrodes to about five-sixths the corresponding distance in the potassium hydroxide solution before we obtain, approximately, as bright a lamp from the current passing through it, and in the case of ammonium hydroxide, we must bring the electrodes so close together that they almost touch, the distance being only one or two hundredths of the distance between the electrodes in the potassium hydroxide solution.
For the degrees of ionization of the three bases we have, approximately, the relation αK : αBa : αNH4 :: dK : dBa : dNH4, if we indicate by dK, dBa, dNH4 the distances between the electrodes in the three solutions when the lamps are of uniform brightness, i.e. when the same quantity of current passes through each solution. In this deduction, the conductivities of the bases at infinite dilution (Λ∞) are taken to be the same, which is roughly true.
The experiment gives us a rough measure of the relative conductivities and the relative degrees of ionization of the three bases. It shows that potassium hydroxide is somewhat more ionized than is barium hydroxide, in equivalent solution, and decidedly more than is ammonium hydroxide.
Limiting the further discussion, at this moment, to potassium hydroxide and ammonium hydroxide, we should find that, since in equimolar solutions, a larger portion of the former is ionized than of the latter, the potassium hydroxide solution must contain the larger proportion or concentration of hydroxide-ion, HO−, which is the characteristic ion of bases. It should, therefore, show the chemical characteristics of a base much more decidedly than the ammonium hydroxide solution. That such is the case can be very simply shown by adding equal quantities (0.1 c.c.) of the 0.1 molar solutions to equal volumes (50 c.c.) of water138 containing some phenolphthaleïn. This is an indicator for bases and acids, like litmus, but it is less sensitive to hydroxide-ion than is litmus. We find that the potassium hydroxide causes a very decided change, producing a deep red color with the phenolphthaleïn, whereas the ammonium hydroxide only produces a pink hue.139 [p079]
In all the chemical changes produced by these alkalies, the same difference in intensity of action is shown, that is here exhibited towards indicators. If, for example, we measure the rate of change in an action, which is slow enough to be measured [p080] and which proceeds quantitatively in proportion to the concentration of hydroxide-ion, we find that the measured rates of change indicate the same ratio in the concentrations of hydroxide-ion in potassium and ammonium hydroxide solutions, as is indicated by quantitative conductivity measurements. An action suitable for the purpose is the saponification of an ester, such as ethyl acetate. Under the influence of an alkali, like potassium hydroxide, ethyl acetate is decomposed, more or less rapidly, into an acetate and alcohol: we have, for instance,
The rate of saponification is found to be proportional to the concentration of hydroxide-ion, and not to the total concentration of the base, and the action may be formulated more accurately as follows:
For ammonium hydroxide we have similarly,
Now, Arrhenius140 proved that the rate of saponification of ethyl acetate by ammonium hydroxide, which is very much slower than the rate of saponification by potassium hydroxide of equivalent concentration, does agree quantitatively, indeed, with the rate demanded by the theory of ionization, when the hydroxide-ion is considered the active component of the bases, to which the saponification is due.
Exp. A rough idea of the difference in the chemical actions of the two bases may be obtained by observing their effects on the ester, methyl acetate, which is decomposed into an acetate and methyl alcohol rather rapidly. To 50 c.c. of (CO2 free) water containing some phenolphthaleïn, 10 c.c. of 0.1 molar potassium hydroxide is added; a similar mixture with 10 c.c. of 0.1 molar ammonium hydroxide solution is prepared. To each of the solutions, 2 c.c. (an excess) of methyl acetate is added (to the ammonium hydroxide solution first), and the mixtures are shaken for a moment. At room temperature, the mixture containing potassium hydroxide will become pale pink in a few minutes, and colorless soon thereafter, while the mixture [p081] containing ammonium hydroxide will still be deep red at the end of 45 minutes.141
In the following tables are summarized some of the results which have been obtained in comparing the activity of bases, in saponifying methyl acetate, and the concentrations of the hydroxide-ion, in the solutions of the bases, as determined by conductivity measurements. The comparisons are made by representing the activity of the hydroxide-ion in a solution of lithium hydroxide by 100 and by expressing the ratio of the activity of a given base to that of the lithium hydroxide in percentages of the activity of the latter. All the bases were used in 0.025 molar concentration, and their degrees of ionization are given in the last column of the table.
Chemical Activity of Bases and Their IonizationA
| Base. | Activity. | Relative Concentration of HO−. |
|---|---|---|
| Lithium hydroxide | 100 | 97 |
| Potassium hydroxide | 98 | 97 |
| Sodium hydroxide | 98 | 97 |
| Ammonium hydroxide | 2 | 2.5 |
| Ethyl ammonium hydroxide | 12 | 16. |
[A] Whetham, Theory of Solutions, p. 338 (1902). (Cf. Walker, Introduction to Physical Chemistry, p. 277 (1899).)
An ester is decomposed also under the influence of acids, in aqueous solution, into an organic acid and an alcohol, and cane sugar is similarly decomposed into glucose and fructose (grape sugar and fruit sugar): C12H22O11 + H2O → C6H12O6 + C6H12O6. Both actions are found to be caused by the influence of the hydrogen ions of the acids used and to proceed, at a given temperature, with a velocity proportional to the concentration of the hydrogen ions. Now, in 0.1 molar solution, acetic acid is very little ionized (1.3%), as compared with hydrochloric acid (91%), the degrees of ionization being determined by conductivity measurements (p. 50); the relation may easily be demonstrated with the aid of the conductivity apparatus used to show the difference in ionization between potassium hydroxide and ammonium hydroxide. In the presence of 0.1 molar hydrochloric acid, the decomposition of cane sugar actually proceeds at 79 times the rate that it does in the presence of 0.1 molar acetic acid. The ratio of the concentrations of the hydrogen-ion in the two [p082] solutions is, in fact, 70 : 1. There is, therefore, close agreement142 between the relative chemical activity of the two acids and the relation demanded, if we assume, on the basis of the theory of ionization (p. 77), that the chemically active components of the acids are their ions and particularly their hydrogen ions.
In the following table, the relative activities of acids, in accelerating the decomposition of methyl acetate by water, are contrasted, in a similar fashion, with their relative conductivities. The conductivities of acids depend to such an extent on the concentration of hydrogen-ion, which moves five times, or more, faster than the anions and carries therefore the greater part of the current, that the conductivities of acids, in equivalent concentrations, may be considered an approximate measure of their relative degrees of ionization and of the concentrations of hydrogen-ion. For the purpose of comparison the activity and the conductivity of molar hydrochloric acid are both represented by 100. All the acids were used in normal solutions.
Chemical Activity of Acids and Their Ionization.A
| Acid. | Activity. | Conductivity. |
|---|---|---|
| Hydrochloric acid | 100 | 100 |
| Nitric acid | 92 | 100 |
| Sulphuric acid | 74 | 65 |
| Acetic acid | 0.3 | 0.4 |
| Formic acid | 1.3 | 1.7 |
| Chloracetic acid | 4.3 | 4.9 |
| Tartaric acid | 2.3 | 2.3 |
[A] Whetham, Theory of Solutions, p. 338.
In the following chapters and, indeed, throughout our further work, we shall continually meet additional instances of the quantitative relation between chemical activity and ionization. In fact, the results obtained in the field of quantitative measurement of chemical action, of which the above are single instances, have demonstrated, more than anything else, the value of the theory of ionization to chemistry and the necessity of taking it into account in expressing the results of chemical action in mathematical terms. [p083]
On the other hand, there are large numbers of compounds, especially among organic substances, which do not appear to ionize to a measurable extent and whose actions, in large part at least, appear to be the actions of non-ionized molecules. It is characteristic that most of these actions take place at slow, very frequently easily measurable, rates of speed. Critical study shows that even for such actions ionization often plays a very important rôle, at least in some of their stages, and throughout the field of organic chemistry the intimate relations between electrical phenomena and chemical activity can be readily recognized.146 But these relations are not obvious ones and do not, as yet, play a dominant rôle. It is because analytical chemistry deals predominantly with the reactions of ionogens, that the study of the reactions of ions will demand our extended attention.
It is evident,150 from Walden's equation showing the relation between the ionizing power and the dielectric constant of a solvent (p. 63), that the presumption is that hydrogen chloride in benzene solution is not absolutely non-ionized, but rather that it is ionized in traces.151 No exact measurements of the [p085] degrees of ionization of hydrogen chloride in benzene solution have been made; that the solution shows an enormous resistance to the passage of the electric current and can be, at best, very little ionized, is all that has been established. In default of exact data, the semiquantitative determination by Kablukoff, showing that a 0.25 molar solution of hydrogen chloride in benzene has a resistance of 120 × 106 ohms, is of interest. From the meager data concerning the dimensions of the electrodes used, one may calculate (with the aid of a not unreasonable assumption as to the limiting value of the conductivity, at infinite solution) that the degree of ionization of the acid in the solution is perhaps of the order 5E−9, and the concentration of hydrogen-ion,152 consequently, roughly 10−9. Now, the evolution of hydrogen by means of zinc, in aqueous solutions, takes place according to the equation Zn ↓, + 2 H+ ⇄ Zn2+ + H2 ↑, and depends on a ratio of the concentrations of zinc-ion and hydrogen-ion153 (Chapters XIV and XV, q.v.). Even if the concentration of hydrogen-ion is very small, zinc will liberate hydrogen, provided the conditions are such that the concentration of zinc-ion cannot reach a large enough value to satisfy the equilibrium ratio, and stop the action. Now, in an alkaline solution, zinc-ion is converted into zincate-ion (Zn2+ + 4 HO− ⇄ ZnO22− + 2 HOH) and a large concentration of zinc-ion cannot accumulate. The consequence is that zinc liberates hydrogen freely even from alkaline solutions, for instance from molar solutions of potassium hydroxide, in which the concentration of hydrogen-ion, roughly 10−14, is very much smaller than that calculated for the benzene solution of hydrogen chloride (namely, 10−9). Now, although the values of the solution-tension constants of elements change most decidedly with a change of solvent, it seems likely154 that their ratios, on which their mutual displacement depends, will not be found materially altered. Zinc chloride being insoluble in benzene, the ratio for equilibrium may not be fulfilled for zinc in contact with a benzene solution of hydrogen chloride. Hence, with that solvent, the evolution of hydrogen may, so far as it goes, very well be due to precisely the same machinery as that operating in aqueous solution. The liberation goes on until the metal is protected against any further action by a film of the solid chloride. It seems, therefore, at least possible, that the evolution of hydrogen observed by Kahlenberg and his collaborators155 is a purely ionic action, the same as the similar [p086] action in aqueous solution has been proved to be by quantitative measurements.156 Only exact measurements, comparable with those made in aqueous solutions, can settle the question at issue, and until such quantitative evidence is forthcoming, a definite conclusion that the action of hydrogen chloride in benzene solution is or is not an ionic action is not warranted by the facts.
Equally interesting are Kahlenberg's observations of interaction between hydrogen chloride in benzene solution and a similar solution of copper oleate. Each solution shows absence of appreciable conductivity, yet, when the solutions are mixed, precipitation of copper chloride occurs instantly. Whether we have here an instantaneous action between non-ionized molecules, as claimed by the observer, or whether the minimal ionization157 of the hydrogen chloride and copper oleate, the existence of which we have a right to assume, is sufficient to account for this rapid action, both components being in solution and intimately mixed, is a question of the greatest interest. But until quantitative measurements of all the factors involved in chemical actions in benzene solution are obtained, a very difficult, but necessary task, which the discoverer of the action omitted to perform, no definite conclusion whatever can be based on such results, interesting as they are. Water, although it is only minimally ionized (tables, Chapter VI), hydrolyzes salts like potassium cyanide and aluminium chloride almost instantly, and it has been rigorously proved that the resulting condition of equilibrium involves the ions of water158 (Chapter X). With the possibility that the well-known enormous speeds of action of ions may completely offset the tremendous reduction in concentration of the hydrogen-ion, in a benzene solution of hydrogen chloride as compared with an aqueous solution, further analysis of the relations is imperative.159 Until such investigations have been carried out, we must consider [p087] it possible that the reactions of hydrogen chloride in benzene solution may be reactions of its non-ionized molecules or reactions of its ions. In view of the undoubted minute concentrations of the latter, as compared with aqueous solutions, and in view of the inertness of non-ionized hydrogen chloride in aqueous solutions as compared with the activity of its ions, a benzene solution of hydrogen chloride should show far less ionic activity than an aqueous solution, and that such is the case is brought out clearly by Kahlenberg's interesting experiments.
Perhaps the most instructive case of this kind, that we can study, is that of iron in ferrous and ferric salts. Exceedingly sensitive tests are known for the ferrous and the ferric ions. Thiocyanates produce an intensely red salt, Fe(SCN)3, when added, for instance, to ferric chloride; potassium ferrocyanide, K4Fe(CN)6, precipitates ferric ferrocyanide, Fe4[Fe(CN)6]3, Prussian blue, from ferric chloride solutions; ammonium hydroxide precipitates quantitatively the insoluble red ferric hydroxide (exps.). With ferrous salts, potassium ferricyanide K3Fe(CN)6 precipitates ferro-ferricyanide Fe3[Fe(CN)6]2, Turnbull's blue; ammonium sulphide precipitates black ferrous sulphide (exps.). Now, in two of the reagents used, potassium ferro- and ferricyanide, iron is present according to the formulæ given. If one should attempt to demonstrate its presence by means of these tests—among the most sensitive and most reliable tests known in analysis—one would fail utterly. Thiocyanates do not produce even the faintest tinge of pink in potassium ferricyanide solution163; ammonium hydroxide does not precipitate any ferric hydroxide (exps.). Ammonium sulphide does not precipitate the least trace of a black sulphide from a ferrocyanide solution, and when the latter is mixed with the ferricyanide solution, no trace, either of Prussian or Turnbull's blue, is shown (exps.). The contrast between the behavior of these salts and ferrous and ferric salts is now sharply and definitely interpreted, as being the result of the contrast in their ionization,—the color tests we use are extremely sensitive tests only for the ferric and ferrous ions, Fe3+ and Fe2+, respectively,—but potassium ferrocyanide ionizes into potassium ions and the negative ferrocyanide ions Fe(CN)64−, and shows the actions of ferrous ions as little as chlorate ions ClO3− exhibit the reactions of chloride ions Cl−. Potassium ferricyanide, in turn, gives rise to trivalent, negative ferricyanide ions Fe(CN)63− and not to ferric [p089] ions.164 If any doubts arise on this point, one can decide the question readily by experiment. When a concentrated solution of potassium ferricyanide is placed in a U-tube under a solution of some colorless electrolyte, such as sodium sulphate, and plates connected with a battery are inserted, there is no difficulty (exp.) in seeing that the yellow ion,165 containing the iron, moves to the positive pole and not to the negative. The iron is, therefore, as a matter of experiment, part of a negatively charged substance.
That iron is really present in these compounds can be shown most effectively if we destroy the salts:
Exp. Dry, pulverized potassium ferrocyanide is intimately mixed with dry potassium carbonate and the mixture heated in a hard glass test tube. When the whole mass has become red-hot, insuring complete decomposition, the hot (not red-hot) tube is plunged into water; the salts are extracted and particles of metallic iron are left undissolved. The action is
If the iron is dissolved in a little dilute hydrochloric acid and oxidized to the ferric condition, by the addition of a few drops of bromine water, the intensely red solution characteristic of ferric salts may be readily obtained, when a thiocyanate is added to the solution.
[114] Loomis. (Cf. Whetham, Theory of Solution, p. 320 (1902).)
[115] Loomis; and E. H. Griffith. (Cf. Whetham, loc. cit.)
[116] Expressed in moles per liter.
[117] Δ1 : Δ2... = C1 : C2...or Δ1 / C1 = Δ2 / C2 = a constant.
[118] Cf. Whetham, loc. cit., pp. 147, 158.
[119] Ibid., p. 320.
[120] In regard to the degrees of ionization, as shown by freezing-point depressions and conductivities of salts, see also A. A. Noyes, Report of the Congress of Arts and Sciences, St. Louis, 1904, Vol. IV, p. 313.
[121] See Chapter XII, in regard to so-called "complex ions" and their salts.
[122] The term "acid ion" is used to designate the "acid radical," when it exists, in solution, as an independent charged particle or ion. "Acid ion" is thus a convenient synonym for anion, just as "metal ion," designating the metal or metal-like radical of a salt, is used as a synonym for cation. The term, acid ion, has been found to convey more quickly and definitely to the student's mind, than does the term anion, which component of an acid or salt is referred to. While it is not, in some respects, an ideal term, yet its use seems justified by its very close relation to the term "acid radical" and by its practical advantages.
[123] The principle was first applied by Hittorf.
[124] This does not preclude the possibility that the ion is combined with more or less water and is Na(H2O)x+; see pp. 42, 65.
[125] Baker, J. Chem. Soc. (London), 65, 611 (1894), 73, 422 (1898). On page 623 of the first article is given a list of chemical actions for which the effect of the presence of moisture has been investigated (Stud.).
[126] Hughes, Phil. Mag., 34, 117 (1892) (Stud.).
[127] Gore, Proc. Royal Soc., 14, 204 (1841). Gore found that aluminium was dissolved and that sodium and potassium were attacked by the gas, even before its liquefaction. It is uncertain whether these positive reactions are reactions of absolutely anhydrous hydrogen chloride or the result of the presence of moisture in the experiments in question, since Cohen [Chem. News, 54, 305 (1896)], drying the gas more carefully than did Gore, found, in contrast to the latter, that metallic sodium may be exposed for several weeks to dry hydrogen chloride gas and retain its lustre. In all experiments demanding the rigorous exclusion of moisture, more weight must be attached to negative results (showing lack of activity) than to positive results. [Cf. the controversy between Baker, loc. cit., and Gutmann, Liebig's Ann., 299, 3 (1898)].
[128] Nernst's Theoretical Chemistry, p. 375. Kablukoff, Z. phys. Chem., 4, 430 (1889).
[129] In regard to the behavior of zinc, see below, p. 84. (Cf. Kahlenberg, J. Phys. Chem., 6, 13 (1902) (Stud.).)
[131] The acid character, in particular, is due to the hydrogen-ion, H+; see below.
[132] The fusion is conveniently made in a platinum dish; the dish and a platinum cathode are connected with the lighting circuit and an electric lamp.
[133] See Smith, Inorganic Chemistry, pp. 550, 569, 578, 588, 608, 610, 683: College Chemistry, 361, 373, 380, 389, 404, 405, 443 (Stud.).
[134] J. Chem. Soc. (Abstracts) (London), 40, 504 (1881).
[135] For positive evidence of the ionizing power of light, see Haber, Z. Elektrochem., 11, 847 (1905). For evidence as to the negligible rôle of ionization in the combination of chlorine and hydrogen, see Mellor, Chemical Statics and Dynamics (1904), p. 290.
[136] The apparatus described by A. A. Noyes and Blanchard for comparing acids is used [J. Am. Chem. Soc., 22, 737 (1900)].
[137] The conductivity depends in this case chiefly on the migration of the fast moving hydroxide ions (p. 56), common to the three bases. There is little difference in the rates at which the cations move.
[138] The water should be free from carbonic acid.
[139] The various indicators show different, specific degrees of sensitiveness to acids (to hydrogen ions) and to bases (to hydroxide ions). That is, different concentrations of hydrogen-ion or of hydroxide-ion are required to change their colors. As they are particularly useful in demonstrating varying concentrations of these ions, they will frequently be used in illustrating conclusions reached in the course of our work, just as they are used extensively in practical analysis. The following tables are intended to give some definite information on this valuable quality. The fourth column of the first table shows the concentration of hydrogen-ion, required to change the color of the indicator from the tint given in the second column to the tint given in the third column. The second table gives, similarly, the concentrations of hydroxide-ion required to produce the changes of tint indicated. The tables refer to results obtained when 0.1 c.c. (about two drops) of a 0.1 to 0.15% solution of the indicator is added to 10 c.c. of the solution examined.
Table of Sensitiveness to Acids (to Hydrogen-ion)
| Indicator. | From | to | Concentration H+. |
|---|---|---|---|
| Phenolphthaleïn | Pink | Colorless | 10E−9 |
| AzolitminA (litmus) | Violet | Violet pink | 1E−6 |
| Methyl orange | Yellow | Reddish orange | 1E−3 – 0.1E−3 |
[A] Azolitmin is an important component of litmus.
Table of Sensitiveness to Bases (to Hydroxide-ion)
| Indicator. | From | to | Concentration HO−. |
|---|---|---|---|
| Phenolphthaleïn | Colorless | Pink | 10E−6 |
| Azolitmin | Violet | Violet blue | 1E−6 – 0.1E−6 |
| Methyl orange | Orange | Yellow | 1E−9 |
It is clear that of the three indicators given in the table, phenolphthaleïn is the most sensitive to acids, methyl orange the most sensitive to bases. An extended table of the sensitiveness of many indicators, on which the above tables are based, is given by Salm, Z. phys. Chem., 57, 471 (1907). The theories (of Ostwald, Bernthsen, and others) regarding the color changes, and the theory (of Ostwald) concerning the sensitiveness of indicators, are discussed (with references to the literature) by Stieglitz, J. Am. Chem. Soc., 25, 1117 (1903). Later modifications of the views on color changes are discussed in papers by Stieglitz, Am. Chem. J. 39, (1908), and by Acree, ibid., 37, 39, 42, and in these papers references to the literature will be found. For investigations on the sensitiveness of indicators, see McCoy, ibid., 31, 508 (1904), Salm, loc. cit., and A. A. Noyes, J. Am. Chem. Soc., 32, 815 (1910).
[140] Z. phys. Chem., 2, 289 (1888). Note the remarks in the footnote following.
[141] The formation of an ammonium salt in the latter action still further reduces the concentration of the hydroxide-ion (Chapter VI) and retards the action; but the solution, in equal measure, becomes less active toward the indicator, phenolphthaleïn (p. 114). The experiment shows, therefore, rather fairly, the relative activities of the bases. The exact work of Arrhenius included consideration of the effect of the ammonium salt, and the clearing up of the mystery of this effect (p. 114) formed one of the greatest triumphs of his theory.
[142] Arrhenius, Electro-chemistry, p. 184 (1902). A second accelerative factor, the so-called "salt effect" (Chap. VI, q. v.), is more pronounced in the case of 0.1 molar hydrochloric acid than in that of 0.1 molar acetic acid, as the result of which the activity of the hydrochloric acid should be increased about ten per cent; the ratio, therefore, of the speeds of reaction, both the degrees of ionization of the acids and the "salt effect" being considered, should be approximately 83 : 1, whereas the ratio found by experiment is 79 : 1.
[143] Vide also A. A. Noyes, Report of the Congress of Arts and Science, Vol. IV, p. 311 (1904).
[144] Haber, Z. für Elektrochem., 10, 775 (1904); see Chapter XII.
[145] This is, essentially, the old Berzelius view of chemical action.
[146] Vide, for instance, Stieglitz, Report of the Congress of Arts and Sciences, St. Louis, IV, 276 (1904); W. A. Noyes, Ibid., 285; Nef, J. Am. Chem. Soc., 30, 645 (1908). For the application of the electron theory to organic compounds, see Falk and Nelson, School of Mines Quarterly, 30, 179, and J. Am. Chem. Soc., 32, 1637 (1910). (Cf. also Chapter XV.)
[147] J. Phys. Chem., 6, 1 (1902), and other papers in the same Journal.
[148] Cf. Patten, ibid., 7, 168 (1903), and Falk and Waters, Am. Chem. J., 31, 398 (1903). According to the latter investigators, the evolution of hydrogen is slow and weak.
[149] Patten, loc. cit.
[150] Students will not be capable of following the argument given in the succeeding passages and would better omit this part until Chapter XV has been studied.
[151] Kablukoff, Z. phys. Chem., 4, 430 (1889). See also Nernst, Theoretical Chemistry, p. 373.
[152] In view of the low order of accuracy of the data, and of the approximate method of calculation, this result is only qualitative, but even with an error of 102 to 104 the argument in the text would hold.
[153] For hydrogen under atmospheric pressure, the equilibrium ratio, [Zn2+] / [H+]2, is, approximately, 1027.
[154] Vide Sackur, Z. Elektrochem., 11, 387 (1905). Kahlenberg holds a different view; ibid.
[155] The negative results obtained with aluminium and magnesium are possibly more interesting than the positive action observed with zinc, but their inactivity may be due to thin films of protective chloride or oxide or to a passive condition (vide Smith's Inorganic Chemistry, pp. 723, 753; College Chemistry, p. 475).
[156] The work of Ostwald, Arrhenius, Nernst and many others shows conclusively that the liberation of hydrogen by metals and the precipitation of metals by one another is a function of ion concentrations (Chapter XIV). Vide Nernst, Theoretische Chemie (1905), p. 245.
[157] See above.
[158] In a 0.1 molar solution of potassium cyanide, the potassium hydroxide formed by the decomposition of the cyanide by water is approximately 0.0013 molar and the concentration of hydrogen-ion is reduced to 10−11 (Chapter X), a value roughly of the same order as that calculated above as a possible concentration of hydrogen-ion in a benzene solution of hydrogen chloride. In spite of this small concentration of hydrogen-ion in the cyanide solution, the reactions in which it is involved are, as far as known, completed in a few moments. Only for much smaller concentrations of ions have any doubts as to their direct action been aroused; in Chapter XII this question, as raised by Haber, is discussed for concentrations of ions of the order of 10−23. Haber considers that ionic concentrations of 10−14 can still account for very fast actions.
[159] Cf. Abegg., Theorie der Elektrolytischen Dissociation (1903), 255; Lehfeldt, Electro-chemistry (1904), 87.
[160] There is probably minimal ionization in all these cases, especially in the case of ammonia (NH3 ⇄ NH2− + H+), but not enough to yield a sufficient supply of hydrogen-ion to show its common properties.
[161] Vide Jorgensen, J. prakt. Chem., 16, 349 (1877).
[162] See Chapter XII in regard to the stability of (PtCl62−) as a complex ion.
[163] Freshly prepared solutions must be used.
[164] See Chapter XII as to the decomposition of the "complex ions."
[165] K+ and CN− are colorless ions. The yellow color of the ion moving to the positive electrode shows the presence of the iron in it—a fact that can be confirmed by testing the solution round the anode for ferricyanide by the method discussed further on in the text.
The theory of ionization, as studied so far, gives us simple, rational explanations of many of our qualitative reactions—explanations which agree with phenomena taken from separate fields of investigation. But, if our study of the theory ceased at the present stage without further elaboration, we should fail to find in it a satisfactory explanation of a number of other important facts of analysis—notably, why certain reactions, the occurrence of which we might anticipate, do not take place. For instance, the addition of a soluble carbonate to a barium chloride solution precipitates almost all the barium as barium carbonate (exp.); we have 2 Na+ + CO32− + Ba2+ + 2 Cl− → BaCO3 ↓ + 2 Na+ + 2 Cl−. But the addition of carbonic acid to barium chloride solutions fails to produce the slightest precipitate (exp.), although carbonic acid also gives rise to the carbonate-ion, CO32−. In the same way silver nitrate readily precipitates silver phosphate from sodium phosphate solutions (exp.), but not from a solution of phosphoric acid (exp.). Hydrogen sulphide precipitates zinc sulphide from a zinc sulphate solution (exp.), Zn2+ + SO42− + 2 H+ + S2− → ZnS ↓ + 2 H+ + SO42−; but the addition of hydrochloric acid effectually prevents the precipitation (exp.), although the hydrogen sulphide is still ionized, as is apparent from the precipitation of copper sulphide when copper sulphate is added to the mixture (exp.). In the negative results, we have instances of a very large number of cases which require closer study, and a further development of the theory, if we wish to interpret them satisfactorily. The line of development to be followed is indicated perhaps most sharply by the following experiment.
Exp. Some sodium tetraborate (borax) is dissolved in a little water and silver nitrate is added to a small part of the solution. A pure white precipitate (silver borate) results. Another portion of the borate solution is diluted with a large quantity of water, and then silver nitrate is added; quite a different result is obtained—a brown precipitate (silver oxide) is formed. [p091]
The change in the quantity of water brought about the difference in result—the quantitative relations were altered thereby. In order to follow intelligently this and the other actions referred to, the study of reactions in solutions must be taken up from the quantitative side—the development heretofore has been essentially qualitative in character. On several occasions we have found that all electrolytes do not ionize equally well, and that the intensity of their action, demonstrated, for instance, for potassium and ammonium hydroxides, varies accordingly. We shall now have to study these relations in greater detail.
For our purpose, the study of two of the fundamental quantitative laws governing action in solution and of their application to analytical phenomena, will be sufficient: these are, the law of chemical or homogeneous equilibrium, in which the law of mass action is included, and the law of physical or heterogeneous equilibrium.
in which A, B, C and D represent four different substances reacting in the molecular proportions indicated by their symbols, which as usual represent molecular weights. And the condition for equilibrium may be expressed in the mathematical equation
[A], [B], [C] and [D] are used to represent the concentrations166 of [p092] the four reacting substances and k is some definite number, called the equilibrium constant.
The law was discovered by Guldberg and Waage in 1867, and, with certain limiting conditions (see below) it has been fully established by extensive experimental work.167 The significance of the law may be interpreted on the basis of the following considerations. If we start with the two substances A and B alone and have one mole of each in one liter (as gas or in solution) at a given temperature, then, all the conditions being given,—the temperature, the concentrations, and the nature of the substances,—the reaction A + B → C + D, leading to the formation of C and D, will proceed with a perfectly definite velocity. The molecules of A and of B move in all directions (kinetic theory of gases and solutions), and molecules of A will collide with molecules of B a definite number of times in unit time and will form a definite number168 of molecules of C and D per minute. The velocity of chemical change of a given substance (chemical velocity) is also measured in terms of moles, and is represented by the number of moles or the fraction of a mole changed per minute. If v′1 stands for the velocity of the action between A and B, under the given conditions, then
where k1 is some number. Now, if the concentration of one of the components, e.g. A, should be doubled, then the chances for collision and for action between molecules of A and B will be twice as great as before and the velocity of the action will be doubled. If only one-tenth of the concentration of A (one-tenth mole) is used, the velocity will only be one-tenth as great as originally, and, in general terms, if [A] moles of A are used per liter, the velocity of the change will be proportional to [A], and equal to k1 × [A]. If the concentration of the other reacting component, B, is now doubled, the chances for action are again doubled, and, in general, the velocity of the action will be proportional also to the concentration [p093] [B] of the second reacting substance. For the velocity, v1 of the action for any concentrations, [A] and [B], of A and B at any moment at a given temperature, we have
Hence, if by the symbols [A] and [B] the concentrations at any given moment are represented, we may say that the velocity of the formation of C and D at that moment169 is proportional to the product of the concentrations of A and B, and to some constant, which is characteristic of the interaction of A and B.
The validity of this conclusion has been fully verified by experiment.170 The case is an instance of the law of mass action, which states that in chemical changes the velocity of the action is proportional at any moment to the molecular concentrations171 of the reacting components, and to a constant, which is characteristic of the chemical nature of the reacting components (and of the temperature).
If we start with the reversed action
the relation may be developed in the same way. Thus the two substances C and D will react upon each other, at the given temperature, with a velocity proportional to a constant, k2, and, at any given moment, proportional also to their respective concentrations at that moment:
Equilibrium will be reached when the substances A and B are formed at any moment from C and D just as rapidly as they are used up to produce C and D, and vice versa. Such is the case, [p094] when the velocities of the two opposite reactions are equal to each other. For the condition of equilibrium, then, v1 must be equal to v2 and therefore
or
In this way the meaning of the fundamental law of chemical equilibrium may be developed from the consideration of the velocities of the reversible actions, such as are involved in all conditions of equilibrium, and the equilibrium constant represents the ratio of the velocity constants of the two opposite reactions. This conclusion has been fully verified by experiment, the equilibrium constant being, as a matter of fact, found equal to the ratio of the velocity constants.172
The relations, so far considered, have been those of the simplest type of reversible reaction. We may now discuss the modifications required for other types of reaction by the law of equilibrium.
When two molecules of any reacting component take part in a reaction—for instance, in A + 2 B ⇄ C + D—the concentration of this component is raised to the second power in the mathematical expression of the law of equilibrium; when three molecules of a component take part, its concentration is raised to the third power, etc.
For instance, hydrogen iodide is decomposed, reversibly, into hydrogen and iodine, according to 2 HI ⇄ H2 + I2. A condition of equilibrium is reached, at a given temperature when
At 440°, the results given in the following table were obtained by Bodenstein. The concentrations are expressed in moles per liter.173 The constant is calcuated according to the equation just given. Analytical errors affect the value of the constant most in the first and last experiments, as a result of the very small concentrations of one component, I2 or H2. [p095]
| [H2] | [I2] | [HI] | K |
|---|---|---|---|
| 0.0268 | 0.000190 | 0.0177 | (0.016) |
| 0.00986 | 0.00203 | 0.0328 | 0.019 |
| 0.00308 | 0.00783 | 0.0337 | 0.021 |
| 0.00175 | 0.0114 | 0.0315 | 0.020 |
| 0.000653 | 0.0204 | 0.0236 | 0.024 |
| 0.000265 | 0.0242 | 0.0202 | (0.016) |
The mechanical significance of the raised powers of the concentrations of components, two or more molecules of which take part in a reaction as indicated, will be discussed further on, in connection with a case of equilibrium between an electrolyte and its ions (Chapter VI, p. 102).
The following experiments may be used to illustrate the significance of the two classes of factors: Phosphorus pentabromide is partially decomposed by heat into the tribromide and bromine (a case of gaseous dissociation):
Phosphorus trichlordibromide is decomposed more or less, in a similar fashion, into the components phosphorus trichloride and bromine, according to the equation
For the condition of equilibrium in the two cases we have
Exp. Two tubes containing equivalent quantities of the two bromides are placed side by side in warm water.178 The tube containing the trichlordibromide is found to be much more intensely colored by free bromine than that containing the pentabromide.
The intensity of the color of the bromine vapor shows that the concentration of bromine, [Br2]″, in the PCl3Br2 tube, is greater than the corresponding concentration, [Br2]′, in the PBr5 tube. As a molecule of pentahalide PX5 dissociates into one molecule of PX3 and one molecule of X2, [PCl3] equals [Br2]″ and is greater than [PBr3], which is equal to [Br2]′. Further, more of the pentabromide than of the trichlordibromide must be left undecomposed, i.e. [PCl3Br2] is smaller than PBr5. Since the factors in the numerator of the second equation are both larger, and the factor in the denominator smaller, than the corresponding factors in the first equation, k2 must be greater than k1. These constants are thus seen to be a measure of the chemical stability of these pentahalides. It is evident, too, that in reactions which depend on the presence of free bromine, such as the bromination of many organic compounds, the trichlordibromide should be more effective than the equivalent quantity of the pentabromide. [p097]
In the second place, if we were to introduce into either tube, for instance into the tube containing the phosphorus trichlordibromide, an excess of one of the dissociation products, say an excess of phosphorus trichloride, then the condition of equilibrium would necessarily be disturbed:
in which the bracketed symbols represent the concentrations of the first experiment. The velocities of the two opposite reactions would be no longer equal, the combination of trichloride with bromine would be accelerated by the increased concentration of the former. Here, equilibrium would only be reëstablished when the trichloride and bromine had combined to a sufficient extent to make
| (y [PCl3] − x) × ([Br2]′ − x) | = k2, |
| ([PCl3Br2] + x) |
in which x represents the number of moles of additional phosphorus trichlordibromide formed in unit volume by the combination of bromine with phosphorus trichloride. The net result is seen to be that an increase in the concentration of the one dissociation product eo ipso reduces the concentration of the other dissociation product.
Exp. A third tube charged with the same quantity of phosphorus trichlordibromide as the tube mentioned above, and with an added excess of phosphorus trichloride, is placed in the warm water next to the tube containing the trichlordibromide. Its color is much paler than that of the latter, owing to the suppression of free bromine.179
The concentration of the free bromine, ([Br2]′ − x), under the new conditions of equilibrium, is smaller than the original concentration [Br2]′—a result confirmed by experience. It is in our power, therefore, arbitrarily to change the concentration of a reacting component, in a case of equilibrium, and thus to affect the reactivity of the system; for instance, for brominating purposes, the new system would be less effective than the original one, and it might be of especial service where bromination is to be avoided.
In the cases studied, are found the two fundamentally important relations expressed by the law of equilibrium: the equilibrium constant is a measure of the stability of a certain system and, in a way, of its reactivity at a given temperature; and the [p098] concentration factors are variables, which we may change to a very considerable extent, so as, to a certain degree, to subject the system to our own purposes. We shall repeatedly have occasion to refer to these two fundamental relations and we shall use them again and again in our analytical work.
If the total concentration of the acid is known, the concentrations of the ions and of the non-ionized acid may be calculated from the conductivity of the solution. For instance, if 60 grams of acetic acid (1 mole) is dissolved in sufficient water to make 10 liters, the equivalent conductivity of the solution (p. 50) is found to be 4.67 reciprocal ohms at 18°. The maximum conductivity of one mole of acetic acid, at infinite dilution, when all the acid would be ionized, would be 347. Therefore, in the acid under examination, 4.67 / 347, or 1.34 per cent, is ionized (p. 50). Since the total concentration of the acid is 0.1 mole per liter and 1.34 per cent is ionized, the concentration of the hydrogen-ion, [H+], is 0.1 × 0.0134, and that of the acetate-ion, [CH3CO2−], is the same. The concentration of the non-ionized acetic acid, [CH3CO2H], is 0.1 × 0.9866. If these values are inserted in the equation for the condition of equilibrium, we have
| (0.1 × 0.0134)2 | = Kionization = 18.2E−6. |
| 0.1 × 0.9866 |
From this experimental result, the equilibrium constant, which is called the ionization constant of the acid, is found to have the value 18.2E−6. If the ratio [H+] × [CH3CO2−] / [CH3CO2H] really is a constant, the same value, within the limits of experimental errors, should be obtained from acetic acid in other concentrations. Now, if the above solution is diluted to ten times its volume, the concentration of the acid is made 0.01 mole per liter, the conductivity [p099] is found to have increased to 14.5 reciprocal ohms, and the percentage of ionized acid is then 14.5 / 347, or 4.17. Here, [H+] and [CH3CO2−] = 0.01 × 0.0417 and [CH3CO2H] = 0.01 × 0.9583. Inserting these values in our general equation and calculating the result, we obtain 18.1E−6 as the value of the constant. In the following table180 are given the molar conductivities, Λ (column 2), of acetic acid of varying concentrations, m (column 1). The degrees of ionization, α, and the ionization constant, calculated according to the equilibrium equation, are given in columns 3 and 4.
Ionization of Acetic Acid. Λ∞ = 347.
| m. | Λ. | 100 α. | K. |
|---|---|---|---|
| 0.1 | 4.67 | 1.34 | 18.2E−6 |
| 0.08 | 5.22 | 1.50 | 18.3E−6 |
| 0.03 | 8.50 | 2.45 | 18.5E−6 |
| 0.01 | 14.50 | 4.17 | 18.1E−6 |
It is evident, that a constant value is found for the ratio [H+] × [CH3CO2−] / [CH3CO2H] and that the ionization of acetic acid, in these dilute solutions, obeys the law of chemical equilibrium.181 The equilibrium constant expresses in definite, quantitative terms the tendency of acetic acid to ionize in dilute solution. Examination of other acids shows that there is an enormous range in the values found for their respective ionization constants. The constants are the best measure of the strength of the acids as acids. Obviously, the more readily acids in equivalent solutions ionize, the greater will be the concentration of the hydrogen-ion to which the characteristic acid properties are due, and the more pronounced (stronger) will be the exhibition of these properties. From the ionization constants one may calculate, for instance, the proportion in which two competing acids will neutralize a base, when the latter is used in quantity insufficient to neutralize both acids. [p100]
Inspection of the equation for acetic acid, which is the typical equilibrium equation for all monobasic acids, shows that the greater the degrees of ionization of acids are in equivalent solutions, i.e. the greater the concentrations of the hydrogen-ion which their ionization produces in equivalent solutions, the larger will be the values of their ionization constants. The acids with the larger constants are, then, the stronger acids.
In the first place, for the strongest acids, such as hydrochloric, nitric, hydrobromic and similar acids, chemists have been unable to determine ionization constants on the basis of the law of chemical equilibrium. Strong acids, strong bases and most salts (see pp. 106–8, below), the three classes comprising all the very readily ionizable electrolytes, do not give constants when the values of the equilibrium ratio,182 [Cation] × [Anion] / [Molecules], are calculated for different concentrations, and they therefore do not ionize simply in accordance with the law of chemical equilibrium. The reasons for this abnormal behavior will be discussed presently (p. 108), when other necessary facts are before us. In order to have, at least, a rough basis for comparison of these strong acids with the weak ones, which do obey the law of chemical equilibrium, the table will give for the strong acids the value of the above ratio as calculated from their ionization in 0.1 molar solutions.
We may ask, however, whether both the hydrogen atoms of carbonic acid show the same tendency to ionize, or, since there is a vast difference in the ease of ionization of different acids, whether there is not also a difference in the ease of ionization of the different hydrogen atoms in a polybasic acid. As a matter of experiment, we find that a molecule of carbonic acid does ionize, first, and more readily, into one hydrogen ion and an acid carbonate ion HCO3−, according to H2CO3 ⇄ H+ + HCO3−.
For this reversible reaction we have184
The value of this constant,185 called the primary ionization constant of carbonic acid, is 0.3E−6.
The acid carbonate-ion HCO3−, in turn, is ionized to a certain extent, producing another hydrogen ion and the carbonate-ion, CO32−. We have HCO3− ⇄ H+ + CO32−, and
The value of this constant186, called the constant of the [p102] secondary ionization of carbonic acid, is 0.07E−9, which has about one four-thousandth of the value of the constant for the primary ionization.
If we combine equations (2) and (3) we have
| [H+] × [HCO3−] × [H+] × [CO32−] | = K1 × K2 |
| ([H2CO3] × [HCO3−]) |
or
This is equation (1), derived originally by the application of the law of mass action to the relation between the carbonate-ion, CO32−, the hydrogen-ion, and carbonic acid, H2CO3.
This relation, and, in particular, the significant squaring of the concentration of the hydrogen-ion, an ion which appears twice in the equation for the formation of carbonic acid from carbonate and hydrogen ions, (2 H+ + CO32− ⇄ H2CO3), may now be interpreted mechanically (p. 92) as follows: For the formation of carbonic acid from a carbonate ion and two hydrogen ions, a carbonate ion must collide and combine first with one hydrogen ion, and the velocity for the formation of this intermediate product, HCO3−, will be proportional to the (total) concentration of the hydrogen ions; the product, HCO3−, to form H2CO3, must collide and combine with a hydrogen ion once more, and this combination will proceed with a velocity again proportional to the (total) concentration of the hydrogen ions. So the velocity for the transformation of CO32− into H2CO3 will be proportional twice over to the (total) concentration of the hydrogen ions—as well as, in the usual fashion, to the concentration of the carbonate ions present at any moment.
It is a general principle that the primary ionization of polyvalent acids occurs more readily than the secondary, and this in turn more readily than the tertiary (if a third ionizable hydrogen atom is present in the acid).
In the case of phosphoric acid, for instance, the primary ionization into the hydrogen-ion and the dihydrogen-phosphate-ion, H2PO4−, takes place so readily that phosphoric acid reacts strongly acid187 to methyl orange,188 the [p103] concentration of hydrogen-ion being sufficiently great to affect this indicator (see Exp. below).
When phosphoric acid is neutralized by one equivalent of a base, say of sodium hydroxide, the salt formed, sodium dihydrogen-phosphate, NaH2PO4, yields sodium-ion and dihydrogen-phosphate-ion, H2PO4−. The latter is ionized somewhat into H+ and the bivalent hydrogen-phosphate-ion, HPO42−. The ionization of the ion H2PO4− is now the chief source of supply of hydrogen-ion (the further ionization of HPO42− is practically negligible here) and it is ionized so little that the solution of NaH2PO4 no longer changes the color of methyl orange (see Exp. below). The solution is, however, acid to the indicator phenolphthaleïn, which is much more sensitive to the hydrogen-ion and will show the presence of much smaller concentrations of it than will methyl orange. The addition of a second equivalent of sodium hydroxide to the solution converts NaH2PO4 into Na2HPO4. This salt gives sodium-ion and the hydrogen-phosphate-ion HPO42−, which, in turn, is ionized only very slightly, producing phosphate-ion PO43−, and again hydrogen-ion. The ionization of HPO42− is so slight, however, and the concentration of the hydrogen-ion, therefore, so minute, that the solution does not react acid even to the sensitive indicator phenolphthaleïn.
Exp. Methyl orange (very little) is added to 10 c.c. of a 0.1 molar solution of phosphoric acid and 10 c.c. of 0.1 molar sodium hydroxide solution is added to the mixture; the color will be found to change from the acid to the neutral tint just as the last drop or two of the alkali are added. Phenolphthaleïn is then added to the mixture and 10 c.c. more of the 0.1 molar sodium hydroxide solution are required to change the color of the mixture to a pronounced pink (alkaline) tint.
Even sulphuric acid, although its two hydrogen atoms are ionized very easily, making sulphuric acid a strong acid, shows a difference in the ease of ionization of the two hydrogen atoms. Since ionization, in general, is favored by dilution, we find that in the case of such a strong acid the difference is most marked in more concentrated solutions, the smaller amount of water starting the ionization in the more favored direction and producing first, chiefly, hydrogen-sulphate ions, HSO4−. When the solution is diluted, the hydrogen-sulphate ions are to a very considerable extent dissociated into sulphate ions and hydrogen ions. The described change in ionization can be roughly followed with the aid of an insoluble sulphate like barium sulphate. Barium sulphate, while very insoluble in water, dissolves in rather strong sulphuric acid to form the acid sulphate, Ba(HSO4)2, the SO42− ion of the sulphate being more or less suppressed by uniting with hydrogen-ion. We have the action
If the solution of the acid sulphate is poured into a large volume of water, barium sulphate is immediately reprecipitated, the hydrogen-sulphate-ion being dissociated, in the dilute solution, into hydrogen-ion and sulphate-ion, SO42−, whose barium salt is so difficultly soluble:
Exp. Finely divided barium sulphate is warmed for a moment with a few cubic centimeters of concentrated sulphuric acid in a test tube, the mixture is allowed to settle, and some of the clear acid is carefully decanted into a large beaker full of water.
It may be added, that while the primary ionization of sulphuric acid does not yield an equilibrium constant for the ratio [H+] × [HSO4] / [H2SO4], even such a strong acid as is sulphuric acid is found to give a fairly good constant189 for [H+] × [SO42−] / [HSO4−]. The value of this constant189 is 0.03.
The Ionization ConstantsA of Acids
| Acid. | Equilibrium Ratio. | K. |
|---|---|---|
| Hydrochloric | [H+]×[Cl−]/[HCl] | (1) |
| Hydrobromic | [H+]×[Br−]/[HBr] | (1) |
| Hydroiodic | [H+]×[I−]/[HI] | (1) |
| Nitric | [H+]×[NO3−]/[HNO3] | (1) |
| ChromicB | [H+]×[HCrO4−]/[H2CrO4] | (1) |
| [H+]×[CrO42−]/[HCrO4−] | 0.6E−6 | |
| SulphuricC,D | [H+]×[HSO4−]/[H2SO4] | (1) |
| [H+]×[SO42−]/[HSO4−] | 0.3E−1 | |
| OxalicE | [H+]×[C2O4−]/[H2C2O4] | 3.8E−2 |
| [H+]×[C2O42−]/[HC2O4−] | 0.5E−4 | |
| PhosphoricF | [H+]×[H2PO4−]/[H3PO4] | 0.1E−1 |
| [H+]×[HPO42−]/[H2PO4−] | 0.2E−6 | |
| [H+]×[PO43−]/[HPO42−] | 0.4E−12 | |
| ArsenicD | [H+]×[H2AsO4−]/[H3AsO4] | 0.5E−2 |
| NitrousB | [H+]×[NO2−]/[HNO2] | 0.5E−3 |
| AceticG | [H+]×[CH3CO2−]/[CH3CO2H] | 1.8E−5 |
| CarbonicH,I | [H+]×[HCO3−]/([H2CO3]+[CO2]) | 0.3E−6 |
| [H+]×[CO32−]/[HCO3−] | 0.7E−10 | |
| Hydrogen SulphideJ,K |
[H+]×[SH−]/[H2S] | 0.9E−7 |
| [H+]×[S2−]/[SH−] | 0.1E−14 | |
| BoricB | [H+]×[H2BO3−]/[H3BO3] | 0.7E−9 |
| Hydrocyanic | [H+]×[CN−]/[HCN] | 0.7E−9 |
| Arsenious | [H+]×[H2AsO3−]/[H3AsO3] | 0.6E−9 |
| WaterL,C | [H+]×[HO−]/[H2O] at 25° | 0.2E−15 |
| at 100° | 0.9E−14 | |
| [H+]×[HO−] at 25° | 1.2E−14 | |
| at 100° | 0.5E−11 |
[A] As explained on p. 100, the bracketed values given for the strong acids are not constants, but express the values of the ratios [H+] × [Anion] / [Acid] for 0.1 molar solutions.
[B] See references, Noyes, ibid., 32, 860 (1910).
[C] Noyes and Eastman, Carnegie Institution Publications, 63, 274 (1907).
[D] Luther, Z. Elektroch, 13, 296 (1907).
[E] Chandler (McCoy), J. Am. Chem. Soc., 30, 713 (1908).
[F] Abbot and Bray, ibid., 31, 760 (1909).
[H] Walker, J. Chem. Soc., (London), 77, 5 (1900).
[I] McCoy, Am. Chem. J., 29, 455 (1903); Stieglitz, Carnegie Institution Publications, 107, 243 (1909).
[J] Auerbach, Z. phys. Chem., 49, 220 (1904).
[K] Knox, in Abegg's laboratory, Trans. Faraday Soc., 4, 43 (1908).
The difference in the tendencies of acids to ionize, as expressed in the table, may be recognized in equivalent solutions by any of the properties dependent on the ionization, such as the conductivity, the chemical activity, the osmotic pressure and allied effects, and so forth. If the conductivities of equal volumes of equivalent (e.g. normal) solutions of hydrochloric, phosphoric and acetic acids are compared (exp.)190, it is readily seen that hydrochloric acid is the best conductor, phosphoric acid a much poorer one, and acetic acid an exceedingly poor one (the conductivity of normal acetic acid is about 1 / 200 that of normal hydrochloric acid, and the conductivity of normal phosphoric acid is about 1 / 14 that of normal hydrochloric acid). Since the conductivity is approximately proportional to the concentration of the hydrogen-ion191 in each of the solutions, it is evident that the hydrochloric acid is ionized to a considerably greater extent than either of the other acids—than acetic acid, in particular. Similarly, if a drop (0.05 c.c.) of molar hydrochloric acid and a drop of molar acetic acid are added to equal volumes (50 c.c.) of a very dilute solution of methyl orange (exp.), the color will be changed decidedly by the hydrochloric acid to a bright pink, but by the acetic acid only to an orange hue. Again, if a precipitate of barium chromate or calcium oxalate is treated with some strong acid, hydrochloric or nitric, for instance, it dissolves readily, while a considerable excess of acetic acid (exp.) only dissolves traces of either precipitate.192 In this way, the chemical behavior of these acids differs in degree, as a result of the different tendencies to ionize, which are expressed in the constants of the table. Advantage is taken, in analysis, of such differences. Acetic acid, for instance, is used when only a slight degree of acidity is desired—as in recognizing barium-ion by its chromate, or oxalic acid by means of its calcium salt. Hydrochloric or nitric acid is used when decided acidity is required—as in the separation of groups by hydrogen sulphide (Chap. XI).
The Ionization ConstantsA of Bases
| Base. | Ratio. | K. |
|---|---|---|
| Potassium hydroxide | [K+]×[HO−]/[KOH] | (1) |
| Sodium hydroxide | [Na+]×[HO−]/[NaOH] | (1) |
| Barium hydroxide | [Ba2+]×[HO−]2/[Ba(OH)2] | (0.03) |
| Strontium hydroxide | [Sr2+]×[HO−]2/[Sr(OH)2] | (0.03) |
| Calcium hydroxideB | [Ca2+]×[HO−]2/[Ca(OH)2] | (0.03) |
| Ammonium hydroxideC,D | [NH4+]×[HO−]/([NH4OH]+[NH3]) | 1.8E−5 |
| HydrazineE | [N2H5+]×[HO−]/([N2H5OH]+[N2H4]) | 0.3E−5 |
| AnilineF | [C6H5NH3+]×[HO−]/ ([C6H5NH3OH]+[C6H5NH2]) |
0.5E−9 |
| Water | [H+]×[HO−]/[H2O] at 25° | 0.2E−15 |
| at 100° | 0.9E−14 | |
| [H+]×[HO−] at 25° | 1.2E−14 | |
| at 100° | 0.5E−11 |
[A] As explained above, the bracketed values under K for strong bases are not constants, but express the values of the ratios for 0.1 molar solutions only. (For the alkaline earths 0.05 molar solutions are referred to.)
[B] Estimated value.
[D] Corrected value, from Bredig's data, Z. phys. Chem., 13, 322 (1894). A. A. Noyes, Carnegie Institution, Publication No. 63, p. 178, finds the value 17.3E−6 for 18°.
[E] Uncorrected value, Bredig, ibid.
[F] Bredig, ibid.; Stieglitz and Derby, Am. Chem. J., 31, 457 (1904).
While the constants of a large number of organic bases194 have been determined few constants of inorganic bases are as yet known. The fact that the majority of inorganic bases are polyvalent and difficultly soluble has made their examination in this respect more difficult. From the study of the decomposition of salts by water (see Chapter X), the trivalent bases, such as [p107] ferric hydroxide and aluminium hydroxide, are found to be much weaker than bivalent bases like cadmium, zinc and lead hydroxides,195 but the data are not sufficient for the calculation of any constants, or for distinguishing between the ionization of the first, second and third hydroxide groups.
The difference in ionization and in chemical activity between a strong base, like sodium or potassium hydroxide, and a weak base, like ammonium hydroxide, has already been discussed and illustrated (see p. 77). In analysis, advantage is frequently taken of these relations.196
| Molar Concentration. |
Conductivity. | Per cent Ionized. |
Ratio. |
|---|---|---|---|
| 0. | 131.2 | 100 | ——— |
| 0.001 | 127.6 | 97.3 | 0.035 |
| 0.01 | 122.5 | 93.4 | 0.130 |
| 0.05 | 115.9 | 88.4 | 0.335 |
| 0.10 | 111.9 | 85.1 | 0.485 |
| 0.20 | 107.7 | 82.1 | 0.754 |
| 0.50 | 102.3 | 77.9 | 1.38 |
| 1.00 | 98.2 | 74.9 | 2.23 |
It would lead too far from our subject to enter into a full discussion of this important question. It will be sufficient here to indicate two directions of inquiry, which promise to lead to an explanation of the apparent contradiction between the demands of the law of chemical equilibrium and the ionization of strong electrolytes.
In the first place, the law of chemical equilibrium is based thermodynamically, i.e. from the point of view of the ultimate energy relations involved, on the assumption that none but negligible forces of attraction or repulsion exist between the molecules, whose concentrations are factors in the equilibrium equations (cf. p. 95).200 Now, in solutions of electrolytes this condition is not strictly fulfilled under any circumstances; the attractions between ions of opposite charge and the repulsions of ions of like charge, as well as the effect of charged particles on neutral molecules, come into play. For strong electrolytes, where the proportion of charged particles is always a large one, the deviations from the simpler conditions to which alone the law is really applicable must be very much greater than for weak electrolytes. It is, therefore, probable that these electrical forces201 are the source of the deviation of the ionization of strong electrolytes from the law of chemical equilibrium: although ionization is a reversible reaction, forces come into play which make the simple law inapplicable, and it is altogether likely, therefore, that we shall find, when all the factors have been investigated, that strong electrolytes should not and cannot obey this law alone.202 In confirmation of this conclusion, recent careful calculations203 have shown that entirely analogous deviations from the equilibrium law become perceptible in rather concentrated solutions of weak electrolytes, such as acetic acid, in which there is an accumulation of charged particles, more nearly akin to that present in dilute solutions of strong electrolytes. So it appears more and more certain that the deviations are a result of the presence of electrically charged components in the solutions, the amount of deviation depending on their concentration.
Now, solid salts have higher dielectric constants than has206 solid water, and the dielectric constant of a compound is usually much higher in the liquid than in the solid form.207 It is possible, therefore, that the presence of salts in the solution increases the dielectric or, at any rate, the ionizing power of the solvent and there are many facts which would be explained by such a behavior. Unfortunately for any decision of the question, determinations of the dielectric constants of salt solutions have given contradictory results; the more recent, and possibly more reliable results of Drude208 indicate that salt solutions show approximately the same dielectric behavior as water itself. Smale, in Nernst's laboratory, on the other hand, obtained results indicating that salt solutions have decidedly higher dielectric constants than pure water.209 A final decision in the matter would be of great importance.210 But, as explained before (p. 64), there are other properties of a solvent which seem to be intimately related to its ionizing power and which may be modified by the presence of salts, i.e. of strong electrolytes. The value obtained for the proportion [Me+] × [X−] / [MeX] grows rapidly with increasing concentration, indicating a disproportionately large ionization in the more concentrated solutions—which is what one would expect, if electrolytes or their ions in some way increased the ionizing power of the medium. In agreement with such a conclusion, Arrhenius found211 that the ionization of weak acids, like acetic acid, is increased by the presence of foreign neutral salts, such as sodium chloride. This means, of course, that the strength of acetic acid, as an acid, is increased likewise.
Exp. 0.5 c.c. of 0.1 molar acetic acid is added to 100 c.c. of a dilute solution of methyl orange in each of three test glasses. When some solid sodium chloride (3 grams, and then 3 grams more—altogether 0.1 mole) is added to the one solution, a plain increase in the intensity of the acid tint is observed.212 The addition of cane sugar to a second solution has no such effect. The addition of sodium chloride to a fourth portion of the methyl orange, to which no acetic acid has been added, shows that its color remains unchanged: the effect on the indicator in the first case, then, is the result of the action of the salt on the acetic acid.213 [p111]
The so-called "salt-effect" on the ionization of ammonium hydroxide may be illustrated in a similar way.
Exp. 0.5 cc of 0.1 molar ammonium hydroxide is added to each of two portions (100 c.c.) of a dilute solution of phenolphthaleïn. When some sodium chloride solution is then added to one of the two portions, the basicity of the solution is distinctly increased. The addition of sodium chloride to a third portion of the phenolphthaleïn solution shows that its own reaction to the indicator is neutral.
If the ionizing power of a solvent is changed by the presence of an electrolyte, then the law of chemical equilibrium, in its simple form, would not apply to the ionization of such electrolytes in varying concentrations—as little as we should expect to obtain the same constant for acetic acid in aqueous solution and in alcoholic solution, the ionizing power of alcohol being much smaller than that of water. The deviation from the law, naturally, would be most marked in the case of those electrolytes which ionize so easily as readily to produce high concentrations of ions.
It may be said that laws based on the electrical properties of salt solutions seem to be the predominating laws governing the ionization of electrolytes and modifying, in certain cases, the chemical laws based on the study of non-electrolytes.214
For the purposes of qualitative analysis, it will suffice to bear in mind the fact that the ionization215 of salts, strong acids and strong bases does not conform to the laws of mass action, and the fact that practically all salts (with the notable exceptions, among common salts, given on p. 107) are very readily ionized in aqueous solution, namely to the extent of 40 to 85% in solutions of such moderate concentration as 0.1 molar.216
If the concentrations of the components are modified in any way, the condition of equilibrium is disturbed and change will result, always toward the restoration of equilibrium. The changes, in the case of purely ionic actions, are found to take place with an enormous velocity, equilibrium being restored almost instantly.
(1) If the solution of acetic acid, represented in the above equation, is diluted by an equal volume of water, the condition of equilibrium is disturbed:
The ratio is smaller than that required for equilibrium, and there will be a change towards increasing the ratio. The acid will ionize more rapidly than it will be formed from the acetate and hydrogen ions (which collide less frequently in the diluted solution) and a new condition of equilibrium will be reached, when more of the acid is ionized. We found, as a matter of fact, that the more a solution of acetic acid is diluted, the larger is the proportion of ionized acid (see p. 99).
(2) If the concentration of the acetate-ion is increased in the solution by the addition of a salt of acetic acid, say sodium acetate, we have
The ratio is larger than allowed by the equilibrium law, and the acetate ions will combine with the hydrogen ions to form acetic acid more rapidly than the ions are formed from it, until equilibrium is reëstablished. In a molar solution of acetic acid, 0.42% of the acid is ionized, and we have
If an equivalent quantity of sodium acetate should be added, i.e. one mole or 82 grams of the salt per liter, the salt being ionized to the extent of 53%, we would have
The equilibrium constant will be satisfied (and the velocity of ionization of the acetic acid will become equal to the velocity of its [p113] formation from its ions) when217 [CH3CO2−] = 0.53, [H+] = 0.000,034 and [CH3CO2H] = 0.999,966. If we use two characteristic places in the decimals, we have
The most significant fact in the new condition of equilibrium is the extremely small concentration of hydrogen-ion in the solution. Since the acid properties of acetic acid are due to its forming hydrogen-ion, we would conclude that such properties of acetic acid are very much weakened by the presence of its own salts. This conclusion has been fully verified by careful quantitative measurements and can be demonstrated as follows218:
Exp. To two of three portions of a dilute solution of methyl orange equal quantities of acetic acid are added (e.g. 0.5 c.c. molar acid), the third portion being reserved to show the color of the neutral solution of the indicator. Now, if into one of the solutions, to which acetic acid has been added, a few crystals of sodium acetate are gradually dropped, the color reverts gradually to the color of the original neutral solution; the concentration of hydrogen-ion becomes so small, that it does not visibly affect this indicator, which is not very sensitive to acids, (H+).219
The solution, according to the views expressed, should still be very slightly acid, and by the use of an indicator (litmus paper) which is much more sensitive to the hydrogen-ion than is methyl orange, no difficulty is found in recognizing this fact also. As a matter of experiment, then, an acid like acetic acid is very much weaker in the presence of its own salts than in their absence, and the equilibrium constant and the concentrations of the components used determine the extent to which the hydrogen-ion is suppressed. The same must be true for all weak acids and similar relations must [p114] hold for all weak bases220—in general, weak acids and weak bases are very much weakened by the addition of their own salts.
The importance of recognizing such changes, in considering analytical reactions, may be illustrated as follows:
Exp. A solution of ferrous acetate (ferrous chloride with an equivalent quantity of sodium acetate) is treated with hydrogen sulphide; a precipitate of black ferrous sulphide is formed. A second portion of the solution is first decidedly acidified with acetic acid: hydrogen sulphide does not precipitate any ferrous sulphide. Some crystals of sodium or ammonium acetate are added to the mixture and a black precipitate of iron sulphide immediately appears around the salt as it dissolves, and on mixing the contents a heavy precipitate of the sulphide throughout the vessel is formed.
It is evident that the addition of a neutral salt, containing the same negative ion as the added acid, may completely reverse the net result of a test with hydrogen sulphide.
(3) If the concentration of the hydrogen ions in the solution of acetic acid is increased by the addition of hydrochloric, or some other strong acid, equilibrium between the acetic acid and its ions will likewise be disturbed and the new condition of equilibrium will show a suppression of the acetate-ion. Instances of such action of a strong acid in suppressing the characteristic ions of weaker acids will be discussed in detail in connection with the analytical applications of hydrogen sulphide (Chap. XI), where the action is of peculiar importance. Strong bases have a similar effect on weak bases.
(4) If one of the ions of acetic acid is suppressed by the addition of some agent, equilibrium is again destroyed and the resulting change is always in the direction of reëstablishing a condition of equilibrium on the basis of the law of equilibrium. Instances of this common case, such as the neutralization of acetic or any other acid by a base, or the driving out of a weak acid, from its salts, by a strong acid, or of a weak base by a strong base, considered from the point of view of the equilibrium law, should be worked out by the student.221 [p115]
(5) The displacement of an acid (or base) in salts by another acid (or base) is subject always to the law that equilibrium is reached, when all the equilibrium constants are satisfied in the system. Very frequently, the application of the law will lead, apparently, to the incorrect conclusion that the stronger acid (or base) will always displace, more or less completely, the weaker222—an inference, out of which grew, indeed, the characterization of acids and bases as strong and weak. Yet, when the laws of equilibrium, as the result of the peculiar values of constants, demand that, on the contrary, a strong acid or base should be displaced by a weak, or even a feeble one, we find that the change in this direction occurs with equal ease. Numerous instances will be given where a weak acid (or a weak base) does this to a certain extent (Chap. X), and others where precipitation of salts facilitates the action of weaker acids greatly by the introduction of new, physical constants. The following case of the liberation of hydrochloric acid by the exceedingly weak acid, hydrocyanic acid, is important because it shows a reversal of the common action without the formation of any precipitate, and especially because it brings out most strikingly the relations between ionization and chemical activity in a case of special importance to analytical chemists.
Exp. Into the parallel tubes of the conductivity apparatus (p. 77) equivalent quantities223 of solutions of mercuric cyanide224 Hg(CN)2, mercuric chloride [p116] HgCl2, and barium chloride BaCl2, are introduced. The barium chloride represents an ordinary salt of the same type as the mercury salts, and the current passing through its solution makes the little lamp glow. The electrodes in the mercuric chloride solution must be brought quite close together before sufficient current will pass through the solution to bring its little lamp to redness. In the case of the cyanide we can, at most, get a faint, dull glow by bringing the electrodes together as closely as we can, without allowing them to touch each other and short-circuit the current.
It is evident that these mercury salts are not as readily ionizable as are ordinary salts. This difference, as may be anticipated, shows itself also in the chemical behavior of their solutions and makes necessary special precautions on the part of the analyst in examining mercury compounds. For instance, whereas mercuric oxide is readily precipitated by the addition of sodium hydroxide to solutions of the nitrate and even of the moderately ionized chloride, one fails to get a precipitate of oxide from the cyanide solution (exp.), and if we relied on this test, we should overlook the mercury entirely. That traces of the mercuric-ion are present, as indicated by the minimal conductivity of the cyanide, is confirmed by the fact that from the cyanide solution the sulphide, which is much less soluble than is the oxide, may be precipitated by the addition of ammonium sulphide (exp.). That the sulphide is in fact less soluble225 than the oxide is shown by the conversion of the latter into the former by the action of ammonium sulphide (exp.).
As a further result of the abnormally slight ionization of these mercury salts, the analyst, unless he is on his guard, may also have difficulty in discovering the presence of their negative ions. Thus, while sodium chloride readily gives hydrogen chloride when treated with concentrated sulphuric acid, mercuric chloride, although it is a soluble salt, does not (exp.), and reliance on this test alone might lead to a gross error.226 In the case of the cyanide, it is correspondingly difficult to recognize the [p117] cyanide-ion (see the laboratory experiment, Part III). The ordinary tests fail to show its presence until the mercury has been removed from the solution by precipitation as a sulphide. Mercuric cyanide being a deadly poison which analysts are liable to meet and have met with in criminal cases, it is clear that a knowledge of these facts is vital to analytical accuracy.
Now, the very slight ionization of mercuric cyanide enables us to realize, in the following experiment, the case where an exceedingly weak acid without the formation of any precipitate involving physical constants, may displace a much stronger acid from its salts. Hydrocyanic acid is one of the weakest acids (table, p. 104), the constant for the ratio [H+] × [CN−] / [HNC] being 0.7E−9. It is so weak an acid that the addition of a dilute solution to methyl orange will not redden the indicator, but will have only a barely perceptible effect on it (exp.). Mercuric chloride solutions also are almost neutral to methyl orange (exp.) (very slight decomposition of the salt by water makes the solution very slightly acid, not enough to produce more than an orange color with methyl orange). Now, mercuric chloride, while it is not very easily ionized, is, we found, very much more readily ionized than is mercuric cyanide. The consequence is that when we add hydrocyanic acid to a mercuric chloride solution, the equilibrium between mercuric chloride and its ions and between hydrocyanic acid and its ions will be decidedly displaced, the mercuric-ion combining with the cyanide-ion to form the scarcely ionizable mercuric cyanide. As a result, more and more of the molecular mercuric chloride and hydrocyanic acid will be ionized; and since the other ions, the chloride and the hydrogen ions, form a readily ionizable electrolyte, hydrochloric acid, these ions (H+ and Cl−) will accumulate in the solution and we shall have sufficient ionized hydrochloric acid liberated to make the solution decidedly acid.
Exp. When the two solutions described above are mixed, a strongly acid solution, colored a bright pink, results.
In the following equations the dark arrows indicate the direction in which the action goes when the solutions are mixed:
[166] Concentrations are usually measured in moles or gram-molecular weights per liter, and a gram-molecular or molar weight of a compound is its molecular weight expressed in grams. Hence the number of grams of a given substance in a liter divided by its molecular weight represents its concentration.
[167] Nernst, Theoretical Chemistry, 423, 433; Ostwald, Lehrbuch, II2, 104, etc., 296; Walker, Introduction to Physical Chemistry (1909), 259, etc.
[168] Not every collision of a molecule of A with one of B is supposed to result in a chemical interaction, but the number of collisions with such a result is considered to be directly proportional to the total number of collisions. Van 't Hoff, Lectures on Physical Chemistry, I, 104.
[169] Since in any chemical action, which has not reached a condition of equilibrium, the concentrations of the reacting substances change continuously, the relation between the velocity of the action and the concentrations, for any moment, is found by the application of the calculus to the experimental data. (Cf. Elements of Calculus, by Young and Linebarger (1900), 168, 181, 240; Mellor, Higher Mathematics for Students of Chemistry and Physics (1902), 197.)
[170] Nernst, loc. cit., 541, etc.; Ostwald, loc. cit., 107, etc.; Walker, loc. cit., 257; Smith, loc. cit., 250, and 180 (Stud.).
[171] If a component takes part more than once in the action, its concentration is raised to the power corresponding to the coefficient expressing the number of its molecules taking part in the action. For instance, for A + 2 B → C + D, v1 = k1 × [A] × [B]2; (see below).
[172] Cf. Van 't Hoff, loc. cit., I, 206.
[173] The concentrations are calculated from the data given by Bodenstein, Z. phys. Chem., 22, 16 (1897). (Cf. Van 't Hoff loc. cit., I, 110.)
[174] The fundamental meaning of the law is most accurately defined in thermodynamic terms, that is, in terms of the work or energy relations connected with changes of gaseous or osmotic pressures.
[175] Van 't Hoff, loc. cit., I, 104, 159, etc.
[176] In regard to the variations of the equilibrium constant with changes of temperature and the relations which govern these changes see Smith's Inorganic Chemistry (1909), p. 260.
[177] The limitations are indicated in the preceding section.
[178] Stieglitz, Am. Chem. J., 23, 406 (1900).
[179] Vide Stieglitz, loc. cit.
[180] The table is based on the results of Noyes and Cooper, given in "The Electrical Conductivity of Aqueous Solutions," Carnegie Institution Publications, No. 63, pp. 138, 141 (1907).
[181] Ostwald [Z. phys. Chem., 2, 278 (1888)], was the first to develop this relation from the conductivity data for so-called "weak acids," and the law of chemical equilibrium, holding in such and similar cases, is often called Ostwald's Law of Dilution.
[182] The equilibrium ratio, used as an illustration in the text, is the equilibrium ratio for monobasic acids. For polybasic acids, the ratio would have the form demanded by the rule given p. 94. For instance, for H2X ⇄ 2 H+ + X2−, the expression [H+]2 × [X2−] / [H2X] should be constant, provided the ionization occurs according to the law of chemical equilibrium in its simplest terms. In point of fact, for strong acids, this ratio holds as little as does the equilibrium ratio for the monobasic acids.
[183] Owing to the instability of carbonic acid, which breaks down into carbon dioxide and water (H2CO3 ⇄ H2O + CO2), the carbonic acid is, in turn, in equilibrium with the carbon dioxide. For the sake of simplicity, this relation is not included in the detailed discussion, and wherever the symbols H2CO3 and [H2CO3] are used, they are intended to represent the total carbonic acid, present as such and as carbon dioxide. The detailed discussion of the complication mentioned will be given in connection with the analogous case of ammonium hydroxide and ammonia, and, as will be shown there, with the significance just attached to the symbols, the relations developed in the text are a rigorous expression of the facts.
[184] [H+], in all the equations used, represents as usual, the total concentration of hydrogen-ion.
[185] Walker and Cornack, J. Chem. Soc. (London), 77, 20 (1900).
[186] McCoy, Am. Chem. J., 29, 437 (1903); Stieglitz, Carnegie Institution Publications, No. 107, p. 245 (1909).
[187] In a solution of phosphoric acid, all the possible forms of ionization, described in the text, occur simultaneously, but the secondary and tertiary forms of ionization, as far as the concentration of the hydrogen-ion is concerned, are entirely subordinate to the primary ionization.
[189] Luther, Z. Elektrochem., 3, 296 (1907). Noyes and Eastman, Carnegie Institution Publications, 63, 274 (1907). Noyes and Stewart, J. Am. Chem. Soc., 32, 1133 (1910).
[191] Hydrogen ions move five to ten times as fast as the anions and carry 80–90 per cent of the current; see p. 56.
[192] The solution of these salts is due to the action of hydrogen ions on their anions; see Chap. VIII.
[193] Goodwin, Z. phys. Chem., 21, 1 (1896).
[194] See Kohlrausch and Holborn, loc. cit., p. 194. Their values for K (last column) must be divided by 100 to express the constants in terms of the same units as those used in the above table.
[195] J. H. Long, J. Am. Chem. Soc., 18, 693 (1896). Ley, Z. phys. Chem., 30, 322 (1899); Bruner, ibid., 32, 133 (1900); Walker, J. Chem. Soc., (London), 67, 585 (1895).
[196] Instances are found in the laboratory experiments, Parts III and IV.
[197] The ionization of salts of other types, e.g. MeX2, Me2Y, etc., likewise fails to conform to the law of chemical equilibrium.
[198] See below (pp. 112–4), also, further, confirmatory evidence, derived from the application of the same law to the influence upon the degree of ionization of weak acids and weak bases, exerted by the presence of their own salts.
[199] See below, in regard to evidence that the disturbing factors, predominant with strong electrolytes, are exhibited in much slighter, but perceptible measure in the case of the weak electrolytes.
[200] See also the interpretation of the law of chemical equilibrium from the viewpoint of the kinetic theory, Nernst, Theoretical Chemistry, p. 428.
[201] For a more detailed discussion of these views, see Lehfeldt's Electrochemistry (1904), pp. 78, 79.
[202] Various empirical laws, expressing the behavior of strong electrolytes, have been suggested: see Nernst, Theoretical Chemistry, p. 498, as to Rudolphi's and van 't Hoff's rules; see also A. A. Noyes, Report of the Congress of Arts and Science, IV, p. 316 (1904).
[203] Wegscheider, Z. phys. Chem., 70 (I), 603 (1909).
[204] It is possible that this effect is only another form of expressing the very relation discussed in the preceding paragraph.
[205] Arrhenius, Z. Elektrochem., 6, 10 (1899); Z. phys. Chem., 31, 197 (1899).
[206] Salts have constants averaging about 7, and running from 5 to 28; the constant for ice is about 3. Landolt, Börstein, Meyerhoffer, Tabellen, p. 766 (1905).
[207] We have: Ice, 3, water (at 0°), 80; glacial acetic acid, 2.8, acetic acid (liquid), 10; cane sugar, 4, cane sugar in aqueous solution (40%), 67.5, (6.5%), 45.3. Ibid.
[208] Z. phys. Chem., 23, 280 (1897).
[209] Wiedemann's Ann., 60, 625 (1897).
[210] See Walden, Z. phys. Chem., 61, 636 (1908), in regard to the difficulties of the problem.
[211] Loc. cit.
[212] Cf. Szyszkowski, Z. phys. Chem., 58, 420 (1907).
[213] Arrhenius made a calculation of the effect, taking into account all the rather involved changes produced by the salt. Loc. cit.
[214] For instance, the principle of "isohydric solutions," discovered by Arrhenius, has been established empirically and it involves relations which are in marked disagreement with the demands of the law of chemical equilibrium. Vide A. A. Noyes, Report of the Congress of Arts and Sciences, IV, p. 318 (1904).
[215] The most reliable estimates of the concentrations of ions in these solutions are based on determinations of the degrees of ionization by means of conductivity measurements (see Chap. IV, and the previous footnote).
[216] Salts MeX ionize more readily (80–85% in 0.1 molar solution) than do salts Me″X2 or Me2X″ (50 to 70% in 0.1 molar solution), and these, again, more readily than salts Me″X″ (about 40% in 0.1 molar solution).
[217] The calculation of the condition of equilibrium can be made, with sufficient accuracy for our purpose, as follows: The denominator 0.9958 in the original proportion, being near its limit (its highest possible value is 1 in a molar solution), cannot change appreciably. Consequently, when the one factor in the numerator, [CH3CO2−], is made 0.53 / 0.0042, or 126 times as large as it was, the other factor, [H+], to maintain a constant proportion, must be made 1 / 126th of its original value and 0.0042 / 126 = 0.000,034. For more exact work, the new concentrations of the three components may be found by solving a simple quadratic equation.
[218] Küster, Z. für Elektrochem., 4, 110 (1897).
[220] See Part III for the application of this principle to ammonium hydroxide and its experimental confirmation. (Cf. Arrhenius, Z. phys. Chem., 2, 28 (1888); Stieglitz, Am. Chem. J., 23, 406 (1900).)
[221] For instance, in the first place, the action of 0.1 mole of HCl on 0.1 mole of C2H3O2Na, dissolved in a liter of water, and, in the second place, the action of 0.1 mole of NaOH on 0.1 mole of NH4Cl, in a liter of water, may be considered. The strong electrolytes (HCl, C2H3O2Na, NaCl, NH4Cl, NaOH) may be taken to be (roughly) 80% ionized. From the concentrations given and the constants involved, the direction and the presumable intensity of the main change in each of the two cases should be determined.
[222] Instances of such displacement are given in the footnote of the previous paragraph.
[223] E.g. 50 c.c. of 0.2 molar solutions.
[224] Mercuric cyanide and mercuric chloride are largely present in aqueous solution as [Hg(CN)2]2 and [HgCl2]2; see Chap. XII.
[225] See Chapter VIII in regard to this proof that mercuric sulphide is less soluble than mercuric oxide and in regard to the question how, by a continuous disturbance of the equilibrium conditions, all the mercury may be precipitated from the cyanide solution as the sulphide, in spite of the very slight degree of ionization of the cyanide.
[226] The chloride is, however, sufficiently ionized to make possible the precipitation of the very insoluble silver chloride, when silver nitrate is added to its solution.
The law governing physical or heterogeneous equilibrium applies to all cases where, at a constant temperature, one and the same chemical substance is present in two or more physical conditions, or "phases," in contact and in equilibrium with each other. We have, for instance, the common case of a liquid, say water, in contact with its vapor, or the liquid in contact with its solid phase (ice) and its vapor; or, we may have a gas, say oxygen, in contact with its solution in some solvent like water. We may have a solid, like cane sugar, in contact with its solution. We may also have a substance like bromine, which is soluble both in chloroform and in water, present in both solutions at the same time, the two solutions being in contact but immiscible. These cases represent the most common types of systems to which the law of physical equilibrium may be applied, although the list has by no means been exhausted. The law of physical or heterogeneous equilibrium states that when one and the same chemical compound is present in two physical states or phases, as expressed in the equation S1 ⇄ S2, then when equilibrium is reached, at a given temperature, the ratio of the concentrations of the substance in the two phases is some constant number:
The bracketed symbols denote concentrations.
It should be noted that the condition of equilibrium is independent of the total quantity227 of substance present in either phase or in both phases; that is, provided the ratio of the concentrations is maintained constant at a given temperature, the quantity of substance present in both phases or in either phase is variable. For instance, the condition of equilibrium between water and [p119] water vapor is independent of the quantity of water or of water vapor present: in a closed liter bottle containing water and water vapor, the ratio of the concentrations is maintained, irrespective of the question whether the bottle contains 10 c.c. of water and 990 c.c. of vapor or 990 c.c. of water and 10 c.c. of vapor.
The law is one of experience; instances of its application are given below. Its probable theoretical significance may be explained mechanically with the aid of the kinetic theory of gases and solutions, as follows: If chloroform is added to a solution of bromine in water, the chloroform takes up part of the bromine and, if the mixture is vigorously shaken, a condition of equilibrium and a definite distribution of bromine between the two solvents will result (exp.228). Now, if one imagines a liter of the aqueous solution to contain one mole of bromine at some given temperature and to cover a liter of chloroform, the whole system being left to itself, then all the conditions affecting the migration of the bromine into the chloroform will be definite ones—the concentration of the bromine, the temperature, the surface between the two solvents—and bromine will pass from the aqueous solution into the chloroform solution at a definite speed. We may call the quantity (in moles) of bromine which would enter the chloroform in one minute, if the concentration of the bromine in the water were kept constant (one mole) throughout the minute, the velocity of migration of the bromine—this velocity, like chemical velocity, representing a quantity, not a distance. The velocity being a definite one under these conditions, we have v1 = k1. Now, if all the conditions are left unaltered, except that the concentration of the bromine is changed, say kept at one-hundredth its original value, then only one one-hundredth as many molecules of bromine as in the first case will come into contact with the chloroform surface in unit time. The chances for migration are one one-hundredth as great, and the quantity entering the chloroform in unit time—the velocity of the [p120] change—will be one one-hundredth of the original velocity. In general, the velocity will be proportional to the concentration of the bromine [Br]aq. in the water at any moment and to the characteristic constant k1.
On the other hand, if a solution of bromine in chloroform is covered with water, bromine enters the water (exp.).229 We would find, by the method of analysis used before, and for the same conditions, that the velocity of migration, v2, of the bromine into the water is also proportional to a characteristic constant, k2, and to the concentration of the bromine in the chloroform [Br]ch.. We have, therefore v2 = [Br]ch. × k2.
Equilibrium between the two solutions will be reached when
from which follows that230 for the condition of equilibrium
Now, at a fixed temperature, a pure liquid has a fixed concentration, its specific gravity being a definite one. Hence, for a fixed temperature, the second term of the constant ratio being definite, the first term, [CHCl3]vap., representing the concentration of the vapor, must also have a fixed, constant value for the condition of equilibrium, i.e. when the space above the liquid is saturated with its vapor. This is in agreement with well-known facts. The concentration of the vapor is usually expressed in terms of its [p121] pressure, and is called the vapor pressure or vapor tension of the liquid at the temperature in question. Tables giving the definite vapor pressures of important liquids at the various fixed temperatures are in common use.
(2) For oxygen in equilibrium with its saturated solution, say in water, at a fixed temperature, we have, according to the law, [O2]gas : [O2]solut. = k.
If the oxygen is under a given pressure at a definite temperature, its concentration [O2]gas is fixed, and consequently the second term, [O2]solut., of the ratio, the concentration of the dissolved oxygen, or its solubility, must also be definite, i.e. oxygen must have a definite solubility in water at a given temperature under a given pressure. If the pressure on the gas is doubled, its concentration is doubled and, to maintain the constant ratio, its solubility must also be doubled—which is in agreement with the facts (Henry's law). If air of the same pressure is taken, in place of pure oxygen, then the concentration of the oxygen (first term of the above ratio) is only about one-fifth as great as for the pure gas, and the water must be saturated with oxygen when it has taken up only one-fifth (second term of the ratio) as much as it would from the pure gas (Dalton's law): Each gas in a mixture is soluble in proportion to its own partial pressure or concentration.
(3) For sugar in equilibrium with its solution in water, i.e. in contact with its saturated solution, at a given temperature, we should have
Since a pure solid like sugar at a given temperature has a definite specific gravity, the concentration of the sugar in the solid condition should also be a definite one. Consequently, according to the law under discussion, the first term, [C12H22O11]aq., of the ratio, the concentration of the sugar in its saturated solution in contact with the solid phase, must also have a definite value. This is in agreement with fact, the concentration of the sugar in the saturated solution, termed its solubility, being a definite one for a given temperature. (See below, p. 123, in regard to the solubility of fine powders.)
Exp. Supersaturated solutions of sodium sulphate and sodium thiosulphate, into which crystals of the salts are dropped, show how the crystal starts crystallization. The crystals develop as branches from the crystal first introduced and from the new crystals formed.
This phenomenon of supersaturation is one which analytical chemists must always take into consideration. Tests which involve the precipitation of substances that are merely difficultly soluble, rather than exceedingly insoluble, or of substances present only in very small quantities, may well lead to entirely wrong conclusions, if precautions are not taken against the possibility of the failure of a precipitate to appear as a consequence of persistent supersaturation. For instance, a common test for the presence of potassium salts consists in the precipitation of potassium acid tartrate by the addition of tartaric acid to the solution of a potassium salt (exp.). The tartrate is somewhat soluble and tends to form supersaturated solutions; if we proceed without due regard for this phenomenon, we may readily have a quantity of potassium salt present and fail to obtain the test for it. Simply mixing tartaric acid and potassium chloride solutions (exp.) may fail to [p123] give any precipitate, and if the test is thrown away and potassium reported absent, a glaring blunder is committed. To insure against the error of supersaturation, we try to start crystallization by the common devices of shaking the solution or "scratching" the walls of the vessel, the object being to facilitate the formation of the first crystal. The surest method is to inoculate a small portion of the mixture with a minute crystal of the substance we expect to be formed. If no precipitate results in a short time, the solution is not supersaturated—it may be too dilute and may require further concentration, but the error of supersaturation has been excluded.
The relation between supersaturated solutions and crystals brings out sharply the fact that physical equilibrium is essentially a condition of equilibrium between the substance at the surface of the solid and the substance in its dissolved state. In terms of the molecular theory, equilibrium is established when the molecules of the crystal surface dissolve as rapidly as molecules from the solution are deposited on the surface. If the concentration of the dissolved molecules is reduced below the point required for equilibrium, the velocity of deposition is diminished. The velocity of solution will then be greater than the velocity of deposition and solution will result. The reversed relations hold when the concentration of the solution is greater than that demanded by equilibrium: the velocity of deposition will be the greater than that of solution and precipitation follows.231
The application of these relations to analysis is as follows: If a crystalline precipitate is in contact with a solvent, e.g. if barium sulphate is in contact with the liquid from which it has been precipitated, then this liquid must be continually in a state of change, not of equilibrium, with respect to the solution and the deposited barium sulphate. The more minute crystals, being a little more soluble than the larger ones, will supersaturate the solution in respect to the larger crystals and the excess will be deposited on these larger crystals and make them grow still larger. This deposition will make the solution unsaturated with respect to the smaller crystals and more of these will dissolve. The process is obviously a continuous one, and must lead in time to the disappearance of the minute crystals and the growth of the larger ones. That is a result which analysts aim to attain,—which in quantitative work it is in fact necessary to attain, since the more minute crystals are likely to pass through filters and be lost in the analysis. The views expressed, and the experimental confirmation of the conclusion reached, form the theory of what is called the "digesting" of precipitates before they are brought on filters. It is clear that every condition facilitating contact between solvent and solid will accelerate the desired change and continuous stirring is therefore desirable. Heating is, as a rule, also to be desired for very insoluble precipitates, as it will, in the majority of cases, facilitate the solution of the undesirable, finer crystals.
In conclusion, these considerations will also indicate the precautions to be observed in the precipitation of difficultly soluble substances. If this is not properly carried out, endless trouble in [p125] the analytical laboratory results. Except when heating is, for some special reason, undesirable—as inducing a chemical change (like hydrolysis) that is not wanted—solutions are brought to the boiling-point, and the precipitant added drop by drop, in order not to supersaturate the solution too strongly. The solution is thus allowed time to deposit its excess as far as possible on the first crystals formed, which it will do rather than to form new, minute ones (see supersaturation, p. 121). Constant stirring is prescribed in order to bring older crystals, as far as possible, into contact with all parts of the slightly supersaturated solution. After the precipitation is complete, it is usually desirable to allow the mixture to "digest" for some time, for the reasons given above—stirring and a high temperature during the process being desirable. (See further Chap. VIII, p. 147, in regard to the use of an excess of precipitant.)
When a difficultly soluble substance is formed in a solution beyond the point of saturation of the solution, the substance in question separates from the solution in a new phase, according to the principles just laid down. Ordinarily, if the substance is a solid, a precipitate is formed; if a gas, a gas escapes; if a liquid, a liquid separates out, which is immiscible with the solution in which it is formed. Occasionally, the condition of supersaturation which precedes the separation is somewhat persistent, but this resistance to the separation of the phase may be overcome by vigorous agitation of the solution or, as in the case of supersaturation with a crystallizable salt, by inoculation of the solution with a particle of the new phase (p. 123).
Under certain conditions, however, a difficultly soluble substance may be produced in a solution, in a concentration far beyond its solubility, without the separation of a precipitate (evolution of a gas or formation of a separate liquid) and also without the formation of a supersaturated solution. Thus, when hydrogen sulphide is passed into an aqueous solution of arsenious oxide, the liquid acquires the yellow to orange color of arsenious sulphide and becomes opalescent. But no precipitate is seen (exp.), in spite of the fact that the sulphide is extremely insoluble and is formed practically quantitatively according to the equation As2O3 + 3 H2S ⇄ As2S3 + 3 H2O. The orange liquid passes through a [p126] filter unchanged (exp.). But if some hydrochloric acid or a salt (e.g. sodium chloride) solution is added to a portion of it, a heavy precipitate of arsenious sulphide is immediately produced (exp.); its quantity is a good indication of the great amount of sulphide that is not precipitated before the addition of the acid or salt. If some pure arsenic sulphide (solid) is added to another portion of the orange liquid, in order to overcome any possible condition of supersaturation, the liquid is found to remain clear (but opalescent), excepting for the few particles of added sulphide (exp.); even when it is vigorously shaken (exp.), or allowed to stand for days, no precipitate is formed. We are therefore not dealing with a case of supersaturation.
A liquid, in which a very insoluble substance appears thus to be in solution far beyond its usual degree of solubility, and yet does not show at all the behavior of a supersaturated solution, is said to contain the substance in the colloidal condition. After a few more instances of the colloidal condition have been presented, the significance of the condition and the meaning of the term used to designate it will be explained.
Exactly as in the case of the other liquids discussed above, in which very insoluble substances appear to be in solution far beyond their usual degree of solubility, so the present liquid does not show the behavior of a supersaturated solution and it is said to contain the ferric hydroxide in the colloidal condition.245
The following measurements of osmotic pressures may be given:246
| Substance. | Concentration Per cent. |
Osmotic Pressure. Cm. Hg. |
|---|---|---|
| Gum arabic | 1 | 6.9 |
| Dextrin | 1 | 16.6 |
| As2S3 | 4 | 1.7 |
| Fe(OH)3 | 1.1 | 0.8 |
| 2.0 | 2.8 | |
| 3.0 | 5.6 | |
| 5.3 | 12.5 | |
| 8.9 | 22.6 |
The last results, obtained with special care to exclude soluble impurities, are more reliable than the older results on gum arabic and dextrin. For the purpose of comparison it may be said that a 1% solution of cane sugar (molecular weight = 342) has an osmotic pressure of 53 cm. Hg at 18°, a 5% solution a pressure of 265 cm.
For our purposes it will be sufficient to define the colloidal condition, on the basis of these results, as the condition of an insoluble substance in which, as far as ordinary observation and the common methods for separation of heterogeneous phases (filtration, sedimentation, etc.) are concerned, the substance appears to be present in a homogeneous clear solution, whereas in reality it is present in a heterogeneous mixture. An extremely finely divided solid suspended in a liquid, or an emulsified liquid suspended in another liquid, are the most common types254 of such mixtures. [p131]
The following colloids, which are of interest in analytical chemistry, are found to carry a negative charge in pure water: Colloidal acids (silicic, stannic), sulphides (As2S3, As2S5, CdS, etc.), salts (AgI, AgCl) and metals (Au, Pt, Ag). It is noteworthy that the suspensions of finely divided clay, kaolin, quartz, carbon, carry the same charge as these colloidal suspensions. On the other hand, metal hydroxides (ferric, aluminium, chromic), and basic substances in general, carry positive charges.
On the other hand, the colloids of one important group are found to be almost without any electric charges;260 the passage of an electric current through their suspensions has little or no effect on them. Perfectly neutral albumen and gelatine are common representatives of this group.
The charge on a colloid seems to be liable to variation with the nature of the liquid in which it is suspended. Colloidal platinum in water is negative, in a mixture of water and alcohol, positive.[2] Of peculiar interest and importance is the fact that some colloids change the character of their charge when the liquid, in which they are suspended, is made to pass from an acid to an alkaline condition, and vice versa.261 For instance, albumen262, colloidal silicic acid263 and colloidal stannic acid264 are negative in alkaline liquids, positive in acid. The relation of these facts to the chemical nature of the substances will be discussed presently.
According to the other of the two theories, here considered, the electrification of the colloid may result from what is known as contact or surface electricity.269 At the surface of two different substances there is always a potential difference.270 In the case of finely divided suspensions, like the colloids, the contact surfaces are enormous, as compared with the surfaces involved in ordinary contact. Whether metals (Au, Pt, Ag) owe their charges to simple contact effects or to their (minimal) tendency to ionize (Chapters XIV and XV) is not known. In fact, no exact knowledge of the source of electrification of any colloid has yet been obtained.
The purple precipitate (purple of Cassius), which is formed when stannous chloride is added to gold chloride (p. 126), contains colloidal gold,276 which, in suspension, is charged with negative electricity, and colloidal stannic acid,276 which in acid solution, presumably, carries a positive charge277: these two colloids mutually precipitate each other in the presence of hydrochloric acid.278
When the precipitate is treated with an alkaline liquid (ammonium hydroxide solution), the charge on the stannic acid becomes negative, both colloids acquire the same charge and the precipitate dissolves, to form the beautifully tinted suspensions of colloidal gold (p. 126). In this condition the colloids (gold and stannic acid) are sensitive to precipitating electrolytes, and the solution is more sensitive to a mixture of magnesium nitrate and ammonium nitrate than to ammonium nitrate alone (exp.), as is to be expected from a negative suspension (see below).
The characteristic difference in behavior between ortho-, pyro- and metaphosphoric acids toward albumen, which is used as a characteristic analytical test to distinguish metaphosphoric acid from the other two acids,279 appears to be due to similar relations280: metaphosphoric acid, which precipitates (coagulates) albumen, is colloidal, ortho- and pyrophosphoric acids are not. The [p135] coagulation seems to be the result of the union of the negative colloid metaphosphoric acid (or a complex negative colloidal ion thereof) with the positive colloid albumen (or a positive colloidal ion thereof).
Thus, colloidal As2S3, carrying a negative charge, is precipitated by the positive ions of added electrolytes. The addition of a few drops of a molar solution of ammonium nitrate (the precipitating ion is NH4+) to 20 c.c. of the colloidal suspension282 produces a slight precipitate; complete precipitation requires 3.5 to 3.6 c.c. of the ammonium nitrate solution.283 Only 0.06 c.c. of an equivalent solution284 of magnesium nitrate (the precipitating ion is Mg2+) is required, and as little as 0.015 c.c. of an equivalent solution of aluminium nitrate285 (the precipitating ion is Al3+) has the same effect (exp.). An increase in valence of the negative ion, which is not the precipitating ion in this case, does not affect the result appreciably: 3.5 c.c. of a solution286 of ammonium sulphate, (NH4)2SO4, equivalent to the solution of NH4NO3, is also required for the complete precipitation of the colloidal As2S3 (exp.), although the one contains the univalent ion, NO3−, the other the bivalent ion, SO42−.
Conversely, a positively charged colloid, like ferric hydroxide, may be precipitated by much smaller quantities287 of bivalent negative ions than of univalent ions, etc. [p136]
In the second place, if precipitations are attempted either in rather dilute solutions or in solutions of little ionized substances (arsenious acid and hydrogen sulphide), the addition of an electrolyte is frequently required to insure precipitation. Thus, the presence of ammonium chloride, or nitrate, in excess, is helpful in the precipitation of the sulphides of the zinc group; the addition of hydrochloric acid (or other electrolyte) is required to effect the precipitation of arsenious sulphide from a solution of the oxide (p. 126).
In the next place, account must be taken, in analytical work, of the fact that colloids carry down with them the precipitating ion by which they are coagulated, a fact which may lead to the loss of ions which, it is intended, should be kept in solution. To a certain extent, this loss may also be avoided by insuring the presence of electrolytes (acids, ammonium salts) in sufficient concentration to cause the coagulation without the aid of the ions which, it is intended, should not be precipitated. In view of the much weaker precipitating power of univalent ions (of hydrochloric acid, ammonium nitrate and chloride), as compared with that of polyvalent ions, which may be present, the acid and ammonium salts must not be used in too small concentrations. In quantitative analysis, when conditions permit it, ammonium or sodium sulphate is frequently substituted for the ammonium salts of the univalent monobasic acids. The washing of the precipitated colloid with such salt solutions gradually removes289 the ions which are precipitated with the colloid and forms a further safeguard against their loss. But this source of loss is avoided only with great difficulty and is seldom absolutely removed.
Finally, the presence of protective colloids, especially of the [p138] gelatine and albumen type, may interfere so decidedly with the common precipitation tests for ions, that their destruction is imperative, before these tests can be applied with any degree of confidence. Thus, the mixing of solutions (0.1 molar) of silver nitrate and hydrochloric acid, each containing one per cent of gelatine, fails to produce the ordinary, characteristic precipitate290 of silver chloride, the reaction which is used to determine the presence of the silver-ion in systematic analysis.
The mixture is opalescent and, in reflected light, looks opaque-white; on somewhat prolonged standing a white milk is produced, but no precipitate. When the mixture is boiled, the same deep white milk is formed, but no coagulated precipitate, the mixture running unchanged through a filter. Hydrogen sulphide converts the mixture into a similar suspension of the black sulphide.
[227] The ratio is affected somewhat by the fineness of division of liquids and solids as a result of surface tension phenomena, as explained below.
[228] An aqueous solution of iodine and potassium iodide shaken with chloroform gives similar results, and the difference in color between the two layers is an advantage for a lecture experiment. But the iodine is partially combined with the iodide, according to KI + I2 ⇄ KI3, or I− + I2 ⇄ I3−, and the theoretical relations are not so simple as for bromine in aqueous and chloroform solutions.
[229] To accelerate the action, the mixture is shaken vigorously. After the separation of the layers, the bromine may be recognized in the aqueous layer by its color, or by the addition of potassium iodide (liberation of iodine).
[230] [Br]aq. and [Br]ch. are used to express the actual concentrations at any given moment we wish to consider, for instance at the moment equilibrium is reached. The ratio k2 / k1 for any substance S is found to be equal to the ratio of the solubilities of the substance in the two solvents. That it must be so can be proved by applying the law of physical equilibrium to the mixed solvents in contact with an excess of the substance, i.e. to its saturated solutions (see below).
[231] Similar relations hold for the condition of equilibrium between a liquid and its vapor.
[232] Curie, Bull. Soc. Min., 8, 145 (1885); Ostwald, Grundlagen der Anal. Chem., p. 22 (1894).
[233] Hulett, Z. Phys. Chem., 37, 384 (1901). See also Ostwald, ibid., 34, 495 (1900), on the solubilities of finely divided mercuric oxide ("yellow oxide") and of larger crystals ("red oxide").
[234] A 1 / 1000 solution of AuCl3, 2 aq., and a 1.2 / 1000 solution of SnCl2, 2 aq., may be used conveniently. When equal volumes of the solutions are mixed, the desired precipitate is formed.
[235] Stannous chloride is usually sufficiently contaminated with stannic salt. Add a few drops of bromine- or chlorine-water to 100 c.c. of a pure stannous chloride solution.
[236] The action is an exceedingly sensitive qualitative test for gold. By a modification of the test Donau was able to detect as little as 2E−9 gram of gold (Monatshefte f. Chem., 25, 545 (1904)).
[237] The nature of the reduction reaction is discussed in Chapters XIV and XV.
[238] Faraday, Proc. Royal Soc., 8, 356 (1857), Phil. Mag. (4), 13, 401 (1857) (Stud.).
[239] Zsigmondy, Liebig's Annalen, 301, 30 (1898).
[240] Bredig, Z. f. Elektrochem., 4, 514, 547 (1898), and Anorganische Fermente, 1901. Colloidal preparations of platinum, silver and many other metals may be prepared in the same way. In ether, colloidal preparations of the alkali metals may be made (Svedberg, Ber. d. chem. Ges., 38, 3616 (1905), 39, 1708 (1906)).
[241] Argentum Credé may be conveniently used. It contains, with the metallic silver, a small percentage of albumen, which is added for reasons discussed below. Brown solutions are formed at once.
[242] First a thin film of black carbon is produced round the metal, then the latter appears in the form of a filigree of silver.
[243] For details of the preparation, see A. A. Noyes, J. Amer. Chem. Soc., 27, 94 (1905).
[244] This process of separation of substances, which do not pass through membranes, from such as do, is called dialysis. It was first used by Graham, Trans. Royal Soc., London, 151, 183–224 (1861) (Stud.).
[245] Graham made the first extended investigations in this field: Trans. Royal Soc., 151, 183 (1861); J. Chem. Soc. (London), 17, 318 (1864) (Stud.). He found that amorphous, gelatinous bodies like ferric hydroxide, aluminium hydroxide, silicic acid, gelatine, glue, dextrin, caramel, albumen and similar bodies do not pass through membranes and may be obtained by dialysis in the colloidal condition. Such substances were called "colloids" by Graham, the name referring to the Latin for gelatine. Substances which pass through membranes readily were found by Graham to resemble in behavior such bodies as are crystallizable when solid; such compounds were classified by him as "crystalloids." That liquids containing substances in the colloidal condition (e.g. arsenious sulphide, gold, silver and many other substances) may be prepared by methods other than dialysis, was found later by many investigators and, in a few cases, previous to Graham, e.g. by Faraday, loc. cit. A brief history of the chemistry of colloids is found as an introduction to Wo. Ostwald's Kolloidchemie, pp. 1–63 (1909).
[246] Cf. Wo. Ostwald, loc. cit., p. 193.
[247] Before Graham's time, and for the few colloidal liquids then known, this view was held by such men as J. B. Richter, Berzelius and Faraday (loc. cit.) (cf. Wo. Ostwald, loc. cit., p. 19). The first extended experimental investigation in support of it was made by Barus and Schneider, Z. phys. Chem., 8, 278 (1891). Bredig was also an early and consistent champion of this view (vide his Anorganische Fermente, 1901).
[248] Cf. Wo. Ostwald, loc. cit., pp. 102–114. Graham considered "colloidal silicic acid a liquid miscible with water in all proportions." According to modern ideas, no true miscibility exists, but a suspension or emulsion is formed (see Ostwald, p. 237).
[249] Siedentopf and Zsigmondy, Drude's Annalen, 10, 1 (1903). Zsigmondy, Colloids and the Ultramicroscope (1909), Chapter V.
[250] Zsigmondy, Z. für Elektrochem., 8, 684 (1902); Siedentopf and Zsigmondy, loc. cit.
[251] Zsigmondy, loc. cit., p. 161. A µµ is 1E−6 mm. The hydrogen molecule is considered to have a diameter of 0.1 µµ (O. E. Meyer), the alcohol molecule one of 0.5 µµ (Zsigmondy, loc. cit., plate IV, p. 157).
[252] Weimarn, Chem. Zentralblatt, 1907, II, p. 1293.
[253] Paal, Ber. d. chem. Ges., 39, 1436, 2859 (1906).
[254] Other varieties of heterogeneous colloidal mixtures are tabulated by Wo. Ostwald, loc. cit., p. 96.
[255] The "Cassius' purple" test for gold is an instance where the colloidal condition is used in analysis for a positive test. See Wo. Ostwald, loc. cit., p. 68, for other, similar applications for positive tests.
[256] Vide Wo. Ostwald's Kolloidchemie, 1909, and the references given by Noyes, loc. cit., p. 86.
[257] A general discussion of the preparation and properties of colloidal mixtures is given by A. A. Noyes, J. Am. Chem. Soc., 27, 86–104 (1905) (Stud.).
[258] Picton and Linder, J. Chem. Soc. (London), 61, 160 (1892), 67, 63 (1895), 71, 568 (1897), etc., and others. Wo. Ostwald, loc. cit., p. 240, gives a list of references.
[259] The arrangement of the experiment is described by Noyes, loc. cit., p. 98.
[260] Cf. Wo. Ostwald, loc. cit., p. 108. Billitzer has found that gelatine is positive in acid solution, negative in alkaline, Z. phys. Chem., 51, 147 (1905). The charges are, however, relatively small ones.
[261] Billitzer, Z. f. Elektrochem., 8, 638 (1902). This is probably true of all amphoteric colloids (Chapter X); it is also true of many other substances, which are not pronouncedly amphoteric. (Cf. Perrin, Comp. rend., 136, 1388 (1903); Billitzer, Z. phys. Chem., 51, 157 (1905).)
[262] Hardy, J. of Physiology, 24, 288 (1899); Z. phys. Chem., 33, 387 (1900).
[263] Billitzer, loc. cit., p. 159; Müller's Allgemeine Chemie der Kolloide, 1907, p. 79.
[265] In a slightly acid solution colloidal silicic acid is negatively charged; in a strong acid solution, positively—a relation which agrees with its predominantly acid character.
[266] The general class of substances, showing both basic and acid properties, of which albumen is a derivative, is described in a footnote on glycocoll, Chapter X, p. 188.
[267] Hardy, loc. cit.
[268] J. Loeb, University of California Publications, Physiology, 2, 149 (1904).
[269] Very little is known about the nature of contact electricity. It is even doubtful whether it is different, in principle, from ionization.
[270] W. Ostwald, Lehrbuch der Chem., 2, (1) 553 (1903).
[271] Hardy, Proc. Royal Soc., 66, 110 (1899); Z. phys. Chem., 33, 391 (1900).
[272] Picton and Linder, J. Chem. Soc. (London), 67, 63 (1895).
[273] Whitney and Ober, J. Am. Chem. Soc., 23, 852–856 (1901) (Stud.).
[274] Picton and Linder, loc. cit. 71, 572 (1897); Lottermoser, Anorganische Kolloide, p. 76; Biltz, Ber. d. chem. Ges., 37, 1095 (1904).
[275] Precipitation is complete only when the colloids are used in the proportions required to neutralize each other's charges [Billitzer, Z. phys. Chem., 51, 140 (1905)]. The proportions to be used must be determined in each case, most simply by trial (Noyes, loc. cit., p. 101), but quantitative methods for determining the charges, by titration, are also known (cf. Billitzer, loc. cit.).
[276] E. A. Schneider, Z. anorg. Chem., 5, 80 (1894).
[277] See the above discussion on silicic acid. Stannic acid has a greater tendency to form a base than has silicic acid.
[278] Zsigmondy, Liebig's Annalen, 301, 361 (1898).
[279] Cf. Fresenius, p. 334, or Smith's Inorganic Chemistry, p. 468.
[280] Mylius, Ber. d. chem. Ges., 36, 775 (1903); Biltz, ibid., 37, 1116 (1904).
[281] J. für prakt. Chem., 25, 431 (1882).
[282] The suspension used is prepared by saturating, with hydrogen sulphide, an aqueous solution of arsenious oxide. The latter is saturated on a steam bath, cooled to 20°, filtered and diluted with an equal volume of water before it is used.
[283] Eight grams of NH4NO3 per 100 c.c.
[284] 0.6 c.c. of a tenth-normal solution is used, containing 1.28 gram Mg(NO3)2, 6 aq., in 100 c.c. Precipitation was found to be incomplete with 0.5 c.c.
[285] 0.15 c.c. of a tenth-normal solution is used, containing 1.2 gram Al(NO3)3, 4 aq., in 100 c.c. Precipitation was found to be incomplete with 0.1 c.c. of the solution.
[286] 3.3 grams (NH4)2SO4 in 100 c.c.
[287] Freundlich found, for instance, that NaCl, KCl, BaCl2, in equivalent concentrations, had practically the same effect on colloidal ferric hydroxide, but only one-fortieth as much of a sulphate (the precipitating ion is SO42− versus Cl−) was required; Z. phys. Chem., 44, 129 (1903).
[288] For other reasons (e.g. to prevent oxidation of the sulphides), hydrogen sulphide is also used in the solution for washing the arsenic group, and ammonium sulphide in that for the zinc group (see Lab. Manual, pp. 101 and 110).
[289] Picton and Linder, loc. cit., and Whitney and Ober, loc. cit.
[290] A. A. Noyes describes a similar experiment with sodium chloride and silver nitrate, loc. cit.
It frequently happens that we have to deal, simultaneously, with conditions of chemical and of physical equilibrium, obtaining in the same system. For instance, a gas like carbon dioxide, in contact with its saturated solution in water, is in equilibrium with the dissolved carbon dioxide, and this, in turn, is in equilibrium with its hydrate, carbonic acid. A substance may be distributed between two solvents and show a different molecular weight in the two (see p. 18); it may exist, in the one, primarily in polymeric form, and only to a slight extent in the simple form, the two forms being in equilibrium (chemical equilibrium). In the other solvent, it may exist only in its simple molecular form, and this will be in equilibrium with the same simple molecular form in the first solvent (physical equilibrium). In matters dealing with the solubility of electrolytes in water, and, therefore, in questions of their precipitation or solution, such simultaneous conditions of chemical and physical equilibrium are constantly occurring. Since qualitative analysis deals to a very considerable extent with just such precipitates of salts, acids and bases, these cases are of particular importance to us.
When water is added to solid silver acetate, the salt will dissolve. If an excess of the acetate is used, equilibrium will result between the solid salt and its solution, when the solution is saturated at the temperature used. As the salt dissolves, it is more or less ionized, and in the saturated solution we have a [p140] condition of chemical equilibrium between the salt and its ions:
If the law of chemical equilibrium is applied to this reversible action, we have (p. 98)
The nonionized silver acetate is present in two phases, in the solid phase and also in solution:
Applying the law of physical equilibrium to this system, we have further (p. 121)
The concentration of a pure solid, as we have seen, may be considered a constant at a given temperature. Consequently, if we consider the question of the size of the solid particles as a minor factor and negligible, we shall conclude, that, for saturated solutions of silver acetate, the concentration of the solid silver acetate being a constant, the concentration of the nonionized or molecular silver acetate, the first term of our constant ratio II, must also have some definite, constant value at a given temperature. We may call this concentration the "molecular solubility" of silver acetate and may put
for a saturated solution of silver acetate in water at the given temperature. Now, since the concentration of the nonionized silver acetate, [CH3COOAg], in the saturated solution also forms the second term of equation I, representing the condition of chemical equilibrium between the acetate and its ions, we obtain, by combining I and III,
Further, if the assumption is made that the presence of foreign electrolytes, in not too concentrated solutions, does not affect either the molecular solubility, Kmol. sol., of silver acetate or its tendency to ionize—as expressed in KIonization—then, the [p141] relation, which has been developed, would hold for saturated aqueous solutions of silver acetate in the presence of foreign electrolytes, as well as for a saturated, pure, aqueous solution. A single, simple equation would thus express the conditions for simultaneous chemical and physical equilibrium between a difficultly soluble ionogen, of the type of silver acetate, and its saturated solutions, at a given temperature, in the presence or the absence of foreign electrolytes.
It appears, however, that while the soundness of this theoretical development of the relations expressed by the solubility-product must be questioned, nevertheless as a matter of experiment, the product of the ion concentrations of a difficultly soluble salt is found, in dilute solutions, to be a constant, or sufficiently close to a constant to satisfy all but the most rigorous requirements.295
It is, in fact, quite evident, that a decreasing value for the second term of the ratio I—namely, for [CH3COOAg], the molecular solubility of the salt—as the total concentration of the electrolytes present increases, together with an increasing value for the whole ratio I under the same conditions, are not incompatible with a constant value of the first term of the ratio. That is, the product of the ion concentrations, [CH3COO−] × [Ag+], may well remain constant (equation IV), or approximately constant, in dilute salt solutions, even if equations I and III do not hold for salt solutions. [p143]
Whether in the case of all difficultly soluble salts, as the total salt concentration increases, the increasing values of the chemical equilibrium ratio (equation I) will be so nicely balanced by the decreasing values of the molecular solubility, that the first term of the first ratio (the solubility-product) will always be constant, is a question demanding further extended investigation.296 The range of the investigation must be extensive, because it must include several other classes297 of salts (e.g. Me2X, MeY2, etc.), for which the first equation has a different form; for instance, for Me2X,
For the present we must remain content with the result of the past investigations and consider the principle of the constant solubility-product to be essentially an empirical one. It is an extremely convenient condensation, into a very simple mathematical form, of the main factors involved in the precipitation and solution of difficultly soluble salts, acids, and bases. It should be used with due knowledge of its character and limitations.
Washburn298 derives the principle of the constancy of the solubility-product, without involving in his derivation the relation between ions and nonionized molecules—a relation which, as was stated above, deviates from the law of chemical equilibrium. The deviation, it will be recalled (p. 109), is generally supposed to be due to the fact that the fundamental kinetic assumption which must be made to derive the law of chemical equilibrium from the kinetic theory, the assumption that there should be none but negligible forces of attraction and repulsion between the molecules (of a gas or solute) which are in equilibrium, is not fulfilled in the case of solutions of strong electrolytes (p. 109). According to Washburn, if it is assumed that the ions of an electrolyte fulfill this fundamental condition and that only the nonionized molecules do not—the latter causing the deviation from the law of chemical equilibrium—then the principle of the solubility-product constant follows.299 He sees an approximate confirmation of the assumption made, in the fact that the principle is found, empirically, to be true, and that other relations, developed on the basis of the same assumption, agree with the observations made. [p144]
This theoretical derivation of the principle, like the derivations of the law of chemical equilibrium and of all our laws of dilute solutions, assumes300 that the nature of the solvent, and consequently of the solution-process, is not changed by added substances, for instance by an excess of the precipitating ionogen. There can be no question, however, that the nature of the solvent must change, as a continuous function, by the addition of electrolytes to solutions. The changed solubilities of inert gases in salt solutions,301 and a mass of other evidence,302 lead to this conclusion. The addition of a half mole of sodium chloride to a liter of water reduces the dissolving power of the liquid towards oxygen at 25° by 15%, i.e. by 30% per mole of salt. A weak electrolyte, such as acetic acid, has practically no effect at this concentration, and so the effect must be chiefly due to the ions of sodium chloride; since the salt, in half-molar solution, is ionized 73%, the reduction in the dissolving power would be 30 / 0.73 = 41% per mole of fully ionized salt. The principle of the constant solubility-product cannot be considered as established for solutions more concentrated than 0.2 to 0.3 molar; but it is evident that, in any comprehensive theoretical formulation of the principle for the range in which it is found empirically to hold, the change in the nature of the solvent, which in some cases is conspicuous in 0.5 molar solution, must be taken into consideration as a factor even in more dilute solutions (say 0.05 to 0.3 molar). It seems at present, quite possible, perhaps even probable, that the constancy, in all but the most dilute solutions, is the result of the approximate balancing of two (or more) opposing factors.303 When we leave the range of concentrations mentioned, and go to more concentrated solutions, these factors seem to be less well balanced and the validity of the principle ceases.304 For the present it will be safe to consider the principle as an empirical one, holding for solutions of total salt content up to 0.25 or 0.3 molar.305 For quite dilute solutions the effect of the electrolyte on the solvent would be negligible, and only to such solutions would the theoretical derivation brought forward by Washburn be applicable.
In such an aqueous solution, containing no foreign salts, the concentration of the silver-ion is equal to the concentration of the acetate-ion, since a molecule of silver acetate, when it ionizes, gives one silver ion for every acetate ion formed. The numerical value of the solubility-product may then be calculated, if the solubility of the salt and its degree of ionization are known. For instance, at 16° one liter of water dissolves 10.07 grams of silver acetate, that is, 10.07 / 167, or 0.0603 gram-molecule (mole). Conductivity measurements show that 70.8% of the salt is ionized in such a solution, and consequently the concentration of the silver-ion is 0.708 × 0.0603, or 0.0427. The concentration of the acetate-ion is the same, and the value of the solubility-product constant, obtained by inserting these quantities in the above equation, is KS.P. = 0.0427 × 0.0427 = 0.00182.
Now, if, to the saturated solution of the silver acetate, there are added a few drops of a concentrated solution of sodium acetate or some crystals of solid sodium acetate, the concentration of the acetate-ion is thereby increased and the condition of equilibrium in the solution is disturbed:
The concentration of the acetate-ion having been increased, the ion will combine more rapidly than before with the silver-ion, and the concentration of the nonionized salt will be increased. The solution being already saturated with nonionized silver acetate, the excess formed must be precipitated. As a matter of fact, a precipitate of silver acetate is readily obtained in this way (exp.). Precipitation will cease when sufficient silver acetate has crystallized out to make the product of the concentrations of the ions again equal to the solubility-product constant. If, after the crystallization is complete and equilibrium has been reëstablished, the acetate-ion is x′ times as concentrated as it was in the pure aqueous solution, the concentration of the silver-ion must be reduced to 1 / x′ its original value:
It is clear that a corresponding result should be obtained when, to the saturated aqueous solution of silver acetate, an excess of the silver-ion is added—for instance by the addition of solid silver nitrate or of a little of a concentrated solution of this salt (exp.). Here again, the product of the ion concentrations is greater than the constant, i.e. [CH3COO−] × y [Ag+] > KS.P., and precipitation results. Silver acetate therefore crystallizes out, until
The following table shows the relations when sodium acetate is added to the saturated solution of silver acetate. Column 1 gives the concentration of the sodium acetate in the solution saturated with silver acetate, column 2 the percentage of the sodium acetate that is ionized, column 3 the total concentration of silver acetate in the saturated solution, column 4 the percentage of it which is ionized, column 5 the concentration of the acetate-ion, column 6 the concentration of the silver-ion and column 7 the value of the solubility-product.
| 1 Na-Acet. |
2 100 p. |
3 Ag-Acet. |
4 100 p′. |
5 [CH3COO−]. |
6 [Ag+]. |
7 KS.P.. |
|---|---|---|---|---|---|---|
| ... | 0.0603 | 70.8 | 0.0427 | 0.0427 | 0.00182 | |
| 0.061 | 78.6 | 0.0392 | 64.5 | 0.0735 | 0.0258 | 0.00185 |
| 0.119 | 75.8 | 0.028 | 59.7 | 0.1065 | 0.0167 | 0.00179 |
| 0.239 | 70.8 | 0.0208 | 52.3 | 0.1727 | 0.0109 | 0.00188 |
The second table shows the relations when an excess of the silver-ion is present, silver nitrate having been added to the saturated silver acetate solution. The columns have the same significance as in the first table, excepting that the first column gives the concentration of silver nitrate present and the second column its degree of ionization.306
It is clear from these results that a difficultly soluble salt is rendered less soluble (see column 3 of the tables) by the presence of another salt, when the [p147] latter has an ion in common with the former. This conclusion has been well established307 for a considerable number of salts.308
| 1 AgNO2. |
2 100 p. |
3 Ag-Acet. |
4 100 p′. |
5 [CH3COO−]. |
6 [Ag+]. |
7 KS.P.. |
|---|---|---|---|---|---|---|
| 0. | ... | 0.0603 | 70.8 | 0.0427 | 0.0427 | 0.00182 |
| 0.061 | 82.0 | 0.0417 | 64.0 | 0.0267 | 0.0767 | 0.00204 |
| 0.119 | 78.4 | 0.0341 | 58.6 | 0.0200 | 0.1142 | 0.00227 |
| 0.239 | 74.0 | 0.0195 | 51.7 | 0.0100 | 0.1809 | 0.00182 |
In passing, we may ask what the approximate loss of dissolved nonionized barium sulphate would amount to. The value of the ratio ([Ba2+] × [SO42−]) : [BaSO4], representing the ionization of barium sulphate, is unknown for the extreme dilution represented [p148] by the saturated solution. If we assume it to be roughly of the order 2000 : 1,309 the solubility of nonionized barium sulphate at 18° would be roughly 0.05 milligram per liter.
As a rule, then, in the absence of complicating conditions,310 an excess of the precipitant promotes the complete precipitation of an ionogen.
Such precautions are still more important in the case of precipitates which are somewhat more soluble than is barium sulphate, and in such cases the question must be considered, whether as a washing fluid, some solution may not be used, which contains an ion in common with the precipitate, and which has, therefore, according to the principle of the solubility-product, a very much smaller dissolving power for the precipitate in question than pure water. That is a resource of the analyst to which recourse is occasionally taken. Lead sulphate, for instance, is washed with a very dilute solution of sulphuric acid, rather than with pure water;312 potassium cobaltinitrite, K3Co(NO2)6, which is used in the separation of cobalt from nickel, is washed313 with a ten per cent solution of potassium acetate, containing a little potassium nitrite. Ammonium phosphomolybdate, used in determinations of phosphates, is washed with a solution of ammonium nitrate. [p149]
The use of such solutions for washing precipitates is limited by the necessity, first, of avoiding salts which interfere with subsequent operations (e.g. which would leave nonvolatile residues in the subsequent ignition of a precipitate, that is to be weighed after ignition) and, second, of avoiding the loss of precipitate by the formation of complex ions between an ion of the precipitate and a component of the washing mixture (see p. 148). But wherever such complications can be excluded, the method is a desirable one.
It has sometimes been recommended to wash a precipitate with a saturated aqueous solution of the precipitate itself, in place of with pure water. It was reasoned that the solution, being already saturated with the salt, would not be able to dissolve any of the precipitate obtained. That is true; but if a saturated solution of a salt, MeX, is placed on a filter still holding an excess of the precipitant, i.e. one of the ions, say X, of the precipitate, then this excess may cause supersaturation of the saturated washing fluid and some of the salt may be precipitated out of the washing fluid. The method, as commonly employed, has therefore the inherent fault, theoretically at least, of being liable to give too high results. If it is to be employed without error, precautions must be taken first to remove, from the precipitate and filter, the mother liquor (containing the excess of precipitant) as completely as possible. If in a given case this can be accomplished, then the danger of precipitating any of the salt (MeX) from the saturated solution is avoided, and the precipitate (MeX ↓) may then be further washed with a saturated solution of the same salt (MeX), with advantage, in certain cases. Thus, in the Lindo-Gladding method314 of determining potassium in the form of potassium chloroplatinate, the source of error, just discussed, has been avoided in the following way: the excess of precipitant, chloroplatinic acid H2PtCl6, which has the ion PtCl62− in common with the precipitate, is first removed from the precipitate by thorough washing of the precipitate with alcohol; subsequently, other impurities, e.g. sulphates, soluble in water but not in alcohol, are washed out with an aqueous solution of ammonium chloride315 that has been saturated with potassium chloroplatinate. The method gives good results.
Since the concentrations of both the silver and the acetate ions are reduced, they will not combine as rapidly as before to form nonionized silver acetate, and the conditions of equilibrium between the latter and its ions must be disturbed. The nonionized salt ionizes, for a moment, more rapidly than it is formed and its concentration will thus be reduced. We, therefore, might expect the solution to become unsaturated in respect to the nonionized form, and the solid salt, if present, should go into solution. In other words, the addition of a salt with two foreign ions should increase the solubility of a difficultly soluble salt (it is understood that no salt is used which would precipitate a new, less soluble salt). This expectation has also been fully confirmed by careful quantitative determinations, especially by A. A. Noyes and his collaborators. The effect may be demonstrated more easily by the addition to silver acetate of an electrolyte which will very thoroughly suppress one of its ions. Nitric acid is such an agent. The hydrogen-ion will very decidedly reduce the concentration of the acetate-ion, acetic acid being a weak acid (table, p. 104). There is no difficulty in recognizing the anticipated effect (exp.).
On the other hand, solution of an ionogen is evidently favored and its precipitation rendered more difficult, if we suppress one (or both) of its ions. Thus barium phosphate, calcium carbonate, silver borate, and many salts of weak acids, that are very difficultly soluble in water, are quite easily soluble in strong acids, which suppress the anions by converting them into little ionized acids. When a precipitate is dissolved by the addition of a reagent, such as an acid, an alkali, ammonia, ammonium sulphide—chemical solvents most frequently used in analytical work—we may, as a general principle, consider that the reagent must affect one or both of the ions of the precipitate in question, suppressing it (or them) and thereby making solution possible. The problem of determining in what way the suppression of the ion is effected, must then be faced. Many occasions to determine such questions318 will arise. [p153]
We have, therefore, a certain degree of control over the precipitation and solution of electrolytes, the control depending upon, and being limited by, the fact that the factors of the product of ion concentrations are variables.
On the other hand, we have little control, in a given solvent, over the question of solution or precipitation as affected by the value of the ion product constant, the remaining term in the equation of the solubility-product for saturated solutions. These constants cover a very wide range of values for the various salts, which are most frequently used in analytical work for the precipitation of the common ions.319 They are subject to variation with the temperature, and, as a rule, as most salts are more soluble at higher than at lower temperatures, the values of the constants increase with the temperature. For exceedingly difficultly soluble salts, the increase is commonly of no practical moment in analytical work, when, by an excess of the precipitant, the ion, which is to be precipitated, can be precipitated quantitatively; the solubility of the nonionized salt, that is precipitated, is so minute (see p. 148) in this case, even at high temperatures, that it is altogether negligible for ordinary purposes.320 On the other hand, precipitates are often used which are not at all extremely insoluble but merely rather difficultly soluble; they are used in spite of their relatively slight insolubility because they are the best available forms for our purposes. Such salts are, for instance, lead chloride, magnesium-ammonium phosphate, potassium chloroplatinate. When these are precipitated, not only must the fact that they are appreciably soluble at ordinary temperature be taken into account, but also the fact that they are very much more soluble at higher temperatures. Lead chloride and potassium chloroplatinate are, for instance, quite soluble in hot water.
As a rule, we select for the form in which a given ion is to be precipitated, a form which, in a saturated aqueous solution, shows the smallest concentration of the ion in question. But if no form is [p154] known which is sufficiently insoluble to give satisfactory quantitative results, then we have recourse to a change in the solvent.
If this relation is combined with that discussed on page 63, according to which the degree of ionization of a given salt, in different solvents, is the same, when the cube roots of its concentrations are directly proportional to the dielectric constants of the solvents (e1 : ∛c1 = e2 : ∛c2 = a constant), then we find, that in saturated solutions of a given salt, in different solvents, the cube roots of the concentrations, or solubilities, are directly proportional to the dielectric constants of the solvents, or, the solubilities are proportional to the third powers of the dielectric constants.
c1 and c2 representing the solubilities, in molar concentrations, in two solvents of dielectric constants e1 and e2.
The following table illustrates the relations for a salt examined by Walden, a derivative of ammonium iodide, namely tetraethyl ammonium iodide (C2H5)4NI. The first column gives the name of the solvent, the second the solubility or concentration in the saturated solution, in terms of the proportion of moles of the solute to the total number of moles present324 [p155] (solute + solvent); the third column gives the dielectric constant, under comparable conditions, and the last column gives the relation e : ∛c.
| Solvent. | Solubility. | e5 | e : ∛c |
|---|---|---|---|
| Water | 0.0332 | 75.0 | 50.5 |
| Nitrobenzene | 0.0020 | 32.2 | 54.8 |
| Ethyl alcohol | 0.00201 | 26.6 | 45.5 |
| Acetone | 0.00072 | 21.8 | 52.8 |
| Amyl alcohol | 0.00031 | 15.0 | 48. |
In view of the difficulties in determining the values for the dielectric constant, the agreement in the values of the last column must be considered satisfactory.325
This important principle forms another striking instance of the supreme influence of electrical relations in determining the behavior of ionogens in solution (see p. 111).
Since, in solutions saturated at the same temperature with a given ionogen, the degree of ionization of the ionogen is the same in both solvents, the proportion of nonionized to ionized salt is also the same. If a salt, e.g. calcium sulphate, is less soluble in alcohol than in water, the alcohol must hold less of the nonionized form, as well as less of the ionized salt, than does an equal volume of water at the same temperature.
The development of further relations, of fundamental importance to analytical chemistry, with the aid of the laws of chemical and physical equilibrium and of the principle of the solubility-product, will be taken up in the study of the reactions of the various analytical groups of ions.
[291] Z. phys. Chem., 4, 372 (1889). See also van 't Hoff, ibid., 3, 484 (1889).
[293] A. A. Noyes, Z. phys. Chem., 9, 618 (1892); Findlay, ibid., 34, 409 (1900).
[294] As foreign salts affect the ionization of poor electrolytes (p. 109), the ratio of equation I would hold as little for poor electrolytes, and would grow larger with an increased concentration of the foreign salts.
[295] Cf. A. A. Noyes, Congress of Arts and Sciences (St. Louis), 4, 321 (1904) and Stieglitz, J. Am. Chem. Soc., 30, 946 (1908) (Stud.), and the references to literature given there. The empirical relation seems to hold for dilute solutions, the total electrolyte concentration of which is not greater than 0.2 to 0.3 gram-equivalent per liter, and, roughly, for concentrations not greater than 0.5 gram-equivalent per liter.
[296] See Stieglitz, loc. cit.
[297] Since the writing of this it has been learned that such investigations have been carried out by Harkins. Cf. J. Am. Chem. Soc., 1911.
[298] J. Am. Chem. Soc., 32, 488 (1910).
[299] Otherwise a perpetuum mobile of the second class (footnote 3, p. 12) could be constructed, which is at variance with experience.
[300] This sentence is quoted from a letter from Dr. Washburn, who is at present investigating moderately concentrated solutions of electrolytes, to determine the range of concentrations in which it is possible to apply the laws of ideal solution.
[301] Cf. Geffcken, Z. Phys. Chem., 49, 257 (1907), and the references given there.
[304] See also Hill, J. Am. Chem. Soc., 32, 1186 (1910). Hill attacks the principle as a whole, but brings no evidence against its validity for solutions of concentrations up to 0.3.
[305] The limit of concentration depends, for constancy, upon the nature of the salts. The calculations, on which the data in the tables on pp. 146–7 are based, involve extrapolations which prevent the results, especially for the more concentrated solutions, being considered as final.
[306] For further illustrations, vide Stieglitz, J. Am. Chem. Soc., 30, p. 947 (1908), and the references given there to the work of Noyes, Findlay, etc.
[307] Some instances are known where the solubility of a salt is increased by the addition of a salt with a common ion. In such cases it is extremely likely that an ion of the salt in question forms a complex ion with a component of the solution. Vide A. A. Noyes, Z. phys. Chem., 6, 241 (1890), and 9, 603 (1892). In Chapter XII we shall discuss, in detail, instances of this nature where the formation of complex ions is particularly susceptible of exact experimental verification.
[308] Especially by Noyes, loc. cit., and later papers; Findlay, loc. cit.
[309] This is the value for a similar ratio for KCl of the same concentration as found, by extrapolation, from the data in the table on p. 108.
[310] Owing to the possibility of the formation of complex ions (Chapter XII), each individual case must be considered by itself and the most favorable conditions for the complete precipitation determined experimentally. The rule mentioned is to be used as a guide, and the reference to the possibility of the formation of complex ions considered as a warning, in the planning of such investigations.
[311] Cf. p. 136, concerning precautions used to prevent precipitates from assuming the colloidal state.
[312] Fresenius, Quantitative Analysis, I, 355 (1904).
[313] Ibid., I, 307.
[314] Official Methods of Analysis, Bulletin 107, p. 11, U. S. Dept. of Agriculture.
[315] The excess of chloroplatinic acid is first washed out of the precipitate primarily to avoid subsequent precipitation of ammonium chloroplatinate, but its removal also avoids the error discussed in the text.
[316] Gay-Lussac's method.
[317] Mulder. See Sutton's Volumetric Analysis, p. 304 (1904).
[318] Vide Chapters XII and XIII.
[319] A table of exact solubilities is given at the end of the Lab. Manual, q.v.
[320] In the most exact quantitative work, as demanded in the determinations of atomic weights, every known loss must, as far as possible, be measured and taken into account. Beautiful instances of such work are found in T. W. Richards' classic determinations of atomic weights. See, for instance, Richards, Carnegie Institution Publications, No. 125 (1910), Determinations of the Atomic Weights of Silver, Lithium and Chlorine (Stud.).
[321] Z. Elektrochem., 11, 797 (1905).
[322] Ibid., 11, 936 (1905), and 12, 725 (1906).
[323] Z. phys. Chem., 55, 707 (1906), and 61, 638 (1907).
[324] If n is the number of moles of solute dissolved in N moles of solute, the concentration of the solute may be expressed as n / (n + N), which is called its "mole fraction." This form of expressing concentrations is in many particulars preferable to the mole / liter form. For very dilute solutions (n is very small compared with N) the two forms become practically identical, but they are not so for more concentrated solutions, and the mole-fraction expression is then easier to treat rigorously.
[325] See Walden, loc cit., for more extended data.
In systematic analysis it is most convenient to make separate examinations for the metal and for the acid ions. The examination for metal ions usually precedes that for the acid ions, and the scheme of analysis for the former will be considered first.
The analytical grouping of the metallic elements is not a natural one, as far as their chemical behavior is concerned. Such a grouping is found in the Periodic System of Mendeléeff and is used in systematic inorganic chemistry.326 The groups in analysis are based chiefly, but not exclusively, on the physical property of greater or smaller solubility of certain salts of the metals. According to the salts chosen, different systems vary somewhat in detail. Frequently elements of the same natural family are also found in the same analytical group, relationship in chemical properties being often coincident with relationship in the physical behavior of the salts of the metals.
In the following list, the common metal ions are arranged in groups, which are given in the order in which they are precipitated in the method of systematic analysis adopted. In each case, a group name and the characteristic reagents used in separating a group from those following it, are given.
Pb2+ (the chloride is somewhat soluble), Ag+, Hg+.
The Copper Group.—Hg2+, (Pb2+), Bi3+, Cu2+, Cd2+.
The Arsenic Group.—As3+, As5+, Sb3+, Sb5+, Sn2+, Sn4+, Pt2+, Pt4+, Au+, Au3+.
The Aluminium Group.—Fe3+, Al3+, Cr3+.
The Zinc Group.—Fe2+, Ni2+, Co2+, Mn2+, Zn2+.
In considering the analytical reactions and the analysis of these groups of metal ions, we shall take up the groups in the order reversed to that given in the table. We shall begin with the group of alkali metals, follow this group with the alkaline earths, then take the aluminium and zinc groups, the copper and silver groups, and finish with the arsenic group. This order is chosen because the chemistry of the reactions involved is simplest in the groups to be studied first and grows more complicated as we advance to those to be studied later.
It is not intended to discuss in detail all the reactions and methods; our attention will be limited rather to the study of typical general relations, and the student is expected to acquire the power to apply the general conclusions reached, to any specific case demanding it. [p159]
The ammonium-ion is recognized, and may be removed from a mixture of the salts of the group, on the basis of a fundamental distinction in its chemical behavior, namely its instability and the instability of its compounds. Sodium-ion and potassium-ion, are recognized, and separated from each other, by physical methods. All ammonium compounds, NH4X, decompose more or less readily into ammonia and the free acids,328 according to the reversible reaction,
The stronger the acid combined with ammonia, the more stable is the salt, and the higher is the temperature, at which the salt decomposes readily and rapidly. Ammonium chloride, one of the most stable of the salts, is decomposed rapidly only at about 350°, which is, however, still below red heat; ammonium carbonate, the salt of a very much weaker acid, decomposes appreciably at ordinary temperatures, and exposed to the air, it gradually disappears as ammonia, carbon dioxide and water. If the acid of the salt is volatile at the dissociation temperature of the salt, the whole salt is volatilized, and if the ammonia and volatile acid vapor reach a colder space, recombination to form the original solid salt occurs to a considerable extent (the "smoking off" of ammonium chloride). If the acid is not volatile, the salt, nevertheless, loses its ammonia at temperatures below red heat, while the acid remains. Sodium-ammonium phosphate, for instance, when heated, loses its ammonia, and sodium-dihydrogen phosphate is left as a nonvolatile residue.
Ammonium happens to form salts which closely resemble the corresponding salts of potassium in physical properties, such as [p160] solubility and insolubility, salts which could readily be mistaken for potassium salts. Advantage is taken of the chemical instability of the ammonium salts, just described, to remove ammonium completely from mixtures, by ignition, before tests for potassium are made.
Water is a far weaker acid (see table, p. 104) than carbonic acid and it is not surprising to find the compound formed by water and ammonia, ammonium hydroxide, one of the least stable of the ammonium compounds. Even at ordinary temperature, the hydroxide is more or less decomposed, according to a reversible reaction of the same type as that found for the ammonium salts, NH4OH ⇄ NH3 + HOH.
Chemists have always been interested in the problem of the exact degree of stability of ammonium hydroxide, and, more particularly, in the problem whether ammonia gives solutions in water showing very much weaker basic strength329 than equivalent solutions of potassium and sodium hydroxides, primarily because only a small proportion of the ammonia is combined with water to form the real base, ammonium hydroxide (which would be present then in much more dilute solution than the alkali metal hydroxides are in the solutions with which the comparison is made), or chiefly because ammonium hydroxide is much less readily ionizable than potassium or sodium hydroxide.
For the reversible action NH3 + HOH ⇄ NH4OH we would have, at a constant temperature, according to the law of chemical equilibrium,
For a dilute solution at a given temperature the concentration of the water may be considered a constant, and therefore
For the ionization of ammonium hydroxide, NH4OH ⇄ NH4+ + HO−, we would have in turn,
This constant represents the real ionization constant of ammonium hydroxide as a base, and its approximate value has only recently been determined by Moore330 and found to be about 5E−5. The ratio [NH3] / [NH4OH] was found to be approximately 2 at 20°. According to this result, ammonium hydroxide is really a much weaker, less readily ionized base than potassium or sodium hydroxide. The efficiency of ammonium hydroxide as a base depends [p161] on both conditions of equilibrium; the first equation states what proportion of ammonium hydroxide can exist, as such, in solution, if a given amount of ammonia is dissolved in a given amount of water, and the second equation shows the proportion of the hydroxide, which is ionized. The equations may be combined331 into one expression,
That is, the ratio of [NH4+] × [HO−] to the total concentration of nonionized ammonium hydroxide and ammonia, is a constant. This constant has the value 0.000,018 at 18° (as given in the table, p. 106) and, as said, comprises in a single expression a statement measuring the efficiency, as a base, of a solution of ammonium hydroxide and ammonia in aqueous solutions. The concentration of the hydroxide-ion, on which the efficiency as a base depends, can be ascertained directly from the expression, provided we know the total concentration of the ammonia and ammonium hydroxide and the concentration and degree of ionization of any ammonium salt, which may be present with the base (see p. 161). These data are easily obtained by direct measurement.
The instability of ammonium hydroxide is used as a means for detecting ammonium-ion in its salts. The latter are treated with some strong base, such as sodium or calcium hydroxide, and the ammonia, liberated by the decomposition of its hydroxide, is recognized by its odor or by the more sensitive test of its action on moist litmus. The delicacy of the test is dependent on the conditions expressed in the equilibrium equation (p. 160).
Sodium and potassium resemble each other so profoundly in the chemical behavior of their compounds, that they are recognized, and separated from each other, by physical methods. A very simple physical test is based on the color of their heated vapors, the color imparted to the nonluminous bunsen flame by the introduction and volatilization of their salts. The sodium flame is so intense that, if sodium is present in any quantity, the color of its flame easily masks the faint color of potassium vapor. The color of the flame is best examined, in such a case, with the aid of a spectroscope, in which the light emitted by the two elements may be readily recognized side by side, or with the aid of cobalt glass, which absorbs the sodium light. [p162]
The ions of the two metals may be separated and identified by means of difficultly soluble salts. There are so few of these in the case of both ions, that recourse must be taken to the salts of comparatively uncommon acids. Potassium chloroplatinate K2PtCl6, precipitated by the addition of chloroplatinic acid H2PtCl6 to concentrated solutions of potassium salts, gives very satisfactory results, both in qualitative and in quantitative work. The acid tartrate, KHC4H4O6, the picrate, KC6H2N3O7, and the cobaltinitrite, K3Co(NO2)6,332 are difficultly soluble and are sometimes used to identify potassium-ion. The corresponding ammonium salts are also difficultly soluble and resemble the potassium salts, and ammonium-ion must therefore be removed, as stated above, if present, before any of these precipitates may be used for the identification of potassium-ion. In the case of sodium-ion, recourse is taken to the salt of a still more uncommon acid; pyroantimonate of sodium, Na2H2Sb2O7, 6 aq., is sufficiently difficultly soluble and characteristic to be used as a means of identifying sodium-ion.
There is a very wide range in the degree of the insolubility of such precipitates as are used in analysis. In the table at the end of Part IV, the exact solubilities of the most important [p163] precipitates of the alkaline earths are given, for 18°, in grams and moles per liter. The values are instructive in a number of respects.
Inspection of the table shows which are the least soluble (in molar terms), and therefore the best salts, for precipitating barium, strontium and calcium, in order to insure the use of the most sensitive tests for the ions of each of these metals. It also shows which salts must be treated with special precautions to escape error. It is further seen, that if the carbonates of these alkaline earths are precipitated by a moderate excess of ammonium carbonate, the addition of a sulphate (for instance ammonium sulphate), to the filtrate from the precipitated carbonates, will only precipitate barium sulphate, the only sulphate whose solubility (and solubility-product) is smaller than that of the corresponding carbonate. In the same way, calcium oxalate is the only oxalate of these three alkaline earths that will be precipitated by ammonium oxalate in the filtrate from the carbonates (see Part III in regard to precautions against difficultly soluble double oxalates of magnesium). Again, calcium sulphate is the only one of the sulphates, which is sufficiently soluble in water to give an immediate heavy precipitate, when the sulphates are shaken for a few moments with water and the filtered solution is treated with a few drops of ammonium oxalate solution.
For a saturated solution of barium sulphate,335 at 18°, in contact with the solid salt, we have, according to the principle of the solubility-product,
and for a saturated solution of strontium sulphate, we have similarly336
Now, we may ask what the conditions are under which both precipitates can be present together in a condition of equilibrium with a supernatant saturated solution. In such a solution we have simultaneously
New symbols, [Ba2+]1, etc., are used for expressing the concentrations, as they are not the same as in the pure aqueous solutions. The much more soluble strontium sulphate makes the concentration of the sulphate-ion very much greater than it is in the saturated solution of pure barium sulphate and diminishes the concentration of the barium-ion proportionately (p. 145). The concentration, [SO42−]1, of the sulphate-ion, representing the actual (total) concentration of the ion in the solution saturated with both salts, appears in both of the new equations. Combining the two equations, we have, for the condition of equilibrium between the two precipitates and the supernatant liquid,
That is, in a solution in equilibrium with both precipitates at 18°, the strontium-ion must be about 2500 times as concentrated as is the barium-ion. If we start with equivalent quantities of barium and strontium chlorides, say in 0.1 molar solutions, and gradually add sulphuric acid or ammonium sulphate, barium sulphate will be precipitated alone,337 until the strontium-ion is in the excess [p165] indicated by the ratio given. After that, strontium sulphate will be precipitated, with traces of barium sulphate, the ratio expressed in the equilibrium equation being maintained in the supernatant liquid. On the other hand, if we start with a solution containing a very large excess of a strontium salt, more than is required by the equilibrium ratio, then strontium sulphate will be precipitated first, until the ratio given is reached.
Even should the more soluble salt be precipitated first from a solution containing, say, equal concentrations of barium and strontium ions, it could not remain in equilibrium with the supernatant liquid and would be converted into the less soluble one, before equilibrium was reached in the system. We can follow similar relations, experimentally, by using precipitates of different colors. Silver chromate Ag2CrO4 is an intensely red precipitate, that is rather difficultly soluble in water (exp.); a liter of water dissolves338 0.0252 gram or 8E−5 mole at 18°. The concentration of the silver-ion in the saturated solution is then 0.00016 mole.339 Silver chloride AgCl, a white salt, is still less soluble in water, a liter of water at 18° dissolving 0.00134 gram or 1E−5 mole, and the concentration of the silver-ion in the saturated solution is, therefore, only 1E−5 mole, as compared with 1.6E−4 in the saturated silver chromate solution. If a mixture of potassium chromate and potassium chloride, containing approximately equal (0.01 molar) concentrations of the two salts, is prepared and silver nitrate solution added, drop by drop, to the mixture, the first permanent precipitate is the white silver chloride (exp.). However, as the silver nitrate solution strikes the surface of the liquid, a red precipitate of the chromate, mixed with chloride, is momentarily seen, where the silver nitrate temporarily produces a local excess of the precipitant. But the red precipitate disappears rapidly and gives way to the white precipitate of the less soluble chloride. The quantitative relations, which may be developed with the aid of the principle of the solubility-product (see below), are such that, if little chromate is used, it may serve as an [p166] indicator to determine quantitatively the moment when all the chloride, within the limits of allowed quantitative error, is precipitated, the first permanent tinge of pink (solid Ag2CrO4), mixed with the yellow color of the solution, being used as the indication that the precipitation of the chloride is complete. Potassium chromate is used as a favorite indicator in quantitative analysis, for this purpose.
The quantitative relations340 for the precipitation may be developed as follows: For a supernatant liquid in which a precipitate of silver chromate just appears permanently, together with the chloride, i.e. for the condition of saturation with both silver salts at 18°, we have
and
and therefore:
For a solution containing one or two drops (0.1 c.c.) of saturated potassium chromate solution per 100 c.c., a proportion frequently used in quantitative analysis, the concentration of the chromate-ion is approximately 2.5E−3 and the chloride-ion will consequently be precipitated until [Cl−] = 3E−6. The chief source of error in the method, then, will not be due to the incompleteness of the prior precipitation of the chloride, but rather to the use of the small excess of silver nitrate required to precipitate sufficient chromate to be visible. This error may be avoided, and is avoided in very accurate work (e.g. in water analysis), by determining, in a blank test, the amount of silver nitrate required to show the change of tint of a pure chromate solution of the concentration to be used in the titration and by titrating to this tint in the determination of the chloride: the volume of silver nitrate (e.g. 0.2 c.c. of a 0.01 molar solution), required to produce the tint in the blank test, is subtracted from the total volume of silver nitrate used in the chloride determination.
We find thus, that the order of precipitation of difficultly soluble salts, which contain a common ion (fractional precipitation), is subject to the equilibrium conditions derived from the application of the principle of the solubility-product to the salts in question.341
It should be further noted that the condition of equilibrium between two precipitates, containing a common ion, and a supernatant liquid, depends on the concentrations in the supernatant liquid, in the liquid phase, and not on the quantities of the solids [p167] present. This conclusion was first reached by Guldberg and Waage, to whom we owe the law of mass action, and was fully confirmed by them. The modern treatment of the subject substitutes ion concentrations, i.e. the concentrations of the active components,342 for the total concentrations used by these investigators.343
That the condition of equilibrium is dependent on the liquid phase can easily be demonstrated if mercurous chloride and mercurous hydroxide are selected as the two precipitates, in order that we may follow changes of concentration in the liquid phase by color changes. For the condition of equilibrium between the two precipitates and the supernatant liquid we may develop the relation
Exp. A few drops of phenolphthaleïn are added to 100 c.c. of a very dilute solution of potassium hydroxide (1 / 500 molar); the usual indication of the presence of the hydroxide-ion is shown and the intensity of the color will be a measure of its concentration. Three identical solutions are prepared and then a pinch of calomel is added to two of the solutions,—their pink color fades decidedly.
Some of the calomel is decomposed into dark-colored mercurous oxide, which is precipitated, and sufficient potassium chloride is formed to bring the ratio [OH−] / [Cl−], in the solution, down to the value required by the constant K. Since no chloride-ion is present at the start, this result can be brought about only by the change indicated. Now, some chloride, say a little of a concentrated solution of potassium chloride, which reacts perfectly neutral, is added to one of the mixtures of the hydroxide and chloride. The concentration of the chloride-ion is increased in the solution, the ratio [OH−] / [Cl−] is made much too small and the condition of equilibrium is disturbed. Consequently, mercurous oxide reacts with potassium chloride, as expressed in the equation HgOH ↓ + KCl → HgCl ↓ + KOH, until the ratio [OH−] / [Cl−] [p168] has the value required by the constant K. The phenolphthaleïn is colored by the increased concentration of the hydroxide-ion and shows the direction of the change.344
The fact that ammonium salts prevent the precipitation of magnesium hydroxide was formerly explained as being due to the formation of "double salts," such as MgCl2,NH4Cl. It is true that such double salts exist, but, if their formation should prevent the precipitation of magnesium hydroxide, possibly by including the magnesium as part of a negative ion or radical,347 MgCl3, then the corresponding double salts of magnesium chloride with potassium and sodium chloride (e.g. MgCl2,KCl), which are just as stable as the ammonium salts, should show the same behavior; but, as a matter of fact, the addition of potassium chloride does not interfere with the precipitation of the hydroxide by either [p169] potassium hydroxide or ammonium hydroxide (exp.). So the explanation is untenable. Obviously, a specific interference of ammonium salts with the precipitating power of ammonium hydroxide is involved. But that is exactly what the law of chemical equilibrium, applied to the ionization of ammonium hydroxide, would demand: As a weak base, which is little ionized in pure aqueous solutions, it is very much weaker as a base, produces a far smaller concentration of the hydroxide-ion, when readily ionizable salts of ammonium are added to the solution,348 and the precipitation of magnesium hydroxide, and of metal hydroxides in general, depends on the concentration of the hydroxide-ion, which is a factor in the solubility-products of bases.
The precipitation of magnesium hydroxide, in particular, depends on the relation of the product [Mg2+] × [HO−]2 to the solubility-product constant of magnesium hydroxide. For the saturated aqueous solution, the product [Mg2+] × [HO−]2 is equal to the solubility-product constant, and from the solubility of magnesium hydroxide (see the table) the value of the constant is found to be 15E−12 at 18°. The concentration of magnesium-ion is 0.000,154 in this solution. In a 0.1 molar solution of magnesium sulphate, which is ionized to the extent of 37.3%, the concentration of magnesium-ion is 0.0373, and it would require a concentration greater than 2E−5 of hydroxide-ion to precipitate any magnesium hydroxide.349 Now, the concentration of the hydroxide-ion, in an ammoniacal solution, can easily be reduced far below this value by the addition of ammonium chloride, nitrate, sulphate or other readily ionizable ammonium salt to the solution, and then magnesium hydroxide will not be precipitated.
In solutions of ammonium hydroxide the concentration of hydroxide ion for 18° is found from the relation [NH4+] × [HO−] : ([NH4OH] + [NH3]) = 18E−6 (p. 161). (1) For ammonium hydroxide, for instance in 0.2 molar solution, and in the absence of any ammonium salt, [HO−] = [NH4+] = 0.0019.350 This concentration of the hydroxide-ion should be more than sufficient to precipitate magnesium hydroxide in a 0.1 molar solution of the sulphate.351
Exp. 100 c.c. of a mixture which should contain magnesium sulphate in 0.1 molar solution would require 246 / (10 × 10) or 2.46 grams of MgSO4, 7 H2O. [p170] This weight of the salt is dissolved in 50 c.c. of water and 50 c.c. of 0.4 molar solution of ammonium hydroxide is added to it. Magnesium hydroxide is precipitated. (The precipitation is incomplete because the ammonium sulphate, formed in the reaction, reduces the ionization of ammonium hydroxide.)
(2) In the presence of 0.25 molar ammonium chloride, the chloride being dissociated to the extent of 80%,352 the concentration of the hydroxide-ion in a 0.2 molar ammonium hydroxide solution is reduced to 18E−6.353 According to the above calculation this is too small a concentration to precipitate magnesium hydroxide in a 0.1 molar solution of the sulphate.
Exp. 1.35 grams ammonium chloride (the weight corresponding to 100 c.c. of a mixture containing ammonium chloride in 0.25 molar solution) is dissolved in 50 c.c. of 0.4 molar ammonium hydroxide and 2.46 grams of magnesium sulphate, dissolved as before in 50 c.c. of water, is added to the mixture. No precipitate of magnesium hydroxide is formed.
In a similar fashion and for the same reason, ammonium salts interfere more or less with the precipitation of other hydroxides, for instance with the precipitation of manganous, nickelous, cobaltous, ferrous, zinc, cupric and cadmium hydroxides. But ammonium salts do not prevent the precipitation of aluminium, chromium and ferric hydroxides, which are much less soluble than the hydroxides just mentioned, and as much weaker bases, (Chap. X) are also much less readily ionized. They are precipitated by smaller concentrations of the hydroxide-ion than are the hydroxides of the first group, and their precipitation may be made quantitative.
Exp. Ferric hydroxide is readily precipitated when 2.7 grams of ferric chloride FeCl3, 6 H2O, the weight of the chloride required to give 100 c.c. of a 0.1 molar solution, is dissolved in as little water as possible. The solution is added to the mixture of magnesium sulphate, ammonium chloride and ammonium hydroxide obtained in the previous experiment, in which no magnesium hydroxide was precipitated.
[326] See Smith, General Inorganic Chemistry, p. 414, General Chemistry for Colleges, p. 277; Remsen, Inorganic Chemistry (advanced course), p. 158.
[327] Mg2+ may also be precipitated as a carbonate with the other ions of the group (see Part III).
[328] In the case of ammonium nitrate a different form of decomposition, namely into nitrous oxide and water, predominates, and, in the case of ammonium nitrite, decomposition into nitrogen and water takes place so readily, that the decomposition of the salt takes that direction chiefly.
[330] T. S. Moore, J. Chem. Soc. (London), 91, 1379 (1907).
[331] From equation (I) we obtain directly, by the application of a simple mathematical transformation, that [NH3] + [NH4OH] / [NH4OH] = kNH3 + 1 = k′, and, therefore, [NH4OH] = [NH3] + [NH4OH] / k′. Inserting this value for [NH4OH] in equation (II) and transferring k′, we have [NH4+] × [HO−] / ([NH3] + [NH4OH]) = kbase / k′ = K.
[332] Water of crystallization, found in many of the precipitates used in qualitative analysis, will, as a rule, be indicated only in the formulas used in Part III, in the study of the reactions of ions.
[333] See Part III as to the method of vaporizing magnesium.
[334] Cf. Findlay, Z. phys. Chem., 34, 409 (1900).
[335] The solubility of barium sulphate at 18°, according to the table, is 0.0023 / 233, or 1E−5 mole per liter, and the salt may be considered completely ionized at this dilution.
[336] The solubility (see the table) is 0.114 / 183.6, or 6.2E−4 mole per liter, 84% of which is ionized (according to conductivity determinations, Kohlrausch and Holborn, loc. cit., p. 200). Hence [Sr2+] = [SO42−] = 0.00062 × 0.84 = 0.0005.
[337] To establish equilibrium, prolonged "digesting" is sometimes required. Double salts, solid solutions and mechanical enclosures are liable to interfere with the completeness of such separations by fractional precipitation. Resolution and reprecipitation will then usually effect a sufficiently accurate separation for most purposes. On account of the possibility of such complications, the conditions for a successful separation, within limits such as those described in the text, must in all cases be investigated.
[338] See the table at the end of Part IV.
[339] The salt may be considered completely ionized at this dilution. Each molecule of silver chromate forms two silver ions when it is ionized. See p. 141 in regard to the form the solubility-product takes in the case of a salt of this type.
[340] The complication, resulting from the hydrolysis of the chromate, is not included in this calculation.
[341] Cf. Findlay, loc. cit.
[342] Even Guldberg and Waage considered the active mass to be the fundamental factor and simply considered the total concentrations to be proportional to the "active masses," since they had no means of determining the proportion of "active" substances in the total concentrations.
[343] See Nernst, Theoretical Chemistry, p. 533, for a fuller discussion of the relations between the new and the old views on this subject.
[344] Dietrich and Wöhler, Z. anorg. Chem., 34, 194 (1903).
[345] On account of the formation of an ammonium salt in the reaction.
[346] Loven, Z. Anorg. Chem., 11, 404 (1896); Herz and Muks, ibid., 38, 138 (1904).
[347] In that case the salts would be called "complex" salts, salts of a complex ion, MgCl3−. See Chapter XII. They are really "double salts"; cf. Smith, General Inorganic Chemistry, p. 536.
[348] See p. 114, and recall the laboratory experiments (Lab. Manual, p. 9, § 6), which may be given as lecture experiments at this point.
[349] Calling x the concentration of the hydroxide-ion, required to saturate a 0.1 molar magnesium sulphate solution with magnesium hydroxide, we have 0.0373 × x2 = 15E−12 and x = 2E−5.
[350] Putting [HO−] = [NH4+] = y, we have y2 : (0.2 − y) = 18E−6. Then y = 0.0019.
[351] 0.0373 × 0.00192 = 0.13E−6, which is considerably larger than the solubility-product constant for magnesium hydroxide, 15E−12.
[352] Kohlrausch and Holborn, p. 159. Minor changes in the degrees of ionization of MgSO4 and NH4Cl (and consequently of NH4OH) occur, when the salts are present together. In a rigorous treatment, the ionization of each salt in the mixture would be calculated with the aid of Arrhenius's principle of isohydric solutions.
The chemistry of the analytical reactions of the alkalies and alkaline earths is extremely simple,—it is essentially the chemistry of well-defined bases and their salts,—and the separations and identifications, as we have seen, depend almost entirely on physical differences rather than on chemical contrasts. In the aluminium and zinc groups, which are precipitated together and which will be discussed together, the chemistry of the reactions becomes very much more complex. Therefore, we shall not, as yet, consider the groups as a whole, but shall first discuss the important analytical reactions of some compounds of aluminium.
According to the best knowledge we have on the subject, the molecule of aluminium hydroxide has the following structure or arrangement of its atoms: Al(─O─H)3.
It is readily seen that the cleavage of the molecules may produce, [p172] either aluminium and hydroxide ions, characteristic ions of a base, or aluminate354 and hydrogen ions, characteristic ions of an acid:
The ionization of the hydroxide both as an acid and as a base is, thus, quite possible on the basis of the molecular structure assigned to it. In fact, all of the so-called oxygen acids are considered to be hydroxides—we have sulphuric acid, O2S(OH)2, phosphoric acid, OP(OH)3, etc.,—exactly as the bases, Mg(OH)2, etc., are hydroxides.
That brings us to the second question, why aluminium hydroxide should show this dual character, whereas, for instance, sodium and magnesium hydroxides, which have similar structures, do not show it. The best answer to this question is found when we consider the properties of the elements and their derivatives in connection with their position in the periodic or natural system of elements, which shows the properties as (periodic) functions of the atomic weights. In the second series of the elements,355 omitting the zero group element neon and taking the elements in the order of increasing atomic weights, we have sodium (23), magnesium (24), aluminium (27), silicon (28), phosphorus (31), sulphur (32), and chlorine (35.5). One of the properties that are shown to be functions dependent on the atomic weight, is the property under discussion, namely the tendency of the (highest) hydroxides of the elements to ionize as bases or acids, respectively. It is clear that the hydroxides of the elements with the lowest atomic weights in the series, sodium and magnesium, show the most pronounced tendency to ionize as bases; the hydroxides of the elements with the highest atomic weights show the most pronounced tendency to ionize as acids—perchloric acid, (HO)ClO3, and sulphuric acid, (HO)2SO2, belong to the strongest acids. In accordance with the underlying principle of the periodic system, the change of [p173] properties, in going from one extreme to the other, is a function of the increase in atomic weight and is not sudden but gradual. And so the basic function, the tendency to produce the hydroxide-ion, is found to grow weaker as one goes from sodium to magnesium and then to aluminium, hydroxide; and the acid function, the tendency to produce the hydrogen-ion, grows markedly stronger, as one goes from phosphoric to sulphuric and perchloric acids. It is not surprising to find the two functions existing together, but in rather weak form, in the case of the intermediate hydroxides, notably in aluminium hydroxide and, to some degree, in silicic acid, the acid character beginning before the basic function has ceased. In accordance with this view, aluminium hydroxide is found to be only a weak, slightly ionized base, and a very weak, even less readily ionizable acid. In the case of silicic acid, which is the next hydroxide one meets as one goes toward the acid end of the series, the conditions are reversed. As the name indicates, it is primarily an acid, but it is a very weak one, and a critical scrutiny of its behavior shows it to have very weak basic functions, much weaker than those of aluminium hydroxide. The question may, indeed, be raised, whether either the basic or the acid properties really die out altogether in the hydroxides, from one end of the series to the other. In view of the small tendency toward sudden changes found in nature, one might suspect traces of basic character to be preserved right through the series to the strongest acids, like perchloric acid. As a matter of fact, later (see Chapter XV), we shall be obliged to consider possible basic functions of the strongest oxygen acids, such as nitric, perchloric, permanganic acids, and one of their most important properties, their behavior as oxidizing agents, will be found to be probably intimately associated with this remnant of basic ionization. On the other hand, fused sodium hydroxide will dissolve sodium with evolution of hydrogen, sodium oxide, Na─O─Na, being formed; and it can readily be shown,356 that in the fused hydroxide there must be at least a few ions NaO−, besides HO−, H+, O2−, and Na+. [p174]
The position of aluminium in the periodic system adequately accounts, then, for the amphoteric character of its hydroxide.357
If, in the second series of the periodic group, one goes back from aluminium to magnesium hydroxide, in accordance with the first general principle laid down a much stronger base is found; and if one then goes, in the magnesium family, to the hydroxide of the element of next lower atomic weight, glucinum or beryllium, one again meets, in accordance with the second principle laid down, a weaker basic and more acidic hydroxide than magnesium hydroxide; in other words, the basic and acid functions revert closely to those exhibited by aluminium hydroxide. Glucinum hydroxide is a pronounced amphoteric hydroxide and resembles aluminium hydroxide so closely that, in the early history of chemistry, it was mistaken for the latter.
If one goes from glucinum back to lithium, in the same series of the periodic system, and from lithium to the element with the next lower atomic weight in the same group, one comes to hydrogen, which forms one of the most important and interesting of the [p175] amphoteric hydroxides, water. The ionization of water, slight as it is, yields hydrogen-ion and hydroxide-ion, the ions characteristic of acids and of bases, and water is placed among the weakest of the acids (see table, p. 104) as well as among the weakest of the bases (table, p. 106). We shall return to these relations, presently, and shall find that the apparent weakness of water, as a base and as an acid, is seemingly very largely due to the fact that water represents only an extremely dilute solution (see p. 66) of the real hydroxide, HOH, or hydrol, and consists very largely of a compound (H2O)2. H2O, or hydrol, is, perhaps, not very much weaker as an acid or as a base, than is aluminium hydroxide.
Lower oxides of elements in the higher (acid-forming) groups show a less pronounced acid-forming character than the higher oxides, and a greater tendency to produce bases as well as acids, and are often amphoteric. Chromium hydroxide is of this type.
In view of all these facts, and in view, also, of the fact that the majority of the seventy-odd elements cannot lie at the ends of the periodic system but are found in the middle, it is not surprising to find that pronounced amphoterism is shown by a large number of metal hydroxides; it is, perhaps, the rule rather than the exception. A considerable number of the elements in the middle of the system are rare elements and that is perhaps the chief reason why this relation does not stand out more prominently in the consideration of the common acids and bases.
As the concentration of pure water, or of the water in dilute solutions, may be considered nearly a constant, we may put
This is the relation most commonly, and most conveniently, used. It is free from all assumptions as to the molecular weight of the nonionized water, the calculation of the concentrations [p177] [H+] and [OH−] being independent of any such assumption. The value of KH2O increases decidedly with an increase in the temperature,362 whereas the ionization constant of an ordinary acid, such as acetic acid, is affected very little by changes in temperature. This peculiar increase of the ionization of water at higher temperatures is undoubtedly due to the increasing dissociation of the complex water molecules into hydrol molecules (see p. 66), which, presumably, are most easily ionized. Now, the value of the constant KH2O, at any temperature, may be determined in some half a dozen different and independent ways, including the conductivity method mentioned, and one of the most remarkable developments of the theory of ionization is that all of these methods lead to concordant results.363
Aside from considerations based on its ionization, water may be shown, by its chemical behavior, to have the functions of an acid and of a base, and the conclusions reached are in complete accord with those reached with the aid of the theory of ionization.
Water will combine with a number of oxides very much in the same manner and sometimes with such vigor, that considerable heat is evolved, as in the slaking of lime (exp.):
Water in this, and similar actions, takes the place of and plays the rôle of, an acid, and the metal hydroxides or bases appear as its salts.364 It is a very weak acid, which can easily be driven out of its salts by any stronger acid (neutralization of bases), but that does not alter the conclusions reached. Considered from the point of view of the theory of ionization, the relation [p178] would be expressed by saying that in the common bases the positive hydrogen ion of water has been replaced by some other positive or metal ion. The salt of any acid could be defined in exactly the same way.
A number of acid oxides combine with water in exactly the same manner, and sometimes with such tremendous vigor, that great care must be taken in bringing the two together, as is the case when sulphur trioxide or phosphorus pentoxide are added to water (Exp.).
It is evident that in such actions water may take the place of, and play the rôle of, an ordinary base, forming the acids, which may well be defined as hydrogen salts.365 It is true that the basic properties of water are so weak, that the metal ion of even a weak base, like ammonium hydroxide, will replace the hydrogen-ion in its salts, the acids, quite readily (HCl + NH4OH ⥂ NH4Cl + H2O). But such a weak base, in turn, will have to give way, of course, to still stronger bases; for instances, NH4Cl + NaOH ⥂ NaCl + NH4OH. From the point of view of the theory of ionization, the hydrogen-ion is positive, like all the other metals ions whose hydroxides are bases.
There should be no difficulty, therefore, in considering water to have the chemical properties of a base as well as of an acid. Its chemical activities as such, weak as they may be, must be satisfied whenever it is present. These activities lead to the hydrolysis or the decomposition of salts by water, in greater or lesser degree, whenever water is used as a solvent for salts.
The decomposition of sodium chloride by water, which one may predict on the basis of these theoretical considerations, may be demonstrated, slight as it is, by the following experiment.367
Exp. A pinch of sodium chloride is brought into a platinum crucible, which is previously heated in a blast lamp to a bright yellow heat (1100°); then 1 c.c. of water is introduced, drop by drop. A steam cushion is formed at once (Leidenfrost's phenomenon). After about half of the water has been evaporated (half a minute), the water is poured into a solution colored with blue litmus; it is changed to red by an excess of hydrochloric acid in the water. The crucible is cooled, and the salt remaining in it is dissolved in a little water and the solution poured into a red litmus solution; the latter turns blue.
The sodium chloride has obviously been partially decomposed, by the water, into its base and its acid; the decomposition is favored by the high temperature and by the fact that the hydrogen chloride [p180] formed can pass through the steam cushion into the water, while the sodium hydroxide is left behind. The removal of a product of the decomposition would favor its progress (see. p. 114).
The conclusions concerning salts of the type of sodium chloride may then be summarized in the statement, that salts formed by the union of a very strong base with an equally strong acid are only very slightly decomposed by water and their solutions show a neutral reaction.
The decomposition of a salt by water into its component base and acid is called hydrolysis and the salt is said to be hydrolyzed in the action.
When the cyanide is dissolved in water, we must obtain, for the same reasons as were developed in the discussion of the hydrolysis of sodium chloride, a little nonionized potassium hydroxide, from the union of potassium ions with hydroxide ions, formed by the water. Potassium hydroxide being a strong, easily ionizable base, there will be only a slight tendency towards this union. Hydrocyanic acid, on the other hand, is an exceedingly weak acid. The value of its ionization constant KHCN = [H+] × [CN−] / [HCN] is only 7E−10, as compared with a similar ratio approximating 1 for potassium hydroxide ([K+] × [HO−] / [KOH] = 1; see the tables, p. 104 and p. 106 and see pp. 106–7). The hydrogen-ion, formed from the water, must therefore combine with cyanide-ion, to form nonionized hydrocyanic acid, much more completely than the hydroxide-ion combines with potassium-ion. With the disappearance of the ions of water, in this case notably of its hydrogen ions, more water must ionize to satisfy the ionization constant [p181] for water (p. 176), and the formation of hydrocyanic acid will continue, towards the satisfying of its own constant. It is important to note that, for the reasons given, the hydrogen-ion of water is used up to a far greater extent than is the hydroxide-ion; the latter therefore accumulates, and this accumulation results in the formation of smaller and smaller concentrations of the hydrogen-ion, by the water. Since [H+] × [HO−] = 1.2E−14 (at 25°; p. 104), as [HO−] grows larger, [H+] must grow proportionally smaller. The suppression of the hydrogen-ion by the accumulation of the hydroxide ion will, ultimately, make [H+] so small, that the equilibrium ratio [H+] × [CN−] / [HCN] will equal the equilibrium constant. Since the union of the hydrogen-ion with the cyanide-ion, to form little ionized hydrocyanic acid, is the main moving cause for the changes, the latter will then come to a standstill and equilibrium will be established. The net result of the action of water on potassium cyanide may be said to consist in the formation of practically nonionized hydrocyanic acid and the liberation of (chiefly) ionized potassium hydroxide, until all the equilibrium constants of the system are satisfied. We note that potassium cyanide solution must react strongly alkaline (exp.) and that a free acid (e.g. HCN) may well exist in the presence of a free base (e.g. KOH), provided the acid is present in a nonionized, and therefore chemically inactive, condition (inactive as an acid).
Ignoring the (practically) unimportant formation of small quantities of nonionized potassium hydroxide, we may summarize the action in a single equation, which shows the main action:
Whereas water, as an acid and as a base, is so exceedingly weak, that it can form but traces of its own salts, sodium hydroxide and hydrochloric acid, when acting on sodium chloride and competing for the base with such a strong acid as hydrochloric acid and for the acid with such a strong base as sodium hydroxide (see p. 179), the result, evidently, is quite different when water competes for a base with so weak an acid as hydrocyanic acid. In this case, we note that a considerable quantity of (ionized) potassium hydroxide, the salt of water in its rôle of an acid, is formed as a result of the action of water on potassium cyanide. [p182]
The theory of ionization, with the aid of the law of chemical equilibrium, gives us the means for accurately defining the relative concentrations of the products, in the final condition of equilibrium.368 For the weak acid, hydrocyanic acid, we have the condition of equilibrium
The symbols [H+], [CN−] and [HCN] denote the final concentrations for the condition of equilibrium, indicated in the equations on p. 180; in such a mixture [H+] is not equal to [CN−], as it is in pure solutions of hydrocyanic acid in water. [CN−], representing the total concentration of the cyanide-ion, is very much larger than [H+], since the salt, potassium cyanide, produces the cyanide-ion in large concentrations.
For water, we have [H+] × [HO−] = KHOH = 1.2E−14, at 25°. Here, again, the symbols represent the final, total concentrations of the ions in the mixture and [HO−] is much larger than [H+], since hydroxide-ion is formed in large quantities, as described above.
Combining the two equations, we have:
The cyanide-ion, whose concentration is expressed by [CN−], is formed practically altogether by the ionization of potassium cyanide, which is an easily ionizable and almost entirely ionized salt; the hydroxide-ion, whose concentration is expressed by [HO−], is formed by the ionization of potassium hydroxide, which is an easily ionizable base, ionized to practically the same degree as is the potassium cyanide in the solution. If we represent the total concentration of the potassium cyanide, ionized and nonionized, at the point of equilibrium, by [KCN] and its degree of ionization by α1, and if we represent, similarly, the total concentration of potassium hydroxide by [KOH] and its degree of ionization by α2, the equilibrium equation may be written:
Since the degrees of ionization of the two strong electrolytes are practically the same, we have further simply
The mathematical equations give us a measure of the extent to which water must decompose or hydrolyze the salt in question, as expressed in the chemical equations (p. 180). The extent of the hydrolysis, clearly, depends on the relative ionization constants of hydrocyanic acid and water, the two acids competing for the base.
From the known values of the constants, one may calculate that, at 25°, in a solution of 6.5 grams potassium cyanide in a liter (0.1 molar), almost 1.3% of the cyanide is decomposed into potassium hydroxide and hydrocyanic acid. Since every molecule of hydrolyzed salt forms one molecule of [p183] the hydroxide and one molecule of the acid, we may put [KOH] = [HCN] = x and [KCN] = 0.1 − x. The ionization constant, KHCN = 7E−10, and KHOH = 1.2E−14, at 25°. Inserting these values into the equation [KCN] / ([HCN] × [KOH]) = KHCN / KHOH we have: (0.1 − x) / x2 = 7E−10 / 1.2E−14. Here x = 0.0013. This is 1.3% of the 0.1 mole of cyanide used.
One may convince himself, as follows, that the constants are satisfied when the decomposition of the cyanide has proceeded to this point: the degrees of ionization of the potassium cyanide and potassium hydroxide, α1 and α2, may be taken as 85% (the same as the degree of ionization of the similar electrolyte KCl in 0.1 molar solution). Then [HO−] = 0.85 × 0.0013 = 0.0011; [CN−] = 0.85 × (0.1 − 0.0013) = 0.083; [H+] = 1.2E−14 / [HO−] = 1.1E−11. For [H+] × [CN−] / [HCN] we have then: 1.1E−11 × 0.083 / (0.0013) or 7E−10, the value for the ionization constant of hydrocyanic acid. It should be noted that, whereas in pure water at 25° [H+] = [HO−] = √(1.2E−14) = 1.1E−7, in the solution under consideration [HO−] has increased to the value 0.0011 and [H+] is only 1.1E−11.
The relation developed for the hydrolysis of potassium cyanide is a general one, holding for the hydrolysis of salts, of the type MeX, of a weak acid with a strong base. It may be expressed in general as follows: for the hydrolysis of a salt according to MeX + HOH ⇄ MeOH + HX, where HX is a weak acid and MEOH a strong base, we have:369
It is clear, from the equation, that the weaker the acid of the salt (measured by the ionization constant KAcid, the numerator on the right), the more will water, ceteris paribus, be able to drive it out of its salt and form its own salt, the base (the smaller the numerator on the right, the larger must be the denominator on the left).
The conclusions may be summarized in the statement that the salts of strong bases with weak acids are more or less decomposed by water (hydrolyzed) and the resulting solutions must react alkaline. We find, as a matter of fact, that aqueous solutions of potassium cyanide, sodium carbonate, sodium sulphide, borax (see the table, p. 104), all react strongly alkaline to litmus (exp.). Conversely, it may be said, that if the sodium or potassium salt of an acid dissolves in water with a decidedly alkaline reaction, it is the salt of a weak, poorly ionized acid.370 [p184]
For MeX + HOH ⇄ MeOH + HX, where MeOH is a weak base and HX a strong acid, we have as before:371
Like all salts, such a salt, say MeX, would ionize very readily, when dissolved in water (the few exceptions to readily ionizable salts are not under consideration), and, in this case, both the positive and the negative ions would have to combine respectively with the hydroxide and the hydrogen ions of water to form the nonionized weak base and the nonionized weak acid, and satisfy two very small constants, KBase and KAcid:
Both the hydrogen and the hydroxide ions of water would disappear, and in approximately equal quantity, if the base and acid were approximately equally weak, and the ions would be regenerated from water with no accumulation of either one to suppress the other, as in the two previous cases considered. Under these circumstances, the decomposition by water must proceed very much further than in the previous cases. For instance, in the hydrolysis of potassium cyanide in 0.1 molar solution, at 25°, we find the concentration of the hydrogen-ion [H+] reduced373 from 1.1E−7, its [p185] value in pure water, to 1.1E−11, as a result of the accumulation of potassium hydroxide (the hydroxide-ion), and only this small value for [H+] appears in the equation for the formation of the free acid, HCN (first equation, p. 182; vide the calculation, p. 183). But, in the present case, the factors [HO−] and [H+], in the equations on p. 184, maintain practically their original value, about the same as in pure water, and the formation of nonionized MeOH and HX must go correspondingly further to satisfy the constants KBase and KAcid. Just how far the action must proceed, can be formulated with the aid of the theory of ionization and the law of chemical equilibrium,374 much in the same way as for the hydrolysis of potassium cyanide.
The final equation, as developed by Arrhenius, reads:
| [Me+] × [X−] | = | α2 [Salt]2 | = | KAcid × KBase | = K, |
| [HX] × [MeOH] | [Acid] × [Base] | KHOH |
in which KAcid and KBase represent the ionization constants of the acid and the base, as given in the tables (pp. 104 and 106), and α is the degree of ionization of the salt.
For the cyanide of a base, which is as weak a base as hydrocyanic acid is an acid, we find that the decomposition by water, at 25° in a 0.1 molar solution, must comprise 99.35%375 of the salt, in order to establish equilibrium. In the case of potassium cyanide, in 0.1 molar solution, only 1.3% of the salt is decomposed (p. 182).
Now, if both the free base and the free acid are very difficultly soluble, then the concentrations [MeOH] and [HX], respectively, in the solution cannot go beyond a certain minute limit. In view,376 then, of the very small value, KBase, of the ratio [Me+] × [HO−] / [MeOH] and the minute value that the second term [MeOH] has under these conditions, the first term [Me+] × [HO−] must have a correspondingly smaller value. It is clear, therefore, that in such a solution neither the nonionized base, MeOH, nor its ion, Me+, can exist in more than minute quantities when the equilibrium constants are satisfied. The same conclusion is reached regarding the [p186] possibility of the existence of the difficultly soluble acid HX and its ion X−, in more than minimal quantities. Since, then, neither the ion Me+ nor the ion X− can be present in more than traces, their salt, MeX, which is considered readily ionizable, also cannot exist in aqueous solutions, except in traces.
The quantitative relations are evident from the equilibrium equation (p. 185): [Me+] × [X−] / ([HX] × [MeOH]) = α2 [Salt]2 / ([Acid] × [Base]) = KAcid × KBase / KHOH = K. It is evident that the concentration of the salt, [Salt], which is capable of existence in aqueous solution, is, in the first place, the smaller the smaller the values for KAcid and KBase are, i.e. the weaker the acid and the base are; and, in the second place, it is the smaller the smaller the values for [Acid] and [Base] are, which, in the present instance, represent the concentrations of the difficultly soluble acid and base in saturated solution, i.e. their solubilities.
We reach the conclusion that salts of very weak bases and very weak acids are very considerably decomposed by water, and, if both the acid and the base are difficultly soluble in water, the decomposition is practically complete. Conversely, such a very weak, difficultly soluble base will not combine with a very weak, difficultly soluble acid to form a salt in the presence of water. An instance of the first kind is found in the case of aluminium sulphide, the salt of a very weak, difficultly soluble base, aluminium hydroxide, with a rather little soluble, weak acid, hydrogen sulphide (see table, p. 104). We find that when a piece of aluminium sulphide, prepared by dry methods, is dropped into water (exp.), a precipitate of aluminium hydroxide is immediately formed and evolution of hydrogen sulphide occurs. We have
An instance where a very weak insoluble acid will not combine, appreciably, with a very weak insoluble base, is found in the case of aluminium hydroxide. A development of the equilibrium equations for its ionization as a base and its ionization as an acid would show, that all the constants would be readily satisfied, when a very minute quantity of dissolved ionized aluminium aluminate is formed. [p187]
Similarly, for the basic ionization,378 Al(OH)3 ⇄ (AlO)+ + HO− + H2O, we have
The formation of traces of nonionized (basic) aluminium aluminate would satisfy the equilibrium requirements for AlO+ + AlO2− ⇄ AlO(AlO2), since the aluminate, like other aluminates, is presumably readily ionizable in aqueous solutions. Aluminium hydroxide, as a base and as an acid, would yield in the first moment greater concentrations of the hydroxide and hydrogen ions than would satisfy the equilibrium constant for water (p. 176); the excess of these ions must combine to form water, until the product of their concentrations is equal to the ionization constant of water. The neutralization of these first quantities of hydrogen and hydroxide ions would destroy the momentary condition of equilibrium between aluminium hydroxide and its ions and would lead to its further ionization, both as a base and as an acid, and to the solution of some aluminium hydroxide (see the above equilibrium equations). However, since AlO+ and AlO2− remain practically uncombined and therefore accumulate in the solution, the concentrations of the hydroxide and hydrogen ions formed grow smaller and smaller; for an increasing excess of the ion AlO+ will allow only smaller and smaller values for [HO−], according to the equilibrium equation for KBase, and, similarly, an increasing excess of the ion AlO2− will permit [H+] to reach only smaller and smaller values, according to the equilibrium equation for KAcid. When the values for [HO−] and [H+] have in this way become small enough to make [HO−] × [H+] = KHOH, equilibrium is reached. It is evident that in such a solution, in the condition of equilibrium, [HO−] is not equal to [AlO+], as it would ordinarily be, according to the ionization equation Al(OH)3 ⇄ AlO+ + HO− + H2O, but is much smaller. Similarly, [H+] is much smaller than [AlO2−].
Just how much aluminium aluminate must be formed by a self-neutralization of the amphoteric hydroxide will depend on the values for KBase and KAcid and on the solubility of aluminium hydroxide (nonionized Al(OH)3). The two equilibrium equations may be combined:
| [AlO+] × [AlO2−] × [H+] × [HO−] | = KBase × KAcid. |
| [Al(OH)3]2 |
Since [H+] × [HO−] = KHOH, and since [AlO+] and [AlO2−] may be taken to represent each the concentration of the practically completely ionized aluminium aluminate AlO(AlO2), we have379
| [Alum. Aluminate]2 | = | KBase × KAcid | , |
| [Alum. Hydroxide]2 | KHOH |
or
| [Alum. Aluminate] | = √ ( | KBase × KAcid | ). |
| [Alum. Hydroxide] | KHOH |
It is clear, that the smaller the ionization constants KBase and KAcid are, and the smaller the solubility of nonionized aluminium hydroxide [Alum. Hydroxide] is, the smaller must be the concentration of the aluminate formed to satisfy the conditions for equilibrium.
Aluminium hydroxide is a typical amphoteric hydroxide, and the relations developed may be applied, mutatis mutandis, to the conditions of equilibrium for analogous amphoteric hydroxides, such as zinc, lead, chromic hydroxides, and so forth. Salt formation or self-neutralization will depend, in every instance, on the strength of the base and the acid formed, and on the solubility of the hydroxide.380
With the aid of the preceding considerations the analytical reactions of aluminium, which are used to separate it from other elements and to identify it, may be readily understood. They will be discussed in connection with the analysis of the "Aluminium and Zinc Groups."
Only one member of this group, zinc, forms an amphoteric hydroxide and advantage is taken of this in identifying zinc.
The members of the aluminium group form hydroxides, which are much weaker bases than are the hydroxides of the bivalent group just considered. Their salts with strong acids are considerably hydrolyzed and react strongly acid, and their salts with very weak acids, like carbonic acid and hydrogen sulphide, are decomposed so readily by water, that only ferric sulphide is capable of existence in its presence. When the sulphide, Al2S3, prepared by heating aluminium with sulphur, is added to water, it is totally decomposed into the hydroxide and hydrogen sulphide (p. 186); and if aluminium chloride is treated with ammonium sulphide in aqueous solution, aluminium hydroxide, and not its sulphide, is precipitated. The latter result may be interpreted in two ways, both of which, in the ultimate analysis, mean that hydrogen sulphide is too weak an acid to form a stable sulphide with aluminium hydroxide in the presence of water, the difficult solubility of aluminium hydroxide and the limited solubility of hydrogen sulphide being favoring factors (see p. 186). In a solution of aluminium chloride, the salt of a very weak base with a strong [p190] acid, more or less of the salt is hydrolyzed, and we have a condition of equilibrium as expressed in the equation AlCl3 + 3 H2O ⇄ Al(OH)3 + 3 HCl. The addition of ammonium sulphide to such a solution would neutralize the free hydrochloric acid, and the action would proceed to completion towards the right, hydrogen sulphide being liberated, by the action of the acid on the ammonium sulphide. As hydrogen sulphide is too weak an acid to combine, appreciably, with aluminium hydroxide, and as the latter is difficultly soluble, the hydroxide is precipitated. According to the degree of dilution, more or less of the hydrogen sulphide also escapes. Besides this interpretation of the precipitation of aluminium hydroxide under these conditions, we may also consider the following: any aluminium sulphide, formed the first moment, would remain largely ionized and would be immediately converted, by the ions of water, into aluminium hydroxide and hydrogen sulphide. The net result of the action is the precipitation of aluminium hydroxide and the evolution of hydrogen sulphide:
A similar result is obtained when the solution of a chromium salt is treated with a solution of ammonium sulphide. Only ferric hydroxide is capable of forming a sulphide, ferric sulphide, Fe2S3, which is precipitated when solutions of ferric salts are treated with ammonium sulphide.382
Ammonium sulphide will, consequently, precipitate aluminium and chromium hydroxides and ferric, ferrous, nickel, cobalt, manganese and zinc sulphides, from a solution of the chlorides of the metals.
Now, both the sulphides and the hydroxides of the alkaline earths and alkalies are sufficiently soluble not to be precipitated by ammonium sulphide, or by a mixture of it with ammonium hydroxide, if ammonium chloride be added to the mixture to prevent the precipitation of magnesium hydroxide (see p. 168), which is the least soluble of the hydroxides of the alkaline earth group. [p191] A mixture of ammonium sulphide, ammonium hydroxide and ammonium chloride will, therefore, precipitate the aluminium and zinc groups together, separating them from the alkaline earth and alkali groups.383
Aluminium Group: Fe2S3, Al(OH)3, Cr(OH)3.
Zinc Group: NiS, CoS, FeS, MnS,385 ZnS.
If such a precipitate is treated, in the cold, for a short time with quite dilute (1 to 1.2 molar) hydrochloric acid, all of the hydroxides and sulphides dissolve, excepting the greater part of the nickel and cobalt sulphides, which dissolve very much more slowly than do the other compounds. Advantage is taken of this fact, to separate these two elements from the remaining members of these groups, and if the treatment is carried out with care, the separation is usually satisfactory. In all cases, however, since it is a question of delayed solution only, at least traces, and sometimes considerably more than traces, of the sulphides of nickel and cobalt go into solution with the other compounds. No sacrifice of analytical accuracy is involved, if this possible loss is kept in mind and provision made for the later detection of these small quantities of nickel and cobalt.
The question of the slow solution, or apparent lack of solubility, of nickel and cobalt sulphides in dilute hydrochloric acid has formed an interesting problem for investigation. While nickel and cobalt sulphides are precipitated by ammonium sulphide, these sulphides, in common with those of all the other members of the zinc group, are not precipitated by hydrogen sulphide in the presence of a small excess of hydrochloric acid.386 We would have [p193]
as representing the condition of equilibrium, if we start with nickel chloride, hydrochloric acid and hydrogen sulphide; the amount of sulphide NiS, formed, is insufficient to supersaturate the solution and form a precipitate. In reversible reactions the final condition of equilibrium must be independent of the order in which components are mixed (p. 91), a conclusion which is borne out by experience. One should expect, then, that nickel sulphide, when treated with dilute hydrochloric acid, would dissolve and give nickel chloride, hydrogen sulphide and an excess of acid, and thus produce the same system, found to be in equilibrium, when one starts with the chloride, hydrogen sulphide and hydrochloric acid. As a matter of fact, the same condition of equilibrium is finally reached, only it is reached slowly,387 much more slowly than ordinarily in such cases, much more slowly, for instance, than with ferrous sulphide, hydrochloric acid and hydrogen sulphide (exp.). By taking advantage of this slow return to equilibrium and by working with the system during the process of slow change (collecting the undissolved nickel and cobalt sulphides on a filter), one can separate the sulphides of nickel and cobalt from the other components of the mixed precipitate, which dissolve much more rapidly.
When zinc chloride, which may be taken as a representative of the bivalent group, is treated with sodium carbonate, a difficultly soluble carbonate is precipitated, since zinc hydroxide, like the remaining bivalent hydroxides, is a sufficiently strong base to form a fairly stable carbonate.388 When ferric chloride, a representative of the trivalent group, is treated with a solution of sodium carbonate, ferric hydroxide, mixed with some basic ferric carbonate389 Fe2(OH)4CO3, is precipitated and carbon dioxide escapes (exp.). The trivalent hydroxides are too weak bases390 to form stable salts with so weak an acid as carbonic acid.
Since the bivalent metal ions are precipitated by sodium carbonate as carbonates and the trivalent ones as hydroxides, the reagent, obviously, cannot be used to separate the two groups. But barium carbonate is so little soluble in water that it will not precipitate manganous, zinc, nickel, cobalious and ferrous carbonates391 from solutions of their chlorides or nitrates. We have, for instance, ZnCl2 + BaCO3 ↓ ⥃ BaCl2 + ZnCO3. Barium carbonate has, however, the same effect on ferric chloride (exp.) and on the other chlorides of the trivalent group, as has sodium carbonate, i.e. it precipitates their hydroxides. By means of barium carbonate [p195] we can, therefore, precipitate the hydroxides of the aluminium group without precipitating the ions of the zinc group. The separation is carried out in a, practically, neutral medium (free carbonic acid in excess is evolved; barium carbonate alone, when treated with water, is slightly alkaline) and thus avoids the error of facilitating the precipitation of the bivalent metals in the shape of salts of the acidic forms of the trivalent metals, i.e. as aluminates, chromites, and so forth. Manganous salts are liable to oxidation to manganic salts, when exposed to the air, especially in alkaline, neutral or slightly acid solutions, and prolonged exposure of the barium carbonate mixture to the air may result in the precipitation of manganic hydroxide, Mn(OH)3, with the other trivalent hydroxides. Provision is made for its detection in the systematic analysis.
We have, in this instance, the case of a very weak, difficultly soluble acid, aluminium hydroxide, forming a salt with a weak, soluble base, ammonium hydroxide. The conditions determining the solubility of aluminium hydroxide in ammonium hydroxide, as an aluminate NH4AlO2, may be shown as follows: for the acid ionization of aluminium hydroxide, Al(OH)3 ⇄ AlO2− + H+ + H2O (p. 172); the solubility-product for a saturated solution is [AlO2−] × [H+] = KAc.S.P.. Further, from [H+] × [HO−] = KHOH, we find [H+] = KHOH / [HO−]. Then [AlO2−] = [HO−] × KAc.S.P. / KHOH, which shows that the solubility of aluminium hydroxide, as aluminate, is proportional to the concentration [HO−] of the hydroxide-ion in the solution. For NH4OH we have [NH4+] × [HO−] / ([NH3] + [NH4OH]) = 0.000,018 (p. 161), and consequently, [HO−] = 0.000,018 × ([NH3] + [NH4OH]) / [NH4+]. Then [HO−] is the smaller, the smaller the excess of ammonium hydroxide used (which is approximately equal to ([NH3] + [NH4OH])) and the greater the concentration [NH4+] of the ammonium-ion, i.e. of the added ammonium salt. The solubility of Al(OH)3, as aluminate, in ammonium hydroxide and ammonium chloride is, therefore, directly proportional to the excess of ammonium hydroxide, and indirectly proportional to the concentration of the ammonium salt present.392
For the sake of a certain simplicity in the result, we will, for the moment, consider aluminium hydroxide to ionize as an acid according to Al(HO)3 ⇄ AlO33− + 3 H+, which would resemble the basic ionization. Then we would have [AlO33−] × [H+]3 = K′Ac.S.P., and, using the relation [H+] = KHOH / [HO−], we have
Adding equations I and II we find
Aluminium hydroxide will be most completely precipitated when [Al3+] + [AlO33−] is a minimum, the values [Al3+] and [AlO33−] measuring the solubility of aluminium as aluminium-ion and as aluminate-ion. If we put [Al3+] + [AlO33−] = y and [HO−] = x, we can find the value x (the concentration of the hydroxide-ion) for which y is a minimum. We have y = KBas.S.P. × x−3 + x3 × K′Ac.S.P. × KHOH−3, and find, by means of the calculus,393 that y is a minimum, when x = +(KHOH3 × KBas.S.P. / K′Ac.S.P.)1/6.
If aluminium hydroxide were as strong an acid as it is a base, i.e. if KBas.S.P. = K′Ac.S.P., we would have, simply, x = [HO−] = ((1.2E−14)3)1/6 = √(1.2E−14) (at 25°), which is the concentration of the hydroxide-ion in pure water at 25° (p. 176). In other words, a perfectly neutral solution would then give us the conditions for as complete a precipitation as possible. But aluminium hydroxide is a stronger base than acid, KBas.S.P. > K′Ac.S.P., and consequently we find for x = [HO−] = (KHOH3 × KBas.S.P. / K′Ac.S.P.)1/6, a value somewhat greater than the concentration of the hydroxide-ion in pure water, i.e. we must use a slightly alkaline medium—which agrees with common practice. In other words, there is less danger of losing aluminium hydroxide in the form of aluminate, owing to the weaker acid character of the hydroxide, than there is of losing it in the form of aluminium-ion. The most favorable degree of alkalinity for the precipitation would depend on the relation of KBas.S.P.. and K′Ac.S.P..
The exact values for KBas.S.P. and K′Ac.S.P., the two solubility-product constants, and for the corresponding ionization constants, which would show the same ratio, are still not known. But, if, for the sake of an illustration, we take recourse to assumed values for these constants, we find that the solubility of aluminium, as aluminium-ion and as aluminate-ion, is, by calculation, as anticipated, a minimum for a solution, which contains the concentration of HO− calculated (for x) in the manner indicated above. And the further interesting conclusion is reached that this minimum loss of aluminium [p198] hydroxide would occur when [Al3+] = [AlO33−]—which would correspond to a saturated solution of aluminium aluminate, Al(AlO3).
When the ionization of aluminium hydroxide, as an acid, is considered to take place according to Al(OH)3 ⇄ AlO2− + H+ + H2O, which agrees best with its real behavior (p. 172), we can find, similarly, that [Al3+] + [AlO2−] is a minimum, when aluminium hydroxide is precipitated in such a way, that an excess x of the hydroxide-ion is used, and x = [HO−] = (3 KHOH × KBas.S.P. / KAc.S.P.)0.25,—where KAc.S.P. represents the solubility-product constant for [AlO2−] × [H+]. That a minimum loss of aluminium hydroxide would be suffered when the favorable excess of the hydroxide-ion (x) is calculated on the basis of the equation as given, may readily be seen by again assuming definite values for KBas.S.P. and KAc.S.P.. It also appears that this minimum loss394 of aluminium includes one-third as many Al3+ ions, as AlO2− ions—a relation corresponding, again, to a saturated solution of aluminium aluminate, Al(AlO2)3.
[354] When all three of the hydrogen atoms in the hydroxide are ionized, an aluminate ion, AlO33− is formed: Al(OH)3 ⇄ AlO33− + 3 H+. But, as in the case of other weak polybasic acids, a single hydrogen atom is far more readily ionized than are the remaining two (p. 102), and the ion Al(OH)2O−, which is formed by the primary ionization, readily loses water and forms the anhydride ion AlO2−. The most important aluminates are derivatives of this ion.
[355] See the table at the back of Smith's Inorganic Chemistry, or p. 149 of Remsen's Inorganic Chemistry.
[356] The displacement of hydrogen by a metal, like sodium, is the result of the displacement of the hydrogen-ion (see Chapters XIV and XV). The hydrogen-ion in fused sodium hydroxide is probably formed chiefly by the secondary ionization of the hydroxide-ion (HO− ⇄ H+ + O2−) (see Chap. XIII). We cannot have positive ions, Na+, with negative ions, O2−, without having some ions NaO−. (O2− + Na+ ⥂ NaO−), NaOH, undoubtedly, is much too weak an acid to form salts with bases in the presence of water. Such salts would be decomposed by water (see below, p. 180), as sodium oxide, indeed, is decomposed; we have Na─O─Na + HOH ⇄ 2 NaOH (see Chapter XIII for a detailed discussion of this action). These relations sufficiently account for the fact that salts of sodium hydroxide, in which it has the functions of an acid, are not commonly formed. (Cf. Abegg, Anorganische Chemie, II, (1) p. 247.)
[357] See J. J. Thomson, Corpuscular Theory of Matter, pp. 103–141.
[358] See Mendeléeff, Principles of Chemistry, I, 22 (1891), in regard to the rôle of "even" and "uneven" series in the system.
[359] In regard to the indications of the amphoteric character of stronger acids, see Chapter XV.
[360] An elaborate treatment of this problem is given by Walker, Z. phys. Chem., 49, 82 (1904), 51, 706 (1905).
[361] Kohlrausch and Heydweiller, Z. phys. Chem., 14, 317 (1894).
[364] This suggests a much broader, natural definition of a base than the conventional one. All salts of very weak acids, to a certain degree, which is determined by the weakness of their acids, do exactly what the ordinary bases do, e.g. neutralize acids. Metal derivatives of acids weaker than water, metal amides, like Zn(NH2)2, metal alkyls, like zinc methyl, Zn(CH3)2, react more vigorously than the hydroxides do, e.g. in neutralizing acids, and water attacks them and acts upon them, exactly as ordinary acids interact with metal hydroxides. We have, for instance, Zn(CH3)2 + 2 HOH → Zn(OH)2 + 2 CH4.
[366] The symbols in heavy type indicate the chief components of the final system. Vide Smith's General Chemistry for Colleges and Inorganic Chemistry, for the form of equations used.
[367] Emich, Ber. d. chem. Ges. 40, 1482 (1901).
[368] Arrhenius, Z. phys. Chem., 5, 16 (1890); Shields, ibid., 12, 167 (1893).
[369] See below for the corresponding equation, developed by Walker for a salt of a weak base and a strong acid.
[370] Potassium sulphate, K2SO4, reacts faintly alkaline in aqueous solution, the secondary ionization of sulphuric acid (table, p. 104) being somewhat weaker than the ionization of potassium hydroxide. We have: K2SO4 + HOH ⇄ KHSO4 + KOH or SO42− + HOH ⇄ HSO4− + HO−.
[371] Walker, Z. phys. Chem., 4, 319, (1889); Arrhenius, loc. cit.; Bredig, ibid., 13, 321 (1894).
[372] Arrhenius, loc. cit.
[374] Arrhenius developed the relation for aniline acetate, loc. cit.
[375] Putting x = [Acid] = [Base], we have [Salt] = (0.1 − x), and (0.1 − x)2 / x2 = (7E−10)2 / 1.2E−14. Then (0.1 − x) / x = 0.0064 and x = .09935, which is 99.35% of the total salt used. The degree of ionization, α, of the salt, in the extremely dilute solution, is taken to be 100%.
[377] See p. 172. The concentration of water may be considered a constant and is included in KAcid (and KBase, below).
[378] Only the primary ionization (of aluminium hydroxide) is considered in the text, because only that is involved, as a rule, in the neutralization of very weak bases by very weak acids (see footnote 2, p. 194). The relations are also simpler and clearer, if we limit the discussion to the formation of a salt AlO(AlO2).
| H3 | N | .CH2.CO | O |
| └ | ─────── | ┘ |
[381] The carbonates are occasionally partially hydrolyzed to basic carbonates.
[382] Stokes, J. Am. Chem. Soc., 29, 304 (1907).
[383] A complication, which leads to the precipitation of alkaline earths, along with these groups, as phosphates and similar insoluble salts (not as hydroxides or sulphides), when phosphate or certain other acid ions are present, is treated in Part IV (q.v.) under the systematic analysis of the groups.
[384] Cf. Fresenius, Quantitative Analysis.
[385] Ammonium sulphide usually precipitates a pink hydrated sulphide of manganese, probably Mn(SH)(OH). Under certain conditions of concentration and temperature, the dark green sulphide MnS is precipitated. In quantitative work the chemist aims to precipitate this green sulphide, which is more easily collected on a filter. (Cf. Fresenius, Quantitative Analysis.)
[386] We shall find that this property of the whole zinc group makes it possible to separate the following groups, the copper and arsenic groups, from the zinc group (see p. 158). The theory of the separation will be discussed in detail in Chapter XI.
[387] Vide Noyes, Bray and Spear, J. Am. Chem. Soc., 30, 483 (1908).
[389] The comparative stability of this basic salt represents an instance of the different ionizing power, or basic strength, of the three hydroxide groups of a trivalent base (see p. 106). The hydrolysis of ferric chloride seems to involve, primarily, only the third or least ionizable of the hydroxide groups of ferric hydroxide, and the hydrolysis, except in extreme dilution, proceeds chiefly according to Fe3+ + 3 Cl− + HOH ⇄ Fe(OH)2+ + 3 Cl− + H+. Vide Goodwin, Z. phys. Chem., 21, 1 (1896). In the case of the salt of the much weaker acid, carbonic acid, the hydrolysis goes further, involving two hydroxide groups of ferric hydroxide and, to some extent, all three.
[390] The extreme insolubility of Al(OH)3, Fe(OH)3 and Cr(OH)3, together with their weakness as bases, facilitates their precipitation (see pp. 185–6).
[391] There is a small degree of hydrolysis (see footnote, p. 189), but the hydroxides of the zinc group are not sufficiently insoluble to be precipitated under these conditions.
[392] Cf. A. A. Noyes, Bray and Spear, J. Am. Chem. Soc., 30, 496 (1908).
[393] Cf. The Elements of the Differential and Integral Calculus, based on Nernst and Schönflies's Lehrbuch, etc., by Young and Linebarger, pp. 363 and 364 (1900).
The sulphides of the metal ions of the zinc group are readily precipitated by ammonium or sodium sulphide, but hydrogen sulphide, in the presence of a small excess of a strong acid, such as hydrochloric acid, does not precipitate any of these sulphides (or any of the sulphides of the aluminium, the alkaline earth and the alkali groups). Under the same conditions the sulphides of the metal ions of the silver group, Ag+, Hg+, Pb2+, of the copper group, Hg2+, Pb2+, Bi3+, Cu2+, Cd2+, and also of the arsenic group, As3+, As5+, Sb3+, Sb5+, Sn2+, Sn4+, Pt2+, Pt4+, Au+, and Au3+, are precipitated. Advantage is taken of these relations in the following way, in systematic analysis: after the separation of the silver group, by precipitation of the difficultly soluble chlorides, hydrogen sulphide, in the presence of an excess of acid, is used to precipitate the sulphides of the ions of the copper and the arsenic groups, the two groups being precipitated together. Hydrogen sulphide, under these conditions, does not precipitate any sulphides of the zinc group or those of any of the remaining groups. Hydrogen sulphide is used, in this way, as one of the most valuable reagents in analytical work, enabling the analyst to separate whole groups of metal ions from other groups. There is also no other agent, equally important, which is more likely to be used in a wrong way and to lead to error.
For the first dissociation, HSH ⇄ H+ + HS−, we have
The value of the constant395 for this primary ionization of hydrogen sulphide is 0.91E−7. It is apparent that hydrogen sulphide, even in the primary ionization, is a very weak acid and produces a very small concentration of hydrosulphide-ion. In a solution, saturated at 25°, the total concentration of hydrogen sulphide is approximately 0.1 molar, and the concentration of hydrosulphide-ion, therefore, in the absence of any foreign acid, at most396 0.95E−4. The concentration of the dissolved, nonionized hydrogen sulphide, [H2S], is practically a constant, if solutions saturated with hydrogen sulphide under a given pressure, say under atmospheric pressure, are considered. For such solutions, then, we may put more simply396
The concentration of hydrosulphide-ion is, therefore, inversely proportional to the concentration of hydrogen-ion. It is clear that the addition of a strong acid, readily yielding concentrations of hydrogen-ion very much greater than 0.95E−4 (the value of [H+] in a saturated aqueous solution of hydrogen sulphide) will, as the result of the greatly increased total hydrogen-ion concentration, reduce the concentration of hydrosulphide-ion to correspondingly low values. For instance, the presence of 0.1 molar hydrochloric acid will increase the concentration of hydrogen-ion close to a thousandfold and will reduce the concentration of hydrosulphide-ion to 0.9E−7.
For the secondary ionization (see p. 101) of hydrogen sulphide, HS− ⇄ H+ + S2−, we have
The value of this constant has recently been determined397 and found to be 1.2E−15. Recalling the fact that the concentrations [H+] and [HS−] of hydrogen-ion and hydrosulphide-ion, [p201] respectively, resulting from the primary ionization, are each398 0.95E−4, we have for the concentration of the sulphide-ion, in aqueous solution saturated with hydrogen sulphide at atmospheric pressure and 25°, [S2−] = 1.2E−15.
Combining equations (II) and (III), we have, further:399
which shows, directly, the relation between the concentration of the sulphide-ion and that of the hydrogen-ion, the relation of primary importance in considering the precipitation of metal sulphides in acid solutions. The concentration of the sulphide-ion is, thus, inversely proportional to the square of the concentration of the hydrogen-ion. A thousandfold increase in the concentration of the latter, which is very nearly the effect produced by the presence of 0.1 molar hydrochloric acid ([H+] = 0.091), reduces the concentration of sulphide-ion in the saturated aqueous solution a millionfold: If we call [S2−]Ac. the concentration of the sulphide-ion in the acid solution, [S2−]Ac. = (1.1E−23) / (0.091)2 = 1.3E−21, whereas, in the absence of acid, as found above, [S2−] = 1.2E−15.
On the other hand, the addition of alkali to hydrogen sulphide, by neutralizing and suppressing the hydrogen-ion, and by forming the salts MeSH and Me2S, will very greatly increase the concentrations of the hydrosulphide-ion and of the sulphide-ion. Since the constant for the secondary ionization of hydrogen sulphide shows that HS− is an exceedingly weak acid, its salts, Me2S, are very largely hydrolyzed, the constant for water being somewhat greater400 than its own. According to Knox, in a 0.1 molar solution of Na2S about 99% of the sulphide is hydrolyzed: Na2S + H2O ⥂ NaSH + NaOH. In spite of this almost complete hydrolysis, sufficient sodium sulphide remains in a solution of this [p202] substance, to yield a concentration of the sulphide-ion that is far greater than that obtained from a solution of hydrogen sulphide. In a 0.1 molar solution of sodium sulphide the concentration of the sulphide-ion is, approximately, [S2−]alk. = 0.9E−3, as compared with [S2−] = 1.2E−15 in a saturated solution of hydrogen sulphide (25°, 760 mm.), and with 1.3E−21 in the same solution in the presence of 0.1 molar hydrochloric acid.
Ammonium sulphide (NH4)2S is the salt of an extremely weak acid with a much weaker base than sodium hydroxide, and it is correspondingly more completely decomposed by water. In a 0.1 molar solution of the sulphide (NH4)2S, we find the approximate concentration401 of the sulphide-ion [S2−]am. = 1.8E−6, as compared with 0.9E−3 in a similar solution of Na2S. But the concentration of sulphide-ion is still enormously greater than its concentrations in hydrogen sulphide in the absence and in the presence of acids (see above).
The following table402 contains a summary of the concentrations of sulphide-ion in the various solutions discussed, as well as its concentration in the presence of 0.2 molar hydrochloric acid. In the separation of the copper and arsenic groups from the zinc and aluminium groups, a concentration of hydrogen-ion corresponding to the presence of 0.15 to 0.25 molar hydrochloric acid is satisfactory for an accurate separation for ordinary purposes.
| Solution. | [S2−] |
|---|---|
| 0.1 molar Na2S: | 0.9E−3 |
| 0.1 molar NaSH: | 0.8E−5 |
| 0.1 molar (NH4)2S: | 1.8E−6 |
| 0.1 molar (NH4)SH: | 1.4E−8 |
| 0.1 molar H2S, sat. aq. sol., 25°: | 1.2E−15 |
| 0.1 molar H2S, 0.1 molar HCl:403 | 1.3E−21 |
| 0.1 molar H2S, 0.2 molar HCl: | 3.5E−22 |
The absolute values of the solubilities of the various sulphides, which are involved in the discussion, are known, with any degree of accuracy, only in a few cases. The aim of the discussion will be, therefore, to develop, rather, the relations in the values involved, which may be readily determined. Wherever absolute quantities can be given, they also will be referred to.
If the solution of zinc sulphate is saturated with hydrogen sulphide, under the same conditions as were used with the ferrous salt solution (exp.), or if we add the zinc sulphate solution to the mixture of ferrous sulphate and hydrogen sulphide (exp.), we immediately obtain heavy white precipitates of zinc sulphide. We would decide, therefore, on the basis of the principle of the solubility-product, that in this case [Zn2+] × [S2−] > KZnS. Since we have used hydrogen sulphide under practically the same conditions, we may consider that [S2−], in this experiment,407 is the same as in the [p205] test with ferrous sulphate, and, by the conditions of the experiment, we have also made [Zn2+] = [Fe2+]. The two factors of the product are, therefore, the same, for the first moment, and we may put [Fe2+] × [S2−] = [Zn2+] × [S2−] = P.
Since P is smaller than KFeS and larger than KZnS, it is clear that the solubility-product constant for zinc sulphide must be smaller than that for ferrous sulphide. The solubility-product constants, for similar salts, are a measure of their solubilities in water. We may obtain their values by determining the solubilities of salts in pure water, whenever the solubility is not affected by other chemical changes. In the present instance, the quantitative measurements, that have been made in this way, are open to question, owing to the considerable hydrolysis which sulphides, as salts of a very weak acid, undergo in solutions of such extreme dilution.408 Until such relations have been taken into account quantitatively, it is better to limit ourselves for the present to the more accessible question of relative solubility.
It is a comparatively easy matter to determine the relative solubility of zinc and ferrous sulphides. If equal quantities of the equivalent solutions are mixed and a precipitant, ammonium sulphide, which would precipitate either sulphide, if its salt were present alone, is carefully and gradually added to the mixture, it will precipitate first the less soluble one (see p. 163); and that one alone can be present permanently (i.e. in equilibrium) in contact with the solution containing the two salts. As a matter of fact,409 [p206] we find that zinc sulphide is precipitated first, under conditions permitting the precipitation of ferrous sulphide if no zinc sulphate were present, and the precipitate of zinc sulphide remains unchanged in the presence of a mixture of the composition indicated (exp.).
It is clear, therefore, that the prediction, based on the conclusion drawn from the application of the principle of the solubility-product, is verified by experiment.
Now, closer examination of the solution of zinc sulphate, from which zinc sulphide has been precipitated by the action of hydrogen sulphide, shows, after the hydrogen sulphide has precipitated as much sulphide as it can and the solution has been passed through a filter, that a very considerable proportion of zinc salt is still present in the filtrate, and we must ask why hydrogen sulphide fails to precipitate the zinc completely. The concentration of the zinc-ion has grown somewhat smaller, but that is not the cause of the nonprecipitation of zinc sulphide under the new conditions, since hydrogen sulphide will precipitate the sulphide, if it is passed into a solution of zinc sulphate which contains even a smaller concentration of zinc-ion than the filtrate, in which it fails to give any further precipitate. If the filtrate is examined, it is found to be strongly acid, since sulphuric acid has been liberated by the action of hydrogen sulphide on zinc sulphate: ZnSO4 + H2S → ZnS ↓ + H2SO4. Sulphuric acid is a strong acid, which is very highly ionized, much more so than the exceedingly weak acid hydrogen sulphide, and consequently, as the precipitation of zinc sulphide proceeds, the concentration of hydrogen-ion in the solution rapidly grows larger and larger. But, the greater the concentration of the hydrogen-ion, the smaller is that of the sulphide-ion, since the product [H+]2 × [S2−] is a constant [equation (IV), p. 201] for a solution kept saturated with hydrogen sulphide. The sulphide-ion is reduced in concentration very much more rapidly than is the zinc-ion.410 As [S2−] is a factor in the [p207] solubility-product of zinc sulphide, it is clear that the value of this product must grow rapidly smaller during the precipitation of zinc sulphide from the solution, and that it may well, eventually, grow too small to surpass the value of the solubility-product constant KZnS. Precipitation of zinc sulphide will then cease. Obviously, the suppression of the sulphide-ion may be accomplished by the addition of hydrochloric, sulphuric or any other strong acid to the zinc sulphate solution in the first place, and then hydrogen sulphide should fail to precipitate any zinc sulphide at all. In fact, if to 50 c.c. of the 0.1 molar zinc sulphate solution 2 c.c. of hexamolar hydrochloric acid is added,411 hydrogen sulphide does not precipitate even a trace of zinc sulphide (exp.).
We have found, then, that 0.1 molar zinc sulphate solution, acidified with a small excess of hydrochloric acid, fails to produce a precipitate of zinc sulphide, when it is saturated with hydrogen sulphide. We must conclude that, under these circumstances, the product of the ion concentrations is smaller than the solubility-product constant for zinc sulphide: ([Zn2+] × [S2−] / x) < KZnS, the new concentration of the sulphide-ion being represented by the symbol [S2−] / x.
It would follow, from these considerations, that the action of hydrochloric or sulphuric acid, in preventing the precipitation of zinc sulphide, depends on their producing a sufficiently high concentration of the hydrogen-ion, to keep the concentration of the sulphide-ion, in a mixture of zinc sulphate and hydrogen sulphide, below the point where the solution could become supersaturated with zinc sulphide. [p208] For exactly similar reasons, none of the sulphides of the zinc group is precipitated by hydrogen sulphide in (sufficiently) acid solutions.
It is evident, further, that, if a solution of zinc acetate (without the addition of any acid) is substituted for the zinc sulphate solution and is treated with hydrogen sulphide, an entirely different result, quantitatively considered, must be obtained. By the action of hydrogen sulphide on the acetate, acetic acid is liberated, according to Zn(CH3CO2)2 + H2S ⥂ ZnS ↓ + 2 CH3COOH. As a weak acid, acetic acid produces much less hydrogen-ion than is formed in equivalent solutions of sulphuric acid. Consequently, a much slighter suppression of the sulphide-ion and a much more complete precipitation of zinc sulphide from the acetate, than from the sulphate solution, must result. Such is the case. Zinc sulphide is, indeed, precipitated quantitatively by hydrogen sulphide from the acetate solution.
This behavior of zinc acetate412—and zinc salts of other weak acids show, of course, the same behavior—represents one of the pitfalls, into which the unwary analytical chemist is liable to fall, when he uses hydrogen sulphide. The separation of groups by hydrogen sulphide depends, as stated, on the fact, that, in the presence of a certain concentration of hydrogen-ion, hydrogen sulphide will not precipitate zinc sulphide and the remaining sulphides of the zinc group. To secure this concentration of hydrogen-ion, some hydrochloric acid is added to solutions, from which hydrogen sulphide is expected to precipitate none but sulphides of the copper and arsenic groups—and, as a rule, the purpose is accomplished, as desired. It is evident, however, that if a solution contains an acetate, say sodium acetate, or the salt of any other weak acid, e.g. a borate or a phosphate, the addition of hydrochloric acid will result, at least at first, in the liberation of the weaker acid and will not produce the excess of hydrogen-ion, required for the analysis. Zinc sulphide, and possibly nickel and cobalt sulphides,412 may, under such conditions, be precipitated with the sulphides of the groups mentioned. Unless provision is made, therefore, to insure a certain excess of hydrogen-ion (p. 213), or unless we are on our guard and look for zinc, nickel and cobalt in [p209] the analysis of the precipitate formed by hydrogen sulphide,413 serious errors obviously could result. To add an inordinately large excess of hydrochloric acid to mixtures, in order to avoid this pitfall, will, as we shall presently see, only throw us more certainly into still another error, to which we are exposed in the use of this important reagent, hydrogen sulphide.
By the conditions of the experiment we started with a concentration of the cadmium-ion, [Cd2+], equal to the concentration, [Zn2+], of the zinc-ion in the zinc sulphate solution, and with the same concentration,415 [S2−] / x, of sulphide-ion as was used when hydrogen sulphide failed to precipitate zinc sulphide. The corresponding factors of the products of the ion concentrations are equal, at the beginning of the two experiments, and we may put ([Cd2+] × [S2−] / x) = ([Zn2+] × [S2−] / x) = P′. We recall the fact, that we have already concluded, on the basis of the principle of the solubility-product, that [Zn2+] × [S2−] / x, or P′, is smaller than KZnS (p. 207), and that [Cd2+] × [S2−] / x, or P′, is greater than KCdS.
P′ being smaller than KZnS and larger than KCdS, it is clear that [p210] KCdS is smaller than KZnS and that cadmium sulphide must be the less soluble of the two sulphides. As a matter of fact, if ammonium sulphide is carefully added to a mixture of equal quantities of the two salt solutions, cadmium sulphide is precipitated first, and when practically all of the cadmium is precipitated, a final precipitate of white zinc sulphide is obtained (exp.; see note, p. 205). Or, if zinc sulphide is first precipitated by the addition of a little ammonium sulphide to 25 c.c. of the 0.1 molar zinc sulphate solution, care being taken to have zinc sulphate in excess, and if 25 c.c. of the 0.1 molar cadmium sulphate solution is then added to the mixture, the white zinc sulphide immediately gives way to the less soluble yellow cadmium sulphide (exp.; see p. 165). Cadmium sulphide is thus proved to be the less soluble of the two sulphides, a result which confirms the prediction made above with the aid of the principle of the solubility-product, and we may indeed conclude that the solubility-product constant KCdS of cadmium sulphide must be smaller than the constant KZnS of zinc sulphide (see pp. 163–168, on fractional precipitation). We are, therefore, also justified in deciding that CdS may well be precipitated from acidulated solutions by hydrogen sulphide, when ZnS is not thus precipitated, simply because KCdS is sufficiently small (CdS is sufficiently insoluble) to make the product of the ion concentrations [Cd2+] × [S2−] / x, in spite of the extremely small value of [S2−] / x, greater than the constant KCdS, whereas the same small value of [S2−] / x makes it impossible for the product [Zn2+] × [S2−] / x to reach the value of the larger constant KZnS, required for the precipitation of ZnS. Since cadmium sulphide may be precipitated quantitatively under the conditions given, it is also evident that it may be precipitated even when the concentration of the cadmium-ion also has a rather small value. The relations, in regard to this point, will be discussed presently.
Solubilities vary from salt to salt, and we have already found that, in the zinc group, zinc sulphide is less soluble than the sulphide of a second member of the group, ferrous sulphide, and that the difference is revealed in a somewhat different behavior of their salts toward hydrogen sulphide, when the action is studied in some detail. Similar differences must be expected to exist among the sulphides of the groups that hydrogen sulphide precipitates even in the presence of an excess of hydrochloric acid. As these differences are the sources of some of the most common and most serious errors which analysts are liable to commit, the detailed study of the action of hydrogen sulphide must be continued a little further.
In fact, if a large excess417 of hydrochloric acid is added to 50 c.c. [p212] of the 0.1 molar solution of cadmium sulphate, hydrogen sulphide fails to precipitate any of the sulphide (exp.).
But, if a few cubic centimeters of a 0.1 molar solution of cupric sulphate (25.0 grams of CuSO4, 5 H2O, per liter) are added to the solution from which hydrogen sulphide fails to precipitate cadmium sulphide, cupric sulphide is at once precipitated. And, if 15 c.c. of concentrated hydrochloric acid are added to 50 c.c. of the 0.1 molar cupric sulphate solution, there results a mixture corresponding to the cadmium sulphate solution from which hydrogen sulphide fails to precipitate CdS; we find that hydrogen sulphide will precipitate the sulphide of copper very readily, even under these adverse conditions (exp.). Cupric sulphide must be even less soluble in water than cadmium sulphide,418 and there is no difficulty in showing that such is the case. If ammonium sulphide, or hydrogen sulphide, is gradually introduced into a mixture of 25 c.c. each of the 0.1 molar sulphate solutions, cupric sulphide is precipitated first, and, if the precipitate is collected in fractions, [p213] pure yellow cadmium sulphide is precipitated last.419 Or, if 25 c.c. of 0.1 molar cupric sulphate is added to the mixture in which a precipitate of cadmium sulphide displaced the more soluble zinc sulphide (p. 210), the yellow sulphide will, in turn, give way to the less soluble black sulphide of copper (exp.).
We find thus that the precipitation of cadmium sulphide, by hydrogen sulphide in acid solution, can be prevented by the presence of an excess of hydrochloric acid, which does not prevent the precipitation of the less soluble cupric sulphide.420 The fact, then, that, in an analysis of some unknown mixture, hydrogen sulphide produces a precipitate in acid solution, must not be considered as evidence that the conditions are such as to insure the precipitation of all the sulphides of the groups, which we intend to precipitate. To avoid error, conditions must be such as to insure the complete precipitation of the more soluble as well as the less soluble sulphides. The sulphides of cadmium and lead, in particular, and, to a lesser degree, the sulphides of antimony and tin, are most liable to remain unprecipitated and thus escape detection in systematic analysis. This is a matter of special importance, also, in detecting traces of the ions of these metals, especially of lead, which is a slow cumulative poison, even when absorbed in minute amounts, and which analysts must therefore be able to detect, even in traces, with absolute certainty. It is clear, from a consideration of the product of the ion concentrations, as affecting the precipitation or nonprecipitation of such a sulphide, that a much smaller excess of acid will prevent the precipitation of the last traces of lead sulphide, and, therefore, of all of it, if only traces are present, than will interfere with the precipitation of the sulphide in bulk.
If an analyst aims to find even smaller quantities of a particular metal ion, e.g. traces of lead, the ordinary method of analysis [p215] may be modified, the source of error in the precipitation of traces of lead sulphide being kept in mind.424
Besides the complications mentioned, and provided against in the way discussed, there is still one more complication in the use of hydrogen sulphide: this is in the matter of the precipitation of arsenic sulphide from solutions containing arsenic in the pentavalent condition. Since the interpretation of this complication and the explanation of the methods for avoiding the errors, which may arise therefrom, are necessarily intimately connected with the chemical behavior of arsenic acid, this subject will be considered in the discussion of the arsenic group (Chapter XIII).
[395] Auerbach, Z. phys. Chem., 49, 220 (1904).
[397] Knox (in Abegg's laboratory), Trans. Faraday Soc., 4, 44 (1908).
[398] The concentration of the hydrogen-ion is really a little greater than that of the hydrosulphide-ion, as a result of the ionization of the latter, but the amount of hydrogen-ion formed in this way (about 1E−15) is so minute, compared with that formed by the primary ionization, that it is negligible.
[399] We can obtain the relation, directly, from H2S ⇄ 2 H+ + S2− and [H+]2 × [S2−] / [H2S] = K = 1.1E−22. For a given pressure of the hydrogen sulphide, [H2S], expressing its solubility (about 0.1 molar at 25°), is constant, and therefore [H+]2 × [S2−] = a constant, as given in equation (IV). Putting [H2S] = 0.1, we have [H+]2 × [S2−] = 0.1 × 1.1E−22 = 1.1E−23.
[400] On account of the great mass of water, we compare (see equation, p. 176) [H+] × [HO−] = 1.2E−14 (at 25°) with [H+] × [S2−] / [HS−] = 1.2E−15.
[401] The calculation was made by the method used by Knox (loc. cit.) for a molar solution. The degree of ionization of the salt was not considered and the correct ionization constant for ammonium hydroxide was used, 1.8E−5 in place of 2.3E−5. The latter, evidently, was used by Knox as the result of overlooking a correction, which Bredig made in his (Bredig's) first calculations of the constant; cf. Bredig, Z. phys. Chem., 13, 293, footnote. The same erroneous constant is found in Kohlrausch and Holborn, loc. cit., p. 194.
[402] For further values and for the method of calculation, see Knox, loc. cit.
[404] Knox's work leads to that conclusion.
[405] The precipitation of sulphides, from a solution containing much more of the hydrosulphide-ion than of the sulphide-ion, is comparable with the precipitation of mercuric oxide, HgO, and of silver oxide, Ag2O, by sodium or potassium hydroxide.
[406] On account of the presence of a small, unknown amount of sulphuric acid in the original solution, resulting from the hydrolysis of ferrous sulphate, the exact value of [S2−] in the first solution cannot be calculated without further examination; but, according to the values given in the table on page 202, the value of x, indicating the growth in the concentration of S2−, is at least 1012, if 2 equivalents of NaOH, and 109, if 2 equivalents of NH4OH are used to convert the 0.1 molar hydrogen sulphide into the corresponding sulphide Me2S, of 0.1 molar concentration.
[407] [S2−] is exactly the same in the two products, when equal volumes of the zinc and ferrous sulphate solutions are mixed and the mixture is saturated with hydrogen sulphide; zinc sulphide is precipitated.
[408] The difference in the values obtained, when hydrolysis is considered or neglected, is very considerable. Vide Bodländer, on the solubility of calcium carbonate, Z. phys. Chem., 35, 23 (1900), and Stieglitz, Carnegie Institution Publications, No. 107, 249 (1909).
[409] In carrying out this fractional precipitation a very dilute solution of ammonium sulphide is used, so as to prevent the mechanical enclosure of black ferrous sulphide, which would discolor the white sulphide. The ammonium sulphide solution should be saturated with hydrogen sulphide, to prevent the precipitation of green ferrous-ferric oxide by an excess of free ammonia. It is best to prepare a set of the precipitates and to preserve them in well-stoppered vessels, and not to try to take the time and care necessary to effect a perfect fractionation as a lecture experiment. The presence of the ferrous sulphate, in the supernatant liquid above the first precipitate of zinc sulphide, may be readily demonstrated by pouring off some of the solution and adding an excess of ammonium sulphide to it. Of course, it is also perfectly legitimate, and easier, to precipitate first zinc sulphide from a pure zinc sulphate solution and then to add ferrous sulphate solution to the mixture and to preserve the mixture. If the zinc sulphide were not the less soluble, it would be rapidly converted into the black ferrous sulphide. (See p. 165, and see below, pp. 210, 213, where similar transformations are carried out as lecture experiments.)
[410] When 10% of the zinc in a 0.1 molar solution has been precipitated, 0.01 molar sulphuric acid has been formed. For the sake of a rough approximation, the acid may be considered completely ionized and then [H+] = 0.02, which is 200 times the value of [H+] in a saturated H2S solution (p. 200); if the presence of a little sulphuric acid in the original zinc sulphate solution, resulting from a slight hydrolysis of the salt, is ignored, the concentration of the sulphide-ion is decreased roughly (200)2 or forty thousandfold, while the concentration of zinc-ion falls 10%. The corrections, that have been indicated, would change the quantities involved, but they would not modify the character of the result.
[411] This proportion of acid, making the concentration of the hydrogen-ion, approximately, [H+] = 0.2, is used, not because it represents the minimum concentration of the hydrogen-ion, which will prevent the precipitation of zinc sulphide in 0.1 molar zinc sulphate solution, but because it represents the practical conditions under which the precipitation of zinc sulphide is avoided, when the copper and arsenic groups are precipitated in qualitative analysis (see p. 213).
[412] Nickel and cobalt sulphides are also precipitated by hydrogen sulphide in the presence of free acetic acid, if sodium or potassium acetate is added, to suppress the hydrogen-ion of the acetic acid (p. 112).
[413] They would be found in the copper group.
[414] The sulphate, of this composition, is obtained by drying the crystallized sulphate in an air bath at 100–105°.
[417] Any immediate precipitation of cadmium sulphide will be prevented by the addition of 10 c.c. of concentrated acid (sp. gr. 1.19) to 50 c.c. of the 0.1 molar solution, and 15 c.c. will completely prevent any precipitation of the sulphide. Of course, a smaller excess would prevent the precipitation of small quantities of the sulphide (e.g. a half milligram of cadmium), which should easily be found in 50 c.c. (see p. 214).
[418] The value of the solubility-product constant for cupric sulphide, at 25°, was determined by Knox (loc. cit.): [Cu2+] × [S2−] = 1.2E−42, corresponding to a concentration of 1.1E−21 of cupric-ion. Mercuric sulphide was found even less soluble: [Hg2+] × [S2−] = 2.8E−54, and its behavior agrees with such a relation (Lab. Manual, p. 50, § 2). The solubility-product constant for lead sulphide, which resembles cadmium sulphide in the fact that a large excess of acid prevents its precipitation, was found to be [Pb2+] × [S2−] = 2.6E−15, the constant being about 1027 times as large as the constant for cupric sulphide. This value for the solubility-product constant for lead sulphide must either be considerably larger than the true value or lead must be easily precipitated as a hydrosulphide, Pb(SH)2, since solutions in which the product of the ion concentrations, [Pb2+] × [S2−], is very much smaller than the constant given, readily precipitate lead sulphide. Thus Noyes and Bray [J. Am. Chem. Soc., 29, 137 (1907)] report it possible to precipitate 1 to 2 milligrams of lead-ion in 100 c.c. of solution (say [Pb2+] = 1E−4) with hydrogen sulphide in the presence of 4 c.c. of hydrochloric acid (sp. gr. 1.12), for which, approximately, [H+] = 0.25. Then (equation (IV), p. 201) [S2−] = (1.1E−23) / (0.25)2 = 1.8E−22, and [Pb2+] × [S2−] = 1E−4 × 1.8E−22 = 1.8E−26, which is a much lower value than that given by Knox, and which still is not claimed to represent the limit of insolubility. Experiments, made in this laboratory, confirm this result and show further, that lead-ion in a concentration of 1E−5 is precipitated in the presence of 0.25 molar hydrochloric acid ([H+] = 0.22). Then [S2−] = 2.3E−22 and [Pb2+] × [S2−] = 2.3E−22 × 10−5 = 2E−27, which does not yet express the limit of insolubility.
[419] The fractions are not prepared in the lecture, but the first fraction is kept suspended in part of the solution of the two sulphates and may be kept so for years. The last fraction is kept in a separate container.
[420] A large excess of acid is liable to interfere with the precipitation of the last traces of cupric sulphide and is avoided in exact work.
[421] Noyes and Bray use, approximately, [H+] = 0.25 [J. Am. Chem. Soc., 29, 137 (1907)]. Tests in this laboratory showed that 1 milligram of cadmium-ion, or of lead-ion, in 100 c.c., is readily precipitated by hydrogen sulphide in the presence of 0.25 molar hydrochloric acid, ([H+] = 0.22).
[422] Kahlbaum's "Krystallviolett," [(CH3)2NC6H4]2C : C6H4N(CH3)2Cl, is referred to.
[423] An indelible ink pencil (violet) may, in most cases, be used in place of the solution. The details for the application of the indicator are given in the instructions for laboratory practice, Lab. Manual, pp. 31, 102, 103.
[424] See Blyth, Poisons, etc., p. 608 (1895), in regard to the detection of traces of lead.
We will now turn to the consideration of a series of reactions involving the behavior of so-called "complex ions," which are very frequently met with in the various analytical groups and which offer valuable methods of separation and identification of ions. The behavior of silver nitrate solution towards ammonia forms a convenient point of attack in taking up the general subject.
If more ammonium hydroxide is added to the mixture, the precipitate dissolves readily. The excess of ammonium hydroxide must increase the concentration of hydroxide-ion and, if no other action occurred, we should, according to the principle of the solubility-product, expect that the precipitate would thereby be slightly increased (p. 145), rather than that it should be dissolved so readily. Since solution results even when the value of the one factor, [HO−], of the product is increased, we must suspect that the value of the other factor, the concentration [Ag+] of silver-ion, is in some way made much smaller by the addition of the excess of ammonium hydroxide. Recalling the fact that aluminium hydroxide is soluble in excess of sodium hydroxide, as the result of its amphoteric character, a solution of sodium aluminate NaAlO2 being obtained, we might suspect that silver hydroxide also has amphoteric properties, i.e. that it might be capable of ionizing into "argentate ions," AgO−, and hydrogen ions, AgOH ⇄ AgO− + H+. If such be the case, the nonionized silver hydroxide is in equilibrium, not only with the solid phase, [p217] but also with two sets of ions,
| Ag+ + HO− ⇄ | AgOH | ⇄ AgO− + H+, |
| ⇅ | ||
| AgOH ↓ |
and we must have two solubility-product constants, one corresponding to the basic ionization (see above) and the other corresponding to the acid ionization, and [AgO−] × [H+] = K′AgOH.
If silver hydroxide have acid properties, the addition of an alkali must suppress the hydrogen-ion and the hydroxide will go into solution as an argentate, MeAgO. We find, however, that sodium or potassium hydroxide, which would form an argentate very much more readily than ammonium hydroxide, has no solvent action on silver hydroxide (exp.); on the contrary, quantitative experiments show that the alkali makes the hydroxide still less soluble than in pure water—as demanded by the solubility-product for the basic ionization. It is thus evident, that the solvent action of ammonium hydroxide is not due to its basic functions. We would suspect that we have here an action, in which ammonia is the active component, the product of a form of dissociation of ammonium hydroxide, of which the fixed alkalies are incapable.
For the condition of equilibrium between ammonia, the silver-ion and the silver-ammonium-ion, we would have426:
Experimental investigations of the quantitative relations, obtaining in ammoniacal solutions containing silver compounds, show that no constant value is obtained for the ratio, as just developed. But the experimental data show equally conclusively,427 that a constant is obtained, when the concentration of the ammonia is raised to the second power, in the mathematical statement.
The significance of this change in the mathematical relation, it will be recalled (p. 94), is that two molecules of ammonia must combine with one silver ion to form an ion [(NH3)2Ag]+, whereas in the formation of the ammonium ion, NH4+, we have a single molecule of ammonia combining with one hydrogen ion. We have then
We would thus have a silver-ammonium ion, [(NH3)2Ag]+, and its hydroxide, silver-ammonium hydroxide, corresponding to the [p219] ammonium ion and its hydroxide, ammonium hydroxide. The properties of ammoniacal solutions of silver oxide are in entire agreement with this conception. The hydroxide is a stronger base than barium hydroxide.428 It forms salts, [(NH3)2Ag]X, in which silver appears as part of a so-called positive "complex ion." The hydroxide, like ammonium hydroxide, is unstable and is only known in solution and in the presence of free ammonia, exactly as is the case for ammonium hydroxide. The mathematical equation expressing the equilibrium conditions for the complex ion,
gives a definite measure of the stability of this complex ion. It is clear, that the larger the constant, the more unstable the complex ion would be, and so the constant is called the Instability Constant429 of the complex silver-ammonium-ion. Bodländer found the value of the constant to be 6.8E−8 at 25°.430
According to the composition of the complex ion, two molecules of ammonia should be required for every molecule of silver nitrate, to produce a solution containing the nitrate of the complex ion: Ag+ + NO3− + 2 NH3 ⇄ [(NH3)2Ag]+ + NO3−. As a matter of fact, 20 c.c. of a molar solution of ammonium hydroxide (= 200 c.c. of a 0.1 molar solution) must be added to 100 c.c. of a 0.1 molar solution of silver nitrate, to convert the silver nitrate into the salt of the complex silver-ammonium-ion. If the ammonium hydroxide solution is allowed to flow slowly, from a pipette, into the silver nitrate solution, we find that the last trace of the precipitated silver hydroxide redissolves just as the last drop or two of the 20 c.c. is added to the mixture (exp.). Working more exactly, Reychler431 found that the addition of ammonia to a silver nitrate solution, in the proportion of two molecules of the former to one of the nitrate, does not change the freezing-point of the solution, and therefore [p220] does not increase the total number of molecules in the solution. This result agrees with the conception that two molecules of ammonia combine with one silver ion to form a complex ion.
The bearing of these relations, which, it will be noted, concern concentrations of silver-ion, can best be seen by working with solutions of definite concentrations.
If the solution we have just prepared is diluted with water to 200 c.c., a 0.05 molar solution of [(NH3)2Ag]NO3 is formed. In such a solution, the concentration, [Ag+], of the silver-ion is only 0.0009,432 whereas in 0.05 molar silver nitrate solution it is 0.0435. It is clear that the reactions of the silver-ion will not be observed as readily in such an ammoniacal solution as in a solution of silver nitrate, which contains the same concentration of total silver. That such is the case, may be readily demonstrated as follows: the addition of 1 c.c. of molar sodium bromate to 10 c.c. of 0.05 molar silver nitrate immediately forms a heavy precipitate of the moderately difficultly soluble bromate, AgBrO3, while the same addition to 10 c.c. of the 0.05 molar silver-ammonium nitrate solution produces no precipitate whatever (exp.). [p221]
A liter of water dissolves 0.025 mole (6 grams) of silver bromate433 at 18°. If the same degree of ionization be assumed for it as for a 0.025 molar solution of the analogous salt, silver nitrate, AgNO3, 90% of the silver bromate in the saturated solution is ionized. The solubility-product constant then is [Ag+] × [BrO3−] = (0.025 × 0.9)2 = 0.0005.
When 1 c.c. of molar sodium bromate is added to 10 c.c. of 0.05 molar silver nitrate, each salt is ionized 80% in the mixture, and [Ag+] = 0.05 × 0.8 × 10 / 11 = 0.037 and [BrO3−] = (1 × 1 / 11) × 0.8 = 0.072. Then the product of the ion concentrations, [Ag+] × [BrO3−] = 0.037 × 0.072 = 0.0027, is considerably larger than the constant 0.0005 and precipitation follows.
But, when 1 c.c. of molar sodium bromate is added to 10 c.c. of a 0.05 molar silver-ammonium nitrate solution, the concentration of silver-ion434 is 0.00085 and the product of the ion concentrations, [Ag+] × [BrO3−] = 0.00085 × 0.072 = 6E−5, is smaller than the constant; the solution will not be saturated with silver bromate and no precipitate is formed.
On the other hand, if 1 c.c. of a 0.1 molar solution of sodium chloride is added to 10 c.c. of 0.05 molar silver-ammonium nitrate solution, a very decided precipitate of silver chloride is formed (exp.). The difference in the action of the sodium bromate and the chloride lies in the fact that silver chloride is 2500 times as insoluble as is silver bromate, and the chloride may be precipitated from solutions containing a very much smaller concentration of the silver-ion than is required for the precipitation of silver bromate.
The quantitative relations for the chloride are as follows: a liter of water dissolves 0.002 gram, or 1.4E−5 mole, of silver chloride at 25°,435 and the solubility-product constant at 25° is [Ag+] × [Cl−] = (1.4E−5)2 = 2E−10. Now, if 1 c.c. of 0.1 molar sodium chloride is added to 10 c.c. of 0.05 molar silver-ammonium nitrate, we have,436 for the first moment, [Ag+] = 8.9E−4 and [p222] [Cl−] = 0.008, and [Ag+] × [Cl−] = 8.9E−4 × 0.008 = 7E−6, which is much larger than the solubility-product constant, and precipitation must take place. The precipitate will be quite a heavy one: as silver-ion is removed from solution, the complex ion must decompose and furnish a new supply of silver-ion, and precipitation must continue until the excess of ammonia, which is liberated by the decomposition of the complex ion (Ag(NH3)2+ + Cl− → AgCl ↓ + 2 NH3), suppresses the silver-ion sufficiently to satisfy, with the diminished concentration of chloride-ion, the solubility-product constant of silver chloride.
It is clear that, while the reactions of silver-ion are not obtained as readily in the ammoniacal solution as in an equivalent solution of silver nitrate (bromate experiment), nevertheless more sensitive tests show that a small portion of the silver still is present as silver-ion in the ammoniacal solution (chloride experiment).
This brings us to our third point, the influence of an excess of ammonia on the concentration of silver-ion and on its reactions. It is evident, from the form of the equilibrium equation (p. 219), that any excess of ammonia must very rapidly reduce the concentration of silver-ion. We may ask what excess will be required to prevent the precipitation of silver chloride in the experiment just tried.
The question may be answered as follows: The concentration of chloride-ion, when 1 c.c. of 0.1 molar sodium chloride is added to 10 c.c. of 0.05 molar [Ag(NH3)2]NO3, no precipitate being formed, will be 0.1 × (1 / 11) × 0.87, the solution being diluted 1 to 11 and the percentage of ionization of a salt MeX being approximately 87% in 0.05 to 0.06 molar concentration. For a solution containing this concentration of chloride-ion, the concentration [Ag+] of silver-ion, which may just be present without leading to the precipitation of silver chloride (i.e. for the saturated solution) is, according to the principle of the solubility-product,
Further, in the presence of an excess of ammonia, practically all of the silver is present in the complex form, and, [Ag(NH3)2+] = 0.05 × 0.87 × 10 / 11 the 0.05 molar solution being diluted 10 parts to 11 and the salt being 87% ionized.
If we call x the concentration of free ammonia required to reduce the concentration of silver-ion to the small value indicated, we may put
| [NH3]2 × [Ag+] | = | x2 × 2E−10 / (0.1 × 0.87 × 1 / 11) | = 6.8E−8. |
| [Ag(NH3)2+] | (0.05 × 0.87 × 10 / 11) |
Solving for x, we obtain x = [NH3] = 0.33. The concentration of free ammonia, necessary to prevent precipitation of silver chloride in this system, is then [p223] 0.33, instead of 0.0018, present in the original solution. Now, 11 c.c. of 0.33 molar ammonia is equal to 11 × 0.33 / 6, or 0.61 c.c. hexamolar ammonia.437
Calculations, based on the solubility-product constant of silver chloride and on the instability constant of silver-ammonium-ion, lead, thus, to the conclusion that an excess of 0.61 c.c. of hexamolar ammonia is required, in 10 c.c. of 0.05 molar [Ag(NH3)2]NO3, to prevent the precipitation of silver chloride by 1 c.c. of 0.1 molar sodium chloride. Conversely, this excess of ammonia will be required to redissolve the precipitate of silver chloride, formed when 1 c.c. of 0.1 molar sodium chloride solution is added to 10 c.c. of 0.05 molar [Ag(NH3)2]NO3. The following experiment shows that such is the case.
Exp. 1 c.c. of 0.1 molar sodium chloride is added to 10 c.c. of 0.05 molar silver-ammonium nitrate, prepared as described on p. 220; hexamolar ammonia is slowly added to the mixture from a 1 c.c. pipette, graduated in twentieths of a cubic centimeter. The precipitate will be seen to be just about completely dissolved when 0.6 to 0.65 c.c. of the ammonia solution has been used.
We find, in this way, that the equilibrium equation for the instability constant of the complex silver-ammonium-ion, together with the principle of the solubility-product, allows a quantitative interpretation of the problem of the behavior of ammoniacal silver solutions, as far as the detection of silver by the precipitation of its salts is concerned.
If a still larger excess of ammonia is used (exp.), even the addition of a 10% solution of sodium chloride fails to precipitate the chloride, and, vice versa, ammonia in excess will readily redissolve a heavy precipitate of silver chloride (exp.). Advantage is taken of this fact in the separation and identification of silver-ion (Laboratory Manual, q. v.).
It is interesting to note that the addition of potassium bromide, iodide or sulphide to the ammoniacal solution, in which sodium chloride fails to precipitate any silver chloride, will still precipitate silver bromide, iodide or sulphide readily (exp.). Judged by the line of argument used above, in contrasting the behavior of silver bromate and silver chloride, these silver salts [p224] must be still less soluble than the chloride. Experiment proves, that such is, indeed, the case.438
Silver iodide is so insoluble, that ammonia439 may be used to separate it, with a considerable degree of accuracy, from silver chloride, and this separation forms the basis of a method to detect chloride-ion in the presence of an iodide. If a solution with a limited concentration of ammonia is used, the method may be extended also to the separation of chlorides from bromides (see Chap. XVI).440
Cupri-ammonium-ion is far more intensely blue than cupric-ion and its color is used as one of the tests to identify copper in its salts. Nickel-ammonium-ion is also blue, a much paler blue, and its color must not be mistaken as indicating the presence of a dilute solution of cupric-ammonium-ion. The same kind of relations obtain for these complex ions as for silver-ammonium-ion. For instance, a salt like cupric phosphate, which is readily precipitated from cupric sulphate solutions, is not precipitated from the ammoniacal solutions containing an excess of ammonia (exp.), while the very much less soluble443 cupric sulphide is readily precipitated even from the ammoniacal solutions (exp.). It may [p225] easily be shown, in the usual way,444 that the sulphide of copper is very much less soluble than its phosphate (exp.).
For the condition of equilibrium between the complex and its components, the relation
would hold. Bodlaender448 determined the value of this constant by measuring the concentrations of the three components under varying conditions. The value found is 1E−21. The value of the instability constant for [Ag(NH3)2+], of analogous composition, is 6.8E−8, a very much larger value than the constant of the [Ag(CN)2−] complex. The latter is, therefore, by far the more stable. It must, consequently, be much more difficult to obtain reactions, such as precipitations, of silver-ion in cyanide than in ammoniacal solutions. In fact, it is impossible to precipitate silver chloride by the addition of sodium chloride to KAg(CN)2 solution (exp.).449 Silver sulphide was found to be a much less [p227] soluble salt than the chloride (p. 224), and ammonium or sodium sulphide solution, when added to the cyanide solution, readily precipitates silver sulphide (exp.). (The sulphide is capable of existence in the solid phase, therefore, under these conditions.) In view of the extremely small concentrations of silver-ion in the cyanide solution, we have here a striking illustration of the extreme insolubility of the sulphide.
According to the equilibrium equation given above, the larger the excess of cyanide-ion in the solution, the smaller must be the concentration of silver-ion which is capable of existence in its presence. In agreement with this conclusion, we find that the addition of an excess of potassium cyanide readily redissolves the precipitated silver sulphide (exp.).450 In other words, even the minute concentration of silver-ion, that must be present in the supernatant liquid above a precipitate of silver sulphide ([Ag+]2 × [S2−] = KSol. Prod., for a saturated liquid), cannot be permanently present with an excess of potassium cyanide. Consequently, the solid phase is incapable of existence in the system.
The equilibrium equations give us, thus, a comprehensive basis for the interpretation of the behavior of cyanide solutions containing silver. First, in accordance with the small value of the constant, we find it very much more difficult to obtain precipitates of silver salts in cyanide, than, say, in ammoniacal solutions; secondly, in accordance with the fact that a very small, but definite, concentration of the silver-ion may still persist in the [p228] system, we find it possible, in the absence of an excess of cyanide, to precipitate such an extremely insoluble silver salt as silver sulphide represents; and finally, in accordance with the form and constant of our equation, we find it possible, by using an excess of potassium cyanide, to suppress the silver-ion to the point where even this extremely insoluble salt can no longer exist.451
When potassium cyanide is added to the deep blue ammoniacal solution of cupric-ammonium sulphate [Cu(NH3)4]SO4, the cupric-ion is reduced453 [p229] to cuprous-ion, and the latter is converted, by an excess of cyanide, into the extremely stable complex ion Cu(CN)32− and its salt, potassium cuprocyanide K2[Cu(CN)3]. The instability constant of the complex ion is: [Cu+] × [CN−]3 / [Cu(CN)32−] = 0.5E−27, and the concentration of cuprous-ion, in a 0.1 molar solution, is approximately454 3.7E−8. Without an excess of cyanide, traces of cuprous sulphide may still be precipitated, but a few drops excess will prevent the precipitation entirely.455
With an excess of potassium cyanide, cadmium forms the salt K2[Cd(CN)4], yielding the ion [Cd(CN)42−]. The instability constant456 of the complex ion is [Cd2+] × [CN−]4 / [Cd(CN)42−] = 1.4E−17. The concentration of cadmium-ion, in a 0.1 molar solution of the salt, is then approximately457 8E−5.
If potassium cyanide is added to an ammoniacal solution, containing both cadmium and copper, until the color of the solution is just discharged, and if two or three drops excess of the cyanide is then used, the addition of ammonium sulphide will precipitate pure cadmium sulphide (exp.), while ammonium sulphide, added to a portion of the original ammoniacal solution, will precipitate a dark mixture of cupric and cadmium sulphide (exp.), in which the yellow color of cadmium sulphide is masked by the black precipitate of cupric sulphide.
If the fact is recalled that the extremely sensitive tests for the ferric-ion fail to reveal the least trace of it in a potassium ferricyanide solution, one must conclude that the ferricyanide-ion must be extremely stable. The conception of the ferricyanide-ion as a complex ion, subject to the above equilibrium conditions, suggests that if a considerable excess of hydrogen-ion is added to its solutions, the concentration of ferric-ion must be increased: since hydrocyanic acid is an extremely weak acid (p. 104), the ratio [H+] × [CN−] / [HCN] having the value 7 / 1010, the addition of some concentrated hydrochloric acid must decidedly suppress the cyanide-ion in a ferricyanide solution and thus lead to an increase in the concentration of the ferric-ion. Under these conditions, direct evidence of the presence of the ferric-ion, and of the fact that the complex ion is a component in a reversible reaction, may, indeed, be obtained, as well as further evidence of the extreme stability of the complex. The presence of traces of ferric-ion may be detected, namely, in the acid solution by the thiocyanate test, applied in its most sensitive form, in which any ferrithiocyanate produced is taken up in ether.
Exp. Potassium ferricyanide, treated with a thiocyanate and ether, does not show the least trace of color; when some concentrated hydrochloric acid is added to the mixture, a perfectly plain, although noticeably faint, pink tint is imparted to the ether solution.
Mercuric cyanide, as we have seen (p. 115), is exceptional in its exceedingly small capacity for ionization. Sherrill461 has found that the dissociation constant for [Hg2+] × [CN−]4 / [Hg(CN)42−] has the extremely small value 0.4E−41. Consequently, mercuric-ion must be even more effective than hydrogen-ion (strong acids), in suppressing the cyanide-ion and liberating the ferrous- or ferric-ion, in solutions of ferrocyanides or ferricyanides. In fact, when a solution of potassium ferrocyanide is warmed, for a moment, with some mercuric oxide, the ferrocyanide complex is to some extent decomposed; the liberated ferrous-ion is oxidized, by the excess of mercuric oxide,462 to ferric-ion, and the presence of the latter, in quantity, is shown by the abundant precipitation of ferric ferrocyanide or Prussian blue, when the mixture is acidified with hydrochloric acid (exp.). [p232]
The second, suggested, course of the action would be the following:
This second action would mean that we could obtain reactions of silver ions, such as the precipitation of silver sulphide, without the intermediate formation of the free ions themselves.
The consequences of the first, the ordinary, conception of such actions as direct actions of silver ions, have been analyzed by Haber465 from the point of view of the velocities of the actions, by which the complex must be formed from its components and be decomposed into them, in order to satisfy the facts concerning the precipitations. [p233]
We may consider, with Haber, a liter of a 0.05 molar solution of K2Ag(CN)3, containing an excess466 of 0.95 mole potassium cyanide. In such a solution, the concentration of silver-ion is reduced to 8E−24 gram-ion per liter. Now, according to the best determinations of the ultimate dimensions of molecules, about 1024 molecules are estimated to be contained in a mole (gram-molecule), and 1024 ions, therefore, in a gram-ion (e.g. in 108 grams of silver-ion there would be 1024 individual silver ions). Then a liter of the solution we are considering would contain, at any moment, only eight individual silver ions, which are different ones from moment to moment, since the reversible reactions Ag+ + 3 CN− ⇄ Ag(CN)32−, are going on continually. Thus 100 c.c. of the solution would not contain even one silver ion all the time, but the requirements of the equilibrium conditions could be met467 by silver ions "flashing up and disappearing" in such a way, that the required average concentration in unit time is maintained. There is nothing irrational in such a conception.
One may ask, however, what must be the velocities, with which the complex is formed from the components, and is resolved into them, in order to satisfy an instability constant466 10−22 and still enable us to obtain a practically instantaneous precipitation, say of silver sulphide, the action being analyzed on the basis of the ordinary conception that only the silver-ion itself, and not the complex ion, is directly active in the formation of the silver sulphide. A condition of equilibrium, in a reversible action, implies that the velocities of the two continuous, opposed reactions are equal (p. 94). For the action Ag+ + 3 CN− → Ag(CN)32− the velocity of formation of the complex is proportional to a characteristic constant, KFormation, to the concentration, [Ag+], of the silver-ion, and to the third power (see p. 94) of the concentration, [CN−], of the cyanide-ion. The velocity of the opposed reaction of decomposition of the complex is proportional to another characteristic constant, KDecomposition, and to the concentration, [Ag(CN)32−], of the complex ion. For the condition of equilibrium, the velocities of the opposed reactions are equal, and we derive the relation:
| [Ag+] × [CN−]3 | = | KDecomposition | = | 1 | . |
| [Ag(CN)32−] | KFormation | 1022 |
The equilibrium constant of the complex ion is, then, the ratio of the velocity constants of its decomposition and formation (see p. 94). Now, the velocity constant, KFormation, represents the concentration, in moles, of the complex ion [Ag(CN)32−],that is formed in unit time from unit concentrations of its components Ag+ and CN−, and it may be considered as the reciprocal of a time constant, TFormation, the time required to form unit concentration of the complex ion, while the components are maintained at unit concentration. The analogous reciprocal relation holds for the velocity constant, KDecomposition, and a time constant, TDecomposition. The equilibrium equation, therefore, expresses also the following relations:468 [p234]
| [Ag+] × [CN−]3 | = | TFormation | = | 1 | . |
| [Ag(CN)32−] | TDecomposition | 1022 |
In words, the time required for the spontaneous decomposition of one mole of the complex is 1022 times as long as the time required to form one mole of the complex, from uniformly unit concentrations of the components. If the concentration of silver-ion is reduced to 1 / 1022 and the concentrations of the cyanide-ion and the complex ion are maintained at 1, the formation of the complex takes place 1022 times as slowly as when [Ag+] = 1, and a condition of equilibrium is produced, the time required to decompose and to form the same amount of the complex being now equal.
This relation of time constants may be used to obtain some idea of the consequences of assuming certain limiting values for one or the other, the ratio being maintained at the value 1 / 1022. If the time constant TFormation for the formation of the complex be taken as one ten-thousandth of a second,469 then, according to Haber, a molar solution of potassium argenticyanide would not be able to form in thousands of years sufficient silver ions to be discovered by any direct test, a result which is not compatible with the precipitation of silver sulphide and of metallic silver in a few minutes, since silver ions could not be supplied rapidly enough. It is evident, thus, that the ratio 1 / 1022 must indicate an exceedingly small value for TFormation, if only silver ions form silver sulphide and silver.
If we assume that the complex is decomposed so fast as to supply new silver ions rapidly enough, to allow us to consider the precipitation of silver and silver sulphide as direct actions of the silver ions, then we may, conservatively, consider TDecomposition to be about 1 / 100 second. Then TFormation would be only 1 / 1024 second. Considering the limiting results for the dimensions of atoms (and ions) and taking account of the fact that the formation of the complex involves electrical changes, that is, in modern terms, changes in position of electrons,470 Haber finds, that to satisfy the above value for the time constant, such changes must involve a motion of electrical charges at a speed about a million times as great as the velocity of light. Such a velocity is, unquestionably, incompatible with our knowledge of the velocities of light and of electrical charges. We must draw the conclusion that the complex argenticyanide-ion probably cannot decompose fast enough into its ions, to enable the latter to be the only components which make it possible to precipitate silver sulphide or metallic silver from its solutions471 (see above, p. 232). That would make it necessary to assume direct action [p235] (as given in equation II, p. 232) between the complex and the precipitating agent, to some extent, at least, the extent being dependent on the concentrations involved in a given case. If further investigations should confirm such a view, we would probably find that both the actions under consideration (equations I and II, p. 232) must proceed simultaneously. The second one would have the advantage of enormously greater concentrations of the reacting components, e.g. of the complex ion; the first one would, probably, be found to have the advantage of an enormously greater velocity constant. The actual velocities of the two reactions have never been measured472 and no final explanation of the relations can be offered. The problem is a very important one, involving the whole question of the mode of ionic action (cf. Chap. V, especially p. 83).
Aside from the theoretical value of the problem that has been raised, the question of immediate moment to us, from the point of view of analytical chemistry, is the question whether such conclusions would invalidate, in any way, the use we have made of the theory of complex ions, in elucidating the question of the precipitation and nonprecipitation of salts of simple ions from solutions of their complex ions.
The existence of a precipitate in contact with a solution is a question of a condition of equilibrium; the question raised, as the result of Haber's calculations, deals simply with the problem of the path, the mechanism by which equilibrium is reached, but the answer to it does not affect the conditions, on which the maintenance of equilibrium depends. All the conclusions, drawn in our discussions of precipitation from solutions of complex ions, are concerned with final conditions for equilibrium, i.e. with the conditions under which a precipitate can exist, and not with the mechanism of its formation. The conclusions reached are valid, therefore, irrespective of what the decision may ultimately be in the question, whether the simple ions alone are acted upon, when their salts are precipitated, or whether the complex ions are also immediately concerned in the action. The precipitation of silver chloride from an ammoniacal solution473 may serve to illustrate this point.
In the first place, the precipitation of silver chloride from an ammoniacal solution, say by sodium chloride, may be considered to be the result of the direct interaction of chloride ions with the small quantity of silver ions present, the complex serving only to renew the supply of silver ions, as the latter are removed from solution, by the precipitation. The course of the action would be expressed by the equations
| 2 NH3 + Ag+ + Cl− ⇄ | AgCl | + 2 NH3. |
| ⇅ | ||
| AgCl ↓ |
When the precipitation is ended and equilibrium established, a trace of silver chloride is in solution, in contact with the precipitate, and, according [p236] to the principle of the solubility-product, we must have [Ag+] × [Cl−] = KAgCl. Bodländer's experiments,474 on the solubility of silver chloride in ammonia, prove that this relation is in perfect agreement with the facts. For the silver-ammonium-ion, the free ammonia and the silver-ion present in the solution, we must have the relation [Ag+] × [NH3]2 / [Ag(NH3)2+] = KInstab. Const.. This relation, according to the experimental evidence, is also found to hold.
Now, we might, on the other hand, assume that the primary or main action, leading to the precipitation of silver chloride, is the interaction of the chloride ions with the complex ions, rather than with silver ions. Silver-ammonium chloride, [Ag(NH3)2]Cl, might first be formed, for instance, and then decompose directly into silver chloride and ammonia. This is the simplest assumption we can make for this kind of action and is sufficiently illustrative of any kind of direct action between the chloride ions and the complex ions. The path of the action would then be expressed by the equations
| 2 NH3 + | AgCl | ⇄ 2 NH3 + Ag+ + Cl−. |
| ⇅ | ||
| AgCl ↓ |
It is clear, from a comparison of this series of equations with equations (1), that they represent the same reversible reactions in a somewhat different order. Since equilibrium conditions for any reversible reaction (e.g. for A + B ⇄ C + D) are independent of the order in which the components (e.g. A, B, C, D) are brought into the system (p. 94), the difference of order, indicated by equations (1) and (2), cannot affect the final condition of equilibrium in the system under discussion. For instance, since we again have silver chloride in contact with its saturated solution, we again must have [Ag+] × [Cl−] = KAgCl, and the experimental confirmation of this relation (and similarly of the relation [Ag+] × [NH3]2 / [Ag(NH3)2+] = K) agrees as well with this second path of the action as with the first. Conversely, since the path, by which the equilibrium is reached, does not affect the condition of equilibrium, it is perfectly legitimate to draw conclusions from equilibrium constants, without assuming to know anything at all about the path by which the condition is reached.475
For analytical work, the vital point is the ultimate condition of equilibrium, which determines whether a precipitate may exist and be formed in a given system or not. The instability constants of the complex ions and the solubility-product constants of precipitates are the constant factors involved in the ultimate conditions for equilibrium, and they do not depend on the path by which equilibrium is reached. Consequently, we find that the application of [p237] the theory of complex ions to analytical problems of precipitation has been in no wise invalidated by the problems presented by Haber. The theory forms now, as before, in fact, the best quantitative basis for the expression of the experimental results. The stability constants, and the concentrations of the components used, determine the limiting concentrations in which a given metal ion is capable of continued existence, and determine, therefore, the question whether an ionogen, of a given solubility, is capable of existence as a solid phase in a given system.
| Ag─N═ | C──C | ═N─K. |
| ╲ ╱ | ||
| C | ||
| ║ | ||
| N | ||
| | | ||
| K |
The other complex cyanide ions, ferrocyanide, ferricyanide, cobalticyanide, etc., are considered to have structures entirely similar to those given to the argenticyanide ions.479
These relations clearly recall the characteristic behavior of ammoniacal and cyanide solutions, in which complex ions are formed, and the interference of the organic compounds with precipitation is of a similar nature—complex ions are formed by metal ions with these organic compounds, and the complexes are, in many instances, sufficiently stable to reduce the concentrations of the metal ions to the point, where only very difficultly soluble salts can be precipitated.
The relations may be illustrated by the discussion of the complex formed by the cupric-ion with tartrates. The structure of sodium tartrate is expressed by NaO2C─CH(OH)─CH(OH)─CO2Na. The underscored hydroxide groups OH are known in organic chemistry as alcohol groups.487 Now, alcohols resemble water in very many properties and, among others, in the capacity to form metal derivatives or alcoholates, in which the hydrogen (ion) of the hydroxide group is replaced by metal ions. The alcoholates correspond, thus, to the metal hydroxides, which are the analogous [p240] derivatives of water. Exactly as there is a vast difference in the readiness with which the various metal hydroxides, or bases, ionize, many of them being only slightly ionizable (the weakest bases), so certain alcoholates are much less readily ionizable than others. The alkali alcoholates are most readily ionized.
When sodium tartrate is mixed with an excess of sodium hydroxide, some of the readily ionizable sodium salt of the alcohol groups of the sodium tartrate is formed and we have:
When cupric sulphate is added to this mixture, a slightly ionizable complex cupri-tartrate-ion is formed by the union of the cupric-ion with the "alcoholate-tartrate-ion":
The complex ion is not perfectly stable and so the action is a reversible one, as indicated in the equation. The greater portion of the copper, however, is present as part of the complex negative ion of cupric-tartaric acid and its salts. This may be demonstrated by subjecting the solution to electrolysis in a U-tube (p. 45). It is readily seen (exp.) that a deep blue ion, obviously containing copper, migrates to the positive pole.488 The concentration of cupric-ion is so small that its hydroxide and its phosphate are not precipitated from the solution by the addition, respectively, of alkali or of a soluble phosphate (exp.). Cupric sulphide, however, is so insoluble that it may be precipitated completely from the solution by the addition of a sulphide (exp.), the concentration of cupric-ion being much smaller in the saturated solution of the sulphide than in the solution of sodium cupri-tartrate.
Citrates, sugars, glycerine, contain alcoholic groups of the same nature as found in the tartrates, and they are capable of forming similar complexes, or little ionizable alcoholates, with metal ions.
Certain organic acids, which contain no alcohol groups,489 are [p241] also capable of forming fairly stable complexes with metal ions: thus, acetates form a complex with lead-ion, that is sufficiently stable to render lead sulphate, which is difficultly soluble in water, readily soluble in ammonium acetate solution490 (exp.). Soluble oxalates readily combine with ferric, ferrous, cupric and other oxalates and interfere, more or less, with the detection of the metal ions, as the result of complex formations.
All of these complexes are decomposed rather readily by the addition of strong acids, whose hydrogen-ion breaks up the complex ions, by suppressing the anions491 of the much weaker organic acids and alcohols. Consequently, these organic compounds do not interfere with tests which may be carried out in strongly acid solution. For instance, the addition of potassium ferrocyanide to a solution of ammonium ferrioxalate (NH4)3Fe(C2O4)3, to which an excess of ammonium oxalate has been added, gives only a slight indication of the presence of ferric-ion (a greenish blue solution is obtained); when hydrochloric acid, in excess, is added to the mixture, Prussian blue, ferric ferrocyanide, is immediately precipitated in quantity (exp.).
[425] The naming of the complex ions, which ammonia forms with metal ions, has not yet been satisfactorily settled. English writers frequently speak of "ammonio-argentic" ion and "ammonio-argentic" nitrate. German writers speak of "Silber-ammoniak" ion (Abegg, Handb. der anorg. Chem., II, 728), which would read "silver-ammonia" ion in English terms. The terminology "silver-ammonium" ion, used in this book, is based on the idea, that all these complex ions are essentially of the same nature as the well-known ammonium-ion, NH4+, the positive charge being, almost certainly, carried by nitrogen in these complex ions, as it is in ammonium-ion. The latter is a complex ion of ammonia with hydrogen-ion. The name "ammonio-argentic" ion does not bring out this close relationship and puts the emphasis on the silver, which is probably little concerned in the reactions of the complex as such. The names "silver-ammonia" ion and "silver-ammonia" nitrate sound badly and do not emphasize the relation to ammonium, potassium, sodium and similar positive ions and their salts. The term "ammonium" is, for the reasons given, used here in a generic sense for all complex ions of ammonia with simple metal ions (such as H+, Ag+, Cu2+, Zn2+ etc.), and the number of ammonia molecules, entering into the composition of a complex ion, is not indicated in the names. A similar nomenclature has long been in vogue, and has worked well, for the complex ions of metal ions with the cyanide-ion (see below). We speak of ferrocyanide, Fe(CN)64−, argenticyanide, Ag(CN)2− and Ag2(CN)32−, etc., without indicating the number of cyanide groups, CN, in the complex, and we use the same generic ending "cyanide" as is used to designate the simple cyanide ion, e.g. to designate the ion formed from potassium cyanide, KCN ⇄ K+ + CN−.
[426] The hydroxide-ion appears with the same coefficient, 1, on both sides of the equilibrium equation and need not be included in the mathematical statement; it would appear as a factor in both terms of the ratio given and would cancel out.
[427] Bodländer and Fittig, Z. phys. Chem., 39, 602 (1903).
[428] Bonsdorff, Ber. d. chem. Ges., 36, 2324 (1903).
[429] It is also frequently called the dissociation constant of the complex ion, indicating the tendency of the complex ion to dissociate into its components.
[430] Two independent experimental methods were used and gave concordant results—one having as its basis the solubility of silver salts (chloride, bromide), the other the electrolytic potentials of silver against ammoniacal silver solutions (see Chap. XV).
[431] Bull. de la Soc. Chim. de Paris, (3), 13, 386 (1895).
[432] We may consider the salt to be ionized to about the same extent as ammonium or potassium nitrate in 0.05 molar solutions, or, approximately, 87%. If we call x the concentration of silver-ion, formed by the decomposition of the silver-ammonium-ion, then 2 x is the concentration of the free ammonia, and (0.05 × 0.87 − x) is the concentration of the complex ion. Since x is a small number in comparison with 0.0435, we may write, with sufficient accuracy for our purposes,
Then, x = [Ag+] = 0.0009.
[433] Kohlrausch and Holborn, loc. cit., p. 202.
[434] The dilution of the silver-ammonium nitrate (10 c.c. to 11 c.c.) and the decrease in ionization due to the added salt reduce the concentration of silver-ion from 0.0009 to 0.00085. [Ag(NH3)2+] = (0.05 × 10 / 11) × 0.8 = 0.0364 and 4 x3 = 6.8E−8 × 0.0364 (see footnote, p. 220). Then x = [Ag+] = 0.00085.
[435] Thiel (cf. Bodländer and Fittig, loc. cit.). The solubility given in the table at the end of the laboratory manual refers to 18°. The constant for the complex ion was determined at 25°.
[436] The combined concentration of the salts is 0.055 and their degree of ionization may be taken as 87%, the same as the degree of ionization of 0.05 to 0.06 molar KNO3. Then [Cl−] = (0.1 × 1 / 11) × 0.87 = 0.008. [Ag(NH3)2+] = (0.05 × 10 / 11) × 0.87 = 0.04 and x = [Ag+] = 0.00089 (see the method of calculation in the footnote, p. 220).
[437] The strong solution of ammonia is used in order to avoid unnecessary dilution, and in the experiment, described below, the dilution of the liquids by the added ammonia is considered negligible.
[438] The following solubilities have been determined at 25°:
| [Ag+] × [Cl−] = 2E−10; | [Ag+] = 1.4E−5. |
| [Ag+] × [I−] = 1E−15; | [Ag+] = 1E−8. |
| [Ag+]2 × [S2−] = 4E−50; | [Ag+] = 4.3E−17. |
[439] 100 c.c. molar ammonia dissolves at 25° only 0.6 milligram of silver iodide (Bodländer, loc. cit., p. 606).
[440] Fresenius, Qualitative Analysis, p. 378.
[441] In regard to Cu(NH3)42+ see Locke and Forssall, Am. Chem. J., 31, 268, 297 (1904), and Dawson, J. Chem. Soc. (London), 89, 1674 (1906).
[442] Euler, Ber. d. chem. Ges., 36, 3403 (1903).
[445] The acid HAg(CN)2, corresponding to the salt, is crystallizable and is a strong acid. It is largely decomposed, by water, into silver cyanide and hydrocyanic acid.
[447] In solutions containing an excess of potassium cyanide greater than 0.05 molar, the salt K2[Ag(CN)3] is formed. The dissociation or instability constant for the complex ion Ag(CN)32− is 1E−22.
[448] Z. anorg. Chem., 39, 222 (1904).
[449] The solubility-product constant for silver chloride at 25° is 2E−10. If the concentration of chloride-ion be made 1.0 by the addition of potassium chloride to a 0.05 molar solution of KAg(CN)2, then the concentration of silver-ion, necessary for the precipitation of the chloride, would be KS.P. / [Cl−] = 2E−10 gram-ion. Neglecting the fact that the complex salt is not completely ionized and putting [Ag(CN)2−] = 0.05, and calling x the concentration of the cyanide-ion just necessary to prevent the precipitation of the chloride, we have:
We find x = 5E−7 mole, or approximately 0.03 milligram potassium cyanide (cyanide-ion) per liter. This minute quantity of free cyanide, if not originally present in the solution used, would be formed by the liberation of potassium cyanide from the complex (according to KAg(CN)2 + KCl → AgCl + 2 KCN) as soon as 2.5E−7 mole, or 0.036 milligram, of silver chloride per liter have been formed, a quantity too small to be perceptible.
When potassium cyanide is added to a silver nitrate solution, the precipitate formed is found to be silver argenticyanide, Ag[Ag(CN)2], the silver salt of the extremely stable complex, rather than the simple salt, silver cyanide, AgCN [cf. Bodländer, Z. anorg. Chem., 39, 223 (1904)]. Ag[Ag(CN)2] is even less soluble than silver chloride, the solubility-product constant for [Ag+] × [Ag(CN)2−] being 2.25E−12. An excess of only 2E−6 mole, or about 0.15 milligram, of potassium cyanide (cyanide-ion) per liter is sufficient to prevent the precipitation of silver cyanide (silver argenticyanide) from a 0.1 molar solution of KAg(CN)2, and, conversely, at least this minute excess of potassium cyanide is used in the preparation of a clear 0.1 molar solution of KAg(CN)2, by the addition of potassium cyanide to silver nitrate, until the silver cyanide, first precipitated, is just redissolved (Bodländer, loc. cit.). This excess, as just explained, is more than sufficient to prevent the precipitation of silver chloride from the cyanide solution, even by a large excess of potassium or sodium chloride. Unless one takes into account, in the manner indicated, this marked influence of a minute excess of cyanide-ion in decidedly reducing the concentration of silver-ion in these solutions, one could be led, wrongly, to infer from the value of the instability constant of the complex ion and that of the solubility-product constant of silver chloride, that silver chloride should still be precipitated by the addition of sodium chloride to a solution of KAg(CN)2.
[450] For this reason potassium cyanide is an excellent cleansing agent for stained silverware (sulphide stains), and, since it is an intense poison, cleaning powders should be examined for it.
[451] For the quantitative relations see Lucas, Z. anorg. Chem., 41, 192 (1904).
[452] See Bodlaender, Z. phys. Chem., 39, 597 (1902); Ber. d. chem. Ges., 36, 3933 (1903).
[453] Potassium cyanide is a powerful reducing agent (see p. 89) and is readily oxidized to potassium cyanate. The action, presumably, takes the following course (see Chapters XIV and XV):
[454] Put [Cu+] = x, and [CN−] = 3 x, and, neglecting the degree of ionization, [Cu(CN)32−] = 0.1, x being so small that it need not be subtracted from 0.1. Then x × (3 x)3 = 0.1 × 0.5E−27, and x = 3.7E−8.
[455] Treadwell and Girsewald, Z. anorg. Chem., 38, 92 (1904).
[456] Euler, Ber. d. chem. Ges., 36, 3404 (1903).
[457] Putting [Cd2+] = y, we have y × (4 y)4 = 0.1E−17, and y = 8E−5. In view of the values of the constants, a small excess of potassium cyanide will have a much smaller suppressing effect on the cadmium-ion than on the cuprous-ion. For the excess [CN−] = 0.01, [Cu+] = 5E−23, [Cd2+] = 10−10 as compared with [Cu+] = 4E−8 in a 0.1 molar solution of the salt K3[Cu(CN)3], and with [Cd2+] = 8E−5 in a 0.1 molar solution of K2Cd(CN)4.
[458] Bromine water is a convenient agent for oxidizing cobaltous to cobaltic ions (see Chapter XV).
[459] The heavy arrows → indicate the main course the reversible actions take, under the influence of the reagents used. Since the oxidation of nickel-ion by bromine is accomplished only after the bromine has oxidized any excess of cyanide used—potassium cyanide is a powerful reducing agent (p. 89)—the addition of cyanide, beyond a very small excess, must be avoided (see laboratory instructions).
[460] E.g. for the precipitation of silver, copper, nickel, cobalt and certain other metals from cyanide solutions; cf. Edgar F. Smith, Electro-Analysis (1907).
[461] Z. phys. Chem., 43, 705 (1903). Vide also Haber, Z. Elektrochem., 11, 847 (1905).
[462] 2 Fe2+ + Hg2+ → 2 Fe3+ + Hg ↓. If the treatment with mercuric oxide is carried to completion the final products of the reaction are ferric hydroxide, mercuric cyanide, mercury and potassium hydroxide (Rose, Z. anal. Chem., 1, 300 (1862)):
[463] Bodlaender, loc. cit.
[464] The solubility-product constant of silver sulphide at 25° is 0.5E−51; for [S2−] = 0.8E−5 (p. 202), we would have in the present case [Ag+]2 × [S2−] = 2E−46, which is greater than the constant. Vide quantitative data by Lucas, loc. cit.
[465] Z. f. Elektrochem., 10, 433 and 773 (1904).
[467] Ostwald, Allgem. Chemie, Vol. II, part 1, p. 881 (1893).
[468] Haber, loc. cit.
[469] Then TDecomposition = 10−4 × 1022 = 1018 seconds, and, since there are 3.15E7 seconds in a year, TDecomposition = 3E10 years.
[471] Since there are still smaller "instability constants" than that of the argenticyanide-ion (e.g. for the gold-cyanide-ion the constant is 1 / 1028), there is a large margin of safety for the plausibility of Haber's argument. For full details, his articles (loc. cit.), and the discussion (by Abegg, Bodlaender, Danneel, ibid.) aroused by them should be consulted.
[472] See Le Blanc and Schick, Z. phys. Chem., 46, 213 (1903), on measurements of the speed of ionic actions. The values obtained agree, in general, with Haber's contention.
[473] The concentrations of silver-ion are large, in comparison with those in cyanide solution, and the action is, most likely, essentially an ionic one; but the argument applies with equal force to cyanide systems.
[474] Loc. cit.
[475] An equilibrium constant, as we have seen, is a ratio of velocity constants of balanced reactions (pp. 94, 233) and involves therefore at least two unknown velocity constants. By determining the actual rate of change with known concentrations of reacting components, i.e. by determining the velocity constants themselves, rather than their ratio, a definite conclusion as to the mechanism or path of a given reaction can often be reached (see p. 80).
[476] Proceedings Amer. Academy, 1892.
[477] In the absence of any added cyanide, it combines with itself. Silver cyanide, according to Bodländer's results, is, in saturated solutions, chiefly (AgCN)2 or Ag[Ag(CN)2], i.e. Ag─[N═C═C═N─Ag].
[479] Werner has developed quite a different theory of the structure of complex ions. (Cf. Nernst, Theoretical Chemistry, p. 374 (1904).)
[480] Sherrill, Z. phys. Chem., 43, 721 (1903).
[481] In Nessler's reagent, Fresenius' Qualitative Analysis, p. 141.
[482] Cf. Remsen, Am. Chem. J., 11, 291 (1899); 14, 81 (1892) (Stud.).
[483] For instance, for arsenious acid we have
and, therefore, [As3+] × [HO−]3 / ([AsO33−] × [HO+]3) = k1. Since [H+] = k′HOH / [HO−] (p. 176), we have further, [As3+] × [HO−]6 / [AsO33−] = k2. And since we may derive the relation [HO−]2 = k3 × [O2−], by considering the primary and the secondary ionization of water (see pp. 246, 278), we have, finally, [As3+] × [O2−]3 / [AsO33−] = K. The constants for the primary and the secondary ionization of water are included in the value of K.
[484] Fitzgerald and Lapworth, J. Chem. Soc. (London), 93, 2163 (1908); Lapworth, ibid., 2187. Vide also Franklin on the characteristics of the NH4+ ion in liquid ammonia, Am. Chem. J., 23, 305 (1900).
[485] See the laboratory instructions, in regard to the precautions used, to avoid errors from this source.
[486] On the other hand, colloidal organic substances, such as casein, glue or albumen, interfere with the precipitation of even the most insoluble sulphides, by producing colloidal suspensions of the latter (see Chap. VII; cf. Müller, Allgemeine Chemie der Kolloide, p. 56 (1907)).
[487] In alcohols the hydroxide group is held by a carbon atom, whose remaining valences are satisfied by hydrogen or carbon atoms, as in ordinary or ethyl alcohol, H3C─CH2(OH).
[488] Küster, Z. Elektrochem., 4, 117 (1897).
[489] The most common organic acids contain the acid group —CO(OH), as in acetic acid, CH3CO(OH). The hydroxide group OH of the alcohols, e.g. in CH3CH2(OH), is still found in these organic acids, but its tendency to form hydrogen-ion is very much increased by the replacement of two hydrogen atoms of the alcohols by the oxygen atom, as found in the acids. To a certain degree, the properties of the alcohol hydroxide are maintained in the properties shown by the acid hydroxide group. Thus, the organic acids, on the whole, are still rather weak acids, and their salts, in many instances, are appreciably less ionizable than the salts of strong inorganic acids. The organic acids, further, may combine, to a certain extent, with water and thus form hydrates (e.g. CH3COOH + H2O ⇄ CH3C(OH)3) containing a number of hydroxide groups: the second and third hydroxide groups must have a very much smaller tendency to form hydrogen ions and ionizable salts, than has the first hydroxide group (p. 102), and the former, thus show, more nearly, the behavior of alcoholic hydroxide groups. Finally, organic acids also show a tendency to combine with themselves, forming complex acids (e.g., (CH3COOH)2 or CH3C(OH)2OOCCH3), from which complex salts may be derived, which may be little ionizable. The power of the organic acids to form complex ions—which they share with many inorganic acids—is most likely intimately connected with the relations described.
[490] Lead acetate, itself, is less ionized than most salts and this property contributes to the solubility of lead sulphate in acetate solutions. (Cf. Noyes and Bray, loc. cit.)
The analytical groups, which we have heretofore discussed, contain elements, whose oxides are preëminently base-forming. The methods of separation of these groups, from each other, involve, primarily, physical492 differences between the groups—in the matter of the relative insolubility of analogous salts. Thus, barium, strontium and calcium carbonates are precipitated, and separated from the alkalies, by means of ammonium carbonate, not because the alkalies do not form carbonates when their salts, in solution, are treated with ammonium carbonate, but wholly because barium, strontium and calcium carbonates are very difficultly, the alkali carbonates easily, soluble in water. The hydroxides of the aluminium group and the sulphides of the zinc group are less soluble than the hydroxides and sulphides of the alkaline earths and alkalies. The sulphides of the copper and the arsenic groups, again, are still less soluble than the sulphides of the zinc group, and thus the former may be precipitated by hydrogen sulphide, even when its precipitating power is reduced by the suppression of its sulphide (and hydrosulphide) ions by the addition of a strong acid.
On the other hand, the separation of the arsenic group (arsenic, antimony, tin, gold and platinum) from the copper group, with which it is precipitated by hydrogen sulphide from acid solutions, depends, essentially, on a chemical difference between the groups. The oxides, especially the higher oxides, of the arsenic group, are preëminently acid-forming; the higher oxides form such acids as arsenic acid, H3AsO4, antimonic acid, H3SbO4, stannic acid, H2SnO3, platinic acid, H2PtO3, and auric acid, HAuO2. These [p243] hydroxides are, however, all more or less weakly basic in character as well. The hydroxides of the lower oxides of the metals are, as one must expect, much more strongly basic, but most of them—arsenious, antimonous and stannous hydroxides—still show sufficient acid character to be distinctly amphoteric in behavior. But, with the exception of arsenious acid, the basic ionization of the hydroxides of the lower oxides is more pronounced than their acid ionization.
The basic ionization of the hydroxides of their lower and higher oxides brings these elements into the plan of analysis for the metal or positive ions in systematic analysis. In the presence of hydrochloric acid they form chlorides, which yield positive ions in sufficient quantity493 to allow their extremely insoluble sulphides to be precipitated by hydrogen sulphide in acid solution, together with the, likewise, very insoluble sulphides of the copper group.
The acid-forming properties of the oxides of the arsenic group are maintained in their sulphides. Again, this is especially evident in the higher sulphides. The element sulphur is substituted for the closely related element oxygen without any profound change in the chemical behavior of the compounds. Advantage is taken of this acid-forming power to separate the sulphides of the arsenic group from the sulphides of the copper group, which either are not acid-forming at all, or exhibit this property only to a very slight degree.494
The higher sulphides of the arsenic group, and arsenious and antimonious sulphides among the lower ones, combine with the alkali sulphides to form soluble alkali salts of sulpho-acids, in the same way as carbon bisulphide does. In the case of arsenious sulphide, for instance, we have the action
The salt, ammonium sulpharsenite, is ionized as follows:
This instability of the sulpho-acids is entirely analogous to the instability of the metal hydrosulphides (p. 203) and to the instability of certain oxygen acids, notably of carbonic acid. Sulpho-carbonic acid, H2CS3, is the best-known free acid of this type. It may be precipitated, undecomposed, as an oil, and its gradual decomposition into hydrogen sulphide and carbon disulphide may be observed.
Exp.—A solution of potassium hydrosulphide is saturated with hydrogen sulphide, in order to prevent hydrolysis and the formation of potassium hydroxide496 (p. 180), as far as possible, and the solution is added to an acid (hydrochloric) solution of methyl orange;497 the acid color is changed to orange, as a result of the almost complete neutralization of the acid. The potassium hydrosulphide (the hydrosulphide-ion HS−) neutralizes the hydrogen-ion (of hydrochloric acid), that converts methyl orange into its pink salt, and hydrogen sulphide is formed, which is too weak an acid to affect the color of the indicator (p. 79).
The objection that potassium sulphide and hydrosulphide are salts, the salts of hydrogen sulphide, might be raised against the conception of their possessing a certain measure of basic functions; but the common oxygen base, potassium hydroxide, is also a salt, the salt of a still weaker acid, water. Indeed, the characteristic properties of ordinary bases are due essentially to the fact, that they are the more or less readily ionizable salts of an extremely weak acid, water, and these properties may well be duplicated by salts of other weak acids, duplicated in a very much weaker way, in proportion as the acids are stronger than water. The difference is, then, really one of degree and not of kind.498
Owing to the fact that hydrogen sulphide is a much stronger acid than water, the action of potassium hydrosulphide on an acid sulphide, like carbon disulphide (equation (2), p. 243), is reversed to a correspondingly greater degree than the action of potassium hydroxide on carbon dioxide499 (equation (1), p. 243). The dissociation constant for the secondary ionization of hydrogen sulphide (HS− ⇄ H+ + S2−) is very much smaller than the constant for the primary ionization (HS− is a much weaker acid than HSH), and so we find that a sulphide like K2S exhibits very much stronger basic functions than do the hydrosulphides, as, for instance, in forming salts with acid-forming sulphides [p246] (equation (3), p. 243) and in neutralizing acids. There can be no question that, if we could have an aqueous solution of potassium oxide, K2O, it would show, similarly, the characteristic actions of strong bases even more powerfully than the hydroxide, KOH; for instance, in acting on acid-forming oxides (equation (1), p. 243), in neutralizing acids, in saponifying esters (p. 81), and so forth. It is, in fact, on account of this property, that potassium oxide is decomposed by water. It is a salt involving the secondary ionization of water, (HO− ⇄ H+ + O2−), which has a much smaller dissociation constant even than the primary ionization (H2O ⇄ H+ + HO−). The oxide, K2O, is decomposed by neutralizing hydrogen ions formed by the primary ionization of water. We have 2 K+ + O2− + H+ + HO− ⥂ 2 K+ + 2 HO−, which is entirely analogous, in principle, to K+ + HO− + H+ + Cl− ⥂ K+ + Cl− + HOH.
The ammonium-ion, appearing with the same coefficient on both sides of the last equation, evidently takes no direct part in the action and we have more simply: Sn4+ + 3 S2− ⇄ SnS32−.
For the condition of equilibrium between the complex and its components we have:501,502
When a solution of arsenic acid, containing the usual small amount of hydrochloric acid (0.3 molar), is treated with hydrogen sulphide at ordinary temperatures, the following three reactions take place, but exceedingly slowly:
Even in the presence of a considerable amount of arsenic acid, precipitation, either of the trisulphide or of the pentasulphide, may not occur for some time, and, unless one takes account of that fact, the dangerous element, arsenic, would easily be overlooked. Heat accelerates both the precipitation of the pentasulphide and the reduction of arsenic acid and the subsequent precipitation of arsenic trisulphide.506
The interesting observation has also been made that, in the presence of an unusually large excess of hydrochloric acid and of a rapid stream of hydrogen sulphide, the precipitation of the pentasulphide (equation (1)) is favored and accelerated.507 For instance, if 100 c.c. of concentrated hydrochloric acid (sp. gr. 1.2) are added to 50 c.c. of a 0.1 molar solution of potassium arseniate and a rapid stream of hydrogen sulphide is passed through the mixture at the ordinary temperature, a copious precipitate is formed within a minute (exp.). The precipitate formed under these conditions [p249] is the pentasulphide.508 On the other hand, a mixture of 5 c.c. of hexanormal hydrochloric acid and 50 c.c. of 0.1 molar potassium arseniate fails, for a long time, to give a precipitate when treated in the same way (exp.).
The acceleration of the precipitation of the pentasulphide by the presence of a large excess of hydrochloric acid forms a problem of peculiar interest and importance, and no complete explanation of it has yet been offered.509 The following considerations lead to one explanation, that has been suggested. Arsenic acid, by virtue of its close relations to antimonic, stannic and arsenious acids, may be assumed to have extremely weak basic, as well as pronounced acid, properties. For its ionization, we would have 3 H+ + AsO43− ⇄ H3AsO4 (+ H2O) ⇄ As(OH)5 ⇄ As5+ + 5 HO−. Further, the precipitation of As2S5 may be assumed to result, ultimately,510 from the action of the sulphide-ion S2− on the positive ion As5+ (2 As5+ + 5 S2− ⇄ As2S5 ↓). The favorable action of the hydrochloric acid might, consequently, be thought to result from the fact, that it facilitates the ionization of arsenic acid as a base and the formation of a salt511 AsCl5. It could thus greatly increase the concentration of the ion As5+ and facilitate its combination with the sulphide-ion.
Treatment of a solution of arsenic acid with a concentrated acid, yielding a large concentration of hydrogen-ion, would carry the series of actions, represented in the above ionization equation for arsenic acid, decidedly toward the right—suppressing the arseniate-ion AsO43− and increasing the concentration of the arsenic-ion As5+. Since we cannot apply the equilibrium laws (or the principle of the solubility-product) to solutions as concentrated as the one under discussion, a quantitative theoretical treatment of the subject cannot be given. The following may be suggested: The action of the acid would be favorable to the precipitation of As2S5 by suppressing the arseniate-ion AsO43− and thus increasing the concentration of the hydroxide As(OH)5, available for ionization as a base and for the production of the ion As5+. But the further favorable effect of the hydrochloric acid, in converting the hydroxide into a salt AsCl5 and increasing thereby the concentration of As5+, would be very largely offset by the action of the acid in suppressing the [p250] sulphide-ion ([S2−] = k / [H+]2; see p. 201). For systems to which the equilibrium laws could be applied, the concentration of As5+ (except for the suppression of the ion AsO43−) would grow, approximately, with the fifth power512 of the concentration of the hydrogen-ion, and the concentration of the sulphide-ion would decrease, approximately, proportionally to the square of the concentration of the hydrogen-ion. Further, the precipitation of As2S5, in a system to which the principle of the solubility-product were applicable, would depend on the relation of the product [As5+]2 × [S2−]5 to the solubility-product constant; it is evident that the value for [As5+]2 would increase proportionally to the tenth power of [H+] and the value of [S2−] decrease proportionally to the tenth power of the same factor [H+]. The two effects would consequently offset each other under such conditions. However, the equilibrium laws cannot legitimately be applied to such concentrated solutions and the relation has been developed only to indicate opposing factors, which must be taken into account. An experimental study of the problem would be extremely interesting.513 Since it involves the question of the minute basic ionization of a moderately strong acid (H3AsO4), which may be open to measurement (see Chap. XVI), the problem is one of particular interest and importance.
The analytical precautions, taken to insure the precipitation, by hydrogen sulphide, of arsenic sulphide, when arsenic is present in quinquivalent form, are based on the observations described; in quantitative analysis, for the sake of securing a precipitate of uniform composition, the aim is to precipitate the pure pentasulphide and a considerable excess of hydrochloric acid is used. In qualitative analysis, where the composition of the precipitate is a matter of indifference and a large excess of acid would seriously interfere with the precipitation of certain sulphides (e.g. CdS, see p. 211), a smaller excess of acid is used and the precipitation of arsenic sulphide is insured by prolonged treatment of a solution with hydrogen sulphide at a high temperature.
[492] The weak basic properties of the hydroxides of the aluminium group, as compared with those of the zinc group, a chemical difference, and the resulting great instability of the carbonates of the former group, are used in the separation of the aluminium from the zinc group, by barium carbonate; but the physical element of extreme insolubility of the trivalent hydroxides enters also as an important factor (see footnote 3, p. 194).
[494] See p. 246, footnote 3, in regard to the action of sodium sulphide on mercuric and bismuth sulphide.
[495] Vide Nilson, J. prakt. Ch., 14, 150 (1876).
[496] Such a solution does not react alkaline to phenolphthaleïn.
[497] Hydrogen sulphide rapidly destroys the indicator and the experiment is best carried out by preparing 50 c.c. of a saturated aqueous solution of hydrogen sulphide, containing 1 or 2 c.c. of normal hydrochloric acid, and by adding a considerable excess of methyl orange to the solution immediately before the addition of potassium hydrosulphide solution, which has been prepared as described in the text.
[498] See the discussion on p. 177. See also the discussion by Remsen on acidic and basic halides, Am. Chem. J., 11, 300 (1889) Stud.
[499] In both cases acid salts, KHCO3 and KHCS3, are also formed.
[500] McCay, Z. anorg. Chem., 29, 36 (1901).
[501] On p. 238 the analogous equation for the condition of equilibrium of the anion of an oxygen acid with its components was developed. Applying the result to the ion SnO32− of stannic acid, H2SnO3, we have:
It is evident, from the form of the equation, that for the stronger oxygen acids, which are most stable as acids and ionize as bases at most in traces, the value of the constant must be extremely small.
[502] Mercuric sulphide is somewhat soluble in potassium and sodium sulphides, forming the salts Me2HgS2, and the complex ion HgS22−. A liter of 0.1 molar Na2S dissolves, at 25°, 1.9 grams (0.0082 mole) of HgS [Knox, Trans. Faraday Society, 4, 36 (1908)]. While the oxide (hydroxide) shows no perceptible tendency toward acid ionization, mercuric salts, it will be recalled, show in many cases an abnormally small tendency to form the mercuric-ion (see p. 115), and the latter also shows a particularly great tendency towards forming very stable complex ions of all kinds (e.g. HgI42−, in K2HgI4, HgCl42− in K2HgCl4, Hg(CN)42−, etc.). Knox found for [Hg2+] × [S2−]2 / [HgS22−] = k, the approximate value of k to be 1 / 1053. Bismuth sulphide is also very sparingly soluble in sodium or potassium sulphide, but not in ammonium sulphide. Solid salts, KBiS2 and NaBiS2 are known [Knox, J. Chem. Soc. (London), 95, 1760 (1909)].
[504] See the discussion of the reaction, given below.
[505] See Chap. XVI, for the interpretation of the reduction as an ionic reaction.
[506] Bunsen, Ann. (Liebig), 192, 305 (1878). Brauner and Tomicek, J. Chem. Soc. (London), 53, 145 (1888). Usher and Travers, ibid., 87, 1370 (1905).
[507] Neher, Z. anal. Chem., 32, 45 (1893).
[508] Neher, loc. cit.
[509] The theory of the relations favoring the precipitation expressed in equation (1) as against the reduction expressed in equation (2), forms a second interesting problem.
[510] Intermediate derivatives, such as H3AsSO3 (p. 246), could be the result of the ionization of As(OH)5, or of AsCl5, in stages (see p. 106). Neher, loc. cit., McCay, loc. cit.
[511] Neher (loc. cit.) suggested that the favorable action of the large excess of hydrochloric acid might well be due to the formation of AsCl5. McCay, J. Am. Chem. Soc., 24, 661 (1902), discusses the ionization of arsenic acid as a base, in connection with the precipitation of As2S5.
[512] As(OH)5 is considered to be an extremely weak base and AsCl5 to be an ionizable salt.
[513] To a certain extent, the effect of the acid may be to coagulate and precipitate the colloidal sulphide. Possibly, also, the concentrated acid renders inactive a considerable portion of the water present (forming oxonium salts OH3Cl, etc., see p. 238), which tends, by hydrolysis, to reverse the formation of the chloride As(OH)5 + 5 HCl ⇄ AsCl5 + 5 H2O. Possibly, the formation of the pentasulphide is not wholly an ionic reaction, its precipitation being always a more or less slow process, and there may be intermediate products whose formation could be accelerated by the presence of acids (see Bredig and Walton, Z. Elektrochem., 9, 114 (1903) for the study of a simple inorganic action involving such catalytic effects of acids).
Oxidation and reduction reactions are frequently met with in analysis, and we shall turn now to the consideration of such reactions, from the point of view of the modern theory of solution and the laws of equilibrium.
Leaving until later the discussion of the most important and most common oxidizing agents, such as oxygen, nitric acid, permanganate, etc., we shall, in order to develop the subject most simply, confine ourselves, for the moment, to the qualitative study of some oxidations and reductions met with early in the study of analytical reactions. One such reaction is the reduction of ferric salts by hydrogen sulphide, and the simultaneous oxidation of the latter to sulphur (exp.). The reaction may be expressed by the equation
If the action is considered to be the result of the interaction of the ionized ferric chloride and hydrogen sulphide, it would be represented by the equation
It is then clear that the reacting components, according to such a conception, are the ferric and the sulphide ions, whose electrical charges mutually discharge each other. Considering only those components whose charges are changed, we have
The reduction of a ferric to a ferrous salt would then be accomplished by the discharge of one of the three positive charges on the ferric ions; the oxidation of hydrogen sulphide to sulphur would be accomplished by the complete discharge of the sulphide ions.
Ferric salts are reduced, much in the same way, by iodides (exp.), iodine being liberated: 2 Fe3+ + 2 I− → 2 Fe2+ + I2.
Reduction then appears to involve a loss of positive charges by ions, oxidation a loss of negative charges. [p252]
Conversely, we frequently have occasion to oxidize ferrous salts to the ferric condition, and among the most convenient reagents for the purpose are chlorine and bromine water (exp.). For instance, we have 2 FeCl2 + Cl2 → 2 FeCl3, or, considering the action from the point of view of the theory of ionization,514 2 Fe2+ + Cl2 → 2 Fe3+ + 2 Cl−. In this case the oxidation of the ferrous to the ferric ion consists in the assumption of an additional positive charge; reduction of chlorine to the chloride-ion consists in the assumption of negative charges by the chlorine atoms.
Ferric salts are reduced, at the negative pole, to ferrous salts:
Exp.—A solution of ferrous chloride, freshly prepared from iron wire, or a freshly prepared solution of ferrous-ammonium sulphate, is placed in a very small beaker; a solution of ferric chloride, acidulated with hydrochloric acid to prevent subsequent complete reduction of the ferric-ion to iron, is brought into a similar beaker. A small amount (5 c.c.) of each solution is tested, the former with potassium thiocyanate and the latter with ferricyanide solution, to show the absence of perceptible quantities of ferric and ferrous ions in them, respectively. Platinum electrodes, consisting best of cylinders of platinum gauze, are introduced into the solutions, the solutions are connected by means of a "salt bridge" (a U-tube filled with a solution of sodium chloride and closed at both ends by plugs of filter paper), and a current of 0.2 ampere is passed through the system, the positive current entering the solution containing the ferrous salt. After the current has been allowed to pass for a minute or two, 5 c.c. is withdrawn, by a pipette, from the meshes of the positive electrode and tested with thiocyanate, and 5 c.c., withdrawn in the same way from the negative electrode, is tested with potassium ferricyanide.
Exp. For instance, some ferric chloride and sodium chloride solution may be put into a small beaker, some sodium chloride solution into a second beaker of the same size, and the two solutions connected, first by means of a "salt-bridge," and then by means of two platinum electrodes dipping into the solutions and connected with the terminals of a sensitive voltmeter.516 If [p254] all of the connections are made, the introduction of the "salt-bridge" being left to the last, a momentary slight motion of the needle is observed, when the bridge is introduced. The needle then falls back to the zero point (see p. 276). If now some hydrogen sulphide water is poured into the beaker containing sodium chloride, a decided, and continuing, deflection of the needle of the voltmeter is immediately observed, showing the passage of an electric current, and it is in the direction anticipated by the consideration of the reaction equation: 2 Fe3+ + S2− → 2 Fe2+ + S ↓. The positive current passes into the voltmeter from the ferric chloride solution, where ferric ions are giving up their charges; the negative current enters the voltmeter from the solution containing the hydrogen sulphide, where sulphide ions are being discharged. The "salt-bridge" is necessary to complete the electrical circuit and prevent any local accumulation of positive or negative electricity (polarization). For instance, as the ferric ions are discharged, an excess of chloride ions would remain in the beaker, rendering the solution negative and preventing the flow of electricity from the electrode, if negative ions did not move off, through the "salt-bridge," into the beaker containing hydrogen sulphide and, simultaneously, positive ions migrate into the beaker containing the ferric salt. Similarly, the accumulation of positive electricity in the hydrogen sulphide solution, on account of the hydrogen ions left free by the discharge of sulphide ions, is prevented by the flow of positive ions (sodium and hydrogen) through the U-tube into the beaker containing the ferric chloride and the flow of negative (chloride) ions into the hydrogen sulphide solution. Thus a current of electricity passes through the whole circuit.
It is thus possible to reduce ferric chloride in one vessel by hydrogen sulphide poured into another vessel,517 and an electric current may be obtained from the simultaneous discharge of the sulphide and ferric ions in the action.
It would appear possible, in fact, to obtain an electrical current from any oxidation-reduction reaction, if the oxidizing and reducing agents can be, experimentally, properly arranged for this purpose.
The mere possibility of a transfer of charges, or electrons, is therefore apparently521 not sufficient to induce an oxidation and reduction reaction—much in the same way as, for instance, the mere presence, simultaneously, of the barium-ion and the carbonate-ion, in itself, does not necessarily lead to the precipitation of barium carbonate (p. 90), although the latter is difficultly soluble. In order to understand the problem of precipitation or nonprecipitation of salts, it was found necessary to examine the question from its quantitative side (p. 91), and, similarly, the solution of the difficulty concerning the occurrence or nonoccurrence of oxidation and reduction reactions, where the possibility of a transfer of electrons is given, will be found in a study of the problem from its quantitative side.
or, since the sulphate-ion is not directly concerned in the action, we have more simply:
Cupric-ion has been reduced, therefore, to metallic copper, the metallic zinc oxidized to zinc-ion, each zinc atom transferring two electrons to a cupric ion.
| Cu | O | SO2, | ||
| ╱ | ╲ | |||
| ╲ | ╱ | |||
| O | ||||
| Zn | O | SO2, | ||
| ╱ | ╲ | |||
| ╲ | ╱ | |||
| O | ||||
If a strip of copper is placed in a solution of mercuric nitrate, copper, in turn, is dissolved, being oxidized to the form of cupric-ion, and mercury is deposited:
We find, then, that cupric-ion has a tendency to give up its charges, to be reduced to the metallic condition; metallic copper, in turn, has a tendency to revert to the ionic condition, to be oxidized and to form cupric-ion. We may consider the two opposed tendencies, shown in these relations, as representing a reversible reaction:
Exp. If an electric current is passed through a copper sulphate solution, copper is deposited on the negative (platinum) electrode; if the current is reversed, the copper vanishes quite as rapidly at what is now the positive pole. [p258]
Since the concentration [Cu ↓] of a pure, dense523 piece of copper may be considered a constant at a given temperature, it would follow, that the first term in our relation would also have a constant definite value for the condition of equilibrium between the metal and its ion. Consequently, for the condition of equilibrium we would have:
Metallic copper would then be in equilibrium, at a given temperature, with solutions containing cupric-ion only if the latter has a perfectly definite, constant concentration. Nernst524 discovered this and similar relations, as a result of a more rigorous analysis of the energy changes involved in the ionization and precipitation of metals, and proved the validity of the relations. The value of the constant,525 which, according to Nernst's [p259] suggestion is called the electrolytic solution-tension constant, is 8E−22 for copper526; that is, copper is directly in equilibrium with a solution containing cupric-ion only if the concentration of the latter is 8E−22 gram-ion per liter.
We see, then, that copper would be directly in equilibrium with solutions of cupric salts only if they contain this exceedingly minute concentration of cupric ions. When such is the case, the ionization of the metal and the formation of the metal, by the deposit of discharging ions, may be considered to proceed with the same velocity (p. 94).
But, if the metal is dipped into a solution of greater concentration of cupric ions than that represented by the constant, say into a solution of 0.1 molar copper sulphate, the velocity of deposition of the metal would be proportionally increased (p. 92), while the velocity of ionization and solution of the metal would remain unchanged. We would consequently have the ions discharging and forming metal more rapidly than they are formed. A condition of change, not of equilibrium, exists. If we [p260] consider the changes that must occur, we see that the ions, discharging on the metal, would charge it with positive electricity, and the positive charge would, in turn, repel from the metal the positive cupric ions remaining in the solution. Equilibrium would be expected to result when the charge on the plate becomes heavy enough to repel from the film, immediately surrounding it, all the cupric ions excepting those representing a concentration of 8E−22, as required by the value of the equilibrium constant. The positive charge on the plate would attract and hold negative sulphate ions, freed by the discharge of cupric ions, in a kind of "double layer," the surface of the metal holding positive charges and the film of liquid in contact with it holding an excess of negative ions. An electric potential would thus be established between the positive metal and the negative solution, bathing it.527 It is evident that the more concentrated the solution of cupric ions, the heavier the charge must be that will be required to repel the cupric ions sufficiently to establish equilibrium.528
If copper is placed in a solution in which the concentration of the cupric ions is smaller than the constant 8E−22, the velocity of ionization will be greater than the velocity of the deposition of the metal. The ions formed, having assumed positive charges, will leave a negative charge on the metal, and, as a result of the electrical attraction, a "double layer," surrounding the metal, will again be formed, the positive ions clinging to the negative metal. Equilibrium will be reached when the concentration of the cupric ions originally present, increased by the new ions formed in this "double layer," will have reached, in the film bathing the plate, the concentration demanded by the equilibrium constant. An electrical potential will be established as before, the metal being negative, the solution, in this case, positive.
By developing the quantitative relations between osmotic forces and the electrical potential, Nernst[3] was able to show that, at room temperature529 (17°–18°), the following logarithmic relation [p261] holds for the potential difference between a metal530 and a solution of its ion, which bathes it:
In this equation εMe, Me-salt is the electrical potential, in volts, existing between the metal Me and the solution of its salt, Me-salt; v is the number of electrical charges transferred from the metal to its ion, and vice versa, in the action Me ⇄ Meion; in the present case, it is identical with the valence of the metal ion, which the metal forms. C is the concentration of this ion in any given case, and K is the concentration represented by the solution-tension constant, i.e. by the equilibrium constant. The logarithm is the common one. In place of the concentrations, K and C, the corresponding osmotic pressures of the metal ion (P and p, as used by Nernst) may be used in the equation, and for solutions in which osmotic pressure and concentration are not strictly proportional, the osmotic pressure should be used by preference (see footnote 4, p. 258). The sign531 given to [p262] εMe, Me-salt, in any given case, shows the sign of the electric charge on the first component named in the subscript, which is the metal, in the present instance.
For the relation between copper and cupric-ion we would have:
When the concentration of cupric-ion is equal to the constant, C = K, the logarithm has the value 0 and the potential difference is 0. When the concentration of cupric-ion is smaller than the constant, C < K, the potential εCu, Cu-salt is negative, i.e. the metal receives a negative charge. This negative charge is the greater, the smaller C is. When C > K, εCu, Cu-salt is positive, the copper plate receives a positive charge, and this positive charge is the greater, the larger the value of C is.
and533
It is also clear, from this equation, that the greater the difference in concentration of the cupric-ion in the two solutions, the greater should be the potential difference produced. The following series of experiments illustrates these relations and confirms the conclusions reached. [p264]
If two electrodes of pure copper are introduced into solutions of cupric sulphate of equal concentration,534 no current is produced, when the solutions are connected by a "salt bridge" and the electrodes with a voltmeter (exp.; the chemometer described on p. 253 is used). If one of the beakers is partially emptied, only a few drops of the solution being left in it, and is then filled with a solution of sodium sulphate, we notice that the voltmeter immediately indicates the establishing of a potential difference—a current is produced. From the experimental arrangement and from the manner of the deflection of the needle of the chemometer, we note, too, that the plate dipping into the more concentrated solution of the cupric-ion is the positive pole, and hence the cupric ions are discharged on it; this solution is therefore growing less concentrated in regard to cupric-ion. In the other vessel, copper is dissolving and the concentration of cupric-ion is increasing. Both changes tend toward equalizing the concentrations in the two solutions and thus toward establishing equilibrium.
The diffusion of ions, from and to the plates, is a very slow process (p. 8), and since the potential produced depends on the momentary concentrations of the liquid films immediately next to the plates, the potential difference, first observed, is seen to disappear rapidly. More decided and lasting potential differences are obtained by introducing reagents, which keep the concentration of the cupric-ion, automatically, at very low values in the one solution, and which thus make us less dependent on the slow diffusion of the ions around the plates. We may add, for instance, sodium hydroxide to a solution of copper sulphate to precipitate cupric hydroxide; cupric hydroxide being a difficultly soluble compound, its saturated solution contains only a very small concentration of [p265] cupric-ion. If we connect, again, copper plates in two equally concentrated solutions of copper sulphate, and add a little more than the equivalent amount of sodium hydroxide to the solution holding the plate connected with the negative post of the voltmeter, cupric hydroxide is thereby precipitated, and we note that a decided difference of potential is established and maintained (exp.). An excess of a concentrated solution of sodium hydroxide should, according to the principle of the solubility-product, reduce the concentration of cupric-ion still more, and the potential is, in fact, thereby increased (exp.). Cupric sulphide is much less soluble than cupric hydroxide, and if we add sodium sulphide (a little more than one equivalent) to the mixture containing the hydroxide, we find that the hydroxide is converted into the less soluble, black sulphide, leaving a still smaller concentration of cupric-ion in this solution, and the potential is again increased (exp.). We found that the complex ions of copper with the cyanide-ion are so extremely stable as to allow of the existence of a concentration of cupric-ion so minute, that copper sulphide cannot be precipitated from cyanide solutions (p. 228). If sufficient potassium cyanide is added to the mixture containing the suspension of cupric sulphide, the sulphide dissolves readily,535 and the largest potential difference, yet noted, is produced.536 We find thus that the behavior of the metal, in contact with these different solutions, agrees with the demands of the theory.
In aqueous solutions, the concentration of zinc-ion with which the metal would be in equilibrium, as found by calculation from the potential difference between zinc and zinc sulphate solutions [p266] of realizable concentrations of zinc-ion, is 1017, a value537 enormously larger than 10−21, the value of the corresponding constant for copper. A zinc rod, in contact with a solution of a zinc salt, like zinc sulphate, will acquire a negative charge, as the metal must ionize much more rapidly than the ion will be discharged, since even a saturated solution would contain only a relatively small concentration of the ion. Copper, as we have seen, placed in a copper sulphate solution of moderate concentration, is charged with positive electricity, the concentration of cupric-ion being very much larger than that required for the condition of equilibrium between the metal and its ion. When zinc, immersed in a zinc sulphate solution, and copper, immersed in a copper sulphate solution, are connected through a metal circuit, e.g. that of a voltmeter, and the solutions are connected by a "salt-bridge" (exp.), a current is established, the positive current flowing from the copper through the metal circuit to the zinc, metallic copper being deposited and zinc going into solution. The combination represents the well-known Daniell cell. We note that in each solution the change in concentration of the ion is towards the solution-tension constant, towards a condition of equilibrium. We may inquire, a little more closely, what would be the condition for equilibrium for such a system. If we imagine a copper plate dipping into a solution containing a concentration of 10−21 of cupric-ion (the solution-tension constant), the metal will be directly in equilibrium with the solution and will not acquire any electrical charge. If we imagine a zinc rod immersed, in the same way, in a solution containing a concentration of zinc-ion of 1017 (this is not practically feasible), the metal and its ion would also be in equilibrium with each other and the metal would not assume any charge. It is evident that, if the zinc and copper and the solutions of their salts were connected, no current would be established, [p267] zinc would not be oxidized to zinc-ion, and cupric-ion would not be reduced. In this condition of equilibrium, then, the ratio of the concentrations of the respective ions in the solutions bathing the metals would be, also, the ratio of the solution-tension constants. This is a general relation for these two metals—the individual concentrations of the ions need not have the value of the solution-tension constants, but equilibrium will be established whenever the ratio of the concentrations of the cupric-ion and the zinc-ion has the same value as the ratio of the solution-tension constants.538 The condition for equilibrium, in mathematical form, is then
The nearer the ratio is to the equilibrium constant, the smaller the potential will be, until, when the constant is reached, it becomes 0. We cannot increase the concentration of zinc-ion indefinitely in order to reach the condition of equilibrium, but we may reduce the concentration of cupric-ion practically at will, as we have seen (p. 265), and we may thus approach the constant. In fact, if we add to the copper sulphate solution of the copper-zinc element, described above, a solution of sodium hydroxide, and thus leave, in the solution, only the small concentration of cupric-ion belonging to the difficultly soluble cupric hydroxide, the potential of the copper-zinc element is decidedly reduced (exp.). If sodium sulphide is added to the cupric hydroxide, to convert the hydroxide into the less soluble sulphide, which yields a smaller concentration of cupric-ion, the potential is again reduced most decidedly (exp.). It has now so small a value that we may readily anticipate that, if the cupric-ion is suppressed so thoroughly, by the addition of potassium cyanide, that even the sulphide cannot persist, the value of the ratio [Zn2+] : [Cu2+] may grow even larger than the [p268] equilibrium constant 1038, and we would have a system in which chemical change in the opposite direction must result from the tendency to establish equilibrium. In fact, if potassium cyanide is added to the mixture surrounding the copper plate, in sufficient quantity to dissolve the sulphide, we find that a current is established in the opposite direction539—zinc is now precipitated at the expense of the solution of metallic copper; that means, that the zinc-ion is being reduced by metallic copper, which in turn is oxidized to cupric-ion (exp.).
We may apply the conclusions, reached, to the action of metallic zinc when it is introduced into the solution of a cupric salt. The oxidation of zinc to the zinc-ion and the reduction of the cupric-ion to copper must be reversible reactions, Zn ↓ + Cu2+ ⇄ Zn2+ + Cu ↓, which will come to a condition of equilibrium, according to the laws of equilibrium, when [Zn2+] : [Cu2+] = K = 1038. The value of this ratio shows that the cupric-ion will be practically completely reduced, and precipitated as copper, by a sufficient quantity of zinc, the trace of cupric-ion, required to maintain the equilibrium ratio, being too minute to be detected. By the study of this oxidation and reduction reaction with the aid of potential differences, as just described, the validity of the relation is subject to demonstration, and the value of the equilibrium constant is brought into definite relation to the solution-tension constants of the metals.
Each element has its own characteristic solution-tension constant (see the table at the end of Chapter XV), and the relation just established for the reduction of cupric-ion, at the expense of the oxidation of metallic zinc, may be applied to any pair of metals and their ions.540
The oxidation and reduction reactions, such as Zn ↓ + Cu2+ ⇄ Cu ↓ + Zn2+, to which we have heretofore limited the discussion of the quantitative relations, are particularly simple actions, involving only two variables (in this case [Cu2+] and [Zn2+]). But the knowledge of the general principles of the quantitative relations will now enable us to answer questions, in connection with more complicated cases, which the qualitative relations alone did not put us into the position of answering (see p. 256).
In considering the question of the possible reduction of ferric to ferrous ions, at the expense of the oxidation of chloride ions to chlorine, we must bear in mind the fact that the reduction of the ferric ions is a reversible process, Fe3+ ⇄ Fe2+, and that the oxidation of chloride ions to chlorine is also a reversible process, 2 Cl− ⇄ Cl2. We will deal first, in some detail, with the action Fe3+ ⇄ Fe2+. For this reversible action we have an equilibrium constant541 [Fe2+] : [Fe3+] = KFerro, Ferri = 1017, which must be [p270] taken into account in all oxidation and reduction reactions involving these ions.542 In a system containing the two ions, the tendency towards reduction of ferric-ion and the tendency toward oxidation of ferro-ion would be directly in equilibrium (i.e. without the intervention of other opposed forces, such as an electric potential, produced by an opposing cell or produced by an opposing action543 of other components in the solution) only when the concentration of ferro-ion is 1017 times as great as the concentration of ferric-ion.
If we connect a 0.1-molar solution of ferric chloride with a 0.1-molar solution of ferrous chloride, by means of a "salt bridge" and a pair of platinum electrodes dipping into the solutions and connected with the voltmeter (see p. 253), a current is produced, the positive current entering the voltmeter from the electrode placed in the ferric chloride solution (exp.). It is evident that, in the effort to establish equilibrium, ferric ions in the ferric chloride solution are reduced at the expense of the oxidation of ferrous ions in the ferrous chloride solution. If we consider only the ratio of the concentration of the ferro-ion to that of the ferric-ion in each of the salt solutions and leave out of consideration, for the moment, other, secondary, electrical forces,544 it is clear that the ratio [p271] [Fe2+]1 : [Fe3+]1 in the ferrous salt solution, considered by itself, is far closer to the point of equilibrium545 than the ratio [Fe2+]2 : [Fe3+]2 in the ferric chloride solution, in which the concentration of ferric-ion is enormously greater than that of ferro-ion, while the equilibrium constant demands that the ferro-ion should be in great excess. The strongest tendency to change must be toward a reduction of the concentration of the ferric-ion in the solution of ferric chloride, which is in agreement with the observed direction of the current. Equilibrium, it may be added, will be reached when the ratio of the concentration of ferro-ion to that of ferric-ion is the same in both solutions.546
The addition of potassium fluoride to the ferric chloride solution converts the ferric-ion into the rather stable complex ferrifluoride-ion FeF63−, whose potassium salt K3FeF6 is formed. The [p272] concentration of ferric-ion being decidedly reduced, the system must be nearer to the condition of equilibrium, the potential must fall (exp.). It is again evident (p. 255) that the oxidizing agent is clearly the ferric-ion, and not the total quantity of the ferric salt in the solution.
For the reduction of ferric salts by iodides (p. 251), we have to consider the reversible tendency of iodide-ion to form iodine and to be formed from iodine: 2 I− ⇄ I2. The constant550 KI−, Iodine for the equilibrium ratio [I−]2 / [I2] is 5.6E29 at 25°. [p274]
The reduction of ferric salts by iodides is a reversible reaction: 2 Fe3+ + 2 I− ⇄ 2 Fe2+ + I2, and the ultimate condition of equilibrium will depend on the values of the constants, KFerro, Ferri and KI−, Iodine, and on the concentrations of the components used. For the condition of equilibrium we have
and for this constant the relation551
| Keq = | KI−, Iodine | = | 5.6E29 | = | 5.6 |
| (KFerro, Ferri)2 | (1017)2 | 105 |
can be established. It is evident, from the value of the constant, that the chief tendency of the reversible reaction will be toward the reduction of the ferric ions and the liberation of iodine, which is in accord with experience (exp., p. 251).
It is interesting to note, again, that the reduction of the ferric salt depends on the reduction of the ferric-ion: the ferric-ion may be suppressed, with the aid of potassium fluoride (see p. 255), and the addition of potassium iodide to a mixture of ferric chloride and potassium fluoride leads to the formation of traces, only, of free iodine (exp.).
For the reaction of chloride-ion on ferric-ion we would have, as in the case of the action of iodide-ion, 2 Fe3+ + 2 Cl− ⇄ 2 Fe2+ + Cl2 and
For this equilibrium constant we have the relation, as determined above (p. 274),
| Keq = | KCl−, Chlorine | = | 2E60 | = 2E26. |
| (KFerro, Ferri)2 | (1017)2 |
It is evident, from the value of the equilibrium constant, that the action of chloride-ion on ferric-ion must result quantitatively so differently from the action of the analogous iodide-ion (p. 275), that the net qualitative results are entirely dissimilar. Whereas in the case of the iodide, liberation of iodine and reduction of the ferric-ion are bound to be the chief and obvious actions, in the case of the chloride-ion, on the other hand, the equilibrium constant demands that there should be no appreciable reduction of the ferric-ion or liberation of chlorine—which is in accordance with our experience (exp., p. 256).
It is noteworthy, however, that the equilibrium relations demand that at least traces of chlorine be liberated, and traces of ferrous salt be formed, since neither [Fe++] nor [Cl2] may have the value 0. If we add some sodium chloride to a solution of sodium sulphate, connected electrically, in the usual way, with a solution of ferric sulphate, a very slight momentary current is produced (exp.). The liberation of the first traces of chlorine and of ferro-ion on the electrodes is necessary, and also sufficient, to satisfy the conditions for equilibrium as expressed by the constant, until diffusion from the electrodes removes these traces.
[514] The oxidation by chlorine may also be represented on the basis of the conception that the chlorine molecule contains a positive and a negative chlorine atom, Cl+Cl−. (Vide W. A. Noyes, J. Am. Chem. Soc., 23, 460 (1901); Stieglitz, ibid., 23, 796 (1901); Walden, Z. phys. Chem., 43, 385 (1903); J. J. Thomson, Corpuscular Theory of Matter, p. 130 (1907)). We may consider the action to take place as follows: 2 Fe2+ + Cl+ → 2 Fe3+ + Cl−.
[515] ε− is used to indicate an electron.
[516] The whole device is an adaptation of Ostwald's "Chemometer" [see Z. phys. Chem., 15, 399 (1894)]. It has been found best to convert a Weston voltmeter into a lecture table apparatus by lengthening its index to 10 inches, with the aid of a very light, hollow aluminium wire carrying an index and playing over a scale 10 inches wide, drawn on glass and divided into 150 divisions. The scale is illuminated by means of five small one-candle-power lamps. The whole is encased in a simple wooden frame. The voltmeter shows a range of 0.7 volt, but, on account of its low resistance (78 ohms), it is used only for qualitative purposes and does not register the true potentials, quantitatively. (Such adaptations of Weston voltmeters may be purchased from the Weston Electrical Instrument Co., or a similar instrument obtained from Hartmann and Braun, Frankfurt a/M, Germany.)
[517] Chemical Action at a Distance, Ostwald, Z. phys. Chem., 9, 540 (1892).
[518] Peters, Z. phys. Chem., 26, 229 (1898).
[519] See below, in regard to the quantitative relations for reactions of this nature.
[520] Exp. Ferric sulphate solution is tested with a ferricyanide.
[521] Rigorous quantitative examination of the relations shows (p. 275) that these reductions and oxidations do take place, but equilibrium is reached when they have proceeded to so slight an extent, that, qualitatively, they are not always obvious or discernible.
[522] A change in the nature of the solvent changes the value of the equilibrium constant, just as it changes the ionization constant of electrolytes. See p. 61 and see remarks by Sackur, Z. Elektrochem., 11, 387 (1905).
[523] For exceedingly thin films of copper we cannot make this assumption, and for such films the conclusions, that follow, are, in fact, found not to hold. (Overbeck. Vide Le Blanc, Electrochemistry, p. 252 (1896)).
[524] Z. phys. Chem., 4, 129 (1889).
[525] The values of this and similar equilibrium constants are derived by means of Nernst's formula (see below) for the potential difference between an element and solutions of its ions. The derivation involves the assumption that this formula expresses correctly the relation between the potential change and the concentration change at all concentrations. This assumption appears to be justified by all experimental indications thus far observed. The constants are of importance, primarily, for the calculations which can be made with their aid (see below), and may, conservatively, be considered to be essentially "calculation factors" ("Rechengrössen," according to Haber. See pp. 232–7, Chapter XII). The constants may be expressed, as in the text, in terms of (molar) concentrations of the ions, or in terms of the osmotic pressures of the ions, a molar solution at 0° producing an osmotic pressure of 22.4 atmospheres. Where osmotic pressure and concentration are not strictly proportional (e.g. for concentrated solutions), the osmotic pressure, rather than the concentration, is the determining factor and, when known, is used in exact calculations. The plan, pursued in the text, is adopted in order to express these constants in the terms used for all the other equilibrium constants. It should be recalled (e.g. p. 30) that in calculations, in general, where pressure and concentration are not strictly proportional, the pressure is the determining factor. A third method of expressing the solution-tension relations consists in giving the potential differences, which exist between elements and solutions of their ions, in which the ions have unit (molar) concentration. These potential differences are functions of the solution-tension constants, as will be discussed below, and the constants, in terms of concentrations or osmotic pressures, may be easily calculated, from the potential differences, with the aid of this function (see below, and see the table at the end of Chapter XV).
[526] According to Wilsmore's tabulation (Z. phys. Chem., 36, 92 (1901)), the potential difference εCu, Cu2+ of copper against a 0.5 molar solution of cupric sulphate, in which [Cu2+] = 0.11, is +0.584 volt. Inserting these values for [Cu2+] and εCu, Cu2+ in the equation εCu, Cu2+ = (0.0575 / 2) log([Cu2+] / K) (see below) and solving the equation for K, we find K = 8E−22. For [Cu2+] = 0.24, εCu, Cu2+ is +0.594 volt and K = 8E−22. In regard to the convention determining the signs used (in the present case εCu, Cu2+ is positive), see the footnote below, p. 262, and in regard to the definition of zero potential, to which the potential differences used in this book refer, see the table and summary at the end of Chapter XV.
[527] Nernst, loc. cit., p. 151.
[528] In other words, the greater the concentration of cupric-ion, the greater its osmotic pressure must be, and the repelling electric force, required to overcome the pressure of the cupric-ion, would be correspondingly greater.
[529] Cf. Nernst, Theoretical Chemistry (1904), pp. 720–723, in regard to the derivation and the general form of his formula.
[530] For elements that form negative ions, e.g. for chlorine, bromine, oxygen, etc., the equation reads (see pp. 273, 275 and the table at the end of Chapter XV):
Note the changed sign of the expression on the right. The difference in sign expresses the fact that, when negative ions discharge on an electrode, they render it negative, and when they are formed by an electrode, they leave the latter positive; for positive ions, it will be recalled, the conditions are just the reverse (see above).
Where a soluble element (e.g. chlorine) or a solution of a metal (e.g. sodium amalgam) is used as an electrode, its concentration, in general, is not constant, as in the case of a pure, solid metal like copper (p. 258). In such cases, the quantity in the denominator of the ratio in the logarithm cannot be expressed by a constant K, but is expressed by K × CElement, CElement being used to indicate the concentration of the element in the experiment in question.
[531] The convention, adopted in the text, for the use of the positive and negative signs in expressing potentials, is that proposed by Luther (cf. Le Blanc's Lehrbuch der Elektrochemie (third edition), p. 212). The sign always denotes the character of the charge on the first component written in the subscript to ε. Thus, for a copper plate in contact with a solution of cupric sulphate, when C > K, the logarithm, log(C / K), has a positive value and εCu, CuSO4 is positive, which means that the metal will be positive, the electrolyte negative. For instance, for [Cu2+] = 1, εCu, CuSO4 is found to be +0.606 (see the table at the end of Chapter XV). εCu, CuSO4 = −εCuSO4, Cu′. By this use of the signs one is never in doubt as to their meaning. Unfortunately, widely different definitions of the signs have been used (cf. Le Blanc, Electrochemistry (1896), pp. 209, 219, and Lehfeldt, Electro-Chemistry (1904), p. 159). Care must be taken, in using the data of original papers, to be informed as to the definition used.
In accordance with the convention as to signs, adopted in this book, the ratio of concentrations (C / K), used in the logarithm of Nernst's formula, is the reciprocal of the ratio usually given. The change has been made in order that the algebraic signs of the values obtained from the application of the formula should be the same as those observed in the experimental arrangements, as demanded by the convention.
[532] When two electrodes are combined to form an electric cell or couple, the potential difference of the couple is always the (algebraic) difference of the two individual electrode potentials, and hence these are subtracted from each other (algebraically). The electrode of the first term of the difference (the minuend) is named first in the subscript of the potential of the couple; then the sign of the difference represents the character of the charge on that electrode, in agreement with the convention (see footnote 2, p. 261). In illustration: two copper electrodes may be taken, each of which, considered by itself, carries a positive charge, because the concentrations of the cupric-ion in the solutions bathing them are both greater than K; when they are combined, each of the two electrodes will tend to send a positive current, in opposite directions, into the metal connecting them. But the potential of the electrode with the heavier charge (the one dipping into the solution containing the greater concentration of cupric-ion) will overcome the potential of the other electrode, and the current will flow, through the connecting metal, with a potential that represents the difference between the two values. If the electrode of the more concentrated solution is named first in the subscript of the potential of the couple, its individual electrode-potential appears as the first term of the difference (the minuend) and is reduced by the value of the electrode-potential of the second electrode; as this is numerically smaller than the value of the minuend, the difference will be positive, showing that the electrode in the stronger solution, named first in the subscript of the potential difference of the couple, carries a positive charge. Further, if the second electrode dips into a solution, in which the concentration of the cupric-ion is smaller than K, the logarithmic expression for its electrode-potential will be found to give a negative value; and the (algebraic) subtraction of this negative quantity from the electrode-potential of the first electrode will give a larger potential difference, for the couple, than that possessed by the first electrode alone—all of which agrees with the experimental results, when such combinations are made.
Where negative elements are concerned, the same convention holds, but the logarithmic expression for the potential of such an electrode carries a negative sign (see footnote 1, p. 261), which must be inserted, algebraically, when the expression is used as a term in the difference under discussion.
[533] If C′ > C″, the logarithm will be positive and εCu′, Cu″ will have a positive value, which means that the copper plate, Cu′, which is named first in the subscript to ε, will be charged positively, when the system works. If C′ < C″, the logarithm will be negative, which means that the first plate, Cu′, mentioned in the subscript, will receive a negative charge, when the system works. The sign is therefore intended, by the convention adopted (p. 261), to express any result for the working system, irrespective of the charge on the individual plates before they are combined. For instance, for C′ = 1 and C″ = 10−10, both plates are positive, before they are connected with each other, since in each case C > K, and εCu, CuX = (0.0575 / 2) log(C / K) = a positive value. When the plates are combined, we find from εCu′, Cu″ = (0.0575 / 2) log(C′ / C″) that the first plate, dipping in the more concentrated solution of cupric-ion, is positive, which is confirmed by experiment.
[534] (1 / 10)-molar cupric sulphate, 100 c.c., containing some sodium sulphate or nitrate, to reduce the resistance, is a convenient concentration.
[535] The copper plate is best freed from adhering sulphide by means of a strong cyanide solution, and re-introduced into the solution.
[536] Küster, Z. Elecktrochem., 4, 110 and 503 (1897).
[537] In a solution of zinc sulphate in which [Zn2+] = 0.114, the potential εZn, ZnSO4= −0.514 (the minus sign indicates that the metal named first in the subscript has a negative charge). Inserting the values for [Zn2+] and εZn, ZnSO4 in the general equation given on p. 261, and solving for K, we find K = 1017. For [Zn2+] = 0.022 and εZn, ZnSO4 = −0.535, we find K = 1016.8. (Cf. Wilsmore's tables, loc. cit.)
[538] Equilibrium will be established whenever the potential of the system is equal to 0. The potential of the system may be calculated according to the equation (see footnote 1, p. 262)
The potential εCu, Zn is 0 whenever [Cu2+] / KCu = [Zn2+] / KZn, i.e. when [Zn2+] / [Cu2+] = KZn / KCu.
For ions of different valence, such as silver and cupric ions, the equilibrium equation assumes a somewhat less simple form. For Cu ↓ + 2 Ag+ ⇄ 2 Ag ↓ + Cu2+, we have [Ag+]2 / [Cu2+] = (KAg)2 / KCu.
[539] Vide Ostwald's Lehrbuch der allgemeinen Chemie, 2d Ed., Vol. II, p. 874, for the historical data on this action. Vide Küster's experiments, Z. Elektrochem., 4, 503 (1897).
[540] See the footnote, p. 267, in regard to the form the equilibrium ratio assumes when metals producing ions of different valence are used.
[541] The value of the constant is calculated from the data given by Peters, Z. phys. Chem., 26, 193 (1898).
[542] The fact that this equilibrium relation has been proved to hold for the action Fe2+ ⇄ Fe3+ and that it must be taken into account in all oxidation-reduction reactions involving these ions, in no wise excludes the possibility that other equilibrium relations can also exist between ferrous and ferric compounds. For instance, ferrous hydroxide Fe(OH)2 may well have a characteristic tendency of its own to assume a further positive charge (lose an electron) according to Fe(OH)2 ⇄ Fe(OH)2+, the potential of which action may, under given conditions, be a main determining factor in the course of an action, e.g. in alkaline mixtures. It is not impossible, even, that we also must consider negative ions FeO22− and their tendency to be oxidized. Evidence would suggest that ferrous hydroxide, or its negative ion FeO22−, may have, indeed, a very great tendency to be oxidized, possibly much greater than the tendency of Fe2+ to form Fe3+. (Cf. Manchot, Z. anorg. Chem., 27, 419 (1901), and McCoy and Bunzel, J. Am. Chem. Soc., 31, 370 (1909)). Closer investigations of these relations, from a quantitative viewpoint, would probably determine this question and bring exceedingly important relations to light.
[543] E.g. by the potential of the action Cl2 ⇄ 2 Cl−.
[544] The potential of a solution of the iron salts is given by ε = 0.058 log(1017 × [Fe3+] / [Fe2+]). In a solution of a ferric salt, if [Fe2+] = 0, the potential would obviously be ∞, which could not present a condition of equilibrium. Equilibrium is established in such a solution, as will be shown further on in the text, by the liberation of chlorine and the formation of ferro-salt, according to 2 Fe3+ + 2 Cl− ⇄ 2 Fe2+ + Cl2, until the potential, resulting from the tendency of chlorine to form chloride-ion, just balances the tendency of the ferric-ion to form ferro-ion. But when a ferric chloride solution is used as the source of supply of positive electricity, as in the experiment described in the text, both the ferric-ion and the chlorine tend to charge the platinum electrode with positive electricity and to revert to a condition of equilibrium in reference to their individual constants. The relations are much like those between a cupric salt solution and a copper plate: if [Cu2+] > KCu2+, equilibrium will be established, as we have seen, by the positive charging of the plate in sufficient degree to oppose the tendency of the cupric-ion to discharge (see p. 259). But when the solution and plate are used as the source of supply for an electric current (p. 264), both the positive charge on the plate, and the tendency of the cupric-ion to discharge and acquire the concentration [Cu2+] = KCu2+, will supply the positive current. In calculations we ignore the positive charge already deposited on the plate and deal only with the concentration of Cu2+. The chlorine, liberated in a solution of ferric chloride, plays practically the same rôle as does the copper plate in a cupric salt solution, and it can be ignored in the discussion of the combination described in the text. In a ferrous salt solution, in a similar manner, some ferric-ion must always be formed by liberation of hydrogen (see p. 282), until equilibrium is reached according to 2 Fe2+ + 2 H+ ⇄ 2 Fe3+ + H2. Hydrogen plays here the same rôle as chlorine does in the ferric chloride solution.
[545] The condition for equilibrium is [Fe2+] : [Fe3+] = 1017, in a solution considered for itself.
[546] This ratio need not be 1017, since we have two solutions combined with each other and the total potential will be expressed by:
| ε = ε1 − ε2 = 0.058 (log | 1017 × [Fe3+]1 | − log | 1017 × [Fe3+]2 | ) |
| [Fe2+]1 | [Fe2+]2 |
| = 0.058 log | [Fe3+]1 × [Fe2+]2 | . |
| [Fe2+]1 × [Fe3+]2 |
Equilibrium is reached when the total potential is 0. Then
| [Fe3+]1 × [Fe2+]2 | = 1 |
| [Fe2+]1 × [Fe3+]2 |
| [Fe2+]1 | = | [Fe2+]2 | . |
| [Fe3+]1 | [Fe3+]2 |
[547] In order to have very decided differences in the speeds of the action in the absence and presence of fluoride, it is best to use an old ferrous sulphate, or ferrous ammonium sulphate, solution which contains considerable ferric salt.
[548] Vide Peters, loc. cit., p. 236.
[549] Ostwald [Lehrbuch d. allgem. Chem., 2d Ed., II, 883 (1893)], first emphasized the fact that potential differences are a measure of oxidizing and reducing powers.
[550] The constant is calculated from the data of Küster and Crotogino on the potential of solutions of iodine in potassium iodide [Z. anorg. Chem., 23, 88 (1900)]. Owing to the formation of complex ions I3−, for which due allowance has not been made in the calculation, and owing to some uncertainty as to the vague definition of the concentration of iodine used, the estimation of the constant can only be considered a rough one. The value given expresses the order of the equilibrium ratio sufficiently well for our present purposes. In a recent paper, Bray and MacKay [J. Am. Chem. Soc., 32, 914 (1910)] have determined the constant for the formation of the complex ion according to I3− ⇄ I2 + I−, which might be used to correct the data of Küster and Crotogino; but in view of other uncertainties and inaccuracies, the correction has not been considered advisable.
Several related methods may be used to calculate the equilibrium constant for [I−]2 : [I2] = K from the data of Küster and Crotogino. Perhaps the simplest method is the following: A solution of iodine ([I] = 1 / 32 normal, and therefore [I2] = 1 / 64 molar) in 1/8 molar potassium iodide, in which, the degree of ionization being taken into account, [I−] = 0.109, was observed to show a potential εI2, I− = +0.860 (the convention as to signs, discussed on p. 261, is used here and the potential, observed against a so-called "calomel electrode," is reduced to the so-called "absolute potential"; cf. Le Blanc, Lehrbuch der Elektrochemie, p. 214). Now, there must be a certain concentration of iodide-ion, which we will call [C], with which iodine of the above concentration would be directly in equilibrium and would give no potential at all (cf. pp. 261 and 258 in regard to copper). With a change in the concentration of the iodide-ion, a potential would be produced according to εI2, I− = 0.0575 log([C] / [I−]). This relation is of exactly the same nature as that developed for the potential of copper plates, immersed in solutions of cupric-ion of different concentrations (but see footnote 1, p. 261, concerning the sign of the new relation). In the present case, we are dealing with univalent ions, I−, in place of bivalent ions Cu2+, and the factor 0.0575 is used instead of 0.0575 / 2 (see p. 261). If we insert the observed values, [I−] = 0.109 and ε = 0.860, of the experiment described above, into the equation εI2, I− = 0.0575 log([C] / [I−]) and solve the equation for [C], we find [C] = 1014. That means, 1 / 64 molar iodine would be directly in equilibrium with a concentration of iodide-ion = 1014 (if this value is inserted for [I−] in the logarithmic equation, the potential is found to be 0). For the condition of equilibrium for I2 ⇄ 2 I−, according to [I−]2 : [I2] = K, we have then (1014)2 : (1 / 64) = K = 6.4E29. Similarly, for [I−] = 0.109 and [I2] = 1 / 512 the potential ε = 0.831 is observed, and the equilibrium constant is found to be 5.1E29. When [I−] = 0.109 and [I2] = 1 / 128, the potential is 0.850 and the constant is calculated to be 5.3E29. The mean value for K is 5.6E29. In these calculations, the formation of ions I3−, affecting the values for [I−] and [I2], has not been considered, and there is some doubt whether the concentrations of iodine, given by Küster and Crotogino, do not represent [I2] rather than [I], as assumed in the calculations. If the former be the case, the mean value of the above experiments would be 2.8E29. The value, used in the text, is considered sufficiently accurate for the purposes of this book.
[551] This relation of the equilibrium constant and the solution-tension constants may be deduced in a manner similar to that for the analogous equilibrium constant for the oxidation of zinc by the cupric-ion, as given in footnote 1, on page 267. The exact value of the equilibrium constant is uncertain, since KI−, Iodine has not yet been determined with a sufficient degree of accuracy; but the value, used, gives the order of the constant sufficiently well for our purposes, especially when it is considered in connection with the constant given below for the same relation, when the chloride-ion is substituted for the iodide-ion.
[552] This is the value of the constant as calculated from the data given by Wilsmore (Z. phys. Chem., 36, 91 (1900)) for the solution-tension of chlorine under atmospheric pressure at 18°. The calculation may be made exactly as in the case of the similar constant for iodine (p. 273). There must be a concentration of chloride-ion, which we will call [C], with which chlorine, of one atmosphere pressure at 18°, would be directly in equilibrium. The potential of chlorine, against any other concentration of chloride-ion, would be εCl2, Cl− = 0.0575 log([C] / [Cl−]). For [Cl−] = 1, ε is +1.694 (see the table at the end of Chapter XV), and inserting these values in our equation and solving it for [C], we find [C] = 2.88E29. That means, that chlorine, at 18° and of atmospheric pressure, would be in equilibrium with chloride-ion of the concentration given. Since chlorine, at this temperature and pressure, has a concentration of 1 / 23.9 moles (at 18°, one mole is contained in 23.9 liters, instead of in 22.4 liters, at O°), we have for the condition of equilibrium: [Cl−]2 : [Cl2] = (2.88E29)2 : (1 / 23.9) = 2E60. [Cl2] represents, thus, in the calculation of this constant, the concentration of chlorine gas (see Chapter XV concerning gas electrodes) and not the concentration of the dissolved chlorine; the latter, however, is proportional to the gas concentration (Chapter VII).
We will turn now to the consideration of the question, how the principles of the theory of electric oxidation and reduction may be applied to the most important oxidizing agent, oxygen, and to such vigorous and common oxidizing agents as permanganates, dichromates, nitric acid, and similar substances.
In this equation [H2] represents the concentration of the hydrogen in contact with the electrode (see below) and with the solution, and [H+] represents the concentration of hydrogen-ion in the solution bathing the electrode. The ionization of hydrogen, at a given temperature, depends, according to this equation, on two variables, the concentration, or pressure, of the gas and the concentration, or osmotic pressure, of the hydrogen-ion in a given solution.
If platinum gauze, coated with platinum black, is charged with hydrogen, then, the greater the pressure of the gas, the more soluble the hydrogen will be in the platinum (p. 121). Such a charged gauze may be used as a hydrogen electrode (Fig. 13, p. 281), the concentration of the hydrogen in which is proportional to the concentration, or pressure, of the hydrogen gas surrounding it; the platinum will allow of the ready transmission of electric charges from and to the hydrogen dissolved in it. [p278]
The value of the constant553 KH+, Hydrogen = [H+]2 / [H2], at 18°, is found to be 5.55E−9, and hydrogen, at 18°, under atmospheric pressure, is directly in equilibrium with hydrogen-ion of the concentration [H+] = 1.52E−5.
If such an electrode, in contact with hydrogen of atmospheric pressure, is dipped into the solution of some neutral salt, say sodium chloride, in which the concentration of the hydrogen-ion, formed by the ionization of water, at 18°, is 0.9E−7, which is less than 1.5E−5, the hydrogen in the electrode must tend to ionize more rapidly than it is formed from the ion, and the electrode must receive a negative charge, exactly as in the case of zinc, placed in a zinc sulphate solution.
For oxygen similar relations may be developed.554 We have: O2 ⇄ 2 O2− and
If we use the relation of the oxide-ion, O2−, to the more stable hydroxide-ion, HO−, we also have:555 [p279]
The value of the constant KHO−, Oxygen is 8.2E49 at 18°, and oxygen of atmospheric pressure at this temperature should be in equilibrium with solutions containing hydroxide-ion at a concentration556 of 1.36E12.
An electrode of platinum gauze, charged with oxygen under atmospheric pressure, when dipped into the solution of a neutral salt, acquires a very strong positive charge, the minute concentration of hydroxide-ion, 0.9E−7, being very much smaller than the value required by the constant, and the oxygen ionizing very much more rapidly, in consequence, than it is formed by the discharge of hydroxide ions (see p. 259). [p280]
When we combine the hydrogen and the oxygen electrodes, dipping into a solution of sodium chloride, we find a current is, in fact, established (the apparatus discussed on p. 281 is used), and it flows in the direction anticipated from the above development, the positive current entering the voltmeter from the oxygen electrode.557
The potential of the hydrogen electrode, for a constant pressure of hydrogen, is dependent on the concentration of hydrogen-ion in the solution surrounding the electrode, exactly as the potential of a copper plate, against a solution of cupric-ion, depends on the concentration, or osmotic pressure, of cupric-ion in the solution in which the plate is immersed. The concentration of hydrogen-ion, in the present instance, is very small (0.9E−7, at 18°), the solution being practically neutral; but the addition of an alkali must reduce its concentration far below even this value, since for water the product of the concentrations of hydrogen-ion and hydroxide-ion is a constant (p. 176) and the increase in the concentration of hydroxide-ion, produced by the addition of alkali, must decrease the concentration of the hydrogen-ion proportionally. We would expect, then, that the potential of the hydrogen electrode must increase, when we add alkali to the solution surrounding it, the hydrogen now ionizing against a much smaller concentration of its ion. Such is in fact the case (exp.), and the increase is found to be subject to a logarithmic function for the relation between potential and the concentration of the ion, similar to that found to hold for copper and its ion.558 In the same way, the potential of the oxygen electrode must depend on the concentration559 of the hydroxide-ion in the solution bathing it. The addition of a strong acid, like sulphuric acid, to this solution, by suppressing the hydroxide-ion, small as its concentration is, should increase the potential of the [p281] electrode and the total potential of the cell. This, in fact, is the case (exp.); the cell working under these conditions shows us the largest potential yet observed.560
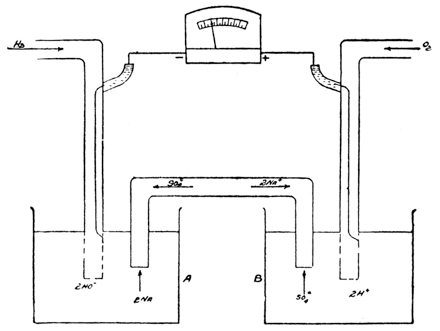
The arrangement of the apparatus and the course of the current are shown in Fig. 14. The glass tube of the hydrogen electrode is connected with a hydrogen generator, the tube of the oxygen electrode with a cylinder or gasometer filled with oxygen. The hydrogen electrode is connected with the negative post of the voltmeter, the oxygen electrode with the positive post. Since the hydrogen ionizes, under the conditions used, more rapidly than it is formed from the small concentration of the hydrogen ions surrounding the hydrogen electrode, hydrogen ions pass from the electrode into solution A, leaving a negative charge on the electrode; there is a migration of sodium ions through the salt bridge (see p. 254) to solution B, and the hydrogen ions formed combine with hydroxide ions and produce water. In a similar way, oxygen passes into solution B in the form of hydroxide ions and these combine with hydrogen ions of the sulphuric acid, forming water; SO42− ions migrate from the solution B through the salt bridge toward solution A and thus prevent polarization (p. 254). While water is an actual product of the action of the cell, working under these conditions, the essential feature of the oxidation of hydrogen is its ionization—H2 → 2 H+; it would be in the same condition of oxidation if the hydrogen ions combined with any negative ions other than HO−, or if they remained ions (as they would, if sodium chloride surrounded the hydrogen electrode). Similarly, the essential feature of the reduction of oxygen is its ionization in the form of HO− ions; in the present [p282] instance, these actually combine with hydrogen ions and form water, but the reduction of oxygen would also be accomplished, if the hydroxide ions remained ionized (as they would, if sodium chloride bathed the oxygen electrode). The formation of water is the result of a union of ions, following the oxidation-reduction reaction, which may be expressed in the following condensed form:
We may recall the fact that a solution of potassium arseniate, to which dilute hydrochloric acid has been added, will remain clear for some time when the mixture is saturated with hydrogen sulphide (exp.). If a considerable excess of concentrated hydrochloric acid is added to this mixture, hydrogen sulphide immediately forms a dense precipitate (exp.) of arsenic pentasulphide—presumably through the union of quinquivalent arsenic-ion with the sulphide-ion: 2 As5+ + 5 S2− ⇄ As2S5 ↓ (see p. 247). This behavior suggested that arsenic acid, although a moderately strong acid, might nevertheless be somewhat amphoteric, might have slight basic properties, as well as its ordinary acid functions. The relation is expressed in the equations:565
Since oxidations by arsenic acid involve its reduction to arsenious acid, containing trivalent,566 in place of quinquivalent arsenic, one might well suspect, that the oxidizing component is the quinquivalent arsenic-ion, As5+, the discharge of two of whose positive charges would cause oxidation (e.g. of iodide-ion), exactly as the discharge of positive charges at the positive pole of an electric current causes oxidation (p. 252): As5+ + 2 I− ⥂ As3+ + I2. [p285]
In a solution of potassium arseniate, we would have only the faintest trace of the ion As5+, since the addition of an alkali to the system, expressed in the above equations, would carry the reversible reactions towards the left. The addition of dilute hydrochloric acid to the system must carry the reactions towards the right and increase the concentration of As5+; the addition of concentrated acid must increase the concentration of As5+ very much more. Even if the concentration of As5+ remained minute, the oxidizing power would be increased proportionally to the ratio of the concentrations in the first and the last solutions. A millionfold increase in concentration, even when we are dealing with very small numbers, would imply a millionfold increase in the activity of the solution. If, then, the oxidizing component of arsenic acid is the quinquivalent ion, As5+, which would tend to discharge two of its positive (oxidizing) charges, arsenic acid should be a much more powerful oxidizing agent in strong acid solution than in alkaline or neutral solutions.
We thus arrive at the conclusion that the addition of hydrochloric acid to a mixture of arseniate and iodide may be effective, in bringing about the reduction of the arseniate and the oxidation of the iodide, primarily because of its action on arsenic acid, perhaps by facilitating its ionization as a base, and that it is not effective through any action on the iodide, for instance by producing free hydroiodic acid, as is often assumed. This conclusion may easily be tested with the aid of the chemometer (see p. 253): potassium arseniate against potassium iodide gives only the faintest possible current, barely perceptible with the aid of a very sensitive voltmeter.567 The addition of hydrochloric acid to the beaker containing the potassium iodide does not increase the potential (it rather decreases it somewhat), whereas the addition of the concentrated acid to the potassium arseniate solution produces a most decided increase in the potential568 (exp.). It is evident, therefore, that the addition of the acid is primarily and directly intended to increase the oxidizing power of the arsenic acid, rather than to increase the reducing power of the iodide. [p286]
The more common methods of expressing oxidation-reduction reactions of this type are illustrated in the following equations:
Both of these forms of expression give the net results of the action correctly. Neither attempts to interpret the interesting and important fact that the reduction of arsenic acid is facilitated by the presence of acids (of hydrogen-ion). It is, at least, also permissible to consider As5+ ions to be present and to express the oxidation-reduction reaction with the aid of this conception,570 as has been done in the previous discussion. In the final analysis, this method seems to have the advantage of showing directly the changes of the valences571 (electric charges) of the atoms involved in the oxidation-reduction, and it also expresses, clearly and definitely, the relation of the hydrogen-ion to the action.571 The following case furnishes an illustration as to how the new point of view works out from the standpoint of a quantitative study of an oxidation-reduction reaction of this type572: uranyl salts, such as the sulphate UO2SO4, are oxidizing reagents, which are readily reduced, particularly in acid solutions, to uranous salts (e.g. to the sulphate, U(SO4)2). The potential of a mixture of uranyl and uranous salts is found573 to depend on the action expressed in the equation UO22+ + 4 H+ + 2 ⊖ ⇄ U4+ + 2 H2O. For the condition of equilibrium (zero potential), it follows that
The value of this constant, at 18°, is found, by calculation,574 to be approximately 1 / 1024. Now, the uranyl-ion UO22+ may be assumed to have the power of ionizing, with the aid of water, to a very slight degree into ions U6+ and HO−, according to
For the ionization of an extremely weak base of this character, we have, further, [U6+] × [HO-]4 / [UO22+] = kbase. And, since [HO−] = KHOH / [H+], we also find, by substitution and by solving for U6+,
In other words, we may substitute [U6+] and a constant factor KHOH4 / kbase for [UO22+] × [H+]4 in the first term (numerator) of the oxidation-reduction equation (3), derived from Luther's quantitative work. We thus obtain:
which must agree just as well with the quantitative data,575 as does the original equilibrium equation (3). It follows, that we may write the chemical equation, for the action in acid solutions, simply U6+ ⇄ U4+, exactly as we have Fe3+ ⇄ Fe2+ (p. 269). [U6+] cannot be measured, as yet, but in the analogous case of Fe3+ ⇄ Fe2+, where both terms of the equilibrium equation are accessible to direct measurement, the experimental evidence distinctly favors576 the views expressed.577
If we bring permanganate, against potassium iodide, into the beakers of the chemometer (p. 253), we find that it is a much more vigorous oxidizing agent than is arsenic acid, and again we find that the addition of acid (sulphuric) to the permanganate solution enormously increases the potential (exp.) and therefore its oxidizing power. The addition of an acid would, obviously, enormously increase the concentration of a positive septavalent ion, if permanganic acid is assumed to be, to a slight extent, base forming and therefore amphoteric:
Similar experiments may be made with ferrous sulphate against permanganate.
The oxidation of ferro-ion, or of iodide-ion, may be represented, most simply, by the equations:
and
Each heptavalent manganese ion is derived from a salt, such as MnX′7 or Mn2Y″7, and, consequently, when two manganese ions Mn7+ are reduced, ten univalent negative ions X′, or five bivalent ions Y″, are liberated and become available for salt formation with the ferric ions, produced, or with the hydrogen ions (from hydroiodic acid) set free by the oxidation of the iodide ions to iodine.
Thus, the oxidation of ferrous sulphate by permanganate, in the presence of sulphuric acid, may be represented, in greater detail, by the equations:
Analogous results are obtained with potassium chromate or dichromate against potassium iodide, ferrous sulphate, hydrogen sulphide, and other reducing agents.
would be facilitated by the high concentration of hydrogen-ion.
Formaldehyde, like other aldehydes, is readily oxidized. A favorite reagent, used in oxidizing it, is an ammoniacal solution of silver nitrate (exp.), the separation of silver from such a solution being a characteristic reaction of aldehydes. The reagent is rendered still more sensitive by the addition of sodium or potassium hydroxide.579 We may ask how we would interpret, from the point of view of the electric theory of oxidation and reduction, the oxidation of formaldehyde and the reduction of silver nitrate to silver, under these conditions. According to the theory, the oxidizing agent in silver nitrate is the silver-ion, the discharge of which gives positive electricity, which the oxidized substance, the formaldehyde, must absorb. But in a silver nitrate solution there is a far larger concentration of the silver-ion than in an ammoniacal solution (p. 220), containing the same total concentration of silver. The complex silver-ammonium-ion Ag(NH3)2+, it may be recalled, is a rather stable one,580 and, consequently, the addition of ammonia to silver nitrate should decidedly weaken its oxidizing power. Still, the practical use of ammonia, especially in combination with sodium hydroxide, is found to be most effective. We are led to suspect that, in spite of the untoward effect of ammonia on the oxidizing power of the silver compound, an alkaline solution is desirable for the sake of the effect of the alkali on formaldehyde, the reducing substance involved. To follow up this conclusion, we must next consider, in some detail, the nature of formaldehyde; we shall presently find that the conclusion, which we have just reached, as to the probably favorable effect of alkali on the reducing power of formaldehyde, will be verified by experiments, which the consideration of formaldehyde will suggest.
The oxidation of formaldehyde may most clearly be formulated on the basis of views, developed by Nef, on the formation of methylene581 derivatives, containing bivalent carbon atoms. A solution [p291] of formalin contains formaldehyde in a variety of forms, in a very complex condition of equilibrium. Of these compounds, the aldehyde, CH2O, probably exists in two forms, which have the same composition and molecular weight, but which differ in the arrangement of the atoms in the molecules (in the structure of the molecules); we probably have CH2═O ⥃ CH(OH), the former of which (CH2═O) is, most likely, by far the more stable and the chief one of these two substances, present under ordinary conditions. The second compound CH(OH) may be present in traces only. One difference, we note, lies in the position of one of the hydrogen atoms in the respective molecules; the second form contains a hydroxide group (OH), which gives it the properties of an acid and renders it capable of forming salts CH(OMe) with bases. But the molecule of this second form also would contain a carbon atom, only two of whose valences are satisfied (by H and OH), two of the ordinary four valences of a carbon atom being thus left free or unsaturated. We may indicate the two free carbon valences in the formula ═CH(OH). Such an unsaturated, bivalent carbon atom ═C would be particularly sensitive to oxidation.582
Besides these two forms, a formalin solution also contains a polymerized form, probably (CH2O)2, which in dilute solution, or under the influence of heat, slowly breaks down into formaldehyde, (CH2O)2 ⇄ 2 CH2O.
The addition of alkali to the mixture probably leads to the formation of the salt ═CH(OMe), thus disturbing all the conditions of equilibrium and leading to the transformation of a very much larger part of the aldehyde into a compound containing the characteristic unsaturated (bivalent) carbon, than was originally present. The aldehyde will thus become more susceptible to oxidation as a result of the enormous increase in the concentration of the oxidizable component. We may assume this to be either the salt, ═CH(OMe), or its negative ion, ═CH(O−), or both, or some analogous derivative. Further, the two free valences of a bivalent carbon atom may be considered to consist of a positive and a negative charge of electricity, either actual or potential,583 and the oxidation will consist [p292] primarily in the absorption of two positive charges, from the oxidizing agent, to convert the negative charge on the carbon atom, say in ±CH(ONa), into a positive charge.584 If the oxidizing agent is alkaline silver nitrate solution, we may formulate the successive actions as follows:
The two positive silver ions correspond to two negative ions, e.g. hydroxide ions HO−, which are set free by the discharge of the silver ions, and which, in turn, will combine with the oxidized carbon atom holding the two positive charges:
The salt formed, HCO2Na, is sodium formate, which is the first isolated product of the oxidation of formaldehyde.
It would appear, from this point of view, that the alkaline nature of the silver nitrate mixture is advantageous primarily because a base is required by the formaldehyde, the reducing agent, to convert it into some readily oxidizable form. And the proved efficiency of the alkaline mixture (see above) makes it appear probable that the advantage gained by this result more than offsets the loss in oxidizing power, suffered by the silver nitrate following the suppression of its real oxidizing component, the silver-ion, when, in the presence of ammonia, the latter is converted largely into the ion, Ag(NH3)2+. Ammonia, in turn, is employed in the oxidizing mixture, essentially with the object of preventing the precipitation of the silver-ion, as silver oxide, by the hydroxide-ion of an alkaline mixture. These conclusions, as well as, in particular, the main conception that in the oxidation of formaldehyde there is an actual transfer of electrical charges, may be fully confirmed with the aid of the chemometer.585
Exp. A small beaker, containing a platinum electrode, which is connected with the positive post of the voltmeter, is half filled with a solution of silver and sodium nitrates. A similar small beaker, containing a platinum electrode leading to the negative post of the voltmeter, is charged with a solution of sodium nitrate (to render the solution a good conductor) and with some formalin. The solutions in the two beakers are connected by means of a salt-bridge containing sodium nitrate. [p293]
Only a very slight current is produced under these conditions; the potential between silver nitrate and formaldehyde is found to be extremely small. If, now, sodium hydroxide is added to the formalin mixture, an enormous increase in potential is observed, proving, unmistakably, that the addition of the alkali to the formalin solution enormously increases the concentration of the reacting, oxidizable component.586
When some ammonia is added to the silver nitrate mixture, we find, as anticipated, that the oxidizing power of the silver solution is greatly reduced, the silver-ion being converted into the complex ion, Ag(NH3)2+; but the potential is still very much greater than the potential between silver nitrate and formalin without any alkali—which shows that the advantage of using alkali with the formaldehyde greatly outweighs the disadvantage of using ammonia with the silver nitrate.
An electric current may also be readily obtained by combining alkaline formaldehyde with other oxidizing agents—for instance with an oxygen electrode (p. 279). We find (exp.) that the oxidation proceeds with remarkable ease under these conditions. Permanganate, dichromate, etc., may be substituted for oxygen, with the same general result.
It also follows, from the conclusions reached, that, under proper experimental conditions, electricity, in the form of a current, must be capable of effecting the oxidation, or the reduction, of organic as well as inorganic compounds (p. 252). Extended investigations have, indeed, shown that electric currents belong to the most important and efficient agents for this purpose, because the oxidation, or the reduction, of the organic compound becomes susceptible to the most exact control through the regulation of the potentials used.587
TABLEA OF EQUILIBRIUM (SOLUTION-TENSION) CONSTANTS (IN MOLAR TERMS) AND OF POTENTIAL DIFFERENCES BETWEEN ELEMENTS AND THEIR IONS IN UNIMOLAR AQUEOUS SOLUTIONS.
| Element, Ion. | E.P.El.,Ion. | KIon. |
|---|---|---|
| K, K+ B | (−2.92) | 6E50 |
| Na, Na+ C | −2.44 | 2.5E42 |
| Ba, Ba2+ | (−2.54) | 2.1E88 |
| Sr, Sr2+ | (−2.49) | 4.0E86 |
| Ca, Ca2+ | (−2.28) | 2.0E79 |
| Mg, Mg2+ | (−2.26) | 4.1E78 |
| Al, Al3+ D | −0.999 ? | 1.3E52 |
| Mn, Mn2+ | −0.798 | 5.7E27 |
| Zn, Zn2+ | −0.493 | 1.4E17 |
| Cd, Cd2+ | −0.143 | 9.5E4 |
| Fe, Fe2+ E | −0.122 ? | 1.8E4 |
| Co, Co2+ F | +0.0138 ? | 0.3314 |
| Ni, Ni2+ G | +0.108 ? | 1.8E−4 |
| Sn, Sn2+ | <+0.085 | <1.1E−3 |
| Pb, Pb2+ | +0.129 | 3.3E−5 |
| H2, H+ H | +0.277 | 1.52E−5 |
| Cu, Cu2+ | +0.606 | 8.3E−22 |
| As, As+++ | <+0.570 | <2.7E−30 |
| Bi, Bi3+ | <+0.668 | <1.4E−35 |
| Sb, Sb3+ | <+0.743 | <1.7E−39 |
| Hg, Hg+ | +1.027 | 1.38E−18 |
| Ag, Ag+ | +1.048 | 6E−19 |
| Pt, Pt4+ | <+1.140 | 5E−80 |
| Au, Au3+ | <+1.356 | <1.8E−71 |
| F3, F− H | (+2.24) | 9.0E88 |
| Cl2, Cl− H | +1.694 | 3.16E29 |
| Br2, Br− | +1.270 | 1.23E22 |
| I2, I− | +0.797 ? | 7.26E13 |
| O2, HO− I | +0.698 | 1.36E12 |
[A] The table is based on Wilsmore's compilation of solution-tension potentials, Z. phys. Chem., 36, 91 (1901).
[B] Values in parentheses have been estimated by indirect measurements.
[C] G. N. Lewis, J. Am. Chem. Soc., 32, 1467 (1910).
[D] Values marked with? are uncertain.
[E] Calculated from the data of Richards and Behr (Z. phys. Chem., 58, 301 (1907)), who found the potential of iron against 0.5 molar FeSO4 to be −0.15 volt. The degree of ionization of 0.5 molar FeSO4 is taken as 22%. [Λ = 25.8 (Kohlrausch and Holborn, loc. cit., p. 152) and Λ∞ is taken as 117, as for ZnSO4 (ibid., p. 200).] On account of the doubtful value for the degree of ionization, the values in the table are marked?, but the value found by Richards and Behr appears to be quite accurate.
[F] Calculated from the data of Schildbach (Z. für Elektroch., 16, 967 (1910)). The same uncertainty as to the degree of ionization exists as that discussed in the previous footnote.
[G] Calculated from the data of E. P. Schoch (Am. Chem. J., 41, 208 (1909)). The same uncertainty as to the degree of ionization exists as that discussed in footnote 5, p. 294.
[H] The values for gaseous elements refer to the gases under one atmosphere pressure.
[I] The potential of oxygen at 18°, 760 mm., against an alkaline solution in which [HO−] = 1. KIon refers to the concentration of HO−, with which oxygen under atmospheric pressure would be directly in equilibrium, at 18°.
The potential differences, given in the table, are based on the assumption that the absolute zero of potential is at such a point, that the so-called standard normal calomel electrode has a value of +0.56 volt relative to this zero (cf. Ostwald, Z. phys. Chem., 36, 97 (1901)). The exact determination of this value is a very difficult matter. Recently Palmaer (ibid., 59, 129 (1907)), located the absolute zero at a point 0.04 volt more positive than the above, making the absolute potential of the normal calomel electrode, approximately, +0.52 volt. To refer potentials, given in this book, to this new zero, one would subtract 0.04 volt from all positive potentials and add 0.04 to the numbers representing negative potentials (e.g. E. P.Zn,Zn2+ would become −0.569 in place of −0.529 volt). Since the equilibrium (solution-tension) constants are calculated from the potential differences referred to the absolute zero (p. 259), any change in the zero involves corresponding changes in the values of the equilibrium constants, as calculated for this book. However, it should be noted that all potential differences would be corrected by the same constant quantity (0.04 volt for Palmaer's zero): all the equilibrium constants for univalent metallic ions would be increased proportionally to a constant factor c (c is very nearly equal to 5, for Palmaer's zero), the equilibrium constants for bivalent metallic ions would be increased proportionally to c2, etc. The equilibrium ratio for two metals and their ions would in no wise be changed by these alterations: e.g. for the equilibrium between zinc and copper and [p296] their ions (p. 267), Kequil. = KZn2+ / KCu2+; the factor c2 would be introduced into both terms of the ratio and would not affect the value of the latter. For the condition of equilibrium between silver and copper and their ions (p. 267) Kequil. = KAg+2 / KCu2+, and since (c)2 = c2, this equilibrium ratio would also not be affected. For elements, which produce negative ions, the corresponding correction factors would be 1 / c, 1 / c2, etc., and the equilibrium relations between two such elements and their ions likewise would remain unchanged. Since these equilibrium relations are the significant ones in this work, and since our conclusions have been based on them, it is clear that a change in the absolute zero would not affect the conclusions reached.
On account of the uncertainty attaching to the determination of the absolute zero of potential, it is preferred, in practice, to report the experimentally determined potentials as measured against a constant, well-defined electrode (such as the calomel electrode or a hydrogen electrode) and thus to eliminate the variation, which a change in the determination of the zero potential would make necessary. However, for an elementary discussion of oxidation-reduction reactions, from the same viewpoint as is used in considering all other reversible chemical actions, the idea of the absolute potential has certain advantages, making a uniform treatment possible.
1. Meaning of KIon. Under KIon is given, for each element, the concentration of its ion, with which the element would be directly in equilibrium at the ordinary temperature (see p. 258). The constants for gaseous elements represent the constants of the gases under atmospheric pressure.
2. The Condition for Equilibrium between Two Elements and Their Ions. The condition of equilibrium in a system of two elements and their ions may be found with the aid of the constants KIon, as follows: For Zn ↓ + Cu2+ ⥂ Zn2+ + Cu ↓ we have for the condition of equilibrium (see p. 267)
Zinc-ion must be present in enormous excess in the condition of equilibrium and zinc will precipitate copper from solutions of cupric salts until this relation is established. The suppression of the cupric-ion—by precipitation in the form of insoluble salts or by conversion into very stable complex ions—makes [Cu2+] exceedingly small and makes it increasingly difficult for zinc to precipitate copper, and, under certain conditions, the ordinary course of the action may be reversed (p. 268).
For Cu ↓ + 2 Ag+ ⥂ Cu2+ + 2 Ag ↓, we have (p. 267)
3. Potential Differences Calculated with the Aid of KIon. For metallic elements, which send out positive ions, in contact with an aqueous solution containing the ion in concentration [C], the potential difference is (see p. 261)
In these equations v represents the valence of the ion. It is clear that for the condition of equilibrium, in which [C] = KIon, the potential is 0. Further, for the potential difference between copper and a cupric salt solution in which [Cu2+] = 1, we would have
4. Meaning of E.P.Element, Ion. Under E.P.Element, Ion the table gives the potential difference in volts, calculated for the element named and an aqueous solution of its ion in unit concentration (one gram-ion per liter). For instance, for zinc and [Zn2+] = 1 (65.4 grams zinc-ion per liter), we have a potential E.P.Zn, Zn2+ = −0.493. The signs used, in accordance with the convention adopted (p. 261), indicate the character of the charge on the element electrode (which is named first in the subscript to E.P.). For instance, zinc in a solution in which [Zn2+] = 1 would acquire a negative charge (p. 266), the potential difference E.P.Zn, Zn2+ being −0.493 according to the table; silver, immersed in a solution in which [Ag+] = 1, would acquire a positive charge, the potential difference E.P.Ag, Ag+ = +1.048.
The potentials given for the gaseous elements represent the potentials of the gases under 760 mm. pressure.
5. Potential Differences Calculated with the Aid of E.P.Element, Ion. The potential corresponding to any concentration [C] of a metal ion may be found from the equation588
and the potential for any concentration [C] of the ions of elements forming negative ions is found588 according to
6. The Condition for Equilibrium between Two Metals and Their Ions, Calculated with the Aid of E.P.Element, Ion. The condition for equilibrium in a system of two metals and their ions is determined by the fact that the potential of the system must be 0 when equilibrium is established. We have, for instance for the two metals zinc and copper and their ions, Zn2+ and Cu2+, for Zn ↓ + Cu2+ ⇄ Cu ↓ + Zn2+ the condition for equilibrium that εCu, Cu2+ − εZn, Zn2+ = 0. According to the equation given in § 5, we have, then, for the condition of equilibrium,
Then
From the last relation we find log([Zn2+] / [Cu2+]) = 38.2261, and therefore, for the condition of equilibrium, [Zn2+] / [Cu2+] = 1.7E38.
7. Equilibrium Constants for Elements with Variable Concentration. The concentration of a pure metal at a given temperature may be considered a constant, except in the case of extremely thin films of the metal (p. 258). The concentration of hydrogen, and of the non-metallic elements given in the table, is variable, and KIon has a definite value only when the concentration of the element is defined (see the preceding table, footnotes 3, 4, p. 295). For certain estimations the equilibrium constants, which show the relation between the two variables, namely the concentration of the element and that of its ion, are very helpful (see pp. 274 and 275). In the following table some of the more important equilibrium constants of this nature are given.
TABLE OF EQUILIBRIUM CONSTANTS.
| Element. | Kequil.. |
|---|---|
| Hydrogen: [H+]2 : [H2] | 5.6E−9 |
| Oxygen: [HO−]4 : [O2] | 8.2E49 |
| Chlorine: [Cl−]2 : [Cl2] | 2E60 |
| IodineA: [I−]2 : [I2] | 5.6E29 |
The significance of the constants is indicated by the ratios given in the table. The relation of these constants to those given in the first table may be seen from the following illustration. For hydrogen we have H2 ⇄ 2 H+. The first table tells us that hydrogen, at 18° under atmospheric pressure, is in equilibrium with its ion when the concentration of hydrogen-ion is 1.52E−5 (under KIon). Now, a mole of hydrogen at 18° occupies 22.4 × 291 / 273 = 23.9 liters under atmospheric pressure, and its concentration (per liter) is therefore 1 / 23.9 mole. Then equilibrium exists, when [H2] = 1 / 23.9 and [H+] = 1.52E−5 and Kequil. = [H+]2 : [H2] = (1.52E−5)2 × 23.9 = 5.6E−9.
[553] These constants are calculated from data given in Wilsmore's tables (loc. cit.) on the solution tension of hydrogen. Hydrogen, at 18° under one atmosphere pressure, produces a potential of εH2, H+ = +0.277 (see p. 261, in regard to the sign) against a solution containing hydrogen-ion in a concentration [H+] = 1 (see the table at the end of this chapter). Now, there must be some concentration of hydrogen-ion, which we will call [C], with which hydrogen at 18° and 760 mm. pressure is directly in equilibrium, with the potential 0. For any concentration of hydrogen-ion [H+], other than [C], a potential is produced according to εH2, H+ = 0.0575 log([H+] / [C]). If we insert into this equation the values [H+] = 1 and the potential ε = +0.277, and if we solve the equation for [C], we find [C] = 1.52E−5. That is the concentration of H+, with which hydrogen of one atmosphere pressure at 18° is directly in equilibrium. Since under these conditions of temperature and pressure [H2] = 1 / 23.9 mole, we have for the condition of equilibrium [H+]2 / [H2] = K : (1.52E−5)2 : (1 / 23.9) = 5.55E−9 = K.
[554] Experimentally the relations for an "oxygen electrode" are much more complicated than for a hydrogen electrode, as a result, apparently, of the oxidation of the metal (e.g. platinum), with the aid of which the electrode is prepared. For a critical review and summary of the more recent results on this point, vide Schoch, J. phys. Chem., 14, 665 (1910). For the purposes of this book it will be sufficient to limit our discussion to the behavior of an ideal oxygen electrode.
[555] The bivalent oxygen ions, O2−, combine with hydrogen ions (formed, for instance, by the ionization of water) and form the more stable hydroxide ions (p. 246): O2− + H+ + HO− ⇄ 2 HO−, or simply, O2− + H+ ⇄ HO−. Then, [O2−] × [H+] / [HO−] = k and [O2−] = k × [HO−] / [H+]. But since we have [H+] × [HO−] = KHOH for the ionization of water (p. 176), we also have:
By substituting this value for the concentration [O2−] of the oxide-ion in equation (1), equation (2) is obtained. The constant K2 includes then the constants k and KHOH.
[556] The constants are calculated from the estimated potential of the oxygen-hydrogen cell, +1.231 volt, at 18°. (Vide G. N. Lewis, Z. phys. Chem., 55, 465 (1906); Nernst and Wartenberg, ibid., 56, 534 (1906); Brönsted, ibid., 65, 91 (1908); and a summary and discussion by Schoch, loc. cit.) At 18° oxygen, under one atmosphere pressure, gives an estimated potential εO2, HO− = +1.508 against an acid solution, in which the concentration of the hydrogen-ion [H+] = 1 (see the table at the end of this chapter). Since at 18° [H+] × [HO−] = 0.81E−14, the value for [HO−] in this acid solution is 0.81E−14. Now, for oxygen, at 18° and 760 mm., there must be some concentration of hydroxide-ion, which we will call [C], at which the tendency of the oxygen to ionize is exactly balanced by the tendency of the hydroxide-ion to form oxygen—at this point the potential is 0. For any concentration [HO−] of the hydroxide-ion, other than [C], a potential will exist εO2, HO− = 0.0575 log([C] / [HO−]). Since for [HO−] = 0.81E−14, we have a potential εO2, HO− = +1.508, these values can be introduced into the equation and the latter solved for [C]. We find thus [C] = 1.36E12, and oxygen, at 18° and 760 mm. pressure, would be directly in equilibrium with a solution in which [HO−] = 1.36E12. At 18° and 760 mm. pressure a liter of oxygen contains 1 / 23.9 mole, and thus we have for the condition of equilibrium [HO−]4 : [O2] = K : (1.36E12)4 : (1 / 23.9) = 8.2E49 = K.
[557] The most convenient form of electrode for this purpose consists (see Fig. 14) of a cylinder (about one inch long) of platinum gauze, which is fused to a glass tube and connected with a wire leading through the tube to some mercury, held in a small branch tube, fused into the main tube near its upper end. The gas is easily conducted to the platinum gauze electrode through such a tube. The cylinder of platinum gauze may be made by joining the ends of rolled gauze with pieces of molten glass. It is coated with platinum black.
[560] See Ostwald, Z. phys. Chem., 11, 521 (1893), Arrhenius, ibid., 11, 805 (1893), and Nernst, ibid., 14, 155 (1893), for a detailed discussion of oxygen-hydrogen gas cells. For more recent work, vide G. N. Lewis, J. Am. Chem. Soc., 28, 158 (1905), where references to other recent investigations are given.
[563] Fredenhagen, Z. anorg. Chem., 29, 424 (1902), has brought interesting experimental evidence of the charging of an electrode with gaseous oxygen, when ferric-ion is the oxidizing agent in aqueous solutions. Whether the oxygen, which is liberated by the action of the ferric-ion on water, 4 Fe3+ + 4 HO− ⇄ 4 Fe2+ + O2 + 2 H2O, is always the intermediate product and the direct oxidizing agent in aqueous solution, can hardly be considered decided by the experiment—it may well be the product of a parallel action, which must take place to a certain extent, according to the laws of equilibrium, in a system containing both Fe3+ and HO− ions. The result hardly proves that oxygen must be the intermediate product in the main action, when ferric ions act as the oxidizing agent. We may consider, for instance, a solution containing an iodide and a ferric salt: iodide ions have a far smaller affinity for their negative charges (electrons) than hydroxide ions have, and, consequently, will transfer their negative charges (electrons) more readily to the ferric ions than the hydroxide ions would. The action, if oxygen were first liberated, would lead to the same ultimate result, but the observation made by Fredenhagen would not prove that the main action would not nevertheless go by the shorter direct path rather than through an intermediate formation of oxygen.
[564] According to the theory, that arsenic acid is an oxidizing agent because it gives up oxygen of a definite pressure, this pressure would be the more effective, the more completely the opposing hydroxide-ion is suppressed by added acid (p. 280; see also p. 272, on the action of ferro-ion on silver-ion in the presence and in the absence of fluorides).
[565] Only the simplest form of basic ionization of arsenic acid is considered. Intermediate ionization into As(OH)4−, As(OH)32−, etc. (see p. 249), is, of course, to be assumed in any complete investigation of the subject.
[566] Arsenious acid As(OH)3, or HAsO2, as well as its anions AsO33− and AsO2−, may have their own characteristic tendencies to assume positive charges and be oxidized to arsenic acid and its derivatives (see footnote 1, p. 270). In alkaline solutions these tendencies, and the potentials corresponding to them, might well be more important factors in determining the course of an action, than the tendency of As3+ to form As5+. The discussion in the text, which deals primarily with acid solutions, does not exclude such relations.
[567] A millivoltmeter is used for this experiment.
[568] See footnote 1, p. 284, in regard to the interpretation of this experiment on the basis of the theory of liberation of oxygen by arsenic acid.
[569] Cf. Smith's General Inorganic Chemistry, p. 712.
[570] The essential feature of this point of view was first published by Abegg, Z. anorg. Chem., 39, 330 (1904), and Z. phys. Chem., 43, 385 (1903); vide also Stieglitz, Am. Chem. J., 39, 51 (footnote) (1908), and Qualitative Analysis Notes, University of Chicago (1905). Abegg's view has recently received support from J. J. Thomson in his Corpuscular Theory of Matter, p. 118.
[571] H+ does not change its valence (charge) in the action, and yet it appears as an essential component in both styles of the current equations for the oxidation-reduction reaction.
[572] A somewhat similar development of these relations, for arsenic acid, has been found in Abegg's Anorg. Chem., III, 3, p. 552 (1907).
[573] Luther and Michie, Z. für Elektroch., 14, 826 (1908).
[574] The calculation is based on the results obtained by Luther and Michie.
[575] The proportion of UO22+ converted into U6+ would be so minute, that in an experimental determination of the concentration [UO22+], the concentration [U6+] would no doubt be a negligible quantity.
[576] Peters, Z. phys. Chem., 26, 193 (1898).
[577] In other instances, the action of the hydrogen-ion in facilitating and accelerating chemical actions (often called its "catalytic effect") has been explained, in a similar fashion, as being based on salt formation, followed by the ionization of the salts formed, the active components being the ions (vide, for instance, Bredig, Z. für Elektroch., 9, 118 and 10, 586 (1904) and Stieglitz, Report of the Congress of Arts and Sciences, St. Louis, 4, 276 (1904) and Am. Chem. J., 39, 29, 415 (1908) and later articles). In many of these cases, the ion concentrations of the reacting components have not yet been accessible to direct measurements, but the viewpoint has been sustained by quantitative studies of analogous reactions, which were selected for study, because the factors involved could be measured (cf. Stieglitz, loc. cit.).
[578] Usher and Priestley, Proc. Roy. Soc., B, 77, 369 (1905); 78, 318 (1908).
[579] Tollens, Ber. d. chem. Ges., 15, 1635 (1882).
[580] [Ag+] × [NH3]2 / [Ag(NH3)2+] = 1 / 107.
[581] Methylene CH2, itself, has never been isolated, but derivatives of it are known, such as the cyanides, C(NH), C(NK) (see pp. 66, 237).
[584] If a negative charge is an electron, a positive charge the absence of an electron in an atom, the bivalent carbon atom loses two electrons, when it is oxidized.
[585] See Stieglitz, Science, 27, 774 (1908).
[586] The oxidation occurs essentially in the same manner as described (p, 292) for the action of formaldehyde on ammoniacal silver solution, when they are brought together in a single vessel. In the present case, where the action is used to produce an electric current, there is a migration of negative ions into the formalin solution through the salt-bridge (p. 254). For every two silver ions discharged on the electrode in the silver nitrate solution, two hydroxide ions are liberated in the formaldehyde solution, as a result of this migration, and they combine with the oxidized carbon atom. The oxidation may be expressed, then, simply as follows:
By comparison with the equations given on p. 292, it is evident, that the only difference lies in the fact that the positive charges, in the present case, are carried to the formaldehyde salt through metal wires and a metal electrode, while previously they were discharged directly by silver ions on the formaldehyde salt.
[587] Cf. Nernst, Theoretical Chemistry (1904), p. 739, and the applications mentioned there.
[588] Le Blanc, Elektrochemie, p. 215; v is the valence of the ion.
The systematic analysis for acid ions is made on a plan differing in an important particular from the systematic analysis for metal ions. The latter, as has been seen, are divided into groups, which, by precipitation or solution of characteristic salts, are successively separated from subsequent groups, before the isolated groups are analyzed. That is, in general, a group of metal ions is examined in the absence of the ions of all other groups. Acid ions are also divided into groups, but, as a rule, the groups are not separated from each other for analysis. The reason for this difference in procedure is found, chiefly, in the fact that foreign acid ions interfere589 to a smaller degree with the specific tests for the ions of a group, than is the case in the analysis for metal ions.
If acids were present only in the form of the free acids or of their alkali salts, the division into groups could naturally and profitably be made to include groups, which are identified by reactions carried out in neutral or alkaline solution, as well as by such as are made in acid solutions. Now, cations other than the alkali ions are liable to interfere with tests designed for alkaline or neutral solutions. For instance, a group of acid ions, in which the phosphate-ion is included, is characterized by the fact that the acids form barium salts, which are soluble in acid but not in neutral or alkaline solutions. The absence or presence of such a group may be recognized, if no cations other than the alkali metal ions are present, by the addition of barium chloride to the solution and by careful neutralization of any free acid, by ammonium [p300] hydroxide. Barium phosphate and the barium salts of the other acids of the group will be precipitated, if their ions are present. It is clear, however, that a number of metal ions must interfere with the test. For instance, a solution of aluminium nitrate or of ferric chloride, treated with barium chloride, and with ammonium hydroxide to neutralize the acid present in the solution as a result of the hydrolysis of the salt, would give a precipitate of aluminium hydroxide or of ferric hydroxide, and not of barium salts. The formation of a precipitate under these conditions evidently will not constitute any basis whatever for reaching a conclusion as to the presence or absence of acid ions, such as can form precipitates of barium salts under the same circumstances.
The treatment with sodium carbonate, while advantageous in certain cases, is not uniformly successful590: it is also frequently complicated by the presence of amphoteric bases or of organic substances, and frequently demands treatments and tests beyond those made with the solution thus prepared. Furthermore, if a group is found to be present, say a group of acid ions forming barium or calcium salts insoluble in water, but soluble in acids,591 all the acids of the group, which have not been found to be present or absent in the analysis for metal ions,592 must be specifically [p301] tested for, although they may all be absent and the only representative of the group present may be an ion previously found in the analysis for metal ions.593 Then, too, when the group is found to be absent by the group test, more sensitive tests for some of the acid ions of the group must still be made to insure their complete absence.594
While much may be said in favor of the systematic analysis for acid ions, based on the preparation of a solution containing only the alkali salts of the anions, and while one should be familiar with the plan and be able to have recourse to it at will, yet the drawbacks mentioned suggest another basis for the analysis.
Since the grouping for both methods of analysis may be made the same, the following grouping of acid ions has been adopted. Only the group characteristics are given; the members of the groups are described in detail in the Laboratory Manual (Part III).
I. Ions of Amphoteric Acids and of Related Acids. This group includes those acids whose amphoteric character, or whose ready reduction by hydrogen or ammonium sulphide, leads to their being found, or indicated, in the systematic analysis for metal ions.
II. The Carbonate Group. This group includes those acids whose physical properties (insolubility), or the physical properties of decomposition products of which (carbon dioxide is a decomposition product of carbonic acid), usually lead to their discovery in the course of the preparation of solutions or of the analysis for cations.
III. The Sulphate Group. The barium salts of this group of acid ions are insoluble in acid solution. Barium nitrate, added to a solution acidified with nitric acid, is the group reagent.
IV. The Chloride Group. The anions of this group form silver salts, which are insoluble in nitric acid. Silver nitrate, added to a solution acidified with nitric acid, is the group reagent.
V. The Phosphate Group. A test for this group, as a whole, can be made only if cations other than the alkali metal ions are absent: the barium salts of the acid ions of the group are insoluble in neutral, but soluble in strongly acid, solutions. Barium nitrate, used with a neutral solution, is the group reagent in the absence of metal ions other than the alkali metal ions. In the presence of other cations, the three members of the group, which are not found in some other group,595 namely: phosphate, borate and fluoride ions, are tested for specifically, and the group test omitted. Phosphate-ion is tested for in nitric acid solution, in the same solution as is used for the tests for groups III and IV. [p303]
VI. The Nitrate Group. The salts of the acids of this group are readily soluble in water and specific tests for the acid ions are made; there is no group test.
VII. The Group of Organic Acids. This group need only be considered when a test for organic matter reveals its presence.
In the following, only a few typical and interesting applications of the principles and theories to acid ions will be given; numerous other applications will suggest themselves in connection with the laboratory work on the acids.
For a solution saturated simultaneously with the three silver salts, the value of the concentration of the silver-ion is the same in the three solubility-products (see p. 164). Consequently, for such a solution, with which the three solid salts are in equilibrium, the ratios of the concentrations of the anions must be: [Cl−] : [Br−] : [I−] = KAgCl : KAgBr : KAgI = 3 × 105 : 1300 : 1. That is, if silver nitrate is added to a mixture of iodides, bromides and chlorides, silver iodide must be precipitated first, until the concentration of bromide-ion, in solution, is 1300 times as great as the concentration of the iodide-ion left in solution. Then bromide and traces of iodide of silver will be precipitated, until the concentration of chloride-ion is 300,000 times as great as the concentration of iodide-ion and some 250 times as great as the concentration of the bromide-ion. In other words, if silver nitrate is added gradually to such a mixture, iodide-ion and bromide-ion will be almost completely removed from solution before a precipitate of silver chloride can be in equilibrium with the solution. This gives us a convenient and rapid method of detecting chlorides, if present, [p304] in more than small quantities, with iodides and bromides. Silver nitrate, a few drops at a time, is added to the solution and the mixture vigorously shaken after each addition. As long as a yellow (AgI) or yellowish (AgBr) silver salt is precipitated on the addition of silver nitrate to the supernatant liquid (the precipitate settles quickly), silver nitrate is added as before; when the color becomes quite pale, the solution is filtered and silver nitrate added a drop at a time; if a pure white precipitate results finally, chloride-ion is present in the mixture (exp.).
The condition of equilibrium between silver-ion, ammonia and silver-ammonium-ion is expressed in the relation:
The concentration of silver-ion, which may exist in an ammoniacal solution, evidently must decrease rapidly with increasing concentrations of the free ammonia. Now, let us imagine only sufficient free ammonia, in solution, added to a mixture of silver chloride, bromide and iodide, to keep the concentration of silver-ion, which can exist in the solution, say at [Ag+] = 6E−9, which is just 1 / 100th of the concentration of silver-ion in a saturated aqueous solution of silver bromide. Such a solution of ammonia, in contact with the three silver salts mentioned, will dissolve silver chloride, if sufficient is present, until [Cl−] = KAgCl / 6E−9 = 0.017 molar. At the same time, silver bromide would be dissolved until [Br−] = KAgBr / 6E−9 = 0.000,06 molar. In other words, silver chloride could be dissolved in some quantity, while silver bromide is dissolved only in traces (the ratio of [Cl−] : [Br−] is again about 250 : 1). When such an ammoniacal extract is acidified with nitric acid, almost pure (white) silver chloride would be precipitated and only traces of bromide would be lost. After the extraction of the chloride, an increased concentration of ammonia would lead, similarly, to a solution in which silver bromide would dissolve readily and only traces of the iodide be lost, and thus a separation of bromide and iodide may be effected.
In Hagar's method, the concentration of ammonia, required to dissolve silver chloride with but traces of bromide, is attained by the use of a solution of ammonium sesqui-carbonate,598 in which free ammonia is present only in small concentration, as a result of the hydrolysis of the salt. After the [p305] extraction of the chloride by this solution, the bromide is extracted with a 5% solution of ammonia.
Ammonium phosphomolybdate, (NH4)3PO4, 12 MoO3, is the salt of a complex phosphomolybdic acid, formed from phosphoric acid, O:P(OH)3, and molybdic acid, O2Mo(OH)2, by a loss of water, much as potassium dichromate is formed from potassium acid chromate [KO(CrO2)OH + HO(CrO2)OK ⇄ KO(CrO2)O(CrO2)OK]. The only difference between the two actions lies in the fact that, in the case of the dichromate, anhydride formation occurs between two molecules of a single acid; in the case of the phosphomolybdate, anhydride formation takes place between molecules of different acids, and a much larger number of molecules is involved. If we suppose the combination between the two acids to proceed symmetrically,601 we may consider the following to be the action:
Intermediate complex acids, containing less molybdic acid, are no doubt formed first (the action is a relatively slow one), and the action proceeds until the formation of an insoluble salt leads to the final precipitation of all of the phosphate in this form. The precipitate shows the characteristic behavior of an acid anhydride—alkalies dissolve it readily and form phosphate and molybdate—e.g. ammonium hydroxide forms [NH4]2HPO4 and (NH4)2MoO4 (exp.). Dichromates, in a similar way, are converted by alkalies into chromates, an action which may readily be followed by the change in color (exp.).
We shall discuss here only one other oxidation-reduction reaction, taken in connection with the laboratory work—the oxidation of hydroiodic acid by exposure to the air and the resistance to oxidation shown by an iodide, such as potassium iodide, under the same conditions. The following method of proximate analysis of the chief relations involved may also be used to interpret the contrast in the behavior of hydroiodic acid and that of hydrobromic or hydrochloric acid (Laboratory Manual, q. v.). In all of these cases the actual relations are rendered more complex in consequence of secondary reactions, than is indicated in the text that follows: it is intended only to outline the most effective of the factors involved and to illuminate the qualitative results observed.
The condition for equilibrium will be
A system in which I− is directly in equilibrium with I2 (for which [I−]12 : [I2]1 = KI−, Iodine = 5.6E29, at room temperature (p. 298)) and in which, at the same time, HO− is directly in equilibrium with O2 (for which at room temperature [HO−]14 : [O2]1 = KHO−, Oxygen = 8.2E49 (p. 298)) would also represent a condition of equilibrium for the four components. We find thus
With the aid of this constant and of equation (2) we can obtain, at least, an approximate interpretation of the results of the exposure of hydroiodic acid and of potassium iodide to the influence of atmospheric oxygen.604 We may [p307] calculate, first, what concentration of free iodine would be required to prevent oxidation of hydroiodic acid, in molar solution, by the oxygen of the air, i.e. to establish equilibrium. We will call x that concentration of I2. As hydroiodic acid is a very strong acid, ionized to the extent of about 80% in molar solution, we may, with sufficient accuracy for our purpose, consider it completely ionized and put [I−] = 1 and [H+] = 1. Since at 25° [H+] × [HO−] = 1.2E−14 (p. 104), we may put [HO−] = 10−14. The concentration of oxygen in the air, at room temperature, may be considered to be approximately [O2] = (1/5) × (1 / 23.9). Inserting all these given values in equation (2), we have
| [I−]4 × [O2] | = | 1 × (1/5) × (1 / 23.9) | = 4 × 109. |
| [I2]2 × [HO−]4 | x2 × (10−14)4 |
Solving for x, we find x = 1022 = [I2]. That is, free iodine of this enormous concentration would be required to prevent oxidation of hydroiodic acid in molar solution by the oxygen of the air at room temperatures. It is obvious that hydroiodic acid must be extremely sensitive to oxidation by exposure to air.
One might estimate, in a similar way, the extent to which hydroiodic acid, of a given concentration, would be oxidized by air before equilibrium would be reached. The process would involve simultaneous changes in three factors—iodide-ion is destroyed, iodine is formed and hydroxide-ion increases, as the result of the neutralization of hydrogen-ion by the hydroxide-ion formed in the action (see above). The solution of the equilibrium equation is too involved for the elementary purposes of this discussion: it leads to the same qualitative conclusion as was just reached.
| [I−]4 × [O2] | = | 1 × (1/5) × (1 / 23.9) | = 4E9. |
| [I2]2 × [HO−]4 | y2 × (2 y)4 |
Solving for y, we find y = 0.007. That is, in molar solution, about 1.4% of the iodide608 would be oxidized (carbonic acid and other acids being excluded); in 5 c.c. (see Lab. Manual, p. 73) 9 milligrams of iodine609 would be liberated to reach a condition of equilibrium.610
It is thus clear that the conditions for equilibrium between a solution of an iodide and air would be satisfied, in the case of an alkali iodide, by the liberation of a mere trace of iodine, whereas, as was previously shown, in the case of hydrogen iodide, a very large proportion of iodine must be liberated before equilibrium could obtain. A careful comparison of the two developments shows that the difference in result610 is plainly due to the higher oxidizing power, the higher potential of oxygen (p. 280), in acid solutions, containing only a minute concentration of hydroxide-ion, as compared with its efficiency in neutral or slightly alkaline solution.
[589] In the few cases when there is interference, it is provided against.
[590] Cf. Fresenius, Qualitative Analysis, p. 520.
[591] The group includes phosphate, borate, fluoride, oxalate, silicate, arsenite, arseniate, chromate and tartrate ions.
[592] The ions of the amphoteric acids, arsenic and arsenious acids, and chromate-ion, which is reduced by hydrogen sulphide to chromium-ion, are found in the systematic analysis for metal ions.
[593] The ions of the amphoteric acids, arsenic and arsenious acids, and chromate-ion, which is reduced by hydrogen sulphide to chromium-ion, are found in the systematic analysis for metal ions.
[594] See Fresenius, loc. cit., p. 511, footnote, and p. 520.
[595] Other acid ions which would show the group test—precipitation of a barium salt in a neutral solution—are determined in other groups, as follows: arsenite, arseniate and chromate ions in the group of amphoteric acids, etc. (I); carbonate and silicate ions in the carbonate group (II); and oxalate and tartrate ions in the group of organic acids (VII).
[596] The constants refer to 18°. The subindices are used to distinguish the (unequal) concentrations of the silver-ion and of the halide ions in the different solutions referred to in the text.
[597] Hagar's method. See Fresenius, loc. cit., pp. 356 and 378.
[598] See Fresenius, loc. cit., pp. 356 and 378, for the preparation of the solution and for details of the method, and see Smith, General Inorganic Chemistry, p. 566, as to the nature of the sesqui-carbonate.
[599] They also form complex ions with substances related to ammonia, such as the organic amines.
[600] Ammonium arsenomolybdate is an analogous salt (see Laboratory Manual, Part III). A similar complex acid, phosphotungstic acid, is used in alkaloidal analysis.
[601] The exact structure of the complex acid is not known.
[602] In the Laboratory Manual a second, similar method is also given.
[603] It is considered that water has a constant concentration in a dilute solution and that for its active components [H+] × [HO−] is a constant (p. 176).
[604] In the calculation which follows, which is meant merely for a rough survey, no account is taken of the formation of complex ions I3−, or of the tendency of hydroiodic acid to decompose spontaneously into iodine and hydrogen: 2 H+ + 2 I− ⇄ H2 + I2, a reaction which could also be studied profitably with the aid of the equilibrium constants for I2 ⇄ 2 I− and for H2 ⇄ 2 H+. The value of the iodide constant is also uncertain (see p. 273).
[605] 4 K+ + 4 I− + O2 + 2 HOH ⇄ 2 I2 + 4 K+ + 4 HO−.
[606] The formation of complex ions I3− and other secondary reactions (formation of hypoiodite, iodate, etc.) are ignored.
[607] y has so small a value that we may consider [I−] practically unchanged.
[608] 0.007 I2 = 0.014 I−.
[609] A mole of I2 = 2 × 127 = 254 grams; 0.007 × 254 × 5 / 1000 = 0.009 gram.
[610] The tendency of iodine to form hypoiodous acid, iodates, etc., is not taken into consideration here and involves another relation.
Numbers marked (†) refer to subjects illustrated by experiments, heavy numbers refer to tables.
Original printed spelling and grammar is generally retained. Footnotes were renumbered and relocated to the ends of chapters. Notes to tables were left in their original locations. Some mathematical and chemical formulas and equations were modified in format or rearranged. Original small caps type Looks like This. The transcriber created the cover image, and hereby releases it to the public domain.
This book uses many uncommon Unicode characters, and careful selection of the ebook reader software and font used to view it is necessary. Some of the uncommon characters not already mentioned are: U+2296 ⊖, U+2295 ⊕, U+221E ∞, U+221B ∛, U+2212 −, U+21C4 ⇄, U+2192 →, U+21C5 ⇅, U+2572 ╲, and U+2571 ╱, etc. A monospaced font will improve the appearance of the data tables. However, the Thin Space U+2009 is used in most of the chemical and mathematical equations, and an exact monospaced font will not display Thin Space correctly. Adobe's "Source Code Pro" is an unusual "monospace font" that does display Thin Space and the data tables correctly.
The archaic form of scientific notation exemplified by "0.0413", is herein simplified either to decimal form—"0.000013"in this example—or to modern scientific E notation, "1.3E−5". In this, "E" means "times ten raised to the power of". Furthermore, E notation has also been substituted herein for many numbers originally printed like this: "a × 10b ".
The name "van't Hoff" was changed to "van 't Hoff" throughout; likewise "Van't" to "Van 't". The hyphen is used inconsistently throughout the book, in words such as "hydrogen-ion" versus "hydrogen ion" or "non-ionized" versus "nonionizied". These have been retained. The word "difficulty" was sometimes employed as an adverb; herein it is converted to "difficultly" in this usage.
Page 45: Changed "permangante" to "permanganate".
Page 81: Removed the unmatched right parenthesis from "the difference in ionization between potassium hydroxide and ammonium hydroxide).".
Page 104: The table notes were reordered and renumbered to match the sequence of note anchors in the table. The anchor in the table title originally linked to a footnote instead of a table note; this footnote was converted to a table note (the first one).
Page 106: The label for the sixth note to the table "The Ionization Constants of Bases" was changed from "3" to "F".
Page 117: The chemical reaction schema, originally comprising two balanced equations and two unbalanced equations using vertical arrows has been rearranged into four balanced equations, with horizontal arrows. Such rearrangements have been silently performed elsewhere.
Page 117: The printed symbol that might be described as "normal leftward arrow over rightward dark arrow (or heavy arrow)" has been represented herein with a more readily available character "⥂"—the Unicode character with hexadecimal number 2942, designated as "U+2942", rightward arrow over short leftward arrow. The same character is used herein for the printed symbol which might be described as "downward dark arrow left beside upward short arrow right"—the equations having been rearranged into a horizontal format—and also for "rightward dark arrow over leftward arrow". A different character U+2943 "⥃" represents "normal rightward arrow over heavy leftward arrow". Rtn to Footnote #459.
Page 125: In the reaction of arsenious oxide with hydrogen sulphide, changed "H3S" to "H2S".
Page 157 "Mendelejeff" changed to "Mendeléeff".
Page 197: Changed "[AlO3−] = y" to "[AlO33−] = y".
Page 226, etc.: Both forms "Bodlaender" and "Bodländer" are retained.
Page 246: Changed "saponifying esters (p. 801)" to "saponifying esters (p. 81)".
Page 252: Substituted "ε−" for a symbol that might be described as "circled epsilon".
Page 283: In the equation showing the oxidation of zinc by cupric ion, the upward arrow originally shown beside the symbol for copper metal is changed to downward arrow.
Page 310: The reference for "mobility" of "Hydroxide-ion" was changed from "156" to "56".