THE FIFTEEN WATT TUNGSTEN LAMP
BY
CLAIR ELMORE ANDERSON
B. S., University of Illinois, 1911
THESIS
Submitted in Partial Fulfillment of the Requirements for the
Degree of
MASTER OF SCIENCE
IN ELECTRICAL ENGINEERING
IN
THE GRADUATE SCHOOL
OF THE
UNIVERSITY OF ILLINOIS
1912

UNIVERSITY OF ILLINOIS
THE GRADUATE SCHOOL
May 31, 1912
I HEREBY RECOMMEND THAT THE THESIS PREPARED UNDER MY SUPERVISION BY CLAIR ELMORE ANDERSON ENTITLED THE FIFTEEN WATT TUNGSTEN LAMP BE ACCEPTED AS FULFILLING THIS PART OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE IN ELECTRICAL ENGINEERING
Ernst Berg
In Charge of Major Work
Ernst Berg
Head of Department
Recommendation concurred in:
Morgan Brooks
Ellery B Paine
J M Bryant
Committee on Final Examination
CONTENTS
1THE 15 WATT TUNGSTEN LAMP
I. INTRODUCTION.
Since the introduction of the tungsten lamp some
five years ago, the manufacturers have attempted continually
to produce smaller and smaller units in the standard voltages.
The latest lamp offered today is the 115 volt, 15 watt,
tungsten, and it is the purpose of this paper to show the
characteristics of this lamp, how it compares with the larger
units as to life under different conditions and its behavior
in general.
First of all, it must be borne in mind that these tests
have been made upon a comparatively small number of lamps,
and for that reason the results should not be taken as absolutely
conclusive. For the life tests, at least 100 lamps
should have been used under each condition, but this was impossible
because of the expense.
Special attention has been given to the phenomenon
of “overshooting”. An entire year could have easily been
spent investigating this subject, and the writer regrets that
lack of time has prevented more elaborate and comprehensive
tests of this strange phenomenon.
2
II. DESCRIPTION OF LAMPS AND TESTS.
The total number of 15 watt lamps tested was 24, one
half of which was obtained directly from the manufacturer
and the other half bought in open market. It is well to
mention at this time that this may have been the cause of
the different qualities as brought out by the life tests.
The lamps were rated at 1.31 watts per horizontal
candle power and were supposed to have a useful life of 1000
hours. The voltage ratings of those obtained from the
factory were 114 - 112 - 110 and those bought in open
market were 115 - 113 - 111. The correct efficiency of
the lamps as found by test was 1.34 watts per candle power.
A shot diagram follows which shows the actual rating of
the lamps at high efficiency.
All readings were made by a Lummer-Brodhun photometer
and the voltmeters and ammeters used were carefully standardized.
The ammeter was placed beyond the voltmeter in order
to get the true current taken by the lamp. The drop across
the ammeter was taken into account in the voltmeter readings.
Life tests were made under two conditions, namely, a
shock test where the lamps received severe vibrations and a
test under ideal conditions, i.e. no jar and constant voltage.
3In order to obtain vibrations for the lamps upon the
shock test, a small motor, with its shaft pulley off set, was
screwed rigidly to a table. The lamps were placed in a
normal position upon the table by means of wooden frames.
The result was that when the motor was running it had a
pounding effect, thus putting the table, consequently the
lamps, in a state of severe vibration. The filaments of the
lamps could be seen violently shaking for some distance.
The test was indeed a hard one, and one that would not be
found in many actual cases. It is very doubtful if railway
lamps are subjected to such a strain and they are of the
heavy filament low voltage type. The following photograph
shows the arrangement above described. Ten 15 watt lamps
were used on this test, the remainder shown being 20 and 25
watt and carbons.

4
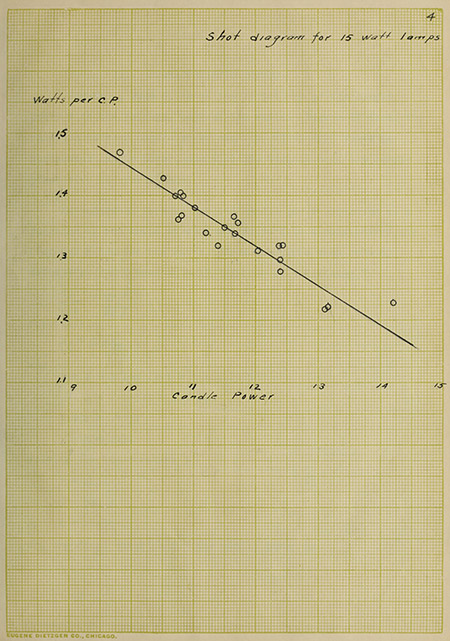
Shot diagram for 15 watt lamps
5
III. CHARACTERISTIC CURVES.
Figure 1, Page 8, shows the variations of the candle
power with the voltage, current and watts. Figure II shows the
relation between candle power and the efficiency, watts per
horizontal candle power, and also the variation of the candle
power with the resistance.
An empirical formula for the candle power expressed as a
function of the watts is cp = KWx where K is a constant of the
lamp and W denotes the watts. From the curve when cp = 5,
watts = 11.1 and when cp = 15, watts = 17.5 dividing
substituting
and
log 3 + x log 11.1 = x log 17.5
.4771 + 1.0453x = 1.2430x
.198x = .4771
x = 2.41
solving for the constant K
5 = K 11.12.41
5 = 332 K
K = .0150
and the final equation for the candle power is
In the same way, the candle power may be expressed
in terms of the voltage and this is found to be
This formula checks precisely with the one used in the
engineering department of the General Electric Company at
their lamp works, Harrison, N.J.
The horizontal distribution curve of a lamp with its
filament mounted as is the modern tungsten is nearly a
circle. This is not true, however, in the case of vertical
distribution and this curve is shown, Figure III. As will
be noted, the tip candle power is only about 23 per cent
of the horizontal.
Life Tests.
The results of the life tests were very surprising.
The lamps upon the test under ideal conditions, namely, no
vibrations and constant voltage, had only an average life of
460 hours, while every one of those upon the shock test are
still burning at the present time, having been burned 300
hours. In order to make the test still more severe, the
lamps were subjected to vibrations without voltage being
impressed, and as yet, not a filament has broken, the total
time being 400 hours. It was impossible to give more time
to these lamps as was done for those under ideal conditions,
for the reason it was thought unadvisable to leave the motor,
which gave the vibrations, running over night.
7The curves have the same general form for the two
conditions but the variations are far more great for the
lamps which were upon the shock test. The reason for this
is that the vibrations were so severe as to shake parts of
the filament together thus giving a partial short circuit,
causing great variations in candle power.
8
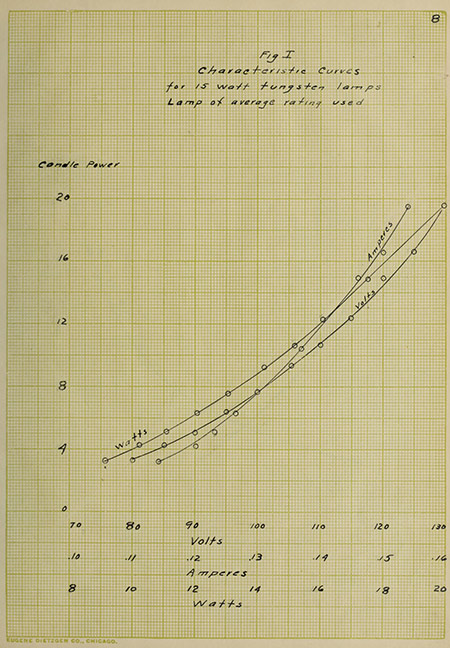
Fig I
Characteristic Curves for 15 watt tungsten lamps
Lamp of average rating used
9
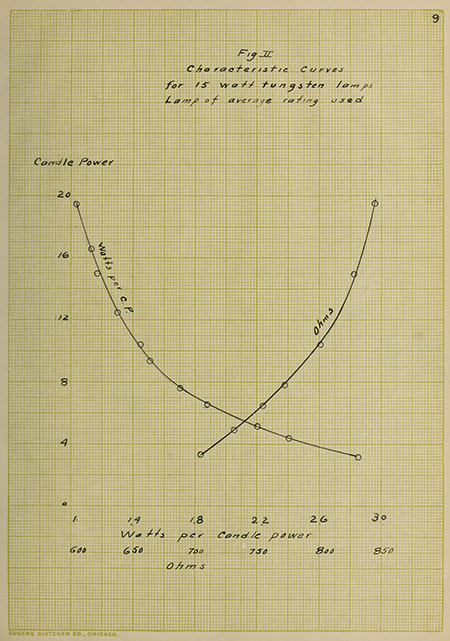
Fig II
Characteristic Curves for 15 watt tungsten lamps
Lamp of average rating used
10
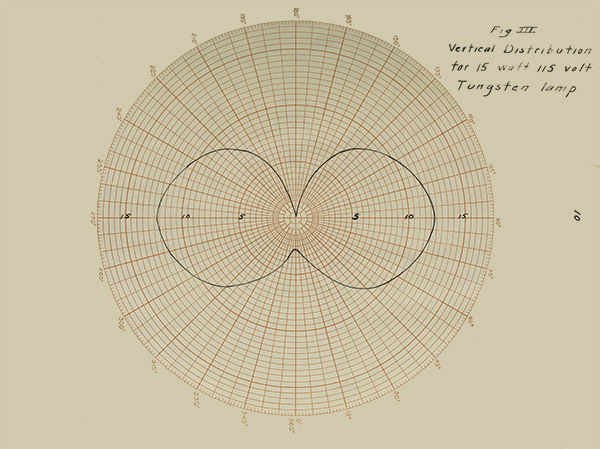
Fig III
Vertical Distribution for 15 watt 115 volt Tungsten lamp
11
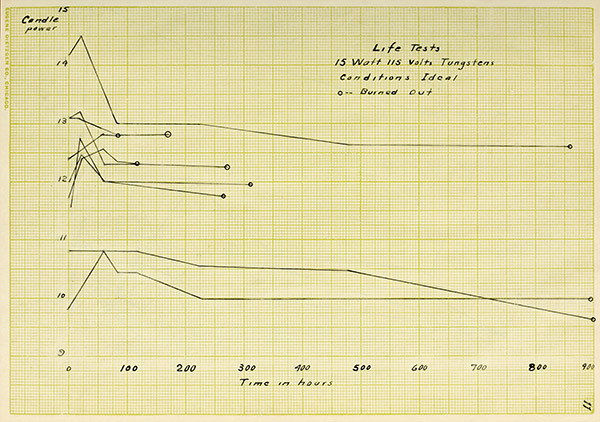
Life Tests
15 Watt 115 Volts Tungstens
Conditions Ideal
o—Burned Out
12
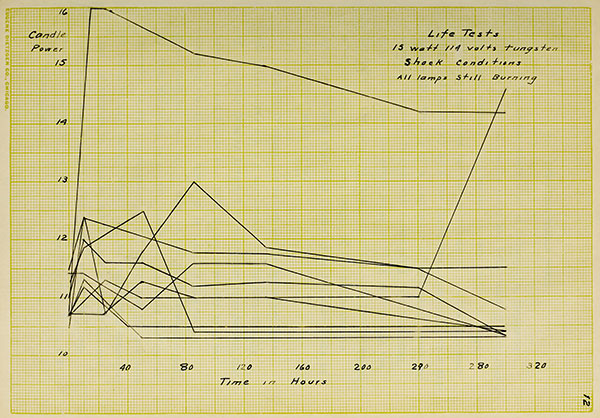
Life Tests
15 watt 114 volts tungsten
Shock Conditions
All lamps still Burning
13
IV. SPHERICAL CANDLE POWER.
Owing to the absence of an integrating photometer,
the mean spherical candle power has been found by Kennelley’s
graphical method. This method is very simple as compared
with Rousseau’s and has the advantage of yielding the mean
spherical intensity as a one dimensional quantity. This dispenses
with the use of a planimeter or equivalent measuring
surface device. It consists essentially in determining
graphically from the given polar curve an evolute and the
involute of the same and then projecting this involute upon
a vertical line. Half the length of the projection is
equal to the mean spherical intensity to the same scale as
the original polar curve.
Figure IV shows the method and is explained thus:
The polar curve O A H B corresponds to the distribution
of intensity from an inverted incandescent lamp having its
base at V and tip at V´. This is not precisely true but
the only variation to speak of is that the tip candle
power does not fall off so much as the curve between B and
O. This variation is slight, however. The mean horizontal
intensity is OH, the diameter of the circle, and in this case
is equal to 12.4 candle power. In the diagram the construction
is adapted to zones of 30° and the radii of the midzones
found i.e. at +75°, +45°, +15°, -15°, -45° -75°.
These are marked by dotted lines O t, O s, O r, O r´, O s´,
O t´ respectively.
14With radius O r and center O, the arc hra is
described through an angle of 30°. The radius Oa is
drawn at the end of the arc. A distance Ab is measured
from a along a O equal to O s, the second midzone radius.
With a center b and radius O s, the arc ac is described
through an angle of 30° so that bc makes an angle of 60°
with the horizontal OH. The line bc is drawn at the end of
this arc. From c towards b, a distance cd is marked off
equal to Ot, the third midzone radius. With center d and
radius O t, the arc ce is described through an angle of
30° so that de makes an angle of 90° with the horizontal
OH. The line de is drawn.
The arc ha´c´e´ is extended from the horizontal to the
vertical beneath in the same manner as above by steps of
30° with centers O, b´, and d´, and radii Or´, OS´ and Ot´
respectively. The curve ecarr´a´c´e´ is now continuous and
complete. A vertical line QQ´ is drawn through the
convenient point H and the points e c a a´ c´ e´ are projected
upon the same. The length HQ, is the upper hemispherical
intensity and the length HQ´ the lower hemispherical
intensity. Their arithmetical mean is the mean spherical
intensity. Since in this case the upper and lower hemispheres
are symmetrical HQ = HQ´ = QQ´/2 = mean spherical intensity.
By measurement this half length is found to be 3.125 inches
and from the scale used this corresponds to 9.67 candle power.
The spherical reduction factor for these lamps is, then
15
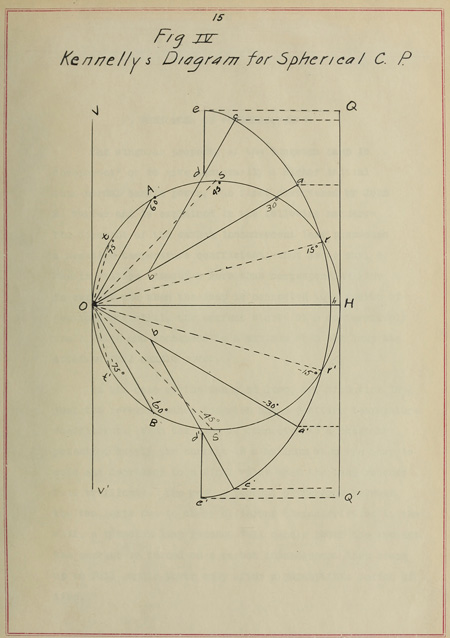
Fig IV
Kennelly’s Diagram for Spherical C. P.
16
V. PHENOMENA OF “OVERSHOOTING”.
The singular property of the tungsten lamp to
“overshoot” or to give temporarily a higher initial
than normal candle power, was first discovered by John
B. Taylor and is explained in the following manner:—The
filament of the carbon incandescent lamp possesses
a negative temperature coefficient; that is to say, a
rise in voltage causes a more than corresponding rise
in current and when the lamp is connected to a source of
constant potential, the current starts at a comparatively
small value and increases to a maximum when the lamp has
attained full candle power.
In the case of the tungsten lamp, the situation is
just the reverse, since tungsten has a positive temperature
coefficient. When the lamp is connected to a constant
potential supply the current is a maximum when the lamp is
cold and decreases to a final value when the lamp reaches
full brilliancy. The most important difference between
the two lamps due to these different characteristics is that
while a tungsten lamp reaches full candle power the instant
the current is turned on a carbon incandescent lamp comes
up to full candle power only after a perceptible period of
time.
17The apparent temporary increase in the candle power of
a tungsten lamp was observed early after the lamp was invented
but it was generally ascribed to some possible
physiological action due to the slow contraction of the pupil
of the eye.
The following curve was obtained by means of the
oscillograph and shows clearly the rush of current for the
first instant after the lamp is turned on. The break in the
curve is due to an imperfection in one of the operating
switches and has nothing to do with any characteristic of
the lamp. The cycle wave was put on merely to obtain the
time.
In order to prove that this overshooting occurs, an
actual photograph of the intensity has been made. This was
obtained by making a box 1´ × 1´ × 3´ absolutely light proof
and arranging a lamp inside so that it could be turned on
and off at will. A slit, fitted with a shutter, was cut in
one end of the box which permitted the light to fall upon a
18revolving oscillograph film. The film holder was attached
to the box with thin metal strips and revolved by means of
a small motor. As is seen the whole arrangement was nothing
more than a large camera.
The following photograph shows the phenomenon quite
clearly, point A denoting where the lamp was turned on.
19
VI. THEORIES OF “OVERSHOOTING.”
The theory given by Taylor to account for the
“overshooting” of tungsten lamps is based on the fact that
there is a small amount of residual gas in the lamp, which
is attracted to the walls of the lamp when it is cold;
and when the lamp is lighted and warms up, this residual gas
is driven off lowering the vacuum. With a high vacuum,
practically all the energy must be radiated from the filament;
conversely, on a lowering of the vacuum, some of the
heat is carried away by convection and conduction. When
all the heat is carried away by radiation the filament runs
at a higher temperature and will give more light.
Another theory is that a cold tungsten filament
lamp absorbs and occludes certain gaseous substances from
the low pressure space within the chamber. Owing to the
presence of these gases the filament shines more brightly
when first brought quickly to incandescence, but after the
gases have been driven off by the heat, the extra luminescence
disappears and can be regained only by prolonged
cooling and rest.
Still another theory, and the one that seems the most
logical to the writer, is that the increase of resistance
accompanying the rise of temperature takes a certain small
interval of time so that when the temperature is rising
20at the rate of thousands of degrees per second, the
resistance lags perceptibly. The resistance does not
suppress the current as quickly as it should and an
extra rush of current and heat energy goes through the
filament, raising the temperature above normal, with a
corresponding increase in brilliancy.
21
VII. AMOUNT OF “OVERSHOOTING”.
In order to determine the amount of over shooting,
the writer has made photographs as shown below. Number
one was made with the lamp under voltage, number two by
using normal voltage and suddenly turning the lamp on by
means of a snap switch, thereby obtaining the overshooting,
and finally number three was made by impressing voltage
above normal. The pictures were obtained by using the
photographic arrangement as before described. All three
prints were made from the same film, that is the three
pictures were made upon one film thus insuring the same
development and printing for all. The print has been cut
merely to allow a closer comparison of the intensities.

It is seen that number three compares favorably with
the overshooting as shown by number two and the candle
power corresponding was found to be approximately 50%
greater than normal. It is not claimed that every lamp
22will overshoot this amount as the degree of vacuum or
other factors of individual lamps may play an important
part in this phenomenon. There is no doubt, however, that
this strange fact really occurs and is not due to
physiological reasons.
23
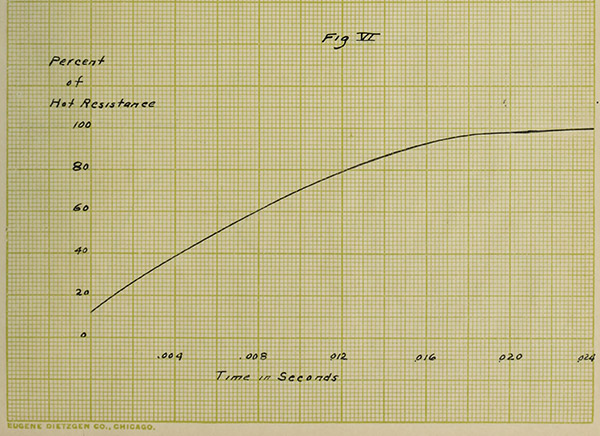
VIII. CURVES OF “OVERSHOOTING”.
In order to prove that the law of resistances,
namely, R = Ro(1 + αt) does not hold for the first instance
after closing the switch on a tungsten lamp, the following
curves have been plotted. Number V. has been taken from
the oscillograph record shown in the first part of this
paper and shows that about .024 second elapses before the
current becomes normal. Knowing the current at any instant
as given by this curve, it is easy to find the resistance
at the same instant by Ohm's law, the electromotive force
being a constant and known value. Curve VI shows this relation.
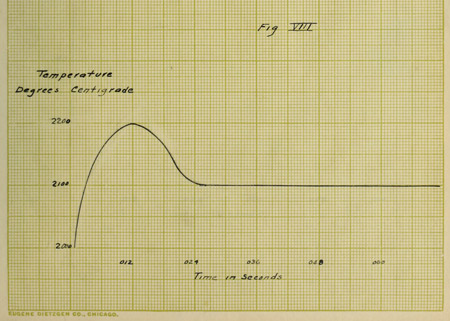
Curves VII and VIII are approximate values and not
absolute. Now from the temperature curve, values are taken
and substituted in the formula for resistance, R = Ro(1 + αt),
the resulting curve being Figure IX. It is seen that curves
VI and IX do not take the same values at all until after a
brief interval of time has elapsed. Curve VI is absolutely
correct, however, as these values have been obtained from the
oscillograph record. Consequently, the assumption upon which
curve IX is based must be incorrect for the first .024th of a
second and the conclusion is that the law of resistances does
not hold. This result tends to strengthen the theory of the
lag of resistivity for the “overshooting” of a tungsten lamp.
24
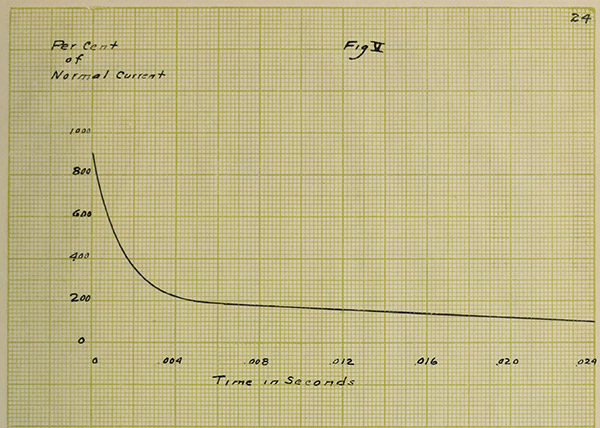
25
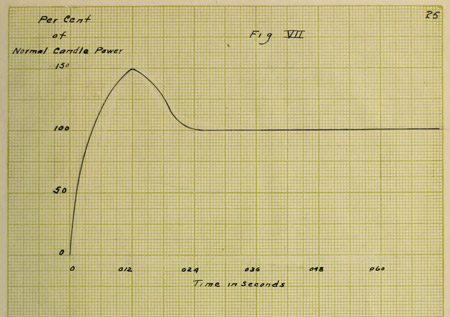
26
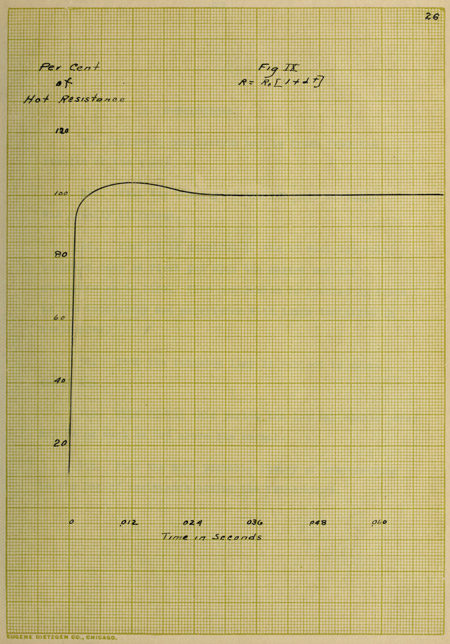
27
IX. CONCLUSIONS.
The following conclusions may be drawn from the
results of the tests.
1st, That the quality of the two sets of lamps
was greatly different.
2d, That it is doubtful if the 15 watt, 115 volt,
tungsten lamp as first put upon the market met the
guarantee as to life. This conclusion is reached by tests
in the laboratory and experience with lamps installed in
residences.
3d, That the tungsten lamp is subject to overshooting.
4th, That during this period the initial candle power
may be as much as 50% above the normal.
5th, That the most probable theory of overshooting
is the lag of resistance behind the temperature.
TRANSCRIBER’S NOTE
Fractions are represented horizontally using the slash / symbol.
The original separated the numerator and denominator
horizontally, separated by a _ line.
Punctuation has been normalized. Except in the following
cases, variations in hyphenation, spelling and spacing have
been retained as they were in the original publication.
Chapter 2:
Lumer-Brodhum photometer —> Lummer-Brodhun photometer
Chapter 4:
What appear to be hand-drawn primes in
the text have been confirmed as:
The arc ha´ce —> The arc ha´c´e´.
e c a a´ c e´ —> e c a a´ c´ e´
Figure IV
There are two points b radiating from point O.
The lower is likely to represent b´.
Chapter 5:
inportant difference between —> important difference between