Fig. 1. Mortality among Feeble-Minded in Institutions Compared With the General Population
Title: Deficiency and Delinquency: An Interpretation of Mental Testing
Author: James Burt Miner
Release date: August 17, 2016 [eBook #52826]
Most recently updated: October 23, 2024
Language: English
Credits: E-text prepared by Richard Tonsing, MWS, Bryan Ness, and the Online Distributed Proofreading Team (http://www.pgdp.net) from page images generously made available by Internet Archive (https://archive.org)
The Project Gutenberg eBook, Deficiency and Delinquency, by James Burt Miner
| Note: | Images of the original pages are available through Internet Archive. See https://archive.org/details/deficiencydelinq00mine |
Transcriber's Note:
The cover image was created by the transcriber and is placed in the public domain.
| Preface | 1 | ||
| Chapter I. INTRODUCTION | 3 | ||
| PART I. PRACTICAL CONSIDERATIONS | |||
| Chapter II. THE FUNCTIONS OF A SCALE IN DIAGNOSIS | 10 | ||
| A. The Meaning of Intellectual Deficiency | 10 | ||
| B. Forms of Mental Deficiency Not Yet Discoverable by Tests | 14 | ||
| C. Doubtful Intellects Accompanied by Delinquency Presumed Deficient | 18 | ||
| Chapter III. THE PERCENTAGE DEFINITION OF INTELLECTUAL DEFICIENCY | 20 | ||
| A. The Definition | 20 | ||
| B. The Assumptions of a Quantitative Definition | 21 | ||
| (a) Deficiency is a Difference in Degree not in Kind | 21 | ||
| (b) As to the Variation in the Frequency of Deficiency at Different Ages | 23 | ||
| (c) As to the Number of Deficients not Detected by Tests | 34 | ||
| (d) Allowance May be Made for Variability | 40 | ||
| Chapter IV. WHAT PERCENTAGE IS FEEBLE-MINDED | 47 | ||
| A. Kinds of Social Care Contemplated | 47 | ||
| B. Estimates of the School Population Versus the General Population | 48 | ||
| C. Desirable Versus Immediately Advisable Social Care | 51 | ||
| D. Percentages Suggested to Harmonize the Estimates | 52 | ||
| E. Comparison With Important Estimates | 56 | ||
| F. The Ability of the Mentally Retarded Especially Those Receiving Special Training | 74 | ||
| xChapter V. ADAPTING THE PERCENTAGE DEFINITION TO THE BINET SCALE | 82 | ||
| A. The Border Region for the Mature | 82 | ||
| (a) Indication from a Random Group | 82 | ||
| (b) The Present Tendency Among Examiners | 95 | ||
| B. The Border Region for the Immature | 104 | ||
| (a) For the Binet 1908 Scale | 104 | ||
| (b) Data for Other Developmental Scales | 110 | ||
| (c) The Change in Interpreting the Borderline for the Immature | 116 | ||
| Chapter VI. DELINQUENTS TESTING DEFICIENT | 122 | ||
| A. At the Glen Farm School for Boys, Hennepin County, Minnesota | 122 | ||
| B. Comparison of Tested Deficiency Among Typical Groups of Delinquents | 127 | ||
| (a) Women and Girl Delinquents in State Institutions | 128 | ||
| (b) Women and Girl Delinquents in Country and City Institutions | 134 | ||
| (c) Men and Boy Delinquents in State Institutions | 141 | ||
| (d) Men and Boy Delinquents in County and City Institutions | 148 | ||
| C. Summary of Tested Deficiency Among Delinquents | 158 | ||
| Chapter VII. CHECKING THE BINET DIAGNOSIS BY OTHER METHODS | 170 | ||
| Chapter VIII. SCHOOL RETARDATION AMONG DELINQUENTS | 177 | ||
| A. In Minneapolis | 177 | ||
| B. School Retardation Among Other Groups of Delinquents | 185 | ||
| Chapter IX. COMPARISON OF THE SCHOOL TEST AND THE BINET TEST | 189 | ||
| A. Practical Uses of the School Test | 190 | ||
| xi | (a) Estimating the Frequency of Deficiency by School Retardation | 190 | |
| (b) School Retardation as a Warning of the Need for Examination | 194 | ||
| (c) School Success as a Check on the Binet Diagnosis | 197 | ||
| B. Checking Deficiency Among Delinquents by the School Test | 199 | ||
| Chapter X. BAD SCHOOL ADJUSTMENT AS A CAUSE OF DELINQUENCY | 203 | ||
| Chapter XI. DEFICIENCY AS A CAUSE OF DELINQUENCY | 210 | ||
| A. The Chances of the Mentally Deficient Becoming Delinquent | 211 | ||
| B. The Correlation of Deficiency and Delinquency | 218 | ||
| C. The Causes of Delinquency | 224 | ||
| (a) Constitutional Factors | 224 | ||
| (b) External Factors | 225 | ||
| (c) Weighing Heredity Against Environment | 229 | ||
| (d) The Criminal Diathesis | 234 | ||
| Chapter XII. SUMMARY AND SUGGESTIONS | 239 | ||
| PART II. THEORETICAL CONSIDERATIONS | |||
| Chapter XIII. THE THEORY OF THE MEASUREMENT OF MENTAL DEVELOPMENT | 252 | ||
| A. Comparison of Units and Scales for Measuring Individual Differences | 254 | ||
| (a) Equivalent Units of Ability When the Distributions are Normal | 254 | ||
| (b) The Year Unit of the Binet Scale | 260 | ||
| (c) Is Tested Capacity Distributed Normally? | 267 | ||
| (d) Equivalent Units of Development When the Form of Distribution is Uncertain | 275 | ||
| B. The Curves of Mental Development | 279 | ||
| xii | (a) The Significance of Average Curves of Development | 280 | |
| (b) Changes in the Rate of Development | 290 | ||
| (c) The Question of Earlier Arrest of Deficient Children | 294 | ||
| Chapter XIV. QUANTITATIVE DEFINITIONS OF THE BORDERLINE | 304 | ||
| A. Different Forms of Quantitative Definitions | 304 | ||
| B. Common Characteristics of Quantitative Definitions | 308 | ||
| C. Practical Advantages of the Percentage Method | 311 | ||
| D. Theoretical Advantage of the Percentage Method with Changes in the Form of the Distributions | 317 | ||
| BIBLIOGRAPHY ON TESTED DELINQUENTS | 324 | ||
| Other References Cited | 329 | ||
| APPENDICES | 344 | ||
| INDEX | 353 | ||
| Tables | ||
|---|---|---|
| I. | Age distribution of deaths in the general population and of feeble-minded in institutions | 30 |
| II. | Mortality of institutional deficients in the United States compared with the general population | 31 |
| III. | Test borderlines with randomly selected Minneapolis 15-year-olds | 89 |
| IV. | Results with the Binet tests for mental ages XI and XII (1908 series) | 98 |
| V. | Percentages of mentally retarded children as tested with the Binet 1908 Scale | 106 |
| VI. | Mental retardation of children as tested with the Binet 1911 Scale | 111 |
| VII. | Borderlines with the Point Scale | 115 |
| VIII. | Test ages of the Glen Lake group of delinquent boys | 124 |
| IX. | Intellectual development relative to life-ages and school positions among the delinquent boys of Glen Lake | 125 |
| X. | Binet 1911 tests of boys consecutively admitted to the Detention Home at Thorn Hill, Allegheny County | 151 |
| XI. | Frequency of tested deficiency among over 9000 delinquents | 159 |
| XII. | Age and grade distribution of elementary school pupils in Minneapolis | 178 |
| XIII. | School retardation of Minneapolis delinquents and elementary school pupils | 179 |
| XIV. | Indices of frequency and amount of school retardation for Minneapolis delinquents and elementary school pupils | 183 |
| XV. | Percentage of pupils 12 and 13 years of age most seriously retarded in school | 193 |
| XVI. | School position of delinquents at Glen Lake relative to their intellectual development | 204 |
| xivXVII. | Goring's data as to the percentage of mental defectives among men convicted of various offenses | 213 |
| XVIII. | Goring's data as to groups of crimes committed most frequently by those mentally deficient | 214 |
| XIX. | Four-fold correlation table for juvenile delinquency and deficiency in Minneapolis | 222 |
| XX. | Average Intelligence Quotients of children of different ability | 296 |
| XXI. | Test records with random 15-year-olds | 344 |
| XXII. | Test records with delinquents at the Glen Lake Farm School | 349 |
| Figures | ||
| 1. | Mortality among feeble-minded in institutions compared with the general population | 32 |
| 2. | School retardation of Minneapolis delinquents compared with elementary school boys | 180 |
| 3. | Hypothetical development curves (normal distributions) | 253 |
| 4. | The question of equivalence of year units | 265 |
| 5. | Hypothetical development curves (changing form of distribution.) | 277 |
| 6. | Tests of the development of memory processes. Medians at each age for the central tendencies of the tests | 285 |
| 7. | Different types of development. Medians at each age for the central tendencies of the tests | 286 |
| 8. | Forty tests of development. Distribution at each age for the central tendencies of the tests | 287 |
| 9. | Relative positions at each age of the median and of corresponding bright and retarded children with the Form Board Test | 299 |
In undertaking in 1912 to examine the mental development of delinquents for the clinic started and supported by the Juvenile Protective League of Minneapolis, in connection with the Juvenile Court, I soon became convinced that a safer method for evaluating the limit of feeble-mindedness with tests was more needed than masses of new data. The researches that have been published in the past three years do not seem to have changed this situation. Numerous studies with psychological tests are already available, but they generally treat of average rather than borderline conditions. In the field of delinquency the work of testing has been carried on with especial activity. Here, as well as elsewhere, the conclusions seem likely to be misleading unless social workers better appreciate the real place of mental tests, their value and their limitations.
The tables of a few hundred juvenile delinquents and school children examined in Minneapolis, which are presented in this book, indicate the occasion rather than the aim of the present study. The purpose is mainly to help clear the ground for other work with mental tests, and especially to put the determination of feeble-mindedness by objective examination with the Binet or other scales on what seems to me a sounder basis. Furthermore, the results of objective testing which have been so rapidly accumulating in the field of delinquency need to be assembled and reorganized in order to avoid confusion. It is especially desirable to discover a conservative basis for objective diagnosis of deficient intellectual capacity in order to prevent very useful testing systems from becoming unjustly discredited and to preserve the advance that has been made.
2The work out of which this monograph grew was begun through the encouragement of Judge Edward F. Waite of the Hennepin County Juvenile Court. His earnest co-operation and my interest in the field of mental testing has led me to continue the study. Judge Waite's insight into his court problems resulted in the early organization of a Juvenile Court clinic (153, 170) in Minneapolis. The clinic is in charge of Dr. Harris Dana Newkirk, who has contributed materially to this study by his thorough medical examination of each of the cases brought to him. To the staff at the probation office I am also much indebted.
The earnest help of Superintendent D. C. MacKenzie, of the Glen Lake Farm School for the juvenile delinquents of Hennepin County, made a close study of our most interesting group of boys much more profitable personally than I have shown here. For detailed expert work in tabulation and in examinations I wish to express my thanks to my advanced students, a half dozen of whom have contributed materially to the data of this book.
As an interpretation of the results which have been obtained with mental tests, this book lies between the topics of deficiency and delinquency. It is an attempt to discover the significance of objective measurements of ability in connection with both of these fields. The pressing practical problem was to find out what positions on a scale for testing mental development were symptomatic of social deficiency. After working out a percentage method for conservatively indicating these borderlines for tested deficiency, it was then possible to reinterpret the test records of over 9000 delinquents who have been examined with some form of the well-known Binet Scale. The size of the problem of the deficient delinquent has thus been determined on a significant scientific plan. The outcome is a new basis for judging the current statements about this problem by those who have used the Binet scale. Scores of investigators by their tireless energy have provided data which may now be compared for many types of delinquents and in many parts of the country. Some sixty studies of deficient delinquents have been thus summarized from the point of view of psychological tests.
Closely related to the problem of the frequency of feeble-mindedness among delinquents is the question of the cause of delinquency. This has further been considered in the light of the most important scientific studies, especially those using the method of correlation. Among these researches stands out the fundamental investigation of the causes of criminality by Goring, a work which has received very inadequate attention in this country, although it involved ten years study of a group of 3000 convicts by the 4best quantitative methods. The careful study of these objective investigations should take the question of the relation of deficiency and delinquency out of the realm of opinion and theory. It may be expected to have an important influence upon the social handling of these problems. In this connection I have added a chapter of suggestions which have grown out of my year's study of the education of deficients and delinquents in European schools and institutions.
To determine the size of the problem of dealing with deficients, especially deficient delinquents, is a task of first importance. In spite of our more conservative basis for judging the results with tests, the necessity of caring for the feeble-minded remains the most vital problem connected with social welfare. The movement for more individual training in our schools, which has been gaining such headway, may also be encouraged by the evidence that maladjustment to school work is also definitely related to delinquency.
It is essential that we should have objective data for determining the borderline of tested deficiency among adults. To meet the present serious lack of knowledge on this point, new data were collected which for the first time afford the means of determining, by the use of a randomly selected group what is a conservative borderline of tested deficiency for those intellectually mature. These data include the Binet test records for all the 15-year-old children who resided in seven school districts in Minneapolis and who had not graduated from the eighth grade.
The urgency of plans for indefinitely segregating certain types of the feeble-minded, especially deficient delinquents, has placed a new emphasis on those quantitative aids to diagnosis. The difficulty of establishing feeble-mindedness before a court has been called to attention by both 5Supt. C. A. Rogers (173)[1] of the Minnesota School for Feeble-Minded, and Supt. Walter E. Fernald (104) of the Massachusetts School. Both of these men recognize that psychological tests are the most hopeful way of improving this situation.
A fundamental feature of the diagnosis of deficiency is the plan here advocated for designating the borderlines on a scale on the basis of a percentage definition of tested deficiency. This involves the distinction of intellectual deficiency from certain rare volitional forms of feeble-mindedness, which the tests do not at present detect. This percentage definition seems to afford the best approach to a test diagnosis. It is apparent that the data are insufficient for finally establishing such a quantitative description of the lower limit for passable intellects on a mental scale. The plan, however, may be easily adjusted to new data, and meanwhile avoids some of the serious current misinterpretations of test results.
While the idea of a quantitative definition of the borderline of deficiency is not new, the percentage method seems to have certain fundamental advantages over either the “intelligence quotient” of Stern (188), the “intelligence coefficient” of Yerkes (226), or the description in terms of deviation, mentioned by Norsworthy (159) and Pearson (164, 166, 167). Several investigators, including Terman (57) and Yerkes (226), are utilizing the percentage method indirectly for describing the borderline of feeble-mindedness, but have inadequately distinguished it from the ratios. While ratio and deviation methods are possibly more serviceable for certain purposes, they are especially faulty near the borderline of deficiency, since they are affected by variations in the units of measurement and in 6the form of distribution from age to age. My paper on a percentage definition and the detailed plan for determining the borderline in the Binet scale, which was read at the meeting of the American Psychological Association in 1915, seems to have been contemporaneous with a similar suggestion by Pintner and Paterson (44). They, however, would restrict the term “feeble-mindedness” to tested deficiency, while I advocate the use of percentage borderlines on a test scale as symptomatic of one form of feeble-mindedness, much as excess of normal temperature on a clinical thermometer is symptomatic of disease.
Although no system of objective tests will ever dispense with the need for expert interpretation in diagnosing individual cases, still there are few who would doubt that it is desirable to reduce the option of expert judgment as much as we reasonably can. This is the scientific method of procedure. The borderline cases, however, which are often most troublesome in their delinquencies, are just those which will longest defy rigid rules. The diagnostician who wants to be as free as possible from external restraint will find in this border field of mental capacity a happy hunting ground. His scientific instincts should make him eager to discover when he leaves the mundane sphere and sallies forth into uncharted realms where he bears the full responsibility of his own opinion. Let me hasten to add that reasoning from objective data in the mass to the diagnosis of an individual case may lead to serious mistakes, unless one keeps alert to detect the exception from the general rule, and unless one understands the numerous sources of error entering into an examination. On the other hand the test results when properly interpreted afford the most important criteria on which to base a prognosis if they are considered in relation to the history of the case and the medical examination.
7By the use of more conservative borderlines for raising the presumption of deficiency and also by designating a doubtful position on the scale, on the plan advocated herein, it is possible to make scales for testing mental capacity more serviceable both to the clinician and to the amateur tester. The latter may use the scales for his own information or may wish to discover whether an examination by an expert in mental development is desirable, without attempting to make a diagnosis himself. The scale may thus take a place in the study of child mentality analogous to the familiar Snellen chart in the testing of vision. For every teacher familiarity with a development scale may thus become as essential and desirable as the knowledge of the chart for eye testing. It should find a place in all progressive schools which do not have the services of a clinician.
The Binet system of tests was used for obtaining new data on groups of juvenile delinquents in Minneapolis and Pittsburgh. The use of this scale, around which the discussion centers, grew out of the necessity for immediate practical results for the clinic at the Minneapolis Juvenile Court which I was called upon to serve. In 1912, when that work began, there was practically nothing approaching norms with children for any other scale of tests. Even today it is plain that there is more data available for interpreting results with the Binet scale than with any other system of tests. While my experience would make me unwilling to advocate the Binet tests as an ideal method for building up a measuring scale, I still feel that it remains the most useful method at present for discovering the fundamental symptoms of intellectual deficiency. The percentage method, here advocated, as the best way available for determining the borderlines with a scale, would be quite as serviceable, however, with any other testing system. 8It has been my aim to contribute to the interpretation of the results of the tests as they are, not to perfecting the arrangement or details of the separate tests.[2] It happens that one of the main objections which has been raised to the Binet scale, the inadequacy of its tests for the older ages, loses its force so far as the diagnosis of feeble-mindedness is concerned for those who accept the borderlines described in this paper.
Some diagnosticians may hesitate to use the Binet scale because of the criticisms it has received. Yerkes and Bridges state: “Indeed, we feel bound to say that the Binet scale has proved worse than useless in a very large number of cases” (226, p. 94). So far as this objection arises from the attempt to use the descriptions of the borderline of feeble-mindedness published with Binet scales, it will meet with a wide response. The difficulty is hardly less, as I shall show, with other scales. The definition of the borderline is certainly the vital point with any objective method for aiding diagnosis. Only by improving methods for determining the borderline can this weakness be attacked. The central contribution of this paper is directed, therefore, to this problem of the interpretation of the borderline, so that objective scales may be made more reliable for purposes of diagnosis.
In Part Two I have added an intensive discussion of the measurement of development and a comparison of the different objective methods for describing the borderline. This may well be omitted by those who are not interested in the technical aspects of these questions. To those who care only for accounts of individual lives, let 9me say that I am contributing nothing herein to that important field which has been covered in authoritative form by Dr. Healy (27) and by Dr. Goddard (112). They will find instead, I hope, the fascination of figures, a picture book in which probability curves take the place of photographs and biographies, in which general tendencies are evaluated and attention is focussed upon the problem of properly diagnosing deficiency and upon plans for the care of the feeble-minded, whether they be potential or actual delinquents.
1. Numbers in parenthesis indicate the references in the bibliography at the close of the book.
2. Those concerned with other features of the Binet scale will find an admirable bibliography by Samuel C. Kohs, Journal of Educational Psychology, April, May and June, 1914, and September, October, November, and December, 1917. Other references are contained in the Bibliography by L. W. Crafts (9).
Whatever form the definition of feeble-mindedness may take, in this country at least[3] the concept has become quite firmly established as describing the condition of those who require social guardianship, because, with training, they do not develop enough mentally to live an independent life in society. The feeble-minded are socially deficient because of a failure to develop mentally. They are proper wards of the state because of this mental deficiency. Goddard says, they are “incapable of functioning properly in our highly organized society” (112, p. 6). The most generally quoted verbal description of the upper line of social unfitness is that of the British Royal Commission on Feeble-Mindedness: “Persons who may be capable of earning a living under favorable circumstances, but are incapable from mental defect existing from birth or from an early age (a) of competing on equal terms with their normal fellows; or (b) of managing themselves and their affairs with ordinary prudence.” It is clear that the intention is to distinguish mental deficiency from senile dementia, from hysteria and from insanity, in which there is a temporary or permanent loss of mental ability rather than a failure to develop. Feeble-mindedness may, however, arise from epilepsy or from other diseases or accidents in early life as well as from an inherent incapacity for development. 11Moreover, mental deficiency, or feeble-mindedness, (I use the terms interchangeably) does not imply that the social unfitness is always caused by intellectual deficiency. Mind is a broader term than intellect, as we shall note in the next section.
This definition of the feeble-minded is the main idea expressed by Witmer (221), Tredgold (204), Pearson (164), and Murdock (164). The historical development of the concept is traced by Rogers (172) and Norsworthy (159). It is criticized by Kuhlmann (140) as impractical and indefinite. The indefiniteness is indicated by such terms as “under favorable circumstances,” “on equal terms,” and “with ordinary prudence.” This objectionable uncertainty as to social fitness can be considerably relieved for those types of feeble-mindedness which involve the inability to pass mental tests, since this result can later be correlated with subsequent social failure and predictions made during childhood on the basis of the tests. Attempts to make the concept of feeble-mindedness more definite have, therefore, naturally taken some quantitative form in relation to objective tests. Binet and the French commission in 1907 (77) called attention to the method in use in Belgium for predicting unfitness objectively on the basis of the amount of retardation in school at different ages. With the appearance in 1908 of the Binet-Simon revised scale for measuring mental development, quantitative descriptions began to be concerned with the borderlines of mental deficiency on scales of tests.
While the quantitative descriptions of tested deficiency do not include all forms of feeble-mindedness, as I shall show in the next section, they have made the diagnosis of the majority of cases much more definite. Nobody would think of returning to the days when the principal objective criteria were signs of Cretinism, Mongolianism, hydrocephalus, 12microcephalus, epilepsy, meningitis, etc., which LaPage (141) has shown are not found among more than 9% of 784 children in the Manchester special schools. The impossibility of agreeing upon subjective estimates of mental capacity without the use of objective criteria is well shown by Binet's methodical comparison of the admission certificates filled out within a few days of each other by the alienists for the institutions of Sainte-Anne, Bicêtre, the Salpêtreire and Vaucluse. These physicians gave their judgments as to whether a case was an idiot, imbecile or higher grade. Binet says: “We have compared several hundreds of these certificates, and we think we may say without exaggeration that they looked as if they had been drawn by chance out of a sack” (77, p. 76).
The rapid accumulation of data with psychological tests has made it possible to take our first halting steps in the direction of greater definiteness in diagnosis by a larger use of objective methods. This increase in significance of the concept of deficiency is fruitful at once in estimating the size of the social problem and planning means for undertaking the care of these unfortunates. We can discover something of the error in the previous subjective estimates of the frequency of feeble-mindedness. We can bring together and compare the work of different investigators, not only in our country, but throughout the world. We can discover, for example, how important the problem of deficiency is among different groups of delinquents, knowing that the differences are not to be explained by differences in expert opinion. Furthermore, we can now determine, with considerable accuracy, whether the diagnosis made by a reliable examiner is independent of his personal opinion.
If we disregard the natural antipathy of many people to anything which tends to limit the charming vagueness 13of their mental outlook, we may endeavor to chart this horizon of tested deficiency with something of the definiteness of figures, which shall at the same time indicate a range of error. As soon as our aim comes to be to plot the borderline on a measuring scale of mental ability, we find that the borderline must be so stated that we can deal with either adults or children. Two sorts of limiting regions must be described, one for mature minds and one for immature minds. The latter will be in the nature of a prediction as to what sort of ability the children will show when they grow up. We must keep in mind, therefore, that we should attempt our quantitative definition for both growing and adult minds. As soon as the growing mind passes the lower limit for the mature it is then guaranteed access to the social seas although it may never swim far from shore nor develop further with advancing years. In seeking greater definiteness, our aim should then be to describe both the limit for the mature individuals and the limit for the immature of each age. In this paper the definition will be restricted to intellectual deficiency, i. e., tested deficiency. It will take the form of describing the positions on a scale below which fall the same lowest percentage of intellects. This percentage definition of intellectual deficiency offers such a simple method of consistently describing the borderlines for mature and immature that it is surprising so little attempt has previously been made to work it out for a system of tests. Although the principle on which the definition is based depends upon the distribution curve of ability, it is concerned only with the lower limit of the distribution. Since the exact form of this distribution is uncertain I have preferred to call it a percentage definition of intellectual deficiency rather than to state the limits in terms of the variability of ability. Moreover the lowest X per cent. 14in mental development requires no further explanation to be understood by the layman.
The first broad conclusion that impresses those who try to use mental scales for diagnosing feeble-mindedness is that the lower types, the idiots and imbeciles, can be detected with great accuracy by an hour's testing. The difficulties pile up as soon as the individual rises above the imbecile group. The practical experience of those in institutions for the feeble-minded here becomes of fundamental importance. They are able to supply the history of exceptions that should make us cautious about our general rules. Certain people whom they have known for years to be unable to adjust themselves socially because their minds have not reached the level of social fitness will yet be able to pass considerably beyond the lower test limit for mature minds. The mental scales can only detect those feeble-minded who cannot succeed with our present tests. This is the basal principle in using any system of tests.
Stated in another way, this first caution for anybody seeking the assistance of a mental scale is that tests may detect a feeble-minded person, but when a person passes them it does not guarantee social fitness. The negative conclusion, “this person is not feeble-minded,” can not be drawn from tests alone. Mental tests at present are positive and not negative scales. This fact will probably always make the expert's judgment essential before the discharge of a suspected case of mental deficiency. When a subject falls below a conservative limit for tested ability a trained psychologist who is familiar with the sources of error in giving tests, even without experience with the 15feeble-minded, should be able to say that this person at present shows as deficient development as the feeble-minded. To conclude however that any subject has a passable mind requires in addition practical experience with feeble-minded people who pass the tests. It is very much easier to state that the tests do not detect all forms of feeble-mindedness than it is to give any adequate description of the sort of feeble-mindedness which they do not as yet detect.
This distinction between the feeble-minded who do well with test scales and those who do not, is well known in the institutions for the feeble-minded. Binet sought to distinguish some of the feeble-minded who escaped the tests by calling them “unstable,” or “ill-balanced,” individuals as Drummond (77) translates the term. To use the historical distinctions of psychology, their minds seem to be undeveloped more on their volitional and emotional sides than on their intellectual side. Weidensall (59) has described another type as “inert.” She found that quite a number of the reformatory women might slide through the tests but fail socially from the fact that “their lives and minds are so constituted that they feel no need to learn the things any child ought to know, though they can and do learn when we teach them.” Again, it seems to be a disturbance of will through the feeling, rather than an intellectual deficiency. Many of the so-called “moral imbeciles” are probably able to pass intellectual tests lasting but a few minutes. Like the unstable or inert they are not failures because of a lack of intellectual understanding of right and wrong, but because of excess or deficiency of their instinctive tendencies especially in the emotional sphere. Such weakness of will may arise either from abnormality of specific instinctive impulses or inability to organize these impulses so that one impulse may 16be utilized to supplement or inhibit another. We may call all this group of cases socially deficient because of a weakness in the volitional, or conative, aspect of mind.
The discrimination of mental activities which are predominately emotional and conative from those in which intellect is mainly emphasized is also well recognized by those who have been making broad studies of tests in other fields than that of feeble-mindedness. Hart and Spearman (123), for example, call attention to the fact that tests passed under the stimulus of test conditions represent what the subject does when keyed up to it rather than what he would do under social conditions. We cannot be sure that speed ability as tested will represent speed preferences. The subject may be able to work rapidly for a few minutes, but in life consistently prefer to work deliberately. Regarding the eighteen tests which they studied with normal and abnormal adults they say: “These tests have been arranged so as to be confined to purely intellectual factors. But in ordinary life, this simplicity is of rare occurrence. For the most part, what we think and believe is dominated by what we feel and want.” Kelley (130) finds by the regression equation that the factor of effort amounts to two-thirds of the weight of that of the intellectual factor in predicting scholarship from teachers' estimates. Webb (217) thinks that he finds by tests a general conative factor comparable to Spearman's general intellective factor.
With the change in point of view that has come from the adoption of the biological conception of the mind the discrimination of the different forms of feeble-mindedness must be recognized as a distinction in the emphasis on intellectual, emotional and conative processes, not a distinction between actually separable forms of mental activity. On account of the organic nature of the mind 17it is well established that various mental processes are mutually dependent. Any disturbance of the emotional processes will tend to affect the thinking and vice versa. Even if we believe that emotions are complex facts, involving vague sensations as well as feelings, and that terms like emotion, memory, reasoning and will are names for classes of mental facts rather than for mental powers, it still remains important to distinguish between feeling, intellect and will, as well as to recognize the interdependence of the mental processes. Common sense seems to agree with psychological descriptions in regarding mind as a broader term than intellect, and feeble-mindedness as a broader term than intellectual feebleness.
Since tests at present tend to reach the intellectual processes more surely than the emotional, we describe those who fail in them as intellectually deficient. The term “intellect” seems to be better than “intelligence” because the latter seems to include information as well as capacity, while the aim of measuring scales has been to eliminate the influence of increasing information with age. To be thoroughly objective, of course, one should talk about “feebleness in tested abilities;” but we would then fail to point out the important fact about our present scales that they detect mainly intellectual deficiency, that they do not reach those forms of feeble-mindedness in which the weakness in such traits as stability, ambition, perseverance, self-control, etc., is not great enough to interfere with the brief intellectual processes necessary for passing tests. Intellectual deficiency will be used hereafter to refer to those social deficients whose feebleness is disclosed by our present test scales.
In the opinion of Kuhlmann these cases of disturbed emotions and will which shade off into different forms of insanity should not be classed as feeble-minded at all, 18although he recognizes that they are commonly placed in this group. He regards them as an intermediate class between the feeble-minded and the insane. He says: “They readily fail in the social test for feeble-mindedness and because of the absence of definite symptoms of insanity are often classed as feeble-minded. In the opinion of the present writer they should not be so classed, because they require a different kind of care and treatment, and have a different kind of capacity for usefulness” (140). So long as this group of what we shall term “conative cases” is discriminated from the intellectually deficient it matters less whether they be regarded as a sub-group of the feeble-minded or as a co-ordinate class. In grouping them with the feeble-minded we have followed the customary classification. An estimate of the size of this group will be considered later in Chapter III.
Conative forms of feeble-mindedness are perhaps the most serious types in the field of delinquency. They are the troublesome portion of the borderland group of deficient delinquents about which there is so much concern. It is important to remember that it is just among these cases that the test judgment is least certain. In this dilemma one principle seems to be sound enough psychologically to be likely to meet with acceptance. I should state this principle as follows: A borderline case which has also shown serious and repeated delinquency should be classed as feeble-minded, the combination of doubtful intellect and repeated delinquency making him socially unfit. This will relieve the practical situation temporarily until tests are perfected which will detect those whose feebleness is specialized in those phases of volition centering around the instinctive passions, control, balance, interest and endurance. 19The principle recognizes that mental weakness is sometimes emphasized in the volitional processes of the mind.
The principle is apparently in conflict with the rule advocated by Dr. Wallin. Referring to the mental levels reached by individuals, he says: “We cannot consider X-, XI-, or XII-year-old criminals as feeble-minded because they happen to be criminals and refuse to consider X-, XI-, and XII-year-old housewives, farmers, laborers and merchants as feeble-minded simply because they are law abiding and successful” (214, p. 707). At another place he insists “that the rule must work both ways” (215, p. 74). Logically it would seem at first that it was a poor rule which did not work both ways. Further consideration will show, I believe, that there has been a confusion of feeble-mindedness with tested deficiency. If all the feeble-minded tested deficient intellectually then the tested level should determine whether or not they were feeble-minded. This, however, is not a correct psychological description of the facts. I prefer, therefore, to allow for those in a defined narrow range of weak intellects to be classed as deficient provided their weakness also manifests itself pronouncedly in the conative sphere.
The principle that all mental deficients need not show the same low degree of intellectual ability is clearly recognized in perhaps the most important legal enactment on deficiency which has been passed in recent years, the British Mental Deficiency Act of 1913. It states regarding “moral imbeciles” that they are persons “who from an early age display some permanent mental defect coupled with strong vicious or criminal propensities on which punishment has had little or no deterrent effect.” It specifically distinguishes them from the group of feeble-minded which require guardianship because of inability to care for themselves.
3. In Great Britain the term is restricted to those above the imbecile group.
In order to direct attention to the quantitative description of intellectual deficiency which is here proposed, let us state the percentage definition in its most general form. Individuals whose mental development tests in the lowest X per cent. of the population are PRESUMABLY INTELLECTUALLY DEFICIENT, unless their deficiency is caused by removable handicaps. Above these is a group of Y per cent. within which the diagnosis of intellectual deficiency is uncertain on the basis of our present tests. The size of the presumably deficient X group is to be determined by the number of intellectually weak which society is at present justified in indefinitely isolating. The doubtfully deficient Y group should include all those who are so intellectually deficient as to be expected to need assistance indefinitely. The feeble-minded, or MENTALLY DEFICIENT, are those who require social care indefinitely because of deficiency in mental development. They include the X group, that portion of the doubtful Y group which is found to require isolation, guardianship or social assistance, and any others not detected by the tests but requiring prolonged social care on account of their failure to develop mentally. Under the principle which we stated at the close of the last section the combination of Y ability and persistent serious delinquency brings the case within the group presumed to be feeble-minded.
Besides the greater definiteness and significance of such a definition of intellectual deficiency, it affords the simplest practical criterion for determining the borderline of passable intellects with a scale of mental tests. A detailed comparison of the percentage plan with other forms of 21quantitative definition will be found in Part Two. We may note here, however, that it guards against a number of the absurdities of current descriptions of the borderline with measuring scales. It is a criterion which may be consistently applied to the borderline of both the immature and the mature. It may be adapted with comparative ease to any system of tests. It aids in comparing the frequency of intellectual deficiency among different groups, for example, among different types of delinquents, regardless of whether the investigators have used the same series of tests, provided only that each series has been standardized for similar random groups.
Any form of quantitative definition, on the other hand, involves certain assumptions which must be defended before it can claim to be of advantage for practical purposes.
Fortunately the tendency to describe the feeble-minded person as if he were a different species from the normal has been definitely attacked by two noteworthy researches, that of Norsworthy (159) and that of Pearson and Jaederholm (164) (167). In these two investigations mentally deficient children either in special classes or in institutions have been compared with groups of normal children from the same localities on the basis of objective tests. The results are uniformly supported by numerous other studies of deficient and normal groups with the Binet and other tests. The conclusion is, therefore, thoroughly established that there is no break in the continuity of mental ability. It grades off gradually from average ability, and continually fewer and fewer individuals are to be found 22at each lower degree of ability. The borderline of deficiency will, therefore, not be a mental condition which clearly separates different kinds of ability, but a limiting degree of capacity to be decided upon by social policy in attempting to care for those who most need social guardianship. Since ability changes gradually in degree it is necessary to indicate a doubtful border region of degrees of ability on which expert judgment must supplement the test diagnosis. Below the doubtful region the diagnosis is clearly supported by objective test criteria, so that the only question to raise is whether the condition is caused by removable handicaps. The percentage definition thus strictly conforms to the best objective studies of mental deficiency in treating deficiency as a difference in degree.
It should, perhaps, be said that this view is in direct conflict with the opinion that mental deficiency is accounted for as a Mendelian simple unit character. The opposing view has been advocated by Davenport (95, p. 310) and others in the publications of the Eugenics Record Office, and accepted by Goddard (112, p. 556). It has been so fully answered by Pearson (164) and Heron of the Galton Laboratory (127) and by Thorndike (198) that there is no occasion to take up the question in detail. We seem to be reaching an understanding so far as our present problem is concerned. If the explanation of the inheritance of mental ability is through Mendelian characters, nevertheless intellectual ability is the result of such a complex combination of units that it may best be thought of in connection with the unimodal distribution of ability adopted in this study. No random measurement of mental ability has ever shown any other form of distribution.
The attempt has also been made by Schmidt (179) to 23find qualitative differences between normal and feeble-minded children by means of tests, and by Louise and George Ordahl (162) to find qualitative differences between levels of intelligence among feeble-minded children. While these studies are very suggestive in pointing out the tests which most clearly indicate differences between individuals, they seem to me to fall far short of showing that the qualitative distinctions are anything more than larger quantitative distinctions. It is not clear that the authors intended them to mean anything more than this, so these studies do not seem to conflict seriously with our assumption that intellectual ability grades off gradually and uninterruptedly from medium ability to that of the lowest idiot.
A quantitative definition of intellectual deficiency would certainly be much simpler if it could be assumed that the percentage of deficients at each age is practically constant during the time when a diagnosis of deficiency is most important, say from 5 to 25 years. Otherwise the objection might be raised that it is impracticable to determine different percentages for each year of immaturity or to formulate our borderlines of ability for a particular age. When the general instinctive origin of intellectual deficiency is considered along with the incurability of the condition, we seem to be theoretically justified in assuming that the variation will be slight from one year of life to the next. This assumption is tacitly made by all those who use Stern's quantitative description of deficiency in terms of the mental quotient. On the other hand, there is a feeling among some of the investigators that there is a sudden influx of feeble-minded at particular 24ages and this position should be examined. Probably more important than this possibility of increase is the question of a decrease in frequency with age on account of the excessive death rate among the deficients.
It is a natural supposition that there is a sudden increase in the proportion of feeble-minded at adolescence. On account of the increased rate of growth at this period we might expect to find greater instability for a few years. It may well be that there is a rather sudden influx of the unstable type of feeble-mindedness at this period. Such an increase may occur without being detected by a series of brief intellectual tests such as the Binet scale. It would be of the conative type of feeble-mindedness that cannot at present be diagnosed by objective tests, the type that requires diagnosis by expert opinion. It is to be noted, however, that Binet, who paid much attention to the unstable type, says: “Since the ill-balanced are so numerous at ten years of age, and even at eight, we conclude that in many cases the mental instability is not the result of the perturbation which precedes puberty. This physiological explanation is not of such general application as is sometimes supposed” (77, p. 18).
Only when an emotional disturbance is so great as to be detectable by mental tests will this influx need to be taken into consideration in stating the borderline for objective tests. The evidence that few cases of feeble-mindedness are not detectable until after ten years of age is all the other way. With the Stanford measuring scale, Terman and his co-workers did not even find a noticeable increase in the variability of the groups at the ages of adolescence (57, p. 555). It is to be remembered also that we are not concerned here with mere instability which corrects itself with more maturity, such as has been described by Bronner among delinquents. This does not, 25of course, amount to an incurable conative deficiency and is not classified under feeble-mindedness.
Goddard has suggested that possibly the moral imbecile group comes into our class of feeble-minded suddenly with a common arrest of development at about the stage reached by the nine-year-old. He notes that “of the twenty-three cases of this sort picked out for us (at Vineland) by the head of the school department, fifteen are in the nine-year-old group, five in the ten-year-old, two in the eleven, and one in the twelve” (113). He regards this evidence, however, as meager and only suggestive. Doll has given evidence of late appearance of retardation in rare cases (100 and 99).
It is to be noted that if a sudden change is found in the percentage of children falling below a certain test standard it is perhaps more likely to mean that there is a change in the difficulty of the tests at that point. For example our Table V shows 1.3% of the nine-year-olds test two or more years retarded, while 18.9% of the ten-year-olds are retarded two years or more. This presumably indicates a change in the relative difficulty of the tests for VII and VIII rather than a change in the frequency of retardation at ages nine and ten. When we turn to Goddard's norms for VII and VIII we find that 81% of the seven-year-old children pass the norm for VII while only 56% of the eight-year-old children pass the norm for VIII.
The Jaederholm data (167) obtained by applying the Binet tests to pupils in the regular school classes and in special classes for the retarded may suggest a possible influx of intellectual deficiency at about 12 years of age or else “more mental stagnation in the intellectually defective” at this life-age and after. If one were to define intellectual deficiency in terms of the standard deviation 26of the regular school children, this data suggests that there is a marked increase in the number of children sent to the special classes at 12 years of age who are -4 S. D. or lower. Roughly speaking it amounts to 36 children at 12 years of age, 36 at 13, and 21 at 14, as compared with 11 at 11 years and 13 at 10 years. On the other hand, this may as well mean that intellectual deficiency becomes greater in degree rather than in frequency at these ages. The latter interpretation is adopted by Pearson for the Jaederholm data, so that it is perhaps not necessary to consider this evidence further. On the average the pupils in the special classes fall about .3 S. D. months further behind regular school children with each added year of life from 5 to 14 inclusive. A third possible interpretation of the greater number showing the degree of deficiency measured by -4 S. D. with the older ages should be mentioned. It is possible that 1 S. D. has not the same significance for 5-year-olds as for 12-year-olds. The distribution of abilities at succeeding ages may be progressively more and more skewed in the direction of deficiency. We shall return to this point in Part Two as showing the advantage of the percentage definition over a definition in terms of the deviation. In connection with the Jaederholm data on special classes one should also consider the fact that younger children are not as likely to be detected by the teachers and sent to the special classes. It is possible also that the difference in difficulty of the tests for different age groups is somewhat obscured by using a year of excess or deficiency as a constant unit as Pearson has in treating this data. The bearing of this difference in difficulty was pointed out above for Goddard's data.
The investigations by Pearson of children in the regular school classes indicate that there is no important shift with maturity in the frequency of those with different 27degrees of ability, when the ability is measured either in terms of years of excess or deficiency with the Jaederholm form of the Binet scale or in terms of estimates of ability relative to children of the same age (166 and 167). In both these studies the correlation of ability with age was shown to be almost zero. For tested ability for 261 school children “r” was .0105, P. E. .0417; with the estimated ability, the correlation ratios were for 2389 boys, .054, P. E. .014; for 2249 girls, .081, P. E. .014. Until we have better data this is certainly the most authoritative quantitative answer to the question of the shift with age in the frequency of the same relative degree of mental capacity.
The best method of empirically settling this question of the early appearance and constancy of deficiency would be to test the same group of children again after they had reached maturity and find out how many of those who tested in the lowest X per cent. still remained in the same relative position. This is, of course, not possible at present, but it certainly should be done before we are dogmatic as to the permanent isolation of the lowest X percentage at any age. The nearest approach to this sort of evidence is Goddard's three annual testings of a group of 346 feeble-minded children with the Binet scale (117, p. 121-131). Among these 109 showed no variation, 123 gained or lost 0.1 or 0.2 year, 18 lost 0.3 or more, and only 96 gained 0.3 or more of a year. With so small a change in absolute tested ability the probability of a change in position relative to normal children seems to be slight. Only one of the 76 who had tested in the idiot group gained as much as a half year in tested age in three years.
It is not possible to settle this question of the constancy of the percentage of intellectual deficiency from one life-age to the next by considering the frequency of different 28ages of children among those who are sent to special classes for retarded pupils. This is evident from the fact that these classes contain a considerable proportion of those who are feeble mentally mainly because of conative disturbances. These would not be detected by our present tests and would not be classed as intellectually deficient. In the second place the pupils for the special classes are usually selected mainly on the advice of their teachers, who cannot, of course, without tests select those who are intellectually deficient except by trying them for a number of years in the regular school classes. This means that a smaller percentage of pupils in the special classes at the younger ages is to be expected.
The figures of the U.S. Census as to the ages of inmates of the institutions for feeble-minded are also of little significance in connection with the question of the variation from age to age. That the number of inmates at the different ages is affected most largely by the pressure of necessity for shifting the care from their homes to the institution is shown by the fact that three-fourths of the admissions are of persons over 10 years of age. It is also indicated by the fact that for the period from 15 to 19 the males are over 20% more frequent than females, while from 30-34 the females are nearly 20% more frequent. Considering those ages most frequently represented in the institutions, 10-24 years, the average variation for the three five-year periods in the percentage of the population of the corresponding ages who are in these institutions is only 0.01%. The middle five-year period has the most, but even if there were a cumulation of feeble-mindedness with age, which is not shown, we would anticipate a change of not more than 0.05% for these 15 years. This would be clearly negligible in considering the general problem.
29That little allowance for the variation from age to age need be made for the number of cases not discoverable at the beginning of school life is further indicated by report of the Minnesota State School for Feeble-Minded. It shows that in only 247 out of its 3040 admissions was the mental deficiency known to commence after six years of age (154). If the number of feeble-minded who should be isolated were found to increase after school age less than one in 10,000 of the population, as this suggests, it would surely be better to neglect this variation from age to age than to emphasize it in dealing with the problem of objective diagnosis and social welfare.
How rare is the onset of feeble-mindedness after five years of age is also shown by the frequency of hereditary causes. In his study of the 300 families represented at Vineland, Goddard places only 19% in his “accidental” group and 2.6% in the group for which the causes are unassigned. The rest are either in the hereditary group, probably hereditary, or with neurotic heredity. Half of the cases in the “accidental” group are due to meningitis. His histories show that only 9 of the “accidental” and unassigned groups were unknown at 5 years of age. This is only 3% of his total feeble-minded group. To these might be added, perhaps, a few from the hereditary groups who did not show their feeble-mindedness at so early an age, but so far as I can judge these would not be of the intellectually deficient type that would be detectable by the Binet scale at any age. They would test high enough intellectually to pass socially and require expert diagnosis to be classed as feeble-minded.
Certain diseases, epilepsy and meningitis, are undoubtedly causes of feeble-mindedness. The evidence, however, seems to be that they are so rare compared with the mass of mental deficiency that after 5 years they may 30well be offset by the excessive death rate among the feeble-minded. That recoveries from feeble-mindedness are insignificant is generally agreed. Among the 20,000 in institutions in 1910 only 55 were returned to the custody of themselves. This is further evidence of the fundamental, if not congenital, nature of the deficiency.
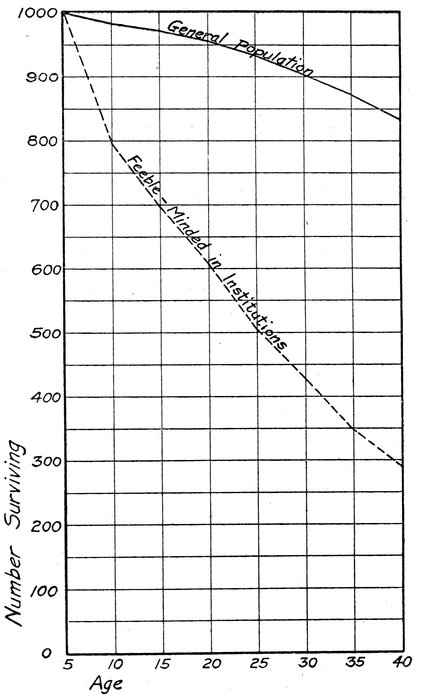
While the evidence submitted above makes it seem fair to assume that the increase in the frequency of a certain degree of intellectual deficiency with age is probably negligible, it is not clear that the decrease with age in the proportion of feeble-minded caused by an excessive death rate may be neglected even for the test ages 5 to 25. By searching the literature it has been possible to assemble the records for nearly 3500 deaths among the feeble-minded in institutions in this country and Great Britain distributed by ages in ten-year periods. This evidence is presented in Table I. The number of cases under five years of age living in the institutions is so small that the deaths under five years are certainly misleading. They have, therefore, been omitted from the table and the distribution calculated for those five years or over (123, 154, 204, 205). Comparison is made with a similar distribution of the total deaths for a period of five years from 1901 to 1904, inclusive, within the area of the United States in which deaths are registered, compiled from the special mortality report of the Bureau of the Census (206). This registration area has a population of about 32,000,000. The general agreement of the distribution of deaths among the four different groups of institutional inmates seems to make it reasonable to assume that the United States group of institutional deaths for the year 1910 is a conservative description of excessive death frequency at the early ages among the feeble-minded in institutions.
| Population | Ages | ||||||
|---|---|---|---|---|---|---|---|
| 5-14 | 15-24 | 25-34 | 35-44 | 45-54 | 55 & over | ||
| Gen'l—U. S. in death registration area | 1,897,492 | 6.1% | 9.6% | 12.8% | 13.0% | 13.6% | 44.9% |
| F. M. 1910 in Institut'ns in U. S. | 840 | 26.6 | 33.0 | 18.9 | 9.1 | 45 & over 12.3 |
|
| F. M. British (Earlswood) | 997 | 34.3 | 41.1 | 10.4 | 6.5 | 3.5 | 55 & over 4.2 |
| F. M. British (Barr) | 613 | 34.7 | 46.8 | 9.5 | 35 & over 9.0 |
||
| F. M. Faribault Minnesota | 982 | 27.6 | 38.0 | 16.1 | 8.6 | 3.5 | 55 & over 6.2 |
| Ages | ||||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | |
| General population | 1000 | 983 | 972 | 956 | 934 | 903 | 872 | 835 |
| Deficients in Institut'ns | 1000 | 795 | 696 | 606 | 503 | 428 | 349 | 290 |
| Per cent. deficient if 1% at age 15 | 1.40 | 1.11 | 1.00 | .75 | ||||

Fig. 1. Mortality among Feeble-Minded in Institutions Compared With the General Population
33A comparison of the death rates of the feeble-minded and the general population at different ages is of prime importance in connection with all attempts at quantitative descriptions of deficiency. Heretofore this has been completely neglected. Fig. 1 and Table II have been prepared to provide a roughly adequate estimate, on the basis of the above data for the United States, as to the survival of 1000 institutional cases of feeble-minded 5 years of age for successive age periods compared with 1000 people in the general population. In constructing this table it was necessary to assume, since the facts were not given, that the age distribution in the registration area of the general population was the same as for the United States as a whole (census of 1910) and that the number of feeble-minded in the institutions at the various age periods was equal to the number enumerated on the first of January plus the admissions during the year 1910, disregarding the number discharged since they are not distributed by ages. The average annual death rate among the institutional cases of feeble-minded 5 years of age and over in the United States in 1910 was 35.19 per thousand, while the corresponding death rate in the general population of the registration area for the five years 1901-1904 inclusive was 13.56. Assuming that the death rates are uniform within the five-year periods, the decline in the proportion of institutional feeble-minded from 5-25 years of age as the result of excessive mortality is indicated by the last line in Table II, after allowing for the mortality in the general population. That this effect of excessive mortality upon the percentage of feeble-minded cannot be neglected between 5 and 25 years of age is apparent unless the mortality among institutional cases is much greater than it is among the deficient generally. As the figures stand the proportion of feeble-minded would be reduced nearly one-half between ages 5 and 25. Only a small part of this reduction probably would be compensated for by new cases developing from accident or disease. On the other hand there is little doubt that the institutions contain an excessive proportion of low grade cases among whom the mortality is much greater. The mortality among institutional cases is, therefore, probably not typical of that among the feeble-minded generally. Nevertheless it is so great that any quantitative definition of deficiency which neglects it entirely is open to serious objection. We shall, therefore, keep this variation in mind in connection with the discussion in the next chapter of the percentage which is deficient, and in the adaptation of the definition to a measuring scale. It is clear that the percentage should be so chosen as to allow best for the possible large effect of excessive mortality among the deficients. Finally, it 34should be said that the percentage definition of feeble-mindedness might be modified to meet a varying percentage from age to age should that ever become desirable.
If most of the feeble-minded for whom society should provide were of the type which is only conative and not detectable by our present objective tests, a quantitative definition would be abortive. We must, therefore, study our assumption that it is worth while to direct our attention to those who are intellectually deficient. We shall attempt to discover how frequent are the primarily conative types.
Before examining the quantitative evidence we may note that it is in conformity with two prominent recent tendencies in psychology to subordinate specialized abilities, as compared with abilities which function commonly in many situations. The first of these tendencies is represented by the fundamental researches of Hart and Spearman (123) (185). This is not the place to set forth the technical work on which their conclusions are based. It may be said, however, that, with 17 different psychological tests, they were unable to discover any important specific mental weakness which distinguished adults who were suffering with any one of various mental abnormalities, including imbecility, manic-depressive insanity, dementia praecox, paranoia, and general paralysis of the insane. This may have been the fault of the tests, but it seems to be more likely that the fault lies in the custom of emphasizing special abilities and disabilities, at least from the point of view of tested capacities. On the other hand, all of these mental abnormalities showed a weakness in general intellectual ability. This is true whether 35this general ability be regarded, as it is by Hart and Spearman, as due to a general fund of brain energy, or whether general ability be taken to refer to the common recurrence of many specific abilities in much of our mental life. Its significance for this study is that a series of varied tests, such as that of Binet, may be expected to give a good estimate of general ability, and its failure to disclose specific disabilities is thus less important.
The second influence in psychology tending to emphasize average tested ability is the establishment of the biological conception of the mind which recognizes the mutual interdependence of the mental processes, organically united through the activity of the brain. So long as intellectual, emotional and volitional processes are all mutually dependent, a disturbance of one aspect of mental life is bound to affect the others. In considering the mutual dependence of the mental processes, it is important to weigh carefully the striking examples which Bronner[4] has brought together, illustrating special abilities and disabilities. She has made an admirable start toward a differential diagnosis of special defects in number work, language ability and other mental activities. The degree of special deficiency which results in social failure could be placed upon an objective basis, but the rarity of special deficiencies as compared with general deficiency will make this a slow task. In the meantime we may rely upon the mutual dependence of the organic processes as a point of view which emphasizes the common spread of deficiency to many activities. Knowledge of a single case of specific disability is sufficient to make us recognize that such cases do occur. On account of the rarity of those cases and the absence of objective criteria, it seems necessary 36to leave the further differentiation to the future, considering here only those cases which may be grouped together as conative, as contrasted with those detected by our general intellectual tests.
Whether the group of primarily conative cases is of any considerable size can be only very roughly estimated at present, since the diagnosis of such cases of feeble-mindedness rests at present almost exclusively on the subjective opinion of the examiner. Before their diagnosis is put upon an objective basis we must have a different form of test directed at such traits of will as initiative, perseverance, stability and self-control. These probably center on the mental side around the instinctive emotional background of interest and the passions, while, on the physical side, they raise the question whether the subject's energy is adequate to endure the strain of competition or whether it shows itself only in sudden bursts.
If the diagnosis of conative cases could be determined objectively, it is possible that most forms of social unfitness would be found highly correlated with intellectual deficiency. On the other hand, when the diagnosis of unfitness for school or social life depends merely upon the opinion of experts or teachers, the inaccuracy of the diagnosis may show a wide discrepancy between the so-called conative and intellectual types of deficiency. Binet, on the basis of his acquaintance with the pupils in special classes, suggested that the number of unstable children is probably equal to the number of those who are intellectually unsuited for the ordinary schools or institutions (77). Since he then places the total number of the two classes at four or five per cent., it is apparent that he is discussing a higher type of ability than is usually included under the term feeble-minded. We can get somewhat better evidence on this question by studying the results 37of Binet tests applied to children cared for in special classes or in institutions for the feeble-minded. Chotzen (90) presents a table of 280 children in the Hilfsschule in Breslau, only 201 of whom, however, he himself diagnosed as feeble-minded, i. e., debile or lower. Of these only 51 were intellectually deficient as indicated by the Binet tests when we include the doubtful cases according to the criteria we have adopted in this study. If we suppose that, in addition to those in the special classes, there would be one intellectually deficient child in an institution for feeble-minded for every child testing deficient, we would then guess that only 40% of the feeble-minded children in Breslau were intellectually deficient. This sort of estimate seems to agree with Binet's belief that half of the children requiring special care, at least during school ages, are cases which are primarily conative.
Pearson has approached the same problem in another way (164) (167). He has used the results of the psychological tests applied by Norsworthy to children in New York in special classes and institutions for feeble-minded compared with those in the regular school classes, and the results of Jaederholm obtained with the Binet tests applied to 301 children in Stockholm in the special classes compared with 261 others selected from the regular classes. He found that “70.5% of normal children fall into the range of intelligence of the so-called mentally defective; and 60.5% of so-called mentally defective children have an intelligence comparable with that of some normal children” (167, p. 23). On the statistical assumption that those in the normal classes would distribute according to the Gaussian normal probability curve he estimates that, with the Binet tests, among those in the special classes “10% to 20%, or those from 4 to 4.5 years and beyond of mental defect, could not be matched at all from 27,000 children” 38(164, p. 46). Another 20 to 30% could be intellectually matched by those in the regular classes having from 3 to 4.5 years of mental deficiency, but they would be matched very rarely. On the assumption that 1% of the children were feeble-minded, not more than about two children in a thousand of this regular school population would be expected to be 3 or more years retarded and thus overlap those of like deficiency in the special classes (167, p. 30). Considering the results of Norsworthy's study he says on similar assumptions: “It seems, therefore, that a carefully planned psychological test, while not sufficing to differentiate 50 to 60% of the mentally defective from the normal child, would suffice to differentiate 40 to 50%” (164, p. 35). Again we come back to the estimate that psychological tests may well be expected to select nearly half of the children at present found in special classes for retarded pupils. Moreover, a considerable part of the overlapping of intellectual deficiency in the regular classes with that in the special classes which he found may be accounted for by the inadequate methods of selection of pupils for the special classes by teachers or examiners who have used no objective tests. Some who were left in the regular classes should undoubtedly have been transferred to special classes and vice versa. There seems to be nothing to indicate that less than half of those properly sent to special classes would be of clear or doubtful intellectual deficiency. If the tests served to select even a smaller proportion of those assigned to special instruction, the “school inefficients” as Pearson calls them, their value as an aid to diagnosis would be demonstrated.
Among groups of delinquents, where we would expect the purely conative cases to be more common, we find that a careful diagnosis of feeble-mindedness on the basis of test data, medical examination and case history indicates 39that conative cases without serious intellectual deficiency are much rarer than intellectually deficient delinquents. At least this is the evidence of one study where such information is available. Kohs at the Chicago House of Correction found among 219 cases over 16 years of age, which he diagnosed as feeble-minded, only 28 tested XI and there were only 52 who did not test either presumably deficient or uncertain intellectually according to our criterion. Another bit of evidence is that collected at the Clearing House for Mental Defectives in connection with the New York Post-Graduate School of Medicine, where 200 consecutive cases (108 males) were examined by Miss Hinckley. Her graphs show that only 15% tested X or above with the Binet revised scale, i. e., above those presumably deficient in intellect. The cases were from 13 to 42 years of age. The clearing house provides an opportunity for social workers to have suspected deficients examined and the few cases over X seems to indicate that the purely conative type is not very commonly met with among the social workers.
When we turn to the institutions for the feeble-minded we find that they are today caring for few solely conative cases. Although I can find no tables which give both the life ages and mental ages of the individual inmates, we can at least be sure that few test so high as X, or above with the Binet scale. This means that only a few have as yet reached the threshold for passable adult intellects, which should be attained by 15 years of age. At the Minnesota state institution for the feeble-minded in Faribault among 1266 inmates, excluding epileptics, 41 tested X; 28, XI; 12, XII; and 8, XIII, a total of 7% (154). At Vineland, N. J., Goddard reported among 382 inmates, 14 tested X; 5, XI; and 7, XII, about 7%. Some of the children who were under 15 in life-age might later develop 40above the limit for intellectual deficiency. Of the 1266 at the Minnesota institution, however, 508 were 15 or over at the time of their admission, so that at least 82% of the 508 were clearly intellectually deficient. Eight per cent. more tested X and were in the doubtful group in intellectual ability according to the criteria we have adopted. This suggests that not more than about 10% of those who are at present isolated in institutions are there for feebleness of will alone. It seems to confirm our presumption that the intellectually deficient discovered by tests form the great majority of the social deficients who need prolonged care or assistance.
The quantitative definition of intellectual deficiency must be made with careful allowance for irregularities among different mental processes, among different individuals, and among different groups. Theoretically it is possible to place the borderline so low that a case with that degree of deficiency and without removable handicaps would be clearly feeble-minded. The chance that the diagnosis would be mistaken could be reduced to any minimum desired. Above this a wider region of doubtful deficiency could then be stated in similar form. This is the plan that we suggest in attempting the percentage definition. Practically, however, the plan assumes that a suitable allowance can actually be made for these variations and raises a number of problems as to variability which should be considered. Four of these sources of variation are discussed below: (1) the variation due to a limited sample of individuals measured, (2) the variation among different communities, (3) the variations arising from sex, race and social differences, (4) the variation of the same individual from one mental process to another. 41We do not have the problem of neglecting these variations, but of adequately allowing for them both in the percentage of presumably deficient and in the doubtful region.
(1) Variation among Samples of Individuals Measured. The error introduced by the fact that measurements are made on a limited rather than an unlimited number of individuals, in establishing the standards with a system of tests, can be taken care of statistically fairly well by applying the theory of probability as to the error of a percentage in a single sample. The range of the error can then be indicated on the measurement scale. This supposes, however, that each sample to be measured is taken from a random group and not from a selected group. Allowance for this error of sampling is therefore complicated by the fact that the usual test data have been obtained from groups of school children, even when there has been no further selection within the school group. Data on school children are certainly reliable only within the years of compulsory school attendance. Ordinarily in this country, they are not reliable for children of 14 years of age or over. Moreover, the point of the scale which is reached by the lowest X percentage of school pupils will exclude a slightly larger percentage of all children of corresponding ages, since the idiots and some imbeciles are not sent to the ordinary schools. This slight discrepancy should be kept in mind. The problem of avoiding selected samples among adults is still more difficult; but we found that it was possible in one community at least to measure all the 15-year-olds in the lowest X percentage in certain districts, as we shall note later. By this age, mental processes are probably very much like those of adults, except for the amount of information and practise.
42(2) Variation among Different Communities. Under any conception of deficiency it is clear that there are relatively more deficients in some communities than others. The percentage should, of course, not be determined for a small community such as a city or county, but for a state or a nation in order to avoid the difficulty of the difference between communities. It would not interfere with the plan for isolating the lowest X percentage of a state even if that meant isolating 10% in one small community and none in another. Indeed, it might be expected to do just that, when one considers the accumulation of deficiency in certain settlements such as Key has shown (131, p. 63). The data on which the borderline with a measuring scale would be established should, of course, not be obtained from communities known to be unusual in respect to the frequency of deficiency.
Since social failure is our final criterion for judging deficiency, we must further consider that it is easier for a person to survive in one environment than in another: in the country, for example, than in the city. This sort of problem has led to considerable confusion. Goddard remarks: “In consequence of this it happens that a man may be intelligent in one environment and unintelligent in another. It is this point which Binet has illustrated by saying 'A French peasant may be normal in a rural community but feeble-minded in Paris.'” (117, p. 573.) Goddard then goes on to suppose that a delinquent with the intelligence of a sixteen year old may be “defective” because he happens “to have got into an environment that requires a twenty-year-old intelligence.” The suggestion that a criminal might be excused on the ground of deficiency because he happened to fall among bad companions is a reductio ad absurdum. Clearly environment must be defined as ordinary environment, available 43environment or by some similar concept, or else the definition of deficiency loses all significance. In another place Goddard more properly suggests that it would be well to “draw one line at that point below which a person of that intelligence is not desirable or useful in any environment” (117, p. 3).
So long as the care of the feeble-minded is a state problem the percentage of passable intellects would apparently be determined for the available environment in that state. The problem of social care cannot mean that the state should care for college men because they cannot survive among college men or in the station of life into which they may have been born. So long as there are environments within the community where they can survive it is a problem of shifting them in their social habitat, not a problem for social care. The same is true for the low grades of intellect. It is not likely, however, that any portion of the community could absorb many more of the low degree intellects. For the problem of social care for the feeble-minded, the question: What environment will allow this individual to survive? becomes the question: Can he survive in any available environment in his community? It would seem very hazardous to suppose that the different opportunities for survival afforded by different localities in a state would be large enough to care for more than the group of doubtful cases which should be allowed for in a quantitative description of the border region.
(3) The Variation with Sex, Race, and Social Position has been carefully called to attention by Yerkes and Bridges in their studies with the Binet Point Scale (225, Chap. V and VI). It may very well be that not as high ability should be expected of certain groups as of others; 44as a matter of moral obligation, they are not as responsible for their conduct or their attainments. On the other hand this does not directly affect the question, what lowest percentage of intellects cannot get along in society? When that percentage is determined for the environment available in the community all those who fall within it might even turn out to be of one sex or of one nationality or of one social position, without affecting the question whether they should be cared for by society, or what grade of intellect is not socially passable? Temporary social handicaps, such as lack of familiarity with the language, lack of training, etc., must, of course, be allowed for so far as they affect the individual's test record. Whether the difference of 5% to 10% in the score of pupils born to non-English-speaking families compared to their companions' (225, p. 66) is due to the temporary handicap of language or to a permanent difference is, however, just the problem which the Yerkes and Bridges study does not answer. The fact that the difference is even greater for older children suggests that it may indicate an inborn difference between the groups compared.
A diagnosis of deficiency should not be made until the examiner is able to estimate whether the removal of training or health handicaps would bring the individual above the borderline. So far as known temporary handicaps affect the standard of the test results with groups they should, of course, also be taken into account. On the other hand, it is clear that the borderline which predicts social failure should not be shifted to allow for differences in permanent handicaps whether those be of race, sex or social position.
(4) The Variation among Different Mental Processes. With our present knowledge the most difficult variation for which we must make allowance at the borderline is the 45variation from one trait or process to another in the same individual. One phase of it was discussed above under “c.” The investigation of Norsworthy throws light on this question. Summarizing her tests she says: “Among idiots there is not an equal lack of mental capacity in all directions. There is something of the same lack of correlation among the traits measured in the case of idiots as there is with ordinary people” (159, p. 68). Again: “The idiots are nearest the central tendency for children in general in the measurements of mental traits which are chiefly tests of maturity, and farther and farther away as measurements are made which are tests of ability to deal with abstract data. They are two and a half times as far from the median for children in general in tests like the genus-species test as they are in tests like the A test or the perception of weight.” Weidensall (60) and Pyle (46) also compare delinquent and normal individuals for different tests, showing a variation with the sort of mental activity compared.
While Norsworthy thus presents evidence of certain specializations of deficiency, she notes, however, that perhaps feeble-mindedness is more typically general than specific and that general deficiency is more important to consider than specific. Even with that test with which her group of retarded and feeble-minded children did best, only 28% of them passed the point which would be excelled by 75% of the children in general. In their worst test only 1% passed this point. It is also to be noticed that those tests in which they most nearly approached ordinary children are for just those simple processes which would be least likely to be of use in the struggle for social existence. As a whole, therefore, there is nothing in her results which shows that any appreciable number of children who were deficient in the average of tested abilities, 46would have good enough special ability along a few lines to make them socially passable. Indeed, for all that we know at present, the borderline for passable ability in each of our various mental processes might vary quite as much as Norsworthy found, without this variation affecting a prediction of failure based upon the average of a series of tests.
On account of the great attention that has been paid to individual differences in recent years, on account of their importance for diagnosis, for determining the causes of deficiency, and for planning for the training of deficients, we have come almost to the point where we forget the significance of the average as the most common condition with which we have to deal. The lack of complete correlation between abilities of an individual does not make us hesitate to use the concept of his average ability; it should not make us neglect or misunderstand the significance of the position of an individual testing low down on the scale. For the problem of social care the borderline position on a scale is immensely more important than higher ability. It seems advisable, therefore, to define this borderline ability with some suitable allowance for variability in mental processes. It is far safer to judge an individual's chance of survival by his average or general tested ability than by the little knowledge that is as yet available regarding special abilities.
4. Augusta F. Bronner. The Psychology of Special Abilities and Disabilities. Boston, 1917, pp. vii, 269.
At first it seems like a hopeless task to try to bring harmony out of the confused estimates of the proportion of the feeble-minded in modern society. Authoritative estimates by commissions or by recognized experts range from less than 0.2% to 5.0% that is, from 2 to 50 per thousand. Further study of these estimates shows that they reflect not so much a difference in expert opinion about the same problem as differences in the problems which were considered in making the estimates. As soon as we compare only those estimates that have been made to answer the question, what percentage of low grade minds should be provided with a certain form of social care? it is rather surprising how much less the discrepancy becomes. An analysis of important estimates will therefore be undertaken in order to try to discover some of the sources of disagreement.
The most significant thing about an estimate is that the estimator is thinking of providing for his group of deficients in a special way. This is the purpose of the estimates. Three important groups of the mentally deficient now demand attention. They are: (1) The group which, for moral and eugenic reasons, society is justified in isolating for life or an indefinite period. (2) The group which needs special simple industrial training in order to get along with social assistance without isolation. These deficients may be cared for in their home towns by special schools, public guardians, and after-care committees. (3) The group which needs special school assistance, but is socially passable after leaving school. These individuals are incapable of competing in school with their fellows, 48but they are able to get along in the simplest employments without social assistance. We may designate these three groups as those needing (1) social isolation, (2) social assistance, and (3) only school assistance. The largest estimates of feeble-mindedness, it will be found, include the third group, while the smallest intend to include only the first group. The first and second groups are clearly below the limit of feeble-mindedness designated by the verbal definition of the British Commission. They are socially unfit. The language of that definition is ambiguous enough to include the third group, but the plan of the Commission, judged by its consideration of the number to be sent to special schools, would regard only the first two classes as feeble-minded. Following this common conception I have regarded those in the third group as above the feeble-minded. It will help to find harmony among the estimates if we estimate separately those mentally deficient enough to need social isolation, social assistance, and only school assistance. This discrimination of the retarded by the kind of social care needed should also make the social definition more useful.
Before we consider the percentage estimates in detail for these different forms of social care, let us note the effect on them of two other considerations. The first of these is the discrepancy between estimates of the proportion of feeble-minded among school children and estimates as to the proportion in the general population. Since feeble-mindedness is regarded as a permanent arrest of mental development occurring at an early age and usually due to hereditary causes, it is plain that a school child who is feeble-minded would be expected to remain 49so for life. Nevertheless we find that estimates of 0.3% of the general population are accompanied by estimates of 1.0% or 2.0% of the school population as feeble-minded. I have not been able to find any careful attempt to account for these discrepancies. The excessive mortality among the feeble-minded is hardly adequate to explain so great a difference.
It is interesting to note some of these comparisons. Goddard, for example, considers it conservative to estimate that 2% of the school population is “feeble-minded” (112, p. 6). In the same publication he says: “There are between 300,000 and 400,000 feeble-minded persons in the United States” (p. 582). Since the elementary school enrollment is about 20,000,000 (208), the feeble-minded school children alone on his first estimate would account for 400,000 feeble-minded in the United States without allowing for any feeble-minded outside of the ages in the elementary school.
The report of the British Royal Commission, published in 1908, forms the starting point for many of the estimates made today. The commission added together the number of school children which were thought to require special classes with the number of defectives found in institutions, prisons and almshouses, or reported by its medical investigators. The total gave 0.46% of the general population as “mentally defective persons,” not including certified lunatics. From this amount should be deducted .06% who were insane but had not been certified as such, leaving 0.4% mentally deficient. This was not regarded by the Commission as an estimate, but was the number actually “enumerated by the medical investigators” in sixteen typical districts studied in England and Wales with a total population of 2,362,222 (83, VIII, p. 192). Turning to the school children we find that in 50the areas investigated there were 436,833 school children of whom 0.79% were found defective. Since this was an enumeration and not an estimate, the commission paid no attention to the discrepancy between 0.79% of the school children and 0.31% of the rest of the population. Tredgold, moreover, based his estimates of the frequency of the mental deficiency in England and Wales on the data of the Royal Commission without attempting to harmonize this discrepancy. This oversight has apparently been one source of the not uncommon difference between the estimates for school children and for the general population. One suspects that the fact that the elementary school population is about a fifth of the general population, has also mistakenly contributed to this error. The discrepancy of three to five times as large a frequency of deficiency among school children as in the general population certainly needs clearing up.
There is an escape from this dilemma which seems more reasonable than to attempt to account for the discrepancy by excessive mortality. When estimates are made concerning the school population the estimator is usually thinking of that group of feeble-minded which needs special school training and probably social assistance afterward. When estimates are made of the general population the estimator is likely to be thinking of that group which must be cared for permanently by society, mainly in institutions or colonies. For some time at least the state cannot be expected to undertake the indefinite care of all the deficients who should have, at once, simple industrial training, in special local schools or classes in order to survive, even with social assistance. This difference in the type of care contemplated seems most naturally to account for the discrepancy found with many writers, between their estimates for the school population and for the general population.
A second source of confusion arises when one investigator is thinking of the number of feeble-minded, the care of whom it is desirable that society should assume, and another is thinking of the feeble-minded, the care of whom it is advisable for society to assume at once. Considered in connection with a specific case the distinction is quite obvious. It is one thing to say that it would be desirable for the state to assume the indefinite care of a particular person, it is quite another thing to say that it would be advisable for the state to assume that care immediately, when one remembers the crowded condition of the institutions, the necessity of caring for the worst cases first, the possibility of the person being cared for by his own family or in a local school, the added public expense, the necessary neglect of other movements for social welfare if society assumes this expense, etc., etc.
When you magnify this problem in the mind of the estimator who is interested in the question of caring for the groups of feeble-minded, the result is that his estimates of the size of the groups are decidedly affected. For example, few would deny that the Site Commission of New York appointed to locate the colony for mental defectives, now known as the Letchworth Village, was emphasizing a program of permanent social care when it estimated the number of feeble-minded in New York. The Commission, “after taking into consideration the figures of the State and National census, and other data collected from institutions,” estimated that there were in New York state possibly 12,300 mentally defective persons (Editor's Note, 205, p. 84). This is less than 0.15% of the population and very low compared with most estimates.
52The low estimates will generally be found to be influenced by considerations of public expense rather than the social unfitness of the lower group. Inasmuch as there are no sharp distinctions between different degrees of mental ability this consideration of public expense is perfectly proper. At the other extreme, however, are the eugenists who are convinced that it is desirable to isolate a large group at the lower range of ability. The member of the legislature will be concerned mainly with the question how much money will the public be willing to appropriate now for the care of these unfortunates. The eugenist will be thinking of an ideal rather far in the future towards which to work.
The diagnostician should take a conservative intermediate ground. He may leave to the court or other authorized tribunal to decide whether the public has the facilities available at present for caring for a particular weak-minded person, but he must decide whether expert scientific opinion at the present time will justify diagnosing this degree of deficiency as suitable for the special care provided for the feeble-minded. Whether it is advisable to care for the particular deficient at home, in a special local school, or in a state institution would be left to the legal authority to decide. Under present conditions, the diagnostician may possibly indicate whether the individual is deficient enough to justify social isolation, or merely to justify sending to a local elementary day school for deficients.
It is from the point of view of the diagnostician that we shall attempt to focus this question of the percentage of feeble-minded. We shall tentatively suggest limits as 53to the degrees of intellectual deficiency which we might be justified in regarding, under the present conditions of scientific knowledge as being low enough in intellectual capacity to justify particular forms of social care. Such estimates will be of value if they help to harmonize the conflicting opinions by bringing them into relation with the above analysis. We shall, therefore, compare the suggested percentages with a number of authoritative statements of the frequency of feeble-mindedness. By considering the differences in the nature of the estimations we may approach nearer to an understanding of the problem.
Since the percentages to be suggested are chosen from the point of view of diagnosis, they do not represent the number for which every community should immediately make financial provision. The expense is a local or a state question. It is so much affected by state conditions and by public policy that it probably must be determined in any state by a special commission. On the other hand, the laws already provide for caring for the feeble-minded in institutions or colonies and in special schools or classes, so that the estimates may help to guide diagnosticians who are called upon to decide whether a particular person might be rightfully regarded as deficient enough intellectually to justify committing him for permanent care to a state institution. In the present practise it is fairly clear that this distinction is made in the minds of different diagnosticians. It may ultimately be desirable that this differentiation between the types of social care be introduced into the law. Until then it will remain the duty of the court to determine what degree of social unfitness is intended by a particular law. The social concept of feeble-mindedness is just now undergoing a rapid evolution so that it would be impossible to predict how it may legally crystallize a generation hence.
54To begin with the lowest group of the feeble-minded, we should consider those whom the state might be clearly justified in isolating indefinitely on the basis of their tested lack of intellectual capacity, the social isolation group. For purposes of comparison let us place this degree of intellectual ability as that possessed by the lowest 0.5% at fifteen years of age. Above these let us estimate a group of uncertain cases so far as isolation is concerned, but cases which the diagnostician would be justified in regarding as intellectually deficient enough to justify sending to special local schools for training the feeble-minded. After special training the majority of these cases might be expected to require social assistance indefinitely. They would form the social assistance group. Isolation would be justified for none of them on the basis of their test records alone. Those in this group who were persistent delinquents would, by that additional fact, fall into the lowest group so far as social care is concerned. Let us estimate this social assistance group tentatively as the next 1.0% at fifteen years of age.
These estimates have been made as at fifteen years of age since the effect of the excessive mortality especially among the isolation group is uncertain and may need to be allowed for in a discussion of the percentage deficient at different ages. If the mortality were as great as has been described among institutional cases in the previous chapter, a rough estimate of the percentage intellectually deficient in the general population places it at less than 0.5%. This estimate may be made by using the estimated deficiency at the median age of those under 15 years of age and at the median age of those 15 years of age and over. According to the age distribution of the 1910 census, there were 32% under 15 years with a median age of 6 years. At age six 0.67% would be presumed as 55low as 0.50% at 15 years. The older group (68% of the population) has a median age of 32 with a corresponding percentage in the isolation group at that age of 0.30%, after allowing for differences in mortality on the plan indicated in Table II. This rough estimate for the lowest group indicates that 0.42% of the general population would be of as low a degree of intellectual capacity as the lowest 0.5% at 15 years. Our plan presumes, therefore, that between 0.4% and 0.5% of the population are unable to pass their entire lives outside of institutions under ordinary conditions; i. e., make an honest living and live within the law even with social assistance and supervision.
The corresponding estimate for those requiring only social assistance would be between 0.8% and 1.0% of the general population above the lowest group. This might vary from approximately 1.34% at 6 years to 0.59% at 32, the median age for those over 14 years. Since the mortality is probably less among deficients not in institutions, as they average higher in ability, the changes in the percentages are probably extreme estimates. We should keep in mind, however, the possibility that with the excessive death rate the lowest 1.0% at 15 may mean an ability corresponding to the lowest 1.34% at 6 years and the lowest 0.60% at 32 years.
The next higher group in intellectual ability is so high as not to require social assistance outside of school. When we ask how large a per cent. we should be justified in placing in this group and separating merely for special instruction in school, we reach a condition which is at present so ill-defined even in the minds of educators that it seems best to fall back on the general advice that our school systems should provide just as nearly individual instruction as the public purse and managing genius can devise. Mannheim, Germany, for example, takes care of 5618 per cent. outside of its regular school classes. The ideal is individual instruction for all. School authorities would be justified in providing special instruction for every degree of mental ability, if the cost would not restrict other more important social undertakings. This less degree of retardation in the group needing only school assistance should not, however, be classed as feeble-minded. We shall see later the percentages for which some authorities have considered it already advisable to provide special school instruction. We need not attempt to estimate the size of this group, as it is beyond the limit of feeble-mindedness.
The purely conative cases are not taken care of in the above estimates, which are intended for tested deficients. If the conative cases unaccompanied by intellectual deficiency should be regarded as frequent enough to replace those in the social assistance group who ultimately care for themselves, plus those subtracted by the excessive death rate, we would have a total of 1.5% of the general population feeble-minded enough to warrant social care of some sort. About 0.5% might justly be isolated. The reasonableness of this program can be judged by comparison with authoritative estimates now to be reviewed. The problem here is whether this is an unreasonable program for the diagnostician to assume as scientifically justified, remembering that these estimates are for tested deficients at 15 years of age and do not include purely conative cases which might occur above these intellectual borderlines.
The Social Isolation Group. We are now ready to consider some of the important estimates which throw light upon the reasonableness of the percentages we have named. 57First, what percentage would we be justified in socially isolating? In the United States Census Report on the Insane and Feeble-Minded in Institutions in 1910, we find that the number then actually in institutions for feeble-minded was only about 0.02% of the population. At the most frequent ages this rises to about 0.05%. It is evident that the number actually isolated is of little significance except as a check on the estimates. The report, however, refers to the special estimate made by the public authorities in Massachusetts which also included feeble-minded in state hospitals for the insane, other asylums, those reported by the overseers of the poor and those enumerated in the general population. The U. S. report says: “The census was not regarded as being complete, but it is of interest to note that if the number of feeble-minded in proportion to the total population was the same for the entire United States as it was in Massachusetts according to this census, the total number of feeble-minded would be over 200,000. Probably this may be regarded as a conservative estimate of the number of feeble-minded in the United States and would indicate that not over one-tenth of the feeble-minded are being cared for in special institutions” (205, p. 183). This estimate, which thus amounts to about 0.2%, may probably be considered as a reasonable program of expansion from the institutional viewpoint. The diagnostician who is considering the individual and not the mass must supplement it by considering who should be isolated if facilities were available. If the census bureau can contemplate institutional care for ten times those at present thus provided for, it gives us some indication of a reasonable limit as to the increase in institutional care that can be assumed to be reasonably contemplated at present.
58Dr. W. D. Cornell, director of medical inspection of the Philadelphia public schools, after the personal examination of those cases which in the opinion of the teachers should be sent to institutions, places the “institution cases” at a minimum of 15 per 10,000 school children. He adds: “The number of evidently feeble-minded above 6 years of age may be said to be 1 to every 500 of the population. These figures are conservative and have been accepted by experts for years.” This then is the minimum estimate and quite clearly refers to institutional cases.
A committee of the Public School Alliance of New Orleans, of which Prof. David Spence Hill was chairman, reported in 1913 a careful census of the public school children in that city the previous year made by the teachers in co-operation with the Newcomb Laboratory of Psychology and Education. Each teacher was asked to state her opinion as to how many in her room were “feeble-minded or insane children who should be under institutional or home care, rather than in the public schools.” Also the number of backward children not in the above class “who urgently need special educational methods in special classes within the special schools.” About a fifth of the total of the 38,000 school children in the city are colored. The grand total showed 0.28% in the first class mentioned above, and 7.7% in the second. Speaking of those “thought by teachers to be feeble-minded” and needing institutional care the report says:
“The figure 0.28 of 1% coincides exactly with the estimate of the Philadelphia Teachers' Association made in 1909 in a census of 150,000 school children. Secondly, while the teacher's estimates are open to revision, nevertheless her judgment, as inevitably evidenced in her attitude toward the child, is the practically effective judgment” 59(157, p. 6). It is a well-known fact that teachers tend to underestimate the frequency of mental deficiency, so that it would certainly be a matter of regret if this were to continue to be the “practically effective judgment.”
Another census of the institutional type of feeble-minded made by the Director of Public Health Charities in Philadelphia and reported in 1910 enumerated 0.2% of the population as in this group. It included cases in the institutions for feeble-minded, the insane hospitals, almshouses, hospital, reformatories, orphanages and known to charity workers (168, p. 13).
One of the most careful surveys of individuals who, because of mental abnormalities, show such social maladjustment as to become the concern of public authorities was made under the auspices of the National Committee for Mental Hygiene in 1916.[5] It selected Nassau County as representative of New York state. Part of the survey consists of an intensive house to house canvass of four districts of about a thousand population each. The result disclosed that 0.54% of the population of this county were socially maladjusted because of “arrests in development” and 0.06% more, because of epilepsy. This was in a population of 115,827.
The Children's Bureau in the U. S. Department of Labor in 1915 made a census of the number of “mental defectives” in the District of Columbia. The census included only those whom we have termed feeble-minded. The report states that 798 individuals, 0.24% of the population, were found to be “in need of institutional treatment; and the number reported, allowing for the margin of error in omission and inclusion, is probably a fair 60representation of the number in the District who should have custodial care” (88, p. 13). Over a quarter of the population of the District is colored. The census was taken in connection with plans for immediate care. The same Bureau also made in 1915 and 1916 a Social Study of Mental Defectives in New Castle County, Delaware.[6] This county had a population of 131,670 and the survey disclosed 212 “positive cases of mental defect” and 361 “questionable cases,” a total of 0.44% of the general population in this county. Among the positive cases, 82.5% were in need of public supervision or institutional care. Among the questionable cases, information was obtained about only 175, and 165 of these were either in institutions, delinquent or uncontrollable, or living in homes where proper care and safeguarding were impossible.
Two other important attempts to enumerate carefully all the feeble-minded in definite areas in the United States have been made in recent years. Lapeer County, Mich., was chosen for such a study, as it was of average size and contained no large city. The census as reported in 1914, showed 36 feeble-minded from that county in the state institution and 116 others living in the county, a total of 1 from every 171 inhabitants (145). A special children's commission was appointed by the state of New Hampshire to investigate the welfare of dependent, defective and delinquent children. Its report in 1914 contained a section by its chairman, Mrs. Lilian C. Streeter, on feeble-mindedness (40). This comes the nearest to a complete enumeration for an entire state which has ever been attempted. The commission tested with the Binet scale the inmates 61of the State Hospital for the Insane, the County Farms, the State Industrial School and the Orphanages within the state. The borderline which it used for the scale was high. It counted all those testing three or more years retarded and under XII as feeble-minded. Taking its figures as they stand we find that they listed 947 as feeble-minded in institutions and 2,019 outside, a total of 0.69% of the inhabitants of the state. Outside the institutions the commission sent a questionnaire to all school superintendents and to chairmen of school boards, physicians, overseers of the poor, county commissioners, probation and truant officers, district nurses and charity workers throughout the state, by which means they listed 792 additional cases. This questionnaire gave the following description of the type of case it was trying to list as feeble-minded.
“The high grade imbecile, frequently known as the moron, is one who can do fairly complicated work without supervision, but who cannot plan, who lacks ordinary prudence, who cannot resist the temptations that are common to humanity. The high grade imbecile is most dangerous because, except to the expert, he is apparently not feeble-minded and is, therefore, usually treated as normal, and permitted to multiply his kind, and to corrupt the community.”
This description would tend to include cases above our isolation group. Besides the questionnaire the commission made an intensive study of 52 towns in which it says practically complete census returns were obtained by consulting doctors, school and town officials. With these supplementary cases it secured a list of 2,019 cases outside of institutions, making a total of 2,966 recorded cases within the state or 0.69% of the population. When it estimated the proportion for the entire state on the basis of the rate of canvass returns to questionnaire returns, 62this proportion rose to 0.95%. The commission does not advocate compulsory isolation for all of these people although it recommends custodial care for the feeble-minded women and girls of child-bearing age, apparently of the degree of deficiency represented by its criteria. This enumeration of 0.69% of the people of a state as feeble-minded is the most liberal general census of the feeble-minded in any large area. It clearly shows the trend of diagnosis since the British Census.
The Extension Department of the Training School at Vineland, N. J., states regarding estimates of the number of feeble-minded in the general population: “Conservative estimates give one in three hundred as the probable present number.” Under the discussion of estimates of the general population I have already cited Goddard's estimate which was approximately 0.3 to 0.4% and the enumeration of 0.4% by the British Royal Commission in 16 districts with over two million population. While all of these estimators are speaking broadly of the feeble-minded, in the general population, we shall not be far wrong in supposing that they are considering mainly those deficients for whom the state might well expect to provide care for life, isolating all those who cannot be eugenically guarded at home. We shall later quote the estimate of Van Sickle, Witmer and Ayres of 0.5% of the school population as “institution cases.”
Our estimate of 0.5% in the group justifying isolation on the ground of intellectual deficiency seems to be conservative and to harmonize fairly this type of estimate.
The Social Assistance Group. Passing now to the next higher group of deficients, those needing special training in order to get along with social assistance, the estimates have been based almost entirely upon the study of school 63children. Francis Warner was the moving spirit in the early investigations in Great Britain, which were made without tests from 1888 to 1894. The census which he directed included about 100,000 school children who passed in review before medical examiners. As cited by Tredgold (204) the estimate growing out of this work was that 1.26% of the school population should have instruction in special classes. Of these 0.28% required special instruction because of physical defects only (204).
About the same time Will S. Monroe (155) on the basis of a questionnaire sent to California teachers, who reported on 10,842 school children, found that they estimated 1,054 of these as mentally dull in school, 268 feebly gifted mentally, and 6 imbeciles and idiots. He summarized his conclusion as follows: “A long experience teaches that every school of fifty pupils has at least one child that can be better and more economically trained in the special institutions than in the public schools.” In his estimate of 2% he was probably thinking of care in special local schools and not permanent isolation.
A government inquiry of school teachers in Switzerland, who had charge of 490,252 school children, reported that 1.2% were so feeble mentally as to need training in special classes. Only about a tenth of this number were then being instructed in separate classes (181, p. 17).
Great Britain first gave legal recognition to the class of feeble-minded above the imbeciles in its Education Act of 1898, following a report of a departmental committee of its National Board of Education growing out of the inquiries of Francis Warner. This committee estimated the proportion of this class as approximately 1% of the elementary school population (181). In discussing the comparative estimates on the general and school populations I have already referred to the estimate of Tredgold 64based upon an elaborate analysis of the most extensive data ever collected,—that gathered by the British Royal Commission on the Care and Control of the Feeble-Minded. While the Commission's investigators enumerated 0.79% among the school as mentally defective, Tredgold's estimate based on his analysis of their report was that 0.83% of the school population in England and Wales were above the grade of imbecile but still feeble-minded (204, p. 157). The variability of the estimates collected by the Royal Commission from various cities probably indicates the subjective character of the standards of deficiency. They varied from an estimate of 0.24% of the elementary school population in Durham to 1.85% in Dublin (204, p. 159). The Commission says regarding estimates as to communities other than those reported by their medical investigator, for Newcastle the “number of feeble-minded children of school age” (morons) was 0.25%, for Leeds the estimate was 0.80%, for London 0.50% or 0.60%, for Bradford 0.50%, for Dublin about 1% and for Birmingham about 1% of the school population. Dr. Francis Warner's general estimate was 0.8%. We have thus variations in estimates from 0.25%, 0.5%, 0.80% to 1% and some 2% (167, p. 90). For the rural areas the estimates were generally less.
A careful estimate has been made with a different method by Karl Pearson on the basis of a classification by teachers of school children in Great Britain into nine different classes each especially defined and extending from the imbecile to the genius. This distribution of the children was then fitted to the normal probability curve. On this basis Pearson estimated that 1.8% would fall in the “very dull group,” defined as having “a mind capable of holding only the simplest facts, and incapable of grasping or reasoning about the relationship between facts; 65the very dull group covers but extends somewhat further up than the mentally defective.” Lower down would be 0.1% in the imbecile group. He says further regarding this estimate: “It is deduced from three series covering between 4000 and 5000 cases, and the three separate results are in several accord. It will, I think, be possibly useful for other inquirers, and it endeavors to give quantitative expression to our verbal definitions of the intellectual categories” (166).[7]
In 1914 Pearson cites estimates of mentally defective children in several cities by teachers and medical officers based upon the recommendation of elementary school children for special schools and classes. These were, for London: boys, 1.59%; girls, 1.09%. For Liverpool: boys, 0.827%; girls, 0.618%. The corresponding figure for both sexes in Stockholm is 1.23%. He concludes that “something between 1% and 2% is true for England. Dr. James Kerr, Medical Research Officer, thinks that the final estimate will be nearer the latter value.”
After giving a table of the percentages at each age in the elementary schools of Stockholm, Pearson says: “Judged from this table it would seem that the most reasonable estimate of the prevalence of mental defect is to be formed when all the mental defectives have been definitely selected and the normal children have not yet begun to leave school, i. e., at the ages 11 and 12. For Stockholm this leads up to a mentally defective percentage of about 1.5” (167, p. 6-8). In another place he says that the members of special classes are selected practically for the same reason, i. e., because they are school inefficients, the bulk 66of whom will, no doubt, unless provided for become “social inefficients” (164, p. 48). Since some were not selected because of intellectual deficiency, our social assistance group should be somewhat smaller.
In 1909-10 the actual number in the schools for mental defectives maintained by the London County Council was 0.9% of the enrollment of the London elementary Schools (143). The 1912 report of the London County Council shows 7357 children enrolled in its local schools for mental defectives, which is 1.1% of the average attendance from 1912-1913 in the elementary county council schools and voluntary schools of London (144, p. 44).
Following a discussion in the Australian Medical Congress of 1911 the Minister of Public Instruction called for returns as to the number of feeble-minded in the Australian public elementary schools between 5½ and 14 years of age inclusive. The questionnaire used the definitions of the British Royal Commission as a description of the various degrees of retardation and brought returns from 2,241 of the state schools, all except 57. For their average attendance of 175,000 children, these teachers classified 1.9% as backward from accidental causes, 2% mentally dull, 0.42% feeble-minded imbeciles or idiots, and 0.6% epileptics. To this would be added 0.19% for children in the idiot asylums. The report states that “the teachers' estimates will thus be realized to be an absolute minimum, dealing only with the intermediate grades, and not including the gross cases (idiots, etc.) on the one hand and the less marked high grades of feeble-minded on the other” (70).
The census made by the Bureau of Health of Philadelphia through the principals of schools in 1909 covered 157,752 elementary school children of whom 1.9% above 67the 0.28% who could “properly be in custodial institutions 'were classed' as backward children who require special instruction by special methods in small special classes” (168).
A survey of the school population in the Locust Point District of Baltimore was made by Dr. C. Macfie Campbell.[8] The district surveyed was, however, not considered typical of Baltimore, but was a sample of an industrial district in which the majority of families are “close to the poverty line, and too often below it.” Out of a school population of 1,281 children, 166 (13%) were “found to have special requirements on account of their mental constitution.” Among these, 22 (1.7%) “showed a pronounced mental defect, which eliminated any prospects of their becoming self-supporting.”
The city of Mannheim (147), which perhaps cares for its exceptional children better than any other in the world, was in 1911-1912 caring for 0.7% of the children in its Volkschule in Hilfsklassen which do not take them beyond the fourth grade. There were 12% more who were backward in school and being taught in Forderklassen where they may reach the sixth grade. Including the exceptionally bright who were also in special classes, 18% all together of its school children were not in the regular Hauptklassen of the eight grades. To these would be added those sent to special institutions. When we estimate, therefore, that we are justified at present in sending 1% of the children in school to special classes because their intellectual deficiency is such that the bulk of them cannot get along without social assistance, we are naming about the proportion already thus cared for in several foreign cities.
68Among the authoritative estimates of the number of feeble-minded, which have been made by estimators who had in mind the evidence from mental tests, is that made by James H. Van Sickle, Lightner Witmer, and Leonard P. Ayres in a bulletin published by the United States Bureau of Education in 1911 (209). They state that, “if all children of the public schools could be ranked, it is probable that a rough classification would group them about as follows—Talented, 4%; Bright, Normal, Slow, 92%; Feeble-Minded, 4%. The 4% may for administrative purposes be divided into two groups. The lower one includes about one-half of one per cent. of the entire school membership.... They are genuinely mentally deficient, and cannot properly be treated in the public schools. They are institution cases, and should be removed to institutions. Ranking just above these are the remaining three and one-half per cent. who are feeble-minded but who could be given a certain amount of training in special classes in the public schools.” The estimate of institutional cases practically coincides with that adopted above in this paper. The extension of the term feeble-minded to include the lowest 4% seems to be extreme. The authors do not suggest what portion of these they think might require social assistance indefinitely, but are interested primarily in provision for special classes in the public schools. If the term feeble-minded were to mean only unfit for regular school classes and not socially unfit, I have already suggested that the limit for special instruction might be increased indefinitely. In Mannheim 18% are not cared for in the regular classes.
The only estimate of feeble-minded which I have found that is so large as this 4% is that of Binet. It is also intended to cover all cases that should be sent to special 69classes regardless of subsequent social survival. His statement as to those who are so abnormal or defective as to be suitable for neither the ordinary school nor the asylum is as follows:
“As to France, precise information has not been available until the last year, when two inquiries were held—one at the instance of the Ministerial Commission, the other organized by the Minister of the Interior. According to the former inquiry we find that the proportion of defectives amounts to scarcely 1% for the boys, and 0.9% for the girls. These percentages are evidently far too small, and we ourselves have discovered, by a small private inquiry, that many schools returned “none” in the questionnaires distributed, although the headmasters have admitted to us that they possessed several genuine defectives. In Paris, M. Vaney, a headmaster, made some investigations by the arithmetic test, which we shall explain presently, and reached the conclusion that 2% of the school population of two districts were backward. If we were to include the ill-balanced, whose number is probably equal to that of the backward, the proportion would be about 4%. Lastly and quite recently a special and most careful inquiry was made at Bordeaux, under the direction of M. Thamin, by alienists and the school medical inspectors, and it was found that the percentage of abnormality amongst the boys was 5.17. Probably the true percentage is somewhere in the neighborhood of 5. All these inquiries are comparable because they deal with the school population” (77, p. 8).
In this estimate of 5%, Binet was considering those to be sent to special classes regardless of whether or not they would require indefinite social assistance after their schooling. It is therefore not directly comparable with our estimate of 1.5% presumably or doubtfully intellectually deficient.
The estimate of Dr. Henry H. Goddard, who has done the most to introduce the Binet Measuring Scale in this 70country, is stated as follows: “It is a conservative statement to declare that 2% of public school children are distinctly feeble-minded, the larger part of them belonging to this high-grade group which we call morons” (118). In another (114) place he says: “The most extensive study ever made of the children of an entire school system of two thousand has shown that 2% of such children are so mentally defective as to preclude any possibility of their ever being made normal and able to take care of themselves as adults.”[9] The study to which he refers gives individual results with the Binet 1908 tests made on 1547 school children in the first six grades (114, p. 43). Since the sixth grade does not include the better children who are twelve years or over in age this group is clearly selected in such a way that it would show an excessive percentage of mentally retarded children. We find in the investigation referred to that he says: “Then we come to those that are four years or more behind their age, and here again experience is conclusive that children who are four years behind are so far back that they can never catch up, or in other words, they are where they are because there is a serious difficulty which can never be overcome—they are feeble-minded. They constitute 3% of the children in these grades.”
Since we have a random selection of school children in his table for only those children who are 6 to 11 years of age inclusive, I find that only 1% at these ages are retarded four years intellectually. On his own basis, therefore, 3% is evidently too large an estimate. Later he seems to have reduced his estimate to 2% of the school population. Of those who test in the lowest 1.5% including our doubtful group, I believe that there is no clear evidence that more than 1% will require even social assistance as adults.
71Many more estimates of the number of feeble-minded among school children might be cited, but they would add little to these authoritative samples. At the present time an estimate by health officers or teachers who are not familiar with the results of mental testing has little significance, as the whole complexion of the problem has been changed since the work of Binet and Simon.[10] We may, however, cite three estimates based upon familiarity with test results, which fairly cover the range of estimates among school children. In connection with the Springfield, Illinois, survey conducted by the National Committee for Mental Hygiene under the direction of the Russel Sage Foundation, we find that three typical schools with a total of 924 pupils were studied. The report states that “the mentally defective children” constituted 3.8% of the number in attendance in March. The number of children in the schools examined, for whom instruction in special classes would be desirable, is about 7% of the entire enrollment of these schools (203, p. 10).
In connection with the Stanford Version of the Binet Scale, Dr. Lewis M. Terman says: “Whenever intelligence tests have been made in any considerable number in the schools, they have shown that not far from 2% of the children enrolled have a grade of intelligence which, however long they live, will never develop beyond the level which is normal to the average child of 11 or 12 years.... The more we learn about such children, the clearer it becomes that they must be looked upon as real defectives (57, p. 10). Again in placing the borderline for feeble-mindedness” with the Intelligence Quotient used, 72he suggests that “definite feeble-mindedness” lies below an I. Q. of 70 which with 1000 quotients was found to exclude about the lowest 1%. Above this is a group with I. Q.'s 70-80 which he describes as “borderline deficiency, sometimes classifiable as dullness, often as feeble-mindedness.” This group would include, as judged by the results of these tests, over 4% more.
Dr. Wallin, who has had wide experience in testing both school children and defectives, states: “I will venture the assertion, after years of teaching in the public schools and clinically examining public school cases, that the oft-repeated statement that 2% of the general school population is defective (if by this is meant feeble-minded), exaggerates the real situation. The actual number is probably about 1%” (211, p. 149).
After reading a paper on “A Percentage Definition of Intellectual Deficiency” before the American Psychological Association in 1915 (151), I was pleased to discover that Prof. Rudolf Pintner and Donald G. Paterson were also about to propose a percentage definition of feeble-mindedness for those who are dealing with mental tests (44). While their idea seems to be fundamentally similar, their paper shows that their conception is to be sharply distinguished in several particulars from that which I am advocating. They would limit the use of the term “feeble-mindedness” to individuals who test in a rather arbitrarily chosen lowest percentage of the population. As opposed to this I suggest continuing the present social definition of feeble-mindedness and supplementing it, for the purpose of aiding in the diagnosis, by indicating the social significance of those testing in certain lowest percentages. Such tested deficients I designate as “intellectually deficient.” It is important to consider their statement and to note what percentage 73they have chosen to regard as feeble-minded. They say:
“It is in order to avoid this vagueness and uncertainty attaching to the term that we suggest a definite psychological concept. The lowest three per cent. of the community at large, that is, the lowest as determined by definitely standardized mental tests, are to be called feeble-minded. Such a definition will be unambiguous and the dividing line between this and other groups will become clearer and clearer as we increase the accuracy of our measuring scales and the adequacy of our standardizations. Furthermore, if evolution is raising the degree of intelligence the three per cent. at the lower end will still remain, for, whatever the degree of their intelligence may be, they will still be feeble-minded as compared with the normal.
“Such a definition will in addition restrict the term to such as are lacking in intelligence and will differentiate them from the moral defectives and the psychopathic personalities, which are at present often confused with the group that we propose to call feeble-minded. An individual may be at the same time a moral defective and feeble-minded, but there is reason to believe that moral deficiency may exist without such intellectual defect as to warrant a diagnosis of feeble-mindedness. The same may be said of the psychopathic personality.
“The further question, whether all those coming within the proposed definition of feeble-mindedness are to be confined in institutions, is purely social and will be determined by the social needs of each community and does not concern us here. It is obvious that many more in addition to the feeble-minded as defined by us will require the restraint of an institution, even though no real mental defect exists.
“It is immaterial for the purposes of this hypothesis whether three or a smaller or larger percentage be designated as feeble-minded. The important point is the agreement upon some fixed percentage, and we have chosen three per cent. as covering presumably all the cases of marked mental deficiency. A brief glance at the chief estimates of the number of feeble-minded in civilized communities would indicate that our percentage is somewhat higher than the conservative writers give, but we shall show later on that it is much lower than the results obtained from groups of children tested by intelligence scales” (44, p. 36).
With those who understand that deficiency is mainly a question of degree, it would seem that there might be some agreement as to the plan for defining tested deficiency. In order to make this plan more useful to those dealing 74with the social care of the feeble-minded, it would be necessary to supplement the bare percentage definition by relating it to expectations of social failure somewhat after the manner I have attempted. In particular it will gain its main value for diagnostic purposes, it seems to me, if the percentage is so chosen that it may receive the support of conservative scientific opinion. To be most useful it seems evident, also, that the percentages must be chosen with regard to the sort of social care which it is anticipated would be justified for the particular degrees of deficiency.
Let us recall the percentages suggested to harmonize the estimates: the lowest 0.5% to be regarded as presumably deficient enough to justify isolation and the next 1% as doubtful, but low enough to warrant special training and probably requiring indefinite social assistance. If these percentages for tested intellectual deficiency have been shown to be fairly conservative estimates in the light of the authoritative judgments with which they have here been compared, the laboriousness of this comparison has been worth while. Further light upon the social assistance group may be thrown by the study of the success of those children who have already had the advantage of training in local classes for the deficient.
That we are not justified in isolating all whom we class as feeble-minded is best indicated by the evidence as to the number of these sent to special local classes for deficients who are able to float socially with the assistance of capable after-care committees. A fair picture of the present situation may be obtained by thinking of these pupils in the help-classes and schools as representing about 75the next 1% above those who have been isolated in institutions. With this picture in mind let us see what has been the outcome of their special instruction and social assistance thereafter.
In his book on Les Enfants Anormaux, Binet collected the evidence available at that time (77, p. 140). He says:
“Mme. Fuster, after a stay in Germany, where she visited some Hilfsschulen and Hilfsklassen (literally, 'help-schools' and 'help-classes') made a communication to the Société de l'Enfant, from which it appears that in the case of 90 classes for defectives in Berlin, 70% to 75% of the defective pupils who were there became able to carry on a trade; 20% to 30% died in the course of study, or returned to their homes, or were sent to medical institutions for idiots.
“According to a more recent inquiry, made under the auspices of M. de Gizycki at Berlin, and published in a book by Paul Dubois, 22% of the children were sent home or to asylums; 11% were apprenticed; 62% worked at occupations which required no knowledge and yielded little pay (laborers, crossing-sweepers, ragmen). If we add together these two last groups, we reach a proportion of 73% of defectives who have been made, or who have become more or less useful....
“Dr. Decroly has kindly arranged at our request a few figures relating to the occupational classification of the girls discharged from a special class in Brussels.... Finally, then, out of nineteen feeble-minded subjects, regarding whom particulars have been supplied, one-half, or 50%, have been apprenticed, or more than half, 75% if we count the defectives who 'work....'
“Through the intervention of an inspector, M. Belot, we have inquired of twenty heads of schools what has become of the defectives whom they notified to us two years ago. We have made these inquiries with regard to sixty-six children only.... If we subtract the two first groups, those about whom the particulars are wanting, and those who have not yet left school, there remain twenty-seven children, of whom seventeen have been apprenticed, or 76%.... Now this proportion is, by an unexpected agreement, identical with that obtained in the classes of Berlin and Brussels.”
A more recent report concerning the Hilfsschulen in Berlin by Rector Fuchs is in close agreement. It indicates 76that from 70% to 80% of the former pupils of these schools make a living after they leave school.
To compare with these reports indicating that about three-fourths of those leaving the special schools of Paris, Berlin and Brussels by social assistance attain occupational classifications, we have less favorable reports from Great Britain. Shuttleworth and Potts (181, p. 23) say:
“At the Conference of After-Care Committees held in Bristol on October 22, 1908, a paper read by Sir William Chance, Chairman of the National Association for the Feeble-Minded, dealing with the reports of the After-Care Committees of Birmingham, Bristol, Leicester, Liverpool, London, Northampton, Oldham and Plymouth. The combined statistics from the nine centers showed that 22% of those who had attended special schools for the mentally defective were in regular work, and 6.8% had irregular work.... To illustrate the necessity for continuous supervision and the futility of temporary care, we cannot do better than quote the records of the Birmingham After-Care Committee, as embodied in their report for 1908, after seven years work. It was found that, 'out of 308 feeble-minded persons who have left school and are still alive, only 19.8% are earning wages at all, and only 3.9% are earning as much as 10 s. per week'” (181).
Tredgold summarizes other data on this question of industrial success as follows:
“We may next turn to the reports of 'After-Care' Committees regarding feeble-minded (moron) pupils of the special schools. In London the proportion of pupils known to be in 'good or promising' employment was 37.5%. Two years previously it had been 45.7%, and Sir George Newman, the Chief Medical Officer to the Board of Education, attributes the falling off to two causes—firstly, insufficient after-care; and secondly, the two additional years. He remarks: 'The longer the test the more severe it is.' In Birmingham, the 'After-Care' Committee compiled information regarding 932 cases which had passed through the schools during the previous ten years. Of these, excluding the normal and dead, 272, or 34%, were engaged in remunerative work. At Liverpool, of 712 children passing through the hands of the 'After-Care' Committee during a period of six years, 85, or 11.9%, were doing remunerative work.
“Finally we may refer to some figures concerning 'After-Care' work compiled by Sir William Chance from the returns of the National Association 77for the Feeble-Minded. These were based upon an inquiry made of sixteen centers of the Association, and referred to a total of 3,283 persons. Of this number, 798 were doing remunerative work, 89 were 'doing work, but not reported;' 202 were useful at home; and 941 were returned as 'useless members of society.' If we exclude 340 who were transferred to normal schools (not being feeble-minded), we have 27% engaged in remunerative work.
“With regard to the term 'remunerative work,' however, it is to be remarked that the person employed is not being paid the standard wage. On the contrary, it is my experience that this is practically never the case, and this is corroborated by the observations of the secretary of the Birmingham center, who says: 'Although some of our cases have been at work for more than ten years, only 34 of the whole number (173) earn as much as 10 s., 2 d., per week. Of these only 6 earn as much as 15 s., and only 2 earn 20 s., which is the highest wages earned.... While it is not very difficult for some of our higher-grade cases to get work when they first leave school, it is almost impossible for them to retain their situations when they get older, and the difference between them and their fellows becomes accentuated. Uncontrolled and often quite improperly cared for, they rapidly deteriorate, the good results obtained by the training and discipline of the special school being under these circumstances distinctly evanescent.... There are few workers over twenty years of age'” (204, p. 425, 435).
The 1912 report of the London County Council (144) covers those who left its special schools for mentally defective children during the years 1908-1912 inclusive. These schools have accommodation for about 1% of the elementary school enrollment. Of 2010 children who left these schools during these five years, and who were still alive, 1357 were employed and 311 more employed when last heard from, a total of 79% employed at last accounts. Those out for five years show about the same proportion employed. This is a more favorable showing and fairly in line with the results of other European help-schools. The average weekly wages of those employed ranged from 4 s. 6 d. for those just out to 10 s. 7810 d. for those leaving five years before. A considerable proportion who live at home thus have been meeting their necessary living expenses as the result of this special training and subsequent assistance.
Dr. Walter E. Fernald reported to the British Royal Commission on the Care and Control of the Feeble-Minded concerning the inmates of the institutions for feeble-minded in the United States. These institutions receive a much lower grade of cases on the whole than the local help-schools abroad: (83, Vol. VIII, p. 159)
“Some of the institutions where only the brightest class of imbeciles are received, and where the system of industrial training has been very carefully carried out, report that from 20% to 30% of the pupils are discharged as absolutely self-supporting. In other words at other institutions, where the lower grade cases are received, the percentage of cases so discharged is considerably less. It is safe to say that not over 10% to 15% of our inmates can be made self-supporting, in the sense of going out into the community and securing and retaining a situation, and prudently spending their earnings.... But it is safe to say that over 50% of the adults of the higher grade who have been under training from childhood are capable, under intelligent supervision, of doing a sufficient amount of work to pay for the actual cost of their support, whether in an institution or at home.”
The wages of the women at the Bedford Reformatory before entering prostitution as given by Davis (133, p. 210) have a direct bearing on the earning capacity of the higher grade feeble-minded. The Binet tests of Bedford women by Weidensall indicate that about 38% of the successive cases admitted to Bedford test in the lowest 0.5% intellectually, and 75% in the lowest 1.5% intellectually. Davis' table shows that for 110 whom she classes as mentally low grade cases at the reformatory, the median wage of those in domestic service, as claimed by the women, was nearly $4.50 before entering prostitution. These feeble-minded women, if their statements of earnings can 79be accepted, are therefore feeble-minded by reason of their low intelligence plus delinquency, and not by reason of inability to earn the necessities of life. The best of these mentally low grade cases earned as high as $5.00 in addition to board and lodging in domestic service and $25.00 outside of domestic service.
In this country we have fewer studies of the results of training the mentally retarded in special local classes and schools. Miss Farrell has made a preliminary report of 350 boys and girls out of the 600 children formerly in the ungraded classes in New York City during the preceding 8 years (102). Omitting seven whose status was unknown and 10 who had died, only 6% were known to have failed to survive socially with assistance. These were in penal or other institutions. On the other hand a strict analysis of her returns shows only 28% earning $5.00 a week or more and thus possibly surviving independently. Of the above group of 333, 86 were at home, 192 employed, 31 unemployed and 3 married.
In Detroit among 100 children over 16 years of age who had attended its special classes and been out of school not over 5 years, 27 had been arrested, but 39 of the boys had been at work and received an average wage of $7.00 per week, while 16 girls had averaged $3.75 in weekly wages, although few held their positions long (97).
Bronner (6) compared a random group of thirty delinquent women at the detention home maintained by the New York Probation Association with an intellectually similar group of 29 women all of whom had been earning their living in domestic service and none of whom had been “guilty of any known wrong doing.” The delinquents were 16 to 22 years of age while the servant group was somewhat older. Only two or three of the delinquent group were worse than the poorest of the servant group in any of the five intellectual tests, so that, if more than this 80number were intellectually deficient, they were no more deficient than those who had survived in society. No Binet scale records were published so that we have no means of determining how many of these delinquents might fall within either of our deficient groups.
The principal deduction from this evidence on the earning capacity of those of low intellectual grade is a caution against demanding the social isolation of all the intellectually weak until we have more definite information as to what portion of them are able to live moral lives, as well as earn their living with social assistance, without being cared for entirely in isolation colonies. That a significant number of the lowest 1.0% intellectually next above the lowest 0.5% have led moral lives and have shown considerable earning capacity after attending special schools, when they are given proper after-care, has probably been demonstrated. They should, therefore, be treated as an uncertain group whose feeble-mindedness would never be decided purely on the ground of the intellectual tests. Most of them will, however, probably be found mentally deficient enough to need at least social assistance and protection.
In concluding this summary on the estimates of the frequency of feeble-mindedness, it need only be added that so far as concerns the use of the percentage definition for fixing the borderline in any particular system of tests the percentages chosen are not essential to the plan. The principles of the method apply whatever percentages might be adopted. For such important purposes as the comparison of the relative frequency of deficiency in different social groups and harmonizing the investigations with different mental scales, agreement upon a particular percentage is not essential. In diagnosis, of course, it is a matter of fundamental importance in order that injustice may not be done individuals. For this 81reason the estimate should be conservative, possibly more conservative even than our tentative 0.5% at 15 years of age. Any investigator who disagrees with the above estimates of the degree of tested deficiency justifying isolation may substitute X per cent. with a doubtful region extending Y per cent. further. Provided such a census were legally authorized and funds available it would be not impossible to get a reliable determination by a house to house canvass showing the number of adult deficients, say 21 years of age, in typical communities, who were not able to survive socially without assistance. This number would then give the key for a conservative percentage and the movement for early care would be immensely advanced.
With the recent introduction of psychological tests into the cantonments of the national army, the goal of symptomatic borderlines as determined by objective tests seems to be almost at hand. Since the men are brought practically at random to the camps by the draft and are under military command, it may be possible to find out the social history of a large enough group at the lower limit of tested ability to establish the question of the necessary capacity for independent moral and social survival. These borderlines could then be transferred from the army tests to positions of equivalent difficulty in other test systems.
The remainder of this study will show some of the advantages of the percentage definition for fixing the borderlines with a system of tests and the result of applying such an interpretation to the particular problem of delinquency. The advantage in increased definiteness should already be evident. When a person is classed as presumably deficient it will mean that he is in the lowest 0.5% in intellectual development or within the lowest 1.5%, if he is a persistent delinquent.
5. Aaron J. Rosanoff. Survey of Mental Disorders in Nassau County, New York. Publication No. 9, National Committee for Mental Hygiene, 1917.
6. Emma O. Lundberg. A Social Study of Mental Defectives in New Castle County Delaware. U. S. Dept. of Labor, Children's Bureau, Publication No. 24, 1917, pp. 38.
7. This statement in 1906 seems to be the earliest attempt at a quantitative definition of deficiency. As I discovered it after the present monograph was practically completed, it furnishes evidence of the natural tendency of attempts at more exact definition to take the percentage form.
8. C. Macfie Campbell. The Sub-Normal Child—A Study of the Children in a Baltimore School District. Mental Hygiene, 1917, I, 96-147.
9. Italics mine.
10. The report of the Massachusetts Commission on Mental Diseases (Vol. I, p. 198) shows that social agencies systematically using mental tests reported 19.2% as mental cases, while those using examinations only for obvious cases reported 1.3%.
Sufficiently large random groups have not been tested with any development scale to make the determination of the borderline on the scale more than tentative. Such borderlines must be looked upon as temporary descriptions to be used in aiding diagnosis until more data are available. Nevertheless, the percentage method of procedure seems to be an improvement over other plans of stating the borderline. So far as the Binet 1908 scale is concerned, when we supplement Goddard's results with 1500 school children by the data for the lower limits of a random group of 653 15-year-olds which we tested, the limits on the scale for passable intellects defined by the percentage method will be found, I believe, not only more conservative, but more reliable than those in current use. Moreover the intended meaning of such borders becomes clear.
The passing limit for adults is unquestionably much more important than that for children since any child who once passes this limit is assured, generally speaking, of social fitness so far as intellect is concerned. He has attained a position intellectually which is sufficiently good to enable him to get along without social assistance unless he is especially deficient in will. This borderline for the mature has been so thoroughly neglected that in none of the common published forms of the Binet scale, except the new Stanford Scale, is there an attempt to define it. This seems almost incredible in view of the general use of the Binet method in diagnosing feeble-mindedness. To be sure, there are discussions of this upper limit, as we shall see, but they have usually not been embodied 83in the actual directions accompanying the scales which get into the hands of amateurs. Most of these directions content themselves with describing borderlines for children with no caution about the final lower limit for social survival.
The borderline for the mature is the first difficulty which a court examiner will encounter when he attempts to obtain assistance from an objective system of measurement. Very little experience will convince one that it is not enough to describe the deficient ability of an adult in terms of years of retardation. It is widely agreed that at some age during adolescence practically all the mental processes are available that will be found in the mature. From that time the advance in ability is made by attaining greater skill in specific activities through training and by increasing knowledge, rather than through a native change in the form of thinking. If mental tests mainly reach capacity for thinking, as they aim to do, rather than amount of knowledge or skill in specific work, then we are conservative in using a randomly selected group at 15 years of age for approximating the borderline on the scale for the mature.
In connection with the new Stanford Scale, Terman says: “Native intelligence, in so far as it can be measured by tests now available, appears to improve but little after the age of 15 or 16 years. It follows that in calculating the I Q (intelligence quotient) of an adult subject, it will be necessary to disregard the years he has lived beyond the point where intelligence attains its final development. Although the location of this point is not exactly known, it will be sufficiently accurate for our purpose to assume its location at 16 years” (57, p. 140).
Yerkes and Bridges in connection with their Point Scale say, “it seems highly probable that the adult level 84is attained as early as the sixteenth year” (225, p. 64). Kuhlmann (138) used 15 years as the divisor in calculating the intelligence quotient of adults and Spearman thinks that the limit of native development is reached about 15 years (184). He says, “That mental ability reaches its full development about the period of puberty is still further evidenced by physiology. For the human brain has been shown to attain its maximum weight between the ages of 10 and 15 years” (184). For the last statement he quotes Vierordt. On the contrary Wallin thinks that we need more evidence for the correctness of these hypotheses before choosing a fixed age as a divisor for adults (215, p. 67).
We are not interested in determining a divisor for an adult intelligence quotient but in fixing a conservative borderline for the mature. Admitting that the mental capacity of those 15-year-olds at the lower limit may not be like adults, nevertheless adults would be more likely to be better than worse. Borderlines for the 15-year-olds, should, therefore, be safe for adults. Moreover, the lower limits with a truly random group of 15-year-olds would probably be more reliable than an assorted group of adults subjectively chosen from different walks in life and combined in an effort to represent a random mature group. The Stanford Scale utilizes such combination of selected adults. It seems, therefore, that we are justified in utilizing the lowest percentages of randomly selected 15-year-olds as a reasonable criterion for describing the limits for adult deficiency. Surely adults below this lower limit for 15-year-olds would have questionable intellectual capacity.
The borderline for the mature being the crucial feature of a developmental scale when used for detecting feeble-mindedness, it seemed imperative to us that some effort 85should be made to obtain records with a random group of older-age children or adults. Goddard's results with school children were not significant above eleven years of age since the personal examinations were confined to children in the sixth grade or below. The twelve year old group in the sixth grade clearly omits the best 12-year-olds, so that the percentage method would have no significance applied to his figures for children above 11 years of age. Moreover it was obvious that the group of public school children 15 years of age or older would not give a picture of the lower end of a random group since many children drop out of school at 14. On the average those that leave are undoubtedly of lower ability than those who remain.
The most valuable data on the borderline for the mature would come from mental examinations of large random groups of adults. The impossibility of gaining the consent of adults for such examinations puts this plan out of consideration. Perhaps the next best method would be to examine all the children of 15 and 16 years of age in typical communities. It happened that we could approach this result in Minneapolis since we there had an excellent school census made from house to house covering all children under 16 years of age. The Minnesota law requires school attendance until 16 years of age unless the child has graduated from the eighth grade. Under the able direction of Mr. D. H. Holbrook of the attendance department the census of children of school age had been made with unusual care. All the children living in each elementary school district in the city were listed in a card index regardless of whether they were attending public, parochial or private schools, or had been excused from attendance for disability or for any other reason. Since we only needed to be sure to examine the lowest few per cent. 86of the children in ability this group of 15-year-olds could be tested by examining all those children in typical school districts in the city who had not graduated from the eighth grade. A third of the 15-year-olds were still in the eighth grade or below. Neither the compulsory attendance law nor the census would have reached the 16-year-old adequately. In most states even the 15-year-olds would have been above the compulsory school age.
There were 653 children, (322 boys,) 15 years of age living in the seven typical districts which were selected objectively for study. Among these there were 196 who had not graduated from the eighth grade. All of these latter children were examined, except one who could not be tested as she was in a hospital on account of illness. Quite a number of the children were in parochial or private schools, two were followed to the state industrial school and a number were examined at home. In order to be sure that we had not missed any institutional cases in these districts the complete list of Minneapolis children at the State School for Feeble-Minded was gone through to get any of low ability who might have been missed.
The seven districts in which the children were to be studied were chosen, with the idea of avoiding any personal bias in their selection, by taking them alphabetically by the name of the schools, except that no district was taken where the normal school attendance of the district was affected by inadequate school facilities so that children had to be transferred either to or from that district to other schools in order to meet crowded conditions. It happened fortunately that none of these schools represented extreme conditions in the city. The average percentage of children in the 69 elementary schools of the city retarded in school position below a standard of 7 years in 87the first grade, 8 in the second, etc., was 24.1% with a mean variation of 6.5%. The percentages retarded in the schools studied were as follows: Adams, 22.7; Bryant, 21.1; Calhoun, 21.7; Corcoran, 29.4; Douglas, 20.4; Garfield, 18.6; Greeley, 26.4.
Kuhlmann's adaptation of the 1911 scale (135) was used as a basis for the examinations, supplemented by the 1908 scale wherever tests had been changed so that other forms of the tests were found in either Kuhlmann's (136) or Goddard's (110) adaptations of the 1908 scale. Since test results with the 1908 scale provide the most data for describing the borderline for the immature, our plan was to use the 1908 form of a test first when the procedure had changed. The supplementary directions were arranged for each age so that the testing could proceed methodically and the results be scored under either the 1908 or 1911 scale with the least possible disturbance of each test. Over a third of the children were tested by myself. The rest were tested by three advanced students in psychology. It is a pleasure to express my thanks to these assistants, Miss Rita McMullan, Miss Lucile Newcomb and Miss Florence Wells. Besides having had brief experience in dealing with exceptional children, they practised testing under my observation until the tests could be given smoothly and I was convinced of their ability to follow directions intelligently and make full records with reasonable accuracy. The results of the tests were all carefully gone over and scored by me. So far as I can judge, the results are quite as accurate as any other published tables, although one must always consider the possible effect of errors of testing. Separate rooms were provided at the schools or homes so that the child could be alone with the examiner during the testing.
In attempting to define the borderlines on these scales 88we might either state the exact scale position in tenths of a year below which 0.5 and 1.5% of the cases fall, or we might merely attempt at present to state the borderlines in rounded terms of years on the scale. The latter plan is the one I have adopted for several reasons. The main reason is that I wish to emphasize that these are still rough boundaries. Besides that, however, a study of the results shows that the cases do not distribute by separate tenths of a year so that exactly these percentages could be picked off, without a questionable smoothing of the curves while the rounded years approach these limits fairly well.
It seems to me that it is best at present to be carefully conservative in describing these borderlines, so that I have chosen them from the available data at the nearest rounded age position which is reasonably sure not to catch more than these limiting percentages. Throughout the tables I have also followed the published directions for the 1908 scale in classing the person in the intellectual age group in which he finally scores all or all but one of the tests. I recognize, of course, that this is an arbitrary limit; but it is the limit fixed by the usual printed directions going with the 1908 scale, which is the only one thus far standardized for the immature on the percentage basis. For those who wish to calculate other borderlines or reconstruct the individual tests of the scale I have provided the complete data for each individual both for the 1908 and 1911 scales in Table XXI, Appendix I. The table also gives the exact ages and school grades of each child.
The summary of the results with the tests for those testing under XII is given in Table III. Life-age[11] at 89the last birthday and not the nearest life-age is used in the table. The children were all between their 15th and 16th birthdays. Following the directions published with the scales, the basal age for calculating the results in the table is taken as the highest at which all or all but one test are passed for the 1908 scale, and the highest at which all were passed for the 1911 scale. Two-tenths is allowed in the table for each test passed above the basal age and 0.1 for an uncertain answer. The children were tested by the long method, beginning with the mental-age group at which the child could pass all the tests and continuing to that age group in which he failed in all.
| 1908 Scale | 1911 Scale | |||
|---|---|---|---|---|
| Scored below | Pass all but one in basal age | Pass all in basal age | ||
| Per cent. | Cases | Per cent. | Cases | |
| IX.0 | 0.0 | 0 | 0.0 | 0 |
| IX.8 | 0.2 | 1 | 0.5 | 3 |
| X.0 | 0.3 | 2 | 0.5 | 3 |
| X.8 | 1.1 | 7 | 1.2 | 8 |
| XI.0 | 1.2 | 8 | 2.0 | 13 |
| XI.8 | 10.0 | 65 | 8.1 | 53 |
| XII.0 | 10.4 | 68 | 13.0 | 85 |
| XII.8 | 23.6 | 153 | 29.1 | 190 |
| XIII or XV | 23.6 | 153 | 29.7 | 194 |
Thrown into percentages of the group of 653 children living in these districts, it is evident that a test score of XI raises any person above the group of intellectual deficients. The percentage that tested this low, i. e., under XI.8, with the 1908 scale, was 10.0 (65 cases) and this would probably be increased if those who had graduated from 90the eighth grade had also been tested. The percentage testing under the same position in the 1911 scale is 8.1 (53 cases). With the 1911 scale there were 32 additional cases testing XI.8 or XI.9. The table indicates that 0.2% of the 15-year-olds tested below IX.8 with the 1908 scale, and 0.5% with the 1911 scale. This defines our scale borderline for the mature who are presumably deficient as below test-age X. These positions are near enough to the lowest 0.5%. The group testing of uncertain ability, age X, (strictly speaking between IX.8 and X.7 inclusive,) includes 0.7 to 0.9%. We thus approach fairly well the rounded age positions which exclude 1.0% above the lowest 0.5%. The total number testing in presumably and uncertain groups is thus 1.1%, 7 cases out of 653, for the 1908 scale and 1.2%, 8 cases, for the 1911 scale. This is to be compared with the percentage definition that the lowest 1.5% are either presumably deficient or uncertain.
At present we are entitled to assume that adults testing below XI, i. e., below X.8, are so low in intellectual development that it is a question whether they have sufficient equipment to survive socially. Fine discriminations with the Binet scale are not possible with our present knowledge. So far as our information goes, if we use the percentage method of defining intellectual deficiency, we may say that adults who test X are in an uncertain group in intellectual ability, with the probability that they will require more or less social care, while those who test IX are deficient enough to need continuous care unless the evidence of the test is contradicted by other facts or is accounted for by the existence of removable handicaps.
It is perhaps not necessary to call attention to the fact that X and XI are used here merely to refer to positions on the Binet scale without regard to what per cent. of 91ordinary 10-and-11-year-old children attain these positions. For example, XI does not imply that most of the children of eleven years of age are above this borderline. Table IV, to be given later, suggests that hardly two-thirds of random 12-year-old children pass this position on the 1908 scale and not half of the 11-year-olds. Thorndike regarded X.8 as normal for a child of 11.6 years of age. (200)
So far as the determination of intellectual deficiency is concerned we should note with emphasis that placing the limit of passable intellects at XI for adults almost entirely removes the common objection to the Binet scale on account of the difficulty of the older age tests. The older age tests become of little consequence because the best of the deficient group have a chance at tests in at least two groups above those of mental age X, so that they can increase their score by passing advanced tests as they could not if they had to test XII.
As a check upon the borderline for those presumably deficient, it is important to note that the only case which tested below this borderline with the 1908 scale was a girl in the 4B grade. She tested exactly IX with each scale and was the only child in the group who was below the fifth grade in school. There can be no question that she was mentally deficient. On the other hand in the group which tested X or above there are several cases which it would be unjust in my opinion to send to an institution for the feeble-minded without some other evidence of mental weakness. Half of them, for example, are in the seventh grade. In Minneapolis this is not as significant as it might be in other cities, since pupils are rarely allowed to remain more than two years in the same grade whether they are able to carry the work of the 92next higher grade or not. Pupils in higher grades may not always be able to do even fifth grade work.
The evidence from the institutions for the feeble-minded indicates that less than 5% of their inmates test XI or over. Of 1266 examinations at the Minnesota School for Feeble-Minded, 3.8% (154); of 378 examined at Vineland, 3.2% (113); of 140 consecutive admissions examined by Huey at Illinois, 5.7% (129). To be sure, a goodly number of these inmates are not eleven years of age, but a majority of them are at least that old and many are older. Of 280 children in the Breslau Hilfsschulen, Chotzen (89) found none reaching XI, and only six who tested X. These few cases in institutions reaching XI or over may well come within our class of those feeble-minded through volitional deficiency.
Goddard's description of the children at the Vineland school for feeble-minded who tested XI with the 1908 scale hardly sounds like an account of social deficiency. He says:
“In the eleven year old group we find only five individuals, but they are children who, for example, can care for the supervisor's room entirely, can take care of animals entirely satisfactorily, and who require little or no supervision. They are, it is true, not quite as expert or trustworthy as those a year older, and yet the difference is very little and the two ages can probably be very well classed together” (113).
The studies of groups are more important for fixing our general rules than individual examples. We must always expect to find exceptional cases where the brief intellectual tests given in an hour or less are not adequate, especially if the testing has been interfered with by the person's emotional condition at the time or by deliberate deception. A number of illustrations have been reported 93of successful adults who have tested X under careful examinations. Such, for example, are three cases of successful farmers tested by Wallin (215) and a normal school student tested by Weidensall (59). There are two examples of persons testing IX with the Binet scale and yet earning a living. Such is the case related by Dr. Glueck of the Italian immigrant making two trips to this country to accumulate wealth for his family by his labor (109), and the case of the boy reported by Miss Schmidt (179). These cases should make us cautious, but they are so rare that it seems best to treat those testing IX at least as exceptions.
The group studies confirm our suggestion that a borderline of X or below will bring in for expert consideration nearly all adults who are feeble-minded from a lack of intellectual ability, while testing IX is a fairly clear indication of such serious deficiency as to justify isolation. That testing X, in the absence of other evidence of conative disturbance, places the case only in an uncertain region so far as isolation is concerned is best indicated by the fact that 1.1% to 1.4% of these 15-year-olds tested this low. We have good evidence that many in special classes, which contain only about the lowest one per cent., afterwards do float in society with or without social assistance. They cannot be presumed to require isolation, as I showed in the previous chapter. It is better to say at present that those testing X require evidence of their deficiency before isolation, except in special classes, is justified. The test diagnosis alone is too uncertain, even when there are no removable handicaps.
As to the reliability of these borderlines, too much emphasis can hardly be put upon the fact that they have been determined for only a single group of 653 in a single community. They are undoubtedly not the exact borderlines, 94although they are the most probable percentage estimates we have at present and were obtained in a group that was as nearly unselected as it is possible to obtain. The method of selection was perfectly objective and excluded no feeble-minded children of this age living in these school districts.
The theory of sampling applied to percentages (228) enables us to say that the standard deviation of the true lowest 0.5% in samples of this size made under the same conditions would not be more than 0.28%.[12] That is to say, if our result were only affected by the size of our sample the chances are about two out of three that the border of the true lowest 0.5 per cent. would lie between the border of the lowest 0.22% and the lowest 0.78% of a very large sample. Assuming that the distribution in this sample represented that of communities generally, the chances would be two out of three that the true border of the lowest 0.5% for like groups in like communities examined under the same conditions would lie between IX.0 and X.6 or X.4 on the 1908 and 1911 scales respectively. Moreover, the chances that a case in the lowest 0.5% in this sample would be above the doubtful group in a larger sample, i. e., get above the lowest 1.5%, would be about 1 in 10,000. On the other hand, the chances that a case above the true lowest 1.5%, i. e., above the uncertain group, would get into the lowest 0.5% in a larger sample, i. e., be classed as clearly deficient intellectually, would be about 18 in 1,000.
So far as the theory of sampling goes it would seem that these borderlines for the mature are sufficiently accurate for correcting present practise. On the other hand, the conditions in Minneapolis so far as deficiency 95is concerned are probably better than in the country as a whole, so that the borderlines here described might very well exclude more than the lowest 0.5% and 1.5% in the country at large. But if we shifted the definition so as to exclude the lowest 0.2% and 1.1% (the percentages empirically found below the limits described), the borders on the Binet 1908 scale would not be changed from the rough measures IX and X which are as accurate as we should expect to define our limits with the present data.
Comparing the suggestions as to the borderline for the mature which have heretofore been made, we find that they have gradually approached the boundary now suggested by the percentage method. In 1910 the American Association for the Study of the Feeble-Minded adopted a tentative classification in which the upper limit of the feeble-minded included those “whose mental development does not exceed that of a child of about twelve years” (64). This was based mainly on the fact that Goddard had found no case at the Vineland school for feeble-minded which tested higher than XII. Huey later than this found only two such cases at the institution at Lincoln, Ill., and Kuhlmann only ten cases at the Minnesota State School for the Feeble-Minded.
There was an early statement by Binet which referred to the practise in Belgium of regarding older school children as deficient when they were three years retarded in their school work (77, p. 41). This practise may have also contributed to this formulation by the American Association. Binet, however, regarded a child of the mentality of twelve as normal. In 1905, before his tests were arranged in age groups, he said:
“Lastly we have noticed that children of twelve years can mostly reply to abstract questions. Provisionally 96we limit mental development at this point. A moron shows himself by his inability to handle verbal abstractions; he does not understand them sufficiently to reply satisfactorily” (76, p. 146).
It is important to consider how the suggestion of XII as the upper limit of feeble-mindedness for adults got into the early practise in this country as the lower borderline for the mature. It is the most serious error which has marred investigations in this field. It seems to have been a case of repeated misunderstanding on the part of examiners for which nobody in particular was to blame. So far as I can determine nobody stated directly in connection with any scale what should be regarded as the lower borderline for the mature. Numerous examiners, however, in reporting their results, concluded that if the feeble-minded tested as high as XII then adults who tested XII were feeble-minded. They were somewhat encouraged in this fallacy by the fact that the 1908 scales suggested three years of retardation as an indication of feeble-mindedness, and the highest age-group of tests was soon shifted to fifteen years.
The trouble seems to have been that early workers failed to recognize that some of the feeble-minded in institutions, the purely conative cases, have passable capacity so far as the brief intellectual tests are concerned. To determine scientifically what is the borderline, we should study randomly selected groups from the general population and determine the positions on the scale below which practically all are socially unfit. Or, as Wallin has suggested, we should find out the degree of tested ability necessary for survival in simple occupations that are afforded by society (216, p. 224). These positions can only be checked by finding the conditions in institutions or special classes. They cannot be determined by tests of 97these abnormal groups alone. Besides the confusion arising from these feeble-minded who are primarily unstable or inert, but with passable intellects, reasoning from the statistics on abnormal groups merely repeats a common fallacy. The fact that some inmates of institutions test XII does not let us know how many outside the institutions who test XII actually survive in society.
The randomly selected groups of children on which Binet tried out his tests were so ridiculously small that he continually cautioned against adopting his suggestions as to borderlines as anything but tentative. For judging the borderline for the mature there were no test results which had not been seriously affected by the methods of selecting the groups, so we collected the data on this random group of Minneapolis 15-year-olds. I trust that this will make any examiner more careful about assuming that adults testing XI are clearly unable to survive socially, unless he is ready to claim that 10% of the general population are unfit socially.
It is to be noted that, taken literally, the description of the American Association is not in terms of the Binet scale, but of the mental development of a normal child of twelve years, although the framers of the resolution undoubtedly had the Binet scale of mental ages in mind. It was soon found that the tests for the older ages in the Binet 1908 scale were too difficult for the places assigned them. This is certainly true with the tests for twelve years and probably with those for eleven. This evidence is assembled in Table IV. The combined results should be used only with great caution since the methods of the investigators differed in detail and the groups were differently chosen. In the groups of children which Bobertag and Bloch and Preiss tested, there had been eliminated some of those who were backward in school, while Goddard's group did not include the best 12-year-olds.
| No. of Cases | Pass tests XII or better | Pass tests XI or better | ||||||
|---|---|---|---|---|---|---|---|---|
| Life-Age | Life-Age | Life-Ages | ||||||
| Investigators | 12 | 11 | 12 | 11 | 12 | |||
| No. | No. | No. | % | No. | % | No. | % | |
| Binet and Simon (School in poor quarter) | ||||||||
| 1908 study | 11 | 2 | 18 | 7 | 64 | |||
| 20 | 13 | 65 | ||||||
| 1911 study | 23 | 15[13] | 65 | |||||
| Bloch and Preiss | 21 | 21 | 100 | 21 | 100 | |||
| (Only pupils up to grade) | 15 | 13 | 87 | |||||
| Bobertag | 33 | 19 | 57 | 29 | 88 | |||
| (Pupils averaged satisfactory) | 34 | 18 | 53 | |||||
| Dougherty | 46 | 9 | 20 | 36 | 78 | |||
| (Includes 8th grade) | 44 | 22 | 50 | |||||
| Goddard | 144 | 39 | 27 | 75 | 52 | |||
| (Includes none above 6th grade) | 166 | 73 | 44 | |||||
| Johnston | 24 | 6 | 25 | ? | ||||
| (Includes some high school pupils) | 29 | 7 | 24 | |||||
| Terman and Childs | 35 | 3 | 9 | 29 | 83 | |||
| (Includes a few in 8th grade) | 44 | 14 | 32 | |||||
| Rogers and McIntyre | 20 | 1 | 5 | 5 | 25 | |||
| 27 | 6 | 22 | ||||||
| Totals | 357 | 379 | 100 | 166 | 217? | |||
Each of the studies indicated in the table, except that of Bloch and Preiss, gives evidence that the XII-year tests are too difficult for 12-year-old children. Moreover, we find that in the 1911 revision of their scale Binet and Simon advanced their 1908 XII-year tests to test-age XV and four out of the five XI-year tests to test-age XII. Passing the XII-year (1908) tests would, therefore, seem to bring a child above the upper limit of feeble-mindedness as defined even by the American Association for the Study of Feeble-mindedness, since it means more than the intelligence of a child of 12.
Goddard still adhered to this borderline of the American Association in 1914 in his work on Feeble-Mindedness. He says: “We have practically agreed to call all persons feeble-minded who do not arrive at an intelligence higher than that of the twelve year old normal child” (p. 573). In the same year Schwegler's “Teachers' Manual” for the use of the Binet scale says that a person who tests XII is a moron if mature (180). Since the evidence of Table IV indicates that 75% of the twelve-year-olds do not test above XI, even those who adhere to the high limit of the intelligence of a 12-year-old should have required an adult to test XI on the Binet scale in order to show deficiency.
In 1911 we find Wallin writing, regarding the 1908 tests, “it is a question whether the line of feeble-mindedness 100should not be drawn between eleven and twelve instead of between twelve and thirteen.... A number of our twelve-year-olds are certainly very slightly, if at all, feeble-minded” (210). Jennings and Hallock (31) and Morrow and Bridgman (39) in testing delinquents reported in 1911 and 1912 that they regarded those passing the tests for twelve years as socially fit. Chotzen (31) thinks that the two children in his group of pupils from a Hilfsschule who test ten and are three years or more retarded are not feeble-minded. Davis thinks that those “showing mentality from ten to twelve years” may possibly not be called mentally defective (133, p. 187).
In 1915 the editors of the magazine “Ungraded” in their recommendations regarding the use of the Binet scale say “a mental age of 10 or above is not necessarily indicative of feeble-mindedness, regardless of how old the examinee may be” (66, p. 7). In the same year Kohs, in reporting the examinations of 335 consecutive cases at the Chicago House of Correction, says: “We find normality to range within the limits 122 and 104 and feeble-mindedness not to extend above the limit 112. In other words, none of our cases testing 113 or over was found, with the aid of other confirmatory data, to be mentally defective. None of our cases testing 103 or below was found to be normal. Of those testing between 104 and 112, our borderline cases, a little less than half were found normal, and somewhat more than half were found feeble-minded” (33). His exponents here refer to number of tests and not to tenths of a test-year. Hinckley (182) reports examinations with the Binet 1911 scale on 200 consecutive cases at the New York Clearing House for Mental Defectives which show that with these suspected cases, which were from 13 to 43 years of age, seven-eighths tested X or below. Referring to adults, Wallin states that he 101has “provisionally placed the limen somewhere between the ages of IX and X” (215). Dr. Mabel Fernald at the Bedford Reformatory laboratory said in 1917, “many of us for some time have been using a standard that only those who rank below ten years mentally can be called feeble-minded with certainty” (16). The reader should also see the admirable review and discussion of the borderlines on the Binet scale in Chap. II of Wallin's Problems of Subnormality. Two descriptions of the scale borderlines in books on mental testing which appeared in 1917 are of interest. In his Clinical Studies in Feeble-Mindedness (p. 76), E. A. Doll says:
“By the Binet-Simon method feeble-mindedness is almost always (probably more than 95 times in a hundred) an accurately safe diagnosis when the person examined exhibits a mental age under 12 years with an absolute retardation of more than three years, or a relative retardation of more than 25 per cent.”
N. J. Melville, in his Standard Method of Testing Juvenile Mentality (p. 10), says:
“Conservative estimates today place the upper limit of feeble-mindedness at least in a legal sense at Binet age ten; others place it at Binet age eleven.... A Binet age score below eleven when accompanied by a sub-age (retardation) of more than three years is usually indicative of serious mental deficiency. Even when accompanied by a slight sub-age score, a Binet age score below eleven may be indicative of potential mental deficiency when the test record reveals a Binet base that is six or more years below the life age.”
In 1916 the new Stanford scale appeared and its tests are arranged so that approximately 50% of each age instead of 75%, test at age or above. Even with this lowering of the scale units, Dr. Terman describes his borderline for “definite feeble-mindedness” as below an intelligence 102quotient of 70. This would mean for his 16-year-old mature borderline a mental age on this scale of XI.2. We have no means of determining to what positions these points on the Stanford scale would correspond on the 1908 or 1911 Binet scales. Dr. Terman says “the adult moron would range from about 7-year to 11-year intelligence” (57). Apparently also referring to the Stanford scale, the physicians at the Pediatric Clinic of that university agree with this borderline and say: “morons are such high grade feeble-minded as never at any age acquire a mental age greater than 10 years” (169). That there is still need for more caution is evidenced by the statement of a prominent clinician in 1916 that “cases prove ultimately to be feeble-minded since they never develop beyond 12 years intelligence” (135).
Most interesting perhaps is the fact that Binet and Simon themselves, the collaborators who first formulated the scale for measuring intelligence by mental ages, after their years of experience with the tests came, by rule of thumb, to regard IX as the highest level reached by those testing deficient. Dr. Simon stated the borderline for the mature in this way in a paper read in England in 1914 and published the next year. He said:
“Provisionally it might be proposed to fix at 9 years the upper level of mental debility.... We have reason to think that a development equivalent to the normal average at 9 years of age is the minimum below which the individual is incapable of getting along without tutelage in the conditions of modern life. A certain number of facts suggest this view and are mutually confirmatory. Nine years is the intellectual level found in the lowest class of domestic servants, in those who are just on the border of a possible existence in economic independence; it is, on the other hand, the highest level met with in general paralytics who come under asylum care on account of their dementia; so long as a general paralytic, setting aside any question of active delirious symptoms, has not fallen below the intellectual level of 9 years, he can keep at liberty; once he has reached that level, he 103ceases to be able to live in society. And lastly, when we examine in our asylums cases of congenital defect, brought under care for the sole reason that their intelligence would not admit of their adapting themselves sufficiently to the complex conditions of life, we find that amongst the most highly developed the level of intelligence does not exceed that of a normal child of 9 years of age” (182).
In connection with their 1911 revision of the scale Binet and Simon had stated that among 20 adults in a hospital where custodial care was provided for the deficient “we found that the best endowed did not surpass the normal level of nine or ten years, and in consequence our measuring scale furnished us something by which to raise before them a barrier that they could not pass” (79, p. 267). They, however, then expressed complete reserve as to the application of this criterion to subjects in different environments on their presumption that deficiency for the laboring class is different from that for other classes in the population.
The Germans seem to have early recognized a lower borderline for the mature than we did in this country for we find Chotzen saying in 1912 that he agreed with Binet's finding that “idiots do not rise above a mental age of three, imbeciles not over seven, and debile not over ten” (89, p. 494). Stern also quotes Binet as declaring that the moron does not progress beyond the mental age of nine (188, p. 70).
The tendency of interpretation indicated by these studies is plainly to lower the borderline for passable mature intellects until it approaches the limits which the percentage definition suggests as reasonable from our available evidence. The percentage plan thus confirms the borderline that has been approached gradually by hit or miss methods. An adult testing IX is presumed deficient, while one testing X is in an uncertain zone. The 104numerous studies of delinquents which have regarded adults who tested XI and even XII as deficient have seriously overestimated the problem of the deficient delinquent, as we shall see in our later chapter on tested delinquents.
In attempting to adapt the percentage method of description to the border region for the immature, it is essential that the tests shall have been tried out on randomly selected groups. Neither teachers nor the examiner should pick out children to be tested, if we are to know much about the region of lowest intellects. While Bobertag's method of choosing typical groups by balancing those backward in school by those advanced, is serviceable for his purpose of determining norms, the personal element of choice involved makes the results thus obtained almost useless in determining the lower limit of ability.
In regard to the diagnosis of intellectual deficiency by the Binet 1908 or 1911 scales, we know much more about the interpretation of results obtained with the 1908 scale than with the 1911 scale. The 1908 scale was therefore used for our examinations of juvenile delinquents. The best available data on which to base a description of the borderline for the immature is that collected by Goddard (119). He says that he “arranged to test the entire school population of one complete school system. This system includes about five thousand population within a small city and as many more outside, so that we have, city and country, a school population of about two thousand children.... In the seventh and eighth grammar grades and the high school, the children were tested in groups.” Since only the first six grades were tested individually 105and only these results are published in sufficient detail to be available, we shall confine this account to the school children below the seventh grade. It must be remembered that any children of the idiot class and possibly some of the low imbeciles would not be included in his figures for they would probably have been excused from school attendance. In a small rural community it is not likely that these would be numerous enough to change the rough borderline materially. We thus have a fairly random group for a small town and its environs.
Since we cannot use Goddard's results for our purpose above the sixth grade, it is plain that we would not sufficiently approach a random distribution for any age above 11 years. In Minneapolis, for example, a recent census showed 28% of the public school children 12 years of age are in the seventh grade or above, while 6% of the better eleven-year-olds would be excluded by including only those below the seventh grade. We have therefore omitted from our calculations all of Goddard's results for children above eleven years of age as too unreliable for purposes of percentage estimations. Even his eleven-year-olds may be affected.
Although it is not clear in the published reports whether the nearest or last birthday was used, Dr. Goddard has informed me that his table shows the results for ages at the last birthday. A child is regarded as six until he has reached his seventh birthday, as is customary. Throughout this book I have followed this method of using age to mean age at last birthday, or avowed age. This is in conformity with the common use of age and with general anthropometric practise. It is less confusing and less subject to mistake or errors of record. On the whole, I believe that in statistical work avowed age is preferable to nearest age.
| Life-Age | No. of cases | Years Retarded | |||
| Two or more | Three or more | Four or more | Five or more | ||
| 5 | 114 | 5.3 | 1.8 | ||
| 6 | 160 | 2.5 | 0.6 | 0.6 | |
| 7 | 197 | 5.6 | 1.5 | 0.5 | 0.0 |
| 8 | 209 | 2.4 | 1.9 | 1.0 | 0.0 |
| 9 | 201 | 1.3 | 0.0 | 0.0 | 0.0 |
| 10 | 222 | 18.9 | 8.1 | 1.4 | 0.0 |
| 11 | 166 | 25.9 | 10.8 | 3.0 | 0.6 |
| 1269 | |||||
In the accompanying Table V Goddard's results are arranged so as to show the percentages at each life-age retarded two or more, three or more, four or more, and five or more years according to the Binet 1908 scale. The heavy black line indicates the upper borderline of the doubtful group according to our interpretation. In spite of irregularities, due mainly to insufficient numbers, the trend of the table is fairly plain. The column of percentages two or more years retarded and to the left of the heavy line suggests that the break comes at ten years of age. Using our tentative criterion of 0.5% presumably deficient and the next 1.0% uncertain intellectually, the outcome of this analysis is a rather striking demonstration of the feasibility of the percentage procedure even when the groups examined at each age are only composed of about 200 cases. I have preferred to take the empirical data at the lower extreme of each age distribution instead of projecting the tail of a smoothed distribution curve for each age.
107Until better data are available we have adopted in practise, as a result of the study of this table, the procedure of considering any child who is ten years of age or over as testing of doubtful capacity if he is four or more years retarded below his chronological age, three or more years retarded if he is under ten years of age. If he shows one additional year of retardation we consider, in the absence of some other explanation of his retardation, that he is presumably intellectually deficient enough to justify a recommendation of isolation. Of course no such recommendation should be made without a complete medical examination, a full knowledge of the history of the case and a checking of the record by further tests at different times when there is any suspicion that the child has not done as well as he might under other conditions.
The fact that we have no data on random groups 12, 13 and 14 years of age leaves a gap which may mean that our criterion of 5 years retardation for presumable deficiency at these ages is too small. It is possible that the shift to 6 years retardation should be made before 15 years, which is the position where our criterion for the borderline for the mature automatically makes the shift. We say a 15-year-old testing X is above the group presumably deficient as he has entered the “doubtful” adult class.
It is also to be remembered that the standard error expected from the results of samples as small as these is 0.5% when the sample is 200 and 0.7% when it is 100. The limits thus might easily shift a year. The suggested borderlines for the immature can at best be regarded only as the most likely under the meager evidence available.
Whether the borderlines for deficiency on the Binet scale should be described in terms of years of retardation is doubtful except, as in this case, for practical convenience. 108It is certainly only a rough indication of the borderlines. When this method has not been followed the most common practise is to use some form of Stern's “intelligence quotient.” An extended discussion of this question is reserved for Part II of this book, to which the reader is referred. It need only be said here that the percentage procedure adapts itself to either method of description. Since the designation of the limits must be very rough until we have much further information from tests upon unselected groups, we have adopted the common method of description in terms of years of retardation, since it seems to afford for the 1908 scale the simplest expression of the borderline until the tests have been much improved. It happens that the empirical results for 5 years of age and over lend themselves to designating the lowest percentages in terms of years of retardation with only a single shift at 9 years of age. An equally accurate designation by the intelligence quotient would be quite complicated if it were adapted equally well to the different life-ages.
The fact that the Binet mental ages do not signify corresponding norms at each age has been frequently pointed out (200). Moreover it is probable that one year of retardation on the scale means a different thing at different chronological ages. With the new Stanford form of the scale, for example, “a year of deviation at age 6 is exactly equivalent to a deviation of 18 months at age 9, and to 2 years at age 12, etc.” (197) when measured in terms of the deviation in ability at these ages. This variation does not interfere, however, with our use of the “years of retardation” merely as a short method for describing empirically the positions on the scale which roughly and conservatively designate the same percentages of children of low ability at various ages. Besides its convenience in 109this respect, there is no question but that such a description does help better than a quotient to convince the public of the seriousness of the deficiency.
A more serious theoretical objection to describing the borderline for the immature in terms of years of retardation is that, when one changes from three to four years of retardation, it is clear that a moron who tests VI at 9 years of age would be supposed to be still only VI at 10 years in order to remain below the borderline, while it is known that there is some, albeit a small, amount of progress made by the higher class deficients at these ages. In the crude state in which the Binet scale still remains, however, we have preferred to waive these theoretical objections in favor of the prevalent custom which has the advantages of simplicity, practical convenience, popular significance and, in this case, equal accuracy.
It is, of course, very desirable that the results obtained by Goddard as well as our Minneapolis results should be checked by data on unselected groups elsewhere. With the 1908 scale the only other data which seems fairly to represent a random selection are those of Terman and Child's (195, p. 69). Since they examined less than 50 at any age, however, their table helps only to check roughly the borderline suggested. The percentages retarded two years or more changed to the basis of calculation we used, indicate that the break comes at 10 years. The percentages from six up to ten years run 0, 3, 7, 6, when they change to 12% or more for the following ages. While the groups are too small to indicate the borderlines for each age, yet, when we group the children from 6-9 years inclusive, under our interpretation we find that a year less than our upper borderline for the uncertain group would give 4.8% of 147 cases. With 142 cases in the group 10, 11, and 12 years old, 5.6% would be caught by 110placing the borderline for the doubtful a year less than we have indicated. Our scale borderlines are thus in harmony with these data.
When we turn to data from randomly selected groups for judging the borderlines with other developmental scales than the 1908 Binet, we find that a group of children in the rural schools of Porter County, Indiana, have been examined with the Goddard adaptation of the Binet 1911 scale (92) and a group of school children in a Minnesota city, with the Kuhlmann adaptation of the 1911 scale (138). The important results with each study are given in Table VI. In the Indiana study the children were examined through the eighth grade. The elimination of older children from school would certainly affect the groups over 13 years of age and probably disturb the results even for the 13-year olds. For this group the results are published only for nearest mental and nearest life-ages. The results are, therefore, not strictly comparable with those of Table V. for the 1908 scale. It is doubtful whether tests on children in the rural schools should be used for indicating borderlines. The table suggests, however, that the borderlines we have indicated for the 1908 scale are not too conservative for the immature tested with the 1911 scale. It is possible, however, that with Goddard's adaptation the break comes at 9 years of age instead of 10.
| Nearest Life-Ages | Total Pupils | Percentages showing the following years of tested retardation according to the nearest mental ages: | |||
|---|---|---|---|---|---|
| Two or more | Three or more | Four or more | Five or more | ||
| 6 | 107 | 2.8 | |||
| 7 | 232 | 6.03 | .43 | ||
| 8 | 234 | 8.12 | 2.12 | .42 | |
| 9 | 216 | 12.04 | 5.54 | 1.84 | .92 |
| 10 | 278 | 19.88 | 3.58 | 1.08 | .36 |
| 11 | 212 | 18.3 | 8.4 | 1.8 | |
| 12 | 243 | 33.9 | 12.9 | 2.6 | |
| 13 | 249 | 63.7 | 27.9 | 8.4 | 2.8 |
| Exact years of retardation. | ||||
|---|---|---|---|---|
| Nearest Life-Age | Total Pupils | 1 or more | 2 or more | 3 or more |
| 6 | 38 | 0 | 0 | 0 |
| 7 | 82 | 4 | 0 | 0 |
| 8 | 95 | 9 | 0 | 0 |
| 9 | 91 | 12 | 2 | 0 |
| 10 | 84 | 16 | 9 | 1 |
| 11 | 88 | 18 | 4 | 0 |
| 12 | 75 | 32 | 8 | 1 |
112Kuhlmann, with the assistance of twenty teachers whom he started in the work and whom he regards as “untrained examiners,” measured “the public school children from the first to the seventh grade, inclusive, in a Minnesota city.” The essential figures from his results are given in Table VI. These results are not directly comparable with those of Goddard using the 1908 scale, since Kuhlmann tabulates the nearest ages instead of the actual ages. His age groups would therefore average a half year younger chronologically than Goddard's. Moreover, the exact amount of retardation to tenths of a year was then calculated from the exact age, and it is to be remembered that the method of calculating the mental age was changed in 1911 so as to start with a basal age in which all tests were passed. The effect of these changes would be that some of those recorded in Kuhlmann's table as two years retarded might easily be a year more retarded under the same methods of calculation that were previously used. Using his method of computation, it is clear that the general borderline for the immature with this scale would not be as low as we have indicated for the 1908 Binet scale. It would apparently be about a year less, i. e., two years of retardation for those six to nine years of age, and three years retardation for those 10 or above in order to fall within our doubtful group. The 13 year old group are not included here. They would not be even approximately random since those who had reached the eighth grade or above were not examined. It is interesting to note that the break in frequency of serious retardation again occurs in the change from those chronologically 9 years of age to those 10 years of age.
The Stanford Revision and Extension of the Binet-Simon Scale (57) has included a percentage designation of the degrees of ability by a classification of intelligence quotients (I Q's). It is interesting to find the percentage method of setting forth the borderlines is utilized to supplement the intelligence quotients in this important revision of the Binet-Simon Scale. It shows how the method may be adapted to testing of intelligence quotients. 113For fixing the borderline for the immature the Stanford scale affords the best means provided by any of the revisions or adaptations of the Binet scale. The amount of data on randomly selected groups of school children, by which these borderlines were determined, is, however, less than with the 1908 Binet Scale as given by Goddard and summarized in our Table V. The Stanford Scale was standardized for the immature by testing 80 to 120 native born school children at each age from 5 to 14 inclusive, a total of 905. While the 1908 scale gives corresponding distributions for 114 to 222 children at each age from 5 to 11 inclusive, a total of 1269. Using the I Q's adopted by Dr. Terman for the Stanford Scale, the lowest 1% of the children were found to reach only an I Q of 70 or below, 2% to reach 73 or below, 5% to reach 78 or below. The author designates below 70 as “definite feeble-mindedness,” 70-80 as “borderline deficiency, sometimes classified as dullness, often as feeble-mindedness.” His “definite feeble-mindedness” thus includes somewhat fewer than our “presumably deficient” and “uncertain groups” combined. The distribution of the intelligence quotients was “found fairly symmetrical at each age from 5 to 14.” The range including the middle 50% of the I Q's, was found practically constant (57, p. 66). The data for the extreme cases have not been published except for ages 6, 9 and 13. For these ages 1% were 75 or below at 6 years, 2% at nine years, and 7% at 13 (197). The results with the extreme cases at each age are the most important factor in fixing the borderline. The combined per cent. results with I Q of 905 children at different ages, which show 0.33% testing 65 or below and 2.3% 75 or below, may be deceptive for separate ages.
It seems clear that the criterion for tested deficiency suggested by our study is more conservative than that of the Stanford scale which says:
114“All who test below 70 I Q by the Stanford revision of the Binet-Simon Scale should be considered feeble-minded, and it is an open question whether it would not be justifiable to consider 75 I Q as the lower limit of “normal” intelligence. Certainly a large proportion falling between 70 and 75 can hardly be classed as other than feeble-minded, even according to the social criterion.” (57, p. 81)
In regard to the borderline for the mature with the Stanford scale it is especially important to note that at present no randomly selected mature group has been tested with this scale so that we are at a loss to know what would be a safe borderline for adults with it. It is peculiarly unsafe, it seems to me, to carry over an intelligence quotient which may shut out the lowest 1% of children who distribute normally, to the uncertain borderline of an adult group composed of thirty business men, 150 migrating unemployed, 150 adolescent delinquents and 50 high school students. By these data it would be impossible to tell what per cent. of a random group of adults would be shut out by this borderline of 70.
| Nearest Ages | 4-5 | 6-7 | 8-9 | 10-11 | 12-13 | 14-15 | 18-on |
| No. of Cases | 84 | 357 | 196 | 161 | 120 | 77 | 284 |
| Presumably deficient | Under .61 0.4% |
Under .61 0.6% |
Under .61 0.7% |
||||
| Doubtful | Under .51 | .61 to .81 | Under .51 | .61 to .71 | Under .51 | Under .61 | .61 to .71 |
| Both | (4.8%) | 1.5% | 1.5% | (5.0%) | 1.7% | 1.3% | (6.3%) |
| Ages | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| No. of Pupils | 71 | 73 | 61 | 71 | 76 | 79 | 60 | 52 |
| Per Cent of Pupils at | 1.4 | 1.4 | 1.5 | 2.7 | 1.3 | 1.3 | 1.7 | 2.0 |
| and Below Points | 11 | 14 | 15 | 21 | 35 | 40 | 33 | 38 |
For the Point Scale for Measuring Mental Ability, prepared by Yerkes, Bridges and Hardwick, we have two sets of data which give the only empirical basis for estimating the percentage borderlines for the various ages (225, 226). These data are restated in terms of percents in Table VII. The first part of the table shows the borderline results with the normal group composed of 829 pupils of the Cambridge schools, 166 pupils of Iowa schools, 237 in the group of Cincinnati 18-year-old working girls and an adult Massachusetts group of 50. The table illustrates how difficult it is to find a common borderline in terms of a ratio, in this case the “coefficient of intelligence,” for a series of life-ages. It certainly seems hazardous to attempt to smooth these empirical borderlines for the different ages by accepting, on the present evidence, the suggestion of the authors that a coefficient of .50 or less at any of these ages indicates the individual is “dependent” and coefficients from .51-70 that he is “inferior,” since the data show the lowest group would include only the lowest 0.04% of 18 years of age and over, while it includes 4.8% of those in their table four and five years of age. Indeed, the authors note that “a few months' difference in age will alter the coefficient of a five or six year old child by ten to thirty per cent.” Under such circumstances it would be better for the present to use the empirical basis suggested from the data of Table VII rather than to attempt to use a uniform borderline coefficient for the various ages. For calculating the coefficient of a particular individual, his point scale record should presumably be divided by the revised norms published by the authors, which are as follows for the nearest life-ages, reading the dots on their graph: 4 yrs. 15 points, 5 yrs. 22, 6 yrs. 28, 7 yrs. 35, 8 yrs. 41, 9 yrs. 50, 10 yrs. 58, 11 yrs. 64, 12 yrs. 70, 13 yrs. 74, 14 yrs. 79, 15 yrs. 81, 16 yrs. 84, 17 yrs. 86, 18 yrs. 88.
116Since all the pupils in Grammar School B, who were not absent during the periods of examination, were examined, the distribution of these 675 pupils may be serviceable for obtaining a rough idea of the borderlines in terms of points at the different ages from 6-13 inclusive. These individuals “constituted the population of a city grammar school in a medium to poor region and including grades from the kindergarten to the eighth, inclusive.” On account of the small number of individuals at each age the errors are large and the limits should be used only with much caution as an indication of the general trend of the table.
All the scales, it should be noted, have been tried out on immature groups composed only of school children. These would not include those children who are so deficient as not to be sent to school. The borderlines determined with school children, therefore, tend to shut out a slightly larger percentage of all children than of school children. They would, therefore, tend to class slightly too many as deficient. Moreover, the groups tested were probably in communities which are somewhat above the average in ability so that we should be doubly cautious in using the borderlines for the immature.
The confusion over the amount of allowable retardation in evaluating the results of Binet tests is illustrated by the variations in practise. In 1908 Binet and Simon said: “On the contrary, a retardation of two years is rare enough; ... Let us admit that every time it occurs, the question may be raised as to whether the child is subnormal, and in what category he should be placed” (79, p. 269). In 1911 they had become much 117more conservative. With their new scale they stated: “We would add that a child should not be considered defective in intelligence no matter how little he knows unless his retardation of intelligence amounts to more than two years” (78). This cautious statement seems to have been converted by the various translators into a rule that every child retarded three years was to be regarded deficient. Drummond, for example, in his translation says: “Should a child's mental age show a retardation of three years as compared with his chronological age, and should there be no evident explanation of this, such as ill health, neglect of school attendance, etc., he is reckoned as deficient mentally” (77, p. 163). Wallin, however, in 1911 kept to the original conservative statement, “children retarded less than three years should probably not be rated as feeble-minded” (211, p. 16).
In his book on Mentally Defective Children, before the 1908 scale had appeared, Binet had adopted the Belgian practise of making a distinction between younger and older children as to the amounts of allowable school retardation before the question of mental deficiency should be raised. As a method of preliminary selection for examination he used a retardation in school position of two years when the child was under 9 years of age and three years when he had passed his ninth birthday (77, p. 42). This practise was carried over into the field of mental tests, and Huey then qualified these limits by the safer allowance of four and three years of tested retardation with the change still at nine years (129).
The German standard, formulated by Bobertag and accepted by Chotzen (89, p. 494), is to place the lower limit for the normal as less than three years retardation at ten years of age or less than two years retardation under that age. The change in the amount of retardation allowed 118came at the same position we advocated instead of at 9 as was earlier suggested.
The early practise in the United States was merely to regard three years retardation as the sign of feeble-mindedness. This custom was even followed in 1914 for all under 16 years of age by Mrs. Streeter in the investigation by the New Hampshire Children's Commission of Institutions in that state. She did not call any feeble-minded who tested over XII (40, p. 79). In both the 1908 and 1911 editions of the Binet scale issued by Goddard, he stated that if a child “is more than three years backward he is mentally defective,” giving no caution about a borderline for the mature. This is a practise which has been followed so far as the immature are concerned, by Goddard's students generally. Kuhlmann carefully avoids the statement of a borderline with both his 1908 and 1911 adaptations of the Binet scale, but he has since advocated using an intelligence quotient of less than .75 with his 1911 scale to indicate feeble-mindedness and leaving a doubtful area from .75 to .80 (140). Stern suggested a borderline of .80 with the intelligence quotient (188). Even a quotient of .75 would call a child feeble-minded by Kuhlmann's 1911 scale if he tested two years retarded at eight and three years retarded at twelve. Haines suggests using, with caution, a borderline with a modified Point Scale which should be at 75% of the average performance measured in points at each age for individuals over thirteen years, and four years retardation for 13 years and younger (26).
Pintner and Paterson collected in one table the test results with the Binet scale published by thirteen different investigators and covering 4,429 children tested (44, p. 49). They do not attempt to readjust these results so as to allow for the very great differences in the methods by 119which the different groups were chosen to be tested or the different uses of actual life-age and nearest life-age. Such a table is, as they recognize, too hazardous to use for determining the borderlines of deficiency. There might be an average difference of at least a year in the mental ages obtained by different investigators when no allowance is made for their different procedures. Nevertheless, it is interesting to note that a mental quotient of .75 is less conservative than the lowest 3% which is the borderline of feeble-mindedness that they suggest. The lowest 3% they find would include, for example, those who were 1.5 years or more retarded at age 5, 2.1 years retarded at 9 and 2.8 years at age 10.
The most important confirmation of the claim that a borderline for the immature should require at least 4 years retardation comes from the Galton biometric laboratory in London. Karl Pearson has furnished a careful statistical treatment of Jaederholm's results in testing all the 301 children in special classes in Stockholm compared with 261 normal children in the same schools. Pearson found that the modified 1911 Binet scale which Jaederholm used could be corrected so that the normal children at each age averaged very closely to their age norms from 7 to 14 years of age. Under these conditions of the scale he generalized on the basis of the children in the Stockholm special classes who were from 7 to 15 years of age, as follows:
“The reader may rest assured that until the mental age of a child is something like four years in arrear of its physical age it is not possible to dogmatically assert, on the basis of the most scientific test yet proposed as a measure of intelligence, that it is feeble-minded. Even then all we can say is that such a child would be unlikely to occur once in 261 normal children, or occurs under ½% in the normal child population.” (167, p. 18).
120In a later paper he says that those children “from 4 to 4.5 years and beyond of mental defect could not be matched at all from 27,000 children,” on the assumption of a normal distribution fitted to the normal Stockholm school children (164, p. 51). He says further:
“It is a matter of purely practical convenience where the division—if there must be an arbitrary one—between the normal and defective child is placed; we suggest that it be placed at either 3 or 4 years of mental defect. But as mental defect increases with the age of the mentally defective the division will be really a function of the child's age” (167, p. 37).
Since he finds the children in the special classes fall further behind the normal children on the average 4 months each year of life, this means that 3 years retardation at 7 years of age would be equivalent to 4 years at 10.
In spite of uncertainty introduced by the use of quotients, the general tendency in interpretation of results with Binet scales has thus been to make a distinction in the amount of retardation signifying deficiency among younger and older children and to require four years retardation, at least for the older ages. Our criterion for the borderline of three years retardation for children under 10 years and four years for 10 years and over, with an extra year to be quite sure that the deficiency is sufficient to justify isolation, seems to be in line with the best practise at present among those who have had much experience with the Binet scale. Fortunately, little harm has been done to the individuals themselves by this uncertainty in the interpretation of the scores with the scale, since only questionable cases have been affected. These have generally been diagnosed, before disposing of the child, by some expert who understands the sources of error in mental tests. On the other hand, shifting the limit of 121allowable retardation by one year makes a great difference in the estimation of the frequency of feeble-mindedness in particular groups, as will be shown in our discussion of deficient delinquents.
11. Throughout this study I shall use the literal translation of the German term “lebensalter,” life-age, instead of the awkward “chronological age.”
12.
| S. E. = | √ | p. q. |
| n |
13. Tests XI were recorded as XII in the 1911 series.
We are now in a position to evaluate the Binet examinations of delinquents. Let us first note our results for a group of 123 consecutive cases at the Hennepin County Detention Home.[14] It is not a detention home in the sense of a place where children are held awaiting the disposition of their cases by the Juvenile Court. It is better described by its unofficial title, The Glen Lake Farm School for Boys. This county training school for delinquents is located on a splendid farm beside a small lake fourteen miles outside of Minneapolis. The boys are sent there by the juvenile court for a few months' training as an intermediate discipline between probation and sentence to the State School at Redwing.
The character of this group of 123 randomly selected delinquents is further indicated by the fact that 69 of them had already been brought into court two or more times, 54 were first offenders. Boys are sent to Glen Lake whenever the nature of their delinquency or the conditions at home, together with the personality of the boy, seem to the court to require this special training. A summary of the offenses for which the boys were brought into court does not, therefore, show the character of the boy as it is known to the court through the evidence and 123the efficient service of the probation officers. It shows, however, that the last offenses for which this group were being disciplined were as follows: Petit larceny 29, truancy 25, incorrigibility 25, burglary 9, grand larceny 6, disorderly conduct 4, malicious destruction of property 4, trespass 3, sweeping grain cars 3, breaking and entering 3, indecent conduct 2, miscellaneous offenses one each 8, total 123. Perhaps a more important indication of the character of the offenders in this group is that they represent about a quarter of the cases brought before the juvenile court during the period of this study, a little over a year. With the exception of a very few cases sent directly to the State Industrial School they may thus be regarded as typically the worst quarter of the delinquent boys under 17 years of age in Minneapolis.
The majority of boys were tested by myself after several year's experience with the clinic in mental development at the University of Minnesota and after examining many other delinquents. Some were tested by assistants from the university clinic, Mrs. Marie C. Nehls and Mr. Harold D. Kitson, who had been specially trained for this. Their detailed reports were carefully gone over and evaluated. The Binet 1908 series (136) was used, except that for tests above XII either tests XIII were used, or later these were supplemented by two other tests, which have been placed in the age XV group or adult groups, in the revisions of the Binet scale published by Goddard (110) or Kuhlmann (135). This variation was of small importance since a boy was regarded as of passable intellect if he scored X.8. We always gave the three tests of the XIII group and the boy was credited with age XIII if he passed two out of the original XIII year tests or four out of five tests given above XII. In accordance with our conservative position the rule of this 1908 scale for scoring 124was followed and the boy credited with the highest age for which he passed all but one test, plus one year for each five higher tests passed. This is the basis of the 1908 form of the scale as standardized by Goddard. Appendix II gives the detailed results for each boy with exact life-age and tenths of test-age on the scale, basal test-age with the tests, grade in school at the first of September when he was of this life-age and offense for which he was being disciplined. It also indicates which boys were repeaters. The results of this table are summarized in Tables VIII and IX. The life-ages at the last birthday are used rather than the nearest ages, since this accords with Goddard's standardization and with the common use of the term “age.” Moreover it seems to conform to the best practise and to be less likely to lead to mistakes. Table IX also shows the school position of each boy. Since a number of the older boys had left school, in order to tabulate their school positions in reference to their life-ages it was necessary to assume that they would have continued to progress normally from the position they held when they left. The Minnesota law requires attendance at school until sixteen years of age unless before that the child graduates from the eighth grade. In this group most of those sixteen years of age and a goodly number of those fifteen years old had left school, so that their school position had to be advanced a year in the table; a very few of the 16-year-olds had to be advanced two years in the table. In all cases the school position is given relative to the first of September when the boy was of the life-age given. Either ages six or seven are taken as satisfactory for the first grade, ages seven or eight for the second grade, and so on with the other grades.
| Life-Ages at Last Birthday | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test-Ages | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Totals |
| VII | 1 | 1 | ||||||||||
| VIII | 1 | 1 | 1 | 3 | ||||||||
| IX | 4 | 2 | 1 | 1 | 1 | 8 | ||||||
| X | 1 | 2 | 2 | 1 | 5 | 2 | 3 | 1 | 17 | |||
| XI | 1 | 2 | 8 | 6 | 9 | 6 | 13 | 3 | 48 | |||
| XII | 1 | 2 | 5 | 4 | 6 | 7 | 3 | 27 | ||||
| XIII | 1 | 4 | 8 | 5 | 18 | |||||||
| Total | 1 | 1 | 0 | 6 | 8 | 13 | 12 | 21 | 18 | 30 | 13 | 123 |
| Life-Ages | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| School Position Grades | No. | 6 | 7 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| + | 1 | XI | |||||||||
| +S | 17 | VIII | VIII | XII | XI | XIII | XIII | ||||
| IX-3 | XI | XII | XI | XII | |||||||
| X | XII-2 | XII | |||||||||
| -S | 21 | X | XI-3 | XIII-2 | XI | XIII | |||||
| IX | XI | X | |||||||||
| X | XII-2 | ||||||||||
| XII | XIII | ||||||||||
| XI | VII | XI | |||||||||
| -1 | 28 | XI | XI-3 | XI | XI-3 | XII | XI | XIII-2 | |||
| IX-1 | VIII | ||||||||||
| X | X | XII | XII | XI-2 | XIII-4 | XI | |||||
| IX | XII | ||||||||||
| -2 | 26 | IX | XII-2 | XII | (X) | XIII-3 | XIII-2 | ||||
| XI | XI-2 | X-2 | XIII | XII-2 | XII | ||||||
| X | XI | XI-5 | |||||||||
| -3 | 19 | XI | (IX) | XII-2 | (X) | XI-2 | |||||
| XI-3 | XI-2 | XI-XII | |||||||||
| X XII | |||||||||||
| -4 | 7 | VIII | XI | (X) | XII | ||||||
| X | XI | ||||||||||
| XII | |||||||||||
| -5 | 4 | (X) | (X) | (IX) | |||||||
| (X) | |||||||||||
| Totals | 123 | 1 | 1 | 6 | 8 | 13 | 12 | 21 | 18 | 30 | 13 |
An Arabic numeral after a Roman numeral indicates the number of cases, when more than one case occurs at any position in the table. Parentheses indicate cases testing presumable deficient or doubtful. S is a satisfactory school grade.
126The summary of the Binet scale testing of this group according to the valuation which we have adopted, shows two clear cases of tested deficiency. One boy who was 13 years of age tested VIII and was the only case sent to the State School for Feeble-Minded from this group. The other was 16 years of age and tested IX. Besides the two presumable deficients, seven other boys were uncertain according to our interpretation, as judged by the Binet tests alone. One of them was 13 and tested IX, the others were 14, 15 and 16 and tested X. This would make a total of 7% possibly socially deficient, since they were all delinquent. This seems to be the largest estimation of deficiency which would be justified on the basis of these test results. To show, however, how important is the interpretation of the results obtained with Binet examinations when treated in gross, it need only be stated that a few years ago, when this study began, it was not uncommon to count all who were retarded three or more years and testing XII or under as feeble-minded. On that absurd basis, there would be 45 such cases (37%). As we have considered at length the reasons for not counting a person as even of doubtful intellect who tests XI or above or is less than three or four years retarded, we do not need to rehearse them here.
Using our conservative basis for interpreting the results of Binet examinations, let us now review the evidence of the proportion of delinquents which is intellectually deficient. We shall compare the available data on groups of tested delinquents which have not been subjectively selected, provided that the data permit of restatement on the basis of the borderlines we have adopted. The evidence of tested deficiency on over 9000 objectively selected delinquents has thus been assembled under approximately the same interpretation of the borderlines. This should help to make it clear how extensive the preparations must be for dealing with this problem of the defective delinquent and where the needs are most pressing. It should also enable us to discover when the estimates have been excessive. We shall confine ourselves to the reports of objective test examinations, so that the estimates do not depend upon the judgment of the examiner alone. A bibliography of these studies is given at the close of the book. How much more has been accomplished in this field in the United States than abroad is illustrated by the fact that repeated search has failed to discover any reports of Binet examinations on representative, randomly selected groups of delinquents in any foreign country. Binet examinations have been made of juvenile delinquents in Breslau (34) and in Frankfurt a. M., and in London (56); but only upon selected cases.
Those who wish to compare the results as to tested deficiency with the subjective opinions of various estimators should consult the reviews of this literature by Bronner (6) and by Gruhle (121). The effect of such a comparison is an increasing conviction that it affords dubious evidence 128of the relative amount of deficiency in different groups of delinquents. Without objective tests, there is no means of telling what amount of mental retardation the different experts would class as feeble-mindedness.
Women in state penitentiaries are a small group among delinquents in institutions. According to one study by Louise E. Ordahl and George Ordahl[15] the frequency of tested deficiency is smaller among them than among women committed to reformatories, who in general commit less serious crimes. All except one of the 50 women prisoners enrolled were tested with the Kuhlmann 1911 revision of the Binet scale. About half were negro women. Only 6 (4 negroes) tested IX or below and were in our group of presumably deficient by the tests. Twenty others (13 negroes) tested one Binet age higher and were in the doubtful group.
If we consider the worst condition so far as intellectual deficiency is concerned, we find it in the reformatories and training schools for women. Dr. Weidensall applied the 1908 Binet scale to 200 consecutive women, 16 years to 30 years of age, as they were admitted to the New York Reformatory for Women at Bedford. Seventy-seven tested IX or under and were within our presumably deficient group. An additional 74 tested X and were in the uncertain group, although if we regard them all as deficient because of their persistent delinquency, we have a total of 75% (59). These results were duplicated by Dr. Fernald (16). She tested 100 other consecutive cases with the 1911 scale and found 41% tested below X, our presumably deficient group. She regards these as “feeble-minded with certainty.”
129Dr. Katherine Bement Davis, the former superintendent at Bedford, estimated herself that among 647 prostitutes who were inmates there, 107 were “feeble-minded (distinctly so);” 26 “border-line neurotic;” 26 “weak-willed, no moral sense;” 11 “wild, truant, run-a-ways.” This makes a total of 26% of this group whom she apparently thought might possibly be classed feeble-minded or of questionable mentality because of deficient intellect or will (11). It is quite clear that the objective tests give a much better basis for comparison of the Bedford group with those which are to follow.
The professional prostitute confined in institutions for delinquents has been carefully studied and tested by the Massachusetts Commission for the Investigation of the White Slave Traffic, So Called (36). Three groups of 100 each were examined “without selection, except that all had a history of promiscuous sex intercourse for pecuniary gain.” One of the groups consisted of young girls under sentence in the State Industrial School for Girls, the House of Refuge and the Welcome House. A second group consisted of those just arrested and awaiting trial in the Suffolk House of Detention in Boston. The third was made up of women serving sentence in the State Reformatory for Women, the Suffolk County Jail and the Suffolk House of Correction. “These three groups represent the young girls who have just begun prostitution, the women plying their trade on the streets at the present time, and the women who are old offenders.”
The Binet tests were applied to 289 of the 300 women examined, and other psychological tests were applied in doubtful cases. The ages ranged from 12 up. Only 10 were under 15 and 32 were 36 years of age or over. The investigators classed no case as feeble-minded which did not test XI or under, but they did not class as feeble-minded 130107 other cases which tested XI and under. The Commission's diagnosis is therefore conservative. It regarded 154 cases (51%) as feeble-minded, 46 in the detention house group and 54 in each of the others. If we ask how many tested below our standard we can not tell exactly, since the report does not state whether X.8 was classed as X or XI. It shows 81 tested IX or under (27%) and these were nearly all, therefore, within the limits of our group presumably deficient. Ninety-nine others tested X, a total of 60% testing below our borderline for presumable and doubtful deficients. Since only 2 cases were under 14 years of age, these figures could not be much disturbed by the younger girls. We can be reasonably sure, then, that at least 27% of these prostitutes should be placed under permanent custodial care, and probably 50% would be more nearly correct.
In a recent report of the Bureau of Analysis and Investigation of the New York State Board of Charities[16] Dr. Jesse L. Herrick reports testing 194 inmates of the state reformatory for women known as the Western House of Refuge. The Stanford Scale was used, 25% tested IX or under with that scale and 14% tested X. In the same bulletin the report is made of Binet ages for 607 inmates of the New York Training School for Girls. Four versions of the scale were used so that the estimates are somewhat affected. Moreover, 97 girls were under 15 years of age. The table of Binet ages indicates 20% testing IX or under and 28% testing X.
Hill and Goddard (30) report examining a group of 56 girls who had been in a reformatory and were under probation with a certain officer. In this entire group they found only four who were not feeble-minded, “as we usually define feeble-mindedness.” Presumably this means 131three or more years retarded, including those who tested XII, so that it cannot be regarded as a conservative estimate. No further data is provided for interpreting the borderline.
Taking up the younger and milder girl delinquents, Dr. Haines reports the examination of an unselected group of 329 at the State Girls Industrial Home near Delaware, Ohio (26). They were all under 21 years of age and represent less hardened delinquents than the older groups at the reformatories for women. The Ohio group was tested with the Binet 1911 scale as well as with the Yerkes-Bridges Point Scale. Counting a result of .8 of a year as placing the case under the next mental age above, as we have in fixing the limits, we find that his results are given with such excellent detail that we may fairly compare the percentages with our standard for the Binet Scale. On this basis 70 of these delinquent girls (21%) are clearly deficient and 55 more are in the uncertain group, a total of 38%.
As a check upon results, we may compare the report of Miss Renz for 100 consecutive admissions to the same institution in 1912, tested with the Binet scale (47). She found 29 tested IX or under, 49 tested X or under, slightly more than was shown by the Haines tests. Miss Renz' report, however, does not show how many of the girls were under 14 years of age and might thus be excluded from the deficient groups.
In the California School for Girls, Grace M. Fernald[17] examined 124 cases as they entered the school. Twenty-four tested under XI with both the Binet 1911 and Stanford revision. This is a further indication of the less frequency of feeble-mindedness in the state schools for girls than in the reformatories for women.
132Dr. H. W. Crane reports the results of the Binet testing at Adrian, the Michigan Industrial School for Girls, which receives only minors and corresponds to the Ohio Industrial Home (37). The Binet 1911 scale was used, but this grouping in mental ages may mean that a few more cases are thus classed deficient than with our standardized borderlines which place the subject in the higher age group when he scores .8. It is to be remembered also that the borderlines for those whose life-ages are under 15 have not been as well standardized with the 1911 scale. The testing was done under the direction of a state commission appointed to investigate the extent of mental defectiveness (37). Dr. Crane was assisted by three other workers. The results at Adrian show, among the 386 inmates, 131 or 34% tested in our groups of presumably or uncertain intellectual deficients. Seventy-seven of these, in our uncertain group, should only class as deficient because also delinquent. The investigators give it as their opinion that 16.7% of the inmates were feeble-minded but not reached by the tests.
The entire population of the Illinois State Training School for Girls at Geneva was tested by Louise E. and George Ordahl.[18] The Kuhlmann revision of the Binet Scale, supplemented by the Stanford Scale, for the older ages, was used. Among the 432 tested 13 per cent. tested below our borderline for the presumably deficient and 22 per cent. more in the doubtful group.
Dr. Otis, resident psychologist at the New Jersey State Home for Girls at Trenton, examined 172 girls between 10 and 20 years of age inclusive (43). Since she said it was “a preliminary testing” and “not many of the smaller girls were included,” we conclude that it was a somewhat 133selected group. She regarded those who stand between eleven and twelve as practically normal and those who stand below ten as without doubt defective. She then publishes three groups: “Defectives,” 45% (77 cases) high grade; “Morons,” 30% (52 cases); and “Presumably Normal,” 25% (43 cases). Since she does not give the distribution of the cases it is not possible to tell how many of her group were less than four years retarded. Her statement of the ages, however, shows that not more than 7 of the defectives could have been less than four years retarded and not more than 12 of the combined group of defectives and morons tested X or over. We may be sure, therefore, that at least 68% of these girls are of questionable intellectual ability according to the conservative standard adopted in this discussion.
Dr. Bridgman has reported the examination of 118 girls, 10 to 21 years of age, successively admitted to the State Training School for Girls at Geneva, Ill. She states that 89% (105 cases) “showed a retardation of three years or more.” The distribution of cases is not given so that it is not possible to tell how many testing X, XI, and XII were classed as feeble-minded or how many tested only three years retarded. The published estimate is undoubtedly extreme, but I have no means of making a more conservative estimate on this group. It is interesting, however, to note that only 14 of the cases were not sexually immoral. These were all cases which were either dependent or sent because uncontrollable at home and all tested as passable intellectually. She states that “according to the Binet tests, 97% of the children (5) sent to this institution because of sexual immorality are feeble-minded as well.” This percentage also would be decidedly discounted on a conservative test standard. In another place Dr. Bridgman makes the 134important statement that of 400 girls admitted to Geneva 60% were suffering from venereal disease (4).
Mr. Bluemel (2) found that 24 out of 50 girls sent from Judge Lindsay's Juvenile Court in Denver to the State Industrial School or the Florence Crittenden Home tested XI or under and four or more years retarded. This is less conservative than our standard, which would exclude those who tested XI as above even the uncertain group in intellect.
Dr. Pyle (46) has tested the 240 girls at the Missouri State Industrial Home for Girls with his standardized group tests. These girls are from 7 to 21 years of age and his table gives the results with each of six tests. The most significant fact for our purpose is that with the different tests from 50 to 88 per cent. fall below the averages of normal individuals who are three years younger. He says, “Our figures would indicate that about one-third of these delinquent girls are normal and about two-thirds subnormal. Most of them are probably high grade morons.” This is based apparently on 69% being the average of the results of six different tests as to the percentages three years or more retarded from their life-ages. He indicates, however, that 38%, similarly calculated, are within the average deviation of the normal groups for their life-ages. This indicates that the lowest 62% test only as low as we should expect to find the lowest 21% of random groups of corresponding ages. They should certainly not be regarded as testing feeble-minded.
When we turn to those who are cared for locally in city or county institutions, we find Sullivan (56) has examined 104 women and girls held temporarily at the Holloway 135jail in London, most of whom were between 16 and 25 years of age. Apparently the cases were especially selected for examination and therefore do not represent the general condition there. He was interested, however, in finding the relative amount of deficiency among different classes of these inmates and he gives the detailed results with the Binet 1908 scale on small groups of these different types which we may classify by our standard as follows:
Twenty non-criminal, either not guilty or guilty of unimportant offenses, who represent, he thinks, the ordinary conditions among the corresponding working class in this community, 3 presumably deficient, 5 uncertain; twenty criminal by reason of the occasion, 1 presumably deficient, 6 uncertain; twelve impulsive criminals, 1 presumably deficient, 2 uncertain; eight moral imbeciles, 2 presumably deficient, 2 uncertain; twenty-four recidivists, 2 presumably deficient, 8 uncertain; twenty prostitutes, 3 presumably deficient, 8 uncertain. Together these different types of women in jail form a motley group of 104 of whom 12 test presumably deficient, 31 uncertain, a total of 41%.
Ordinary prostitutes are about as frequently deficient as are those in reformatory institutions, if we may judge by an important study of women who were sex offenders but not in institutions for delinquents. The report is by Dr. Clinton P. McCord, health director of the Board of Education at Albany (35). One group consisted of fifty cases of sex offenders who were not legally delinquents at the time but were living in houses of ill-fame. Their ages ranged from 22 to 41 with an average age of 27. Nine of these (18%) tested IX or under with the Binet 1911 and 18 tested X, a total of 54% presumably and doubtfully deficient. Another 38 cases were staying at a House of Shelter where most of them had been sent by 136the courts. Nineteen of these tested IX or under (50%), while 13 more tested X, a total of 84%. Since their ages ranged from 12 to 40 years with an average of 18 we cannot tell how many might be above the borderline on account of an age less than 15 years, but probably very few. A third group consisted of 9 street walkers and 3 wayward girls. Among these 7 tested presumably or doubtfully deficient.
The McCord study of prostitutes not legally delinquent at the time of examination is confirmed by the Virginia State Board of Charities and Corrections in a special report to the General Assembly which gives the results of examining the prostitutes in an entire segregated district in one of the Virginia cities (58). Its table shows that, among 120 of these women, 43, or 36%, tested approximately under our borderline for the presumably deficient, while 67 cases, or 56%, tested below approximately our borderline for the presumably passable intellects.
These results are similar to Weidensall's[19] findings among the unselected group of unmarried mothers in the Cincinnati General Hospital. While she does not give the number tested with the Yerkes-Bridges scale, she indicates that 48% tested as low-grade morons or worse, which should correspond to a test age of IX or lower. Twenty-two per cent. had intelligence coefficients of .50 or less and 32%, from .51 to .70. A Study of Fifty Feeble-Minded Prostitutes[20] by Mary E. Paddon gives an admirable summary of the social history of prostitutes who tested deficient.
137Dr. Bronner has made a careful study with Binet tests of a younger group of randomly selected girls at the Cook County Detention Home which is connected with the juvenile court at Chicago. The group included 133 girls 10-17 years of age inclusive, who were held awaiting a hearing or were temporarily cared for in the detention home. The Binet tests were given to all who did not show clearly that they were of passable mentality by completing the sixth grade or above without retardation, and passing school tests in long division and writing from dictation. A 14-year-old child “passing all the 10-year-old tests and some, but not all, of the 12-year-old tests,” was regarded as doubtful. She was not classed as feeble-minded without further testing and study. Dr. Bronner does not state her criterion for the borderline with the younger children, but we may judge that her borderline was more likely than ours to have classed a child in the presumably deficient group. Her summary shows only 15 girls “probably feeble-minded” (11.2%), and 2 others “possibly” so. From her description we may suppose that the “probable” group were comparable with our test standard of presumably deficient, plus perhaps a few conative cases.
Mention should also be made of the work of Dr. Bronner to which we referred under the earnings of the mentally retarded (6). This group of 30 randomly selected delinquent women at a local detention home in New York tested, with two or three possible exceptions, no lower than a similar group of women servants who had never been offenders. Her data do not enable us to determine how many would fall below our borderlines.
Stenquist, Thorndike, and Trabue (54) report the results with the Binet 1911 tests, under a slightly modified procedure, for 75 randomly selected dependent and 4 138delinquent girls cared for by a certain county, excluding those children within the county sent to an institution for the feeble-minded. The children were from 9 to 16 years of age, with a medium age of 11 years. The line between the delinquent and dependent groups with these younger children becomes rather obscure. They state: “A child may, in the county in question, become a public charge by commitment by an officer of the poor-law on grounds of destitution, or by an officer of the courts on grounds of delinquency.... The decisive factor is often simply whether the parents are more successful in getting justices to commit their children than in getting poor-law officers to do so.” With the detailed records which they give it is possible to apply our standard even for the immature, although it is certainly less adequate for those under 15 years of age tested by the 1911 scale. I have translated their corrected Binet ages back to the original test ages, since their summary of retardation in terms of years below average ability at each age is not comparable with our borderline. Among the 79 girls who are mostly dependent, there are 5 girls, or, 6%, who fall within our presumably deficient group and 8 in the doubtful group, a total of 16%. So far as serious deficiency is concerned the situation is undoubtedly worse among delinquents than among corresponding groups of dependents. The figures of these investigators show this for their group of boys, to which we shall refer later.
Certain other groups of women and girls have been examined with the Binet or other tests, but the results are of little significance for judging the problem of deficiency objectively, since the individuals were either selected for examination because they were thought to be abnormal mentally or because there are not adequate norms for determining the borderlines with the particular tests used. 139At the New York State Training School for Girls in Hudson, we find that 208 selected cases who were not profiting by their training were examined with the 1911 scale. They ranged in life-age from 12 to 20. We cannot determine how many were under 14 years of age, or how much effect might have been produced by selecting dull cases; but 44 tested IX or under and 52 tested X (158). Dr. Spaulding (183) used Binet and other psychological tests on a group of 400 inmates of the Massachusetts Reformatory for Women at South Framingham; but she gives only her judgment based on the examination and history of the cases so that we have no data on this group for comparison. Her statement that 16.8% showed “marked mental defect, i. e., the moron group” and 26.8% showed “mental subnormality (slight mental defect)” is an excellent illustration of the best type of subjective judgment on consecutive cases, since she is familiar with test results. For her purpose of deciding how to care for the women it is of undoubted value, but for comparative purposes it is clear that it is impossible to tell how her subjective opinion would agree with that of an equally competent diagnostician, or what is meant by her terms “feeble-minded” or “subnormal.” For scientific purposes the Binet results for her group would be of much value, for we should like to know whether the conditions at Bedford are typical among the women's reformatories for the older offenders.
Dr. Rowland used psychological tests other than the Binet scale with a group of 35 at the Bedford Reformatory for Women, but there are no adequate norms for the comparison of her results with the general conditions (49). Baldwin (1) has shown that delinquent colored girls, 13 to 21 years of age, in the girls' division of the Pennsylvania Reformatory school at Sleighton Farm are inferior to white 140girls in the same institution in a learning test. As cited by Gruhle (121), Cramer (10) used an Ebbinghaus completion test, definition tests, etc. with 376 delinquent girls in Hanover, but there are no borderlines for comparison. As cited by Bronner, von Grabe gave several psychological tests to 62 prostitutes treated in the city hospital in Hamburg and compared them with a control group of 30 (6).
The most striking conclusion that comes out of the study of this evidence of frequent deficiency among delinquent girls and women is the close association between sex offenses and deficiency. One hundred and four out of 118 consecutive admissions at the Illinois training school were known to be sexually immoral. At Bedford 94 out of 100 consecutive cases had records of immorality, while three-fourths of the same group tested questionable in intellect by our standards (11). This evidence, taken with the report of the Massachusetts' Commission and the tests of sex offenders who were not at the time legally delinquents, reported by McCord, and the Virginia Commission, leaves little doubt that there is an excess of deficiency among this type of offender. Many of these deficient girls probably at first drift into the life of prostitution. They are passive rather than active agents. This distinction in the nature of the offense accounts for some of the difference between the sexes in this form of delinquency. Furthermore our public attitude in matters of social hygiene has made the isolation of the female sex more common. Part of this may be due to the greater difficulty of proof in the case of men and boys, but in part it undoubtedly means that men have not been held to as high a moral standard as women in this regard. The greater frequency of deficient sex offenders among girls, does not mean that girls are more likely than boys to be active sex offenders. They are, however, more likely to 141be isolated for such offenses, and also more likely to be passive offenders.
The greater amount of deficiency found among female delinquents than among corresponding groups of males is thus easily accounted for by frequent association between deficiency and sex delinquency on the part of girls and women. The combination of legal sex delinquency and deficiency is due both to a native sex difference and a difference in social attitude toward the two sexes as to this form of offense. Whichever may be the main cause of the facts found, it is clear that deficiency is, today, most serious among female offenders. It is so serious that some of our reformatories for women might even prove to be practically institutions for deficient delinquents. It is in this type of institution without doubt, that the immediate problem of the deficient delinquent is most pressing. Permanent guardianship, if not isolation, for at least a third of the inmates of an institution like Bedford which shows this amount of clear tested deficiency, under our very conservative standard, would seem to be a wise move in social hygiene. It should be undertaken at once with vigor. A more fundamental change in our social attack of this problem means state guardianship before adolescence for all girls testing presumably deficient under our standard, when their deficiency is not due to removable handicaps.
For the purpose of judging the importance of the question of feeble-mindedness among the most serious criminals, those committed to the state prison, we have a very important study by Rossy (48). Three hundred cases were taken at random with the exception of a few selected cases on which a report was requested. In this group, 142thirty prisoners could not be examined either because of language difficulties or because of their refusal to be tested. The Point Scale of Yerkes and Bridges was used and the results are presented in terms of mental ages on that scale. The examiner considered all those testing XI or under as feeble-minded and found 22% of the 300 in this class. This is less conservative than even our doubtful standard, but I estimate that 16% would fall within our doubtful and presumably deficient groups. This includes 11% who test X or under with the Point Scale plus 54% of those who tested XI. This estimate is made on the basis of the tables given by Haines (26), comparing Binet 1911 results with those of the Point Scale on the same individuals. It adds the proportion of those testing XI with Point Scale, who would test nearer X with the Binet 1911 scale.
Ordahl[21] examined 51 convicts in the penitentiary at Joliet, Ill. They “were selected in a manner thought to secure fair representation of the prison population as a whole.” The Kuhlmann 1911 Binet scale was used and supplemented by tests for 13 to 18 years taken from the Stanford scale. It is possible that selection affected the results with this small group, since 25% showed test ages of IX or under and 36% tested X or under.
Haines tested with the Point Scale 87 consecutive admissions to the Ohio penitentiary (24). He found 18% tested below a record corresponding to X.6 on the Goddard 1911 scale, which is about the upper limit of our doubtful group.
That a smaller proportion of the state prison inmates is found intellectually deficient than is found among the inmates of the industrial schools is not surprising. 143This may be due to various causes. Among these may be mentioned the failure to recognize feeble-mindedness, heretofore, among the younger delinquents while the adult feeble-minded were more carefully isolated in their proper institutions. The deficient adults have also been reduced in frequency by the excessive mortality. Probably the feeble-minded are not so likely to plan or commit felony as lesser crimes and misdemeanors. Moreover the adult feeble-minded may be more stable and less inclined to delinquency than adolescents. Whatever may be the explanation, deficiency generally does not seem to be as common among the inmates of a state prison as among minor delinquents in states which are in the forefront in the care of their feeble-minded.
The state reformatories reach a class of delinquents between those of the state prisons and the state industrial schools. In Minnesota all the inmates of the reformatory except 80, who were disqualified by inability to speak English or otherwise, were tested by Dr. E. F. Green. Men are sent there only between the ages of 16 and 30, so that his table of mental and life-ages gives us the opportunity to apply our criteria accurately. Thirteen per cent. of the 370 examined tested IX or under and were presumably deficient, while 22% more were in the uncertain group testing X (22).
In a report of the Binet results with 996 inmates of the Iowa Reformatory, which Warden C. C. McClaughry kindly sent me, 200 tested IX or under and 146 tested X, a total of 35% including the doubtful group. The range of ages was from 16 to 49. The Warden notes that the tests were not made by an experienced psychologist. “In many cases it is suspected that the crafty criminal was endeavoring to lower his standing as to mentality in the hope of excusing or mitigating his crime in the eyes 144of the Board of Parole.” The results, however, agree well with what has been found in similar institutions.
Supt. Frank Moore of the New Jersey Reformatory at Rahway says, “Nearly every young man who has entered our institution in the last eighteen months has been tested by this system (Binet), and the results have shown that at least 46 per cent. were mentally subnormal” (38). By his discussion this seems to mean that they tested below XII which would mean that all those testing XI were less deficient than our standard for doubtful cases. These young men were from 16-25 years of age and 17.5% of them had had one year or less in school. Ten per cent. could not be examined because of unfamiliarity with English. A later report in 1912 regarding the same institution (42) says that 600 of the inmates have been examined with the Binet tests in two years, but does not state how these were selected. Of those examined we are told “48% are of the moron type of mental defectives, ranging in mentality from three to eight years, below the average normal adult.” Again, no further information is given so that it is impossible to allow for those testing X or XI or for the cases only three years retarded. Both of these estimates at the New Jersey Reformatory are excessive when judged by conservative borderlines.
Dr. Fernald has applied 11 objective tests to a representative group of 100 inmates at the Massachusetts Reformatory (15) but the norms for the tests which he used were obtained, for the most part, by testing a dozen boys so that the line which he draws for the limit of the defectives is largely a matter of his expert opinion and the estimation loses objective character. He estimates that 26% of his group whose ages run from 15 to 35 inclusive were defective. Beanblossom[22] has published an account of 145tests on 2000 inmates of the Indiana Reformatory. Some of the Binet tests as well as other tests were used but the published results do not admit of reinterpretation.
Comparing the reports from the Minnesota, Iowa, and New Jersey reformatories with the tested deficiency found in institutions for women delinquents on the basis of the same borderline with the scale, the records indicate clearly that the percentage of feeble-mindedness is greater in the reformatories for women. At the Bedford Reformatory for women, for example, Dr. Weidensall's results show that the corresponding borderline to that used in the New Jersey men's reformatory which reported 46% deficient, would class 100% at Bedford as feeble-minded, where only one case in 200 tested as high as XII. A conservative estimate of tested deficiency in men's reformatories from the above data would be from 15 to 20%.
In the state institutions for minor delinquents, usually called industrial schools, we have several studies of representative groups with sufficient data to make objective interpretations comparable with our standard. In Ohio, Dr. Haines (26) reports on the examination of 671 delinquent boys 10 to 19 years of age at the Boys' Industrial School near Lancaster. Interpreted as we have indicated for the Ohio Institution for girls, we find 100, or 15%, in the group testing presumably deficient and 179 in the doubtful group, a total of 42% clear and questionable.
In the corresponding Michigan Industrial School at Lansing, Dr. Crane (37) shows by his table of mental and life-ages that 52 out of the 801 unselected inmates, or 6% are presumably deficient and 171 below the presumably passable, or 21%. This is only a slightly greater number than our criterion would provide, if .8 of a year were not classed in the next higher mental age by these examiners. The age of those examined ran from 10 to 17.
146T. L. Kelley in his “Mental Aspects of Delinquency”[23] gives the results for an extensive series of measurements and tests on about three hundred boys in the Texas State Juvenile Training School. On the basis of an analysis of his tests he estimates that 20% of the boys there should be in a school for the feeble-minded. Interpreting his original data for the 1911 Binet tests on the same basis as our own, 8% fall within the clearly deficient group and 9% in the doubtful. The latter on account of their delinquencies might also be included as feeble-minded.
The 215 inmates of the Whittier State School in California were examined by J. Harold Williams with the Stanford revision of the Binet scale (61). The boys were 10 to 22 years of age, median 16 years. He states that 32% were feeble-minded in the sense of having Intelligence Quotients less than .75. This is a standard which would include about 2% of those tested with the scale, so that we may consider the bulk of them as within our presumably deficient and uncertain groups combined. He also states that approximately 14% tested below X with the Stanford Revised Scale. In another paper he shows that the amount of feeble-mindedness was much different among the different races represented in the institution. With 150 cases according to his standard there were 6% feeble-minded among the whites, 48% among the colored, and 60% among the Mexican and Indian races. In this group 64% were native whites, 21% of Indian or Mexican descent and 15% colored. “While the negro population of California constitute but 0.9% of the total, yet the results of this study indicate that more than 15% of the juvenile delinquents committed to the state institution are of that race.” It is, of course, of fundamental importance in regard to all estimates 147of feeble-mindedness among delinquents to consider the racial conditions at the particular institution.
A New Hampshire Commission tested the children in its State Industrial School. Its table shows that among the 113 boys tested at least 37% were presumably or doubtfully deficient. To these should be added some 14 years of age and over who tested X, in order to have the total number below our borderline for the presumably passable cases. The published table does not separate these from the 13-year-olds (40). Hauck and Sisson report in School and Society for September, 1911, tests made at the Idaho Industrial School, which receives both boys and girls from 9 to 21 years of age, including some children who would be classed as dependents but can not be cared for elsewhere in the state. Supposing that our standard applied to the 1911 scale which was used, among 201 tested there were 5 presumably deficient and 13 doubtful.
A partially selected group of 341 inmates at the St. Charles, Ill., State School for Boys chosen in such a way that it naturally would somewhat increase the frequency of deficiency, was tested by Dr. Ordahl with Kuhlman's form of the 1911 scale supplemented by the Stanford Scale above XII. The results showed 11% in the presumably deficient group and 20% in the doubtful group (41).
One of the main uses of the objective scale is to demonstrate that the same conditions do not prevail in various institutions which, except for this objective evidence, might be expected to care for the same type of inmates. This is illustrated by the comparison of the above studies in Ohio and Michigan with that made at a similar state school for delinquent boys in Indiana reported by Hickman (12, 28). The Binet 1911 tests, Goddard's adaptation, 148were applied to 229 new boys 8 to 17 years of age inclusive, admitted to the Indiana Boys School at Plainfield. Among these, 68 boys (30%) tested below our borderline for the clearly deficient and 53 more within the doubtful region, a total of 48%. There seems little doubt that this represents a significant difference from the condition at the corresponding Ohio and Michigan schools where only 15% and 6% respectively tested clearly deficient on a corresponding standard. An interesting commentary on the necessity of reinterpreting the borderline for feeble-mindedness on the scale arises when we note that Hickman says: “One hundred and sixty-six, or about 75% of the whole number tested, tested as much as three years or more below normal, and therefore would be classed as feeble-minded to a greater or less degree.”
It seems likely that in city and county institutions deficiency is most common among repeaters in the jails or workhouses. One study has been made of a randomly selected group of repeaters who were in the jail of a Virginia city for fixed sentences of not more than a year. The examinations are summarized in the Special Report of the Virginia State Board of Charities and Corrections (58). In this Virginia city 50 whites of both sexes and 50 negroes of both sexes were examined. Among the whites, 18 tested IX or under and 5 more tested X. Among the negroes, 24 tested IX or under and 10 tested X. The percentages would be just twice these numbers, a total of 61% below passable capacity in this group of 100. If such is the condition in other jails in other parts of the country, it indicates one of the most serious hot beds of deficiency among delinquents. The repeaters in this 149city jail during three years were responsible for 60% of the commitments to jail, although only about one-fourth of the 33,306 arrests in this city during the three years resulted in commitment to jail. The feeble-mindedness among the repeaters, therefore, may be little indication of the frequency of deficiency among those arrested in the city. The repeaters represented only a third of those committed to jail during this period and this third was probably the most deficient among those committed, since recidivism goes with deficiency. Moreover, those committed to jail are probably more likely to be deficient than those who escape jail sentences. To assume, therefore, that 61% of this city's delinquents were of doubtful ability would be clearly unjustified, and yet this sort of reasoning about the frequency of deficient delinquents has been all too common.
Gilliland[24] tested one hundred male inmates of the Columbus, Ohio, Workhouse (28 negroes) selected so as to attempt to represent the different offenses about in their proportions. He gives the results in point scores with the Yerkes-Bridges scale, which may be translated only roughly into Binet 1911 ages by Haines' data, as I have indicated for the study by Rossy. All were 18 years of age or over, so that I estimate 14% would fall into our presumably deficient group including only the proportion of those under 64 points who would test as Binet IX or less. The doubtful group would include 17% more, including the proportion under 66 points who would test X or under.
Among the local institutions supported by the county or city, the most serious delinquency is probably found in the 150group reported by Kohs at the Chicago House of Correction (33). He tested with the 1911 Binet scale 335 consecutive cases between 17 and 21 years of age. Among these were 72 cases (21%) who tested clearly deficient according to our standard, and 95 cases doubtful, a total of 50% at least uncertain in intellectual ability.
Through the courtesy of Catherine Mathews, who made the examinations for the psychological clinic of the University of Pittsburgh, which is under the direction of Dr. G. C. Bassett, I am able to give the records of 125 consecutive admissions to the Allegheny County Detention Home. The institution is known as the Thorn Hill School. It is situated some miles outside of Pittsburgh and provides on the cottage plan for about 300 boys. The boys are sent from the Juvenile Court for milder training than that at the state school. The school has also been found to furnish a necessary place to care for cases of feeble-minded delinquent boys who cannot be immediately admitted to the state institution on account of its crowded condition. A detention home is also provided in the city for juvenile court children awaiting trial or the disposition of their cases. These are not included in the Thorn Hill group.
Among the 125 consecutive cases at Thorn Hill, omitting two cases which are probably dementia praecox, there were 37, or 29%, who tested presumably deficient according to our standard, and a total of 68 cases, or 55%, presumably and doubtfully deficient. It is to be remembered that our standard for the immature was arranged for the 1908 scale and not the 1911 scale which was used here, although the difference would be slight.
The accompanying Table X shows the distribution, omitting the dementia praecox cases. It classes .8 as in the next higher test age and shows the last birthday for life-age. In interpreting these figures it is highly important to remember that Thorn Hill is necessarily used at present to shelter deficient boys who are dependent or delinquent and cannot be otherwise provided for. This is undoubtedly a wise temporary relief until the state takes proper care of these unfortunates. Under the cottage system which prevails at Thorn Hill the segregation can be made with little interference with the main purpose of an institution for delinquents. It is apparent that any deductions made from the large frequency of feeble-mindedness among these delinquents without considering the particular local conditions under which they are found, would be wholly unjustified. A similar local condition probably explains the high percentage of tested deficiency among the following group of boys in the Newark, N. J., detention home.
152A representative group of 100 in the detention home at Newark, “chosen entirely at random,” was examined by Mrs. Gifford, and reported by herself and Dr. Goddard (17). In this group of 100 there were 66 between the ages of 14 and 17 who were at least four years retarded mentally. Moreover, among these 66 “none tested over eleven and only a few at that age.” Only average mental ages are published, so that we cannot tell how many tested XI or X, but the statement quoted shows that few of these 66 would test XI, and would thus be above our doubtful class. We may, perhaps, suppose that about 66% of this group in the Newark detention home tested as low as the randomly selected group at Thorn Hill, Pittsburgh.
That the explanation of the excessive amount of deficiency found at Newark lies in the inadequate provision for recognized feeble-mindedness in that community is indicated by the Fourteenth Annual Report of the Newark City Home. It states that “the lack of a state institution for defective children made it necessary to commit to the City Home many children, who, on account of physical defects and psychic disturbances, have become juvenile delinquents.” A statistical table shows that of 181 boys, 151 were either illiterate or below the fifth grade in school in spite of the fact that the average age of the boys at the school is 13 years. This shows clearly that the differences between the test results at this institution and those in Minneapolis, Chicago, and elsewhere, is not the result of different methods of giving the tests. It seems to be mainly due to inadequate state provision for recognized feeble-minded children.
Among the more serious juvenile court offenders we have a group of 1000 recidivists referred to Dr. William Healy at the Psychopathic Institute connected with the 153Chicago Juvenile Court. The cases are not tabulated separately for the sexes as to mentality. They were all under 21 and averaged between 15 and 16 years of age. While he used the Binet tests quite generally, as well as his own and Miss Fernald's series (125), Dr. Healy has not summarized his data in reference to the test standards. Nevertheless, according to his experience after the results of the test examinations were known, he classified only 89 of these cases as moron and 8 imbecile, a total of only 9.7% feeble-minded. Another group above these amounting to 7.9% was classed as of “subnormal mentality—considerable more educability than the feeble-minded” (27, p. 139).
From the same psychopathic laboratory comes the estimates of Dr. Bronner (7) of a group of less serious offenders, some of whom were in court for the first time, a group at the Cook County Detention Home connected with the Juvenile Court in Chicago, where cases are held for trial or until other disposition can be made of them. I have already reported her results with the Binet tests for the girls in this group. Using the same standard which was there described, she found among 337 boys 7 to 16 years of age 7% “probably feeble-minded,” and 2.4% doubtful, a total of 9.4% “possibly feeble-minded.” As nearly as I can tell from the description of the borderline which she used with the tests, a boy was perhaps slightly more likely to be regarded as testing probably deficient than by our standard for the presumably deficient. Inasmuch as Miss Bronner worked with Dr. Healy, this may throw some light on the test standard which he had in mind in connection with his more serious offenders.
By means of Bluemel's study of different classes of juvenile delinquents who passed through Judge Lindsay's 154Juvenile Court in Denver, we are able to compare the intellectual ability of a group which was on probation, about half of whom were first offenders, with groups sent to the Boys' and Girls' State Industrial Schools (2). Although the report does not so state, I should judge that the cases were objectively selected. The published data is not adequate to state the results on the basis of our conservative borderlines; but we can note the cases which tested XI or below and were four or more years retarded with the 1911 Binet Scale (Goddard's modification). This only differs from my broadest interpretation by also including those that test XI. On this basis 6 of the 100 probationers were possibly deficient; 9 of the 50 boys sent to the State Industrial School, and 24 of the 50 girls sent to the State Industrial School or Florence Crittenden Home. These are all somewhat excessive estimates of the amounts of deficiency in this group as judged by the interpretation we have been using. A more telling comparison of the mentality of these groups may be made by weighting each retarded case by the tests according to the number of years he is retarded. The amount of retardation alone averages 1.3 years for the group of probationers, 1.8 for the boys at the state school, and 3.8 years of the institutional group of girl delinquents. Fifty first offenders among the probation group average 1.1 years retarded. The girls and the more serious juvenile delinquents in these younger groups show more retardation.
The Stenquist, Thorndike, and Trabue study of children 9 to 16 years of age, who were county charges as delinquents or dependents in a single county, provides results for a group of 104 delinquent boys. Translating their records as I have explained for the girls in the group, we find 11 of these presumably deficient and 18 doubtful, 155a total of 28%. So far as their delinquency is concerned these probably correspond to the local institution groups. While there is little difference in the average mentality of the groups of delinquent and dependent children in this county shown by tests there is apparently some difference in the frequency of serious deficiency. In their corresponding group of 63 dependent boys who were county charges, 2 are in the presumably deficient group and 10 in the doubtful, a total of 19%. Miss Merrill found only 0.8% in our presumably deficient group and 1.6% uncertain in a group of 250 dependent children at the Minnesota State home (149).
Dr. Pintner reports the examination of 100 cases in the Columbus, Ohio, Juvenile Court who were in the detention home waiting to be disposed of or held for trial.[25] He does not say whether they were selected cases among those in the home, but we may presume that they were more serious offenders than the usual juvenile court cases not in the home. Their ages ranged from 7 to 20 years. He used the Binet 1911 series and allowed double credit for any test passed in the XV or adult series. By placing his borderline so that a person testing 3.1 years retarded if he scored under XII would be regarded as feeble-minded, Dr. Pintner found 46% feeble-minded in this group. Under the same standard about 20% of the Minneapolis group would be classed as feeble-minded, instead of 2 to 7% under our more conservative borderlines.
In a preliminary report of the doctorate examination of Dr. Olga L. Bridgman (132) I find that she reports testing 205 delinquents and 133 dependent children sent to the psychological clinic of the University of California. She found 36% of the delinquent and 26% of the dependent 156cases thus especially selected for clinical examination to be “definitely feeble-minded,” but the preliminary report does not enable one to judge the standard used for her borderline (3).
Ordahl's study[26] of 61 cases who were wards of the San Jose Juvenile Court is not comparable with other groups since both sexes, both dependents and delinquents and ages from 3 to 44 were included.
Dr. Hickson (8) reports concerning some 2700 cases selected especially for examination from those passing through the municipal court in Chicago, in the divisions of the Boys Court, the Morals Court and the Domestic Relations Court. His tables state only average mental ages, and he classes 728 boys who average XI.11 as morons, so that I am unable to make any comparisons with his data.
Dr. Walter S. Cornell (92) published in 1912 the results of Binet tests on 100 cases at the Philadelphia House of Detention among whom 64% tested three or more years below normal and 41% four years or more below normal. We are unable to tell how many of these tested X or above and were thus of questionable deficiency. He also gives the results merely with the years of retardation for a group of 73 “mildly delinquent boys of Miss Wood's special school and the Children's Bureau (mostly truants).” Of this group 46% were three years or more and 25% four or more years retarded according to the tests. Again we are unable to judge how the cases were selected or what was the mental age distribution so as to discover those that fall under our borderlines, especially under the borderline of XI for the mature.
Psychological examinations have been employed in connection 157with the children at the Seattle Juvenile Court. Although the results are not presented in a form which can be compared with other localities, Dr. Merrill, the physician who directs the general clinic, is of the opinion that feeble-mindedness was the cause of the delinquency of only 6% of 421 consecutive cases (148). Previously in the same court, Dr. Smith, the psychologist, on the basis of tests, reported among 200 consecutive cases only 11 cases as feeble-minded, 5 as mentally defective, and 8 as “moral imbeciles,” a total of 13.5% (53).
Frau Dosai-Révész (13) gave a number of tests to 40 boys, 9 to 16 years of age, selected from the boys training school of the Children's Protective League in Hungary. The cases which she classified as morally feeble-minded were found to test between the normal and the feeble-minded groups.
As yet only the preliminary announcement has appeared of a study of a thousand delinquent boys and girls with the Point Scale which has been made by Bird T. Baldwin. It is to be published as a Swarthmore College Monograph (Psychol. Bull., 1917, 14, p. 78).
The reader should also consult the series of articles by L. W. Crafts and E. A. Doll appearing in the Journal of Delinquency beginning with May, 1917, on “The Proportion of Mental Defectives among Juvenile Delinquents.” It is especially valuable as a critique of the conditions desirable for exact comparison of the results of different investigations.
A Bibliography of Feeble-Mindedness in Relation to Juvenile Delinquency, compiled by L. W. Crafts, may be found in the Journal of Delinquency, Vol. I, No. 4. In Chap. II of his Problems of Subnormality, Dr. Wallin gives an admirable review of numerous studies of tested groups.
In bringing together these studies in which we can make somewhat comparable estimates of tested deficiency covering over 9000 delinquents, it seems possible to analyze further the question of the deficient delinquent. Comparison of the amounts of deficiency on an objective basis is scientifically a big step in advance from a reliance upon the subjective opinion of experts who cannot possibly have the same standard of deficiency in their minds. The results of the comparable investigations, on the basis of the above reinterpretation of the borderlines, are brought together in Table XI. The frequency of tested deficiency which is found among about the lowest 0.5 and 1.5% respectively of the population generally is there shown for these different groups of delinquents. This review of the studies thus assembled enables us to correct a number of impressions that have become prevalent by the early studies, as well as to formulate the general data in regard to the deficient delinquent in a manner that places the practical control of this problem on a safer foundation. We shall summarize the data under four heads.
| Percentages | ||||
|---|---|---|---|---|
| Group and Investigator | No. of Cases | Presumably deficient | Doubtful | Both |
| Women and Girls | ||||
| State Institutions | ||||
| Penitentiaries | ||||
| Illinois Penitentiary (L. E. and G. Ordahl) Negro | 26 | 15 | 27 | 42 |
| Illinois Penitentiary (L. E. and G. Ordahl) White | 23 | 9 | 30 | 39 |
| Reformatories | ||||
| Bedford Reformatory, N. Y. (Weidensall) | 200 | 38 | 37 | 75 |
| Bedford Reformatory, N. Y. (M. R. Fernald) | 100 | 41 | 24 | 65 |
| Western House of Refuge, N. Y. (Herrick) | 194 | (25) | (14) | (39) |
| Training Schools | ||||
| State Home for Girls, N. J. (Otis) Partially selected | 172 | (68) | ||
| Girls Industrial Home, Ohio (Renz) | 100 | (29) | (20) | (49) |
| State Industrial School and Florence Crittenden Home, Colo. (Bluemel) | 50 | (48) | ||
| N. Y. Training School for Girls (Hall) | 607 | (20) | (28) | (48) |
| Girls Industrial Home, Ohio (Haines) | 329 | 21 | 17 | 38 |
| Illinois State Training School for girls (L. E. and G. Ordahl) | 432 | 13 | 22 | 35 |
| Industrial School for Girls, Mich. (Crane) | 386 | 14 | 20 | 34 |
| California School for Girls (G. M. Fernald) | 124 | 19 | ||
| County and City | ||||
| Sex Offenders | ||||
| Sex Offenders not under arrest, Albany, N. Y. (McCord) | 88 | 32 | 35 | 67 |
| Unmarried mothers, Cincinnati General Hospital (Weidensall) | (48) | |||
| Professional prostitutes, Mass. (State Commission) | 300 | 27 | 33 | 60 |
| Prostitutes in a segregated district in a Virginia City (State Commission) | 120 | 36 | 20 | 56 |
| Juveniles | ||||
| Cook County Juvenile Detention Home, Chicago (Bronner) | 133 | 11 | ||
| 160 | ||||
| Men and Boys | ||||
| State Institutions | ||||
| Penitentiaries | ||||
| Illinois Penitentiary (Ordahl) | 51 | (25) | (11) | (36) |
| Ohio Penitentiary (Haines) | 87 | 18 | ||
| State Prison, Mass. (Rossy) | 300 | 16 | ||
| Reformatories | ||||
| State Reformatory, Minnesota (Green) | 370 | 13 | 22 | 35 |
| State Reformatory, Iowa (Report) | 996 | 20 | 15 | 35 |
| Training Schools | ||||
| Indiana Boys School (Hickman) | 229 | 30 | 18 | 48 |
| Boys Industrial School, Ohio (Haines) | 671 | 15 | 27 | 42 |
| State Industrial School, Colo. (Bluemel) | 50 | (18) | ||
| Whittier State School, Calif. (Williams) | 215 | (14) | (18) | (32) |
| State School for Boys, Ill. (Ordahl) | 341 | (11) | (20) | (31) |
| Industrial School, Mich. (Crane) | 801 | 6 | 15 | 21 |
| State Industrial School, N. H. (Streeter) | 147 | (37+) | ||
| Texas State Juvenile Training School (Kelley) | 296 | 8 | 9 | 17 |
| County and City | ||||
| Jails and Workhouses | ||||
| Repeaters in jail in a Virginia city (State Commission) Negro | 50[27] | 48 | 20 | 68 |
| Repeaters in jail in a Virginia city (State Commission) White | 50[27] | 36 | 10 | 46 |
| Chicago House of Correction (Kohs) | 335 | 21 | 29 | 50 |
| Columbus, O., Workhouse, 28 Negroes (Gilliland) | 100 | (14) | (17) | (31) |
| Juveniles | ||||
| Newark Detention Home, N. J. (Gifford and Goddard) | 100 | 66[28] | ||
| Allegheny County Juveniles Detention Home, Pa. (Mathews) | 125 | 29[28] | 26[28] | 55[28] |
| Boys cared for by the county (Stenquist, Thorndike and Trabue) Delinquents | 104 | 11 | 17 | 28 |
| Cook County Detention Home, Chicago (Bronner) | 337 | 7 | ||
| Glen Lake Farm School for Boys, Hennepin County, Minn. (Miner) | 123 | 2 | 5 | 7 |
| Probationers, Juvenile Court (Bluemel) | 100 | (6) | ||
Parentheses indicate percentages or selection on a somewhat different basis.
1611. Intellectual deficiency as a social problem is undoubtedly at present most serious among women and girls who are sex offenders. It is this fact which accounts for the excessive amount of deficiency found in the industrial schools for girls, and the reformatories for women. It is not necessary to repeat the discussion of the reasons for this which were considered at the close of the studies of women delinquents. The most closely corresponding class of male delinquents is probably the “vags,” as Aschaffenburg suggests (68, p. 162). The vagrants form a much smaller portion of the inmates of the institutions for male delinquents than do the prostitutes in the institutions for women and girls. The little evidence we have indicates, moreover, that as a class the ne'er-do-wells average higher in ability than the prostitutes. They are, probably, a more mixed group. As reported by Terman (57), Mr. Kollin found among 150 “hoboes” at least 20 per cent. belonged to the “moron grade of mental deficiency.” * * * “The above findings have been fully paralleled by Mr. Glen Johnson and Professor Eleanor Rowland, of Reed College, who tested 108 unemployed charity cases in Portland, Oregon” (57, p. 18). Since these investigators used the Stanford Scale, the borderline was probably set at the position where it would exclude about 1% of the ordinary population, a little more conservative than our doubtful group. We should know more about deficiency among the typical “Weary Willies,” since it is likely that courts are accustomed to assume that vagrancy is a habit which can be corrected by a term in the workhouse. There is little doubt that mental deficients fill up the recruiting stations for the prostitutes and “vags.” It is with these classes that the most intensive social work should be done in the campaign for early isolation of the unfit.
2. Institutions which care for the same type of delinquents show pronounced variation in the amount of tested deficiency. Compare the Indiana Boys' School with the Michigan Industrial School for Boys. Thirty per cent. tested presumably deficient in the former as against 6% in the latter; or 48% in the former and 21% in the latter tested below our borderline for the presumably passable intellects. This difference can hardly be explained by errors in testing. It marks a significant difference between the care of the mentally deficient in the two states. 162The difference in the success of states in isolating their feeble-minded is best shown by comparing the Newark and Pittsburgh institutions for boys from the juvenile courts on the one hand, and the local groups of boy delinquents from Hennepin County, Minn., and Cook County, Ill., on the other. In one case over 60% and in the other less than 10% were below the same borderline. In other words, the courts in Newark and Pittsburgh were deliberately sending mental deficients to their local institutions for delinquents because there was no better place available, not because they mistook deficiency for delinquency. The better diagnosis of deficiency by test criteria is, however, the first step in demonstrating this situation so that public sentiment for an adequate state care for the feeble-minded may be in accord with a conservative statement of the present conditions. Moreover, we have made real progress when we have demonstrated objectively that the difference in the character of the inmates of corresponding institutions is not a mere matter of opinion.
3. Unfortunately for social reform, a wholly incorrect impression seems to have spread abroad that half of the delinquents in juvenile courts are feeble-minded. Exaggeration of the condition retards rather than assists a sane public policy regarding the indefinite isolation of those demonstrably deficient by psychological tests. The mistaken impression apparently started with the study of Goddard and Gifford as to the condition found among boys at the Newark Detention Home. Two-thirds of these boys tested approximately below our borderline for clearly passable intellects. I should not be inclined seriously to question calling these two-thirds in the Newark Home feeble-minded, since I am willing to class those in our doubtful group as feeble-minded provided 163that they are persistent delinquents. The deductions which were drawn from this startling discovery seem, however, to have slipped into the literature of the subject without anybody noting that they were unjustified by the facts. In the first place the condition at Newark Detention Home may reflect a peculiar local situation analogous to that at Pittsburgh in which deficient boys had to be cared for in the detention home because no other institution was available for these feeble-minded. Under these recognized local conditions, it would seem that the general situation might be better represented by the conditions of deficiency found since then in Cook and Hennepin counties than by the conditions at Newark. We at least know that Newark and Pittsburgh represent special and not ordinary conditions among those in local detention homes, unless the situation is very different in the East from that in the West.
Besides regarding the condition in the Newark Detention Home as representative of the general condition in detention homes elsewhere, it was argued that the condition in the detention home represented the condition among the ordinary cases of delinquents before the juvenile courts. The groups in detention homes are undoubtedly extreme both as to the seriousness of their delinquency and as to their deficiency. Since Goddard published his paper following the Newark study considerable additional evidence has been made available. But even without this contradictory data, it was a big jump to assume that the condition in the local detention home represented the frequency of deficiency among the ordinary cases which come before the juvenile courts.
Either Dr. Goddard overlooked this distinction between serious offenders who are often repeaters and the ordinary offenders, or he took the questionable position that the 164difference was unimportant. On the basis of the tests of cases in the detention home in Newark, which we have quoted, he says that “by actual test 66% of the children in the Juvenile Courts of Newark are feeble-minded.” Again after quoting the results of examinations of delinquents at several institutions, he says: “Suppose we take the very lowest figure that any of these studies suggests, namely 25%, and see for a moment where it leads us. Twenty-five per cent. of the children who come before the Juvenile Court[A] are feeble-minded. The figures cannot be less than that” (19).
This paper was subsequently referred to by Dr. Fernald, physician at the Massachusetts Reformatory, as follows: “It has been found by the most eminent research workers in this field that probably not less than 25% of the criminals who come before our courts are feeble-minded and that a much larger percentage of the children brought before the Juvenile Court are defective” (103).[29]
The incorrectness of the assumption that detention home cases show no more deficiency than ordinary juvenile court cases could not at the time be demonstrated. Since then, however, there have been several objective studies. In Minneapolis we found that relatively twice as large a proportion of the serious offenders sent to the county detention home were either three or four years retarded in school as we found among the ordinary juvenile offenders taken consecutively. The data will be presented later under our discussion of the school test. We also found that if we compared the results of Binet examinations at the Minnesota reformatory (22) with those at the county detention home, tested deficiency is about five times as common among the older and more established offenders 165at the reformatory. At Chicago serious deficiency was less frequent among those in the detention home than among more serious recidivists. Bluemel, as we have also noted, found that the frequency of tested retardation was decidedly greater among boys in Denver sent to the State Industrial School than among those only put on probation in that city. The investigation of Stenquist, Thorndike and Trabue shows that serious deficiency is less among dependent boys than among delinquents in the same county. Cornell found less truant boys deficient than delinquent boys, in the Philadelphia House of Detention. In Chicago, Denver and Minneapolis, moreover, less than 10% of the more serious cases in the detention homes were found deficient. This evidence all tends to contradict the assumption that a large proportion of the ordinary children brought before the juvenile court is feeble-minded.
Ernest K. Coulter, as Clerk of the Children's Court of New York County, has raised his voice in protest against charging the Juvenile Courts with dealing mainly with feeble-minded children. He says:
“The writer, who has seen at close range 80,000 children pass through the largest Children's Court in the world, has little patience with the sentimentalist who would pounce on every other juvenile delinquent as a mental defective” (94, p. 68).
Unless we are to convert valuable propaganda for isolating the feeble-minded from good kindling wood into shavings, we must remove this cloud which has been cast upon the mentality of the ordinary children who are brought before juvenile courts of the country. Travis, (202) years ago, may have been nearer right when he said that 95% of the children who come before the Juvenile Court are normal. Surely this agrees better with 166the conditions found in Chicago, Denver, and Minneapolis. Possibly these western cities, however, show unusually good conditions. The evidence as to the peculiar local situations in Newark and Pittsburgh makes one confident that their detention home conditions do not at all represent the frequency of mental deficiency among ordinary juvenile offenders in these cities. I see nothing in the present evidence from mental tests to indicate that the frequency of mental deficients who might justly be sent to institutions from among the ordinary children who come before the juvenile courts of the country, would be over 10 per cent.
4. What shall we say as to the general frequency of deficiency among delinquents of all classes? How about the impression that a large proportion of them are not responsible because of their deficiency and that the condition is worse among juveniles? Note some of the published statements: “Probably 80% of the children in the Juvenile Courts in Manhattan and Bronx are feeble-minded.” “Preliminary surveys have shown that from 60% to 70% of these adolescents [sent to the industrial schools in one state] are retarded in their mental development and are to be classed as morons.” “Forty to 50% of our juvenile delinquents are without a doubt feeble-minded.” “The best estimate and the result of the most careful studies indicate that somewhere in the neighborhood of 50% of all criminals are feeble-minded.” “Nearly half of those punished for their wickedness are in reality paying the penalty for their stupidity.” “More than a quarter of the children in juvenile courts are defective.” “One-third of all delinquents are as they are because they are feeble-minded.” “It is extremely significant in the study of juvenile delinquency that practically one-third of our delinquent children are actually feeble-minded.”
167Fortunately, some of these writers are already beginning to qualify and modify their views, and some of these statements misstate the idea of the investigators, but it is difficult to correct the impression that has been gathered from those who speak with authority. In the face of the fact that mental deficiency is undoubtedly the most important single factor to be considered today in the institutional care of delinquents, one hesitates to correct even the most exaggerated impressions as to its importance. On the other hand, it seems time to modify opinions which raise false hopes as to solving the problem of delinquency by caring for the feeble-minded. Above all it is important to lay a surer foundation on which a platform for the social care of these unfortunates may be securely built.
In the first place, it is necessary to recognize that after all the feeble-minded are properly cared for by society the problem of the ordinary delinquent may still remain with us in much of its present proportions. Surely the isolation of the deficient children will hardly scratch the surface of the problem of first offenders as it comes before the juvenile courts of the country. To this it should be replied that the first offenders are not, after all, the troublesome cases before our courts. If we study the different groups of delinquents which have been tested, we notice that they represent highly selected groups among the ordinary offenders whether these be adults or minor delinquents. The only parallelism which can be traced at all is between prostitutes and vagrants and some of the institutional groups. We should stop assuming that the institutional delinquents represent the ordinary offenders. The present evidence points to the conclusion that it is the repeaters, not the first offenders either in the juvenile or criminal courts, who are most likely to be deficient. 168Nevertheless, 68% of the boys brought before the Chicago Juvenile Court during its first ten years were first offenders (142), while 89% of 4143 boys in the Juvenile Court in Minneapolis were first offenders (105). We know almost nothing about the frequency of deficiency among the first offenders brought before our courts and yet the bulk of delinquents are undoubtedly first offenders.
On the other hand, the repeaters do account for a considerable portion of the cases before the courts, especially the municipal courts, because each offender appears time and time again. In the Virginia city cited, for example, repeaters furnished 60% of the jail commitments for three years. This is probably also an indication of the workhouse situation, which is best represented by such a study as that of Kohs. The proportions of offenses accounted for by deficiency would, therefore, be much larger than the proportion of offenders who are deficient. While the offenses of repeaters might not commonly be serious crimes, they afford a serious problem because of their bulk and because temporary restraint is of little use when the offender is mentally weak. As Aschaffenburg says: “We must not forget that it is not the murderers, not the swindlers, on a large scale, not the assassins of people in high places, and not the sexual murderers, that determine the criminal physiognomy of our day, but the thieves and pickpockets, the swindlers and abusers of children, the tramps and the prostitutes” (68, p. 181).
The best that we can do is to study Table XI, which gives us a classified list of different types of delinquents in institutions. If we should pick out in it such institutions as represent to us the typical conditions in the country we could get an idea of what we might expect from groups of offenders of each type. For example, we might say that the Massachusetts State prison is typical of such 169institutions, and it contained possibly 16% who were deficient. Picking the Ohio Boys Industrial School as typical of its class, it had between 15% and 42% deficient, depending on how conservative you wish to be in your diagnosis. So one might go through the list stating the expectation for each type of institutional delinquent. If these were then weighted according to the number of delinquents of each class in the country sent to them, we would have some idea of the frequency of deficiency among those who reach the institutions. Merely to average the columns in Table XI would give only a false impression. The seriousness of the situation is amply demonstrated among repeaters and the inmates of certain institutions. Each superintendent should be put upon inquiry as to his own charges.
Nothing which I have said in caution as to the importance of deficiency in solving the problem of delinquency can be taken for a moment to signify that the effort for the isolation of the deficient is misspent. Elimination of a generation of deficients will not solve the problem of delinquency, but in no other way is there open such a clear and definite method of reducing that problem. The better care and prevented procreation of even a tenth of the delinquents who would propagate deficiency, would mean the most scientific advance in attacking the problem of delinquency. A safe public policy can be formulated which would at first provide for appropriate permanent care of at least that number of delinquents in institutions who by test are presumably deficient. This perfectly obvious first step promises to tax our facilities for years.
14. During the months when these examinations were made we failed to test six boys, four of whom were sent to relatives outside of the state. One other could not be tested because of his unfamiliarity with the English language.
15. Louise Ordahl and George Ordahl. A Study of 49 Female Convicts. Journal of Delinquency, 1917, 2, 331-351.
16. Eugenics and Social Welfare Bulletin No. XI, 1917, p. 73.
17. Grace M. Fernald. Report of the Psychological Work at the California School for Girls. J. of Delinquency, 1916, 1, 22-32.
18. Ordahl, Louise E. and George. A Study of Delinquent and Dependent Girls. J. of Delinquency, 1918, III, 41-73.
19. Jean Weidensall. The Mentality of the Unmarried Mother. National Conference of Social Work, 1917.
20. J. of Deficiency, 1918, III, 1-11.
21. George Ordahl. A Study of Fifty-Three Male Convicts. J. of Delinquency, 1916, 1, 1-21.
22. M. L. Beanblossom. Mental Examination of Two Thousand Delinquent Boys and Young Men. Indiana Reformatory Print, 1916, p. 23.
23. Bull. No. 1713, University of Texas, 1917, p. 125.
24. A. R. Gilliland. The Mental Ability of One Hundred Inmates of the Columbus, (O.) Workhouse. J. of Crim. Law and Crim., 1917, 7, pp. 857-866.
25. R. Pintner. One Hundred Juvenile Delinquents Tested by the Binet Scale. Ped. Sem., 1914, XXI, 523-531.
26. George Ordahl. Mental Defectives and the Juvenile Court. J. of Delinquency, 1917, II, 1-13.
27. Both sexes.
28. Local conditions explain the excessive amount of deficiency.
29. Italics mine.
The Binet scale in its various forms provides only part of the objective evidence as to the mental inferiority of delinquents, although it affords the best means at present of interpreting the borderline of deficiency. Among the other investigations in which psychological tests have been tried with delinquents in comparison with normal subjects, the recent study of the Mentality of the Criminal Women by Weidensall is the most important so far as estimating the frequency of deficiency is concerned (60). It affords an admirable check upon our conclusions from the Binet examinations, since she gives in detail the results with a random group of 88 women inmates of the Bedford (N. Y.) Reformatory, which is quite comparable with the group of 200 which she tested with the Binet scale, and which we have already considered.
For our purpose, the most important comparisons are those between the group of women in the reformatory and the group of 15-year-old Cincinnati working girls tested by Woolley with the same tests. Weidensall's Table 92 shows for three tests the percentages of the Bedford women who tested below the lowest 1% of these girls. For the opposites test, 20% were below this borderline; for a test on the completion of sentences, 12%; for the memory span for digits, 29%. She also shows that 17% of the delinquent group were poorer than any of the working girls and 30.7% as poor as the poorest 5.7% of these working girls, when their mentality is measured by the number of the tests in which their ability is at or above that of the median working girl of fifteen. This 30.7% is probably most nearly comparable in ability with the lowest 0.5% of the general population.
171Kelley's monograph on Mental Aspects of Delinquency, to which reference was made in the last chapter, gives the results with boys in the Texas Juvenile Training School for the completion test and his own construction test, as well as for a number of physical measurements, sensory and motor tests. He has used various data from which to provide norms for comparison. In connection with the Psychopathic Institute at the Chicago Juvenile Court, Healy and Fernald (125) have published an elaborate series of tests with suggestions as to how they may be employed for analyzing a child's mental ability and estimating his mental capacity. Schmidt has partially standardized these tests (178). Guy G. Fernald (15) tried out a dozen different tests and recommends seven of them for testing delinquents who are of adolescent age or older. Haines has sought the diagnostic value with girl delinquents of a dozen tests including Fernald's test of moral judgment. Weidensall (218), Smedley (51), Rowland (49), Porteus (45), and Whipple and Fraser (220, p. 663), have published results with certain tests tried with delinquents. With none of these tests can we adequately define the borderline of feeble-minded intellects.
There is no series of tests which has been employed outside the field of delinquency which diagnoses the borderline cases objectively so well as the Binet scale. The tests of Weyandt (219), Rossolimo (175), Rybakow (176), and Knox (134) are without definable limits based on unselected groups. Those employed by Dr. Norsworthy, while scientifically better scored for describing the borderline, were not arranged with this in view (160). Carpenter has published norms obtained with Squire's tests on 50 pupils of each age from 7 to 14. Single tests like the form board (87), Knox's cube test (134), the substitution test (1), and the A test (160) have been tried with delinquent 172or feeble-minded groups as well as with normal people. Under the direction of the New York Board of Charities an excellent beginning has been made in determining norms for eleven different tests (158). Stenquist, Thorndike and Trabue (54) have furnished developmental norms for several tests. Gilbert (108) and Smedley (51) at an earlier date provided age norms and deviations for certain tests. Mrs. Woolley has provided the percentile distribution for a series of mental and physical tests with 14-and 15-year-old children leaving the public schools to go to work (222) (223). In England a goodly number of different tests have been tried out on small groups or on children of particular ages (84) (63) (224). Pyle has obtained norms and variations with a series of group tests. It approaches nearest to the Binet as a developmental scale for the immature, but these tests have not been tried as individual tests and so could hardly be used safely for individual diagnosis. A graphic summary of the developmental curves for most of these tests on children will be found in Chapter XIII.
In no case do we find any tests except the Binet scales which have reached a stage of practical usefulness for the diagnosis of deficiency except as supplementary aids for checking the Binet indication with children of particular ages. The emphasis has almost universally been placed on determining the central tendencies of children of different ages and not on the lower limits of the distributions. Considering mental tests apart from the Binet scale, in all the extended literature which has been brought together in books like Whipple's Manual of Mental Tests (220), one may seek in vain for tests which have reached the position of defining the limits of serious mental deficiency. This indicates, of course, the difficulty as well as the newness of the problem, although the quantity of 173work that is being done shows the great interest aroused. From all of this mass of research on mental tests one may gather much that is useful in analyzing the character of a mental defect. Many of the tests admirably aid in elaborating the subjective impression of the examiner. The failure to do this systematically has been one of the main criticisms raised against the Binet scale. This and the incorrectness of the borderline described in the published scale seem to be the main objections made by Miss Schmidt to the Binet Method. She voiced the objection of the Juvenile Psychopathic Institute in Chicago to the tests as follows: “It has been the experience of the writer, and it may be added of all others who have worked in this laboratory, where practical results are demanded, that the Binet tests cannot furnish an adequate means through which to come to conclusions for the disposition, classification, or treatment of the cases which come for diagnosis” (179).
Dr. Merrill of the Seattle court also seems unfriendly to the Binet scale when he says: “Any system of tests by which alone[30] it is attempted to classify the child as being of a given mental age involves the fallacy of pseudo-exactness, and needs carefully to be avoided” (148). Nobody would seriously urge that real exactness of definition leads to confusion. It is just the looseness of definition of borderline with the Binet Scale which has led to most of the mistakes with it. Perhaps Dr. Merrill has not discovered that the scale works just as well when used as a graded series of tests without the designation of mental ages at all. The latter is merely a convenience. On the other hand, we should agree when he says, that “no scale of tests can give a valid measure of the child's intelligence unless supplemented by a consideration of his history,” especially if he includes in the child's history a medical diagnosis.
174The objection that the Binet tests do not analyze the source of the child's mental defect is of course important if one were considering whether a better scale might not be devised. It is rather beside the point, however, when one remembers that it is not the purpose of this scale to determine the causes of deficiency, but only to say whether a deficiency in general intelligence is present and to what degree. The causes of the disturbance must then be determined by an expert. Moreover, if one classifies the Binet tests as Meumann has done one may often get valuable clues as to whether the deficiency is mainly in information or in mental process. In seeking the causes of the disturbance, the expert should not overlook the standardization of the Rosanoff and Kent Association Test which has been available for delinquent, feeble-minded and normal children (174). It is one of the most important supplementary means for mental analysis which has yet been standardized for practical use. The most complete tables on children's reactions for this test have been published in a Psychological Monograph by Woodrow and Lowell.
The importance of more accurate psychological tests in studying mental disturbance is well illustrated by comparing the results that may be obtained with the Binet tests with the desultory, unstandardized tests such as one finds in Dr. Schaefer's Allgemeine gerichtliche Psychiatrie für Juristen, Mediziner, and Pädagogen (177), or Dr. Cimbal's Taschenbuch (91) prepared for physicians and jurists. Suggestive as these books are for disclosing different mental activities, they give no means of evaluating the disclosures. They show the puerile stage in diagnosis which had been reached before standardized tests were available.
Among those who are engaged in practical clinical work for determining mental development the Binet Scale has advocates who are quite as ardent as critics we have noted. Goddard, Kuhlmann (139), Wallin (213), and Towne 175(201), have all used it in the practical examination of hundreds of cases and heartily commend its use in connection with delinquents, as does Healy for the earlier ages (27, p. 80). On the other hand there is a growing sentiment that the examinations should only be entrusted to experts in mental development. It is felt that the physician who has not had enough training in a psychological laboratory to understand the snares of mental tests, and very few have had this opportunity, ought to refer this question to a clinical psychologist as the best physicians now do when such experts are available. Perhaps nobody is so well equipped to judge a child's mental development without diagnostic tests as his school teacher, although Terman has shown that the teacher's judgment may be seriously at fault when he has not learned to dissociate mental capacity from the age and size of the child (196). In an editorial in the Journal of Criminology, Dr. Gault (106, p. 322) expresses the opinion that “dissatisfaction with mental tests as a means of diagnosis” is traceable to the fact “that what the lay mind recognizes as palpable errors are often made by half-trained 'investigators,' 'research directors' and even by men and women whose only qualification is that they have been trained for six weeks in a psychological clinic.” Dr. Wallin demands that the tests should be used for diagnosis only by the psychologist with clinical experience.
The American Psychological Association has cautioned against diagnosis by those inadequately trained and adopted the following resolution at its 1915 meeting:
“Whereas, psychological diagnosis requires thorough technical training in all phases of mental testing, thorough acquaintance with the facts of mental development and with the various degrees of mental retardation.
“And whereas, there is evident tendency to appoint for this work persons whose training in clinical psychology and acquaintance with genetic and educational psychology are inadequate:
176“Be it resolved, that this Association discourages the use of mental tests for practical psychological diagnosis by individuals psychologically unqualified for the work.”
Binet's suggestion as to the diagnosis of mental development seems to be best. He says that “the selection of defectives calls for three varieties of experience—that of teachers, of doctors, and of psychologists” (77, p. 38). These three points of view may be combined in a committee as in France, or the decision may rest with a specialist in mental development whose judgment should only be given after he has all the information which the medical, educational, and social diagnosis can provide to supplement his test records and his evaluation of the causes of the condition found.
Those who are considering the legal isolation of the feeble-minded, especially defective delinquents, and superintendents who wish a safe rule for transferring school children to special classes or schools for the mentally retarded should keep a committee plan in mind. A legal requirement embodying an examination by such a commission could easily be framed. In my opinion the expert in mental development should be required at least to have the equivalent of a year of graduate work with his major time in testing. On the other hand very desirable information as to children that require examination may be obtained by a teacher who uses a mental scale intelligently. In the hands of an amateur it may perform an analogous service to that of a vision chart in discovering children who require expert examination of their eyes. The danger lies in the novice not knowing his limitations. Few who have had experience with tests can doubt, however, the much greater danger of inadequate diagnosis of mental development on the part of physicians who give opinions about mental deficiency without having had experience with test scales.
30. Italics mine.
Besides the estimates of deficiency based on tests, the school records may furnish valuable objective evidence about mental retardation among delinquents. The school environment is the first prominent social environment to which the child must adjust himself. If he fails in this while in regular attendance we have an important indication of mental deficiency. With laws which require attendance at school, we may even estimate the mental character of groups, on the basis of success in school, provided that we use proper caution as to the effects of late entrance and of absence from school. Moreover, whether retardation in school shows mental deficiency or not, it certainly sets forth a vital problem in connection with delinquency. We shall first consider the school retardation of delinquents and leave the problem of checking the tests by school records until later.
In order to study school retardation we tabulated the school position of 236 boys and 95 girls consecutively found delinquent in the Minneapolis juvenile court. To make the results more significant we did not include any cases dismissed at their hearing in court. Comparison with more serious delinquents is made by means of the group of 100 juvenile repeaters and 123 from the Glen Lake Farm School. The school position and actual age of each delinquent was compared with the age and grade distribution among Minneapolis elementary school children. The latter was determined by a census made the same year the returns for which included about 15,000 of 178each sex (see Table XII).[31] The ages and grades were recorded for the beginning of September, when the school year opens, and the census was taken late in the year after all the children had been registered in school. That different groups can only be properly compared when the age-grade distributions are made for the same time in the year is clear when one remembers that the ages are changing throughout the school year while the grades remain the same for at least half the year. The census was taken for another purpose so that it unfortunately does not include the high school pupils. Since the frequency and amount of retardation increases for older ages which occur relatively more frequently in the groups of delinquents the comparison somewhat exaggerates the difference between the groups. This difference in the relative ages of the groups is allowed for, however, in a later table on which the discussion will be based. The school positions of the various groups of delinquents and of ordinary school children are given in Table XIII and graphically in Figure 2.
| Ages | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Grades | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18+ | Totals |
| I | 61 | 1656 | 629 | 144 | 44 | 7 | 4 | 4 | 4 | 2 | 1 | 2556 | |||
| II | 1 | 151 | 979 | 650 | 221 | 92 | 28 | 11 | 4 | 2 | 1 | 2140 | |||
| III | 12 | 169 | 724 | 606 | 290 | 106 | 44 | 9 | 10 | 4 | 3 | 2 | 2140 | ||
| IV | 140 | 628 | 635 | 344 | 184 | 66 | 34 | 13 | 2 | 2046 | |||||
| V | 2 | 120 | 489 | 541 | 371 | 190 | 88 | 36 | 9 | 1 | 1847 | ||||
| VI | 5 | 94 | 428 | 594 | 380 | 223 | 96 | 20 | 1 | 1 | 1842 | ||||
| VII | 7 | 97 | 422 | 458 | 397 | 204 | 60 | 6 | 2 | 1635 | |||||
| VIII | 112 | 308 | 499 | 346 | 142 | 27 | 6 | 1444 | |||||||
| 62 | 1819 | 1777 | 1650 | 1624 | 1614 | 1552 | 1742 | 1419 | 1235 | 702 | 236 | 45 | 12 | 15489 | |
| Ages | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Grades | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18+ | Totals |
| I | 45 | 1642 | 493 | 117 | 38 | 9 | 6 | 3 | 1 | 1 | 1 | 1 | 2356 | ||
| II | 143 | 890 | 582 | 159 | 63 | 27 | 6 | 5 | 1 | 1 | 1877 | ||||
| III | 10 | 165 | 755 | 553 | 193 | 77 | 27 | 12 | 4 | 1796 | |||||
| IV | 6 | 168 | 727 | 618 | 290 | 132 | 446 | 18 | 8 | 1 | 2014 | ||||
| V | 12 | 133 | 573 | 611 | 309 | 131 | 44 | 15 | 4 | 1 | 1833 | ||||
| VI | 7 | 132 | 493 | 519 | 330 | 179 | 80 | 17 | 1 | 3 | 1761 | ||||
| VII | 6 | 113 | 447 | 554 | 342 | 173 | 29 | 5 | 2 | 1671 | |||||
| VIII | 6 | 109 | 432 | 577 | 348 | 96 | 12 | 8 | 1588 | ||||||
| 45 | 1795 | 1554 | 1634 | 1617 | 1594 | 1623 | 1552 | 1510 | 1166 | 626 | 146 | 18 | 16 | 14896 | |
| Summary | Percentages | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BOYS | Number | Retardation | Advanced | Satisfactory | Retarded | |||||||||||
| Per Cent | Av. Am't | 2 | 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
| Ordinary pupils | 15489 | 70 | 0.37 Yr. | 0.2 | 6.1 | 36.3 | 30.0 | 15.9 | 7.6 | 2.7 | 1.2 | |||||
| Ordinary delinquents | 236 | 27 | 1.34 Yr. | 2.5 | 9.7 | 17.4 | 30.1 | 24.6 | 9.7 | 3.4 | 1.3 | 0.9 | 0.4 | |||
| Recidivists | 100 | 74 | 1.77 Yr. | 1.0 | 1.0 | 6.0 | 18.0 | 17.0 | 25.0 | 18.0 | 11.0 | 3.0 | ||||
| County Farm School | 123 | 68 | 1.66 Yr. | 0.8 | 13.8 | 17.1 | 22.8 | 21.1 | 15.4 | 5.7 | 3.3 | |||||
| GIRLS | ||||||||||||||||
| Ordinary Pupils | 14879 | 23 | 0.27 Yr. | 0.3 | 6.8 | 40.0 | 30.2 | 14.0 | 5.9 | 1.8 | 0. | |||||
| Ordinary Delinquents | 95 | 91 | 2.57 Yr. | 1.1 | 0.0 | 2.1 | 5.3 | 15.8 | 32.6 | 20.0 | 8.4 | 9.4 | 1.1 | 2.1 | 2.1 | |
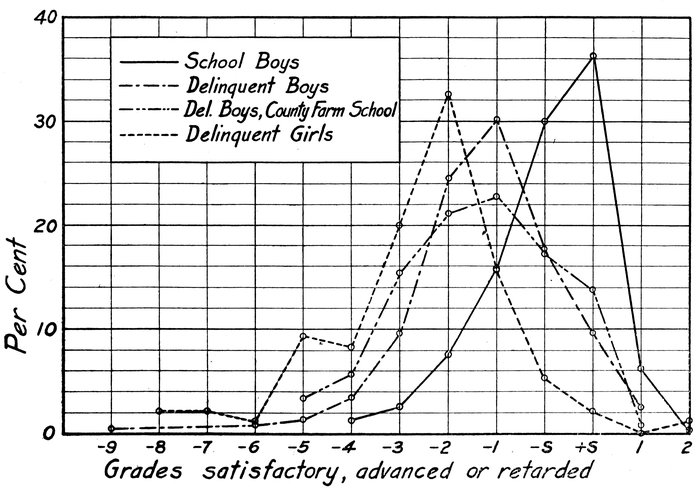
Fig. 2. School Retardation of Minneapolis Delinquents Compared With Elementary School Boys.
181In the Minneapolis group of elementary school children it will be found that there is about as much chance of a child being in either of the two most common ages for a grade. Among the boys, for example, 36% were in the series represented by age 6 in the first grade, 7 in the second grade, 8 in the third grade, etc., while 30% were in the series represented by one year older for each grade. It is, therefore, reasonable to regard either 6 or 7 as a satisfactory age in the first grade, 7 or 8 in the second, when one estimates the amount of retardation in this group. The allowance of two ages as satisfactory for a grade is in conformity with the practise of Strayer (189). The necessity of taking these ages at either the beginning or the end of the school year, and not merely “in the grade,” is emphasized by the report of the New York City Committee on School Inquiry (72). Ayres (71) also considers only those pupils over-age who are over 7 in the first grade, 8 in the second, etc., so that this may be regarded as fairly well established as a standard for measuring the retardation in school position of groups of children.
The summary of results in Table XIII shows that 70% of the ordinary delinquent boys were retarded in school position as compared with 27% among the Minneapolis boys in the elementary schools, 91% of the ordinary delinquent 182girls as compared with 23% of the Minneapolis girls of these schools. When one compares the age distribution of the delinquent groups, given in Table XIII with that of the Minneapolis school children in Table XII, it is clear that an allowance should be made for the much larger proportion of older children in the delinquent groups. This may be done by determining the percentage retarded at each age and in each group and then calculating indices of retardation by weighting the percentage retarded at each age in the proportion to the number of delinquents at that age. Table XIV gives these results for the ages 8 to 15 inclusive.
For example, in calculating the indices 39 and 70 for the frequency of retardation among ordinary delinquent boys as compared with elementary school boys, the percentages retarded at each life-age for each of these groups was multiplied by the number of ordinary delinquent boys at this age, as shown lower in the table, and the totals divided by the number of ordinary delinquents, 213. The average frequency of the retardation of a school group which compares in ages with the delinquent group was thus determined. In calculating the indices of amount of retardation the same procedure is followed except that the average number of years retarded is found for each age and this is multiplied by the number of delinquents at that age. The 16-year-olds are omitted because of the inadequacy of the school census for this age. According to the standard which regards 7 years as satisfactory in the first grade there can be no retardation under eight years of age. Since some of the pupils 13 years of age and over have reached high school and so do not show in the Minneapolis table the percentage of retardation for children 13-15 years is based on the assumption that the number of children at these ages will be the same as the average number for 11 and 12 years. No credit could be allowed for those advanced in school positions on account of the incompleteness of the Minneapolis census for older ages. The comparison is, therefore, on the basis of retardation alone.
| RETARDATION | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Percentage Retarded at Each Life-Age | |||||||||
| Index | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| School Boys | 39% | 8 | 16 | 24 | 31 | 35 | 40 | 45 | 43 |
| Delinquent Boys | 70% | 0 | 44 | 50 | 67 | 58 | 60 | 77 | 93 |
| School Boys | 36% | ||||||||
| Glen Lake Boys | 86% | 17 | 50 | 46 | 66 | 81 | 61 | 87 | |
| School Girls | 35% | 7 | 12 | 16 | 25 | 31 | 33 | 37 | 93 |
| Delinquent Girls | 90% | 0 | 100 | 50 | 50 | 75 | 83 | 95 | 100 |
| Index | Average Amount of Retardation in Years | ||||||||
| School Boys | .61 Yr. | .09 | .19 | .31 | .43 | .54 | .63 | .78 | .64 |
| Delinquent Boys | 1.27 Yr. | .00 | .66 | .50 | .86 | 1.09 | 1.11 | 1.23 | 2.11 |
| School Boys | .54 Yr. | ||||||||
| Glen Lake Boys | 1.54 Yr. | .17 | .50 | .62 | 1.25 | 1.86 | 2.11 | 2.03 | |
| School Girls | .64 Yr. | .07 | .15 | .22 | .34 | .45 | .50 | .59 | .82 |
| Delinquent Girls | 2.29 Yr. | .00 | 1.00 | 1.00 | 1.00 | 1.25 | 2.25 | 2.05 | 2.84 |
| Totals | Number of Children at Each Life-Age | ||||||||
| School Boys | 13,123 | 1650 | 1624 | 1614 | 1552 | 1742 | 1647 | 1647 | 1647 |
| Delinquent Boys | 213 | 3 | 9 | 6 | 21 | 25 | 47 | 56 | 46 |
| Glen Lake Boys | 108 | 0 | 6 | 8 | 13 | 12 | 21 | 18 | 30 |
| School Girls | 12,781 | 1634 | 1617 | 1594 | 1623 | 1552 | 1587 | 1587 | 1587 |
| Delinquent Girls | 82 | 2 | 1 | 2 | 2 | 4 | 12 | 21 | 338 |
Index equals the sum of retardation at each age multiplied by the number of delinquents at that age divided by the total number of delinquents.
From the indices of frequency of retardation in Table XIV it will be seen that retardation of one or more years below the standard of age 7 in the first grade is nearly twice as common among the ordinary delinquent boys as among a group of school boys of corresponding ages, while it is fully 2½ times as great among the ordinary girl delinquents as among a corresponding group of school girls, when estimated on the same basis.
To understand the significance of this comparison one should consider the relative difference which is shown between school children and delinquents in the statistics of health, defective sight, nose and throat obstructions, etc. The percentages of consecutive delinquents showing 184other defective or diseased conditions has never, so far as the writer is aware, been found to be double that among the school children generally when figured on a corresponding basis. Medical inspection shows that for other conditions than retardation the frequency of defects and disease found among representative groups of ordinary juvenile delinquents can often be equaled in the poorer schools of the city. To find a factor relatively twice as common among delinquents as among school children, when the frequencies are as great as with retardation, means a variation that is unquestionably significant. This is, of course, not an argument against the detection and treatment of handicaps that can be benefited by the physician. It only suggests the relative size of the two problems.
In considering the frequency of school retardation among delinquents in Minneapolis, it will be noted that the most serious condition is clearly among the girls, 90% of whom are below grade as compared with the index of 35% for the corresponding group of school girls.
One may estimate that the chance of a Minneapolis boy who is retarded in school getting into juvenile court is about 3½ times that of a boy who is up-to-grade. But the chance of a girl who is retarded in school getting into juvenile court is about 17 times as great as that of a girl who is up to grade. This calculation is easily made on the assumption that the indices of Table XIV are typical for a single year, knowing that about 194 in 10,000 school boys in Minneapolis get into the court annually and 21 in 10,000 school girls.
The best measure of the difference in school attainment cannot be shown, however, without considering the amounts instead of the frequency of retardation in the groups compared. We should regard two years retardation 185as twice as serious as one year and make a corresponding allowance for each additional year of retardation. Thus weighting our results we find in the indices of Table XIV that the boys 8-15 years of age in the Glen Lake Farm School group of delinquents have on the average lost 1.54 of a year through retardation in school attainment compared with the satisfactory standard of 7 in the first grade. The ordinary delinquent boys have lost on the average 1.27 of a year, while the indices for Minneapolis school boys of corresponding ages are—.54 and—.61 of a year respectively. Among the ordinary delinquent girls the average amount of retardation on the same basis is 2.29 years as compared with .64 of a year among the school girls of corresponding age distribution.
The indices for the amount of school retardation are the most significant figures in any of these tables, although they are based on too few numbers to afford more than rough comparisons. It is, however, a fairly reliable estimate to say that retardation in school attainment in Minneapolis is about twice as great among ordinary delinquent boys and among the detention home group while it is three times as great among ordinary delinquent girls as among corresponding groups of elementary school children. If we had been able to credit the groups with those in advance of the expected position for their ages the difference would have been even greater.
In view of the fact that retardation in school offers an important check upon the question of the frequency of mental deficiency among groups, besides stating a different training problem of its own, it is curious that it has not been more systematically studied in connection with 186delinquency. Few investigations include any reference to the question. Auden (69) reports that among 263 committed to Borstal institutions (juvenile reformatories) in England for the year ending March 31, 1909, 71% (186) had not reached the fourth standard, corresponding to the fourth school grade. These were delinquents between 16 and 21 years of age. The next year 402 out of 554 (72%) had not reached the fourth grade. Not one person had reached the eighth grade and only 13 the seventh grade. In the Minneapolis detention home group only 23 out of the 103 over ten years of age were below the fourth grade.
Cornell gives the distribution of 236 boys in special disciplinary classes of two Philadelphia schools (93). These classes are for truant and difficult boys 8 to 14 years of age inclusive. While they are not technically delinquents the problem is similar and they show even more serious school retardation than the Minneapolis group. Summarizing his results according to the standard which counts ages six or seven as satisfactory in the first grade, and so on, we find 12.3% satisfactory; 12.3% retarded one year; 26.7% retarded two years; 30.1% retarded three years; 15.8% retarded four years; 2.5% retarded 5 years; and 0.4% retarded 6 years. Eighty-eight per cent. are thus behind a satisfactory position in the grades, and 48.8% three or more years behind. This is to be compared with 70 and 16% among ordinary Minneapolis delinquent boys (Table XIII).
Among 647 prostitutes at the Bedford (N. Y.) Reformatory 48% either could not read or write any language or had not finished the primary grades. Seven per cent. had graduated from the grammar grades. Among 610 prostitutes in other reformatories reported in the same work, only 23% had finished the fifth grade. Among 877 street 187cases from which information was obtained 814 had no more education than ability to read and write, 53 had graduated from the grammar grades or had some special education (133). Another report by Weidensall we shall consider in the next chapter.
The attending physician (60) of the Morals Court in Chicago inquired “of as many of the defendants as she could, who were charged with being public prostitutes, as to what ages they had left school.” Among 3546 cases which passed before the court in seven months the report covers 494 cases. Of these only 17 had gone beyond the fifth grade in school, only one was a high school graduate (161). Among 100 girls at the Ohio Industrial School, 11 to 18 years of age, median age 15 years, 50% were in the third or fourth grade and 54% had failed of promotion three or more times (55).
Drucker gives the age-grade distribution of 100 randomly selected minor offenders, 15 to 22 years of age, in the Cook County (Ill.) jail. This shows that 41 of these were below the eighth grade and three or more years retarded at the age they left school. They might well be examined for deficiency. Among 86 who left school at 14 or after, 24 were in the fifth grade or below (101). Among 100 consecutive admissions to the Ohio State Girls Industrial Home, Renz reports 25% in the third grade and 25% in the fourth grade, 15% in the fifth grade; 29% failed of promotion 4.5 to 6 years and 25% more failed of promotion 3 years (47). Storer reports on the same groups (55). Bluemel finds that 100 probationers in the Denver Juvenile Court were retarded in school 2 years on the average as compared with an average school retardation among the school boys of Denver of 1 year (2). At the New Jersey State Home for Girls among a group of 163 selected cases 102 had not reached the fifth grade although their average age was 17 (12).
188The school distributions by age is given for 215 delinquents in the California State School at Whittier for boys by Williams (62) in sufficient detail to make it usable for estimating the frequency of deficiency on a plan we shall consider shortly. Regarding age seven as satisfactory for the first grade, and so on, only 7 of these boys had reached this standard. Supposing that those older should have attained at least the grade which is satisfactory for the 14-year-old, and those younger the corresponding grades, we find that 29% were four or more years below this standard and 14% were five years below this standard. In the next section we shall endeavor to find out how the school records might also be used as symptomatic of mental capacity.
31. The tables of Minneapolis school children were prepared by Mr. Andrew J. Lein and of delinquents by Miss Lydia B. Christ, to whom I am much indebted.
There has been considerable discussion of the question whether psychological testing should be expected to conform to the ranking of pupils in school. This discussion however, does not attack the question in which we are especially interested, i. e., how to get the best information from both. If the school level were measured by the progress made in school by passable work and not by the school position attained often merely through age or size, Binet would be right in expecting that in general they would correspond among groups of children in the public schools. Agreement with real school progress could, therefore, be taken as a criterion of a good series of tests, as it has been by Binet and Bobertag. On the other hand Meumann and Abelson were right in objecting to the proof of the value of tests by agreement with the school level, if they limited their objection to tests applied to exceptional children and to using school position as a final test of school level. Lack of correspondence with our group of delinquents is, of course, no indication of a weakness in the Binet scale. In numerous instances they had been promoted in school because of age without doing passable work. The reader should also see the evidence of the teacher's bad judgment of a pupil's ability assembled by Terman and by Terman and Knollen (196).
Terman has calculated the correlation between intelligence quotients determined by the Binet scale and the teacher's estimates of scholastic or of general ability. These gave coefficients of .48 and .45. Doll has found for Goddard's data on school children that the correlation of school grades is closer with life-age than with test-age, .84 as compared with .73 (12). This indicates an 190influence of life-age upon promotion. In a school for deficients Burt found the correlation of teachers' estimates with Binet ages was .55, with mental retardation or excess .59, with intellectual quotient .48. He quotes McIntyre and Rogers as finding coefficients about .5 for similar calculations with normal school children in Scotland (85). Starch has shown that measured by the combined ability in reading, writing and spelling a third of the pupils are in a grade behind and a third are in a grade ahead of their ability (186).
However much we might disagree as to how close a correlation might be expected between the Binet tests and school level, independent of the relation to life-ages, or which is the better test, it is certain that they afford two different symptoms of mental deficiency. It becomes our immediate problem, therefore, to discover how the most information may be gained from a careful interpretation of the test of school level. If we had sufficient data, three sorts of checks might be formulated. 1. What amount of school retardation will give us the best estimate of mental deficiency among groups? 2. What amount of school retardation should put an individual's mentality in question so that he should be examined? 3. What amount of school success should put in question a Binet diagnosis?
We shall first take up the question of utilizing information about school retardation in estimating the frequency of mental deficiency among groups of delinquents. It is 191perfectly clear that retardation in school position is not always an indication of mental retardation. A child may be behind the position in school reached by the children of his age merely because he has not attended school so long as his companions. A census of school progress which we took in Minnesota indicates that in general a large part, perhaps half, of the retardation in school is to be thus explained even under compulsory attendance laws. Some allowance is also to be made for physical handicaps, such as defects of sight and hearing which are not corrected, illness which does not cause prolonged absence, frequent change of schools, bad home conditions, etc. Aside from absence, however, there can be no question that greater or less degrees of mental retardation is the main cause of retardation in school. Moreover a dull mind is often the reason for beginning school at an older age and for staying away from an unsuitable school environment as much as the law will permit. In any particular case, it is to be noted, however, that all of the excuses for backwardness in school are not likely to account for more than one or two years of lagging for other reasons than dullness.
We cannot hope at present to get nearly so accurate a judgment about the frequency of deficiency in groups by means of any school test as by the psychological tests. Nevertheless, I believe that it may furnish us some supplementary evidence. The main difficulty in formulating any general rule for interpretation of the school level is that very different plans of promotion prevail in different school systems. It is not uncommon, for example, to find that a child will be promoted to a higher grade regardless of his ability provided that he has spent two years with the same teacher. This practise, of course, makes it impossible to judge a particular individual's 192ability by the school grade he has attained without knowing how he reached it. Nevertheless, spending two years in each grade will begin to show in a general distribution of pupils by the time we deal with 12-year-olds. I have gone over the tables of school retardation of pupils provided by Strayer for several hundred cities in the United States and I find that the percentage method of approach gives us at least a rough cue as to what might be expected by any general principle of interpretation (189).
Using age 7 as satisfactory in the first grade, 8 in the second, and so on, we find that among 319 cities of all sizes, half of them had 2% or more retarded four or more years in school position. This condition was about the same for cities less than 25,000 as with the larger cities. On the basis of school position for groups of children of all the school ages it would, therefore, be safer to make a low estimate of the frequency of mental deficiency on the basis of five or more years of scholastic retardation in the groups and regard 4 years or more of school retardation as a maximum estimate. Since most children leave school at 14 it is generally best to regard all older as only 14 years of age when estimating deficiency. I have not been able to check this by school and test records on a group of children through all the grades. Goddard's published records do not give the mental ages for those four or more years retarded scholastically. Moreover, he only included those in the sixth grade and below. For a group of young children this estimate would undoubtedly be too low. The delinquent groups, however, are all older. Most of them, if they lived in this country have gone to school until they were at least 14 years of age. Wallin (211) and Strong (190) also give records of school position to check the Binet rating.
| Percentages Retarded | ||
|---|---|---|
| 4 or more grades | 5 or more grades | |
| Cincinnati, Ohio—June 1907 | 8.8% | 2.5% |
| Cleveland, Ohio—1909-1910 | 3.0 | 0.9 |
| Des Moines, Iowa—1915 | 1.0 | 0.2 |
| Memphis, Tenn.—June 1908 | 6.6 | 1.5 |
| Minneapolis, Minn.—June 1915 | 1.3 | 0.5 |
| Pittsburgh, Pa.—1913 | 4.7 | 1.1 |
| Springfield, Mass.—Sept. 1907 | 1.2 | 0.1 |
| Reading, Pa.—1906-1909 | 2.2 | 0.4 |
The distributions for Cincinnati, Memphis and Springfield are taken from Ayres' Laggards in Our Schools. That for Minneapolis is from unpublished data. That for Reading is from Snyder's Retardation in Reading Public Schools. The others are from Superintendents' reports.
By considering only pupils in the public schools who are 12 and 13 years of age, the last years in which practically all are in school, we can get a check upon this method of estimating for delinquent groups. I have compared the age-grade distributions for those of these ages in eight cities showing the percentages retarded 4 or more and 5 or more years. They are given in Table XV. These records indicate that at least five or more years retardation below a standard of age 7 in the first grade for all who are 12 years of age or over might be taken for a low estimate of the frequency of deficiency, and four or more years retardation for a maximum estimate. Except under special circumstances those who are older than 14 years should be considered as if the highest grade attained was at 14 years of age. These borderlines of school retardation for the purpose of estimating the frequency of deficiency check fairly well with estimates for the Minneapolis and other groups of delinquents which have been tested by the Binet scale, as we shall note later in this chapter.
194In order that the school test of mental deficiency should be as good as the Binet system it would have to provide a standard of school progress relative to length of attendance instead of school position relative to age. If one could say that a child was not above the lowest 0.5% of the children of his age in the progress which he had made in school relative to the time actually spent in school, one would then have an excellent standard for judging feeble-mindedness for any child who had been in school for some years. It would be better if an uncertain region were also defined. By the time that a child's ability has been passed upon for four or five years and by different teachers, even from the point of view of the needs of school work, one has a criterion for mental ability in a particular community applied under long observation, which no system of brief tests can hope to equal for some time to come. Such a standard, however, is unfortunately not available since we have too little information about school progress relative to attendance. Even if it were available, psychological tests would still be an important check upon the school judgment on account of the excessive value put upon mere memorizing in school and on account of the emotional repulsion to the school developed by some children of ability. Mental tests would be necessary, moreover, for the younger ages.
Even if no more is known than a person's grade in school at any age over eleven it is an important cue as to his mentality. Here our problem is not estimating deficiency among groups but the discovery of deficient individuals. We wish to find the highest grade in school in which we are at all likely to find children under present 195conditions who test in the lowest 1.5% for their ages. Our records on 653 15-year-olds indicate that a pupil of this age who tests doubtful is very rarely retarded less than 3 years in school. It occurred only twice when tested ability was judged by the 1911 tests, four times judged by the 1908 scale. None of the 15-year-olds who tested presumably deficient were retarded less than three years. In Minneapolis, as in many cities, the custom prevails of promoting, regardless of passable work, after two years have been spent in a grade.
We suggest, therefore, to be perfectly safe, it is well for every child in court to be examined who is two years retarded in school below the standard age of 7 in the first grade and is not able to carry work above the seventh grade. This will include a considerable number of children at the lower border of those presumably passable.
Binet used this standard of two years retardation in recommending examination for children 9 years of age or over (3 years below age 6 in the first grade) (77, p. 44). He adopted it from Belgium. It is also quite commonly followed in this country. The New Jersey law provides for special classes in any school district where there are ten or more children four or more years behind grade. This probably means behind the theoretical position of age 6 in the first grade, one year worse retarded than we suggest examining. Goddard says in one place that “a child who has been in school regularly and is two or three years behind his grade is so suspicious that it is almost certain that he is feeble-minded” (116). But later he is much more conservative and says, “The child who is fourteen years old and cannot pass an examination in fourth grade work is almost surely feeble-minded” (34). As judged by Strayer's tables the suggestion that examination is desirable for those two years behind a standard of 196age 7 in the first grade would tend to bring in for examination about 18% of the school boys in half of the cities of 25,000 population and over. This would not be too severe a burden for courts which would be interested only in that portion of these retardates who were brought into court.
This school test may be made of decidedly practical use by those working in juvenile courts where most of the cases are with children over this age. It can be applied in a very simple manner by subtracting 8 from the child's age and only passing without testing those who are in a grade in school higher than the number remaining. For example, if the child is 13 years of age, subtracting 8 gives 5. Now, if the child is in the fifth grade or lower, or entered such a grade at the time he was of this age, one should investigate the question of feeble-mindedness. Unless more than one year of the retardation is explained by the person's absence from school since he was six years of age, he should always be turned over to an expert for examination. This retardation of two years in school attainment below the standard of seven in the first grade may indicate feeble-mindedness if the child has been attending school constantly, although the chances are perhaps 6 to 1 that it does not. It is very desirable that we should have more adequate data on this point. A cautious court, however, would inquire into the mental ability of any child—at least two years retarded in school, i. e., any child the number of whose school grade is not higher than the remainder after subtracting 8 from his life-age at the time that he entered his last grade or who is not actually carrying the school work of an advanced grade. This latter caution we must now consider.
The school test can give us still another practical cue as to feeble-mindedness in examining children. Ability to carry successfully school work of some grade certainly could be used as a systematic criterion of passable intellectual ability. What school grade indicates this is not at present possible to determine except as a rough practical check. With the great irregularity in school grading at present known to exist, it certainly would not be possible to say that fifth grade work indicates a passable intellect, although some of the oldest local schools for deficients, like those in Mannheim, do not pretend to carry children above the fourth grade work. Speaking of the school success of the intellectually deficient, Binet said: “One may draw the conclusion, which is of practical value, that one need not seek children of this group in the senior divisions of the primary schools” (77, p. 44). This would correspond to the sixth and seventh grades in this country. Tredgold gives a careful description of the highest work in a London special day-school for the highest grades of deficients. It shows that even fifth grade work would be beyond what is actually taught the children in this school. He says:
“The work done by this class consists of reading and writing, equivalent to normal Standard II; compound addition and subtraction up to 1000, and simple multiplication and division. Excluding a few children—who, in my opinion, are not really defective—it may be said that the scholastic acquirements of none of these children come up to the Standard II. In occupations and manual work they are decidedly better, and a considerable portion of the children of this class can cut out and make simple artificial flowers, knit rugs and weave baskets, with a really very creditable amount of dexterity, 198which redounds in no small measure to the patient, persevering and systematic care of their teacher” (14, p. 173).
Some of our group with doubtful intellects do better than this. When considering the borderlines with the Binet tests we decided that a child was presumably passable if he scored a test-age of XI. This score would not be made by 11-year-olds as a group, but could probably be attained by 12-year-olds. We may then ask what is the corresponding school position attained by 12-year-olds who have been continuously in school. At the same time we must ask whether the lowest 1.5% of the children of any single age can attain this school grade since it should be high enough to exclude the deficients, no matter how long they have attended school. We happen to have this information for a random group of Minneapolis elementary school pupils on the basis of census of school progress per years of schooling. Considering only the children who had been in school since they were six years of age, we found that 82% of 186 12-year-olds and 92% of 174 13-year-olds had reached the seventh grade, and that the lowest 1.5% of neither age nor of any of the older ages could apparently carry the work of this grade no matter how long they had remained in school. Our records included older pupils who were in their eleventh year of attendance on the elementary schools.
Another indication that reaching the seventh grade is presumptive evidence of passable intellects is found in the fact that none of our group of 653 15-year-olds testing presumably deficient with the Binet scale and only four of the six who tested doubtful intellectually had reached the seventh grade. On the other hand those that think that a 15-year-old testing XI is deficient will be interested to find that 42 out of 51 who tested XI with the 1908 scale 199were in the seventh grade or above. We are convinced, therefore, that it is a conservative position to take that either passing the Binet tests XI in the 1908 series or ability to pass successfully the seventh grade in school is good evidence of a passable intellect. The rule, of course, does not apply to those who are passed along to the seventh grade because of their size or age regardless of ability to carry the work.
Let us see what the rough preliminary estimates on the basis of school retardation would indicate for the Minneapolis delinquents. We may disregard the upper limit of 14 years since compulsory attendance in Minnesota for backward pupils continues until age 16. For the limits of five and four years of retardation in school below the standard of 7 years in the first grade we would have estimates of 2.6% to 6% of deficiency among the ordinary cases of delinquent boys and 14.7% to 23.1% among the ordinary delinquent girls. Among the recidivist group of boy offenders 3% to 11% would be below these borderlines. Among the Glen Lake School group 12% are four years or more and 4% five years or more retarded. This last is to be compared with our judgment on the basis of individual examinations with the Binet scale in which we concluded that 2% were presumably deficient and 5% doubtful as to deficiency. The estimates on the basis of school retardation are somewhat too large. This would certainly be true for older delinquents. In as much as the laws for compulsory school attendance usually do not enforce attendance after 14 years of age, it would probably be better generally to treat all over 14 years of age as if they were of this age at the time of leaving school. 200This limiting age of 14 checks more closely with the mental examination records reported by Williams (149) and Ordahl (41) for groups of delinquents in the California state schools.
With her unselected group of 88 women at the Bedford reformatory, Weidensall found that 39% had not completed the fifth B grade (60, p. 23). This is not far from the estimate of presumable deficiency among such inmates on our borderline with the Binet scale. Considering the actual years of school retardation relative to years of attendance, so far as she was able to discover, and adding the 8 who never attended school, we have 20% five or more years retarded in school and 28% four or more years retarded (60, p. 251). She says further regarding the bi-modal distribution of ability which she found among her group:
“The division which alone served to separate the better from the poorer subjects was that of the grade completed upon leaving school. Those who had accomplished the completion of at least 5B grade formed a curve which paralleled very closely that of the Cincinnati girl of fifteen, while those who had not succeeded in passing 5B comprised the majority of those who collected at the poorer mode of the Bedford 88 curves. Throughout, the grade completed has proved to be more often a measure of our subjects' ability to progress in school, less often a measure of their opportunity to attend school.”
The administrative officers of institutions may make rough estimates of the frequency of serious deficiency among their charges by regarding all over 14 as if they were 14 years of age or under, disregarding those under 12 years of age, tabulating the highest school positions reached, and finding the frequency of those four or more and five or more grades retarded below a standard of age 7 for the first grade. It would be well for each court 201also thus to make an estimate of the size of the problem of deficiency in its jurisdiction. According to the second suggestion which we have made, the Minneapolis Juvenile Court, for example, should plan to examine for mental deficiency all those two or more years retarded in school or about 20% of the boys found delinquent and nearly half of the girls. The prospect would be that the number sifted out as having feeble intellects will be less than 10% of the ordinary run of cases.
Let us study a little further into the detention home cases tested by the Binet scale and see what additional light their school position throws upon the question whether or not they are defective delinquents. Four years retardation in school position would have called attention to both of our sure cases of feeble-mindedness. On the other hand, it would have brought in for examination only 4 out of the 7 doubtful cases. Three years of school retardation would have sifted out all but one. Two years school retardation, the rule suggested above, would have detected all those who tested doubtful. It would have required 56 examinations in this group to have found the eight cases suspicious under our test criteria. We also find that, among the random 15-year-olds not delinquent, examining all those 3 years retarded would have discovered all that tested even doubtful intellectually.
Applying the rule that ability to carry seventh grade work is a good indication of a passable intellect, we find that none of our Glen Lake delinquents testing either presumably deficient or doubtful had reached the seventh grade. On the other hand, if one were disposed to object to saying that a person who passes Binet tests XI (1908) has a passable intellect, one finds in reply that 16 out of the 22 Glen Lake delinquent cases testing XI and three or more years retarded intellectually, i. e., presumably passable, were carrying seventh grade work or better.
202In examining individuals the importance of checking each of these tests with the other seems perfectly clear. If a boy fails in the Binet tests and shows better school ability one should certainly be cautious in his diagnosis. On the other hand a boy who is seriously behind in school may be found by the Binet scale to have a better intellect, so that the inquiry must be further extended to determine the cause of his school retardation. Retardation in school is generally not as fundamental a symptom of deficiency as retardation in the tests because of the numerous other causes of delay in school.
After allowance for the external causes of backwardness in school one finds that the test of progress in school and the Binet examination not rarely reach two different sides of the nature of unusual children found in juvenile court. Working with these exceptional children, Dr. Kramer observed that school performances were often notably different from ability in the tests. After checking the two tests against each other in examining 59 cases sent to him from the Society for the Care of Delinquent and Dependent Children in Breslau and 59 children at the psychiatric clinic in Berlin, he says regarding the result of this comparison:
“For the valuation of the Binet method, it shows us that the first objection which occurs to one, that the method tests only school knowledge, is not correct. On the contrary it was found that we had to do in high degree with that which was independent of what the child had learned in school and with real abilities which the normal child is accustomed to acquire by a certain age uninfluenced by training and instruction.”
He emphasizes, however, that to answer practical questions regarding the training of a child, “we must not only examine into the understanding but the total personality must be taken into consideration” (184, p. 519).
The comparison of the Binet and school tests for our group of serious delinquents suggests another important comparison. Many delinquents are found to be apparently wrongly placed in school relative to their intellectual development. They form a group for which not isolation but training is needed, a group notably larger than that which should be sent to institutions for the feeble-minded. This bad adjustment of juvenile delinquents to their school work is not the same problem as backwardness in school. It means attendance in school classes unsuited to the child's mental ability. In a paper before the Minnesota Annual Conference of Charities and Corrections in 1910, I briefly forecasted this problem (152). It is now clearly indicated by the records of the group of delinquents at the Glen Lake Farm Training School. This comparison is made in Table XVI.
| School position worse | Alike[32] | Better | Total | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 3 yr. | 2 yr. | 1 yr. | 1 yr. | 2 yr. | 3 yr. | 4 yr. | |||
| 1 | 8 | 21 | 21 | 29 | 16 | 4 | 2 | 2 | 104 |
In order to be thoroughly conservative in estimating this problem of maladjustment to school work, let us not only allow for two mental ages to be satisfactory for each grade, as indicated in the table, but in addition omit all cases which might be credited with an intellectual development above XII. This eliminates the objection to considering higher age tests, for nobody questions that tests XII or above indicate at least a 12-year-old intellect. After these extremely liberal allowances we still find 54 of the 104 boys in the detention home testing less than XIII who were in school grades the work of which was presumably not suited to their intellectual level. Seventeen of the boys (16%) were at least two years out of adjustment to their school work. If we disregard those who were trying to carry work too difficult for their capacity because placed a year or more ahead of their ability, we find 30 out of adjustment because at least one grade behind the class suited to their intellects. Over a quarter of our detention-home group was thus placed in school a year or more below grades attended by the pupils of corresponding intellectual development. It may be said that some of those behind their proper intellectual position in school may have been kept back because of instability, laziness, or other volitional characteristics which might fail to show in tests of intellectual performance. This is probably rare, and, when found, it often means merely that the pupil requires more attention to secure results.
That our delinquents are not unique in their maladjustment to school as judged by their tested abilities, is indicated by the report of Ordahl on the school position of the special group of 341 delinquents in the state school at St. Charles, California. The median of their school positions, counting seven years as satisfactory for the first grade, fell a grade and a half below that which their tested mental development seemed to justify. He notes that “mentality is not alone responsible” for their low grades in school. Moreover, he believes that it shows the necessity for a more objective pedagogical method in dealing with them (41, p. 81).
205Only a prolonged trial of special instruction for those presumably behind their proper grade would finally determine how large is this evil of maladjustment. Such an experiment could be satisfactorily carried out only with the co-operation of the board of education. It would mean the employment for some years of expert teachers to train those delinquents found behind their intellectual level in school. Until that time we shall have to take the estimate from psychological tests which indicated that, in our group of serious juvenile delinquents, presumably 29% of those compared had been held back by the school machinery. Since the retardation of these pupils may be attributed to a late start in school life or prolonged absence, the inadequacy of the schools so far as these pupils are concerned may be supposed to lie in their failure to promote pupils quickly up to the school position of their equals. On account of the expense of special teachers such pupils presumably could not be given a chance to make up the school subjects which they had missed and could not be advanced to the grades requiring this knowledge. Whenever this is the case or under any circumstances which keep the pupil behind the school class of his intellectual equals, we have a fundamental cause of distaste for school work. No wonder that such pupils dislike school, become disgruntled and stubborn, run away and rebel at the treatment they receive under the traditional school system. One can hardly blame a self-respecting boy, forced to remain behind his peers, for breaking away from the lock step, playing truant and seeking his education in the streets.
The trouble is not with the school authorities alone. They are doing about as well as can be expected with the funds which the people have been willing to provide. The public must be educated up to the recognition of the 206fact that every child in the school should be allowed to progress as rapidly as his abilities permit. The public schools of Mannheim, Germany, are the great illustration of what can be done to bring the school instruction close to the varying degrees of capacity among the pupils. In the Mannheim schools children may carry from four to eight years of the regular curriculum in eight years, and the brighter pupils may also take additional subjects. The Industrial School in Cleveland has demonstrated that some 14-year-old boys two years backward in school may, with special help, be successfully prepared for high school with about as much likelihood that they will continue the high school course as the ordinary boys (107).
It is self-evident that a boy with ability to carry a higher grade of work cannot ordinarily be allowed to skip one or two classes without special instruction and be expected to succeed with studies which require preliminaries that he has had no opportunity to learn. The necessary knowledge and sufficient skill in particular habits of thought needed could probably be acquired in a brief time under the right sort of special instruction. It is not sufficient that special classes for pupils mentally backward should be provided in the schools. They will not take care of this problem, which has to do mainly with pupils intellectually capable of carrying the work of a higher grade than that in which they are placed. These children can now be found by means of mental tests and they should be assisted in making up the intermediate work by collecting them into redemption groups, so to speak, where they can have individual instruction. In the public schools of Faribault, Minnesota, the plan of thus picking out older minds in a class and promoting them one or two grades with very little extra instruction has been successfully tried in an experimental way.
207If all of the children in a school system who are thus seriously out of intellectual adjustment cannot be cared for, it is plain that the children in danger of delinquency might well receive the first attention, since the lack of adjustment with these may cause the most serious social consequences. That the problem is more acute among the serious offenders in juvenile court than among school children generally is indicated by a comparison with Goddard's figures for school children generally in a typical community tested with the same scale. If we select from his tables only that group of mental ages which could actually be in a class ahead or behind their mental development, we find that only 20% of this group would be outside the standard of 6 and 7 years in the first grade, etc., as compared with 52% of our detention home group on the same basis. On the other hand Terman's records with the Stanford scale (193) indicate 44% of ordinary children similarly maladjusted to school. This condition should probably be regarded, therefore, as a supplementary stimulus for delinquency rather than a fundamental cause comparable with mental retardation.
While this lack of adjustment is undoubtedly the most pressing training problem connected with juvenile delinquency, we must not expect that when it is solved we shall have eliminated the problem of mental backwardness of delinquents as a class. The most that we could expect from perfect adjustment of the school work to mental ability would be that the average amount of school retardation for the group would be materially reduced. How much retardation in school relative to the life-ages would still remain, cannot be determined on account of the uncertainty of the tests for older ages and the factor of volition. For the mentally deficient pupils still remaining behind the regular pupils it is necessary to provide 208other special classes. In these classes or schools the feeble-minded children would remain for their entire school course.
That the correction of the lack of adjustment is a much more agreeable and hopeful task than the care for deficients is shown by the facts regarding the detention home group in Table IX. There is at least the possibility that 10 of the school laggards in this group of serious delinquents might be brought up to a satisfactory grade. Discount this prospect as you may, it is still to be compared with the fact that no actually feeble-minded boy can ever, by special instruction, be brought up to a satisfactory school grade. Moreover, we might expect that 30 of the 84 laggards might, by special help, catch up one or more grades.
That the correction of lack of school adjustment is a bigger problem in connection with juvenile delinquency than the detection and isolation of the mentally unfit can only be said in relation to the numbers affected. Taking the lowest estimate of those in the detention home group out of adjustment with their school environment it was at least 30, while only 9 of that group fell below the borderline of passable intellects and only 2 were surely feeble-minded. If one guessed as we have on the basis of school position that a maximum 6% of the ordinary juvenile delinquents in Minneapolis might be feeble-minded, who would venture to guess that ill-adjustment of school to mental ability affects so small a proportion? On the other hand one feeble-minded person, through the transmission of his deficiency, may, perhaps, do more damage to society than many intelligent delinquents. Who shall say? Certainly both the isolation of the feeble-minded and the adjustment of school training are vitally important problems in the care of juvenile delinquents 209today. Nobody can say that one is more important than the other except from a special point of view. From the eugenics standpoint feeble-mindedness is more important; from the point of view of the numbers affected and the skill required for training the child, there can be little question but that the correction of bad adjustment to school environment is the bigger problem. When one considers how much of the child's time is spent out of school, at home, with playfellows, or at work we cannot be sure that other external influences might not ultimately be found to be more important in connection with juvenile delinquency than either the school life or mental incapacity. The further consideration of the causes of delinquency we shall now make the subject of a broader inquiry.
32. Mental ages VI and VII regarded as satisfactory for the first grade, etc.
In a preceding chapter we have shown the frequency of tested deficiency among various types of delinquents. We may now further consider the significance of this association of delinquency with deficiency. The best plan for discovering its meaning is provided by the technical method of correlation. The data in the published reports of the score or more of investigations which I have reported is wholly inadequate for following out this method. We must, therefore, for the present content ourselves with noting what has been discovered by the better analysis of similar data which was supplemented by the necessary information as to the distribution of the different types of crime in the corresponding general populations. To this we can add certain correlations in connection with the small Minneapolis group of tested juvenile delinquents.
We are indeed fortunate to have the fundamental work of Dr. Charles Goring on “The English Convict,” from which to formulate a point of view regarding the relation of deficiency and delinquency. This work represents ten years labor in making observations, collecting, tabulating, and statistically evaluating data on 3000 convicted men, who were found in the English convict prisons where they had been sent after conviction in the higher courts because guilty of grave or repeated offenses. It was carried out with the co-operation of a corps of workers who had the help of Professor Karl Pearson and his assistants at the Biometric Laboratory of the University of London, in the statistical reduction of the almost overwhelming mass of data. By the large use of partial 211correlation the relative influence of various factors upon criminality was investigated as it never had been before. It is, of course, not possible to reproduce here the conclusions of this monumental work which should be made more widely available in the libraries of this country. We shall, however, select certain conclusions which bear most directly upon our problem and which rest upon well established statistical deductions, and compare them with a few other studies which have contributed interesting side lights upon the causes of delinquency.
“Every feeble-minded person is a potential criminal,” says Goddard in his work on Feeble-Mindedness (112, 514), and this sentiment finds an echo in the emotions of many social workers. On the other hand we have the careful work of Bronner in which she compares by their test records a group of delinquent women with groups selected from night classes and the servant class who had never been known to be immoral. On the average she finds that the delinquents do not test below her servant group. She says:
“Thus, though our delinquents are not as capable as their sisters, many of them from congested districts, who in other ways are proving themselves ambitious [the group from night classes,] yet they are no less equipped intellectually than others who are earning a livelihood and caring for themselves without coming in conflict with the law in the least. Whatever their mental status might be, measured by other means, the fact remains that there is no necessary correlation between their immoral or criminal tendencies and their intellectual ability and that others, no more endowed than they, are fighting 212life's battles without manifesting the same immoral or criminal tendencies” (112, p. 43).
What portion of these moral household servants of equal ability with the delinquents may later fall under temptation, we, of course, cannot say. Neither can we say that any of the delinquents would test deficient, since we do not know the border lines of deficiency with the tests which were used. The conclusion, however, is clear that, if corresponding grades of intellect may be delinquent or not at maturity, we must be cautious in assuming that the lowest grades of intellects would all become delinquent if not under supervision.
What chances we are running by allowing feeble-minded individuals to be abroad might be determined if we could find out the probability of tested deficients becoming delinquent. This question cannot be answered by showing for a single year or a period of years that crimes are relatively more common among the defective classes, although such figures give some impression of the danger of deficiency to the community.
Kinberg, for example, calculates that in Sweden during the years 1901-1907 murder was relatively 200 times as common as among those not in institutions, but lacking criminal responsibility through insanity or deficiency, as among those who were responsible, arson was 72.5 as common, manslaughter 12.63 times, other injuries to property than arson 6.55, rape 6.1 times, infanticide 4.59 times, larceny 0.99 times, and fraud 0.26 times (132). The data were based upon the reports of the Royal College of Health which makes the diagnosis as to criminal responsibility that is required for all cases in which this question arises. Such examinations, it is estimated, miss at least 15% of the deficient criminals.
213Goring gives a table which shows what crimes are most likely to be committed by deficients. He found that 10% of the convicts in England and Wales were definitely treated in prison as deficient, and he estimated that 0.5% of the non-criminal population were equally deficient. His table is based upon the tabulation of 8,290 crimes past and present of 948 English convicts (Fig. XXXIX, p. 258). It is given below:
| Firing of stack | 52.9% |
| Wilful damage, including maiming of animals | 22.2 |
| Arson | 16.7 |
| Rape (child) | 15.8 |
| Robbery with violence | 15.6 |
| Unnatural (sexual) offenses | 14.3 |
| Blackmail | 14.3 |
| Fraud | 12.8 |
| Stealing (and poaching) | 11.2 |
| Burglary | 10.0 |
| Murder and murderous intent | 9.5 |
| Rape (adult) | 6.7 |
| Receiving | 5.1 |
| Manslaughter | 5.0 |
| Coining | 3.3 |
| Wounding, intent to wound, striking superior officer | 2.9 |
| Embezzlement, forgery, fraudulence as trustee, bigamy, performing illegal surgical operation | 0.0 |
| General population | 0.5 |
Another table from Goring shows which groups of crime are most likely to be committed by the deficients compared with the frequency of that type of crime in the general population. It is reproduced in part below.
| Nature of crimes | Total criminals | Mentally defective | Percentages of mental defectives among those committing various crimes | Percentages of general population committing the several offenses |
|---|---|---|---|---|
| Malicious damage to property | 55 | 22 | 40.00 | 0.406 |
| Stealing and burglary | 442 | 45 | 10.18 | 4.180 |
| Sexual offences | 101 | 13 | 12.87 | 0.199 |
| Violence to the person | 183 | 11 | 6.01 | 1.606 |
| Forgery, coining and fraud | 167 | 4 | 2.40 | 0.722 |
| Total | 948 | 95 | 10.00 | 7.203 |
Some very striking instances of recidivism on the part of the feeble-minded were summarized by Dr. Smalley in his evidence before the Royal Commission (83). He said:
“Against 130 out of 333 weak-minded prisoners who were unfit for ordinary penal discipline by reason of mental deficiency, no previous conviction had been recorded; but for this absence of record their nomadic habits might in part account. Against fifty-six 1 conviction had been recorded, against twenty-eight 2; the remainder varied from 4 to 105 convictions. About half had been convicted from 5 to 10 times.... Dr. Hamblin Smith, Medical Officer of Stafford Prison, as the result of a special inquiry into 100 mentally defective prisoners, found that 100 had a combined record of 1,104 convictions, or an average of 11 per prisoner, and this number was regarded as being below the actual truth. Ten of the prisoners had over 30 convictions. Dr. W. R. Dawson found that in the two prisons in Dublin 12.21 per cent. of the inmates were defectives. The average number of previous convictions for the females was 44.13. Many of them ran into hundreds, and one was in prison for the two-hundred and thirty-sixth time, and she was only twenty-nine years old.”
215So far as I can discover nobody has directly attacked the specific problem, what percentage of individuals of a given degree of deficiency who are not under supervision, become legally delinquent at some time in their lives. A slight contribution to the empirical study of the problem is made in the reports of the follow-up work in connection with pupils formerly in special classes in the public schools which I reviewed in Chap. IV, f. We have also a telling report by Bullard of the New York Prison Association published by Moore in 1911 (156). It follows the records of 85 feeble-minded boys and men 16-29 years of age, paroled from the Elmira State Reformatory in 1904. The whereabouts of 3 were unknown and 2 died. Of the remaining eighty, 31 were arrested again and 6 others violated their parole. One was arrested 19 times in this short period.
The best approach to this problem of measuring the potential delinquency among deficients is afforded by Goring's four-fold table for calculating the correlation between deficiency and criminality in the male population of England and Wales (20, p. 259). By means of the annual data on first convictions of crime at different ages and the probable length of life among criminals and in the general population he has been able to predict a potential criminality on the part of 7.2% of the general male population. In other words, the best estimate seems to be that about 7 in every hundred males in England and Wales will be convicted of crime at some time in their lives. About 10% of the convicts in England for a series of years have been isolated in prison treatment because of deficiency. If we now also assume with him that 0.46% of the non-criminal population is mentally deficient, we arrive at the table which enables us to determine, on these assumptions, that it is most likely that 63% of the deficients 216will be convicted of crime at some time in their lives. If instead of taking this estimate of 10% of the criminals being deficient we had taken 20%, then the probability of a deficient individual being convicted of crime would rise to .77.
On the basis of our summary of tested delinquents in the last chapter it seems extremely conservative to suppose that 10% of the manifest and potential criminals are as deficient mentally as the lowest 1.5% of the general population. Even with this assumption we find that the chances would be 48 out of a hundred that a person of this degree of deficiency would be convicted of crime.
These estimates, I believe, afford a telling argument for the indefinite isolation of at least those who are in the lowest 0.5% mentally on the ground of their potential criminality, independently of any question of the danger to society from the hereditary transmission of the diathesis of deficient delinquency.
We have heard much in recent years of the particular danger of allowing the better grade of feeble-minded, especially the morons, to be abroad in the community. Time and again it is asserted that it is this class of deficients which is most likely to become delinquent. There is a widespread confusion here between the statement that criminals in absolute numbers are drawn more frequently from the moron class and the statement that morons are relatively more likely than imbeciles or idiots to become delinquent. To the first alternative there would be no objection since morons are much more frequent than the lower grades of deficiency. On the other hand if morons are relatively more likely to be delinquent than imbeciles, then we should expect those just above the morons in ability to be more likely than morons to be delinquent. The technical answer to the 217problem whether the lower grades of deficiency are more likely to become delinquent could be best reached by discovering the correlation of delinquency with the different grades of deficiency.
Goring's data throw some light on this question since he has found the correlation between grades of intelligence and the degree of recidivism and also between intelligence and the frequency of bad reports in the penal institutions where the convicts were held. In both cases the tendency is clear for the weak-minded and imbecile to be more frequently convicted and to be reported more frequently for bad conduct than for the higher grades of intelligence which he classifies as unintelligent, fairly intelligent and intelligent. The correlation coefficient with frequency of convictions relative to time out of prison is -.16 and with frequency of bad reports is -.33. The correlation ratios are slightly higher in both cases. On the other hand the more intelligent are likely to be given longer sentences, the correlation being +.10.[33] It might be contended that his distinction between the lowest grades of intelligence is not objective and not very clear; but that the general tendency of the regression lines would be reversed at the lower extreme seems very improbable. In other words there is some reason to suppose that, relative to their numbers, the idiots and imbeciles would be more likely to be delinquent than the more intelligent feeble-minded provided none was confined in an institution. No idiot and few, if any, imbeciles could survive honestly in any environment without assistance.
How closely the degrees of immorality are associated with the degrees of deficiency remains one of the most 218important problems to be answered authoritatively by the correlation of these traits when properly measured. That the greater degrees of immorality and of deficiency are on the whole associated and not opposed we have good reason to believe, but there are undoubtedly examples in which the degree of immorality or delinquency is out of proportion to the degree of deficiency. The fact that certain instances are found of moral imbeciles without corresponding intellectual deficiency, which has been noted by Stern (188, p. 75) and by Anton (67), does not of course determine the direction of the tendencies. We must base our deductions as to the danger of delinquency among lower and higher grades of deficients on our knowledge of the general tendencies. Are morons, relative to their numbers, more dangerous to the community than lower grade deficients? We must not make the absurd deduction that because morons are most numerous they are most likely to be delinquent and should therefore be most carefully isolated or supervised.
Modern statistical methods afford the ultimate quantitative tool for determining the cause of delinquency, whether or not we also require that the data should be assembled under experimentally controlled conditions. The rapid strides which have been made in answering this fundamental question of criminology may be judged by noting the treatment of it in such a work as Goring's compared with the impressionistic literary style which has prevailed. Illustrations of particular cases, opinions subconsciously formulated by experts from wide experience in dealing with delinquents, even the votes of the majority of leaders in the field, give way before the acid 219test of measurement of tendencies in human traits just as poorer methods succumbed in the Middle Ages in the realm of the physical sciences. Quantitative determinations can no longer be brushed aside with a smile on the supposition that statisticians are the biggest liars. They must be answered by better data or more refined methods. The form of the discussion of social questions has changed. Correlation is a powerful new weapon for attacking these problems which promises to go far beyond the range of earlier blundering methods.
While partial correlation affords an ideal approach to answering the question of causation, it has been used only to a very limited extent. The necessary data for comparing the closeness of relationship of various suggested causes of delinquency are not available and too few who are interested in social problems have appreciated the significance of the method. We should, therefore, lay especial emphasis on the measurement of the correlation of deficiency and criminality by Goring. He laboriously assembled the only data which are sufficiently extensive to allow much reliance to be placed upon their statistical reduction. In his use of correlation, moreover, he acted under advice from the main center for this work at the Galton Laboratory in London.
If those who were “mentally defective” under Goring's designation were always convicted of crime and none of those who were not defective were ever convicted of crime, the measure of the relationship between criminality and deficiency would be expressed by a correlation coefficient of +1.00. If there were no relationship whatever between deficiency and criminality the coefficient would be 0.00. If the deficients were never convicted of crime and the non-deficients were always criminal the coefficient would be -1.00. Intermediate degrees in the 220relationship of these tendencies would then be represented by decimals which would be either positive or negative, depending upon whether the traits were associated together or were opposed. The coefficient which he found for the male population was +.6553, which was much higher than that for any other constitutional or environmental factor which he measured.
In calculating this correlation Goring regarded 10% of the criminal male population as defective. He found that this was in agreement with the common tendency in English convict prisons to class officially about this portion of the criminals as defectives and needing care. He also assumed that 0.46% of the non-criminal male population in England and Wales was defective, the proportion suggested by the report of the Royal Commission on Feeble-mindedness. By a careful computation he calculated that 7.2% of the males either have been or will be convicted of crime before they die. He then constructed the four-fold table on the basis of these estimates as applied to the 948 convicts whom he examined as to their mental condition. The coefficient was then calculated by Pearson's method for a four-fold table. This method assumes that the mental ability and the tendency to criminality are distributed normally in the population and that the difference in numbers between the criminal and the non-criminal, deficient and non-deficient are not too great. In case the percentage of defectives among the criminals were taken as 20% instead of 10% the correlation would be increased to .79.
Using the same four-fold method we may calculate the correlation between deficiency and juvenile delinquency among Minneapolis boys. It is necessary to make a good estimate of the proportion of boys who annually become delinquent in Minneapolis for the first time, and 221of the proportion of these boys who are correspondingly deficient. Fortunately these comparisons can be made fairly accurately on the basis of the reports for the year 1915 and of our tests of juvenile delinquents. We may use a minimum and a maximum estimate of deficiency among the delinquents corresponding to those that tested below borderlines which represented the lowest 0.5% and the lowest 1.5% of the population of corresponding ages. We need to assume that the frequency of tested deficiency among the boys found delinquent would correspond within these limits to the frequency among the Glen Lake group. The indices for the amount of school retardation in these two groups (Table XIV) indicate that this is a liberal estimate. We must also assume that the proportion of juvenile delinquents for the year 1915 may be regarded as typical for a series of years. The number of new cases of boys in juvenile court in 1915 was within 18 of the median number for the last four years. The result of these estimates is Table XIX for the minimum estimate of deficiency. A similar table for the maximum estimate of deficiency would be the same, except that the proportion of all boys of these ages who were deficient would be 1.5%, and of the delinquent group, 7.3%.
The computation of the correlations by Pearson's tetrachoric r shows the relationship between juvenile delinquency and deficiency among boys to be .16, P. E. .07, on the minimum estimate of deficiency. On the maximum estimate the correlation is .29, P. E. .05. In order to make a closer comparison between Goring's calculation and my own I have recalculated the correlation for his group on the assumption that 0.5% of the general male population were deficient and that 1.29% would be convicted felons of the type among which he found 10% to be deficient. This brings the minimum correlation for his figures to .59, P. E. .03.
| Non-Deficient | Deficient | Total | |
|---|---|---|---|
| Non-Delinquent | 22,305 | 109 | 22,414 |
| Delinquent | 268 | 4 | 272 |
| Total | 22,573 | 113 | 22,686 |
The total number of boys is taken from the census of school children for 1915-16 compiled by the attendance department of the Board of Education. It includes those in public, parochial and private schools and those not attending. The number of delinquent boys is taken from the report of the Juvenile Court of Hennepin County, Tables H and I. The number of repeaters and the proportion of delinquent cases dismissed at the hearing are subtracted from the total number of new cases.
The difference between a correlation of .29, the highest I found, and .59, Goring's lowest result, indicates that conviction for felony in Great Britain is more closely associated with deficiency than juvenile delinquency is associated with deficiency in such communities as Minneapolis. It is to be remembered, however, that Goring's calculation gave the convicts a life-time in which to be convicted, while ours gave the boys only 16 years. The relation of potential delinquency after 16 years of age to deficiency might be greater among Minneapolis males than the corresponding relation we found among the boys; but the difference in these correlations is more easily explained by supposing that the type of serious delinquency represented by sentences to penal servitude, in England at least, is more closely related to deficiency than are the lighter forms of delinquency found among the youth of an American city.
223The most significant fact demonstrated by the correlations between juvenile delinquency and deficiency is that there is a positive relationship which is significant in amount. With the maximum estimate the correlation is nearly 6 times its error. This is the first time that the relationship has actually been calculated in connection with any group of juveniles. We can say that when a Minneapolis boy is below the average in tested ability for his age, he is most likely to be .16 to .29 of the same amount below the average in legal conduct, both measurements being in corresponding units.
What then, is the significance of correlation in answering the problem of causation? So far as the statistical method itself is concerned it shows only a mathematical functional relation between the conditions measured, not a physiological relationship. In other words a correlation between deficiency and delinquency might be explained by both conditions being related to some more fundamental factor which might be the causal factor involved. One cannot reason from correlation to direct causal connection. On the other hand, by correlation we may directly compare the relation between any one trait and various factors. We can find out, for example, whether the association of delinquency with deficiency is closer than the association of delinquency with other factors which it has been suggested are causes of delinquency. Goring's work allows us to compare the correlation of the tendency to be convicted of crime with deficiency and with many other constitutional and environmental factors which have been measured, and thus our attention may at once be directed to that factor which the present evidence indicates as most fundamental. Unless the measurement of the various factors is shown to be seriously faulty or incomplete the outcome should 224determine our point of view as to the main cause of delinquency, until new evidence is forthcoming. This is the problem of the next section.
As we have noted above, the correlation of delinquency with various factors should give us a scientific point of view as to the main causal influence in criminality. Thanks to Dr. Goring this work has recently been carried far. His findings mark a new and higher scientific level in the study of criminology. No data are now available which modify his position in any important regard. I shall, therefore, attempt to give his evidence in the briefest possible manner, hoping that it may lead to a closer reading of his basal investigation.
First comparing a dozen factors in the individual's own constitution which may be measured by the death rates, Goring found the tendency to be convicted of crime was correlated most closely with alcoholism, .39; sexual profligacy (syphilis and aneurism), .31; and epilepsy, .26; while it was found to correlate with intelligence, .66. The closeness of the relationship of defective physique to criminality was expressed by coefficients of .18 and .19. Among the inner factors investigated were many of Lombroso's characteristics of the so-called criminal physiognomy of which so much use is made by phrenologists, such as asymmetries, projection of the chin, complexion, form of the face and features, kind of hair, tattooing, left-handedness, temperament, etc.
Following this analysis, we find that alcoholism, epilepsy, and probably social profligacy are closely associated with intelligence as well. By means of partial correlations 225he shows that when individuals of the same degrees of intelligence are compared there is only slight additional relation between alcoholism or epilepsy and criminality. The relations to these other conditions are therefore accidental, depending upon the fact that deficients are more likely to be alcoholic and epileptic, the fundamental constitutional factor being intelligence. Among over forty physical and mental factors, the only other condition which he found to have significant relation to criminality is a generally defective physique as shown by height and weight, neither of which is correlated with intelligence.
Regarding the above inner factors he summarizes his conclusion as follows:
“Our final conclusion is that English criminals are selected by a physical condition, and a mental constitution which are independent of each other—that the one significant physical association with criminality is a generally defective physique; and that the one vital mental constitutional factor in the etiology of crime is defective intelligence” (20, p. 263.).
Turning now to certain factors which might be supposed to be important mainly as environmental influences, Goring studied the length of imprisonment and the frequency of reconvictions for crime relative to the periods of freedom as two measures of the degree of recidivism among his criminal group. He measured the correlation between the degree of recidivism and such outer factors as formal education classified by the kind of school training, whether received in the elementary school, secondary school, or at a compulsory industrial or reformatory school for delinquents, also formal education as measured by the age at leaving school; effective education as 226measured by the grade in school reached at the time of leaving and by the educational grade assigned the convict in the prison school; regularity of employment classified under the headings regular, occasional, voluntarily unemployed, unemployable; alcoholism under estimates as to the convicts' intemperance, temperance or abstinence; family life, in which the standard of life was classified as well-to-do, prosperous poor, poor, very poor, and destitute; the influence of maternal authority measured by the age at death of the mother, order of the subject in the family, and number in the family, thus reaching the question of only sons and of size of family; nationality; and finally the relation of age at which the first sentence was received and the nature of the sentence to subsequent convictions.
The significance of the relation of these external influences upon the degree of recidivism is not directly comparable with the influence of these factors upon the tendency to be convicted or not to be convicted of crime at all, as he carefully explains. Since the distribution of the above factors in the population at large is not known, the relationship to criminality in general could not be measured for the outer factors as it was for the inner factors discussed previously. Reserving, then, our judgment as to how closely these environmental factors may be related to the criminal tendency not represented by recidivism, we can reach important conclusions as to their relation to the degree of recidivism. Only one of the coefficients was found to be large enough to be twice its probable error, so that as a whole they were not at all significant. He summarizes his conclusions as follows:
“The relative values of these contrasted coefficients demonstrate effectively and conclusively one truth: that an adverse environment is related much more intimately 227to the intelligence of the convicts than it is to the degree of their recidivism, or to the nature of the crimes they commit. Moreover, since mental defectiveness is closely related to crime, an easily imagined corollary to this truth is that the mental defectiveness of the convict is antecedent to his environmental misfortunes, rather than that his unfortunate circumstances have been responsible for the mental defectiveness of the convict, and his lapse into crime....”
“From the general trend of the results tabulated above, our interim conclusion is that, relatively to its origin in the constitution of the malefactor, and especially in his mentally defective constitution, crime in this country is only to a trifling extent (if to any) the product of social inequality, or of adverse environment, or of other manifestations of what may be comprehensively termed 'the force of circumstances'” (20, p. 287-288).
The caution which we have noted above, as to the influence of outer factors having been measured in relation to recidivism rather than to criminality, becomes more important when we find that the correlation of high intelligence with frequency of convictions is also low, only -.16 and to fractions of a year imprisoned +.10. Since the relation of intelligence to criminality in the general population is +.66, we cannot be at all sure that these outer factors, or some of them, might not also be much more closely related to criminality than they are to recidivism. Besides this caution we might also urge that some of the most important outer influences have not yet been evaluated by correlations. We know nothing, as yet, except by inference about the correlation of delinquency with the influence of bad companions outside the home, bad school adjustment, the effect of broken families aside from the early death of the mother, absence of proper recreation, and many other stimuli for delinquency which social workers have been studying for years by less conclusive methods.
228Just to recall the frequency of some of these other conditions associated with the environment of the youth we may note that Aschaffenburg says that Abanel found in Paris “among 600 criminals under twenty years of age in 303 cases the family life of the parents was destroyed owing to death, divorce, desertion, illicit relations, or to some similar cause” (208, p. 133). Again he states that in 1841 Father Mathew, by making 1,800,000 total abstainers temporarily reduced serious crimes in Ireland from 12,096 to 773 per annum in a period of three years. Miss Rhoades by a personal evaluation of many factors involved in each of 81 random cases of juvenile delinquency in Chicago found that the main cause in 67 cases was some home condition and in 9 others it was a special temptation in street gangs, while only in 5 was the main cause mental subnormality (171). That nearly half of the juvenile delinquents come from broken families, affected by death, divorce, or desertion has been frequently shown. A study of more than a thousand successive cases in the Minneapolis juvenile court by Miss Finkle showed that 39% of them were from families not normally constituted, families in which one of the natural parental guardians of the children had been removed (105). We also have an important study of the relation of the delinquent child to his home by Breckenridge and Abbot (82).
While there is always a possibility of finding some other factor closely related to delinquency and independent of capacity, nevertheless we should hardly urge this possibility at the present time as overweighing the accumulation of negative evidence which has been assembled in recent years, especially at the Galton Laboratory. We should remember that many so-called outer influences are, like the temptation to drink, related to the incapacity 229which precedes the temptations. There is also good reason to suppose that many bad environmental surroundings result from rather than cause deficiency. Even broken homes may be a result of incapacity, to which undoubtedly early death is related. The first essential for social philosophers is to recognize that so-called environmental factors may have their corresponding inborn correlates. This is almost invariable with home conditions. The problem is to weigh the relative importance of these outer and inner factors on the same individuals.
Both subjective and objective methods have been used in trying to determine whether heredity or environment has the most influence upon criminality. The earlier and subjective method is one for which Gruhle is perhaps the leading advocate. By this method an expert with wide experience judges the relative effect of inner and outer causes of delinquency in particular cases. In his study of 105 minor delinquents in a German industrial school Gruhle, after a thorough and systematic clinical and sociological study of each person, gave his judgment whether heredity or environment was the main cause of delinquency in the case. In his summary he concluded that in 9 cases the fundamental cause was found in the environment, in 8 cases in environment plus a subordinate influence of heredity, in 41 environment and heredity were balanced, in 20 cases heredity was the main influence but environment was a subordinate factor and in 21 heredity was considered the causal factor. This shows that, when each case was estimated separately, in his opinion heredity on the whole turned out to be more important than environment for this group. By the same subjective method Gruhle weighs the influence of family taints 230such as mental abnormalities, deficiency, and drunkenness as against the hereditary influence in crime, and comes to the surprising result that in 9 cases where both parents were abnormal mentally or drunken in only two cases was heredity the predominant cause of the delinquency, while in 7 cases where neither parent showed these taints the delinquency was invariably explained by heredity. The group whose delinquencies were in his opinion mainly due to heredity showed, curiously enough, less family taints from nearly every point of view. He concludes:
“The knowledge that so many of the criminal youths are abnormal is indeed very significant for the therapeutic treatment of the social offenders, for the choice of the ways which should be used to improve the youths; but this knowledge has no significance for establishing the causes of delinquency.... The abnormal parents really have more children who are abnormal and under the average in capacity, but their children are actually more seldom delinquent because of the natural tendencies than the children of normal parents” (121).
Healy has followed a similar plan in subjectively weighing the influence of various factors as causes of the delinquency of 823 recidivists before the Psychopathic Institute at the Chicago Juvenile Court. Although he does not directly estimate hereditary and environmental factors as such, his summary of these estimates of separate cases shows the main cause of delinquency in 455 of these cases to be some form of mental abnormality or peculiarity. Abnormal physical conditions, including excessive sex development accounted for 40 more. His other causes, which embraced only 26% of the cases, might possibly be regarded as directly environmental. They included defective home conditions, including alcoholism, bad companions, mental conflicts, improper sex experience and habits, etc.
231Thus we find that the two most important expert estimates of individual cases after exhaustive study apparently agree in placing the main causal influence on factors which are predominately inner rather than outer. The most serious objection to this method of approaching the problem is that we have no way of determining how far such a result is the effect of the expert's unintentional bias. Gruhle's analysis of his delinquent group, however, raises very clearly the question whether the total influence of heredity may not be markedly greater in the production of delinquency than merely the heredity influence through mental deficiency and abnormalities in the families.
A better method of evaluating the relative influence of heredity and environment would avoid the danger of subjective bias by studying objectively measured factors. With either the subjective or objective method correlation affords a better way of statistically handling the results. The best approach to an objective study of the inner and outer causes of delinquency by the correlation methods is furnished by Goring. The ingenuity of the biometrical procedure in applying correlation to resolving this perennial question of heredity and environment must be recognized by all who take the time to understand its methods. We can only briefly consider the results of Goring's chapter on “The Relative Influence of 'Inheritance' and 'Contagion' upon the Occurrence of Crime and the Production of Criminals.”
This work conclusively demonstrates that crime runs in families. The probable value of the correlation between conviction for crime on the part of the father and son was found to be .60, while the correlation between mother and son was only slightly less. The tendency to resemble brothers in criminality was shown by the 232probable fraternal correlations of .45. Whether this family resemblance is mainly through nature or nurture is the problem.
In analyzing the influence of the home he uses partial correlation and finds that the correlation between age at first conviction and the number of convictions for a constant period of time after the first conviction is -.243. “From the value and sign of this coefficient, we see that the earlier in life a child commits a criminal offence, and is consequently removed from his home, the worse criminal does he become; and, accordingly, we conclude that criminal proclivities are more bred in the home than inoculated there” (119, p. 368). This argues against the predominant influence of the home training or example as explaining family resemblance in criminality. Nevertheless, it would seem that the result might also be interpreted as meaning that the contact with other delinquents and official discipline outside the home at a more impressionable age notably increases the tendency to recidivism.
Besides the argument as to the earlier removal from home, we have a test of the question whether those kinds of crime that are most influenced by contagion show closer correlation within the family. His statement of the results is as follows:
“Our table 177, above, starting with crimes of fraud, passes to stealing and burglary—professional crimes, where the influence of criminal contagion should be the most intense; and then progressively to violence, arson and sexual offenses, in which last it is difficult to understand how the influence of example could have any effect at all. We can understand the influence of parental training in the original moulding of a professional burglar or thief, and, to a certain extent, it is conceivable that the constant spectacle of the lack of control in parents might 233lead their offspring to emulate them in acts of unlawful violence. But, that parental example could play any part of importance in the perpetration by their offspring of crimes such as arson and wilful damage to property, and, particularly, of sexual offenses, is not reasonably to be supposed. As seen in the above table, 177, the parental correlation for sexual crimes, and crimes for wilful damage to property is from .45 to .5; for stealing, it is from .48 to .58. We would assume then, from this evidence, that the tendency of the inherited factor in criminality is from .45 to .5, and the intensity of criminal contagion is anything between .05 and .1” (20, p. 367).
Other evidence as to the relative influence of heredity and training, which Goring suggests, is in connection with the difference in influence of the two parents. If the contagion were from either the mother or father alone, the difference in resemblance to that parent and the other might indicate the strength of the contagion. The difference amounts to about .05. This again, in his opinion, gives some idea of the relative importance of nature and nurture within the family. The measure would not be complete unless the hereditary tendency to resemble mother and father were equal and the contagion were all from one parent.
Husbands and wives tend strongly to resemble each other in crime, the correlation being .6378. This resemblance is of course not due to heredity. Goring believes that it is not due to contagion and argues that besides the subjective tendency for the criminals to associate together, there is here a large element of conscious choice of a mate among the criminal classes, especially as the criminal woman shows the tendency most clearly and would not be able easily to get a non-criminal husband.
This work of Goring illustrates how an important beginning has been made in applying the correlation method to objective records, in order to weigh the relative importance 234of hereditary and environmental sources of crime. Perhaps its most important support is the close agreement between his conclusions as to the importance of the native diathesis of criminality and other studies by the biometric school as to the family tendencies in physical traits such as stature, eye color, tuberculosis, insanity, and deafness. These all tend to show a correlation between parents and children or brothers and sisters of about .5 as compared with relations to environmental factors which tend to be less than .1 (165).
If one accepts the point of view that the cause of crime is to be considered analogous to that of pulmonary tuberculosis, his understanding of the etiology of crime gains immensely. The old question of whether the criminal is born or made is answered, “both.” But the emphasis from our present data is on the inborn tendencies. Moreover, being born with the criminal diathesis does not mean that a person is predestined to commit crime, but that he is more likely than his neighbor to be infected by the contagion of delinquency. We have only to catch the trend of recent scientific research to extend our vision further. The criminal does not lack a simple unit character which would otherwise make him whole as some of the disciples of Mendel seem to argue. Neither is the criminal diathesis a simple instinctive tendency like the tendency to make a specific response to a specific stimulus, e. g., to wink when an object approaches the eye; the criminal is not charged with a specific propensity to commit murder or to steal. The safety of those who are more susceptible lies in keeping away from the contagion of bad example and temptations to fall, toward which he is generally less resistant than others. Specific training in 235strengthening and guarding his weakest spots may in time build up a resistance to temptations, the amount of which we cannot yet measure. His hope lies in the recognition of his weakness and the adjustment of his living so that his whole organism may support the breach in his make-up during the struggle with himself and with society.
In this complex diathesis which means greater susceptibility to temptations, there is little doubt that mental deficiency is the main factor. Aschaffenburg has well expressed one effect of this particular causal factor: “The weak-minded are generally children of the moment.... The lessons of experience, which serve normal persons as a guide, in later events, soon fade, be cause they cannot be fitted into the existing condition of the ideas. The inability to understand, much less to form general points of view, is the direct result of mental weakness” (20, p. 180). Lacking the ability to organize their experience, fixed punishments have little restraining influence. Only prolonged training and supervision can save them from being the victims of the moment. Even the large majority above the grade of ability which would justify indefinite supervision still show their stupidity in the offenses they commit. Goring gives an instance of a watch repairer who was legally punished nine times for pawning watches entrusted to him to repair. Who would doubt that native stupidity is an important cause of the recidivism which is so common a criticism of our present forms of legal discipline? It is stated, for example, that 10,000 of those convicted in one year in England had been convicted more than twenty times before (165, p. 59). Even with school punishments the same association of bad conduct and stupidity holds. Kemsies has shown, as quoted by Terman, that the 16% ranking lowest in 236a group of pupils received 80% of the punishments, while the brightest third received almost none (194).
That the criminal diathesis is not limited to mental deficiency is demonstrated by Goring's results. He shows its smaller correlation with deficient physical size, alcoholism and suicidal tendency with such pathological conditions as insanity and epilepsy, independent of their relations to mental deficiency. In this connection Gruhle's opinion that the hereditary tendency to crime was greater among his non-defective families may be borne in mind.
That mental ability, and especially mental deficiency, is primarily a question of inherited capacity rather than training, is now indicated by a number of fundamental objective studies of the correlation of abilities within the family, which have been analyzed to show the relative influence of inborn and external factors. Among these studies Thorndike's investigation of the tested abilities of twins compared with brothers and sisters in the same family is the most objective, and is very convincing (199). He has also summarized the evidence so well that it is not necessary to go into the question here (198). One of the most important facts is that equal practise under the same conditions increases the difference between individuals rather than makes them more alike. The work of the English biometricians appearing in Biometrika and the monographs from the Eugenics Laboratory is the most important in this field, and cannot be summarized here. It includes family resemblance in both pathological and healthy mental traits (126).
As compared with these studies the attempt to show that feeble-mindedness is inherited, because many of those in institutions for the feeble-minded are from families showing mental taints, lacks cogency, since we are still uninformed as to what portion of the offspring of 237parents with and without deficient minds are deficient. Even if 85% of the children in institutions for the feeble-minded have tainted parents this does not mean that we know what percentage of deficient parents have deficient offspring. It is this latter fact that we must know in order to predict the danger of defective offspring from deficient parents. From what we know about the correlation of parents and offspring in mental ability, it is clear that the more deficient are the parents, the more likely it is that their offspring are deficient. Children of morons are, therefore, not so likely to be deficient as are children of parents with lower grades of ability. From the eugenic point of view, it is, therefore, most important first to protect society from propagation by the lowest grades of deficients, provided that all grades of deficients are equally likely to have children when left unrestrained in society. Since mental and moral qualities are probably correlated positively, the same emphasis would be placed on first isolating the lowest grades in order to reduce inheritance of criminality. The eugenic emphasis waits, however, on the discovery whether the greater tendency for the lowest types to be produced by the lowest types is overbalanced by any tendency of deficients or delinquents of lower degrees to be less productive when unrestrained in society.
The conception of a criminal diathesis does not stop merely with the notion that there is an inborn predisposition to crime. It considers further that offenses do not occur except under the stimulus of certain situations, even if such stimuli may be even more common than the tubercle-bacillus. The important question which it now puts to science is, “How much may the actual outbreak of delinquency be reduced with better methods of social prophylaxis?” Even if, “the chief tasks of social hygiene” 238are the “struggle against alcohol and against poor economic conditions,” as Aschaffenburg believes (68, p. 228), the chief emphasis from the best scientific work still seems to be that the problems of alcoholism, poverty and crime are more closely related to internal than to the external conditions which have thus far been measured. Guarding against the propagation of mental deficiency thus seems to be the most direct and hopeful method of attack, while the removal of infecting temptations, and training for greater resistance, should receive hearty, albeit subordinate emphasis.
33. See the next section for the significance of these coefficients of correlation.
1. In our attempt to interpret the volume of results concerning tested delinquents, we have accepted the common conception that the feeble-minded are those who, through lack of mental development, are social deficients. They cannot survive in society without supervision. In the words of the English Mental Deficiency Act, “they require care, supervision, and control for their own protection or for the protection of others.” Our present scales of development tests do not detect those deficients whose failure is not directly due to intellectual incapacity. We have called those not detected by tests “purely conative cases,” to distinguish them from the tested deficients, who were said to be “intellectually deficient.” These conative cases would not be feeble-minded except for their incapacity for prolonged acts of will. Deficiency thus specialized in volition is so unusual, however, that the study of tested deficients gives us a useful picture of the problem of feeble-mindedness. To get a general view of the relation of deficiency to delinquency we determined conservative borderlines with the Binet scale and then reinterpreted on a common conservative basis the results obtained in more than a score of investigations covering thousands of objectively selected delinquents who had been tested. This has enabled us very largely to remove the question of the frequency of deficient delinquents from the realm of subjective opinion. We may now be certain that under present conditions the problem of deficiency is most pressing in institutions for female offenders. The evidence also points to the greater frequency of deficiency among prostitutes and repeaters, rather than among ordinary juvenile delinquents. 240We have thus been able to restate the problem of the deficient delinquent more conservatively and to modify some of the current conceptions. This enables us to direct our efforts more intelligently, with greater foresight, and more hope of success.
2. A still broader outcome of this interpretative study is to increase the precision of the test scales for use in the diagnosis of social deficiency. This has been accomplished by an extended reconsideration of the borderlines of deficiency on test scales, particularly the Binet scale. A percentage definition of tested deficiency is suggested for determining the borderline below which an individual may be presumed to be so deficient as to justify isolation, and for setting off a distance above this on the scale for which the test diagnosis of social deficiency should be regarded as uncertain. By this means it is hoped that the developmental scale may be made safer and more useful as an instrument for diagnosing feeble-mindedness.
A quantitative definition for tested deficiency has its main justification in its success in discovering social deficients and in predicting social failure. With this in mind the percentages suggested as representing the social deficients or uncertain cases in the community were chosen after a careful search through the evidence as to the success of children who had been in special classes or institutions and an extensive résumé and analysis of the best expert estimates of the frequency of social deficiency. The conclusion was that these percentages may tentatively be placed so that those who would at 15 years of age be in the lowest 0.5% in tested ability among a randomly selected group, may be presumed to be so deficient as to justify isolation. Above these the next 1.0% may be regarded as uncertain, since the bulk of them would require some supervision or guardianship during 241life. These two borderlines have then been located on the Binet scale for both the immature and the mature so far as possible from the available data. In particular these borderlines for the mature have been found for the first time on the basis of a randomly selected group. Besides the records of Minneapolis delinquents these Binet borderlines for a typical random population of 643 15-year-olds is the main contribution of new data in the study.
The practical consideration of these borderlines in Part One and their location on the test scale emphasizes that a test diagnosis is only symptomatic, that the suggested borderlines on the Binet scale are determined from limited data which may not be verified in other communities, that the scale itself is imperfect, and that the results should be checked by other tests, especially by the school retardation, a new example of which is given for the Minneapolis delinquents. The plan of the percentage method of describing the borderlines readily allows for adjustment to more complete data or better developmental scales. The alternative to the use of a test record as symptomatic of deficiency is dependence upon the history of the case or physical signs, such as are found among Mongolians, cretins, epileptics, etc. These signs have been found among only about 13% of the deficient children (141). Expert opinion given on the history of the case is clearly less reliable than such opinion checked by even a crude objective test standard. In Part Two of this study the theoretical background for the percentage definition is compared with that of other quantitative definitions on the basis of the conceptions of mental measurement and mental development.
3. In attempting to suggest methods for diagnosis and control, which our summary of the scientific data makes necessary, we shall be led beyond the evidence presented 242in this study. To those to whom these suggestions may seem remoted from the foregoing pages, it may be said that they are the result not only of a review of the available research work, but also an outcome of several years observation of the practical handling of this problem both in this country and abroad. In that study I was led to visit several scores of institutions and schools for delinquent or deficient children in Austria, England, France, Germany, Italy and Switzerland. The methods suggested below for the case of the deficient delinquent are only modifications of what has been observed in actual operation.
An adequate diagnosis of deficiency involves not only the accurate knowledge of the present mental condition of the individual, but an understanding of the causes of that condition. This requires a complete family and social history of the individual and a knowledge of the medically removable handicaps. It would seem, therefore, that such a diagnosis may be best made by a commission which shall include a physician as well as a psychologist, or else by an expert in mental development who is provided with adequate facilities and assistance for discovering other handicaps than innate incapacity. For the group of uncertain and conative cases a final diagnosis should, if possible, be made only after prolonged observation in a temporary home school.
Frankfurt a. M. in Germany seems to have been the first to provide a specialized observation cottage for uncertain cases among children. This was established in 1900 and is much used by the juvenile court. Although it has a separate building and an isolated division of the grounds it is, however, connected with the local hospital for the insane. An improvement in this respect was made with the first provincial school for psychopathic children 243under compulsory training established near Leipzig at Kleinmeusdorf. This serves also as a distribution station and has two observation divisions through which all fürsorge children in the province pass. Only the psychopathic cases remain indefinitely. Detention homes for juvenile delinquents in this country quite generally are used for temporary quarters for cases to be observed, although these are not isolated from the other children. If an entirely separate observation institution is not possible, a more definitely recognized probationary period for observation of the uncertain cases should be arranged within other institutions. The efforts for clearing-houses for mental defectives such as that in New York City and the Ohio Bureau of Juvenile Research will help to distribute individuals to their proper institutions. The ideal is a separate observation home where all cases in which the question of mental deficiency and mental disease is raised may be sent before the individual is labeled. The effect of commitment to an institution for the feeble-minded, insane, or delinquent can be guarded against much better if the observation home is entirely isolated from all other institutions. The separate institution, however, is more difficult to obtain than a separate division or cottage in an existing institution. The latter forms a valuable intermediate step and is better than merely giving uncertain cases additional attention when other duties permit.
As a matter of legal procedure, diagnosis raises the troublesome question of expert advice in court. Two decisions have to be made about each case. First, is the individual deficient enough to justify isolation or guardianship? Second, considering the means of care available in the particular community, how should the deficient be cared for? The first is primarily a question which requires 244expert knowledge in mental development and should be so handled. The second decision requires knowledge about the individual's home and about the facilities for guardianship or isolation. It should be left with the authorities thus informed. This will usually be the court unless there is a commissioner or a committee especially charged with this duty.
An important advance in the legal definition of criminal responsibility of deficients should be made by avoiding all subtle questions of psychological analysis such as would be involved in deciding, for example, under the New York statute whether the accused “was laboring under such a defect of reason as not to know the nature and quality of the act he was doing or know the nature of the act as wrong.” Obsolete legal descriptions could easily be cleared away by adopting the statement of the law suggested by the Committee of the Institute of Criminal Law and Criminology for criminal responsibility and insanity. In substance such a law would then state that the accused was mentally deficient “so as not to be responsible ... for his acts or omissions at the time when the act or omission charged was made.” The New York law places an emphasis on knowledge which should be placed on will, only one feature of which is an understanding of the situation.
4. What should be the aim in the care and control of deficients and delinquents after diagnosis also depends upon a proper understanding of the causes of these conditions. We have summarized some of the best and most recent investigations in which a notable advance toward solving this problem has been made by means of the correlation method. This has proved to be a new and vigorous force for directing social progress. By no other method have we approached so near the solution of the 245cause of delinquency. It enables us to restate the problem of criminality as mainly a problem in the treatment of a hereditary criminal diathesis in which mental deficiency is the largest factor. These recent scientific measurements have deprived neither the eugenist nor the euthenist of the opportunity for service. There is plenty of congenial work to be done by those whose sympathies may exaggerate the influence of heredity, contagion, or training. As in the control of tuberculosis, so with the diathesis of delinquency, some effect is produced by predisposition, by training, and by external influences. Unless the present evidence, however, is outweighed by improved data obtained in the future, the most strategic point for attacking persistent delinquency is through the relation to deficiency, with heredity holding the heights.
With the immediate campaign against delinquency centered against the propagation of the social deficients, we have the atmosphere cleared so that it is possible to turn attention to the best means of attaining this end. Sterilization, isolation, or guardianship, by force or by consent, which of these methods promises best? This is not a question for detailed discussion here. We may, however, call attention to the strides that have been made by such legislation as the British Mental Deficiency Act of 1913 and to the summary of the laws of the several states in our country published at the University of Washington, Seattle. The question whether sterilization is desirable must at present be settled apparently by the judgment whether the benefit in reducing the propagation of the unfit outweighs the danger to morality through the temptation of known sterility. The question of isolation of the sexes by either sterilization or segregation resolves itself into the question of accuracy of diagnosis and prognosis. Our review of the uncertainties of 246diagnosis should make us cautious. When we consider the social survival of many of those trained in the public school classes for deficients and when a dozen girls discharged from the Massachusetts institution for the feeble-minded succeeded in getting along in society (164, p. 49), it would seem wise to place the emphasis on first isolating those about whose danger to the community through delinquency or propagation of deficiency there would be the least question. This would mean those of uncertain mentality who were already repeated delinquents or in imminent danger and those who were of the lowest grades of deficiency, not the morons who were of uncertain moral and mental ability. Among the clearly deficient there is no question but that the emphasis should be to isolate first the girls and women of child-bearing age, since their chance of obtaining mates is greater than that of the deficient males. With doubtful cases public guardianship, such as that provided by the British Mental Deficiency Act of 1913, affords a promising remedy. Even those who are of uncertain ability should, when in danger, be provided with whatever protection guardianship can give. In this connection a suggestion of Dr. Goddard in the Survey, March 2, 1912, may be utilized. A court in returning an individual who is of uncertain ability to his family or guardian may well warn them: “We shall leave him in your custody, but we insist that you shall care for him, shall be responsible for him throughout his life, shall see that he does not get into mischief, and above all that he does not become a parent. Whenever the time comes that we find you are incapable of performing or are neglecting this duty, then we shall take him and place him in a colony.”
The question where to isolate the deficient delinquent, whom Kuhlmann says is “equally well placed or misplaced 247in the institution for the feeble-minded and the reformatory,” (140) is answered in substance by Supt. Murdoch of the State Institution for the Feeble-Minded in Western Pennsylvania. He suggests that in large states the deficient delinquents might be cared for in an institution which should bear the same relation to the state institutions for the feeble-minded and the penal institutions as is now held by the asylums for the criminal insane. Where a separate institution is not possible the affiliation with the institutions for either the delinquents or the deficients may be tried by means of colonies especially set apart in them. In Massachusetts these divisions for the deficient delinquent are connected with the institutions for delinquents.
5. Turning to external influences upon delinquency, we find that their effect has been measured mainly in connection with the tendency to repeat criminal acts. It has been shown by Goring that even such important influences as the example of criminality in the home, kind and amount of schooling, irregularity of employment, alcoholism, size of family, low standard of living, early death of mother, etc., have generally been found not to increase notably the tendency to recidivism while they do correlate decidedly with deficiency. Nevertheless, it has not been determined whether these external factors may not have an important influence upon the first manifestation of the criminal diathesis even though they tend only slightly to increase recidivism. Should these external influences prove to be not more than a fifth as important as deficiency and heredity, which now seems to be indicated, we need to hunt for other outer influences which may really prove to be more important.
Among bad external influences as yet unmeasured is maladjustment to school among those of passable ability. 248We have given some evidence as to this which we found among a group of delinquent boys at a county farm school, when their test records were compared with their positions in school. As a possible serious source of delinquency, bad adjustment to school work should be studied further, since it is a matter that could be easily corrected by the assistance of special teachers. With the earlier discovery of deficient children by means of mental tests, it should also be possible more definitely to direct the training so as to build up resistance to worldly temptations. How much could be done in this direction we cannot yet say. We have undoubtedly wasted much effort in the past in trying to create intellectual capacity in those who are innately deficient in intellect. Fortunately we are now directing our attention to training them to acquire passable ability in simple occupations, or to adjust themselves to the life of a colony. In the education of the mentally weak the most promising field is undoubtedly with the conative cases with passable intellects. At Templin, outside of Berlin, there has been established the first home school devoted entirely to the training of such unstable and inert boys. This specialized institution for conative cases, which was founded by a philanthropic society at the suggestion of Prof. Thiedor Ziehen, marks a most important advance step in the problem of training the mentally deficient. The results of specific training for the social adjustment of the intellectually and of the volitionally deficient will be awaited with great interest.
6. Shall the public authorities have the power to compel isolation and special training at local or state schools? These powers have already been provided by laws in a number of states. Thus far the law has not outstripped scientific knowledge. How far the authorities should 249use their discretion under these laws to force isolation is a question which calls for the utmost good judgment on their part. In case the parents or guardians of the socially deficient can be convinced of the desirability of such isolation, this procedure is undoubtedly to be urged. When the guardian has once consented to the isolation of his charge, he should not be permitted to remove the individual from such care without the consent of the proper public authority, which would of course be reviewable in court. During this period of uncertainty as to the prognosis of social deficiency, such a procedure would perhaps be preferable to forced isolation in most cases, since the authorities might be less troubled by the frequent annoyance of legal actions begun by parents who had their children forcibly removed to institutions. In some states unscrupulous attorneys have deliberately stirred up parents to try to get back their children who had been taken away by force, thus seriously interfering with the administration of laws for compulsory isolation. Without the possibility of compulsory isolation of the socially deficient for an indefinite time, we shall perpetuate the disgraceful spectacle now observable in many states which cannot legally prevent a feeble-minded parent removing a feeble-minded girl from an institution to which she may be brought back a few years later with one or more illegitimate, feeble-minded children. Our legal omissions should not thus handicap the wisdom of society. The 1917 codification of the Minnesota laws relating to defective, delinquent and deficient children should be seen by those who are interested in the legal aspects of these questions. It was brought about by the Minnesota Child Welfare Commission, of which Judge Edward F. Waite was chairman.
7. In case we suddenly segregate for life all those who are so deficient that we are justified in isolating them, 250would that solve the problem of delinquency for the next generation? Although this would be the most important attack which could be made on the most important known cause of delinquency, we must still answer that the results would hardly be comparable with a jail delivery. There is nothing to be gained by turning our backs upon the facts. Goring has estimated that 7.2% of the male population of England and Wales commit crime before death. We could not possibly suppose that more than 1% of the male population could be justly isolated for deficiency. Even if all the deficients committed crime, at least six-sevenths of the criminals in these countries, about which we have the best means of estimating, are presumably individuals who could not be isolated for deficiency.
Moreover, Goring's estimates regarding the British convicts enable us to judge that only about 25% of the criminals of this generation inherit a predisposition to crime from parents who were the criminals of the last generation (20, p. 336). Nobody has suggested isolating all persistent delinquents. We could not expect that the isolation of both the deficients and delinquents would completely remove the diathesis of delinquency from society. The predisposition is received not only from the deficients and delinquents, but also to some extent from those above the borderlines. We could not raise the borderlines of deficiency without isolating many whose social deficiency or delinquency it would be presumptuous to predict. We should not look forward, therefore, to the sudden elimination of the problem of delinquency even when it is attacked at its most vital spot. On the other hand Dr. Hart, in a bulletin of the Russell Sage Foundation, has worked out a practical plan which would isolate the lowest 0.3% of the girls and women 251of child-bearing age in this country within five to ten years. Some similar plan for isolating all deficient delinquents would materially lessen the cost of recidivism in the present generation.
The most hopeful sign is that we are no longer content merely to guess at the relative importance of the sources of delinquency and deficiency, but our efforts to promote social welfare are directed by scientific investigations which are utilizing new and more efficient methods of research.
In defining the borderline of feeble-mindedness it will be found that certain assumptions are usually tacitly made as to the form of the curves of normal and retarded development. These assumptions which are often based on vague conceptions of mental measurements should be brought clearly to mind if we are to compare the relative merits of different scales of mental tests or different ways of stating the borderlines of deficiency. With this in view it is proposed to take up in this second part of the monograph a brief technical discussion of the units of mental measurement, the equivalent individual differences at different ages, and the curves of mental development. The bearing of these conceptions on the various quantitative definitions of tested deficiency, including the percentage definition, will then be discussed in the following chapter. Practical advice as to individual diagnosis or group comparisons has been confined to Part One, so that those who are not concerned with the theoretical assumptions on which the conception of mental development and the interpretations of tested deficiency are based should omit Part Two.
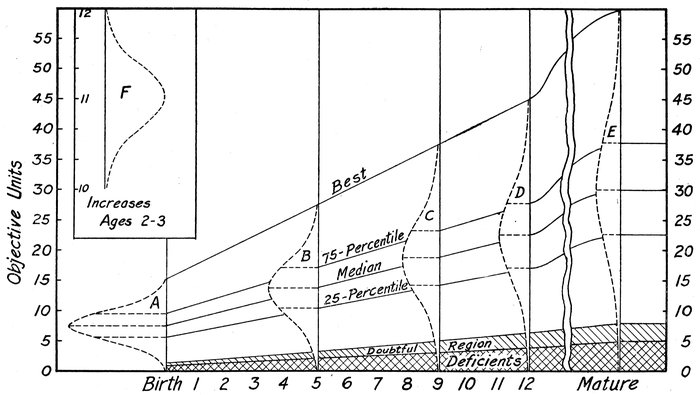
Fig. 3. Hypothetical Development Curves (Normal Distribution)
254When we try to picture to ourselves the significance of individual differences and mental development we are at once forced to think in terms of graphs showing the distribution of abilities at particular periods of life and the changes from one life-age to another. To simplify the discussion I have presented in Fig. 3 the graphic picture of the conditions on the simplest hypothesis, namely, that mental capacity at each age is distributed in the form of the normal probability curve extending to zero ability and that individuals retain their same relative capacity on the scale of objective units.
In considering the curves of development it is desirable first to notice the differences between measurement in equal physical units and measurement in equivalent units of ability or of development. The difference in the point of view of the two forms of measurement is so pronounced that I can hardly hope to make myself clear to those who are not somewhat familiar with such terms as “distribution curves,” “frequency surfaces,” “standard deviation,” and other phrases connected with the theory of probability, which are treated at length in such books as Thorndike's “Mental and Social Measurements” and Yule's “Introduction to the Theory of Statistics.” We often, by mistake, regard the growth of an inch in height, for example, as always representing an equivalent unit of growth. This will lead us into rather serious misconceptions unless we are careful, for it is perfectly evident that the growth of an inch in height has a very different significance for the three-year-old boy than for the eight-year-old. Half of the three-year-old boys grow about 3 inches during a year while at eight years of age not more than about one in seven grow that much. Moreover it 255is not always satisfactory to regard the same relative increase in physical size as an equivalent unit of development. To say that a boy 20 inches tall who grows 1-10 in height shows an increase in development equivalent to a boy of 50 inches who grows one-tenth, may be quite misleading. Nearly every 20-inch child grows one-tenth in height in a year while not one in fourteen of the boys who are 50 inches in height may grow at that physical rate. In considering human traits, and especially developmental traits, it would seem to conduce to more significant thought if we gave up at times our habit of thinking in terms of equal or relative physical units and thought instead in terms of more equivalent biological units.
In the measurement of mental ability, moreover, it is exceedingly difficult to utilize equal physical units. Most of the objective units which are commonly called alike are clearly not equal even in the physical sense. “Spelling one word,” for example, is not equal to spelling another “one word;” but only equal to spelling the same word. Out of such units of amount accomplished, it is, of course, not possible to build a satisfactory scale without referring to some other concepts of measurement. Some tests, however, are scored in equal units. When the measurements for example, are in the units of time it takes to perform the same task under the same outward conditions we have the possibility of a scale of equal objective units. Such a scale is approached by the results with the form board test which give the number of seconds it takes children to place blocks of different shapes in their proper openings.
Even the unit of time may be deceptive in name, as it is with the Binet scale. A year of time is, of course, the same physical unit and the task proposed with the 256Binet scale is always the same, but the other essential with this scale, the children of each age who pass the tests at each age norm, varies decidedly. “Test-age five,” for example, means 44% of the children pass and “test-age eleven” means 88% pass, even with approximately random samples of children of these life-ages. This question of the equality of the Binet age units will have to be considered further, therefore, in connection with the other concept of equivalence used in psychology.
In order to determine equivalent units of activity we find that a number of different concepts have been utilized. With some of the scales for measuring educational products, such as Thorndike's Scale for Handwriting, equal units of merit in handwriting mean differences judged equal by relatively the same proportion of competent judges. This form of unit has not been used, however, in any scale of mental development thus far proposed.
In the measurement of mental ability the most commonly accepted idea of equivalent units is that they are provided by the units of standard deviation for a series of measurements which distribute in the normal form. The meaning of these units may be understood by referring to Fig. 3 which shows Gaussian or normal distributions of abilities of individuals at various periods of life in curves A, B, C, D and E. The straight lines of the measurement scales form the bases of these distribution curves. These graphs represent the normal form of distribution usually expected when any fundamental ability is measured in a random group. If the number of cases at each unit of measurement are plotted by a point placed relatively as far above the scale, used as a base line, as the number of cases found at that unit of the scale, it will be discovered that these points arrange themselves in the form of a symmetrical curve high at the middle and flaring out 257along the base-line scale. This bell-shaped curve, known as a normal probability curve, shows that the largest number of cases occurs at the middle or average measurement. From this middle point on the scale the number of cases falls off gradually and symmetrically in both directions. Distances along the base line of this distribution surface may then be measured in terms of the standard deviation regarded as unity. This S. D. is the best measure of the scatter of the deviations. It is the square root of the average of the squares of the deviations of the separate measurements from the average of all the measurements. There are approximately four units of the standard deviation between the average and either extreme when the distribution is normal, as in Fig. 3. Only six cases in one hundred thousand fall outside these limits.
The studies of biological traits suggest that a unit of the standard deviation is the most important measure we have for equivalent degrees of any trait which distributes normally. It measures the same portion of the total distance from the lowest to the highest ability on any objective scale so long as the distribution of measurements is in the normal form. It thus affords the best interchangeable unit from measurements at one life-age to those at another, provided that the distributions keep close to the form of the normal probability curve. This is the assumption on which practically all the developmental scales have been based. The difference in ability between an individual at the average and at -1 S. D. (standard deviation) below the average is equivalent to that between the last individual and one at -2 S. D. The same distances along the base line of different distribution surfaces measured in terms of their respective deviations set off equivalent portions at each age so long as the distributions are normal. For example individuals 258measuring between -2 and -3 S. D. in any distribution in Fig. 3 are equivalent in ability to those lying between -2 and -3 S. D. in any other of these normal distribution surfaces. Later we shall consider equivalent units when the form of the distribution of ability is not normal or is unknown.
We may now compare the relations of the units in the physical scale, shown at the left of the figure, to units of the scales for adults or for the immature of any age, expressed in units of the standard deviation from the averages of these groups. Relative ability measured on the physical scale or any one of the distribution scales in Fig. 3 will be found identical since they all start from the same zero point and the distributions are all normal. But the ability of an individual in one distribution can hardly be compared with that of an individual in another distribution in a biologically significant way by their actual positions on the physical scale. A physical unit, does not measure the same sort of fact of development in a scale for the immature that it measures in the scale for adults or that it measures in another dynamic scale for the immature. This can be seen when a physical unit is compared with the amount of standard deviation which it measures in the different scales. Moreover, the correspondence of relative distances on the physical scale and any one of these other scales will not hold the moment the distributions do not start from the same point or are unsymmetrical.
It does not seem seriously wrong to suppose that there are some individuals at any age who have no more mental ability than the baby of the poorest mental ability at birth. At any rate our intelligence scales are hardly fine enough to measure the difference in intellectual capacity between the dullest adult idiots and the dullest idiot 259babies. We shall, therefore, here assume that mental capacity extends to zero at each age. The importance of this will be evident when we consider the question whether the distributions of ability are symmetrical around the average point at each age. Postponing for the present the discussion of unsymmetrical or skewed distributions, we may consider the several meanings of stages of development.
In applying the concept of the probability curve we should distinguish between individuals who have attained their mature mental capacity and those who are still maturing. The former would be represented by a random group of adults (Distribution E, Fig. 3) the latter by a group of nine-year-olds (Distribution C). If we say, for example, that a child has reached a certain stage of development we might have in mind the final distribution of mature capacity or the distribution of capacity among those of his particular age or of all ages. When we compare stages of development we must, therefore, be careful to indicate the distribution surface to which we are referring.
An increase in development may refer to at least five different things depending upon the scale of measurement to which reference is made. Besides an increase measured by the physical scale, the scales for adults, for the immature or for all ages, to which we have already referred, it may mean an increase judged by the distribution of increases which individuals of the same life-age and capacity make in the same period of time. This last meaning may be the most significant, although it has never been used. It has reference to a distribution surface of increases such as is represented in Distribution F, Fig. 3. This is intended to show the increases in one year of all two-year-old children who had average ability at 2 years, on the assumption 260that at 3 years these children would on the average equal the average of all three-year-olds. It is clear that when these increases are measured in objective units the latter have a still different significance from that assigned to them in connection with other scales. An increase of one objective unit here might represent twice the standard deviation, while it only represents 0.2 of the standard deviation in another distribution.
A sharp disagreement of opinion as to whether the Binet year units can be regarded equivalent has arisen between Karl Pearson, Director of the Galton Laboratory in London, and certain psychologists who have used the Binet scale. Cyril Burt, for example, says, as quoted by Pearson:
“Except for rough and popular purposes, any measurement of mental capacity in terms of age is unsatisfactory.... The unit fluctuates in its significance all along the scale. When the child is just beginning to walk and talk, when he is 7 or 8, when he is 10 to 11, when he is on the verge of puberty—at these different periods a retardation of a single year means very different things” (164, p. 36).
A number of good psychologists including Yerkes, Terman, and Kuhlmann, agree with Burt in maintaining that a year of retardation at different ages has very different significance.
With this statement of Burt, Pearson takes issue, saying:
“Can the psychologist to the London County Council ever have seen the growth curves of children, or would he write thus?... There is no valid reason to suppose that a year's growth in mental power may not 261be taken for all practical purposes to mean the same unit for ages of 6 to 15, the period for which Binet and Jaederholm have used the tests” (164, p. 44).
Like many other apparently opposite statements both contain truth. The conflict arises apparently, first from a disagreement between the data obtained with the Jaederholm form of the scale, on which Pearson bases his statement, and data obtained with other forms of the scale; second, from a discrepancy in the points of view. Pearson stresses the fact that the mental year-marks equal average growth increment with the Jaederholm scale (167). He shows that the regression of years of mental excess (or deficiency) on increase of life-age is a straight line, just as he found it with physical measurements. Moreover, the standard deviation of the mental measurements for the entire group of normal school children, 6-14 years of age, was found to be about one year of mental age (.96 year for the corrected data) (167). To which Pearson's opponents might reply, these facts are of comparatively little significance unless the deviations for the separate ages are alike in terms of these year units on the scale. Neither linear regression nor the balancing of years of excess by years of deficiency at each age indicates that the deviations of the separate ages are alike in terms of the year units. The new Stanford scale, for example, shows both of these conditions and yet the range of months of life-ages which sets off the middle 50% of the children of the different tested ages increased decidedly from 6 to 14 years of age. The middle half of the tested ages, for example, at age VI on the scale include a randomly selected group of six-year-old children whose range of life-age is ten months, at age VIII on the scale this range is 13.4 months, at X it is 16 months, at XII, 20 months, and at XIV, 26 months. “The number of 6-year-old children 262testing 'at age' is approximately twice as great as the number of 12-year-olds testing at age, and 50% greater than in the case of the 9-year-olds” (196, p. 557).
To this argument Pearson might reply that he had not overlooked the question of variation in the deviations from one age to the next for he has a footnote in which he states regarding the Jaederholm data: “There are, however, relatively little differences in these mental age standard-deviations of the normal children beyond what we may attribute to the effect of random sampling” (164, p. 46). In this respect, then, the Jaederholm data differ notably from Terman's data obtained with random groups with the Stanford scale and, as I shall show, from data obtained by Goddard with the 1908 Binet scale, the two largest groups of Binet test data which have been collected. Even with the Jaederholm data on efficient school children, although the largest difference between the standard deviations of different age groups is only about twice its probable error, it is notable that 24 of his 39 7-year-olds are included within an interval of the middle year of tested age, while only 9 of his 35 11-year-olds are included within the same middle year interval.
Taking Goddard's data for the 1908 scale for the separate ages from 5-11 at which probably the factor of selection for his groups may be neglected, I have calculated the standard deviations from his Table I and find them as follows:
| Life-Ages | |||||||
|---|---|---|---|---|---|---|---|
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| Standard deviations in Mental Excess or Deficiency | 1.10 | .98 | .93 | .99 | 1.04 | 1.23 | 1.19 |
The differences between the deviations for ages 7 and 11 or between ages 8 and 10, are more than three times their standard errors, so that we would not be justified 263in assuming that the standard deviations of the separate ages measured in terms of years of excess are equivalent. There seems to be a tendency for the deviations to increase, at least from age 7 to 10 and 11.
The comparison of the year units on the Binet scale with the diagrams in Fig. 3 shows that if the scale at each life-age shut out the same lowest proportion, say half, of the children of that age, then the year units might be regarded as equal in the sense of equal average growth increments, as Pearson suggests. A child 7 years of age testing VII would be at least one annual average-growth unit higher in mental development than one of 6 years testing VI, and so with each age until the limit of development had been reached. This is the condition approximated closely for children by the new Stanford scale and the corrected Jaederholm data. Since there is little prospect, however, even with a scale perfected so far as its age norms are concerned, that the total distributions for each of the different years would be the same multiple of the year-units, the main significance of the age units is in permitting the statement that a child had reached the tested development normal for the children of a certain age.
It is also legitimate to use years of retardation as a short way of expressing rough borderlines when they happen thus to afford an easy method of empirically describing equivalent borderlines for a particular scale. This is what I have done for convenience in Part One of this book. I certainly do not mean to contend that four-years retardation has theoretically the same significance at different ages, in terms of the deviation of the separate ages. To me the Binet years are no more than names for certain positions on the scale.
To most psychologists who have been dealing with the 264measurement of mental development, I believe that the most significant concept of equivalent units would be in terms of the deviations for each age provided that the form of the distributions remained normal. But the deviations vary so much in the terms of the year units that it is not likely that they will be willing to accept a year of excess or deficiency as an equivalent unit for different ages with the common forms of the scale in use in English-speaking countries. Moreover, below the age of 6 and above 15, the limits which Pearson discusses, there is good reason to expect the year unit to vary still further. This Pearson recognizes for the complete developmental curve. It is only at the intermediate years, in which the average increases are most constant in relation to the deviations of the separate ages, that the year unit may be at all serviceable in measuring the deviation of a child from the norm of his age.
With the scales in use in this country the Binet year units are not equivalent in the sense in which they are usually spoken of as equivalent. We should recognize this and emphasize it. Even if the norms at each age marked off the same proportion of the individuals, as shown in A and B of Fig. 4, unless we knew that the forms of distribution were always alike, we should not know that the distance between successive age norms was the same on any sort of objective scale other than average age increments. Moreover, we would not have an objective scale of equal units applicable to measuring the deviation of children of any one age. The average annual increments would not necessarily represent the same proportion of the total distance from the lowest to the highest ability at different ages even if the distributions were all normal. With normal distributions it would also be necessary to demonstrate empirically that the annual average growth increment between successive ages always bore a constant relation to the deviations at these adjacent ages as shown in B of Fig. 4 where the increment is equal to 1 S. D. at each age. This could not possibly hold when the increment lessened near maturity.
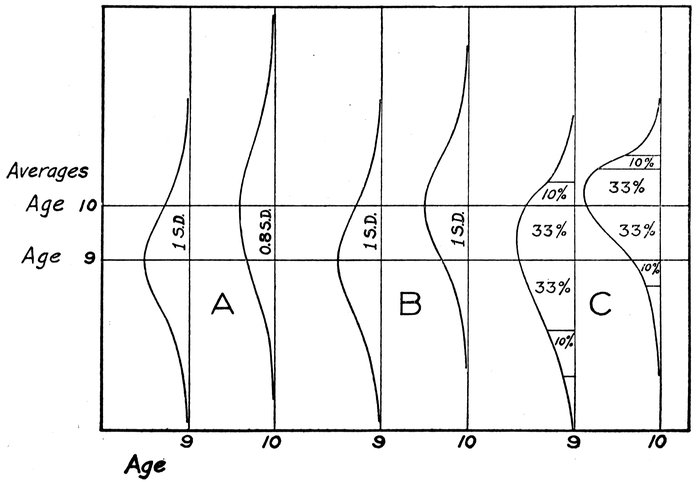
Fig. 4. The Question of Equivalence of Year Units.
266If the distributions of ability were variously skewed, the year units of excess or deficiency would not be shown to be equivalent at the different ages even if the proportion of individuals one year accelerated was equal to the number one year retarded, two years accelerated equal to those two years retarded, etc., at each age and the norm at each age shut out the same proportions of the age group. This is shown in C of Fig. 4 in which the year units are clearly not equal steps from lowest to highest ability even for the same age and yet the usual criteria which have been suggested for discovering the equivalence of the units are fulfilled. Whether the actual distribution of ability is skewed or normal cannot be determined by the Binet scale, of course, on account of the uncertain and probably varying size of its year units in measuring deviations at any age.
With the empirical evidence against the equivalence of the year units and the impossibility of determining their equivalence unless we first know that ability is distributed normally at each age, it is certainly hazardous to assume that individual deviations measured in terms of year units are equivalent at different ages.
It may be noted that it is quite as hazardous to suppose that the units of the Point scale are equivalent in any theoretical or practical sense. This question will be discussed later in Chap. XIII, B, (b).
Before leaving the question of the significance of units on a scale described in terms of the standard deviation we should ask whether tested mental abilities have been found to distribute normally, i. e., in the form of the symmetrical Gaussian curve with each extreme the same distance from the middle measurement. Contrary to the usual supposition in this matter, it seems as if the evidence was somewhat against this assumption, although neither position can be asserted at all dogmatically on the basis of our present data. A résumé of this evidence which I have given below makes it appear that the assumption of a normal distribution will not conflict with a practical use of normal probability tables for medium degrees of ability, but may quite seriously interfere with such use for the borderline of deficiency. There is little doubt, as Pearson believes, that the bulk of the children now in special classes for the retarded in the public schools would fall within the lower range of a normal distribution fitted to the general population. On the other hand, there is likely to be a respectable minority of the deficients which will be beyond such a normal curve. These facts are sufficiently evident, I believe, to make it impossible to base quantitative descriptions of borderline of deficiency on a hypothesis of normal distribution.
The best evidence on this point is probably the data of Norsworthy with eleven tests on groups of 100 to 150 feeble-minded children in institutions and special classes and 250 to 900 normal children. She expressed the position of each child in terms of the deviation of the group of normal children of his age for each test. Pearson has presented her data graphically on the assumption that her defective group represented 0.3% of a general population 268of 50,000 children, and then fitted a normal distribution curve to her data with her normal group. The result makes it evident, especially for the intelligence tests, that the defective group would better be described as part of a skewed distribution. To less extent this is also true for the maturity and memory tests (15, p. 30). Norsworthy's own table of data show that 43 of the 74 feeble-minded taking the intelligence tests were over -5 times the probable error of their ages below the averages of the normal children, a criterion which she proposes as indicating ability outside of that included in the normal species. Moreover, 9 children score between -22 P. E. and -32 P. E. which is far beyond any conceivable extension of the normal curve. Her figure for the composite results of all her mental tests is also manifestly skewed toward deficiency although she hesitates to adopt this conclusion, and was content with showing that they grade off into the distribution of normal children.
The other data, which I have found, that indicate that tested ability, when measured in equal physical units for the same task, is skewed toward deficiency, have to do with tests that are pre-eminently for psychomotor activities rather than intellectual. They consist of Sylvester's and Young's results with the form board test on Philadelphia school children, Stenquist's results with his construction test, and Smedley's results with the ergograph test on Chicago school children. Here we may apply the better criterion of the distance of the quartiles above and below the median of the group. These positions would be less likely, through extreme records, to be affected by chance conditions during the testing.
It is to be remembered that if the records of school pupils appear to be normally distributed this would not settle our problem, since it is apparent that idiots and many 269imbeciles are not sent to the public schools at all. The lowest children at any age would not be represented in the regular school groups. On the other hand, the brightest children are not generally drawn away from the public schools at least before 14 years of age in this country. We shall confine ourselves, therefore, to school-children 6-13 years of age. If we find that they show ability skewed toward deficiency the results will underestimate rather than over-estimate the skewness.
Sylvester (191) tested with the form board a group of 1537 children in the Philadelphia public schools, from 80 to 221 at each age from 5 to 14 inclusive. “Except that no especially backward or peculiar children were included there was no selection.” This study gives, with the complete distribution tables, the number of seconds required for the same task by the children at each age. If we find that the limit of the lower 25 percentile was farther from the median than the limit of the upper 25 percentile we can be reasonably sure that the difference would be still greater if the excluded deficient and backward children were also included. By calculating the quartiles and their differences from the medians at each age, I find that for only two of the eight ages is the upper quartile farther from the median than the lower quartile. The average excess of the distances of the lower quartile is .64 of a second. At only age 7 is the difference three times its probable error, 2.1 seconds, P. E. .67. The form board distributions thus tend to be slightly skewed toward deficiency. The errors of the quartiles were found by the method given in Yule's Introduction to the Theory of Statistics, Chap. XVII, which assumes normal distribution, so that they are too small. The skewness is more manifest when the extreme measurements are compared with medians at each age. It is not possible, unfortunately, 270to compare his group of normal children with those in the special classes since he did not use the same method of giving the test.
Since it was not important to compare the amounts of skewness in different data, I have not attempted the more elaborate calculations of coefficients of skewness. These would give the results a more elegant statistical expression. The simpler method I have here used affords more convincing evidence of asymmetry for the non-mathematical reader.
Young has published the results with Witmer's form board test on approximately two hundred Philadelphia children for each age, giving the results for the sexes separately for each half year of life-age (227). This affords 36 different groups in which he gives the median and upper and lower quintiles for the shortest time records. The lowest quintile is farther from the median in 25 cases, equal in 6 and less than the upper quintile in only 6 of the 36 comparisons. This skewness would have been even greater if children of the special classes had not been excluded from his groups.
Stenquist's results (54) with his construction test are scored in arbitrary units in which allowance is made for the quality of the score, but we should expect no constant effect on the form of the distribution from the character of these units of measurement. At ages 6 to 13 he tested from 27 to 74 pupils randomly selected from the public schools, a total of over 400. For six of these eight ages the lower quartile is farther from the median than the upper quartile, when calculated from his distribution table. The number of cases at each age, however, is so small that the largest difference, 15 units, is not three times its probable error, 6.
271Smedley gave his ergograph test to about 700 school children of each of the ages we are considering. Since he tested so many more subjects than any other investigator this should provide the most valuable data on the question of distribution with a test recorded in the same physical units for the same task. Unfortunately, his results for two succeeding years are so directly contradictory to each other that they seem to have no significance for our problem. The simplest explanation of this contradiction is that the groups tested may have been selected on a different basis each year.
A casual observation of his standard percentile curves for the ergograph test at the different ages gives the impression that the distributions are decidedly skewed toward deficiency, but this impression is not justified by a careful analysis of his results (51). In the table which accompanies his standard percentile curves, giving his total results for the two years, we find that there is a sharp disagreement between the distributions of the boys and the girls. The distributions for the boys at each age between 6 and 13 years show a greater distance, measured in kilogram-centimeters, from the median to the 80-percentile than from the median to the 20-percentile, in 5 ages out of 8. The total difference is also slightly greater between the median and the upper 80-percentile. On the other hand, the table for the girls at these ages shows the 20-percentile farther from the median in 5 out of 8 ages, with a total difference considerably greater than that shown for the boys. Usually the differences were small compared with their errors. With the boys only at age 13 was the difference in favor of the 80-percentile three times its probable error, while with the girls the four oldest ages show the distance of the 20-percentile greater by three times its probable error.
A comparison with the reports of Smedley on this test for the previous year (Report No. 2), leaves his results still more uncertain. While he does not give the medians at each age, we may make less satisfactory comparisons between the distance of the 10-percentile from the 25-percentile and the distance of the 90-percentile from the 75-percentile. If we do this, we find the distance is uniformly greater at the upper end of the distributions for each age both for the boys and girls. The Smedley results are, therefore, decidedly contradictory. The first 272year shows distributions skewed toward excellence and total results for two years show distributions skewed mainly toward deficiency.
Broadly considered, the Binet records with school children point to a skewed distribution toward deficiency when large allowance is made for the difference in value of the year units. It is extremely rare to find a child testing 4 years in advance of his life-age, while 15-year-old idiots are presumed to test 12-year-units or more under a mature standard.
Pearson believes that “the Gaussian curve will be found to describe effectively the distribution of mental excess and defect” for intermediate ages as measured by Jaederholm's form of the Binet scale. The data on which Pearson places reliance are Jaederholm's results in testing 261 normal children 6-14 years of age in the Stockholm schools and 301 backward children in the special help classes of the same city. The best fit of a normal curve to the data was obtained with a group of 100 8-year-old children, in which case the chances were even that samples from a normal distribution would fit. With his larger normal and backward groups combined in proper proportions in one population the chances were 20 to 1 that such a distribution as was actually found would not fit into the Gaussian distribution. He admits that “this is not a very good result,” although it is better than when the Gaussian curve is fitted to either the normal or the backward group alone. In a subsequent paper he gives each child a score relative to the standard deviation of the normal child of his own age, a method comparable to his treatment of Norsworthy's data. He then finds that “10% to 20% or those from 4 to 4.5 years and beyond of mental defect could not be matched at all from 27,000 children” (164, p. 46). In each case the distributions actually found were skewed somewhat toward deficiency. Furthermore, 273when he suggests that -4 S. D. may be used as a borderline for tested deficiency, he recognized that the mental ability of children is skewed so far as the empirical data are concerned. With a normal distribution there would not be two children in 100,000 who would fall below this borderline. Nevertheless, the normal curve serves for most practical purposes to describe the middle ranges of ability.
Pearson thinks that the skewed distributions of his data may possibly be explained by the drawing off of older children of better ability to the “Vorgymnasium,” or to the higher-grade schools, by the incompleteness of the higher age testing, or by the “possibility of the existence of a really anomalous group of mental defectives, who, while continuously graded inter se, and continuously graded with the normal population as far as intelligence tests indicate, are really heterogeneous in origin, and differentiated from the remainder of the mentally defective population” (164, p. 34). The last hypothesis, of course, supposes that mental ability is skewed and suggests the cause. He supplements this explanation by stating that the heterogeneous cause of the “social inefficiency” of the deficients may not be connected directly with the intellect but affect rather the conative side of the mind. A skewed distribution under biological principles of interpretation supposes a single cause or group of causes especially affecting a portion of the population.
It is also to be noted that the apparent form of distribution may be the result of the nature of the test and the units in which it is scored. Some tests might not discriminate equally well a difference in ability at the lower and at the upper ranges of ability. If the test were too easy the group might bunch at the upper portion of the scale and the distribution appear to be skewed toward the lower extreme where there were only a few cases. 274If too difficult a test were used the form of distribution might shift in the opposite direction, most of the group ranking low. It is extremely difficult to formulate mental tests so that they will equally well measure differences at each degree of ability. This objection should not hold, however, if the scoring were in units of time for the same task, as with the form board test. The essential characteristics of a test in order that it may indicate the form of a distribution is that the units of scoring shall be objectively equal under some reasonable interpretation and that they shall be fine enough to discriminate ability at each position on the scale. Under such conditions the variations in the difficulty of tests should not obscure the form of the distribution of the ability tested.
Turning to the analogy of measurements of physical growth, a strong argument may be made for the hypothesis of shifting forms of distribution. As Boas points out regarding measurements of the body at adolescence, owing to the rapid increase of the rate of growth the distribution of the amounts of growth is asymmetrical, “the asymmetry of annual growth makes also all series of measurements of statures, weights, etc., asymmetrical.” Moreover, “acceleration and retardation of growth affects all the parts of the body at the same time, although not all to the same extent.... Rapid physical and rapid mental growth go hand in hand” (80). There is no reason to suppose that the brain is free from this phenomenon of asymmetrical distribution of annual increments of growth among children of the same age when the rate of growth is changing as at adolescence. It is therefore to be expected that the separate age distributions would be skewed at early ages and at adolescence even if the distribution should be normal with a static population. The presumption from physical measurements is that the form of distribution shifts with age.
275Again we may note that if some of the idiots reach an arrest of development before any of the normal individuals, as several investigators contend, this would imply that the distributions must be skewed unless there is a curious corresponding acceleration of growth on the part of geniuses to balance this lagging by idiots.
In spite of these arguments and the evidence of asymmetry of measurements at least at some periods of life it is to be noted that current opinion is probably contrary to this hypothesis, although, as I believe, because it has been concerned mainly with those who are not of extreme ability. For all large medium ranges of ability slight skewness might well be negligible. It is interesting to note that Galton says that “eminently gifted men are raised as much above mediocrity as idiots are depressed below it” (159, p. 19). Measured by intelligence quotients with the Stanford scale, Terman finds among school children that deviations below normal are not more common than those above (197, p. 555). Burt, following a suggestion of Cattell as to college men, however, seems to incline to the opinion that the general distribution of ability, like wages, is skewed toward the upper end. He adds, “In crude language, dullards outnumber geniuses, just as paupers outnumber millionaires” (85).
For our problem of units and scales of measurement, an asymmetrical distribution sets a very difficult problem. It may be that this very difficulty has been one of the main reasons for slowness in recognizing the drift of the evidence. In order to set forth the difference in the conception of measurement when distributions become asymmetrical I have presented this hypothesis in connection 276with the curves of development in Fig. 5. It will be noted that if the distributions of mental capacity vary in symmetry, the units of standard deviation change in significance from one form of distribution to another. Minus 2 S. D. may exclude very different portions of groups differently distributed, while it would always exclude the same proportion if the distributions had the same symmetry, or skewness.
Under conditions of variable symmetry there is a sense in which the same relative physical score in units running from zero ability to the best ability would always have an equivalent objective meaning, but this might not express equivalent development conditions at different ages. For example, with shifting forms of distribution, to say that a child of six years had reached three-fifths of the best development for his age on an objective scale might give no significant indication of how nearly he was keeping pace with those three-fifths of the best ability of another age. Neither would his position in units of the deviation of ability at his age give this information without knowledge of the form of the distribution of ability at his age. With varying forms of distribution at different stages of development this would afford an insurmountable difficulty.
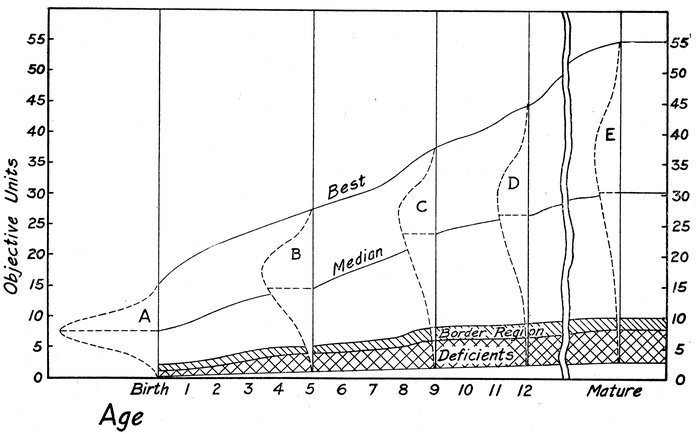
Fig. 5. Hypothetical Development Curves (Changing Forms of Distribution)
278With unknown or varying types of distribution it is desirable to utilize percentiles as equivalent units for comparing individuals at different stages of development. They differ somewhat from ranks in an order of noticeable differences. With an indefinitely large group, such ranks would mark off only those cases which were indistinguishable in merit. These units would be numbered in order from the highest to the lowest in ranks of just distinguishable merit, a different number of individuals conceivably occurring at the single steps. Psychologically the percentiles are somewhat less significant because they are not conceivable in steps of just noticeable differences. Percentiles have less value in comparing abilities in the same distribution, but have decided advantages when comparing corresponding abilities in different distributions. Except at points where merit is indistinguishable, they signify that a certain proportion of a group is ahead in the struggle for existence. They are thus units of relative rank. Moreover, they are directly translatable into units of the deviation in case the form of the distribution of ability has been determined. This is a special advantage if the forms of distribution turn out to be normal or even uniform.
In using percentiles it is to be remembered that equal differences between percentiles are not comparable in the same distribution except in the sense of the same extra proportions of the group to be met in competition. A change in the degree of ability from the lowest percentile to the lowest 2 percentile would be very different from the change in the degree represented by the 50 percentile to the next percentile above. Differences in the ability of individuals ranking near each other in the middle of the same percentile series would be distinguished with difficulty while it would be easy to make such discriminations at the extremes.
The special value of the percentile units in measurement of ability lies in the comparison of individuals of corresponding position in corresponding groups in which the ability may not be assumed to distribute alike. The concept that 995 out of every 1000 randomly selected individuals at his age are ahead of a particular individual in the struggle for existence has very definite and significant meaning which is quite comparable from one period of life to another regardless of the form of the distribution. 279We shall return to this question of equivalent units in distributions of unlike symmetry when we compare the definitions of the borderlines of deficiency in terms of intelligence quotient, coefficient of intelligence, standard deviation and percentage. Corresponding percentages of corresponding groups have a more useful definite significance of equivalence than any other units of measurement of mental ability available when the forms of distribution vary at different stages of development or are uncertain, as seems to be true with tested abilities.
When we endeavor to make our ideas of mental development more definite, we are assisted by thinking of the various stages in graphic form. This is especially true when trying to think of the position of the deficient individuals, relative to the average individuals and to genius.
In diagrammatically presenting these concepts in Fig. 3 and Fig. 5 we do not wish to assume that all the principles on which the developmental curves have been plotted have been decided. If they make clearer the points still under discussion and direct the discussion to specific features so that more data may be brought to bear upon the empirical determination of their characteristics, they will serve a useful purpose. For our present ends, we shall consider only certain features which have a bearing upon the interpretation of developmental scales and the quantitative definition of the borderline.
In the graphic presentation of the curves of development in Figures 3 and 5 the relative position at various ages has been suggested hypothetically for those of the best ability and median, or middle ability, as well as the borderline of the deficients.
280It is evident that these graphs should represent equivalent ability at each stage of development measured by as objective a scale of measurement as possible. In the graphs this scale is assumed to be composed of physical units with its zero at zero ability. The deficient group is distinguished by the portion with a grated shading. The distribution curves of individual ability we have already mentioned in connection with scales of measurement. Fig. 3 is constructed on the assumption of a normal distribution of ability at each age extending to the same zero ability. Fig. 5 on the assumption of distributions of varying form.
Otis has given a very able logical analysis of certain concepts underlying the testing of mental development (163). His discussion differs from the present in its aim to determine the proper mental age for particular tests, a question which I have not considered. It also supplements the present discussion by showing the changing value of the same intelligence quotient with normal distributions of ability under certain assumptions as to range of ability and decrease in the annual increments of ability with age.
Some investigators are apparently inclined to question the significance of any curve of mental development on account of the very different forms of development which they have found in particular cases. A quotation from Goddard will state this problem:
“It seems to me that there is considerable evidence that there are a good many children that develop at a normal rate up to a certain age and then slow down; 281some slowing down gradually and others rapidly. This is possibly accounted for by accidental conditions. Dr. Healy's case of traumatic feeble-mindedness is a good illustration of this. We have quite a good many cases, not a large percentage as yet, where it is pretty clear that they have developed very nearly normally up to the age of seven, eight or nine, so that I am very skeptical as to the possibility of formulating a rule for determining the rate of development. Many cases are uniform in slowness while others vary a great deal; some slow up more rapidly than others as has already been stated....
“Morons are not usually discovered until twelve or fourteen years of age. The picture to me of the development of the feeble-minded is rather that these different types develop each in his own way very much as the physical side develops. Different families have different determiners of development. Just as it was determined before I was born that I should be five feet, ten inches tall, I developed that height and no further. In the same way, probably, that determiner carries with it the determination of the rate of development and the time. This carries with it the fact that I should have been an average boy from birth. As a matter of fact I was very much under-size until I was fifteen or sixteen years of age. Then I shot up. Other cases are over-size. It may be a false analogy, but it seems to me to illustrate the rate at which these cases develop” (111).
This view raises clearly the question how far the curve of average development represents a common tendency of different individuals in development. Are the individual curves of development so varied in form that an average curve does nothing but obscure their significance? The study of individual curves of growth in height and weight by Baldwin indicates that the bigger children tend to develop earlier, the smaller later (73). The individual curves of mental development may be analogous. If so, the average curves may not adequately represent the common tendencies of development. Nevertheless, it is to be remembered that with height and weight the average 282curves do retain a decided usefulness, which nobody, I suppose, would seriously question.
An analogous problem arises when we consider the question of variations in the maturity of different mental processes. Besides the question whether the average curve is useful in view of the variation among individuals in their rates of maturity for the same process, the psychologists have a still more difficult problem about curves of general ability. These curves are built by combining the results of numerous psycho-physical tests which are very different in type. We need to raise the question whether the type of process measured by memory for digits, for example, matures at the same rate as those processes measured by other memory tests: in general, how much a single test or combination of tests represents a common process. Furthermore, we need to inquire whether processes measured by memory tests mature like those measured by tests emphasizing reasoning, imagination, motor ability and other groups of activities. We thus have the problems of the different rates of maturity of the different tested processes in the same individual and of common tendencies among these specific processes.
In order more clearly to present this problem of the significance of developmental curves for different processes, I have brought together the age norms from 8 to 14 years for 40 tests as given by different investigators. No norms were included which were not based on tests of at least 25 individuals. After 14 years the data which have been collected are open to the objection that the norms for the older ages would be seriously affected by the fact that they were obtained upon children remaining in school, usually in the elementary school, i. e., upon groups, among which a large portion of those of better or of poorer ability had been eliminated. The relative position of the norms for 283older ages are, therefore, not comparable with those of children who are of the ages of compulsory attendance. The results published are inadequate below 8 years for most of the tests, so I have not extended the curves to earlier ages. In 14 instances the data for boys and girls were only given separately. In these I have used the norms for the boys. A prepubertal break in a combined curve may, therefore, indicate a sex difference. In most cases the norms were given for the sexes combined, and the difference is unimportant for the points considered.
The variation in age norms with different tests is shown graphically in Figures 6, 7 and 8. In order that the various tests may be plotted on the same scale, so as to compare changes in development for the different tested processes, I have used the average increase in ability from 8 to 9 years of age for each test as a common measure and arbitrarily plotted the slant of the curve between these ages at 45 degrees. The increase from 8 to 9 is represented by 10 units on the objective scale to the left of the graphs. On this basis it is possible roughly to compare changes in the absolute annual increase at different ages for the same test and for different tests. It assumes that the units in which each test is scored are equivalent for that test. An average difference between the basal ages or between any two ages cannot be assumed to be accompanied by the same distribution of increases. Moreover, the 8-year norm is at different distances from zero for the different tests so that the relative increase from 8 to 9 cannot be regarded alike for the different tests. The method, however, is sufficiently accurate for illustrating the very different forms of the developmental curves which might be expected if they were measured by absolute increases from year to year. Even the variation in the slant of the lines at the different ages gives a graphic picture 284which will assist in interpreting the significance of average curves of general ability. As the curves stand, they show the norms for each age for any test, as if placed on its own objective scale, and the various objective scales have been harmonized on the assumption that the norms at 8 and 9 years are accurate. We thus have a simple representation of the absolute changes in the abilities tested from age to age by the same tests relative to a single objective scale. It will not give a seriously erroneous picture for any tested ability so long as the units in which the particular test is scored may be presumed to be objectively equal.
The tests on which Figures 6, 7, and 8 were based included practically all which were reported in the researches used. They were as follows: Norsworthy (159), perception of 100-gram weight, cancelling A's (boys), ideas remembered from four simple sentences, memory of related and of unrelated words, part-wholes, genus-species, opposites and reverse of opposites given the next day, “a-t” test. J. Allen Gilbert (108), taps in 5 seconds, fatigue in tapping, visual reaction time, color-discrimination reaction time, reproduction of 2-second interval. Smedley (51, No. 3), strength of right-hand grip (boys), taps in 30 seconds (boys), ergograph; visual, auditory, audio-visual, and audio-visual-articulatory memory for digits. W. H. Pyle, Standards of Mental Efficiency (J. of Educ. Psychol., 1913, IV., 61-70), uncontrolled association, opposites, part-wholes, genus-species, digit-symbol and symbol-digit substitution, memory for concrete and for abstract words, memory of Marble Statue selection, (only boys' norms used for each). Pyle and Anderson combined by Whipple (220) two word-building tests (boys). Anderson as given by Whipple memory for letter squares. D. F. Carpenter, Mental Age Tests (J. of Educ. Psychol., 1913, IV., 538-544), substitution of colors in forms and of numbers in forms, perception time in marking A's, concentration, i. e., difference in time of last test under distraction, memory of pictures of objects, all tests devised by Carrie R. Squire. Stenquist (54), construction test. Sylvester (191), form-board test.
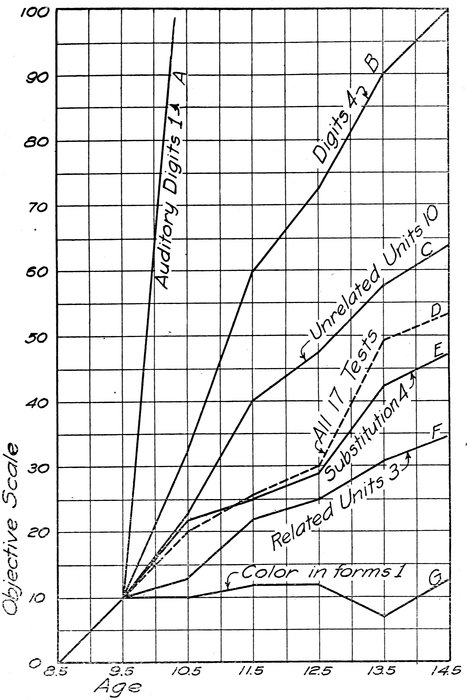
Fig. 6. Tests of the Development of Memory Processes. Medians at Each Age of the Central Tendencies of the Tests.
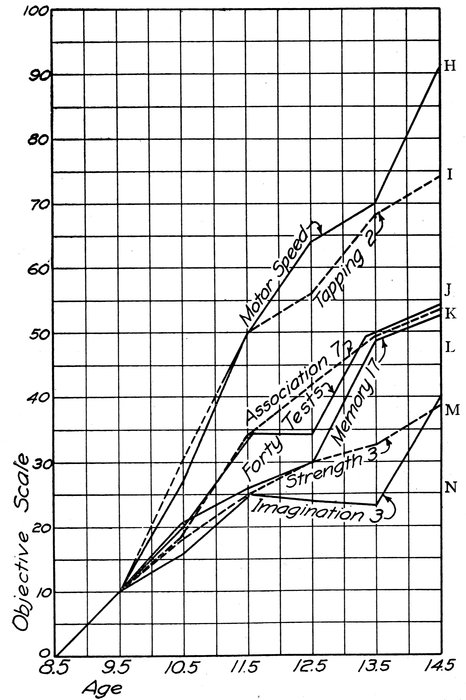
Fig. 7. Different Types of Development. Medians at Each Age of the Central Tendencies of the Tests.

Fig. 8. Forty Curves of Development. Distribution at Each Age of the Central Tendencies of the Tests.
288In Fig. 6 curves A and B are Smedley's tests; curve C includes in addition Norsworthy's unrelated words, Pyle's memory for concrete and abstract terms, Anderson's letter-squares, Carpenter's memory for pictures, and Gilbert's for the time interval; curve E includes Pyle's two and Carpenter's two substitution tests; curve F includes Pyle's Marble Statue and Norsworthy's memory for related words and for sentences; curve S is Norsworthy's; curve D is the combination of these 17 tests.
In Fig. 7 curve H includes Gilbert's visual reaction time, Norsworthy's A and a-t tests, Carpenter's two A tests; curve I includes Gilbert's and Smedley's tapping tests; curve J is the median of the central tendencies of all 40 tests; curve K includes Norsworthy's two opposites and her part-whole and genus-species tests, the Pyle opposites, genus-species and part-whole tests; curve L is the same as D, curve M includes Smedley's strength of grip and ergograph tests and Gilbert's fatigue of tapping; curve N includes Pyle and Anderson's word building tests and Pyle's uncontrolled word association test.
In Fig. 8 curve P is Gilbert's visual reaction time test, curve S is Norsworthy's test for memory of unrelated words, the other curves are the median and quartiles for the central tendencies of all 40 tests after each was expressed at each age in terms of the gain from 8 to 9 years taken as a unit.
Several points are to be noted about the nature of the curves for different tests. In Fig. 6 showing the curves for different forms of memory tests, that for the memory of digits is very different in character from that for memory of related material. The most extreme differences in the time of maturity are shown by the test for memory for digits presented orally and the substitution of color in forms, the former continues to increase so rapidly relative to the absolute increase from 8 to 9 years that it cannot be represented in the graph reaching 539 units of the scale by 14 years of age, while improvement in ability in the latter is not measured after 9 years. We cannot take time to discuss how much of the differences between the various curves may be due to the nature of the tests themselves, the form of scoring the results, or the condition under which they were given, selection of subjects, etc. The conclusion is safe, however, that when groups of three or four tests of similar type show such marked differences 289as those for memory of digits and memory for related material we may expect similar differences in the rates of maturity of the corresponding processes.
From Fig. 7 we may learn that tests emphasizing functions such as speed of motor or perceptual motor reaction, curves H and I, are notably different in their form from curves for tests of imaginative processes, curve N. As we group tests together covering larger ranges of activity we approach the median curve for general ability. Note the median curve for 17 memory tests (curve L) compared with the median for the 40 tests (curve J). By empirical studies we might pick out types of tests which would most closely represent the maturity of average ability. For example, the median for the substitution tests, curve E, resembles the median for the memory tests, curve D, more closely than does that of the 4 digit tests, curve B. Curve K, for 7 association tests, resembles the median for the 40 tests, curve J, much more closely than the curve for the perceptual-motor speed tests, curve H. This difference can not be explained by the use of 7 instead of 5 tests in calculating the central tendency of the group. It probably means that the sort of psycho-physical processes usually tested more closely represent on the average the abilities shown in association tests than they do the abilities shown by speed of motor reaction. The significance of this sort of analysis for those constructing a scale for measuring intellectual ability is obvious.
Fig. 8 shows the median and quartile range for the central tendencies of the 40 tests and gives examples of two extremely different tests, visual reaction time and memory for unrelated words. How closely these particular tests represent fundamental differences in the maturity of different processes, we cannot, of course, be sure without prolonged research; but nobody would question that 290analogous differences would be found in different processes. When we think of curves of general ability we must, therefore, keep in mind the light which might be thrown on them by an analysis of the various processes tested in the particular scale used.
Another feature of all developmental curves which is apparent as soon as the causes of development are considered, is that growth in an individual is the result of several factors. These include the native capacity, the rate at which that capacity manifests itself instinctively, and the external stimuli which encourage or retard that manifestation. To some extent these factors vary independently. Our curves of development will never completely express all the facts until they analyse out all these factors for each of the processes. In the meantime we shall be able to think of general trends of development by considering average curves. The fact that they represent combinations of unanalyzed factors must, however, make us very cautious in interpreting our norms.
There has been considerable discussion of the form of the curves of mental development. The logical aspects of the curves on the assumption of normal distribution of ability at each age and uniform age of maturity have been treated by Otis (163) and the bearing of these assumptions upon the Binet scale pointed out. Thorndike has plotted the developmental curves for a dozen tests on the basis of the variability at 12 years of age used as unit and gives a chapter in his Educational Psychology to the changes with maturity (198, Chap. XI). Bobertag suggests that the rates of development of normal and deficient children are analogous to the upward progress of two projectiles fired from such different heights that the force of gravity 291would retard the lower projectile more than the upper (81). This analogy supposes that the rate of maturity would continually decrease and that those who were feebler mentally would be arrested in their developmental earlier. Bobertag, Kuhlmann (137, 138) and Otis give evidence from the results of Binet testing that the rate of development decreases with age. The percentages of older children passing certain positions on the Binet scale or certain tests taken from it were found to change less at year intervals for the older ages. This evidence is not conclusive unless we know that the positions compared are at the same point in the distributions of ability at the beginning of the periods of growth. The same percentage change at a point farther away from the central tendency would mean a larger growth than at the middle of the distribution, when judged either in reference to a physical scale or to units of deviation.
While recognizing that the complete curve of mental development is logarithmic in form Pearson contends that, when measured by Jaederholm's adaptation of the Binet scale, development is adequately represented by a straight line from 6 to 15 years of age (164). As this conclusion is based upon the use, as equivalent units, of years of excess and deficiency at all these ages the data lacks the cogency of a scale of equal physical units.
With the Point Scale it is not known whether the units in different parts of the scale are equivalent. Without assuming that they are equal it is impossible to discover the form of curves of development from the records of children at a series of ages. Yerkes and Wood publish a curve of the increase of intellectual ability based upon point-scale measurements, which resembles in form the hypothetical curves. They say:
292“The point-scale method has the merit of indicating directly the rate, or annual increments of intellectual growth. We do not claim for our measurements a high degree of accuracy, especially in the case of the early years of childhood. But even the roughly determined curve of intellectual growth from four to eighteen years, which we present below, has considerable interest for the genetic psychologist and for the psychological examiner. We have ascertained that whether measured by the ratio of the increment of increase, year by year, to the norm for the appropriate year or by the ratio of the extreme range of scores to appropriate year norms, intellectual development rapidly diminishes in rate, at least from the fifth year onward” (169, p. 603).
Waiving the question whether annual increases or the range of measurements relative to the age norms would be satisfactory indications of the change in the rate of growth, it seems to be fairly clear that neither of these criteria would be adequate unless we first knew that the units in which they were measured were equivalent at different portions of the scale. To show that the point scale units are even theoretically equivalent it would seem to be necessary to assume, on the basis of normal distribution of ability, that each unit of the deviation for each age distribution either equaled the same number of scale units or the same proportion of the total distance from lowest to highest ability at each age measured in the point-scale units. The originators of the scale do not seem to have planned it with this in view. Moreover, the difficulty of empirically demonstrating such equivalence of units on a point scale or any form of the Binet scale prevents its use for indicating curves of mental development, however serviceable it may be for other purposes.
The simplest demonstration of the form of the development curves is applying the same test, scored in equal physical units, to children of different ages. In Figs. 6, 2937, and 8 the evidence from tests was assembled for ages 8 to 14 inclusive. It is probable, however, that the form of these development curves, when the unit of measurement was anything but time taken for the same task, has been affected by the difference in the real value of units called by the same name, e. g., giving the opposite of one word is not always equal to giving the opposite of another.
The best developmental curves empirically determined are probably those for the form board presented by Sylvester (191), Wallin (212) and Young (227) since in each of these cases the same test was presented at all ages and the scores were in equal physical units of seconds. It can hardly be supposed, however, that the form board curves alone would be typical of average mental development. To know something about the general curve of mental development we need a combination of a number of mental tests scored on scales of equal units. These may be either equal physical units or units on scales for mental development similar to those of Thorndike and others for measuring educational products, handwriting, arithmetic, spelling, etc.
That either a straight line or a simple curve would represent the development of ability from birth to maturity is very doubtful. When we consider the entire developmental curve from birth nobody doubts that there is a change in the rate of development at the time of the arrest of instinctive changes at adolescence. There are probably fluctuations in the rate before this final arrest. Pintner and Paterson also assume a complex curve of development (44). Whether the fluctuations should be allowed for in the description of the borderline of deficiency is the important question in our study. With measurements of bodily growth we noted that changes in the rate of maturity are accompanied by a skewness of distribution of 294ability at the ages affected. The same effect may be expected with mental measurements. The percentage method of defining the borderline of deficiency has an advantage when the form of distribution at any age is uncertain (See Chap. XIV, d.). Since the changes in the rate of development are most likely to be important at the prepubertal and adolescent ages the description of the borderline in terms of deviation or quotient may be expected to be most uncertain at this period. Moreover, none of the quantitative definitions of the borderline, except the percentage method, remain equivalent if rates of development of normal and deficient children change relative to each other, a question we shall now consider.
It has been assumed by Bobertag (81), Stern (88), Goddard (117) and others that deficient children reach their maturity earlier than normal children. If this were true the curves of mental development for the average and for the deficient children should not be expected to retain their same relative positions after the idiots had begun to show arrested development. Moreover, unless this arrest were compensated by some peculiar form of accelerated growth among those above normal ability, we might expect that the distributions of ability would change in form at the various ages after arrest had begun. A relative increase in the distance of older deficients from the average as compared with younger deficients may be interpreted as meaning either the earlier cessation of growth of the deficients or a change in the relative rates of growth of individuals of different mental capacity. When fully considered the present evidence from the Binet tests fails, I believe, to demonstrate the earlier arrest of 295the deficients, although it is undoubtedly true that the Binet scale may not be fine enough to measure the improvement of idiots. We shall take up certain investigations that bear upon this point.
Goddard has reported tests upon the same group of 346 inmates in an institution for the feeble-minded who were tested three years in succession (117). The paper suggests that the idiots, as a group increased less in absolute ability than those of higher mental age. The average gain for 55 idiots who tested I or II mentally was about half a test in the two years. In order to reach our present problem, however, we must know that the idiots, for example, developed relatively less mentally than did those of the higher grades of ability in the imbecile and moron groups of the same life-ages. This question cannot be answered from the paper. It probably cannot be adequately answered from mental age results on account of the irregularity in the value of the year units at different points on the Binet scales.
Bobertag summarizes Chotzen's data obtained by the examination of the children in the Breslau Hilfsschulen with the Binet scale. He believes that the position on an objective scale attained by the average of these retarded children is progressively lower with advancing age relative to the average position attained by normal children, assuming that the quotient for normal children remained constant at each age. The average intelligence quotients of all the children in the special schools (exclusive of those testing III or less) was 0.79 for those 8 years of age, 0.72 for those 9 years, 0.70 at 10, and 0.67 at 11-12 (81, p. 534).
Stern also compiled a table from Chotzen's results which shows this decrease in intelligence quotients with life-age separately for each group of those whom Chotzen 296by his expert diagnosis regarded as imbeciles, morons, doubtful, and not feeble-minded although attending the special schools (188, p. 80). This table is reproduced here as Table XX. On the surface it suggests that the quotients of the extreme groups are nearer together at the older ages, instead of being farther apart. The objection to this evidence from the Binet scale is that the norms are not equivalent for different ages on the scale used. Since the objective norms on the Binet scale are more difficult to attain at the older ages this variation would tend to make older children show lower quotients than the same children would show at younger ages, so that such tables are quite uncertain in significance.
| Life-Age | Not Feeble-Minded | Doubtful Defect | Morons | Imbeciles |
|---|---|---|---|---|
| 8 | 0.92 | 0.84 | 0.76 | 0.71 |
| 9 | 0.85 | 0.81 | 0.77 | 0.67 |
| 10 | (0.80) | (0.80) | 0.74 | 0.62 |
| 11 | (0.73) | (0.68) | 0.71 | (0.64) |
| 12 | (0.75) | (0.75) | (0.73) | (0.61) |
| 13 | (0.73) |
The Jaederholm data with his form of the Binet scale, as treated by Pearson, shows a straight regression line for the backward children which falls below the normal development line on the average four months of mental age for each additional year of life from 7-14 (167). Accepting Pearson's interpretation that a year of excess or deficiency and a year of growth is a constant unit, we find that the deficient group from special classes was falling continually behind the normals with increase of age a relatively greater distance from any rational reference point. Pearson accounts for this change in the distance between the 297two groups of normal and backward children, as I understand his paper, by supposing that with increase in age more and more normal children become deficient. It would seem that this data would be more easily explained by supposing that the distributions became skewed toward deficiency for the older ages, rather than that the distributions remained normal and became flatter.
The best evidence as to the relative positions of the curves for deficients and those for average ability would be provided by using psychological tests that could be adequately scored in terms of equal physical units for the same task. The position of various lower percentiles relative to the average or to an assumed reference point could then be compared on the same objective scale. I have reviewed studies of this type in discussing skewed distributions in Chap. XIII, A, c. I there reached the conclusion that the weight of the evidence was that the distributions were slightly skewed in the direction of deficiency, although the evidence was not conclusive. We are now raising the further question whether this skewness increases with age.
On account of the difficulty of determining the points for zero ability in terms of the physical scales used, let us see what conclusion might be reached if we calculated the relative distance of median and low ability of equivalent degree from the scores of the same higher degree of ability assumed as a reference point at the various ages. There seems to be no reason in the theory of measurement why the highest score instead of the lowest score in random samples might not be used for a reference point for comparing the distances between normal and deficient children at different ages. Instead of using the highest single score, it would be better to use the upper quartile or quintile since it would be less affected by a chance error in giving the test.
298Applying this method to determining the relative position of median and retarded ability I have calculated the data for the form board test cited previously from Sylvester (191) and from Young (227). This affords the only adequate evidence of which I know, derived from tests scored in equal physical units given to sufficiently large groups to indicate whether or not the retarded group changes its relative position from the normal group at different ages. The comparison is shown in Fig. 9. With Sylvester's data the distance of the lower quartile in ability from the median is compared with the distance of the upper quartile from the median, the latter distance being taken as a unit. With Young's data for Witmer's form board the quintile is used instead of the quartile and each sex is given separately. Since Young's table shows the scores for half ages, it was necessary to take the average of the two scores, thus giving the approximate score for the middle of the complete age group. The graph discloses no pronounced tendency for the retarded group to fall relatively farther behind the median with increase in age. There are, however, notable fluctuations in the relative positions of the groups so that at 7 years with Young's data for boys and at 13 years for Sylvester's curve the retarded group is twice as far from the median relative to the distance between the median and the corresponding better group as it is at some other times. It is possible that the curves for the older groups of those of poorer ability are too high since it is likely that more of the actually deficient children tend to be dropped from the public school classes with increase in age. Nevertheless, so far as the evidence at present goes it is not sufficient to determine whether the backward and the corresponding better group show a general change in their relative distances from the median with approach to maturity.

Fig. 9. Relative Positions at Each Age of the Median and of Corresponding Bright and Retarded Children with the Form Board Test.
300On the other hand the curves indicate the tendency for the distributions to be skewed toward deficiency and for the relative distances to fluctuate as we should expect if the accelerations in growth occurred at different ages for those of different ability. The data of Young suggest that there may be sex differences in the age of acceleration, the backward girls showing accelerations, relative to the upper group at ages 7 and 12, a year or more before the boys. For Sylvester's data the ratio of the distance between the median and the lower quartile divided by the distance between the median and the upper quartile for each of the age groups is as follows: 5 yrs. 1.8, 6 yrs. 2.4, 7 yrs. 3.0, 8 yrs. 2.0, 9 yrs. 2.2, 10 yrs. 2.4, 11 yrs. 2.0, 12 yrs. 1.8, 13 yrs. 3.0, 14 yrs. 2.1. For Young's data the corresponding ratios are—Boys: 6 yrs. 1.5, 7 yrs. 1.9, 8 yrs. 1.5, 9 yrs. 0.8, 10 yrs. 1.6, 11 yrs. 1.2, 12 yrs. 1.4, 13 yrs. 1.0, 14 yrs. 1.3. Girls: 6 yrs. 1.7, 7 yrs. 1.0, 8 yrs. 1.5, 9 yrs. 0.9, 10 yrs. 1.0, 11 yrs. 1.3, 12 yrs. 0.9, 13 yrs. 1.5, 14 yrs. 1.4. Changes in the rate of growth causing asymmetrical distributions are to be expected throughout the periods of growth. A fundamental skewness toward deficient mental capacity, therefore, would be indicated only if it were found at maturity or at ages when the average rate is decreasing, when the more capable individuals would theoretically approach relatively nearer the deficients if the latter accelerated later.
So far as physical growth is concerned Baldwin (74, 75) has shown with repeated annual measurements on the same group of children that the period of adolescent acceleration shifts from 12½ years for the tallest boy to 16 years for the shortest boy. For the tallest girl the maximum height was attained at 14½, for the shortest at 17 years, 3 months. Maturity may be reached at 11 years by a tall well nourished girl, while with a short girl light 301in weight it may be delayed until 16. “Children above medium height between the chronological ages of 6-18 grow in stature and in physiological maturity in advance of those below the medium height, and they may be physiologically from one to four or five years older than those below the medium height. Those above the medium height have their characteristic pubescent changes and accelerations earlier than those below; there is a relative shifting of the accelerated period according to the individuals' relative heights” (74).
Doll presents evidence from the physical measurements of a large feeble-minded group in institutions which he suggests shows that the shorter among them cease growing earlier. When the height of these feeble-minded is measured in relation to the Smedley percentiles of the height of normal children of their corresponding ages, he finds a correlation of -.20 between age and percentiles of height, the taller relative to normals being younger. He says: “This confirms Goddard's similar conclusion, but negatives for the feeble-minded at least, the theory affirmed by some writers, that children who grow at a retarded rate continue their growth to a later age” (98 p. 51). On the contrary this minus correlation is more likely to mean only that the Smedley norms on school children are too high for the older ages because of the excess of taller children who remain for the high school work. This would give the minus correlation without supposing that the taller individuals continue their growth to a later age, as he thinks.
Moreover, a total longer period of physical growth for smaller, less normal, children has been demonstrated. Boas (80) says: “Among the poor the period of diminishing growth which precedes adolescence is lengthened and the acceleration of adolescence sets in later; therefore, the 302whole period of growth is lengthened but the total amount of growth during the larger period is less than during the shorter period of the well-to-do” (80). A reversal in growth tendency between brain capacity and size of body, which is supposed when the mentally deficient are said to arrest earlier, would be one of the most puzzling paradoxes in the study of development. We should, therefore, be exceedingly cautious before accepting the hypothesis of the earlier maturity of deficient children.
A complicated situation is presented when we come to represent graphically the effect on the distributions of these differences in growth among those of different intellectual capacity. In the hypothetical diagrams, Fig. 5, it is shown how arrest of development might be presented graphically in relation to the distribution curves, ability being measured on the same physical scale. The earlier acceleration and earlier maturity of those of better ability are indicated. The distributions are shown as skewed at all ages after birth. Equivalent units of mental development at different ages can be found only in corresponding percentages of the groups, not in the units of the deviation or in development quotients relative to the averages at different ages. In other words the lowest 0.5% continues to be an equivalent unit while -3 S. D. measures different portions of the group and different portions of the distance from lowest to highest ability. Corresponding percentages retain one common significance, namely, that the same proportion of the group is ahead in the struggle for survival, regardless of the form of the distribution.
It is hoped that the discussion of the statistical problems connected with the quantitative study of mental development has given more meaning to the different attempts to devise scales for measuring mental ability. It should be 303noted that the same relative development at different ages, expressed relative to the distance from lowest to highest ability measured in equal objective units, does not correspond to the same relative development measured in percentages of the groups, as soon as the forms of the distributions change. The theoretical considerations show that we have available at once a perfectly definite and clear method of stating relative development in terms of corresponding percentages of corresponding groups. If the groups distribute normally these units are translatable into units of the standard deviation of the group. If the distributions change in symmetry the only equivalent units of deficiency available are in terms of corresponding percentages reading from either end of the group. On the other hand percentile units are not equivalent in amount of change for the same distribution, so they are of most importance for comparing different age distributions of uncertain forms.
Until we have a scale of equal objective units for mental ability, it is not possible to obtain a measure of relative development which shall take into account the amount of relative change. We must be content to measure the change in percentile rank (changes in serial position) of an individual relative to those of his own age.
Having clarified our conceptions of mental development and brought them into harmony with certain suppositions regarding the distribution of ability and its change from year to year, we are in a better position to evaluate in the following chapter the different objective methods of defining the borderline of feeble-mindedness.
On the basis of the detailed conception of the developmental curves and distributions of ability at different ages, which we have been considering, we can now compare the percentage method with other quantitative methods of describing the borderline on developmental test scales.
The earliest form of the quantitative description of the borderline on a scale of tests, was in terms of a fixed unit of years of retardation. This was taken over apparently from the rough method of selecting school children to be examined for segregation in special classes by choosing those who were two or three grades behind the common position for children of their ages. As this amount of school retardation was greater for older children, an additional year of retardation was required after the child had reached 9 years of age. I believe that nobody would seriously defend a practice of making an abrupt turning point of this kind, except on grounds of practical convenience. The theory of stating the borderline in terms of a fixed absolute unit of retardation is so crude that it has now been generally superseded by methods which make the amount of retardation a function of the age.
In order to relate the definition to the age of the child, at least during the period of growth, Stern suggested the “intelligence quotient,” consisting of the tested age divided by the life-age (188). This has been adopted by Kuhlmann with his revision of the Binet scale (139) and by Terman with the new Stanford scale (197). With the 305Point scale Yerkes utilized a similar ratio method for stating borderlines by what he calls a “coefficient of intelligence.” He defines it as “the ratio of an individual's point-scale score to the expected score, or norm” (226, p. 595). Haines also uses these coefficients, dividing the individual's score on the Point scale by the average number of points scored by those of his age (26). The difference between the “quotient” and the “coefficient” seems to be mainly empirical since they are theoretically alike in principle provided the scales by which they are determined are composed of equal units. Empirically, however, the units of the point scale would have to be compared with the 0.1 year units of the Binet scale to determine which showed the greater uniformity within its own scale. The coefficient has an advantage over the quotient in that the scale norms for the different ages would automatically become readjusted with additional data, and that physiological age norms could be more readily stated if they were ever available.
The suggestion of defining the borderline of tested deficiency in terms of a multiple of the standard deviation of ability of children who are efficient in school was made by Pearson in 1914. Tested inefficients did not with him include all inefficients, as he recognized other sources of deficiency. He had previously suggested a scale of mental ability in units called “mentaces”, 100 of which were equivalent to a unit of the standard deviation of all ability assumed to be normally distributed. On this scale of mentaces the imbeciles were 300 mentaces or more below average ability and would be expected to occur once among 1000 individuals chosen at random. Very dull, including some mentally defective individuals, were also to be found from 208 to 300 mentaces below the average (166, p. 109). Defining the borderline in terms of the deviation 306of a normal population was definitely forecasted by Norsworthy, although she did not specifically discuss the problem of the borderline. She indicated that if children tested below -5 P.E., they might be regarded as outside the normal group.
The following quotation from Pearson will make the method of stating the borderline in terms of a multiple of the deviation clearer:
“Now the question is, what we mean by a 'special or differentiated race': I should define it to mean that we could not obtain it by any selection from the large mass of the normal material. Now in the case of the mentally defective, we could easily obtain children of their height, weight, and temperature among the normals. We could, out of 50,000 normal children, obtain children practically with the same powers of perception and memory as the feeble-minded, as judged by Norsworthy's data. But not out of 50,000, nor out of 100,000 normal children, could we obtain children with the same defect of intelligence as some 50% of the feeble-minded children. In other words, when the deviation of a so-called feeble-minded child from the average intelligence of a normal-minded child is six times the quartile or probable deviation of the group of normal children of the same age, it falls practically outside the risk of being an extreme variation of the normal population. Now six times the quartile variation is almost exactly four times the standard deviation or the variability in intelligence of the normal child, and in the next material I am going to discuss [Jaederholm's], we have shown that the standard deviation in intelligence of the normal child is just about one year of mental growth” (164, p. 35).
With the Jaederholm data obtained in testing children in the regular and in the special classes in Stockholm by a modified form of the Binet scale, Pearson found that a year of excess or defect in intelligence was practically a uniform unit from 7 to 12 years of age and was about equivalent to the standard deviation of normal children measured in these year units. He, therefore, uses a year unit and the standard deviation as interchangeable for these data. He does not, however, always make it clear 307whether he means that the equivalence of the year units is determined by the standard deviation of the children of all these ages grouped together in one distribution, as it is in determining the regression lines, or by the equivalence of the standard deviations of the separate ages, especially when these two deviations are not equal in terms of the year units on the scale. I shall assume, however, that he would use the deviations of the separate years in case of such an inequality of the two concepts.
The quotation from Pearson, which we have given above, indicates that he would determine the borderline on the scale by the standard deviation of 'normal' children. In his case he actually used children who were efficient in school, as contrasted with those in special classes. On the other hand, he argues at length that all mental ability, including that of the social inefficients, is distributed in the form of the normal curve (167). Under this assumption it is, therefore, little theoretical change in his position to suppose that the borderline might be described in terms of the standard deviation of a random sample of the population. Defining the borderline in terms of a multiple of the deviation of a random sample at each age thus becomes directly comparable with the other forms of the quantitative definition, supposing that all refer to conditions to be found in a completely random sample. It is in this sense that I shall refer to the method of defining the borderline in terms of a multiple of the deviation.
The percentage method of defining the borderline seems to have been the spontaneous natural working out of the problem in the minds of several investigators. At the same time that I suggested this method in a paper before the American Psychological Association (151) Pintner and Paterson had prepared a paper suggesting a percentage definition of feeble-mindedness (44) and Terman had worked 308out his use of the quotient so that the borderline in terms of the quotient was given equivalent form in terms of percentage. Nobody, however, seems to have attempted to work out the details of the method as in the present monograph.
As a point of detail it is to be remembered that in translating percentages into terms of the deviation, the size of the group for which the percentages are determined is important if the groups are small, since the same percentage lies above slightly different multiples of the standard deviation with different sized groups. On this point the reader may see a paper by Cajori and the references cited there (86).
In distinction from qualitative methods of describing the mentally deficient, all quantitative definitions assume that those of deficient mentality do not represent a different species of mind; but that they are only the extreme representatives of a condition of mental ability which grades up gradually to medium ability. The deficient are not an anomalous group such as we find with some mental diseases. Except for the comparatively rare cases of traumatic or febrile origin, the deficient individual is a healthy individual so far as his nervous system is concerned, even though his capacity for brain activity is below that of those who socially survive. They are not as a group abnormal in the sense of diseased, but only unusual in the sense of being extreme variations from medium ability in a distribution which is uninterrupted in continuity. This distinction has been fully discussed by Goring in his work on The English Convict, which those who are interested in a full mathematical discussion of the significance of mental deficiency are urged to read.
309Schmidt urges that the deficients are qualitatively different in being “unable to plan”, and then suggests tests which most markedly bring out this distinction between deficient and normal children (178). As I have said before, however, this seems rather to be a failure to recognize that such an attempt to find tests which “qualitatively” distinguish the two groups is only an effort to pick those tests which best make measurable the differences between individuals at the extreme of mental ability. As such it is a valuable contribution to this problem. If it is intended as an attempt to set up a qualitative distinction in a mathematical or biological sense, between deficient and passable ability, it seems to me wholly to fail. As I take it, a “qualitative” distinction with Schmidt is only a bigger quantitative distinction and is intended only to mean this.
None of those who advocate quantitative definitions would contend, I believe, as some of their opponents seem to think, that such definitions afford a final diagnosis for particular cases. In attempting to place the borderlines on a scale of tests, this is always done with the clear recognition that such borders are only symptomatic of deficiency. The diagnosis of “social inefficiency,” to use Pearson's term, rests upon many facts among which the test result is only one, albeit the most important.
Other characteristics which each of the above quantitative definitions, except that of a constant absolute amount of deficiency, have in common, or might easily have if they were stated in their best forms, include the possibility of adaptation to any developmental scale, the suggestion of borderlines for both the mature and immature, the distinction of a group which might be regarded as presumably deficient from one that was of better but doubtful ability and of this from a still better group which was presumably socially efficient.
Perhaps the most curious and important thing about these definitions is that they are all substantially identical, except in their terminology so long as general mental capacity is found to distribute in the form of the normal probability curve and to extend to absolute zero ability 310at each age. This can easily be seen by comparing the distribution curves in Fig. 3. The position of the percentage borderline would always represent the same distance from the average in terms of the standard deviation of each age and the same ratio when the life-age of arrest of development had been determined as the largest divisor. Under these conditions, therefore, these main statements of the quantitative definition agree in supposing that the same proportion of the individuals of each life-age would test deficient. Those who advocate any of these quantitative definitions logically commit themselves to assuming that the percentage of deficients at each age is practically constant, unless they suppose the symmetry of distribution varies or does not extend to the same zero point.
If the distributions do not extend to the same zero points of lowest ability on an objective scale (see Fig. 5), the ratio is clearly at a disadvantage compared with either of the other methods, since it assumes that the same percentage of average ability is an equivalent measure. This does not hold when the lowest ability at different ages is not at the same point on the scale of objective units. For example, .7 of an average 100 units above 0 is not equivalent to .7 of an average 150 points above a zero ability of 30 points on the objective scale. The idea of regarding percentages of averages as equivalent is therefore generally avoided in mental measurement. In case the position of the absolute zero points of ability may be different, the distance from the average should be stated in terms of the deviation. In this respect the method of the deviation or the lowest percentage are equally good so long as the form of distribution does not change.
1. With the percentages fixed at the lowest 0.5% as presumably deficient and the next 1.0% doubtful, these borderlines for tested deficiency have the advantage of being more conservative than those at present advocated. On the basis of our empirical knowledge this is an important reason for urging borderlines on the scales at least as low as those suggested herein. Disregarding the extremely high borderlines which have fallen into disuse, we still find that social deficiency is often presumed for those testing above the lowest 1%. With the new Stanford scale, Terman presumes “definite feeble-mindedness” below an Intelligence Quotient of .70, below which he finds that 1% of 1000 unselected children fell. I Q's from .70 to .80 would include his uncertain group, which he describes as “border-line deficiency, sometimes classified as dullness, often as feeble-mindedness” (57, p. 79). His tables show 5% below an I Q of .78. We have no results with a random group of adults by which to judge how many would be below these borders. When the I Q has been applied to scores with other scales a larger percentage has often been found to be excluded. Fernald has shown that Haines' suggestion of a coefficient of .75 with the Point scale would exclude 16% of 100 Cincinnati girls selected at random from among those who left school at 14 years to go to work (16).
Unless the examiner wishes to assume that social inefficiency is more frequent than it has been demonstrated by the practical tests of life, the success of those who have low quotients should make him exceedingly cautious about accepting the various borderlines which have been suggested by those who have not tested their criteria by the percentage method. It is not merely that the borderlines should be lowered, but that they should be lowered 312under some consistent plan so that we should know as much as is possible about their significance in the prediction of ultimate social inefficiency, and that we should be able to readjust them on the basis of new data or to new scales.
With the Point scale Yerkes and Wood say regarding “the coefficient of intelligence .70, which we accept as the upper limit of intellectual inadequacy or inferiority”: “Our data indicate that grades of intellectual ability measured by the coefficient .70 or less are socially burdensome, ineffective, and usually a menace to racial welfare” (226). With the most reliable part of their data, that for children from 8-13, this coefficient excludes the lowest 8.39%. Moreover, the lowest group for which they suggest a borderline, the dependents, falls at .50 or below and includes 1.05%.
2. A second practical advantage of the percentage borderlines on the scale is that they make no assumption as to the uniformity of the norms for the different ages. Except for the Stanford and the Jaederholm scales, there is little evidence that the age norms exclude equivalent portions of the children at the different life ages.
Goddard's Table I gives the data from which the following percentages of those who pass the norm are calculated, not counting those above 11 years, since the older groups are clearly affected by selection:—5 yrs., 88%; 6 yrs., 79%; 7 yrs., 81%; 8 yrs., 51%; 9 yrs., 60%; 10 yrs., 73%; 11 yrs., 44%. Kuhlmann's figures when using his own revised scale with public school children including the seventh grade, are:—6 yrs., 100%; 7 yrs., 95%; 8 yrs., 90%; 9 yrs., 87%; 10 yrs., 81%; 11 yrs., 80%; 12 yrs., 57%. It is clear that any change in the test norm from age to age must disturb the quotient which is based on these norms, although it would not affect the intelligence coefficient with the Point scale.
3133. A third advantage of the percentage method arises from the fact that we cannot presume that the same ratio in terms of the scale units will exclude the same degrees of ability at different ages even when the norms for these ages are properly adjusted. The earlier results with the Stanford revision show a large variation as to the percentage excluded by the same I Q at different ages. For example, an I Q of .76 would have shut out 1% of 117 non-selected 6-year-olds, 2% of 113 9-year-olds and 7% of 98 13-year-olds. The lowest 1% of the last group was below a borderline of .66 (197).
With widely varying norms of the other scales, the I Q borderlines show much greater variation. In a recent review of the evidence, including Descoudres' report (96) on retesting the same children for several years Stern recognizes that an I Q index is not constant after 12 years (187). Doll records decided changes in quotients for the same individual at different ages (99). So far as the 1908 scale is concerned, using Goddard's data, our Table V shows that at five years of age the lowest 1.8% would fall at or below a quotient of .40, at eight years the lowest 1.9% would show a quotient of .62 or less, and at 15 years the lowest 2.8% fall below a quotient of .75. The rough tentative approximation of scale limits which I have suggested for the lowest 1.5% shows that a series of quotients for children from 5 to 15 years of age would be below .75 at every age and below .65 for half of these ages. For the presumably deficient group the quotients would be still lower in order to be as conservative as the borderlines that I have suggested with the Binet scale as at present standardized.
With the coefficient of intelligence and the Point scale, the Yerkes and Wood data show that their borderline of .70 excluded 13% of 196 children 8 and 9 years of age, 314while it excluded only 5% of each of the next two groups of double ages. With the group of 237 18-year-old Cincinnati working girls it excluded only 3% (226).
The data at present available thus indicate that we should not expect to find the same ratio at different ages excluding similar percentages. If the ratios have a value for comparing individuals of different ages, they seem to fluctuate so decidedly from age to age that they can hardly be trusted for stating the borderlines of deficiency without empirical confirmation for each age.
Pearson found that the children of the older ages in the special classes were more and more deficient, measured in terms of the standard deviation of the normal group. This shift on the average was four months of mental age downward for each year of life during the period 7-14 which he studied. It makes uncertain the definition of the borderline in terms of a constant multiple of the deviation or of a constant quotient, unless this shift is shown to be due to imperfections of the tests which can be corrected, or to changes in the selection of the tested groups at advanced ages.
Pearson's suggestion of -4 S. D. as a borderline with the Jaederholm data gives some very curious results with the group of children in the special schools at Stockholm. Under his interpretation at life-ages 8-11 from 0 to 5.2% of the pupils in these classes would be regarded as deficient, while for life-ages 12-14, 15.2% to 44.4% are beyond -4 S. D. In passing it is to be noted that if one accepted Pearson's suggestion that the borderline should be fixed at -4 S. D., in case the distribution of mental capacity were strictly normal, only four children in 100,000 would be found deficient, according to the probability tables.
With the method of the standard deviation it would be necessary either to show that the deviation was constant 315in terms of the year units or else to restate the borderline for different ages in terms of the scale units. The irregularity of the norms with the Binet scale could also be allowed for, of course, by stating different quotients for the different ages, but when this readjustment is required for either the ratio or the deviation in terms of the scale units, these methods lose all their advantage of simplicity. Instead of one ratio or one multiple of the years of deviation, we might have a different statement for each life-age. With the percentage method there would be only one statement of the borderline for all ages in terms of percentage, although the scale positions change which shut out the same lowest percentage.
4. All the quotient methods of defining the borderline encounter a serious practical difficulty in fixing the borderline for the mature, so that it will be equivalent to that for the immature. With the Stanford scale in calculating the quotient for adults, no divisor is used over 16 years. Yerkes and Bridges also think that this is about the time that the development of capacity ceases. Kuhlmann and others use 15 as the highest divisor. Wallin objects to either of these ages being used as the age of arrest of mental development (15, p. 67). Both the methods of the standard deviation and percentage have a similar difficulty, in that the borderline for the mature has to be empirically determined on a test scale. In this dilemma, however, the data collected with the random group of 15-year-olds in Minneapolis and published in the present study, places the borderline for the mature on either the 1908 or 1911 Binet scale in a much safer position, so far as empirical data is concerned, than the borderline for the mature for any other scale. This is true whether that borderline be then stated in terms of either the quotient or percentage methods. Translated into terms of the quotient, our percentage 316borderlines for the mature with these scales, below X for presumably deficient and below XI for the uncertain, would amount to quotients .60 and .66 on the basis of our findings with this random group of children who have presumably about reached adult development. Pearson does not attempt to define any borderline for the adults on the basis of the deviation, since Jaederholm tested only children. Moreover, this is not possible empirically with our group of 15-year-olds, since we tested only the lower extreme of this group.
Unfortunately, the borderlines of the mature for the Stanford and other scales depend upon empirical results obtained not with random groups, but upon a composite of selected groups of adults built up by the investigator on an estimate that this combined group represents a random selection among those with a typical advance in development, an almost superhuman task. Fortunately the empirical determination of this borderline for the mature might be improved later by obtaining data on less selected groups. The clearer significance of the empirical data for the borderline for the mature which I have presented for the Binet 1908 and 1911 scales from a random group of 15-year-olds seems to be an important practical advantage. It provides an empirical basis for judging the implication of test results with adults. It gives adults the benefit of the doubt if they improve after 15 years of age.
5. Compared as to their popular significance, there is no doubt that the lowest 0.5% of the individuals of a particular age has very much more significance to those not familiar with detailed statistical practise than a coefficient or a multiple of the standard deviation. A statement that an adult has only the tested ability of a child of 7 years is certainly much more impressive than his score in other 317quantitative terms. It will probably always be desirable, therefore, to supplement any other method of scoring by a statement of the individual's test age.
With our present series of tests, the percentage method will best provide a concept of the equivalence of the borderlines at different ages provided the form of the distribution does not remain uniform. I discussed this question briefly in connection with units of measurement. In considering curves of development, I assembled some of the evidence which makes the assumption of normal distribution or even of a constant skewness at least uncertain. In my opinion the weight of the evidence is against the hypothesis that the distributions retain a constant form during the period of development. If this were clearly demonstrated, both the ratio methods and deviation would fail to express equivalent borderlines for the different ages with the Binet scales. A fixed multiple of the standard deviation or a fixed quotient would exclude different percentages of the population at each age when the skewness varied. By reference to Figures 3 and 5, it can be seen that, if our physical units in which we expressed the measurement were uniform and ability always extended to the same absolute zero point, it is true that .01 of the physical units reached by the best at each age would be the same relative amount of ability of the best at each age, stated in physical units, regardless of the form of the distributions. Such a concept, however, has an unknown biological or social significance so far as I can see, except for a constant form of distribution. The same relative physical score compared with the highest at each age, theoretically 318might exclude the lowest 40% of one age group, for example, and only 10% of another group provided the distribution varied enough in form. The concept of the same relative amount of ability measured in physical units, so soon as the form of distribution varies from age to age, thus loses significance in terms of the struggle for existence. In that struggle, a vital question is—do the individuals at different ages have to struggle to overcome the same relative number of opponents of better ability at their age? If they do, the individuals might properly be regarded as in equivalent positions in the struggle for social survival, disregarding how far the next better individual is above them on the objective scale. This is the concept accepted by the percentage definition of the borderline as the best available under uncertain forms of distribution.
The recent rapid perfection of objective scales to measure educational products, like ability in handwriting, etc., in equal units running to an absolute zero of ability, suggests that it might be possible ultimately to state the borderline of deficiency in terms of the same relative objective distance between the best and zero ability at each age on a scale of general ability. This ideal could be approached, for example, with the Sylvester form-board test in which the units are seconds required to complete the same task, if we could agree upon a maximum number of seconds without success which should mean no ability, and if this zero should remain the same at each age. It would only be necessary to take, for example, the best position or the median or the upper quartile at each age as the other point of reference. We could then say that a borderline in physical units was always, for example, .01 of the median record at each age above zero. Such a method would provide relatively equal objective borderlines at each age 319and it would afford a measure which would take into account the ability of the individuals to be competed against instead of merely counting them as the percentage method must. It would be better than a description in units of the standard deviation in that its significance would be more easily understood if the form of distribution varied with age.
To demonstrate its worth, however, this method of defining the borderline in terms of the same proportion of the physical difference between zero and the median at each age, would also have to provide a better prediction of ultimate social failure. It would have to be shown that individuals below the relative objective borderline at maturity were below the same relative objective borderline during immaturity. Moreover, it would have to be shown that this relationship was closer than it would be with percentile records. It is a form of this relative objective measurement which Otis advocates in his “absolute intelligence quotient,” which he proposes as logically the best measure of ability. It consists of the ratio of the score of the individual measured in equal absolute units of intelligence, divided by his age (163).
While a relative objective borderline might under certain circumstances afford a better criterion than the same lowest percentage of individuals, there are two very serious practical difficulties which at present make it impossible. In the first place, with the exception of a few motor tests, there are no test results with children of different ages measured in terms of equal objective units for the same task. Even if the Binet year units are equal, as applied to the same task, there is no accurate means of dividing the year units into smaller physical units on the basis of scores with the tests. This makes the use of the Binet scale impossible and we should be forced back upon 320such tests as the form-board, the ergograph, etc., for which we should have to agree upon an absolute zero of ability. Moreover, mental tests do not lend themselves to measurement in terms merely of rapidity in doing the same task or in terms of other equal physical units since the quality of the work also has to be evaluated and this is usually done in units assumed arbitrarily to measure equivalent degrees of perfection.
The second practical difficulty which at present makes a relative objective borderline impossible is that we know nothing as to the prediction of social failure and success from relative positions on the objective scale used even with the few isolated tests that might be made available. Until we have data on this question, as well as scales of tests for native ability that are measurable to zero ability in objective terms, the percentage method affords the only available way of stating equivalent borderlines when the form of distribution changes.
If the age of arrest of development shifts either earlier or later with different degrees of capacity, then there seems to be no logical escape from a change in the form of distribution. Stern recognized this when he concluded that idiots reach an arrest of development earlier than those better endowed, so he stated that his quotient would not hold for them. He said:
“The feeble-minded child, it must be remembered, not only has a slower rate of development than the normal child, but also reaches a stage of arrest at an age when the normal child's intelligence is still pushing forward in its development. At this time, then, the cleft between the two will be markedly widened.
“From this consideration it follows that the mental quotient can hold good as an index of feeble-mindedness only during that period when the development of the feeble-minded individual is still in progress. It is for this reason 321that there is no use in calculating the quotient for idiots, because, in their case the stage of arrested development has been entered upon long before the ages at which they are being subjected to examination” (188).
Perhaps the most interesting characteristic of the percentage method is that it automatically adjusts itself to any form of distribution. In case the distributions of ability turn out to be normal for each age and the arrests of development for different degrees of ability distribute alike, then the borderline fixed by the percentage method becomes identical with the corresponding borderlines by the quotient, deviation, or relative objective distance. It can be directly translated into a quotient or a multiple of the standard deviation. This fact affords a good check upon the empirical borderlines fixed by the percentage method for different ages. If the distribution is normal, the lowest 1.5% and 0.5% would be identical with -2.17 S. D. and -2.575 S. D. in samples of 10,000 cases. We may check these percentage borderlines by Goddard's results for ages 5-11 tested with the 1908 Binet scale. I have given the standard deviation for the ages 5-11 with this data in Chap. XIII a, 2. Applying the criterion of 2.575 S. D. to these deviations, we find that to be in the lowest 0.5%, if the distribution were normal, would be about a year less of deficiency than we have suggested, while Pearson's borderline of -4 S. D. would be close to that we suggest. The empirical data thus suggest that the assumption of a normal distribution is faulty at the borderline or else Goddard's data is incorrect for fixing the limits on the scales. I have already given the evidence for supposing that the distribution is skewed during the years of growth.
When approximately random samples are not available, a multiple of the deviation of an efficient group such as 322-4 S. D. at the particular age seems to afford a practical way of discovering a tentative borderline until a random sample can be measured. The serious theoretical objections to such a procedure as a regular method is that the efficient group would be selected by the subjective standard of somebody's opinion and that the form of distribution of ability may vary from age to age.
Recalling the practical advantages of the percentage method which we enumerated in the preceding section, we can now better understand the value of a method that is not disturbed by the form of distribution of mental capacity which may ultimately be found to prevail at different ages. It is safer at present to assume that the distributions do change enough in form at the lower end seriously to affect the borderlines of deficiency as defined by other methods. If, however, the form of distribution remains uniform, it would first be necessary for those advocating the use of any of the other quantitative definitions to show that the units of their scales are equal under some reasonable hypothesis. A ratio or a deviation statable only in scale units which are not demonstrably equal is a hazard, with the chances badly weighted against its reliability. So far as both the Binet and the Point scales are concerned we have found that the units are not equal. A quotient or coefficient arrived at by assuming their equality is sure to mean seriously erroneous fluctuations in the borderlines.
Referring to the percentage method, Yerkes and Wood say: “Frequency of occurrence is unquestionably a useful datum, which should be presented, if not instead of, then in addition to, certain other statistical indices which possess greater scientific value” (226). These other indices require both equal scale units and uniform distributions from age to age. The ratio and deviation methods 323fail at present in both of these particulars, so that it seems necessary to depend upon the percentage definition of tested deficiency, incomplete as that may be.
This leaves us in the unfortunate situation that the borderline positions on the scale will have to be stated separately for each age and will have to be found empirically. Moreover, we shall need to determine more accurately in what lowest percentage an individual must test in order reasonably to predict that he will require social care for the good of himself and society.
As soon as anybody can discover a means of defining the borderline, which is equally accurate and significant, and which, in addition to counting the proportion of better individuals to be met in the competition of life, will also evaluate the distance they are above the borderline, we all shall be eager to accept this better criterion of deficiency. A form which it might take is that of relative objective distance between zero and median ability. If measurable in equal objective units, this would be independent of the form of distribution and would improve the quantitative description of equivalent deficiency, provided that it also forecasted future social failure as well as the percentage method.
What form of stating the borderline of tested deficiency may ultimately meet with approval, a verbal definition of feeble-mindedness will never remain an ideal scientific statement until it finds expression in quantitative terms.
1. Baldwin, Bird T. The Learning of Delinquent Adolescent Girls as shown by a Substitution Test. J. of Educ. Psychol., 1913, 4, 317-332.
2. Blumel, C. S. Binet Tests on the Two Hundred Juvenile Delinquents. Training School Bull., 1915, 12, 187-193.
3. Bridgman, Olga Louise. An Experimental Study of Abnormal Children with Special Reference to the Problems of Delinquency and Dependency. Announcement of Examination for Ph.D., Stanford University, Calif.
4. Bridgman, Olga Louise. Delinquency and Mental Deficiency. Survey, 1914, 32, 302.
5. Bridgman, Olga Louise. Mental Deficiency and Delinquency. J. of Amer. Med. Assoc., 1913, 62, 471-472.
6. Bronner, Augusta F. A Comparative Study of the Intelligence of Delinquent Girls. Columbia Contrib. to Educ. 1914, No. 68, pp. v + 95.
7. Bronner, Augusta F. A Research on the Proportion of Mental Defectives Among Delinquents. J. of Crim. Law and Criminol., Nov. 1914.
8. Chicago Municipal Court. The Psychopathic Laboratory Eighth and Ninth Annual Reports for the years Dec. 1, 1913, to Dec. 5, 1915, inclusive, pp. 34-48.
9. Crafts, L. W. Bibliography of Feeble-Mindedness in its Social Aspects. Monog. Sup., J. of Psycho-Asthenics, 1916, 1, No. 3, pp. 72. A Bibliography on the Relations of Crime and Feeble-Mindedness. J. of Crim. Law and Criminol., 1916, 7, 544-555.
10. Cramer, A. Bericht an das Landesdirektorium ueber die psychiatrisch-neurologische Untersuchung der F. Z. in 325dem Stephansstift bei Hannover, u. s. w., Klin. Jahrb., Jena, 1907, 18.
11. Davis, Katherine Bement. Feeble-minded Women in Reformatory Institutions. Survey, 1912, 27, 1849-1851.
12. Doll, E. A. Supplementary Analysis of H. B. Hickman's Study of Delinquents. The Training School, 1915, 11, 165-168.
13. Dosai-Révész, Frau. Experimenteller Beitrag zu Psychologie der moralisch verkommenen Kinder. Zsch. f. angew. Psychol., 1911, 5, 272-330.
14. Eastman, Frederic C. and Rosanoff, A. J. Association in Feeble-Minded and Delinquent Children. Amer. J. of Insanity, 1912, 69, 125-141.
15. Fernald, Guy G. The Defective Delinquent Class: Differentiating Tests. Amer. J. of Insanity, 1912, 68, 523-594.
16. Fernald, Mabel R. Practical Applications of Psychology to the Problems of a Clearing House. J. of Crim. Law and Criminol., 1917, 7, 722-731.
17. Gifford, Mrs. E. G. and Goddard, Henry H. Defective Children in the Juvenile Court. The Training School, 1912, 9, 132-134.
18. Goddard, Henry H. The Criminal Imbecile. Macmillan, New York, 1915, p. 157.
19. Goddard, Henry H. The Responsibility of Children in Juvenile Court. J. of Crim. Law and Criminol., 1912, 3, No. 3.
20. Goring, Charles. The English Convict. A Statistical Study. Wyman & Sons, Ltd., London, 1913, pp. 440.
21. Grabe, E. Von. Prostitution, Kriminalität, und Psychopathie. Archiv. für kriminal Anthropologie und Kriminalistik, 1912, 48 ff.
32622. Green, E. F. Report of Physician and Psychologist on the Reformatory Population of St. Cloud, Minn. J. of Crim. Law and Criminol., 1913, 4, 420-421.
23. Green, E. F. The Defective Delinquents. Minnesota State Reformatory, St. Cloud, 1913, pp. 7.
24. Haines, Thomas H. Feeble-Mindedness Among Adult Delinquents. J. of Crim. Law and Criminol., 1917, 7, 702-721.
25. Haines, Thomas H. Point Scale Ratings of Delinquent Boys and Girls. Psychol. Rev., 1915, 22, 104-109.
26. Haines, Thomas H. Relative Value of Point Scale and Year-Scale Measurements of One Thousand Minor Delinquents. J. of Exper. Psychol., 1916, 1, 51-82.
27. Healy, William. The Individual Delinquent. Little, Brown & Co., Boston, 1915, pp. xvii + 830.
28. Hickman, H. B. Delinquent and Criminal Boys Tested by the Binet Scale. The Training-School Bull., 1915, 11, 159-164.
29. Hickson, William J. The Defective Delinquent. J. of Crim. Law and Criminol., 1914, 5, 397-403.
30. Hill, Helen F. and Goddard, H. H. Delinquent Girls Tested by the Binet Scale. The Training School, 1911, 8, 50-56.
31. Jennings, H. M. and Hallock, A. L. Binet-Simon Tests at the George Junior Republic. J. of Educ. Psychol., 1913, 4, 471-475.
32. Jones, Arthur M. The Relation of the Psychiatrist to the Juvenile Court. Wis. Med. J., 1914, 13, August.
33. Kohs, Samuel C. The Practicability of the Binet Scale and the Question of the Borderline Case. Bull. No. 23, 1915, Research Dep't., Chicago House of Correction, pp. 23.
34. Kramer, Franz. Intelligenzprüfungen an abnormen Kindern. Monatschrift für Psychiatrie and Neurologie, 1913, 33, 500-519.
32735. McCord, Clinton P. One Hundred Female Offenders. J. of Crim. Law and Criminol., 1915, 6, 385-407.
36. Massachusetts. Report of the Commission for the Investigation of the White Slave Traffic. House Report No. 2281, 1914, pp. 86.
37. Michigan. Report of the Commission to Investigate the Extent of Feeble-mindedness, Epilepsy and Insanity and other Conditions of Mental Defectiveness in Michigan, 1916, State Printers, Lansing, pp. 175.
38. Moore, Frank. Mentally Defective Delinquents. Proc. of Nat. Conf. of Char. and Cor., 1911, 65-68.
39. Morrow, Louise, and Bridgman, Olga. Delinquent Girls Tested by the Binet-Scale. The Training School, 1912, 9, May.
40. New Hampshire. Children's Commission Report to the Governor and Legislature of New Hampshire. Concord, 1914, pp. 136.
41. Ordahl, George. A Study of 341 Delinquent Boys. J. of Delinquency, 1916, 1, 72-86.
42. Orton, G. L. and Moore, Frank. The Procreative Regulation of Defectives and Delinquents. J. of Amer. Med. Assoc., 1912, 58, No. 26.
43. Otis, Margaret. The Binet Tests Applied to Delinquent Girls. Psychol. Clinic, 1913, 7, 127-134.
44. Pintner, Rudolf, and Paterson, Donald G. A Psychological Basis for the Diagnosis of Feeble-mindedness. J. of Crim. Law and Criminol., 1916, 7, 32-55.
45. Porteus, S. D. Mental Tests with Delinquents and Australian Aboriginal Children. Psychol. Rev., 1917, 24, 32-42.
46. Pyle, W. H. A Study of Delinquent Girls. Psychol. Clinic, 1914, 8, 143-148.
47. Renz, Emile. A Study of the Intelligence of Delinquents and the Eugenic Significance of Mental Defect. The Training School Bull., 1914, 11, 37-39.
32848. Rossy, C. S. Report on the First Three Hundred Cases Examined at the Massachusetts State Prison. Bull. No. 17 of the Mass. State Brd. of Insanity, 1915.
49. Rowland, Eleanor. Report of Experiments at the State Reformatory for Women at Bedford, N. Y. Psychol. Rev. 1913, 20, 244-249.
50. Schlapp, Max G., and Hollingworth, Letta Stetter. The Mentally Defectives as Cases in the Courts of New York City. Bull. of U. S. Bur. of Educ., 1915, No. 50, 150-157; N. Y. Med. Rec., Feb. 27, 1915.
51. Smedley, Fred. W. Child Study Reports No. 2 and No. 3, 1901, 1902. Chicago Public Schools.
52. Smith, M. H. The Binet-Simon Method and the Intelligence of Adult Prisoners. Lancet, 1915, 17, 120.
53. Smith, Stevenson. First Annual Report of the Bailey and Babette Gatzert Foundation for Child Welfare. Bull. of the Univ. of Wash. No. 60, 1912.
54. Stenquist, J. L.; Thorndike, E. L.; Trabue, M. R. The Intellectual Status of Children who are Public Charges. Archiv. of Psychol., 1915, No. 33, pp. 52.
55. Storer, Mary. The Defective Delinquent Girl. J. of Psycho-Asthenics, 1914, 19, 23-30.
56. Sullivan, W. C. La mesure de developpement intellectual chez les jeunes delinquantes. L'année psychol., 1912, 18, 341-361.
57. Terman, Lewis M. The Measurement of Intelligence. An Explanation of and a Complete Guide for the use of the Stanford Revision and Extension of the Binet-Simon Intelligence Scale. Houghton Mifflin, Boston, 1916, pp. xviii + 362.
58. Virginia. State Board of Charities and Corrections. A Special Report to the General Assembly of 1916 on Weak-Mindedness in the State of Virginia; together with a Plan for the Training, Segregation, and Prevention of the Procreation of the Feeble-Minded. Richmond, Va., 1916, pp. 128.
32959. Weidensall, Jean. Psychol. Tests as Applied to Criminal Women. Psychol. Rev., 1914, 21, 370-375.
60. Weidensall, Jean. The Mentality of the Criminal Woman. Educ. Psychol. Monog., Warwick & York, Baltimore, 1916, pp. xx + 322.
61. Williams, J. Harold. A Study of 150 Delinquent Boys. Bull. No. 1. Research Laboratory of the Buckel Foundation, Stanford University, Cal., Feb. 1915, pp. 15.
62. Williams, J. Harold. Intelligence and Delinquency. A Study of Two Hundred and Fifteen Cases. J. of Crim. Law and Criminol., 1916, 6, 696-705.
63. Abelson, A. R. The Measurement of Mental Ability of Backward Children. Brit. J. of Psychol., 1911, 4, 268-314.
64. American Association for the Study of the Feeble-Minded. Report of Committee on Classification of Feeble-Minded. Chippewa Falls, 1909. J. of Psycho-Asthenics, 1910, 15, 61.
65. Anderson, V. V. The Laboratory in the Study and Treatment of Crime. J. of Crim. Law and Criminol., 1915, 5, 840-850.
66. Anonymous. Recommendations on the Binet. Ungraded, 1915, 1, 7.
67. Anton, G. Das moralische Fühlen und Begreifen bei Imbezilen und bei kriminellen Degenerierten, Hermann, Juristisch-psychiatrische Grenzfragen, 1912, 8, Heft. 4, 5.
68. Aschaffenburg, Gustav. Crime and Its Repression. Translated by Adalbert Albrecht. Modern Crim. Sci. Series. Little, Brown & Co., Boston, 1913, pp. xxviii + 331.
69. Auden, George A. Feeble-Mindedness and Juvenile Crime. J. of Crim. Law. and Criminol., 2, 228-238.
33070. Australian Minister of Public Instruction. Report for 1911-12. Albert J. Mullett, Melbourne, 1913.
71. Ayres, Leonard P. Laggards in Our Schools. Russell Sage Foundation, New York, 1909, pp. xii + 236.
72. Bachman, Frank P. Supplementary Report on Overage and the Method of Determining Overage. New York.
73. Baldwin, Bird T. Individual Differences in the Correlation of Physical Growth of Elementary and High School Pupils. J. of Educ. Psychol., 2, 315-341.
74. Baldwin, Bird T. Physical Growth and School Progress. Bull. U. S. Bur. of Educ., 1914, No. 10.
75. Baldwin, Bird T. The Normal Child. Its Physical Growth and Mental Development. Pop. Sci. Mo., 1914, 75, 550-567.
76. Binet, Alfred. Application of the New Methods to the Diagnosis of the Intellectual Level Among Normal and Subnormal Children in Institutions and in the Primary Schools. L'année psychol., 1905, 245-236. Translated by Elizabeth S. Kite in The Development of Intelligence in Children. The Training School, Vineland, N. J., 1916, pp. 336.
77. Binet, Alfred, and Simon, Th. Mentally Defective Children. Translated by Drummond, W. B. Longmans Green & Co., London, 1914, pp. viii + 180.
78. Binet, A. and Simon, Th. Method of Measuring the Development of the Intelligence of Young Children. Translated by Clara H. Town. Courier, Lincoln, Ill., 1913.
79. Binet, Alfred, and Simon, Th. The Development of Intelligence in Children. Translated by Elizabeth S. Kite. The Training School, Vineland, N. J., 1916, pp. 329.
80. Boas, Franz. Growth, Monroe Cyclop. of Educ.
33181. Bobertag, Otto. Ueber Intelligenz Prüfungen (nach der Methode von Binet und Simon). Zsch. f. Angew. Psychol., 1916, 6, 531 ff.
82. Breckenridge, Sophonisba P., and Abbott, Edith. The Delinquent Child and the Home. Charities Publication Committee, New York, 1912, pp. 355.
83. British Royal Commission on the Care and Control of the Feeble-Minded. Report of the Commission. Wyman and Sons, Ltd. London, 1908, 8 vols.
84. Burt, Cyril. Experimental Tests of General Intelligence. Brit. J. of Psychol., 1910, 3, 94-177.
85. Burt, Cyril. The Measurement of Intelligence by the Binet Tests. Eugenics Rev., 1914, 6, 36-50, 140-152.
86. Cajori, Florian. A New Marking System and Means of Measuring Mathematical Abilities. Science, 1915, 39, 874-881.
87. Carpenter, D. F. Mental Age Tests. J. of Educ. Psychol., 1913, 4, 538-544.
88. Children's Bureau of the U. S. Department of Labor. Mental Defectives in the District of Columbia. Children's Bull., 1915, No. 13, pp. 39.
89. Chotzen, F. Die Bedeutung der Intelligenzprüfungsmethode von Binet und Simon für die Hilfsschule. Hilfsschule, 1915, 5, 153-162.
90. Chotzen, F. Die Intelligenzprüfungsmethode von Binet-Simon bei Schwachsinnigen Kindern. Zsch. für angew. Psychol., 1912, 6, 411-494.
91. Cimbal, W. Taschenbuch zur Untersuchung nerväser und psychischer Krankheit under Krankheits-ver-dachtiger Zustädige. J. Springer, Berlin, 1909.
92. Clark, Taliaferro; Collins, George L.; and Treadway, W. L. Rural School Sanitation Including Physical and Mental Status of School Children in Porter County, Indiana. U. S. Public Health Bull., 1916, No. 77, pp. 125.
33293. Cornell, Walter S. Health and Medical Inspection of School Children. F. A. Davis Co., Phila., 1912, pp. xiv + 614.
94. Coulter, Ernest K. Mentally Defective Delinquents and the Law. Proc. Nat. Conf. Char. and Cor., 1911.
95. Davenport, C. B.; Castle, Wm. Ernest; Coulter, John Merle; East, Edward Murray; and Tower, Wm. Lawrence. Heredity and Eugenics. Univ. of Chicago Press, 1912.
96. Descoudres, A. Les tests de Binet-Simon comme mesure du developpement des enfants anormaux. Archiv. de psychol., 1915, 15, 225-254.
97. Detroit Board of Education. Seventy-Second Annual Report for the year ending June 30, 1915.
98. Doll, E. A. Anthropometry as an aid to Mental Diagnosis. Pub. of the Research Dept. The Training School, Vineland, N. J., 1916, No. 8, pp. 91.
99. Doll, E. A. Note on the “Intelligence Quotient.” The Training School, Vineland, No. 7, Jan. 1916.
100. Doll, E. A. Preliminary Note on the Diagnosis of Potential Feeble-Mindedness. Training School Bull., 1916, May.
101. Drucker, A. P. A Study of One Hundred Juvenile Adult Offenders in the Cook County Jail. Chicago, Ill. J. of Crim. Law and Criminol., 1913, 4, 47-57.
102. Farrell, Elizabeth E. A Preliminary Report on the Careers of Three Hundred Fifty Children Who Have Left Ungraded Classes. J. of Psycho-Asthenics, 1915, 20, Nos. 1 and 2.
103. Fernald, Guy G. The Recidivist. J. of Crim. Law and Criminol., 3, 866-875.
104. Fernald, Walter E. The Imbecile with Criminal Instincts. Amer. J. of Insanity, 1909, 65, No. 4.
333105. Finkle, Kate T. Significant Figures from the Juvenile Court of Hennepin County. Proc. Minn. Acad. of Soc. Sci., 1910.
106. Gault, Robert H. Editorial. J. of Crim. Law and Crimol., 1913, 4, 322.
107. Gault, Robert H. Preventives of Delinquency. J. of Crim. Law and Criminol., 1914, 4, 637.
108. Gilbert, J. Allen. Researches on the Mental and Physical Development of School-Children. Stud. from the Yale Psychol. Lab., 1894, 2, 40-100.
109. Glueck, Bernard. The Mentally Defective Immigrant. N. Y. Medical J., 1913, 98, 760-796.
110. Goddard, Henry H. Binet's Measuring Scale for Intelligence. The Training School, 1910, 6, No. 11.
111. Goddard, Henry H. Discussion of Degree of Mental Deficiency in Children as Expressed by the Relation of Age to Mental Age. J. of Psycho-Asthenics, 1913, 17, 143 ff.
112. Goddard, Henry H. Feeble-mindedness: Its Causes and Consequences. Macmillan, N. Y., 1914, pp. xii + 599.
113. Goddard, Henry H. Four Hundred Feeble-Minded Children Classified by the Binet Method. J. of Psycho-Asthenics, 1910, 15, 28.
114. Goddard, Henry H. School Training of Defective Children. World Book Co., New York, 1914, pp. xi + 97.
115. Goddard, Henry H. The Binet-Simon Measuring Scale for Intelligence. Revised Edition, 1911. Department of Psychological Research, The Training School, Vineland, N. J.
116. Goddard, Henry H. The Diagnosis of Feeble-Mindedness. Illinois Med. J., Sept. 1913.
117. Goddard, Henry H. The Improvability of Feeble-Minded Children. J. of Psycho-Asthenics, 1913, 17, 121-131.
334118. Goddard, Henry H. The Prevention of Feeble-Mindedness. Transactions of the 15th Internat. Cong. of Hygiene and Demography.
119. Goddard, Henry H. Two Thousand Normal Children Measured by the Binet Measuring Scale for Intelligence. Ped. Sem., 1911, 18, 232-259.
120. Goring, Charles. On the Inheritance of the Diatheses of Phthisis and Insanity. A Statistical Study based upon the Family History of 1,500 Criminals. Biometric Laboratory Pub., Drapers' Co. Research Memoirs, Biometric Series No. V.
121. Gruhle, Hans W. Die Ursachen der jugendlichen Verwahlosung and Kriminalität. J. Springer, Berlin, 1912, pp. iv + 454. Reviewed by J. B. Miner in J. of Crim. Law and Criminol., March, 1913.
122. Haines, Thomas H. Diagnostic Values of Some Performance Tests. Psychol. Rev., 1915, 22, 299-305.
123. Hart, B. and Spearman, C. Mental Tests of Dementia. J. of Abnorm. Psychol., 1914, 9, 217-264.
124. Healy, William. Mental Defects and Delinquency. Proc. of the Nat. Confer. Char. and Cor., 1911, 38, 59-63.
125. Healy, William and Fernald, Grace M. Tests for Practical Mental Classification. Psychol. Monog., 1911, No. 54, p. 53.
126. Heron, David. A First Study of the Statistics of Insanity and the Inheritance of the Insane Diathesis. Eugenics Laboratory Publications, Memoir Series No. 11. Dulau & Co., Ltd.
127. Heron, David. Mendelism and the Problem of Mental Defect. A Criticism of Recent American Work. Questions of the Day and Fray 1914, No. XII, p. 51.
128. Hinckley, Alice C. The Binet Tests Applied to Individuals Over Twelve Years of Age. J. of Educ. Psychol., 1915, 6, 43-58.
335129. Huey, Edmund Burke. Backward and Feeble-Minded Children. Educ. Psychol. Monog. Warwick and York, 1912.
130. Kelley, Truman Lee. Educational Guidance. Columbia Contributions to Educ., 1914, No. 71, pp. xi + 116.
131. Key, Wilhelmine E. Feeble-Minded Citizens in Pennsylvania. Public Charities Assoc. of Penn., 1915, Pub. No. 16, pp. 63.
132. Kinberg, Olaf. Obligatory Psychiatric Examination of Certain Classes of Accused Persons. J. of Crim. Law and Criminol., 1912, 2, 858-867.
133. Kneeland, G. J. Commercialized Prostitution in New York City. Century Co., 1913.
134. Knox, Howard A. Alien Mental Defectives, A Collection of Papers. C. H. Stoelting Co., Chicago.
135. Kuhlmann, F. A Revision of the Binet-Simon System of Measuring the Intelligence of Children. Monog. Sup. to J. of Psycho-Asthenics, 1, No. 1, pp. 41.
136. Kuhlmann, F. Binet and Simon's System for Measuring the Intelligence of Children. J. of Psycho-Asthenics, 1911, 15, Nos. 3 and 4.
137. Kuhlmann, F. Degree of Mental Deficiency in Children as Expressed by the Relation of Age to Mental Age. J. of Psycho-Asthenics, 1913, 17, 132-144.
138. Kuhlmann, F. Some Results of Examining a Thousand Public School Children with a Revision of the Binet-Simon Tests of Intelligence by Untrained Examiners. Jour. of Psycho-Asthenics, 1914, 18, 150-179, 233-269.
139. Kuhlmann, F. The Binet and Simon Tests of Intelligence in Grading Feeble-Minded Children. J. of Psycho-Asthenics, 1912, 16, 173-193.
140. Kuhlmann, F. What Constitutes Feeble-Mindedness? J. of Psycho-Asthenics, 1915, 19, 214-236.
336141. LaPage, C. Paget. Feeble-mindedness in Children of School Age. Manchester Univ. Press, 1911, pp. viii + 359.
142. Lindsay, S. M. Juvenile Delinquency. Monroe's Cyclopedia of Education.
143. London County Council. Annual Report, 1909-10.
144. London County Council. Annual Report, 1912, Chap. XLI. Special Schools, Industrial and Reformatory Schools and Places of Detention. Also Board of Education, Statistics of Public Educ. in Eng. and Wales, Part 1, Educ. Statistics, 1912-13.
145. McKinnie, Adele E. The Feeble-Minded in One Michigan County. J. of Psycho-Asthenics, 1914, 18, 142-146.
146. MacMillan, D. P. The Physical and Mental Examination of Public School Pupils in Chicago. Charities, Dec. 22, 1906.
147. Manheim. Bericht ueber den stand der dem Volksschulrektorat unterstellten Stadtischen Schulern in Manheim in den Schuljahren 1909-10, 1910-11, 1911-12.
148. Merrill, Lilburn. The Clinical Classification of Delinquent Children According to Causative Pathology. Seattle, Wash., 1913.
149. Merrill, Maud. A Chart of Mental Examinations. Quarterly, Representing the Minnesota Educational Philanthropic Correctional and Penal Institutions. State Board of Control, St. Paul, Nov., 1915, pp. 78.
150. Meumann, Ernst. Vorlesungen zur Einjuehrung in die experimentelle Paedagogik and ihre psychologishen Grundlagen., 1913, 2 vol.
151. Miner, James Burt. A Percentage Definition of Intellectual Deficiency. Psychol. Bull., 1916, 13, 89-90.
152. Miner, James Burt. The Discovery of Capacity in Backward Children. Proceedings of the Twentieth 337Minnesota State Conference of Charities and Correction, 1911, 150 ff.
153. Miner, James Burt. The Scientific Study of Juvenile Delinquents in Minneapolis. J. of Crim. Law and Criminol., 1913, 3, 781-782.
154. Minnesota State School for Feeble-Minded. Biennial Report for 1912.
155. Monroe, Will S. Feeble-Minded Children in Public Schools. Proceedings of the Assoc. of Med'l. Officers of Amer. Institutions for Idiotic and Feeble-Minded Persons, at Fort Wayne, Ind., May, 1894, pp. 11.
156. Moore, Anne. The Feeble-Minded in New York. A Report Prepared for the Public Education Association of New York, United Charities Building, N. Y. City, 1911, pp. iii + 57.
157. New Orleans. Public School Alliance. Report of the Committee on Exceptional Children in the Public Schools of New Orleans, March, 1913.
158. New York State Board of Charities. Eleven Mental Tests Standardized. Eugenics and Social Welfare, 1915. Bull. No. 5, Albany, pp. 87.
159. Norsworthy, Naomi. Psychology of Mentally Deficient Children. Archives of Psychol., 1906, No. 1.
160. Norsworthy, Naomi. The A Test with the Feeble-Minded. The Training School, June, 1913, 10, No. 4.
161. Olson, Harry. A Constructive Policy Whereby the Social Evil May Be Reduced. Barnard and Miller, Chicago, 1913.
162. Ordahl, Louise Ellison, and Ordahl, George. Qualitative Differences Between Levels of Intelligence in Feeble-Minded Children. J. of Psycho-Asthenics. Monog. Sup., 1915, 1, No. 2, pp. 50.
163. Otis, Arthur S. Some Logical Aspects of the Binet Scale. Psychol. Rev., 1916, 23, 129-152, 165-179.
338164. Pearson, Karl. Mendelism and the Problem of Mental Defect. III. On the Graduated Character of Mental Defect and on the Need for Standardizing Judgments as to the Grade of Social Inefficiency Which Shall Involve Segregation. Questions of the Day and Fray, 1914, No. IX.
165. Pearson, Karl. On Certain Errors with Regard to Multiple Correlation Occasionally made by those who have not Adequately Studied this Subject. Biometrika, 1914, 10, 181-187.
166. Pearson, Karl. On the Relationship of Intelligence to Size and Shape of Head and to other Physical and Mental Characters. Biometrika, 1906, 5, 105-146.
167. Pearson, Karl, and Jaederholm, Gustav A. Mendelism and the Problem of Mental Defect. II. On the Continuity of Mental Defect. Questions of the Day and Fray, 1914, No. VIII.
168. Philadelphia Department of Public Health and Charities. The Number of the Feeble-Minded, 1910.
169. Porter, Langley; Huffaker, A.; and Retter, A. Physical Survey of Supposedly Normal Children. J. of Amer. Med. Assoc., 1915, 45, 675-678.
170. Reed, Mrs. Frederick W. Research Work in the Minneapolis Juvenile Court. Amer. Rev. of Rev., Aug., 1913, 48, 214-217.
171. Rhoades, Mabel Carter. A Case Study of Delinquent Boys in the Juvenile Court of Chicago. Univ. of Chicago Press, 1907, pp. 25.
172. Rogers, A. C. Classification of the Feeble-Minded Based on Mental Age. Bull. of Amer. Acad. of Med., 1912. 13.
173. Rogers, A. C. Discussion of the Mentally Defective and the Courts. J. of Psycho-Asthenics, 1910, 15, 58.
339174. Rosanoff, Isabel R. and Rosanoff, A. J. A Study of Association in Children. Psychol. Rev., 1913, 20, 43-89.
175. Rossolimo, G. Die psychologischen Profile, zur Methodik der quantitativen Untersuchung der psychischen Vorgänze in normalen und pathologischen Fällen. Klinik f. psychische u. nevöse Krankeiten, 1911, 6, Heft. 2.
176. Rybakow, Th. Atlas zur psychologischen Untersuchungen auf gesund und geistes Kranken.
177. Schaefer, H. Allgemeine gerichtliche Psychiatrie für Juristen, Mediziner und Pädogogen. Ernst Hoffman, Berlin, 1910.
178. Schmidt, Clara. Standardization of Tests for Defective Children. Psychol. Monog., 1915, 19, No. 3.
179. Schmidt, Clara. The Binet-Simon Tests of Mental Ability, Discussion and Criticism. Ped. Sem., 1912, 19, 186-200.
180. Schwegler, Raymond A. A Teacher's Manual for the use of the Binet-Simon Scale of Intelligence. Kansas State Printing Office, Topeka, 1914, pp. 56.
181. Shuttleworth, G. E. and Potts, W. A. Mentally Deficient Children. 3rd Ed. Blakistons Son & Co., 1910, pp. 236.
182. Simon, Th. Measurement of Intelligence. Eugenics. Rev., 1915, 6, 291-307.
183. Spaulding, Edith R. The Results of Mental and Physical Examinations of Four Hundred Women Offenders, with Particular Reference to their Treatment during Commitment. J. of Crim. Law and Criminol., 1915, 5, 704-717.
184. Spearman, C. The Heredity of Abilities. Eugenics Review, 1914, 6, 219-237.
185. Spearman, C. The Theory of Two Factors. Psychol. Rev., 1914, 21, 101-115.
340186. Starch, Daniel. The Measurement of Efficiency in Spelling and the Overlapping of Grades in Combined Measurements of Reading, Writing and Spelling. J. of Educ. Psychol., 1915, 6, 167-186.
187. Stern, William. Der Intelligenz quotient als Mass der kindlichen Intelligenz, inbesondere der unter normalen. Zsch. f. angew Psychol., 1916, 11, 1-18.
188. Stern, William. Psychological Methods of Testing Intelligence. Trans. by G. M. Whipple. Psychol. Monographs, Warwick and York, Baltimore, 1914.
189. Strayer, George Drayton. Age and Grade Census of Schools and Colleges. Bull. of the U. S. Bureau of Educ., 1911, No. 5, pp. 144.
190. Strong, Alice C. Three Hundred Fifty White and Colored Children Measured by the Binet-Simon Measuring Scale of Intelligence. A Comparative Study. Ped. Sem., 1913, 20, 485-515.
191. Sylvester, Reuel Hall. The Form Board Test. Psychol. Monog., 1913, No. 65, pp. 56.
192. Terman, Lewis M. The Binet Scale and the Diagnosis of Feeble-Mindedness. J. of Crim. Law and Criminol., 1916, 4, 530-543.
193. Terman, Lewis M. The Mental Hygiene of Exceptional Children. Ped. Sem., 1915, 22, 537-539.
194. Terman, Lewis M. The Significance of Intelligence Tests for Mental Hygiene. J. of Psycho-Asthenics, 1914, 18, 119-127.
195. Terman, Lewis M. and Childs, H. G. A Tentative Revision and Extension of the Binet-Simon Measuring Scale of Intelligence. J. of Educ. Psychol., 1912, 3, 61-74, 133-143, 198-208, 277-289.
196. Terman, Lewis M. and Knollin, H. E. Some Problems Relating to the Detection of Borderline Cases of Mental Deficiency. J. of Psycho-Asthenics, 1915, 20, 1-15.
341197. Terman, Lewis M.; Lyman, Grace; Ordahl, George; Galbreath, Neva; and Talbert, Wilford. The Stanford Revision of the Binet-Simon Scale, and Some Results from its Application to One Thousand Non-Selected Children. J. of Educ. Psychol., 1915, 6, 551-564.
198. Thorndike, Edward L. Educational Psychology. Revised Edition. Columbia, Teachers' College, N. Y. City, 1914, pp. x + 408.
199. Thorndike, Edward L. Measurement of Twins. Archives of Psychol., 1905, No. 1, pp. 64.
200. Thorndike, Edward L. The Significance of the Binet Mental Ages. Psychol. Clinic, 1914, 8, 185-189.
201. Towne, Clara H. Mental Types of Juvenile Delinquents, Considered in Relation to Treatment. J. of Crim. Law and Criminol., 1913, 4, 83-89.
202. Travis, Thomas. The Young Malefactor. N. Y., 1908.
203. Treadway, Walter L. Care of Mental Defectives, the Insane, and Alcoholics in Springfield, Illinois. The Springfield Survey, No. VIII, 1914, pp. ix + 46.
204. Tredgold, A. F. Mental Deficiency (Amentia). 2nd Ed. Revised and Enlarged. Bailliere, Tindall & Cox, London, 1914, pp. xv + 491.
205. United States Bureau of Census, Dept. of Commerce. Insane and Feeble-Minded in Institutions in 1910, 1914.
206. United States Bureau of Census, Dept. of Commerce. U. S. Special Report of Census Office on Mortality. Government Printing Office, 1916.
207. United States Bureau of Census, Department of Commerce. United States Life Tables, 1910. Prepared under the Supervision of James W. Glover, Government Printing Office, 1916.
208. United States Commissioner of Education. Annual Report, 1914.
342209. Van Sickle, James H.; Witmer, Lightner; Ayres, Leonard P. Provisions for Exceptional Children in Public Schools. Bull. of U. S. Bur. of Educ., 1911, No. 14, pp. 92.
210. Wallin, J. E. Wallace. Eight Months of Psycho-Clinical Research at the New Jersey State Village for Epileptics, with Some Results for the Binet-Simon Testing. Trans. of the Nat. Assoc. for the Study of Epilepsy, 1911, 29-43.
211. Wallin, J. E. Wallace. Mental Health of the School Child. Yale Univ. Press, 1914, pp. 463 + ix.
212. Wallin, J. E. Wallace. Psycho-Motor Norms for Practical Diagnosis. Psychol. Monog., 1916, 22, No. 2, pp. 102.
213. Wallin, J. E. Wallace. Re-Averments Respecting Psycho-Clinical Norms and Scales of Development. Psycho. Clinic, 1913, 7, 89-97.
214. Wallin, J. E. Wallace. Who is Feeble-Minded? J. of Crim. Law and Criminol., 1915, 6, 706-716.
215. Wallin, J. E. Wallace. Who is Feeble-Minded? A Reply to Mr. Kohs. J. of Crim. Law and Criminol., 1916, 7, 56-78.
216. Wallin, J. E. Wallace, and Kohs, Samuel C. Who is Feeble-Minded? A Rejoinder and a Rebuttal. J. of Crim. Law and Criminol., 7, 219-226.
217. Webb, E. Character and Intelligence. Brit. J. of Psychol., Monog. Sup., 1915, 3, pp. ix + 99.
218. Weidensell, Jean. Criminology and Delinquency. Annual Summary, Psychol. Bull., 1913, 10, 230-236.
219. Weyandt, Prof. Dr. Ein Schwachsinns-Prüfungskasten von Prof. Dr. Weyandt. Zsch. f. Erforschung and Behandlung des jugendlichen Schwachsinns, 1910, 4, Reprint by P. Johannes Muller, Charlottenburg 5.
220. Whipple, Guy Montrose. Manual of Mental and Physical Tests. Warwick and York, Baltimore, 1915, 2 vols.
343221. Witmer, Lightner. Children With Mental Defect Distinguished from Mentally Defective Children. The Psychol. Clinic., 1913, 7, 175-182.
222. Woolley, Helen Thompson. A New Scale of Mental and Physical Measurements for Adolescents and Some of its Uses. J. of Educ. Psychol., 1915, 6, 521-550.
223. Woolley, Helen Thompson and Fischer, Charlotte R. Mental and Physical Measurements of Working Children. Psychol. Monog., 1914, 18, No. 1.
224. Wyatt, Stanley. The Quantitative Investigation of Higher Mental Processes. Brit. J. of Psychol., 1913, 6, 104-133.
225. Yerkes, Robert M.; Bridges, James W.; and Hardwick, Rose S. A Point Scale for Measuring Mental Ability. Warwick and York, Baltimore, 1915, pp. viii + 218.
226. Yerkes, Robert M., and Wood, Louise. Methods of Expressing Results of Measurements of Intelligence. Coefficient of Intelligence. J. of Educ. Psychol., 1916, 7, 593-606.
227. Young, Herman H. The Witmer Formboard. Psychol. Clinic, 1916, 10, 93-111.
228. Yule, J. Udny. An Introduction to the Theory of Statistics. Charles Griffen and Co., London, 1911, pp. xiii + 376.
34. Additional references on tested delinquents will be found as footnotes in Chapter VI.
| No. | Sex | Age Mo. | Grade | Kuhlmann 1911, all passed in lowest age given | 1911 Score | Other Kuhlmann or Goddard 1908 tests passed | 1908 Score | |
|---|---|---|---|---|---|---|---|---|
| 1 | F | 4 | 8 A | XI, | XII 1,2,4,5. XV 1,2,5 | XII.4 | XI 2. XIII 1 | XIII ⅔ |
| 2 | M | 1 | 8 A | XI, | XII 1,2,4,5 | XI.8 | None | XII.0 |
| 3 | M | 10 | 8 A | XI, | XII 1,2,3,4. XV 1,3,4 | XII.4 | XIII 1 | XIII ⅔ |
| 4 | M | 5 | 8 A | XI, | XII 1,2,3,4. XV 3,5 | XII.2 | None | XII.2 |
| 5 | M | 8 | 8 A | IX, | X 2,3,4. XI 1,2,3,4. XII 1,2,3,4. XV 4 | XI.4 | IX 2,3,4,5. X 1,2,4. XI 2 | XII.0 |
| 6 | F | 0 | 8 A | XI, | XII 1,2,4. XV 3 | XI.4 | None | XII.2 |
| 7 | M | 0 | 8 A | XI, | XII 1,2,4. XV 1,3 | XII.0 | XIII 1 | XIII |
| 8 | F | 4 | 8 A | XI, | XII 1,2,3,4. XV 3,4 | XII.4 | XIII 1 | XII.2 |
| 9 | M | 9 | 7 A | XI, | XII 1,2,3. XV 1,3 | XII.0 | XI 2, XII 3. XIII 1 | XI.6 |
| 10 | M | 10 | 8 A | XI, | XII 1,2,4. XIII 1 | XI.8 | XI 2. XII 3 | XII.0 |
| 11 | F | 0 | 5 B | IX, | X 2,3,4. XI 2,3. XII 1,2,4,5 | X.8 | IX 2,3,4,5. X 1,2,4. XI 2 | XII.0 |
| 12 | M | 11 | 6 B | VIII, | IX 2,3,4,5. X 2,4. XI 3. XII 1 | IX.6 | VIII 1,5. IX 2,3,4,5. X 1. XI 2 | X.0 |
| 13 | F | 10 | 7 A | XI, | XII 2,3,4. XV 2? | XI.9 | XI 2. XV 1? | XII.2 |
| 14 | M | 11 | 7 A | XI, | XII 1,2,3,4 | XII.0 | XI 2. XV 1? | XII.0 |
| 15 | F | 4 | 7 A | XII, | XV 2,3 | XII.6 | XV 1. | XIII.0 |
| 16 | M | 8 | 7 A | XII, | XV 1 | XII.2 | None | XII.0 |
| 17 | F | 8 | 8 B | X, | XI 2,3,4. XII 1,2,3,4 | XI.4 | X 1.2,4. XI 2 | XII.0 |
| 18 | M | 3 | 8 B | IX, | X 2,3,4. XI 1,2,3,4. XII 1,2,5 | XI.0 | VIII 1,5. IX 2,3,4. X 1,2,4. XI 2 | XI.4 |
| 19 | M | 10 | 8 B | XII, | XV 1,4,5? | XII.5 | None | XII.2 |
| 20 | F | 3 | 8 B | XII, | XV 5 | XII.2 | None | XII.0 |
| 21 | F | 3 | 8 B | XI, | XII 2,3,4 | XI.6 | XI 2 | XI.4 |
| 22 | F | 11 | 8 B | XI, | XII 2,4,5 | XI.6 | XI 2 | XI.4 |
| 23 | F | 1 | 8 B | XI, | XII 2,3,4,5. XV 3 | XII.4 | X 1. XI 2 | XII.2 |
| 24 | M | 2 | 8 A | XI, | XII 1,2,3,4. XV 3 | XII.0 | XI 2 | XII.2 |
| 25 | F | 3 | 8 A | XI, | XII 1,2,3,4. XV 1,3,5 | XII.4 | XII 3 | XII.2 |
| 26 | M | 2 | 8 A | XI, | XII 1,2,3 | XI.6 | XI 2 | XI.4 |
| 27 | M | 11 | 6 A | X, | XI 2,3,4,5. XII 2,4,5 | XI.4 | VIII 1,3,5. IX 2,3,5. X 1,2,4. XI 2 | XI.4 |
| 28 | F | 8 | 6 A | XI, | XII 2,3,4,5 | XI.8 | XI 2 | XI.4 |
| 29 | M | 4 | 7 B | XI, | XII 2,3,4,5 | XI.6 | XI 2 | XII.0 |
| 30 | F | 1 | 7 B | XI, | XII 2,4. XV 1,3 | XI.8 | XI 2 | XI.6 |
| 31 | M | 7 | 7 B | XI, | XII 1,2,5. XV 3 | XI.8 | XI 2 | XI.6 |
| 32 | F | 4 | 7 A | X, | XI 3,4,5. XII 1,4. XV 1 | XI.2 | X 1.2,4. XI 2 | XI.0 |
| 33 | F | 0 | 7 A | XI, | XII 1,2,5. XV 1 | XI.8 | IX 2. X 1,2,4. XI 2 | XI.4 |
| 34 | F | 0 | 8 B | X, | XI I,2,3,4. XII 1,2,4. XV 3 | XI.6 | X 1,2,4. XI 2 | XII.2 |
| 34535 | F | 9 | 8 A | X, | XI 2?,3,4. XII 2,3,5 | XI.3 | X 1,2,4. XI 2 | XI.1 |
| 36 | F | 8 | 8 A | XI, | XII 1,2,3,4. XV 3,4 | XII.2 | XI 2 | XII.2 |
| 37 | M | 2 | 8 A | XII, | XVI | XII.2 | XIII 3 | XII.0 |
| 38 | F | 6 | 8 A | XI, | XII 2. XV 3? | XII.2 | None | XII.0 |
| 39 | M | 2 | 8 A | XII, | XV 3,4 | XII.4 | None | XII.2 |
| 40 | F | 0 | 8 A | XII, | XV 1,3,5 | XII.6 | XII 3. XIII 1 | XIII.0 |
| 41 | F | 7 | 8 B | XII, | XV 2,3,5 | XII.6 | None | XIII.0 |
| 42 | M | 11 | 8 B | XI, | XII 2,3,4, XV 1,2,3,5 | XII.4 | XI 2 | XIII.0 |
| 43 | F | 0 | 8 A | XI, | XI.0 | XI 2 | XI.0 | |
| 44 | F | 1 | 8 B | XI, | XII 1,2,3,4 | XII.0 | XI 2 | XII.2 |
| 45 | M | 5 | 8 B | XI, | XII 1,2,3,5 | XI.8 | XI 2 | XI.4 |
| 46 | F | 7 | 8 B | XI, | XII 1,2,3. XV 3 | XI.8 | XI 2 | XI.6 |
| 47 | F | 1 | 8 B | XII, | XV 5 | XII.2 | None | XII.0 |
| 48 | M | 7 | 8 B | XII, | XV 1,3 | XII.4 | XII 3 | XIII.0 |
| 49 | F | 8 | 7 B | VIII, | IX 2,3,4,5. X 2,3,4,5. XI 2,5 | X.0 | VIII 1,5. IX 2,3,5. X 1 | IX.8 |
| 50 | F | 0 | 7 A | XI, | XII 1,2,3. XV 1 | XII.0 | XIII 1 | XI.6 |
| 51 | M | 11 | 7 A | XI, | XII 2,3,4. XV 2,3 | XII.0 | XI 2 | XIII.0 |
| 52 | F | 11 | 8 A | XI, | XII 2,5. XV 5? | XI.5 | XI 2 | XI.2 |
| 53 | M | 4 | 8 A | XI, | XII 1,2,5. XV 4,5 | XII.0 | XI 2 | XI.6 |
| 54 | M | 11 | 8 B | XII, | XV 5 | XII.2 | None | XII.0 |
| 55 | F | 3 | 7 A | VII, | VIII 2,4,5. IX 2,4. X 2,4,5. XI 1,2. XII 1,2 | IX.4 | VI 2,6. VII3,7. VIII1,3,5. IX2. X4, XI2 | X.8 |
| 56 | M | 1 | 8 A | XI | XII 1,2. XV 2,3,5 | XII.0 | XI 2 | XI.8 |
| 57 | M | 10 | 8 A | XII, | XV 1,2 | XII.4 | XII 2 | XII.2 |
| 58 | M | 0 | 8 A | XI, | XII 2,3. XV 1,3 | XI.8 | XI 2. XII 3. XIII 1 | XI.8 |
| 59 | M | 0 | 8 A | XI, | XII 1,2,4. XV 5 | XI.8 | XI 2 | XII.2 |
| 60 | M | 11 | 8 A | XI, | XII 1,2,3,4. XV 2 | XII.0 | None | XII.2 |
| 61 | M | 0 | 8 A | XII, | XV 1,2,3,4 | XII.8 | XI 2. XIII 1 | XIII.0 |
| 62 | M | 0 | 8 B | XI, | XII 1,2,3,4. XV 2,3,4 | XII.4 | XI 2 | XIII.0 |
| 63 | F | 10 | 7 A | XI, | XII 1,4,5. XV 1 | XI.8 | XI 2. XIII 1 | XI.6 |
| 64 | F | 0 | 7 A | XII, | XV 3 | XII.4 | None | XII.2 |
| 65 | F | 9 | 8 A | XI, | XII 1,2,3,4. XV 1,2,3 | XII.4 | XI 2. XIII 1 | XIII.0 |
| 66 | F | 7 | 8 A | XI, | XII 1,2,3,5. XV 1,3,4,5 | XII.6 | XI 2. XIII 1 | XIII.0 |
| 67 | M | 3 | 8 B | XII, | XV 2,3,4? | XII.5 | None | XIII.0 |
| 68 | M | 4 | 8 A | XII, | XV 2 | XII.2 | None | XII.2 |
| 69 | M | 2 | 8 A | XII, | XV 2,3?,4 | XII.5 | None | XII.2 |
| 70 | M | 0 | 7 A | XII, | XV 2,4 | XII.4 | None | XII.2 |
| 71 | F | 6 | 8 A | X, | XI 1,2,3,4. XII 1,2. XV 3 | XI.4 | XIII 1 | XI.6 |
| 72 | F | 2 | 8 A | XI, | XII 1,2,3,4. XV 3,4 | XII.2 | XI 2 | XII.2 |
| 73 | F | 10 | 8 A | XII, | XV 1,3,4,5 | XII.8 | XIII 1 | XIII.0 |
| 74 | F | 7 | 8 A | XI, | XII 1,2,4,5 | XI.8 | XI 2 | XI.6 |
| 75 | F | 4 | 7 B | XI, | XII 1,2 | XI.4 | XI 2 | XI.4 |
| 76 | F | 2 | 8 B | XI, | XII 1,2,3 | XI.6 | X2. XI 2 | XII.0 |
| 77 | F | 11 | 7 B | X, | XII 1,4,5 | XI.2 | IX 5. X 4. XI 1 | XI.4 |
| 34678 | F | 4 | 8 A | XII, | XV 2,3 | XII.4 | None | XIII.0 |
| 79 | F | 8 | 8 A | XI, | XII 2,4. XV 3,4 | XI.8 | None | XI.6 |
| 80 | F | 1 | 8 A | XI, | XII 1,2,3,5 | XI.8 | XI 2 | XI.4 |
| 81 | M | 9 | 8 A | XI, | XII 1,2,3,4 | XI.8 | XI 2 | XII.0 |
| 82 | F | 5 | 8 A | XII, | XV 3,4 | XII.4 | XII 3 | XII.2 |
| 83 | F | 5 | 8 A | XI, | XV 3,4? | XII.3 | None | XII.2 |
| 84 | F | 1 | 6 A | XI, | XII 1,2,4,5. XV 2 | XII.0 | XI 2 | XII.2 |
| 85 | M | 3 | 8 A | XV, | XV.0 | XIII 1 | XIII.0 | |
| 86 | M | 4 | 8 B | XI, | XII 1,2,3,5. XV 1,2 | XII.2 | XI 2. XII 3. XIIII | XIII.0 |
| 87 | F | 4 | 8 A | XI, | XII 1 | XI.2 | XI 2 | XI.2 |
| 88 | F | 5 | 8 A | X, | XI 2,3,4,5. XII 1,2 | XI.8 | VIII 1,3,5. IX 2,3,5. X 1,2,4. XI 2. XII 3 | XIII.0 |
| 89 | M | 0 | 8 B | XI, | XII 2,5. XV 1,3,5 | XII.0 | XII 3 | XI.4 |
| 90 | F | 0 | 7 A | X, | XI 2,3. XII 1,2,4,5. XV 1,2,3,4? | XI.9 | IX 2,3,5. X 1,2,4. XI 2. XII 3 | XIII.0 |
| 91 | F | 6 | 7 A | VIII, | IX 2,3,4,5. X 2,4,5. XI 1,2,3. XII 1,2 | X.4 | VIII 1,3,5. IX 2,5. X 1,4 | XI.4 |
| 92 | F | 11 | 8 A | X, | XI 2,3,4. XII 2. XV 3 | XI.0 | X 1,2,4. XI 2 | XI.4 |
| 93 | F | 0 | 7 B | IX, | X 2,3,4,5. XI 1,5. XII 2,3,5 | X.8 | IX 2,3,4,5. X 1,2. XI 2 | X.6 |
| 94 | F | 9 | 6 A | IX, | X 2,3,4,5. XI 1,3,4,5. XII 1,2,4. XV 3? | XI.3 | IX 2,3,4,5. X 1,2,4. XI 2 | XII.1 |
| 95 | M | 6 | 8 A | X, | XI 1,2,4,5. XII 1,2,3. XV 2,3,4. | XII.0 | X 1,2,4 XI 2 | XIII.0 |
| 96 | M | 10 | 7 A | XI, | XII 1,2,4. XV 1,3,5 | XII.2 | None | XII.2 |
| 97 | F | 6 | 7 B | X, | XI 4,5. XII 2,5 | X.8 | IX 2,3,4,5. X 1,2. XI 2 | X.6 |
| 98 | M | 1 | 7 A | XI, | XII 1,2,4,5. XV 3,4 | XII.2 | None | XII.2 |
| 99 | F | 1 | 8 A | XI, | XII 1,2. XV 2,3 | XI.8 | None | XIII.0 |
| 100 | M | 0 | 8 A | XI, | XII 2,3,4,5. XV 1,2,3 | XII.4 | None | XIII.0 |
| 101 | F | 3 | 6 A | XI, | XII 1,2,3?,4?,5. XV 1,3,4 | XII.4 | None | XI.7 |
| 102 | F | 3 | 8 A | XI, | XII 1,2,4,5 | XI.8 | None | XII.0 |
| 103 | F | 0 | 8 A | XI, | XII 1,2,5. XV 1,3 | XII.0 | XIII 1 | XI.6 |
| 104 | M | 0 | 8 B | XI, | XII 2,3,4. XV 3 | XI.8 | None | XII.2 |
| 105 | F | 10 | 8 A | XI, | XII 1,2,3,4. XV 4 | XII.0 | XII 3 | XII.0 |
| 106 | F | 3 | 6 A | XII, | XV 1,3,4,5 | XII.8 | XIII 1 | XIII.0 |
| 107 | F | 1 | 8 A | IX, | X 2,4,5. XI 2,3,4,5. XII 1,2,3. XV 2,3 | XI.4 | IX 1. X 1,2 | XIII.0 |
| 108 | F | 8 | 8 A | IX, | X 2,3,4,5. XI 3,4,5. XII 1,2,5. XV 3 | XI.2 | IX 2,3,5. X 1,2,4 | XI.2 |
| 109 | F | 2 | 8 A | XI, | XII 1,2,4,5. XV 1 | XII.0 | None | XII.0 |
| 110 | F | 6 | 7 B | IX, | X 2,3?,5. XI 2,3,4. XII 1,3. XV 1,3 | X.9 | IX 2,3,5. X 2,4. XII 3 | X.8 |
| 111 | F | 2 | 6 A | XII, | XV 1,3,4,5 | XII.8 | XII 3. XIII 1 | XIII.0 |
| 112 | M | 1 | 5 A | IX, | X 1,2,3,5. XI 2,3,4. XII 2 | X.6 | IX 2,3,4?,5. X 1,2,4? | X.5 |
| 113 | F | 0 | 6 A | XI, | XII 1,2,3. XV 1,3,4 | XII.2 | XI 2 | XI.6 |
| 114 | M | 8 | 8 A | XII, | XV 1,3,5 | XII.6 | XIII 1 | XIII.0 |
| 115 | F | 8 | 8 A | XI, | XII 1,2,3,4. XV 3 | XII.0 | XIII 1 | XII.2 |
| 116 | M | 2 | 7 B | XI, | XII 2,3,5 | XI.6 | XI 2. XII 3 | XI.4 |
| 117 | F | 5 | 8 B | XI, | XII 1,2,4,5 | XI.8 | XIII 1 | XI.6 |
| 118 | M | 0 | 7 A | XII, | XV 1,2 | XII.2 | None | XII.2 |
| 347119 | F | 9 | 8 A | XV | XV.0 | None | XIII.0 | |
| 120 | F | 9 | 8 B | XI, | XII 1,2,3,4. XV 3 | XII.0 | XI 2 | XII.2 |
| 121 | M | 4 | 7 B | XII, | XV 1,5 | XII.2 | XII 3 | XII.4 |
| 122 | F | 3 | 8 A | XII, | XV 4,5 | XII.4 | None | XII.0 |
| 123 | M | 5 | 8 B | XII, | XII.0 | None | XII.0 | |
| 124 | M | 1 | 8 A | XII, | XV 3,4 | XII.0 | None | XII.0 |
| 125 | M | 8 | 6 A | X, | XI 1,2,3,4. XII 2,4 | XII.4 | None | XII.2 |
| 126 | M | 8 | 8 A | XI, | XII 2,4. XV 2,3,4 | XI.2 | X 1,2,4. XI 2 | XIII.0 |
| 127 | F | 4 | 8 A | XI, | XII 2,4. XV 3,4 | XII.0 | XI 2 | XI.8 |
| 128 | F | 9 | 8 A | X, | XI 1,3,4,5. XII 1,2,3,4. XV 3 | XI.8 | X 1,2,4. XI 2. XII 3? | XII.2 |
| 129 | F | 10 | 7 A | XI, | XII1,2,3,5. XV 3,5 | XII.2 | XI 2 | XI.6 |
| 130 | F | 4 | 7 B | XI, | XII 1,2,3. XV 3 | XI.8 | None | XI.6 |
| 131 | M | 3 | 7 A | VII, | VIII 1,3,5. IX 1,2,3,4. X 2,3,4,5. XI 1,4,5. XII 1,2,3. XV 4? | X.5 | VII 3,4,7. VIII 1,3,5. IX 2,3,4,5. X 2,4. XIII 1 | XI.4 |
| 132 | F | 3 | 7 B | VIII, | IX 1,2,3?,4,5. X 1,3,4?,5. XI 1,3,4,5. XII 1,2,3,4 | XI.2 | IX 1,2. X 2,1,4. XI 2? XII 3 | XII. |
| 133 | M | 7 | 7 A | XI, | XII 1,2,3,5 | XI.8 | None | XI.6 |
| 134 | M | 1 | 8 B | VIII, | IX 1,2,3,4. X 1,2,3,4. XI 1,2,3,5. XII 2,3,4. XV 2,3 | XI.6 | IX 2,3,4,5. X 1,2,4. XI 2 | XIII.0 |
| 135 | F | 1 | 8 A | X, | XI 2,3,4,5. XII 1,2,4. XV 3,4,5 | XII.0 | X 1,2,4. XI 2 | XII.2 |
| 136 | F | 5 | 8 A | XI, | XII 1,2,3,4?. XV 1,3,4,5 | XII.5 | XI 1. XII 3. XIII 1 | XIII.0 |
| 137 | M | 6 | 8 I | XI, | XII 2. XV 2 | XI.4 | XI 2 | XI.4 |
| 138 | F | 4 | 8 A | XI, | XII 1,4,5. XV 1,3,4 | XII.2 | XI 2 | XI.6 |
| 139 | M | 3 | 8 A | XII, | XV 1,3 | XII.4 | None | XII.2 |
| 140 | M | 4 | 8 A | XI, | XII 1,2,3. XV 3 | XI.8 | XI 2 | XI.6 |
| 141 | F | 7 | 7 A | X, | XI 2,3,4,5. XII 2,5. XV 2,3 | XI.6 | X 4. XI 2 | XIII.0 |
| 142 | M | 0 | 8 A | XII, | XV 3,4,5 | XII.6 | None | XII.2 |
| 143 | F | 2 | 5 A | X, | XI I,2,3. XII 5 | X.8 | X 1,2,4. XI 2 | XI.0 |
| 144 | M | 8 | 8 A | XII, | XV 2,3,5 | XII.6 | None | XIII.0 |
| 145 | F | 11 | 8 B | XII, | XV 3 | XII.2 | None | XII.2 |
| 146 | M | 10 | 8 A | XV | XV.0 | XIII 1 | XIII.0 | |
| 147 | F | 2 | 7 B | XI, | XII 1,2,4,5. XV 3,5 | XII.2 | XI 2 | XII.2 |
| 148 | F | 7 | 8 A | XI, | XII 1,2,3,5. XV 3,5 | XII.2 | XI 2 | XI.6 |
| 149 | M | 0 | 8 B | XII | XII.0 | None | XII.0 | |
| 150 | F | 4 | 8 A | XI, | XII 2. XV 3,5 | XI.6 | XI 2 | XI.4 |
| 151 | F | 7 | 8 A | XI, | XII 1,2,3,4. XV 3 | XII.0 | XI 2 | XII.2 |
| 152 | F | 5 | 8 B | XI, | XII 2,3,4,5. XV 1,3 | XII.2 | XI 2. XIII 1 | XIII.0 |
| 153 | M | 2 | 8 A | XII, | XV 2,3,4,5 | XII.8 | None | XIII.0 |
| 154 | F | 0 | 4 B | VIII, | IX 2,3,4,5. X 1 | IX.0 | VII 3,4,7. VIII 1,3. IX 2,5. X 4 | IX.0 |
| 155 | M | 7 | 7 A | XI, | XII 2,5 | XI.4 | XI 2 | XI.2 |
| 156 | M | 6 | 8 B | XII, | XV 3 | XII.2 | None | XII.2 |
| 157 | F | 0 | 8 A | XII, | XV 1,3 | XII.4 | XII 3. XIII 1 | XIII.0 |
| 158 | M | 2 | 8 B | XII, | XV 1,2,3,4 | XII.8 | XII 3 | XIII.5 |
| 159 | F | 1 | 7 B | X, | XI 1,2,3,4. XII 1,2,4 | XI.6 | X 1,2,4. XI 2 | XII.0 |
| 160 | F | 6 | 8 B | XII, | XV 3,5 | XII.4 | None | XII.2 |
| 348161 | M | 1 | 8 A | XII, | XV 1 | XII.2 | XII 3. XIII 1 | XII.2 |
| 162 | F | 4 | 8 A | XII | XII.4 | XII 3?. XIII 1 | XII.2 | |
| 163 | F | 6 | 8 B | XI, | XII 1,2,3,4. XV 3,4 | XII.2 | None | XII.2 |
| 164 | F | 10 | 8 A | XI, | XII 1,2,5 | XI.6 | XI 2 | XI.4 |
| 165 | M | 8 | 8 A | X, | XI 1,2,3. XII 2,3,4,5 | XI.4 | VIII 1,3,5. IX 2,3,4,5. X 1,4. XI 2 | XI.4 |
| 166 | F | 1 | 7 A | X, | XI 3,4,5. XII 1,2,3,4. XV 1,3 | XI.8 | X 1,2,4. XI 2 | XII.2 |
| 167 | M | 8 | 6 B | XI, | XII 2,3 | XI.8 | XI 2. XII 3 | XI.6 |
| 168 | M | 10 | 6 A | X, | XI 1,3,4,5. XII 1,2,3,5. XV 2,5 | XII.0 | X 1,2,4. XI 2 | XI.6 |
| 169 | M | 10 | 6 B | XI, | XII 1,4?,5. XV 2? | XI.6 | XI 2 | XI.4 |
| 170 | M | 10 | 8 A | XI, | XII 3,4,5. XV 5 | XI.8 | None | XI.4 |
| 171 | M | 1 | 8 A | XII, | XV 2,4 | XII.4 | None | XII.2 |
| 172 | M | 3 | 8 A | X, | XI 2,3,4. XI 1,2,3,4 | XI.4 | X 1,2,4 | XII.0 |
| 173 | F | 4 | 8 A | X, | XI 1,3,4,5. XII 1,2,4,5. XV 1,4,5 | XII.2 | X 1,2,4. XIII 1 | XII.2 |
| 174 | F | 2 | 8 A | XI, | XII 1,2,4,5. XV 1,3 | XII.2 | XII 3. XIII 1 | XIII.0 |
| 175 | F | 4 | 8 A | XI, | XII 1,2,4. XV 1 | XI.8 | XI 2 | XII.2 |
| 176 | F | 4 | 8 A | XI, | XII 1,2,4,5. XV 1,4 | XII.2 | XI 1 | XII.0 |
| 177 | M | 3 | 8 A | X, | XI 1,2,3,4. XII 1,2,4. XV 3 | XI.6 | X 1,2,4. XI 1 | XII.2 |
| 178 | M | 6 | 8 A | XII, | XV 1,3 | XII.4 | XI 2. XII 3?. XIII 1 | XIII.0 |
| 179 | F | 2 | 8 B | XI, | XII 1,2,3. XV 3 | XII.2 | None | XII.2 |
| 180 | F | 2 | 8 B | XII, | XV 1,3 | XII.4 | None | XII.2 |
| 181 | F | 2 | 8 B | XI, | XII 1,2,4,5. XV 3,4 | XII.2 | XI 2 | XII.2 |
| 182 | F | 6 | 8 B | XI, | XII 1,2,4,5. XV 3 | XII.0 | XI 2 | XII.2 |
| 183 | F | 0 | 8 B | XI, | XII 2,3,4,5. XV 2,3 | XII.2 | None | XIII.0 |
| 184 | M | 5 | 7 A | XI, | XII 4,5 | XI.6 | XI 2 | XI.4 |
| 185 | M | 2 | 7 A | XI, | XII 2,3,4. XV 1 | XI.4 | XI 2 | XI.8 |
| 186 | F | 9 | 7 B | XI, | XII 2,3. XV 1,2,3,4? | XII.1 | XI 2 | XIII.0 |
| 187 | M | 8 | 7 A | XII, | XV 3 | XII.2 | XI 2 | XII.2 |
| 188 | M | 2 | 7 B | XI, | XII 1,2,4,5. XV 1,2,3 | XII.4 | XI 2 | XIII.0 |
| 189 | M | 4 | 7 B | XI, | XII 2,3,4,5 | XI.8 | XI 2 | XI.4 |
| 190 | M | 2 | 6 B | XI, | XII 4,5 | XI.4 | IX 2,3,4,5. X 1,2,4. XI 2 | XI.2 |
| 191 | F | 1 | 7 B | IX, | X 1,2,3,4. XI 3,5. XII 4,5 | X.6 | IX 2,3,5. X 1,2,4. XI 2 | X.6 |
| 192 | F | 1 | 8 A | XI, | XII 1,2,3,4. XV 1,3 | XII.2 | XI 2 | XII.2 |
| 193 | M | 10 | 8 B | X, | XI 1,2,5. XII 2,4,5 | XI.2 | IX 2,3,4,5. X 1,2,4. XI 2 | XI.0 |
| 194 | M | 8 | 8 B | XI, | XII 1,2,3,4. XV 1,3 | XII.2 | XI 2 | XII.2 |
| 195 | M | 3 | 7 B | XI, | XII 1,2,3. XV 1 | XI.8 | XI 2. XII 3 | XI.6 |
| 196 | F | 2 | 8 B | XI, | XII 2 | XI.2 | XI 2 | XI.2 |
| Life-Age | Basal | School Grade | ||||
|---|---|---|---|---|---|---|
| No. | Yr. | Mo. | Test-Age | Test-Age | Sept. 1 of Life-Age | Offense |
| 1 | 9 | 10 | VIII.8 | VIII[35] | 3 B | Truancy |
| [36]2 | 16 | 7 | XIII | XIII | 12 A | Grand larceny |
| 3 | 10 | 1 | X.8 | IX[35] | 3 A | Truancy |
| 4 | 12 | 4 | XII | XII | 4 A | Truancy |
| 5 | 14 | 3 | XII.2 | XII | 7 A | Petit larceny |
| [36]6 | 14 | 8 | XIII | XIII[35] | 9 B | Assault & battery |
| 7 | 16 | 3 | XIII | XIII | 9 B | Check, no funds |
| 8 | 15 | 7 | XIII | XIII | 7 A | Burglary |
| [36]9 | 15 | 0 | XI.6 | XI[35] | 8 B | Petit larceny |
| [36]10 | 9 | 9 | IX.2 | VIII | 2 B | Truancy |
| [36]11 | 14 | 5 | XII | XII | 9 B | Petit larceny |
| 12 | 12 | 2 | XI.2 | XI | 4 A | Incorrigibility |
| [36]13 | 16 | 0 | XIII | XIII[35] | 8 A | Petit larceny |
| 14 | 13 | 8 | IX.6 | VIII[35] | 4 B | Breaking & entering |
| [36]15 | 15 | 10 | X.6 plus | X | 4 A | Incorrigibility |
| [36]16 | 15 | 9 | X.6 | IX[35] | 5 B | Breaking & entering |
| [36]17 | 11 | 1 | XI.4 | XI[35] | 5 B | Incorrigibility |
| [36]18 | 14 | 10 | XII.2 | XII | 5 A | Indecent conduct |
| [36]19 | 15 | 11 | XIII | XIII | 8 A | Truancy |
| 20 | 13 | 2 | VIII.4 | VII | 3 B | Grand larceny |
| 21 | 14 | 1 | XIII | XIII | 8 B | Petit larceny |
| [36]22 | 13 | 9 | XI.6 | XI[35] | 6 B | Petit larceny |
| 23 | 11 | 0 | XI.2 | XI | 4 B | Incorrigibility |
| 24 | 16 | 11 | XI.6 | XI | 7 A | Petit larceny |
| 25 | 12 | 6 | XI.2 | XI[35] | 7 B | Truancy |
| [36]26 | 12 | 9 | XI.2 | X | 4 B | Incorrigibility |
| Life-Age | Basal | School | ||||
| No. | Yr. | Mo. | Test-Age | Test-Age | Grade | Offense |
| [36]27 | 11 | 0 | X.4 | X | 5 A | Petit larceny |
| [36]28 | 15 | 7 | XIII | XIII | 8 A | Truancy |
| 29 | 14 | 9 | XII | XII | 5 A | Truancy |
| [36]30 | 11 | 11 | XII | XII | 6 B | Truancy |
| 350[36]31 | 11 | 4 | IX.8 | IX[35] | 4 B | Truancy |
| [36]32 | 15 | 7 | XII | XII | 7 | Vagrancy |
| [36]33 | 13 | 9 | XI.4 | XI[35] | 5 | Grand larceny |
| [36]34 | 13 | 8 | X.8 | X | 5 A | Petit larceny |
| 35 | 16 | 6 | XII.2 | XII | 8 A | Burglary |
| [36]36 | 10 | 8 | IX.8 | VIII[35] | 3 B | Incorrigibility |
| [36]37 | 14 | 10 | XI.6 | XI[35] | 7 B | Grand larceny |
| [36]38 | 13 | 8 | XIII.0 | XIII | 8 B | Disorderly conduct |
| [36]39 | 14 | 1 | X.8 | X[35] | 4 B | Truancy |
| 40 | 15 | 2 | XI.6 | XI | 7 B | Petit larceny |
| [36]41 | 9 | 9 | X.2 | X | 4 B | Truancy |
| 42 | 11 | 5 | XI.4 | XI | 5 B | Incorrigibility |
| [36]43 | 7 | 8 | VII.6 | VII | 2 B | Petit larceny |
| [36]44 | 13 | 11 | XI.6 | XI | 8 B | Grand larceny |
| [36]45 | 15 | 1 | XI.6 | XI[35] | 9 B | Burglary |
| 46 | 13 | 10 | XII | XII | 5 B | Incorrigibility |
| [36]47 | 10 | 6 | IX.2 | IX[35] | 5 B | Truancy |
| 48 | 14 | 1 | X.2 | X[35] | 6 B | Burglary |
| 49 | 14 | 3 | XIII | XIII[35] | 8 B | Burglary |
| 50 | 14 | 7 | XII.2 | XII[35] | 8 B | Burglary |
| [36]51 | 13 | 2 | XII.2 | XII | 8 B | Malicious destruction of property |
| 52 | 13 | 6 | X.2 | X | 7 B | Petit larceny |
| [36]53 | 13 | 7 | XI.6 | XI | 6 A | Burglary |
| 54 | 14 | 3 | XI.6 | XI[35] | 5 A | Incorrigibility |
| 55 | 6 | 0 | VII.8 | VII[35] | 1 B | Petit larceny |
| 56 | 15 | 0 | XII.2 | XII | 8 B | Incorrigibility |
| [36]57 | 12 | 0 | XI | XI | 6 A | Petit larceny |
| [36]58 | 15 | 0 | XI.4 | XI[35] | 7 A | Petit larceny |
| 59 | 15 | 9 | X.4 | X[35] | 6 B | Petit larceny |
| 60 | 15 | 1 | XIII | XIII | 7 A | Petit larceny |
| [36]61 | 11 | 3 | XI.4 | XI | 4 A | Truancy |
| 62 | 12 | 0 | XI | X | 3 A | Truancy |
| [36]63 | 15 | 3 | XIII | XII I | 8 B | Petit larceny |
| [36]64 | 16 | 1 | VIII.8 | VIII | 5 B | Trespass |
| 65 | 16 | 4 | XII | XII | 6 B | Incorrigibility |
| [36]66 | 15 | 0 | XI.4 | XI[35] | 6 B | Trespass |
| [36]67 | 14 | 5 | IX.9 | IX[35] | 3 A | Incorrigibility |
| 68 | 16 | 0 | XI.4 | XI | 9 B | Disorderly conduct |
| 351[36]69 | 16 | 0 | XIII | XIII | 8 B | Grand larceny |
| [36]70 | 15 | 7 | XI.4 | XI[35] | 7 B | Jumping on train |
| 71 | 15 | 8 | XI.6 | XI[35] | 6 A | Disorderly conduct |
| 72 | 16 | 7 | XIII | XIII[35] | 10 | Taking auto. |
| [36]73 | 15 | 11 | XII.2 | XII | 6 A | Truancy |
| [36]74 | 13 | 1 | X.4 | X[35] | 3 A | Truancy |
| [36]75 | 14 | 10 | XI.6 | XI | 5 A | Truancy |
| [36]76 | 11 | 4 | VIII.8 | VIII | 3 A | Incorrigibility |
| [36]77 | 10 | 3 | XI | XI | 4 A | Petit larceny |
| [36]78 | 13 | 4 | X.8 | X[35] | 4 A | Petit larceny |
| 79 | 15 | 5 | XII | XII | 7 A | Indecent Conduct |
| [36]80 | 15 | 4 | XI.4 | XI[35] | 5 A | Furnishing Liquor |
| [36]81 | 11 | 0 | XII | XII | 5 B | Malicious destruction of property |
| [36]82 | 12 | 5 | IX.8 | IX[35] | 4 B | Petit larceny |
| [36]83 | 11 | 7 | XI.4 | XI | 4 A | Truancy |
| 84 | 13 | 8 | XI | XI[35] | 6 B | Incorrigibility |
| 85 | 16 | 4 | XII | XII | 11 A | Petit larceny |
| 86 | 11 | 4 | XI.4 | XI[35] | 5 A | Malicious destruction of property |
| [36]87 | 13 | 9 | XI.4 | XI | 6 B | Petit larceny |
| [36]88 | 14 | 0 | XI.2 | XI | 8 A | Burglary |
| 89 | 16 | 5 | X | X | 5 B | Taking auto plug |
| 90 | 14 | 9 | XIII | XIII | 6 A | Petit larceny |
| 91 | 13 | 10 | X.4 | X | 4 B | Carrying dangerous weapons |
| [36]92 | 15 | 4 | XI.6 | XI[35] | 6 B | Truancy |
| 93 | 15 | 11 | XIII | XIII | 8 B | Truancy |
| 94 | 12 | 10 | XII | XII | 4 B | Incorrigibility |
| [36]95 | 10 | 10 | IX.2 | VIII[35] | 3 A | Petit larceny |
| [36]96 | 12 | 4 | XII.2 | XII | 7 B | Petit larceny |
| [36]97 | 15 | 7 | XIII | XIII | 9 A | Burglary |
| 98 | 14 | 9 | XII | XII | 8 B | Incorrigibility |
| [36]99 | 11 | 0 | XI.2 | XI[35] | 5 B | Incorrigibility |
| 100 | 13 | 7 | X.2 | X | 5 B | Petit larceny |
| 101 | 10 | 9 | VIII | VII | 3 B | Breaking & entering |
| [36]102 | 15 | 1 | XIII | XIII | 7 A | Truancy |
| 103 | 15 | 5 | XI.6 | XI[35] | 10 B | Incorrigibility |
| 104 | 9 | 7 | IX | VIII[35] | 4 B | Incorrigibility |
| 352105 | 15 | 10 | XI.6 | XI | 7 A | Receiving stolen property |
| 106 | 15 | 10 | XII.2 | XII | 5 B | Incorrigibility |
| 107 | 12 | 2 | XII.2 | XII | 7 B | Vagrancy |
| 108 | 13 | 1 | X.8 | X | 5 B | Truancy |
| [36]109 | 13 | 9 | X.6 | X[35] | 5 B | Petit larceny |
| [36]110 | 15 | 10 | XI.4 | XI | 6 A | Malicious destruction of property |
| [36]111 | 12 | 6 | XI.2 | XI | 5 B | Petit larceny |
| 112 | 10 | 9 | XII | XII | 4 A | Sweeping grain car |
| 113 | 15 | 2 | XIII | XIII | 9 B | Trespass |
| 114 | 12 | 10 | XII.2 | XII | 5 B | Incorrigibility |
| 115 | 14 | 7 | XI.6 | XI[35] | 7 B | Incorrigibility |
| [36]116 | 15 | 10 | XI.4 | XI | 7 A | Incorrigibility |
| [36]117 | 13 | 9 | XII | XII | 4 A | Incorrigibility |
| [36]118 | 9 | 1 | XI.2 | XI[35] | 5 B | Incorrigibility |
| [36]119 | 16 | 11 | XI | X[35] | 7 B | Disorderly conduct |
| [36]120 | 13 | 3 | XII.2 | XII | 6 B | Truancy |
| [36]121 | 9 | 9 | IX.6 | VIII[35] | 4 B | Sweeping grain car |
| [36]122 | 11 | 9 | X.8 | X | 3 B | Sweeping grain car |
| [36]123 | 10 | 3 | X.2 | X | 4 A | Truancy |
35. Passed all tests at the basal age. The others passed all but one test at the basal age.
36. Repeater.