Title: Mathematische Geographie für Lehrerbildungsanstalten
Author: Erwin Eggert
Release date: December 20, 2020 [eBook #64085]
Most recently updated: October 18, 2024
Language: German
Credits: The Online Distributed Proofreading Team at https://www.pgdp.net
Anmerkungen zur Transkription
Das Original ist in Fraktur gesetzt. Im Original gesperrter Text ist so ausgezeichnet. Im Original in Antiqua gesetzter Text ist so markiert.
Das Buch verwendet unübliche Akzente und mathematische Zeichen, die insbesondere auf E-Book-Readern nicht immer korrekt dargestellt werden.
Weitere Anmerkungen zur Transkription befinden sich am Ende des Buches.
Herausgegeben von
E. Eggert,
Königl. Seminar-Direktor zu Cottbus.
Gänzliche Umarbeitung von
Lorch-Eggerts Mathematischer Geographie.
10. (5.) Auflage.
Mit 47 Holzschnitten.
Berlin 1912.
Union Deutsche Verlagsgesellschaft
Abteilung Dürrscher Seminarverlag.
Druck der Union Deutsche Verlagsgesellschaft in Stuttgart.
Nach dem Erscheinen der ministeriellen Bestimmungen vom 1. Juli 1901 erschien es mir klar, daß eine neue Auflage der von mir im Jahre 1898 umgearbeiteten Mathematischen Geographie von Lorch sich nicht mit dem Ausmerzen und Verbessern einiger Mängel und Versehen begnügen dürfe. Die erhöhten Ziele in der Geographie und im Rechnen erforderten eine gänzliche Umgestaltung des Werkchens. So erscheint es denn hier sozusagen als ein neues Buch. In der sechsten Auflage hatten trotz starker Änderungen und Erweiterungen immer noch größere Abschnitte ihre ursprüngliche Gestalt behalten, wie sie ihnen von Lorch gegeben war; jetzt hat das Buch von Lorchs Werk kaum mehr als die streng anschauliche Darstellungsweise, eine größere Anzahl Figuren und einige Sätze Text behalten. Wenn es in einigen umfangreicheren Abschnitten noch mit der sechsten Auflage übereinstimmt, so handelt es sich um Stellen, die dort schon von mir stark geändert oder neu eingeschoben waren. Zunächst ist der Stoff wesentlich anders angeordnet, besonders in den zwei ersten Kapiteln, die, wie ich hoffe, jetzt übersichtlicher erscheinen werden. Kapitel 3 und 4 der alten Auflage sind zu einem vereinigt, vom fünften Kapitel der alten Auflage ab ist alles neu gestaltet. Überall ist das rein mathematische Element stärker betont, um dem vermehrten Wissen der Seminaristen auch auf diesem Gebiete fruchtbare Anwendung zu geben. Ganz oder fast ganz neu sind die §§ 9, 11, 12, 13, 14, 16, 18, 22, 24, 25, 26, 27, 33 und die Kapitel 5, 6 und 8. Daß der Titel das Buch jetzt nur als ein Lehrbuch für Seminare und nicht mehr, wie früher, auch für Mittelschulen usw. bezeichnet, bedarf keiner Begründung.
Alle Bemerkungen und Ausstellungen der Kritik sind berücksichtigt, soweit sie berechtigt erschienen. Ob das Buch in seiner neuen Gestalt überall das richtige Maß getroffen hat, wird sich erst erweisen müssen. Im großen ganzen hoffe ich es, und wenn es hier und da vielleicht zuviel bieten sollte, so dürfte das kaum ein Fehler sein; manches, was der Lehrer aus Mangel an Zeit übergeht, kann strebsamen Schülern, die es selbständig nachlesen, eine Anregung zu weiterem Studium sein.
Ganz besonderen Dank schulde ich für zahlreiche Winke und Ratschläge über Auswahl und Anordnung des Stoffes meinem lieben hiesigen Kollegen, Herrn Seminarlehrer Heinze, dem ich auch an dieser Stelle meinen herzlichsten Dank sage. Jeden weiteren guten Rat aus Kollegenkreisen werde ich mit Freuden begrüßen.
So möge denn das Buch in der neuen Gestalt sich die alten Freunde erhalten und neue gewinnen und an seinem Teile beitragen zu einer fruchtbaren Gestaltung des Unterrichts in der mathematischen Geographie in Seminar und Volksschule!
Friedeberg Nm., im März 1904.
E. Eggert.
Nach der gründlichen Umarbeitung des Buches vor drei Jahren schienen mir wesentliche Änderungen jetzt nicht nötig. Hinzugekommen sind eine kurze Einleitung über Wesen, Aufgabe und Hilfsmittel der mathematischen Geographie, ein kleiner geschichtlicher Anhang und einige neue Figuren. Außerdem erfuhren die §§ 16, 25, 27, 28, 33 Umänderungen und Erweiterungen. Im übrigen habe ich mich auf sorgfältige Ausmerzung einiger Unklarheiten und Ungenauigkeiten und auf noch eingehendere Gliederung des Stoffes beschränkt.
Friedeberg Nm., im März 1907.
E. Eggert.
Eine Änderung in der Anlage des Werkchens habe ich nicht vorgenommen, da dieselbe allgemeine Anerkennung gefunden hat. In Einzelheiten habe ich vielfach kleinere Verbesserungen ausgeführt und die Winke beachtet, die ich in den mir zugänglichen Kritiken fand oder von Kollegen erhielt. Eine nochmalige Umgestaltung erfuhren die §§ 12 und 14 bis 18 unter Benutzung der wertvollen Abhandlung von Binder, Ein wunder Punkt unserer geographischen Schulbücher (Geographischer Anzeiger, 8. Jahrgang, S. 127 ff.). In verschiedenen Figuren wurden die schlecht gezeichneten Ellipsen verbessert.
Zum Schlusse habe ich Herrn Seminarlehrer Kruckenberg in Aurich für freundschaftliche Hinweise auf einzelne Mängel bestens zu danken.
Cottbus, im Februar 1910.
E. Eggert.
Diese Auflage ist ein wenig veränderter Abdruck der neunten. Kleine Verbesserungen und kurze Einschaltungen wurden in den §§ 9, 26, 28, 29, 30 und 34 vorgenommen.
Cottbus, im März 1912.
E. Eggert.
| Seite | ||
| Einleitung | 5 | |
| Erstes Kapitel. Die Himmelskugel | 6 | |
| § 1. | Der Horizont | 6 |
| § 2. | Das Himmelsgewölbe | 7 |
| § 3. | Die Himmelskugel | 11 |
| Zweites Kapitel. Die scheinbaren Bewegungen der Himmelskörper | 12 | |
| § 4. | Die scheinbare tägliche Bewegung der Sonne | 12 |
| § 5. | Die scheinbare tägliche Bewegung des Mondes | 14 |
| § 6. | Die scheinbare tägliche Bewegung der Sterne | 15 |
| § 7. | Der scheinbare jährliche Lauf der Sonne | 17 |
| § 8. | Die Dämmerung | 19 |
| § 9. | Die scheinbaren Bewegungen der Gestirne für einige bemerkenswerte Punkte der Erdoberfläche | 20 |
| § 10. | Die Ekliptik | 24 |
| § 11. | Ortsbestimmungen am Himmel mittels des Äquators oder der Ekliptik | 28 |
| Drittes Kapitel. Die Erde und ihre Bewegungen | 30 | |
| § 12. | Gestalt der Erde | 30 |
| § 13. | Einteilung der Erdoberfläche und Ortsbestimmungen auf derselben | 32 |
| § 14. | Die wahre Gestalt und die Größe der Erde | 38 |
| § 15. | Rotation der Erde | 41 |
| § 16. | Beweise für die Rotation der Erde | 42 |
| § 17. | Beweise für die Rotation von Westen nach Osten | 46 |
| § 18. | Die fortschreitende Bewegung (Revolution) der Erde | 49 |
| § 19. | Die Stellung der Erdachse zur Erdbahn | 53 |
| § 20. | Folgen der Rotation und der Revolution der Erde | 54 |
| Viertes Kapitel. Der Mond und der Kalender | 58 | |
| § 21. | Die Bewegungen des Mondes | 58 |
| § 22. | Die Mondphasen | 61 |
| § 23. | Lage der Mondbahn zur Ekliptik | 62 |
| § 24. | Die Mondfinsternisse | 63 |
| § 25. | Die Sonnenfinsternisse | 66 |
| § 26. | Physikalische Beschaffenheit des Mondes | 68 |
| § 27. | Der Kalender | 71 |
| Fünftes Kapitel. Die Planeten | 74 | |
| § 28. | Zahl und Bewegungen der Planeten | 74 |
| § 29. | Die physikalische Beschaffenheit der einzelnen Planeten | 77 |
| Sechstes Kapitel. Kometen und Meteore | 81 | |
| § 30. | Die Kometen oder Haarsterne | 81 |
| § 31. | Die Meteore | 83 |
| Siebentes Kapitel. Die Sonne und das Sonnensystem | 84 | |
| § 32. | Physikalische Beschaffenheit der Sonne | 84 |
| § 33. | Die Bewegungsgesetze unseres Planetensystems | 89 |
| § 34. | Die Entstehung des Sonnensystems | 92 |
| Achtes Kapitel. Die Fixsterne | 93 | |
| § 35. | Wesen, Größe, Entfernungen und Arten der Fixsterne | 93 |
| § 36. | Spektralanalyse der Fixsterne | 95 |
| § 37. | Bewegungen der Fixsterne | 96 |
| § 38. | Wie orientiert man sich am Sternenhimmel? | 97 |
| Anhang. Bedeutende Astronomen | 100 | |
| Empfehlenswerte Werke zur Fortbildung | 100 | |
1. Wesen und Aufgaben der mathematischen Geographie. Die mathematische Geographie kann als ein Grenzgebiet zwischen Erdkunde und Mathematik bezeichnet werden. Sie beschäftigt sich mit der Erde und ihren Beziehungen zu anderen Weltkörpern. Aber ihre Untersuchungen erstrecken sich nur auf die mathematischen Eigenschaften und Beziehungen der Erde, insofern diese einen bestimmten Raum einnimmt, eine bestimmte Gestalt besitzt, ihre Punkte bestimmte Entfernungen voneinander haben, sie selbst in jedem Augenblicke eine bestimmte Stellung zu anderen Weltkörpern einnimmt usw. Die Hauptaufgaben der mathematischen Geographie werden daher folgende sein: 1. Bestimmung der Gestalt und Größe der Erde, 2. Bestimmung der Lage von Punkten auf der Erdoberfläche, 3. Bestimmung der augenblicklichen Lage der Erde im Weltraume. Die letzte Aufgabe setzt Bekanntschaft mit den etwaigen Bewegungen der Weltkörper und ihren Bahnen voraus.
Dieses Buch enthält außerdem auch noch Beobachtungen und Mitteilungen über die physische Beschaffenheit der Gestirne. Das sind zwar Stoffe, die streng genommen nicht der mathematischen Geographie angehören, sondern der Sternkunde oder Astronomie; aber beide Wissenschaften berühren sich so vielfach miteinander, daß das Wissenswerte aus der zweiten am besten in Verbindung mit der ersten gelehrt wird.
2. Hilfsmittel der mathematischen Geographie. Die mathematische Geographie wird sich einerseits auf mathematische Lehrsätze und Berechnungen, anderseits als Naturwissenschaft auf Erfahrungen, Beobachtungen und Versuche gründen. Zu diesen bedarf sie bestimmter Instrumente. Da sie es mehrfach mit Bewegungen zu tun hat, die sich in der Zeit vollziehen, so kann sie die Uhr und das Pendel nicht entbehren. Neben diesen für Erdkunde, Astronomie und Physik in gleichem Maße grundlegenden Hilfsmitteln ist in erster Linie das Fernrohr zu nennen. Unmittelbar nach seiner Erfindung durch Galilei im Jahre 1609 wurden von diesem und anderen bedeutende astronomische Entdeckungen gemacht, und die Zahl derselben hat beständig zugenommen, unsere Kenntnis des Sternhimmels ist immer genauer geworden, je mehr die Fernrohre verbessert wurden. In neuerer Zeit hat man auch die Photographie in den Dienst der Sternkunde gestellt und für diesen Zweck besondere Apparate hergestellt, in welchen photographische Kamera und Fernrohr verbunden sind. Das Studium der physischen Beschaffenheit der Fixsterne und der Sonne beruht wesentlich auf Spektralanalyse; deshalb spielt auch das Spektroskop eine Rolle in der Astronomie. Endlich sind für Ortsbestimmungen auf der Erde und im Weltraum Instrumente zum Messen von Winkeln nötig. Die wichtigsten sind der Spiegelsextant und der Theodolit.[6] Der Spiegelsextant ist eine Verbindung von zwei Spiegeln und einem Fernrohr auf einem Kreissextanten (dem sechsten Teil einer Kreislinie), an dem die Hälfte des zu messenden Winkels abgelesen werden kann. Der Theodolit ist eine Verbindung von zwei Fernrohren, von denen das eine um eine senkrechte, das andere um eine wagerechte Achse drehbar ist. Die Drehungswinkel können an geteilten Kreisen genau abgelesen werden.
1. Wesen. Befinden wir uns im Freien auf einer Stelle, die ringsum weite, ungehinderte Aussicht bietet, also frei von Bergen u. dgl. ist, so überblicken wir einen Teil der Erdoberfläche. Dieser erscheint als eine Ebene mit kreisähnlicher Grenzlinie. Am vollkommensten ist der Kreis natürlich auf einem großen See oder auf dem Meere bei Windstille. Die Grenzlinie der überschauten Erdoberfläche nennen wir Horizont. Dieses griechische Wort heißt genau die »Begrenzende« (Linie nämlich); es wird aber gewöhnlich übersetzt durch das Wort Gesichtskreis. Die überschaute Fläche selbst heißt Horizontfläche oder Horizontebene. Eine gerade Linie, die in der Horizontebene liegt, wird eine horizontale Linie genannt.

2. Verschiedenheit nach der Lage des Standpunktes auf der Erdoberfläche. Wir selbst stehen im Mittelpunkte des Horizontes, und dieser Mittelpunkt heißt unser Standpunkt oder Standort.
So weit wir von unserem Standpunkte aus wandern, stets bleiben wir im Mittelpunkte des Horizontes. Natürlich ist demnach an jedem Orte der Erdoberfläche oder, was dasselbe ist, für jeden anderen Standpunkt auch der Horizont ein anderer. Für den Standpunkt a (Fig. 1) ist es Kreislinie I, für den Standpunkt b Kreislinie II.

3. Verschiedenheit nach der Höhe des Standpunktes. Stelle ich mich in senkrechter Richtung über dem Standpunkte a (Fig. 2) einige Meter höher auf, etwa auf einem Gerüste, so sehe ich viel weiter in die Ferne, mein Horizont wird also größer. Erhöhe ich das Gerüst noch mehr, so wird auch der Gesichtskreis noch größer. Natürlich haben diese Kreise alle drei denselben Mittelpunkt (vgl. Fig. 2). Also je höher der Standpunkt, desto größer der Horizont.
1. Scheitelpunkt, Scheitellinie, Scheitelkreis. Richten wir nun von unserem Standpunkte aus unsere Blicke nach oben, so sehen wir den Himmel über uns wie ein Halbkugelgewölbe, das sich über der Horizontalebene erhebt und auf dem Horizonte ruht. Wir selbst stehen im Mittelpunkte des Gewölbes und zwar senkrecht auf der Horizontalebene, wie sich durch ein herniedergelassenes Lot leicht zeigen läßt. Bezeichnen wir diese Richtung von unserem Standpunkte aus durch eine gerade Linie, so trifft diese das Himmelsgewölbe in einem Punkte über unserem Scheitel; er heißt Scheitelpunkt oder Zenit, und die gerade Linie, die Standpunkt und Zenit verbindet, heißt Scheitellinie. Ein Kreis um unseren Standpunkt als Mittelpunkt, dessen Ebene durch die Scheitellinie und dessen Peripherie durch den Zenit geht heißt Scheitelkreis oder Vertikalkreis, (vertex lat. = Scheitel).
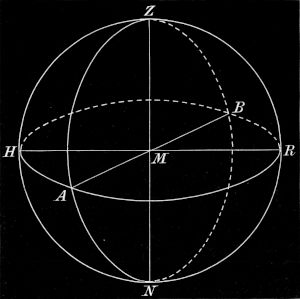
In Fig. 3 ist M unser Standpunkt, der Kreis HARBH der Horizont, Z der Zenit, ZM die Scheitellinie; die Kreise HZRNH und AZBNA sind Scheitelkreise, der Halbkreis HZR bedeutet zugleich das Himmelsgewölbe.
Ein Blick auf die Figur lehrt ferner: 1. Alle Vertikalkreise stehen senkrecht auf der Horizontebene 2. Die Ebene eines Scheitelkreises schneidet die Horizontalebene in einer geraden Linie, welche den Horizont halbiert, so daß die Endpunkte dieser Linie 180° voneinander entfernt sind. Die Ebenen der Scheitelkreise HZRNH und AZBNA z. B. schneiden die Horizontebene in den geraden Linien HR und AB. 3. Umgekehrt halbiert auch der Horizont jeden Scheitelkreis, so daß von dem Scheitelkreise 180° über und 180° unter dem Horizonte liegen. 4. Die Scheitelkreishälfte über dem Horizonte wird wieder durch den Zenit halbiert, folglich sind alle Punkte des Horizonts 90° vom Zenit entfernt.

2. Bestimmung der Himmelsgegenden. a) Durch den Polarstern. Um in der Horizontebene die Lage bestimmter Gegenstände (Häuser, Bäume) und[8] Punkte zueinander zu bestimmen, hat man zuerst gewisse Richtungen festgelegt, die unser geradeaus sehendes Auge verfolgt. Für den Abend und die Nacht kann man dazu, wenn es sternhell ist, einen Stern am Himmelsgewölbe benutzen, den Polarstern. Während nämlich alle Sterne scheinbar ihre Lage am Himmel verändern, bleibt dieser immer ziemlich auf demselben Flecke stehen. Um ihn aufzufinden, mögen folgende Angaben dienen. Wir sehen an jedem sternhellen Abend ziemlich hoch am Himmel sieben helle Sterne, die eine Figur bilden, wie sie Fig. 4 darstellt. Die ganze Figur hat aber zum Horizont zu verschiedenen Zeiten eine verschiedene Stellung. Wie in Fig. 4 zeigt sie sich uns an Abenden des Spätherbstes. Diese Sterne, die wegen ihres Glanzes und ihrer eigenartigen Stellung sehr leicht aufzufinden sind, bilden mit einer Anzahl von weniger hellen Sternen ein sogenanntes Sternbild, den Großen Bären. Verbindet man die beiden mit a und b bezeichneten Sterne dieses Sternbildes durch eine gerade Linie, so trifft deren Verlängerung den Polarstern c.
Denken wir uns die gerade Linie zwischen unserem Auge und dem Polarstern auf unsere Horizontebene projiziert, so nennen wir die Richtung dieser Projektion Norden, die entgegengesetzte Richtung – hinter uns – Süden. Ziehen wir von unserem Standpunkte aus in der Horizontebene eine gerade Linie rechtwinklig zur Nordsüdlinie nach links, so heißt die durch diese Linie bezeichnete Richtung Westen, und die Verlängerung jener Linie nach rechts zeigt nach Osten.
Nord, Süd, West und Ost sind die vier Haupthimmelsgegenden.
Die Halbierungslinien der vier rechten Winkel zwischen der Nordsüdlinie und der Westostlinie zeigen nach den ersten Nebenhimmelsgegenden, die Halbierungslinien der so entstandenen acht Winkel von 45° nach den zweiten Nebenhimmelsgegenden;
b) Durch die Sonne. Am Tage kann man die Himmelsgegenden mit Hilfe der Sonne feststellen. Beobachten wir sie an verschiedenen Tagen, so zeigt sich, daß sie morgens zwar nicht immer an demselben Punkte, aber doch immer in derselben Gegend, der Ostgegend des Horizontes, am Himmelsgewölbe erscheint,[9] sich an diesem immer höher hebt, bis sie mittags um 12 Uhr den höchsten Punkt ihrer Bahn erreicht hat und dann sinkt, um abends in der Westgegend unter dem Horizonte zu verschwinden. An welcher Stelle des Himmelsgewölbes auch an verschiedenen Tagen mittags der höchste Punkt der Sonnenbahn liegen mag, immer weist die Projektion der geraden Linie zwischen unserem Auge und diesem höchsten Punkte auf die Horizontalebene genau von unserem Standpunkte nach Süden, mit anderen Worten: sie fällt in die Nordsüdlinie, die man deswegen auch Mittagslinie nennt. Da jeder Ort seinen eigenen Horizont und seinen eigenen Zenit hat, hat er auch seine eigene Mittagslinie. Offenbar würde man nach Feststellung dieser Linie alle Himmelsgegenden durch bloße Winkelkonstruktionen bestimmen können. – Aber wie kann man auf einfache Weise die Lage der Mittagslinie eines Ortes bestimmen? Je höher die Sonne steht, desto kürzer ist der Schatten aller Gegenstände, die senkrecht auf der Horizontebene stehen, und umgekehrt. Stellte man also bei Sonnenschein auf eine horizontale Fläche senkrecht einen Stab und beobachtete genau die Länge der Schatten auf der Fläche, so wäre der kürzeste aller Schatten die Mittagslinie. Diese Beobachtung bietet aber praktische Schwierigkeiten und würde sehr unsicher sein; daher ist folgendes Verfahren besser.
Auf einem horizontalen Brette wird ein mehrere Zoll langer Stab senkrecht befestigt, nachdem man vorher um seinen Standort eine größere Anzahl konzentrischer Kreise gezogen hat. Die Einrichtung heißt Gnṓmōn. Vormittags fällt der Schatten mehr nach Westen, nachmittags mehr nach Osten, mittags genau nach Norden; vormittags wird er allmählich kürzer, nachmittags allmählich länger; vormittags wird er also durch die äußeren Kreislinien mit größerem Halbmesser hindurch nach den inneren zurück und dabei gleichzeitig von Westen nach Norden herum, nachmittags von den inneren Kreisen durch die äußeren vorwärts und dabei gleichzeitig von Norden nach Osten herum gehen. Den Kreis, den der Schatten vormittags um eine bestimmte Stunde schneidet, schneidet er um ebensoviel nach 12 Uhr wieder. Bezeichnet man zwei solche Schnittpunkte desselben Kreises, verbindet sie und halbiert die Verbindungslinie, so ist die Linie, die durch den Halbierungspunkt und den Standpunkt des Stabes geht, die Mittagslinie.
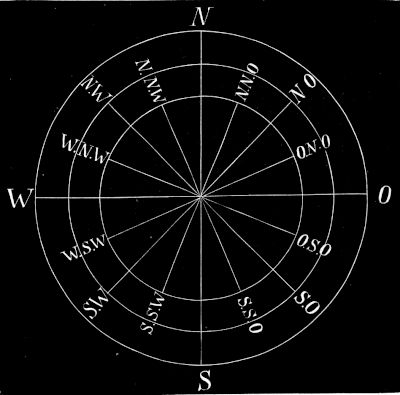
Hat man die Lage der Mittagslinie gefunden, so kann man leicht die Himmelsgegenden genau bestimmen. Das Nordende der Mittagslinie heißt Nordpunkt, das Südende derselben Südpunkt; beide Punkte sind 180° voneinander entfernt und halbieren den Horizont. Durch Halbierung der zwei Horizonthälften erhält man Ostpunkt und Westpunkt; die gerade Linie zwischen diesen beiden Punkten heißt die Ostwestlinie. Durch Mittagslinie und Ostwestlinie wird der Horizont in vier gleiche Teile geteilt, welche Quadranten heißen. Die vier Punkte heißen Kardinalpunkte. Sie sind je 90° voneinander entfernt. Halbieren wir jeden zwischen zwei Himmelsgegenden liegenden Bogen des betreffenden Kreisausschnittes auf unserer Horizontebene, so entstehen Nordost, Nordwest, Südost und Südwest. Ähnlich entstehen dann die zweiten Nebengegenden usw. Bei der Namengebung stehen die Hauptgegenden immer voran. Man erkennt die Namen aus Fig. 5. Diese heißt die Windrose.
c) Durch die Magnetnadel. Ein weiteres, sehr bequemes Mittel, zu jeder Zeit die Mittagslinie festzustellen, bietet die Magnetnadel, deren Spitze bei uns bekanntlich nach der Nordgegend weist und zwar 10° westlich von der Mittagslinie.
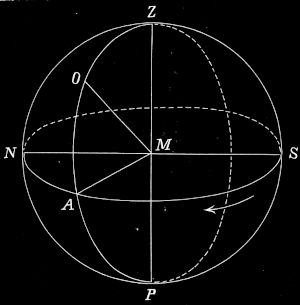
3. Höhe und Azimut. Um zu zeigen, wie man den augenblicklichen Ort eines Sternes am Himmelsgewölbe bestimmt, benutzen wir Fig. 6. Der Kreis NASN ist der Horizont, N der Nord-, S der Südpunkt, NS die Nordsüdlinie, Z der Zenit, ZM die Scheitellinie, O der Ort des Sternes. Wir denken uns durch O den Scheitelkreis OAPZ gelegt. Diejenige Hälfte dieses Kreises, die durch den Punkt O geht (ZOAP), schneidet den Horizont in A. Nun mißt man zunächst den Bogen SA des Horizontes vom Südpunkte S in westlicher (durch den Pfeil bezeichneter) Richtung bis A, dem der Winkel SMA entspricht. Diesen Bogen nennt man den Azimut des Ortes (Sternes) O; man mißt ihn über den ganzen Horizont von 0° bis 360°. Dann mißt man den Bogen AO des Scheitelkreises, dem der Winkel AMO entspricht. Da dieser Bogen angibt, wie hoch der Ort sich über den Horizont erhebt, so nennt man ihn die Höhe des Ortes. Offenbar haben alle Orte auf einem Kreise am Himmelsgewölbe, dessen Ebene parallel zur Horizontebene liegt, gleiche Höhe. Solche Kreise, auf denen natürlich die Scheitellinie senkrecht steht, heißen Höhenkreise. Die Höhe wird vom Horizonte an gemessen, geht also von 0° bis 90°, der Höhe des Zenits. An die Stelle der Höhe kann auch ihr Komplement treten, der Bogen OZ. Man nennt ihn die Zenitdistanz. Offenbar kann man den Ort eines Sternes am Himmelsgewölbe genau bestimmen, wenn man seinen Azimut und seine Höhe kennt.
1. Fußpunkt, Achse des Horizontes. Wie wir wissen, scheint der Himmel an den verschiedensten Standpunkten als Halbkugel auf unserem Horizont zu ruhen. Daraus, daß diese Beobachtung für alle Punkte der Erde gilt, ergibt sich: Der Himmel erscheint als eine Kugel, die die Erde umgibt und zur Hälfte als Himmelsgewölbe über, zur Hälfte unter dem Horizonte liegt. Unser Standpunkt ist der Mittelpunkt der Kugel, und die Verlängerung der Scheitellinie durch diesen Mittelpunkt trifft die unsichtbare Hälfte der Himmelskugel unter dem Horizonte in einem Punkte senkrecht unter uns; dieser Punkt heißt Fußpunkt oder Nadir. Die gerade Linie zwischen Zenit und Nadir, die auf dem Horizonte senkrecht steht, heißt die Achse des Horizontes. In Fig. 6 bedeutet der Kreis NZSPN die Himmelskugel, P den Nadir, ZP die Achse des Horizontes.
2. Natürlicher, scheinbarer und wahrer Horizont. Eigentlich ist unser Standpunkt nicht im mathematisch genauen Sinne der Mittelpunkt der Himmelskugel. Aus dem geographischen Unterrichte in der Volksschule ist ja schon bekannt, daß die Erde nicht, wie man aus dem Augenschein nach § 1 schließen möchte, eine Scheibe ist, sondern die Gestalt einer Kugel hat. Das mag hier einmal, trotzdem erst im dritten Kapitel die Beweise dafür zusammengestellt sind,[12] vorausgesetzt werden. Der Himmel erscheint nun als eine viel größere konzentrische Hohlkugel. Der Halbmesser der Erde ist sehr groß, aber dennoch verschwindend klein gegen den Halbmesser der Himmelskugel.
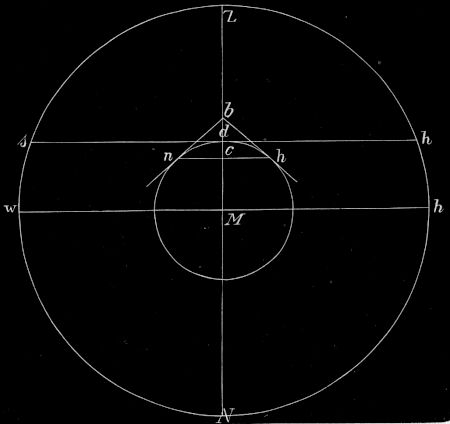
In Fig. 7 ist der kleine Kreis die Erde, der große die Himmelskugel, d mein Standpunkt, b die Augenhöhe. Der Deutlichkeit wegen ist die Linie db im Verhältnis zur Erdkugel und diese im Verhältnis zur Himmelskugel unendlich vielmal zu groß gezeichnet. Ich überblicke von der Erdkugel die Kugelkappe ndh; diese ist begrenzt durch Berührungsebenen, die ich von b aus an die Kugel legen kann. Die Grenzlinie dieser Kugelkappe ist der Kreis nh. Er ist der Horizont, von dem bisher die Rede war, und heißt der natürliche Horizont. Da db im Vergleich zur Erdkugel verschwindend klein ist, so ist es auch das überblickte Stück ndh; es erscheint deshalb eben und weicht in Wirklichkeit unendlich wenig von der Ebene nch ab. Also fällt auch Punkt c mit d und die Ebene nch mit der Berührungs- oder Tangentialebene in d fast zusammen. Diese Tangentialebene schneidet das Himmelsgewölbe in einem Kreise sh; ihn nennt man den scheinbaren oder astronomischen Horizont. Das Stück sZh ist der für uns sichtbare Teil der Himmelskugel. Legt man zu der Tangentialebene durch den Mittelpunkt der Erde eine parallele Ebene, so schneidet diese die Himmelskugel in dem Kreise wh; ihn nennt man den wahren Horizont. Da nun der Halbmesser der Erde im Vergleich zu dem der Himmelskugel verschwindend klein ist, so ist auch die Höhe der Zone, die von den Kreisen sh und wh am Himmel begrenzt wird, verschwindend klein im Vergleich zur Höhe des Himmelsgewölbes. Man kann also annehmen, daß der wahre und scheinbare Horizont zusammenfallen, und setzt in der astronomischen Geographie für das von uns in Wirklichkeit überblickte Stück der Himmelskugel ohne weiteres die Halbkugel wZh.
1. Der Tagbogen. Daß die Sonne zu verschiedenen Tageszeiten in verschiedenen Höhen über dem Horizonte steht, also scheinbar täglich eine Bewegung am Himmelsgewölbe ausführt, ist schon bei der Feststellung der Mittagslinie beobachtet worden (vgl. § 2). Diese Bewegung wollen wir jetzt genauer betrachten. Wir sehen die Sonne nur während des Tages. Zuerst erblicken wir sie in einem Punkte des Horizontes in der Morgengegend und sagen dann: »Die Sonne geht auf.« Der Punkt des Horizontes, in dem der Mittelpunkt der Sonnenscheibe aufgeht, heißt ihr Aufgangspunkt. Von ihm aus erhebt sie sich immer höher, bis sie mittags den höchsten Punkt in ihrer Bahn erreicht. Dann senkt sie sich in einer dem Aufsteigen entgegengesetzten Richtung dem Horizonte wieder zu, bis sie ihren Untergangspunkt erreicht und verschwindet. Daraus, daß diese Beobachtung überall[13] auf der Erde zu machen ist, schließen wir: Vom Untergangspunkt aus setzt die Sonne, für uns ungesehen, ihren Weg unter unserem Horizonte fort und durchläuft an einem Tage einen vollständigen Kreis an der Himmelskugel.
Der über dem Horizonte liegende Teil der Sonnenbahn, der vom Aufgangs- bis zum Untergangspunkte – also bei Tage – durchlaufen wird, erscheint als ein Kreisbogen und heißt der Tagbogen. Der höchste Punkt im Tagbogen heißt der obere Kulminationspunkt. Er liegt genau in der Mitte zwischen Aufgangs- und Untergangspunkt und teilt den Tagbogen in zwei gleiche Teile, welche Vormittags- und Nachmittagsbogen heißen. Der Weg der Sonne, den sie unter dem Horizonte und nachts zurücklegt, heißt Nachtbogen; in seiner Mitte liegt der untere Kulminationspunkt; dieser liegt dem oberen gerade gegenüber und teilt den Nachtbogen in Vor- und Nachmitternachtsbogen. Tag- und Nachtbogen bilden zusammen einen Kreis, der in 24 Stunden = 1 Tag von der Sonne durchlaufen wird und zwar von Osten nach Westen; er heißt Tagkreis und steht schief auf unserem Horizont.
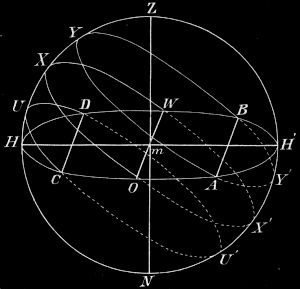
2. Meridian. In Fig. 8 ist Kreis HZH´NH = Himmelskugel; Kreis HOH´WH = Horizont von Berlin; m = Standpunkt (Berlin); Kreis AYBY´A = Tagkreis der Sonne für den 21. Juni, Kreis OXWX´O = Tagkreis der Sonne für den 21. März und den 23. September, CUDU´C = Tagkreis der Sonne für den 21. Dezember. Man erkennt: 1. Die Tagkreise der verschiedenen Tage sind verschieden. 2. Sie sind aber unter demselben Winkel gegen den Horizont eines bestimmten Standpunktes geneigt; für Berlin beträgt der Winkel 37½°. 3. Daraus ergibt sich weiter, daß die Ebenen der Tagkreise untereinander parallel sind. 4. Auch die Aufgangspunkte (A, O, C) und die Untergangspunkte (B, W, D) für die verschiedenen Tage sind verschieden. 5. Endlich sind auch Tag- und Nachtbogen nicht immer einander gleich, wohl aber Vor- und Nachmittags-(Vor- und Nachmitternachts-)bogen. Den längsten Tagbogen beschreibt die Sonne am Himmelsgewölbe am 21. Juni (AYB), den kürzesten am 21. Dezember (CUD); nur am 21. März und am 23. September sind alle vier Teile des Tagkreises einander gleich. 6. U, X, Y sind die oberen, U´, X´, Y´ die unteren Kulminationspunkte der drei Kreise. Auch die Kulminationspunkte sind also für die verschiedenen Tage verschieden; aber sie liegen stets in demselben Vertikalkreise oder: Die Sonne kulminiert für einen bestimmten Standpunkt an allen Tagen des Jahres in demselben Vertikalkreise. Man nennt ihn, da die obere Kulmination der Sonne in ihm mittags eintritt, den Meridian oder Mittagskreis des Ortes. Anstatt zu sagen: »Die Sonne kulminiert für den Ort,« kann man somit auch sagen: »Die Sonne steht im Meridian des[14] Ortes.« Kreis HZH´NH (Fig. 8) ist der Meridian von Berlin. Dieser soll fernerhin bei allen weiteren Betrachtungen zugrunde gelegt werden, wenn nichts Besonderes angegeben wird.
3. Meridian und Mittagslinie. Die Ebene des Meridians steht als Ebene eines Scheitelkreises senkrecht auf der Horizontebene und schneidet diese in einer geraden Linie, die durch den Standpunkt geht und den Horizont halbiert. Diese gerade Linie wollen wir noch näher betrachten. Nach einem bekannten Lehrsatze der Stereometrie liegen alle Senkrechten, die man aus einem Punkte einer Ebene auf eine sie senkrecht schneidende Ebene fällt, ganz in der ersten Ebene; ihre Fußpunkte gehören also beiden Ebenen an, d. h. die Verbindungslinie der Fußpunkte zweier solcher Senkrechten fällt mit der Schnittlinie der zwei Ebenen zusammen. Nun ist aber nach § 2 die Mittagslinie nichts anderes als die Verbindungslinie der Fußpunkte zweier Senkrechten, die aus Punkten der Meridianebene auf die sie senkrecht schneidende Horizontalebene gefällt sind, nämlich der Scheitellinie und der Senkrechten aus dem oberen Kulminationspunkt der Sonne auf die Horizontalebene; also schneidet die Meridianebene die Horizontebene in der Mittags- oder Nordsüdlinie, oder die Meridianebene ist, wie die Mittagslinie, genau von Süden nach Norden gerichtet.
1. Dauer. a) Auch der Mond beschreibt täglich (und scheinbar!) von Osten nach Westen einen Tagkreis, welcher denselben schiefen Winkel mit dem Horizont bildet wie der Tagkreis der Sonne und auch wie dieser vom Horizont in zwei Teile geteilt wird; auch er geht täglich auf und unter und kulminiert zweimal im Meridian wie die Sonne. b) Ebenso sind seine Tagkreise an den verschiedenen Tagen verschieden. c) Aber in bezug auf die Zeit des Auf- und Unterganges und der Kulminationen weicht er von der Sonne ab; denn diese Ereignisse erfolgen beim Monde im Laufe eines Monats zu den verschiedensten Tageszeiten. Das liegt daran, daß er zu seinem Tagkreise nicht wie die Sonne nur 24 Stunden, sondern 24 Stunden und 50 Minuten, also fast eine Stunde mehr braucht.
2. Phasen. Auch die scheinbare Gestalt des Mondes wechselt. Man unterscheidet unter seinen mannigfaltigen Gestalten vier Hauptwechsel oder Phasen (griech. = Erscheinungen), nämlich Neumond, erstes Viertel, Vollmond und letztes Viertel.
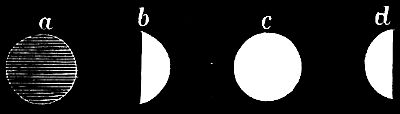
(Siehe Fig. 9) a = Neumond; b = erstes Viertel; c = Vollmond; d = letztes Viertel.
Der Neumond ist dunkel; das erste Viertel zeigt die rechte Hälfte erleuchtet, der Vollmond die ganze Scheibe, das letzte Viertel die linke Hälfte. Dieser Wechsel vollzieht sich in 29½ Tagen.
(Der zunehmende Mond, vom Neumond bis Vollmond, erinnert bei uns an
den oberen Teil des 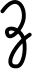 , der abnehmende, vom Vollmond bis Neumond, an den
linken Teil eines geschriebenen
, der abnehmende, vom Vollmond bis Neumond, an den
linken Teil eines geschriebenen 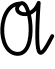 .)
.)
1. Fixsterne. Die meisten Sterne behalten ihre Stellung zueinander; das können wir z. B. an der Stellung der Sterne des Großen Bären (s. § 2) zueinander und zum Polarstern beobachten. Nur wenige Sterne ändern ihre Stellung zu anderen Sternen. Die Sterne, die ihre Stellung zueinander nicht ändern, nennt man aus diesem Grunde Fixsterne (lat. fixus = angeheftet, nämlich scheinbar am Himmelsgewölbe).
2. Tagkreise. Alle Sterne ohne Ausnahme ändern ihre Stellung zum Horizonte beständig, und zwar rücken sie von Osten nach Westen fort, gerade wie die Sonne und der Mond. Jeder Stern durchläuft in etwa 24 Stunden (die Fixsterne genauer in 23 Stunden 56 Minuten) einen Kreis und alle einzelnen Kreise laufen miteinander und mit den Tagkreisen von Sonne und Mond parallel, sind also, wie diese, gegen den Horizont geneigt. Für Berlin beträgt diese Neigung, wie in § 4 gezeigt wurde, 37½°. Daher kulminieren auch alle Sterne wie die Sonne und der Mond im Meridian unseres Standpunktes (s. § 4).
3. Himmelsachse und Himmelsäquator. Da Sonne, Mond und alle Sterne täglich parallele Kreise zu durchlaufen scheinen, so macht es den Eindruck, als drehe sich die ganze Himmelskugel täglich um einen ihrer Durchmesser. Dieser steht auf den Ebenen aller jener parallelen Kreise senkrecht, enthält ihre Mittelpunkte und heißt Himmels- oder Weltachse; seine Endpunkte in der Himmelskugel (Pole) heißen Himmels- oder Weltpole. Der Polarstern liegt dem einen Himmelspole sehr nahe, etwa nur 1½° von ihm entfernt. Dieser Pol ist der Nordpol, der andere der Südpol des Himmels. (Genau genommen ist die Projektion der Weltachse auf die Horizontebene die Nordsüdlinie. Sie weicht aber nach dem eben Gesagten von der Projektion der Linie zwischen Auge und Polarstern auf die Horizontebene [s. § 2] nur unmerklich ab.)
Unter den Parallelkreisen, die von den Sternen durchlaufen werden, ist der größte derjenige, dessen Mittelpunkt zugleich der Mittelpunkt der Weltachse ist. Er teilt die Himmelskugel in eine nördliche und eine südliche Hälfte und heißt Himmelsäquator (Äquator lat. = Gleichmacher, Gleicher). Die Parallelkreise werden nach beiden Polen zu immer kleiner. Deshalb sind auch die Tagkreise der Sterne als Parallelkreise an Größe sehr verschieden. Der Polarstern durchläuft einen so kleinen Kreis, daß man diesen kaum wahrnimmt. Je weiter die Sterne von ihm entfernt sind, desto größer sind ihre Kreise, also im Himmelsäquator am[16] größten, wie schon gezeigt wurde. Von da zum Südpole werden sie wieder kleiner. Es gibt Sterne am Himmel, die für einen bestimmten Ort der Erdoberfläche nicht untergehen; für uns gilt das z. B. vom Polarstern und den Sternen im Sternbild des Großen Bären. Solche Sterne heißen für diesen Ort Zirkumpolarsterne. Der Horizont und seine Achse wechseln für jeden Standpunkt, die Himmelsachse, also auch die Pole und der Äquator, sind für alle Standpunkte dieselben.
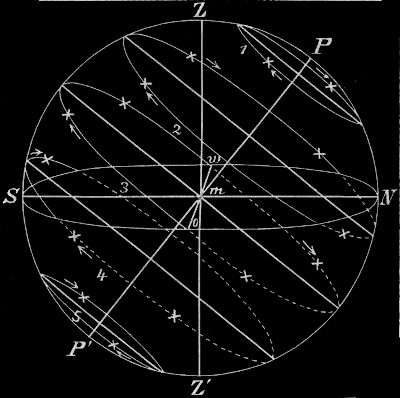
(Vgl. Fig. 10.) Kreis SZNZ´S = Himmelskugel, Kreis SoNwS = Horizont, PP´ = Weltachse, P = Nordpol, P´ = Südpol, m = Standpunkt. Stern 1 = Zirkumpolarstern, die Bahn von Stern 2 liegt größtenteils, die von Stern 3, der sich im Äquator bewegt, zur Hälfte über dem Horizont, die von Stern 4 größtenteils, die von Stern 5 ganz unter dem Horizont.
Weil die Kreise der Sterne an Größe verschieden sind, alle aber in derselben Zeit – ca. 24 Stunden – durchlaufen werden, so muß die scheinbare Geschwindigkeit der Sterne verschieden sein.
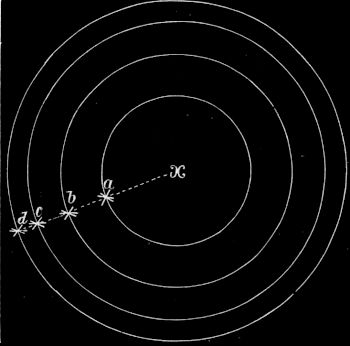
(Siehe Fig. 11.) x = Pol. Stern a durchläuft 360° in ca. 24 Stunden = 1440 Minuten, also 1° in 4 Minuten (= 1440/360), b, c, d desgleichen; aber der Kreis des Sternes b, d. i. sein Weg, ist größer als der des Sternes a. Ebenso ist der Weg des Sternes c größer als der des Sternes b usw.
Die größte scheinbare Geschwindigkeit haben Sterne, die im Himmelsäquator stehen.
4. Neue Definition des Meridians. Da die Kulminationspunkte eines jeden Parallelkreises um 180° voneinander entfernt liegen, so gehen die Verbindungslinien dieser Punkte als Durchmesser der Parallelkreise alle durch die Weltachse. Die Endpunkte dieser Durchmesser liegen aber als Kulminationspunkte im Meridian unseres Standpunktes, demnach die Durchmesser alle in der Ebene, die man durch den Meridian legen kann. In dieser Ebene muß dann also auch die Weltachse liegen. Daraus ergibt sich: der Meridian ist derjenige Vertikalkreis, der durch die Pole der Weltachse geht.
Für unseren Standpunkt ist in Fig. 10 also der Kreis SZPNZ´P´S, der die Himmelskugel bedeutet, zugleich der Meridian.
5. Neigung der Himmelsachse gegen den Horizont; Polhöhe. Die Neigung der Himmelsachse gegen den Horizont hängt natürlich ab von der Neigung des Äquators. Diese beträgt, wie bei allen Tagkreisen, für Berlin 37½°. Sie wird dargestellt (Fig. 10) durch den Bogen vom Südpunkte S des Horizontes bis zum oberen Schnittpunkte des Meridians SZPNZ´P´S mit dem Äquator 3; der Bogen von hier aus zum Nordpol P beträgt 90°, also beträgt der Bogen von P[17] bis zum Nordpunkte des Horizontes zusammen mit dem ersten Bogen von 37½° ebenfalls 90°, er selbst ist demnach = 90° − 37½° = 52½°. Dieser Bogen ist die Polhöhe; sie ist stets das Komplement der Neigung des Äquators gegen den Horizont und gibt zugleich die Neigung der Himmelsachse gegen den Horizont an. Auch der Abstand des Nordpols vom Zenit ist das Komplement der Polhöhe, also für Berlin 37½°, und überall liegt der Äquator so viel Grad unter dem Nordpunkte des Horizontes, als der Nordpol unter dem Zenit liegt. Zugleich ergibt sich, daß der Tagkreis, der, im Meridian gemessen, um die Polhöhe (52½°) vom Pol entfernt ist, die Grenze der Zirkumpolarsterne bildet; denn die untere Kulmination der Sterne, die diesen Kreis durchlaufen, findet im Nordpunkte des Horizontes statt.
1. Tagkreis der Sonne für den 21. März. Am 21. März können wir beobachten, daß die Sonne um 6 Uhr morgens im Ostpunkte auf-, um 6 Uhr abends im Westpunkte untergeht. Daher gehört die Ostwestlinie, mithin auch unser Standpunkt, der Mittelpunkt der Himmelskugel, dem Tagkreise des 21. März an. Dieser Tagkreis ist also, wie jeder Kugelkreis, dessen Ebene durch den Kugelmittelpunkt geht, ein größter Kreis der Himmelskugel und ist, wie die Tagkreise aller Gestirne, für Berlin unter einem Winkel von 37½° gegen den Horizont geneigt. Der größte Kreis aber, der diese Neigung gegen den Horizont hat, ist nach § 6 der Himmelsäquator. Die Sonne durchläuft somit am 21. März den Himmelsäquator, und die Mittagshöhe der Sonne ist an diesem Tage überall gleich der Äquatorhöhe (37½°; Bogen HX in Fig. 8). Wie alle größten Kreise halbieren Horizont und Äquator einander; daher ist am 21. März der Tagbogen gleich dem Nachtbogen, Tag und Nacht sind gleich, es ist Frühlings-Tag- und Nachtgleiche (Äquinoktium). Mit dem 21. März beginnt der Frühling.
In Fig. 8 ist OXW der Tag-, WX´O der Nachtbogen für den 21. März; H ist der Südpunkt, H´ der Nordpunkt des Horizontes. Vom Zenit ist die Sonne an diesem Tage mittags um 90° − 37½° = 52½° entfernt. (Bogen XZ [Winkel XmZ] = Bogen HZ − HX = 90° − 37½°.) Der Abstand heißt die Zenitdistanz. Um Mitternacht steht die Sonne 37½° unter dem Horizont (Bogen H´X´ in Fig. 8).
2. Verschiebung der Tagkreise. Setzen wir unsere Beobachtungen täglich fort, und zwar von demselben Standpunkte aus, so entdecken wir, daß die Sonne täglich früher aufgeht, und zwar nicht mehr im Ostpunkte, sondern immer mehr nördlich davon, auch daß sie zu Mittag immer höher steigt, und endlich, daß sie auch immer mehr nördlich vom Westpunkte untergeht.
Daraus folgt, daß der Tagkreis der Sonne nicht mehr der Äquator sein kann, sondern ein Kreis, der nördlich vom Äquator liegt. Die Sonne ist also nach Norden zu gerückt, die Tage sind länger, die Nächte sind kürzer geworden.
Die Entfernung des Aufgangspunktes vom Ostpunkte heißt Morgenweite (Bogen OA in Fig. 8); die Entfernung des Untergangspunktes vom Westpunkte heißt Abendweite (Bogen WB in Fig. 8).
3. Tagkreis für den 21. Juni. So geht es fort bis zum 21. Juni, an welchem Tage die nördliche Abweichung der Sonne vom Äquator mit 41° ihr Maximum erreicht. Am 21. Juni geht die Sonne um 3¾ Uhr morgens auf und um 8¼ Uhr abends unter, steht also 16½ Stunden über dem Horizonte: es ist der längste Tag und die kürzeste Nacht. Der Tagkreis der Sonne ist 23½° nördlich vom Äquator; der Abstand wird dargestellt durch den Bogen XY, dem der Winkel XmY entspricht, oder durch den Bogen X´Y´. Es befindet sich also die Mittagshöhe 37½° + 23½° = 61° (Bogen HX + XY = HY) über dem Horizonte, und die Zenitdistanz beträgt nur 90° − 61° = 29° (Bogen HZ − HY = YZ).
Um Mitternacht steht die Sonne dann nur 37½° − 23½° = 14° unter dem Horizonte (Bogen H´Y´ = H´X´ − X´Y´).
Nun wendet sich die Sonne wieder dem Äquator zu, man nennt deshalb jenen am 21. Juni beschriebenen Kreis den Wendekreis, und zwar, weil er nördlich vom Äquator liegt, den nördlichen Wendekreis.
Am 21. Juni ist Sommersonnenwende oder Sommersolstitium. Mit dem 21. Juni beginnt der Sommer.
4. Tagkreis für den 23. September. Vom 21. Juni ab werden Abend- und Morgenweite und Mittagshöhe der Sonne immer kleiner. Es erfolgt späterer Sonnenaufgang und früherer Sonnenuntergang; die Tage werden kürzer, die Nächte länger, bis am 23. September der Äquator wieder erreicht und wie am 21. März durchlaufen wird. Die Sonne geht 6 Uhr morgens im Ostpunkte auf und 6 Uhr abends im Westpunkte unter; die Mittagshöhe beträgt wieder 37½° (Äquatorhöhe).
Es ist das Herbstäquinoktium eingetreten, und der Herbst beginnt. Vom 23. September ab durchläuft die Sonne Tagkreise, die südlich vom Äquator liegen; dabei gehen Tagkreis, Morgen- und Abendweite täglich mehr nach Süden, die Mittagshöhe sinkt täglich mehr unter 37½°, die Tage werden kürzer, die Nächte länger bis zum 21. Dezember.
5. Tagkreis für den 21. Dezember. An diesem Tage beträgt die (südliche!) Morgen- und Abendweite 41° (Bogen OC und WD): die Sonne geht um 8¼ Uhr morgens auf und um 3¼ Uhr nachmittags unter; sie verweilt also 16½ Stunden unter dem Horizonte. Wir haben den kürzesten Tag und die längste Nacht. Der Tagkreis liegt 23½° südlich vom Äquator; der Abstand wird dargestellt durch den Bogen XU, dem der Winkel XmU entspricht, oder durch den Bogen X´U´. Die Mittagshöhe beträgt nur 37½° − 23½° = 14° (Bogen HU = HX − XU). Um Mitternacht ist die Sonne 37½° + 23½° = 61° unter dem Horizonte (Bogen H´U´ = H´X´ + X´U´). Die Zenitdistanz beträgt 90° − 14° = 76° (Bogen HZ − HU = UZ).
Der Tagkreis des 21. Dezembers heißt der südliche Wendekreis; denn von nun an wendet sich die Sonne wieder dem Äquator zu. Der 21. Dezember heißt der Tag der Wintersonnenwende oder des Wintersolstitiums.
Die südlichen Morgen- und Abendweiten werden nun wieder immer kleiner, die Mittagshöhe wird größer, die Tage nehmen zu und die Nächte ab, bis am 21. März die Tag- und Nachtgleiche wieder eintritt, weil an diesem Tage die Sonne den Äquator wieder erreicht.
1. Wesen. Ehe die Sonne im Horizonte erscheint, kündigt sie ihre Ankunft durch einen lichten Schein an; man sagt: »Der Tag graut«, oder: »Es ist Morgendämmerung«. Ähnlich gibt es eine Abenddämmerung nach Sonnenuntergang.
2. Ursache. Diese Erscheinungen wären nicht da, wenn die Erde nicht von einem Dunstkreise (Atmosphäre, Lufthülle) umgeben wäre. Diese Atmosphäre ist nicht vollkommen durchsichtig, so daß die Sonnenstrahlen frei hindurchgehen könnten, sondern sie wirft einen Teil der auf sie fallenden Strahlen zurück (reflektiert sie). Wenn daher die Sonne mit ihren Strahlen noch nicht oder nicht mehr die Erdoberfläche direkt erleuchten kann, so sendet sie der Erde immer noch Strahlen zu vermittelst der die Erde umgebenden Luftschichten, welche das empfangene Licht zurückwerfen. Ginge nun die Atmosphäre ins Unendliche fort, so würde die Dämmerung nie erlöschen. Weil aber die Dämmerung wirklich aufhört, so muß auch die Atmosphäre eine obere Grenze haben.
Je höher, desto dünner ist die Luft. Je näher die Sonne dem Horizonte, desto niedriger und darum desto dichter sind die von der Sonne beschienenen Luftschichten. Je tiefer die Sonne sinkt, desto höher liegen die von ihr noch getroffenen Luftschichten und desto dünner sind sie auch, desto mehr Licht lassen sie deshalb hindurch, und desto weniger werfen sie zurück. Darum wird das Licht mit sinkender Sonne immer matter.
3. Dämmerungszone. Steht die Sonne tiefer als 18° (im Scheitelkreise gemessen!) unter dem Horizonte, so hört die Dämmerung gänzlich auf. Die nun noch von der Sonne getroffenen Luftschichten haben eine Höhe von etwa 70 km. Die Atmosphäre wird also auch eine Höhe (Dicke) von etwa 70 km haben oder wenigstens über diese Grenze hinaus so dünn werden, daß sie uns bemerkbare reflektierte Lichtmengen nicht mehr zusendet. Aus verschiedenen Gründen nimmt man allerdings das letztere an und schätzt die Dicke der Atmosphäre auf etwa 350 km.
Denken wir uns einen Kreis unter dem Horizonte, und zwar 18° von ihm entfernt und parallel mit ihm, so heißt dieser der Dämmerungskreis, und die zwischen ihm und dem Horizonte liegende Zone (Gürtel) heißt die Dämmerungszone. Solange die Sonne darin verweilt, ist Dämmerung, und zwar die astronomische.
4. Dauer der Dämmerung. Ginge die Sonne senkrecht unter, so brauchte sie 18 × 4 Minuten (da sie 4 Minuten Zeit braucht, um 1° zu durchlaufen; vgl. die Bem. zu Fig. 11 in § 6!) = 1 Stunde 12 Minuten, um die Dämmerungszone zu durchlaufen. Weil aber für unseren Horizont die Sonne schief auf- und untergeht, so wird (für uns!) die Dämmerung bedeutend verlängert. Ihre Dauer ist jedoch nicht immer gleich lang. Die kürzeste Dämmerung ist für uns am 1. März und 12. Oktober, die längste am 16. Mai und 31. Juli. Die bürgerliche Dämmerung ist die Zeit vor Aufgang oder nach Untergang der Sonne, in der man im Zimmer schon oder noch ohne Licht lesen kann.
5. Die hellen Nächte. Am 21. Juni steht die Sonne um Mitternacht, wie wir gesehen haben, nur 14° unter dem Horizonte; deshalb ist an diesem Tage die ganze Nacht hindurch Dämmerung. Offenbar gibt es aber vor und[20] nach dem 21. Juni je einen Tag, an dem die Entfernung der Sonne vom Horizonte um Mitternacht = 18° ist; das sind für uns der 16. Mai und der 31. Juli. Zwischen diesen beiden Tagen geht die Abenddämmerung in die Morgendämmerung über, es ist somit nie ganz finster. Das ist die Zeit der hellen Nächte, in denen wir selbst nachts den Stand der Sonne am hellen Scheine des Himmels erkennen.
1. Die schiefe Sphäre. Wir haben gesehen, daß für Berlin Sonne, Mond und Sterne unter einer Neigung von 37½° gegen den Horizont, also schief aufgehen: daher nennen wir die Himmelskugel, die sich über diesem Horizonte um die Weltachse dreht, die schiefe Sphäre (griechisch = Kugel).
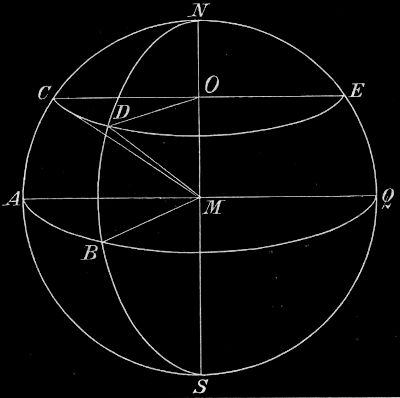
2. Erdachse und Erdäquator. Wesentlich anders stellen sich die scheinbaren Bewegungen der Gestirne für andere Punkte der Erdoberfläche dar. Für einige dieser Punkte wollen wir uns das durch Figuren klarmachen, nachdem wir folgende Erwägungen angestellt haben. Da der Himmel als eine mit der Erdkugel (s. § 3) konzentrische Kugel erscheint, so wird die Himmelsachse auch durch den Erdmittelpunkt gehen und die Oberfläche der Erde in den Endpunkten eines Erddurchmessers treffen; dieser heißt Erdachse, seine Endpunkte sind der Nord- und Südpol der Erde. Die Ebene des Himmelsäquators schneidet die Erde in einem größten Kreise, der auf der Erdachse senkrecht steht; er heißt Äquator der Erde. Offenbar würde ein Beobachter, dessen Standpunkt ein Pol der Erde wäre, den entsprechenden Himmelspol und ein Beobachter, der in einem Punkte des Erdäquators stände, einen Punkt des Himmelsäquators als Zenit haben. Jeder größte Kreis, der durch die Himmelspole geht, steht senkrecht auf dem Himmelsäquator, und seine Ebene schneidet die Erdoberfläche in einem größten Kreise, der durch die Erdpole geht und auf dem Erdäquator senkrecht steht. Zieht man von irgend einem Punkte eines solchen Kreises der Himmelskugel einen Halbmesser, so schneidet er den entsprechenden Kreis der Erdoberfläche in einem Punkte, der ebensoviel Grad, in seinem Kreise gemessen, über dem Erdäquator liegt, als der Himmelspunkt, in seinem Kreise gemessen, über dem Himmelsäquator. Ein Beobachter, der in dem Punkte auf der Erde stände, hätte den entsprechenden Himmelspunkt als Zenit über sich. Wer also 23½° nördlich vom Erdäquator steht, hat einen Punkt im nördlichen Wendekreis als Zenit. –
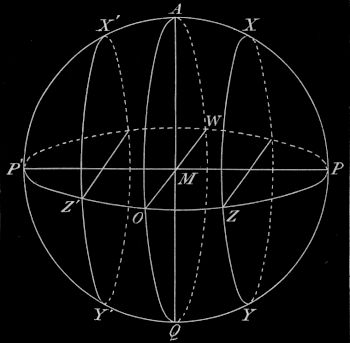
3. Die scheinbaren Bewegungen der Gestirne in der geraden Sphäre. In Fig. 12 stellt PZOZ´P´WP den Horizont des Beobachters auf den Äquator der Erde dar. Sein Zenit A ist ein Punkt des Äquators des Himmels AOQWA. Die Himmelsachse PP´ ist ein Durchmesser des Horizontes, und da der Vertikalkreis PYQY´P´X´AXP durch die Pole geht, ist er der Meridian; also fallen für den Beobachter unter dem Äquator Nordpunkt und Südpunkt des Horizontes mit dem Nord- und Südpol des Himmels zusammen. Wie der Äquator, so stehen natürlich die Tagkreise aller Gestirne senkrecht auf dem Horizonte, d. h. Sonne, Mond und Sterne gehen für den Äquatorbewohner senkrecht auf und unter;[21] die Himmelskugel ist für ihn die senkrechte oder gerade Sphäre. Alle Gestirne stehen 12 Stunden über und 12 Stunden unter dem Horizont mit Ausnahme derjenigen, die etwa genau in den Himmelspolen stehen; diese stehen stets im Nord- und Südpunkte des Horizontes. Zirkumpolarsterne gibt es nicht. Stets sind Tag und Nacht gleich. Am 21. März geht die Sonne im Ostpunkte auf, durchläuft den Äquator des Himmels, steht also mittags im Zenit, und geht im Westpunkte unter. Bis zum 21. Juni gehen Auf- und Untergangspunkte der Sonne immer weiter nach Norden herum, die Tagkreise werden kleiner. Am 21. Juni betragen Morgen- und Abendweite 23½°. Ebensoweit steht an diesem Tage die Sonne mittags vom Zenit nach Norden, ihre Mittagshöhe beträgt also 90° − 23½° = 66½°. Vom 21. Juni bis zum 23. September werden die Tagkreise wieder größer, die Morgen- und Abendweiten kleiner; am 23. September durchläuft die Sonne wieder den Äquator und steht mittags zum zweiten Male im Jahre im Zenit. Bis zum 21. Dezember gehen Auf-, Untergangs- und Kulminationspunkt der Sonne immer mehr nach Süden herum, die Tagkreise werden kleiner. Am 21. Dezember betragen Morgen- und Abendweite und Zenitdistanz wieder 23½°, die Mittagshöhe ist 66½°. Nun wachsen die Tagkreise wieder, Morgen- und Abendweiten nehmen ab, bis am 21. März der Äquator wieder erreicht ist. Offenbar werfen die Bewohner des Äquators am 21. März und am 23. September mittags keinen Schatten; vom 21. März bis zum 23. September fällt ihr Schatten mittags nach Süden, vom 23. September bis zum 21. März nach Norden, während in unserer Gegend, wie schon gezeigt, der Schatten mittags stets nach Norden fällt. Daher sagt man: wir sind einschattig, die Äquatorbewohner zweischattig. Die Dämmerung ist am Äquator viel kürzer als bei uns. Sie beträgt z. B. am 21. März und am 23. September 1 Stunde 23 Minuten (s. § 8).
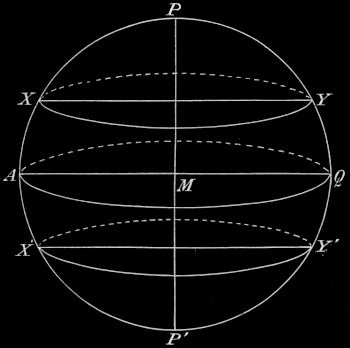
4. Die scheinbaren Bewegungen der Gestirne in der parallelen Sphäre. Fig. 13 zeigt die Verhältnisse für einen Beobachter, den wir uns im Nordpol der Erde denken. Sein Zenit ist der Nordpol des Himmels, der Himmelsäquator fällt mit dem Horizont zusammen. Alle Gestirne durchlaufen daher täglich Kreise, die parallel zum Horizont sind; die Sphäre des Poles ist die parallele Sphäre. Die Höhe eines Sternes ist zu allen Stunden dieselbe; Sterne, Sonne und Mond kulminieren nie. Es gibt weder Nord- und Süd- noch Ost- und Westpunkte. Die Sterne der nördlichen Himmelshalbkugel sind alle Zirkumpolarsterne, die Sterne im Himmelsäquator stehen stets im, die Sterne der südlichen Himmelshalbkugel stets unter dem Horizonte. Die Sonne steht am 21. März und am 23. September den ganzen Tag im Horizonte; an allen anderen Tagen sind[22] ihre Tagbogen zum Horizonte parallel; vom 21. März bis zum 21. Juni steigt sie dabei allmählich bis zu 23½° über den Horizont und sinkt dann bis zum 23. September wieder zum Horizont herab. In diesen 6 Monaten ist also stets die Sonne über dem Horizonte, es ist Tag, in der Zeit vom 28. September bis zum 21. März ist die Sonne unter dem Horizonte, es ist 6 Monate Nacht. Den tiefsten Stand, 23½° unter dem Horizonte, erreicht die Sonne am 21. Dezember. Die kleinste Zenitdistanz ist am 21. Juni; sie beträgt 90° − 23½° = 66½°. Aus § 8 ergibt sich noch, daß im größeren Teile der Nachtmonate, und zwar zu Anfang und zu Ende dieser Zeit, Dämmerung herrscht. In 24 Stunden beschreibt der Schatten einen Kreis um den Nordpol der Erde. Ein Beobachter in diesem Punkte wäre umschattig.
Ohne weiteres leuchtet ein, daß für den Südpol der Erde die Verhältnisse sich umkehren: Tag vom 23. September bis zum 21. März usw.
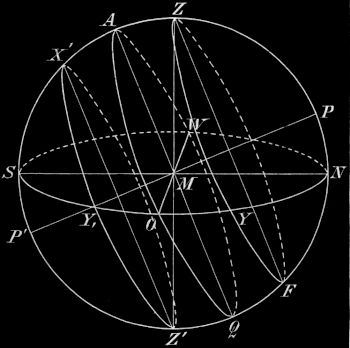
5. Unter den Wendekreisen. Mit Hilfe der Fig. 14 wollen wir uns auf einen Punkt der Erde versetzt denken, der 23½° nördlich von ihrem Äquator liegt. Für ihn liegt der Zenit Z im Wendekreise des Krebses, der obere Kulminationspunkt des Himmelsäquators 23½° südlich vom Zenit, der Nordpol des Himmels P um ebensoviel über dem Nordpunkte N des Horizontes. Die Sphäre ist schief; ihr Neigungswinkel gegen den Horizont (= Bogen SA) beträgt 90° − 23½° = 66½°. Dies ist zugleich die Mittagshöhe für den 21. März und den 23. September. Morgen- und Abendweite für den 21. Juli und 21. Dezember sind größer als am Äquator, aber kleiner als für den Horizont Berlins (vgl. Fig. 8). Die Zu- und Abnahme der Tage erfolgt zwischen denselben Terminen wie für den Horizont von Berlin; doch weicht die Dauer des längsten und des kürzesten Tages nicht so stark von der mittleren Dauer (12 Stunden) ab wie bei[23] uns. Die Sonne geht am 21. Juni um 5¼ Uhr morgens auf und um 6¾ Uhr abends unter, steht also 13½ Stunden über dem Horizonte (gegen 16½ Stunden für Berlin); am 21. Dezember geht sie um 6¾ Uhr morgens auf und um 5¼ Uhr abends unter. Die Differenz zwischen längstem und kürzestem Tage beträgt also 3 Stunden (für Berlin 9 Stunden). Einmal im Jahre, am 21. Juni, steht die Sonne mittags im Zenit. Auch am Tage des niedrigsten Sonnenstandes, am 21. Dezember (Kreis X´Y´Z´X´) ist die Mittagshöhe noch 66½° − 23½° = 43° gegen 14° für den Horizont von Berlin, die Zenitdistanz 90° − 43° = 47°; um Mitternacht steht die Sonne an diesem Tage im Nadir. Die Dämmerung ist wenig länger als unter dem Äquator, eine Zeit der hellen Nächte gibt es nicht, da die Sonne um Mitternacht 43° bis 90° unter dem Horizonte liegt. Die Zirkumpolarsterne sind nicht mehr als 23½° vom Nordpol des Himmels entfernt; unsichtbar bleiben nur die Sterne, die 23½° und weniger vom Südpol entfernt sind. Die Erdbewohner, die 23½° nördlich vom Äquator der Erde wohnen, sind einschattig und werfen am 21. Juni mittags überhaupt keinen Schatten.
Natürlich kehren sich für einen Bewohner der Erde, der 23½° südlich von ihrem Äquator wohnt, die Verhältnisse wieder um.
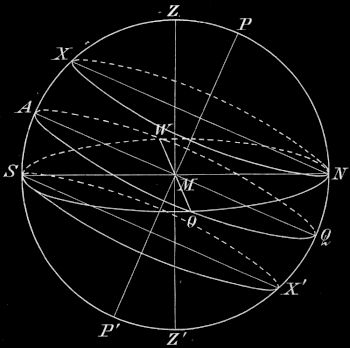
6. Unter den Polarkreisen. Gehen wir nun noch zu einem Punkte der Erde nördlich von Berlin, der 66½° nördlich vom Äquator liegt (Fig. 15). Der Zenit liegt in einem Parallelkreise der Himmelskugel 66½° nördlich vom Äquator des Himmels, den man nördlichen Polarkreis nennt; die Zenitdistanz beträgt daher 23½°, desgleichen die Schiefe der Sphäre und die Neigung des Äquators gegen den Horizont. Alle Sterne, die nicht mehr als 66½° vom Nordpol des Himmels entfernt sind, sind Zirkumpolarsterne, alle, die nicht mehr als 66½° vom Südpol entfernt sind, bleiben unsichtbar. Die Zu- und Abnahme der Tagesdauer, die Morgen- und Abendweiten sind viel bedeutender als für den Horizont von Berlin. Einmal im Jahre, am 21. Juni, geht die Sonne nicht unter, sondern streift nur in ihrem tiefsten Stande den Horizont; es ist 24 Stunden Tag; ebenso ist einmal, am 21. Dezember, 24 Stunden Nacht. Die Morgen- und Abendweite beträgt am 21. Juni 90°; an diesem Tage sind auch die Bewohner aller Punkte der Erde in 66½° Entfernung von ihrem Äquator umschattig. Da in der Zeit vom 21. März bis zum 23. September der untere Kulminationspunkt der Sonne weniger als 23½° unter dem Nordpunkte des Horizontes liegt, so ist der größere Teil dieses Halbjahres eine Zeit der hellen Nächte.
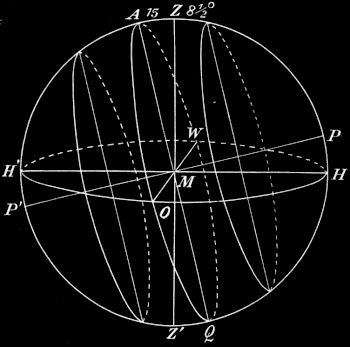
7. Zwischen Äquator und Wendekreis; zwischen Polarkreis und Pol. Ein Blick auf die Figuren 16 und 17, die die Verhältnisse darstellen für einen Punkt, der dem Äquator näher liegt als 23½° (15°), und für einen Punkt, der weiter als 66½° (80°) von ihm entfernt ist, lehrt noch folgendes:
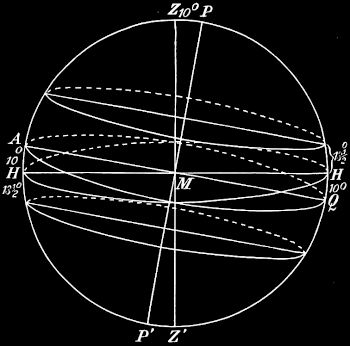
Für alle Punkte der Erde, die weniger als 23½° vom Äquator entfernt sind, steht die Sonne zweimal im Jahre mittags im Zenit, für die nördliche Halbkugel einmal zwischen 21. März und 21. Juni und einmal zwischen 21. Juni und 23. September. Die Bewohner solcher Punkte sind zweischattig. Die Mittagshöhe am Tage des niedrigsten Sonnenstandes ist größer als 43°, die Zenitdistanz kleiner als 47°. Für alle Punkte, die weiter als 66½° vom Äquator entfernt sind, geht die Sonne für die nördliche Halbkugel von einem Tage zwischen 21. März und 21. Juni an bis zu einem Tage zwischen 21. Juni und 23. September nicht mehr unter. Die Bewohner sind für diese Zeit umschattig. Von einem Tage zwischen 23. September und 21. Dezember an bis zu einem Tage zwischen 21. Dezember und 21. März geht die Sonne nicht mehr auf. Die Tage liegen dem 21. März und 23. September um so näher, je näher der Punkt dem Nordpol der Erde liegt. Für die südliche Halbkugel sind hieraus die entsprechenden Verhältnisse ohne weiteres zu folgern.
1. Nachweis der scheinbaren jährlichen Bewegung der Sonne aus der Beobachtung der Sterne. Wir wissen, daß die Sonne die scheinbare tägliche Umdrehung der Himmelskugel mit allen Gestirnen von Osten nach Westen[25] mitmacht; wir wissen auch, daß sie außerdem noch eine jährliche Bewegung zu machen scheint, weil sie täglich an einer anderen Stelle auf- und untergeht. Dieses jährliche Auf- und Absteigen zwischen den Wendekreisen läßt sich auch aus der Beobachtung der Sterne erkennen.
Beobachten wir eine uns bekannte Sterngruppe kurz nach Sonnenuntergang über der Gegend des Horizontes, wo die Sonne unterging, und setzen unsere Beobachtung mehrere Wochen fort, so bemerken wir, daß die Sterngruppe täglich tiefer nach dem westlichen Rande des Horizontes zu erscheint und sich zuletzt unseren Blicken ganz entzieht, während nach und nach immer andere Sterngruppen gleich nach Sonnenuntergang an der Stelle erscheinen, wo vorher die erste Gruppe stand. Nach Wochen oder Monaten erblicken wir dieselbe Gruppe am östlichen Himmel kurz vor Aufgang der Sonne. Hier erscheint sie jetzt bei Anbruch der Morgendämmerung täglich etwas höher über dem Horizonte. Während also die Sterngruppe früher östlich von der Sonne stand und deshalb nach ihr unterging, steht sie jetzt westlich von ihr und geht deshalb vor ihr auf. Diese Beobachtung ist unzähligemal und an verschiedenen Sternen und Sterngruppen gemacht worden. Demnach ändert die Sonne ihre Stellung zu den Sternen im Laufe des Jahres; dabei ändern die Sterne ihre Stellung zueinander nicht. Jene Änderung ist also nur dadurch erklärlich, daß die Sonne scheinbar hinter den nach Westen sich bewegenden Sternen zurückbleibt, oder anders ausgedrückt: die Sonne macht außer ihrer scheinbaren Tagesbewegung noch eine zweite scheinbare Bewegung in einer Richtung, die der Richtung ihres Tagkreises und des Tagkreises der Gestirne entgegengesetzt ist, d. h. von Westen nach Osten. Aus diesen Beobachtungen der Gestirne ergibt sich noch weiter, daß wir in den verschiedenen Jahreszeiten andere Sterne am Himmel erblicken. (Unser Sternbild verschwand auf Wochen oder Monate und kam wieder.) Auch die Zirkumpolarsterne, z. B. die Sterne des Großen Bären, nehmen in den verschiedenen Jahreszeiten eine verschiedene Lage zum Horizonte ein. Also ändert sich der Anblick des gestirnten Himmels fortwährend in den verschiedenen Jahreszeiten; aber genau nach Verlauf eines Jahres erscheinen uns dieselben Sterne an demselben Orte am Himmel. Daraus folgt, daß die Sonne zu ihrem Umlaufe am Himmel ein Jahr gebraucht.
2. Der Jahreskreis der Sonne. Welchen Weg schlägt die Sonne dabei ein? Der Umlauf erfolgt in einem Kreise, dessen Lage man dadurch bestimmt, daß man diejenigen Sterne beobachtet, welche um Mitternacht der Sonne gerade gegenüberstehen. Die Alten nannten diesen Kreis aus Gründen, die später erst nachgewiesen werden können, Ekliptik, d. h. »Mangel des Lichtes«.
3. Schiefe der Ekliptik. Welche Lage hat nun diese jährliche Bahn der Sonne am Himmel?
Es ist uns bekannt, daß die Sonne täglich ihren Auf- und Untergangspunkt und ihre Mittagshöhe ändert (für unseren Horizont!). Folglich kann ihre Bahn kein Parallelkreis sein, weil diese Kreise, ebenso wie der Äquator des Himmels, bei der täglichen Umdrehung des Himmelsgewölbes den Horizont und den Meridian immer wieder in demselben Punkte schneiden. Die Sonne wandert tatsächlich von einem Parallelkreise zum anderen; deshalb muß ihre Bahn schief gegen die Parallelkreise, also auch gegen den Äquator liegen.
Aber wie schief? Zweimal jährlich (21. März und 23. September) durchläuft die Sonne als Tagkreis den Äquator; ihre Jahresbahn muß deshalb den[26] Äquator in zwei Punkten schneiden. Am weitesten entfernt vom Äquator ist die Sonne am 21. Juni und am 21. Dezember, nämlich einmal 23½° nach Norden, das andere Mal 23½° nach Süden zu, d. h. die Jahres-Sonnenbahn schneidet den Äquator unter einem Winkel von 23½° und halbiert ihn, ist also, wie der Äquator, ein größter Kreis. Natürlich halbiert diesen auch der Äquator. Der Winkel von 23½° heißt die Schiefe der Ekliptik.
Die ganze Zone, in welcher sämtliche Tagkreise der Sonne innerhalb eines Jahres sich vollziehen, ist also 23½° + 23½° = 47° breit und liegt zwischen den Wendekreisen. Die Ekliptik wird, wie jeder Kreis, in 360 Grade geteilt. Da diese in 365 Tagen durchlaufen werden, so rückt die Sonne täglich 360/365 Grad fort (= 0,986°).
4. Einteilung der Ekliptik. Dadurch, daß die zwei größten Kreise, Äquator und Ekliptik, einander halbieren, entsteht eine nördliche und eine südliche Hälfte der Ekliptik. Die zwei Durchschnittspunkte sind 180° voneinander entfernt. Wenn die Sonne durch diese zwei Punkte hindurchgeht, so ist Tag- und Nachtgleiche; deshalb heißen die zwei Punkte die Äquinoktialpunkte und zwar Frühlings- und Herbst-Äquinoktialpunkt. Genau in der Mitte zwischen[27] denselben liegt der nördlichste und südlichste Punkt der Ekliptik; den nördlichsten erreicht die Sonne am 21. Juni, den südlichsten am 21. Dezember.
Weil die Sonne in beiden Punkten still steht d. h. aufhört zu steigen oder (im Süden!) zu fallen, so heißen sie auch Solstitialpunkte, d. h. Sonnenstillstandspunkte, und zwar der eine Sommer- und der andere Wintersolstitialpunkt. Die Sonne geht innerhalb eines Jahres, indem sie die Ekliptik durchläuft, durch zwölf verschiedene Sterngruppen (Sternbilder) hindurch. Diese liegen also in einem Gürtel zu beiden Seiten der Ekliptik, den man Tierkreis oder Zodiakus genannt hat. Die Sternbilder haben aber ungleiche Länge; darum teilten schon die Alten die Ekliptik in zwölf gleiche Teile und nannten diese Teile Zeichen, gaben ihnen aber die Namen der zwölf Sternbilder; man muß also scheiden zwischen Sternbild und Zeichen.
I. Jedes Zeichen nimmt 360/12 Grade = 30 Grade ein. Man zählt von Westen nach Osten, und zwar beginnt man mit dem Frühlingspunkte, dem Zeichen des Widders, welches also von 0° bis 30° reicht. Sie folgen so: 1. Widder, 2. Stier, 3. Zwillinge, 4. Krebs, 5. Löwe, 6. Jungfrau, 7. Wage, 8. Skorpion, 9. Schütze, 10. Steinbock, 11. Wassermann, 12. Fische. Ihre entsprechenden Zeichen sind
II.
III.
IV. In bezug auf die Lage zum Horizonte teilt man sie ein:
a) Nr. 10–12 und 1–3 = 6 aufsteigende Zeichen. (Vom Winter- bis zum Sommersolstitium.)
b) Nr. 4–9 = 6 absteigende Zeichen. (Vom Sommer- bis zum Wintersolstitium.)
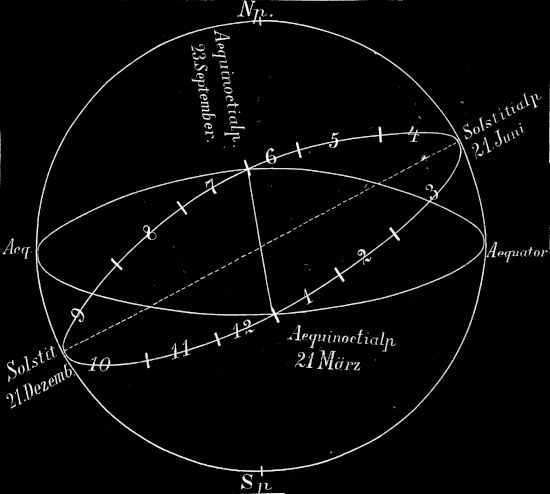
(Siehe Fig. 18.)
Weil die Sonne am 21. Juni den nördlichen Wendekreis durchläuft und zugleich in das Zeichen des Krebses tritt, heißt der nördliche Wendekreis auch Wendekreis des Krebses. Ebenso erklärt es sich, daß man den südlichen Wendekreis auch Wendekreis des Steinbocks nennt.
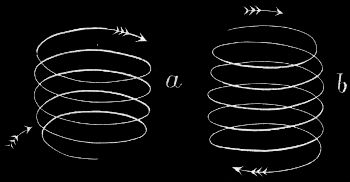
5. Genaue Form der Tagkreise der Sonne. Tägliche und jährliche Bewegung der Sonne finden gleichzeitig statt. Deshalb sind die Tagkreise keine geschlossenen Kreise; vielmehr muß die Bewegung der Sonne schraubenförmig sein, und zwar sind die Windungen beim Hinabsteigen vom nördlichen Wendekreise zum südlichen andere, als beim Heraufsteigen vom südlichen zum nördlichen Wendekreise.[28] Beim Heraufsteigen vom 21. Dezember bis zum 21. Juni ist der Weg die sogenannte linke Schraube (Fig. 19 a), beim Hinabsteigen vom 21. Juni bis 21. Dezember die sogenannte rechte Schraube (Fig. 19 b). Daraus folgt, daß unsere bisherigen Beobachtungen über die Tagkreise der Sonne nicht ganz genau sind, denn:
1. Die Tagkreise der Sonne können mit dem Äquator nicht genau parallel sein.
2. Morgen- und Abendweite desselben Tages sind nicht genau einander gleich.
Außerdem ergibt sich:
3. Die Sonne durchläuft nicht zweimal genau denselben Tagkreis.
6. Präzession der Tag- und Nachtgleichen. Auch die Äquinoktialpunkte behalten ihr Lage nicht genau. Der Frühlingspunkt schreitet vielmehr langsam nach Westen, nämlich etwa 50¼ Sekunden in einem Jahre, also 1° in ca. 72 Jahren; die ganze Ekliptik würde er in so viel Jahren durchlaufen, als 50¼´´ in 360° enthalten sind, d. i. in rund 25 800 Jahren. Diese Verschiebung der Äquinoktialpunkte nennt man die Präzession der Äquinoktien, d. h. Vorrücken der Nachtgleichen (lat.). Sie hat natürlich im Laufe der Zeiten die Zeichen wesentlich gegen die entsprechenden Tierbilder verschoben, so daß jetzt der Anfang vom Zeichen des Widders im Sternbilde der Fische steht. In diesem Sternbilde also erscheint die Sonne am 21. März. Vor mehr als 2000 Jahren, als der Alexandriner Hipparch die Sternbilder benannte, lag der Frühlingspunkt noch ca. 30° weiter östlich, d. i. wirklich im Sternbilde des Widders.
1. Rektaszension und Deklination; Stundenwinkel. Aus § 2 wissen wir, daß man mit Hilfe von Horizont und Höhenkreis den augenblicklichen Ort eines Sternes bestimmen kann.
Weil der Äquator die scheinbare tägliche Rotation der Himmelskugel um die Weltachse mitmacht, ändern die Sterne ihre Lage zu ihm nicht, und eine Bestimmung dieser Lage würde also unveränderliche Größen liefern, eine absolute Ortsbestimmung am Himmelsgewölbe sein.
Wie die Ebene eines durch Zenit und Nadir gelegten Kreises auf der Ebene des Horizontes senkrecht steht, so steht die Ebene eines durch die Pole der Weltachse gelegten Kreises auf der Ebene des Äquators senkrecht. Solche Kreise heißen Deklinations- oder Stundenkreise. Man legt nun durch den Stern, dessen Ort bestimmt werden soll, den Stundenkreis und mißt zunächst im Äquator den Bogen vom Frühlingspunkt nach Osten herum bis zum Schnittpunkt des Äquators mit dem Stundenkreise; dieser Bogen heißt die Rektaszension (lateinisch = gerade Aufsteigung) des Sternes, die demnach in umgekehrter Richtung wie der Azimut[29] gemessen wird. Dann mißt man den Bogen des Deklinationskreises vom Äquator bis zum Stern, die Deklination. Die Rektaszension geht von 0° bis 360°, die Deklination von 0° bis 90°; beide bestimmen den Ort eines Sternes am Himmelsgewölbe. Statt der Rektaszension dient auch wohl zur Ortsbestimmung der Stundenwinkel, d. i. der Bogen des Äquators vom oberen Kulminationspunkte nach Westen herum bis zum Schnittpunkte mit dem Stundenkreise. Er heißt Stundenwinkel aus folgendem Grunde: Astronomisch rechnet man den Tag von der oberen Kulmination bis wieder zur oberen Kulmination, und die Grade des Stundenwinkels können daher zum Bestimmen der Tageszeit dienen (1° = 4 Minuten).
2. Astronomische Länge und Breite. Die Astronomen benutzen für astronomische Rechnungen noch eine dritte Ortsbestimmung am Himmel. Wir denken uns auf der Ebene der Ekliptik in dem Mittelpunkte ein Lot errichtet, die Achse der Ekliptik; diese trifft die Himmelskugel in den Polen der Ekliptik. Kreise, die durch diese zwei Punkte gehen, stehen senkrecht auf der Ekliptik; sie heißen Breitenkreise. Man legt nun durch den Stern einen solchen Breitenkreis[30] und mißt zunächst den Bogen der Ekliptik vom Frühlingspunkt nach Osten (wie bei der Rektaszension) bis zum Schnittpunkte der Ekliptik mit dem Breitenkreise, die astronomische Länge des Sternes, und dann den Bogen des Breitenkreises von der Ekliptik bis zum Stern, die astronomische Breite. Beide Bogen bestimmen auch den Ort des Sternes.
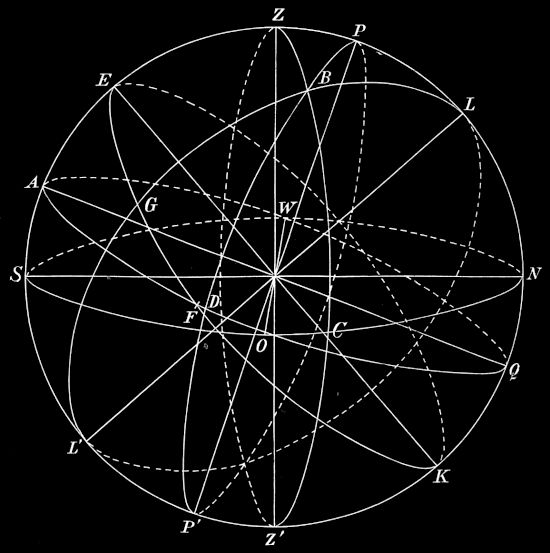
In Fig. 20 ist B der Ort eines Sternes, Kreis SOCNWS der Horizont, Kreis AFDOQWA der Äquator, EGFKE die Ekliptik, Z der Zenit, PP´ die Himmelsachse, LL´ die Achse der Ekliptik, F der Frühlingspunkt, S der Südpunkt des Horizontes; Kreis ZBCZ´Z ist der Höhenkreis, Kreis PBDP´P der Stundenkreis, LBGL´L der Breitenkreis des Sternes. Daher ist Bogen SWNC der Azimut, Bogen CB die Höhe, Bogen FD die Rektaszension, Bogen DB die Deklination, Bogen AWQOD der Stundenwinkel, Bogen FKEG die astronomische Länge, Bogen GB die astronomische Breite des Sternes B.
1. Ältere Ansichten. Homer (950 v. Chr.) hielt die Erde für eine ruhende Scheibe, umflossen vom Ozean. Thales von Milet (650 v. Chr.) hielt sie für eine auf dem Wasser schwimmende Scheibe, und dessen Schüler Anaximander glaubte, sie sei ein Zylinder, dessen kreisförmige Grundfläche bewohnt sei. Pythagoras (zwischen 580 und 500 v. Chr.) und Aristoteles (384–322 v. Chr.) hielten die Erde für eine Kugel, obgleich sie das nicht beweisen konnten.
2. Die Erde hat Kugelgestalt.
A. Beobachtungen, die das nahe legen. a) Man sagt gewöhnlich, daß der Horizont überall als Kreislinie erscheint. Das ist freilich nicht richtig; denn nur in den seltensten Fällen ist der Ausblick nach allen Seiten frei, und auch dann kann man durch bloße Beobachtung niemals feststellen, daß alle Punkte der Linie des Horizontes vom Standpunkte gleich weit entfernt sind. Aber man kann wenigstens sagen, daß bei freier Aussicht der Horizont eine kreisähnliche Linie ist.
b) Wir haben gesehen, daß überall auf der Erde bei Erhöhung des Standpunktes auch der Horizont größer wird. Dieses Wachstum müßte zwar auch vor sich gehen, wenn die Erde eine Scheibe wäre, aber viel schneller, als es in Wirklichkeit geschieht.
Daß und wie der Horizont sich bei einer scheibenförmigen und bei einer kugelförmigen Erde vergrößern muß, zeigen folgende Berechnungen.

I. Angenommen, die Erde sei eine Scheibe. In Fig. 21 sei BA = h die Höhe des Beobachters über der Erdoberfläche, C ein Punkt, der eben noch sichtbar ist, also ein Punkt des Horizontes; BC nennt man dann die Gesichtsweite.[31] Da die Gegenstände für das Auge erst verschwinden, wenn der Gesichtswinkel kleiner als 2´ ist, so ist ∢ BCA = 2´ und h/BC = sin 2´, also BC = h/(sin 2´). Offenbar wird BC um so größer, je größer h wird. Durch Berechnung ergibt sich für h = 1 m BC = 1,7 km, für h = 10 m BC = 17 km, für h = 100 m BC = 170 km usw.
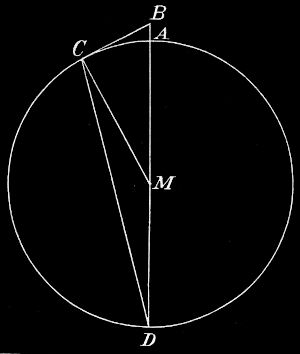
II. Angenommen, die Erde sei eine Kugel. In Fig. 22 sei BA = h die Höhe des Beobachters über der Erdoberfläche; die Tangente BC ist dann die Gesichtsweite. MA = MD = MC = R seien Halbmesser der Erdkugel, so ist in dem rechtwinkligen Dreieck BCM
| BC² | = | MB² − MC² |
| = | (R + h)² − R² | |
| = | R² + 2Rh + h² − R² | |
| = | 2Rh + h² | |
| = | (2R + h) · h. |
Also
BC = √((2R + h)h).
Da h auch für die höchsten Punkte der Erdoberfläche gegen 2R verschwindend klein ist, so kann man ohne merkbaren Fehler statt 2R + h in der Formel einfach 2R setzen und erhält
BC = √(2R · h).
Wie wir in § 14 finden werden, ist 2R etwa = 12 750 km. Daraus ergibt sich für h = 1 m BC = 3,57 km, für h = 10 m BC = 11,2 km, für h = 100 m BC = 35,7 km usw.
c) Stehen wir am Meeresufer und nähert sich uns ein Schiff, so sehen wir zuerst den Wimpel auf der Mastspitze, dann die Takelage, dann den Bord des Schiffes; es sieht aus, als führe das Schiff zu uns herauf. Fährt ein Schiff von uns fort, so ist die Erscheinung gerade die umgekehrte, und es sieht aus, als ob das Schiff hinabführe. Ebenso sehen wir zuerst die Kirchturmspitze, wenn wir uns einem Orte nähern, und sie entschwindet zuletzt unseren Blicken, wenn wir uns von dem Orte entfernen. Wäre die Erdoberfläche eine Scheibe, so müßte der Gegenstand, sobald er in den Horizont tritt, ganz erscheinen.
B. Beobachtungen, die beweisen, daß die Erde doppelt gekrümmt ist. a) Wäre die Erde eine ebene Scheibe, so müßte diese Ebene für jeden Standpunkt zugleich Horizontebene sein. Dann müßte aber auch die Ebene des unveränderlichen Himmelsäquators und ebenso die auf ihr senkrechte Himmelsachse gegen die unveränderliche Horizontebene für alle Punkte der Erde dieselbe Neigung haben. Aus § 9 wissen wir jedoch schon, daß dem nicht so ist. Vielmehr liegt bei einer vom Äquator der Erde genau nach Norden gerichteten Reise, also einer Reise[32] durch lauter Punkte, die gleichzeitig Mittag haben oder deren Zenite alle auf demselben Himmelsmeridian liegen, der Polarstern zuerst im Horizont und steigt dann immer höher, so daß also die Polhöhe fortwährend zunimmt und der Pol sich dem Zenit nähert. Der Sternhimmel wird überhaupt ein anderer. Während im Äquator der Erde im Laufe einer Nacht die Sterne beider Himmelskugeln sichtbar sind oder werden, verschwinden bei der Reise nach Norden allmählich immer mehr Sterne der südlichen Himmelshalbkugel unter dem Horizont, d. h. ihr Tagkreis erreicht den Horizont nicht mehr. Ähnlich wächst die Polhöhe des Südpols des Himmels, und die Sterne seiner nördlichen Halbkugel verschwinden unter dem Horizont bei einer Reise vom Äquator der Erde nach Süden.
b) Wäre die Erde eine Scheibe, so müßte für alle ihre Orte die Sonne gleichzeitig aufgehen. Reisen wir aber beispielsweise von Dresden nach Saratow in Rußland, d. i. ziemlich genau von Westen nach Osten, und stellen unsere Uhr genau nach der Sonne, so werden wir in Saratow finden, daß sie gegen eine dort nach der Sonne gestellte Uhr etwa 2 Stunden nachgeht. Umgekehrt ist es, wenn wir von Osten nach Westen reisen. Es folgt daraus, daß den östlichen Orten die Sonne früher aufgeht, als den westlichen, und zwar um so früher, je weiter jene nach Osten liegen. Demnach ist die Erde auch von Westen nach Osten gekrümmt.
C. Beobachtungen, die beweisen, daß die Erde nahezu Kugelgestalt hat. a) Man hat nicht nur festgestellt, daß die Polhöhe fortwährend wächst, wenn man vom Äquator nach den Polen reist. Vielmehr ist durch genaue trigonometrische Messungen an verschiedenen Stellen der Erde nachgewiesen, daß die Polhöhe jedesmal um einen nahezu gleichen Betrag zunimmt, wenn man um ein gleiches Stück vom Äquator der Erde nach Norden oder Süden reist. Daher muß die Krümmung der Erdoberfläche von Norden nach Süden nahezu gleichmäßig sein.
b) Ebenso hat man mit Hilfe der besten Uhren (Chronometer) bei Reisen von Westen nach Osten gefunden, daß jedesmal gleiche Unterschiede in der Zeit des Sonnenaufgangs sich ergeben, wenn man immer wieder ein gleiches Stück genau nach Osten reist. Die Erdoberfläche ist also nicht nur, wie wir sahen, von Norden nach Süden, sondern auch von Osten nach Westen gleichmäßig gekrümmt, d. h. die Erde ist (nahezu) eine Kugel.
1. Die Meridiane. Aus § 9 kennen wir schon die Erdachse mit den beiden Polen und den Äquator der Erde nebst ihren Beziehungen zu der Himmelsachse, den Himmelspolen und dem Himmelsäquator. Auf dem Globus (lat. = Kugel), dem Modell der Erdkugel, ist der Äquator eingezeichnet; ebenso sind die Pole gekennzeichnet. Außerdem finden wir aber noch zwei Gruppen Kreislinien darauf. Die eine besteht aus lauter größten Kreisen, die sämtlich durch die beiden Pole gehen, also auf dem Äquator senkrecht stehen; die andere Gruppe besteht aus lauter Kreisen, die parallel zum Äquator verlaufen, also von diesem aus nach Norden und Süden zu immer kleiner werden und, wie der Äquator, von den Kreisen der ersten Gruppe rechtwinklig geschnitten werden. Zur Erklärung dieser Kreise gehen wir auf die Betrachtung des Himmels zurück. Auch auf der[33] Himmelskugel dachten wir uns Kreise durch die Pole verlaufend, nämlich die Stundenkreise; natürlich schneiden die Ebenen derselben die Erdoberfläche in Kreisen der ersten Gruppe, die durch die Pole der Erde gehen. Für alle Bewohner eines solchen Kreises der Erde geht demnach ein und derselbe Stundenkreis durch ihren Zenit, d. h. er ist ihr gemeinsamer Himmelsmeridian, und ihre Mittagslinien liegen alle in der Ebene desselben. Offenbar haben also alle Punkte der einen Hälfte eines solchen Kreises vom Nordpol bis zum Südpol zu derselben Zeit Mittag und alle Punkte der anderen Hälfte 12 Stunden später. Aus diesem Grunde nennt man die Linien auf der Erde auch Meridiane oder Mittagskreise. Sie verlaufen nach den vorhergehenden Ausführungen genau von Norden nach Süden. Ihre Zahl wird durch die Gradeinteilung des Kreises bestimmt. Man teilt nämlich den Äquator der Erde in 360 Grad und legt durch den 0ten (360sten) Teilpunkt den ersten Kreis, der natürlich zugleich durch den 180sten Teilpunkt geht; der zweite geht durch den ersten und 181sten Teilpunkt. So erhält man 180 Meridiane, die die Erdoberfläche in 360 Kugelzweiecke teilen. Natürlich kann man diese Einteilung noch weiter führen, indem man auch durch die Minuten- und Sekundenteilpunkte des Äquators Meridiane legt. Stücke von solchen Meridianen finden wir auf Spezialwandkarten, d. h. Wandkarten von ziemlich kleinen Teilen der Erdoberfläche. Um die Meridiane ein für allemal festzulegen, hat man den 0ten Meridian durch einen bestimmten Punkt der Erde gelegt. Früher wählte man dazu ziemlich allgemein den Meridian, der 30´ östlich von Ferro verläuft, einer von den Kanarischen Inseln an der westafrikanischen Küste; jetzt legen die meisten Landkarten und Globen den 0ten Meridian durch Greenwich bei London (17½° östlich von Ferro), andere auch wohl durch Paris (20° östlich von Ferro). In diesem Buche wird stets unter dem 0ten Meridian der von Greenwich verstanden werden. Jede Meridianebene teilt offenbar die Erde in zwei Halbkugeln; die Halbkugel östlich vom Meridian von Ferro nennt man die östliche, die andere die westliche Halbkugel. Offenbar ist ferner die Mittagslinie eines Punktes der Erdoberfläche ein Stück seines Meridians oder genauer die durch den Punkt an seinen Meridian gelegte Tangente.
2. Die Parallelkreise. Alle Kreise der zweiten Gruppe verlaufen parallel zueinander und zum Äquator; deshalb heißen sie Parallelkreise. Da sie alle auf den Meridianen senkrecht stehen, verlaufen sie genau von Osten nach Westen. Auch ihre Zahl wird durch die Gradeinteilung des Kreises bestimmt. Man teilt irgendeinen Viertelmeridian der Erde vom Äquator bis zum Nordpol in 90 Grade und ebenso den Viertelmeridian vom Äquator bis zum Südpol. Die äußersten Teilpunkte fallen mit den Polen zusammen; durch alle übrigen legt man dann parallel zum Äquator je einen Kreis. So erhält man nördlich und südlich vom Äquator je 89 Parallelkreise, die vom Äquator aus nach Norden und nach Süden immer kleiner werden, und je einen Punkt, den Pol.
Natürlich kann auch diese Einteilung noch weitergeführt werden, indem man durch die Minuten- und Sekundenteilpunkte des Meridians Parallelkreise legt. Durch das Ausgehen vom Äquator sind auch die Parallelkreise festgelegt. Selbstverständlich teilen die Meridiane nicht nur den Äquator, sondern auch jeden Parallelkreis und umgekehrt diese jeden Meridian in 360 Grade. Die Meridiangrade sind alle gleichlang (s. aber § 14), nämlich 111 km, ebensolang ist ein Gradbogen des Äquators. Dagegen werden die Grade der Parallelkreise immer[34] kürzer, je weiter diese Kreise vom Äquator liegen. Man kann aber die Längen dieser Grade berechnen, wenn man weiß, wie viel Grad sie vom Äquator entfernt sind. In Fig. 23 sei M der Mittelpunkt der Erde, Halbkreis ABQ der halbe Äquator, Halbkreis CDE ein halber Parallelkreis, AB und CD seien je ein Gradbogen dieser beiden Kreise, der Erdradius (MA, MB, MC, MD) sei = R, der Radius des Parallelkreises (CO, DO) = r und ∢ CMA (= MCO) = φ°. Dann ist
| Bogen CD : Bogen AB | = | r : R |
| r | = | R cos φ, |
also
Bogen CD : Bogen AB = cos φ : 1
oder
| Bogen CD | = | Bogen AB · cos φ |
| = | 111 cos φ km. |
Für den Parallelkreis von Berlin ist φ = 52½°. Es ergibt sich als Länge eines Gradbogens auf diesem Kreise 67,5 km.
Auch den Parallelkreisen auf der Erdoberfläche entsprechen Kreise auf der Himmelskugel, nämlich die zum Himmelsäquator parallelen Tagkreise der Gestirne, die also Parallelkreise des Himmels sind. Aus den Betrachtungen des § 9 ergibt sich noch folgendes: Die Erdhalbmesser, die durch verschiedene Punkte eines und desselben Parallelkreises gehen, treffen verlängert auf lauter Punkte eines und desselben Parallelkreises der Himmelskugel, und dieser ist um ebensoviel Grade vom Himmelsäquator entfernt, als der Parallelkreis der Erde vom Äquator. Da der getroffene Punkt der Himmelskugel zugleich der Zenit des entsprechenden Punktes der Erde ist, so ergibt sich: Der Zenit eines jeden Punktes der Erde liegt ebensoviel Bogengrade vom Himmelsäquator entfernt, als der Punkt selbst vom Erdäquator.
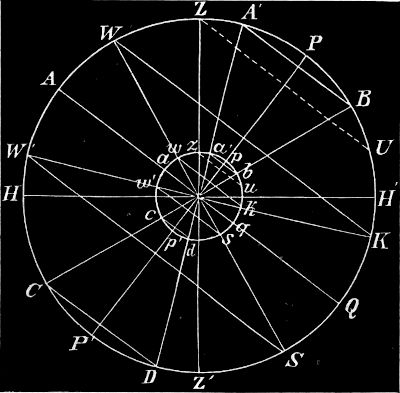
Fig. 24 bringt diese Verhältnisse zur Anschauung: Der große Kreis ist die Himmelskugel, der kleine die Erdkugel. PP´ = Himmelsachse, P = Nordpol,[35] P´ = Südpol des Himmels; pp´ = Erdachse, p = Nordpol, p´ = Südpol der Erde; AQ = Himmelsäquator, aq = Äquator der Erde; z ist unser Standpunkt, Z unser Zenit. Der große Kreis ist auch unser Himmels-, der kleine unser Erdmeridian; a´b, zu, wk, w´s, cd sind Parallelkreise der Erde, A´B, ZU, WK, W´S, CD die entsprechenden Parallelkreise des Himmels.
3. Geographische Länge und Breite. Die eben besprochene Einteilung der Erdoberfläche dient zur Ortsbestimmung auf der Erde. Man mißt vom Nullmeridian aus den Bogenabstand eines Ortes in seinem Parallelkreise, und zwar nach Osten oder Westen, je nachdem dieser Abstand nach der einen oder anderen dieser Richtungen weniger als 180° beträgt. Diesen Bogenabstand nennt man die geographische Länge des Ortes. Dann mißt man im Meridian des Ortes seinen Bogenabstand vom Äquator; dieser Abstand ist die geographische Breite des Ortes. Die Parallelkreise werden auch Grade der Breite, die Meridiane Grade der Länge genannt; das Stück der Erdoberfläche zwischen zwei benachbarten Parallelkreisen ist ein Breitengrad, das Stück zwischen zwei benachbarten Meridianen ein Längengrad.
Die geographische Länge ist eine östliche oder eine westliche (abgekürzt ö. L. und w. L.), die geographische Breite eine nördliche oder eine südliche (abgekürzt n. Br. und s. Br.). Da die Breite vom Äquator gemessen wird, so meint man, wenn man von »hohen Breiten« spricht, die Gegenden in der Nähe der Pole, die »niederen Breiten« liegen nahe dem Äquator. Offenbar ist durch genaue Angabe der Länge und Breite die Lage eines Ortes auf der Erde völlig bestimmt. Berlin hat 52½° n. Br. und 13½° ö. L. Nach diesen Angaben kann ich es leicht auf Globus oder Landkarte auffinden.
Die Namen Breite und Länge sind historisch zu erklären. Den Alten war von der Erdoberfläche ein Stück bekannt, das etwa die Gestalt eines Rechtecks hatte. Seine Ausdehnung von Westen nach Osten war bedeutend größer als von Süden nach Norden. Da man nun gewöhnlich die größere Ausdehnung Länge, die kleinere Breite nennt, so nannte der Astronom und Geograph Ptolemäus (um 140 n. Chr.) die westöstliche Ausdehnung die Länge, die südnördliche die Breite.
4. Bestimmung der geographischen Länge und Breite. I a. Zum leichten Feststellen der geographischen Breite dient folgendes. Bei der Betrachtung der Parallelkreise fanden wir, daß der Bogenabstand eines Ortes vom Äquator, d. i. seine geographische Breite, gleich dem Bogenabstand seines Zenits vom Himmelsäquator ist. Dieser ist aber wiederum das Komplement der Höhe des Himmelsäquators, wie aus Fig. 24 zu ersehen, und da auch die Polhöhe des Ortes ein Komplement dieser Höhe ist, so ergibt sich: Die geographische Breite eines Ortes ist gleich seiner Polhöhe. Diese aber kann man mit Hilfe des Sextanten oder des Theodolits unmittelbar messen.
b. Am 21. März und am 23. September durchläuft die Sonne den Äquator; daher ist an diesen Tagen ihre Mittagshöhe gleich der Äquatorhöhe. Die Mittagshöhe der Sonne finden wir aber durch Messen des Schattens, den ein vertikal stehender Stab mittags wirft. Zeichnet man nämlich ein rechtwinkliges Dreieck aufs Papier, dessen Katheten sich wie die Länge des Stabes zu seinem Schatten verhalten, so ist es dem aus dem Stab, dem Schatten und der Verbindungslinie ihrer Endpunkte gebildeten Dreieck ähnlich, also der Winkel, den die Hypotenuse mit der dem Schatten entsprechenden Kathete bildet und der ohne weiteres mit dem[36] Transporteur gemessen werden kann, gleich der Sonnenhöhe, und sein Komplement gibt die geographische Breite. An anderen als den zwei genannten Tagen stimmt freilich diese Messung nicht, sondern man muß bei uns den gemessenen Winkel in der Zeit vom 21. März bis zum 23. September um die Deklination der Sonne für den betreffenden Tag vermindern, in der übrigen Zeit vermehren. Die Deklination findet sich vielfach in Kalendern verzeichnet.
c. Ein anderes Verfahren ergibt sich aus folgender Überlegung: In Fig. 24 ist A´B der Tagkreis eines Zirkumpolarsternes. Bogen A´H´ ist seine Höhe bei der oberen, Bogen BH´ bei der unteren Kulmination, Bogen PH´ die Polhöhe für den Standort z. Nun ist Bogen PH´ = Bogen PB + BH´ = ½ Bogen A´B + Bogen BH´ = ½(Bogen A´B + 2BH´) = ½(Bogen A´B + BH´ + BH´) = ½(Bogen A´H´ + BH´), d. h. die Polhöhe, also auch die geographische Breite eines Ortes ist das arithmetische Mittel zwischen der Höhe der oberen und unteren Kulmination eines Zirkumpolarsternes. Ist z. B. die obere Kulmination eines solchen Sternes 65°, die untere 40°, so ist die geographische Breite gleich (65° + 40°)/2 = 52½°. Die Höhe der beiden Kulminationen kann aber wieder mit dem Sextanten oder dem Theodolit gemessen werden.
II. Zur Bestimmung der geographischen Länge dienen die Chronometer, besonders genau gearbeitete, von Temperaturschwankungen in ihrem Gange nicht beeinflußte Uhren. Die Schiffe führen solche Chronometer mit sich; sie sind nach der Ortszeit des Abfahrtsortes gestellt, d. h. sie zeigen 12 Uhr, wenn dort die Sonne durch den Meridian geht. Damit sie bei allen Schwankungen des Schiffes in wagerechter Lage bleiben, werden sie wie der Kompaß in einem Cardanischen Ringe aufgehängt. Wir fanden schon, daß die Sonne in 4 Minuten 1° durchläuft. Daher wird sie bei uns 4 Minuten später aufgehen und kulminieren als in einem 1° östlicher gelegenen Punkte. Zeigt demnach ein Schiffschronometer an einer Stelle der Fahrt im Augenblicke der oberen Kulmination der Sonne 2 Uhr nachmittags, so liegt der Ort soviel Längengrade westlich vom Ausfahrtsorte, als 4 Minuten in 2 Stunden = 120 Minuten enthalten sind, d. h. 30°.
5. Die Zonen der Erde. a) Begrenzung der Zonen. Wir wissen schon aus § 9, welche Bedeutung die Orte auf den Wendekreisen des Himmels und auf den Polarkreisen für die Himmelsbeobachtung haben. Ihnen entsprechen auch auf der Erde ein nördlicher und ein südlicher Wendekreis oder ein Wendekreis des Krebses und ein Wendekreis des Steinbocks (23½° n. und s. Br.) und ein nördlicher und südlicher Polarkreis (66½° n. und s. Br.). Diese vier Kreise, die auch auf dem Globus verzeichnet sind, teilen die Erdoberfläche in drei Kugelzonen (Zone griech. = Gürtel) und zwei Kugelkappen. Alle fünf Teile werden kurzweg Zonen genannt.
b) Beleuchtung und Erwärmung in den Zonen. Wir erkannten schon in § 9: Zwischen den zwei Wendekreisen fallen die Sonnenstrahlen an zwei Tagen, auf den Wendekreisen an einem Tage im Jahre mittags senkrecht auf die Erde und weichen an den anderen Tagen nie über 47° von dieser Richtung ab. Zwischen je einem Wendekreise und dem nächsten Polarkreise fallen die Strahlen stets schräg auf die Erde, und zwar um so schräger, je weiter der getroffene Ort von den Wendekreisen entfernt ist. Auf den Polarkreisen herrscht zwar einmal im Jahre volle 24 Stunden Tag, aber auch einmal ebenso lange Nacht, und[37] zwischen den Polarkreisen und den Polen herrscht sogar länger als 24 Stunden, auf den Polen sogar sechs Monate lang hintereinander Tag, aber auch ebenso lange Nacht; vor allem aber fallen von den Polarkreisen bis zu den Polen die Strahlen immer schräger auf. – Nun lehrt die Erfahrung, daß bei sonst gleichen Verhältnissen eine Fläche durch Sonnenstrahlen um so stärker erwärmt wird, je mehr die Richtung der Strahlen der senkrechten Richtung nahe kommt; daher wird die Durchschnittstemperatur der Erde in der Zone zwischen den Wendekreisen höher sein als in den zwei Zonen zwischen Wendekreis und nächstem Polarkreis und in diesen wieder höher als in der nördlichsten und südlichsten Zone. Wir wissen ferner, daß in der Zone zwischen den Wendekreisen die Zahl der Stunden, in denen die Erde überhaupt von Sonnenstrahlen getroffen wird, in der Jahreszeit des höchsten Sonnenstandes verhältnismäßig wenig (am Äquator selbst gar nicht) höher ist als in der Zeit des niedrigsten Sonnenstandes. In der Zone zwischen Wendekreis und Polarkreis wird dagegen der Unterschied immer bedeutender, je höher die geographische Breite. Jenseits der Polarkreise sind diese Unterschiede, wie sich aus dem Vorhergehenden ergibt, noch bedeutender. Daher wird die Erwärmung in der Zone um den Äquator in allen Jahreszeiten ziemlich gleichmäßig, in den übrigen Zonen im Sommer viel stärker als im Winter sein. Am stärksten ist dieser Unterschied an den Polen. Also unterscheiden sich die fünf Zonen der Erde 1. in der Höhe der Durchschnittstemperatur des Jahres, 2. in der Gleichmäßigkeit der Erwärmung in den verschiedenen Jahreszeiten.
c) Namen der Zonen. Die erste Zone nennt man deshalb die heiße Zone oder, da man die Wendekreise, zwischen denen sie liegt, auch mit dem griechischen Namen Tropen (trépo griech. = wenden) bezeichnet, die tropische Zone oder das Gebiet der Tropen: die beiden nächsten Zonen heißen nördliche und südliche gemäßigte Zone, die beiden kältesten nördliche und südliche kalte Zone oder wegen ihrer Lage um die Pole herum auch die Polargegenden. Weil endlich die nördliche kalte Zone von allen Zonen der Erde dem Sternbilde des Bären (griech. arktos) am nächsten liegt, heißt sie die arktische Zone, die südliche kalte Zone heißt die antarktische (anti griech. = gegen, entgegen). Der Flächeninhalt der beiden gemäßigten Zonen zusammen ist mehr als sechsmal, der der heißen Zone mehr als viermal so groß als der Flächeninhalt der beiden kalten Zonen zusammen[1].
[1] Über die Wirkungen der Unterschiede in der Erwärmung, die in das Gebiet der physischen Geographie gehören, vgl. Heinze, Physische Geographie, 3. Aufl., § 23.
6. Gegenfüßler, Gegenwohner, Nebenwohner. 1. Gegenfüßler (griech. Antipoden) wohnen auf entgegengesetzten Hälften eines Meridians, also einer auf der östlichen, der andere auf der westlichen Halbkugel; sie haben also entgegengesetzte Tageszeit. Sie wohnen zugleich auf entgegengesetzten Parallelkreisen, also einer auf der nördlichen, der andere auf der südlichen Halbkugel; sie haben also entgegengesetzte Jahreszeit.
In Fig. 24 wohnen in w und s Gegenfüßler, ebenso in a und q, in c und b. Wie man sieht, wohnen sie stets an den Endpunkten eines Erddurchmessers. Die Bewohner von Cordoba in Spanien haben auf der Nordinsel von Neuseeland ihre Gegenfüßler.
2. Die Gegenwohner wohnen auf demselben Halbmeridian, also beide auf der östlichen oder beide auf der westlichen Halbkugel, aber auf entgegengesetztem Parallelkreise, also die einen auf der nördlichen, die anderen auf der südlichen Halbkugel; sie haben dieselbe Tageszeit, aber entgegengesetzte Jahreszeit. In Fig. 24 wohnen in w und w´, in c und a´ Gegenwohner. Die Bewohner von Tokio in Japan und Adelaide in Südaustralien sind nahezu Gegenwohner.
3. Die Nebenwohner wohnen auf entgegengesetztem Halbmeridian, also die einen auf der östlichen, die anderen auf der westlichen Halbkugel, aber auf demselben Parallelkreise, also beide auf der nördlichen oder beide auf der südlichen Halbkugel. Sie haben entgegengesetzte Tageszeit, aber dieselbe Jahreszeit. In Fig. 24 wohnen in w und k, in z und u, in w´ und s Nebenwohner. Die Bewohner von Santo Domingo auf Haiti haben auf der Insel Hainan, südw. von Canton, ihre Nebenwohner.
1. Beweise für die Abplattung der Erde. Die Erde hat nicht genau die Gestalt einer Kugel, sondern ist an den Polen etwas abgeplattet. Das folgt aus verschiedenen Beobachtungen:
a) Der französische Astronom Richer reiste 1672 von Paris (49° n. Br.) nach Cayenne (5° n. Br.), um dort Beobachtungen des Planeten Mars auszuführen. Er hatte eine genau regulierte Pendeluhr mit einem Sekundenpendel bei sich, d. h. mit einem Pendel, das in Paris in einer Sekunde eine Schwingung machte, also im Tage 24 × 60 × 60 = 86 400 Schwingungen. In Cayenne bemerkte er, daß das Pendel seiner Uhr täglich 148 Schwingungen weniger machte als in Paris, daß also die Uhr 148 Sekunden nachging. Erst als er das Pendel um etwa 22/3 mm kürzer machte, ging die Uhr wieder richtig. Nach Paris zurückgekehrt, fand Richer, daß seine Uhr täglich 148 Sekunden vorging; er brachte das Pendel auf die frühere Länge, und die Uhr ging wieder richtig. Dieselbe Erfahrung ist hernach bei Reisen von Norden nach Süden und umgekehrt vielfach gemacht worden, stets schwang das Pendel bei einer Reise nach den Polen zu schneller, nach dem Äquator zu langsamer. Die bewegende Kraft des Pendels ist nun die Schwerkraft, und sie wirkt erfahrungsmäßig um so stärker, je näher der angezogene Körper dem Mittelpunkt der Erde ist. Mit Recht folgerten daher Newton (1643–1727) und Huygens (1629–1695), daß die Punkte der Erdoberfläche in den höheren Breiten dem Mittelpunkte der Erde näher sind, als die Punkte um den Äquator; folglich ist die Erde an den Polen abgeplattet (s. aber § 16, Anm.).
b) Die Abplattung ist durch Gradmessungen direkt erwiesen. Wäre die Erde eine Kugel, so müßten nicht nur alle Grade des Äquators und alle Grade eines und desselben Parallelkreises untereinander gleich sein, was in der Tat der Fall ist, sondern auch alle Grade desselben Meridians, gleichgültig, in welcher geographischen Breite sie gemessen wären. Anders aber muß es sein, wenn die Erde an den Polen abgeplattet ist. Ein Kreis ist um so stärker gekrümmt, je kleiner der Radius ist; ein Gradbogen mit größerem Radius erscheint also flacher, als ein Gradbogen mit kleinerem Radius. Ist also wirklich die Erde nach den Polen[39] zu abgeplattet, d. h. erscheint sie dorthin weniger gekrümmt, als am Äquator, so kann man den Meridian ansehen als zusammengesetzt aus lauter Gradbogen, deren Radien vom Äquator nach den Polen zu beständig wachsen. Die Länge eines Gradbogens auf einer Kreislinie hängt nun ab von der Länge des Halbmessers; denn da die Peripherie oder ein Bogen von 360° = 2π · r ist, so ist ein Bogen von 1° = π/180 · r. Der Bogen ist also um so länger, je länger der Radius ist. Daraus ergibt sich sofort: Ist die Erde an den Polen abgeplattet, so muß die Länge eines Meridiangrades vom Äquator nach den Polen zu wachsen. Das ist in der Tat der Fall. In der Mitte des 18. Jahrhunderts haben französische Gelehrte in Peru, Frankreich und Lappland Gradmessungen angestellt und fanden die Länge eines Meridiangrades in Peru 110,608 km, in Frankreich 111,212 km, in Lappland 111,949 km. Damit war die Abplattung direkt bewiesen[2].
[2] Über das Verfahren bei solcher schwierigen und mühevollen Messung s. Heinze, a. a. O. § 2 Anm.
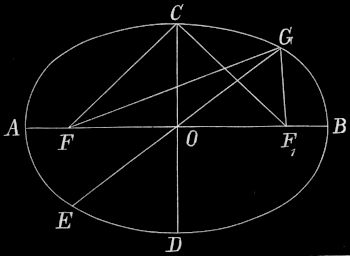
2. Die wahre Gestalt der Erde. Während also alle Breitengrade Kreise sind, sind die Meridiane keine Kreise; sie sind vielmehr Ellipsen. Eine Ellipse ist eine geschlossene, krumme Linie, innerhalb deren, ebenso wie innerhalb eines Kreises sich ein Punkt befindet, der alle geraden Linien halbiert, die man durch ihn von einem Punkte der krummen Linie zum andern zieht. Wie beim Kreise nennt man jenen Punkt Mittelpunkt, die geraden Linien Durchmesser. Diese sind aber nicht untereinander gleich, wie im Kreise; es gibt einen größten und einen kleinsten Durchmesser; dieselben stehen senkrecht aufeinander und heißen große und kleine Achse der Ellipse. In der großen Achse liegen zwei besondere Punkte in gleicher Entfernung vom Mittelpunkte; zieht man von diesen beiden nach irgend einem Punkte der Ellipse die beiden Verbindungslinien, so ist ihre Summe für alle Punkte dieselbe, nämlich gleich der großen Achse. Diese beiden Punkte in der Hauptachse heißen Brennpunkte. Ihr Abstand vom Mittelpunkt heißt Exzentrizität, ihr kürzester Abstand von der Peripherie der Ellipse heißt Brennweite. Fig. 25 ist eine Ellipse, O ist ihr Mittelpunkt, AB, EG, CD sind Durchmesser, AB ist die große, CD die kleine Achse, F und F1 sind die Brennpunkte, FC + CF1 = FG + GF1 = AB, FO ist die Exzentrizität, FA die Brennweite. Die Meridiane sind natürlich alle kongruente Ellipsen, die große Achse ist ein Äquatordurchmesser, die kleine die Erdachse. Denkt man sich eine halbe Ellipse, etwa CAD in Fig. 25 um ihre kleine Achse gedreht bis zur ursprünglichen Lage, so beschreibt die halbe Ellipsenlinie eine solche Fläche, wie es die Oberfläche der Erde ist. Jeder Punkt der Ellipse, z. B. A, E, beschreibt dabei einen Kreis, entsprechend einem Parallelkreis der Erde, der Endpunkt der halben großen Achse (A) den größten, entsprechend dem Äquator. Alle Schnitte längs der Drehachse schneiden[40] die Fläche in Ellipsen, die alle gleiche Achsen haben mit der Ellipse, deren Hälfte durch ihre Drehung die Fläche beschrieb. Ihnen entsprechen die Meridiane der Erde. Einen Körper, den eine solche Fläche begrenzt, nennt man Umdrehungs- oder Rotationsellipsoid, auch Sphäroid (griech. = kugelähnlich). Die Erde ist also ein Sphäroid, die Meridiane sind Ellipsen mit geringer Exzentrizität und großer Brennweite, d. h. nahezu Kreise. Genau ist freilich auch das noch nicht. Die Arbeiten der seit 1861 tätigen europäischen Gradmessung führten zu folgendem Ergebnis: Die Erdoberfläche ist allseitig gekrümmt und setzt sich aus Flächen von wechselnder Krümmung zusammen, die allmählich ineinander übergehen. Man nennt diese Fläche ein Geoid (griech. = erdähnlich).
3. Die Größe der Erde und ihrer Abplattung. Ein Grad des Äquators ist 111,305 km lang; daraus ergibt sich der Umfang des Äquators (= 360°) = 360 · 111,305 = rund 40 070 km. Da der Umfang eines Kreises = 2rπ, so ist 2r = Umfang/π, der Durchmesser des Äquators also = 40 070/π = 12 754,8 km, der Halbmesser = 6377,4 km. Sieht man die Erde als Kugel an, so ergibt sich daraus als Inhalt ihrer Oberfläche = 4r²π = 2rπ · 2r = Äquatorumfang × Äquatordurchmesser = 40 070 · 12 754,8 = 511 077 778 qkm, als Körperinhalt der Erde ca. 1086 Milliarden cbkm. Aber diese Ergebnisse sind zu groß, da die Erde abgeplattet ist. Mit Hilfe der höheren Mathematik sind aus den verschiedenen Längen der Meridiangrade in verschiedenen geographischen Breiten auch der Umfang eines Meridians = 40 003 km und die Länge seiner kleinsten Achse, d. i. die Länge der Erdachse (Polardurchmesser) = 12 712,3 km berechnet. Der größte und der kleinste Halbmesser der Erde sind also:
| Äquatorialhalbmesser | = | 6377,4 km, |
| Polarhalbmesser | = | 6356,1 km; |
| ihr Unterschied | = | 21,3 km. |
Man bezeichnet als die Abplattung eines Sphäroids den Bruch (a − b)/a, wo a und b die große und die kleine Achse bedeuten. Offenbar ist sie um so kleiner, je kleiner a − b ist, also je weniger die große und kleine Achse voneinander verschieden sind. Für die Erde beträgt die Abplattung nur 21,3/6377,4 = 1/299, ist also sehr gering. Die höhere Mathematik lehrt auch die Berechnung der Oberfläche und des Körperinhaltes eines Sphäroids aus seinen beiden Achsen; sie betragen für die Erde
| Oberfläche der Erde | = | 509 950 714 qkm, |
| Körperinhalt der Erde | = | 1083 Milliarden cbkm, |
also nicht unerheblich weniger, als wenn man die Erde als Kugel und als deren Durchmesser den Äquatorialdurchmesser ansieht.
Der höchste Berg der Erde ist 8840 m hoch; der größte Durchmesser der Erde ist also rund 1440mal so groß. Auf einem Globus, dessen Durchmesser fast ¾ m lang wäre, würde daher der höchste Berg in entsprechender Größe nur ½ mm groß sein. Die Berge ändern also an der Kugelgestalt der Erde so wenig, wie die kleinen Unebenheiten einer Eierschale an der Gestalt des Eies. Auch die Abplattung ändert daran wenig; schon in einer Entfernung von wenigen Erddurchmessern wird daher die Erde durchaus als Kugel erscheinen.
1. Möglichkeit der Rotation. a) Sitzt man in einem Eisenbahnzuge und richtet den Blick aufs Fenster, so scheint es, als ob der Zug stillstände und die überblickten Felder und Telegraphenstangen vorbeiflögen. Diese scheinbare Bewegung geschieht in einer Richtung, die der Richtung der wirklichen Bewegung des Zuges entgegengesetzt ist. Ähnliche Beobachtungen kann man noch in großer Zahl machen. So glaubt man sich selber zu drehen, wenn man unter der sich langsam herumdrehenden Kuppel einer Sternwarte steht. Immer erfolgt bei solchen Beobachtungen die scheinbare Bewegung in einer Richtung, die der Richtung der wirklichen Bewegung entgegengesetzt ist. Unsere Beobachtung kann uns also täuschen. Wir beobachten nun, daß scheinbar die ganze Himmelskugel mit der Sonne und all ihren Sternen sich täglich von Osten nach Westen um die Erde herumschwingt. Das könnte wirklich so sein; es kann aber auch nach dem, was wir eben fanden, seinen Grund darin haben, daß sich die Erde täglich um eine Achse dreht; diese Achse müßte natürlich mit der Achse der scheinbaren Drehung des Himmelsgewölbes zusammenfallen, d. h. es müßte die Erdachse sein. Auch müßte die Bewegung der scheinbaren Bewegung entgegengesetzt, also von Westen nach Osten erfolgen. Weil man früher wegen Mangels guter Instrumente über die Entfernung der einzelnen Sterne von der Erde ganz im unklaren war, so nahm man ohne weiteres an, daß die Bewegung der Himmelskugel eine wirkliche sei; man setzte also alle Fixsterne in gleicher Entfernung von der Erde an die Fläche eines kristallenen Gewölbes und ließ sie mit diesem durch eine unbekannte Kraft um die Erde herumgeführt werden. Nach Entdeckung des Fernrohres im Anfang des 17. Jahrhunderts erkannte man bald, daß die Entfernungen der Sterne von der Erde sehr verschieden seien und daß sie daher mit sehr verschiedenen Geschwindigkeiten sie umkreisen müßten. Dann aber wäre es doch kaum zu begreifen, daß trotzdem alle genau in derselben Zeit diese Umkreisung ausführen sollten.
b) Wenn die Sonne und die Sterne um die Erde herumliefen, so müßte die Geschwindigkeit der meisten umlaufenden Sterne ganz ungeheuer sein. Die Sonne ist, wie man aus gewissen Fernrohrbeobachtungen berechnet hat, rund 150 000 000 km von der Erde entfernt; sie müßte also, wenn sie den Äquator durchläuft (21. März, 23. September), in 24 Stunden einen Weg von 2π · 150 000 000 km, demnach in 1 Sekunde 11 000 km durchlaufen. Der Fixstern Sirius ist 1 000 000mal so weit von uns entfernt als die Sonne, und da die Umfänge der Kreise sich wie die Radien verhalten, so müßte der Sirius bei der Umkreisung der Erde in 24 Stunden und demnach auch in einer Sekunde eine Bahn beschreiben, die 1 000 000mal so groß wäre als die entsprechende Bahn der Sonne, d. h. seine Geschwindigkeit betrüge rund 11 000 000 000 km in der Sekunde, also eine Strecke, gegen welche die riesige Geschwindigkeit des Lichtes (300 000 km in der Sekunde) ganz verschwindet! Das ist gar nicht denkbar.
c) Wo eine Wirkung ist, da muß auch eine Ursache sein, und zwar muß die Ursache der Wirkung entsprechen. Woher sollte nun die ungeheure bewegende Kraft kommen? Sie müßte doch von der Erde als dem Mittelpunkte des ganzen Weltsystems kommen. Aber wie klein ist die Erde im Vergleich zu den Massen, auf die sie so gewaltige Wirkungen ausüben müßte! Ist ja doch die Sonne an Masse 324 000mal so groß wie die Erde!
Aus solchen Betrachtungen ergab sich die Möglichkeit, ja die Wahrscheinlichkeit, daß sich nicht die Sterne um die Erde bewegen, sondern daß die Erde sich um ihre Achse drehe. Danach müßte man sagen: Die Erde bewegt sich um ihre Achse, sie »rotiert« von Westen nach Osten. Die scheinbare Rotation des ganzen Fixsternhimmels von Osten nach Westen ist also eine natürliche Folge der Rotation der Erdkugel von Westen nach Osten. Sie bewirkt, daß uns am östlichen Himmel beständig neue Sterne auf- und gesehene Sterne am westlichen Himmel untergehen. Die Atmosphäre nimmt an der Rotation teil.
Der Einwand, daß wir von der Rotation nichts spüren, ist nicht stichhaltig. Wenn wir in einem Kahne oder auf einem Dampfer sitzen und von diesem Fahrzeuge sanft, ohne Schwanken und Schaukeln bewegt werden, so haben wir, sobald wir die Augen schließen, das Gefühl, als ständen wir still, selbst wenn die Bewegung ziemlich schnell vor sich geht. Die Erdbewegung ist noch viel gleichmäßiger, daher äußerst sanft, und deshalb spüren wir nichts davon.
2. Dauer der Rotation. Wenn die Erde wirklich rotiert, so geschieht das natürlich in derselben Zeit, in welcher der Himmel mit all seinen Gestirnen sich einmal um die Erde herumzuschwingen scheint: in 23 Stunden 56 Minuten und 4 Sekunden. In dieser Zeit durchläuft jeder Punkt der Erdoberfläche, ausgenommen die Pole, einen ganzen Kreis = 360°. Die Achsendrehung der Erde ist eine vollkommen gleichmäßige Bewegung; denn die scheinbare Bewegung der Sterne erfolgt ja, wie wir wissen, auch ganz gleichmäßig, in 4 Minuten wird immer ein Grad des Tagkreises durchlaufen. Natürlich ist für die verschiedenen Punkte der Erdoberfläche die Rotationsgeschwindigkeit sehr verschieden. Am größten ist sie am Äquator; hier durchläuft ein Punkt in einem Tage den Umfang des Äquators = 40 070 km, also in einer Sekunde 1/86 164 Tag 40 070/86 164 km = 465,04 m. (So rasch fliegt etwa eine Büchsenkugel.) Aus unseren Berechnungen in § 13, 2 ergibt sich, daß der Parallelkreis in der geographischen Breite φ gleich ist dem Produkt aus der Länge des Äquators und dem cos φ, also = 40 070 · cos φ km. Hier durchläuft also ein Punkt in einer Sekunde 40 070/86 164 · cos φ km. Hiernach rotiert Berlin bei einer Breite von 52½° immer noch mit einer Geschwindigkeit von 283 m in der Sekunde.
Der augenfälligste Beweis für die Rotation stammt von dem französischen Physiker Foucault.
I. a) Er geht davon aus, daß ein schwingendes Pendel stets in derselben Vertikalebene schwingt. Das ergibt sich schon aus dem Beharrungsgesetze, kann aber auch tatsächlich durch einen Versuch nachgewiesen werden, der etwa folgendermaßen anzuordnen wäre. Auf einem horizontalen Brette ruht eine Scheibe, von deren Mittelpunkte eine Achse in das Brett führt, so daß die Scheibe um diesen Mittelpunkt drehbar ist. Auf der Scheibe ist in den Endpunkten eines Durchmessers ein vertikaler Bügel befestigt; dieser wird also an einer Drehung der Scheibe teilnehmen mit Ausnahme des Punktes in ihm, der von einer auf der[43] Scheibe im Mittelpunkte errichteten Senkrechten, der Drehachse der ganzen Vorrichtung getroffen wird. Von diesem Punkte hängt ein Pendel nach dem Mittelpunkte der Scheibe zu herab. Auf dem Grundbrette steht neben der Scheibe senkrecht aufwärts ein Stift. Hebt man das Pendel nach diesem Stifte hin und läßt es los, so schwingt es über den Mittelpunkt der Scheibe hinaus und zurück in einer durch den Stift, den Scheibenmittelpunkt und den Aufhängepunkt bezeichneten Vertikalebene. In dieser schwingt es nun unverändert weiter, wenn man auch die Scheibe samt dem Bügel um ihre Achse im Kreise herumdreht. Dabei wird es natürlich nach und nach über allen Scheibendurchmessern schwingen. Verschiebt man die ganze Vorrichtung samt dem Grundbrette nur seitlich, so wird die Schwingungsebene ihre Richtung nicht ändern, also nur parallel zu ihrer früheren Lage liegen.
b) Denken wir uns nun den Versuch noch etwas anders eingerichtet. Die Scheibe sei der Fußboden eines geschlossenen Raumes (Zimmers), der Aufhängepunkt liege in der Zimmerdecke, der Bügel ist dann überflüssig. Das ganze Zimmer sei in derselben Weise drehbar wie das Gestell, und diese Bewegung erfolge sanft, ohne alle Erschütterungen und Schwankungen; dann wird natürlich jemand, der im Zimmer ist, von der Drehung, an der er teilnimmt, nichts merken, sondern den Eindruck gewinnen, daß sich die Schwingungsebene des Pendels in dem scheinbar ruhenden Raume fortwährend herumdreht, und zwar in einer der wirklichen Drehung des Zimmers entgegengesetzten Richtung.
II. Rotiert nun die Erde wirklich in rund 24 Stunden um ihre Achse, so würden für eine solche Pendelvorrichtung, die genau über dem Nordpol stände, genau dieselben Bedingungen vorliegen, wie in dem beschriebenen Versuche. Das Pendel würde über den Pol hin zunächst über einem bestimmten Meridian schwingen; aber schon nach 4 Minuten würden die Punkte des Meridians sich um 1° gedreht haben, und das Pendel schwänge jetzt über dem nächsten Meridian hin. Schwänge es lange genug, so würden sich alle 360 Halbmeridiane unter ihm herumdrehen; ein Beobachter aber, der ja, ohne es zu bemerken, diese Bewegung mitmachte, würde, wie jener Beobachter des Versuches im Zimmer, den Eindruck haben, daß die Schwingungsebene des Pendels um die Erdachse in einer der wirklichen Rotation der Erde entgegengesetzten Richtung rotierte und erst nach 24 Stunden wieder ihre alte Lage einnähme.
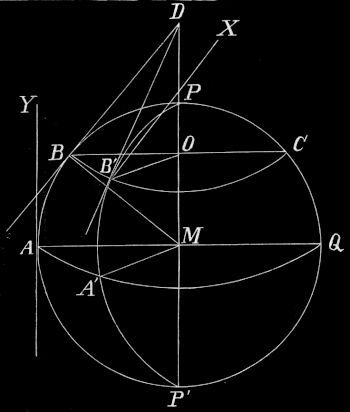
III. Daß auch an anderen Stellen der Erdoberfläche eine scheinbare Drehung der Schwingungsebene zu bemerken sein müßte, zeigt Fig. 26, in der PP´ die Achse,[44] Bogen AA´Q den halben Äquator der Erde, Bogen BB´C den halben Parallelkreis, Kreis PBAP´QCP den Meridian des Ortes B bedeutet. Das Pendel schwinge zunächst über dem Meridian von B oder, was dasselbe, über der Nordsüdlinie. Da diese Linie einerseits der Horizontalebene angehört, d. h. der Ebene, die die Erdkugel in B berührt, anderseits der Meridianebene, so kann sie mit dem Meridian nur Punkt B gemein haben, mit anderen Worten: sie ist die Tangente des Meridians im Punkte B, also die gerade Linie BD. Diese steht auf dem Kreishalbmesser BM senkrecht und muß deshalb die Achse, mit der sie in derselben Ebene (Meridianebene) liegt, schneiden. Dreht sich nun die Erde um ihre Achse, so wird Punkt B in seinem Parallelkreise fortschreiten und nach einiger Zeit in B´ angelangt sein; der Halbmeridian von B ist dann PB´A´P´, die Nordsüdlinie B´D. Die Schwingungsebene des Pendels aber muß noch immer parallel zu ihrer ersten Lage sein; das Pendel wird also über einer Linie B´X schwingen, die zu BD parallel ist und demnach von der Nordsüdlinie um einen Winkel XB´D abweicht, der als Wechselwinkel gleich B´DB ist. Würde dieser Versuch im geschlossenen Raume ausgeführt, so müßte sich demnach für die Zuschauer die Schwingungsebene scheinbar von Osten über Süden nach Westen drehen.
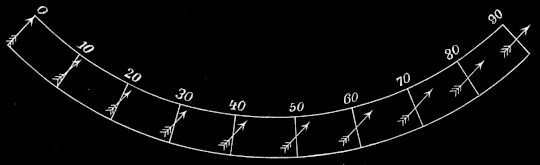
Auch die Fig. 27 veranschaulicht sehr deutlich die allmähliche scheinbare Drehung der Schwingungsebene. Die beiden konzentrischen Kreisbogen seien Stücke zweier voneinander nur um den Bruchteil einer Sekunde entfernten Parallelkreise der Erde, die zwischen ihnen gezogenen zehn geraden Linien 0, 10, 20 usw. sehr kurze und darum als geradlinig anzusehende Stücke von Meridianen oder, mit anderen Worten, die Nordsüdlinien der entsprechenden Punkte der Erde. Die untereinander parallelen Pfeile geben die unveränderliche Richtung der Schwingung des Pendels an. Schwingt also das Pendel bei der Linie 0 noch über der Nordsüdlinie, so weicht es mehr und mehr davon ab, wenn es durch die Rotation der Erde nach und nach in die Gegend der Linien 10, 20, 30, 40 … 90 kommt.
IV. Diese scheinbare Drehung der Schwingungsebene hat nun eben Foucault 1851 durch direkten Versuch im Pantheon zu Paris vorgeführt und damit die Rotation der Erde unwiderleglich bewiesen. Er brauchte dazu natürlich ein Pendel, das möglichst lange schwang, d. h. ein langes verhältnismäßig schweres Fadenpendel. Als solches diente ihm eine 62 m lange und kaum 1 mm dicke Klaviersaite, die von der Kuppel herabhing und am unteren Ende eine 24 kg schwere Bleikugel trug; diese ging in eine lange Spitze aus. Unter dem ruhenden Pendel war der Mittelpunkt einer Gradeinteilung, und 4 m von diesem an den Enden[45] eines Durchmessers der Gradeinteilung lag auf zwei Tischen je eine Sandschicht. Das Pendel schwang zunächst über einem bestimmten Durchmesser von Norden nach Süden und zog dabei eine Furche durch den Sand. Sehr bald aber zog es eine andere Furche, es schwang mehr von Nordost nach Südwest über einem anderen Durchmesser; seine Schwingungsebene war wirklich scheinbar von Osten über Süden nach Westen herumgegangen.
V. Nur für die Punkte des Äquators zeigt das Pendel die Bewegung der Erde nicht an. Hier steht ja die Nordsüdlinie, die in Fig. 26 für die Stellung des Punktes A gezeichnet ist (AY), stets auf der Ebene des Äquators senkrecht. Da nun auch die Erdachse senkrecht auf der Ebene des Äquators steht, so sind die Nordsüdlinien aller Punkte des Äquators zur Erdachse parallel, oder: die Nordsüdlinie eines Äquatorpunktes bewegt sich bei der Drehung der Erde stets parallel zu ihrer vorherigen Lage weiter, sie ändert ihre Richtung nicht. Da nun aber auch die Schwingungsebene des Pendels sich nur parallel zu ihrer vorherigen Lage verschiebt, so wird das Pendel, das über der Nordsüdlinie schwingt, stets darüber bleiben und nicht in seiner Schwingungsrichtung davon abweichen.
VI. Der Winkel, um den sich die Schwingungsebene des Pendels in einer Stunde scheinbar drehen muß, läßt sich unter der Voraussetzung berechnen, daß die Erde in 24 Stunden rotiert. Das Ergebnis dieser Berechnung stimmt für die zahlreichen Orte, an denen man die Abweichung beobachtet hat, mit den Ergebnissen der Beobachtung so vorzüglich überein, daß die Drehung der Erde in 24 Stunden damit zweifellos erwiesen ist. Die Berechnung gestaltet sich folgendermaßen: Der Winkel, um den sich das Pendel in einer Stunde scheinbar drehen muß, ist in Fig. 26 der Winkel DB´X unter der Voraussetzung, daß B in einer Stunde nach B´ gelangt, er ist als Wechselwinkel an Parallelen gleich ∢ B´DB. Dieser, dessen Gradzahl wir x nennen wollen, kann aber als Zentriwinkel eines um D mit dem Halbmesser DB geschlagenen Kreises gelten; sein Bogen BB´ ist dann gleich
(π · BD)/180 · x; [Bogen von 1° = (π · Radius)/180].
Derselbe Bogen ist aber auch ein Teil des Parallelkreises von O; sein Zentriwinkel BOB´ ist der Winkel, um den sich Punkt B in einer Stunde gedreht hat. Für eine Drehung von 24 Stunden beträgt dieser für alle Punkte der Erde 360°, also für eine Stunde 15°. Somit ist der Bogen BB´ auch = (π · BO)/180 · 15°. Wir haben damit die Gleichung:
(π · BD)/180 · x = (π · BO)/180 · 15°,
woraus folgt:
x = 15° · BO/BD.
Nun ist
BO/BD = sin BDO,
∢ BDO = 1R − BMD, und da auch die geographische Breite von B, d. i. der Winkel BMA, den wir φ nennen wollen, 1R − BMD, so ist
∢ BDO = φ,
also
BO/BD = sin φ
und
x = 15° · sin φ.
Hat die scheinbare Drehung weniger oder mehr als eine Stunde gewährt, so hat natürlich ∢ BOB´ einen anderen Wert, den wir allgemein α nennen wollen. Dann ist x = α · sin φ.
Für Berlin ist φ = 52°30´; also dreht sich hier die Schwingungsebene des Pendels in einer Stunde scheinbar um 15° · sin 52°30´, d. i. 11,9° oder 11°54´, in einem Tage (α = 360°) um 360° · sin 52°30´ = 285°36´. Einen völligen Kreis oder eine Drehung von 360° wird sie also scheinbar in 360/11,9, d. i. rund in 30 Stunden beschreiben, während sie, wie gezeigt, am Pol nur 24 Stunden dazu gebraucht. Näher am Äquator ist der Drehungswinkel für eine Stunde noch kleiner, also die Zeit einer ganzen Drehung noch länger. Auf dem Wendekreise z. B. dreht sich die Schwingungsebene des Pendels in einer Stunde scheinbar um 15° · sin 23°30´, d. i. rund 6°, beschreibt also in ca. 360/6 = 60 Stunden einen vollen Kreis.
Die Formel x = 15° · sin φ paßt auch für Pol und Äquator. Für jenen ist φ = 90°, also sin φ = 1, und daher x = 15°, woraus sich weiter als Dauer einer ganzen scheinbaren Umdrehung der Schwingungsebene am Pol 360/15 = 24 Stunden ergibt. Für den Äquator ist φ = 0, also sin φ = 0 und auch x = 0, d. h. hier findet keine scheinbare Drehung der Schwingungsebene des Pendels statt.
Anmerkung. Durch die Rotation der Erde erklärt sich folgende Beobachtung. Richer entdeckte, wie wir schon wissen, daß die Schwingungszeit des Pendels mit Annäherung an den Äquator sich verlangsamte. Genaue Rechnungen haben nun ergeben, daß die durch zahlreiche Gradmessungen gefundene Größe der Abplattung der Erde allein eine etwas geringere Vergrößerung der Schwingungszeit des Pendels verursachen müßte, als sie durch die Beobachtung festgestellt ist. Es muß also noch eine Ursache mitwirken. Dies ist die Schwungkraft (Zentrifugalkraft); sie wird, da die Erde um ihre Achse rotiert, gar nicht auf die beiden Pole, sonst aber auf alle Punkte der Oberfläche wirken, am stärksten auf die Punkte des größten, auf der Rotationsachse senkrechten Kugelkreises, des Äquators, da die Schwungkraft, wie aus der Physik bekannt, wie der Radius der Bahn wächst. Ebenso muß natürlich die Schwungkraft auf ein mit der Erde rotierendes Pendel wirken, d. i. das Pendel wird am Äquator ein starkes Streben haben, sich von der Erde zu entfernen, wodurch ebenfalls, wie durch die stärkere Wölbung der Erde am Äquator, die Schwerkraft in ihrer Wirkung beeinträchtigt werden muß. Weiter nach den Polen zu wird die Schwungkraft weniger, an den Polen selbst gar nicht wirken. Berechnet man nun die Verlangsamung, die die Pendelschwingungen am Äquator erfahren müssen, weil Rotation und Abplattung der Erde gleichzeitig die Ursache sind, so ergeben sich dieselben Größen, wie sie die Erfahrung geliefert hat.
Auch die Behauptung, daß die Rotation von Westen nach Osten geschieht, ist schon bewiesen; denn
1. weil die scheinbare Bewegung des Himmels von Osten nach Westen geht, so muß die wirkliche Rotation der Erde von Westen nach Osten gehen;
2. weil beim Pendelversuch Foucaults die scheinbare Drehung der Schwingungsebene von Osten nach Westen stattfand, muß die wirkliche Rotation der Erde von Westen nach Osten gehen.
3. Beweis durch Fallversuche. Als die Rotation der Erde noch nicht so allgemein als bewiesen anerkannt war wie heute, sagten Gegner, wenn die Erde wirklich von Westen nach Osten rotiere, so könne ein aus der Höhe fallender Körper nicht in dem Punkte den Boden erreichen, der senkrecht unter dem Abgangspunkte des Körpers liege, sondern er müsse, weil ja die Erde während seines Falles unter ihm von Westen nach Osten sich fortbewegt habe, westlich von jenem Punkte zu Boden fallen; es falle aber tatsächlich jeder Körper lotrecht zur Erde; folglich rotiere die Erde nicht.
In diesem Einwande stecken zwei Fehler, einer in der Schlußfolgerung, die ein Naturgesetz nicht beachtet, ein zweiter in der Beobachtung, daß wirklich jeder Körper genau lotrecht falle.
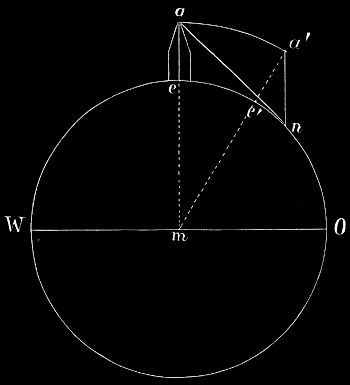
Den ersten Fehler hat Newton nachgewiesen, und zwar so: Es ist bewiesen, daß jeder Körper dem Gesetze der Beharrung unterworfen ist. Nach diesem Gesetze ändert ein bewegter Körper seine Geschwindigkeit und seine Richtung nicht, wenn nicht eine bisher nicht wirksame Kraft auf ihn einwirkt und seine Richtung und Geschwindigkeit ändert. In Fig. 28 ist der Kreis die Erde, ea ist ein Turm; von seiner Spitze a soll ein Körper herabfallen; e ist der Punkt, welcher lotrecht unter a liegt. Rotiert die Erde wirklich und beschreibt e den Bogen ee´ nach Osten in der Zeit, in welcher der Körper zur Erde fällt, so beschreibt a den Bogen aa´ in derselben Zeit. Die Spitze a hat also eine größere Geschwindigkeit als der Fußpunkt e. Diese Geschwindigkeit teilt der Körper vor seinem Fallen von a aus und muß sie nach dem Beharrungsgesetz beibehalten; daher muß er, wenn die Erde wirklich rotiert, in einem Punkte zur Erde fallen, der so weit von e entfernt ist, als a´ von a, d. h. er muß Punkt n treffen, so daß etwa die Linie an seinen Weg zur Erde bezeichnet; er muß also um das Stück e´n nach Osten fallen und nicht westlich von e´, wie die Gegner der Rotation behaupteten.
Aber auch ihre Behauptung, daß der Körper lotrecht nach e´ falle, muß falsch sein, wenn die Erde rotiert. Das ist sie auch, wie zum ersten Male in den Jahren 1801 bis 1803 Benzenberg durch Versuche in dem Turme der Michaeliskirche in Hamburg bei einer Fallhöhe von 76,3 m gezeigt hat. Später hat man öfter von hohen Türmen herab oder in tiefe Bergwerksschächte hinein Körper fallen[48] lassen und dabei eine östliche Abweichung des Ankunftspunktes von dem lotrecht unter dem Abgangspunkte gelegenen Punkte gefunden, die sich bei 160 m Tiefe auf 2,6 cm belief. Natürlich werden so kleine Abweichungen nur bei besonders sorgfältiger Beobachtung wahrgenommen.
4. Beweis durch die Richtung der Passatwinde. Der Erdboden und die darüber befindliche Luftschicht wird am Äquator viel stärker erwärmt als an den Polen. Daher dehnt sich hier die Luft stark aus und steigt nach oben über die obere Grenze der Atmosphäre; der Luftdruck wird geringer. In den oberen Schichten strömt dann die Luft als Äquatorialstrom nach den Polen zu, wo sie sich weniger hoch erhebt, ab. Auf dem Wege nach den Polen kühlt sich die Luft mehr und mehr ab, sinkt allmählich zu Boden und strömt nun von den Polen, wo der Druck der Luft wegen ihrer größeren Dichtigkeit höher ist, als Polarstrom zum Äquator. Allerdings hat sich der Äquatorialstrom schon in einer Breite von ca. 30° so abgekühlt, daß ein guter Teil seiner Luft schon hier niedersinkt und zum Äquator zurückströmt, während der Rest des Stromes in den höheren Breiten sich mit dem Polarstrome stark mischt, so daß hier wechselnde Luftströmungen, also auch wechselnde Winde herrschen. Zwischen dem 30. Grad n. Br. und dem 30. Grad s. Br. aber wehen ganz regelmäßig in den unteren Luftschichten Winde von den Polen nach dem Äquator zu, in den oberen Schichten in umgekehrter Richtung.
Hätte nun die Erde keine Achsendrehung, so würde in den niederen Breiten die von den Polen kommende Luft in der Richtung der Meridiane zum Äquator, die vom Äquator kommende darüber in der entgegengesetzten Richtung zum Pole strömen; es würde also auf der nördlichen Halbkugel in den höheren Luftschichten Südwind, in den tieferen Nordwind, auf der südlichen Halbkugel in den höheren Luftschichten Nordwind, in den tieferen Südwind wehen. Dem widerspricht die Erfahrung. Die Schiffahrt hat längst bezeugt, daß in niederen Breiten in den unteren Luftschichten auf der nördlichen Halbkugel beständig Nordostwind, auf der südlichen Südostwind weht; man nennt diese Winde den Nordost- und den Südostpassat. Ebenso ist durch Beobachtung der Federwolken, die in großer Höhe ziehen, das Wehen des Südwestwindes in den oberen Luftschichten der nördlichen Halbkugel und das Wehen des Nordwestwindes in den oberen Luftschichten der südlichen Halbkugel nachgewiesen. Man nennt diese Winde Gegenpassate oder Antipassate. Eine andere bekannte Erscheinung, die das Wehen des Gegenpassates beweist, kann man bei dem Vulkan Cotopaxi in Südamerika, nahe am Äquator, beobachten. Sein Rauch steigt anfangs nach Nordwesten, aber in einer Höhe von 6500 m wendet er sich plötzlich in die entgegengesetzte Richtung. Diese Erscheinung der Passate ist nur durch die Rotation der Erde von Westen nach Osten zu erklären. Infolge der Rotation müssen nämlich, wie schon mehrfach ausgesprochen wurde, die Punkte am Äquator die größte, die weiter nach den Polen zu gelegenen Punkte geringere Rotationsgeschwindigkeit haben. Die Luft teilt im ganzen die Geschwindigkeit der Punkte, über denen sie sich befindet, d. h. die Luftteile der Polarluftströme bringen eine geringere Geschwindigkeit mit, als sie die Punkte der Erde haben, über die sie nach dem Äquator hinstreichen, und sie suchen ihre Geschwindigkeit auch nach dem Beharrungsgesetze beizubehalten. Deshalb muß die dem Äquator zuströmende Luft, wenn die schon nachgewiesene Rotation der Erde wirklich von Westen nach Osten erfolgt, westlich gegen die Orte unter niederen Breiten zurückbleiben; die Erdkugel[49] muß unter dem Luftstrome weg nach Osten vorauseilen, d. h. für die niederen Breiten scheint der Polarstrom nicht nach Süden, sondern mehr nach Südwesten zu wehen, also von Nordosten zu kommen. Ebenso muß auf der südlichen Halbkugel ein Südostwind wehen. Der Äquatorialstrom dagegen muß wegen seiner größeren Geschwindigkeit den Orten unter höheren Breiten, über die er hinstreicht, nach Osten vorauskommen, also auf der nördlichen Halbkugel aus Südwesten, auf der südlichen aus Nordwesten wehen. Diese theoretischen Erwägungen liefern uns somit ein Ergebnis, das mit der Beobachtung völlig übereinstimmt. Also rotiert die Erde tatsächlich von Westen nach Osten.
1. Möglichkeit der Revolution. Den täglichen Umschwung der Sonne usw. haben wir durch die Rotation der Erde erklärt gefunden. Aber damit ist noch nicht erklärt die zweite scheinbare Bewegung der Sonne, die jährliche, mit der es zusammenhängt, daß sie nicht wie alle Fixsterne in 23 Stunden 56 Minuten, sondern erst in 24 Stunden eine scheinbare Rotation ausführt. Daß die Sonne in der Ekliptik täglich ziemlich einen Grad (s. § 10) von Westen nach Osten fortschreitet (scheinbar!), würde sich erklären lassen, wenn die Sonne wirklich in Jahresfrist in der Ekliptik um die ruhende, nur rotierende Erde sich bewegte; es würde sich aber auch erklären lassen, wenn sich die Sache umgekehrt verhielte und die Erde um die ruhende Sonne herum in einem Jahre ebenfalls von Westen nach Osten kreiste. Wäre der Kreis in Fig. 18, der die Ekliptik darstellt, die Jahresbahn der Erde, so stände die Sonne im Mittelpunkte. Uns aber würde sie von dem jedesmaligen Standpunkte der Erde aus in der Verlängerung des von der Erde zur Sonne gezogenen Halbmessers am Himmelsgewölbe zu stehen scheinen, wo für uns ja alle Gestirne scheinbar stehen. Stände z. B. die Erde im Sommerwendepunkte, träte sie also eben ins Zeichen des Krebses, so schiene uns die Sonne im Winterwendepunkte zu stehen und eben ins Zeichen des Steinbocks zu treten. Ginge die Erde zum Zeichen des Löwen weiter, so schiene uns die Sonne nach Osten bis zum Zeichen des Wassermannes fortzurücken usf. Während also die Erde im Tierkreise von Westen über Süden nach Osten wirklich herumginge, würde die Sonne die Ekliptik in derselben Richtung scheinbar durchlaufen. Daß dies die richtige Erklärung der Beobachtung ist, wird wahrscheinlich durch das Massenverhältnis zwischen Erde und Sonne. Sie sind 150 000 000 km voneinander entfernt, und die Sonne ist an Masse 324 000mal so groß als die Erde. Nun muß jede Bewegung eine Kraft als Ursache haben, und die Kraft hängt natürlich von der Masse ab; folglich muß wohl die Erde von der Sonne und nicht umgekehrt die Sonne von der Erde bewegt werden.
Diese Bewegung der Erde, Revolution genannt, ist aber auch durch Beobachtungen, Überlegungen und Berechnungen wirklich nachgewiesen.
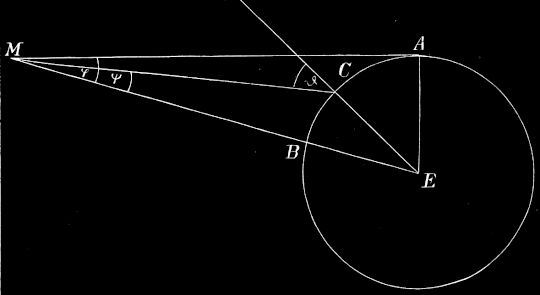
2. Beweise für die Revolution. a) Die Jahresparallaxe der Fixsterne. 1. Ist in Fig. 29 Punkt E der Mittelpunkt, der Kreis ein Meridian der Erde, M der Mittelpunkt des Mondes, so wird zu derselben Zeit für die Punkte A und B der Mond an ganz verschiedenen Stellen des Himmelsgewölbes zu stehen scheinen, für A im Horizonte, für B im Zenit; MA ist Tangente am[50] Meridian, MB geht verlängert durch den Mittelpunkt der Erde, ist eine Zentrallinie. Den Winkel, den die Zentrallinie mit einer Tangente vom Mittelpunkte des Mondes an die Erde bildet, in der Figur ∢ EMA = φ, nennt man die Horizontalparallaxe des Mondes (Parallaxe, griech. = Abweichung). 2. Der Winkel, den die Zentrale mit einer von M nach einem beliebigen anderen Punkte C des Meridians gelegten Linie bildet, hier ∢ CME = ψ, heißt die Höhenparallaxe des Mondes, da von C aus der Mond nicht im Horizont, sondern in einer gewissen Höhe sichtbar ist. 3. Die Horizontalparallaxe φ läßt sich folgendermaßen feststellen: ∢ AEB (Bogen AB) ist offenbar die Differenz oder die Summe der geographischen Breiten der Orte A und B, je nachdem sie beide auf derselben oder auf verschiedenen Seiten des Äquators liegen, und er ist die geographische Breite des einen der beiden Orte selbst, wenn der andere auf dem Äquator liegt, also findet sich φ als Komplement dieses Winkels. 4. Dem Winkel BEA entspricht für C der Winkel CEB. Da ∢ θ als Außenwinkel des Dreiecks MEC = ∢ CEB + ψ ist, so ist die Höhenparallaxe ψ = θ − ∢ CEB, d. i. die Zenitdistanz des Mondes (oder der Sonne) für den Punkt C vermindert um die Differenz oder die Summe der geographischen Breiten von B und C. 5. Da man den Halbmesser der Erde kennt, so ist klar, daß man mit Hilfe der Horizontal- oder mit Hilfe der Höhenparallaxe die Entfernungen des Mondes und der Sonne von der Erde, in der Figur ME, bestimmen kann. Ist r der Halbmesser der Erde, so ist ja
r/ME = sin φ,
also
ME = r/(sin φ)
und
r/ME = (sin ψ)/(sin (2R − θ)) = (sin ψ)/(sin θ) (Sinussatz),
also
ME = (r sin θ)/(sin ψ).
6. Die Höhen- und Horizontalparallaxe eines Gestirnes wird nun aber offenbar um so kleiner, je weiter es von der Erde entfernt ist; für sehr entfernte Gestirne[51] wird es schließlich erscheinen, als wären MA und ME parallel, d. h. für diese Gestirne ist die Parallaxe nicht mehr meßbar, nicht mehr von 0° zu unterscheiden. Das trifft für alle Fixsterne zu. Als aber im 16. Jahrhundert die Ansicht hervortrat, daß die Erde um die Sonne kreise, da lag der Gedanke nahe, daß es dann doch eine Jahresparallaxe der Fixsterne geben müsse. Beschreibt nämlich die Erde in einem Jahre einen Kreis mit dem gewaltigen Halbmesser von 150 000 000 km (Abstand der Sonne von der Erde), so müßten doch die Fixsterne in derselben Richtung am Himmel in einem Jahre auch für uns Kreise, allerdings sehr kleine Kreise, zu beschreiben und daher ihre Stelle am Himmelsgewölbe zu verändern scheinen. Wäre z. B. in Fig. 30 ELE´E die Erdbahn, also O die Sonne, so müßte der Stern S im Laufe des Jahres am Himmel den Kreis FL´F´F zu beschreiben scheinen, und ∢ ESE´ wäre dann als Jahresparallaxe zu bezeichnen. In der Tat wurde seit Galilei nach solchen Jahresparallaxen gesucht, und als sie trotz der genauesten Beobachtungen für keinen Fixstern entdeckt wurden, als keiner einen noch so kleinen Kreis am Himmelsgewölbe zu beschreiben schien, da benutzten das anfangs die Anhänger der alten Meinung als Beweis gegen die Revolution der Erde. Freilich wurde die Zahl derselben immer kleiner; man wurde sich immer klarer darüber, daß dieses scheinbare Fehlen der Jahresparallaxe nur die ungeheuren Entfernungen der Fixsterne beweise, gegen die selbst die Sonnenweite, d. i. der Halbmesser der Erdbahn, verschwindet; aber erst mit den vorzüglichen Meßinstrumenten des 19. Jahrhunderts gelang es, und zwar zum ersten Male im Jahre 1832, für die der Erde nächsten Fixsterne parallaktische Bewegungen nachzuweisen und die Parallaxen zu messen. Selbst die größte bisher gefundene Parallaxe macht allerdings wenig über ¾ Bogensekunden aus; aber daß sie nachgewiesen ist, ist ein sicherer Beweis für die Bewegung der Erde um die Sonne.

b) Die Aberration des Lichtes. Schon 1727 entdeckte der Engländer Bradley die sogenannte Aberration (lat. = Abirrung) des Lichtes. Er beschäftigte sich damals auch mit dem Suchen nach Fixsternparallaxen und beobachtete deshalb seit 1725 denselben Zirkumpolarstern. Dabei richtete er sein Fernrohr so auf den Stern, daß ein Strahl desselben durch die Achse des Rohres in sein Auge gelangte. Als er aber am folgenden Tage um dieselbe Zeit die Beobachtung fortsetzen wollte, war der Strahl von der Richtung des vorhergehenden Tages etwas abgelenkt; das in horizontaler Richtung um eine Achse drehbare Fernrohr mußte, damit der Strahl wieder ins Auge gelangte, etwas gegen die Lichtstrahlen in der Richtung gedreht werden, in der sich die Erde bewegt. Der Fixstern hatte also scheinbar eine kleine Bewegung gemacht. Ähnlich geschah es bei den folgenden Beobachtungen, die lange fortgesetzt wurden. Nach einem Jahre aber hatte das Fernrohr seine erste Lage wieder, der Stern erschien an seiner ersten Stelle. Er hatte scheinbar eine sehr kleine und sehr flache Ellipse beschrieben, die mit der[52] Ekliptik parallel war. Daraus und aus der Wiederkehr der Erscheinung genau im Laufe eines Jahres schloß Bradley mit Recht, daß sie mit der Bewegung der Erde zusammenhing. Aber das erkannte er auch sogleich, daß es sich um keine parallaktische Bewegung handelte. Denn einerseits erschien dafür die große Achse der Ellipse etwas groß, 40,9´´, und das wäre ja die Parallaxe gewesen; anderseits hätte der Fixstern gerade dann am Ende der großen Achse der Ellipse erscheinen müssen, wenn er am Ende der kleinen stand. Späteren Beobachtern fiel es auch auf, daß die große Achse der Ellipse auch für andere Sterne stets dieselbe Länge hatte, wie verschieden auch die kleine war. Bradley selbst hat die richtige Erklärung seiner Beobachtung gegeben. Ein Lichtstrahl braucht eine Sekunde, um 300 000 km zu machen. Es vergeht also auch ein sehr kleiner Zeitteil, während der Strahl durch das Fernrohr streicht. Bewegt sich die Erde wirklich, so bewegt sich mit ihr in jener sehr kurzen Zeit auch das Fernrohr etwas in der Richtung ihrer Bahn. Wird also das Fernrohr genau auf den Standort des Sternes gerichtet, so kann der Strahl nicht in der Richtung der Achse einfallen, sondern muß durch die gleichzeitige Bewegung des Rohres etwas abgelenkt werden; man muß das Rohr vielmehr in der Richtung der Erdbewegung etwas, allerdings sehr wenig, verschieben. Das tut man also bei jeder derartigen Beobachtung, wenn auch unbewußt. Wenn sich nun die Erde gar nicht oder in gerader Linie weiter bewegte, so würde bei Bradleys Beobachtung das Fernrohr stets die Richtung des ersten Tages behalten haben; denn dann würden wegen der außerordentlichen Kleinheit der Jahresparallaxe alle Linien, die man sich von der Erde an den verschiedenen Tagen zum Fixsterne gezogen denken kann, parallel erscheinen, also auch alle Strahlen, die an den verschiedenen Tagen in das Rohr fallen würden. Nun war ja aber täglich, wie wir sahen, jene kleine Drehung des Fernrohrs nötig. Diese Drehung ist überhaupt nur dadurch zu erklären, daß die Erde sich bewegt und zwar in einer krummlinigen Bahn. Somit ist die Bewegung der Erde bewiesen. Die Verschiebungen eines Jahres zeigten außerdem, daß die Bahn der Erde kreisähnlich, genauer elliptisch ist und in einem Jahre zurückgelegt wird.
3. Schnelligkeit der Bewegung. Da die Erde um ihre Achse rotiert, liegt der Gedanke nahe, daß die Revolution vielleicht durch ein bloßes Abrollen der Erde in ihrer Bahn erfolge, wie etwa eine Kugel sich auf der Kegelbahn bewegt. Offenbar müßte dann nach einer Rotation die Erde in ihrer Bahn um eine Strecke fortgerückt sein, die gleich ihrem Umfang ist, d. h. die in der Bahn zurückgelegte Strecke müßte genau so lang sein wie der Weg, den ein Punkt des Äquators bei der Rotation macht. Nun ist die elliptische Erdbahn fast ein Kreis; dieser beträgt, da der Durchmesser 300 000 000 km lang ist, 300π Millionen oder rund 942 000 000 km. Ein Schnellzug, der in 1 Sekunde etwa 25 m macht, würde rund 1200 Jahre brauchen, um diese Bahn zu durchlaufen! Die Erde durchläuft sie in einem Jahre, bewegt sich also in 1 Sekunde
942 000 000/(365 × 24 × 60 × 60) = 30 km
fort; ein Punkt des Äquators macht bei der Rotation in 1 Sekunde nur 463,7 m, d. h. die Erde bewegt sich 64mal so schnell in ihrer Bahn, als sie rotiert. Die Bewegung ist also nicht ein bloßes Abrollen, sondern gleichzeitig ein Fortrücken.
4. Stellung der Sonne in der Ebene der Erdbahn. Die Mittelpunkte von Erde und Sonne liegen natürlich in der Ebene der elliptischen Erdbahn, aber die Sonne steht nicht im Mittelpunkte der Ellipse, sondern in dem einen Brennpunkte, weil die Erde nicht bloß von der Sonne, sondern auch von anderen Himmelskörpern angezogen wird. Die Folge davon ist, daß die Entfernung der Erde von der Sonne im Laufe des Jahres sich beständig ändert.
Der der Sonne am nächsten stehende Punkt der Erdbahn heißt die Sonnennähe oder das Pĕrihēl; der entfernteste Punkt heißt die Sonnenferne oder das Aphel (spr. Afhēl). (Perihel und Aphel griech. von pĕri und apŏ́ = um und weg und Hḗlios = Sonne.) Beide zusammen heißen die Apsiden, die sie verbindende gerade Linie heißt die Apsidenlinie.
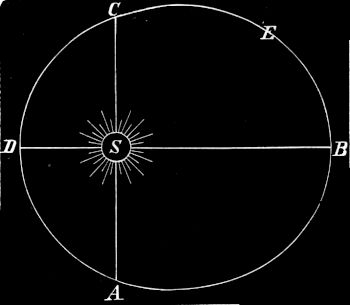
In Fig. 31 bedeutet Ellipse E die Erdbahn, S die Sonne, D ist das Perihel, B das Aphel, DB die Apsidenlinie; doch ist der Unterschied zwischen Perihel und Aphel verhältnismäßig klein und lange nicht so bedeutend, wie es der größeren Deutlichkeit wegen Fig. 31 darstellt. Die Exzentrizität der Erdbahn ist nämlich gering, etwa 1/60 der halben großen Achse, was ja allerdings auch noch 150/60 = 2½ Millionen km ausmacht. Der Unterschied zwischen Perihel und Aphel beträgt demnach 5 000 000 km. Die Erde steht im Winter ihrer nördlichen Halbkugel im Perihel, im Sommer im Aphel.
Die Ekliptik ist nicht die Erdbahn selbst, sondern der größte Kreis, in dem ihre Ebene die Himmelskugel schneidet, also gleichsam die Projektion der Erdbahn auf die Himmelskugel.
1. Unveränderlichkeit ihrer Richtung. Die Erdachse macht natürlich die Revolution um die Sonne mit; aber sie ändert bei dieser Bewegung ihre Lage im Weltraume, ihre Richtung nicht; denn die Ebene des Erdäquators ist ein Teil der Ebene des Himmelsäquators; dieser hat immer dieselbe Neigung gegen die Ebene der Ekliptik; daher muß auch der Erdäquator stets dieselbe Neigung gegen die Ebene der Ekliptik haben; dann aber hat auch die Erdachse, die auf der Äquatorebene senkrecht steht, eine unveränderliche Neigung gegen die Ebene der Ekliptik, d. h. sie bewegt sich parallel zu sich selbst um die Sonne. Damit ist es auch wohl vereinbar, daß sie sich scheinbar gar nicht bewegt, da ja die Himmelspole, in denen ihre Verlängerung die Himmelskugel trifft, stets dieselben zu sein scheinen. In Wirklichkeit ist das nicht so, sondern die Erdachse zeigt zu verschiedenen Zeiten des Jahres nach verschiedenen Punkten des Himmels; doch können diese höchstens um[54] den Durchmesser der Erdbahn, 300 000 000 km voneinander entfernt sein. Wir wissen nun, wie klein die Jahresparallaxe der nächsten Fixsterne ist. Erscheinen aber zwei von den Enden eines Durchmessers der Erdbahn nach einem Sterne gezogene Linien so gut wie parallel, so erscheinen für uns auch umgekehrt zwei Punkte des Himmelsgewölbes als einer, wenn sie 300 000 000 km voneinander entfernt sind.
Also: Indem die Erde sich um die Sonne bewegt, behält ihre Achse stets dieselbe Lage im Weltraume bei; sie bleibt stets nach derselben Himmelsgegend gesichtet, d. h. sie bleibt sich stets parallel.
Allerdings ist hier eine kleine Einschränkung nötig. Die Lage der Erdachse und somit auch die Lage des Erdäquators zur Erdbahn ändert sich doch beim Laufe der Erde um die Sonne um einen äußerst kleinen Betrag, der allerdings erst nach längeren Zeiträumen bemerkbar wird. Deshalb ändert sich auch die Lage der Himmelspole am Himmelsgewölbe und die des Himmelsäquators zur Ekliptik. Vor 1000 Jahren war der Nordpol des Himmels weiter vom Polarstern entfernt, als heute; im Laufe der Jahrhunderte wird er sich ihm noch mehr nähern, sich aber dann im Laufe von Jahrtausenden von ihm um mehrere Grade entfernen. Ja, in 25 800 Jahren beschreibt der Nordpol des Himmels, also auch der der Erde einen vollständigen kleinen Kreis; daher werden wir in 12 000 Jahren einen ganz anderen Polarstern haben; die Erdachse wird dann nämlich nach einer Stelle in der Nähe der Wega zeigen, eines der hellsten Sterne der nördlichen Himmelshalbkugel. Die damit zusammenhängende Änderung der Lage des Himmelsäquators gegen die Ekliptik bewirkt, daß auch die Durchschnittspunkte beider Kreise, d. h. die Äquinoktialpunkte eine andere Lage in der Ekliptik erhalten; und zwar schreiten dieselben in der Richtung von Osten nach Westen fort, also gegen die Ordnung der Zeichen. Mit einem Worte, wir haben hier die Erklärung für die Präzession der Äquinoktien, die sich ja auch in 25 800 Jahren vollzieht.
Sehen wir von dieser geringen Verschiebung der Richtung der Erdachse ab, so bleibt noch eine Frage zu beantworten.
2. Welche Neigung hat die Erdachse gegen die Ebene der Erdbahn? Die Ekliptik bildet mit dem Äquator des Himmels einen Winkel von 23½°; die Himmelsachse steht auf dem Äquator senkrecht; also beträgt der Winkel zwischen Himmelsachse und Ekliptik und demnach auch der Neigungswinkel der Erdachse gegen die Erdbahn 90° − 23½° = 66½°. (Vgl. Fig. 18. Der Bogen von Np bis zum Solstitialpunkt des 21. Juni gibt den gesuchten Winkel.)
1. Die Tageszeiten. Der Wechsel der Tageszeiten und ihr für verschiedene Punkte der Erde verschiedener Eintritt beruht auf der Rotation der Erde.
a) Die Erde ist ein von Natur dunkler Körper, der sein Licht von der Sonne empfängt. Daher wird nur die der Sonne zugewandte Erdhälfte beleuchtet, sie hat Tag; die von der Sonne abgewandte Erdhälfte liegt in dem hinter der undurchsichtigen Erdkugel entstehenden Schatten, empfängt kein Licht von der Sonne, sie hat Nacht. Die äußersten Lichtstrahlen, die die Erde noch treffen, berühren sie in einem größten Kreise; er heißt Beleuchtungsgrenze; in ihm stoßen Licht[55] und Schatten zusammen. Hätte die Erde keine Atmosphäre, so müßte hier auch eine ganz scharfe Lichtgrenze sein, wie beim Monde, der keine Atmosphäre hat. Wir wissen aber schon, daß die Atmosphäre durch die Brechung auch solchen Punkten der Erde noch Sonnenstrahlen zuführt, die jenseits der Beleuchtungsgrenze liegen, d. h. die direkt keine Sonnenstrahlen mehr empfangen. Wir kennen ja bereits die Dämmerungszone. Wirkliche Nacht ist daher nur auf 100/289 der Erdoberfläche.
Ständen Erde und Sonne still, so hätte die eine Hälfte der Erde beständig Tag, die andere Nacht; so aber geht infolge der Rotation der Erde die Sonne für jeden Punkt der Erde auf und wieder unter, es ist Wechsel zwischen Tag und Nacht.
b) Tritt irgendein Meridian der Erde eben in die Beleuchtungsgrenze, so muß der um einen Längengrad östlicher gelegene Meridian bei der Rotation von Westen nach Osten diese Grenze schon 4 Minuten früher erreicht haben. An jedem um 1° östlicher gelegenen Orte der Erdoberfläche geht die Sonne 4 Minuten früher auf; er hat auch 4 Minuten früher Mittag, ist überhaupt in seiner Zeitrechnung 4 Minuten voraus. (S. § 13.) Reist man also von seinem Wohnorte einen Grad nach Osten, so hat man dort 4 Minuten früher Sonnenaufgang als zu Hause, bei einer Reise, die sich auf 2 Grade erstreckt, 8 Minuten. Notierte man bei einer Reise um die Erde, also durch 360 Grade, in östlicher Richtung bei jedem Sonnenaufgang ein neues Datum, so wäre man bei der Heimkehr mit seinem Kalender um 360 × 4 = 1440 Minuten = 24 Stunden, d. i. um einen vollen Tag vor dem Orte der Abfahrt voraus. Umgekehrt bringt eine Reise von Osten nach Westen um die Erde um einen Tag zurück. Als eins der Schiffe Magellans nach seiner von Spanien aus nach Westen ausgeführten Weltumseglung nach 3 Jahren zurückkehrte, schrieb man auf dem Schiffe den 6. September 1522, in Spanien den 7. September. Wäre die Reise nach Osten erfolgt, so hätte man auf dem Schiffe den 8. September geschrieben. Nach Osten zu verfrüht man gleichsam den Sonnenaufgang, nach Westen zu verspätet man ihn. Daher verschiedenes Datum in ostwestlich weit voneinander entfernten Orten.
2. Die ungleiche Dauer der Tageszeiten und der Wechsel der Jahreszeiten. Die ungleiche Dauer, die Tag und Nacht in verschiedenen Breiten und zu verschiedenen Jahreszeiten haben, und der Wechsel der Jahreszeiten beruhen auf der Revolution der Erde und der Neigung der Erdachse gegen die Erdbahn.
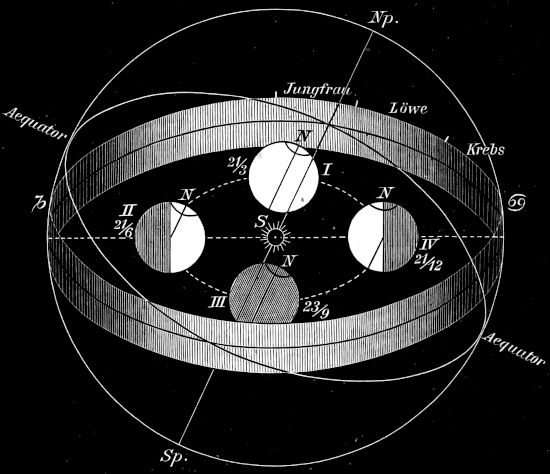
Fig. 32 läßt den Wechsel der Jahreszeiten erkennen.
S = Sonne; die punktierte Ellipse = Erdbahn; der schattierte Gürtel, etwa 20° breit, = Tierkreis; der schwarze Kreis in seiner Mitte, der den Himmelsäquator halbiert, = Ekliptik: Np = Nordpol, Sp = Südpol. – I = Erdstellung am 21. März, II am 21. Juni, III am 23. September, IV am 21. Dezember. Ersichtlich ist auch der Parallelismus in den Stellungen der Erdachse.
Nord- und Südpol sind gleich weit von der Sonne entfernt; nördliche und südliche Halbkugel sind halb beleuchtet, halb dunkel, also sind Tag und Nacht auf der ganzen Erde gleich lang. Für die Pole steht die Sonne 24 Stunden im Horizont; der Äquator wird mittags senkrecht von der Sonne beschienen;[56] südlich und nördlich vom Äquator fallen die Sonnenstrahlen schief auf die Erde. Auf dem Wege bis zur Stellung II wendet sich die nördliche Erdhalbkugel immer mehr der Sonne zu, die südliche Erdhalbkugel wendet sich immer mehr von der Sonne ab; daher geht die Sonne scheinbar nach Norden, und es werden für die nördliche Halbkugel 1. die Tage immer länger, die Nächte immer kürzer, 2. die Winkel, unter denen die Sonnenstrahlen auffallen, und die Mittagshöhen immer größer, die Zenitdistanzen immer kleiner. Daher wird für diese Halbkugel die Erwärmung immer stärker, sie hat Frühling. Für die südliche Halbkugel werden 1. die Tage kürzer, die Nächte länger, 2. die Winkel, unter denen die Sonnenstrahlen auffallen, spitzer, die Zenitdistanzen größer. Ihre Erwärmung nimmt also ab, sie hat Herbst. Die Sonne geht scheinbar (bis zum 21. Juni) durch die Zeichen: Widder, Stier, Zwillinge; also geht die Erde wirklich durch die Zeichen: Wage, Skorpion, Schütze.
Die nördliche Halbkugel ist so weit als möglich der Sonne zugewandt, die südliche so weit als möglich von ihr abgewandt. Auf dem Äquator sind, wie an allen Tagen, Tag und Nacht gleich, auf allen anderen Punkten der Erde ungleich.[57] Alle Örter der nördlichen Halbkugel haben den längsten Tag und die kürzeste Nacht; umgekehrt ist es auf der südlichen Halbkugel. Der Unterschied zwischen Tag und Nacht für einen Ort ist um so größer, je weiter er vom Äquator entfernt ist. Der nördliche Wendekreis wird mittags senkrecht beschienen, seine Bewohner sind am Mittag unschattig; in allen Örtern nördlich davon hat die Sonne die größte Mittagshöhe, die sie dort erreichen kann; am Äquator steht die Sonne nur 66½° hoch; dafür fällt sie aber auch 90° − 66½° = 23½° über den Nordpol hinaus, das heißt bis zum äußersten Rande des nördlichen Polarkreises. Dieser liegt ganz im Lichte, hat 24 Stunden Tag; der südliche Polarkreis liegt ganz im Schatten, hat 24 Stunden Nacht. Für die nördliche Halbkugel beginnt der Sommer, für die südliche der Winter.
Die Erde geht bis zum 23. September durch die Zeichen: Steinbock, Wassermann und Fische. Vom 21. März bis 23. September ist am Nordpole Tag, am 21. Juni ist der Mittag dieses 6 Monate dauernden Tages. Am Südpole ist 6 Monate Nacht.
Tag und Nacht sind auf der Erde gleich. Sonst alles entgegengesetzt der I. Erdstellung.
Die Erde geht bis zum 21. Dezember durch die Zeichen: Widder, Stier, Zwillinge.
Seit dem 23. September sind auf der südlichen Halbkugel die Tage immer länger, auf der nördlichen kürzer geworden als die Nächte. Am 21. Dezember ist auf der südlichen Halbkugel der längste, auf der nördlichen der kürzeste Tag. Der südliche Polarkreis liegt im Lichte, der nördliche im Schatten. Der südliche Wendekreis wird senkrecht beschienen. Für die südliche Halbkugel beginnt der Sommer, für die nördliche der Winter.
Die Erde geht bis zum 21. März durch die Zeichen: Krebs, Löwe, Jungfrau.
Vom 21. Dezember ab nehmen die Tage auf der nördlichen Halbkugel wieder zu, auf der südlichen ab, bis am 21. März wieder Tag- und Nachtgleiche eintritt.
3. Die ungleiche Dauer der Jahreszeiten. Wie der Fall der Körper durch die Anziehungskraft der Erde bewirkt wird, so wird die Revolution der Erde durch die Anziehungskraft der Sonne verursacht: daher regelt diese Kraft auch die Geschwindigkeit der Erde. Wie wir wissen, schwingt das Pendel an den Polen schneller als am Äquator der Erde, weil es dort wegen der Abplattung der Erde ihrem Mittelpunkte näher ist als am Äquator. Die Stärke der Anziehung auf der Erde ist also von der Entfernung vom Mittelpunkte abhängig. Nun wirkt aber die Anziehung im ganzen Weltall nach denselben Gesetzen; daher ist die Anziehung der Sonne und deshalb auch die Geschwindigkeit der Erde im Perihel größer als im Aphel. Die Bewegung der Erde wird langsamer von D (Fig. 31) über A nach B, wo sie am langsamsten ist, sie wird schneller von B über C nach D, wo sie am schnellsten ist.
Daher muß der im Perihel liegende Teil der Erdbahn, Bogen CDA in Fig. 31, schneller von der Erde durchlaufen werden, als der im Aphel liegende Teil, Bogen ABC. Weil nun aber das Perihel nahezu mit der Winter-, das[58] Aphel nahezu mit der Sommersonnenwende zusammenfällt, und weil eine Jahreszeit astronomisch vorüber ist, wenn die Sonne scheinbar 90° der Ekliptik in bezug auf Äquinoktial- und Solstitialpunkte durchlaufen hat, so fällt die Dauer des Winterhalbjahres (Herbst und Winter) nahezu mit der Zeit zusammen, in der die Erde den Bogen CDA durchläuft, die Dauer des Sommerhalbjahres mit der Zeit, die die Erde für den Bogen ABC gebraucht. Tatsächlich ist auch unser Sommerhalbjahr etwa 7 Tage länger als das Winterhalbjahr. Auf der südlichen Halbkugel ist es umgekehrt.
Wegen der Präzession des Frühlingspunktes sind auch diese Verhältnisse nicht dauernd so; man hat berechnet, daß im Jahre 6470 nach Chr. die beiden Halbjahre gleich sein werden.
[3] Für die Veranschaulichung der Erscheinungen, die in diesem Kapitel zur Sprache kommen, empfiehlt sich der Gebrauch eines Telluriums mit Lunarium.
1. A. Die scheinbare Bewegung. a) Wir sahen schon, daß der Mond eine scheinbare tägliche Bewegung um die Erde von Osten nach Westen macht, wie die Sonne und die Fixsterne. b) Die Dauer einer solchen scheinbaren Bewegung um die Erde mißt man am besten von einer oberen Kulmination bis zur nächsten. Zwischen zwei oberen Kulminationen vergehen nun bei einem Fixstern 23 Stunden 56 Minuten, bei der Sonne 24 Stunden, beim Monde 24 Stunden 50 Minuten. Geht also der Mond einmal um Mitternacht durch den Meridian, so tritt erst etwa eine Stunde nach der nächsten Mitternacht wieder ein solcher Durchgang ein. c) Beobachtet man die scheinbare tägliche Bewegung des Mondes einige Tage nacheinander, so macht man noch eine Bemerkung. Er durchläuft, gerade wie die Sonne, nicht immer denselben Kreis am Himmel. Ging er vielmehr an einem Tage etwa im Ostpunkte auf und durchlief den Äquator des Himmels, so geht er am nächsten Tage nicht mehr genau im Ostpunkte auf, sondern etwas seitwärts davon, also nach Süden oder Norden zu, und durchläuft einen kleineren zum Äquator parallelen Kreis. Weicht sein Aufgangspunkt nach Süden ab, so wächst die Abweichung in etwa 7 Tagen ungefähr bis zum Wendekreise des Steinbocks, verringert sich dann wieder, so daß nach ungefähr 7 Tagen aufs neue der Äquator vom Mond durchlaufen wird. Dann folgt die Abweichung nach Norden zu bis etwa zum Wendekreis des Krebses usw.
B. Die Erklärung der scheinbaren Bewegung. a) Die scheinbare tägliche Bewegung des Mondes erklärten wir uns schon, wie die aller Gestirne, durch die Rotation der Erde. b) Es fällt in die Augen, daß den beiden Abweichungen in der scheinbaren täglichen Bewegung des Mondes von der der Fixsterne[59] zwei ähnliche schon bekannte Erscheinungen bei der scheinbaren täglichen Bewegung der Sonne entsprechen. Diese erklärten sich aus einer zweiten Bewegung der Erde, ihrer Revolution um die Sonne. Daß der Mond in seiner Kulmination hinter Fixsternen und Sonne zurückbleibt, wird sich also wahrscheinlich ähnlich erklären. Aber schon das Größenverhältnis zwischen Mond und Erde macht es wahrscheinlich, daß diese Bewegung vom Monde um die Erde ausgeführt wird. In der Tat bewegt sich der Mond von Westen nach Osten um die Erde; die krumme Linie, die er beschreibt, ist die Mondbahn. Diese Bewegung ist eine wirkliche monatliche. c) Ist das der Fall, so muß der Mond auch, wie die Erde bei ihrer Revolution, seine Stellung zu den Fixsternen ändern. Das tut er. Seine Bahn weicht von der Ekliptik so wenig ab, daß er auch den Tierkreis durchläuft. Sah man ihn nun an einem bestimmten Tage an einer bestimmten Stelle in einem Sternbilde des Tierkreises, so ist er am nächsten Tage schon in der Richtung des Tierkreises um etwa 13° fortgerückt. Nach 27 Tagen 7¾ Stunden hat er den ganzen Tierkreis durchlaufen und erscheint wieder in seiner ersten Stellung. Diese Zeit nennt man einen siderischen Monat. (Sidera lat. = die Sterne!) Wegen dieser wirklichen Bewegung geschieht die scheinbare tägliche Bewegung des Mondes, wie bei der Sonne, nicht in geschlossenen Kreisen, sondern in Schraubenlinien.
2. Die wirkliche Bewegung des Mondes a) um die Erde. Sie erfolgt, wie wir eben hörten, in 27 Tagen 7¾ Stunden; b) um seine Achse. Der Mond wendet uns stets dieselbe Seite zu. Denken wir uns, wir wollten um einen Tisch herum gehen und dabei ständig das Gesicht nach ihm richten. Offenbar ist das nur möglich, wenn wir uns während einer Umkreisung des Tisches genau einmal um uns selbst drehen. Ebenso muß es beim Monde sein: der Mond rotiert in einem siderischen Monat, während er die Erde einmal umkreist, auch einmal um seine Achse. Wegen der Gleichzeitigkeit beider Bewegungen bezeichnet man sie zusammen als die Rotation des Mondes; c) um die Sonne. Der Mond wandert zugleich mit der Erde um die Sonne herum; diese Bewegung des Mondes heißt Mondrevolution. Daraus folgt, daß der Mond in den 27 Tagen 7¾ Stunden, in denen er den Tierkreis durchläuft, noch nicht wieder dieselbe Stellung zur Verbindungslinie zwischen Erde und Sonne erreicht, die er beim Beginn seines Umlaufs um die Erde hatte. In dieser Zeit ist ja die Erde auch um mehr als 27° in ihrer Bahn fortgerückt, also etwa ein Sternbild weiter, und der Mond erhält deshalb die alte Stellung zur Sonne erst wieder nach etwa 29½ Tagen. Diese Zeit heißt der synodische Monat. (Synodus, griech. = Zusammenkunft, nämlich mit der Sonne!)
3. Die Entfernung des Mondes von der Erde. Die Entfernung des Mondes von der Erde wechselt. Das beweist die Horizontalparallaxe, die bald größer, bald kleiner ist. Er hat also eine Erdnähe (griech. Perigäum) und eine Erdferne (griech. Apogäum). Der mittlere Wert seiner Horizontalparallaxe beträgt etwa 57´20´´. Daraus ergibt sich als seine mittlere Entfernung von der Erde nach § 18 r/(sin 57´20´´), worin r den Halbmesser der Erde bedeutet. Das ist = 59,97r oder rund 60r. Hieraus ergibt sich als mittlere Entfernung des Mondes ca. 384 000 km.
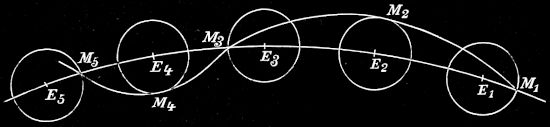
4. Die Gestalt der Mondbahn. Stände die Erde still, so würde die Bahn des Mondes um sie eine Ellipse sein. Nun geht aber die Erde, während sie vom Monde umkreist wird, selbst in ihrer elliptischen Bahn weiter. Ihr Mittelpunkt durchläuft etwa 1/12 derselben während eines Mondumlaufes, und an dieser Bewegung nimmt der Mond teil. Man kann sich den Vorgang an Fig. 33 klar machen. Angenommen, ein Punkt bewege sich in dem Bogenstück E1E2E3E4E5 und werde gleichzeitig umkreist von einem zweiten Punkte, dessen Bahn einer der kleinen Kreise wäre, wenn der erste Punkt still stände. Da sich dieser bewegt, so wird der zweite Punkt in der Zeit, in der er ¼ eines der kleinen Kreise durchlaufen müßte, etwa von M1 bis M2, in der Zeit, in der er einen halben Kreis durchlaufen müßte, von M1 bis M3 gelangen usw. Verbindet man die verschiedenen Stellungen, die der zweite Punkt einnimmt, während der erste von E1 durch E2, E3 usw. fortschreitet, so ergibt sich als seine Bahn die Schlangenlinie M1M2M3M4M5. Denselben Fall haben wir offenbar bei der Bewegung des Mondes um die fortschreitende Erde; in der Fig. 33 würden die Punkte E verschiedene Stellungen des Erdmittelpunktes, die Punkte M die entsprechenden Stellungen des Mondmittelpunktes bedeuten. Der Weg des Mondes gleicht demnach einer Schlangenlinie. Allerdings sieht diese in Wirklichkeit anders aus, als in der Figur. Die Schlangenwindungen sind nämlich viel länger und flacher, schmiegen sich viel enger an die Erdbahn, die Ekliptik, an und kehren der Sonne nicht, wie es in Fig. 33 scheint, bei Neumond eine konvexe, sondern immer eine konkave Biegung zu. Fig. 34 zeigt ein der Wirklichkeit mehr entsprechendes Bild für die Dauer eines Monats. Die ausgezogene Kurve, in der die Mittelpunkte der kleinen Kreise liegen, ist ein Stück der Erdbahn, die punktierte ein Stück der Mondbahn.

1. Entstehung der Mondphasen. Der Mond hat, wie alle Gestirne, Kugelgestalt. Jedermann weiß aber, daß er nicht immer als leuchtende Scheibe erscheint, sondern bald sichelförmig, bald als halbkreisförmig leuchtende Fläche. (S. § 5.) Das ist folgendermaßen zu erklären. Der Mond ist ein dunkler Körper, daher ist immer nur die Seite erleuchtet und leuchtend, die er der Sonne zuwendet. Das ist nicht immer dieselbe Seite, während er der Erde immer dieselbe Seite zukehrt. Hierin finden die verschiedenen Lichtgestalten des Mondes, griech. Mondphasen, ihre Erklärung.

Die Bahn des Mondes weicht, wie wir in § 23 genauer sehen werden, von der Ebene der Ekliptik etwas, aber sehr wenig ab. Wir können darum ohne großen Fehler an Stelle des Mondmittelpunktes dessen Projektion auf die Ebene der Ekliptik setzen, in der die Mittelpunkte von Erde und Sonne liegen. Tun wir dies und denken uns außerdem die Erde als stillstehend und vom Monde von Westen nach Osten umkreist, so kann Fig. 35 zur Erklärung der Mondphasen dienen.
Steht der Mond so, daß die Projektion seines Mittelpunktes mit den Mittelpunkten von Erde und Sonne in einer geraden Linie liegt und zwischen Erde und Sonne fällt, so ist es klar, daß der Mond uns seine dunkle Hälfte zukehrt, der Sonne die erhellte. Dann steht der Mond in Konjunktion (lat. = Verbindung) mit der Sonne, und wir haben Neumond. (Phase 1.)
Nun geht der Mond von Westen nach Osten. Nach etwa 3½ Tagen bilden die zwei geraden Linien vom Mittelpunkte der Erde zu dem der Sonne und zu dem projizierten Mittelpunkte des Mondes einen spitzen Winkel von 45°; dann sehen wir ¼ der uns zugewandten Mondhälfte erleuchtet, und zwar sichelförmig (weil[62] der Mond eine Kugel ist) und auf der westlichen (der unter dem Horizonte stehenden Sonne zugewendeten) Seite des Mondes. (Phase 2.)
Nach weiteren 3½ Tagen bilden dieselben zwei Linien einen rechten Winkel, und wir erblicken die westliche Hälfte der uns zugewandten Mondhälfte erleuchtet. Wir haben erstes Viertel. (Phase 3.)
Nach 3½ Tagen entsteht folgerecht Phase 4.
Nach ferneren 3½ Tagen steht die Erde zwischen Sonne und Mond, und die Projektion seines Mittelpunktes liegt wieder mit den Mittelpunkten von Erde und Sonne in einer geraden Linie; dann erblicken wir die uns zugewendete Mondhälfte völlig erleuchtet. Der Mond steht in Opposition (lat. = Entgegenstellung) zur Sonne. (Phase 5.)
Wie die Verdunkelung des Mondes in Phase 6, 7 und 8 sich vollzieht, wird aus dem Gesagten genugsam erhellt.
2. Die Auf- und Untergangszeiten des Mondes in den verschiedenen Phasen. Wenn der Mond an einem Tage mit der Sonne gleichzeitig kulminiert, so wird er, wie wir schon wissen, am nächsten Tage etwa 50 Minuten später als die Sonne kulminieren. Ähnlich verhält es sich mit den Zeiten des Auf- und Unterganges beider Gestirne, aber nicht genau so; denn da der Mond in 27 Tagen 7 Stunden ungefähr dieselben Kreise an der Himmelskugel scheinbar durchläuft, die die Sonne in einem Jahr durchläuft, so werden sie selten beide denselben Kreis an demselben Tag durchlaufen, und daher werden sie an demselben Tage auch selten beide gleich lange über dem Horizonte stehen. Am 21. März würde z. B. Neumond im Äquator, erstes Viertel ungefähr im Wendekreise des Krebses, Vollmond im Äquator, letztes Viertel etwa im Wendekreise des Steinbocks stattfinden, und die übrigen Phasen lägen zwischen diesen Grenzen; am 21. Juni fänden die entsprechenden Phasen im Wendekreise des Krebses, im Äquator, im Wendekreise des Steinbocks und im Äquator statt usw. Die Differenzen zwischen den Aufgangszeiten beider Gestirne und ebenso die zwischen ihren Untergangszeiten werden deshalb andere sein, als die Differenzen ihrer Kulminationszeiten. Aber wenn man von Zeitunterschieden von einiger Größe absehen will, so kann man im allgemeinen doch sagen:
Die Stellung des Vollmondes zu der Verbindungslinie von Erde und Sonne ergibt schon, daß der Vollmond um die Zeit des Sonnenunterganges aufgehen und um Sonnenuntergang untergehen muß; der Vollmond scheint also, wie man regelmäßig beobachten kann, die ganze Nacht. Der Neumond geht ungefähr gleichzeitig mit der Sonne auf und unter; er bleibt unsichtbar und steht scheinbar in ihrer Nähe während des ganzen Tages.
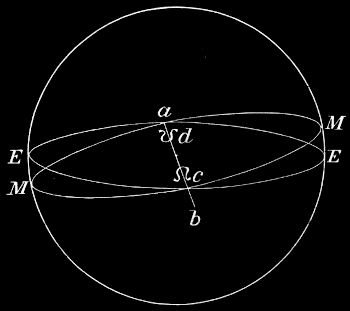
Die Ebene der Mondbahn fällt nicht mit der Ebene der Ekliptik zusammen, sondern weicht um einen Winkel von 5° ab. In Fig. 36 ist EE die Ekliptik; MM die Projektion der Mondbahn auf die Himmelskugel; ab ist die bis zum Himmel verlängerte gerade Linie, in welcher die Ebene der Erdbahn von der Ebene der Mondbahn durchschnitten wird: sie heißt die Knotenlinie. Ihre Endpunkte heißen Knoten, und zwar c aufsteigender, d absteigender Knoten. Indem[63] der Mond einen Knoten passiert, geht er auch scheinbar durch die Ekliptik; aufsteigend erhebt er sich über die Ekliptik, absteigend senkt er sich unter dieselbe herab.
c heißt Drachenkopf, d heißt Drachenschwanz. Die Zeit zwischen zwei aufeinander folgenden Ständen des Mondes im Drachenkopfe heißt ein Drachenmonat oder drakonischer Monat. Er dauert 27 Tage 5 Stunden 2 Minuten 36 Sekunden, ist also etwas kürzer als ein siderischer Monat. Das liegt daran, daß die Knoten nicht feststehende Punkte der Ekliptik sind. Weil nämlich nicht nur die Anziehungskraft der Erde, sondern auch die der ferneren Sonne auf den Mond wirkt, wird er bei jedem Umlaufe um die Erde etwas früher in die Erdbahn hineingezogen, als beim vorhergehenden Umlaufe. Daher bewegen sich die Knoten der Richtung der Mondrotation entgegen, d. h. von Osten nach Westen in der Ekliptik. Dabei dreht sich die Knotenlinie natürlich allmählich im Kreise herum. Die Zeit, in der sie einen ganzen Kreis beschreibt, in der also auch die Knoten in die erste Lage zurückkehren, beträgt rund 19 Jahre; deshalb fallen dann die Mondphasen wieder ziemlich auf dieselben Tage.

1. Entstehung. Wie jeder dunkle, von einer Lichtquelle beleuchtete Körper, werfen auch Erde und Mond in den von der Sonne abgewandten Raum Schatten. Da die Lichtquelle, die Sonne, in beiden Fällen eine größere, der beleuchtete Körper eine kleinere Kugel ist, so gibt es, wie aus Fig. 37 sofort ersichtlich, einen kegelförmigen, in eine Spitze auslaufenden Kernschatten und einen kegelstumpfförmigen, sich verbreiternden Halbschatten. Mondfinsternisse werden entstehen, wenn die Erde sich so zwischen Sonne und Mond stellt, daß der Mond in den Erdschatten tritt. Wie wir aus Fig. 35 erkennen können, ist das nur möglich bei Vollmond, also wenn der Mond in Opposition zur Sonne steht.
In Fig. 37 bedeutet der Kreis um S die Sonne, E die Erde, M den Mond in drei verschiedenen Stellungen seiner Bahn um die Erde. Der dunkel schraffierte Raum hinter E ist der Kernschatten, der heller schraffierte der Halbschatten der Erde. In jenen fällt kein Licht von der Sonne, und die Sonne ist von ihm aus nicht sichtbar; in den Halbschatten fällt weniger Licht, als auf die der Sonne zugewandte Seite der Erde, und von der Sonne ist hier nur ein Teil sichtbar.
2. Verlauf. Der Mond wird aber erst dunkel, wenn er in den Kernschatten der Erde tritt. Dieser ist, wie gezeigt, ein spitz zulaufender Kegel; daher muß er auf dem Monde stets als eine dunkle Scheibe erscheinen, die ihn ganz oder zum Teil verdunkelt. Da der Mond täglich 13° an den Fixsternen von Westen nach Osten vorüberzieht, die Erde aber nicht 1°, so taucht er sich zuerst mit seiner[64] östlichen Seite in den Erdschatten, und uns erscheint es, als ob der Erdschatten der Bewegungsrichtung des Mondes entgegen, also von Osten nach Westen, d. h. von der Erde gesehen, von links nach rechts über den Mond hinwegrückte.
3. Arten. Man unterscheidet partiale (teilweise) und totale (gänzliche) Mondfinsternisse. Liegen die Mittelpunkte von Sonne, Erde und Mond in einer geraden Linie, so entsteht eine zentrale Mondfinsternis. Diese ist stets eine totale, wie sich aus folgender Rechnung ergibt. Fig. 37 läßt erkennen, daß sich der Halbmesser der Sonne zu dem der Erde verhält, wie die Summe aus dem Abstand zwischen Sonne und Erde und der Länge des Erdschattens zur Länge des Erdschattens. Man hat nun berechnet, daß der Halbmesser der Sonne etwa 108½mal so groß ist als der der Erde. Demnach muß auch die Summe aus dem Abstand beider Körper voneinander und der Länge des Erdschattens das 108½fache dieser Länge betragen, oder, wenn wir die Länge des Erdschattens mit x bezeichnen, so ist
150 000 000 + x = (108½)x,
woraus sich ergibt: x = rund 1 394 000 km.
Weiter verhält sich, wie wieder unmittelbar aus Fig. 37 zu ersehen ist, der Erdhalbmesser zum Halbmesser des Schattens in der Entfernung des Mondes von der Erde wie die Länge des Erdschattens zur Differenz zwischen dieser und dem Abstand zwischen Mond und Erde, oder, wenn wir den Erdhalbmesser r und den Halbmesser des Schattens an der angegebenen Stelle x nennen, so ist
r : x = 1 394 000 : (1 394 000 − 382 000)
oder rund = 1 394 000 : 1 000 000, woraus sich ergibt: x ist ungefähr = (5/7)r, der Durchmesser des Schattens an jener Stelle also = (10/7)r = 9100 km. Der Durchmesser des Mondes ist auf 3480 km berechnet worden, d. h. der Durchmesser des Schattens beträgt an der Stelle, wo der Mond durch ihn verfinstert werden kann, etwa das 22/3fache des Monddurchmessers. Daher wird der Mond bei einer zentralen Finsternis stets ganz verfinstert.
4. Sichtbarkeit. Für alle Orte der Erde, für die bei einer Mondfinsternis der Mond überhaupt sichtbar ist, d. h. für die ganze Halbkugel, über deren Horizont er dann steht, die also Nacht hat, ist auch die Mondfinsternis sichtbar. Das ergibt unmittelbar Fig. 37. Sie ist auch, absolut angesehen, in demselben Augenblicke sichtbar, wenn auch für Orte unter verschiedenen Meridianen zu verschiedenen Stunden.
5. Bedingungen der Mondfinsternis. Lägen Erdbahn und Mondbahn in derselben Ebene, so müßte bei jedem Vollmonde der Mond in den Kernschatten der Erde treten, und es müßte eine zentrale Finsternis entstehen. Weil aber die Mondbahnebene mit der Erdbahnebene einen Winkel von 5° bildet und sie[65] schneidet, so geht der Mond bald über, bald unter dem Erdschatten weg, ohne daß eine Mondfinsternis entsteht.
Offenbar tritt also eine zentrale Mondfinsternis, wie in Fig. 37, nur ein, wenn gerade bei Vollmond der Mond in einem seiner Knoten steht. Diese Finsternis ist, wie wir eben sahen, auch stets eine totale.
Weil aber der Erdschatten in der Entfernung des Mondes von der Erde einen 22/3mal so großen Durchmesser hat als der Mond, so ist eine Mondfinsternis auch dann noch möglich, wenn der Mond zur Zeit des Vollmondes nur in der Nähe eines Knotens steht. Sie kann sogar noch total sein, wenn die Entfernung des Mondes vom Knoten etwa 5° beträgt; bei einer Entfernung von mehr als 13° ist auch eine partiale Mondfinsternis nicht mehr möglich.
6. Dauer der Mondfinsternis. Die Breite des Schattens der Erde in der Entfernung des Mondes ist nicht immer ganz dieselbe, da die Entfernung zwischen Sonne und Erde, ebenso wie die zwischen Mond und Erde nicht immer ganz dieselbe ist. Der Schatten ist am breitesten, wenn die Erde im Aphel und der Mond im Perigäum steht. In solchem Falle wird auch die Mondfinsternis am längsten dauern. Eine ungefähre Berechnung der Dauer einer zentralen Mondfinsternis ist folgendermaßen möglich. Der Durchmesser des Mondes erscheint von der Erde aus unter einem Winkel von 30´, daher die in derselben Entfernung etwa 22/3 oder rund dreimal so große Breite des Erdschattens unter einem Winkel von 90´. Nun durchläuft der Mond in 271/3 Tagen 360°, also 30´ in (82 · 24)/(3 · 360 · 2) = 41/45 oder rund 1 Stunde. Bei einer zentralen Finsternis wird also der Mond, nachdem sein Ostrand eben in den Erdschatten eingetaucht ist, etwa eine Stunde gebrauchen, bis er völlig verfinstert ist. Dann hat er noch 60´ des Schattens zu durchlaufen, bleibt also noch etwa 2 Stunden ganz verfinstert und tritt nach einer weiteren Stunde ganz aus dem Schatten heraus. Das ergäbe für die Gesamtdauer einer totalen Mondfinsternis rund 4 Stunden. Genauere Rechnungen ergeben, daß eine totale Mondfinsternis in ihrem ganzen Verlaufe höchstens 4 Stunden 38 Minuten, eine partiale nicht über 2 Stunden 18 Minuten dauert.
7. Häufigkeit der Mondfinsternisse. Weil der Vollmond nur zweimal im Jahre in der Nähe der Knoten sich befindet, so können auch höchstens zwei Mondfinsternisse in einem Jahre stattfinden, die dann etwa ein halbes Jahr auseinander liegen. In Wirklichkeit finden in 19 Jahren durchschnittlich 29 Mondfinsternisse statt, jedesmal eine im auf-, die andere im absteigenden Knoten.
8. Farbe des verfinsterten Mondes. Der Mond hat keine Atmosphäre (s. § 26); hätte auch die Erde keine, so müßte der verfinsterte Mond ganz unsichtbar sein. In Wirklichkeit sieht man die Scheibe in matt rötlichem Schimmer leuchten. Weil die Erde eine Atmosphäre hat, so ist sie für andere Himmelskörper mit einem rötlichen Ringe (unserer Dämmerungszone!) umgeben; dieser sendet Licht in den Schattenraum der Erde, also auch zum verfinsterten Monde, und zwar um so mehr, je mehr Wasserdampf unsere Atmosphäre zufällig gerade enthält. Daher lauten auch die Berichte über die Farbe der Mondscheibe bei Verfinsterungen sehr verschieden; sie erscheint rosa-, kupfer-, hoch-, grau- oder blaurot. Manchmal fehlt eine Färbung so gut wie ganz; daher war am 25. April 1642 der Mond gar nicht mehr zu erblicken, ebenso 1816 einmal.
1. Entstehung. Die Sonnenfinsternisse müßten eigentlich Erdfinsternisse heißen; denn sie entstehen, wenn der Mond bei Tage so zwischen Erde und Sonne tritt, daß deren Strahlen einen Teil der ihr zugewandten Erdhälfte nicht treffen können, oder anders ausgedrückt, daß der Mondschatten die Erde trifft.

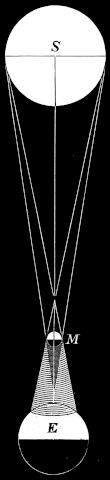
Die Figuren 38 und 39, in denen Kreis S die Sonne, M den Mond, E die Erde bedeutet, lassen erkennen, daß das nur möglich ist, wenn der Mond in Konjunktion zur Sonne steht, also bei Neumond. Die Erde wird also durch den Schatten des Mondes verdunkelt, die Sonne bleibt hell, wenn auch vor dem Monde nicht sichtbar.
2. Verlauf. Der Mond läuft mit der Erde von Westen nach Osten um die Sonne, aber schneller als die Erde, da die von ihm durchlaufene Schlangenlinie länger als die elliptische Erdbahn ist. Darum bedeckt er erst den Westrand der Sonne und zieht nach Osten zu über sie hin.
3. Sichtbarkeit. Eine Sonnenfinsternis ist nicht für alle Orte der Erdoberfläche, denen die Sonne überhaupt sichtbar ist, oder, was dasselbe ist, nicht für die ganze Halbkugel, die gerade Tag hat, sichtbar. Die Erde ist ja viel größer als der Mond selbst, also ihr Durchmesser erst recht größer, als der Durchmesser des Kernschattens vom Monde dort ist, wo er die Erde trifft. Ja, ihr Durchmesser ist sogar größer, als der des Halbschattens vom Monde an dieser Stelle ist. Also kann gleichzeitig von drei Orten, die alle drei Tag haben, dem einen die Sonne ganz, dem anderen zum Teil, dem dritten gar nicht verfinstert erscheinen. Das[67] zeigt auch ein Blick auf Fig. 38. Da der Mondschatten von Westen nach Osten über die Erde hinstreicht, wird die Sonnenfinsternis auch für Orte, denen sie sichtbar ist, nicht gleichzeitig eintreten, sondern für westlich gelegene früher.
4. Bedingungen der Sonnenfinsternis. Auch eine Sonnenfinsternis findet natürlich nicht mit jedem Neumonde statt, sondern nur, wenn der Mond gleichzeitig in oder nahe bei einem Knoten steht.
Es sind dann aber noch keineswegs immer die Bedingungen für eine völlige Verfinsterung der Sonne erfüllt; oft ist die Verfinsterung vielmehr für alle Punkte, denen sie überhaupt sichtbar ist, nur eine teilweise. Dann trifft eben der Kernschatten des Mondes die Erde nicht, sondern nur der Halbschatten. Diesen Fall stellt Fig. 39 dar. Er tritt ein, wenn zur Zeit der Sonnenfinsternis die Erde im Perihel und der Mond im Apogäum steht. Nennen wir nämlich den Halbmesser der Sonne s, den des Mondes m, den Abstand zwischen Sonne und Mond, den man als Differenz von Sonnen- und Mondweite finden kann, a, die Länge des Schattenkegels x, so folgt aus Fig. 38 oder 39 sofort
s : m = (a + x) : x,
woraus sich ergibt
x = (a · m)/(s − m).
Nun hat a seinen kleinsten Wert, wenn die Erde im Perihel, der Mond im Apogäum steht, nämlich 147 680 000 km − 410 000 km, woraus sich ergibt: x ungefähr = 370 000 km gegenüber dem Abstande des Mondes von der Erde im Apogäum = 410 000 km. Also hier erreicht der Kernschatten des Mondes die Erde wirklich nicht. Dagegen ist bei der umgekehrten Stellung, Erde im Aphel und Mond im Perigäum (s. Fig. 38), der Kernschatten des Mondes länger als der Abstand des Mondes von der Erde, nämlich jener über 380 000 km, dieser noch nicht 370 000 km. Somit ergibt sich für diese Stellung der Himmelskörper die Möglichkeit einer totalen Sonnenfinsternis.
Unmöglich ist eine Sonnenfinsternis, wenn der Neumond 19° vom Knoten entfernt ist; gewiß ist sie, wenn die Entfernung bloß 13° beträgt. Total kann die Finsternis bei 7–13° Entfernung des Neumondes vom Knoten sein.

5. Arten. Die Sonnenfinsternis ist, wie sich aus dem Vorhergehenden ergibt, entweder für verschiedene Gegenden verschieden, nämlich teils partial, teils total (Fig. 38), oder für alle Gegenden, denen sie sichtbar wird, partial (Fig. 39). Im zweiten Falle ist die Finsternis für den Punkt der Erdoberfläche, durch den die Verbindungslinie der Mittelpunkte von Sonne, Mond und Erde geht, ringförmig, d. h. der sichtbare Teil der Sonne bildet um den verfinsterten Teil einen Kreisring. In Fig. 40 zeigt a das Sonnenbild bei einer partialen, b bei einer totalen und e bei einer ringförmigen Verfinsterung. Die Finsternisse in Fig. 40 b und c sind zugleich zentral.
6. Dauer der Sonnenfinsternisse. Die längste Dauer einer totalen Sonnenfinsternis für die ganze Erde kann 4 Stunden 38 Minuten sein, dagegen für einen einzelnen Ort, und zwar für den Äquator, höchstens 7 Minuten 38 Sekunden. Eine Sonnenfinsternis (Anfang bis Ende) kann für die ganze Erde 7 Stunden dauern. Wenn die Erde nicht zugleich mit dem Monde von Westen nach Osten rotierte, so würde die Zeit der Finsternis für einen einzelnen Ort noch kürzer sein.
7. Häufigkeit der Sonnenfinsternisse. In 19 Jahren gibt es durchschnittlich 41 Sonnenfinsternisse für die ganze Erde. Dagegen ereignen sich für einen bestimmten Ort die Sonnenfinsternisse dreimal so selten als Mondfinsternisse. Eine totale Sonnenfinsternis tritt für denselben Ort der Erde nur etwa alle 200 Jahre ein.
8. Eigentümliche Erscheinungen bei den Sonnenfinsternissen. Vor Eintritt einer totalen Verfinsterung, solange die Sonne noch Sichelgestalt hat, erscheinen die Lichter, die durch das Laub der Bäume fallen und sonst kreisrund sind, auch sichelförmig. Unmittelbar vor der totalen Verfinsterung huschen unheimliche fliegende Schattenbänder mit gewaltiger Schnelligkeit über die Landschaft hin, deren Ursache noch nicht klar ist und vor denen namentlich die Tiere sich entsetzen. Mit Eintritt der völligen Finsternis wird der Himmel schwärzlichblau, die Luft kühlt sich rasch ab, es beginnt zu tauen, Wolken bilden sich, die Vögel fliegen in ihr Versteck, Blumen schließen ihre Kelche, ein unheimliches Gefühl ergreift den Menschen. Bei heiterem Himmel sieht man um den dunklen Mond einen glänzenden Ring von grünlichweißem Lichte, aus dem lebhaft rote Gebilde oft sehr weit in den Weltraum hinaustreten. Diese Lichterscheinungen gehören natürlich der Sonne an und sollen in § 32 näher besprochen werden.
Partielle Sonnenfinsternisse vermindern die Tageshelle je nach dem Umfange der Verfinsterung; man kann sie am besten durch dunkel gefärbte Gläser wahrnehmen.
Bemerkung. Aus der Lage der Mondbahn zur Ekliptik ergibt sich, daß alle Finsternisse sich in der Nähe der Ekliptik ereignen müssen; daher ihr schon in § 10 erklärter Name.

1. Größe und Gestalt. Der Durchmesser des Mondes erscheint von der Erde aus gesehen unter einem Winkel von 30´, also der Halbmesser unter einem Winkel von 15´. Ist der Kreis um M der Mond, E ein Punkt der Erde, so kann man bei der großen Entfernung ohne merklichen Fehler die Linie AE (Fig. 41), die zu einem Endpunkte des auf EM senkrechten Durchmessers AB führt, als Tangente ansehen, also:
| AM | = | EM · tg 15´ und |
| AB | = | 2 · EM · tg 15´. |
Da EM, der Abstand des Mondes von der Erde, bekannt ist, kann man hieraus den Durchmesser des Mondes bestimmen. Nach möglichst genauer Bestimmung beträgt er rund 3480 km, sein Umfang also π · 3480 km = 11 000 km; seine Oberfläche, die daraus ja leicht zu berechnen ist, ist kleiner als Asien, seine Dichtigkeit halb so groß als die der Erde.
Aus theoretischen Gründen ist man zu der Annahme gekommen, daß der Mond polar und äquatorial ein wenig abgeplattet ist; doch haben die genauesten Beobachtungen mit den besten Fernrohren keinen sicheren Anhalt dafür gegeben. Er erscheint durchaus kugelförmig. Ist eine Abplattung vorhanden, so muß sie sehr gering sein.
2. Die Oberfläche des Mondes. Wegen seiner Nähe ist die Oberfläche des Mondes verhältnismäßig genau bekannt. Unsere Fernrohre gestatten eine 3000–5000fache Vergrößerung und nähern uns den 384 000 km entfernten Mond auf 80–100 km. Im allgemeinen benutzt man aber zur Beobachtung des Mondes höchstens 450fache Vergrößerungen, bei denen Oberflächenteile, die durch Helligkeit oder Dunkelheit sich von ihrer Umgebung abheben, bei einem Durchmesser von 550 m noch wohl erkennbar sind.
Im ersten Viertel bemerkt man eine große Zerrissenheit der Lichtgrenze; man sieht leuchtende Punkte außer allem Zusammenhange mit dem hellen Teile des Mondes selbst in der dunklen Seite, während zugleich solche isolierte Lichtstellen mit dem hellen Teile durch Lichtstreifen wie durch Brücken verbunden sind. Sodann sieht man in der Nähe hellerer Flecke im hellen Teile schwarze Flecke, die so lang sind, daß sie in die Schattenseite hineinreichen. Jene helleren Flecke sind Berge, die schwarzen deren Schatten. Die Lichtstärke des Mondes ist überall gleich.
Am anderen Tage schon bietet sich ein anderes Bild dar. Die Schatten sind kürzer geworden, weil die Berge senkrechter von der Sonne beschienen werden. Der Vollmond sieht wieder ganz anders aus, weil die Sonne für den Mittelpunkt der Mondscheibe im Zenit steht und diese Gegenden ohne Schatten sind, und weil die Schatten auch nach den Rändern der Mondscheibe hin nur gering sind. Die Berge erscheinen nur undeutlich.
Das letzte Viertel ist wieder dem ersten ähnlich. Folglich hat der Mond eine sehr unebene Oberfläche mit Bergen und Tälern. Mehr als 1000 Mondberge sind gemessen mit Hilfe ihres Schattens; darunter sind 39 über 4500 m hoch, einige 7200 m, einer, wie der Gaurisankar, 8800 m. Das sind in Anbetracht der Kleinheit des Mondes außerordentliche Höhen.
Schon mit bloßem Auge unterscheidet man dunkle Flecke auf dem Monde. Im Fernrohre erkennt man sie als umfangreiche Ebenen, die meist grau oder grünlich erscheinen. Sie liegen meist tiefer als die gewöhnlich helleren gebirgigen Teile und werden Meere genannt, weil man sie früher dafür hielt. Unter den Gebirgen herrscht das Massengebirge vor, Bergketten sind selten. In den grauen Flächen, den Ebenen, erheben sich häufig sogenannte Bergadern, niedrige, 450–600 km lange Bergrücken, die dunkel erscheinen. Die häufigste Form der Bergbildung ist die Ringform. Große ringförmige Erhebungen umgrenzen tiefere, selten ganz ebene Stellen der Mondoberfläche. Man unterscheidet Wallebenen, Ringgebirge und Krater. Die Umrandung der Wallebenen hat einen gewaltigen Durchmesser, bis zu 220 km, und hat in allen Teilen ziemlich gleiche Höhe; der eingeschlossene Teil ist wenig oder gar nicht niedriger als die übrige Mondoberfläche und meist mit Erhebungen besetzt. Das Ringgebirge[70] ist enger, wenn es auch noch bis zu 90 km Durchmesser zeigt; der eingeschlossene Teil ist ziemlich viel tiefer als die äußere Umgebung, über die sich die Wälle nicht allzuhoch erheben, und hat in der Mitte meist einen oder mehrere kegelförmige Berge, die niedriger als die Umwallung sind. Die engeren Ringgebirge mit besonders tiefen Innenflächen heißen Krater. Die Kettengebirge heißen meist nach irdischen Gebirgen (Anden, Kordilleren), die Ringgebirge nach berühmten Männern (Tycho, Kopernikus, Kepler, Plato). –
Eine höchst eigenartige Erscheinung auf der Mondoberfläche sind die Rillen, meist gerade, 75–200 km lange Linien, die quer durch alle Unebenheiten, selbst durch Krater sich hinziehen. Es sind offenbar Spalten, da man bei schräger Beleuchtung im Innern den Schatten eines ihrer Ränder wahrnimmt. Sie erreichen 300–600 m und werden auf Tiefen von 100–400 m geschätzt. Man kennt an 400 solcher Rillen. Über die Entstehung und das Wesen dieser Erscheinungen sind die Forscher noch sehr verschiedener Meinung.
3. Das Fehlen der Atmosphäre. Der Mond hat keine Atmosphäre. Beweise: a) Für jeden Körper, der eine Atmosphäre hat, werden die schräg auffallenden Strahlen wegen des weiteren Weges durch die Atmosphäre stärker abgeschwächt, als die senkrecht auffallenden. Für den Mond kommen die Sonnenstrahlen, die seinen Rand treffen, von seinem Horizont, also schräger, als an anderen Stellen. Demnach müßte der Rand matter leuchten als die Mitte. Das ist nicht der Fall.
b) Die Schatten der Mondberge sind ganz schwarz und nicht grau, wie sie beim Vorhandensein einer Atmosphäre sein müßten.
c) Das Licht der Fixsterne, die hinter dem wandelnden Monde verschwinden, müßte vorher schon abgeschwächt werden, da es seine Atmosphäre durchdringen müßte, und auch zunächst wieder abgeschwächt erscheinen. Die Sterne verschwinden aber und erscheinen wieder plötzlich ohne Lichtschwächung.
d) Aus der Optik ist bekannt, daß wir wegen der astronomischen Strahlenbrechung unserer Atmosphäre die Sonne noch kurz nach ihrem Untergange und schon kurz vor ihrem Aufgange sehen. Ebenso müßten die Fixsterne noch kurz nach und schon kurz vor ihrem Verschwinden hinter dem Monde sichtbar sein. Das aber ist nicht der Fall, wie durch Vergleichung der durch Beobachtung gefundenen Zeit mit der aus der Geschwindigkeit und dem Durchmesser des Mondes berechneten Zeit nachgewiesen ist.
e) Die Spektralanalyse zeigt, daß die Spektren der Planeten, die wie der Mond ihr Licht von der Sonne empfangen, zwar dem Sonnenspektrum sehr ähnlich sind, aber doch einige neue Linien enthalten. Das kommt daher, daß die Sonnenstrahlen, nachdem sie von der Oberfläche der Planeten zurückgeworfen sind, noch die absorbierenden Gase der Planetenatmosphäre durchlaufen. Das Spektrum des Mondes aber stimmt ganz mit dem Sonnenspektrum überein; ihm fehlt also die Atmosphäre.
Eine Folge dieses Fehlens der Atmosphäre ist, daß der Mond auch am Tage keinen durch eine Atmosphäre blau gefärbten, sondern einen schwarzen Himmel hat, daß ihm die Sonne und die Sterne viel heller leuchten als uns. Auch kann kein flüssiges Wasser auf dem Monde vorhanden sein, da es sofort verdunsten würde. Er ist jedenfalls als ein starrer Körper anzusehen, auf dem jedes Leben unmöglich sein muß.
1. Entstehung. Das Bedürfnis, die Zeit in größere und kleinere Abschnitte zu teilen, ist uralt. Zu einer solchen Zeiteinteilung gaben besonders die Sonne und der Mond Veranlassung, und so entstand der Kalender. (Das Wort kommt vom lateinischen Zeitwort calare = ausrufen; die römischen Priester mußten den Tag des eingetretenen Neumondes – also den Monatsanfang – öffentlich ausrufen; deshalb wurde dieser Tag Calendae genannt, und hiervon kommt unmittelbar unser Wort Kalender.)
2. Grundlage. Unserem Kalender liegt das tropische Jahr zugrunde, d. h. die Zeit des Sonnenlaufs von Frühlingsknoten zu Frühlingsknoten = 365 Tage 5 Stunden 48 Minuten 48 Sekunden.
3. Der Tag. a) Sonnen- und Sterntag. Als kürzestes natürliches Zeitmaß gilt die Zeit von einer Kulmination der Sonne bis zur nächsten; man nennt sie einen Tag, genauer Sonnentag. So heißt er zum Unterschiede vom Sterntag, der ja um etwa 4 Minuten kürzer ist. Wir wissen, daß die größere Länge des Sonnentages davon kommt, daß die Erde nicht nur von Westen nach Osten rotiert, sondern gleichzeitig in dieser Richtung fortrückt, was ein scheinbares Fortrücken der Sonne in der Ekliptik zur Folge hat. Nun bewegt sich aber die Erde nicht gleichmäßig in ihrer Bahn, sondern im Perihel schneller als im Aphel; daher wird auch die Sonne in der Ekliptik an verschiedenen Tagen verschieden weit vorrücken. Ja, wenn sie sogar täglich um denselben Bogen in der Ekliptik vorrückte, so würden die entsprechenden Bogen im Äquator doch ungleich sein, weil die Ekliptik gegen den Äquator geneigt ist. Zur Zeit der Sonnenwenden, wo die Ekliptikbögen eines Tages ziemlich parallel zum Äquator liegen, rückt die Sonne in einem Tage mehr nach Osten vor, als zur Zeit der Nachtgleichen, wo die stärkste Neigung zwischen Ekliptik- und Äquatorbogen besteht. Also sind die wahren Sonnentage verschieden lang, weil die Erde ihre Jahresbahn nicht mit gleichmäßiger Geschwindigkeit durchläuft und die Ekliptik schief gegen den Äquator liegt. Deshalb sind sie auch zur Zeiteinteilung ungeeignet, und unser bürgerlicher Tag ist der mittlere Sonnentag, d. h. die Zeit zwischen zwei Kulminationen einer gedachten Sonne, die mit gleichförmiger Geschwindigkeit den Äquator in derselben Zeit durchliefe, in der die wahre Sonne jetzt mit ungleichförmiger Geschwindigkeit die Ekliptik durchläuft. Eine gute Räderuhr gibt diesen Tag an, eine Sonnenuhr den wahren Sonnentag. Der Tag wird in 24 Stunden, die Stunde in 60 Minuten, die Minute in 60 Sekunden eingeteilt.
Der bürgerliche Tag geht von Mitternacht zu Mitternacht und zählt zweimal von 1 Uhr bis 12 Uhr.
Die Astronomen rechnen nach den kürzeren Sterntagen, und der astronomische Tag geht von Mittag zu Mittag. Er zählt 1 – 2 – 3 – – 12 – 13 usw. Uhr bis 24. Er führt das Datum des vorhergehenden bürgerlichen Tages bis 24 Uhr, d. h. bis 12 Uhr mittags fort.
b) Die Zeitgleichung. Viermal im Jahre, am 14. April, 14. Juni, 31. August, 23. Dezember stimmen mittlere und wahre Sonnenzeit überein. Den Unterschied zwischen der mittleren und wahren Zeit nennt man die Zeitgleichung und gibt ihr das positive Vorzeichen, wenn man sie zur wahren Zeit addieren[72] muß, um die mittlere zu erhalten, das negative, wenn man subtrahieren muß. Ist also für einen bestimmten Tag die Zeitgleichung als +11 angegeben, so heißt das: Am wahren Mittag zeigt die Räderuhr schon 12 Uhr 11 Minuten. Die Zeitgleichung ist vom 23. Dezember bis zum 14. April und vom 14. Juni bis zum 31. August positiv, vom 14. April bis zum 14. Juni und vom 31. August bis zum 23. Dezember negativ. Ihre größten Zahlenwerte erreicht sie am 11. Februar, wo sie +15 Minuten, und am 2. November, wo sie -16 Minuten beträgt. Hieraus erklärt es sich, daß man das Zunehmen der Tage im Februar und ihr Abnehmen im November am stärksten nachmittags bemerkt.
c) Mitteleuropäische Zeit. Natürlich geht auch bei der Rechnung nach mittleren Sonnentagen, wie beim wahren Sonnentage, die Uhr der östlicher gelegenen Orte vor unserer vor, die der westlicher gelegenen nach, d. h. jeder Ort hat seine besondere Ortszeit. Das hat bei dem gewaltigen Verkehr der Gegenwart aber viel Unbequemlichkeiten im Gefolge, namentlich für den Eisenbahnverkehr und den Eisenbahndienst. Daher hat man schon vor Jahren vorgeschlagen, die Erde in 24 Stundenzonen, also Zonen von 15° Breite (15 · 4 Minuten!), einzuteilen und für jede solche Zone unbekümmert um die Ortszeit die Uhren übereinstimmen, von denen der Nachbarzone aber um eine Stunde abweichen zu lassen. Eine solche Zone sollte sich 7½° östlich und 7½° westlich von Greenwich erstrecken und Greenwicher Zeit haben; für die östlich davon gelegene würde die Zeit des 15. Meridians östlich von Greenwich, das ist ziemlich genau die Ortszeit von Stargard in Pommern, die Einheitszeit sein. Da dieser Zone fast ganz Deutschland angehört, mit Ausnahme eines schmalen Striches im Westen, der etwa durch eine Linie Leer, Dortmund, Neuwied, Pirmasens, Kolmar zu begrenzen wäre, so wurde im Jahre 1893 für Deutschland die Stargarder Zeit unter dem Namen mitteleuropäische Zeit als Einheitszeit eingeführt. Schweden hat dieselbe Einheitszeit schon seit 1879. Die wahre Ortszeit von Aachen ist um mehr als eine halbe Stunde hinter ihr zurück, die von Königsberg um mehr als 20 Minuten voraus. Frankreich hat sich dieser Zoneneinteilung, nach der es mit England gleiche Zeit haben würde, nicht angeschlossen, sondern benutzt als Einheitszeit die Zeit des Meridians der Pariser Sternwarte und weicht deshalb von der englischen Zeit um 10 Minuten ab. Rußland aber regelt seine Zeit ebenfalls unter Benutzung des Meridians von Greenwich und ist uns in der Uhr um eine Stunde voraus.
4. Die Woche. Viele Völker haben 7 Tage als größeren Zeitabschnitt – Woche – zusammengefaßt, am frühesten wohl die Semiten. Wahrscheinlich ist das auf Grund der Mondbeobachtung geschehen. (Ungefähr die Zeit von einer Phase bis zur nächsten.)
Die Namen der Wochentage sind Überreste der Astrologie (Wahrsagerei aus dem Stand der Gestirne), und zwar sind die Tage benannt nach Saturn, Jupiter, Mars, Sonne, Venus, Merkur und Mond. Nach der Meinung der Chaldäer und Ägypter beherrschen diese in der genannten Reihenfolge die einzelnen Stunden des Tages. Nach dem die erste Stunde des Tages beherrschenden Planeten erhielt der Tag seinen Namen. Bei den Ägyptern war unser Sonnabend der erste Wochentag. Saturn aber beherrschte die erste Stunde dieses Tages, deshalb hieß er Saturnstag (englisch heute noch Saturday), Jupiter beherrschte die zweite Stunde usw., folglich kam auf die Sonne die 25. Stunde, d. h. die erste Stunde des nächsten Tages, der also Sonntag genannt wurde. Montag = Mondstag, Dienstag =[73] Tag des (Kriegsgottes) Mars, dem der deutsche Gott Ziu entsprach, also Ziustag, woraus Dienstag entstand. An die Stelle des Merkurtages (Wodantages, engl. Wednesday) trat die Benennung Mittwoch. Der Jupiterstag wurde Donnerstag vom Gott Donar; der Venustag wurde Freitag von der Göttin Freia.
5. Der Monat. Der Name kommt von »Mond«. Im Altertum war ein Monat der synodische Monat, also die Zeit von einer bestimmten Stellung des Mondes zur Sonne bis zur Wiederkehr derselben Stellung, z. B. von Neumond zu Neumond, also 29½ Tage lang; man gab aber dem Monat in der Zeitrechnung bald 29, bald 30 Tage, um mit vollen Tagen zu rechnen. Zwölf solche Monate sind also 354 Tage.
Die Namen der Monate sind lateinischen Ursprungs. Januar von Janus, dem Gotte der Zeit, dem der erste Tag dieses Monats bei den Römern geweiht war. Februar von februare = reinigen, da das Reinigungsfest der Römer in diesem Monate gefeiert wurde. März von Mars. April von aperire = öffnen, nämlich der Blüten. Mai von der Göttin Maja. Juni von der Göttin Juno. Der Juli von Julius Cäsar; er hieß früher Quintilis, der fünfte, nämlich nach dem 1. März, mit dem die Römer das Jahr begannen. August vom Kaiser Augustus; er hieß früher Sextilis, der sechste. September = der siebente; Oktober = der achte; November = der neunte; Dezember = der zehnte.
Karls d. Gr. Monatsnamen sind: Wintermonat, Hornung, Lenz-, Oster-, Wonne-, Brach-, Heu-, Ernte-, Herbst-, Wein- und Heil- oder Christmonat.
6. Das Jahr. Die meisten Völker rechneten wohl anfangs nach Mondjahren zu 354 Tagen, die Mohammedaner tun das heute noch. Da aber bei dieser Rechnung das Datum des Frühlingsäquinoktiums und der übrigen wichtigen Tage um 11 Tage vorrückte, so zeigte sich namentlich bei den ackerbautreibenden Völkern schon früh das Verlangen, ihre Zeitrechnung mit dem Laufe der Sonne, der für ihre Beschäftigung so wichtig war, in Einklang zu bringen. Die Ägypter rechneten daher bald nach Sonnenjahren, und zwar vom ersten Aufgange des Sirius vor Sonnenaufgang am Morgenhimmel bis zu demselben Termin. Das gab 365 Tage. Sie zählten nun 11 Monate zu je 30, den zwölften zu 35 Tagen. Die Griechen halfen sich durch Einführung des sogenannten Metonschen Zyklus, den der Athener Meton um 450 v. Chr. vorschlug. Dieser Zyklus umfaßte 19 Jahre, zählte zwar immer noch den Monat mit abwechselnd 29 und 30 Tagen, schob aber im 3., 5., 8., 11., 13., 16. und 19. Jahre je einen Schaltmonat und in bestimmten Zwischenräumen noch einen Schalttag ein, so daß das Jahr im Durchschnitt nur etwa eine halbe Stunde zu lang wurde.
Diese ziemlich verwickelte Zeitrechnung der Griechen übernahmen die Römer in einer weniger vollkommenen Gestalt. Daher war bis zum Jahre 46 vor Christus der römische Kalender ganz in Unordnung. Cäsar setzte auf den Rat des Astronomen Sosigenes dem Jahre 46 noch zwei Schaltmonate von zusammen 67 Tagen hinzu, so daß der nächste 1. Januar richtig gemäß dem Sonnenstande fiel. Nun führte Cäsar die Rechnung nach Sonnenjahren ein und nahm ein Jahr von 365 Tagen und 6 Stunden an, so daß auf je 3 Jahre je 365 Tage, auf das 4. Jahr 366 Tage kamen und der 29. Februar der Schalttag wurde. Die Monate wurden teils zu 30, teils zu 31 Tagen gerechnet bis auf den Februar, der damals der letzte Monat im Jahre war. Das ist der julianische Kalender.
Das tropische Jahr ist in Wirklichkeit etwas kürzer als das julianische Jahr, und zwar um 6 Stunden weniger 5 Stunden 48 Minuten 48 Sekunden, d. i. mehr[74] als 11 Minuten; man schaltete also alle 4 Jahre fast 45 Minuten zuviel ein durch den Schalttag; das macht in etwa 130 Jahren schon einen ganzen Tag aus, in 390 oder rund in 400 Jahren 3 Tage, die man hinter der wirklichen Sonnenzeit zurückblieb, so daß im Jahre 1582 das Datum des Frühlingsäquinoktiums im Kalender auf den 11. März fiel. Der Kalender war also 10 Tage zurückgeblieben und hätte sogar um 12 Tage zurück sein müssen, wenn nicht schon das Konzil zu Nizäa 325 eine Änderung vorgenommen hätte. Deshalb bestimmte Papst Gregor XIII., daß nach dem 4. Oktober 1582 sofort der 15. Oktober geschrieben wurde. Jedes vierte Jahr sollte auch ferner ein Schaltjahr bleiben; aber, um den Frühlingspunkt unverrückt zu erhalten, sollten innerhalb 400 Jahren diejenigen Schaltjahre, deren Zahl wohl durch 100, nicht aber durch 400 ohne Rest teilbar wäre, als gewöhnliche Jahre gelten, z. B. 1600 = Schaltjahr, 1700, 1800, 1900 nicht = Schaltjahr. So wurden die 3 Tage ausgeschaltet, um die der julianische Kalender in 400 Jahren etwa zurückbleibt. Demnach gibt es in 400 Jahren 303 gewöhnliche Jahre (Gemeinjahre) und 97 Schaltjahre. Erst in 3846 Jahren gibt es nach dem gregorianischen Kalender wieder zwischen Kalender und Sonne eine Abweichung von 1 Tag. Dieser Kalender fand übrigens anfangs nur in römisch-katholischen Ländern Eingang; in Deutschland wird erst seit 1700 nach ihm gerechnet. Die griechisch-katholischen Länder haben sogar heute noch den julianischen Kalender beibehalten, so daß z. B. in Rußland das Datum gegen unseren Kalender jetzt um 13 Tage zurückgeblieben ist.
1. Wesen. Wir wissen schon, daß die meisten Sterne ihre Lage zueinander nicht verändern. Beobachtet man jedoch längere Zeit, etwa mehrere Monate nacheinander, die Sternbilder des Tierkreises, so wird man vereinzelt auch Sterne wahrnehmen, die ihre Lage zu den Sternen der Sternbilder verändern. Diese Sterne müssen also nicht nur an der scheinbaren Rotation der Himmelskugel teilnehmen, sondern außerdem noch eine eigene, wirkliche Bewegung haben. Weitere Beobachtungen haben ergeben, daß diese Sterne die Sonne umkreisen, Licht und Wärme von ihr erhalten, nicht funkeln (szintillieren) und uns in Scheibenform erscheinen. Man nennt sie Planeten oder Wandelsterne. Auch die Erde ist ein solcher Planet, der, von anderen Planeten gesehen, als leuchtender Stern erscheinen wird.
2. Haupt- und Nebenplaneten. Die meisten uns bekannten Planeten bewegen sich nur um die Sonne, 24 bewegen sich um einen von jenen Planeten und mit ihm um die Sonne. Jene heißen Hauptplaneten, diese Nebenplaneten, auch Satelliten, Trabanten, Monde. Einer davon ist der Mond unserer Erde.
3. Zahl. Vor Erfindung des Fernrohres durch Galilei (1609) kannte man[75] nur 6 Planeten und einen Nebenplaneten, den Mond der Erde. Seitdem sind viele hundert neue Planeten und 26 Nebenplaneten entdeckt worden. Von Nebenplaneten umkreisen die Erde einer, den Mars 2, den Jupiter 8, den Saturn 10, den Uranus 4, den Neptun einer. Sie führen diese Bewegung von Westen nach Osten aus, bis auf je einen Mond des Jupiter, des Saturn und den Mond des Neptun, die von Osten nach Westen kreisen.
Die Entdeckung des 6., 7. und 8. Jupitermondes und des 8., 9. und 10. Saturnmondes stammt aus den Jahren 1902–1908 und ist der Himmelsphotographie zu verdanken; der 9. Mond des Saturn kann in keinem der besten Fernrohre der Welt gesehen werden.
4. Namen und Entfernungen. Die Namen der Planeten, die vor der Erfindung des Fernrohres bekannt waren, sind: Merkur, Venus, Erde, Mars, Jupiter, Saturn. Dazu kam, im Jahre 1781 von Friedrich Wilhelm Herschel entdeckt, der Uranus. Die Entfernung des Merkur von der Sonne beträgt rund 60, die des Uranus rund 3000 Millionen km. Für die Entfernungen der sechs ersten von diesen Planeten von der Sonne hatte man ein merkwürdiges Zahlenverhältnis gefunden. In möglichst runden Zahlen sind diese Größen nämlich folgendermaßen darzustellen:
| Merkur | 60 + | 0 · 45 | = | 60 | Millionen Kilometer |
| Venus | 60 + | 1 · 45 | = | 105 | Millionen Kilometer |
| Erde | 60 + | 2 · 45 | = | 150 | Millionen Kilometer |
| Mars | 60 + | 4 · 45 | = | 240 | Millionen Kilometer |
| Jupiter | 60 + | 16 · 45 | = | 780 | Millionen Kilometer |
| Saturn | 60 + | 32 · 45 | = | 1500 | Millionen Kilometer |
Das sah so gesetzmäßig aus, daß man früh auf die Vermutung kam, zwischen Mars und Jupiter, wo die Stufe 60 + 8 · 45 fehlte, müsse noch ein Planet vorhanden sein. Diese Vermutung wurde bestärkt, als sich die Entfernung für den Uranus = 60 + 64 · 45 = 2940 Millionen km herausstellte. Durch einen Zufall wurde wirklich 1801 zwischen Mars und Jupiter ein neuer, aber im Vergleich zu den anderen sehr kleiner Planet entdeckt. In wenigen Jahren folgte die Entdeckung noch mehrerer solcher kleinen Planeten zwischen Mars und Jupiter. Heute ist die Zahl der bekannten Planeten dieser Art nicht mehr weit von 1000 entfernt; eine genaue Zahl anzugeben, ist zwecklos, da in jedem Jahr eine große Anzahl neuer entdeckt wird. Ihre Entfernungen von der Sonne sind zwar sehr verschieden (zwischen 300 000 000 und 600 000 000 km), aber fast alle bewegen sich zwischen Mars und Jupiter. Man nennt sie kleine Planeten oder Planetoiden.
Eigentümliche Unregelmäßigkeiten im Laufe des Uranus legten den Astronomen die Vermutung nahe, daß in noch weiterer Entfernung von der Sonne noch ein Planet sich befinde, und der Franzose Leverrier berechnete 1846 aus jenen Unregelmäßigkeiten den Ort, wo man ihn suchen müsse. Es war ein gewaltiger Triumph der Astronomie, daß noch in demselben Jahre Galle in Berlin den Planeten wirklich auffand, und zwar am Abend des Tages, an dem er Leverriers briefliche Aufforderung zum Aufsuchen des Sternes erhalten hatte. Dieser Planet heißt Neptun; er ist rund 4 500 000 000 km von der Sonne entfernt.
5. Arten. Die Planeten, die näher an der Sonne stehen als die Erde, nennt man untere, die entfernteren obere Planeten. Jene können nie in Opposition[76] mit der Sonne stehen, d. h. so, daß die Erde zwischen ihnen und der Sonne steht, sondern nur in oberer oder unterer Konjunktion, d. h. so, daß entweder die Sonne zwischen ihnen und der Erde oder sie zwischen der Sonne und Erde erscheinen. Die oberen Planeten können in Opposition oder oberer Konjunktion mit der Sonne stehen. – Man scheidet auch wohl die Planeten zwischen Sonne und Planetoidenzone als innere, die jenseits der Planetoidenzone gelegenen als äußere Planeten.
6. Umlaufszeit. Die Umlaufszeiten der Planeten sind folgende:
| Merkur | 88 Tage, |
| Venus | 225 Tage, |
| Erde | 1 Jahr, |
| Mars | 1 Jahr, 322 Tage, |
| Jupiter | 11 Jahre, 315 Tage, |
| Saturn | 29 Jahre, 167 Tage, |
| Uranus | 84 Jahre, 7 Tage, |
| Neptun | 164 Jahre, 285 Tage. |
Die Umlaufszeiten der Planetoiden liegen zwischen 3 und 8 Jahren.
7. Bahnen. Alle Planeten bewegen sich um die Sonne von Westen über Süden nach Osten in Ellipsen, in deren einem Brennpunkte die Sonne steht. Für alle gibt es also ein Perihel und ein Aphel. Die vorher angegebenen Entfernungen von der Sonne sind stark abgerundete mittlere Entfernungen.
Keine Planetenbahn fällt mit irgend einer zweiten in dieselbe Ebene. Daher sind also auch alle Planetenbahnen gegen die Ekliptik geneigt. Die Neigungswinkel sind aber so klein, daß die Bahnen sämtlich innerhalb des Tierkreises liegen. Nur einige Planetoiden machen eine Ausnahme.
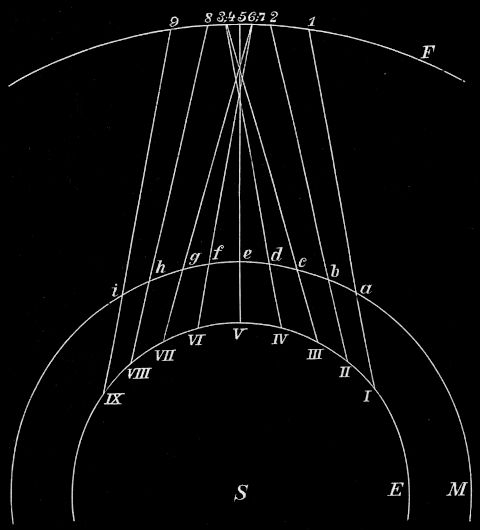
8. Rückläufigkeit. Nach dem Augenschein sollte man meinen, daß die Bahnen der Planeten viel verwickeltere krumme Linien seien. Beachten wir z. B. eine Zeitlang die Venus und zeichnen täglich in eine Sternkarte den Ort ein, wo sie am Fixsternhimmel beobachtet wurde, so wird sich nicht nur finden, daß die Bewegung des Planeten mit sehr ungleichen Geschwindigkeiten zu erfolgen scheint; vielmehr wird es sogar den Eindruck machen, als stehe der Stern, nachdem er anfangs von Westen nach Osten fortgeschritten, einige Tage fast still und bewege sich höchstens etwas von Norden nach Süden, um dann plötzlich von Osten nach Westen weiter zu wandern, nach einiger Zeit wieder stillzustehen und endlich den Weg von Westen nach Osten fortzusetzen. Der Stern wird so scheinbar eine ganze Schleife durchlaufen. Die Bewegung von Westen nach Osten nennt man rechtläufig (recht = richtig), die von Osten nach Westen rückläufig. Ähnliche Beobachtungen kann man auch an den Bahnen der oberen Planeten machen. Fig. 42 soll uns diese merkwürdige Erscheinung erklären. In S stehe die Sonne, die Kreisbogen E, M, F seien Stücke der Erdbahn, der Marsbahn und des Fixsternhimmels. Die Planetenbahnen sind also der Einfachheit wegen kreisförmig angenommen. Wir beobachten die Bewegungen des Mars einige Zeit vor und nach der Opposition. Den Stellungen der Erde in I, II, III … IX entsprechen die gleichzeitigen Stellungen des Mars in a, b, c … i; die Stellung V–e ist die der Opposition. Steht die Erde in I, so sieht der Beobachter den Stern in der Verlängerung von I–a, also in 1 am Fixsternhimmel. Ist die Erde bis II fortgerückt, so erscheint dem Beobachter der Mars in 2, er ist also rechtläufig[77] fortgewandert. Diese Wanderung setzt er fort bis 3. Dort aber scheint er einige Zeit stillzustehen; denn auch von IV aus sieht ihn der Beobachter noch an dieser Stelle. Von nun an zieht er offenbar rückläufig weiter über 5 bis 6, steht hier wieder scheinbar still und schlägt nun wieder die rechtläufige Bewegung ein. Zum völligen Verständnis ist noch zu beachten, daß E und M nicht in derselben Ebene liegen, sondern daß ihre Ebenen etwas gegeneinander geneigt sind; daher wird die rückläufige Bewegung von 4 nach 5 nicht an denselben Fixsternen vorübergehen, wie vorher die rechtläufige auf dieser Strecke, sondern es werden Schleifen entstehen.
9. Rotation. Bei einigen Planeten ist auch eine Rotation um ihre Achse nachgewiesen durch Beobachtung von Flecken auf ihrer Oberfläche. Der Merkur braucht zu einer Rotation wahrscheinlich so viel Zeit, wie zu einer Revolution, 88 Tage, würde sich also zur Sonne wie der Mond zur Erde verhalten. Von der Venus glaubte der berühmte italienische Astronom Schiaparelli 1892 dasselbe nachgewiesen zu haben; doch haben noch neuere Forschungen die ältere Annahme wahrscheinlicher gemacht, daß die Rotation der Venus etwa 24 Stunden währe; ungefähr ebensolange dauert eine Rotation des Mars. Jupiter rotiert in ca. 10 Stunden. Bedenkt man, daß dieser Stern 310mal so groß wie Erde ist, so ergibt sich, daß ein Punkt seines Äquators mit rasender Geschwindigkeit rotieren muß. Auch die Rotation des Saturn dauert ca. 10 Stunden. Von den übrigen Planeten ist eine Rotation noch nicht erwiesen, aber wahrscheinlich.
1. Merkur und Venus. Von der Beschaffenheit der unteren Planeten weiß man noch nicht viel; denn sie sind nur kurze Zeit am Tage zu beobachten. Das liegt zunächst an ihrer geringen Entfernung von der Sonne, die bewirkt, daß sie beide wenig vor oder nach ihr auf- und untergehen und daher entweder nur einige Zeit vor Sonnenaufgang am östlichen oder nur einige Zeit nach Sonnenuntergang[78] am westlichen Himmel sichtbar werden. Die Venus erscheint, besonders wenn sie der Erde nahe in ihrer Bahn ist, als größter, leuchtendster Stern und ist bekannt unter dem Namen Morgen- oder Abendstern.
Im Fernrohr zeigen beide Sterne Phasen wie der Mond. Das ist leicht erklärlich: Zur Zeit der unteren Konjunktion kehren sie uns, wie der Mond in Konjunktion ihre unbeleuchtete Seite zu, sind also gerade, wenn sie uns am nächsten stehen, unsichtbar; von da auf dem Wege zur oberen Konjunktion gelangen sie durch die Sichelform zum ersten Viertel, werden in der oberen Konjunktion voll usw.
In der unteren Konjunktion gehen beide zuweilen, wie der Mond bei Sonnenfinsternissen, zwischen Erde und Sonne hindurch und erscheinen als schwarze Flecke auf der Sonne. Die Durchgänge der Venus sind besonders wichtig für die genaue Berechnung der Entfernung der Sonne von der Erde.
Der Merkur ist sehr klein, sein Halbmesser beträgt nur 2400 km; er hätte etwa 19mal in der Erde Platz. Seine Dichte beträgt 4/5 von der der Erde.
Daß er eine Atmosphäre hat, ist noch nicht sicher erwiesen, aber wahrscheinlich. Nehmen wir dies an, so kann man folgende Vermutung über ihn anstellen. Ein Teil wird zwar stets von der Sonne abgekehrt sein, wie ein Teil des Mondes von der Erde; aber die ewige Nacht wird ziemlich hell sein; denn die atmosphärische Strahlenbrechung wird ihr mehr Licht zuführen als uns in hellen Sommernächten, da die Lichtwirkung der Sonnenstrahlen wegen der Nähe der Sonne siebenmal so stark ist als bei uns. Ebenso verhält es sich mit der Wärmewirkung der Sonnenstrahlen. Daher wird die stets beleuchtete Seite glühend heiß sein, die Nachtseite angenehm erwärmt durch die zu ihr als der kühleren herumströmenden warmen Winde.
Der Halbmesser der Venus beträgt 6300 km; sie ist also ungefähr ebenso groß wie die Erde. Auch ihre Dichtigkeit ist ungefähr die der Erde.
Eine Atmosphäre ist ziemlich sicher auf ihr nachgewiesen, besonders überzeugend bei Venusdurchgängen, wo die dunkle Venusscheibe, kurz bevor sie vor die Sonnenscheibe trat, durch einen hellen sie umgebenden Ring sichtbar wurde. Dieser kann nur als das durch atmosphärische Reflexion um den ganzen Planeten herumgeführte Sonnenlicht erklärt werden, dessen Wirkung ja bei der größeren Nähe auch hier noch stärker ist als auf der Erde. Die Atmosphäre der Venus scheint beständig starke Wolkenbildung zu haben und viel Wasserdampf zu enthalten, was ja bei der starken Erwärmung natürlich wäre. Man kann also annehmen, daß auf diesem Planeten eine feuchte Treibhauswärme herrscht, bei der jedoch menschenähnliche Wesen und Pflanzenwuchs wohl bestehen könnten.
2. Mars. Der Mars ist uns unter allen Planeten am bekanntesten, da er der Erde bei besonders günstigen Umständen bis auf 55 000 000 km nahe kommen kann und gerade, wenn er ihr nahe ist, in der Opposition, seine vollbeleuchtete Scheibe die ganze Nacht zeigt. Er ist kenntlich an seinem roten Lichte.
Sein Halbmesser beträgt 3370 km, seine Dichtigkeit etwa 4/5 von der der Erde. Eine Abplattung hat weder bei ihm noch bei Merkur und Venus mit Sicherheit nachgewiesen werden können.
Eine Atmosphäre, die der irdischen sehr ähnlich ist, wurde bisher allgemein angenommen; aber neuere Beobachtungen der Lick-Sternwarte widersprechen dieser Annahme und haben zu der Auffassung geführt, daß die Marsatmosphäre, wenn sie überhaupt vorhanden ist, höchstens ¼ der Dichte unserer Atmosphäre erreichen kann.
Auf der Oberfläche des Planeten unterscheidet man deutlich zwei Arten umfangreicher Flecke, rötlichgelbe und blaugraue; jene überwiegen und bilden auf der nördlichen Halbkugel des Mars größere zusammenhängende Massen, während auf der südlichen Hälfte die grauen Flecke überwiegen, aber auch noch durch größere eingelagerte gelbe Flecke unterbrochen werden. Man nimmt meistens an, daß die gelben Flecke Festland, die grauen Wasser sind. Dieses ist dann auf dem Mars in verhältnismäßig geringer Menge vorhanden und bildet nur auf der südlichen Halbkugel ein größeres Meer. Auch dies scheint nicht tief zu sein, so daß es den Eindruck macht, als ob auf weitere Strecken das Land durch das Wasser hindurchschimmerte. Noch wunderbarer ist das Auftreten der sogenannten Kanäle auf dem Mars. Das sind schnurgerade graue Linien, oft mehrere tausend Kilometer lang, die das ganze Land wie ein Netz durchziehen. Sie verbinden das südliche Meer mit kleineren Wasserbecken im Lande und dem kleinen Meer um den Nordpol. Man hat sie und ihre wechselnde Gestalt auf die Jahreszeiten zurückgeführt. Diese müssen wegen der starken Neigung des Äquators gegen die Bahn des Mars und wegen der starken Exzentrizität der Marsbahn viel bedeutendere Gegensätze bewirken als bei uns und zum Sommer starke Schneeschmelzen bringen, besonders auf der südlichen Halbkugel, die zur Zeit des Perihels Sommer hat. Das ergibt sich auch aus einer weiteren Beobachtung. An den beiden Polen und auch an anderen Stellen des Mars zeigen sich zeitweise große weiße Flecke von wechselnder Ausdehnung, die sich an den Polen dauernd halten. Man wird sie als Schnee oder Eis ansehen müssen. Dafür spricht auch der Umstand, daß nach starker Nebelbildung in der Atmosphäre des Mars manchmal weite Strecken des Landes für kurze Zeit weiß erscheinen, als sei Schnee gefallen. Die großen Wassermengen, die also zu Beginn der wärmeren Jahreszeit namentlich auf der wasserreichen südlichen Halbkugel durch die Schneeschmelze sich sammeln würden, könnten aber nicht, wie auf der Erde, sich frei nach dem Äquator zu ergießen. Ein Ausgleich wäre nur über das Festland hin möglich, und dieser geschieht, so nimmt man an, durch jene Kanäle. Aber es gibt noch eine Erscheinung, die auch bei dieser Annahme rätselhaft bleibt; das ist die Verdoppelung der Kanäle. Zeitweise erscheinen die Kanäle plötzlich als zwei parallele Linien, die, um überhaupt von uns noch als getrennt wahrgenommen zu werden, mindestens 60 km voneinander entfernt sein müssen. Kein Erklärungsversuch hat bisher diesen Vorgang befriedigend gedeutet.
Man hat auch wegen des geradlinigen Verlaufes der Kanäle, die wie ein möglichst praktisches Netz zur Verbindung und Bewässerung erscheinen, folgern wollen, daß vernünftige Wesen den Mars bevölkern oder bevölkert haben und die Schöpfer dieser Kanäle sind. Zwar ist die Durchschnittstemperatur auf dem Mars niedriger als auf der Erde, aber die Möglichkeit zum Leben ist auch für menschenähnliche Geschöpfe vorhanden, wenigstens in der Nähe der Kanäle, wenn auch die gelben Flächen wohl wegen des Wassermangels auf dem Planeten als Wüste angesehen werden müssen; aber der Annahme, daß die Kanäle Werke der Kunst und nicht der Natur sind, ist doch ihre riesige Ausdehnung sehr hinderlich. Vorläufig muß ihre Entstehung also als unaufgeklärt bezeichnet werden.
Manche Astronomen halten übrigens die Marskanäle und -meere nur für optische Erscheinungen, also nicht für wirklich vorhanden. Nachgewiesen ist mit Hilfe der modernen, besseren Instrumente, daß nicht, wie man früher annahm, alle Kanäle[80] sich verdoppeln, und daß manche Kanäle, die man mit kleineren Fernrohren nachgewiesen zu haben glaubte, gar nicht vorhanden sind.
3. Jupiter. Seine Leuchtkraft ist in Opposition fast so stark wie die des Mars in Opposition, in Konjunktion bedeutend stärker, auch stärker als die des hellsten Fixsternes. In tiefer Nacht ist er also der hellste Stern, da dann die Venus nie sichtbar ist.
Sein Halbmesser beträgt über 70 000 km, seine Oberfläche ist 118mal so groß als die der Erde. Er ist bei weitem der größte Planet, und seine Masse ist 2½mal so groß als die aller übrigen Planeten zusammen. Daher bewirkt er bedeutende Störungen in der Bahn des Saturn. Seine Abplattung ist sehr bedeutend, etwa 1/15,6, was für die schon erwähnte rasende Rotation seiner Äquatorteile spricht. Seine Dichtigkeit ist gering, noch nicht ¼ der Dichtigkeit der Erde. Man schließt daraus, daß seine Oberfläche noch sehr weich und dünn sein muß.
Wahrnehmen kann man von dieser Oberfläche nichts; denn aus zahlreichen Gründen und Beobachtungen ergibt sich, daß er von einer sehr dichten Atmosphäre umgeben ist. Daher nehmen wir durch das Fernrohr nur die Wolkenbildungen derselben wahr. Charakteristisch für die Atmosphäre des Jupiter sind parallel zum Äquator in ihr verlaufende dunkle Streifen, die am Äquator ein breites Band bilden. Offenbar handelt es sich um Wolkenbildungen, deren Anordnung in der schnellen Rotation ihre Erklärung findet.
Die Neigung des Äquators zur Bahn ist unbedeutend; daher können die Verschiedenheiten der Jahreszeiten nicht bedeutend sein.
4. Saturn. Er leuchtet mit mattem, weißem Lichte. Sein Halbmesser beträgt etwa 60 000 km; er ist nächst Jupiter der größte Planet. Seine Dichtigkeit beträgt nur 1/7 von der der Erde und ist nicht größer als die des Alkohols. Die Abplattung ist 1/10; kein Planet ist so stark abgeplattet.
Im übrigen hat er mit dem Jupiter viel Ähnlichkeit; die dichte Atmosphäre, die die Oberfläche unsichtbar macht, die Streifen, die wohl nur wegen der größeren Entfernung nicht so stark hervortreten, mit einem breiten Gürtel am Äquator, finden sich auch bei ihm.
Was ihn aber im Teleskop von jedem anderen Gestirn unterscheidet, ist sein Ringsystem. Genau um den Äquator legt sich eine Schar leuchtender konzentrischer Ringe, die sich in drei Gruppen mit größeren Zwischenräumen sondern. Am hellsten ist der mittlere, am mattesten der innerste Ring. Um diese Ringe legt sich keine Atmosphäre. Die Breite des ganzen Systems beträgt 277 000 km, der Abstand des innersten Ringes von dem Planeten über 11 000 km. Da der Äquator gegen die Ekliptik geneigt ist, sehen wir ziemlich die halbe Umlaufszeit, also ca. 14 Jahre, die obere Seite des Ringes; dann erscheint er kurze Zeit fast wie ein Strich, verschwindet ganz, was seine geringe Dicke gegenüber dem gewaltigen Durchmesser beweist, und zeigt dann die untere Seite. Mit Hilfe der Spektralanalyse hat man nachgewiesen, daß der Ring um den Saturn rotiert, aber nicht als Ganzes; denn dann müßten die äußersten Teile die größte Geschwindigkeit haben. Das Gegenteil ist aber der Fall, die innersten Teile haben die größte Geschwindigkeit. Daher nehmen manche Forscher an, daß der Ring aus zahllosen sehr kleinen getrennten Trabanten besteht, von denen[81] natürlich die nächsten als die am stärksten vom Planeten angezogenen am schnellsten rotieren müssen.
5. Uranus. Er leuchtet in mattgrünem Lichte. Sein Halbmesser beträgt etwa 27 000 km, seine Dichtigkeit ¼ der Erddichtigkeit. Eine Abplattung ist nicht mit Sicherheit erwiesen.
Eine sehr dichte Atmosphäre ist nach spektroskopischen Untersuchungen sicher vorhanden. Von der Oberfläche oder von Bewegungen in der Atmosphäre ist wegen der weiten Entfernung nichts wahrzunehmen.
6. Neptun. Über diesen Planeten sind wegen seiner gewaltigen Entfernung besondere Angaben nicht zu machen. Sein Halbmesser beträgt etwa 25 000 km.
1. Gestalt. Von alters her sind die Kometen wegen ihrer Gestalt Gegenstand der Phantasie und des Aberglaubens gewesen.
Man unterscheidet an ihnen die Nebelhülle mit dem Kern oder Kopf und den Schweif; doch gibt es auch schweiflose Kometen. Man hat auch Kometen mit mehreren Kernen beobachtet, z. B. 1860 und 1873.

Der Schweif, meist besenförmig sich ausbreitend, leuchtet weniger als der Kopf. Auch die fächerförmige Gestalt ist schon beobachtet worden (Fig. 43 und 44).

Die Gestalt ist veränderlich. Taucht ein Komet im Weltraume auf, so erscheint er erst wie ein Nebelfleck. Je mehr er sich der Sonne nähert, desto größer und glänzender wird er, und im Kopfe beginnt der Vorgang, dessen Ergebnis der Schweif ist. Vom Kopfe werden leuchtende Massen ausgestoßen, die meist zur Sonne hin gerichtet sind. Die ausstoßende Kraft erlahmt allmählich, die ausgestoßenen Massen werden durch eine Repulsivkraft der Sonne zurückgestoßen und zum Schweife geformt, der oft sehr lang wird. (Die Erscheinung hat Ähnlichkeit mit einem Springbrunnen.)
Die Schweifbildung erfährt zuweilen eine Wiederholung. Bei Annäherung an[82] die Sonne wird der Kopf kleiner, ja beim Kometen von 1819 verschwand er gänzlich, d. h. er wurde ganz zum Schweife verwendet. Der Schweif ist meist der Sonne abgewandt.
Es kommt vor, daß der Kern ganz zerrissen wird und aus einem Kometen mehrere werden, die dann alle in derselben Bahn sich bewegen.
2. Zahl. Sie sind lange nicht alle mit dem bloßen Auge erkennbar. Ihre Zahl muß recht groß sein; man kennt etwa 800. Mit unseren vervollkommneten Instrumenten werden jetzt alle Jahre Kometen entdeckt.
3. Bahnen. Ihre Bahnen sind aufs verschiedenste gegen die Ekliptik geneigt und gehen teils von Westen nach Osten, teils von Osten nach Westen. Ihre Exzentrizität ist sehr bedeutend; daher erscheinen sie wie Parabeln, krumme, nicht geschlossene Linien mit einem Brennpunkte; doch es ist wahrscheinlich, daß die meisten Kometen sich in sehr flachen Ellipsen bewegen, in deren einem Brennpunkte die Sonne steht. Natürlich ist deshalb die Geschwindigkeit in den verschiedenen Teilen der Bahn sehr verschieden und in der Nähe der Sonne so groß, daß sie uns nur kurze Zeit sichtbar bleiben. Sicher bewegen sich die siebzehn Kometen, die periodisch wiederkehren oder wenigstens früher wiedergekehrt sind, in Ellipsen. Zu ihnen gehören:
4. Masse. Ihre Masse ist sehr gering, aber ihr Volumen sehr groß; sie sind also sehr wenig dicht. Fixsterne erscheinen darum auch durch ihren Schweif hindurch fast gar nicht verdunkelt.
5. Wesen. Die Ansichten über das Wesen der Kometen sind noch sehr geteilt. Auf Grund spektroskopischer Untersuchungen findet man jetzt öfters folgende Annahme: Der Kern ist aus vielen kleinen Steinen gebildet und von einer Atmosphäre aus Kohlenwasserstoff und Kohlenoxyd umgeben. Nähert sich diese Masse hinreichend der Sonne, so entwickeln sich in der dieser zugekehrten Seite unter dem Einfluß der Wärme gewaltige Gasmassen, die nach der Sonne zu fliegen.[83] Diese Gase sind durch die Reibung im Innern elektrisch geworden, werden von der gleichnamigen Elektrizität abgestoßen, die infolge der Ausbrüche in der Sonne (Protuberanzen), von denen bei der Sonnenfinsternis die Rede war, auch auf deren Oberfläche angesammelt ist. So biegen die Dämpfe allmählich hinter dem Kern um und bilden den Schweif.
Diese Annahme würde es auch durch den Einfluß der Sonnenhitze erklärlich machen, daß zuweilen die Kerne zerreißen und mehrere Kometen entstehen.
Das Zurückweichen der Dämpfe hinter den Kometenkern und die Bildung des Schweifes wird auch durch eine von dem Engländer Maxwell aufgestellte und von dem Schweden Svante Arrhenius durch Versuche nachgewiesene Theorie erklärt, nach der das Licht einen Druck ausübt, dessen abstoßende Kraft auf sehr kleine Massen stärker wirkt als die Anziehung des leuchtenden Körpers.
1. Arten. Zu den Meteoren rechnet man die Sternschnuppen und die sogenannten Feuerkugeln.
2. Erscheinung. a) Sternschnuppen sind mild leuchtende Funken mit langem, schmalem Schweif, die wie ein lichter Streif mit großer Geschwindigkeit durch den Raum eilen und kaum eine Sekunde sichtbar sind. Lichtstärke und Lichtfarbe sind verschieden. Ihre Zahl ist sehr groß, täglich 300 bis 400 Millionen. Man sieht jedoch die wenigsten. Es erscheinen mehr nach der Mitternacht, am meisten gegen Morgen. Ihre Höhe über der Erdoberfläche beträgt im Durchschnitt 70 bis 120 km; doch steigen einige bis 8 km zum Erdboden herab. Jedenfalls treten sie stets in die Atmosphäre der Erde ein. Ihre Bahn ist fast nur eine absteigende. Ihre Geschwindigkeit beträgt in einer Sekunde 40 bis 60 km.
b) Feuerkugeln sind große, blendend in sehr verschiedenen Farben leuchtende Körper von verschiedener Gestalt, meist mit glänzendem Schweife, die mit der Geschwindigkeit der Sternschnuppen durch die Luft fliegen, manchmal unter lautem Getöse, meist in ziemlicher Höhe, zerplatzen und dann wohl zum Teil in Dampf aufgehen, zuweilen aber auch größere oder kleinere feste Bruchstücke auf die Erde fallen lassen. Die Steine heißen Meteorite oder Aërolithe (griech. = Luftsteine).
3. Arten der Sternschnuppen. In allen Nächten fallen sporadische, vereinzelte Sternschnuppen. Viel wichtiger und interessanter sind die periodisch wiederkehrenden Sternschnuppenschwärme, die oft einen Anblick von wunderbarer Pracht gewähren. Es ist sicher, daß diese Schwärme in geschlossenen Bahnen die Sonne umkreisen und dabei zu bestimmter Zeit die Bahn der Erde schneiden. Sie machen den Eindruck, als kämen sie alle von einer bestimmten Stelle der Himmelskugel her, die man den Radiationspunkt nennt. Das erklärt sich daraus, daß die Bahnen aller dieser Meteore nahezu parallel sind und daher für einen Beobachter, etwa wie die Schienen einer Eisenbahnstrecke, in weiter Ferne zusammenzulaufen scheinen. Nach den Sternbildern, in denen der Radiationspunkt zu liegen scheint, bezeichnet man die Schwärme. Die bekanntesten sind folgende: Der Perseidenschwarm aus dem Sternbilde des Perseus, der alljährlich in den Nächten des 10. und 11. August eine mäßige Anzahl Sternschnuppen bringt. Viel prächtiger ist der Leonidenschwarm (Löwenschwarm), seit 1799, wo ihn[84] Alexander von Humboldt zum ersten Male beobachtete, bekannt. Er ist alle 33 bis 34 Jahre um den 12. bis 14. November wiedergekehrt; seine Bahn ist als zusammenfallend mit der eines bekannten Kometen nachgewiesen, 1866 erschien er zu einer genau vorausgesagten Zeit, aber 1899 blieb er wider Erwarten aus oder brachte wenigstens keinen nennenswerten Meteorfall. Alle sechs bis sieben Jahre endlich kehrt, seit 1841 beobachtet, in der Bahn des Bielaschen Kometen der Andromedaschwarm Ende November oder Anfang Dezember wieder, ist aber seit dem letzten stärkeren Auftreten im Jahre 1892 wenig mehr hervorgetreten.
4. Arten der Meteorite. Die Meteorite enthalten entweder vorwiegend Eisen (ca. 90%), oder sie sind Steine, die hauptsächlich aus Kieselerde, Magnesin, Tonerde und Schwefel bestehen. Das Meteoreisen zeigt, mit verdünnter Salpetersäure geätzt, eigentümliches kristallinisches Gefüge, die Widmannstättenschen Figuren.
5. Erklärung. Alle diese Erscheinungen werden angesehen als kosmische (im Weltraum sich bewegende) Massen, die in den Bereich unserer Sonne geraten und so bleibend oder vorübergehend ihrer Anziehung unterliegen. Die periodischen Sternschnuppenschwärme sind jedenfalls vielfach aufgelöste Kometen. Damit wird nicht nur das Ausbleiben des Bielaschen Kometen seit 1856 verständlich, sondern auch das Ausbleiben von Sternschnuppenschwärmen, die sich wahrscheinlich immer mehr auseinanderziehen und gleichmäßig auf die Bahn verteilen.
Das Leuchten erklärt sich aus der Geschwindigkeit, mit der diese Körper in unsere Atmosphäre eindringen, und dem dadurch veranlaßten Widerstand der Atmosphäre, der ihre Bewegung verlangsamt und an ihrer Rinde in Licht und Wärme umsetzt, wobei die erhitzte Luft mit glühenden, vom Meteor losgerissenen Teilchen als Schweif folgt. Je nachdem die Meteore den Widerstand der Luft überwinden können oder nicht, treten sie wieder heraus aus der Atmosphäre oder verlieren ihre ganze Geschwindigkeit und fallen zur Erde, wobei häufig wegen des starken Gegensatzes zwischen der erhitzten Rinde und dem kalten Kerne die Explosion erfolgt.
1. Größenverhältnisse. Der Durchmesser der Sonne ist 108½mal so groß als der der Erde, also etwa 1 383 000 km lang. Ihren Umfang würde ein Schnellzug mit einer Geschwindigkeit von 25 m in der Sekunde erst in 5½ Jahren zurücklegen. Die Oberfläche ist 11 800mal so groß als die der Erde. Ihr Volumen ist 1 280 000mal so groß als das der Erde, ihre Masse 324 000mal so groß als die der Erde und 700mal so groß als die aller Planeten zusammen. Aus dem Verhältnis von Masse und Oberfläche ergibt sich ihre Dichtigkeit = 324 000/1 280 000 = ¼ der Dichtigkeit der Erde.
2. Die Granulation der Oberfläche. Für das menschliche Auge gibt es nichts Glänzenderes als die Sonne. Ihr Licht blendet so, daß alle Beobachtungen unter Abblendung des grellen Lichtes geschehen müssen. Betrachtet man so die Sonne durch ein Fernrohr, so erscheint ihre Oberfläche nicht als gleichmäßig helle Scheibe, sondern es wechseln auf ihr hellere und dunklere Fleckchen ab. Bei starker Vergrößerung hat man etwa den Eindruck, als lägen über der leuchtenden Sonne eine Unzahl von Wölkchen. Man nennt diese Erscheinung Granulation der Oberfläche.
3. Die Sonnenflecke. a) Verlauf eines Flecks. In den meisten Zeiten erscheinen auf der Sonnenscheibe dunkle Stellen, welche Sonnenflecke genannt werden. Gestalt und Größe derselben wechseln beständig, sie haben aber eine stufenmäßige Entwicklung. Ihren Anfang bezeichnet gewöhnlich eine gewisse Unruhe in der Schicht glühender Gase, die die Sonne zunächst umgibt, dem sogenannten Lichtgewölk oder der Photosphäre (griech. = Lichtgebiet), wobei sich kleine dunkle Flecke oder sogenannte Poren auf der Granulation bilden. Eine derselben gewinnt die Oberhand und erweitert sich allmählich zu einem größeren, scheinbar ganz schwarzen Fleck von zuweilen rundlicher, meist sehr unregelmäßiger, zackiger Form. Die eigentliche Farbe ist aber braungrau, und der Fleck strahlt noch Licht aus. Das zeigt sich z. B. beim Durchgang der wirklich schwarzen Venusscheibe. In dem Kernfleck sind wieder hellere und dunklere Stellen zu unterscheiden. Die Kernflecke sind meist von einer schmäleren oder breiteren Lichteinfassung, Lichthof oder Penumbra genannt, umgeben, welche nach außen scharf abgegrenzt ist und eine strahlige Struktur hat. Der innere Teil der Penumbra erscheint stets heller leuchtend als der äußere. Die Form der Penumbra ist nicht immer dem Kernfleck ähnlich, vielmehr oft auf der östlichen Seite zerklüftet.
Will ein Fleck sich schließen, so strömen Lichtmengen aus dem Lichthofe von allen Seiten herbei, und zwar anfangs ziemlich genau nach der Mitte des Flecks. Dabei bilden sich dann oft Lichtstreifen, die quer über den Kernfleck ziehen und wie Brücken über dem Abgrunde schweben. Diese Brücken lösen sich wie Wolken allmählich auf, und ihre Reste schwimmen wie ein Lichtpunkt auf dunklem Grunde. Manche Teile des Kernflecks überziehen sich mit sogenannten Schleiern, die oft ein rosenfarbiges Licht haben und meist nach kurzer Zeit verschwinden. Ist der Fleck seinem Ende nahe, so geschieht das Hinzuströmen der Lichtmassen unregelmäßiger, bis er endlich ganz verschwunden ist.
b) Zonen der Sonnenflecke. Nicht oder doch selten erscheinen sie in der Nähe des Sonnenäquators, am häufigsten zwischen 10 und 30° nördlicher und südlicher Breite.
c) Perioden der Sonnenflecke. Schwabe hat von 1826 bis 1850 eine gewisse Periodizität der Flecke beobachtet. Wolff in Zürich fand eine 11½jährige Periode. Es zeigt sich deutliche Übereinstimmung zwischen den Schwankungen der Häufigkeit der Sonnenflecke und den Schwankungen der Deklinationsnadel, für die auch eine 11jährige Periode existiert. Da aber diese Schwankungen ebenso wie die Häufigkeit des Polarlichts auf der Erde mit den Wirkungen des Erdmagnetismus zusammenhängen, so ist es nicht wunderbar, daß auch zwischen Sonnenfleckenperiode und der ebenfalls 11jährigen Polarlichtperiode große Übereinstimmung herrscht.
d) Größe der Sonnenflecke. Die Größe der Sonnenflecke ist sehr verschieden. Manche zeigen sich selbst im Fernrohre nur als sehr kleine Öffnungen, Poren; andere kann man hinter farbigen Brillengläsern schon mit bloßem Auge[86] wahrnehmen. 1779 sah Herschel einen Fleck, der 18,3 cm scheinbaren, also ca. 200 000 km wirklichen Durchmesser hatte.
e) Dauer der Sonnenflecke. Sie ist verschieden, bis zu 6, ja 8 Monaten, beträgt aber meistens nur einige Tage. Der vom Astronomen Schwabe 1850 am 5. September beobachtete Sonnenfleck vergrößerte sich an einem Tage um 160 000 km. Welche unendliche Schnelligkeit also in der Bewegung der einzelnen Teilchen! Die Flecke bleiben auch nicht an derselben Stelle, sondern sie gehen vom östlichen zum westlichen Sonnenrande. Je mehr sich ein Fleck dem Rande nähert, desto breiter erscheint die dem Rande nächste graue Einfassung, und desto schmäler wird die andere Seite. Auch der Kernfleck erscheint schmäler, bis er zuletzt verschwindet. Diese Änderungen sind nur zum Teil wirklich, zum Teil sind sie perspektivischer Natur und hängen von dem Winkel ab, unter dem wir den Fleck und seine Umrandung sehen.
4. Die Rotation der Sonne. Da sich alle Sonnenflecke auf der Sonnenoberfläche von Osten nach Westen bewegen, so ist damit erwiesen, daß die Sonne von Osten nach Westen rotiert. Man hat die Dauer dieser Rotation auf 25 Tage festgesetzt; doch ist diese Angabe zu bestimmt. Wir können nur sagen, daß die Rotationszeit von 25 bis 28 Tagen nicht viel abweichen wird. Die Beobachtungen sind nämlich schwierig, weil die Zahl der Flecke, die während einer ganzen Umdrehung vorhanden sind, klein ist, und weil die Flecke zweifellos noch außer der Rotation, die sie mitmachen, eine eigene Bewegung haben, so daß sie nach den Polen der Sonne zu längere Zeit zu einer Umkreisung gebrauchen als am Äquator.
5. Die Sonnenfackeln. In der Umgebung der Flecke finden sich oft Stellen, die sich durch erhöhten Lichtglanz auszeichnen. Man nennt sie Sonnenfackeln. Sie scheinen oft die Vorläufer von Sonnenflecken zu sein und gleichsam die Stelle zu bezeichnen, wo später Flecke hervorbrechen werden. Ihre Gestalt und Größe sind verschieden. In der Mitte sehen sie wie geballtes Lichtgewölk aus; nach den Rändern verlaufen sie nicht selten aderförmig.
6. Die Atmosphäre der Sonne.
a) Vorhandensein. Daß die Sonne eine Atmosphäre hat, ergibt ein Blick auf eine Sonnenphotographie, wie sie jetzt in vorzüglicher Weise hergestellt werden. Darauf erscheinen deutlich die Ränder viel matter als die Mitte, und das ist ja, wie wir aus der Betrachtung des Mondes (§ 26) wissen, ein sicherer Beweis für das Vorhandensein einer Atmosphäre. Wir können sie aber auch unmittelbar sehen, wenn bei einer totalen Sonnenfinsternis die Mondscheibe uns das direkte Sonnenlicht bedeckt.
b) Teile. Die Atmosphäre besteht aus drei Hüllen. 1. Zunächst dem Kern der Sonne liegt die Photosphäre, die Schicht leuchtender Gase, der die Erscheinung der Sonnenflecke angehört (S. 3 a). Die beiden anderen Gebiete konnte man früher nur bei einer Sonnenfinsternis unterscheiden. Zu ihnen gehört 2. die Chromosphäre mit den Protuberanzen. Unmittelbar am Mondrande erscheint zunächst eine dünne, lebhaft rote Schicht. Man kann sie jetzt bei gewöhnlichem Sonnenschein mittels des Spektroskops besser wahrnehmen als bei einer Sonnenfinsternis, da dann die Mondscheibe sie zum Teil verdeckt. Sie heißt Chromosphäre (griech. von chrōma = Farbe). Aus ihr sieht man lebhaft rote Gebilde hervorbrechen, die Protuberanzen (lat. = Hervorragungen). Früher konnte man sie auch nur bei Sonnenfinsternissen wahrnehmen; die Spektralanalyse hat uns die Mittel gegeben, sie auch bei hellem Sonnenschein zu beobachten. Man weiß jetzt, daß sie sich schnell entwickeln und verändern und oft wie großartige vulkanische Ausbrüche[87] erscheinen, die sich mit ungeheurer Geschwindigkeit zu gewaltigen Höhen erheben. Man will Protuberanzen von ca. 170 000, ja 1893 sogar eine Protuberanz von 480 000 km Höhe (= 1/3 Sonnendurchmesser) beobachtet haben.
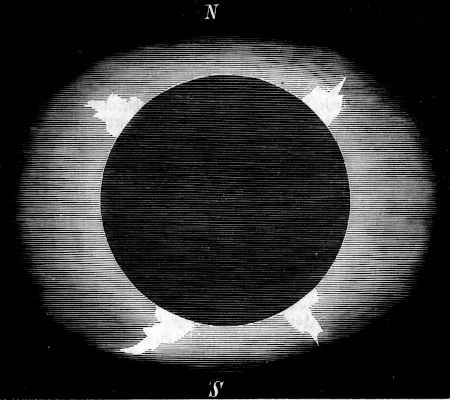
Um die Chromosphäre legt sich 3. die Corona (lat. = Kranz) (s. Fig. 45). Sie ist der glänzende Ring von grünlichweißem Lichte, welcher den dunklen Mond bei totalen Sonnenfinsternissen umsäumt; sie ist auch schon gelblich oder rötlich gesehen worden. Ihre Breite ist am geringsten an den Polen der Sonne, am ausgedehntesten in den mittleren Breiten; ihr Glanz ist unmittelbar am Monde am hellsten.
7. Die Spektralanalyse der Sonne. Die Sonne liefert ein Farbenspektrum, aber kein zusammenhängendes; bei näherem Zusehen zeigt es sich vielmehr von einer gewaltigen Zahl dunkler Linien durchbrochen. Man kennt sie lange und nennt sie nach ihrem Entdecker Fraunhofersche Linien; aber erst die Spektralanalyse hat die Ursache dieser Linien nachgewiesen. Dieses Absorptionsspektrum kann nach den sicheren Erfahrungen der Spektralanalyse nur von einem weißglühenden Körper stammen, dessen Licht vor der Zerlegung im Prisma durch matter leuchtende Gase gegangen ist. Wir können demnach sofort folgende Folgerungen aus der Beschaffenheit des Sonnenspektrums ziehen. Der Kern der Sonne ist weißglühend, fest oder flüssig. Ihn umgibt zunächst eine Atmosphäre leuchtender Gase, die Photosphäre, deren Temperatur, wie im Kern, so hoch ist, daß sich die Grundstoffe noch im Zustande[88] der Dissoziation befinden, d. h. chemische Prozesse sind dort unmöglich. Die unteren Schichten der Photosphäre liefern uns das eigentliche Sonnenlicht; die oberen sind so viel kühler, daß hier die Absorption von Strahlen stattfindet. Hier ist also die Ursache der Fraunhoferschen Linien zu suchen; Beweis: bei totalen Sonnenfinsternissen werden auf einen Augenblick alle Fraunhoferschen Linien leuchtend, sobald die Mondscheibe die unteren Schichten der Photosphäre bedeckt. In den oberen Schichten der Photosphäre glühen, wie uns die Fraunhoferschen Linien lehren, die Gase aller leichteren Metalle, die auch auf der Erde zu finden sind; die schwereren Metalle mögen nicht fehlen, werden aber wohl in tieferen Schichten der Sonne vorkommen. Von Metallen, deren Linien man früher nur im Sonnenspektrum kannte, sind in den letzten Jahren durch die Spektralanalyse viele auch in Gesteinen der Erde entdeckt und dann chemisch daraus gewonnen und untersucht worden. Daher kann man schon jetzt sagen: die Sonne besteht im wesentlichen wahrscheinlich aus denselben Grundstoffen wie die Erde. Die oberen, kühleren Schichten der Photosphäre sind auch das Gebiet der Granulation, die man jetzt meistens als Niederschläge, Wolken von Metalldämpfen, ansieht. Sie entsprächen dann etwa den Federwolken unserer Atmosphäre, die in großer Höhe dahinziehen. Die zweite Gashülle der Sonne, die Chromosphäre, ist bei Sonnenfinsternissen ebenfalls spektroskopisch untersucht worden. Sie zeigt ein Linienspektrum, besteht also aus glühenden Gasen. Es glühen in ihr hauptsächlich Wasserstoff und zwei andere Stoffe, die man Helium und Coronium nennt. Beide waren bis vor kurzem unbekannt; jetzt ist das Helium, ein Metall, auch auf der Erde in einem Mineral des hohen Nordens entdeckt. Selbst in unserer Luft sind Spuren davon. Die dritte Gashülle, die Corona, ist von sehr geringer Dichtigkeit und enthält vorwiegend Coronium, das man, wie gesagt, auf der Erde noch nicht gefunden hat. Es muß aber ein sehr leichtes Gas sein, das deshalb wohl in sehr hohen Schichten unserer Atmosphäre vorhanden sein kann. Früher hielt man Chromosphäre und Corona für bloße Lichterscheinungen, durch Brechungen in sehr bewegter Atmosphäre bewirkt; die Beobachtung ihres Spektrums hat gezeigt, daß sie Gase sind. Dasselbe gilt von den Protuberanzen. Sie haben dasselbe Spektrum wie die Chromosphäre, werden also, wie die Beobachtung schon früher zu ergeben schien, aus ihr herausgeschleudert. Die Fackeln haben das gewöhnliche Sonnenspektrum, nur heller. Man hält sie deshalb für Erhebungen in der Photosphäre und nimmt an, daß sie durch gewaltige Bewegungen im Innern emporgetrieben werden, und daß sie bisweilen zerreißen und Dämpfe aus dem Innern in die Chromosphäre treten lassen. Diese würden dann wieder die Protuberanzen emporschleudern. So wäre es erklärlich, daß öfters Spuren von Metalldämpfen in den Protuberanzen sind, und daß diese Ausbrüche stets im Gebiete der Fackeln erscheinen. Über die Sonnenflecke läßt uns bisher auch die Spektralanalyse noch im unklaren; aber gewisse Beobachtungen (große Breite der dunklen Linien in ihrem Spektrum, plötzliches Aufflammen heller Linien in diesen breiten, dunklen Linien der Flecke) lassen es wahrscheinlich erscheinen, daß die Sonnenflecke wirkliche Öffnungen in der Photosphäre sind, die einen Blick ins Sonneninnere gestatten. Aus ihnen scheinen Ausbrüche von leuchtenden Massen zu kommen. Dann wären also Fackeln, Flecke, Protuberanzen drei Abschnitte eines Ausbruches aus dem Innern der Sonne.
8. Die Sonne als Quelle des Lichtes und der Wärme. Ohne Sonne kein Leben! Sie allein bewirkt die Schwingungen des den Weltraum erfüllenden[89] Äthers, der uns die Lichtempfindungen vermittelt. Sie leuchtet wie sonst kein Licht. 300 000 Vollmonde würden kaum so viel Licht geben wie die eine Sonne. Wenn eine Ebene von der Größe der Erdoberfläche mit einer 10 m dicken Eisschicht bedeckt wäre, so würde diese in einer Minute schmelzen, wenn alle Strahlen der Sonne auf die Eisschicht gelenkt würden.
Es ist möglich, daß die Sonne sich abkühlt; aber dann muß sie sich auch zusammenziehen. Dadurch würde aber wieder Wärme erzeugt, und wenn sie ihre Dichtigkeit bis auf die Dichtigkeit der Erde steigerte, so würde dadurch der Verlust der Ausstrahlung für 17 000 000 Jahre ersetzt werden. Außerdem wird der Wärmeverlust wenigstens zum Teil durch Meteorite ersetzt, von denen bei ihrer großen Zahl und ihren exzentrischen Bahnen recht viele in die Sonne fallen werden.
Neuerdings sind viele Forscher geneigt, als wichtigste Quelle für den Ausgleich des Wärmeverlustes der Sonne chemische Vorgänge in der Sonne selbst anzusehen. Man hat nämlich durch sorgfältige Untersuchungen des neuerdings entdeckten chemischen Elementes Radium festgestellt, daß dieses allmählich in ein anderes Element, Helium, zerfällt, und daß dabei ungewöhnlich viel Wärme frei wird. Da nun in der Chromosphäre der Sonne viel Helium vorhanden ist, so schließt man mit gutem Grunde auch auf viel Radium in tieferen Schichten, und zwar in solcher Menge, daß es, wie man sagt, erst in Billionen von Jahren in Helium übergeführt sein wird.
9. Das Tierkreis- oder Zodiakallicht. Unter besonders günstigen Umständen kann bei uns ein geübtes Auge im Frühling nach der Abenddämmerung am westlichen, im Herbst kurz vor der Morgendämmerung am östlichen Himmel einen schwachen Lichtschimmer wahrnehmen. Dieser hat Pyramidengestalt; die Grundfläche liegt am Horizonte dort, wo nahe unter ihm die Sonne steht, die Achse liegt in der Ekliptik, so daß sich das Licht durch die Sternbilder des Tierkreises hinzieht. Daher hat es den Namen Tierkreis- oder Zodiakallicht. Viel schöner zeigt es sich fast allnächtlich unter den Tropen, weil hier die Ekliptik höher über den Horizont steigt. Das Wesen dieser Erscheinung ist noch nicht bekannt. Neuerdings neigt man dazu, einen Ring von dünn verteilten kleinen Massenteilchen anzunehmen, der nach Art des Saturnringes die Sonne in der Entfernung der Erde umgibt und das Sonnenlicht, wie die Planeten, Monde und der Saturnring, zurückwirft.
1. Verschiedene Systeme. a) Ptolemäus zu Alexandria, 125 n. Chr., hat zuerst ein wirkliches Sonnen-, eigentlich sogar Weltsystem: Um die im Mittelpunkte ruhende Erde kreisen 7 Wandelsterne: Mond, Merkur, Venus, Sonne, Mars, Jupiter und Saturn; das Ganze umschließt die Fixsternsphäre.
b) Das ägyptische System: Mond, Sonne, Mars, Jupiter und Saturn drehen sich um die ruhende Erde, Merkur und Venus zuerst um die Sonne, dann mit dieser um die Erde.
c) Kopernikus (geb. 1473 zu Thorn, gest. 1543 zu Frauenburg): Die Sonne ist der Mittelpunkt der Planetenbahnen, und diese sind Kreise, die nach außen immer weiter voneinander entfernt liegen in folgender Reihenfolge: Merkur, Venus,[90] Erde usw. Ähnliches lehrte schon um 270 v. Chr. Aristarch von Samos, fand aber keine Anerkennung.
d) Tycho de Brahe (gest. 1601 in Dänemark): Die Erde ist der Mittelpunkt der Welt; um sie laufen Mond und Sonne; die Sonne bildet den Mittelpunkt für die Bahnen der Planeten, zu denen also danach die Erde nicht gehört.
Dieser Versuch, zwischen dem ptolemäischen und dem kopernikanischen System zu vermitteln, war ein Rückschritt; denn gerade das Grundgesetz, daß die Sonne der Mittelpunkt ist, um den mit den anderen Planeten sich auch die Erde dreht, ist das Bleibende am kopernikanischen System. Um dieser Entdeckung willen nennen wir eben unser Sonnensystem das kopernikanische. Die Bahnen, die Kopernikus den einzelnen Planeten zuschrieb, waren durchaus falsch, weil er die Gesetze ihrer Bewegung nicht kannte.
2. Keplers Gesetze: Die drei Gesetze, nach denen sich die Planeten um die Sonne bewegen, verdanken wir Johann Kepler (geb. 1571 zu Weil in Württemberg, gest. 1630 in Regensburg). Er hat sie durch äußerst mühevolle Rechnungen und Zeichnungen gefunden, die deswegen so schwierig waren, weil er noch nicht das letzte höhere Gesetz gefunden hatte, aus dem seine drei Gesetze sich ergeben. Hier soll nur das zweite bewiesen werden, weil es einen leichten physikalisch-geometrischen Beweis zuläßt. Die Gesetze lauten:
a) Die Bahnen der Planeten sind Ellipsen, in deren einem gemeinsamen Brennpunkte die Sonne steht.
b) Die Leitstrahlen, d. h. die Verbindungslinie der Sonne mit den Planeten, beschreiben in gleichen Zeiten gleiche Flächenräume.
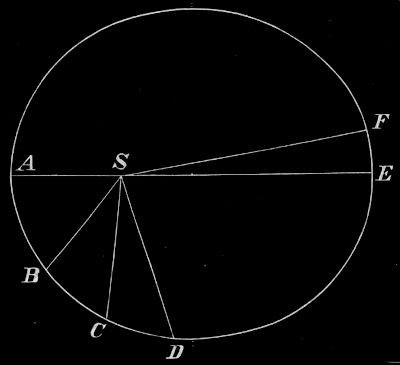
In Fig. 46 bedeutet S = Mittelpunkt der Sonne, Ellipse ABCDEFA = Bahn eines Planeten, SA, SB, SC, SD, SE, SF sind Leitstrahlen nach verschiedenen Stellungen des Planeten. Das zweite Gesetz besagt nun: Durchläuft der Planet den Ellipsenbogen AB in derselben Zeit wie die Bogen BC, CD, EF, so sind die Flächen ABS, BCS, CDS, EFS einander gleich.
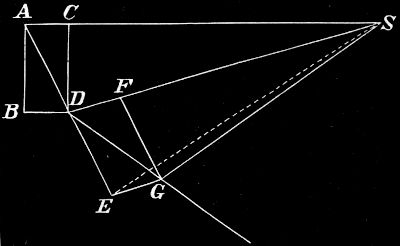
In Fig. 47 sei S = Sonne, A = Punkt einer Planetenbahn. Die Stücke der Ellipse, die der Planet in sehr kurzen Zeitteilchen, vielleicht in Sekunden, beschreibt, kann man ohne merklichen Fehler als gerade Linien ansehen. Angenommen, die Richtung und Geschwindigkeit, mit denen der Planet in A ankommt, würden bewirken, daß er in der nächsten Sekunde nach dem Beharrungsgesetze die Linie AB zurücklegte, und in derselben Zeit würde die Anziehungskraft der Sonne ihn von A bis C ziehen, so würde er nach einem allgemeinen Naturgesetze in der Sekunde in Wirklichkeit die Diagonale AD des Parallelogramms ABDC durchlaufen. Daher müßte er nach dem Beharrungsgesetze in der nächsten Sekunde in der Richtung von AD weiter bis E gehen, so daß DE = AD, wenn nicht in derselben Zeit die[91] Anziehungskraft der Sonne ihn in gerader Linie nach F zu führen strebte. Somit durchläuft der Planet in der nächsten Sekunde die Diagonale DG des Parallelogramms DEGF. Nun ist aber Dreieck ADS = DES, weil Grundlinie AD = DE und die zugehörige Höhe, das Lot von S auf AE, gemeinsam ist; Dreieck DES = DGS, weil Grundlinie DS gemeinsam ist und die gegenüberliegenden Ecken E und G auf der zu DS parallelen Linie EG liegen. Daher ist auch Dreieck ADS = DGS. Das sind aber die Flächenräume, die der Leitstrahl in zwei aufeinanderfolgenden gleichen Zeitteilchen beschreibt. Natürlich sind in Wirklichkeit die Dreiecke viel schmäler als in der Figur, und die Linien AD, DG usw. bilden keine gebrochene Linie, sondern einen Ellipsenbogen. Sind aber alle diese kleinen Teildreiecke gleich, so sind auch die aus je einer gleichen Anzahl davon gebildeten größeren Flächen (Wege von Stunden, Tagen oder anderen gleichen Zeiteinheiten) untereinander gleich.
c) Die Quadratzahlen der Umlaufszeiten zweier Planeten verhalten sich wie die Kubikzahlen ihrer mittleren Abstände von der Sonne.
Betrüge also die Umlaufszeit eines Planeten t1 Tage und sein mittlerer Abstand von der Sonne s1 km, und wären für einen zweiten Planeten die entsprechenden Größen t2 und s2, so verhält sich stets
t1² : t2² = s1³ : s2³.
Ein Beispiel zur Erläuterung: Die Umlaufszeiten des Merkur und der Erde sind, auf zwei Stellen berechnet, genau = 87,97 und 365,26 Tage; die mittlere Entfernung des Merkur von der Sonne beträgt 0,3871, wenn die der Erde = 1 gesetzt wird; es muß sich also verhalten:
87,97² : 365,26² = 0,3871³ : 1³.
In der Tat sind beide Verhältnisse = 1 : 17,2.
3. Newtons Gravitationsgesetz. Auch Keplers Entdeckung konnte noch nicht befriedigen. Seine drei Gesetze lieferten zwar Ergebnisse, die den Beobachtungen genau entsprechen, aber das Höchste wäre doch der Nachweis eines allgemein gültigen Gesetzes gewesen, aus dem jene Gesetze sich alle ableiten lassen. Diese Aufgabe hat der Engländer Isaak Newton (geb. 1643, gest. 1727) gelöst durch den strengen Nachweis des Gesetzes, daß die Schwerkraft oder Anziehungskraft, nach der sich alle Bewegungen (Fall, Wurf, Pendelschwingung) auf der Erde regeln, nicht bloß auf der Erde, sondern im ganzen Weltall stets in gleicher Weise wirkt.
Diese Wirkungsweise läßt sich kleiden in das Gravitationsgesetz: Zwei Körper ziehen einander an im geraden Verhältnis ihrer Massen und im umgekehrten Verhältnis der Quadratzahlen ihrer Entfernungen.
Danach würde also nicht nur die Erde den fallenden Stein anziehen, sondern auch dieser die Erde, und das tut er auch; allein wegen des ungeheuren Übermaßes[92] der Masse der Erde wird der Stein wohl selbst stark bewegt werden, aber keine nennenswerte Bewegung der Erde bewirken. Genau so ist es mit der Sonne und den Planeten, deren gesamte Masse nur 1/700 der Sonnenmasse ausmacht. Das Gravitationsgesetz stellt also notwendig die Sonne als den regierenden Mittelpunkt des Planetensystems hin, es erklärt die schnellere Revolution der Planeten, die der Sonne nahe liegen. Es ist, wie gesagt, auch möglich, die Keplerschen Gesetze einheitlich aus dem einen Gravitationsgesetze abzuleiten, man kann nachweisen, daß auch die Bewegung der Trabanten um ihre Planeten nach diesem Gesetze erfolgt; kurz, es ist der Schlüssel zu allen Bewegungserscheinungen unseres Weltsystems.
1. Die Kant-Laplacesche Hypothese oder Nebularhypothese. Über die Entstehung des Sonnensystems kann es nur Vermutungen, aber kein sicheres Wissen geben. Die meiste Anerkennung hat die Kant-Laplacesche Hypothese gefunden.
Hiernach ist die ganze Masse, aus der die Sonne und alle Planeten und Nebenplaneten wurden, anfangs eine rotierende, glühende Gaskugel von geringer Dichtigkeit und daher von riesiger Ausdehnung gewesen, so daß sie bis über die heutige Bahn des Neptun hinaus den Raum erfüllte. Bei ihrer gewaltigen Wärmeausstrahlung zog sich diese Masse zusammen, was eine schnellere Rotation zur Folge hatte. Hieraus ergab sich eine starke Abplattung, die schließlich am Äquator ein solches Überwiegen der Zentrifugalkraft über die Kohäsion bewirkte, daß Teile am Äquator sich aus der Masse lösten und als äquatorialer Ring weiter an der Notation teilnahmen. Dieser Ring kühlte sich schnell weiter ab und zwar ungleich wegen der stärkeren Wärmeausstrahlung am äußeren Rande, so daß er zerriß. Die Teile gestalteten sich durch Schwer- und Schwungkraft wieder kugelförmig, rotierten weiter und umkreisten auch den Mittelkörper, die Sonne, wie sie es als Teile des Ringes getan hatten. Das waren also die Planeten, aus denen durch erneute Zusammenziehung, Abplattung usw. ihre Monde sich lösten. Die Planeten und Monde kühlten sich durch Wärmestrahlung weiter ab, wurden flüssig, fest. –
2. Was spricht für die Hypothese? Für die Hypothese spricht die Spektralanalyse, die uns in der Sonne im wesentlichen dieselbe Elemente nachgewiesen hat, die wir auf der Erde finden. Auch die Meteoriten enthalten nur Elemente, wie sie auch die Erde aufzuweisen hat. Die Planeten und Monde sind in ihrer Dichte nach der Größe der Masse verschieden, der Erdmond ist starr, die Erde nur in der Kruste erhärtet, die größten Planeten sind noch weich, zum Teil leichter als Öl. Endlich kann man, wie wir im nächsten Kapitel sehen werden, in der Fixsternwelt mancherlei beobachten, was den Gedanken nahelegt, daß wir es dabei mit Sonnensystemen zu tun haben, die sich eben erst in ähnlicher Weise bilden. Nichtsdestoweniger sind auch aus Gelehrtenkreisen manche Bedenken gegen die Hypothese vorgebracht worden. Vor allem wird betont, daß die Drehung der Urnebelmasse wegen ihrer ungeheuren Ausdehnung eine äußerst langsame gewesen sein müsse. Daher sei es unerklärlich, woher die zur Abtrennung des äquatorialen[93] Ringes nötige Geschwindigkeit gekommen und wo diese Drehungsenergie geblieben sein solle. Neuerdings ist der folgende, sehr gewichtige Einwand erhoben worden. Nach der Kant-Laplaceschen Hypothese müßten alle Planeten die Sonne und alle Monde ihre Planeten in derselben Richtung umkreisen; es steht aber fest, daß der 8. Jupitertrabant und der äußerste (nach der Zeitfolge der Entdeckung der 9.) Saturntrabant in der den übrigen Bewegungen entgegengesetzten Richtung kreisen. Man hat auch andere Hypothesen aufgestellt; aber es ist bisher nicht gelungen, eine solche zu finden, die ein gleiches oder gar ein größeres Maß von Wahrscheinlichkeit hätte, als die Nebularhypothese.
1. Wesen und wirkliche Größe. Wir sahen schon, daß die überwiegende Mehrzahl der sichtbaren Sterne Fixsterne sind, d. h. Sterne, die ihre gegenseitige Lage nicht zu ändern, also still zu stehen scheinen. Sie leuchten im eigenen Lichte und zeichnen sich aus durch ein mehr oder weniger lebhaftes Funkeln (Szintillieren, lat. scintilla = der Funke), was man darauf zurückführt, daß ihr Licht sehr bewegliche, in ihrer Dichtigkeit schnell wechselnde Luftschichten durcheilt, ehe es zu uns kommt. Auch in den stärksten Fernrohren erscheinen diese Sterne nicht als Scheiben, sondern nur als Punkte, so daß man über ihre wirkliche Größe nichts sagen kann. Wohl aber ergibt sich, daß sie in ungeheuren Entfernungen von der Erde stehen müssen.
2. Scheinbare Größe. Man teilt die Fixsterne gewöhnlich nach dem Grade ihrer Helligkeit in Sterne erster, zweiter usw. Größe ein. Sterne sechster Größe kann nur noch ein gutes Auge ohne Fernrohr erkennen. Natürlich gibt diese Helligkeit allein noch keinen Anhalt über die Größe der Sterne, da sie ja auch von ihrer Entfernung mit abhängt. Die Astronomie führt die Messungen der Lichtstärke mit sehr sorgfältig gearbeiteten Photometern (griech. = Lichtmesser) aus und unterscheidet zwischen den Sternen erster, zweiter usw. Größe noch Zwischenstufen, spricht also von 2,1. oder 3,6. Größe.
3. Entfernungen der Fixsterne. Da die Fixsterne im Fernrohre als Punkte erscheinen, so haben sie keine Horizontalparallaxe. Aber man kann die Jahresparallaxe der nächsten Fixsterne bestimmen und zur Berechnung ihrer Entfernungen von der Erde benutzen. Diese Bestimmungen sind indes mühsam und unsicher und erst für wenige Sterne durchgeführt. Jedenfalls ist auch der nächste Fixstern noch mehr als 30 Billionen Kilometer oder 200 000 Sonnenweiten von uns entfernt. Das Licht, das in einer Sekunde 300 000 km zurücklegt und in 8 Minuten von der Sonne zur Erde gelangt, braucht zu der Reise von jenem Fixsterne mehr als 3 Jahre. Das Licht des hellsten Fixsternes, des Sirius, braucht[94] fast 14 Jahre, das des Polarsternes 43, das der Capella im Sternbilde des Fuhrmanns 70 Jahre, um zur Erde zu gelangen. Welche Feuerbälle, die auf solche Entfernungen so helles Licht spenden!
4. Veränderliche Sterne. Einige Fixsterne erscheinen teils in unregelmäßigem, teils in ganz bestimmtem Wechsel bald heller, bald dunkler; andere hat man ganz plötzlich hell aufflammen, aber dann wieder schnell dunkler werden sehen, ohne daß sich der Vorgang wiederholt hätte. Sogar ganz neue Sterne sind schon aufgetaucht und stets wieder nach einigen Jahren verschwunden. Über die Gründe dieser Erscheinungen hat man bisher nur Vermutungen. Interessant ist eine Erklärung, durch die man eine bestimmte Art der Veränderlichkeit verständlich zu machen sucht. Als Beispiel dient der Algol, ein Stern zweiter Größe im Sternbilde des Perseus. Dieser hat in einem Zeitraum von etwa 3 Tagen 8¼ Stunden, in denen zuerst sein Glanz 4 Stunden lang bis zur vierten Größe abnimmt, ¼ Stunde dabei bleibt, dann wieder bis zur zweiten Größe zunimmt. Man hat nun die Vermutung ausgesprochen, daß es sich um eine Art Verfinsterung durch einen in regelmäßigen Zwischenräumen an dem Fixstern vorübergehenden dunklen Stern, also einen Trabanten des Fixsternes, handle. Auch wäre die Erklärung möglich, daß auf Sternen mit periodischer Verdunkelung schon eine Abkühlung begonnen hat, die an einem Teile der Oberfläche schon bis zur Bildung einer dunklen Rinde gediehen ist. Natürlich ist dabei vorausgesetzt, daß der Stern rotiert; das nimmt man aber nach dem Muster der Sonne und der Planeten auch von allen Fixsternen an.
5. Nebelflecke. Ganz eigenartige Erscheinungen, von denen man in klarer Nacht eine Anzahl mit bloßem Auge wahrnehmen kann, sind die Nebelflecke. Das Fernrohr und das Spektroskop belehren uns, daß es sich hier um zweierlei Gebilde handelt. a) Die einen lösen sich in guten Teleskopen in einzelne Sterne auf und zeigen wie die Sonne zusammenhängende Farbenspektren, woraus sich auch ergibt, daß es sich um eine Anzahl glühender fester oder flüssiger Körper, Sterne, handelt. Diese Flecke nennt man Sternhaufen. Ein solcher Sternhaufen ist z. B. die Plejadengruppe, in der man die hellsten Sterne schon mit bloßem Auge erkennt. b) Andere Nebelflecke lösen sich auch im größten Teleskop nicht in Sterne auf und liefern im Spektroskop Linienspektren, sind also zweifellos Gasmassen. Sie nennt man echte Nebelflecke. Der Gedanke liegt nahe, daß die Hypothese von Kant und Laplace, wenn sie für unser Planetensystem richtig ist, auch für das ganze Weltall gilt. Dann hätten wir hier zukünftige Planetensysteme in verschiedenen Stufen der Entwickelung vor uns. Der berühmte Nebel im Orion zeigt noch ein wildes Durcheinander; andere Nebel haben mehr kugelige Form, man nennt sie planetarische Nebel. In einzelnen treten helle Stellen hervor, die sich im Spektrum schon als wirkliche Sterne erweisen; andere, wie der Ringnebel im Sternbilde der Leier, zeugen von starker Rotation, die den größeren Teil der Masse in der Peripherie zusammengedrängt hat. Noch deutlicher tritt eine Rotation des ganzen Nebels nach einer bestimmten Richtung in der Form der Spiralnebel hervor, die sich als lange Spirale um den Mittelpunkt herumlegen. Über die Form dieser Nebel haben wir besonders durch die Vervollkommnung der Photographie sichere Kenntnis erhalten. Natürlich nehmen wir sie nicht so wahr, wie sie heute sind; denn ihre Entfernungen sind zu groß, als daß sie noch gemessen werden könnten. Ihr Licht gebraucht wohl Jahrtausende, um bis zu uns zu gelangen.
6. Die Milchstraße. Jeder kennt das geheimnisvolle, mildleuchtende Band, das sich fast in einem größten Kreise um den ganzen Himmel zieht, die Milchstraße. Schon geringe Vergrößerungen zeigen, daß sie sich in eine Fülle kleiner Sterne auflöst; aber auch die stärkste Vergrößerung und die beste Photographie genügt nicht, um diese Fülle von Sternen zu scheiden und zu entwirren; immer wieder treten hinter den herausgelösten Sternen neue Nebelmassen auf. Wir haben es also sicherlich mit einem gewaltigen Sternhaufen oder einer Anhäufung vieler Haufen zu tun, und es liegt die Annahme nahe, daß dieser Sternhaufen uns verhältnismäßig viel näher liegt als die bekannten, meist nur im Fernrohre wahrnehmbaren Sternhaufen; daher eben die Unmöglichkeit, ihn zu übersehen. Ja, wegen seiner Stellung nahezu in einem größten Kreise der Himmelskugel scheint der Gedanke sich zu ergeben, daß unsere Sonne selbst ihm angehört.
1. Farbe des Fixsternlichtes. Die meisten Fixsterne strahlen in weißem Lichte; doch hat man schon im Altertum mit bloßem Auge wahrgenommen, daß es auch Fixsterne mit rotem Lichte gibt. Zu diesen gehört z. B. die Beteigeuze, einer der hellsten Sterne im Sternbilde des Orion. Genauere Beobachtung hat ergeben, daß die Fixsterne in den verschiedensten Farben leuchten, besonders in mannigfaltigen Schattierungen von Rot und Gelb. Da nun jedenfalls der Kern aller Fixsterne weißglühend ist, so muß man annehmen, daß diese verschiedenartige Färbung mit verschiedenartiger Beschaffenheit ihrer Atmosphären zusammenhängt. Einige Klarheit über diese Atmosphären gibt die Spektralanalyse.
2. Einteilung der Fixsterne auf Grund spektroskopischer Untersuchungen. Nach der Beschaffenheit ihrer Spektra teilt Professor Vogel die Fixsterne in drei Klassen. Alle liefern bandartige Farbenspektra, wodurch die Annahme, daß alle einen weißglühenden Kern enthalten, sich bestätigt.
a) Das Spektrum der ersten Klasse zeigt nur die Linien des Wasserstoffes, absorbiert oder leuchtend, oder höchstens treten neben den sehr kräftigen Wasserstofflinien die Linien einiger Leichtmetalle schwach hervor. Diese Sterne zeigen das reinste Weiß in ihrem Licht. Unser hellster Fixstern, der Sirius, gehört zu ihnen.
b) Das Spektrum der zweiten Klasse enthält eine reiche Schar von Absorptionslinien, besonders der Leichtmetalle, die ebenso scharf vortreten wie die Wasserstofflinien. Zu ihnen gehört die Sonne.
c) Das Spektrum der dritten Klasse zeigt neben den Absorptionslinien breite Absorptionsbänder, das Kennzeichen von glühenden Gasen chemischer Verbindungen. Hierher gehören die roten Sterne.
Man faßt diese drei Klassen als drei verschiedene Entwickelungsstufen auf. Die Fixsterne der ersten Klasse sind noch so heiß, daß die Metalldämpfe, die jedenfalls in der Atmosphäre vorhanden sind, noch gar nicht oder wenig imstande sind, das Licht ihrer charakteristischen Linien zu absorbieren. In der zweiten Klasse ist die Abkühlung so weit vorgeschritten, daß die Metalldämpfe der Atmosphäre sich durch Absorption deutlich bemerkbar machen. In der dritten Klasse ist die Glühhitze so weit gesunken, daß nicht mehr bloß chemische Elemente in den Körpern glühen, sondern schon Verbindungen zustande gekommen sind.
1. Doppelsterne. Die Frage liegt nahe, ob wohl mehr Fixsterne so wie unser Fixstern, die Sonne, von Planeten umkreist werden. Allerdings ist darauf kaum jemals eine Antwort zu erwarten, da das Licht beleuchteter Körper viel zu schwach ist, um aus jenen Fernen zu uns zu dringen. Aber daß es auch bei den Fixsternen Bewegung nach dem Gravitationsgesetze gibt, daß also Newtons Gesetz ein wirkliches Weltgesetz ist, das zeigen uns die Doppelsterne. Im Fernrohre lösen sich nämlich verschiedene Fixsterne in zwei Sterne auf. Manche davon sind freilich nur optische Doppelsterne, d. h. Sterne von großer gegenseitiger Entfernung, die für uns nur in derselben Gesichtslinie liegen; von einer großen Anzahl aber steht fest, daß sie einander wirklich nahestehen und umkreisen oder vielmehr beide sich um einen gemeinsamen, zwischen ihnen liegenden Schwerpunkt bewegen. Solch ein physischer Doppelstern ist z. B. der zweite Stern in der Deichsel des Großen Wagens (Bären).
2. Einzelbewegung anderer Fixsterne. Bezeichnet man die Stellung eines Fixsternes in längeren Zwischenräumen, etwa von Jahrzehnten, genau im Meridian, so zeigt sich, daß dieselbe sich ändert. Also stehen die Fixsterne nur scheinbar still; in Wahrheit haben sie alle Eigenbewegung. Daß es sich hier um eine wirkliche Bewegung handelt und nicht um eine scheinbare, ergibt sich daraus, daß ihre Richtung und Geschwindigkeit für jeden Stern eine andere ist. Man kann sogar feststellen, ob und wie weit sich dabei der Stern auf uns zu oder von uns fort bewegt. Das macht die Betrachtung der Sternspektra möglich.
Bekanntlich richtet sich nach der Zahl der Ätherschwingungen, die in einer Sekunde in unser Auge gelangen, die Art der Farbenempfindung. Die Zahl wächst in der Reihenfolge der Farben des Spektrums vom Rot zum Violett, so daß für Rot 430, für Violett 800 Billionen Schwingungen nötig sind. Offenbar wird nun von einem Fixsterne, der sich uns mit gewaltiger Geschwindigkeit nähert, eine größere, von einem sich ebenso entfernenden Fixsterne eine kleinere Zahl von Ätherschwingungen in der Sekunde zu uns gelangen, als von einem solchen, der beständig dieselbe Entfernung behält, sowie etwa von der Lokomotivpfeife eines heranbrausenden Eisenbahnzuges mehr, von einem abfahrenden Zuge weniger Luftwellen in der Sekunde in unser Ohr kommen, als von einem stillstehenden Zuge, oder wie einen gegen den Wellengang fahrenden Kahn mehr, einen mit ihm fahrenden Kahn weniger Wellen treffen, als einen verankerten Kahn in derselben Zeit. Daher wird das Spektrum eines auf uns zueilenden Fixsternes schon rot leuchten in einem Gebiete, das im Spektrum eines Fixsternes, dessen Entfernung von uns sich nicht ändert, nur ultrarote Strahlen erhält, d. h. es verschiebt sich nach Rot zu. Daraus ergibt sich sofort, daß die feststehenden Absorptionslinien eines Gases, z. B. des Wasserstoffes, in jenem Spektrum nach der entgegengesetzten Seite, nach Violett zu, verschoben erscheinen. Umgekehrt müssen diese Linien im Spektrum eines sich entfernenden Sternes nach Rot zu verschoben erscheinen. Solche Verschiebungen im Vergleich zum Sonnenspektrum hat nun die Spektralanalyse für zahlreiche Fixsterne zweifellos festgestellt und zwar für jeden andere. Die mittlere Entfernung der Sonne von uns kann sich nicht ändern, da wir jede etwaige Eigenbewegung[97] derselben mitmachen würden. Im Vergleich zum Sonnenspektrum zeigt nun das Spektrum des Sirius z. B. die Absorptionslinien nach dem roten Ende hin verschoben; also entfernt er sich von unserem Planetensystem. Sogar die Geschwindigkeit dieser Bewegung ist für den Sirius festgestellt worden.
3. Bewegung der Sonne. Jetzt liegt die Frage nahe, ob nicht auch vielleicht die Sonne mit ihrer ganzen Planetenschar sich im Raum vorwärts bewegt. Auch das ist nachgewiesen; die Sonne bewegt sich mit einer Geschwindigkeit von ca. 50 km in der Sekunde auf eine Gegend im Sternbilde des Herkules zu. Ja, es scheint sogar festzustehen, daß die Bewegung vieler anderer Fixsterne auf dieselbe Gegend gerichtet ist, so daß wir es vielleicht mit einem ganzen Fixsternsysteme zu tun haben.
1. Sternbilder. Seit den ältesten Zeiten hat die geheimnisvolle Majestät des Sternenhimmels die Augen der Menschen angezogen, und man hat früh angefangen, hervorragend helle Sterne mit Namen zu versehen, um dann von diesen Sternen aus sich leichter am Himmel zu orientieren. Wie wir schon wissen, wurden auch ganze Gruppen von Fixsternen zu Sternbildern zusammengefaßt und mit Namen belegt. Diese nahm man teils von Figuren, die die Phantasie in den Fixsterngruppen zu sehen glaubte, teils von mythischen, sagenhaften und berühmten Personen. Alle möglichen Sprachen sind an dieser Namengebung beteiligt, besonders Chaldäisch, Griechisch und Arabisch. Die Bilder des Tierkreises, die schon aufgezählt wurden, haben ihre Namen wahrscheinlich zum guten Teile von den Jahresarbeiten des Landmannes erhalten. Die Astronomie bezeichnet in den Sternbildern wieder die einzelnen Sterne nach ihrer Helligkeit mit den ersten Buchstaben des griechischen Alphabets.
2. Aufsuchen einiger Sterne und Sternbilder. Zum leichten Auffinden einiger besonders bekannten Sterne und Sternbilder dienen folgende Bemerkungen. Wir beginnen mit dem Sternbilde des Großen Bären oder Großen Wagens, das allbekannt und leicht aufzufinden ist wegen der Helligkeit und eigenartigen Stellung seiner Sterne und weil es stets die ganze Nacht am Himmel steht. Es besteht aus drei Sternen zweiter und einem Sterne dritter Größe, die im Viereck stehen, und drei Sternen zweiter Größe, die im Bogen von dem Viereck ausgehen. Das Ganze erinnert an einen Wagen. Einige kleinere Sternchen gehören noch mit zu dem Sternbilde; doch können wir diese übergehen; erwähnenswert ist höchstens noch ein Sternchen über dem Mittelstern der Deichsel, das Reiterlein genannt. Verlängern wir die Verbindungslinie der beiden Hinterräder etwa um vier Achsenlängen, so kommen wir auf den Polarstern, einen Stern zweiter Größe, der selbst wieder die Deichselspitze des Kleinen Bären oder Wagens bildet; die Sterne darin stehen ähnlich wie im Großen Bären, sind aber weniger hell. Verlängert man die Linie von dem helleren Vorderrade des Großen Bären zum Polarstern über diesen hinaus etwa um sich selbst, so stößt man auf einen Stern zweiter Größe, den äußersten von vier Sternen zweiter und einem Stern dritter Größe, die in der Gestalt eines lateinischen W zum Teil in der Milchstraße stehen, das Sternbild Kassiopeia. Eine Linie, die die beiden unteren,[98] dem Polarstern abgekehrten Räder des Großen Bären verbindet, führt, in der Richtung der Deichsel verlängert, auf einen prachtvollen Stern erster Größe, den Arktur im Sternbilde des Boṓtes (griech. = Ochsentreiber). Die Verbindungslinie des ersten und letzten Sternes der Deichsel des Großen Wagens führt nach der entgegengesetzten Seite hin auf einen Stern erster Größe, nahe am Äquator gelegen, Beteigeuze. Dieser Stern gehört dem schönsten Sternbilde des Himmels an, das halb nördlich, halb südlich vom Äquator liegt, dem Orion. Erkennbar ist es an seinen sieben hervorragendsten Sternen. Von diesen bilden vier ein schiefes längliches Viereck; in der einen Diagonale liegt Beteigeuze und, südlich vom Äquator, ebenfalls ein Stern erster Größe, Rigel. In der Mitte des Vierecks stehen dicht nebeneinander in schräger Linie drei Sterne zweiter Größe, der Gürtel des Orion oder Jakobsstab. Gerade diese machen durch ihre Stellung das Sternbild besonders kenntlich. Die Verlängerung des Jakobsstabes nach der Seite der Beteigeuze hin trifft den Sirius, den hellsten aller Fixsterne, im Sternbilde des Großen Hundes. Ziemlich auf der Mitte zwischen Rigel und Polarstern liegt der Stern erster Größe Capella (lat. Böckchen) im Fuhrmann. Zwischen Fuhrmann und Orion schiebt sich nach der dem Großen Hunde entgegengesetzten Seite ein Sternbild des Tierkreises, der Stier mit dem Sterne erster Größe Aldebaran, ein. Ein zweites Sternbild des Tierkreises finden wir auf der Mitte zwischen dem unteren Hinterrade des Großen Wagens und dem Sirius. Hier liegt nämlich der Stern erster Größe Pollux, der mit dem daneben stehenden Sterne zweiter Größe Kastor dem Sternbilde der Zwillinge angehört. Das Sternbild des Löwen treffen wir durch Verlängerung der Vorderachse des Großen Wagens über den helleren der beiden Sterne hinaus in seinem hellsten Sterne (erster Größe) Regulus. Dieselbe Linie geht, nach der entgegengesetzten Seite verlängert, ganz nahe an zwei Sternen erster Größe vorbei, die mit einem anderen nicht allzuweit davon stehenden Sterne erster Größe in einem Dreieck liegen; der erste ist die Wega in der Leier, der zweite, entfernteste, der Atair im Adler, der dritte der Deneb im Schwan.
3. Sternkarten. Zu genaueren Beobachtungen sind Sternkarten unentbehrlich. Eine bessere Karte des nördlichen Sternhimmels enthält wenigstens 24 Meridiane, die Stundenkreise, in der Projektion als divergente Linsen vom Nordpole aus erscheinend, den Äquator und einige Deklinationskreise, als konzentrische Kreise um den Pol erscheinend, und die halbe Ekliptik. Da die 24 Meridiane je 360/24 = 15° voneinander liegen, so ist klar, daß die Sterne auf dem einen immer eine Stunde früher kulminieren, als die auf dem nächsten nach Osten zu. Sind die Linien nicht als Stundenkreise, sondern nach Graden der Rektaszension bezeichnet, so ist festzuhalten, daß ein Grad immer einen Unterschied von 4 Minuten in der Kulmination bedeutet. Der 0te Stundenkreis, von dem aus man im Äquator die Rektaszension mißt, als der zum Frühlingspunkte gehende, ist dadurch sicher am Himmel gekennzeichnet, daß er durch β der Kassiopeia geht, den Stern, den wir vorher mit unserer Verbindungslinie vom γ des Großen Bären durch den Polarstern her trafen.
Diese Verbindungslinie lehrt übrigens auch, daß γ des Großen Bären 180° Rektaszension hat, oder daß er 12 Stunden nach β der Kassiopeia kulminiert. Offenbar beginnt nun für einen Ort ein Sterntag, wenn der 0te Stundenkreis[99] oder β der Kassiopeia kulminiert, d. h. durch den Ortsmeridian geht, der durch Zenit und Polarstern gelegt zu denken ist. Weiß man diese Stunde, so ist es nicht schwer, aus der vorher auf der Karte abgelesenen Rektaszension zu berechnen, wann ein anderer Stern, den man beobachten möchte, im Meridian stehen wird. Die Schwierigkeit liegt darin, daß Sternzeit und Sonnenzeit nur zweimal zusammenfallen. Aber man kann, davon ausgehend, daß am 22. September für beide Zeiten der Tag um Mitternacht beginnt, sich eine Tabelle anlegen. Nach dieser würde der Sterntag am 23. September um 11 Uhr 56 Minuten, am 24. September um 11 Uhr 52 Minuten, am 6. Oktober um 11 Uhr nachts, am 22. März um 12 Uhr mittags beginnen. Außerdem wird freilich noch die Ortszeit in mitteleuropäische Zeit umgerechnet werden müssen, weil nach dieser meistens die Uhren gestellt sein werden. Auch die Deklination des Sternes liefert uns die Karte. Diese kann ja bekanntlich am Himmel mit Instrumenten gemessen werden. Für gröbere Bestimmungen genügt eine Abschätzung im Meridian. Bei einiger Übung ist das nicht zu schwer, wenn man den Äquator festhalten kann. Dieser ist der größte zur Himmelsachse senkrechte Kreis, der durch δ des Orion, den oberen von Beteigeuze abgewandten Gürtelstern, geht. Kulminationszeit und Deklination aber lassen uns leicht den Stern, den wir suchen, auffinden. Anfänger stört gewöhnlich der Umstand, daß der Sternhimmel an jedem Abend anders erscheint, daß die Sterne, die um eine bestimmte Stunde kulminieren, am nächsten Abend um dieselbe Zeit die Kulmination schon hinter sich haben, daß in der Gegend des Himmelsäquators im Laufe des Jahres immer neue Sternbilder sichtbar und dann wieder unsichtbar werden. Für sie ist der Gebrauch drehbarer Sternkarten sehr empfehlenswert. Auf diesen kann man ziemlich genau sehen, wie um eine beliebige Stunde an einem beliebigen Tage der Fixsternhimmel aussieht.
4. Orte wissenschaftlicher Beobachtung. Zur wissenschaftlichen Beobachtung des Sternenhimmels sind große Sternwarten mit den mannigfaltigsten Meß-, Photographie-, Spektral- und Fernsehapparaten nötig. Solche Sternwarten gibt es in den meisten Universitätsstädten. Genannt seien die von Berlin, Leipzig, Straßburg, Wien, Greenwich, Nizza, Pulkowa bei Petersburg, die Sternwarte der Harvard-Universität in Cambridge bei Boston, die Licksternwarte auf dem Mount Hamilton in Kalifornien; ganz bestimmten Gebieten, z. B. der Beobachtung und Berechnung der Eigenbewegung der Fixsterne, dient das vorzüglich eingerichtete astrophysikalische Observatorium zu Potsdam.
Meyer, Dr. M. Wilhelm, Das Weltgebäude. Eine gemeinverständliche Himmelskunde. Leipzig und Wien. 2. Aufl. 1908.
Ule, Die Wunder der Sternenwelt. Ein Ausflug in den Himmelsraum. 5. Aufl. Bearbeitet von Dr. Hermann J. Klein. Leipzig 1909.
Diesterwegs Populäre Himmelskunde und mathematische Geographie. Neu bearbeitet von Dr. M. Wilhelm Meyer. 21. Aufl. Hamburg 1909.
Klein, Handbuch der allgemeinen Himmelsbeschreibung nach dem Standpunkte der astronomischen Wissenschaft am Schlusse des 19. Jahrhunderts. 3. Aufl. Braunschweig 1901.
Geißler, Anschauliche Grundlagen der mathematischen Erdkunde zum Selbstverstehen und zur Unterstützung des Unterrichts. Leipzig 1904.
Martus, Astronomische Erdkunde. 3. Aufl. Dresden 1904.
Günther, S., Handbuch der mathematischen Geographie. Stuttgart 1890.
Weitere Anmerkungen zur Transkription
Das Cover wurde aus dem Originalumschlag des Buches und der Titelseite zusammengesetzt und steht unter der Public Domain.
Offensichtliche Fehler wurden stillschweigend korrigiert. Die Darstellung der Ellipsen wurde vereinheitlicht.
Korrekturen:
S. 94: Sternbild → Stern
ein Stern zweiter Größe im Sternbilde des Perseus