
Title: The atom and the Bohr theory of its structure
an elementary presentation
Author: Helge Holst
Hendrik Anthony Kramers
Author of introduction, etc.: Ernest Rutherford
Translator: Rachel T. Lindsay
Robert Bruce Lindsay
Release date: May 5, 2023 [eBook #70708]
Most recently updated: May 22, 2023
Language: English
Original publication: United States: Alfred A. Knopf, 1923
Credits: deaurider and the Online Distributed Proofreading Team at https://www.pgdp.net (This file was produced from images generously made available by The Internet Archive)
Original Title:
“Bohr’s Atomteori, almenfatteligt fremstillet”
Translated from
the Danish by R. B. Lindsay,
Fellow of the American-Scandinavian Foundation,
1923, and Rachel T. Lindsay

THE ATOM AND
THE BOHR THEORY
OF ITS STRUCTURE
An Elementary Presentation
BY
H. A. KRAMERS
LECTURER AT THE INSTITUTE OF THEORETICAL PHYSICS
IN THE UNIVERSITY OF COPENHAGEN
AND
HELGE HOLST
LIBRARIAN AT THE ROYAL TECHNICAL COLLEGE OF COPENHAGEN
WITH A FOREWORD BY
SIR ERNEST RUTHERFORD, F.R.S.

NEW YORK
ALFRED A. KNOPF
1923
PRINTED IN GREAT BRITAIN BY
MORRISON AND GIBB LTD., EDINBURGH
At the close of the nineteenth century and the beginning of the twentieth, our knowledge of the activities in the interior of matter experienced a development which surpassed the boldest hopes that could have been entertained by the chemists and physicists of the nineteenth century. The smallest particles of chemistry, the atoms of the elements, which hitherto had been approached merely by inductive thought, now became tangible realities, so to speak, which could be counted and whose tracks could be photographed. A series of remarkable experimental investigations, stimulated largely by the English physicist, J. J. Thomson, had disclosed the existence of negatively charged particles, the so-called electrons, ¹/₂₀₀₀ the mass of the smallest atom of the known elements. A theory of electrons, based on Maxwell’s classical electrodynamical theory and developed mainly through the labours of Lorentz in Holland and Larmor in England, had brought the problem of atomic structure into close connection with the theory of radiation. The experiments of Rutherford proved, beyond a doubt, that atoms were composed simply of light, negative electric particles, and small heavy, positive electric particles. The new “quantum theory” of Planck was proving itself very powerful in overcoming grave difficulties in the theory of radiation. The time thus seemed ripe for a comprehensive investigation of the fundamental problem of physics—the constitution of matter, and an explanation in terms of simple general laws of the physical and chemical properties of the atoms of the elements.
During the first ten years of the new century the problem was attacked with great zeal by many scientists, and many interesting atomic models were developed and studied. But most of these had more significance for chemistry than for physics, and it was not until 1913 that the work of the Danish physicist, Niels Bohr, paved the way for a really physical investigation of the problem in a remarkable series of papers on the spectrum and atomic structure of hydrogen. The ideas of Bohr, founded as they were on the quantum theory, were startling and revolutionary, but their immense success in explaining the facts of experience after a time won for them the wide recognition of the scientific world, and stimulated work by other investigators along similar lines. The past decade has witnessed an enormous development at the hands of scientists in all parts of the world of Bohr’s original conceptions; but through it all Bohr has remained the leading spirit, and the theory which, at the present time, gives the most comprehensive view of atomic structure may, therefore, most properly bear the name of Bohr.
It is the object of this book to give the reader a glimpse of the fundamental conceptions of this theory, together with some of the most significant results it has attained. The book is designed to meet the needs of those who wish to keep abreast of modern developments in science, but have neither time nor inclination to delve into the highly mathematical abstract literature in which the developments are usually concealed. It is with this in mind that the first four chapters have been devoted to a general survey of those parts of physics and chemistry which have close connection with atomic theory. No attempt has been made at a mathematical development, and the physical meaning of such mathematical formulæ as do occur has been clearly emphasized in the text. It is hoped, however, that even those readers whose acquaintance with atomic theory is more than casual, will find the book a stimulus to further study of the Bohr theory.
Here we wish to record our best thanks to Mr. and Mrs. Lindsay for the ability and the great care with which they have carried out the translation from the Danish original.
During the last decade there has been a great advance in our knowledge of the structure of the atom and of the relation between the atoms of the chemical elements. In the later stages, science owes much to the remarkable achievements of Professor Niels Bohr and his co-workers in Copenhagen. For the first time, we have been given a consistent theory to explain the arrangement and motion of the electrons in the outer atom. The theory of Bohr is not only able to account in considerable detail for the variation in the properties of the elements exemplified by the periodic law, but also for the main features of the spectra, both X-ray and optical, shown by all elements.
This volume, written by Dr. Kramers and Mr. Holst, gives a simple and interesting account of our knowledge of atomic structure, with special reference to the work of Professor Bohr. Dr. Kramers is in an especially fortunate position to give a first-hand account of this subject, for he has been a valued assistant to Professor Bohr in developing his theories, and has himself made important original contributions to our knowledge in this branch of inquiry.
I can confidently recommend this book to English readers as a clearly written and accurate account of the development of our ideas on atomic structure. It is written in simple language, and the essential ideas are explained without mathematical calculations. This book should prove attractive not only to the general scientific reader, but also to the student who wishes to gain a broad general idea of this subject before entering into the details of the mathematical theory.
Cavendish Laboratory,
Cambridge, 8th October 1923.
CONTENTS
| chap. | PAGE | |
| Preface | vii | |
| Foreword | xi | |
| I. | Atoms and Molecules | 1 |
| II. | Light Waves and the Spectrum | 34 |
| III. | Ions and Electrons | 61 |
| IV. | The Nuclear Atom | 83 |
| V. | The Bohr Theory of the Hydrogen Spectrum | 105 |
| VI. | Various Applications of the Bohr Theory | 153 |
| VII. | Atomic Structure and the | |
| Chemical Properties of the Elements | 180 | |
| Interpretation of Symbols and Physical Constants | 209 | |
| COLOURED PLATES |
||
| I. | Spectrum Plates according to the Original | |
| Drawings of Bunsen and Kirchhoff | At end | |
| II. | Principal Features of Atomic Structure in Some | |
| of the Elements—Atomic Structure of Radium | At end | |
THE ATOM AND
THE BOHR THEORY
OF ITS STRUCTURE
[Pg 1]
As early as 400 b.c. the Greek philosopher, Democritus, taught that the world consisted of empty space and an infinite number of small invisible particles. These particles, differing in form and magnitude, by their arrangements and movements, by their unions and disunions, caused the existence of physical bodies with different characteristics, and also produced the observed variations in these bodies. This theory, which no doubt antedated Democritus, later became known as the Atomic Theory, since the particles were called atoms, i.e. the “indivisible.”
But the atomic conception was not the generally accepted one in antiquity. Aristotle (384-322 b.c.) was not an atomist, and denied the existence of discontinuous matter; his philosophy had a tremendous influence upon the ideas of the ancients, and even upon the beliefs of the Middle Ages. It must be confessed that his conception of the continuity of matter seemed to agree best with [Pg 2] experiment, because of the apparent homogeneity of physical substances such as metal, glass, water and air. But even this apparent homogeneity could not be considered entirely inconsistent with the atomic theory, for, according to the latter, the atoms were so small as to be invisible. Moreover, the atomic theory left the way open for a more complete understanding of the properties of matter. Thus when air was compressed and thereafter allowed to expand, or when salt was dissolved in water producing an apparently new homogeneous liquid, salt water, or when silver was melted by heat, or light changed colour on passing through wine, it was clear that something had happened in the interior of the substances in question. But complete homogeneity is synonymous with inactivity. How is it possible to obtain a definite idea of the inner activity lying at the bottom of these changes of state, if we do not think of the phenomenon as an interplay between the different parts of the apparently homogeneous matter? Thus, in the examples above, the decrease in the volume of the air might be considered as due to the particles drawing nearer to each other; the dissolving of salt in water might be looked upon as the movement of the salt particles in between the water particles and the combination of the two kinds; the melting of silver might naturally appear to be due to the loosening of bonds between the individual silver particles.
The atomic theory had thus a sound physical basis, and proved particularly attractive to those philosophers who tried to explain the mysterious activity of matter in terms of exact measurements. The atomic hypothesis was never completely overthrown, being supported after the time of Aristotle by Epicurus (c. 300 b.c.), [Pg 3] who introduced the term “atom,” and by the Latin poet, Lucretius (c. 75 b.c.) in his De Rerum Natura. Even in the Middle Ages it was supported by men of independent thought, such as Nicholas of Autrucia, who assumed that all natural activities were due to unions or disunions of atoms. It is interesting to note that in 1348 he was forced to retract this heresy. With the impetus given to the new physics by Galileo (1600) the atomic view gradually spread, sometimes explicitly stated as atomic theory, sometimes as a background for the ideas of individual philosophers. Various investigators developed comprehensive atomic theories in which they attempted to explain nearly everything from purely arbitrary hypotheses; they occasionally arrived at very curious and amusing conceptions. For example, about 1650 the Frenchman, Pierre Gassendi, following some of the ancient atomists, explained the solidity of bodies by assuming a hook-like form of atom so that the various atoms in a solid body could be hooked together. He thought of frost as an element with tetrahedral atoms, that is, atoms with four plane faces and with four vertices each; the vertices produced the characteristic pricking sensation in the skin. A much more thorough treatment of the atomic theory was given by Boscovich (1770). He saw that it was unnecessary to conceive of the atoms as spheres, cubes, or other sharply defined physical bodies; he considered them simply as points in space, mathematical points with the additional property of being centres of force. He assumed that any two atoms influenced each other with a force which varied, according to a complicated formula, with the distance between the centres. But the [Pg 4] time was hardly ripe for such a theory, inspired as it evidently was by Newton’s teachings about the gravitational forces between the bodies of the universe. Indeed there were no physical experiments whose results could, with certainty, be assumed to express the properties of the individual atoms.

Fig. 1.—The four elements and the four fundamental characteristics.
In the meantime atomic investigations of a very different nature had been influencing the new science of chemistry, in which the atomic theory was later to prove itself extraordinarily fruitful. It was particularly unfortunate that in chemistry, concerned as it is with the inner activities of the elements, Aristotle’s philosophy was long the prevailing one. He adopted and developed the famous theory of the four “elements,” namely, the dry and cold earth, the cold and damp water, the damp and warm air, the warm and dry fire. These “elements” must not be confused with the chemical elements known at the present day; they were merely representatives of the different consistent combinations of [Pg 5] the four fundamental qualities, dryness and wetness, heat and cold. From the symmetry in the system these were supposed to be the principles by means of which all the properties of matter could be explained. Neither the four “elements” nor the four fundamental qualities could be clearly defined; they were vague ideas to be discussed in long dialectic treatises, but were founded upon no physical quantities which could be measured.
A system of chemistry which had its theoretical foundations in the Greek elemental conceptions naturally had to work in the dark. Undoubtedly this uncertainty contributed to the relatively insignificant results of all the labour expended in the Middle Ages on chemical experiments, many of which had to do with the attempt to transmute the base metals into gold. Naturally there were many important contributions to chemistry, and the theories were changed and developed in many ways in the course of time. The alchemists of the Middle Ages thought that metal consisted only of sulphur and quicksilver; but the interpretation of this idea was influenced by the Greek elemental theory which was maintained at the same time; thus these new metal “elements” were considered by many merely as the expressions of certain aspects of the metallic characteristics, rather than as definite substances, identical with the elements bearing these names. It is, however, necessary to guard against attributing to a single conception too great influence on the historical development of the chemical and physical sciences. That the growth of the latter was hindered for so long a time was due more to the uncritical faith in authority and to the whole characteristic psychological point of view [Pg 6] which governed Western thought in the centuries preceding the Renaissance.
Robert Boyle (1627-1691) is one of the men to whom great honour is due for brushing aside the old ideas about the elements which had originated in obscure philosophical meditations. To him an element was simply a substance which by no method could be separated into other substances, but which could unite with other elements to form chemical compounds possessing very different characteristics, including that of being decomposable into their constituent elements. Undoubtedly Boyle’s clear conception of this matter was connected with his representation of matter as of an atomic nature. According to the atomic conception, the chemical processes do not depend upon changes within the element itself, but rather in the union or disunion of the constituent atoms. Thus when iron sulphide is produced by heating iron and sulphur together, according to this conception, the iron atoms and the sulphur atoms combine in such a way that each iron atom links itself with a sulphur atom. There is then a definite meaning in the statement that iron sulphide consists of iron and sulphur, and that these two substances are both represented in the new substance. There is also a definite meaning, for instance, in the statement that iron is an element, namely, that by no known means can the iron be broken down into different kinds of atoms which can be reunited to produce a substance different from iron.
The clarity which the atomic interpretation gave to the conception of chemical elements and compounds was surely most useful to chemical research in the following years; but before the atomic theory could [Pg 7] play a really great rôle in chemistry, it had to undergo considerable development. In the time of Boyle, and even later, there was still uncertainty as to which substances were the elements. Thus, water was generally considered as an element. According to the so-called phlogiston theory developed by the German Stahl (1660-1734), a theory which prevailed in chemistry for many years, the metals were chemical compounds consisting of a gaseous substance, phlogiston, which was driven off when the metals were heated in air, and the metallic oxide which was left behind. It was not until the latter half of the eighteenth century that the foundation was laid for the new chemical science by a series of discoveries and researches carried on by the Swedish scientist Scheele, the Englishmen Priestley and Cavendish, and particularly by the Frenchman Lavoisier. It was then discovered that water is a chemical compound of the gaseous elements oxygen and hydrogen, that air is principally a mixture (not a compound) of oxygen and nitrogen, that combustion is a chemical process in which some substance is united with oxygen, that metals are elements, while metallic oxides, on the other hand, are compounds of metal and oxygen, etc. Of special significance for the atomic theory was the fact that Lavoisier made weighing one of the most powerful tools of scientific chemistry.
Weighing had indeed been used previously in chemical experiments, but the experimenters had been satisfied with very crude precision, and the results had little influence on chemical theory. For example, the phlogiston theory was maintained in spite of the fact that it was well known that metallic oxide weighed more than the metal from which it was [Pg 8] obtained. Lavoisier now showed, by very careful weighings, that chemical combinations or decompositions can never change the total weight of the substances involved; a given quantity of metallic oxide weighs just as much as the metal and the oxygen taken individually, or vice versa. From the point of view of the atomic theory, this obviously means that the weight of individual atoms is not changed in the combinations of atoms which occur in the chemical processes. In other words, the weight of an atom is an invariable quantity. Here, then, we have the first property of the atom itself to be established by experiment—a property, indeed, which most atomists had already tacitly assumed.
Moreover, by the practice of weighing it was determined that to every chemical combination there corresponds a definite weight ratio among the constituent parts. This also had been previously accepted by most chemists as highly probable; but it must be admitted that the law at one time was assailed from several sides.
In comparing the weight ratios in different chemical compounds certain rules were, in the meantime, obtained. In many ways the most important of these, the so-called law of multiple proportions, was enunciated in the beginning of the last century by the Englishman, John Dalton. As an example of this law we may take two compounds of carbon and hydrogen called methane or marsh gas and ethylene, in which the quantities of hydrogen compounded with the same quantity of carbon are as two is to one. Another example may be seen in the compounds of carbon and oxygen. In the two compounds of carbon and oxygen, carbon monoxide and carbon dioxide, the weight ratios between the carbon and oxygen are [Pg 9] respectively as three to four and three to eight. A definite quantity of carbon has thus in carbon dioxide combined with just twice as much oxygen as in carbon monoxide. No less than five oxygen compounds with nitrogen are known, where with a given quantity of nitrogen the oxygen is combined in ratios of one, two, three, four and five.
These simple number relations can be explained very easily by the atomic theory, by assuming, first, that all atoms of the same element have the same weight; and second, that in a chemical combination between two elements the atoms combine to form an atomic group characteristic of the compound in question—a compound atom, as Dalton called it, or a molecule, as the atomic group is now called. These molecules consist of comparatively few atoms, as, for example, one of each kind, or one of one kind and two, three or four of another, or two of one kind and three or four of another, etc. When three elements are involved in a chemical compound the molecule must contain at least three atoms, but there may be four, five, six or more. The law of multiple proportions thus takes on a more complicated character, but it remains apparent even in this case.
When Dalton in the beginning of last century formulated the theory of the formation of chemical compounds from the atoms of the elements, he at once turned atomic theory into the path of more practical research, and it was soon evident that chemical research had then obtained a valuable tool. It may be said that Dalton’s atomic theory is the firm foundation upon which modern chemistry is built. [Pg 10]
Simple

Binary

Ternary

Quaternary

[Pg 11]
Fig. 2.—Representation of a part of Dalton’s atomic table (of 1808) where the atom of each element has its own symbol, and chemical compounds are indicated by the union of the atoms of the elements into groups by 2, 3, 4 ... (binary, ternary, quaternary ... atoms). Below are given the designations of the different atoms, and in parentheses the atomic weight given by Dalton with that of hydrogen as unity and the designations of the indicated atomic groups.
Atoms of the Elements.—1. Hydrogen (1); 2. Azote (5); 3. Carbon (5); 4. Oxygen (7); 5. Phosphorus (9); 6. Sulphur (13); 7. Magnesia (20); 8. Lime (23); 9. Soda (28); 10. Potash (42); 11. Strontites (46); 12. Barytes (68); 13. Iron (38); 14. Zinc (56); 15. Copper (56); 16. Lead (95); 17. Silver (100); 18. Platina (100); 19. Gold (140); 20. Mercury (167).
Chemical Compounds.—21. Water; 22. Ammonia; 23. 26. 27. and 30. Oxygen compounds of Azote; 24. 29. and 33. Hydrogen compounds of Carbon; 25. Carbon monoxide; 28. Carbon dioxide; 31. Sulphuric acid; 32. Hydro-sulphuric acid.
While Dalton’s theory could not give information about the absolute weights in grams of the atoms of various elements, it could say something about the relative atomic weights, i.e., the ratios of the weights of the different kinds of atoms, although it is true that these ratios could not always be determined with certainty. If, for example, the ratio between the oxygen and hydrogen in water is found to be as eight to one, then the weight ratio between the oxygen atom and the hydrogen atom will be as eight to one, if the water molecule is composed of one oxygen atom and one hydrogen atom (as Dalton supposed, see Fig. 2). But it will be as sixteen to one, if the water molecule is composed of one oxygen and two hydrogen atoms (as we now know to be the case). On the other hand, a ratio of seven to one will be compatible with the experimental ratio of eight to one only if we assume that the water molecule consists of fifteen atoms, eight of oxygen and seven of hydrogen, a very improbable hypothesis. In another case let us compare the quantities of oxygen and of hydrogen which are compounded with the same quantities of carbon in the two substances, carbon monoxide and methane respectively. On the assumption that the molecules in question have a simple structure, we can draw conclusions about the ratio of the atomic weights of hydrogen and oxygen. Now, if a ratio such as seven to [Pg 12] one or fourteen to one is obtained while the analysis of water gives eight to one or sixteen to one, then either the structure of the molecule is more complicated than was assumed, or the analyses must be improved by more careful experiments. We can thus understand that the atomic theory can serve as a controlling influence on the analysis of chemical compounds.
In order to choose between the different possible ratios of atomic weights, for example, the eight to one or the sixteen to one in the case of oxygen and hydrogen, Dalton had to make certain arbitrary assumptions. The first of these is that two elements of which only one compound is known appear with but one atom each in a molecule. Partly on account of this assumption and partly on account of the incompleteness of his analyses, Dalton’s values of the ratios of the atomic weights of the atoms and his pictures of the structure of molecules differ from those of the present day, as is obvious from Fig. 2.
A much firmer foundation for the choice made appears later in the Avogadro Law; starting with the fact that different gases show great similarity in their physical conduct—for instance, all expand by an increase of ¹/₂₇₃ of their volume with an increase in temperature from 0° C. to 1° C.—the Italian, Avogadro, in 1811, put forward the hypothesis that equal volumes of all gases at the same temperature and pressure contain equal numbers of molecules. A few examples suffice to show the usefulness of this rule.
When one volume of the gas chlorine unites with one volume of hydrogen there result two volumes of the gas, hydrogen chloride, at the same temperature and pressure. According to Avogadro’s Law one molecule of [Pg 13] chlorine and one molecule of hydrogen unite to become two molecules of hydrogen chloride, and since each of these two molecules must contain at least one atom of hydrogen and one atom of chlorine, it follows that one molecule of chlorine must contain two atoms of chlorine and that one molecule of hydrogen must contain two atoms of hydrogen. From this one can see that even in the elements the atoms are united into molecules. It is now well established that most elements have diatomic molecules, though some, including mercury and many other metals, are monatomic. When oxygen and hydrogen unite to form water, one litre of oxygen and two litres of hydrogen produce two litres of water vapour at same temperature and pressure. Accordingly, one molecule of oxygen and two molecules of hydrogen form two molecules of water. If the oxygen molecule is diatomic like the hydrogen, then one molecule of water contains one atom of oxygen and two atoms of hydrogen. Since the weight ratio between the oxygen and hydrogen in water is eight to one, the atomic weight of oxygen must be sixteen times that of hydrogen.
Through such considerations, supported by certain other rules, it has gradually proved possible to obtain reliable figures for the ratios between the atomic weights of all known elements and the atomic weight of hydrogen. For convenience it was customary to assign the number 1 to the latter and to call the ratio between the weight of the atom of a given element and the weight of the hydrogen atom the atomic weight of the element in question. Thus the atomic weight of oxygen is 16, that of carbon 12, because one carbon atom weighs as much as 12 hydrogen atoms. Nitrogen has the atomic weight 14, sulphur 32, copper 63.6, etc. [Pg 14]
A summary of the chemical properties and chemical compounds was greatly facilitated by the symbolic system initiated by the Swedish chemist, Berzelius. In this system the initial of the Latin name of the element (sometimes with one other letter from the Latin name) is made to indicate the element itself, an atom of the element, and its atomic weight with respect to hydrogen as unity, while a small subscript to the initial designates the number of atoms to be used. For example, in the chemical formula for sulphuric acid, H₂SO₄, the symbolic formula means that this substance is a chemical compound of hydrogen, sulphur and oxygen, that the acid molecule consists of two atoms of hydrogen, one atom of sulphur and four atoms of oxygen, and that the weight ratios between the three constituent parts is as 2×1 = 2 to 32 to 4×16 = 64, or as 1:16:32. To say that the chemical formula of zinc chloride is ZnCl₂ means that the zinc chloride molecule consists of one atom of zinc and two atoms of chlorine. Furthermore the changes which take place in a chemical process may be indicated in a very simple way. Thus the decomposition of water into hydrogen and oxygen may be represented by the so-called chemical “equation” 2H₂O ⇾ 2H₂+O₂, where H₂ and O₂ signify the molecules of hydrogen and oxygen respectively. Conversely, the combination of hydrogen and oxygen to form water will be given by the equation 2H₂+O₂ ⇾ 2H₂O.
As a consequence of the development of the atomic theory the atoms of the elements became, so to speak, the building stones of which the elements and the chemical compounds are built. It can also be said that the atoms are the smallest particles which the chemists reckon with in [Pg 15] the chemical processes, but it does not follow from the theory that these building stones in themselves are indivisible. The theory leaves the way open to the idea that they are composed of smaller parts. A belief founded on such an idea was indeed enunciated by the Englishman, Prout, a short time after Dalton had developed his atomic theory. Prout assumed that the hydrogen atoms were the fundamental ones, and that the atoms of the other elements consisted of a smaller or larger number of the atoms of hydrogen. This might explain the fact that within the limits of experimental error, many atomic weights seemed to be integral multiples of that of hydrogen—16 for oxygen, 14 for nitrogen, and 12 for carbon, etc. This led to the possibility that the same might hold for all elements, and this hypothesis gave impetus to very careful determinations of atomic weights. These, however, showed that the assumption of the integral multiples could not be verified. It therefore seemed as if Prout’s hypothesis would have to be given up. It has, however, recently come into its own again, although the situation is more complicated than Prout had imagined (see p. 97).
Dalton’s atomic theory gave no information about the atoms except that the atoms of each element had a definite constant weight, and that they could combine to form molecules in certain simple ratios. What the forces are which unite them into such combinations, and why they prefer certain unions to others, were very perplexing problems, which could only be solved when chemical and physical research had collected a great mass of information as a surer source of speculation.
From the knowledge of atomic weights it was easy to calculate what [Pg 16] weight ratios might be found to exist in chemical compounds, the molecules of which consisted of simple atomic combinations. Thus many compounds which were later produced in the laboratory were first predicted theoretically, but only a small part of the total number of possible compounds (corresponding to simple atomic combinations) could actually be produced. Clearly it was one of the greatest problems of chemistry to find the laws governing these cases.
It had early been known that the elements seemed to fall into two groups, characterized by certain fundamental differences, the metals and the metalloids. In addition, there were recognized two very important groups of chemical compounds, i.e. acids and bases, possessing the property of neutralizing each other to form a third group of compounds, the so-called salts. The phenomenon called electrolysis, in which an electric current separates a dissolved salt or an acid into two parts which are carried respectively with and against the direction of the current, indicates strongly that the forces holding the atoms together in the molecule are of an electrical nature, i.e. of the same nature as those forces which bring together bodies of opposite electrical charges. One is led to denote all metals as electropositive and all metalloids as electronegative, which means that in a compound consisting of a metal and a metalloid the metal appears with a positive charge and the metalloid with a negative charge. The chemist Berzelius did a great deal to develop electrical theories for chemical processes. Great difficulties, however, were encountered, some proving for the time being insurmountable. Such a difficulty, for example, is the circumstance that two atoms of the same kind (like two hydrogen atoms) can unite into a diatomic molecule, [Pg 17] although one might expect them to be similarly electrified and to repel rather than attract each other.
Another circumstance playing a very important part in determining the chemical compounds which are possible, is the consideration of what is called valence.
As mentioned above, one atom of oxygen combines with two atoms of hydrogen to form water, while one atom of chlorine combines with but one atom of hydrogen to form hydrogen chloride. The oxygen atom thus seems to be “equivalent” to two hydrogen atoms or two chlorine atoms, while one chlorine atom is “equivalent” to one hydrogen atom. The atoms of hydrogen and chlorine are for this reason called monovalent, while that of oxygen is called divalent. Again an acid is a chemical compound containing hydrogen, in which the hydrogen can be replaced by a metal to produce a metallic salt. Thus, when zinc is dissolved by sulphuric acid to form hydrogen and the salt zinc sulphate, the hydrogen of the acid is replaced by the zinc and the chemical change may be expressed by the formula
Zn+H₂SO₄ ⇾ H₂+ZnSO₄
In this, one atom of zinc changes place with two atoms of hydrogen. The zinc atom is therefore divalent. This is consistent with the fact that one zinc atom will combine with one oxygen atom to form zinc oxide. To take another example, if silver is dissolved in nitric acid, one atom of silver is exchanged for one atom of hydrogen. Silver, therefore, is monovalent, and we should expect that one atom of oxygen would unite with two atoms of silver. Some elements are trivalent, as, for example, nitrogen, which combines with hydrogen to form ammonia, NH₃; others, [Pg 18] again, are tetravalent, such as carbon, which unites with hydrogen to form marsh gas CH₄, and with oxygen to form carbon dioxide CO₂. A valence greater than seven or eight has not been found in any element.

Fig. 3.—Rough illustrations of the valences of the elements.
A. Hydrogen chloride (HCl); B. Water (H₂O); C. Methane (CH₄); D. Ethylene (C₂H₄).
If we consider the matter rather roughly and more or less as Gassendi did, we can explain the concept of valence by assuming that the atoms possess hooks; thus hydrogen and chlorine are each furnished with one [Pg 19] hook, oxygen and zinc with two hooks, nitrogen with three hooks, etc. When a hydrogen atom and a chlorine atom are hooked together, there are no free hooks left, and consequently the compound is said to be saturated. When one hydrogen atom is hooked into each of the hooks of an oxygen or carbon atom the saturation is also complete (see Fig. 3, A, B, C).
The matter is not so simple as this, however, since the same element can often appear with different valences. Iron may be divalent, trivalent or hexavalent in different compounds. In many cases, however, where an examination of the weight ratios seems to show that an element has changed its valence, this is not really true. It was mentioned previously that carbon forms another compound with hydrogen in addition to CH₄, namely, ethylene, containing half as much hydrogen in proportion to the same amount of carbon. With the aid of Avogadro’s Law, it is found that the ethylene molecule is not CH₂ but C₂H₄. Thus we can say that the two carbon atoms in the molecule are held together by two pairs of hooks, and consequently the compound can be expressed by the formula
| H - C - H |
| | | |
| H - C - H |
where the dashes correspond to hooks (cf. Fig. 3, D). Such a formula is called a structural formula.
Even if we are not allowed to think of the atoms in the molecules as held together by hooks, it is well to have some sort of concrete picture of molecular structure. It is possible to represent the tetravalent carbon atom in the form of a tetrahedron, and to consider the united atoms or atomic groups as placed at the four vertices. With such a spatial representation we can get an idea about many chemical questions which otherwise would be difficult to explain. We know, for [Pg 20] example, that two compound molecules having the same kind and number of atoms and the same bonds (and hence the same structural formulæ), may yet be different in that they are images of each other like a pair of gloves. Substances whose molecules are symmetrical in this way can be distinguished from each other by their different action on the passage of light. This molecular chemistry of space, or stereo-chemistry as it is called, has proved of great importance in explaining difficult problems in organic chemistry, i.e. the chemistry of carbon. Although there have never been many chemists who really have believed the carbon atom to be a rigid tetrahedron, we must admit that in this way it has been possible to get on the track of the secrets of atomic structure.
In comparing the properties of the elements with their atomic weights, there has been discovered a peculiar relation which remained for a long time without explanation, but which later suggested a certain connection between the inner structure of an atom and its chemical properties. We refer to the natural or periodic system of the elements which was enunciated in 1869 by the Russian chemist, Mendelejeff, and about the same time and independently by the German, Lothar Meyer. This system will be understood most clearly by examining the table on p. 23, where the elements with their respective atomic weights and chemical symbols are arranged in numbered columns so that the atomic weights increase upon reading the table from left to right or from top to bottom. It will be seen that in each of the nine columns there are collected elements with related properties, forming what may be called chemical families. The table as here given is of a recent [Pg 21] date and differs from the old table of Mendelejeff, both in the greater number of elements and in the particulars of the arrangement. With each element there is associated a number which indicates its position in the series with respect to increasing atomic weight. Thus hydrogen has the number 1, helium 2, etc., up to uranium, the atom of which is the heaviest of any known element, and to which the number 92 is given. In each of the columns the elements fall naturally into two sub-groups, and this division is indicated in the table by placing the chemical symbols to the right or left in the column.
On close examination it becomes evident that the regularity in the system is not entirely simple. First of all some cases will be found where the atomic weight of one element is greater than that of the following element. (The cases of argon and potassium on the one hand and cobalt and nickel on the other are examples.) Such an interchange is absolutely necessary if the elements which belong to the same chemical family are to be placed in the same column. As a second instance of irregularity, attention must be called to Column VIII. in the table. While in the first score or so of elements it is always found that two successive elements have different properties and clearly belong to distinct chemical families, in the so-called iron group (iron, cobalt and nickel) we meet with a case where successive elements resemble each other in many respects (for instance, in their magnetic properties). Since there are two more such “triads” in the periodic system, however, we cannot properly call this an irregularity. But in addition to these difficulties there is what we may even call a kind of inelegance presented by the so-called “rare earths” group. In [Pg 22] this group there follow after lanthanum thirteen elements whose properties are rather similar, so that it is very difficult to separate them from each other in the mixtures in which they occur in the minerals of nature. (In the table these elements are enclosed in a frame.)
On the other hand, the apparent absence of an element in certain places in the table (indicated by a dash) cannot by any means be looked upon as irregular. In Mendelejeff’s first system there were many vacant spaces. With the help of his table Mendelejeff was, to some extent, able to predict the properties of the missing elements. An example of this is the case of the element between gallium and arsenic. This is called germanium, and was discovered to have precisely the properties which had been predicted for it—a discovery which was one of the greatest triumphs in favour of the reality of the periodic system. On the whole, the elements discovered since the time of Mendelejeff have found their natural positions in the table. This is seen, for example, in the case of the so-called “inactive gases” of the atmosphere, helium, argon, neon, xenon, krypton and niton, which have the common property of being able to form no chemical combinations whatever. Their valence is therefore zero, and in the table they are placed by themselves in a separate column headed with zero.
To explain the mystery of the periodic system, it was necessary to make clear not only the regularity of it, but also the apparent irregularities which seemed to be arbitrary individual peculiarities of certain elements or groups. In the periodic system, chemistry laid down some rather searching tests for future theories of atomic structure. [Pg 23]
THE PERIODIC OR NATURAL SYSTEM
OF THE ELEMENTS
| 0 | I. | II. | III. | IV. | V. | VI. | VII. | VIII. |
|---|---|---|---|---|---|---|---|---|
| 1 Hydrogen H 1·008 |
||||||||
| 2 Helium He 4·00 |
3 Lithium Li 6·94 |
4 Beryllium Be 9·1 |
5 Boron B 11·0 |
6 Carbon C 12·0 |
7 Nitrogen N 14·0 |
8 Oxygen O 16 |
9 Fluorine F 19·0 |
|
| 10 Neon Ne 20·2 |
11 Sodium Na 23·0 |
12 Magnesium Mg 24·3 |
13 Aluminium Al 27·1 |
14 Silicon Si 28·3 |
5 Phosphorus P 31·0 |
16 Sulphur S 32·1 |
17 Chlorine Cl 35·5 |
|
| 18 Argon A 39·9 |
19 Potassium K 39·1 |
20 Calcium Ca 40·1 |
21 Scandium Sc 44·1 |
22 Titanium Ti 48·1 |
23 Vanadium V 51·0 |
24 Chromium Cr 52·0 |
25 Manganese Mn 54·9 |
26 Iron 27 Cobalt Fe 55·8 Co 59·0 28 Nickel Ni 58.7 |
| 29 Copper Cu 63·6 |
30 Zinc Zn 65·4 |
31 Gallium Ga 69·9 |
32 Germanium Ge 72·5 |
33 Arsenic As 75·0 |
34 Selenium Se 79·2 |
35 Bromine Br 79·9 |
||
| 36 Krypton Kr 82·9 |
37 Rubidium Rb 85·4 |
38 Strontium Sr 87·6 |
39 Yttrium Y 88·7 |
40 Zirconium Zr 90·6 |
41 Niobium Nb 93·5 |
42 Molybdenum Mo 96·0 |
43 — | 44 Ruthenium 45 Rhodium Ru 101·7 Rh 102·9 46 Palladium Pd 106·7 |
| 47 Silver Ag 107·9 |
48 Cadmium Cd 112·4 |
49 Indium In 114·8 |
50 Tin Sn 118·7 |
51 Antimony Sb 120·2 |
52 Tellurium Te 127·5 |
53 Jodine J 126·9 |
||
| 54 Xenon X 130·2 |
55 Caesium Cs 132·8 |
56 Barium Ba 137·3 |
57 Lanthanum La 139·0 |
58 Cerium 59 Praseodymium 60 Neodymium
61 —62 Samarium Ce 140·2 Pr 140·6 Nd 144·3 Sm 150·4 |
||||
| 63 Europium
64 Gadolinium
65 Terbium
66 Dysprosium Eu 152·0 Gd 157·3 Tb 159·2 Dy 162·5 |
||||||||
| 67 Holmium 68 Erbium 69 Thulium
70 Ytterbium71 Cassiopeium Ho 163·5Er 167·7 Tm 168·5 Yb 173·0Cp 175·0 |
||||||||
| 72 Hafnium Hf 179 |
73 Tantalum Ta 181·5 |
74 Tungsten W 184·0 |
75 — | 76 Osmium 77 Iridium Os 190·9 Ir 192·1 78 Platinum Pt 195·2 |
||||
| 79 Gold Au 197·2 |
80 Mercury Hg 200·6 |
81 Thallium Tl 204·0 |
82 Lead Pb 207·2 |
83 Bismuth Bi 209·0 |
84 Polonium Po 210·0 |
85 — | ||
| 86 Niton Ni 222·0 |
87 — | 88 Radium Ra 226·0 |
89 Actinium Ac? |
90 Thorium Th 232 |
91 Protactinium Pa? |
92 Uranium U 238 |
||
[Pg 24]
From a consideration of the chemical properties of the elements we shall now turn to an examination of the physical characteristics, although in a certain sense chemistry itself is but one special phase of physics.
If matter is really constructed of independently existing particles—atoms and molecules—the interplay of the individual parts must determine not only the chemical activities, but also the other properties of matter. Since most of these properties are different for different substances, or in other words are “molecular properties,” it is reasonable to suppose that in many cases explanations can be more readily given by considering the molecules as the fundamental parts. It is natural that the first attempts to develop a molecular theory concerned gases, for their physical properties are much simpler than those of liquids or solids. This simplicity is indeed easily understood on the molecular theory. When a liquid by evaporation is transformed into a gas, the same weight of the element has a volume several hundred times greater than before. The molecules, packed together tightly in the liquid, in the gas are separated from each other and can move freely without influencing each other appreciably. When two of them come very close to each other, mutually repulsive forces will arise to prevent collision. Since it must be assumed that in such a “collision” the individual molecules do not change, they can then to a certain extent be considered as elastic bodies, spheres for instance.
From considerations of this nature the kinetic theory of gases developed. According to this a mass of gas consists of an immense [Pg 25] number of very small molecules. Each molecule travels with great velocity in a straight line until it meets an obstruction, such as another molecule or the wall of the containing vessel; after such an encounter the molecule travels in a second direction until it collides again, and so on. The pressure of the gas on the wall of the container is the result of the very many collisions which each little piece of wall receives in a short interval of time. The magnitude of the pressure depends upon the number, mass and velocity of the molecules. The velocity will be different for the individual molecules in a gas, even if all the molecules are of the same kind, but at a given temperature an average velocity can be determined and used. If the temperature is increased, this average molecular velocity will be increased, and if at the same time the volume is kept constant, the pressure of the gas on the walls will be increased. If the temperature and the average velocity remain constant while the volume is halved, there will be twice as many molecules per cubic centimetre as before. Therefore, on each square centimetre of the containing wall there will be twice as many collisions, and consequently the pressure will be doubled. Boyle’s Law, that the pressure of a gas at a given temperature is inversely proportional to its volume, is thus an immediate result of the molecular theory.
The molecular theory also throws new light upon the correspondence between heat and mechanical work and upon the law of the conservation of energy, which about the middle of the nineteenth century was enunciated by the Englishman, Joule, the Germans, Mayer and Helmholtz, and the Dane, Colding. A brief discussion of heat and energy will be [Pg 26] given here, since some conception of these phenomena is necessary in understanding what follows.
To lift a stone of 5 pounds through a distance of 10 feet demands an expenditure of work amounting to 5 × 10 = 50 foot-pounds; but the stone is now enabled to perform an equally large amount of work in falling back these 10 feet. The stone, by its height above the earth and by the attraction of the earth, now has in its elevated position what is called “potential” energy to the amount of 50 foot-pounds. If the stone as it falls lifts another weight by some such device as a block and tackle, the potential energy lost by the falling stone will be transferred to the lifted one. If the apparatus is frictionless, the falling stone can lift 5 pounds 10 feet or 10 pounds 5 feet, etc., so that all the 50 foot-pounds of potential energy will be stored in the second stone. If instead of being used to lift the second stone, the original stone is allowed to fall freely or to roll down an inclined plane without friction, the velocity will increase as the stone falls, and, as the potential energy is lost, another form of energy, known as energy of motion or kinetic energy, is gained. Conversely, a body when it loses its velocity can do work, such as stretching a spring or setting another body in motion. Let us suppose that the stone is fastened to a cord and is swinging like a pendulum in a vacuum where there is no resistance to its motion. The pendulum will alternately sink and rise again to the same height. As the pendulum sinks, the potential energy will be changed into kinetic energy, but as it rises again the kinetic will be exchanged for potential. Thus there is no loss of energy, but merely a continuous exchange between the two forms. [Pg 27]
If a moving body meets resistance, or if its free fall is halted by a fixed body, it might seem as if, at last, the energy were lost. This, however, is not the case, for another transformation occurs. Every one knows that heat is developed by friction, and that heat can produce work, as in a steam-engine. Careful investigations have shown that a given amount of mechanical work will always produce a certain definite amount of heat, that is, 400 foot-pounds of work, if converted into heat, will always produce 1 B.T.U. of heat, which is the amount necessary to raise the temperature of 1 pound of water 1° F. Conversely, when heat is converted into work, 1 B.T.U. of heat “vanishes” every time 400 foot-pounds of work are produced. Heat then is just a special form of energy, and the development of heat by friction or collision is merely a transformation of energy from one form to another.
With the assistance of the molecular theory it becomes possible to interpret as purely mechanical the transformation of mechanical work into heat energy. Let us suppose that a falling body strikes a piston at the top of a gas-filled cylinder, closed at the bottom. If the piston is driven down, the gas will be compressed and therefore heated, for the speed of the molecules will be increased by collisions with the piston in its downward motion. In this example the kinetic energy given to the piston by the exterior falling body is used to increase the kinetic energy of the molecules of the gas. When the molecules contain more than one atom, attention must also be given to the rotations of the atoms in a molecule about each other. A part of any added kinetic energy in the gas will be used to increase the energy of the atomic rotations. [Pg 28]
The next step is to assume that, in solids and liquids, heat is purely a molecular motion. Here, too, the development of heat after collision with a moving body should be treated as a transformation of the kinetic energy of an individual, visible body into an inner kinetic energy, divided among the innumerable invisible molecules of the heated solid or liquid. In considering the internal conduct of gases it is unnecessary (at least in the main) to consider any inner forces except the repulsions in the collisions of the molecules. In solids and liquids, however, the attractions of the tightly packed molecules for each other must not be neglected. Indeed the situation is too complicated to be explained by any simple molecular theory. Not all energy transformations can be considered as purely mechanical. For instance, heat can be produced in a body by rays from the sun or from a hot fire, and, conversely, a hot body can lose its heat by radiation. Here, also, we are concerned with transformations of energy; therefore the law for the conservation of energy still holds, i.e. the total amount of energy can neither be increased nor decreased by transformations from one form to another. For the production of 1 B.T.U. of heat a definite amount of radiation energy is required; conversely, the same amount of radiation energy is produced when 1 B.T.U. of heat is transformed into radiation. This change cannot, however, be explained as the result of mechanical interplay between bodies in motion.
The mechanical theory of heat is very useful when we restrict ourselves to the transfer of heat from one body to another, which is in contact with it. When applied to gases the theory leads directly to Avogadro’s Law. If two masses of gas have the same temperature, i.e., if no [Pg 29] exchange of heat between them takes place even if they are in contact with each other, then the average value of the kinetic energy of the molecules must be the same in both gases. If one gas is hydrogen and the other oxygen, the lighter hydrogen molecules must have a greater velocity than the heavier oxygen molecules; otherwise they cannot have the same kinetic energy (the kinetic energy of a body is one-half the product of the mass and the square of the velocity). Since the pressure of a gas depends upon the kinetic energy of the molecules and upon their number per cubic centimetre, at the same temperature and pressure equal volumes must contain equal numbers of oxygen and of hydrogen molecules. As Joule showed in 1851, from the mass of a gas per cubic centimetre and from its pressure per square centimetre, the average velocity of the molecules can be calculated. For hydrogen at 0° C. and atmospheric pressure the average velocity is about 5500 feet per second; for oxygen under the same conditions it is something over 1300 feet per second.
All these results of the atomic and molecular theory, however, gave no information about the absolute weight of the individual atoms and molecules, nor about their magnitude nor the number of molecules in a cubic centimetre at a given temperature and pressure. As long as such questions were unsolved there was a suggestion of unreality in the theory. The suspicion was easily aroused that the theory was merely a convenient scheme for picturing a series of observations, and that atoms and molecules were merely creations of the imagination. The theory would seem more plausible if its supporters could say how large and how heavy the atoms and molecules were. The molecular theory of [Pg 30] gases showed how to solve these problems which chemistry had been powerless to solve.
Let us assume that the temperature of a mass of gas is 100° C. at a certain altitude, and 0° C. one metre lower, i.e., the molecules have different average velocities in the two places. The difference between the velocities will gradually decrease and disappear on account of molecular collisions. We might expect this “levelling out” process or equilibration to proceed very rapidly because of the great velocity of the molecules, but we must consider the fact that the molecules are not entirely free in their movements. In reality they will travel but very short distances before meeting other molecules, and consequently their directions of motion will change. It is easy to understand that the difference between the velocities of the molecules of the gas will not disappear so quickly when the molecules move in zigzag lines with very short straight stretches. The greater velocity in one part of the gas will then influence the velocity in the other part only through many intermediate steps. Gases are therefore poor conductors of heat. When the molecular velocity of a gas and its conductivity of heat are known, the average length of the small straight pieces of the zigzag lines can be calculated—in other words, the length of the mean free path. This length is very short; for oxygen at standard temperature and pressure it is about one ten-thousandth of a millimetre, or 0·1 μ, where μ is 0·001 millimetre or one micron.
In addition to the velocity of the molecules, the length of the mean free path depends upon the average distance between the centres of two neighbouring molecules (in other words, upon the number of molecules [Pg 31] per cubic centimetre) and upon their size. There is difficulty in defining the size of molecules because, as a rule, each contains at least two atoms; but it is helpful to consider the molecules, temporarily, as elastic spheres. Even with this assumption we cannot yet determine their dimensions from the mean free path, since there are two unknowns, the dimensions of the molecules and their number per cubic centimetre. Upon these two quantities depends, however, also the volume which will contain this number of molecules, if they are packed closely together. If we assume that we meet such a packing when the substance is condensed in liquid form, this volume can be calculated from a knowledge of the ratio between the volume in liquid form and the volume of the same mass in gaseous form (at 0° C. and atmospheric pressure). Then from this result and the length of the mean free path the two unknowns can be determined. Although the assumptions are imperfect, they serve to give an idea about the dimensions of the molecules; the results found in this way are of the same order of magnitude as those derived later by more perfect methods of an electrical nature.
The radius of a molecule, considered as a sphere, is of the order of magnitude 0·1 μμ, where μμ means 10⁻⁶ millimetre or 0·001 micron. Even if a molecule is by no means a rigid sphere, the value given shows that the molecule is almost unbelievably small, or, in other words, that it can produce appreciable attraction and repulsion in only a very small region in space.
The number of molecules in a cubic centimetre of gas at 0° C. and [Pg 32] atmospheric pressure has been calculated with fair accuracy as approximately 27 × 10¹⁸. From this number and from the weight of a cubic centimetre of a given gas the weight of one molecule can be found. One hydrogen molecule weighs about 1·65 × 10⁻²⁴ grams, and one gram of hydrogen contains about 6 × 10²³ atoms and 3 × 10²³ molecules. The weight of the atoms of the other elements can be found by multiplying the weight of the hydrogen atom by the relative atomic weight of the element in question—16 for oxygen, 14 for nitrogen, etc. If the pressure on the gas is reduced as much as possible (to about one ten-millionth of an atmosphere) there will still be 3 × 10¹² molecules in a cubic centimetre, and the average distance between molecules will be about one micron. The mean free path between two collisions will be considerable, about two metres, for instance, in the case of hydrogen. [Pg 33]
The values found for the number, weight and dimensions of molecules are either so very large or so extremely small that many people, instead of having more faith in the atomic and molecular theory, perhaps may be more than ever inclined to suppose the atoms and molecules to be mere creations of the imagination. In fact, it is only two or three decades ago that some physicists and chemists—led by the celebrated German scientist, Wilhelm Ostwald—denied the existence of atoms and molecules, and even went so far as to try to remove the atomic theory from science. When these sceptics, in defence of their views, said that the atoms and molecules were, and for ever would be, completely inaccessible to observation, it had to be admitted at that time that they were seemingly sure of their argument, in this one objection at any rate.
A series of remarkable discoveries at the close of the nineteenth century so increased our knowledge of the atoms and improved the methods of studying them that all doubts about their existence had to be silenced. However incredible it may sound, we are now in a position to examine many of the activities of a single atom, and even to count atoms, one by one, and to photograph the path of an individual atom. All these discoveries depend upon the behaviour of atoms as electrically charged, moving under the influence of electrical forces. This subject will be developed in another section after a discussion of some phenomena of light, an understanding of which is necessary for the appreciation of the theory of atomic structure proposed by Niels Bohr.
In the molecular theory of gases, where we have to do with neutral molecules, much progress has in the last years been made by the Dane, Martin Knudsen, in his experiments at a very low pressure, when the molecules can travel relatively far without colliding with other molecules. While his researches give information on many interesting and important details, his work gives at the same time evidence of a very direct nature concerning the existence of atoms and molecules.
[Pg 34]
There have been several theories about the nature of light. The great English physicist, Isaac Newton (1642-1727), who was a pioneer in the study of light as well as in that of mechanics, favoured an atomic explanation of light; i.e., he thought that it consisted of particles or light corpuscules which were emitted from luminous bodies like projectiles from a cannon. In contrast to this “emission” theory was the wave theory of Newton’s contemporary, the Dutch scientist, Huygens. According to him, light was a wave motion passing from luminous bodies into a substance called the ether, which filled the otherwise empty universe and permeated all bodies, at least all transparent ones. In the nineteenth century the wave theory, particularly through the work of the Englishman, Young, and the Frenchman, Fresnel, came to prevail over the emission theory. Since the wave theory plays an important part in the following chapters, a discussion of the general characteristics of all wave motions is appropriate here. The examples will include water waves on the surface of a body of water, and sound waves in air. [Pg 35]

Fig. 4.—Photograph of the interference between two similar wave systems.

Fig. 5.—A section of the same picture enlarged.
(From Grimsehl, Lehrbuch der Physik.)
Let us suppose that we are in a boat which is anchored on a body of water and let us watch the regular waves which pass us. If there is neither wind nor current, a light body like a cork, lying on the surface, rises with the wave crests and sinks with the troughs, going forward slightly with the former and backward with the latter, but remaining, on the whole, in the same spot. Since the cork follows the surrounding water particles, it shows their movements, and we thus see that the individual particles are in oscillation, or more accurately, in circulation, one circulation being completed during the time in which the wave motion advances a wave-length, i.e., the distance from one crest to the next. This interval of time is called the time of oscillation, or the period. If the number of crests passed in a given time is counted, the oscillations of the individual particles in the same time can be determined. The number of oscillations in the unit of time, which we here may take to be one minute, is called the [Pg 36] frequency. If the frequency is forty and the wave-length is three metres, the wave progresses 3 × 40 = 120 metres in one minute. The velocity with which the wave motion advances, or in other words its velocity of propagation, is then 120 metres per minute. We thus have the rule that velocity of propagation is equal to the product of frequency and wave-length (cf. Fig. 8).
On the surface of a body of water there may exist at the same time several wave systems; large waves created by winds which have themselves perhaps died down, small ripples produced by breezes and running over the larger waves, and waves from ships, etc. The form of the surface and the changes of form may thus be very complicated; but the problem is simplified by combining the motions of the individual wave systems at any given point. If one system at a given time gives a crest and another at the same instant also gives a crest at the same point, the two together produce a higher crest. Similarly, the resultant of two simultaneous troughs is a deeper trough; a crest from one system and a simultaneous trough from the other partially destroy or neutralize each other. A very interesting yet simple case of such “interference” of two wave systems is obtained when the systems have equal wave-lengths and equal amplitudes. Such an interference can be produced by throwing two stones, as much alike as possible, into the water at the same time, at a short distance from each other. When the two sets of wave rings meet there is created a network of crests and troughs. Figs. 4 and 5 show photographs of such an interference, produced by setting in oscillation two spheres which were suspended over a body of water. [Pg 37]

Fig. 6.—Schematic representation of an interference.
In Fig. 6 there is a schematic representation of an interference of the same nature. Let us examine the situation at points along the lower boundary line. At 0, which is equidistant from the two wave centres, there is evidently a wave crest in each system; therefore there is a resultant crest of double the amplitude of a single crest if the two systems have the same amplitude. Half a period later there is a trough in each system with a resultant trough of twice the amplitude of a single trough. Thus higher crests and deeper troughs alternate. The same situation is found at point 2, a wave-length farther from the left than from the right wave centre; in fact, these results are found at all points such as 2, 2′, 4 and 4′, where the difference in distance [Pg 38] from the two wave centres is an even number of wave-lengths. At the point 1, on the other hand, where the difference between the distance from the centres is one-half a wave-length, a crest from one system meets a trough from the other, and the resultant is neither crest nor trough but zero. There is the same result at points 1′, 3, 3′, 5, 5′, etc., where the difference between the distances from the two wave centres is an odd number of half wave-lengths. By throwing a stone into the water in front of a smooth wall an interference is obtained, similar to the one described above. The waves are reflected from the wall as if they came from a centre at a point behind the wall and symmetrically placed with respect to the point where the stone actually falls.

Fig. 7.—Waves which are reflected by a board and pass through a hole in it.
When a wave system meets a wall in which there is a small hole, this opening acts as a new wave centre, from which, on the other side of the wall, there spread half-rings of crests and troughs. But if the waves are small and the opening is large in proportion to the wave-length, the case is essentially different. Let us suppose that wave rings originate at every point of the opening. As a result of the co-operation of all these wave systems the crests and troughs will advance, just as before, in the original direction of propagation, [Pg 39] i.e., along straight lines drawn from the original wave centre through the opening; lines of radiation, we may call them. It can be shown, however, that as these lines of radiation deviate more and more from the normal to the wall, the interference between wave systems weakens the resultant wave motion. If the deviation from the normal to the wall is increased, the weakening varies in magnitude, provided that the waves are sufficiently small; but even if the wave motions at times may thus “flare up” somewhat, still on the whole they will decrease as the deviation from the normal to the wall is increased. The smaller the waves in comparison to the opening, the more marked is the decrease of the wave motions as the distance from the normal to the wall is increased, and the more nearly the waves will move on in straight lines. That light moves in straight lines, so that opaque objects cast sharp shadows, is therefore consistent with the wave theory, provided the light waves are very small; though it is reasonable to expect that on the passage of light through narrow openings there will be produced an appreciable bending in the direction of the rays. This supposition agrees entirely with experiment. As early as the middle of the seventeenth century, the Italian Grimaldi discovered such a diffraction of light which passes through a narrow opening into a dark room. [Pg 40]

Fig. 8.—Schematic representation of a wave.
A and B denote crests; C denotes a trough.
λ = wave-length. α = amplitude of wave.
If T denotes the time the wave takes to travel
from A to B, and ν = 1/T the frequency, the
wave velocity v will be equal to λ/T = λν.
Points P and P′ are points in the same phase.
In both light and sound the use of such terms as wave and wave motion is figurative, for crests and troughs are lacking. But this choice of terms is commendable, because sound and light possess an essential property similar to one possessed by water waves. What happens when a tuning-fork emits sound waves into the surrounding air, is that the air particles are set in oscillation in the direction of the propagation of sound. All the particles of air have the same period as the tuning-fork, and the number of oscillations per second determines the pitch of the note produced; but the air particles at different distances from the tuning-fork are not all simultaneously in the same phase or condition of oscillation. If one particle, at a certain distance from the source of sound and at a given time, is moving most rapidly away from the source, then at the same time there is another particle, somewhat farther along the direction of propagation, which is moving towards the source most rapidly. This alternation of direction will exist all along the path of the sound. Where the particles are approaching each other, the air is in a state of condensation, and where the particles are drawing apart, the air is in a state of rarefaction. While the individual particles are oscillating in approximately the same place, the condensations and rarefactions, like troughs and crests in water, advance with a velocity [Pg 41] which is called the velocity of sound. If we call the distance between two consecutive points in the same phase a wave-length, and the number of oscillations in a period of time the frequency, then, as in the case of water waves, the velocity of propagation will be equal to the product of frequency and wave-length.
Light, like sound, is a periodic change of the conditions in the different points of space. These changes which emanate from the source of light, in the course of one period advance one wave-length, i.e., the distance between two successive points in the same phase and lying in the direction of propagation. As in the cases of sound and water waves, the velocity of propagation or the velocity of light is equal to the product of frequency and wave-length. If this velocity is indicated by the letter c, the frequency by ν and the wave-length by λ, then
| c = νλ or ν = | c | or λ = | c |
| λ | ν |
The velocity of light in free space is a constant, the same for all wave-lengths. It was first determined by the Danish astronomer Ole Rømer (1676) by observations of the moons of Jupiter. According to the measurements of the present day the velocity of light is about 1,000,000,000 feet or 300,000 kilometres per second. In centimetres it is thus about 3 × 10¹⁰.
Efforts have been made to consider light waves, like sound waves, as produced by the oscillations of particles, not of the air, but of a particular substance, the “ether,” filling and permeating everything; but all attempts to form definite representations of the material properties of the ether and of the movements of its particles have been unsuccessful. The electromagnetic theory of light, enunciated about [Pg 42] fifty years ago by the Scottish physicist, Maxwell, has furnished information of an essentially different character concerning the nature of light waves.
Let us suppose that electricity is oscillating in a conductor connecting two metal spheres, for instance. The spheres, therefore, have, alternately, positive and negative charges. Then according to Maxwell’s theory we shall expect that in the surrounding space there will spread a kind of electromagnetic wave with a velocity equal to that of light. Wherever these waves are, there should arise electric and magnetic forces at right angles to each other and to the direction of propagation of the waves; the forces should change direction in rhythm with the movements of electricity in the emitting conductor. By way of illustration let us assume that we have somewhere in space an immensely small and light body or particle with an electric charge. If, in the region in question, an electromagnetic wave motion takes place, then the charged particle will oscillate as a result of the periodically changing electrical forces. The particle here plays the same rôle as the cork on the surface of the water (cf. p. 35); the charged body thus makes the electrical oscillations in space apparent just as the cork shows the oscillations of the water. In addition to the electrical forces there are also magnetic forces in an electromagnetic wave. We can imagine that they are made apparent by using a very small steel magnet instead of the charged body. According to Maxwell’s theory, the magnet exposed to the electromagnetic wave will perform rapid oscillations. Maxwell came to the conclusion that light consisted of electromagnetic waves of a similar nature, but much more delicate than could possibly be produced and made visible directly by electrical means. [Pg 43]
In the latter part of the nineteenth century the German physicist, H. Hertz, succeeded in producing electromagnetic waves with oscillations of the order of magnitude of 100,000,000 per second, corresponding to wave-lengths of the order of magnitude of several metres.
| ( λ = | c | = | 3 × 10¹⁰ | = 300 cm. ) |
| ν | 10⁸ |
Moreover, he proved the existence of the oscillating electric forces by producing electric sparks in a circle of wire held in the path of the waves. He showed also that these electromagnetic waves were reflected and interfered with each other according to the same laws as in the case of light waves. After these discoveries there could be no reasonable doubt that light waves were actually electromagnetic waves, but so small that it would be totally impossible to examine the oscillations directly with the assistance of electric instruments.
But there was in this work of Hertz no solution of the problems about the nature of ether and the processes underlying the oscillations. More and more, scientists have been inclined to rest satisfied with the electromagnetic description of light waves and to give up speculation on the nature of the ether. Indeed, within the last few years, specially through the influence of Einstein’s theory of relativity, many doubts have arisen as to the actual existence of the ether. The disagreement about its existence is, however, more a matter of definition than of reality. We can still talk about light as consisting of ether waves if we abandon the old conception of the ether as a rigid elastic body with definite material properties, such as specific gravity, hardness and elasticity.
It has been said that the wave-length of light is much shorter than [Pg 44] that of the Hertzian waves. This does not mean that all light waves have the same wave-length and frequency. The light which comes to us from the sun is composed of waves of many different wave-lengths and frequencies, to each of which corresponds a particular colour.
In this respect also light may be compared with sound. In whatever way a sound is produced, it is in general of a complicated nature, composed of many distinct notes, each with its characteristic wave-length and frequency. Naturally the air particles cannot oscillate in several different ways simultaneously. At a given time, however, we can think of the condensation and rarefactions of the air or the oscillations of the particles corresponding to different tones, as compounded with each other in a way similar to that in which the resultant crests and troughs are produced on a body of water with several coexistent wave systems. When we say that the complicated wave-movement emitted from some sound-producing instrument consists of different tones, this does not only mean that we may imagine it purely mathematically as resolved into a series of simpler wave systems. The resolution may also take place in a more physical way. Let us assume that we have a collection of strings each of which will produce a note of particular pitch. Now, if sound waves meet this collection of strings, each string is set in oscillation by the one wave in the compound sound wave which corresponds to it. Each string is then said to act as a resonator for the note in question. The notes which set the resonator strings in oscillation sound more loudly in the neighbourhood of the resonators; but, as the wave train continues on its journey the tones taken out by [Pg 45] the strings will become weak in contrast to those notes which found no corresponding strings. The resonator is said to absorb the notes with which it is in pitch.
Light which is composed of different colours, i.e., of wave systems with different wave-lengths, can also be resolved or dispersed, but by a method different from that in the case of sound.
When light passes from one medium to another, as from air to glass or vice versa, it is refracted, i.e., the direction of the light rays is changed; but if the light is composed of different colours the refraction is accompanied by a “spreading” of the colours which is called dispersion. If we look through a glass prism so that the light from the object examined must pass in and out through two faces of the prism which make not too great an angle with each other, the light-producing object is not only displaced by the refraction, but has coloured edges. Newton was the first to explain the relation of the production of the colours to refraction. He made an experiment with sunlight, which he sent through a narrow opening into a dark room. The sunlight was then by a glass prism transformed or dispersed into a band of colour, a spectrum consisting of all the colours of the rainbow, red, yellow, green, blue and violet, in the order named, and with continuous transition stages between neighbouring colours. [Pg 46]

Fig. 9.—Prism spectroscope.
To the right is seen the collimator,
to the left the telescope,
in the foreground a scheme for
illuminating the cross-wire.
(From an old print.)
In Newton’s original experiment the different wave-lengths were but imperfectly separated. A spectrum with pure wave-lengths can be obtained with a spectroscope (cf. Fig. 9). The light to be investigated illuminates an adjustable vertical slit in one end of a long tube, called the collimator, with a lens in the other end. If the slit is in the focal plane of the lens, the light at any point in the slit goes in parallel rays after meeting the lens. It then meets a prism, with vertical edges, placed on a little revolving platform. The rays, refracted by the prism, go in a new direction into a telescope whose objective lens gives in its focal plane, for every colour, a clear vertical image of the slit. These images can be examined through the ocular of the telescope; but since the different colours are not [Pg 47] refracted equally, each coloured image of the slit has its own place. The totality of the slit images then forms a horizontal spectrum of the same height as the individual images. By revolving the collimator different parts of the spectrum can be put in the middle of the field of view. To facilitate measurements in the spectrum there is in the focal plane of the collimator a sliding cross-wire with an adjusting screw or a vertical strand of spider web.
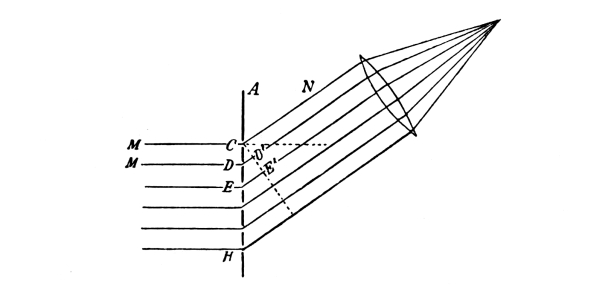
Fig. 10.—The mode of operation of a grating.
A, grating; C, D, E ... H, slits; M M, incident rays. When D D′, E E′ ... are a whole number of wave-lengths, the light waves which move in the direction indicated by C N and are collected by a lens, at the focal point will all be in the same phase and therefore will reinforce each other. In other directions the light action from one slit is compensated by that from another.
Instead of using the refraction of light in a prism to separate the wave-lengths, we can use the interference which arises when a bundle of parallel light waves passes through a ruled grating, consisting of a great many very fine parallel lines, equidistant from each other; such a grating can be made by ruling lines with a diamond point on the metal coating of a silvered plate of glass. From each line there are sent out [Pg 48] light waves in all directions; but if we are considering light of one definite colour (a given wave-length, monochromatic light), the interference among the waves from all the slits practically destroys all waves except in the direction of the original rays and in the directions making certain angles with the former, dependent upon the wave-length and the distance between two successive lines (the grating space). Monochromatic light can be obtained by using as the source of light a spirit flame, coloured yellow with common salt (sodium chloride). If the slit in a spectroscope is lighted with a yellow light from such a flame, and if a grating normal to the direction of the rays is substituted for the prism, then in the telescope there is seen a yellow image of the slit, and on each side of it one, two, three or more yellow images. If sunlight is used the central image is white, since all the colours are here assembled. The other images become spectra because the different colours are unequally refracted. In these grating spectra, which according to their distance from the central line are called spectra of the first, second or third order, the violet part lies nearest to the central line, the red part farthest away. Since the deflection is the greater the greater the wave-length, then violet light must have the shortest wave-length and red the greatest. From the amount of the refraction and the size of the grating space the wave-length of the light under investigation can be calculated.
For the yellow light from our spirit flame the wave-length is about 0·000589 mm. or 0·589 μ or 589 μμ. In centimetres the wave-length is 0·0000589 cm.; from the formula ν = c/λ, ν = 526 × 10¹². The frequency is thus almost inconceivably large. For the most distant red [Pg 49] and violet in the spectrum the wave-lengths are respectively about 800 μμ and 400 μμ, and the frequencies 375 × 10¹² and 750 × 10¹² oscillations per second.
In scientific experiments a grating of specular metal with parallel rulings is substituted for the transparent grating. The spectrum is then given by the reflected light from the parts between the rulings. Specular gratings can be made by ruling on a concave mirror, which focuses the rays so that a glass lens is unnecessary. Gratings with several hundred lines or rulings to the millimetre give excellent spectra, with strength of light and marked dispersion. The preparation of the first really good gratings is due to the experimental skill of the American, Rowland, who in 1870 built a dividing engine from which the greater part of the good gratings now in use originate. The contribution which Rowland thereby made to physical science can hardly be over-estimated.
In the early part of the nineteenth century Wollaston, in England, and later Fraunhofer in Germany, discovered dark lines in the solar spectrum, a discovery which meant that certain colours were missing. The most noticeable of these so-called “Fraunhofer Lines” were named with the letters A, B, C, D, E, F, G, H, from red to violet. It was later discovered that some of the lines were double, that the D-line, for instance, can be resolved into D₁ and D₂; other letters, such as b and h, were introduced to denote new lines. With improvements in the methods of experiment and research the number of lines has increased to hundreds and even thousands. The light from a glowing [Pg 50] solid or liquid element forms, on the other hand, a continuous spectrum, i.e. a spectrum which has no dark lines. An illustration of the solar spectrum with the strongest Fraunhofer lines is given at the end of the book.
In contrast to the solar spectrum with dark lines on a bright background are the so-called line spectra, which consist of bright lines on a dark background. The first known line spectrum was the one given by light from the spirit flame coloured with common salt, mentioned in connection with monochromatic light. As has been said, this spectrum had just one yellow line which was later found to consist of two lines close to each other. It is sodium chloride which colours the flame yellow. The colour is due, not to the chlorine, but to the sodium, for the same double yellow line can be produced by using other sodium salts not compounded with chlorine. The yellow light is therefore called sodium light. No. 7 in the table of spectra at the end of the book shows the spectrum produced by sodium vapour in a flame. (On account of the small scale in the figure it is not shown that the yellow line is double.)
Another interesting discovery was soon made, namely, that the sodium line has exactly the same wave-length as the light lacking in the solar spectrum, where the double D-line is located. About 1860 Kirchhoff and Bunsen explained this remarkable coincidence as well as others of the same nature. They showed by direct experiment that if sodium vapour is at a high temperature it can not only send out the yellow light, but also absorb light of the same wave-length when rays from a still warmer glowing body pass through the vapour. This phenomenon is something like that in the case of sound waves where a resonator absorbs the pitch [Pg 51] which it can emit itself. The existence of the dark D-line in the solar spectrum must then mean that in the outer layer of the sun there is sodium vapour present of lower temperature than the white-hot interior of the sun, and that the light corresponding to the D-line is absorbed by the vapour. Several ingenious experiments, which cannot be described here, have given further evidence in favour of this explanation.
In the other line spectra, just as in that from the common salt flame, definite lines correspond to definite elements and not to chemical compounds. The emission of these lines is then not a molecular characteristic, but an atomic one. The line spectra of metals can often be produced by vaporizing a metallic salt in a spirit flame or in a hot, colourless gas flame (from a Bunsen burner). It is even better to use an electric arc or strong electric sparks. The atoms from which gaseous molecules are formed can also be made to emit light which by means of the spectroscope is shown to consist of a line spectrum. These results are obtained by means of electric discharges of various kinds, arcs, and spark discharges through tubes where the gas is in a rarefied state.
The other Fraunhofer lines in the solar spectrum correspond to bright lines in the line spectra of certain elements which exist here on earth. These Fraunhofer lines must then be assumed to be caused by the absorption of light by the elements in question. This may be explained by the presence of these elements as gases in the solar atmosphere, through which passes the light from the inner layer. This inner surface would in itself emit a continuous spectrum. [Pg 52]
The work of Kirchhoff and Bunsen put at the disposal of science became a new tool of incalculable scope. First and foremost, spectrum examinations were taken into the service of chemistry as spectrum analysis. It has thus become possible to analyse quantities of matter so small that the general methods of chemistry would be quite powerless to detect them. It is also possible by spectrum analysis to detect minute traces of an element; several elements were in this way first discovered by the spectroscope. Moreover, chemical analysis has been extended to the study of the sun and stars. The spectral lines have given us answers to many problems of physics—problems which formerly seemed insoluble. Last but not least spectrum analysis has given us a key to the deepest secrets of the atom, a key which Niels Bohr has taught us how to use.
In the discussion of the spectrum we have hitherto restricted ourselves to the visible spectrum limited on the one side by red and on the other by violet. But these boundaries are in reality fortuitous, determined by the human eye. The spectrum can be studied by other methods than those of direct observation. The more indirect methods include the effect of the rays on photographic plates and their heating effect on fine conducting wires for electricity, held in various parts of the spectrum. It has thus been discovered that beyond the visible violet end of the spectrum there is an ultra-violet region with strong photographic activity and an infra-red region producing marked heat effects. There are both dark and light spectral lines in these new parts of the spectrum. The fact that glass is not transparent to ultra-violet or infra-red rays has been an obstacle in the experiments, but the difficulty can be overcome by using other substances, such as [Pg 53] quartz or rock salt, for the prisms and lenses, or by substituting concave gratings. By special means it has been possible to detect rays with wave-lengths as great as 300 μ and as small as about 0·02 μ, corresponding to frequencies between 10¹², and 15 × 10¹⁵ vibrations per second, while the wave-lengths of the luminous rays lie between 0·8 and 0·4 μ. The term “light wave” is often used to refer to the ultra-violet and infra-red rays which can be shown in the spectra produced by prisms or gratings.
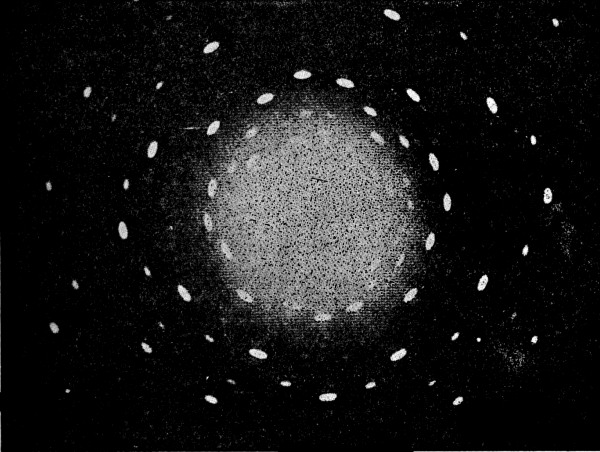
Fig. 11.—Photographic
effect of X-rays, which are
passed through the atom grating
in a magnesia crystal.
The electrically produced electromagnetic waves, as already mentioned, have wave-lengths much greater than 300 μ. In wireless telegraphy there are generally used wave-lengths of one kilometre or more, corresponding to frequencies of 300,000 vibrations per second or less. By direct electrical methods it has, however, not been possible to obtain [Pg 54] wave-lengths less than about one-half a centimetre, a length differing considerably from the 0·3 millimetre wave of the longest infra-red rays. Wave-lengths much less than 0·02 μ or 20 μμ exist in the so-called Röntgen rays or X-rays with wave-lengths as small as 0·01 μμ corresponding to a frequency of 30 × 10¹⁸. These rays cannot possibly be studied even with the finest artificially made gratings, but crystals, on account of the regular arrangement of the atoms, give a kind of natural grating of extraordinary fineness. With the use of crystal gratings success has been attained in decomposing the Röntgen rays into a kind of spectrum, in measuring the wave-lengths of the X-rays and in studying the interior structure of the crystals. The German Laue, the discoverer of the peculiar action of crystals on X-rays (1912), let the X-rays beams pass through the crystal, obtaining thereby photographs of the kind illustrated in Fig. 11. Later on essential progress was due to the Englishmen, W. H. and W. L. Bragg, who worked out a method of investigation by which beams of X-rays are reflected from crystal faces. The greatest wave-length which it has been possible to measure for X-rays is about 1·5 μμ, which is still a long way from the 20 μμ of the furthermost ultra-violet rays.
It may be said that the spectrum since Fraunhofer has been made not only longer but also finer, for the accuracy of measuring wave-lengths has been much increased. It is now possible to determine the wave-length of a line in the spectrum to about 0·001 μμ or even less, and to measure extraordinarily small changes in wave-lengths, caused by different physical influences.
In addition to the continuous spectra emitted by glowing solids or liquids, and to the line spectra emitted by gases, and to the [Pg 55] absorption spectra with dark lines, there are spectra of still another kind. These are the absorption spectra which are produced by the passage of white light through coloured glass or coloured fluids. Here instead of fine dark lines there are broader dark absorption bands, the spectrum being limited to the individual bright parts. There are also the band spectra proper, which, like the line spectra, are purely emission spectra, given by the light from gases under particular conditions; these seem to consist of a series of bright bands which follow each other with a certain regularity (cf. Fig. 12). With stronger dispersion the bands are shown to consist of groups of bright lines.
Fig. 12.—Spectra
produced by discharges of different character
through a glass
tube containing nitrogen at a pressure of ¹/₂₀
that of
the atmosphere. Above, a band spectrum;
below, a line spectrum.
Since the line spectra are most important in the atomic theory, we shall examine them here more carefully.
The line spectra of the various elements differ very much from each other with respect to their complexity. While many metals give a great number of lines (iron, for instance, gives more than five thousand), others give only a few, at least in a simple spectroscope. With a more [Pg 56] powerful spectroscope the simplicity of structure is lost, since weaker lines appear and other lines which had seemed single are now seen to be double or triple. Moreover, the number of lines is increased by extending the investigation to the ultra-violet and infra-red regions of the spectrum. The sodium spectrum, at first, seemed to consist of one single yellow line, but later this was shown to be a double line, and still later several pairs of weaker double lines were discovered. The kind and number of lines obtained depends not only upon the efficiency of the spectroscope, but also upon the physical conditions under which the spectrum is obtained.
The eager attempts of the physicists to find laws governing the distribution of the lines have been successful in some spectra. For instance, the line spectra of lithium, sodium, potassium and other metals can be arranged into three rows, each consisting of double lines. The difference between the frequencies of the two “components” of the double lines was found to be exactly the same for most of the lines in one of these spectra, and for the spectra of different elements there was discovered a simple relationship between this difference in frequency and the atomic weight of the element in question. But this regularity was but a scrap, so to speak; scientists were still very far from a law which could exactly account for the distribution of lines in a single series, not to mention the lines in an entire spectrum or in all the spectra.
The first important step in this direction was made about 1885 by the Swiss physicist, Balmer, in his investigations with the hydrogen spectrum, the simplest of all the spectra. In the visible part there are just three lines, one red, one green-blue and one violet, corresponding to the Fraunhofer lines C, F and h. These hydrogen [Pg 57] lines are now generally known by the letters Hα, Hᵦ and Hᵧ. In the ultra-violet region there are many lines also.
Balmer discovered that wave-lengths of the red and of the green hydrogen line are to each other exactly as two integers, namely, as 27 to 20, and that the wave-lengths of the green and violet lines are to each other as 28 to 25. Continued reflection on this correspondence led him to enunciate a rule which can be expressed by a simple formula. When frequency is substituted for wave-length Balmer’s formula is written as
| ν = K | 1 | - | 1 | , | ||
| 4 | n² |
where ν is the frequency of a hydrogen line, K a constant equal to 3·29 × 10¹⁵ and n an integer. If n takes on different values, ν becomes the frequency for the different hydrogen lines. If n = 1 ν is negative, for n = 2 ν is zero. These values of n therefore have no meaning with regard to ν. But if n = 3, then ν gives the frequency for the red hydrogen line Hα; n = 4 gives the frequency of the green line Hᵦ and n = 5 that of the violet line Hᵧ. Gradually more than thirty hydrogen lines have been found, agreeing accurately with the formula for different values of n. Some of these lines were not found in experiment, but were discovered in the spectrum of certain stars; the exact agreement of these lines with Balmer’s formula was strong evidence for the belief that they are due to hydrogen. The formula thus proved itself valuable in revealing the secrets of the heavens.
As n increases 1/n² approaches zero, and can be made as close to zero as desired by letting n increase indefinitely. In mathematical [Pg 58] terminology, as n = ∞, 1/n² = 0 and ν = K/4 = 823 × 10¹², corresponding to a wave-length of 365 μμ. Physically this means that the line spectrum of hydrogen in the ultra-violet is limited by a line corresponding to that frequency. Near this limit the hydrogen lines corresponding to Balmer’s formula are tightly packed together. For n = 20 ν differs but little from K/4, and the distance between two successive lines corresponding to an increase of 1 in n becomes more and more insignificant. Fig. 13, where the numbers indicate the wave-lengths in the Ångström unit (0·1 μμ), shows the crowding of the hydrogen lines towards a definite boundary. The following table, where K has the accurate value of 3·290364 × 10¹⁵, shows how exactly the values calculated from the formula agree with experiment.
Fig. 13.—Lines in the hydrogen spectrum corresponding to the Balmer series.
Table of some of the Lines of the Balmer Series
| ν = K(1/4 - 1/n²) = ν (calculated). |
ν (found). | λ (found). | |
|---|---|---|---|
| n = 3 | K(¼ - ¹/₉ ) = 456,995 bills | 456,996 bills | 656·460 μμ Hα |
| n = 4 | K(¼ - ¹/₁₆ ) = 616,943 “ | 616,943 “ | 486·268 “ Hᵦ |
| n = 5 | K(¼ - ¹/₂₅ ) = 690,976 “ | 690,976 “ | 434·168 “ Hᵧ |
| n = 6 | K(¼ - ¹/₃₆ ) = 731,192 “ | 731,193 “ | 410·288 “ Hδ |
| n = 7 | K(¼ - ¹/₄₉ ) = 755,440 “ | 755,441 “ | 397·119 “ Hε |
| n = 20 | K(¼ - ¹/₄₀₀) = 814,365 “ | 814,361 “ | 368·307 “ |
[Pg 59] From arguments in connection with the work of the Swedish scientist, Rydberg, in the spectra of other elements, Ritz, a fellow countryman of Balmer’s, has made it seem probable that the hydrogen spectrum contains other lines besides those corresponding to Balmer’s formula. He assumed that the hydrogen spectrum, like other spectra, contains several series of lines and that Balmer’s formula corresponds to only one series. Ritz then enunciated a more comprehensive formula, the Balmer-Ritz formula:
| ν = K | 1 | - | 1 | , | ||
| n″ ² | n′ ² |
where K has the same value as before, and both n′ and n″ are integers which can pass through a series of different values. For n″ = 2, the Balmer series is given; to n″ = 1, and n′ = 2, 3 ... ∞ there corresponds a second series which lies entirely in the ultra-violet region, and to n″ = 3, n′ = 4, 5 ... ∞ a series lying entirely in the infra-red. Lines have actually been found belonging to these series.
Formulæ, similar to the Ritz one, have been set up for the line spectra of other elements, and represent pretty accurately the distribution of the lines. The frequencies are each represented by the difference between two terms, each of which contains an integer, which can pass through a series of values. But while the hydrogen formula, except for the n′s, depends only upon one constant quantity K and its terms have the simple form K/n², the formula is more complicated with the other elements. The term can often be written, with a high degree of exactness, as K/(n + α)², where K is, with considerable accuracy, the [Pg 60] same constant as in the hydrogen formula. For a given element α can assume several different values; therefore the number of series is greater and the spectrum is even more complicated than that of hydrogen.
All these formulæ are, however, purely empirical, derived from the values of wave-lengths and frequencies found in spectrum measurements. They represent certain more or less simple bookkeeping rules, by which we can register both old and new lines, enter them in rows, arrange them according to a definite system. But from the beginning there could be no doubt that these rules had a deeper physical meaning which it was not yet possible to know. There was no visible correspondence between the spectral line formulæ and the other physical characteristics of the elements which emitted the spectra; not even in their form did the formulæ show any resemblance to formulæ obtained in other physical branches.
[Pg 61]
The fundamental phenomena of electricity, which were first made the subject of careful study about two centuries ago, are that certain substances can be electrified by friction so that somehow they can attract light bodies, and that the charges of electricity may be either “positive” or “negative.” Bodies with like charges repel each other, while those with unlike charges attract each other, and either partially or entirely neutralize each other when they are brought close together. Moreover, it had long ago been discovered that in some substances electricity can move freely from place to place, while in others there is resistance to the movement. The former bodies are now called conductors and include metals, while the latter are called insulators, glass, porcelain and air being members of this class.
In order to explain the phenomena some imagined that there were two kinds of “electric substances” or “fluids”; and since no change in weight could be discovered in a body when it was electrified, it was, in general, assumed that the electric fluids were weightless. In the [Pg 62] normal, neutral body it was believed that these fluids were mixed in equal quantities, thereby neutralizing each other; on this account they were supposed to be of opposite characteristics, so one was called positive and the other negative. According to a second theory, there was assumed to be just one kind of electricity, which was present in a normal amount in neutral bodies; positive electricity was caused by a superfluity of the fluid; negative, by a deficit. In both theories it was possible to talk of the amount of positive or negative electricity which a body contained or with which it was “charged,” because the supporters of the one-fluid idea understood by the terms positive and negative a superfluity and a deficit, respectively, of the one fluid. In both theories it was possible to talk about the direction of the electric current in a conductor, since the supporters of the two-fluid theory understood by “direction” that in which the electric forces sent the positive electricity, or the opposite to that in which the negative would be sent. It could not be decided whether positive electricity went in the one direction or the negative in the other, or whether each simultaneously moved in its own direction. Both theories were quite arbitrary in designating the electric charge in glass, which was rubbed with woollen cloth, as positive. On the whole, neither theory seemed to have any essential advantage over the other; the difference between them seemed to lie more in phraseology than in actual fact.
That the positive and negative states of electricity could not be taken as “symmetric” seemed, however, to follow from the so-called discharge phenomena, in which electricity, with the emission of light, streams [Pg 63] out into the air from strongly charged (positive or negative) bodies, or passes through the air between positive and negative bodies in sparks, electric arcs or in some other way. In a discharge in air between a metal point and a metal plate, for instance, a bush-shaped glow is seen to extend from the point when the charge there is positive, while only a little star appears when the charge is negative.
Naturally, we cannot discuss here the many electric phenomena and laws, and must be satisfied with a brief description of those which are of importance in the atomic theory.
In this latter category belongs Coulomb’s Law, formulated about 1785. According to this law, the repulsions or attractions between two electrically charged bodies are directly as the product of the charges and inversely as the square of the distance between them (as in the case of the gravitational attraction between two neutral bodies, according to Newton’s Law). The unit in measuring electric charges can be taken as that amount which will repel an equal amount of electricity of the same kind at unit distance with unit force. If we use the scientific or “absolute” system, in which the unit of length is one centimetre, that of time one second and that of mass one gram, then the unit of force is one dyne, which is a little greater than the earth’s attraction on a milligram weight. Let us suppose that two small bodies with equal charges of positive (or negative) electricity are at a distance of one centimetre from each other. If they repel each other with a charge of one dyne, then the amount of electricity with which each is charged is called the absolute electrostatic unit of electricity. If one body has a charge three times as great and the [Pg 64] other has a charge four times as great, the repulsion is 3 × 4 = 12 times greater. If the distance between the bodies is increased from one to five, the repulsion is twenty-five times as small, since 5² = 25. If the charge of one body is substituted by a negative one of same magnitude the repulsion becomes an attraction of the same magnitude.
In the early part of the nineteenth century methods were found for producing a steady electric current in metal wires. In 1820, the Danish physicist, H. C. Ørsted, discovered that an electric current influences a magnet in a characteristic way, and that, conversely, the current is affected by the forces emanating from the magnet, by a magnetic field in other words. The French scientist, Ampère, soon afterwards formulated exact laws for the electromagnetic forces between magnets and currents. In 1831, the English physicist, Faraday, discovered that an electric current is induced in a wire when currents or magnets in its neighbourhood are moved or change strength. Faraday’s views on electric and magnetic fields of force around currents and magnets were further of fundamental importance to the electromagnetic wave theory as developed by Maxwell. The branch of physics dealing with all these phenomena is now generally known as electrodynamics.
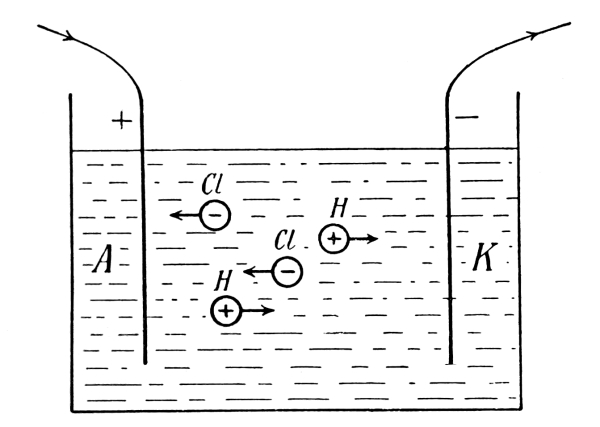
Fig. 14.—Picture of electrolysis of hydrogen chloride.
A, anode; K,
cathode;
H, hydrogen atoms;
Cl, chlorine atoms.
Faraday also studied the chemical effects which an electric current produces upon being conducted between two metal plates, called electrodes, which are immersed in a solution of salts or acids. The current separates the salt or acid into two parts which are carried by the electric forces in two opposite directions. This separation is [Pg 65] called electrolysis. If the liquid is dilute hydrochloric acid (HCl), the hydrogen goes with the current to the negative electrode, the cathode, and takes the positive electricity with it, while the chlorine goes against the current and takes the negative electricity to the positive electrode, the anode. We must then assume with the Swedish scientist, Arrhenius, that, under the influence of the water, the molecules of hydrogen chloride always are separated into positive hydrogen atoms and negative chlorine atoms, and that the electric forces from the anode and the cathode carry these atoms respectively with and against the current. The electrically charged wandering atoms are called ions, i.e. wanderers. The positive electricity taken by the hydrogen atoms to the cathode goes into the metal conductor, while the anode must receive from the metal conductor an equal amount of positive electricity to be given to the chlorine atoms to neutralize them. The negative charge of a chlorine atom must then be as large as [Pg 66] the positive charge of a hydrogen atom. These assumptions imply that equal numbers of the two kinds of atoms are present in the whole quantity of atoms transferred in any period of time.
Faraday found that the quantity of hydrogen which in the above experiment is transferred to the cathode in a given time is proportional to the quantity of electricity transferred in the same time. A gram of hydrogen always takes the same amount of electricity with it. By experiment this amount of electricity can be determined, and, since the weight in grams of the hydrogen atom is known, it is possible to calculate the amount of one atom. In electrostatic units it is 4·77 × 10⁻¹⁰, i.e., 477 billionth[1] parts. A chlorine atom then carries with it 4·77 × 10⁻¹⁰ electrostatic units of negative electricity. Since its atomic weight is 35·5, then 35·5 grams of chlorine will take as much electricity as 1 gram of hydrogen. The ratio e/m between the charge e and the mass m is then 35·5 times as great for hydrogen as for chlorine.
[1] Billion used here to mean one million million, and trillion to mean one million billion.
We have temporarily restricted ourselves to the electrolysis of hydrogen chloride. Let us now assume that we have chloride of zinc (ZnCl₂), which, by electrolysis, is separated into chlorine and zinc. Each atom of chlorine will, as before, carry 4·77 × 10⁻¹⁰ units of negative electricity to the anode; but since zinc is divalent (cf. p. 17) and one atom of zinc is joined to two of chlorine, therefore one atom of zinc must carry a charge of 2 × 4·77 × 10⁻¹⁰ units of positive electricity to the cathode. An atom or a group of atoms, with valence of three, in electrolysis carries 3 × 4·77 × 10⁻¹⁰ units, etc. [Pg 67]
We see then, that the quantity of electricity which accompanies the atoms in electrolysis is always 4·77 × 10⁻¹⁰ electrostatic units or an integral multiple thereof. This suggests the thought that electricity is atomic and that the quantity 4·77 × 10⁻¹⁰ units is the smallest amount of electricity which can exist independently, i.e., the elementary quantum of electricity or the “atom of electricity.” The atom of a monovalent element, when charged or ionized, should have one atom of electricity; a divalent, two, etc. On the two-fluid theory it was most reasonable to assume that there were two kinds of atoms of electricity representing, respectively, positive and negative electricity. In Fig. 15 there is given, in accordance with the two-fluid theory, a rough picture of a chlorine ion and a hydrogen ion and their union into a molecule.
Fig. 15.—Provisional
representation
(according to the two-fluid theory) of
A, a hydrogen ion; and
B, a chlorine ion; and
C, a molecule of hydrogen chloride.
The atoms of electricity seemed to differ essentially from the usual atoms of the elements in their apparent inability to live independently; they seemed to exist only in connection with the atoms of the elements. They would seem much more real if they could exist [Pg 68] independently. That such existence really is possible, has been discovered by the study of the motion of electricity in gases.
Fig. 16.—Vacuum tube with cathode rays and a shadow-producing cross.
P and N, conducting wires for the electric current;
a, cathode; b, anode and shadow-producer; c, d, the shadow.
Fig. 17.—Vacuum tube, where a bundle of
cathode rays are deviated by electric forces.
A, anode; K, cathode.
It has previously been said that air is an insulator for electricity, a statement which is, in general, true; however, as has also been said, electric sparks and arcs can pass through air. Moreover, it has been discovered that exhausted air is a very good conductor, so that a strong current can pass between two metal electrodes in a glass tube where the air is exhausted, if the electrodes are connected to an outer conductor by metal wires fused into the glass. In these vacuum tubes there are produced remarkable light effects, at first inexplicable. When the air is very much exhausted, to a hundred thousandth of the atmospheric pressure or less, strong electric forces (large difference of potential between the electrodes) are needed to produce an electric [Pg 69] discharge. Such a discharge assumes an entirely new character; in the interior of the glass tube there is hardly any light to be seen, but the glass wall opposite the negative electrode (the cathode) glows with a greenish tint (fluorescence). If a small metal plate is put in the tube between the cathode and the glass wall, a shadow is cast on the wall, just as if light were produced by rays, emitted from the cathode at right angles to its surface (cf. Fig. 16). The English physicist, Crookes, was one of the first to study these cathode rays. He assumed that they are not ether waves like the light rays, but that they consist of particles which are hurled from the cathode with great velocity in straight lines; they light the wall by their collisions with it. There was soon no doubt as to the correctness of Crookes’ theory. The cathode rays are evidently particles of negative electricity, which by repulsions are driven from the cathode (the negative electrode). A metal plate bombarded by the rays becomes charged negatively. Let us suppose that we have a small bundle of cathode rays, obtained by passing the rays from the cathode K (cf. Fig. 17) through two narrow openings S₁ and S. It can then be shown [Pg 70] that the bundle of rays is deviated not only by electric forces, but also by magnetic action from a magnet which is held near the glass. In the figure there is shown a deviation of the kind mentioned, caused by making the plates at B and C respectively positive and negative; since B attracts the negative particles and C repels them, the light spot produced by the bundle of rays is moved from M to M₁. The magnetic deviation is in agreement with Ørsted’s rules for the reciprocal actions between currents and magnets, if we consider the bundle of rays produced by moving electric particles as an electric current. (Since the electric particles travelling in the direction of the rays are negative, and since it is customary by the expression “direction of current” to understand the direction opposite to that in which the negative electricity moves, then, in the case of the cathode rays just mentioned, the direction of the current must be opposite to that of the rays.)
From measurements of the magnetic and electric deviations it is possible to find not only the velocity of the particles, but also the ratio e/m between the charge e of the particle and its mass m. The velocity varies with the potential at the cathode, and may be very great, 50,000 km. per second, for instance (about one-sixth the speed of light), or more. It has been found that e/m always has the same value, regardless of the metal of the cathode and of the gas in the tube; this means that the particles are not atoms of the elements, but something quite new. It has also been found that e/m is about two thousand times as large as the ratio between the charge and the mass of the hydrogen atom in electrolysis. If we now assume that e is just the elementary quantum of electricity 4·77 × 10¹⁰, which in magnitude [Pg 71] amounts to the charge of the hydrogen atom in electrolysis (but is negative), then m must have about ¹/₂₀₀₀ the mass of the hydrogen atom. This assumption as to the size of e has been justified by experiments of more direct nature. The experiments with charge and mass of electrons which have in particular been carried out by the English physicist, J. J. Thomson, give reason then to suppose these quite new and unknown particles to be free atoms of negative electricity; they have been given the name of electrons. Gradually more information about them has been acquired. Thus it has been possible in various ways to determine directly the charge on the electron, independently of its mass. Special mention must be made of the brilliant investigations of the American, Millikan, on the motion of very small electrified oil-drops through air under the influence of an electric force. To Millikan is due the above-mentioned value of e, which is accurate to one part in five hundred. Further, the mass of the electron has been more exactly calculated as about ¹/₁₈₃₅ that of the hydrogen atom. Their magnitude has also been learned; the radius of the electron is estimated as 1·5 × 10⁻¹³ cm. or 1·5 × 10⁻⁶ μμ, an order of magnitude one ten-thousandth that of the molecule or atom.
After the atom of negative electricity had been isolated, in the form of cathode rays, the next suggestion was that corresponding positive electric particles might be discharged from the anode in a vacuum tube. By special methods success has been attained in showing and studying rays of positive particles. In order to separate them from the negative cathode ray particles the German scientist, Goldstein, let the positive particles pass through canals in the cathode; they are therefore called [Pg 72] canal rays. The velocity of the particles is much less than that of the cathode rays, and the ratio e/m between charge and mass is much smaller and varies according to the gas in the tube. In experiments where the tube contains hydrogen, rays are always found for which e/m, as in electrolysis, is about ¹/₂₀₀₀ of the ratio in the cathode rays. Therefore there can be scarcely any doubt that these canal rays are made up of charged hydrogen atoms or hydrogen ions. The values found with other gases indicate that the particles are atoms (or molecules sometimes) of the elements in question, with charges one or more times the elementary quantum of electricity (4·77 × 10⁻¹⁰ electrostatic units). Research in this field has also been due in particular to J. J. Thomson. From his results, as well as from those obtained by other methods, it follows that positive electricity, unlike negative, cannot appear of its own accord, but is inextricably connected to the atoms of the elements.
The earlier conceptions of a one or two-fluid explanation of the phenomena of electricity appear now in a new light. We are led to think of a neutral atom as consisting of one mass charged with positive electricity together with as many electrons negatively charged as are sufficient to neutralize the positive. If the atom loses one, two or three electrons, it becomes positive with a charge of one, two or three elementary quanta of electricity, or for the sake of simplicity and brevity we say that the atom has one, two or three “charges.” If, on the other hand, it takes up one, two or three extra electrons it has one, two or three negative charges. Fig. 18 [Pg 73] can give help in understanding these ideas, but it must not be thought that the electrons are arranged in the way indicated. The substances, which appear as electropositive in electrolysis—i.e. hydrogen and metals—should then be such that their atoms easily lose one or more electrons, while the electronegative elements should, on the other hand, easily take up extra electrons. Elements should be monovalent or divalent according as their atoms are apt to lose or to take up one or two electrons. From investigations with the vacuum tube it appears, however, that the atoms of the same element can in this respect behave in more ways than would be expected from electrolysis or chemical valence.

Fig. 18.—Provisional representation (according to the electron theory) of
A, a neutral atom; B,
the same atom with two positive charges (a divalent positive ion)
and C, the same atom with two negative charges (a divalent negative ion).
When an electric current passes through a metal wire, it must be assumed that the atoms of the metal remain in place, while the electrical forces carry the electrons in a direction opposite to that which usually is considered as the direction of the current (cf. p.70). The motion of the electrons must not be supposed to proceed [Pg 74] without hindrance, but rather as the result of a complicated interplay, by no means completely understood, whereby the electrons are freed from and caught by the atoms and travel backwards and forwards, in such a way that through every section of the metal wire a surplus of electrons is steadily passing in the direction opposite to the so-called direction of the current. The number of surplus electrons which in every second passes through a section of the thin metal wire in an ordinary twenty-five candle incandescent light, at 220 volts, amounts to about one trillion (10¹⁸), or 1000 million (10⁹) in 0·000,000,001 of a second. If the metal conducting wire ends in the cathode of a vacuum tube, the electrons carried through the wire pass freely into the tube as cathode rays from the cathode.
This motion of electricity agrees best with the one-fluid theory, since the electrons, which here alone accomplish the passage of the electricity, may be considered as the fundamental parts of electricity. In this respect the choice of the terms positive and negative is very unfortunate, since a body with a negative charge actually has a surplus of electrons. Moreover, the electrons really have mass; but since the mass of a single electron is only ¹/₁₈₃₅ that of the atom of the lightest element, hydrogen, and since in an electrified body which can be weighed by scale there is always but an infinitesimal number of charged atoms, it is easy to understand that, formerly, electricity seemed to be without weight.
In electrolysis, where the motion of electricity is accomplished by positive and negative ions, we have a closer connection with the two-fluid theory. In motions of electricity through air the situation suggests both the one-fluid and the two-fluid theories, since the passage of electricity is sometimes carried on exclusively by the [Pg 75] electrons, and sometimes partly by them and partly by larger positive and negative ions, i.e., atoms or molecules with positive and negative charges.
Proceeding on the assumption that the electric and optical properties of the elements are determined by the activity of the electric particles, the Dutch physicist Lorentz and the English physicist Larmor succeeded in formulating an extraordinarily comprehensive “electron theory,” by which the electrodynamic laws for the variations in state of the ether were adapted to the doctrine of ions and electrons. This Lorentz theory must be recognized as one of the finest and most significant results of nineteenth century physical research.
It was one of the most suggestive problems of this theory to account for the emission of light waves from the atom. From the previously described electromagnetic theory of light (cf. p. 42) it follows that an electron oscillating in an atom will emit light waves in the ether, and that the frequency ν of these waves will naturally be equal to the number of oscillations of the electron in a second. If this last quantity is designated as ω, then
ν = ω
It may then be supposed that the electrons in the undisturbed atom are in a state of rest, comparable with that of a ball in the bottom of a bowl. When the atom in some way is “shaken,” one or more of the electrons in the atom begins to oscillate with a definite frequency, just as the ball might roll back and forth in the bowl if the bowl was shaken. This means that the atom is emitting light waves, [Pg 76] which, for each individual electron have a definite wave-length corresponding to the frequency of the oscillations, and that, in the spectrum of the emitted light, the observed spectral lines correspond to these wave-lengths.
Strong support for this view was afforded by Zeeman’s discovery of the influence of a magnetic field upon spectral lines. Zeeman, a Dutch physicist, discovered, about twenty-five years ago, that when a glowing vacuum tube is placed between the poles of a strong electromagnet, the spectral lines in the emitted light are split so that each line is divided into three components with very little distance between them. It was one of the great triumphs of the electron theory that Lorentz was able to show that such an effect was to be expected if it was assumed that the oscillations of light were produced by small oscillating electric particles within the atom. From the experiments and from the known laws concerning the reciprocal actions of a magnet and an electric current (here the moving particle), the theory enabled Lorentz to find not only the ratio e/m between the electric charge of each of these particles and its mass, but also the nature of the charge. He could conclude from Zeeman’s experiment that the charge is negative and that the ratio e/m is the same as that found for the cathode rays. After this there could not well be doubt that the electrons in the atoms were the origin of the light which gives the lines of the spectrum. It seemed, however, quite unfeasible for the theory to explain the details in a spectrum—to derive, for instance, Balmer’s formula, or to show why hydrogen has these lines, copper those, etc. These difficulties, combined with the great number of lines in the different spectra, seemed to mean that there were many electrons [Pg 77] in an atom and that the structure of an atom was exceedingly complicated.
As has been said, the electrons in a vacuum tube cause its wall to emit a greenish light when they strike it. Upon meeting the glass wall or a piece of metal (the anticathode) placed in the tube the electrons cause also the emission of the peculiar, penetrating rays called Röntgen rays in honour of their discoverer, or more commonly X-rays. They may be described as ultra-violet rays with exceedingly small wave-lengths (cf. p. 54). When, further, the electrons meet gas molecules in the tube they break them to pieces, separating them into positive and negative ions (ionization). The positive ions are the ones which appear in the canal rays. The ions set in motion by electrical forces can break other gas molecules to pieces, thus assisting in the ionization process. At the same time the gas molecules and atoms are made to produce disturbances in the ether, and thus to cause the light phenomena which arise in a tube which is not too strongly exhausted.
The free air can be ionized in various ways; this ionization can be detected because the air becomes more or less conducting. In fact, electric forces will drive the positive and negative ions through the air in opposite directions, thus giving rise to an electric current. If the ionization process is not steadily continued, the air gradually loses its conductivity, since the positive and negative ions recombine into neutral atoms or molecules. Ionization can be produced by flames, [Pg 78] since the air rising from a flame contains ions. A strong ionization can also be brought about by X-rays and by ultra-violet rays. In the higher strata of the atmosphere the ultra-violet rays of the sun exercise an ionizing influence. Most of all, however, the air is ionized by rays from the so-called radioactive substances which in very small quantities are distributed about the world.
The characteristic radiation from these substances was discovered in the last decade of the nineteenth century by the French physicist, Becquerel, and afterwards studied by M. and Mme. Curie. From the radioactive uranium mineral, pitchblende, the latter separated the many times more strongly radioactive element radium. The proper nature of the rays was later explained, particularly through the investigations of the English physicists, Rutherford, Soddy and Ramsay. These rays, which can produce heat effects, photographic effects and ionization, are of three quite different classes, and accordingly are known as α-rays, β-rays, and γ-rays. The last named, like the X-rays, are ultra-violet rays, but they have often even shorter wave-lengths and a much greater power of penetration than the usual X-rays. The β-rays are electrons which are ejected with much greater velocity than the cathode rays; in some cases their velocity goes up to 99·8 per cent. that of light. The α-rays are positive atomic ions, which move with a velocity varying according to the emitting radioactive element from ¹/₂₀ to almost ¹/₁₀ that of light. It has further been proved that the α-particles are atoms of the element helium, which has the atomic weight 4, and that they possess two positive charges, i.e., they must take up two electrons to produce a neutral helium atom. [Pg 79]
There is no doubt that the process which takes place in the emission of radiation from the radioactive elements is a transformation of the element, an explosion of the atoms accompanied by the emission either of double-charged helium atoms or of electrons, and the forming of the atoms of a new element. The energy of the rays is an internal atomic energy, freed by these transformations. The element uranium, with the greatest of all known atomic weights (238), passes, by several intermediate steps, into radium with atomic weight 226; from radium there comes, after a series of steps, lead, or, in any case, an element which, in all its chemical properties, behaves like lead. We shall go no further into this subject, merely remarking that the transformations are quite independent of the chemical combinations into which the radioactive elements have entered, and of all external influences.
When α-particles from radium are sent against a screen with a coating of especially prepared zinc sulphide, on this screen, in the dark, there can be seen a characteristic light phenomenon, the so-called scintillation, which consists of many flashes of light. Each individual flash means that an α-particle, a helium atom, has hit the screen. In this bombardment by atoms the individual atom-projectiles are made visible in a manner similar to that in which the individual raindrops which fall on the surface of a body of water are made visible by the wave rings which spread from the places where the drops meet the water. This flash of light was the first effect of the individual atom to be available for investigation and observation. The incredibility of anything so small as an atom producing a visible effect is lessened [Pg 80] when, instead of paying attention merely to the small size or mass of the atom, its kinetic energy is considered; this energy is proportional to the square of the velocity, which is here of overwhelming magnitude. For the most rapid α-particles the velocity is 2·26 × 10⁹ cm. per second; their kinetic energy is then about ⁴/₃₀ of the kinetic energy of a weight of one milligram of a substance at a velocity of one centimetre per second. This energy may seem very small, but, at least, it is not a magnitude of “inconceivable minuteness,” and it is sufficient under the conditions given above to produce a visible light effect. We must here also consider the extreme sensitiveness of the eye.

Fig. 19.—Photograph
of paths described by
α-particles (positive helium ions) emitted
from a radioactive substance.
[Pg 81] More practical methods of revealing the effects of the individual α-particles and of counting them are founded on their very strong ionization power. By strengthening the ionization power of α-particles, Rutherford and Geiger were able to make the air in a so-called ionization chamber so good a conductor that an individual α-particle caused a deflection in an electrical apparatus, an electrometre.
Fig. 20.—Photograph
of the path of a
β-particle (an electron).
(Both 19 and 20 are photographs by C. T. R. Wilson.)
With a more direct method the English scientist C. T. R. Wilson has shown the paths of the α-particles by making use of the characteristic property of ions, that in damp air they attract the neutral water [Pg 82] molecules which then form drops of water with the ions as nuclei. In air which is completely free of dust and ions the water vapour is not condensed, even if the temperature is decreased so as to give rise to supersaturation, but as soon as the air is ionized the vapour condenses into a fog. When Wilson sent α-particles through air, supersaturated with water vapour, the vapour condensed into small drops on the ions produced by the particles; the streaks of fog thus obtained could be photographed. Fig. 19 shows such a photograph of the paths of a number of atoms. When a streak of fog ends abruptly it does not mean that the α-particles have suddenly halted, but that their velocity has decreased so that they can no longer break the molecules of air to pieces, producing ions. The paths of the β-particles have been photographed in the same way, although an electron of the β-particles has a mass about 7000 times smaller than that of a helium atom; the electron has, however, a far greater velocity than the helium atom. This velocity causes the ions to be farther apart, so that each drop of water formed around the individual ions can appear in the photograph by itself (cf. Fig. 20).
[Pg 83]
We are now brought face to face with the fundamental question, hardly touched upon at all in the previous part of this work, namely, that of the construction and mode of operation of the atomic mechanism itself. In the first place we must ask: What is the “architecture” of the atom, that is, what positions do the positive and negative particles take up with respect to each other, and how many are there of each kind? In the second place, of what sort are the processes which take place in an atom, and how can we make them interpret the physical and chemical properties of the elements? In this chapter we shall keep essentially to the first question, and consider especially the great contribution which Rutherford made in 1911 to its answer in his discovery of the positive atomic nucleus and in the development of what is known as the Rutherford atomic model or nuclear atom.
Rutherford’s discovery was the result of an investigation which, in its main outlines, was carried out as follows: a dense stream of [Pg 84] α-particles from a powerful radium preparation was sent into a highly exhausted chamber through a little opening. On a zinc sulphide screen, placed a little distance behind the opening, there was then produced by this bombardment of atomic projectiles, a small, sharply defined spot of light. The opening was next covered by a thin metal plate, which can be considered as a piece of chain mail formed of densely-packed atoms. The α-particles, working their way through the atoms, easily traversed this “piece of mail” because of their great velocity. But now it was seen that the spot of light broadened out a little and was no longer sharply limited. From this fact one could conclude that the α-particles in passing among the many atoms in the metal plate suffered countless, very small deflections, thus producing a slight spreading of the rays. It could also be seen that some, though comparatively few, of the α-particles broke utterly away from the stream, and travelled farther in new directions, some, indeed, glancing back from the metal plate in the direction in which they had come (cf. Fig. 21). The situation was approximately as if one had discharged a quantity of small shot through a wall of butter, and nearly all the pellets had gone through the wall in an almost unchanged direction, but that one or two individual ones had in some apparently uncalled for fashion come travelling back from the interior of the butter. One might naturally conclude from this circumstance that here and there in the butter were located some small, hard, heavy objects, for example, some small pellets with which some of the projectiles by chance had collided. Accordingly, it seemed as if there were located in the metal sheet some small hard objects. These [Pg 85] could hardly be the electrons of the metal atoms, because α-particles, as has been stated before, are helium atoms with a mass over seven thousand times that of a single electron; and if such an atom collided with an electron, it would easily push the electron aside without itself being deviated materially in its path. Hardly any other possibility remained than to assume that what the α-particles had collided with was the positive part of the atom, whose mass is of the same order of magnitude as the mass of the helium atom (cf. Fig. 21). A mathematical investigation showed that the large deflections were produced because the α-particles in question had passed, on their way, through a tremendously strong electric field of the kind which will exist about an electric charge concentrated into a very small space and acting on other charges according to Coulomb’s Law. When, in the [Pg 86] foregoing, the word “collision” is used, it must not be taken to mean simply a collision of elastic spheres; rather the two particles (the α-particle and the positive particle of the metal atom) come so near to each other in the flight of the former that the very great electrical forces brought into play cause a significant deflection of the α-particles from their original course.

Fig. 21.—Tracks of α-particles in the interior of matter. While 1 and 3 undergo small deflections by collisions with electrons, 2 is sharply deflected by a positive nucleus.
Rutherford was thus led to the hypothesis that nearly all of the mass of the atom is concentrated into a positively charged nucleus, which, like the electrons, is very small in comparison with the size of the whole atom; while the rest of the mass is apportioned among a number of negative electrons which must be assumed to rotate about the nucleus under the attraction of the latter, just as the planets rotate about the sun. Under this hypothesis the outer limits of the atom must be regarded as given by the outermost electron orbits. The assumption of an atom of this structure makes it at once intelligible why, in general, the α-particles can travel through the atom without being deflected materially by the nuclear repulsion, and why the very great deflections occur as seldom as is indicated by experiment. This latter circumstance has, on the other hand, no explanation in the atomic model previously suggested by Lord Kelvin and amplified by J. J. Thomson, in which the positive electricity was assumed to be distributed over the whole volume of the atom, while the electrons were supposed to move in rings at varying distances from the centre of the atom.
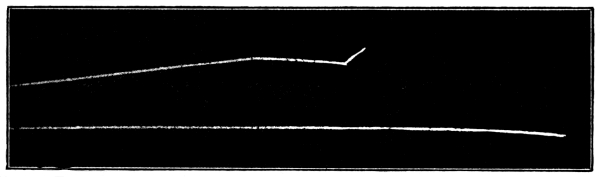
Fig. 22.—Photograph of the
paths of two α-particles
(positive helium ions).
One collides with an atomic nucleus.
The same characteristic phenomenon made evident in the passage of α-particles through substances by the investigations of Rutherford appears in a more direct way in Wilson’s researches discussed on p. 81. [Pg 87] His photographs of the paths of α-particles through air supersaturated with water vapour (see Fig. 22) show pronounced kinks in the paths of individual particles. Thus in the figure referred to, there are shown the paths of two α-particles. One of these is almost a straight line (with a very slight curvature), while the other shows a very perceptible deflection as it approaches the immediate neighbourhood of the nucleus of an atom, and finally a very abrupt kink; at the latter place it is clear that the α-particle has penetrated very close to the nucleus. If one examines the picture more closely, there will be seen a very small fork at the place where the kink is located. Here the path seems to have divided into two branches, a shorter and a longer. This leads one at once to suspect that a collision between two bodies has taken place, and that after the collision each body has travelled its own path, just as if, to return to the analogy of the bombardment of the butter wall, one had been able to drive two pellets out of the butter by shooting in only one. Or, to take perhaps a more familiar example, when a moving billiard ball collides at random with a stationary one, after the collision they both move off in different [Pg 88] directions. So, when the α-particle hits at random the atomic nucleus, both particle and nucleus move off in different directions; though in this case, since the nucleus has the much greater mass of the two, it moves more slowly, after the collision, than the α-particle, and has, therefore, a much shorter range in the air than the lighter, swifter α-particle. Had the gas in which the collisions took place been hydrogen, for example, the recoil paths of the hydrogen nuclei would have been longer than those of the α-particles, because the mass of the hydrogen nucleus is but one quarter the mass of the α-particle (helium atom).
The collision experiments on which Rutherford’s theory is founded are of so direct and decisive a character that one can hardly call it a theory, but rather a fact, founded on observation, showing conclusively that the atom is built after the fashion indicated. Continued researches have amassed a quantity of important facts about atoms. Thus, Rutherford was able to show that the radius of the nucleus is of the order of magnitude 10⁻¹² to 10⁻¹³cm. This means really that it is only when an α-particle approaches so near the centre of an atom that forces come into play which no longer follow Coulomb’s Law for the repulsion between two point charges of the same sign (in contrast to the case in the ordinary deflections of α-particles). It should be remarked, however, that in the case of the hydrogen nucleus theoretical considerations give foundation for the assumption that its radius is really many times smaller than the radius of the electron, which is some 2000 times lighter; experiments by which this assumption can be tested are not at hand at present. [Pg 89]
It is not necessary to have recourse to a new research to determine the masses of the nuclei of various atoms, because the mass of the nucleus is for all practical purposes the mass of the atom. Accordingly, if the mass of the hydrogen nucleus is taken as unity, the atomic mass is equal to the atomic weight as previously defined. The individual electrons which accompany the nucleus are so light that their mass has relatively little influence (within the limits of experimental accuracy) on the total mass of the atom.
On the other hand, a problem of the greatest importance which immediately suggests itself is to determine the magnitude of the positive charge of the nucleus. This naturally must be an integral multiple of the fundamental quantum of negative electricity, namely, 4·77 × 10⁻¹⁰ electrostatic units, or if we prefer to call this simply the “unit” charge, then the nuclear charge must be an integer. Otherwise a neutral atom could not be formed of a nucleus and electrons, for in a neutral atom the number of negative electrons which move about the nucleus must be equal to the number of positive charges in the nucleus. The determination of this number is, accordingly, equivalent to the settling of the important question, how many electrons surround the nucleus in the normal neutral state of the atom of the element in question.
The answer to the question is easiest in the case of the helium atom. For when this is expelled as an α-particle, it carries, as Rutherford was able to show, a positive charge of two units—in other words, two electrons are necessary to change the positive ion into a neutral atom. [Pg 90] At the same time there is every reason to suppose that the α-particle is simply a helium nucleus deprived of its electrons; it follows, therefore, that the electron system of the neutral helium atom consists of two electrons. Since the atomic weight of helium is four, the number of electrons is consequently one-half the atomic weight. Rutherford’s investigation of the deflections of α-particles in passing through various media had already led him to believe that for many other elements, to a considerable approximation, the nuclear charge and hence the number of electrons was equal to half the atomic weight. Hydrogen, of course, must form an exception, since its atomic weight is unity. The positive charge on the hydrogen nucleus is one elementary quantum, and in the neutral state of the atom, only one electron rotates about it. Fig. 23 gives a representation of the structure of the hydrogen atom, and the structures of the two types of hydrogen ions formed respectively by the loss and gain of an electron. In the picture, the position of the electron is, of course, arbitrary, and for the sake of simplicity its path is supposed to be circular.

Fig. 23.—Schematic representation of the nuclear atom.
A, a neutral hydrogen atom;
B, a positive, and C, a negative hydrogen ion;
K, atomic nuclei; E, electrons.
[Pg 91] As has just been indicated, Rutherford’s rule for the number of electrons is only an approximation. A Dutch physicist, van den Broek, conceived in the meantime the idea that the number of electrons in the atom of an element is equal to its order number in the periodic table (its “atomic number,” as it is now called). Especially through a systematic investigation of the X-ray spectra characteristic of the different elements this has proved to be the correct rule. In fact, using Bragg’s reflection method of X-rays from crystal surfaces (cf. p. 54), the Englishman, Moseley, made in 1914 the far-reaching discovery that these spectra possess an exceptionally simple structure, which made it possible in a simple way to attach an order number to each element (given on p. 23). On the basis of Bohr’s theory, established a year before, it could be directly proved that this order number must be identical with the number of positive elementary charges on the nucleus.
The number which formerly indicated simply the position of an element in the periodic system has thus obtained a profound physical significance, and in comparison the atomic weight has come to have but a secondary meaning. The inversion of argon and potassium in the periodic system (mentioned on p. 21), which seemed to be an exception to the regularity displayed by the system as a whole, obtains an easy explanation on the van den Broek rule; for to explain the inversion we need only assume that potassium has one electron more than argon, though its atomic weight is less than that of argon. We see at once that the atomic weight and number of electrons (or what is the same thing—the nuclear charge) are not directly correlated to each other. [Pg 92] And since the periodic system based on the atomic number represents the correct arrangement of the elements according to their respective properties (especially their chemical properties), we are led naturally to the conclusion that it is the atomic number and not the atomic weight that determines chemical characteristics.
The conception of the relatively great importance of the atomic number as compared with the atomic weight has in recent years received overwhelming support from the researches of Soddy, Fajans, Russell, Hevesy and others who have discovered the existence of so-called isotope elements (from the Greek isos = same, and topos = place), substances with different nuclear masses (atomic weights) and different radioactive properties (if there are any), but with the same nuclear charge, the same number of electrons and, consequently, occupying the same place in the periodic system. Two such isotopes are practically equivalent in all their chemical properties as well as in most of their physical characteristics. One of the oldest examples of isotopes is provided by ordinary lead with the atomic weight 207·2 and the substance found in pitchblende with the atomic weight 206, but identical, chemically, with ordinary lead. This latter form of lead has already been referred to on p. 79 as the end product of radioactive disintegrations, and hence it is sometimes called radium lead.
By his investigations of canal rays the English physicist Aston has just recently shown that many substances which have always been assumed to be simple elements, are in reality mixtures of isotopes. The atomic weight of chlorine determined in the usual way is 35·5, but in the [Pg 93] discharge tube two kinds of chlorine atoms appear, having atomic weights 35 and 37 respectively; and it must be assumed that these two kinds of chlorine are present in all the compounds of chlorine known on the earth in the ratio of, roughly, three to one. To separate such mixtures into their constituent parts is extremely difficult, precisely because the constituents have identical properties apart from a small difference in density, which stands in direct connection with the atomic weight. Such a separation was first carried out successfully by the Danish chemist, Brønsted, in collaboration with the Hungarian chemist, Hevesy (1921). These two scientists were able to separate a large quantity of mercury of density 13·5955 into two portions of slightly different densities. All the different isotopes of which mercury is a mixture were, indeed, not wholly separated; they were represented in the two portions in different proportions. Thus, in one of the first attempts, the density of the one part was 13·5986 and of the other 13·5920 (at 0° C).
It is a perfectly reasonable supposition that it is the electron system which determines the external properties of the atom, that is, those properties which depend on the interplay of two or more atoms. For the electron, rotating about the nucleus at a considerable distance, separates, so to speak, the nucleus from the surrounding space, and must therefore be assumed to be the organ which connects the atom with the rest of the universe. One might also expect the structure of the electron system to depend wholly on the nuclear charge, i.e. on the atomic number and not on the mass of the nucleus, since it is the nuclear electrical attraction which holds the electrons in their orbits and not the relatively insignificant gravitational attraction. [Pg 94]
It thus becomes intelligible that the properties of the elements can be divided into two sharply defined classes, namely: (1) properties of the nucleus, and (2) properties of the electron system in the atom. The credit for first recognizing the sharp distinction between these two classes, a distinction fundamental for a detailed study of the atom, is due to Niels Bohr.
The properties of the nucleus determine—(a) the radioactive processes, or explosions of the nucleus, and related processes; (b) collisions, where two nuclei approach extremely near to each other; and (c) weight which, as mentioned above, stands in direct connection with atomic weight. The properties of the electron system are, on the other hand, the determining factors in all other physical and chemical activities, and, as has been stated, are functions, we may say, of the atomic number of the given element. The Bohr theory may be said to concern itself with the chemical and physical properties of the atom with the exception of those which have to do with the nucleus. We shall consequently devote our attention in the next chapters to the electron system. But before turning to this we shall dwell a little further upon the atomic nucleus.
That the nucleus is not an elementary indivisible particle but a system of particles, is clearly shown by the radioactive processes in which α-particles and β-particles (electrons) are shot out of the nuclei of [Pg 95] radioactive elements. Bohr was the first to see clearly that not only the α-particles emitted in such cases come from the nucleus, but that the β-particles also have their source there. There is now no doubt that, in addition to the outer electrons of the atom, which are the determining factor in the atomic number, there must also be, in the radioactive substances at any rate, special nuclear electrons which lead a more hidden existence in the interior of the nucleus. One can easily understand that isotopes may result as products of radioactive disintegration. For example, let us suppose that a nucleus emits first an α-particle (i.e. a helium nucleus with two positive charges), and thereafter sends out two electrons, each with its negative charge, in two new disintegrations. The nuclear charge in the resultant atom will then obviously be the same as before, because the loss of the two electrons exactly neutralizes that of the α-particle. But the atomic weight will be diminished by four units (i.e. the weight of the helium nucleus, remembering also that the electrons have but very negligible masses). Among the radioactive substances are recognized many examples of isotope elements, with atomic weights differing precisely by four. The radioactive element uranium is the element with the greatest atomic weight (238), and atomic number (92), and consequently with the greatest nuclear charge. Almost all the other radioactive substances are those with high atomic numbers in the periodic system. The cause of radioactivity must be sought in the hypothesis that the nuclei of the radioactive elements are very complicated systems with small stability, and therefore break down rather easily into less complicated and more stable systems with the emission of some of their constituent particles; [Pg 96] the corpuscular rays thus produced possess a considerable amount of kinetic energy.
Accordingly, by analogy, the nuclei of the non-radioactive elements may be assumed to be composed of nuclear electrons and positive particles; hydrogen alone excepted. The simplest assumption is that the hydrogen nucleus is the real quantum or atom of positive electricity, just as the electron is the atom of negative electricity. On this theory all substances are built up of two kinds only of fundamental particles, namely, hydrogen nuclei and electrons. That these particles may themselves consist of constituent parts is, of course, an open possibility, but such speculation is beyond our experience up to the present. In every nucleus there are more positive hydrogen nuclei than there are negative electrons, so that the nucleus has a residual positive charge of a magnitude equal to the difference between the number of hydrogen nuclei and nuclear electrons.
If we now pass from hydrogen which has the atomic weight, atomic number and nuclear charge of unity, we next encounter helium with the atomic weight 4, atomic number and nuclear charge 2. The helium nucleus should therefore consist of 4 hydrogen nuclei, which would together account for the atomic weight of 4. But since these represent 4 positive charges, there must also be present in the nucleus 2 negative electrons to make the resultant nuclear charge equal to 2. We could indeed hardly conceive of a system composed of 4 positive hydrogen nuclei alone; for the forces of repulsion would soon drive the separate parts asunder. The two electrons can, so to speak, serve to hold the system together. [Pg 97] Fig. 24 gives a rough representation of the helium atom. It must be carefully noted that the picture is purely schematic and the distances arbitrary. The helium nucleus, composed of 4 hydrogen nuclei and 2 electrons, seems to possess extreme stability, and it is not improbable that helium nuclei occur as higher units in the structure of the nuclei of not only the radioactive substances but also the other elements. We shall perhaps be very near the truth in saying that all nuclei are built up of combinations of hydrogen nuclei, helium nuclei and electrons.

Fig. 24.—Schematic
representation of a helium atom.
K, nuclear system with
four hydrogen nuclei and two nuclear
electrons; E,
electrons in the outer electron system.
In nitrogen, with the atomic weight 14 and atomic number 7, the nucleus should consist of 14 hydrogen nuclei (with 12 of them compounded, perhaps, into 3 helium nuclei) and 7 nuclear electrons, reducing the resultant positive nuclear charge from 14 to 7. Uranium, with atomic number 92 and atomic weight 238, should have a nucleus composed of 238 hydrogen nuclei and 146 electrons, and so on for the others. We see at once that the conception of the nucleus here propounded leads us back to the old hypothesis of Prout (see p. 15) that all atomic weights should be integral multiples of that of hydrogen. This hypothesis [Pg 98] apparently disagreed with atomic weight measurements, but the isotope researches have vanquished this difficulty; thus it has been mentioned before that chlorine with an atomic weight of 35·5 appears to be a mixture of isotopes with atomic weights 35 and 37, and other cases have a similar explanation. Yet the rule cannot be wholly and completely exact. For, in the first place, the mass of the electrons must contribute something, though this contribution is far too small to be measured. But there is also a second matter which plays a part here. This is the law enunciated by Einstein in his relativity theory, that every increase or decrease in the energy of a body is correlated with an increase or decrease in the mass of the body, proportional to the energy change. We must, therefore, expect that the masses of the various atomic nuclei will depend not only on the number of hydrogen nuclei (and electrons), but also on the energy represented in the attractions and repulsions between the particles of the system, and in their mutual motions, or the energy which comes into play in the formation and disintegration of nuclear systems. This is presumably closely connected, although in a way which is not clearly understood, with the fact, that if the atomic weights of the elements are to come out integers, that of hydrogen must not be taken as 1 but as 1·008; that is, the atomic weight unit must be chosen a little smaller than the atomic weight of hydrogen (cf. table, p. 23).
We shall now treat very briefly two questions which have profoundly [Pg 99] interested many people, because they are concerned with possible practical applications of our new knowledge of atoms.
The first question is this: Can one not, from this knowledge, bring about the transformation of one element into another? In answering this, it can, of course, be said immediately that among the radioactive substances such transformations are constantly taking place without human interference, and we certainly have no right to state offhand that it will be impossible for man ever to bring about such a transformation artificially. For example, if we could succeed in getting one hydrogen nucleus loose from the nucleus of mercury, the latter would thereby be changed into a gold nucleus. Such a thing is not only conceivable, but in the last few years it has become a reality, though, to be sure, not with the substances here mentioned. In 1919 Rutherford, by bombarding nitrogen (N = 14) with α-particles, was able to knock loose some hydrogen nuclei from the nitrogen nucleus; perhaps he succeeded thereby in changing the nitrogen nuclei into carbon nuclei (C = 12) by the breaking off of two hydrogen nuclei from each nitrogen nucleus. But to disintegrate very few nitrogen nuclei, Rutherford had to employ a formidable bombardment with hundreds of thousands of projectiles (α-particles); and even if he had ended with gold instead of carbon, this would have been, from the economic point of view, a very foolish way of making gold; and at the present time we know of no other artificial method for the transformation of elements. That Rutherford’s investigation has, in any case, extraordinarily great interest and scientific value is another matter. [Pg 100]
The second question is whether one cannot liberate and utilize the energy latent in the interior of the atom. This question, which was suggested in the first instance by the discovery of radium, has recently attracted considerable attention because of reports that, according to Einstein’s relativity theory, one gram of any substance by virtue of its mass alone must contain a quantity of energy equal to that produced by the burning of 3000 tons of coal. The meaning of this statement is this: it has already been mentioned that according to the relativity theory a decrease in the energy of a body brings about a decrease in its mass; it is immaterial in what form the energy is given up, whether as heat, elastic oscillations, or the like; all that is said is, that to a certain decrease in mass, will correspond a perfectly definite emission of energy in some form. If we now could imagine the whole mass of one gram of a substance to be “destroyed” (i.e. caused to disappear utterly as a physical substance), and to reappear as heat energy, for example, then we could compute from the known relation between mass and energy, that the heat energy thus brought about would be equivalent to that obtained by the burning of 3000 tons of coal. But in order that all this energy should be developed, even the hydrogen nuclei and the electrons would have to be “destroyed,” and no phenomenon is known, supporting the supposition that such a “destruction” of the fundamental particles of a substance is possible, or that it is possible to transform these particles into other types of energy. A thought like this must rather be stamped as fantasy, the origin of which is to be found in a misunderstanding of a purely scientific mode of expression. [Pg 101]
The case is essentially different with those quantities of energy which must be assumed to be freed or absorbed in the transformation of one nuclear system into another, that is, in elemental transformations. Though these are far smaller in amount, the radioactive processes indicate that they are not wholly to be despised. For one gram of radium will upon complete disintegration to non-radioactive material give off as much energy as is equivalent to 460 kg. of coal. But even here we must confess that it will take about 1700 years for only half of the radium to be transformed. It is not at all impossible that other elemental transformations might lead to just as great energy developments as appear in the disintegration of radioactive substances. Let us imagine that four hydrogen nuclei, which together have a mass of 4 × 1·008 = 4·032, and two electrons could join together to form a helium nucleus with atomic weight very close to 4. This process would thus result in a loss of mass which must be assumed to appear in another form of energy. The amount of energy obtainable in this way from one gram of hydrogen would be considerably more than that given off by the disintegration of one gram of radium.
There can hardly exist any doubt that in nature there occur not only disintegrations, but also (perhaps in the interior of the stars) building-up processes in which compound nuclei result from simple ones. It is therefore natural to suppose that by exerting on hydrogen exceptional conditions of temperature, pressure, electrical changes, etc., we could succeed by experiments here on earth in forming helium from it with the development of considerable energy. But at the same time it is very likely that even under favourable circumstances such [Pg 102] a process would take place with very great slowness, because the formation of a helium nucleus might well be a very infrequent occurrence; it would probably be the result of a certain succession of collisions between hydrogen nuclei and electrons, a combination whose probability of occurrence in a certain number of collisions is infinitely less than the probability of winning the largest prize in a lottery with the same number of chances. Nature has time enough to wait for “wins,” while mankind unfortunately has not. We know concerning the disintegration of the radioactive substances that it is of the character here indicated; of the great number of atoms to be found in a very small mass of a radioactive substance, now one explodes and now another. But why fortune should pick out one particular atom is as difficult to understand as why in a lottery one particular number should prove to be the lucky one rather than any other. Our only understanding of the whole matter rests on the law of averages, or probability as we may call it. We know that of a billion radium atoms (10¹²) on the average thirteen explode every second; and even if in any single collection of a billion a few more or a few less may explode, the average of thirteen per second per billion will always be maintained in dealing with larger and larger numbers of atoms, as, for example, with a thousand billion or a million billion. For other radioactive substances we get wholly different averages for the number of atoms disintegrating per second; but in no case are we able to penetrate into the inner character of the process of disintegration itself. And what holds true of the radioactive substances will also hold true probably for elemental changes of all kinds; Rutherford with his hundreds of thousands of α-particle projectiles was able to make [Pg 103] sure of but a few lucky “shots.” The whole matter must at this stage be looked upon as governed wholly by chance.
One interested in speculating on what would happen if it were possible to bring about artificially a transformation of elements propagating itself from atom to atom with the liberation of energy, would find food for serious thought in the fact that the quantities of energy which would be liberated in this way would be many, many times greater than those which we now know of in connection with chemical processes. There is then offered the possibility of explosions more extensive and more violent than any which the mind can now conceive. The idea has been suggested that the world catastrophes represented in the heavens by the sudden appearance of very bright stars may be the result of such a release of sub-atomic energy, brought about perhaps by the “super-wisdom” of the unlucky inhabitants themselves. But this is, of course, mere fanciful conjecture.
It seems clear, however, that we need have no fear that in investigating the problem of atomic energy we are releasing forces which we cannot control, because we can at present see no way to liberate the energy of atomic nuclei beyond that which Nature herself provides, to say nothing of a practical solution of the energy problem. The time has certainly not yet come for the technician to follow in the theoretical investigator’s footsteps in this branch of science. One hesitates, however, to predict what the future may bring forth.
Interesting and significant as is the insight which Rutherford and others have opened up into the inner workings of the nucleus, the study [Pg 104] of the electron system of the atom bears more intimately upon the various branches of physical and chemical science, and hence presents greater possibilities of attaining, in a less remote future, to discoveries of practical significance.
[Pg 105]
Even if Rutherford had not yet succeeded in giving a complete answer to the first of the questions propounded in the previous chapter, namely, that concerning the positions of the positive and negative particles of the atom, one might at any rate hope that his general explanation of the structure of the atom—that is, the division into the nucleus and surrounding electrons, and the determination of the number of electrons in the atoms of the various elements—would furnish a good foundation for the answer to the second question about the connection between the atomic processes and the physical and chemical properties of matter. But in the beginning this seemed so far from being true that it appeared almost hopeless to find a solution of the problem of the atom in this way.
We shall best understand the meaning of this if we consider the simplest of the elemental atoms, namely, the atom of hydrogen with its positive nucleus and its one electron revolving about the nucleus. How could it be possible to explain from such a simple structure the many [Pg 106] sharp spectral lines given by the Balmer-Ritz formula (p. 57)? As has previously been mentioned, the classical electron theory seemed to demand a very complicated atomic structure for the explanation of these lines. According to the electron theory, the atoms may be likened to stringed instruments which are capable of emitting a great number of tones, and in these atoms the electrons are naturally supposed to correspond to the “strings.” But the hydrogen atom has only one electron, and it hardly seems credible that in a mass of hydrogen the individual atoms would be tuned for different “tones,” with definite frequencies of vibration.
Now, it certainly cannot be concluded from the analogy with the stringed instrument that a single electron can emit light of only a single frequency at one time, corresponding to a single spectral line. For a plucked string will, as we know, give rise to a simple tone only if it vibrates in a very definite and particularly simple way; in general it will emit a compound sound which may be conceived as made up of a “fundamental” and its so-called “overtones,” or “harmonies” whose frequencies are 2, 3, ... times that of the fundamental (i.e. integral multiples of the latter). These overtones may arise even separately because the string, instead of vibrating as a whole, may be divided into 2, 3, ... equally long vibrating parts, giving respectively 2, 3, ... times as great frequencies of vibration. We call such vibrations “harmonic oscillations.” The simultaneous existence of these different modes of oscillation of the string may be thought of in the same way as the simultaneous existence of wave systems of different wave-lengths on the surface of water. Corresponding to the possibility [Pg 107] of resolving the motion of the string into its “harmonic components,” the compound sound waves produced by the string can be resolved by resonators (cf. p. 44) into tones possessing the frequencies of these components.
According to the laws of electrodynamics the situation with the electron revolving about the hydrogen nucleus might be expected to be somewhat similar to that described above in connection with the vibrating string. If the orbit of the electron were a circle, it should emit into the ether electromagnetic waves of a single definite wave-length and corresponding frequency, ν, equal to ω, the frequency of rotation of the electron in its orbit; that is, the number of revolutions per second. But just as a planet under the attraction of the sun, varying inversely as the square of the distance, moves in an ellipse with the sun at one focus, so the electron, under the attraction of the positive nucleus, which also follows the inverse square law, will in general be able to move in an ellipse with the nucleus at one focus. The electromagnetic waves which are emitted from such a moving electron may on the electron theory be considered as composed of light waves corresponding to a series of harmonic oscillations with the frequencies:
ν₁ = ω, ν₂ = 2ω, ν₃ = 3ω ... and so on,
where ω, as before, is the frequency of revolution of the electron. According as the actual orbit deviates more or less from a circle, the frequencies ν₂, ν₃ ... will appear stronger or weaker in the compound light waves emitted. But the actual distribution of spectral lines in the real hydrogen spectrum presents no likeness whatever to this distribution of frequencies.
[Pg 108] From this it is evident that no agreement can be reached between the classical electron theory on the one hand and the Rutherford atom model on the other. Indeed, the disagreement between the two is really far more fundamental than has just been indicated. According to Lorentz’s explanation of the emission of light waves, the electrons in a substance (see again p. 75) should have certain equilibrium positions, and should oscillate about these when pushed out of them by some external impulse. The energy which is given to the electron by such an impulse is expended in the emission of the light waves and is thus transformed into radiation energy in the emitted light, while the electrons fall to rest again unless they receive in the meantime a new impulse. We can get an understanding of what these impulses in various cases may be by thinking of them, in the case of a glowing solid, for example, as due to the collisions of the molecules; or in the case of the glowing gas in a discharge tube, from the collisions of electrons and ions. The oscillating system represented by the electron (the “oscillator”) will possess under these circumstances great analogy with a string which after being set into vibration by a stroke gradually comes back to rest, while the energy expended in the stroke is emitted in the form of sound waves. Although the vibrations of the string become weaker after a while, the period of the vibrations will remain unchanged; the string vibrations like pendulum oscillations have an invariable period, and the same will be the case with the frequency of the electron if the force which pulls it back into its equilibrium position is directly proportional to the displacement from this position (the “harmonic motion” force). [Pg 109]
Rutherford’s atomic model is, however, a system of a kind wholly different from the “oscillator” of the electron theory. The one revolving hydrogen electron will find a position of “rest” or equilibrium only in the nucleus itself, and if it once becomes united with the latter it will not easily escape; it will then probably become a nuclear electron, and such a process would be nothing less than a transformation of elements (see p. 79). On the other hand, it follows necessarily from the fundamental laws of electrodynamics that the revolving electron must emit radiation energy, and, because of the resultant loss of energy, must gradually shrink its path and approach nearer the nucleus. But since the nuclear attraction on the electron is inversely proportional to the square of the distance, the period of revolution will be gradually decreased and hence the frequency of revolution ω, and the frequency of the emitted light will gradually increase. The spectral lines emitted from a great number of atoms should, accordingly, be distributed evenly from the red end of the spectrum to the violet, or in other words there should be no line spectrum at all. It is thus clear that Rutherford’s model was not only unable to account for the number and distribution of the spectral lines; but that with the application of the ordinary electrodynamic laws it was quite impossible to account for the existence even of spectral lines. Indeed, it had to be admitted that an electrodynamic system of the kind indicated was mechanically unstable and therefore an impossible system; and this would apply not merely to the hydrogen atom, but to all nuclear atoms with positive nuclei and systems of revolving electrons.
However one looks at the matter, there thus appears to be an [Pg 110] irremediable disagreement between the Rutherford theory of atomic structure and the fundamental electrodynamic assumptions of Lorentz’s theory of electrons. As has been emphasized, however, Rutherford founded his atomic model on such a direct and clear-cut investigation that any other interpretation of his experiments is hardly possible. If the result to which he attained could not be reconciled with the theory of electrodynamics, then, as has been said, this was so much the worse for the theory.
It could, however, hardly be expected that physicists in general would be very willing to give up the conceptions of electrodynamics, even if its basis was being seriously damaged by Rutherford’s atomic projectiles. Surmounted by its crowning glory—the Lorentz electron theory—the classical electrodynamics stood at the beginning of the present century a structure both solid and spacious, uniting in its construction nearly all the physical knowledge accumulated during the centuries, optics as well as electricity, thermodynamics as well as mechanics. With the collapse of such a structure one might well feel that physics had suddenly become homeless.
In a field completely different from the above the conclusion had also been reached that there was something wrong with the classical electrodynamics. Through his very extended speculations on thermodynamic equilibrium in the radiation process, Planck (1900) had reached the point of view expressed in his quantum theory, which was just as irreconcilable with the fundamental electrodynamic laws as the Rutherford atom. [Pg 111]
A complete representation of this theory would lead us too far; we shall merely give a short account of the foundations on which it rests.
By a black body is generally understood a body which absorbs all the light falling upon it, and, accordingly, can reflect none. Physicists, however, denote by the term “perfect black body” in an extended sense, a body which at all temperatures absorbs all the radiation falling upon it, whether this be in the form of visible light, or ultra-violet, or infra-red radiation. From considerations which were developed some sixty years ago by Kirchhoff, it can be stated that the radiation which is emitted by such a body when heated does not depend on the nature of the body but merely on its temperature, and that it is greater than that emitted by any other body whatever at the same temperature. Such radiation is called temperature radiation or sometimes “black” radiation, though the latter term is apt to be misleading, since a “perfect black body” emitting black radiation may glow at white heat. It may be of interest to note here the fundamental law deduced by Kirchhoff, which may best be illustrated by saying that good absorbers of radiation are also good radiators. An instructive experiment illustrating this is performed by painting a figure in lampblack on a piece of white porcelain. The lampblack surface is clearly a better absorber of radiant energy than the white porcelain. When the whole is heated in a blast flame, the lampblack figure glows much more brightly than the surrounding porcelain, thus showing that at the same temperature it is also the better radiator. Following the same law we conclude that highly reflecting bodies are not good radiators, a fact that has practical significance in house heating. The perfect black [Pg 112] body, then, being the best absorber of radiation, is also the best radiator.
In actual practice no body is absolutely black. Even a body coated with lampblack reflects about 10 per cent. of the light waves incident on it. The Danish physicist Christiansen remarked long ago that a real black body could be produced only if an arrangement could be made whereby the incident waves could be reflected several times in succession before finally being emitted. To take the case of lampblack, three such reflections would reduce the re-emission from the lampblacked body to only ⁴/₁₀₀₀ of the radiation initially falling on it. This type of black body was finally realized by making a cavity in an oven having as its only opening a very small peep-hole, and keeping the temperature of the wall of the oven uniform. If a ray is sent into the cavity through the peep-hole, it will become, so to speak, captured, because, when once inside it will suffer countless reflections from the walls of the cavity, having more and more of its energy absorbed at each reflection. Very little of the radiation thus entering will ever get out again, and consequently such a body will act very much like a “perfect black body” according to the theoretical definition above. Accordingly, the radiation which is emitted from such a glowing cavity through the peep-hole will be black or practically black radiation.
The cavity itself will be criss-crossed in all directions by radiation emitted from one part of the inner surface of the cavity and absorbed by (and partially reflected from) other parts of the surface. When the walls of the cavity are kept at a fixed and uniform temperature there will automatically be produced a state of equilibrium in which every [Pg 113] cubic centimetre of the cavity will contain a definite quantity of radiation energy, dependent only on the temperature of the walls. Further, in the equilibrium state the radiation energy will be distributed in a perfectly definite way (dependent as before on the temperature only) among the various types of radiation corresponding to different wave-lengths and frequencies. If there is too much radiation of one kind and too little of another, the walls of the cavity will absorb more of the first kind than they emit, and emit more of the second kind than they absorb, and so the state will vary until the right proportion for equilibrium is attained.
This distribution of the radiation over widely differing wave-lengths can be investigated by examining spectroscopically the light emitted from the peep-hole in the cavity. Then, by means of a bolometer or some other instrument, the heat development in the different portions of the spectrum can be measured. At a temperature of 1500° C., for example, one will find that the maximum energy is represented for rays of wave-length in the close vicinity of 1·8 μ, i.e. in the extreme infra-red. If the temperature is raised, the energy maximum travels off in the direction of the violet end of the spectrum; if the temperature is lowered, it will move farther down into the infra-red.
It is also possible to make a theoretical calculation of the distribution of energy in the spectrum of the black-body radiation at a given temperature. But the results obtained do not agree with experiment. The English physicists, Rayleigh and Jeans, developed on the basis of the classical electrodynamic laws and by apparently convincing arguments a distribution law according to which actual [Pg 114] radiation equilibrium becomes impossible, since if it were true the energy in the radiation would tend more and more to go over to the region of short wave-lengths and high frequencies, and this shifting would apparently go on indefinitely. The theory thus leads to results which are not only in disagreement with experiment, but which must be looked upon as extremely unreasonable in themselves.
Planck, however, had vanquished these difficulties and had obtained a radiation law in agreement with experiment by introducing an extremely curious hypothesis. Like Lorentz, he thought of radiation as produced through the medium of small vibrating systems or oscillators, which could emit or absorb rays of a definite frequency ν. But while, according to the Lorentz theory and the classical electrodynamics, radiation can be emitted in infinitely small quantities (i.e. small without limit), Planck assumed that an oscillator can emit and absorb energy only in certain definite quantities called quanta, where the fundamental quantum of radiation is dependent on the frequency of the oscillator, varying directly with the latter. If thus we denote the smallest quantity of energy which an oscillator of frequency ν can emit or absorb by E, then we can write
E = hν,
where h is a definite constant fixed for all frequencies. Accordingly the cavity can receive radiation energy of frequency ν from the radiating oscillators in its wall, or transfer energy to these in no smaller quantity than hν. The total energy of that kind emitted or absorbed at any given time will always be an integral multiple of hν. Oscillators with a frequency 1½ times as great will emit energy in quanta which are 1½ times larger, and so on. [Pg 115]
The quantity h is independent, not only of the wave-length, but also of the temperature and nature of the emitting body. This constant, the so-called Planck constant, is thus a universal constant. If one uses the “absolute” units of length, mass and time (see table, p. 210), its value comes out as 6·54 × 10⁻²⁷. For the frequency 750 × 10¹² vibrations per second, corresponding to the extreme violet in the visible spectrum, the Planck energy quantum thus becomes about 5 × 10⁻¹² erg, or 3·69 × 10⁻¹⁹ foot-pounds (note that the “erg” is the “absolute” unit of work, or the amount of work done when a body is moved through a distance of 1 cm. by a force of one dyne acting in the direction of the motion, while the “foot-pound” is the work done when a force of 1 pound moves a body 1 foot in the direction of the force). For light belonging to the red end of the spectrum, the energy is about half as great. If we pass, however, to the highest frequencies and the shortest wave-lengths which are known, namely those corresponding to the “hardest” (i.e. most penetrating) γ-rays (see p. 78), we meet with energy quanta which are a million times larger, i.e. 2 × 10⁻⁶ erg, although they are still very small compared to any amount of energy measurable mechanically.
This remarkable theory of quanta, which in the hands of Planck still possessed a rather abstract character, proved under Einstein’s ingenious treatment to have the greatest significance in many problems which, like heat radiation, had provided physicists with many difficulties. For by assuming that energy in general could only be given up and taken in in quanta, certain facts about the specific heats of bodies could be accounted for—facts which the older physics had [Pg 116] proved powerless to explain. The Planck energy quanta, as Einstein showed, could also explain in a very direct and satisfactory way the photoelectric effect, as it is called. This effect consists in the freeing of electrons from a metal plate which ultra-violet rays are allowed to strike. The maximum velocity with which these electrons are propelled from the plate is found to be independent of the intensity of the incident light, but dependent simply on the frequency of the radiation. Careful measurements have indeed shown, as Einstein predicted, that the incident light really does utilize an energy quantum hν to free each electron and give it velocity (cf. p. 172). Of the different methods which nowadays are at hand, the photoelectric effect constitutes one of the best means of determining the value of h. It has been applied for that purpose by Millikan, to whose ingenious experiments the most accurate direct determination of h is actually due.
All this lay completely outside the laws of electrodynamics, and pointed to the existence of unknown and more fundamental laws. But, for the time being, physicists had to be satisfied merely with a recognition of the fact that these mysterious energy quanta play a very significant part in many phenomena.
A decade ago physics, as regards radiation problems, was in a very unsettled state; with four separate branches of knowledge, each of which seemed firm and well-founded enough in itself, but which had no common connecting link, indeed, were even to some extent inconsistent with each other. The first of these was the classical electrodynamics surmounted by the felicitous electron theory of Lorentz and Larmor. The second was the empirical knowledge of the spectra resting on the work [Pg 117] of Balmer, Ritz and Rydberg. The third was Rutherford’s nuclear atom model. And the fourth was Planck’s quantum theory of heat radiation. It was quite evident that progress in the theory of radiation and the structure of the atom was hopeless as long as these four points of view remained uncorrelated.
Such was the situation when, in 1913, Bohr published his atomic theory, in which he was able with great ingenuity to unite the nuclear atom, the Balmer-Ritz formula and the quantum theory. As far as electrodynamics is concerned, the impossibility of retaining that in its classical form was presented in a much clearer way than ever before. But, as will presently be evident, the Bohr theory has a very definite connection with the classical theory, and Bohr’s attempts to preserve and develop this connection have proved to be of the greatest significance for his theory. In spite of the fundamental rupture with the old ideas, the Bohr theory strives to absorb all that is useful in the classical point of view.
At the head of the theory appear the two fundamental hypotheses or postulates on the properties of the atom. [Pg 118]
The first postulate states that for each atom or atomic system there exists a number of definite states of motion, called “stationary states,” in which the atom (or atomic system) can exist without radiating energy. A finite change in the energy content of the atom can take place only in a process in which the atom passes completely from one stationary state to another.
The second postulate states that if such a transition takes place with the emission or absorption of electromagnetic light waves, these waves will have a definite frequency, the magnitude of which is determined by the change in the energy content of the atom. If we denote the change in energy by E and the frequency by ν we may write
| E = hν, or ν = | E |
| h |
where h is the Planck constant. In consequence of the second postulate the emission as well as the absorption of energy by the atom always takes place in quanta.
The two postulates say nothing concerning the nature of the motion in the stationary states. In the applications, however, a connection with the Rutherford atomic model is established. Confining our attention first to the hydrogen atom, the system with which we are concerned consists, accordingly, of a positive nucleus and one electron revolving about it. The various states of motion which the electron can assume in virtue of the first postulate are a series of orbits at different distances from the nucleus. In each of these “stationary orbits” the electron follows the general mechanical laws of motion; i.e. under the nuclear attraction which is inversely proportional to the square of the distance, the electron describes an ellipse with the nucleus at one focus, as has previously been stated; but in contradiction with the classical electrodynamics it will emit no radiation while moving in this orbit. Fig. 25 shows a series of these orbits, to which the numbers 1, 2, 3, 4 have been attached, and which for simplicity are represented as circular. [Pg 119]

Fig. 25.—The
Bohr model of the hydrogen atom in
the simplified form
(with circles instead of ellipses).
If the electron passes from an outer orbit to an inner one; for example, if it goes from number 4 to number 2, or from number 2 to number 1, the electric force which attracts it to the nucleus will do work just as the force of gravity does work when a stone falls to the ground. A part of this work is used to increase the kinetic energy of the electron, making its velocity in the inner orbit greater than in the outer, but the rest of the work is transformed into radiation energy which is emitted from the atom in the form of monochromatic light. In consequence of the second postulate the frequency of the emitted radiation is proportional to the energy loss. When the electron has reached the innermost orbit (the one denoted by 1 in the figure), it cannot get any nearer the nucleus and hence cannot emit any more radiation unless it first is impelled to pass from its inner orbit to an outer orbit again by the absorption of external energy sufficient to bring about this change. Once in the outer orbit again, it is in a state to produce radiation by falling in a second time. The innermost [Pg 120] orbit represents thus the electron’s equilibrium state, and corresponds to the normal state of the atom.
If we try to illustrate the matter with an analogy from the theory of sound, we can do so by comparing the atom not with a stringed instrument, but with a hypothetical musical instrument of a wholly different kind. Let us imagine that we have placed one over another and concentrically a series of circular discs of progressively smaller radii, and let us suppose that a small sphere can move around any one of these without friction and without emitting sound. In such a motion the system may be said to be in a “stationary state.” Sooner or later the sphere may fall from the first disc on to one lower down and continue to roll around on the second, having emitted a sound, let us assume, by its fall. By passing thus from one stationary state to another it loses a quantity of energy equal to the work which would be necessary to raise it again to the disc previously occupied, and to bring it back to the original state of motion. We can assume that the energy which is lost in the fall reappears in a sound wave emitted by the instrument, and that the pitch of the sound emitted is proportional to the energy sent out. If, moreover, we imagine that the lowermost disc is grooved in such a way that the sphere cannot fall farther, then this fanciful instrument can provide a very rough analogy with the Bohr atom. We must beware, however, of stretching the analogy farther than is here indicated.
It must be specially emphasized here that the frequency of the sound emitted in the above example has no connection with the frequency of revolution of the sphere. In the Bohr atom, likewise, the frequency of [Pg 121] revolution ω of the electron in its stationary orbit has no direct connection with the frequency of the radiation emitted when the electron passes from this orbit to another. This is a very surprising break with all previous views on radiation, a break whose revolutionary character should not be under-estimated. But, however unreasonable it might seem to give up the direct connection between the revolutional frequency and the radiation frequency, it was absolutely necessary if the Rutherford atomic model was to be preserved. And as we shall now see, the new point of view of the Bohr theory leads naturally to an interpretation of the Balmer-Ritz formula, which had previously not been connected with any other physical theory.
The quantity of energy E, which the atom gives up when the electron passes from an outer to an inner orbit, or which, conversely, is taken in when the electron passes from an inner to an outer orbit, may, as has been indicated, be regarded as the difference between the energy contents of the atom in the two stationary states. This difference may be expressed in the following way. Let us imagine that we eject the electron from a given orbit (e.g. No. 2 in the diagram) so that it is sent to “infinity,” or, in other words, is sent so far away from the nucleus that the attraction of the latter becomes negligible. To bring about this removal of the electron from the atom demands a certain amount of energy, which we can call the ionizing work corresponding to the stationary orbit in question. We may here designate it as A₂. To eject the electron from the orbit No. 4 will demand a smaller amount of ionizing work, A₄. The difference A₂ - A₄ is accordingly the work which [Pg 122] must be done to transfer the electron from the orbit No. 2 to the orbit No. 4. This is, however, exactly equal to the quantity E of energy which will be emitted as light when the electron passes from orbit No. 4 to orbit No. 2. If we call the frequency of this light ν, then from the relations E = hν and E = A₂ - A₄, we have
hν = A₂ - A₄
If, now, in place of this specific example using the stationary orbits 2 and 4 we take any two orbits designated by the numbers n″ (for the inner) and n′ (for the outer), we can write for the frequency of the radiation emitted for a transition between these arbitrary states
| hν = Aₙ″ - Aₙ′ or ν = | Aₙ″ | - | Aₙ′ |
| h | h |
We have now reached the point where we ought to bring in the Balmer-Ritz formula for the distribution of the lines in the hydrogen spectrum. This formula may be written (see p. 59)
| ν = | K | - | K |
| n″ ² | n′ ² |
We can now see very clearly the similarity between the formula derived from the spectrum investigations and that derived from the two Bohr postulates. In both formulæ the frequency appears as the difference between two terms which are characterized in both cases by two integral numbers, in the first formula, numbers denoting two stationary orbits in the Bohr model for hydrogen, and in the second the two numbers which in the Balmer-Ritz formula for the hydrogen spectrum characterize, respectively, a series and one of the lines of the [Pg 123] series. To obtain complete agreement we have merely to equate the corresponding terms in the two formulæ. Thus we have for any arbitrary integer n
| Aₙ | = | K | or Aₙ = | hK |
| h | n ² | n ² |
For the innermost stationary orbit, for which n = 1, the ionizing work A₁ will accordingly be equal to the product of the constants h and K of Planck and Balmer respectively; and for the orbits No. 2, No. 3, No. 4, etc., the values will be respectively ¼, ¹/₉, ¹/₁₆, etc., of this product. From the charges on the nucleus and the electron, which are both equal to the elementary quantum e of electricity (see p. 90), and from the ionizing energy for a given orbit we can now find by the use of simple mechanical considerations the radius of the orbit. If we denote the radii of the orbits 1, 2, 3 ... by a₁, a₂, a₃ ..., we then obtain for the diameters 2a₁, 2a₂, 2a₃ ... the values 2a₁ = 1·056 × 10⁻⁸ cm. (or approximately 2a₁ = 10⁻⁸ cm.), 2a₂ = 4 × 10⁻⁸ cm., 2a₃ = 9 × 10⁻⁸ cm., etc. It is seen that the radii of the orbits are in the proportion 1, 4, 9 ..., or in other words the squares of the integers which determine the orbit numbers. It is in this proportion that the circles in Fig. 25 are drawn. We must remember, however, that we have here for the moment been thinking of the orbits as circles, while in reality they must in general be assumed to be ellipses. The foregoing considerations will, however, still hold with the single change that 2aₙ will now mean, instead of the diameter of a circle, the major axis of an ellipse.
Let us return to the formulæ
| ν = | Aₙ″ | - | Aₙ′ | and ν = | K | - | K |
| h | h | n″ ² | n′ ² |
[Pg 124] Here n″ denotes in the first formula the index number for the inner of the two orbits between which the transition is supposed to take place, while in the second formula n″ denotes a definite series in the hydrogen spectrum. If n″ is 2 while n′ takes on the values 3, 4, 5 ... ∞ then in the Bohr model of the hydrogen atom this corresponds to a series of transitions to the orbit No. 2 from the orbits 3, 4, 5 ..., while in the hydrogen spectrum this corresponds to the lines in the Balmer series, namely, the red line (Hα) corresponding to the transition 3-2, the blue-green line (Hβ) to 4-2, the violet line (Hγ) to 5-2 and so on. If we now put n″ = 1 while n′ takes the values 2, 3, 4 ..., we get in the atom transitions to the orbit No. 1 from the orbits No. 2, 3, 4 ..., corresponding in the spectrum to what is called the Lyman series in the ultra-violet (named after the American physicist Lyman, who has carried on extensive researches in the ultra-violet region of the spectrum). Thus every line in the hydrogen spectrum is represented by a transition between two definite stationary states in the hydrogen atom, since this transition will give the frequency corresponding to the line in question.
At first sight this would seem perhaps to be such an extraordinary satisfactory result that it would prove an overwhelming witness in favour of the Bohr theory. A little more careful thought, on the other hand, would perhaps cause a complete reversion from enthusiasm and lead some to say that the whole thing has not the slightest value, because the stationary states were so chosen that agreement might be made with the Balmer-Ritz formula. This last consideration, indeed, states the [Pg 125] truth in so far that the agreement between the formula and the theory, at least as developed here up to this point, is of a purely formal nature. In the Bohr postulates the frequencies of the emitted radiation are determined by a difference between two of a series of energy quantities, characterizing the stationary states, just as in the Balmer-Ritz formula they appear as a difference between two of a series of terms (K, K/4, K/9, ...) each characterized by its integer. Now by characterizing the quantities of energy in the stationary states by a series of integers (in itself a wholly arbitrary procedure) complete agreement between the Bohr stationary states idea and the spectral formulæ can be attained. It is not even necessary to introduce the Rutherford atomic model to attain this end. By bringing in this specific model, one might join the new theory to the knowledge already gained of the atomic structure, and, so to speak, crystallize the hitherto undefined or only vaguely defined stationary states into more definite form as revolution in certain concrete orbits. This would then lead to a more comprehensive conception of atomic structure. But the theory unfortunately would still be rather arbitrary, since there would seem to be no justification for picking out certain fixed orbits with definite diameters or major axes to play a special rôle. One cannot wonder then that many scientists considered the Bohr theory unacceptable, or at any rate were inclined to look upon it simply as an arbitrary, unreasonable conception which really explained nothing.
Naturally, Bohr himself clearly recognized the formal nature of the agreement between the Balmer-Ritz formula and his postulates. But Bohr was the first to see that the quantum theory afforded the possibility of [Pg 126] bringing about such an agreement, and he saw, moreover, that the agreement was not merely fortuitous, but contained within it something really fundamental, on which one could build further. That atomic processes on his theory took on an unreasonable character (compared with the classical theory) was nothing to worry about, for Bohr had come to the clear recognition that it was completely impossible to understand from known laws the Planck-Einstein “quantum radiation,” or to deduce the properties of the spectrum from the Rutherford atom alone. He therefore saw that his theory was really not introducing new improbabilities, but was only causing the fundamental nature of the contradictions which had previously hindered development in this field to appear in a clearer light.
But in addition to this the choice of the dimensions of the stationary states was by no means so arbitrary as might appear in the foregoing. In his first presentation of the theory of the hydrogen spectrum, Bohr had derived his results from certain considerations connected with the quantum theory—considerations of a purely formal nature, indeed, just as those developed in the preceding, but leading to agreement with the spectral formulæ. He, moreover, called attention to the fact that the values obtained for the orbital dimensions were of the same order of magnitude as those which could be expected on wholly different grounds. The diameter of the innermost orbit, i.e., that which defines the outer limit of the atom in the normal state, was found to be, as has been noted above, about 10⁻⁸ cm., i.e., of the same order of magnitude as the values obtained for the diameters of molecules on the [Pg 127] kinetic theory of gases (see p. 27). The stationary states corresponding to very high quantum numbers one could expect to meet only when hydrogen was very attenuated, for otherwise there could be no room for the large orbits. We note that the 32nd orbit must have a diameter 32² (or over 1000 times) as great as the innermost orbit. Since, now, lines with high number in a hydrogen series correspond on the Bohr theory to transitions from orbits of high number to an inner orbit, it became understandable why only comparatively few lines of the Balmer series are ordinarily observed in the discharge tube, while many more lines are observed in the spectra of certain stars. For in such stars the possibility is left open for hydrogen to exist in a very attenuated state, and yet in such large masses that the lines in question can become strong enough for observation. In fact, one must assume that in a great mass of hydrogen a very large number of atoms send out simultaneously light of the wave-length corresponding to one line. For the ionizing work, i.e., the work necessary to eject the electron completely from the normal state and thus make the atom into a positive ion, the Bohr theory gives a value of the same order of magnitude as the so-called “ionization potentials” which have been found by experiment for various gases. An exact correspondence between theory and experiment could for hydrogen not be attained with certainty, because the hydrogen atoms in hydrogen gas under ordinary conditions always appear united in molecules.
In his very first paper, however, Bohr had studied Balmer’s formula also from another point of view, and had derived in this way an expression for the Rydberg constant K which agreed with experiment. [Pg 128] These considerations have reference to the above-mentioned connection of the theory with the classical theory of electrodynamics.
Such a connection had previously been known to exist in the fact that, for long wave-lengths, the radiation formula of Planck reduces practically to the Rayleigh Jeans Law which can be derived from electrodynamics. This is related to the fact that when ν is small (long wave-lengths), the energy quantum hν is very small, and hence the character of the radiation emitted will approach more and more nearly to a continuous “unquantized” radiation. One might then expect that the Bohr theory also should lead in the limit of long wave-lengths and small frequencies to results resembling those of the ordinary electrodynamic theory of the radiation process. On the Bohr theory we get the long wave-lengths for transitions between two stationary states of high numbers (numbers which also differ little from each other). Thus suppose n is a very large number. Then the transition from the orbit n to the orbit n - 1 will give rise to radiation of great wave-length. For in this case Aₙ and Aₙ₋₁ differ very little, and accordingly hν is very small, as must ν be also. According to the electrodynamic theory of radiation, the revolving electron should emit radiation whose frequency is equal to the electron’s frequency of revolution. According to the Bohr theory it is impossible to fulfil this condition exactly, since radiation results from a transition between two stationary orbits in each of which the electron has a distinct revolutional frequency. But if n is a large number, the difference between the frequencies of revolution ωₙ and ωₙ₋₁ for the two orbits n and n - 1, respectively, becomes very small; for [Pg 129] example, for n = 100, it is only 3 per cent. For a certain high value of n, then, the frequency of the emitted radiation can therefore be approximately equal to the frequency of revolution of the electron in both the two orbits, between which the transition takes place. But even if this proved correct for values of n about 100, one could not be sure beforehand whether it would work out right for still larger values of n, for example, 1000.
In order to investigate this latter point we must look into the formulæ for the revolutional frequency ω in a stationary orbit and for the radiation frequency ν. Since, according to the Bohr theory, we can apply the usual laws of mechanics to revolution in a stationary orbit, it is an easy matter to find an expression for ω. From a short mathematical calculation we can deduce that ω = R/n³, where R is the frequency of revolution for the first orbit (n = 1). We find ν, on the other hand, by substituting in the Balmer-Ritz formula the numbers n and n - 1, and a simple calculation shows that for great values of n, the expression for ν will approach in the limit the simple form ν = 2K/n³. For large orbit numbers, ν accordingly varies as ω, i.e., inversely proportional to the third power of n, and by equating R and 2K, we find that the values for ν and ω tend more and more to become equal.
In this way the value of K, the Balmer constant, may be computed. It is found that
| K = 2π²e⁴ | m |
| h³ |
where e is the charge on the electron, m the mass of the electron, and h is Planck’s constant. Upon the substitution of the experimental values for these quantities, a value of K is determined which agrees with the experimental value (from the spectral lines investigation) of 3·29 × 10¹⁵ within the accuracy to which e, m and h are [Pg 130] obtainable. This agreement has from the very first been a significant support for the Bohr theory.
One might now object that we have here considered radiation due to a transition between two successive stationary states, e.g., No. 100 and No. 99, or the like (a “single jump” we might call it). On the other hand, for transitions between states whose numbers differ by 2, 3, 4 or more (as in a double jump, or a triple jump) the agreement found above will wholly disappear, and doubt be cast on its value. For in such cases of high orbit numbers the frequency of revolution will remain approximately the same even for a difference of 2, 3, 4 or more in orbit number; but the radiation frequency for a double jump will be nearly twice that for a single jump, while that for a triple jump will be nearly three times, etc. Accordingly, for approximately the same revolutional frequency ω we shall have in these cases for the radiation frequency very nearly ν₁ = ω, ν₂ = 2ω, ν₃ = 3ω, etc. We must, however, remember that when the orbit in the stationary states is not a circle, but an ellipse (as must in general be assumed to be the case), the classical electrodynamics require that the electron emits besides the “fundamental” radiation of frequency ν₁ = ω, the overtones of frequencies ν₂ = 2ω, ν₃ = 3ω .... We then also here see the outward similarity between the Bohr theory and the classical electrodynamics. We may say that the radiation of frequency ν, produced by a single jump, corresponds to the fundamental harmonic component in the motion of the electron, while the radiation of frequency ν₂, emitted by a double jump, corresponds to the first overtone, etc.
The similarity is, however, only of a formal nature, since the [Pg 131] processes of radiation, according to the Bohr theory, are of quite different nature than would be expected from the laws of electrodynamics. In order to show how fundamental is the difference, even where the similarity seems greatest, let us assume that we have a mass of hydrogen with a very large number of atoms in orbits, corresponding to very high numbers, and that the revolutional frequency can practically be set equal to the same quantity ω. There may take place transitions between orbits with the difference 1, 2, 3 ... in number, and as the result of these different transitions we shall find, by spectrum analysis, in the emitted radiation frequencies which are practically ω, 2ω, 3ω, etc. According to the radiation theory of electrodynamics we should also get these frequencies and the spectral lines corresponding to them. It must, however, be assumed that they are produced by the simultaneous emission from every individual radiating atom of a fundamental and a series of overtones. According to the Bohr theory, on the other hand, each individual radiating atom at a given time emits only one definite line corresponding to a definite frequency (monochromatic radiation).
We can now realize that the Bohr theory takes us into unknown regions, that it points towards fundamental laws of nature about which we previously had no ideas. The fundamental postulates of electrodynamics, which for a long time seemed to be the fundamental laws of the physical world itself, by which there was hope of explaining the laws of mechanics and of light and of everything else, were disclosed by the Bohr theory as merely superficial and only applicable to large-scale phenomena. The apparently exact account of the activities of nature, [Pg 132] obtained by the formulæ of electrodynamics, often veiled processes of a nature entirely different from those the formulæ were supposed to describe.
One might then express some surprise that the laws of electrodynamics could have been obtained at all and interpreted as the most fundamental of all laws. It must, however, be remembered that the Bohr theory for large wave-lengths, i.e., the slow oscillations, leads to a formal agreement with electrodynamics. It must, moreover, be remembered that the laws of electrodynamics are established on the basis of large-scale electric and magnetic processes which do not refer to the activities of separate atoms, but in which very great numbers of electrons are carried in a certain direction in the electric conductors or vibrate in oscillations which are extremely slow compared with light oscillations. Moreover, the observed laws, even if they can account for many phenomena in light, early showed their inability to explain the nature of the spectrum and many other problems connected with the detailed structure of matter. Indeed the more this structure was studied, the greater became the difficulties, the stronger the evidence that the solution cannot be obtained in the classical way.
If we ask whether Bohr has succeeded in setting up new fundamental laws, which can be quantitatively formulated, to replace the laws of electrodynamics and to be used in the derivation of everything that happens in the atom and so in all nature, this question must receive a negative answer. The motion of the electron in a given stationary state may, at any rate to a considerable extent, be calculated by the laws of mechanics. We do not know, however, why certain orbits are, in this way, preferred over others, nor why the electrons jump from outer to [Pg 133] inner orbits, nor why they sometimes go from one stationary orbit to the next and sometimes jump over one or more orbits, nor why they cannot come any closer to the nucleus than the innermost orbit, nor why, in these transitions, they emit radiation of a frequency determined according to the rules mentioned.
It must not be forgotten that in science we must always be patient with the question “Why?” We can never get to the bottom of things. On account of the nature of the problem, answers cannot be given to the questions why the smallest material particles (for the time being hydrogen nuclei and electrons)—the elementary physical individuals—exist, or why the fundamental laws for their mutual relationships—the most elementary relationships existing between them—are of this or that nature; a satisfactory answer would necessarily refer to something even more elementary. We cannot claim more than a complete description of the relative positions and motions of the fundamental particles and of the laws governing their mutual action and their interplay with the ether.
If we examine our knowledge of the atomic processes in the light of this ideal we are tempted, however, to consider it as boundless ignorance. We are inconceivably far from being able to give a description of the atomic mechanism, such as would enable us to follow, for example, an electron from place to place during its entire motion, or to consider the stationary states as links in the whole instead of isolated “gifts from above.” During the transition from one stationary state to another we have no knowledge at all of the existence of the electron, indeed we do not even know whether it exists at that time or [Pg 134] whether it perhaps is dissolved in the ether to be re-formed in a new stationary state. But even if we turn aside from such a paradoxical consideration, it must be recognized that we do not know what path the electron follows between two stationary orbits nor how long a time the transition takes. As has been done in this book, the transition is often denoted as a jump, and many are inclined to believe that the electron in its entire journey from a distant outer orbit to the innermost spends the greatest part of the time in the stationary orbits, while each transition takes but an infinitesimally short time. This, however, in itself does not follow from the theory, nor is it implied in the expression “the stationary states.” These states may in a certain sense be considered as way stations; but when we ask whether an electron stays long in the station, or whether the stationary state is simply a transfer point where the electron changes its method of travelling so that the frequency of its radiation is changed, these are other matters, and we cannot here go into the considerations connected with them.
To get an idea of some of the difficulties inherent in the attempt to make concrete pictures of the nature of the processes, let us again consider the analogy between the Bohr atom of hydrogen and a special kind of musical instrument in which sounds are produced by the fall of a small sphere between discs at various heights (see p. 120). It will be most natural here to think of the sounds as developed by the sphere when it hits the lower disc, and to think of the tones of higher pitch as given by the harder blows, corresponding to the larger energy (determinative of the pitch) released by the fall. We can, however, by no means transfer such a picture to the atomic model. For in the latter [Pg 135] we cannot think of the stationary state as a material thing which the electron can hit, and it is also unreasonable to imagine that the radiation is not emitted until the moment when the transition is over and the electron has arrived in its new stationary state. We must, on the contrary, assume that the emission of radiation takes place during the whole transition, whether the latter consumes a shorter or longer time. If it were the case that a transition always took place between two successive stationary states, it would then be possible to use the musical instrument to illustrate the matter. Let us denote the discs from the lowest one up with the numbers 1, 2, 3, ... corresponding to the stationary states 1, 2, 3, ... and for the moment consider a fall from disc 6 to disc 5. We can now imagine that the space between the two discs is in some way tuned for a definite note. Thus we might place between the discs a series of sheets of paper having such intervals between them that the sphere in its fall strikes their edges at equal intervals of time, e.g., ¹/₁₀₀ second. The disturbance then set up will produce a sound with the frequency 100 vibrations per second. If the distance between the discs 5 and 4 is double that between 6 and 5, the sphere in the fall from 5 to 4 will lose double the energy lost in the descent from 6 to 5, and will therefore emit a note of double frequency. The sheets of paper in the space between 5 and 4 must then be packed more tightly than between 6 and 5. And so the space between any two discs may thus be said to have its own particular classification or “tuning.” In analogy with this we might think of the space about a hydrogen nucleus divided by the stationary states into [Pg 136] sections each with its own “tuning.” But apart from the intrinsic peculiarity of such an arrangement and the particular difficulties it will meet in trying to explain the more complicated phenomena to be mentioned later, the one fact that the electron in a transition from one stationary state to another can jump over one or more intervening stationary orbits, makes such a representation impossible. If the sphere in the given example could fall from disc 6 to disc 4, it should during the whole descent emit a note of higher pitch than in the descent from 6 to 5. But this could not possibly take place, if the space from 6 to 5, which must be traversed en route to 4, is tuned for a lower note. The same consideration applies to the hydrogen atom. Naturally it is not impossible to continue the effort to illustrate the matter in some concrete manner (one might, for example, imagine separate channels each with its own particular tuning between the same two discs). But in all these attempts the situation must become more and more complicated rather than more simple.
On the whole it is very difficult to understand how a hydrogen atom, where the electron makes a transition from orbit 6 to orbit 4, can during the entire transition emit a radiation with a frequency different from that when the electron goes from orbit 6 to orbit 5. Although it seems as if the two electrons in making the transition are at first under identical conditions, still, nevertheless, the one which is going to orbit 4 emits from the first a radiation different from that emitted by the one going to orbit 5. Even from the very beginning the electron seems to arrange its conduct according to the goal of its motion and also according to future events. But such a gift is wont to be the privilege of thinking beings that can anticipate certain future [Pg 137] occurrences. The inanimate objects of physics should observe causal laws in a more direct manner, i.e., allow their conduct to be determined by their previous states and the contemporaneous influences on them.
There is a difficulty of a similar nature in the fact that from the same stationary orbit the electron sometimes starts for a single jump, another time for a double jump, and so on. From certain considerations it is often possible to propound laws for the probability of the different jumps, so that for a great quantity of atoms it is possible to calculate the strengths (intensities) of the corresponding spectral lines. But we can no more give the reason why one given electron at a given time determines to make a double jump while another decides to make a single jump or not to jump at all, than we can say why a certain radium nucleus among many explodes at a given moment (cf. p. 102). This similarity between the occurrence of radiation processes on the Bohr theory and of the radioactive processes has especially been emphasized by Einstein.
It must, by no means, be said that the causal laws do not hold for the atomic processes, but the hints given here indicate how difficult it will be to reach an understanding—in the usual sense—of these processes and consequently of the processes of physics in general. There is much that might indicate that, on the whole, it is impossible to obtain a consistent picture of atomic processes in space and time with the help of the motions of the nuclei and the electrons and the variations in the state of the ether, and with the application of such fundamental conceptions of physics as mass, electric charge and energy. [Pg 138]
Even if this were the case, it does not follow that a comprehensive description in time and space of the physical processes is impossible in principle; but the hope of attaining such a description must perhaps be allied to the representation of “physical individuals” or material particles of an even lower order of magnitude than the smallest particles now known—electrons and hydrogen nuclei—and to ideas of more fundamental nature than those now known; we are here outside our present sphere of experience.
From all the above remarks it would be very easy to get the impression that the Bohr theory, while it gives us a glimpse into depths previously unsuspected, at the same time leads us into a fog, where it is impossible to find the way. This is very far from being the case. On the contrary, it has thrown new light on a host of physical phenomena of different kinds so that they now appear in a coherence previously unattainable. That this light is not deceptive follows from the fact that the theory, which has been gradually developed by Bohr and many other investigators, has made it possible to predict and to account for many phenomena with remarkable accuracy and in complete agreement with experimental observation. The fundamental concepts are, on the one hand, the stationary states, where the usual laws of mechanics can be applied (although only within certain limits), and, on the other, the “quantum rule” for transitions between the states. But at the very beginning it has been necessary in many respects to grope in the dark, guided in part by the experimental results and in part by various assumptions, often very arbitrary. [Pg 139]
For Bohr himself, a most important guide has been the so-called correspondence principle, which expresses the previously mentioned connection with the classical electrodynamics. It is difficult to explain in what it consists, because it cannot be expressed in exact quantitative laws, and it is, on this account, also difficult to apply. In Bohr’s hands it has been extraordinarily fruitful in the most varied fields; while other more definite and more easily applicable rules of guidance have indeed given important results in individual cases, they have shown their limitations by failing in other cases. We can here merely indicate what the correspondence principle is.
As has been said (cf. p. 130), it has been found that in the limiting region (sufficiently low frequencies) where the Bohr theory and the classical electrodynamics are merged in their outward features, a series of frequencies ν₁, ν₂, ν₃ for monochromatic radiation, emitted by different atoms in the single jumps, double jumps, etc., of the electrons, are equal to the frequencies ω, 2ω, 3ω ... which, according to the laws of electrodynamics, are contained in each of these atoms respectively as fundamental and the first, second ... overtones in the motion of the electron. Farther away from this region the two sets of frequencies are no longer equally large, but it is easy to understand, from the foregoing, the meaning of the statement that, for example, the radiation of a triple jump with the frequency ν₃ “corresponds” to the second overtone 3ω in the revolution of the electron. It is this correspondence which Bohr traces back to the regions where there is even a great difference in two successive orbits and where the frequency produced by a transition between these orbits is very different from the frequencies of revolution in the two orbits or their [Pg 140] overtones. He expresses himself as follows: “The probability for the occurrence of single, double, triple jumps, etc., is conditioned by the presence in the motion of the atom of the different constituent harmonic vibrations having the frequency of the fundamental, first overtone, second overtone, etc., respectively.”
In order to understand how this “correspondence,” apparently so indefinite, can be used to derive important results, we shall give an illustration. Let us assume that the mechanical theory for the revolution of an electron in the hydrogen atom had led to the result that the orbits of the electrons always had to be circles. According to the laws of electrodynamics, the motion of the electron would in this case never give any overtones, and, according to the correspondence principle, there could not appear among the frequencies emitted by hydrogen any which would correspond to the overtones, i.e., there would not be any double jumps, triple jumps, etc., produced, but the only transitions would be those between successive stationary orbits. The investigation of the spectrum shows, however, that multiple jumps occur as well as single jumps, and this fact may be taken as evidence that the orbits in the hydrogen atom are not usually circles. Let us next assume that, instead, we had obtained the result that the orbits of the electrons are always ellipses of a certain quite definite eccentricity, corresponding to certain definite ratios in intensity between the overtones and the fundamentals; that, for instance, the intensity of the classical radiation due to the first overtone is in all states of motion always one-half that due to the fundamental, the intensity due to the second overtone always one-third that due to the [Pg 141] fundamental, etc. Then the radiation actually emitted should, according to the correspondence principle, be such that the intensities of the lines corresponding to the double and triple jumps, which start from a given stationary state, are respectively one-half and one-third of the intensity corresponding to a single jump from the same state.
By these examples we can obtain an idea of how the correspondence principle may in certain cases account for various facts, as to what spectral lines cannot be expected to appear at all, although they would be given by a particular transition, and concerning the distribution of intensities in those which really appear. The illustration given above, however, has really nothing much to do with actual problems, and objections may be raised to the rough way in which the illustration has been handled. The correspondence principle has its particular province in more complicated electron motions than those which appear in the unperturbed hydrogen atom—motions which, unlike the simple elliptical motion, are not composed of a series of harmonic oscillations (ω, 2ω, 3ω ...) but may be considered as compounded of oscillations whose frequencies have other ratios. The correspondence principle has, in such cases, given rise to important discoveries and predictions which agree completely with the observations.
We have dwelt thus long upon the difficult correspondence principle, because it is one of Bohr’s deepest thoughts and chief guides. It has made possible a more consistent presentation of the whole theory, and it bids fair to remain the keystone of its future development. But from these general considerations we shall now proceed to more special [Pg 142] phases of the problem and examine one of the first great triumphs in which the theory showed its ability to lead the way where previously there had been no path.
In 1897 the American astronomer, Pickering, discovered in the spectrum of a star, in addition to the usual lines given by the Balmer series, a series of lines each of which lay about midway between two lines of the Balmer series; the frequencies of these lines could be represented by a formula which was very similar to the Balmer formula; it was necessary merely to substitute n = 3½, 4½, 5½, etc., in the formula on p. 57 instead of n = 3, 4, 5, etc. It was later discovered that in many stars there was a line corresponding to n″ = ³/₂ or n′ = 2 in the usual Balmer-Ritz formula (p. 59). It was considered that these must be hydrogen lines, and that the spectral formula for this element should properly be written
| ν = K | 1 | - | 1 | ||
| (n″/2) ² | (n′/2) ² |
where n″ and n′ can assume integral values. This was done since it was not to be believed that the spectral properties of chemically different elements could be so similar. This view was very much strengthened when Fowler, in 1912, discovered the Pickering lines in the light from a vacuum tube containing a mixture of hydrogen and helium. It could not quite be understood, however, why the new lines did not in general appear in the hydrogen spectrum.
According to the Bohr theory for the hydrogen spectrum it was impossible—except by giving up the agreement (cf. p. 129) [Pg 143] with electrodynamics in the region of high orbit numbers—to attribute to the hydrogen atom the emission of lines corresponding to a formula where the whole numbers were halved. The formula given above might, however, also be written as
| ν = 4K | 1 | - | 1 | ||
| n″ ² | n′ ² |
If the earlier calculations had been carried out a little more generally, i.e., if instead of equating the nuclear charge with 1 elementary electric quantum e, as in hydrogen, it had been equated with Ne where N is an integer, then the frequency might have been written as
| ν = N²K | 1 | - | 1 | ||
| n″ ² | n′ ² |
This formula is evidently the same as that just given when N equals 2. Now we know that helium has the atomic number and nuclear charge 2 (cf. p. 90); a normal neutral helium atom has two electrons and it is, therefore, very different from a hydrogen atom. If, however, a helium atom has lost one electron and therefore has become a positive ion with one charge, it is a system like the hydrogen atom with only one single electron moving about the nucleus. It differs in its “outer” characteristics from the hydrogen atom only in having a nuclear charge twice as great, i.e. its spectral formula must be given with N = 2, or N² = 4. The formula for the supposed hydrogen lines would consequently fit the case of a helium atom which has lost an electron. Bohr was aware of this, and he therefore suggested that the lines in question were due, not to hydrogen, but to helium. [Pg 144]
At first all the authorities in the field of spectroscopy were against this view; but most of the doubt was dispelled when Evans showed that the lines could be produced in a vacuum tube where there was only helium with not a trace of hydrogen.
In a letter to Nature in September 1913, Fowler objected to the Bohr theory on the ground that the disputed line-formula did not exactly correspond to the formula with 4K, but that there was a slight disagreement. Bohr’s answer was immediate. He called attention to the fact that—since temporarily he had sought only a first approximation—in his calculations he had taken the mass of the nucleus to be infinite in comparison to the mass of the electron, so that the nucleus could be considered exactly at the focus of the ellipse described by the electron. In reality, he said, it must be assumed that nucleus and electron move about their common centre of gravity, just as in the motion in the solar system it must be assumed that not the centre of the sun, but the centre of gravity of the entire system remains fixed. This motion of the nucleus leads to the introduction of a factor M/(M + m) in the expression for the constant K given on p. 129, where M is the mass of the nucleus and m that of the electron, which in hydrogen is ¹/₁₈₃₅ that of the nucleus. In helium, M is four times as large as in hydrogen, so that the given factor here has a slightly different value. The difference in the values for K for the hydrogen and for the helium spectrum which was found by Fowler, is 0·04 per cent., which agrees exactly with the theoretical difference.
Bohr thus turned Fowler’s objection into a strong argument in favour of the theory. [Pg 145]
During the first years after 1913, Bohr was practically alone in working out his theory, at that time still assailed by many, and in showing its application to many problems. In 1916, however, the theorists in other countries, led by the well-known Munich professor, Sommerfeld, began to associate themselves with the Bohr theory, and their investigations gave rise to much essential progress. We shall here mention some of the most important contributions.
In the theory for the hydrogen spectrum propounded above, it was assumed that we had to do with a single series of stationary orbits, each characterized by its quantum number. But as shown by theoretical investigations each of the stationary orbits must, when more detail is asked for, also be indicated by an additional quantum number. [Pg 146]

Fig. 26.—A compound
electron motion produced
by the very rapid rotation of an
elliptical orbit.
This is closely connected with the fact that the motion of the electron is not quite so simple as previously assumed. We have assumed that the electron moves about the nucleus just as a planet moves about the sun (according to Kepler’s Laws), in an ellipse with the sun at one focus, since the electron is influenced by an attraction inversely proportional to the square of the distance, just as the planets are attracted by the sun according to Newton’s Law. We must, however, remember that we are here concerned with the electric attraction which at a given distance is determined, not by mass, but by the electric charges in question. If the latter remain unchanged, while the mass of the electron varies, the motion will be changed, because the same force has less effect upon a greater mass. According to the Einstein principle of relativity, the mass of the electrons, in accordance with ideas expounded long ago by J. J. Thomson, will not be constant, but to a certain extent depend upon the velocity, which will vary from place to place, when the orbit is an ellipse. As a result of this, the motion becomes a central motion of more general nature than a Kepler ellipse. Since the influence of the change of mass is very small, the orbit can still be considered as an approximate Kepler ellipse; but the major axis will slowly rotate in the plane of the orbit. In reality, the orbit will not therefore be closed, but will have the character which is shown in Fig. 26; this, however, corresponds to a much more rapid rotation of the major axis than that which actually takes place in the hydrogen atom, where—even in case of the swiftest rotation—the [Pg 147] electron will revolve about 40,000 times round the nucleus at the same time as the major axis turns round once.
If the electron moves in a fixed Kepler ellipse, the energy content of the atom will be determined by the major axis of the ellipse only. If these axes for the stationary states with quantum numbers 1, 2, 3 ... are respectively denoted by 2a₁, 2a₂, 2a₃ ... the frequency, for instance, in the transition from No. 3 to No. 2—since it is determined by the loss of energy—will be the same whether the orbits are circles or ellipses. If, on the other hand, the electron moves in an ellipse which itself rotates slowly, the energy content, as can be shown mathematically, will depend not only upon the major axis of the ellipse, but also to a slight degree upon its eccentricity, or, in other words, on its minor axis. Then in the transition 3-2 we shall get different energy losses and consequently different frequencies, according as the ellipse is more or less elongated. If it were the case that the eccentricity of the ellipses for a certain quantum number could take arbitrary values, then in the transition between two numbers we could get frequencies which may take any value within a certain small interval, i.e., a mass of hydrogen with its great quantity of atoms would give diffuse spectral lines, i.e. lines which are broadened over a small continuous spectral interval. This is, however, not the case; but long before the appearance of the Bohr theory it had been discovered that the hydrogen lines, which we hitherto have considered as single, possess what is called a fine structure. With a spectroscopic apparatus of high resolving power each line can be separated into two lying very close to each other. This fine structure [Pg 148] can now be explained by the fact that in a stationary state with quantum number 3 and major axis of the orbit 2a₃, for instance, the eccentricity of the orbit has neither one single definite value nor all possible values, but, on the contrary, it has several discrete values of definite magnitude, to which there correspond slightly different but definite values of the energy content of the atom. It is now possible to designate the series of stationary orbits, which have the major axis 2a₃ with the principal quantum number 3, with subscripts giving the auxiliary quantum number for stationary orbits corresponding to the different eccentricities, so that the series is known as 3₁, 3₂, 3₃. Instead of a single line corresponding to the transition 3-2, there are then obtained several spectral lines lying closely together and corresponding to transitions such as 3₃-2₂, 3₂-2₁, etc. By theoretical considerations, requiring considerable mathematical qualifications, but of essentially the same formal nature as those Bohr had originally applied to the determination of the stationary orbits in hydrogen, Sommerfeld was led to certain formal quantum rules which permit the fixing of the stationary states of the hydrogen atom corresponding to such a double set of quantum numbers. The results he obtained as regards the fine structure of the hydrogen lines agree with observation inside the limit of experimental error.
Although Sommerfeld’s methods have also been very fruitful when applied to the spectra of other elements, they were still of a purely formal and rather arbitrary nature; it is, therefore, of great importance that the Leiden professor, Ehrenfest, and Bohr succeeded later in handling the problem from a more fundamental point of view, Bohr making use of [Pg 149] the correspondence principle previously mentioned. It should be said here, by way of suggestion, that Bohr used the fact that the motions of the electrons are not simple periodic but “multiple periodic.” We see this most simply if we think of the revolution of the electrons in the elliptical orbit as representing one period, and the rotation for the major axis of the ellipse as representing a second period.

Fig. 27.—The model
of the hydrogen atom
with stationary orbits corresponding to
principal
quantum numbers and auxiliary quantum numbers.
Fig. 27 shows a number of the possible stationary orbits in the hydrogen atom according to Sommerfeld’s theory; for the sake of simplicity the orbits are drawn as completely closed ellipses. If we examine, for instance, the orbits with principal quantum number 4, we have here three more or less elongated ellipses, 4₁, 4₂, 4₃, and the [Pg 150] circle 4₄; in all of them the major axis has the same length, and the length of the major axis is to that of the minor axis as the principal quantum number is to the auxiliary quantum number (for the circle 4: 4 = 1). On the whole, to a principal quantum number n there correspond the auxiliary quantum numbers 1, 2 ... n, and the orbit for which the auxiliary quantum number equals the principal quantum number is a circle. We see that in the more complicated hydrogen atom model there is possibility for a much greater number of different transitions than in the simple model (Fig. 25, p. 119). Some of the transitions are indicated by arrows. Since the energy content of the atom is almost the same for orbits with the same principal quantum number and different auxiliary quantum numbers, three transitions like 3₃-2₂, 3₂-2₁ and 3₁-2₂ will give about the same frequency, and therefore spectral lines which lie very close together. In a transition like 4₄-4₃ the emitted energy quantum hν, and also ν, will be so extremely small that the corresponding line will be too far out in the infra-red for any possibility of observing it.
It must be pointed out that the above considerations only hold if the hydrogen atoms, strictly speaking, are undisturbed. Thus, very small external forces, which may be due to the neighbourhood of other atoms, etc., will be sufficient to cause changes in the eccentricity of the stationary orbits. In such a case the above definition of the auxiliary quantum number becomes obviously illusory, and the original character of the fine structure disappears. This is in agreement with the experiments, since the Sommerfeld fine structure can be found only when the conditions in the discharge tube are especially quiet and favourable. [Pg 151]

Fig. 28.—The
splitting of three hydrogen lines
under the influence of a
strong electric field.
As previously mentioned (p. 76), the spectral lines are split into three components when the atoms emitting lights are exposed to magnetic forces. The agreement found here between observation and the Lorentz electron theory was considered as strong evidence of the correctness of the latter. According to the Bohr theory, the picture upon which this explanation rested must be abandoned entirely; but fortunately it has been shown that the Bohr theory leads to the same results; and, moreover, Bohr, with the assistance of the correspondence principle, has been able to set forth the more fundamental reason for this agreement.
The German scientist, Stark, showed, in 1912, that hydrogen lines are also split by electric fields of force. In Fig. 28 [Pg 152] it is shown how very complicated this phenomenon is; here the classical electron theory could not at all explain what happened. This phenomenon could also be accounted for by the extended Bohr theory (with the introduction of more than one quantum number), as it was shown independently by Epstein and by Schwarzschild in 1916; further, the correspondence principle has again shown its superiority, since it makes possible an approximate determination of the different intensities of the different lines. A calculation carried out by H. A. Kramers has shown that the theory gives a remarkably good agreement with the experiments.
Not until we think of the extraordinary accuracy of the measurements which are obtained by spectrum analysis, can we thoroughly appreciate the importance of the quantitative agreement between theory and observation in the hydrogen spectrum that has just been mentioned. Moreover, we must remember how completely helpless we previously were in the strange puzzles offered even by the simplest of all spectra, that of hydrogen.
[Pg 153]
We have dwelt at length upon the theory of the hydrogen spectrum because it was particularly in this relatively simple spectrum that the Bohr theory first showed its fertility. Moreover, by studying the case of the hydrogen atom with its one electron, it is easier to gain insight into the fundamental ideas of the Bohr theory and its revolutionary character. Naturally, the theory is limited neither to the hydrogen atom nor to spectral phenomena, but has a much more general application. As has already been said, it takes, as its problem, the explanation of every one of the physical and chemical properties of all the elements, with the exception of those properties known to be nuclear (cf. p. 94). This very comprehensive problem can naturally, even in its main outlines, be solved but gradually and by the co-operation of many scientists, and it is quite impossible to go very deeply into the great work which has already been accomplished, and into the difficulties which Bohr and the others working on the problem have overcome. We must be content with showing some especially significant features. [Pg 154]
While the neutral hydrogen atom consists simply of a positive nucleus and one electron revolving about the nucleus, the other elements, in the neutral state, have from two up to 92 electrons in the system of electrons revolving around the nucleus. Even 2 electrons, as in the helium atom, make the situation far more complicated, since we have in this case a system of 3 bodies which mutually attract or repel each other. We are thus confronted with what, in astronomy, is known as the three-body problem, a problem considered with respect by all mathematicians on account of its difficulties. In astronomy, the difficulties are restricted very much when the mass of one body is many times greater than that of the others, as in the case of the mass of the sun in relation to that of the other planets. Here, by comparatively simple methods, it is possible to calculate the motions inside a finite time-interval with a high degree of approximation even when there are not two but many planets involved.
We might now be tempted to believe that in the atom we had to deal with comparatively simple systems—solar systems on small scale—since the mass of the nucelus is many times greater than that of the electrons. But even if the suggested comparison illustrates the position of the nucleus as the central body which holds the electrons together by its power of attraction, the comparison in other respects is misleading. While the orbits of the planets in the solar system may be at any distance whatsoever from the sun, and the motions of the planets are everywhere governed by the laws of mechanics, the atomic processes, [Pg 155] according to the Bohr theory, are characterized by certain stationary states, and only in these can the laws of mechanics possibly be applied. But in addition, the forces between nucleus and electrons are determined not at all by the masses, but rather by the electric charges. In the helium atom the nuclear charge is only double that of an electron, and the attraction of the nucleus for an electron will therefore be only twice as large as the repulsions between two electrons at the same distance apart. This repulsion under these circumstances will, therefore, also have great influence on the ensuing motion. In elements with higher atomic numbers the nuclear charge has greater predominance over the electron charges; but, on the other hand, there are then more electrons. The situation is in each case more complicated than in the hydrogen atom.
Nevertheless, the line spectra of the elements of higher atomic number show how the lines, as in the hydrogen spectrum, are arranged in series although in a more complicated manner (cf. p. 59); in any case in many instances there is great similarity between the radiation from the hydrogen atom and that from the more complicated atoms. Thus in the line spectra of many elements, just as in that of hydrogen, the frequency ν of every line can be expressed as a difference between two terms, involving certain integers which can pass through a series of values. From the combinations of terms, two at a time, the values of ν corresponding to the different spectral lines can be derived. This so-called combination principle enunciated by the Swiss physicist, Ritz, can evidently be directly interpreted on the basis of Bohr’s postulates, since the different combinations may be assumed to [Pg 156] correspond to definite atomic processes, in which there is a transition between two stationary states, each of which corresponds to a spectral term.
Moreover, the terms (cf. p. 59) may often be approximately given by the Rydberg formula
| K |
| (n + α) ² |
where K has about the same value as in hydrogen, and α can take on a series of values α₁, α₂ ... αₖ, while n takes on integer values. Since we thus determine the different lines by assigning values to the two integers n and k in each term, we have in this respect something like the fine structure in the hydrogen spectrum, where the stationary states are determined by a principal quantum number and an auxiliary quantum number. The spectra of which we are speaking here, and for which the terms have the form given above, are often called arc spectra, because they are emitted particularly in the light from the electric arc or from the vacuum tube. We must expect that the similarity which exists in the law for the distribution of spectral lines will correspond to a similarity in the atomic processes of hydrogen and the other elements.
The hydrogen atom emits radiation corresponding to the different spectral lines when an electron from an outer stationary orbit jumps, with a spring of varying size, to an orbit with lower number, and at last finds rest in the innermost orbit in a normal state, where the energy of the atom is as small as possible. Similarly, we must assume that the electrons in other atoms, during processes of radiation, may proceed in towards the nucleus until they are collected as tightly as [Pg 157] possible about the nucleus, corresponding to the normal state of the atom, where its energy content is as small as possible: “capture” of electrons by the nucleus. The region in space which, in the normal state, includes the entire electron system, must be assumed to be of the same order of magnitude as the dimensions of the atom and molecule which are derived from the kinetic theory of gases. This normal state may be called a “quiescent” state, since the atom cannot emit radiation until it has been excited by the introduction of energy from without. This excitation process consists of freeing one (or more) electrons, in some way or other, from the normal state and either removing it out to a stationary orbit farther away from the nucleus or ejecting it completely from the atom. Not all electrons can be equally easily removed from the quiescent state. Those moving in small orbits near the nucleus will be tighter bound than those moving in larger orbits farther from the nucleus. The arc spectrum is now caused by driving one of the most loosely bound electrons out into an orbit farther from the nucleus or removing it completely from the atom. In the latter case the rest of the atom, which with the loss of the negative electron becomes a positive ion, easily binds another electron, which, with the emission of radiation, corresponding to lines of the series spectrum, can approach closer to the nucleus.
Let us now assume, first, that this radiating electron moves at so great a distance from the nucleus and the other electrons that the entire inner system can be considered as concentrated in one point; then the situation is quite as if we had to deal with a hydrogen atom. [Pg 158] If the atomic number is as high as 29 (copper), for instance, the nuclear charge will consist of twenty-nine elementary quanta of positive electricity; but since there are twenty-eight electrons in the inner system, the resultant effect is that of only one elementary quantum of positive electricity, as in the case of a hydrogen nucleus. The spectral lines which are emitted in the jumps between the more distant paths will be practically the same as hydrogen lines. But, since in the jumps between these distant orbits, very small energy quanta will be emitted, the frequencies are very small, the wave-lengths very great, i.e., the lines in question lie far out in the infra-red. [Pg 159]

Fig. 29.—Different
stationary orbits which the
outermost (11th) electron of
sodium may describe.
When the electron has come in so close to the nucleus that the distances in the inner system cannot be assumed to be small in comparison to the distance of the outer electron from the nucleus, the situation is changed. The force with which the nucleus and the inner electrons together will work upon the outer electron will be appreciably different from the inverse square law of attraction of a point charge. The consequence of this difference is that the major axis in the ellipse of the electron rotates slowly in the plane of the orbit as described in case of the theory of the fine structure of the hydrogen lines (cf. p. 146), and even if the cause is different the result is the same; the orbit of the outer electron in the stationary states will be characterized by a quantum number n and an auxiliary quantum number k. If the electron comes still closer to the nucleus, its motion is even more complicated. When the electron in its revolution is nearest the nucleus it will be able to dive into the region of the inner electrons, and we can get motions like those shown in Fig. 29 for one of the eleven sodium electrons. The inner dotted circle is the boundary of the inner system which is given by the nucleus and the ten electrons remaining in the “quiescent” state—little disturbed by the restless No. 11. In the figure we can see greater or smaller parts of No. 11’s different stationary orbits with principal quantum numbers 3 and 4. We shall not account further for the different orbits and the spectral lines produced by the [Pg 160] transitions between orbits, but shall merely remark that the yellow sodium line, which corresponds to the Fraunhofer D-line (cf. p. 49), is produced by the transition 3₂-3₁, between two orbits with the same principal quantum number. The sketch shows to a certain degree how fully many details of the atomic processes can already be explained. The theory can even give a natural explanation of why the D-line is double.
We have restricted ourselves to the case where only one electron is removed from the normal state of the neutral atom. It may, however, happen that two electrons are ejected from the atom so that it becomes a positive ion with two charges. When an electron from the outside is approaching this doubly charged ion it will, at a distance, be acted upon as if the ion were a helium nucleus with two positive charges. The situation, in other words, will be as in the case of the false hydrogen spectrum (cf. p. 142), where the constant K in the formula for the hydrogen spectrum is replaced by another which is very close to 4K. But if the atom is not one of helium, but one with a higher atomic number, the stationary orbits of the outer electron which approach closely to the nucleus will not coincide exactly with those in the ionized helium atom, corresponding to the fact that the terms in the formula for the spectrum, instead of the simple form 4K/n², have the more complicated form 4K/(n + α)². Spectra of this nature are often called spark spectra, since they appear especially strong in electric sparks; they appear also in light from vacuum tubes, when an interruptor is placed in the circuit, making the discharge intermittent and more intense.
An atom with several electrons can, however, be much more violently [Pg 161] excited from its quiescent state when an electron in the inner region of the atom is ejected by a swiftly moving electron (a cathode ray particle or a β-particle from radium) which travels through the atom. Such an invasion produces a serious disturbance in the stability of the electron system; a reconstruction follows, in which one of the outer, more loosely bound electrons takes the vacant position. In the transitions, in which these outer electrons come in, rather large energy quanta are emitted. The emitted radiation has therefore a very high frequency; monochromatic X-rays are thus emitted. Since these have their origin in processes far within the atom, it can be understood that the different elements have different characteristic X-ray spectra, which can give very valuable information about the structure of the electron system (cf. p. 91).
Between these X-ray spectra and the series spectra previously mentioned there lie, as connecting links, those spectra which are produced when electrons are ejected from a group in the atom which does not belong to the innermost group, but does not, on the other hand, belong in the outermost group in the normal atom. We have very little experimental knowledge about such spectra, because the spectral lines involved have wave-lengths lying between about 1·5 μμ and 100 μμ. Rays with these wave-lengths are absorbed very easily by all possible substances; they have very little effect on photographic plates, where they are absorbed by the gelatine coating before they have an opportunity to influence the molecules susceptible to light. But there can be scarcely any doubt that, in the course of a few years, experimental technique will have reached such efficiency that this domain of the spectrum, so important [Pg 162] for the atomic theory, will also become accessible to experiment. In individual cases, wave-lengths as small as 20 μμ have already been obtained by Millikan.
Of entirely different character from these spectra are the band spectra. They are in general produced by electric discharges through gases which are not very highly attenuated (cf. p. 55); they are not due to purely atomic processes, but can be designated as molecular spectra. Their special character is due to motions in the molecule, not only motions of the electrons, but also oscillations and rotations of the nuclei about each other. We shall not go into these problems here; in what follows we shall investigate a certain type of band spectra somewhat more closely in connection with the absorption of radiation.
While the band spectra with a spectroscope of high resolving power can be more or less completely resolved into lines, this is not the case with the continuous spectra. They are emitted not only by glowing solids (cf. p. 54), but also by many gaseous substances. When such gases are exposed to electric discharges they emit, in addition to the line spectra and band spectra, continuous spectra which in certain parts of the spectrum furnish a background for bright lines which come out more strongly. It might seem impossible to correlate these with the Bohr theory; but in reality a spectrum does not always have to consist of sharp lines. This can at once be seen from the correspondence principle. If the motions in the stationary states are of such nature that they can be resolved into a number of discrete harmonic oscillations each with its own period (for instance the orbit of an electron in a rotating ellipse; cf. p. 149), [Pg 163] then, according to the correspondence principle, in the transition between two such stationary states there are produced sharp spectral lines “corresponding” to these harmonic components. But not all motions of atomic systems can be thus resolved into a number of definite harmonic oscillations. When this cannot be done, the stationary states cannot be expected to be such that transitions between them produce radiation which can be resolved into sharp lines.
A simple example, where it is easily intelligible that the Bohr theory will not lead to sharp lines, is obtained in a simple consideration of the hydrogen atom. Let us examine the lines belonging to the Balmer series which are produced when an electron passes to the No. 2 orbit from an orbit with higher orbit number, which is farther from the nucleus. As has been said, we obtain here an upper limit for the frequency corresponding to a value of the outer orbit number which is infinite; this means, in reality, that the electron in one jump comes in from a distance so great that the attraction of the nucleus is infinitely small. The energy released by such a jump is the same as the ionizing energy A₂ which is required to eject the electron from the orbit No. 2 and drive it from the atom. It is here assumed, however, that the electron out in the distance was practically at rest. If the captured electron has a certain initial velocity outside, it will have a corresponding kinetic energy A. When in one jump this electron comes from the outside into orbit No. 2, the energy lost by the electron and emitted in the form of radiation will be the sum of the ionizing energy A₂ and the original kinetic energy A. The frequency ν will then become greater than that corresponding to A₂; and since the velocity of the [Pg 164] electron before it is captured is not restricted to certain definite values, neither is the value of ν. The radiation from a great quantity of hydrogen atoms which are binding electrons in this way will, in the spectrum, not be concentrated in certain lines, but will be distributed over a region in the ultra-violet which lies outside of the limit calculated from the Balmer formula; still in a certain sense this continuous spectrum is correlated with the Balmer series. In the spectra from certain stars there has actually been discovered a continuous spectrum, which lies beyond the limits of the Balmer series and may be said to continue it.
Also the X-rays, which are generally used in medicine, have varying frequencies; this is caused by the fact that some of the electrons which, in an X-ray tube, strike the atoms of the anticathode and travel far into it at a high speed, lose a part or all of their velocity without ejecting inner electrons. The lost kinetic energy then appears directly as radiation. These remarks ought to be sufficient to show that the radiation, for instance, from a glowing body, where the interplay of atoms and molecules is very complicated, can give a continuous spectrum.
The excitation of an atom in the normal state (cf. p. 157), by which one of its electrons is removed to an outer stationary orbit, may be caused by a foreign electron which strikes the atom. A study of collisions between atoms and free electrons is therefore of the greatest importance when investigating more closely the conditions by which series spectra are produced.
These investigations can be carried out by giving free electrons definite velocities by letting them pass through an electric field, [Pg 165] where the “difference of potential” is known in the path traversed by the electrons. When an electron moves through a region with a difference of potential of one volt (the usual technical unit), the kinetic energy of the electron will be increased by a definite amount (of 1·6 × 10⁻¹² erg). If its initial velocity is zero, its passage through this field will make the velocity 600 km. per second; if the potential difference were 4 volts, 9 volts, etc., the velocity obtained by the electron would be 2, 3, etc., times larger. For the sake of brevity we shall say that the kinetic energy of an electron is, for instance, 15 volts, when we mean that the kinetic energy is as great as would be given by a difference of potential of 15 volts.
In 1913 the German physicist Franck began a series of experiments by methods which made it possible to regulate accurately the velocity of the electrons, and to determine the kinetic energy before and after collisions with atoms. He first applied the methods to mercury vapour, where the conditions are particularly simple, since the mercury molecules consist of only one atom. Franck bombarded mercury vapour with electrons all of which had the same velocity. He then showed that if the kinetic energy of the electrons was less than 4·9 volts the collisions with the atoms were completely “elastic,” i.e., the direction of the electron could be changed by the collision, but not its velocity. If, however, the velocity of the impinging electrons was increased so much that it was somewhat larger than 4·9 volts, there was an abrupt change in the situation, since many of the collisions became completely inelastic, i.e., the colliding electron lost its entire velocity and gave up its entire kinetic energy to the atom. If the initial velocity was even greater, so that the kinetic energy of the [Pg 166] colliding electron was 6 volts, for instance, then when the collision took place there would always be lost a kinetic energy of 4·9 volts, since the electrons would either preserve their kinetic energy intact or have it reduced to 1·1 volt (cf. Fig. 30).
Fig. 30.—Schematic drawing of Franck’s experiment with electron collisions. G is a glowing metal wire which emits electrons. If between G and the wire net T there is a difference of potential of 6 volts, the electrons will pass through the holes of the net with great velocity out into the space R, where there is mercury vapour. a represents a free electron F and a mercury atom Hg before the collision, while b represents them after the collision; with the collision F loses a kinetic energy corresponding to 4·9 volts; at the same time a bound electron B in the atom goes over to a larger stationary orbit.
This remarkable phenomenon can be understood from the Bohr theory if we assume that to send the most loosely bound electron in the mercury atom out to the nearest outer stationary orbit there is required an energy of 4·9 volts, since in that case, according to the first postulate, an energy of less than this magnitude cannot be absorbed by the atom. The use of the word “understanding” must here be qualified; if the forces [Pg 167] which influence the free electron as it comes into the electron system of the mercury atom are no other than the usual repulsion from the electrons and the attraction from the nucleus, the conduct of the colliding electron can in no way be explained by the laws of mechanics. But what happens is in agreement with the characteristic stability of the stationary states, and Bohr had prophesied how it would happen. Curiously enough Franck believed in the beginning that his experiment disagreed with the Bohr theory because he made the mistake of supposing that what happened was merely ionization, i.e., complete disruption of a bound electron from a mercury atom.
Franck’s experiments showed, moreover, that mercury vapour, as soon as the inelastic collisions appeared, began to emit ultra-violet light of a definite wave-length, namely, 253·7 μμ. The product of the frequency ν of this light and Planck’s constant h agrees exactly with the energy quantum possessed by an electron which has passed a potential difference of 4·9 volts; but this also agrees with what might be expected, according to the Bohr theory, from the radiation the removed electron would emit upon returning to the normal state. The energy which is respectively absorbed and emitted in the two transitions must be indeed hν.
Since an electron can not only be driven out to the next stationary orbit, but also to an even more distant one (or entirely ejected) and thence can come in again in one or more jumps, it is evident that a far more complicated situation may arise. The Franck experiment, which now has been extended to many other elements, clearly gives extraordinarily valuable information in such cases. In mercury it has been found that [Pg 168] the energy a free electron must have in order to eject an electron from an atom and turn the atom into a positive ion, corresponds to a difference of potential of 10·8 volts, a value which Bohr had predicted. At the same time that Franck’s experiments, in this respect and in others, have strengthened the Bohr theory in the most satisfactory way, they have also advanced its development very much. Indeed it may be said that they have been of the greatest help in atomic research. Even if the spectroscope has greater importance, the investigations on electron collisions make the realities in the Bohr theory accessible to study in a more direct and palpable manner.

Fig. 31.—Stratification of light in a vacuum tube.
The peculiarities in the electron collisions appear most clearly in an old and well-known phenomenon of light, namely, the stratification of the light in a vacuum tube (Fig. 31). This stratification, which previously seemed so incomprehensible, agrees exactly with the feature so fundamental in the atomic theory that a free electron cannot give energy under a certain quantum to an atom. We can imagine that, in the non-illuminated central space between the bright strata, the electrons each time under the influence of the outer electric field obtain the amount of kinetic energy which must serve to excite the atoms of the attenuated vapour.
As has been said (p. 161), electron collisions may cause the emission [Pg 169] of characteristic X-rays; but to produce them very great energy is required. Therefore the electrons which are to produce this effect must have an opportunity to pass freely through a certain region under the influence of a proportionately strong electric field (with potential of from 1000 to 100,000 volts and more). The electrons find such a field in a highly exhausted X-ray tube, where the electrons under strong potential are driven from the cathode against the anticathode, into which they penetrate deeply.
In the experiments previously described it was the electron collisions which furnished the energy required to excite the atoms, i.e., to carry them from the normal state over into a stationary state with greater energy. This “excitation energy” may, however, also be furnished to the atoms in the form of radiation energy; we shall now examine this case more closely.
Let us assume that to transfer an atom from the normal state to another stationary state, or, in other words, to transfer one of the electrons to an outer stationary orbit, a certain quantity of energy E is demanded; then the radiation emitted by the atom when it returns to the normal state will have a frequency ν depending upon the relation E=hν or ν=E/h, where h, as usual, is the Planck constant. But just as the atom in the transition from the stationary state to the normal state can emit radiation only with the definite frequency ν, then the opposite transition can only be performed by absorption of radiation with the same frequency; when this happens the absorbed radiation energy has exactly the value E=hν. [Pg 170]
This reciprocity, which may be considered as a direct consequence of the Bohr postulates, agrees with what has been said (cf. p. 50) about the correspondence between the lines in the line spectrum of an element and the dark absorption lines of that element—e.g., the Fraunhofer lines in the solar spectrum. Let us examine, as an example, the yellow sodium line, the D-line. Light with the corresponding frequency, 526 × 10¹² vibrations per second, is emitted by a sodium atom, when the loosest bound electron goes over from a stationary orbit with quantum numbers 3₂ to the orbit 3₁, which belongs to the normal state of the sodium atom. The transition in the opposite direction, 3₁ to 3₂, can take place under absorption of radiation only when in the light from some other source of light, which passes the sodium atoms, there are found rays with the frequency 526 × 10¹². Even if there is present radiation energy with some other frequency, the sodium atoms take no notice of this energy; they absorb only rays with the frequency stated, and every time an atom absorbs energy from a ray the energy taken is always an energy quantum of the magnitude hν, i.e. about 6·54 × 10⁻²⁷ × 526 × 10¹² = 3·44 × 10⁻¹² ergs (1 erg is the unit of energy used in the determination of h). When there are present a large number of sodium atoms (as, for instance, in the previously mentioned common salt flame), the transition 3₁ to 3₂ can take place in some atoms, the transition 3₂ to 3₁ in others; therefore, at the same time there can be absorption and radiation of the light in question. Whether absorption or radiation at any given time has the upper hand depends upon various conditions (temperature, etc.).
For the sake of simplicity we have here tacitly understood that there [Pg 171] can be but one definite transition (from the normal state) corresponding to the assumption that the sodium spectrum had no other lines than the D-line. In reality this is not the case, and there can equally occur absorption of rays with larger frequencies belonging to other spectral lines in the sodium atom and corresponding to other possible transitions between stationary states in the sodium atom. If the temperature of the sodium vapour is sufficiently low, in which case almost all the atoms are in the normal state, it is evident that in the absorption only those lines will appear which correspond to transitions from the normal state, and which therefore form only a part of all the lines of the sodium spectrum. We thus obtain an explanation of the previously enigmatical circumstance that not all spectral lines which can appear in emission will be found in absorption. At the same time we get, in absorption experiments, valuable information about the structure of the atom beyond what the observations in the emission spectra are able to give.
Interesting phenomena may arise owing to the fact that the jumps between the stationary states of the atom sometimes, as we know, take place in single jumps, sometimes in double or multiple jumps, so that the intermediate stationary states are jumped over. There is then evidently a possibility that absorption can take place, for instance, with a double jump of an electron, which may later return to the original stationary orbit in two single jumps. The absorbed radiation energy will then appear in emission with two frequencies which are entirely different from the frequency of the absorbed rays (this latter in this case will be the sum of the other two). When an element is illuminated with a certain kind of rays, it can, in other words, emit [Pg 172] in return rays of a different nature. Such changes of frequencies have also been observed in experiment; they contain, in principle, an explanation of the characteristic phenomenon called fluorescence.
We shall not go further into this problem, but dwell for a time on the characteristic phenomenon of absorption which is known as the photoelectric effect. In this phenomenon (cf. p. 116) a metal plate, by illumination with ultra-violet light, is made to send out electrons with velocities the maximum value of which is independent of the strength of the illumination, but depends only on the frequency of the rays. What happens is that some of the electrons in the metal which otherwise have, as their function, the conduction of the electric current, by absorbing radiation energy, free themselves from the metal and leave it with a certain velocity. The reason why the rays for most metals must be ultra-violet (i.e. have a high frequency and consequently correspond to a proportionately large energy quantum) depends upon the fact that the energy quantum absorbed by the electrons must be large enough to carry out the work of freeing the electrons. But as long as the frequency of the rays (and therefore their energy quantum) is no less than what is needed for the freeing process, it does not need to have certain fixed values. If the energy quantum hν which the rays can give off is greater than is required to free the electrons, the surplus becomes kinetic energy in the electrons, which thus acquire a velocity which is the greater the greater the frequency ν, and which coincides with the maximum velocity observed in the experiments. What happens here is evidently something which can be [Pg 173] considered as the reverse of the process which leads to the production of the continuous hydrogen spectrum (described on p. 163). In the latter case, electrons with different velocities are bound by the hydrogen atoms, which thus emit rays with frequencies increasing with increasing velocity, while, vice versa, in the photoelectric effect rays with different frequencies free the electrons and give them velocities increasing with increasing frequencies.
It must be acknowledged that there is something very curious in this effect. If the electromagnetic waves, as has been assumed, are distributed evenly over the field of radiation, it is not easy to understand why they give energy to some atoms and not to others, and why the selected ones always—with a given frequency—acquire a definite energy quantum, independent of the intensity of the radiation. For small intensities of the incident radiation, the atom, in order to acquire the proper quantum, must absorb energy from a greater part of the field of radiation (or for a longer time) than for large intensities. When the atoms acquire energy in electron collisions, the situation is apparently easier to understand, since in this case the colliding electrons give their kinetic energy to definite atoms, namely, those which they strike.
Einstein, in 1905, when there was not yet any talk of the nuclear atom or the Bohr theory, enunciated his theory of light quanta, according to which the energy of radiation is not only emitted and absorbed by the atoms in certain quanta, with magnitudes determined by the frequency ν, but is also present in the field of radiation in such quanta. When an atom emits an energy quantum hν, this energy will not spread out in waves on all sides, but will travel in a definite [Pg 174] direction—like a little lump of energy, we might say. These light quanta, as they are called, can, like the electrons, hit certain atoms.
But even if in this theory the difficulties mentioned are, apparently, overcome, far greater difficulties are introduced; indeed it may be said that the whole wave theory becomes shrouded in darkness. The very number ν which characterizes the different kinds of rays loses its significance as a frequency and the phenomena of interference—reflection, dispersion, diffraction, and so on—which are so fundamental in the wave theory of the propagation of light, and on which, for instance, the mechanism of the human eye is based, receive no explanation in the theory of light quanta.
For instance, in order to understand that grating spectra can be produced at all, we must think of a co-operation of the light from all the rulings (cf. Fig. 10, p. 47), and this co-operation cannot arise if all the slits at a given moment do not receive light emitted from the same atom. In a bundle of rays which comes in at right angles to a grating, we must, in order to explain the interference, assume that the state of oscillation at a given moment is the same in all slits, that, for instance, there are wave crests in all at the same time, if we borrow a picture from the representation of water waves. Only in this case there can behind the grating at certain fixed places—for which the difference in the wave-length of the distances from successive slits is a whole number of wave-lengths—steadily come wave crests from all the slits at one moment and wave troughs from all at another moment (the classical explanation of the “mechanism” of a grating). If we imagine, however, that some slits are hit by light quanta from one atom [Pg 175] and others from a second atom, it is pure chance if there are wave crests simultaneously in all slits, because the different atoms in a source of light emit light at different times, depending purely on chance. An understanding of the observed effect of a grating on light seems then out of question.
The theory of light quanta may thus be compared with medicine which will cause the disease to vanish but kill the patient. When Einstein, who has made so many essential contributions in the field of the quantum theory, advocated these remarkable representations about the propagation of radiation energy he was naturally not blind to the great difficulties just indicated. His apprehension of the mysterious light in which the phenomena of interference appear on his theory is shown in the fact that in his considerations he introduces something which he calls a “ghost” field of radiation to help to account for the observed facts. But he has evidently wished to follow the paradoxical in the phenomena of radiation out to the end in the hope of making some advance in our knowledge.
This matter is introduced here because the Einstein light quanta have played an important part in discussions about the quantum theory, and some readers may have heard about them without being clear as to the real standing of the theory of light quanta. The fact must be emphasized that this theory in no way has sprung from the Bohr theory, to say nothing of its being a necessary consequence of it.
In the Bohr theory, absorption and radiation must be said to be completely reciprocal processes, i.e. processes of essentially the same nature, but proceeding in opposite directions. In itself it cannot [Pg 176] be said to be more incomprehensible that an atom absorbs energy from a field of radiation in agreement with the Bohr postulates than that it emits energy into the field; but in both cases we naturally encounter the great difficulties mentioned in Chap. V.
We have hitherto restricted ourselves to the purely atomic processes. But just as in the emission of radiation we meet spectra which owe their characteristics to molecular processes (band spectra, cf. p. 162), we have also absorption spectra with characteristics depending essentially upon motions of the atomic nuclei in the molecules. A particularly interesting and instructive example of this nature is met with in the infra-red region of the spectrum in certain broad absorption lines or absorption bands, which are due to gases having molecules containing several atoms. In hydrogen chloride, for instance, there is found, in the region of the spectrum which corresponds to a wave-length of about 3·5 μ, such an absorption band, which by more accurate investigation has been shown to consist of a great number of absorption lines.
The explanation of this collection of lines must be sought in the motions which the hydrogen nucleus and the chlorine nucleus perform, as they in part vibrate with respect to each other and in part rotate about their common centre of gravity. Just as in the case of the motions of the electrons in the atom, there are also certain stationary states for the nuclear motions. When the molecule absorbs radiation energy it will go from one of these states to another, where the energy content is greater. This absorption of energy proceeds according to the quantum rule, i.e., the product of the Planck constant h and the [Pg 177] frequency ν for the absorbed radiation must be equal to the difference in energy between the two stationary states; only those rays which have frequencies fulfilling this condition are absorbed.

Fig. 32.—Schematic representation of possible motions in a molecule of hydrogen chloride. O is the centre of gravity of the molecule. The black circles give the states of equilibrium of the nuclei, the circles s their outer positions in oscillating, and the circles r positions during the rotation of the nuclei.
In hydrogen chloride, at standard temperature, the molecules will be in different stationary states of rotation (cf. the remarks on p. 27), corresponding to different definite values of the rotation frequency, while the nuclei, on the other hand, must be assumed to be at rest with reference to each other, i.e., they preserve their mutual distance. In Fig. 32, H and Cl indicate the circles which the two nuclei will describe about the centre of gravity; here, however, it must be remarked that the hydrogen circle is drawn too small in comparison with [Pg 178] that of chlorine. If heat rays with all possible wave-lengths around 3·5 μ are sent through the hydrogen chloride, that radiation energy will be absorbed which can in part set the nuclei in oscillation and in part change the state of rotation. Let us for a moment assume that only the former change could happen. Then a ray with wave-length 3·46 μ would be absorbed, this frequency corresponding to the energy in the stationary state of oscillation into which the molecule goes; this frequency is very nearly equal to the frequency with which the nuclei vibrate relatively to each other. In reality, at the same time that the nucleus is set in oscillation, there will always be a change in the state of rotation—consisting either in an increase or in a decrease in the velocity of rotation. The energy absorbed, and therefore the frequency for the radiation absorbed, is thereby changed a little, so that in the spectrum of the rays sent through we do not obtain an absorption line corresponding to 3·46 μ, but a line somewhat removed from that. Since there are, however, many stationary states of rotation to start from, and since in some molecules there is one transition, in others another, we get many absorption lines on each side of 3·46 μ.
Even before Bohr propounded his theory, at a time when the quantum theory did not yet have a clarified form, the Danish chemist, Niels Bjerrum, had predicted that the infra-red absorption lines ought to have such a structure. This structure must be interpreted in the above way which differs somewhat from Bjerrum’s ideas, but his prediction was essentially strengthened by investigations, and it was one of the most significant features in the development of the quantum theory prior to 1913. The first to detect the structure of the infra-red absorption [Pg 179] bands was the Swedish physicist, Eva von Bahr. Her experiments were later extended in a most significant way by the work of Imes and other American investigators. They enable us to calculate exactly the distance between the two nuclei in the molecule.
It may be asked what becomes of the energy which the hydrogen chloride molecule thus absorbs, and whether it necessarily after a longer or shorter time must be re-emitted as radiation. The latter is not the case. In a collision between molecules or atoms, the energy which one molecule (or atom) has absorbed by radiation can undoubtedly be transferred to another molecule, the velocity of which is thereby increased. The theoretical necessity of the occurrence of such collisions was clearly shown for the first time in a very significant investigation by two of Bohr’s students, Klein and Rosseland. Without collisions of this nature the radiation energy absorbed could never be transformed into heat energy. Here we come to a very great and important field, which has a very close connection with the theory of the chemical processes and to a better explanation of which the more recent experiments of Franck and his co-workers have made important contributions.
[Pg 180]
We have hitherto restricted ourselves mainly to those applications of the Bohr theory which have a direct connection with the processes of radiation. We have shown how fertile the theory has proved to be, how many problems, previously inexplicable, have been solved, and what exact agreement has been established between experiment and theory in this comprehensive field. We may now ask how the theory accounts for the chemical behaviour of the different elements. As early as 1913, Bohr, in connection with his researches on spectral phenomena, had considered the chemical properties of the elements and had pointed out interesting possibilities.

Fig. 33.—Early
representation of the formation
of a hydrogen molecule (Bohr, 1913).
In his discussion of hydrogen, Bohr suggested a model for the structure of its molecule, which we shall give here, because, by a simple example, it illustrates how two neutral atoms may form a molecule (cf. p. 13). In Fig. 33, a, K₁E₁ and K₂E₂ are two neutral hydrogen [Pg 181] atoms which are approaching each other with the orbits of the two electrons parallel. The nucleus K₁ and the electron E₂ then attract each other as do the nucleus K₂ and the electron E₁. The two electrons repel each other as do the two nuclei; but when the electrons are in opposite positions of their orbits, the forces of attraction outweigh the effect of the forces of repulsion. Calculation shows that when the atoms are allowed to approach each other the positions of the atoms will be as is shown in Fig. 33, b, where the orbits are closer to each other than the nuclei. Finally, for small distances of the two nuclei, the two orbits will be merged into one, as is shown in Fig. 33, c. This orbit will be slightly larger than the original ones. The two hydrogen atoms may, in this way, combine into one molecule. In fact, an [Pg 182] equilibrium position can be found for which the nuclei are held together, in spite of their mutual repulsion, by the attractive forces existing between them and the electrons which are moving in their common orbit. It must, however, be assumed, for reasons which cannot be given here, that the hydrogen molecule is, in reality, constructed somewhat differently; probably the orbits of the electrons make an angle with each other.
The formation of a hydrogen molecule may also be supposed to occur when a positive hydrogen ion, i.e., a hydrogen nucleus, and a negative hydrogen ion, i.e., a hydrogen nucleus with two electrons, are drawn together by their mutual attractions. The forces of attraction would be much stronger than in the first example given, and the formation of a neutral molecule would not take place in the same way. More energy would also be released, but the final result will be the same.
Just as in the case of the hydrogen molecule, other molecules may be formed from atoms belonging to the same or to different elements. The method of formation of molecules varies according as it is a union of neutral molecules in the normal state, or a union of positive and negative ions. Conversely, by chemical decomposition a molecule can be separated either into neutral parts or into ions. If, for instance, common salt (sodium chloride, NaCl) is dissolved in water, the salt molecules are, under the influence of the water molecules, decomposed in Na-ions with one positive charge and Cl-ions with one negative charge, corresponding to the monovalent electropositive character of sodium and the monovalent electronegative character of chlorine. [Pg 183]
The possibilities are, however, far from being exhausted by these two methods of composition and decomposition. An atom may exist not only in the normal state where it has its complete number of electrons collected as tightly as possible about the nucleus, and in the ionized state with one or more too many or too few electrons; but in a neutral atom one or more of the outer electrons may be in a stationary orbit at a greater distance from the nucleus than corresponds to the normal stationary state. It is easy to understand that an atom in such an “excited” or (as it is called in chemistry) active state often finds it easier to act in concert with other atoms than when it is in the normal state; in this latter state the atom is often more like a little compact lump of neutral substance than in the active state.
It will, in any case, be understood that the interplay between the atoms, which reveals itself in the chemical processes or reactions between different elements, offers many opportunities for the Bohr theory to give in the future a more detailed explanation than was possible to the earlier theories of chemistry. We must also mention the fact that it has become possible to elucidate in main features the phenomena, hitherto unexplained, of the chemical effects of light, as on a photographic plate (photochemistry) and of catalysis, which consists in bringing about, or accelerating, the chemical interaction between two substances by the presence of a third substance which does not itself enter in the compound, and often needs only to be present in very small quantities. It must, however, be emphasized that at present we do not yet possess a detailed theory of molecular constitution comparable with our knowledge of the structure of the atoms. [Pg 184]
Instead of inquiring how the chemical processes may take place, we shall now study the general correlation between the chemical properties and the atomic numbers of the elements, a correlation which has found its empirical expression in the natural or periodic system of the elements (cf. p. 23). The explanation of the puzzles of this system must be said to be one of the finest results which Bohr has obtained, and it constitutes a striking evidence in favour of the quantum theory of atoms.
There is nothing new in the idea of connecting the arrangement of the elements in the periodic system with an arrangement of particles in the atom in regular groups, the character of which varies, so to say, periodically with increasing number of particles. In the atom model of Lord Kelvin and J. J. Thomson (cf. p. 86), with the positive electricity distributed over the volume of the whole atom, Thomson tried to explain certain leading characteristics of the periodic system by imagining the electrons as arranged in several circular rings about the centre of the atom. He pointed out that the stability of the electronic configurations of this type varied in a remarkable periodic way with the number of electrons in the atom. By considerations of this nature Thomson was able to enunciate a series of analogies to the behaviour of the elements in the periodic system as regards the tendency of the neutral atoms to lose one or more electrons (electropositive elements) or to take up one or more electrons (electronegative elements). But, setting aside possible objections to his considerations and calculations, the connection with the system [Pg 185] was very loose and general, and his theory lost its fundamental support when his atomic model had to give way to Rutherford’s. With Bohr’s theory the demand for a stable system of electrons was placed in an entirely new light.
In his treatise of 1913, Bohr tried to give an explanation of the structure of the atom, by thinking of the electrons as moving in a larger or smaller number of circular rings about the nucleus. His theory did not exclude the possibility of orbits of electrons having different directions in space instead of lying in one plane or being parallel. The tendency of the considerations was to attain a definite, unique determination of the structure of the atom, as is demanded by the pronounced stability of the chemical and physical properties of the elements. The results were, however, rather unsatisfactory, and it became more and more clear that the bases of the quantum theory were not sufficiently developed to lead in an unambiguous way to a definite picture of the atom. Nowadays the simple conception of the electrons moving in circular rings in the field of the nucleus is definitely abandoned, and replaced by a picture of atomic constitution of which we shall speak presently.
In the following years the general conception of the group distribution of the electrons in the atom formed the basis of many theoretical investigations, which in various respects have led to a closer understanding of chemical and physical facts. The German physicist, Kossel, showed that the characteristic X-ray spectra of the elements, which are due to a process of reconstruction of the atom subsequent to the removal of one or more of the innermost electrons (cf. p. 161), [Pg 186] give a most striking support to the assumption that the electrons are distributed in different groups in which they are bound with different strength to the atom.
The connection between the electron groups and the chemical valence properties of the atoms, to which Thomson had first drawn attention and which also played an important part in Bohr’s early considerations, was further developed in a significant way by Kossel, as well as by Lewis and by Langmuir in America. These chemical theories had, however, little or no connection with the quantum theory of atomic processes; even the special features of the Rutherford atom, which are of essential importance in the theory of the hydrogen spectrum and of other spectra, played only a subordinate part.
In 1920 Bohr showed how, by the development of the quantum theory which had taken place in the meantime, and the main features of which consisted in the introduction of more than one quantum number for the determination of the stationary states and in the establishment of the correspondence principle, the problem of the structure of the atom had appeared in a new light. In fact, he outlined a general picture of atomic constitution, based on the quantum theory, which in a remarkable way accounted for the properties of the elements. In order to decide doubtful questions, he has often had to call to his aid the observed properties of elements, and it must be readily admitted that the finishing touches of the theory are still lacking. But from his general starting-point he has been able to outline the architecture of even the most complex atomic structures and to explain, not only the known regularities, but also the apparent irregularities of the periodic system of the elements. [Pg 187]
The method Bohr used in his attempt to solve the problem was to study how a neutral normal atom may gradually be formed by the successive capturing and binding of the individual electrons in the field of force about the nucleus of the atom. He began by assuming that he had a solitary nucleus with a positive charge of a given magnitude. To this nucleus free electrons are now added, one after the other, until the nucleus has taken on the number sufficient to neutralize the nuclear charge. Each individual electron undergoes a “binding” process, i.e. it can move in different possible stationary orbits about the nucleus and the electrons already bound. With the emission of radiation it can go from stationary states with greater energy to others with less energy, ending its journey by remaining in the orbit which corresponds to the least possible energy. We may designate this state of least energy as the normal state of the system, which, however, is only a positive atomic ion, so long as all the electrons needed for neutralization are not yet captured.
From the exposition in the preceding chapter it will be seen that the ordinary series spectra (arc spectra) may be considered as corresponding to the last stage in this formation process, since the emission of each line in such a spectrum is due to a transition between two stationary states in each of which N-1 electrons are bound in their normal state, i.e. as tight as possible, by the nucleus, while the Nth electron moves in an orbit mainly outside the region of the other electrons. In the same way the spark spectra give witness of the last stage but one of the formation process of the atom, since here N-2 electrons are bound in their normal state while an N-1th electron moves [Pg 188] in an orbit large compared with the dimensions of the orbits of the inner electrons. From these remarks it will be clear that the study of the series spectra is of great importance for the closer investigation of the process of formation of the atom outlined above. Furthermore, the general ideas of the correspondence principle, which directly connects the possibility of transition from one stationary state to another with the motion of the electron, has been very useful in throwing light on the individual capturing processes and on the stability of the electronic configurations formed by these. In what follows we cannot, however, reproduce Bohr’s arguments at length; we must satisfy ourselves with some hints here and there, and for the rest restrict ourselves to giving some of the principal results.
Before going farther we shall recall what has previously been said about the quantum numbers. In the undisturbed hydrogen atom, the stationary orbits can be numbered with the principal quantum numbers 1, 2, 3 ... n. But to each principal quantum number there corresponds not one but several states, each with its auxiliary quantum number 1, 2, 3 ... k, k at the most being equal to the principal quantum number. In a similar way, the stationary orbits of the electrons in an atom containing several electrons can be indicated by two quantum numbers, the 3₂ orbit, for instance, being that with principal quantum number 3 and auxiliary quantum number 2. But while in the hydrogen atom the principal quantum number n, in the stationary orbits which are slowly rotating ellipses, is very simply connected with the length of the major axis of the ellipse, and k: n is the ratio between [Pg 189] the minor and major axes, still in other atoms with complex systems of electrons the significance of the principal quantum number is not so simple and the orbit of an electron consists of a sequence of loops of more complicated form (cf. Fig. 29). We must satisfy ourselves with the statement that a definition of their significance can be given, but only by mathematical-physical considerations which we cannot enter into here. It may, however, be stated that, if we restrict ourselves to a definite atom, the rule will hold that, among a series of orbits with the same auxiliary quantum number but different principal quantum numbers, that orbit in which the electron attains a greater distance from the nucleus has the higher number. Another rule which holds is, that an orbit with a small auxiliary quantum number in comparison with its principal quantum number (as 4₁ for instance, cf. Fig. 29), will consist of very oblong loops with a very great difference between the greatest and least distances of the electron from the nucleus, while the orbit will be a circle when the two quantum numbers are the same as for 1₁, 2₂, 3₃. Although each orbit has two quantum numbers, we often speak simply of the 1-, 2-, 3- ... n-quantum orbits, meaning here the orbits with the principal quantum numbers 1, 2, 3 ... n.
The one electron of hydrogen will, upon being captured, first be at “rest” when it reaches the 1₁-path, and we might perhaps be led to expect that in the atoms with greater nuclear charges the electrons in the normal state also would be in the one quantum orbit 1₁, because to this corresponds the least energy in hydrogen. This assumption formed actually the basis of Bohr’s work of 1913 on the structure of the heavier atoms. It cannot be maintained, however. Considerations of [Pg 190] theoretical and empirical nature lead to the assumption that the electrons which already are gathered about the nucleus can make room only to a certain extent for new ones, moving in orbits of the same principal quantum number. Those electrons which are captured later are kept at an appropriate distance; they are, for instance, prevented from passing from a 3-quantum orbit to a 2-quantum one, if the number of electrons moving in 2-quantum orbits has reached a certain maximum value. When it is said that the captured electrons end in the stationary state which corresponds to the least energy, it must, therefore, mean, not the 1-quantum orbit, but the innermost possible under the existing circumstances. The final result will be that the electrons are distributed in groups, which are characterized each by their quantum numbers in such a way that passing from the nucleus to the surface of the atom, the successive groups correspond to successive integer values of the quantum number, the innermost group being characterized by the quantum number one. Moreover, each group is subdivided into sub-groups corresponding to the different values which the auxiliary quantum number may take.
That the electrons first collected keep the latecomers at an appropriate distance must be understood with reservations; a new electron moving in an elongated orbit can very well come into the territory already occupied; in fact, it may come closer to the nucleus than some of the innermost groups of electrons. In case an outer electron thus dives into the inner groups, it makes a very short visit, travelling about the nucleus like a comet which at one time on its elongated orbit comes in among the planets and perhaps draws closer to [Pg 191] the sun than the innermost planet, but during the greater part of its travelling time moves in distant regions beyond the boundaries of the planetary system. It is a very important characteristic of the Bohr theory of atomic architecture that the outer electrons thus penetrate far into the interior of the atom and thus chain the whole system together.
Such a “comet electron” has, however, a motion of a very different nature from that of a comet in the solar system. Let us suppose that the nuclear charge is 55 (Caesium), that there already are fifty-four electrons gathered tightly about the nucleus, and that No. 55 in an orbit consisting of oblong loops moves far away from the nucleus, but at certain times comes in close to it. Then, for the greater part of its orbit, this electron will be subject to approximately the same attraction as the attraction towards one single charge, as a hydrogen nucleus; but when No. 55 comes within the fifty-four electrons it will for a very short time be influenced by the entire nuclear charge 55. Together with the nearness of the nucleus, this will cause No. 55 to acquire a remarkably high velocity and to move in an orbit quite different from the elliptical one it followed outside. Moreover, the great velocity of the electron during its short visit to the nucleus is in a considerable degree determinative of its principal quantum number; this will be higher than would be expected from the dimensions of the outer part of the orbit if we supposed the motion to take place about a hydrogen nucleus (cf. Figs. 27 and 29).
After these general remarks we shall try in a few lines to sketch the Bohr theory of the structure of the atomic systems from the simplest to the most complicated. We shall not examine the entire periodic system [Pg 192] with its ninety-two elements, but here and there we shall bring to light a trait which will illustrate the problem—partly in connection with the schematic representations in the atomic diagrams at the end of the book.
The curves drawn represent parts of the orbital loops of the electrons in the neutral atoms of different elements. Although the attempt has been made to give a true picture of these orbits as regards their dimensions, the drawings must still be considered as largely symbolic. Thus in reality the orbits do not lie in the same plane, but are oriented in different ways in space. It would have been impracticable to show the different planes of the orbits in the figure. Moreover, there is still a good deal of uncertainty as to the relative positions of these planes. On this account the orbits belonging to the same sub-group, i.e., designated by the same quantum numbers, are placed in a symmetric scheme in the sketch. For groups of circular orbits the rule has been followed to draw only one of them as a circle, while the others in the simpler atoms are drawn in projection as ellipses within the circle, and in the more complicated atoms are omitted entirely. The two circular orbits of the helium atom are both drawn in projection as ellipses. Further, for the sake of clearness, no attempt has been made to draw the inner loops of the non-circular orbits of electrons which dive into the interior of the atom. In lithium only, the inner loop of the orbit of the 2₁ electron has been shown by dotted lines.
In order to distinguish the groups of orbits with different principal [Pg 193] quantum numbers two colours have been used, red and black, the red indicating the orbits with uneven quantum numbers, as 1, 3, 5, the black those with even quantum numbers, as 2, 4, 6. Wherever possible the nucleus is indicated by a black dot; but in the sketches of atoms with higher atomic numbers the 1-quantum orbits are merged into one little cross and the nucleus has been omitted. It should be noticed that the radium atom is drawn on a scale twice as great as that for the other atoms.
We shall begin with the capture of the first electron. If the nucleus is a hydrogen nucleus the hydrogen atom is completed when the electron has come into the 1₁ orbit, a circle with diameter of about 10⁻⁸ cm. (cf. the diagram). If the nucleus had had a greater nuclear charge the No. 1 electron would have behaved in the same way, but the radius of its orbit would have been less in the same ratio as the nuclear charge was greater. For a lead nucleus, with charge (atomic number) 82, the radius of the 1₁ orbit is ¹/₈₂ that of the hydrogen 1₁ orbit. Since atoms with high atomic numbers thus collect the electrons more tightly about them it is understandable that, in spite of their greater number of electrons, they can be of the same order of magnitude as the simpler atoms.
Let us now examine the helium atom. The first electron, which its nucleus (charge 2) catches, moves as shown in a circle 1₁, but with a smaller radius than in the case of the hydrogen atom. Electron No. 2 can be caught in different ways, and the closer study of the conditions prevailing here, which are still comparatively simple since there are only two electrons, has been of greatest importance in the further development of the whole theory. We cannot go into it here, but must [Pg 194] content ourselves with saying that the stable final result of the binding of the second electron consists in the two electrons moving in circular 1-quantum orbits of the same size with their planes making an angle with each other (cf. the diagram). This state has a very stable character, and the helium atom is therefore very disinclined to interplay with other atoms, with other helium atoms as well as with those of other elements. Helium is therefore monatomic and a chemically inactive gas.
In all atomic nuclei with higher charges than the helium nucleus the first two orbits are also bound into two 1-quantum circular orbits at an angle with each other; this group cannot take up any new electron having the same principal quantum number. It takes on an independent existence and forms the innermost electron group in all atoms of atomic number higher than 2.
Electron No. 3 will accordingly not be bound in the same group with 1 and 2. It must be satisfied with a 2-quantum orbit, 2₁, which consists of oblong loops, and, when nearest the nucleus, comes into the territory of the 1-quantum orbits. It is but loosely bound compared to the first two electrons, and the lithium atom, which has only three electrons, can therefore easily let No. 3 loose so that the atom becomes a positive ion. Lithium is therefore a strongly electropositive monovalent metal. The element beryllium (No. 4) will probably have two electrons in the orbits 2₁; it will therefore be divalent. But during the short visit of these electrons to the nucleus they are subject to a greater nuclear charge than in lithium. The 2₁ electrons are therefore, in beryllium, more firmly bound than in [Pg 195] lithium, and the electropositive character of beryllium is therefore less marked.
We have something essentially new in the boron atom (atomic No. 5) where the two electrons No. 3 and No. 4 are taken into 2₁ orbits, but where No. 5 will very probably be bound in a circular 2₂ orbit. How the conditions will be in the normal state of the following atoms preceding neon is not known with certainty. We only know that the electrons coming after the first two will be captured in 2-quantum orbits, the dimensions of which get smaller, according as the atomic number increases.
The neon atom (compare the diagram) has a particularly stable structure, both “closed” and symmetric, which besides two 1₁-orbits contains four electrons in 2₁ orbits and four electrons in 2₂ orbits. As regards the four electrons in 2₁ orbits, they do not have symmetrical positions at every moment or move simultaneously either towards or away from the nucleus; on the contrary, it must be assumed that the electrons come closest to the nucleus at different moments at equal intervals of time.
The name of inert or inactive gases is given to the entire series of helium (2), neon (10), argon (18), krypton (36), xenon (54) and niton (86), the O-column in the periodic system given in the table on p. 23. All these elements are monatomic and quite unwilling to enter into chemical compounds with other elements (although there is about 1 per cent. of argon in the air about us this element has, on this account, escaped the observation of chemists until about 1895, when it was discovered by the English chemist, Ramsay). This complete chemical inactivity is explained by the fact that the atoms of all these [Pg 196] elements have a nicely finished “architecture” with all the electrons firmly bound in symmetrical configurations. They may be said to form the mile posts of the periodic system, and to be the ideals towards which the other atoms aspire. The table shows how the electrons in the atoms of these gases are divided among the types of orbits corresponding to the different quantum numbers.
Table showing the Distribution of the Electrons
of different Orbital Types in the Neutral Atoms
of the Inactive Gases.
| Atomic Number |
Quantum Numbers. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1₁ | 2₁ | 2₂ | 3₁ | 3₂ | 3₃ | 4₁ | 4₂ | 4₃ | 4₄ | ||
| Helium | 2 | 2 | 2 | ||||||||
| Neon | 10 | 2 | 4 | 4 | |||||||
| Argon | 18 | 2 | 4 | 4 | 4 | 4 | - | ||||
| Krypton | 36 | 2 | 4 | 4 | 6 | 6 | 6 | 4 | 4 | - | - |
| Xenon | 54 | 2 | 4 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | - |
| Niton | 86 | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 |
| ? | 118 | 2 | 4 | 4 | 6 | 6 | 6 | 8 | 8 | 8 | 8 |
| Atomic Number |
Quantum Numbers. | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5₁ | 5₂ | 5₃ | 5₄ | 5₅ | 6₁ | 6₂ | 6₃ | 6₄ | 6₅ | 6₆ | 7₁ | 7₂ | 7₃ | ||
| Helium | 2 | ||||||||||||||
| Neon | 10 | ||||||||||||||
| Argon | 18 | ||||||||||||||
| Krypton | 36 | ||||||||||||||
| Xenon | 54 | 4 | 4 | - | - | - | |||||||||
| Niton | 86 | 6 | 6 | 6 | - | - | 4 | 4 | - | - | - | - | |||
| ? | 118 | 8 | 8 | 8 | 8 | - | 6 | 6 | 6 | - | - | - | 4 | 4 | - |
The elements fluorine, oxygen and nitrogen can attain the ideal neon-architecture by binding respectively one, two and three additional electrons. Naturally they do not become neon atoms, but merely negative atomic ions with single, double or triple charge; and their tendency in this direction appears in their character of monovalent, divalent and trivalent electronegative elements respectively. If we return to carbon it can probably not become a tetravalent negative ion by binding four free electrons; but in the typical carbon compound, methane (CH₄), the neon ideal is realized in another manner. In fact, it is reasonable to assume that the four electrons of the hydrogen atoms together with the [Pg 197] six of the carbon atom give approximately a neon-architecture. The four hydrogen nuclei naturally cannot be combined with the carbon nucleus; the mutual repulsions keep them at a distance. They will probably assume very symmetrical positions within the electron system which holds them together. The nitrogen atom may in a similar way find completion in a neutral molecule with neon-architecture, if it unites with three hydrogen atoms to form ammonia NH₃; but the three hydrogen nuclei, although having symmetrical positions, will not lie in the same plane as the nitrogen nucleus. The electric centre of gravity for the positive nuclei will therefore not coincide with the centre of gravity for the negative electron system. The molecule obtains thus what might be called a positive and a negative pole, and this dipolar character appears in the electrical action of ammonia (its dielectric constant). Something similar holds true for the water molecule, where, in a neon-architecture of electrons, in addition to the oxygen nucleus in the centre there are two hydrogen nuclei which are not co-linear with the oxygen nucleus.
If we go on from neon in the periodic system we come to sodium (11). When the sodium nucleus captures electron No. 11, this cannot find room in the neon-architecture formed by the first ten electrons. Since the eleventh electron thus cannot find a place in either a 2₁ or a 2₂ orbit, it is bound in a 3₁ orbit (cf. Fig. 29 and diagram at the end). The atom then has a character like that of the lithium atom, and we can therefore understand the chemical relationship between the two elements, which are both monovalent electropositive metals.
We shall not dwell longer upon the individual elements of the atomic series. If we pass from neon through sodium (11), magnesium (12), [Pg 198] aluminium (13), etc., to argon (18), we get what is essentially a repetition of the situation in the series from lithium to neon. We first get two orbits of the 3₁ type in magnesium, a 3₂ orbit is for the first time added in aluminium, and for the atomic number 18, eight 3-quantum orbits, together with the eight orbits of the inner 2-quantum group and the two of the innermost 1-quantum group, give the symmetric architecture of argon (cf. table on p. 196, and diagram at the end).
The architecture of the argon atom is in a certain sense less complete than that of the neon atom. In argon there are indeed four orbits of the 3₁ type and four of the 3₂ type, but the third kind of 3-quantum orbit, the circular 3₃ one, is missing. Nor does it appear in the next element, potassium (19). The electron No. 19 prefers, instead of the 3₃ orbit, the 4₁ orbit, which consists of oblong loops and which gives a firmer binding because it dives in among the electrons bound earlier, while the circle 3₃ would lie outside them all. We thus obtain an atom of type similar to the lithium and sodium atoms. But the slighted 3₃ path lies, so to speak, on the watch to steal a place for itself in the neutral atom, and this has grave results for the subsequent development. Even in calcium (20), after the first eighteen electrons are bound in the argon architecture, both the nineteenth and the twentieth go into a 4₁ orbit, and the behaviour of calcium is like that of magnesium. But since the increasing nuclear charge means for the electron No. 19 a decrease in the dimensions and an increase in the binding of the orbits corresponding to the quantum number 3₃, a point will finally be attained where the 3₃ orbit of the nineteenth electron lies within the boundaries of what may be called the argon system, [Pg 199] i.e., the architecture corresponding to the first eighteen electrons, and corresponds to a stronger binding than a 4₁ orbit would do. In scandium (21) the 3₃-type orbit occurs for the first time in the neutral atom and will not only come into competition with the 4₁ type, but will also cause a disturbance in the 3-quantum groups, which in the following elements must undergo reconstruction. As long as this lasts the situation is very complicated and uncertain. When the reorganization is almost completed, we come to the blotting out of chemical differences, particularly known from the triad, iron, cobalt and nickel. Moreover, there comes a fluctuation in the valency of the elements. Iron can, as has been said, be divalent, trivalent or hexavalent. This oscillation in valency begins in titanium.
We should perhaps expect that the reconstruction would be completed long before nickel (28) is reached, because even with twenty-two electrons we could get four orbits of each of the 3-quantum types (3₁, 3₂ and 3₃); but from the chemical facts we are led to assume that in a completed group of 3-quantum orbits there can be room for six electrons in each sub-group. At first sight we should, then, expect the end of the reconstruction with nickel, which has indeed eighteen electrons more than neon where the group of 2-quantum orbits was completed. We might expect that nickel would be an inert element in the series with helium, neon, and argon. On the contrary, nickel merely imitates cobalt. This is explained by the fact that the group of eighteen 3-quantum orbits, although it has a symmetric architecture, is weakly constructed if the nuclear charge is not sufficiently large. The binding of this group is too weak for it to exist as the outer group in [Pg 200] a neutral atom. In nickel the electrons, in a less symmetrical manner, will probably arrange themselves with seventeen 3-quantum orbits and one 4-quantum orbit.
The group of eighteen 3-quantum orbits becomes stable, however, when the nuclear charge is equal to or larger than 29, in which case it can become the outer group in a positive ion. In this we find the explanation of the properties of the atom of copper. The neutral copper atom has its twenty-ninth electron bound in a 4₁ orbit consisting of oblong loops (cf. diagram at the end); this electron can easily be freed and leaves a positive monovalent copper ion with a symmetrical architecture. Even under these circumstances, although possessing a certain stability, the ion is not very firmly constructed. Thus the fact that copper can be both monovalent and divalent, must be explained by the assumption that for a nuclear charge 29, the 3-quantum group still easily loses an electron.
When we come to zinc (30) the group of eighteen is more firmly bound; zinc is a pronounced divalent metal which in its properties reminds us of calcium and magnesium. From zinc (30) to krypton (36) we have a series of elements which in a certain way repeat the series from magnesium (12) to argon (18).
In Fig. 34 is shown Bohr’s arrangement of the periodic system in which the systematic correlation of the properties of the element appears somewhat clearer than in the usual plan (cf. p. 23). It shows great similarity with an arrangement proposed nearly thirty years ago by the Danish chemist, Julius Thomsen. The elements from scandium to nickel, where, in the neutral atom, the electron group of 3-quantum orbits is in a state of reconstruction, are placed in a frame; the neutral oblique lines connect elements which are “homologous,” i.e., similar in chemical and physical (spectral) respect. [Pg 201]
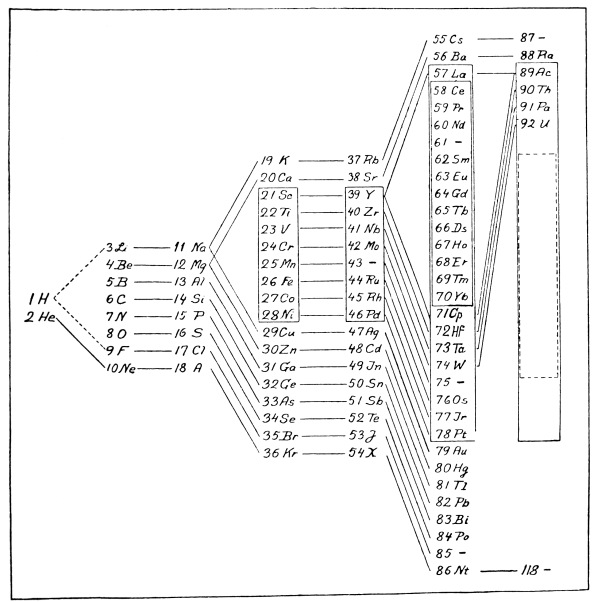
Fig. 34.—The periodic system of the elements. The elements where an inner group of orbits is in a stage of reconstruction are framed. The oblique lines connect elements which in physical and chemical respects have similar properties.
[Pg 202] In krypton (36) we again have a stable architecture with an outer group of eight electrons, four in 4₁ orbits and four in 4₂ orbits. Owing to the appearance of 4₃ orbits in the normal state of the atoms of elements with atomic number higher than 38, there follows in the fifth period of the natural system a reconstruction and provisional completion of the 4-quantum orbits to a group of eighteen electrons, which shows a great simplicity with the completion of the 3-quantum group in the fourth period. In Fig. 34 the elements where the 4-quantum group is in a state of reconstruction are framed. The 4-quantum group with eighteen electrons is of more stable construction than the group of eighteen 3-quantum orbits in the elements with an atomic number lower by eighteen. This is due to the fact that all the orbits in the first-mentioned group are oblong and therefore moored, so to say, in the inner groups, while in the complete group of 3-quantum orbits there are six circular orbits. This is the reason why silver, in contrast to copper, is monovalent.
The next inactive gas is xenon (54), which outside of the 4-quantum group has a group of eight electrons in 5-quantum orbits, four in 5₁ orbits and four in 5₂ orbits. We notice that in xenon the group of 4-quantum orbits still lacks the 4₄ orbits. On the theory we must, therefore, expect to meet a new process of completion and reconstruction when proceeding in the system of the elements. The theoretical argument is similar to that which applies in the case of the completion of the 3-quantum group which takes place in the fourth period of the natural system. In fact, in the formation of the normal [Pg 203] atoms of the elements next after xenon, caesium, 55, and barium, 56, the fifty-four electrons first captured will form a xenon configuration, while the fifty-fifth electron will be bound in a 6₁ orbit, consisting of very oblong loops, which represents a much stronger binding than a circular 4₄ orbit. Calculation shows, however, that with increasing nuclear charge there must soon appear an element for which a 4₄ orbit will represent a stronger binding than any other orbit. This is actually the case in cerium (58), and starting from this element we meet a series of elements where, in the normal neutral atom, the 4-quantum group is in a state of reconstruction. This reconstruction must occur far within the atom, since the group of eighteen 4-quantum orbits in xenon is already covered by an outer group of eight 5-quantum orbits. The result is a whole series of elements with very slight outward differences between their neutral atoms, and therefore with very similar properties. This is the rare earths group, which in such a strange way seemed to break down the order of the natural system (cf. p. 21), but which thus finds its natural explanation in the quantum theory of the structure of the atom.
The elements in which the 4-quantum group is in a state of reconstruction are, in Fig. 34, enclosed in the inner frame in the sixth period. Moreover, in the outer frame all elements are enclosed where the group of 5-quantum orbits is in a state of reconstruction, which started, even before cerium in lanthanum (57), where the fifty-fifth electron in the normal state is bound in a 5₃ orbit. The element cassiopeium, with atomic number 71, which is the last of the rare earths, stands just outside the inner frame, because in the normal neutral atom of this element the 4-quantum group is just completed; this [Pg 204] group, instead of eighteen electrons with six electrons in each sub-group, consists now of thirty-two electrons with eight electrons in each sub-group. The theory was able to predict that the element with atomic number 72, which until a short time ago had never been found, and the properties of which had been the subject of some discussion, must in its chemical properties differ considerably from the trivalent rare earths and show a resemblance to the tetravalent elements zirconium (40), and thorium (90). This expectation has recently been confirmed by the work of Hevesy and Coster in Copenhagen, who have observed, by means of X-ray investigations, that most zircon minerals contain considerable quantities (1 to 10 per cent.) of an element of atomic number 72, which has chemical properties resembling very much those of zirconium, and which on this account had hitherto not been detected by chemical investigation. A preliminary investigation of the atomic weight of this new element, for which its discoverers have proposed the name hafnium (Hafnia = Copenhagen), gave values lying between 178-180, in accordance with what might be expected from the atomic weight of the elements (71) and (73). (Cf. p. 23.)
The further completion of the groups of 5- and 6-quantum orbits, which in the rare earths had temporarily come to a standstill, is resumed in hafnium and goes on in a way very similar to that in which the 4- and 5-quantum groups in the fifth, and the 3- and 4-quantum groups in the fourth period underwent completion. Thus the reconstruction of the 5-quantum group which began in lanthanum, and which receives a characteristic expression in the triad of the platinum metals, has come to a provisional conclusion in gold (79), gold being the first [Pg 205] element outside the two frames which, in Fig. 34, appear in the sixth period. The neutral gold atom possesses, in its normal state—besides two 1-quantum orbits, eight 2-quantum orbits, eighteen 3-quantum orbits, thirty-two 4-quantum orbits and eighteen 5-quantum orbits—one loosely bound electron in a 6₁ orbit.
In niton (86), finally, we meet again an inactive gas, the structure of the atom of which is indicated in the table on p. 196.
In this element the difference between nuclear and electron properties appears very conspicuously, since the structure of the electron system is particularly stable, while that of the nucleus is unstable. Niton, in fact, is a radioactive element which is known in three isotopic forms; one of these is the disintegration product of radium, the so-called radium emanation; it then has a very brief life. In the course of four days over half of the nuclei in a given quantity of radium emanation will explode.
In the diagram at the end of the book, as an example of an atom with very complicated structure, there is given a schematic representation of the atom of the famous element radium, on a scale twice as large as the one used in the other atoms. It follows clearly enough, from what has been said in Chap. IV., that the structure of the electron system has nothing to do with the radioactivity. All the remarkable radiation activities are due to the nucleus itself. There has not even been room in the figure to draw the nucleus; the 1-quantum orbits consist only of a small cross, and in the other groups we have contented ourselves with summary indications. The electron system, with [Pg 206] its eighty-eight electrons, is, however, in itself very interesting, with its symmetry in the number of electrons in the different groups. In the different quantum groups from 1 to 7 there are found respectively two, eight, eighteen, thirty-two, eighteen, eight and two electrons. The last group is naturally of a very different nature from the first; they are “valence electrons,” which easily get loose and leave behind a positive radium ion with stable niton architecture. Radium then belongs to the family of the divalent metals, magnesium, calcium, strontium and barium.
Four places from radium is uranium (92) and the end of the journey, if we restrict ourselves to the elements which are known to exist. One could very well continue the building-up process still further and discuss what structure would have to be assumed for the atoms of the elements with higher atomic numbers. That they cannot exist is not the fault of the electron system but of the nuclei, which would become too complicated and too large to be stable. In the table on p. 196 there is shown the probable structure of the atom of the inert gas following niton; it must be assumed to have one hundred and eighteen electrons distributed in groups of two, eight, eighteen, thirty-two, thirty-two, eighteen and eight among the quantum groups from 1 to 7.
As has been said, in all this symmetrical structure of the atoms of the elements, Bohr has in many cases had to rely upon general considerations of the information that observation gives about the properties of the individual elements. It must, however, not be forgotten that the backbone of the theory is and remains the general laws of the quantum theory, applied to the nucleus atom in the same way [Pg 207] as they originally were applied to the hydrogen atom, leading thereby to the interpretation of the hydrogen spectrum.
We have, further, a most striking evidence as to the correctness of Bohr’s ideas in the fact that not only do the pictures of the atoms which he has drawn agree with the known chemical facts about the elements, but they are also able to explain in the most satisfactory manner possible the most essential features of the characteristic X-ray spectra of the different elements, a field we shall not enter upon here.
In all that has been said above we have been considering the Bohr theory simply as a means of gaining a deeper understanding of the laws which determine activities in the atomic world. Perhaps we shall now be asked if we can “utilize” the theory, or, in other words, if it can be put to practical use.
To this natural and not unwarranted question we may first give the very general answer, that progress in our knowledge of the laws of nature always contributes sooner or later, directly or indirectly, to increase our mastery over nature. But the connection between science and practical application may be more or less conspicuous, the path from science to practical application more or less smooth. It must be admitted that the Bohr theory, in its present state of development, hardly leads to results of direct practical application. But since it shows the way to a more thorough understanding of the details in a great number of physical and chemical processes, where the peculiar properties of the different elements play parts of decided importance, then in reality it offers a wealth of possibilities for making [Pg 208] predictions about the course of the processes—predictions which undoubtedly in the course of time will be of practical use in many ways. In this connection the discovery of the element hafnium, discussed on p. 204, may be mentioned. It must be for the future to show what the Bohr theory can do for technical practice. [Pg 209]
[Pg 210]
Below is given an explanation of the different symbols which occur at various places in the book; also the values of important physical constants.
1 m. = 1 metre; 1 cm. = 1 centimetre = 0·394 inches.
1 μ = 1 micron = 1/1000 of a millimetre = 0·0001 cm. = 10⁻⁴ cm.
1 μμ = 1/1,000,000 of a millimetre = 10⁻⁷ cm.
1 cm.³ = 1 cubic centimetre.
1 g. = 1 gram; 1 kg. = 1 kilogram = 2·2 pounds.
1 kgm. = 1 kilogrammetre (the work or the energy required to lift 1 kg. 1 m.).
1 erg = 1·02 × 10⁻⁸ kgm. = 7·48 × 10⁻⁸ foot-pounds.
λ represents wave-length.
ν represents frequency (number of oscillations in 1 second).
ω represents frequency of rotation (number of rotations in 1 second).
n represents an integer (particularly the Bohr quantum numbers).
The velocity of light is c = 3 × 10¹⁰ cm. per second = 9·9 × 10⁸ feet per second.
The wave-length of yellow sodium light is 0·589 μ = 589 μμ = 2·32 × 10⁻⁵ inches.
The frequency of yellow sodium light is 526 × 10¹² vibrations per second.
The number of molecules per cm.³ at 0° C. and atmospheric pressure is about 27 × 10¹⁸.
The number of hydrogen atoms in 1 g. is about 6·10²³.
The mass of a hydrogen atom is 1·65 × 10⁻²⁴ g.
The elementary quantum of electricity is 4·77 × 10⁻¹⁰ “electrostatic units.”
The negative electric charge of an electron is 1 elementary quantum (1 negative charge).
The positive electric charge of a hydrogen nucleus is 1 elementary quantum (1 positive charge).
The mass of an electron is ¹/₁₈₃₅ that of the hydrogen atom.
The diameter of an electron is estimated to be about 3 × 10⁻¹³ cm.
The diameter of the atomic nucleus is of the order of magnitude 10⁻¹³ to 10⁻¹² cm.
The diameter of a hydrogen atom in the normal state (the diameter of the first stationary orbit in Bohr’s model) is 1·056 × 10⁻⁸ cm.
The Balmer constant K = 3·29 × 10¹⁵.
The Planck constant h = 6·54 × 10⁻²⁷.
An energy quantum is E = hν.
The Balmer-Ritz formula for the frequencies of the lines in the hydrogen spectrum is
| ν = K | 1 | - | 1 | ||
| n″ ² | n′ ² |
DIAGRAMS OF SPECTRA
AFTER BUNSEN AND KIRCHHOFF
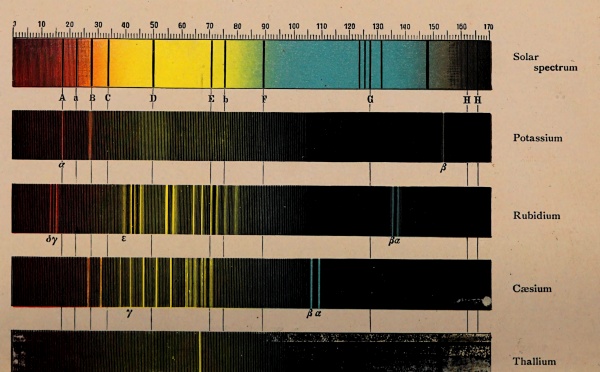

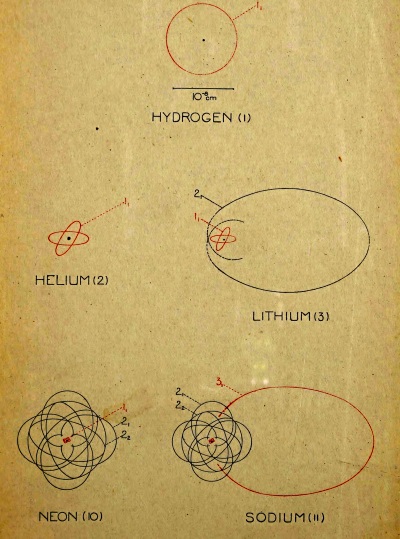

MAIN LINES OF
THE ATOMIC STRUCTURE
OF SOME ELEMENTS

STRUCTURE OF THE RADIUM ATOM
Transcriber’s Notes:
The cover image was created by the transcriber, and is in the public domain.
The illustrations have been moved so that they do not break up paragraphs and so that they are next to the text they illustrate.
Typographical and punctuation errors have been silently corrected.
Page 41: “1,000,000 feet or 300,000 kilometres per second” changed to “1,000,000,000 feet or 300,000 kilometres per second”