The Project Gutenberg EBook of Encyclopaedia Britannica, 11th Edition,
Volume 11, Slice 6, by Various
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
Title: Encyclopaedia Britannica, 11th Edition, Volume 11, Slice 6
"Geodesy" to "Geometry"
Author: Various
Release Date: September 17, 2011 [EBook #37461]
Language: English
Character set encoding: ISO-8859-1
*** START OF THIS PROJECT GUTENBERG EBOOK ENCYCLOPAEDIA BRITANNICA ***
Produced by Marius Masi, Don Kretz and the Online
Distributed Proofreading Team at http://www.pgdp.net
|
Transcriber’s note:
|
A few typographical errors have been corrected. They
appear in the text like this, and the
explanation will appear when the mouse pointer is moved over the marked
passage. Sections in Greek will yield a transliteration
when the pointer is moved over them, and words using diacritic characters in the
Latin Extended Additional block, which may not display in some fonts or browsers, will
display an unaccented version.
Links to other EB articles: Links to articles residing in other EB volumes will
be made available when the respective volumes are introduced online.
|
THE ENCYCLOPÆDIA BRITANNICA
A DICTIONARY OF ARTS, SCIENCES, LITERATURE AND GENERAL INFORMATION
ELEVENTH EDITION
VOLUME XI SLICE VI
Geodesy to Geometry
Articles in This Slice
607
GEODESY (from the Gr. γῆ, the earth, and δαίειν, to divide),
the science of surveying (q.v.) extended to large tracts of country,
having in view not only the production of a system of maps of
very great accuracy, but the determination of the curvature of
the surface of the earth, and eventually of the figure and
dimensions of the earth. This last, indeed, may be the sole
object in view, as was the case in the operations conducted in
Peru and in Lapland by the celebrated French astronomers
P. Bouguer, C.M. de la Condamine, P.L.M. de Maupertuis,
A.C. Clairault and others; and the measurement of the meridian
608
arc of France by P.F.A. Méchain and J.B.J. Delambre had
for its end the determination of the true length of the “metre”
which was to be the legal standard of length of France (see
Earth, Figure of the).
The basis of every extensive survey is an accurate triangulation,
and the operations of geodesy consist in the measurement, by
theodolites, of the angles of the triangles; the measurement of
one or more sides of these triangles on the ground; the determination
by astronomical observations of the azimuth of the whole
network of triangles; the determination of the actual position
of the same on the surface of the earth by observations, first for
latitude at some of the stations, and secondly for longitude; the
determination of altitude for all stations.
For the computation, the points of the actual surface of the
earth are imagined as projected along their plumb lines on the
mathematical figure, which is given by the stationary sea-level,
and the extension of the sea through the continents by a system
of imaginary canals. For many purposes the mathematical
surface is assumed to be a plane; in other cases a sphere of
radius 6371 kilometres (20,900,000 ft.). In the case of extensive
operations the surface must be considered as a compressed
ellipsoid of rotation, whose minor axis coincides with the earth’s
axis, and whose compression, flattening, or ellipticity is about
1/298.
Measurement of Base Lines.
To determine by actual measurement on the ground the length of a
side of one of the triangles (“base line”), wherefrom to infer the
lengths of all the other sides in the triangulation, is not the least
difficult operation of a trigonometrical survey. When the problem
is stated thus—To determine the number of times that a certain
standard or unit of length is contained between two finely marked
points on the surface of the earth at a distance of some miles asunder,
so that the error of the result may be pronounced to lie between
certain very narrow limits,—then the question demands very
serious consideration. The representation of the unit of length by
means of the distance between two fine lines on the surface of a bar
of metal at a certain temperature is never itself free from uncertainty
and probable error, owing to the difficulty of knowing at any moment
the precise temperature of the bar; and the transference of this
unit, or a multiple of it, to a measuring bar will be affected not
only with errors of observation, but with errors arising from uncertainty
of temperature of both bars. If the measuring bar be not
self-compensating for temperature, its expansion must be determined
by very careful experiments. The thermometers required for this
purpose must be very carefully studied, and their errors of division
and index error determined.
In order to avoid the difficulty in exactly determining the temperature
of a bar by the mercury thermometer, F.W. Bessel introduced
in 1834 near Königsberg a compound bar which constituted a
metallic thermometer.1 A zinc bar is laid on an iron bar two toises
long, both bars being perfectly planed and in free contact, the zinc
bar being slightly shorter and the two bars rigidly united at one end.
As the temperature varies, the difference of the lengths of the bars,
as perceived by the other end, also varies, and affords a quantitative
correction for temperature variations, which is applied to reduce the
length to standard temperature. During the measurement of the
base line the bars were not allowed to come into contact, the interval
being measured by the insertion of glass wedges. The results of the
comparisons of four measuring rods with one another and with the
standards were elaborately computed by the method of least-squares.
The probable error of the measured length of 935 toises (about
6000 ft.) has been estimated as 1/863500 or 1.2 μ (μ denoting a
millionth). With this apparatus fourteen base lines were measured
in Prussia and some neighbouring states; in these cases a somewhat
higher degree of accuracy was obtained.
The principal triangulation of Great Britain and Ireland has seven
base lines: five have been measured by steel chains, and two,
more exactly, by the compensation bars of General T.F. Colby, an
apparatus introduced in 1827-1828 at Lough Foyle in Ireland. Ten
base lines were measured in India in 1831-1869 by the same apparatus.
This is a system of six compound-bars self-correcting for temperature.
The bars may be thus described: Two bars, one of brass and the
other of iron, are laid in parallelism side by side, firmly united at
their centres, from which they may freely expand or contract; at
the standard temperature they are of the same length. Let AB be
one bar, A′B′ the other; draw lines through the corresponding
extremities AA′ (to P) and BB′ (to Q), and make A′P = B′Q, AA′
being equal to BB′. If the ratio A′P/AP equals the ratio of the coefficients
of expansion of the bars A′B′ and AB, then, obviously,
the distance PQ is constant (or nearly so). In the actual instrument
P and Q are finely engraved dots 10 ft. apart. In practice the bars,
when aligned, are not in contact, an interval of 6 in. being allowed
between each bar and its neighbour. This distance is accurately
measured by an ingenious micrometrical arrangement constructed
on exactly the same principle as the bars themselves.
The last base line measured in India had a length of 8913 ft. In
consequence of some suspicion as to the accuracy of the compensation
apparatus, the measurement was repeated four times, the operations
being conducted so as to determine the actual values of the probable
errors of the apparatus. The direction of the line (which is at Cape
Comorin) is north and south. In two of the measurements the brass
component was to the west, in the others to the east; the differences
between the individual measurements and the mean of the four were
+0.0017, −0.0049, −0.0015, +0.0045 ft. These differences are
very small; an elaborate investigation of all sources of error shows
that the probable error of a base line in India is on the average
±2.8 μ. These compensation bars were also used by Sir Thomas
Maclear in the measurement of the base line in his extension of
Lacaille’s arc at the Cape. The account of this operation will be
found in a volume entitled Verification and Extension of Lacaille’s
Arc of Meridian at the Cape of Good Hope, by Sir Thomas Maclear,
published in 1866. A rediscussion has been given by Sir David
Gill in his Report on the Geodetic Survey of South Africa, &c., 1896.
A very simple base apparatus was employed by W. Struve in his
triangulations in Russia from 1817 to 1855. This consisted of four
wrought-iron bars, each two toises (rather more than 13 ft.) long;
one end of each bar is terminated in a small steel cylinder presenting
a slightly convex surface for contact, the other end carries a contact
lever rigidly connected with the bar. The shorter arm of the lever
terminates below in a polished hemisphere, the upper and longer
arm traversing a vertical divided arc. In measuring, the plane end
of one bar is brought into contact with the short arm of the contact
lever (pushed forward by a weak spring) of the next bar. Each bar
has two thermometers, and a level for determining the inclination
of the bar in measuring. The manner of transferring the end of a
bar to the ground is simply this: under the end of the bar a stake
is driven very firmly into the ground, carrying on its upper surface
a disk, capable of movement in the direction of the measured line
by means of slow-motion screws. A fine mark on this disk is
brought vertically under the end of the bar by means of a theodolite
which is planted at a distance of 25 ft. from the stake in a direction
perpendicular to the base. Struve investigated for each base the
probable errors of the measurement arising from each of these seven
causes: Alignment, inclination, comparisons with standards, readings
of index, personal errors, uncertainties of temperature, and the
probable errors of adopted rates of expansion. He found that
±0.8 μ was the mean of the probable errors of the seven bases
measured by him. The Austro-Hungarian apparatus is similar;
the distance of the rods is measured by a slider, which rests on one
of the ends of each rod. Twenty-two base lines were measured in
1840-1899.
General Carlos Ibañez employed in 1858-1879, for the measurement
of nine base lines in Spain, two apparatus similar to the
apparatus previously employed by Porro in Italy; one is complicated,
the other simplified. The first, an apparatus of the brothers Brunner
of Paris, was a thermometric combination of two bars, one of platinum
and one of brass, in length 4 metres, furnished with three levels and
four thermometers. Suppose A, B, C three micrometer microscopes
very firmly supported at intervals of 4 metres with their axes vertical,
and aligned in the plane of the base line by means of a transit
instrument, their micrometer screws being in the line of measurement.
The measuring bar is brought under say A and B, and those micrometers
read; the bar is then shifted and brought under B and C. By
repetition of this process, the reading of a micrometer indicating the
end of each position of the bar, the measurement is made.
Quite similar apparatus (among others) has been employed by the
French and Germans. Since, however, it only permitted a distance
of about 300 m. to be measured daily, Ibañez introduced a simplification;
the measuring rod being made simply of steel, and provided
with inlaid mercury thermometers. This apparatus was used in
Switzerland for the measurement of three base lines. The accuracy
is shown by the estimated probable errors: ±0.2 μ to ±0.8 μ.
The distance measured daily amounts at least to 800 m.
A greater daily distance can be measured with the same accuracy
by means of Bessel’s apparatus; this permits the ready measurement
of 2000 m. daily. For this, however, it is important to notice
that a large staff and favourable ground are necessary. An important
improvement was introduced by Edward Jäderin of Stockholm,
who measures with stretched wires of about 24 metres long;
these wires are about 1.65 mm. in diameter, and when in use are
stretched by an accurate spring balance with a tension of 10 kg.2
The nature of the ground has a very trifling effect on this method.
The difficulty of temperature determinations is removed by employing
wires made of invar, an alloy of steel (64%) and nickel (36%)
which has practically no linear expansion for small thermal changes
609
at ordinary temperatures; this alloy was discovered in 1896 by
Benôit and Guillaume of the International Bureau of Weights and
Measures at Breteuil. Apparently the future of base-line measurements
rests with the invar wires of the Jäderin apparatus; next
comes Porro’s apparatus with invar bars 4 to 5 metres long.
Results have been obtained in the United States, of great importance
in view of their accuracy, rapidity of determination and
economy. For the measurement of the arc of meridian in longitude
98° E., in 1900, nine base lines of a total length of 69.2 km. were
measured in six months. The total cost of one base was $1231.
At the beginning and at the end of the field-season a distance of
exactly 100 m. was measured with R.S. Woodward’s “5-m. ice-bar”
(invented in 1891); by means of the remeasurement of this
length the standardization of the apparatus was done under the same
conditions as existed in the case of the base measurements. For
the measurements there were employed two steel tapes of 100 m.
long, provided with supports at distances of 25 m., two of 50 m.,
and the duplex apparatus of Eimbeck, consisting of four 5-m. rods.
Each base was divided into sections of about 1000 m.; one of these,
the “test kilometre,” was measured with all the five apparatus,
the others only with two apparatus, mostly tapes. The probable
error was about ±0.8 μ, and the day’s work a distance of about
2000 m. Each of the four rods of the duplex apparatus consists of
two bars of brass and steel. Mercury thermometers are inserted
in both bars; these serve for the measurement of the length of the
base lines by each of the bars, as they are brought into their consecutive
positions, the contact being made by an elastic-sliding
contact. The length of the base lines may be calculated for each
bar only, and also by the supposition that both bars have the same
temperature. The apparatus thus affords three sets of results,
which mutually control themselves, and the contact adjustments
permit rapid work. The same device has been applied to the older
bimetallic-compensating apparatus of Bache-Würdemann (six
bases, 1847-1857) and of Schott. There was also employed a single
rod bimetallic apparatus on F. Porro’s principle, constructed by the
brothers Repsold for some base lines. Excellent results have been
more recently obtained with invar tapes.
The following results show the lengths of the same German base
lines as measured by different apparatus:
| | metres. |
| Base at Berlin | 1864 | Apparatus of | Bessel | 2336·3920 |
| ” ” | 1880 | ” | Brunner | ·3924 |
| Base at Strehlen | 1854 | ” | Bessel | 2762·5824 |
| ” ” | 1879 | ” | Brunner | ·5852 |
| Old base at Bonn | 1847 | ” | Bessel | 2133·9095 |
| ” ” | 1892 | ” | ” | ·9097 |
| New base at Bonn | 1892 | ” | ” | 2512·9612 |
| ” ” | 1892 | ” | Brunner | ·9696 |
It is necessary that the altitude above the level of the sea of every
part of a base line be ascertained by spirit levelling, in order that
the measured length may be reduced to what it would have been
had the measurement been made on the surface of the sea, produced
in imagination. Thus if l be the length of a measuring bar, h its
height at any given position in the measurement, r the radius of
the earth, then the length radially projected on to the level of the
sea is l(1 − h/r). In the Salisbury Plain base line the reduction to
the level of the sea is −0.6294 ft.
 |
| Fig. 1. |
The total number of base lines measured in Europe up to the
present time is about one hundred and ten, nineteen of which do
not exceed in length 2500 metres, or about 1½ miles, and three—one
in France, the others in Bavaria—exceed
19,000 metres. The question
has been frequently discussed whether
or not the advantage of a long base is
sufficiently great to warrant the expenditure
of time that it requires, or
whether as much precision is not obtainable
in the end by careful triangulation
from a short base. But the answer
cannot be given generally; it must
depend on the circumstances of each
particular case. With Jäderin’s apparatus,
provided with invar wires, bases
of 20 to 30 km. long are obtained without
difficulty.
In working away from a base line ab,
stations c, d, e, f are carefully selected so
as to obtain from well-shaped triangles
gradually increasing sides. Before, however,
finally leaving the base line, it is
usual to verify it by triangulation thus:
during the measurement two or more
points, as p, q (fig. 1), are marked in the
base in positions such that the lengths of
the different segments of the line are
known; then, taking suitable external stations, as h, k, the angles of
the triangles bhp, phq, hqk, kqa are measured. From these angles
can be computed the ratios of the segments, which must agree, if all
operations are correctly performed, with the ratios resulting from
the measures. Leaving the base line, the sides increase up to 10,
30 or 50 miles occasionally, but seldom reaching 100 miles. The
triangulation points may either be natural objects presenting themselves
in suitable positions, such as church towers; or they may be
objects specially constructed in stone or wood on mountain tops
or other prominent ground. In every case it is necessary that the
precise centre of the station be marked by some permanent mark.
In India no expense is spared in making permanent the principal
trigonometrical stations—costly towers in masonry being erected.
It is essential that every trigonometrical station shall present a fine
object for observation from surrounding stations.
Horizontal Angles.
In placing the theodolite over a station to be observed from, the
first point to be attended to is that it shall rest upon a perfectly
solid foundation. The method of obtaining this desideratum must
depend entirely on the nature of the ground; the instrument must
if possible be supported on rock, or if that be impossible a solid
foundation must be obtained by digging. When the theodolite is
required to be raised above the surface of the ground in order to
command particular points, it is necessary to build two scaffolds,—the
outer one to carry the observatory, the inner one to carry the
instrument,—and these two edifices must have no point of contact.
Many cases of high scaffolding have occurred on the English Ordnance
Survey, as for instance at Thaxted church, where the tower, 80 ft.
high, is surmounted by a spire of 90 ft. The scaffold for the observatory
was carried from the base to the top of the spire; that
for the instrument was raised from a point of the spire 140 ft. above
the ground, having its bearing upon timbers passing through the
spire at that height. Thus the instrument, at a height of 178 ft.
above the ground, was insulated, and not affected by the action of
the wind on the observatory.
At every station it is necessary to examine and correct the adjustments
of the theodolite, which are these: the line of collimation
of the telescope must be perpendicular to its axis of rotation; this
axis perpendicular to the vertical axis of the instrument; and the
latter perpendicular to the plane of the horizon. The micrometer
microscopes must also measure correct quantities on the divided
circle or circles. The method of observing is this. Let A, B, C ...
be the stations to be observed taken in order of azimuth; the
telescope is first directed to A and the cross-hairs of the telescope
made to bisect the object presented by A, then the microscopes or
verniers of the horizontal circle (also of the vertical circle if necessary)
are read and recorded. The telescope is then turned to B, which
is observed in the same manner; then C and the other stations.
Coming round by continuous motion to A, it is again observed, and
the agreement of this second reading with the first is some test of
the stability of the instrument. In taking this round of angles—or
“arc,” as it is called on the Ordnance Survey—it is desirable
that the interval of time between the first and second observations
of A should be as small as may be consistent with due care. Before
taking the next arc the horizontal circle is moved through 20° or
30°; thus a different set of divisions of the circle is used in each
arc, which tends to eliminate the errors of division.
It is very desirable that all arcs at a station should contain one
point in common, to which all angular measurements are thus
referred,—the observations on each arc commencing and ending
with this point, which is on the Ordnance Survey called the “referring
object.” It is usual for this purpose to select, from among the
points which have to be observed, that one which affords the best
object for precise observation. For mountain tops a “referring
object” is constructed of two rectangular plates of metal in the
same vertical plane, their edges parallel and placed at such a distance
apart that the light of the sky seen through appears as a vertical line
about 10″ in width. The best distance for this object is from
1 to 2 miles.
This method seems at first sight very advantageous; but if,
however, it be desired to attain the highest accuracy, it is better,
as shown by General Schreiber of Berlin in 1878, to measure only
single angles, and as many of these as possible between the directions
to be determined. Division-errors are thus more perfectly eliminated,
and errors due to the variation in the stability, &c., of the instruments
are diminished. This method is rapidly gaining precedence.
The theodolites used in geodesy vary in pattern and in size—the
horizontal circles ranging from 10 in. to 36 in. in diameter. In
Ramsden’s 36-in. theodolite the telescope has a focal length of
36 in. and an aperture of 2.5 in., the ordinarily used magnifying
power being 54; this last, however, can of course be changed at the
requirements of the observer or of the weather. The probable
error of a single observation of a fine object with this theodolite
is about 0″.2. Fig. 2 represents an altazimuth theodolite of an
improved pattern used on the Ordnance Survey. The horizontal
circle of 14-in. diameter is read by three micrometer microscopes;
the vertical circle has a diameter of 12 in., and is read by two microscopes.
In the great trigonometrical survey of India the theodolites
used in the more important parts of the work have been of 2 and
3 ft. diameter—the circle read by five equidistant microscopes.
Every angle is measured twice in each position of the zero of the
horizontal circle, of which there are generally ten; the entire
610
number of measures of an angle is never less than 20. An examination
of 1407 angles showed that the probable error of an observed
angle is on the average ±0″.28.
For the observations of very distant stations it is usual to employ
a heliotrope (from the Gr. ἥλιος, sun; τρόπος, a turn), invented by
Gauss at Göttingen in 1821. In its simplest form this is a plane
mirror, 4, 6, or 8 in. in diameter, capable of rotation round a horizontal
and a vertical axis. This mirror is placed at the station to be observed,
and in fine weather it is kept so directed that the rays of the
sun reflected by it strike the distant observing telescope. To the
observer the heliotrope presents the appearance of a star of the
first or second magnitude, and is generally a pleasant object for
observing.
Observations at night, with the aid of light-signals, have been
repeatedly made, and with good results, particularly in France
by General François Perrier, and more recently in the United
States by the Coast and Geodetic Survey; the signal employed
being an acetylene bicycle-lamp, with a lens 5 in. in diameter.
Particularly noteworthy are the trigonometrical connexions of
Spain and Algeria, which were carried out in 1879 by Generals
Ibañez and Perrier (over a distance of 270 km.), of Sicily and Malta
in 1900, and of the islands of Elba and Sardinia in 1902 by Dr
Guarducci (over distances up to 230 km.); in these cases artificial
light was employed: in the first case electric light and in the two
others acetylene lamps.
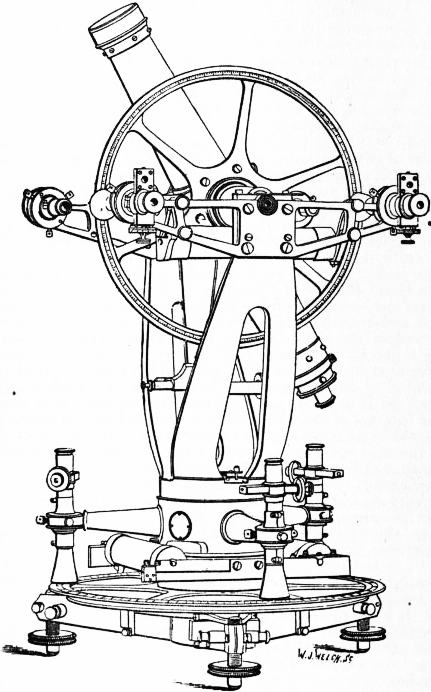 |
| Fig. 2.—Altazimuth Theodolite. |
Astronomical Observations.
The direction of the meridian is determined either by a theodolite
or a portable transit instrument. In the former case the operation
consists in observing the angle between a terrestrial object—generally
a mark specially erected and capable of illumination at night—and
a close circumpolar star at its greatest eastern or western
azimuth, or, at any rate, when very near that position. If the
observation be made t minutes of time before or after the time of
greatest azimuth, the azimuth then will differ from its maximum
value by (450t)² sin 1″ sin 2δ/sin z, in seconds of angle, omitting
smaller terms, δ being the star’s declination and z its zenith distance.
The collimation and level errors are very carefully determined
before and after these observations, and it is usual to arrange the
observations by the reversal of the telescope so that collimation
error shall disappear. If b, c be the level and collimation errors,
the correction to the circle reading is b cot z ± c cosec z, b being
positive when the west end of the axis is high. It is clear that any
uncertainty as to the real state of the level will produce a corresponding
uncertainty in the resulting value of the azimuth,—an
uncertainty which increases with the latitude and is very large
in high latitudes. This may be partly remedied by observing in
connexion with the star its reflection in mercury. In determining
the value of “one division” of a level tube, it is necessary to bear
in mind that in some the value varies considerably with the temperature.
By experiments on the level of Ramsden’s 3-foot theodolite,
it was found that though at the ordinary temperature of 66° the
value of a division was about one second, yet at 32° it was about
five seconds.
In a very excellent portable transit used on the Ordnance Survey,
the uprights carrying the telescope are constructed of mahogany,
each upright being built of several pieces glued and screwed together;
the base, which is a solid and heavy plate of iron, carries a reversing
apparatus for lifting the telescope out of its bearings, reversing it
and letting it down again. Thus is avoided the change of temperature
which the telescope would incur by being lifted by the hands
of the observer. Another form of transit is the German diagonal
form, in which the rays of light after passing through the object-glass
are turned by a total reflection prism through one of the transverse
arms of the telescope, at the extremity of which arm is the
eye-piece. The unused half of the ordinary telescope being cut away
is replaced by a counterpoise. In this instrument there is the
advantage that the observer without moving the position of his eye
commands the whole meridian, and that the level may remain on
the pivots whatever be the elevation of the telescope. But there is
the disadvantage that the flexure of the transverse axis causes a
variable collimation error depending on the zenith distance of the
star to which it is directed; and moreover it has been found that in
some cases the personal error of an observer is not the same in the
two positions of the telescope.
To determine the direction of the meridian, it is well to erect two
marks at nearly equal angular distances on either side of the north
meridian line, so that the pole star crosses the vertical of each mark
a short time before and after attaining its greatest eastern and
western azimuths.
If now the instrument, perfectly levelled, is adjusted to have its
centre wire on one of the marks, then when elevated to the star,
the star will traverse the wire, and its exact position in the field at
any moment can be measured by the micrometer wire. Alternate
observations of the star and the terrestrial mark, combined with
careful level readings and reversals of the instrument, will enable
one, even with only one mark, to determine the direction of the
meridian in the course of an hour with a probable error of less than
a second. The second mark enables one to complete the station
more rapidly and gives a check upon the work. As an instance,
at Findlay Seat, in latitude 57° 35′, the resulting azimuths of the
two marks were 177° 45′ 37″.29 ± 0″.20 and 182° 17′ 15″.61 ± 0″.13,
while the angle between the two marks directly measured by a
theodolite was found to be 4° 31′ 37″.43 ± 0″.23.
 |
| Fig. 3. |
We now come to the consideration of the determination of time
with the transit instrument. Let fig. 3 represent the sphere stereographically
projected on the plane of
the horizon,—ns being the meridian,
we the prime vertical, Z, P the zenith
and the pole. Let p be the point in
which the production of the axis of
the instrument meets the celestial
sphere, S the position of a star when
observed on a wire whose distance
from the collimation centre is c. Let
a be the azimuthal deviation, namely,
the angle wZp, b the level error so
that Zp = 90° − b. Let also the hour
angle corresponding to p be 90° − n,
and the declination of the same = m,
the star’s declination being δ, and the
latitude φ. Then to find the hour
angle ZPS = τ of the star when observed, in the triangles pPS, pPZ
we have, since pPS = 90 + τ − n,
− Sin c = sin m sin δ + cos m cos δ sin (n − τ),
Sin m = sin b sin φ − cos b cos φ sin a,
Cos m sin n = sin b cos φ + cos b sin φ sin a.
|
And these equations solve the problem, however large be the errors
of the instrument. Supposing, as usual, a, b, m, n to be small,
we have at once τ = n + c sec δ + m tan δ, which is the correction to
the observed time of transit. Or, eliminating m and n by means
of the second and third equations, and putting z for the zenith
distance of the star, t for the observed time of transit, the corrected
time is t + (a sin z + b cos z + c) / cos δ. Another very convenient form
for stars near the zenith is τ = b sec φ + c sec δ + m (tan δ − tan φ).
Suppose that in commencing to observe at a station the error of the
chronometer is not known; then having secured for the instrument
a very solid foundation, removed as far as possible level and collimation
errors, and placed it by estimation nearly in the meridian,
let two stars differing considerably in declination be observed—the
instrument not being reversed between them. From these two
stars, neither of which should be a close circumpolar star, a good
approximation to the chronometer error can be obtained; thus
611
let ε1, ε2, be the apparent clock errors given by these stars if δ1, δ2
be their declinations the real error is
ε = ε1 + (ε1 − ε2) (tan φ − tan δ1) / (tan δ1 − tan δ2).
Of course this is still only approximate, but it will enable the observer
(who by the help of a table of natural tangents can compute ε in a
few minutes) to find the meridian by placing at the proper time,
which he now knows approximately, the centre wire of his instrument
on the first star that passes—not near the zenith.
The transit instrument is always reversed at least once in the
course of an evening’s observing, the level being frequently read and
recorded. It is necessary in most instruments to add a correction
for the difference in size of the pivots.
The transit instrument is also used in the prime vertical for the
determination of latitudes. In the preceding figure let q be the point
in which the northern extremity of the axis of the instrument
produced meets the celestial sphere. Let nZq be the azimuthal
deviation = a, and b being the level error, Zq = 90° − b; let also
nPq = τ and Pq = ψ. Let S′ be the position of a star when observed
on a wire whose distance from the collimation centre is c, positive
when to the south, and let h be the observed hour angle of the star,
viz. ZPS′. Then the triangles qPS′, gPZ give
−Sin c = sin δ cos ψ − cos δ sin ψ cos (h + τ),
Cos ψ = sin b sin φ + cos b cos φ cos a,
Sin ψ sin τ = cos b sin a.
|
Now when a and b are very small, we see from the last two equations
that ψ = φ − b, a = τ sin ψ, and if we calculate φ′ by the formula
cot φ′ = cot δ cos h, the first equation leads us to this result—
φ = φ′ + (a sin z + b cos z + c) / cos z,
the correction for instrumental error being very similar to that
applied to the observed time of transit in the case of meridian
observations. When a is not very small and z is small, the formulae
required are more complicated.
 |
| Fig. 4.—Zenith Telescope constructed
for the International Stations at Mizusawa, Carloforte, Gaithersburg and
Ukiah, by Hermann Wanschaff, Berlin. |
The method of determining latitude by transits in the prime
vertical has the disadvantage of being a somewhat slow process,
and of requiring a very precise knowledge of the time, a disadvantage
from which the zenith telescope is free. In principle this instrument
is based on the proposition
that when the meridian
zenith distances of
two stars at their upper
culminations—one being
to the north and the other
to the south of the zenith—are
equal, the latitude
is the mean of their
declinations; or, if the
zenith distance of a star
culminating to the south
of the zenith be Z, its
declination being δ, and
that of another culminating
to the north with
zenith distance Z′ and
declination δ′, then clearly
the latitude is ½(δ + δ′) +
½(Z − Z′). Now the zenith
telescope does away with
the divided circle, and
substitutes the measurement
micrometrically of
the quantity Z′ − Z.
In fig. 4 is shown a
zenith telescope by H.
Wanschaff of Berlin,
which is the type used
(according to the Central
Bureau at Potsdam) since
about 1890 for the determination
of the variations
of latitude due to different,
but as yet imperfectly
understood, influences.
The instrument is supported
on a strong tripod,
fitted with levelling
screws; to this tripod is
fixed the azimuth circle
and a long vertical steel
axis. Fitting on this axis
is a hollow axis which
carries on its upper end a
short transverse horizontal
axis with a level. This
latter carries the telescope, which, supported at the centre of its
length, is free to rotate in a vertical plane. The telescope is thus
mounted eccentrically with respect to the vertical axis around
which it revolves. Two extremely sensitive levels are attached to
the telescope, which latter carries a micrometer in its eye-piece,
with a screw of long range for measuring differences of zenith distance.
Two levels are employed for controlling and increasing the
accuracy. For this instrument stars are selected in pairs, passing
north and south of the zenith, culminating within a few minutes
of time and within about twenty minutes (angular) of zenith distance
of each other. When a pair of stars is to be observed, the
telescope is set to the mean of the zenith distances and in the plane
of the meridian. The first star on passing the central meridional
wire is bisected by the micrometer; then the telescope is rotated
very carefully through 180° round the vertical axis, and the second
star on passing through the field is bisected by the micrometer on
the centre wire. The micrometer has thus measured the difference
of the zenith distances, and the calculation to get the latitude is
most simple. Of course it is necessary to read the level, and the
observations are not necessarily confined to the centre wire. In
fact if n, s be the north and south readings of the level for the south
star, n′, s′ the same for the north star, l the value of one division
of the level, m the value of one division of the micrometer, r, r′ the
refraction corrections, μ, μ′ the micrometer readings of the south
and north star, the micrometer being supposed to read from the
zenith, then, supposing the observation made on the centre wire,—
φ = ½ (δ + δ′) + ½ (μ − mu′)m + ¼ (n + n′ − s − s′)l + ½ (r − r′).
It is of course of the highest importance that the value m of the
screw be well determined. This is done most effectually by observing
the vertical movement of a close circumpolar star when at its greatest
azimuth.
In a single night with this instrument a very accurate result,
say with a probable error of about 0″.2, could be obtained for
latitude from, say, twenty pair of stars; but when the latitude is
required to be obtained with the highest possible precision, two
nights at least are necessary. The weak point of the zenith telescope
lies in the circumstance that its requirements prevent the selection
of stars whose positions are well fixed; very frequently it is necessary
to have the declinations of the stars selected for this instrument
specially observed at fixed observatories. The zenith telescope is
made in various sizes from 30 to 54 in. in focal length; a 30-in.
telescope is sufficient for the highest purposes and is very portable.
The net observation probable-error for one pair of stars is only
±0″.1.
The zenith telescope is a particularly pleasant instrument to
work with, and an observer has been known (a sergeant of Royal
Engineers, on one occasion) to take every star in his list during
eleven hours on a stretch, namely, from 6 o’clock P.M. until 5 A.M.,
and this on a very cold November night on one of the highest points
of the Grampians. Observers accustomed to geodetic operations
attain considerable powers of endurance. Shortly after the commencement
of the observations on one of the hills in the Isle of Skye
a storm carried away the wooden houses of the men and left the
observatory roofless. Three observatory roofs were subsequently
demolished, and for some time the observatory was used without a
roof, being filled with snow every night and emptied every morning.
Quite different, however, was the experience of the same party when
on the top of Ben Nevis, 4406 ft. high. For about a fortnight the
state of the atmosphere was unusually calm, so much so, that a
lighted candle could often be carried between the tents of the men
and the observatory, whilst at the foot of the hill the weather was
wild and stormy.
The determination of the difference of longitude between two
stations A and B resolves itself into the determination of the local
time at each of the stations, and the comparison by signals of the
clocks at A and B. Whenever telegraphic lines are available these
comparisons are made by telegraphy. A small and delicately-made
apparatus introduced into the mechanism of an astronomical clock
or chronometer breaks or closes by the action of the clock an electric
circuit every second. In order to record the minutes as well as
seconds, one second in each minute, namely that numbered 0 or 60,
is omitted. The seconds are recorded on a chronograph, which
consists of a cylinder revolving uniformly at the rate of one revolution
per minute covered with white paper, on which a pen having a slow
movement in the direction of the axis of the cylinder describes a
continuous spiral. This pen is deflected through the agency of an
electromagnet every second, and thus the seconds of the clock are
recorded on the chronograph by offsets from the spiral curve. An
observer having his hand on a contact key in the same circuit can
record in the same manner his observed times of transits of stars.
The method of determination of difference of longitude is, therefore,
virtually as follows. After the necessary observations for instrumental
corrections, which are recorded only at the station of observation,
the clock at A is put in connexion with the circuit so as to
write on both chronographs, namely, that at A and that at B.
Then the clock at B is made to write on both chronographs. It is
clear that by this double operation one can eliminate the effect of the
small interval of time consumed in the transmission of signals, for
the difference of longitude obtained from the one chronograph
will be in excess by as much as that obtained from the other will be
in defect. The determination of the personal errors of the observers
in this delicate operation is a matter of the greatest importance,
as therein lies probably the chief source of residual error.
612
These errors can nevertheless be almost entirely avoided by using
the impersonal micrometer of Dr Repsold (Hamburg, 1889). In
this device there is a movable micrometer wire which is brought by
hand into coincidence with the star and moved along with it; at
fixed points there are electrical contacts, which replace the fixed
wires. Experiments at the Geodetic Institute and Central Bureau
at Potsdam in 1891 gave the following personal equations in the case
of four observers:—
| | Older Procedure. | New Procedure. |
| A − B | −0s.108 | −0s.004 |
| A − G | −0s.314 | −0s.035 |
| A − S | −0s.184 | −0s.027 |
| B − G | −0s.225 | +0s.013 |
| B − S | −0s.086 | −0s.023 |
| G − S | +0s.109 | −0s.006 |
These results show that in the later method the personal equation
is small and not so variable; and consequently the repetition of
longitude determinations with exchanged observers and apparatus
entirely eliminates the constant errors, the probable error of such
determinations on ten nights being scarcely ±0s.01.
Calculation of Triangulation.
The surface of Great Britain and Ireland is uniformly covered by
triangulation, of which the sides are of various lengths from 10 to
111 miles. The largest triangle has one angle at Snowdon in Wales,
another on Slieve Donard in Ireland, and a third at Scaw Fell in
Cumberland; each side is over a hundred miles and the spherical
excess is 64″. The more ordinary method of triangulation is, however,
that of chains of triangles, in the direction of the meridian and
perpendicular thereto. The principal triangulations of France,
Spain, Austria and India are so arranged. Oblique chains of triangles
are formed in Italy, Sweden and Norway, also in Germany
and Russia, and in the United States. Chains are composed sometimes
merely of consecutive plain triangles; sometimes, and more
frequently in India, of combinations of triangles forming consecutive
polygonal figures. In this method of triangulating, the sides of the
triangles are generally from 20 to 30 miles in length—seldom exceeding
40.
The inevitable errors of observation, which are inseparable from
all angular as well as other measurements, introduce a great difficulty
into the calculation of the sides of a triangulation. Starting from a
given base in order to get a required distance, it may generally be
obtained in several different ways—that is, by using different sets
of triangles. The results will certainly differ one from another,
and probably no two will agree. The experience of the computer
will then come to his aid, and enable him to say which is the most
trustworthy result; but no experience or ability will carry him
through a large network of triangles with anything like assurance.
The only way to obtain trustworthy results is to employ the method
of least squares. We cannot here give any illustration of this method
as applied to general triangulation, for it is most laborious, even for
the simplest cases.
Three stations, projected on the surface of the sea, give a spherical
or spheroidal triangle according to the adoption of the sphere or
the ellipsoid as the form of the surface. A spheroidal triangle differs
from a spherical triangle, not only in that the curvatures of the sides
are different one from another, but more especially in this that,
while in the spherical triangle the normals to the surface at the angular
points meet at the centre of the sphere, in the spheroidal triangle
the normals at the angles A, B, C meet the axis of revolution of the
spheroid in three different points, which we may designate α, β, γ
respectively. Now the angle A of the triangle as measured by a
theodolite is the inclination of the planes BAα and CAα, and the angle
at B is that contained by the planes ABβ and CBβ. But the planes
ABα and ABβ containing the line AB in common cut the surface in
two distinct plane curves. In order, therefore, that a spheroidal
triangle may be exactly defined, it is necessary that the nature of the
lines joining the three vertices be stated. In a mathematical point
of view the most natural definition is that the sides be geodetic or
shortest lines. C.C.G. Andrae, of Copenhagen, has also shown
that other lines give a less convenient computation.
K.F. Gauss, in his treatise, Disquisitiones generales circa superficies
curvas, entered fully into the subject of geodetic (or geodesic)
triangles, and investigated expressions for the angles of a geodetic
triangle whose sides are given, not certainly finite expressions, but
approximations inclusive of small quantities of the fourth order, the
side of the triangle or its ratio to the radius of the nearly spherical
surface being a small quantity of the first order. The terms of the
fourth order, as given by Gauss for any surface in general, are very
complicated even when the surface is a spheroid. If we retain small
quantities of the second order only, and put A, B, C for the angles
of the geodetic triangle, while A, B, C are those of a plane triangle
having sides equal respectively to those of the geodetic triangle,
then, σ being the area of the plane triangle and a, b, c the measures
of curvature at the angular points,
A = A + σ(2a + b + c) / 12,
B = B + σ(a + 2b + c) / 12,
C = C + σ(a + b + 2c) / 12.
|
For the sphere a = b = c, and making this simplification, we obtain the
theorem previously given by A.M. Legendre. With the terms of the
fourth order, we have (after Andrae):
| A − A = | ε |
+ | σ |
k ( | m² − a² |
k + | a − k |
), |
| 3 | 3 |
20 | 4k |
| B − B = | ε |
+ | σ |
k ( | m² − b² |
k + | b − k |
), |
| 3 | 3 |
20 | 4k |
| C − C = | ε |
+ | σ |
k ( | m² − c² |
k + | c − k |
), |
| 3 | 3 |
20 | 4k |
in which ε = σk {1 + (m²k / 8)}, 3m² = a² + b² + c², 3k = a + b + c. For the
ellipsoid of rotation the measure of curvature is equal to 1/ρn,
ρ and n being the radii of curvature of the meridian and perpendicular.
It is rarely that the terms of the fourth order are required. As a
rule spheroidal triangles are calculated as spherical (after Legendre),
i.e. like plane triangles with a decrease of each angle of about ε/3;
ε must, however, be calculated for each triangle separately with its
mean measure of curvature k.
The geodetic line being the shortest that can be drawn on any
surface between two given points, we may be conducted to its most
important characteristics by the following considerations: let p, q
be adjacent points on a curved surface; through s the middle point
of the chord pq imagine a plane drawn perpendicular to pq, and let
S be any point in the intersection of this plane with the surface;
then pS + Sq is evidently least when sS is a minimum, which is
when sS is a normal to the surface; hence it follows that of all
plane curves on the surface joining p, q, when those points are indefinitely
near to one another, that is the shortest which is made
by the normal plane. That is to say, the osculating plane at any
point of a geodetic line contains the normal to the surface at that
point. Imagine now three points in space, A, B, C, such that AB =
BC = c; let the direction cosines of AB be l, m, n, those of BC l’,
m′, n′, then x, y, z being the co-ordinates of B, those of A and C will
be respectively—
x − cl : y − cm : z − cn
x + cl′ : y + cm′ : z + cn′.
|
Hence the co-ordinates of the middle point M of AC are x + ½c(l′ − l),
y + ½c(m′ − m), z + ½c(n′ − n), and the direction cosines of BM are
therefore proportional to l′ − l: m′ − m: n′ − n. If the angle made
by BC with AB be indefinitely small, the direction cosines of BM
are as δl : δm : δn. Now if AB, BC be two contiguous elements of
a geodetic, then BM must be a normal to the surface, and since δl,
δm, δn are in this case represented by δ(dx/ds), δ(dy/ds), δ(dz/ds),
and if the equation of the surface be u = 0, we have
| d²x |
/ | du |
= | d²y |
/ | du |
= | d²z |
/ | du |
, |
| ds² | dx |
ds² | dy |
ds² | dz |
which, however, are equivalent to only one equation. In the case
of the spheroid this equation becomes
which integrated gives ydx − xdy = Cds. This again may be put in
the form r sin a = C, where a is the azimuth of the geodetic at any
point—the angle between its direction and that of the meridian—and
r the distance of the point from the axis of revolution.
From this it may be shown that the azimuth at A of the geodetic
joining AB is not the same as the astronomical azimuth at A of B
or that determined by the vertical plane AαB. Generally speaking,
the geodetic lies between the two plane section curves joining A and
B which are formed by the two vertical planes, supposing these points
not far apart. If, however, A and B are nearly in the same latitude,
the geodetic may cross (between A and B) that plane curve which
lies nearest the adjacent pole of the spheroid. The condition of
crossing is this. Suppose that for a moment we drop the consideration
of the earth’s non-sphericity, and draw a perpendicular from
the pole C on AB, meeting it in S between A and B. Then A being
that point which is nearest the pole, the geodetic will cross the plane
curve if AS be between ¼AB and 3⁄8AB. If AS lie between this last
value and ½AB, the geodetic will lie wholly to the north of both
plane curves, that is, supposing both points to be in the northern
hemisphere.
The difference of the azimuths of the vertical section AB and of
the geodetic AB, i.e. the astronomical and geodetic azimuths, is
very small for all observable distances, being approximately:—
Geod. azimuth = Astr. azimuth −1/12 [e²/(1 − e²)] [(s²/ρn (cos²φ sin 2α + (s/4a) | sin 2φ sin α)],
in which: e and a are the numerical eccentricity
and semi-major axis respectively of the meridian ellipse, φ and α are
the latitude and azimuth at A, s = AB, and ρ and n are the radii of
curvature of the meridian and perpendicular at A. For s = 100
kilometres, only the first term is of moment; its value is 0″.028
cos² φ sin 2α, and it lies well within the errors of observation. If we
imagine the geodetic AB, it will generally trisect the angles between
the vertical sections at A and B, so that the geodetic at A is near
613
the vertical section AB, and at B near the section BA.3 The
greatest distance of the vertical sections one from another is
e²s³ cos² φ0 sin 2α0/16a², in which φ0 and α0 are the mean latitude
and azimuth respectively of the middle point of AB. For the value
s = 64 kilometres, the maximum distance is 3 mm.
An idea of the course of a longer geodetic line may be gathered
from the following example. Let the line be that joining Cadiz and
St Petersburg, whose approximate positions are—
| Cadiz. | St Petersburg. |
| Lat. 36° 22′ N. | 59° 56′ N. |
| Long. 6° 18′ W. | 30° 17′ E. |
If G be the point on the geodetic corresponding to F on that one
of the plane curves which contains the normal at Cadiz (by “corresponding”
we mean that F and G are on a meridian) then G is to
the north of F; at a quarter of the whole distance from Cadiz GF
is 458 ft., at half the distance it is 637 ft., and at three-quarters it is
473 ft. The azimuth of the geodetic at Cadiz differs 20″ from that
of the vertical plane, which is the astronomical azimuth.
The azimuth of a geodetic line cannot be observed, so that the
line does not enter of necessity into practical geodesy, although
many formulae connected with its use are of great simplicity and
elegance. The geodetic line has always held a more important place
in the science of geodesy among the mathematicians of France,
Germany and Russia than has been assigned to it in the operations
of the English and Indian triangulations. Although the observed
angles of a triangulation are not geodetic angles, yet in the calculation
of the distance and reciprocal bearings of two points which
are far apart, and are connected by a long chain of triangles, we may
fall upon the geodetic line in this manner:—
If A, Z be the points, then to start the calculation from A, we
obtain by some preliminary calculation the approximate azimuth
of Z, or the angle made by the direction of Z with the side AB or
AC of the first triangle. Let P1 be the point where this line intersects
BC; then, to find P2, where the line cuts the next triangle
side CD, we make the angle BP1P2 such that BP1P2 + BP1A = 180°.
This fixes P2, and P3 is fixed by a repetition of the same process;
so for P4, P5 .... Now it is clear that the points P1, P2, P3 so computed
are those which would be actually fixed by an observer with
a theodolite, proceeding in the following manner. Having set the
instrument up at A, and turned the telescope in the direction of
the computed bearing, an assistant places a mark P1 on the line
BC, adjusting it till bisected by the cross-hairs of the telescope at
A. The theodolite is then placed over P1, and the telescope turned
to A; the horizontal circle is then moved through 180°. The
assistant then places a mark P2 on the line CD, so as to be bisected
by the telescope, which is then moved to P2, and in the same manner
P3 is fixed. Now it is clear that the series of points P1, P2, P3
approaches to the geodetic line, for the plane of any two consecutive
elements Pn−1 Pn, Pn Pn+1 contains the normal at Pn.
If the objection be raised that not the geodetic azimuths but the
astronomical azimuths are observed, it is necessary to consider that
the observed vertical sections do not correspond to points on the
sea-level but to elevated points. Since the normals of the ellipsoid
of rotation do not in general intersect, there consequently arises an
influence of the height on the azimuth. In the case of the measurement
of the azimuth from A to B, the instrument is set to a point A′
over the surface of the ellipsoid (the sea-level), and it is then adjusted
to a point B′, also over the surface, say at a height h′. The vertical
plane containing A′ and B′ also contains A but not B: it must
therefore be rotated through a small azimuth in order to contain B.
The correction amounts approximately to −e²h′ cos²φ sin 2α/2a;
in the case of h′ = 1000 m., its value is 0″.108 cos²φ sin 2α.
This correction is therefore of greater importance in the case of
observed azimuths and horizontal angles than in the previously
considered case of the astronomical and the geodetic azimuths. The
observed azimuths and horizontal angles must therefore also be
corrected in the case, where it is required to dispense with geodetic
lines.
When the angles of a triangulation have been adjusted by the
method of least squares, and the sides are calculated, the next
process is to calculate the latitudes and longitudes of all the stations
starting from one given point. The calculated latitudes, longitudes
and azimuths, which are designated geodetic latitudes, longitudes
and azimuths, are not to be confounded with the observed latitudes,
longitudes and azimuths, for these last are subject to somewhat
large errors. Supposing the latitudes of a number of stations in the
triangulation to be observed, practically the mean of these determines
the position in latitude of the network, taken as a whole. So the
orientation or general azimuth of the whole is inferred from all the
azimuth observations. The triangulation is then supposed to be
projected on a spheroid of given elements, representing as nearly as
one knows the real figure of the earth. Then, taking the latitude
of one point and the direction of the meridian there as given—obtained,
namely, from the astronomical observations there—one
can compute the latitudes of all the other points with any degree of
precision that may be considered desirable. It is necessary to employ
for this purpose formulae which will give results true even for the
longest distances to the second place of decimals of seconds, otherwise
there will arise an accumulation of errors from imperfect calculation
which should always be avoided. For very long distances, eight
places of decimals should be employed in logarithmic calculations;
if seven places only are available very great care will be required to
keep the last place true. Now let φ, φ′ be the latitudes of two stations
A and B; α, α* their mutual azimuths counted from north by east
continuously from 0° to 360°; ω their difference of longitude
measured from west to east; and s the distance AB.
First compute a latitude φ1 by means of the formula φ1 = φ
+ (s cos α)/ρ, where ρ is the radius of curvature of the meridian at the
latitude φ; this will require but four places of logarithms. Then,
in the first two of the following, five places are sufficient—
| ε = | s² |
sin α cos a, η = | s² |
sin² α tan φ1, |
| 2ρn | 2ρn |
| φ′ − φ = | s |
cos (α − 2⁄3ε) − η, |
| rho0 |
| ω = | s sin (alpha − 1⁄3ε) |
, |
| n cos (φ′ + 1⁄3η) |
α* − α = ω sin (φ′ + 2⁄3η) − ε + 180°.
Here n is the normal or radius of curvature perpendicular to the
meridian; both n and ρ correspond to latitude φ1, and ρ0 to latitude
½(φ + φ′). For calculations of latitude and longitude, tables of the
logarithmic values of ρ sin 1″, n sin 1″, and 2 n ρ sin 1″ are necessary.
The following table contains these logarithms for every ten minutes
of latitude from 52° to 53° computed with the elements a = 20926060
and a : b = 295 : 294 :—
| Lat. | Log. 1/ρ sin 1″. | Log. 1/n sin 1″. | Log. 1/2ρn sin 1″. |
| ° ′ | | | |
| 52 0 | 7.9939434 | 7.9928231 | 0.37131 |
| 10 | 9309 | 8190 | 29 |
| 20 | 9185 | 8148 | 28 |
| 30 | 9060 | 8107 | 26 |
| 40 | 8936 | 8065 | 24 |
| 50 | 8812 | 8024 | 23 |
| 53 0 | 8688 | 7982 | 22 |
The logarithm in the last column is that required also for the
calculation of spherical excesses, the spherical excess of a triangle
being expressed by a b sin C/(2ρn) sin 1″.
It is frequently necessary to obtain the co-ordinates of one point
with reference to another point; that is, let a perpendicular arc be
drawn from B to the meridian of A meeting it in P, then, α being
the azimuth of B at A, the co-ordinates of B with reference to A are
AP = s cos (α − 2⁄3ε), BP = s sin (α − 1⁄3ε),
where ε is the spherical excess of APB, viz. s² sin α cos α multiplied
by the quantity whose logarithm is in the fourth column of the above
table.
If it be necessary to determine the geographical latitude and
longitude as well as the azimuths to a greater degree of accuracy
than is given by the above formulae, we make use of the following
formula: given the latitude φ of A, and the azimuth α and the
distance s of B, to determine the latitude φ′ and longitude ω of B,
and the back azimuth α′. Here it is understood that α′ is symmetrical
to α, so that α* + α′ = 360°.
Let
θ = sΔ / a, where Δ = (1 − e² sin² φ)1/2
and
| ξ = | e² θ² |
cos² φ sin 2α, ξ′ = | e² θ³ |
cos² φ cos² α; |
| 4 (1 − e²) | 6 (1 − e²) |
ξ, ξ′ are always very minute quantities even for the longest distances;
then, putting κ = 90° − φ,
| tan | α′ + ξ − ω |
= | sin ½(κ − θ − ξ′) |
cot | α |
| 2 | sin ½(κ + θ + ξ′) |
2 |
| tan | α′ + ξ − ω |
= | cos ½(κ − θ − ξ′) |
cot | α |
| 2 | cos ½(κ + θ + ξ′) |
2 |
| φ′ − φ = | s sin ½(α′ + ξ − α) |
( 1 + | θ² |
cos² | α′ − α |
); |
| ρ0 sin ½(α′ + ξ + α) | 12 |
2 |
here ρ0 is the radius of curvature of the meridian for the mean
latitude ½(φ + φ′). These formulae are approximate only, but they
are sufficiently precise even for very long distances.
For lines of any length the formulae of F.W. Bessel (Astr. Nach.,
1823, iv. 241) are suitable.
If the two points A and B be defined by their geographical
614
co-ordinates, we can accurately calculate the corresponding astronomical
azimuths, i.e. those of the vertical section, and then proceed,
in the case of not too great distances, to determine the length and
the azimuth of the shortest lines. For any distances recourse must
again be made to Bessel’s formula.4
Let α, α′ be the mutual azimuths of two points A, B on a spheroid,
k the chord line joining them, μ, μ′ the angles made by the chord
with the normals at A and B, φ, φ′, ω their latitudes and difference of
longitude, and (x² + y²)/a² + z² b² = 1 the equation of the surface;
then if the plane xz passes through A the co-ordinates of A and B
will be
| x = (a/Δ) cos φ, | x′ = (a/Δ’) cos φ′ cos ω, |
| y = 0 | y′ = (a/Δ’) cos φ′ sin ω, |
| z = (a/Δ) (1 − e²) sin φ, | z′ = (a/Δ′) (1 − e²) sin φ′, |
where Δ = (1 − e² sin² φ)1/2, Δ′ = (1 − e² sin² φ′)1/2, and e is the eccentricity.
Let f, g, h be the direction cosines of the normal to that
plane which contains the normal at A and the point B, and whose
inclinations to the meridian plane of A is = α; let also l, m, n and
l’, m’, n’ be the direction cosines of the normal at A, and of the
tangent to the surface at A which lies in the plane passing through
B, then since the first line is perpendicular to each of the other two
and to the chord k, whose direction cosines are proportional to
x′ − x, y′ − y, z′ − z, we have these three equations
| f (x′ − x) + gy′ + h (z′ − z) = 0 |
| fl + gm + hn = 0 |
| fl′ + gm′ + hn′ = 0. |
Eliminate f, g, h from these equations, and substitute
| l = cos φ | l′ = − sin φ cos α |
| m = 0 | m′ = sin α |
| n = sin φ | n′ = cos φ cos α, |
and we get
(x′ − x) sin φ + y′ cot α − (z′ − z) cos φ = 0.
The substitution of the values of x, z, x′, y′, z′ in this equation will
give immediately the value of cot α; and if we put ζ, ζ’ for the
corresponding azimuths on a sphere, or on the supposition e = 0,
the following relations exist
| cot α − cot ζ = e² | cos φ Q |
| cos φ′ Δ |
| cot α′ − cot ζ′ = −e² | cos φ′ Q |
|
| cos φ Δ′ |
Δ′ sin φ − Δ sin φ′ = Q sin ω.
If from B we let fall a perpendicular on the meridian plane of A,
and from A let fall a perpendicular on the meridian plane of B,
then the following equations become geometrically evident:
| k sin μ sin α = (a/Δ′) cos φ′ sin ω |
| k sin μ′ sin α′ = (a/Δ) cos φ sin ω. |
Now in any surface u = 0 we have
k² = (x′ − x)² + (y′ − y)² + (z′ − z)²
| −cos μ = [ (x′ − x) | du |
+ (y′ − y) | du |
+ (z′ − z) | du |
] / k ( | du² |
+ | du² |
+ | du² |
) | 1/2 |
| dx | dy |
dz | dx² |
dy² | dz² |
| cos μ′ = [ (x′ − x) | du |
+ (y′ − y) | du |
+ (z′ − z) | du |
] / k ( | du² |
+ | du² |
+ | du² |
) | 1/2 | . |
| dx′ | dy′ |
dz′ | dx′² |
dy′² | dz′² |
In the present case, if we put
then
| k² |
= 2U − e² ( | z′ − z |
) | ² |
| a² | b |
cos μ = (a/k) ΔU; cos μ′ = (a/k) Δ′U.
Let u be such an angle that
| (1 − e²)½ sin φ = Δ sin u |
| cos φ = Δ cos u, |
then on expressing x, x′, z, z′ in terms of u and u′,
U = 1 − cos u cos u′ cos ω − sin u sin u′;
also, if v be the third side of a spherical triangle, of which two
sides are ½π − u and ½π − u′ and the included angle ω, using a subsidiary
angle ψ such that
sin ψ sin ½v = e sin ½ (u′ − u) cos ½ (u′ + u),
we obtain finally the following equations:—
| k | = 2a cos ψ sin ½v |
| cos μ | = Δ sec ψ sin ½v |
| cos μ′ | = Δ′ sec ψ sin ½v |
| sin μ sin α | = (a/k) cos u′ sin ω |
| sin μ′ sin α′ | = (a/k) cos u sin ω. |
These determine rigorously the distance, and the mutual zenith
distances and azimuths, of any two points on a spheroid whose
latitudes and difference of longitude are given.
By a series of reductions from the equations containing ζ, ζ′ it
may be shown that
α + α′ = ζ + ζ′ + ¼e4ω (φ′ − φ)² cos4 φ0 sin φ0 + ...,
where φ0 is the mean of φ and φ′, and the higher powers of e are
neglected. A short computation will show that the small quantity
on the right-hand side of this equation cannot amount even to
the thousandth part of a second for k < 0.1a, which is, practically
speaking, zero; consequently the sum of the azimuths α + α′ on the
spheroid is equal to the sum of the spherical azimuths, whence
follows this very important theorem (known as Dalby′s theorem).
If φ, φ′ be the latitudes of two points on the surface of a spheroid, ω
their difference of longitude, α, α′ their reciprocal azimuths,
tan ½ω = cot ½ (α + α′) {cos ½ (φ′ − φ) / sin ½ (φ′ + φ)}.
The computation of the geodetic from the astronomical azimuths
has been given above. From k we can now compute the length s
of the vertical section, and from this the shortest length. The
difference of length of the geodetic line and either of the plane
curves is
e4s5 cos4 φ0 sin² 2α0/360 a4.
At least this is an approximate expression. Supposing s = 0.1a,
this quantity would be less than one-hundredth of a millimetre.
The line s is now to be calculated as a circular arc with a mean radius r
along AB. If φ0 = ½ (φ + φ′), α0 = ½ (180° + α − α′), Δ0 = (1 − e² sin² φ0)1/2,
then 1/r = Δ0/a [1 + (e²/(1 − e²) cos² φ0 cos² α0], and approximately sin (s/2r) =
k/2r. These formulae give, in the case of k = 0.1a, values certain to
eight logarithmic decimal places. An excellent series of formulae
for the solution of the problem, to determine the azimuths, chord
and distance along the surface from the geographical co-ordinates,
was given in 1882 by Ch. M. Schols (Archives Néerlandaises, vol. xvii.).
Irregularities of the Earth’s Surface.
In considering the effect of unequal distribution of matter in the
earth’s crust on the form of the surface, we may simplify the matter
by disregarding the considerations of rotation and eccentricity.
In the first place, supposing the earth a sphere covered with a film of
water, let the density ρ be a function of the distance from the centre
so that surfaces of equal density are concentric spheres. Let now a
disturbance of the arrangement of matter take place, so that the
density is no longer to be expressed by ρ, a function of r only, but is
expressed by ρ + ρ′, where ρ′ is a function of three co-ordinates θ, φ, r.
Then ρ′ is the density of what may be designated disturbing matter;
it is positive in some places and negative in others, and the whole
quantity of matter whose density is ρ′ is zero. The previously
spherical surface of the sea of radius a now takes a new form. Let
P be a point on the disturbed surface, P′ the corresponding point
vertically below it on the undisturbed surface, PP′ = N. The
knowledge of N over the whole surface gives us the form of the
disturbed or actual surface of the sea; it is an equipotential surface,
and if V be the potential at P of the disturbing matter ρ′, M the
mass of the earth (the attraction-constant is assumed equal to unity)
| M |
+ V = C = | M |
− | M |
N + V. |
| a + N | a |
a² |
As far as we know, N is always a very small quantity, and we have
with sufficient approximation N = 3V/4πδa, where δ is the mean
density of the earth. Thus we have the disturbance in elevation
of the sea-level expressed in terms of the potential of the disturbing
matter. If at any point P the value of N remain constant when we
pass to any adjacent point, then the actual surface is there parallel
to the ideal spherical surface; as a rule, however, the normal at P is
inclined to that at P′, and astronomical observations have shown
that this inclination, the deflection or deviation, amounting
ordinarily to one or two seconds, may in some cases exceed 10″,
or, as at the foot of the Himalayas, even 60″. By the expression
“mathematical figure of the earth” we mean the surface of the sea
produced in imagination so as to percolate the continents. We
see then that the effect of the uneven distribution of matter in the
crust of the earth is to produce small elevations and depressions on
the mathematical surface which would be otherwise spheroidal.
No geodesist can proceed far in his work without encountering the
irregularities of the mathematical surface, and it is necessary that
he should know how they affect his astronomical observations. The
whole of this subject is dealt with in his usual elegant manner by
Bessel in the Astronomische Nachrichten, Nos. 329, 330, 331, in a
paper entitled “Ueber den Einfluss der Unregelmässigkeiten der
Figur der Erde auf geodätische Arbeiten, &c.” But without entering
into further details it is not difficult to see how local attraction at
any station affects the determinations of latitude, longitude and
azimuth there.
Let there be at the station an attraction to the north-east throwing
the zenith to the south-west, so that it takes in the celestial sphere a
position Z′, its undisturbed position being Z. Let the rectangular
components of the displacement ZZ′ be ξ measured southwards
615
and η measured westwards. Now the great circle joining Z′ with
the pole of the heavens P makes there an angle with the meridian
PZ = η cosec PZ′ = η sec φ, where φ is the latitude of the station.
Also this great circle meets the horizon in a point whose distance
from the great circle PZ is η sec φ sin φ = η tan φ. That is, a meridian
mark, fixed by observations of the pole star, will be placed that
amount to the east of north. Hence the observed latitude requires
the correction ξ; the observed longitude a correction η sec φ; and
any observed azimuth a correction η tan φ. Here it is supposed
that azimuths are measured from north by east, and longitudes
eastwards. The horizontal angles are also influenced by the deflections
of the plumb-line, in fact, just as if the direction of the vertical
axis of the theodolite varied by the same amount. This influence,
however, is slight, so long as the sights point almost horizontally
at the objects, which is always the case in the observation of distant
points.
The expression given for N enables one to form an approximate
estimate of the effect of a compact mountain in raising the sea-level.
Take, for instance, Ben Nevis, which contains about a couple of
cubic miles; a simple calculation shows that the elevation produced
would only amount to about 3 in. In the case of a mountain mass
like the Himalayas, stretching over some 1500 miles of country with
a breadth of 300 and an average height of 3 miles, although it is difficult
or impossible to find an expression for V, yet we may ascertain
that an elevation amounting to several hundred feet may exist
near their base. The geodetical operations, however, rather negative
this idea, for it was shown by Colonel Clarke (Phil. Mag., 1878)
that the form of the sea-level along the Indian arc departs but slightly
from that of the mean figure of the earth. If this be so, the action
of the Himalayas must be counteracted by subterranean tenuity.
Suppose now that A, B, C, ... are the stations of a network of
triangulation projected on or lying on a spheroid of semiaxis major
and eccentricity a, e, this spheroid having its axis parallel to the axis
of rotation of the earth, and its surface coinciding with the mathematical
surface of the earth at A. Then basing the calculations
on the observed elements at A, the calculated latitudes, longitudes
and directions of the meridian at the other points will be the true
latitudes, &c., of the points as projected on the spheroid. On
comparing these geodetic elements with the corresponding astronomical
determinations, there will appear a system of differences
which represent the inclinations, at the various points, of the actual
irregular surface to the surface of the spheroid of reference. These
differences will suggest two things,—first, that we may improve the
agreement of the two surfaces, by not restricting the spheroid of
reference by the condition of making its surface coincide with the
mathematical surface of the earth at A; and secondly, by altering
the form and dimensions of the spheroid. With respect to the first
circumstance, we may allow the spheroid two degrees of freedom,
that is, the normals of the surfaces at A may be allowed to separate
a small quantity, compounded of a meridional difference and a
difference perpendicular to the same. Let the spheroid be so placed
that its normal at A lies to the north of the normal to the earth’s
surface by the small quantity ξ and to the east by the quantity η.
Then in starting the calculation of geodetic latitudes, longitudes and
azimuths from A, we must take, not the observed elements φ, α,
but for φ, φ + ξ, and for α, α + η tan φ, and zero longitude must be
replaced by η sec φ. At the same time suppose the elements of the
spheroid to be altered from a, e to a + da, e + de. Confining our
attention at first to the two points A, B, let (φ′), (α′), (ω) be the
numerical elements at B as obtained in the first calculation, viz.
before the shifting and alteration of the spheroid; they will now
take the form
(φ′) + fξ + gη + hda + kde,
(α′) + f′ξ + g′η + h′da + k′de,
ω + f″ξ + g″η + h″da + k″de,
|
where the coefficients f, g, ... &c. can be numerically calculated.
Now these elements, corresponding to the projection of B on the
spheroid of reference, must be equal severally to the astronomically
determined elements at B, corrected for the inclination of the surfaces
there. If ξ′, η′ be the components of the inclination at that
point, then we have
| ξ′ | = (φ′) − φ′ + fξ + gη + hda + kde, |
| η′ tan φ′ | = (α′) − α′ + f′ξ + g′η + h′da + k′de, |
| η′ sec φ′ | = (ω) − ω + f″ξ + g″η + h″da + k″de, |
where φ′, α′, ω are the observed elements at B. Here it appears
that the observation of longitude gives no additional information,
but is available as a check upon the azimuthal observations.
If now there be a number of astronomical stations in the triangulation,
and we form equations such as the above for each point,
then we can from them determine those values of ξ, η, da, de, which
make the quantity ξ² + η² + ξ′² + η′² + ... a minimum. Thus we
obtain that spheroid which best represents the surface covered by the
triangulation.
In the Account of the Principal Triangulation of Great Britain and
Ireland will be found the determination, from 75 equations, of the
spheroid best representing the surface of the British Isles. Its
elements are a = 20927005 ± 295 ft., b : a − b = 280 ± 8; and it is so
placed that at Greenwich Observatory ξ = 1″.864, η = −0″.546.
Taking Durham Observatory as the origin, and the tangent plane
to the surface (determined by ξ = −0″.664, η = −4″.117) as the plane
of x and y, the former measured northwards, and z measured vertically
downwards, the equation to the surface is
.99524953 x² + .99288005 y² + .99763052 z² − 0.00671003xz − 41655070z = 0.
Altitudes.
The precise determination of the altitude of his station is a matter
of secondary importance to the geodesist; nevertheless it is usual
to observe the zenith distances of all trigonometrical points. Of
great importance is a knowledge of the height of the base for its reduction
to the sea-level. Again the height of a station does influence
a little the observation of terrestrial angles, for a vertical line at B
does not lie generally in the vertical plane of A (see above). The
height above the sea-level also influences the geographical latitude,
inasmuch as the centrifugal force is increased and the magnitude and
direction of the attraction of the earth are altered, and the effect
upon the latitude is a very small term expressed by the formula
h (g′ − g) sin 2 φ/ag, where g, g′ are the values of gravity at the equator
and at the pole. This is h sin 2 φ/5820 seconds, h being in metres,
a quantity which may be neglected, since for ordinary mountain
heights it amounts to only a few hundredths of a second. We
can assume this amount as joined with the northern component of
the plumb-line perturbations.
The uncertainties of terrestrial refraction render it impossible to
determine accurately by vertical angles the heights of distant points.
Generally speaking, refraction is greatest at about daybreak; from
that time it diminishes, being at a minimum for a couple of hours
before and after mid-day; later in the afternoon it again increases.
This at least is the general march of the phenomenon, but it is by
no means regular. The vertical angles measured at the station on
Hart Fell showed on one occasion in the month of September a
refraction of double the average amount, lasting from 1 P.M. to 5 P.M.
The mean value of the coefficient of refraction k determined from a
very large number of observations of terrestrial zenith distances in
Great Britain is .0792 ± .0047; and if we separate those rays which
for a considerable portion of their length cross the sea from those
which do not, the former give k = .0813 and the latter k = .0753.
These values are determined from high stations and long distances;
when the distance is short, and the rays graze the ground, the amount
of refraction is extremely uncertain and variable. A case is noted
in the Indian survey where the zenith distance of a station 10.5 miles
off varied from a depression of 4′ 52″.6 at 4.30 P.M. to an elevation
of 2′ 24″.0 at 10.50 P.M.
If h, h′ be the heights above the level of the sea of two stations,
90° + δ, 90° + δ′ their mutual zenith distances (δ being that observed
at h), s their distance apart, the earth being regarded as a sphere of
radius = a, then, with sufficient precision,
| h′ − h = s tan ( s | 1 − 2k |
− δ), h − h′ = s tan ( s | 1 − 2k |
− δ′). |
| 2a | 2a |
If from a station whose height is h the horizon of the sea be observed
to have a zenith distance 90° + δ, then the above formula gives for h
the value
Suppose the depression δ to be n minutes, then h = 1.054n² if
the ray be for the greater part of its length crossing the sea; if
otherwise, h = 1.040n². To take an example: the mean of eight
observations of the zenith distance of the sea horizon at the top of
Ben Nevis is 91° 4′ 48″, or δ = 64.8; the ray is pretty equally disposed
over land and water, and hence h = 1.047n² = 4396 ft. The
actual height of the hill by spirit-levelling is 4406 ft., so that the error
of the height thus obtained is only 10 ft.
The determination of altitudes by means of spirit-levelling is
undoubtedly the most exact method, particularly in its present
development as precise-levelling, by which there have been determined
in all civilized countries close-meshed nets of elevated points
covering the entire land.
(A. R. C; F. R. H.)
1 An arrangement acting similarly had been previously introduced
by Borda.
2 Geodetic Survey of South Africa, vol. iii. (1905), p. viii; Les Nouveaux
Appareils pour la mesure rapide des bases géod., par J. René Benoît
et Ch. Éd. Guillaume (1906).
3 See a paper “On the Course of Geodetic Lines on the Earth’s
Surface” in the Phil. Mag. 1870; Helmert, Theorien der höheren
Geodäsie, 1. 321.
4 Helmert, Theorien der höheren Geodäsie, 1. 232, 247.
GEOFFREY, surnamed Martel (1006-1060), count of Anjou,
son of the count Fulk Nerra (q.v.) and of the countess Hildegarde
or Audegarde, was born on the 14th of October 1006. During his
father’s lifetime he was recognized as suzerain by Fulk l’Oison
(“the Gosling”), count of Vendôme, the son of his half-sister
Adela. Fulk having revolted, he confiscated the countship,
which he did not restore till 1050. On the 1st of January 1032
he married Agnes, widow of William the Great, duke of Aquitaine,
and taking arms against William the Fat, eldest son and successor
of William the Great, defeated him and took him prisoner at
Mont-Couër near Saint-Jouin-de-Marnes on the 20th of September
1033. He then tried to win recognition as dukes of Aquitaine for
the sons of his wife Agnes by William the Great, who were still
minors, but Fulk Nerra promptly took up arms to defend his
suzerain William the Fat, from whom he held the Loudunois and
616
Saintonge in fief against his son. In 1036 Geoffrey Martel had to
liberate William the Fat, on payment of a heavy ransom, but the
latter having died in 1038, and the second son of William the
Great, Odo, duke of Gascony, having fallen in his turn at the
siege of Mauzé (10th of March 1039) Geoffrey made peace with his
father in the autumn of 1039, and had his wife’s two sons recognized
as dukes. About this time, also, he had interfered in the
affairs of Maine, though without much result, for having sided
against Gervais, bishop of Le Mans, who was trying to make
himself guardian of the young count of Maine, Hugh, he had been
beaten and forced to make terms with Gervais in 1038. In 1040
he succeeded his father in Anjou and was able to conquer Touraine
(1044) and assert his authority over Maine (see Anjou). About
1050 he repudiated Agnes, his first wife, and married Grécie, the
widow of Bellay, lord of Montreuil-Bellay (before August 1052),
whom he subsequently left in order to marry Adela, daughter of a
certain Count Odo. Later he returned to Grécie, but again left
her to marry Adelaide the German. When, however, he died on
the 14th of November 1060, at the monastery of St Nicholas at
Angers, he left no children, and transmitted the countship to
Geoffrey the Bearded, the eldest of his nephews (see ANJOU).
See Louis Halphen, Le Comté d’Anjou au XIe siècle (Paris, 1906).
A summary biography is given by Célestin Port, Dictionnaire
historique, géographique et biographique de Maine-et-Loire (3 vols.,
Paris-Angers, 1874-1878), vol. ii. pp. 252-253, and a sketch of the
wars by Kate Norgate, England under the Angevin Kings (2 vols.,
London, 1887), vol. i. chs. iii. iv.
(L. H.*)
GEOFFREY, surnamed Plantagenet [or Plantegenet]
(1113-1151), count of Anjou, was the son of Count Fulk the Young
and of Eremburge (or Arembourg of La Flèche); he was born on
the 24th of August 1113. He is also called “le bel” or “the
handsome,” and received the surname of Plantagenet from the
habit which he is said to have had of wearing in his cap a sprig of
broom (genêt). In 1127 he was made a knight, and on the 2nd of
June 1129 married Matilda, daughter of Henry I. of England, and
widow of the emperor Henry V. Some months afterwards he
succeeded to his father, who gave up the countship when he
definitively went to the kingdom of Jerusalem. The years of his
government were spent in subduing the Angevin barons and in
conquering Normandy (see Anjou). In 1151, while returning
from the siege of Montreuil-Bellay, he took cold, in consequence of
bathing in the Loir at Château-du-Loir, and died on the 7th of
September. He was buried in the cathedral of Le Mans. By his
wife Matilda he had three sons: Henry Plantagenet, born at Le
Mans on Sunday, the 5th of March 1133; Geoffrey, born at
Argentan on the 1st of June 1134; and William Long-Sword, born
on the 22nd of July 1136.
See Kate Norgate, England under the Angevin Kings (2 vols.,
London, 1887), vol. i. chs. v.-viii.; Célestin Port, Dictionnaire
historique, géographique et biographique de Maine-et-Loire (3 vols.,
Paris-Angers, 1874-1878), vol. ii. pp. 254-256. A history of
Geoffrey le Bel has yet to be written; there is a biography of him
written in the 12th century by Jean, a monk of Marmoutier, Historia
Gaufredi, ducis Normannorum et comitis Andegavorum, published by
Marchegay et Salmon; “Chroniques des comtes d’Anjou” (Société
de l’histoire de France, Paris, 1856), pp. 229-310.
(L. H.*)
GEOFFREY (1158-1186), duke of Brittany, fourth son of the
English king Henry II. and his wife Eleanor of Aquitaine, was
born on the 23rd of September 1158. In 1167 Henry suggested a
marriage between Geoffrey and Constance (d. 1201), daughter and
heiress of Conan IV., duke of Brittany (d. 1171); and Conan not
only assented, perhaps under compulsion, to this proposal, but
surrendered the greater part of his unruly duchy to the English
king. Having received the homage of the Breton nobles,
Geoffrey joined his brothers, Henry and Richard, who, in alliance
with Louis VII. of France, were in revolt against their father; but
he made his peace in 1174, afterwards helping to restore order in
Brittany and Normandy, and aiding the new French king, Philip
Augustus, to crush some rebellious vassals. In July 1181 his
marriage with Constance was celebrated, and practically the
whole of his subsequent life was spent in warfare with his brother
Richard. In 1183 he made peace with his father, who had come
to Richard’s assistance; but a fresh struggle soon broke out for
the possession of Anjou, and Geoffrey was in Paris treating for
aid with Philip Augustus, when he died on the 19th of August
1186. He left a daughter, Eleanor, and his wife bore a
posthumous son, the unfortunate Arthur.
GEOFFREY (c. 1152-1212), archbishop of York, was a bastard
son of Henry II., king of England. He was distinguished from
his legitimate half-brothers by his consistent attachment and
fidelity to his father. He was made bishop of Lincoln at the age
of twenty-one (1173); but though he enjoyed the temporalities
he was never consecrated and resigned the see in 1183. He then
became his father’s chancellor, holding a large number of lucrative
benefices in plurality. Richard nominated him archbishop of
York in 1189, but he was not consecrated till 1191, or enthroned
till 1194. Geoffrey, though of high character, was a man of
uneven temper; his history in chiefly one of quarrels, with the
see of Canterbury, with the chancellor William Longchamp, with
his half-brothers Richard and John, and especially with his
canons at York. This last dispute kept him in litigation before
Richard and the pope for many years. He led the clergy in their
refusal to be taxed by John and was forced to fly the kingdom in
1207. He died in Normandy on the 12th of December 1212.
See Giraldus Cambrensis, Vita Galfridi; Stubbs’s prefaces to
Roger de Hoveden, vols. iii. and iv. (Rolls Series).
(H. W. C. D.)
GEOFFREY DE MONTBRAY (d. 1093), bishop of Coutances
(Constantiensis), a right-hand man of William the Conqueror, was
a type of the great feudal prelate, warrior and administrator at
need. He knew, says Orderic, more about marshalling mailed
knights than edifying psalm-singing clerks. Obtaining, as a young
man, in 1048, the see of Coutances, by his brother’s influence
(see Mowbray), he raised from his fellow nobles and from their
Sicilian spoils funds for completing his cathedral, which was
consecrated in 1056. With bishop Odo, a warrior like himself,
he was on the battle-field of Hastings, exhorting the Normans to
victory; and at William’s coronation it was he who called on
them to acclaim their duke as king. His reward in England was a
mighty fief scattered over twelve counties. He accompanied
William on his visit to Normandy (1067), but, returning, led a
royal force to the relief of Montacute in September 1069. In 1075
he again took the field, leading with Bishop Odo a vast host
against the rebel earl of Norfolk, whose stronghold at Norwich
they besieged and captured.
Meanwhile the Conqueror had invested him with important
judicial functions. In 1072 he had presided over the great
Kentish suit between the primate and Bishop Odo, and about the
same time over those between the abbot of Ely and his despoilers,
and between the bishop of Worcester and the abbot of Ely, and
there is some reason to think that he acted as a Domesday
commissioner (1086), and was placed about the same time in
charge of Northumberland. The bishop, who attended the
Conqueror’s funeral, joined in the great rising against William
Rufus next year (1088), making Bristol, with which (as
Domesday shows) he was closely connected and where he had
built a strong castle, his base of operations. He burned Bath and
ravaged Somerset, but had submitted to the king before the end
of the year. He appears to have been at Dover with William in
January 1090, but, withdrawing to Normandy, died at Coutances
three years later. In his fidelity to Duke Robert he seems to
have there held out for him against his brother Henry, when the
latter obtained the Cotentin.
See E.A. Freeman, Norman Conquest and William Rufus; J.H.
Round, Feudal England; and, for original authorities, the works of
Orderic Vitalis and William of Poitiers, and of Florence of Worcester;
the Anglo-Saxon Chronicle; William of Malmesbury’s Gesta pontificum,
and Lanfranc’s works, ed. Giles; Domesday Book.
(J. H. R.)
GEOFFREY OF MONMOUTH (d. 1154), bishop of St Asaph
and writer on early British history, was born about the year 1100.
Of his early life little is known, except that he received a liberal
education under the eye of his paternal uncle, Uchtryd, who was
at that time archdeacon, and subsequently bishop, of Llandaff.
In 1129 Geoffrey appears at Oxford among the witnesses of an
Oseney charter. He subscribes himself Geoffrey Arturus;
from this we may perhaps infer that he had already begun his
experiments in the manufacture of Celtic mythology. A first
edition of his Historia Britonum was in circulation by the year
617
1139, although the text which we possess appears to date from
1147. This famous work, which the author has the audacity
to place on the same level with the histories of William of
Malmesbury and Henry of Huntingdon, professes to be a translation
from a Celtic source; “a very old book in the British
tongue” which Walter, archdeacon of Oxford, had brought
from Brittany. Walter the archdeacon is a historical personage;
whether his book has any real existence may be fairly questioned.
There is nothing in the matter or the style of the Historia to
preclude us from supposing that Geoffrey drew partly upon
confused traditions, partly on his own powers of invention, and
to a very slight degree upon the accepted authorities for early
British history. His chronology is fantastic and incredible;
William of Newburgh justly remarks that, if we accepted the
events which Geoffrey relates, we should have to suppose that
they had happened in another world. William of Newburgh
wrote, however, in the reign of Richard I. when the reputation
of Geoffrey’s work was too well established to be shaken by such
criticisms. The fearless romancer had achieved an immediate
success. He was patronized by Robert, earl of Gloucester, and
by two bishops of Lincoln; he obtained, about 1140, the archdeaconry
of Llandaff “on account of his learning”; and in
1151 was promoted to the see of St Asaph.
Before his death the Historia Britonum had already become a
model and a quarry for poets and chroniclers. The list of
imitators begins with Geoffrey Gaimar, the author of the Estorie
des Engles (c. 1147), and Wace, whose Roman de Brut (1155) is
partly a translation and partly a free paraphrase of the Historia.
In the next century the influence of Geoffrey is unmistakably
attested by the Brut of Layamon, and the rhyming English
chronicle of Robert of Gloucester. Among later historians who
were deceived by the Historia Britonum it is only needful to
mention Higdon, Hardyng, Fabyan (1512), Holinshed (1580)
and John Milton. Still greater was the influence of Geoffrey
upon those writers who, like Warner in Albion’s England (1586),
and Drayton in Polyolbion (1613), deliberately made their
accounts of English history as poetical as possible. The stories
which Geoffrey preserved or invented were not infrequently
a source of inspiration to literary artists. The earliest English
tragedy, Gorboduc (1565), the Mirror for Magistrates (1587), and
Shakespeare’s Lear, are instances in point. It was, however,
the Arthurian legend which of all his fabrications attained the
greatest vogue. In the work of expanding and elaborating this
theme the successors of Geoffrey went as far beyond him as he
had gone beyond Nennius; but he retains the credit due to the
founder of a great school. Marie de France, who wrote at the
court of Henry II., and Chrétien de Troyes, her French contemporary,
were the earliest of the avowed romancers to take
up the theme. The succeeding age saw the Arthurian story
popularized, through translations of the French romances, as
far afield as Germany and Scandinavia. It produced in England
the Roman du Saint Graal and the Roman de Merlin, both from
the pen of Robert de Borron; the Roman de Lancelot; the Roman
de Tristan, which is attributed to a fictitious Lucas de Gast. In
the reign of Edward IV. Sir Thomas Malory paraphrased and
arranged the best episodes of these romances in English prose.
His Morte d’Arthur, printed by Caxton in 1485, epitomizes the
rich mythology which Geoffrey’s work had first called into life,
and gave the Arthurian story a lasting place in the English
imagination. The influence of the Historia Britonum may be
illustrated in another way, by enumerating the more familiar
of the legends to which it first gave popularity. Of the twelve
books into which it is divided only three (Bks. IX., X., XI.) are
concerned with Arthur. Earlier in the work, however, we have
the adventures of Brutus; of his follower Corineus, the vanquisher
of the Cornish giant Goemagol (Gogmagog); of Locrinus and
his daughter Sabre (immortalized in Milton’s Comus); of Bladud
the builder of Bath; of Lear and his daughters; of the three
pairs of brothers, Ferrex and Porrex, Brennius and Belinus,
Elidure and Peridure. The story of Vortigern and Rowena
takes its final form in the Historia Britonum; and Merlin makes
his first appearance in the prelude to the Arthur legend. Besides
the Historia Britonum Geoffrey is also credited with a Life of
Merlin composed in Latin verse. The authorship of this work
has, however, been disputed, on the ground that the style is distinctly
superior to that of the Historia. A minor composition, the
Prophecies of Merlin, was written before 1136, and afterwards incorporated
with the Historia, of which it forms the seventh book.
For a discussion of the manuscripts of Geoffrey’s work, see Sir
T.D. Hardy’s Descriptive Catalogue (Rolls Series), i. pp. 341 ff. The
Historia Britonum has been critically edited by San Marte (Halle,
1854). There is an English translation by J.A. Giles (London, 1842).
The Vita Merlini has been edited by F. Michel and T. Wright (Paris,
1837). See also the Dublin Univ. Magazine for April 1876, for an
article by T. Gilray on the literary influence of Geoffrey; G. Heeger’s
Trojanersage der Britten (1889); and La Borderie’s Études historiques
bretonnes (1883).
(H. W. C. D.)
GEOFFREY OF PARIS (d. c. 1320), French chronicler, was
probably the author of the Chronique métrique de Philippe le
Bel, or Chronique rimée de Geoffroi de Paris. This work, which
deals with the history of France from 1300 to 1316, contains
7918 verses, and is valuable as that of a writer who had a personal
knowledge of many of the events which he relates. Various short
historical poems have also been attributed to Geoffrey, but there
is no certain information about either his life or his writings.
The Chronique was published by J.A. Buchon in his Collection des
chroniques, tome ix. (Paris, 1827), and it has also been printed in
tome xxii. of the Recueil des historiens des Gaules et de la France
(Paris, 1865). See G. Paris, Histoire de la littérature française au
moyen âge (Paris, 1890); and A. Molinier, Les Sources de l’histoire de
France, tome iii. (Paris, 1903).
GEOFFREY THE BAKER (d. c. 1360), English chronicler,
is also called Walter of Swinbroke, and was probably a secular
clerk at Swinbrook in Oxfordshire. He wrote a Chronicon
Angliae temporibus Edwardi II. et Edwardi III., which deals
with the history of England from 1303 to 1356. From the beginning
until about 1324 this work is based upon Adam Murimuth’s
Continuatio chronicarum, but after this date it is valuable and
interesting, containing information not found elsewhere, and
closing with a good account of the battle of Poitiers. The author
obtained his knowledge about the last days of Edward II. from
William Bisschop, a companion of the king’s murderers, Thomas
Gurney and John Maltravers. Geoffrey also wrote a Chroniculum
from the creation of the world until 1336, the value of
which is very slight. His writings have been edited with notes
by Sir E.M. Thompson as the Chronicon Galfridi le Baker de
Swynebroke (Oxford, 1889). Some doubt exists concerning
Geoffrey’s share in the compilation of the Vita et mors Edwardi
II., usually attributed to Sir Thomas de la More, or Moor, and
printed by Camden in his Anglica scripta. It has been maintained
by Camden and others that More wrote an account of Edward’s
reign in French, and that this was translated into Latin by
Geoffrey and used by him in compiling his Chronicon. Recent
scholarship, however, asserts that More was no writer, and that
the Vita et mors is an extract from Geoffrey’s Chronicon, and
was attributed to More, who was the author’s patron. In the
main this conclusion substantiates the verdict of Stubbs, who
has published the Vita et mors in his Chronicles of the reigns of
Edward I. and Edward II. (London, 1883). The manuscripts
of Geoffrey’s works are in the Bodleian library at Oxford.
GEOFFRIN, MARIE THÉRÈSE RODET (1699-1777), a
Frenchwoman who played an interesting part in French literary
and artistic life, was born in Paris in 1699. She married, on the
19th of July 1713, Pierre François Geoffrin, a rich manufacturer
and lieutenant-colonel of the National Guard, who died in 1750.
It was not till Mme Geoffrin was nearly fifty years of age that we
begin to hear of her as a power in Parisian society. She had
learned much from Mme de Tencin, and about 1748 began to
gather round her a literary and artistic circle. She had every
week two dinners, on Monday for artists, and on Wednesday for
her friends the Encyclopaedists and other men of letters. She
received many foreigners of distinction, Hume and Horace
Walpole among others. Walpole spent much time in her society
before he was finally attached to Mme du Deffand, and speaks of
her in his letters as a model of common sense. She was indeed
somewhat of a small tyrant in her circle. She had adopted the
pose of an old woman earlier than necessary, and her coquetry, if
618
such it can be called, took the form of being mother and mentor to
her guests, many of whom were indebted to her generosity for
substantial help. Although her aim appears to have been to
have the Encyclopédie in conversation and action around her, she
was extremely displeased with any of her friends who were so
rash as to incur open disgrace. Marmontel lost her favour after
the official censure of Bélisaire, and her advanced views did not
prevent her from observing the forms of religion. A devoted
Parisian, Mme Geoffrin rarely left the city, so that her journey to
Poland in 1766 to visit the king, Stanislas Poniatowski, whom she
had known in his early days in Paris, was a great event in her life.
Her experiences induced a sensible gratitude that she had been
born “Française” and “particulière.” In her last illness her
daughter, Thérèse, marquise de la Ferté Imbault, excluded her
mother’s old friends so that she might die as a good Christian, a
proceeding wittily described by the old lady: “My daughter is
like Godfrey de Bouillon, she wished to defend my tomb from
the infidels.” Mme Geoffrin died in Paris on the 6th of October
1777.
See Correspondance inédite du roi Stanislas Auguste Poniatowski et
de Madame Geoffrin, edited by the comte de Mouÿ (1875); P. de
Ségur, Le Royaume de la rue Saint-Honoré, Madame Geoffrin et sa
fille (1897); A. Tornezy, Un Bureau d’esprit au XVIIIe siècle: le
salon de Madame Geoffrin (1895); and Janet Aldis, Madame Geoffrin,
her Salon and her Times, 1750-1777 (1905).
GEOFFROY, ÉTIENNE FRANÇOIS (1672-1731), French
chemist, born in Paris on the 13th of February 1672, was first
an apothecary and then practised medicine. After studying at
Montpellier he accompanied Marshal Tallard on his embassy to
London in 1698 and thence travelled to Holland and Italy.
Returning to Paris he became professor of chemistry at the
Jardin du Roi and of pharmacy and medicine at the Collège de
France, and dean of the faculty of medicine. He died in Paris on
the 6th of January 1731. His name is best known in connexion
with his tables of affinities (tables des rapports), which he presented
to the French Academy in 1718 and 1720. These were lists,
prepared by collating observations on the actions of substances
one upon another, showing the varying degrees of affinity exhibited
by analogous bodies for different reagents, and they retained
their vogue for the rest of the century, until displaced by the
profounder conceptions introduced by C.L. Berthollet. Another
of his papers dealt with the delusions of the philosopher’s stone,
but nevertheless he believed that iron could be artificially formed
in the combustion of vegetable matter. His Tractatus de materia
medica, published posthumously in 1741, was long celebrated.
His brother Claude Joseph, known as Geoffroy the younger
(1685-1752), was also an apothecary and chemist who, having a
considerable knowledge of botany, devoted himself especially to
the study of the essential oils in plants.
GEOFFROY, JULIEN LOUIS (1743-1814), French critic, was
born at Rennes in 1743. He studied in the school of his native
town and at the Collège Louis le Grand in Paris. He took orders
and fulfilled for some time the humble functions of an usher,
eventually becoming professor of rhetoric at the Collège Mazarin.
A bad tragedy, Caton, was accepted at the Théâtre Français, but
was never acted. On the death of Élie Fréron in 1776 the other
collaborators in the Année littéraire asked Geoffroy to succeed him,
and he conducted the journal until in 1792 it ceased to appear.
Geoffroy was a bitter critic of Voltaire and his followers, and
made for himself many enemies. An enthusiastic royalist,
he published with Fréron’s brother-in-law, the abbé Thomas
Royou (1741-1792), a journal, L’Ami du roi (1790-1792),
which possibly did more harm than good to the king’s cause by its
ill-advised partisanship. During the Terror Geoffroy hid in the
neighbourhood of Paris, only returning in 1799. An attempt to
revive the Année littéraire failed, and Geoffroy undertook the
dramatic feuilleton of the Journal des débats. His scathing
criticisms had a success of notoriety, but their popularity was
ephemeral, and the publication of them (5 vols., 1819-1820) as
Cours de littérature dramatique proved a failure. He was also the
author of a perfunctory Commentaire on the works of Racine
prefixed to Lenormant’s edition (1808). He died in Paris on the
27th of February 1814.
GEOFFROY SAINT-HILAIRE, ÉTIENNE (1772-1844), French
naturalist, was the son of Jean Gèrard Geoffroy, procurator and
magistrate of Étampes, Seine-et-Oise, where he was born on the
15th of April 1772. Destined for the church he entered the
college of Navarre, in Paris, where he studied natural philosophy
under M.J. Brisson; and in 1788 he obtained one of the canonicates
of the chapter of Sainte Croix at Étampes, and also a
benefice. Science, however, offered him a more congenial career,
and he gained from his father permission to remain in Paris, and
to attend the lectures at the Collège de France and the Jardin des
Plantes, on the condition that he should also read law. He
accordingly took up his residence at Cardinal Lemoine’s college,
and there became the pupil and soon the esteemed associate of
Brisson’s friend, the abbé Haüy, the mineralogist. Having,
before the close of the year 1790, taken the degree of bachelor in
law, he became a student of medicine, and attended the lectures of
A.F. de Fourcroy at the Jardin des Plantes, and of L.J.M.
Daubenton at the Collège de France. His studies at Paris were at
length suddenly interrupted, for, in August 1792, Haüy and the
other professors of Lemoine’s college, as also those of the college
of Navarre, were arrested by the revolutionists as priests, and
confined in the prison of St Firmin. Through the influence of
Daubenton and others Geoffroy on the 14th of August obtained
an order for the release of Haüy in the name of the Academy;
still the other professors of the two colleges, save C.F. Lhomond,
who had been rescued by his pupil J.L. Tallien, remained in
confinement. Geoffroy, foreseeing their certain destruction if
they remained in the hands of the revolutionists, determined if
possible to secure their liberty by stratagem. By bribing one of
the officials at St Firmin, and disguising himself as a commissioner
of prisons, he gained admission to his friends, and entreated them
to effect their escape by following him. All, however, dreading
lest their deliverance should render the doom of their fellow-captives
the more certain, refused the offer, and one priest only,
who was unknown to Geoffroy, left the prison. Already on the
night of the 2nd of September the massacre of the proscribed had
begun, when Geoffroy, yet intent on saving the life of his friends
and teachers, repaired to St Firmin. At 4 o’clock on the morning
of the 3rd of September, after eight hours’ waiting, he by means
of a ladder assisted the escape of twelve ecclesiastics, not of the
number of his acquaintance, and then the approach of dawn and
the discharge of a gun directed at him warned him, his chief
purpose unaccomplished, to return to his lodgings. Leaving Paris
he retired to Étampes, where, in consequence of the anxieties of
which he had lately been the prey, and the horrors which he had
witnessed, he was for some time seriously ill. At the beginning
of the winter of 1792 he returned to his studies in Paris, and in
March of the following year Daubenton, through the interest of
Bernardin de Saint Pierre, procured him the office of sub-keeper
and assistant demonstrator of the cabinet of natural history,
vacant by the resignation of B.G.E. Lacépède. By a law
passed in June 1793, Geoffroy was appointed one of the twelve
professors of the newly constituted museum of natural history,
being assigned the chair of zoology. In the same year he
busied himself with the formation of a menagerie at that
institution.
In 1794 through the introduction of A.H. Tessier he entered
into correspondence with Georges Cuvier, to whom, after the
perusal of some of his manuscripts, he wrote: “Venez jouer
parmi nous le rôle de Linné, d’un autre législateur de l’histoire
naturelle.” Shortly after the appointment of Cuvier as assistant
at the Muséum d’Histoire Naturelle, Geoffroy received him into
his house. The two friends wrote together five memoirs on
natural history, one of which, on the classification of mammals,
puts forward the idea of the subordination of characters upon
which Cuvier based his zoological system. It was in a paper
entitled “Histoire des Makis, ou singes de Madagascar,” written
in 1795, that Geoffroy first gave expression to his views on “the
unity of organic composition,” the influence of which is perceptible
in all his subsequent writings; nature, he observes,
presents us with only one plan of construction, the same in
principle, but varied in its accessory parts.
619
In 1798 Geoffroy was chosen a member of the great scientific
expedition to Egypt, and on the capitulation of Alexandria in
August 1801, he took part in resisting the claim made by the
British general to the collections of the expedition, declaring that,
were that demand persisted in, history would have to record
that he also had burnt a library in Alexandria. Early in January
1802 Geoffroy returned to his accustomed labours in Paris. He
was elected a member of the academy of sciences of that city
in September 1807. In March of the following year the emperor,
who had already recognized his national services by the award
of the cross of the legion of honour, selected him to visit the
museums of Portugal, for the purpose of procuring collections
from them, and in the face of considerable opposition from the
British he eventually was successful in retaining them as a
permanent possession for his country. In 1809, the year after
his return to France, he was made professor of zoology at the
faculty of sciences at Paris, and from that period he devoted
himself more exclusively than before to anatomical study. In
1818 he gave to the world the first part of his celebrated Philosophie
anatomique, the second volume of which, published in
1822, and subsequent memoirs account for the formation of
monstrosities on the principle of arrest of development, and of
the attraction of similar parts. When, in 1830, Geoffroy proceeded
to apply to the invertebrata his views as to the unity of
animal composition, he found a vigorous opponent in Georges
Cuvier, and the discussion between them, continued up to the
time of the death of the latter, soon attracted the attention of
the scientific throughout Europe. Geoffroy, a synthesist, contended,
in accordance with his theory of unity of plan in organic
composition, that all animals are formed of the same elements,
in the same number, and with the same connexions: homologous
parts, however they differ in form and size, must remain associated
in the same invariable order. With Goethe he held that there
is in nature a law of compensation or balancing of growth, so
that if one organ take on an excess of development, it is at the
expense of some other part; and he maintained that, since
nature takes no sudden leaps, even organs which are superfluous
in any given species, if they have played an important part in
other species of the same family, are retained as rudiments,
which testify to the permanence of the general plan of creation.
It was his conviction that, owing to the conditions of life, the
same forms had not been perpetuated since the origin of all
things, although it was not his belief that existing species are
becoming modified. Cuvier, who was an analytical observer of
facts, admitted only the prevalence of “laws of co-existence”
or “harmony” in animal organs, and maintained the absolute
invariability of species, which he declared had been created
with a regard to the circumstances in which they were placed,
each organ contrived with a view to the function it had to
fulfil, thus putting, in Geoffroy’s considerations, the effect for
the cause.
In July 1840 Geoffroy became blind, and some months later
he had a paralytic attack. From that time his strength gradually
failed him. He resigned his chair at the museum in 1841, and
died at Paris on the 19th of June 1844.
Geoffroy wrote: Catalogue des mammifères du Muséum National
d’Histoire Naturelle (1813), not quite completed; Philosophie anatomique—t.
i., Des organes respiratoires (1818), and t. ii., Des monstruosités
humaines (1822); Système dentaire des mammifères et des
oiseaux (1st pt., 1824); Sur le principe de l’unité de composition
organique (1828); Cours de l’histoire naturelle des mammifères
(1829); Principes de philosophie zoologique (1830); Études progressives
d’un naturaliste (1835); Fragments biographiques (1832);
Notions synthétiques, historiques et physiologiques de philosophie
naturelle (1838), and other works; also part of the Description de
l’Égypte par la commission des sciences (1821-1830); and, with
Frédéric Cuvier (1773-1838), a younger brother of G. Cuvier, Histoire
naturelle des mammifères (4 vols., 1820-1842); besides numerous
papers on such subjects as the anatomy of marsupials, ruminants
and electrical fishes, the vertebrate theory of the skull, the opercula
of fishes, teratology, palaeontology and the influence of surrounding
conditions in modifying animal forms.
See Vie, travaux, et doctrine scientifique d’Étienne Geoffroy Saint-Hilaire,
par son fils M. Isidore Geoffroy Saint-Hilaire (Paris and
Strasburg, 1847), to which is appended a list of Geoffroy’s works;
and Joly, in Biog. universelle, t. xvi. (1856).
GEOFFROY SAINT-HILAIRE, ISIDORE (1805-1861), French
zoologist, son of the preceding, was born at Paris on the 16th of
December 1805. In his earlier years he showed an aptitude for
mathematics, but eventually he devoted himself to the study
of natural history and of medicine, and in 1824 he was appointed
assistant naturalist to his father. On the occasion of his taking
the degree of doctor of medicine in September 1829, he read a
thesis entitled Propositions sur la monstruosité, considérée chez
l’homme et les animaux; and in 1832-1837 was published his
great teratological work, Histoire générale et particulière des
anomalies de l’organisation chez l’homme et les animaux, 3 vols.
8vo. with 20 plates. In 1829 he delivered for his father the second
part of a course of lectures on ornithology, and during the three
following years he taught zoology at the Athénée, and teratology
at the École pratique. He was elected a member of the academy
of sciences at Paris in 1833, was in 1837 appointed to act as
deputy for his father at the faculty of sciences in Paris, and in
the following year was sent to Bordeaux to organize a similar
faculty there. He became successively inspector of the academy
of Paris (1840), professor of the museum on the retirement of
his father (1841), inspector-general of the university (1844),
a member of the royal council for public instruction (1845), and
on the death of H.M.D. de Blainville, professor of zoology
at the faculty of sciences (1850). In 1854 he founded the
Acclimatization Society of Paris, of which he was president.
He died at Paris on the 10th of November 1861.
Besides the above-mentioned works, he wrote: Essais de zoologie
générale (1841); Vie ... d’Étienne Geoffroy Saint-Hilaire (1847);
Acclimatation et domestication des animaux utiles (1849; 4th ed.,
1861); Lettres sur les substances alimentaires et particulièrement sur
la viande de cheval (1856); and Histoire naturelle générale des règnes
organiques (3 vols., 1854-1862), which was not quite completed.
He was the author also of various papers on zoology, comparative
anatomy and palaeontology.
GEOGRAPHY (Gr. γῆ, earth, and γράφειν, to write), the
exact and organized knowledge of the distribution of phenomena
on the surface of the earth. The fundamental basis of geography
is the vertical relief of the earth’s crust, which controls all
mobile distributions. The grander features of the relief of the
lithosphere or stony crust of the earth control the distribution
of the hydrosphere or collected waters which gather into the
hollows, filling them up to a height corresponding to the volume,
and thus producing the important practical division of the
surface into land and water. The distribution of the mass of
the atmosphere over the surface of the earth is also controlled
by the relief of the crust, its greater or lesser density at the surface
corresponding to the lesser or greater elevation of the surface.
The simplicity of the zonal distribution of solar energy on the
earth’s surface, which would characterize a uniform globe, is
entirely destroyed by the dissimilar action of land and water
with regard to radiant heat, and by the influence of crust-forms
on the direction of the resulting circulation. The influence of
physical environment becomes clearer and stronger when the
distribution of plant and animal life is considered, and if it is
less distinct in the case of man, the reason is found in the modifications
of environment consciously produced by human effort.
Geography is a synthetic science, dependent for the data with
which it deals on the results of specialized sciences such as
astronomy, geology, oceanography, meteorology, biology and
anthropology, as well as on topographical description. The
physical and natural sciences are concerned in geography only
so far as they deal with the forms of the earth’s surface, or as
regards the distribution of phenomena. The distinctive task of
geography as a science is to investigate the control exercised by
the crust-forms directly or indirectly upon the various mobile
distributions. This gives to it unity and definiteness, and renders
superfluous the attempts that have been made from time to
time to define the limits which divide geography from geology
on the one hand and from history on the other. It is essential
to classify the subject-matter of geography in such a manner as
to give prominence not only to facts, but to their mutual relations
and their natural and inevitable order.
The fundamental conception of geography is form, including
620
the figure of the earth and the varieties of crustal relief. Hence
mathematical geography (see Map), including cartography as
a practical application, comes first. It merges into physical
geography, which takes account of the forms of the lithosphere
(geomorphology), and also of the distribution of the hydrosphere
and the rearrangements resulting from the workings of solar
energy throughout the hydrosphere and atmosphere (oceanography
and climatology). Next follows the distribution of plants
and animals (biogeography), and finally the distribution of
mankind and the various artificial boundaries and redistributions
(anthropogeography). The applications of anthropogeography
to human uses give rise to political and commercial geography,
in the elucidation of which all the earlier departments or stages
have to be considered, together with historical and other purely
human conditions. The evolutionary idea has revolutionized
and unified geography as it did biology, breaking down the old
hard-and-fast partitions between the various departments, and
substituting the study of the nature and influence of actual
terrestrial environments for the earlier motive, the discovery
and exploration of new lands.
History of Geographical Theory
The earliest conceptions of the earth, like those held by the primitive
peoples of the present day, are difficult to discover and almost
impossible fully to grasp. Early generalizations, as far as they were
made from known facts, were usually expressed in symbolic language,
and for our present purpose it is not profitable to speculate on the
underlying truths which may sometimes be suspected in the old
mythological cosmogonies.
The first definite geographical theories to affect the western world
were those evolved, or at least first expressed, by the Greeks.1
The earliest theoretical problem of geography was the
Early Greek ideas.
Flat earth of Homer.
form of the earth. The natural supposition that the earth
is a flat disk, circular or elliptical in outline, had in the
time of Homer acquired a special definiteness by the
introduction of the idea of the ocean river bounding the whole, an
application of imperfectly understood observations. Thales of
Miletus is claimed as the first exponent of the idea of a
spherical earth; but, although this does not appear to be
warranted, his disciple Anaximander (c. 580 B.C.) put
forward the theory that the earth had the figure of a solid body
hanging freely in the centre of the hollow sphere of the starry heavens.
The Pythagorean school of philosophers adopted the theory of a
spherical earth, but from metaphysical rather than scientific reasons;
their convincing argument was that a sphere being the most perfect
solid figure was the only one worthy to circumscribe the dwelling-place
of man. The division of the sphere into parallel zones and
some of the consequences of this generalization seem to have presented
themselves to Parmenides (c. 450 B.C.); but these ideas did
not influence the Ionian school of philosophers, who in their treatment
of geography preferred to deal with facts demonstrable by
Hecataeus.
Herodotus.
travel rather than with speculations. Thus Hecataeus,
claimed by H.F. Tozer2 as the father of geography on
account of his Periodos, or general treatise on the earth, did not
advance beyond the primitive conception of a circular disk. He
systematized the form of the land within the ring of ocean—the
οἰκουμένη, or habitable world—by recognizing two continents:
Europe to the north, and Asia to the south of the midland sea.
Herodotus, equally oblivious of the sphere, criticized and
ridiculed the circular outline of the oekumene, which he
knew to be longer from east to west than it was broad from north to
south. He also pointed out reasons for accepting a division of the
land into three continents—Europe, Asia and Africa. Beyond the
limits of his personal travels Herodotus applied the characteristically
Greek theory of symmetry to complete, in the unknown, outlines
The idea of symmetry.
of lands and rivers analogous to those which had been
explored. Symmetry was in fact the first geographical
theory, and the effect of Herodotus’s hypothesis that the
Nile must flow from west to east before turning north in
order to balance the Danube running from west to east before turning
south lingered in the maps of Africa down to the time of Mungo
Park.3
To Aristotle (384-322 B.C.) must be given the distinction of founding
scientific geography. He demonstrated the sphericity of the
earth by three arguments, two of which could be tested by observation.
These were: (1) that the earth must be spherical, because
Aristotle and the sphere.
of the tendency of matter to fall together towards a common
centre; (2) that only a sphere could always throw a
circular shadow on the moon during an eclipse; and (3)
that the shifting of the horizon and the appearance of
new constellations, or the disappearance of familiar stars, as one
travelled from north to south, could only be explained on the hypothesis
that the earth was a sphere. Aristotle, too, gave greater
definiteness to the idea of zones conceived by Parmenides, who had
pictured a torrid zone uninhabitable by reason of heat, two frigid
zones uninhabitable by reason of cold, and two intermediate temperate
zones fit for human occupation. Aristotle defined the temperate
zone as extending from the tropic to the arctic circle, but there is
some uncertainty as to the precise meaning he gave to the term
“arctic circle.” Soon after his time, however, this conception was
clearly established, and with so large a generalization the mental
horizon was widened to conceive of a geography which was a science.
Aristotle had himself shown that in the southern temperate zone
winds similar to those of the northern temperate zone should blow,
but from the opposite direction.
While the theory of the sphere was being elaborated the efforts of
practical geographers were steadily directed towards ascertaining
the outline and configuration of the oekumene, or habitable
world, the only portion of the terrestrial surface known
Fitting the oekumene to the sphere.
to the ancients and to the medieval peoples, and still
retaining a shadow of its old monopoly of geographical
attention in its modern name of the “Old World.” The
fitting of the oekumene to the sphere was the second theoretical
problem. The circular outline had given way in geographical
opinion to the elliptical with the long axis lying east and west, and
Aristotle was inclined to view it as a very long and relatively narrow
band almost encircling the globe in the temperate zone. His argument
as to the narrowness of the sea between West Africa and East
Asia, from the occurrence of elephants at both extremities, is difficult
to understand, although it shows that he looked on the distribution
of animals as a problem of geography.
Pythagoras had speculated as to the existence of antipodes, but
it was not until the first approximately accurate measurements of
the globe and estimates of the length and breadth of the
oekumene were made by Eratosthenes (c. 250 B.C.) that
Problem of the Antipodes.
the fact that, as then known, it occupied less than a quarter
of the surface of the sphere was clearly recognized. It was
natural, if not strictly logical, that the ocean river should be extended
from a narrow stream to a world-embracing sea, and here again
Greek theory, or rather fancy, gave its modern name to the greatest
feature of the globe. The old instinctive idea of symmetry must
often have suggested other oekumene balancing the known world
in the other quarters of the globe. The Stoic philosophers, especially
Crates of Mallus, arguing from the love of nature for life, placed an
oekumene in each quarter of the sphere, the three unknown world-islands
being those of the Antoeci, Perioeci and Antipodes. This
was a theory not only attractive to the philosophical mind, but
eminently adapted to promote exploration. It had its opponents,
however, for Herodotus showed that sea-basins existed cut off from
the ocean, and it is still a matter of controversy how far the pre-Ptolemaic
geographers believed in a water-connexion between the
Atlantic and Indian oceans. It is quite clear that Pomponius Mela
(c. A.D. 40), following Strabo, held that the southern temperate zone
contained a habitable land, which he designated by the name
Antichthones.
Aristotle left no work on geography, so that it is impossible to
know what facts he associated with the science of the earth’s surface.
The word geography did not appear before Aristotle,
the first use of it being in the Περὶ κόσμων, which is one
Aristotle’s geographical views.
of the writings doubtfully ascribed to him, and H. Berger
considers that the expression was introduced by Eratosthenes.4
Aristotle was certainly conversant with many
facts, such as the formation of deltas, coast-erosion, and to a certain
extent the dependence of plants and animals on their physical
surroundings. He formed a comprehensive theory of the variations
of climate with latitude and season, and was convinced of the necessity
of a circulation of water between the sea and rivers, though,
like Plato, he held that this took place by water rising from the sea
through crevices in the rocks, losing its dissolved salts in the process.
He speculated on the differences in the character of races of mankind
living in different climates, and correlated the political forms of
communities with their situation on a seashore, or in the neighbourhood
of natural strongholds.
Strabo (c. 50 B.C.-A.D. 24) followed Eratosthenes rather than
Aristotle, but with sympathies which went out more to the human
interests than the mathematical basis of geography. He
Strabo.
compiled a very remarkable work dealing, in large measure
from personal travel, with the countries surrounding the Mediterranean.
He may be said to have set the pattern which was followed
in succeeding ages by the compilers of “political geographies”
621
dealing less with theories than with facts, and illustrating rather than
formulating the principles of the science.
Claudius Ptolemaeus (c. A.D. 150) concentrated in his writings the
final outcome of all Greek geographical learning, and passed it across
the gulf of the middle ages by the hands of the Arabs,
to form the starting-point of the science in modern times.
Ptolemy.
His geography was based more immediately on the work of his
predecessor, Marinus of Tyre, and on that of Hipparchus, the
follower and critic of Eratosthenes. It was the ambition of Ptolemy
to describe and represent accurately the surface of the oekumene,
for which purpose he took immense trouble to collect all existing
determinations of the latitude of places, all estimates of longitude,
and to make every possible rectification in the estimates of distances
by land or sea. His work was mainly cartographical in its aim,
and theory was as far as possible excluded. The symmetrically
placed hypothetical islands in the great continuous ocean disappeared,
and the oekumene acquired a new form by the representation of the
Indian Ocean as a larger Mediterranean completely cut off by land
from the Atlantic. The terra incognita uniting Africa and Farther
Asia was an unfortunate hypothesis which helped to retard exploration.
Ptolemy used the word geography to signify the description
of the whole oekumene on mathematical principles, while chorography
signified the fuller description of a particular region, and
topography the very detailed description of a smaller locality. He
introduced the simile that geography represented an artist’s sketch
of a whole portrait, while chorography corresponded to the careful
and detailed drawing of an eye or an ear.5
The Caliph al-Mamūn (c. A.D. 815), the son and successor of
Hārūn al-Rashīd, caused an Arabic version of Ptolemy’s great
astronomical work (Σύνταξις μεγίστη) to be made, which is known
as the Almagest, the word being nothing more than the Gr. μεγίστη
with the Arabic article al prefixed. The geography of Ptolemy was
also known and is constantly referred to by Arab writers. The
Arab astronomers measured a degree on the plains of Mesopotamia,
thereby deducing a fair approximation to the size of the earth.
The caliph’s librarian, Abu Jafar Muhammad Ben Musa, wrote a
geographical work, now unfortunately lost, entitled Rasm el Arsi (“A
Description of the World”), which is often referred to by subsequent
writers as having been composed on the model of that of Ptolemy.
The middle ages saw geographical knowledge die out in Christendom,
although it retained, through the Arabic translations of
Ptolemy, a certain vitality in Islam. The verbal interpretation
of Scripture led Lactantius (c. A.D. 320) and
Geography in the middle ages.
other ecclesiastics to denounce the spherical theory of the
earth as heretical. The wretched subterfuge of Cosmas
(c. A.D. 550) to explain the phenomena of the apparent
movements of the sun by means of an earth modelled on the plan
of the Jewish Tabernacle gave place ultimately to the wheel-maps—the
T in an O—which reverted to the primitive ignorance of the
times of Homer and Hecataeus.6
The journey of Marco Polo, the increasing trade to the East and
the voyages of the Arabs in the Indian Ocean prepared the way for
the reacceptance of Ptolemy’s ideas when the sealed books of the
Greek original were translated into Latin by Angelus in 1410.
The old arguments of Aristotle and the old measurements of
Ptolemy were used by Toscanelli and Columbus in urging a westward
voyage to India; and mainly on this account did the
Revival of geography.
crossing of the Atlantic rank higher in the history of
scientific geography than the laborious feeling out of the
coast-line of Africa. But not until the voyage of Magellan shook
the scales from the eyes of Europe did modern geography begin to
advance. Discovery had outrun theory; the rush of new facts
made Ptolemy practically obsolete in a generation, after having been
the fount and origin of all geography for a millennium.
The earliest evidence of the reincarnation of a sound theoretical
geography is to be found in the text-books by Peter Apian and
Sebastian Münster. Apian in his Cosmographicus liber,
published in 1524, and subsequently edited and added to
Apianus.
by Gemma Frisius under the title of Cosmographia, based the whole
science on mathematics and measurement. He followed Ptolemy
closely, enlarging on his distinction between geography and chorography,
and expressing the artistic analogy in a rough diagram.
This slender distinction was made much of by most subsequent
writers until Nathanael Carpenter in 1625 pointed out that the
difference between geography and chorography was simply one of
degree, not of kind.
Sebastian Münster, on the other hand, in his Cosmographia
universalis of 1544, paid no regard to the mathematical basis of
geography, but, following the model of Strabo, described
Münster.
the world according to its different political divisions,
and entered with great zest into the question of the productions
of countries, and into the manners and costumes of the various
peoples. Thus early commenced the separation between what were
long called mathematical and political geography, the one subject
appealing mainly to mathematicians, the other to historians.
Throughout the 16th and 17th centuries the rapidly accumulating
store of facts as to the extent, outline and mountain and river
systems of the lands of the earth were put in order by the generation
of cartographers of which Mercator was the chief; but the writings
of Apian and Münster held the field for a hundred years without a
serious rival, unless the many annotated editions of Ptolemy might
be so considered. Meanwhile the new facts were the subject of
original study by philosophers and by practical men without reference
to classical traditions. Bacon argued keenly on geographical
matters and was a lover of maps, in which he observed and reasoned
upon such resemblances as that between the outlines of South
America and Africa.
Philip Cluver’s Introductio in geographiam universam tam veterem
quam novam was published in 1624. Geography he defined as
“the description of the whole earth, so far as it is known
to us.” It is distinguished from cosmography by dealing
Cluverius.
with the earth alone, not with the universe, and from chorography
and topography by dealing with the whole earth, not with a country
or a place. The first book, of fourteen short chapters, is concerned
with the general properties of the globe; the remaining six books
treat in considerable detail of the countries of Europe and of the
other continents. Each country is described with particular regard
to its people as well as to its surface, and the prominence given to
the human element is of special interest.
A little-known book which appears to have escaped the attention
of most writers on the history of modern geography was published
at Oxford in 1625 by Nathanael Carpenter, fellow of
Carpenter.
Exeter College, with the title Geographie delineated forth
in Two Bookes, containing the Sphericall and Topicall parts thereof.
It is discursive in its style and verbose; but, considering the period
at which it appeared, it is remarkable for the strong common sense
displayed by the author, his comparative freedom from prejudice,
and his firm application of the methods of scientific reasoning to
the interpretation of phenomena. Basing his work on the principles
of Ptolemy, he brings together illustrations from the most recent
travellers, and does not hesitate to take as illustrative examples
the familiar city of Oxford and his native county of Devon. He
divides geography into The Spherical Part, or that for the study of
which mathematics alone is required, and The Topical Part, or the
description of the physical relations of parts of the earth’s surface,
preferring this division to that favoured by the ancient geographers—into
general and special. It is distinguished from other English
geographical books of the period by confining attention to the
principles of geography, and not describing the countries of the
world.
A much more important work in the history of geographical
method is the Geographia generalis of Bernhard Varenius, a German
medical doctor of Leiden, who died at the age of twenty-eight
in 1650, the year of the publication of his book.
Varenius.
Although for a time it was lost sight of on the continent, Sir Isaac
Newton thought so highly of this book that he prepared an annotated
edition which was published in Cambridge in 1672, with the addition
of the plates which had been planned by Varenius, but not produced
by the original publishers. “The reason why this great man took
so much care in correcting and publishing our author was, because
he thought him necessary to be read by his audience, the young
gentlemen of Cambridge, while he was delivering lectures on the same
subject from the Lucasian Chair.”7 The treatise of Varenius is a
model of logical arrangement and terse expression; it is a work of
science and of genius; one of the few of that age which can still be
studied with profit. The English translation renders the definition
thus: “Geography is that part of mixed mathematics which explains
the state of the earth and of its parts, depending on quantity, viz.
its figure, place, magnitude and motion, with the celestial appearances,
&c. By some it is taken in too limited a sense, for a bare
description of the several countries; and by others too extensively,
who along with such a description would have their political constitution.”
Varenius was reluctant to include the human side of geography in
his system, and only allowed it as a concession to custom, and in
order to attract readers by imparting interest to the sterner details
of the science. His division of geography was into two parts—(i.)
General or universal, dealing with the earth in general, and explaining
its properties without regard to particular countries; and (ii.) Special
or particular, dealing with each country in turn from the chorographical
or topographical point of view. General geography was divided
into—(1) the Absolute part, dealing with the form, dimensions,
position and substance of the earth, the distribution of land and
water, mountains, woods and deserts, hydrography (including all
the waters of the earth) and the atmosphere; (2) the Relative part,
including the celestial properties, i.e. latitude, climate zones, longitude,
&c.; and (3) the Comparative part, which “considers the
622
particulars arising from comparing one part with another”; but
under this head the questions discussed were longitude, the situation
and distances of places, and navigation. Varenius does not treat
of special geography, but gives a scheme for it under three heads—(1)
Terrestrial, including position, outline, boundaries, mountains,
mines, woods and deserts, waters, fertility and fruits, and living
creatures; (2) Celestial, including appearance of the heavens and
the climate; (3) Human, but this was added out of deference to
popular usage.
This system of geography founded a new epoch, and the book—translated
into English, Dutch and French—was the unchallenged
standard for more than a century. The framework was capable of
accommodating itself to new facts, and was indeed far in advance
of the knowledge of the period. The method included a recognition
of the causes and effects of phenomena as well as the mere fact of
their occurrence, and for the first time the importance of the vertical
relief of the land was fairly recognized.
The physical side of geography continued to be elaborated after
Varenius’s methods, while the historical side was developed separately.
Both branches, although enriched by new facts, remained
stationary so far as method is concerned until nearly the end of the
18th century. The compilation of “geography books” by uninstructed
writers led to the pernicious habit, which is not yet wholly
overcome, of reducing the general or “physical” part to a few
pages of concentrated information, and expanding the particular
or “political” part by including unrevised travellers’ stories and
uncritical descriptions of the various countries of the world. Such
books were in fact not geography, but merely compressed travel.
The next marked advance in the theory of geography may be
taken as the nearly simultaneous studies of the physical earth
carried out by the Swedish chemist, Torbern Bergman,
acting under the impulse of Linnaeus, and by the German
Bergman.
philosopher, Immanuel Kant. Bergman’s Physical Description of
the Earth was published in Swedish in 1766, and translated into
English in 1772 and into German in 1774. It is a plain, straightforward
description of the globe, and of the various phenomena
of the surface, dealing only with definitely ascertained facts in the
natural order of their relationships, but avoiding any systematic
classification or even definitions of terms.
The problems of geography had been lightened by the destructive
criticism of the French cartographer D’Anville (who had purged
the map of the world of the last remnants of traditional
fact unverified by modern observations) and rendered
Kant.
richer by the dawn of the new era of scientific travel, when Kant
brought his logical powers to bear upon them. Kant’s lectures on
physical geography were delivered in the university of Königsberg
from 1765 onwards.8 Geography appealed to him as a valuable
educational discipline, the joint foundation with anthropology of
that “knowledge of the world” which was the result of reason
and experience. In this connexion he divided the communication
of experience from one person to another into two categories—the
narrative or historical and the descriptive or geographical; both
history and geography being viewed as descriptions, the former a
description in order of time, the latter a description in order of
space.
Physical geography he viewed as a summary of nature, the basis
not only of history but also of “all the other possible geographies,”
of which he enumerates five, viz. (1) Mathematical geography, which
deals with the form, size and movements of the earth and its place
in the solar system; (2) Moral geography, or an account of the
different customs and characters of mankind according to the region
they inhabit; (3) Political geography, the divisions according to
their organized governments; (4) Mercantile geography, dealing
with the trade in the surplus products of countries; (5) Theological
geography, or the distribution of religions. Here there is a clear and
formal statement of the interaction and causal relation of all the
phenomena of distribution on the earth’s surface, including the influence
of physical geography upon the various activities of mankind
from the lowest to the highest. Notwithstanding the form of this
classification, Kant himself treats mathematical geography as preliminary
to, and therefore not dependent on, physical geography.
Physical geography itself is divided into two parts: a general,
which has to do with the earth and all that belongs to it—water, air
and land; and a particular, which deals with special products of
the earth—mankind, animals, plants and minerals. Particular
importance is given to the vertical relief of the land, on which the
various branches of human geography are shown to depend.
Alexander von Humboldt (1769-1859) was the first modern geographer
to become a great traveller, and thus to acquire an extensive
stock of first-hand information on which an improved
system of geography might be founded. The impulse
Humboldt.
given to the study of natural history by the example of Linnaeus;
the results brought back by Sir Joseph Banks, Dr Solander and the
two Forsters, who accompanied Cook in his voyages of discovery;
the studies of De Saussure in the Alps, and the lists of desiderata
in physical geography drawn up by that investigator, combined to
prepare the way for Humboldt. The theory of geography was
advanced by Humboldt mainly by his insistence on the great
principle of the unity of nature. He brought all the “observable
things,” which the eager collectors of the previous century had been
heaping together regardless of order or system, into relation with the
vertical relief and the horizontal forms of the earth’s surface. Thus
he demonstrated that the forms of the land exercise a directive
and determining influence on climate, plant life, animal life and on
man himself. This was no new idea; it had been familiar for
centuries in a less definite form, deduced from a priori considerations,
and so far as regards the influence of surrounding circumstances
upon man, Kant had already given it full expression. Humboldt’s
concrete illustrations and the remarkable power of his personality
enabled him to enforce these principles in a way that produced
an immediate and lasting effect. The treatises on physical geography
by Mrs Mary Somerville and Sir John Herschel (the latter written
for the eighth edition of the Encyclopaedia Britannica) showed the
effect produced in Great Britain by the stimulus of Humboldt’s work.
Humboldt’s contemporary, Carl Ritter (1779-1859), extended and
disseminated the same views, and in his interpretation of “Comparative
Geography” he laid stress on the importance of
forming conclusions, not from the study of one region by
Ritter.
itself, but from the comparison of the phenomena of many places.
Impressed by the influence of terrestrial relief and climate on human
movements, Ritter was led deeper and deeper into the study of history
and archaeology. His monumental Vergleichende Geographie, which
was to have made the whole world its theme, died out in a wilderness
of detail in twenty-one volumes before it had covered more of the
earth’s surface than Asia and a portion of Africa. Some of his
followers showed a tendency to look on geography rather as an
auxiliary to history than as a study of intrinsic worth.
During the rapid development of physical geography many
branches of the study of nature, which had been included in the
cosmography of the early writers, the physiography of
Linnaeus and even the Erdkunde of Ritter, had been
Geography as a natural science.
so much advanced by the labours of specialists that
their connexion was apt to be forgotten. Thus geology,
meteorology, oceanography and anthropology developed
into distinct sciences. The absurd attempt was, and sometimes
is still, made by geographers to include all natural science in geography;
but it is more common for specialists in the various detailed
sciences to think, and sometimes to assert, that the ground of
physical geography is now fully occupied by these sciences. Political
geography has been too often looked on from both sides as a mere
summary of guide-book knowledge, useful in the schoolroom, a poor
relation of physical geography that it was rarely necessary to
recognize.
The science of geography, passed on from antiquity by Ptolemy,
re-established by Varenius and Newton, and systematized by Kant,
included within itself definite aspects of all those terrestrial phenomena
which are now treated exhaustively under the heads of geology,
meteorology, oceanography and anthropology; and the inclusion
of the requisite portions of the perfected results of these sciences in
geography is simply the gathering in of fruit matured from the seed
scattered by geography itself.
The study of geography was advanced by improvements in cartography
(see Map), not only in the methods of survey and projection,
but in the representation of the third dimension by means
of contour lines introduced by Philippe Buache in 1737, and the
more remarkable because less obvious invention of isotherms
introduced by Humboldt in 1817.
The “argument from design” had been a favourite form of
reasoning amongst Christian theologians, and, as worked out by
Paley in his Natural Theology, it served the useful purpose
of emphasizing the fitness which exists between all the
The teleological argument in geography.
inhabitants of the earth and their physical environment.
It was held that the earth had been created so as to fit
the wants of man in every particular. This argument was
tacitly accepted or explicitly avowed by almost every writer on the
theory of geography, and Carl Ritter distinctly recognized and
adopted it as the unifying principle of his system. As a student of
nature, however, he did not fail to see, and as professor of geography
he always taught, that man was in very large measure conditioned
by his physical environment. The apparent opposition of the
observed fact to the assigned theory he overcame by looking upon
the forms of the land and the arrangement of land and sea as instruments
of Divine Providence for guiding the destiny as well as for
supplying the requirements of man. This was the central theme of
Ritter’s philosophy; his religion and his geography were one, and
the consequent fervour with which he pursued his mission goes far
to account for the immense influence he acquired in Germany.
The evolutionary theory, more than hinted at in Kant’s “Physical
Geography,” has, since the writings of Charles Darwin, become the
unifying principle in geography. The conception of the
development of the plan of the earth from the first
The theory of evolution in geography.
cooling of the surface of the planet throughout the long
geological periods, the guiding power of environment on
the circulation of water and of air, on the distribution
of plants and animals, and finally on the movements of man, give
to geography a philosophical dignity and a scientific completeness
623
which it never previously possessed. The influence of environment
on the organism may not be quite so potent as it was once believed
to be, in the writings of Buckle, for instance,9 and certainly man,
the ultimate term in the series, reacts upon and greatly modifies his
environment; yet the fact that environment does influence all
distributions is established beyond the possibility of doubt. In
this way also the position of geography, at the point where physical
science meets and mingles with mental science, is explained and
justified. The change which took place during the 19th century
in the substance and style of geography may be well seen by comparing
the eight volumes of Malte-Brun’s Géographie universelle
(Paris, 1812-1829) with the twenty-one volumes of Reclus’s Géographie
universelle (Paris, 1876-1895).
In estimating the influence of recent writers on geography it is
usual to assign to Oscar Peschel (1826-1875) the credit of having
corrected the preponderance which Ritter gave to the historical
element, and of restoring physical geography to its old pre-eminence.10
As a matter of fact, each of the leading modern exponents of theoretical
geography—such as Ferdinand von Richthofen, Hermann
Wagner, Friedrich Ratzel, William M. Davis, A. Penck, A. de
Lapparent and Elisée Reclus—has his individual point of view,
one devoting more attention to the results of geological processes,
another to anthropological conditions, and the rest viewing the
subject in various blendings of the extreme lights.
The two conceptions which may now be said to animate the theory
of geography are the genetic, which depends upon processes of
origin, and the morphological, which depends on facts of form and
distribution.
Progress of Geographical Discovery
Exploration and geographical discovery must have started from
more than one centre, and to deal justly with the matter one ought
to treat of these separately in the early ages before the whole civilized
world was bound together by the bonds of modern intercommunication.
At the least there should be some consideration of four
separate systems of discovery—the Eastern, in which Chinese and
Japanese explorers acquired knowledge of the geography of Asia,
and felt their way towards Europe and America; the Western, in
which the dominant races of the Mexican and South American
plateaus extended their knowledge of the American continent
before Columbus; the Polynesian, in which the conquering races
of the Pacific Islands found their way from group to group; and
the Mediterranean. For some of these we have no certain information,
and regarding others the tales narrated in the early records
are so hard to reconcile with present knowledge that they are better
fitted to be the battle-ground of scholars championing rival theories
than the basis of definite history. So it has come about that the
only practicable history of geographical exploration starts from the
Mediterranean centre, the first home of that civilization which has
come to be known as European, though its field of activity has long
since overspread the habitable land of both temperate zones, eastern
Asia alone in part excepted.
From all centres the leading motives of exploration were probably
the same—commercial intercourse, warlike operations, whether
resulting in conquest or in flight, religious zeal expressed in pilgrimages
or missionary journeys, or, from the other side, the avoidance
of persecution, and, more particularly in later years, the
advancement of knowledge for its own sake. At different times one
or the other motive predominated.
Before the 14th century B.C. the warrior kings of Egypt had carried
the power of their arms southward from the delta of the Nile well-nigh
to its source, and eastward to the confines of Assyria. The
hieroglyphic inscriptions of Egypt and the cuneiform inscriptions of
Assyria are rich in records of the movements and achievements of
armies, the conquest of towns and the subjugation of peoples; but
though many of the recorded sites have been identified, their discovery
by wandering armies was isolated from their subsequent
history and need not concern us here.
The Phoenicians are the earliest Mediterranean people in the
consecutive chain of geographical discovery which joins pre-historic
time with the present. From Sidon, and later from its
more famous rival Tyre, the merchant adventurers of
The Phoenicians.
Phoenicia explored and colonized the coasts of the Mediterranean
and fared forth into the ocean beyond. They traded also
on the Red sea, and opened up regular traffic with India as well
as with the ports of the south and west, so that it was natural for
Solomon to employ the merchant navies of Tyre in his oversea trade.
The western emporium known in the scriptures as Tarshish was
probably situated in the south of Spain, possibly at Cadiz, although
some writers contend that it was Carthage in North Africa. Still
more diversity of opinion prevails as to the southern gold-exporting
port of Ophir, which some scholars place in Arabia, others at one or
another point on the east coast of Africa. Whether associated
with the exploitation of Ophir (q.v.) or not the first great voyage of
African discovery appears to have been accomplished by the Phoenicians
sailing the Red Sea. Herodotus (himself a notable traveller
in the 5th century B.C.) relates that the Egyptian king Necho of
the XXVIth Dynasty (c. 600 B.C.) built a fleet on the Red Sea,
and confided it to Phoenician sailors with the orders to sail southward
and return to Egypt by the Pillars of Hercules and the Mediterranean
sea. According to the tradition, which Herodotus quotes
sceptically, this was accomplished; but the story is too vague to
be accepted as more than a possibility.
The great Phoenician colony of Carthage, founded before 800 B.C.,
perpetuated the commercial enterprise of the parent state, and extended
the sphere of practical trade to the ocean shores of Africa
and Europe. The most celebrated voyage of antiquity undertaken
for the express purpose of discovery was that fitted out by the
senate of Carthage under the command of Hanno, with the intention
of founding new colonies along the west coast of Africa. According
to Pliny, the only authority on this point, the period of the voyage
was that of the greatest prosperity of Carthage, which may be taken
as somewhere between 570 and 480 B.C. The extent of this voyage
is doubtful, but it seems probable that the farthest point reached
was on the east-running coast which bounds the Gulf of Guinea
on the north. Himilco, a contemporary of Hanno, was charged
with an expedition along the west coast of Iberia northward, and
as far as the uncertain references to this voyage can be understood,
he seems to have passed the Bay of Biscay and possibly sighted the
coast of England.
The sea power of the Greek communities on the coast of Asia
Minor and in the Archipelago began to be a formidable rival to the
Phoenician soon after the time of Hanno and Himilco,
and peculiar interest attaches to the first recorded Greek
The Greeks.
voyage beyond the Pillars of Hercules. Pytheas, a
navigator of the Phocean colony of Massilia (Marseilles), determined
the latitude of that port with considerable precision by the somewhat
clumsy method of ascertaining the length of the longest day, and
when, about 330 B.C., he set out on exploration to the northward
in search of the lands whence came gold, tin and amber, he followed
this system of ascertaining his position from time to time. If on
each occasion he himself made the observations his voyage must
have extended over six years; but it is not impossible that he
ascertained the approximate length of the longest day in some cases
by questioning the natives. Pytheas, whose own narrative is not
preserved, coasted the Bay of Biscay, sailed up the English Channel
and followed the coast of Britain to its most northerly point. Beyond
this he spoke of a land called Thule, which, if his estimate of the
length of the longest day is correct, may have been Shetland, but
was possibly Iceland; and from some confused statements as to a
sea which could not be sailed through, it has been assumed that
Pytheas was the first of the Greeks to obtain direct knowledge of
the Arctic regions. During this or a second voyage Pytheas entered
the Baltic, discovered the coasts where amber is obtained and returned
to the Mediterranean. It does not seem that any maritime
trade followed these discoveries, and indeed it is doubtful whether
his contemporaries accepted the truth of Pytheas’s narrative;
Strabo four hundred years later certainly did not, but the critical
studies of modern scholars have rehabilitated the Massilian explorer.
The Greco-Persian wars had made the remoter parts of Asia
Minor more than a name to the Greek geographers before the time
of Alexander the Great, but the campaigns of that conqueror
Alexander the Great.
from 329 to 325 B.C. opened up the greater Asia
to the knowledge of Europe. His armies crossed the plains
beyond the Caspian, penetrated the wild mountain passes north-west
of India, and did not turn back until they had entered on the
Indo-Gangetic plain. This was one of the few great epochs of
geographical discovery.
The world was henceforth viewed as a very large place stretching
far on every side beyond the Midland or Mediterranean Sea, and the
land journey of Alexander resulted in a voyage of discovery in the
outer ocean from the mouth of the Indus to that of the Tigris,
thus opening direct intercourse between Grecian and Hindu civilization.
The Greeks who accompanied Alexander described with care
the towns and villages, the products and the aspect of the country.
The conqueror also intended to open up trade by sea between Europe
and India, and the narrative of his general Nearchus records this
famous voyage of discovery, the detailed accounts of the chief
pilot Onesicritus being lost. At the beginning of October 326 B.C.
Nearchus left the Indus with his fleet, and the anchorages sought for
each night are carefully recorded. He entered the Persian Gulf,
and rejoined Alexander at Susa, when he was ordered to prepare
another expedition for the circumnavigation of Arabia. Alexander
died at Babylon in 323 B.C., and the fleet was dispersed without
making the voyage.
The dynasties founded by Alexander’s generals, Seleucus, Antiochus
and Ptolemy, encouraged the same spirit of enterprise which
their master had fostered, and extended geographical knowledge
in several directions. Seleucus Nicator established the Greco-Bactrian
empire and continued the intercourse with India. Authentic
information respecting the great valley of the Ganges was supplied
by Megasthenes, an ambassador sent by Seleucus, who reached the
remote city of Patali-putra, the modern Patna.
The Ptolemies in Egypt showed equal anxiety to extend the
bounds of geographical knowledge. Ptolemy Euergetes (247-222 B.C.)
624
rendered the greatest service to geography by the protection and
The Ptolemies.
encouragement of Eratosthenes, whose labours gave the first approximate
knowledge of the true size of the spherical
earth. The second Euergetes and his successor Ptolemy
Lathyrus (118-115 B.C.) furnished Eudoxus with a fleet
to explore the Arabian sea. After two successful voyages, Eudoxus,
impressed with the idea that Africa was surrounded by ocean on the
south, left the Egyptian service, and proceeded to Cadiz and other
Mediterranean centres of trade seeking a patron who would finance
an expedition for the purpose of African discovery; and we learn
from Strabo that the veteran explorer made at least two voyages
southward along the coast of Africa. The Ptolemies continued to
send fleets annually from their Red Sea ports of Berenice and Myos
Hormus to Arabia, as well as to ports on the coasts of Africa and
India.
The Romans did not encourage navigation and commerce with
the same ardour as their predecessors; still the luxury of Rome,
which gave rise to demands for the varied products
of all the countries of the known world, led to an active
The Romans.
trade both by ships and caravans. But it was the military
genius of Rome, and the ambition for universal empire, which led,
not only to the discovery, but also to the survey of nearly all Europe,
and of large tracts in Asia and Africa. Every new war produced
a new survey and itinerary of the countries which were conquered,
and added one more to the imperishable roads that led from every
quarter of the known world to Rome. In the height of their power
the Romans had surveyed and explored all the coasts of the Mediterranean,
Italy, Greece, the Balkan Peninsula, Spain, Gaul, western
Germany and southern Britain. In Africa their empire included
Egypt, Carthage, Numidia and Mauritania. In Asia they held
Asia Minor and Syria, had sent expeditions into Arabia, and were
acquainted with the more distant countries formerly invaded by
Alexander, including Persia, Scythia, Bactria and India. Roman
intercourse with India especially led to the extension of geographical
knowledge.
Before the Roman legions were sent into a new region to extend
the limits of the empire, it was usual to send out exploring expeditions
to report as to the nature of the country. It is narrated by Pliny
and Seneca that the emperor Nero sent out two centurions on such
a mission towards the source of the Nile (probably about A.D. 60),
and that the travellers pushed southwards until they reached vast
marshes through which they could not make their way either on
foot or in boats. This seems to indicate that they had penetrated
to about 9° N. Shortly before A.D. 79 Hippalus took advantage of
the regular alternation of the monsoons to make the voyage from
the Red Sea to India across the open ocean out of sight of land.
Even though this sea-route was known, the author of the Periplus
of the Erythraean Sea, published after the time of Pliny, recites the
old itinerary around the coast of the Arabian Gulf. It was, however,
in the reigns of Severus and his immediate successors that Roman
intercourse with India was at its height, and from the writings of
Pausanias (c. 174) it appears that direct communication between
Rome and China had already taken place.
After the division of the Roman empire, Constantinople became
the last refuge of learning, arts and taste; while Alexandria continued
to be the emporium whence were imported the commodities
of the East. The emperor Justinian (483-565), in whose reign the
greatness of the Eastern empire culminated, sent two Nestorian
monks to China, who returned with eggs of the silkworm concealed
in a hollow cane, and thus silk manufactures were established in
the Peloponnesus and the Greek islands. It was also in the reign
of Justinian that Cosmas Indicopleustes, an Egyptian merchant,
made several voyages, and afterwards composed his Χριστιανικὴ τοπογραφία (Christian Topography), containing, in addition to his
absurd cosmogony, a tolerable description of India.
The great outburst of Mahommedan conquest in the 7th century
was followed by the Arab civilization, having its centres at Bagdad
and Cordova, in connexion with which geography again
received a share of attention. The works of the ancient
The Arabs.
Greek geographers were translated into Arabic, and starting with a
sound basis of theoretical knowledge, exploration once more made
progress. From the 9th to the 13th century intelligent Arab
travellers wrote accounts of what they had seen and heard in distant
lands. The earliest Arabian traveller whose observations have come
down to us is the merchant Sulaiman, who embarked in the Persian
Gulf and made several voyages to India and China, in the middle of
the 9th century. Abu Zaid also wrote on India, and his work is the
most important that we possess before the epoch-making discoveries
of Marco Polo. Masudi, a great traveller who knew from personal
experience all the countries between Spain and China, described the
plains, mountains and seas, the dynasties and peoples, in his Meadows
of Gold, an abstract made by himself of his larger work News of the
Time. He died in 956, and was known, from the comprehensiveness
of his survey, as the Pliny of the East. Amongst his contemporaries
were Istakhri, who travelled through all the Mahommedan
countries and wrote his Book of Climates in 950, and Ibn Haukal,
whose Book of Roads and Kingdoms, based on the work of Istakhri,
was written in 976. Idrisi, the best known of the Arabian geographical
authors, after travelling far and wide in the first half of
the 12th century, settled in Sicily, where he wrote a treatise descriptive
of an armillary sphere which he had constructed for Roger II.,
the Norman king, and in this work he incorporated all accessible
results of contemporary travel.
The Northmen of Denmark and Norway, whose piratical adventures
were the terror of all the coasts of Europe, and who established
themselves in Great Britain and Ireland, in France and
Sicily, were also geographical explorers in their rough but
The Northmen.
practical way during the darkest period of the middle ages.
All Northmen were not bent on rapine and plunder; many were
peaceful merchants. Alfred the Great, king of the Saxons in
England, not only educated his people in the learning of the past
ages; he inserted in the geographical works he translated many
narratives of the travel of his own time. Thus he placed on record
the voyages of the merchant Ulfsten in the Baltic, including particulars
of the geography of Germany. And in particular he told of
the remarkable voyage of Other, a Norwegian of Helgeland, who
was the first authentic Arctic explorer, the first to tell of the rounding
of the North Cape and the sight of the midnight sun. This voyage
of the middle of the 9th century deserves to be held in happy memory,
for it unites the first Norwegian polar explorer with the first English
collector of travels. Scandinavian merchants brought the products
of India to England and Ireland. From the 8th to the 11th century
a commercial route from India passed through Novgorod to the
Baltic, and Arabian coins found in Sweden, and particularly in
the island of Gotland, prove how closely the enterprise of the Northmen
and of the Arabs intertwined. Five-sixths of these coins
preserved at Stockholm were from the mints of the Samanian
dynasty, which reigned in Khorasan and Transoxiana from about
A.D. 900 to 1000. It was the trade with the East that originally gave
importance to the city of Visby in Gotland.
In the end of the 9th century Iceland was colonized from Norway;
and about 985 the intrepid viking, Eric the Red, discovered Greenland,
and induced some of his Icelandic countrymen to settle on its inhospitable
shores. His son, Leif Ericsson, and others of his followers
were concerned in the discovery of the North American coast (see
Vinland), which, but for the isolation of Iceland from the centres
of European awakening, would have had momentous consequences.
As things were, the importance of this discovery passed unrecognized.
The story of two Venetians, Nicolo and Antonio Zeno, who gave a
vague account of voyages in the northern seas in the end of the 13th
century, is no longer to be accepted as history.
At length the long period of barbarism which accompanied and
followed the fall of the Roman empire drew to a close in Europe.
The Crusades had a favourable influence on the intellectual
state of the Western nations. Interesting regions,
Close of the dark ages.
known only by the scant reports of pilgrims, were made
the objects of attention and study; while religious zeal,
and the hope of gain, combined with motives of mere curiosity,
induced several persons to travel by land into remote regions of the
East, far beyond the countries to which the operations of the crusaders
extended. Among these was Benjamin of Tudela, who set out from
Spain in 1160, travelled by land to Constantinople, and having
visited India and some of the eastern islands, returned to Europe
by way of Egypt after an absence of thirteen years.
Joannes de Plano Carpini, a Franciscan monk, was the head of
one of the missions despatched by Pope Innocent to call the chief
and people of the Tatars to a better mind. He reached
the headquarters of Batu, on the Volga, in February
Asiatic journeys.
1246; and, after some stay, went on to the camp of the
great khan near Karakorum in central Asia, and returned safely
in the autumn of 1247. A few years afterwards, a Fleming named
Rubruquis was sent on a similar mission, and had the merit of being
the first traveller of this era who gave a correct account of the Caspian
Sea. He ascertained that it had no outlet. At nearly the same
time Hayton, king of Armenia, made a journey to Karakorum in
1254, by a route far to the north of that followed by Carpini and
Rubruquis. He was treated with honour and hospitality, and
returned by way of Samarkand and Tabriz, to his own territory.
The curious narrative of King Hayton was translated by Klaproth.
While the republics of Italy, and above all the state of Venice,
were engaged in distributing the rich products of India and the Far
East over the Western world, it was impossible that motives of
curiosity, as well as a desire of commercial advantage, should not be
awakened to such a degree as to impel some of the merchants to
visit those remote lands. Among these were the brothers Polo, who
traded with the East and themselves visited Tatary. The recital
of their travels fired the youthful imagination of young Marco Polo,
son of Nicolo, and he set out for the court of Kublai Khan, with his
father and uncle, in 1265. Marco remained for seventeen years
in the service of the Great Khan, and was employed on many
important missions. Besides what he learnt from his own observation,
he collected much information from others concerning
countries which he did not visit. He returned to Europe possessed
of a vast store of knowledge respecting the eastern parts of the
world, and, being afterwards made a prisoner by the Genoese, he
dictated the narrative of his travels during his captivity. The
work of Marco Polo is the most valuable narrative of travels that
appeared during the middle ages, and despite a cold reception and
many denials of the accuracy of the record, its substantial truthfulness
has been abundantly proved.
625
Missionaries continued to do useful geographical work. Among
them were John of Monte Corvino, a Franciscan monk, Andrew of
Perugia, John Marignioli and Friar Jordanus, who visited the west
coast of India, and above all Friar Odoric of Pordenone. Odoric
set out on his travels about 1318, and his journeys embraced parts
of India, the Malay Archipelago, China and even Tibet, where he
was the first European to enter Lhasa, not yet a forbidden city.
Ibn Batuta, the great Arab traveller, is separated by a wide space
of time from his countrymen already mentioned, and he finds his
proper place in a chronological notice after the days of Marco Polo,
for he did not begin his wanderings until 1325, his career thus coinciding
in time with the fabled journeyings of Sir John Mandeville.
While Arab learning flourished during the darkest ages of European
ignorance, the last of the Arab geographers lived to see the dawn of
the great period of the European awakening. Ibn Batuta went by
land from Tangier to Cairo, then visited Syria, and performed the
pilgrimages to Medina and Mecca. After exploring Persia, and again
residing for some time at Mecca, he made a voyage down the Red
sea to Yemen, and travelled through that country to Aden. Thence
he visited the African coast, touching at Mombasa and Quiloa, and
then sailed across to Ormuz and the Persian Gulf. He crossed
Arabia from Bahrein to Jidda, traversed the Red sea and the desert
to Syene, and descended the Nile to Cairo. After this he revisited
Syria and Asia Minor, and crossed the Black sea, the desert from
Astrakhan to Bokhara, and the Hindu Kush. He was in the service
of Muhammad Tughluk, ruler of Delhi, about eight years, and was
sent on an embassy to China, in the course of which the ambassadors
sailed down the west coast of India to Calicut, and then visited the
Maldive Islands and Ceylon. Ibn Batuta made the voyage through
the Malay Archipelago to China, and on his return he proceeded
from Malabar to Bagdad and Damascus, ultimately reaching Fez,
the capital of his native country, in November 1349. After a journey
into Spain he set out once more for Central Africa in 1352, and
reached Timbuktu and the Niger, returning to Fez in 1353. His
narrative was committed to writing from his dictation.
The European country which had come the most completely
under the influence of Arab culture now began to send forth explorers
to distant lands, though the impulse came not from the
Moors but from Italian merchant navigators in Spanish
Spanish exploration.
service. The peaceful reign of Henry III. of Castile is
famous for the attempts of that prince to extend the
diplomatic relations of Spain to the remotest parts of the earth.
He sent embassies to all the princes of Christendom and to the
Moors. In 1403 the Spanish king sent a knight of Madrid, Ruy
Gonzalez de Clavijo, to the distant court of Timur, at Samarkand.
He returned in 1406, and wrote a valuable narrative of his travels.
Italians continued to make important journeys in the East
during the 15th century. Among them was Nicolo Conti, who
passed through Persia, sailed along the coast of Malabar, visited
Sumatra, Java and the south of China, returned by the Red sea,
and got home to Venice in 1444 after an absence of twenty-five years.
He related his adventures to Poggio Bracciolini, secretary to Pope
Eugenius IV.; and the narrative contains much interesting information.
One of the most remarkable of the Italian travellers was
Ludovico di Varthema, who left his native land in 1502. He went
to Egypt and Syria, and for the sake of visiting the holy cities became
a Mahommedan. He was the first European who gave an account
of the interior of Yemen. He afterwards visited and described
many places in Persia, India and the Malay Archipelago, returning
to Europe in a Portuguese ship after an absence of five years.
In the 15th century the time was approaching when the discovery
of the Cape of Good Hope was to widen the scope of geographical
enterprise. This great event was preceded by the general
utilization in Europe of the polarity of the magnetic
Portuguese exploration—Prince Henry the Navigator.
needle in the construction of the mariner’s compass.
Portugal took the lead along this new path, and foremost
among her pioneers stands Prince Henry the Navigator
(1394-1460), who was a patron both of exploration and
of the study of geographical theory. The great westward
projection of the coast of Africa, and the islands to the north-west
of that continent, were the principal scene of the work of the mariners
sent out at his expense; but his object was to push onward and
reach India from the Atlantic. The progress of discovery received
a check on his death, but only for a time. In 1462 Pedro de Cintra
extended Portuguese exploration along the African coast and discovered
Sierra Leone. Fernan Gomez followed in 1469, and opened
trade with the Gold Coast; and in 1484 Diogo Cão discovered the
mouth of the Congo. The king of Portugal next despatched Bartolomeu
Diaz in 1486 to continue discoveries southwards; while, in the
following year, he sent Pedro de Covilhão and Affonso de Payva
to discover the country of Prester John. Diaz succeeded in rounding
the southern point of Africa, which he named Cabo Tormentoso—the
Cape of Storms—but King João II., foreseeing the realization of the
long-sought passage to India, gave it the stimulating and enduring
name of the Cape of Good Hope. Payva died at Cairo; but Covilhão,
having heard that a Christian ruler reigned in the mountains of
Ethiopia, penetrated into Abyssinia in 1490. He delivered the letter
which João II. had addressed to Prester John to the Negus Alexander
of Abyssinia, but he was detained by that prince and never allowed
to leave the country.
The Portuguese, following the lead of Prince Henry, continued to
look for the road to India by the Cape of Good Hope. The same
end was sought by Christopher Columbus, following the
suggestion of Toscanelli, and under-estimating the diameter
Columbus.
of the globe, by sailing due west. The voyages of Columbus
(1492-1498) resulted in the discovery of the West Indies and North
America which barred the way to the Far East. In 1493 the pope,
Alexander VI., issued a bull instituting the famous “line of demarcation”
running from N. to S. 100 leagues W. of the Azores, to the
west of which the Spaniards were authorized to explore and to the
east of which the Portuguese received the monopoly of discovery.
The direct line of Portuguese exploration resulted in the discovery
of the Cape route to India by Vasco da Gama (1498), and in 1500
to the independent discovery of South America by Pedro Alvarez
Cabral. The voyages of Columbus and of Vasco da Gama were so
important that it is unnecessary to detail their results in this place.
See Columbus, Christopher; Gama, Vasco da.
The three voyages of Vasco da Gama (who died on the scene of his
labours, at Cochin, in 1524) revolutionized the commerce of the
East. Until then the Venetians held the carrying trade
Vasco da Gama.
of India, which was brought by the Persian Gulf and Red
sea into Syria and Egypt, the Venetians receiving the
products of the East at Alexandria and Beirut and distributing
them over Europe. This commerce was a great source of wealth
to Venice; but after the discovery of the new passage round the
Cape, and the conquests of the Portuguese, the trade of the East
passed into other hands.
The discoveries of Columbus awakened a spirit of enterprise in
Spain which continued in full force for a century; adventurers
flocked eagerly across the Atlantic, and discovery followed
discovery in rapid succession. Many of the companions
Spaniards in America.
of Columbus continued his work. Vicente Yañez Pinzon
in 1500 reached the mouth of the Amazon. In the same
year Alonso de Ojeda, accompanied by Juan de la Cosa, from whose
maps we learn much of the discoveries of the 16th century navigators,
and by a Florentine named Amerigo Vespucci, touched the
coast of South America somewhere near Surinam, following the shore
as far as the Gulf of Maracaibo. Vespucci afterwards made three
voyages to the Brazilian coast; and in 1504 he wrote an account
of his four voyages, which was widely circulated, and became the
means of procuring for its author at the hands of the cartographer
Waldseemüller in 1507 the disproportionate distinction of giving his
name to the whole continent. In 1508 Alonso de Ojeda obtained the
government of the coast of South America from Cabo de la Vela
to the Gulf of Darien; Ojeda landed at Cartagena in 1510, and
sustained a defeat from the natives, in which his lieutenant, Juan
de la Cosa, was killed. After another reverse on the east side of the
Gulf of Darien Ojeda returned to Hispaniola and died there. The
Spaniards in the Gulf of Darien were left by Ojeda under the command
of Francisco Pizarro, the future conqueror of Peru. After
suffering much from famine and disease, Pizarro resolved to leave,
and embarked the survivors in small vessels, but outside the harbour
they met a ship which proved to be that of Martin Fernandez Enciso,
Ojeda’s partner, coming with provisions and reinforcements. One
of the crew of Enciso’s ship, Vasco Nuñez de Balboa, the future discoverer
of the Pacific Ocean, induced his commander to form a
settlement on the other side of the Gulf of Darien. The soldiers
became discontented and deposed Enciso, who was a man of learning
and an accomplished cosmographer. His work Suma de Geografia,
which was printed in 1519, is the first Spanish book which gives an
account of America. Vasco Nuñez, the new commander, entered
upon a career of conquest in the neighbourhood of Darien, which
ended in the discovery of the Pacific Ocean on the 25th of September
1513. Vasco Nuñez was beheaded in 1517 by Pedrarias de Avila,
who was sent out to supersede him. This was one of the greatest
calamities that could have happened to South America; for the
discoverer of the South sea was on the point of sailing with a little
fleet into his unknown ocean, and a humane and judicious man would
probably have been the conqueror of Peru, instead of the cruel and
ignorant Pizarro. In the year 1519 Panama was founded by
Pedrarias; and the conquest of Peru by Pizarro followed a few years
afterwards. Hernan Cortes overran and conquered Mexico from
1518 to 1521, and the discovery and conquest of Guatemala by
Alvarado, the invasion of Florida by De Soto, and of Nueva Granada
by Quesada, followed in rapid succession. The first detailed account
of the west coast of South America was written by a keenly observant
old soldier, Pedro de Cieza de Leon, who was travelling in South
America from 1533 to 1550, and published his story at Seville
in 1553.
The great desire of the Spanish government at that time was
to find a westward route to the Moluccas. For this purpose Juan
Diaz de Solis was despatched in October 1515, and in
January 1516 he discovered the mouth of the Rio de la
Pacific Ocean.
Plata. He was, however, killed by the natives, and his
ships returned. In the following year the Portuguese Ferdinando
Magalhães, familiarly known as Magellan, laid before Charles V.,
at Valladolid, a scheme for reaching the Spice Islands by sailing
westward. He started on the 21st of September 1519, entered the
strait which now bears his name in October 1520, worked his way
through between Patagonia and Tierra del Fuego, and entered on
626
the vast Pacific which he crossed without sighting any of its innumerable
island groups. This was unquestionably the greatest of
the voyages which followed from the impulse of Prince Henry, and it
was rendered possible only by the magnificent courage of the commander
in spite of rebellion, mutiny and starvation. It was the
6th of March 1521 when he reached the Ladrone Islands. Thence
Magellan proceeded to the Philippines, and there his career ended
in an unimportant encounter with hostile natives. Eventually a
Biscayan named Sebastian del Cano, sailing home by way of the
Cape of Good Hope, reached San Lucar in command of the “Victoria”
on the 6th of September 1522, with eighteen survivors;
this one ship of the squadron which sailed on the quest succeeded
in accomplishing the first circumnavigation of the globe. Del Cano
was received with great distinction by the emperor, who granted
him a globe for his crest, and the motto Primus circumdedisti me.
While the Spaniards were circumnavigating the
world and completing their knowledge of the coasts of
Central and South America, the Portuguese were actively
Portuguese in Africa and the East.
engaged on similar work as regards Africa and the East
Indies.
With Abyssinia the mission of Covilhão led to further intercourse.
In April 1520 Vasco da Gama, as viceroy of the Indies, took a fleet
into the Red sea, and landed an embassy consisting of Dom Rodriguez
de Lima and Father Francisco Alvarez, a priest whose detailed narrative
is the earliest and not the least interesting account we possess
of Abyssinia. It was not until 1526 that the embassy was dismissed;
and not many years afterwards the negus entreated the help of the
Portuguese against Mahommedan invaders, and the viceroy sent an
expeditionary force, commanded by his brother Cristoforo da Gama,
with 450 musketeers. Da Gama was taken prisoner and killed, but
his followers enabled the Christians of Abyssinia to regain their
power, and a Jesuit mission remained in the country. The Portuguese
also established a close connexion with the kingdom of Congo
on the west side of Africa, and obtained much information respecting
the interior of the continent. Duarte Lopez, a Portuguese settled
in the country, was sent on a mission to Rome by the king of Congo,
and Pope Sixtus V. caused him to recount to his chamberlain,
Felipe Pigafetta, all he had learned during the nine years he had been
in Africa, from 1578 to 1587. This narrative, under the title of
Description of the Kingdom of Congo, was published at Rome by
Pigafetta in 1591. A map was attached on which several great
equatorial lakes are shown, and the empire of Monomwezi or Unyamwezi
is laid down. The most valuable work on Africa about
this time is, however, that written by the Moor Leo Africanus in
the early part of the 16th century. Leo travelled extensively in
the north and west of Africa, and was eventually taken by pirates
and sold to a master who presented him to Pope Leo X. At the
pope’s desire he translated his work on Africa into Italian.
In Further India and the Malay Archipelago the Portuguese
acquired predominating influence at sea, establishing factories on
the Malabar coast, in the Persian Gulf, at Malacca, and in the Spice
Islands, and extending their commercial enterprises from the Red
sea to China. Their missionaries were received at the court of
Akbar, and Benedict Goes, a native of the Azores, was despatched
on a journey overland from Agra to China. He started in 1603,
and, after traversing the least-known parts of Central Asia, he
reached the confines of China. He appears to have ascended from
Kabul to the plateau of the Pamir, and thence onwards by Yarkand,
Khotan and Aksu. He died on the journey in March 1607; and
thus, as one of the brethren pronounced his epitaph, “seeking
Cathay he found heaven.”
The activity and love of adventure, which became a passion for
two or three generations in Spain and Portugal, spread to other
countries. It was the spirit of the age; and England,
Holland and France were fired by it. English enterprise
English, Dutch and French.
was first aroused by John and Sebastian Cabot, father
and son, who came from Venice and settled at Bristol
in the time of Henry VII. The Cabots received a patent in 1496,
empowering them to seek unknown lands; and John Cabot discovered
Newfoundland and part of the coast of America. Sebastian
afterwards made a voyage to Rio de la Plata in the service of Spain,
but he returned to England in 1548 and received a pension from
Edward VI. At his suggestion a voyage was undertaken for the discovery
of a north-east passage to Cathay, with Sir Hugh Willoughby
as captain-general of the fleet and Richard Chancellor as pilot-major.
They sailed in May 1553, but Willoughby and all his crew
perished on the Lapland coast. Chancellor, however, was more
fortunate. He reached the White Sea, performed the journey
overland to Moscow, where he was well received, and may be said
to have been the founder of the trade between Russia and England.
He returned to Archangel and brought his ship back in safety to
England. On a second voyage, in 1556, Chancellor was drowned;
and three subsequent voyages, led by Stephen Burrough, Arthur
Pet and Charles Jackman, in small craft of 50 tons and under,
carried on an examination of the straits which lead into the Kara
sea.
The French followed closely on the track of John Cabot, and
Norman and Breton fishermen frequented the banks of Newfoundland
at the beginning of the 16th century. In 1524 Francis I. sent
Giovanni da Verazzano of Florence on an expedition of discovery
to the coast of North America; and the details of his voyage were
embodied in a letter addressed by him to the king of France from
Dieppe, in July 1524. In 1534 Jacques Cartier set out to continue
the discoveries of Verazzano, and visited Newfoundland and the
Gulf of St Lawrence. In the following year he made another
voyage, discovered the island of Anticosti, and ascended the St
Lawrence to Hochelaga, now Montreal. He returned, after passing
two winters in Canada; and on another occasion he also failed to
establish a colony. Admiral de Coligny made several unsuccessful
endeavours to form a colony in Florida under Jean Ribault
of Dieppe, René de Laudonnière and others, but the settlers
were furiously assailed by the Spaniards and the attempt was
abandoned.
The reign of Elizabeth is famous for the gallant enterprises that
were undertaken by sea and land to discover and bring to light the
unknown parts of the earth. The great promoter of
geographical discovery in the Elizabethan period was
The Elizabethan era.
Richard Hakluyt (1553-1616), who was active in the formation
of the two companies for colonizing Virginia in
1606; and devoted his life to encouraging and recording similar
undertakings. He published much, and left many valuable papers
at his death, most of which, together with many other narratives,
were published in 1622 in the great work of the Rev. Samuel Purchas,
entitled Hakluytus Posthumus, or Purchas his Pilgrimes.
It is from these works that our knowledge of the gallant deeds of
the English and other explorers of the Elizabethan age is mainly
derived. The great and splendidly illustrated collections of voyages
and travels of Theodorus de Bry and Hulsius served a similar useful
purpose on the continent of Europe. One important object of
English maritime adventurers of those days was to discover a route
to Cathay by the north-west, a second was to settle Virginia, and a
third was to raid the Spanish settlements in the West Indies. Nor
was the trade to Muscovy and Turkey neglected; while latterly
a resolute and successful attempt was made to establish direct
commercial relations with India.
The conception of the north-western route to Cathay now leads
the story of exploration, for the first time as far as important and
sustained efforts are concerned, towards the Arctic seas. This part
of the story is fully told under the heading of Polar Regions, and
only the names of Martin Frobisher (1576), John Davis (1585),
Henry Hudson (1607) and William Baffin (1616) need be mentioned
here in order to preserve the complete conspectus of the history of
discovery. The Dutch emulated the British in the Arctic seas during
this period, directing their efforts mainly towards the discovery of
a north-east passage round the northern end of Novaya Zemlya;
and William Barents or Barendsz (1594-1597) is the most famous
name in this connexion, his boat voyage along the coast of Novaya
Zemlya after losing his ship and wintering in a high latitude, being
one of the most remarkable achievements in polar annals.
Many English voyages were also made to Guinea and the West
Indies, and twice English vessels followed in the track of Magellan,
and circumnavigated the globe. In 1577 Francis Drake, who had
previously served with Hawkins in the West Indies, undertook his
celebrated voyage round the world. Reaching the Pacific through
the Strait of Magellan, Drake proceeded northward along the west
coast of America, resolved to attempt the discovery of a northern
passage from the Pacific to the Atlantic. The coast from the
southern extremity of the Californian peninsula to Cape Mendocino
had been discovered by Juan Rodriguez Cabrillo and Francisco de
Ulloa in 1539. Drake’s discoveries extended from Cape Mendocino
to 48° N., in which latitude he gave up his quest, sailed across the
Pacific and reached the Philippine Islands, returning home round
the Cape of Good Hope in 1580.
Thomas Cavendish, emulous of Drake’s example, fitted out three
vessels for an expedition to the South sea in 1586. He took the
same route as Drake along the west coast of America. From Cape
San Lucas Cavendish steered across the Pacific, seeing no land until
he reached the Ladrone Islands. He returned to England in 1588.
The third English voyage into the Pacific was not so fortunate.
Sir Richard Hawkins (1593) on reaching the bay of Atacames, in 1°N.
in 1594, was attacked by a Spanish fleet, and, after a desperate
naval engagement, was forced to surrender. Hawkins declared
his object to be discovery and the survey of unknown lands, and
his voyage, though terminating in disaster, bore good fruit. The
Observations of Sir Richard Hawkins in his Voyage into the South Sea,
published in 1622, are very valuable. It was long before another
British ship entered the Pacific Ocean. Sir John Narborough took
two ships through the Strait of Magellan in 1670 and touched on
the coast of Chile, but it was not until 1685 that Dampier sailed over
the part of the Pacific where Hawkins met his defeat.
The exploring enterprise of the Spanish nation did not wane
after the conquest of Peru and Mexico, and the acquisition of the
vast empire of the Indies. It was spurred into renewed activity
by the audacity of Sir John Hawkins in the West Indies, and by
the appearance of Drake, Cavendish and Richard Hawkins in the
Pacific.
In the interior of South America the Spanish conquerors had
explored the region of the Andes from the isthmus of Panama to
Chile. Pedro de Valdivia in 1540 made an expedition into the
country of the Araucanian Indians of Chile, and was the first to
627
explore the eastern base of the Andes in what is now Argentine
Patagonia. In 1541 Francisco de Orellana discovered the whole
course of the Amazon from its source in the Andes to the Atlantic.
A second voyage on the Amazon was made in 1561 by the mad pirate
Lope de Aguirre; but it was not until 1639 that a full account was
written of the great river by Father Cristoval de Acuña, who ascended
it from its mouth and reached the city of Quito.
The voyage of Drake across the Pacific was preceded by that of
Alvaro de Mendaña, who was despatched from Peru in 1567 to
discover the great Antarctic continent which was believed
to extend far northward into the South sea, the search
Spaniards in the Pacific.
for which now became one of the leading motives of
exploration. After a voyage of eighty days across the
Pacific, Mendaña discovered the Solomon Islands; and the expedition
returned in safety to Callao. The appearance of Drake on
the Peruvian coast led to an expedition being fitted out at Callao,
to go in chase of him, under the command of Pedro Sarmiento. He
sailed from Callao in October 1579, and made a careful survey of
the Strait of Magellan, with the object of fortifying that entrance
to the South sea. The colony which he afterwards took out from
Spain was a complete failure, and is only remembered now from the
name of “Port Famine,” which Cavendish gave to the site at which
he found the starving remnant of Sarmiento’s settlers. In June
1595 Mendaña sailed from the coast of Peru in command of a second
expedition to colonize the Solomon Islands. After discovering the
Marquesas, he reached the island of Santa Cruz of evil memory,
where he and many of the settlers died. His young widow took
command of the survivors and brought them safely to Manila.
The viceroys of Peru still persevered in their attempts to plant a
colony in the hypothetical southern continent. Pedro Fernandez
de Quiros, who was pilot under Mendaña and Luis Vaez de Torres,
were sent in command of two ships to continue the work of exploration.
They sailed from Callao in December 1605, and discovered
several islands of the New Hebrides group. They anchored in a bay
of a large island which Quiros named “Australia del Espiritu Santo.”
From this place Quiros returned to America, but Torres continued
the voyage, passed through the strait between Australia and New
Guinea which bears his name, and explored and mapped the southern
and eastern coasts of New Guinea.
The Portuguese, in the early part of the 17th century (1578-1640),
were under the dominion of Spain, and their enterprise was
to some extent damped; but their missionaries extended geographical
knowledge in Africa. Father Francisco Paez acquired great influence
in Abyssinia, and explored its highlands from 1600 to 1622. Fathers
Mendez and Lobo traversed the deserts between the coast of the
Red sea and the mountains, became acquainted with Lake Tsana,
and discovered the sources of the Blue Nile in 1624-1633.
But the attention of the Portuguese was mainly devoted to vain
attempts to maintain their monopoly of the trade of India against
the powerful rivalry of the English and Dutch. The
English enterprises were persevering, continuous and
Rivalry in the East.
successful. James Lancaster made a voyage to the Indian
Ocean from 1591 to 1594; and in 1599 the merchants and adventurers
of London resolved to form a company, with the object of
establishing a trade with the East Indies. On the 31st of December
1599 Queen Elizabeth granted the charter of incorporation to the
East India Company, and Sir James Lancaster, one of the directors,
was appointed general of their first fleet. He was accompanied
by John Davis, the great Arctic navigator, as pilot-major. This
voyage was eminently successful. The ships touched at Achin in
Sumatra and at Java, returning with full ladings of pepper in 1603.
The second voyage was commanded by Sir Henry Middleton; but
it was in the third voyage, under Keelinge and Hawkins, that the
mainland of India was first reached in 1607. Captain Hawkins
landed at Surat and travelled overland to Agra, passing some time
at the court of the Great Mogul. In the voyage of Sir Edward
Michelborne in 1605, John Davis lost his life in a fight with a Japanese
junk. The eighth voyage, led by Captain Saris, extended the
operations of the company to Japan; and in 1613 the Japanese
government granted privileges to the company; but the British
retired in 1623, giving up their factory. The chief result of this
early intercourse between Great Britain and Japan was the interesting
series of letters written by William Adams from 1611 to 1617. From
the tenth voyage of the East India Company, commanded by
Captain Best, who left England in 1612, dates the establishment of
permanent British factories on the coast of India. It was Captain
Best who secured a regular firman for trade from the Great Mogul.
From that time a fleet was despatched every year, and the company’s
operations greatly increased geographical knowledge of India
and the Eastern Archipelago. British visits to Eastern countries,
at this time, were not confined to the voyages of the company.
Journeys were also made by land, and, among others, the entertaining
author of the Crudities, Thomas Coryate, of Odcombe in
Somersetshire, wandered on foot from France to India, and died
(1617) in the company’s factory at Surat. In 1561 Anthony Jenkinson
arrived in Persia with a letter from Queen Elizabeth to the shah.
He travelled through Russia to Bokhara, and returned by the
Caspian and Volga. In 1579 Christopher Burroughs built a ship
at Nizhniy Novgorod and traded across the Caspian to Baku; and
in 1598 Sir Anthony and Robert Shirley arrived in Persia, and
Robert was afterwards sent by the shah to Europe as his ambassador.
He was followed by a Spanish mission under Garcia de Silva, who
wrote an interesting account of his travels; and to Sir Dormer
Cotton’s mission, in 1628, we are indebted for Sir Thomas Herbert’s
charming narrative. In like manner Sir Thomas Roe’s mission
to India resulted not only in a large collection of valuable reports
and letters of his own, but also in the detailed account of his chaplain
Terry. But the most learned and intelligent traveller in the East,
during the 17th century, was the German, Engelbrecht Kaempfer,
who accompanied an embassy to Persia, in 1684, and was afterwards
a surgeon in the service of the Dutch East India Company. He
was in the Persian Gulf, India and Java, and resided for more than
two years in Japan, of which he wrote a history.
The Dutch nation, as soon as it was emancipated from Spanish
tyranny, displayed an amount of enterprise, which, for a long time,
was fully equal to that of the British. The Arctic voyages
of Barents were quickly followed by the establishment of
Dutch exploration, 16th-17th centuries.
a Dutch East India Company; and the Dutch, ousting
the Portuguese, not only established factories on the
mainland of India and in Japan, but acquired a preponderating
influence throughout the Malay Archipelago. In 1583 Jan
Hugen van Linschoten made a voyage to India with a Portuguese
fleet, and his full and graphic descriptions of India, Africa, China
and the Malay Archipelago must have been of no small use to his
countrymen in their distant voyages. The first of the Dutch Indian
voyages was performed by ships which sailed in April 1595, and
rounded the Cape of Good Hope. A second large Dutch fleet sailed
in 1598; and, so eager was the republic to extend her commerce
over the world that another fleet, consisting of five ships of Rotterdam,
was sent in the same year by way of Magellan’s Strait, under
Jacob Mahu as admiral, with William Adams as pilot. Mahu died
on the passage out, and was succeeded by Simon de Cordes, who
was killed on the coast of Chile. In September 1599 the fleet had
entered the Pacific. The ships were then steered direct for Japan,
and anchored off Bungo in April 1600. In the same year, 1598, a
third expedition was despatched under Oliver van Noort, a native
of Utrecht, but the voyage contributed nothing to geography. The
Dutch Company in 1614 again resolved to send a fleet to the Moluccas
by the westward route, and Joris Spilbergen was appointed to the
command as admiral, with a commission from the States-General.
He was furnished with four ships of Amsterdam, two of Rotterdam
and one from Zeeland. On the 6th of May 1615 Spilbergen entered
the Pacific Ocean, and touched at several places on the coast of Chile
and Peru, defeating the Spanish fleet in a naval engagement off
Chilca. After plundering Payta and making requisitions at Acapulco,
the Dutch fleet crossed the Pacific and reached the Moluccas in
March 1616.
The Dutch now resolved to discover a passage into the Pacific
to the south of Tierra del Fuego, the insular nature of which had
been ascertained by Sir Francis Drake. The vessels fitted out for
this purpose were the “Eendracht,” of 360 tons, commanded by
Jacob Lemaire, and the “Hoorn,” of 110 tons, under Willem
Schouten. They sailed from the Texel on the 14th of June 1615,
and by the 20th of January 1616 they were south of the entrance
of Magellan’s Strait. Passing through the strait of Lemaire they
came to the southern extremity of Tierra del Fuego, which was
named Cape Horn, in honour of the town of Hoorn in West Friesland,
of which Schouten was a native. They passed the cape on the 31st
of January, encountering the usual westerly winds. The great merit
of this discovery of a second passage into the South sea lies in the
fact that it was not accidental or unforeseen, but was due to the
sagacity of those who designed the voyage. On the 1st of March
the Dutch fleet sighted the island of Juan Fernandez; and, having
crossed the Pacific, the explorers sailed along the north coast of
New Guinea and arrived at the Moluccas on the 17th of September
1616.
There were several early indications of the existence of the great
Australian continent, and the Dutch endeavoured to obtain further
knowledge concerning the country and its extent; but only its
northern and western coasts had been visited before the time of
Governor van Diemen. Dirk Hartog had been on the west coast
in latitude 26° 30′ S. in 1616. Pelsert struck on a reef called “Houtman’s
Abrolhos” on the 4th of June 1629. In 1697 the Dutch
captain Vlamingh landed on the west coast of Australia, then called
New Holland, in 31° 43′ S., and named the Swan river from the black
swans he discovered there. In 1642 the governor and council of
Batavia fitted out two ships to prosecute the discovery of the south
land, then believed to be part of a vast Antarctic continent, and
entrusted the command to Captain Abel Jansen Tasman. This
voyage proved to be the most important to geography that had been
undertaken since the first circumnavigation of the globe. Tasman
sailed from Batavia in 1642, and on the 24th of November sighted
high land in 42° 30′ S., which was named van Diemen’s Land, and
after landing there proceeded to the discovery of the western coast
of New Zealand; at first called Staten Land, and supposed to be connected
with the Antarctic continent from which this voyage proved
New Holland to be separated. He then reached Tongatabu, one
of the Friendly Islands of Cook; and returned by the north coast
of New Guinea to Batavia. In 1644 Tasman made a second voyage
to effect a fuller discovery of New Guinea.
628
The French directed their enterprise more in the direction of
North America than of the Indies. One of their most distinguished
explorers was Samuel Champlain, a captain in the navy,
French in North America.
who, after a remarkable journey through Mexico and the
West Indies from 1599 to 1602, established his historic
connexion with Canada, to the geographical knowledge
of which he made a very large addition.
The principles and methods of surveying and position finding
had by this time become well advanced, and the most remarkable
example of the early application of these improvements
is to be found in the survey of China by Jesuit missionaries.
Missionaries in the East.
They first prepared a map of the country round Peking,
which was submitted to the emperor Kang-hi, and,
being satisfied with the accuracy of the European method of surveying,
he resolved to have a survey made of the whole empire on the
same principles. This great work was begun in July 1708, and the
completed maps were presented to the emperor in 1718. The
records preserved in each city were examined, topographical information
was diligently collected, and the Jesuit fathers checked their
triangulation by meridian altitudes of the sun and pole star and by a
system of remeasurements. The result was a more accurate map of
China than existed, at that time, of any country in Europe. Kang-hi
next ordered a similar map to be made of Tibet, the survey being
executed by two lamas who were carefully trained as surveyors
by the Jesuits at Peking. From these surveys were constructed
the well-known maps which were forwarded to Duhalde, and which
D’Anville utilized for his atlas.
Several European missionaries had previously found their way
from India to Tibet. Antonio Andrada, in 1624, was the first
European to enter Tibet since the visit of Friar Odoric
The 18th century.
in 1325. The next journey was that of Fathers Grueber
and Dorville about 1660, who succeeded in passing from
China, through Tibet, into India. In 1715 Fathers Desideri and
Freyre made their way from Agra, across the Himalayas, to Lhasa,
and the Capuchin Friar Orazio della Penna resided in that city
from 1735 until 1747. But the most remarkable journey in this
direction was performed by a Dutch traveller named Samuel van de
Putte. He left Holland in 1718, went by land through Persia to
India, and eventually made his way to Lhasa, where he resided for a
long time. He went thence to China, returned to Lhasa, and was
in India in time to be an eye-witness of the sack of Delhi by Nadir
Asia.
Shah in 1737. In 1743 he left India and died at Batavia
on the 27th of September 1745. The premature death
of this illustrious traveller is the more to be lamented because his
vast knowledge died with him. Two English missions sent by
Warren Hastings to Tibet, one led by George Bogle in 1774, and the
other by Captain Turner in 1783, complete Tibetan exploration in
the 18th century.
From Persia much new information was supplied by Jean Chardin,
Jean Tavernier, Charles Hamilton, Jean de Thévenot and Father
Jude Krusinski, and by English traders on the Caspian. In 1738
John Elton traded between Astrakhan and the Persian port of
Enzelî on the Caspian, and undertook to build a fleet for Nadir
Shah. Another English merchant, named Jonas Hanway, arrived
at Astrabad from Russia, and travelled to the camp of Nadir at
Kazvin. One lasting and valuable result of Hanway’s wanderings
was a charming book of travels. In 1700 Guillaume Delisle published
his map of the continents of the Old World; and his successor
D’Anville produced his map of India in 1752. D’Anville’s map
contained all that was then known, but ten years afterwards Major
Rennell began his surveying labours, which extended over the
period from 1763 to 1782. His survey covered an area 900 m. long
by 300 wide, from the eastern confines of Bengal to Agra, and from
the Himalayas to Calpi. Rennell was indefatigable in collecting
geographical information; his Bengal atlas appeared in 1781, his
famous map of India in 1788 and the memoir in 1792. Surveys
were also made along the Indian coasts.
Arabia received very careful attention, in the 18th century,
from the Danish scientific mission, which included Carsten Niebuhr
among its members. Niebuhr landed at Loheia, on the coast of
Yemen, in December 1762, and went by land to Sana. All the other
members of the mission died, but he proceeded from Mokha to
Bombay. He then made a journey through Persia and Syria to
Constantinople, returning to Copenhagen in 1767. His valuable
work, the Description of Arabia, was published in 1772, and was
followed in 1774-1778 by two volumes of travels in Asia. The great
traveller survived until 1815, when he died at the age of eighty-two.
James Bruce of Kinnaird, the contemporary of Niebuhr, was
equally devoted to Eastern travel; and his principal geographical
work was the tracing of the Blue Nile from its source to
its junction with the White Nile. Before the death of
Africa.
Bruce an African Association was formed, in 1788, for collecting
information respecting the interior of that continent, with Major
Rennell and Sir Joseph Banks as leading members. The association
first employed John Ledyard (who had previously made an extraordinary
journey into Siberia) to cross Africa from east to west
on the parallel of the Niger, and William Lucas to cross the Sahara
to Fezzan. Lucas went from Tripoli to Mesurata, obtained some
information respecting Fezzan and returned in 1789. One of the
chief problems the association wished to solve was that of the existence
and course of the river Niger, which was believed by some
authorities to be identical with the Congo. Mungo Park, then an
assistant surgeon of an Indiaman, volunteered his services, which
were accepted by the association, and in 1795 he succeeded in
reaching the town of Segu on the Niger, but was prevented from
continuing his journey to Timbuktu. Five years later he accepted
an offer from the government to command an expedition into the
interior of Africa, the plan being to cross from the Gambia to the
Niger and descend the latter river to the sea. After losing most of
his companions he himself and the rest perished in a rapid on the
Niger at Busa, having been attacked from the shore by order of a
chief who thought he had not received suitable presents. His work,
however, had established the fact that the Niger was not identical
with the Congo.
While the British were at work in the direction of the Niger, the
Portuguese were not unmindful of their old exploring fame. In
1798 Dr F.J.M. de Lacerda, an accomplished astronomer, was
appointed to command a scientific expedition of discovery to the
north of the Zambesi. He started in July, crossed the Muchenja
Mountains, and reached the capital of the Cazembe, where he died
of fever. Lacerda left a valuable record of his adventurous journey;
but with Mungo Park and Lacerda the history of African exploration
in the 18th century closes.
In South America scientific exploration was active during this
period. The great geographical event of the century, as regards
that continent, was the measurement of an arc of the
meridian. The undertaking was proposed by the French
South America.
Academy as part of an investigation with the object
of ascertaining the length of the degree near the equator and near the
pole respectively so as to determine the figure of the earth. A
commission left Paris in 1735, consisting of Charles Marie de la
Condamine, Pierre Bouguer, Louis Godin and Joseph de Jussieu
the naturalist. Spain appointed two accomplished naval officers,
the brothers Ulloa, as coadjutors. The operations were carried on
during eight years on a plain to the south of Quito; and, in addition
to his memoir on this memorable measurement, La Condamine
collected much valuable geographical information during a voyage
down the Amazon. The arc measured was 3° 7′ 3″ in length;
and the work consisted of two measured bases connected by a series
of triangles, one north and the other south of the equator, on the
meridian of Quito. Contemporaneously, in 1738, Pierre Louis
Moreau de Maupertuis, Alexis Claude Clairaut, Charles Etienne
Louis Camus, Pierre Charles Lemonnier and the Swedish physicist
Celsius measured an arc of the meridian in Lapland.
The British and French governments despatched several expeditions
of discovery into the Pacific and round the world during the
18th century. They were preceded by the wonderful
and romantic voyages of the buccaneers. The narratives
The Pacific Ocean.
of such men as Woodes Rogers, Edward Davis, George
Shelvocke, Clipperton and William Dampier, can never
fail to interest, while they are not without geographical value.
The works of Dampier are especially valuable, and the narratives
of William Funnell and Lionel Wafer furnished the best accounts
then extant of the Isthmus of Darien. Dampier’s literary ability
eventually secured for him a commission in the king’s service;
and he was sent on a voyage of discovery, during which he explored
part of the coasts of Australia and New Guinea, and discovered the
strait which bears his name between New Guinea and New Britain,
returning in 1701. In 1721 Jacob Roggewein was despatched on a
voyage of some importance across the Pacific by the Dutch West
India Company, during which he discovered Easter Island on the
6th of April 1722.
The voyage of Lord Anson to the Pacific in 1740-1744 was of a
predatory character, and he lost more than half his men from scurvy;
while it is not pleasant to reflect that at the very time when the
French and Spaniards were measuring an arc of the meridian at
Quito, the British under Anson were pillaging along the coast of the
Pacific and burning the town of Payta. But a romantic interest
attaches to the wreck of the “Wager,” one of Anson’s fleet, on a
desert island near Chiloe, for it bore fruit in the charming narrative
of Captain John Byron, which will endure for all time. In 1764
Byron himself was sent on a voyage of discovery round the world,
which led immediately after his return to the despatch of another
to complete his work, under the command of Captain Samuel Wallis.
The expedition, consisting of the “Dolphin” commanded by
Wallis, and the “Swallow” under Captain Philip Carteret, sailed in
September 1766, but the ships were separated on entering the Pacific
from the Strait of Magellan. Wallis discovered Tahiti on the 19th
of June 1767, and he gave a detailed account of that island. He
returned to England in May 1768. Carteret discovered the Charlotte
and Gloucester Islands, and Pitcairn Island on the 2nd of July 1767;
revisited the Santa Cruz group, which was discovered by Mendaña
and Quiros; and discovered the strait separating New Britain from
New Ireland. He reached Spithead again in February 1769. Wallis
and Carteret were followed very closely by the French expedition
of Bougainville, which sailed from Nantes in November 1766.
Bougainville had first to perform the unpleasant task of delivering
up the Falkland Islands, where he had encouraged the formation
of a French settlement, to the Spaniards. He then entered the
Pacific, and reached Tahiti in April 1768. Passing through the New
629
Hebrides group he touched at Batavia, and arrived at St Malo after
an absence of two years and four months.
The three voyages of Captain James Cook form an era in the history
of geographical discovery. In 1767 he sailed for Tahiti, with the
object of observing the transit of Venus, accompanied
by two naturalists, Sir Joseph Banks and Dr Solander,
Captain Cook.
a pupil of Linnaeus, as well as by two astronomers. The
transit was observed on the 3rd of June 1769. After exploring
Tahiti and the Society group, Cook spent six months surveying New
Zealand, which he discovered to be an island, and the coast of New
South Wales from latitude 38° S. to the northern extremity. The
belief in a vast Antarctic continent stretching far into the temperate
zone had never been abandoned, and was vehemently asserted by
Charles Dalrymple, a disappointed candidate nominated by the
Royal Society for the command of the Transit expedition of 1769.
In 1772 the French explorer Yves Kerguelen de Tremarec had discovered
the land that bears his name in the South Indian Ocean
without recognizing it to be an island, and naturally believed it
to be part of the southern continent.
Cook’s second voyage was mainly intended to settle the question
of the existence of such a continent once for all, and to define the
limits of any land that might exist in navigable seas towards the
Antarctic circle. James Cook at his first attempt reached a south
latitude of 57° 15′. On a second cruise from the Society Islands,
in 1773, he, first of all men, crossed the Antarctic circle, and was
stopped by ice in 71° 10′ S. During the second voyage Cook visited
Easter Island, discovered several islands of the New Hebrides and
New Caledonia; and on his way home by Cape Horn, in March 1774,
he discovered the Sandwich Island group and described South
Georgia. He proved conclusively that any southern continent
that might exist lay under the polar ice. The third voyage was
intended to attempt the passage from the Pacific to the Atlantic by
the north-east. The “Resolution” and “Discovery” sailed in
1776, and Cook again took the route by the Cape of Good Hope.
On reaching the North American coast, he proceeded northward,
fixed the position of the western extremity of America and surveyed
Bering Strait. He was stopped by the ice in 70° 41′ N., and named
the farthest visible point on the American shore Icy Cape. He then
visited the Asiatic shore and discovered Cape North. Returning to
Hawaii, Cook was murdered by the natives. On the 14th of February
1779, his second, Captain Edward Clerke, took command, and
proceeding to Petropavlovsk in the following summer, he again
examined the edge of the ice, but only got as far as 70° 33′ N. The
ships returned to England in October 1780.
In 1785 the French government carefully fitted out an expedition
of discovery at Brest, which was placed under the command of
François La Pérouse, an accomplished and experienced officer.
After touching at Concepcion in Chile and at Easter Island, La
Pérouse proceeded to Hawaii and thence to the coast of California,
of which he has given a very interesting account. He then crossed
the Pacific to Macao, and in July 1787 he proceeded to explore the
Gulf of Tartary and the shores of Sakhalin, remaining some time at
Castries Bay, so named after the French minister of marine. Thence
he went to the Kurile Islands and Kamchatka, and sailed from the
far north down the meridian to the Navigator and Friendly Islands.
He was in Botany Bay in January 1788; and sailing thence, the
explorer, his ship and crew were never seen again. Their fate was
long uncertain. In September 1791 Captain Antoine d’Entrecasteaux
sailed from Brest with two vessels to seek for tidings.
He visited the New Hebrides, Santa Cruz, New Caledonia and Solomon
Islands, and made careful though rough surveys of the Louisiade
Archipelago, islands north of New Britain and part of New Guinea.
D’Entrecasteaux died on board his ship on the 20th of July 1793,
without ascertaining the fate of La Pérouse. Captain Peter Dillon
at length ascertained, in 1828, that the ships of La Pérouse had been
wrecked on the island of Vanikoro during a hurricane.
The work of Captain Cook bore fruit in many ways. His master,
Captain William Bligh, was sent in the “Bounty” to convey breadfruit
plants from Tahiti to the West Indies. He reached Tahiti in
October 1788, and in April 1789 a mutiny broke out, and he, with
several officers and men, was thrust into an open boat in mid-ocean.
During the remarkable voyage he then made to Timor, Bligh
passed amongst the northern islands of the New Hebrides, which
he named the Banks Group, and made several running surveys.
He reached England in March 1790. The “Pandora,” under
Captain Edwards, was sent out in search of the “Bounty,” and
discovered the islands of Cherry and Mitre, east of the Santa Cruz
group, but she was eventually lost on a reef in Torres Strait. In
1796-1797 Captain Wilson, in the missionary ship “Duff,” discovered
the Gambier and other islands, and rediscovered the islands known
to and seen by Quiros, but since called the Duff Group. Another
result of Captain Cook’s work was the colonization of Australia.
On the 18th of January 1788 Admiral Phillip and Captain Hunter
arrived in Botany Bay in the “Supply” and “Sirius,” followed by
six transports, and established a colony at Port Jackson. Surveys
were then undertaken in several directions. In 1795 and 1796
Matthew Flinders and George Bass were engaged on exploring work
in a small boat called the “Tom Thumb.” In 1797 Bass, who had
been a surgeon, made an expedition southwards, continued the work
of Cook from Ram Head, and explored the strait which bears his
name, and in 1798 he and Flinders were surveying on the east coast
of Van Diemen’s land.
Yet another outcome of Captain Cook’s work was the voyage of
George Vancouver, who had served as a midshipman in Cook’s
second and third voyages. The Spaniards under Quadra had begun
a survey of north-western America and occupied Nootka Sound,
which their government eventually agreed to surrender. Captain
Vancouver was sent out to receive the cession, and to survey the
coast from Cape Mendocino northwards. He commanded the old
“Discovery,” and was at work during the seasons of 1792, 1793 and
1794, wintering at Hawaii. Returning home in 1795, he completed
his narrative and a valuable series of charts.
The 18th century saw the Arctic coast of North America reached
at two points, as well as the first scientific attempt to reach the
North Pole. The Hudson Bay Company had been incorporated
in 1670, and its servants soon extended their
Arctic regions.
operations over a wide area to the north and west of
Canada. In 1741 Captain Christopher Middleton was ordered to
solve the question of a passage from Hudson Bay to the westward.
Leaving Fort Churchill in July 1742, he discovered the Wager river
and Repulse Bay. He was followed by Captain W. Moor in 1746,
and Captain Coats in 1751, who examined the Wager Inlet up to the
end. In November 1769 Samuel Hearne was sent by the Hudson
Bay Company to discover the sea on the north side of America,
but was obliged to return. In February 1770 he set out again from
Fort Prince of Wales; but, after great hardships, he was again
forced to return to the fort. He started once more in December
1771, and at length reached the Coppermine river, which he surveyed
to its mouth, but his observations are unreliable. With the same
object Alexander Mackenzie, with a party of Canadians, set out from
Fort Chippewyan on the 3rd of June 1789, and descending the great
river which now bears the explorer’s name reached the Arctic sea.
In February 1773 the Royal Society submitted a proposal to the
king for an expedition towards the North Pole. The expedition was
fitted out under Captains Constantine Phipps and Skeffington
Lutwidge, and the highest latitude reached was 80° 48′ N., but no
opening was discovered in the heavy Polar pack. The most important
Arctic work in the 18th century was performed by the
Russians, for they succeeded in delineating the whole of the northern
coast of Siberia. Some of this work was possibly done at a still
earlier date. The Cossack Simon Dezhneff is thought to have made a
voyage, in the summer of 1648, from the river Kolyma, through
Bering Strait (which was rediscovered by Vitus Bering in 1728) to
Anadyr. Between 1738 and 1750 Manin and Sterlegoff made their
way in small sloops from the mouth of the Yenesei as far north as
75° 15′ N. The land from Taimyr to Cape Chelyuskin, the most
northern extremity of Siberia, was mapped in many years of patient
exploration by Chelyuskin, who reached the extreme point
(77° 34′ N.) in May 1742. To the east of Cape Chelyuskin the
Russians encountered greater difficulties. They built small vessels
at Yakutsk on the Lena, 900 m. from its mouth, whence the first
expedition was despatched under Lieut. Prontschichev in 1735. He
sailed from the mouth of the Lena to the mouth of the Olonek,
where he wintered, and on the 1st of September 1736 he got as far
as 77° 29′ N., within 5 m. of Cape Chelyuskin. Both he and his
young wife died of scurvy, and the vessel returned. A second
expedition, under Lieut. Laptyev, started from the Lena in 1739,
but encountered masses of drift ice in Chatanga bay, and with this
ended the voyages to the westward of the Lena. Several attempts
were also made to navigate the sea from the Lena to the Kolyma.
In 1736 Lieut. Laptyev sailed, but was stopped by the drift ice in
August, and in 1739, during another trial, he reached the mouth
of the Indigirka, where he wintered. In the season of 1740 he
continued his voyage to beyond the Kolyma, wintering at Nizhni
Kolymsk. In September 1740 Vitus Bering sailed from Okhotsk
on a second Arctic voyage with George William Steller on board
as naturalist. In June 1741 he named the magnificent peak on the
coast of North America Mount St Elias and explored the Aleutian
Islands. In November the ship was wrecked on Bering Island;
and the gallant Dane, worn out with scurvy, died there on the
8th of December 1741. In March 1770 a merchant named Liakhov
saw a large herd of reindeer coming from the north to the Siberian
coast, which induced him to start in a sledge in the direction whence
they came. Thus he reached the New Siberian or Liakhov Islands,
and for years afterwards the seekers for fossil ivory resorted to them.
The Russian Captain Vassili Chitschakov in 1765 and 1766 made two
persevering attempts to penetrate the ice north of Spitsbergen,
and reached 80° 30′ N., while Russian parties twice wintered at Bell
Sound.
In reviewing the progress of geographical discovery thus far, it
has been possible to keep fairly closely to a chronological order.
But in the 19th century and after exploring work was so
generally and steadily maintained in all directions, and
Geographical societies.
was in so many cases narrowed down from long journeys
to detailed surveys within relatively small areas, that it
becomes desirable to cover the whole period at one view for certain
great divisions of the world. (See Africa; Asia; Australia; Polar
Regions; &c.) Here, however, may be noticed the development
of geographical societies devoted to the encouragement of exploration
and research. The first of the existing geographical societies was
630
that of Paris, founded in 1825 under the title of La Société de
Géographie. The Berlin Geographical Society (Gesellschaft für
Erdkunde) is second in order of seniority, having been founded in
1827. The Royal Geographical Society, which was founded in
London in 1830, comes third on the list; but it may be viewed as a
direct result of the earlier African Association founded in 1788.
Sir John Barrow, Sir John Cam Hobhouse (Lord Broughton), Sir
Roderick Murchison, Mr Robert Brown and Mr Bartle Frere formed
the foundation committee of the Royal Geographical Society, and
the first president was Lord Goderich. The action of the society in
supplying practical instruction to intending travellers, in astronomy,
surveying and the various branches of science useful to collectors,
has had much to do with advancement of discovery. Since the war
of 1870 many geographical societies have been established on the
continent of Europe. At the close of the 19th century there were
upwards of 100 such societies in the world, with more than 50,000
members, and over 150 journals were devoted entirely to geographical
subjects.11 The great development of photography has been a notable
aid to explorers, not only by placing at their disposal a faithful and
ready means of recording the features of a country and the types
of inhabitants, but by supplying a method of quick and accurate
topographical surveying.
The Principles of Geography
As regards the scope of geography, the order of the various
departments and their inter-relation, there is little difference of
opinion, and the principles of geography12 are now generally accepted
by modern geographers. The order in which the various subjects
are treated in the following sketch is the natural succession from
fundamental to dependent facts, which corresponds also to the
evolution of the diversities of the earth’s crust and of its inhabitants.
The fundamental geographical conceptions are mathematical, the
relations of space and form. The figure and dimensions of the
earth are the first of these. They are ascertained by a
combination of actual measurement of the highest
Mathematical geography.
precision on the surface and angular observations of the
positions of the heavenly bodies. The science of geodesy
is part of mathematical geography, of which the arts of surveying
and cartography are applications. The motions of the earth
as a planet must be taken into account, as they render possible
the determination of position and direction by observations of the
heavenly bodies. The diurnal rotation of the earth furnishes two
fixed points or poles, the axis joining which is fixed or nearly so in its
direction in space. The rotation of the earth thus fixes the directions
of north and south and defines those of east and west. The angle
which the earth’s axis makes with the plane in which the planet
revolves round the sun determines the varying seasonal distribution
of solar radiation over the surface and the mathematical zones of
climate. Another important consequence of rotation is the deviation
produced in moving bodies relatively to the surface. In the form
known as Ferrell’s Law this runs: “If a body moves in any direction
on the earth’s surface, there is a deflecting force which arises from
the earth’s rotation which tends to deflect it to the right in the
northern hemisphere but to the left in the southern hemisphere.”
The deviation is of importance in the movement of air, of ocean
currents, and to some extent of rivers.13
In popular usage the words “physical geography” have come
to mean geography viewed from a particular standpoint rather
than any special department of the subject. The popular
meaning is better conveyed by the word physiography, a
Physical geography.
term which appears to have been introduced by Linnaeus,
and was reinvented as a substitute for the cosmography of the middle
ages by Professor Huxley. Although the term has since been limited
by some writers to one particular part of the subject, it seems best
to maintain the original and literal meaning. In the stricter sense,
physical geography is that part of geography which involves the
processes of contemporary change in the crust and the circulation
of the fluid envelopes. It thus draws upon physics for the explanation
of the phenomena with the space-relations of which it is specially
concerned. Physical geography naturally falls into three divisions,
dealing respectively with the surface of the lithosphere—geomorphology;
the hydrosphere—oceanography; and the atmosphere—climatology.
All these rest upon the facts of mathematical geography,
and the three are so closely inter-related that they cannot
be rigidly separated in any discussion.
Geomorphology is the part of geography which deals with terrestrial
relief, including the submarine as well as the subaërial portions
of the crust. The history of the origin of the various forms belongs
to geology, and can be completely studied only by geological
Geomorphology.
methods. But the relief of the crust is not a finished piece of sculpture;
the forms are for the most part transitional, owing
their characteristic outlines to the process by which they
are produced; therefore the geographer must, for strictly
geographical purposes, take some account of the processes which are
now in action modifying the forms of the crust. Opinion still differs
as to the extent to which the geographer’s work should overlap that
of the geologist.
The primary distinction of the forms of the crust is that between
elevations and depressions. Granting that the geoid or mean
surface of the ocean is a uniform spheroid, the distribution of land
and water approximately indicates a division of the surface of the
globe into two areas, one of elevation and one of depression. The
increasing number of measurements of the height of land in all
continents and islands, and the very detailed levellings in those
countries which have been thoroughly surveyed, enable the average
elevation of the land above sea-level to be fairly estimated, although
many vast gaps in accurate knowledge remain, and the estimate
is not an exact one. The only part of the sea-bed the configuration
of which is at all well known is the zone bordering the coasts where
the depth is less than about 100 fathoms or 200 metres, i.e. those
parts which sailors speak of as “in soundings.” Actual or projected
routes for telegraph cables across the deep sea have also been sounded
with extreme accuracy in many cases; but beyond these lines of
sounding the vast spaces of the ocean remain unplumbed save for
the rare researches of scientific expeditions, such as those of the
“Challenger,” the “Valdivia,” the “Albatross” and the “Scotia.”
Thus the best approximation to the average depth of the ocean is
little more than an expert guess; yet a fair approximation is probable
for the features of sub-oceanic relief are so much more uniform than
those of the land that a smaller number of fixed points is required
to determine them.
The chief element of uncertainty as to the largest features of the
relief of the earth’s crust is due to the unexplored area in the Arctic
region and the larger regions of the Antarctic, of which
we know nothing. We know that the earth’s surface if
Crustal relief.
unveiled of water would exhibit a great region of elevation
arranged with a certain rough radiate symmetry round the north
pole, and extending southwards in three unequal arms which taper
to points in the south. A depression surrounds the little-known
south polar region in a continuous ring and extends northwards in
three vast hollows lying between the arms of the elevated area. So
far only is it possible to speak with certainty, but it is permissible
to take a few steps into the twilight of dawning knowledge and
indicate the chief subdivisions which are likely to be established
in the great crust-hollow and the great crust-heap. The boundary
between these should obviously be the mean surface of the
sphere.
Sir John Murray deduced the mean height of the land of the globe
as about 2250 ft. above sea-level, and the mean depth of the oceans
as 2080 fathoms or 12,480 ft. below sea-level.14 Calculating the area
of the land at 55,000,000 sq. m. (or 28.6% of the surface), and that
of the oceans as 137,200,000 sq. m. (or 71.4% of the surface), he
found that the volume of the land above sea-level was 23,450,000
cub. m., the volume of water below sea-level 323,800,000, and the
total volume of the water equal to about 1⁄666th of the volume of the
whole globe. From these data, as revised by A. Supan,15 H.R. Mill
calculated the position of mean sphere-level at about 10,000 ft. or
1700 fathoms below sea-level. He showed that an imaginary
spheroidal shell, concentric with the earth and cutting the slope
between the elevated and depressed areas at the contour-line of 1700
fathoms, would not only leave above it a volume of the crust equal
to the volume of the hollow left below it, but would also divide the
surface of the earth so that the area of the elevated region was
equal to that of the depressed region.16
A similar observation was made almost simultaneously by
Romieux,17 who further speculated on the equilibrium between the
weight of the elevated land mass and that of the total
waters of the ocean, and deduced some interesting relations
Areas of the crust according to Murray.
between them. Murray, as the result of his study,
divided the earth’s surface into three zones—the continental
area containing all dry land, the transitional area including
the submarine slopes down to 1000 fathoms, and the abysmal area
consisting of the floor of the ocean beyond that depth; and Mill
proposed to take the line of mean-sphere level, instead of the empirical
depth of 1000 fathoms, as the boundary between the transitional
and abysmal areas.
An elaborate criticism of all the existing data regarding the
volume relations of the vertical relief of the globe was made in
1894 by Professor Hermann Wagner, whose recalculations of volumes
631
and mean heights—the best results which have yet been obtained—led
to the following conclusions.18
The area of the dry land was taken as 28.3% of the surface of the
globe, and that of the oceans as 71.7%. The mean height deduced
for the land was 2300 ft. above sea-level, the mean depth
of the sea 11,500 ft. below, while the position of mean-sphere
Areas of the crust according to Wagner.
level comes out as 7500 ft. (1250 fathoms) below
sea-level. From this it would appear that 43% of the
earth’s surface was above and 57% below the mean
level. It must be noted, however, that since 1895 the soundings
of Nansen in the north polar area, of the “Valdivia,” “Belgica,”
“Gauss” and “Scotia” in the Southern Ocean, and of various
surveying ships in the North and South Pacific, have proved that
the mean depth of the ocean is considerably greater than had been
supposed, and mean-sphere level must therefore lie deeper than the
calculations of 1895 show; possibly not far from the position deduced
from the freer estimate of 1888. The whole of the available data
were utilized by the prince of Monaco in 1905 in the preparation of a
complete bathymetrical map of the oceans on a uniform scale,
which must long remain the standard work for reference on ocean
depths.
By the device of a hypsographic curve co-ordinating the vertical
relief and the areas of the earth’s surface occupied by each zone of
elevation, according to the system introduced by Supan,19 Wagner
showed his results graphically.
This curve with the values reduced from metres to feet is reproduced
below.
Wagner subdivides the earth’s surface, according to elevation,
into the following five regions:
Wagner’s Divisions of the Earth’s Crust:
| Name. | Per cent of
Surface. | From | To |
| Depressed area | 3 | Deepest. | −16,400 feet. |
| Oceanic plateau | 54 | −16,400 feet. | − 7,400 feet. |
| Continental slope | 9 | − 7,400 feet. | − 660 feet. |
| Continental plateau | 28 | − 660 feet. | + 3,000 feet. |
| Culminating area | 6 | + 3,300 feet. | Highest. |
The continental plateau might for purposes of detailed study be
divided into the continental shelf from -660 ft. to sea-level, and
lowlands from sea-level to +660 ft. (corresponding to
the mean level of the whole globe).20 Uplands reaching
from 660 ft. to 2300 (the approximate mean level of
the land), and highlands, from 2300 upwards, might
also be distinguished.

A striking fact in the configuration of the crust is
that each continent, or elevated mass of the crust, is
diametrically opposite to an ocean basin or great depression;
the only partial exception being in the case of southern
Arrangement of world-ridges and hollows.
South America, which is antipodal to eastern Asia.
Professor C. Lapworth has generalized the grand features
of crustal relief in a scheme of attractive simplicity. He
sees throughout all the chaos of irregular crust-forms the
recurrence of a certain harmony, a succession of folds or
waves which build up all the minor features.21 One
great series of crust waves from east to west is crossed by a
second great series of crust waves from north to south, giving rise
by their interference to six great elevated masses (the continents),
arranged in three groups, each consisting of a northern and a
southern member separated by a minor depression. These elevated
masses are divided from one another by similar great depressions.
He says: “The surface of each of our great continental masses of
land resembles that of a long and broad arch-like form, of
which we see the simplest type in the New World. The
surface of the North American arch is sagged downwards
Lapworth’s fold-theory.
in the middle into a central depression which
lies between two long marginal plateaus, and these
plateaus are finally crowned by the wrinkled crests which form its
two modern mountain systems. The surface of each of our ocean
floors exactly resembles that of a continent turned upside down.
Taking the Atlantic as our simplest type, we may say that the
surface of an ocean basin resembles that of a mighty trough or
syncline, buckled up more or less centrally in a medial ridge, which
is bounded by two long and deep marginal hollows, in the cores
of which still deeper grooves sink to the profoundest depths. This
complementary relationship descends even to the minor features
of the two. Where the great continental sag sinks below the ocean
level, we have our gulfs and our Mediterraneans, seen in our type
continent, as the Mexican Gulf and Hudson Bay. Where the
central oceanic buckle attains the water-line we have our oceanic
islands, seen in our type ocean, as St Helena and the Azores. Although
the apparent crust-waves are neither equal in size nor
symmetrical in form, this complementary relationship between
them is always discernible. The broad Pacific depression seems to
answer to the broad elevation of the Old World—the narrow trough
of the Atlantic to the narrow continent of America.”
The most thorough discussion of the great features of terrestrial
relief in the light of their origin is that by Professor E. Suess,22 who
points out that the plan of the earth is the result of
two movements of the crust—one, subsidence over
Suess’s theory.
wide areas, giving rise to oceanic depressions and leaving
the continents protuberant; the other, folding along comparatively
narrow belts, giving rise to mountain ranges. This theory of crust
blocks dropped by subsidence is opposed to Lapworth’s theory of
vast crust-folds, but geology is the science which has to decide
between them.
Geomorphology is concerned, however, in the suggestions which
have been made as to the cause of the distribution of heap and
hollow in the larger features of the crust. Élie de Beaumont, in
his speculations on the relation between the direction of mountain
ranges and their geological age and character, was feeling towards a
comprehensive theory of the forms of crustal relief; but his ideas
were too geometrical, and his theory that the earth is a spheroid
built up on a rhombic dodecahedron, the pentagonal faces of which
determined the direction of mountain ranges, could not be proved.23
The “tetrahedral theory” brought forward by Lowthian Green,24
that the form of the earth is a spheroid based on a regular tetrahedron,
is more serviceable, because it accounts for three very
interesting facts of the terrestrial plan—(1) the antipodal
position of continents and ocean basins; (2) the triangular
outline of the continents; and (3) the excess of
sea in the southern hemisphere. Recent investigations
have recalled attention to the work of Lowthian Green,
but the question is still in the controversial stage.25 The
study of tidal strain in the earth’s crust by Sir George
Darwin has led that physicist to indicate the possibility
of the triangular form and southerly direction of the
continents being a result of the differential or tidal
attraction of the sun and moon. More recently Professor
A.E.H. Love has shown that the great features of the
relief of the lithosphere may be expressed by spherical
harmonics of the first, second and third degrees, and their
formation related to gravitational action in a sphere of
unequal density.26
In any case it is fully recognized that the plan of the earth is so
clear as to leave no doubt as to its being due to some general cause
which should be capable of detection.
If the level of the sea were to become coincident with the mean
level of the lithosphere, there would result one tri-radiate land-mass
of nearly uniform outline and one continuous sheet of water
632
broken by few islands. The actual position of sea-level lies so near
The continents.
the summit of the crust-heap that the varied relief of the upper
portion leads to the formation of a complicated coast-line
and a great number of detached portions of land.
The hydrosphere is, in fact, continuous, and the land is
all in insular masses: the largest is the Old World of Europe,
Asia and Africa; the next in size, America; the third, possibly,
Antarctica; the fourth, Australia; the fifth, Greenland. After
this there is a considerable gap before New Guinea, Borneo, Madagascar,
Sumatra and the vast multitude of smaller islands descending
in size by regular gradations to mere rocks. The contrast between
island and mainland was natural enough in the days before the
discovery of Australia, and the mainland of the Old World was
traditionally divided into three continents. These “continents,”
“parts of the earth,” or “quarters of the globe,” proved to be
convenient divisions; America was added as a fourth, and subsequently
divided into two, while Australia on its discovery was classed
sometimes as a new continent, sometimes merely as an island, sometimes
compromisingly as an island-continent, according to individual
opinion. The discovery of the insularity of Greenland might again
give rise to the argument as to the distinction between island and
continent. Although the name of continent was not applied to
large portions of land for any physical reasons, it so happens that
there is a certain physical similarity or homology between them
which is not shared by the smaller islands or peninsulas.
The typical continental form is triangular as regards its sea-level
outline. The relief of the surface typically includes a central plain,
sometimes dipping below sea-level, bounded by lateral
highlands or mountain ranges, loftier on one side than
Homology of continents.
on the other, the higher enclosing a plateau shut in by
mountains. South America and North America follow
this type most closely; Eurasia (the land mass of Europe and Asia)
comes next, while Africa and Australia are farther removed from
the type, and the structure of Antarctica and Greenland is unknown.
If the continuous, unbroken, horizontal extent of land in a continent
is termed its trunk,27 and the portions cut up by inlets or
channels of the sea into islands and peninsulas the limbs, it is possible
to compare the continents in an instructive manner.
The following table is from the statistics of Professor H. Wagner,28
his metric measurements being transposed into British units:
Comparison of the Continents.
| | Area
total
mil.
sq. m. | Mean
height,
feet. | Area
trunk,
mil.
sq. m. | Area
penin-
sulas,
mil.
sq. m. | Area
islands,
mil.
sq. m. | Area
limbs,
mil.
sq. m. | Area
limbs,
per
cent. |
| Old World | 35.8 | 2360 | | | | | |
| New World | 16.2 | 2230 | | | | | |
| Eurasia | 20.85 | 2620 | 15.42 | 4.09 | 1.34 | 5.43 | 26 |
| Africa | 11.46 | 2130 | 11.22 | .. | 0.24 | 0.24 | 2.1 |
| North America | 9.26 | 2300 | 6.92 | 0.78 | 1.56 | 2.34 | 25 |
| South America | 6.84 | 1970 | 6.76 | 0.02 | 0.06 | 0.08 | 1.1 |
| Australia | 3.43 | 1310 | 2.77 | 0.16 | 0.50 | 0.66 | 19 |
| Asia | 17.02 | 3120 | 12.93 | 3.05 | 1.04 | 4.09 | 24 |
| Europe | 3.83 | 980 | 2.49 | 1.04 | 0.30 | 1.34 | 35 |
The usual classification of islands is into continental and oceanic.
The former class includes all those which rise from the continental
shelf, or show evidence in the character of their rocks of
having at one time been continuous with a neighbouring
Islands.
continent. The latter rise abruptly from the oceanic abysses.
Oceanic islands are divided according to their geological character
into volcanic islands and those of organic origin, including coral
islands. More elaborate subdivisions according to structure, origin and
position have been proposed.29 In some cases a piece of land is only
an island at high water, and by imperceptible gradation the form
passes into a peninsula. The typical peninsula is connected with the
mainland by a relatively narrow isthmus; the name is, however, extended
to any limb projecting from the trunk of the mainland, even
when, as in the Indian peninsula, it is connected by its widest part.
Small peninsulas are known as promontories or headlands, and
the extremity as a cape. The opposite form, an inlet of the sea, is
known when wide as a gulf, bay or bight, according
to size and degree of inflection, or as a fjord or ria when
Coasts.
long and narrow. It is convenient to employ a specific name for a
projection of a coast-line less pronounced than a peninsula, and for
an inlet less pronounced than a bay or bight; outcurve and incurve
may serve the turn. The varieties of coast-lines were reduced to an
exact classification by Richthofen, who grouped them according to
the height and slope of the land into cliff-coasts (Steilküsten)—narrow
beach coasts with cliffs, wide beach coasts with cliffs, and
low coasts, subdividing each group according as the coast-line runs
parallel to or crosses the line of strike of the mountains, or is not
related to mountain structure. A further subdivision depends on
the character of the inter-relation of land and sea along the shore
producing such types as a fjord-coast, ria-coast or lagoon-coast.
This extremely elaborate subdivision may be reduced, as Wagner
points out, to three types—the continental coast where the sea comes
up to the solid rock-material of the land; the marine coast, which is
formed entirely of soft material sorted out by the sea; and the composite
coast, in which both forms are combined.
On large-scale maps it is necessary to show two coast-lines, one
for the highest, the other for the lowest tide; but in small-scale
maps a single line is usually wider than is required to
represent the whole breadth of the inter-tidal zone.
Coast-lines.
The measurement of a coast-line is difficult, because
the length will necessarily be greater when measured on a large-scale
map where minute irregularities can be taken into account.
It is usual to distinguish between the general coast-line measured
from point to point of the headlands disregarding the smaller bays,
and the detailed coast-line which takes account of every inflection
shown by the map employed, and follows up river entrances to the
point where tidal action ceases. The ratio between these two
coast-lines represents the “coastal development” of any region.
While the forms of the sea-bed are not yet sufficiently well known
to admit of exact classification, they are recognized to be as a rule
distinct from the forms of the land, and the importance
of using a distinctive terminology is felt. Efforts have
Submarine forms.
been made to arrive at a definite international agreement
on this subject, and certain terms suggested by a committee were
adopted by the Eighth International Geographical Congress at New
York in 1904.30 The forms of the ocean floor include the “shelf,”
or shallow sea margin, the “depression,” a general term applied to
all submarine hollows, and the “elevation.” A depression when of
great extent is termed a “basin,” when it is of a more or less round
form with approximately equal diameters, a “trough” when it is
wide and elongated with gently sloping borders, and a “trench”
when narrow and elongated with steeply sloping borders, one of
which rises higher than the other. The extension of a trough or
basin penetrating the land or an elevation is termed an “embayment”
when wide, and a “gully” when long and narrow; and the
deepest part of a depression is termed a “deep.”
A depression of small extent when steep-sided is
termed a “caldron,” and a long narrow depression
crossing a part of the continental border is termed
a “furrow.” An elevation of great extent which
rises at a very gentle angle from a surrounding
depression is termed a “rise,” one which is relatively
narrow and steep-sided a “ridge,” and one
which is approximately equal in length and breadth
but steep-sided a “plateau,” whether it springs
direct from a depression or from a rise. An elevation
of small extent is distinguished as a “dome”
when it is more than 100 fathoms from the surface,
a “bank” when it is nearer the surface than
100 fathoms but deeper than 6 fathoms, and a
“shoal” when it comes within 6 fathoms of the
surface and so becomes a serious danger to shipping.
The highest point of an elevation is termed
a “height,” if it does not form an island or one
of the minor forms.
The forms of the dry land are of infinite variety, and have been
studied in great detail.31 From the descriptive or topographical
point of view, geometrical form alone should be considered;
Land forms.
but the origin and geological structure of
land forms must in many cases be taken into account
when dealing with the function they exercise in the control of
mobile distributions. The geographers who have hitherto given
most attention to the forms of the land have been trained as geologists,
and consequently there is a general tendency to make origin
or structure the basis of classification rather than form alone.
The fundamental form-elements may be reduced to the six
proposed by Professor Penck as the basis of his double system of
classification by form and origin.32 These may be looked
The six elementary land forms.
upon as being all derived by various modifications or
arrangements of the single form-unit, the slope or inclined
plane surface. No one form occurs alone, but always
grouped together with others in various ways to make up districts,
regions and lands of distinctive characters. The form-elements are:
633
1. The plain or gently inclined uniform surface.
2. The scarp or steeply inclined slope; this is necessarily of
small extent except in the direction of its length.
3. The valley, composed of two lateral parallel slopes inclined
towards a narrow strip of plain at a lower level which itself slopes
downwards in the direction of its length. Many varieties of this
fundamental form may be distinguished.
4. The mount, composed of a surface falling away on every side
from a particular place. This place may either be a point, as
in a volcanic cone, or a line, as in a mountain range or ridge of
hills.
5. The hollow or form produced by a land surface sloping inwards
from all sides to a particular lowest place, the converse of a mount.
6. The cavern or space entirely surrounded by a land surface.
These forms never occur scattered haphazard over a region,
but always in an orderly subordination depending on their mode
of origin. The dominant forms result from crustal
movements, the subsidiary from secondary reactions
Geology and land forms.
during the action of the primitive forms on mobile distributions.
The geological structure and the mineral composition
of the rocks are often the chief causes determining the
character of the land forms of a region. Thus the scenery of a limestone
country depends on the solubility and permeability of the
rocks, leading to the typical Karst-formations of caverns, swallow-holes
and underground stream courses, with the contingent phenomena
of dry valleys and natural bridges. A sandy beach or desert
owes its character to the mobility of its constituent sand-grains,
which are readily drifted and piled up in the form of dunes. A
region where volcanic activity has led to the embedding of dykes or
bosses of hard rock amongst softer strata produces a plain broken by
abrupt and isolated eminences.33
It would be impracticable to go fully into the varieties of each
specific form; but, partly as an example of modern geographical
classification, partly because of the exceptional importance
of mountains amongst the features of the land, one
Classification of mountains.
exception may be made. The classification of mountains
into types has usually had regard rather to geological
structure than to external form, so that some geologists would even
apply the name of a mountain range to a region not distinguished
by relief from the rest of the country if it bear geological evidence
of having once been a true range. A mountain may be described
(it cannot be defined) as an elevated region of irregular surface
rising comparatively abruptly from lower ground. The actual
elevation of a summit above sea-level does not necessarily affect its
mountainous character; a gentle eminence, for instance, rising a
few hundred feet above a tableland, even if at an elevation of say
15,000 ft., could only be called a hill.34 But it may be said that
any abrupt slope of 2000 ft. or more in vertical height may justly
be called a mountain, while abrupt slopes of lesser height may
be called hills. Existing classifications, however, do not take
account of any difference in kind between mountain and hills,
although it is common in the German language to speak of Hügelland,
Mittelgebirge and Hochgebirge with a definite significance.
The simple classification employed by Professor James Geikie35
into mountains of accumulation, mountains of elevation and mountains
of circumdenudation, is not considered sufficiently thorough
by German geographers, who, following Richthofen, generally
adopt a classification dependent on six primary divisions, each of
which is subdivided. The terms employed, especially for the subdivisions,
cannot be easily translated into other languages, and the
English equivalents in the following table are only put forward
tentatively:—
Richthofen’s Classification of Mountains36
I. Tektonische Gebirge—Tectonic mountains.
(a) Bruchgebirge oder Schollengebirge—Block mountains.
1. Einseitige Schollengebirge oder Schollenrandgebirge—Scarp or tilted block mountains.
(i.) Tafelscholle—Table blocks.
(ii.) Abrasionsscholle—Abraded blocks.
(iii.) Transgressionsscholle—Blocks of unconformable strata.
2. Flexurgebirge—Flexure mountains.
3. Horstgebirge—Symmetrical block mountains.
(b) Faltungsgebirge—Fold mountains.
1. Homöomorphe Faltungsgebirge—Homomorphic fold mountains.
2. Heteromorphe Faltungsgebirge—Heteromorphic fold mountains.
II. Rumpfgebirge oder Abrasionsgebirge—Trunk or abraded mountains.
III. Ausbruchsgebirge—Eruptive mountains.
IV. Aufschüttungsgebirge—Mountains of accumulation.
V. Flachböden—Plateaux.
(a) Abrasionsplatten—Abraded plateaux.
(b) Marines Flachland—Plain of marine erosion.
(c) Schichtungstafelland—Horizontally stratified tableland.
(d) Übergusstafelland—Lava plain.
(e) Stromflachland—River plain.
(f) Flachböden der atmosphärischen Aufschüttung—Plains of aeolian formation.
VI. Erosionsgebirge—Mountains of erosion.
|
From the morphological point of view it is more important to
distinguish the associations of forms, such as the mountain mass
or group of mountains radiating from a centre, with the
valleys furrowing their flanks spreading towards every
Mountain forms.
direction; the mountain chain or line of heights, forming a
long narrow ridge or series of ridges separated by parallel valleys;
the dissected plateau or highland, divided into mountains of circumdenudation
by a system of deeply-cut valleys; and the isolated
peak, usually a volcanic cone or a hard rock mass left projecting after
the softer strata which embedded it have been worn away (Monadnock
of Professor Davis).
The geographical distribution of mountains is intimately associated
with the great structural lines of the continents of which they form
the culminating region. Lofty lines of fold mountains
form the “backbones” of North America in the Rocky
Distribution of mountains.
Mountains and the west coast systems, of South America
in the Cordillera of the Andes, of Europe in the Pyrenees,
Alps, Carpathians and Caucasus, and of Asia in the mountains of
Asia Minor, converging on the Pamirs and diverging thence in the
Himalaya and the vast mountain systems of central and eastern
Asia. The remarkable line of volcanoes around the whole coast
of the Pacific and along the margin of the Caribbean and Mediterranean
seas is one of the most conspicuous features of the globe.
If land forms may be compared to organs, the part they serve in
the economy of the earth may, without straining the term, be
characterized as functions. The first and simplest
Functions of land forms.
Land waste.
function of the land surface is that of guiding loose
material to a lower level. The downward pull of gravity
suffices to bring about the fall of such material, but the
path it will follow and the distance it will travel before coming to
rest depend upon the land form. The loose material may, and in
an arid region does, consist only of portions of the higher
parts of the surface detached by the expansion and
contraction produced by heating and cooling due to
radiation. Such broken material rolling down a uniform scarp
would tend to reduce its steepness by the loss of material in the
upper part and by the accumulation of a mound or scree against
the lower part of the slope. But where the side is not a uniform
scarp, but made up of a series of ridges and valleys, the tendency
will be to distribute the detritus in an irregular manner, directing
it away from one place and collecting it in great masses in another,
so that in time the land form assumes a new appearance. Snow
accumulating on the higher portions of the land, when compacted
into ice and caused to flow downwards by gravity, gives rise, on
Glaciers.
account of its more coherent character, to continuous
glaciers, which mould themselves to the slopes down
which they are guided, different ice-streams converging to send
forward a greater volume. Gradually coming to occupy definite
beds, which are deepened and polished by the friction, they impress
a characteristic appearance on the land, which guides them as they
traverse it, and, although the ice melts at lower levels, vast quantities
of clay and broken stones are brought down and deposited in terminal
moraines where the glacier ends.
Rain is by far the most important of the inorganic mobile distributions
upon which land forms exercise their function of guidance
and control. The precipitation of rain from the aqueous
Rain.
vapour of the atmosphere is caused in part by vertical
movements of the atmosphere involving heat changes and apparently
independent of the surface upon which precipitation occurs; but in
greater part it is dictated by the form and altitude of the land surface
and the direction of the prevailing winds, which itself is largely
influenced by the land. It is on the windward faces of the highest
ground, or just beyond the summit of less dominant heights upon the
leeward side, that most rain falls, and all that does not evaporate
or percolate into the ground is conducted back to the sea by a route
which depends only on the form of the land. More mobile and more
searching than ice or rock rubbish, the trickling drops are guided by
the deepest lines of the hillside in their incipient flow, and as these
River systems.
lines converge, the stream, gaining strength, proceeds in
its torrential course to carve its channel deeper and entrench
itself in permanent occupation. Thus the stream-bed,
from which at first the water might be blown away into a new
channel by a gale of wind, ultimately grows to be the strongest line
of the landscape. As the main valley deepens, the tributary stream-beds
are deepened also, and gradually cut their way headwards,
enlarging the area whence they draw their supplies. Thus new
land forms are created—valleys of curious complexity, for example—by
634
the “capture” and diversion of the water of one river by another,
leading to a change of watershed.37 The minor tributaries become
more numerous and more constant, until the system of torrents
has impressed its own individuality on the mountain side. As
the river leaves the mountain, ever growing by the accession of
tributaries, it ceases, save in flood time, to be a formidable instrument
of destruction; the gentler slope of the land surface gives to
it only power sufficient to transport small stones, gravel, sand and
ultimately mud. Its valley banks are cut back by the erosion of
minor tributaries, or by rain-wash if the climate be moist, or left
steep and sharp while the river deepens its bed if the climate be
arid. The outline of the curve of a valley’s sides ultimately depends
on the angle of repose of the detritus which covers them, if there
has been no subsequent change, such as the passage of a glacier
along the valley, which tends to destroy the regularity of the cross-section.
The slope of the river bed diminishes until the plain compels
the river to move slowly, swinging in meanders proportioned to its
size, and gradually, controlled by the flattening land, ceasing to
transport material, but raising its banks and silting up its bed by
the dropped sediment, until, split up and shoaled, its distributaries
struggle across its delta to the sea. This is the typical river of which
there are infinite varieties, yet every variety would, if time were
given, and the land remained unchanged in level relatively to the sea,
ultimately approach to the type. Movements of the land
Adjustment of rivers to land.
either of subsidence or elevation, changes in the land by
the action of erosion in cutting back an escarpment or
cutting through a col, changes in climate by affecting the
rainfall and the volume of water, all tend to throw the
river valley out of harmony with the actual condition of
its stream. There is nothing more striking in geography than the
perfection of the adjustment of a great river system to its valleys
when the land has remained stable for a very lengthened period.
Before full adjustment has been attained the river bed may be
broken in places by waterfalls or interrupted by lakes; after adjustment
the bed assumes a permanent outline, the slope diminishing
more and more gradually, without a break in its symmetrical descent.
Excellent examples of the indecisive drainage of a new land surface,
on which the river system has not had time to impress itself, are to be
seen in northern Canada and in Finland, where rivers are separated
by scarcely perceptible divides, and the numerous lakes frequently
belong to more than one river system.
The action of rivers on the land is so important that it has been
made the basis of a system of physical geography by Professor
W.M. Davis, who classifies land surfaces in terms of
the three factors—structure, process and time.38 Of
The geographical cycle.
these time, during which the process is acting on the
structure, is the most important. A land may thus be
characterized by its position in the “geographical cycle”, or cycle
of erosion, as young, mature or old, the last term being reached
when the base-level of erosion is attained, and the land, however
varied its relief may have been in youth or maturity, is reduced to
a nearly uniform surface or peneplain. By a re-elevation of a
peneplain the rivers of an old land surface may be restored to
youthful activity, and resume their shaping action, deepening the
old valleys and initiating new ones, starting afresh the whole course
of the geographical cycle. It is, however, not the action of the
running water on the land, but the function exercised by the land
on the running water, that is considered here to be the special
province of geography. At every stage of the geographical cycle
the land forms, as they exist at that stage, are concerned in guiding
the condensation and flow of water in certain definite ways. Thus,
for example, in a mountain range at right angles to a prevailing
sea-wind, it is the land forms which determine that one side of the
range shall be richly watered and deeply dissected by a complete
system of valleys, while the other side is dry, indefinite in its valley
systems, and sends none of its scanty drainage to the sea. The
action of rain, ice and rivers conspires with the movement of land
waste to strip the layer of soil from steep slopes as rapidly as it
forms, and to cause it to accumulate on the flat valley bottoms, on
the graceful flattened cones of alluvial fans at the outlet of the gorges
of tributaries, or in the smoothly-spread surface of alluvial plains.
The whole question of the régime of rivers and lakes is sometimes
treated under the name hydrography, a name used by some writers
in the sense of marine surveying, and by others as synonymous with
oceanography. For the study of rivers alone the name potamology39
has been suggested by Penck, and the subject being of much practical
importance has received a good deal of attention.40
The study of lakes has also been specialized under the name of
limnology (see Lake).41 The existence of lakes in hollows of the land
depends upon the balance between precipitation and evaporation.
A stream flowing into a hollow will tend to fill it up, and
Lakes and internal drainage.
the water will begin to escape as soon as its level rises high
enough to reach the lowest part of the rim. In the case
of a large hollow in a very dry climate the rate of
evaporation may be sufficient to prevent the water from ever rising
to the lip, so that there is no outflow to the sea, and a basin of internal
drainage is the result. This is the case, for instance, in the Caspian
sea, the Aral and Balkhash lakes, the Tarim basin, the Sahara, inner
Australia, the great basin of the United States and the Titicaca
basin. These basins of internal drainage are calculated to amount
to 22% of the land surface. The percentages of the land surface
draining to the different oceans are approximately—Atlantic, 34.3%;
Arctic sea, 16.5%; Pacific, 14.4%; Indian Ocean, 12.8%.42
The parts of a river system have not been so clearly defined as is
desirable, hence the exaggerated importance popularly attached to
“the source” of a river. A well-developed river system
has in fact many equally important and widely-separated
Terminology of river systems.
sources, the most distant from the mouth, the highest,
or even that of largest initial volume not being necessarily
of greater geographical interest than the rest.
The whole of the land which directs drainage towards one river is
known as its basin, catchment area or drainage area—sometimes,
by an incorrect expression, as its valley or even its watershed.
The boundary line between one drainage area and others is rightly
termed the watershed, but on account of the ambiguity which has
been tolerated it is better to call it water-parting or, as in America,
divide. The only other important term which requires to be noted
here is talweg, a word introduced from the German into French
and English, and meaning the deepest line along the valley, which
is necessarily occupied by a stream unless the valley is dry.
The functions of land forms extend beyond the control of the
circulation of the atmosphere, the hydrosphere and the water which
is continually being interchanged between them; they are exercised
with increased effect in the higher departments of biogeography and
anthropogeography.
The sum of the organic life on the globe is termed by some geographers
the biosphere, and it has been estimated that the whole
mass of living substance in existence at one time would
cover the surface of the earth to a depth of one-fifth of
Biogeography.
an inch.43 The distribution of living organisms is a
complex problem, a function of many factors, several of which
are yet but little known. They include the biological nature of
the organism and its physical environment, the latter involving
conditions in which geographical elements, direct or indirect, preponderate.
The direct geographical elements are the arrangement
of land and sea (continents and islands standing in sharp contrast)
and the vertical relief of the globe, which interposes barriers of a
less absolute kind between portions of the same land area or oceanic
depression. The indirect geographical elements, which, as a rule,
act with and intensify the direct, are mainly climatic; the prevailing
winds, rainfall, mean and extreme temperatures of every
locality depending on the arrangement of land and sea and of land
forms. Climate thus guided affects the weathering of rocks, and
so determines the kind and arrangement of soil. Different species
of organisms come to perfection in different climates; and it may
be stated as a general rule that a species, whether of plant or animal,
once established at one point, would spread over the whole zone
of the climate congenial to it unless some barrier were interposed
to its progress. In the case of land and fresh-water organisms
the sea is the chief barrier; in the case of marine organisms, the
land. Differences in land forms do not exert great influence on the
distribution of living creatures directly, but indirectly such land
forms as mountain ranges and internal drainage basins are very
potent through their action on soil and climate. A snow-capped
mountain ridge or an arid desert forms a barrier between different
forms of life which is often more effective than an equal breadth of
sea. In this way the surface of the land is divided into numerous
natural regions, the flora and fauna of each of which include some
distinctive species not shared by the others. The distribution of
life is discussed in the various articles in this Encyclopaedia dealing
with biological, botanical and zoological subjects.44
635
The classification of the land surface into areas inhabited by
distinctive groups of plants has been attempted by many phyto-geographers,
but without resulting in any scheme of
general acceptance. The simplest classification is perhaps
Floral zones.
that of Drude according to climatic zones, subdivided
according to continents. This takes account of—(1) the Arctic-Alpine
zone, including all the vegetation of the region bordering
on perpetual snow; (2) the Boreal zone, including the temperate
lands of North America, Europe and Asia, all of which are substantially
alike in botanical character; (3) the Tropical zone, divided
sharply into (a) the tropical zone of the New World, and (b) the
tropical zone of the Old World, the forms of which differ in a significant
degree; (4) the Austral zone, comprising all continental
land south of the equator, and sharply divided into three regions
the floras of which are strikingly distinct—(a) South American,
(b) South African and (c) Australian; (5) the Oceanic, comprising
all oceanic islands, the flora of which consists exclusively of forms
whose seeds could be drifted undestroyed by ocean currents or
carried by birds. To these might be added the antarctic, which is
still very imperfectly known. Many subdivisions and transitional
zones have been suggested by different authors.
From the point of view of the economy of the globe this classification
by species is perhaps less important than that by mode
of life and physiological character in accordance with
environment. The following are the chief areas of
Vegetation areas.
vegetational activity usually recognized: (1) The ice-deserts
of the arctic and antarctic and the highest mountain regions,
where there is no vegetation except the lowest forms, like that
which causes “red snow.” (2) The tundra or region of intensely
cold winters, forbidding tree-growth, where mosses and lichens
cover most of the ground when unfrozen, and shrubs occur of
species which in other conditions are trees, here stunted to the
height of a few inches. A similar zone surrounds the permanent
snow on lofty mountains in all latitudes. The tundra passes by
imperceptible gradations into the moor, bog and heath of warmer
climates. (3) The temperate forests of evergreen or deciduous trees,
according to circumstances, which occupy those parts of both
temperate zones where rainfall and sunlight are both abundant.
(4) The grassy steppes or prairies where the rainfall is diminished
and temperatures are extreme, and grass is the prevailing form of
vegetation. These pass imperceptibly into—(5) the arid desert,
where rainfall is at a minimum, and the only plants are those modified
to subsist with the smallest supply of water. (6) The tropical forest,
which represents the maximum of plant luxuriance, stimulated by
the heaviest rainfall, greatest heat and strongest light. These
divisions merge one into the other, and admit of almost indefinite
subdivision, while they are subject to great modifications by human
interference in clearing and cultivating. Plants exhibit the controlling
power of environment to a high degree, and thus vegetation is
usually in close adjustment to the bolder geographical features of
a region.
The divisions of the earth into faunal regions by Dr P.L. Sclater
have been found to hold good for a large number of groups of animals
as different in their mode of life as birds and mammals,
and they may thus be accepted as based on nature.
Faunal realms.
They are six in number: (1) Palaearctic, including
Europe, Asia north of the Himalaya, and Africa north of the Sahara;
(2) Ethiopian, consisting of Africa south of the Atlas range, and
Madagascar; (3) Oriental, including India, Indo-China and the
Malay Archipelago north of Wallace’s line, which runs between
Bali and Lombok; (4) Australian, including Australia, New Zealand,
New Guinea and Polynesia; (5) Nearctic or North America, north
of Mexico; and (6) Neotropical or South America. Each of these
divisions is the home of a special fauna, many species of which
are confined to it alone; in the Australian region, indeed, practically
the whole fauna is peculiar and distinctive, suggesting a prolonged
period of complete biological isolation. In some cases, such as the
Ethiopian and Neotropical and the Palaearctic and Nearctic regions,
the faunas, although distinct, are related, several forms on opposite
sides of the Atlantic being analogous, e.g. the lion and puma, ostrich
and rhea. Where two of the faunal realms meet there is usually,
though not always, a mixing of faunas. These facts have led some
naturalists to include the Palaearctic and Nearctic regions in one,
termed Holarctic, and to suggest transitional regions, such as the
Sonoran, between North and South America, and the Mediterranean,
between Europe and Africa, or to create sub-regions, such as Madagascar
and New Zealand. Oceanic islands have, as a rule, distinctive
faunas and floras which resemble, but are not identical with, those of
other islands in similar positions.
The study of the evolution of faunas and the comparison of the
faunas of distant regions have furnished a trustworthy
instrument of pre-historic geographical research, which
Biological distribution as a means of geographical research.
enables earlier geographical relations of land and sea to
be traced out, and the approximate period, or at least the
chronological order of the larger changes, to be estimated.
In this way, for example, it has been suggested that a
land, “Lemuria,” once connected Madagascar with the
Malay Archipelago, and that a northern extension of
the antarctic land once united the three southern continents.
The distribution of fossils frequently makes it possible to map out
approximately the general features of land and sea in long-past
geological periods, and so to enable the history of crustal relief to be
traced.45
While the tendency is for the living forms to come into harmony
with their environment and to approach the state of equilibrium
by successive adjustments if the environment should
happen to change, it is to be observed that the action
Reaction of organisms on environment.
of organisms themselves often tends to change their
environment. Corals and other quick-growing calcareous
marine organisms are the most powerful in this
respect by creating new land in the ocean. Vegetation of all sorts
acts in a similar way, either in forming soil and assisting in breaking
up rocks, in filling up shallow lakes, and even, like the mangrove,
in reclaiming wide stretches of land from the sea. Plant life,
utilizing solar light to combine the inorganic elements of water,
soil and air into living substance, is the basis of all animal life.
This is not by the supply of food alone, but also by the withdrawal
of carbonic acid from the atmosphere, by which vegetation maintains
the composition of the air in a state fit for the support of animal
life. Man in the primitive stages of culture is scarcely to be distinguished
from other animals as regards his subjection to environment,
but in the higher grades of culture the conditions of control
and reaction become much more complicated, and the department
of anthropogeography is devoted to their consideration.
The first requisites of all human beings are food and protection,
in their search for which men are brought into intimate relations
with the forms and productions of the earth’s surface.
The degree of dependence of any people upon environment
Anthropogeography.
varies inversely as the degree of culture or civilization,
which for this purpose may perhaps be defined as the power
of an individual to exercise control over the individual and over
the environment for the benefit of the community. The development
of culture is to a certain extent a question of race, and although
forming one species, the varieties of man differ in almost imperceptible
gradations with a complexity defying classification (see Anthropology).
Professor Keane groups man round four leading types,
which may be named the black, yellow, red and white, or the Ethiopic,
Mongolic, American and Caucasic. Each may be subdivided,
though not with great exactness, into smaller groups, either according
to physical characteristics, of which the form of the head is most
important, or according to language.
The black type is found only in tropical or sub-tropical countries,
and is usually in a primitive condition of culture, unless educated
by contact with people of the white type. They follow
the most primitive forms of religion (mainly fetishism),
Types of man.
live on products of the woods or of the chase, with the
minimum of work, and have only a loose political organization.
The red type is peculiar to America, inhabiting every climate from
polar to equatorial, and containing representatives of many stages
of culture which had apparently developed without the aid or
interference of people of any other race until the close of the 15th
century. The yellow type is capable of a higher culture, cherishes
higher religious beliefs, and inhabits as a rule the temperate zone,
although extending to the tropics on one side and to the arctic
regions on the other. The white type, originating in the north
temperate zone, has spread over the whole world. They have
attained the highest culture, profess the purest forms of monotheistic
religion, and have brought all the people of the black type
and many of those of the yellow under their domination.
The contrast between the yellow and white types has been softened
by the remarkable development of the Japanese following the
assimilation of western methods.
The actual number of human inhabitants in the world has been
calculated as follows:
| | By Continents.46 | | By Race.47 |
| Asia | 875,000,000 | White (Caucasic) | 770,000,000 |
| Europe | 392,000,000 | Yellow (Mong.) | 540,000,000 |
| Africa | 170,000,000 | Black (Ethiopic) | 175,000,000 |
| America | 143,000,000 | Red (American) | 22,000,000 |
| Australia and Polynesia | 7,000,000 | | ————— |
| | ————— | Total | 1,507,000,000 |
| Total | 1,587,000,000 | | |
In round numbers the population of the world is about
1,600,000,000, and, according to an estimate by Ravenstein,48 the
maximum population which it will be possible for the earth to
maintain is 6000 millions, a number which, if the average rate of
increase in 1891 continued, would be reached within 200 years.
While highly civilized communities are able to evade many of
the restrictions of environment, to overcome the barriers to intercommunication
interposed by land or sea, to counteract the adverse
636
influence of climate, and by the development of trade even to
inhabit countries which cannot yield a food-supply, the mass of
mankind is still completely under the control of those conditions
which in the past determined the distribution and the mode of life
of the whole human race.
In tropical forests primitive tribes depend on the collection of
wild fruits, and in a minor degree on the chase of wild animals, for
their food. Clothing is unnecessary; hence there is
little occasion for exercising the mental faculties beyond
Influence of environment on man.
the sense of perception to avoid enemies, or the inventive
arts beyond what is required for the simplest
weapons and the most primitive fortifications. When
the pursuit of game becomes the chief occupation of a people there
is of necessity a higher development of courage, skill, powers of
observation and invention; and these qualities are still further
enhanced in predatory tribes who take by force the food, clothing
and other property prepared or collected by a feebler people. The
fruit-eating savage cannot stray beyond his woods which bound
his life as the water bounds that of a fish; the hunter is free to
live on the margin of forests or in open country, while the robber
or warrior from some natural stronghold of the mountains sweeps
over the adjacent plains and carries his raids into distant lands.
Wide grassy steppes lead to the organization of the people as nomads
whose wealth consists in flocks and herds, and their dwellings
are tents. The nomad not only domesticates and turns to his
own use the gentler and more powerful animals, such as sheep,
cattle, horses, camels, but even turns some predatory creatures,
like the dog, into a means of defending their natural prey. They
hunt the beasts of prey destructive to their flocks, and form armed
bands for protection against marauders or for purposes of aggression
on weaker sedentary neighbours. On the fertile low grounds along
the margins of rivers or in clearings of forests, agricultural communities
naturally take their rise, dwelling in villages and cultivating
the wild grains, which by careful nurture and selection have been
turned into rich cereals. The agriculturist as a rule is rooted to
the soil. The land he tills he holds, and acquires a closer connexion
with a particular patch of ground than either the hunter or the herdsman.
In the temperate zone, where the seasons are sharply contrasted,
but follow each other with regularity, foresight and self-denial
were fostered, because if men did not exercise these qualities seed-time
or harvest might pass into lost opportunities and the tribes would
suffer. The more extreme climates of arid regions on the margins of
the tropics, by the unpredictable succession of droughts and floods,
confound the prevision of uninstructed people, and make prudence
and industry qualities too uncertain in their results to be worth
cultivating. Thus the civilization of agricultural peoples of the
temperate zone grew rapidly, yet in each community a special type
arose adapted to the soil, the crop and the climate. On the seashore
fishing naturally became a means of livelihood, and dwellers
by the sea, in virtue of the dangers to which they are exposed from
storm and unseaworthy craft, are stimulated to a higher degree of
foresight, quicker observation, prompter decision and more energetic
action in emergencies than those who live inland. The building
and handling of vessels also, and the utilization of such uncontrollable
powers of nature as wind and tide, helped forward mechanical
invention. To every type of coast there may be related a special
type of occupation and even of character; the deep and gloomy
fjord, backed by almost impassable mountains, bred bold mariners
whose only outlet for enterprise was seawards towards other lands—the
viks created the vikings. On the gently sloping margin of the
estuary of a great river a view of tranquil inland life was equally
presented to the shore-dweller, and the ocean did not present the
only prospect of a career. Finally the mountain valley, with its
patches of cultivable soil on the alluvial fans of tributary torrents,
its narrow pastures on the uplands only left clear of snow in summer,
its intensified extremes of climates and its isolation, almost equal to
that of an island, has in all countries produced a special type of
brave and hardy people, whose utmost effort may bring them comfort,
but not wealth, by honest toil, who know little of the outer
world, and to whom the natural outlet for ambition is marauding
on the fertile plains. The highlander and viking, products of the
valleys raised high amid the mountains or half-drowned in the sea,
are everywhere of kindred spirit.
It is in some such manner as these that the natural conditions
of regions, which must be conformed to by prudence and utilized
by labour to yield shelter and food, have led to the growth of peoples
differing in their ways of life, thought and speech. The initial
differences so produced are confirmed and perpetuated by the
same barriers which divide the faunal or floral regions, the sea,
mountains, deserts and the like, and much of the course of past
history and present politics becomes clear when the combined
results of differing race and differing environment are taken into
account.49
The specialization which accompanies the division of labour has
important geographical consequences, for it necessitates communication
between communities and the interchange of their products.
Density of population.
Trade makes it possible to work mineral resources
in localities where food can only be grown with great
difficulty and expense, or which are even totally barren
and waterless, entirely dependent on supplies from distant sources.
The population which can be permanently supported by a given
area of land differs greatly according to the nature of the resources
and the requirements of the people. Pastoral communities are
always scattered very thinly over large areas; agricultural populations
may be almost equally sparse where advanced methods of
agriculture and labour-saving machinery are employed; but where
a frugal people are situated on a fertile and inexhaustible soil, such
as the deltas and river plains of Egypt, India and China, an enormous
population may be supported on a small area. In most cases,
however, a very dense population can only be maintained in regions
where mineral resources have fixed the site of great manufacturing
industries. The maximum density of population which a given
region can support is very difficult to determine; it depends partly
on the race and standard of culture of the people, partly on the
nature and origin of the resources on which they depend, partly
on the artificial burdens imposed and very largely on the climate.
Density of population is measured by the average number of people
residing on a unit of area; but in order to compare one part of the
world with another the average should, strictly speaking, be taken
for regions of equal size or of equal population; and the portions
of the country which are permanently uninhabitable ought to be
excluded from the calculation.50 Considering the average density
of population within the political limits of countries, the following
list is of some value; the figures for a few smaller divisions of
large countries are added (in brackets) for comparison:
Average Population on 1 sq. m. (For 1900 or 1901.)
| Country. | Density
of pop. | Country. | Density
of pop. |
| (Saxony) | 743* | Ceylon | 141** |
| Belgium | 589* | Greece | 97 |
| Java | 568** | European Turkey | 90 |
| (England and Wales) | 558 | Spain | 97 |
| (Bengal) | 495** | European Russia | 55** |
| Holland | 436 | Sweden | 30 |
| United Kingdom | 344 | United States | 25 |
| Japan | 317 | Mexico | 18 |
| Italy | 293 | Norway | 18 |
| China proper | 270** | Persia | 15 |
| German Empire | 270 | New Zealand | 7 |
| Austria | 226 | Argentina | 5 |
| Switzerland | 207 | Brazil | 4.5 |
| France | 188 | Eastern States of | |
| Indian Empire | 167** | Australia | 3 |
| Denmark | 160** | Dominion of Canada | 1.5 |
| Hungary | 154** | Siberia | 1 |
| Portugal | 146 | West Australia | 0.2 |
| * Almost exclusively industrial. |
| ** Almost exclusively agricultural. |
The movement of people from one place to another without the
immediate intention of returning is known as migration, and according
to its origin it may be classed as centrifugal (directed
from a particular area) and centripetal (directed towards
Migration.
a particular area). Centrifugal migration is usually a matter of
compulsion; it may be necessitated by natural causes, such as a
change of climate leading to the withering of pastures or destruction
of agricultural land, to inundation, earthquake, pestilence or to an
excess of population over means of support; or to artificial causes,
such as the wholesale deportation of a conquered people; or to
political or religious persecution. In any case the people are driven
out by some adverse change; and when the urgency is great they
may require to drive out in turn weaker people who occupy a desirable
territory, thus propagating the wave of migration, the direction of
which is guided by the forms of the land into inevitable channels.
Many of the great historic movements of peoples were doubtless due
to the gradual change of geographical or climatic conditions; and the
slow desiccation of Central Asia has been plausibly suggested as the
real cause of the peopling of modern Europe and of the medieval
wars of the Old World, the theatres of which were critical points on
the great natural lines of communication between east and west.
In the case of centripetal migrations people flock to some particular
place where exceptionally favourable conditions have been found to
exist. The rushes to gold-fields and diamond-fields are typical instances;
the growth of towns on coal-fields and near other sources
of power, and the rapid settlement of such rich agricultural districts
as the wheat-lands of the American prairies and great plains are
other examples.
There is, however, a tendency for people to remain rooted to the
637
land of their birth, when not compelled or induced by powerful
external causes to seek a new home.
Thus arises the spirit of patriotism, a product of purely geographical
conditions, thereby differing from the sentiment of loyalty,
which is of racial origin. Where race and soil conspire to
evoke both loyalty and patriotism in a people, the moral
Political geography.
qualities of a great and permanent nation are secured.
It is noticeable that the patriotic spirit is strongest in those places
where people are brought most intimately into relation with the land;
dwellers in the mountain or by the sea, and, above all, the people of
rugged coasts and mountainous archipelagoes, have always been
renowned for love of country, while the inhabitants of fertile plains
and trading communities are frequently less strongly attached to
their own land.
Amongst nomads the tribe is the unit of government, the political
bond is personal, and there is no definite territorial association
of the people, who may be loyal but cannot be patriotic. The idea
of a country arises only when a nation, either homogeneous or
composed of several races, establishes itself in a region the boundaries
of which may be defined and defended against aggression from
without. Political geography takes account of the partition of the
earth amongst organized communities, dealing with the relation of
races to regions, and of nations to countries, and considering the
conditions of territorial equilibrium and instability.
The definition of boundaries and their delimitation is one of the
most important parts of political geography. Natural boundaries
are always the most definite and the strongest, lending
themselves most readily to defence against aggression.
Boundaries.
The sea is the most effective of all, and an island state is
recognized as the most stable. Next in importance comes a mountain
range, but here there is often difficulty as to the definition of
the actual crest-line, and mountain ranges being broad regions, it
may happen that a small independent state, like Switzerland or
Andorra, occupies the mountain valleys between two or more great
countries. Rivers do not form effective international boundaries,
although between dependent self-governing communities they are
convenient lines of demarcation. A desert, or a belt of country
left purposely without inhabitants, like the mark, marches or
debatable lands of the middle ages, was once a common means
of separating nations which nourished hereditary grievances. The
“buffer-state” of modern diplomacy is of the same ineffectual
type. A less definite though very practical boundary is that formed
by the meeting-line of two languages, or the districts inhabited
by two races. The line of fortresses protecting Austria from Italy
lies in some places well back from the political boundary, but
just inside the linguistic frontier, so as to separate the German
and Italian races occupying Austrian territory. Arbitrary lines,
either traced from point to point and marked by posts on the ground,
or defined as portions of meridians and parallels, are now the most
common type of boundaries fixed by treaty. In Europe and Asia
frontiers are usually strongly fortified and strictly watched in times
of peace as well as during war. In South America strictly defined
boundaries are still the exception, and the claims of neighbouring
nations have very frequently given rise to war, though now more
commonly to arbitration.51
The modes of government amongst civilized peoples have little
influence on political geography; some republics are as arbitrary
and exacting in their frontier regulations as some absolute
monarchies. It is, however, to be noticed that absolute
Forms of government.
monarchies are confined to the east of Europe and to
Asia, Japan being the only established constitutional
monarchy east of the Carpathians. Limited monarchies are (with
the exception of Japan) peculiar to Europe, and in these the degree
of democratic control may be said to diminish as one passes eastwards
from the United Kingdom. Republics, although represented
in Europe, are the peculiar form of government of America and
are unknown in Asia.
The forms of government of colonies present a series of transitional
types from the autocratic administration of a governor
appointed by the home government to complete democratic
self-government. The latter occurs only in the temperate possessions
of the British empire, in which there is no great preponderance
of a coloured native population. New colonial forms have been
developed during the partition of Africa amongst European powers,
the sphere of influence being especially worthy of notice. This
is a vaguer form of control than a protectorate, and frequently
amounts merely to an agreement amongst civilized powers to respect
the right of one of their number to exercise government within
a certain area, if it should decide to do so at any future time.
The central governments of all civilized countries concerned with
external relations are closely similar in their modes of action, but
the internal administration may be very varied. In this respect a
country is either centralized, like the United Kingdom or France,
or federated of distinct self-governing units like Germany (where
the units include kingdoms, at least three minor types of monarchies,
municipalities and a crown land under a nominated governor), or the
United States, where the units are democratic republics. The ultimate
cause of the predominant form of federal government may be
the geographical diversity of the country, as in the cantons occupying
the once isolated mountain valleys of Switzerland, the racial diversity
of the people, as in Austria-Hungary, or merely political expediency,
as in republics of the American type.
The minor subdivisions into provinces, counties and parishes, or
analogous areas, may also be related in many cases to natural
features or racial differences perpetuated by historical causes. The
territorial divisions and subdivisions often survive the conditions
which led to their origin; hence the study of political geography is
allied to history as closely as the study of physical geography is allied
to geology, and for the same reason.
The aggregation of population in towns was at one time mainly
brought about by the necessity for defence, a fact indicated by the
defensive sites of many old towns. In later times,
towns have been more often founded in proximity to
Towns.
valuable mineral resources, and at critical points or nodes on lines
of communication. These are places where the mode of travelling
or of transport is changed, such as seaports, river ports and railway
termini, or natural resting-places, such as a ford, the foot of a
steep ascent on a road, the entrance of a valley leading up from a
plain into the mountains, or a crossing-place of roads or railways.52
The existence of a good natural harbour is often sufficient to
give origin to a town and to fix one end of a line of land communication.
In countries of uniform surface or faint relief, roads and railways
may be constructed in any direction without regard to the configuration.
In places where the low ground is marshy,
roads and railways often follow the ridge-lines of hills,
Lines of communication.
or, as in Finland, the old glacial eskers, which run parallel
to the shore. Wherever the relief of the land is pronounced,
roads and railways are obliged to occupy the lowest ground
winding along the valleys of rivers and through passes in the mountains.
In exceptional cases obstructions which it would be impossible
or too costly to turn are overcome by a bridge or tunnel, the magnitude
of such works increasing with the growth of engineering skill
and financial enterprise. Similarly the obstructions offered to
water communication by interruption through land or shallows are
overcome by cutting canals or dredging out channels. The economy
and success of most lines of communication depend on following
as far as possible existing natural lines and utilizing existing natural
sources of power.53
Commercial geography may be defined as the description of the
earth’s surface with special reference to the discovery, production,
transport and exchange of commodities. The transport
concerns land routes and sea routes, the latter being
Commercial geography.
the more important. While steam has been said to
make a ship independent of wind and tide, it is still
true that a long voyage even by steam must be planned so as to
encounter the least resistance possible from prevailing winds and
permanent currents, and this involves the application of oceanographical
and meteorological knowledge. The older navigation by
utilizing the power of the wind demands a very intimate knowledge
of these conditions, and it is probable that a revival of sailing
ships may in the present century vastly increase the importance of
the study of maritime meteorology.
The discovery and production of commodities require a knowledge
of the distribution of geological formations for mineral products,
of the natural distribution, life-conditions and cultivation
or breeding of plants and animals and of the labour market. Attention
must also be paid to the artificial restrictions of political geography,
to the legislative restrictions bearing on labour and trade
as imposed in different countries, and, above all, to the incessant
fluctuations of the economic conditions of supply and demand and
the combinations of capitalists or workers which affect the market.54
The term “applied geography” has been employed to designate
commercial geography, the fact being that every aspect of scientific
geography may be applied to practical purposes, including the
purposes of trade. But apart from the applied science, there is an
aspect of pure geography which concerns the theory of the relation
of economics to the surface of the earth.
It will be seen that as each successive aspect of geographical
science is considered in its natural sequence the conditions become
638
Conclusion.
more numerous, complex, variable and practically important.
From the underlying abstract mathematical considerations all
through the superimposed physical, biological, anthropological,
political and commercial development of the
subject runs the determining control exercised by crust-forms
acting directly or indirectly on mobile distributions; and this
is the essential principle of geography.
(H. R. M.)
1 A concise sketch of the whole history of geographical method or
theory as distinguished from the history of geographical discovery
(see later section of this article) is only to be found in the introduction
to H. Wagner’s Lehrbuch der Geographie, vol. i. (Leipzig, 1900),
which is in every way the most complete treatise on the principles of
geography.
2 History of Ancient Geography (Cambridge, 1897), p. 70.
3 See J.L. Myres, “An Attempt to reconstruct the Maps used by
Herodotus,” Geographical Journal, viii. (1896), p. 605.
4 Geschichte der wissenschaftlichen Erdkunde der Griechen (Leipzig,
1891), Abt. 3, p. 60.
5 Bunbury’s History of Ancient Geography (2 vols., London, 1879),
Müller’s Geographi Graeci minores (2 vols., Paris, 1855, 1861) and
Berger’s Geschichte der wissenschaftlichen Erdkunde der Griechen
(4 vols., Leipzig, 1887-1893) are standard authorities on the Greek
geographers.
6 The period of the early middle ages is dealt with in Beazley’s
Dawn of Modern Geography (London; part i., 1897; part ii., 1901;
part iii., 1906); see also Winstedt, Cosmos Indicopleustes (1910).
7 From translator’s preface to the English version by Mr Dugdale
(1733), entitled A Complete System of General Geography, revised
by Dr Peter Shaw (London, 1756).
8 Printed in Schriften zur physischen Geographie, vol. vi. of
Schubert’s edition of the collected works of Kant (Leipzig, 1839).
First published with notes by Rink in 1802.
9 History of Civilization, vol. i. (1857).
10 See H.J. Mackinder in British Association Report (Ipswich),
1895, p. 738, for a summary of German opinion, which has been
expressed by many writers in a somewhat voluminous literature.
11 H. Wagner’s year-book, Geographische Jahrbuch, published at
Gotha, is the best systematic record of the progress of geography
in all departments; and Haack’s Geographen Kalender, also published
annually at Gotha, gives complete lists of the geographical societies
and geographers of the world.
12 This phrase is old, appearing in one of the earliest English works
on geography, William Cuningham’s Cosmographical Glasse conteinyng
the pleasant Principles of Cosmographie, Geographie, Hydrographie
or Navigation (London, 1559).
13 See also S. Günther, Handbuch der mathematischen Geographie
(Stuttgart, 1890).
14 “On the Height of the Land and the Depth of the Ocean,” Scot.
Geog. Mag. iv. (1888), p. 1. Estimates had been made previously by
Humboldt, De Lapparent, H. Wagner, and subsequently by Penck
and Heiderich, and for the oceans by Karstens.
15 Petermanns Mitteilungen, xxv. (1889), p. 17.
16 Proc. Roy. Soc. Edin. xvii. (1890) p. 185.
17 Comptes rendus Acad. Sci. (Paris, 1890), vol. iii. p. 994.
18 “Areal und mittlere Erhebung der Landflächen sowie der Erdkruste”
in Gerland’s Beiträge zur Geophysik, ii. (1895) p. 667. See
also Nature, 54 (1896), p. 112.
19 Petermanns Mitteilungen, xxxv. (1889) p. 19.
20 The areas of the continental shelf and lowlands are approximately
equal, and it is an interesting circumstance that, taken as a
whole, the actual coast-line comes just midway on the most nearly
level belt of the earth’s surface, excepting the ocean floor. The configuration
of the continental slope has been treated in detail by
Nansen in Scientific Results of Norwegian North Polar Expedition,
vol. iv. (1904), where full references to the literature of the subject
will be found.
21 British Association Report (Edinburgh, 1892), p. 699.
22 Das Antlitz der Erde (4 vols., Leipzig, 1885, 1888, 1901). Translated
under the editorship of E. de Margerie, with much additional
matter, as La Face de la terre, vols. i. and ii. (Paris, 1897, 1900), and
into English by Dr Hertha Sollas as The Face of the Earth, vols. i.
and ii. (Oxford, 1904, 1906).
23 Élie de Beaumont, Notice sur les systèmes de montagnes (3 vols.,
Paris, 1852).
24 Vestiges of the Molten Globe (London, 1875).
25 See J.W. Gregory, “The Plan of the Earth and its Causes,”
Geog. Journal, xiii. (1899) p. 225; Lord Avebury, ibid. xv. (1900)
p. 46; Marcel Bertrand, “Déformation tétraédrique de la terre et
déplacement du pôle,” Comptes rendus Acad. Sci. (Paris, 1900),
vol. cxxx. p. 449; and A. de Lapparent, ibid. p. 614.
26 See A.E.H. Love, “Gravitational Stability of the Earth,” Phil.
Trans. ser. A. vol. ccvii. (1907) p. 171.
27 Rumpf, in German, the language in which this distinction was
first made.
28 Lehrbuch der Geographie (Hanover and Leipzig, 1900), Bd. i. S.
245, 249.
29 See, for example, F.G. Hahn’s Insel-Studien (Leipzig, 1883).
30 See Geographical Journal, xxii. (1903) pp. 191-194.
31 The most important works on the classification of land forms are
F. von Richthofen, Führer für Forschungsreisende (Berlin, 1886);
G. de la Noë and E. de Margerie, Les Formes du terrain (Paris, 1888);
and above all A. Penck, Morphologie der Erdoberfläche (2 vols.,
Stuttgart, 1894). Compare also A. de Lapparent, Leçons de géographie
physique (2nd ed., Paris, 1898), and W.M. Davis, Physical
Geography (Boston, 1899).
32 “Geomorphologie als genetische Wissenschaft,” in Report of
Sixth International Geog. Congress (London, 1895), p. 735 (English
Abstract, p. 748).
33 On this subject see J. Geikie, Earth Sculpture (London, 1898);
J.E. Marr, The Scientific Study of Scenery (London, 1900); Sir A.
Geikie, The Scenery and Geology of Scotland (London, 2nd ed., 1887);
Lord Avebury (Sir J. Lubbock), The Scenery of Switzerland (London,
1896) and The Scenery of England (London, 1902).
34 Some geographers distinguish a mountain from a hill by origin;
thus Professor Seeley says “a mountain implies elevation and a hill
implies denudation, but the external forms of both are often identical.”
Report VI. Int. Geog. Congress (London, 1895), p. 751.
35 “Mountains,” in Scot. Geog. Mag. ii. (1896) p. 145.
36 Führer für Forschungsreisende, pp. 652-685.
37 See, for a summary of river-action, A. Phillipson, Studien über
Wasserscheiden (Leipzig, 1886); also I.C. Russell, River Development,
(London, 1898) (published as The Rivers of North America, New York,
1898).
38 W.M. Davis, “The Geographical Cycle,” Geog. Journ. xiv.
(1899) p. 484.
39 A. Penck, “Potamology as a Branch of Physical Geography,”
Geog. Journ. x. (1897) p. 619.
40 See, for instance, E. Wisotzki, Hauptfluss und Nebenfluss
(Stettin, 1889). For practical studies see official reports on the
Mississippi, Rhine, Seine, Elbe and other great rivers.
41 F.A. Forel, Handbuch der Seenkunde: allgemeine Limnologie
(Stuttgart, 1901); F.A. Forel, “La Limnologie, branche de la géographie,”
Report VI. Int. Geog. Congress (London, 1895), p. 593;
also Le Léman (2 vols., Lausanne, 1892, 1894); H. Lullies, “Studien
über Seen,” Jubiläumsschrift der Albertus-Universität (Königsberg,
1894); and G.R. Credner, “Die Reliktenseen,” Petermanns Mitteilungen,
Ergänzungshefte 86 and 89 (Gotha., 1887, 1888).
42 J. Murray, “Drainage Areas of the Continents,” Scot. Geog. Mag.
ii. (1886) p. 548.
43 Wagner, Lehrbuch der Geographie (1900), i. 586.
44 For details, see A.R. Wallace, Geographical Distribution of
Animals and Island Life; A. Heilprin, Geographical and Geological
Distribution of Animals (1887); O. Drude, Handbuch der Pflanzengeographie;
A. Engler, Entwickelungsgeschichte der Pflanzenwelt;
also Beddard, Zoogeography (Cambridge, 1895); and Sclater, The
Geography of Mammals (London, 1899).
45 See particularly A. de Lapparent, Traité de géologie (4th ed.,
Paris, 1900).
46 Estimate for 1900. H. Wagner, Lehrbuch der Geographie, i.
P. 658.
47 Estimate for year not stated. A.H. Keane in International
Geography, p. 108.
48 In Proc. R. G. S. xiii. (1891) p. 27.
49 On the influence of land on people see Shaler, Nature and
Man in America (New York and London, 1892); and Ellen C.
Semple’s American History and its Geographic Conditions (Boston,
1903).
50 See maps of density of population in Bartholomew’s great large-scale
atlases, Atlas of Scotland and Atlas of England.
51 For the history of territorial changes in Europe, see Freeman,
Historical Geography of Europe, edited by Bury (Oxford), 1903;
and for the official definition of existing boundaries, see Hertslet,
The Map of Europe by Treaty (4 vols., London, 1875, 1891); The
Map of Africa by Treaty (3 vols., London, 1896). Also Lord Curzon’s
Oxford address on Frontiers (1907).
52 For numerous special instances of the determining causes of
town sites, see G.G. Chisholm, “On the Distribution of Towns
and Villages in England,” Geographical Journal (1897), ix. 76,
x. 511.
53 The whole subject of anthropogeography is treated in a masterly
way by F. Ratzel in his Anthropogeographie (Stuttgart, vol. i. 2nd
ed., 1899, vol. ii. 1891), and in his Politische Geographie (Leipzig,
1897). The special question of the reaction of man on his environment
is handled by G.P. Marsh in Man and Nature, or Physical
Geography as modified by Human Action (London, 1864).
54 For commercial geography see G.G. Chisholm, Manual of Commercial
Geography (1890).
GEOID (from Gr. γῆ, the earth), an imaginary surface employed
by geodesists which has the property that every element
of it is perpendicular to the plumb-line where that line cuts it.
Compared with the “spheroid of reference” the surface of the
geoid is in general depressed over the oceans and raised over
the great land masses. (See Earth, Figure of the.)
GEOK-TEPE, a former fortress of the Turkomans, in Russian
Transcaspia, in the oasis of Akhal-tekke, on the Transcaspian
railway, 28 m. N.W. of Askabad. It consisted of a walled
enclosure 1¾ m. in circuit, the wall being 18 ft. high and 20 to
30 ft. thick. In December 1880 the place was attacked by
6000 Russians under General Skobelev, and after a siege of
twenty-three days was carried by storm, although the defenders
numbered 25,000. A monument and a small museum commemorate
the event.
GEOLOGY (from Gr. γῆ, the earth, and λόγος, science), the
science which investigates the physical history of the earth.
Its object is to trace the structural progress of our planet from
the earliest beginnings of its separate existence, through its
various stages of growth, down to the present condition of
things. It seeks to determine the manner in which the evolution
of the earth’s great surface features has been effected. It unravels
the complicated processes by which each continent has
been built up. It follows, even into detail, the varied sculpture
of mountain and valley, crag and ravine. Nor does it confine
itself merely to changes in the inorganic world. Geology shows
that the present races of plants and animals are the descendants
of other and very different races which once peopled the earth.
It teaches that there has been a progressive development of the
inhabitants, as well as one of the globe on which they have
dwelt; that each successive period in the earth’s history, since
the introduction of living things, has been marked by characteristic
types of the animal and vegetable kingdoms; and that,
however imperfectly the remains of these organisms have been
preserved or may be deciphered, materials exist for a history
of life upon the planet. The geographical distribution of existing
faunas and floras is often made clear and intelligible by geological
evidence; and in the same way light is thrown upon some of
the remoter phases in the history of man himself. A subject
so comprehensive as this must require a wide and varied basis
of evidence. It is one of the characteristics of geology to gather
evidence from sources which at first sight seem far removed
from its scope, and to seek aid from almost every other leading
branch of science. Thus, in dealing with the earliest conditions
of the planet, the geologist must fully avail himself of the
labours of the astronomer. Whatever is ascertainable by
telescope, spectroscope or chemical analysis, regarding the constitution
of other heavenly bodies, has a geological bearing.
The experiments of the physicist, undertaken to determine
conditions of matter and of energy, may sometimes be taken
as the starting-points of geological investigation. The work
of the chemical laboratory forms the foundation of a vast and
increasing mass of geological inquiry. To the botanist, the
zoologist, even to the unscientific, if observant, traveller by land
or sea, the geologist turns for information and assistance.
But while thus culling freely from the dominions of other
sciences, geology claims as its peculiar territory the rocky
framework of the globe. In the materials composing that
framework, their composition and arrangement, the processes
of their formation, the changes which they have undergone,
and the terrestrial revolutions to which they bear witness, lie
the main data of geological history. It is the task of the geologist
to group these elements in such a way that they may be made
to yield up their evidence as to the march of events in the
evolution of the planet. He finds that they have in large
measure arranged themselves in chronological sequence,—the
oldest lying at the bottom and the newest at the top. Relics
of an ancient sea-floor are overlain by traces of a vanished
land-surface; these are in turn covered by the deposits of a
former lake, above which once more appear proofs of the return
of the sea. Among these rocky records lie the lavas and ashes
of long-extinct volcanoes. The ripple left upon the shore, the
cracks formed by the sun’s heat upon the muddy bottom of a
dried-up pool, the very imprint of the drops of a passing rainshower,
have all been accurately preserved, and yield their
evidence as to geographical conditions often widely different
from those which exist where such markings are now found.
But it is mainly by the remains of plants and animals imbedded
in the rocks that the geologist is guided in unravelling the
chronological succession of geological changes. He has found
that a certain order of appearance characterizes these organic
remains, that each great group of rocks is marked by its own
special types of life, and that these types can be recognized,
and the rocks in which they occur can be correlated even in
distant countries, and where no other means of comparison
would be possible. At one moment he has to deal with the bones
of some large mammal scattered through a deposit of superficial
gravel, at another time with the minute foraminifers and ostracods
of an upraised sea-bottom. Corals and crinoids crowded and
crushed into a massive limestone where they lived and died,
ferns and terrestrial plants matted together into a bed of coal
where they originally grew, the scattered shells of a submarine
sand-bank, the snails and lizards which lived and died within
a hollow-tree, the insects which have been imprisoned within
the exuding resin of old forests, the footprints of birds and
quadrupeds, the trails of worms left upon former shores—these,
and innumerable other pieces of evidence, enable the geologist
to realize in some measure what the faunas and floras of successive
periods have been, and what geographical changes the site of
every land has undergone.
It is evident that to deal successfully with these varied
materials, a considerable acquaintance with different branches
of science is needful. Especially necessary is a tolerably wide
knowledge of the processes now at work in changing the surface
of the earth, and of at least those forms of plant and animal
life whose remains are apt to be preserved in geological deposits,
or which in their structure and habitat enable us to realize what
their forerunners were. It has often been insisted that the
present is the key to the past; and in a wide sense this assertion
is eminently true. Only in proportion as we understand the
present, where everything is open on all sides to the fullest investigation,
can we expect to decipher the past, where so much is
obscure, imperfectly preserved or not preserved at all. A
study of the existing economy of nature ought thus to be the
foundation of the geologist’s training.
While, however, the present condition of things is thus employed,
we must obviously be on our guard against the danger
of unconsciously assuming that the phase of nature’s operations
which we now witness has been the same in all past time, that
geological changes have always or generally taken place in former
ages in the manner and on the scale which we behold to-day,
and that at the present time all the great geological processes,
which have produced changes in the past eras of the earth’s
history, are still existent and active. As a working hypothesis
we may suppose that the nature of geological processes has
remained constant from the beginning; but we cannot postulate
that the action of these processes has never varied in energy.
The few centuries wherein man has been observing nature
obviously form much too brief an interval by which to measure
the intensity of geological action in all past time. For aught
we can tell the present is an era of quietude and slow change,
compared with some of the eras which have preceded it. Nor
perhaps can we be quite sure that, when we have explored
every geological process now in progress, we have exhausted
all the causes of change which, even in comparatively recent
times, have been at work.
In dealing with the geological record, as the accessible solid
part of the globe is called, we cannot too vividly realize that at
639
the best it forms but an imperfect chronicle. Geological history
cannot be compiled from a full and continuous series of documents.
From the very nature of its origin the record is necessarily
fragmentary, and it has been further mutilated and obscured
by the revolutions of successive ages. And even where the
chronicle of events is continuous, it is of very unequal value in
different places. In one case, for example, it may present us
with an unbroken succession of deposits many thousands of
feet in thickness, from which, however, only a few meagre facts
as to geological history can be gleaned. In another instance
it brings before us, within the compass of a few yards, the
evidence of a most varied and complicated series of changes
in physical geography, as well as an abundant and interesting
suite of organic remains. These and other characteristics of
the geological record become more apparent and intelligible as
we proceed in the study of the science.
Classification.—For systematic treatment the subject may be
conveniently arranged in the following parts:—
1. The Historical Development of Geological Science.—Here
a brief outline will be given of the gradual growth of geological
conceptions from the days of the Greeks and Romans down to
modern times, tracing the separate progress of the more important
branches of inquiry and noting some of the stages which in each
case have led up to the present condition of the science.
2. The Cosmical Aspects of Geology.—This section embraces
the evidence supplied by astronomy and physics regarding the
form and motions of the earth, the composition of the planets
and sun, and the probable history of the solar system. The
subjects dealt with under this head are chiefly treated in separate
articles.
3. Geognosy.—An inquiry into the materials of the earth’s
substance. This division, which deals with the parts of the
earth, its envelopes of air and water, its solid crust and the
probable condition of its interior, especially treats of the more
important minerals of the crust, and the chief rocks of which
that crust is built up. Geognosy thus lays a foundation of knowledge
regarding the nature of the materials constituting the mass
of the globe, and prepares the way for an investigation of the
processes by which these materials are produced and altered.
4. Dynamical Geology studies the nature and working of the
various geological processes whereby the rocks of the earth’s
crust are formed and metamorphosed, and by which changes
are effected upon the distribution of sea and land, and upon
the forms of terrestrial surfaces. Such an inquiry necessitates
a careful examination of the existing geological economy of
nature, and forms a fitting introduction to an inquiry into the
geological changes of former periods.
5. Geotectonic or Structural Geology has for its object the
architecture of the earth’s crust. It embraces an inquiry into the
manner in which the various materials composing this crust
have been arranged. It shows that some have been formed
in beds or strata of sediment on the floor of the sea, that others
have been built up by the slow aggregation of organic forms,
that others have been poured out in a molten condition or in
showers of loose dust from subterranean sources. It further
reveals that, though originally laid down in almost horizontal
beds, the rocks have subsequently been crumpled, contorted
and dislocated, that they have been incessantly worn down,
and have often been depressed and buried beneath later
accumulations.
6. Palaeontological Geology.—This branch of the subject,
starting from the evidence supplied by the organic forms which
are found preserved in the crust of the earth, includes such
questions as the relations between extinct and living types,
the laws which appear to have governed the distribution of life
in time and in space, the relative importance of different genera
of animals in geological inquiry, the nature and use of the
evidence from organic remains regarding former conditions
of physical geography. Some of these problems belong also to
zoology and botany, and are more fully discussed in the articles
Palaeontology and Palaeobotany.
7. Stratigraphical Geology.—This section might be called
geological history. It works out the chronological succession
of the great formations of the earth’s crust, and endeavours to
trace the sequence of events of which they contain the record.
More particularly, it determines the order of succession of the
various plants and animals which in past time have peopled
the earth, and thus ascertains what has been the grand march
of life upon this planet.
8. Physiographical Geology, proceeding from the basis of
fact laid down by stratigraphical geology regarding former
geographical changes, embraces an inquiry into the origin and
history of the features of the earth’s surface—continental ridges
and ocean basins, plains, valleys and mountains. It explains
the causes on which local differences of scenery depend, and
shows under what very different circumstances, and at what
widely separated intervals, the hills and mountains, even of a
single country, have been produced.
Most of the detail embraced in these several sections is
relegated to separate articles, to which references are here
inserted. The following pages thus deal mainly with the general
principles and historical development of the science:—
Part I.—Historical Development
Geological Ideas among the Greeks and Romans.—Many geological
phenomena present themselves in so striking a form that they could
hardly fail to impress the imagination of the earliest and rudest
races of mankind. Such incidents as earthquakes and volcanic
eruptions, destructive storms on land and sea, disastrous floods and
landslips suddenly strewing valleys with ruin, must have awakened
the terror of those who witnessed them. Prominent features of
landscape, such as mountain-chains with their snows, clouds and
thunderstorms, dark river-chasms that seem purposely cleft open in
order to give passage to the torrents that rush through them, crags
with their impressive array of pinnacles and recesses must have
appealed of old, as they still do, to the awe and wonder of those
who for the first time behold them. Again, banks of sea-shells in
far inland districts would, in course of time, arrest the attention of
the more intelligent and reflective observers, and raise in their minds
some kind of surmise as to how such shells could ever have come
there. These and other conspicuous geological problems found
their earliest solution in legends and myths, wherein the more
striking terrestrial features and the elemental forces of nature were
represented to be the manifestation of the power of unseen supernatural
beings.
The basin of the Mediterranean Sea was especially well adapted,
from its physical conditions, to be the birth-place of such fables.
It is a region frequently shaken by earthquakes, and contains two
distinct centres of volcanic activity, one in the Aegean Sea and one
in Italy. It is bounded on the north by a long succession of lofty
snow-capped mountain-ranges, whence copious rivers, often swollen
by heavy rains or melted snows, carry the drainage into the sea.
On the south it boasts the Nile, once so full of mystery; likewise
wide tracts of arid desert with their dreaded dust storms. The
Mediterranean itself, though an inland sea, is subject to gales,
which, on exposed coasts, raise breakers quite large enough to give a
vivid impression of the power of ocean waves. The countries that
surround this great sheet of water display in many places widely-spread
deposits full of sea shells, like those that still live in the
neighbouring bays and gulfs. Such a region was not only well fitted
to supply subjects for mythology, but also to furnish, on every side,
materials which, in their interest and suggestiveness, would appeal
to the reason of observant men.
It was natural, therefore, that the early philosophers of Greece
should have noted some of these geological features, and should have
sought for other explanations of them than those to be found in the
popular myths. The opinions entertained in antiquity on these
subjects may be conveniently grouped under two heads: (1) Geological
processes now in operation, and (2) geological changes in
the past.
1. Contemporary Processes.—The geological processes of the present
time are partly at work underground and partly on the surface of the
earth. The former, from their frequently disastrous
character, received much attention from Greek and
Earthquakes and volcanoes.
Roman authors. Aristotle, in his Meteorics, cites the
speculations of several of his predecessors which he rejects
in favour of his own opinion to the effect that earthquakes are due
to the generation of wind within the earth, under the influence of the
warmth of the sun and the internal heat. Wind, being the lightest
and most rapidly moving body, is the cause of motion in other
bodies, and fire, united with wind, becomes flame, which is endowed
with great rapidity of motion. Aristotle looked upon earthquakes
and volcanic eruptions as closely connected with each other, the
discharge of hot materials to the surface being the result of a severe
earthquake, when finally the wind rushes out with violence, and
sometimes buries the surrounding country under sparks and cinders,
640
as had happened at Lipari. These crude conceptions of the nature
of volcanic action, and the cause of earthquakes, continued to prevail
for many centuries. They are repeated by Lucretius, who, however,
following Anaximenes, includes as one of the causes of earthquakes
the fall of mountainous masses of rock undermined by time, and the
consequent propagation of gigantic tremors far and wide through
the earth. Strabo, having travelled through the volcanic districts
of Italy, was able to recognize that Vesuvius had once been an
active volcano, although no eruption had taken place from it within
human memory. He continued to hold the belief that volcanic
energy arose from the movement of subterranean wind. He believed
that the district around the Strait of Messina, which had formerly
suffered from destructive earthquakes, was seldom visited by them
after the volcanic vents of that region had been opened, so as to
provide an escape for the subterranean fire, wind, water and burning
masses. He cites in his Geography a number of examples of widespread
as well as local sinkings of land, and alludes also to the uprise
of the sea-bottom. He likewise regards some islands as having been
thrown up by volcanic agency, and others as torn from the mainland
by such convulsions as earthquakes.
The most detailed account of earthquake phenomena which has
come down to us from antiquity is that of Seneca in his Quaestiones
Naturales. This philosopher had been much interested in the
accounts given him by survivors and witnesses of the earthquake
which convulsed the district of Naples in February A.D. 63. He
distinguished several distinct movements of the ground: 1st, the
up and down motion (succussio); 2nd, the oscillatory motion (inclinatio);
and probably a third, that of trembling or vibration.
While admitting that some earthquakes may arise from the collapse
of the walls of subterranean cavities, he adhered to the old idea,
held by the most numerous and important previous writers, that
these commotions are caused mainly by the movements of wind
imprisoned within the earth. As to the origin of volcanic outbursts
he supposed that the subterranean wind in struggling for an outlet,
and whirling through the chasms and passages, meets with great
store of sulphur and other combustible substances, which by mere
friction are set on fire. The elder Pliny reiterates the commonly
accepted opinion as to the efficacy of wind underground. In
discussing the phenomena of earthquakes he remarks that towns
with many culverts and houses with cellars suffer less than others,
and that at Naples those houses are most shaken which stand on
hard ground. It thus appears that with regard to subterranean
geological operations, no advance was made during the time of the
Greeks and Romans as to the theoretical explanation of these phenomena;
but a considerable body of facts was collected, especially
as to the effects of earthquakes and the occurrence of volcanic
eruptions.
The superficial processes of geology, being much less striking than
those of subterranean energy, naturally attracted less attention in
antiquity. The operations of rivers, however, which so
intimately affect a human population, were watched with
Action of rivers.
more or less care. Herodotus, struck by the amount of
alluvial silt brought down annually by the Nile and spread over the
flat inundated land, inferred that “Egypt is the gift of the river.”
Aristotle, in discussing some of the features of rivers, displays considerable
acquaintance with the various drainage-systems on the
north side of the Mediterranean basin. He refers to the mountains
as condensers of the atmospheric moisture, and shows that the largest
rivers rise among the loftiest high grounds. He shows how sensibly
the alluvial deposits carried down to the sea increase the breadth
of the land, and cites some parts of the shores of the Black Sea,
where, in sixty years, the rivers had brought down such a quantity
of material that the vessels then in use required to be of much
smaller draught than previously, the water shallowing so much that
the marshy ground would, in course of time, become dry land.
Strabo supplies further interesting information as to the work of
rivers in making their alluvial plains and in pushing their deltas
seaward. He remarks that these deltas are prevented from advancing
farther outward by the ebb and flow of the tides.
2. Past Processes.—The abundant well-preserved marine shells
exposed among the upraised Tertiary and post-Tertiary deposits in
the countries bordering the Mediterranean are not infrequently
alluded to in Greek and Latin literature.
Occurrences of fossils.
Xenophanes of Colophon (614 B.C.) noticed the occurrence
of shells and other marine productions inland among the
mountains, and inferred from them that the land had risen out of
the sea. A similar conclusion was drawn by Xanthus the Lydian
(464 B.C.) from shells like scallops and cockles, which were found far
from the sea in Armenia and Lower Phrygia. Herodotus, Eratosthenes,
Strato and Strabo noted the vast quantities of fossil shells in
different parts of Egypt, together with beds of salt, as evidence that
the sea had once spread over the country. But by far the most
philosophical opinions on the past mutations of the earth’s surface
are those expressed by Aristotle in the treatise already cited. Reviewing
the evidence of these changes, he recognized that the sea
now covers tracts that were once dry land, and that land will one
day reappear where there is now sea. These alternations are to be
regarded as following each other in a certain order and periodicity.
But they are apt to escape our notice because they require successive
periods of time, which, compared with our brief existence, are of
enormous duration, and because they are brought about so imperceptibly
that we fail to detect them in progress. In a celebrated
passage in his Metamorphoses, Ovid puts into the mouth of the
philosopher Pythagoras an account of what was probably regarded
as the Pythagorean view of the subject in the Augustan age. It
affirms the interchange of land and sea, the erosion of valleys by
descending rivers, the washing down of mountains into the sea, the
disappearance of the rivers and the submergence of land by earthquake
movements, the separation of some islands from, and the union
of others with, the mainland, the uprise of hills by volcanic action,
the rise and extinction of burning mountains. There was a time
before Etna began to glow, and the time is coming when the mountain
will cease to burn.
From this brief sketch it will be seen that while the ancients had
accumulated a good deal of information regarding the occurrence of
geological changes, their interpretations of the phenomena were to
a considerable extent mere fanciful speculation. They had acquired
only a most imperfect conception of the nature and operation of the
geological processes; and though many writers realized that the
surface of the earth has not always been, and will not always remain,
as it is now, they had no glimpse of the vast succession of changes
of that surface which have been revealed by geology. They built
hypotheses on the slenderest basis of fact, and did not realize the
necessity of testing or verifying them.
Progress of Geological Conceptions in the Middle Ages.—During the
centuries that succeeded the fall of the Western empire little progress
was made in natural science. The schoolmen in the monasteries
and other seminaries were content to take their science from the
literature of Greece and Rome. The Arabs, however, not only
collected and translated that literature, but in some departments
made original observations themselves. To one of the most illustrious
of their number, Avicenna, the translator of Aristotle, a treatise has
been ascribed, in which singularly modern ideas are expressed
regarding mountains, some of which are there stated to have been
produced by an uplifting of the ground, while others have been left
prominent, owing to the wearing away of the softer rocks around
them. In either case, it is confessed that the process would demand
long tracts of time for its completion.
After the revival of learning the ancient problem presented by
fossil shells imbedded in the rocks of the interior of many countries
received renewed attention. But the conditions for its solution
were no longer what they had been in the days of the philosophers
of antiquity. Men were not now free to adopt and teach any doctrine
they pleased on the subject. The Christian church had meanwhile
arisen to power all over Europe, and adjudged as heretics all
who ventured to impugn any of her dogmas. She taught that the
land and the sea had been separated on the third day of creation,
before the appearance of any animal life, which was not created until
the fifth day. To assert that the dry land is made up in great part
of rocks that were formed in the sea, and are crowded with the
remains of animals, was plainly to impugn the veracity of the Bible.
Again, it had come to be the orthodox belief that only somewhere
about 6000 years had elapsed since the time of Adam and Eve.
If any thoughtful observer, impressed with the overwhelming force
of the evidence that the fossiliferous formations of the earth’s crust
must have taken long periods of time for their accumulation, ventured
to give public expression to his conviction, he ran considerable
risk of being proceeded against as a heretic. It was needful, therefore,
to find some explanation of the facts of nature, which would not
run counter to the ecclesiastical system of the day. Various such
interpretations were proposed, doubtless in an honest endeavour at
reconciliation. Three of these deserve special notice: (1) Many
able observers and diligent collectors of fossils persuaded themselves
that these objects never belonged to organisms of any kind, but
should be regarded as mere “freaks of nature,” having no more
connexion with any once living creature than the frost patterns
on a window. They were styled “formed” or “figured” stones,
“lapides sui generis,” and were asserted to be due to some inorganic
imitative process within the earth or to the influence of the stars.
(2) Observers who could not resist the evidence of their senses that
the fossil shells once belonged to living animals, and who, at the
same time, felt the necessity of accounting for the presence of marine
organisms in the rocks of which the dry land is largely built up,
sought a way out of the difficulty by invoking the Deluge of Noah.
Here was a catastrophe which, they said, extended over the whole
globe, and by which the entire dry land was submerged even up to
the tops of the high hills. True, it only lasted one hundred and fifty
days, but so little were the facts then appreciated that no difficulty
seems to have been generally felt in crowding the accumulation of
the thousands of feet of fossiliferous formations into that brief space
of time. (3) Some more intelligent men in Italy, recognizing that
these interpretations could not be upheld, fell back upon the idea
that the rocks in which fossil shells are imbedded might have been
heaped up by repeated and vigorous eruptions from volcanic centres.
Certain modern eruptions in the Aegean Sea and in the Bay of Naples
had drawn attention to the rapidity with which hills of considerable
size could be piled around an active crater. It was argued that if
Monte Nuovo near Naples could have been accumulated to a height
of nearly 500 ft. in two days, there seemed to be no reason against
believing that, during the time of the Flood, and in the course of the
641
centuries that have elapsed since that event, the whole of the fossiliferous
rocks might have been deposited. Unfortunately for this
hypothesis it ignored the fact that these rocks do not consist of
volcanic materials.
So long as the fundamental question remained in dispute as to
the true character and history of the stratified portion of the earth’s
crust containing organic remains, geology as a science could not
begin its existence. The diluvialists (those who relied on the hypothesis
of the Flood) held the field during the 16th, 17th and a great
part of the 18th century. They were looked on as the champions of
orthodoxy; and, on that account, they doubtless wielded much
more influence than would have been gained by them from the
force of their arguments. Yet during those ages there were not
wanting occasional observers who did good service in combating the
prevalent misconceptions, and in preparing the way for the ultimate
triumph of truth. It was more especially in Italy, where many of
the more striking phenomena of geology are conspicuously displayed,
that the early pioneers of the science arose, and that for several
generations the most marked progress was made towards placing
the investigations of the past history of the earth upon a basis of
careful observation and scientific deduction. One of the first of
Leonardo da Vinci; Fracastorio; Falloppio.
these leaders was Leonardo da Vinci (1452-1519), who,
besides his achievements in painting, sculpture, architecture
and engineering, contributed some notable observations
regarding the great problem of the origin of fossil
shells. He ridiculed the notion that these objects could
have been formed by the influence of the stars, and maintained
that they had once belonged to living organisms, and therefore
that what is now land was formerly covered by the sea.
Girolamo Fracastorio (1483-1553) claimed that the shells could
never have been left by the Flood, which was a mere temporary
inundation, but that they proved the mountains, in which they
occur, to have been successively uplifted out of the sea. On the
other hand, even an accomplished anatomist like Gabriello Falloppio
(1523-1562) found it easier to believe that the bones of elephants,
teeth of sharks, shells and other fossils were mere earthy inorganic
concretions, than that the waters of Noah’s Flood could ever nave
reached as far as Italy.
By much the most important member of this early band of Italian
writers was undoubtedly Nicolas Steno (1631-1687), who, though
born in Copenhagen, ultimately settled in Florence.
Having made a European reputation as an anatomist,
Nicolas Steno.
his attention was drawn to geological problems by finding
that the rocks of the north of Italy contained what appeared to be
sharks’ teeth closely resembling those of a dog-fish, of which he had
published the anatomy. Cautiously at first, for fear of offending
orthodox opinions, but afterwards more boldly, he proclaimed his
conviction that those objects had once been part of living animals,
and that they threw light on some of the past history of the earth.
He published in 1669 a small tract, De solido intra solidum naturaliter
contento, in which he developed the ideas he had formed of this
history from an attentive study of the rocks. He showed that the
stratified formations of the hills and valleys consist of such materials
as would be laid down in the form of sediment in turbid water;
that where they contain marine productions this water is proved
to have been the sea; that diversities in their composition point to
commingling of currents, carrying different kinds of sediment of
which the heaviest would first sink to the bottom. He made original
and important observations on stratification, and laid down some
of the fundamental axioms in stratigraphy. He reasoned that as
the original position of strata was approximately horizontal, when
they are found to be steeply inclined or vertical, or bent into arches,
they have been disrupted by subterranean exhalations, or by the
falling in of the roofs of underground cavernous spaces. It is to
this alteration of the original position of the strata that the inequalities
of the earth’s surface, such as mountains, are to be ascribed,
though some have been formed by the outburst of fire, ashes and
stones from inside the earth. Another effect of the dislocation has
been to provide fissures, which serve as outlets for springs. Steno’s
anatomical training peculiarly fitted him for dealing authoritatively
with the question of the nature and origin of the fossils contained
in the rocks. He had no hesitation in affirming that, even if no shells
had ever been found living in the sea, the internal structure of these
fossils would demonstrate that they once formed parts of living
animals. And not only shells, but teeth, bones and skeletons of
many kinds of fishes had been quarried out of the rocks, while some
of the strata had skulls, horns and teeth of land-animals. Illustrating
his general principles by a sketch of what he supposed to have been
the past history of Tuscany, he added a series of diagrams which
show how clearly he had conceived the essential elements of stratigraphy.
He thought he could perceive the records of six successive
phases in the evolution of the framework of that country, and was
inclined to believe that a similar chronological sequence would be
found all over the world. He anticipated the objections that would
be brought against his views on account of the insuperable difficulty
in granting the length of time that would be required for all the
geographical vicissitudes which his interpretation required. He
thought that many of the fossils must be as old as the time of the
general deluge, but he was careful not to indulge in any speculation
as to the antiquity of the earth.
To the Italian school, as especially typified in Steno, must be
assigned the honour of having thus begun to lay firmly and truly
the first foundation stones of the modern science of
geology. The same school included Antonio Vallisneri
Lazzaro Moro.
(1661-1730), who surpassed his predecessors in his wider
and more exact knowledge of the fossiliferous rocks that form the
backbone of the Italian peninsula, which he contended were formed
during a wide and prolonged submergence of the region, altogether
different from the brief deluge of Noah. There was likewise Lazzaro
Moro (1687-1740), who did good service against the diluvialists,
but the fundamental feature of his system of nature lay in the
preponderant part which, unaware of the great difference between
volcanic materials and ordinary sediment, he assigned to volcanic
action in the production of the sedimentary rocks of the earth’s
crust. He supposed that in the beginning the globe was completely
surrounded with water, beneath which the solid earth lay as a smooth
ball. On the third day of creation, however, vast fires were kindled
inside the globe, whereby the smooth surface of stone was broken
up, and portions of it, appearing above the water, formed the earliest
land. From that time onward, volcanic eruptions succeeded each
other, not only on the emerged land, but on the sea-floor, over which
the ejected material spread in an ever augmenting thickness of
sedimentary strata. In this way Moro carried the history of the
stratified rocks beyond the time of the Flood back to the Creation,
which was supposed to have been some 1600 years earlier; and he
brought it down to the present day, when fresh sedimentary deposits
are continually accumulating. He thus incurred no censure from
the ecclesiastical guardians of the faith, and he succeeded in attracting
increased public attention to the problems of geology. The
influence of his teaching, however, was subsequently in great part
due to the Carmelite friar Generelli, who published an eloquent
exposition of Moro’s views.
The Cosmogonists and Theories of the Earth.—While in Italy
substantial progress was made in collecting information regarding
the fossiliferous formations of that country, and in forming conclusions
concerning them based upon more or less accurate observations,
the tendency to mere fanciful speculation, which could not be
wholly repressed in any country, reached a remarkable extravagance
in England. In proportion as materials were yet lacking from
which to construct a history of the evolution of our planet in accordance
with the teaching of the church, imagination supplied the place
of ascertained fact, and there appeared during the last twenty years
of the 18th century a group of English cosmogonists, who, by the
sensational character of their speculations, aroused general attention
both in Britain and on the continent. It may be doubted, however,
whether the effect of their writings was not to hinder the advance
of true science by diverting men from the observation of nature into
barren controversy over unrealities. It is not needful here to do
more than mention the names of Thomas Burnet, whose Sacred
Theory of the Earth appeared in 1681, and William Whiston, whose
New Theory of the Earth was published in 1696. Hardly less fanciful
than these writers, though his practical acquaintance with rocks
and fossils was infinitely greater, was John Woodward, whose
Essay towards a Natural History of the Earth dates from 1695. More
important as a contribution to science was the catalogue of the large
collection of fossils, which he had made from the rocks of England
and which he bequeathed to the university of Cambridge. This
catalogue appeared in 1728-1729 with the title of An attempt towards
a Natural History of the Fossils of England.
A striking contrast to these cosmogonists is furnished by another
group, which arose in France and Germany, and gave to the world
the first rational ideas concerning the probable primeval
evolution of our globe. The earliest of these pioneers was
Descartes.
the illustrious philosopher René Descartes (1596-1650). He propounded
a scheme of cosmical development in which he represented
the earth, like the other planets, to have been originally a mass of
glowing material like the sun, and to have gradually cooled on the
outside, while still retaining an incandescent, self-luminous nucleus.
Yet with this noble conception, which modern science has accepted,
Descartes could not shake himself free from the time-honoured
error in regard to the origin of volcanic action. He thought that
certain exhalations within the earth condense into oil, which, when
in violent motion, enters into the subterranean cavities, where it
passes into a kind of smoke. This smoke is from time to time ignited
by a spark of fire and, pressing violently against its containing
walls, gives rise to earthquakes. If the flame breaks through to the
surface at the top of a mountain, it may escape with enormous
energy, hurling forth much earth mingled with sulphur or bitumen,
and thus producing a volcano. The mountain might burn for a
long time until at last its store of fuel in the shape of sulphur or
bitumen would be exhausted. Not only did the philosopher refrain
from availing himself of the high internal temperature of the globe
as the source of volcanic energy, he even did not make use of it as
the cause of the ignition of his supposed internal fuel, but speculated
on the kindling of the subterranean fires by the spirits or gases
setting fire to the exhalations, or by the fall of masses of rock and
the sparks produced by their friction or percussion.
The ideas of Descartes regarding planetary evolution were enlarged
and made more definite by Wilhelm Gottfried Leibnitz (1646-1716),
whose teaching has largely influenced all subsequent speculation
642
on the subject. In his great tract, the Protogaea (published in 1749,
Leibnitz.
thirty-three years after his death), he traced the probable passage
of our earth from an original condition of incandescent
vapour into that of a smooth molten globe, which, by
continuous cooling, acquired an external solid crust and rugose
surface. He thought that the more ancient rocks, such as granite
and gneiss, might be portions of the earliest outer crust; and that as
the external solidification advanced, immense subterranean cavities
were left which were filled with air and water. By the collapse of
the roofs of these caverns, valleys might be originated at the surface,
while the solid intervening walls would remain in place and form
mountains. By the disruption of the crust, enormous bodies of
water were launched over the surface of the earth, which swept vast
quantities of sediment together, and thus gave rise to sedimentary
deposits. After many vicissitudes of this kind, the terrestrial forces
calmed down, and a more stable condition of things was established.
An important feature in the cosmogony of Leibnitz is the
prominent place which he assigned to organic remains in the stratified
rocks of the crust. Ridiculing the foolish attempts to account for
the presence of these objects by calling them “sports of nature,”
he showed that they are to be regarded as historical monuments;
and he adduced a number of instances wherein successive platforms
of strata, containing organic remains, bear witness to a series of
advances and retreats of the sea. He recognized that some of the
fossils appeared to have nothing like them in the living world of
to-day, but some analogous forms might yet be found, he thought,
in still unexplored parts of the earth; and even if no living representatives
should ever be discovered, many types of animals might
have undergone transformation during the great changes which had
affected the surface of the earth. In spite of his clear realization
of the vast store of potential energy residing within the highly heated
interior of the earth, Leibnitz continued to regard volcanic action
as due to the combustion of inflammable substances enclosed within
the terrestrial crust, such as stone-coal, naphtha and sulphur.
Appealing to a much wider public than Descartes or Leibnitz, and
basing his speculations on a wider acquaintance with the organic
and inorganic realms of nature, G.L.L. de Buffon (1707-1788)
was undoubtedly one of the most influential forces
Buffon.
that in Europe guided the growth of geological ideas during the
18th century. He published in 1749 a Theory of the Earth, in which
he adopted views similar to those of Descartes and Leibnitz as to
planetary evolution; but though he realized the importance of
fossils as records of former conditions of the earth’s surface, he
accounted for them by supposing that they had been deposited from
a universal ocean, a large part of which had subsequently been
engulfed into caverns in the interior of the globe. Thirty years
later, after having laboured with skill and enthusiasm in all branches
of natural history, he published another work, his famous Époques
de la nature (1778), which is specially remarkable as the first attempt
to deal with the history of the earth in a chronological manner, and
to compute, on a basis of experiment, the antiquity of the several
stages of this history. His experiments were made with globes of
cast iron, and could not have yielded results of any value for his
purpose; but in so far as his calculations were not mere random
guesses but had some kind of foundation on experiment, they
deserve respectful recognition. He divided the history of our earth
into six periods of unequal duration, the whole comprising a period
of some 70,000 or 75,000 years. He supposed that the stage of
incandescence, before the globe had consolidated to the centre,
lasted 2936 years, and that about 35,000 years elapsed before the
surface had cooled sufficiently to be touched, and therefore to be
capable of supporting living things. Terrestrial animal life, however,
was not introduced until 55,000 or 60,000 years after the beginning
of the world or about 15,000 years before our time. Looking into
the future, he foresaw that, by continued refrigeration, our globe
will eventually become colder than ice, and this fair face of nature,
with its manifold varieties of plant and animal life, will perish after
having existed for 132,000 years.
Buffon’s conception of the operation of the geological agents did
not become broader or more accurate in the interval between the
appearance of his two treatises. He still continued to believe in
the lowering of the ocean by subsidence into vast subterranean
cavities, with a consequent emergence of land. He still looked on
volcanoes as due to the burning of “pyritous and combustible
stones,” though he now called in the co-operation of electricity.
He calculated that the first volcanoes could not arise until some
50,000 years after the beginning of the world, by which time a
sufficient extent of dense vegetation had been buried in the earth
to supply them with fuel. He appears to have had but an imperfect
acquaintance with the literature of his own time. At least there
can be little doubt that had he availed himself of the labours of his
own countryman, Jean Etienne Guettard (1715-1786), of Giovanni
Arduíno (1714-1795) in Italy, and of Johann Gottlob Lehmann
(d. 1767) and George Christian Füchsel (1722-1773) in Germany, he
would have been able to give to his “epochs” a more definite succession
of events and a greater correspondence with the facts of nature.
Among the writers of the 18th century, who formed philosophical
conceptions of the system of processes by which the life of our earth
as a habitable globe is carried on, a foremost place must be assigned
to James Hutton (1726-1797). Educated for the medical profession,
James Hutton.
he studied at Edinburgh and at Paris, and took his doctor’s degree
at Leiden. But having inherited a small landed property in
Berwickshire, he took to agriculture, and after putting
his land into excellent order, let his farm and betook
himself to Edinburgh, there to gratify the scientific
tastes which he had developed early in life. He had been more
especially led to study minerals and rocks, and to meditate on the
problems which they suggest as to the constitution and history of
the earth. His journeys in Britain and on the continent of Europe
had furnished him with material for reflection; and he had gradually
evolved a system or theory in which all the scattered facts
could be arranged so as to show their mutual dependence and their
place in the orderly mechanism of the world. He used to discuss
his views with one or two of his friends, but refrained from publishing
them to the world until, on the foundation of the Royal Society of
Edinburgh, he communicated an outline of his doctrine to that
learned body in 1785. Some years later he expanded this first essay
into a larger work in two volumes, which were published in 1795
with the title of Theory of the Earth, with Proofs and Illustrations.
Hutton’s teaching has exercised a profound influence on modern
geology. This influence, however, has arisen less from his own
writings than from the account of his doctrines given by
his friend John Playfair in the classic work entitled
John Playfair.
Illustrations of the Huttonian Theory, published in 1802.
Hutton wrote in so prolix and obscure a style as rather to repel than
attract readers. Playfair, on the other hand, expressed himself in
such clear and graceful language as to command general attention,
and to gain wide acceptance for his master’s views. Unlike the
older cosmogonists, Hutton refrained from trying to explain the
origin of things, and from speculations as to what might possibly
have been the early history of our globe. He determined from the
outset to interpret the past by what can be seen to be the present
order of nature; and he refused to admit the operation of causes
which cannot be shown to be part of the actual terrestrial system.
Like other observers who had preceded him, he recognized in the
various rocks composing the dry land evidence of former geographical
conditions very different from those which now prevail. He saw
that the vast majority of rocks consist of hardened sediments and
must have been deposited in the sea. He could distinguish among
them an older or Primary series, and a younger or Secondary series;
and did not dispute the existence of a Tertiary series claimed by
Peter Simon Pallas (1741-1811). He believed that these various
aqueous accumulations had been consolidated by subterranean heat,
that the oldest and lowest rocks had suffered most from this action,
that into these more deep-seated masses subsequent veins and
larger bodies of molten matter were injected from below, and thus
that what was originally loose detritus eventually became changed
in such crystalline schists as are now found in mountain-chains.
In the course of these terrestrial revolutions sedimentary strata,
originally more or less nearly horizontal, have been pushed upward,
dislocated, crumpled, placed on end, and even elevated to form
ranges of lofty mountains. Hutton looked upon these disturbances
as due to the expansive power of subterranean heat; but he did not
attempt to sketch the mechanism of the process, and he expressly
declined to offer any conjecture as to how the land so elevated
remains in that position. He thought that the interior of our
planet may “be a fluid mass, melted, but unchanged by the action
of heat”; and, far from connecting volcanoes with the combustion of
inflammable substances, as had been the prevalent belief for so many
centuries, he looked upon them as a beneficent provision of “spiracles
to the subterranean furnace, in order to prevent the unnecessary
elevation of land and fatal effects of earthquakes.”
A distinguishing feature of the Huttonian philosophy is to be
seen in the breadth of its conceptions regarding the geological
operations continually in progress on the surface of the globe.
Hutton saw that the land is undergoing a ceaseless process of degradation,
through the influence of the air, frost, rain, rivers and the sea,
and that in course of time, if no countervailing agency should intervene,
the whole of the dry land will be washed away into the sea.
But he also perceived that this universal erosion is not everywhere
carried on at the same rate; that it is specially active along the
channels of torrents and rivers, and that, owing to this difference
these channels are gradually deepened and widened, until the
complicated valley-system of a country is carved out. He recognized
that the detritus worn away from the land must be spread out over
the floor of the sea, so as to form there strata similar to those that
compose most of the dry land. As he could detect in the structure
of land convincing evidence that former sea floors had been elevated
to form the continents and islands of to-day, he could look forward
to future ages, when the same subterranean agency which had raised
up the present land would again be employed to uplift the bed of
the existing ocean, thus to renew the surface of our earth as a
habitable globe, and to start a fresh cycle of erosion and deposition.
Though Hutton was not unaware that organic remains abound in
many of the stratified rocks, he left them out of consideration in
the elaboration of his theory. It was otherwise with
one of his French contemporaries, the illustrious J.B.
Lamarck.
Lamarck (1744-1829), who, after having attained great eminence as
a botanist, turned to zoology when he was nearly fifty years of age,
and before long rose to even greater distinction in that department
643
of science. His share in the classification and description of the
mollusca and in founding invertebrate palaeontology, his theory
of organic evolution and his philosophical treatment of many
biological questions have been tardily recognized, but his contributions
to geology have been less generally acknowledged. When he
accepted the “professorship of zoology; of insects, of worms and of
microscopic animals” at the Museum of Natural History, Paris,
in 1793, he at once entered with characteristic ardour and capacity
into the new field of research then opened to him. In dealing with
the mollusca he considered not merely the living but also the extinct
forms, especially the abundant, varied and well-preserved genera
and species furnished by the Tertiary deposits of the Paris basin,
of which he published descriptions and plates that proved of essential
service in the stratigraphical work of Cuvier and Alexandre
Brongniart (1770-1847). His labours among these relics of ancient
seas and lakes led him to ponder over the past history of the globe,
and as he was seldom dilatory in making known the opinions he had
formed, he communicated some of his conclusions to the National
Institute in 1799. These, including a further elaboration of his
views, he published in 1802 in a small volume entitled Hydrogéologie.
This treatise, though it did not reach a second edition and has
never been reprinted, deserves an honourable place in geological
literature. Its object, the author states, was to present some important
and novel considerations, which he thought should form
the basis of a true theory of the earth. He entirely agreed with the
doctrine of the subaerial degradation of the land and the erosion of
valleys by running water. Not even Playfair could have stated this
doctrine more emphatically, and it is worthy of notice that Playfair’s
Illustrations of the Huttonian Theory appeared in the same year
with Lamarck’s book. The French naturalist, however, carried his
conclusions so far as to take no account of any great movements of
the terrestrial crust, which might have produced or modified the
main physical features of the surface of the globe. He thought that
all mountains, except such as were thrown up by volcanic agency or
local accidents, have been cut out of plains, the original surfaces of
which are indicated by the crests and summits of these elevations.
Lamarck, in reflecting upon the wide diffusion of fossil shells and
the great height above the sea at which they are found, conceived
the extraordinary idea that the ocean basin has been scoured out
by the sea, and that, by an impulse communicated to the waters
through the influence chiefly of the moon, the sea is slowly eating
away the eastern margins of the continents, and throwing up detritus
on their western coasts, and is thus gradually shifting its basin
round the globe. He would not admit the operation of cataclysms;
but insisted as strongly as Hutton on the continuity of natural
processes, and on the necessity of explaining former changes of the
earth’s surface by causes which can still be seen to be in operation.
As might be anticipated from his previous studies, he brought living
things and their remains into the forefront of his theory of the earth.
He looked upon fossils as one of the chief means of comprehending
the revolutions which the surface of the earth has undergone;
and in his little volume he again and again dwells on the vast
antiquity to which these revolutions bear witness. He acutely
argues, from the condition of fossil shells, that they must have lived
and died where their remains are now found.
In the last part of his treatise Lamarck advances some peculiar
opinions in physics and chemistry, which he had broached eighteen
years before, but which had met with no acceptance among the
scientific men of his time. He believed that the tendency of all
compound substances is to decay, and thereby to be resolved into
their component constituents. Yet he saw that the visible crust
of the earth consists almost wholly of compound bodies. He therefore
set himself to solve the problem thus presented. Perceiving
that the biological action of living organisms is constantly forming
combinations of matter, which would never have otherwise come
into existence, he proceeded to draw the extraordinary conclusion
that the action of plant and animal life (the Pouvoir de la vie) upon
the inorganic world is so universal and so potent, that the rocks and
minerals which form the outer part of the earth’s crust are all,
without exception, the result of the operations of once living bodies.
Though this sweeping deduction must be allowed to detract from
the value of Lamarck’s work, there can be no doubt that he realized,
more fully than any one had done before him, the efficacy of plants
and animals as agents of geological change.
The last notable contributor to the cosmological literature of
geology was another illustrious Frenchman, the comparative anatomist
Cuvier (1769-1832). He was contemporary with
Lamarck, but of a very different type of mind. The
Cuvier.
brilliance of his speculations, and the charm with which he expounded
them, early gained for him a prominent place in the society of Paris.
He too was drawn by his zoological studies to investigate fossil
organic remains, and to consider the former conditions of the earth’s
surface, of which they are memorials. It was among the vertebrate
organisms of the Paris basin that he found his chief material, and
from them that he prepared the memoirs which led to him being
regarded as the founder of vertebrate palaeontology. But beyond
their biological interest, they awakened in him a keen desire to
ascertain the character and sequence of the geographical revolutions
to which they bear witness. He approached the subject from an
opposite and less philosophical point of view than that of Lamarck,
coming to it with certain preconceived notions, which affected all
his subsequent writings. While Lamarck was by instinct an evolutionist,
who sought to trace in the history of the past the operation
of the same natural processes as are still at work, Cuvier, on the
other hand, was a catastrophist, who invoked a succession of vast
cataclysms to account for the interruptions in the continuity of the
geological record.
In a preliminary Discourse prefixed to his Recherches sur les
ossemens fossiles (1821) Cuvier gave an outline of what he conceived
to have been the past history of our globe, so far as he had been able
to comprehend it from his investigations of the Tertiary formations
of France. He believed that in that history evidence can be
recognized of the occurrence of many sudden and disastrous revolutions,
which, to judge from their effects on the animal life of the
time, must have exceeded in violence anything we can conceive at
the present day, and must have been brought about by other agencies
than those which are now in operation. Yet, in spite of these
catastrophes, he saw that there has been an upward progress in the
animal forms inhabiting the globe, until the series ended in the
advent of man. He could not, however, find any evidence that one
species has been developed from another, for in that case there should
have been traces of intermediate forms among the stratified formations,
where he affirmed that they had never been found. A
prominent position in the Discourse is given to a strenuous argument
to disprove the alleged antiquity of some nations, and to show that
the last great catastrophe occurred not more than some 5000 or
6000 years ago. Cuvier thus linked himself with those who in
previous generations had contended for the efficacy of the Deluge.
But his researches among fossil animals had given him a far wider
outlook into the geological past, and had opened up to him a succession
of deeply interesting problems in the history of life upon the
earth, which, though he had not himself material for their solution,
he could foresee would be cleared up in the future.
Gradual Shaping of Geology into a Distinct Branch of Science.—It
will be seen from the foregoing historical sketch that it was only
after the lapse of long centuries, and from the labours of many
successive generations of observers and writers, that what we now
know as the science of geology came to be recognized as a distinct
department of natural knowledge, founded upon careful and extended
study of the structure of the earth, and upon observation of
the natural processes, which are now at work in changing the earth’s
surface. The term “geology,”1 descriptive of this branch of the
investigation of nature, was not proposed until the last quarter of
the 18th century by Jean André De Luc (1727-1817) and Horace
Benedict De Saussure (1740-1749). But the science was then in a
markedly half-formed condition, theoretical speculation still in large
part supplying the place of deductions from a detailed examination
of actual fact. In 1807 a few enterprising spirits founded the
Geological Society of London for the special purpose of counteracting
the prevalent tendency and confining their intention “to
investigate the mineral structure of the earth.” The cosmogonists
and framers of Theories of the Earth were succeeded by other schools
of thought. The Catastrophists saw in the composition of the crust
of the earth distinct evidence that the forces of nature were once
much more stupendous in their operation than they now are, and
that they had from time to time devastated the earth’s surface;
extirpating the races of plants and animals, and preparing the ground
for new creations of organized life. Then came the Uniformitarians,
who, pushing the doctrines of Hutton to an extreme which he did
not propose, saw no evidence that the activity of the various geological
causes has ever seriously differed from what it is at present.
They were inclined to disbelieve that the stratified formations of
the earth’s crust furnish conclusive evidence of a gradual progression,
from simple types of life in the oldest strata to the most
highly developed forms in the youngest; and saw no reason why
remains of the higher vertebrates should not be met with among
the Palaeozoic formations. Sir Charles Lyell (1797-1875) was the
great leader of this school. His admirably clear and philosophical
presentations of geological facts which, with unwearied industry,
he collected from the writings of observers in all parts of the world,
impressed his views upon the whole English-speaking world, and
gave to geological science a coherence and interest which largely
accelerated its progress. In his later years, however, he frankly
accepted the views of Darwin in regard to the progressive character
of the geological record.
The youngest of the schools of geological thought is that of the
Evolutionists. Pointing to the whole body of evidence from inorganic
and organic nature, they maintain that the history of our
planet has been one of continual and unbroken development from
the earliest cosmical beginnings down to the present time, and that
the crust of the earth contains an abundant, though incomplete,
record of the successive stages through which the plant and animal
644
kingdoms have reached their existing organization. The publication
of Darwin’s Origin of Species in 1859, in which evolution was made
the key to the history of the animal and vegetable kingdoms, produced
an extraordinary revolution in geological opinion. The older
schools of thought rapidly died out, and evolution became the
recognized creed of geologists all over the world.
Development of Opinion regarding Igneous Rocks.—So long as the
idea prevailed that volcanoes are caused by the combustion of
inflammable substances underground, there could be no rational
conception of volcanic action and its products. Even so late as
the middle of the 18th century, as above remarked, such a good
observer as Lazzaro Moro drew so little distinction between volcanic
and other rocks that he could believe the fossiliferous formations
to have been mainly formed of materials ejected from eruptive vents.
After his time the notion continued to prevail that all the rocks which
form the dry land were laid down under water. Even streams of
lava, which were seen to flow from an active crater, were regarded
only as portions of sedimentary or other rocks, which had been
melted by the fervent heat of the burning inflammable materials
that had been kindled underground. In spite of the speculations
of Descartes and Leibnitz, it was not yet generally comprehended
that there exists beneath the terrestrial crust a molten magma,
which, from time to time, has been injected into that crust, and has
pierced through it, so as to escape at the surface with all the energy
of an active volcano. What we now recognize to be memorials of
these former injections and propulsions were all confounded with the
rocks of unquestionably aqueous origin. The last great teacher by
whom these antiquated doctrines were formulated into a system
Werner.
and promulgated to the world was Abraham Gottlob
Werner (1749-1815), the most illustrious German mineralogist
and geognost of the second half of the 18th century. While
still under twenty-six years of age, he was appointed teacher of
mining and mineralogy at the Mining Academy of Freiberg in Saxony—a
post which he continued to fill up to the end of his life. Possessed
of great enthusiasm for his subject, clear, methodical and eloquent
in his exposition of it, he soon drew around him men from all parts
of the world, who repaired to study under the great oracle of what
he called geognosy (Gr. γῆ, the earth, γνῶσις, knowledge) or earth-knowledge.
Reviving doctrines that had been current long before
his time, he taught that the globe was once completely surrounded
with an ocean, from which the rocks of the earth’s crust were
deposited as chemical precipitates, in a certain definite order over
the whole planet. Among these “universal formations” of aqueous
origin were included many rocks, which have long been recognized
to have been once molten, and to have risen from below into the
upper parts of the terrestrial crust. Werner, following the old
tradition, looked upon volcanoes as modern features in the history
of the planet, which could not have come into existence until a
sufficient amount of vegetation had been buried to furnish fuel for
their maintenance. Hence he attached but little importance to
them, and did not include in his system of rocks any division of
volcanic or igneous materials. From the predominant part assigned
by him to the sea in the accumulation of the materials of the visible
part of the earth, Werner and his school were known as “Neptunists.”
But many years before the Saxon professor began to teach, clear
evidence had been produced from central France that basalt, one
of the rocks claimed by him as a chemical precipitate and
a universal formation, is a lava which has been poured
Origin of basalt.
out in a molten state at various widely separated periods
of time and at many different places. So far back as 1752 J.E.
Guettard (1715-1786) had shown that the basaltic rocks of Auvergne
are true lavas, which have flowed out in streams from groups of
once active cones. Eleven years later the observation was confirmed
and greatly extended by Nicholas Desmarest (1725-1815), who,
during a long course of years, worked out and mapped the complicated
volcanic records of that interesting region, and demonstrated
to all who were willing impartially to examine the evidence the true
volcanic nature of basalt. These views found acceptance from some
observers, but they were vehemently opposed by the followers of
Werner, who, by the force of his genius, made his theoretical conceptions
predominate all over Europe. The controversy as to the
origin of basalt was waged with great vigour during the later decades
of the 18th century. Desmarest took no part in it. He had accumulated
such conclusive proof of the correctness of his deductions,
and had so fully expounded the clearness of the evidence in their
favour furnished by the region of Auvergne, that, when any one
came to consult him on the subject, he contented himself with giving
the advice to “go and see.” While the debate was in progress
on the continent, the subject was approached from a new and
independent point of view by Hutton in Scotland. This illustrious
philosopher, as already stated, realized the importance of the internal
heat of the globe in consolidating the sedimentary rocks, and believed
that molten material from the earth’s interior has been protruded
from below into the overlying crust. Some of the material thus
injected could be recognized, he thought, in granite and in the
various dark massive rocks which, known in Scotland under the
name of “whinstone,” were afterwards called “Trap,” and are now
grouped under various names, such as basalt, dolerite and diorite.
So important a share did Hutton thus assign to the internal heat in
the geological evolution of the planet, that he and those who adopted
the same opinions were styled “Plutonists,” or, especially where
they concerned themselves with the volcanic origin of basalt, “Vulcanists.”
The geological world was thus divided into two hostile
camps, that of the Neptunists or Wernerians, and that of the
Plutonists, Vulcanists or Huttonians.
After many years of futile controversy the first serious weakening
of the position of the dominant Neptunist school arose from the
defection of some of the most prominent of Werner’s pupils. In
particular Jean François D’Aubuisson de Voisins (1769-1819), who
had written a treatise on the aqueous origin of the basalts of Saxony,
went afterwards to Auvergne, where he was speedily a convert to
the views expounded by Desmarest as to the volcanic nature of
basalt. Having thus to relinquish one of the fundamental articles
of the Freiberg faith, he was subsequently led to modify his adherence
to others until, as he himself confessed, his views came almost wholly
to agree with those of Hutton. Not less complete, and even more
important, was the conversion of the great Leopold von Buch (1774-1853).
He, too, was trained by Werner himself, and proved to be
the most illustrious pupil of the Saxon professor. Full of admiration
for the Neptunism in which he had been reared, he, in his earliest
separate work, maintained the aqueous origin of basalt, and contrasted
the wide field opened up to the spirit of observation by his
master’s teaching with the narrower outlook offered by “the volcanic
theory.” But a little further acquaintance with the facts of nature
led Von Buch also to abandon his earlier prepossessions. It was a
personal visit to the volcanic region of Auvergne that first opened
his eyes, and led him to recant what he had believed and written
about basalt. But the abandonment of so essential a portion of the
Wernerian creed prepared the way for further relinquishments.
When a few years later he went to Norway and found to his astonishment
that granite, which he had been taught to regard as the oldest
chemical precipitate from the universal ocean, could there be seen
to have broken through and metamorphosed fossiliferous limestones,
and to have sent veins into them, his faith in Werner’s order of the
succession of the rocks in the earth’s crust received a further momentous
shock. While one after another of the Freiberg doctrines
crumbled away before him, he was now able to interrogate nature
on a wider field than the narrow limits of Saxony, and he was thus
gradually led to embrace the tenets of the opposite school. His
commanding position, as the most accomplished geologist on the
continent, gave great importance to his recantation of the Neptunist
creed. His defection indeed was the severest blow that this creed
had yet sustained. It may be said to have rung the knell of
Wernerianism, which thereafter rapidly declined in influence, while
Plutonism came steadily to the front, where it has ever since remained.
Although Desmarest had traced in Auvergne a long succession
of volcanic eruptions, of which the oldest went back to a remote
period of time, and although he had shown that this succession,
coupled with the records of contemporaneous denudation, might
be used in defining epochs of geological history, it was not until
many years after his day that volcanic action came to be recognized
as a normal part of the mechanism of our globe, which had been in
operation from the remotest past, and which had left numerous
records among the rocks of the terrestrial crust. During the progress
of the controversy between the two great opposing factions in the
later portion of the 18th and the first three decades of the 19th
century, those who espoused the Vulcanist cause were intent on
proving that certain rocks, which are intercalated among the
stratified formations and which were claimed by the Neptunists as
obviously formed by water, are nevertheless of truly igneous origin.
These observers fixed their eyes on the evidence that the material of
such rocks, instead of having been deposited from aqueous solution,
had once been actually molten, and had in that condition been thrust
between the strata, had enveloped portions of them, and had indurated
or otherwise altered them. They spoke of these masses
as “unerupted lavas”; and undoubtedly in innumerable instances
they were right. But their zeal to establish an intrusive origin led
them to overlook the proofs that some intercalated sheets of igneous
material had not been injected into the strata, but had been poured
out at the surface as truly volcanic discharges, and therefore belonged
to the ancient periods represented by the strata between which they
are interposed. It may readily be supposed that any proofs of the
contemporaneous intercalation of such sheets would be eagerly
seized upon by the Neptunists in favour of their aqueous theory.
The influence of the ancient belief that “burning mountains”
could only rise from the combustion of subterranean inflammable
materials extended even into the ranks of the Vulcanists, so far at
least as to lead to a general acquiescence in the assumption that
volcanoes appeared to belong to a late phase in the history of the
planet. It was not until after considerable progress had been made
in determining the palaeontological distinctions and order of succession
of the stratified formations of the earth’s crust that it became
possible to trace among these formations a succession of volcanic
episodes which were contemporaneous with them. In no part of
the world has an ampler record of such episodes been preserved than
in the British Isles. It was natural, therefore, that the subject
should there receive most attention. As far back as 1820 Ami Boué
(1794-1881) showed that the Old Red Sandstone of Scotland includes
a great series of volcanic rocks, and that other rocks of volcanic
origin are associated with the Carboniferous formations. H.T.
645
de la Beche (1796-1855) afterwards traced proofs of contemporaneous
eruptions among the Devonian rocks of the south-west of England.
Adam Sedgwick (1785-1873) showed, first in the Lake District,
and afterwards in North Wales, the presence of abundant volcanic
sheets among the oldest divisions of the Palaeozoic series; while
Roderick Impey Murchison (1792-1871) made similar discoveries
among the Lower Silurian rocks. From the time of these pioneers
the volcanic history of the country has been worked out by many
observers until it is now known with a fulness as yet unattained
in any other region.
Growth of Opinion regarding Earthquakes.—We have seen how
crude were the conceptions of the ancients regarding the causes of
volcanic action, and that they connected volcanoes and earthquakes
as results of the commotion of wind imprisoned within subterranean
caverns and passages. One of the earliest treatises, in which the
phenomena of terrestrial movements were discussed in the spirit
of modern science, was the posthumous collection of papers by
Robert Hooke (1635-1703), entitled Lectures and Discourses of
Earthquakes and Subterranean Eruptions, where the probable agency
of earthquakes in upheaving and depressing land is fully considered,
but without any definite pronouncement as to the author’s conception
of its origin. Hooke still associated earthquakes with volcanic
action, and connected both with what he called “the general congregation
of sulphurous subterraneous vapours.” He conceived
that some kind of “fermentation” takes place within the earth,
and that the materials which catch fire and give rise to eruptions
or earthquakes are analogous to those that constitute gunpowder.
The first essay wherein earthquakes are treated from the modern
point of view as the results of a shock that sends waves through the
crust of the earth was written by the Rev. John Michell, and communicated
to the Royal Society in the year 1760. Still under the
old misconception that volcanoes are due to the combustion of
inflammable materials, which he thought might be set on fire by the
spontaneous combustion of pyritous strata, he supposed that, by the
sudden access of large bodies of water to these subterranean fires,
vapour is produced in such quantity and with such force as to give
rise to the shock. From the centre of origin of this shock waves,
he thought, are propagated through the earth, which are largest
at the start and gradually diminish as they travel outwards. By
drawing lines at different places in the direction of the track of these
waves, he believed that the place of common intersection of these
lines would be nearly the centre of the disturbance. In this way he
showed that the great Lisbon earthquake of 1755 had its focus under
the Atlantic, somewhere between the latitudes of Lisbon and Oporto,
and he estimated that the depth at which it originated could not
be much less than 1 m., and probably did not exceed 3 m. Michell,
however, misconceived the character of the waves which he described,
seeing that he believed them to be due to the actual propagation of
the vapour itself underneath the surface of the earth. A century
had almost passed after the date of his essay before modern scientific
methods of observation and the use of recording instruments began
to be applied to the study of earthquake phenomena. In 1846 Robert
Mallet (1810-1881) published an important paper “On the Dynamics
of Earthquakes” in the Transactions of the Royal Irish Academy.
From that time onward he continued to devote his energies to the
investigation, studying the effects of the Calabrian earthquake of
1857, experimenting on the transmission of waves of shock through
various materials, caused by exploding charges of gunpowder, and
collecting all the information to be obtained on the subject. His
writings, and especially his work in two volumes on The First
Principles of Observational Seismology, must be regarded as having
laid the foundations of this branch of modern geology (see Earthquake;
Seismometer).
History of the Evolution of Stratigraphical Geology.—Men had long
been familiar with the evidence that the present dry land once lay
under the sea, before they began to realize that the rocks, of which
the land consists, contain a record of many alternations of land and
sea, and relics of a long succession of plants and animals from early
and simple types up to the manifold and complex forms of to-day.
In countries where coal-mining had been prosecuted for generations,
it had been recognized that the rocks consist of strata superposed
on each other in a definite order, which was found to extend over
the whole of a district. As far back as 1719 John Strachey drew
attention to this fact in a communication published in the Philosophical
Transactions. John Michell (1760), in the paper on earthquakes
already cited, showed that he had acquired a clear understanding
of the order of succession among stratified formations, and
perceived that to disturbances of the terrestrial crust must be ascribed
the fact that the lower or older and more inclined strata form the
mountains, while the younger and more horizontal strata are spread
over the plains.
In Italy G. Arduíno (1713-1795) classified the rocks in the north
of the peninsula as Primitive, Secondary, Tertiary and Volcanic.
A similar threefold order was announced for the Harz and Erzgebirge
by J.G. Lehmann in 1756. He recognized in that region an ancient
series of rocks in inclined or vertical strata, which rise to the tops
of the hills and descend to an unknown depth into the interior.
These masses, he thought, were contemporaneous with the making
of the world. Next came the Flötzgebirge, consisting of younger
sediments, disposed in flat or gently inclined sheets which overlie
the first and more disturbed series, and are full of petrified remains
of plants and animals. Lastly he included the mountains which
have from time to time been formed by local accidents. Still more
advanced were the conceptions of G.C. Füchsel, who in the year
1762 published in Latin A History of the Earth and the Sea, based on
a History of the Mountains of Thuringia; and in 1773, in German,
a Sketch of the most Ancient History of the Earth and Man. In these
works he described the stratigraphical relations and general characters
of the various geological formations in his little principality;
and taking them as indicative of a general order of succession, he
traced what he believed to have been a series of revolutions through
which the earth has passed. In interpreting this geological history,
he laid great stress on the evidence of the fossils contained in the
rocks. He recognized that the various formations differ from each
other in their enclosed organic remains, and that from these differences
the existence of former sea-bottoms and land surfaces can
be determined.
The labours of these pioneers paved the way for the advent
of Werner. Though the system evolved by this teacher claimed to
discard theory and to be established on a basis of observed facts,
it rested on a succession of hypotheses, for which no better foundation
could be shown than the belief of their author in their validity.
Starting from the extremely limited stratigraphical range displayed
in the geological structure of Saxony, he took it as a type for the rest
of the globe, persuading himself and impressing upon his followers
that the rocks of that small kingdom were to be taken as examples
of his “universal formations.” The oldest portion of the series,
classed by him as “Primitive,” consisted of rocks which he maintained
had been deposited from chemical solution. Yet they
included granite, gneiss, basalt, porphyry and serpentine, which,
even in his own day, were by many observers correctly regarded
as of igneous origin. A later group of rocks, to which he gave the
name of “Transition,” comprised, in his belief, partly chemical,
partly mechanical sediments, and contained the earliest fossil
organic remains. A third group, for which he reserved Lehmann’s
name “Flötz,” was made up chiefly of mechanical detritus, while
youngest of all came the “Alluvial” series of loams, clays, sands,
gravels and peat. It was by the gradual subsidence of the ocean
that, as he believed, the general mass of the dry land emerged, the
first-formed rocks being left standing up, sometimes on end, to form
the mountains, while those of later date, less steeply inclined,
occupied successively lower levels down to the flat alluvial accumulations
of the plains. Neither Werner, nor any of his followers,
ventured to account for what became of the water as the sea-level
subsided, though, in despite of their antipathy to anything like
speculation, they could not help suggesting, as an answer to the
cogent arguments of their opponents, that “one of the celestial
bodies which sometimes approach near to the earth may have been
able to withdraw a portion of our atmosphere and of our ocean.”
Nor was any attempt made to explain the extraordinary nature of
the supposed chemical precipitates of the universal ocean. The
progress of inquiry even in Werner’s lifetime disproved some of
the fundamental portions of his system. Many of the chemical
precipitates were shown to be masses that had been erupted in a
molten state from below. His order of succession was found not
to hold good; and though he tried to readjust his sequence and to
introduce into it modifications to suit new facts, its inherent artificiality
led to its speedy decline after his death. It must be conceded,
however, that the stress which he laid upon the fact that the
rocks of the earth’s crust were deposited in a definite order had an
important influence in directing attention to this subject, and in
preparing the way for a more natural system, based not on mere
mineralogical characters, but having regard to the organic remains,
which were now being gathered in ever-increasing numbers and
variety from stratified formations of many different ages and from
all parts of the globe.
It was in France and in England that the foundations of stratigraphy,
based upon a knowledge of organic remains, were first
successfully laid. Abbé J.L. Giraud-Soulavie (1752-1813), in his
Histoire naturelle de la France méridionale, which appeared in seven
volumes, subdivided the limestones of Vivarais into five ages, each
marked by a distinct assemblage of shells. In the lowest strata,
representing the first age, none of the fossils were believed by him
to have any living representatives, and he called these rocks “Primordial.”
In the next group a mingling of living with extinct forms
was observable. The third age was marked by the presence of
shells of still existing species. The strata of the fourth series were
characterized by carbonaceous shales or slates, containing remains
of primordial vegetation, and perhaps equivalents of the first three
calcareous series. The fifth age was marked by recent deposits
containing remains of terrestrial vegetation and of land animals.
It is remarkable that these sagacious conclusions should have been
formed and published at a time when the geologists of the Continent
were engaged in the controversy about the origin of basalt, or in
disputes about the character and stratigraphical position of the
supposed universal formations, and when the interest and importance
of fossil organic remains still remained unrecognized by the vast
majority of the combatants.
The rocks of the Paris basin display so clearly an orderly
arrangement, and are so distinguished for the variety and perfect
646
preservation of their enclosed organic remains, that they could not
fail to attract the early notice of observers. J. É. Guettard, G.F.
Rouelle (1703-1770), N. Desmarest, A.L. Lavoisier (1743-1794)
and others made observations in this interesting district. But it
was reserved for Cuvier (1769-1832) and A. Brongniart (1770-1847)
to work out the detailed succession of the Tertiary formations, and
to show how each of these is characterized by its own peculiar
assemblage of organic remains. The later progress of investigation
has slightly corrected and greatly amplified the tabular arrangement
established by these authors in 1808, but the broad outlines of the
Tertiary stratigraphy of the Paris basin remain still as Cuvier and
Brongniart left them. The most important subsequent change
in the classification of the Tertiary formations was made by Sir
Charles Lyell, who, conceiving in 1828 the idea of a classification
of these rocks by reference to their relative proportions of living
and extinct species of shells, established, in collaboration with
G.P. Deshayes, the now universally accepted divisions Eocene,
Miocene and Pliocene.
Long before Cuvier and Brongniart published an account of their
researches, another observer had been at work among the Secondary
formations of the west of England, and had independently discovered
that the component members of these formations were each
distinguished by a peculiar group of organic remains; and that this
distinction could be used to discriminate them over all the region
through which he had traced them. The remarkable man who
arrived at this far-reaching generalization was William Smith (1769-1839),
a land surveyor who, in the prosecution of his professional
business, found opportunities of traversing a great part of England,
and of putting his deductions to the test. As the result of these
journeys he accumulated materials enough to enable him to produce
a geological map of the country, on which the distribution and
succession of the rocks were for the first time delineated. Smith’s
labours laid the foundation of stratigraphical geology in England
and he was styled even in his lifetime the “Father of English
geology.” From his day onward the significance of fossil organic
remains gained rapidly increasing recognition. Thus in England
the outlines traced by him among the Secondary and Tertiary
formations were admirably filled in by Thomas Webster (1773-1844);
while the Cretaceous series was worked out in still greater detail
in the classic memoirs of William Henry Fitton (1780-1861).
There was one stratigraphical domain, however, into which William
Smith did not enter. He traced his sequence of rocks down into the
Coal Measures, but contented himself with only a vague reference
to what lay underneath that formation. Though some of these
underlying rocks had in various countries yielded abundant fossils,
they had generally suffered so much from terrestrial disturbances,
and their order of succession was consequently often so much
obscured throughout western Europe, that they remained but little
known for many years after the stratigraphy of the Secondary and
Tertiary series had been established. At last in 1831 Murchison
began to attack this terra incognita on the borders of South Wales,
working into it from the Old Red Sandstone, the stratigraphical
position of which was well known. In a few years he succeeded in
demonstrating the existence of a succession of formations, each
distinguished by its own peculiar assemblage of organic remains
which were distinct from those in any of the overlying strata. To
these formations he gave the name of Silurian (q.v.). From the
key which his researches supplied, it was possible to recognize in
other countries the same order of formations and the same sequence
of fossils, so that, in the course of a few years, representatives of the
Silurian system were found far and wide over the globe. While
Murchison was thus engaged, Sedgwick devoted himself to the more
difficult task of unravelling the complicated structure of North
Wales. He eventually made out the order of the several formations
there, with their vast intercalations of volcanic material. He named
them the Cambrian system (q.v.), and found them to contain fossils,
which, however, lay for some time unexamined by him. He at
first believed, as Murchison also did, that his rocks were all older
than any part of the Silurian series. It was eventually discovered
that a portion of them was equivalent to the lower part of that
series. The oldest of Sedgwick’s groups, containing distinctive
fossils, retain the name Cambrian, and are of high interest, as they
enclose the remains of the earliest faunas which are yet well known.
Sedgwick and Murchison rendered yet another signal service to
stratigraphical geology by establishing, in 1839, on a basis of
palaeontological evidence supplied by W. Lonsdale, the independence
of the Devonian system (q.v.).
For many years the rocks below the oldest fossiliferous deposits
received comparatively little attention. They were vaguely described
as the “crystalline schists” and were often referred to as parts of
the primeval crust in which no chronology was to be looked for.
W.E. Logan (1798-1875) led the way, in Canada, by establishing
there several vast series of rocks, partly of crystalline schists and
gneisses (Laurentian) and partly of slates and conglomerates
(Huronian). Later observers, both in Canada and the United
States, have greatly increased our knowledge of these rocks, and
have shown their structure to be much more complex than was at
first supposed (see Archean System).
During the latter half of the 19th century the most important
development of stratigraphical geology was the detailed working
out and application of the principle of zonal classification to the
fossiliferous formations—that is, the determination of the sequence
and distribution of organic remains in these formations, and the
arrangement of the strata into zones, each of which is distinguished
by a peculiar assemblage of fossil species (see under Part VI.). The
zones are usually named after one especially characteristic species.
This system of classification was begun in Germany with reference
to the members of the Jurassic system (q.v.) by A. Oppel (1856-1858)
and F.A. von Quenstedt (1858), and it has since been extended
through the other Mesozoic formations. It has even been found to
be applicable to the Palaeozoic rocks, which are now subdivided
into palaeontological zones. In the Silurian system, for example, the
graptolites have been shown by C. Lapworth to furnish a useful
basis for zonal subdivisions. The lowest fossiliferous horizon in the
Cambrian rocks of Europe and North America is known as the
Olenellus zone, from the prominence in it of that genus of trilobite.
Another conspicuous feature in the progress of stratigraphy
during the second half of the 19th century was displayed by the rise
and rapid development of what is known as Glacial geology. The
various deposits of “drift” spread over northern Europe, and the
boulders scattered across the surface of the plains had long attracted
notice, and had even found a place in popular legend and superstition.
When men began to examine them with a view to ascertain
their origin, they were naturally regarded as evidences of the
Noachian deluge. The first observer who drew attention to the
smoothed and striated surfaces of rock that underlie the Drifts was
Hutton’s friend, Sir James Hall, who studied them in the lowlands
of Scotland and referred them to the action of great debacles of
water, which, in the course of some ancient terrestrial convulsion,
had been launched across the face of the country. Playfair, however,
pointed out that the most potent geological agents for the transportation
of large blocks of stone are the glaciers. But no one was
then bold enough to connect the travelled boulders with glaciers
on the plains of Germany and of Britain. Yet the transporting
agency of ice was invoked in explanation of their diffusion. It
came to be the prevalent belief among the geologists of the first
half of the 19th century, that the fall of temperature, indicated by
the gradual increase in the number of northern species of shells
in the English Crag deposits, reached its climax during the time
of the Drift, and that much of the north and centre of Europe was
then submerged beneath a sea, across which floating icebergs and
floes transported the materials of the Drift and dropped the scattered
boulders. As the phenomena are well developed around the Alps,
it was necessary to suppose that the submergence involved the
lowlands of the Continent up to the foot of that mountain chain—a
geographical change so stupendous as to demand much more
evidence than was adduced in its support. At last Louis Agassiz
(1807-1873), who had varied his palaeontological studies at Neuchâtel
by excursions into the Alps, was so much struck by the proofs of
the former far greater extension of the Swiss glaciers, that he pursued
the investigation and satisfied himself that the ice had formerly
extended from the Alpine valleys right across the great plain of
Switzerland, and had transported huge boulders from the central
mountains to the flanks of the Jura. In the year 1840 he visited
Britain and soon found evidence of similar conditions there. He
showed that it was not by submergence in a sea cumbered with
floating ice, but by the former presence of vast glaciers or sheets of
ice that the Drift and erratic blocks had been distributed. The idea
thus propounded by him did not at once command complete approval,
though traces of ancient glaciers in Scotland and Wales were soon
detected by native geologists, particularly by W. Buckland, Lyell,
J.D. Forbes and Charles Maclaren. Robert Chambers (1802-1871)
did good service in gathering additional evidence from Scotland and
Norway in favour of Agassiz’s views, which steadily gained adherents
until, after some quarter of a century, they were adopted by the
great majority of geologists in Britain, and subsequently in other
countries. Since that time the literature of geology has been swollen
by a vast number of contributions in which the history of the Glacial
period, and its records both in the Old and New World, have been
fully discussed.
Rise and Progress of Palaeontological Geology.—As this branch of
the science deals with the evidence furnished by fossil organic
remains as to former geographical conditions, it early attracted
observers who, in the superficial beds of marine shells found at some
distance from the coast, saw proofs of the former submergence of
the land under the sea. But the occurrence of fossils embedded in
the heart of the solid rocks of the mountains offered much greater
difficulties of explanation, and further progress was consequently
slow. Especially baneful was the belief that these objects were
mere sports of nature, and had no connexion with any once living
organisms. So long as the true organic origin of the fossil plants and
animals contained in the rocks was in dispute, it was hardly possible
that much advance could be made in their systematic study, or in
the geological deductions to be drawn from them. One good result
of the controversy, however, was to be seen in the large collections
of these “formed stones” that were gathered together in the cabinets
and museums of the 17th and 18th centuries. The accumulation
and comparison of these objects naturally led to the production of
treatises in which they were described and not unfrequently illustrated
by good engravings. Switzerland was more particularly
647
noted for the number and merit of its works of this kind, such as that
of K.N. Lang (Historia lapidum figuratorum Helvetiae, 1708) and
those of Johann Jacob Scheuchzer (1672-1733). In England, also,
illustrated treatises were published both by men who looked on
fossils as mere freaks of nature, and by those who regarded them as
proofs of Noah’s flood. Of the former type were the works of Martin
Lister (1638-1712) and Robert Plot (Natural History of Oxfordshire,
1677). The Celtic scholar Edward Llwyd (1660-1709) wrote a Latin
treatise containing good plates of a thousand fossils in the Ashmolean
Museum, Oxford, and J. Woodward, in 1728-1729, published his
Natural History of the Fossils of England, already mentioned, wherein
he described his own extensive collection, which he bequeathed to
the University of Cambridge, where it is still carefully preserved.
The most voluminous and important of all these works, however,
appeared at a later date at Nuremberg. It was begun by G.W.
Knorr (1705-1761), who himself engraved for it a series of plates,
which for beauty and accuracy have seldom been surpassed. After
his death the work was continued by J.E.I. Walch (1725-1778), and
ultimately consisted of four massive folio volumes and nearly 300
plates under the title of Lapides diluvii universalis testes. Although
the authors supposed their fossils to be relics of Noah’s flood, their
work must be acknowledged to mark a distinct onward stage in the
palaeontological department of geology.
It was in France that palaeontological geology began to be cultivated
in a scientific spirit. The potter Bernard Palissy, as far back
as 1580, had dwelt on the importance of fossil shells as monuments
of revolutions of the earth’s surface; but the observer who first
undertook the detailed study of the subject was Jean Etienne
Guettard, who began in 1751 to publish his descriptions of fossils
in the form of memoirs presented to the Academy of Sciences of
Paris. To him they were not only of deep interest as monuments
of former types of existence, but they had an especial value as
records of the changes which the country had undergone from sea
to land and from land to sea. More especially noteworthy was a
monograph by him which appeared in 1765 bearing the title “On
the accidents that have befallen Fossil Shells compared with those
which are found to happen to shells now living in the Sea.” In this
treatise he showed that the fossils have been encrusted with barnacles
and serpulae, have been bored into by other organisms, and have
often been rounded or broken before final entombment; and he
inferred that these fossils must have lived and died on the sea-floor
under similar conditions to those which obtain on the sea-floor
to-day. His argument was the most triumphant that had ever
been brought against the doctrine of lusus naturae, and that of the
efficacy of Noah’s flood—doctrines which still held their ground in
Guettard’s day. When Soulavie, Cuvier and Brongniart in France,
and William Smith in England, showed that the rock formations
of the earth’s crust could be arranged in chronological order, and
could be recognized far and wide by means of their enclosed organic
remains, the vast significance of these remains in geological research
was speedily realized, and palaeontological geology at once entered
on a new and enlarged phase of development. But apart from
their value as chronological monuments, and as witnesses of former
conditions of geography, fossils presented in themselves a wide
field of investigation as types of life that had formerly existed, but
had now passed away. It was in France that this subject first took
definite shape as an important branch of science. The mollusca of
the Tertiary deposits of the Paris basin became, in the hands of
Lamarck, the basis on which invertebrate palaeontology was founded.
The same series of strata furnished to Cuvier the remains of extinct
land animals, of which, by critical study of their fragmentary bones
and skeletons, he worked out restorations that may be looked on
as the starting-point of vertebrate palaeontology. These brilliant
researches, rousing widespread interest in such studies, showed how
great a flood of light could be thrown on the past history of the earth
and its inhabitants. But the full significance of these extinct types
of life could not be understood so long as the doctrine of the immutability
of species, so strenuously upheld by Cuvier, maintained its
sway among naturalists. Lamarck, as far back as the year 1800,
had begun to propound his theory of evolution and the transformation
of species; but his views, strongly opposed by Cuvier and the
great body of naturalists of the day, fell into neglect. Not until
after the publication in 1859 of the Origin of Species by Charles
Darwin were the barriers of old prejudice in this matter finally
broken down. The possibility of tracing the ancestry of living forms
back into the remotest ages was then perceived; the time-honoured
fiction that the stratified formations record a series of catastrophes
and re-creations was finally dissipated; and the earth’s crust was
seen to contain a noble, though imperfect, record of the grand
evolution of organic types of which our planet has been the theatre.
Development of Petrographical Geology.—Theophrastus, the favourite
pupil of Aristotle, wrote a treatise On Stones, which has come
down to our own day, and may be regarded as the earliest work on
petrography. At a subsequent period Pliny, in his Natural History,
collected all that was known in his day regarding the occurrence
and uses of minerals and rocks. But neither of these works is
of great scientific importance, though containing much interesting
information. Minerals from their beauty and value attracted
notice before much attention was paid to rocks, and their study
gave rise to the science of mineralogy long before geology came
into existence. When rocks began to be more particularly scrutinized,
it was chiefly from the side of their usefulness for building
and other economic purposes. The occurrence of marine shells in
many of them had early attracted attention to them. But their
varieties of composition and origin did not become the subject of
serious study until after Linnaeus and J.G. Wallerius in the 18th
century had made a beginning. The first important contribution
to this department of the science was that of Werner, who in 1786
published a classification and description of rocks in which he
arranged them in two divisions, simple and compound, and further
distinguished them by various external characters and by their
relative age. The publication of this scheme may be said to mark
the beginning of scientific petrography. Werner’s system, however,
had the serious defect that the chronological order in which he
grouped the rocks, and the hypothesis by which he accounted for
them as chemical precipitates from the original ocean, were both
alike contrary to nature. It was hardly possible indeed that much
progress could be made in this branch of geology until chemistry
and mineralogy had made greater advances; and especially until
it was possible to ascertain the intimate chemical and mineralogical
composition, and the minute structure of rocks. The study, however,
continued to be pursued in Germany, where the influence of Werner’s
enthusiasm still led men to enter the petrographical rather than the
palaeontological domain. The resources of modern chemistry were
pressed into the service, and analyses were made and multiplied to
such a degree that it seemed as if the ultimate chemical constitution
of every type of rock had now been thoroughly revealed. The
condition of the science in the middle of the 19th century was well
shown by J.L.A. Roth, who in 1861 collected about 1000 trustworthy
analyses which up to that time had been made. But though
the chemical elements of the rocks had been fairly well determined,
the manner in which they were combined in the compound rocks
could for the most part be only more or less plausibly conjectured.
As far back as 1831 an account was published of a process devised by
William Nicol of Edinburgh, whereby sections of fossil wood could be
cut, mounted on glass, and reduced to such a degree of transparency
as to be easily examined under a microscope. Henry Sorby, of
Sheffield, having seen Nicol’s preparations, perceived how admirably
adapted the process was for the study of the minute structure and
composition of rocks. In 1858 he published in the Quarterly Journal
of the Geological Society a paper “On the Microscopical Structure of
Crystals.” This essay led to a complete revolution of petrographical
methods and gave a vast impetus to the study of rocks. Petrology
entered upon a new and wider field of investigation. Not only were
the mineralogical constituents of the rocks detected, but minute
structures were revealed which shed new light on the origin and
history of these mineral masses, and opened up new paths in
theoretical geology. In the hands of H. Vogelsang, F. Zirkel,
H. Rosenbusch, and a host of other workers in all civilized countries,
the literature of this department of the science has grown to a
remarkable extent. Armed with the powerful aid of modern optical
instruments, geologists are now able with far more prospect of success
to resume the experiments begun a century before by de Saussure
and Hall. G.A. Daubrée, C. Friedel, E. Sarasin, F. Fouqué and
A. Michel Lévy in France, C. Doelter y Cisterich and E. Hussak of
Gratz, J. Morozewicz of Warsaw and others, have greatly advanced
our knowledge by their synthetical analyses, and there is every
reason to hope that further advances will be made in this field of
research.
Rise of Physiographical Geology.—Until stratigraphical geology
had advanced so far as to show of what a vast succession of rocks the
crust of the earth is built up, by what a long and complicated series
of revolutions these rocks have come to assume their present positions,
and how enormous has been the lapse of time which all these changes
represent, it was not possible to make a scientific study of the surface
features of our globe. From ancient times it had been known that
many parts of the land had once been under the sea; but down even
to the beginning of the 19th century the vaguest conceptions continued
to prevail as to the operations concerned in the submergence
and elevation of land, and as to the processes whereby the present
outlines of terrestrial topography were determined. We have seen,
for instance, that according to the teaching of Werner the oldest
rocks were first precipitated from solution in the universal ocean to
form the mountains, that the vertical position of their strata was
original, that as the waters subsided successive formations were
deposited and laid bare, and that finally the superfluous portion of the
ocean was whisked away into space by some unexplained co-operation
of another planetary body. Desmarest, in his investigation of the
volcanic history of Auvergne, was the first observer to perceive by
what a long process of sculpture the present configuration of the land
has been brought about. He showed conclusively that the valleys have
been carved out by the streams that flow in them, and that while
they have sunk deeper and deeper into the framework of the land,
the spaces of ground between them have been left as intervening
ridges and hills. De Saussure learnt a similar lesson from his studies
of the Alps, and Hutton and Playfair made it a cardinal feature in
their theory of the earth. Nevertheless the idea encountered so
much opposition that it made but little way until after the middle
of the 19th century. Geologists preferred to believe in convulsions
of nature, whereby valleys were opened and mountains were
648
upheaved. That the main features of the land, such as the great
mountain-chains, had been produced by gigantic plication of the
terrestrial crust was now generally admitted, and also that minor
fractures and folds had probably initiated many of the valleys.
But those who realized most vividly the momentous results achieved
by ages of subaerial denudation perceived that, as Hutton showed,
even without the aid of underground agency, the mere flow of water
in streams across a mass of land must in course of time carve out
just such a system of valleys as may anywhere be seen. It was
J.B. Jukes who, in 1862, first revived the Huttonian doctrine,
and showed how completely it explained the drainage-lines in the
south of Ireland. Other writers followed in quick succession until,
in a few years, the doctrine came to be widely recognized as one of
the established principles of modern geology. Much help was derived
from the admirable illustrations of land-sculpture and river-erosion
supplied from the Western Territories and States of the American
Union.
Another branch of physiographical geology which could only come
into existence after most of the other departments of the science
had made large progress, deals with the evolution of the framework
of each country and of the several continents and oceans of the globe.
It is now possible, with more or less confidence, to trace backward
the history of every terrestrial area, to see how sea and land have
there succeeded each other, how rivers and lakes have come and
gone, how the crust of the earth has been ridged up at widely
separated intervals, each movement determining some line of
mountains or plains, how the boundaries of the oceans have shifted
again and again in the past, and thus how, after so prolonged a series
of revolutions, the present topography of each country, and of the
globe as a whole, has been produced. In the prosecution of this
subject maps have been constructed to show what is conjectured
to have been the distribution of sea and land during the various
geological periods in different parts of the world, and thus to indicate
the successive stages through which the architecture of the land has
been gradually evolved. The most noteworthy contribution to this
department of the science is the Antlitz der Erde of Professor Suess
of Vienna. This important and suggestive work has been translated
into French and English.
Part II.—Cosmical Aspects
Before geology had attained to the position of an inductive
science, it was customary to begin investigations into the
history of the earth by propounding or adopting some more
or less fanciful hypothesis in explanation of the origin of our
planet, or even of the universe. Such preliminary notions were
looked upon as essential to a right understanding of the manner
in which the materials of the globe had been put together. One
of the distinguishing features of Hutton’s Theory of the Earth
consisted in his protest that it is no part of the province of
geology to discuss the origin of things. He taught that in the
materials from which geological evidence is to be compiled
there can be found “no traces of a beginning, no prospect of an
end.” In England, mainly to the influence of the school which
he founded, and to the subsequent rise of the Geological Society
of London, which resolved to collect facts instead of fighting
over hypotheses, is due the disappearance of the crude and
unscientific cosmologies by which the writings of the earlier
geologists were distinguished.
But there can now be little doubt that in the reaction against
those visionary and often grotesque speculations, geologists
were carried too far in an opposite direction. In allowing
themselves to believe that geology had nothing to do with
questions of cosmogony, they gradually grew up in the conviction
that such questions could never be other than mere speculation,
interesting or amusing as a theme for the employment of the
fancy, but hardly coming within the domain of sober and
inductive science. Nor would they soon have been awakened
out of this belief by anything in their own science. It is still
true that in the data with which they are accustomed to deal,
as comprising the sum of geological evidence, there can be
found no trace of a beginning, though the evidence furnished
by the terrestrial crust shows a general evolution of organic
forms from some starting-point which cannot be seen. The
oldest rocks which have been discovered on any part of the
globe have probably been derived from other rocks older than
themselves. Geology by itself has not yet revealed, and is little
likely ever to reveal, a trace of the first solid crust of our globe.
If, then, geological history is to be compiled from direct evidence
furnished by the rocks of the earth, it cannot begin at the
beginning of things, but must be content to date its first chapter
from the earliest period of which any record has been preserved
among the rocks.
Nevertheless, though geology in its usual restricted sense has
been, and must ever be, unable to reveal the earliest history of
our planet, it no longer ignores, as mere speculation, what is
attempted in this subject by its sister sciences. Astronomy,
physics and chemistry have in late years all contributed to cast
light on the earlier stages of the earth’s existence, previous to
the beginning of what is commonly regarded as geological history.
But whatever extends our knowledge of the former conditions
of our globe may be legitimately claimed as part of the domain of
geology. If this branch of inquiry, therefore, is to continue
worthy of its name as the science of the earth, it must take
cognizance of these recent contributions from other sciences.
It must no longer be content to begin its annals with the records
of the oldest rocks, but must endeavour to grope its way through
the ages which preceded the formation of any rocks. Thanks
to the results achieved with the telescope, the spectroscope and
the chemical laboratory, the story of these earliest ages of our
earth is every year becoming more definite and intelligible.
Up to the present time no definite light has been thrown by
physics on the origin and earliest condition of our globe. The
famous nebular theory (q.v.) of Kant and Laplace sketched the
supposed evolution of the solar system from a gaseous nebula,
slowly rotating round a more condensed central portion of its
mass, which eventually became the sun. As a consequence of
increased rapidity of rotation resulting from cooling and contraction,
the nebula acquired a more and more lenticular form,
until at last it threw off from its equatorial protuberance a ring
of matter. Subsequently the same process was repeated, and
other similar rings successively separated from the parent mass.
Each ring went through a corresponding series of changes until
it ultimately became a planet, with or without one or more
attendant satellites. The intimate relationship of our earth
to the sun and the other planets was, in this way, shown. But
there are some serious physical difficulties in the way of the
acceptance of the nebular hypothesis. Another explanation
is given by the meteoritic hypothesis, according to which, out
of the swarms of meteorites with which the regions of space are
crowded, the sun and planets have been formed by gradual
accretion.
According to these theoretical views we should expect to find
a general uniformity of composition in the constituent matter
of the solar system. For many years the only available evidence
on this point was derived from the meteorites (q.v.) which so
constantly fall from outer space upon the surface of the earth.
These bodies were found to consist of elements, all of which had
been recognized as entering into the constitution of the earth.
But the discoveries of spectroscopic research have made known
a far more widely serviceable method of investigation, which
can be applied even to the luminous stars and nebulae that lie
far beyond the bounds of the solar system. By this method
information has been obtained regarding the constitution of the
sun, and many of our terrestrial metals, such as iron, nickel and
magnesium, have been ascertained to exist in the form of incandescent
vapour in the solar atmosphere. The present
condition of the sun probably represents one of the phases
through which stars and planets pass in their progress towards
becoming cool and dark bodies in space. If our globe was at
first, like its parent sun, an incandescent mass of probably
gaseous matter, occupying much more space than it now fills,
we can conceive that it has ever since been cooling and contracting
until it has reached its present form and dimensions, and that
it still retains a high internal temperature. Its oblately spheroidal
form is such as would be assumed by a rotating mass of matter
in the transition from a vaporous and self-luminous or liquid
condition to one of cool and dark solidity. But it has been
claimed that even a solid spherical globe might develop, under
the influence of protracted rotation, such a shape as the earth
at present possesses.
The observed increase of temperature downwards in our
649
planet has hitherto been generally accepted as a relic and proof
of an original high temperature and mobility of substance.
Recently, however, the validity of this proof has been challenged
on the ground that the ascertained amount of radium in the
rocks of the outer crust is more than sufficient to account for
the observed downward increase of temperature. Too little,
however, is known of the history and properties of what is
called radium to afford a satisfactory ground on which to
discard what has been, and still remains, the prevalent belief
on this subject.
An important epoch in the geological history of the earth
was marked by the separation of the moon from its mass (see
Tide). Whether the severance arose from the rupture of a
surrounding ring or the gradual condensation of matter in such
a ring, or from the ejection of a single mass of matter from the
rapidly rotating planet, it has been shown that our satellite
was only a few thousand miles from the earth’s surface, since
when it has retreated to its present distance of 240,000 m. Hence
the influence of the moon’s attraction, and all the geological
effects to which it gives rise, attained their maximum far back
in the development of the globe, and have been slowly diminishing
throughout geological history.
The sun by virtue of its vast size has not yet passed out of
the condition of glowing gas, and still continues to radiate heat
beyond the farthest planet of the solar system. The earth,
however, being so small a body in comparison, would cool down
much more quickly. Underneath its hot atmosphere a crust
would conceivably begin to form over its molten surface, though
the interior might still possess a high temperature and, owing
to the feeble conducting power of rocks, would remain intensely
hot for a protracted series of ages.
Full information regarding the form and size of the earth,
and its relations to the other planetary members of the solar
system, will be found in the articles Planet and Solar System.
For the purposes of geological inquiry the reader will bear in
mind that the equatorial diameter of our globe is estimated to
be about 7925 m., and the polar diameter about 7899 m.; the
difference between these two sums representing the amount of
flattening at the poles (about 26½ m.). The planet has been
compared in shape to an orange, but it resembles an orange
which has been somewhat squeezed, for its equatorial circumference
is not a regular circle but an ellipse, of which the major
axis lies in long. 8° 15′ W.—on a meridian which cuts the north-west
corner of America, passing through Portugal and Ireland,
and the north-east corner of Asia in the opposite hemisphere.
The rotation of the earth on its axis exerts an important
influence on the movements of the atmosphere, and thereby
affects the geological operations connected with these movements.
The influence of rotation is most marked in the great aerial
circulation between the poles and the equator. Currents of
air, which set out in a meridional direction from high latitudes
towards the equator, come from regions where the velocity due
to rotation is small to where it is greater, and they consequently
fall behind. Thus, in the northern hemisphere a north wind,
as it moves away from its northern source of origin, is gradually
deflected more and more towards the west and becomes a north-east
current; while in the opposite hemisphere a wind making
from high southern latitudes towards the equator becomes,
from the same cause, a south-east current. Where, on the
other hand, the air moves from the equatorial to the polar regions
its higher velocity of rotation carries it eastward, so that on the
south side of the equator it becomes a north-west current and
on the north side a south-west current. It is to this cause that
the easting and westing of the great atmospheric currents are
to be attributed, as is familiarly exemplified in the trade winds.
The atmospheric circulation thus deflected influences the
circulation of the ocean. The winds which persistently blow
from the north-east on the north side of the equator, and from
the south-east on the south side, drive the superficial waters
onwards, and give rise to converging oceanic currents which
unite to form the great westerly equatorial current.
A more direct effect of terrestrial rotation has been claimed
in the case of rivers which flow in a meridional direction. It has
been asserted that those, which in the northern hemisphere
flow from north to south, like the Volga, by continually passing
into regions where the velocity of rotation is increasingly greater,
are thrown more against their western than their eastern banks,
while those whose general course is in an opposite direction, like
the Irtisch and Yenesei, press more upon their eastern sides.
There cannot be any doubt that the tendency of the streams
must be in the directions indicated. But when the comparatively
slow current and constantly meandering course of most rivers
are taken into consideration, it may be doubted whether the
influence of rotation is of much practical account so far as
river-erosion is concerned.
One of the cosmical relations of our planet which has been
more especially prominent in geological speculations relates to
the position of the earth’s axis of rotation. Abundant evidence
has now been obtained to prove that at a comparatively late
geological period a rich flora, resembling that of warm climates
at the present day, existed in high latitudes even within less than
9° of the north pole, where, with an extremely low temperature
and darkness lasting for half of the year, no such vegetation could
possibly now exist. It has accordingly been maintained by
many geologists that the axis of rotation must have shifted,
and that when the remarkable Arctic assemblage of fossil plants
lived the region of their growth must have lain in latitudes much
nearer to the equator of the time.
The possibility of any serious displacement of the rotational
axis since a very early period in the earth’s history has been
strenuously denied by astronomers, and their arguments have
been generally, but somewhat reluctantly, accepted by geologists,
who find themselves confronted with a problem which has
hitherto seemed insoluble. That the axis is not rigidly stable,
however, has been postulated by some physicists, and has now
been demonstrated by actual observation and measurement.
It is admitted that by the movement of large bodies of water
the air over the surface of the globe, and more particularly by
the accumulation of vast masses of snow and ice in different
regions, the position of the axis might be to some extent shifted;
more serious effects might follow from widespread upheavals
or depressions of the surface of the lithosphere. On the assumption
of the extreme rigidity of the earth’s interior, however, the
general result of mathematical calculation is to negative the
supposition that in any of these ways within the period represented
by what is known as the “geological record,” that is,
since the time of the oldest known sedimentary formations, the
rotational axis has ever been so seriously displaced as to account
for such stupendous geological events as the spread of a luxuriant
vegetation far up into polar latitudes. If, however, the inside
of the globe possesses a great plasticity than has been allowed,
the shifting of the axis might not be impossible, even to such an
extent as would satisfy the geological requirements. This
question is one on which the last word has not been said, and
regarding which judgment must remain in suspense.
In recent years fresh information bearing on the minor devagations
of the pole has been obtained from a series of several
thousand careful observations made in Europe and North
America. It has thus been ascertained that the pole wanders
with a curiously irregular but somewhat spiral movement,
within an amplitude of between 40 and 50 ft., and completes
its erratic circuit in about 428 days. It was not supposed that
its movement had any geological interest, but Dr John Milne
has recently pointed out that the times of sharpest curvature
in the path of the pole coincide with the occurrence of large
earthquakes, and has suggested that, although it can hardly be
assumed that this coincidence shows any direct connexion
between earthquake frequency and changes in the position of
the earth’s axis, both effects may not improbably arise from
the same redistribution of surface material by ocean currents
and meteorological causes.
If for any reason the earth’s centre of gravity were sensibly
displaced, momentous geological changes would necessarily
ensue. That the centre of gravity does not coincide with the
650
centre of figure of the globe, but lies to the south of it, has long
been known. This greater aggregation of dense material in the
southern hemisphere probably dates from the early ages of the
earth’s consolidation, and it is difficult to believe that any
readjustment of the distribution of this material in the earth’s
interior is now possible. But certain rearrangements of the
hydrosphere on the surface of the globe may, from time to time,
cause a shifting of the centre of gravity, which will affect the
level of the ocean. The accumulation of enormous masses of
ice around the pole will give rise to such a displacement, and
will thus increase the body of oceanic water in the glaciated
hemisphere. Various calculations have been made of the effect
of the transference of the ice-cap from one pole to the other, a
revolution which may possibly have occurred more than once
in the past history of the globe. James Croll estimated that if
the mass of ice in the southern hemisphere be assumed to be
1000 ft. thick down to lat. 60°, its removal to the opposite
hemisphere would raise the level of the sea 80 ft. at the north pole,
while the Rev. Osmond Fisher made the rise as much as 409 ft.
The melting of the ice would still further raise the sea-level by
the addition of so large a volume of water to the ocean. To
what extent superficial changes of this kind have operated in
geological history remains an unsolved problem, but their
probable occurrence in the past has to be recognized as one of
the factors that must be considered in tracing the revolutions of
the earth’s surface.
The Age of the Earth.—Intimately connected with the relations
of our globe to the sun and the other members of the solar system
is the question of the planet’s antiquity—a subject of great
geological importance, regarding which much discussion has
taken place since the middle of the 19th century. Though an
account of this discussion necessarily involves allusion to departments
of geology which are more appropriately referred to in
later parts of this article, it may perhaps be most conveniently
included here.
Geologists were for many years in the habit of believing that
no limit could be assigned to the antiquity of the planet, and that
they were at liberty to make unlimited drafts on the ages of the
past. In 1862 and subsequent years, however, Lord Kelvin
(then Sir William Thomson) pointed out that these demands were
opposed to known physical facts, and that the amount of time
required for geological history was not only limited, but must
have been comprised within a comparatively narrow compass.
His argument rested on three kinds of evidence: (1) the internal
heat and rate of cooling of the earth; (2) the tidal retardation
of the earth’s rotation; and (3) the origin and age of the sun’s
heat.
1. Applying Fourier’s theory of thermal conductivity, Lord
Kelvin contended that in the known rate of increase of temperature
downward and beneath the surface, and the rate of loss
of heat from the earth, we have a limit to the antiquity of the
planet. He showed, from the data available at the time, that
the superficial consolidation of the globe could not have occurred
less than 20 million years ago, or the underground heat would
have been greater than it is; nor more than 400 million years
ago, otherwise the underground temperature would have shown
no sensible increase downwards. He admitted that very wide
limits were necessary. In subsequently discussing the subject,
he inclined rather towards the lower than the higher antiquity,
but concluded that the limit, from a consideration of all the
evidence, must be placed within some such period of past time
as 100 millions of years.
2. The argument from tidal retardation proceeds on the
admitted fact that, owing to the friction of the tide-wave, the
rotation of the earth is retarded, and is, therefore, much slower
now than it must have been at one time. Lord Kelvin affirmed
that had the globe become solid some 10,000 million years ago,
or indeed any high antiquity beyond 100 million years, the
centrifugal force due to the more rapid rotation must have given
the planet a very much greater polar flattening than it actually
possesses. He admitted, however, that, though 100 million
years ago that force must have been about 3% greater than now,
yet “nothing we know regarding the figure of the earth, and
the disposition of land and water, would justify us in saying
that a body consolidated when there was more centrifugal
force by 3% than now, might not now be in all respects like
the earth, so far as we know it at present.”
3. The third argument, based upon the age of the sun’s heat,
is confessedly less to be relied on than the two previous ones.
It proceeds upon calculations as to the amount of heat which
would be available by the falling together of masses from space,
which gave rise by their impact to our sun. The vagueness of
the data on which this argument rests may be inferred from
the fact that in one passage P.G. Tait placed the limit of time
during which the sun has been illuminating the earth as, “on
the very highest computation, not more than about 15 or 20
millions of years”; while, in another sentence of the same
volume, he admitted that, “by calculations in which there is
no possibility of large error, this hypothesis [of the origin of the
sun’s heat by the falling together of masses of matter] is
thoroughly competent to explain 100 millions of years’ solar
radiation at the present rate, perhaps more.” In more recently
reviewing his argument, Lord Kelvin expressed himself in
favour of more strictly limiting geological time than he had at
first been disposed to do. He insists that the time “was more
than 20 and less than 40 millions of years and probably much
nearer 20 than 40.” Geologists appear to have reluctantly
brought themselves to believe that perhaps, after all, 100 millions
of years might suffice for the evolution of geological history.
But when the time was cut down to 15 or 20 millions they
protested that such a restricted period was insufficient for that
evolution, and though they did not offer any effective criticism
of the arguments of the physicists they felt convinced that there
must be some flaw in the premises on which these arguments
were based.
By degrees, however, there have arisen among the physicists
themselves grave doubts as to the validity of the physical
evidence on which the limitation of the earth’s age has been
founded, and at the same time greater appreciation has been
shown of the signification and strength of the geological proofs
of the high antiquity of our planet. In an address from the
chair of the Mathematical Section of the British Association in
1886, Professor (afterwards Sir) George Darwin reviewed the
controversy, and pronounced the following deliberate judgment
in regard to it: “In considering these three arguments I have
adduced some reasons against the validity of the first [tidal
friction], and have endeavoured to show that there are elements
of uncertainty surrounding the second [secular cooling of the
earth]; nevertheless, they undoubtedly constitute a contribution
of the first importance to physical geology. Whilst, then, we
may protest against the precision with which Professor Tait
seeks to deduce results from them, we are fully justified in
following Sir William Thomson, who says that ‘the existing
state of things on the earth, life on the earth—all geological
history showing continuity of life—must be limited within some
such period of past time as 100 million years’.” Lord Kelvin
has never dealt with the geological and palaeontological objections
against the limitation of geological time to a few millions of years.
But Professor Darwin, in the address just cited, uttered the
memorable warning: “At present our knowledge of a definite
limit to geological time has so little precision that we should do
wrong summarily to reject theories which appear to demand
longer periods of time than those which now appear allowable.”
In his presidential address to the British Association at Cape
Town in 1905 he returned to the subject, remarking that the
argument derived from the increase of underground temperature
“seems to be entirely destroyed” by the discovery of the
properties of radium. He thinks that “it does not seem extravagant
to suppose that 500 to 1000 million years may have
elapsed since the birth of the moon.” He has “always believed
that the geologists were more nearly correct than the physicists,
notwithstanding the fact that appearances were so strongly
against them,” and he concludes thus: “It appears, then, that
the physical argument is not susceptible of a greater degree of
651
certainty than that of the geologists, and the scale of geological
time remains in great measure unknown” (see also Tide, chap.
viii.).
In an address to the mathematical section of the American
Association for the Advancement of Science in 1889, the vice-president
of the section, R.S. Woodward, thus expressed himself
with regard to the physical arguments brought forward by Lord
Kelvin and Professor Tait in limitation of geological time:
“Having been at some pains to look into this matter, I feel
bound to state that, although the hypothesis appears to be the
best which can be formulated at present, the odds are against
its correctness. Its weak links are the unverified assumptions of
an initial uniform temperature and a constant diffusivity. Very
likely these are approximations, but of what order we cannot
decide. Furthermore, if we accept the hypothesis, the odds
appear to be against the present attainment of trustworthy
numerical results, since the data for calculation, obtained
mostly from observations on continental areas, are far too
meagre to give satisfactory average values for the entire mass
of the earth.”
Still more emphatic is the protest made from the physical
side by Professor John Perry. He has attacked each of the
three lines of argument of Lord Kelvin, and has impugned the
validity of the conclusions drawn from them. The argument
from tidal retardation he dismisses as fallacious, following in
this contention the previous criticism of the Rev. Maxwell Close
and Sir George Darwin. In dealing with the argument based on
the secular cooling of the earth, he holds it to be perfectly
allowable to assume a much higher conductivity for the interior
of the globe, and that such a reasonable assumption would enable
us greatly to increase our estimate of the earth’s antiquity.
As for the third argument, from the age of the sun’s heat, he
points out that the sun may have been repeatedly fed by a
supply of meteorites from outside, while the earth may have been
protected from radiation, and been able to retain much of its
heat by being enveloped in a dense atmosphere. Remarking
that “almost anything is possible as to the present internal
state of the earth,” he concludes thus: “To sum up, we can
find no published record of any lower maximum age of life on
the earth, as calculated by physicists, than 400 millions of years.
From the three physical arguments Lord Kelvin’s higher limits
are 1000, 400 and 500 million years. I have shown that we have
reasons for believing that the age, from all these, may be very
considerably underestimated. It is to be observed that if we
exclude everything but the arguments from mere physics, the
probable age of life on the earth is much less than any of the above
estimates; but if the palaeontologists have good reasons for
demanding much greater times, I see nothing from the physicists’
point of view which denies them four times the greatest of these
estimates.”
A fresh line of argument against Lord Kelvin’s limitation of
the antiquity of our globe has recently been started by the
remarkable discoveries in radio-activity. From the ascertained
properties of radium it appears to be possible that our estimates
of solar heat, as derived from the theory of gravitation, may
have to be augmented ten or twenty times; that stores of
radium and similar bodies within the earth may have indefinitely
deferred the establishment of the present temperature
gradient from the surface inward; that consequently the earth
may have remained for long ages at a temperature not greatly
different from that which it now possesses, and hence that the
times during which our globe has supported animal and vegetable
life may be very much longer than that allowed in the estimates
previously made by physicists from other data (see Radioactivity).
The arguments from the geological side against the physical
contention that would limit the age of our globe to some 10
or 20 millions of years are mainly based on the observed rates of
geological and biological changes at the present time upon land
and sea, and on the nature, physical history and organic contents
of the stratified crust of the earth. Unfortunately, actual
numerical data are not obtainable in many departments of
geological activity, and even where they can be procured they
do not yet rest on a sufficiently wide collection of accurate and
co-ordinated observations. But in some branches of dynamical
geology, material exists for, at least, a preliminary computation
of the rate of change. This is more especially the case in respect
of the wide domain of denudation. The observational records
of the action of the sea, of springs, rivers and glaciers are becoming
gradually fuller and more trustworthy. A method of making
use of these records for estimating the rate of denudation of
the land has been devised. Taking the Mississippi as a general
type of river action, it has been shown that the amount of
material conveyed by this stream into the sea in one year is
equivalent to the lowering of the general surface of the drainage
basin of the river by 1⁄6000 of a foot. This would amount to one
foot in 6000 years and 1000 ft. in 6 million years. So that at
the present rate of waste in the Mississippi basin a whole continent
might be worn away in a few millions of years.
It is evident that as deposition and denudation are simultaneous
processes, the ascertainment of the rate at which solid
material is removed from the surface of the land supplies some
necessary information for estimating the rate at which new
sedimentary formations are being accumulated on the floor of
the sea, and for a computation of the length of time that would
be required at the present rate of change for the deposition of all
the stratified rocks that enter into the composition of the crust
of our globe. If the thickness of these rocks be assumed to be
100,000 ft., and if we could suppose them to have been laid down
over as wide an area as that of the drainage basins from the
waste of which they were derived, then at the present rate of
denudation their accumulation would require some 600 millions
of years. But, as Dr A.R. Wallace has justly pointed out, the
tract of sea-floor over which the material derived from the waste
of the terrestrial surface is laid down is at present much less than
that from which this material is worn away. We have no means,
however, of determining what may have been the ratio between
the two areas in past time. Certainly ancient marine sedimentary
rocks cover at the present day a much more extensive area than
that in which they are now being elaborated. If we take the
ratio postulated by Dr Wallace—1 to 19—the 100,000 ft. of
sedimentary strata would require 31 millions of years for their
accumulation. It is quite possible, however, that this ratio may be
much too high. There are reasons for believing that the proportion
of coast-line to land area has been diminishing during geological
time; in other words, that in early times the land was
more insular and is now more continental. So that the 31
millions of years may be much less than the period that would be
required, even on the supposition of continuous uninterrupted
denudation and sedimentation, during the whole of the time
represented by the stratified formations.
But no one who has made himself familiar with the actual
composition of these formations and the detailed structure of the
terrestrial crust can fail to recognize how vague, imperfect and
misleading are the data on which such computations are founded.
It requires no prolonged acquaintance with the earth’s crust to
impress upon the mind that one all-important element is omitted,
and indeed can hardly be allowed for from want of sufficiently
precise data, but the neglect of which must needs seriously
impair the value of all numerical calculations made without it.
The assumption that the stratified formations can be treated as
if they consisted of a continuous unbroken sequence of sediments,
indicating a vast and uninterrupted process of waste and deposition,
is one that is belied on every hand by the actual structure
of these formations. It can only give us a minimum of the time
required; for, instead of an unbroken series, the sedimentary
formations are full of “unconformabilities”—gaps in the
sequence of the chronological records—as if whole chapters
and groups of chapters had been torn out of a historical work.
It can often be shown that these breaks of continuity must have
been of vast duration, and actually exceeded in chronological
importance thick groups of strata lying below and above them
(see Part VI.). Moreover, even among the uninterrupted strata,
where no such unconformabilities exist, but where the sediments
652
follow each other in apparently uninterrupted sequence, and
might be thought to have been deposited continuously at the
same general rate, and without the intervention of any pause, it
can be demonstrated that sometimes an inch or two of sediment
might, on certain horizons, represent the deposit of an enormously
longer period than a hundred or a thousand times the same
amount of sediment on other horizons. A prolonged study of
these questions leads to a profound conviction that in many
parts of the geological record the time represented by sedimentary
deposits may be vastly less than the time which is not
so represented.
It has often been objected that the present rate of geological
change ought not to be taken as a measure of the rate in past
time, because the total sum of terrestrial energy has been steadily
diminishing, and geological processes must consequently have
been more vigorous in former ages than they are now. Geologists
do not pretend to assert that there has been no variation
or diminution in the activities of the various processes which
they have to study. What they do insist on is that the
present rate of change is the only one which we can watch and
measure, and which will thus supply a statistical basis for any
computations on the subject. But it has been dogmatically
affirmed that because terrestrial energy has been diminishing
therefore all kinds of geological work must have been more
vigorously and more rapidly carried on in former times than
now; that there were far more abundant and more stupendous
volcanoes, more frequent and more destructive earthquakes,
more gigantic upheavals and subsidences, more powerful oceanic
waves and tides, more violent atmospheric disturbances with
heavier rainfall and more active denudation.
It is easy to make these assertions, and they look plausible;
but, after all, they rest on nothing stronger than assumption.
They can be tested by an appeal to the crust of the earth, in
which the geological history of our planet has been so fully recorded.
Had such portentous manifestations of geological
activity ever been the normal condition of things since the
beginning of that history, there ought to be a record of them in
the rocks. But no evidence for them has been found there,
though it has been diligently sought for in all quarters of the
globe. We may confidently assert that while geological changes
may quite possibly have taken place on a gigantic scale in the
earliest ages of the earth’s existence, of which no geological record
remains, there is no proof that they have ever done so since the
time when the very oldest of the stratified formations were
deposited. There is no need to maintain that they have always
been conducted precisely on the same scale as now, or to deny
that they may have gradually become less vigorous as the general
sum of terrestrial energy has diminished. But we may unhesitatingly
affirm that no actual evidence of any such progressive
diminution of activity has been adduced from the geological
record in the crust of the earth: that, on the contrary, no appearances
have been detected there which necessarily demand the
assumption of those more powerful operations postulated by
physicists, or which are not satisfactorily explicable by reference
to the existing scale of nature’s processes.
That this conclusion is warranted even with regard to the innate
energy of the globe itself will be seen if we institute a comparison
between the more ancient and the more recent manifestations of
that energy. Take, for example, the proofs of gigantic plication,
fracture and displacement within the terrestrial crust. These,
as they have affected the most ancient rocks of Europe, have
been worked out in great detail in the north-west of Scotland.
But they are not essentially different from or on a greater scale
than those which have been proved to have affected the Alps,
and to have involved strata of so recent a date as the older
Tertiary formations. On the contrary, it may be doubted
whether any denuded core of an ancient mountain-chain reveals
traces of such stupendous disturbances of the crust as those
which have given rise to the younger mountain-chains of the
globe. It may, indeed, quite well have been the rule that instead
of diminishing in intensity of effect, the consequences of terrestrial
contraction have increased in magnitude, the augmenting
thickness of the crust offering greater resistance to the stresses,
and giving rise to vaster plications, faults, thrust-planes and
metamorphism, as this growing resistance had to be overcome.
The assertion that volcanic action must have been more
violent and more persistent in ancient times than it is now has
assuredly no geological evidence in its support. It is quite true
that there are vastly more remains of former volcanoes scattered
over the surface of the globe than there are active craters now,
and that traces of copious eruptions of volcanic material can be
followed back into some of the oldest parts of the geological
record. But we have no proof that ever at any one time in
geological history there have been more or larger or more vigorous
volcanoes than those of recent periods. It may be said that the
absence of such proof ought not to invalidate the assertion until
a far wider area of the earth’s surface has been geologically
studied. But most assuredly, as far as geological investigation
has yet gone, there is an overwhelming body of evidence to show
that from the earliest epochs in geological history, as registered
in the stratified rocks, volcanic action has manifested itself very
much as it does now, but on a less rather than on a greater scale.
Nowhere can this subject be more exhaustively studied than in
the British Isles, where a remarkably complete series of volcanic
eruptions has been chronicled ranging from the earliest Palaeozoic
down to older Tertiary time. The result of a prolonged study
of British volcanic geology has demonstrated that, even to
minute points of detail, there has been a singular uniformity in
the phenomena from beginning to end. The oldest lavas and
ashes differ in no essential respect from the youngest. Nor have
they been erupted more copiously or more frequently. Many
successive volcanic periods have followed each other after prolonged
intervals of repose, each displaying the same general
sequence of phenomena and similar evidence of gradual diminution
and extinction. The youngest, instead of being the feeblest,
were the most extensive outbursts in the whole of this prolonged
series.
If now we turn for evidence of the alleged greater activity
of all the epigene or superficial forces, and especially for proofs
of more rapid denudation and deposition on the earth’s surface,
we search for it in vain among the stratified formations of the
terrestrial crust. Had the oldest of these rocks been accumulated
in a time of great atmospheric perturbation, of torrential rains,
colossal tides and violent storms, we might surely expect to find
among the sediments some proof of such disturbed meteorological
and geographical conditions. We should look, on the one hand,
for tumultuous accumulations of coarse unworn detritus, rapidly
swept by rains, floods and waves from land to sea, and on the
other hand, for an absence of any evidence of the tranquil and
continuous deposit of such fine laminated silt as could only
settle in quiet water. But an appeal to the geological record
is made in vain for any such proofs. The oldest sediments, like
the youngest, reveal the operation only of such agents and such
rates of activity as are still to be witnessed in the accumulation
of the same kind of deposits. If, for instance, we search the
most ancient thick sedimentary formation in Britain—the
Torridon Sandstone of north-west Scotland, which is older than
the oldest fossiliferous deposits—we meet with nothing which
might not be found in any Palaeozoic, Mesozoic or Cainozoic
group of similar sediments. We see an accumulation, at least
8000 or 10,000 ft. thick, of consolidated sand, gravel and mud,
such as may be gathering now on the floor of any large mountain-girdled
lake. The conglomerates of this ancient series are not
pell-mell heaps of angular detritus, violently swept away from
the land and huddled promiscuously on the sea-floor. They are,
in general, built up of pebbles that have been worn smooth,
rounded and polished by prolonged attrition in running water,
and they follow each other on successive platforms with intervening
layers of finer sediment. The sandstones are composed
of well water-worn sand, some of which has been laid down so
tranquilly that its component grains have been separated out in
layers according to their specific gravity, in such manner that
they now present dark laminae in which particles of magnetic
iron, zircon and other heavy minerals have been sifted out
653
together, just as iron-sand may be seen gathered into thin sheets
on sandy beaches at the present day. Again, the same series
of primeval sediments includes intercalations of fine silt, which
has been deposited as regularly and intermittently there as it
has been among the most recent formations. These bands of
shale have been diligently searched for fossils, as yet without
success; but they may eventually disclose organic remains older
than any hitherto found in Europe.
We now come to the consideration of the palaeontological
evidence as to the value of geological time. Here the conclusions
derived from a study of the structure of the sedimentary formations
are vastly strengthened and extended. In the first place,
the organization of the most ancient plants and animals furnishes
no indication that they had to contend with any greater violence
of storm, flood, wave or ocean-current than is familiar to their
modern descendants. The oldest trees, shrubs, ferns and
club-mosses display no special structures that suggest a difference
in the general conditions of their environment. The most
ancient crinoids, sponges, crustaceans, arachnids and molluscs
were as delicately constructed as those of to-day, and their
remains are often found in such perfect preservation as to show
that neither during their lifetime nor after their death were they
subject to any greater violence of the elements than their living
representatives now experience. Of much more cogency,
however, is the evidence supplied by the grand upward succession
of organic forms, from the most ancient stratified rocks up to
the present day. No biologist now doubts for a moment that
this marvellous succession is the result of a gradual process of
evolution from lower to higher types of organization. There
may be differences of opinion as to the causes which have governed
this process and the order of the steps through which it has
advanced, but no one who is conversant with the facts will now
venture to deny that it has taken place, and that, on any possible
explanation of its progress, it must have demanded an enormous
lapse of time. In the Cambrian or oldest fossiliferous formations
there is already a large and varied fauna, in which the leading
groups of invertebrate life are represented. On no tenable
hypothesis can these be regarded as the first organisms that
came into being on our planet. They must have had a long
ancestry, and as Darwin first maintained, the time required for
their evolution may have been “as long as, or probably far
longer than, the whole interval from the Silurian [Cambrian]
age to the present day.” The records of these earliest eras of
organic development have unfortunately not survived the
geological revolutions of the past; at least, they have not yet
been recovered. But it cannot be doubted that they once
existed and registered their testimony to the prodigious lapse of
time prior to the deposition of the most ancient fossiliferous
formations which have escaped destruction.
The impressive character of the evidence furnished by the
sequence of organic forms throughout the great series of fossiliferous
strata can hardly be fully realized without a detailed and
careful study of the subject. Professor E.B. Poulton, in an
address to the zoological section of the British Association at
the Liverpool Meeting in 1896, showed how overwhelming are
the demands which this evidence makes for long periods of time,
and how impossible it is of comprehension unless these demands
be conceded. The history of life upon the earth, though it will
probably always be surrounded with great and even insuperable
difficulties, becomes broadly comprehensible in its general
progress when sufficient time is granted for the evolution
which it records; but it remains unintelligible on any other
conditions.
Taken then as a whole, the body of evidence, geological and
palaeontological, in favour of the high antiquity of our globe
is so great, so manifold, and based on such an ever-increasing
breadth of observation and reflection, that it may be confidently
appealed to in answer to the physical arguments which would
seek to limit that antiquity to ten or twenty millions of years.
In the present state of science it is out of our power to state
positively what must be the lowest limit of the age of the earth.
But we cannot assume it to be much less, and it may possibly
have been much more, than the 100 millions of years which Lord
Kelvin was at one time willing to concede.2
Part III.—Geognosy. The Investigation of the Nature
and Composition of the Materials of which the
Earth Consists
This division of the science is devoted to a description of the
parts of the earth—of the atmosphere and ocean that surround
the planet, and more especially of the solid materials that underlie
these envelopes and extend downwards to an unknown distance
into the interior. These various constituents of the globe are
here considered as forms of matter capable of being analysed,
and arranged according to their composition and the place they
take in the general composition of the globe.
Viewed in the simplest way the earth may be regarded as
made up of three distinct parts, each of which ever since an
early period of planetary history has been the theatre of important
geological operations. (1) An envelope of air, termed
the atmosphere, which surrounds the whole globe; (2) A lower
and less extensive envelope of water, known as the hydrosphere
(Gr. ὕδωρ, water) which, constituting the oceans and seas,
covers nearly three-fourths of the underlying solid surface of the
planet; (3) A globe, called the lithosphere (Gr. λίθος, stone),
the external part of which, consisting of solid stone, forms the
crust, while underneath, and forming the vast mass of the
interior, lies the nucleus, regarding the true constitution of
which we are still ignorant.
1. The Atmosphere.—The general characters of the atmosphere
are described in separate articles (see especially Atmosphere;
Meteorology). Only its relations to geology have here to be
considered. As this gaseous envelope encircles the whole
globe it is the most universally present and active of all the
agents of geological change. Its efficacy in this respect arises
partly from its composition, and the chemical reactions which
it effects upon the surface of the land, partly from its great
variations in temperature and moisture, and partly from its
movements.
Many speculations have been made regarding the chemical
composition of the atmosphere during former geological periods.
There can indeed be little doubt that it must originally have differed
greatly from its present condition. If the whole mass of the planet
originally existed in a gaseous state, there would be practically no
atmosphere. The present outer envelope of air may be considered
to be the surviving relic of this condition, after all the other constituents
have been incorporated into the hydrosphere and lithosphere.
The oxygen, which now forms fully a half of the outer
crust of the earth, was doubtless originally, whether free or in
combination, part of the atmosphere. So, too, the vast beds of coal
found all over the world, in geological formations of many different
ages, represent so much carbonic acid once present in the air. The
chlorides and other salts in the sea may likewise partly represent
materials carried down out of the atmosphere in the primitive
condensation of the aqueous vapour, though they have been continually
increased ever since by contributions from the drainage of
the land. It has often been suggested that, during the Carboniferous
period, the atmosphere must have been warmer and more charged
with aqueous vapour and carbon dioxide than at the present day,
to admit of so luxuriant a flora as that from which the coal-seams
were formed. There seems, however, to be at present no method
of arriving at any certainty on this subject. Lastly, the amount of
carbonic acid absorbed in the weathering of rocks at the surface, and
the consequent production of carbonates, represents an enormous
abstraction of this gas.
As at present constituted, the atmosphere is regarded as a
654
mechanical mixture of nearly four volumes of nitrogen and one of
oxygen, together with an average of 3.5 parts of carbon dioxide in
every 10,000 parts of air, and minute quantities of various other
gases and solid particles. Of the vapours contained in it by far the
most important is that of water which, although always present,
varies greatly in amount according to variations in temperature.
By condensation the water vapour appears in visible form as dew,
mist, cloud, rain, hail, snow and ice, and in these forms includes and
carries down some of the other vapours, gases and solid particles
present in the air. The circulation of water from the atmosphere to
the land, from the land to the sea, and again from the sea to the
land, forms the great geological process whereby the habitable
condition of the planet is maintained and the surface of the land
is sculptured (Part IV.).
2. The Hydrosphere.—The water envelope covers nearly
three-fourths of the surface of the earth, and forms the various
oceans and seas which, though for convenience of reference
distinguished by separate names, are all linked together in one
great body. The physical characters of this vast envelope are
discussed in separate articles (see Ocean and Oceanography).
Viewed from the geological standpoint, the features of the
sea that specially deserve attention are first the composition of
its waters, and secondly its movements.
Sea-water is distinguished from that of ordinary lakes and rivers
by its greater specific gravity and its saline taste. Its average
density is about 1.026, but it varies even within the same ocean,
being least where large quantities of fresh water are added from
rain or melting snow and ice, and greatest where evaporation is most
active. That sea-water is heavier than fresh arises from the greater
proportion of salts which it contains in solution. These salts constitute
about three and a half parts in every hundred of water.
They consist mainly of chlorides of sodium and magnesium, the
sulphates of magnesium, calcium and potassium, with minuter
quantities of magnesium bromide and calcium carbonate. Still
smaller proportions of other substances have been detected, gold for
example having been found in the proportion of 1 part in 15,180,000.
That many of the salts have existed in the sea from the time of
its first condensation out of the primeval atmosphere appears to
be probable. It is manifest, however, that, whatever may have
been the original composition of the oceans, they have for a vast
section of geological time been constantly receiving mineral matter
in solution from the land. Every spring, brook and river removes
various salts from the rocks over which it moves, and these substances,
thus dissolved, eventually find their way into the sea.
Consequently sea-water ought to contain more or less traceable
proportions of every substance which the terrestrial waters can
remove from the land, in short, of probably every element present
in the outer shell of the globe, for there seems to be no constituent
of this earth which may not, under certain circumstances, be held
in solution in water. Moreover, unless there be some counteracting
process to remove these mineral ingredients, the ocean water ought
to be growing, insensibly perhaps, but still assuredly, saltier, for the
supply of saline matter from the land is incessant.
To the geologist the presence of mineral solutions in sea-water is
a fact of much importance, for it explains the origin of a considerable
part of the stratified rocks of the earth’s crust. By evaporation
the water has given rise to deposits of rock-salt, gypsum and other
materials. The lime contained in solution, whether as sulphate or
carbonate, has been extracted by many tribes of marine animals,
which have thus built up out of their remains vast masses of solid
limestone, of which many mountain-chains largely consist.
Another important geological feature of the sea is to be seen
in the fact that its basins form the great receptacles for the detritus
worn away from the land. Besides the limestones, the visible parts
of the terrestrial crust are, in large measure, composed of sedimentary
rocks which were originally laid down on the sea-bottom. Moreover,
by its various movements, the sea occupies a prominent place
among the epigene or superficial agents which produce geological
changes on the surface of the globe.
3. The Lithosphere.—Beneath the gaseous and liquid envelopes
lies the solid part of the planet, which is conveniently regarded
as consisting of two parts,—(a) the crust, and (b) the interior
or nucleus.
It was for a long time a prevalent belief that the interior of the
globe is a molten mass round which an outer shell has gradually
formed through cooling. Hence the term “crust”
was applied to this external solid envelope, which
The crust.
was variously computed to be 10, 20, or more miles in thickness.
The portion of this crust accessible to human observation was
seen to afford abundant evidence of vast plications and corrugations
of its substance, which were regarded as only explicable
on the supposition of a thin solid collapsible shell floating on a
denser liquid interior. When, however, physical arguments
were adduced to show the great rigidity of the earth as a whole,
the idea of a thin crust enclosing a molten nucleus was reluctantly
abandoned by geologists, who found the problem of the earth’s
interior to be incapable of solution by any evidence which their
science could produce. They continued, however, to use the
term “crust” as a convenient word to denote the cool outer
layer of the earth’s mass, the structure and history of which
form the main subjects of geological investigation. More
recently, however, various lines of research have concurred in
suggesting that, whatever may be the condition of the interior,
its substance must differ greatly from that of the outer shell,
and that there may be more reason than appeared for the
retention of the name of crust. Observations on earthquake
motion by Dr John Milne and others, show that the rate and
character of the waves transmitted through the interior of the
earth differ in a marked degree from those propagated along the
crust. This difference indicates that rocky material, such as
we know at the surface, may extend inwards for some 30 m.,
below which the earth’s interior rapidly becomes fairly homogeneous
and possesses a high rigidity. From measurements
of the force of gravity in India by Colonel S.G. Burrard, it has
been inferred that the variations in density of the outer parts of
the earth do not descend farther than 30 or 40 m., which might
be assumed to be the limit of the thickness of the crust. Recent
researches in regard to the radio-active substances present
in rocks suggest that the crust is not more than 50 m. thick,
and that the interior differs from it in possessing little or no
radio-active material.
Though we cannot hope ever to have direct acquaintance with
more than the mere outside skin of our planet, we may be led
to infer the irregular distribution of materials within
the crust from the present distribution of land and
The interior.
water, and the observed differences in the amount of
deflection of the plumb-line near the sea and near mountain-chains.
The fact that the southern hemisphere is almost wholly
covered with water appears explicable only on the assumption
of an excess of density in the mass of that portion of the planet.
The existence of such a vast sheet of water as that of the Pacific
Ocean is to be accounted for, as Archdeacon J.H. Pratt pointed
out, by the presence of “some excess of matter in the solid
parts of the earth between the Pacific Ocean and the earth’s
centre, which retains the water in its place, otherwise the ocean
would flow away to the other parts of the earth.” A deflection
of the plumb-line towards the sea, which has in a number of
cases been observed, indicates that “the density of the crust
beneath the mountains must be less than that below the plains,
and still less than that below the ocean-bed.” Apart therefore
from the depression of the earth’s surface in which the oceans
lie, we must regard the internal density, whether of crust or
nucleus, to be somewhat irregularly arranged, there being an
excess of heavy materials in the water hemisphere, and beneath
the ocean-beds, as compared with the continental masses.
In our ignorance regarding the chemical constitution of the
nucleus of our planet, an argument has sometimes been based
upon the known fact that the specific gravity of the globe
as a whole is about double that of the crust. This has been
held by some writers to prove that the interior must consist of
much heavier material and is therefore probably metallic. But
the effect of pressure ought to make the density of the nucleus
much higher, even if the interior consisted of matter no heavier
than the crust. That the total density of the planet does not
greatly exceed its observed amount seems only explicable on
the supposition that some antagonistic force counteracts the
effects of pressure. The only force we can suppose capable of so
acting is heat. But comparatively little is yet known regarding
the compression of gases, liquids and solids under such vast
pressures as must exist within the nucleus.
That the interior of the earth possesses a high temperature
is inferred from the evidence of various sources. (1) Volcanoes,
which are openings that constantly, or intermittently, give out
hot vapours and molten lava from reservoirs beneath the crust.
Besides active volcanoes, it is known that former eruptive vents
655
have been abundantly and widely distributed over the globe
from the earliest geological periods down to our own day.
(2) Hot springs are found in many parts of the globe, with
temperatures varying up to the boiling point of water. (3)
From mines, tunnels and deep borings into the earth it has
been ascertained that in all quarters of the globe below the
superficial zone of invariable temperature, there is a progressive
increase of heat towards the interior. The rate of this increase
varies, being influenced, among other causes, by the varying
conductivity of the rocks. But the average appears to be
about 1° Fahr. for every 50 or 60 ft. of descent, as far down as
observations have extended. Though the increase may not
advance in the same proportion at great depths, the inference
has been confidently drawn that the temperature of the nucleus
must be exceedingly high.
The probable condition of the earth’s interior has been a fruitful
source of speculation ever since geology came into existence;
but no general agreement has been arrived at on the subject.
Three chief hypotheses have been propounded: (1) that the
nucleus is a molten mass enclosed within a solid shell; (2) that,
save in local vesicular spaces which may be filled with molten
or gaseous material, the globe is solid and rigid to the centre;
(3) that the great body of the nucleus consists of incandescent
vapours and gases, especially vaporous iron, which under the
gigantic pressure within the earth are so compressed as to confer
practical rigidity on the globe as a whole, and that outside this
main part of the nucleus the gases pass into a shell of molten
magma, which, in turn, shades off outwards into the comparatively
thin, cool solidified crust. Recent seismological observations
have led to the inference that the outer crust, some 30 to
45 m. thick, must rapidly merge into a fairly homogeneous
nucleus which, whatever be its constitution, transmits undulatory
movements through its substance with uniform velocity and is
believed to possess a high rigidity.
The origin of the earth’s high internal temperature has been
variously accounted for. Most usually it has been assumed to
be the residue of the original “tracts of fluent heat” out of
which the planet shaped itself into a globe. According to another
supposition the effects of the gradual gravitational compression
of the earth’s mass have been the main source of the high
temperature. Recent researches in radio-activity, to which
reference has already been made, have indicated another possible
source of the internal heat in the presence of radium in the
rocks of the crust. This substance has been detected in all
igneous rocks, especially among the granites, in quantity
sufficient, according to the Hon. R.J. Strutt, to account for the
observed temperature-gradient in the crust, and to indicate
that this crust cannot be more than 45 m. thick, otherwise the
outflow of heat would be greater than the amount actually
ascertained. Inside this external crust containing radio-active
substances, it is supposed, as already stated, that the nucleus
consists of some totally different matter containing little or no
radium.
Constitution of the Earth’s Crust.—As the crust of the earth contains
the “geological record,” or stony chronicle from which geology
interprets the history of our globe, it forms the main subject of study
to the geologist. The materials of which this crust consists are
known as minerals and rocks. From many chemical analyses,
which have been made of these materials, the general chemical
constitution of, at least, the accessible portion of the crust has been
satisfactorily ascertained. This information becomes of much
importance in speculations regarding the early history of the globe.
Of the elements known to the chemist the great majority form but a
small proportion of the composition of the crust, which is mainly
built up of about twenty of them. Of these by far the most important
are the non-metallic elements oxygen and silicon. The former
forms about 47% and the latter rather more than 28% of the
original crust, so that these two elements make up about three-fourths
of the whole. Next after them come the metals aluminium
(8.16%), iron (4.64), calcium (3.50), magnesium (2.62), sodium
(2.63), and potassium (2.35). The other twelve elements included
in the twenty vary in amount from a proportion of 0.41% in the
case of titanium, to not more than 0.01% of chlorine, fluorine,
chromium, nickel and lithium. The other fifty or more elements
exist in such minute proportions in the crust that, probably, not
one of them amounts to as much as 0.01%, though they include
the useful metals, except iron. Taking the crust, and the external
envelopes of the ocean and the air, we thus perceive that these
outer parts of our planet consist of more than three-fourths of non-metals
and less than one-fourth of metals.
The combinations of the elements which are of most importance
in the constitution of the terrestrial crust consist of oxides. From
the mean of a large number of analyses of the rocks of the lower or
primitive portion of the crust, it has been ascertained that silica
(SiO2) forms almost 60% and alumina (Al2O3) upwards of 15% of
the whole. The other combinations in order of importance are
lime (CaO) 4.90%, magnesia (MgO) 4.36, soda (Na2O) 3.55, ferrous
oxide (FeO) 3.52, potash (K2O) 2.80, ferric oxide (Fe2O3) 2.63, water
(H2O) 1.52, titanium oxide (TiO2) 0.60, phosphoric acid (P2O5)
0.22; the other combinations of elements thus form less than 1%
of the crust.
These different combinations of the elements enter into further
combinations with each other so as to produce the wide assortment
of simple minerals (see Mineralogy). Thus, silica and alumina are
combined to form the aluminous silicates, which enter so largely
into the composition of the crust of the earth. The silicates of
magnesia, potash and soda constitute other important families of
minerals. A mass of material composed of one, but more usually
of more than one mineral, is known as a rock. Under this term
geologists are accustomed to class not only solid stone, such as
granite and limestone, but also less coherent materials such as clay,
peat and even loose sand. The accessible portion of the earth’s
crust consists of various kinds of rocks, which differ from each other
in structure, composition and origin, and are therefore susceptible
of diverse classifications according to the point of view from which
they are considered. The details of this subject will be found in
the article Petrology.
Classification of Rocks.—Various systems of classification of rocks
have been proposed, but none of them is wholly satisfactory. The
most useful arrangement for most purposes of the geologist is one
based on the broad differences between them in regard to their mode
of origin. From this point of view they may be ranged in three
divisions:
1. In the first place, a large number of rocks may be described
as original or underived, for it is not possible to trace them back to
any earlier source. They belong to the primitive constitution of the
planet, and, as they have all come up from below through the crust,
they serve to show the nature of the material which lies immediately
below the outer parts of that crust. They include the numerous
varieties of lava, which have been poured out in a molten state from
volcanic vents, also a great series of other rocks which, though they
may never have been erupted to the surface, have been forced
upward in a melted condition into the other rocks of the crust and
have solidified there. From their mode of origin this great class of
rocks has been called “igneous” or “eruptive.” As they generally
show no definite internal structure save such as may result from
joints, they have been termed “massive” or “unstratified,” to
distinguish them from those of the second division which are
strongly marked out by the presence of a stratified structure. The
igneous rocks present a considerable range of composition. For
the most part they consist mainly of aluminous silicates, some of
them being highly acid compounds with 75% or more of silica.
But they also include highly basic varieties wherein the proportion
of silica sinks to 40%, and where magnesia greatly predominates
over alumina. The textures of igneous rocks likewise comprise a
wide series of varieties. On the one hand, some are completely
vitreous, like obsidian, which is a natural glass. From this extreme
every gradation may be traced through gradual increase of the
products of devitrification, until the mass may become completely
crystalline. Again, some crystalline igneous rocks are so fine in
grain as not to show their component crystals save under the microscope,
while in others the texture is so coarse as to present the
component minerals in separate crystals an inch or more in length.
These differences indicate that, at first, the materials of the rock
may have been as completely molten as artificial glass, and that
the crystalline condition has been subsequently developed by cooling,
and the separation of the chemical constituents into definite crystalline
minerals. Many of the characters of igneous rocks have been
reproduced experimentally by fusing together their minerals, or the
constituents of their minerals, in the proper proportion. But it has
not yet been found possible to imitate the structure of such rocks
as granite. Doubtless these rocks consolidated with extreme
slowness at great depths below the surface, under vast pressures
and probably in the presence of water or water-vapour—conditions
which cannot be adequately imitated in a laboratory.
Though the igneous rocks occupy extensive areas in some countries,
they nevertheless cover a much smaller part of the whole surface of
the land than is taken up by the second division or stratified rocks.
But they increase in quantity downwards and probably extend
continuously round the globe below the other rocks. This important
series brings before us the relations of the molten magma within the
earth to the overlying crust and to the outer surface. On the one
hand, it includes the oldest and most deep-seated extravasations
of that magma, which have been brought to light by ruptures and
upheavals of the crust and prolonged denudation. On the other,
it presents to our study the varied outpourings of molten and
fragmentary materials in the discharges of modern and ancient
656
volcanoes. Between these two extremes of position and age, we
find that the crust has been, as it were, riddled with injections of
the magma from below. These features will be further noticed in
Part V. of this article.
2. The “sedimentary” or “stratified rocks” form by much the
larger part of the dry land of the globe, and they are prolonged to
an unknown distance from the shores under the bed of the sea.
They include those masses of mineral matter which, unlike the
igneous rocks, can be traced back to a definite origin on the surface
of the earth. Three distinct types may be recognized among them:
(a) By far the largest proportion of them consists of different kinds
of sediment derived from the disintegration of pre-existing rocks.
In this “fragmental” group are placed all the varieties of shingle,
gravel, sand, clay and mud, whether these materials remain in a
loose incoherent condition, or have been compacted into solid stone.
(b) Another group consists of materials that have been deposited by
chemical precipitation from solution in water. The white sinter
laid down by calcareous springs is a familiar example on a small
scale. Beds of rock-salt, gypsum and dolomite have, in some
regions, been accumulated to a thickness of many thousand feet,
by successive precipitations of the salt contained in the water of
inland seas. (c) An abundant and highly important series of sedimentary
formations has been formed from the remains of plants and
animals. Such accumulations may arise either from the transport
and deposit of these remains, as in the case of sheets of drift-wood,
and banks of drifted sea-shells, or from the growth and decay of
the organisms on the spot, as happens in peat bogs and in coral-reefs.
As the sedimentary rocks have for the most part been laid down
under water, and more especially on the sea-floor, they are often
spoken of as “aqueous,” in contradistinction to the igneous rocks.
Some of them, however, are accumulated by the drifting action of
wind upon loose materials, and are known as “aeolian” formations.
Familiar instances of such wind-formed deposits are the sand-dunes
along many parts of the sea coast. Much more extensive in area are
the sands of the great deserts in the arid regions of the globe.
It is from the sedimentary rocks that the main portion of geological
history is derived. They have been deposited one over another
in successive strata from a remote period in the development of
the globe down to the present time. From this arrangement they
have been termed “stratified,” in contrast to the unstratified or
igneous series. They have preserved memorials of the geographical
revolutions which the surface of the earth has undergone; and
above all, in the abundant fossils which they have enclosed, they
furnish a momentous record of the various tribes of plants and
animals which have successively flourished on land and sea. Their
investigation is thus the most important task which devolves upon
the geologist.
3. In the third place comes a series of rocks which are not now
in their original condition, but have undergone such alteration as
to have acquired new characters that more or less conceal their
first structures. Some of them can be readily recognized as altered
igneous masses; others are as manifestly of sedimentary origin;
while of many it is difficult to decide what may have been their
pristine character. To this series the term “metamorphic” has
been applied. Its members are specially distinguished by a prevailing
fissile, or schistose, structure which they did not at first possess, and
which differs from anything found in unaltered igneous or sedimentary
rocks. This fissility is combined with a more or less pronounced
crystalline structure. These changes are believed to be the result
of movements within the crust of the earth, whereby the most solid
rocks were crushed and sheared, while, at the same time, under the
influence of a high temperature and the presence of water, they
underwent internal chemical reactions, which led to a rearrangement
and recomposition of their mineral constituents and the production
of a crystalline structure (see Metamorphism).
Among the less altered metamorphic rocks of sedimentary origin,
the successive laminae of deposit of the original sediment can be
easily observed; but they are also traversed by a new set of divisional
planes, along which they split across the original bedding.
Together with this superinduced cleavage there have been developed
in them minute hairs, scales and rudimentary crystals. Further
stages of alteration are marked by the increase of micaceous scales,
garnets and other minerals, especially along the planes of cleavage,
until the whole rock becomes crystalline, and displays its chief
component minerals in successive discontinuous folia which merge
into each other, and are often crumpled and puckered. Massive
igneous rocks can be observed to have undergone intense crushing
and cleavage, and to have ultimately assumed a crystalline foliated
character. Rocks which present this aspect are known as schists
(q.v.). They range from the finest silky slates, or phyllites, up to the
coarsest gneisses, which in hand-specimens can hardly be distinguished
from granites. There is indeed every reason to believe
that such gneisses were probably originally true granites, and that
their foliation and recrystallization have been the result of metamorphism.
The schists are more especially to be found in the heart of
mountain-chains, and in regions where the lowest and oldest parts
of the earth’s crust have, in the course of geological revolutions,
been exposed to the light of day. They have been claimed by some
writers to be part of the original or primitive surface of our globe
that first consolidated on the molten nucleus. But the progress of
investigation all over the world has shown that this supposition
cannot be sustained. The oldest known rocks present none of the
characters of molten material that has cooled and hardened in the
air, like the various forms of recent lava. On the contrary, they
possess many of the features characteristic of bodies of eruptive
material that have been injected into the crust at some depth underground,
and are now visible at the surface, owing to the removal
by denudation of the rocks under which they consolidated. In their
less foliated portions they can be recognized as true eruptive rocks.
In many places gneisses that possess a thoroughly typical foliation
have been found to pierce ancient sedimentary formations as intrusive
bosses and veins.
Part IV.—Dynamical Geology
This section of the science includes the investigation of those
processes of change which are at present in progress upon the
earth, whereby modifications are made on the structure and
composition of the crust, on the relations between the interior
and the surface, as shown by volcanoes, earthquakes and other
terrestrial disturbances, on the distribution of oceans and
continents, on the outlines of the land, on the form and depth
of the sea-bottom, on climate, and on the races of plants and
animals by which the earth is tenanted. It brings before us,
in short, the whole range of activities which it is the province of
geology to study, and leads us to precise notions regarding their
relations to each other and the results which they achieve. A
knowledge of this branch of the subject is thus the essential
groundwork of a true and fruitful acquaintance with the principles
of geology, seeing that it necessitates a study of the present order
of nature, and thus provides a key for the interpretation of the
past.
The whole range of operations included within the scope of
inquiry in this branch of the science may be regarded as a vast
cycle of change, into which we may break at any point, and
round which we may travel, only to find ourselves brought
back to our starting-point. It is a matter of comparatively
small moment at what part of the cycle we begin our inquiries.
We shall always find that the changes we see in action have
resulted from some that preceded, and give place to others
which follow them.
At an early time in the earth’s history, anterior to any of the
periods of which a record remains in the visible rocks, the chief
sources of geological action probably lay within the earth itself.
If, as is generally supposed, the planet still retained a great
store of its initial heat, it was doubtless the theatre of great
chemical changes, giving rise, perhaps, to manifestations of
volcanic energy somewhat like those which have so marvellously
roughened the surface of the moon. As the outer layers of the
globe cooled, and the disturbances due to internal heat and
chemical action became less marked, the conditions would
arise in which the materials for geological history were accumulated.
The influence of the sun, which must always have
operated, would then stand out more clearly, giving rise to that
wide circle of superficial changes wherein variations of temperature
and the circulation of air and water over the surface of the
earth come into play.
In the pursuit of his inquiries into the past history and into
the present régime of the earth, the geologist must needs keep
his mind ever open to the reception of evidence for kinds
and especially for degrees of action which he had not before
imagined. Human experience has been too short to allow him
to assume that all the causes and modes of geological change
have been definitively ascertained. On the earth itself there may
remain for future discovery evidence of former operations by
heat, magnetism, chemical change or otherwise, which may
explain many of the phenomena with which geology has to deal.
Of the influences, so many and profound, which the sun exerts
upon our planet, we can as yet only perceive a little. Nor can
we tell what other cosmical influences may have lent their aid in
the evolution of geological changes.
Much useful information regarding many geological processes
has been obtained from experimental research in laboratories
and elsewhere, and much more may be confidently looked for
657
from future extensions of this method of inquiry. The early
experiments of Sir James Hall, already noticed, formed the
starting-point for numerous subsequent researches, which have
elucidated many points in the origin and history of rocks. It
is true that we cannot hope to imitate those operations of nature
which demand enormous pressures and excessively high temperatures
combined with a long lapse of time. But experience
has shown that in regard to a large number of processes, it is
possible to imitate nature’s working with sufficient accuracy
to enable us to understand them, and so to modify and control
the results as to obtain a satisfactory solution of some geological
problems.
In the present state of our knowledge, all the geological
energy upon and within the earth must ultimately be traced
back to the primeval energy of the parent nebula or sun. There
is, however, a certain propriety and convenience in distinguishing
between that part of it which is due to the survival of some of
the original energy of the planet and that part which arises
from the present supply of energy received day by day from the
sun. In the former case we have to deal with the interior of
the earth, and its reaction upon the surface; in the latter, we
deal with the surface of the earth and to some extent with its
reaction on the interior. This distinction allows of a broad
treatment of the subject under two divisions:
I. Hypogene or Plutonic Action: The changes within the
earth caused by internal heat, mechanical movement and
chemical rearrangements.
II. Epigene or Surface Action: The changes produced on the
superficial parts of the earth, chiefly by the circulation of air
and water set in motion by the sun’s heat.
DIVISION I.—HYPOGENE OR PLUTONIC ACTION
In the discussion of this branch of the subject we must carry
in our minds the conception of a globe still possessing a high
internal temperature, radiating heat into space and consequently
contracting in bulk. Portions of molten rocks from inside are
from time to time poured out at the surface. Sudden shocks
are generated by which destructive earthquakes are propagated
through the diameter of the globe as well as to and along
its surface. Wide geographical areas are pushed up or sink
down. In the midst of these movements remarkable changes
are produced upon the rocks of the crust; they are plicated,
fractured, crushed, rendered crystalline and even fused.
(A) Volcanoes and Volcanic Action.
This subject is discussed in the article Volcano, and only a
general view of its main features will be given here. Under the term
volcanic action (vulcanism, vulcanicity) are embraced all the
phenomena connected with the expulsion of heated materials from
the interior of the earth to the surface. A volcano may be defined
as a conical hill or mountain, built up wholly or mainly of materials
which have been ejected from below, and which have accumulated
around the central vent of eruption. As a rule its truncated summit
presents a cup-shaped cavity, termed the crater, at the bottom of
which is the opening of the main funnel or pipe whereby communication
is maintained with the heated interior. From time to
time, however, in large volcanoes rents are formed on the sides of
the cone, whence steam and other hot vapours and also streams of
molten lava are poured forth. On such rents smaller or parasitic
cones are often formed, which imitate the operations of the parent
cone and, after repeated eruptions, may rise to hills hundreds of
feet in height. In course of centuries the result of the constant
outpouring of volcanic materials may be to build up a large mountain
like Etna, which towers above the sea to a height of 10,840 feet, and
has some 200 minor cones along its flanks.
But all volcanic eruptions do not proceed from central orifices.
In Iceland it has been observed that, from fissures opened in the
ground and extending for long distances, molten material has issued
in such abundance as to be spread over the surrounding country
for many miles, while along the lines of fissure small cones or hillocks
of fragmentary material have accumulated round more active parts
of the rent. There is reason to believe that in the geological past
this fissure-type of eruption has repeatedly been developed, as well
as the more common form of central cones like Vesuvius or Etna.
In the operations of existing volcanoes only the superficial manifestations
of volcanic action are observable. But when the rocks of
the earth’s crust are studied, they are found to enclose the relics
of former volcanic eruptions. The roots of ancient volcanoes have
thus been laid bare by geological revolutions; and some of the
subterranean phases of volcanic action are thereby revealed which
are wholly concealed in an active volcano. Hence to obtain as
complete a conception as possible of the nature and history of
volcanic action, regard must be had, not merely to modern volcanoes,
but to the records of ancient eruptions which have been preserved
within the crust.
The substances discharged from volcanic vents consist of—(1)
Gases and vapours: which, dissolved in the molten magma of the
interior, take the chief share in volcanic activity. They include
in greatest abundance water-gas, which condenses into the clouds
of steam so conspicuous in volcanic eruptions. Hydrochloric acid
and sulphuretted hydrogen are likewise plentiful, together with
many other substances which, sublimed by the high internal temperature,
take a solid form on cooling at the surface. (2) Molten
rock or lava: which ranges from the extremely acid type of the
obsidians and rhyolites with 70% or more of silica, to the more basic
and heavy varieties such as basalts and leucite-lavas with much iron,
and sometimes no more than 45% of silica. The specific gravity
of lavas varies between 2.37 and 3.22, and the texture ranges from
nearly pure glass, like obsidian, to a coarse granitoid compound,
as in some rhyolites. (3) Fragmentary materials, which are sometimes
discharged in enormous quantity and dispersed over a wide extent
of country, the finer particles being transported by upper air-currents
for hundreds of miles. These materials arise either from the explosion
of lava by the sudden expansion of the dissolved vapours and gases,
as the molten rock rises to the surface, or from the breaking up and
expulsion of portions of the walls of the vent, or of the lava, which
happens to have solidified within these walls. They vary from the
finest impalpable dust and ashes, through increasing stages of
coarseness up to huge “bombs” torn from the upper surface of the
molten rock in the vent, and large blocks of already solidified lava,
or of non-volcanic rock detached from the sides of the pipe up which
the eruptions take place.
Nothing is yet known as to the determining cause of any particular
volcanic eruption. Some vents, like that of Stromboli, in the
Mediterranean, are continually active, and have been so ever since
man has observed them. Others again have been only intermittently
in eruption, with intervals of centuries between their periods of
activity. We are equally in the dark as to what has determined
the sites on which volcanic action has manifested itself. There is
reason, indeed, to believe that extensive fractures of the terrestrial
crust have often provided passages up which the vapours, imprisoned
in the internal magma, have been able to make their way, accompanied
by other products. Where chains of volcanoes rise along
definite lines, like those of Sumatra, Java, and many other tracts
both in the Old and the New World, there appears to be little doubt
that their linear distribution should be attributed to this cause.
But where a volcano has appeared by itself, in a region previously
exempt from volcanic action, the existence of a contributing fissure
cannot be so confidently presumed. The study of certain ancient
volcanoes, the roots of which have been exposed by long denudation,
has shown an absence of any visible trace of their having availed
themselves of fractures in the crust. The inference has been drawn
that volcanic energy is capable of itself drilling an orifice through the
crust, probably at some weaker part, and ejecting its products at
the surface. The source of this energy is to be sought in the enormous
expansive force of the vapours and gases dissolved in the magma.
They are kept in solution by the enormous pressure within the earth;
but as the lava approaches the surface and this pressure is relieved
these dissolved vapours and gases rush out with explosive violence,
blowing the upper part of the lava column into dust, and allowing
portions of the liquid mass below to rise and escape, either from the
crater or from some fissure which the vigour of explosion has opened
on the side of the cone. So gigantic is the energy of these pent-up
vapours, that, after a long period of volcanic quiescence, they
sometimes burst forth with such violence as to blow off the whole of
the upper part or even one side of a large cone. The history of
Vesuvius, and the great eruptions of Krakatoa in 1883 and of
Bandaizan in 1888 furnish memorable examples of great volcanic
convulsions. It has been observed that such stupendous discharges
of aeriform and fragmentary matter may be attended with the
emission of little or no lava. On the other hand, some of the largest
outflows of lava have been accompanied by comparatively little
fragmentary material. Thus, the great lava-floods of Iceland in
1783 spread for 40 m. away from their parent fissure, which was
marked only by a line of little cones of slag.
The temperature of lava as it issues from underground has been
measured more or less satisfactorily, and affords an indication of
that existing within the earth. At Vesuvius it has been ascertained
to be more than 2000° Fahr. At first the molten rock glows with a
white light, which rapidly reddens, and disappears under the rugged
brown and black crust that forms on the surface. Underneath this
badly conducting crust, the lava cools so slowly that columns of
steam have been noticed rising from its surface more than 80 years
after its eruption.
Considerable alteration in the topography of volcanic regions
may be produced by successive eruptions. The fragmentary
materials are sometimes discharged in such abundance as to cover
the ground for many miles around with a deposit of loose ashes,
cinders and slag. Such a deposit accumulating to a depth of many
658
feet may completely bury valleys and water-courses, and thus
greatly affect the drainage. The coarsest materials accumulate
nearest to the vent that emits them. The finer dust is not infrequently
hurled forth with such an impetus as to be carried for
thousands of feet into the tracks of upper air-currents, whereby it
may be borne for hundreds of miles away from the vent so as ultimately
to fall to the ground in countries far removed from any active
volcano. Outflows of lava, from their greater solidity and durability,
produce still more serious and lasting changes in the external features
of the ground over which they flow. As they naturally seek the
lowest levels, they find their way into the channels of streams.
If they keep along the channels, they seal them up under a mass of
compact stone which the running water, if not wholly diverted
elsewhere, will take many long centuries to cut through. If, on the
other hand, the lava crosses a stream, it forms a massive dam,
above which the water is ponded back so as to form a lake.
As the result of prolonged activity a volcanic cone is gradually
built up by successive outflows of lava and showers of dust and
stones. These materials are arranged in beds, or sheets, inclined
outwards from the central vent. On surrounding level ground the
alternating beds are flat. In course of time, deep gullies are cut on
the outer slopes of the cone by rain, and by the heavy showers that
arise from the condensation of the copious discharges of steam
during eruptions. Along the sides of these ravines instructive
sections may be studied of the volcanic strata. The larger rivers of
some volcanic regions have likewise eroded vast gorges in the more
horizontal lavas and ashes of the flatter country, and have thus laid
bare stupendous cliffs, along which the successive volcanic sheets
can be seen piled above each other for many hundred feet. On a
small scale, some of these features are well displayed among the
rivers that drain the volcanic tracts of central France; on a great
scale, they are presented in the course of the Snake river, and other
streams that traverse the great volcanic country of western North
America. Similar volcanic scenery has been produced in western
Europe by the action of denudation in dissecting the flat Tertiary
lavas of Scotland, the Faeroe Isles and Iceland.
Of special interest to the geologist are those volcanoes which have
taken their rise on the sea-bottom; for the volcanic intercalations
among the stratified formations of the earth’s crust are almost
entirely of submarine origin. Many active volcanoes situated on
islands have begun their eruptions below sea-level. Both Vesuvius
and Etna sprang up on the floor of the Mediterranean sea, and have
gradually built up their cones into conspicuous parts of the dry land.
Examples of a similar history are to be found among the volcanic
islands of the Pacific Ocean. In some of these cases a movement
of elevation has carried the submarine lavas, tuffs and agglomerates
above sea-level, and has furnished opportunities of comparing these
materials with those of recent subaerial origin, and also with the
ancient records of submarine eruptions which have been preserved
among the stratified formations. From the evidence thus supplied,
it can be shown that the materials ejected from modern submarine
volcanic vents closely resemble those accumulated by subaerial
volcanoes; that the dust, ashes and stones become intermingled or
interstratified with coral-mud, or other non-volcanic deposit of the
sea-bottom, that vesicular lavas may be intercalated among them
as on land, and that between the successive sheets of volcanic
origin, layers of limestone may be laid down which are composed
chiefly, or wholly, of the remains of calcareous marine organisms.
Though active volcanoes are widely distributed over the globe,
and are especially abundant around the vast basin of the Pacific
Ocean, they afford an incomplete picture of the extent to which
volcanic action has displayed itself on the surface of our planet.
When the rocks of the land are attentively studied they disclose
proofs of that action in many districts where there is now no outward
sign of it. Not only so, but they reveal that volcanoes have been in
eruption in some of these districts during many different periods of
the past, back to the beginnings of geological history. The British
Islands furnish a remarkable example of such a series of ancient
eruptions. From the Cambrian period all through Palaeozoic times
there rose at intervals in that country a succession of volcanic centres
from some of which thousands of feet of lavas and tuffs were discharged.
Again in older Tertiary times the same region witnessed
a stupendous outpouring of basalt, the surviving relics of which
are more than 3000 ft. thick, and cover many hundreds of square
miles. Similar evidence is supplied in other countries both in the
Old and the New world. Hence it is proved that, in the geological
past, volcanic action has been vigorous at long intervals on the same
sites during a vast series of ages, though no active vents are to be
seen there now. The volcanoes now active form but a small proportion
of the total number which has appeared on the surface of
the earth.
With regard to the cause of volcanic action much has been
speculated, but little can be confidently affirmed. That water in
the form of occluded gas plays the chief part in forcing the lava
column up a volcanic chimney, and in the violent explosions that
accompany the rise of the molten material, is generally admitted.
But opinions differ as to the source of this water. According to
some investigators, it should be regarded as in large measure of
meteoric origin, derived from the descent of rain into the earth, and
its absorption by the molten magma in the interior. Others, contending
that the supply so furnished, even if it could reach and be
dissolved in the magma, would yet be insufficient to furnish the
prodigious quantity of aqueous vapour discharged during an eruption,
maintain that the water belongs to the magma itself. They point
to the admitted fact that many substances, particularly metals in
a state of fusion, can absorb large quantities of vapours and gases
without chemical combination, and on cooling discharge them with
eruptive phenomena somewhat like those of volcanoes. This
question must be regarded as one of the still unsolved problems of
geology.
(B) Movements of the Earth’s Crust.
Among the hypogene forces in geological dynamics an important
place must be assigned to movements of the terrestrial crust. Though
the expression “the solid earth” has become proverbial, it appears
singularly inappropriate in the light of the results obtained in recent
years by the use of delicate instruments of observation. With the
facilities supplied by these instruments (see Seismometer), it has
been ascertained that the ground beneath our feet is subject to
continual slight tremors, and feeble pulsations of longer duration,
some of which may be due to daily or seasonal variations of temperature,
atmospheric pressure or other meteorological causes.
The establishment of self-recording seismometers all over the world
has led to the detection of many otherwise imperceptible shocks,
over and above the appreciable earth-waves propagated from earthquake
centres of disturbance. Moreover, it has been ascertained
that some parts of the surface of the land are slowly rising, while
others are falling with reference to the sea-level. From time to
time the surface suffers calamitous devastation from earthquakes,
when portions of the crust under great strain suddenly give way.
Lastly, at intervals, probably separated from each other by vast
periods of time, the terrestrial crust undergoes intense plication
and fracture, and is consequently ridged up into mountain-chains.
No event of this kind has been witnessed since man began to record
his experiences. But from the structure of mountains, as laid open
by prolonged denudation, it is possible to form a vivid conception
of the nature and effects of these most stupendous of all geological
revolutions.
In considering this department of geological inquiry it will be
convenient to treat it under the following heads: (1) Slow depression
and upheaval; (2) Earthquakes; (3) Mountain-making; (4)
Metamorphism of rocks.
1. Slow Depression and Upheaval.—On the west side of Japan
the land is believed to be sinking below the sea, for fields are replaced
by beaches of sand or shingle, while the depth of the sea off shore
has perceptibly increased. A subsidence of the south of Sweden has
taken place in comparatively recent times, for streets and foundations
of houses at successive levels are found below high-water mark.
The west coast of Greenland over an extent of more than 600 m.
is sinking, and old settlements are now submerged. Proofs of
submergence of land are furnished by “submerged forests,” and
beds of terrestrial peat now lying at various depths below the level
of the sea, of which many examples have been collected along the
shores of the British Isles, Holland and France. Interesting evidence
that the west of Europe now stands at a lower level than it did at a
late geological period is supplied in the charts of the North Sea and
Atlantic, which show that the valleys of the land are prolonged
under the sea. These valleys have been eroded out of the rocks by
the streams which flow in them, and the depth of their submerged
portions below the sea level affords an indication of the extent of the
subsidence.
The uprise of land has been detected in various parts of the world.
One of the most celebrated instances is that of the shores of the Gulf
of Bothnia, where, at Stockholm, the elevation, between the years
1774 and 1875, appears to have been 48 centimetres (18½ in.) in
a century. But on the west side of Sweden, fronting the Skager Rak,
the coast, between the years 1820 and 1870, rose 30 centimetres,
which is at the rate of 60 centimetres, or nearly 2 ft. in a century.
In the region of the Great Lakes in the interior of Canada and the
United States it has been ascertained that the land is undergoing a
slow tilt towards the south-west, of which the mean rate appears to
be rather less than 6 in. in a century. If this rate of change should
continue the waters of Lake Michigan, owing to the progress of the
tilt, will, in some 500 or 600 years, submerge the city of Chicago,
and eventually the drainage of the lakes will be diverted into the
basin of the Mississippi. Proof of recent emergence of land is supplied
by what are called “raised beaches” or “strand-lines,” that is,
lines of former shores marked by sheets of littoral deposits, or
platforms cut by shore-waves in rock and flanked by old sea-cliffs
and lines of sea-worn caves. Admirable examples of these features
are to be seen along the west coast of Europe from the south of
England to the north of Norway. These lines of old shores become
fainter in proportion to their antiquity. In Britain they occur at
various heights, the platforms at 25, 50 and 100 ft. being well
marked.
The cause of these slow upward and downward movements of the
crust of the earth is still imperfectly understood. Upheaval might
conceivably be produced by an ascent of the internal magma, and the
consequent expansion of the overlying crust by heat; while depression
might follow any subsidence of the magma, or its displacement
659
to another district. If, as is generally believed, the globe is still
contracting, the shrinkage of the surface may cause both these
movements. Subsidence will be in excess, but between subsiding
tracts lateral thrust may suffice to push upward intervening more
solid and stable ground; but no solution of the problem yet proposed
is wholly satisfactory.
2. Earthquakes.—As this subject is discussed in a separate article
it will be sufficient here to take note of its more important geological
bearings. It was for many centuries taken for granted that earthquakes
and volcanoes are due to a common cause. We have seen
that in classical antiquity they were looked on as the results of the
movements of wind imprisoned within the earth. Long after this
notion was discarded, and a more scientific appreciation of volcanic
action was reached, it was still thought that earthquakes should be
regarded as manifestations of the same source of energy as that
which displays itself in volcanic eruptions. It is true that earthquakes
are frequent in districts of active volcanoes, and they may
undoubtedly be often due there to the explosions of the magma,
or to the rupture of rocks caused by its ascent towards the surface.
But such shocks are comparatively local in their range and feeble
in their effects. There is now a general agreement that between the
great world-shaking earthquakes and volcanic phenomena, no
immediate and intimate relationship can be traced, though they may
be connected in ways which are not yet perceived. Some of the
more recent great earthquakes on land have proved that the waves
of shock are produced by the sudden rupture or collapse of rocks
under great strain, either along lines of previous fracture or of new
rents in the terrestrial crust; and that such ruptures may occur at
a remote distance from any volcano. Thus the recent disastrous
San Francisco earthquake has been recognized to have resulted from
a slipping of ground along the line of an old fault, which has been
traced for a long distance in California generally parallel to the
coast. The position of this fault at the surface has long been clearly
followed by its characteristic topography. After the earthquake
these superficial features were found to have been removed by the
same cause that had originated them. For some 300 m. on the track
of this old fault-line a renewed slipping was seen to have taken place
along one or both sides, and the ground at the surface was ruptured
as well as displaced horizontally. Obviously, the jar occasioned by
the sudden and simultaneous subsidence of a portion of the earth’s
crust several hundred miles long, must be far more serious than
could be produced by an earthquake radiating from a single local
volcanic focus.
From their disastrous effects on buildings and human lives, an
exaggerated importance has been imputed to earthquakes as agents
of geological change. Experience shows that even after a severe
shock which may have destroyed numerous towns and villages,
together with thousands of their inhabitants, the face of the country
has suffered scarcely any perceptible change, and that, in the course
of a year or two, when the ruined houses and prostrate trees have
been cleared away, little or no obvious trace of the catastrophe may
remain. Among the more enduring records of a great earthquake
may be enumerated (a) landslips, which lay bare hillsides, and sometimes
pond back the drainage of valleys so as to give rise to lakes;
(b) alterations of the topography, as in fissuring of the ground, or in
the production of inequalities whereby the drainage is affected;
new valleys and new lakes may thus be formed, while previously
existing lakes may be emptied; (c) permanent changes of level,
either in an upward or downward direction.
3. Mountain-making.—This subject may be referred to here for
the striking evidence which it supplies of the importance of movements
of the earth’s crust among geological processes. The structure
of a great mountain-chain such as the Alps proves that the crust
of the earth has been intensely plicated, crumpled and fractured.
Vast piles of sedimentary strata have been folded to such an extent
as to occupy now only half of their original horizontal extent. This
compression in the case of the Alps has been computed to amount
to as much as 120,000 metres or 74 English miles, so that two points
on the opposite sides of that chain have been brought by so much
nearer to each other than they were originally before the movements.
Besides such intense plication, extensive rupturing of the crust has
taken place in the same range of mountains. Not only have the
most ancient rocks been squeezed up into the central axis of the
chain, but huge slices of them have been torn away from the main
body, and thrust forward for many miles, so as now actually to
form the summits of mountains, which are almost entirely composed
of much younger formations. If these colossal disturbances occurred
rapidly, they would give rise to cataclysms of inconceivable
magnitude over the surface of the globe. No record has been discovered
of such accompanying devastation. But whether sudden
and violent, or prolonged and gradual, such stupendous upturnings
of the crust did undoubtedly take place, as is clearly revealed in
innumerable natural sections, which have been laid open by the
denudation of the crests and sides of the mountains.
4. Metamorphism of Rocks (see Metamorphism).—During the
movements to which the crust of the earth has been subject, not
only have the rocks been folded and fractured, but they have likewise,
in many regions, acquired new internal structures, and have
thus undergone a process of “regional metamorphism.” This
rearrangement of their substance has been governed by conditions
which are probably not yet all recognized, but among them we should
doubtless include a high temperature, intense pressure, mechanical
movement resulting in crushing, shearing and foliation, and the
presence of water in their pores. It is among igneous rocks that the
progressive stages of metamorphism can be most easily traced.
Their definite original structure and mineral composition afford a
starting-point from which the investigation may be begun and
pursued. Where an igneous rock has been invaded by metamorphic
changes, it may be observed to have been first broken down into
separate lenticles, the cores of which may still retain, with little or
no alteration, the original characteristic minerals and crystalline
structure of the rock. Between these lenticles, the intervening
portions have been crushed down into a powder or paste, which
seems to have been squeezed round and past them, and shows a
laminated arrangement that resembles the flow-structure in lavas.
As the degree of metamorphism increases, the lenticles diminish in
size, and the intervening crushed and foliated matrix increases in
amount, until at last it may form the entire mass of the rock. While
the original minerals are thus broken down, new varieties make
their appearance. Of these, among the earliest to present themselves
are usually the micas, that impart their characteristic silvery sheen
to the surfaces of the folia along which they spread. Younger
felspars, as well as mica, are developed, and there arise also sillimanite,
garnet, andalusite and many others. The texture becomes
more coarsely crystalline, and the segregation of the constituent
minerals more definite along the lines of foliation. From the finest
silky phyllites a graduation may be traced through successively
coarser mica-schists, until we reach the almost granitic texture of
the coarsest gneisses.
Regional metamorphism has arisen in the heart of mountain-chains,
and in any other district where the deformation of the crust
has been sufficiently intense. There is another type of alteration
termed “contact-metamorphism,” which is developed around
masses of igneous rock, especially where these have been intruded in
large bosses among stratified formations. It is particularly displayed
around masses of granite, where sandstones are found altered into
quartzite, shales and grits into schistose compounds, and where sometimes
fossils are still recognizable among the metamorphic minerals.
DIVISION II.—EPIGENE OR SUPERFICIAL ACTION
It is on the surface of the globe, and by the operation of agents
working there, that at present the chief amount of visible geological
change is effected. In considering this branch of inquiry,
we are not involved in a preliminary difficulty regarding the very
nature of the agencies as is the case in the investigation of
plutonic action. On the contrary, the surface agents are carrying
on their work under our very eyes. We can watch it in all its
stages, measure its progress, and mark in many ways how
accurately it represents similar changes which, for long ages
previously, must have been effected by the same means. But
in the systematic treatment of this subject we encounter a
difficulty of another kind. We discover that while the operations
to be discussed are numerous and readily observable, they are so
interwoven into one great network that any separation of them
under different subdivisions is sure to be more or less artificial
and to convey an erroneous impression. While, therefore, under
the unavoidable necessity of making use of such a classification
of subjects, we must always bear in mind that it is employed
merely for convenience, and that in nature superficial geological
action must be continually viewed as a whole, since the work of
each agent has constant reference to that of the others, and is
not properly intelligible unless that connexion be kept in view.
The movements of the air; the evaporation from land and
sea; the fall of rain, hail and snow; the flow of rivers and
glaciers; the tides, currents and waves of the ocean; the growth
and decay of organized existence, alike on land and in the depths
of the sea;—in short, the whole circle of movement, which is
continually in progress upon the surface of our planet, are the
subjects now to be examined. It is desirable to adopt some
general term to embrace the whole of this range of inquiry. For
this end the word epigene (Gr. ἐπί, upon) has been suggested as
a convenient term, and antithetical to hypogene (Gr. ὑπό, under),
or subterranean action.
A simple arrangement of this part of Geological Dynamics is
in three sections:
A. Air.—The influence of the atmosphere in destroying and
forming rocks.
B. Water.—The geological functions of the circulation of
water through the air and between sea and land, and the
action of the sea.
660
C. Life.—The part taken by plants and animals in preserving,
destroying or reproducing geological formations.
The words destructive, reproductive and conservative,
employed in describing the operations of the epigene agents, do
not necessarily imply that anything useful to man is destroyed,
reproduced or preserved. On the contrary, the destructive
action of the atmosphere may turn barren rock into rich soil,
while its reproductive effects sometimes turn rich land into
barren desert. Again, the conservative influence of vegetation
has sometimes for centuries retained as barren morass what
might otherwise have become rich meadow or luxuriant woodland.
The terms, therefore, are used in a strictly geological
sense, to denote the removal and re-deposition of material, and
its agency in preserving what lies beneath it.
(A) The Air.
As a geological agent, the air brings about changes partly by its
component gases and partly by its movements. Its destructive
action is both chemical and mechanical. The chemical changes are
probably mainly, if not entirely, due to the moisture of the air,
and particularly to the gases, vapours and organic matter which
the moisture contains. Dry air seems to have little or no appreciable
influence in promoting these reactions. As the changes in question
are similar to those much more abundantly brought about by rain
they are described in the following section under the division on rain.
Among the more recognizable mechanical changes effected in
the atmosphere, one of considerable importance is to be seen in the
result of great and rapid changes of temperature. Heat expands
rocks, while cold contracts them. In countries with a great annual
range of temperature, considerable difficulty is sometimes experienced
in selecting building materials liable to be little affected by the
alternate expansion and contraction, which prevents the joints of
masonry from remaining close and tight. In dry tropical climates,
where the days are intensely hot and the nights extremely cold, the
rapid nocturnal contraction produces a strain so great as to rival
frost in its influence upon the surface of exposed rocks, disintegrating
them into sand, or causing them to crack or peel off in skins or
irregular pieces. Dr Livingstone found in Africa (12° S. lat., 34° E.
long.) that surfaces of rock which during the day were heated up to
137° Fahr., cooled so rapidly by radiation at night that, unable to
sustain the strain of contraction, they split and threw off sharp
angular fragments from a few ounces to 100 or 200 ℔ in weight.
In temperate regions this action, though much less pronounced,
still makes itself felt. In these climates, however, and still more in
high latitudes, somewhat similar results are brought about by frost.
By its motion in wind the air drives loose sand over rocks, and in
course of time abrades and smoothes them. “Desert polish” is
the name given to the characteristic lustrous surface thus imparted.
Holes are said to be drilled in window glass at Cape Cod by the same
agency. Cavities are now and then hollowed out of rocks by the
gyration in them of little fragments of stone or grains of sand kept
in motion by the wind. Hurricanes form important geological
agents upon land in uprooting trees, and thus sometimes impeding
the drainage of a country and giving rise to the formation of peat
mosses.
The reproductive action of the air arises partly from the effect
of the chemical and mechanical disintegration involved in the
process of “weathering,” and partly from the transporting power
of wind and of aerial currents. The layer of soil, which covers so
much of the surface of the land, is the result of the decay of the
underlying rocks, mingled with mineral matter blown over the ground
by wind, or washed thither by rain, and with the mouldering remains
of plants and animals. The extent to which fine dust may be
transported over the surface of the land can hardly be realized in
countries clothed with a covering of vegetation, though even there,
in dry weather during spring, clouds of dust may often be seen
blown away by wind from bare ploughed fields. Intercepted by the
leaves of plants and washed down to their roots by rain, this dust
goes to increase the soil below. In arid climates, where dust clouds
are dense and frequent, enormous quantities of fine mineral particles
are thus borne along and accumulated. The remarkable deposit
of “Loess,” which is sometimes more than 1500 ft. thick and covers
extensive areas in China and other countries, is regarded as due to
the drifting of dust by wind. Again the dunes of sand so abundant
along the inner side of sandy sea-beaches in many different parts
of the world are attributable to the same action.
(B) Water.
In treating of the epigene action of water in geological processes
it will be convenient to deal first with its operations in traversing
the land, and then with those which it performs in the sea. The
circulation of water from land to sea and again from sea to land
constitutes the fundamental cause of most of the daily changes by
which the surface of the land is affected.
1. Rain.—Rain effects two kinds of changes upon the surface of
the land. It acts chemically upon soils and stones, and sinking under
ground continues a great series of similar reactions there. It acts
mechanically, by washing away loose materials, and thus powerfully
affecting the contours of the land. Its chemical action depends
mainly upon the nature and proportion of the substances which, in
descending to the earth, it abstracts from the atmosphere. Rain
always absorbs a little air, which, in addition to its nitrogen and
oxygen, contains carbonic acid, and in minute proportions, sodium
chloride, sulphuric acid and other ingredients, especially inorganic
dust, organic particles and living germs. Probably the most generally
efficient of these constituents are oxygen, carbonic acid and organic
matter. Armed with these reagents, rain effects a chemical decomposition
of the rocks on which it falls, and through which it sinks
underground. The principal changes thus produced are as follows:
(a) Oxidation.—Owing to the prominence of oxygen in rain-water,
and its readiness to unite with any substance which can contain
more of it, a thin oxidized pellicle is formed on the surface of many
rocks on which rain falls, and this oxidized layer if not at once
washed off, sinks deeper until a crust is formed over the stone. A
familiar illustration of this action is afforded by the rust, or oxide,
which forms on iron when exposed to moisture, though this iron
may be kept long bright if allowed to remain screened from moist
air and rain. (b) Deoxidation.—Organic matter having an affinity
for more oxygen decomposes peroxides by depriving them of some
part of their share of that element and reducing them to protoxides.
These changes are especially noticeable among the iron oxides so
abundantly diffused among rocks. Hence rain-water, in sinking
through soil and obtaining such organic matter, becomes thereby
a reducing agent. (c) Solution.—This may take place either by the
simple action of the water, as in the solution of rock-salt, or by the
influence of the carbonic acid present in the rain. (d) Formation of
Carbonates.—A familiar example of the action of carbonic acid
in rain is to be seen in the corrosion of exposed marble slabs. The
carbonic acid dissolves some of the lime, which, as a bicarbonate,
is held in solution in the carbonated water, but is deposited again
when the water loses its carbonic acid or evaporates. It is not
merely carbonates, however, which are liable to this kind of destruction.
Even silicates of lime, potash and soda, combinations existing
abundantly as constituents of rocks, are attacked; their silica is
liberated, and their alkalis or alkaline earths, becoming carbonates,
are removed in solution. (e) Hydration.—Some minerals, containing
little or no water, and therefore called anhydrous, when exposed to
the action of the atmosphere, absorb water, or become hydrous,
and are then usually more prone to further change. Hence the rocks
of which they form part become disintegrated.
Besides the reactions here enumerated, a considerable amount of
decay may be observed as the result of the presence of sulphuric
and nitric acid in the air, especially in that of large towns and
manufacturing districts, where much coal is consumed. Metallic
surfaces, as well as various kinds of stone, are there corroded, while
the mortar of walls may often be observed to be slowly swelling out
and dropping off, owing to the conversion of the lime into sulphate.
Great injury is likewise done from a similar cause to marble monuments
in exposed graveyards.
The general result of the disintegrating action of the air and of
rain, including also that of plants and animals, to be noticed in the
sequel, is denoted by the term “weathering.” The amount of decay
depends partly on conditions of climate, especially the range of
temperature, the abundance of moisture, height above the sea and
exposure to prevalent winds. Many rocks liable to be saturated
with rain and rapidly dried under a warm sun are apt to disintegrate
at the surface with comparative rapidity. The nature and progress
of the weathering are mainly governed by the composition and
texture of the rocks exposed to it. Rocks composed of particles
liable to little chemical change from the influence of moisture are
best fitted to resist weathering, provided they possess sufficient
cohesion to withstand the mechanical processes of disintegration.
Siliceous sandstones are excellent examples of this permanence.
Consisting wholly or mainly of the durable mineral quartz, they are
sometimes able so to withstand decay that buildings made of them
still retain, after the lapse of centuries, the chisel-marks of the
builders. Some rocks, which yield with comparative rapidity to
the chemical attacks of moisture, may show little or no mark of
disintegration on their surface. This is particularly the case with
certain calcareous rocks. Limestone when pure is wholly soluble
in acidulated water. Rain falling on such a rock removes some of it
in solution, and will continue to do so until the whole is dissolved
away. But where a limestone is full of impurities, a weathered crust
of more or less insoluble particles remains after the solution of the
calcareous part of the stone. Hence the relative purity of limestones
may be roughly determined by examining their weathered surfaces,
where, if they contain much sand, the grains will be seen projecting
from the calcareous matrix, and where, should the rock be very
ferruginous, the yellow hydrous peroxide, or ochre, will be found as
a powdery crust. In limestones containing abundant encrinites,
shells, or other organic remains, the weathered surface commonly
presents the fossils standing out in relief. The crystalline arrangement
of the lime in the organic structures enables them to resist
disintegration better than the general mechanically aggregated
matrix of the rock. An experienced fossil collector will always
search well such weathered surfaces, for he often finds there, delicately
661
picked out by the weather, minute and frail fossils which are wholly
invisible on a freshly broken surface of the stone. Many rocks
weather with a thick crust, or even decay inwards for many feet or
yards. Basalt, for example, often shows a yellowish-brown ferruginous
layer on its surface, formed by the conversion of its felspar
into kaolin, and the removal of its calcium silicate as carbonate,
by the hydration of its olivine and augite and their conversion into
serpentine, or some other hydrous magnesian silicate, and by the
conversion of its magnetite into limonite. Granite sometimes shows
in a most remarkable way the distance to which weathering can
reach. It may occasionally be dug into for a depth of 20 or 30 ft.,
the quartz crystals and veins retaining their original positions, while
the felspar is completely kaolinized. It is to the endlessly varied
effects of weathering that the abundant fantastic shapes assumed
by crags and other rocky masses are due. Most varieties of rock
have their own characteristic modes of weathering, whereby they
may be recognized even from a distance. To some of these features
reference will be made in Part VIII.
The mechanical action of rain, which is intimately bound up with
its chemical action, consists in washing off the fine superficial
particles of rocks which have been corroded and loosened by the
process of weathering, and in thus laying open fresh portions to the
same influences of decay. The detritus so removed is partly carried
down into the soil which is thereby enriched, partly held in suspension
in the little runnels into which the rain-drops gather as they begin
to flow over the land, partly pushed downwards along the surface
of sloping ground. A good deal of it finds its way into the nearest
brooks and rivers, which are consequently made muddy by heavy
rain.
It is natural that a casual consideration of the subject should lead
to an impression that, though the general result of the fall of rain
upon a land-surface must lead to some amount of disintegration and
lowering of that surface, the process must be so slow and slight as
hardly to be considered of much importance among geological
operations. But further attention will show such an impression to
be singularly erroneous. It loses sight of the fact that a change
which may be hardly appreciable within a human lifetime, or even
within the comparatively brief span of geological time embraced in
the compass of human history, may nevertheless become gigantic
in its results in the course of immensely protracted periods. An
instructive lesson in the erosive action of rain may be found in the
pitted and channelled surface of ground lying under the drip of the
eaves of a cottage. The fragments of stone and pebbles of gravel
that form part of the soil can there be seen sticking out of the ground,
because being hard they resist the impetus of the falling drops,
protecting for a time the earth beneath them, while that which
surrounded and covered them is washed away. From this familiar
illustration the observer may advance through every stage in the
disappearance of material which once covered the surface, until he
comes to examples where once continuous and thick sheets of solid
rock have been reduced to a few fragments or have been entirely
removed. Since the whole land surface over which rain falls is
exposed to this waste, the superficial covering of decayed rock or
soil, as Hutton insisted, is constantly, though imperceptibly, travelling
outward and downward to the sea. In this process of transport
rain is an important carrying agent, while at the same time it serves
to connect the work of the other disintegrating forces, and to make
it conducive to the general degradation of the land. Though this
decay is general and constant, it is obviously not uniform. In some
places where, from the nature of the rock, from the flatness of the
ground, or from other causes, rain works under great difficulties,
the rate of waste may be extremely slow. In other places it may
be rapid enough to be appreciable from year to year. A survey of
this department of geological activity shows how unequal wasting
by rain, combined with the operations of brooks and rivers, has
produced the details of the present relief of the land, those tracts
where the destruction has been greatest forming hollows and valleys,
others, where it has been less, rising into ridges and hills (Part VIII.).
Rain-action is not merely destructive, but is accompanied with
reproductive effects, chief of which is the formation of soil. In
favourable situations it has gathered together accumulations of loam
and earth from neighbouring higher ground, such as the “brick-earth,”
“head,” and “rain-wash” of the south of England—earthy
deposits, sometimes full of angular stones, derived from the subaerial
waste of the rocks of the neighbourhood.
2. Underground Water.—Of the rain which falls upon the land
one portion flows off into brooks and rivers by which the water is
conducted back to the ocean; the larger part, however, sinks into
the ground and disappears. It is this latter part which has now
to be considered. Over and above the proportion of the rainfall
which is absorbed by living vegetation and by the soil, there is a
continual filtering down of the water from the surface into the rocks
that lie below, where it partly lodges in pores and interstices, and
partly finds its way into subterranean joints and fissures, in which
it performs an underground circulation, and ultimately issues once
more at the surface in the form of springs (q.v.). In the course of
this circulation the water performs an important geological task.
Not only carrying down with it the substances which the rain has
abstracted from the air, but obtaining more acids and organic
matter from the soil, it is enabled to effect chemical changes in the
rocks underneath, and especially to dissolve limestone and other
calcareous formations. So considerable is the extent of this solution
in some places that the springs which come to the surface, and begin
there to evaporate and lose some of their carbonic acid, contain more
dissolved lime than they can hold. They consequently deposit it
in the form of calcareous tuff or sinter (q.v.). Other subterranean
waters issue with a large proportion of iron-salts in solution which
form deposits of ochre. The various mineral springs so largely
made use of for the mitigation or cure of diseases owe their properties
to the various salts which they have dissolved out of rocks
underground. As the result of prolonged subterranean solution in
limestone districts, passages and caves (q.v.), sometimes of great
width and length, are formed. When these lie near the surface their
roofs sometimes fall in and engulf brooks and rivers, which then
flow for some way underground until the tunnels conduct them back
again to daylight on some lower ground.
Besides its chemical activity water exerts among subterranean
rocks a mechanical influence which leads to important changes in
the topography of the surface. In removing the mineral matter,
either in solution or as fine sediment, it sometimes loosens the support
of overlying masses of rock which may ultimately give way on sloping
ground, and rush down the declivities in the form of landslips.
These destructive effects are specially frequent on the sides of valleys
in mountainous countries and on lines of sea-cliff.
3. Brooks and Rivers.—As geological agents the running waters
on the face of the land play an important part in epigene
changes. Like rain and springs they have both a chemical and a
mechanical action. The latter receives most attention, as it undoubtedly
is the more important; but the former ought not to be
omitted in any survey of the general waste of the earth’s surface.
The water of rivers must possess the powers of a chemical solvent
like rain and springs, though its actual work in this respect can be
less easily measured, seeing that river water is directly derived from
rain and springs, and necessarily contains in solution mineral substances
supplied to it by them and not by its own operation. Nevertheless,
it is sometimes easy to prove that streams dissolve chemically
the rocks of their channels. Thus, in limestone districts the base
of the cliffs of river ravines may be found eaten away into tunnels,
arches, and overhanging projections, presenting in their smooth
surfaces a great contrast to the angular jointed faces of the same
rock, where now exposed to the influence only of the weather on the
higher parts of the cliff.
The mechanical action of rivers consists (a) in transporting mud,
sand, gravel and blocks of stone from higher to lower levels; (b)
in using these loose materials to widen and deepen their channels
by erosion; (c) in depositing their load of detritus wherever possible
and thus to make new geological formations.
(a) Transporting Power.—River-water is distinguished from that
of springs by being less transparent, because it contains more or less
mineral matter in suspension, derived mainly from what is washed
down by rain, or carried in by brooks, but partly also from the
abrasion of the water-channels by the erosive action of the rivers
themselves. The progress of this burden of detritus may be instructively
followed from the mountain-tributaries of a river down to
the mouth of the main stream. In the high grounds the water-courses
may be observed to be choked with large fragments of rock
disengaged from the cliffs and crags on either side. Traced downwards
the blocks are seen to become gradually smaller and more rounded.
They are ground against each other, and upon the rocky sides and
bottom of the channel, getting more and more reduced as they
descend, and at the same time abrading the rocks over or against
which they are driven. Hence a great deal of débris is produced,
and is swept along by the onward and downward movement of the
water. The finer portions, such as mud and fine sand, are carried
in suspension, and impart the characteristic turbidity to river-water;
the coarser sand and gravel are driven along the river-bottom.
The proportion of suspended mineral matter has been
ascertained with more or less precision for a number of rivers. As
an illustrative example of a river draining a vast area with different
climates, forms of surface and geological structure the Mississippi
may be cited. The average proportion of sediment in its water was
ascertained by Humphreys and Abbot to be 1⁄1500 by weight or
1⁄2900 by volume. These engineers found that, in addition to this
suspended material, coarse detritus is constantly being pushed
forward along the bed of the river into the Gulf of Mexico, to an
amount which they estimated at about 750,000,000 cubic ft. of
sand, earth and gravel; they concluded that the Mississippi carries
into the gulf every year an amount of mechanically transported
sediment sufficient to make a prism one square mile in area and
268 ft. in height.
(b) Excavating Power.—It is by means of the sand, gravel and
stones which they drive against the sides and bottoms of their
channels that streams have hollowed out the beds in which they
flow. Not only is the coarse detritus reduced in size by the friction
of the stones against each other, but, at the same time, these materials
abrade the rocks against which they are driven by the current.
Where, owing to the shape of the bottom of the channel, the stones
are caught in eddies, and are kept whirling round there, they become
more and more worn down themselves, and at the same time scour
out basin-shaped cavities, or “pot-holes,” in the solid rock below.
662
The uneven bed of a swiftly flowing stream may in this way be
honeycombed with such eroded basins which coalesce and thus
appreciably lower the surface of the bed. The steeper the channel,
other conditions being equal, the more rapid will be the erosion.
Geological structure also affects the character and rate of the excavation.
Where the rocks are so arranged as to favour the formation
and persistence of a waterfall, a long chasm may be hollowed out
like that of the Niagara below the falls, where a hard thick bed of
nearly flat limestone lies on softer and more easily eroded shales.
The latter are scooped out from underneath the limestone, which
from time to time breaks off in large masses and the waterfall
gradually retreats up stream, while the ravine is proportionately
lengthened. To the excavating power of rivers the origin of the
valley systems of the dry land must be mainly assigned (see Part VIII.).
(c) Reproductive Power.—So long as a stream flows over a steep
declivity its velocity suffices to keep the sediment in suspension,
but when from any cause, such as a diminution of slope, the velocity
is checked, the transporting power is lessened and the sediment
begins to fall to the bottom and to remain there. Hence various
river-formed or “alluvial” deposits are laid down. These sometimes
cover considerable spaces at the foot of mountains. The
floors of valleys are strewn with detritus, and their level may thereby
be sensibly raised. In floods the ground inundated on either side
of a stream intercepts some part of the detritus, which is then spread
over the flood-plain and gradually heightens it. At the same time
the stream continues to erode the channel, and ultimately is unable
to reach the old flood-plain. It consequently forms a new plain at
a lower level, and thus, by degrees, it comes to be flanked on either
side by a series of successive terraces or platforms, each of which
marks one of its former levels. Where a river enters a large body of
water its current is checked. Some of its sediment is consequently
dropped, and by slow accumulation forms a delta (q.v.). On land,
every lake in mountain districts furnishes instances of this kind of
alluvium. But the most important deltas are those formed in the
sea at the mouths of the larger rivers of the globe. Off many coast-lines
the detritus washed from the land gathers into bars, which
enclose long strips of water more or less completely separated from
the sea outside and known as lagoons. A chain of such lagoon-barriers
stretches for hundreds of miles round the Gulf of Mexico
and the eastern shores of the United States.
4. Lakes.—These sheets of water, considered as a whole, do not
belong to the normal system of drainage on the land whereby valleys
are excavated. On the contrary they are exceptional to it; for
the constant tendency of running water is to fill them up, or to drain
them by wearing down the barriers that contain them at their
outflow. Some of them are referable to movements of the terrestrial
crust whereby depressions arise on the surface of the land, as has
been noted after earthquakes. Others have arisen from solution
such as that of rock-salt or of limestone, the removal of which by
underground water causes a subsidence of the ground above. A
third type of lake-basin occurs in regions that are now or have once
been subject to the erosive action of glaciers (see under next subdivision,
Terrestrial Ice). Many small lakes or tarns have been
caused by the deposit of débris across a valley as by landslips or
moraines. Considered from a geological point of view, lakes perform
an important function in regulating the drainage of the ground below
their outfall and diminishing the destructive effects of floods, in
filtering the water received from their affluent streams, and in
providing undisturbed areas of deposit in which thick and extensive
lacustrine formations may be accumulated. In the inland basins
of some dry climates the lakes are salt, owing to excess of evaporation,
and their bottoms become the sites of chemical deposits, particularly
of chlorides of sodium and magnesium, and calcium sulphate and
carbonate.
5. Terrestrial Ice.—Each of the forms assumed by frozen water
has its own characteristic action in geological processes. Frost has
a powerful influence in breaking up damp soils and surfaces of stone
in the pores or cracks of which moisture has lodged. The water in
freezing expands, and in so doing pushes asunder the component
particles of soil or stone, or widens the space between the walls of
joints or crevices. When the ice melts the loosened grains remain
apart ready to be washed away by rain or blown off by wind, while
by the widening of joints large blocks of rock are detached from
the faces of cliffs. Where rivers or lakes are frozen over the ice
exerts a marked pressure on their banks; and when it breaks up
large sheets of it are driven ashore, pushing up quantities of gravel
and stones above the level of the water. The piling up of the disrupted
ice against obstructions in rivers ponds back the water, and
often leads to destructive floods when the ice barriers break. Where
the ice has formed round boulders in shallow water, or at the bottom
(“anchor-ice”), it may lift these up when the frost gives way,
and may transport them for some distance. Ice formed in the
atmosphere, and descending to the ground in the form of hail, often
causes great destruction to vegetation and not infrequently to
animal life. Where the frozen moisture reaches the earth as snow,
it serves to protect rock, soil and vegetation from the effects of
frost; but on sloping ground it is apt to give rise to destructive
avalanches or landslips, while indirectly, by its rapid melting, it
may cause serious floods in rivers.
But the most striking geological work performed by terrestrial
ice is that achieved by glaciers (q.v.) and ice-sheets. These vast
masses of moving ice, when they descend from mountains where the
steeper rocks are clear of snow, receive on their surface the débris
detached by frost from the declivities above, and bear these materials
to lower levels or to the sea. Enormous quantities of rock-rubbish
are thus transported in the Alps and other high mountain ranges.
When the ice retreats the boulders carried by it are dropped where
it melts, and left there as memorials of the former extension of the
glaciers. Evidence of this nature proves the much wider extent of
the Alpine ice at a comparatively recent geological date. It can
also be shown that detritus from Scandinavia has been ice-borne to
the south-east of England and far into the heart of Europe.
The ice, by means of grains of sand and pieces of stone which it
drags along, scores, scratches and polishes the surfaces of rock
underneath it, and, in this way, produces the abundant fine sediment
that gives the characteristic milky appearance to the rivers that
issue from the lower ends of glaciers. By such long-continued
attrition the rocks are worn down, portions of them of softer nature,
or where the ice acts with especial vigour, are hollowed out into
cavities which, on the disappearance of the ice, may be filled with
water and become tarns or lakes. Rocks over which land-ice has
passed are marked by a peculiar smooth, flowing outline, which
forms a contrast to the more rugged surface produced by ordinary
weathering. They are covered with groovings, which range from
the finest striae left by sharp grains of sand to deep ruts ground out
by blocks of stone. The trend of these markings shows the direction
in which the ice flowed. By their evidence the position and movement
of former glaciers in countries from which the ice has entirely
vanished may be clearly determined (see Glacial Period).
6. The Sea.—The physical features of the sea are discussed in
separate articles (see Ocean and Oceanography). The sea must
be regarded as the great regulator of temperature and climate over
the globe, and as thus exerting a profound influence on the distribution
of plant and animal life. Its distinctly geological work is partly
erosive and partly reproductive. As an eroding agent it must to
some extent effect chemical decompositions in the rocks and sediments
over which it spreads; but these changes have not yet been
satisfactorily studied. Undoubtedly, its chief destructive power
is of a mechanical kind, and arises from the action of its waves in
beating upon shore-cliffs. By the alternate compression and
expansion of the air in crevices of the rocks on which heavy breakers
fall, and by the hydraulic pressure which these masses of sea-water
exert on the walls of the fissures into which they rush, large masses
of rock are loosened and detached, and caves and tunnels are drilled
along the base of sea-cliffs. Probably still more efficacious are the
blows of the loose shingle, which, caught up and hurled forward by
the waves, falls with great force upon the shore rocks, battering
them as with a kind of artillery until they are worn away. The
smooth surfaces of the rocks within reach of the waves contrasted
with their angular forms above that limit bear witness to the amount
of waste, while the rounded forms of the boulders and shingle show
that they too are being continually reduced in size. Thus the sea,
by its action on the coasts, produces much sediment, which is swept
away by its waves and currents and strewn over its floor. Besides
this material, it is constantly receiving the fine silt and sand carried
down by rivers. As the floor of the ocean is thus the final receptacle
for the waste of the land, it becomes the chief era on the surface of
the globe for the accumulation of new stratified formations. And
such has been one of its great functions since the beginning of
geological time, as is proved by the rocks that form the visible part
of the earth’s crust, and consist in great part of marine deposits.
Chemical precipitates take place more especially in enclosed parts
of the sea, where concentration of the water by evaporation can take
place, and where layers of sodium chloride, calcium sulphate and
carbonate, and other salts are laid down. But the chief marine
accumulations are of detrital origin. Near the land and for a variable
distance extending sometimes to 200 or 300 m. from shore the
deposits consist chiefly of sediments derived from the waste of the
land, the finer silts being transported farthest from their source.
At greater depths and distances the ocean floor receives a slow deposit
of exceedingly fine clay, which is believed to be derived from the
decomposition of pumice and volcanic dust from insular or submarine
volcanoes. Wide tracts of the bottom are covered with
various forms of ooze derived from the accumulation of the remains
of minute organisms.
(C) Life.
Among the agents by which geological changes are carried on
upon the surface of the globe living organisms must be enumerated.
Both plants and animals co-operate with the inorganic agents in
promoting the degradation of the land. In some cases, on the other
hand, they protect rocks from decay, while, by the accumulation of
their remains, they give rise to extensive formations both upon the
land and in the sea. Their operations may hence be described as
alike destructive, conservative and reproductive. Under this heading
also the influence of Man as a geological agent deserves notice.
(a) Plants.—Vegetation promotes the disintegration of rocks and
soil in the following ways: (1) By keeping the surfaces of stone
moist, and thus promoting both mechanical and chemical dissolution,
as is especially shown by liverworts, mosses and other moisture-loving
plants. (2) By producing through their decay carbonic and
663
other acids, which, together with decaying organic matter taken up
by passing moisture, become potent in effecting the chemical decomposition
of rocks and in promoting the disintegration of soils. (3)
By inserting their roots or branches between joints of rock, which
are thereby loosened, so that large slices may be eventually wedged
off. (4) By attracting rain, as thick woods, forests and peat-mosses
do, and thus accelerating the general waste of a country by running
water. (5) By promoting the decay of diseased and dead plants and
animals, as when fungi overspread a damp rotting tree or the carcase
of a dead animal.
That plants also exert a conservative influence on the surface of
the land is shown in various ways. (1) The formation of a stratum
of turf protects the soil and rocks underneath from being rapidly
disintegrated and washed away by atmospheric action. (2) Many
plants, even without forming a layer of turf, serve by their roots or
branches to protect the loose sand or soil on which they grow from
being removed by wind. The common sand-carex and other arenaceous
plants bind the loose sand-dunes of our coasts, and give them a
permanence, which would at once be destroyed were the sand laid
bare again to storms. The growth of shrubs and brushwood along
the course of a stream not only keeps the alluvial banks from being
so easily undermined and removed as would otherwise be the case,
but serves to arrest the sediment in floods, filtering the water and
thereby adding to the height of the flood plain. (3) Some marine
plants, like the calcareous nullipores, afford protection to shore
rocks by covering them with a hard incrustation. The tangles and
smaller Fuci which grow abundantly on the littoral zone break the
force of the waves or diminish the effects of ground swell. (4)
Forests and brushwood protect the soil, especially on slopes, from
being washed away by rain or ploughed up by avalanches.
Plants contribute by the aggregation of their remains to the
formation of stratified deposits. Some marine algae which secrete
carbonate of lime not only encrust rocks but give rise to sheets of
submarine limestone. An analogous part is played in fresh-water
lakes by various lime-secreting plants, such as Chara. Long-continued
growth of vegetation has, in some regions, produced thick
accumulations of a dark loam, as in the black cotton soil (regur) of
India, and the black earth (tchernozom) of Russia. Peat-mosses
are formed in temperate and arctic climates by the growth of marsh-loving
plants, sometimes to a thickness of 40 or 50 ft. In tropical
regions the mangrove swamps on low moist shores form a dense
jungle, sometimes 20 m. broad, which protects these shores from the
sea until, by the arrest of sediment and the constant contribution of
decayed vegetation, the spongy ground is at last turned into firm
soil. Some plants (diatoms) can abstract silica and build it into
their framework, so that their remains form a siliceous deposit or
ooze which covers spaces of the deep sea-floor estimated at more
than ten millions of square miles in extent.
(b) Animals.—These exert a destructive influence in the following
ways: (1) By seriously affecting the composition and arrangement
of the vegetable soil. Worms bring up the lower portions of the
soil to the surface, and while thus promoting its fertility increase
its liability to be washed away by rain. Burrowing animals, by
throwing up the soil and subsoil, expose these to be dried and blown
away by the wind. At the same time their subterranean passages
serve to drain off the superficial water and to injure the stability
of the surface of the ground above them. In Britain the mole and
rabbit are familiar examples. (2) By interfering with or even diverting
the flow of streams. Thus beaver-dams check the current of
water-courses, intercept floating materials, and sometimes turn
streams into new channels. The embankments of the Mississippi
are sometimes weakened to such an extent by the burrowings of the
cray-fish as to give way and allow the river to inundate the surrounding
country. Similar results have happened in Europe from
subterranean operations of rats. (3) Some mollusca bore into stone
or wood and by the number of contiguous perforations greatly
weaken the material. (4) Many animals exercise a ruinously
destructive influence upon vegetation. Of the numerous plagues
of this kind the locust, phylloxera and Colorado beetle may be cited.
The most important geological function performed by animals is
the formation of new deposits out of their remains. It is chiefly by
the lower grades of the animal kingdom that this work is accomplished,
especially by molluscs, corals and foraminifera. Shell-banks
are formed abundantly in such comparatively shallow and enclosed
basins as that of the North Sea, and on a much more extensive scale
on the floor of the West Indian seas. By the coral polyps thick
masses of limestones have been built up in the warmer seas of the
globe (see Coral Reefs). The floor of the Atlantic and other oceans
is covered with a fine calcareous ooze derived mainly from the
remains of foraminifera, while in other regions the bottom shows a
siliceous ooze formed almost entirely of radiolaria. Vertebrate
animals give rise to phosphatic deposits formed sometimes of their
excrement, as in guano and coprolites, sometimes of an accumulation
of their bones.
(c) Man.—No survey of the geological workings of plant and
animal life upon the surface of the globe can be complete which does
not take account of the influence of man—an influence of enormous
and increasing consequence in physical geography, for man has
introduced, as it were, an element of antagonism to nature. His
interference shows itself in his relations to climate, where he has
affected the meteorological conditions of different countries: (1)
By removing forests, and laying bare to the sun and winds areas
which were previously kept cool and damp under trees, or which,
lying on the lee side, were protected from tempests. It is supposed
that the wholesale destruction of the woodlands formerly existing
in countries bordering the Mediterranean has been in part the cause
of the present desiccation of these districts. (2) By drainage, whereby
the discharged rainfall is rapidly removed, and the evaporation is
lessened, with a consequent diminution of rainfall and some increase
in the general temperature of a country. (3) By the other processes
of agriculture, such as the transformation of moor and bog into
cultivated land, and the clothing of bare hillsides with green crops
or plantations of coniferous and hardwood trees.
Still more obvious are the results of human interference with the
flow of water: (1) By increasing or diminishing the rainfall man
directly affects the volume of rivers. (2) By his drainage operations
he makes the rain to run off more rapidly than before, and thereby
increases the magnitude of floods and of the destruction caused by
them. (3) By wells, bores, mines, or other subterranean works he
interferes with the underground waters, and consequently with the
discharge of springs. (4) By embanking rivers he confines them to
narrow channels, sometimes increasing their scour, and enabling
them to carry their sediment further seaward, sometimes causing
them to deposit it over the plains and raise their level. (5) By his
engineering operations for water-supply he abstracts water from its
natural basins and depletes the streams.
In many ways man alters the aspect of a country: (1) By changing
forest into bare mountain, or clothing bare mountains with forest.
(2) By promoting the growth or causing the removal of peat-mosses.
(3) By heedlessly uncovering sand-dunes, and thereby setting in
motion a process of destruction which may convert hundreds of
acres of fertile land into waste sand, or by prudently planting the
dunes with sand-loving vegetation and thus arresting their landward
progress. (4) By so guiding the course of rivers as to make them
aid him in reclaiming waste land, and bringing it under cultivation.
(5) By piers and bulwarks, whereby the ravages of the sea are
stayed, or by the thoughtless removal from the beach of stones
which the waves had themselves thrown up, and which would have
served for a time to protect the land. (6) By forming new deposits
either designedly or incidentally. The roads, bridges, canals,
railways, tunnels, villages and towns with which man has covered
the surface of the land will in many cases form a permanent record
of his presence. Under his hand the whole surface of civilized
countries is very slowly covered with a stratum, either formed
wholly by him or due in great measure to his operations and containing
many relics of his presence. The soil of ancient towns has
been increased to a depth of many feet by their successive destructions
and renovations.
Perhaps the most subtle of human influences are to be seen in the
distribution of plant and animal life upon the globe. Some of man’s
doings in this domain are indeed plain enough, such as the extirpation
of wild animals, the diminution or destruction of some forms of
vegetation, the introduction of plants and animals useful to himself,
and especially the enormous predominance given by him to the
cereals and to the spread of sheep and cattle. But no such extensive
disturbance of the normal conditions of the distribution of life can
take place without carrying with it many secondary effects, and
setting in motion a wide cycle of change and of reaction in the
animal and vegetable kingdoms. For example, the incessant
warfare waged by man against birds and beasts of prey in districts
given up to the chase leads sometimes to unforeseen results. The
weak game is allowed to live, which would otherwise be killed off
and give more room for the healthy remainder. Other animals
which feed perhaps on the same materials as the game are by the
same cause permitted to live unchecked, and thereby to act as a
further hindrance to the spread of the protected species. But the
indirect results of man’s interference with the régime of plants and
animals still require much prolonged observation.
Part V.—Geotectonic or Structural Geology
From a study of the nature and composition of minerals and
rocks, and an investigation of the different agencies by which
they are formed and modified, the geologist proceeds to inquire
how these materials have been put together so as to build up the
visible part of the earth’s crust. He soon ascertains that they
have not been thrown together wholly at random, but that they
show a recognizable order of arrangement. Some of them,
especially those of most recent growth, remain in their original
condition and position, but, in proportion to their antiquity,
they generally present increasing alteration, until it may no
longer be possible to tell what was their pristine state. As by
far the largest accessible portion of the terrestrial crust consists of
stratified rocks, and as these furnish clear evidence of most of the
modifications to which they have been subjected in the long
course of geological history, it is convenient to take them into
664
consideration first. They possess a number of structures which
belong to the original conditions in which they were accumulated.
They present in addition other structures which have been superinduced
upon them, and which they share with the unstratified
or igneous rocks.
1. Original Structures
(a) Stratified Rocks.—This extensive and important series is
above all distinguished by possessing a prevailing stratified
arrangement. Their materials have been laid down in laminae,
layers and strata, or beds, pointing generally to the intermittent
deposition of the sediments of which they consist. As this
stratification was, as a rule, originally nearly or quite horizontal,
it serves as a base from which to measure any subsequent disturbance
which the rocks have undergone. The occurrence of
false-bedding, i.e. bands of inclined layers between the normal
planes of stratification, does not form any real exception; but
indicates the action of shifting currents whereby the sediment
was transported and thrown down. Other important records of
the original conditions of deposit are supplied by ripple-marks,
sun-cracks, rain-prints and concretions.
From the nature of the material further light is cast on the geographical
conditions in which the strata were accumulated. Thus,
conglomerates indicate the proximity of old shore-lines, sandstones
mark deposits in comparatively shallow water, clays and shales
point to the tranquil accumulation of fine silt at a greater depth
and further from land, while fossiliferous limestones bear witness to
clearer water in which organisms flourished at some distance from
deposits of sand and mud. Again, the alternation of different kinds
of sediment suggests a variability in the conditions of deposition,
such as a shifting of the sediment-bearing currents and of the areas
of muddy and clear water. A thick group of conformable strata,
that is, a series of deposits which show no discordance in their
stratification, may usually be regarded as having been laid down on
a sea-floor that was gently sinking. Here and there evidence is
obtainable of the limits or of the progress of the subsidence by what
is called “overlap.” Of the absolute length of time represented by
any strata or groups of strata no satisfactory estimates can yet be
formed. Certain general conclusions may indeed be drawn, and
comparisons may be made between different series of rocks. Sandstones
full of false-bedding were probably accumulated more rapidly
than finely-laminated shales or clays. It is not uncommon in certain
Carboniferous formations to find coniferous and other trunks embedded
in sandstone. Some of these trees seem to have been carried
along and to have sunk, their heavier or root end touching the
bottom and their upper end slanting upward in the direction of the
current, exactly as in the case of the snags of the Mississippi. In
other cases the trees have been submerged while still in their positions
of growth. The continuous deposit of sand at last rose above the
level of the trunks and buried them. It is clear then that the rate
of deposit must have been sometimes sufficiently rapid to allow
sand to accumulate to a depth of 30 ft. or more before the decay
of the wood. Modern instances are known where, under certain
circumstances, submerged trees may last for some centuries, but
even the most durable must decay in what, after all, is a brief space
of geological time. Since continuous layers of the same kind of
deposit suggest a persistence of geological conditions, while numerous
alternations of different kinds of sedimentary matter point to
vicissitudes or alternations of conditions, it may be supposed that
the time represented by a given thickness of similar strata was less
than that shown by the same thickness of dissimilar strata, because
the changes needed to bring new varieties of sediment into the area
of deposit would usually require the lapse of some time for their
completion. But this conclusion may often be erroneous. It will
be best supported when, from the very nature of the rocks, wide
variations in the character of the water-bottom can be established.
Thus a group of shales followed by a fossiliferous limestone would
almost always mark the lapse of a much longer period than an equal
depth of sandy strata. A thick mass of limestone, made up of
organic remains which lived and died upon the spot, and whose
remains are crowded together generation above generation, must
have demanded many years or centuries for its formation.
But in all speculations of this kind we must bear in mind that the
length of time represented by a given depth of strata is not to be
estimated merely from their thickness or lithological character.
The interval between the deposit of two successive laminae of shale
may have been as long as, or even longer than, that required for
the formation of one of the laminae. In like manner the interval
needed for the transition from one stratum or kind of strata to
another may often have been more than equal to the time required
for the formation of the strata on either side. But the relative
chronological importance of the bars or lines in the geological
record can seldom be satisfactorily discussed merely on lithological
grounds. This must mainly be decided on the evidence of organic
remains, as shown in Part VI., where the grouping of the stratified
rocks into formations and systems is described.
(b) Igneous Rocks.—As part of the earth’s crust these rocks
present characters by which they are strongly differentiated
from the stratified series. While the broad petrographical
distinctions of their several varieties remain persistent, they
present sufficient local variations of type to point to the existence
of what have been called petrographic provinces, in each of
which the eruptive masses are connected by a general family
relationship, differing more or less from that of a neighbouring
province. In each region presenting a long chronological series
of eruptive rocks a petrographical sequence can be traced, which
is observed to be not absolutely the same everywhere, though its
general features may be persistent. The earliest manifestations
of eruptive material in any district appear to have been most
frequently of an intermediate type between acid and basic,
passing thence into a thoroughly acid series and concluding
with an effusion of basic material.
Considered as part of the architecture of the crust of the earth,
igneous rocks are conveniently divisible into two great series:
(1) those bodies of material which have been injected into the
crust and have solidified there, and (2) those which have reached
the surface and have been ejected there, either in a molten state
as lava or in a fragmental form as dust, ashes and scoriae. The
first of these divisions represents the plutonic, intrusive or
subsequent phase of eruptivity; the second marks the volcanic,
interstratified or contemporaneous phase.
1. The plutonic or intrusive rocks, which have been forced into
the crust and have consolidated there, present a wide range of texture
from the most coarse-grained granites to the most perfect natural
glass. Seeing that they have usually cooled with extreme slowness
underground, they are as a general rule more largely crystalline
than the volcanic series. The form assumed by each individual
body of intrusive material has depended upon the shape of the space
into which it has been injected, and where it has cooled and become
solid. This shape has been determined by the local structure of
the earth’s crust on the one hand and by the energy of the eruptive
force on the other. It offers a convenient basis for the classification
of the intrusive rocks, which, as part of the framework of the crust,
may thus be grouped according to the shape of the cavity which
received them, as bosses, sills, dikes and necks.
Bosses, or stocks, are the largest and most shapeless extravasations
of erupted material. They include the great bodies of granite which,
in most countries of the world, have risen for many miles through
the stratified formations and have altered the rocks around them
by contact-metamorphism. Sills, or intrusive sheets, are bed-like
masses which have been thrust between the planes of sedimentary
or even of igneous rocks. The term laccolite has been applied to
sills which are connected with bosses. Intrusive sheets are distinguishable
from true contemporaneously intercalated lavas by not
keeping always to the same platform, but breaking across and
altering the contiguous strata, and by the closeness of their texture
where they come in contact with the contiguous rocks, which, being
cold, chilled the molten material and caused it to consolidate on its
outer margins more rapidly than in its interior. Dikes or veins
are vertical walls or ramifying branches of intrusive material which
has consolidated in fissures or irregular clefts of the crust. Necks
are volcanic chimneys which have been filled up with erupted
material, and have now been exposed at the surface after prolonged
denudation has removed not only the superficial volcanic masses
originally associated with them, but also more or less of the upper
part of the vents. Plutonic rocks do not present evidence of their
precise geological age. All that can be certainly affirmed from
them is that they must be younger than the rocks into which they
have been intruded. From their internal structure, however, and
from the evidence of the rocks associated with them, some more or
less definite conjectures may be made as to the limits of time within
which they were probably injected.
2. The interstratified or volcanic series is of special importance
in geology, inasmuch as it contains the records of volcanic action
during the past history of the globe. It was pointed out in Part I.
that while towards the end of the 18th and in the beginning of the
19th century much attention was paid by Hutton and his followers
to the proofs of intrusion afforded by what they called the “unerupted
lavas” within the earth’s crust, these observers lost sight
of the possibility that some of these rocks might have been erupted
at the surface, and might thus be chronicles of volcanic action in
former geological periods. It is not always possible to satisfactorily
discriminate between the two types of contemporaneously intercalated
and subsequently injected material. But rocks of the
former type have not broken into or involved the overlying strata,
and they are usually marked by the characteristic structures of
superficial lavas and by their association with volcanic tuffs. By
665
means of the evidence which they supply, it has been ascertained
that volcanic action has been manifested in the globe since the
earliest geological periods. In the British Isles, for example, the
volcanic record is remarkably full for the long series of ages from
Cambrian to Permian time, and again for the older Tertiary period.
2. Subsequently induced Structures
After their accumulation, whether as stratified or eruptive
masses, all kinds of rocks have been subject to various changes,
and have acquired in consequence a variety of superinduced
structures. It has been pointed out in the part of this article
dealing with dynamical geology that one of the most important
forms of energy in the evolution of geological processes is to be
found in the movements that take place within the crust of the
earth. Some of these movements are so slight as to be only
recognizable by means of delicate instruments; but from this
inferior limit they range up to gigantic convulsions by which
mountain-chains are upheaved. The crust must be regarded as
in a perpetual state of strain, and its component materials are
therefore subject to all the effects which flow from that condition.
It is the one great object of the geotectonic division of geology to
study the structures which have been developed in consequence
of earth-movements, and to discover from this investigation the
nature of the processes whereby the rocks of the crust have been
brought into the condition and the positions in which we now
find them. The details of this subject will be found in separate
articles descriptive of each of the technical terms applied to the
several kinds of superinduced structures. All that need be
offered here is a general outline connecting the several portions
of the subject together.
One of the most universal of these later structures is to be seen
in the divisional planes, usually vertical or highly inclined, by which
rocks are split into quadrangular or irregularly shaped blocks.
To these planes the name of joints has been given. They are of
prime importance from an industrial point of view, seeing that the
art of quarrying consists mainly in detecting and making proper
use of them. Their abundance in all kinds of rocks, from those of
recent date up to those of the highest antiquity, affords a remarkable
testimony to the strains which the terrestrial crust has suffered.
They have arisen sometimes from tension, such as that caused by
contraction from the drying and consolidation of an aqueous sediment
or from the cooling of a molten mass; sometimes from torsion
during movements of the crust.
Although the stratified rocks were originally deposited in a more
or less nearly horizontal position on the floor of the sea, where now
visible on the dry land they are seldom found to have retained their
flatness. On the contrary, they are seen to have been generally
tilted up at various angles, sometimes even placed on end (crop,
dip, strike). When a sufficiently large area of ground is examined,
the inclination into which the strata have been thrown may be
observed not to continue far in the same direction, but to turn over
to the opposite or another quarter. It can then be seen that in
reality the rocks have been thrown into undulations. From the
lowest and flattest arches where the departure from horizontality
may be only trifling, every step may be followed up to intense
curvature, where the strata have been compressed and plicated as
if they had been piles of soft carpets (anticline, syncline, monocline,
geo-anticline, geo-syncline, isoclinal, plication, curvature, quaquaversal).
It has further happened abundantly all over the surface of
the globe that relief from internal strain in the crust has been obtained
by fracture, and the consequent subsidence or elevation of one or
both sides of the fissure. The differential movement between the
two sides may be scarcely perceptible in the feeblest dislocation,
but in the extreme cases it may amount to many thousand feet
(fault, fissure, dislocation, hade, slickensides). The great faults in a
country are among its most important structural features, and as
they not infrequently continue to be lines of weakness in the crust
along which sudden slipping may from time to time take place, they
become the lines of origin of earthquakes. The San Francisco
earthquake of 1906, already cited, affords a memorable illustration
of this connexion.
It is in a great mountain-chain that the extraordinary complication
of plicated and faulted structures in the crust of the earth can
be most impressively beheld. The combination of overturned folds
with rupture has been already referred to as a characteristic feature
in the Alps (Part IV.). The gigantic folds have in many places been
pushed over each other so as to lie almost flat, while the upper limb
has not infrequently been driven for many miles beyond the lower
by a rupture along the axis. In this way successive slices of a thick
series of formations have been carried northwards on the northern
slope of the Alps, and have been piled so abnormally above each
other that some of their oldest members recur several times on
different thrust-planes, the whole being underlain by Tertiary
strata (see Alps). Further proof of the colossal compression to
which the rocks have been subjected is afforded by their intense
crumpling and corrugation, and by the abundantly faulted and
crushed condition to which they have been reduced. Similar
evidence as to stresses in the terrestrial crust and the important
changes which they produce among the rocks may also be obtained
on a smaller scale in many non-mountainous countries.
Another marked result of the compression of the terrestrial crust
has been induced in some rocks by the production of the fissile
structure which is typically shown in roofing-slate (cleavage).
Closely connected with this internal rearrangement has been the
development of microscopic microlites or crystals (rutile, mica, &c.)
in argillaceous slates which were undoubtedly originally fine marine
mud and silt. From this incipient form of metamorphism successive
stages may be traced through the various kinds of argillite and
phyllite into mica-schist, and thence into more crystalline gneissoid
varieties (foliation, slate, mica-schist, gneiss). The Alps afford
excellent illustrations of these transformations.
The fissures produced in the crust are sometimes clean, sharply
defined divisional planes, like cracks across a pane of glass. Much
more usually, however, the rocks on either side have been broken up
by the friction of movement, and the fault is marked by a variable
breadth of this broken material. Sometimes the walls have separated
and molten rock has risen from below and solidified between them
as a dike. Occasionally the fissures have opened to the surface,
and have been filled in from above with detritus, as in the sandstone-dikes
of Colorado and California. In mineral districts the fissures
have been filled with various spars and ores, forming what are known
as mineral veins.
Where one series of rocks is covered by another without any
break or discordance in the stratification they are said to be conformable.
But where the older series has been tilted up or visibly
denuded before being overlain by the younger, the latter is termed
unconformable. This relation is one of the greatest value in
structural geology, for it marks a gap in the geological record, which
may represent a vast lapse of time not there recorded by strata.
Part VI.—Paleontological Geology
This division of the science deals with fossils, or the traces
of plants and animals preserved in the rocks of the earth’s crust,
and endeavours to gather from them information as to the history
of the globe and its inhabitants. The term “fossil” (Lat.
fossilis, from fodere, to dig up), meaning literally anything
“dug up,” was formerly applied indiscriminately to any mineral
substance taken out of the earth’s crust, whether organized or
not. Since the time of Lamarck, however, the meaning of the
word has been restricted, so as to include only the remains or
traces of plants and animals preserved in any natural formation
whether hard rock or superficial deposit. It includes not merely
the petrified structures of organisms, but whatever was directly
connected with or produced by these organisms. Thus the
resin which was exuded from trees of long-perished forests
is as much a fossil as any portion of the stem, leaves, flowers
or fruit, and in some respects is even more valuable to the
geologist than more determinable remains of its parent trees,
because it has often preserved in admirable perfection the insects
which flitted about in the woodlands. The burrows and trails
of a worm preserved in sandstone and shale claim recognition as
fossils, and indeed are commonly the only indications to be met
with of the existence of annelid life among old geological formations.
The droppings of fishes and reptiles, called coprolites,
are excellent fossils, and tell their tale as to the presence and
food of vertebrate life in ancient waters. The little agglutinated
cases of the caddis-worm remain as fossils in formations from
which, perchance, most other traces of life may have passed
away. Nay, the very handiwork of man, when preserved in
any natural manner, is entitled to rank among fossils; as
where his flint-implements have been dropped into the pre-historic
gravels of river-valleys or where his canoes have been
buried in the silt of lake-bottoms.
A study of the land-surfaces and sea-floors of the present time
shows that there are so many chances against the conservation
of the remains of either terrestrial or marine animals and plants
that if, as is probable, the same conditions existed in former geological
periods, we should regard the occurrence of organic remains among
the stratified formations of the earth’s crust as generally the result
of various fortunate accidents.
Let us consider, in the first place, the chances for the preservation
of remains of the present fauna and flora of a country. The surface
of the land may be densely clothed with forest and abundantly
peopled with animal life. But the trees die and moulder into soil.
666
The animals, too, disappear, generation after generation, and leave
few or no perceptible traces of their existence. If we were not aware
from authentic records that central and northern Europe were
covered with vast forests at the beginning of our era, how could we
know this fact? What has become of the herds of wild oxen, the
bears, wolves and other denizens of primeval Europe? How could
we prove from the examination of the surface soil of any country
that those creatures had once abounded there? The conditions for
the preservation of any relics of the plant and animal life of a terrestrial
surface must obviously be always exceptional. They are
supplied only where the organic remains can be protected from the
air and superficial decay. Hence they may be observed in (1) the
deposits on the floors of lakes; (2) in peat-mosses; (3) in deltas at
river-mouths; and (4) under the stalagmite of caverns in limestone
districts. But in these and other favourable places a mere infinitesimal
fraction of the fauna or flora of a land-surface is likely to be
entombed or preserved.
In the second place, although in the sea the conditions for the
preservation of organic remains are in many respects more favourable
than on land, they are apt to be frustrated by many adverse circumstances.
While the level of the land remains stationary, there can
be but little effective entombment of marine organisms in littoral
deposits; for only a limited accumulation of sediment will be formed
until subsidence of the sea-floor takes place. In the trifling beds of
sand or gravel thrown up on a stationary shore, only the harder and
more durable forms of life, such as gastropods and lamellibranchs,
which can withstand the triturating effects of the beach waves, are
likely to remain uneffaced.
Below tide-marks, along the margin of the land where sediment
is gradually deposited, the conditions are more favourable for the
preservation of marine organisms. In the sheets of sand and mud
there laid down the harder parts of many forms of life may be
entombed and protected from decay. But only a small proportion
of the total marine fauna may be expected to appear in such deposits.
At the best, merely littoral and shallow-water forms will occur, and,
even under the most favourable conditions, they will represent but
a fraction of the whole assemblage of life in these juxta-terrestrial
parts of the ocean. As we recede from the land the rate of deposition
of sediment on the sea-floor must become feebler, until, in the remote
central abysses, it reaches a hardly appreciable minimum. Except,
therefore, where some kind of ooze or other deposit is accumulating
in these more pelagic regions, the conditions must be on the whole
unfavourable for the preservation of any adequate representation
of the deep-sea fauna. Hard durable objects, such as teeth and
bones, may slowly accumulate, and be protected by a coating of
peroxide of manganese, or of some of the silicates now forming here
and there over the deep-sea bottom; or the rate of growth of the
abysmal deposit may be so tardy that most of the remains of at
least the larger animals will disappear, owing to decay, before they
can be covered up and preserved. Any such deep-sea formation,
if raised into land, would supply but a meagre picture of the whole
life of the sea.
It would thus appear that the portion of the sea-floor best suited
for receiving and preserving the most varied assemblage of marine
organic remains is the area in front of the land, to which rivers and
currents bring continual supplies of sediment. The most favourable
conditions for the accumulation of a thick mass of marine fossiliferous
strata will arise when the area of deposit is undergoing a gradual
subsidence. If the rate of depression and that of deposit were equal,
or nearly so, the movement might proceed for a vast period without
producing any great apparent change in marine geography, and even
without seriously affecting the distribution of life over the sea-floor
within the area of subsidence. Hundreds or thousands of feet of
sedimentary strata might in this way be heaped up round the continents,
containing a fragmentary series of organic remains belonging
to those forms of comparatively shallow-water life which had hard
parts capable of preservation. There can be little doubt that such
has, in fact, been the history of the main mass of stratified formations
in the earth’s crust. By far the largest proportion of these piles
of marine strata has unquestionably been laid down in water of no
great depth within the area of deposit of terrestrial sediment.
The enormous thickness to which they attain seems only explicable
by prolonged and repeated movements of subsidence, interrupted,
however, as we know, by other movements of a contrary kind.
Since the conditions for the preservation of organic remains exist
more favourably under the sea than on land, marine organisms must
be far more abundantly conserved than those of the land. This is
true to-day, and has, as far as known, been true in all past geological
time. Hence for the purposes of the geologist the fossil remains of
marine forms of life far surpass all others in value. Among them
there will necessarily be a gradation of importance, regulated chiefly
by their relative abundance. Now, of all the marine tribes which
live within the juxta-terrestrial belt of sedimentation, unquestionably
the Mollusca stand in the place of pre-eminence as regards their
aptitude for becoming fossils. They almost all possess a hard, durable
shell, capable of resisting considerable abrasion and readily passing
into a mineralized condition. They are extremely abundant both as
to individuals and genera. They occur on the shore within tide
mark, and range thence down into the abysses. Moreover, they
appear to have possessed these qualifications from early geological
times. In the marine Mollusca, therefore, we have a common ground
of comparison between the stratified formations of different periods.
They have been styled the alphabet of palaeontological inquiry.
There are two main purposes to which fossils may be put in
geological research: (1) to throw light upon former conditions
of physical geography, such as the presence of land, rivers,
lakes and seas, in places where they do not now exist, changes
of climate, and the former distribution of plants and animals;
and (2) to furnish a guide in geological chronology whereby
rocks may be classified according to relative date, and the facts
of geological history may be arranged and interpreted as a
connected record of the earth’s progress.
1. As examples of the first of these two directions of inquiry
reference may be made to (a) former land-surfaces revealed by the
occurrence of layers of soil with tree-stumps and roots still in the
position of growth (see Purbeckian); (b) ancient lakes proved by
beds of marl or limestone full of lacustrine shells; (c) old sea-bottoms
marked by the occurrence of marine organisms; (d) variations in
the quality of the water, such as freshness or saltness, indicated by
changes in the size and shape of the fossils; (e) proximity to former
land, suggested by the occurrence of abundant drift-wood in the
strata; (f) former conditions of climate, different from the present,
as evidenced by such organisms as tropical types of plants and
animals intercalated among the strata of temperate or northern
countries.
2. In applying fossils to the determination of geological chronology
it is first necessary to ascertain the order of superposition of the
rocks. Obviously, in a continuous series of undisturbed sedimentary
deposits the lowest must necessarily be the oldest, and the plants or
animals which they contain must have lived and died before any of
the organisms that occur in the overlying strata. This order of
superposition having been settled in a series of formations, it is
found that the fossils at the bottom are not quite the same as those
at the top of the series. Tracing the beds upward, we discover that
species after species of the lowest platforms disappears, until perhaps
not one of them is found. With the cessation of these older species
others make their entrance. These, in turn, are found to die out,
and to be replaced by newer forms. After patient examination of
the rocks, it has been ascertained that every well-marked “formation,”
or group of strata, is characterized by its own species or
genera, or by a general assemblage, or facies, of organic forms.
Such a generalization can only, of course, be determined by actual
practical experience over an area of some size. When the typical
fossils of a formation are known, they serve to identify that formation
in its progress across a country. Thus, in tracts where the true
order of superposition cannot be determined, owing to the want of
sections or to the disturbed condition of the rocks, fossils serve as a
means of identification and furnish a guide to the succession of the
rocks. They even demonstrate that in some mountainous ground
the beds have been turned completely upside down, where it
can be shown that the fossils in what are now the uppermost
strata ought properly to lie underneath those in the beds below
them.
It is by their characteristic fossils that the stratified rocks of the
earth’s crust can be most satisfactorily subdivided into convenient
groups of strata and classed in chronological order. Each “formation”
is distinguished by its own peculiar assemblage of organic
remains, by means of which it can be followed and recognized, even
amid the crumplings and dislocations of a disturbed region. The
same general succession of organic types can be observed over a
large part of the world, though, of course, with important modifications
in different countries. This similarity of succession has been
termed homotaxis, a term which expresses the fact that the order
in which the leading types of organized existence have appeared
upon the earth has been similar even in widely separated regions.
It is evident that, in this way, a reliable method of comparison
is furnished, whereby the stratified formations of different parts of
the earth’s crust can be brought into relation with each other.
Had the geologist continued to remain, as in the days of Werner,
hampered by the limitations imposed by a reliance on mere lithological
characters, he would have made little or no progress in
deciphering the record of the successive phases of the history of
the globe chronicled in the crust. Just as, at the present time,
sheets of gravel in one place are contemporaneous with sheets of
mud at another, so in the past all kinds of sedimentation have been
in progress simultaneously, and those of one period may not be
distinguishable in themselves from those of another. Little or no
reliance can be placed upon lithological resemblances or differences
in comparing the sedimentary formations of different countries.
In making use of fossil evidence for the purpose of subdividing
the stratified rocks of the earth’s crust, it is found to be applicable
to the smaller details of stratigraphy as well as to the definition of
large groups of strata. Thus a particular stratum may be marked
by the occurrence in it of various fossils, one or more of which may
be distinctive, either from occurring in no other bed above and
below or from special abundance in that stratum. One or more of
these species is therefore used as a guide to the occurrence of the bed
667
in question, which is called by the name of the most abundant
species. In this way what is called a “geological horizon,” or
“zone,” is marked off, and its exact position in the series of formations
is fixed.
Perhaps the most distinctive feature in the progress of palaeontological
geology during the last half century has been the recognition
and wide application of this method of zonal stratigraphy, which,
in itself, was only a further development of William Smith’s famous
idea, “Strata identified by Organized Fossils.” It was first carried
out in detail by various palaeontologists in reference to the Jurassic
formations, notably by F.A. von Quenstedt and C.A. Oppel in
Germany and A.D. d’Orbigny in France. The publication of
Oppel’s classic work Die Juraformation Englands, Frankreichs und
des südwestlichen Deutschlands (1856-1858) marked an epoch in the
development of stratigraphical geology. Combining what had been
done by various observers with his own laborious researches in
France, England, Württemberg and Bavaria, he drew up a classification
of the Jurassic system, grouping its several formations into zones,
each characterized by some distinctly predominant fossil after which
it was named (see Lias). The same method of classification was
afterwards extended to the Cretaceous series by A.D. d’Orbigny,
E. Hébert and others, until the whole Mesozoic rocks from the
Trias to the top of the Chalk has now been partitioned into zones,
each named after some characteristic species or genus of fossils.
More recently the principle has been extended to the Palaeozoic
formations, though as yet less fully than to the younger parts of the
geological record. It has been successfully applied by Professor C.
Lapworth to the investigation of the Silurian series (see Silurian;
Ordovician System). He found that the species of graptolites
have each a comparatively narrow vertical range, and they may
consequently be used for stratigraphical purposes. Applying the
method, in the first instance, to the highly plicated Silurian rocks of
the south of Scotland, he found that by means of graptolites he was
able to work out the structure of the ground. Each great group of
strata was seen to possess its own graptolitic zones, and by their
means could be identified not only in the original complex Scottish
area, but in England and Wales and in Ireland. It was eventually
ascertained that the succession of zones in Great Britain could be
recognized on the Continent, in North America and even in Australia.
The brachiopods and trilobites have likewise been made use of for
zonal purposes among the oldest sedimentary formations. The
most ancient of the Palaeozoic systems has as its fitting base the
Olenellus zone.
Within undefined and no doubt variable geographical limits
palaeontological zones have been found to be remarkably persistent.
They follow each other in the same general order, but not always
with equal definiteness. The type fossil may appear in some districts
on a higher or a lower platform than it does in others. Only to a
limited degree is there any coincidence between lithological variations
in the strata and the sequence of the zones. In the Jurassic formations,
indeed, where frequent alternations of different sedimentary
materials are to be met with, it is in some cases possible to trace a
definite upward or downward limit for a zone by some abrupt
change in the sedimentation, such as from limestone to shale. But
such a precise demarcation is impossible where no distinct bands of
different sediments are to be seen. The zones can then only be
vaguely determined by finding their characteristic fossils, and noting
where these begin to appear in the strata and where they cease.
It would seem, therefore, that the sequence of palaeontological
zones, or life-horizons, has not depended merely upon changes in
the nature of the conditions under which the organisms lived. We
should naturally expect that these changes would have had a marked
influence; that, for instance, a difference should be perceptible
between the character of the fossils in a limestone and that of those
in a shale or a sandstone. The environment, when a limestone was
in course of deposition, would generally be one of clear water,
favourable for a more vigorous and more varied fauna than where
a shale series was accumulating, when the water would be discoloured,
and only such animals would continue to live in it, or on
the bottom, as could maintain themselves in the midst of mud.
But no such lithological reason, betokening geographical changes
that would affect living creatures, can be adduced as a universally
applicable explanation of the occurrence and limitation of palaeontological
zones. One of these zones may be only a few inches, or
feet or yards in vertical extent, and no obvious lithological or other
cause can be seen why its specially characteristic fossils should
not be found just as frequently in the similar strata above and
below. There is often little or no evidence of any serious change
in the conditions of sedimentation, still less of any widespread
physical disturbance, such as the catastrophes by which the
older geologists explained the extinction of successive types of
life.
It has been suggested that, where the life-zones are well defined,
sedimentation has been extremely slow, and that though these zones
follow each other with no break in the sedimentation, they were
really separated by prolonged intervals of time during which organic
evolution could come effectively into play. But it is not easy to
explain how, for example in the Lower Lias, there could have been
a succession of prodigious intervals, when practically no sediment
was laid down, and yet that the strata should show no sign of contemporaneous
disturbance or denudation, but succeed each other
as if they had been accumulated by one continuous process of
deposit. It must be admitted that the problem of life-zones in
stratigraphical geology has not yet been solved.
As Darwin first cogently showed, the history of life has been very
imperfectly registered in the stratified parts of the earth’s crust.
Apart from the fact that, even under the most favourable conditions,
only a small proportion of the total flora and fauna of any period
would be preserved in the fossil state, enormous gaps occur where
no record has survived at all. It is as if whole chapters and books
were missing from a historical work. Some of these lacunae are
sufficiently obvious. Thus, in some cases, powerful dislocations have
thrown considerable portions of the rocks out of sight. Sometimes
extensive metamorphism has so affected them that their original
characters, including their organic contents, have been destroyed.
Oftenest of all, denudation has come into play, and vast masses of
fossiliferous rock have been entirely worn away, as is demonstrated
by the abundant unconformabilities in the structure of the earth’s
crust.
While the mere fact that one series of rocks lies unconformably
on another proves the lapse of a considerable interval between their
respective dates, the relative length of this interval may sometimes
be proved by means of fossil evidence, and by this alone. Let us
suppose, for example, that a certain group of formations has been
disturbed, upraised, denuded and covered unconformably by a
second group. In lithological characters the two may closely resemble
each other, and there may be nothing to show that the gap represented
by their unconformability is of an important character. In
many cases, indeed, it would be quite impossible to pronounce any
well-grounded judgment as to the amount of interval, even measured
by the vague relative standards of geological chronology. But if
each group contains a well-preserved suite of organic remains, it
may not only be possible, but easy, to say exactly how much of the
geological record has been left out between the two sets of formations.
By comparing the fossils with those obtained from regions where the
geological record is more complete, it may be ascertained, perhaps,
that the lower rocks belong to a certain platform or stage in geological
history which for our present purpose we may call D, and that the
upper rocks can in like manner be paralleled with stage H. It would
be then apparent that at this locality the chronicles of three great
geological periods E, F, and G were wanting, which are elsewhere
found to be intercalated between D and H. The lapse of time represented
by this unconformability would thus be equivalent to that
required for the accumulation of the three missing formations in
those regions where sedimentation was more continuous.
Fossil evidence may be made to prove the existence of gaps which
are not otherwise apparent. As has been already remarked, changes
in organic forms must, on the whole, have been extremely slow in
the geological past. The whole species of a sea-floor could not pass
entirely away, and be replaced by other forms, without the lapse
of long periods of time. If then among the conformable stratified
formations of former ages we encounter sudden and abrupt changes
in the facies of the fossils, we may be certain that these must mark
omissions in the record, which we may hope to fill in from a more
perfect series elsewhere. The complete biological contrasts between
the fossil contents of unconformable strata are sufficiently explicable.
It is not so easy to give a satisfactory account of those which occur
where the beds are strictly conformable, and where no evidence can
be observed of any considerable change of physical conditions at the
time of deposit. A group of strata having the same general lithological
characters throughout may be marked by a great discrepance
between the fossils above and below a certain line. A few species
may pass from the one into the other, or perhaps every species may
be different. In cases of this kind, when proved to be not merely
local but persistent over wide areas, we must admit, notwithstanding
the apparently undisturbed and continuous character of the original
deposition of the strata, that the abrupt transition from the one facies
of fossils to the other represents a long interval of time which has not
been recorded by the deposit of strata. A.C. Ramsay, who called
attention to these gaps, termed them “breaks in the succession of
organic remains.” He showed that they occur abundantly among
the Palaeozoic and Secondary rocks of England. It is obvious, of
course, that such breaks, even though traceable over wide regions,
were not general over the whole globe. There have never been any
universal interruptions in the continuity of the chain of being,
so far as geological evidence can show. But the physical changes
which caused the breaks may have been general over a zoological
district or minor region. They no doubt often caused the complete
extinction of genera and species which had a small geographical
range.
From all these facts it is clear that the geological record, as it now
exists, is at the best but an imperfect chronicle of geological history.
In no country is it complete. The lacunae of one region must be
supplied from another. Yet in proportion to the geographical
distance between the localities where the gaps occur and those
whence the missing intervals are supplied, the element of uncertainty
in our reading of the record is increased. The most desirable
method of research is to exhaust the evidence for each area or
province, and to compare the general order of its succession as a
whole with that which can be established for other provinces.
668
Part VII.—Stratigraphical Geology
This branch of the science arranges the rocks of the earth’s
crust in the order of their appearance, and interprets the sequence
of events of which they form the records. Its province is to
cull from the other departments of geology the facts which may
be needed to show what has been the progress of our planet,
and of each continent and country, from the earliest times of
which the rocks have preserved any memorial. Thus from
mineralogy and petrography it contains information regarding
the origin and subsequent mutations of minerals and rocks.
From dynamical geology it learns by what agencies the materials
of the earth’s crust have been formed, altered, broken, upheaved
and melted. From geotectonic geology it understands the
various processes whereby these materials were put together
so as to build up the complicated crust of the earth. From
palaeontological geology it receives in well-determined fossil
remains a clue by which to discriminate the different stratified
formations, and to trace the grand onward march of organized
existence upon this planet. Stratigraphical geology thus
gathers up the sum of all that is made known by the other
departments of the science, and makes it subservient to the
interpretation of the geological history of the earth.
The leading principles of stratigraphy may be summed up
as follows:
1. In every stratigraphical research the fundamental requisite
is to establish the order of superposition of the strata. Until
this is accomplished it is impossible to arrange the dates, and
make out the sequence of geological history.
2. The stratified portion of the earth’s crust, or what has been
called the “geological record,” can be subdivided into natural
groups, or series of strata, characterized by distinctive organic
remains and recognizable by these remains, in spite of great
changes in lithological character from place to place. A bed,
or a number of beds, linked together by containing one or more
distinctive species or genera of fossils is termed a zone or horizon,
and usually bears the name of one of its more characteristic
fossils, as the Planorbis-zone of the Lower Lias, which is so
called from the prevalence in it of the ammonite Psiloceras
planorbis. Two or more such zones related to each other by the
possession of a number of the same characteristic species or
genera have been designated beds or an assise. Two or more
sets of beds or assises similarly related form a group or stage; a
number of groups or stages make a series, formation or section,
and a succession of formations may be united into a system.
3. Some living species of plants and animals can be traced
downwards through the more recent geological formations;
but the number which can be so followed grows smaller as the
examination is pursued into more ancient deposits. With their
disappearance other species or genera present themselves which
are no longer living. These in turn may be traced backward into
earlier formations, till they too cease and their places are taken by
yet older forms. It is thus shown that the stratified rocks contain
the records of a gradual progression of organic forms. A species
which has once died out does not seem ever to have reappeared.
4. When the order of succession of organic remains among the
stratified rocks has been determined, they become an invaluable
guide in the investigation of the relative age of rocks and the
structure of the land. Each zone and formation, being characterized
by its own species or genera, may be recognized by their
means, and the true succession of strata may thus be confidently
established even in a country wherein the rocks have been
shattered by dislocation, folded, inverted or metamorphosed.
5. Though local differences exist in regard to the precise zone
in which a given species of organism may make its first appearance,
the general order of succession of the organic forms found in the
rocks is never inverted. The record is nowhere complete in any
region, but the portions represented, even though extremely
imperfect, always follow each other in their proper chronological
order, unless where disturbance of the crust has intervened to
destroy the original sequence.
6. The relative chronological value of the divisions of the
geological record is not to be measured by mere depth of strata.
While it may be reasonably assumed that, in general, a great
thickness of stratified rock must mark the passage of a long
period of time, it cannot safely be affirmed that a much less
thickness elsewhere must represent a correspondingly diminished
period. The need for this caution may sometimes be made
evident by an unconformability between two sets of rocks, as
has already been explained. The total depth of both groups
together may be, say 1000 ft. Elsewhere we may find a single
unbroken formation reaching a depth of 10,000 ft.; but it would
be unwarrantable to assume that the latter represents ten times
the length of time indicated by the former two. So far from
this being the case, it might not be difficult to show that the
minor thickness of rock really denotes by far the longer geological
interval. If, for instance, it could be proved that the upper
part of both the sections lies on one and the same geological
platform, but that the lower unconformable series in the one
locality belongs to a far lower and older system of rocks than the
base of the thick conformable series in the other, then it would
be clear that the gap marked by the unconformability really
indicates a longer period than the massive succession of deposits.
7. Fossil evidence furnishes the chief means of comparing the
relative value of formations and groups of rock. A “break in
the succession of organic remains,” as already explained, marks
an interval of time often unrepresented by strata at the place
where the break is found. The relative importance of these
breaks, and therefore, probably, the comparative intervals
of time which they mark, may be estimated by the difference
of the facies or general character of the fossils on each side.
If, for example, in one case we find every species to be dissimilar
above and below a certain horizon, while in another locality only
half of the species on each side are peculiar, we naturally infer,
if the total number of species seems large enough to warrant
the inference, that the interval marked by the former break
was much longer than that marked by the second. But we may
go further and compare by means of fossil evidence the relation
between breaks in the succession of organic remains and the
depth of strata between them.
Three formations of fossiliferous strata, A, C, and H, may occur
conformably above each other. By a comparison of the fossil
contents of all parts of A, it may be ascertained that, while some
species are peculiar to its lower, others to its higher portions, yet the
majority extend throughout the formation. If now it is found that
of the total number of species in the upper portion of A only one-third
passes up into C, it may be inferred with some plausibility that the
time represented by the break between A and C was really longer
than that required for the accumulation of the whole of the formation
A. It might even be possible to discover elsewhere a thick intermediate
formation B filling up the gap between A and C. In like
manner were it to be discovered that, while the whole of the formation
C is characterized by a common suite of fossils, not one of the species
and only one half of the genera pass up into H, the inference could
hardly be resisted that the gap between the two formations marks
the passage of a far longer interval than was needed for the deposition
of the whole of C. And thus we reach the remarkable conclusion
that, thick though the stratified formations of a country may be,
in some cases they may not represent so long a total period of time
as do the gaps in their succession,—in other words, that non-deposition
was more frequent and prolonged than deposition, or that the
intervals of time which have been recorded by strata have not been
so long as those which have not been so recorded.
In all speculations of this nature, however, it is necessary
to reason from as wide a basis of observation as possible, seeing
that so much of the evidence is negative. Especially needful
is it to bear in mind that the cessation of one or more species
at a certain line among the rocks of a particular district may
mean nothing more than that, onward from the time marked
by that line, these species, owing to some change in the conditions
of life, were compelled to migrate or became locally extinct or,
from some alteration in the conditions of fossilization, were no
longer imbedded and preserved as fossils. They may have
continued to flourish abundantly in neighbouring districts for
a long period afterward. Many examples of this obvious
truth might be cited. Thus in a great succession of mingled
marine, brackish-water and terrestrial strata, like that of the
Carboniferous Limestone series of Scotland, corals, crinoids
669
and brachiopods abound in the limestones and accompanying
shales, but disappear as the sandstones, ironstones, clays, coals
and bituminous shales supervene. An observer meeting for the
first time with an instance of this disappearance, and remembering
what he had read about breaks in succession, might be
tempted to speculate about the extinction of these organisms,
and their replacement by other and later forms of life, such as
the ferns, lycopods, estuarine or fresh-water shells, ganoid
fishes and other fossils so abundant in the overlying strata.
But further research would show him that high above the plant-bearing
sandstones and coals other limestones and shales might
be observed, once more charged with the same marine fossils
as before, and still farther overlying groups of sandstones, coals
and carbonaceous beds followed by yet higher marine limestones.
He would thus learn that the same organisms, after being
locally exterminated, returned again and again to the same
area. After such a lesson he would probably pause before too
confidently asserting that the highest bed in which we can
detect certain fossils marks their final appearance in the history
of life. Some breaks in the succession may thus be extremely
local, one set of organisms having been driven to a different part
of the same region, while another set occupied their place until
the first was enabled to return.
8. The geological record is at the best but an imperfect
chronicle of the geological history of the earth. It abounds
in gaps, some of which have been caused by the destruction of
strata owing to metamorphism, denudation or otherwise, others
by original non-deposition, as above explained. Nevertheless
from this record alone can the progress of the earth be traced.
It contains the registers of the appearance and disappearance
of tribes of plants and animals which have from time to time
flourished on the earth. Only a small proportion of the total
number of species which have lived in past time have been thus
chronicled, yet by collecting the broken fragments of the record
an outline at least of the history of life upon the earth can be
deciphered.
It cannot be too frequently stated, nor too prominently kept
in view, that, although gaps occur in the succession of organic
remains as recorded in the rocks, they do not warrant the conclusion
that any such blank intervals ever interrupted the progress
of plant and animal life upon the globe. There is every reason
to believe that the march of life has been unbroken, onward and
upward. Geological history, therefore, if its records in the
stratified formations were perfect, ought to show a blending
and gradation of epoch with epoch. But the progress has been
constantly interrupted, now by upheaval, now by volcanic
outbursts, now by depression. These interruptions serve as
natural divisions in the chronicle, and enable the geologist to
arrange his history into periods. As the order of succession
among stratified rocks was first made out in Europe, and as many
of the gaps in that succession were found to be widespread over
the European area, the divisions which experience established
for that portion of the globe came to be regarded as typical,
and the names adopted for them were applied to the rocks of
other and far distant regions. This application has brought out
the fact that some of the most marked breaks in the European
series do not exist elsewhere, and, on the other hand, that some
portions of that series are much more complete than the corresponding
sections in other regions. Hence, while the general
similarity of succession may remain, different subdivisions and
nomenclature are required as we pass from continent to continent.
The nomenclature adopted for the subdivisions of the geological
record bears witness to the rapid growth of geology. It is a
patch-work in which no system nor language has been adhered
to, but where the influences by which the progress of the science
has been moulded may be distinctly traced. Some of the earliest
names are lithological, and remind us of the fact that mineralogy
and petrography preceded geology in the order of birth—Chalk,
Oolite, Greensand, Millstone Grit. Others are topographical,
and often recall the labours of the early geologists of England—London
Clay, Oxford Clay, Purbeck, Portland, Kimmeridge beds.
Others are taken from local English provincial names, and
remind us of the debt we owe to William Smith, by whom so
many of them were first used—Lias, Gault, Crag, Cornbrash.
Others of later date recognize an order of superposition as
already established among formations—Old Red Sandstone,
New Red Sandstone. By common consent it is admitted that
names taken from the region where a formation or group of rocks
is typically developed are best adapted for general use.
Cambrian, Silurian, Devonian, Permian, Jurassic are of this
class, and have been adopted all over the globe.
But whatever be the name chosen to designate a particular
group of strata, it soon comes to be used as a chronological or
homotaxial term, apart altogether from the stratigraphical
character of the strata to which it is applied. Thus we speak
of the Chalk or Cretaceous system, and embrace under that
term formations which may contain no chalk; and we may
describe as Silurian a series of strata utterly unlike in lithological
characters to the formations in the typical Silurian country.
In using these terms we unconsciously allow the idea of relative
date to arise prominently before us. Hence such a word as
“chalk” or “cretaceous” does not suggest so much to us the
group of strata so called as the interval of geological history
which these strata represent. We speak of the Cretaceous,
Jurassic, and Cambrian periods, and of the Cretaceous fauna,
the Jurassic flora, the Cambrian trilobites, as if these adjectives
denoted simply epochs of geological time.
The stratified formations of the earth’s crust, or geological
record, are classified into five main divisions, which in their
order of antiquity are as follows: (1) Archean or Pre-Cambrian,
called also sometimes Azoic (lifeless) or Eozoic (dawn of life);
(2) Palaeozoic (ancient life) or Primary; (3) Mesozoic (middle
life) or Secondary; (4) Cainozoic (recent life) or Tertiary;
(5) Quaternary or Post-Tertiary. These divisions are further
ranged into systems, formations, groups or stages, assises and
zones. Accounts of the various subdivisions named are given
in separate articles under their own headings. In order, however,
that the sequence of the formations and their parallelism in
Europe and North America may be presented together a stratigraphical
table is given on next page.
Part VIII.—Physiographical Geology
This department of geological inquiry investigates the origin
and history of the present topographical features of the land.
As these features must obviously be related to those of earlier
time which are recorded in the rocks of the earth’s crust, they
cannot be satisfactorily studied until at least the main outlines
of the history of these rocks have been traced. Hence physiographical
research comes appropriately after the other branches
of the science have been considered.
From the stratigraphy of the terrestrial crust we learn that
by far the largest part of the area of dry land is built up of marine
formations; and therefore that the present land is not an
aboriginal portion of the earth’s surface, but has been overspread
by the sea in which its rocks were mainly accumulated. We
further discover that this submergence of the land did not
happen once only, but again and again in past ages and in all
parts of the world. Yet although the terrestrial areas varied
much from age to age in their extent and in their distribution,
being at one time more continental, at another more insular,
there is reason to believe that these successive diminutions and
expansions have on the whole been effected within, or not far
outside, the limits of the existing continents. There is no
evidence that any portion of the present land ever lay under the
deeper parts of the ocean. The abysmal deposits of the ocean-floor
have no true representatives among the sedimentary
formations anywhere visible on the land. Nor, on the other
hand, can it be shown that any part of the existing ocean
abysses ever rose above sea-level into dry land. Hence geologists
have drawn the inference that the ocean basins have probably
been always where they now are; and that although the continental
areas have often been narrowed by submergence and by
denudation, there has probably seldom or never been a complete
disappearance of land. The fact that the sedimentary formations
of each successive geological period consist to so large an
extent of mechanically formed terrigenous detritus, affords
good evidence of the coexistence of tracts of land as well as of
extensive denudation.
670
The Geological Record or Order of Succession of the Stratified
Formations of the Earth’s Crust.
| | | Europe. | North America. |
Quaternary
or
Post-Tertiary. |
Recent,
Post-glacial
or Human. |
Historic, up to the present time.
Prehistoric, comprising deposits of the Iron, Bronze, and later Stone Ages.
Neolithic—alluvium, peat, lake-dwellings, loess, &c.
Palaeolithic—river-gravels, cave-deposits, &c. |
Similar to the European development, but with scantier traces of the presence of man. |
| Pleistocene or Glacial. |
Older Loess and valley-gravels; cave-deposits.
Strand-lines or raised beaches; youngest moraines.
Upper Boulder-clays; eskers; marine sands and clays.
Interglacial deposits.
Lower boulder-clay or Till, with striated rock-surfaces below. |
As in Europe, it is hardly possible to assign a definite chronological place to
each of the various deposits of this period, terrestrial and marine. They generally resemble the
European series. The characteristic marine, fluviatile and lacustrine terraces, which
overlie the older drifts, have been classed as the Champlain Group. |
| Cainozoic or Tertiary. |
Pliocene. |
Newer:—English Forest-Bed Group; Red and Norwich Crag; Amstelian and Scaldesian groups
of Belgium and Holland; Sicilian and Astian of France and Italy.
Older:—English Coralline Crag; Diestian of Belgium; Plaisancian of southern France and Italy. |
On the Atlantic border represented by the marine Floridian series; in the interior
by a subaerial and lacustrine series; and on the Pacific border by the thick marine series of San Francisco. |
| Miocene. |
Wanting in Britain; well developed in France, S. E. Europe and Italy; divisible
into the following groups in descending order: (1) Pontian; (2) Sarmatian; (3) Tortonian; (4) Helvetian;
(5) Langhian (Burdigalian). |
Represented in the Eastern States by a marine series (Yorktown or Chesapeake, Chipola
and Chattahoochee groups), and in the interior by the lacustrine Loup Fork (Nebraska), Deep
River, and John Day groups. |
| Oligocene. |
In Britain the “fluvio-marine series” of the Isle of Wight;
also the volcanic plateaux of Antrim and Inner Hebrides and those of the Faeroe Isles and Iceland. In
continental Europe the following subdivisions have been established in descending order:
(1) Aquitanian, (2) Stampian (Rupelian), (3) Tongrain (Sannoisian). |
On the Atlantic border no equivalents have been satisfactorily
recognised, but on the Pacific side there are marine deposits in N. W. Oregon, which
may represent this division. In the interior the equivalent is believed to be the fresh-water
White River series, including (1) Protoceras beds, (2) Oreodon beds,
and (3) Titanothervum beds. |
| Eocene. |
Barton sands and clays; Ludian series of France.
Bracklesham Beds; Lutetian (Calcaire grossier and Caillasses) of Paris basin.
London clay, Woolwich and Reading Beds; Thanet sands; Ypresian or Londinian of N. France and Belgium;
Sparnacian and Thanetian groups |
Woodstock and Aquia Creek groups of Potomac River; Vicksburg, Jackson,
Claiborne, Buhrstone, and Lignitic groups of Mississippi.
In the interior a thick series of fresh-water formations, comprising, in descending order,
the Uinta, Bridger, Wind River, Wasatch, Torrejon, and Puerco groups.
On the Pacific side the marine Tejon series of Oregon and California. |
| Mesozoic or Secondary. |
Cretaceous. Upper. |
Danian—wanting in Britain; uppermost limestone of Denmark.
Senonian—Upper Chalk with Flints of England; Aturian and Emscherian stages on the European continent.
Turonian—Middle Chalk with few flints, and comprising the Angoumian and Ligerian stages.
Cenomanian—Lower Chalk and Chalk Marl.
Albian—Upper Greensand and Gault. |
On the Atlantic border both marine strata and others containing a
terrestrial flora represent the Cretaceous series of formations.
In the interior there is also a commingling of marine with lacustrine deposits. At the top lies the
Laramie or Lignitic series with an abundant terrestrial flora, passing down into the lacustrine
and brackish-water Montana series. Of older date, the Colorado series contains an abundant
marine fauna, yet includes also some Niobrara marls and limestones are likewise of marine
origin, but the lower members of the series (Benton and Dakota) show another great representation of
fresh-water sedimentation with lignites and coals.
In California a vast succession of marine deposits (Shasta-Chico) represents the Cretaceous system;
and in western British N. America coal-seams also occur. |
| Cretaceous. Lower. |
Aptian—Lower Greensand; Marls and limestones of Provence, &c.
Urgonian (Barremian)—Atherfield clay; massive Hippurite limestones of southern France.
Neocomian—Weald clay and Hastings sand; Hauterivian and Valanginian sub-stages of
Switzerland and France. |
| |
| Jurassic. |
Purbeckian—Purbeck beds; Münder Mergel; largely present in Westphalia.
Portlandian—Portland group of England, represented in S. France by the thick Tithonian limestones.
Kimmeridgian— Kimmeridge Clay of England; Virgulian and Pterocerian groups of
N. France; represented by thick limestones in the Mediterranean basin.
Corallian—Coral Rag, Coralline Oolite; Sequanian stages of the Continent,
comprising the sub-stages of Astartian and Rauracian.
Oxfordian—Oxford Clay; Axgovian and Neuvizyan stages.
Callovian—Kellaways Rock, Divesian sub-stage of N. France.
Bathonian—series of English strata from Cornbrash down to Fuller’s Earth.
Bajocian—Inferior Oolite of England.
Lassic—divisible into (1) Upper Lias or Toarcian, (2) Middle Lias, Marlstone or Charmouthian, (3) Lower
Lias of Sinemurian and Hettangian. |
Representatives of the Middle and lower Jurassic formations have been found in
California and Oregon, and farther north among the Arctic islands.
Strata containing Lower Jurassic marine fossils appear in Wyoming and Dakota; and above them come
the Atlantosaurus and Baptanodon beds, which have yielded so large a
variety of deinosaurs and other vertebrates, and especially the remains of a number of genera
of small mammals. |
| Triassic. |
In Germany and western Europe this division represents the deposits of
inland seas or lagoons, and is divisible into the following stages in descending
order: (1) Rhaetic, (2) Keuper, (3) Muschelkalk, (4) Bunter. In the eastern Alps and the Mediterranean
basin the contemporaneous sedimentary formations are those of open clear sea, in which a thickness of many
thousand feet of strata was accumulated. |
In New York, Connecticut, New Brunswick, and Nova Scotia a series of red sandstone
(Newark series) contains land-plants and labyrinthodonts like the lagoon type of central
and western Europe. On the Pacific slope, however, marine equivalents occur, representing
the pelagic type of south-eastern Europe. |
| Palaeozoic or Primary. |
Permian. |
Thuringian—Zechstein, Magnesian Limestone; named from its development
in Thuringia; well represented also in Saxony, Bavaria and Bohemia.
Saxonian—Rothliegendes Group; Red Sandstones, &c.
Autunian—where the strata present the lagoon facies, well displayed at Autun
in France; where the marine type is predominant, as in Russia, the group has been termed Artinskian. |
To this division of the geological record the Upper Barren
Measures of the coal-fields of Pennsylvania, Prince Edward Island, Nova Scotia and
New Brunswick have been assigned.
Farther south in Kansas, Texas, and Nebraska the representatives of the division have an
abundant marine fauna. |
| Carboniferous. |
Stephanian or Uralian—represented in Russia by marine formations, and in
central and western Europe by numerous small basins containing a peculiar
flora and in some places a great variety of insects.
Westphalian or Moscovian—Coal-measures, Millstone Grit.
Culm or Dinantian—Carboniferous Limestone and Calciferous Sandstone series. |
Upper productive Coal-measures.
Lower Barren measures.
Lower productive Coal-measures.
Pottsville conglomerate.
Mauch Chunk shales; limestones of Chester, St Louis, &c.
Pocono series; Kinderhook limestone. |
| Devonian and Old Red Sandstone. |
Devonian type. |
Old Red Sandstone type. |
|
Upper
Famennian.
Frasnian. |
Yellow and red sandstone with Holoptychius,
Bothriolepis, &c. |
Catskill red sandstone; Old Red Sandstone type: the strata below show the
Devonian type.
Chemung Group.
Genesee Group. |
Middle
Givetian.
Eifelian. |
Caithness Flagstones with Osteolepus, Dipterus,
Homosteus, &c. |
Hamilton Group.
Marcellus Group. |
Lower
Coblentizian.
Gedinnian. |
Red and purple sandstones and conglomerates with Cephalaspis,
Pteraspis, |
Corniferous Limestone.
Onondaga Limestone.
Upper Helderberg Group.
Oriskany Sandstone. |
| Silurian. |
Upper
Ludlow Group.
Wenlock Group.
Llandovery Group. |
Lower Helderberg Group.
Water-Lime.
Niagara Shale and Limestone.
Clinton Group.
Medina Group. |
Lower (Ordovician)
Ludlow Group.
Wenlock Group.
Llandovery Group. |
Cincinnati Group.
Utica Group.
Trenton Group.
Chazy Group.
Calciferous Group. |
| Cambrian. |
Upper or Olenus series—Tremadoc slates and Lingula Flags.
Middle or Pardoxides series—Menevian Group.
Lower or Olenellus series—Llanberis and Harlech Group, and Olenellus-zone. |
Upper or Potsdam series with Olenus and Dicelocephalus fauna.
Middle or Acadian series with Paradoxides fauna.
Lower or Georgian series with Olenellus fauna. |
| Archean, Pre-Cambrian Eozoic. |
|
In Scotland, underneath the Cambrian Olenellus group, lies unconformably
a mass of red sandstone and conglomerate (Torridonian) 8000 or 10,000 ft. thick, which rests with a strong
gneisses and schists (Lewisian). A thick series of slates and phyllites lies below the oldest Palaeozoic rocks
in central Europe, with coarse gneisses below. |
In Canada and the Lake Superior region of the United States a vast succession of
rocks of Pre-Cambrian age has been grouped into the following subdivisions in descending order: (1) Keweenwan,
lying unconformably on (2) Animikie, separated by a strong unconformability from
(3) Upper Huronian, (4) Lower Huronian with an unconformable base, (5) Goutchiching,
(6) Laurentian. In the eastern part of Canada, Newfoundland, &c., and also in Montana,
sedimentary formations of great thickness below the lowest Cambrian zone have
been found to contain some obscure organisms. |
671
From these general considerations we proceed to inquire how
the existing topographical features of the land arose. Obviously
the co-operation of the two great geological agencies of hypogene
and epigene energy, which have been at work from the beginning
of our globe’s decipherable history, must have been the cause
to which these features are to be assigned; and the task of the
geologist is to ascertain, if possible, the part that has been taken
by each. There is a natural tendency to see in a stupendous
piece of scenery, such as a deep ravine, a range of hills, a line of
precipice or a chain of mountains, evidence only of subterranean
convulsion; and before the subject was taken up as a matter
of strict scientific induction, an appeal to former cataclysms
was considered a sufficient solution of the problems presented
by such features of landscape. The rise of the modern
Huttonian school, however, led to a more careful examination
of these problems. The important share taken by erosion in the
determination of the present features of landscape was then
recognized, while a fuller appreciation of the relative parts
played by the hypogene and epigene causes has gradually been
reached.
1. The study of the progress of denudation at the present
time has led to the conclusion that even if the rate of waste
were not more rapid than it is to-day, it would yet suffice in a
comparatively brief geological period to reduce the dry land to
below the sea-level. But not only would the area of the land be
diminished by denudation, it could hardly fail to be more or
less involved in those widespread movements of subsidence,
during which the thick sedimentary formations of the crust
appear to have been accumulated. It is thus manifest that there
must have been from time to time during the history of our
globe upward movements of the crust, whereby the balance
between land and sea was redressed. Proofs of such movements
have been abundantly preserved among the stratified formations.
We there learn that the uplifts have usually followed each other
at long intervals between which subsidence prevailed, and thus
that there has been a prolonged oscillation of the crust over the
great continental areas of the earth’s surface.
An examination of that surface leads to the recognition of two
great types of upheaval. In the one, the sea-floor, with all its
thick accumulations of sediment, has been carried upwards,
sometimes for several thousand feet, so equably that the strata
retain their original flatness with hardly any sensible disturbance
for hundreds of square miles. In the other type the solid crust
has been plicated, corrugated and dislocated, especially along
particular lines, and has attained its most stupendous disruption
in lofty chains of mountains. Between these two phases of uplift
many intermediate stages have been developed, according to
the direction and intensity of the subterranean force and the
varying nature and disposition of the rocks Of the crust.
(a) Where the uplift has extended over wide spaces, without
appreciable deformation of the crust, the flat strata have given
rise to low plains, or if the amount of uprise has been great
enough, to high plains, plateaux or tablelands. The plains of
Russia, for example, lie for the most part on such tracts of
equably uplifted strata. The great plains of the western interior
of the United States form a great plateau or tableland, 5000 or
6000 ft. above the sea, and many thousands of square miles in
extent, on which the Rocky Mountains have been ridged up.
(b) It is in a great mountain-chain that the complicated
structures developed during disturbances of the earth’s crust
can best be studied (see Parts IV. and V. of this article), and
where the influence of these structures on the topography of the
surface is most effectively displayed. Such a chain may be the
result of one colossal disturbance; but those of high geological
antiquity usually furnish proofs of successive uplifts with more
or less intervening denudation. Formed along lines of continental
displacement in the crust, they have again and again given
relief from the strain of compression by fresh crumpling, fracture
and uprise. The chief guide in tracing these successive stages
of growth is supplied by unconformability. If, for example, a
mountain-range consists of upraised Silurian rocks, upon the
upturned and denuded edges of which the Carboniferous Limestone
lies transgressively, it is clear that its original upheaval
must have taken place in the period of geological time represented
by the interval between the Silurian and the Carboniferous
Limestone formations. If, as the range is followed along its
course, the Carboniferous Limestone is found to be also highly
inclined and covered unconformably by the Upper Coal-measures,
a second uplift of that portion of the ground can be proved to
have taken place between the time of the Limestone and that of
the Upper Coal-measures. By this simple and obvious kind of
evidence the relative ages of different mountain-chains may
be compared. In most great chains, however, the rocks have
been so intensely crumpled, and even inverted, that much
labour may be required before their true relations can be determined.
The Alps furnish an instructive example of the long series of
revolutions through which a great mountain-system may have
passed before reaching its present development. The first
beginnings of the chain may have been upraised before the
oldest Palaeozoic formations were laid down. There are at
least traces of land and shore-lines in the Carboniferous period.
Subsequent submergences and uplifts appear to have occurred
during the Mesozoic periods. There is evidence that thereafter
the whole region sank deep under the sea, in which the older
Tertiary sediments were accumulated, and which seems to
have spread right across the heart of the Old World. But after
the deposition of the Eocene formations came the gigantic
disruptions whereby all the rocks of the Alpine region were
folded over each other, crushed, corrugated, fractured and
displaced, some of their older portions, including the fundamental
gneisses and schists, being squeezed up, torn off, and pushed
horizontally for many miles over the younger rocks. But this
upheaval, though the most momentous, was not the last which
the chain has undergone, for at a later epoch in Tertiary time
renewed disturbance gave rise to a further series of ruptures
and plications. The chain thus successively upheaved has
been continuously exposed to denudation and has consequently
lost much of its original height. That it has been left in a state
of instability is indicated by the frequent earthquakes of the
Alpine region, which doubtless arise from the sudden snapping
of rocks under intense strain.
A distinct type of mountain due to direct hypogene action is
to be seen in a volcano. It has been already pointed out (Part IV.
sect. 1) that at the vents which maintain a communication
between the molten magma of the earth’s interior and the
surface, eruptions take place whereby quantities of lava and
fragmentary materials are heaped round each orifice of
discharge. A typical volcanic mountain takes the form of a
perfect cone, but as it grows in size and its main vent is choked,
while the sides of the cone are unable to withstand the force of
the explosions or the pressure of the ascending column of lava,
eruptions take place laterally, and numerous parasitic cones
arise on the flanks of the parent mountain. Where lava flows
out from long fissures, it may pile up vast sheets of rock, and
bury the surrounding country under several thousand feet of
solid stone, covering many hundreds of square miles. In this
way volcanic tablelands have been formed which, attacked by
the denuding forces, are gradually trenched by valleys and
ravines, until the original level surface of the lava-field may be
almost or wholly lost. As striking examples of this physiographical
type reference may be made to the plateau of Abyssinia,
the Ghats of India, the plateaux of Antrim, the Inner Hebrides
and Iceland, and the great lava-plains of the western territories
of the United States.
2. But while the subterranean movements have upraised
portions of the surface of the lithosphere above the level of the
ocean, and have thus been instrumental in producing the existing
tracts of land, the detailed topographical features of a landscape
672
are not solely, nor in general even chiefly, attributable to these
movements. From the time that any portion of the sea-floor
appears above sea-level, it undergoes erosion by the various
epigene agents. Each climate and geological region has its own
development of these agents, which include air, aridity, rapid and
frequent alternations of wetness and dryness or of heat and
cold, rain, springs, frosts, rivers, glaciers, the sea, plant and
animal life. In a dry climate subject to great extremes of
temperature the character and rate of decay will differ from
those of a moist or an arctic climate. But it must be remembered
that, however much they may vary in activity and in the results
which they effect, the epigene forces work without intermission,
while the hypogene forces bring about the upheaval of land only
after long intervals. Hence, trifling as the results during a
human life may appear, if we realize the multiplying influence
of time we are led to perceive that the apparently feeble superficial
agents can, in the course of ages, achieve stupendous
transformations in the aspect of the land. If this efficacy may
be deduced from what can be seen to be in progress now, it
may not less convincingly be shown, from the nature of the
sedimentary rocks of the earth’s crust, to have been in progress
from the early beginnings of geological history. Side by side
with the various upheavals and subsidences, there has been a
continuous removal of materials from the land, and an equally
persistent deposit of these materials under water, with the
consequent growth of new rocks. Denudation has been aptly
compared to a process of sculpturing wherein, while each of the
implements employed by nature, like a special kind of graving
tool, produces its own characteristic impress on the land, they
all combine harmoniously towards the achievement of their
one common task. Hence the present contours of the land
depend partly on the original configuration of the ground, and
the influence it may have had in guiding the operations of the
erosive agents, partly on the vigour with which these agents
perform their work, and partly on the varying structure and
powers of resistance possessed by the rocks on which the erosion
is carried on.
Where a new tract of land has been raised out of the sea
by such an energetic movement as broke up the crust and
produced the complicated structure and tumultuous external
forms of a great mountain chain, the influence of the hypogene
forces on the topography attains its highest development.
But even the youngest existing chain has suffered so greatly
from denudation that the aspect which it presented at the time
of its uplift can only be dimly perceived. No more striking
illustration of this feature can be found than that supplied by
the Alps, nor one where the geotectonic structures have been
so fully studied in detail. On the outer flanks of these mountains
the longitudinal ridges and valleys of the Jura correspond with
lines of anticline and syncline. Yet though the dominant
topographical elements of the region have obviously been
produced by the plication of the stratified formations, each
ridge has suffered so large an amount of erosion that the younger
rocks have been removed from its crest where the older members
of the series are now exposed to view, while on every slope
proofs may be seen of extensive denudation. If from these
long wave-like undulations of the ground, where the relations
between the disposition of the rocks below and the forms of
the surface are so clearly traceable, the observer proceeds
inwards to the main chain, he finds that the plications and
displacements of the various formations assume an increasingly
complicated character; and that although proofs of great
denudation continue to abound, it becomes increasingly difficult
to form any satisfactory conjecture as to the shape of the ground
when the upheaval ended or any reliable estimate of the amount
of material which has since then been removed. Along the
central heights the mountains lift themselves towards the sky
like the storm-swept crests of vast earth-billows. The whole
aspect of the ground suggests intense commotion, and the
impression thus given is often much intensified by the twisted
and crumpled strata, visible from a long distance, on the crags
and crests. On this broken-up surface the various agents of
denudation have been ceaselessly engaged since it emerged
from the sea. They have excavated valleys, sometimes along
depressions provided for them by the subterranean disturbances,
sometimes down the slopes of the disrupted blocks of ground.
So powerful has been this erosion that valleys cut out along
lines of anticline, which were natural ridges, have sometimes
become more important than those in lines of syncline, which
were structurally depressions. The same subaerial forces have
eroded lake-basins, dug out corries or cirques, notched the
ridges, splintered the crests and furrowed the slopes, leaving
no part of the original surface of the uplifted chain
unmodified.
It has often been noted with surprise that features of
underground structure which, it might have been confidently
anticipated, should have exercised a marked influence on the
topography of the surface have not been able to resist the
levelling action of the denuding agents, and do not now affect
the surface at all. This result is conspicuously seen in coal-fields
where the strata are abundantly traversed by faults. These
dislocations, having sometimes a displacement of several hundred
feet, might have been expected to break up the surface into
a network of cliffs and plains; yet in general they do not modify
the level character of the ground above. One of the most
remarkable faults in Europe is the great thrust which bounds
the southern edge of the Belgian coal-field and brings the
Devonian rocks above the Coal-measures. It can be traced
across Belgium into the Boulonnais, and may not improbably
run beneath the Secondary and Tertiary rocks of the south of
England. It is crossed by the valleys of the Meuse and other
northerly-flowing streams. Yet so indistinctly is it marked
in the Meuse valley that no one would suspect its existence from
any peculiarity in the general form of the ground, and even an
experienced geologist, until he had learned the structure of the
district, would scarcely detect any fault at all.
Where faults have influenced the superficial topography,
it is usually by giving rise to a hollow along which the subaerial
agents and especially running water can act effectively. Such
a hollow may be eventually widened and deepened into a valley.
On bare crags and crests, lines of fault are apt to be marked by
notches or clefts, and they thus help to produce the pinnacles
and serrated outlines of these exposed uplands.
It was cogently enforced by Hutton and Playfair, and independently
by Lamarck, that no co-operation of underground
agency is needed to produce such topography as may be seen
in a great part of the world, but that if a tract of sea-floor were
upraised into a wide plain, the fall of rain and the circulation
of water over its surface would in the end carve out such a system
of hills and valleys as may be seen on the dry land now. No
such plain would be a dead-level. It would have inequalities
on its surface which would serve as channels to guide the drainage
from the first showers of rain. And these channels would be
slowly widened and deepened until they would become ravines
and valleys, while the ground between them would be left projecting
as ridges and hills. Nor would the erosion of such a system
of water-courses require a long series of geological periods for
its accomplishment. From measurements and estimates of the
amount of erosion now taking place in the basin of the Mississippi
river it has been computed that valleys 800 ft. deep might be
carved out in less than a million years. In the vast tablelands
of Colorado and other western regions of the United States an
impressive picture is presented of the results of mere subaerial
erosion on undisturbed and nearly level strata. Systems of
stream-courses and valleys, river gorges unexampled elsewhere
in the world for depth and length, vast winding lines of escarpment,
like ranges of sea-cliffs, terraced slopes rising from plateau
to plateau, huge buttresses and solitary stacks standing like
islands out of the plains, great mountain-masses towering into
picturesque peaks and pinnacles cleft by innumerable gullies,
yet everywhere marked by the parallel bars of the horizontal
strata out of which they have been carved—these are the orderly
symmetrical characteristics of a country where the scenery is
due entirely to the action of subaerial agents on the one hand and
673
the varying resistance of perfectly regular stratified rocks on the
other.
The details of the sculpture of the land have mainly depended
on the nature of the materials on which nature’s erosive tools
have been employed. The joints by which all rocks are traversed
have been especially serviceable as dominant lines down which
the rain has filtered, up which the springs have risen and into
which the frost wedges have been driven. On the high bare
scarps of a lofty mountain the inner structure of the mass is laid
open, and there the system of joints even more than faults is
seen to have determined the lines of crest, the vertical walls of
cliff and precipice, the forms of buttress and recess, the position
of cleft and chasm, the outline of spire and pinnacle. On the
lower slopes, even under the tapestry of verdure which nature
delights to hang where she can over her naked rocks, we may
detect the same pervading influence of the joints upon the forms
assumed by ravines and crags. Each kind of stone, too, gives
rise to its own characteristic form of scenery. Massive crystalline
rocks, such as granite, break up along their joints and often
decay into sand or earth along their exposed surfaces, giving
rise to rugged crags with long talus slopes at their base. The
stratified rocks besides splitting at their joints are especially
distinguished by parallel ledges, cornices and recesses, produced
by the irregular decay of their component strata, so that they
often assume curiously architectural types of scenery. But
besides this family feature they display many minor varieties of
aspect according to their lithological composition. A range of
sandstone hills, for example, presents a marked contrast to one
of limestone, and a line of chalk downs to the escarpments
formed by alternating bands of harder and softer clays and
shales.
It may suffice here merely to allude to a few of the more
important parts of the topography of the land in their relation
to physiographical geology. A true mountain-chain, viewed
from the geological side, is a mass of high ground which owes its
prominence to a ridging-up of the earth’s crust, and the intense
plication and rupture of the rocks of which it is composed. But
ranges of hills almost mountainous in their bulk may be formed
by the gradual erosion of valleys out of a mass of original high
ground, such as a high plateau or tableland. Eminences which
have been isolated by denudation from the main mass of the
formations of which they originally formed part are known as
“outliers” or “hills of circumdenudation.”
Tablelands, as already pointed out, may be produced either
by the upheaval of tracts of horizontal strata from the sea-floor
into land; or by the uprise of plains of denudation, where rocks
of various composition, structure and age have been levelled
down to near or below the level of the sea by the co-operation
of the various erosive agents. Most of the great tablelands
of the globe are platforms of little-disturbed strata which have
been upraised bodily to a considerable elevation. No sooner,
however, are they placed in that position than they are attacked
by running water, and begin to be hollowed out into systems of
valleys. As the valleys sink, the platforms between them grow
into narrower and more definite ridges, until eventually the
level tableland is converted into a complicated network of hills
and valleys, wherein, nevertheless, the key to the whole arrangement
is furnished by a knowledge of the disposition and effects
of the flow of water. The examples of this process brought to
light in Colorado, Wyoming, Nevada and the other western
regions by Newberry, King, Hayden, Powell and other explorers,
are among the most striking monuments of geological operations
in the world.
Examples of ancient and much decayed tablelands formed by
the denudation of much disturbed rocks are furnished by the
Highlands of Scotland and of Norway. Each of these tracts of
high ground consists of some of the oldest and most dislocated
formations of Europe, which at a remote period were worn down
into a plain, and in that condition may have lain long submerged
under the sea and may possibly have been overspread there
with younger formations. Having at a much later time been
raised several thousand feet above sea-level the ancient platforms
of Britain and Scandinavia have been since exposed to denudation,
whereby each of them has been so deeply channeled into
glens and fjords that it presents to-day a surface of rugged
hills, either isolated or connected along the flanks, while only
fragments of the general surface of the tableland can here and
there be recognized amidst the general destruction.
Valleys have in general been hollowed out by the greater
erosive action of running water along the channels of drainage.
Their direction has been probably determined in the great
majority of cases by irregularities of the surface along which
the drainage flowed on the first emergence of the land. Sometimes
these irregularities have been produced by folds of the
terrestrial crust, sometimes by faults, sometimes by the irregularities
on the surface of an uplifted platform of deposition or of
denudation. Two dominant trends may be observed among
them. Some are longitudinal and run along the line of flexures
in the upraised tract of land, others are transverse where the
drainage has flowed down the slopes of the ridges into the longitudinal
valleys or into the sea. The forms of valleys have been
governed partly by the structure and composition of the rocks,
and partly by the relative potency of the different denuding
agents. Where the influence of rain and frost has been slight,
and the streams, supplied from distant sources, have had
sufficient declivity, deep, narrow, precipitous ravines or gorges
have been excavated. The canyons of the arid region of the
Colorado are a magnificent example of this result. Where, on
the other hand, ordinary atmospheric action has been more
rapid, the sides of the river channels have been attacked, and
open sloping glens and valleys have been hollowed out. A
gorge or defile is usually due to the action of a waterfall, which,
beginning with some abrupt declivity or precipice in the course
of the river when it first commenced to flow, or caused by some
hard rock crossing the channel, has eaten its way backward.
Lakes have been already referred to, and their modes of origin
have been mentioned. As they are continually being filled up
with the detritus washed into them from the surrounding
regions they cannot be of any great geological antiquity, unless
where by some unknown process their basins are from time to
time widened and deepened.
In the general subaerial denudation of a country, innumerable
minor features are worked out as the structure of the rocks
controls the operations of the eroding agents. Thus, among
comparatively undisturbed strata, a hard bed resting upon
others of a softer kind is apt to form along its outcrop a line of
cliff or escarpment. Though a long range of such cliffs resembles
a coast that has been worn by the sea, it may be entirely due to
mere atmospheric waste. Again, the more resisting portions of
a rock may be seen projecting as crags or knolls. An igneous
mass will stand out as a bold hill from amidst the more decomposable
strata through which it has risen. These features,
often so marked on the lower grounds, attain their most conspicuous
development among the higher and barer parts of the
mountains, where subaerial disintegration is most rapid. The
torrents tear out deep gullies from the sides of the declivities.
Corries or cirques are scooped out on the one hand and naked
precipices are left on the other. The harder bands of rock
project as massive ribs down the slopes, shoot up into prominent
aiguilles, or help to give to the summits the notched saw-like
outlines they so often present.
The materials worn from the surface of the higher are spread
out over the lower grounds. The streams as they descend begin
to drop their freight of sediment when, by the lessening of their
declivity, their carrying power is diminished. The great plains
of the earth’s surface are due to this deposit of gravel, sand and
loam. They are thus monuments at once of the destructive and
reproductive processes which have been in progress unceasingly
since the first land rose above the sea and the first shower of rain
fell. Every pebble and particle of their soil, once part of the
distant mountains, has travelled slowly and fitfully to lower
levels. Again and again have these materials been shifted,
ever moving downward and sea-ward. For centuries, perhaps,
they have taken their share in the fertility of the plains and
674
have ministered to the nurture of flower and tree, of the bird of
the air, the beast of the field and of man himself. But their
destiny is still the great ocean. In that bourne alone can they
find undisturbed repose, and there, slowly accumulating in
massive beds, they will remain until, in the course of ages,
renewed upheaval shall raise them into future land, there once
more to pass through the same cycle of change.
(A. Ge.)
Literature.—Historical: The standard work is Karl A. von
Zittel’s Geschichte der Geologie und Paläontologie (1899), of which
there is an abbreviated, but still valuable, English translation;
D’Archiac, Histoire des progrès de la géologie, deals especially with
the period 1834-1850; Keferstein, Geschichte und Literatur der
Geognosie, gives a summary up to 1840; while Sir A. Geikie’s
Founders of Geology (1897; 2nd ed., 1906) deals more particularly
with the period 1750-1820. General treatises: Sir Charles Lyell’s
Principles of Geology is a classic. Of modern English works, Sir A.
Geikie’s Text Book of Geology (4th ed., 1903) occupies the first place;
the work of T.C. Chamberlin and R.D. Salisbury, Geology; Earth
History (3 vols., 1905-1906), is especially valuable for American
geology. A. de Lapparent’s Traité de géologie (5th ed., 1906), is the
standard French work. H. Credner’s Elemente der Geologie has gone
through several editions in Germany. Dynamical and physiographical
geology are elaborately treated by E. Suess, Das Antlitz
der Erde, translated into English, with the title The Face of the Earth.
The practical study of the science is treated of by F. von Richthofen,
Führer für Forschungsreisende (1886); G.A. Cole, Aids in Practical
Geology (5th ed., 1906); A. Geikie, Outlines of Field Geology (5th ed.,
1900). The practical applications of Geology are discussed by
J.V. Elsden, Applied Geology (1898-1899). The relations of Geology
to scenery are dealt with by Sir A. Geikie, Scenery of Scotland (3rd ed.,
1901); J.E. Marr, The Scientific Study of Scenery (1900); Lord
Avebury, The Scenery of Switzerland (1896); The Scenery of England
(1902); and J. Geikie, Earth Sculpture (1898). A detailed bibliography
is given in Sir A. Geikie’s Text Book of Geology. See also
the separate articles on geological subjects for special references to
authorities.
1 In De Luc’s Lettres physiques et morales sur les montagnes (1778),
the word “cosmology” is used for our science, the author stating
that “geology” is more appropriate, but it “was not a word in use.”
In a completed edition, published in 1779, the same statement is
made, but “geology” occurs in the text; in the same year De
Saussure used the word without any explanation, as if it were
well known.
2 The subject of the age of the earth has also been discussed by
Professor J. Joly and Professor W.J. Sollas. The former geologist,
approaching the question from a novel point of view, has estimated
the total quantity of sodium in the water of the ocean and the
quantity of that element received annually by the ocean from the
denudation of the land. Dividing the one sum by the other, he
arrives at the result that the probable age of the earth is between
90 and 100 millions of years (Trans. Roy. Dublin Soc. ser. ii. vol. vii.,
1899, p. 23: Geol. Mag., 1900, p. 220). Professor Sollas believes
that this limit exceeds what is required for the evolution of geological
history, that the lower limit assigned by Lord Kelvin falls short of
what the facts demand, and that geological time will probably be
found to have been comprised within some indeterminate period
between these limits. (Address to Section C, Brit. Assoc. Report,
1900; Age of the Earth, London, 1905.)
GEOMETRICAL CONTINUITY. In a report of the Institute
prefixed to Jean Victor Poncelet’s Traité des propriétés projectives
des figures (Paris, 1822), it is said that he employed “ce
qu’il appelle le principe de continuité.” The law or principle
thus named by him had, he tells us, been tacitly assumed as
axiomatic by “les plus savans géomètres.” It had in fact been
enunciated as “lex continuationis,” and “la loi de la continuité,”
by Gottfried Wilhelm Leibnitz (Oxf. N.E.D.), and previously
under another name by Johann Kepler in cap. iv. 4 of his Ad
Vitellionem paralipomena quibus astronomiae pars optica traditur
(Francofurti, 1604). Of sections of the cone, he says, there are
five species from the “recta linea” or line-pair to the circle.
From the line-pair we pass through an infinity of hyperbolas to
the parabola, and thence through an infinity of ellipses to the
circle. Related to the sections are certain remarkable points
which have no name. Kepler calls them foci. The circle has
one focus at the centre, an ellipse or hyperbola two foci equidistant
from the centre. The parabola has one focus within it,
and another, the “caecus focus,” which may be imagined to be
at infinity on the axis within or without the curve. The line from it
to any point of the section is parallel to the axis. To carry out
the analogy we must speak paradoxically, and say that the line-pair
likewise has foci, which in this case coalesce as in the circle
and fall upon the lines themselves; for our geometrical terms
should be subject to analogy. Kepler dearly loves analogies, his
most trusty teachers, acquainted with all the secrets of nature,
“omnium naturae arcanorum conscios.” And they are to be
especially regarded in geometry as, by the use of “however
absurd expressions,” classing extreme limiting forms with an
infinity of intermediate cases, and placing the whole essence of a
thing clearly before the eyes.
Here, then, we find formulated by Kepler the doctrine of the
concurrence of parallels at a single point at infinity and the
principle of continuity (under the name analogy) in relation to the
infinitely great. Such conceptions so strikingly propounded in
a famous work could not escape the notice of contemporary
mathematicians. Henry Briggs, in a letter to Kepler from
Merton College, Oxford, dated “10 Cal. Martiis 1625,” suggests
improvements in the Ad Vitellionem paralipomena, and gives
the following construction: Draw a line CBADC, and let an
ellipse, a parabola, and a hyperbola have B and A for focus and
vertex. Let CC be the other foci of the ellipse and the hyperbola.
Make AD equal to AB, and with centres CC and radius in each
case equal to CD describe circles. Then any point of the ellipse
is equidistant from the focus B and one circle, and any point of
the hyperbola from the focus B and the other circle. Any point
P of the parabola, in which the second focus is missing or infinitely
distant, is equidistant from the focus B and the line
through D which we call the directrix, this taking the place of
either circle when its centre C is at infinity, and every line CP
being then parallel to the axis. Thus Briggs, and we know not
how many “savans géomètres” who have left no record, had
already taken up the new doctrine in geometry in its author’s
lifetime. Six years after Kepler’s death in 1630 Girard Desargues,
“the Monge of his age,” brought out the first of his remarkable
works founded on the same principles, a short tract entitled
Méthode universelle de mettre en perspective les objets donnés
réellement ou en devis (Paris, 1636); but “Le privilége étoit de
1630.” (Poudra, Œuvres de Des., i. 55). Kepler as a modern
geometer is best known by his New Stereometry of Wine Casks
(Lincii, 1615), in which he replaces the circuitous Archimedean
method of exhaustion by a direct “royal road” of infinitesimals,
treating a vanishing arc as a straight line and regarding a curve
as made up of a succession of short chords. Some 2000 years
previously one Antipho, probably the well-known opponent of
Socrates, has regarded a circle in like manner as the limiting
form of a many-sided inscribed rectilinear figure. Antipho’s
notion was rejected by the men of his day as unsound, and when
reproduced by Kepler it was again stoutly opposed as incapable
of any sort of geometrical demonstration—not altogether without
reason, for it rested on an assumed law of continuity rather
than on palpable proof.
To complete the theory of continuity, the one thing needful
was the idea of imaginary points implied in the algebraical
geometry of René Descartes, in which equations between variables
representing co-ordinates were found often to have imaginary
roots. Newton, in his two sections on “Inventio orbium”
(Principia i. 4, 5), shows in his brief way that he is familiar with
the principles of modern geometry. In two propositions he uses
an auxiliary line which is supposed to cut the conic in X and Y,
but, as he remarks at the end of the second (prop. 24), it may not
cut it at all. For the sake of brevity he passes on at once with the
observation that the required constructions are evident from the
case in which the line cuts the trajectory. In the scholium
appended to prop. 27, after saying that an asymptote is a tangent
at infinity, he gives an unexplained general construction for the
axes of a conic, which seems to imply that it has asymptotes.
In all such cases, having equations to his loci in the background,
he may have thought of elements of the figure as passing into the
imaginary state in such manner as not to vitiate conclusions
arrived at on the hypothesis of their reality.
Roger Joseph Boscovich, a careful student of Newton’s works,
has a full and thorough discussion of geometrical continuity in
the third and last volume of his Elementa universae matheseos
(ed. prim. Venet, 1757), which contains Sectionum conicarum
elementa nova quadam methodo concinnata et dissertationem de
transformatione locorum geometricorum, ubi de continuitatis
lege, et de quibusdam infiniti mysteriis. His first principle is
that all varieties of a defined locus have the same properties, so
that what is demonstrable of one should be demonstrable in like
manner of all, although some artifice may be required to bring
out the underlying analogy between them. The opposite
extremities of an infinite straight line, he says, are to be regarded
as joined, as if the line were a circle having its centre at the
infinity on either side of it. This leads up to the idea of a veluti
plus quam infinita extensio, a line-circle containing, as we say,
the line infinity. Change from the real to the imaginary state is
contingent upon the passage of some element of a figure through
zero or infinity and never takes place per saltum. Lines being
some positive and some negative, there must be negative rectangles
and negative squares, such as those of the exterior
diameters of a hyperbola. Boscovich’s first principle was that
of Kepler, by whose quantumvis absurdis locutionibus the boldest
675
applications of it are covered, as when we say with Poncelet
that all concentric circles in a plane touch one another in two
imaginary fixed points at infinity. In G.K. Ch. von Staudt’s
Geometrie der Lage and Beiträge zur G. der L. (Nürnberg, 1847,
1856-1860) the geometry of position, including the extension of
the field of pure geometry to the infinite and the imaginary, is
presented as an independent science, “welche des Messens nicht
bedarf.” (See Geometry: Projective.)
Ocular illusions due to distance, such as Roger Bacon notices
in the Opus majus (i. 126, ii. 108, 497; Oxford, 1897), lead up to
or illustrate the mathematical uses of the infinite and its reciprocal
the infinitesimal. Specious objections can, of course, be
made to the anomalies of the law of continuity, but they are
inherent in the higher geometry, which has taught us so much
of the “secrets of nature.” Kepler’s excursus on the “analogy”
between the conic sections hereinbefore referred to is given at
length in an article on “The Geometry of Kepler and Newton”
in vol. xviii. of the Transactions of the Cambridge Philosophical
Society (1900). It had been generally overlooked, until attention
was called to it by the present writer in a note read in 1880 (Proc.
C.P.S. iv. 14-17), and shortly afterwards in The Ancient and
Modern Geometry of Conics, with Historical Notes and Prolegomena
(Cambridge 1881).
(C. T.*)
GEOMETRY, the general term for the branch of mathematics
which has for its province the study of the properties of
space. From experience, or possibly intuitively, we characterize
existent space by certain fundamental qualities, termed axioms,
which are insusceptible of proof; and these axioms, in conjunction
with the mathematical entities of the point, straight line,
curve, surface and solid, appropriately defined, are the premises
from which the geometer draws conclusions. The geometrical
axioms are merely conventions; on the one hand, the system
may be based upon inductions from experience, in which case
the deduced geometry may be regarded as a branch of physical
science; or, on the other hand, the system may be formed by
purely logical methods, in which case the geometry is a phase
of pure mathematics. Obviously the geometry with which we
are most familiar is that of existent space—the three-dimensional
space of experience; this geometry may be termed Euclidean,
after its most famous expositor. But other geometries exist,
for it is possible to frame systems of axioms which definitely
characterize some other kind of space, and from these axioms
to deduce a series of non-contradictory propositions; such
geometries are called non-Euclidean.
It is convenient to discuss the subject-matter of geometry
under the following headings:
I. Euclidean Geometry: a discussion of the axioms of existent
space and of the geometrical entities, followed by a synoptical
account of Euclid’s Elements.
II. Projective Geometry: primarily Euclidean, but differing
from I. in employing the notion of geometrical continuity (q.v.)—points
and lines at infinity.
III. Descriptive Geometry: the methods for representing upon
planes figures placed in space of three dimensions.
IV. Analytical Geometry: the representation of geometrical
figures and their relations by algebraic equations.
V. Line Geometry: an analytical treatment of the line regarded
as the space element.
VI. Non-Euclidean Geometry: a discussion of geometries
other than that of the space of experience.
VII. Axioms of Geometry: a critical analysis of the foundations
of geometry.
Special subjects are treated under their own headings: e.g.
Projection, Perspective; Curve, Surface; Circle, Conic
Section; Triangle, Polygon, Polyhedron; there are also
articles on special curves and figures, e.g. Ellipse, Parabola,
Hyperbola; Tetrahedron, Cube, Octahedron, Dodecahedron,
Icosahedron; Cardioid, Catenary, Cissoid, Conchoid, Cycloid,
Epicycloid, Limaçon, Oval, Quadratrix, Spiral, &c.
History.—The origin of geometry (Gr. γῆ, earth, μέτρον, a
measure) is, according to Herodotus, to be found in the etymology
of the word. Its birthplace was Egypt, and it arose from the
need of surveying the lands inundated by the Nile floods. In
its infancy it therefore consisted of a few rules, very rough and
approximate, for computing the areas of triangles and quadrilaterals;
and, with the Egyptians, it proceeded no further, the
geometrical entities—the point, line, surface and solid—being
only discussed in so far as they were involved in practical affairs.
The point was realized as a mark or position, a straight line as a
stretched string or the tracing of a pole, a surface as an area;
but these units were not abstracted; and for the Egyptians
geometry was only an art—an auxiliary to surveying.1 The
first step towards its elevation to the rank of a science was made
by Thales (q.v.) of Miletus, who transplanted the elementary
Egyptian mensuration to Greece. Thales clearly abstracted
the notions of points and lines, founding the geometry of the
latter unit, and discovering per saltum many propositions concerning
areas, the circle, &c. The empirical rules of the Egyptians
were corrected and developed by the Ionic School which he
founded, especially by Anaximander and Anaxagoras, and in
the 6th century B.C. passed into the care of the Pythagoreans.
From this time geometry exercised a powerful influence on
Greek thought. Pythagoras (q.v.), seeking the key of the
universe in arithmetic and geometry, investigated logically the
principles underlying the known propositions; and this resulted
in the formulation of definitions, axioms and postulates which,
in addition to founding a science of geometry, permitted a
crystallization, fractional, it is true, of the amorphous collection
of material at hand. Pythagorean geometry was essentially a
geometry of areas and solids; its goal was the regular solids—the
tetrahedron, cube, octahedron, dodecahedron and icosahedron—which
symbolized the five elements of Greek cosmology.
The geometry of the circle, previously studied in Egypt and
much more seriously by Thales, was somewhat neglected, although
this curve was regarded as the most perfect of all plane figures
and the sphere the most perfect of all solids. The circle, however,
was taken up by the Sophists, who made most of their discoveries
in attempts to solve the classical problems of squaring the circle,
doubling the cube and trisecting an angle. These problems,
besides stimulating pure geometry, i.e. the geometry of constructions
made by the ruler and compasses, exercised considerable
influence in other directions. The first problem led to the
discovery of the method of exhaustion for determining areas.
Antiphon inscribed a square in a circle, and on each side an
isosceles triangle having its vertex on the circle; on the sides
of the octagon so obtained, isosceles triangles were again constructed,
the process leading to inscribed polygons of 8, 16 and
32 sides; and the areas of these polygons, which are easily
determined, are successive approximations to the area of the
circle. Bryson of Heraclea took an important step when he
circumscribed, in addition to inscribing, polygons to a circle,
but he committed an error in treating the circle as the mean of
the two polygons. The method of Antiphon, in assuming that
by continued division a polygon can be constructed coincident
with the circle, demanded that magnitudes are not infinitely
divisible. Much controversy ranged about this point; Aristotle
supported the doctrine of infinite divisibility; Zeno attempted
to show its absurdity. The mechanical tracing of loci, a principle
initiated by Archytas of Tarentum to solve the last two problems,
was a frequent subject for study, and several mechanical curves
were thus discovered at subsequent dates (cissoid, conchoid,
quadratrix). Mention may be made of Hippocrates, who,
besides developing the known methods, made a study of similar
figures, and, as a consequence, of proportion. This step is
important as bringing into line discontinuous number and
continuous magnitude.
A fresh stimulus was given by the succeeding Platonists, who,
accepting in part the Pythagorean cosmology, made the study
of geometry preliminary to that of philosophy. The many
discoveries made by this school were facilitated in no small
measure by the clarification of the axioms and definitions, the
logical sequence of propositions which was adopted, and, more
especially, by the formulation of the analytic method, i.e. of
assuming the truth of a proposition and then reasoning to a
676
known truth. The main strength of the Platonist geometers
lies in stereometry or the geometry of solids. The Pythagoreans
had dealt with the sphere and regular solids, but the pyramid,
prism, cone and cylinder were but little known until the Platonists
took them in hand. Eudoxus established their mensuration,
proving the pyramid and cone to have one-third the content
of a prism and cylinder on the same base and of the same height,
and was probably the discoverer of a proof that the volumes of
spheres are as the cubes of their radii. The discussion of sections
of the cone and cylinder led to the discovery of the three curves
named the parabola, ellipse and hyperbola (see Conic Section);
it is difficult to over-estimate the importance of this discovery;
its investigation marks the crowning achievement of Greek
geometry, and led in later years to the fundamental theorems
and methods of modern geometry.
The presentation of the subject-matter of geometry as a connected
and logical series of propositions, prefaced by Ὅροι or
foundations, had been attempted by many; but it is to Euclid
that we owe a complete exposition. Little indeed in the Elements
is probably original except the arrangement; but in this Euclid
surpassed such predecessors as Hippocrates, Leon, pupil of
Neocleides, and Theudius of Magnesia, devising an apt logical
model, although when scrutinized in the light of modern mathematical
conceptions the proofs are riddled with fallacies. According
to the commentator Proclus, the Elements were written with
a twofold object, first, to introduce the novice to geometry, and
secondly, to lead him to the regular solids; conic sections found
no place therein. What Euclid did for the line and circle,
Apollonius did for the conic sections, but there we have a discoverer
as well as editor. These two works, which contain the greatest
contributions to ancient geometry, are treated in detail in
Section I. Euclidean Geometry and the articles Euclid; Conic
Section; Appolonius. Between Euclid and Apollonius there
flourished the illustrious Archimedes, whose geometrical discoveries
are mainly concerned with the mensuration of the
circle and conic sections, and of the sphere, cone and cylinder,
and whose greatest contribution to geometrical method is the
elevation of the method of exhaustion to the dignity of an instrument
of research. Apollonius was followed by Nicomedes, the
inventor of the conchoid; Diocles, the inventor of the cissoid;
Zenodorus, the founder of the study of isoperimetrical figures;
Hipparchus, the founder of trigonometry; and Heron the elder,
who wrote after the manner of the Egyptians, and primarily
directed attention to problems of practical surveying.
Of the many isolated discoveries made by the later Alexandrian
mathematicians, those of Menelaus are of importance. He
showed how to treat spherical triangles, establishing their
properties and determining their congruence; his theorem on
the products of the segments in which the sides of a triangle
are cut by a line was the foundation on which Carnot erected
his theory of transversals. These propositions, and also those
of Hipparchus, were utilized and developed by Ptolemy (q.v.),
the expositor of trigonometry and discoverer of many isolated
propositions. Mention may be made of the commentator Pappus,
whose Mathematical Collections is valuable for its wealth of
historical matter; of Theon, an editor of Euclid’s Elements and
commentator of Ptolemy’s Almagest; of Proclus, a commentator
of Euclid; and of Eutocius, a commentator of Apollonius and
Archimedes.
The Romans, essentially practical and having no inclination
to study science qua science, only had a geometry which sufficed
for surveying; and even here there were abundant inaccuracies,
the empirical rules employed being akin to those of the Egyptians
and Heron. The Hindus, likewise, gave more attention to
computation, and their geometry was either of Greek origin or
in the form presented in trigonometry, more particularly connected
with arithmetic. It had no logical foundations; each
proposition stood alone; and the results were empirical. The
Arabs more closely followed the Greeks, a plan adopted as a
sequel to the translation of the works of Euclid, Apollonius,
Archimedes and many others into Arabic. Their chief contribution
to geometry is exhibited in their solution of algebraic
equations by intersecting conics, a step already taken by the
Greeks in isolated cases, but only elevated into a method by Omar
al Hayyami, who flourished in the 11th century. During the
middle ages little was added to Greek and Arabic geometry.
Leonardo of Pisa wrote a Practica geometriae (1220), wherein
Euclidean methods are employed; but it was not until the 14th
century that geometry, generally Euclid’s Elements, became
an essential item in university curricula. There was, however,
no sign of original development, other branches of mathematics,
mainly algebra and trigonometry, exercising a greater fascination
until the 16th century, when the subject again came into favour.
The extraordinary mathematical talent which came into being
in the 16th and 17th centuries reacted on geometry and gave rise
to all those characters which distinguish modern from ancient
geometry. The first innovation of moment was the formulation
of the principle of geometrical continuity by Kepler. The notion
of infinity which it involved permitted generalizations and
systematizations hitherto unthought of (see Geometrical
Continuity); and the method of indefinite division applied to
rectification, and quadrature and cubature problems avoided
the cumbrous method of exhaustion and provided more accurate
results. Further progress was made by Bonaventura Cavalieri,
who, in his Geometria indivisibilibus continuorum (1620), devised
a method intermediate between that of exhaustion and
the infinitesimal calculus of Leibnitz and Newton. The logical
basis of his system was corrected by Roberval and Pascal; and
their discoveries, taken in conjunction with those of Leibnitz,
Newton, and many others in the fluxional calculus, culminated
in the branch of our subject known as differential geometry
(see Infinitesimal Calculus; Curve; Surface).
A second important advance followed the recognition that
conics could be regarded as projections of a circle, a conception
which led at the hands of Desargues and Pascal to modern
projective geometry and perspective. A third, and perhaps the
most important, advance attended the application of algebra to
geometry by Descartes, who thereby founded analytical geometry.
The new fields thus opened up were diligently explored, but the
calculus exercised the greatest attraction and relatively little
progress was made in geometry until the beginning of the 19th
century, when a new era opened.
Gaspard Monge was the first important contributor, stimulating
analytical and differential geometry and founding descriptive
geometry in a series of papers and especially in his lectures at the
École polytechnique. Projective geometry, founded by Desargues,
Pascal, Monge and L.N.M. Carnot, was crystallized by
J.V. Poncelet, the creator of the modern methods. In his
Traité des propriétés des figures (1822) the line and circular points
at infinity, imaginaries, polar reciprocation, homology, cross-ratio
and projection are systematically employed. In Germany,
A.F. Möbius, J. Plücker and J. Steiner were making far-reaching
contributions. Möbius, in his Barycentrische Calcul (1827),
introduced homogeneous co-ordinates, and also the powerful
notion of geometrical transformation, including the special
cases of collineation and duality; Plücker, in his Analytisch-geometrische
Entwickelungen (1828-1831), and his System der
analytischen Geometrie (1835), introduced the abridged notation,
line and plane co-ordinates, and the conception of generalized
space elements; while Steiner, besides enriching geometry in
numerous directions, was the first to systematically generate
figures by projective pencils. We may also notice M. Chasles,
whose Aperçu historique (1837) is a classic. Synthetic geometry,
characterized by its fruitfulness and beauty, attracted most
attention, and it so happened that its originally weak logical
foundations became replaced by a more substantial set of axioms.
These were found in the anharmonic ratio, a device leading to
the liberation of synthetic geometry from metrical relations,
and in involution, which yielded rigorous definitions of imaginaries.
These innovations were made by K.J.C. von Staudt.
Analytical geometry was stimulated by the algebra of invariants,
a subject much developed by A. Cayley, G. Salmon, S.H. Aronhold,
L.O. Hesse, and more particularly by R.F.A. Clebsch.
The introduction of the line as a space element, initiated by
677
H. Grassmann (1844) and Cayley (1859), yielded at the hands of
Plücker a new geometry, termed line geometry, a subject
developed more notably by F. Klein, Clebsch, C.T. Reye and
F.O.R. Sturm (see Section V., Line Geometry).
Non-euclidean geometries, having primarily their origin in the
discussion of Euclidean parallels, and treated by Wallis, Saccheri
and Lambert, have been especially developed during the 19th
century. Four lines of investigation may be distinguished:—the
naïve-synthetic, associated with Lobatschewski, Bolyai,
Gauss; the metric differential, studied by Riemann, Helmholtz,
Beltrami; the projective, developed by Cayley, Klein, Clifford;
and the critical-synthetic, promoted chiefly by the Italian
mathematicians Peano, Veronese, Burali-Forte, Levi Civittà,
and the Germans Pasch and Hilbert.
(C. E.*)
I. Euclidean Geometry
This branch of the science of geometry is so named since its
methods and arrangement are those laid down in Euclid’s
Elements.
§ 1. Axioms.—The object of geometry is to investigate the
properties of space. The first step must consist in establishing
those fundamental properties from which all others follow by
processes of deductive reasoning. They are laid down in the
Axioms, and these ought to form such a system that nothing
need be added to them in order fully to characterize space, and
that nothing may be omitted without making the system incomplete.
They must, in fact, completely “define” space.
§ 2. Definitions.—The axioms of Euclidean Geometry are
obtained from inspection of existent space and of solids in
existent space,—hence from experience. The same source
gives us the notions of the geometrical entities to which the
axioms relate, viz. solids, surfaces, lines or curves, and points.
A solid is directly given by experience; we have only to abstract
all material from it in order to gain the notion of a geometrical
solid. This has shape, size, position, and may be moved. Its
boundary or boundaries are called surfaces. They separate one
part of space from another, and are said to have no thickness.
Their boundaries are curves or lines, and these have length
only. Their boundaries, again, are points, which have no
magnitude but only position. We thus come in three steps
from solids to points which have no magnitude; in each step
we lose one extension. Hence we say a solid has three dimensions,
a surface two, a line one, and a point none. Space itself, of which
a solid forms only a part, is also said to be of three dimensions.
The same thing is intended to be expressed by saying that a
solid has length, breadth and thickness, a surface length and
breadth, a line length only, and a point no extension whatsoever.
Euclid gives the essence of these statements as definitions:—
Def. 1, I. A point is that which has no parts, or which has no magnitude.
Def. 2, I. A line is length without breadth.
Def. 5, I. A superficies is that which has only length and breadth.
Def. 1, XI. A solid is that which has length, breadth and thickness.
It is to be noted that the synthetic method is adopted by
Euclid; the analytical derivation of the successive ideas of
“surface,” “line,” and “point” from the experimental realization
of a “solid” does not find a place in his system, although
possessing more advantages.
If we allow motion in geometry, we may generate these
entities by moving a point, a line, or a surface, thus:—
The path of a moving point is a line.
The path of a moving line is, in general, a surface.
The path of a moving surface is, in general, a solid.
|
And we may then assume that the lines, surfaces and solids,
as defined before, can all be generated in this manner. From
this generation of the entities it follows again that the boundaries—the
first and last position of the moving element—of a line are
points, and so on; and thus we come back to the considerations
with which we started.
Euclid points this out in his definitions,—Def. 3, I., Def. 6, I.,
and Def. 2, XI. He does not, however, show the connexion
which these definitions have with those mentioned before.
When points and lines have been defined, a statement like
Def. 3, I., “The extremities of a line are points,” is a proposition
which either has to be proved, and then it is a theorem, or which
has to be taken for granted, in which case it is an axiom. And
so with Def. 6, I., and Def. 2, XI.
§ 3. Euclid’s definitions mentioned above are attempts to
describe, in a few words, notions which we have obtained by
inspection of and abstraction from solids. A few more notions
have to be added to these, principally those of the simplest
line—the straight line, and of the simplest surface—the flat
surface or plane. These notions we possess, but to define them
accurately is difficult. Euclid’s Definition 4, I., “A straight
line is that which lies evenly between its extreme points,” must
be meaningless to any one who has not the notion of straightness
in his mind. Neither does it state a property of the straight
line which can be used in any further investigation. Such a
property is given in Axiom 10, I. It is really this axiom, together
with Postulates 2 and 3, which characterizes the straight line.
Whilst for the straight line the verbal definition and axiom
are kept apart, Euclid mixes them up in the case of the plane.
Here the Definition 7, I., includes an axiom. It defines a plane
as a surface which has the property that every straight line
which joins any two points in it lies altogether in the surface.
But if we take a straight line and a point in such a surface, and
draw all straight lines which join the latter to all points in the
first line, the surface will be fully determined. This construction
is therefore sufficient as a definition. That every other straight
line which joins any two points in this surface lies altogether
in it is a further property, and to assume it gives another axiom.
Thus a number of Euclid’s axioms are hidden among his first
definitions. A still greater confusion exists in the present
editions of Euclid between the postulates and axioms so called,
but this is due to later editors and not to Euclid himself. The
latter had the last three axioms put together with the postulates
(αἰτήματα), so that these were meant to include all assumptions
relating to space. The remaining assumptions, which relate to
magnitudes in general, viz. the first eight “axioms” in modern
editions, were called “common notions” (κοιναὶ ἔννοιαι).
Of the latter a few may be said to be definitions. Thus the eighth
might be taken as a definition of “equal,” and the seventh
of “halves.” If we wish to collect the axioms used in Euclid’s
Elements, we have therefore to take the three postulates, the
last three axioms as generally given, a few axioms hidden in the
definitions, and an axiom used by Euclid in the proof of Prop.
4, I, and on a few other occasions, viz. that figures may be
moved in space without change of shape or size.
§ 4. Postulates.—The assumptions actually made by Euclid
may be stated as follows:—
(1) Straight lines exist which have the property that any one of
them may be produced both ways without limit, that through any
two points in space such a line may be drawn, and that any two of
them coincide throughout their indefinite extensions as soon as two
points in the one coincide with two points in the other. (This
gives the contents of Def. 4, part of Def. 35, the first two Postulates,
and Axiom 10.)
(2) Plane surfaces or planes exist having the property laid down
in Def. 7, that every straight line joining any two points in such a
surface lies altogether in it.
(3) Right angles, as defined in Def. 10, are possible, and all right
angles are equal; that is to say, wherever in space we take a plane,
and wherever in that plane we construct a right angle, all angles
thus constructed will be equal, so that any one of them may be made
to coincide with any other. (Axiom 11.)
(4) The 12th Axiom of Euclid. This we shall not state now, but
only introduce it when we cannot proceed any further without it.
(5) Figures maybe freely moved in space without change of shape
or size. This is assumed by Euclid, but not stated as an axiom.
(6) In any plane a circle may be described, having any point in
that plane as centre, and its distance from any other point in that
plane as radius. (Postulate 3.)
The definitions which have not been mentioned are all
“nominal definitions,” that is to say, they fix a name for a
thing described. Many of them overdetermine a figure.
§ 5. Euclid’s Elements (see Euclid) are contained in thirteen
books. Of these the first four and the sixth are devoted to
“plane geometry,” as the investigation of figures in a plane is
generally called. The 5th book contains the theory of proportion
678
which is used in Book VI. The 7th, 8th and 9th books are purely
arithmetical, whilst the 10th contains a most ingenious treatment
of geometrical irrational quantities. These four books will be
excluded from our survey. The remaining three books relate to
figures in space, or, as it is generally called, to “solid geometry.”
The 7th, 8th, 9th, 10th, 13th and part of the 11th and 12th
books are now generally omitted from the school editions of the
Elements. In the first four and in the 6th book it is to be understood
that all figures are drawn in a plane.
Book I. of Euclid’s “Elements.”
§ 6. According to the third postulate it is possible to draw in
any plane a circle which has its centre at any given point, and its
radius equal to the distance of this point from any other point
given in the plane. This makes it possible (Prop. 1) to construct
on a given line AB an equilateral triangle, by drawing first a circle
with A as centre and AB as radius, and then a circle with B as
centre and BA as radius. The point where these circles intersect—that
they intersect Euclid quietly assumes—is the vertex of the
required triangle. Euclid does not suppose, however, that a circle
may be drawn which has its radius equal to the distance between
any two points unless one of the points be the centre. This implies
also that we are not supposed to be able to make any straight line
equal to any other straight line, or to carry a distance about in space.
Euclid therefore next solves the problem: It is required along a
given straight line from a point in it to set off a distance equal to
the length of another straight line given anywhere in the plane.
This is done in two steps. It is shown in Prop. 2 how a straight line
may be drawn from a given point equal in length to another given
straight line not drawn from that point. And then the problem
itself is solved in Prop. 3, by drawing first through the given point
some straight line of the required length, and then about the same
point as centre a circle having this length as radius. This circle
will cut off from the given straight line a length equal to the required
one. Nowadays, instead of going through this long process, we
take a pair of compasses and set off the given length by its aid.
This assumes that we may move a length about without changing it.
But Euclid has not assumed it, and this proceeding would be fully
justified by his desire not to take for granted more than was necessary,
if he were not obliged at his very next step actually to make this
assumption, though without stating it.
§ 7. We now come (in Prop. 4) to the first theorem. It is the
fundamental theorem of Euclid’s whole system, there being only a
very few propositions (like Props. 13, 14, 15, I.), except those in the
5th book and the first half of the 11th, which do not depend upon
it. It is stated very accurately, though somewhat clumsily, as
follows:—
If two triangles have two sides of the one equal to two sides of the
other, each to each, and have also the angles contained by those sides
equal to one another, they shall also have their bases or third sides
equal; and the two triangles shall be equal; and their other angles
shall be equal, each to each, namely, those to which the equal sides are
opposite.
That is to say, the triangles are “identically” equal, and one
may be considered as a copy of the other. The proof is very simple.
The first triangle is taken up and placed on the second, so that the
parts of the triangles which are known to be equal fall upon each
other. It is then easily seen that also the remaining parts of one
coincide with those of the other, and that they are therefore equal.
This process of applying one figure to another Euclid scarcely uses
again, though many proofs would be simplified by doing so. The
process introduces motion into geometry, and includes, as already
stated, the axiom that figures may be moved without change of
shape or size.
If the last proposition be applied to an isosceles triangle, which
has two sides equal, we obtain the theorem (Prop. 5), if two sides
of a triangle are equal, then the angles opposite these sides are equal.
Euclid’s proof is somewhat complicated, and a stumbling-block
to many schoolboys. The proof becomes much simpler if we consider
the isosceles triangle ABC (AB = AC) twice over, once as a triangle
BAC, and once as a triangle CAB; and now remember that AB, AC
in the first are equal respectively to AC, AB in the second, and the
angles included by these sides are equal. Hence the triangles are
equal, and the angles in the one are equal to those in the other, viz.
those which are opposite equal sides, i.e. angle ABC in the first
equals angle ACB in the second, as they are opposite the equal
sides AC and AB in the two triangles.
There follows the converse theorem (Prop. 6). If two angles in
a triangle are equal, then the sides opposite them are equal,—i.e. the
triangle is isosceles. The proof given consists in what is called a
reductio ad absurdum, a kind of proof often used by Euclid, and
principally in proving the converse of a previous theorem. It
assumes that the theorem to be proved is wrong, and then shows
that this assumption leads to an absurdity, i.e. to a conclusion
which is in contradiction to a proposition proved before—that
therefore the assumption made cannot be true, and hence that
the theorem is true. It is often stated that Euclid invented this
kind of proof, but the method is most likely much older.
§ 8. It is next proved that two triangles which have the three sides
of the one equal respectively to those of the other are identically equal,
hence that the angles of the one are equal respectively to those of the
other, those being equal which are opposite equal sides. This is Prop. 8,
Prop. 7 containing only a first step towards its proof.
These theorems allow now of the solution of a number of problems,
viz.:—
To bisect a given angle (Prop. 9).
To bisect a given finite straight line (Prop. 10).
To draw a straight line perpendicularly to a given straight line
through a given point in it (Prop. 11), and also through a given point
not in it (Prop. 12).
The solutions all depend upon properties of isosceles triangles.
§ 9. The next three theorems relate to angles only, and might have
been proved before Prop. 4, or even at the very beginning. The
first (Prop. 13) says, The angles which one straight line makes with
another straight line on one side of it either are two right angles or
are together equal to two right angles. This theorem would have
been unnecessary if Euclid had admitted the notion of an angle
such that its two limits are in the same straight line, and had besides
defined the sum of two angles.
Its converse (Prop. 14) is of great use, inasmuch as it enables us
in many cases to prove that two straight lines drawn from the same
point are one the continuation of the other. So also is
Prop. 15. If two straight lines cut one another, the vertical or opposite
angles shall be equal.
§ 10. Euclid returns now to properties of triangles. Of great
importance for the next steps (though afterwards superseded by a
more complete theorem) is
Prop. 16. If one side of a triangle be produced, the exterior angle
shall be greater than either of the interior opposite angles.
Prop. 17. Any two angles of a triangle are together less than two
right angles, is an immediate consequence of it. By the aid of these
two, the following fundamental properties of triangles are easily
proved:—
Prop. 18. The greater side of every triangle has the greater angle
opposite to it;
Its converse, Prop. 19. The greater angle of every triangle is subtended
by the greater side, or has the greater side opposite to it;
Prop. 20. Any two sides of a triangle are together greater than the
third side;
And also Prop. 21. If from the ends of the side of a triangle there
be drawn two straight lines to a point within the triangle, these shall
be less than the other two sides of the triangle, but shall contain a greater
angle.
§ 11. Having solved two problems (Props. 22, 23), he returns to two
triangles which have two sides of the one equal respectively to two
sides of the other. It is known (Prop. 4) that if the included angles
are equal then the third sides are equal; and conversely (Prop. 8),
if the third sides are equal, then the angles included by the first
sides are equal. From this it follows that if the included angles are
not equal, the third sides are not equal; and conversely, that if the
third sides are not equal, the included angles are not equal. Euclid
now completes this knowledge by proving, that “if the included
angles are not equal, then the third side in that triangle is the greater
which contains the greater angle”; and conversely, that “if the third
sides are unequal, that triangle contains the greater angle which contains
the greater side.” These are Prop. 24 and Prop. 25.
§ 12. The next theorem (Prop. 26) says that if two triangles have
one side and two angles of the one equal respectively to one side and
two angles of the other, viz. in both triangles either the angles adjacent
to the equal side, or one angle adjacent and one angle opposite it, then
the two triangles are identically equal.
This theorem belongs to a group with Prop. 4 and Prop. 8. Its
first case might have been given immediately after Prop. 4, but the
second case requires Prop. 16 for its proof.
§ 13. We come now to the investigation of parallel straight lines,
i.e. of straight lines which lie in the same plane, and cannot be made
to meet however far they be produced either way. The investigation
which starts from Prop. 16, will become clearer if a few names be
explained which are not all used by Euclid. If two straight lines
be cut by a third, the latter is now generally called a “transversal”
of the figure. It forms at the two points where it cuts the given lines
four angles with each. Those of the angles which lie between the
given lines are called interior angles, and of these, again, any two
which lie on opposite sides of the transversal but one at each of the
two points are called “alternate angles.”
We may now state Prop. 16 thus:—If two straight lines which
meet are cut by a transversal, their alternate angles are unequal. For
the lines will form a triangle, and one of the alternate angles will
be an exterior angle to the triangle, the other interior and opposite
to it.
From this follows at once the theorem contained in Prop. 27.
If two straight lines which are cut by a transversal make alternate
angles equal, the lines cannot meet, however far they be produced,
hence they are parallel. This proves the existence of parallel
lines.
Prop. 28 states the same fact in different forms. If a straight
line, falling on two other straight lines, make the exterior angle equal
to the interior and opposite angle on the same side of the line, or make
679
the interior angles on the same side together equal to two right angles,
the two straight lines shall be parallel to one another.
Hence we know that, “if two straight lines which are cut by a
transversal meet, their alternate angles are not equal”; and hence
that, “if alternate angles are equal, then the lines are parallel.”
The question now arises, Are the propositions converse to these
true or not? That is to say, “If alternate angles are unequal, do
the lines meet?” And “if the lines are parallel, are alternate
angles necessarily equal?”
The answer to either of these two questions implies the answer
to the other. But it has been found impossible to prove that the
negation or the affirmation of either is true.
The difficulty which thus arises is overcome by Euclid assuming
that the first question has to be answered in the affirmative. This
gives his last axiom (12), which we quote in his own words.
Axiom 12.—If a straight line meet two straight lines, so as to make
the two interior angles on the same side of it taken together less than
two right angles, these straight lines, being continually produced, shall
at length meet on that side on which are the angles which are less than
two right angles.
The answer to the second of the above questions follows from this,
and gives the theorem Prop. 29:—If a straight line fall on two parallel
straight lines, it makes the alternate angles equal to one another, and
the exterior angle equal to the interior and opposite angle on the same
side, and also the two interior angles on the same side together equal
to two right angles.
§ 14. With this a new part of elementary geometry begins. The
earlier propositions are independent of this axiom, and would be
true even if a wrong assumption had been made in it. They all
relate to figures in a plane. But a plane is only one among an infinite
number of conceivable surfaces. We may draw figures on any one
of them and study their properties. We may, for instance, take a
sphere instead of the plane, and obtain “spherical” in the place of
“plane” geometry. If on one of these surfaces lines and figures
could be drawn, answering to all the definitions of our plane figures,
and if the axioms with the exception of the last all hold, then all
propositions up to the 28th will be true for these figures. This is
the case in spherical geometry if we substitute “shortest line” or
“great circle” for “straight line,” “small circle” for “circle,” and
if, besides, we limit all figures to a part of the sphere which is less
than a hemisphere, so that two points on it cannot be opposite ends
of a diameter, and therefore determine always one and only one great
circle.
For spherical triangles, therefore, all the important propositions
4, 8, 26; 5 and 6; and 18, 19 and 20 will hold good.
This remark will be sufficient to show the impossibility of proving
Euclid’s last axiom, which would mean proving that this axiom is
a consequence of the others, and hence that the theory of parallels
would hold on a spherical surface, where the other axioms do hold,
whilst parallels do not even exist.
It follows that the axiom in question states an inherent difference
between the plane and other surfaces, and that the plane is only
fully characterized when this axiom is added to the other assumptions.
§ 15. The introduction of the new axiom and of parallel lines leads
to a new class of propositions.
After proving (Prop. 30) that “two lines which are each parallel
to a third are parallel to each other,” we obtain the new properties
of triangles contained in Prop. 32. Of these the second part is the
most important, viz. the theorem, The three interior angles of every
triangle are together equal to two right angles.
As easy deductions not given by Euclid but added by Simson
follow the propositions about the angles in polygons, they are given
in English editions as corollaries to Prop. 32.
These theorems do not hold for spherical figures. The sum of the
interior angles of a spherical triangle is always greater than two
right angles, and increases with the area.
§ 16. The theory of parallels as such may be said to be finished
with Props. 33 and 34, which state properties of the parallelogram,
i.e. of a quadrilateral formed by two pairs of parallels. They are—
Prop. 33. The straight lines which join the extremities of two equal
and parallel straight lines towards the same parts are themselves equal
and parallel; and
Prop. 34. The opposite sides and angles of a parallelogram are
equal to one another, and the diameter (diagonal) bisects the parallelogram,
that is, divides it into two equal parts.
§ 17. The rest of the first book relates to areas of figures.
The theory is made to depend upon the theorems—
Prop. 35. Parallelograms on the same base and between the same
parallels are equal to one another; and
Prop. 36. Parallelograms on equal bases and between the same
parallels are equal to one another.
As each parallelogram is bisected by a diagonal, the last theorems
hold also if the word parallelogram be replaced by “triangle,” as is
done in Props. 37 and 38.
It is to be remarked that Euclid proves these propositions only
in the case when the parallelograms or triangles have their bases in
the same straight line.
The theorems converse to the last form the contents of the next
three propositions, viz.: Props, 40 and 41.—Equal triangles, on
the same or on equal bases, in the same straight line, and on the same
side of it, are between the same parallels.
That the two cases here stated are given by Euclid in two separate
propositions proved separately is characteristic of his method.
§ 18. To compare areas of other figures, Euclid shows first, in
Prop. 42, how to draw a parallelogram which is equal in area to a
given triangle, and has one of its angles equal to a given angle. If the
given angle is right, then the problem is solved to draw a “rectangle”
equal in area to a given triangle.
Next this parallelogram is transformed into another parallelogram,
which has one of its sides equal to a given straight line, whilst its angles
remain unaltered. This may be done by aid of the theorem in
Prop. 43. The complements of the parallelograms which are about
the diameter of any parallelogram are equal to one another.
Thus the problem (Prop. 44) is solved to construct a parallelogram
on a given line, which is equal in area to a given triangle, and which
has one angle equal to a given angle (generally a right angle).
As every polygon can be divided into a number of triangles, we
can now construct a parallelogram having a given angle, say a
right angle, and being equal in area to a given polygon. For each
of the triangles into which the polygon has been divided, a parallelogram
may be constructed, having one side equal to a given straight
line and one angle equal to a given angle. If these parallelograms
be placed side by side, they may be added together to form a single
parallelogram, having still one side of the given length. This is
done in Prop. 45.
Herewith a means is found to compare areas of different polygons.
We need only construct two rectangles equal in area to the given
polygons, and having each one side of given length. By comparing
the unequal sides we are enabled to judge whether the areas are
equal, or which is the greater. Euclid does not state this consequence,
but the problem is taken up again at the end of the second book,
where it is shown how to construct a square equal in area to a given
polygon.
Prop. 46 is: To describe a square on a given straight line.
§ 19. The first book concludes with one of the most important
theorems in the whole of geometry, and one which has been celebrated
since the earliest times. It is stated, but on doubtful authority,
that Pythagoras discovered it, and it has been called by his name.
If we call that side in a right-angled triangle which is opposite the
right angle the hypotenuse, we may state it as follows:—
Theorem of Pythagoras (Prop. 47).—In every right-angled triangle
the square on the hypotenuse is equal to the sum of the squares of the
other sides.
And conversely—
Prop. 48. If the square described on one of the sides of a triangle be
equal to the squares described on the other sides, then the angle contained
by these two sides is a right angle.
On this theorem (Prop. 47) almost all geometrical measurement
depends, which cannot be directly obtained.
Book II.
§ 20. The propositions in the second book are very different in
character from those in the first; they all relate to areas of rectangles
and squares. Their true significance is best seen by stating them in
an algebraic form. This is often done by expressing the lengths of
lines by aid of numbers, which tell how many times a chosen unit
is contained in the lines. If there is a unit to be found which is contained
an exact number of times in each side of a rectangle, it is
easily seen, and generally shown in the teaching of arithmetic, that
the rectangle contains a number of unit squares equal to the product
of the numbers which measure the sides, a unit square being the
square on the unit line. If, however, no such unit can be found,
this process requires that connexion between lines and numbers
which is only established by aid of ratios of lines, and which is therefore
at this stage altogether inadmissible. But there exists another
way of connecting these propositions with algebra, based on modern
notions which seem destined greatly to change and to simplify
mathematics. We shall introduce here as much of it as is required
for our present purpose.
At the beginning of the second book we find a definition according
to which “a rectangle is said to be ‘contained’ by the two sides
which contain one of its right angles”; in the text this phraseology
is extended by speaking of rectangles contained by any two straight
lines, meaning the rectangle which has two adjacent sides equal to
the two straight lines.
We shall denote a finite straight line by a single small letter,
a, b, c, ... x, and the area of the rectangle contained by two lines
a and b by ab, and this we shall call the product of the two lines a
and b. It will be understood that this definition has nothing to do
with the definition of a product of numbers.
We define as follows:—
The sum of two straight lines a and b means a straight line c which
may be divided in two parts equal respectively to a and b. This sum
is denoted by a + b.
The difference of two lines a and b (in symbols, a-b) means a line
c which when added to b gives a; that is,
a − b = c if b + c = a.
The product of two lines a and b (in symbols, ab) means the area
680
of the rectangle contained by the lines a and b. For aa, which
means the square on the line a, we write a².
§ 21. The first ten of the fourteen propositions of the second book
may then be written in the form of formulae as follows:—
| Prop. | 1. | a (b + c + d + ... ) = ab + ac + ad + ... |
| ” | 2. | ab + ac = a² if b + c = a. |
| ” | 3. | a (a + b) = a² + ab. |
| ” | 4. | (a + b)² = a² + 2ab + b². |
| ” | 5. | (a + b)(a − b) + b² = a². |
| ” | 6. | (a + b)(a − b) + b² = a². |
| ” | 7. | a² + (a − b)² = 2a (a − b) + b². |
| ” | 8. | 4(a + b)a + b² = (2a + b)². |
| ” | 9. | (a + b)² + (a − b)² = 2a² + 2b². |
| ” | 10. | (a + b)² + (a − b)² = 2a² + 2b². |
It will be seen that 5 and 6, and also 9 and 10, are identical. In
Euclid’s statement they do not look the same, the figures being
arranged differently.
If the letters a, b, c, ... denoted numbers, it follows from algebra
that each of these formulae is true. But this does not prove them in
our case, where the letters denote lines, and their products areas
without any reference to numbers. To prove them we have to
discover the laws which rule the operations introduced, viz. addition
and multiplication of segments. This we shall do now; and we shall
find that these laws are the same with those which hold in algebraical
addition and multiplication.
§ 22. In a sum of numbers we may change the order in which
the numbers are added, and we may also add the numbers together
in groups and then add these groups. But this also holds for the
sum of segments and for the sum of rectangles, as a little consideration
shows. That the sum of rectangles has always a meaning
follows from the Props. 43-45 in the first book. These laws about
addition are reducible to the two—
a + b = b + a
(1),
a + (b + c) = a + b + c
(2);
or, when expressed for rectangles,
ab + ed = ed + ab
(3),
ab + (cd + ef) = ab + cd + ef
(4).
The brackets mean that the terms in the bracket have been added
together before they are added to another term. The more general
cases for more terms may be deduced from the above.
For the product of two numbers we have the law that it remains
unaltered if the factors be interchanged. This also holds for our
geometrical product. For if ab denotes the area of the rectangle
which has a as base and b as altitude, then ba will denote the area
of the rectangle which has b as base and a as altitude. But in a
rectangle we may take either of the two lines which contain it as
base, and then the other will be the altitude. This gives
ab = ba
(5).
In order further to multiply a sum by a number, we have in algebra
the rule:—Multiply each term of the sum, and add the products
thus obtained. That this holds for our geometrical products is
shown by Euclid in his first proposition of the second book, where
he proves that the area of a rectangle whose base is the sum of a
number of segments is equal to the sum of rectangles which have
these segments separately as bases. In symbols this gives, in the
simplest case,
a(b + c) = ab + ac
and
(b + c)a = ba + ca
(6).
To these laws, which have been investigated by Sir William Hamilton
and by Hermann Grassmann, the former has given special names.
He calls the laws expressed in
(1) and (3) the commutative law for addition;
(5) the commutative law for multiplication;
(2) and (4) the associative laws for addition;
(6) the distributive law.
|
§ 23. Having proved that these six laws hold, we can at once
prove every one of the above propositions in their algebraical form.
The first is proved geometrically, it being one of the fundamental
laws. The next two propositions are only special cases of the first.
Of the others we shall prove one, viz. the fourth:—
(a + b)² = (a + b)(a + b) = (a + b)a + (a + b)b
by (6).
But
(a + b)a = aa + ba
by (6),
= aa + ab
by (5);
and
(a + b)b = ab + bb
by (6).
Therefore
| (a + b)² | = aa + ab + (ab + bb) |
| | = aa + (ab + ab) + bb |
| | = aa + 2ab + bb |
by (4).
This gives the theorem in question.
In the same manner every one of the first ten propositions is
proved.
It will be seen that the operations performed are exactly the same
as if the letters denoted numbers.
Props. 5 and 6 may also be written thus—
(a + b)(a − b) = a² − b².
Prop. 7, which is an easy consequence of Prop. 4, may be transformed.
If we denote by c the line a + b, so that
c = a + b, a = c − b,
we get
| c² + (c − b)² | = 2c(c − b) + b² |
| | = 2c² − 2bc + b². |
Subtracting c² from both sides, and writing a for c, we get
(a − b)² = a² − 2ab + b².
In Euclid’s Elements this form of the theorem does not appear,
all propositions being so stated that the notion of subtraction does
not enter into them.
§ 24. The remaining two theorems (Props. 12 and 13) connect
the square on one side of a triangle with the sum of the squares on
the other sides, in case that the angle between the latter is acute or
obtuse. They are important theorems in trigonometry, where it is
possible to include them in a single theorem.
§ 25. There are in the second book two problems, Props. 11 and 14.
If written in the above symbolic language, the former requires to
find a line x such that a(a − x) = x². Prop. 11 contains, therefore,
the solution of a quadratic equation, which we may write x² + ax = a².
The solution is required later on in the construction of a regular
decagon.
More important is the problem in the last proposition (Prop. 14).
It requires the construction of a square equal in area to a given
rectangle, hence a solution of the equation
x² = ab.
In Book I., 42-45, it has been shown how a rectangle may be constructed
equal in area to a given figure bounded by straight lines.
By aid of the new proposition we may therefore now determine a
line such that the square on that line is equal in area to any given
rectilinear figure, or we can square any such figure.
As of two squares that is the greater which has the greater side,
it follows that now the comparison of two areas has been reduced
to the comparison of two lines.
The problem of reducing other areas to squares is frequently met
with among Greek mathematicians. We need only mention the
problem of squaring the circle (see Circle).
In the present day the comparison of areas is performed in a
simpler way by reducing all areas to rectangles having a common
base. Their altitudes give then a measure of their areas.
The construction of a rectangle having the base u, and being equal
in area to a given rectangle, depends upon Prop. 43, I. This therefore
gives a solution of the equation
ab = ux,
where x denotes the unknown altitude.
Book III.
§ 26. The third book of the Elements relates exclusively to properties
of the circle. A circle and its circumference have been defined
in Book I., Def. 15. We restate it here in slightly different words:—
Definition.—The circumference of a circle is a plane curve such
that all points in it have the same distance from a fixed point in
the plane. This point is called the “centre” of the circle.
Of the new definitions, of which eleven are given at the beginning
of the third book, a few only require special mention. The first,
which says that circles with equal radii are equal, is in part a theorem,
but easily proved by applying the one circle to the other. Or it
may be considered proved by aid of Prop. 24, equal circles not being
used till after this theorem.
In the second definition is explained what is meant by a line
which “touches” a circle. Such a line is now generally called a
tangent to the circle. The introduction of this name allows us to
state many of Euclid’s propositions in a much shorter form.
For the same reason we shall call a straight line joining two points
on the circumference of a circle a “chord.”
Definitions 4 and 5 may be replaced with a slight generalization
by the following:—
Definition.—By the distance of a point from a line is meant the
length of the perpendicular drawn from the point to the line.
§ 27. From the definition of a circle it follows that every circle
has a centre. Prop. 1 requires to find it when the circle is given,
i.e. when its circumference is drawn.
To solve this problem a chord is drawn (that is, any two points in
the circumference are joined), and through the point where this is
bisected a perpendicular to it is erected. Euclid then proves, first,
that no point off this perpendicular can be the centre, hence that the
centre must lie in this line; and, secondly, that of the points on the
perpendicular one only can be the centre, viz. the one which bisects
the parts of the perpendicular bounded by the circle. In the second
part Euclid silently assumes that the perpendicular there used does
cut the circumference in two, and only in two points. The proof
therefore is incomplete. The proof of the first part, however, is
exact. By drawing two non-parallel chords, and the perpendiculars
which bisect them, the centre will be found as the point where these
perpendiculars intersect.
§ 28. In Prop. 2 it is proved that a chord of a circle lies altogether
within the circle.
681
What we have called the first part of Euclid’s solution of Prop. 1
may be stated as a theorem:—
Every straight line which bisects a chord, and is at right angles to it,
passes through the centre of the circle.
The converse to this gives Prop. 3, which may be stated thus:—
If a straight line through the centre of a circle bisect a chord, then
it is perpendicular to the chord, and if it be perpendicular to the chord
it bisects it.
An easy consequence of this is the following theorem, which is
essentially the same as Prop. 4:—
Two chords of a circle, of which neither passes through the centre,
cannot bisect each other.
These last three theorems are fundamental for the theory of the
circle. It is to be remarked that Euclid never proves that a straight
line cannot have more than two points in common with a circumference.
§ 29. The next two propositions (5 and 6) might be replaced by
a single and a simpler theorem, viz:—
Two circles which have a common centre, and whose circumferences
have one point in common, coincide.
Or, more in agreement with Euclid’s form:—
Two different circles, whose circumferences have a point in common,
cannot have the same centre.
That Euclid treats of two cases is characteristic of Greek mathematics.
The next two propositions (7 and 8) again belong together. They
may be combined thus:—
If from a point in a plane of a circle, which is not the centre, straight
lines be drawn to the different points of the circumference, then of all
these lines one is the shortest, and one the longest, and these lie both in
that straight line which joins the given point to the centre. Of all the
remaining lines each is equal to one and only one other, and these
equal lines lie on opposite sides of the shortest or longest, and make
equal angles with them.
Euclid distinguishes the two cases where the given point lies within
or without the circle, omitting the case where it lies in the circumference.
From the last proposition it follows that if from a point more
than two equal straight lines can be drawn to the circumference,
this point must be the centre. This is Prop. 9.
As a consequence of this we get
If the circumferences of the two circles have three points in common
they coincide.
For in this case the two circles have a common centre, because
from the centre of the one three equal lines can be drawn to points
on the circumference of the other. But two circles which have a
common centre, and whose circumferences have a point in common,
coincide. (Compare above statement of Props. 5 and 6.)
This theorem may also be stated thus:—
Through three points only one circumference may be drawn; or,
Three points determine a circle.
Euclid does not give the theorem in this form. He proves, however,
that the two circles cannot cut another in more than two points
(Prop. 10), and that two circles cannot touch one another in more points
than one (Prop. 13).
§ 30. Propositions 11 and 12 assert that if two circles touch, then
the point of contact lies on the line joining their centres. This gives
two propositions, because the circles may touch either internally
or externally.
§ 31. Propositions 14 and 15 relate to the length of chords. The
first says that equal chords are equidistant from the centre, and that
chords which are equidistant from the centre are equal;
Whilst Prop. 15 compares unequal chords, viz. Of all chords the
diameter is the greatest, and of other chords that is the greater which
is nearer to the centre; and conversely, the greater chord is nearer to
the centre.
§ 32. In Prop. 16 the tangent to a circle is for the first time introduced.
The proposition is meant to show that the straight line
at the end point of the diameter and at right angles to it is a tangent.
The proposition itself does not state this. It runs thus:—
Prop. 16. The straight line drawn at right angles to the diameter
of a circle, from the extremity of it, falls without the circle; and no
straight line can be drawn from the extremity, between that straight
line and the circumference, so as not to cut the circle.
Corollary.—The straight line at right angles to a diameter drawn
through the end point of it touches the circle.
The statement of the proposition and its whole treatment show
the difficulties which the tangents presented to Euclid.
Prop. 17 solves the problem through a given point, either in the
circumference or without it, to draw a tangent to a given circle.
Closely connected with Prop. 16 are Props. 18 and 19, which
state (Prop. 18), that the line joining the centre of a circle to the point
of contact of a tangent is perpendicular to the tangent; and conversely
(Prop. 19), that the straight line through the point of contact
of, and perpendicular to, a tangent to a circle passes through the centre
of the circle.
§ 33. The rest of the book relates to angles connected with a
circle, viz. angles which have the vertex either at the centre or
on the circumference, and which are called respectively angles
at the centre and angles at the circumference. Between these
two kinds of angles exists the important relation expressed as
follows:—
Prop. 20. The angle at the centre of a circle is double of the angle
at the circumference on the same base, that is, on the same arc.
This is of great importance for its consequences, of which the
two following are the principal:—
Prop. 21. The angles in the same segment of a circle are equal to
one another;
Prop. 22. The opposite angles of any quadrilateral figure inscribed
in a circle are together equal to two right angles.
Further consequences are:—
Prop. 23. On the same straight line, and on the same side of it, there
cannot be two similar segments of circles, not coinciding with one
another;
Prop. 24. Similar segments of circles on equal straight lines are
equal to one another.
The problem Prop. 25. A segment of a circle being given to describe
the circle of which it is a segment, may be solved much more easily
by aid of the construction described in relation to Prop. 1, III.,
in § 27.
§ 34. There follow four theorems connecting the angles at the
centre, the arcs into which they divide the circumference, and the
chords subtending these arcs. They are expressed for angles, arcs
and chords in equal circles, but they hold also for angles, arcs and
chords in the same circle.
The theorems are:—
Prop. 26. In equal circles equal angles stand on equal arcs, whether
they be at the centres or circumferences;
Prop. 27. (converse to Prop. 26). In equal circles the angles which
stand on equal arcs are equal to one another, whether they be at the
centres or the circumferences;
Prop. 28. In equal circles equal straight lines (equal chords) cut
off equal arcs, the greater equal to the greater, and the less equal to
the less;
Prop. 29 (converse to Prop. 28). In equal circles equal arcs are
subtended by equal straight lines.
§ 35. Other important consequences of Props. 20-22 are:—
Prop. 31. In a circle the angle in a semicircle is a right angle;
but the angle in a segment greater than a semicircle is less than a right
angle; and the angle in a segment less than a semicircle is greater than
a right angle;
Prop. 32. If a straight line touch a circle, and from the point of
contact a straight line be drawn cutting the circle, the angles which
this line makes with the line touching the circle shall be equal to the
angles which are in the alternate segments of the circle.
§ 36. Propositions 30, 33, 34, contain problems which are solved
by aid of the propositions preceding them:—
Prop. 30. To bisect a given arc, that is, to divide it into two equal
parts;
Prop. 33. On a given straight line to describe a segment of a circle
containing an angle equal to a given rectilineal angle;
Prop. 34. From a given circle to cut off a segment containing an
angle equal to a given rectilineal angle.
§ 37. If we draw chords through a point A within a circle, they
will each be divided by A into two segments. Between these segments
the law holds that the rectangle contained by them has the
same area on whatever chord through A the segments are taken.
The value of this rectangle changes, of course, with the position
of A.
A similar theorem holds if the point A be taken without the circle.
On every straight line through A, which cuts the circle in two points
B and C, we have two segments AB and AC, and the rectangles
contained by them are again equal to one another, and equal to the
square on a tangent drawn from A to the circle.
The first of these theorems gives Prop. 35, and the second Prop.
36, with its corollary, whilst Prop. 37, the last of Book III., gives
the converse to Prop. 36. The first two theorems may be combined
in one:—
If through a point A in the plane of a circle a straight line be drawn
cutting the circle in B and C, then the rectangle AB.AC has a constant
value so long as the point A be fixed; and if from A a tangent AD can
be drawn to the circle, touching at D, then the above rectangle equals the
square on AD.
Prop. 37 may be stated thus:—
If from a point A without a circle a line be drawn cutting the circle
in B and C, and another line to a point D on the circle, and AB.AC =
AD², then the line AD touches the circle at D.
It is not difficult to prove also the converse to the general proposition
as above stated. This proposition and its converse may be
expressed as follows:—
If four points ABCD be taken on the circumference of a circle, and
if the lines AB, CD, produced if necessary, meet at E, then
EA·EB = EC·ED;
and conversely, if this relation holds then the four points lie on a circle,
that is, the circle drawn through three of them passes through the
fourth.
That a circle may always be drawn through three points, provided
that they do not lie in a straight line, is proved only later on in
Book IV.
682
Book IV.
§ 38. The fourth book contains only problems, all relating to
the construction of triangles and polygons inscribed in and circumscribed
about circles, and of circles inscribed in or circumscribed
about triangles and polygons. They are nearly all given for their
own sake, and not for future use in the construction of figures, as
are most of those in the former books. In seven definitions at the
beginning of the book it is explained what is understood by figures
inscribed in or described about other figures, with special reference
to the case where one figure is a circle. Instead, however, of saying
that one figure is described about another, it is now generally said
that the one figure is circumscribed about the other. We may then
state the definitions 3 or 4 thus:—
Definition.—A polygon is said to be inscribed in a circle, and the
circle is said to be circumscribed about the polygon, if the vertices
of the polygon lie in the circumference of the circle.
And definitions 5 and 6 thus:—
Definition.—A polygon is said to be circumscribed about a circle,
and a circle is said to be inscribed in a polygon, if the sides of the
polygon are tangents to the circle.
§ 39. The first problem is merely constructive. It requires to
draw in a given circle a chord equal to a given straight line, which
is not greater than the diameter of the circle. The problem is not
a determinate one, inasmuch as the chord may be drawn from any
point in the circumference. This may be said of almost all problems
in this book, especially of the next two. They are:—
Prop. 2. In a given circle to inscribe a triangle equiangular to a
given triangle;
Prop. 3. About a given circle to circumscribe a triangle equiangular
to a given triangle.
§ 40. Of somewhat greater interest are the next problems, where
the triangles are given and the circles to be found.
Prop. 4. To inscribe a circle in a given triangle.
The result is that the problem has always a solution, viz. the
centre of the circle is the point where the bisectors of two of the
interior angles of the triangle meet. The solution shows, though
Euclid does not state this, that the problem has but one solution;
and also,
The three bisectors of the interior angles of any triangle meet in a
point, and this is the centre of the circle inscribed in the triangle.
The solutions of most of the other problems contain also theorems.
Of these we shall state those which are of special interest; Euclid
does not state any one of them.
§ 41. Prop. 5. To circumscribe a circle about a given triangle.
The one solution which always exists contains the following:—
The three straight lines which bisect the sides of a triangle at right
angles meet in a point, and this point is the centre of the circle circumscribed
about the triangle.
Euclid adds in a corollary the following property:—
The centre of the circle circumscribed about a triangle lies within,
on a side of, or without the triangle, according as the triangle is
acute-angled, right-angled or obtuse-angled.
§ 42. Whilst it is always possible to draw a circle which is inscribed
in or circumscribed about a given triangle, this is not the case with
quadrilaterals or polygons of more sides. Of those for which this
is possible the regular polygons, i.e. polygons which have all their
sides and angles equal, are the most interesting. In each of them a
circle may be inscribed, and another may be circumscribed about it.
Euclid does not use the word regular, but he describes the polygons
in question as equiangular and equilateral. We shall use the name
regular polygon. The regular triangle is equilateral, the regular
quadrilateral is the square.
Euclid considers the regular polygons of 4, 5, 6 and 15 sides.
For each of the first three he solves the problems—(1) to inscribe
such a polygon in a given circle; (2) to circumscribe it about a
given circle; (3) to inscribe a circle in, and (4) to circumscribe a
circle about, such a polygon.
For the regular triangle the problems are not repeated, because
more general problems have been solved.
Props. 6, 7, 8 and 9 solve these problems for the square.
The general problem of inscribing in a given circle a regular
polygon of n sides depends upon the problem of dividing the circumference
of a circle into n equal parts, or what comes to the same
thing, of drawing from the centre of the circle n radii such that the
angles between consecutive radii are equal, that is, to divide the
space about the centre into n equal angles. Thus, if it is required
to inscribe a square in a circle, we have to draw four lines from the
centre, making the four angles equal. This is done by drawing
two diameters at right angles to one another. The ends of these
diameters are the vertices of the required square. If, on the other
hand, tangents be drawn at these ends, we obtain a square circumscribed
about the circle.
§ 43. To construct a regular pentagon, we find it convenient first
to construct a regular decagon. This requires to divide the space
about the centre into ten equal angles. Each will be 1⁄10th of a right
angle, or 1⁄5th of two right angles. If we suppose the decagon constructed,
and if we join the centre to the end of one side, we get an
isosceles triangle, where the angle at the centre equals 1⁄5th of two
right angles; hence each of the angles at the base will be 2⁄5ths of
two right angles, as all three angles together equal two right angles.
Thus we have to construct an isosceles triangle, having the angle at
the vertex equal to half an angle at the base. This is solved in
Prop. 10, by aid of the problem in Prop. 11 of the second book. If
we make the sides of this triangle equal to the radius of the given
circle, then the base will be the side of the regular decagon inscribed
in the circle. This side being known the decagon can be constructed,
and if the vertices are joined alternately, leaving out half their
number, we obtain the regular pentagon. (Prop. 11.)
Euclid does not proceed thus. He wants the pentagon before
the decagon. This, however, does not change the real nature of
his solution, nor does his solution become simpler by not mentioning
the decagon.
Once the regular pentagon is inscribed, it is easy to circumscribe
another by drawing tangents at the vertices of the inscribed pentagon.
This is shown in Prop. 12.
Props. 13 and 14 teach how a circle may be inscribed in or circumscribed
about any given regular pentagon.
§ 44. The regular hexagon is more easily constructed, as shown
in Prop. 15. The result is that the side of the regular hexagon
inscribed in a circle is equal to the radius of the circle.
For this polygon the other three problems mentioned are not
solved.
§ 45. The book closes with Prop. 16. To inscribe a regular
quindecagon in a given circle. If we inscribe a regular pentagon
and a regular hexagon in the circle, having one vertex in common,
then the arc from the common vertex to the next vertex of the
pentagon is 1⁄5th of the circumference, and to the next vertex of the
hexagon is 1⁄6th of the circumference. The difference between these
arcs is, therefore, 1⁄5 − 1⁄6 = 1⁄30th of the circumference. The latter may,
therefore, be divided into thirty, and hence also in fifteen equal parts,
and the regular quindecagon be described.
§ 46. We conclude with a few theorems about regular polygons
which are not given by Euclid.
The straight lines perpendicular to and bisecting the sides of any
regular polygon meet in a point. The straight lines bisecting the angles
in the regular polygon meet in the same point. This point is the centre
of the circles circumscribed about and inscribed in the regular polygon.
We can bisect any given arc (Prop. 30, III.). Hence we can divide
a circumference into 2n equal parts as soon as it has been divided
into n equal parts, or as soon as a regular polygon of n sides has been
constructed. Hence—
If a regular polygon of n sides has been constructed, then a regular
polygon of 2n sides, of 4n, of 8n sides, &c., may also be constructed.
Euclid shows how to construct regular polygons of 3, 4, 5 and 15
sides. It follows that we can construct regular polygons of
| 3, | 6, | 12, | 24 | sides |
| 4, | 8, | 16, | 32 | ” |
| 5, | 10, | 20, | 40 | ” |
| 15, | 30, | 60, | 120 | ” |
The construction of any new regular polygon not included in one
of these series will give rise to a new series. Till the beginning of the
19th century nothing was added to the knowledge of regular polygons
as given by Euclid. Then Gauss, in his celebrated Arithmetic,
proved that every regular polygon of 2n + 1 sides may be constructed
if this number 2n + 1 be prime, and that no others except those
with 2m (2n + 1) sides can be constructed by elementary methods.
This shows that regular polygons of 7, 9, 13 sides cannot thus be
constructed, but that a regular polygon of 17 sides is possible; for
17 = 24 + 1. The next polygon is one of 257 sides. The construction
becomes already rather complicated for 17 sides.
Book V.
§ 47. The fifth book of the Elements is not exclusively geometrical.
It contains the theory of ratios and proportion of quantities in
general. The treatment, as here given, is admirable, and in every
respect superior to the algebraical method by which Euclid’s theory
is now generally replaced. We shall treat the subject in order to
show why the usual algebraical treatment of proportion is not really
sound. We begin by quoting those definitions at the beginning of
Book V. which are most important. These definitions have given
rise to much discussion.
The only definitions which are essential for the fifth book are
Defs. 1, 2, 4, 5, 6 and 7. Of the remainder 3, 8 and 9 are more
than useless, and probably not Euclid’s, but additions of later editors,
of whom Theon of Alexandria was the most prominent. Defs. 10
and 11 belong rather to the sixth book, whilst all the others are
merely nominal. The really important ones are 4, 5, 6 and 7.
§ 48. To define a magnitude is not attempted by Euclid. The
first two definitions state what is meant by a “part,” that is, a
submultiple or measure, and by a “multiple” of a given magnitude.
The meaning of Def. 4 is that two given quantities can have
a ratio to one another only in case that they are comparable as to
their magnitude, that is, if they are of the same kind.
Def. 3, which is probably due to Theon, professes to define a ratio,
but is as meaningless as it is uncalled for, for all that is wanted is
given in Defs. 5 and 7.
In Def. 5 it is explained what is meant by saying that two magnitudes
have the same ratio to one another as two other magnitudes,
683
and in Def. 7 what we have to understand by a greater or a less ratio.
The 6th definition is only nominal, explaining the meaning of the
word proportional.
Euclid represents magnitudes by lines, and often denotes them
either by single letters or, like lines, by two letters. We shall use
only single letters for the purpose. If a and b denote two magnitudes
of the same kind, their ratio will be denoted by a : b; if c and d are
two other magnitudes of the same kind, but possibly of a different
kind from a and b, then if c and d have the same ratio to one another
as a and b, this will be expressed by writing—
a : b :: c : d.
Further, if m is a (whole) number, ma shall denote the multiple
of a which is obtained by taking it m times.
§ 49. The whole theory of ratios is based on Def. 5.
Def. 5. The first of four magnitudes is said to have the same ratio
to the second that the third has to the fourth when, any equimultiples
whatever of the first and the third being taken, and any equimultiples
whatever of the second and the fourth, if the multiple of the first be less
than that of the second, the multiple of the third is also less than that of
the fourth; and if the multiple of the first is equal to that of the second,
the multiple of the third is also equal to that of the fourth; and if the
multiple of the first is greater than that of the second, the multiple of
the third is also greater than that of the fourth.
It will be well to show at once in an example how this definition
can be used, by proving the first part of the first proposition in the
sixth book. Triangles of the same altitude are to one another as
their bases, or if a and b are the bases, and α and β the areas, of two
triangles which have the same altitude, then a : b :: α : β.
To prove this, we have, according to Definition 5, to show—
if ma > nb, then mα > nβ,
if ma = nb, then mα = nβ,
if ma < nb, then mα < nβ.
|
That this is true is in our case easily seen. We may suppose that
the triangles have a common vertex, and their bases in the same
line. We set off the base a along the line containing the bases
m times; we then join the different parts of division to the vertex,
and get m triangles all equal to α. The triangle on ma as base equals,
therefore, mα. If we proceed in the same manner with the base b,
setting it off n times, we find that the area of the triangle on the
base nb equals nβ, the vertex of all triangles being the same. But
if two triangles have the same altitude, then their areas are equal
if the bases are equal; hence mα = nβ if ma = nb, and if their bases
are unequal, then that has the greater area which is on the greater
base; in other words, mα is greater than, equal to, or less than
nβ, according as ma is greater than, equal to, or less than nb, which
was to be proved.
§ 50. It will be seen that even in this example it does not become
evident what a ratio really is. It is still an open question whether
ratios are magnitudes which we can compare. We do not know
whether the ratio of two lines is a magnitude of the same kind as the
ratio of two areas. Though we might say that Def. 5 defines equal
ratios, still we do not know whether they are equal in the sense of
the axiom, that two things which are equal to a third are equal to
one another. That this is the case requires a proof, and until this
proof is given we shall use the :: instead of the sign = , which, however,
we shall afterwards introduce.
As soon as it has been established that all ratios are like magnitudes,
it becomes easy to show that, in some cases at least, they
are numbers. This step was never made by Greek mathematicians.
They distinguished always most carefully between continuous
magnitudes and the discrete series of numbers. In modern times
it has become the custom to ignore this difference.
If, in determining the ratio of two lines, a common measure can
be found, which is contained m times in the first, and n times in
the second, then the ratio of the two lines equals the ratio of the
two numbers m : n. This is shown by Euclid in Prop. 5, X. But the
ratio of two numbers is, as a rule, a fraction, and the Greeks did
not, as we do, consider fractions as numbers. Far less had they
any notion of introducing irrational numbers, which are neither
whole nor fractional, as we are obliged to do if we wish to say that
all ratios are numbers. The incommensurable numbers which are
thus introduced as ratios of incommensurable quantities are nowadays
as familiar to us as fractions; but a proof is generally omitted
that we may apply to them the rules which have been established
for rational numbers only. Euclid’s treatment of ratios avoids this
difficulty. His definitions hold for commensurable as well as for
incommensurable quantities. Even the notion of incommensurable
quantities is avoided in Book V. But he proves that the more
elementary rules of algebra hold for ratios. We shall state all
his propositions in that algebraical form to which we are now accustomed.
This may, of course, be done without changing the character
of Euclid’s method.
§. 51. Using the notation explained above we express the first
propositions as follows:—
Prop. 1. If
a = ma′, b = mb′, c = mc′,
then
a + b + c = m(a′ + b′ + c′).
Prop. 2. If
a = mb, and c = md,
e = nb, and f = nd,
|
then a + e is the same multiple of b as c + f is of d, viz.:—
a + e = (m + n)b, and c + f = (m + n)d.
Prop. 3. If a = mb, c = md, then is na the same multiple of b
that nc is of d, viz. na = nmb, nc = nmd.
Prop. 4. If
a : b :: c : d,
then
ma : nb :: mc : nd.
Prop. 5. If
a = mb, and c = md,
then
a − c = m(b − d).
Prop. 6. If
a = mb, c = md,
then are a − nb and c − nd either equal to, or equimultiples of, b
and d, viz. a − nb = (m − n)b and c − nd = (m − n)d, where m − n may
be unity.
All these propositions relate to equimultiples. Now follow propositions
about ratios which are compared as to their magnitude.
§ 52. Prop. 7. If a = b, then a : c :: b : c and c : a :: c : b.
The proof is simply this. As a = b we know that ma = mb; therefore
if
ma > nc, then mb > nc,
if
ma = nc, then mb = nc,
if
ma < nc, then mb < nc,
therefore the first proportion holds by Definition 5.
Prop. 8. If
a > b, then a : c > b : c,
and
c : a < c : b.
The proof depends on Definition 7.
Prop. 9 (converse to Prop. 7). If
a : c :: b : c,
or if
c : a :: c : b, then a = b.
Prop. 10 (converse to Prop. 8). If
a : c > b : c, then a > b,
and if
c : a < c : b, then a < b.
Prop. 11. If
a : b :: c : d,
and
a : b :: e : f,
then
c : d :: e : f.
In words, if too ratios are equal to a third, they are equal to one
another. After these propositions have been proved, we have a
right to consider a ratio as a magnitude, for only now can we consider
a ratio as something for which the axiom about magnitudes
holds: things which are equal to a third are equal to one another.
We shall indicate this by writing in future the sign = instead
of ::. The remaining propositions, which explain themselves, may
then be stated as follows:
§ 53. Prop. 12. If
a : b = c : d = e : f,
then
a + c + e : b + d + f = a : b.
Prop. 13. If
a : b = c : d and c : d > e : f,
then
a : b > e : f.
Prop. 14. If
a : b = c : d, and a > c, then b > d.
Prop. 15. Magnitudes have the same ratio to one another that
their equimultiples have—
ma : mb = a : b.
Prop. 16. If a, b, c, d are magnitudes of the same kind, and if
a : b = c : d,
then
a : c = b : d.
Prop. 17. If
a + b : b = c + d : d,
then
a : b = c : d.
Prop. 18 (converse to 17). If
a : b = c : d
then
a + b : b = c + d : d.
Prop. 19. If a, b, c, d are quantities of the same kind, and if
a : b = c : d,
then
a − c : b − d = a : b.
§ 54. Prop. 20. If there be three magnitudes, and another three,
which have the same ratio, taken two and two, then if the first be greater
than the third, the fourth shall be greater than the sixth: and if equal,
equal; and if less, less.
If we understand by
a : b : c : d : e : ... = a′ : b′ : c′ : d′ : e′ : ...
that the ratio of any two consecutive magnitudes on the first side
equals that of the corresponding magnitudes on the second side,
we may write this theorem in symbols, thus:—
If a, b, c be quantities of one, and d, e, f magnitudes of the same
or any other kind, such that
a : b : c = d : e : f,
and if
a > c, then d > f,
but if
a = c, then d = f,
and if
a < c, then d < f.
Prop. 21. If
a : b = e : f and b : c = d : e,
or if
a : b : c = 1/f : 1/e : 1/d,
684
and if
a > c, then d > f,
but if
a = c, then d = f,
and if
a < c, then d < f.
By aid of these two propositions the following two are proved.
§ 55. Prop. 22. If there be any number of magnitudes, and as
many others, which have the same ratio, taken two and two in order,
the first shall have to the last of the first magnitudes the same ratio
which the first of the others has to the last.
We may state it more generally, thus:
If
a : b : c : d : e: ... = a′ : b′ : c′ : d′ : e′ : ... ,
then not only have two consecutive, but any two magnitudes on
the first side, the same ratio as the corresponding magnitudes on
the other. For instance—
a : c = a′ : c′; b : e = b′ : e′, &c.
Prop. 23 we state only in symbols, viz.:—
a : b : c : d : e : ... = 1/a′ : 1/b′ : 1/c′ : 1/d′ : 1/e′ ...,
then
a : c = c′ : a′,
b : e = e′ : b′,
and so on.
Prop. 24 comes to this: If a : b = c : d and e : b = f : d, then
a + e : b = c + f : d.
Some of the proportions which are considered in the above propositions
have special names. These we have omitted, as being of
no use, since algebra has enabled us to bring the different operations
contained in the propositions under a common point of view.
§ 56. The last proposition in the fifth book is of a different
character.
Prop. 25. If four magnitudes of the same kind be proportional,
the greatest and least of them together shall be greater than the other
two together. In symbols—
If a, b, c, d be magnitudes of the same kind, and if a : b = c : d,
and if a is the greatest, hence d the least, then a + d > b + c.
§ 57. We return once again to the question. What is a ratio?
We have seen that we may treat ratios as magnitudes, and that all
ratios are magnitudes of the same kind, for we may compare any
two as to their magnitude. It will presently be shown that ratios
of lines may be considered as quotients of lines, so that a ratio appears
as answer to the question, How often is one line contained in another?
But the answer to this question is given by a number, at least in
some cases, and in all cases if we admit incommensurable numbers.
Considered from this point of view, we may say the fifth book of the
Elements shows that some of the simpler algebraical operations
hold for incommensurable numbers. In the ordinary algebraical
treatment of numbers this proof is altogether omitted, or given by
a process of limits which does not seem to be natural to the subject.
Book VI.
§ 58. The sixth book contains the theory of similar figures.
After a few definitions explaining terms, the first proposition gives
the first application of the theory of proportion.
Prop. 1. Triangles and parallelograms of the same altitude are to
one another as their bases.
The proof has already been considered in § 49.
From this follows easily the important theorem
Prop. 2. If a straight line be drawn parallel to one of the sides
of a triangle it shall cut the other sides, or those sides produced, proportionally;
and if the sides or the sides produced be cut proportionally,
the straight line which joins the points of section shall be parallel to
the remaining side of the triangle.
§ 59. The next proposition, together with one added by Simson
as Prop. A, may be expressed more conveniently if we introduce a
modern phraseology, viz. if in a line AB we assume a point C between
A and B, we shall say that C divides AB internally in the ratio
AC : CB; but if C be taken in the line AB produced, we shall say
that AB is divided externally in the ratio AC : CB.
The two propositions then come to this:
Prop. 3. The bisector of an angle in a triangle divides the opposite
side internally in a ratio equal to the ratio of the two sides including
that angle; and conversely, if a line through the vertex of a triangle
divide the base internally in the ratio of the two other sides, then that
line bisects the angle at the vertex.
Simson’s Prop. A. The line which bisects an exterior angle of a
triangle divides the opposite side externally in the ratio of the other
sides; and conversely, if a line through the vertex of a triangle divide
the base externally in the ratio of the sides, then it bisects an exterior
angle at the vertex of the triangle.
If we combine both we have—
The two lines which bisect the interior and exterior angles at one
vertex of a triangle divide the opposite side internally and externally
in the same ratio, viz. in the ratio of the other two sides.
§ 60. The next four propositions contain the theory of similar
triangles, of which four cases are considered. They may be stated
together.
Two triangles are similar,—
1. (Prop. 4). If the triangles are equiangular:
2. (Prop. 5). If the sides of the one are proportional to those of
the other;
3. (Prop. 6). If two sides in one are proportional to two sides in
the other, and if the angles contained by these sides are equal;
4. (Prop. 7). If two sides in one are proportional to two sides in
the other, if the angles opposite homologous sides are equal, and if
the angles opposite the other homologous sides are both acute, both right
or both obtuse; homologous sides being in each case those which are
opposite equal angles.
An important application of these theorems is at once made to
a right-angled triangle, viz.:—
Prop. 8. In a right-angled triangle, if a perpendicular be drawn
from the right angle to the base, the triangles on each side of it are
similar to the whole triangle, and to one another.
Corollary.—From this it is manifest that the perpendicular
drawn from the right angle of a right-angled triangle to the base
is a mean proportional between the segments of the base, and also
that each of the sides is a mean proportional between the base and
the segment of the base adjacent to that side.
§ 61. There follow four propositions containing problems, in
language slightly different from Euclid’s, viz.:—
Prop. 9. To divide a straight line into a given number of equal
parts.
Prop. 10. To divide a straight line in a given ratio.
Prop. 11. To find a third proportional to two given straight lines.
Prop. 12. To find a fourth proportional to three given straight
lines.
Prop. 13. To find a mean proportional between two given straight
lines.
The last three may be written as equations with one unknown
quantity—viz. if we call the given straight lines a, b, c, and the
required line x, we have to find a line x so that
Prop. 11.
a : b = b : x;
Prop. 12.
a : b = c : x;
Prop. 13.
a : x = x : b.
We shall see presently how these may be written without the
signs of ratios.
§ 62. Euclid considers next proportions connected with parallelograms
and triangles which are equal in area.
Prop. 14. Equal parallelograms which have one angle of the one
equal to one angle of the other have their sides about the equal angles
reciprocally proportional; and parallelograms which have one angle
of the one equal to one angle of the other, and their sides about the equal
angles reciprocally proportional, are equal to one another.
Prop. 15. Equal triangles which have one angle of the one equal
to one angle of the other, have their sides about the equal angles reciprocally
proportional; and triangles which have one angle of the one equal
to one angle of the other, and their sides about the equal angles reciprocally
proportional, are equal to one another.
The latter proposition is really the same as the former, for if, as
in the accompanying diagram,
in the figure belonging to the
former the two equal parallelograms
AB and BC be bisected
by the lines DF and EG, and
if EF be drawn, we get the
figure belonging to the latter.
It is worth noticing that
the lines FE and DG are
parallel. We may state therefore
the theorem—
If two triangles are equal in
area, and have one angle in the one vertically opposite to one angle
in the other, then the two straight lines which join the remaining two
vertices of the one to those of the other triangle are parallel.
§ 63. A most important theorem is
Prop. 16. If four straight lines be proportionals, the rectangle
contained by the extremes is equal to the rectangle contained by the
means; and if the rectangle contained by the extremes be equal to the
rectangle contained by the means, the four straight lines are proportionals.
In symbols, if a, b, c, d are the four lines, and
if
a : b = c : d,
then
ad = bc;
and conversely, if
ad = bc,
then
a : b = c : d,
where ad and bc denote (as in § 20), the areas of the rectangles
contained by a and d and by b and c respectively.
This allows us to transform every proportion between four lines
into an equation between two products.
It shows further that the operation of forming a product of two
lines, and the operation of forming their ratio are each the inverse
of the other.
If we now define a quotient a/b of two lines as the number which
multiplied into b gives a, so that
685
we see that from the equality of two quotients
follows, if we multiply both sides by bd,
ad = cb.
But from this it follows, according to the last theorem, that
a : b = c : d.
Hence we conclude that the quotient a/b and the ratio a : b are
different forms of the same magnitude, only with this important
difference that the quotient a/b would have a meaning only if a and
b have a common measure, until we introduce incommensurable
numbers, while the ratio a : b has always a meaning, and thus gives
rise to the introduction of incommensurable numbers.
Thus it is really the theory of ratios in the fifth book which enables
us to extend the geometrical calculus given before in connexion
with Book II. It will also be seen that if we write the ratios in
Book V. as quotients, or rather as fractions, then most of the theorems
state properties of quotients or of fractions.
§ 64. Prop. 17. If three straight lines are proportional the rectangle
contained by the extremes is equal to the square on the mean; and
conversely, is only a special case of 16. After the problem, Prop.
18, On a given straight line to describe a rectilineal figure similar
and similarly situated to a given rectilineal figure, there follows another
fundamental theorem:
Prop. 19. Similar triangles are to one another in the duplicate
ratio of their homologous sides. In other words, the areas of similar
triangles are to one another as the squares on homologous sides.
This is generalized in:
Prop. 20. Similar polygons may be divided into the same number
of similar triangles, having the same ratio to one another that the
polygons have; and the polygons are to one another in the duplicate
ratio of their homologous sides.
§ 65. Prop. 21. Rectilineal figures which are similar to the same
rectilineal figure are also similar to each other, is an immediate consequence
of the definition of similar figures. As similar figures
may be said to be equal in “shape” but not in “size,” we may state
it also thus:
“Figures which are equal in shape to a third are equal in shape
to each other.”
Prop. 22. If four straight lines be proportionals, the similar
rectilineal figures similarly described on them shall also be proportionals;
and if the similar rectilineal figures similarly described on four
straight lines be proportionals, those straight lines shall be proportionals.
This is essentially the same as the following:—
If
a : b = c : d,
then
a² : b² = c² : d².
§ 66. Now follows a proposition which has been much discussed
with regard to Euclid’s exact meaning in saying that a ratio is
compounded of two other ratios, viz.:
Prop. 23. Parallelograms which are equiangular to one another,
have to one another the ratio which is compounded of the ratios of their
sides.
The proof of the proposition makes its meaning clear. In symbols
the ratio a : c is compounded of the two ratios a : b and b : c, and if
a : b = a′ : b′, b : c = b″ : c″, then a : c is compounded of a′ : b′ and
b″ : c″.
If we consider the ratios as numbers, we may say that the one
ratio is the product of those of which it is compounded, or in symbols,
| a |
= | a |
· | b |
= | a′ |
· | b″ |
, if | a |
= | a′ |
and | b |
= | b″ |
. |
| c | b |
c | b′ |
c″ | b |
b′ | c |
c″ |
The theorem in Prop. 23 is the foundation of all mensuration of
areas. From it we see at once that two rectangles have the ratio
of their areas compounded of the ratios of their sides.
If A is the area of a rectangle contained by a and b, and B that
of a rectangle contained by c and d, so that A = ab, B = cd, then
A : B = ab : cd, and this is, the theorem says, compounded of the
ratios a : c and b : d. In forms of quotients,
This shows how to multiply quotients in our geometrical calculus.
Further, Two triangles have the ratios of their areas compounded
of the ratios of their bases and their altitude. For a triangle is equal
in area to half a parallelogram which has the same base and the
same altitude.
§ 67. To bring these theorems to the form in which they are usually
given, we assume a straight line u as our unit of length (generally
an inch, a foot, a mile, &c.), and determine the number α which
expresses how often u is contained in a line a, so that α denotes the
ratio a : u whether commensurable or not, and that a = αu. We
call this number α the numerical value of a. If in the same manner
β be the numerical value of a line b we have
a : b = α : β;
in words: The ratio of two lines (and of two like quantities in general)
is equal to that of their numerical values.
This is easily proved by observing that a = αu, b = βu, therefore
a : b = αu : βu, and this may without difficulty be shown to equal α : β.
If now a, b be base and altitude of one, a′, b′ those of another
parallelogram, α, β and α′, β′ their numerical values respectively,
and A, A′ their areas, then
| A |
= | a |
· | b |
= | α |
· | β |
= | αβ |
. |
| A′ | a′ |
b′ | α′ |
β′ | α′β′ |
In words: The areas of two parallelograms are to each other as the
products of the numerical values of their bases and altitudes.
If especially the second parallelogram is the unit square, i.e. a
square on the unit of length, then α′ = β′ = 1, A′ = u², and we have
This gives the theorem: The number of unit squares contained in
a parallelogram equals the product of the numerical values of base
and altitude, and similarly the number of unit squares contained in
a triangle equals half the product of the numerical values of base
and altitude.
This is often stated by saying that the area of a parallelogram is
equal to the product of the base and the altitude, meaning by this
product the product of the numerical values, and not the product as
defined above in § 20.
§ 68. Propositions 24 and 26 relate to parallelograms about
diagonals, such as are considered in Book I., 43. They are—
Prop. 24. Parallelograms about the diameter of any parallelogram
are similar to the whole parallelogram and to one another; and its
converse (Prop. 26), If two similar parallelograms have a common
angle, and be similarly situated, they are about the same diameter.
Between these is inserted a problem.
Prop. 25. To describe a rectilineal figure which shall be similar to
one given rectilinear figure, and equal to another given rectilineal
figure.
§ 69. Prop. 27 contains a theorem relating to the theory of
maxima and minima. We may state it thus:
Prop. 27. If a parallelogram be divided into two by a straight line
cutting the base, and if on half the base another parallelogram be constructed
similar to one of those parts, then this third parallelogram is
greater than the other part.
Of far greater interest than this general theorem is a special case
of it, where the parallelograms are changed into rectangles, and
where one of the parts into which the parallelogram is divided is
made a square; for then the theorem changes into one which is
easily recognized to be identical with the following:—
Of all rectangles which have the same perimeter the square has the
greatest area.
This may also be stated thus:—
Of all rectangles which have the same area the square has the least
perimeter.
§ 70. The next three propositions contain problems which may
be said to be solutions of quadratic equations. The first two are,
like the last, involved in somewhat obscure language. We transcribe
them as follows:
Problem.—To describe on a given base a parallelogram, and to
divide it either internally (Prop. 28) or externally (Prop. 29) from
a point on the base into two parallelograms, of which the one has
a given size (is equal in area to a given figure), whilst the other
has a given shape (is similar to a given parallelogram).
If we express this again in symbols, calling the given base a, the
one part x, and the altitude y, we have to determine x and y in the
first case from the equations
(a − x)y = k²,
k² being the given size of the first, and p and q the base and altitude
of the parallelogram which determine the shape of the second of the
required parallelograms.
If we substitute the value of y, we get
or,
ax − x² = b²,
where a and b are known quantities, taking b² = pk²/q.
The second case (Prop. 29) gives rise, in the same manner, to the
quadratic
ax + x² = b².
The next problem—
Prop. 30. To cut a given straight line in extreme and mean ratio,
leads to the equation
ax + x² = a².
686
This is, therefore, only a special case of the last, and is, besides,
an old acquaintance, being essentially the same problem as that
proposed in II. 11.
Prop. 30 may therefore be solved in two ways, either by aid of
Prop. 29 or by aid of II. 11. Euclid gives both solutions.
§ 71. Prop. 31 (Theorem). In any right-angled triangle, any
rectilineal figure described on the side subtending the right angle is
equal to the similar and similarly-described figures on the sides containing
the right angle,—is a pretty generalization of the theorem of
Pythagoras (I. 47).
Leaving out the next proposition, which is of little interest, we
come to the last in this book.
Prop. 33. In equal circles angles, whether at the centres or the
circumferences, have the same ratio which the arcs on which they stand
have to one another; so also have the sectors.
Of this, the part relating to angles at the centre is of special
importance; it enables us to measure angles by arcs.
With this closes that part of the Elements which is devoted to
the study of figures in a plane.
Book XI.
§ 72. In this book figures are considered which are not confined
to a plane, viz. first relations between lines and planes in space,
and afterwards properties of solids.
Of new definitions we mention those which relate to the perpendicularity
and the inclination of lines and planes.
Def. 3. A straight line is perpendicular, or at right angles, to a
plane when it makes right angles with every straight line meeting it
in that plane.
The definition of perpendicular planes (Def. 4) offers no difficulty.
Euclid defines the inclination of lines to planes and of planes to
planes (Defs. 5 and 6) by aid of plane angles, included by straight
lines, with which we have been made familiar in the first books.
The other important definitions are those of parallel planes,
which never meet (Def. 8), and of solid angles formed by three or
more planes meeting in a point (Def. 9).
To these we add the definition of a line parallel to a plane as a
line which does not meet the plane.
§ 73. Before we investigate the contents of Book XI., it will be
well to recapitulate shortly what we know of planes and lines from
the definitions and axioms of the first book. There a plane has
been defined as a surface which has the property that every straight
line which joins two points in it lies altogether in it. This is equivalent
to saying that a straight line which has two points in a plane
has all points in the plane. Hence, a straight line which does not
lie in the plane cannot have more than one point in common with
the plane. This is virtually the same as Euclid’s Prop. 1, viz.:—
Prop. 1. One part of a straight line cannot be in a plane and another
part without it.
It also follows, as was pointed out in § 3, in discussing the definitions
of Book I., that a plane is determined already by one straight
line and a point without it, viz. if all lines be drawn through the
point, and cutting the line, they will form a plane.
This may be stated thus:—
A plane is determined—
1st, By a straight line and a point which does not lie on it;
2nd, By three points which do not lie in a straight line; for if two
of these points be joined by a straight line we have case 1;
3rd, By two intersecting straight lines; for the point of intersection
and two other points, one in each line, give case 2;
4th, By two parallel lines (Def. 35, I.).
The third case of this theorem is Euclid’s
Prop. 2. Two straight lines which cut one another are in one plane,
and three straight lines which meet one another are in one plane.
And the fourth is Euclid’s
Prop. 7. If two straight lines be parallel, the straight line drawn
from any point in one to any point in the other is in the same plane
with the parallels. From the definition of a plane further follows
Prop. 3. If two planes cut one another, their common section is a
straight line.
§ 74. Whilst these propositions are virtually contained in the
definition of a plane, the next gives us a new and fundamental
property of space, showing at the same time that it is possible to
have a straight line perpendicular to a plane, according to Def. 3.
It states—
Prop. 4. If a straight line is perpendicular to two straight lines
in a plane which it meets, then it is perpendicular to all lines in the plane
which it meets, and hence it is perpendicular to the plane.
Def. 3 may be stated thus: If a straight line is perpendicular
to a plane, then it is perpendicular to every line in the plane which
it meets. The converse to this would be
All straight lines which meet a given straight line in the same point,
and are perpendicular to it, lie in a plane which is perpendicular to
that line.
This Euclid states thus:
Prop. 5. If three straight lines meet all at one point, and a straight
line stands at right angles to each of them at that point, the three straight
lines shall be in one and the same plane.
§ 75. There follow theorems relating to the theory of parallel
lines in space, viz.:—
Prop. 6. Any two lines which are perpendicular to the same plane
are parallel to each other; and conversely
Prop. 8. If of two parallel straight lines one is perpendicular to a
plane, the other is so also.
Prop. 7. If two straight lines are parallel, the straight line which
joins any point in one to any point in the other is in the same plane as
the parallels. (See above, § 73.)
Prop. 9. Two straight lines which are each of them parallel to the
same straight line, and not in the same plane with it, are parallel to
one another; where the words, “and not in the same plane with
it,” may be omitted, for they exclude the case of three parallels
in a plane, which has been proved before; and
Prop. 10. If two angles in different planes have the two limits of
the one parallel to those of the other, then the angles are equal. That
their planes are parallel is shown later on in Prop. 15.
This theorem is not necessarily true, for the angles in question
may be supplementary; but then the one angle will be equal to
that which is adjacent and supplementary to the other, and this
latter angle will also have its limits parallel to those of the first.
From this theorem it follows that if we take any two straight
lines in space which do not meet, and if we draw through any point
P in space two lines parallel to them, then the angle included by
these lines will always be the same, whatever the position of the
point P may be. This angle has in modern times been called the
angle between the given lines:—
By the angles between two not intersecting lines we understand the
angles which two intersecting lines include that are parallel respectively
to the two given lines.
§ 76. It is now possible to solve the following two problems:—
To draw a straight line perpendicular to a given plane from a given
point which lies
1. Not in the plane (Prop. 11).
2. In the plane (Prop. 12).
The second case is easily reduced to the first—viz. if by aid of
the first we have drawn any perpendicular to the plane from some
point without it, we need only draw through the given point in the
plane a line parallel to it, in order to have the required perpendicular
given. The solution of the first part is of interest in itself. It depends
upon a construction which may be expressed as a theorem.
If from a point A without a plane a perpendicular AB be drawn to the
plane, and if from the foot B of this perpendicular another perpendicular
BC be drawn to any straight line in the plane, then the straight line
joining A to the foot C of this second perpendicular will also be perpendicular
to the line in the plane.
The theory of perpendiculars to a plane is concluded by the
theorem—
Prop. 13. Through any point in space, whether in or without a
plane, only one straight line can be drawn perpendicular to the plane.
§ 77. The next four propositions treat of parallel planes. It is
shown that planes which have a common perpendicular are parallel
(Prop. 14); that two planes are parallel if two intersecting straight
lines in the one are parallel respectively to two straight lines in the
other plane (Prop. 15); that parallel planes are cut by any plane in
parallel straight lines (Prop. 16); and lastly, that any two straight
lines are cut proportionally by a series of parallel planes (Prop. 17).
This theory is made more complete by adding the following
theorems, which are easy deductions from the last: Two parallel
planes have common perpendiculars (converse to 14); and Two
planes which are parallel to a third plane are parallel to each other.
It will be noted that Prop. 15 at once allows of the solution of
the problem: “Through a given point to draw a plane parallel to
a given plane.” And it is also easily proved that this problem
allows always of one, and only of one, solution.
§ 78. We come now to planes which are perpendicular to one
another. Two theorems relate to them.
Prop. 18. If a straight line be at right angles to a plane, every
plane which passes through it shall be at right angles to that plane.
Prop. 19. If two planes which cut one another be each of them
perpendicular to a third plane, their common section shall be perpendicular
to the same plane.
§ 79. If three planes pass through a common point, and if they
bound each other, a solid angle of three faces, or a trihedral angle,
is formed, and similarly by more planes a solid angle of more faces,
or a polyhedral angle. These have many properties which are quite
analogous to those of triangles and polygons in a plane. Euclid
states some, viz.:—
Prop. 20. If a solid angle be contained by three plane angles, any
two of them are together greater than the third.
But the next—
Prop. 21. Every solid angle is contained by plane angles, which
are together less than four right angles—has no analogous theorem
in the plane.
We may mention, however, that the theorems about triangles
contained in the propositions of Book I., which do not depend
upon the theory of parallels (that is all up to Prop. 27), have their
corresponding theorems about trihedral angles. The latter are
formed, if for “side of a triangle” we write “plane angle” or
“face” of trihedral angle, and for “angle of triangle” we substitute
“angle between two faces” where the planes containing the
solid angle are called its faces. We get, for instance, from I. 4, the
687
theorem, If two trihedral angles have the angles of two faces in the one
equal to the angles of two faces in the other, and have likewise the angles
included by these faces equal, then the angles in the remaining faces are
equal, and the angles between the other faces are equal each to each, viz.
those which are opposite equal faces. The solid angles themselves are
not necessarily equal, for they may be only symmetrical like the
right hand and the left.
The connexion indicated between triangles and trihedral angles
will also be recognized in
Prop. 22. If every two of three plane angles be greater than the
third, and if the straight lines which contain them be all equal, a triangle
may be made of the straight lines that join the extremities of those equal
straight lines.
And Prop. 23 solves the problem, To construct a trihedral angle
having the angles of its faces equal to three given plane angles, any two
of them being greater than the third. It is, of course, analogous to the
problem of constructing a triangle having its sides of given length.
Two other theorems of this kind are added by Simson in his
edition of Euclid’s Elements.
§ 80. These are the principal properties of lines and planes in
space, but before we go on to their applications it will be well to
define the word distance. In geometry distance means always
“shortest distance”; viz. the distance of a point from a straight
line, or from a plane, is the length of the perpendicular from the
point to the line or plane. The distance between two non-intersecting
lines is the length of their common perpendicular, there being
but one. The distance between two parallel lines or between two
parallel planes is the length of the common perpendicular between
the lines or the planes.
§ 81. Parallelepipeds.—The rest of the book is devoted to the
study of the parallelepiped. In Prop. 24 the possibility of such
a solid is proved, viz.:—
Prop. 24. If a solid be contained by six planes two and two of
which are parallel, the opposite planes are similar and equal parallelograms.
Euclid calls this solid henceforth a parallelepiped, though he
never defines the word. Either face of it may be taken as base,
and its distance from the opposite face as altitude.
Prop. 25. If a solid parallelepiped be cut by a plane parallel to
two of its opposite planes, it divides the whole into two solids, the base
of one of which shall be to the base of the other as the one solid is to the
other.
This theorem corresponds to the theorem (VI. 1) that parallelograms
between the same parallels are to one another as their bases.
A similar analogy is to be observed among a number of the remaining
propositions.
§ 82. After solving a few problems we come to
Prop. 28. If a solid parallelepiped be cut by a plane passing
through the diagonals of two of the opposite planes, it shall be cut in
two equal parts.
In the proof of this, as of several other propositions, Euclid
neglects the difference between solids which are symmetrical like
the right hand and the left.
Prop. 31. Solid parallelepipeds, which are upon equal bases, and
of the same altitude, are equal to one another.
Props. 29 and 30 contain special cases of this theorem leading up
to the proof of the general theorem.
As consequences of this fundamental theorem we get
Prop. 32. Solid parallelepipeds, which have the same altitude, are
to one another as their bases; and
Prop. 33. Similar solid parallelepipeds are to one another in the
triplicate ratio of their homologous sides.
If we consider, as in § 67, the ratios of lines as numbers, we may
also say—
The ratio of the volumes of similar parallelepipeds is equal to the
ratio of the third powers of homologous sides.
Parallelepipeds which are not similar but equal are compared by
aid of the theorem
Prop. 34. The bases and altitudes of equal solid parallelepipeds
are reciprocally proportional; and if the bases and altitudes be reciprocally
proportional, the solid parallelepipeds are equal.
§ 83. Of the following propositions the 37th and 40th are of
special interest.
Prop. 37. If four straight lines be proportionals, the similar solid
parallelepipeds, similarly described from them, shall also be proportionals;
and if the similar parallelepipeds similarly described
from four straight lines be proportionals, the straight lines shall be
proportionals.
In symbols it says—
If a : b = c : d, then a³ : b³ = c³: d³.
Prop. 40 teaches how to compare the volumes of triangular
prisms with those of parallelepipeds, by proving that a triangular
prism is equal in volume to a parallelepiped, which has its altitude
and its base equal to the altitude and the base of the triangular
prism.
§ 84. From these propositions follow all results relating to the
mensuration of volumes. We shall state these as we did in the case
of areas. The starting-point is the “rectangular” parallelepiped,
which has every edge perpendicular to the planes it meets, and
which takes the place of the rectangle in the plane. If this has all
its edges equal we obtain the “cube.”
If we take a certain line u as unit length, then the square on u is
the unit of area, and the cube on u the unit of volume, that is to
say, if we wish to measure a volume we have to determine how
many unit cubes it contains.
A rectangular parallelepiped has, as a rule, the three edges unequal,
which meet at a point. Every other edge is equal to one
of them. If a, b, c be the three edges meeting at a point, then we
may take the rectangle contained by two of them, say by b and c,
as base and the third as altitude. Let V be its volume, V′ that of
another rectangular parallelepiped which has the edges a′, b, c,
hence the same base as the first. It follows then easily, from Prop.
25 or 32, that V : V′ = a : a′; or in words,
Rectangular parallelepipeds on equal bases are proportional to their
altitudes.
If we have two rectangular parallelepipeds, of which the first has
the volume V and the edges a, b, c, and the second, the volume V′
and the edges a′, b′, c′, we may compare them by aid of two new
ones which have respectively the edges a′, b, c and a′, b′, c, and the
volumes V1 and V2. We then have
V : V1 = a : a′; V1 : V2 = b : b′, V2 : V′ = c : c′.
Compounding these, we have
V : V′ = (a : a′) (b : b′) (c : c′),
or
| V |
= | a |
· | b |
· | c |
. |
| V′ | a′ |
b′ | c′ |
Hence, as a special case, making V′ equal to the unit cube U on u
we get
| V |
= | a |
· | b |
· | c |
= α·β·γ, |
| U | u |
u | u |
where α, β, γ are the numerical values of a, b, c; that is, The number
of unit cubes in a rectangular parallelepiped is equal to the product
of the numerical values of its three edges. This is generally expressed
by saying the volume of a rectangular parallelepiped is
measured by the product of its sides, or by the product of its base
into its altitude, which in this case is the same.
Prop. 31 allows us to extend this to any parallelepipeds, and Props.
28 or 40, to triangular prisms.
The volume of any parallelepiped, or of any triangular prism, is
measured by the product of base and altitude.
The consideration that any polygonal prism may be divided into
a number of triangular prisms, which have the same altitude and
the sum of their bases equal to the base of the polygonal prism,
shows further that the same holds for any prism whatever.
Book XII.
§ 85. In the last part of Book XI. we have learnt how to compare
the volumes of parallelepipeds and of prisms. In order to determine
the volume of any solid bounded by plane faces we must determine
the volume of pyramids, for every such solid may be decomposed
into a number of pyramids.
As every pyramid may again be decomposed into triangular
pyramids, it becomes only necessary to determine their volume.
This is done by the
Theorem.—Every triangular pyramid is equal in volume to one
third of a triangular prism having the same base and the same
altitude as the pyramid.
This is an immediate consequence of Euclid’s
Prop. 7. Every prism having a triangular base may be divided
into three pyramids that have triangular bases, and are equal to one
another.
The proof of this theorem is difficult, because the three triangular
pyramids into which the prism is divided are by no means equal in
shape, and cannot be made to coincide. It has first to be proved
that two triangular pyramids have equal volumes, if they have
equal bases and equal altitudes. This Euclid does in the following
manner. He first shows (Prop. 3) that a triangular pyramid may
be divided into four parts, of which two are equal triangular pyramids
similar to the whole pyramid, whilst the other two are equal triangular
prisms, and further, that these two prisms together are
greater than the two pyramids, hence more than half the given
pyramid. He next shows (Prop. 4) that if two triangular pyramids
are given, having equal bases and equal altitudes, and if each be
divided as above, then the two triangular prisms in the one are
equal to those in the other, and each of the remaining pyramids in
the one has its base and altitude equal to the base and altitude of
the remaining pyramids in the other. Hence to these pyramids the
same process is again applicable. We are thus enabled to cut out
of the two given pyramids equal parts, each greater than half the
original pyramid. Of the remainder we can again cut out equal
parts greater than half these remainders, and so on as far as we like.
This process may be continued till the last remainder is smaller
than any assignable quantity, however small. It follows, so we
should conclude at present, that the two volumes must be equal, for
they cannot differ by any assignable quantity.
To Greek mathematicians this conclusion offers far greater
688
difficulties. They prove elaborately, by a reductio ad absurdum,
that the volumes cannot be unequal. This proof must be read in
the Elements. We must, however, state that we have in the above
not proved Euclid’s Prop. 5, but only a special case of it. Euclid
does not suppose that the bases of the two pyramids to be compared
are equal, and hence he proves that the volumes are as the bases.
The reasoning of the proof becomes clearer in the special case, from
which the general one may be easily deduced.
§ 86. Prop. 6 extends the result to pyramids with polygonal
bases. From these results follow again the rules at present given
for the mensuration of solids, viz. a pyramid is the third part of a
triangular prism having the same base and the same altitude. But
a triangular prism is equal in volume to a parallelepiped which
has the same base and altitude. Hence if B is the base and h the
altitude, we have
| Volume of prism | = Bh, |
| Volume of pyramid | = 1⁄3Bh, |
statements which have to be taken in the sense that B means the
number of square units in the base, h the number of units of length
in the altitude, or that B and h denote the numerical values of base
and altitude.
§ 87. A method similar to that used in proving Prop. 5 leads to
the following results relating to solids bounded by simple curved
surfaces:—
Prop. 10. Every cone is the third part of a cylinder which has the
same base, and is of an equal altitude with it.
Prop. 11. Cones or cylinders of the same altitude are to one another
as their bases.
Prop. 12. Similar cones or cylinders have to one another the triplicate
ratio of that which the diameters of their bases have.
Prop. 13. If a cylinder be cut by a plane parallel to its opposite
planes or bases, it divides the cylinder into two cylinders, one of which
is to the other as the axis of the first to the axis of the other; which
may also be stated thus:—
Cylinders on the same base are proportional to their altitudes.
Prop. 14. Cones or cylinders upon equal bases are to one another
as their altitudes.
Prop. 15. The bases and altitudes of equal cones or cylinders are
reciprocally proportional, and if the bases and altitudes be reciprocally
proportional, the cones or cylinders are equal to one another.
These theorems again lead to formulae in mensuration, if we
compare a cylinder with a prism having its base and altitude equal to
the base and altitude of the cylinder. This may be done by the
method of exhaustion. We get, then, the result that their bases are
equal, and have, if B denotes the numerical value of the base, and
h that of the altitude,
| Volume of cylinder | = Bh, |
| Volume of cone | = 1⁄3Bh. |
§ 88. The remaining propositions relate to circles and spheres.
Of the sphere only one property is proved, viz.:—
Prop. 18. Spheres have to one another the triplicate ratio of that
which their diameters have. The mensuration of the sphere, like
that of the circle, the cylinder and the cone, had not been settled
in the time of Euclid. It was done by Archimedes.
Book XIII.
§ 89. The 13th and last book of Euclid’s Elements is devoted to
the regular solids (see Polyhedron). It is shown that there are
five of them, viz.:—
1. The regular tetrahedron, with 4 triangular faces and 4 vertices;
2. The cube, with 8 vertices and 6 square faces;
3. The octahedron, with 6 vertices and 8 triangular faces;
4. The dodecahedron, with 12 pentagonal faces, 3 at each of the
20 vertices;
5. The icosahedron, with 20 triangular faces, 5 at each of the
12 vertices.
It is shown how to inscribe these solids in a given sphere, and
how to determine the lengths of their edges.
§ 90. The 13th book, and therefore the Elements, conclude with
the scholium, “that no other regular solid exists besides the five
ones enumerated.”
The proof is very simple. Each face is a regular polygon, hence
the angles of the faces at any vertex must be angles in equal regular
polygons, must be together less than four right angles (XI. 21), and
must be three or more in number. Each angle in a regular triangle
equals two-thirds of one right angle. Hence it is possible to form
a solid angle with three, four or five regular triangles or faces.
These give the solid angles of the tetrahedron, the octahedron and
the icosahedron. The angle in a square (the regular quadrilateral)
equals one right angle. Hence three will form a solid angle, that
of the cube, and four will not. The angle in the regular pentagon
equals 6⁄5 of a right angle. Hence three of them equal 18⁄5 (i.e. less
than 4) right angles, and form the solid angle of the dodecahedron.
Three regular polygons of six or more sides cannot form a solid
angle. Therefore no other regular solids are possible.
(O. H.)
II. Projective Geometry
It is difficult, at the outset, to characterize projective geometry
as compared with Euclidean. But a few examples will at least
indicate the practical differences between the two.
In Euclid’s Elements almost all propositions refer to the magnitude
of lines, angles, areas or volumes, and therefore to measurement.
The statement that an angle is right, or that two straight
lines are parallel, refers to measurement. On the other hand,
the fact that a straight line does or does not cut a circle is independent
of measurement, it being dependent only upon the
mutual “position” of the line and the circle. This difference
becomes clearer if we project any figure from one plane to another
(see Projection). By this the length of lines, the magnitude
of angles and areas, is altered, so that the projection, or shadow,
of a square on a plane will not be a square; it will, however,
be some quadrilateral. Again, the projection of a circle will not
be a circle, but some other curve more or less resembling a circle.
But one property may be stated at once—no straight line can cut
the projection of a circle in more than two points, because no
straight line can cut a circle in more than two points. There
are, then, some properties of figures which do not alter by
projection, whilst others do. To the latter belong nearly all
properties relating to measurement, at least in the form in which
they are generally given. The others are said to be projective
properties, and their investigation forms the subject of projective
geometry.
Different as are the kinds of properties investigated in the old
and the new sciences, the methods followed differ in a still
greater degree. In Euclid each proposition stands by itself;
its connexion with others is never indicated; the leading ideas
contained in its proof are not stated; general principles do not
exist. In the modern methods, on the other hand, the greatest
importance is attached to the leading thoughts which pervade
the whole; and general principles, which bring whole groups of
theorems under one aspect, are given rather than separate propositions.
The whole tendency is towards generalization.
A straight line is considered as given in its entirety, extending
both ways to infinity, while Euclid never admits anything but
finite quantities. The treatment of the infinite is in fact another
fundamental difference between the two methods: Euclid avoids
it; in modern geometry it is systematically introduced.
Of the different modern methods of geometry, we shall treat
principally of the methods of projection and correspondence which
have proved to be the most powerful. These have become independent
of Euclidean Geometry, especially through the Geometrie
der Lage of V. Staudt and the Ausdehnungslehre of Grassmann.
For the sake of brevity we shall presuppose a knowledge of
Euclid’s Elements, although we shall use only a few of his propositions.
§ 1. Geometrical Elements. We consider space as filled with points,
lines and planes, and these we call the elements out of which our
figures are to be formed, calling any combination of these elements a
“figure.”
By a line we mean a straight line in its entirety, extending both
ways to infinity; and by a plane, a plane surface, extending in all
directions to infinity.
We accept the three-dimensional space of experience—the space
assumed by Euclid—which has for its properties (among others):—
Through any two points in space one and only one line may be
drawn;
Through any three points which are not in a line, one and only one
plane may be placed;
The intersection of two planes is a line;
A line which has two points in common with a plane lies in the
plane, hence the intersection of a line and a plane is a single point; and
Three planes which do not meet in a line have one single point in
common.
These results may be stated differently in the following form:—
I. A plane is determined— |
A point is determined— |
1. By three points which do not lie in a line;
2. By two intersecting lines;
3. By a line and a point which does not lie in it. |
1. By three planes which do not pass through a line;
2. By two intersecting lines
3. By a plane and a line which does not lie in it. |
A line is determined— |
|
1. By two points; |
2. By two planes. |
689
It will be observed that not only are planes determined by points,
but also points by planes; that therefore the planes may be considered
as elements, like points; and also that in any one of the
above statements we may interchange the words point and plane,
and we obtain again a correct statement, provided that these
statements themselves are true. As they stand, we ought, in
several cases, to add “if they are not parallel,” or some such words,
parallel lines and planes being evidently left altogether out of
consideration. To correct this we have to reconsider the theory of
parallels.
 |
| Fig. 1. |
§ 2. Parallels. Point at Infinity.—Let us take in a plane a line p
(fig. 1), a point S not in this line, and a line q drawn through S.
Then this line q will meet
the line p in a point A. If
we turn the line q about S
towards q’, its point of
intersection with p will
move along p towards B,
passing, on continued turning,
to a greater and greater
distance, until it is moved
out of our reach. If we
turn q still farther, its continuation
will meet p, but
now at the other side of
A. The point of intersection
has disappeared to
the right and reappeared
to the left. There is one intermediate position where q is parallel
to p—that is where it does not cut p. In every other position it
cuts p in some finite point. If, on the other hand, we move the point
A to an infinite distance in p, then the line q which passes through
A will be a line which does not cut p at any finite point. Thus we
are led to say: Every line through S which joins it to any point
at an infinite distance in p is parallel to p. But by Euclid’s 12th
axiom there is but one line parallel to p through S. The difficulty in
which we are thus involved is due to the fact that we try to reason
about infinity as if we, with our finite capabilities, could comprehend
the infinite. To overcome this difficulty, we may say that all points
at infinity in a line appear to us as one, and may be replaced by a
single “ideal” point.
We may therefore now give the following definitions and axiom:—
Definition.—Lines which meet at infinity are called parallel.
Axiom.—All points at an infinite distance in a line may be considered
as one single point.
Definition.—This ideal point is called the point at infinity in the
line.
The axiom is equivalent to Euclid’s Axiom 12, for it follows from
either that through any point only one line may be drawn parallel
to a given line.
This point at infinity in a line is reached whether we move a
point in the one or in the opposite direction of a line to infinity.
A line thus appears closed by this point, and we speak as if we
could move a point along the line from one position A to another
B in two ways, either through the point at infinity or through finite
points only.
It must never be forgotten that this point at infinity is ideal;
in fact, the whole notion of “infinity” is only a mathematical
conception, and owes its introduction (as a method of research) to
the working generalizations which it permits.
§ 3. Line and Plane at Infinity.—Having arrived at the notion of
replacing all points at infinity in a line by one ideal point, there is no
difficulty in replacing all points at infinity in a plane by one ideal
line.
To make this clear, let us suppose that a line p, which cuts two
fixed lines a and b in the points A and B, moves parallel to itself
to a greater and greater distance. It will at last cut both a and
b at their points at infinity, so that a line which joins the two points
at infinity in two intersecting lines lies altogether at infinity. Every
other line in the plane will meet it therefore at infinity, and thus it
contains all points at infinity in the plane.
All points at infinity in a plane lie in a line, which is called the line
at infinity in the plane.
It follows that parallel planes must be considered as planes
having a common line at infinity, for any other plane cuts them in
parallel lines which have a point at infinity in common.
If we next take two intersecting planes, then the point at infinity
in their line of intersection lies in both planes, so that their lines
at infinity meet. Hence every line at infinity meets every other
line at infinity, and they are therefore all in one plane.
All points at infinity in space may be considered as lying in one
ideal plane, which is called the plane at infinity.
§ 4. Parallelism.—We have now the following definitions:—
Parallel lines are lines which meet at infinity;
Parallel planes are planes which meet at infinity;
A line is parallel to a plane if it meets it at infinity.
Theorems like this—Lines (or planes) which are parallel to a third
are parallel to each other—follow at once.
This view of parallels leads therefore to no contradiction of
Euclid’s Elements.
As immediate consequences we get the propositions:—
Every line meets a plane in one point, or it lies in it;
Every plane meets every other plane in a line;
Any two lines in the same plane meet.
§ 5. Aggregates of Geometrical Elements.—We have called points,
lines and planes the elements of geometrical figures. We also say
that an element of one kind contains one of the other if it lies in it
or passes through it.
All the elements of one kind which are contained in one or two
elements of a different kind form aggregates which have to be
enumerated. They are the following:—
I. Of one dimension.
1. The row, or range, of points formed by all points in a line,
which is called its base.
2. The flat pencil formed by all the lines through a point in
a plane. Its base is the point in the plane.
3. The axial pencil formed by all planes through a line
which is called its base or axis.
II. Of two dimensions.
1. The field of points and lines—that is, a plane with all its
points and all its lines.
2. The pencil of lines and planes—that is, a point in space
with all lines and all planes through it.
III. Of three dimensions.
The space of points—that is, all points in space.
The space of planes—that is, all planes in space.
IV. Of four dimensions.
The space of lines, or all lines in space.
§ 6. Meaning of “Dimensions.”—The word dimension in the above
needs explanation. If in a plane we take a row p and a pencil with
centre Q, then through every point in p one line in the pencil will
pass, and every ray in Q will cut p in one point, so that we are
entitled to say a row contains as many points as a flat pencil lines,
and, we may add, as an axial pencil planes, because an axial pencil
is cut by a plane in a flat pencil.
The number of elements in the row, in the flat pencil, and in the
axial pencil is, of course, infinite and indefinite too, but the same in
all. This number may be denoted by ∞. Then a plane contains
∞² points and as many lines. To see this, take a flat pencil in a
plane. It contains ∞ lines, and each line contains ∞ points, whilst
each point in the plane lies on one of these lines. Similarly, in a
plane each line cuts a fixed line in a point. But this line is cut at
each point by ∞ lines and contains ∞ points; hence there are ∞²
lines in a plane.
A pencil in space contains as many lines as a plane contains
points and as many planes as a plane contains lines, for any plane
cuts the pencil in a field of points and lines. Hence a pencil contains
∞² lines and ∞² planes. The field and the pencil are of two
dimensions.
To count the number of points in space we observe that each
point lies on some line in a pencil. But the pencil contains ∞²
lines, and each line ∞ points; hence space contains ∞³ points.
Each plane cuts any fixed plane in a line. But a plane contains
∞² lines, and through each pass ∞ planes; therefore space contains
∞³ planes.
Hence space contains as many planes as points, but it contains
an infinite number of times more lines than points or planes. To
count them, notice that every line cuts a fixed plane in one point.
But ∞² lines pass through each point, and there are ∞² points in the
plane. Hence there are ∞4 lines in space. The space of points
and planes is of three dimensions, but the space of lines is of four
dimensions.
A field of points or lines contains an infinite number of rows and
flat pencils; a pencil contains an infinite number of flat pencils
and of axial pencils; space contains a triple infinite number of
pencils and of fields, ∞4 rows and axial pencils and ∞5 flat pencils—or,
in other words, each point is a centre of ∞² flat pencils.
§ 7. The above enumeration allows a classification of figures.
Figures in a row consist of groups of points only, and figures in
the flat or axial pencil consist of groups of lines or planes. In the
plane we may draw polygons; and in the pencil or in the point,
solid angles, and so on.
We may also distinguish the different measurements We have—
In the row, length of segment;
In the flat pencil, angles;
In the axial pencil, dihedral angles between two planes;
In the plane, areas;
In the pencil, solid angles;
In the space of points or planes, volumes.
|
Segments of a Line
§ 8. Any two points A and B in space determine on the line through
them a finite part, which may be considered as being described by
a point moving from A to B. This we shall denote by AB, and
distinguish it from BA, which is supposed as being described by a
point moving from B to A, and hence in a direction or in a “sense”
opposite to AB. Such a finite line, which has a definite sense, we
shall call a “segment,” so that AB and BA denote different segments,
which are said to be equal in length but of opposite sense. The one
sense is often called positive and the other negative.
690
In introducing the word “sense” for direction in a line, we have
the word direction reserved for direction of the line itself, so that
different lines have different directions, unless they be parallel,
whilst in each line we have a positive and negative sense.
We may also say, with Clifford, that AB denotes the “step” of
going from A to B.
 |
| Fig. 2. |
§ 9. If we have three points A, B, C in a line (fig. 2), the step AB
will bring us from A to B, and the step
BC from B to C. Hence both steps are
equivalent to the one step AC. This is
expressed by saying that AC is the
“sum” of AB and BC; in symbols—
AB + BC = AC,
where account is to be taken of the
sense.
This equation is true whatever be the
position of the three points on the line.
As a special case we have
AB + BA = 0,
(1)
and similarly
AB + BC + CA = 0,
(2)
which again is true for any three points in a line.
We further write
AB = −BA.
where − denotes negative sense.
We can then, just as in algebra, change subtraction of segments
into addition by changing the sense, so that AB − CB is the same
as AB + (−CB) or AB + BC. A figure will at once show the truth
of this. The sense is, in fact, in every respect equivalent to the
“sign” of a number in algebra.
§ 10. Of the many formulae which exist between points in a line
we shall have to use only one more, which connects the segments
between any four points A, B, C, D in a line. We have
BC = BD + DC, CA = CD + DA, AB = AD + DB;
or multiplying these by AD, BD, CD respectively, we get
BC · AD = BD · AD + DC · AD = BD · AD − CD · AD
CA · BD = CD · BD + DA · BD = CD · BD − AD · BD
AB · CD = AD · CD + DB · CD = AD · CD − BD · CD.
|
It will be seen that the sum of the right-hand sides vanishes, hence
that
BC · AD + CA · BD + AB · CD = 0
(3)
for any four points on a line.
 |
| Fig. 3. |
§ 11. If C is any point in the line AB, then we say that C divides
the segment AB in the ratio AC/CB, account being taken of the
sense of the two segments AC and CB. If C lies between A and B
the ratio is positive, as AC and CB have the same sense. But if
C lies without the segment AB, i.e. if C divides AB externally, then
the ratio is negative.
To see how the value of
this ratio changes with
C, we will move C along
the whole line (fig. 3),
whilst A and B remain fixed. If C lies at the point A, then AC = 0,
hence the ratio AC : CB vanishes. As C moves towards B, AC
increases and CB decreases, so that our ratio increases. At the
middle point M of AB it assumes the value +1, and then increases
till it reaches an infinitely large value, when C arrives at B. On
passing beyond B the ratio becomes negative. If C is at P we have
AC = AP = AB + BP, hence
| AC |
= | AB |
+ | BP |
= − | AB |
− 1. |
| CB | PB |
PB | BP |
In the last expression the ratio AB : BP is positive, has its greatest
value ∞ when C coincides with B, and vanishes when BC becomes
infinite. Hence, as C moves from B to the right to the point at
infinity, the ratio AC : CB varies from −∞ to −1.
If, on the other hand, C is to the left of A, say at Q, we have
AC = AQ = AB + BQ = AB − QB, hence AC/CB = AB/QB − 1.
Here AB < QB, hence the ratio AB : QB is positive and always
less than one, so that the whole is negative and < 1. If C is at
the point at infinity it is −1, and then increases as C moves to the
right, till for C at A we get the ratio = 0. Hence—
“As C moves along the line from an infinite distance to the left to
an infinite distance at the right, the ratio always increases; it starts
with the value −1, reaches 0 at A, +1 at M, ∞ at B, now changes
sign to −∞, and increases till at an infinite distance it reaches
again the value −1. It assumes therefore all possible values from
-∞ to +∞, and each value only once, so that not only does every
position of C determine a definite value of the ratio AC : CB, but also,
conversely, to every positive or negative value of this ratio belongs one
single point in the line AB.
[Relations between segments of lines are interesting as showing an
application of algebra to geometry. The genesis of such relations
from algebraic identities is very simple. For example, if a, b, c, x
be any four quantities, then
| a |
+ | b |
+ | c |
= | x |
; |
| (a − b)(a − c)(x − a) | (b − c)(b − a)(x − b) |
(c − a)(c − b)(x − c) | (x − a)(x − b)(x − c) |
this may be proved, cumbrously, by multiplying up, or, simply, by
decomposing the right-hand member of the identity into partial
fractions. Now take a line ABCDX, and let AB = a, AC = b, AD = c,
AX = x. Then obviously (a − b) = AB − AC = −BC, paying regard
to signs; (a − c) = AB − AD = DB, and so on. Substituting these
values in the identity we obtain the following relation connecting
the segments formed by five points on a line:—
| AB |
+ | AC |
+ | AD |
= | AX |
. |
| BC · BD · BX | CD · CB · CX |
DB · DC · DX | BX · CX · DX |
Conversely, if a metrical relation be given, its validity may be
tested by reducing to an algebraic equation, which is an identity
if the relation be true. For example, if ABCDX be five collinear
points, prove
| AD · AX |
+ | BD · BX |
+ | CD · CX |
= 1. |
| AB · AC | BC · BA |
CA · CB |
Clearing of fractions by multiplying throughout by AB · BC · CA,
we have to prove
−AD · AX · BC − BD · BX · CA − CD · CX · AB = AB · BC · CA.
Take A as origin and let AB = a, AC = b, AD = c, AX = x. Substituting
for the segments in terms of a, b, c, x, we obtain on simplification
a²b − ab² = −ab² + a²b, an obvious identity.
An alternative method of testing a relation is illustrated in the
following example:— If A, B, C, D, E, F be six collinear points,
then
| AE · AF |
+ | BE · BF |
+ | CE · CF |
+ | DE · DF |
= 0. |
| AB · AC · AD | BC · BD · BA |
CD · CA · CB | DA · DB · DC |
Clearing of fractions by multiplying throughout by AB · BC · CD · DA,
and reducing to a common origin O (calling OA = a, OB = b, &c.),
an equation containing the second and lower powers of OA ( = a),
&c., is obtained. Calling OA = x, it is found that x = b, x = c, x = d
are solutions. Hence the quadratic has three roots; consequently
it is an identity.
The relations connecting five points which we have instanced above
may be readily deduced from the six-point relation; the first by
taking D at infinity, and the second by taking F at infinity, and then
making the obvious permutations of the points.]
Projection and Cross-ratios
§ 12. If we join a point A to a point S, then the point where the
line SA cuts a fixed plane π is called the projection of A on the
plane π from S as centre of projection. If we have two planes π
and π′ and a point S, we may project every point A in π to the
other plane. If A′ is the projection of A, then A is also the projection
of A′, so that the relations are reciprocal. To every figure
in π we get as its projection a corresponding figure in π′.
We shall determine such properties of figures as remain true for
the projection, and which are called projective properties. For this
purpose it will be sufficient to consider at first only constructions in
one plane.
 |
| Fig. 4. |
Fig. 5. |
Let us suppose we have given in a plane two lines p and p′ and a
centre S (fig. 4); we may then project the points in p from S to p′.
Let A′, B′ ... be the projections of A, B ..., the point at infinity in
p which we shall denote by I will be projected into a finite point
691
I′ in p′, viz. into the point where the parallel to p through S cuts
p′. Similarly one point J in p will be projected into the point
J′ at infinity in p′. This point J is of course the point where the
parallel to p′ through S cuts p. We thus see that every point in p
is projected into a single point in p′.
Fig. 5 shows that a segment AB will be projected into a segment
A′B′ which is not equal to it, at least not as a rule; and
also that the ratio AC : CB is not equal to the ratio
A′C′ : C′B′ formed by the projections. These ratios
will become equal only if p and p′ are parallel, for
in this case the triangle SAB is similar to the triangle
SA′B′. Between three points in a line and their projections
there exists therefore in general no relation.
But between four points a relation does exist.
§ 13. Let A, B, C, D be four points in p, A′, B′,
C, D′ their projections in p′, then the ratio of the two
ratios AC : CB and AD : DB into which C and D
divide the segment AB is equal to the corresponding
expression between A′, B′, C′, D′. In symbols we have
| AC |
: | AD |
= | A′C′ |
: | A′D′ |
. |
| CB | DB |
C′B′ | D′B′ |
This is easily proved by aid of similar triangles.
 |
| Fig. 6. |
Through the points A and B on p draw parallels to p′, which cut
the projecting rays in
C2, D2, B2 and A1, C1,
D1, as indicated in
fig. 6. The two triangles
ACC2 and BCC1 will be
similar, as will also be
the triangles ADD2 and
BDD1.
The proof is left to
the reader.
This result is of fundamental
importance.
The expression
AC/CB : AD/DB has been
called by Chasles the
“anharmonic ratio of the
four points A, B, C, D.”
Professor Clifford proposed
the shorter name of “cross-ratio.” We shall adopt the
latter. We have then the
Fundamental Theorem.—The cross-ratio of four points in a
line is equal to the cross-ratio of their projections on any other line
which lies in the same plane with it.
§ 14. Before we draw conclusions from this result, we must investigate
the meaning of a cross-ratio somewhat more fully.
If four points A, B, C, D are given, and we wish to form their
cross-ratio, we have first to divide them into two groups of two,
the points in each group being taken in a definite order. Thus,
let A, B be the first, C, D the second pair, A and C being the first
points in each pair. The cross-ratio is then the ratio AC : CB
divided by AD : DB. This will be denoted by (AB, CD), so that
| (AB, CD) = | AC |
: | AD |
. |
| CB | DB |
This is easily remembered. In order to write it out, make first
the two lines for the fractions, and put above and below these
the letters A and B in their places, thus, A/*B : A/*B; and then fill
up, crosswise, the first by C and the other by D.
§ 15. If we take the points in a different order, the value of the
cross-ratio will change. We can do this in twenty-four different
ways by forming all permutations of the letters. But of these
twenty-four cross-ratios groups of four are equal, so that there are
really only six different ones, and these six are reciprocals in pairs.
We have the following rules:—
I. If in a cross-ratio the two groups be interchanged, its value
remains unaltered, i.e.
(AB, CD) = (CD, AB) = (BA, DC) = (DC, BA).
II. If in a cross-ratio the two points belonging to one of the two
groups be interchanged, the cross-ratio changes into its reciprocal, i.e.
(AB, CD) = 1/(AB, DC) = 1/(BA, CD) = 1/(CD, BA) = 1/(DC, AB).
From I. and II. we see that eight cross-ratios are associated with
(AB, CD).
III. If in a cross-ratio the two middle letters be interchanged,
the cross-ratio α changes into its complement 1 − α, i.e. (AB, CD) =
1 − (AC, BD).
[§ 16. If λ = (AB, CD), μ = (AC, DB), ν = (AD, BC), then λ, μ, ν
and their reciprocals 1/λ, 1/μ, 1/ν are the values of the total number
of twenty-four cross-ratios. Moreover, λ, μ, ν are connected by the
relations
λ + 1/μ = μ + 1/ν = ν + 1/λ =
−λμν = 1;
this proposition may be proved by substituting for λ, μ, ν and
reducing to a common origin. There are therefore four equations
between three unknowns; hence if one cross-ratio be given, the
remaining twenty-three are determinate. Moreover, two of the
quantities λ, μ, ν are positive, and the remaining one negative.
The following scheme shows the twenty-four cross-ratios expressed
in terms of λ, μ, ν.]
(AB, CD)
(BA, DC)
(CD, AB)
(DC, BA) | λ | 1 − μ | 1/(1 − ν) |
(AD, BC)
(BC, AD)
(CB, DA)
(DA, CB) | (λ − 1)/λ | μ/(μ − 1) | ν |
(AC, DB)
(BD, CA)
(CA, BD)
(DB, AC) | 1/(1 − λ) | 1/μ | (ν − 1)/ν |
(AC, BD)
(BD, AC)
(CA, DB)
(DB, CA) | 1 − λ | μ | ν/(ν − 1) |
(AB, DC)
(BA, CD)
(CD, BA)
(DC, AB) | 1/λ | 1/(1 − μ) | 1 − ν |
(AD, CB)
(BC, DA)
(CB, AD)
(DA, BC) | λ/(λ − 1) | (μ − 1)/μ | 1/ν |
§ 17. If one of the points of which a cross-ratio is formed is the
point at infinity in the line, the cross-ratio changes into a simple
ratio. It is convenient to let the point at infinity occupy the last
place in the symbolic expression for the cross-ratio. Thus if I is a
point at infinity, we have (AB, CI) = −AC/CB, because AI : IB = −1.
Every common ratio of three points in a line may thus be expressed
as a cross-ratio, by adding the point at infinity to the group
of points.
Harmonic Ranges
§ 18. If the points have special positions, the cross-ratios may
have such a value that, of the six different ones, two and two become
equal. If the first two shall be equal, we get λ = 1/λ, or λ² = 1,
λ = ±1.
If we take λ = +1, we have (AB, CD) = 1, or AC/CB = AD/DB;
that is, the points C and D coincide, provided that A and B are
different.
If we take λ = −1, so that (AB, CD) = −1, we have AC/CB =
−AD/DB. Hence C and D divide AB internally and externally in the
same ratio.
The four points are in this case said to be harmonic points, and
C and D are said to be harmonic conjugates with regard to A and B.
But we have also (CD, AB) = −1, so that A and B are harmonic
conjugates with regard to C and D.
The principal property of harmonic points is that their cross-ratio
remains unaltered if we interchange the two points belonging to one
pair, viz.
(AB, CD) = (AB, DC) = (BA, CD).
For four harmonic points the six cross-ratios become equal two
and two:
| λ = −1, 1 − λ = 2, | λ |
= ½, | 1 |
= −1, | 1 |
= ½, | λ − 1 |
= 2. |
| λ − 1 | λ |
1 − λ | λ |
Hence if we get four points whose cross-ratio is 2 or ½, then they
are harmonic, but not arranged so that conjugates are paired. If
this is the case the cross-ratio = −1.
§ 19. If we equate any two of the above six values of the cross-ratios,
we get either λ = 1, 0, ∞, or λ = −1, 2, ½, or else λ becomes
a root of the equation λ² − λ + 1 = 0, that is, an imaginary cube root of
−1. In this case the six values become three and three equal, so
that only two different values remain. This case, though important
in the theory of cubic curves, is for our purposes of no interest,
whilst harmonic points are all-important.
§ 20. From the definition of harmonic points, and by aid of § 11,
the following properties are easily deduced.
If C and D are harmonic conjugates with regard to A and B,
then one of them lies in, the other without AB; it is impossible
to move from A to B without passing either through C or through
D; the one blocks the finite way, the other the way through infinity.
This is expressed by saying A and B are “separated” by
C and D.
For every position of C there will be one and only one point
D which is its harmonic conjugate with regard to any point pair
A, B.
If A and B are different points, and if C coincides with A or B,
D does. But if A and B coincide, one of the points C or D, lying
between them, coincides with them, and the other may be anywhere
in the line. It follows that, “if of four harmonic conjugates two
coincide, then a third coincides with them, and the fourth may be any
point in the line.”
If C is the middle point between A and B, then D is the point at
infinity; for AC : CB = +1, hence AD : DB must be equal to −1.
The harmonic conjugate of the point at infinity in a line with regard
to two points A, B is the middle point of AB.
This important property gives a first example how metric properties
are connected with projective ones.
[§ 21. Harmonic properties of the complete quadrilateral and quadrangle.
692
 |
| Fig. 7. |
Fig. 8. |
A figure formed by four lines in a plane is called a complete quadrilateral,
or, shorter, a four-side. The four sides meet in six points,
named the “vertices,” which may be joined by three lines (other
than the sides), named the “diagonals” or “harmonic lines.” The
diagonals enclose the “harmonic triangle of the quadrilateral.” In
fig. 7, A′B′C′, B′AC, C′AB, CBA′ are the sides, A, A′, B, B′, C, C′
the vertices, AA′, BB′, CC′ the harmonic lines, and αβγ the harmonic
triangle of the quadrilateral. A figure formed by four coplanar
points is named a complete quadrangle, or, shorter, a four-point.
The four points may be joined by six lines, named the “sides,”
which intersect in three other points, termed the “diagonal or
harmonic points.” The harmonic points are the vertices of the
“harmonic triangle of the complete quadrangle.” In fig. 8, AA′,
BB′ are the points, AA′, BB′, A′B′, B′A, AB, BA′ are the sides,
L, M, N are the diagonal points, and LMN is the harmonic triangle
of the quadrangle.
The harmonic property of the complete quadrilateral is: Any
diagonal or harmonic line is harmonically divided by the other
two; and of a complete quadrangle: The angle at any harmonic
point is divided harmonically by the joins to the other harmonic
points. To prove the first theorem, we have to prove (AA′, βγ),
(BB′, γα), (CC′, βα) are harmonic. Consider the cross-ratio (CC′, αβ).
Then projecting from A on BB′ we have A(CC′, αβ) = A(B′B, αγ).
Projecting from A′ on BB′, A′(CC′, αβ) = A′(BB′, αγ). Hence
(B′B, αγ) = (BB′, αγ), i.e. the cross-ratio (BB′, αγ) equals that of its
reciprocal; hence the range is harmonic.
The second theorem states that the pencils L(BA, NM), M(B′A, LN),
N(BA, LM) are harmonic. Deferring the subject of harmonic pencils
to the next section, it will suffice to state here that any transversal
intersects an harmonic pencil in an harmonic range. Consider the
pencil L(BA, NM), then it is sufficient to prove (BA′, NM′) is harmonic.
This follows from the previous theorem by considering A′B
as a diagonal of the quadrilateral ALB′M.]
This property of the complete quadrilateral allows the solution
of the problem:
To construct the harmonic conjugate D to a point C with regard to two
given points A and B.
Through A draw any two lines, and through C one cutting the
former two in G and H. Join these points to B, cutting the former
two lines in E and F. The point D where EF cuts AB will be the
harmonic conjugate required.
This remarkable construction requires nothing but the drawing
of lines, and is therefore independent of measurement. In a similar
manner the harmonic conjugate of the line VA for two lines VC,
VD is constructed with the aid of the property of the complete
quadrangle.
§ 22. Harmonic Pencils.—The theory of cross-ratios may be extended
from points in a row to lines in a flat pencil and to planes in
an axial pencil. We have seen (§ 13) that if the lines which join four
points A, B, C, D to any point S be cut by any other line in A′, B′, C′,
D′, then (AB, CD) = (A′B′, C′D′). In other words, four lines in a
flat pencil are cut by every other line in four points whose cross-ratio
is constant.
Definition.—By the cross-ratio of four rays in a flat pencil is
meant the cross-ratio of the four points in which the rays are cut
by any line. If a, b, c, d be the lines, then this cross-ratio is denoted
by (ab, cd).
Definition.—By the cross-ratio of four planes in an axial pencil
is understood the cross-ratio of the four points in which any line
cuts the planes, or, what is the same thing, the cross-ratio of the
four rays in which any plane cuts the four planes.
In order that this definition may have a meaning, it has to be
proved that all lines cut the pencil in points which have the same
cross-ratio. This is seen at once for two intersecting lines, as their
plane cuts the axial pencil in a flat pencil, which is itself cut by
the two lines. The cross-ratio of the four points on one line is
therefore equal to that on the other, and equal to that of the four
rays in the flat pencil.
If two non-intersecting lines p and q cut the four planes in A, B,
C, D and A′, B′, C′, D′, draw a line r to meet both p and q, and
let this line cut the planes in A″, B″, C″, D″. Then (AB, CD) =
(A′B′, C′D′), for each is equal to (A″B″, C″D″).
§ 23. We may now also extend the notion of harmonic elements,
viz.
Definition.—Four rays in a flat pencil and four planes in an axial
pencil are said to be harmonic if their cross-ratio equals -1, that is,
if they are cut by a line in four harmonic points.
If we understand by a “median line” of a triangle a line which
joins a vertex to the middle point of the opposite side, and by a
“median line” of a parallelogram a line joining middle points of
opposite sides, we get as special cases of the last theorem:
The diagonals and median lines of a parallelogram form an harmonic
pencil; and
At a vertex of any triangle, the two sides, the median line, and the
line parallel to the base form an harmonic pencil.
Taking the parallelogram a rectangle, or the triangle isosceles,
we get:
Any two lines and the bisections of their angles form an harmonic
pencil. Or:
In an harmonic pencil, if two conjugate rays are perpendicular,
then the other two are equally inclined to them; and, conversely, if
one ray bisects the angle between conjugate rays, it is perpendicular to
its conjugate.
This connects perpendicularity and bisection of angles with
projective properties.
§ 24. We add a few theorems and problems which are easily proved
or solved by aid of harmonics.
An harmonic pencil is cut by a line parallel to one of its rays in
three equidistant points.
Through a given point to draw a line such that the segment
determined on it by a given angle is bisected at that point.
Having given two parallel lines, to bisect on either any given
segment without using a pair of compasses.
Having given in a line a segment and its middle point, to draw
through any given point in the plane a line parallel to the given line.
To draw a line which joins a given point to the intersection of two
given lines which meet off the drawing paper (by aid of § 21).
Correspondence. Homographic and Perspective Ranges
§ 25. Two rows, p and p′, which are one the projection of the
other (as in fig. 5), stand in a definite relation to each other, characterized
by the following properties.
1. To each point in either corresponds one point in the other; that
is, those points are said to correspond which are projections of one
another.
2. The cross-ratio of any four points in one equals that of the corresponding
points in the other.
3. The lines joining corresponding points all pass through the same
point.
If we suppose corresponding points marked, and the rows brought
into any other position, then the lines joining corresponding points
will no longer meet in a common point, and hence the third of the
above properties will not hold any longer; but we have still a
correspondence between the points in the two rows possessing the first
two properties. Such a correspondence has been called a one-one
correspondence, whilst the two rows between which such correspondence
has been established are said to be projective or homographic.
Two rows which are each the projection of the other are therefore
projective. We shall presently see, also, that any two projective
rows may always be placed in such a position that one appears as
the projection of the other. If they are in such a position the rows
are said to be in perspective position, or simply to be in perspective.
§ 26. The notion of a one-one correspondence between rows may
be extended to flat and axial pencils, viz. a flat pencil will be said
to be projective to a flat pencil if to each ray in the first corresponds
one ray in the second, and if the cross-ratio of four rays in one equals
that of the corresponding rays in the second.
Similarly an axial pencil may be projective to an axial pencil.
But a flat pencil may also be projective to an axial pencil, or either
pencil may be projective to a row. The definition is the same in each
case: there is a one-one correspondence between the elements, and
four elements have the same cross-ratio as the corresponding ones.
§ 27. There is also in each case a special position which is called
perspective, viz.
1. Two projective rows are perspective if they lie in the same
plane, and if the one row is a projection of the other.
2. Two projective flat pencils are perspective—(1) if they lie in
the same plane, and have a row as a common section; (2) if they
lie in the same pencil (in space), and are both sections of the same
axial pencil; (3) if they are in space and have a row as common
section, or are both sections of the same axial pencil, one of the
conditions involving the other.
3. Two projective axial pencils, if their axes meet, and if they
have a flat pencil as a common section.
4. A row and a projective flat pencil, if the row is a section of the
pencil, each point lying in its corresponding line.
5. A row and a projective axial pencil, if the row is a section of the
pencil, each point lying in its corresponding line.
6. A flat and a projective axial pencil, if the former is a section
of the other, each ray lying in its corresponding plane.
That in each case the correspondence established by the position
indicated is such as has been called projective follows at once from
the definition. It is not so evident that the perspective position may
always be obtained. We shall show in § 30 this for the first three
693
cases. First, however, we shall give a few theorems which relate to
the general correspondence, not to the perspective position.
§ 28. Two rows or pencils, flat or axial, which are projective to a
third are projective to each other; this follows at once from the
definitions.
§ 29. If two rows, or two pencils, either flat or axial, or a row and a
pencil, be projective, we may assume to any three elements in the one
the three corresponding elements in the other, and then the correspondence
is uniquely determined.
For if in two projective rows we assume that the points A, B, C
in the first correspond to the given points A′, B′, C′ in the second,
then to any fourth point D in the first will correspond a point D′
in the second, so that
(AB, CD) = (A′B′, C′D′).
But there is only one point, D′, which makes the cross-ratio
(A′B′, C′D′) equal to the given number (AB, CD).
The same reasoning holds in the other cases.
§ 30. If two rows are perspective, then the lines joining corresponding
points all meet in a point, the centre of projection; and
the point in which the two bases of the rows intersect as a point
in the first row coincides with its corresponding point in the
second.
This follows from the definition. The converse also holds,
viz.
If two projective rows have such a position that one point in the one
coincides with its corresponding point in the other, then they are perspective,
that is, the lines joining corresponding points all pass through
a common point, and form a flat pencil.
For let A, B, C, D ... be points in the one, and A′, B′, C′,
D′ ... the corresponding points in the other row, and let A be made
to coincide with its corresponding point A′. Let S be the point where
the lines BB′ and CC′ meet, and let us join S to the point D in the
first row. This line will cut the second row in a point D″, so that
A, B, C, D are projected from S into the points A, B′, C′, D″. The
cross-ratio (AB, CD) is therefore equal to (AB′, C′D″), and by hypothesis
it is equal to (A′B′, C′D′). Hence (A′B′, C′D″) = (A′B′, C′D′),
that is, D″ is the same point as D′.
§ 31. If two projected flat pencils in the same plane are in perspective,
then the intersections of corresponding lines form a row,
and the line joining the two centres as a line in the first pencil
corresponds to the same line as a line in the second. And conversely,
If two projective pencils in the same plane, but with different centres,
have one line in the one coincident with its corresponding line in the
other, then the two pencils are perspective, that is, the intersection of
corresponding lines lie in a line.
The proof is the same as in § 30.
§ 32. If two projective flat pencils in the same point (pencil in
space), but not in the same plane, are perspective, then the planes
joining corresponding rays all pass through a line (they form an
axial pencil), and the line common to the two pencils (in which
their planes intersect) corresponds to itself. And conversely:—
If two flat pencils which have a common centre, but do not lie
in a common plane, are placed so that one ray in the one coincides
with its corresponding ray in the other, then they are perspective,
that is, the planes joining corresponding lines all pass through a
line.
§ 33. If two projective axial pencils are perspective, then the intersection
of corresponding planes lie in a plane, and the plane common
to the two pencils (in which the two axes lie) corresponds to itself.
And conversely:—
If two projective axial pencils are placed in such a position that a
plane in the one coincides with its corresponding plane, then the two
pencils are perspective, that is, corresponding planes meet in lines
which lie in a plane.
The proof again is the same as in § 30.
§ 34. These theorems relating to perspective position become
illusory if the projective rows of pencils have a common base. We
then have:—
In two projective rows on the same line—and also in two projective
and concentric flat pencils in the same plane, or in two
projective axial pencils with a common axis—every element in the
one coincides with its corresponding element in the other as soon
as three elements in the one coincide with their corresponding
elements in the other.
Proof (in case of two rows).—Between four elements A, B, C, D
and their corresponding elements A′, B′, C′, D′ exists the relation
(ABCD) = (A′B′C′D′). If now A′, B′, C′ coincide respectively with
A, B, C, we get (AB, CD) = (AB, CD′), hence D and D′ coincide.
The last theorem may also be stated thus:—
In two projective rows or pencils, which have a common base
but are not identical, not more than two elements in the one can
coincide with their corresponding elements in the other.
Thus two projective rows on the same line cannot have more
than two pairs of coincident points unless every point coincides
with its corresponding point.
 |
| Fig. 9. |
 |
| Fig. 10. |
 |
| Fig. 11. |
It is easy to construct two projective rows on the same line,
which have two pairs of corresponding points coincident. Let the
points A, B, C as points belonging to the one row correspond to A,
B, and C′ as points in the second. Then A and B coincide with their
corresponding points, but C does not. It is, however, not necessary
that two such rows
have twice a point
coincident with its corresponding
point; it is
possible that this happens
only once or not
at all. Of this we shall
see examples later.
§ 35. If two projective
rows or pencils are in
perspective position, we
know at once which
element in one corresponds
to any given
element in the other.
If p and q (fig. 9) are
two projective rows, so
that K corresponds to
itself, and if we know
that to A and B in p
correspond A′ and B′ in q, then the point S, where AA′ meets BB′,
is the centre of projection, and hence, in order to find the point C′
corresponding to C, we have only to join C to S; the point C′,
where this line cuts q, is the point required.
If two flat pencils, S1 and S2, in a plane are perspective (fig. 10),
we need only to know two pairs, a, a′ and b, b′, of corresponding
rays in order to find the
axis s of projection. This
being known, a ray c′ in
S2, corresponding to a given
ray c in S1, is found by
joining S2 to the point
where c cuts the axis s.
A similar construction
holds in the other cases
of perspective figures.
On this depends the
solution of the following
general problem.
§ 36. Three pairs of corresponding
elements in two
projective rows or pencils
being given, to determine
for any element in one
the corresponding element
in the other.
We solve this in the two cases of two projective rows and of two
projective flat pencils in a plane.
Problem I.—Let A, B, C be
three points in a row s, A′, B′, C′
the corresponding points in a
projective row s′, both being in a
plane; it is required to find for
any point D in s the corresponding
point D′ in s′.
Problem II.—Let a, b, c be
three rays in a pencil S, a′, b′, c′
the corresponding rays in a projective
pencil S′, both being in
the same plane; it is required to
find for any ray d in S the corresponding
ray d′ in S′.
The solution is made to depend on the construction of an auxiliary
row or pencil which is perspective to both the given ones. This is
found as follows:—
Solution of Problem I.—On the line joining two corresponding
points, say AA′ (fig. 11), take any two points, S and S′, as centres
of auxiliary pencils.
Join the intersection B1
of SB and S′B′ to the
intersection C1 of SC
and S′C′ by the line s1.
Then a row on s1 will
be perspective to s with
S as centre of projection,
and to s′ with S′
as centre. To find now
the point D′ on s′ corresponding
to a point
D on s we have only to
determine the point D1,
where the line SD cuts
s1, and to draw S′D1;
the point where this line
cuts s′ will be the required
point D′.
Proof.—The rows s
and s′ are both perspective
to the row s1, hence
they are projective to
one another. To A, B,
C, D on s correspond
A1, B1, C1, D1 on s1, and
to these correspond A′, B′, C′, D′ on s′; so that D and D′ are
corresponding points as required.
694
 |
| Fig. 12. |
 |
| Fig. 13. |
Solution of Problem II.—Through the intersection A of two
corresponding rays a and a′ (fig. 12), take two lines, s and s′, as
bases of auxiliary rows. Let S1
be the point where the line b1,
which joins B and B′, cuts the
line c1, which joins C and C′.
Then a pencil S1 will be perspective
to S with s as axis of
projection. To find the ray d′ in
S′ corresponding to a given ray d
in S, cut d by s at D; project
this point from S1 to D′ on s′
and join D′ to S′. This will be
the required ray.
Proof.—That the pencil S1 is
perspective to S and also to S′
follows from construction. To
the lines a1, b1, c1, d1 in S1 correspond
the lines a, b, c, d in S and
the lines a′, b′, c′, d′ in S′, so that d
and d′ are corresponding rays.
In the first solution the two
centres, S, S′, are any two points
on a line joining any two corresponding
points, so that the solution
of the problem allows of a great many different constructions.
But whatever construction be used, the point D′, corresponding to D,
must be always the same, according to the theorem in § 29. This
gives rise to a number of theorems, into which, however, we shall
not enter. The same remarks hold for the second problem.
§ 37. Homological Triangles.—As a further application of the
theorems about perspective rows and pencils we shall prove the
following important theorem.
Theorem.—If ABC and A′B′C′ (fig. 13) be two triangles, such that
the lines AA′, BB′, CC′ meet in a point S, then the intersections of
BC and B′C′, of CA and C′A′, and of AB and A′B′ will lie in a line.
Such triangles are said to be homological, or in perspective. The
triangles are “co-axial” in virtue of the property that the meets of
corresponding sides are collinear and copolar, since the lines joining
corresponding vertices are concurrent.
Proof.—Let a, b, c denote the lines AA′, BB′, CC′, which meet at
S. Then these may be taken as bases of projective rows, so that
A, A′, S on a correspond to B, B′, S on b, and to C, C′, S on c. As
the point S is common to all, any two of these rows will be perspective.
| If | S1 be the centre of projection of rows | b and c, |
| | S2 ” ” ” | c and a, |
| | S3 ” ” ” | a and b, |
and if the line S1S2 cuts a in A1, and b in B1, and c in C1, then A1, B1
will be corresponding points
in a and b, both corresponding
to C1 in c. But a and b are
perspective, therefore the line
A1B1, that is S1S2, joining
corresponding points must
pass through the centre of
projection S3 of a and b. In
other words, S1, S2, S3 lie in a
line. This is Desargues’ celebrated
theorem if we state it
thus:—
Theorem of Desargues.—If
each of two triangles has one
vertex on each of three concurrent
lines, then the intersections
of corresponding sides
lie in a line, those sides
being called corresponding which are opposite to vertices on the
same line.
The converse theorem holds also, viz.
Theorem.—If the sides of one triangle meet those of another in
three points which lie in a line, then the vertices lie on three lines
which meet in a point.
The proof is almost the same as before.
§ 38. Metrical Relations between Projective Rows.—Every row
contains one point which is distinguished from all others, viz.
the point at infinity. In two projective rows, to the point I at
infinity in one corresponds a point I′ in the other, and to the point
J′ at infinity in the second corresponds a point J in the first. The
points I′ and J are in general finite. If now A and B are any two
points in the one, A′, B′ the corresponding points in the other row,
then
(AB, JI) = (A′B′, J′I′),
or
AJ/JB : AI/IB = A′J′/J′B′ : A′I′/I′B′.
But, by § 17,
AI/IB = A′J′/J′B′ = −1;
therefore the last equation changes into
AJ · A′I′ = BJ · B′I′,
that is to say—
Theorem.—The product of the distances of any two corresponding
points in two projective rows from the points which correspond to
the points at infinity in the other is constant, viz. AJ · A′I′ = k.
Steiner has called this number k the Power of the correspondence.
[The relation AJ · A′I′ = k shows that if J, I′ be given then the
point A′ corresponding to a specified point A is readily found; hence
A, A′ generate homographic ranges of which I and J′ correspond to
the points at infinity on the ranges. If we take any two origins O,
O′, on the ranges and reduce the expression AJ · A′I′ = k to its algebraic
equivalent, we derive an equation of the form αxx′ + βx + γx′
+ δ = 0. Conversely, if a relation of this nature holds, then points
corresponding to solutions in x, x′ form homographic ranges.]
§ 39. Similar Rows.—If the points at infinity in two projective
rows correspond so that I′ and J are at infinity, this result loses its
meaning. But if A, B, C be any three points in one, A′, B′, C′ the
corresponding ones on the other row, we have
(AB, CI) = (A′B′, C′I′),
which reduces to
AC/CB = A′C′/C′B′ or AC/A′C′ = BC/B′C′,
that is, corresponding segments are proportional. Conversely, if
corresponding segments are proportional, then to the point at
infinity in one corresponds the point at infinity in the other. If we call
such rows similar, we may state the result thus—
Theorem.—Two projective rows are similar if to the point at
infinity in one corresponds the point at infinity in the other, and
conversely, if two rows are similar then they are projective, and the
points at infinity are corresponding points.
From this the well-known propositions follow:—
Two lines are cut proportionally (in similar rows) by a series of
parallels. The rows are perspective, with centre of projection at
infinity.
If two similar rows are placed parallel, then the lines joining
homologous points pass through a common point.
§ 40. If two flat pencils be projective, then there exists in either,
one single pair of lines at right angles to one another, such that the
corresponding lines in the other pencil are again at right angles.
 |
| Fig. 14. |
To prove this, we place the pencils in perspective position (fig. 14)
by making one ray coincident
with its corresponding
ray. Corresponding rays
meet then on a line p. And
now we draw the circle which
has its centre O on p, and
which passes through the
centres S and S′ of the two
pencils. This circle cuts p in
two points H and K. The
two pairs of rays, h, k, and
h′, k′, joining these points to
S and S′ will be pairs of
corresponding rays at right
angles. The construction
gives in general but one
circle, but if the line p is
the perpendicular bisector
of SS′, there exists an infinite
number, and to every
right angle in the one pencil corresponds a right angle in the
other.
Principle of Duality
§ 41. It has been stated in § 1 that not only points, but also planes
and lines, are taken as elements out of which figures are built up.
We shall now see that the construction of one figure which possesses
certain properties gives rise in many cases to the construction of
another figure, by replacing, according to definite rules, elements
of one kind by those of another. The new figure thus obtained will
then possess properties which may be stated as soon as those of the
original figure are known.
We obtain thus a principle, known as the principle of duality
or of reciprocity, which enables us to construct to any figure not
containing any measurement in its construction a reciprocal figure,
as it is called, and to deduce from any theorem a reciprocal theorem,
for which no further proof is needed.
It is convenient to print reciprocal propositions on opposite sides
of a page broken into two columns, and this plan will occasionally
be adopted.
We begin by repeating in this form a few of our former statements:—
Two points determine a line. |
Two planes determine a line. |
Three points which are not in a line determine a plane. |
Three planes which do not pass through a line determine a point. |
A line and a point without it determine a plane. |
A line and a plane not through it determine a point. |
Two lines in a plane determine a point. |
Two lines through a point determine a plane. |
These propositions show that it will be possible, when any figure
is given, to construct a second figure by taking planes instead of
points, and points instead of planes, but lines where we had lines.
695
For instance, if in the first figure we take a plane and three points
in it, we have to take in the second figure a point and three planes
through it. The three points in the first, together with the three
lines joining them two and two, form a triangle; the three planes
in the second and their three lines of intersection form a trihedral
angle. A triangle and a trihedral angle are therefore reciprocal
figures.
Similarly, to any figure in a plane consisting of points and lines
will correspond a figure consisting of planes and lines passing through
a point S, and hence belonging to the pencil which has S as centre.
The figure reciprocal to four points in space which do not lie
in a plane will consist of four planes which do not meet in a point.
In this case each figure forms a tetrahedron.
§ 42. As other examples we have the following:—
| To a row | is reciprocal | an axial pencil, |
| to a flat pencil | ” | a flat pencil, |
| to a field of points and lines | ” | a pencil of planes and lines, |
| to the space of points | ” | the space of planes. |
For the row consists of a line and all the points in it, reciprocal to
it therefore will be a line with all planes through it, that is, an axial
pencil; and so for the other cases.
This correspondence of reciprocity breaks down, however, if we
take figures which contain measurement in their construction. For
instance, there is no figure reciprocal to two planes at right angles,
because there is no segment in a row which has a magnitude as
definite as a right angle.
We add a few examples of reciprocal propositions which are easily
proved.
Theorem.—If A, B, C, D are any four points in space, and if
the lines AB and CD meet, then all four points lie in a plane,
hence also AC and BD, as well as AD and BC, meet. |
Theorem.—If α, β, γ, δ are four planes in space, and if the
lines αβ and γδ meet, then all four planes lie in a point (pencil),
hence also αγ and βδ, as well as αδ and βγ, meet. |
Theorem.—If of any number of lines every one meets every other,
whilst all do not
lie in a point, then all lie in a plane. |
lie in a plane, then all lie in a point (pencil). |
§ 43. Reciprocal figures as explained lie both in space of three
dimensions. If the one is confined to a plane (is formed of elements
which lie in a plane), then the reciprocal figure is confined to a pencil
(is formed of elements which pass through a point).
But there is also a more special principle of duality, according to
which figures are reciprocal which lie both in a plane or both in a
pencil. In the plane we take points and lines as reciprocal elements,
for they have this fundamental property in common, that two
elements of one kind determine one of the other. In the pencil,
on the other hand, lines and planes have to be taken as reciprocal,
and here it holds again that two lines or planes determine one plane
or line.
Thus, to one plane figure we can construct one reciprocal figure
in the plane, and to each one reciprocal figure in a pencil. We
mention a few of these. At first we explain a few names:—
A figure consisting of n points in a plane will be called an n-point. |
A figure consisting of n lines in a plane will be called an n-side. |
A figure consisting of n planes in a pencil will be called an n-flat. |
A figure consisting of n lines in a pencil will be called an n-edge. |
It will be understood that an n-side is different from a polygon
of n sides. The latter has sides of finite length and n vertices, the
former has sides all of infinite extension, and every point where
two of the sides meet will be a vertex. A similar difference exists
between a solid angle and an n-edge or an n-flat. We notice particularly—
A four-point has six sides, of which two and two are opposite,
and three diagonal points, which are intersections of opposite sides. |
A four-side has six vertices, of which two and two are opposite,
and three diagonals, which join opposite vertices. |
A four-flat has six edges, of which two and two are opposite,
and three diagonal planes, which pass through opposite edges. |
A four-edge has six faces, of which two and two are opposite,
and three diagonal edges, which are intersections of opposite faces. |
A four-side is usually called a complete quadrilateral, and a four-point
a complete quadrangle. The above notation, however, seems
better adapted for the statement of reciprocal propositions.
§ 44.
If a point moves in a plane it describes a plane curve. |
If a line moves in a plane it envelopes a plane curve (fig. 15). |
If a plane moves in a pencil it envelopes a cone. |
If a line moves in a pencil it describes a cone. |
A curve thus appears as generated either by points, and then we
call it a “locus,” or by lines, and then we call it an “envelope.”
In the same manner a cone, which means here a surface, appears
either as the locus of lines passing through a fixed point, the “vertex”
of the cone, or as the envelope of planes passing through the same
point.
 |
| Fig. 15. |
To a surface as locus of points corresponds, in the same manner,
a surface as envelope of planes; and to
a curve in space as locus of points corresponds
a developable surface as envelope
of planes.
It will be seen from the above that
we may, by aid of the principle of
duality, construct for every figure a
reciprocal figure, and that to any
property of the one a reciprocal property
of the other will exist, as long
as we consider only properties which
depend upon nothing but the positions and intersections of the
different elements and not upon measurement.
For such propositions it will therefore be unnecessary to prove
more than one of two reciprocal theorems.
Generation of Curves and Cones of Second Order
or Second Class
§ 45. Conics.—If we have two projective pencils in a plane,
corresponding rays will meet, and their point of intersection will
constitute some locus which we have to investigate. Reciprocally,
if two projective rows in a plane are given, then the lines which join
corresponding points will envelope some curve. We prove first:—
Theorem.—If two projective flat pencils lie in a plane, but
are neither in perspective nor concentric, then the locus of
intersections of corresponding rays is a curve of the second
order, that is, no line contains more than two points of the locus. |
Theorem.—If two projective rows lie in a plane, but are
neither in perspective nor on a common base, then the envelope
of lines joining corresponding points is a curve of the second
class, that is, through no point pass more than two of the enveloping lines. |
Proof.—We draw any line t. This cuts each of the pencils in a
row, so that we have on t two rows, and these are projective
because the pencils are projective. If corresponding rays
of the two pencils meet on the line t, their intersection will be a
point in the one row which coincides with its corresponding
point in the other. But two projective rows on the same base
cannot have more than two points of one coincident with
their corresponding points in the other (§ 34). |
Proof.—We take any point T and join it to all points in each
row. This gives two concentric pencils, which are projective
because the rows are projective. If a line joining corresponding
points in the two rows passes through T, it will be a line in the
one pencil which coincides with its corresponding line in the
other. But two projective concentric flat pencils in the same
plane cannot have more than two lines of one coincident with their
corresponding line in the other (§ 34). |
It will be seen that the proofs are reciprocal, so that the one may
be copied from the other by simply interchanging the words point
and line, locus and envelope, row and pencil, and so on. We shall
therefore in future prove seldom more than one of two reciprocal
theorems, and often state one theorem only, the reader being recommended
to go through the reciprocal proof by himself, and to supply
the reciprocal theorems when not given.
§ 46. We state the theorems in the pencil reciprocal to the last,
without proving them:—
Theorem.—If two projective flat pencils are concentric, but
are neither perspective nor coplanar, then the envelope of the
planes joining corresponding rays is a cone of the second class;
that is, no line through the common centre contains more
than two of the enveloping planes. |
Theorem.—If two projective axial pencils lie in the same
pencil (their axes meet in a point), but are neither perspective
nor co-axial, then the locus of lines joining corresponding
planes is a cone of the second order; that is, no plane in the
pencil contains more than two of these lines. |
§ 47. Of theorems about cones of second order and cones of second
class we shall state only very few. We point out, however, the
following connexion between the curves and cones under consideration:
The lines which join any point in space to the points on a curve
of the second order form a cone of the second order. |
Every plane section of a cone of the second order is a curve of
the second order. |
The planes which join any point in space to the lines enveloping
a curve of the second class envelope themselves a cone of the second class. |
Every plane section of a cone of the second class is a curve of
the second class. |
By its aid, or by the principle of duality, it will be easy to obtain
theorems about them from the theorems about the curves.
We prove the first. A curve of the second order is generated by
two projective pencils. These pencils, when joined to the point in
space, give rise to two projective axial pencils, which generate the
cone in question as the locus of the lines where corresponding planes
meet.
696
§48.
Theorem.—The curve of second order which is generated by two
projective flat pencils passes through the centres of the two pencils. |
Theorem.—The envelope of second class which is generated
by two projective rows contains the bases of these rows as enveloping
lines or tangents. |
Proof.—If S and S′ are the two pencils, then to the ray SS′ or p′
in the pencil S′ corresponds in the pencil S a ray p, which is
different from p′, for the pencils are not perspective. But p and
p′ meet at S, so that S is a point on the curve, and similarly S′. |
Proof.—If s and s′ are the two rows, then to the point ss′ or P′
as a point in s′ corresponds in s a point P, which is not coincident
with P′, for the rows are not perspective. But P and P′ are
joined by s, so that s is one of the enveloping lines, and similarly s′. |
It follows that every line in one of the two pencils cuts the curve
in two points, viz. once at the centre S of the pencil, and once
where it cuts its corresponding ray in the other pencil. These two
points, however, coincide, if the line is cut by its corresponding
line at S itself. The line p in S, which corresponds to the line
SS′ in S′, is therefore the only line through S which has but one
point in common with the curve, or which cuts the curve in two
coincident points. Such a line is called a tangent to the curve,
touching the latter at the point S, which is called the “point of
contact.”
In the same manner we get in the reciprocal investigation the
result that through every point in one of the rows, say in s, two
tangents may be drawn to the curve, the one being s, the other the
line joining the point to its corresponding point in s′. There is,
however, one point P in s for which these two lines coincide. Such
a point in one of the tangents is called the “point of contact” of the
tangent. We thus get—
Theorem.—To the line joining the centres of the projective
pencils as a line in one pencil corresponds in the other the
tangent at its centre. |
Theorem.—To the point of intersection of the bases of two
projective rows as a point in one row corresponds in the other the
point of contact of its base. |
§ 49. Two projective pencils are determined if three pairs of
corresponding lines are given. Hence if a1, b1, c1 are three lines in a
pencil S1, and a2, b2, c2 the corresponding lines in a projective pencil
S2, the correspondence and therefore the curve of the second order
generated by the points of intersection of corresponding rays is
determined. Of this curve we know the two centres S1 and S2,
and the three points a1a2, b1b2, c1c2, hence five points in all. This
and the reciprocal considerations enable us to solve the following
two problems:
Problem.—To construct a curve of the second order, of which five
points S1, S2, A, B, C are given. |
Problem.—To construct a curve of the second class, of which five
tangents u1, u2, a, b, c are given. |
In order to solve the left-hand problem, we take two of the given
points, say S1 and S2, as centres of pencils. These we make projective
by taking the rays a1, b1, c1, which join S1 to A, B, C respectively,
as corresponding to the rays a2, b2, c2, which join S2 to A, B, C
respectively, so that three rays meet their corresponding rays at
the given points A, B, C. This determines the correspondence of
the pencils which will generate a curve of the second order passing
through A, B, C and through the centres S1 and S2, hence through
the five given points. To find more points on the curve we have to
construct for any ray in S1 the corresponding ray in S2. This has
been done in § 36. But we repeat the construction in order to deduce
further properties from it. We also solve the right-hand problem.
Here we select two, viz. u1, u2 of the five given lines, u1, u2, a, b, c,
as bases of two rows, and the points A1, B1, C1 where a, b, c cut u1
as corresponding to the points A2, B2, C2 where a, b, c cut u2.
We get then the following solutions of the two problems:
Solution.—Through the point
A draw any two lines, u1 and u2
(fig. 16), the first u1 to cut the
pencil S1 in a row AB1C1, the
other u2 to cut the pencil S2 in a
row AB2C2. These two rows will
be perspective, as the point A
corresponds to itself, and the
centre of projection will be the
point S, where the lines B1B2
and C1C2 meet. To find now for
any ray d1 in S1 its corresponding
ray d2 in S2, we determine the
point D1 where d1 cuts u1, project
this point from S to D2 on u2 and
join S2 to D2. This will be the
required ray d2 which cuts d1 at
some point D on the curve. |
Solution.—In the line a take
any two points S1 and S2 as
centres of pencils (fig. 17), the
first S1 (A1B1C1) to project the
row u1, the other S2 (A2B2C2) to
project the row u2. These two
pencils will be perspective, the
line S1A1 being the same as the
corresponding line S2A2, and the
axis of projection will be the line
u, which joins the intersection B
of S1B1 and S2B2 to the intersection
C of S1C1 and S2C2. To find
now for any point D1 in u1 the
corresponding point D2 in u2, we
draw S1D1 and project the point
D where this line cuts u from S2
to u2. This will give the required
point D2, and the line d joining D1
to D2 will be a new tangent to the
curve. |
§ 50. These constructions prove, when rightly interpreted, very
important properties of the curves in question.
 |
| Fig. 16. |
If in fig. 16 we draw in the pencil S1 the ray k1 which passes
through the auxiliary centre S, it will be found that the corresponding
ray k2 cuts it on u2. Hence—
Theorem.—In the above construction the bases of the auxiliary
rows u1 and u2 cut the curve
where they cut the rays S2S and
S1S respectively. |
Theorem.—In the above construction (fig. 17) the tangents to
the curve from the centres of the auxiliary pencils S1 and S2 are the
lines which pass through u2u and
u1u respectively. |
As A is any given point on the curve, and u1 any line through
it, we have solved the problems:
Problem.—To find the second point in which any line through a
known point on the curve cuts the curve. |
Problem.—To find the second tangent which can be drawn
from any point in a given tangent to the curve. |
If we determine in S1 (fig. 16) the ray corresponding to the ray
S2S1 in S2, we get the tangent at S1. Similarly, we can determine
the point of contact of the tangents u1 or u2 in fig. 17.
 |
| Fig. 17. |
 |
| Fig. 18. |
§ 51. If five points are given, of which not three are in a line,
then we can, as has just been shown, always draw a curve of the
second order through them; we select two of the points as centres of
projective pencils, and then one such curve is determined. It will
be presently shown that we get always the same curve if two other
points are taken as centres of pencils, that therefore five points
determine one curve of the second order, and reciprocally, that five
tangents determine one curve of the second class. Six points taken
at random will therefore not lie on a curve of the second order. In
order that this may be the case a certain condition has to be satisfied,
and this condition is easily obtained
from the construction in
§ 49, fig. 16. If we consider the
conic determined by the five
points A, S1, S2, K, L, then the
point D will be on the curve if,
and only if, the points on D1, S,
D2 be in a line.
This may be stated differently
if we take AKS1DS2L (figs. 16
and 18) as a hexagon inscribed
in the conic, then AK and DS2
will be opposite sides, so will be
KS1 and S2L, as well as S1D and
LA. The first two meet in D2,
the others in S and D1 respectively. We may therefore state the
required condition, together with the reciprocal one, as follows:—
697
Pascal’s Theorem.—If a hexagon be inscribed in a curve of the
second order, then the intersections of opposite sides are three points in a line. |
Brianchon’s Theorem.—If a hexagon be circumscribed about
a curve of the second class, then the lines joining opposite vertices
are three lines meeting in a point. |
These celebrated theorems, which are known by the names of
their discoverers, are perhaps the most fruitful in the whole theory
of conics. Before we go over to their applications we have to show
that we obtain the same curve if we take, instead of S1, S2, any two
other points on the curve as centres of projective pencils.
§ 52. We know that the curve depends only upon the correspondence
between the pencils S1 and S2, and not upon the special construction
used for finding new points on the curve. The point A
(fig. 16 or 18), through which the two auxiliary rows u1, u2 were
drawn, may therefore be changed to any other point on the curve.
Let us now suppose the curve drawn, and keep the points S1, S2,
K, L and D, and hence also the point S fixed, whilst we move A
along the curve. Then the line AL will describe a pencil about
L as centre, and the point D1 a row on S1D perspective to the
pencil L. At the same time AK describes a pencil about K and D2
a row perspective to it on S2D. But by Pascal’s theorem D1 and
D2 will always lie in a line with S, so that the rows described by D1
and D2 are perspective. It follows that the pencils K and L will
themselves be projective, corresponding rays meeting on the curve.
This proves that we get the same curve whatever pair of the five
given points we take as centres of projective pencils. Hence—
Only one curve of the second order can be drawn which passes through five given points. |
Only one curve of the second class can be drawn which touches five given lines. |
We have seen that if on a curve of the second order two points
coincide at A, the line joining them becomes the tangent at A.
If, therefore, a point on the curve and its tangent are given, this
will be equivalent to having given two points on the curve. Similarly,
if on the curve of second class a tangent and its point of
contact are given, this will be equivalent to two given tangents.
We may therefore extend the last theorem:
Only one curve of the second order can be drawn, of which
four points and the tangent at one of them, or three points and the
tangents at two of them, are given. |
Only one curve of the second class can be drawn, of which four
tangents and the point of contact at one of them, or three tangents
and the points of contact at two of them, are given. |
§ 53. At the same time it has been proved:
If all points on a curve of the second order be joined to any
two of them, then the two pencils thus formed are projective, those
rays being corresponding which meet on the curve. Hence— |
All tangents to a curve of second class are cut by any two of
them in projective rows, those being corresponding points which
lie on the same tangent. Hence— |
The cross-ratio of four rays joining a point S on a curve of
second order to four fixed points A, B, C, D in the curve is independent
of the position of S, and is called the cross-ratio of the
four points A, B, C, D. |
The cross-ratio of the four points in which any tangent u is
cut by four fixed tangents a, b, c, d is independent of the position of
u, and is called the cross-ratio of the four tangents a, b, c, d. |
If this cross-ratio equals −1 the four points are said to be
four harmonic points. |
If this cross-ratio equals −1 the four tangents are said to be
four harmonic tangents. |
We have seen that a curve of second order, as generated by
projective pencils, has at the centre of each pencil one tangent;
and further, that any point on the curve may be taken as centre of
such pencil. Hence—
A curve of second order has at every point one tangent. |
A curve of second class has on every tangent a point of contact. |
§ 54. We return to Pascal’s and Brianchon’s theorems and their
applications, and shall, as before, state the results both for curves
of the second order and curves of the second class, but prove them
only for the former.
Pascal’s theorem may be used when five points are given to find
more points on the curve, viz. it enables us to find the point where
any line through one of the given points cuts the curve again. It
is convenient, in making use of Pascal’s theorem, to number the
points, to indicate the order in which they are to be taken in forming
a hexagon, which, by the way, may be done in 60 different ways.
It will be seen that 1 2 (leaving out 3) 4 5 are opposite sides,
so are 2 3 and (leaving out 4) 5 6, and also 3 4 and (leaving
out 5) 6 1.
If the points 1 2 3 4 5 are given, and we want a 6th point on a
line drawn through 1, we know all the sides of the hexagon with
the exception of 5 6, and this is found by Pascal’s theorem.
If this line should happen to pass through 1, then 6 and 1 coincide,
or the line 6 1 is the tangent at 1. And always if two consecutive
vertices of the hexagon approach nearer and nearer, then the side
joining them will ultimately become a tangent.
We may therefore consider a pentagon inscribed in a curve of
second order and the tangent at one of its vertices as a hexagon,
and thus get the theorem:
Every pentagon inscribed in a curve of second order has the
property that the intersections of two pairs of non-consecutive
sides lie in a line with the point where the fifth side cuts the tangent
at the opposite vertex. |
Every pentagon circumscribed about a curve of the second class
has the property that the lines which join two pairs of non-consecutive
vertices meet on that line which joins the fifth vertex
to the point of contact of the opposite side. |
This enables us also to solve the following problems.
Given five points on a curve of second order to construct the
tangent at any one of them. |
Given five tangents to a curve of second class to construct the
point of contact of any one of them. |
 |
| Fig. 19. |
If two pairs of adjacent vertices coincide, the hexagon becomes a
quadrilateral, with tangents at two vertices. These we take to be
opposite, and get the following theorems:
If a quadrilateral be inscribed in a curve of second order, the
intersections of opposite sides, and also the intersections of the
tangents at opposite vertices, lie in a line (fig. 19). |
If a quadrilateral be circumscribed about a curve of second
class, the lines joining opposite vertices, and also the lines joining
points of contact of opposite sides, meet in a point. |
 |
| Fig. 20. |
If we consider the hexagon made up of a triangle and the tangents
at its vertices, we get—
If a triangle is inscribed in a curve of the second order, the
points in which the sides are cut by the tangents at the opposite
vertices meet in a point. |
If a triangle be circumscribed about a curve of second class,
the lines which join the vertices to the points of contact of the
opposite sides meet in a point (fig. 20). |
§ 55. Of these theorems, those about the quadrilateral give rise to
a number of others. Four points A, B, C, D may in three different
ways be formed into a quadrilateral, for we may take them in the
order ABCD, or ACBD, or ACDB, so that either of the points
B, C, D may be taken as the vertex opposite to A. Accordingly we
may apply the theorem in three different ways.
Let A, B, C, D be four points on a curve of second order (fig. 21),
and let us take them as forming a quadrilateral by taking the points
in the order ABCD, so that A, C and also B, D are pairs of opposite
vertices. Then P, Q will be the points where opposite sides meet,
698
and E, F the intersections of tangents at opposite vertices. The
four points P, Q, E, F lie therefore in a line. The quadrilateral
ACBD gives us in the same way the four points Q, R, G, H in a line,
and the quadrilateral ABDC a line containing the four points R, P,
I, K. These three lines form a triangle PQR.
The relation between the points and lines in this figure may be
expressed more clearly if we consider ABCD as a four-point inscribed
in a conic, and the tangents at these points as a four-side circumscribed
about it,—viz. it will be seen that P, Q, R are the diagonal points
of the four-point ABCD, whilst the sides of the triangle PQR are
the diagonals of the circumscribing four-side. Hence the theorem—
Any four-point on a curve of the second order and the four-side
formed by the tangents at these points stand in this relation that the
diagonal points of the four-point lie in the diagonals of the four-side.
And conversely,
If a four-point and a circumscribed four-side stand in the above
relation, then a curve of the second order may be described which passes
through the four points and touches there the four sides of these figures.
 |
| Fig. 21. |
That the last part of the theorem is true follows from the fact
that the four points A, B, C, D and the line a, as tangent at A, determine
a curve of the second order, and the tangents to this curve at
the other points B, C, D are given by the construction which leads
to fig. 21.
The theorem reciprocal to the last is—
Any four-side circumscribed about a curve of second class and the
four-point formed by the points of contact stand in this relation that the
diagonals of the four-side pass through the diagonal points of the
four-point. And conversely,
If a four-side and an inscribed four-point stand in the above relation,
then a curve of the second class may be described which touches the sides
of the four-side at the points of the four-point.
§ 56. The four-point and the four-side in the two reciprocal
theorems are alike. Hence if we have a four-point ABCD and a
four-side abcd related in the manner described, then not only may
a curve of the second order be drawn, but also a curve of the second
class, which both touch the lines a, b, c, d at the points A, B, C, D.
The curve of second order is already more than determined by the
points A, B, C and the tangents a, b, c at A, B and C. The point D
may therefore be any point on this curve, and d any tangent to the
curve. On the other hand the curve of the second class is more
than determined by the three tangents a, b, c and their points of
contact A, B, C, so that d is any tangent to this curve. It follows
that every tangent to the curve of second order is a tangent of a
curve of the second class having the same point of contact. In
other words, the curve of second order is a curve of second class,
and vice versa. Hence the important theorems—
Every curve of second order is a curve of second class. |
Every curve of second class is a curve of second order. |
The curves of second order and of second class, having thus been
proved to be identical, shall henceforth be called by the common
name of Conics.
For these curves hold, therefore, all properties which have been
proved for curves of second order or of second class. We may
therefore now state Pascal’s and Brianchon’s theorem thus—
Pascal’s Theorem.—If a hexagon be inscribed in a conic, then
the intersections of opposite sides lie in a line.
Brianchon’s Theorem.—If a hexagon be circumscribed about a
conic, then the diagonals forming opposite centres meet in a point.
§ 57. If we suppose in fig. 21 that the point D together with the
tangent d moves along the curve, whilst A, B, C and their tangents
a, b, c remain fixed, then the ray DA will describe a pencil about
A, the point Q a projective row on the fixed line BC, the point F
the row b, and the ray EF a pencil about E. But EF passes always
through Q. Hence the pencil described by AD is projective to the
pencil described by EF, and therefore to the row described by F on
b. At the same time the line BD describes a pencil about B projective
to that described by AD (§ 53). Therefore the pencil BD
and the row F on b are projective. Hence—
If on a conic a point A be taken and the tangent a at this point, then
the cross-ratio of the four rays which join A to any four points on the
curve is equal to the cross-ratio of the points in which the tangents at
these points cut the tangent at A.
§ 58. There are theorems about cones of second order and second
class in a pencil which are reciprocal to the above, according to § 43.
We mention only a few of the more important ones.
The locus of intersections of corresponding planes in two projective
axial pencils whose axes meet is a cone of the second order.
The envelope of planes which join corresponding lines in two
projective flat pencils, not in the same plane, is a cone of the second
class.
Cones of second order and cones of second class are identical.
Every plane cuts a cone of the second order in a conic.
A cone of second order is uniquely determined by five of its edges
or by five of its tangent planes, or by four edges and the tangent plane
at one of them, &c. &c.
Pascal’s Theorem.—If a solid angle of six faces be inscribed in a
cone of the second order, then the intersections of opposite faces
are three lines in a plane.
Brianchon’s Theorem.—If a solid angle of six edges be circumscribed
about a cone of the second order, then the planes through
opposite edges meet in a line.
Each of the other theorems about conics may be stated for cones
of the second order.
 |
| Fig. 22. |
§ 59. Projective Definitions of the Conics.—We now consider the
shape of the conics. We know that any line in the plane of the conic,
and hence that the line at infinity, either has no point in common
with the curve, or one (counting for two coincident points) or two
distinct points. If the line at infinity has no point on the curve the
latter is altogether finite, and is called an Ellipse (fig. 21). If the line
at infinity has only one point in common with the conic, the latter
extends to infinity, and has the line at infinity a tangent. It is
called a Parabola (fig. 22). If, lastly, the line at infinity cuts the
curve in two points, it
consists of two separate
parts which each extend
in two branches to the
points at infinity where
they meet. The curve is
in this case called an
Hyperbola (see fig. 20).
The tangents at the
two points at infinity
are finite because the
line at infinity is not
a tangent. They are
called Asymptotes. The
branches of the hyperbola
approach these lines
indefinitely as a point on
the curves moves to infinity.
§ 60. That the circle
belongs to the curves of
the second order is seen
at once if we state in
a slightly different form the theorem that in a circle all angles at
the circumference standing upon the same arc are equal. If two
points S1, S2 on a circle be joined to any other two points A and B
on the circle, then the angle included by the rays S1A and S1B is
equal to that between the rays S2A and S2B, so that as A moves
along the circumference the rays S1A and S2A describe equal and
therefore projective pencils. The circle can thus be generated by
two projective pencils, and is a curve of the second order.
699
If we join a point in space to all points on a circle, we get a (circular)
cone of the second order (§ 43). Every plane section of this cone is a
conic. This conic will be an ellipse, a parabola, or an hyperbola,
according as the line at infinity in the plane has no, one or two points
in common with the conic in which the plane at infinity cuts the
cone. It follows that our curves of second order may be obtained
as sections of a circular cone, and that they are identical with the
“Conic Sections” of the Greek mathematicians.
§ 61. Any two tangents to a parabola are cut by all others in
projective rows; but the line at infinity being one of the tangents,
the points at infinity on the rows are corresponding points, and the
rows therefore similar. Hence the theorem—
The tangents to a parabola cut each other proportionally.
Pole and Polar
§ 62. We return once again to fig. 21, which we obtained in § 55.
If a four-side be circumscribed about and a four-point inscribed
in a conic, so that the vertices of the second are the points of contact
of the sides of the first, then the triangle formed by the diagonals
of the first is the same as that formed by the diagonal points of the
other.
Such a triangle will be called a polar-triangle of the conic, so that
PQR in fig. 21 is a polar-triangle. It has the property that on the
side p opposite P meet the tangents at A and B, and also those at C
and D. From the harmonic properties of four-points and four-sides
it follows further that the points L, M, where it cuts the lines AB
and CD, are harmonic conjugates with regard to AB and CD
respectively.
If the point P is given, and we draw a line through it, cutting
the conic in A and B, then the point Q harmonic conjugate to P
with regard to AB, and the point H where the tangents at A and B
meet, are determined. But they lie both on p, and therefore this
line is determined. If we now draw a second line through P, cutting
the conic in C and D, then the point M harmonic conjugate to P
with regard to CD, and the point G where the tangents at C and D
meet, must also lie on p. As the first line through P already determines
p, the second may be any line through P. Now every two
lines through P determine a four-point ABCD on the conic, and
therefore a polar-triangle which has one vertex at P and its opposite
side at p. This result, together with its reciprocal, gives the
theorems—
All polar-triangles which have one vertex in common have also the
opposite side in common.
All polar-triangles which have one side in common have also the
opposite vertex in common.
§ 63. To any point P in the plane of, but not on, a conic corresponds
thus one line p as the side opposite to P in all polar-triangles which
have one vertex at P, and reciprocally to every line p corresponds
one point P as the vertex opposite to p in all triangles which have p
as one side.
We call the line p the polar of P, and the point P the pole of the
line p with regard to the conic.
If a point lies on the conic, we call the tangent at that point its
polar; and reciprocally we call the point of contact the pole of
tangent.
§ 64. From these definitions and former results follow—
The polar of any point P not on the conic is a line p, which has
the following properties:— |
The pole of any line p not a tangent to the conic is a point
P, which has the following properties:— |
| 1. On every line through P which cuts the conic, the polar
of P contains the harmonic conjugate of P with regard to those
points on the conic. |
1. Of all lines through a point on p from which two tangents
may be drawn to the conic, the pole P contains the line which is
harmonic conjugate to p, with regard to the two tangents. |
| 2. If tangents can be drawn from P, their points of contact lie
on p. |
2. If p cuts the conic, the tangents at the intersections
meet at P. |
| 3. Tangents drawn at the points where any line through P
cuts the conic meet on p; and conversely, |
3. The point of contact of tangents drawn from any point
on p to the conic lie in a line with P; and conversely, |
| 4. If from any point on p, tangents be drawn, their points
of contact will lie in a line with P. |
4. Tangents drawn at points where any line through P cuts the
conic meet on p. |
| 5. Any four-point on the conic which has one diagonal point at
P has the other two lying on p. |
5. Any four-side circumscribed about a conic which has one
diagonal on p has the other two meeting at P. |
The truth of 2 follows from 1. If T be a point where p cuts the
conic, then one of the points where PT cuts the conic, and which
are harmonic conjugates with regard to PT, coincides with T; hence
the other does—that is, PT touches the curve at T.
That 4 is true follows thus: If we draw from a point H on the
polar one tangent a to the conic, join its point of contact A to the
pole P, determine the second point of intersection B of this line with
the conic, and draw the tangent at B, it will pass through H, and
will therefore be the second tangent which may be drawn from H to
the curve.
§ 65. The second property of the polar or pole gives rise to the
theorem—
| From a point in the plane of a conic, two, one or no tangents
may be drawn to the conic, as its polar has two,
one, or no points in common with the curve. |
A line in the plane of a conic has two, one or no points in
common with the conic, according as two, one or no tangents
can be drawn from its pole to the conic. |
Of any point in the plane of a conic we say that it was without,
on or within the curve according as two, one or no tangents to the
curve pass through it. The points on the conic separate those within
the conic from those without. That this is true for a circle is known
from elementary geometry. That it also holds for other conics
follows from the fact that every conic may be considered as the
projection of a circle, which will be proved later on.
The fifth property of pole and polar stated in § 64 shows how
to find the polar of any point and the pole of any line by aid of the
straight-edge only. Practically it is often convenient to draw three
secants through the pole, and to determine only one of the diagonal
points for two of the four-points formed by pairs of these lines and
the conic (fig. 22).
These constructions also solve the problem—
From a point without a conic, to draw the two tangents to the
conic by aid of the straight-edge only.
For we need only draw the polar of the point in order to find the
points of contact.
§ 66. The property of a polar-triangle may now be stated thus—
In a polar-triangle each side is the polar of the opposite vertex,
and each vertex is the pole of the opposite side.
 |
| Fig. 23. |
If P is one vertex of a polar-triangle, then the other vertices, Q
and R, lie on the polar p of P. One of these vertices we may choose
arbitrarily. For if from
any point Q on the polar
a secant be drawn cutting
the conic in A and D (fig.
23), and if the lines joining
these points to P cut the
conic again at B and C,
then the line BC will pass
through Q. Hence P and
Q are two of the vertices
on the polar-triangle which
is determined by the four-point
ABCD. The third
vertex R lies also on the
line p. It follows, therefore,
also—
If Q is a point on the polar
of P, then P is a point on the
polar of Q; and reciprocally,
If q is a line through the
pole of p, then p is a line
through the pole of q.
This is a very important theorem. It may also be stated
thus—
If a point moves along a line describing a row, its polar turns about
the pole of the line describing a pencil.
This pencil is projective to the row, so that the cross-ratio of four
poles in a row equals the cross-ratio of its four polars, which pass
through the pole of the row.
To prove the last part, let us suppose that P, A and B in fig. 23
remain fixed, whilst Q moves along the polar p of P. This will
make CD turn about P and move R along p, whilst QD and RD
describe projective pencils about A and B. Hence Q and R describe
projective rows, and hence PR, which is the polar of Q, describes a
pencil projective to either.
§ 67. Two points, of which one, and therefore each, lies on the
polar of the other, are said to be conjugate with regard to the conic;
and two lines, of which one, and therefore each, passes through the
pole of the other, are said to be conjugate with regard to the conic.
Hence all points conjugate to a point P lie on the polar of P; all lines
conjugate to a line p pass through the pole of p.
If the line joining two conjugate poles cuts the conic, then the
poles are harmonic conjugates with regard to the points of intersection;
hence one lies within the other without the conic, and all
points conjugate to a point within a conic lie without it.
Of a polar-triangle any two vertices are conjugate poles, any two
sides conjugate lines. If, therefore, one side cuts a conic, then
one of the two vertices which lie on this side is within and the other
without the conic. The vertex opposite this side lies also without,
for it is the pole of a line which cuts the curve. In this case therefore
one vertex lies within, the other two without. If, on the
other hand, we begin with a side which does not cut the conic,
then its pole lies within and the other vertices without. Hence—
Every polar-triangle has one and only one vertex within the conic.
We add, without a proof, the theorem—
The four points in which a conic is cut by two conjugate polars
are four harmonic points in the conic.
§ 68. If two conics intersect in four points (they cannot have
more points in common, § 52), there exists one and only one
700
four-point which is inscribed in both, and therefore one polar-triangle
common to both.
Theorem.—Two conics which intersect in four points have always
one and only one common polar-triangle; and reciprocally,
Two conics which have four common tangents have always one
and only one common polar-triangle.
Diameters and Axes of Conics
§ 69. Diameters.—The theorems about the harmonic properties
of poles and polars contain, as special cases, a number of important
metrical properties of conics. These are obtained if either the pole
or the polar is moved to infinity,—it being remembered that the
harmonic conjugate to a point at infinity, with regard to two points
A, B, is the middle point of the segment AB. The most important
properties are stated in the following theorems:—
The middle points of parallel chords of a conic lie in a line—viz. on
the polar to the point at infinity on the parallel chords.
This line is called a diameter.
The polar of every point at infinity is a diameter.
The tangents at the end points of a diameter are parallel, and are
parallel to the chords bisected by the diameter.
All diameters pass through a common point, the pole of the line at
infinity.
All diameters of a parabola are parallel, the pole to the line at
infinity being the point where the curve touches the line at infinity.
In case of the ellipse and hyperbola, the pole to the line at infinity
is a finite point called the centre of the curve.
A centre of a conic bisects every chord through it.
The centre of an ellipse is within the curve, for the line at infinity
does not cut the ellipse.
The centre of an hyperbola is without the curve, because the line at
infinity cuts the curve. Hence also—
From the centre of an hyperbola two tangents can be drawn to the
curve which have their point of contact at infinity. These are called
Asymptotes (§ 59).
To construct a diameter of a conic, draw two parallel chords and
join their middle points.
To find the centre of a conic, draw two diameters; their intersection
will be the centre.
§ 70. Conjugate Diameters.—A polar-triangle with one vertex at
the centre will have the opposite side at infinity. The other two
sides pass through the centre, and are called conjugate diameters,
each being the polar of the point at infinity on the other.
Of two conjugate diameters each bisects the chords parallel to the
other, and if one cuts the curve, the tangents at its ends are parallel to
the other diameter.
Further—
Every parallelogram inscribed in a conic has its sides parallel to
two conjugate diameters; and
Every parallelogram circumscribed about a conic has as diagonals two
conjugate diameters.
This will be seen by considering the parallelogram in the first
case as an inscribed four-point, in the other as a circumscribed
four-side, and determining in each case the corresponding polar-triangle.
The first may also be enunciated thus—
The lines which join any point on an ellipse or an hyperbola to the
ends of a diameter are parallel to two conjugate diameters.
§ 71. If every diameter is perpendicular to its conjugate the conic is
a circle.
For the lines which join the ends of a diameter to any point on
the curve include a right angle.
A conic which has more than one pair of conjugate diameters at right
angles to each other is a circle.
 |
| Fig. 24. |
Let AA′ and BB′ (fig. 24) be one pair of conjugate diameters at
right angles to each other, CC and DD′ a second pair. If we draw
through the end point A of one
diameter a chord AP parallel to
DD′, and join P to A′, then PA and
PA′ are, according to § 70, parallel to
two conjugate diameters. But PA is
parallel to DD′, hence PA′ is parallel
to CC, and therefore PA and PA′
are perpendicular. If we further
draw the tangents to the conic at A
and A′, these will be perpendicular
to AA′, they being parallel to the
conjugate diameter BB′. We know
thus five points on the conic, viz. the
points A and A′ with their tangents,
and the point P. Through these a
circle may be drawn having AA′ as
diameter; and as through five points
one conic only can be drawn, this circle must coincide with the
given conic.
§ 72. Axes.—Conjugate diameters perpendicular to each other
are called axes, and the points where they cut the curve vertices
of the conic.
In a circle every diameter is an axis, every point on it is a vertex;
and any two lines at right angles to each other may be taken as a
pair of axes of any circle which has its centre at their intersection.
 |
| Fig. 25. |
If we describe on a diameter AB of an ellipse or hyperbola a circle
concentric to the conic, it will cut the latter in A and B (fig. 25).
Each of the semicircles in which it is divided by AB will be partly
within, partly without the curve, and must cut the latter therefore
again in a point. The circle and the conic have thus four points
A, B, C, D, and therefore
one polar-triangle, in common
(§ 68). Of this the
centre is one vertex, for
the line at infinity is the
polar to this point, both
with regard to the circle
and the other conic. The
other two sides are conjugate
diameters of both,
hence perpendicular to
each other. This gives—
An ellipse as well as an
hyperbola has one pair of
axes.
This reasoning shows at
the same time how to construct
the axis of an ellipse
or of an hyperbola.
A parabola has one axis,
if we define an axis as a diameter perpendicular to the chords
which it bisects. It is easily constructed. The line which bisects
any two parallel chords is a diameter. Chords perpendicular to it
will be bisected by a parallel diameter, and this is the axis.
§ 73. The first part of the right-hand theorem in § 64 may be
stated thus: any two conjugate lines through a point P without a
conic are harmonic conjugates with regard to the two tangents
that may be drawn from P to the conic.
If we take instead of P the centre C of an hyperbola, then the
conjugate lines become conjugate diameters, and the tangents
asymptotes. Hence—
Any two conjugate diameters of an hyperbola are harmonic conjugates
with regard to the asymptotes.
As the axes are conjugate diameters at right angles to one another,
it follows (§ 23)—
The axes of an hyperbola bisect the angles between the asymptotes.
 |
| Fig. 26. |
Let O be the centre of the hyperbola (fig. 26), t any secant which
cuts the hyperbola in C, D and the asymptotes in E, F, then the
line OM which bisects the chord CD is a diameter conjugate to the
diameter OK which is parallel to the secant t, so that OK and OM
are harmonic with regard to the asymptotes. The point M therefore
bisects EF. But by construction M bisects CD. It follows
that DF = EC, and ED = CF; or
On any secant of an hyperbola the segments between the curve and the
asymptotes are equal.
If the chord is changed into a tangent, this gives—
The segment between the asymptotes on any tangent to an hyperbola
is bisected by the point of contact.
The first part allows a simple solution of the problem to find any
number of points on an hyperbola, of which the asymptotes and one
point are given. This is equivalent to three points and the tangents
at two of them. This construction requires measurement.
§ 74. For the parabola, too, follow some metrical properties. A
diameter PM (fig. 27) bisects every chord conjugate to it, and the
pole P of such a chord BC lies on the diameter. But a diameter cuts
the parabola once at infinity. Hence—
The segment PM which joins the middle point M of a chord of a parabola
to the pole P of the chord is bisected by the parabola at A.
 |
| Fig. 27. |
§ 75. Two asymptotes and any two tangents to an hyperbola
may be considered as a quadrilateral circumscribed about the
701
hyperbola. But in such a quadrilateral the intersections of the
diagonals and the points of contact of opposite sides lie in a line
(§ 54). If therefore DEFG
(fig. 28) is such a quadrilateral,
then the diagonals
DF and GE will meet on
the line which joins the
points of contact of the
asymptotes, that is, on the
line at infinity; hence they
are parallel. From this
the following theorem is
a simple deduction:
All triangles formed by a
tangent and the asymptotes
of an hyperbola are equal in
area.
If we draw at a point P
(fig. 28) on an hyperbola
a tangent, the part HK
between the asymptotes
is bisected at P. The
parallelogram PQOQ′
formed by the asymptotes and lines parallel to them through
P will be half the triangle OHK, and will therefore be constant.
If we now take the asymptotes OX and OY as oblique
axes of co-ordinates, the lines OQ and QP will be the co-ordinates of
P, and will satisfy the equation xy = const. = a².
 |
| Fig. 28. |
For the asymptotes as axes of co-ordinates the equation of the hyperbola
is xy = const.
Involution
 |
| Fig. 29. |
§ 76. If we have two projective rows, ABC on u and A′B′C′ on
u′, and place their bases on the same line, then each point in this
line counts twice, once as a point in the row u and once as a point
in the row u′. In fig. 29 we denote the points as points in the one
row by letters above the line A, B, C ..., and as points in the second
row by A′, B′, C′ ... below the
line. Let now A and B′ be the
same point, then to A will correspond
a point A′ in the second,
and to B′ a point B in the first
row. In general these points A′
and B will be different. It may, however, happen that they coincide.
Then the correspondence is a peculiar one, as the following theorem
shows:
If two projective rows lie on the same base, and if it happens that to one
point in the base the same point corresponds, whether we consider the
point as belonging to the first or to the second row, then the same will
happen for every point in the base—that is to say, to every point in the
line corresponds the same point in the first as in the second row.
 |
| Fig. 30. |
In order to determine the correspondence, we may assume three
pairs of corresponding points in two projective rows. Let then
A′, B′, C′, in fig. 30, correspond to
A, B, C, so that A and B′, and also
B and A′, denote the same point.
Let us further denote the point
C′ when considered as a point in
the first row by D; then it is to
be proved that the point D′, which corresponds to D, is the same
point as C. We know that the cross-ratio of four points is equal
to that of the corresponding row. Hence
(AB, CD) = (A′B′, C′D′)
but replacing the dashed letters by those undashed ones which
denote the same points, the second cross-ratio equals (BA, DD′),
which, according to § 15, equals (AB, D′D); so that the equation
becomes
(AB, CD) = (AB, D′D).
This requires that C and D′ coincide.
§ 77. Two projective rows on the same base, which have the above
property, that to every point, whether it be considered as a point in
the one or in the other row, corresponds the same point, are said
to be in involution, or to form an involution of points on the line.
We mention, but without proving it, that any two projective
rows may be placed so as to form an involution.
An involution may be said to consist of a row of pairs of points,
to every point A corresponding a point A′, and to A′ again the
point A. These points are said to be conjugate, or, better, one point
is termed the “mate” of the other.
From the definition, according to which an involution may be
considered as made up of two projective rows, follow at once the
following important properties:
1. The cross-ratio of four points equals that of the four conjugate
points.
2. If we call a point which coincides with its mate a “focus”
or “double point” of the involution, we may say: An involution
has either two foci, or one, or none, and is called respectively a
hyperbolic, parabolic or elliptic involution (§ 34).
3. In an hyperbolic involution any two conjugate points are
harmonic conjugates with regard to the two foci.
For if A, A′ be two conjugate points, F1, F2 the two foci, then to the
points F1, F2, A, A′ in the one row correspond the points F1, F2, A′, A
in the other, each focus corresponding to itself. Hence (F1F2, AA′) =
(F1F2, A′A)—that is, we may interchange the two points AA′ without
altering the value of the cross-ratio, which is the characteristic
property of harmonic conjugates (§ 18).
4. The point conjugate to the point at infinity is called the
“centre” of the involution. Every involution has a centre, unless
the point at infinity be a focus, in which case we may say that
the centre is at infinity.
In an hyperbolic involution the centre is the middle point between
the foci.
5. The product of the distances of two conjugate points A, A′
from the centre O is constant: OA · OA′ = c.
For let A, A′ and B, B′ be two pairs of conjugate points, the
centre, I the point at infinity, then
(AB, OI) = (A′B′, IO),
or
OA · OA′ = OB · OB′.
In order to determine the distances of the foci from the centre,
we write F for A and A′ and get
OF² = c; OF = ±√c.
Hence if c is positive OF is real, and has two values, equal and
opposite. The involution is hyperbolic.
If c = 0, OF = 0, and the two foci both coincide with the centre.
If c is negative, √c becomes imaginary, and there are no foci.
Hence we may write—
| In an hyperbolic involution, | OA · OA′ = k², |
| In a parabolic involution, | OA · OA′ = 0, |
| In an elliptic involution, | OA · OA′ = −k². |
From these expressions it follows that conjugate points A, A′ in an
hyperbolic involution lie on the same side of the centre, and in an
elliptic involution on opposite sides of the centre, and that in a
parabolic involution one coincides with the centre.
In the first case, for instance, OA · OA′ is positive; hence OA
and OA′ have the same sign.
It also follows that two segments, AA′ and BB′, between pairs of
conjugate points have the following positions: in an hyperbolic
involution they lie either one altogether within or altogether without
each other; in a parabolic involution they have one point in common;
and in an elliptic involution they overlap, each being partly within
and partly without the other.
Proof.—We have OA . OA′ = OB · OB′ = k² in case of an hyperbolic
involution. Let A and B be the points in each pair which are
nearer to the centre O. If now A, A′ and B, B′ lie on the same side of
O, and if B is nearer to O than A, so that OB < OA, then OB′ > OA′;
hence B′ lies farther away from O than A′, or the segment AA′ lies
within BB′. And so on for the other cases.
6. An involution is determined—
(α) By two pairs of conjugate points. Hence also
(β) By one pair of conjugate points and the centre;
(γ) By the two foci;
(δ) By one focus and one pair of conjugate points;
(ε) By one focus and the centre.
|
7. The condition that A, B, C and A′, B′, C′ may form an involution
may be written in one of the forms—
(AB, CC′) = (A′B′, C′C),
or
(AB, CA′) = (A′B′, C′A),
or
(AB, C′A′) = (A′B′, CA),
for each expresses that in the two projective rows in which A, B, C
702
and A′, B′, C′ are conjugate points two conjugate elements may be
interchanged.
8. Any three pairs. A, A′, B, B′, C, C′, of conjugate points are
connected by the relations:
| AB′ · BC′ · CA′ |
= | AB′ · BC · C′A′ |
= | AB · B′C′ · CA′ |
= | AB · B′C · C′A′ |
= −1. |
| A′B · B′C · C′A | A′B · B′C′ · CA |
A′B′ · BC · C′A | A′B′ · BC′ · CA |
These relations readily follow by working out the relations in (7)
(above).
§ 78. Involution of a quadrangle.—The sides of any four-point are
cut by any line in six points in involution, opposite sides being cut in
conjugate points.
Let A1B1C1D1 (fig. 31) be the four-point. If its sides be cut by
the line p in the points A, A′, B, B′, C, C′, if further, C1D1 cuts the
line A1B1 in C2, and if we project the row A1B1C2C to p once from
D1 and once from C1, we get (A′B′, C′C) = (BA, C′C).
Interchanging in the last cross-ratio the letters in each pair we get
(A′B′, C′C) = (AB, CC′). Hence by § 77 (7) the points are in involution.
The theorem may also be stated thus:
The three points in which any line cuts the sides of a triangle and the
projections, from any point in the plane, of the vertices of the triangle
on to the same line are six points in involution.
 |
| Fig. 31. |
Or again—
The projections from any point on to any line of the six vertices
of a four-side are six points in involution, the projections of opposite
vertices being conjugate points.
This property gives a simple means to construct, by aid of the
straight edge only, in an involution of which two pairs of conjugate
points are given, to any point its conjugate.
§ 79. Pencils in Involution.—The theory of involution may at once
be extended from the row to the flat and the axial pencil—viz. we say
that there is an involution in a flat or in an axial pencil if any line
cuts the pencil in an involution of points. An involution in a pencil
consists of pairs of conjugate rays or planes; it has two, one or no
focal rays (double lines) or planes, but nothing corresponding to a
centre.
An involution in a flat pencil contains always one, and in general
only one, pair of conjugate rays which are perpendicular to one
another. For in two projective flat pencils exist always two corresponding
right angles (§ 40).
Each involution in an axial pencil contains in the same manner
one pair of conjugate planes at right angles to one another.
As a rule, there exists but one pair of conjugate lines or planes
at right angles to each other. But it is possible that there are
more, and then there is an infinite number of such pairs. An involution
in a flat pencil, in which every ray is perpendicular to its
conjugate ray, is said to be circular. That such involution is
possible is easily seen thus: if in two concentric flat pencils each
ray on one is made to correspond to that ray on the other which
is perpendicular to it, then the two pencils are projective, for if
we turn the one pencil through a right angle each ray in one coincides
with its corresponding ray in the other. But these two projective
pencils are in involution.
A circular involution has no focal rays, because no ray in a pencil
coincides with the ray perpendicular to it.
§ 80. Every elliptical involution in a row may be considered as a
section of a circular involution.
In an elliptical involution any two segments AA′ and BB′ lie
partly within and partly without each other (fig. 32). Hence two
circles described on AA′ and BB′ as diameters will intersect in two
points E and E′. The line EE′ cuts the base of the involution at a
point O, which has the property that OA . OA′ = OB · OB′, for
each is equal to OE . OE′. The point O is therefore the centre of
the involution. If we wish to construct to any point C the conjugate
point C′, we may draw the circle through CEE′. This will cut the
base in the required point C′ for OC · OC′ = OA · OA′. But EC and
EC′ are at right angles. Hence the involution which is obtained
by joining E or E′ to the points
in the given involution is circular.
This may also be expressed
thus:
 |
| Fig. 32. |
Every elliptical involution has
the property that there are two
definite points in the plane from
which any two conjugate points
are seen under a right angle.
At the same time the following
problem has been solved:
To determine the centre and
also the point corresponding
to any given point in an elliptical involution of which two pairs of
conjugate points are given.
§ 81. Involution Range on a Conic.—By the aid of § 53, the points
on a conic may be made to correspond to those on a line, so that the
row of points on the conic is projective to a row of points on a line.
We may also have two projective rows on the same conic, and these
will be in involution as soon as one point on the conic has the same
point corresponding to it all the same to whatever row it belongs.
An involution of points on a conic will have the property (as follows
from its definition, and from § 53) that the lines which join conjugate
points of the involution to any point on the conic are conjugate lines
of an involution in a pencil, and that a fixed tangent is cut by the
tangents at conjugate points on the conic in points which are again
conjugate points of an involution on the fixed tangent. For such
involution on a conic the following theorem holds:
The lines which join corresponding points in an involution on a conic
all pass through a fixed point; and reciprocally, the points of intersection
of conjugate lines in an involution among tangents to a conic
lie on a line.
 |
| Fig. 33 |
We prove the first part only. The involution is determined by
two pairs of conjugate points, say by A, A′ and B, B′ (fig. 33). Let
AA′ and BB′
meet in P. If we
join the points in
involution to any
point on the conic,
and the conjugate
points to another
point on the conic,
we obtain two
projective pencils.
We take A and
A′ as centres of
these pencils, so
that the pencils
A(A′BB′) and
A′(AB′B) are projective,
and in
perspective position,
because AA′
corresponds to
A′A. Hence corresponding
rays
meet in a line, of which two points are found by joining AB′ to
A′B and AB to A′B′. It follows that the axis of perspective is the
polar of the point P, where AA′ and BB′ meet. If we now wish
to construct to any other point C on the conic the corresponding
point C′, we join C to A′ and the point where this line cuts p to A.
The latter line cuts the conic again in C′. But we know from the
theory of pole and polar that the line CC′ passes through P. The
point of concurrence is called the “pole of the involution,” and
the line of collinearity of the meets is called the “axis of the
involution.”
Involution Determined by a Conic on a Line.—Foci
§ 82. The polars, with regard to a conic, of points in a row p form
a pencil P projective to the row (§ 66). This pencil cuts the base of
the row p in a projective row.
If A is a point in the given row, A′ the point where the polar of
A cuts p, then A and A′ will be corresponding points. If we take
A′ a point in the first row, then the polar of A′ will pass through
A, so that A corresponds to A′—in other words, the rows are in
involution. The conjugate points in this involution are conjugate
points with regard to the conic. Conjugate points coincide only if
the polar of a point A passes through A—that is, if A lies on the
conic. Hence—
A conic determines on every line in its plane an involution, in which
those points are conjugate which are also conjugate with regard to the
conic.
If the line cuts the conic the involution is hyperbolic, the points of
intersection being the foci.
If the line touches the conic the involution is parabolic, the two foci
coinciding at the point of contact.
If the line does not cut the conic the involution is elliptic, having no
foci.
703
If, on the other hand, we take a point P in the plane of a conic,
we get to each line a through P one conjugate line which joins P
to the pole of a. These pairs of conjugate lines through P form an
involution in the pencil at P. The focal rays of this involution are
the tangents drawn from P to the conic. This gives the theorem
reciprocal to the last, viz:—
A conic determines in every pencil in its plane an involution, corresponding
lines being conjugate lines with regard to the conic.
If the point is without the conic the involution is hyperbolic, the
tangents from the points being the focal rays.
If the point lies on the conic the involution is parabolic, the tangent
at the point counting for coincident focal rays.
If the point is within the conic the involution is elliptic, having no
focal rays.
It will further be seen that the involution determined by a conic
on any line p is a section of the involution, which is determined by
the conic at the pole P of p.
§ 83. Foci.—The centre of a pencil in which the conic determines
a circular involution is called a “focus” of the conic.
In other words, a focus is such a point that every line through it is
perpendicular to its conjugate line. The polar to a focus is called a
directrix of the conic.
From the definition it follows that every focus lies on an axis, for
the line joining a focus to the centre of the conic is a diameter to
which the conjugate lines are perpendicular; and every line joining
two foci is an axis, for the perpendiculars to this line through the foci
are conjugate to it. These conjugate lines pass through the pole of
the line, the pole lies therefore at infinity, and the line is a diameter,
hence by the last property an axis.
It follows that all foci lie on one axis, for no line joining a point
in one axis to a point in the other can be an axis.
As the conic determines in the pencil which has its centre at a focus
a circular involution, no tangents can be drawn from the focus to
the conic. Hence each focus lies within a conic; and a directrix does
not cut the conic.
Further properties are found by the following considerations:
§ 84. Through a point P one line p can be drawn, which is with
regard to a given conic conjugate to a given line q, viz. that line
which joins the point P to the pole of the line q. If the line q is made
to describe a pencil about a point Q, then the line p will describe a
pencil about P. These two pencils will be projective, for the line
p passes through the pole of q, and whilst q describes the pencil Q,
its pole describes a projective row, and this row is perspective to
the pencil P.
We now take the point P on an axis of the conic, draw any line
p through it, and from the pole of p draw a perpendicular q to p.
Let q cut the axis in Q. Then, in the pencils of conjugate lines,
which have their centres at P and Q, the lines p and q are conjugate
lines at right angles to one another. Besides, to the axis as a ray
in either pencil will correspond in the other the perpendicular to the
axis (§ 72). The conic generated by the intersection of corresponding
lines in the two pencils is therefore the circle on PQ as diameter,
so that every line in P is perpendicular to its corresponding line
in Q.
To every point P on an axis of a conic corresponds thus a point
Q, such that conjugate lines through P and Q are perpendicular.
We shall show that these point-pairs P, Q form an involution.
To do this let us move P along the axis, and with it the line p,
keeping the latter parallel to itself. Then P describes a row, p a
perspective pencil (of parallels), and the pole of p a projective row.
At the same time the line q describes a pencil of parallels perpendicular
to p, and perspective to the row formed by the pole of p. The point
Q, therefore, where q cuts the axis, describes a row projective to the
row of points P. The two points P and Q describe thus two projective
rows on the axis; and not only does P as a point in the first
row correspond to Q, but also Q as a point in the first corresponds
to P. The two rows therefore form an involution. The centre of
this involution, it is easily seen, is the centre of the conic.
A focus of this involution has the property that any two conjugate
lines through it are perpendicular; hence, it is a focus to the conic.
Such involution exists on each axis. But only one of these can
have foci, because all foci lie on the same axis. The involution on
one of the axes is elliptic, and appears (§ 80) therefore as the section
of two circular involutions in two pencils whose centres lie in the
other axis. These centres are foci, hence the one axis contains two
foci, the other axis none; or every central conic has two foci which lie
on one axis equidistant from the centre.
The axis which contains the foci is called the principal axis; in
case of an hyperbola it is the axis which cuts the curve, because the
foci lie within the conic.
In case of the parabola there is but one axis. The involution
on this axis has its centre at infinity. One focus is therefore at
infinity, the one focus only is finite. A parabola has only one
focus.
 |
| Fig. 34. |
§ 85. If through any point P (fig. 34) on a conic the tangent PT
and the normal PN (i.e. the perpendicular to the tangent through
the point of contact) be drawn, these will be conjugate lines with
regard to the conic, and at right angles to each other. They will
therefore cut the principal axis in two points, which are conjugate
in the involution considered in § 84; hence they are harmonic
conjugates with regard to the foci. If therefore the two foci F1 and
F2 be joined to P, these lines will be harmonic with regard to the
tangent and normal. As the latter are perpendicular, they will
bisect the angles between the other pair. Hence—
The lines joining any point on a conic to the two foci are equally
inclined to the tangent and normal at that point.
In case of the parabola this becomes—
The line joining any point on a parabola to the focus and the diameter
through the point, are equally inclined to the tangent and normal at
that point.
From the definition of a focus it follows that—
The segment of a tangent between the directrix and the point of
contact is seen from the focus belonging to the directrix under a right
angle, because the lines joining the focus to the ends of this
segment are conjugate with regard to the conic, and therefore
perpendicular.
With equal ease the following theorem is proved:
The two lines which join the points of contact of two tangents each
to one focus, but not both to the same, are seen from the intersection of
the tangents under equal angles.
§ 86. Other focal properties of a conic are obtained by the following
considerations:
 |
| Fig. 35. |
Let F (fig. 35) be a focus to a conic, f the corresponding directrix,
A and B the points of contact of two tangents meeting at T, and P
the point where the
line AB cuts the directrix.
Then TF will be
the polar of P (because
polars of F and T meet
at P). Hence TF and
PF are conjugate lines
through a focus, and
therefore perpendicular.
They are further harmonic
conjugates with
regard to FA and FB
(§§ 64 and 13), so that
they bisect the angles
formed by these lines.
This by the way
proves—
The segments between
the point of intersection
of two tangents to a conic
and their points of contact
are seen from a focus
under equal angles.
If we next draw
through A and B lines
parallel to TF, then the
points A1, B1 where
these cut the directrix
will be harmonic conjugates
with regard to P
and the point where FT
cuts the directrix. The
lines FT and FP bisect
therefore also the angles
between FA1 and FB1.
From this it follows
easily that the triangles
FAA1 and FBB1 are
equiangular, and therefore similar, so that FA : AA1 = FB : BB1.
The triangles AA1A2 and BB1B2 formed by drawing perpendiculars
from A and B to the directrix are also similar, so that AA1 : AA2 =
= BB1 : BB2. This, combined with the above proportion, gives
FA : AA2 = FB : BB2. Hence the theorem:
The ratio of the distances of any point on a conic from a focus and
the corresponding directrix is constant.
To determine this ratio we consider its value for a vertex on the
principal axis. In an ellipse the focus lies between the two vertices
on this axis, hence the focus is nearer to a vertex than to the corresponding
directrix. Similarly, in an hyperbola a vertex is nearer
704
to the directrix than to the focus. In a parabola the vertex lies
halfway between directrix and focus.
It follows in an ellipse the ratio between the distance of a point
from the focus to that from the directrix is less than unity, in the
parabola it equals unity, and in the hyperbola it is greater than
unity.
It is here the same which focus we take, because the two foci
lie symmetrical to the axis of the conic. If now P is any point on
the conic having the distances r1 and r2 from the foci and the distances
d1 and d2 from the corresponding directrices, then r1/d1 = r2/d2 = e,
where e is constant. Hence also (r1 ± r2) / (d1 ± d2) = e.
In the ellipse, which lies between the directrices, d1 + d2 is constant,
therefore also r1 + r2. In the hyperbola on the other hand d1 − d2 is
constant, equal to the distance between the directrices, therefore
in this case r1 − r2 is constant.
If we call the distances of a point on a conic from the focus its
focal distances we have the theorem:
In an ellipse the sum of the focal distances is constant; and in an
hyperbola the difference of the focal distances is constant.
This constant sum or difference equals in both cases the length of
the principal axis.
Pencil of Conics
§ 87. Through four points A, B, C, D in a plane, of which no three
lie in a line, an infinite number of conics may be drawn, viz. through
these four points and any fifth one single conic. This system of
conics is called a pencil of conics. Similarly, all conics touching four
fixed lines form a system such that any fifth tangent determines one
and only one conic. We have here the theorems:
| The pairs of points in which any line is cut by a system of
conics through four fixed points are in involution. |
The pairs of tangents which can be drawn from a point to
a system of conics touching four fixed lines are in involution. |
 |
| Fig. 36. |
We prove the first theorem only. Let ABCD (fig. 36) be the
four-point, then any line t will cut two opposite sides AC, BD in
the points E, E′, the pair AD, BC in points F, F′, and any conic
of the system in M, N, and we have A(CD, MN) = B(CD, MN).
If we cut these pencils by t we get
(EF, MN) = (F′E′, MN)
or
(EF, MN) = (E′F′, NM).
But this is, according to § 77 (7), the condition that M, N are
corresponding points in the involution determined by the point pairs
E, E′, F, F′ in which the line t cuts pairs of opposite sides of the
four-point ABCD. This involution is independent of the particular
conic chosen.
§ 88. There follow several important theorems:
Through four points two, one, or no conics may be drawn which touch
any given line, according as the involution determined by the given
four-point on the line has real, coincident or imaginary foci.
Two, one, or no conics may be drawn which touch four given lines
and pass through a given point, according as the involution determined
by the given four-side at the point has real, coincident or imaginary
focal rays.
For the conic through four points which touches a given line has
its point of contact at a focus of the involution determined by the
four-point on the line.
As a special case we get, by taking the line at infinity:
Through four points of which none is at infinity either two or no
parabolas may be drawn.
The problem of drawing a conic through four points and touching
a given line is solved by determining the points of contact on the
line, that is, by determining the foci of the involution in which the
line cuts the sides of the four-point. The corresponding remark
holds for the problem of drawing the conics which touch four lines
and pass through a given point.
Ruled Quadric Surfaces
§ 89. We have considered hitherto projective rows which lie in
the same plane, in which case lines joining corresponding points
envelop a conic. We shall now consider projective rows whose
bases do not meet. In this case, corresponding points will be joined
by lines which do not lie in a plane, but on some surface, which
like every surface generated by lines is called a ruled surface. This
surface clearly contains the bases of the two rows.
If the points in either row be joined to the base of the other, we
obtain two axial pencils which are also projective, those planes
being corresponding which pass through corresponding points in the
given rows. If A′, A be two corresponding points, α, α′ the planes in
the axial pencils passing through them, then AA′ will be the line
of intersection of the corresponding planes α, α′ and also the line
joining corresponding points in the rows.
If we cut the whole figure by a plane this will cut the axial pencils
in two projective flat pencils, and the curve of the second order
generated by these will be the curve in which the plane cuts the
surface. Hence
The locus of lines joining corresponding points in two projective
rows which do not lie in the same plane is a surface which contains the
bases of the rows, and which can also be generated by the lines of intersection
of corresponding planes in two projective axial pencils. This
surface is cut by every plane in a curve of the second order, hence either
in a conic or in a line-pair. No line which does not lie altogether on
the surface can have more than two points in common with the surface,
which is therefore said to be of the second order or is called a ruled
quadric surface.
That no line which does not lie on the surface can cut the surface
in more than two points is seen at once if a plane be drawn through
the line, for this will cut the surface in a conic. It follows also that
a line which contains more than two points of the surface lies altogether
on the surface.
§ 90. Through any point in space one line can always be drawn
cutting two given lines which do not themselves meet.
If therefore three lines in space be given of which no two meet,
then through every point in either one line may be drawn cutting
the other two.
If a line moves so that it always cuts three given lines of which no
two meet, then it generates a ruled quadric surface.
Let a, b, c be the given lines, and p, q, r ... lines cutting them in the
points A, A′, A″ ...; B, B′, B″ ...; C, C′, C″ ... respectively; then
the planes through a containing p, q, r, and the planes through b containing
the same lines, may be taken as corresponding planes in two
axial pencils which are projective, because both pencils cut the line
c in the same row, C, C′, C″ ...; the surface can therefore be generated
by projective axial pencils.
Of the lines p, q, r ... no two can meet, for otherwise the lines
a, b, c which cut them would also lie in their plane. There is a single
infinite number of them, for one passes through each point of a.
These lines are said to form a set of lines on the surface.
If now three of the lines p, q, r be taken, then every line d cutting
them will have three points in common with the surface, and will
therefore lie altogether on it. This gives rise to a second set of lines
on the surface. From what has been said the theorem follows:
A ruled quadric surface contains two sets of straight lines. Every
line of one set cuts every line of the other, but no two lines of the same
set meet.
Any two lines of the same set may be taken as bases of two projective
rows, or of two projective pencils which generate the surface. They are
cut by the lines of the other set in two projective rows.
The plane at infinity like every other plane cuts the surface either
in a conic proper or in a line-pair. In the first case the surface is
called an Hyperboloid of one sheet, in the second an Hyperbolic
Paraboloid.
The latter may be generated by a line cutting three lines of which
one lies at infinity, that is, cutting two lines and remaining parallel
to a given plane.
Quadric Surfaces
§ 91. The conics, the cones of the second order, and the ruled
quadric surfaces complete the figures which can be generated by
projective rows or flat and axial pencils, that is, by those aggregates
of elements which are of one dimension (§§ 5, 6). We shall
now consider the simpler figures which are generated by aggregates of
two dimensions. The space at our disposal will not, however, allow
us to do more than indicate a few of the results.
§ 92. We establish a correspondence between the lines and planes
in pencils in space, or reciprocally between the points and lines in
two or more planes, but consider principally pencils.
In two pencils we may either make planes correspond to planes
and lines to lines, or else planes to lines and lines to planes. If
hereby the condition be satisfied that to a flat, or axial, pencil
corresponds in the first case a projective flat, or axial, pencil, and in
the second a projective axial, or flat, pencil, the pencils are said to be
projective in the first case and reciprocal in the second.
For instance, two pencils which join two points S1 and S2 to the
different points and lines in a given plane π are projective (and
in perspective position), if those lines and planes be taken as
705
corresponding which meet the plane π in the same point or in the
same line. In this case every plane through both centres S1 and S2
of the two pencils will correspond to itself. If these pencils are
brought into any other position they will be projective (but not
perspective).
The correspondence between two projective pencils is uniquely
determined, if to four rays (or planes) in the one the corresponding
rays (or planes) in the other are given, provided that no three rays of
either set lie in a plane.
Let a, b, c, d be four rays in the one, a′, b′, c′, d′ the corresponding
rays in the other pencil. We shall show that we can find for every
ray e in the first a single corresponding ray e′ in the second. To
the axial pencil a (b, c, d ...) formed by the planes which join a to
b, c, d ..., respectively corresponds the axial pencil a′ (b′, c′, d′ ... ),
and this correspondence is determined. Hence, the plane a′e′ which
corresponds to the plane ae is determined. Similarly the plane
b′e′ may be found and both together determine the ray e′.
Similarly the correspondence between two reciprocal pencils is
determined if for four rays in the one the corresponding planes in
the other are given.
§ 93. We may now combine—
1. Two reciprocal pencils.
Each ray cuts its corresponding plane in a point, the locus
of these points is a quadric surface.
2. Two projective pencils.
Each plane cuts its corresponding plane in a line, but a
ray as a rule does not cut its corresponding ray. The
locus of points where a ray cuts its corresponding ray
is a twisted cubic. The lines where a plane cuts its
corresponding plane are secants.
3. Three projective pencils.
The locus of intersection of corresponding planes is a
cubic surface.
Of these we consider only the first two cases.
§ 94. If two pencils are reciprocal, then to a plane in either corresponds
a line in the other, to a flat pencil an axial pencil, and so on.
Every line cuts its corresponding plane in a point. If S1 and S2 be
the centres of the two pencils, and P be a point where a line a1 in the
first cuts its corresponding plane α2, then the line b2 in the pencil S2
which passes through P will meet its corresponding plane β1 in P. For
b2 is a line in the plane α2. The corresponding plane β1 must therefore
pass through the line a1, hence through P.
The points in which the lines in S1 cut the planes corresponding
to them in S2 are therefore the same as the points in which the lines
in S2 cut the planes corresponding to them in S1.
The locus of these points is a surface which is cut by a plane in a
conic or in a line-pair and by a line in not more than two points unless
it lies altogether on the surface. The surface itself is therefore called a
quadric surface, or a surface of the second order.
To prove this we consider any line p in space.
The flat pencil in S1 which lies in the plane drawn through p
and the corresponding axial pencil in S2 determine on p two projective
rows, and those points in these which coincide with their
corresponding points lie on the surface. But there exist only two,
or one, or no such points, unless every point coincides with its
corresponding point. In the latter case the line lies altogether on
the surface.
This proves also that a plane cuts the surface in a curve of the
second order, as no line can have more than two points in common
with it. To show that this is a curve of the same kind as those
considered before, we have to show that it can be generated by
projective flat pencils. We prove first that this is true for any
plane through the centre of one of the pencils, and afterwards that
every point on the surface may be taken as the centre of such pencil.
Let then α1 be a plane through S1. To the flat pencil in S1 which
it contains corresponds in S2 a projective axial pencil with axis
a2 and this cuts α1 in a second flat pencil. These two flat pencils
in α1 are projective, and, in general, neither concentric nor perspective.
They generate therefore a conic. But if the line a2 passes
through S1 the pencils will have S1 as common centre, and may
therefore have two, or one, or no lines united with their corresponding
lines. The section of the surface by the plane α1 will be accordingly
a line-pair or a single line, or else the plane α1 will have only the
point S1 in common with the surface.
Every line l1 through S1 cuts the surface in two points, viz. first
in S1 and then at the point where it cuts its corresponding plane.
If now the corresponding plane passes through S1, as in the case
just considered, then the two points where l1 cuts the surface coincide
at S1, and the line is called a tangent to the surface with S1 as point
of contact. Hence if l1 be a tangent, it lies in that plane τ1 which
corresponds to the line S2S1 as a line in the pencil S2. The section
of this plane has just been considered. It follows that—
All tangents to quadric surface at the centre of one of the reciprocal
pencils lie in a plane which is called the tangent plane to the surface
at that point as point of contact.
To the line joining the centres of the two pencils as a line in one
corresponds in the other the tangent plane at its centre.
The tangent plane to a quadric surface either cuts the surface in
two lines, or it has only a single line, or else only a single point in
common with the surface.
In the first case the point of contact is said to be hyperbolic, in the
second parabolic, in the third elliptic.
§ 95. It remains to be proved that every point S on the surface
may be taken as centre of one of the pencils which generate the
surface. Let S be any point on the surface Φ′ generated by the
reciprocal pencils S1 and S2. We have to establish a reciprocal
correspondence between the pencils S and S1, so that the surface
generated by them is identical with Φ. To do this we draw two
planes α1 and β1 through S1, cutting the surface Φ in two conics
which we also denote by α1 and β1. These conics meet at S1, and
at some other point T where the line of intersection of α1 and β1
cuts the surface.
In the pencil S we draw some plane σ which passes through T,
but not through S1 or S2. It will cut the two conics first at T, and
therefore each at some other point which we call A and B respectively.
These we join to S by lines a and b, and now establish the
required correspondence between the pencils S1 and S as follows:—To
S1T shall correspond the plane σ, to the plane α1 the line a, and
to β1 the line b, hence to the flat pencil in α1 the axial pencil a.
These pencils are made projective by aid of the conic in α1.
In the same manner the flat pencil in β1 is made projective to the
axial pencil b by aid of the conic in β1, corresponding elements being
those which meet on the conic. This determines the correspondence,
for we know for more than four rays in S1 the corresponding planes
in S. The two pencils S and S1 thus made reciprocal generate a
quadric surface Φ′, which passes through the point S and through
the two conics α1 and β1.
The two surfaces Φ and Φ′ have therefore the points S and S1 and
the conics α1 and β1 in common. To show that they are identical,
we draw a plane through S and S2, cutting each of the conics α1 and
β1 in two points, which will always be possible. This plane cuts
Φ and Φ′ in two conics which have the point S and the points where
it cuts α1 and β1 in common, that is five points in all. The conics
therefore coincide.
This proves that all those points P on Φ′ lie on Φ which have the
property that the plane SS2P cuts the conics α1, β1 in two points
each. If the plane SS2P has not this property, then we draw a plane
SS1P. This cuts each surface in a conic, and these conics have in
common the points S, S1, one point on each of the conics α1, β1, and
one point on one of the conics through S and S2 which lie on both
surfaces, hence five points. They are therefore coincident, and our
theorem is proved.
§ 96. The following propositions follow:—
A quadric surface has at every point a tangent plane.
Every plane section of a quadric surface is a conic or a line-pair.
Every line which has three points in common with a quadric surface
lies on the surface.
Every conic which has five points in common with a quadric surface
lies on the surface.
Through two conics which lie in different planes, but have two points
in common, and through one external point always one quadric surface
may be drawn.
§ 97. Every plane which cuts a quadric surface in a line-pair is a
tangent plane. For every line in this plane through the centre of
the line-pair (the point of intersection of the two lines) cuts the
surface in two coincident points and is therefore a tangent to the
surface, the centre of the line-pair being the point of contact.
If a quadric surface contains a line, then every plane through this
line cuts the surface in a line-pair (or in two coincident lines). For
this plane cannot cut the surface in a conic. Hence:—
If a quadric surface contains one line p then it contains an infinite
number of lines, and through every point Q on the surface, one line
q can be drawn which cuts p. For the plane through the point Q
and the line p cuts the surface in a line-pair which must pass through
Q and of which p is one line.
No two such lines q on the surface can meet. For as both meet p
their plane would contain p and therefore cut the surface in a
triangle.
Every line which cuts three lines q will be on the surface; for it
has three points in common with it.
Hence the quadric surfaces which contain lines are the same as the
ruled quadric surfaces considered in §§ 89-93, but with one important
exception. In the last investigation we have left out of consideration
the possibility of a plane having only one line (two coincident
lines) in common with a quadric surface.
§ 98. To investigate this case we suppose first that there is one
point A on the surface through which two different lines a, b can be
drawn, which lie altogether on the surface.
If P is any other point on the surface which lies neither on a nor
b, then the plane through P and a will cut the surface in a second
line a′ which passes through P and which cuts a. Similarly there
is a line b′ through P which cuts b. These two lines a′ and b′ may
coincide, but then they must coincide with PA.
If this happens for one point P, it happens for every other point
Q. For if two different lines could be drawn through Q, then by the
same reasoning the line PQ would be altogether on the surface,
hence two lines would be drawn through P against the assumption.
From this follows:—
If there is one point on a quadric surface through which one, but only
one, line can be drawn on the surface, then through every point one line
706
can be drawn, and all these lines meet in a point. The surface is a cone
of the second order.
If through one point on a quadric surface, two, and only two, lines
can be drawn on the surface, then through every point two lines may
be drawn, and the surface is ruled quadric surface.
If through one point on a quadric surface no line on the surface can
be drawn, then the surface contains no lines.
Using the definitions at the end of § 95, we may also say:—
On a quadric surface the points are all hyperbolic, or all parabolic,
or all elliptic.
As an example of a quadric surface with elliptical points, we
mention the sphere which may be generated by two reciprocal
pencils, where to each line in one corresponds the plane perpendicular
to it in the other.
§ 99. Poles and Polar Planes.—The theory of poles and polars
with regard to a conic is easily extended to quadric surfaces.
Let P be a point in space not on the surface, which we suppose
not to be a cone. On every line through P which cuts the surface
in two points we determine the harmonic conjugate Q of P with
regard to the points of intersection. Through one of these lines we
draw two planes α and β. The locus of the points Q in α is a line a,
the polar of P with regard to the conic in which α cuts the surface.
Similarly the locus of points Q in β is a line b. This cuts a, because
the line of intersection of α and β contains but one point Q. The
locus of all points Q therefore is a plane. This plane is called the
polar plane of the point P, with regard to the quadric surface. If P
lies on the surface we take the tangent plane of P as its polar.
The following propositions hold:—
1. Every point has a polar plane, which is constructed by drawing
the polars of the point with regard to the conics in which two planes
through the point cut the surface.
2. If Q is a point in the polar of P, then P is a point in the polar
of Q, because this is true with regard to the conic in which a plane
through PQ cuts the surface.
3. Every plane is the polar plane of one point, which is called the
Pole of the plane.
The pole to a plane is found by constructing the polar planes of
three points in the plane. Their intersection will be the pole.
4. The points in which the polar plane of P cuts the surface are
points of contact of tangents drawn from P to the surface, as is easily
seen. Hence:—
5. The tangents drawn from a point P to a quadric surface form a
cone of the second order, for the polar plane of P cuts it in a conic.
6. If the pole describes a line a, its polar plane will turn about
another line a′, as follows from 2. These lines a and a′ are said to be
conjugate with regard to the surface.
§ 100. The pole of the line at infinity is called the centre of the
surface. If it lies at the infinity, the plane at infinity is a tangent
plane, and the surface is called a paraboloid.
The polar plane to any point at infinity passes through the centre,
and is called a diametrical plane.
A line through the centre is called a diameter. It is bisected at the
centre. The line conjugate to it lies at infinity.
If a point moves along a diameter its polar plane turns about the
conjugate line at infinity; that is, it moves parallel to itself, its centre
moving on the first line.
The middle points of parallel chords lie in a plane, viz. in the polar
plane of the point at infinity through which the chords are drawn.
The centres of parallel sections lie in a diameter which is a line
conjugate to the line at infinity in which the planes meet.
Twisted Cubics
§ 101. If two pencils with centres S1 and S2 are made projective,
then to a ray in one corresponds a ray in the other, to a plane a
plane, to a flat or axial pencil a projective flat or axial pencil, and
so on.
There is a double infinite number of lines in a pencil. We shall
see that a single infinite number of lines in one pencil meets its
corresponding ray, and that the points of intersection form a curve
in space.
Of the double infinite number of planes in the pencils each will
meet its corresponding plane. This gives a system of a double
infinite number of lines in space. We know (§ 5) that there is a
quadruple infinite number of lines in space. From among these we
may select those which satisfy one or more given conditions. The
systems of lines thus obtained were first systematically investigated
and classified by Plücker, in his Geometrie des Raumes. He uses the
following names:—
A treble infinite number of lines, that is, all lines which satisfy one
condition, are said to form a complex of lines; e.g. all lines cutting
a given line, or all lines touching a surface.
A double infinite number of lines, that is, all lines which satisfy
two conditions, or which are common to two complexes, are said to
form a congruence of lines; e.g. all lines in a plane, or all lines
cutting two curves, or all lines cutting a given curve twice.
A single infinite number of lines, that is, all lines which satisfy
three conditions, or which belong to three complexes, form a ruled
surface; e.g. one set of lines on a ruled quadric surface, or developable
surfaces which are formed by the tangents to a curve.
It follows that all lines in which corresponding planes in two
projective pencils meet form a congruence. We shall see this congruence
consists of all lines which cut a twisted cubic twice, or of
all secants to a twisted cubic.
§ 102. Let l1 be the line S1S2 as a line in the pencil S1. To it
corresponds a line l2 in S2. At each of the centres two corresponding
lines meet. The two axial pencils with l1 and l2 as axes are projective,
and, as, their axes meet at S2, the intersections of corresponding
planes form a cone of the second order (§ 58), with S2 as
centre. If π1 and π2 be corresponding planes, then their intersection
will be a line p2 which passes through S2. Corresponding to it in
S1 will be a line p1 which lies in the plane π1, and which therefore
meets p2 at some point P. Conversely, if p2 be any line in S2 which
meets its corresponding line p1 at a point P, then to the plane l2p2
will correspond the plane l1p1, that is, the plane S1S2P. These
planes intersect in p2, so that p2 is a line on the quadric cone generated
by the axial pencils l1 and l2. Hence:—
All lines in one pencil which meet their corresponding lines in the
other form a cone of the second order which has its centre at the centre
of the first pencil, and passes through the centre of the second.
From this follows that the points in which corresponding rays
meet lie on two cones of the second order which have the ray joining
their centres in common, and form therefore, together with the line
S1S2 or l1, the intersection of these cones. Any plane cuts each of the
cones in a conic. These two conics have necessarily that point in
common in which it cuts the line l1, and therefore besides either
one or three other points. It follows that the curve is of the third
order as a plane may cut it in three, but not in more than three,
points. Hence:—
The locus of points in which corresponding lines on two projective
pencils meet is a curve of the third order or a “twisted cubic” k, which
passes through the centres of the pencils, and which appears as the
intersection of two cones of the second order, which have one line in
common.
A line belonging to the congruence determined by the pencils is a
secant of the cubic; it has two, or one, or no points in common with
this cubic, and is called accordingly a secant proper, a tangent, or a
secant improper of the cubic. A secant improper may be considered,
to use the language of coordinate geometry, as a secant with
imaginary points of intersection.
§ 103. If a1 and a2 be any two corresponding lines in the two
pencils, then corresponding planes in the axial pencils having a1 and
a2 as axes generate a ruled quadric surface. If P be any point on
the cubic k, and if p1, p2 be the corresponding rays in S1 and S2 which
meet at P, then to the plane a1p1 in S1 corresponds a2p2 in S2. These
therefore meet in a line through P.
This may be stated thus:—
Those secants of the cubic which cut a ray a1, drawn through the
centre S1 of one pencil, form a ruled quadric surface which passes through
both centres, and which contains the twisted cubic k. Of such surfaces
an infinite number exists. Every ray through S1 or S2 which is not a
secant determines one of them.
If, however, the rays a1 and a2 are secants meeting at A, then the
ruled quadric surface becomes a cone of the second order, having
A as centre. Or all lines of the congruence which pass through a point
on the twisted cubic k form a cone of the second order. In other words,
the projection of a twisted cubic from any point in the curve on to
any plane is a conic.
If a1 is not a secant, but made to pass through any point Q in
space, the ruled quadric surface determined by a1 will pass through
Q. There will therefore be one line of the congruence passing through
Q, and only one. For if two such lines pass through Q, then the lines
S1Q and S2Q will be corresponding lines; hence Q will be a point on
the cubic k, and an infinite number of secants will pass through it.
Hence:—
Through every point in space not on the twisted cubic one and only
one secant to the cubic can be drawn.
§ 104. The fact that all the secants through a point on the cubic
form a quadric cone shows that the centres of the projective pencils
generating the cubic are not distinguished from any other points on
the cubic. If we take any two points S, S′ on the cubic, and draw
the secants through each of them, we obtain two quadric cones,
which have the line SS′ in common, and which intersect besides
along the cubic. If we make these two pencils having S and S′ as
centres projective by taking four rays on the one cone as corresponding
to the four rays on the other which meet the first on the
cubic, the correspondence is determined. These two pencils will
generate a cubic, and the two cones of secants having S and S′ as
centres will be identical with the above cones, for each has five
rays in common with one of the first, viz. the line SS′ and the four
lines determined for the correspondence; therefore these two cones
intersect in the original cubic. This gives the theorem:—
On a twisted cubic any two points may be taken as centres of projective
pencils which generate the cubic, corresponding planes being
those which meet on the same secant.
Of the two projective pencils at S and S′ we may keep the first
fixed, and move the centre of the other along the curve. The pencils
will hereby remain projective, and a plane α in S will be cut by its
corresponding plane α′ always in the same secant a. Whilst S′
moves along the curve the plane α′ will turn about a, describing an
axial pencil.
707
Authorities.—In this article we have given a purely geometrical
theory of conics, cones of the second order, quadric surfaces, &c. In
doing so we have followed, to a great extent, Reye’s Geometrie der
Lage, and to this excellent work those readers are referred who wish
for a more exhaustive treatment of the subject. Other works
especially valuable as showing the development of the subject are:
Monge, Géométrie descriptive: Carnot, Géométrie de position
(1803), containing a theory of transversals; Poncelet’s great work
Traité des propriétés projectives des figures (1822); Möbins, Barycentrischer
Calcul (1826); Steiner, Abhängigkeit geometrischer
Gestalten (1832), containing the first full discussion of the projective
relations between rows, pencils, &c.; Von Staudt, Geometrie der
Lage (1847) and Beiträge zur Geometrie der Lage (1856-1860), in
which a system of geometry is built up from the beginning without
any reference to number, so that ultimately a number itself gets
a geometrical definition, and in which imaginary elements are
systematically introduced into pure geometry; Chasles, Aperçu
historique (1837), in which the author gives a brilliant account of
the progress of modern geometrical methods, pointing out the
advantages of the different purely geometrical methods as compared
with the analytical ones, but without taking as much account of
the German as of the French authors; Id., Rapport sur les progrès
de la géométrie (1870), a continuation of the Aperçu; Id., Traité de
géométrie supérieure (1852); Cremona, Introduzione ad una teoria
geometrica delle curve piane (1862) and its continuation Preliminari
di una teoria geometrica delle superficie (German translations by
Curtze). As more elementary books, we mention: Cremona,
Elements of Projective Geometry, translated from the Italian by
C. Leudesdorf (2nd ed., 1894); J.W. Russell, Pure Geometry (2nd ed.,
1905).
(O. H.)
III. Descriptive Geometry
This branch of geometry is concerned with the methods for
representing solids and other figures in three dimensions by
drawings in one plane. The most important method is that
which was invented by Monge towards the end of the 18th
century. It is based on parallel projections to a plane by rays
perpendicular to the plane. Such a projection is called orthographic
(see Projection, § 18). If the plane is horizontal the
projection is called the plan of the figure, and if the plane is
vertical the elevation. In Monge’s method a figure is represented
by its plan and elevation. It is therefore often called drawing
in plan and elevation, and sometimes simply orthographic
projection.
§ 1. We suppose then that we have two planes, one horizontal,
the other vertical, and these we call the planes of plan and of elevation
respectively, or the horizontal and the vertical plane, and
denote them by the letters π1 and π2. Their line of intersection is
called the axis, and will be denoted by xy.
If the surface of the drawing paper is taken as the plane of the
plan, then the vertical plane will be the plane perpendicular to it
through the axis xy. To bring this also into the plane of the drawing
paper we turn it about the axis till it coincides with the horizontal
plane. This process of turning one plane down till it coincides with
another is called rabatting one to the other. Of course there is no
necessity to have one of the two planes horizontal, but even when
this is not the case it is convenient to retain the above names.
 |
| Fig. 37. |
Fig. 38. |
The whole arrangement will be better understood by referring to
fig. 37. A point A in space is there projected by the perpendicular
AA1 and AA2 to the planes π1 and π2 so that A1 and A2 are the
horizontal and vertical projections of A.
If we remember that a line is perpendicular to a plane that is
perpendicular to every line in the plane if only it is perpendicular
to any two intersecting lines in the plane, we see that the axis which
is perpendicular both to AA1 and to AA2 is also perpendicular to
A1A0 and to A2A0 because these four lines are all in the same plane.
Hence, if the plane π2 be turned about the axis till it coincides with
the plane π1, then A2A0 will be the continuation of A1A0. This
position of the planes is represented in fig. 38, in which the line A1A2
is perpendicular to the axis x.
Conversely any two points A1, A2 in a line perpendicular to the
axis will be the projections of some point in space when the plane
π2 is turned about the axis till it is perpendicular to the plane π1,
because in this position the two perpendiculars to the planes π1
and π2 through the points A1 and A2 will be in a plane and therefore
meet at some point A.
Representation of Points.—We have thus the following method
of representing in a single plane the position of points in space:—we
take in the plane a line xy as the axis, and then any pair of points
A1, A2 in the plane on a line perpendicular to the axis represent a
point A in space. If the line A1A2 cuts the axis at A0, and if at A1
a perpendicular be erected to the plane, then the point A will be in
it at a height A1A = A0A2 above the plane. This gives the position
of the point A relative to the plane π1. In the same way, if in a
perpendicular to π2 through A2 a point A be taken such that A2A =
A0A1, then this will give the point A relative to the plane π2.
 |
| Fig. 39. |
§ 2. The two planes π1, π2 in their original position divide space
into four parts. These are called the four quadrants. We suppose
that the plane π2 is turned as indicated in
fig. 37, so that the point P comes to Q and
R to S, then the quadrant in which the
point A lies is called the first, and we say
that in the first quadrant a point lies above
the horizontal and in front of the vertical
plane. Now we go round the axis in the
sense in which the plane π2 is turned and
come in succession to the second, third
and fourth quadrant. In the second a
point lies above the plane of the plan and
behind the plane of elevation, and so on.
In fig. 39, which represents a side view of
the planes in fig. 37 the quadrants are
marked, and in each a point with its projection
is taken. Fig. 38 shows how these are represented when
the plane π2 is turned down. We see that
A point lies in the first quadrant if the plan lies below, the elevation
above the axis; in the second if plan and elevation both lie above; in
the third if the plan lies above, the elevation below; in the fourth if plan
and elevation both lie below the axis.
If a point lies in the horizontal plane, its elevation lies in the axis
and the plan coincides with the point itself. If a point lies in the
vertical plane, its plan lies in the axis and the elevation coincides
with the point itself. If a point lies in the axis, both its plan and
elevation lie in the axis and coincide with it.
Of each of these propositions, which will easily be seen to be true,
the converse holds also.
§ 3. Representation of a Plane.—As we are thus enabled to represent
points in a plane, we can represent any finite figure by representing
its separate points. It is, however, not possible to represent a plane
in this way, for the projections of its points completely cover the
planes π1 and π2, and no plane would appear different from any other.
But any plane α cuts each of the planes π1, π2 in a line. These are
called the traces of the plane. They cut each other in the axis at the
point where the latter cuts the plane α.
A plane is determined by its two traces, which are two lines that meet
on the axis, and, conversely, any two lines which meet on the axis
determine a plane.
If the plane is parallel to the axis its traces are parallel to the axis.
Of these one may be at infinity; then the plane will cut one of the
planes of projection at infinity and will be parallel to it. Thus a
plane parallel to the horizontal plane of the plan has only one finite
trace, viz. that with the plane of elevation.
 |
| Fig. 40. |
If the plane passes through the axis both its traces coincide with the
axis. This is the only case in which the representation of the plane
by its two traces fails. A third plane of projection is therefore
introduced, which is best taken perpendicular to the other two.
We call it simply the third plane and denote it by π3. As it is
perpendicular to π1, it may be
taken as the plane of elevation,
its line of intersection γ with π1
being the axis, and be turned
down to coincide with π1. This
is represented in fig. 40. OC is
the axis xy whilst OA and OB
are the traces of the third plane.
They lie in one line γ. The plane
is rabatted about γ to the horizontal
plane. A plane α through
the axis xy will then show in it
a trace α3. In fig. 40 the lines OC
and OP will thus be the traces
of a plane through the axis xy,
which makes an angle POQ with
the horizontal plane.
We can also find the trace
which any other plane makes
with π3. In rabatting the plane
π3 its trace OB with the plane π2 will come to the position OD.
Hence a plane β having the traces CA and CB will have with the
third plane the trace β3, or AD if OD = OB.
708
It also follows immediately that—
If a plane α is perpendicular to the horizontal plane, then every point
in it has its horizontal projection in the horizontal trace of the plane,
as all the rays projecting these points lie in the plane itself.
Any plane which is perpendicular to the horizontal plane has its
vertical trace perpendicular to the axis.
Any plane which is perpendicular to the vertical plane has its horizontal
trace perpendicular to the axis and the vertical projections of all
points in the plane lie in this trace.
§ 4. Representation of a Line.—A line is determined either by two
points in it or by two planes through it. We get accordingly two
representations of it either by projections or by traces.
First.—A line a is represented by its projections a1 and a2 on the
two planes π1 and π2. These may be any two lines, for, bringing
the planes π1, π2 into their original position, the planes through these
lines perpendicular to π1 and π2 respectively will intersect in some line
a which has a1, a2 as its projections.
Secondly.—A line a is represented by its traces—that is, by the points
in which it cuts the two planes π1, π2. Any two points may be taken
as the traces of a line in space, for it is determined when the planes
are in their original position as the line joining the two traces. This
representation becomes undetermined if the two traces coincide in
the axis. In this case we again use a third plane, or else the projections
of the line.
The fact that there are different methods of representing points
and planes, and hence two methods of representing lines, suggests
the principle of duality (section ii., Projective Geometry, § 41). It
is worth while to keep this in mind. It is also worth remembering
that traces of planes or lines always lie in the planes or lines which
they represent. Projections do not as a rule do this excepting when
the point or line projected lies in one of the planes of projection.
Having now shown how to represent points, planes and lines,
we have to state the conditions which must hold in order that these
elements may lie one in the other, or else that the figure formed by
them may possess certain metrical properties. It will be found that
the former are very much simpler than the latter.
Before we do this, however, we shall explain the notation used;
for it is of great importance to have a systematic notation. We
shall denote points in space by capitals A, B, C; planes in space
by Greek letters α, β, γ; lines in space by small letters a, b, c;
horizontal projections by suffixes 1, like A1, a1; vertical projections
by suffixes 2, like A2, a2; traces by single and double dashes α′ α″,
a′, a″. Hence P1 will be the horizontal projection of a point P in
space; a line a will have the projections a1, a2 and the traces a′ and
a″; a plane α has the traces α′ and α″.
§ 5. If a point lies in a line, the projections of the point lie in the
projections of the line.
If a line lies in a plane, the traces of the line lie in the traces of the
plane.
These propositions follow at once from the definitions of the
projections and of the traces.
If a point lies in two lines its projections must lie in the projections
of both. Hence
If two lines, given by their projections, intersect, the intersection of
their planes and the intersection of their elevations must lie in a line
perpendicular to the axis, because they must be the projections of
the point common to the two lines.
Similarly—If two lines given by their traces lie in the same plane
or intersect, then the lines joining their horizontal and vertical traces
respectively must meet on the axis, because they must be the traces
of the plane through them.
§ 6. To find the projections of a line which joins two points A, B
given by their projections A1, A2 and B1, B2, we join A1, B1 and A2,
B2; these will be the projections required. For example, the
traces of a line are two points in the line whose projections are
known or at all events easily found. They are the traces themselves
and the feet of the perpendiculars from them to the axis.
 |
| Fig. 41. |
Hence if a′ a″ (fig. 41) are the traces of a line a, and if the perpendiculars
from them cut the axis in P and Q respectively, then the
line a′Q will be the horizontal and
a″P the vertical projection of the
line.
Conversely, if the projections
a1, a2 of a line are given, and if
these cut the axis in Q and P
respectively, then the perpendiculars
Pa′ and Qa″ to the axis
drawn through these points cut the
projections a1 and a2 in the traces
a′ and a″.
To find the line of intersection of
two planes, we observe that this
line lies in both planes; its traces
must therefore lie in the traces
of both. Hence the points where the horizontal traces of the given
planes meet will be the horizontal, and the point where the vertical
traces meet the vertical trace of the line required.
§ 7. To decide whether a point A, given by its projections, lies in
a plane α, given by its traces, we draw a line p by joining A to some
point in the plane α and determine its traces. If these lie in the
traces of the plane, then the line, and therefore the point A, lies
in the plane; otherwise not. This is conveniently done by joining
A1 to some point p′ in the trace α′; this gives p1; and the point
where the perpendicular from p′ to the axis cuts the latter we join
to A2; this gives p2. If the vertical trace of this line lies in the
vertical trace of the plane, then, and then only, does the line p, and
with it the point A, lie in the plane α.
§ 8. Parallel planes have parallel traces, because parallel planes are
cut by any plane, hence also by π1 and by π2, in parallel lines.
Parallel lines have parallel projections, because points at infinity
are projected to infinity.
If a line is parallel to a plane, then lines through the traces of the
line and parallel to the traces of the plane must meet on the axis, because
these lines are the traces of a plane parallel to the given plane.
§ 9. To draw a plane through two intersecting lines or through two
parallel lines, we determine the traces of the lines; the lines joining
their horizontal and vertical traces respectively will be the horizontal
and vertical traces of the plane. They will meet, at a finite point
or at infinity, on the axis if the lines do intersect.
To draw a plane through a line and a point without the line, we
join the given point to any point in the line and determine the plane
through this and the given line.
To draw a plane through three points which are not in a line, we
draw two of the lines which each join two of the given points and
draw the plane through them. If the traces of all three lines AB,
BC, CA be found, these must lie in two lines which meet on the
axis.
§ 10. We have in the last example got more points, or can easily
get more points, than are necessary for the determination of the
figure required—in this case the traces of the plane. This will
happen in a great many constructions and is of considerable importance.
It may happen that some of the points or lines obtained
are not convenient in the actual construction. The horizontal
traces of the lines AB and AC may, for instance, fall very near
together, in which case the line joining them is not well defined.
Or, one or both of them may fall beyond the drawing paper, so that
they are practically non-existent for the construction. In this case
the traces of the line BC may be used. Or, if the vertical traces of
AB and AC are both in convenient position, so that the vertical
trace of the required plane is found and one of the horizontal traces
is got, then we may join the latter to the point where the vertical
trace cuts the axis.
The draughtsman must remember that the lines which he draws
are not mathematical lines without thickness, and therefore every
drawing is affected by some errors. It is therefore very desirable
to be able constantly to check the latter. Such checks always
present themselves when the same result can be obtained by different
constructions, or when, as in the above case, some lines must meet
on the axis, or if three points must lie in a line. A careful draughtsman
will always avail himself of these checks.
§ 11. To draw a plane through a given point parallel to a given
plane α, we draw through the point two lines which are parallel to
the plane α, and determine the plane through them; or, as we
know that the traces of the required plane are parallel to those of
the given one (§ 8), we need only draw one line l through the point
parallel to the plane and find one of its traces, say the vertical trace
l″; a line through this parallel to the vertical trace of α will be the
vertical trace β″ of the required plane β, and a line parallel to the
horizontal trace of α meeting β″ on the axis will be the horizontal
trace β′.
 |
| Fig. 42. |
Let A1 A2 (fig. 42) be the given point, α′ α″ the given plane, a
line l1 through A1, parallel to α′ and a horizontal line l2 through
A2 will be the projections of
a line l through A parallel
to the plane, because the
horizontal plane through
this line will cut the plane
α in a line c which has its
horizontal projection c1
parallel to α′.
§ 12. We now come to
the metrical properties of
figures.
A line is perpendicular
to a plane if the projections
of the line are perpendicular
to the traces of the plane. We prove it for the horizontal
projection. If a line p is perpendicular to a plane α, every plane
through p is perpendicular to α; hence also the vertical plane which
projects the line p to p1. As this plane is perpendicular both to the
horizontal plane and to the plane α, it is also perpendicular to their
intersection—that is, to the horizontal trace of α. It follows that
every line in this projecting plane, therefore also p1, the plan of p, is
perpendicular to the horizontal trace of α.
To draw a plane through a given point A perpendicular to a given
line p, we first draw through some point O in the axis lines γ′, γ″
perpendicular respectively to the projections p1 and p2 of the given
line. These will be the traces of a plane γ which is perpendicular
to the given line. We next draw through the given point A a plane
parallel to the plane γ; this will be the plane required.
709
Other metrical properties depend on the determination of the real
size or shape of a figure.
In general the projection of a figure differs both in size and shape
from the figure itself. But figures in a plane parallel to a plane
of projection will be identical with their projections, and will thus
be given in their true dimensions. In other cases there is the
problem, constantly recurring, either to find the true shape and
size of a plane figure when plan and elevation are given, or, conversely,
to find the latter from the known true shape of the figure
itself. To do this, the plane is turned about one of its traces till it
is laid down into that plane of projection to which the trace belongs.
This is technically called rabatting the plane respectively into the
plane of the plan or the elevation. As there is no difference in the
treatment of the two cases, we shall consider only the case of rabatting
a plane α into the plane of the plan. The plan of the figure is
a parallel (orthographic) projection of the figure itself. The results
of parallel projection (see Projection, §§ 17 and 18) may therefore
now be used. The trace α′ will hereby take the place of what
formerly was called the axis of projection. Hence we see that corresponding
points in the plan and in the rabatted plane are joined by
lines which are perpendicular to the trace α′ and that corresponding
lines meet on this trace. We also see that the correspondence is
completely determined if we know for one point or one line in the
plan the corresponding point or line in the rabatted plane.
Before, however, we treat of this we consider some special cases.
§ 13. To determine the distance between two points A, B given by their
projections A1, B1 and A2, B2, or, in other words, to determine the true
length of a line the plan and elevation of which are given.
 |
| Fig. 43. |
 |
| Fig. 44. |
Solution.—The two points A, B in space lie vertically above their
plans A1, B1 (fig. 43) and A1A = A0A2, B1B =
B0B2. The four points
A, B, A1, B1 therefore form a plane
quadrilateral on the base A1B1 and
having right angles at the base.
This plane we rabatt about A1B1
by drawing A1A and B1B perpendicular
to A1B1 and making
A1A = A0A2, B1B = B0B2. Then
AB will give the length required.
The construction might have
been performed in the elevation
by making A2A = A0A1 and
B2B = B0B1 on lines perpendicular
to A2B2. Of course AB must have
the same length in both cases.
This figure may be turned into
a model. Cut the paper along
A1A, AB and BB1, and fold the
piece A1ABB1 over along A1B1 till
it stands upright at right angles to the horizontal plane. The points
A, B will then be in their true position in space relative to
π1. Similarly
if B2BAA2 be cut out and turned along A2B2 through a right
angle we shall get AB in its true position relative to the plane
π2. Lastly we fold the whole plane of the paper along the axis x
till the plane π2 is at right angles to π1. In this position the two
sets of points AB will coincide if the drawing has been accurate.
Models of this kind can be made in many cases and their construction
cannot be too highly recommended in order to realize
orthographic projection.
§ 14. To find the angle between two given lines a, b of which the
projections a1, b1 and a2, b2 are given.
Solution.—Let a1, b1 (fig. 44) meet in P1, a2, b2 in T, then if the line
P1T is not perpendicular to the axis the two lines will not meet. In
this case we draw a line parallel
to b to meet the line a. This is
easiest done by drawing first the
line P1P2 perpendicular to the
axis to meet a2 in P2, and then
drawing through P2 a line c2
parallel to b2; then b1, c2 will be
the projections of a line c which
is parallel to b and meets a in P.
The plane α which these two
lines determine we rabatt to the
plan. We determine the traces
a′ and c′ of the lines a and c;
then a′c′ is the trace α′ of their
plane. On rabatting the point
P comes to a point S on the line
P1Q perpendicular to a′c′, so
that QS = QP. But QP is the hypotenuse of a triangle PP1Q with
a right angle P1. This we construct by making QR = P0P2; then
P1R = PQ. The lines a′S and c′S will therefore include angles equal
to those made by the given lines. It is to be remembered that two
lines include two angles which are supplementary. Which of these
is to be taken in any special case depends upon the circumstances.
To determine the angle between a line and a plane, we draw through
any point in the line a perpendicular to the plane (§ 12) and determine
the angle between it and the given line. The complement of this
angle is the required one.
To determine the angle between two planes, we draw through any
point two lines perpendicular to the two planes and determine the
angle between the latter as above.
In special cases it is simpler to determine at once the angle between
the two planes by taking a plane section perpendicular to the intersection
of the two planes and rabatt this. This is especially the
case if one of the planes is the horizontal or vertical plane of projection.
Thus in fig. 45 the angle P1QR is the angle which the plane α
makes with the horizontal plane.
§ 15. We return to the general case of rabatting a plane α of
which the traces α′ α″ are given.
 |
| Fig. 45. |
Here it will be convenient to determine first the position which
the trace α″—which is a line in α—assumes when rabatted. Points
in this line coincide with their elevations. Hence it is given in
its true dimension, and we can measure off along it the true distance
between two points in it. If therefore (fig. 45) P is any point in α″
originally coincident with
its elevation P2, and if O
is the point where α″ cuts
the axis xy, so that O is
also in α′, then the point P
will after rabatting the
plane assume such a position
that OP = OP2. At
the same time the plan is
an orthographic projection
of the plane α. Hence the
line joining P to the plan
P1 will after rabatting be
perpendicular to α′. But
P1 is known; it is the foot
of the perpendicular from
P2 to the axis xy. We
draw therefore, to find P,
from P1 a perpendicular P1Q to α′ and find on it a point P such that
OP = OP2. Then the line OP will be the position of α″ when
rabatted. This line corresponds therefore to the plan of
α″—that
is, to the axis xy, corresponding points on these lines being those
which lie on a perpendicular to α′.
We have thus one pair of corresponding lines and can now find
for any point B1 in the plan the corresponding point B in the rabatted
plane. We draw a line through B1, say B1P1, cutting α′ in C. To it
corresponds the line CP, and the point where this is cut by the projecting
ray through B1, perpendicular to α′, is the required point B.
Similarly any figure in the rabatted plane can be found when the
plan is known; but this is usually found in a different manner
without any reference to the general theory of parallel projection.
As this method and the reasoning employed for it have their peculiar
advantages, we give it also.
Supposing the planes π1 and π2 to be in their positions in space
perpendicular to each other, we take a section of the whole figure
by a plane perpendicular to the trace α′ about which we are going
to rabatt the plane α. Let this section pass through the point Q in
α′. Its traces will then be the lines QP1 and P1P2 (fig. 9). These
will be at right angles, and will therefore, together with the section
QP2 of the plane α, form a right-angled triangle QP1P2 with the
right angle at P1, and having the sides P1Q and P1P2 which both
are given in their true lengths. This triangle we rabatt about its
base P1Q, making P1R = P1P2. The line QR will then give the true
length of the line QP in space. If now the plane α be turned about
α′ the point P will describe a circle about Q as centre with radius
QP = QR, in a plane perpendicular to the trace α′. Hence when the
plane α has been rabatted into the horizontal plane the point P will
lie in the perpendicular P1Q to α′, so that QP = QR.
If A1 is the plan of a point A in the plane α, and if A1 lies in QP1,
then the point A will lie vertically above A1 in the line QP. On
turning down the triangle QP1P2, the point A will come to A0, the
line A1A0 being perpendicular to QP1. Hence A will be a point in
QP such that QA = QA0.
If B1 is the plan of another point, but such that A1B1 is parallel
to α′, then the corresponding line AB will also be parallel to α′.
Hence, if through A a line AB be drawn parallel to α′, and B1B
perpendicular to α′, then their intersection gives the point B. Thus
of any point given in plan the real position in the plane α, when
rabatted, can be found by this second method. This is the one
most generally given in books on geometrical drawing. The first
method explained is, however, in most cases preferable as it gives
the draughtsman a greater variety of constructions. It requires a
somewhat greater amount of theoretical knowledge.
If instead of our knowing the plan of a figure the latter is itself
given, then the process of finding the plan is the reverse of the
above and needs little explanation. We give an example.
§ 16. It is required to draw the plan and elevation of a polygon of
which the real shape and position in a given plane α are known.
 |
| Fig. 46. |
We first rabatt the plane α (fig. 46) as before so that P1 comes to
P, hence OP1 to OP. Let the given polygon in α be the figure
ABCDE. We project, not the vertices, but the sides. To project
the line AB, we produce it to cut α′ in F and OP in G, and draw GG1
perpendicular to α′; then G1 corresponds to G, therefore FG1 to FG.
In the same manner we might project all the other sides, at least
710
those which cut OF and OP in convenient points. It will be best,
however, first to produce all the sides to cut OP and α′ and then to
draw all the projecting rays through A, B, C ... perpendicular to
α′, and in the same
direction the lines
G, G1, &c. By
drawing FG we
get the points A1,
B1 on the projecting
ray through A
and B. We then
join B to the point
M where BC produced
meets the
trace α′. This
gives C1. So we
go on till we have
found E1. The
line A1 E1 must
then meet AE in
α′, and this gives
a check. If one
of the sides cuts
α′ or OP beyond
the drawing paper
this method fails,
but then we may
easily find the projection
of some
other line, say of
a diagonal, or
directly the projection
of a point,
by the former
methods. The
diagonals may
also serve to check
the drawing, for two corresponding diagonals must meet in the
trace α′.
Having got the plan we easily find the elevation. The elevation
of G is above G1 in α″, and that of F is at F2 in the axis. This
gives the elevation F2G2 of FG and in it we get A2B2 in the verticals
through A1 and B1. As a check we have OG = OG2. Similarly the
elevation of the other sides and vertices are found.
§ 17. We proceed to give some applications of the above principles
to the representation of solids and of the solution of problems
connected with them.
Of a pyramid are given its base, the length of the perpendicular from
the vertex to the base, and the point where this perpendicular cuts the
base; it is required first to develop the whole surface of the pyramid
into one plane, and second to determine its section by a plane which
cuts the plane of the base in a given line and makes a given angle
with it.
1. As the planes of projection are not given we can take them as we
like, and we select them in such a manner that the solution becomes
as simple as possible. We take the plane of the base as the horizontal
plane and the vertical plane perpendicular to the plane of the section.
Let then (fig. 47) ABCD be the base of the pyramid, V1 the plan of
the vertex, then the elevations of A, B, C, D will be in the axis at
A2, B2, C2, D2, and the vertex at some point V2 above V1 at a known
distance from the axis. The lines V1A, V1B, &c., will be the plans
and the lines V2A2, V2B2, &c., the elevations of the edges of the
pyramid, of which thus plan and elevation are known.
We develop the surface into the plane of the base by turning
each lateral face about its lower edge into the horizontal plane by
the method used in § 14. If one face has been turned down, say
ABV to ABP, then the point Q to which the vertex of the next
face BCV comes can be got more simply by finding on the line
V1Q perpendicular to BC the point Q such that BQ = BP, for these
lines represent the same edge BV of the pyramid. Next R is
found by making CR = CQ, and so on till we have got the last vertex—in
this case S. The fact that AS must equal AP gives a convenient
check.
2. The plane α whose section we have to determine has its horizontal
trace given perpendicular to the axis, and its vertical trace
makes the given angle with the axis. This determines it. To find
the section of the pyramid by this plane there are two methods
applicable: we find the sections of the plane either with the faces
or with the edges of the pyramid. We use the latter.
As the plane α is perpendicular to the vertical plane, the trace
α″ contains the projection of every figure in it; the points E2, F2,
G2, H2 where this trace cuts the elevations of the edges will therefore
be the elevations of the points where the edges cut α. From these
we find the plans E1, F1, G1, H1, and by joining them the plan
of the section. If from E1, F1 lines be drawn perpendicular to AB,
these will determine the points E, F on the developed face in which
the plane α cuts it; hence also the line EF. Similarly on the other
faces. Of course BF must be the same length on BP and on BQ.
If the plane α be rabatted to the plan, we get the real shape of the
section as shown in the figure in EFGH. This is done easily by
making F0F = OF2, &c. If the figure representing the development
of the pyramid, or better a copy of it, is cut out, and if the lateral
faces be bent along the lines AB, BC, &c., we get a model of the pyramid
with the section marked on its faces. This may be placed on
its plan ABCD and the plane of elevation bent about the axis x.
The pyramid stands then in front of its elevations. If next the plane
α with a hole cut out representing the true section be bent along the
trace α′ till its edge coincides with α″, the edges of the hole ought to
coincide with the lines EF, FG, &c., on the faces.
§ 18. Polyhedra like the pyramid in § 17 are represented by the
projections of their edges and vertices. But solids bounded by
curved surfaces, or surfaces themselves, cannot be thus represented.
For a surface we may use, as in case of the plane, its traces—that
is, the curves in which it cuts the planes of projection. We may
also project points and curves on the surface. A ray cuts the
surface generally in more than one point; hence it will happen
that some of the rays touch the surface, if two of these points coincide.
The points of contact of these rays will form some curve on the surface,
and this will appear from the centre of projection as the boundary
of the surface or of part of the surface. The outlines of all surfaces
of solids which we see about us are formed by the points at which
rays through our eye touch the surface. The projections of these
contours are therefore best adapted to give an idea of the shape of a
surface.
 |
| Fig. 47. |
Thus the tangents drawn from any finite centre to a sphere form
a right circular cone, and this will be cut by any plane in a conic.
It is often called the projection of a sphere, but it is better called
the contour-line of the sphere, as it is the boundary of the projections
of all points on the sphere.
If the centre is at infinity the tangent cone becomes a right
circular cylinder touching the sphere along a great circle, and if
the projection is, as in our case, orthographic, then the section of
this cone by a plane of projection will be a circle equal to the great
circle of the sphere. We get such a circle in the plan and another in
the elevation, their centres being plan and elevation of the centre of
the sphere.
Similarly the rays touching a cone of the second order will lie
in two planes which pass through the vertex of the cone, the contour-line
of the projection of the cone consists therefore of two lines
meeting in the projection of the vertex. These may, however,
be invisible if no real tangent rays can be drawn from the centre of
projection; and this happens when the ray projecting the centre
of the vertex lies within the cone. In this case the traces of the
cone are of importance. Thus in representing a cone of revolution
with a vertical axis we get in the plan a circular trace of the surface
whose centre is the plan of the vertex of the cone, and in the elevation
the contour, consisting of a pair of lines intersecting in the elevation
of the vertex of the cone. The circle in the plan and the pair of lines
in the elevation do not determine the surface, for an infinite number
of surfaces might be conceived which pass through the circular trace
and touch two planes through the contour lines in the vertical plane.
The surface becomes only completely defined if we write down to
the figure that it shall represent a cone. The same holds for all
711
surfaces. Even a plane is fully represented by its traces only under
the silent understanding that the traces are those of a plane.
§ 19. Some of the simpler problems connected with the representation
of surfaces are the determination of plane sections and of
the curves of intersection of two such surfaces. The former is
constantly used in nearly all problems concerning surfaces. Its
solution depends of course on the nature of the surface.
To determine the curve of intersection of two surfaces, we take a
plane and determine its section with each of the two surfaces,
rabatting this plane if necessary. This gives two curves which lie
in the same plane and whose intersections will give us points on
both surfaces. It must here be remembered that two curves in
space do not necessarily intersect, hence that the points in which
their projections intersect are not necessarily the projections of
points common to the two curves. This will, however, be the case
if the two curves lie in a common plane. By taking then a number
of plane sections of the surfaces we can get as many points on their
curve of intersection as we like. These planes have, of course, to
be selected in such a way that the sections are curves as simple as
the case permits of, and such that they can be easily and accurately
drawn. Thus when possible the sections should be straight lines
or circles. This not only saves time in drawing but determines all
points on the sections, and therefore also the points where the two
curves meet, with equal accuracy.
§ 20. We give a few examples how these sections have to be
selected. A cone is cut by every plane through the vertex in lines,
and if it is a cone of revolution by planes perpendicular to the
axis in circles.
A cylinder is cut by every plane parallel to the axis in lines, and
if it is a cylinder of revolution by planes perpendicular to the axis
in circles.
A sphere is cut by every plane in a circle.
Hence in case of two cones situated anywhere in space we take
sections through both vertices. These will cut both cones in lines.
Similarly in case of two cylinders we may take sections parallel to
the axis of both. In case of a sphere and a cone of revolution with
vertical axis, horizontal sections will cut both surfaces in circles
whose plans are circles and whose elevations are lines, whilst vertical
sections through the vertex of the cone cut the latter in lines and
the sphere in circles. To avoid drawing the projections of these
circles, which would in general be ellipses, we rabatt the plane and
then draw the circles in their real shape. And so on in other cases.
Special attention should in all cases be paid to those points in
which the tangents to the projection of the curve of intersection are
parallel or perpendicular to the axis x, or where these projections
touch the contour of one of the surfaces.
(O. H.)
IV. Analytical Geometry
1. In the name geometry there is a lasting record that the
science had its origin in the knowledge that two distances may
be compared by measurement, and in the idea that measurement
must be effectual in the dissociation of different directions as well
as in the comparison of distances in the same direction. The
distance from an observer’s eye of an object seen would be
specified as soon as it was ascertained that a rod, straight to the
eye and of length taken as known, could be given the direction
of the line of vision, and had to be moved along it a certain
number of times through lengths equal to its own in order to
reach the object from the eye. Moreover, if a field had for two
of its boundaries lines straight to the eye, one running from south
to north and the other from west to east, the position of a point
in the field would be specified if the rod, when directed west,
had to be shifted from the point one observed number of times
westward to meet the former boundary, and also, when directed
south, had to be shifted another observed number of times
southward to meet the latter. Comparison by measurement,
the beginning of geometry, involved counting, the basis of arithmetic;
and the science of number was marked out from the
first as of geometrical importance.
But the arithmetic of the ancients was inadequate as a science
of number. Though a length might be recognized as known
when measurement certified that it was so many times a standard
length, it was not every length which could be thus specified
in terms of the same standard length, even by an arithmetic
enriched with the notion of fractional number. The idea of
possible incommensurability of lengths was introduced into
Europe by Pythagoras; and the corresponding idea of irrationality
of number was absent from a crude arithmetic, while there
were great practical difficulties in the way of its introduction.
Hence perhaps it arose that, till comparatively modern times,
appeal to arithmetical aid in geometrical reasoning was in all
possible ways restrained. Geometry figured rather as the helper
of the more difficult science of arithmetic.
2. It was reserved for algebra to remove the disabilities of
arithmetic, and to restore the earliest ideas of the land-measurer
to the position of controlling ideas in geometrical investigation.
This unified science of pure number made comparatively little
headway in the hands of the ancients, but began to receive
due attention shortly after the revival of learning. It expresses
whole classes of arithmetical facts in single statements, gives
to arithmetical laws the form of equations involving symbols
which may mean any known or sought numbers, and provides
processes which enable us to analyse the information given by an
equation and derive from that equation other equations, which
express laws that are in effect consequences or causes of a law
started from, but differ greatly from it in form. Above all, for
present purposes, it deals not only with integral and fractional
number, but with number regarded as capable of continuous
growth, just as distance is capable of continuous growth. The
difficulty of the arithmetical expression of irrational number,
a difficulty considered by the modern school of analysts to have
been at length surmounted (see Function), is not vital to it.
It can call the ratio of the diagonal of a square to a side, for
instance, or that of the circumference of a circle to a diameter,
a number, and let a or x denote that number, just as properly
as it may allow either letter to denote any rational number
which may be greater or less than the ratio in question by a
difference less than any minute one we choose to assign.
Counting only, and not the counting of objects, is of the essence
of arithmetic, and of algebra. But it is lawful to count objects,
and in particular to count equal lengths by measure. The
widened idea is that even when a or x is an irrational number
we may speak of a or x unit lengths by measure. We may give
concrete interpretation to an algebraical equation by allowing
its terms all to mean numbers of times the same unit length,
or the same unit area, or &c. and in any equation lawfully
derived from the first by algebraical processes we may do the
same. Descartes in his Géométrie (1637) was the first to systematize
the application of this principle to the inherent first
notions of geometry; and the methods which he instituted have
become the most potent methods of all in geometrical research.
It is hardly too much to say that, when known facts as to a
geometrical figure have once been expressed in algebraical
terms, all strictly consequential facts as to the figure can be
deduced by almost mechanical processes. Some may well be
unexpected consequences; and in obtaining those of which
there has been suggestion beforehand the often bewildering
labour of constant attention to the figure is obviated. These
are the methods of what is now called analytical, or sometimes
algebraical, geometry.
3. The modern use of the term “analytical” in geometry has
obscured, but not made obsolete, an earlier use, one as old as
Plato. There is nothing algebraical in this analysis, as distinguished
from synthesis, of the Greeks, and of the expositors
of pure geometry. It has reference to an order of ideas in
demonstration, or, more frequently, in discovering means to
effect the geometrical construction of a figure with an assigned
special property. We have to suppose hypothetically that the
construction has been performed, drawing a rough figure which
exhibits it as nearly as is practicable. We then analyse or
critically examine the figure, treated as correct, and ascertain
other properties which it can only possess in association with
the one in question. Presently one of these properties will often
be found which is of such a character that the construction of
a figure possessing it is simple. The means of effecting synthetically
a construction such as was desired is thus brought to light by
what Plato called analysis. Or again, being asked to prove a
theorem A, we ascertain that it must be true if another theorem
B is, that B must be if C is, and so on, thus eventually finding
that the theorem A is the consequence, through a chain of intermediaries,
of a theorem Z of which the establishment is easy.
This geometrical analysis is not the subject of the present article;
but in the reasoning from form to form of an equation or system
712
of equations, with the object of basing the algebraical proof
of a geometrical fact on other facts of a more obvious character,
the same logic is utilized, and the name “analytical geometry”
is thus in part explained.
4. In algebra real positive number was alone at first dealt
with, and in geometry actual signless distance. But in algebra
it became of importance to say that every equation of the first
degree has a root, and the notion of negative number was introduced.
The negative unit had to be defined as what can be
added to the positive unit and produce the sum zero. The
corresponding notion was readily at hand in geometry, where
it was clear that a unit distance can be measured to the left
or down from the farther end of a unit distance already measured
to the right or up from a point O, with the result of reaching O
again. Thus, to give full interpretation in geometry to the
algebraically negative, it was only necessary to associate distinctness
of sign with oppositeness of direction. Later it was discovered
that algebraical reasoning would be much facilitated, and that
conclusions as to the real would retain all their soundness, if a pair
of imaginary units ±√−1 of what might be called number were
allowed to be contemplated, the pair being defined, though not
separately, by the two properties of having the real sum 0 and
the real product 1. Only in these two real combinations do they
enter in conclusions as to the real. An advantage gained was
that every quadratic equation, and not some quadratics only,
could be spoken of as having two roots. These admissions of
new units into algebra were final, as it admitted of proof that all
equations of degrees higher than two have the full numbers of
roots possible for their respective degrees in any case, and that
every root has a value included in the form a + b √−1, with a, b,
real. The corresponding enrichment could be given to geometry,
with corresponding advantages and the same absence of danger,
and this was done. On a line of measurement of distance we
contemplate as existing, not only an infinite continuum of points
at real distances from an origin of measurement O, but a doubly
infinite continuum of points, all but the singly infinite continuum
of real ones imaginary, and imaginary in conjugate pairs, a
conjugate pair being at imaginary distances from O, which have
a real arithmetic and a real geometric mean. To geometry
enriched with this conception all algebra has its application.
5. Actual geometry is one, two or three-dimensional, i.e.
lineal, plane or solid. In one-dimensional geometry positions
and measurements in a single line only are admitted. Now
descriptive constructions for points in a line are impossible
without going out of the line. It has therefore been held that
there is a sense in which no science of geometry strictly confined
to one dimension exists. But an algebra of one variable can be
applied to the study of distances along a line measured from a
chosen point on it, so that the idea of construction as distinct
from measurement is not essential to a one-dimensional geometry
aided by algebra. In geometry of two dimensions, the
flat of the land-measurer, the passage from one point O to any
other point, can be effected by two successive marches, one east
or west and one north or south, and, as will be seen, an algebra
of two variables suffices for geometrical exploitation. In
geometry of three dimensions, that of space, any point can be
reached from a chosen one by three marches, one east or west,
one north or south, and one up or down; and we shall see that
an algebra of three variables is all that is necessary. With
three dimensions actual geometry stops; but algebra can supply
any number of variables. Four or more variables have been
used in ways analogous to those in which one, two and three
variables are used for the purposes of one, two and three-dimensional
geometry, and the results have been expressed in
quasi-geometrical language on the supposition that a higher
space can be conceived of, though not realized, in which four
independent directions exist, such that no succession of marches
along three of them can effect the same displacement of a point
as a march along the fourth; and similarly for higher numbers
than four. Thus analytical, though not actual, geometries exist
for four and more dimensions. They are in fact algebras furnished
with nomenclature of a geometrical cast, suggested by convenient
forms of expression which actual geometry has, in return for
benefits received, conferred on algebras of one, two and three
variables.
We will confine ourselves to the dimensions of actual geometry,
and will devote no space to the one-dimensional, except incidentally
as existing within the two-dimensional. The analytical
method will now be explained for the cases of two and three
dimensions in succession. The form of it originated by Descartes,
and thence known as Cartesian, will alone be considered in much
detail.
I. Plane Analytical Geometry.
 |
| Fig. 48. |
Fig. 49. |
6. Coordinates.—It is assumed that the points, lines and figures
considered lie in one and the same plane, which plane therefore need
not be in any way referred to. In the plane a point O, and two lines
x′Ox, y′Oy, intersecting in O, are taken once for all, and regarded as
fixed. O is called the origin, and x′Ox, y′Oy the axes of x and y
respectively. Other positions in the plane are specified in relation
to this fixed origin and these fixed axes. From any point P we
suppose PM drawn parallel to the axis of y to meet the axis of x in
M, and may also suppose PN drawn parallel to the axis of x to meet
the axis of y in N, so that OMPN is a parallelogram. The position
of P is determined when we know OM (= NP) and MP (= ON).
If OM is x times the unit of a scale of measurement chosen at pleasure,
and MP is y times the unit, so that x and y have numerical values,
we call x and y the (Cartesian) coordinates of P. To distinguish
them we often speak of y as the ordinate, and of x as the abscissa.
It is necessary to attend to signs; x has one sign or the other
according as the point P is on one side or the other of the axis of y,
and y one sign or the other according as P is on one side or the other
of the axis of x. Using the letters N, E, S, W, as in a map, and
considering the plane as divided into four quadrants by the axes,
the signs are usually taken to be:
| x | y | For quadrant |
| + | + | N E |
| + | − | S E |
| − | + | N W |
| − | − | S W |
A point is referred to as the point (a, b), when its coordinates are
x = a, y = b. A point may be fixed, or it may be variable, i.e. be
regarded for the time being as free to move in the plane. The
coordinates (x, y) of a variable point are algebraic variables, and are
said to be “current coordinates.”
The axes of x and y are usually (as in fig. 48) taken at right angles
to one another, and we then speak of them as rectangular axes,
and of x and y as “rectangular coordinates” of a point P; OMPN
is then a rectangle. Sometimes, however, it is convenient to use
axes which are oblique to one another, so that (as in fig. 49) the angle
xOy between their positive directions is some known angle ω
distinct from a right angle, and OMPN is always an oblique parallelogram
with given angles; and we then speak of x and y as “oblique
coordinates.” The coordinates are as a rule taken to be rectangular
in what follows.
7. Equations and loci. If (x, y) is the point P, and if we are
given that x = 0, we are told that, in fig. 48 or fig. 49, the point M lies
at O, whatever value y may have, i.e. we are told the one fact that
P lies on the axis of y. Conversely, if P lies anywhere on the axis
of y, we have always OM = 0, i.e. x = 0. Thus the equation x = 0 is
one satisfied by the coordinates (x, y) of every point in the axis of y,
and not by those of any other point. We say that x = 0 is the
equation of the axis of y, and that the axis of y is the locus represented
by the equation x = 0. Similarly y = 0 is the equation of the
axis of x. An equation x = a, where a is a constant, expresses that
P lies on a parallel to the axis of y through a point M on the axis
of x such that OM = a. Every line parallel to the axis of y has an
equation of this form. Similarly, every line parallel to the axis of x
has an equation of the form y = b, where b is some definite constant.
These are simple cases of the fact that a single equation in the
current coordinates of a variable point (x, y) imposes one limitation
on the freedom of that point to vary. The coordinates of a point
713
taken at random in the plane will, as a rule, not satisfy the equation,
but infinitely many points, and in most cases infinitely many real
ones, have coordinates which do satisfy it, and these points are
exactly those which lie upon some locus of one dimension, a straight
line or more frequently a curve, which is said to be represented by
the equation. Take, for instance, the equation y = mx, where m
is a given constant. It is satisfied by the coordinates of every point
P, which is such that, in fig. 48, the distance MP, with its proper sign,
is m times the distance OM, with its proper sign, i.e. by the coordinates
of every point in the straight line through O which we
arrive at by making a line, originally coincident with x′Ox, revolve
about O in the direction opposite to that of the hands of a watch
through an angle of which m is the tangent, and by those of no other
points. That line is the locus which it represents. Take, more
generally, the equation y = φ(x), where φ(x) is any given non-ambiguous
function of x. Choosing any point M on x′Ox in fig. 1, and
giving to x the value of the numerical measure of OM, the equation
determines a single corresponding y, and so determines a single
point P on the line through M parallel to y′Oy. This is one point
whose coordinates satisfy the equation. Now let M move from the
extreme left to the extreme right of the line x′Ox, regarded as
extended both ways as far as we like, i.e. let x take all real values
from −∞ to ∞. With every value goes a point P, as above, on
the parallel to y′Oy through the corresponding M; and we thus find
that there is a path from the extreme left to the extreme right of
the figure, all points P along which are distinguished from other
points by the exceptional property of satisfying the equation by
their coordinates. This path is a locus; and the equation y = φ(x)
represents it. More generally still, take an equation f(x, y) = 0
which involves both x and y under a functional form. Any particular
value given to x in it produces from it an equation for the determination
of a value or values of y, which go with that value of x in specifying
a point or points (x, y), of which the coordinates satisfy the
equation f(x, y) = 0. Here again, as x takes all values, the point or
points describe a path or paths, which constitute a locus represented
by the equation. Except when y enters to the first degree only in
f(x, y), it is not to be expected that all the values of y, determined
as going with a chosen value of x, will be necessarily real; indeed
it is not uncommon for all to be imaginary for some ranges of values
of x. The locus may largely consist of continua of imaginary
points; but the real parts of it constitute a real curve or real curves.
Note that we have to allow x to admit of all imaginary, as well as
of all real, values, in order to obtain all imaginary parts of the
locus.
A locus or curve may be algebraically specified in another way;
viz. we may be given two equations x = f(θ), y = F(θ), which express
the coordinates of any point of it as two functions of the same
variable parameter θ to which all values are open. As θ takes all
values in turn, the point (x, y) traverses the curve.
It is a good exercise to trace a number of curves, taken as defined
by the equations which represent them. This, in simple cases, can
be done approximately by plotting the values of y given by the
equation of a curve as going with a considerable number of values
of x, and connecting the various points (x, y) thus obtained. But
methods exist for diminishing the labour of this tentative process.
Another problem, which will be more attended to here, is that of
determining the equations of curves of known interest, taken as
defined by geometrical properties. It is not a matter for surprise
that the curves which have been most and longest studied geometrically
are among those represented by equations of the simplest
character.
 |
| Fig. 50. |
8. The Straight Line.—This is the simplest type of locus. Also
the simplest type of equation in x and y is Ax + By + C = 0, one of
the first degree. Here the coefficients A, B, C are constants. They
are, like the current coordinates, x, y, numerical. But, in giving
interpretation to such an equation, we must of course refer to
numbers Ax, By, C of unit magnitudes of the same kind, of units
of counting for instance, or unit lengths or unit squares. It will
now be seen that every straight
line has an equation of the first
degree, and that every equation
of the first degree represents a
straight line.
It has been seen (§ 7) that lines
parallel to the axes have equations
of the first degree, free
from one of the variables. Take
now a straight line ABC inclined
to both axes. Let it make a
given angle α with the positive
direction of the axis of x, i.e. in
fig. 50 let this be the angle
through which Ax must be revolved
counter-clockwise about
A in order to be made coincident
with the line. Let C, of
coordinates (h, k), be a fixed point
on the line, and P(x, y) any other point upon it. Draw the ordinates
CD, PM of C and P, and let the parallel to the axis of x through C
meet PM, produced if necessary, in R. The right-angled triangle
CRP tells us that, with the signs appropriate to their directions
attached to CR and RP,
RP = CR tan α, i.e. MP − DC = (OM − OD) tan α,
and this gives that
y − k = tan α (x − h),
an equation of the first degree satisfied by x and y. No point not
on the line satisfies the same equation; for the line from C to any
point off the line would make with CR some angle β different from α,
and the point in question would satisfy an equation y − k = tan β(x − h),
which is inconsistent with the above equation.
The equation of the line may also be written y = mx + b, where
m = tan α, and b = k − h tan α. Here b is the value obtained for y
from the equation when 0 is put for x, i.e. it is the numerical measure,
with proper sign, of OB, the intercept made by the line on the axis
of y, measured from the origin. For different straight lines, m and b
may have any constant values we like.
Now the general equation of the first degree Ax + By + C = 0 may
be written y = −(A/B)x − C/B, unless B = 0, in which case it represents a
line parallel to the axis of y; and −A/B, −C/B are values which
can be given to m and b, so that every equation of the first degree
represents a straight line. It is important to notice that the general
equation, which in appearance contains three constants A, B, C, in
effect depends on two only, the ratios of two of them to the third.
In virtue of this last remark, we see that two distinct conditions
suffice to determine a straight line. For instance, it is easy from the
above to see that
is the equation of a straight line determined by the two conditions
that it makes intercepts OA, OB on the two axes, of which a and b
are the numerical measures with proper signs: note that in fig. 50 a
is negative. Again,
| y − y1 = | y2 − y1 |
(x − x1), |
| x2 − x1 |
i.e.
(y1 − y2) x − (x1 − x2) y + x1y2 − x2y1 = 0,
represents the line determined by the data that it passes through
two given points (x1, y1) and (x2, y2). To prove this find m in the
equation y − y1 = m(x − x1) of a line through (x1, y1), from the condition
that (x2, y2) lies on the line.
In this paragraph the coordinates have been assumed rectangular.
Had they been oblique, the doctrine of similar triangles would have
given the same results, except that in the forms of equation y − k = m(x − h),
y = mx + b, we should not have had m = tan α.
9. The Circle.—It is easy to write down the equation of a given
circle. Let (h, k) be its given centre C, and ρ the numerical measure
of its given radius. Take P (x, y) any point on its circumference,
and construct the triangle CRP, in fig. 50 as above. The fact that
this is right-angled tells us that
CR² + RP² = CP²,
and this at once gives the equation
(x − h)² + (y − k)² = ρ².
A point not upon the circumference of the particular circle is at some
distance from (h, k) different from ρ, and satisfies an equation
inconsistent with this one; which accordingly represents the circumference,
or, as we say, the circle.
The equation is of the form
x² + y² + 2Ax + 2By + C = 0.
Conversely every equation of this form represents a circle: we have
only to take −A, −B, A² + B² − C for h, k, ρ² respectively, to obtain
its centre and radius. But this statement must appear too unrestricted.
Ought we not to require A² + B² − C to be positive?
Certainly, if by circle we are only to mean the visible round circumference
of the geometrical definition. Yet, analytically, we
contemplate altogether imaginary circles, for which ρ² is negative,
and circles, for which ρ = 0, with all their reality condensed into
their centres. Even when ρ² is positive, so that a visible round
circumference exists, we do not regard this as constituting the
whole of the circle. Giving to x any value whatever in (x − h)² + (y − k)² = ρ²,
we obtain two values of y, real, coincident or imaginary,
each of which goes with the abscissa x as the ordinate of a point,
real or imaginary, on what is represented by the equation of the
circle.
The doctrine of the imaginary on a circle, and in geometry generally,
is of purely algebraical inception; but it has been in its entirety
accepted by modern pure geometers, and signal success has attended
the efforts of those who, like K.G.C. von Staudt, have striven to
base its conclusions on principles not at all algebraical in form,
though of course cognate to those adopted in introducing the
imaginary into algebra.
A circle with its centre at the origin has an equation x² + y² = ρ².
In oblique coordinates the general equation of a circle is
x² + 2xy cos ω + y² + 2Ax + 2By + C = 0.
10. The conic sections are the next simplest loci; and it will be
seen later that they are the loci represented by equations of the
second degree. Circles are particular cases of conic sections; and
714
they have just been seen to have for their equations a particular
class of equations of the second degree. Another particular class
of such equations is that included in the form (Ax + By + C)(A′x +
B′y + C′) = 0, which represents two straight lines, because the product
on the left vanishes if, and only if, one of the two factors does, i.e.
if, and only if, (x, y) lies on one or other of two straight lines. The
condition that ax² + 2hxy + by² + 2gx + 2fy + c = 0, which is often
written (a, b, c, f, g, h)(x, y, I)² = 0, takes this form is abc + 2fgh − af² −
bg² − ch² = 0. Note that the two lines may, in particular cases, be
parallel or coincident.
Any equation like F1(x, y) F2(x, y) ... Fn(x, y) = 0, of which
the left-hand side breaks up into factors, represents all the loci
separately represented by F1(x, y) = 0, F2(x, y) = 0, ... Fn(x, y) = 0.
In particular an equation of degree n which is free from x represents
n straight lines parallel to the axis of x, and one of degree n which
is homogeneous in x and y, i.e. one which upon division by xn, becomes
an equation in the ratio y/x, represents n straight lines through
the origin.
Curves represented by equations of the third degree are called
cubic curves. The general equation of this degree will be written
(*)(x, y, I)³ = 0.
 |
| Fig. 51. |
11. Descriptive Geometry.—A geometrical proposition is either
descriptive or metrical: in the former case the statement of it is
independent of the idea of magnitude (length, inclination, &c.),
and in the latter it has reference to this idea. The method of coordinates
seems to be by its inception essentially metrical. Yet
in dealing by this method with descriptive propositions we are
eminently free from metrical considerations, because of our power to
use general equations, and
to avoid all assumption that
measurements implied are
any particular measurements.
12. It is worth while to
illustrate this by the instance
of the well-known
theorem of the radical centre
of three circles. The theorem
is that, given any three circles
A, B, C (fig. 51), the common
chords αα′, ββ′, γγ′ of the
three pairs of circles meet in
a point.
The geometrical proof is
metrical throughout:—
Take O the point of intersection
of αα′, ββ′, and joining
this with γ′, suppose that γ′O does not pass through γ, but that it
meets the circles A, B in two distinct points γ2, γ1 respectively. We
have then the known metrical property of intersecting chords of a
circle; viz. in circle C, where αα′, ββ′, are chords meeting at a point O,
Oα·Oα′ = Oβ·Oβ′,
where, as well as in what immediately follows, Oα, &c. denote, of
course, lengths or distances.
Similarly in circle A,
Oβ·Oβ′ = Oγ2·Oγ′,
and in circle B,
Oα·Oα′ = Oγ1·Oγ′.
Consequently Oγ1·Oγ′ = Oγ2·Oγ′, that is, Oγ1 = Oγ2, or the points
γ1 and γ2 coincide; that is, they each coincide with γ.
We contrast this with the analytical method:—
Here it only requires to be known that an equation Ax + By + C = 0
represents a line, and an equation x² + y² + Ax + By + C = 0 represents
a circle. A, B, C have, in the two cases respectively, metrical
significations; but these we are not concerned with. Using S to
denote the function x² + y² + Ax + By + C, the equation of a circle is
S = o. Let the equation of any other circle be S′, = x² + y² + A′x + B′y + C′ = 0;
the equation S-S′ = 0 is a linear equation (S − S′ is in
fact = (A − A′)x + (B − B′)y + C-C), and it thus represents a line;
this equation is satisfied by the coordinates of each of the points of
intersection of the two circles (for at each of these points S = 0 and
S′ = 0, therefore also S − S′ = 0); hence the equation S − S′ = 0 is
that of the line joining the two points of intersection of the two circles,
or say it is the equation of the common chord of the two circles.
Considering then a third circle S″, = x² + y² + A″x + B″y + C″ = 0, the
equations of the common chords are S − S′ = 0, S − S″ = 0, S′ − S″ = 0
(each of these a linear equation); at the intersection of the first and
second of these lines S = S′ and S = S″, therefore also S′ = S″, or the
equation of the third line is satisfied by the coordinates of the point
in question; that is, the three chords intersect in a point O, the coordinates
of which are determined by the equations S = S′ = S″.
It further appears that if the two circles S = 0, S′ = 0 do not intersect
in any real points, they must be regarded as intersecting in two
imaginary points, such that the line joining them is the real line
represented by the equation S − S′ = 0; or that two circles, whether
their intersections be real or imaginary, have always a real common
chord (or radical axis), and that for any three circles the common
chords intersect in a point (of course real) which is the radical centre.
And by this very theorem, given two circles with imaginary intersections,
we can, by drawing circles which meet each of them in
real points, construct the radical axis of the first-mentioned two
circles.
13. The principle employed in showing that the equation of the
common chord of two circles is S − S′ = 0 is one of very extensive
application, and some more illustrations of it may be given.
Suppose S = 0, S′ = 0 are lines (that is, let S, S′ now denote linear
functions Ax + By + C, A′x + B′y + C′), then S − kS′ = 0 (k an arbitrary
constant) is the equation of any line passing through the point
of intersection of the two given lines. Such a line may be made to
pass through any given point, say the point (x0, y0); if S0, S′0 are
what S, S′ respectively become on writing for (x, y) the values (x0, y0),
then the value of k is k = S0 ÷ S′0. The equation in fact is SS′0 − S0S′ = 0;
and starting from this equation we at once verify it a posteriori;
the equation is a linear equation satisfied by the values of (x, y)
which make S = 0, S′ = 0; and satisfied also by the values (x0, y0);
and it is thus the equation of the line in question.
If, as before, S = 0, S′ = 0 represent circles, then (k being arbitrary)
S − kS′ = 0 is the equation of any circle passing through the two
points of intersection of the two circles; and to make this pass
through a given point (x0, y0) we have again k = S0 ÷ S′0. In the
particular case k = 1, the circle becomes the common chord (more
accurately it becomes the common chord together with the line
infinity; see § 23 below).
If S denote the general quadric function,
S = ax2 + 2hxy + by2 + 2fy + 2gx + c,
then the equation S = 0 represents a conic; assuming this, then, if
S′ = 0 represents another conic, the equation S − kS′ = 0 represents
any conic through the four points of intersection of the two conics.
 |
| Fig. 52. |
14. The object still being to illustrate the mode of working with
coordinates for descriptive purposes,
we consider the theorem
of the polar of a point in regard
to a circle. Given a circle and
a point O (fig. 52), we draw
through O any two lines meeting
the circle in the points A, A′ and
B, B′ respectively, and then
taking Q as the intersection of
the lines AB′ and A′B, the
theorem is that the locus of the
point Q is a right line depending
only upon O and the circle, but independent of the
particular lines OAA′ and OBB′.
Taking O as the origin, and for the axes any two lines through O
at right angles to each other, the equation of the circle will be
x2 + y2 + 2Ax + 2By + C = 0;
and if the equation of the line OAA′ is taken to be y = mx, then the
points A, A′ are found as the intersections of the straight line with
the circle; or to determine x we have
x2 (1 + m2) + 2x (A + Bm) + C = 0.
If(x1, y1) are the coordinates of A, and (x2, y2) of A′, then the roots
of this equation are x1, x2, whence easily
| 1 |
+ | 1 |
= −2 | A + Bm |
. |
| x1 | x2 |
C |
And similarly, if the equation of the line OBB′ is taken to be y = m′x1
and the coordinates of B, B′ to be (x3, y3) and (x4, y4) respectively,
then
| 1 |
+ | 1 |
= −2 | A + Bm′ |
. |
| x3 | x4 |
C′ |
We have then by § 8
x (y1 − y4) − y (x1 − x4) + x1y4 − x4y1 = 0,
x (y2 − y3) − y (x2 − x3) + x2y3 − x3y2 = 0,
|
as the equations of the lines AB′ and A′B respectively. Reducing
by means of the relations y1 − mx1 = 0, y2 − mx2 = 0, y3 − m′x3 = 0,
y4 − m′x4 = 0, the two equations become
x (mx1 − m′x4) − y (x1 − x4) + (m′ − m) x1x4 = 0,
x (mx2 − m′x3) − y (x2 − x3) + (m′ − m) x2x3 = 0,
|
and if we divide the first of these equations by x1x4, and the second
by x2x3 and then add, we obtain
| x { m ( | 1 |
+ | 1 |
) − m′ ( | 1 |
+ | 1 |
) } − y { | 1 |
+ | 1 |
− ( | 1 |
+ | 1 |
) } + 2m′ − 2m = 0, |
| x3 | x4 |
x1 | x2 |
x3 | x4 |
x1 | x2 |
or, what is the same thing,
| ( | 1 |
+ | 1 |
) (y − m′x) − ( | 1 |
+ | 1 |
) (y − mx) + 2m′ − 2m = 0, |
| x1 | x2 |
x3 | x4 |
which by what precedes is the equation of a line through the point Q.
Substituting herein for 1/x1 + 1/x2, 1/x3 + 1/x4 their foregoing values, the
equation becomes
−(A + Bm) (y − m′x) + (A + Bm′) (y − mx) + C (m′ − m) = 0;
that is,
(m − m′) (Ax + By + C) = 0;
715
or finally it is Ax + By + C = 0, showing that the point Q lies in a line
the position of which is independent of the particular lines OAA′,
OBB′ used in the construction. It is proper to notice that there is
no correspondence to each other of the points A, A′ and B, B′; the
grouping might as well have been A, A′ and B′, B; and it thence
appears that the line Ax + By + C = 0 just obtained is in fact the line
joining the point Q with the point R which is the intersection of
AB and A′B′.
15. In § 8 it has been seen that two conditions determine the
equation of a straight line, because in Ax + By + C = 0 one of the
coefficients may be divided out, leaving only two parameters to be
determined. Similarly five conditions instead of six determine an
equation of the second degree (a, b, c, f, g, h)(x, y, 1)² = 0, and nine
instead of ten determine a cubic (*)(x, y, 1)³ = 0. It thus appears
that a cubic can be made to pass through 9 given points, and that
the cubic so passing through 9 given points is completely determined.
There is, however, a remarkable exception. Considering two given
cubic curves S = 0, S′ = 0, these intersect in 9 points, and through
these 9 points we have the whole series of cubics S − kS′ = 0, where
k is an arbitrary constant: k may be determined so that the cubic
shall pass through a given tenth point (k = S0 ÷ S′0, if the coordinates
are (x0, y0), and S0, S′0 denote the corresponding values of S, S′).
The resulting curve SS′0 − S′S0 = 0 may be regarded as the cubic
determined by the conditions of passing through 8 of the 9 points
and through the given point (x0, y0); and from the equation it
thence appears that the curve passes through the remaining one of
the 9 points. In other words, we thus have the theorem, any cubic
curve which passes through 8 of the 9 intersections of two given
cubic curves passes through the 9th intersection.
The applications of this theorem are very numerous; for instance,
we derive from it Pascal’s theorem of the inscribed hexagon. Consider
a hexagon inscribed in a conic. The three alternate sides
constitute a cubic, and the other three alternate sides another cubic.
The cubics intersect in 9 points, being the 6 vertices of the hexagon,
and the 3 Pascalian points, or intersections of the pairs of opposite
sides of the hexagon. Drawing a line through two of the Pascalian
points, the conic and this line constitute a cubic passing through 8
of the 9 points of intersection, and it therefore passes through the
remaining point of intersection—that is, the third Pascalian point;
and since obviously this does not lie on the conic, it must lie on the
line—that is, we have the theorem that the three Pascalian points
(or points of intersection of the pairs of opposite sides) lie on a
line.
16. Metrical Theory resumed. Projections and Perpendiculars.—It
is a metrical fact of fundamental importance, already used in § 8,
that, if a finite line PQ be projected on any other line OO′ by perpendiculars
PP′, QQ′ to OO′, the length of the projection P′Q′ is
equal to that of PQ multiplied by the cosine of the acute angle
between the two lines. Also the algebraical sum of the projections
of the sides of any closed polygon upon any line is zero, because as a
point goes round the polygon, from any vertex A to A again, the
point which is its projection on the line passes from A′ the projection
of A to A′ again, i.e. traverses equal distances along the line in
positive and negative senses. If we consider the polygon as consisting
of two broken lines, each extending from the same initial
to the same terminal point, the sum of the projections of the lines
which compose the one is equal, in sign and magnitude, to the sum
of the projections of the lines composing the other. Observe that
the projection on a line of a length perpendicular to the line is
zero.
Let us hence find the equation of a straight line such that the
perpendicular OD on it from the origin is of length ρ taken as
positive, and is inclined to the axis of x at an angle xOD = α,
measured counter-clockwise from Ox. Take any point P(x, y) on
the line, and construct OM and MP as in fig. 48. The sum of the
projections of OM and MP on OD is OD itself; and this gives the
equation of the line
x cos α + y sin α = ρ.
Observe that cos α and sin α here are the sin α and −cos α, or the
−sin α and cos α of § 8 according to circumstances.
We can write down an expression for the perpendicular distance
from this line of any point (x′, y′) which does not lie upon it. If the
parallel through (x′, y′) to the line meet OD in E, we have x′ cos α + y′ sin α = OE,
and the perpendicular distance required is OD − OE,
i.e. ρ − x′ cos α − y′ sin α; it is the perpendicular distance taken
positively or negatively according as (x′, y′) lies on the same side
of the line as the origin or not.
The general equation Ax + By + C = 0 may be given the form
x cos α + y sin α − ρ = 0 by dividing it by √(A² + B³). Thus (Ax′ +
By′ + C) ÷ √(A² + B²) is in absolute value the perpendicular distance
of (x′, y′) from the line Ax + By + C = 0. Remember, however, that
there is an essential ambiguity of sign attached to a square root.
The expression found gives the distance taken positively when
(x′, y′) is on the origin side of the line, if the sign of C is given to
√(A² + B²).
17. Transformation of Coordinates.—We often need to adopt new
axes of reference in place of old ones; and the above principle of
projections readily expresses the old coordinates of any point in
terms of the new.
 |
| Fig. 53. |
Suppose, for instance, that we want to take for new origin the
point O′ of old coordinates OA = h, AO′ = k, and for new axes of
X and Y lines through O′ obtained by rotating parallels to the old
axes of x and y through an angle θ counter-clockwise. Construct
(fig. 53) the old and new coordinates
of any point P. Expressing
that the projections,
first on the old axis of x and
secondly on the old axis of y, of
OP are equal to the sums of the
projections, on those axes respectively,
of the parts of the broken
line OO′M′P, we obtain:
x = h + X cos θ + Y cos (θ + ½π) =
h + X cos θ − Y sin θ,
and
y = k + X cos (½π − θ) + Y cos θ =
k + X sin θ + Y cos θ.
Be careful to observe that these
formulae do not apply to every
conceivable change of reference from one set of rectangular axes to
another. It might have been required to take O′X, O′Y′ for the
positive directions of the new axes, so that the change of directions
of the axes could not be effected by rotation. We must then write
−Y for Y in the above.
Were the new axes oblique, making angles α, β respectively with
the old axis of x, and so inclined at the angle β − α, the same method
would give the formulae
x = h + X cos α + Y cos β, y = k + X sin α + Y sin β.
18. The Conic Sections.—The conics, as they are now called, were
at first defined as curves of intersection of planes and a cone; but
Apollonius substituted a definition free from reference to space of
three dimensions. This, in effect, is that a conic is the locus of a
point the distance of which from a given point, called the focus, has
a given ratio to its distance from a given line, called the directrix
(see Conic Section). If e : 1 is the ratio, e is called the eccentricity.
The distances are considered signless.
Take (h, k) for the focus, and x cos α + y sin α − p = 0 for the
directrix. The absolute values of √{(x − h)² + (y − k)²} and p − x cos α −
y sin α are to have the ratio e : 1; and this gives
(x − h)² + (y − k)² = e² (p − x cos α − y sin α)²
as the general equation, in rectangular coordinates, of a conic.
It is of the second degree, and is the general equation of that
degree. If, in fact, we multiply it by an unknown λ, we can, by
solving six simultaneous equations in the six unknowns λ, h, k, e, p, α,
so choose values for these as to make the coefficients in the equation
equal to those in any equation of the second degree which may be
given. There is no failure of this statement in the special case
when the given equation represents two straight lines, as in § 10,
but there is speciality: if the two lines intersect, the intersection
and either bisector of the angle between them are a focus and
directrix; if they are united in one line, any point on the line and a
perpendicular to it through the point are: if they are parallel,
the case is a limiting one in which e and h² + k² have become infinite
while e−2(h² + k²) remains finite. In the case (§ 9) of an equation
such as represents a circle there is another instance of proceeding
to a limit: e has to become 0, while ep remains finite: moreover α
is indeterminate. The centre of a circle is its focus, and its directrix
has gone to infinity, having no special direction. This last fact
illustrates the necessity, which is also forced on plane geometry by
three-dimensional considerations, of treating all points at infinity
in a plane as lying on a single straight line.
Sometimes, in reducing an equation to the above focus and directrix
form, we find for h, k, e, p, tan α, or some of them, only imaginary
values, as quadratic equations have to be solved; and we have in
fact to contemplate the existence of entirely imaginary conics.
For instance, no real values of x and y satisfy x² + 2y² + 3 = 0. Even
when the locus represented is real, we obtain, as a rule, four sets of
values of h, k, e, p, of which two sets are imaginary; a real conic
has, besides two real foci and corresponding directrices, two others
that are imaginary.
In oblique as well as rectangular coordinates equations of the
second degree represent conics.
19. The three Species of Conics.—A real conic, which does not
degenerate into straight lines, is called an ellipse, parabola or hyperbola
according as e <, = , or > 1. To trace the three forms it is
best so to choose the axes of reference as to simplify their equations.
In the case of a parabola, let 2c be the distance between the given
focus and directrix, and take axes referred to which these are the
point (c, 0) and the line x = − c. The equation becomes (x − c)² + y² =
(x + c)², i.e. y² = 4cx.
In the other cases, take a such that a(e ~ e−1) is the distance of focus
from directrix, and so choose axes that these are (ae, 0) and x = ae-1,
thus getting the equation(x − ae)² + y² = e²(x − ae-1)², i.e. (1 − e²)x² + y² =
a²(1 − e²). When e < 1, i.e. in the case of an ellipse, this may be
written x²/a² + y²/b² = 1, where b² = a²(1 − e²); and when e > 1, i.e.
in the case of an hyperbola, x²/a² − y²/b² = 1, where b² = a²(e² − 1).
716
The axes thus chosen for the ellipse and hyperbola are called the
principal axes.
In figs. 54, 55, 56 in order, conics of the three species, thus referred,
are depicted.
 |
| Fig. 54 |
Fig. 55 |
 |
| Fig. 56. |
The oblique straight lines in fig. 56 are the asymptotes x/a = ±y/b
of the hyperbola, lines to which the curve tends with unlimited
closeness as it goes to infinity. The hyperbola would have an equation
of the form xy = c if referred to its asymptotes as axes, the coordinates
being then oblique, unless a = b, in which case the hyperbola
is called rectangular. An ellipse has two imaginary asymptotes.
In particular a circle x² + y² = a², a particular ellipse, has for asymptotes
the imaginary lines x = ±y √−1. These run from the centre
to the so-called circular points at infinity.
20. Tangents and Curvature.—Let (x′, y′) and (x′ + h, y′ + k) be
two neighbouring points P, P′ on a curve. The equation of the line
on which both lie is h(y − y′) = k(x − x′). Now keep P fixed, and let
P′ move towards coincidence with it along the curve. The connecting
line will tend towards a limiting position, to which it can
never attain as long as P and P′ are distinct. The line which
occupies this limiting position is the tangent at P. Now if we subtract
the equation of the curve, with (x′, y′) for the coordinates in it,
from the like equation in (x′ + h, y′ + k), we obtain a relation in h
and k, which will, as a rule, be of the form 0 = Ah + Bk + terms of
higher degrees in h and k, where A, B and the other coefficients
involve x′ and y′. This gives k/h = −A/B + terms which tend to
vanish as h and k do, so that −A : B is the limiting value tended to
by k : h. Hence the equation of the tangent is B(y − y′) + A(x − x′) = 0.
The normal at (x′, y′) is the line through it at right angles to the
tangent, and its equation is A(y − y′) − B(x − x′) = 0.
In the case of the conic (a, b, c, f, g, h) (x, y, 1)² = 0 we find that
A/B = (ax′ + hy′ + g)/(hx′ + by′ + f).
We can obtain the coordinates of Q, the intersection of the normals
QP, QP′ at (x′, y′) and (x′ + h, y′ + k), and then, using the limiting
value of k : h, deduce those of its limiting position as P′ moves up
to P. This is the centre of curvature of the curve at P (x′, y′), and
is so called because it is the centre of the circle of closest contact
with the curve at that point. That it is so follows from the facts
that the closest circle is the limit tended to by the circle which touches
the curve at P and passes through P′, and that the arc from P to P′
of this circle lies between the circles of centre Q and radii QP, QP′,
which circles tend, not to different limits as P′ moves up to P, but
to one. The distance from P to the centre of curvature is the radius
of curvature.
21. Differential Plane Geometry.—The language and notation of the
differential calculus are very useful in the study of tangents and
curvature. Denoting by (ξ, η) the current coordinates, we find,
as above, that the tangent at a point (x, y) of a curve is η − y =
(ξ − x)dy/dx, where dy/dx is found from the equation of the curve. If
this be f(x, y) = 0 the tangent is (ξ − x) (∂f/∂x) + (η − y) (∂f/∂y) = 0. If ρ
and (α, β) are the radius and centre of curvature at (x, y), we find that
q(α − x) = −p(1 + p²), q(β − y) = 1 + p², q²ρ² = (1 + p²)³, where p, q denote
dy/dx, d²y/dx² respectively. (See Infinitesimal Calculus.)
In any given case we can, at all events in theory, eliminate x, y
between the above equations for α − x and β − y, and the equation
of the curve. The resulting equation in (α, β) represents the locus
of the centre of curvature. This is the evolute of the curve.
22. Polar Coordinates.—In plane geometry the distance of any
point P from a fixed origin (or pole) O, and the inclination xOP of OP
to a fixed line Ox, determine the point: r, the numerical measure
of OP, the radius vector, and θ, the circular measure of xOP, the
inclination, are called polar coordinates of P. The formulae x =
r cos θ, y = r sin θ connect Cartesian and polar coordinates, and make
transition from either system to the other easy. In polar coordinates
the equations of a circle through O, and of a conic with O as focus,
take the simple forms r = 2a cos (θ − α), r{1 − e cos (θ − α)} = l. The
use of polar coordinates is very convenient in discussing curves
which have properties of symmetry akin to that of a regular polygon,
such curves for instance as r = a cos m θ, with m integral, and also the
curves called spirals, which have equations giving r as functions of
θ itself, and not merely of sin θ and cos θ. In the geometry of
motion under central forces the advantage of working with polar
coordinates is great.
23. Trilinear and Areal Coordinates.—Consider a fixed triangle
ABC, and regard its sides as produced without limit. Denote, as
in trigonometry, by a, b, c the positive numbers of units of a chosen
scale contained in the lengths BC, CA, AB, by A, B, C the angles,
and by Δ the area, of the triangle. We might, as in § 6, take CA,
CB as axes of x and y, inclined at an angle C. Any point P (x, y)
in the plane is at perpendicular distances y sin C and x sin C from
CA and CB. Call these β and α respectively. The signs of β and α
are those of y and x, i.e. β is positive or negative according as P lies
on the same side of CA as B does or the opposite, and similarly for α.
An equation in (x, y) of any degree may, upon replacing in it x and y
by α cosec C and β cosec C, be written as one of the same degree in
(α, β). Now let γ be the perpendicular distance of P from the third
side AB, taken as positive or negative as P is on the C side of AB or
not. The geometry of the figure tells us that aα + bβ + cγ = 2Δ.
By means of this relation in α, β, γ we can give an equation considered
countless other forms, involving two or all of α, β, γ. In
particular we may make it homogeneous in α, β, γ: to do this we
have only to multiply the terms of every degree less than the highest
present in the equation by a power of (aα + bβ + cγ)/2Δ just sufficient
to raise them, in each case, to the highest degree.
We call (α, β, γ) trilinear coordinates, and an equation in them
the trilinear equation of the locus represented. Trilinear equations
are, as a rule, dealt with in their homogeneous forms. An advantage
thus gained is that we need not mean by (α, β, γ) the actual measures
of the perpendicular distances, but any properly signed numbers
which have the same ratio two and two as these distances.
In place of α, β, γ it is lawful to use, as coordinates specifying
the position of a point in the plane of a triangle of reference ABC,
any given multiples of these. For instance, we may use x = aα/2Δ,
y = bβ/2Δ, z = cγ/2Δ, the properly signed ratios of the triangular
areas PBC, PCA, PAB to the triangular area ABC. These are called
the areal coordinates of P. In areal coordinates the relation which
enables us to make any equation homogeneous takes the simple
form x + y + z = 1; and, as before, we need mean by x, y, z, in a
homogeneous equation, only signed numbers in the right ratios.
Straight lines and conics are represented in trilinear and in areal,
because in Cartesian, coordinates by equations of the first and
second degrees respectively, and these degrees are preserved when
the equations are made homogeneous. What must be said about
points infinitely far off in order to make universal the statement,
to which there is no exception as long as finite distances alone are
considered, that every homogeneous equation of the first degree
represents a straight line? Let the point of areal coordinates
(x′, y′, z′) move infinitely far off, and mean by x, y, z finite quantities
in the ratios which x′, y′, z′ tend to assume as they become infinite.
The relation x′ + y′ + z′ = 1 gives that the limiting state of things
tended to is expressed by x + y + z = 0. This particular equation of
the first degree is satisfied by no point at a finite distance; but we
see the propriety of saying that it has to be taken as satisfied by
all the points conceived of as actually at infinity. Accordingly the
special property of these points is expressed by saying that they lie
on a special straight line, of which the areal equation is x + y + z = 0.
In trilinear coordinates this line at infinity has for equation aα + bβ +
cγ = 0.
On the one special line at infinity parallel lines are treated as
meeting. There are on it two special (imaginary) points, the circular
points at infinity of § 19, through which all circles pass in the same
sense. In fact if S = O be one circle, in areal coordinates,
S + (x + y + z)(lx + my + nz) = 0 may, by proper choice of l, m, n, be
made any other; since the added terms are once lx + my + nz, and
have the generality of any expression like a′x + b′y + c′ in Cartesian
coordinates. Now these two circles intersect in the two points where
either meets x + y + z = 0 as well as in two points on the radical axis
lx + my + nz = 0.
24. Let us consider the perpendicular distance of a point (α′, β′, γ′)
from a line lα + mβ + nγ. We can take rectangular axes of Cartesian
coordinates (for clearness as to equalities of angle it is best to
choose an origin inside ABC), and refer to them, by putting expressions
p − x cos θ − y sin θ, &c., for α &c.; we can then apply § 16 to
get the perpendicular distance; and finally revert to the trilinear
notation. The result is to find that the required distance is
(lα′ + mβ′ + nγ′) / {l, m, n},
where {l, m, n}² = l² + m² + n² − 2mn cos A − 2nl cos B − 2lm cos C.
In areal coordinates the perpendicular distance from (x′, y′, z′)
717
to lx + my + nz = 0 is 2Δ(lx′ + my′ + nz′)/{al, bm, cn}. In both cases
the coordinates are of course actual values.
Now let ξ, η, ζ be the perpendiculars on the line from the vertices
A, B, C, i.e. the points (1, 0, 0), (0, 1, 0), (0, 0, 1), with signs in
accord with a convention that oppositeness of sign implies distinction
between one side of the line and the other. Three applications
of the result above give
ξ/l = 2Δ / {al, bm, cn} = η/m = ζ/n;
and we thus have the important fact that ξx′ + ηy′ + ζz′ is the
perpendicular distance between a point of areal coordinates (x′y′z′)
and a line on which the perpendiculars from A, B, C are ξ, η, ζ
respectively. We have also that ξx + ηy + ζz = 0 is the areal equation
of the line on which the perpendiculars are ξ, η, ζ; and, by equating
the two expressions for the perpendiculars from (x′, y′, z′) on the
line, that in all cases {aξ, bη, cζ}² = 4Δ².
25. Line-coordinates. Duality.—A quite different order of ideas
may be followed in applying analysis to geometry. The notion of a
straight line specified may precede that of a point, and points may
be dealt with as the intersections of lines. The specification of
a line may be by means of coordinates, and that of a point by an
equation, satisfied by the coordinates of lines which pass through it.
Systems of line-coordinates will here be only briefly considered.
Every such system is allied to some system of point-coordinates;
and space will be saved by giving prominence to this fact, and not
recommencing ab initio.
Suppose that any particular system of point-coordinates, in which
lx + my + nz = 0 may represent any straight line, is before us: notice
that not only are trilinear and areal coordinates such systems, but
Cartesian coordinates also, since we may write x/z, y/z for the
Cartesian x, y, and multiply through by z. The line is exactly
assigned if l, m, n, or their mutual ratios, are known. Call (l, m, n)
the coordinates of the line. Now keep x, y, z constant, and let the
coordinates of the line vary, but always so as to satisfy the equation.
This equation, which we now write xl + ym + zn = 0, is satisfied by
the coordinates of every line through a certain fixed point, and by
those of no other line; it is the equation of that point in the line-coordinates
l, m, n.
Line-coordinates are also called tangential coordinates. A curve
is the envelope of lines which touch it, as well as the locus of points
which lie on it. A homogeneous equation of degree above the first
in l, m, n is a relation connecting the coordinates of every line which
touches some curve, and represents that curve, regarded as an
envelope. For instance, the condition that the line of coordinates
(l, m, n), i.e. the line of which the allied point-coordinate equation
is lx + my + nz = 0, may touch a conic (a, b, c, f, g, h) (x, y, z)² = 0,
is readily found to be of the form (A, B, C, F, G, H) (l, m, n)² = 0,
i.e. to be of the second degree in the line-coordinates. It is not hard
to show that the general equation of the second degree in l, m, n
thus represents a conic; but the degenerate conics of line-coordinates
are not line-pairs, as in point-coordinates, but point-pairs.
The degree of the point-coordinate equation of a curve is the
order of the curve, the number of points in which it cuts a straight
line. That of the line-coordinate equation is its class, the number
of tangents to it from a point. The order and class of a curve are
generally different when either exceeds two.
26. The system of line-coordinates allied to the areal system of
point-coordinates has special interest.
The l, m, n of this system are the perpendiculars ξ, η, ζ of § 24;
and x′ξ + y′η + z′ζ = 0 is the equation of the point of areal coordinates
(x′, y′, z′), i.e. is a relation which the perpendiculars from the vertices
of the triangle of reference on every line through the point, but no
other line, satisfy. Notice that a non-homogeneous equation of the
first degree in ξ, η, ζ does not, as a homogeneous one does, represent
a point, but a circle. In fact x′ξ + y′η + z′ζ = R expresses the constancy
of the perpendicular distance of the fixed point x′ξ + y′η +
z′ζ = 0 from the variable line (ξ, η, ζ), i.e. the fact that (ξ, η, ζ) touches
a circle with the fixed point for centre. The relation in any ξ, η, ζ
which enables us to make an equation homogeneous is not linear,
as in point-coordinates, but quadratic, viz. it is the relation {aξ, bη,
cζ}² = 4Δ² of § 24. Accordingly the homogeneous equation of the
above circle is
4Δ² (x′ξ + y′η + z′ζ)² = R² {aξ, bη, cζ}².
Every circle has an equation of this form in the present system of
line-coordinates. Notice that the equation of any circle is satisfied
by those coordinates of lines which satisfy both x′ξ + y′η + z′ζ = 0,
the equation of its centre, and {aξ, bη, cζ}² = 0. This last equation,
of which the left-hand side satisfies the condition for breaking up
into two factors, represents the two imaginary circular points at
infinity, through which all circles and their asymptotes pass.
There is strict duality in descriptive geometry between point-line-locus
and line-point-envelope theorems. But in metrical geometry
duality is encumbered by the fact that there is in a plane one special
line only, associated with distance, while of special points, associated
with direction, there are two: moreover the line is real, and the
points both imaginary.
II. Solid Analytical Geometry.
27. Any point in space may be specified by three coordinates.
We consider three fixed planes of reference, and generally, as in all
that follows, three which are at right angles two and two. They
intersect, two and two, in lines x′Ox, y′Oy, z′Oz, called the axes
of x, y, z respectively, and divide all space into eight parts called
octants. If from any point P in space we draw PN parallel to
zOz′ to meet the plane xOy in N, and then from N draw NM parallel
to yOy′ to meet x′Ox in M, the coordinates (x, y, z) of P are the
numerical measures of OM, MN, NP; in the case of rectangular
coordinates these are the perpendicular distances of P from the three
planes of reference. The sign of each coordinate is positive or
negative as P lies on one side or the other of the corresponding
plane. In the octant delineated the signs are taken all positive.
 |
| Fig. 57. |
Fig. 58. |
In fig. 57 the delineation is on a plane of the paper taken parallel
to the plane zOx, the points of a solid figure being projected on that
plane by parallels to some chosen line through O in the positive
octant. Sometimes it is clearer to delineate, as in fig. 58, by projection
parallel to that line in the octant which is equally inclined to
Ox, Oy, Oz upon a plane of the paper perpendicular to it. It is
possible by parallel projection to delineate equal scales along Ox,
Oy, Oz by scales having any ratios we like along lines in a plane
having any mutual inclinations we like.
 |
| Fig. 59. |
For the delineation of a surface of simple form it frequently
suffices to delineate the sections by the coordinate planes; and, in
particular, when the surface has symmetry about each coordinate
plane, to delineate the
quarter-sections belonging
to a single
octant. Thus fig. 59
conveniently represents
an octant of the
wave surface, which
cuts each coordinate
plane in a circle and
an ellipse. Or we may
delineate a series of
contour lines, i.e. sections
by planes parallel
to xOy, or some other
chosen plane; of course
other sections may be
indicated too for
greater clearness. For
the delineation of a
curve a good method
is to represent, as
above, a series of points
P thereof, each accompanied by its ordinate PN, which serves to
refer it to the plane of xy. The employment of stereographic
projection is also interesting.
28. In plane geometry, reckoning the line as a curve of the first
order, we have only the point and the curve. In solid geometry,
reckoning a line as a curve of the first order, and the plane as a surface
of the first order, we have the point, the curve and the surface;
but the increase of complexity is far greater than would hence at
first sight appear. In plane geometry a curve is considered in
connexion with lines (its tangents); but in solid geometry the curve
is considered in connexion with lines and planes (its tangents and
osculating planes), and the surface also in connexion with lines and
planes (its tangent lines and tangent planes); there are surfaces
arising out of the line—cones, skew surfaces, developables, doubly
and triply infinite systems of lines, and whole classes of theories
which have nothing analogous to them in plane geometry: it is thus
a very small part indeed of the subject which can be even referred
to in the present article.
In the case of a surface we have between the coordinates (x, y, z)
a single, or say a onefold relation, which can be represented by a
single relation ƒ(x, y, z) = 0; or we may consider the coordinates
expressed each of them as a given function of two variable parameters
p, q; the form z = ƒ(x, y) is a particular case of each of these
modes of representation; in other words, we have in the first mode
ƒ(x, y, z) = z − ƒ(x, y), and in the second mode x = p, y = q for the
expression of two of the coordinates in terms of the parameters.
718
In the case of a curve we have between the coordinates (x, y, z) a
twofold relation: two equations ƒ(x, y, z) = 0, φ(x, y, z) = 0 give
such a relation; i.e. the curve is here considered as the intersection
of two surfaces (but the curve is not always the complete intersection
of two surfaces, and there are hence difficulties); or, again, the coordinates
may be given each of them as a function of a single variable
parameter. The form y = φ(x), z = ψ(x), where two of the coordinates
are given in terms of the third, is a particular case of each of these
modes of representation.
29. The remarks under plane geometry as to descriptive and
metrical propositions, and as to the non-metrical character of the
method of coordinates when used for the proof of a descriptive
proposition, apply also to solid geometry; and they might be
illustrated in like manner by the instance of the theorem of the radical
centre of four spheres. The proof is obtained from the consideration
that S and S′ being each of them a function of the form x² + y² + z² +
ax + by + cz + d, the difference S-S′ is a mere linear function of the
coordinates, and consequently that S-S′ = 0 is the equation of the
plane containing the circle of intersection of the two spheres S = 0
and S′ = 0.
 |
| Fig. 60. |
30. Metrical Theory.—The foundation in solid geometry of the
metrical theory is in fact the before-mentioned theorem that if a
finite right line PQ be projected upon any other line OO′ by lines
perpendicular to OO′, then the length of the
projection P′Q′ is equal to the length of PQ
into the cosine of its inclination to P′Q′—or
(in the form in which it is now convenient
to state the theorem) the perpendicular
distance P′Q′ of two parallel planes is equal
to the inclined distance PQ into the cosine
of the inclination. The principle of § 16,
that the algebraical sum of the projections of
the sides of any closed polygon on any line is
zero, or that the two sets of sides of the
polygon which connect a vertex A and a
vertex B have the same sum of projections
on the line, in sign and magnitude, as we pass
from A to B, is applicable when the sides do
not all lie in one plane.
31. Consider the skew quadrilateral QMNP,
the sides QM, MN, NP being respectively
parallel to the three rectangular axes Ox,
Oy, Oz; let the lengths of these sides be
ξ, η, ζ, and that of the side QP be = ρ; and
let the cosines of the inclinations (or say the cosine-inclinations) of
ρ to the three axes be α, β, γ; then projecting successively on
the three sides and on QP we have
ξ, η, ζ = ρα, ρβ, ργ,
and
ρ = αξ + βη + γζ,
whence ρ² = ξ² + η² + ζ², which is the relation between a distance ρ
and its projections ξ, η, ζ upon three rectangular axes. And from
the same equations we obtain α² + β² + γ² = 1, which is a relation connecting
the cosine-inclinations of a line to three rectangular axes.
Suppose we have through Q any other line QT, and let the cosine-inclinations
of this to the axes be α′, β′, γ′, and δ be its cosine-inclination
to QP; also let ρ be the length of the projection of QP
upon QT; then projecting on QT we have
ρ = α′ξ + β′η + γ′ζ = ρδ.
And in the last equation substituting for ξ, η, ζ their values ρα,
ρβ, ργ we find
δ = αα′ + ββ′ + γγ′,
which is an expression for the mutual cosine-inclination of two
lines, the cosine-inclinations of which to the axes are α, β, γ and
α′, β′, γ′ respectively. We have of course α² + β² + γ² = 1 and
α′² + β′² + γ′² = 1; and hence also
1 − δ² = (α² + β² + γ²)(α′² + β′² + γ′²) − (αα′ + ββ′ + γγ′)²,
= (βγ′ − β′γ)² + (γα′ − γ′α)² + (αβ′ − α′β)²;
so that the sine of the inclination can only be expressed as a square
root. These formulae are the foundation of spherical trigonometry.
32. Straight Lines, Planes and Spheres.—The foregoing formulae
give at once the equations of these loci.
For first, taking Q to be a fixed point, coordinates (a, b, c), and
the cosine-inclinations (α, β, γ) to be constant, then P will be a
point in the line through Q in the direction thus determined; or,
taking (x, y, z) for its coordinates, these will be the current coordinates
of a point in the line. The values of ξ, η, ζ then are
x − a, y − b, z − c, and we thus have
| x − a |
= | y − b |
= | z − c |
(= ρ), |
| α | β |
γ |
which (omitting the last equation, = ρ) are the equations of the line
through the point (a, b, c), the cosine-inclinations to the axes being
α, β, γ, and these quantities being connected by the relation
α² + β² + γ² = 1. This equation may be omitted, and then α, β, γ,
instead of being equal, will only be proportional, to the cosine-inclinations.
Using the last equation, and writing
x, y, z = a + αρ, b + βρ, c + γρ,
these are expressions for the current coordinates in terms of a
parameter ρ, which is in fact the distance from the fixed point
(a, b, c).
It is easy to see that, if the coordinates (x, y, z) are connected by
any two linear equations, these equations can always be brought
into the foregoing form, and hence that the two linear equations
represent a line.
Secondly, taking for greater simplicity the point Q to be coincident
with the origin, and α′, β′, γ′, p to be constant, then p is the perpendicular
distance of a plane from the origin, and α′, β′, γ′ are the cosine-inclinations
of this distance to the axes (α′² + β′² + γ′² = 1). P is
any point in this plane, and taking its coordinates to be (x, y, z) then
(ξ, η, ζ) are = (x, y, z), and the foregoing equation p = α′ξ + β′η + γ′ζ
becomes
α′x + β′y + γ′z = p,
which is the equation of the plane in question.
If, more generally, Q is not coincident with the origin, then,
taking its coordinates to be (a, b, c), and writing p1 instead of p, the
equation is
α′ (x − a) + β′ (y − b) + γ′ (z − c) = p1;
and we thence have p1 = p − (aα′ + bβ′ + cγ′), which is an expression
for the perpendicular distance of the point (a, b, c) from the plane
in question.
It is obvious that any linear equation Ax + By + Cz + D = O between
the coordinates can always be brought into the foregoing form,
and hence that such an equation represents a plane.
Thirdly, supposing Q to be a fixed point, coordinates (a, b, c),
and the distance QP = ρ, to be constant, say this is = d, then, as
before, the values of ξ, η, ζ are x − a, y − b, z − c, and the equation
ξ² + η² + ζ² = ρ² becomes
(x − a)² + (y − b)² + (z − c)² = d²,
which is the equation of the sphere, coordinates of the centre = (a, b, c),
and radius = d.
A quadric equation wherein the terms of the second order are
x² + y² + z², viz. an equation
x² + y² + z² + Ax + By + Cz + D = 0,
can always, it is clear, be brought into the foregoing form; and it
thus appears that this is the equation of a sphere, coordinates of
the centre −½A, −½B, −½C, and squared radius = ¼(A² + B² + C²) − D.
33. Cylinders, Cones, ruled Surfaces.—If the two equations of a
straight line involve a parameter to which any value may be given,
we have a singly infinite system of lines. They cover a surface, and
the equation of the surface is obtained by eliminating the parameter
between the two equations.
If the lines all pass through a given point, then the surface is a
cone; and, in particular, if the lines are all parallel to a given line,
then the surface is a cylinder.
Beginning with this last case, suppose the lines are parallel to
the line x = mz, y = nz, the equations of a line of the system are
x = mz + a, y = nz + b,—where a, b are supposed to be functions of
the variable parameter, or, what is the same thing, there is between
them a relation ƒ(a, b) = 0: we have a = x − mz, b = y − nz, and the
result of the elimination of the parameter therefore is ƒ(x − mz,
y − nz) = 0, which is thus the general equation of the cylinder the
generating lines whereof are parallel to the line x = mz, y = nz. The
equation of the section by the plane z = 0 is ƒ(x, y) = 0, and conversely
if the cylinder be determined by means of its curve of intersection
with the plane z = 0, then, taking the equation of this curve to be
ƒ(x, y) = 0, the equation of the cylinder is ƒ(x − mz, y − nz) = 0. Thus,
if the curve of intersection be the circle (x − α)² + (y − β)² = γ², we
have (x − mz − α)² + (y − nz − β)² = γ² as the equation of an oblique
cylinder on this base, and thus also (x − α)² + (y − β)² = γ² as the
equation of the right cylinder.
If the lines all pass through a given point (a, b, c), then the equations
of a line are x − a = α(z − c), y − b = β(z − c), where α, β are
functions of the variable parameter, or, what is the same thing,
there exists between them an equation ƒ(α, β) = 0; the elimination
of the parameter gives, therefore, ƒ[(x − a)/(x − c′), (y − b)/(z − c)] = 0; and this
equation, or, what is the same thing, any homogeneous equation
ƒ(x − a, y − b, z − c) = 0, or, taking f to be a rational and integral
function of the order n, say (*)(x − a, y − b, z − c)n = 0, is the general
equation of the cone having the point (a, b, c) for its vertex. Taking
the vertex to be at the origin, the equation is (*)(x, y, z)n = 0; and,
in particular, (*)(x, y, z)² = 0 is the equation of a cone of the second
order, or quadricone, having the origin for its vertex.
34. In the general case of a singly infinite system of lines, the
locus is a ruled surface (or regulus). Now, when a line is changing
its position in space, it may be looked upon as in a state of turning
about some point in itself, while that point is, as a rule, in a state of
moving out of the plane in which the turning takes place. If instantaneously
it is only in a state of turning, it is usual, though not
strictly accurate, to say that it intersects its consecutive position.
A regulus such that consecutive lines on it do not intersect, in this
sense, is called a skew surface, or scroll; one on which they do is
called a developable surface or torse.
Suppose, for instance, that the equations of a line (depending on
719
the variable parameter θ) are x/a + y/c = θ
(1 + y/b), x/a − z/c = (1/θ)(1 − y/b);
then, eliminating θ we have x²/a² − z²/c² = 1 − y²/b², or say, x²/a² + y²/b² − z²/c² = 1,
the equation of a quadric surface, afterwards called the hyperboloid
of one sheet; this surface is consequently a scroll. It is to be remarked
that we have upon the surface a second singly infinite
series of lines; the equations of a line of this second system (depending
on the variable parameter φ) are
| x |
+ | z |
= φ ( 1 − | y |
), | x |
− | z |
= | 1 |
( 1 + | y |
). |
| a | c |
b | a |
c | φ |
b |
It is easily shown that any line of the one system intersects every
line of the other system.
Considering any curve (of double curvature) whatever, the tangent
lines of the curve form a singly infinite system of lines, each line
intersecting the consecutive line of the system,—that is, they form
a developable, or torse; the curve and torse are thus inseparably
connected together, forming a single geometrical figure. An osculating
plane of the curve (see § 38 below) is a tangent plane of the torse
all along a generating line.
35. Transformation of Coordinates.—There is no difficulty in
changing the origin, and it is for brevity assumed that the origin
remains unaltered. We have, then, two sets of rectangular axes,
Ox, Oy, Oz, and Ox1, Oy1, Ozx1, the mutual cosine-inclinations being
shown by the diagram—
| | x | y | z |
| x1 | α | β | γ |
| y1 | α | β′ | γ′ |
| z1 | α″ | β″ | γ″ |
that is, α, β, γ are the cosine-inclinations of
Ox1 to Ox, Oy, Oz;
α′, β′, γ′ those of Oy1, &c.
And this diagram gives also the linear expressions of the coordinates
(x1, y1, z1) or (x, y, z) of either set in terms of those of the
other set; we thus have
| x1 = α x + β y + γ z, | x = αx1 + α′y1 + α″z1, |
| y1 = α′x + β′y + γ′z, | y = βx1 + β′y1 + β″z1, |
| z1 = α″x + β″y + γ″z, | z = γx1 + γ′y1 + γ″z1, |
which are obtained by projection, as above explained. Each of
these equations is, in fact, nothing else than the before-mentioned
equation p = α′ξ + β′η + γ′ζ, adapted to the problem in hand.
But we have to consider the relations between the nine coefficients.
By what precedes, or by the consideration that we must have
identically x² + y² + z² = x1² + y1² + z1², it appears that these satisfy
the relations—
| α² | + β² | + γ² | = 1, | α² + | α′² | + α″² | = 1, |
| α′² | + β′² | + γ′² | = 1, | β² | + β′² | + β″² | = 1, |
| α″² | + β″² | + γ″² | = 1, | γ² | + γ′² | + γ″² | = 1, |
| α′a″ | + β′β″ | + γ′γ″ | = 0, | βγ | +β′γ′ | + β″γ″ | = 0, |
| α″α | + β″β | + γ″γ | = 0, | γα | + γ′α′ | + γ″α″ | = 0, |
| αα′ | + ββ′ | + γγ′ | = 0, | αβ | +α′β′ | + α″β″ | = 0, |
either set of six equations being implied in the other set.
It follows that the square of the determinant
| α, | β, | γ |
| α′, | β′, | γ′ |
| α″, | β″, | γ″ |
is = 1; and hence that the determinant itself is = ±1. The distinction
of the two cases is an important one: if the determinant is
= + 1, then the axes Ox1, Oy1, Oz1 are such that they can by a
rotation about O be brought to coincide with Ox, Oy, Oz respectively;
if it is = −1, then they cannot. But in the latter case, by
measuring x1, y1, z1 in the opposite directions we change the signs of
all the coefficients and so make the determinant to be = + 1; hence
the former case need alone be considered, and it is accordingly
assumed that the determinant is = +1. This being so, it is found
that we have the equality α = β′γ″ − β″γ′, and eight like ones,
obtained from this by cyclical interchanges of the letters α, β, γ,
and of unaccented, singly and doubly accented letters.
36. The nine cosine-inclinations above are, as has been seen,
connected by six equations. It ought then to be possible to express
them all in terms of three parameters. An elegant means of doing
this has been given by Rodrigues, who has shown that the tabular
expression of the formulae of transformation may be written
| | x | y | z |
| x1 | 1 + λ² − μ² − ν² | 2(λμ − ν) | 2(νλ + μ) |
| y1 | 2(λμ + ν) | 1 − λ² + μ² − ν² | 2(μν + λ) |
| z1 | 2(νλ − μ) | 2(μν + λ) | 1 − λ² − μ² + ν² |
| ÷ (1 + λ² + μ² + ν²), |
the meaning being that the coefficients in the transformation are
fractions, with numerators expressed as in the table, and the common
denominator.
37. The Species of Quadric Surfaces.—Surfaces represented by
equations of the second degree are called quadric surfaces. Quadric
surfaces are either proper or special. The special ones arise when the
coefficients in the general equation are limited to satisfy certain
special equations; they comprise (1) plane-pairs, including in
particular one plane twice repeated, and (2) cones, including in
particular cylinders; there is but one form of cone, but cylinders
may be elliptic, parabolic or hyperbolic.
A discussion of the general equation of the second degree shows
that the proper quadric surfaces are of five kinds, represented
respectively, when referred to the most convenient axes of reference,
by equations of the five types (a and b positive):
| (1) | z = x²/2a + y²/2b, elliptic paraboloid. |
| (2) | z = x²/2a − y²/2b, hyperbolic paraboloid. |
| (3) | x²/a² + y²/b² + z²/c² = 1, ellipsoid. |
| (4) | x²/a² + y²/b² − z²/c² = 1, hyperboloid of one sheet. |
| (5) | x²/a² + y²/b² − z²/c² = −1, hyperboloid of two sheets. |
 |
| Fig. 61. |
It is at once seen that these are distinct surfaces; and the equations
also show very readily the
general form and mode of generation
of the several surfaces.
In the elliptic paraboloid (fig. 61)
the sections by the planes of zx and
zy are the parabolas
having the common axes Oz; and
the section by any plane z = γ
parallel to that of xy is the ellipse
so that the surface is generated by
a variable ellipse moving parallel to itself along the parabolas as
directrices.
 |
| Fig. 62. |
Fig. 63. |
 |
| Fig. 64. |
In the hyperbolic paraboloid (figs. 62 and 63) the sections by the
planes of zx, zy are the parabolas z = x²/2a, z = − y²/2b, having the opposite
axes Oz, Oz′, and the section by a plane z = γ parallel to that of
xy is the hyperbola γ = x²/2a − y²/2b, which has its transverse axis parallel
to Ox or Oy according as γ is positive or negative. The surface is thus
generated by a variable hyperbola moving parallel to itself along
the parabolas as directrices. The form is best seen from fig. 63,
which represents the sections
by planes parallel to
the plane of xy, or say the
contour lines; the continuous
lines are the sections
above the plane of
xy, and the dotted lines
the sections below this
plane. The form is, in
fact, that of a saddle.
In the ellipsoid (fig. 64)
the sections by the planes
of zx, zy, and xy are each
of them an ellipse, and the
section by any parallel
plane is also an ellipse.
The surface may be considered
as generated by
an ellipse moving parallel to itself along two ellipses as directrices.
720
In the hyperboloid of one sheet (fig. 65), the sections by the planes
of zx, zy are the hyperbolas
| x² |
− | z² |
= 1, | y² |
− | z² |
= 1, |
| c² | c² |
b² | c² |
having a common conjugate axis zOz′; the section by the plane of
x, y, and that by any parallel plane, is an ellipse; and the surface
may be considered as generated by a variable ellipse moving parallel
to itself along the two hyperbolas as directrices. If we imagine two
equal and parallel circular disks, their points connected by strings
of equal lengths, so that these are the generators of a right circular
cylinder, and if we turn one of the disks about its centre through an
angle in its plane, the strings in their new positions will be one
system of generators of a hyperboloid of one sheet, for which a = b;
and if we turn it through the same angle in the opposite direction,
we get in like manner the generators of the other system; there will
be the same general configuration when a ≠ b. The hyperbolic
paraboloid is also covered by two systems of rectilinear generators
as a method like that used in § 34 establishes without difficulty.
The figures should be studied to see how they can lie.
 |
| Fig. 65. |
Fig. 66. |
In the hyperboloid of two sheets (fig. 66) the sections by the planes
of zx and zy are the hyperbolas
| z² |
− | x² |
= 1, | z² |
− | y² |
= 1, |
| c² | a² |
c² | b² |
having a common transverse axis along z′Oz; the section by any
plane z = ±γ parallel to that of xy is the ellipse
| x² |
+ | y² |
= | γ² |
− 1, |
| a² | b² |
c² |
provided γ² > c², and the surface, consisting of two distinct portions
or sheets, may be considered as generated by a variable ellipse
moving parallel to itself along the hyperbolas as directrices.
38. Differential Geometry of Curves.—For convenience consider the
coordinates (x, y, z) of a point on a curve in space to be given as
functions of a variable parameter θ, which may in particular be one
of themselves. Use the notation x′, x″ for dx/dθ, d²x/dθ², and similarly
as to y and z. Only a few formulae will be given. Call the
current coordinates (ξ, η, ζ).
The tangent at (x, y, z) is the line tended to as a limit by the
connector of (x, y, z) and a neighbouring point of the curve when the
latter moves up to the former: its equations are
(ξ − x)/x′ = (η − y)/y′ = (ζ − z)/z′.
The osculating plane at (x, y, z) is the plane tended to as a limit by
that through (x, y, z) and two neighbouring points of the curve as
these, remaining distinct, both move up to (x, y, z): its one equation
is
(ξ − x) (y′z″ − y″z′) + (η − y) (z′x″ − z″x′) + (ζ − z) (x′y″ − x″y′) = 0.
The normal plane is the plane through (x, y, z) at right angles to the
tangent line, i.e. the plane
x′(ξ − x) + y′ (η − y) + z′ (ζ − z) = 0.
It cuts the osculating plane in a line called the principal normal.
Every line through (x, y, z) in the normal plane is a normal. The
normal perpendicular to the osculating plane is called the binormal.
A tangent, principal normal, and binormal are a convenient set of
rectangular axes to use as those of reference, when the nature of a
curve near a point on it is to be discussed.
Through (x, y, z) and three neighbouring points, all on the curve,
passes a single sphere; and as the three points all move up to (x, y, z)
continuing distinct, the sphere tends to a limiting size and position.
The limit tended to is the sphere of closest contact with the curve at
(x, y, z); its centre and radius are called the centre and radius of
spherical curvature. It cuts the osculating plane in a circle, called the
circle of absolute curvature; and the centre and radius of this circle
are the centre and radius of absolute curvature. The centre of
absolute curvature is the limiting position of the point where the
principal normal at (x, y, z) is cut by the normal plane at a neighbouring
point, as that point moves up to (x, y, z).
39. Differential Geometry of Surfaces.—Let (x, y, z) be any chosen
point on a surface ƒ(x, y, z) = 0. As a second point of the surface
moves up to (x, y, z), its connector with (x, y, z) tends to a limiting
position, a tangent line to the surface at (x, y, z). All these tangent
lines at (x, y, z), obtained by approaching (x, y, z) from different
directions on a surface, lie in one plane
| ∂ƒ |
(ξ − x) + | ∂ƒ |
(η − y) + | ∂ƒ |
(ζ − z) = 0. |
| ∂x | ∂y |
∂z |
This plane is called the tangent plane at (x, y, z). One line through
(x, y, z) is at right angles to the tangent plane. This is the normal
| (ξ − x) / | ∂ƒ |
= (η − y) / | ∂ƒ |
= (ζ − z) / | ∂ƒ |
. |
| ∂x | ∂y |
∂z |
The tangent plane is cut by the surface in a curve, real or imaginary,
with a node or double point at (x, y, z). Two of the tangent lines
touch this curve at the node. They are called the “chief tangents”
(Haupt-tangenten) at (x, y, z); they have closer contact with the
surface than any other tangents.
In the case of a quadric surface the curve of intersection of a
tangent and the surface is of the second order and has a node,
it must therefore consist of two straight lines. Consequently a
quadric surface is covered by two sets of straight lines, a pair through
every point on it; these are imaginary for the ellipsoid, hyperboloid
of two sheets, and elliptic paraboloid.
A surface of any order is covered by two singly infinite systems
of curves, a pair through every point, the tangents to which are all
chief tangents at their respective points of contact. These are
called chief-tangent curves; on a quadric surface they are the above
straight lines.
40. The tangents at a point of a surface which bisect the angles
between the chief tangents are called the principal tangents at the
point. They are at right angles, and together with the normal
constitute a convenient set of rectangular axes to which to refer the
surface when its properties near the point are under discussion.
At a special point which is such that the chief tangents there run
to the circular points at infinity in the tangent plane, the principal
tangents are indeterminate; such a special point is called an umbilic
of the surface.
There are two singly infinite systems of curves on a surface, a
pair cutting one another at right angles through every point upon it,
all tangents to which are principal tangents of the surface at their
respective points of contact. These are called lines of curvature,
because of a property next to be mentioned.
As a point Q moves in an arbitrary direction on a surface from
coincidence with a chosen point P, the normal at it, as a rule, at
once fails to meet the normal at P; but, if it takes the direction of a
line of curvature through P, this is instantaneously not the case.
We have thus on the normal two centres of curvature, and the
distances of these from the point on the surface are the two principal
radii of curvature of the surface at that point; these are also the radii
of curvature of the sections of the surface by planes through the
normal and the two principal tangents respectively; or say they are
the radii of curvature of the normal sections through the two principal
tangents respectively. Take at the point the axis of z in the direction
of the normal, and those of x and y in the directions of the principal
tangents respectively, then, if the radii of curvature be a, b (the signs
being such that the coordinates of the two centres of curvature are
z = a and z = b respectively), the surface has in the neighbourhood
of the point the form of the paraboloid
and the chief-tangents are determined by the equation 0 = x²/2a + y²/2b.
The two centres of curvature may be on the same side of the point
or on opposite sides; in the former case a and b have the same sign,
the paraboloid is elliptic, and the chief-tangents are imaginary;
in the latter case a and b have opposite signs, the paraboloid is
hyperbolic, and the chief-tangents are real.
The normal sections of the surface and the paraboloid by the same
plane have the same radius of curvature; and it thence readily
follows that the radius of curvature of a normal section of the surface
by a plane inclined at an angle θ to that of zx is given by the equation
| 1 |
= | cos² θ |
+ | sin² θ |
. |
| ρ | a |
b |
The section in question is that by a plane through the normal
and a line in the tangent plane inclined at an angle θ to the principal
tangent along the axis of x. To complete the theory, consider the
section by a plane having the same trace upon the tangent plane,
but inclined to the normal at an angle φ; then it is shown without
difficulty (Meunier’s theorem) that the radius of curvature of this
inclined section of the surface is = ρ cos φ.
Authorities.—The above article is largely based on that by
Arthur Cayley in the 9th edition of this work. Of early and important
recent publications on analytical geometry, special mention
721
is to be made of R. Descartes, Géométrie (Leyden, 1637); John
Wallis, Tractatus de sectionibus conicis nova methodo expositis (1655,
Opera mathematica, i., Oxford, 1695); de l’Hospital, Traité analytique
des sections coniques (Paris, 1720); Leonhard Euler, Introductio in
analysin infinitorum, ii. (Lausanne, 1748); Gaspard Monge, “Application
d’algèbre à la géométrie” (Journ. École Polytech., 1801);
Julius Plücker, Analytisch-geometrische Entwickelungen, 3 Bde.
(Essen, 1828-1831); System der analytischen Geometrie (Berlin,
1835); G. Salmon, A Treatise on Conic Sections (Dublin, 1848;
6th ed., London, 1879); Ch. Briot and J. Bouquet, Leçons de géométrie
analytique (Paris, 1851; 16th ed., 1897); M. Chasles, Traité
de géométrie supérieure (Paris, 1852); Wilhelm Fiedler, Analytische
Geometrie der Kegelschnitte nach G. Salmon frei bearbeitet (Leipzig,
5te Aufl., 1887-1888); N.M. Ferrers, An Elementary Treatise on
Trilinear Coordinates (London, 1861); Otto Hesse, Vorlesungen
aus der analytischen Geometrie (Leipzig, 1865, 1881); W.A. Whitworth,
Trilinear Coordinates and other Methods of Modern Analytical
Geometry (Cambridge, 1866); J. Booth, A Treatise on Some New
Geometrical Methods (London, i., 1873; ii., 1877); A. Clebsch-F.
Lindemann, Vorlesungen über Geometrie, Bd. i. (Leipzig, 1876,
2te Aufl., 1891); R. Baltser, Analytische Geometrie (Leipzig, 1882);
Charlotte A. Scott, Modern Methods of Analytical Geometry (London,
1894); G. Salmon, A Treatise on the Analytical Geometry of three
Dimensions (Dublin, 1862; 4th ed., 1882); Salmon-Fiedler, Analytische
Geometrie des Raumes (Leipzig, 1863; 4te Aufl., 1898); P.
Frost, Solid Geometry (London, 3rd ed., 1886; 1st ed., Frost and
J. Wolstenholme). See also E. Pascal, Repertorio di matematiche
superiori, II. Geometria (Milan, 1900), and articles now appearing
in the Encyklopädie der mathematischen Wissenschaften, Bd. iii. 1, 2.
(E. B. El.)
V. Line Geometry
Line geometry is the name applied to those geometrical
investigations in which the straight line replaces the point as
element. Just as ordinary geometry deals primarily with points
and systems of points, this theory deals in the first instance
with straight lines and systems of straight lines. In two dimensions
there is no necessity for a special line geometry, inasmuch
as the straight line and the point are interchangeable by the
principle of duality; but in three dimensions the straight line
is its own reciprocal, and for the better discussion of systems
of lines we require some new apparatus, e.g., a system of coordinates
applicable to straight lines rather than to points.
The essential features of the subject are most easily elucidated
by analytical methods: we shall therefore begin with the notion
of line coordinates, and in order to emphasize the merits of the
system of coordinates ultimately adopted, we first notice a
system without these advantages, but often useful in special
investigations.
In ordinary Cartesian coordinates the two equations of a straight
line may be reduced to the form y = rx + s, z = tx + u, and r, s, t, u
may be regarded as the four coordinates of the line. These coordinates
lack symmetry: moreover, in changing from one base of
reference to another the transformation is not linear, so that the
degree of an equation is deprived of real significance. For purposes
of the general theory we employ homogeneous coordinates; if
x1y1z1w1 and x2y2z2w2 are two points on the line, it is easily verified
that the six determinants of the array
are in the same ratios for all point-pairs on the line, and further,
that when the point coordinates undergo a linear transformation
so also do these six determinants. We therefore adopt these six
determinants for the coordinates of the line, and express them by the
symbols l, λ, m, μ, n, ν where l = x1w2 − x2w1, λ = y1z2 − y2z1, &c.
There is the further advantage that if a1b1c1d1 and a2b2c2d2 be two
planes through the line, the six determinants
are in the same ratios as the foregoing, so that except as regards a
factor of proportionality we have λ = b1c2 − b2c1, l = c1d2 − c2d1, &c.
The identical relation lλ + mμ + nν = o reduces the number of independent
constants in the six coordinates to four, for we are only
concerned with their mutual ratios; and the quadratic character
of this relation marks an essential difference between point geometry
and line geometry. The condition of intersection of two lines is
lλ′ + l′λ + mμ′ + m′μ + nν′ + n′ν = 0
where the accented letters refer to the second line. If the coordinates
are Cartesian and l, m, n are direction cosines, the quantity on the
left is the mutual moment of the two lines.
Since a line depends on four constants, there are three distinct types
of configurations arising in line geometry—those containing a triply-infinite,
a doubly-infinite and a singly-infinite number of lines; they
are called Complexes, Congruences, and Ruled Surfaces or Skews
respectively. A Complex is thus a system of lines satisfying one
condition—that is, the coordinates are connected by a single relation;
and the degree of the complex is the degree of this equation supposing
it to be algebraic. The lines of a complex of the nth degree which
pass through any point lie on a cone of the nth degree, those which
lie in any plane envelop a curve of the nth class and there are n lines
of the complex in any plane pencil; the last statement combines
the former two, for it shows that the cone is of the nth degree and
the curve is of the nth class. To find the lines common to four
complexes of degrees n1, n2, n3, n4, we have to solve five equations, viz.
the four complex equations together with the quadratic equation
connecting the line coordinates, therefore the number of common
lines is 2n1n2n3n4. As an example of complexes we have the lines
meeting a twisted curve of the nth degree, which form a complex
of the nth degree.
A Congruence is the set of lines satisfying two conditions: thus
a finite number m of the lines pass through any point, and a finite
number n lie in any plane; these numbers are called the degree
and class respectively, and the congruence is symbolically written
(m, n).
The simplest example of a congruence is the system of lines
constituted by all those that pass through m points and those that
lie in n planes; through any other point there pass m of these lines,
and in any other plane there lie n, therefore the congruence is of
degree m and class n. It has been shown by G.H. Halphen that the
number of lines common to two congruences is mm′ + nn′, which may
be verified by taking one of them to be of this simple type. The
lines meeting two fixed lines form the general (1, 1) congruence;
and the chords of a twisted cubic form the general type of a (1, 3)
congruence; Halphen’s result shows that two twisted cubics have
in general ten common chords. As regards the analytical treatment,
the difficulty is of the same nature as that arising in the theory of
curves in space, for a congruence is not in general the complete
intersection of two complexes.
A Ruled Surface, Regulus or Skew is a configuration of lines
which satisfy three conditions, and therefore depend on only one
parameter. Such lines all lie on a surface, for we cannot draw one
through an arbitrary point; only one line passes through a point of
the surface; the simplest example, that of a quadric surface, is
really two skews on the same surface.
The degree of a ruled surface qua line geometry is the number of
its generating lines contained in a linear complex. Now the number
which meets a given line is the degree of the surface qua point geometry,
and as the lines meeting a given line form a particular case
of linear complex, it follows that the degree is the same from whichever
point of view we regard it. The lines common to three complexes
of degrees, n1n2n3, form a ruled surface of degree 2n1n2n3;
but not every ruled surface is the complete intersection of three
complexes.
In the case of a complex of the first degree (or linear complex)
the lines through a fixed point lie in a plane called the polar plane
or nul-plane of that point, and those lying in a fixed plane
pass through a point called the nul-point or pole of the
Linear complex.
plane. If the nul-plane of A pass through B, then the
nul-plane of B will pass through A; the nul-planes of all points on
one line l1 pass through another line l2. The relation between l1 and
l2 is reciprocal; any line of the complex that meets one will also
meet the other, and every line meeting both belongs to the complex.
They are called conjugate or polar lines with respect to the complex.
On these principles can be founded a theory of reciprocation with
respect to a linear complex.
This may be aptly illustrated by an elegant example due to A.
Voss. Since a twisted cubic can be made to satisfy twelve conditions,
it might be supposed that a finite number could be drawn to touch
four given lines, but this is not the case. For, suppose one such can
be drawn, then its reciprocal with respect to any linear complex
containing the four lines is a curve of the third class, i.e. another
twisted cubic, touching the same four lines, which are unaltered
in the process of reciprocation; as there is an infinite number of
complexes containing the four lines, there is an infinite number of
cubics touching the four lines, and the problem is poristic.
The following are some geometrical constructions relating to the
unique linear complex that can be drawn to contain five arbitrary
lines:
To construct the nul-plane of any point O, we observe that the
two lines which meet any four of the given five are conjugate lines
of the complex, and the line drawn through O to meet them is
therefore a ray of the complex; similarly, by choosing another
four we can find another ray through O: these rays lie in the nul-plane,
and there is clearly a result involved that the five lines so
obtained all lie in one plane. A reciprocal construction will enable
us to find the nul-point of any plane. Proceeding now to the metrical
properties and the statical and dynamical applications, we remark
that there is just one line such that the nul-plane of any point on it
is perpendicular to it. This is called the central axis; if d be the
shortest distance, θ the angle between it and a ray of the complex,
then d tan θ = p, where p is a constant called the pitch or parameter.
Any system of forces can be reduced to a force R along a certain line,
and a couple G perpendicular to that line; the lines of nul-moment
722
for the system form a linear complex of which the given line is the
central axis and the quotient G/R is the pitch. Any motion of a
rigid body can be reduced to a screw motion about a certain line,
i.e. to an angular velocity ω about that line combined with a linear
velocity u along the line. The plane drawn through any point
perpendicular to the direction of its motion is its nul-plane with
respect to a linear complex having this line for central axis, and the
quotient u/ω for pitch (cf. Sir R.S. Ball, Theory of Screws).
The following are some properties of a configuration of two linear
complexes:
The lines common to the two-complexes also belong to an infinite
number of linear complexes, of which two reduce to single straight
lines. These two lines are conjugate lines with respect to each of
the complexes, but they may coincide, and then some simple modifications
are required. The locus of the central axis of this system
of complexes is a surface of the third degree called the cylindroid,
which plays a leading part in the theory of screws as developed
synthetically by Ball. Since a linear complex has an invariant of
the second degree in its coefficients, it follows that two linear complexes
have a lineo-linear invariant. This invariant is fundamental:
if the complexes be both straight lines, its vanishing is the condition
of their intersection as given above; if only one of them be a straight
line, its vanishing is the condition that this line should belong to the
other complex. When it vanishes for any two complexes they
are said to be in involution or apolar; the nul-points P, Q of any
plane then divide harmonically the points in which the plane meets
the common conjugate lines, and each complex is its own reciprocal
with respect to the other. As regards a configuration of these
linear complexes, the common lines from one system of generators
of a quadric, and the doubly infinite system of complexes containing
the common lines, include an infinite number of straight lines which
form the other system of generators of the same quadric.
If the equation of a linear complex is Al + Bm + Cn + Dλ + Eμ +
Fν = 0, then for a line not belonging to the complex we may regard
the expression on the left-hand side as a multiple of the
moment of the line with respect to the complex, the word
General line coordinates.
moment being used in the statical sense; and we infer
that when the coordinates are replaced by linear functions
of themselves the new coordinates are multiples of the moments
of the line with respect to six fixed complexes. The essential features
of this coordinate system are the same as those of the original one,
viz. there are six coordinates connected by a quadratic equation,
but this relation has in general a different form. By suitable choice
of the six fundamental complexes, as they may be called, this connecting
relation may be brought into other simple forms of which
we mention two: (i.) When the six are mutually in involution it can
be reduced to x1² + x2² + x3² + x4² + x5² + x6² = 0; (ii.) When the first
four are in involution and the other two are the lines common to
the first four it is x1² + x2² + x3² + x4² − 2x5x6 = 0. These generalized
coordinates might be explained without reference to actual magnitude,
just as homogeneous point coordinates can be; the essential
remark is that the equation of any coordinate to zero represents a
linear complex, a point of view which includes our original system,
for the equation of a coordinate to zero represents all the lines
meeting an edge of the fundamental tetrahedron.
The system of coordinates referred to six complexes mutually
in involution was introduced by Felix Klein, and in many cases is
more useful than that derived directly from point coordinates; e.g.
in the discussion of quadratic complexes: by means of it Klein has
developed an analogy between line geometry and the geometry of
spheres as treated by G. Darboux and others. In fact, in that
geometry a point is represented by five coordinates, connected by a
relation of the same type as the one just mentioned when the five
fundamental spheres are mutually at right angles and the equation
of a sphere is of the first degree. Extending this to four dimensions
of space, we obtain an exact analogue of line geometry, in which
(i.) a point corresponds to a line; (ii.) a linear complex to a hypersphere;
(iii.) two linear complexes in involution to two orthogonal
hyperspheres; (iv.) a linear complex and two conjugate lines to
a hypersphere and two inverse points. Many results may be obtained
by this principle, and more still are suggested by trying to extend
the properties of circles to spheres in three and four dimensions.
Thus the elementary theorem, that, given four lines, the circles
circumscribed to the four triangles formed by them are concurrent,
may be extended to six hyperplanes in four dimensions; and then
we can derive a result in line geometry by translating the inverse
of this theorem. Again, just as there is an infinite number of spheres
touching a surface at a given point, two of them having contact of a
closer nature, so there is an infinite number of linear complexes
touching a non-linear complex at a given line, and three of these
have contact of a closer nature (cf. Klein, Math. Ann. v.).
Sophus Lie has pointed out a different analogy with sphere
geometry. Suppose, in fact, that the equation of a sphere of radius
r is
x² + y² + z² + 2ax + 2by + 2cz + d = 0,
so that r² = a² + b² + c² − d; then introducing the quantity e to make
this equation homogeneous, we may regard the sphere as given by
the six coordinates a, b, c, d, e, r connected by the equation a² +
b² + c² − r² − de = 0, and it is easy to see that two spheres touch, if
the polar form 2aa1 + 2bb1 + 2cc1 − 2rr1 − de1 − d1e vanishes. Comparing
this with the equation x1² + x2² + x3² + x4² − 2x5x6 = 0 given
above, it appears that this sphere geometry and line geometry are
identical, for we may write a = x1, b = x2, c = x3, r = x4δ − 1, d = x5,
e = ½x6; but it is to be noticed that a sphere is really replaced by two
lines whose coordinates only differ in the sign of x4, so that they are
polar lines with respect to the complex x4 = 0. Two spheres which
touch correspond to two lines which intersect, or more accurately
to two pairs of lines (p, p′) and (q, q′), of which the pairs (p, q) and
(p′, q′) both intersect. By this means the problem of describing a
sphere to touch four given spheres is reduced to that of drawing a
pair of lines (t, t′) (of which t intersects one line of the four pairs
(pp′), (qq′), (rr′), (ss′), and t′ intersects the remaining four). We
may, however, ignore the accented letters in translating theorems,
for a configuration of lines and its polar with respect to a linear
complex have the same projective properties. In Lie’s transformation
a linear complex corresponds to the totality of spheres cutting a
given sphere at a given angle. A most remarkable result is that lines
of curvature in the sphere geometry become asymptotic lines in
the line geometry.
Some of the principles of line geometry may be brought into
clearer light by admitting the ideas of space of four and five
dimensions.
Thus, regarding the coordinates of a line as homogeneous coordinates
in five dimensions, we may say that line geometry is
equivalent to geometry on a quadric surface in five dimensions.
A linear complex is represented by a hyperplane section; and if
two such complexes are in involution, the corresponding hyperplanes
are conjugate with respect to the fundamental quadric. By projecting
this quadric stereographically into space of four dimensions
we obtain Klein’s analogy. In the same way geometry in a linear
complex is equivalent to geometry on a quadric in four dimensions;
when two lines intersect the representative points are on the same
generator of this quadric. Stereographic projection, therefore,
converts a curve in a linear complex, i.e. one whose tangents all
belong to the complex, into one whose tangents intersect a fixed
conic: when this conic is the imaginary circle at infinity the curve
is what Lie calls a minimal curve. Curves in a linear complex have
been extensively studied. The osculating plane at any point of such
a curve is the nul-plane of the point with respect to the complex,
and points of superosculation always coincide in pairs at the points
of contact of stationary tangents. When a point of such a curve is
given, the osculating plane is determined, hence all the curves through
a given point with the same tangent have the same torsion.
The lines through a given point that belong to a complex of the
nth degree lie on a cone of the nth degree: if this cone has a double
line the point is said to be a singular point. Similarly,
Non-linear complexes.
a plane is said to be singular when the envelope of the
lines in it has a double tangent. It is very remarkable
that the same surface is the locus of the singular points
and the envelope of the singular planes: this surface is called the
singular surface, and both its degree and class are in general 2n(n − 1)²,
which is equal to four for the quadratic complex.
The singular lines of a complex F = 0 are the lines common to F
and the complex
| δF |
| δF |
+ | δF |
| δF |
+ | δF |
| δF |
= 0. |
| δl | δλ |
δm | δμ |
δn | δν |
As already mentioned, at each line l of a complex there is an infinite
number of tangent linear complexes, and they all contain the lines
adjacent to l. If now l be a singular line, these complexes all reduce
to straight lines which form a plane pencil containing the line l.
Suppose the vertex of the pencil is A, its plane a, and one of its lines
ξ, then l′ being a complex line near l, meets ξ, or more accurately
the mutual moment of l′, and is of the second order of small quantities.
If P be a point on l, a line through P quite near l in the plane
a will meet ξ and is therefore a line of the complex; hence the
complex-cones of all points on l touch a and the complex-curves
of all planes through l touch l at A. It follows that l is a double
line of the complex-cone of A, and a double tangent of the complex-curve
of a. Conversely, a double line of a cone or curve is a singular
line, and a singular line clearly touches the curves of all planes
through it in the same point. Suppose now that the consecutive
line l′ is also a singular line, A′ being the allied singular point, a′
the singular plane and ξ′ any line of the pencil (A′, a′) so that ξ′ is
a tangent line at l′ to the complex: the mutual moments of the
pairs l′, ξ and l, ξ are each of the second order; hence the plane a′
meets the lines l and ξ′ in two points very near A. This being true
for all singular planes, near a the point of contact of a with its
envelope is in A, i.e. the locus of singular points is the same as the
envelope of singular planes. Further, when a line touches a complex
it touches the singular surface, for it belongs to a plane pencil like
(Aa), and thus in Klein’s analogy the analogue of a focus of a hyper-surface
being a bitangent line of the complex is also a bitangent line
of the singular surface. The theory of cosingular complexes is thus
brought into line with that of confocal surfaces in four dimensions,
and guided by these principles the existence of cosingular quadratic
complexes can easily be established, the analysis required being
almost the same as that invented for confocal cyclides by Darboux
723
and others. Of cosingular complexes of higher degree nothing is
known.
Following J. Plücker, we give an account of the lines of a quadratic
complex that meet a given line.
The cones whose vertices are on the given line all pass through
eight fixed points and envelop a surface of the fourth degree; the
conics whose planes contain the given line all lie on a surface of the
fourth class and touch eight fixed planes. It is easy to see by elementary
geometry that these two surfaces are identical. Further,
the given line contains four singular points A1, A2, A3, A4, and the
planes into which their cones degenerate are the eight common
tangent planes mentioned above; similarly, there are four singular
planes, a1, a2, a3, a4, through the line, and the eight points into
which their conics degenerate are the eight common points above.
The locus of the pole of the line with respect to all the conics in
planes through it is a straight line called the polar line of the given
one; and through this line passes the polar plane of the given line
with respect to each of the cones. The name polar is applied in the
ordinary analytical sense; any line has an infinite number of polar
complexes with respect to the given complex, for the equation of the
latter can be written in an infinite number of ways; one of these
polars is a straight line, and is the polar line already introduced.
The surface on which lie all the conics through a line l is called the
Plücker surface of that line: from the known properties of (2, 2)
correspondences it can be shown that the Plücker surface of l cuts l1
in a range of the same cross ratio as that of the range in which the
Plücker surface of l1 cuts l. Applying this to the case in which l1
is the polar of l, we find that the cross ratios of (A1, A2,
A3, A4) and (a1, a2, a3, a4) are equal. The identity of the locus of the A′s with the
envelope of the a′s follows at once; moreover, a line meets the
singular surface in four points having the same cross ratio as that
of the four tangent planes drawn through the line to touch the surface.
The Plücker surface has eight nodes, eight singular tangent
planes, and is a double line. The relation between a line and its
polar line is not a reciprocal one with respect to the complex; but
W. Stahl has pointed out that the relation is reciprocal as far as the
singular surface is concerned.
To facilitate the discussion of the general quadratic complex we
Quadratic complexes.
introduce Klein’s canonical form. We have, in fact, to
deal with two quadratic equations in six variables; and by
suitable linear transformations these can be reduced to the
form
| a1x12 | + a2x22 | + a3x32 | + a4x42 | + a5x52 | + a6x62 | = 0 |
| x12 | + x22 | + x32 | + x42 | + x52 | + x62 | = 0 |
subject to certain exceptions, which will be mentioned later.
Taking the first equation to be that of the complex, we remark
that both equations are unaltered by changing the sign of any coordinate;
the geometrical meaning of this is, that the quadratic
complex is its own reciprocal with respect to each of the six fundamental
complexes, for changing the sign of a coordinate is equivalent
to taking the polar of a line with respect to the corresponding
fundamental complex. It is easy to establish the existence of
six systems of bitangent linear complexes, for the complex
l1x1 + l2x2 + l3x3 + l4x4 + l5x5 + l6x6 = 0 is a bitangent when
| l1 = 0, and | l2² |
+ | l3² |
+ | l4² |
+ | l5² |
+ | l6² |
= 0, |
| a2 − a1 | a3 − a1 |
a4 − a1 | a5 − a1 |
a6 − a1 |
and its lines of contact are conjugate lines with respect to the first
fundamental complex. We therefore infer the existence of six systems
of bitangent lines of the complex, of which the first is given by
| x1 = 0, | x2² |
+ | x3² |
+ | x4² |
+ | x5² |
+ | x6² |
= 0, |
| a2 − a1 | a3 − a1 |
a4 − a1 | a5 − a1 |
a6 − a1 |
Each of these lines is a bitangent of the singular surface, which is
therefore completely determined as being the focal surface of the
(2, 2) congruence above. It is thence easy to verify that the two
complexes Σax2 = 0 and Σbx2 = 0 are cosingular if br = arλ + μ/arν + ρ.
The singular surface of the general quadratic complex is the
famous quartic, with sixteen nodes and sixteen singular tangent
planes, first discovered by E.E. Kümmer.
We cannot give a full account of its properties here, but we deduce
at once from the above that its bitangents break up into six (2, 2)
congruences, and the six linear complexes containing these are
mutually in involution. The nodes of the singular surface are points
whose complex cones are coincident planes, and the complex conic
in a singular tangent plane consists of two coincident points. This
configuration of sixteen points and planes has many interesting
properties; thus each plane contains six points which lie on a conic,
while through each point there pass six planes which touch a quadric
cone. In many respects the Kümmer quartic plays a part in three
dimensions analogous to the general quartic curve in two; it further
gives a natural representation of certain relations between hyperelliptic
functions (cf. R.W.H.T. Hudson, Kümmer’s Quartic, 1905).
As might be expected from the magnitude of a form in six variables,
the number of projectivally distinct varieties of quadratic complexes
is very great; and in fact Adolf Weiler, by whom the
Classification of quadratic complexes.
question was first systematically studied on lines indicated
by Klein, enumerated no fewer than forty-nine different
types. But the principle of the classification is so important,
and withal so simple, that we give a brief sketch
which indicates its essential features.
We have practically to study the intersection of two quadrics
F and F′ in six variables, and to classify the different cases arising
we make use of the results of Karl Weierstrass on the equivalence
conditions of two pairs of quadratics. As far as at present required,
they are as follows: Suppose that the factorized form of the determinantal
equation Disct (F + λF′) = 0 is
(λ − α)s1 + s2 + s3 ... (λ − β)t1 + t2 + t3 + ... ...
where the root α occurs s1 + s2 + s3 ... times in the determinant,
s2 + s3 ... times in every first minor, s3 + ... times in every second
minor, and so on; the meaning of each exponent is then perfectly
definite. Every factor of the type (λ − α)s is called an elementartheil
(elementary divisor) of the determinant, and the condition of equivalence
of two pairs of quadratics is simply that their determinants have
the same elementary divisors. We write the pair of forms symbolically
thus [(s1s2 ...), (t1t2 ...), ...], letters in the inner brackets
referring to the same factor. Returning now to the two quadratics
representing the complex, the sum of the exponents will be six,
and two complexes are put in the same class if they have the same
symbolical expression; i.e. the actual values of the roots of the
determinantal equation need not be the same for both, but their
manner of occurrence, as far as here indicated, must be identical in
the two. The enumeration of all possible cases is thus reduced
to a simple question in combinatorial analysis, and the actual study
of any particular case is much facilitated by a useful rule of Klein’s
for writing down in a simple form two quadratics belonging to a
given class—one of which, of course, represents the equation connecting
line coordinates, and the other the equation of the complex.
The general complex is naturally [111111]; the complex of tangents
to a quadric is [(111), (111)] and that of lines meeting a conic is
[(222)]. Full information will be found in Weiler’s memoir, Math.
Ann. vol. vii.
The detailed study of each variety of complex opens up a vast
subject; we only mention two special cases, the harmonic complex
and the tetrahedral complex.
The harmonic complex, first studied by Battaglini, is generated
in an infinite number of ways by the lines cutting two quadrics
harmonically. Taking the most general case, and referring the
quadrics to their common self-conjugate tetrahedron, we can find its
equation in a simple form, and verify that this complex really
depends only on seventeen constants, so that it is not the most
general quadratic complex. It belongs to the general type in so far
as it is discussed above, but the roots of the determinant are in involution.
The singular surface is the “tetrahedroid” discussed by
Cayley. As a particular case, from a metrical point of view, we have
L.F. Painvin’s complex generated by the lines of intersection of
perpendicular tangent planes of a quadric, the singular surface now
being Fresnel’s wave surface. The tetrahedral or Reye complex is
the simplest and best known of proper quadratic complexes. It is
generated by the lines which cut the faces of a tetrahedron in a
constant cross ratio, and therefore by those subtending the same
cross ratio at the four vertices. The singular surface is made up of
the faces or the vertices of the fundamental tetrahedron, and each
edge of this tetrahedron is a double line of the complex. The
complex was first discussed by K.T. Reye as the assemblage of lines
joining corresponding points in a homographic transformation of
space, and this point of view leads to many important and elegant
properties. A (metrically) particular case of great interest is the
complex generated by the normals to a family of confocal quadrics,
and for many investigations it is convenient to deal with this complex
referred to the principal axes. For example, Lie has developed
the theory of curves in a Reye complex (i.e. curves whose tangents
belong to the complex) as solutions of a differential equation of the
form (b − c)xdydz + (c − a)ydzdx + (a − b)zdxdy = 0, and we can simplify
this equation by a logarithmic transformation. Many theorems
connecting complexes with differential equations have been given
by Lie and his school. A line complex, in fact, corresponds to a
Mongian equation having ∞3 line integrals.
As the coordinates of a line belonging to a congruence are functions
of two independent parameters, the theory of congruences is analogous
to that of surfaces, and we may regard it as a fundamental
inquiry to find the simplest form of surface into which
Congruences.
a given congruence can be transformed. Most of those
whose properties have been extensively discussed can be represented
on a plane by a birational transformation. But in addition to the
difficulties of the theory of algebraic surfaces, a subject still in its
infancy, the theory of congruences has other difficulties in that a
congruence is seldom completely represented, even by two equations.
A fundamental theorem is that the lines of a congruence are in
general bitangents of a surface; in fact, since the condition of intersection
of two consecutive straight lines is ldλ + dmdμ + dndν = 0, a
line l of the congruence meets two adjacent lines, say l1 and l2.
Suppose l, l1 lie in the plane pencil (A1a1) and l, l2 in the plane pencil
(A2a2), then the locus of the A′s is the same as the envelope of the
a′s, but a2 is the tangent plane at A1 and a1 at A2. This surface is
called the focal surface of the congruence, and to it all the lines l
are bitangent. The distinctive property of the points A is that two
of the congruence lines through them coincide, and in like manner
the planes a each contain two coincident lines. The focal surface
consists of two sheets, but one or both may degenerate into curves;
724
thus, for example, the normals to a surface are bitangents of the
surface of centres, and in the case of Dupin’s cyclide this surface
degenerates into two conics.
In the discussion of congruences it soon becomes necessary to
introduce another number r, called the rank, which expresses the
number of plane pencils each of which contains an arbitrary line
and two lines of the congruence. The order of the focal surface is
2m(n − 1) − 2r, and its class is m(m − 1) − 2r. Our knowledge of
congruences is almost exclusively confined to those in which either
m or n does not exceed two. We give a brief account of those of
the second order without singular lines, those of order unity not
being especially interesting. A congruence generally has singular
points through which an infinite number of lines pass; a singular
point is said to be of order r when the lines through it lie on a cone
of the rth degree. By means of formulae connecting the number of
singular points and their orders with the class m of quadratic congruence
Kümmer proved that the class cannot exceed seven. The
focal surface is of degree four and class 2m; this kind of quartic
surface has been extensively studied by Kümmer, Cayley, Rohn and
others. The varieties (2, 2), (2, 3), (2, 4), (2, 5) all belong to at
least one Reye complex; and so also does the most important class
of (2, 6) congruences which includes all the above as special cases.
The congruence (2, 2) belongs to a linear complex and forty different
Reye complexes; as above remarked, the singular surface is
Kümmer’s sixteen-nodal quartic, and the same surface is focal for
six different congruences of this variety. The theory of (2, 2)
congruences is completely analogous to that of the surfaces called
cyclides in three dimensions. Further particulars regarding quadratic
congruences will be found in Kümmer’s memoir of 1866, and
the second volume of Sturm’s treatise. The properties of quadratic
congruences having singular lines, i.e. degenerate focal surfaces, are
not so interesting as those of the above class; they have been
discussed by Kümmer, Sturm and others.
Since a ruled surface contains only ∞¹ elements, this theory is
practically the same as that of curves. If a linear complex contains
more than n generators of a ruled surface of the nth degree,
it contains all the generators, hence for n = 2 there are
Ruled surfaces.
three linearly independent complexes, containing all the
generators, and this is a well-known property of quadric surfaces.
In ruled cubics the generators all meet two lines which may or may
not coincide; these two cases correspond to the two main classes of
cubics discussed by Cayley and Cremona. As regards ruled quartics,
the generators must lie in one and may lie in two linear complexes.
The first class is equivalent to a quartic in four dimensions and is
always rational, but the latter class has to be subdivided into the
elliptic and the rational, just like twisted quartic curves. A quintic
skew may not lie in a linear complex, and then it is unicursal, while of
sextics we have two classes not in a linear complex, viz. the elliptic
variety, having thirty-six places where a linear complex contains
six consecutive generators, and the rational, having six such
places.
The general theory of skews in two linear complexes is identical
with that of curves on a quadric in three dimensions and is known.
But for skews lying in only one linear complex there are difficulties;
the curve now lies in four dimensions, and we represent it in three by
stereographic projection as a curve meeting a given plane in n points
on a conic. To find the maximum deficiency for a given degree would
probably be difficult, but as far as degree eight the space-curve
theory of Halphen and Nöther can be translated into line geometry
at once. When the skew does not lie in a linear complex at all the
theory is more difficult still, and the general theory clearly cannot
advance until further progress is made in the study of twisted
curves.
References.—The earliest works of a general nature are Plücker,
Neue Geometrie des Raumes (Leipzig, 1868); and Kümmer, “Über
die algebraischen Strahlensysteme,” Berlin Academy (1866). Systematic
development on purely synthetic lines will be found in the
three volumes of Sturm, Liniengeometrie (Leipzig, 1892, 1893, 1896);
vol. i. deals with the linear and Reye complexes, vols. ii. and iii.
with quadratic congruences and complexes respectively. For a
highly suggestive review by Gino Loria see Bulletin des sciences
mathématiques (1893, 1897). A shorter treatise, giving a very
interesting account of Klein’s coordinates, is the work of Koenigs,
La Géométrie réglée et ses applications (Paris, 1898). English treatises
are C.M. Jessop, Treatise on the Line Complex (1903); R.W.H.T.
Hudson, Kümmer’s Quartic (1905). Many references to memoirs on
line geometry will be found in Hagen, Synopsis der höheren Mathematik,
ii. (Berlin, 1894); Loria, Il passato ed il presente delle principali
teorie geometriche (Milan, 1897); a clear résumé of the principal
results is contained in the very elegant volume of Pascal, Repertorio
di mathematiche superiori, ii. (Milan, 1900). Another treatise dealing
extensively with line geometry is Lie, Geometrie der Berührungstransformationen
(Leipzig, 1896). Many memoirs on the subject have
appeared in the Mathematische Annalen; a full list of these will be
found in the index to the first fifty volumes, p. 115. Perhaps the
two memoirs which have left most impression on the subsequent
development of the subject are Klein, “Zur Theorie der Liniencomplexe
des ersten und zweiten Grades,” Math. Ann. ii.; and Lie,
“Über Complexe, insbesondere Linien- und Kugelcomplexe,”
Math. Ann. v.
(J. H. Gr.)
VI. Non-Euclidean Geometry
The various metrical geometries are concerned with the
properties of the various types of congruence-groups, which are
defined in the study of the axioms of geometry and of their
immediate consequences. But this point of view of the subject
is the outcome of recent research, and historically the subject
has a different origin. Non-Euclidean geometry arose from the
discussion, extending from the Greek period to the present day,
of the various assumptions which are implicit in the traditional
Euclidean system of geometry. In the course of these investigations
it became evident that metrical geometries, each internally
consistent but inconsistent in many respects with each other
and with the Euclidean system, could be developed. A short
historical sketch will explain this origin of the subject, and
describe the famous and interesting progress of thought on the
subject. But previously a description of the chief characteristic
properties of elliptic and of hyperbolic geometries will be given,
assuming the standpoint arrived at below under VII. Axioms
of Geometry.
First assume the equation to the absolute (cf. loc. cit.) to
be w² − x² − y² − z² = 0. The absolute is then real, and the
geometry is hyberbolic.
The distance (d12) between the two points (x1, y1, z1, w1) and (x2, y2,
z2, w2) is given by
cosh (d12/γ) = (w1w2 − x1x2 − y1y2 − z1z2) / {(w1² − x1² − y1² − z1²)
(w2² − x2² − y2² − z2²)}1/2
(1)
The only points to which the metrical geometry applies are those
within the region enclosed by the quadric; the other points are
“improper ideal points.” The angle (θ12) between two planes,
l1x + m1y + n1z + r1w = 0 and l2x + m2y + n2z + r2w = 0, is given by
cos θ12 = (l1l2 + m1m2 + n1n2 − r1r2) / {(l1² + m1² + n1² − r1²)
(l2² + m2² + n2² − r2²)}1/2
(2)
These planes only have a real angle of inclination if they possess a
line of intersection within the actual space, i.e. if they intersect.
Planes which do not intersect possess a shortest distance along a line
which is perpendicular to both of them. If this shortest distance is
δ12, we have
cosh (δ12/γ) = (l1l2 + m1m2 + n1n2 − r1r2) / {(l1² + m1² + n1² − r1²)
(l2² + m2² + n2² − r2²)}1/2
(3)
 |
| Fig. 67. |
Thus in the case of the two planes one and only one of the two, θ12
and δ12, is real. The same considerations hold for coplanar straight
lines (see VII. Axioms of Geometry). Let O (fig. 67) be the point
(0, 0, 0, 1), OX the line y = 0,
z = 0, OY the line z = 0, x = 0, and
OZ the line x = 0, y = 0. These are
the coordinate axes and are at
right angles to each other. Let
P be any point, and let ρ be the
distance OP, θ the angle POZ, and
φ the angle between the planes
ZOX and ZOP. Then the coordinates
of P can be taken to be
sinh (ρ/γ) sin θ cos φ, sinh (ρ/γ) sin θ
sin φ, sinh (ρ/γ) cos θ, cosh (ρ/γ).
If ABC is a triangle, and the
sides and angles are named according
to the usual convention, we have
sinh (a/γ) / sin A = sinh (b/γ) / sin B = sinh (c/γ) / sin C,
(4)
and also
cosh (a/γ) = cosh (b/γ) cosh (c/γ) − sinh (b/γ) sinh (c/γ) cos A,
(5)
 |
| Fig. 68. |
with two similar equations. The sum of the three angles of a triangle
is always less than two right angles. The area of the triangle ABC
is λ²(π − A − B − C). If the base BC of a triangle is kept fixed
and the vertex A moves in the fixed plane ABC so that the area
ABC is constant, then the locus of A is a line of equal distance from
BC. This locus is not a straight line. The whole theory of similarity
is inapplicable; two triangles are either congruent, or their angles
are not equal two by two. Thus the elements of a triangle are
determined when its three angles are
given. By keeping A and B and the
line BC fixed, but by making C move
off to infinity along BC, the lines BC
and AC become parallel, and the sides
a and b become infinite. Hence from
equation (5) above, it follows that two
parallel lines (cf. Section VII. Axioms of
Geometry) must be considered as making a zero angle with each
other. Also if B be a right angle, from the equation (5), remembering
that, in the limit,
cosh (a/γ) / cosh (b/γ) = cosh (a/γ) / sinh (b/γ) = 1,
725
we have
cos A = tanh (c/2γ)
(6).
The angle A is called by N.I. Lobatchewsky the “angle of parallelism.”
The whole theory of lines and planes at right angles to each other
is simply the theory of conjugate elements with respect to the
absolute, where ideal lines and planes are introduced.
Thus if l and l′ be any two conjugate lines with respect to the
absolute (of which one of the two must be improper, say l′), then
any plane through l′ and containing proper points is perpendicular
to l. Also if p is any plane containing proper points, and P is its
pole, which is necessarily improper, then the lines through P are
the normals to P. The equation of the sphere, centre (x1, y1, z1, w1)
and radius ρ, is
(w1² − x1² − y1² − z1²) (w² − x² − y² − z²) cosh² (ρ/γ) =
(w1w − x1x − y1y − z1z)²
(7).
The equation of the surface of equal distance (σ) from the plane
lx + my + nz + rw = 0 is
(l² + m² + n² − r²) (w² − x² − y² − z²) sinh² (σ/γ) =
(rw + lx + my + nz)²
(8).
A surface of equal distance is a sphere whose centre is improper;
and both types of surface are included in the family
k² (w² − x² − y² − z²) = (ax + by + cz + dw)²
(9).
But this family also includes a third type of surfaces, which can
be looked on either as the limits of spheres whose centres have
approached the absolute, or as the limits of surfaces of equal distance
whose central planes have approached a position tangential to the
absolute. These surfaces are called limit-surfaces. Thus (9) denotes
a limit-surface, if d² − a² − b² − c² = 0. Two limit-surfaces only
differ in position. Thus the two limit-surfaces which touch the plane
YOZ at O, but have their concavities turned in opposite directions,
have as their equations
w² − x² − y² − z² = (w ± x)².
The geodesic geometry of a sphere is elliptic, that of a surface of
equal distance is hyperbolic, and that of a limit-surface is parabolic
(i.e. Euclidean). The equation of the surface (cylinder) of equal
distance (δ) from the line OX is
(w² − x²) tanh² (δ/γ) − y² − z² = 0.
This is not a ruled surface. Hence in this geometry it is not possible
for two straight lines to be at a constant distance from each other.
Secondly, let the equation of the absolute be x² + y² + z² +
w² = 0. The absolute is now imaginary and the geometry is
elliptic.
The distance (d12) between the two points (x1, y1, z1, w1) and
(x2, y2, z2, w2) is given by
cos (d12/γ) = ± (x1x2 + y1y2 + z1z2 + w1w2) /
{(x1² + y1² + z1² + w1²)
(x2² + y2² + z2² + w2²)}1/2
(10).
Thus there are two distances between the points, and if one is d12,
the other is πγ-d12. Every straight line returns into itself, forming
a closed series. Thus there are two segments between any two
points, together forming the whole line which contains them; one
distance is associated with one segment, and the other distance with
the other segment. The complete length of every straight line is
πγ.
The angle between the two planes l1x + m1y + n1z + r + 1w = 0 and
l2x + m2y + n2z + r2w = 0 is
cos θ12 = (l1l2 + m1m2 + n1n2 + r1r2) /
{(l1² + m1² + n1² +r1²)
(l2² + m2² + n2² + r2²)}1/2
(11).
The polar plane with respect to the absolute of the point (x1, y1, z1, w1)
is the real plane x1x + y1y + z1z + w1w = 0, and the pole of the plane
l1x + m1y + n1z + r1w = 0 is the point (l1, m1, n1, r1). Thus (from
equations 10 and 11) it follows that the angle between the polar
planes of the points (x1, ...) and (x2, ...) is d12/γ, and that the
distance between the poles of the planes (l1, ...) and (l2, ...) is
γθ12. Thus there is complete reciprocity between points and planes
in respect to all properties. This complete reign of the principle
of duality is one of the great beauties of this geometry. The theory
of lines and planes at right angles is simply the theory of conjugate
elements with respect to the absolute. A tetrahedron self-conjugate
with respect to the absolute has all its intersecting elements (edges
and planes) at right angles. If l and l′ are two conjugate lines, the
planes through one are the planes perpendicular to the other. If
P is the pole of the plane p, the lines through P are the normals to
the plane p. The distance from P to p is ½πγ. Thus every sphere
is also a surface of equal distance from the polar of its centre, and
conversely. A plane does not divide space; for the line joining any
two points P and Q only cuts the plane once, in L say, then it is
always possible to go from P to Q by the segment of the line PQ
which does not contain L. But P and Q may be said to be separated
by a plane p, if the point in which PQ cuts p lies on the shortest
segment between P and Q. With this sense of “separation,” it is
possible2 to find three points P, Q, R such that P and Q are separated
by the plane p, but P and R are not separated by p, nor are Q
and R.
Let A, B, C be any three non-collinear points, then four triangles
are defined by these points. Thus if a, b, c and A, B, C are the
elements of any one triangle, then the four triangles have as their
elements:
| (1) | a, | b, | c, | A, | B, | C. |
| (2) | a, | πγ − b, | πγ − c, | A, | π − B, | π − C. |
| (3) | πγ − a, | b, | πγ − c, | π − A, | B, | π − C. |
| (4) | πγ − a, | πγ − b, | c, | π − A, | π − B, | C. |
The formulae connecting the elements are
sin A/sin (a/γ) = sin B/sin (b/γ) = sin C/sin (c/γ),
(12)
and
cos (a/γ) = cos (b/γ) cos (c/γ) + sin (b/γ) sin (c/γ) cos A,
(13)
with two similar equations.
Two cases arise, namely (I.) according as one of the four triangles
has as its sides the shortest segments between the angular points,
or (II.) according as this is not the case. When case I. holds there
is said to be a “principal triangle.”3 If all the figures considered lie
within a sphere of radius ¼πγ only case I. can hold, and the principal
triangle is the triangle wholly within this sphere, also the peculiarities
in respect to the separation of points by a plane cannot then arise.
The sum of the three angles of a triangle ABC is always greater than
two right angles, and the area of the triangle is γ²(A + B + C − π).
Thus as in hyperbolic geometry the theory of similarity does not
hold, and the elements of a triangle are determined when its three
angles are given. The coordinates of a point can be written in the
form
sin (ρ/γ) sin Φ cos φ, sin (ρ/γ) sin Φ sin φ, sin (ρ/γ) cos Φ, cos (ρ/γ),
where ρ, Φ and φ have the same meanings as in the corresponding
formulae in hyperbolic geometry. Again, suppose a watch is laid
on the plane OXY, face upwards with its centre at O, and the line
12 to 6 (as marked on dial) along the line YOY. Let the watch be
continually pushed along the plane along the line OX, that is, in
the direction 9 to 3. Then the line XOX being of finite length, the
watch will return to O, but at its first return it will be found to be
face downwards on the other side of the plane, with the line 12 to 6
reversed in direction along the line YOY. This peculiarity was first
pointed out by Felix Klein. The theory of parallels as it exists in
hyperbolic space has no application in elliptic geometry. But
another property of Euclidean parallel lines holds in elliptic geometry,
and by the use of it parallel lines are defined. For the equation
of the surface (cylinder) of equal distance (δ) from the line
XOX is
(x² + w²) tan² (δ/γ) − (y² + z²) = 0.
This is also the surface of equal distance, ½πγ-δ, from the line
conjugate to XOX. Now from the form of the above equation this
is a ruled surface, and through every point of it two generators pass.
But these generators are lines of equal distance from XOX. Thus
throughout every point of space two lines can be drawn which are
lines of equal distance from a given line l. This property was discovered
by W.K. Clifford. The two lines are called Clifford’s right
and left parallels to l through the point. This property of parallelism
is reciprocal, so that if m is a left parallel to l, then l is a left
parallel to m. Note also that two parallel lines l and m are not
coplanar. Many of those properties of Euclidean parallels, which do
not hold for Lobatchewsky’s parallels in hyperbolic geometry, do
hold for Clifford’s parallels in elliptic geometry. The geodesic
geometry of spheres is elliptic, the geodesic geometry of surfaces of
equal distance from lines (cylinders) is Euclidean, and surfaces of
revolution can be found4 of which the geodesic geometry is hyperbolic.
But it is to be noticed that the connectivity of these surfaces
is different to that of a Euclidean plane. For instance there are only
∞² congruence transformations of the cylindrical surfaces of equal
distance into themselves, instead of the ∞³ for the ordinary plane.
It would obviously be possible to state “axioms” which these
geodesics satisfy, and thus to define independently, and not as loci,
quasi-spaces of these peculiar types. The existence of such Euclidean
quasi-geometries was first pointed out by Clifford.5
In both elliptic and hyperbolic geometry the spherical
geometry, i.e. the relations between the angles formed by lines
and planes passing through the same point, is the same as the
“spherical trigonometry” in Euclidean geometry. The constant
γ, which appears in the formulae both of hyperbolic and elliptic
geometry, does not by its variation produce different types of
geometry. There is only one type of elliptic geometry and one
type of hyperbolic geometry; and the magnitude of the constant
γ in each case simply depends upon the magnitude of the arbitrary
unit of length in comparison with the natural unit of length
726
which each particular instance of either geometry presents.
The existence of a natural unit of length is a peculiarity common
both to hyperbolic and elliptic geometries, and differentiates
them from Euclidean geometry. It is the reason for the failure
of the theory of similarity in them. If γ is very large, that is,
if the natural unit is very large compared to the arbitrary unit,
and if the lengths involved in the figures considered are not large
compared to the arbitrary unit, then both the elliptic and
hyperbolic geometries approximate to the Euclidean. For from
formulae (4) and (5) and also from (12) and (13) we find, after
retaining only the lowest powers of small quantities, as the
formulae for any triangle ABC,
a / sin A = b / sin B = c / sin C,
and
a² = b² + c² − 2bc cos A,
with two similar equations. Thus the geometries of small
figures are in both types Euclidean.
History.—“In pulcherrimo Geometriae corpore,” wrote Sir
Henry Savile in 1621, “duo sunt naevi, duae labes nec quod
sciam plures, in quibus eluendis et emaculendis cum
veterum tum recentiorum ... vigilavit industria.”
Theory of parallels before Gauss.
These two blemishes are the theory of parallels and
the theory of proportion. The “industry of the
moderns,” in both respects, has given rise to important branches
of mathematics, while at the same time showing that Euclid
is in these respects more free from blemish than had been
previously credible. It was from endeavours to improve the
theory of parallels that non-Euclidean geometry arose; and
though it has now acquired a far wider scope, its historical
origin remains instructive and interesting. Euclid’s “axiom
of parallels” appears as Postulate V. to the first book of his
Elements, and is stated thus, “And that, if a straight line falling
on two straight lines make the angles, internal and on the same
side, less than two right angles, the two straight lines, being
produced indefinitely, meet on the side on which are the
angles less than two right angles.” The original Greek is
καὶ ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐντὸς καὶ ἐπὶ τὰ
αὐτὰ μέρη γωνίας δύο ὀρθῶν ἐλάσσονας ποιῇ, ἐκβαλλομένας τὰς
δύο εὐθείας ἐπ᾽ ἄπειρον συμπίπτειν, ἐφ᾽ ἃ μέρη εἰσὶν αἱ τῶν δύο
ὀρθῶν ἐλάσσονες.
To Euclid’s successors this axiom had signally failed to appear
self-evident, and had failed equally to appear indemonstrable.
Without the use of the postulate its converse is proved in Euclid’s
28th proposition, and it was hoped that by further efforts the
postulate itself could be also proved. The first step consisted
in the discovery of equivalent axioms. Christoph Clavius in
1574 deduced the axiom from the assumption that a line whose
points are all equidistant from a straight line is itself straight.
John Wallis in 1663 showed that the postulate follows from the
possibility of similar triangles on different scales. Girolamo
Saccheri (1733) showed that it is sufficient to have a single
triangle, the sum of whose angles is two right angles. Other
equivalent forms may be obtained, but none shows any essential
superiority to Euclid’s. Indeed plausibility, which is chiefly
aimed at, becomes a positive demerit where it conceals a real
assumption.
A new method, which, though it failed to lead to the desired
goal, proved in the end immensely fruitful, was invented by
Saccheri, in a work entitled Euclides ab omni naevo
vindicatus (Milan, 1733). If the postulate of parallels
Saccheri.
is involved in Euclid’s other assumptions, contradictions must
emerge when it is denied while the others are maintained. This
led Saccheri to attempt a reductio ad absurdum, in which he
mistakenly believed himself to have succeeded. What is interesting,
however, is not his fallacious conclusion, but the non-Euclidean
results which he obtains in the process. Saccheri
distinguishes three hypotheses (corresponding to what are now
known as Euclidean or parabolic, elliptic and hyperbolic geometry),
and proves that some one of the three must be universally
true. His three hypotheses are thus obtained: equal
perpendiculars AC, BD are drawn from a straight line AB,
and CD are joined. It is shown that the angles ACD, BDC are
equal. The first hypothesis is that these are both right angles;
the second, that they are both obtuse; and the third, that they
are both acute. Many of the results afterwards obtained by
Lobatchewsky and Bolyai are here developed. Saccheri fails
to be the founder of non-Euclidean geometry only because he
does not perceive the possible truth of his non-Euclidean hypotheses.
Some advance is made by Johann Heinrich Lambert in his
Theorie der Parallellinien (written 1766; posthumously published
1786). Though he still believed in the necessary
truth of Euclidean geometry, he confessed that, in
Lambert.
all his attempted proofs, something remained undemonstrated.
He deals with the same three hypotheses as Saccheri, showing
that the second holds on a sphere, while the third would hold on
a sphere of purely imaginary radius. The second hypothesis
he succeeds in condemning, since, like all who preceded Bernhard
Riemann, he is unable to conceive of the straight line as finite
and closed. But the third hypothesis, which is the same as
Lobatchewsky’s, is not even professedly refuted.6
Non-Euclidean geometry proper begins with Karl Friedrich
Gauss. The advance which he made was rather philosophical
than mathematical: it was he (probably) who first
recognized that the postulate of parallels is possibly
Three periods of non-Euclidean geometry.
false, and should be empirically tested by measuring
the angles of large triangles. The history of non-Euclidean
geometry has been aptly divided by Felix
Klein into three very distinct periods. The first—which contains
only Gauss, Lobatchewsky and Bolyai—is characterized by its
synthetic method and by its close relation to Euclid. The
attempt at indirect proof of the disputed postulate would seem
to have been the source of these three men’s discoveries; but
when the postulate had been denied, they found that the results,
so far from showing contradictions, were just as self-consistent
as Euclid. They inferred that the postulate, if true at all, can
only be proved by observations and measurements. Only one
kind of non-Euclidean space is known to them, namely, that
which is now called hyperbolic. The second period is analytical,
and is characterized by a close relation to the theory of surfaces.
It begins with Riemann’s inaugural dissertation, which regards
space as a particular case of a manifold; but the characteristic
standpoint of the period is chiefly emphasized by Eugenio
Beltrami. The conception of measure of curvature is extended
by Riemann from surfaces to spaces, and a new kind of space,
finite but unbounded (corresponding to the second hypothesis
of Saccheri and Lambert), is shown to be possible. As opposed
to the second period, which is purely metrical, the third period
is essentially projective in its method. It begins with Arthur
Cayley, who showed that metrical properties are projective
properties relative to a certain fundamental quadric, and that
different geometries arise according as this quadric is real,
imaginary or degenerate. Klein, to whom the development of
Cayley’s work is due, showed further that there are two forms
of Riemann’s space, called by him the elliptic and the spherical.
Finally, it has been shown by Sophus Lie, that if figures are to be
freely movable throughout all space in ∞6 ways, no other
three-dimensional spaces than the above four are possible.
Gauss published nothing on the theory of parallels, and it
was not generally known until after his death that he had
interested himself in that theory from a very early
date. In 1799 he announces that Euclidean geometry
Gauss.
would follow from the assumption that a triangle can be drawn
greater than any given triangle. Though unwilling to assume
this, we find him in 1804 still hoping to prove the postulate of
parallels. In 1830 he announces his conviction that geometry
is not an a priori science; in the following year he explains that
non-Euclidean geometry is free from contradictions, and that,
in this system, the angles of a triangle diminish without limit
when all the sides are increased. He also gives for the
727
circumference of a circle of radius r the formula πk(er/k − er −/k),
where k is a constant depending upon the nature of the space. In
1832, in reply to the receipt of Bolyai’s Appendix, he gives an
elegant proof that the amount by which the sum of the angles of a
triangle falls short of two right angles is proportional to the area
of the triangle. From these and a few other remarks it appears
that Gauss possessed the foundations of hyperbolic geometry,
which he was probably the first to regard as perhaps true. It
is not known with certainty whether he influenced Lobatchewsky
and Bolyai, but the evidence we possess is against such a view.7
The first to publish a non-Euclidean geometry was Nicholas
Lobatchewsky, professor of mathematics in the new university
of Kazañ.8 In the place of the disputed postulate
he puts the following: “All straight lines which, in
Lobatchewsky.
a plane, radiate from a given point, can, with respect
to any other straight line in the same plane, be divided into
two classes, the intersecting and the non-intersecting. The
boundary line of the one and the other class is called parallel
to the given line.” It follows that there are two parallels to the
given line through any point, each meeting the line at infinity,
like a Euclidean parallel. (Hence a line has two distinct points
at infinity, and not one only as in ordinary geometry.) The
two parallels to a line through a point make equal acute angles
with the perpendicular to the line through the point. If p be
the length of the perpendicular, either of these angles is denoted
by Π(p). The determination of Π(p) is the chief problem (cf.
equation (6) above); it appears finally that, with a suitable
choice of the unit of length,
tan ½ Π(p) = e−p.
Before obtaining this result it is shown that spherical trigonometry
is unchanged, and that the normals to a circle or a sphere
still pass through its centre. When the radius of the circle or
sphere becomes infinite all these normals become parallel, but the
circle or sphere does not become a straight line or plane. It
becomes what Lobatchewsky calls a limit-line or limit-surface.
The geometry on such a surface is shown to be Euclidean, limit-lines
replacing Euclidean straight lines. (It is, in fact, a surface
of zero measure of curvature.) By the help of these propositions
Lobatchewsky obtains the above value of Π(p), and thence the
solution of triangles. He points out that his formulae result
from those of spherical trigonometry by substituting ia, ib, ic,
for the sides a, b, c.
John Bolyai, a Hungarian, obtained results closely corresponding
to those of Lobatchewsky. These he published in an appendix
to a work by his father, entitled Appendix Scientiam
spatii absolute veram exhibens: a veritate aut falsitate
Bolyai.
Axiomatis XI. Euclidei (a priori haud unquam decidenda) independentem:
adjecta ad casum falsitatis, quadratura circuli
geometrica.9 This work was published in 1831, but its conception
dates from 1823. It reveals a profounder appreciation of the
importance of the new ideas, but otherwise differs little from
Lobatchewsky’s. Both men point out that Euclidean geometry
as a limiting case of their own more general system, that the
geometry of very small spaces is always approximately Euclidean,
that no a priori grounds exist for a decision, and that observation
can only give an approximate answer. Bolyai gives also, as his
title indicates, a geometrical construction, in hyperbolic space,
for the quadrature of the circle, and shows that the area of the
greatest possible triangle, which has all its sides parallel and all
its angles zero, is πι², where i is what we should now call the
space-constant.
The works of Lobatchewsky and Bolyai, though known and
valued by Gauss, remained obscure and ineffective until, in 1866,
they were translated into French by J. Hoüel. But
Riemann.
at this time Riemann’s dissertation, Über die Hypothesen,
welche der Geometrie zu Grunde liegen,10 was already about to be
published. In this work Riemann, without any knowledge of
his predecessors in the same field, inaugurated a far more profound
discussion, based on a far more general standpoint; and by
its publication in 1867 the attention of mathematicians and
philosophers was at last secured. (The dissertation dates from
1854, but owing to changes which Riemann wished to make in it,
it remained unpublished until after his death.)
Riemann’s work contains two fundamental conceptions, that
of a manifold and that of the measure of curvature of a continuous
manifold possessed of what he calls flatness in the smallest parts.
By means of these conceptions space is made to appear
Definition of a manifold.
at the end of a gradual series of more and more specialized
conceptions. Conceptions of magnitude, he explains,
are only possible where we have a general conception
capable of determination in various ways. The manifold consists
of all these various determinations, each of which is an element
of the manifold. The passage from one element to another may
be discrete or continuous; the manifold is called discrete or
continuous accordingly. Where it is discrete two portions of
it can be compared, as to magnitude, by counting; where
continuous, by measurement. But measurement demands
superposition, and consequently some magnitude independent
of its place in the manifold. In passing, in a continuous manifold,
from one element to another in a determinate way, we pass
through a series of intermediate terms, which form a one-dimensional
manifold. If this whole manifold be similarly
caused to pass over into another, each of its elements passes
through a one-dimensional manifold, and thus on the whole
a two-dimensional manifold is generated. In this way we can
proceed to n dimensions. Conversely, a manifold of n dimensions
can be analysed into one of one dimension and one of (n − 1)
dimensions. By repetitions of this process the position of an
element may be at last determined by n magnitudes. We may
here stop to observe that the above conception of a manifold
is akin to that due to Hermann Grassmann in the first edition
(1847) of his Ausdehnungslehre.11
Both concepts have been elaborated and superseded by the
modern procedure in respect to the axioms of geometry, and by
the conception of abstract geometry involved therein.
Riemann proceeds to specialize the manifold by considerations
Measure of curvature.
as to measurement. If measurement is to
be possible, some magnitude, we saw, must be independent of
position; let us consider manifolds in which lengths of lines are
such magnitudes, so that every line is measurable by every
other. The coordinates of a point being x1, x2, ... xn, let us confine
ourselves to lines along which the ratios dx1 : dx2 : ... : dxn
alter continuously. Let us also assume that the element of
length, ds, is unchanged (to the first order) when all its points
undergo the same infinitesimal motion. Then if all the increments
dx be altered in the same ratio, ds is also altered in this ratio.
Hence ds is a homogeneous function of the first degree of the
increments dx. Moreover, ds must be unchanged when all the
dx change sign. The simplest possible case is, therefore, that in
which ds is the square root of a quadratic function of the dx.
This case includes space, and is alone considered in what follows.
It is called the case of flatness in the smallest parts. Its further
discussion depends upon the measure of curvature, the second
of Riemann’s fundamental conceptions. This conception, derived
from the theory of surfaces, is applied as follows. Any one of
the shortest lines which issue from a given point (say the origin)
is completely determined by the initial ratios of the dx. Two
such lines, defined by dx and δx say, determine a pencil, or one-dimensional
series, of shortest lines, any one of which is defined
728
by λdx + μδx, where the parameter λ : μ may have any value.
This pencil generates a two-dimensional series of points, which
may be regarded as a surface, and for which we may apply
Gauss’s formula for the measure of curvature at any point.
Thus at every point of our manifold there is a measure of curvature
corresponding to every such pencil; but all these can be found
when n·n − 1/2 of them are known. If figures are to be freely
movable, it is necessary and sufficient that the measure of
curvature should be the same for all points and all directions
at each point. Where this is the case, if α be the measure of
curvature, the linear element can be put into the form
ds = √(Σdx²) / (1 + ¼αΣx²).
If α be positive, space is finite, though still unbounded, and
every straight line is closed—a possibility first recognized by
Riemann. It is pointed out that, since the possible values of
a form a continuous series, observations cannot prove that our
space is strictly Euclidean. It is also regarded as possible that,
in the infinitesimal, the measure of curvature of our space should
be variable.
There are four points in which this profound and epoch-making
work is open to criticism or development—(1) the idea of a manifold
requires more precise determination; (2) the introduction
of coordinates is entirely unexplained and the requisite presuppositions
are unanalysed; (3) the assumption that ds is the
square root of a quadratic function of dx1, dx2, ... is arbitrary;
(4) the idea of superposition, or congruence, is not adequately
analysed. The modern solution of these difficulties is properly
considered in connexion with the general subject of the axioms
of geometry.
The publication of Riemann’s dissertation was closely followed
by two works of Hermann von Helmholtz,12 again undertaken
in ignorance of the work of predecessors. In these a
Helmholtz.
proof is attempted that ds must be a rational integral
quadratic function of the increments of the coordinates. This
proof has since been shown by Lie to stand in need of correction
(see VII. Axioms of Geometry). Helmholtz’s remaining works
on the subject13 are of almost exclusively philosophical interest.
We shall return to them later.
The only other writer of importance in the second period is
Eugenio Beltrami, by whom Riemann’s work was brought into
connexion with that of Lobatchewsky and Bolyai.
As he gave, by an elegant method, a convenient
Beltrami.
Euclidean interpretation of hyperbolic plane geometry, his
results will be stated at some length14. The Saggio shows that
Lobatchewsky’s plane geometry holds in Euclidean geometry
on surfaces of constant negative curvature, straight lines being
replaced by geodesics. Such surfaces are capable of a conformal
representation on a plane, by which geodesics are represented
by straight lines. Hence if we take, as coordinates on the surface,
the Cartesian coordinates of corresponding points on the plane,
the geodesics must have linear equations.
Hence it follows that
ds² = R²w−4 {(α² − v²) du² + 2uvdudv + (α² − u²)dv²}
where w² = α² − u² − v², and −1/R² is the measure of curvature
of our surface (note that k = γ as used above). The angle between
two geodesics u = const., v = const. is θ, where
cos θ = uv / √ {(α² − u²) (α² − v²)}, sin θ = aw / √ {(a² − u²) (a² − v²)}.
Thus u = 0 is orthogonal to all geodesies v = const., and vice versa.
In order that sin θ may be real, w² must be positive; thus geodesics
have no real intersection when the corresponding straight
lines intersect outside the circle u² + v² = α². When they intersect on
this circle, θ = 0. Thus Lobatchewsky’s parallels are represented
by straight lines intersecting on the circle. Again, transforming
to polar coordinates u = r cos μ, v = r sin μ, and calling ρ the geodesic
distance of u, v from the origin, we have, for a geodesic through the
origin,
| dρ = Radr / (a² − r²), ρ = ½R log | a + r |
, r = a tan h (ρ / R). |
| a − r |
Thus points on the surface corresponding to points in the plane
on the limiting circle r = a, are all at an infinite distance from the
origin. Again, considering r constant, the arc of a geodesic circle
subtending an angle μ at the origin is
σ = Rrμ / √ (a² − r²) = μR sin h (ρ/R),
whence the circumference of a circle of radius ρ is 2πR sin h (ρ/R).
Again, if α be the angle between any two geodesics
V − v = m (U − u), V − v = n (U − u),
then
tan α = a (n − m)w / {(1 + mn)a² − (v − mu) (v − nu)}.
Thus α is imaginary when u, v is outside the limiting circle, and
is zero when, and only when, u, v is on the limiting circle. All
these results agree with those of Lobatchewsky and Bolyai. The
maximum triangle, whose angles are all zero, is represented in the
auxiliary plane by a triangle inscribed in the limiting circle. The
angle of parallelism is also easily obtained. The perpendicular
to v = 0 at a distance δ from the origin is u = a tan h (δ/R), and the
parallel to this through the origin is u = v sin h (δ/R). Hence Π (δ),
the angle which this parallel makes with v = 0, is given by
tan Π(δ) . sin h (δ/R) = 1, or tan ½Π(δ) = e−δ/R
which is Lobatchewsky’s formula. We also obtain easily for the
area of a triangle the formula R²(π − A − B − C).
Beltrami’s treatment connects two curves which, in the earlier
treatment, had no connexion. These are limit-lines and curves
of constant distance from a straight line. Both may be regarded
as circles, the first having an infinite, the second an imaginary
radius. The equation to a circle of radius ρ and centre u0v0 is
(a² − uu0 − vv0)² = cos h² (ρ/R) w0²w² = C²w²
(say).
This equation remains real when ρ is a pure imaginary, and remains
finite when w0 = 0, provided ρ becomes infinite in such a way that
w0 cos h (ρ/R) remains finite. In the latter case the equation represents
a limit-line. In the former case, by giving different values to C,
we obtain concentric circles with the imaginary centre u0v0. One of
these, obtained by putting C = 0, is the straight line a² − uu0 − vv0 = 0.
Hence the others are each throughout at a constant distance from
this line. (It may be shown that all motions in a hyperbolic plane
consist, in a general sense, of rotations; but three types must
be distinguished according as the centre is real, imaginary or at
infinity. All points describe, accordingly, one of the three types of
circles.)
The above Euclidean interpretation fails for three or more dimensions.
In the Teoria fondamentale, accordingly, where n dimensions
are considered, Beltrami treats hyperbolic space in a purely analytical
spirit. The paper shows that Lobatchewsky’s space of any number
of dimensions has, in Riemann’s sense, a constant negative measure
of curvature. Beltrami starts with the formula (analogous to that
of the Saggio)
ds² = R²x−2 (dx² + dx1² + dx2² + ... + dxn²)
where
x² + x1² + x2² + ... + xn² = a².
He shows that geodesics are represented by linear equations between
x1, x2, ..., xn, and that the geodesic distance ρ between two
points x and x′ is given by
| cos h | ρ |
= | a² − x1x′1 − x2x′2 − ... − xnx′n |
| R | {(a² − x1² − x2² − ... − xn²) (a² − x′1² − x′2² − ... − x′n²)}1/2 |
(a formula practically identical with Cayley’s, though obtained by
a very different method). In order to show that the measure of
curvature is constant, we make the substitutions
x1 = rλ1, x2 = rλ2 ... xn = rλn, where Σλ² = 1.
Hence
ds² = (Radr / a² − r²)² + R²r²dΔ² / (a² − r²).
where
dΔ² = Σdλ².
Also calling ρ the geodesic distance from the origin, we have
| cos h (ρ/R) = | a |
, sin h (ρ/R) = | r |
. |
| √(a² − r²) | √(a² − r²) |
Hence
ds² = dρ² + (R sin h (ρ/R))² dΔ².
Putting
z1 = ρλ1, z2 = ρλ2, ... zn = ρλn,
we obtain
| ds² = Σdz² + | 1 |
{ ( | R |
sinh | ρ |
) | ² |
− 1 } Σ (zidzk − zkdzi)². |
| ρ² | ρ |
R | |
Hence when ρ is small, we have approximately
| ds² = Σdz² + | 1 |
Σ (zidzk − zkdzi)² |
| 3R² |
(1).
Considering a surface element through the origin, we may choose
our axes so that, for this element,
z3 = z4 = ... = zn = 0.
Thus
| dz1² + dz2² + | 1 |
(z1dz2 − z2dz1)² |
| 3R² |
(2).
Now the area of the triangle whose vertices are (0, 0), (z1, z2),
(dz1, dz2) is ½(z1, dz2 − z2dz1). Hence the quotient when the terms of
the fourth order in (2) are divided by the square of this triangle is
729
4/3R²; hence, returning to general axes, the same is the quotient
when the terms of the fourth order in (1) are divided by the square
of the triangle whose vertices are (0, 0, ... 0), (z1, z2, z3, ... zn),
(dz1, dz2, dz3 ... dzn). But −¾ of this quotient is defined by Riemann
as the measure of curvature.15 Hence the measure of curvature is
−1/R², i.e. is constant and negative. The properties of parallels,
triangles, &c., are as in the Saggio. It is also shown that the analogues
of limit surfaces have zero curvature; and that spheres of
radius ρ have constant positive curvature 1/R² sinh² (ρ/R), so that
spherical geometry may be regarded as contained in the pseudo-spherical
(as Beltrami calls Lobatchewsky’s system).
The Saggio, as we saw, gives a Euclidean interpretation
confined to two dimensions. But a consideration of the auxiliary
plane suggests a different interpretation, which may be
extended to any number of dimensions. If, instead
Transition to the projective method.
of referring to the pseudosphere, we merely define
distance and angle, in the Euclidean plane, as those
functions of the coordinates which gave us distance and angle
on the pseudosphere, we find that the geometry of our plane has
become Lobatchewsky’s. All the points of the limiting circle
are now at infinity, and points beyond it are imaginary. If we
give our circle an imaginary radius the geometry on the plane
becomes elliptic. Replacing the circle by a sphere, we obtain
an analogous representation for three dimensions. Instead of
a circle or sphere we may take any conic or quadric. With this
definition, if the fundamental quadric be Σxx = 0, and if Σxx′
be the polar form of Σxx, the distance ρ between x and x′ is
given by the projective formula
cos(ρ/k) = Σxx′ / {Σxx·Σx′x′}1/2.
That this formula is projective is rendered evident by observing
that e−2iρ/k is the anharmonic ratio of the range consisting of
the two points and the intersections of the line joining them with
the fundamental quadric. With this we are brought to the third
or projective period. The method of this period is due to Cayley;
its application to previous non-Euclidean geometry is due to
Klein. The projective method contains a generalization of discoveries
already made by Laguerre16 in 1853 as regards Euclidean
geometry. The arbitrariness of this procedure of deriving
metrical geometry from the properties of conics is removed by
Lie’s theory of congruence. We then arrive at the stage of
thought which finds its expression in the modern treatment of
the axioms of geometry.
The projective method leads to a discrimination, first made
by Klein,17 of two varieties of Riemann’s space; Klein calls
these elliptic and spherical. They are also called the
polar and antipodal forms of elliptic space. The latter
The two kinds of elliptic space.
names will here be used. The difference is strictly
analogous to that between the diameters and the points
of a sphere. In the polar form two straight lines in a plane
always intersect in one and only one point; in the antipodal
form they intersect always in two points, which are antipodes.
According to the definition of geometry adopted in section VII.
(Axioms of Geometry), the antipodal form is not to be termed
“geometry,” since any pair of coplanar straight lines intersect
each other in two points. It may be called a “quasi-geometry.”
Similarly in the antipodal form two diameters always determine
a plane, but two points on a sphere do not determine a great
circle when they are antipodes, and two great circles always
intersect in two points. Again, a plane does not form a boundary
among lines through a point: we can pass from any one such
line to any other without passing through the plane. But a great
circle does divide the surface of a sphere. So, in the polar form,
a complete straight line does not divide a plane, and a plane does
not divide space, and does not, like a Euclidean plane, have two
sides.18 But, in the antipodal form, a plane is, in these respects,
like a Euclidean plane.
It is explained in section VII. in what sense the metrical
geometry of the material world can be considered to be determinate
and not a matter of arbitrary choice. The scientific
question as to the best available evidence concerning the nature
of this geometry is one beset with difficulties of a peculiar kind.
We are obstructed by the fact that all existing physical science
assumes the Euclidean hypothesis. This hypothesis has been
involved in all actual measurements of large distances, and in all
the laws of astronomy and physics. The principle of simplicity
would therefore lead us, in general, where an observation conflicted
with one or more of those laws, to ascribe this anomaly,
not to the falsity of Euclidean geometry, but to the falsity of the
laws in question. This applies especially to astronomy. On the
earth our means of measurement are many and direct, and so
long as no great accuracy is sought they involve few scientific
laws. Thus we acquire, from such direct measurements, a
very high degree of probability that the space-constant, if not
infinite, is yet large as compared with terrestrial distances. But
astronomical distances and triangles can only be measured by
means of the received laws of astronomy and optics, all of which
have been established by assuming the truth of the Euclidean
hypothesis. It therefore remains possible (until a detailed proof
of the contrary is forthcoming) that a large but finite space-constant,
with different laws of astronomy and optics, would
have equally explained the phenomena. We cannot, therefore,
accept the measurements of stellar parallaxes, &c., as conclusive
evidence that the space-constant is large as compared with stellar
distances. For the present, on grounds of simplicity, we may
rightly adopt this view; but it must remain possible that, in
view of some hitherto undiscovered discrepancy, a slight correction
of the sort suggested might prove the simplest alternative.
But conversely, a finite parallax for very distant stars, or a
negative parallax for any star, could not be accepted as conclusive
evidence that our geometry is non-Euclidean, unless it were
shown—and this seems scarcely possible—that no modification
of astronomy or optics could account for the phenomenon.
Thus although we may admit a probability that the space-constant
is large in comparison with stellar distances, a conclusive
proof or disproof seems scarcely possible.
Finally, it is of interest to note that, though it is theoretically
possible to prove, by scientific methods, that our geometry is
non-Euclidean, it is wholly impossible to prove by such methods
that it is accurately Euclidean. For the unavoidable errors of
observation must always leave a slight margin in our measurements.
A triangle might be found whose angles were certainly
greater, or certainly less, than two right angles; but to prove
them exactly equal to two right angles must always be beyond our
powers. If, therefore, any man cherishes a hope of proving the
exact truth of Euclid, such a hope must be based, not upon
scientific, but upon philosophical considerations.
Bibliography.—The bibliography appended to section VII. should
be consulted in this connexion. Also, in addition to the citations
already made, the following works may be mentioned.
For Lobatchewsky’s writings, cf. Urkunden zur Geschichte der
nichteuklidischen Geometrie, i., Nikolaj Iwanowitsch Lobatschefsky,
by F. Engel and P. Stäckel (Leipzig, 1898). For John Bolyai’s
Appendix, cf. Absolute Geometrie nach Johann Bolyai, by J. Frischauf
(Leipzig, 1872), and also the new edition of his father’s large work,
Tentamen ..., published by the Mathematical Society of Budapest;
the second volume contains the appendix. Cf. also J. Frischauf,
Elemente der absoluten Geometrie (Leipzig, 1876); M.L. Gérard, Sur
la géométrie non-Euclidienne (thesis for doctorate) (Paris, 1892);
de Tilly, Essai sur les principes fondamentales de la géométrie et de la
mécanique (Bordeaux, 1879); Sir R.S. Ball, “On the Theory of
Content,” Trans. Roy. Irish Acad. vol. xxix. (1889); F. Lindemann,
“Mechanik bei projectiver Maasbestimmung,” Math. Annal. vol.
vii.; W.K. Clifford, “Preliminary Sketch of Biquaternions,” Proc.
of Lond. Math. Soc. (1873), and Coll. Works; A. Buchheim, “On the
Theory of Screws in Elliptic Space,” Proc. Lond. Math. Soc. vols. xv.,
xvi., xvii.; H. Cox, “On the Application of Quaternions and
Grassmann’s Algebra to different Kinds of Uniform Space,” Trans.
Camb. Phil. Soc. (1882); M. Dehn, “Die Legendarischen Sätze über
die Winkelsumme im Dreieck,” Math. Ann. vol. 53 (1900), and
“Über den Rauminhalt,” Math. Annal. vol. 55 (1902).
For expositions of the whole subject, cf. F. Klein, Nicht-Euklidische
Geometrie (Göttingen, 1893); R. Bonola, La Geometria non-Euclidea
(Bologna, 1906); P. Barbarin, La Géométrie non-Euclidienne (Paris,
1902); W. Killing, Die nicht-Euklidischen Raumformen in analytischer
Behandlung (Leipzig, 1885). The last-named work also deals with
geometry of more than three dimensions; in this connexion cf. also
G. Veronese, Fondamenti di geometria a più dimensioni ed a più specie
730
di unità rettilinee ... (Padua, 1891, German translation, Leipzig,
1894); G. Fontené, L’Hyperespace à (n-1) dimensions (Paris, 1892);
and A.N. Whitehead, loc. cit. Cf. also E. Study, “Über nicht-Euklidische
und Liniengeometrie,” Jahr. d. Deutsch. Math. Ver.
vol. xv. (1906); W. Burnside, “On the Kinematics of non-Euclidean
Space,” Proc. Lond. Math. Soc. vol. xxvi. (1894). A bibliography
on the subject up to 1878 has been published by G.B. Halsted,
Amer. Journ. of Math. vols. i. and ii.; and one up to 1900 by R.
Bonola, Index operum ad geometriam absolutam spectantium ...
(1902, and Leipzig, 1903).
(B. A. W. R.; A. N. W.)
VII. Axioms of Geometry
Until the discovery of the non-Euclidean geometries (Lobatchewsky,
1826 and 1829; J. Bolyai, 1832; B. Riemann, 1854),
geometry was universally considered as being exclusively
the science of existent space. (See section
Theories of space.
VI. Non-Euclidean Geometry.) In respect to the
science, as thus conceived, two controversies may be noticed.
First, there is the controversy respecting the absolute and
relational theories of space. According to the absolute theory,
which is the traditional view (held explicitly by Newton), space
has an existence, in some sense whatever it may be, independent
of the bodies which it contains. The bodies occupy space, and
it is not intrinsically unmeaning to say that any definite body
occupies this part of space, and not that part of space, without
reference to other bodies occupying space. According to the
relational theory of space, of which the chief exponent was
Leibnitz,19 space is nothing but a certain assemblage of the relations
between the various particular bodies in space. The idea of
space with no bodies in it is absurd. Accordingly there can be
no meaning in saying that a body is here and not there, apart
from a reference to the other bodies in the universe. Thus, on
this theory, absolute motion is intrinsically unmeaning. It is
admitted on all hands that in practice only relative motion is
directly measurable. Newton, however, maintains in the
Principia (scholium to the 8th definition) that it is indirectly
measurable by means of the effects of “centrifugal force” as
it occurs in the phenomena of rotation. This irrelevance of
absolute motion (if there be such a thing) to science has led to
the general adoption of the relational theory by modern men
of science. But no decisive argument for either view has at
present been elaborated.20 Kant’s view of space as being a form
of perception at first sight appears to cut across this controversy.
But he, saturated as he was with the spirit of the Newtonian
physics, must (at least in both editions of the Critique) be classed
with the upholders of the absolute theory. The form of perception
has a type of existence proper to itself independently
of the particular bodies which it contains. For example he
writes:21 “Space does not represent any quality of objects by
themselves, or objects in their relation to one another, i.e. space
does not represent any determination which is inherent in the
objects themselves, and would remain, even if all subjective
conditions of intuition were removed.”
The second controversy is that between the view that the
axioms applicable to space are known only from experience,
and the view that in some sense these axioms are
given a priori. Both these views, thus broadly stated,
Axioms.
are capable of various subtle modifications, and a discussion
of them would merge into a general treatise on epistemology.
The cruder forms of the a priori view have been made quite
untenable by the modern mathematical discoveries. Geometers
now profess ignorance in many respects of the exact axioms
which apply to existent space, and it seems unlikely that a
profound study of the question should thus obliterate a priori
intuitions.
Another question irrelevant to this article, but with some
relevance to the above controversy, is that of the derivation
of our perception of existent space from our various types of
sensation. This is a question for psychology.22
Definition of Abstract Geometry.—Existent space is the subject
matter of only one of the applications of the modern science of
abstract geometry, viewed as a branch of pure mathematics.
Geometry has been defined23 as “the study of series of two or more
dimensions.” It has also been defined24 as “the science of cross
classification.” These definitions are founded upon the actual
practice of mathematicians in respect to their use of the term
“Geometry.” Either of them brings out the fact that geometry
is not a science with a determinate subject matter. It is concerned
with any subject matter to which the formal axioms may apply.
Geometry is not peculiar in this respect. All branches of pure
mathematics deal merely with types of relations. Thus the
fundamental ideas of geometry (e.g. those of points and of
straight lines) are not ideas of determinate entities, but of any
entities for which the axioms are true. And a set of formal
geometrical axioms cannot in themselves be true or false, since
they are not determinate propositions, in that they do not refer
to a determinate subject matter. The axioms are propositional
functions.25 When a set of axioms is given, we can ask (1)
whether they are consistent, (2) whether their “existence
theorem” is proved, (3) whether they are independent. Axioms
are consistent when the contradictory of any axiom cannot be
deduced from the remaining axioms. Their existence theorem
is the proof that they are true when the fundamental ideas are
considered as denoting some determinate subject matter, so
that the axioms are developed into determinate propositions.
It follows from the logical law of contradiction that the proof
of the existence theorem proves also the consistency of the
axioms. This is the only method of proof of consistency. The
axioms of a set are independent of each other when no axiom
can be deduced from the remaining axioms of the set. The
independence of a given axiom is proved by establishing the
consistency of the remaining axioms of the set, together with the
contradictory of the given axiom. The enumeration of the
axioms is simply the enumeration of the hypotheses26 (with
respect to the undetermined subject matter) of which some at
least occur in each of the subsequent propositions.
Any science is called a “geometry” if it investigates the
theory of the classification of a set of entities (the points) into
classes (the straight lines), such that (1) there is one and only
one class which contains any given pair of the entities, and (2)
every such class contains more than two members. In the two
geometries, important from their relevance to existent space,
axioms which secure an order of the points on any line also
occur. These geometries will be called “Projective Geometry”
and “Descriptive Geometry.” In projective geometry any
two straight lines in a plane intersect, and the straight lines
are closed series which return into themselves, like the circumference
of a circle. In descriptive geometry two straight lines in
a plane do not necessarily intersect, and a straight line is an open
series without beginning or end. Ordinary Euclidean geometry
is a descriptive geometry; it becomes a projective geometry
when the so-called “points at infinity” are added.
Projective Geometry.
Projective geometry may be developed from two undefined
fundamental ideas, namely, that of a “point” and that of a
“straight line.” These undetermined ideas take different
specific meanings for the various specific subject matters to
which projective geometry can be applied. The number of the
axioms is always to some extent arbitrary, being dependent
upon the verbal forms of statement which are adopted. They will
731
be presented27 here as twelve in number, eight being “axioms
of classification,” and four being “axioms of order.”
Axioms of Classification.—The eight axioms of classification
are as follows:
1. Points form a class of entities with at least two members.
2. Any straight line is a class of points containing at least
three members.
3. Any two distinct points lie in one and only one straight
line.
4. There is at least one straight line which does not contain
all the points.
5. If A, B, C are non-collinear points, and A′ is on the straight
line BC, and B′ is on the straight line CA, then the straight lines
AA′ and BB′ possess a point in common.
Definition.—If A, B, C are any three non-collinear points, the
plane ABC is the class of points lying on the straight lines joining
A with the various points on the straight line BC.
6. There is at least one plane which does not contain all the
points.
7. There exists a plane α, and a point A not incident in α,
such that any point lies in some straight line which contains
both A and a point in α.
Definition.—Harm. (ABCD) symbolizes the following conjoint
statements: (1) that the points A, B, C, D are collinear, and (2)
that a quadrilateral can be found with one pair of opposite sides
intersecting at A, with the other pair intersecting at C, and with its
diagonals passing through B and D respectively. Then B and D are
said to be “harmonic conjugates” with respect to A and C.
8. Harm. (ABCD) implies that B and D are distinct points.
In the above axioms 4 secures at least two dimensions, axiom
5 is the fundamental axiom of the plane, axiom 6 secures at
least three dimensions, and axiom 7 secures at most three
dimensions. From axioms 1-5 it can be proved that any two
distinct points in a straight line determine that line, that any
three non-collinear points in a plane determine that plane, that
the straight line containing any two points in a plane lies wholly
in that plane, and that any two straight lines in a plane intersect.
From axioms 1-6 Desargue’s well-known theorem on triangles
in perspective can be proved.
The enunciation of this theorem is as follows: If ABC and
A′B′C′ are two coplanar triangles such that the lines AA′, BB′,
CC′ are concurrent, then the three points of intersection of BC and
B′C′ of CA and C′A′, and of AB and A′B′ are collinear; and
conversely if the three points of intersection are collinear, the three
lines are concurrent. The proof which can be applied is the usual
projective proof by which a third triangle A″B″C″ is constructed
not coplanar with the other two, but in perspective with each
of them.
It has been proved28 that Desargues’s theorem cannot be deduced
from axioms 1-5, that is, if the geometry be confined to two
dimensions. All the proofs proceed by the method of producing a
specification of “points” and “straight lines” which satisfies
axioms 1-5, and such that Desargues’s theorem does not hold.
It follows from axioms 1-5 that Harm. (ABCD) implies Harm.
(ADCB) and Harm. (CBAD), and that, if A, B, C be any three
distinct collinear points, there exists at least one point D such that
Harm. (ABCD). But it requires Desargues’s theorem, and hence
axiom 6, to prove that Harm. (ABCD) and Harm. (ABCD′) imply
the identity of D and D′.
The necessity for axiom 8 has been proved by G. Fano,29 who
has produced a three dimensional geometry of fifteen points,
i.e. a method of cross classification of fifteen entities, in which
each straight line contains three points, and each plane contains
seven straight lines. In this geometry axiom 8 does not hold.
Also from axioms 1-6 and 8 it follows that Harm. (ABCD)
implies Harm. (BCDA).
Definitions.—When two plane figures can be derived from one
another by a single projection, they are said to be in perspective.
When two plane figures can be derived one from the other by a finite
series of perspective relations between intermediate figures, they
are said to be projectively related. Any property of a plane figure
which necessarily also belongs to any projectively related figure, is
called a projective property.
The following theorem, known from its importance as “the
fundamental theorem of projective geometry,” cannot be proved30
from axioms 1-8. The enunciation is: “A projective correspondence
between the points on two straight lines is completely determined
when the correspondents of three distinct points on one line
are determined on the other.” This theorem is equivalent31
(assuming axioms 1-8) to another theorem, known as Pappus’s
Theorem, namely: “If l and l′ are two distinct coplanar lines, and
A, B, C are three distinct points on l, and A′, B′, C′ are three distinct
points on l′, then the three points of intersection of AA′ and B′C,
of A′B and CC′, of BB′ and C′A, are collinear.” This theorem is
obviously Pascal’s well-known theorem respecting a hexagon
inscribed in a conic, for the special case when the conic has degenerated
into the two lines l and l′. Another theorem also
equivalent (assuming axioms 1-8) to the fundamental theorem is
the following:32 If the three collinear pairs of points, A and A′,
B and B′, C and C′, are such that the three pairs of opposite sides
of a complete quadrangle pass respectively through them, i.e. one
pair through A and A′ respectively, and so on, and if also the three
sides of the quadrangle which pass through A, B, and C, are concurrent
in one of the corners of the quadrangle, then another quadrangle
can be found with the same relation to the three pairs of points,
except that its three sides which pass through A, B, and C, are not
concurrent.
Thus, if we choose to take any one of these three theorems as an
axiom, all the theorems of projective geometry which do not require
ordinal or metrical ideas for their enunciation can be proved. Also
a conic can be defined as the locus of the points found by the usual
construction, based upon Pascal’s theorem, for points on the conic
through five given points. But it is unnecessary to assume here
any one of the suggested axioms; for the fundamental theorem can
be deduced from the axioms of order together with axioms 1-8.
Axioms of Order.—It is possible to define (cf. Pieri, loc. cit.)
the property upon which the order of points on a straight line
depends. But to secure that this property does in fact range
the points in a serial order, some axioms are required. A straight
line is to be a closed series; thus, when the points are in order,
it requires two points on the line to divide it into two distinct
complementary segments, which do not overlap, and together
form the whole line. Accordingly the problem of the definition
of order reduces itself to the definition of these two segments
formed by any two points on the line; and the axioms are
stated relatively to these segments.
Definition.—If A, B, C are three collinear points, the points on the
segment ABC are defined to be those points such as X, for which
there exist two points Y and Y′ with the property that Harm.
(AYCY′) and Harm. (BYXY′) both hold. The supplementary
segment ABC is defined to be the rest of the points on the line.
This definition is elucidated by noticing that with our ordinary
geometrical ideas, if B and X are any two points between A and C,
then the two pairs of points, A and C, B and X, define an involution
with real double points, namely, the Y and Y′ of the above definition.
The property of belonging to a segment ABC is projective, since
the harmonic relation is projective.
The first three axioms of order (cf. Pieri, loc. cit.) are:
9. If A, B, C are three distinct collinear points, the supplementary
segment ABC is contained within the segment BCA.
10. If A, B, C are three distinct collinear points, the common
part of the segments BCA and CAB is contained in the supplementary
segment ABC.
11. If A, B, C are three distinct collinear points, and D lies
In the segment ABC, then the segment ADC is contained
within the segment ABC.
From these axioms all the usual properties of a closed order
follow. It will be noticed that, if A, B, C are any three collinear
points, C is necessarily traversed in passing from A to B by one
route along the line, and is not traversed in passing from A to B
along the other route. Thus there is no meaning, as referred
to closed straight lines, in the simple statement that C lies
between A and B. But there may be a relation of separation
between two pairs of collinear points, such as A and C, and
B and D. The couple B and D is said to separate A and C, if
732
the four points are collinear and D lies in the segment complementary
to the segment ABC. The property of the separation
of pairs of points by pairs of points is projective. Also it can be
proved that Harm. (ABCD) implies that B and D separate
A and C.
Definitions.—A series of entities arranged in a serial order, open
or closed, is said to be compact, if the series contains no immediately
consecutive entities, so that in traversing the series from any one
entity to any other entity it is necessary to pass through entities
distinct from either. It was the merit of R. Dedekind and of
G. Cantor explicitly to formulate another fundamental property of
series. The Dedekind property33 as applied to an open series can
be defined thus: An open series possesses the Dedekind property,
if, however, it be divided into two mutually exclusive classes u and
v, which (1) contain between them the whole series, and (2) are
such that every member of u precedes in the serial order every
member of v, there is always a member of the series, belonging to one
of the two, u or v, which precedes every member of v (other than
itself if it belong to v), and also succeeds every member of u (other
than itself if it belong to u). Accordingly in an open series with the
Dedekind property there is always a member of the series marking
the junction of two classes such as u and v. An open series is continuous
if it is compact and possesses the Dedekind property. A
closed series can always be transformed into an open series by taking
any arbitrary member as the first term and by taking one of the two
ways round as the ascending order of the series. Thus the definitions
of compactness and of the Dedekind property can be at once transferred
to a closed series.
12. The last axiom of order is that there exists at least one
straight line for which the point order possesses the Dedekind
property.
It follows from axioms 1-12 by projection that the Dedekind
property is true for all lines. Again the harmonic system ABC,
where A, B, C are collinear points, is defined34 thus: take the
harmonic conjugates A′, B′, C′ of each point with respect to
the other two, again take the harmonic conjugates of each of
the six points A, B, C, A′, B′, C′ with respect to each pair of the
remaining five, and proceed in this way by an unending series
of steps. The set of points thus obtained is called the harmonic
system ABC. It can be proved that a harmonic system is
compact, and that every segment of the line containing it
possesses members of it. Furthermore, it is easy to prove that
the fundamental theorem holds for harmonic systems, in the
sense that, if A, B, C are three points on a line l, and A′, B′, C′
are three points on a line l′, and if by any two distinct series
of projections A, B, C are projected into A′, B′, C′, then any point
of the harmonic system ABC corresponds to the same point of
the harmonic system A′B′C′ according to both the projective
relations which are thus established between l and l′. It now
follows immediately that the fundamental theorem must hold for
all the points on the lines l and l′, since (as has been pointed out)
harmonic systems are “everywhere dense” on their containing
lines. Thus the fundamental theorem follows from the axioms
of order.
A system of numerical coordinates can now be introduced,
possessing the property that linear equations represent planes
and straight lines. The outline of the argument by which this
remarkable problem (in that “distance” is as yet undefined) is
solved, will now be given. It is first proved that the points on
any line can in a certain way be definitely associated with all
the positive and negative real numbers, so as to form with them
a one-one correspondence. The arbitrary elements in the
establishment of this relation are the points on the line associated
with 0, 1 and ∞.
This association35 is most easily effected by considering a
class of projective relations of the line with itself, called by
F. Schur (loc. cit.) prospectivities.
 |
| Fig. 69. |
 |
| Fig. 70. |
 |
| Fig. 71. |
 |
| Fig. 72. |
Let l (fig. 69) be the given line, m and n any two lines intersecting
at U on l, S and S′ two points on n. Then a projective relation
between l and itself is formed by projecting l from S on to m, and
then by projecting m from S′ back on to l. All such projective
relations, however m, n, S and S′ be varied, are called “prospectivities,”
and U is the double point of the prospectivity. If a point
O on l is related to A by a prospectivity, then all prospectivities,
which (1) have the same double point
U, and (2) relate O to A, give the same
correspondent (Q, in figure) to any
point P on the line l; in fact they are
all the same prospectivity, however
m, n, S, and S′ may have been varied
subject to these conditions. Such
a prospectivity will be denoted by
(OAU²).
The sum of two prospectivities,
written (OAU²) + (OBU²), is defined
to be that transformation of the line
l into itself which is obtained by first applying the prospectivity
(OAU²) and then applying the prospectivity (OBU²). Such a
transformation, when the two summands have the same double
point, is itself a prospectivity with that double point.
With this definition of addition it can be proved that prospectivities
with the same double point satisfy all the axioms of magnitude.
Accordingly they can be associated in a one-one correspondence
with the positive and negative real numbers. Let E
(fig. 70) be any point on l, distinct from O and U. Then the
prospectivity (OEU²) is associated with unity, the prospectivity
(OOU²) is associated with zero,
and (OUU²) with ∞. The prospectivities
of the type (OPU²),
where P is any point on the segment
OEU, correspond to the positive
numbers; also if P′ is the
harmonic conjugate of P with
respect to O and U, the prospectivity
(OP′U²) is associated with
the corresponding negative number.
(The subjoined figure explains this
relation of the positive and negative
prospectivities.) Then any
point P on l is associated with the same number as is the prospectivity
(OPU²).
It can be proved that the order of the numbers in algebraic order
of magnitude agrees with the order on the line of the associated
points. Let the numbers, assigned according to the preceding
specification, be said to be associated with the points according to
the “numeration-system (OEU).” The introduction of a coordinate
system for a plane is now managed
as follows: Take any triangle OUV
in the plane, and on the lines OU
and OV establish the numeration
systems (OE1U) and (OE2V), where
E1 and E2 are arbitrarily chosen.
Then (cf. fig. 71) if M and N are
associated with the numbers x and
y according to these systems, the
coordinates of P are x and y. It then
follows that the equation of a straight
line is of the form ax + by + c = 0. Both coordinates of any point on
the line UV are infinite. This can be avoided by introducing
homogeneous coordinates X, Y, Z, where x = X/Z, and y = Y/Z, and
Z = 0 is the equation of UV.
The procedure for three dimensions is similar. Let OUVW
(fig. 72) be any tetrahedron, and associate points on OU, OV, OW
with numbers according to the numeration
systems (OE1U), (OE2V), and
(OE3W). Let the planes VWP, WUP,
UVP cut OU, OV, OW in L, M, N respectively;
and let x, y, z be the numbers
associated with L, M, N respectively.
Then P is the point (x, y, z). Also
homogeneous coordinates can be introduced
as before, thus avoiding the
infinities on the plane UVW.
The cross ratio of a range of four
collinear points can now be defined
as a number characteristic of that range. Let the coordinates of any
point Pr of the range P1 P2 P3 P4 be
| λra + μr + a′ |
, | λrb + μrb′ |
, | λrc + μrc′ |
, (r = 1, 2, 3, 4) |
| λr + μr | λr + μr |
λr + μr |
and let (λrμs) be written for λrμs -λsμr. Then the cross ratio
{P1 P2 P3 P4} is defined to be the number
(λ1μ2)(λ3μ4) / (λ1μ4)(λ3μ2).
The equality of the cross ratios of the ranges (P1 P2 P3 P4) and
(Q1 Q2 Q3 Q4) is proved to be the necessary and sufficient condition
for their mutual projectivity. The cross ratios of all harmonic
ranges are then easily seen to be all equal to -1, by comparing with
the range (OE1UE′1) on the axis of x.
Thus all the ordinary propositions of geometry in which distance
and angular measure do not enter otherwise than in cross ratios
can now be enunciated and proved. Accordingly the greater part of
the analytical theory of conics and quadrics belongs to geometry
733
at this stage The theory of distance will be considered after the
principles of descriptive geometry have been developed.
Descriptive Geometry.
Descriptive geometry is essentially the science of multiple
order for open series. The first satisfactory system of axioms
was given by M. Pasch.36 An improved version is due to G.
Peano.37 Both these authors treat the idea of the class of points
constituting the segment lying between two points as an undefined
fundamental idea. Thus in fact there are in this system two
fundamental ideas, namely, of points and of segments. It is
then easy enough to define the prolongations of the segments,
so as to form the complete straight lines. D. Hilbert’s38 formulation
of the axioms is in this respect practically based on the same
fundamental ideas. His work is justly famous for some of the
mathematical investigations contained in it, but his exposition of
the axioms is distinctly inferior to that of Peano. Descriptive
geometry can also be considered39 as the science of a class of
relations, each relation being a two-termed serial relation, as
considered in the logic of relations, ranging the points between
which it holds into a linear open order. Thus the relations are
the straight lines, and the terms between which they hold are
the points. But a combination of these two points of view
yields40 the simplest statement of all. Descriptive geometry is
then conceived as the investigation of an undefined fundamental
relation between three terms (points); and when the relation
holds between three points A, B, C, the points are said to be “in
the [linear] order ABC.”
O. Veblen’s axioms and definitions, slightly modified, are as
follows:—
1. If the points A, B, C are in the order ABC, they are in the
order CBA.
2. If the points A, B, C are in the order ABC, they are not
in the order BCA.
3. If the points A, B, C are in the order ABC, A is distinct
from C.
4. If A and B are any two distinct points, there exists a point
C such that A, B, C are in the order ABC.
Definition.—The line AB (A ≠ B) consists of A and B, and of all
points X in one of the possible orders, ABX, AXB, XAB. The
points X in the order AXB constitute the segment AB.
5. If points C and D (C ≠ D) lie on the line AB, then A lies on
the line CD.
6. There exist three distinct points A, B, C not in any of the
orders ABC, BCA, CAB.
 |
| Fig. 73. |
7. If three distinct points A, B, C (fig. 73) do not lie on the
same line, and D and E are two distinct points in the orders
BCD and CEA, then a point F exists
in the order AFB, and such that
D, E, F are collinear.
Definition.—If A, B, C are three
non-collinear points, the plane ABC
is the class of points which lie on any
one of the lines joining any two of the
points belonging to the boundary of
the triangle ABC, the boundary being
formed by the segments BC, CA and
AB. The interior of the triangle ABC is formed by the points in
segments such as PQ, where P and Q are points respectively on
two of the segments BC, CA, AB.
8. There exists a plane ABC, which does not contain all the
points.
Definition.—If A, B, C, D are four non-coplanar points, the space
ABCD is the class of points which lie on any of the lines containing
two points on the surface of the tetrahedron ABCD, the surface
being formed by the interiors of the triangles ABC, BCD, DCA,
DAB.
9. There exists a space ABCD which contains all the points.
10. The Dedekind property holds for the order of the points
on any straight line.
It follows from axioms 1-9 that the points on any straight line
are arranged in an open serial order. Also all the ordinary
theorems respecting a point dividing a straight line into two
parts, a straight line dividing a plane into two parts, and a plane
dividing space into two parts, follow.
Again, in any plane α consider a line l and a point A (fig. 74).
 |
| Fig. 74. |
Let any point B divide l into two half-lines l1 and l2. Then it can
be proved that the set of half-lines, emanating from A and intersecting
l1 (such as m), are bounded by two half-lines, of which ABC
is one. Let r be the other. Then it can be proved that r does not
intersect l1. Similarly for the half-line,
such as n, intersecting l2. Let s be its
bounding half-line. Then two cases are
possible. (1) The half-lines r and s are
collinear, and together form one complete
line. In this case, there is one and
only one line (viz. r + s) through A and
lying in α which does not intersect l.
This is the Euclidean case, and the
assumption that this case holds is the
Euclidean parallel axiom. But (2) the
half-lines r and s may not be collinear.
In this case there will be an infinite
number of lines, such as k for instance, containing A and lying in α,
which do not intersect l. Then the lines through A in α are divided
into two classes by reference to l, namely, the secant lines which
intersect l, and the non-secant lines which do not intersect l. The
two boundary non-secant lines, of which r and s are respectively
halves, may be called the two parallels to l through A.
The perception of the possibility of case 2 constituted the starting-point
from which Lobatchewsky constructed the first explicit
coherent theory of non-Euclidean geometry, and thus created a
revolution in the philosophy of the subject. For many centuries
the speculations of mathematicians on the foundations of geometry
were almost confined to hopeless attempts to prove the “parallel
axiom” without the introduction of some equivalent axiom.41
Associated Projective and Descriptive Spaces.—A region of a
projective space, such that one, and only one, of the two supplementary
segments between any pair of points within it lies
entirely within it, satisfies the above axioms (1-10) of descriptive
geometry, where the points of the region are the descriptive
points, and the portions of straight lines within the region are
the descriptive lines. If the excluded part of the original projective
space is a single plane, the Euclidean parallel axiom also
holds, otherwise it does not hold for the descriptive space of the
limited region. Again, conversely, starting from an original
descriptive space an associated projective space can be constructed
by means of the concept of ideal points.42 These are also
called projective points, where it is understood that the simple
points are the points of the original descriptive space. An
ideal point is the class of straight lines which is composed of two
coplanar lines a and b, together with the lines of intersection of
all pairs of intersecting planes which respectively contain a and b,
together with the lines of intersection with the plane ab of all
planes containing any one of the lines (other than a or b) already
specified as belonging to the ideal point. It is evident that, if
the two original lines a and b intersect, the corresponding ideal
point is nothing else than the whole class of lines which are
concurrent at the point ab. But the essence of the definition is
that an ideal point has an existence when the lines a and b do
not intersect, so long as they are coplanar. An ideal point is
termed proper, if the lines composing it intersect; otherwise it
is improper.
A theorem essential to the whole theory is the following: if
any two of the three lines a, b, c are coplanar, but the three lines
are not all coplanar, and similarly for the lines a, b, d, then c
and d are coplanar. It follows that any two lines belonging to an
ideal point can be used as the pair of guiding lines in the definition.
An ideal point is said to be coherent with a plane, if any of the
lines composing it lie in the plane. An ideal line is the class of
ideal points each of which is coherent with two given planes.
734
If the planes intersect, the ideal line is termed proper, otherwise
it is improper. It can be proved that any two planes, with which
any two of the ideal points are both coherent, will serve as the
guiding planes used in the definition. The ideal planes are
defined as in projective geometry, and all the other definitions
(for segments, order, &c.) of projective geometry are applied
to the ideal elements. If an ideal plane contains some proper
ideal points, it is called proper, otherwise it is improper. Every
ideal plane contains some improper ideal points.
It can now be proved that all the axioms of projective geometry
hold of the ideal elements as thus obtained; and also that the
order of the ideal points as obtained by the projective method
agrees with the order of the proper ideal points as obtained from
that of the associated points of the descriptive geometry. Thus
a projective space has been constructed out of the ideal elements,
and the proper ideal elements correspond element by element with
the associated descriptive elements. Thus the proper ideal
elements form a region in the projective space within which the
descriptive axioms hold. Accordingly, by substituting ideal
elements, a descriptive space can always be considered as a
region within a projective space. This is the justification for the
ordinary use of the “points at infinity” in the ordinary Euclidean
geometry; the reasoning has been transferred from the original
descriptive space to the associated projective space of ideal
elements; and with the Euclidean parallel axiom the improper
ideal elements reduce to the ideal points on a single improper ideal
plane, namely, the plane at infinity.43
Congruence and Measurement.—The property of physical space
which is expressed by the term “measurability” has now to be
considered. This property has often been considered as essential
to the very idea of space. For example, Kant writes,44 “Space
is represented as an infinite given quantity.” This quantitative
aspect of space arises from the measurability of distances, of
angles, of surfaces and of volumes. These four types of quantity
depend upon the two first among them as fundamental. The
measurability of space is essentially connected with the idea of
congruence, of which the simplest examples are to be found in
the proofs of equality by the method of superposition, as used
in elementary plane geometry. The mere concepts of “part”
and of “whole” must of necessity be inadequate as the foundation
of measurement, since we require the comparison as to
quantity of regions of space which have no portions in common.
The idea of congruence, as exemplified by the method of superposition
in geometrical reasoning, appears to be founded upon
that of the “rigid body,” which moves from one position to
another with its internal spatial relations unchanged. But unless
there is a previous concept of the metrical relations between the
parts of the body, there can be no basis from which to deduce
that they are unchanged.
It would therefore appear as if the idea of the congruence, or
metrical equality, of two portions of space (as empirically suggested
by the motion of rigid bodies) must be considered as a
fundamental idea incapable of definition in terms of those
geometrical concepts which have already been enumerated.
This was in effect the point of view of Pasch.45 It has, however,
been proved by Sophus Lie46 that congruence is capable of
definition without recourse to a new fundamental idea. This
he does by means of his theory of finite continuous groups (see
Groups, Theory of), of which the definition is possible in terms
of our established geometrical ideas, remembering that coordinates
have already been introduced. The displacement
of a rigid body is simply a mode of defining to the senses a one-one
transformation of all space into itself. For at any point of
space a particle may be conceived to be placed, and to be rigidly
connected with the rigid body; and thus there is a definite
correspondence of any point of space with the new point occupied
by the associated particle after displacement. Again two successive
displacements of a rigid body from position A to position
B, and from position B to position C, are the same in effect as one
displacement from A to C. But this is the characteristic “group”
property. Thus the transformations of space into itself defined
by displacements of rigid bodies form a group.
Call this group of transformations a congruence-group. Now
according to Lie a congruence-group is defined by the following
characteristics:—
1. A congruence-group is a finite continuous group of one-one
transformations, containing the identical transformation.
2. It is a sub-group of the general projective group, i.e. of
the group of which any transformation converts planes into
planes, and straight lines into straight lines.
3. An infinitesimal transformation can always be found satisfying
the condition that, at least throughout a certain enclosed
region, any definite line and any definite point on the line are
latent, i.e. correspond to themselves.
4. No infinitesimal transformation of the group exists, such
that, at least in the region for which (3) holds, a straight line,
a point on it, and a plane through it, shall all be latent.
The property enunciated by conditions (3) and (4), taken
together, is named by Lie “Free mobility in the infinitesimal.”
Lie proves the following theorems for a projective space:—
1. If the above four conditions are only satisfied by a group
throughout part of projective space, this part either (α) must be the
region enclosed by a real closed quadric, or (β) must be the whole of
the projective space with the exception of a single plane. In case
(α) the corresponding congruence group is the continuous group for
which the enclosing quadric is latent; and in case (β) an imaginary
conic (with a real equation) lying in the latent plane is also latent,
and the congruence group is the continuous group for which the
plane and conic are latent.
2. If the above four conditions are satisfied by a group throughout
the whole of projective space, the congruence group is the continuous
group for which some imaginary quadric (with a real equation) is
latent.
By a proper choice of non-homogeneous co-ordinates the equation
of any quadrics of the types considered, either in theorem 1 (α), or in
theorem 2, can be written in the form 1 + c(x² + y² + z²) = 0, where c is
negative for a real closed quadric, and positive for an imaginary
quadric. Then the general infinitesimal transformation is defined
by the three equations:
| dx/dt = u − ω3y + ω2z + cx (ux + vy + wz), | (A) |
| dy/dt = v − ω1z + ω3x + cy (ux + vy + wz), |
| dz/dt = w − ω2x + ω1y + cz (ux + vy + wz). |
In the ease considered in theorem 1 (β), with the proper choice of
co-ordinates the three equations defining the general infinitesimal
transformation are:
| dx/dt = u − ω3y + ω2z, | (B) |
| dy/dt = v − ω1z + ω3x, |
| dz/dt = w − ω2x + ω1y. |
In this case the latent plane is the plane for which at least one of
x, y, z are infinite, that is, the plane 0.x + 0.y + 0.z + a = 0; and the
latent conic is the conic in which the cone x² + y² + z² = 0 intersects
the latent plane.
It follows from theorems 1 and 2 that there is not one unique
congruence-group, but an indefinite number of them. There is
one congruence-group corresponding to each closed real quadric,
one to each imaginary quadric with a real equation, and one to
each imaginary conic in a real plane and with a real equation.
The quadric thus associated with each congruence-group is
called the absolute for that group, and in the degenerate case
of 1 (β) the absolute is the latent plane together with the latent
imaginary conic. If the absolute is real, the congruence-group
is hyperbolic; if imaginary, it is elliptic; if the absolute is a
plane and imaginary conic, the group is parabolic. Metrical
geometry is simply the theory of the properties of some particular
congruence-group selected for study.
The definition of distance is connected with the corresponding
congruence-group by two considerations in respect to a range of five
points (A1, A2, P1, P2, P3), of which A1 and A2 are on the absolute.
Let {A1P1A2P2} stand for the cross ratio (as defined above) of the
range (A1P1A2P2), with a similar notation for the other ranges.
Then
(1)
log {A1P1A2P2} + log {A1P2A2P3} = log {A1P1A2P3},
and
(2), if the points A1, A2, P1, P2 are transformed into A′1, A′2, P′1, P′2
by any transformation of the congruence-group, (α) {A1P1A2P2 =
{A′1P′1A′2P′2}, since the transformation is projective, and (β) A′1, A′2
are on the absolute since A1 and A2 are on it. Thus if we define
735
the distance P1P2 to be ½k log {A1P1A2P2}, where A1 and A2 are the
points in which the line P1P2 cuts the absolute, and k is some constant,
the two characteristic properties of distance, namely, (1) the
addition of consecutive lengths on a straight line, and (2) the invariability
of distances during a transformation of the congruence-group,
are satisfied. This is the well-known Cayley-Klein projective
definition47 of distance, which was elaborated in view of the addition
property alone, previously to Lie’s discovery of the theory of congruence-groups.
For a hyperbolic group when P1 and P2 are in the
region enclosed by the absolute, log {A1P1A2P2} is real, and therefore
k must be real. For an elliptic group A1 and A2 are conjugate
imaginaries, and log {A1P1A2P2} is a pure imaginary, and k is chosen
to be κ/ι, where κ is real and ι = √ −.
Similarly the angle between two planes, p1 and p2, is defined to be
(1/2ι) log (t1p1t2p2), where t1 and t2 are tangent planes to the absolute
through the line p1p2. The planes t1 and t2 are imaginary for an
elliptic group, and also for an hyperbolic group when the planes p1
and p2 intersect at points within the region enclosed by the absolute.
The development of the consequences of these metrical definitions
is the subject of non-Euclidean geometry.
The definitions for the parabolic case can be arrived at as limits
of those obtained in either of the other two cases by making k
ultimately to vanish. It is also obvious that, if P1 and P2 be the
points (x1, y1, z1) and (x2, y2, z2), it follows from equations (B) above
that {(x1 − x2)² + (y1 − y2)² + (z1 − z2)²}1/2 is unaltered by a congruence
transformation and also satisfies the addition property for collinear
distances. Also the previous definition of an angle can be adapted
to this case, by making t1 and t2 to be the tangent planes through
the line p1p2 to the imaginary conic. Similarly if p1 and p2 are intersecting
lines, the same definition of an angle holds, where t1 and t2
are now the lines from the point p1p2 to the two points where the
plane p1p2 cuts the imaginary conic. These points are in fact the
“circular points at infinity” on the plane. The development of
the consequences of these definitions for the parabolic case gives the
ordinary Euclidean metrical geometry.
Thus the only metrical geometry for the whole of projective
space is of the elliptic type. But the actual measure-relations
(though not their general properties) differ according to the
elliptic congruence-group selected for study. In a descriptive
space a congruence-group should possess the four characteristics
of such a group throughout the whole of the space. Then form
the associated ideal projective space. The associated congruence-group
for this ideal space must satisfy the four conditions
throughout the region of the proper ideal points. Thus the
boundary of this region is the absolute. Accordingly there can
be no metrical geometry for the whole of a descriptive space
unless its boundary (in the associated ideal space) is a closed
quadric or a plane. If the boundary is a closed quadric, there
is one possible congruence-group of the hyperbolic type. If
the boundary is a plane (the plane at infinity), the possible
congruence-groups are parabolic; and there is a congruence-group
corresponding to each imaginary conic in this plane,
together with a Euclidean metrical geometry corresponding to
each such group. Owing to these alternative possibilities, it
would appear to be more accurate to say that systems of quantities
can be found in a space, rather than that space is a quantity.
Lie has also deduced48 the same results with respect to congruence-groups
from another set of defining properties, which
explicitly assume the existence of a quantitative relation (the
distance) between any two points, which is invariant for any
transformation of the congruence-group.49
The above results, in respect to congruence and metrical
geometry, considered in relation to existent space, have led to the
doctrine50 that it is intrinsically unmeaning to ask which system
of metrical geometry is true of the physical world. Any one of
these systems can be applied, and in an indefinite number of ways.
The only question before us is one of convenience in respect to
simplicity of statement of the physical laws. This point of view
seems to neglect the consideration that science is to be relevant
to the definite perceiving minds of men; and that (neglecting
the ambiguity introduced by the invariable slight inexactness
of observation which is not relevant to this special doctrine)
we have, in fact, presented to our senses a definite set of transformations
forming a congruence-group, resulting in a set of
measure relations which are in no respect arbitrary. Accordingly
our scientific laws are to be stated relevantly to that particular
congruence-group. Thus the investigation of the type (elliptic,
hyperbolic or parabolic) of this special congruence-group is a
perfectly definite problem, to be decided by experiment. The
consideration of experiments adapted to this object requires some
development of non-Euclidean geometry (see section VI.,
Non-Euclidean Geometry). But if the doctrine means that,
assuming some sort of objective reality for the material universe,
beings can be imagined, to whom either all congruence-groups
are equally important, or some other congruence-group is specially
important, the doctrine appears to be an immediate deduction
from the mathematical facts. Assuming a definite congruence-group,
the investigation of surfaces (or three-dimensional loci
in space of four dimensions) with geodesic geometries of the form
of metrical geometries of other types of congruence-groups forms
an important chapter of non-Euclidean geometry. Arising
from this investigation there is a widely-spread fallacy, which
has found its way into many philosophic writings, namely, that
the possibility of the geometry of existent three-dimensional
space being other than Euclidean depends on the physical
existence of Euclidean space of four or more dimensions. The
foregoing exposition shows the baselessness of this idea.
Bibliography.—For an account of the investigations on the
axioms of geometry during the Greek period, see M. Cantor, Vorlesungen
über die Geschichte der Mathematik, Bd. i. and iii.; T.L.
Heath, The Thirteen Books of Euclid’s Elements, a New Translation
from the Greek, with Introductory Essays and Commentary, Historical,
Critical, and Explanatory (Cambridge, 1908)—this work is the standard
source of information; W.B. Frankland, Euclid, Book I., with a
Commentary (Cambridge, 1905)—the commentary contains copious
extracts from the ancient commentators. The next period of really
substantive importance is that of the 18th century. The leading
authors are: G. Saccheri, S.J., Euclides ab omni naevo vindicatus
(Milan, 1733). Saccheri was an Italian Jesuit who unconsciously
discovered non-Euclidean geometry in the course of his efforts to
prove its impossibility. J.H. Lambert, Theorie der Parallellinien
(1766); A.M. Legendre, Éléments de géométrie (1794). An adequate
account of the above authors is given by P. Stäckel and F. Engel,
Die Theorie der Parallellinien von Euklid bis auf Gauss (Leipzig,
1895). The next period of time (roughly from 1800 to 1870) contains
two streams of thought, both of which are essential to the modern
analysis of the subject. The first stream is that which produced the
discovery and investigation of non-Euclidean geometries, the second
stream is that which has produced the geometry of position, comprising
both projective and descriptive geometry not very accurately
discriminated. The leading authors on non-Euclidean geometry
are K.F. Gauss, in private letters to Schumacher, cf. Stäckel and
Engel, loc. cit.; N. Lobatchewsky, rector of the university of Kazan,
to whom the honour of the effective discovery of non-Euclidean
geometry must be assigned. His first publication was at Kazan
in 1826. His various memoirs have been re-edited by Engel;
cf. Urkunden zur Geschichte der nichteuklidischen Geometrie by
Stäckel and Engel, vol. i. “Lobatchewsky.” J. Bolyai discovered
non-Euclidean geometry apparently in independence of Lobatchewsky.
His memoir was published in 1831 as an appendix to a
work by his father W. Bolyai, Tentamen juventutem.... This
memoir has been separately edited by J. Frischauf, Absolute Geometrie
nach J. Bolyai (Leipzig, 1872); B. Riemann, Über die Hypothesen,
welche der Geometrie zu Grunde liegen (1854); cf. Gesamte Werke, a
translation in The Collected Papers of W.K. Clifford. This is a
fundamental memoir on the subject and must rank with the work of
Lobatchewsky. Riemann discovered elliptic metrical geometry,
and Lobatchewsky hyperbolic geometry. A full account of Riemann’s
ideas, with the subsequent developments due to Clifford,
F. Klein and W. Killing, will be found in The Boston Colloquium for
1903 (New York, 1905), article “Forms of Non-Euclidean Space,”
by F.S. Woods. A. Cayley, loc. cit. (1859), and F. Klein, “Über die
sogenannte nichteuklidische Geometrie,” Math. Annal. vols. iv.
and vi. (1871 and 1872), between them elaborated the projective
theory of distance; H. Helmholtz, “Über die thatsächlichen
Grundlagen der Geometrie” (1866), and “Über die Thatsachen, die
der Geometrie zu Grunde liegen” (1868), both in his Wissenschaftliche
Abhandlungen, vol. ii., and S. Lie, loc. cit. (1890 and 1893), between
them elaborated the group theory of congruence.
The numberless works which have been written to suggest equivalent
alternatives to Euclid’s parallel axioms may be neglected as
being of trivial importance, though many of them are marvels of
geometric ingenuity.
The second stream of thought confined itself within the circle of
ideas of Euclidean geometry. Its origin was mainly due to a
736
succession of great French mathematicians, for example, G. Monge,
Géométrie descriptive (1800); J.V. Poncelet, Traité des proprietés
projectives des figures (1822); M. Chasles, Aperçu historique sur
l’origine et le développement des méthodes en géométrie (Bruxelles, 1837),
and Traité de géométrie supérieure (Paris, 1852); and many others.
But the works which have been, and are still, of decisive influence on
thought as a store-house of ideas relevant to the foundations of
geometry are K.G.C. von Staudt’s two works, Geometrie der Lage
(Nürnberg, 1847); and Beiträge zur Geometrie der Lage (Nürnberg,
1856, 3rd ed. 1860).
The final period is characterized by the successful production of
exact systems of axioms, and by the final solution of problems
which have occupied mathematicians for two thousand years. The
successful analysis of the ideas involved in serial continuity is due to
R. Dedekind, Stetigkeit und irrationale Zahlen (1872), and to G.
Cantor, Grundlagen einer allgemeinen Mannigfaltigkeitslehre (Leipzig,
1883), and Acta math. vol. 2.
Complete systems of axioms have been stated by M. Pasch, loc.
cit.; G. Peano, loc. cit.; M. Pieri, loc. cit.; B. Russell, Principles of
Mathematics; O. Veblen, loc. cit.; and by G. Veronese in his treatise,
Fondamenti di geometria (Padua, 1891; German transl. by A. Schepp,
Grundzüge der Geometrie, Leipzig, 1894). Most of the leading memoirs
on special questions involved have been cited in the text; in addition
there may be mentioned M. Pieri, “Nuovi principii di geometria
projettiva complessa,” Trans. Accad. R. d. Sci. (Turin, 1905);
E.H. Moore, “On the Projective Axioms of Geometry,” Trans.
Amer. Math. Soc., 1902; O. Veblen and W.H. Bussey, “Finite
Projective Geometries,” Trans. Amer. Math. Soc., 1905; A.B.
Kempe, “On the Relation between the Logical Theory of Classes
and the Geometrical Theory of Points,” Proc. Lond. Math. Soc.,
1890; J. Royce, “The Relation of the Principles of Logic to the
Foundations of Geometry,” Trans. of Amer. Math. Soc., 1905;
A. Schoenflies, “Über die Möglichkeit einer projectiven Geometrie
bei transfiniter (nichtarchimedischer) Massbestimmung,” Deutsch.
M.-V. Jahresb., 1906.
For general expositions of the bearings of the above investigations,
cf. Hon. Bertrand Russell, loc. cit.; L. Couturat, Les Principes
des mathématiques (Paris, 1905); H. Poincaré, loc. cit.; Russell
and Whitehead, Principia mathematica (Cambridge, Univ. Press).
The philosophers whose views on space and geometric truth deserve
especial study are Descartes, Leibnitz, Hume, Kant and J.S.
Mill.
(A. N. W.)
1 For Egyptian geometry see Egypt, § Science and Mathematics.
2 Cf. A.N. Whitehead, Universal Algebra, Bk. vi. (Cambridge,
1898).
3 Cf. A.N. Whitehead, loc. cit.
4 Cf. A.N. Whitehead, “The Geodesic Geometry of Surfaces in
non-Euclidean Space,” Proc. Lond. Math. Soc. vol. xxix.
5 Cf. Klein, “Zur nicht-Euklidischen Geometrie,” Math. Annal.
vol. xxxvii.
6 On the theory of parallels before Lobatchewsky, see Stäckel und
Engel, Theorie der Parallellinien von Euklid bis auf Gauss (Leipzig,
1895). The foregoing remarks are based upon the materials collected
in this work.
7 See Stäckel und Engel, op. cit., and “Gauss, die beiden Bolyai,
und die nicht-Euklidische Geometrie,” Math. Annalen, Bd. xlix.;
also Engel’s translation of Lobatchewsky (Leipzig, 1898), pp. 378 ff.
8 Lobatchewsky’s works on the subject are the following:—“On
the Foundations of Geometry,” Kazañ Messenger, 1829-1830;
“New Foundations of Geometry, with a complete Theory of
Parallels,” Proceedings of the University of Kazañ, 1835 (both in
Russian, but translated into German by Engel, Leipzig, 1898);
“Géométrie imaginaire,” Crelle’s Journal, 1837; Theorie der
Parallellinien (Berlin, 1840; 2nd ed., 1887; translated by Halsted,
Austin, Texas, 1891). His results appear to have been set forth in a
paper (now lost) which he read at Kazañ in 1826.
9 Translated by Halsted (Austin, Texas, 4th ed., 1896.)
10 Abhandlungen d. Königl. Ges. d. Wiss. zu Göttingen, Bd. xiii.;
Ges. math. Werke, pp. 254-269; translated by Clifford, Collected
Mathematical Papers.
11 Cf. Gesamm. math. und phys. Werke, vol. i. (Leipzig, 1894).
12 Wiss. Abh. vol. ii. pp. 610, 618 (1866, 1868).
13 Mind, O.S., vols. i. and iii.; Vorträge und Reden, vol. ii. pp. 1,
256.
14 His papers are “Saggio di interpretazione della geometria non-Euclidea,”
Giornale di matematiche, vol. vi. (1868); “Teoria fondamentale
degli spazii di curvatura costante,” Annali di matematica,
vol. ii. (1868-1869). Both were translated into French by J. Hoüel,
Annales scientifiques de l’École Normale supérieure, vol. vi. (1869).
15 Beltrami shows also that this definition agrees with that of Gauss.
16 “Sur la théorie des foyers,” Nouv. Ann. vol. xii.
17 Math. Annalen, iv. vi., 1871-1872.
18 For an investigation of these and similar properties, see Whitehead,
Universal Algebra (Cambridge, 1898), bk. vi. ch. ii. The polar
form was independently discovered by Simon Newcomb in 1877.
19 For an analysis of Leibnitz’s ideas on space, cf. B. Russell, The
Philosophy of Leibnitz, chs. viii.-x.
20 Cf. Hon. Bertrand Russell, “Is Position in Time and Space
Absolute or Relative?” Mind, n.s. vol. 10 (1901), and A.N. Whitehead,
“Mathematical Concepts of the Material World,” Phil. Trans.
(1906), p. 205.
21 Cf. Critique of Pure Reason, 1st section: “Of Space,” conclusion
A, Max Müller’s translation.
22 Cf. Ernst Mach, Erkenntniss und Irrtum (Leipzig); the relevant
chapters are translated by T.J. McCormack, Space and Geometry
(London, 1906); also A. Meinong, Über die Stellung der Gegenstandstheorie
im System der Wissenschaften (Leipzig, 1907).
23 Cf. Russell, Principles of Mathematics, § 352 (Cambridge, 1903).
24 Cf. A.N. Whitehead, The Axioms of Projective Geometry, § 3
(Cambridge, 1906).
25 Cf. Russell, Princ. of Math., ch. i.
26 Cf. Russell, loc. cit., and G. Frege, “Über die Grundlagen der
Géométrie,” Jahresber. der Deutsch. Math. Ver. (1906).
27 This formulation—though not in respect to number—is in all
essentials that of M. Pieri, cf. “I principii della Geometria di Posizione,”
Accad. R. di Torino (1898); also cf. Whitehead, loc. cit.
28 Cf. G. Peano, “Sui fondamenti della Geometria,” p. 73, Rivista
di matematica, vol. iv. (1894), and D. Hilbert, Grundlagen der Geometrie
(Leipzig, 1899); and R.F. Moulton, “A Simple non-Desarguesian
Plane Geometry,” Trans. Amer. Math. Soc., vol. iii. (1902).
29 Cf. “Sui postulati fondamentali della geometria projettiva,”
Giorn. di matematica, vol. xxx. (1891); also of Pieri, loc. cit., and
Whitehead, loc. cit.
30 Cf. Hilbert, loc. cit.; for a fuller exposition of Hilbert’s proof
cf. K.T. Vahlen, Abstrakte Geometrie (Leipzig, 1905), also Whitehead,
loc. cit.
31 Cf. H. Wiener, Jahresber. der Deutsch. Math. Ver. vol. i. (1890);
and F. Schur, “Über den Fundamentalsatz der projectiven Geometrie,”
Math. Ann. vol. li. (1899).
32 Cf. Hilbert, loc. cit., and Whitehead, loc. cit.
33 Cf. Dedekind, Stetigkeit und irrationale Zahlen (1872).
34 Cf. v. Staudt, Geometrie der Lage (1847).
35 Cf. Pasch, Vorlesungen über neuere Geometrie (Leipzig, 1882), a
classic work; also Fiedler, Die darstellende Geometrie (1st ed., 1871,
3rd ed., 1888); Clebsch, Vorlesungen über Geometrie, vol. iii.;
Hilbert, loc. cit.; F. Schur, Math. Ann. Bd. lv. (1902); Vahlen,
loc. cit.; Whitehead, loc. cit.
36 Cf. loc. cit.
37 Cf. I Principii di geometria (Turin, 1889) and “Sui fondamenti
della geometria,” Rivista di mat. vol. iv. (1894).
38 Cf. loc. cit.
39 Cf. Vailati, Rivista di mat. vol. iv. and Russell, loc. cit. § 376.
40 Cf. O. Veblen, “On the Projective Axioms of Geometry,”
Trans. Amer. Math. Soc. vol. iii. (1902).
41 Cf. P. Stäckel and F. Engel, Die Theorie der Parallellinien von
Euklid bis auf Gauss (Leipzig, 1895).
42 Cf. Pasch, loc. cit., and R. Bonola, “Sulla introduzione degli
enti improprii in geometria projettive,” Giorn. di mat. vol. xxxviii.
(1900); and Whitehead, Axioms of Descriptive Geometry (Cambridge,
1907).
43 The original idea (confined to this particular case) of ideal
points is due to von Staudt (loc. cit.).
44 Cf. Critique, “Trans. Aesth.” Sect. I.
45 Cf. loc. cit.
46 Cf. Über die Grundlagen der Geometrie (Leipzig, Ber., 1890);
and Theorie der Transformationsgruppen (Leipzig, 1893), vol. iii.
47 Cf. A. Cayley, “A Sixth Memoir on Quantics,” Trans. Roy. Soc.,
1859, and Coll. Papers, vol. ii.; and F. Klein, Math. Ann. vol. iv.,
1871.
48 Cf. loc. cit.
49 For similar deductions from a third set of axioms, suggested in
essence by Peano, Riv. mat. vol. iv. loc. cit. cf. Whitehead, Desc.
Geom. loc. cit.
50 Cf. H. Poincaré, La Science et l’hypothèse, ch. iii.
End of the Project Gutenberg EBook of Encyclopaedia Britannica, 11th
Edition, Volume 11, Slice 6, by Various
*** END OF THIS PROJECT GUTENBERG EBOOK ENCYCLOPAEDIA BRITANNICA ***
***** This file should be named 37461-h.htm or 37461-h.zip *****
This and all associated files of various formats will be found in:
http://www.gutenberg.org/3/7/4/6/37461/
Produced by Marius Masi, Don Kretz and the Online
Distributed Proofreading Team at http://www.pgdp.net
Updated editions will replace the previous one--the old editions
will be renamed.
Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties. Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark. Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission. If you
do not charge anything for copies of this eBook, complying with the
rules is very easy. You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research. They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks. Redistribution is
subject to the trademark license, especially commercial
redistribution.
*** START: FULL LICENSE ***
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
http://gutenberg.org/license).
Section 1. General Terms of Use and Redistributing Project Gutenberg-tm
electronic works
1.A. By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works. Nearly all the individual works in the
collection are in the public domain in the United States. If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed. Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work. You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are in
a constant state of change. If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work. The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
1.E.2. If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges. If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder. Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form. However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form. Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that
- You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg-tm works calculated using the method
you already use to calculate your applicable taxes. The fee is
owed to the owner of the Project Gutenberg-tm trademark, but he
has agreed to donate royalties under this paragraph to the
Project Gutenberg Literary Archive Foundation. Royalty payments
must be paid within 60 days following each date on which you
prepare (or are legally required to prepare) your periodic tax
returns. Royalty payments should be clearly marked as such and
sent to the Project Gutenberg Literary Archive Foundation at the
address specified in Section 4, "Information about donations to
the Project Gutenberg Literary Archive Foundation."
- You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg-tm
License. You must require such a user to return or
destroy all copies of the works possessed in a physical medium
and discontinue all use of and all access to other copies of
Project Gutenberg-tm works.
- You provide, in accordance with paragraph 1.F.3, a full refund of any
money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days
of receipt of the work.
- You comply with all other terms of this agreement for free
distribution of Project Gutenberg-tm works.
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark. Contact the
Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection. Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH 1.F.3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium with
your written explanation. The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund. If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund. If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS' WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTIBILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law. The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg-tm
Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers. It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need, are critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at http://www.pglaf.org.
Section 3. Information about the Project Gutenberg Literary Archive
Foundation
The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation's EIN or federal tax identification
number is 64-6221541. Its 501(c)(3) letter is posted at
http://pglaf.org/fundraising. Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations. Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
business@pglaf.org. Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at http://pglaf.org
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
gbnewby@pglaf.org
Section 4. Information about Donations to the Project Gutenberg
Literary Archive Foundation
Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To
SEND DONATIONS or determine the status of compliance for any
particular state visit http://pglaf.org
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including checks, online payments and credit card donations.
To donate, please visit: http://pglaf.org/donate
Section 5. General Information About Project Gutenberg-tm electronic
works.
Professor Michael S. Hart is the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone. For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included. Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility:
http://www.gutenberg.org
This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.







































































