
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.
Title: Die Naturwissenschaften in ihrer Entwicklung und in ihrem Zusammenhange, II. Band
Von Galilei bis zur Mitte des XVIII. Jahrhunderts
Author: Friedrich Dannemann
Release Date: February 7, 2017 [eBook #54127]
Language: German
Character set encoding: UTF-8
***START OF THE PROJECT GUTENBERG EBOOK DIE NATURWISSENSCHAFTEN IN IHRER ENTWICKLUNG UND IN IHREM ZUSAMMENHANGE, II. BAND***
| Note: | Images of the original pages are available through Internet Archive. See https://archive.org/details/naturwissenschaf02dann |
DARGESTELLT VON
FRIEDRICH DANNEMANN
ZWEITE AUFLAGE
II. BAND:
VON GALILEI BIS ZUR MITTE DES XVIII. JAHRHUNDERTS
MIT 132 ABBILDUNGEN IM TEXT UND MIT EINEM BILDNIS VON GALILEI

LEIPZIG
VERLAG VON WILHELM ENGELMANN
1921
Alle Rechte, insbesondere das der Übersetzung, vorbehalten.
Copyright 1921 by Wilhelm Engelmann, Leipzig.
Druck von Breitkopf & Härtel in Leipzig.
Dannemann, Die Naturwissenschaften. II. Bd. 2. Auflage.

HERRN PROF. DR.
EDMUND O. VON LIPPMANN
AUS DANKBARKEIT FÜR SEINE
MITWIRKUNG BEI DER HERAUSGABE
DER NEUEN AUFLAGE
GEWIDMET
Der zweite Band befaßt sich in der Hauptsache mit den im 17. Jahrhundert entstandenen Grundlagen der neueren Naturwissenschaft. Es sind die Schöpfungen eines Galilei, Newton, Huygens und zahlreicher anderer Forscher ersten Ranges, die wir in diesem Zeitraum der Entwicklung der Wissenschaften entstehen sehen. Die grundlegenden Arbeiten jener Männer sind durch »Ostwalds Klassiker der exakten Wissenschaften« heute weiteren Kreisen in erläuterten Ausgaben und, wo es erforderlich war, in deutscher Übersetzung zugänglich gemacht. Der zweite Band nimmt, wie es auch die folgenden tun werden, auf diese Ausgaben oft Bezug, so daß die Absicht des Verfassers, in seinem Werke gewissermaßen einen Rahmen für »Ostwalds Klassiker« zu schaffen, mehr als im ersten Bande zum Ausdruck kommt.
Bezüglich der übrigen Gesichtspunkte, die bei der Abfassung des Werkes in Betracht kamen, muß auf das Vorwort zum ersten Bande hingewiesen werden. Der Verfasser hofft, daß es ihm gelungen ist, auch in dem zweiten Bande die Geschichte der Wissenschaften im Rahmen der Gesamtentwicklung darzustellen und ein Buch zu schaffen, mit dem nicht nur dem Historiker, sondern auch dem Arzte, dem Techniker, dem Lehrenden und Studierenden, kurz jedem, der an den Naturwissenschaften lebhafteren Anteil nimmt, gedient ist. War es doch sein Bestreben, die Entwicklung der Naturwissenschaften in ihren noch heute wertvollen Grundlagen, sowie in ihren Beziehungen zu den übrigen Wissenschaften, insbesondere zur Philosophie, zur Mathematik, zur Heilkunde und zur Technik darzustellen.
An der Überwachung des Satzes haben sich wieder die Herren Geh. Hofrat Prof. Dr. E. Wiedemann (Erlangen), Prof. Dr. E. O. v. Lippmann (Halle a. S.), dem der vorliegende Band gewidmet ist, und Prof. Dr. J. Würschmidt (Erlangen) beteiligt. Ich bin ihnen für zahlreiche Verbesserungen und Zusätze zum größten Dank verpflichtet. Auch sonst gingen mir manche Anregungen teils in Besprechungen, teils persönlich zu, die ich hier dankbar anerkenne.
München, im Frühjahr 1921.
Friedrich Dannemann.
1. Altertum und Neuzeit.
(S. 1–10.)
1. Einleitendes. – 2. Rückblick. – 3. Einfluß der alten Literatur. – 4. Mittelalterliche und neuere Denkweise. – 5. Allgemeingeschichtliches. – 7. Neugestaltung des wissenschaftlichen Lebens. – 8. Reformation und Humanismus. – 10. Erweiterung des Weltbildes.
2. Neuzeitliche Forschungsmittel.
(S. 11–19.)
11. Das Mikroskop. – 13. Das Fernrohr. – 16. Keplers Teleobjektiv. – 17. Verbesserungen der Fernrohre. – 18. Auge und Vorgang des Sehens.
3. Galileis grundlegende Schöpfungen.
(S. 20–80.)
20. Allgemeingeschichtliches. – 21. Leben und Entwicklungsgang Galileis. – 24. Galileis astronomische Entdeckungen. – 27. Wissenschaft und Kirche. – 30. Galileis Eintreten für die koppernikanische Lehre. – 38. Galileis Inquisitionsprozeß. – 41. Galileis letzte Lebensjahre. – 43. Galileis Untersuchungen über die Kohäsion und über das Gewicht der Luft. – 46. Die Fallbewegung. – 54. Die Pendelbewegung. – 58. Der Wurf. – 62. Das Prinzip der virtuellen Geschwindigkeiten. – 65. Mängel der Galilei'schen Mechanik. – 67. Galilei untersucht die Festigkeit der Körper. – 70. Die Mechanik der Flüssigkeiten und der Gase. – 74. Galileis Untersuchungen über den Schall. – 76. Galileis optische und magnetische Untersuchungen. – 78. Galileis Persönlichkeit und Schriften.
4. Die Ausbreitung der induktiven Forschungsweise.
(S. 81–112.)
81. Die Versuche der Florentiner Akademie. – 92. Grundlegende optische Untersuchungen. – 96. Die Erforschung der Elektrizität und des Magnetismus. – 105. Die Begründung einer Philosophie der Erfahrung. – 110. Die Denkweise des 17. Jahrhunderts.
5. Die Astronomie im Zeitalter Keplers.
(S. 113–152.)
113. Keplers Entwicklungsgang. – 117. Keplers Konstruktion der Planetensphären. – 119. Fortschritte der Beobachtungskunst. – 127. Die Entdeckung der Keplerschen Gesetze. – 133. Keplers weitere astronomische Leistungen. – 139. Keplers Verdienste um die Optik. – 150. Keplers Nachfolger auf dem Gebiete der Astronomie.
6. Die Förderung der Naturwissenschaften durch die Fortschritte der Mathematik.
(S. 153–173.)
153. Fortschritte der Rechenkunst. – 156. Die Lehre von den Gleichungen. – 157. Die Begründung der analytischen Geometrie. – 160. Maxima- und Minimaaufgaben. – 162. Das Prinzip der kleinsten Wirkung. – 165. Die Anfänge der Infinitesimalrechnung. – 167. Quadraturen und Kubaturen. – 169. Cavalieris Satz und Guldins Regel. – 171. Die Arithmetik des Unendlichen. – 172. Differential- und Integralrechnung. – 173. Die Methode der Fluxionen.
7. Die Beziehungen der Naturwissenschaft zur neueren Philosophie.
(S. 174–188.)
174. Philosophie, Mathematik und Naturwissenschaft. – 177. Atome und Korpuskeln. – 179. Kraft und Stoff. – 181. Die cartesianische Physik. – 182. Hobbes und Spinoza. – 183. Newtons Prinzipien. – 185. Cartesianer und Newtonianer. – 187. Descartes und Leibniz.
8. Der Ausbau der Physik der flüssigen und der gasförmigen Körper.
(S. 189–214.)
189. Die Begründung der Hydrostatik. – 192. Anfänge einer Dynamik der Flüssigkeiten. – 194. Die Erfindung des Quecksilberbarometers. – 196. Pascals Versuche. – 200. Die Erfindung der Luftpumpe. – 206. Das Wasserbarometer. – 209. Wägung der Luft und Versuche im Vakuum. – 211. Die Entdeckung des Boyle-Mariotte'schen Gesetzes.
9. Die weitere Entwicklung der Iatrochemie und die Begründung der wissenschaftlichen Chemie durch Boyle.
(S. 215–230.)
215. Neue Ziele der Chemie. – 217. Die Entdeckungen der Alchemisten. – 219. Das erste Lehrbuch der Chemie. – 221. Der Einfluß der Chemie auf die Gewerbe. – 225. Die Begründung der Chemie als Wissenschaft. – 227. Die Anfänge der antiphlogistischen Lehre.
10. Der Ausbau der Botanik und der Zoologie nach dem Wiederaufleben der Wissenschaften.
(S. 231–242.)
231. Fortschritte der Botanik. – 234. Anfänge der natürlichen und der künstlichen Systematik. – 236. Die Begründung einer Morphologie der Pflanzen. – 240. Fortschritte der Zoologie.
11. Die Begründung der großen wissenschaftlichen Akademien.
(S. 243–253.)
243. Allgemeines. – 245. Die Royal Society. – 247. Die Pariser Akademie der Wissenschaften. – 249. Die Preußische Akademie der Wissenschaften. – 252. Preisaufgaben, Akademieschriften.
12. Newton.
(S. 254–285.)
254. Newtons Werdegang. – 255. Fortschritte der praktischen Optik. – 258. Die Untersuchung des Sonnenspektrums. – 261. Newtons Farbentheorie. – 266. Emissions- und Wellentheorie. – 273. Die Entdeckung des Gravitationsgesetzes. – 277. Newtons »Prinzipien«. – 281. Newtons Weltanschauung.
13. Huygens und die übrigen Zeitgenossen Newtons.
(S. 286–345.)
286. Huygens' Werdegang. – 288. Der Ausbau der Wellentheorie des Lichtes. – 293. Das Huygens'sche Prinzip. – 296. Doppelbrechung und Polarisation. – 302. Die Erfindung der Pendeluhr. – 309. Förderung der Theorie des Pendels. – 313. Untersuchungen über die Zentrifugalkraft. – 316. Die Abplattung der Erde. – 318. Die Begründung einer Theorie des Stoßes. – 320. Lebendige Kraft und Erhaltung der Kraft. – 323. Weiteres Schicksal der Lehre von der Erhaltung der Kraft. – 326. Mariottes Entdeckungen. – 330. Halleys astronomische und physikalische Forschungen. – 337. Die Entdeckungen Cassinis. – 340. Deutschland während der Newton-Huygens-Periode.
14. Unter dem Einfluß der chemischen und der physikalischen Forschung entstehen die Grundlagen der neueren Mineralogie und Geologie.
(S. 346–362.)
346. Allgemeines. – 347. Stenos kristallographische und geologische Untersuchungen. – 351. Die Entwicklung der Ansichten über das Erdinnere. – 353. Anfänge der Paläontologie. – 355. Weitere geologische und mineralogische Fortschritte. – 357. Die Chemie im Zeitalter der Phlogistontheorie.
15. Das Emporblühen der Anatomie und der Physiologie.
(S. 363–372.)
363. Die Lehre vom Kreislauf des Blutes. – 368. Tieferes Eindringen in den Bau der Organe. – 369. Anatomie und Mechanik.
16. Die ersten Ergebnisse der mikroskopischen Erforschung der niederen Tiere.
(S. 373–390.)
373. Der Bau und die Entwicklung der Insekten. – 378. Urzeugung und Entwicklung. – 383. Anfänge der Embryologie. – 386. Die Entdeckung mikroskopisch kleiner Organismen. – 388. Mikroskopie und Anatomie.
17. Die Begründung der Pflanzenanatomie und der Lehre von der Sexualität der Pflanzen.
(S. 391–404.)
391. Einleitendes. – 393. Grews Anatomie der Pflanzen. – 395. Anatomie und Physiologie. – 399. Die Sexualität der Pflanzen.
18. Der weitere Ausbau der Mechanik, Optik und Akustik.
(S. 404–443.)
404. Naturwissenschaft und Mathematik. – 408. Die Begründung der mathematischen Physik. – 415. Mathematik und Astronomie. – 419. Eulers Äthertheorie. – 422. Die Begründung der analytischen Mechanik. – 427. Fortschritte der Mathematik. – 429. Die Grundformeln der analytischen Mechanik. – 432. Die Begründung der Photometrie. – 438. Fortschritte der Akustik.
19. Die Astronomie nach der Begründung der Gravitationsmechanik.
(S. 444–464.)
444. Die Abplattung der Erde. – 447. Die Grundlagen des metrischen Systems. – 452. Sonnenparallaxe, Erddichte und Aberration. – 458. Weitere Fortschritte der Astronomie. – 460. Astronomie und Kartographie.
20. Mineralogie und Geologie im 18. Jahrhundert.
(S. 465–488.)
465. Die Begründung der Mineralchemie. – 467. Die Aufstellung eines Systems der Mineralien. – 470. Die Unterscheidung der Gebirgsglieder. – 474. Die Aufstellung von Perioden der Erdgeschichte. – 476. Weitere Fortschritte der Geologie. – 483. Neptunismus und Vulkanismus. – 486. Die Begründung der Paläontologie.
21. Die Naturwissenschaften und das Zeitalter der Aufklärung.
(S. 489–493.)
Verzeichnis der im II. Bande enthaltenen Abbildungen S. 494
Namen- und Sachverzeichnis S. 501
Ergänzungen, Zusätze und Berichtigungen S. 507
Aus den Besprechungen der ersten Auflage S. 509
Ein Ereignis, das gewöhnlich als ein Wendepunkt in der Geschichte der Wissenschaften betrachtet wird, und mit dem auch wir den ersten Abschnitt unserer Darstellung abschlossen, ist die Aufstellung des heliozentrischen Weltsystems durch Koppernikus. Man darf jedoch nicht außer Acht lassen, daß der Umschwung allmählich erfolgte, und daß man auf allen Wissensgebieten zunächst an das Vorhandene anknüpfte. Auch ging für die einzelnen Zweige die Befreiung aus den Formen des mittelalterlichen Denkens durchaus nicht gleichzeitig vor sich. Zuerst war es die Astronomie, die einen erhöhten Standpunkt gewann. Ihr folgten die Physik seit dem 17. und die Chemie seit dem 18. Jahrhundert, während die Biologie erst im Laufe des 19. Jahrhunderts auf den Rang einer exakten Wissenschaft erhoben wurde.
Eine große Zahl von Aufgaben, deren Bewältigung man mit dem Beginn der Neuzeit in Angriff nahm, hatte sich schon das Altertum gestellt. Während des Mittelalters verlor man sie fast sämtlich aus den Augen. Die Neuzeit nahm sie nahezu dort, wo das Altertum stehen geblieben, wieder auf. Zum Teil führte sie diese Aufgaben ihrer Lösung entgegen, sie knüpfte aber auch an die gelösten und an die schwebenden neue Probleme an, die noch unsere Zeit vollauf beschäftigen, so daß letztere das Gefühl beseelt, daß sich ein Ende in der Kette der Entdeckungen und Erfindungen nirgends absehen läßt.
Ein kurzer Rückblick soll uns zunächst das Erbe vergegenwärtigen, das die neuere Zeit vom Altertum übernommen hat. Die Elemente der Mathematik waren in der Hauptsache entwickelt und am vollständigsten durch Euklid zusammengefaßt worden. Hieran schlossen sich die Untersuchungen des Archimedes und des Apollonios, die insbesondere die wichtige Lehre von den Kegelschnitten begründeten. Das »Almagest« genannte Hauptwerk des Ptolemäos enthielt die Grundzüge der ebenen und der sphärischen Trigonometrie. Das heutige Ziffernsystem und die Anfänge[S. 2] der Algebra verdankte man, als Schöpfungen einer späteren Zeit, vorzugsweise den Indern und den Arabern.
Die Alten hatten ferner gezeigt, in welcher Weise sich die Mathematik auf astronomische und mechanische Probleme anwenden läßt. Das Werk des Ptolemäos und vor allem die Schriften des Archimedes bieten zahlreiche Beispiele dafür. Über den Lauf der Gestirne hatte man eine große Summe von Beobachtungen gesammelt; ferner lagen für eine richtige astronomische Theorie Ansätze vor, die nur der weiteren Entwicklung harrten. Die Methoden und die Instrumente waren im wesentlichen noch dieselben, deren sich die Griechen bedient hatten. Auch gab es im Beginn der neueren Zeit für die Astronomie keine Aufgabe, die sich nicht schon die Alten gestellt hätten. Die Bestimmung des Umfangs der Erdkugel, ihr Verhältnis zu den übrigen Himmelskörpern, eine genaue Topographie des Fixsternhimmels, genaue Zeit- und Ortsbestimmung, die Vorhersage astronomischer Ereignisse, wie der Finsternisse, alles das waren Gegenstände, mit denen sich schon das Altertum, insbesondere die alexandrinische Periode, eingehend beschäftigt hatte, und von denen die neuere Zeit vorzugsweise durch das Hauptwerk des Ptolemäos Kenntnis erhielt.
Die auf uns gekommenen Berichte über Jahrtausende zurückliegende Finsternisse haben einen doppelten Wert. Einmal sind sie geeignet, einen Prüfstein für die neueren, einen weit kürzeren Zeitraum umfassenden Berechnungen zu bieten. Ferner geben sie ein Mittel an die Hand, um weit zurückliegende geschichtliche Ereignisse chronologisch zu ordnen1. Mitunter hat es sich in den alten Berichten offenbar nur um Verfinsterungen gehandelt, die durch plötzlich auftretende Gewitterwolken veranlaßt waren. Im ganzen haben aber die Berechnungen von Mond- und Sonnenfinsternissen, die bis zum Jahre 900 v. Chr. zurückreichen, für die Geschichte des Altertums und für die astronomische Wissenschaft gleich wertvolle Ergebnisse geliefert2.
Auch die Statik und die Optik, Gebiete, die sich für die den Alten am meisten zusagende deduktive Behandlung besonders eigneten, empfing die Neuzeit in einer, bis zu einem gewissen Grade wissenschaftlich durchgebildeten Form, während bezüglich[S. 3] der übrigen Teile der Physik nur die Kenntnis von mehr oder minder wertvollen Einzelbeobachtungen übermittelt wurde, deren richtige Deutung und weiterer Verfolg der neueren Periode vorbehalten blieb. Es gilt dies namentlich von den magnetischen und den elektrischen Erscheinungen, sowie von dem Verhalten der Gase und Dämpfe, über deren Studium wir Heron von Alexandrien ausführliche Mitteilungen verdanken.
Auch die Chemie ist in ihren Anfängen auf das Altertum zurückzuführen. Ist es auch häufig nicht mehr möglich, im einzelnen zu entscheiden, welche Kenntnisse das Mittelalter den späteren Alexandrinern verdankte und welche es selbständig erwarb, so muß doch anerkannt werden, daß die Chemie im Mittelalter ganz besonders gepflegt und auch in mancher Hinsicht durch neue Entdeckungen bereichert wurde. Die Chemie in ihrer ersten, unvollkommenen Gestalt war so sehr eine Wissenschaft des Mittelalters, daß sie weit über den Beginn der neueren Zeit hinaus sich nach den in jener Periode gesteckten Zielen bewegte und sich erst spät den Denkformen der neueren Zeit anpaßte.
Auf dem Gebiete der beschreibenden Naturwissenschaften knüpfte man gleichfalls dort an, wo das Altertum aufgehört hatte. Nachdem das Studium der alten Schriftsteller die erste Anregung gegeben, wandte man sich aber in steigendem Maße der eigenen, auf keine Autorität zurückgreifenden Beobachtung zu, der sich durch die Erweiterung des gesamten Gesichtskreises und infolge der Entwicklung der exakten Wissenschaften ein überreiches, den Alten verschlossen gebliebenes Feld eröffnete.
Die im Altertum geschaffenen Ansätze waren im Mittelalter nicht etwa gänzlich verschollen. Man muß vielmehr annehmen, daß im Orient überhaupt keine völlige Unterbrechung stattfand. Die Wissenschaft der Alten empfing der Orient vorzugsweise aus den Händen der dort ansässig gewordenen Griechen. Man verstand es, dieses Erbe nicht nur zu erhalten, sondern es auch auszubauen und es durch Zuführung neuer Elemente, z. B. aus Indien, zu vermehren. Mit dem 9. und 10. Jahrhundert begannen die arabisch schreibenden Gelehrten des Orients auf den Gebieten der Naturwissenschaften und der Heilkunde selbständig zu werden, während sie sich vorher auf die Aneignung der älteren Werke beschränkt hatten. Ihre Blütezeit erlebte die arabische Literatur im 11. Jahrhundert. Den christlichen Völkern des Mittelalters flossen die Kenntnisse der Alten zuerst aus spärlicher und trüber, dann aber aus immer reinerer Quelle. Was ihre Entfaltung zunächst[S. 4] hinderte, war einmal die jähe Unterbrechung, welche die Kulturentwicklung Europas durch die Völkerwanderung und den Sturz des römischen Kaiserreiches erlitten, ferner aber der eigentümliche, auf das Kirchlich-Dogmatische und Mystische gerichtete, der Natur abholde Geist, der das christliche Mittelalter kennzeichnete. Unter seiner Herrschaft konnte nur ganz allmählich eine die Dogmen beiseite schiebende und die Dinge selbst ins Auge fassende Forschung aufkommen.
Die Welterklärung des Mittelalters drehte sich im wesentlichen um den Streit, ob die Begriffe bloße Namen seien (Nominalisten), oder ob sie als etwas wirklich Vorhandenes, als Wesenheiten, den Dingen und Vorgängen zugrunde lägen (Realisten). Die Realisten, in denen die Philosophie Platons ihre Fortsetzung fand, haben der Naturauffassung des eigentlichen Mittelalters den Stempel aufgeprägt. Die als wirkliche Wesen betrachteten Begriffe (universalia ante res«) spielten damals etwa die Rolle unserer heutigen Naturgesetze. Sie sind es, denen wir noch während der Übergangszeit in dem Archeus des Paracelsus und in der Erd- und Weltseele Keplers begegnen. Als der Realismus3 herrschte, waren die Sterne, die Pflanzen, ja selbst die Steine, kurz jeder Körper, der Schauplatz für das Treiben einer Unzahl von Geistern. Dies rührte daher, daß man der substantiellen Form, ein Wort, das etwa die Bedeutung der platonischen Idee besitzt, reale Existenz beilegte, anstatt in ihr eine Schöpfung des eigenen Verstandes zu erblicken. Das Nächste war dann, daß eine ungezügelte Phantasie diesen wesenhaft gewordenen Begriffen die Attribute der Persönlichkeit beilegte und einen Mystizismus erzeugte, der eine Forschung nach den natürlichen Ursachen unter Anerkennung des Kausalitätsgesetzes gar nicht aufkommen ließ. Die Umwälzung, welche die Überwindung des mittelalterlichen Geistes und die Begründung der neueren Philosophie und Naturforschung bedeutet, bestand darin, daß an Stelle jener substantiellen Formen und ihrer mystischen Auswüchse die bloße Regel, das Naturgesetz, trat. Die Regel mußte aus der Beobachtung vieler Einzelfälle entnommen werden, daher rührte die Forderung, induktiv zu verfahren, eine Forderung, die an der Schwelle des neuen Zeitraumes von vielen Seiten und nicht etwa bloß von Francis Bacon erhoben wurde. Die Regel ließ sich ferner mathematisch[S. 5] fassen. So entstand eine enge Verbindung der Mathematik mit der Naturwissenschaft, durch welche die neuere Zeit sich gleichfalls von den früheren Perioden abhebt. In der Philosophie war es Bacon, in der Naturwissenschaft vor allem Galilei, welche die substantiellen Formen der Scholastiker beseitigten und an ihre Stelle das immaterielle Naturgesetz stellten.
Die Entwicklung der Wissenschaft war während des Mittelalters fast noch mehr als im Altertum auch dadurch sehr gehindert, daß zwischen ihr und der Technik eine nur geringe Berührung stattfand. Der weltfremde Gelehrte des Mittelalters beschränkte sich im wesentlichen darauf, daß er die alten Schriftsteller und ihre Kommentatoren studierte und in maßloser Überschätzung des Wortwissens etymologischen Betrachtungen nachging, ohne auf die eigene Beobachtung Wert zu legen. Auf diese Weise erwuchsen aus der vorhandenen Literatur zwar neue Schriften, es fehlte ihnen aber an neuem Inhalt. Der mitten im Leben stehende Gewerbetreibende dagegen beobachtete und erfand, aber er schrieb nicht. Seine Kenntnisse pflanzten sich vorwiegend durch mündliche Überlieferung fort. So begann, um einen Zweig der Technik herauszugreifen, schon in früher Zeit ein reger Bergbau in Böhmen. Von dort aus breitete er sich über Schlesien aus. Im 11. Jahrhundert begann man in Ungarn, im Harz und im Mansfeldischen Bergwerke einzurichten. Gleichzeitig entstanden Hütten- und Salinenwerke. Dasjenige von Wieliczka z. B. wird seit dem 13. Jahrhundert betrieben. Welchen Nutzen hätte die Naturwissenschaft aus diesen Unternehmungen ziehen können! Und welch befruchtenden Einfluß hätte sie wiederum auf die Technik auszuüben vermocht! Diese Wechselwirkung blieb solange aus, bis der Buchdruck aufkam. Von diesem Zeitpunkt an sehen wir auch den Techniker schriftstellerisch wirken. Er stellte seiner ganzen Eigenart gemäß die eigene Beobachtung und Erfindung in den Vordergrund und beschränkte sich hinsichtlich der literarischen Überlieferungen darauf, sie als Hilfsmittel für seine eigene Arbeit und nicht, wie der Gelehrte, als Mittelpunkt zu betrachten.
Von großem Einfluß auf die Umgestaltung der gesamten europäischen Verhältnisse war auch die Verwendung des schon im 13. Jahrhundert bekannt gewordenen Pulvers zu kriegerischen Zwecken. Es ist nicht unwahrscheinlich, daß sein Gebrauch zum Fortschleudern von Geschossen von einem Mönch namens Berthold[S. 6] (um 1300) herrührt4. Jedenfalls erfolgte die Verbreitung der Feuerwaffen von Deutschland aus, wo vermutlich schon um die Mitte des 14. Jahrhunderts die ersten Pulverfabriken eingerichtet wurden.
Für die Richtung, welche die Entwicklung der Wissenschaft und der gesamten Kultur in der Neuzeit nahm, ist endlich noch ein allgemeingeschichtliches Moment hervorzuheben. Der Sitz der politischen Macht und der geistigen Bildung wanderte nämlich von ihren alten Stätten, dem Orient und den Mittelmeerländern nach dem Nordwesten und der Mitte Europas, nach England, Frankreich und Deutschland. Dieser Zug von Osten nach Westen ist indessen kein blindes Walten des Schicksals. Er wird dadurch hervorgerufen, daß sich dem Westen Europas gegenüber ein neuer Weltteil erschließt, während der Osten dem Andrängen aus Asien hervorbrechender Stämme (Mongolen und Türken) erliegt.
So sehen wir besonders in den beiden großen Hauptstädten nördlich und südlich des Kanals neue Brennpunkte des wissenschaftlichen Lebens entstehen. Und fortan gelten die Gestade der Nordsee dem Geschichtsschreiber5 »als die vornehmste Werkstätte des allgemeinen Geistes des menschlichen Geschlechtes, seiner staatenbildenden, ideenhervorbringenden, die Natur beherrschenden Tätigkeit«.
In dieser Tätigkeit wurde der Mensch der neueren Geschichte durch nichts in dem Maße gefördert, wie durch das Emporblühen der Naturwissenschaften. Sie waren es, die durch ihren Erkenntnisinhalt und durch ihre zahllosen Anwendungen auf allen Gebieten neue Gedanken hervorriefen und das gesamte Leben, sowie die Lebensanschauungen umgestalteten. Das Mittelalter hatte vorzugsweise gesammelt, was an Resten der untergegangenen Kultur des Altertums übrig geblieben war. In der Neuzeit dagegen entfaltete sich immer machtvoller das Bestreben »die Dinge aus den Dingen selbst« kennen zu lernen, wie ein oft gebrauchter Ausdruck lautet. Dadurch gelangte man zu dem eigentlichen Kern der Wissenschaft, deren Wesen das der vorurteilslosen Kritik und der eindringenden Forschung ist. Zwar hat man sich nur nach und nach von den überkommenen herrschenden Vorstellungen[S. 7] frei zu machen gewußt. Selbst Männer wie Koppernikus, Galilei, Kepler und Newton waren nicht unbeeinflußt von ihnen. Die größten Hemmungen bereiteten die kirchlichen Dogmen, die im Mittelalter die Wissenschaft schon aus dem Grunde eingeengt hatten, weil sie fast ausschließlich in den Händen der Geistlichen lag. Erst dadurch, daß die Wissenschaft weltlich wurde, daß sie der engen Haft der Klöster entrann und an besondere, ihrer Pflege bestimmten Stätten, die Universitäten, verpflanzt wurde, daß sie mit dem praktischen Leben in Fühlung trat und mit der selbständig und ohne alle Buchgelehrsamkeit sich entfaltenden Technik in Beziehung kam, waren die Voraussetzungen zu einer Um- und Neugestaltung des gesamten wissenschaftlichen Lebens gegeben. Unter dem Einfluß dieses Lebens hätte sich Europa, wenn die mittelalterlichen Einrichtungen des staatlichen Lebens nicht übermächtig gewesen wären, eigentlich zu einer Art Völkerfamilie entwickeln müssen, da alle Voraussetzungen zu einer Kulturgemeinschaft gegeben waren. Unter den Gelehrten aller europäischen Länder herrschte wenigstens das Gefühl der engen Zusammengehörigkeit. Konnte sich doch der besonders von Leibniz gehegte Gedanke hervorwagen, sämtliche gelehrten Akademien, die als Schöpfungen der Neuzeit entstanden waren, zu einer europäischen Gesamtakademie zu vereinigen. Auch daß eine einzige Sprache, die Lateinische nämlich, die Gebildeten aller Länder verband, war ein Vorzug, dessen die neuere Zeit durch nationalistische Absonderung nach und nach verlustig gegangen ist. Infolge dieses Zusammenschlusses war ferner der Wetteifer zwischen den einzelnen Ländern, insbesondere zwischen Frankreich, England und den Niederlanden gleich groß. Trotz ihrer Kleinheit verdienen die letzteren besondere Anerkennung. Ihre Beteiligung am Welthandel, das Emporblühen von Städten, die ein Hort der Freiheit, der Kunst und blühender Gewerbe waren, befähigten die Niederländer auf allen Gebieten schon an der Schwelle der Neuzeit zu Leistungen ersten Ranges. Zu diesen ist vor allem zu rechnen: die Erfindung des Fernrohrs und des Mikroskops, die Gründung hervorragender Hochschulen, wie derjenigen von Leiden und Utrecht, sowie die Entwicklung des Buchgewerbes auf eine Höhe, von der heute noch die Schätze der Plantinschen Druckerei in Antwerpen und die Buchausgaben der Familie Elzevir Zeugnis ablegen. Auch dadurch haben die Niederlande sich unvergänglichen Ruhm erworben, daß sie Descartes und anderen Großen im Reiche der Wissenschaft[S. 8] eine Zuflucht boten, wenn politischer oder religiöser Fanatismus ihnen die Heimat verleideten.
Politische und konfessionelle Spaltungen waren es auch, die Deutschland anfangs daran hinderten, sich dem edlen, zwischen den übrigen europäischen Ländern entbrannten Wettbewerbe mit Erfolg anzuschließen. Zunächst mußten die Folgen des dreißig Jahre währenden Religionskrieges überwunden werden, ehe Deutschland seinen vollen Anteil an der neuzeitlichen Entwicklung der Wissenschaften beitragen konnte. Man hätte eigentlich von einem Lande, in dem die Reformation ihren Anfang nahm und der Humanismus zu großer Blüte gelangte, mehr erwarten können. Der Einfluß dieser beiden Bewegungen auf die Entwicklung der Naturwissenschaften war indessen nicht so groß, wie man oft annimmt. Mit Recht ist darauf hingewiesen worden, daß die Reformation in gewissem Sinne für die Wissenschaften sogar einen Rückschritt bedeutete, indem sie die transzendente Richtung wieder verstärkte. Die protestantische Kirche verhielt sich, wie ihr Auftreten gegen Koppernikus und Kepler zeigte, den naturwissenschaftlichen Fortschritten gegenüber häufig sogar feindlich. Was die Reformation Fortschrittliches im Gefolge hatte, war, daß sie den Autoritätsglauben und damit eine der größten Fesseln der naturwissenschaftlichen Forschung, einschränken half. Ihn gänzlich zu beseitigen ist vergebliches Bemühen geblieben, da er zu tief in der Natur des Menschen wurzelt.
Ebensowenig wie die Reformation war auch der Humanismus allein imstande, für die Wissenschaften ein neues Zeitalter heraufzuführen. Der Boden auf dem er erwuchs, waren die Universitäten, während an dem Gebäude der neueren Naturwissenschaften viele Männer von geistig freiem Blick arbeiteten, die abseits von dem am alten Herkommen festhaltenden Leben der Universitäten standen. Es sei nur auf Koppernikus, Kepler, Tycho, Guericke, auf Agricola, Leeuwenhoek, Grew und viele andere, die uns in diesem Werke begegnen, hingewiesen. Mitunter verhielten sich die Universitäten gegen die naturwissenschaftliche Forschung geradezu ablehnend. Namentlich in Frankreich, wo Staat und Kirche sich zur Unterdrückung freier geistiger Bewegungen vereinigten, war dies zu Beginn der Neuzeit der Fall. Dies für die Wissenschaft verhängnisvolle Bündnis hemmte auch in Italien den durch Galilei und seine Schule eingeleiteten Fortschritt, so daß Italien die Führung, die es auf geistigem Gebiete anfangs hatte, bald[S. 9] an die nördlichen Länder Europas, insbesondere an England und die Niederlande abtreten mußte.
Der Schaden, den die staatliche unter dem Einfluß der Kirche ausgeübte Bevormundung der Forschung antat, wurde mitunter dadurch wieder aufgehoben, daß der neuzeitliche Staat die Wissenschaft förderte, wenn er sich einen unmittelbaren Nutzen von ihr versprach. So entstanden Sternwarten, die bisher meist der privaten Liebhaberei entsprangen, sowie Akademien unter Aufwendung staatlicher Mittel. Unter den Sternwarten sind besonders die von Paris (gegründet im Jahre 1667) und Greenwich (gegründet 1675) zu nennen. Ihrem Muster schlossen sich diejenigen von Berlin, von Petersburg und Wien im 18. Jahrhundert an.
Die Akademien, denen der vorliegende Band einen besonderen Abschnitt widmet, bildeten sich anfangs durch freien Zusammenschluß hervorragender Forscher. Die Regierungen unterstützten die neue Einrichtung, von der sie mehr als von den Universitäten praktisch verwertbare Ergebnisse erhofften, und nahmen sie zumeist in ihre Obhut oder schufen Neugründungen. Unter den in den nördlichen Ländern gestifteten Akademien sind besonders die Royal Society (Gründungsjahr 1662) und die 1666 durch den Minister Colbert ins Leben gerufene Académie des Sciences zu nennen. Im 18. Jahrhundert folgten Berlin (1700) und Petersburg (1725). Erwähnung verdient auch die erste, rein naturwissenschaftliche Akademie, die 1652 unter dem Namen der Kaiserlich Leopoldinischen Akademie in Deutschland gegründet wurde und, wie die übrigen, heute noch besteht.
Zu den genannten Forschungsmitteln gesellten sich die in der Regel von den Akademien herausgegebenen periodischen Zeitschriften, unter denen vor allem die Berichte der Royal Society und die seit 1682 in Deutschland erscheinende »Acta Eruditorum« zu nennen sind6.
Vor allem aber ist der neue, in den Arbeiten eines Galilei, Guericke, Kepler und Newton seinen Höhepunkt erreichende Abschnitt in der Entwicklung der Naturwissenschaften dadurch gekennzeichnet, daß man die wichtigsten Hilfsmittel zur Verschärfung der Sinne erfand und infolgedessen einen weit tieferen Einblick wie bisher in die Erscheinungen zu tun vermochte. Was die früheren Zeitalter an solchen Mitteln besaßen, erhob sich wenig über den Rang einfacher, durch handwerksmäßiges Schaffen[S. 10] hergestellter Werkzeuge. Jetzt treten uns auf wissenschaftlichen Grundsätzen beruhende, der planmäßigen Forschung dienende Instrumente in größerer Zahl entgegen.
Was nützten alle Bemühungen, in die Natur der Wärmeerscheinungen einzudringen, solange man kein Thermometer besaß? Das 17. Jahrhundert erfand es. Die Philosophen hatten zahllose Spekulationen angestellt über den leeren Raum, über das Wesen der Luft, über die Frage, ob sie Gewicht besitzt oder mit einem Streben vom Erdmittelpunkte fort begabt ist. Da trat Guericke auf, der nichts vom Disputieren auf dem Gebiete der Naturwissenschaften hielt. Er baute seine Luftpumpe und bewies das Vorhandensein des Luftdruckes durch den berühmten Versuch mit den Magdeburger Halbkugeln. Er wog die Luft, untersuchte mit seinem Wasserbarometer die Schwankungen ihres Druckes und vermochte aus ihnen das Wetter vorherzusagen. An die Stelle des Wasserbarometers trat dann das bequemere Quecksilberbarometer. Zur Luftpumpe gesellte Guericke die Elektrisiermaschine. Das Fernrohr wurde in den Dienst der Astronomie gestellt. Das Mikroskop erschloß dem Biologen eine neue Welt. Die Sinne wurden nicht nur bewaffnet und zu höheren Leistungen befähigt; es wurden auch ganz neue Gebiete der Wahrnehmung erschlossen, beispielsweise die Luftdruckschwankungen, die doch etwas sind, wofür wir keinen unmittelbaren Sinn besitzen. Höchstens ein dumpfes Gefühl läßt besonders starke Schwankungen ahnen, während das Barometer die geringste Änderung des atmosphärischen Druckes anzeigt.
So hat sich seit dem 17. Jahrhundert infolge der Erfindung neuer Forschungsmittel eine bedeutende Vertiefung und Erweiterung des Weltbildes vollzogen. Gewiß vermochten auch die Instrumente nicht den letzten Schleier von den Dingen zu ziehen. Es zeugt indes von schlechter Kenntnis der Aufgaben der Naturwissenschaft, das von ihr zu verlangen. Alle Forschung ist Menschenwerk und somit an die körperlichen und geistigen Grenzen des menschlichen Erkennens gebunden. Die Instrumente tragen nur bis an diese Grenzen, und die echte Forschung bleibt sich ihrer stets bewußt.
Gleich an der Schwelle dieser Periode treten uns die beiden wichtigsten unter den neuzeitlichen Forschungsmitteln, das zusammengesetzte Mikroskop und das Fernrohr, entgegen. Ersteres wurde um 1590, letzteres um 1608 erfunden.
Die Glaslinse und ihre vergrößernde Kraft waren zwar seit alters bekannt. Auch waren die Erscheinungen, welche die verschiedenen Arten der Spiegel darboten, da sie sich einer Erklärung durch geometrische Konstruktion zugänglich erwiesen, stets ein Lieblingsgegenstand der Mathematiker. Die Zusammenfügung mehrerer Linsen, in der das Eigentümliche des zusammengesetzten Mikroskops und des Fernrohrs besteht, scheint dagegen anfangs ohne einen leitenden Gedanken als ein bloßes Spiel des Zufalls stattgefunden zu haben. Obgleich die Geschichte jener Instrumente sehr verwickelt ist und mehrere Völker Prioritätsansprüche erheben, ist doch soviel festgestellt, daß der Ruhm beider Erfindungen den Niederländern gebührt, bei denen die Glas- und Steinschleiferei schon im Mittelalter in Blüte stand und die Herstellung von Linsen zwecks Verfertigung von Brillen gewerbsmäßig betrieben wurde7.
Es würde viel zu weit führen, wenn wir uns hier mit der Abwägung aller Prioritätsansprüche befassen wollten8. Nicht nur Roger Bacon und Porta wurden auf Grund dunkler Stellen ihrer Werke für die Erfinder des Fernrohrs gehalten, sondern im Hinblick auf Matthäus 4, 8 wurde das neue Werkzeug sogar für[S. 12] eine Erfindung des Teufels ausgegeben9. Letzteres sei nicht etwa der bloßen Kuriosität wegen angeführt, sondern um die mißbräuchliche Anwendung zu zeigen, die, wie wir noch des öfteren sehen werden, von der Bibel gemacht wurde. In den meisten Fällen geschah dies, um, wie einst dem Emporblühen des Humanismus, der heranwachsenden Naturwissenschaft Hemmnisse zu bereiten. Dies Bestreben hat zwar einzelnen Vertretern der Wissenschaft Verfolgungen eingetragen. Für den gesamten Gang der Entwicklung, der vom Dunkel zum Lichte führte, sollte es indes belanglos bleiben.
Bei Bacon kann es sich nur um prophetische Aussprüche handeln, Porta deutet indessen schon darauf hin, daß sich durch eine Vereinigung von Glaslinsen besondere optische Wirkungen erzielen lassen; doch scheint es sich bei seinem Vorschlage um eine Art Brille gehandelt zu haben10. Irrtümliche Nachrichten, welche die Bekanntschaft mit dem Fernrohr vor dem 17. Jahrhundert bezeugen sollen, sind auch dadurch entstanden, daß man sich schon im Mittelalter, ja selbst im Altertum, beim Beobachten der Gestirne leerer Röhren bediente, um seitliches Licht abzuhalten.
Das erste zusammengesetzte Mikroskop bestand aus der Vereinigung einer Bikonvex- mit einer Bikonkavlinse. Erstere diente als Objektiv, letztere als Okular. Dieses Instrument wurde sehr wahrscheinlich11 von dem holländischen Glasschleifer Zacharias Jansen um das Jahr 1590 erfunden. Eins der ältesten Exemplare beschrieb Borelius. Es war 1½ Fuß lang. Das Rohr hatte zwei Zoll Durchmesser. Auf das Fußgestell gelegte kleine Gegenstände erschienen beim Hineinblicken in das Instrument stark vergrößert12.
Die heutigen zusammengesetzten Mikroskope sind bekanntlich anders eingerichtet. Sie bestehen aus zwei Sammellinsen oder aus zwei Linsensystemen, von denen jedes wie eine einzige Sammellinse wirkt. Die dem Gegenstande genäherte Linse a erzeugt ein physisches Bild, das durch die zweite Linse b wie durch eine Lupe betrachtet wird (s. Abb. 1). Diese Konstruktion kam jedoch erst später auf, wir begegnen ihr nicht vor dem zweiten Jahrzehnt des 17. Jahrhunderts.
Auch das Fernrohr bestand in seiner ersten Einrichtung, die nach glaubwürdigen Zeugnissen von dem holländischen Brillenmacher Franz Lippershey herrührt, in der Verbindung einer Konvexlinse als Objektiv mit einer Konkavlinse als Okular. Diese Vereinigung wird bekanntlich noch jetzt als holländisches Fernrohr bezeichnet und in binokularer Ausführung den heutigen Operngläsern zugrunde gelegt. Auch hier leitete wohl der Zufall auf die Erfindung. Es wird nämlich erzählt, Lippershey habe seine Linsenkombination auf die Wetterfahne eines nahen Kirchturmes gerichtet und sei von der vergrößernden Wirkung überrascht gewesen.

Dafür, daß Lippershey in Middelburg das Fernrohr erfunden hat, sprechen Zeugnisse von Männern des 17. Jahrhunderts und auch behördliche Dokumente. In einem solchen wird Lippershey auf eine Bewerbung um ein Privilegium geantwortet, er möge sein Fernrohr so verbessern, daß man dadurch gleichzeitig mit beiden Augen sehen könne. Dies Verlangen soll Lippershey im Dezember des Jahres 1608 erfüllt haben, während die erste Einsendung seines aus Kristallinsen verfertigten Fernrohrs nach neueren Untersuchungen14 im Herbst 1608 erfolgt sein soll.
Die Kunde von der wunderbaren Erfindung, verbreitete sich mit großer Schnelligkeit. In Frankreich wurden schon im November des Jahres 1610 die Jupitermonde mit dem neuen Instrumente[S. 14] beobachtet. Nach Italien gelangte das Gerücht von der epochemachenden Erfindung im Jahre 1609, in Deutschland soll das Fernrohr schon 1608 zum Kaufe angeboten worden sein15.
In Italien, wo Galilei auf der Höhe seines Schaffens stand, fand die Nachricht den geeignetsten Boden. Mit welchem Eifer Galilei sich der Sache annahm, hat er selbst in einer kleinen Schrift erzählt, die über die ersten, ihm gelungenen astronomischen Entdeckungen berichtet. Es heißt dort16: »Vor etwa zehn Monaten kam das Gerücht zu unseren Ohren, ein Niederländer habe ein Instrument erfunden, vermittelst dessen man entfernte Dinge so deutlich wie nahe gelegene sehe. Das veranlaßte mich, darauf zu sinnen, wie ich zur Verfertigung eines solchen Instruments gelangen könnte. Von den Gesetzen der Dioptrik geleitet, verfiel ich darauf, an den Enden eines Rohres zwei Gläser anzubringen, ein plankonvexes und ein plankonkaves. Als ich das Auge dem letzteren näherte, sah ich die Gegenstände etwa dreimal so nahe und neunmal vergrößert. Da ich weder Arbeit noch Kosten scheute, bin ich soweit gekommen, ein solch vortreffliches Instrument zu erhalten, daß mir die Sachen fast 1000mal so groß und 30mal näher erscheinen, als wenn man sie mit bloßem Auge betrachtet.«
Das Fernrohr, das Galilei anfertigte, war also gleichfalls ein holländisches, während das eigentliche astronomische Fernrohr wie das zusammengesetzte Mikroskop zwei Sammellinsen besitzt. Die Konstruktion des astronomischen Fernrohrs wurde von Kepler in seiner Dioptrik17 (s. Abb. 2) angegeben, dem hervorragendsten Werk, das zu Beginn der neueren Zeit über die Brechung des Lichtes geschrieben wurde.
Im letzten Teile der »Dioptrik« befaßt sich Kepler mit der Wirkung der verschiedenen Linsenkombinationen. Gleich die erste Aufgabe, die er sich stellt, enthält die Konstruktion des astronomischen Fernrohrs. Sie lautet: »Durch zwei Konvexlinsen eine Vergrößerung des Gegenstandes bei vollkommener Deutlichkeit herbeizuführen, aber in umgekehrter Lage«18. Kepler nimmt an, das Objektivglas AB sei in solcher Entfernung von dem Gegenstande CE, daß sein umgekehrtes Bild undeutlich sein würde. »Stellt man nun zwischen das Auge und dieses undeutliche Bild, und zwar nahe dahinter eine zweite Sammellinse OP, so wird letztere die von D und F kommenden Strahlen konvergent und das Bild dadurch deutlich machen.« Auch wird dieses durch das Okular erzeugte Bild, wie Kepler dartut, größer erscheinen als das Bild das »die dem Auge nächststehende Linse (OP) von der entfernteren Linse (AB) erhalten hatte«19.
Das astronomische Fernrohr verdrängte binnen kurzem das holländische, weil es zwei Vorzüge besitzt. Einmal gewährt das astronomische Fernrohr ein größeres Gesichtsfeld. Ferner ermöglicht es die Anwendung eines Fadenkreuzes, mit dem das zwischen Objektiv und Okular erzeugte reelle Bild zur Deckung gebracht werden kann.
Daß sich durch Einfügung einer dritten Konvexlinse das umgekehrte Bild, das ein solches Fernrohr liefert, in ein aufrechtes verwandeln läßt, hat Kepler gleichfalls dargetan20. Merkwürdigerweise wurde das nach ihm benannte astronomische Fernrohr jedoch nicht von ihm selbst, sondern erst einige Jahre später nach den Angaben der Dioptrik von Scheiner, dem wir in der Lebensgeschichte Galileis noch begegnen werden, zum ersten Male angefertigt. Auch das aus drei Konvexlinsen bestehende terrestrische Fernrohr hat Scheiner21 zuerst hergestellt.
Kepler gab in seiner »Dioptrik« auch die erste Theorie des holländischen, aus der Verbindung einer Konvex- mit einer Konkavlinse bestehenden Fernrohrs (Abb. 3). Er zeigte nämlich, daß die verschwommenen Bilder, die eine dicht vor das Auge gesetzte[S. 16] Konkavlinse (LM) liefert, deutlich und größer werden, wenn eine Konvexlinse (NO) in einer bestimmten Entfernung vor die Konkavlinse gehalten wird22. Im Zusammenhang mit seiner Beweisführung steht der durch Abb. 3 gleichfalls erläuterte Satz, daß Strahlen, die durch eine Konvexlinse NO konvergent gemacht sind und noch vor ihrem Schnittpunkt auf eine Konkavlinse LM fallen, so gebrochen werden, daß entweder der Schnittpunkt weiter hinaus verlegt wird (nach A) oder die Strahlen parallel gemacht (AʹAʺ) oder endlich divergent weiter geschickt werden (ξK).
Kepler erläutert ferner, wie sich durch die Kombination einer Konkav- mit einer Konvexlinse reelle Bilder erhalten lassen, die größer sind als die mit einer Konvexlinse allein erhaltenen Bilder. Diese von Kepler vorgeschlagene Vereinigung (Abb. 4) hat erst vor kurzem den Anlaß zur Erfindung des Teleobjektivs gegeben. Kepler verfolgt den Gang von drei Strahlenbündeln, die von den Punkten CAE des Gegenstandes kommen. Die Konkavlinse wird an eine Stelle gebracht, an der die Konvexlinse GH ein verschwommenes Bild geben würde. Indem nun die Konkavlinse (LN) die Büschel kurz vor der Spitze auffängt und die Büschel zu den Spitzen SPT formt, erzeugt sie ein deutliches, reelles Bild, das größer ist als das in FBD durch die Konvexlinse allein hervorgerufene.
Außer den hier hervorgehobenen wichtigen Sätzen über die Wirkung von Linsenkombinationen bringt Kepler noch eine Fülle anderer, bezüglich deren jedoch auf die »Dioptrik« verwiesen werden muß. Um das Fernrohr zu verkürzen, empfiehlt er z. B. zwei gleiche Sammellinsen, die möglichst nahe hintereinander stehen als Objektiv zu wählen. Auch der Vorschlag, das Rohr des Fernrohres verschiebbar zu machen, um es den Augen anzupassen, rührt von Kepler her23.
Das Jahr, in dem das astronomische oder Keplersche Fernrohr zur Ausführung gelangte, hat sich nicht genau ermitteln lassen. Es geschah wohl zwischen 1613 und 1617, und zwar, wie schon erwähnt, durch Scheiner24. Er hat sich um die Begründung der Optik und um die Erfindung und Verbesserung der optischen Instrumente zur Zeit des Wiederauflebens der Naturwissenschaften neben Kepler die größten Verdienste erworben. Scheiner war ferner einer der ersten, der das Fernrohr zu astronomischen Beobachtungen benutzte. Im April oder Mai des Jahres 1611 erblickte er die fast zur selben Zeit von Fabricius und Galilei gesehenen Sonnenflecken25. Gebührt ihm auch nicht die Priorität dieser Entdeckung, so war er es doch, der in jahrewährender Arbeit mehrere tausend Beobachtungen über die neue, so viel Aufsehen erregende Erscheinung anstellte. Diese Beobachtungen wären nicht möglich gewesen, wenn Scheiner nicht als erster an dem Fernrohr besondere Blendgläser angebracht hätte. Sie bestanden in geschliffenen, farbigen Platten, die er vor den Linsen befestigte. Seine ersten Versuche, die Linsen selbst aus farbigem Glase herzustellen und so das Licht zu schwächen, gab er bald wieder auf. Vielleicht ist Galilei dadurch erblindet, daß er noch keine Blendgläser gebrauchte26.
Einen zusammenfassenden Bericht über seine Beobachtungen veröffentlichte Scheiner 1630 unter dem Titel »Rosa Ursina«27.[S. 18] Es wird noch an anderer Stelle davon die Rede sein. Hier sei nur hervorgehoben, daß diese Schrift die erste Nachricht von der Scheiner gelungenen Erfindung des astronomischen, aus zwei konvexen Linsen hergestellten Fernrohres brachte. Die Möglichkeit einer solchen Konstruktion hatte, wie oben erwähnt, zwar Kepler angegeben. Die Ausführung und die erste Anwendung verdanken wir indessen Scheiner. Er erzählt in der Rosa Ursina, er habe mit dem neuen Instrument vor 13 Jahren (also 1617) dem Kaiser die Sonnenflecken gezeigt.
Scheiner wandte auch eine Linsenkombination unter dem Namen Helioskop zur objektiven Darstellung astronomischer Vorgänge an. Er zeigte z. B. die Sonnenflecken gleichzeitig einer größeren Anzahl von Personen, indem er sein Helioskop aus einem dunklen Zimmer gegen die Sonne richtete und hinter dem Instrument eine weiße Platte anbrachte, auf der dann die Sonnenscheibe mit ihren Flecken sichtbar wurde.
Bei diesem Stand der optischen Forschung war es selbstverständlich, daß man sich auch dem uns von der Natur verliehenen Organ und dem Vorgange des Sehens zuwandte. So bewies Scheiner die Ähnlichkeit des Auges mit der Camera obscura durch folgenden Versuch: Er entfernte die Häute an der hinteren Wand eines Ochsenauges bis auf die Netzhaut und brachte eine Kerze in einiger Entfernung vor dem so präparierten Auge an. Das umgekehrte Bild der Kerzenflamme konnte dann auf der Netzhaut von einem hinter dem Auge befindlichen Standpunkt wahrgenommen werden28. Später (im Jahre 1625) stellte Scheiner den gleichen Versuch mit demselben Ergebnis am menschlichen Auge an.
Scheiner ließ sich bei seiner Beschäftigung mit optischen Fragen von dem Gedanken leiten, daß das Auge ein nach den Prinzipien der Optik gebautes Organ und deshalb besonders geeignet sei, die Grundlehren der Optik zu entwickeln. So entstand das Werk, das die soeben erwähnten Beobachtungen enthält. Es führt den, jenen Gedanken Scheiners zum Ausdruck bringenden Titel »Oculus, hoc est fundamentum opticum« und ist grundlegend für die physiologische Optik geworden.
Scheiner beginnt mit der eingehenden anatomischen Beschreibung des Auges. Dann folgt eine Untersuchung des Brechungsvermögens der verschiedenen Medien, welche die Strahlen nach ihrem Eintritt in das Auge durchdringen müssen, um zu der Netzhaut[S. 19] zu gelangen. Letztere ist nach Scheiner und nach Kepler, entgegen früheren Meinungen, welche die Wahrnehmung des Bildes in den Glaskörper oder gar in die Linse verlegten, der eigentliche Sitz des Sehvermögens. Scheiner zeigte, daß das Brechungsvermögen der wässerigen Feuchtigkeit mit demjenigen des Wassers und dasjenige der Linse mit dem des Glases nahezu übereinstimmt, während das Brechungsvermögen des Glaskörpers zwischen dem der erstgenannten Medien liegt. Der Gang des Lichtstrahls wird dann von seinem Eintritt in das Auge, bis er die Netzhaut trifft, verfolgt. Die entsprechenden Kapitelüberschriften geben am besten einen Überblick über den Gang und die Ausführlichkeit der von Scheiner unternommenen Untersuchung. Sie lauten: Brechung des Lichtstrahls beim Übergang aus der Luft in die Hornhaut, Brechung beim Übergang aus der Hornhaut in die wässerige Feuchtigkeit, Vergleich der das Auge zusammensetzenden Medien hinsichtlich ihrer Dichte, Brechung des Lichtes beim Übergang aus der wässerigen Feuchtigkeit in die Kristallinse, Brechung an der Grenze von Kristallinse und Glaskörper, und endlich Brechung an der Grenze von Glaskörper und Netzhaut29.
Scheiner gab ferner die erste zutreffende Antwort auf die Frage, wie es kommt, daß das Auge nahe und entfernte Gegenstände deutlich zu sehen vermag. Dieses, als Akkommodationsfähigkeit bezeichnete Vermögen erklärte Scheiner daraus, daß die Gestalt der Linse sich ändert, indem die Linse sich für nahe Gegenstände stärker wölbt, für entferntere dagegen sich abflacht.
Von den zahlreichen Versuchen, die Scheiner über das Sehen anstellte, sei folgender hervorgehoben. In ein Papierblatt werden mit der Nadel mehrere kleine Öffnungen gestochen, die sich so nahe beieinander befinden, daß die entstehende Figur die Pupille an Größe nicht übertrifft. Bringt man das Blatt dann nahe an das Auge und hält einen Gegenstand, etwa eine Nadelspitze, dahinter, so sieht man von ihm so viel Bilder, als das Papier Öffnungen besitzt. Die Erscheinung erklärt sich daraus, daß sich die von der Nadelspitze ausgehenden Strahlen vor oder hinter der Netzhaut kreuzen.
Auf dem Boden Italiens hatte das Wiederaufleben der Antike stattgefunden, dort entstanden durch Galilei und seine Schüler auch die Grundlagen der neueren Naturwissenschaft. Zu der Zeit, als sich das Dunkel des Mittelalters zu lichten begann, war Italien in zahlreiche Republiken und Fürstentümer zerfallen, die in kriegerischem, sowie in friedlichem Wettbewerb um die Herrschaft rangen. Ihre Nahrung zogen diese kleinen Staatsgebilde vorwiegend aus dem Handel und dem Gewerbe. Seitdem sich die italienischen Seefahrer der Bussole und der geographischen Karten bedienten, hatte sich ein steigender Verkehr nach der Levante entwickelt. Eine Folge davon war das Emporblühen des Kunstgewerbes. Venedigs Glasgegenstände, sowie die Majoliken und Metallgüsse anderer italienischen Städte galten als unübertroffen. Auf solchem Boden erwuchs auch die Kunst eines Lionardo da Vinci, Raphael und Michel Angelo, nachdem im Beginn dieses Zeitalters Dante und Petrarca ihre unvergänglichen Dichtungen geschaffen. In dem Maße, wie die Blüte der Kunst sich ihrem Ende zuneigte, begann der wissenschaftliche Geist seine Schwingen zu regen. An demselben Tage, an dem Michel Angelo die Augen für immer schloß, erblickte Galilei das Licht der Welt. Die Natur, sagt Libri30, schien damit andeuten zu wollen, daß die Kunst das Scepter an die Wissenschaft abgetreten habe.
Galileo Galilei31 wurde am 18. Februar (alten Stils), nach neueren Forschungen wahrscheinlich am 15. Februar, des Jahres 1564 in Pisa geboren. Diese Stadt war im Mittelalter eine freie[S. 21] gewesen; zur Zeit Galileis befand sie sich unter florentinischer Herrschaft, die damals in den Händen des berühmten Geschlechts der Mediceer ruhte. Der Vater Galileis, Vincenzio Galilei, ein verarmter Edelmann, besaß eine große Vorliebe für Musik und Mathematik. Offenbar hat Galilei von ihm seine auf die Naturwissenschaften und gegen den Autoritätsglauben gerichteten geistigen Anlagen empfangen. Bezeichnend hierfür ist, daß Galileis Vater auch schon die Form des Dialogs bevorzugte und einen solchen über die alte und die neuere Musik verfaßte, sowie, daß er sich darin gegen die Berufung auf Autoritäten aussprach.
Der junge Galilei ragte durch Lernbegierde, sowie durch Selbständigkeit des Denkens unter seinen Altersgenossen hervor. Er widmete sich in Pisa zunächst dem Studium der Medizin, einer Wissenschaft, die in ihrer damaligen Verfassung wenig geeignet war, einen Geist wie denjenigen Galileis zu fesseln. Es wird erzählt, daß er vor der Tür den Vorträgen eines Mathematikers lauschte und von den Hörern einige Brocken zu erhaschen suchte. Sobald der Mathematiker davon erfuhr, nahm er sich des jungen Menschen an und bewirkte, daß dieser das Studium der Heilkunde mit dem der Mathematik und der Physik vertauschte.
Auf dem Gebiete der Physik herrschten damals die aristotelischen Lehren noch so gut wie unangefochten. Sie wurden in Italien zu jener Zeit wie ein Evangelium betrachtet32. Als Galilei den »Aristoteles« zu lesen begann, hatte er sich über viele Naturvorgänge schon eigene Meinungen gebildet. Er war nun in hohem[S. 22] Grade erstaunt, daß diese mit den herrschenden Lehren des griechischen Philosophen so wenig im Einklang waren. Bei weiterer Prüfung verwandelte sich dieses Staunen in Zweifel und endlich in völlige Abkehr von den als unrichtig erkannten, älteren Lehrmeinungen.
Als Fünfundzwanzigjähriger bestieg Galilei die Lehrkanzel und trat nun öffentlich als Gegner der aristotelischen Physik auf. Da er dabei mit großer Kühnheit die eigene wissenschaftliche Überzeugung über die Autorität stellte, machte er sich in Pisa, wo man ihn des beharrlichen Verfechtens seiner Meinung wegen den Zänker nannte, auf die Dauer unmöglich. Mit Freuden folgte er deshalb einem vom venetianischen Senat an ihn ergangenen Ruf an die Universität Padua, wo er im Dezember des Jahres 1592 seine Antrittsvorlesung hielt.
Die Eigenart Galileis, seine Ansichten auf eigene Beobachtungen und zweckmäßig ersonnene Versuche zu stützen, hat sich schon in den ersten Jahren seiner Tätigkeit in Pisa geäußert. So ließ er Holz, Marmor und Blei aus bedeutender Höhe herabfallen und zeigte, daß, entgegen der Behauptung der Aristoteliker, die Fallzeit für Körper von verschiedenem Gewicht dieselbe sei. »Daß dies der Ansicht vieler widerspricht«, sagt er in seiner Jugendarbeit, die von dem Fall der Körper handelt (De motu gravium), »ist mir ganz gleichgültig, wenn es nur mit der Vernunft und der Erfahrung übereinstimmt«.
Durch den Luftzug in Schwingungen versetzte Lampen sollen seine später zu besprechenden Forschungen über die Pendelbewegung veranlaßt haben. Es wird erzählt, Galilei habe, als er eine an einer langen Kette schwankende Lampe im Dom seiner Vaterstadt beobachtete, die Schwingungszeit aus der Zahl seiner Pulsschläge ermittelt und auf diese Weise den Isochronismus der Pendelschwingungen entdeckt, d. h. die Tatsache, daß Schwingungen von kleinerem und größerem Ausschlag bei unveränderter Länge des Pendels die gleiche Zeit beanspruchen.
Euklid, Apollonios und Archimedes boten ihm während dieser Zeit des wissenschaftlichen Heranreifens die meiste Anregung. Aus dem Schüler wurde aber bald ein Meister, der seine Lehrer überflügelte. Nicht in dem Erlernen, sondern in der Weiterentwicklung der Wissenschaft erblickte Galilei seine Aufgabe. Wo Erstarrung eingetreten war, galt es, durch neue Wege und bessere Methoden den Fortschritt der Erkenntnis herbeizuführen. In dieser Richtung sehen wir ihn in wachsendem Maße sich betätigen,[S. 23] seitdem er das Lehramt in Padua angetreten. Auch war er schon frühzeitig der koppernikanischen Lehre zugetan. In einem 1597 an Kepler geschriebenen Briefe bekennt er nämlich, daß er »seit vielen Jahren« Anhänger der neuen Weltanschauung sei.
Dieser Brief, in dem er Kepler für die Übersendung des »Prodomus«, der Erstlingsarbeit des großen Deutschen, seinen Dank ausspricht, ist für die Stellung, die beide Männer zu ihren Zeitgenossen einnahmen, so bezeichnend, daß er im Auszuge hier Platz finden möge. »Ich preise mich glücklich«, schreibt Galilei, »in dem Suchen nach Wahrheit einen so großen Bundesgenossen gefunden zu haben. Es ist wirklich erbärmlich, daß es so wenige gibt, die nach dem Wahren streben und bereit sind, von der verkehrten Art zu philosophieren abzugehen. Aber es ist hier nicht am Platz, die Jämmerlichkeit unserer Zeit zu beklagen, sondern Dir zu Deinen herrlichen Forschungen Glück zu wünschen. Ich tue das um so lieber, als ich seit vielen Jahren Anhänger der koppernikanischen Lehre bin. Sie erklärt mir die Ursache vieler Erscheinungen, die aus der allgemein gültigen Ansicht ganz unbegreiflich sind. Ich habe zur Widerlegung der letzteren viele Gründe gesammelt, doch wage ich es nicht, sie ans Licht der Öffentlichkeit zu bringen. Wahrlich, ich würde es wagen, wenn es mehr solche Männer, wie Du bist, gäbe. Da dies aber nicht der Fall ist, so spare ich es mir auf«33.
Galilei hatte allen Grund vorsichtig zu sein, denn ein Jahr, nachdem er diese Zeilen geschrieben, wurde Giordano Bruno, der begeisterte Verfechter der koppernikanischen Lehre, der römischen Inquisition ausgeliefert, um später seine Kühnheit auf dem Scheiterhaufen zu büßen34.
Die Befreiung aus den Banden der Scholastik fand auch darin ihren Ausdruck, daß Galilei, obwohl er das Latein, die Sprache des Mittelalters, beherrschte, in Wort und Schrift sich meist der Muttersprache bediente. Dank für dieses Unterfangen erwies ihm jedoch nur die lernbegierige Jugend, welche dem begeisterten Verkünder einer neuen Zeit in Scharen zuströmte. Auch Gustav Adolf, der als Kronprinz in Italien weilte, soll, nach Vivianis Erzählung, sich in Padua unter seinen Zuhörern befunden haben35.
Zu einem Zusammenstoß zwischen Galilei und den Scholastikern kam es, als 1604 plötzlich der neue Stern erschien, über den Kepler und Fabricius (siehe an späterer Stelle) so eingehend berichtet haben. Da nach der Lehre des Aristoteles der Himmel unveränderlich sein und die Sphäre des Veränderlichen erst unterhalb des Mondes beginnen sollte, so wurde der neue Stern in diese Sphäre verlegt. Dagegen wandte sich Galilei, indem er aus denselben Gründen wie Kepler darauf hinwies, daß sich der neue Himmelskörper weit außerhalb der Sphären der Planeten zwischen den Fixsternen befinden müsse.
Wir sahen, welche Rolle Galilei in der Geschichte des Fernrohrs spielte. Die Erfindung dieses Instruments veranlaßte ihn, sich seit dem Jahre 1608 mit großem Eifer und Erfolge astronomischen Beobachtungen zu widmen. Von besonderer Wichtigkeit war die Entdeckung, daß vier kleinere Weltkörper den Jupiter umkreisen. Dieses Gestirn mit seinen Trabanten bot ihm nämlich einen Analogiebeweis für die Richtigkeit der koppernikanischen Weltansicht36.
»Ich bin vor Verwunderung ganz außer mir«, schrieb Galilei
damals, »und sage Gott unendlichen Dank, daß es ihm gefallen
hat, so große und allen Jahrhunderten unbekannte Wunder durch
mich entdecken zu lassen. Daß der Mond ein der Erde gleicher
Körper sei, dessen war ich schon versichert. Auch habe ich eine
Menge nie gesehener Fixsterne, welche die Zahl derer, die man
mit bloßem Auge sehen kann, mehr als zehnmal übertrifft, entdeckt
und weiß nun, was die Milchstraße ist. Ferner habe ich gefunden,
daß Saturn aus drei Kugeln besteht, die sich fast berühren,
nie ihre Stelle gegeneinander verändern und längs des Tierkreises
in einer Reihe, wie
![]() stehen, dergestalt, daß der mittlere
die anderen dreimal an Größe übertrifft«37.
stehen, dergestalt, daß der mittlere
die anderen dreimal an Größe übertrifft«37.
Von der Gleichgültigkeit und dem Widerstande, dem damals die größten Entdeckungen begegneten, zeugt eine Stelle in einem Briefe Galileis an Kepler. Sie lautet: »Als ich den Professoren am Gymnasium zu Florenz die Jupitertrabanten durch mein Fernrohr zu zeigen wünschte, wollten sie weder diese noch das Rohr sehen. Diese Menschen glauben, in der Natur sei keine Wahrheit zu suchen, sondern nur in der Vergleichung der Texte«38.
Ausführlicher hat Galilei über seine astronomischen Entdeckungen in dem »Himmelsboten«39 berichtet, einem Buch, das großes Aufsehen erregte, aber auch eine ganze Schar von Gegnern in Bewegung setzte.
Eine weitere Stütze erhielt das koppernikanische System durch die Entdeckung, daß ein Planet wie die Venus, ähnlich wie der Mond, Lichtgestalten aufweist. Sie erschien nämlich bald als leuchtende Scheibe, bald war sie von halbkreis- oder sichelförmiger Gestalt. Letzteres war der Fall, wenn sie ihre von der Sonne beleuchtete Hälfte nicht voll dem Beschauer zukehrte. Damit war einer der Nachweise geliefert, den die Gegner des Koppernikus forderten. Die Fixsterne erschienen Galilei dagegen nur als leuchtende Punkte und sind es trotz aller Zunahme der vergrößernden Kraft des Fernrohrs bis auf den heutigen Tag geblieben. Sobald Galilei indes das bewaffnete Auge auf den Himmel richtete, erkannte er, daß die Zahl der Fixsterne viele Male die Zahl der mit bloßem Auge sichtbaren Sterne übertrifft40.
Den Ruhm, die Sonnenflecken entdeckt zu haben, mußte Galilei jedoch mit mehreren zeitgenössischen Astronomen teilen41. Die Sonnenflecken hatten sich selbst Kepler in eigentümlicher Weise bemerkbar gemacht, ohne daß er sich dabei eines Fernrohrs bedient hätte42. Der aus der Bewegung der Flecken gezogene Schluß, daß die Sonne sich dreht, war eine weitere Tatsache,[S. 26] die zur Stütze der neuen Weltansicht herangezogen werden konnte.
Als Galilei seine astronomischen Entdeckungen begann, richtete auch der Deutsche Johann Fabricius43 das kurz zuvor in Holland erfundene Fernrohr auf den Himmel. Diesem Fabricius gebührt hinsichtlich der Sonnenflecken sogar die Priorität der Entdeckung, um die zwischen Galilei und Scheiner mit so großer Heftigkeit gestritten wurde. In einer 1611 erschienenen Schrift44 berichtet Fabricius über seine Beobachtung mit folgenden Worten: »Als ich den Rand der Sonne aufmerksam betrachtete, zeigte sich mir unerwartet ein schwärzlicher Fleck. Zuerst glaubte ich, es sei eine vorüberziehende Wolke. Am nächsten Morgen erschien aber beim ersten Anblick der Fleck wieder, indes schien er ein wenig seine Stellung verändert zu haben. Darauf herrschte drei Tage trübes Wetter. Als wir wieder heiteren Himmel bekamen, war der Fleck von Ost nach West gerückt, und kleinere waren an seine Stelle getreten. Darauf entzog sich der große Fleck am entgegengesetzten Rande nach und nach den Blicken. Daß den kleineren dasselbe bevorstand, sah man aus ihrer Bewegung. Eine unbestimmte Hoffnung ließ mich die Wiederkehr der Flecken erwarten. Und in der Tat, nach 10 Tagen begann der größere Fleck am östlichen Rande von neuem hervorzutreten«.
Neben Galilei und Fabricius verdient auch Scheiner45 als Astronom, der die Sonnenflecken selbständig entdeckte, genannt zu werden. Er berichtete über seine Beobachtungen in einigen, an den Bürgermeister von Augsburg gerichteten Briefen46, welche die Mitteilung enthielten, Scheiner habe im April des Jahres 1611 dunkle Flecken auf der Sonnenscheibe wahrgenommen. Der Bürgermeister sandte diese Briefe an Galilei, um dessen Meinung zu erfahren und erhielt von Galilei die Antwort, er habe dieselbe Erscheinung schon im Oktober 1610 wahrgenommen und sie auch anderen gezeigt. Scheiner war im Zweifel, ob die Flecke sich[S. 27] auf oder dicht über dem Sonnenkörper befänden. Trotzdem schloß er aus ihrer Bewegung, die er mit größter Ausdauer verfolgte, auf eine Drehung der Sonne. Zuerst hatte er an eine optische Täuschung oder an einen Fehler seines Instruments gedacht. Erst nachdem er acht Fernrohre auf die Sonne gerichtet, und sie ihm und den herbeigerufenen Zeugen stets dasselbe gezeigt hatten, glaubte er seiner Sache sicher zu sein.
Als Ursache der eigentümlichen Erscheinung gab es zwei Möglichkeiten, die beide eingehend erörtert wurden. Entweder gehörten die Flecken dem Sonnenkörper an – und diese Ansicht vertrat von vornherein Fabricius – oder man hatte es mit dunklen, die Sonne umkreisenden Körpern zu tun, eine Annahme, die besonders unter denjenigen Astronomen Anhänger fand, welche die neue Erscheinung mit der aristotelischen Lehre von der Reinheit der Sonne in Einklang zu bringen suchten. Fortgesetzte Beobachtungen verhalfen jedoch der ersten Ansicht zum Siege. Blieb es auch unentschieden, welchen Ursprung die Flecken besitzen, so zögerte man doch nicht, nachdem man sie als Teile der Sonne erkannt hatte, aus ihrer Bewegung auf eine Achsendrehung dieses Weltkörpers zu schließen, sowie daraus die Dauer jener Bewegung und die Lage des Sonnenäquators abzuleiten.
Um diese Zeit wurden auch die ersten Nebel entdeckt, und zwar zunächst diejenigen, die bei sehr klarer Luft mit unbewaffnetem Auge als ganz blasse Lichtschimmer wahrgenommen werden können. Es sind das die Nebel im Orion und in der Andromeda. Ersterer wird 1618 zuerst erwähnt. Den Andromedanebel entdeckte Simon Marius im Jahre 1612.
Diese Fülle von astronomischen Entdeckungen hatte zur Folge, daß die Frage nach der Richtigkeit des koppernikanischen Systems in den Mittelpunkt der Erörterung gerückt wurde. Alles was in Italien an Frömmelei, an scholastischem Dünkel und an Neid gegen den Ruhm Galileis herrschte, vereinigte sich, um unter dem Vorgeben, die von Koppernikus begründete und von Galilei verteidigte Lehre sei der heiligen Schrift zuwider, den großen Entdecker zu Fall zu bringen. Es ist dies eins der dunkelsten Blätter in der Geschichte der Wissenschaften. Jene angeblich religiösen Bedenken gegen den Fortschritt der letzteren hat keiner mit solch treffenden Worten zurückgewiesen wie Galilei selbst. Es geschah[S. 28] dies in einem Briefe, aus dem hier einige Stellen47 Platz finden mögen:
»Wir bringen das Neue nicht, um die Geister zu verwirren, sondern um sie aufzuklären, nicht um die Wissenschaft zu zerstören, sondern um sie wahrhaft zu begründen. Unsere Gegner aber nennen, was sie nicht widerlegen können, falsch und ketzerisch, indem sie sich aus erheucheltem Religionseifer einen Schild machen und die heilige Schrift zur Dienerin ihrer Absichten erniedrigen.
Wer sich an den nackten, grammatischen Sinn halten wollte, müßte die Bibel Widersprüche zeihen, wenn sie von Gottes Auge, Hand oder Zorn redet. Wenn aber solches, der Fassungskraft des Volkes entsprechend, vorkommt, um wieviel mehr mußte diese bei Gegenständen berücksichtigt werden, die von der Wahrnehmung der Menge weit abliegen und nicht das Seelenheil betreffen, wie es auf dem Gebiete der Naturwissenschaften der Fall ist. Hier muß man nicht mit der Autorität der Bibel beginnen, sondern mit der Wahrnehmung und dem Beweis. Da die Bibel vieles figürlich sagt, so darf das, was Wahrnehmung und Beweis uns ersichtlich machen, nicht durch solche Stellen der heiligen Schrift in Zweifel gezogen werden, die einen doppelten Sinn haben. Vor allem muß man sich der Tatsache versichern; ihr kann die Bibel nicht entgegen sein, sonst würde Gott sich selbst widersprechen. Die Bibel redet, wie das damalige Volk die Sache ansah. Hätte sie der Erde Bewegung und der Sonne Ruhe beigelegt, so würde das die Fassungskraft der Menge verwirrt haben. Wo hat aber die Bibel die neue Lehre verdammt? Man setzt das Ansehen der Bibel aufs Spiel, wenn man die Sache anders nimmt und, statt nach erwiesenen Tatsachen den Sinn der Schrift zu deuten, lieber die Natur zwingen, den Versuch leugnen, den Beweis verschmähen will.
Das Verbieten der Wissenschaft selbst aber wäre gegen die Bibel, die an hundert Stellen lehrt, wie der Ruhm und die Größe Gottes wunderbar aus allen seinen Werken hervorleuchten und vor allem im offenen Buche des Himmels zu lesen sind. Und glaube niemand, daß das Lesen der erhabensten Gedanken, die auf diesen Blättern geschrieben stehen, damit getan sei, daß man bloß den Glanz der Sterne angafft. Da sind so tiefe Geheimnisse[S. 29] und so erhabene Begriffe, daß die Nachtarbeiten und Studien von hundert und aber hundert der schärfsten Geister in tausendjährigem Forschen noch nicht durchgedrungen sind und die Lust des Forschens und Findens ewig währt.«
Trotz aller Bemühungen und Vermittlungsversuche, die Galilei zugunsten der heliozentrischen Weltansicht unternahm, fanden in Rom, wo man ihm anfangs geneigt war, von fanatischen Mönchen ausgehende Anschuldigungen schließlich Gehör. Im Jahre 1616 kam es zum Verbot aller Schriften, welche die Bewegung der Erde behaupteten. Galilei wurde befohlen, seine Meinung aufzugeben; wenigstens sollte er sich enthalten, diese Meinung zu verteidigen oder zu lehren. Im Übertretungsfalle werde man ihn einkerkern. Das Werk des Koppernikus aber wurde einer entsprechenden Änderung unterzogen. Das bezügliche Dekret lautete: »Behaupten, die Sonne stehe unbeweglich im Mittelpunkt der Welt, ist töricht, philosophisch falsch und, weil ausdrücklich der heiligen Schrift zuwider, förmlich ketzerisch. Behaupten, die Erde stehe nicht im Mittelpunkt der Welt und habe sogar eine tägliche Umdrehung, ist philosophisch falsch und zum mindesten ein irriger Glaube.«
Die Ironie des Schicksals fügte es, daß zur selben Zeit, als Galilei diesen Kampf gegen Unwissenheit und Autoritätsglauben führte, das heliozentrische System, dem bis dahin noch manche Unvollkommenheiten anhafteten, durch die Arbeiten Keplers auf den Rang einer wohlbegründeten Theorie erhoben wurde.
Galilei lehrte, als das soeben erwähnte Dekret erschien, nicht mehr in Padua. In seinem engeren Vaterlande, in Florenz, war ein Fürst, den er als Prinzen unterrichtet hatte, zur Regierung gelangt. Dieser wünschte dem Lehrer seine Dankbarkeit zu beweisen und ihn als Zierde des eigenen Landes wirken zu sehen. Galilei ließ sich gern zur Rückkehr bewegen, da er mit seiner neuen Anstellung nicht die Verpflichtung übernahm, Vorträge zu halten, sondern ausschließlich seiner wissenschaftlichen Tätigkeit leben durfte. Länger als ein Jahrzehnt hat er diese ungestört ausgeübt. Zwar starb sein hochherziger Gönner. Doch gestalteten sich in Rom selbst die Verhältnisse günstiger, indem mit Urban VIII. ein von regem Eifer für die astronomische Wissenschaft beseelter Mann den päpstlichen Stuhl einnahm. Urban hatte sogar Gedichte auf die Entdeckung der Jupitertrabanten verfaßt und brachte Galilei großes Wohlwollen entgegen. Alle Bemühungen des letzteren, den Papst von der Richtigkeit der[S. 30] koppernikanischen Lehre zu überzeugen und eine Zurücknahme der kirchlichen Entscheidung vom Jahre 1616 herbeizuführen, waren jedoch vergeblich.
Unterdessen schrieb Galilei in der Stille seines Landhauses den »Dialog über die beiden hauptsächlichsten Weltsysteme«, ein Buch, das die glänzendste Verteidigung der koppernikanischen Lehre darstellt48.
Der Dialog, der aus vier umfangreichen Gesprächen oder Tagen, wie Galilei sich ausdrückt, besteht, ist eins der merkwürdigsten Werke, das je geschrieben worden ist. Handelt es sich doch nicht darum, zu entscheiden, welches von den beiden Weltsystemen das richtige sei, sondern um die Darlegung einer Methode wissenschaftlichen Forschens und Denkens, die zu dem bisher meist geübten Verfahren in einem schroffen Gegensatze stand. Der Geist, der sich in diesem Buche ausspricht, bezeichnet eine Überwindung der bisherigen Stufe, einen Schritt vorwärts, den die Menschheit auf dem Wege des Denkens machte, wenn auch manches schon vor Galilei im Keime vorhanden war. Mit Recht ist daher Galileis Dialog als eins der wichtigsten Dokumente in der Geschichte des menschlichen Geistes bezeichnet worden.
Die Gesprächsform wählte Galilei in diesem und auch in späteren Werken teils aus ästhetischen, teils aus didaktischen Gründen. Auch mag ihn das Vorbild der platonischen Dialoge dazu veranlaßt haben. Außerdem sprachen Opportunitätsrücksichten für diese Art der Veröffentlichung. Von den sich unterredenden Personen sind Salviati und Sagredo Freunde und Anhänger Galileis, denen er im Dialog ein Denkmal setzt, indem er sie zu Trägern seiner Ansichten macht. Simplicio, eine fingierte Persönlichkeit, ist der Verfechter der zu Galileis Zeiten überwuchernden, dem blinden Autoritätsglauben huldigenden Buchgelehrsamkeit49.
Im ersten Gespräch wird die Lehre des Aristoteles von der besonderen, im Gegensatz zu allem Irdischen stehenden Natur der Himmelskörper angefochten. Das Erscheinen neuer Sterne und die Sonnenflecken dienen Galilei als wichtige Beweisstücke gegen die aristotelische Ansicht von der Unveränderlichkeit des Himmels. Gegen die von Aristoteles behauptete vollkommene Kugelgestalt der Gestirne führt Galilei die durch ihn entdeckten Berge des Mondes ins Feld. Die Unvergänglichkeit ist ferner nach ihm ein Attribut aller Materie und nicht etwa der himmlischen allein. »Ich habe«, läßt er Salviati sagen, »nie eine Umwandlung der Stoffe ineinander begreifen können, vermöge deren ein Körper als vernichtet zu gelten hat und ein völlig verschiedener Körper aus ihm hervorgegangen sein soll. Ich halte es für möglich, daß die Umwandlung durch eine bloße Veränderung in der Anordnung der Teile geschieht, ohne daß etwas vernichtet oder etwas Neues erzeugt wird.«
So sehen wir Galilei in die, aus a priori aufgestellten Sätzen abgeleiteten Lehren des Aristoteles, dessen Methode bis dahin die herrschende gewesen war, erfolgreich Bresche legen. Bewundernswert ist der Geist, mit dem er jede Spitzfindigkeit der Aristoteliker, die er dem Simplicio in den Mund legt, ad absurdum führt. Wenn Simplicio sich zu dem Ausspruch versteigt, Aristoteles könne keinen Denkfehler machen, da er der Erfinder der Logik sei, so ist Galilei sofort mit dem treffenden Einwand bei der Hand, es könne jemand sehr wohl ein guter Instrumentenmacher sein, ohne deshalb kunstgeübt auf seinen Instrumenten spielen zu können50.
Was nun die Frage anbetrifft, ob sich sämtliche Himmelskörper in 24 Stunden um die Erde, oder letztere in der gleichen Zeit sich um sich selbst bewegt, so gibt Galilei zu, daß allerdings beide Annahmen auf den ersten Blick wohl die beobachteten Erscheinungen erklären können. Die Gründe, die sich für eine Drehung der Erde anführen ließen, seien jedoch überwältigend.
»Wenn wir«, meint Galilei, »nur den ungeheuren Umfang der Sternensphäre betrachten, im Vergleiche zu der Kleinheit des Erdballs, der in jener viele Millionen mal enthalten ist, und sodann an die Geschwindigkeit der Bewegung denken, infolge deren[S. 32] in einem Tage eine ganze Umdrehung des Himmel sich vollziehen müßte, so kann ich mir nicht einreden, daß die Himmelssphäre sich dreht, der Erdball dagegen in Ruhe bleibt.« Wolle man aber jene gewaltige Bewegung dem Himmel beilegen, so müsse man notwendigerweise diese als entgegengesetzt den besonderen Bewegungen der sämtlichen Planeten betrachten, die alle ihre eigene Bewegung von West nach Ost besäßen und zwar eine sehr langsame. Lasse man dagegen die Erde sich um sich selbst bewegen, so falle jener Gegensatz der Bewegungen fort.
Eine dritte Schwierigkeit bestehe darin, daß, je größer die Sphäre sei, der Umlauf um so längere Zeit in Anspruch nehme. Saturn, dessen Bahn an Größe die aller Planeten übertreffe, vollende seinen Umlauf in dreißig Jahren. Jupiter beschreibe seinen eigenen Kreislauf in zwölf Jahren, Mars in zweien, der Mond endlich, das uns nächste Gestirn, innerhalb eines Monats. Dasselbe hatten Galilei die Jupitertrabanten gelehrt, für die sich als Umlaufszeiten für den innersten Trabanten 42 Stunden, für den folgenden 3½ Tage, den nächsten 7 und den äußersten endlich 16 Tage ergeben hatten.
Wolle man nun die Erde ruhen lassen, so müsse man von dem ganz kurzen Umlauf des Mondes zu immer größeren übergehen, zu dem zweijährigen des Mars, dem zwölfjährigen des Jupiter, dem dreißigjährigen des Saturn, dann aber plötzlich zu einer unvergleichlich viel größeren Sphäre, der man gleichwohl eine volle Umdrehung in 24 Stunden beilegen müsse. Nehme man aber eine Bewegung der Erde an, so werde die Geschwindigkeit der Perioden aufs beste gewahrt: Von der trägsten Sphäre des Saturn gelange man dann zu den ganz unbeweglichen Fixsternen.
Als weitere Schwierigkeit der Ptolemäischen Weltanschauung führt Galilei die gewaltige Ungleichheit in den Bewegungen der Fixsterne an, von denen einige sich außerordentlich schnell in ungeheuren Kreisen drehen müßten, andere langsam in kleinen Kreisen, da sich die einen in größerer, die anderen in geringerer Entfernung vom Himmelspole befänden.
Noch verwickelter aber werde die Sache dadurch, daß die Fixsterne in ihrer Stellung langsamen Änderungen unterworfen seien. »Diejenigen nämlich,« führt er aus, »die vor Jahrtausenden im Äquator standen und folglich bei ihrer Bewegung größte Kreise beschrieben, müssen, weil sie heutzutage mehrere Grade von ihm entfernt sind, sich langsamer und in kleineren Kreisen bewegen. Auch wird es sogar geschehen, daß einer von denen, die sich bisher[S. 33] stets bewegt haben, schließlich mit dem Pole zusammenfällt und dann feststeht, nach einiger Zeit der Ruhe aber wiederum anfängt sich zu bewegen.«
Bezüglich der Entstehung des Sonnensystems hatte Galilei sich eine Ansicht gebildet, welche der auf Laplace und Kant zurückzuführenden Anschauung, nach der die Planeten aus der Sonne hervorgegangen sind, genau entgegengesetzt ist. Galilei stellte sich vor, der göttliche Baumeister habe zuerst die Sonne gebildet und ihr einen festen Platz verliehen. Dann seien aus seiner Hand die Planeten hervorgegangen. Diese hätten sich von dem Orte ihrer Entstehung mit wachsender Geschwindigkeit nach der Sonne hinbewegt. Dann seien sie, wiederum durch göttlichen Eingriff, an einem bestimmten Punkte mit der bis dahin erlangten Geschwindigkeit aus der Fall- in eine Drehbewegung versetzt worden. Nach Galilei sind z. B. Jupiter und Saturn von demselben Punkte nach der Sonne hin gefallen. Da Jupiter tiefer fiel, erlangte er eine größere Geschwindigkeit, mit der er sich jetzt innerhalb der Bahn des langsamer umlaufenden Saturns um die Sonne bewegt.
Man kann noch weiter gehen, meint Galilei, und aus dem Verhältnis der Geschwindigkeiten von Jupiter und Saturn, die sich ja aus dem Abstand von der Sonne und der Umlaufszeit ergeben, und aus dem Maße der Beschleunigung einer nach dem Zentrum gerichteten Bewegung berechnen, in welcher Entfernung von diesem Zentrum der Ort sich befunden hat, von dem die Planeten ausgingen.
Dafür, daß die Erde und die Himmelskörper gleichartiger Natur seien, führt Galilei besonders die Gebirge des Mondes ins Feld. Sind doch die Gestirne nach der neuen Lehre Erden wie unsere Erde, während sie vorher, wenn auch nicht mehr als göttliche, so doch als übernatürliche Wesen gegolten hatten. In diesem Versetzen der Erde unter die Sterne, unter Aufgabe des anthropozentrischen Standpunktes, liegt eben das Umwälzende, die befangene Menge Aufregende, der neuen Weltanschauung.
Galilei wies auch darauf hin, daß die Sonnenflecken eine verhältnismäßig geringe Beständigkeit besitzen. Er sah sie entstehen und sich allmählich wieder auflösen und verschwinden51. Daraus nahm Galilei besonders Anlaß, sich gegen die Lehre von der Unwandelbarkeit der Gestirne und gegen die Vorstellung,[S. 34] daß das Beständige und Unveränderliche das Vollkommenere sei, zu wenden. Hierin zeigt sich vor allem der Wandel, den das Weltbild an der Schwelle der Neuzeit erfährt. Die Starrheit, die es im Altertum und ganz besonders im Mittelalter besessen, weicht der Vorstellung, daß überall ein Werden, eine Entwicklung vor sich geht. Und dieser Entwicklungsgedanke ist es, der bis auf den heutigen Tag an Kraft und Ausdehnung stetig zugenommen hat und in der Gegenwart nicht nur die wissenschaftlichen, sondern auch alle übrigen, selbst die metaphysischen Vorstellungen beherrscht.
Galilei verleiht diesem Gedanken in folgenden Worten Ausdruck: »Ich kann nur mit dem größten Widerstreben hören, daß die Eigenschaften des Unwandelbaren und Unveränderlichen als etwas Vornehmes und Vollkommenes gelten und im Gegensatz dazu die Veränderlichkeit als etwas Unvollkommenes betrachtet wird. Ich halte die Erde für höchst vornehm gerade wegen der Wandlungen, die sich auf ihr abspielen, und dasselbe gilt von dem Monde, vom Jupiter und anderen Weltkugeln.«
Worin diese Wandlungen der Gestirne beständen, vermöge sich die mächtigste Einbildungskraft nicht vorzustellen. Deshalb tritt Galilei auch der Annahme, daß die Gestirne den irdischen Geschöpfen ähnliche Lebewesen beherbergen, entgegen.
Den Fixsternen hatte man vor Galilei, durch die Irradiation verleitet, eine bedeutende scheinbare Größe zugeschrieben und sie für verhältnismäßig nahe Weltkörper gehalten. Durch Koppernikus und mehr noch durch Galilei, der sie zuerst als bloße Lichtpünktchen wahrnahm, wurden sie in unermeßliche Fernen gerückt, zumal, nachdem Galilei gezeigt hatte, daß sie in Wahrheit einen wenigstens tausendmal geringeren scheinbaren Durchmesser besitzen, als es infolge der Irradiation den Anschein hat52. Während nämlich noch Tycho für einen Fixstern erster Größe einen scheinbaren Durchmesser von 2 Minuten gemessen zu haben glaubte, eben weil er auf die Irradiation keine Rücksicht nahm, gibt Galilei für den Durchmesser eines solchen Sternes als obere Grenze den Wert von 5 Sekunden an. Spätere Untersuchungen haben ergeben, daß sich für die Fixsterne überhaupt kein scheinbarer Durchmesser nachweisen läßt.
Dafür, daß nicht nur auf der Sonne, sondern auch in der unendlich viel weiter entfernten Region der Fixsterne Entwicklung,[S. 35] Vernichtung, kurz ein den irdischen Vorgängen ähnlicher Wechsel besteht, führt Galilei das plötzliche Erscheinen neuer Sterne in den Jahren 1572 und 1604 ins Feld. Für das Sonnensystem dagegen bezeugen ihm nicht nur die am Zentralkörper auftretenden, ihre Form und Größe ändernden Flecken, sondern auch das Auftauchen und das Verschwinden von Kometen, daß überall in der Welt ein natürliches Geschehen stattfindet und daß der Himmel keine über das Naturgesetz hinausgehende Sonderstellung einnimmt. Außer den astronomischen Gründen, welche der vorkoppernikanischen Astronomie für eine Bewegung der Gestirne um die im Weltzentrum ruhende Erde zu sprechen schienen, gab es für diese Annahme noch einige physikalische Scheingründe, die Galilei gleichfalls widerlegte53. Aristoteles und seine Anhänger behaupteten nämlich, daß der senkrechte Fall die Ruhe der Erde beweise. Rotiere diese nämlich, so könne ein senkrecht emporgeworfener Körper nicht längs derselben Linie an den nämlichen Ort zurückkehren, von dem aus er geworfen wurde. Während der für das Steigen und Fallen erforderlichen Zeit habe sich der Ort, wenn eine Rotation vorhanden sei, um ein bedeutendes Stück nach Osten verschoben, der Körper müsse also nach Westen abweichen. Dem widerspräche aber die Beobachtung. Der zweite Einwurf besagte, daß die Erde, wenn sie rotiere, alle nicht in der Nähe der Pole befindlichen Gegenstände vermöge der Schwungkraft von ihrer Oberfläche abschleudern müsse.
Dem ersten Einwurf gegenüber hebt Galilei hervor, daß der Turm, von dem man den Stein herabfallen läßt, sich mit der gleichen Geschwindigkeit nach Osten bewegt wie der Stein. Ein ähnliches Verhalten zeige sich, wenn man einen schweren Körper von dem Maste eines ruhenden und eines schnell fahrenden Schiffes herabfallen lasse. In beiden Fällen treffe nämlich der Körper dieselbe Stelle am Fuße des Mastes. Scharfsinnig hebt Galilei hervor, daß eine kleine Abweichung, die bei diesem Experiment eintreten könne, auf Rechnung des Luftwiderstandes gesetzt werden müsse. Die Luft sei nämlich in bezug auf das fahrende Schiff in Ruhe, während beim Fall von einem Turm sowohl der Turm und der Körper, als auch das Medium an der Erdumdrehung in völlig gleicher Weise teilnähmen. Das Medium könne unter diesen Umständen also auf die Bewegung des fallenden Körpers nicht störend einwirken, wie es bei dem bewegten Schiffe bei großer[S. 36] Geschwindigkeit möglich sei. Es ist also immer wieder der erweiterte Begriff des Beharrungsvermögens, der bei Galilei bald mehr, bald minder deutlich zum Ausdruck kommt, ein Begriff, der seinen Gegnern fehlte und daher ihre Einwürfe gegen die koppernikanische Ansicht von ihrem Standpunkte aus als berechtigt erscheinen ließ.
Den zweiten Einwurf, daß in der Nähe des Äquators befindliche Körper bei einer Rotation von der Erde abgeschleudert werden müßten, widerlegt Galilei gleichfalls. Er zeigt nämlich, daß die Schwungkraft in Anbetracht der verhältnismäßig geringen Rotationsgeschwindigkeit so klein ist, daß ihre Wirkung durch die Schwerkraft viele Male übertroffen wird54.
Nachdem Galilei die ältere Weltanschauung abgelehnt und die von ihren Anhängern erhobenen Einwürfe beseitigt hat, bringt er eine ausführliche Darstellung des koppernikanischen Systems. Für dieses System spreche mehr wie alles andere der Umstand, daß das Stehenbleiben, Rückwärts- und Vorwärtsgehen der Planeten aus der jährlichen Bewegung der Erde folge. Aufgabe der Astronomie sei es, Rechenschaft von den Erscheinungen zu geben, und das habe die geozentrische Lehre nicht vermocht, da sie zu den ungereimtesten Theorien gegriffen habe, um die Stillstände und die Rückgänge der Planeten zu erklären.
Dem Einwurf, daß die von Koppernikus behauptete Ortsveränderung der Erde um ihren doppelten Abstand von der Sonne parallaktische Verschiebungen am Fixsternhimmel zur Folge haben müsse, wußte Galilei durch die Annahme zu begegnen55, daß die Fixsternsphäre wenigstens 10000 Sonnenweiten vom Sonnensystem entfernt sei. Infolgedessen entziehe sich eine durch die Erdbewegung hervorgebrachte, äußerst geringfügige Verschiebung der Fixsterne unserer Beobachtung.
Die bisher erwähnten Anzeichen, die für eine Bewegung der Erde sprachen, bezogen sich sämtlich auf Himmelserscheinungen. Irdische Vorgänge schienen für den Nachweis, ob die Erde sich dreht oder fest steht, nicht in Betracht zu kommen. Nur an dem Wasser, meinte Galilei, das infolge seiner Flüssigkeit gewissermaßen »unter eigener Botmäßigkeit« stehe, ließe sich vielleicht ein Anzeichen finden, aus dem man entnehmen könne, ob die Erde sich dreht oder nicht. Ein solches Anzeichen erblickte[S. 37] Galilei in den Gezeiten. Wenn auch erst Newton imstande war, eine befriedigende Theorie der Gezeiten zu geben, so verdienen doch Galileis scharfsinnige Betrachtungen über diesen Gegenstand unsere Beachtung56. Man muß sich vergegenwärtigen, daß Galilei die Gravitation der Weltkörper zur Erklärung der Gezeiten noch nicht verwerten konnte, weil man von einer zwischen den Weltkörpern wirkenden Kraft wohl eine dunkle Ahnung, aber noch keine festgegründete Lehre besaß. Galilei setzte also noch keine anziehende Kraft des Mondes voraus, sondern erklärte die Gezeiten folgendermaßen: Ist der Erdball unbeweglich, so kann keine Ebbe und Flut stattfinden. Gibt man der Erde aber die Bewegungen, die Koppernikus ihr zuschreibt, so muß das Meer in einer den Beobachtungen entsprechenden Weise der Ebbe und der Flut unterliegen. Und zwar geschieht dies nach Galilei, weil, infolge der Zusammensetzung der jährlichen Bewegung mit der Drehung, gewisse Teile der Erdoberfläche in ihrer absoluten Bewegung beschleunigt, andere dagegen verzögert werden. Nehmen wir mit Galilei an, in A befinde sich die Sonne. Der große Kreis sei die Erdbahn und der kleine die Erde selbst. Bewegt sich letztere von B nach C, während sie gleichzeitig in der Richtung DEFG rotiert, so erkennt man ohne weiteres, daß sich der Punkt D der Erdoberfläche, absolut genommen, am schnellsten bewegt, während derselbe Punkt, wenn er in F angelangt ist, seine geringste[S. 38] Geschwindigkeit besitzt, weil dort die tägliche Bewegung der jährlichen entgegengesetzt und deshalb von ihr in Abzug zu bringen ist. Ähnlich wie nun in einem bewegten Wasserbecken, dessen Geschwindigkeit sich ändert, das Wasser auf der einen Seite steigen und auf der anderen fallen wird, ähnlich muß nach Galilei der erwähnte Einfluß ein Steigen und ein Fallen der Wassermasse im Meeresbecken hervorrufen. Daß dieser Schluß zutrifft, läßt sich nicht in Abrede stellen, und es ist wohl möglich, daß die erwähnte Verschiedenheit der Geschwindigkeiten in D und F (Abb. 5) von Einfluß ist. Da jedoch die Geschwindigkeit der jährlichen Bewegung viele Male größer ist als die Rotationsgeschwindigkeit eines in der Nähe des Äquators gelegenen Punktes, so kann der von Galilei behauptete Einfluß jedenfalls nur gering sein und höchstens Nebenerscheinungen veranlassen. Galilei unterschätzte nämlich jenes Verhältnis, da er den Durchmesser der Sonnenbahn etwa 20mal zu klein annahm57.
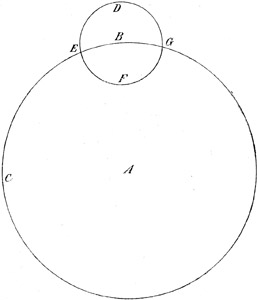
Der »Dialog« ist, wie wir sahen, eins der merkwürdigsten und in seinen Folgen wichtigsten Bücher, die je geschrieben wurden59. Es nimmt für seine Zeit dieselbe Bedeutung ein, welche die »Kreisbewegungen« des Koppernikus für das 15. Jahrhundert und Newtons »Prinzipien« für das auf Galilei folgende Zeitalter besitzen. Diese drei Werke bezeichnen Fortschritte in der Entwicklung der Weltanschauung, d. h. des Weltbildes, der Vorstellungen vom Kosmos, wie sie seitdem kaum wieder gemacht wurden. Wir haben uns deshalb mit dem Inhalt des »Dialogs« eingehender befaßt und wollen nun auch seine Geschichte kennen lernen. Wenn je von einem Buche, so gilt nämlich von diesem das bekannte Wort: Habent sua fata libelli. Auch hat wohl selten ein Werk in solchem Maße das Schicksal seines Verfassers bestimmt, wie es der »Dialog« getan hat.
Mit dem Verbot vom Jahre 1616 suchte sich Galilei dadurch abzufinden, daß er die Lehre des Koppernikus nicht als eigene Meinung vortrug, sondern sie einer der sich unterredenden Personen,[S. 39] dem Salviati, in den Mund legte, während das ptolemäische System von Simplicio verteidigt wurde. Jeder Einsichtige konnte indessen leicht erkennen, daß mit Salviati der Verfasser selbst gemeint sei.
Trotzdem erteilte die römische Zensurbehörde, nachdem auf ihren Wunsch einige Änderungen vorgenommen waren, die Erlaubnis zum Druck des »Dialogs«. Das Buch erschien 1632. Es erregte großes Aufsehen, rief aber auch die Tätigkeit der Feinde und Neider Galileis von neuem wach. Insbesondere war es der Jesuit Scheiner, derselbe, mit dem Galilei einen Prioritätsstreit hinsichtlich der Entdeckung der Sonnenflecken ausgefochten hatte60, der gegen ihn mit allen Mitteln zu Felde zog und die Angelegenheit vor die Inquisition zu bringen suchte. Die freundliche Gesinnung, die Urban VIII. bisher gegen Galilei gehegt, verstand man in das Gegenteil zu verkehren. Man redete dem Papste nämlich ein, in Simplicio, dem ungeschickten Verteidiger der ptolemäischen Ansicht, habe Galilei ihn zu verspotten gesucht.
Es würde hier zu weit führen, wenn wir uns mit den Einzelheiten des gegen Galilei in Szene gesetzten Inquisitionsverfahrens näher befassen wollten61. Der siebzigjährige, durch Krankheit gebeugte Greis, dem sein Vaterland unsterblichen Ruhm verdankt, wurde gezwungen, nach Rom zu reisen. Dort mußte das weitere Verfahren ihn bald überzeugen, daß es hier nur zwei Wege gab. Entweder er teilte das Schicksal Giordano Brunos, der 1600 in Rom den Scheiterhaufen bestiegen hatte, oder er widerrief den Inhalt seines ganzen bisherigen Lebens, indem er nach der Forderung der Inquisition die Lehre des Koppernikus als irrtümlich abschwor und verfluchte. Galilei wählte das letztere. Er beugte sich dem Zwange. Auch mochte ihn die Überzeugung leiten, daß sein Märtyrertod ebensowenig der Wissenschaft wie der Kirche zum Vorteil gereichen könne. Die Abschwörungsformel, die er nach Androhung der Tortur, unter schmachvollen Formen – er war nur mit einem Hemd bekleidet – aussprechen mußte, bildet das unwürdigste Gegenstück zu den Worten, mit denen er[S. 40] selbst in dem oben mitgeteilten Briefe Duldsamkeit gepredigt. Sie lautet62 nach einigen Kürzungen: »Ich beuge meine Knie vor den ehrwürdigen General-Inquisitoren, berühre das heilige Evangelium und versichere, daß ich glaube und in Zukunft alles glauben werde, was die Kirche für wahr erkennt und lehrt.
Mir war von der heiligen Inquisition befohlen, daß ich die falsche Lehre von der Bewegung der Erde und dem Stillstand der Sonne weder glauben noch lehren dürfe, weil sie der heiligen Schrift zuwider sei. Trotzdem habe ich ein Buch geschrieben, und es sogar drucken lassen, in dem ich diese verdammte Lehre vortrage und mit großer Stärke Gründe zu ihren Gunsten vorbringe. Ich bin deswegen der Ketzerei für verdächtig erklärt worden.
Um nun jedem katholischen Christen den mit Recht gegen mich gefaßten Verdacht zu benehmen, schwöre ich ab und verfluche ich die erwähnten Irrtümer und Ketzereien und überhaupt jeden anderen Irrtum und jede Meinung, die gegen die Lehre der Kirche ist. Zugleich schwöre ich, in Zukunft nie etwas mündlich oder schriftlich zu äußern, das mich in einen gleichen Verdacht bringen könnte. Sondern ich will, wenn ich irgendwo Ketzerei finde oder vermute, es gleich dem heiligen Gericht anzeigen.« Der ganze berechnete, fanatische Haß der kirchlichen Machthaber geht aus dem letzten Satze hervor, durch den Galilei auch noch zum Angeber gegen jede weitere Regung der freien Forschung gemacht werden sollte.
Das Galilei zugeschriebene Wort: »Und sie bewegt sich doch« ist gewiß nicht bei diesem Anlaß gesprochen worden63. Daß es jedoch im Grunde seines Herzens erklungen, wer möchte daran zweifeln!
Der gegen Galilei geführte Inquisitionsprozeß ist nicht nur kulturgeschichtlich eine der merkwürdigsten Begebenheiten. Er muß auch späteren Zeiten immer wieder als warnendes Beispiel hingestellt werden, da er mit erschreckender Deutlichkeit zeigt, wohin Unduldsamkeit und religiöser Fanatismus in ihren letzten Konsequenzen geführt haben und immer wieder führen können, wenn nicht durch die stetig wachsende Einsicht weiterer Kreise der trüben Flut ein starker Damm entgegengesetzt wird.
Die Jahre, welche Galilei nach diesen Ereignissen noch gelebt hat, waren voll Bitternis. Die Inquisition wies ihm ein Landhaus bei Florenz als Wohnsitz an, erstreckte jedoch ihre Überwachung auf seine persönlichen Angelegenheiten, so daß er, wenn auch nicht dem Namen nach, so doch tatsächlich, ihr Gefangener blieb. In Galileis Wunsch, nach Florenz übersiedeln zu dürfen, willigte man erst ein, nachdem sein Augenleiden zu völliger Erblindung geführt hatte.
Dennoch war die Schaffenskraft Galileis, die in steigendem Maße, trotz seiner Niederlage in dem Inquisitionsprozeß, die Bewunderung der Zeitgenossen errang, keineswegs gelähmt. Zwar beschäftigten ihn nach seiner Verurteilung nur noch solche astronomische Aufgaben, bei denen keine Erneuerung des Streites mit der römischen Kirche zu befürchten war. So fuhr er, ungeachtet seines beginnenden Augenleidens, mit teleskopischen Untersuchungen fort und entdeckte die Libration des Mondes64. Unter Libration versteht man kleine Schwankungen des Mondes in seiner Stellung zur Erde, die bewirken, daß, vom Erdmittelpunkte aus betrachtet, nicht stets derselbe Punkt der Mondoberfläche im Zentrum der Mondscheibe gesehen wird. Man unterscheidet Libration in Länge (in der Ebene des Mondäquators) und Libration in Breite (senkrecht zur Ebene des Mondäquators). Aber auch abgesehen von derartigen Schwankungen wird die Mondscheibe, von verschiedenen Punkten der Erdoberfläche aus beobachtet oder für denselben Ort zu verschiedenen Tageszeiten, nicht genau dieselbe sein. Es ist dies eine nur scheinbare, parallaktisch genannte Libration. Galilei wies auf letztere hin und entdeckte die Libration in Breite. Die Libration in Länge bemerkte erst Hevel, der bedeutendste Selenograph der neueren Zeit65.
Auch das Problem der Längenbestimmung, das für alle schiffahrttreibenden Nationen die größte Bedeutung hatte, beschäftigte Galilei von neuem. Sein Lieblingsplan, die Verfinsterungen der Jupitermonde zu diesem Zwecke zu verwerten, wurde, nachdem er zwei Jahrzehnte geruht hatte, wieder aufgenommen66.[S. 42] Im Grunde war es derselbe Gedanke, der schon die Alten bei ihren Längenbestimmungen leitete. Periodisch wiederkehrende Himmelsereignisse, die von einem großen Teile der Erde gesehen werden, bieten in beiden Fällen einen Anhalt zur Ermittelung des Zeitunterschiedes für den in Betracht kommenden und einen seiner geographischen Länge nach bekannten Ort. Im Altertum hatte man sich hierzu des Eintritts der Mondfinsternisse bedient. Doch ist ein solches Ereignis so selten, daß es für die Schifffahrt nicht von Belang sein kann. Die Umlaufszeiten der Jupitermonde sind dagegen von so kurzer Dauer, daß fast in jeder Nacht einer derselben durch den Zentralkörper verfinstert wird. Ist nun, schloß Galilei, die Umlaufsbewegung dieser Monde genau bekannt und in Tabellen für den täglichen Gebrauch der Seefahrer niedergelegt, so stellt das System des Jupiters sozusagen eine im Weltraum schwebende, der Beobachtung durch gute Teleskope zugängliche Uhr dar, aus deren Vergleich mit einer nach der Sonne gestellten Uhr der Längenunterschied zwischen dem Ort, auf den sich die Tabellen beziehen, und demjenigen, an dem sich das Schiff befindet, gefunden werden kann. Galilei wußte für seine Methode die Vereinigten Staaten von Holland zu gewinnen und stellte ihnen Ephemeriden der Jupitertrabanten, sowie hinlänglich genau gehende Uhren in Aussicht. Zunehmendes körperliches Leiden brachte jedoch seine Bemühungen, die auch ohnehin schwerlich zu einem Gelingen geführt haben würden, zum Stillstande. Erst im 18. Jahrhundert waren Theorie und Praxis weit genug fortgeschritten, um die Mittel zur Lösung des so überaus wichtigen und schwierigen Problems an die Hand zu geben.
Über das weitere Schicksal des Dialogs, des astronomischen Hauptwerks Galileis, sei noch bemerkt, daß es mit anderen das koppernikanische Weltsystem betreffenden Schriften bis ins 19. Jahrhundert auf dem Index der von der Kirche verbotenen Bücher blieb. Vergebens bemühte sich um die Mitte des 18. Jahrhunderts der große französische Astronom Lalande, die Streichung dieser Schriften aus dem Index durchzusetzen. Erst 1822 entschied das Kardinalskollegium, daß fortan die koppernikanische Lehre in den katholischen Ländern unbeanstandet verkündet werden dürfe. »So endete nach zwei Jahrhunderten dieser denkwürdige Streit der Kirche gegen den vorwärts schreitenden Menschengeist mit einer kläglichen Niederlage der ersteren«67.
Wir gelangen jetzt zu Galileis Arbeiten auf dem Gebiete der Mechanik. Diese Arbeiten waren in solchem Maße grundlegend, daß Galilei in seinem Hauptwerk über diesen Gegenstand, den »Unterredungen«, mit Recht von neuen Wissenszweigen sprechen durfte. Die Zeitgenossen zwar, soweit sie nicht vom Fanatismus geblendet waren, bewunderten vorwiegend seine Leistungen auf astronomischem Gebiete. Die Nachwelt hat jedoch erkannt, daß die Begründung des dynamischen Teiles der Mechanik eine Geistestat von weit höherem Range und weit größerer Bedeutung für den Fortschritt der menschlichen Erkenntnis war, als jene Beobachtungen, von denen, ohne das Verdienst Galileis zu schmälern, gesagt werden kann, daß sie jedes andere, mit einem guten Fernrohr bewaffnete Auge gleichfalls gemacht haben würde. Die »Unterredungen« dagegen bezeichnen den bedeutendsten Fortschritt der Mechanik seit Archimedes.
Mit mechanischen Problemen hatte sich Galilei, anknüpfend an Archimedes und im Kampfe gegen die irrigen Ansichten der Peripatetiker, während seiner ganzen Laufbahn beschäftigt. Nach seiner Verurteilung unternahm er es, die Ergebnisse seiner Forschungen zu dem genannten Hauptwerk68 zusammenzufassen. Bei dieser Arbeit hatte er wenigstens keine Belästigung von seiten kurzsichtiger Gegner zu befürchten.
Das Werk ist wie der »Dialog« in Gesprächsform abgefaßt. Simplicio verficht die Ansichten des Aristoteles. Sagredo und insbesondere Salviati entwickeln dagegen die Lehren Galileis.
Die neuen Prinzipien, die Galilei in die Naturwissenschaft einführte, betreffen vor allem die Dynamik oder die Lehre von der Bewegung der Körper, deren Ansätze wir bereits bei Lionardo da Vinci und einigen andern Forschern vorfanden69. Durch seine Untersuchung des Falles, der Wurf- und der Pendelbewegung zeigte Galilei, wie durch die Vereinigung von messender Beobachtung[S. 44] mit dem mathematischen Beweisverfahren an die Stelle unklarer, schwankender Begriffe wissenschaftliche Erkenntnis gesetzt werden kann. Er schuf so die Methode, die auf naturwissenschaftlichem Gebiete allein zur Auffindung der Wahrheit führt und der im weiteren Verfolg alle bewundernswerten Fortschritte der neueren Zeit zu danken sind.
»Der oberflächlichen Beobachtung ist es zwar nicht entgangen, daß die Geschwindigkeit frei fallender Körper mit der Fallzeit zunimmt. In welchem Maße aber die Beschleunigung stattfindet, ist bisher nicht ausgesprochen worden. Denn soviel ich weiß, hat niemand bewiesen, daß die vom fallenden Körper in gleichen Zeiten zurückgelegten Strecken sich zueinander wie die ungeraden Zahlen verhalten.« Mit diesen Worten leitet Galilei den dritten Abschnitt70 seiner »Unterredungen« ein. »Man hat beobachtet«, so fährt er fort, »daß die Wurfgeschosse eine gewisse Kurve beschreiben, daß letztere aber eine Parabel ist, hat niemand gelehrt. Daß aber dieses sich so verhält und noch vieles andere nicht minder Wissenswerte, soll von mir bewiesen werden. Zu dem, was noch zu tun übrig bleibt, wird die Bahn geebnet, nämlich zur Errichtung einer sehr weiten, außerordentlich wichtigen Wissenschaft, deren Anfangsgründe die vorliegende Arbeit bietet, in deren tiefere Geheimnisse einzudringen aber Geistern vorbehalten bleibt, die mir überlegen sind.« In diesen Worten sprechen sich zwei schöne Eigenschaften Galileis aus, Wertschätzung eigener Errungenschaften gepaart mit wahrer Bescheidenheit.
Wir wollen jetzt die wesentlichsten Punkte der »Unterredungen« einer kurzen Betrachtung unterziehen. Die Peripatetiker hatten eine Reihe von Naturerscheinungen, wie das Saugen, das Aneinanderhaften glatter Platten, das Aufsteigen von Flüssigkeiten in der Pumpe usw. darauf zurückgeführt, daß die Natur kein Vakuum, d. h. keinen leeren Raum zulasse. In Ermangelung eines mechanischen Prinzips dichtete man auf solche Weise der Natur ein psychisches Vermögen an. In dieser Vakuumtheorie bleibt Galilei noch befangen; aus ihr sucht er z. B. die Kohäsion zu erklären.
Die Kohäsion ist nach Galileis Ansicht auf zwei Ursachen zurückzuführen, einmal auf das Widerstreben der Natur, einen leeren Raum zuzulassen. Zweitens müsse ein Mittel angenommen[S. 45] werden, das die Teilchen der Körper fest miteinander verbinde. »Um dies zu beweisen,« sagt Galilei, »nehme man zwei völlig glatt polierte Marmorplatten. Legt man die eine auf die andere, so lassen sie sich leicht gegeneinander verschieben, offenbar ein Beweis, daß kein Bindemittel sie vereinigt. Gegen jede Trennung aber tritt ein Widerstand auf, so daß die obere Platte die untere tragen kann.« Ein solcher Widerstand, der so fühlbar zwischen den Platten sich zeige, sei ohne Zweifel auch zwischen den Teilen eines festen Körpers vorhanden und zum Teil wenigstens die Ursache ihres Zusammenhanges71.
Ein wesentlicher Fortschritt den bloßen Spekulationen seiner Vorgänger gegenüber ist es, daß Galilei überall das Experiment anwendet und daher auch die Größe des Widerstandes, den das Vakuum hervorruft, zu bestimmen sucht. Dies geschieht, indem ein Kolben aus einem mit Wasser gefüllten, die Öffnung nach unten kehrenden Zylinder herausgezogen und die Größe des hierzu erforderlichen Gewichts ermittelt wird (siehe Abb. 6). Galilei kennt auch die Erscheinung, daß das Wasser mittelst Pumpen nur auf eine Höhe von 18 Ellen gehoben werden kann. Tatsächlich wird in beiden Fällen die Größe des Luftdrucks gemessen. Durch Versuche gewonnene Ergebnisse besitzen also immer Wert, gleichgültig, ob die daran geknüpfte Theorie sie richtig deutet oder nicht.
Daß Galilei das Steigen von Flüssigkeiten und verwandte Erscheinungen nicht auf den Luftdruck zurückführte, ist um so verwunderlicher, als ihm die Tatsache, daß die Luft Gewicht besitzt, bekannt war. Aristoteles hatte der Luft und dem Feuer absolute Leichtigkeit, d. h. das Bestreben, sich in gerader Linie vom Mittelpunkt der Erde fortzubewegen, zugeschrieben. Wäre diese Annahme richtig, so würde, wie Galilei72 anführt, daraus folgen, daß beim Verdichten der Luft die Leichtigkeit und damit das Streben nach oben zunimmt. Der Versuch lehrte indes das Gegenteil. Galilei nahm einen Glaskolben und preßte mittelst[S. 46] einer Spritze Luft hinein. Dann wurde der Kolben auf einer genauen Wage ins Gleichgewicht gebracht. Öffnete man ihn jetzt, so trat die zusammengepreßte Luft heraus, und das Gefäß wurde merklich leichter, so daß von der Tara etwas fortgenommen werden mußte, um das Gleichgewicht wieder herzustellen. »Unzweifelhaft ist das Gewicht des Fortgenommenen«, sagt Galilei, »genau gleich dem der Luft, die gewaltsam hineingepreßt war«73.
Hatte man einmal die Luft als einen schweren Körper erkannt, so lag die Frage nahe, wie groß ihr Gewicht im Verhältnis zu demjenigen anderer Stoffe, z. B. des Wassers, sei. Auch diese Aufgabe, das spezifische Gewicht der Luft zu bestimmen, löste Galilei durch den Versuch74. Er preßte Wasser in einen mit Luft gefüllten Kolben, bis er zu dreiviertel seines Inhalts mit Wasser angefüllt war, ohne daß die Luft entweichen konnte. Das Gewicht dieses Gefäßes mit seinem Inhalt wurde bestimmt. Darauf wurde eine die komprimierte Luft abschließende Haut durchstochen, um diejenige Luftmenge, die vorher drei Viertel des Kolbens eingenommen hatte, entweichen zu lassen. Galilei wog jetzt wieder und fand einen dem Gewichte jener Luftmenge entsprechenden Unterschied. War diese Bestimmung bei den damaligen Hilfsmitteln und den der Methode anhaftenden Unvollkommenheiten auch keine genaue, so ergab sich doch, daß die Luft sehr viel leichter als das Wasser ist75.
Größeres als in der Physik der gasförmigen Körper, deren experimenteller Ausbau insbesondere auf deutschem Boden durch Otto von Guericke erfolgte, hat Galilei dadurch geleistet, daß er den Begriff der gleichmäßig beschleunigten Bewegung erörterte und durch Versuche nachwies, daß der Fall über die schiefe Ebene eine derartige Bewegung sei.
Zur genaueren Untersuchung der Fallbewegung wurde Galilei durch die Behauptung des Aristoteles geführt, daß verschiedene Körper in ein- und demselben Mittel mit verschiedener Geschwindigkeit sich bewegen sollten, und zwar proportional den Gewichten. Demnach müßten z. B. zwei Steine, deren Gewichte sich wie 1 : 10 verhalten, wenn man sie gleichzeitig 100 Ellen hoch herabfallen läßt, so verschieden in ihrer Bewegung sein, daß bei der Ankunft des größeren der kleinere erst 10 Ellen zurückgelegt haben würde. Galilei bezweifelte dies. Man darf jedoch nicht annehmen, daß sich nicht schon früher Zweifel geregt hätten. Es fehlte selbst nicht an älteren Versuchen zur Nachprüfung der aristotelischen Lehre76. Ja, Philoponos, der alexandrinische Kommentator des Aristoteles, bemerkte schon tausend Jahre vor Galilei, daß jene Lehre durch Versuche widerlegt werde. Philoponos tut dies mit folgenden Worten77: »Nach Aristoteles müssen, wenn das Medium, durch welches die Bewegung stattfindet, dasselbe ist, die Fallzeiten sich wie die Gewichte der bewegten Körper verhalten. Das ist aber, wie der Augenschein besser als jeder logische Beweis dartut, gänzlich falsch. Läßt man nämlich zwei an Schwere sehr verschiedene Körper gleichzeitig aus derselben Höhe herabfallen, so wird man sehen, daß die Fallzeiten sich nicht wie die Gewichte verhalten, sondern daß nur eine sehr geringe Verschiedenheit in bezug auf die Zeiten stattfindet«.
Um eine Entscheidung herbeizuführen, ließ Galilei, wie Viviani berichtet hat, vom schiefen Turm zu Pisa, der sich für Fallversuche trefflich eignete, eine halbpfündige Kugel und eine hundertpfündige Bombe herabfallen. Dabei eilte letztere nur um wenige Zoll voran78.
Die Verschiedenheiten in der Geschwindigkeit freifallender Körper führt Galilei lediglich auf den Widerstand der Luft zurück. Wenn man diesen Widerstand aufheben, mit anderen Worten einen luftleeren Raum herstellen könne, »so würden alle Körper gleich schnell fallen«.
Für Galilei blieb der Nachweis dieses Satzes, für den er nur einen hohen Grad von Wahrscheinlichkeit annehmen konnte, eine wissenschaftliche Utopie. Erst nach der Erfindung der Luftpumpe wurde dieser Nachweis zu einem Versuch, der in jedem elementaren Physikunterricht angestellt wird.
Wir wenden uns jetzt Galileis Versuchen und Betrachtungen über das Gesetz der Fallbewegung zu. Sie sind von größter Wichtigkeit, weil sie den Ausgangspunkt für die Entwicklung der Dynamik bilden. Galilei behandelte seine Aufgabe zuerst rein phoronomisch, d. h. als Problem der Bewegungslehre. Er stellte der gleichförmigen die gleichförmig beschleunigte Bewegung gegenüber und schuf den Begriff der gleichförmigen Beschleunigung79. Gleichförmig beschleunigt nennt Galilei diejenige Bewegung, bei der von Anfang an in gleichen Zeiten gleiche Geschwindigkeitszunahmen erfolgen.
Daß sich die Geschwindigkeit fallender Körper stetig vergrößert, konnte der frühesten Beobachtung nicht entgehen. Indessen von dieser Beobachtung bis zur Auffindung von Gesetz und Ursache war ein weiter Weg. Rein begrifflich hatte sich mit der gleichförmig beschleunigten Bewegung um die Mitte des 14. Jahrhunderts schon Oresme, einer der hervorragendsten Mathematiker des Mittelalters, befaßt. In einem um dieselbe Zeit entstandenen Kommentare heißt es, die Zeit, in der eine Wegstrecke bei gleichförmig beschleunigter Bewegung zurückgelegt werde, sei gleich der Zeit, in der dieselbe Strecke bei einer gleichförmigen Bewegung zurückgelegt werde, für welche die Geschwindigkeit das Mittel aus der geringsten und der größten Geschwindigkeit sei. Derartige begriffliche Untersuchungen sind von Einfluß auf Galilei gewesen, der sich zunächst mit der scholastischen Physik vertraut gemacht hatte80. Letztere erblickte die Ursache des Fallens in einer verborgenen Qualität, in einem dem Körper innewohnenden Streben nach »seinem Orte«. Die auf solche Weise hervorgerufene Bewegung sollte schneller werden, indem die Luft, die sich über[S. 49] dem fallenden Körper stets wieder zusammenschließt, dabei fortgesetzt einen neuen Antrieb ausübe. Im vollsten Gegensatz dazu behauptete Galilei, daß die Luft kein Mittel zur Beschleunigung sei, sondern vielmehr durch ihren Widerstand die Fallbewegung verzögere. Die experimentelle Probe konnte Galilei, wie gesagt, nicht machen, da ihm die Luftpumpe noch nicht zur Verfügung stand. War die Ansicht der älteren Physiker richtig, so hätten die Körper nach Fortnahme der Luft sich gleichförmig bewegen müssen, während doch, wie Galilei voraussah und spätere Versuche bewiesen, die Körper im luftleeren Raum erst recht deutlich die gleichförmig beschleunigte Bewegung erkennen lassen.
Sehr ausführlich sucht Galilei darzutun, daß der fallende Körper nach Verlauf des ersten, sehr kleinen Zeitteilchens eine von Null kaum verschiedene Geschwindigkeit besitzt. Daß der Körper seine Bewegung »mit unendlich großer Langsamkeit« beginnt, schließt Galilei auch aus dem Verhalten beim senkrechten Wurf. Man könne nicht zweifeln, daß der Zuwachs an Geschwindigkeit beim Fall in derselben Ordnung vor sich gehe, wie die Abnahme beim senkrechten Wurf. Bei letzterem werde die Geschwindigkeit allmählich ganz vernichtet. Bevor der Stein zur Ruhe komme, müsse er daher alle Grade der Langsamkeit durchgemacht haben.
Um zu einer richtigen Vorstellung von der Fall- und von der Wurfbewegung zu gelangen, bedurfte es einer Erweiterung des Trägheitsgesetzes. Daß ein ruhender Körper im Zustande der Ruhe beharrt und nur durch die Wirkung einer Kraft in den Zustand der Bewegung übergeht, war ein Satz, den Galilei nicht erst zu entdecken brauchte. Dieser Satz war stets, stillschweigend oder ausgesprochen, die Voraussetzung mechanischer Erörterungen gewesen. Wohl aber blieb es Galilei vorbehalten, irrtümliche und unklare Vorstellungen, die man sich über den Zustand der Bewegung gebildet hatte, zu berichtigen oder zu klären. Vor ihm herrschte die Meinung, jede Bewegung müsse auch ohne äußere Hindernisse endlich aufhören, wenn sie nicht durch eine Kraft unterhalten werde. Galilei dagegen erweiterte das Trägheitsgesetz dahin, daß ein sich bewegender Körper weder seine Geschwindigkeit noch seine Richtung ändert, wenn nicht eine Kraft auf ihn einwirkt. Wirkt aber eine Kraft, so ist, wie Galilei gleichfalls erkannte, die Größe ihrer Wirkung die gleiche, einerlei ob der Körper ruht oder sich bewegt. Da nun beim freien Fall eine Kraft ununterbrochen wirkt, so werden sich ihre Wirkungen stetig[S. 50] summieren, da jede einmal hervorgerufene Wirkung, dem Trägheitsgesetz zufolge, erhalten bleibt. Diese Summation bewirkt Galilei auf folgende Weise: AB stelle die Zeit t vor, in der ein Körper eine bestimmte Strecke, mit der Ruhelage beginnend, mit gleichförmig beschleunigter Bewegung zurücklegt. Die Gesamtzeit teile man in Zeitteilchen und trage die einem jeden entsprechenden Geschwindigkeitsbeträge senkrecht auf AB ab. EB sei die Endgeschwindigkeit v. Verbindet man dann sämtliche Endpunkte der senkrecht zu AB errichteten Strecken, so erhält man die Linie AE, die mit EB (v) und AB (t) ein Dreieck bildet. Errichtet man dann über FB = ½ EB = ½ v ein Parallelogramm, so erhält man zwei flächengleiche Figuren ABE und ABFG. Beide sind, wie aus der Größe der Stücke AB, EB und FB folgt, gleich (v·t)/2. Innerhalb der Zeit t legt somit ein Körper bei gleichförmig beschleunigter Bewegung den gleichen Weg zurück, als ob er sich während der Zeit t mit der sich stets gleichbleibenden Geschwindigkeit v/2 bewegt hätte. »Denn«, sagt Galilei, »was bei der beschleunigten Bewegung während der ersten Zeithälfte an Bewegung fehlt, entsprechend den Parallelen im kleinen Dreieck AGJ, wird während der zweiten Hälfte der Bewegung ersetzt durch den Überschuß, den die Parallelen in dem AGJ flächengleichen kleinen Dreieck EFJ vorstellen.«
Aus der auf solche Weise gewonnenen Grundvorstellung, nach welcher der Weg bei einer gleichförmig beschleunigten Bewegung gleich dem Produkt aus der Zeit und der halben Endgeschwindigkeit ist (s = v/2·t), folgen nun die übrigen Fallgesetze rein mathematisch. So bewies denn Galilei im Anschluß an dieses Grundgesetz den Satz, daß, wenn ein Körper von der Ruhelage aus gleichförmig beschleunigt fällt, die in bestimmten Zeiten zurückgelegten Strecken sich wie die Quadrate der Zeiten verhalten. Wird nämlich v = gt, so ist s = (g/2)·t2. Daraus schloß Galilei weiter, daß sich die Fallstrecken, die in gleichen Zeiten zurückgelegt werden, wie die ungeraden Zahlen 1, 3, 5, 7 ... verhalten[S. 51] müssen. Dies ergibt sich, wenn wir die Unterschiede der Fallräume für t = 1, 2, 3, 4 ... bilden.
Die Größe der Beschleunigung für den freien Fall zu bestimmen, gelang Galilei noch nicht. So gibt er an, eine eiserne Kugel sei nach wiederholt angestellten Versuchen aus einer Höhe von 100 Ellen, das sind etwa 60 m, in 5 Sekunden herabgefallen81. In Wahrheit würde der Fallraum für diese Zeit aber mehr als das Doppelte (122 m) betragen. Galilei konnte zwar den Einfluß des Luftwiderstandes noch nicht in Rechnung ziehen, nichtsdestoweniger ist der Fehler, den er beging, auffallend groß, da sich aus seinen Versuchen für die Beschleunigung nur der Wert von 5 m ergab. Erst Huygens stellte fest, daß der Geschwindigkeitszuwachs 10 m beträgt, so daß ein Körper nach Ablauf der 1., 2., 3. ... Sekunde eine Geschwindigkeit von 10, 20, 30 ... Metern besitzt. Solche Größen ließen sich durch unmittelbare Beobachtung nicht gut messen. Galilei suchte deshalb nach einem Mittel, die Fallgeschwindigkeit zu vermindern. Als solches schien ihm die schiefe Ebene besonders geeignet. Es sei bekannt, so führt er aus, daß die Geschwindigkeiten ein und desselben Körpers bei verschiedenen Neigungen der Ebene verschieden groß seien. Den größten Wert habe die Geschwindigkeit bei senkrechter Richtung. Die Geschwindigkeit sei um so geringer, je mehr die Ebene vom Lot abweiche. Es zeige sich also, daß der Impuls, die Energie oder die Tendenz zum Fall82 durch die Ebene, auf welche der Körper sich stützt, vermindert werde. Galilei bestimmt auch die Abhängigkeit der Impulse von den Neigungswinkeln und zeigt, daß der Impuls, den der Körper beim freien Fall erhält, und derjenige, der längs der schiefen Ebene wirkt (der in ihrer Richtung wirkenden Seitenkraft oder Komponente, würden wir heute sagen), sich wie die Länge zur Höhe der schiefen Ebene verhalten83.
Die schiefe Ebene war somit, weil dem geringeren Impulse auch ein geringerer Geschwindigkeitszuwachs entspricht, vortrefflich geeignet, die Schlüsse, zu denen Galilei über den Verlauf einer gleichförmig beschleunigten Bewegung gekommen war, experimentell auf ihre Richtigkeit zu prüfen. »Denn«, sagt er, »die Prinzipien sind durch Versuche zu erhärten, und diese bilden die Grundlage für den ganzen späteren Aufbau.«
Über seine Versuche mit der schiefen Ebene gibt uns Galilei folgenden Bericht84: In einem Brett von 12 Ellen Länge wurde eine Rinne von einem halben Zoll Breite hergestellt. Sie wurde gerade gezogen und mit sehr glattem Pergament ausgekleidet. Das Brett wurde darauf an dem einen Ende gehoben, bald eine, bald zwei Ellen hoch. Sodann ließ Galilei eine glatt polierte Messingkugel durch die Rinne laufen und bestimmte die Fallzeit für die ganze Länge der Rinne. Ließ er dagegen die Kugel nur durch ¼ der Rinne laufen, so erforderte dies genau die halbe Zeit. Die Strecken verhielten sich somit wie 1 : 4, wenn die Fallzeiten in dem Verhältnis 1 : 2 standen; allgemeiner ausgedrückt: die Strecken verhielten sich wie die Quadrate der Zeiten. Daß dieses Gesetz nicht nur in dem gewählten Beispiel seine Richtigkeit hat, sondern eine für alle Fälle zutreffende Regel ist, wurde durch hundertfache Wiederholung unter jedesmaliger Abänderung der Strecke und des Neigungswinkels dargetan.
Zur genaueren Bestimmung der Fallzeit diente folgende Vorrichtung: Ein größeres Gefäß war mit Wasser gefüllt und besaß eine enge Öffnung im Boden, durch die sich ein feiner Strahl ergoß. Dieser wurde während jeder Beobachtungszeit in ein kleineres Gefäß geleitet. Die auf solche Weise aufgefangene Flüssigkeitsmenge wog man mittels einer sehr genauen Wage. Aus den Differenzen der Wägungen ergab sich das Verhältnis der Gewichte. Es entsprach dem Verhältnis der Zeiten mit solcher Genauigkeit, daß die zahlreichen Beobachtungen niemals merklich voneinander abwichen.
Wir haben Galileis Versuchen mit der schiefen Ebene eine etwas größere Ausführlichkeit gewidmet, weil sie eine der ersten, bis zur Auffindung des Naturgesetzes durchgeführten Versuchsreihen darstellen.
Galilei erkannte auch, daß die Geschwindigkeiten, die beim Falle über die schiefe Ebene erlangt werden, nur von der Höhe und nicht von der Neigung abhängen. Ein Körper wird demnach, wenn er von C nach A und ein anderes Mal von C nach D gelangt (Abb. 8), in A und in D die gleiche Geschwindigkeit haben. Und zwar ist die Geschwindigkeit dieselbe, als wenn der Körper im freien Fall von C nach B gelangt wäre.
Daß die Geschwindigkeiten eines Körpers, der durch die Schwerkraft auf beliebiger Bahn zur selben Horizontalebene hinabsteigt, unter der Voraussetzung, daß keine Widerstände die Bewegung hemmen, sämtlich gleich sind, bewies Galilei noch durch folgenden Versuch. Er ließ das einfache Pendel AB vor einer Wand schwingen, so daß es den Bogen CBD beschrieb. Das Pendel wird dann, indem es durch den Bogen BD ansteigt, fast bis zur Horizontalebene CD gelangen und nur ein kleines Stück darunter bleiben, einzig und allein deshalb, weil infolge des Widerstandes der Luft und des Fadens das Pendel an der genauen Rückkehr in dieselbe Horizontalebene gehindert wird.
Befestigt man darauf bei E einen Nagel in der unmittelbar hinter dem Pendel befindlichen Wand, so wird das Pendel dadurch gezwungen, den Bogen BG um E als Mittelpunkt zu beschreiben. Es wird aber, von der erwähnten kleinen Ungenauigkeit abgesehen, wieder dieselbe Horizontalebene CD erreichen. Das gleiche ist der Fall, wenn der Nagel in F angebracht wird. Nur wird das Pendel diesmal wieder einen anderen Bogen und zwar BJ durchlaufen. Es sind folglich alle Momente und alle Geschwindigkeiten, mit denen sich das Pendel durch B bewegt, gleich groß. Wenn wir die Bewegung in D, G oder J anfangen lassen, so wird das Pendel auf der anderen Seite stets bis C steigen. Folglich sind auch alle Momente, beziehungsweise Geschwindigkeiten, die beim Durchlaufen der so verschiedenen Bahnen DB, GB, JB hervorgerufen werden, einander gleich.
An dieser Stelle begegnet uns also im Grunde schon, angewandt auf den Fall der Pendelbewegung, jene Vorstellung, welche unter der Bezeichnung des Prinzips von der Erhaltung der Kraft das Fundament der gesamten Naturerklärung bildet. Ist doch die Erkenntnis, daß ein frei fallender Körper infolge der erlangten Geschwindigkeit gerade zu seiner ursprünglichen Höhe wieder emporzusteigen vermag, für alle späteren Vorstellungen, die man sich über die Erhaltung der Kraft gebildet hat, grundlegend geblieben. Es erübrigte nur, die an dem einzelnen Körper gewonnene Erkenntnis auf ein System von Körpern[S. 54] zu übertragen, eine Erweiterung des Prinzips, die, wie sich später zeigen wird, Huygens vollzog.
Wir wollen jetzt die leitenden Gesichtspunkte und Versuche kennen lernen, die Galilei zur Erklärung der Pendel- und der Wurfbewegung geführt haben, und uns dabei eng an die von ihm selbst gegebene Darstellung anschließen.
Galilei hatte bei seinen Versuchen neben einer Verringerung der Beschleunigung stets eine Herabminderung des Widerstandes im Auge. »Läßt man zwei an Gewicht verschiedene Körper fallen,« so führt er aus, »etwa eine Kork- und eine Bleikugel, so wird die Luft, die stets verdrängt und zur Seite geschoben werden muß, einen größeren Einfluß auf den leichteren Körper ausüben als auf den mit einem heftigeren Antrieb begabten schwereren. Der erste wird infolgedessen zurückbleiben.«
Wenn auch der Widerstand der Luft durch die Verlangsamung, welche der Fall bei der schiefen Ebene erfährt, hinreichend vermindert wird, so ließ sich doch nicht verkennen, daß durch die Berührung mit dieser Ebene ein neuer Widerstand auftrat. Gab es nun ein Mittel, den Einfluß dieses Widerstandes zu beseitigen? Das letztere wurde erreicht, indem man die Kork- sowie die Bleikugel an zwei gleichen, feinen Fäden von 4–5 Ellen Länge aufhing. Entfernte man dann beide Körper aus der Ruhelage und ließ sie gleichzeitig los, so wurden Kreisbögen von gleichen Halbmessern beschrieben. Die Kugeln schwangen über ihre ursprüngliche Lage hinaus und kehrten auf denselben Wegen zurück. Nachdem sie sehr oft hin- und hergegangen waren, zeigte sich deutlich, daß die Bewegung des schwereren Körpers so sehr mit derjenigen des leichteren übereinstimmte, daß kaum eine Verschiedenheit zu bemerken war. Die Pendelbewegung stellte sich somit als eine Fallbewegung dar, bei welcher der Widerstand des Mittels sehr eingeschränkt und der bei einer geneigten Ebene vorhandene Reibungswiderstand vermieden ist.
Noch eine weitere Ähnlichkeit zwischen der Pendelbewegung und dem Fall über die schiefe Ebene ließ sich erkennen: Galilei hatte gezeigt85, daß ein Körper, welcher längs der zu einem beliebigen Bogen gehörigen Sehne herabfällt, z. B. von A, B, C, D oder E nach F, die gleiche Zeit gebraucht, einerlei ob der entsprechende[S. 55] Bogen volle 180° oder weniger beträgt. Auch für ein um A schwingendes Pendel ergab sich, daß es in der gleichen Zeit, in der es den Weg E1F (der Sehne EF entsprechend) zurücklegt, bei größerem Ausschlage die Strecke D1F (entsprechend der Sehne DF) durchfällt. Hatte man z. B. das Bleipendel um 50° von dem Lote entfernt86 und ließ man es frei schwingen, so beschrieb es jenseits des Lotes gleichfalls nahezu 50°, im ganzen also 100°. Zurückkehrend, beschrieb es einen etwas kleineren Bogen und gelangte nach einer großen Anzahl von Schwingungen endlich zur Ruhe. Jede dieser Schwingungen kam in einer sich stets gleich bleibenden Zeit zustande, sowohl die von 50° Ausschlag, wie diejenigen von 20° oder 10°. Die Geschwindigkeit nahm also allmählich ab, da in gleichen Zeiten immer kleinere Bögen beschrieben wurden87.
Ganz denselben Vorgang nahm Galilei bei der Korkkugel wahr, wenn er sie an einem ebenso langen Faden befestigte. Nur daß die Korkkugel nach einer kleineren Zahl von Schwingungen zur Ruhe kam. Alle Schwingungen geschahen in gleichen Zeiten, und zwar in derselben Zeit wie die Schwingungen der Bleikugel.
Für größere Ausschläge des Pendels besitzt, wie man später erkannte, dieses Gesetz nicht mehr die volle Gültigkeit, da der Kreisbogen keine Isochrone, d. h. keine Kurve gleicher Schwingungsdauer ist. Huygens wies später nach, daß dies aber für die Zykloide zutrifft. Da die Krümmung beider Kurven in der Nähe der Ruhelage F jedoch (s. Abb. 11) nahezu gleich ist, so[S. 56] gilt das Gesetz von der Isochronie der Pendelschwingungen für kleine Ausschlagswinkel mit hinreichender Genauigkeit. Auffallend bleibt es allerdings, daß Galilei den bei größeren Winkeln eintretenden Unterschied nicht erwähnt. Es geschah dies wohl daher, weil er ihn allein auf den wachsenden Widerstand des Mediums bei der schnelleren Bewegung durch einen größeren Kreisbogen zurückführte. Überhaupt beschränkt sich Galilei vorwiegend auf die experimentelle Erforschung der Pendelbewegung, während ihre mathematische Analyse späteren Jahrzehnten vorbehalten blieb. Wieder war es Huygens, dem wir die Formel für diese Bewegung, sowie die Verwendung des Pendels in den Uhren verdanken. Der Gedanke, das Pendel zur Zeitmessung zu verwenden, ist Galilei indessen auch schon gekommen88.
Auch die Heilkunde hatte sich zu Anfang des 17. Jahrhunderts dieses Gedankens bemächtigt. So findet sich ein zur Pulszählung dienendes Instrument in einem 1602 erschienenen Buche beschrieben. Es bestand89 aus einer Bleikugel, die der Arzt an einer langen Schnur hielt. Man brachte die Schwingungen dieses Pendels mit dem Puls in Übereinstimmung und las dann die Pendellänge an einer Skala ab.
Galilei hat seinem Sohne und seinem Schüler Viviani, wie aus dessen Aufzeichnungen hervorgeht, kurz vor seinem Tode sogar die Konstruktion einer Pendeluhr entwickelt.
Sie besaß folgende Einrichtung. An dem Pendel AB (Abb. 12) ist eine starke Borste C befestigt. Diese greift in eine Lücke des Zahnrades D, das sich auf der Achse F drehen kann. Es ist ersichtlich, daß die Borste bei jedem Hin- und Hergehen des Pendels dem Rädchen eine Drehung um einen Zahn erteilt. Diese Drehung ließ sich leicht auf ein Zählwerk übertragen. Nur bedurfte das Pendel, damit es nicht schließlich stillstand, von Zeit zu Zeit eines Anstoßes. Galileis Bemühen mußte sich ganz[S. 57] naturgemäß darauf richten, diesen Anstoß durch eine mechanische Vorrichtung herbeizuführen. Abb. 13 gibt Galileis Zeichnung wieder, die er kurz vor seinem Tode anfertigen ließ90. Über die[S. 58] Prioritätsansprüche ist man geteilter Ansicht. Jedenfalls hat Huygens die Pendeluhr unabhängig von Galileis Vorarbeiten erfunden.
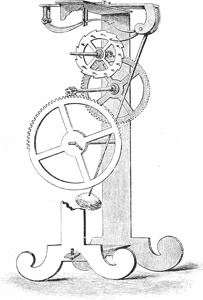
Galilei dehnte seine Untersuchungen auch auf Pendel verschiedener Länge aus und fand, daß ein Pendel, um doppelt so langsam zu schwingen wie ein anderes, viermal so lang sein muß, während der neunfachen Länge eine dreimal so große Schwingungszeit entspricht, so daß sich also die Pendellängen wie die Quadrate der entsprechenden Schwingungszeiten verhalten92.
Man vermöge daher, fügt Galilei hinzu, sofort die Länge eines Pendels von beliebiger Länge zu berechnen, auch wenn sein Aufhängepunkt unsichtbar sei und man nur das untere Ende beobachten könne. Galilei gibt dazu folgendes Beispiel: »Während mein Gehilfe einige Schwingungen zählt, beobachte ich die Schwingungszahl eines anderen Pendels von genau einer Elle Länge. Angenommen mein Gehilfe habe 20 Schwingungen gezählt, während ich 240 erhalten habe. Die Quadrate dieser Zahlen sind 400 und 57600. Das lange Pendel enthält somit 57600 solcher Teile, von denen 400 auf eine Elle gehen. Seine Länge ist also 57600 : 400 gleich 144 Ellen.«
Nachdem die Pendelbewegung als eine Modifikation der Fallbewegung erkannt war, ergab sich dem Scharfsinn Galileis dasselbe für den Wurf. Bezüglich dieses Vorganges war die bloße Spekulation zu den ungereimtesten Ansichten gelangt. Einige Klarheit findet sich zwar schon bei den Vorläufern Galileis93. Diesem blieb es jedoch vorbehalten, auf Grund der von ihm erkannten Prinzipien eine wahre und erschöpfende Analyse der Wurfbewegung zu geben. Es war dies zunächst das Prinzip der Trägheit oder des Beharrungsvermögens. Danach ist die Bewegung auf einer unbegrenzten horizontalen Ebene, wenn alle Widerstände ausgeschlossen sind, gleichförmig und unaufhörlich94. Wird dann, so lautet das zweite Prinzip, der in Bewegung begriffene Körper einer Kraft unterworfen, so setzt sich die neue Bewegung, die aus der Wirkung jener Kraft hervorgeht, mit der ersten, schon bestehenden zusammen.
Wahrscheinlich hat Galilei diese beiden Grundprinzipien der Mechanik, nämlich das Trägheitsgesetz und das Gesetz von der gegenseitigen Unabhängigkeit der auf einen Körper einwirkenden Kräfte, aufgestellt, um das Koppernikanische System darauf zu stützen. Man geht sogar so weit, diese Prinzipien weniger als das Ergebnis von Versuchen, denn als Folgerungen aus dem Koppernikanischen System anzusehen95. Richtiger ist wohl, daß Galilei die Ergebnisse der Erforschung irdischer mechanischer Vorgänge mit den nach der Theorie des Koppernikus gedeuteten Himmelserscheinungen in gutem Einklang fand.
Im Grunde genommen handelt es sich bei Galileis Untersuchung des Wurfes zunächst um die Anwendung des Gesetzes vom Parallelogramm der Bewegungen, das uns bei ihm zum erstenmal als allgemeines Prinzip begegnet, und noch nicht um das Gesetz vom Parallelogramm der Kräfte, das sich zuerst in voller Klarheit in Newtons Prinzipien ausgesprochen findet. Andererseits betrachtete aber schon Galilei die erzeugten Bewegungen nicht rein phoronomisch, sondern er faßte sie auch als Wirkungen von Kräften auf. Mit Recht aber gilt es als einer der wichtigsten Fortschritte der Mechanik, daß Galilei die Umstände, welche die Bewegungen veranlassen, in ihren Wirkungen als unabhängig voneinander erkannte. Newton selbst hat ihn deshalb als den Entdecker des Satzes vom Parallelogramm der Kräfte bezeichnet96. Wären Galilei indessen die in diesem Satz enthaltenen Vorstellungsweisen so geläufig gewesen wie die Zusammensetzung der Bewegungen, so würde er den Satz vom Parallelogramm der Kräfte auf statische Probleme, wie sie z. B. das Verhalten der Körper auf der schiefen Ebene darbietet, angewandt haben. Sehen wir jetzt an einem besonderen Fall, wie Galilei die von ihm erkannten, soeben erwähnten Prinzipien anwendet.
Ist die horizontale Ebene, auf der ein Körper sich dem Gesetz der Trägheit zufolge fortbewegt, nicht unendlich, sondern begrenzt, so wird der Körper, am Ende der Ebene angelangt, sich zwar weiter bewegen, zu seiner gleichförmigen unzerstörbaren Bewegung wird sich indes die durch die Schwerkraft erzeugte gesellen, so daß eine zusammengesetzte Bewegung entsteht. Solcher Art nun ist die Wurfbewegung. Der Körper wird eine Bahn von stetiger[S. 60] Krümmung beschreiben, und zwar, wie sich leicht zeigen läßt, eine Halbparabel.
Die horizontale Ebene, längs der sich der Körper gleichförmig fortbewegt, sei AB. Am Ende B der Ebene fehlt die Stütze, und der Körper unterliegt infolge seiner Schwere einer Bewegung längs der Senkrechten BN. Man denke sich AB nach E hin fortgesetzt und teile gewisse gleiche Strecken BC, CD, DE darauf ab. Gelangt der Körper infolge seiner gleichförmigen Bewegung nach C, so denken wir uns das durch den Fall bedingte Stück CJ hinzugefügt. Der Körper wird sich somit nach Ablauf derjenigen Zeit, welche der Bewegung von B nach C entspricht, im Punkte J befinden. Während der Körper infolge der gleichförmigen Bewegung von C nach D gelangt, also dasselbe Stück zurücklegt wie vorher, ist die Fallstrecke gleich 3CJ oder der Gesamtfallraum DF gleich 4CJ. Hat endlich nach Ablauf des dritten Zeitteils der Körper infolge der gleichmäßigen Bewegung die dreifache Strecke BE zurückgelegt, so würde ihn der Fall von B nach L geführt haben, welche Strecke das Neunfache von CJ ist usf. Nun verhalten sich die Quadrate von BC, BD und BE, welche Stücke man als die Ordinaten der Kurvenpunkte J, F und H bezeichnet, wie die Strecken CJ, DF und EH, nämlich wie 1 : 4 : 9. Diese Strecken CJ, DF und EH sind die Abszissen der Punkte J, F und H. Die analytische Geometrie lehrt aber, daß alle Punkte, deren Abszissen sich verhalten wie die Quadrate der zugehörigen Ordinaten, einer Parabel angehören97.
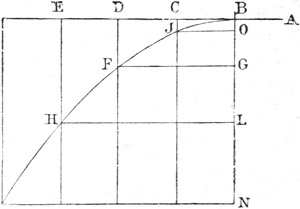
Galilei zeigte dann, daß der schräg aufwärts gerichtete Wurf nichts neues darbietet, sondern in der gleichen Weise aus zwei Bewegungen hervorgeht, deren Zusammensetzung als Wurfbahn[S. 61] wieder eine Parabel liefert. Er bestimmt auch die Parabelamplituden (Wurfweiten) und weist nach, daß Körper, die mit gleicher Anfangsgeschwindigkeit (»gleichen Impulsen«) unter Winkeln abgeschossen werden, die nach oben und unten gleich viel von 45° abweichen, dieselbe Wurfweite besitzen99.
Aus der Tatsache, daß beim Spannen eines Seiles auch zwei Kräfte wirken, nämlich die horizontale Spannkraft und das in vertikaler Richtung wirkende Gewicht des Seiles, leitet Galilei die Erscheinung ab, daß das Seil stets die Form einer krummen Linie annimmt und bei einiger Länge nicht vollkommen horizontal ausgespannt werden kann. Galilei ist oft des Irrtums geziehen worden, daß er jene Linie, die später Kettenlinie genannt wurde, mit der Parabel verwechselt habe. Er sagt aber ausdrücklich, daß nicht gleiche, sondern nur ähnliche Verhältnisse vorlägen und das gespannte Seil sich der parabolischen Form nur nähere100.
Obgleich Galilei sehr wohl wußte, daß die Wurflinie durch den Luftwiderstand bedeutende Änderungen erfährt, hat er letzteren bei seinen Ableitungen doch außer Betracht gelassen. Daß die Ergebnisse der Theorie in der Wirklichkeit durch eine Reihe von Nebenumständen beeinflußt werden, ohne jedoch deshalb ihren Wert zu verlieren, war ihm vollkommen klar. Er selbst beweist in aller Ausführlichkeit, daß genau genommen weder die durch den Stoß hervorgerufene Bewegung gleichförmig, noch die Fallbewegung gleichförmig beschleunigt, noch die Wurfkurve eine Parabel ist. Letzteres treffe schon deshalb nicht zu, weil die Richtung der Schwerkraft nicht sich gleich bleibt, sondern sämtliche Lote nach dem Erdmittelpunkte zusammenlaufen. Bei weiten Würfen aus Geschützen müsse dieser Umstand die Form der Kurve, ganz abgesehen von dem Widerstand der Luft, schon merklich beeinflussen. Wir sehen, daß hier schon im Keime das Problem der Zentralbewegung, deren Gesetze erst Newton und Huygens ermittelten, gegeben ist. Die durch den Stoß hervorgerufene, der Theorie nach gleichförmige Bewegung wird aber, wie Galilei weiter ausführt, durch den Luftwiderstand nicht nur verzögert, sondern schließlich ganz vernichtet; und zwar geschehe dies um so schneller, je leichter der Körper sei. Jede Fallbewegung müsse[S. 62] endlich, auch bei den schwersten Körpern, infolge des mit der Geschwindigkeit sehr stark anwachsenden Widerstandes der Luft in eine gleichförmige Bewegung übergehen. Um dies zu entscheiden, empfiehlt Galilei, je eine Kugel aus großer und aus geringer Höhe senkrecht herabzuschießen. Obgleich der Theorie nach im ersten Fall die Wirkung eine größere sein müsse, so werde man doch das Umgekehrte finden, weil der Luftwiderstand die Geschwindigkeit, die dem Geschoß durch die Kraft des Pulvers erteilt werde, auf dem größeren Wege bedeutender hemme als auf dem kleineren101. Beim schrägen Wurf müsse aus demselben Grunde die Gestalt der Wurfkurve um so mehr von der Parabel abweichen, je größer die Anfangsgeschwindigkeit sei. Die Nebenumstände, die bei der Wurfbewegung in Betracht kommen, hat Galilei somit erkannt und ihre Wirkung richtig ermessen. Er kommt indessen zu der Ansicht, daß über all die unendlich verschiedenen Möglichkeiten, die hinsichtlich der Schwere, der Geschwindigkeit und der Form des geworfenen Körpers bestehen, keine Theorie gegeben werden könne. Es bedurfte einer bedeutenden Fortentwicklung der mathematischen Analyse und der Experimentierkunst, um das »ballistische« Problem zu bewältigen und die wirkliche Bahn eines geworfenen Körpers, die »ballistische Kurve« zu bestimmen. Erst im 18. Jahrhundert haben Johann Bernoulli und andere102 eine angenäherte Lösung dieser Aufgabe gefunden103.
Hiermit verlassen wir Galileis Untersuchungen über die Fall- und Wurfbewegung, welche den dritten und vierten Tag seiner »Unterredungen« ausfüllen und hier nur skizzenhaft geschildert werden konnten. Diese Untersuchungen werden mit Recht als die hervorragendste Leistung Galileis bezeichnet. Erst wenn man berücksichtigt, daß Galilei auf diesem Gebiete kaum etwas anderes vorfand als irrige Meinungen, vermag man den Ausspruch Lagranges zu würdigen, daß ein außerordentliches Genie dazu gehörte, um diesen Teil der »Unterredungen«, den man nie genug bewundern könne, zu verfassen.
Wie wir sahen, liegen die Hauptverdienste Galileis auf dem Gebiete der Dynamik. Ja, er hat diesen Teil der Mechanik, von dem vor ihm nur einige verhältnismäßig unbedeutende, durch Lionardo da Vinci, Tartaglia, Benedetti und andere geschaffene Ansätze vorhanden waren, erst von Grund aus geschaffen. Die Fundamente der Statik hatte die neuere Zeit dagegen aus dem Altertum überliefert bekommen. Doch war auf diesem Gebiete von Archimedes bis Galilei so wenig geschehen, daß letzterem auch hier nicht nur die schärfere Begründung der schon bekannten Sätze, sondern auch die Auffindung mancher neuen Wahrheit vorbehalten blieb.
Vor allem verdanken wir Galilei jene eigentümliche Verbindung statischer und dynamischer Grundsätze, die wir heute als das Prinzip der virtuellen, d. h. möglichen Geschwindigkeiten oder Verschiebungen bezeichnen. Man versteht darunter die Geschwindigkeiten, welche die Punkte eines Systems, an dem sich Kräfte das Gleichgewicht halten, in dem Momente annehmen würden, in dem das Gleichgewicht gestört wird. Das neue Prinzip besagt, daß die im Gleichgewicht befindlichen Kräfte sich umgekehrt wie jene Wege oder Verschiebungen verhalten. Findet die zunächst nur gedachte Verschiebung wirklich statt, so ist die bei der einen Bewegung geleistete Arbeit gleich derjenigen, die bei der entgegengesetzten Bewegung geleistet würde. Wie an Hand dieser Vorstellungsweise verborgene statische Beziehungen als bestimmte Verhältnisse hervortreten, möge an einigen Beispielen aus Galileis Schriften gezeigt werden. So ergibt sich die Bedingung für das Gleichgewicht am Hebel aus dem Prinzip der virtuellen Geschwindigkeiten104 folgendermaßen: Zwei Kräfte P und Q (Abb. 15) greifen an den Armen des Hebels ACB unter einem rechten Winkel an. Die Verschiebungen bei einer Störung des Gleichgewichts sind AD und BE. Diese können für einen sehr kleinen Winkel als gerade, zu ACB senkrechte Stücke betrachtet werden. Es verhalten sich dann die Kräfte, wenn Gleichgewicht besteht, umgekehrt[S. 64] wie diese Verschiebungen (P : Q = BE : AD). Auf solche Weise erkannte Galilei die Wahrheit, daß bei jeder Maschine das, was an Kraft gewonnen wird, an Weg wieder verloren geht.
In ähnlicher Weise dehnt Galilei die Betrachtung an Hand des neuen Prinzips, das er, ohne es mit einem besonderen Ausdruck zu benennen, bei allen statischen Untersuchungen anwendet, auf den Flaschenzug und auf die schiefe Ebene aus. Das Gleichgewicht auf letzterer untersucht er für den Fall, daß ihre Länge das Doppelte der Höhe beträgt (Abb. 16). Es ist dann P = Q/2. Wie Galilei hervorhebt, wird das Gleichgewicht auch durch die mögliche Annäherung und Entfernung der Gewichte in bezug auf den Erdmittelpunkt bestimmt105. Sinkt nämlich P um h, so steigt Q längs AB um h/2. Die Produkte aus dem bewegten Gewicht und der Bewegung in vertikaler Richtung P · h und Q h/2 sind aber gleich, da ja P = Q/2 ist.
Durch die Ermittlung der möglichen Verschiebungen findet Galilei auch das Verhältnis von Kraft und Last beim Flaschenzug. Er gelangt unter der Voraussetzung, daß die Wege s und w der Kraft und der Last sich verhalten wie die Zahl der Seilstücke, über welche sich die Last verteilt, zu der Gleichung P · s = Q · w. An Stelle vorher zur Beurteilung des Gleichgewichts allein maßgebender statischer Momente benützt Galilei für diesen Zweck die Produkte aus den Gewichten und den Falltiefen, d. h. die Arbeit, und erkennt als die Bedingung des Gleichgewichts den Satz, daß die Arbeit der Kraft (Kraft mal Kraftweg) gleich der Arbeit der Last (Last mal Lastweg) ist.
Die Gleichung P · s = Q · w führt auf die Proportion P : Q = w : s. In Worten: Wenn zwei Kräfte im Gleichgewicht stehen, so verhalten sie sich umgekehrt wie die entsprechenden Wege. Oder auch: Was man mit einer Maschine an Kraft ersparen kann, geht an Weg verloren. Man hat diesen Grundsatz wohl nach Descartes benannt. In Wahrheit aber ist auch er auf Galilei zurückzuführen.
Die wesentlichste Unfertigkeit, welche für die Mechanik trotz dieser Erfolge zunächst noch bestehen blieb, war der Mangel einer klaren Einsicht in das Gesetz vom Parallelogramm der Kräfte. Galilei kannte zwar das Parallelogrammgesetz, er wandte es aber, wie wir bei seiner Untersuchung der Wurfbewegung sahen, nur zur Zusammensetzung von Bewegungen an. Dagegen findet sich bei ihm kein Fall einer statischen Anwendung des Prinzips von der Zusammensetzung der Kräfte.
Unfertig waren auch die Vorstellungen, zu denen Galilei hinsichtlich des Wesens und der Wirkung des Stoßes gelangte. Seine dynamischen Untersuchungen waren erfolgreich, solange er sich auf die Wirkung von Kräften auf eine einzige Masse beschränkte, wie es bei der Fall-, der Pendel- und der Wurfbewegung zutrifft. Bei der Stoßbewegung liegt nun eine Aufgabe höherer Ordnung vor, da es sich hier um das Verhalten von wenigstens zwei Massen unter der Wirkung von Kräften handelt. Die Schwierigkeit dieses Problems ahnte schon das Altertum, als es die Frage aufwarf, warum ein kleiner Stoß auf einen Keil viel mehr ausrichten könne als ein großer Druck106. Galilei widmete dem Problem einen ganzen Abschnitt seiner »Unterredungen«. Und wenn er es auch nicht auf mathematisch formulierte Gesetze zurückzuführen vermochte, so ist doch der Grad der Einsicht, zu dem er gelangte, ein hoher und für die weiteren Fortschritte bedeutsamer gewesen.
Mit voller Klarheit spricht es Galilei aus, daß die Kraft beim Stoße von zwei Umständen abhängt, die beide die zu messende Energie bestimmen, nämlich von der Masse des stoßenden Körpers und von seiner Geschwindigkeit. Galilei hebt hervor, daß jeder Stoß Arbeit leistet, während das ruhende Gewicht keine Arbeit leistet. Daher rührt auch seine Vorstellung, daß die Kraft des Stoßes im Verhältnis zur Kraft des bloßen Druckes gleichsam unendlich sei, weil bei letzterem der eine, die Energie mitbestimmende Faktor, die Geschwindigkeit nämlich, gleich Null ist.
Galilei braucht daher für das ruhende, nur einen Druck ausübende Gewicht mitunter den bekannt gewordenen Ausdruck totes[S. 66] Gewicht (Peso morto). Seine Anschauung entspricht durchaus der heutigen Vorstellungsweise, nach welcher die Bewegungsgröße eine andere Dimension als der Druck besitzt und letzterer sich somit zum Moment des Stoßes wie die Linie zur Fläche verhält. Wenn also Galilei sagt, die Kraft des Stoßes sei im Verhältnis zur Kraft des Druckes unbegrenzt groß107, so liegt darin nichts Unklares, wie man ihm wohl vorgeworfen hat. Man muß vielmehr in diesem Ergebnis die glänzende Verstandesschärfe Galileis anerkennen und zugeben, daß das Wesen der Sache ohne die Anwendung einer mathematischen Formel kaum zutreffender ausgedrückt werden konnte.
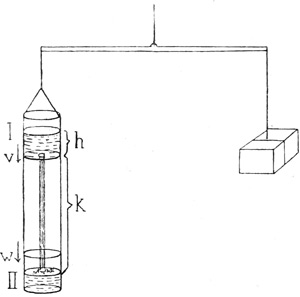
In seine Betrachtungen über das Wesen des Stoßes hat Galilei einen Versuch eingeflochten, der zu den später entdeckten Kräftebeziehungen, die sich innerhalb eines Systems von Körpern darbieten, hinüberleitet. Galilei brachte an einer Wage zwei übereinander befindliche Eimer durch ein Gegengewicht ins Gleichgewicht. Von diesen Eimern war der obere mit Wasser gefüllt, der untere dagegen leer. Darauf ließ er das Wasser durch eine im Boden des oberen Eimers vorhandene Öffnung in den unteren Eimer fließen und beobachtete, ob durch den Stoß des Wassers auf den unteren Eimer das Gleichgewicht gestört wird. Es zeigte sich folgender unerwarteter Verlauf. Während das Wasser aus dem oberen Eimer in den unteren lief, blieb der Gleichgewichtszustand des ganzen Systems trotz des Anpralls der Flüssigkeit vollkommen erhalten. Die Seite mit den Eimern senkte sich nicht um eines Haares Breite. In dem Augenblicke, in welchem das Ausfließen begann, senkte sich das Gegengewicht jedoch, das System erschien also sogar leichter. Sobald aber das Wasser den[S. 67] unteren Eimer erreicht hatte, ging das System in den ursprünglichen Gleichgewichtszustand zurück.
Galilei nennt diesen Versuch zwar sinnreich, vermochte sich aber die Erscheinung doch nicht recht zu erklären. Wir wissen, daß das anfängliche Steigen des mit den Eimern beschwerten Wagearmes auf den Reaktionsdruck des ausfließenden Wassers zurückzuführen ist. Eine zweite Druckverminderung tritt für diesen linken Arm der Wage dadurch ein, daß das Gewicht des in der Luft schwebenden, also noch im Fall begriffenen Wassers nicht wirksam ist. Beide, ein Steigen des linken Armes bewirkende Druckverminderungen werden aber von dem Augenblicke an, in dem der Strahl den Boden des unteren Eimers erreicht, durch die Wirkung des Stoßes vollkommen ausgeglichen.
Grundlegend sind auch Galileis Untersuchungen über die Festigkeit gewesen, wenn er auch unter dem Einfluß der Lehre vom Horror vacui zu unrichtigen Vorstellungen gelangt ist.
Zunächst stellte er sich die Aufgabe, die Zugfestigkeit und die Bruchfestigkeit zu bestimmen und ihr Verhältnis zu ermitteln. Es waren Erfahrungen des praktischen Lebens, insbesondere der Bau- und der Maschinentechnik, welche den Ausgangspunkt für diese Untersuchungen bildeten. Es sei eine bekannte Erfahrung, meint Galilei, daß eine Maschine mitunter im Kleinen als Modell wohl gelinge, im Großen ausgeführt, aber nicht bestehen könne. Eine größere Maschine, in den gleichen Proportionen wie eine kleine hergestellt, besitze nämlich eine viel geringere Festigkeit. So könne man auch kleine Obelisken und Säulen handhaben und aufrichten ohne die Gefahr des Zerbrechens, während sehr große infolge der eigenen großen Last bei jedem Zufall Gefahr liefen, zu bersten. Nicht nur für Maschinen und Kunstwerke, sondern auch für alle Naturkörper bestehe daher eine notwendige Grenze, über die man nicht hinausgehen könne, wenn das Material dasselbe bleibt und auch die Proportionen gewahrt werden. So würden bei einem Baume von 200 Ellen Höhe zweifelsohne die Zweige unter ihrem Eigengewicht abbrechen; es müßte denn die Materie widerstandsfähiger gewählt, oder es müßten die Verhältnisse geändert, z. B. bei sehr großen Tieren die Knochen unförmlich dick gestaltet werden. Aus diesem Grunde fänden sich die Riesen des Tierreiches nur im Wasser, weil dort ihr Gewicht durch den Auftrieb[S. 68] ausgeglichen würde. Andererseits finde man, daß bei einer Verminderung des Körpers die Kräfte nicht im gleichen Maße abnehmen, sondern sogar relativ größer sind. Z. B. könne ein kleiner Hund drei andere von gleicher Größe tragen, während ein Pferd wohl kaum imstande sei, auch nur ein einziges Pferd auf seinem Rücken fortzuschleppen.
Es sind das für die Einsicht in die Mechanik der Tiere und der Pflanzen sehr wichtige Bemerkungen, die wir Galilei verdanken. Zu ihnen fügt er die weitere Einsicht, daß auch die Anordnung der Materie die Festigkeit in hohem Grade bedingt. Die Kunst und die Natur, sagt er, bedienten sich der hohlen Körper in tausend Fällen. Denn hier werde ohne Gewichtsvermehrung die Festigkeit bedeutend gesteigert. Als Beispiele führt er die Knochen und die Grashalme an. Galilei begnügt sich aber nicht mit der allgemeinen Beobachtung dieser Tatsache, sondern er zeigt auch, daß sich die Bruchfestigkeiten zweier Zylinder von gleicher Masse und Länge (Abb. 18), von denen der eine hohl, der andere massiv ist, zueinander wie ihre Durchmesser verhalten.
Auch für die oben erwähnten Beobachtungen über die Inanspruchnahme größerer und kleinerer Gegenstände, Organismen und Maschinen findet Galilei den Grund in einem Satz der Festigkeitslehre. Dieser besagt, daß der Widerstand der Körper gegen das Zerbrechen, wenn die Formverhältnisse dieselben bleiben, nicht mit der Masse, sondern in geringerem Maße wächst. Während nämlich die Massen prismatischer Körper sich wie die dritten Potenzen der ähnlichen Seiten verhalten, wächst der Widerstand gegen das Zerbrechen nur wie die Quadrate dieser Seiten.
Seine Theorie der Bruchfestigkeit begründet Galilei in folgender Weise. Denken wir uns (Abb. 19) einen parallelepipedischen Balken in einer Mauer befestigt und mit Q belastet, so können wir ihn als einen Winkelhebel STU betrachten, dessen Drehpunkt T ist. An dem Arme TU wirkt die Last Q, an TS wirkt der Gesamtwiderstand aller Fasern. TS ist die Hälfte der Höhe h des Prismas, TU ist seine Länge. Setzen wir die Momente gleich, so ist der Gesamtwiderstand X multipliziert mit h/2 = Q · l. Der[S. 69] Gesamtwiderstand ist aber gleich einer Konstanten für die Einheit des Querschnittes, multipliziert mit dem Querschnitt (b · h), also gleich K · bh. Die Gleichung, eine der wichtigsten der technischen Mechanik, nimmt also die Form an:
K · bh · h/2 = Q · l
oder die Bruchfestigkeit (oder relative Festigkeit) des Balkens wird ausgedrückt durch Q = ½ K · (bh2)/l. Galilei nahm bei seiner Ableitung auf die Elastizität der Fasern noch keine Rücksicht. Für Körper wie Glas und Stein ist dies zulässig, da man für diesen Fall die Annahme, welche Galilei allgemein macht, gelten lassen darf, die Annahme nämlich, daß die Fasern sich vor dem Abreißen nicht verändern, während sie in Wirklichkeit sich ja zum Teil ausdehnen, zum Teil verkürzen und nur in einer gewissen Zone (neutrale Fasern) ihre Länge beibehalten, so daß das Zerreißen aller Fasern nicht gleichzeitig stattfindet, wie Galilei voraussetzt. Unter Berücksichtigung der Elastizität der Körper gilt daher in der heutigen Mechanik ein kleinerer, in der Form aber dem von Galilei gefundenen ganz entsprechender Wert:
(1/6 K (bh2)/l).
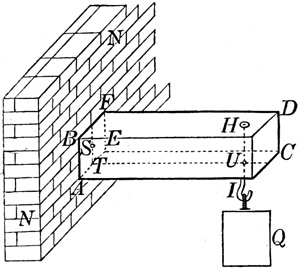
An diese Untersuchung anknüpfend, zeigt Galilei nun weiter, weshalb ein Prisma auf schmaler Basis eine größere Bruchfestigkeit besitzt als ein solches auf breiter (siehe Abb. 20). In beiden Fällen bleibt der Hebelarm (BD) der Last unverändert. Auch der Widerstand ändert sich nicht, da er in beiden Fällen gleich dem Widerstande aller Fasern der Basis AB ist. Was sich dagegen ändert, ist der Hebelarm des Widerstandes. Er ist im ersten Falle die Hälfte von AC,[S. 70] im zweiten dagegen nur die Hälfte von BC. Dem größeren Hebelarm entspricht aber ein größeres Moment, und diesem wieder eine größere relative Festigkeit.
Auch der Mechanik der flüssigen Körper, die seit Archimedes keine Förderung erfahren hatte, wurde von Galilei zuerst wieder Beachtung geschenkt. Zunächst stellte er in seiner Schrift über die schwimmenden Körper110 eine Nachprüfung der von Archimedes gefundenen hydrostatischen Gesetze an und bestätigte ihre Richtigkeit. Dadurch gelangte, gegenüber der unrichtigen Behauptung der Aristoteliker, daß das Schwimmen eines Körpers vor allem von seiner Form abhänge, die richtige Erkenntnis wieder zur Geltung. Diese Erkenntnis gipfelt darin, daß das Schwimmen vom spezifischen Gewicht abhängt, und daß ein Körper schwimmt, wenn sein spezifisches Gewicht kleiner ist als dasjenige der verdrängten Flüssigkeit. Die Aristoteliker waren zu ihrem Trugschluß durch die bekannte Erscheinung geführt worden, daß dünne Metallplatten auf dem Wasser schwimmen. Galilei machte demgegenüber darauf aufmerksam, daß solche Platten in einer Vertiefung auf der Oberfläche des Wassers ruhen und daß sie untersinken und nicht wieder emporsteigen, sobald sie ganz in die Flüssigkeit eingetaucht werden. Eine Erklärung des Schwimmens dünner Metallplatten oder Nadeln auf einer spezifisch leichteren Flüssigkeit vermochte erst das 18. Jahrhundert nach der Entdeckung der Oberflächenspannung zu geben. Letztere gab auch Aufschluß über eine Erscheinung, über die Galilei sich keine Rechenschaft zu geben vermochte, die Erscheinung nämlich, daß Wassermassen auf Blättern sich im Zusammenhang erhalten, ohne zu zerfließen.
Um das Sinken und Steigen von Körpern in Flüssigkeiten aus dem spezifischen Gewichte der Flüssigkeiten zu erklären, stellte Galilei folgenden Versuch an. Er brachte eine Wachskugel in reines Wasser und bemerkte, daß sie untersank. Erhöhte er darauf das spezifische Gewicht der Flüssigkeit, indem er Salz darin löste, so stieg die Kugel bei einem bestimmten Konzentrationsgrade wieder empor.
Galilei entwickelte ferner für die Beschaffenheit der Flüssigkeiten eine Auffassung, die bis auf den heutigen Tag allen Untersuchungen[S. 71] auf dem Gebiete der Hydromechanik als Grundlage gedient hat. Danach bestehen die Flüssigkeiten aus isolierten Teilchen, die sehr beweglich sind und deshalb dem geringsten Drucke folgen. Infolgedessen pflanzt sich jeder Druck durch die ganze Masse der Flüssigkeit fort.
In dem Bestreben, die Mechanik der Flüssigkeiten auf die zunächst an festen Körpern gewonnenen Grundsätze der allgemeinen Mechanik zurückzuführen, wandte Galilei zum ersten Male das Prinzip der virtuellen Geschwindigkeiten auf hydrostatische Verhältnisse an. Er schuf damit für dieses Gebiet ein neues Beweisverfahren, das besonders durch Pascal in seiner ganzen Bedeutung erfaßt und in vollem Umfange angewandt wurde.
Archimedes hatte für die Untersuchung der statischen Verhältnisse den Begriff des statischen Moments geschaffen und bei der Erklärung der einfachen Maschinen sein Augenmerk vornehmlich auf die Gewichte und ihre Abstände vom Drehpunkt gerichtet. Stevin und Galilei dagegen faßten die statischen Verhältnisse vom dynamischen Gesichtspunkt auf und betrachteten die Gewichte und deren bei einer Verschiebung des Systems auftretende, also virtuelle, Falltiefen oder vertikale Verschiebungsgrößen als maßgebend für die Beurteilung der Gleichgewichtsbedingungen. Dieses Prinzip der virtuellen Geschwindigkeiten oder Verschiebungen, wie man es genannt hat, läuft im Grunde genommen auf den Satz hinaus, daß Gleichgewicht besteht, wenn die Arbeit der Kraft gleich der Arbeit der Last ist, da ja das Produkt aus dem Gewicht und der vertikalen Verschiebung als die geleistete Arbeit betrachtet wird.
Am einfachsten und durchsichtigsten gestaltet sich bei Galilei die Anwendung des Prinzips der virtuellen Geschwindigkeiten in dem Falle, in dem es sich um das Eintauchen eines prismatischen Körpers in ein gleichfalls prismatisches mit Flüssigkeit gefülltes Gefäß handelt. Galilei vergleicht die Verschiebung oder, was sich dafür auch setzen läßt, die Geschwindigkeit des Prismas mit derjenigen Verschiebung, die der Flüssigkeitsspiegel in entgegengesetzter Richtung erfährt. Offenbar verhalten sich die Verschiebungen oder die Geschwindigkeiten des Prismas und des Spiegels umgekehrt wie die entsprechenden Flächen, nämlich die Grundfläche des Prismas und die Oberfläche des Flüssigkeitsspiegels. Wird das Prisma wieder herausgezogen, so findet in entsprechender Weise ein Sinken des Spiegels statt. Das Produkt aus Gewicht und Geschwindigkeit des eingetauchten Körpers wird dann, wenn[S. 72] Gleichgewicht bestehen soll, gleich dem Produkte aus Gewicht und Geschwindigkeit der gehobenen Flüssigkeitsmasse gesetzt und so das Prinzip der virtuellen Geschwindigkeiten zur Anwendung gebracht. Galilei dehnte es auch auf das Verhalten der Flüssigkeiten in kommunizierenden Röhren aus. Die Analogie zwischen diesem Verhalten und dem soeben geschilderten Vorgang konnte ihm nicht entgehen. Entspricht doch dem Eintauchen des Prismas und dem dadurch bewirkten Emporheben des Spiegels ein Herabdrücken der Flüssigkeit in der engeren und ein Steigen in der weiteren Röhre, wobei sich gleichfalls die Verschiebungen umgekehrt wie die Querschnitte verhalten.
Auch mit Erfindungen hat Galilei die Hydromechanik bereichert. Er erfand eine hydrostatische Schnellwage und konstruierte eine hydraulische Maschine, für die ihm Venedig ein Patent verlieh111.
Wir haben hiermit die Art der Behandlung, die Galilei den Problemen der Mechanik angedeihen ließ, kennen gelernt und werden ihm die Berechtigung, von neuen Wissenszweigen zu sprechen, voll zugestehen müssen. Durchdrungen von der Bedeutung des erschlossenen, auf der innigen Verknüpfung des Versuches mit der mathematischen Ableitung beruhenden neuen Weges, ruft er am Schlusse seines dritten Gespräches aus: »Die in dieser Abhandlung vorgeführten Sätze werden, wenn sie in die Hände anderer gelangen, immer wieder zu neuen, wunderbaren Erkenntnissen führen. Und es wäre denkbar, daß in solcher Weise eine würdevolle Behandlung sich allmählich auf alle Gebiete der Natur erstreckte«. Diese Vorahnung sollte schon ein Menschenalter nach Galileis Hinscheiden durch die Taten eines Newton, Huygens und anderer Forscher der Erfüllung nahe gebracht werden. Indes schon Galilei selbst hat sich durchaus nicht auf die Mechanik beschränkt, sondern, wenn auch in bescheidenem Maße und mit geringerem Erfolge, seine Untersuchungen den übrigen Gebieten der Naturlehre zugewendet.
Daß die Luft sich beim Erwärmen ausdehnt, war schon dem Altertum bekannt. Beruhen doch auf diesem Verhalten manche physikalische Schaustücke Herons. Galilei scheint trotz allen Dunkels, das die Geschichte des Thermometers umgibt, der erste gewesen zu sein, der diese Ausdehnung zum Messen des[S. 73] Wärmezustandes benutzt hat. Zwar enthalten seine Schriften, soweit sie noch erhalten sind, kaum mehr als eine Andeutung über diesen Gegenstand. So heißt es im »Dialog« an einer Stelle, man dürfe nicht zweifeln, daß heißes Eisen beim Erkalten eher von 10 Grad auf 9 Grad sich abkühle als von 10 auf 6. Indes ist unter Grad hier jedenfalls nur eine ganz unbestimmt gelassene Einheit zu verstehen.
Angaben der älteren Biographien weisen darauf hin, daß Galilei schon vor 1597, als er sich mit den Werken Herons beschäftigte, ein Thermoskop herstellte, das er bei seinen Vorträgen zeigte112. Es bestand aus einer unten offenen und oben in eine Kugel endigenden Röhre (Abb. 21), in der sich eine Flüssigkeit auf- und abbewegte. Letzteres geschah, sobald die in der Kugel eingeschlossene Luft erwärmt oder abgekühlt wurde, da sie dementsprechend einen größeren oder kleineren Raum einnahm. Gleichzeitig mußte sich aber auch jede Schwankung des Luftdrucks an diesem Instrument bemerkbar machen. Infolgedessen waren nur innerhalb eines kurzen Zeitraumes angestellte Versuche vergleichbar.
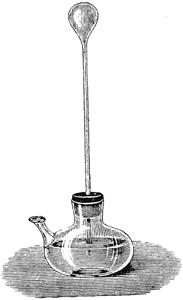
Eine Verbesserung dieses Instrumentes bestand darin, daß man der Röhre eine horizontale Lage gab und die Luft nur durch ein Flüssigkeitströpfchen absperrte. Letzteres wurde bei den durch Wärmeunterschiede hervorgerufenen Volumschwankungen hin- und herbewegt114. Ein Freund Galileis115 kam schon auf den trefflichen Gedanken, ein solches, seinen Zwecken entsprechend abgeändertes Thermoskop zur Bestimmung der Körperwärme von Kranken zu benutzen.
Galilei hat auch unter den Neueren zuerst sich eingehender mit akustischen Untersuchungen beschäftigt. Zwar rührt das erste neuere Werk116 über diesen Gegenstand von Mersenne her, während die Untersuchungen Galileis nur gelegentliche Bemerkungen über akustische Dinge bringen. Man muß jedoch annehmen, daß Mersenne, der mit Galilei in regem Verkehr stand, seine Kenntnisse im wesentlichen Galilei verdankte. Mersenne gebührt das Verdienst, die Forschungsergebnisse des Meisters ausführlicher dargestellt und durch eigene Untersuchungen vervollständigt zu haben.
Galilei behandelte im Anschluß an die von ihm entdeckten Gesetze der Pendelschwingungen die Saitenschwingungen und zwar zunächst das Phänomen des Mitschwingens117, das im physikalischen Denken nicht geschulte Zeitgenossen aus einer Art Sympathie erklären zu können glaubten118. Die Abhängigkeit der Tonhöhe von der Schwingungszahl erkannte Galilei durch folgenden Versuch. Er fuhr mit einem scharfen Eisen über eine Messingplatte. Jedesmal, wenn er dabei einen deutlichen Ton erhielt, waren auf der Platte, entsprechend den Schwingungen des Eisens, eine Menge feiner Striche in völlig gleichen Abständen eingegraben. Erzielte er durch Ändern der Geschwindigkeit einen höheren Ton, so waren die Striche gedrängter; wurde der Ton dagegen tiefer, so nahmen die Abstände zu und zeigten dadurch eine geringere Zahl von Schwingungen an. Diese Schwingungen machten sich auch dadurch bemerklich, daß das Eisen, jedesmal wenn beim Hinwegstreichen über die Messingplatte ein Ton entstand, in der Faust erzitterte, so daß die Hand ein Schauer durchfuhr. Der Vorgang, sagt Galilei, sei genau derselbe, als wenn wir flüstern und laut sprechen. Nur im letzteren Falle empfinde man im Kehlkopf und im Schlunde ein Zittern.
Die Zahl der in der Zeiteinheit bei bestimmten Tönen entstandenen Striche bot nun Galilei das Mittel, einen vorher nur in seiner physiologischen Wirkung bekannten Vorgang der messenden physikalischen Untersuchung zu unterwerfen. Zunächst richtete[S. 75] es Galilei so ein, daß zwei bestimmte Töne, die er auf seiner Messingplatte durch schnelleres und langsameres Streichen erzeugte, den Zusammenklang bildeten, den man in der Musik als Quinte bezeichnet. Als Galilei darauf die Striche zählte und ihre Entfernung ausmaß, fand er, daß auf 30 Striche, d. h. Schwingungen, des einen Tones 45 Striche oder Schwingungen des anderen kamen.
Bisher hatte man die Tonhöhe nur in ihrer Abhängigkeit von der Länge der schwingenden Saiten betrachtet und auch hierbei einfache Beziehungen entdeckt. Galilei erkannte als das Grundgesetz der Akustik, daß die Höhe eines Tones von der Anzahl der Schwingungen abhängt, welche der tönende Körper in der Zeiteinheit macht. Er fand durch jenen einfachen, soeben geschilderten Versuch, daß diese Schwingungszahlen für den Grundton, die Quarte, die Quinte und die Oktave sich verhalten wie 1 : 4/3 : 3/2 : 2 = 6 : 8 : 9 : 12.
Galilei untersuchte ferner die Töne schwingender Saiten in ihren Beziehungen zur physikalischen Beschaffenheit dieser Saiten. Das Ergebnis war folgendes: Bei gleicher Spannung und Beschaffenheit entsteht die Oktave durch Verkürzung der Saite auf die Hälfte. Bei gleicher Länge und Beschaffenheit erhält man die Oktave, wenn man die Spannung vervierfacht. Will man bei gleicher Länge und Spannung die Oktave erhalten, indem man die Saite feiner wählt, so muß man ihre Dicke auf ein Viertel reduzieren. Indessen wird das akustische Verhältnis, wie Galilei hervorhebt, nicht durch die Länge, die Spannung und den Querschnitt der Saite verursacht, sondern durch die Zahl der Schwingungen oder Lufterschütterungen, die unser Trommelfell treffen und es im gleichen Tempo mitschwingen lassen.
Für diese Erscheinung des Mitschwingens oder der Resonanz gibt Galilei folgende Erklärung: Die Schwingungen der Saite versetzen die Luft in Bewegung. Jede mit der angeschlagenen gleich gestimmte Saite fängt, weil sie im selben Tempo zu vibrieren vermag, beim ersten Impulse an, sich ein wenig mit zu bewegen. Es werden nun aber ein zweiter, dritter und viele andere Impulse hinzugefügt; und weil sämtliche Impulse die Saite zur passenden Zeit treffen, so wird schließlich die Schwingung der mitschwingenden Saite ebenso ergiebig wie diejenige der angeschlagenen.
Auch die Erscheinung der Konsonanz und der Dissonanz sucht Galilei aus dem Verhältnis der Schwingungszahlen und aus der Beschaffenheit des Gehörorgans zu erklären. Konsonant seien diejenigen Töne, die in einer gewissen Ordnung das Trommelfell erschüttern. Dissonante Töne dagegen bewirkten, daß die Knorpel des Trommelfells sich in steter Qual befänden, weil die Erschütterungen, die solche Töne hervorriefen, nicht rhythmisch zusammenträfen.
Auch auf die Erscheinung der stehenden Wellen machte Galilei aufmerksam. Er füllte ein Glas zum Teil mit Wasser und brachte das Glas durch Streichen zum Tönen. Es zeigten sich dann Erhöhungen und Vertiefungen der Oberfläche, die bestehen blieben, solange der Ton dauerte. Sprang der Ton in die höhere Oktave über, so zerfiel jede Welle in zwei Wellen.
Mit optischen Untersuchungen hat sich Galilei, abgesehen von seiner Mitwirkung bei der Erfindung des Fernrohrs, kaum beschäftigt. Doch zeugt es von Divinationsgabe, daß er eine endliche Geschwindigkeit des Lichtes annahm, obgleich sein Versuch, sie zu messen, scheiterte. Der Versuch selbst war so gut ausgedacht, daß wir ihn trotzdem schildern wollen, weil er sich im Prinzip mit der später von Fizeau erdachten erfolgreichen Versuchsanordnung deckt119.
In beiden Fällen handelt es sich nämlich um ein rasches Hin- und Hersenden von Lichtsignalen zwischen zwei weit voneinander entfernten Orten. Bei Galilei erhielten zwei Personen Laternen. Sie wurden zunächst auf kurze Entfernung einander gegenübergestellt. Jeder hatte dann sein Licht wiederholt aufzudecken und sofort wieder abzublenden. Das kurze Aufdecken erfolgte jedesmal, wenn der eine Beobachter das Licht des zweiten Beobachters erblickte. Darauf wurde der Abstand zwischen beiden Personen auf eine Meile vergrößert und das Experiment wiederholt. Wäre dann die Beantwortung der Signale in einem langsameren Tempo erfolgt, so hätte man daraus auf die Zeit, die das Licht zu seiner Fortpflanzung gebraucht, schließen können. Die Entfernung war indessen zu gering und der Wechsel erfolgte nicht rasch und nicht gleichmäßig genug. Infolgedessen verlief der Versuch ohne[S. 77] Ergebnis. Wir werden später sehen, daß Fizeau ein solches erzielte, ohne die Entfernung erheblich zu vergrößern, und zwar dadurch, daß er eine mechanische Vorrichtung ersann, die einen gleichmäßigen Wechsel der Signale innerhalb des Bruchteils einer Sekunde ermöglichte.
Zur Beschäftigung mit den magnetischen Erscheinungen wurde Galilei durch das Studium des Gilbertschen Werkes veranlaßt. Er ließ sich dabei von dem Bestreben leiten, den Magnetismus, auf dessen kosmische Bedeutung Gilbert zum ersten Male hingewiesen hatte, zur Erklärung astronomischer Vorgänge zu verwerten. Betrachtungen über den Magnetismus bilden daher einen nicht unwesentlichen Teil seines großen Dialogs über die Weltsysteme120. Das erwähnte Bestreben offenbart sich darin, daß er die unveränderliche Richtung der Erdachse aus der magnetischen Natur der Erde zu erklären sucht und darauf hinweist, daß der Mond »wie durch magnetische Kraft gebannt« stets ein und dieselbe Seite der Erde zukehre121. Gilbert ging darin noch weiter und suchte auch die Drehung der Erde um ihre Achse aus dem Magnetismus zu erklären. Er nahm an, daß jede magnetische Kugel, wenn keine Widerstände sie daran hindern, sich um sich selbst drehen müsse. Diese Ansicht vermochte der in mechanischen Dingen Gilbert weit überlegene Galilei indessen nicht zu teilen. Wohl aber erblickt er in den Bewegungen, welche die Erde nach der koppernikanischen Lehre ausführt, eine Analogie zu den Bewegungen des Magneten, der »in ähnlicher, vielleicht in derselben Weise« eine horizontale und eine vertikale Kreisbewegung (infolge der Deklination und Inklination) besitze122.
In der Erkenntnis, daß »der Magnet dem menschlichen Verstande ein weites Forschungsfeld« darbiete, hat sich Galilei auch mit der Tragkraft des Magneten, sowie mit der Herstellung von Armaturen und ihrer Wirkung eingehender befaßt. Durch Armierung eines Magnetsteins verstärkte er seine Kraft auf das Achtfache. Den Grund dieser Erscheinung erblickt er in dem Umstand, daß die geglättete Armatur das angezogene Eisenstück in viel mehr Punkten berühre als die gröbere und rauhere Substanz des Magnetsteins. In einem anderen Falle123 will Galilei durch Armierung[S. 78] die Tragfähigkeit auf das Achtzigfache gesteigert und bewirkt haben, daß der Magnet 26mal soviel trug, als er Gewicht besaß.
Im vorstehenden haben wir die Verdienste Galileis um die Begründung der neueren Naturwissenschaft kennen gelernt und gesehen, wie überall das mathematische und induktive Verfahren durch diesen Mann zum Durchbruch kam. Fast sämtliche Gebiete der Naturlehre empfingen die kräftigste Anregung. Vor allem aber wurde das ganze Gebiet dieser Wissenschaft von den Auswüchsen metaphysischer Betrachtungsweise, mit denen es vorher so sehr verquickt war, befreit. Galileis Eigenart entsprach es nämlich, daß er sich stets der Grenzen der Naturforschung bewußt blieb und sich darauf beschränkte, die Erscheinungen in ihrem Verlaufe und in ihrem Zusammenhange mit verwandten Vorgängen scharf zu erfassen, ohne in ein unfruchtbares Suchen nach den letzten Gründen zu verfallen. Eine solche Beschränkung ist für die Erneuerung der Naturwissenschaft, wie sie im Beginn des 17. Jahrhunderts erfolgte, von höchstem Werte gewesen. Bevor wir uns dem weiteren Ausbau des von Galilei geschaffenen Lehrgebäudes zuwenden, scheint es geboten, auch der Persönlichkeit des einzigartigen Mannes gerecht zu werden.
Galilei war nach den Berichten seiner Zeitgenossen groß, stark gebaut und von ehrwürdigem Aussehen (siehe das Titelbild). Die Stirn war hoch, der Blick voll Feuer und seine Rede angenehm und ausdrucksvoll. Dabei war er kein einseitiger Gelehrter. Die Erholungsstunden widmete er der Musik und der Malerei. Sogar einige Sonette sind von ihm vorhanden. Diese künstlerische Veranlagung Galileis kam in seinen Schriften dadurch zum Ausdruck, daß sie neben ihrer wissenschaftlichen Bedeutung sprachlich zu dem Vollendetsten gehören, was die italienische Literatur des 17. Jahrhunderts hervorgebracht hat. Gelehrte Unterhaltungen führte Galilei nur mit seinen Freunden, suchten Unberufene ihn in solche hineinzuziehen, so wußte er geschickt abzulenken.
Die gegen ihn gerichteten Verfolgungen setzten sich bis über das Grab hinaus fort. Sogar das letztere wurde ihm streitig gemacht. Erst ein Jahrhundert nach Galileis Tode wurde seinem letzten Wunsche gewillfahrt, indem man die irdischen Überreste[S. 79] des großen Forschers in der Kirche Santa Croce zu Florenz bestattete. Ein prächtiges Denkmal schmückt jetzt diesen Ort. Von gleicher Tragik war das Geschick der handschriftlichen Hinterlassenschaft Galileis. Von seinem Sohne sehr vernachlässigt, von einem Enkel in einer skrupulösen Anwandlung zum Teil verbrannt, gelangte sie endlich in die Hände Vivianis, der Galilei die letzten schlimmen Lebensjahre ertragen geholfen. Vivianis Absicht, diese Geistesschätze durch eine Herausgabe zu heben, wurde jedoch vereitelt. In Florenz, wo mit dem Enkel desjenigen Mediceers, der Galilei in seinem Lande eine Ehrenstätte bereitete, Andächtelei und Priesterherrschaft den Thron bestiegen hatten, war der Name des großen Mannes geradezu verhaßt geworden. Viviani sah sich schließlich in der Furcht, daß ihm auf obrigkeitlichen Befehl die Schriften abgenommen werden könnten, genötigt, sie einem Verstecke anzuvertrauen. Erst im nachfolgenden Jahrhundert wurden Galileis Manuskripte wieder entdeckt. Sie sollten schon als Makulatur in die Hände eines Krämers wandern, als man noch rechtzeitig ihren Wert erkannte und wenigstens einen Teil in die Bibliothek zu Florenz hinüberrettete.
Eine Gesamtausgabe der Werke Galileis124 erschien um die Mitte des 19. Jahrhunderts. Eine auf Grund der eingehendsten Vorarbeiten veranstaltete neue Ausgabe besorgte Favaro. Sie wurde durch staatliche Mittel ermöglicht und umfaßt zwanzig große Bände125.
Um das Bekanntwerden der Werke Galileis hat sich ein Straßburger Professor namens Bernegger verdient gemacht. Bernegger unterhielt mit Galilei und mit Kepler einen lebhaften Briefwechsel126 und übersetzte mehrere Schriften Galileis ins Lateinische, um sie dadurch der gelehrten Welt zugänglicher zu machen. Galilei selbst hatte nämlich seine Werke zum großen[S. 80] Teil in der Muttersprache veröffentlicht. Sein Hauptwerk, der »Dialog« über die beiden hauptsächlichsten Weltsysteme (Deutsch von E. Strauß im Jahre 1891 herausgegeben), erschien in der lateinischen, von Bernegger besorgten Ausgabe schon 1635, also nur wenige Jahre nach der ersten Veröffentlichung durch Galilei127.
Der vorige Abschnitt war ausschließlich einer Darstellung und Würdigung der von Galilei geschaffenen Grundlagen der neueren Wissenschaft gewidmet. Es gilt jetzt zu zeigen, wie sich das neue Verfahren der Naturforschung in Italien und bald darauf auch in den nördlichen Ländern Europas ausbreitete.
Zunächst fand Galilei in Italien eine Anzahl begeisterter Schüler, die sein Werk fortsetzten, wenn ihnen auch nur ein bescheideneres Können verliehen war. Vivianis und seiner Bemühungen haben wir schon gedacht. Ferner ist Torricelli zu nennen, der vor allem zur Fortsetzung der Arbeiten Galileis berufen war. Beide Männer hatten während der qualvollen Monate, welche der Auflösung des Meisters vorhergingen, mit diesem in unmittelbarem Verkehr gestanden und pietätvoll aufgezeichnet, was den unermüdlichen Geist während der letzten Spanne seines Erdenwallens beschäftigte. Sie umstanden mit den Angehörigen das Sterbebett, an dem leider auch die Bevollmächtigten der Inquisition nicht fehlten.
An Torricelli und Viviani schlossen sich eine Anzahl von gleichem Streben erfüllter Männer an. So entstand in Florenz ein Verein, der sich die Aufgabe stellte, die Natur auf dem Wege des Experimentes zu erforschen.
Unter den Mitgliedern dieser Accademia del Cimento128 (Schule des Versuches) sind folgende hervorzuheben: Der Anatom Borelli,[S. 82] welcher die Mechanik auf das Gebiet der Physiologie ausdehnte; der aus Dänemark gebürtige Steno, dessen Untersuchung der toskanischen Gebirge die neuere Geologie einleitete; ferner Redi, bekannt geworden durch seine Experimente über die Urzeugung; Domenico Cassini, der Galileis astronomische Arbeiten fortsetzte und später in Paris die Leitung der neu errichteten Sternwarte übernahm. Diese Männer, die uns im weiteren Verlaufe der Geschichte noch wiederholt begegnen werden, stellten gemeinsam in dem Zeitraum von etwa 1657 bis 1667 eine Fülle grundlegender, meist physikalischer Versuche an, ohne sich dabei von theoretischen Erwägungen leiten zu lassen. Zwar liegt darin eine gewisse Einseitigkeit und ein Abweichen vom Geiste Galileis, der nirgends zu einem bloßen Experimentator herabsinkt. Trotzdem war das Unternehmen bei dem damaligen Mangel sicherer empirischer Grundlagen ein höchst verdienstvolles.
Die Accademia del Cimento bestand nur zehn Jahre. Dann wurde sie infolge der in Florenz aufkommenden hierarchischen Strömung wieder aufgelöst129. Gleichzeitig wurden jedoch die von ihren Mitgliedern erhaltenen Resultate bekannt gegeben130. Da die betreffende Schrift für die weitere Entwicklung der experimentellen Physik von großer Bedeutung war, so soll hier einiges daraus mitgeteilt werden. Sie beginnt mit der Beschreibung und der Gebrauchsanweisung wichtiger Meßinstrumente. Vor allem sind hier das Thermometer, das Hygrometer, das Aräometer und das Pendel zu nennen.
Der umfangreichste Abschnitt trägt die Überschrift: Versuche über den natürlichen Druck der Luft. Er enthält die Beschreibung des Barometers und schildert zahlreiche, im Vakuum angestellte Versuche.
Ein Abschnitt handelt von der Herstellung und Wirkung der Kältemischungen. Ein anderer enthält den ersten Versuch über Wärmestrahlung. Eine größere Eismasse wurde in einiger Entfernung von einem Hohlspiegel aufgestellt. Brachte man dann ein empfindliches Thermometer in den Brennpunkt des Spiegels,[S. 83] so sank die Quecksilbersäule unter die Temperatur der umgebenden Luft. Die weiteren Abschnitte handeln von der Ausdehnung der festen Körper durch die Wärme, von der Zusammendrückbarkeit des Wassers, der Fortpflanzungsgeschwindigkeit des Schalles und des Lichtes, dem Magnetismus, der Elektrizität und der Wurfbewegung. Die Akademiker zogen also alle Gebiete der Physik in den Bereich ihrer Versuche. Allerdings war der Erfolg sehr verschieden. Während man, wie wir sogleich im einzelnen sehen werden, auf dem Gebiete der Mechanik die wertvollsten Aufschlüsse erlangte, waren die Ergebnisse auf den Gebieten des Magnetismus und der Elektrizitätslehre nur gering.
Wir wenden uns den wichtigsten Untersuchungen, Entwürfen und Entdeckungen der Florentiner Physiker zu und geben zunächst in Abb. 22 ein Gefäßbarometer in der zur Zeit der Akademie gebräuchlichen Form wieder. Seine Teilung wurde durch eingebrannte Glasperlen bewerkstelligt.

Daß die Quecksilbersäule von der auf dem Quecksilberspiegel CBD lastenden Luft getragen wird, bewiesen die Akademiker folgendermaßen: Sie verbanden den kleinen, in der Abbildung links befindlichen Ansatz luftdicht mit einer Spritze. Zogen sie den Kolben heraus, so sank das Quecksilber in der Röhre beträchtlich, wurde dagegen durch Hineindrücken[S. 84] des Kolbens auf die in dem weiten Gefäß befindliche Luft ein Druck ausgeübt, so stieg das Quecksilber entsprechend dem größeren auf CBD lastenden Gesamtdruck über A hinaus.
Der Apparat (Abb. 22) eignete sich auch vortrefflich, um die Abhängigkeit der Gasspannung von der Temperatur nachzuweisen. Als die Florentiner Physiker nämlich den kleinen Ansatz hermetisch schlossen und die über dem Quecksilberniveau abgesperrte Luftmenge durch Eis abkühlten, bemerkten sie, daß das Quecksilber in der Röhre fiel, während es beim Erwärmen der abgeschlossenen Luft entsprechend der durch die Temperatursteigerung erzeugten Druckzunahme stieg.
Um Versuche im Vakuum anzustellen, bedienten sich die Akademiker, in Ermangelung einer Luftpumpe, der in Abb. 23 dargestellten, ohne weiteres verständlichen Vorrichtung. Sie erweiterten den oberen Teil des Barometers zu einem Gefäß, das durch einen Deckel luftdicht geschlossen werden konnte. An diesem Deckel wurden Gegenstände befestigt und deren Verhalten untersucht, nachdem man in dem Apparat die Torricellische Leere in der bekannten Weise hergestellt hatte. So wurde z. B., wie die Abbildung andeutet, eine nur wenig Luft enthaltende, zugebundene Blase in das Vakuum gebracht und auf diese Weise erkannt, daß sie infolge einer der Luft zukommenden Expansivkraft erheblich anschwillt. Durch einen ähnlichen Versuch wurde nachgewiesen, daß das Steigen von Flüssigkeiten in engen Röhren auch im Vakuum stattfindet, also mit dem Luftdruck in keiner Beziehung steht.

Die erste Erwähnung findet das Emporsteigen der Flüssigkeiten in engen Röhrchen bei Lionardo da Vinci (1490). Die genauere Untersuchung dieser unter dem Namen Kapillarität bekannten Erscheinung erfolgte indessen erst im 17. Jahrhundert durch das Akademiemitglied Borelli. Borellis Werk über diesen Gegenstand133 erschien gesondert von den Veröffentlichungen der Akademiker, an deren Kapillaritätsversuchen er Teil genommen[S. 85] hatte. Was Borelli darin schildert, sind die heute jedermann geläufigen, bis zum 17. Jahrhundert indessen infolge ihrer Unscheinbarkeit übersehenen Kapillaritätserscheinungen. Sie waren selbst Pascal noch nicht bekannt. In seinem berühmten Werk »Über das Gleichgewicht der Flüssigkeiten«134 behauptet er nämlich, eine Flüssigkeit setze sich in kommunizierenden Röhren stets ins Gleichgewicht, wie auch der Durchmesser dieser Röhren beschaffen sei. Offenbar kann es sich hier nur um eine vorgefaßte Meinung und nicht um das Ergebnis einer Prüfung handeln, die Pascal sofort von der Unrichtigkeit seiner Behauptung überzeugt hätte. Borelli entdeckte nicht nur das Ansteigen, sondern auch den Zusammenhang mit der Beschaffenheit der Röhre. War letztere im Innern feucht, so erfolgte das Ansteigen rascher. Die Höhe erwies sich ferner abhängig von dem Durchmesser der Röhre. Borelli fand, daß die Steighöhe dem Durchmesser umgekehrt proportional ist (h : hʹ= dʹ : d). Zog er die Röhre aus der Flüssigkeit heraus, so blieb so viel davon im Innern hängen, wie der Steighöhe entspricht.
Borelli entdeckte auch die mit der Kapillarität zusammenhängende Erscheinung, daß sich schwimmende Körper (Holzplatten oder sehr leichte auf dem Wasser schwimmen bleibende Metallplatten) innerhalb einer gewissen Entfernung gegenseitig anziehen, wenn sie von der Flüssigkeit benetzt werden (Abb. 24). Dagegen fand er Abstoßung, wenn der eine Körper benetzt wird, der andere aber nicht. Eine befriedigende Erklärung dieser merkwürdigen Erscheinungen vermochte das 17. Jahrhundert noch nicht zu geben. Die erste Theorie der Kapillarität begegnet uns um die Mitte des 18. Jahrhunderts135.
Die Mitglieder der Akademie stellten auch das erste wirkliche Thermometer her. Das von Galilei zum Messen der Temperatur gebrauchte Instrument war nur ein Thermoskop, d. h. es zeigte nur ein Mehr oder Minder von Wärme an. Auch machte sich an ihm jede Schwankung des Luftdrucks bemerkbar.
Ähnliche Thermoskope erfanden auch Guericke und Drebbel. Guerickes Apparat bestand aus einer mit Luft gefüllten Metallkugel, an die sich unten eine U-förmig gebogene, zur Hälfte mit Flüssigkeit gefüllte Röhre anschloß (Abb. 25). In dieser Röhre befand sich ein Schwimmer, der wieder durch einen über eine Rolle geschlungenen Faden, wie die Abbildung zeigt, mit einer schwebenden Figur verbunden war. Letztere bewegte sich auf- und abwärts in dem Maße, in dem die Flüssigkeit, entsprechend den Volumänderungen der in der Kugel eingeschlossenen Luft, fiel und stieg.
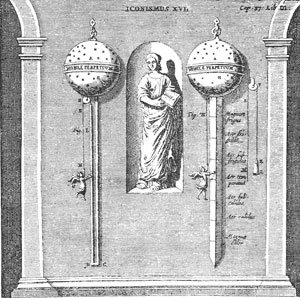
Eine ähnliche Vorrichtung, bei der eine Flüssigkeit durch die Temperaturschwankungen eines mit Luft gefüllten Gefäßes[S. 87] zum Steigen und Fallen gebracht wurde, verfertigte Drebbel137. Er bezeichnete seinen Apparat als ein Perpetuum mobile und suchte den Glauben zu erwecken, daß es sich hier um eine der Ebbe und Flut des Meeres entsprechende Erscheinung handle138. Galilei erhielt im Jahre 1612 Kenntnis von dem Apparate Drebbels, der bis in die neuere Zeit hinein für den Erfinder des Thermometers gegolten hat. Ein wirkliches Thermometer, das vom Wechsel des Luftdruckes nicht merklich beeinflußt wurde, war erst das Instrument, dessen sich die Accademia del Cimento bei ihren Untersuchungen bediente (siehe Abb. 27). Höchst wahrscheinlich waren Galilei und Drebbel, ohne von einander zu[S. 88] wissen, zur selben Vorstufe gelangt139. Wem dagegen die Erfindung des eigentlichen Thermometers zu verdanken ist, weiß man nicht. Das Instrument wurde schon 1641, also vor der Gründung der Akademie in Italien gebraucht. Die grundsätzliche Neuerung, um deren Zustandekommen sich vielleicht mehrere Physiker der Florentiner Schule verdient gemacht haben, bestand darin, daß die Kugel und die Röhre luftleer gemacht und letztere oben, anfangs durch Siegellack und später durch Zuschmelzen, vollkommen geschlossen wurde. Auf diese Weise war der Luftdruck, der bei den Apparaten Galileis, Drebbels und Guerickes neben den Temperaturveränderungen die Schwankungen der Flüssigkeit veranlaßte, ausgeschlossen.
Als Flüssigkeit, deren Ausdehnung zum Messen der Wärme diente, benutzte man Weingeist. Die Skala besaß zwar hundert Teile; doch waren die Angaben sehr schwankend, da man keine festen, leicht bestimmbaren Punkte zugrunde legte, sondern für die niedrigste, sowie die höchste in Toskana beobachtete Temperatur gewisse Punkte der Skala festsetzte. Erst nach der Auflösung der Akademie brachte eines ihrer Mitglieder141 die noch heute gebräuchlichen Fundamentalpunkte, nämlich den Schmelzpunkt und den Siedepunkt des Wassers, in Vorschlag. Die Verfertigung der Thermometer wird in den Abhandlungen der Accademia del Cimento mit folgenden Worten beschrieben: »Zunächst hat der Glasbläser eine Kugel von geeigneter Größe herzustellen und ihr eine Röhre anzufügen. Die Füllung geschieht folgendermaßen: Die Kugel wird erhitzt und dann plötzlich das offene Ende in Weingeist getaucht, der langsam hineinsteigt. Das letzte Nachfüllen wird mit einem Trichter besorgt, der einen ganz dünn ausgezogenen Hals hat. Das Rohr wird vorher in gleiche Teile geteilt und jeder Teilstrich durch eine eingebrannte, weiße Glasperle bezeichnet. Dann wird das Thermometer erwärmt und endlich, nachdem der Weingeist den gewünschten höchsten Stand erreicht hat, vollkommen geschlossen.« Weitere Versuche betrafen[S. 89] die Ausdehnung des Wassers beim Gefrieren und seine Zusammendrückbarkeit. Man füllte ein metallenes Gefäß142 mit Wasser, verschloß das Gefäß und brachte es in eine Kältemischung, deren Anwendung zu wissenschaftlichen Zwecken gleichfalls ein Verdienst der Akademie ist. Die Ausdehnung des Wassers bei seiner Umwandlung in Eis erfolgte mit solch unwiderstehlicher Gewalt, daß das Gefäß zersprang, ein Versuch, der ja in den Bestand der Vorlesungsversuche des heutigen Physikunterrichts übergegangen ist.
Auch das Maß der beim Gefrieren eintretenden Ausdehnung bestimmten die Akademiker; und zwar fanden sie, daß sich das Wasser bei diesem Vorgang im Verhältnis von 8 : 9 ausdehnt. Ihre Kältemischung stellten sie aus Schnee her, dem sie Kochsalz, Salpeter oder Salmiak beimengten.
Daß sich beim Auflösen von Salpeter die Temperatur erniedrigt, war wohl schon im 16. Jahrhundert bekannt geworden. Als merkwürdig und unerklärlich erwähnt Descartes die Kältemischungen aus Salz und Schnee in seiner Schrift über die Meteore143. An den Nachweis, daß das Wasser sich auszudehnen vermag, mußte sich die Frage knüpfen, ob diese Flüssigkeit auch zusammengedrückt werden kann. Um darüber eine Entscheidung herbeizuführen, schloß man Wasser in eine silberne Kugel ein und suchte ihre Form durch Pressen und Hämmern zu verändern144. Dabei bedeckte sich ganz wider Erwarten die Kugel mit Wasser (siehe Abb. 28), das offenbar durch das Silber hindurchgepreßt worden war.

Wie Galilei, so mühten sich die Akademiker auch ab, die Schall- und Lichtgeschwindigkeit zu bestimmen. Ihr Verfahren, die Schallgeschwindigkeit zu messen, bestand darin, daß sie die Zeit, die zwischen dem Aufblitzen und dem Knall eines entfernten Geschützes verfließt, durch Pendelschwingungen ermittelten. Auf[S. 90] die Temperatur der Luft wurde hierbei noch keine Rücksicht genommen. Ihr Ergebnis, 1111 Par. Fuß in der Sekunde, kam dem wahren Werte näher als die früheren Bestimmungen. Indessen glaubten die Akademiker irrigerweise, aus den von ihnen erhaltenen Werten schließen zu dürfen, daß der Wind auf die Schallgeschwindigkeit keinen Einfluß habe.
Die Bemühungen, die Geschwindigkeit des Lichtes zu ermitteln, konnten zu keinem Ergebnis führen, da man noch zu keiner neuen Methode gelangt war, sondern das von Galilei vorgeschlagene Signalverfahren benutzte.
Endlich sei noch erwähnt, daß die Akademie manchen Satz, den Galilei nur ausgesprochen, aber noch nicht auf seine Richtigkeit geprüft hatte, durch das Experiment erhärtete. So wurde eine Kugel von einem hohen Turme horizontal fortgeschossen, während man gleichzeitig eine gleich große Kugel von demselben Standort frei herabfallen ließ. Es zeigte sich, daß beide Kugeln, wie Galilei behauptet, zur selben Zeit aufschlugen.
Einige Überreste des physikalischen Apparats, den die Akademiker für ihre Versuche geschaffen, finden sich noch in Florenz146. Die Akademie selbst, die sich mit unvergänglichem Ruhm bedeckt hat, wurde schließlich auf Betreiben der römischen Kurie geschlossen. Zum Glück war religiöse Unduldsamkeit nicht mehr imstande, die Fackel der Wissenschaft zum Erlöschen zu bringen. Fast zur selben Zeit als die Florentiner Akademie aufgelöst wurde, entstanden nämlich nach ihrem Vorbilde die großen Akademien in London und Paris, die ihre glorreiche Laufbahn bis auf den heutigen Tag fortgesetzt haben und nebst zahlreichen Schwestergesellschaften Hochburgen wissenschaftlicher, von keinerlei Rücksichten gehemmter Forschung bilden.
Mit optischen Dingen hat sich unter den Mitgliedern der Akademie besonders Torricelli beschäftigt. Er stellte winzige Glaskügelchen her und lehrte sie als einfache Mikroskope von bedeutendem Vergrößerungsvermögen gebrauchen. Er befaßte sich ferner mit geometrischen Untersuchungen über die Wirkung der Linsen und konstruierte Teleskope, welche diejenigen Galileis übertrafen147. Aber nicht nur die Schüler und die Anhänger Galileis beschritten eifrig den Weg des Versuches, sondern auch seine Gegner, die ihm besonders aus der Ecclesia militans erstanden,[S. 91] verfolgten häufig denselben Weg. Es war immerhin ein Zugeständnis dieser Kreise an den Geist der neueren Zeit, daß man nicht mehr, wie in früheren Jahrhunderten, den Bannstrahl und scholastisches Gezänke für ausreichend hielt, um das Emporkommen neuer Wahrheiten zu unterdrücken. Ein solcher Gegner Galileis und der koppernikanischen Lehre war der Jesuit Riccioli. Er hat sich trotz dieser Gegnerschaft Verdienste um die Astronomie und die Mechanik erworben.
Giovanni Battista Riccioli (1598–1671) unternahm es, in Gemeinschaft mit Grimaldi, die Gesetze des Falles, die von Galilei nur für die schiefe Ebene experimentell nachgewiesen waren, für den freien Fall zu prüfen. Beide Männer ließen um 1640 von einem Turm Kugeln aus verschiedener Höhe herabfallen und maßen, während der eine oben, der andere unten stand, die Zeit. Um letztere zu messen, bedienten sie sich kleiner Pendel, die 6 Schwingungen in der Sekunde machten. Riccioli unternahm seine Versuche in der Absicht, Galilei zu widerlegen und selbst das wahre Gesetz des Falles zu finden. Um die Werke Galileis lesen zu können, mußte er die Erlaubnis seiner Oberen einholen, da Galileis Schriften von der Indexkongregation verboten waren. Ricciolis Ergebnisse sind in folgender Tabelle wiedergegeben:
| Anzahl der Pendelschwingungen | Fallhöhe in Fuß | Fallraum in gleichen Zeiten | Verhältnis der Fallstrecken |
| 5 | 10 | 10 | 1 |
| 10 | 40 | 30 | 3 |
| 15 | 90 | 50 | 5 |
| 20 | 160 | 70 | 7 |
| 25 | 250 | 90 | 9 |
Ricciolis und Grimaldis Fallversuche entsprachen also vollkommen dem von Galilei für den Fall über die schiefe Ebene gefundenen, für den freien Fall aber noch nicht bewiesenen Gesetz. Es macht dem Charakter beider Forscher alle Ehre, daß sie ihre eigene Niederlage unumwunden eingestanden und die Anhänger Galileis von den Versuchsergebnissen in Kenntnis setzten.
Spätere Versuche Ricciolis bezweckten, den Einfluß der Luft auf fallende Körper zu ermitteln. Schon Galilei hatte den Widerstand der Luft für größere Geschwindigkeiten als recht erheblich[S. 92] angenommen und zum Beweise dieser Annahme einen Versuch vorgeschlagen, den aber erst die Mitglieder der Accademia del Cimento zur Ausführung brachten. Galilei schlug vor, man solle eine Flintenkugel aus einer Höhe von 100 Ellen senkrecht auf eine Eisenplatte herab schießen und diesen Versuch in einer Entfernung von wenigen Ellen wiederholen. Es sei wahrscheinlich, daß im ersteren Falle die Kugel infolge der längeren Wirkung des Luftwiderstandes mit geringerer Geschwindigkeit auf das Eisen treffen werde als im zweiten, obgleich bei dem Schuß aus größerer Entfernung die durch das Pulver erhaltene Geschwindigkeit durch den Fall noch wesentlich vergrößert werde. Ob diese Vermutung richtig sei, müsse sich an der größeren oder geringeren Formveränderung der Kugel ergeben. Die Akademie fand diese Vermutung bestätigt, denn die aus großer Höhe herabgeschossene Kugel war tatsächlich weniger verändert148.
Bemerkenswert sind auch Ricciolis Versuche über diesen Gegenstand. Er stellte zwei Tonkugeln von gleichem Gewicht her, von denen die eine massiv war und 10 Zoll Durchmesser besaß, während die andere hohl war und einen Durchmesser von 20 Zoll hatte. Beide Kugeln ließ Riccioli von der Höhe des Campanile zu Bologna herabfallen. Dabei zeigte es sich, daß die massive Kugel die 280 röm. Fuß betragende Strecke in 3,2 Sekunden durchlief, während die hohle 4,2 Sekunden brauchte. Ferner stellte Riccioli Fallversuche mit Kugeln von Blei, Ton, Wachs und Holz an und beobachtete, daß der spezifisch schwerere Körper schneller als der spezifisch leichtere fällt.
Riccioli war zwar ein Gegner des koppernikanischen Systems. Er hat sich aber um die Astronomie trotzdem verdient gemacht, indem er unter dem Titel Almagestum novum (1651) ein bedeutendes, eine Menge von Tatsachen bietendes Sammelwerk dieser Wissenschaft herausgab.
Auch für die Lehre vom Licht wurden um diese Zeit neue experimentelle Grundlagen geschaffen. Das geschah vor allem durch Grimaldi.
Francesco Maria Grimaldi wurde 1618 in Bologna geboren, wirkte dort als Lehrer der Mathematik und starb 1663.[S. 93] Er war ein sehr gelehrter Mann und ein hervorragender Beobachter. Sein Hauptgebiet war die Optik, in die er tiefer einzudringen verstand als irgend jemand vor ihm. Das Werk, in dem Grimaldi seine Beobachtungen und Lehren über diesen Gegenstand zusammenfaßte, erschien erst einige Jahre nach seinem Tode unter dem Titel Physico-Mathesis de lumine, coloribus et iride149. In diesem Buche findet sich nicht nur die erste Beschreibung des durch ein Prisma erzeugten Sonnenspektrums150, es wird darin auch über merkwürdige Erscheinungen berichtet, welche dem Gesetz der geradlinigen Fortpflanzung des Lichtes zu widersprechen schienen, und mit dem Namen der Beugung belegt wurden.
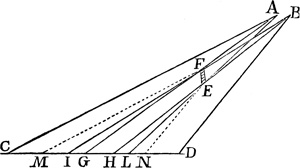
Grimaldi ließ Sonnenlicht durch eine feine Öffnung in ein dunkles Zimmer fallen und brachte in das so erhaltene Lichtbündel einen undurchsichtigen Körper (s. Abb. 29). Fing man vermittelst eines Schirmes CD den Schatten auf, so besaß dieser eine größere Breite (MN), als der Konstruktion entsprach. Ferner war der Schatten von farbigen Streifen umgeben, die seiner Begrenzung parallel liefen und sich auch in das Innere des Schattens erstreckten. Ließ Grimaldi durch die Öffnungen CD und GH (siehe Abb. 30) einen Lichtkegel fallen, der von dem Schirm IK aufgefangen wurde, so besaßen die Grundflächen dieses Kegels nicht den Durchmesser NO, den die geometrische Konstruktion auf Grund der geradlinigen[S. 94] Fortpflanzung des Lichtes fordert, sondern einen größeren Durchmesser IK.
Diese Erscheinungen, insbesondere die zuerst beschriebene, die offenbar nicht mit der infolge der Brechung auftretenden Farbenzerstreuung identisch war, veranlaßte Grimaldi, das Licht als eine wellenförmige Bewegung zu betrachten. »Wie sich um einen Stein, den man ins Wasser wirft, kreisförmige Wellen bilden«, sagt er, »ebenso entstehen um den Schatten des undurchsichtigen Gegenstandes jene glänzenden Streifen. Und so wie jene kreisförmigen Wellen nichts anderes sind als angehäuftes Wasser, um das sich eine Furche hinzieht, so sind auch die glänzenden Streifen nichts anderes als das Licht selbst, das durch eine heftige Zerstreuung ungleichmäßig verteilt und durch schattige Intervalle getrennt wird. So wie endlich die kreisförmigen Wasserwellen breiter werden, wenn sie sich von der Quelle ihrer Erregung entfernen, ebenso bemerken wir dasselbe an den glänzenden Streifen, je weiter sie von dem Anfange ihrer Erregung abstehen«152.
Wir finden hier die erste Andeutung der Undulations- oder Wellentheorie des Lichtes, die in der neuesten Zeit zur vollen Geltung gelangte, da sie nicht nur sämtliche Lichterscheinungen erklärte, sondern in manchen Fällen sogar bisher unbekannte Phänomene vorherzusagen gestattete.
Der Gedanke, daß das Licht aus einer feinen Flüssigkeit bestehe, die in wellenförmiger Bewegung begriffen sei, kehrt in Grimaldis Ausführungen immer wieder. Auch die wichtige Beobachtung, daß »Licht zu Licht addiert«, wie es später bei Arago lautet, Finsternis geben kann, hat Grimaldi zuerst gemacht: »Ein erleuchteter Körper kann dunkel werden«, sagt er153, »wenn zu dem Licht, das er empfängt, noch neues Licht hinzutritt«. In dem Laden eines verdunkelten Zimmers wurden zwei Löcher angebracht, durch welche Licht fiel. Jeder Lichtkegel gab für sich auf dem weißen Schirm einen hellen, gegen die Ränder rötlichen[S. 95] Fleck. Ließ Grimaldi nun die Lichtkegel teilweise übereinander greifen, (s. Abb. 31) so fand er, daß die Kreisbögen, welche den Mittelraum des von den übergreifenden Rändern eingeschlossenen Stückes begrenzen, dunkel erscheinen. Durch diese Versuche war die Interferenz des Lichtes entdeckt. Auf den Gedanken, das weiße Licht aus farbigem zusammenzusetzen, ist Grimaldi noch nicht gekommen. Durch weitere Versuche hat er aber dargetan, daß weißes Licht durch bloße Reflexion, wie er sich ausdrückt, in farbiges Licht verwandelt werden kann. Zu diesem Zwecke, ließ Grimaldi154 das Sonnenlicht auf eine feingeritzte Metallplatte und von dort auf einen Schirm fallen. Es zeigten sich durch Beugung entstandene farbige Streifen. Wir begegnen also schon hier an der Schwelle der neueren Physik dem Verfahren, mittelst dessen heute die Gitter zur Erzeugung eines Beugungspektrums hergestellt werden.
Grimaldi selbst hat aus dem Verhalten seiner geritzten Platte gegen das Licht schon die im Tierreich an Federn, Insektenflügeln usw. so häufig vorkommenden Schillerfarben erklärt, eine Untersuchung, welche die neuere Zoologie wieder aufnahm und die Brücke155 zu einem vorläufigen Abschluß brachte.
Der zuletzt erwähnte Versuch mußte in Grimaldi schon die Überzeugung wachrufen, daß die Farben Bestandteile des weißen Lichtes und nicht etwas den Körpern Eigentümliches sind. Die Farben, sagt er wiederholt, seien nichts vom Lichte Verschiedenes, das etwa in den farbigen Körper ohne die Gegenwart des Lichtes vorhanden wäre. Die Ursache der Körperfarben erblickt Grimaldi vielmehr in dem, was wir heute den molekularen Bau der Körper nennen würden. Er meint nämlich156, ihre Ursache beruhe wahrscheinlich auf der Lage der Poren, also auf dem Gefüge der Stoffe, wodurch gerade diejenige Farbe, die dem betreffenden Körper eigentümlich sei, zurückgeworfen werde. Die Farbe selbst, so führt er weiter aus, ist danach eine durch die Natur des reflektierenden Körpers hervorgerufene Modifikation des Lichtes und besteht wahrscheinlich in einer Änderung der Bewegungsform und der Geschwindigkeit des letzteren. Wie die Töne durch die Verschiedenartigkeit der Luftschwingungen hervorgerufen würden, so würden auch die Farben dadurch erzeugt, daß das Auge von Erzitterungen des Lichtes getroffen werde, deren Geschwindigkeit[S. 96] verschieden groß sei und so die Unterschiede der Farben bedinge. Alles das sind Anschauungen, die für die weitere Entwicklung der Optik grundlegend gewesen sind.
Daß Grimaldi zwischen der Auffassung, ob das Licht stofflicher Natur sei oder in einem reinen Bewegungsvorgang bestehe, noch nicht scharf genug zu unterscheiden vermochte, tut dem Werte seiner Versuche keinen, und dem Werte der an diese Versuche geknüpften Lehren nur geringen Abbruch157. Man findet daher bei den bedeutendsten Physikern des 17. Jahrhunderts, vor allem bei Hooke und Newton, manche Spuren seiner Anregungen, wenn auch beide Forscher auf diese Anregungen in ihren Werken nicht immer hinweisen158.
Nicht nur in Italien, sondern auch in den übrigen Kulturländern hatte das induktive Verfahren Wurzel geschlagen. Teils unabhängig von Galilei und seiner Schule, teils angeregt von dieser, erstand eine stetig wachsende Schar von Forschern, welche die Unfruchtbarkeit der alten Methode erkannten und mit vereinten Kräften die Naturwissenschaften in das neue Fahrwasser hinüberzulenken strebten. Während in Italien diese Wissenschaften durch das Verhalten der in mittelalterlicher Denkweise beharrenden Kreise, wenn auch nicht unterdrückt, so doch in hohem Grade gehemmt wurden, erwies sich im Verlauf des 17. Jahrhunderts der Boden Englands und der Niederlande für ihre Entwicklung besonders günstig. Im nördlichen Europa waren durch die Reformation die Fesseln des blinden Autoritätsglaubens gesprengt worden. Zwar wurde diese Bewegung bald durch neue Schranken eingedämmt. In Deutschland ließen sie auch die politischen Verhältnisse weniger zum Durchbruch kommen. Eine tiefgehende Wirkung blieb jedoch nicht aus. Sie trat auch in den Geisteserzeugnissen jener Zeit zutage. In England vor allem fand seit dem Zeitalter Elisabeths eine Neugestaltung der gesamten Lebensverhältnisse, sowie eine Ausdehnung des Gesichtskreises und des Machtbereiches statt, die eine in diesem Lande[S. 97] nie vorher in solchem Maße gesehene Entfaltung aller Kräfte zur Folge hatten. »Unter den Waffen«, sagt der Geschichtsschreiber dieser Periode159 »wuchs der Handel. Die Erhaltung des Friedens im Innern erfüllte das Land mit Wohlstand und Reichtum; man sah Paläste aufsteigen, wo sonst Hütten gestanden hatten«. Hier war es, wo damals das Wort »Wissen ist Macht«160 erklang. Und daß dieses Wort seitdem gewürdigt wurde, ist eine der Ursachen von Englands Emporblühen gewesen, das, wie Bacon es einmal ausdrückte, seine natürliche Stellung in der Welt gewann.
Der bedeutendste Forscher, der uns zu Beginn der neueren Zeit auf dem Boden Englands begegnet, ist Gilbert. Ihm verdanken wir die erste wissenschaftliche Behandlung der elektrischen und der magnetischen Erscheinungen. Das Ergebnis seiner Untersuchungen hat Gilbert in dem Werke161 »Über den Magneten« niedergelegt. William Gilbert wurde in Colchester im Jahre 1540162 geboren. Er lebte seit 1573 als Arzt in London und wurde von der Königin Elisabeth zu ihrem Leibarzt ernannt. Er starb in London im Jahre 1603.
Zu seinen Untersuchungen wurde Gilbert durch die »Magia naturalis« Portas, besonders aber durch den Umstand angeregt, daß die Magnetnadel und der Erdmagnetismus für die Schifffahrt von solch außerordentlicher Bedeutung geworden waren. Während aber Porta seine Darstellung der physikalischen Erscheinungen noch mit phantastischem und abenteuerlichem Beiwerk vermengte, betrat Gilbert gleich Galilei den Weg der von Vorurteilen und unbegründeten Voraussetzungen absehenden, auf Versuche sich aufbauenden Forschung. Das Ergebnis dieser Bemühungen war ein wissenschaftliches, die Grundlagen für ein weites Gebiet enthaltendes Werk, mit dessen Inhalt wir uns der Hauptsache nach bekannt machen wollen.
Gilbert gebrauchte für seine Versuche kräftige Magnetsteine von geeigneter Größe und gab ihnen die Kugelform. »Der so geformte Stein« sagt er, »ist das getreue und vollkommene Ebenbild[S. 98] der Erde; wir wollen ihn daher Terrella163 nennen«. Um die Pole des Magneten zu finden, nahm er die Terrella in die Hand und legte einen dünnen Eisendraht über den Stein. Letzteren bezeichnete er dort, wo der Draht haftete, mit Kreide. Darauf brachte er die Mitte des Drahtes an eine andere Stelle, sowie an eine dritte und an eine vierte, und versah jedesmal den Stein in der Längsrichtung des Drahtes mit einem Strich. »Diese Striche«, sagt Gilbert, »werden den Meridianen vergleichbare Linien auf der Terrella darstellen. Und es wird sich deutlich zeigen, daß sie in den Polen der Terrella zusammenlaufen.« In gleichem Abstande von diesen Polen der Terrella ließ sich dann ein größter Kreis ziehen, der dem Äquator entsprach.
Ein anderes Verfahren, die Pole aufzufinden, besteht nach Gilbert darin, daß man sich einer Magnetnadel bedient, die mit einer Vertiefung versehen und auf der Spitze einer Nadel so angebracht ist, daß sie sich frei bewegen kann. Diese Vorrichtung wird so auf den Stein AB in C gestellt, daß sich die Nadel im Gleichgewicht befindet (Abb. 32). Darauf wird die Richtung der ruhenden Nadel mit Kreide bezeichnet, dann das Instrument auf eine andere Stelle gebracht und die Richtung wieder vermerkt. »Geschieht dies an recht vielen Stellen, so wird man aus dem Zusammenlauf der Linien den einen Pol an dem Punkte A, den andern bei B finden. Den Pol selbst zeigt die dem Steine genäherte Nadel dadurch[S. 99] an, daß sie sich rechtwinklig zur Oberfläche einstellt und auf den Pol und somit nach dem Mittelpunkt des Steines hinweist.«
Für seine Versuche über die Teilung des Magneten wählte Gilbert einen länglichen Magnetstein AD, mit dem Nordpol A und dem Südpol D, und teilte ihn in zwei gleiche Teile. Darauf ließ er den Teil AB in einem Gefäß auf Wasser schwimmen. Er bemerkte, daß der Nordpol A nach Süden zeigte und D nach Norden. B und C aber, die vorher miteinander verbunden gewesen, waren jetzt zum Nord- und Südpol geworden. Der Südpol B zog den Nordpol C an. »War kein Hindernis vorhanden und das Gewicht aufgehoben, wie es auf der Oberfläche des Wassers der Fall ist, so näherten sich diese Pole und vereinigten sich. Näherte man jedoch den Pol A dem Pole C des anderen Steines, so flohen sie einander.« Es handelte sich bei diesen Schilderungen Gilberts nicht etwa immer um ganz neue Entdeckungen. Wir finden aber vor ihm keine solche klare, wissenschaftlich zu nennende Darstellung. Einen Vorläufer besaß Gilbert in Petrus Peregrinus, dessen im Jahre 1269 entstandene Abhandlung »Über den Magneten« die älteste im Abendlande angestellte Untersuchung über diesen Gegenstand und zugleich eins der frühesten Zeugnisse dafür ist, daß die Anfänge der experimentellen Forschung bis auf das Mittelalter zurückzuführen sind164.
Von dem Inhalt der Schrift des Petrus Peregrinus erhalten wir durch folgende Kapitelüberschriften eine ungefähre Vorstellung: Auf welche Weise der Magnet Eisen anzieht. – Wie das mit dem Magneten berührte Eisen nach den Himmelspolen gerichtet wird. – Über die wechselseitige Anziehung des Nord- und Südpols. – Vorschrift, die Pole aufzufinden. Sie lautet: Man bringe den Magnetstein in ein hölzernes Gefäß. Dieses läßt man in einem größeren mit Wasser gefüllten Behälter schwimmen. Der Stein dreht dann das Gefäß, wie ein Seemann sein Schiff dreht, bis die Pole sich nach den Himmelsrichtungen einstellen.
Von den magnetischen Erscheinungen wußte Gilbert die elektrischen wohl zu unterscheiden, während vor ihm in dieser Hinsicht eine große Unklarheit herrschte. Bis zu seiner Zeit[S. 100] kannte man die elektrische Anziehung fast nur am Bernstein. Durch Gilberts Versuche wurde bewiesen, daß sich diese Kraft auf alle festen Substanzen und sogar auf Flüssigkeiten erstreckt. Tropfen, denen Gilbert elektrisierte Körper näherte, erhoben sich auf ihrer Unterlage. Die Einwirkung der Elektrizität auf Metalle stellte Gilbert fest, indem er diese in der Form leicht beweglicher Nadeln anwandte und zeigte, daß sie von elektrisierten Körpern angezogen werden. Daß zwischen den letzteren auch eine Abstoßung stattfindet, ist von Gilbert übersehen worden. Ganz unbekannt blieb ihm die elektrische Abstoßung jedoch nicht, da er wenigstens die Beobachtung machte, daß die Flamme sich von einem elektrisierten Körper fortbewegt.
Gilbert elektrisierte außer dem Bernstein auch Diamant, Saphir, Rubin, Opal, Amethyst, Beryll, Bergkristall, Schwefel und Harz. Er wies nach, daß all diese Substanzen nicht nur Spreu anziehen, sondern auch sämtliche Metalle, Holz, Blätter, Steine, Erde, sogar Wasser und Öl, kurz, »alles, was durch unsere Sinne wahrgenommen werden kann«. Um aber durch Versuche festzustellen, wie diese Anziehung stattfindet und welches die Stoffe sind, die alle Körper auf solche Weise anziehen, richtete er sich einen 3–4 Zoll langen Zeiger aus Metall her und brachte diesen auf der Spitze einer Nadel, ähnlich wie bei einem Kompaß, leicht beweglich an. Näherte er nun diesem Zeiger Bernstein oder Bergkristall, nachdem er sie gerieben hatte, so geriet der Zeiger sofort in Bewegung.
Der Magnet, bemerkt Gilbert, äußere seinen Magnetismus ohne vorhergehendes Reiben, sowohl im trockenen als im feuchten Zustande, in der Luft wie im Wasser, ja selbst, wenn die dichtesten Körper, seien es Platten aus Holz und Stein oder Scheiben aus Metall, dazwischen gebracht seien. Der Magnet wirke aber nur auf magnetische Körper, während elektrische Substanzen alles anzögen. Auch vermöge der Magnet bedeutende Lasten zu tragen, während der elektrisierte Körper nur sehr kleine Gewichte bewege165.
Die magnetischen Erscheinungen waren infolge der Verwendung, welche die Boussole seit dem 12. Jahrhundert in Europa sowohl für die Schiffahrt als auch beim Bergbau erfahren hatte166, weit mehr als die elektrischen beachtet worden. So konnte die als Deklination bezeichnete Abweichung der Nadel aus der Nord-Südrichtung[S. 101] einem aufmerksamen Beobachter nicht wohl entgehen. Columbus hatte die Änderungen der Deklination auf seiner Reise nach Westen bemerkt und war sogar auf den Gedanken gekommen, diese Änderungen zur Bestimmung der geographischen Länge zu benutzen. Er beobachtete 200 Seemeilen über Ferro hinaus eine westliche Deklination von fünf Graden. Bei der weiteren Fahrt nach Westen vergrößerte sich diese Abweichung, während sie in Europa damals östlich war. Die Neigung der um eine horizontale Achse drehbaren Magnetnadel war gleichfalls bereits bekannt. Gilbert selbst teilt mit, daß ihre Größe im Jahre 1576 für London gleich 71° 50ʹ gefunden sei167.
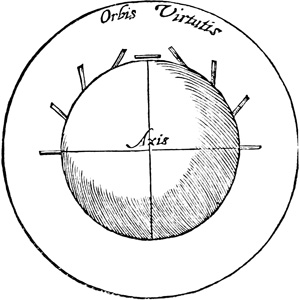
Gilberts wesentlichstes Verdienst bestand darin, daß er alle erdmagnetischen Erscheinungen unter einem Gesichtspunkt vereinigte, indem er die Erdkugel für einen einzigen großen Magneten erklärte. Zu dieser Auffassung gelangte er, als er das Verhalten der Nadel gegen einen kugelförmigen Magneten eingehend untersuchte und es mit dem Verhalten der Magnetnadel gegen die Erde verglich. Daraus, daß die Nadel sich an den Polen eines kugelförmigen Magneten senkrecht zur Oberfläche einstellt (s. Abb. 34), schloß Gilbert, daß die Inklination in den nördlichen Teilen der Erde größer sein müsse als in London, eine Vermutung, die später durch Hudson während seiner Entdeckungsreisen in den polaren Gegenden Amerikas bestätigt wurde. Hudson fand nämlich im Jahre 1608 schon unter dem 75. Grad nördlicher Breite eine nahezu senkrechte Einstellung der Inklinationsnadel. Dies war der Annahme Gilberts nicht ganz entsprechend.[S. 102] Er meinte nämlich, der magnetische Nordpol müsse mit dem geographischen zusammenfallen, wie er ja auch die tägliche Drehung als eine Folge des Erdmagnetismus auffaßte. Galilei, der Gilbert schätzte und seine Ergebnisse im wesentlichen gelten ließ, wies jedoch die Ansicht, daß jede freischwebende, magnetische Kugel sich um ihre Achse drehen müsse, als irrtümlich zurück.
Von dem Nachweis, daß die Erde ein kugelförmiger Magnet ist, war es nur ein Schritt zu dem Gedanken, daß auch die übrigen Weltkörper, insbesondere der Mond und die Sonne, mit magnetischer Kraft begabt seien169. Gilbert zögerte nicht, diesen Schluß zu ziehen und als Anhänger des koppernikanischen Systems die Bewegung der Weltkörper, sowie die Erscheinung von Ebbe und Flut auf den Magnetismus zurückzuführen. Hierin folgte ihm auch Kepler, dessen Ansichten über die magnetische Kraft der Sonne wir später kennen lernen werden.
Da Gilbert die geographischen Pole mit den magnetischen zusammenfallen ließ, bedurfte die Erscheinung der Deklination einer besonderen Erklärung. Gilbert, dem noch wenig Beobachtungsmaterial zur Verfügung stand, hielt die Verteilung von Wasser und Land für die Ursache jener Abweichung der Nadel. Seiner Meinung nach mußte im Innern größerer Kontinente, wo der Einfluß des Meeres aufhörte, auch die Deklination verschwinden. Die wenigen Beobachtungen, welche die Seefahrer damals gesammelt hatten, waren geeignet, diese irrige Ansicht zu unterstützen.
Zwar wußte Gilbert noch keine eigentliche Theorie der von ihm gefundenen Tatsachen zu geben, wenn er auch die elektrischen Erscheinungen in ähnlicher Weise, wie es schon das Altertum versucht hatte, auf Ausflüsse zurückführte. Wie man die Luft als einen Ausfluß der Erde betrachten müsse, so beruhe die Elektrisierbarkeit der Körper darauf, daß eine gewisse feinste Flüssigkeit, die erforderlich sei, um den Zusammenhang der Körper zu bewirken, infolge der Reibung aus ihnen herausgetrieben werde. Dieses Fluidum sollte die elektrische Anziehung leichter Körper vermitteln, ebenso wie nach Gilberts Ansicht die Luft es ist, welche die ihrer Unterstützung beraubten Körper veranlaßt, sich dem Mittelpunkt der Erde zu nähern. Diese Vorstellung von einer oder mehreren Flüssigkeiten als Trägern der elektrischen Erscheinungen,[S. 103] die uns bei den Alten und bei Gilbert im Keime begegnet, wurde vom 18. Jahrhundert, das sich in hervorragendem Maße der Erforschung der Reibungselektrizität zuwandte, festgehalten und zu einer wissenschaftlichen Theorie entwickelt.
Hinsichtlich der magnetischen Erscheinungen verzichtete Gilbert auf eine physikalische Erklärung. Er hielt diese Erscheinungen für die Folge einer Beseelung der Materie. Jenseits der Ausflüsse, welche die elektrischen Vorgänge veranlassen sollten, befinde sich der leere Raum, das Vakuum, durch das hindurch unmöglich eine materielle Einwirkung stattfinden könne. Daher nahm Gilbert – und auch hierin folgte dem Physiker der Astronom Kepler – in den Weltkörpern eine Art seelischer Kraft an. Das große Rätsel von der Wirkung der Materie in die Ferne begegnet uns also schon hier an der Schwelle der neueren Naturwissenschaft170.
Der Mangel an klaren theoretischen Vorstellungen beeinträchtigt indessen nicht den Wert experimentell gewonnener Ergebnisse. Und diese sind es, die wir Gilbert in reichem Maße verdanken. Hervorgehoben seien noch seine Versuche mit bewaffneten oder armierten Magneten. Letztere stellte er dadurch her, daß er die Pole eines natürlichen Magneten mit Eisenkappen bedeckte (siehe Abb. 35). Es zeigt sich, daß die Tragkraft durch eine derartige Armierung bedeutend zunimmt. So trug ein Magnet vor der Armierung 2 und nach der Armierung 12 Unzen Eisen. Die Abbildung zeigt uns einen armierten Magneten, der zwei andere von gleicher Größe trägt171.

Mit dem Werke Gilberts kaum in Parallele zu stellen ist das dickleibige Buch eines gelehrten Deutschen, das wenige Jahrzehnte[S. 104] später (1634) erschien. Es führt den Titel »Magnes sive de arte magnetica« und hat den in Würzburg eine Professur bekleidenden Jesuitenpater Athanasius Kircher zum Verfasser. Kircher steht mit Porta, Schwenter und ähnlichen vom Forschergeist der neuen Zeit noch weniger erfüllten Männern auf einer Stufe. Er ist kein Physiker wie Gilbert oder Galilei, sondern schildert mit vielen Worten überraschende naturwissenschaftliche Erscheinungen und den Laien fesselnde, naturwissenschaftliche Spielereien. Wir haben Kirchers gesamtes, auch die Optik und andere Zweige der Naturlehre betreffendes Wirken schon in einem früheren, jene Übergangszeit behandelnden Abschnitt gewürdigt (Bd. I. S. 427). Hier sei als von Bedeutung nur noch hervorgehoben, daß er die Stärke des Magneten mittelst der Wage zu bestimmen suchte. Einen großen Umfang in Kirchers Werk nehmen seine Vorschläge ein, mit Hilfe des Magnetismus Krankheiten zu heilen. Auch manche Erscheinungen der Tierwelt, z. B. die Züge der Vögel, werden auf diese Naturkraft zurückgeführt. Ein besonderer Abschnitt ist dem Magnetismus der Liebe (Magnetismus amoris) gewidmet. Das Buch schließt mit der Betrachtung, daß Gott totius naturae magnes, der Magnet der gesamten Natur, sei.
Ganz hiervon abweichend und mit derjenigen Gilberts und Galileis verwandt war die Geistesart eines anderen Deutschen, Ottos von Guerickes, der nicht nur die Luftpumpe erfand, sondern zu den ersten Erforschern der magnetischen und ganz besonders der elektrischen Erscheinungen zu rechnen ist. Von Guericke rührt auch die erste, zwar noch sehr einfache Elektrisiermaschine her. Sie findet sich in seinem Werke »De vacuo spatio« abgebildet (siehe Abb. 36) und beschrieben. Zu ihrer Herstellung füllte Guericke eine Glaskugel mit geschmolzenem Schwefel. Nach dem Erkalten wurde das Glas zerschlagen und die so erhaltene Schwefelkugel auf eine Achse gesteckt, die auf zwei Stützen ruhte. Als Reibzeug diente die trockene Hand; ein Konduktor fehlte noch. Immerhin war es die erste maschinelle Vorrichtung zum Erzeugen von Elektrizität. Die geriebene Kugel zog Papier, Federn und andere leichte Gegenstände an und führte sie mit sich herum. Wassertropfen, die man in ihre Nähe brachte, gerieten in eine wallende Bewegung. Auch wurden ein Leuchten und ein Geräusch wahrgenommen, wenn man der Schwefelkugel nach dem Reiben den Finger näherte. Vermittelst dieser Maschine entdeckte Guericke auch die von Gilbert noch übersehene Abstoßung[S. 105] gleichnamig elektrisierter Körper. Ferner bemerkte er, daß ein von der Kugel abgestoßener Körper wieder angezogen wird, nachdem er mit dem Finger oder mit dem Boden in Berührung gekommen ist. Brachte er z. B. eine Feder zwischen die elektrisierte Kugel und den Fußboden, so hüpfte diese Feder auf und nieder. Auch daß sich die Elektrizität der Kugel vermittelst eines leinenen Fadens fortleiten läßt, wurde von Guericke nachgewiesen.

Guericke beobachtete sogar schon, daß Körper elektrisch werden, wenn man sie der geriebenen Schwefelkugel nur nähert. Er war also ein Vorläufer von Aepinus, der als der eigentliche Erforscher der Influenzerscheinungen betrachtet werden muß. Leider fand Guericke auf diesem Gebiete nicht die Beachtung, die man seiner Luftpumpe und den Magdeburger Halbkugeln zollte. Die Laien vermochten ihm hier nicht zu folgen, und die Gelehrten ließen Guerickes Entdeckungen der Vergessenheit anheimfallen174.
In ganz anderer Weise wie Galilei und Gilbert machte sich zur selben Zeit der Engländer Francis Bacon (1561–1626) um die Erneuerung der Naturwissenschaften verdient. Hatte Gilbert gleich Galilei aufbauend und durch die Tat geschaffen, so wirkte Bacon mehr zerstörend und durch das Wort. Er war[S. 106] es, der die damalige geistige Atmosphäre von jenen Trübungen reinigen half, die ihr aus der aristotelisch-scholastischen Periode noch anhafteten. Dabei unterstützte ihn eine klare und gefällige Ausdrucksweise. Mit beredten Worten kämpft er in seinem Hauptwerk, dem neuen Organon175, gegen alles, was die Menschheit von der Ausübung des induktiven Verfahrens bisher zurückgehalten hatte. Es sind das nach ihm vor allem die »Idole« oder falschen Begriffe, die zum Teil in der Natur des Menschen begründet sind, teils aber aus dem Zusammenleben entspringen.
Nicht der menschliche Sinn ist bei Bacon das Maß der Dinge. Vielmehr geschehen alle Auffassungen der Sinne und des Verstandes nach der Natur des Menschen und nicht nach der Natur des Weltalls. Der menschliche Verstand gleicht »einem Spiegel mit unebener Fläche, der seine Natur mit den Strahlen der Gegenstände vermengt«. Aber auch die Eigenart der einzelnen Menschen bedinge wieder eine besondere Auffassung. Ferner beeinflusse die so oft unzutreffende Benennung von Sachen und Vorgängen den Geist in merkwürdiger Weise, so daß »bloße Worte die Menschen zu zahllosen leeren Streitigkeiten und Erdichtungen verleiten«. Der größte Anlaß zu Irrtümern rühre aber von den Täuschungen der Sinne her. Alles, was die Sinne erschüttere, werde über das gestellt, bei dem dies nicht unmittelbar der Fall sei, wenn auch letzteres das Wichtigere sein sollte. Darauf müsse man es z. B. zurückführen, daß die Natur der gewöhnlichen Luft fast unbekannt sei. Die wahre Erklärung der Natur vollziehe sich durch passende Versuche, wobei die Sinne nur über den Versuch, der Versuch aber über die Natur das Urteil zu sprechen habe.
Das Ziel der Wissenschaften besteht nach Bacon darin, das menschliche Leben mit neuen Erfindungen und Hilfsmitteln zu bereichern. Doch könne man auf einen weiteren Fortschritt nur hoffen, wenn die Naturwissenschaft vorzugsweise solche Versuche aufnehme, die zwar keinen unmittelbaren Nutzen gewähren, aber zur Entdeckung der Ursachen und der Gesetze dienen. Ferner sei nicht nur die Zahl der Versuche zu vermehren, sondern es müsse durch eine neue Methode eine bestimmte Regel eingeführt werden. Ein unbestimmtes, sich selbst überlassenes Experimentieren sei ein reines Umhertappen und verwirre nur die Menschen,[S. 107] anstatt sie zu belehren. Wenn aber die Naturforschung nach einer festen Regel in Ordnung und Zusammenhang vorschreite, so lasse sich Besseres für die Wissenschaft erhoffen.
Manche der bisherigen Erfindungen seien derart, daß niemand vorher eine Ahnung von ihnen gehabt, sondern dergleichen als Unmöglichkeiten betrachtet haben würde. Bacon erinnert an die Erfindung der Feuerwaffen und des Kompasses. Man dürfe daher hoffen, daß die Natur in ihrem Busen noch vieles verborgen halte, was mit dem bisher Gefundenen keine Verwandtschaft und Ähnlichkeit habe, sondern weitab von den Wegen der Einbildungskraft liege. Unzweifelhaft werde es im Laufe der Jahrhunderte zum Vorschein kommen, ebenso wie es mit dem Früheren auch geschehen sei. Aber auf dem von ihm gezeigten Wege werde dies schneller und sicherer geschehen.
Trotz dieser unleugbar richtigen Grundsätze einer Philosophie der Erfahrung würde es verkehrt sein, Bacon für einen Naturforscher oder gar, wie es auch wohl geschehen ist, für den eigentlichen Begründer der neueren Naturwissenschaft zu halten. Das, was er forderte, war durch Galilei, Gilbert und andere längst Wirklichkeit geworden. In allen Ländern regte sich ein neuer, dem experimentellen Verfahren zugewandter Geist. Bacons Verdienst war es, daß er diesen in einer klaren, oft prophetischen Weise zum Ausdruck brachte. Wir dürfen ihn also nicht als den Erfinder, wohl aber als einen beredten Verkünder der induktiven Forschungsweise bezeichnen. Es sei daher noch einiges über die Eigenart und den Lebensgang dieses merkwürdigen Mannes mitgeteilt.
Francis Bacon wurde am 22. Januar 1561 in London geboren. Er bekundete frühzeitig eine hervorragende Begabung. Mit 13 Jahren bezog er die Universität, mit 16 Jahren veröffentlichte er seine erste Schrift, in der er bereits sein Lebenswerk, den Kampf gegen die scholastische Philosophie, aufnahm. Die Anregung dazu ist Bacon von verschiedenen Seiten gekommen. An vielen Orten waren während des 16. Jahrhunderts Männer aufgetreten, die sich dem Einfluß der aristotelischen Lehren zu entziehen und selbständig an das Studium der Natur zu gehen strebten. Unter ihnen ist vor allem der Italiener Telesio zu nennen, dessen Hauptwerk »De natura rerum« im Jahre 1565 erschienen war176.[S. 108] Sowohl Bacon als auch Giordano Bruno zollten dem Telesio große Anerkennung.
Bei einem Aufenthalt in Frankreich hatte Bacon dagegen in Palissy einen Mann kennen gelernt, der ohne die Kenntnis der griechischen und lateinischen Quellen sich der Erforschung der Natur widmete und durch seine Erfindungen und Entdeckungen die Aufmerksamkeit der gelehrten Kreise Frankreichs auf sich gezogen hatte. Palissy machte wichtige Erfindungen auf dem Gebiete der Keramik und beschrieb ein von ihm angelegtes Mineralienkabinett. Er bekämpfte die Alchemie, erklärte die Versteinerungen für Überreste von Lebewesen und entwickelte in seiner Abhandlung über die Gewässer und die Quellen ein klares geologisches Verständnis. Dieser seltene Mann177 hielt in Paris Vorträge, denen auch Bacon beiwohnte.
Von Beruf war Bacon Staatsmann. Eine glänzende Beredsamkeit, vereinigt mit einem oft allzu geschmeidigen Wesen, unterstützte sein ehrgeiziges Streben. Sprach er, so hatte er seine Zuhörer so in der Gewalt, daß jeder fürchtete, er möchte schon am Ende angekommen sein. Staffel auf Staffel erklimmend, dabei wenig wählerisch in seinen Mitteln, gelangte Bacon schließlich zur höchsten Würde, indem ihn der König zum Großkanzler und zum Baron von Verulam erhob. Dies geschah zu einer Zeit, als sich in England die Anzeichen bevorstehender politischer Umwälzungen immer mehr geltend machten und der Widerstand des Parlaments gegen die Krone und deren Vertreter in stetem Wachsen begriffen war. Eins der ersten, indessen nicht schuldlosen Opfer dieses Streites ist Bacon geworden.
Damals war die Unsitte, Beamten Geldgeschenke zu machen, in England sehr verbreitet. Auch Bacon nahm solche entgegen, um den Aufwand, den seine Stellung mit sich brachte, zu bestreiten. Bacon wurde infolgedessen der Bestechlichkeit bezichtigt, wenn[S. 109] er auch beteuerte, bei seiner amtlichen Tätigkeit auf die Schenker niemals Rücksicht genommen zu haben. Das Parlament hielt jedoch Bestechlichkeit in mehr als zwanzig Fällen für erwiesen, und das Haus der Lords verurteilte den Kanzler und obersten Richter Englands zum Verlust seiner Stelle. Niemals dürfe Bacon wieder ein öffentliches Amt bekleiden, noch im Parlament sitzen, auch solle er aus der Nähe des Hofes verbannt sein, so lautete das harte, wenn auch gerechte Urteil178. Die Verurteilung geschah im Jahre 1621. Den Rest seines Lebens verbrachte Bacon in der Zurückgezogenheit, mit der Abfassung philosophischer Werke beschäftigt.
Obgleich Bacon auf Experimente drang und lehrte, daß alle Philosophie von der Erfahrung ausgehen müsse, hat er keinen Versuch von Bedeutung angestellt. Sein mathematisches und physikalisches Wissen war selbst für seine Zeit gering. Er kannte die Werke Galileis und Gilberts, hatte jedoch zu ihrem eingehenden Studium offenbar keine Muße gefunden. Während Galilei mit dem Fernrohr den Himmel durchforschte, zweifelte Bacon, ob Instrumente von Nutzen seien179. Auch blieb er Zeit seines Lebens ein Gegner der koppernikanischen Lehre. Ebensowenig fanden die Fortschritte der Mechanik, die wir Galilei und seinen Schülern verdanken, die Beachtung Bacons. Auf diesem Gebiete beharrte er gänzlich in den Fesseln der Scholastik, die er im übrigen bekämpfte. Man höre nur seine Ausführungen über die Bewegung des Zitterns. »Sie ist,« heißt es180, »die einer ewigen Gefangenschaft, in der die Körper nicht ihrer Natur entsprechend gestellt sind, sich aber auch nicht ganz schlecht befinden. Sie bewegen sich deshalb hin und her, weil sie weder mit ihrem Stand zufrieden sind, noch es wagen, weiter vorzuschreiten.« Als eine Bewegung solcher Art faßte er z. B. diejenige des Herzens auf. Ja, er kennt sogar eine »Bewegung aus Abscheu vor Bewegung«. Daß er an dem aristotelischen Begriff der Leichtigkeit und Schwere festhielt und z. B. zu untersuchen empfahl, ob die Luft ein absolut leichter oder ein schwerer Körper sei, darf uns daher nicht wunder nehmen181.
Trotz seines Unvermögens, Eigenes in der von ihm gewollten Richtung zu vollbringen, ist Bacons Einfluß nicht zu unterschätzen. Seine Werke haben manche tüchtige Kraft ermuntert, sich in den Dienst der großen, von Bacon in den Vordergrund gerückten Aufgabe zu stellen, der Aufgabe nämlich, die wahre Herrschaft des Menschen dadurch zu begründen, daß letzterer sich zum Herren der Naturkräfte mache. In der Philosophie ist Bacon der Urheber derjenigen Richtung, die von der Erfahrung ausgeht und als Realismus bezeichnet wird. Auch auf die Pädagogik hat sich sein Einfluß erstreckt. Comenius, der Vater der neueren Pädagogik, wurde in erster Linie durch Bacons Schriften veranlaßt, das größte Gewicht auf die Anschauung zu legen. »Die Jugend recht unterrichten«, sagt Comenius, »heißt nicht ihr einen Mischmasch von Worten, Phrasen, Sentenzen und Meinungen einstopfen, sondern ihr das Verständnis für die Dinge öffnen. Warum sollen wir nicht statt fremder Bücher das lebendige Buch der Natur aufschlagen?182 Fast niemand lehrt Physik durch Anschauung und Experiment. Alle unterrichten durch mündlichen Vortrag des aristotelischen Werkes oder eines anderen.«
Neben Italien, Frankreich, den Niederlanden und England hat sich auch Deutschland an der Neubegründung der Naturwissenschaften beteiligt. Hier war das koppernikanische System[S. 111] entstanden; von hier aus hatte die Reformationsbewegung einen großen Teil der europäischen Menschheit ergriffen. Zwar drohte die befreiende Kraft, welche dieser Bewegung innewohnte, unter neuen starren Formen, sowie in endlosen Religionskämpfen zu ersticken. Die evangelische Hierarchie war nicht weniger darauf bedacht, die Lehrfreiheit zu beschränken, wie es in Italien durch den katholischen Klerus geschah. Ebensowenig wie in diesem Lande hätte es an deutschen Hochschulen ein Gelehrter wagen dürfen, sich zur koppernikanischen Weltanschauung zu bekennen. Dazu kam in den protestantischen Ländern ein solch weitgehender Haß gegen den Katholizismus, daß selbst vernünftige Neuerungen, wenn sie von Rom ausgingen, zurückgewiesen wurden. So erging es z. B. der von Gregor XIII. im Jahre 1582 ins Leben gerufenen Reform des Kalenders. Bis dahin hatte die Christenheit mit dem julianischen Jahr von 365¼ Tagen gerechnet, obgleich schon Hipparch und Ptolemäos wußten, daß die Dauer des Jahres geringer ist. Alle Bemühungen, den stetig wachsenden Fehler des Kalenders zu beseitigen, an denen auch Koppernikus lebhaften Anteil genommen, waren vergeblich geblieben. Dieser Fehler belief sich zur Zeit Gregors schon auf 10 Tage. Er wurde dadurch ausgemerzt, daß man die Tage vom 5. bis zum 15. Oktober 1582 ausfallen ließ und anordnete, daß in Zukunft die Säkularjahre, sofern sie nicht durch 400 teilbar sind, gewöhnliche Jahre bleiben sollten183.
Die allgemeine Annahme des gregorianischen Kalenders wurde besonders durch Kepler befürwortet, der 1613 als Begleiter des Kaisers auf dem Reichstage zu Regensburg erschien. Die protestantischen Stände betrachteten jedoch die Frage als eine Religionssache und lehnten jeden Vermittlungsvorschlag ab. Volle hundert Jahre dauerte es, bis der Verwirrung ein Ende bereitet wurde und dank den Bemühungen eines Leibniz die Kalenderreform in den protestantischen Gegenden Deutschlands Eingang fand184.
Wie bezüglich des Kalenders und des koppernikanischen Systems, so übte damals in allen Dingen eine noch nicht hinlänglich geläuterte Religiosität einen überwiegenden Einfluß aus. Indem[S. 112] sie sich auch mit politischen Interessen verquickte und den Gegensatz des alten und des neuen Bekenntnisses in Kriegen und Verfolgungen zum Ausdruck brachte, wie sie die Menschheit blutiger und zerstörender kaum gesehen, verlieh dieser auf Irrwegen befindliche Religionseifer dem 17. Jahrhundert sein eigentümliches Gepräge. Bevor jedoch in Deutschland der dreißigjährige und in England der Bürgerkrieg entfesselt wurde, Begebenheiten, die in der Entwicklung dieser Länder einen langen Stillstand herbeigeführt und viele Keime in ihrem Ansatz zerstört haben, hatte der wissenschaftliche Sinn dort schon in solchem Maße Wurzel geschlagen, daß er wohl gehemmt, nicht aber wieder vernichtet werden konnte. Während des 16. und des 17. Jahrhunderts lief die geistige Entwicklung, zumal in Deutschland darauf hinaus, die scholastisch-aristotelische Denkweise zurückzudrängen und zunächst das humanistisch-philologische, dann aber auch das naturwissenschaftliche Element an deren Stelle zu setzen. Zwar blieb das Denken der großen Masse, dem Gesetz der Trägheit zufolge, das auch auf geistigem Gebiete seine Geltung hat, zunächst noch in den alten Banden befangen. Indes nahm während der Generationen, welche dem deutschen Religionskriege vorangingen, die Zahl der selbständig denkenden Männer stetig zu. Gleichzeitig erlebten Kunst, Gewerbfleiß und Handel einen bedeutenden Aufschwung und wirkten befruchtend auf viele Zweige der Wissenschaft.
Einen Beweis, welches Ansehen Aristoteles trotzdem noch immer genoß, bietet die Geschichte der Entdeckung der Sonnenflecken. Als nämlich im Jahre 1611 der Jesuit Scheiner sie fast gleichzeitig mit Fabricius und Galilei auffand, meinte sein geistlicher Vorgesetzter, es könne sich hier nur um Fehler der Gläser oder der Augen handeln, da er den Aristoteles zweimal durchgelesen und nichts von derartigen Dingen gefunden habe. Scheiner ließ sich jedoch durch dieses Urteil nicht beeinflussen. Er stellte etwa 2000 Beobachtungen185 über die Sonne zusammen und dehnte seine Forschungen mit Erfolg auf den Vorgang des Sehens und die Beschaffenheit des Auges aus.
Koppernikus hatte das heliozentrische Weltsystem gegründet. Durch deutsche Geistesarbeit sollte es auch seinen weiteren Ausbau erfahren und auf den Boden unzweifelhafter Gewißheit erhoben werden. Zu dieser Tat war Johannes Kepler berufen, der bedeutendste Astronom, den Deutschland im 17. Jahrhundert hervorgebracht hat. Nicht nur die Forschungen Keplers, sondern auch sein Lebensgang verdienen eingehender gewürdigt zu werden.
Johannes Kepler wurde am 27. Dezember 1571 in dem württembergischen Städtchen Weil geboren. Schon im frühesten Lebensalter begann für ihn eine Kette von Widerwärtigkeiten, die sich durch sein ganzes Leben hindurch fortsetzen sollten. Es ist ein eigenartiges Stück Kulturgeschichte, das uns dieser Lebensgang darbietet. Keplers schwächlicher Körper wurde wiederholt von Krankheiten heimgesucht. Im Elternhause herrschte ehelicher Zwist. Der Vater nahm Kriegsdienste. Nach seiner Rückkehr verlor er durch Übernahme einer Bürgschaft seine geringe Habe. Später zog er von neuem hinaus. Er fiel im Kampfe gegen die Türken. Nach einer freudlosen Jugend wurde Kepler, da er seines schwächlichen Körpers wegen für einen praktischen Beruf untauglich war, in eine Klosterschule und darauf in das theologische Stift zu Tübingen geschickt.
»Was auf dem Gebiete der Geometrie und der Astronomie vorkam«, schrieb Kepler später186, »begriff ich ohne Schwierigkeit. Ich wurde auf Kosten des Herzogs von Württemberg unterhalten. Meine Fortschritte in der Gelehrsamkeit bewies mein Mysterium cosmographicum.« Es ist dies Keplers im Jahre 1596[S. 114] erschienenes astronomisches Erstlingswerk, das uns nach Inhalt und Bedeutung noch beschäftigen wird.
Die Anregung zu mathematischen und astronomischen Studien empfing Kepler durch den in Tübingen lehrenden Mästlin. Mästlin (1550–1631) bekleidete dort die Professur für Mathematik und Astronomie. Er war ein Anhänger der koppernikanischen Lehre und soll auch Galilei für diese gewonnen haben. Mästlin hat das »aschfarbene« Licht des Mondes daraus erklärt, daß das Sonnenlicht von der Erde auf den Mond zurückgeworfen werde.

Zwischen Mästlin und Kepler entwickelte sich ein freundschaftliches Verhältnis. In dem Maße, wie Keplers Interesse für die Astronomie zunahm, wurde er der damals herrschenden Theologie entfremdet. Letztere war nämlich im evangelischen Württemberg zu einer Orthodoxie erstarrt, die jede freie Regung hemmte und in Dogmen zum Ausdruck kam, die in das wahrhaft[S. 115] religiöse Gemüt Keplers keinen Eingang fanden. Als Kepler sich dazu noch als ein Anhänger der koppernikanischen Lehre bekannte, war es um seine theologische Laufbahn geschehen. Er wurde als ungeeignet für den Kirchendienst bezeichnet und konnte von Glück sagen, daß er durch Mästlin eine Stelle in Graz erhielt. Hier mußte er Mathematik und Rhetorik vortragen, sowie den Kalender schreiben, wobei die Voraussage des Wetters und der politischen Ereignisse von besonderer Wichtigkeit war. Mit welch schwerem Herzen mag der so aufrichtige Mann oft dies Geschäft erledigt haben, das er selbst als die »eitelste, aber notwendige Amtsarbeit« bezeichnete! »Mutter Astronomie müßte gewißlich Hunger leiden«, sagte er ein anderes Mal, »wenn die Tochter Astrologie nicht das Brot erwürbe.« Daß Kepler übrigens in gewissem Sinne eine Einwirkung kosmischer Vorgänge auf irdische Begebenheiten für möglich hielt, ersieht man aus dem Schlußabschnitt seines »ausführlichen Berichtes über den im Jahre 1607 erschienenen Kometen und dessen Bedeutung«188. Kepler führt darin aus, er wolle nicht unbedingt in Abrede stellen, daß durch Kometen Seuchen hervorgerufen werden könnten. Wenn nämlich der Schwanz die Erde berühre, so könne es geschehen, daß die Luft verunreinigt werde. Da dies aber selten vorkomme, so müsse man nach einem anderen Grunde suchen, um eine etwaige natürliche Wirkung der Kometen zu erklären. »Ist etwas daran«, so fährt er fort, »daß nach der Ordnung der Natur Überschwemmung, Trockenheit oder Pestilenz durch einen Kometen verursacht und also vorbedeutet werden, so muß dies folgendermaßen zugehen: Wenn im Himmel etwas Seltsames entsteht, so empfinden dies alle Kräfte der natürlichen Dinge. Diese Sympathie mit dem Himmel erstreckt sich besonders auf die Kraft, die in der Erde steckt und ihre inneren Zustände beherrscht. Die Folge ist, daß diese Kraft feuchte Dämpfe emportreibt, wodurch Regen und Überschwemmung und schließlich allgemeine Seuchen entstehen.«
Auch der Mensch, wenn er selbst blind wäre, besitze doch dergleichen empfindliche und auf den Himmel aufmerkende Kräfte, die durch einen im Himmel auftauchenden Kometen ebenfalls beunruhigt würden und nicht allein zu unnatürlichen Bewegungen des Geblütes und infolgedessen zu Krankheiten, sondern auch zu[S. 116] starken Gemütserregungen Veranlassung geben könnten. Diese Auffassung Keplers ist weit verschieden von dem abergläubischen Hang zur Sterndeuterei, der seine Zeit beherrschte. Sind es doch gerade Keplers Forschungen gewesen, welche der Astrologie den Boden entzogen haben. »Die sogenannten Irrsterne,« sagt einer seiner Biographen189, »die durch ihre Bewegungen die Schicksale bestimmen sollten, irrten nun nicht mehr, und die mystische Deutung, welche die Astrologie diesem Umherschweifen gab, verlor jeden Anhalt.«
Trotzdem war Kepler, wenn er als Astronom sein Brot verdienen wollte, zum astrologischen Frondienst gezwungen. Dieser Umstand brachte ihn auch in Berührung mit zwei geschichtlichen Persönlichkeiten, mit Kaiser Rudolf II. und Wallenstein, deren Hang zur Astrologie bekannt genug geworden ist. Ein glücklicher Zufall fügte es, daß die von Kepler seinem ersten Kalender einverleibten Prophezeiungen, ein strenger Winter nämlich und der Ausbruch von Unruhen, wirklich eintrafen. Ein Erfolg dieser Art wurde damals von der urteilslosen Menge höher eingeschätzt als die Abfassung eines gelehrten Buches.
Die freie Entfaltung der Wissenschaft wurde zu Keplers Zeit auch durch das Fehlen desjenigen ethischen Momentes, das wir als akademische Lehrfreiheit bezeichnen, und das wir auch heute noch immer gegen rückwärts gerichtete Bestrebungen verteidigen müssen, in hohem Grade gehemmt. Eine Lehrfreiheit konnte sich nur in dem Maße entwickeln, in dem der Streit mit Worten und das gegenseitige Ausspielen von Autoritäten durch die greifbaren und logisch verknüpften Ergebnisse der exakten Forschung zurückgedrängt wurden. Der letzteren ist es zu danken, daß das αὐτὸς ἒφα (Er, d. h. der Meister, hat's gesagt) allmählich verstummte und eine neue, die Wahrheit kündende Sprache an dessen Stelle trat, die Sprache nämlich, in welcher die Natur auf die an sie gerichteten Fragen Antwort gibt.
Zu der Zeit, die wir kennzeichnen, konnte ein Mästlin von dem Senat der evangelischen Universität Tübingen gezwungen werden, die Astronomie entgegen seiner Überzeugung nach dem System des Ptolemäos zu lehren und gegen den gregorianischen Kalender zu schreiben. Als er zauderte, erteilte man ihm einen Verweis. Mästlin mußte sich fügen, wenn er nicht seine Stelle verlieren wollte. Er entledigte sich der aufgezwungenen Arbeit,[S. 117] indem er einige unbedeutende Mängel des Kalenders rügte. In eine neue Verlegenheit geriet Mästlin, als Kepler ihm von Graz seine erste astronomische Arbeit, das Mysterium cosmographicum190, zusandte, damit sie in Tübingen im Druck erschiene. Der Senat erhob Einwendungen, weil die dem Werke zugrunde liegende Lehre von der Bewegung der Erde das Ansehen der heiligen Schrift schädigen könne. »Was ist zu tun?« schrieb Kepler darauf an Mästlin. »Ich denke, wir machen es wie die Pythagoreer und teilen nur uns gegenseitig mit, was wir entdecken. Ich möchte Dir um meinetwillen keine Feinde machen.« Die Schwierigkeiten wurden schließlich überwunden. Das Werk erschien, und der jugendliche Verfasser sandte es an Tycho und an Galilei, die bedeutendsten zeitgenössischen Astronomen, mit denen er auch später in Verbindung blieb.
Das Bestreben, das Kepler nicht nur bei der Abfassung seiner ersten Schrift, sondern auch bei allen übrigen Arbeiten beherrschte, gipfelt darin, einfache arithmetische oder geometrische Beziehungen zwischen den Entfernungen und den Geschwindigkeiten der Planeten nachzuweisen. Die Lösung des ersten Teiles dieser Aufgabe hat er in seinem »Mysterium« vergeblich gesucht, während ihm die Bewältigung des zweiten Problems nach großen Mühen gelungen ist.
Als Kepler seine wissenschaftliche Tätigkeit begann, war die Naturwissenschaft von pythagoreischen und platonischen, auf Zahl und Maß sich gründenden Spekulationen überwuchert. Dieser Geist war es, der auch in Keplers Erstlingswerk zum Ausdruck kam.
Die Zahl der damals bekannten Planeten betrug sechs: Merkur, Venus, Erde, Mars, Jupiter, Saturn. Den Grund für diese Zahl glaubte Kepler in der Existenz der fünf regelmäßigen Körper gefunden zu haben, die er zwischen die für kugelförmig gehaltenen Planetensphären einschaltete. Wir wollen ihn dieses Mysterium, auf das er so stolz war, daß er einmal äußerte, er würde die Ehre dieser Entdeckung nicht um den Besitz des Kurfürstentums Sachsen preisgeben, selbst verkünden lassen: »Die Erdbahn liefert[S. 118] die Sphäre, die das Maß aller übrigen ist. Um diese Sphäre (η in Abb. 38) beschreibe ein Dodekaëder. In der Sphäre, welche dieses umschließt, liegt die Bahn des Mars (♂ in Abb. 38). Um die Marssphäre beschreibe man ein Tetraëder. Eine diesem Körper umschriebene Kugelfläche würde die Bahn des Jupiter enthalten (s. Abb. 39, γ). Letztere umschließe mit einem Würfel; die umschriebene Sphäre (α) enthält die Bahn des Saturn (♄). Ferner errichte innerhalb der irdischen Sphäre ein Ikosaëder; die demselben eingeschriebene Kugelfläche enthält die Bahn der Venus (s. Abb. 38, ♀). Beschreibt man innerhalb ihrer Sphäre ein Oktaëder, so umschließt das letztere die Sphäre des Merkur.«
Kepler legt also eine Folge von sechs Kugelflächen zugrunde, denen die fünf regulären Körper ein- bzw. umgeschrieben sind. Es zeigte sich, daß die Radien jener sechs Sphären ungefähr den von Koppernikus ermittelten verhältnismäßigen Entfernungen der Planeten entsprachen. Die von Koppernikus berechneten Werte weichen indes von den später geltenden erheblich ab. Auch wurde die Annahme, daß die Planeten sich in Kreisen bewegen, von Kepler selbst durch die mühevolle Arbeit der nachfolgenden Jahre widerlegt. Das »Mysterium« war daher nur ein Versuch, dem man indessen seine Berechtigung nicht absprechen darf. Besteht doch die Tätigkeit des Forschers, wenn es sich um einen Fortschritt von grundlegender Bedeutung handelt, meist in der Aufstellung einer neuen Idee und der sich daran anschließenden Prüfung, ob das gesamte Tatsachenmaterial sich in den Rahmen dieser Idee einfügen läßt. Ähnlich verfuhr auch Galilei. Zunächst entwickelte er aus dem Begriff der gleichförmig beschleunigten Bewegung alle Umstände derselben. Dann zeigte er durch den Versuch, daß die Körper beim Fall über die schiefe Ebene ein Verhalten zeigen, das dem Begriff der gleichförmig beschleunigten Bewegung entspricht. Auch unsere heutige Naturwissenschaft besteht in der Vereinigung von Gedankenerzeugnissen,[S. 119] die sich als Systeme, Hypothesen und Theorien darstellen, mit der Summe des zurzeit bekannten Tatsachenmaterials. Weder die Gebilde einer nicht genügend gestützten Spekulation, noch die Erfahrungstatsachen allein sind Wissenschaft. Kepler selbst gesteht einmal, er habe 19 Hypothesen ersonnen und wieder verworfen, ehe er zu der wahren, den Tatsachen entsprechenden Vorstellung gelangt sei.
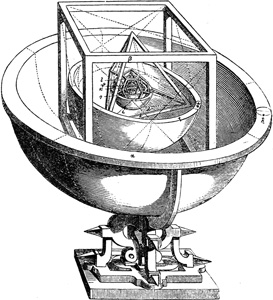
Keplers Aufenthalt in Steiermark dauerte nicht lange. Der von Jesuiten erzogene Erzherzog Ferdinand, der spätere Kaiser Ferdinand der Zweite, wurde einige Jahre nach der Veröffentlichung des »Mysteriums« Keplers Landesherr. Als solcher begann er den Protestantismus mit der Wurzel auszurotten. Wie[S. 120] ein Verbrecher wurde Kepler, der sich in Graz eine glückliche Häuslichkeit gegründet hatte, des Landes verwiesen. Dieses Ereignis, so traurig es für den Betroffenen war, hatte das Gute im Gefolge, daß es Kepler in persönliche Berührung mit Tycho, dem Meister der astronomischen Beobachtungskunst, brachte. Erst dadurch, daß Kepler Tychos Beobachtungen verwerten konnte, wurde es ihm möglich, seine Lebensaufgabe, die in der Erforschung der wahren Bewegung der Planeten bestand, zu erfüllen.
Tycho Brahe191 stammte aus Schweden. Er wurde im Jahre 1546 geboren und zeigte schon als Jüngling, angeregt durch die Beobachtung einer Sonnenfinsternis und das Studium des Almagest, ein großes Interesse für die Himmelskunde. Auch der Alchemie war er zugetan. Ja, er hoffte, durch sie die zur Errichtung einer Sternwarte erforderlichen Mittel zu bekommen.
Als Tycho eines Abends im November des Jahres 1572 sein alchemistisches Laboratorium verließ und den Blick auf den ihm wohlbekannten Sternenhimmel lenkte, nahm er einen neuen, vorher nicht gesehenen Stern in der Cassiopeia wahr. Andere hatten diesen Stern schon einige Tage vor Tycho gesehen. Einen Monat später hatte das neue Gestirn an Glanz den Jupiter fast erreicht. Im Frühling des Jahres 1572 erschien es als Stern erster Größe; darauf nahm es stetig ab. Im Beginn des folgenden Jahres besaß es kaum mehr als 5. Größe, um im Jahre 1574 ganz zu verschwinden.
Die Astronomen gerieten über dieses Vorkommnis in eine leicht begreifliche Erregung. Da man mit Aristoteles den Fixsternen ein wandelloses Sein zuschrieb, glaubten die meisten, die Erscheinung habe innerhalb der planetaren Region stattgefunden. Daran knüpften sich die unsinnigsten Vermutungen. Nach einigen war das in Frage kommende Gestirn sogar vom Jupiter in Brand gesteckt worden. Demgegenüber wies Tycho nach, daß der neue Stern sich jenseits der äußersten Planetensphäre befunden haben müsse, da er seine Stellung zu den Fixsternen nicht verändert habe. Der Zufall fügte es, daß das plötzliche Aufleuchten eines Sternes innerhalb des kurzen Zeitraums von 1572–1604 wiederholt[S. 121] vorkam, wodurch den Astronomen die Wichtigkeit genauer Fixsternverzeichnisse von neuem nahegelegt wurde.
Keine Wissenschaft ist so sehr durch fürstliche Gunst gefördert worden wie die Astronomie. Allerdings hat dabei oft weniger das Interesse für den Gegenstand den Ausschlag gegeben, als der Glaube, daß in den Sternen das Schicksal geschrieben sei. Dies erfuhr auch Tycho. Durch die Freigebigkeit des dänischen Königs192 wurde er in den Stand gesetzt, auf einem zwischen Schonen und Seeland gelegenen Inselchen193 eine Sternwarte zu errichten, wie sie die Welt in gleicher Großartigkeit noch nicht gesehen. Diese Warte erhielt den Namen Uranienborg. Sie blieb 20 Jahre die Arbeitsstätte Tychos, dem sich hervorragende Mitarbeiter zugesellten. Tychos größtes Verdienst bestand darin, daß er den astronomischen Messungen einen bis dahin nicht erreichten Grad von Genauigkeit verlieh und auf diese Weise den Grund für jeden weiteren astronomischen Fortschritt legte. Um die Rektaszension eines Sternes zu finden, hatte man bisher am Tage den Abstand des Mondes von der Sonne bestimmt und in der darauffolgenden Nacht die Stellung des Mondes mit derjenigen der Sterne verglichen. Eine weit größere Sicherheit wurde dadurch erreicht, daß Tycho die Venus, die mitunter am Tage sichtbar ist, zu diesem Zwecke verwertete, anstatt des seine Stellung rasch ändernden Mondes. Der Unterschied der Rektaszensionen zweier Sterne ergibt sich aus der Zeit, die zwischen ihren Kulminationen verfließt. Ein hierauf sich gründendes Verfahren zur Ortsbestimmung der Gestirne setzt aber die Benutzung genau gehender Uhren voraus. Tychos Augenmerk war daher schon auf eine möglichst scharfe Bestimmung des Zeitablaufs gerichtet. Da er jedoch auf Sanduhren und auf Räderuhren ohne Pendelvorrichtung angewiesen war, ließ sich diese Aufgabe nur unvollkommen lösen.
Besonders übertraf Tycho seine Vorgänger in der Genauigkeit des Winkelmessens. Zuerst benutzte er einen Kreuzstab. Später (1569) ließ er einen riesigen Quadranten aus Holz verfertigen, den uns Abb. 40 zeigt. Die Teilung befand sich auf einem Messingreif, dessen Halbmesser sich auf 6 m belief. Die Ablesung erfolgte mittels eines an einem Metallfaden herabhängenden Lotes. Die Beobachtungen erfolgten durch die beiden Lochvisiere.[S. 122] Infolge der gewaltigen Dimensionen des an einem vertikalen drehbaren Eichenpflock befestigten Quadranten war die Genauigkeit der Messung eine beträchtliche.
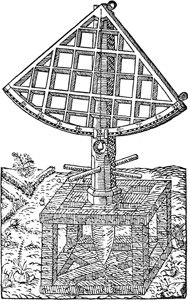
Tychos Riesenquadrant war unter freiem Himmel aufgestellt und daher nicht lange brauchbar. Einen handlichen, kleineren, von Tycho konstruierten Apparat, dessen Einrichtung und Gebrauch ohne weiteres verständlich ist, zeigt Abb. 41. Die Schenkel dieses Apparates besaßen eine Länge von 1,6 m.
Das Urbild des heutigen Theodoliten endlich war Tychos Azimutalquadrant, dessen Einrichtung Abb. 42 (s. S. 124) erläutert. Der Apparat bestand aus Messing und war, trotzdem er weit geringere Dimensionen aufwies, als sie der Riesenquadrant besaß, doch von solcher Genauigkeit, daß sich die Winkel bis auf die Minute daran ablesen ließen.
Tycho ließ ferner eine Himmelskugel aus Kupfer anfertigen, die etwa 1000 Sterne in der nach seinen Messungen berichtigten Stellung zeigte. Die Kreise dieser Kugel waren gleichfalls in Minuten geteilt. Dementsprechend erforderte ihre Herstellung auch die Summe von 5000 Talern.
Zur Annahme des koppernikanischen Systems konnte Tycho sich nicht verstehen, da ihm wie keinem anderen die Schwierigkeiten bekannt waren, welche diesem System noch entgegenstanden. Eine Bewegung, die im Laufe eines halben Jahres den Ort der Erde um das Doppelte ihres Abstandes von der Sonne verändere, müsse, so schloß Tycho mit Recht, auch eine Änderung in der gegenseitigen Stellung der Fixsterne bewirken. »Eine jährliche Bewegung195«, schreibt er, »würde die Fixsternsphäre196 in eine solche Ferne rücken, daß die von der Erde beschriebene Bahn im Vergleich zu jener Entfernung verschwindend klein sein müßte. Hältst Du es für möglich, daß der Raum zwischen der Sonne, dem angeblichen Zentrum der Welt, und dem Saturn noch nicht 1/700 des Abstandes der Fixsternsphäre betrage? Zudem müßte dieser[S. 124] Raum sternenleer sein. Dies ist notwendig der Fall, wenn die jährliche Bahn der Erde, von den Fixsternen betrachtet, nur den Durchmesser einer Minute haben soll. Dann werden aber schon die Fixsterne dritter Größe, deren scheinbarer Durchmesser[S. 125] gleichfalls eine Minute beträgt, an Umfang gleich der Erdbahn sein.« Dieser Einwand Tychos wurde dadurch hinfällig, daß, wie man nach der Erfindung des Fernrohrs wahrnahm, die Fixsterne überhaupt keinen scheinbaren Durchmesser besitzen, sondern als bloße Lichtpunkte erscheinen, eine Tatsache, die wieder für die Behauptung der Koppernikaner sprach, daß sich die Fixsterne in ungeheurer Entfernung befänden. Der von Tycho geforderte Nachweis einer Parallaxe, deren Größe zugleich einen Schluß auf die Entfernung der Fixsterne gestattet hätte, sollte, wie wir später sehen werden, erst im 19. Jahrhundert dem Scharfsinn und der Beobachtungskunst eines Bessel gelingen197. Tychos Bemühungen, eine Parallaxe nachzuweisen, um dadurch die koppernikanische Lehre auf ihre Richtigkeit zu prüfen, blieben ohne Erfolg.
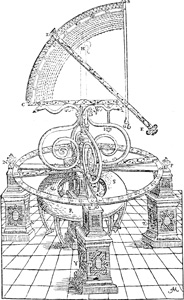
Außer den astronomischen Bedenken machte sich bei Tycho der koppernikanischen Lehre gegenüber auch ein für jene Zeit charakteristischer Mangel an richtigen mechanischen Begriffen geltend. So erhebt er den landläufigen Einwand, daß ein fallender Körper, wenn die Erde sich bewege, unmöglich in lotrechter Richtung die Oberfläche treffen könne. Ferner meint er, die »träge, dicke« Erde sei zu den Bewegungen, die Koppernikus ihr zuschreibe, viel zu ungeschickt.
Andererseits sah Tycho aber wohl ein, daß die Erscheinungen, welche die Planeten zeigen, sich besser mit der neuen Lehre als mit der geozentrischen Ansicht vereinigen ließen. Er stellte deshalb199 ein neues System auf, das zwischen dem geozentrischen und dem heliozentrischen eine vermittelnde Stellung einnahm. Danach sollte sich die Sonne in einem exzentrischen Kreise um die im Mittelpunkte ruhende Erde bewegen, die Planeten sollten indes gleichzeitig die Sonne umkreisen (s. Abb. 43, S. 126). Tychos System fand nur geringen Beifall. Kaum einer unter den angeseheneren Astronomen nahm es an.
Als Tycho auf der Höhe seines Ruhmes stand, ereilte ihn ein trauriges Geschick. Sein hoher Gönner starb200, und nun erhoben sich zahlreiche Feinde und Neider. Auf ihr Betreiben hin wurden Tycho die für die Uranienborg bestimmten Gelder entzogen mit der Begründung, seine Untersuchungen seien nicht nur nutzlos, sondern sogar »voll schädlicher Kuriosität«. Dem großen[S. 126] Forscher, den Bessel später einen König unter den Astronomen nannte, wurde von der Regierung bedeutet, er möge sich mit dergleichen Arbeiten nicht mehr befassen201. Damit war das Schicksal der Uranienborg besiegelt. Die Verblendung, welche der aufstrebenden Naturwissenschaft so manchen Schaden zugefügt, hatte wieder einen ihrer unrühmlichen, zum Glück aber auch erfolglosen Siege errungen. Tycho, der schließlich sogar tätlichen Angriffen[S. 127] ausgesetzt war, rettete von seinen Instrumenten und Aufzeichnungen das Wertvollste und kehrte seinem Vaterlande den Rücken. Wiederum war es fürstliche Gunst, die ihm und seiner Wissenschaft eine neue Stätte bereitete. Auf Veranlassung Kaiser Rudolfs des Zweiten siedelte Tycho nach Prag über. Dort wurde er zum kaiserlichen Astronomen ernannt.
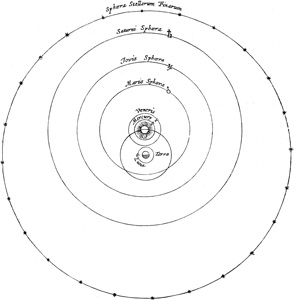
Von Prag aus erfolgte im Jahre 1599 Tychos Ruf an Kepler, dessen Schicksale wir bis zu dem Zeitpunkte verfolgt haben, in dem die Unduldsamkeit der Kirche den in gesicherten Verhältnissen lebenden Mann in eine hilflose Lage versetzt hatte. Kepler wurde Tychos Hilfsrechner und erhielt die Erlaubnis, das umfangreiche Beobachtungsmaterial Tychos nach eigenem Ermessen zu verwerten.
»Ich halte es«, schrieb Kepler später203 »für eine Fügung der Vorsehung, daß bei meiner Ankunft gerade der Mars untersucht wurde. Durch die Bewegungen dieses Gestirnes müssen wir zu den Geheimnissen der Astronomie gelangen oder darin beständig unwissend bleiben«. Der Mars machte nämlich von jeher unter den Planeten die größten Schwierigkeiten, was sich daraus erklärt, daß seine Bahn am meisten vom Kreise abweicht. Andererseits bietet dieser Himmelskörper den Vorteil, daß man seinen Umlauf in wenigen Jahren beobachten kann, während die übrigen äußeren Planeten eine weit längere Beobachtungszeit erfordern.
Tychos Marsbeobachtungen erstreckten sich über einen Zeitraum von 16 Jahren. Sie verteilten sich ferner auf die ganze Bahn des Planeten und waren bis auf einige Minuten richtig, besaßen also eine bisher unerreichte Genauigkeit204.
Daran, daß die Himmelskörper kreisförmige Bahnen beschreiben, hatte vor Kepler niemand gezweifelt. Kepler war der erste, der diesen, fast als Axiom betrachteten Grundsatz verließ. Zunächst untersuchte er, ob sich bessere Resultate unter der Annahme ergeben würden, daß die Bahn des Planeten die Form eines Ovals besäße. Endlich, als sich eine genügende Übereinstimmung zwischen Rechnung und Beobachtung auch dadurch nicht erreichen ließ, kam er auf den Gedanken, anstatt des[S. 128] Ovals die Ellipse zugrunde zu legen. Und siehe da, während nach den von Koppernikus entworfenen Tafeln der beobachtete Ort des Mars im Jahre 1608 um nahezu 5 Grad von dem berechneten abwich, zeigte Kepler in seinem ein Jahr später herausgegebenen Hauptwerk: »Über die Bewegungen des Mars«205, daß der Fehler fast ganz verschwindet, wenn man den Planeten eine Ellipse beschreiben läßt, in deren einem Brennpunkte sich die Sonne befindet.
Wenige Entdeckungen sind in solchem Maße das Ergebnis mühevoller, Jahrzehnte dauernder Arbeit gewesen wie diese Entdeckung Keplers. In der an den Kaiser gerichteten Widmung führt er in scherzhaftem Tone folgendes aus: Die Astronomen hätten bisher den Mars nicht zu überwältigen vermocht. Dem trefflichen Heerführer Tycho indessen sei es in zwanzigjährigen Nachtwachen gelungen, alle Listen des Feindes auszukundschaften. Dadurch habe Kepler Mut bekommen. Und es sei ihm gelungen, Mars gefügig zu machen. Er biete nun dem Kaiser seine Dienste an, auch die Verwandtschaft des Mars, nämlich Jupiter, Venus und Merkur, in gleicher Weise zu bezwingen, doch möge man die Schatzkammer anweisen, daß sie ihm die Mittel zu diesem Feldzug auszahle. Die letzten Worte gestatten einen Schluß auf die ständige Not, in der sich Kepler bis an das Ende seines Lebens befand. Tycho war bald nach Keplers Eintreffen gestorben206 und letzterer zu seinem Nachfolger ernannt. Die Schatzkammer des Kaisers befand sich indessen meist im Zustande der Erschöpfung, wofür insbesondere die Goldkocher sorgten, die Rudolfs Hang zur Alchemie auszunutzen verstanden. Kepler klagt: »Ich stehe ganze Tage in der Hofkammer und bin für die Studien nichts. Ich stärke mich jedoch mit dem Gedanken, daß ich nicht dem Kaiser allein, sondern dem ganzen menschlichen Geschlechte diene, daß ich nicht nur für die Gegenwart, sondern auch für die Nachwelt arbeite«.
Nach dem Tode Kaiser Rudolfs wurde Keplers Lage noch schlimmer. Er erhielt eine Anstellung in Linz, wo er Mathematik lehren und Vermessungen überwachen mußte. Trotz aller Widerwärtigkeiten verlor er jedoch sein großes Ziel nicht aus den Augen. Das unwürdigste Schauspiel, das uns in der Lebensgeschichte Keplers begegnet, ist der gegen seine Mutter geführte Hexenprozeß.[S. 129] Eine kurze Darstellung desselben läßt uns nicht nur einen Einblick in die damals herrschenden Rechtszustände tun, sie bezeugt auch den bewundernswerten Charakter Keplers. Die Mutter des großen Astronomen lebte in einem kleinen schwäbischen Städtchen. Eine ihrer Nachbarinnen erkrankte und verbreitete das Gerede, sie sei von Frau Kepler behext worden. Der Vogt des Ortes wußte die Angelegenheit zu einem Hexenprozeß aufzubauschen. Erschwerend wirkte dabei der Umstand, daß die Angeklagte bei einer Verwandten erzogen war, die man als Hexe verbrannt hatte. Einzig und allein ihrem Sohn Johannes, der von Linz herbeieilte, gelang es, die Mutter vor der Folter und dem Scheiterhaufen zu bewahren. Die übrigen Söhne hatten sich zurückgezogen, und mit Kepler befreundete Juristen besaßen nicht den Mut, für die arme, verfolgte Frau einzutreten, die bald, nachdem sie freigesprochen, infolge der erlittenen Behandlung starb. Gibt es unter den Gestalten, in denen menschliche Größe uns begegnet, eine solche, der wir größere Bewunderung zollen können, als Kepler? Die eigene Sicherheit gering schätzend, zieht er gegen den Wust eines mittelalterlichen Gerichtsverfahrens zu Felde, um die Mutter zu retten207. Und während der dadurch verursachten, jahrelangen Aufregung enthüllt er die Gesetze, nach denen sich der Lauf der Welten regelt.
Unermüdlich hatte Kepler während der ersten Jahrzehnte des 17. Jahrhunderts trotz seiner untergeordneten Amtstätigkeit, die ihn nicht einmal vor der Sorge um das tägliche Brot bewahrte, zwei Aufgaben verfolgt. Einmal galt es, auf Grund der eigenen und der Beobachtungen Tychos Planetentafeln zu entwerfen, welche die bisherigen ungenauen Tafeln übertrafen. Die zweite,[S. 130] höhere Aufgabe bestand in der Begründung einer mit dem System des Koppernikus in Einklang stehenden Theorie der Planetenbewegung. Beide Aufgaben hat Kepler glänzend gelöst und daneben noch Wertvolles auf den Gebieten der Mathematik und der Optik geleistet.
Die neuen Tafeln, die in Anerkennung der Verdienste Kaiser Rudolfs um die Förderung der Astronomie die rudolfinischen genannt wurden, erschienen erst gegen das Ende Keplers208. Während der letzten Jahre ihrer Abfassung konnte die mühevolle Arbeit durch die von Bürgi und Neper erfundenen Logarithmen verringert werden209. Fast ein Jahrhundert blieben die rudolfinischen Tafeln ein unentbehrliches Hilfsmittel der Astronomen, dann erst wurden sie durch neue, bessere ersetzt.
Koppernikus hatte sich darauf beschränkt, eine zum Teil noch mit den Mängeln der geozentrischen Ansicht behaftete bloße Beschreibung des Planetensystems zu geben. Kepler war dagegen bestrebt, gesetzmäßige Beziehungen innerhalb dieses Systems aufzudecken. Das Mißlingen seiner ersten Versuche ist darauf zurückzuführen, daß es ihm noch an genügendem Beobachtungsmaterial fehlte. Erst durch die Verbindung mit Tycho gelangte er in den Besitz desselben, und im Jahre 1609, also ein Jahrzehnt nach Tychos Tode, veröffentlichte er die Entdeckung, daß die Planetenbahnen Ellipsen seien. Damit war das seit alters geheiligte Axiom von der Kreisbewegung beseitigt. Ebensowenig konnte die Ansicht, daß die Bewegung der Himmelskörper eine gleichförmige sei, aufrecht erhalten werden. Kepler wies nach, daß ein Planet sich in der Sonnennähe schneller als in der Sonnenferne bewegt. Die Geschwindigkeiten stehen nach ihm in einem solchen Verhältnis, daß die Flächenstücke, die von dem Leitstrahl, d. h. der den Planeten mit der Sonne verbindenden Geraden, beschrieben werden, für gleiche Zeiten gleiche Größe besitzen. (Siehe Abb. 44.)
Damit waren die Gesetze enthüllt, nach denen die Bewegung jedes einzelnen Planeten vor sich geht210. Es galt noch die[S. 131] Beziehung zu finden, die alle Planeten verknüpft und sie als Glieder eines Systems erscheinen läßt. Die Lösung dieses Problems wurde erst nach einem weiteren Jahrzehnt mühevoller Arbeit gefunden und 1619 in der »Weltharmonie« bekannt gegeben.
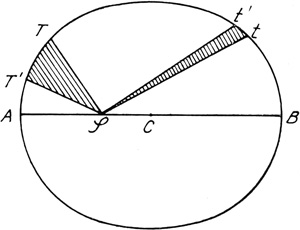
Seit dem Jahre 1595 brütete Kepler, wie er sich selbst einmal ausdrückt, mit der ganzen Kraft seines Geistes über die Einrichtung des Koppernikanischen Systems. Unablässig suchte er von drei Dingen die Ursache zu ergründen, nämlich von der Anzahl, der Entfernung und der Bewegung der Planeten211. Endlich konnte er ausrufen: »Dasjenige, dem ich den größten und besten Teil meines Lebens gewidmet habe, ist jetzt gefunden und die Wahrheit auf eine Weise erkannt, die selbst meine glühendsten Wünsche übersteigt«212. Die als drittes Keplersches Gesetz bekannte Beziehung zwischen den Umlaufszeiten und den Entfernungen zweier Planeten lautet dahin, daß sich die Quadrate der Umlaufszeiten wie die dritten Potenzen der mittleren Abstände von der Sonne verhalten213. Besitzt z. B. ein Planet eine Umlaufszeit von 27 Jahren, so läßt sich nach diesem Gesetze folgern, daß er neunmal so weit wie die Erde von der Sonne entfernt ist, denn 12 : 272 = 1 : 729 = 13 : 93. Dieses Verhältnis findet sich beim Saturn annähernd verwirklicht. Er hat eine Umlaufszeit von 30 Jahren, und seine Entfernung von der Sonne ist dementsprechend etwas größer als neun Halbmesser der Erdbahn. Wir erkennen aus dieser Betrachtung, daß die genaue Bestimmung des Abstandes der Erde von der Sonne von der größten Bedeutung ist. Kepler kannte die absolute Größe dieses Abstandes noch nicht. Er setzte ihn in seinen Berechnungen gleich eins, benutzte also für die Entfernungen der Planeten nur die relativen Werte.
Die naheliegende Gefahr, die entdeckten Gesetze nach Art der Pythagoreer als Ursachen zu betrachten, vermied Kepler. Versteht man unter der Entdeckung der Ursache einer Erscheinung ihre Zurückführung auf andere, in ihrer Gesetzmäßigkeit erkannte Vorgänge, so war Kepler schon bemüht, auch nach dieser Richtung die Planetenbewegungen zu untersuchen. Die endgültige Bewältigung dieses Problems blieb jedoch Newton vorbehalten. Ihm gelang es, die Zentralbewegung gleich der Fall- und Wurfbewegung aus der Schwere zu erklären. Daß die Schwerkraft nicht nur an der Oberfläche der Erde, sondern auf kosmische Entfernungen hin wirkt, hat indessen schon Kepler ausgesprochen. Seiner Ansicht nach würden zwei Körper, auf die kein dritter wirkt, aufeinander zueilen und sich vereinigen. Und zwar würden sich, wie er ausführt, die zurückgelegten Wege umgekehrt wie die Massen der betreffenden Körper verhalten. »Liefe der Mond nicht um die Erde, so würde sich die Erde nach dem Monde um den 54. Teil des Abstandes beider Weltkörper bewegen, und der Mond würde sich um die übrigen 53 Teile nach der Erde senken. Dann würden sie aufeinander treffen, vorausgesetzt, daß beide gleiche Dichte besitzen214«.
Erklären ließ sich die Bewegung der Planeten jedoch erst, als man das Gesetz vom Beharrungsvermögen auch auf sie ausdehnte, wie es Galilei bezüglich aller irdischen Bewegungen getan hatte. Kepler war nämlich noch in dem Irrtum befangen, daß die Planeten zu ihrer Bewegung um die Sonne eines fortgesetzten Antriebes bedürften. Dieser sollte in der Sonnenrotation gegeben sein, die Kepler daher schon als Erklärungsprinzip forderte, bevor ihr Vorhandensein beobachtet war. Drehte sich die Sonne nicht um sich selbst, so würden nach Keplers Meinung die Planeten diesen Zentralkörper nicht umkreisen, sondern sich auf ihn stürzen, während doch in der Tat die Sonnenrotation aufhören könnte, ohne daß die Bewegungen der Planeten eine Änderung erführen. Zu erklären blieb dann noch die ungleiche Dauer, welche die Umläufe der Planeten beanspruchen. Kepler äußert sich darüber mit folgenden Worten: »Hätten die Planeten nicht ein natürliches Widerstreben, so ließe sich keine Ursache angeben,[S. 133] warum sie nicht der Achsendrehung der Sonne aufs genaueste folgen sollten. Nun aber gehen zwar alle Planeten nach der Richtung, in der die Sonne rotiert, aber der eine langsamer als der andere. Sie vermengen nämlich nach gewissen Verhältnissen mit der Geschwindigkeit des Bewegers die Trägheit ihrer eigenen Masse«215. Die bewegende Kraft der Sonne, die sich auf die Planeten erstrecken sollte, wurde von Kepler als eine Art Magnetismus betrachtet. Er berief sich dabei auf Gilbert, der ja auch die Erde als einen Magneten angesehen habe. Wie der Magnet die Nadel, so sollte nach Kepler die Sonne vermöge ihrer Rotation die Erde und die übrigen Planeten mit sich herumführen.
Kepler wußte, daß die Lichtintensitäten sich umgekehrt wie die Quadrate der Entfernungen des beleuchteten Gegenstandes von der Lichtquelle verhalten. Er erörtert daher die Frage, ob die Wirkungen jener bewegenden Kraft der Sonne sich nicht etwa ebenso verhalten, streift damit also schon an die Entdeckung des Newtonschen Gravitationsgesetzes.
Kepler besitzt auch ein gewisses Anrecht auf die Entdeckung der Sonnenflecken. Es war am 28. Mai des Jahres 1607, zu einer Zeit, als das Fernrohr noch nicht erfunden war, als Kepler in seinem Tagebuche eine seltsame Beobachtung vermerkte216. Er war nämlich mit älteren, aus der Zeit Karls des Großen stammenden Nachrichten bekannt geworden, nach welchen man Merkur vor der Sonne als kleinen schwarzen Fleck gesehen haben wollte217. Um zu prüfen, ob dies möglich sei, verfuhr Kepler an einem Tage, an dem Sonne und Merkur in Konjunktion standen, folgendermaßen: Er ließ die Sonnenstrahlen durch eine enge Öffnung in ein dunkles Zimmer treten und fing das Sonnenbild vermittelst eines Papierschirmes auf (s. Abb. 45, S. 134). Zur großen Überraschung Keplers zeigte sich ein kleiner, verschwommener Fleck, den er für Merkur hielt.
Ohne Zweifel hat es sich in diesem, wie in jenem älteren Falle, um Sonnenflecken gehandelt, da Merkur, wie spätere Rechnungen ergeben haben, am Tage der Beobachtung sich nicht vor der Sonnenscheibe befand und auch zu klein ist, um sich bei einer Konjunktion in der geschilderten Weise bemerklich zu machen.
Mehrfach hat sich Kepler auch mit den Kometen beschäftigt, die er und Tycho unter die Himmelskörper versetzten, während die meisten sie für atmosphärische Erscheinungen hielten. »Man möge es mir«, sagt er, »nicht übelnehmen, daß ich eine neue Ansicht einführe oder vielmehr der alten Lehre des Anaxagoras und des Demokrit folge und dem Himmel zuschreibe, was man bisher nicht glauben wollte, daß nämlich darin ebensowohl etwas Neues entstehen kann, wie hier auf der Erde«. Nach Kepler soll nämlich die überall befindliche himmlische Luft, der Äther, durch Zusammenziehung aus sich heraus die Kometen entstehen lassen, von denen der Himmel so voll sei, wie das Meer voll von Fischen. Kepler setzte sich damit in Widerspruch mit Aristoteles, der den meisten damals noch als Autorität galt. Aristoteles schrieb nämlich den Himmelskörpern ein wandelloses Sein zu und ließ die Welt des Werdens und Vergehens erst unter dem Monde beginnen. Die Planeten bekunden dagegen nach ihm, zumal durch ihre ungleichmäßige Bewegung, eine mittlere Stellung zwischen beiden Regionen. Diese Lehre des Aristoteles wurde besonders durch das Aufleuchten neuer Fixsterne in den Jahren 1572, 1600 und 1604 und deren späteres allmähliches Verschwinden widerlegt.
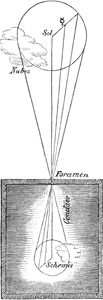
Über den Stern vom Jahre 1604 hat Kepler ausführlich berichtet. Er zeigte, daß auch dieser neue, im Sternbilde der Schlange entstandene Stern seine Stellung zu den Fixsternen nicht veränderte. Daraus schloß er, daß es sich nicht etwa um einen Planeten oder[S. 135] einen Kometen handeln könne. »Wollte Gott, daß diejenigen, die ein langes Gewäsch vom Ursprung dieses Sternes machen, zuvor Tychos Ausführungen über den Stern vom Jahre 1572 lesen möchten, damit sie mit so kindischen Gedanken, als sollte dieser Stern vom Jupiter oder Mars angezündet worden sein, daheim blieben.« So schreibt Kepler in seinem Bericht über einen ungewöhnlichen neuen Stern, der im Oktober 1604 erschien. Ein Faksimileabdruck dieses Berichtes wurde zusammen mit dem Faksimiledruck einer Schrift, in der David Fabricius über den neuen Stern von 1604 berichtete, vor kurzem veröffentlicht219. Die Schrift von Fabricius erschien 1606 in Magdeburg unter dem Titel »Himmlischer Herold«.
Es gewährt einen besonderen Reiz zu sehen, in welcher Weise die beiden Forscher ein und denselben Gegenstand behandelt haben. Dort David Fabricius, der überzeugte Astrolog, der die Bedeutung des Wundersterns seinen staunenden Landsleuten auslegt; hier Kepler, der sich in sehr skeptischer Weise über die Bedeutung des neuen Gestirns ausspricht220. Was der Stern zu bedeuten habe, schreibt Kepler, sei schwerlich zu ergründen. Entweder bedeute er uns Menschen nichts oder er habe solch hohe wichtige Dinge zu bedeuten, daß sie aller Menschen Sinn und Vernunft überträfen.
Eine gewisse Wirkung auf die Menschen äußere ein solcher Stern insofern, als die ganze Natur eine verborgene Art habe, die vom Himmel kommenden Lichtstrahlen zu verspüren und sich danach zu regeln. Sehr wohl könne auch ein Potentat durch das Erscheinen des neuen Sternes zu einem Wagnis ermuntert oder auch von einem solchen abgeschreckt werden, indem er das neue Licht als ein vom Himmel selbst gegebenes Zeichen betrachte.
Nicht ohne Humor bemerkt Kepler, viel zu bedeuten habe der Stern auch dadurch, daß er den Verlegern viel Arbeit und Gewinn bringe, denn fast jeder Theologe, Philosoph oder Astronom werde seine besondere Ansicht darüber haben und damit herauskommen wollen.
Zu diesen gehörte auch der friesische Prediger und Astronom David Fabricius221. Er hat über den neuen Stern drei Abhandlungen[S. 136] veröffentlicht. Nach seiner Schilderung ist der Stern am 30. September 1604 bald nach Sonnenuntergang gegen Südwesten von verschiedenen Astronomen in Deutschland, Böhmen und Italien zuerst gesehen worden. Fabricius sah ihn, da um jene Zeit in Friesland der Himmel bewölkt war, erst am 3. Oktober. Er konnte bis zum Oktober 1605, also ein ganzes Jahr beobachtet werden. Der neue Stern übertraf nach dem Zeugnis des Fabricius alle Fixsterne, ja sogar den Jupiter und auch die Nova von 1572 an Größe und flimmerte »wie ein großes Licht, das vom Winde bewegt wird«.
Seine Größe nahm von Monat zu Monat allmählich ab, so daß er »im Anfang des Jahres 1605 mit der Spica in der Jungfrau von gleicher Größe gewesen ist. Im März war er 3. und im Juli 4. Größe« usw. Darüber, daß sich der Stern jenseits der Sphäre der Planeten befand, zweifelte auch Fabricius nicht. Schon das starke Flimmern beweist ihm, daß man es hier mit einem Fixstern zu tun habe. Deshalb sei auch die »Meinung zahlreicher Gelehrter, daß die Erscheinung von irdischen Dünsten herrühre, als falsch und ungereimt zu verwerfen«.
Fest steht dagegen für Fabricius, daß »je und allerwege neue Sterne und Kometen Vorboten von zukünftigem Unglück und Veränderung gewesen sind«. Ganz besonders deute »der jetzige Wunderstern auf große wichtige Sachen«, weil er alle Vorgänger an Größe übertreffe, und weil bald nach seinem Erscheinen und zwar fast am Orte seines Erscheinens die große Konjunktion von Saturn und Jupiter eingetreten sei. Fabricius sucht dann nachzuweisen, daß diese alle achthundert Jahre wiederkehrende Konjunktion von großer Bedeutung für die Geschicke der Menschheit gewesen. In die Zeit der Konjunktion vom[S. 137] Jahre 800 falle das Auftreten Karls des Großen und die große Konjunktion zu Beginn unserer Zeitrechnung falle mit dem Anfange des Christentums und »großen Veränderungen in vielen Königreichen und Ländern zusammen«. Auch die jetzige große Konjunktion (Fabricius nennt sie den achthundertjährigen Reichstag der beiden obersten himmlischen Kurfürsten) deute auf bevorstehende große Veränderungen hin. Die Bedeutung dieser Konjunktion werde durch das gleichzeitige Erscheinen eines neuen Sternes besonders hervorgehoben. Zum Schlüsse gibt Fabricius der Hoffnung Ausdruck, daß die in Aussicht stehenden Veränderungen dem deutschen Volke ein Zeitalter des Friedens und der Gerechtigkeit bringen möchten. Deshalb nennt er seine Schrift auch den Glücksboten.
Nachdem das koppernikanische System durch Kepler eine festere Gestalt gewonnen, bedurfte es einer zusammenhängenden neuen Darstellung des gesamten astronomischen Lehrgebäudes. Dieser Aufgabe unterzog sich Kepler durch die Veröffentlichung seiner »Epitome astronomiae Copernicanae«222. Damit erschien das erste astronomische Lehrbuch, welches das koppernikanische System zugrunde legte, fast hundert Jahre nach der Aufstellung des letzteren.
Nach Keplers Tode gab sein Sohn im Jahre 1634 ein zweites, für Lehrzwecke bestimmtes Werk des großen Astronomen heraus, in dem letzterer es unternimmt, mit dichterischer Phantasie die astronomischen Erscheinungen so darzustellen, wie sie einem Beobachter auf dem Monde erscheinen würden. Das Buch ist betitelt »Keplers Traum oder nachgelassenes Werk über die Astronomie des Mondes« und verdient als »eine der merkwürdigsten Schriften aus der Reformationszeit der Sternkunde« mehr als bisher beachtet zu werden223. Kepler schildert darin in phantasievoller Weise eine Reise nach dem Monde, ein Gedanke, der vor und nach ihm häufiger näher ausgeführt wurde. Als Brücke dient den Dämonen, die den Reisenden begleiten, der bei Finsternissen den Mond und die Erde verbindende Schattenkegel. Vom Monde aus werden darauf die Himmelserscheinungen beobachtet, und es zeigt sich, daß mit der Veränderung des Standpunktes sich eine, von der irdischen völlig abweichende, neue Astronomie ergibt. An[S. 138] die Astronomie des Mondes schließen sich Mitteilungen über die Oberflächengestalt und die Natur dieses Weltkörpers, den Kepler mit den Wesen seiner Phantasie bevölkert.
Erhöht wird der Wert dieser, ein Vierteljahrhundert vor ihrer Herausgabe entstandenen Schrift, durch Anmerkungen, die Kepler ihr nach und nach beifügte. In diesen Anmerkungen findet sich nämlich vieles, das auf den damaligen Stand der Astronomie und der übrigen Zweige der Naturwissenschaft ein helles Licht wirft224.
Der Herausgeber nennt »Keplers Traum« eine in die schönste Form gekleidete astronomische Offenbarung, ja das hohe Lied der koppernikanischen Lehre. In den Anmerkungen, die Kepler in den Jahren 1620 bis 1630 niedergeschrieben hat, begegnet uns zum ersten Male die Behauptung225, daß die vom Monde reflektierten Strahlen neben der Licht- auch eine Wärmewirkung ausüben. Kepler glaubte sogar die Wärme der Mondstrahlen im Brennpunkte eines parabolischen Hohlspiegels als warmen Hauch fühlen zu können. Neuere Messungen haben jedoch gezeigt, daß die vom Monde ausgestrahlte Wärme nicht größer ist als diejenige, die eine Kerze auf 21 Fuß Entfernung ausstrahlt. Bei Kepler begegnet uns ferner schon die Ansicht, daß das Leben keineswegs auf die Erde beschränkt sei. Wie sich die Menschen und die Tiere der Beschaffenheit ihres Landes und ihrer Provinz anpaßten, so werde es sich auch mit den lebenden Wesen auf dem Monde verhalten226.
Das Jahr 1619, in dem Kepler durch die Entdeckung des dritten Gesetzes der Planetenbewegung sein Lebenswerk krönte, war für die spätere Gestaltung seiner äußeren Lage kein günstiges. In diesem Jahre kam nämlich der fanatische Ferdinand II. auf den Kaiserthron. Die Verfolgungen der Protestanten mehrten sich. Im Jahre 1626 wurde Kepler gedrängt, seine dürftig besoldete Stelle aufzugeben. Von diesem Zeitpunkte an führte der schon alternde Mann ein sorgenvolles unstetes Leben. Er hatte an rückständigem Gehalt nicht weniger als 12000 Gulden zu fordern. Man entledigte sich des unbequemen Mahners, indem man diese Schuld dem zum Herzog von Mecklenburg ernannten Wallenstein übertrug. Letzterer suchte Kepler wieder mit einer Professur in Rostock abzuspeisen.
Nach dem Sturze Wallensteins begab sich Kepler nach Regensburg, um dort auf dem Reichstage seine Forderungen geltend zu machen. Den ausgestandenen Entbehrungen und Aufregungen war sein geschwächter Körper jedoch nicht mehr gewachsen. Er erlag ihnen bald nach seiner Ankunft in Regensburg, am 15. November 1630. Die letzte Ruhestätte hat man ihm vor den Toren dieser Stadt bereitet. Zwei Jahre später tobte dort die Furie des dreißigjährigen Krieges, wodurch jede Spur von Keplers Grab verwischt wurde. Während der nächsten zwei Jahrhunderte die auf ihn folgten, hat Deutschland, von Leibniz abgesehen, keinen Mathematiker und Astronomen gehabt, der sich auch nur annähernd hätte mit Kepler messen können. Auch die hervorragenden ausländischen Forscher, die im 18. Jahrhundert der Berliner Akademie angehörten, (Euler, d'Alembert u. a.) blieben ohne Einfluß auf die Wiederbelebung der mathematischen Wissenschaften in Deutschland227. Eine Änderung, die uns später noch beschäftigen soll, trat fast unvermittelt mit Gauß ein, dem sich zahlreiche hervorragende Mathematiker auf deutschem Boden hinzugesellten.
Wie der literarische Nachlaß Galileis, so erfuhr auch derjenige Keplers ein besonderes Schicksal. Keplers Sohn kam nur dazu, das Somnium herauszugeben. Keplers Enkel verkaufte alles an den Astronomen Hevel. Hevels Sternwarte wurde durch einen Brand vernichtet, doch wurden Keplers Manuskripte zum Glück gerettet. Sie wechselten noch mehrfach den Besitzer, bis sie, auf Veranlassung Eulers, Katharina II. für 2000 Rubel kaufte und der Petersburger Akademie überwies. Hier und später in der Sternwarte zu Pulkowa ruhten die Manuskripte unbenutzt, bis endlich ein Landsmann Keplers, Chr. Frisch in Stuttgart, die so lange vernachlässigten Schätze zu heben verstand. Als Frucht einer dreißigjährigen Arbeit gab er von 1858 bis 1871 das gesamte, ihm zugängliche, gedruckte und ungedruckte Material mit Einleitungen und Erläuterungen versehen als Opera omnia Joannis Kepleri in acht Bänden heraus.
Nach dieser Darstellung des Lebensganges und der astronomischen Leistungen Keplers wollen wir seine Verdienste um die Optik, als eine der wichtigsten Hilfswissenschaften der Astronomie,[S. 140] ins Auge fassen. Von besonderem Interesse mußte für den Astronomen das Problem der Brechung sein, an dem sich schon das Altertum mit einigem Erfolg versucht hatte. Beruhte doch auf dieser Erscheinung die astronomische Refraktion, deren genauere Bestimmung für die beobachtende Astronomie sehr wichtig war, sowie die Konstruktion des Fernrohrs, um dessen Verbesserung Kepler sich gleichfalls verdient gemacht hat.
Die Ergebnisse seiner optischen Untersuchungen hat er in zwei Werken niedergelegt, von denen das eine unter dem Titel »Supplemente zum Vitellio«228 die gesamte Lehre vom Lichte betrifft, während sich das zweite, die »Dioptrik«229, vorzugsweise mit der Brechung beschäftigt. Was Euklid im Altertum und was in späterer Zeit Alhazen auf dem Gebiete der Optik geleistet haben, wird bei weitem übertroffen durch die grundlegenden, in den genannten Werken enthaltenen Untersuchungen Keplers. Daß dieser mit dem Gesetz der Lichtintensität bereits vertraut war, haben wir bei der Erörterung seiner astronomischen Ansichten230 bereits erfahren. Kepler hat dieses wichtige Gesetz zuerst in voller Klarheit ausgesprochen231, und zwar geschieht dies in seiner ersten, dem Kaiser Rudolph gewidmeten optischen Schrift, den »Supplementen zum Vitellio«232, mit deren Inhalt wir uns zunächst beschäftigen wollen.
Das erste Kapitel handelt von der Natur des Lichtes. Bemerkenswert sind die Aussprüche, daß das Licht imstande sei, sich ins Unbegrenzte fortzupflanzen (Prop. III); daß ferner das Licht keine Zeit beanspruche, sondern sich momentan ausbreite (Prop. V)233.
Den Hauptsatz der Photometrie finden wir (in Prop. IX) in folgenden Worten ausgesprochen234: »In dem Maße, wie die Kugelfläche, von deren Mittelpunkt das Licht ausgeht, größer oder kleiner ist, verhält sich die Stärke oder Dichte der Lichtstrahlen, die auf die kleinere, zur Stärke derjenigen Strahlen, die auf die größere Kugelfläche fallen.«
Die Farben vermochte Kepler noch nicht zu erklären; er nahm an, daß sie aus den verschiedenen Graden der Durchsichtigkeit und Dichte entständen, auch huldigte er der irrtümlichen Ansicht, die Brechung werde dadurch veranlaßt, daß dem dichteren Mittel ein größerer Widerstand und demgemäß ein größeres Brechungsvermögen zukomme. Indessen wurde Kepler schon bald nach dem Erscheinen seiner Schrift darauf aufmerksam gemacht, daß das weniger dichte Öl das Licht weit stärker bricht als das Wasser235.
Wie Maurolykus befaßte sich auch Kepler mit der Frage, weshalb hinter verschieden gestalteten Öffnungen stets ein rundes Sonnenbild entsteht. Auf die richtige Erklärung kam er durch folgende geometrische Konstruktion236: »Ich nahm ein Buch, das mir die Stelle des leuchtenden Körpers vertreten sollte, und legte es hin. Zwischen diesem Buch und einer Wand stellte ich eine Tafel mit einer winkligen Öffnung auf. Nun befestigte ich an der einen Ecke des Buches einen Faden, zog ihn durch die Öffnung hindurch und beschrieb, indem der Faden längs den Grenzen dieser Öffnung bewegt wurde, mit Kreide, die an dem Ende des Fadens angebracht war, eine Figur auf der Wand. Diese Figur war der Öffnung ähnlich. Dies wiederholte ich, indem ich den Faden an sämtlichen Ecken und mehreren anderen Stellen des Buches befestigte. Aus sämtlichen Figuren, die ich erhielt, entstand schließlich eine einzige, welche die Gestalt des Buches hatte.«
Das dritte Kapitel enthält außer den Grundlagen der Katoptrik eine Erörterung der Umstände, von denen unser Urteil über die Entfernung eines Gegenstandes abhängt. Ohne uns dessen bewußt[S. 142] zu werden, nehmen wir, wie Kepler ausführt, die Entfernung der beiden Augen zu Hilfe und ermitteln den Ort des Gegenstandes durch ein Dreieck, dessen Grundlinien jener Abstand der Augen, und dessen Seiten die von jedem Auge nach dem Gegenstande gezogenen Gesichtslinien sind237.
In den beiden letzten Abschnitten seiner Optik vom Jahre 1604 behandelt Kepler die Brechung, insbesondere die astronomische Strahlenbrechung, für die er eine Tabelle entwirft, und die Theorie des Sehens. Da diese Gegenstände der Optik indessen in Keplers Dioptrik vom Jahre 1611 wieder behandelt werden, wollen wir uns auf diese spätere Darstellung beschränken.
Einen Anlaß, sich von neuem mit der Optik zu beschäftigen, bot Kepler die im Jahre 1609 in Holland gemachte Erfindung des Fernrohrs. Das Ergebnis seiner, nur durch geringfügige experimentelle Hilfsmittel unterstützten Erwägungen war seine »Dioptrik«. Durch sie insbesondere ist Kepler zum Begründer der neueren Optik geworden. Er ist auf diesem Gebiete das gewesen, was Galilei für die Mechanik und Gilbert für die Elektrizitätslehre war. Leider wurde dies Verdienst Keplers im Vergleich zu den Leistungen anderer Forscher viel zu wenig gewürdigt. Während Galilei z. B. durch seine Beschäftigung mit der Optik Ruhm und Gewinn erntete, ohne diese Wissenschaft wesentlich zu bereichern, trugen Keplers höchst wertvolle Arbeiten, die der Wissenschaft einen neuen Ansporn gaben, nichts dazu bei, das traurige Los des großen deutschen Forschers zu bessern238.
Keplers Dioptrik239 ist vor kurzem durch eine Übersetzung240 zugänglich gemacht. Wir wollen sie der im nachfolgenden gegebenen Darstellung der wichtigsten Errungenschaften zugrunde legen, die wir Kepler auf den Gebieten der Brechung, der optischen Instrumente und der Theorie des Sehens verdanken.
Will man sich das Verdienst Keplers nur diese Dinge vergegenwärtigen, so muß man bedenken, daß man zu jener Zeit mit dem Problem der Brechung noch so wenig bekannt war, daß man[S. 143] das Verhältnis zwischen dem Einfalls- und dem Brechungswinkel als konstant annahm. Ferner war die herrschende Theorie vom Sehen durchaus unrichtig, und bezüglich der optischen Instrumente war eine Theorie überhaupt noch nicht vorhanden.
In seiner Vorrede zur Dioptrik erklärt Kepler, die Erfindung des Fernrohrs habe in ihm den Wunsch entstehen lassen, die Grundlagen dieser Erfindung auf geometrische Gesetze zurückzuführen und so für die Dioptrik das zu leisten, was Euklid für die Katoptrik geschaffen habe.
Als Erfahrungsgrundsatz stellte Kepler folgende Regel an die Spitze: Strahlen, die in ein dichteres Medium eintreten, nähern sich nach der Brechung innerhalb des Körpers der Senkrechten, die auf der Grundfläche im Einfallspunkte errichtet wird. Diese Brechung bleibt dieselbe, ob nun die Strahlen ein- oder austreten.
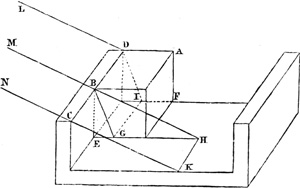
Beim Messen der Brechung verfuhr Kepler folgendermaßen: Er bestimmte die Schattenlänge von BE (siehe EH in Abb. 46) und schob dann einen Würfel der zu untersuchenden Substanz gegen die senkrechte Platte BDE. Infolge der Brechung des Lichtes trat dann eine Verkürzung des Schattens um das Stück GH ein, aus deren Größe er das Verhältnis zwischen dem Einfalls- und dem Brechungswinkel berechnete. Dabei machte Kepler die Entdeckung, daß ein durch Glas gehender Lichtstrahl, dessen Einfallswinkel an der Grenze zwischen Glas und Luft größer ist als 42°, nicht in die Luft tritt, sondern an der Grenze beider Medien nach dem Gesetz der Reflexion total zurückgeworfen wird242.
Trotz zahlreicher Messungen der Einfalls- und der zugehörigen Brechungswinkel vermochte Kepler indessen keine gesetzmäßige Beziehung zwischen beiden Größen zu finden. Zunächst ermittelte[S. 144] er, daß das Brechungsvermögen von Bergkristall und Glas ungefähr übereinstimmt. Betrug der Einfallswinkel 0°-30°, so war nach seinen Messungen das Verhältnis von Einfallswinkel und Brechungswinkel ungefähr konstant. Die bisher auch für größere Winkel angenommene Proportionalität fand Kepler jedoch nicht bestätigt. »Bei einer Neigung von 30°«, heißt es nämlich243 »beträgt die Refraktion 10°. Nach demselben Maße müßte zu einer Neigung von 90° eine Refraktion von 30° gehören; das Experiment ergibt aber 48°«244. Zwar suchte schon Kepler das Brechungsverhältnis zu einer trigonometrischen Funktion in Beziehung zu bringen, doch gelang dies erst einige Jahrzehnte später den Bemühungen von Snellius und Descartes. Snellius entdeckte nämlich (Abb. 47), daß der Weg (CA) eines Lichtstrahls, der aus Luft in Wasser tritt und auf eine senkrechte Wand BA fällt, sich zu dem Wege (CB), den derselbe Strahl ohne Ablenkung von seiner Eintrittsstelle bis zu jener Wand zurückgelegt haben würde, stets wie 3 : 2 verhält. Mit dem heute gebräuchlichen Ausdruck für dieses Gesetz, nach dem der Sinus des Einfallswinkels (DCE) zum Sinus des Brechungswinkels (ACF) in einem bestimmten Verhältnis (für Luft und Wasser 3 : 2) steht, war Snellius noch nicht vertraut245. In diese[S. 145] Form wurde das Brechungsgesetz erst durch den französischen Philosophen und Mathematiker Descartes246 gebracht.
Obgleich Kepler weder im Besitze des strengen Brechungsgesetzes noch des Gesetzes der konjugierten Brennweiten war, das, wie wir sehen werden, erst Halley ableitete, war er doch imstande, eine im großen und ganzen zutreffende Lehre von der Wirkung der Linsen und der Linsensysteme zu geben. Er läßt zunächst parallele Strahlen auf eine plankonvexe Glaslinse fallen und findet, indem er das Brechungsverhältnis 3 : 2 zugrunde legt, daß sie sich in einer Entfernung von ungefähr dem dreifachen Krümmungshalbmesser schneiden. Für die beiderseits gleiche bikonvexe Glaslinse fällt der Brennpunkt nach einem späteren Satze der Dioptrik247 etwa mit dem Krümmungsmittelpunkt zusammen. Auch in diesem Falle nahm Kepler mit einer für geringe Öffnungen der Linse hinreichenden Genauigkeit an, daß sich beim Glase der Einfallswinkel zum Brechungswinkel wie 3 : 2 verhält, während dies Verhältnis ja tatsächlich nicht für die Winkel selbst, sondern für ihre Sinuswerte zutrifft. Es entging Kepler nicht, daß die vom Rande der Linse kommenden Strahlen mit den aus der Mitte kommenden nicht genau zusammentreffen248, eine Erscheinung, die unter dem Namen der sphärischen Abweichung bekannt ist. Sie tritt auch an den sphärischen Hohlspiegeln auf und wurde bezüglich dieser schon von Roger Bacon erwähnt. Daß sie infolge der Brechung an einer Glaskugel auftritt, hatte übrigens schon Maurolykus dargetan, so daß Keplers Verdienst in dieser Hinsicht nicht groß ist. Von ihm rührt indessen der Gedanke her, den Linsen statt der sphärischen eine hyperbolische Form zu geben, um dadurch die sphärische Abweichung aufzuheben. Er nahm nämlich mit den Anatomen seiner Zeit an, daß die Linse unseres Auges auf der hinteren Seite eine hyperbolische Gestalt habe und infolgedessen scharfe Bilder gebe, während durch die sphärische Abweichung das Bild an Schärfe verliert.
Bei seinen Ableitungen der für die Linse und für Linsenkombinationen geltenden Regeln verwendet Kepler meist zwei[S. 146] Strahlenkegel, deren gemeinschaftliche Basis die Linse ist, während die Spitzen mit einem Punkte des Gegenstandes und dem entsprechenden Bildpunkte zusammenfallen. Die nebenstehende Abbildung enthält drei solcher Strahlenbündel, wie Kepler jedes Kegelpaar bezeichnet. Da dem Punkte E des Gegenstandes im Bilde der Punkt F, dem Punkte C dagegen der Punkt D entspricht, so ist der Satz, daß eine Linse umgekehrte Bilder liefert, ohne weiteres ersichtlich. Dieses von Kepler verfolgte Konstruktionsverfahren war eine von ihm herrührende Neuerung. Seine Vorgänger auf dem Gebiete der Optik hatten stets einzelne Strahlen verfolgt, während uns bei Kepler zum ersten Male das aus unzähligen Strahlen bestehende Strahlenbündel als Konstruktionsmittel begegnet. Mit dessen Hilfe war er imstande, die Lage und die Größe der Bilder weit richtiger zu ermitteln, als es vor ihm geschah. Kepler entdeckte beispielsweise die Eigenschaft der bikonvexen Linsen, von einem Gegenstande, der sich in der doppelten Brennweite befindet, ein gleich großes Bild in der gleichen Entfernung auf der entgegengesetzten Seite zu erzeugen.
Besondere Verdienste hat sich Kepler auch um die Theorie des Sehens erworben. Er erklärte die Netzhaut für denjenigen Teil des Auges, der das von der Linse erzeugte Bild auffängt, und vertrat die Ansicht, es müsse, nach Fortnahme der undurchsichtigen äußeren Häute des Auges, auf der Netzhaut ein umgekehrtes, verkleinertes Bild des Gegenstandes zu sehen sein. Diese Annahme Keplers hat später Scheiner249 durch den Versuch[S. 147] bestätigt. Da Kepler, nachdem zahlreiche Versuche anderer vorhergegangen, als der erste eine richtige Theorie des Sehens entwickelte, so wollen wir bei seiner sowohl in der ersten Schrift250 als in der Dioptrik251 gegebenen Darstellung dieses Vorganges noch etwas verweilen.
Keplers Vorläufer auf diesem Gebiete waren Maurolykus und Porta. Beide nahmen an, daß von jedem Punkte des leuchtenden Gegenstandes ein Strahl durch die Pupille ins Auge gelange. Das erzeugte Bild sollte nach Porta auf die Kristallinse, nach Maurolykus hinter diese fallen. Nach Keplers zutreffender Annahme gehen dagegen von jedem Punkte des Gegenstandes Strahlenkegel aus, deren gemeinschaftliche Grundfläche die Pupille ist. Sämtliche Strahlenkegel werden, ähnlich wie es Abbildung 49 zeigt, durch die Kristallinse des Auges so gebrochen, daß sie hinter dieser Linse gleichfalls Kegel bilden, deren Spitzen auf der Netzhaut liegen. Letztere befindet sich an der Stelle des Schirmes der Camera obscura und ist »in einem hohlen Bogen von allen Seiten her um die Kristallinse ausgespannt«.
Sehr zutreffend und an die neuesten Theorien anklingend ist das, was Kepler über die Tätigkeit der Netzhaut sagt. Wir wollen hier mit einigen Abkürzungen seine eigenen Worte bringen: »Das Sehen«, sagt er, »ist eine Gefühlstätigkeit der gereizten und mit Sehgeist erfüllten Netzhaut; oder auch: Sehen heißt die Reizung der Netzhaut fühlen. Die Netzhaut wird mit den farbigen Strahlen der sichtbaren Welt bemalt«. Die Veränderung der Netzhaut ist jedoch nach Keplers Annahme keine nur oberflächliche, sondern eine stoffliche. In der Netzhaut befinde sich nämlich ein außerordentlich feiner Stoff, »der Sehgeist«. Auf diesen wirke das durch die Linse gesammelte Licht zersetzend in der nämlichen Weise, wie etwa brennbare Stoffe durch die Brenngläser verändert würden. Das so entstandene Bild sei auch von einiger Dauer. Als Beweis dafür führt Kepler die Nachbilder an, die sich zeigen, wenn man »sich von einem angeschauten Lichtglanz abwendet«. Eine Bestätigung hat diese Anschauung später durch die Entdeckung des chemisch veränderlichen Sehpurpurs gefunden252.
Vollkommen richtig bemerkt Kepler, daß die Abbildung des Gegenstandes auf der Netzhaut noch nicht den ganzen Sehakt ausmache, sondern, daß das Bild »durch einen geistigen Strom« in das Gehirn übergehen und dort an den Sitz des Sehvermögens abgeliefert werden müsse.
Daß nur ein einziges Bild zur Wahrnehmung gelangt, hat seinen Grund nach Kepler253 darin, daß beide Netzhäute in gleicher Weise gereizt werden. Dementsprechend würden auch, wenn sie in ungleicher Weise gereizt würden, zwei Bilder wahrgenommen. Auch mit der Frage, weshalb wir trotz der umgekehrten Netzhautbilder die Gegenstände aufrecht sehen, hat sich Kepler beschäftigt. Doch vermochte er hierauf keine befriedigende Antwort zu geben. »Das Oben und Unten der Gegenstände,« meinte er, »lernen wir schon aus der Bewegung der Augen unterscheiden, da wir sie in die Höhe richten, wenn wir einen hoch befindlichen Gegenstand und nach unten, wenn wir einen tief gelegenen sehen wollen254.«
Ferner erklärte Kepler die Kurzsichtigkeit und die Übersichtigkeit. Die Ärzte des Altertums handeln zwar auch schon von der Kurzsichtigkeit. Sie führten indessen diesen Zustand, gegen den sie kein Mittel besaßen, auf eine Schwäche der vom Auge ausgehenden Ausströmung zurück255. Wie die Ursache der Kurzsichtigkeit, so blieb den Alten auch das Wesen des Sehvorgangs verborgen. Bei einem kurzsichtigen Auge schneiden sich, wie Kepler richtig ausführt, die von jedem Punkte eines Gegenstandes ausgehenden Strahlen schon innerhalb des zwischen der Linse und der Netzhaut befindlichen Glaskörpers. Sie breiten sich hinter ihrem Durchschnittspunkte wieder aus und geben daher auf der Netzhaut Lichtkreise an Stelle von Lichtpunkten. Ähnlich verhält sich das übersichtige Auge. Es bricht die Strahlen nicht stark genug, so daß die Spitzen der Strahlenkegel hinter der Netzhaut liegen256. Da mit der Entfernung des Gegenstandes von der Linse sich auch die Bildweite ändert, so blieb noch zu erklären, durch welchen Vorgang ein normales Auge imstande ist,[S. 149] die Bilder entfernter und naher Gegenstände mit gleicher Schärfe wahrzunehmen. Kepler meinte, daß dieser, als Akkommodation bezeichnete, Vorgang durch eine Verschiebung der Linse oder der Netzhaut geschehe257, während Descartes der später als richtig erkannten Ansicht zuneigte, daß die Linse infolge eines auf sie ausgeübten, wechselnden Druckes bald mehr, bald weniger gekrümmt sei258. »Da die Netzhaut«, führt Kepler aus, »in ein und derselben Lage nicht zugleich von nahen und fernen Gegenständen scharfe Bilder erhalten kann und doch bei den Menschen, die nah und fern deutlich sehen, gleich scharfe Bilder erhält, so muß die Netzhaut inbezug auf die in der kristallenen Feuchtigkeit liegende Linse eine Ortsveränderung erleiden.« Es sei wahrscheinlich, meint Kepler, daß ein kräftiges, jugendliches Auge, wie es eine deutliche Bewegung in der Pupille zeige, so auch hinter der Linse die Fähigkeit habe, den Augapfel dergestalt zu verändern, daß der Augengrund sich der Linse nähere oder von ihr zurückweiche, je nach der Entfernung der Gegenstände, auf die das Auge eingestellt werde. Vielleicht befinde sich der Sitz dieser Bewegung aber auch in jener Haut, welche die Linse in der kristallenen Feuchtigkeit festhalte und jene eigentümlichen, als Ziliarfortsätze bezeichneten, schwarzen Strahlen aussende. Kepler nahm auch an, daß das Innere des Auges flüssig sei, damit die von ihm geforderten Formveränderungen vor sich gehen könnten. Er erzählt, daß er sich mit der Erklärung des Sehens mehrere Jahre fast ausschließlich beschäftigt habe. Dafür gebührt ihm aber auch der Ruhm, der Begründer der physiologischen Optik zu sein. – Keplers Verdienste um die Theorie der optischen Instrumente haben wir an der Hand seiner »Dioptrik« schon in einem früheren Abschnitt259 gewürdigt.
Descartes und Kepler waren der Meinung, daß das Licht zu seiner Fortpflanzung keine Zeit beanspruche. Ersterer stützte sich dabei nicht ausschließlich auf die Wahrnehmung irdischer Vorgänge, sondern zog auch astronomische Erscheinungen in Betracht. Da er jedoch nur die Verfinsterungen des Mondes ins Auge faßte, so konnte sich bei der verhältnismäßig geringen Entfernung dieses Weltkörpers, die das Licht in einer Sekunde durcheilt, nur ein negatives Resultat ergeben260.
Unter den Männern, welche die astronomische Wissenschaft als Nachfolger Keplers mit Erfolg gepflegt haben, ist vor allem Hevel zu nennen. Johann Hevel261 wurde 1611 in Danzig geboren. Sein Lebensgang erinnert in mancher Hinsicht an denjenigen Guerickes. Hevel stammte gleichfalls aus einer alten, vermögenden Familie seiner Vaterstadt. Er studierte in Leyden Rechtswissenschaft, machte ausgedehnte Reisen, auf denen er Beziehungen zu hervorragenden Ausländern anknüpfte und bekleidete, nach Danzig zurückgekehrt, das Amt eines Ratsherrn. Die Anregung zu astronomischen Arbeiten, denen sich Hevel neben seinen Berufsgeschäften aus Liebhaberei widmete, empfing er von einem seiner Danziger Lehrer. Hevel mußte ihm auf dem Totenbette das Versprechen geben, den gemeinsam gepflegten Studien treu zu bleiben. Er baute 1641 eine Sternwarte und verfertigte nicht nur alle Instrumente, deren er sich bediente – sogar die Linsen schliff er selbst – sondern besorgte auch die Herstellung der Kupferplatten für seine Abbildungen und deren Druck.
Zum Messen benutzte Hevel noch nicht das Fernrohr, obgleich die übrigen Astronomen ihre Meßapparate schon mit dem neuen Instrument versehen hatten, sondern er bediente sich mit einem gewissen Eigensinn ausschließlich der für das unbewaffnete Auge eingerichteten Diopter. Trotzdem erreichte er eine große Genauigkeit. Ja, Halley, der Hevel im Auftrage der Royal Society besuchte, mußte sogar zugeben, daß seine mit dem Fernrohr erhaltenen Messungen mit denjenigen Hevels bis auf die Bogenminute übereinstimmten und oft nur um wenige Sekunden davon abwichen.
Das größte Verdienst Hevels bestand darin, daß er die ersten genauen Karten vom Monde zeichnete und damit einen neuen Zweig der astronomischen Wissenschaft, die Selenographie, begründete. Hevels Werk262 über den Mond erschien als das Ergebnis einer sich über viele Jahre erstreckenden, mühevollen Arbeit im Jahre 1647. Es ist mit Recht als eines der ehrwürdigsten Denkmäler ausdauernder wissenschaftlicher Tätigkeit bezeichnet worden263. Leider sind die von Hevel für dieses Werk gestochenen Kupferplatten[S. 151] infolge der Pietätlosigkeit seiner Erben verloren gegangen. Die dunklen Flecken des Mondes (Abb. 50) hielt Hevel noch für Wasseransammlungen; er benannte sie deshalb Mare frigoris (Eismeer), Oceanus procellarum (stürmischer Ozean) usw. Um die Berge und Gebirge des Mondes zu bezeichnen, bediente er sich geographischer Namen. Es begegnen uns daher auf dem Monde der Vesuv, die Apenninen, die Karpathen usw. Zum großen Schaden für die Wissenschaft wurde Hevels Sternwarte 1679 durch eine Feuersbrunst zerstört, der auch viele Bücher und Aufzeichnungen zum Opfer fielen.
Hevel war auch ein fleißiger Kometenforscher. Es war ihm vergönnt von 1652–1683 neun größere Kometen zu beobachten. Die hierdurch und durch andere gewonnenen Aufzeichnungen über[S. 152] 400 Kometen hat er in seiner Cometographie vom Jahre 1668 veröffentlicht.
Hevel starb im Jahre 1687. Er hatte einen ausgedehnten Briefwechsel mit den bedeutendsten Gelehrten seiner Zeit unterhalten. Die von Hevel gesammelten Briefe umfaßten viele Folianten, sind aber von seinen Erben für einen Spottpreis verkauft worden264. In einer Geschichte der Wissenschaften verdient dies Verhalten verurteilt zu werden, zur Warnung für spätere Geschlechter und zur Mahnung an die Pflichten, welche der Staat hat, wenn dem einzelnen das Verständnis abgeht.
Die unmittelbar auf Kepler folgende Generation schuf auch die mit der Physik und mit der Astronomie in engem Zusammenhange stehende allgemeine Geographie. Ihr Begründer ist Bernhard Varenius und das Werk, durch das er dies vollbrachte, seine »Geographia generalis« (1650)265. Der große Fortschritt, den wir bei Varenius finden, besteht vor allein darin, daß er nicht lediglich schildert und beschreibt, sondern in erster Linie vergleicht. Sein Werk wird daher mit Recht dem zweihundert Jahre später erschienenen Kosmos A. v. Humboldts zur Seite gestellt.
Die Entdeckungen der großen Erneuerer der Naturwissenschaften sind zum großen Teil der Anwendung der Mathematik auf physikalische und astronomische Probleme zu verdanken. Der Fortschritt in der von Galilei und Kepler eingeschlagenen Richtung war daher nicht nur an die Ausbildung und Ausbreitung des induktiven Verfahrens, sondern auch an die Weiterentwicklung der Mathematik geknüpft. Letztere nahm denn auch in diesem Zeitalter unter der Mitwirkung der bedeutendsten Naturforscher einen kräftigen Aufschwung, der in der nachfolgenden Periode durch Newton, Leibniz, Descartes und Huygens eine Fortsetzung erfuhr.
In dem Maße, wie die Genauigkeit der Beobachtungen zunahm, war auch die Berechnung der Ergebnisse zeitraubender und mühseliger geworden, so daß man das Bedürfnis fühlte, an die Stelle des Multiplizierens und Dividierens großer Zahlen eine Vereinfachung treten zu lassen. Diesem wurde durch die Erfindung der Logarithmen genügt, durch die jene Operationen auf das viel schneller zu bewerkstelligende Addieren und Subtrahieren zurückgeführt wurden. Zur Berechnung astronomischer Tafeln wandte Kepler zum erstenmal im Jahre 1620 die Logarithmen an, die nach einem Ausspruch von Laplace das Leben des Astronomen verlängern, indem sie die Arbeit von Monaten auf Stunden abkürzen.
Ein großes Verdienst um die für die Allgemeinheit wie für die Wissenschaft gleichwichtige Fortbildung der Rechenkunst erwarb sich auch der Holländer Simon Stevin266, dessen Lebensgang und physikalische Forschungen wir an späterer Stelle kennen lernen werden. Stevin ist die erste systematische Darstellung des Rechnens mit Dezimalbrüchen zu verdanken. Dabei verfehlte[S. 154] er nicht, auf den Wert der dezimalen Schreib- und Rechnungsweise hinzuweisen und im Zusammenhange damit von den Regierungen die Einführung dezimaler Münz-, Maß- und Gewichtssysteme zu fordern, ein Wunsch, der erst zweihundert Jahre später durch die Männer der französischen Revolution verwirklicht wurde.
Stevins Schreibweise für die Dezimalbrüche ist noch eine umständliche. Er fügte nämlich jeder Ziffer die Stelle, die sie einnimmt, als Index bei. Der Dezimalbruch 0,3469 z. B. nimmt bei ihm folgende Form an: 3① 4② 6③ 9④. Fast zur selben Zeit entstand aber nach Vietas Vorschlag die heutige Schreibweise unter Anwendung des Kommas.
Mit Zinsberechnungen war man schon im Altertum bekannt. Bei den Indern und den italienischen Kaufleuten des Mittelalters begegnen uns auch Zinseszinsberechnungen. Stevin gebührt das Verdienst, zuerst267 Tafeln für die Berechnung von Zinsen und Zinseszinsen veröffentlicht zu haben.
Von größtem Einfluß auf die weitere Entwicklung der Mathematik, wie auf die mathematische Behandlung der Naturwissenschaften war auch die Fortbildung der algebraischen Zeichensprache und des wichtigsten Gebietes der Algebra, der Lehre von den Gleichungen.
Wir haben in früheren Abschnitten erfahren, daß in der ältesten Periode die Mathematik der Zeichen entbehrte und alle Rechnungen und Beziehungen in Worten zum Ausdruck brachte. Bald traten jedoch Fachausdrücke und Abkürzungen und endlich besondere Zeichen auf. So stellten sich gegen den Ausgang des 15. Jahrhunderts, als man in Italien noch für Plus und Minus die Abkürzungen p und m brauchte, die Zeichen + und - ein268.
Das Zeichen = für die Gleichsetzung ist noch jüngeren Datums. Es begegnet uns ein halbes Jahrhundert später und wird von dem Erfinder269 damit begründet, daß nichts gleicher sei als ein[S. 155] Paar paralleler Strichelchen. Klammern, Wurzel- und Unendlichkeitszeichen sind noch später entstanden.
Der bedeutendste Fortschritt in der Ausbildung der Algebra zu einer auf internationaler Kurzschrift beruhenden Sprache geschah durch den Franzosen Vieta mit seiner Einführung allgemeiner Buchstabengrößen270. Bei ihm begegnen uns auch die ersten Anfänge einer Verknüpfung der Algebra mit der Geometrie, indem er die Wurzeln gegebener Gleichungen geometrisch darstellen lehrte. Auch das Verfahren, die Zahl π durch eine unendliche Reihe zu ermitteln, rührt von Vieta her. Er hat auf diesem Wege π bis auf 10 Dezimalen berechnet.
Franziskus Vieta wurde 1540 im Poitou geboren und starb 1603 in Paris. Er wirkte unter Heinrich IV. als Parlamentsrat und später als Mitglied des Königlichen Geheimen Rates. Vieta gilt als der hervorragendste französische Mathematiker des 16. Jahrhunderts.
Mit allgemeinen Sätzen war man in der Arithmetik schon lange vor Vieta bekannt geworden. Wollte man aber eine für das ganze Bereich der konkreten Zahlen gültige Regel ausdrücken, so mußte dies in Worten geschehen. Ein Beispiel diene zur Erläuterung. Ausdrücke von der Form 3 (4 + 2) = 3 · 6 = 3 · 4 + 3 · 2 = 12 + 6 = 18 lassen sich für beliebig viele konkrete Fälle bilden. Man hatte auch daraus den allgemeinen Satz entnommen, daß eine Summe mit einer Zahl multipliziert wird, indem man entweder zuerst summiert und die erhaltene Zahl mit der gegebenen Zahl multipliziert, oder auch, indem man die Summanden einzeln mit der gegebenen Zahl multipliziert und die erhaltenen Produkte dann addiert. Diese umständliche Regel ließ sich in der mit Buchstabengrößen arbeitenden Algebra, zumal bald nach Vieta der Gebrauch von Klammern aufkam, auf folgenden, ohne weiteres verständlichen, sämtliche möglichen konkreten Fälle umfassenden Ausdruck bringen:
a (b + c) = a · b + a · c.
Vieta unternahm es auch, die Trigonometrie mit der Algebra zu verknüpfen, indem er lehrte, wie sich nach algebraischem Verfahren die trigonometrischen Funktionen umformen und in mannigfache Beziehungen bringen lassen. Auf diese Weise entstand durch ihn derjenige Teil der Trigonometrie, den man auch wohl als Goniometrie bezeichnet. So leitete er die Formeln für[S. 156] sin n α und cos n α ab und zeigte z. B., daß sin 3 α = sin α · cos 2 α + cos α · sin 2 α ist271.
Der zweite große Fortschritt auf dem Gebiete der Algebra betraf die Lehre von den Gleichungen. Vieta war noch der Meinung, daß nur die positiven Wurzelwerte einer Gleichung eine Lösung darstellen. Daß auch die negativen Wurzeln reell sind und überhaupt jede Gleichung so viel Wurzeln hat, als ihr Grad anzeigt, erkannten erst die Mathematiker des 17. Jahrhunderts.
Daß jede Gleichung n. Grades n Wurzeln besitzt, folgerte der Niederländer Girard 1629 in seinem Werke »Neue Entdeckungen auf dem Gebiete der Algebra« aus dem von ihm erkannten Zusammenhange zwischen den Wurzeln einer Gleichung mit ihren Koeffizienten272. Dieser Zusammenhang ergab sich daraus, daß die Entstehung einer Gleichung n. Grades durch die Multiplikation von n Faktoren ersten Grades nachgewiesen wurde, eine Erkenntnis, deren mathematischer Ausdruck Xn = (x - α1)(x - α2)(x - α3) ... (x - αn) lautet, wenn wir mit Xn das Polynom der Gleichung und mit α1, α2, α3, αn die Wurzeln bezeichnen.
Nachdem Girard das Bildungsgesetz der Gleichungen erkannt hatte, erhielten auch die imaginären Wurzeln, mit denen man früher nichts anzufangen wußte, gleichsam ihre Daseinsberechtigung. Wenn Girard z. B. findet, daß eine bestimmte Gleichung vierten Grades neben zwei reellen noch zwei imaginäre Wurzeln liefert, so läßt er sich durch das Auftreten der letzteren nicht beirren, sondern erläutert es dahin, daß diese Wurzeln es eben sind, welche dem Bildungsgesetz Genüge leisten.
In der ersten Hälfte des 17. Jahrhunderts begann man mit den negativen Zahlen und mit der Null zu rechnen. Auch hierin hat Girard neben dem gleich zu nennenden Descartes Bahnbrechendes geleistet. Girard bemerkt, die negative Lösung werde geometrisch durch Rückwärtsschreiten dargestellt273. Dieser Gedanke findet sich bei Descartes für eine Reihe von Aufgaben verwertet. Er sowie Girard erklären die negativen Wurzeln geometrisch als Strecken, deren Richtung derjenigen entgegengesetzt[S. 157] ist, welche die den positiven Wurzeln entsprechenden Strecken angeben274.
Auf Gleichungen dritten Grades kamen schon die Alten durch das Problem der Würfelverdopplung (Bd. I. S. 85). Auch Archimedes wurde auf eine kubische Aufgabe geführt, als er eine Kugel durch eine Ebene so zu zerlegen suchte, daß die beiden Teile der Kugel in einem bestimmten Verhältnis stehen. Die Folge war, daß sich auch die Araber mit Gleichungen dritten Grades beschäftigten, ohne indessen andere als geometrische Lösungen zu finden. Die algebraische Auflösung dieser Gleichungen war daher eins der wichtigsten Probleme der neueren Mathematik. Seine Bewältigung gelang zu Beginn des 16. Jahrhunderts275, indem man eine Regel fand, um die Gleichung x3 + ax = b zu lösen. Bekannt gegeben wurde diese Lösung durch Cardano (Cardanische Formel). Er hatte sie indes nicht selbst gefunden, sondern verdankte sie Tartaglia. Es ergibt sich, daß eine Gleichung dritten Grades drei Wurzeln hat und daß die Summe dieser Wurzeln gleich dem Koeffizienten von x2 ist. Bei diesen Untersuchungen war man gezwungen, auch Wurzeln aus negativen Zahlen zu berücksichtigen und mit solchen »imaginären« Werten wie mit algebraischen Zahlen zu rechnen.
Mit einer Gleichung vierten Grades haben sich zuerst arabische Mathematiker beschäftigt. Die Lösung gelang durch Konstruktion276. Die algebraische Lösung dagegen blieb einem Schüler Cardanos277 vorbehalten. Er führte die biquadratische Gleichung auf eine kubische zurück.
Diese Erfolge des 16. Jahrhunderts bewirkten, daß man im 17. und 18. sich eifrig um die Lösung von Gleichungen fünften und höheren Grades mühte. Alle Anstrengungen waren jedoch vergeblich. Sie führten schließlich zu dem negativen Ergebnis, daß es unmöglich sei, solche Gleichungen algebraisch aufzulösen278.
Eine ganz ungeahnte Wichtigkeit erhielt die Lehre von den Gleichungen, als Descartes diesen Teil der Algebra mit der Geometrie[S. 158] in die engste Beziehung setzte und dadurch die Grundlagen der analytischen Geometrie der Ebene schuf. Descartes zeigte, daß jede gesetzmäßig entstandene Kurve auf eine Gleichung zurückgeführt werden kann, aus der sämtliche Eigenschaften der Kurve sich durch Rechnung ableiten lassen. Gesetzmäßig entsteht eine Kurve, wenn sie als der geometrische Ort aller Punkte zu betrachten ist, die einer bestimmten Bedingung genügen. Jene Bedingung drückt Descartes durch eine unbestimmte Gleichung zwischen zwei voneinander abhängigen Größen x und y aus, die er durch Linien darstellt. Den Grundgedanken des auf diesen Voraussetzungen beruhenden Verfahrens279 spricht er in folgenden Worten aus: »Indem man der Linie y der Reihe nach unendlich viele verschiedene Größen beilegt, erhält man auch unendlich viele Werte für die Linie x.« Auf diese Weise sind aber, wie Descartes hinzufügt, unendlich viele Punkte bestimmt, welche der gegebenen Gleichung genügen. Verbindet man diese Punkte, so erhält man eine Kurve als das geometrische Bild jener Gleichung.
Die Möglichkeit einer analytischen Geometrie des Raumes wurde von Descartes nur angedeutet. Er bemerkt nämlich, eine dreidimensionale Kurve sei völlig bestimmt, wenn man von jedem ihrer Punkte zwei Lote auf zwei zueinander senkrechte Ebenen fälle. Auf diesen entständen dadurch ebene Kurven, die uns einen vollkommenen Begriff von dem Verlauf der Raumkurve gäben.
Descartes knüpfte zwar unmittelbar an Vieta an, den wir als den Schöpfer der algebraischen Geometrie kennen gelernt haben. Auf den Grundgedanken seines Verfahrens wurde er aber durch das Studium der Alten geführt. In der Einleitung zu seiner »Geometrie« erzählt Descartes, er habe sich mit einer Aufgabe des Pappus beschäftigt, deren vollständige Lösung den Alten nicht gelungen sei. Den Grund dafür habe er darin gefunden, daß die Aufgabe eine unbestimmte, d. h. die Zahl der Gleichungen kleiner als die der Unbekannten war. Eine Lösung ließ sich, wie Descartes erkannte, nur dadurch ermöglichen, daß man für die überzählige Unbekannte oder die überzähligen Unbekannten bestimmte Werte annahm, wodurch dann jedesmal auch die andere oder die anderen Unbekannten bestimmt waren. Allerdings ergaben sich dann soviel Lösungen, so oft man diese Operation vornahm, und statt eines bestimmten Punktes erhielt man eine Reihe[S. 159] von Punkten oder eine Linie, deren Punkte der gestellten Aufgabe genügten. Der große Fortschritt der Descartes'schen Methode bestand darin, daß fortan geometrische Gebilde der Rechnung unterworfen und alle geometrischen Aufgaben allgemein gelöst werden konnten, während das Altertum nur geometrische Einzelfälle betrachtete.
Auch neue, für die Weiterentwicklung der Mathematik in ihrer Anwendung auf die Naturwissenschaften höchst wichtige Probleme wurden durch das analytische Verfahren zugänglich. Eins der ersten, mit dem sich schon Descartes befaßte und an dem sich vorzugsweise die Infinitesimalrechnung entwickelt hat, war die Tangentenaufgabe. Descartes stellte sie zunächst in der Fassung, daß er für einen gegebenen Punkt einer Kurve die zur Tangente senkrechte Linie, die Normale, suchte. Ein Jahr nach dem Erscheinen seiner »Geometrie« sehen wir ihn jedoch schon mit der Konstruktion der Tangente an die Zykloide beschäftigt, jener Kurve, auf die zuerst Galilei aufmerksam geworden war280. Descartes' Verfahren, unbestimmte Gleichungen geometrisch zu deuten, lehrte alsbald eine Fülle neuer Kurven kennen. Erwähnt seien nur die von ihm entdeckte logarithmische Spirale und das gleichfalls von ihm gefundene und nach ihm benannte Cartesische Blatt, dessen Gleichung x3 + y3 = a · x · y lautet.
Die Geometrie der Ebene wurde insbesondere durch Fermat, diejenige des Raumes erst ein Jahrhundert später durch Clairaut (1713–1765) weiter ausgebaut.
Fermats Verdienste um die Fortbildung der Mathematik zur wichtigsten Hilfsdisziplin der Naturwissenschaften sind so hervorragend, daß wir bei diesem Manne und seinen Leistungen etwas verweilen müssen.
Pierre Fermat wurde 1601 in der Nähe von Toulouse geboren. Er starb dort im Jahre 1665. Wir wollen versuchen Fermat, dem man den Ruhm zuerkannt hat, der bedeutendste französische Mathematiker281 zu sein, als Mitbegründer der analytischen Geometrie zu würdigen, mit deren Problemen er sich bereits 10 Jahre vor dem Erscheinen des Descartes'schen Werkes beschäftigte. Auch Fermat knüpfte wie Descartes an die alte Mathematik an. Fermat bemühte sich nämlich, eine verloren gegangene und nur in Bruchstücken durch Pappus bekannt gewordene[S. 160] Schrift des Euklid, die sogenannten Porismen282, wieder herzustellen.
Fermats für die analytische Geometrie grundlegende Arbeit zeichnet sich der »Geometrie« des Descartes gegenüber durch größere Klarheit und erschöpfende Behandlung aus. Nirgends findet sich bei Descartes eine solch klare Darstellung des Grundgedankens, wie Fermat sie gleich zu Beginn seiner Arbeit gibt. Die Gleichungen, sagt er, können in bequemer Weise dargestellt werden, wenn wir zwei Strecken unter einem gegebenen Winkel, als den man am passendsten den rechten nimmt, aneinandersetzen und einen Anfangspunkt wählen. Diesen Nullpunkt bezeichnet Fermat mit N. Die Strecke, die er von dort abträgt, wird mit A (unser x), die dazu senkrechte mit E (unser y) bezeichnet. Die konstanten Werte (a, b, c usw.) werden bei ihm durch B, D, G ausgedrückt. Die Gleichung einer Geraden, welche durch den Nullpunkt geht, begegnet uns bei Fermat zum ersten Male. Sie lautet D · A = B · E. (unser ax = by). Die Parabelgleichung schreibt er A2 = D · E (unser x2 = ay), die Kreisgleichung B2 - A2 = E2 (heute r2 - x2 = y2) usw.283.
Fermat war einer der ersten, der eine allgemeine Methode fand, die Maxima- und Minimaaufgaben zu lösen. Zum ersten Male begegnet uns ein hierher gehöriges Problem, und zwar in geometrischer Fassung, bei Euklid284. Es läuft, modern ausgedrückt, darauf hinaus, für x · (a - x) den größten Wert zu finden. Die Lösung ergibt, daß dies Produkt ein Maximum ist, wenn x = a/2 gesetzt wird. Daß der Kreis bei gegebenem Umfang unter allen ebenen Figuren die größte Fläche, und die Kugel bei gegebener[S. 161] Oberfläche unter allen Körpern den größten Rauminhalt besitzt, war den Alten gleichfalls bekannt.
Unter den neueren Mathematikern haben sich, von vereinzelten Fällen abgesehen285, zuerst Kepler, Cavalieri und Fermat mit den in ihrer Anwendung auf das physikalische Gebiet so außerordentlich wichtigen Maxima- und Minimabestimmungen beschäftigt. Mit Keplers und mit Cavalieris Verdienst um die Begründung der neueren Mathematik werden wir uns später befassen.
Fermats Methode ist diejenige, die auch heute wohl noch für eine elementare Behandlung von Maxima- und Minimaaufgaben Anwendung findet286. Er setzt nämlich an Stelle einer Unbekannten x einen neuen Wert x - Δ, in welchem Δ (Fermat braucht dafür die Bezeichnung E) als eine von Null nur wenig abweichende Größe betrachtet wird.
Nachdem er den Ausdruck umgeformt, wird der Übergang von Δ zur Null vollzogen und der für x gesuchte Wert ermittelt.
Ein Beispiel Fermats, bei dem wir jedoch von seiner Ausdrucksweise absehen, möge sein Verfahren erläutern. Für x2 (a - x) wird nach dem Wert von x gefragt, für den dieses Produkt den größten Wert annimmt. Für x wird x + Δ gesetzt und wir erhalten:
x2 (a - x) = (x + Δ)2 (a - x - Δ).
Die Ausrechnung und Umformung ergibt:
2ax - 3x2 + Δ (a - 3x - Δ) = 0.
Wird darin Δ = 0 gesetzt, so erhalten wir:
2ax - 3x2 = 0
und daraus:
x = 2/3 a.
Der von Fermat gelehrten Methode fehlte noch ein bestimmtes Kennzeichen dafür, ob der erhaltene Wert ein Maximum[S. 162] oder ein Minimum ist. Dies allgemein zu entscheiden, vermochte man erst mit Hilfe des von Leibniz herrührenden Verfahrens der Differentialrechnung.
In dem Bestreben, die von ihm gefundene Methode auf die Naturlehre anzuwenden, wurde Fermat zu seinem Prinzip von der geringsten Wirkung287 geführt. Fermats Satz läuft darauf hinaus, daß die Natur, »die große Arbeiterin, die unserer Instrumente und Maschinen nicht bedarf«, alle Geschehnisse mit einem Minimum von Aufwand ablaufen lasse. Dieser Gedanke war auch den Alten nicht fremd. So erklärten sie die Form der Bienenzellen aus dem Streben der Natur, möglichst an Material zu sparen288. Der alexandrinische Physiker Heron äußerte einen ähnlichen Gedanken in bezug auf das Reflexionsgesetz. Er wies nämlich darauf hin, daß die Reflexion des Lichtes von A nach B auf dem kürzesten Wege erfolgt, wenn der Reflexionspunkt C die Lage hat, daß der Einfallswinkel ACD gleich dem Austrittswinkel BCD ist, da jede andere Verbindung der Punkte A und B mit der spiegelnden Fläche, z. B. die Verbindung AC1B (Abb. 51), länger ist.
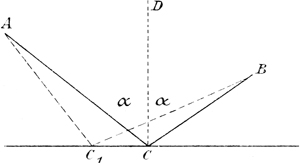
Diese Betrachtungsweise übertrug Fermat zunächst auf das damals im Mittelpunkte der Erörterung stehende Brechungsgesetz. Fermats Gedankengang war etwa folgender: Daß der Lichtstrahl beim Übergang von dem dünneren zum dichteren Medium gebrochen wird, rührt daher, daß das Licht in letzterem einen größeren Widerstand findet und sich infolgedessen langsamer bewegt. Je größer nämlich der Widerstand ist, um so länger wird die für seine Überwindung beanspruchte Zeit sein. Die im Sinne des Prinzips der kleinsten Aktion gestellte Frage lautete also: Welchen Weg muß der Lichtstrahl nehmen, um mit dem geringsten Gesamtwiderstande, der sich aus den Widerständen in den beiden[S. 163] Medien summiert, oder was auf dasselbe hinausläuft, da ja dem kleineren Widerstande eine kürzere Zeit entspricht, um innerhalb der kürzesten Zeit von A nach B zu gelangen (Abb. 52)? Fermat findet mit Hilfe seines Verfahrens, daß dieses Minimum stattfindet, wenn sich der Sinus des Einfallswinkels zum Sinus des Brechungswinkels wie die Geschwindigkeiten in den zugehörigen Medien verhalten (sin α : sin β = v1 : v2 = n).
Fermat schloß auch umgekehrt aus dem Gesetz als einer feststehenden Tatsache auf die Zulässigkeit seines, immerhin einen gewissen metaphysischen Zug aufweisenden Prinzips. Denn metaphysisch war das Prinzip, so lange es darauf hinauslief, an die Stelle des ursächlichen Wirkens der Natur gewissermaßen ein überlegtes, aus Vernunftgründen entspringendes Handeln zu setzen.
Das Prinzip der kleinsten Wirkung ist für die weitere Folge von nicht geringem Einfluß gewesen, obgleich es das »unbestimmteste von allen Prinzipien«289 ist, aus dem man das Wirken der Natur zu erklären sucht. Auch Huygens benutzte den Fermatschen Satz. Bei der nahen Beziehung, in der Huygens zu Leibniz stand, hat man wohl vermutet, daß der letztere seine Lehre von der prästabilierten Harmonie in Anlehnung an die Gedanken Fermats geschaffen hat. Die Mathematiker und die Physikotheologen des 18. Jahrhunderts hielten gleichfalls an diesem Prinzip fest und suchten seine Allgemeingültigkeit dadurch nachzuweisen, daß sie zahlreiche Einzelfälle daraus ableiteten. Auf solche Weise äußerte das Prinzip eine sehr anregende und fruchtbare Wirkung. Viele Untersuchungen über größte und kleinste Werte, die man im 18. Jahrhundert unternahm, waren von dem Bestreben geleitet,[S. 164] die Naturvorgänge aus dem Prinzip der kleinsten Wirkung zu erklären. Hand in Hand damit erwuchs in der Variationsrechnung ein besonderer Zweig der Mathematik, der sich mit Maxima- und Minima-Aufgaben befaßte und allgemeingültige Regeln für ihre Lösung erkennen ließ. Einen vorläufigen Abschluß fanden diese Untersuchungen, an denen sich auch Johann und Jacob Bernoulli beteiligten, in Eulers Schrift vom Jahre 1744290. Welchen Standpunkt Euler dem Fermatschen Prinzip gegenüber einnahm, ersehen wir aus folgenden, jenem Hauptwerk entnommenen Worten: »Da die Einrichtung der Welt die vorzüglichste ist, wird nichts in ihr angetroffen, woraus nicht irgend eine Maximum- oder Minimumeigenschaft hervorleuchtet. Deshalb kann kein Zweifel bestehen, daß alle Wirkungen in der Welt durch die Methode der Maxima und Minima aus den Zwecken wie aus den wirkenden Ursachen selbst abgeleitet werden können«.
Inzwischen mehrten sich die Beobachtungen, daß auch für die organische Welt Fermats Satz als Stütze dienen könne. Der Bau der Knochen, der Federn und der Halme: alles schien darauf hinzudeuten, daß die Natur von ihren Mitteln den zweckmäßigsten und sparsamsten Gebrauch macht und insbesondere bei dem Aufbau der organischen Körper gewissermaßen nach einem Sparsamkeitsgesetz verfährt, das sich als ein besonderer Fall des in der Optik und in der Mechanik beobachteten Prinzips der kleinsten Wirkung darstellt. Letzteres wurde dann auch um die Mitte des 18. Jahrhunderts von Maupertuis zur Grundlage der gesamten Naturlehre gemacht und in folgende Worte gekleidet: »Wenn in der Natur eine Veränderung vor sich geht, so ist der für diese Veränderung erforderliche Aufwand der möglichst kleinste«291.
Wie wir später sehen werden, wurde diese, in ihren Anfängen bis ins Altertum zurückreichende Vorstellung, die Fermat klarer formulierte und das 18. Jahrhundert weiter entwickelte, erst durch schärfere mechanische Prinzipien verdrängt, als Lagrange die Neubegründung der Mechanik unternahm.
Wir kehren noch einmal zu Fermat zurück, um seine Verdienste um die Begründung der Zahlentheorie, der Kombinationslehre und der Wahrscheinlichkeitsrechnung wenigstens kurz zu erwähnen.[S. 165] Schienen auch diese Gebiete zuerst rein mathematisch zu sein, so sind sie im Laufe ihrer Entwicklung doch in den Dienst der Naturwissenschaften getreten. Ganz besonders gilt dies von der Wahrscheinlichkeitsrechnung. Ihre ersten Anfänge begegnen uns im 15. und 16. Jahrhundert. Sie knüpfen an die Glücksspiele an.
Die Begründer der Wahrscheinlichkeitsrechnung als einer mathematischen Disziplin sind Fermat und sein Zeitgenosse Pascal (1623–1662). Pascal wurde die Frage vorgelegt, bei wieviel Würfen man Aussicht habe, mit zwei Würfeln den Sechserpasch zu werfen. Als das wichtigste Mittel zur Bewältigung der Probleme der Wahrscheinlichkeitsrechnung schufen Pascal und Fermat die Kombinatorik, deren Anfänge uns schon bei den Indern begegnen.
Was Fermats Verdienst um die Theorie der Zahlen anbelangt, so sei daran erinnert, daß auch auf diesem Gebiete ein Satz, und zwar ein fundamentaler, seinen Namen führt.
Um die Fortentwicklung der Kombinationslehre haben sich im 18. Jahrhundert Jacob Bernoulli und im 19. Laplace und Gauß die hervorragendsten Verdienste erworben.
Zur selben Zeit, als Descartes neben die alte Euklidische die analytische Geometrie setzte, begegnen uns die Anfänge einer dritten geometrischen Betrachtungsweise, derjenigen der Zentralprojektion. Aus ihr hat sich im 19. Jahrhundert auf Grund der Untersuchungen Poncelets und Steiners die projektivische Geometrie entwickelt292, deren Sätze sich durch einen hohen Grad von Allgemeingültigkeit vor denjenigen der Euklidischen und der analytischen Geometrie auszeichnen.
In den Anfang des 17. Jahrhunderts fallen auch die ersten Schritte zur Begründung einer mathematischen Methode, deren Ausgestaltung zu einem der mächtigsten Hilfsmittel der Naturforschung Newton und Leibniz vorbehalten blieb. Dies ist die Infinitesimalrechnung. Unter den Männern, die hier als Vorläufer zu nennen sind, nimmt Kepler neben dem Italiener Cavalieri, einem Schüler Galileis, die erste Stelle ein. Schon die Alten, insbesondere Archimedes, hatten bemerkt, daß manche geometrische[S. 166] Aufgaben mit Hilfe der Elementarmathematik nicht gelöst werden können. Dies hatte auf die Anwendung eines unter dem Namen der Exhaustionsmethode bekannten Verfahrens geführt, vermittelst dessen z. B. Archimedes293 die Quadratur der Parabel gelang. Auch die von Archimedes und früheren angestellte Berechnung des Kreisumfanges mit Hilfe der ein- und umgeschriebenen Vielecke zeigt uns, wie man schon im Altertum, wenn auch in umständlicher Weise, die Rektifikation einer Kurve vorzunehmen wußte294. Nach neueren Entdeckungen (s. Bd. I S. 164) besaß Archimedes sogar schon ein Verfahren, das der Integration, wie man sie heute ausübt, in seinem Wesen schon entsprach.
Der Fortschritt der Astronomie und der Physik war an die Entwicklung eines Verfahrens geknüpft, das eine allgemein gültige Lösung für die Ausmessung von Kurven, der von Kurven eingeschlossenen Flächen, sowie der durch Bewegung solcher Flächen entstandenen Körper ermöglichte. Wie wichtig mußte es z. B. für Kepler sein, den Umfang der Ellipse aus der großen (a) und der kleinen (b) Achse berechnen zu können295. Er hat sich auch hieran versucht und gibt den Wert für diesen Umfang als nahezu gleich π (a + b) an. Daß es sich hier um eine Annäherung handelt, hebt Kepler ausdrücklich hervor. Auch wird ihm zweifelsohne bekannt gewesen sein, daß der Ausdruck nur gebraucht werden darf, wenn a und b wenig voneinander verschieden sind296.
Mit der Bestimmung des Rauminhaltes von Rotationskörpern befaßt sich Kepler in seiner Doliometrie297 oder Faßberechnung. Lagrange hat später von diesem Buche gerühmt, daß es ähnlich wie die Sandesrechnung des Archimedes an einem gewöhnlichen Gegenstande die erhabensten Gedanken entwickele. Ein besonderer Umstand veranlaßte Kepler, seine Betrachtungen gerade an die Raumbestimmung von Fässern anzuknüpfen. Er hatte[S. 167] nämlich beim Einkauf von Wein beobachtet, daß die Händler den Inhalt der Fässer bestimmten, indem sie einen Meßstab durch den Spund bis zu den gegenüber befindlichen Dauben führten, ohne auf die Krümmung der letzteren Rücksicht zu nehmen. Ein dem Fasse an Inhalt gleicher Körper entsteht, wenn der Längsschnitt um die Achse rotiert. Keplers Grundgedanke bestand nun darin, derartige Rotationskörper in eine unendliche Zahl von Elementarteilen zu zerlegen und diese zu summieren, eine Untersuchung, die er in der »Doliometrie« auf etwa 90 Fälle ausdehnte.
Bei der Quadratur von Flächen hatten sich Archimedes und Euklid der »Exhaustionsmethode« bedient, deren Wesen wir an früherer Stelle kennen lernten. Kepler dagegen bediente sich bei seinen Quadraturen und Kubaturen unendlich kleiner Größen und ging dabei von Vorstellungen aus, welche die alten Mathematiker im allgemeinen vermieden hatten. So gelten für ihn unendlich kleine Bogen als gerade Linien, unendlich schmale Ebenen als Linien und unendlich dünne Ebenen als Körper, eine Vorstellung, die später auch Cavalieri seinen Integrationen zugrunde legte.
Als Beispiel diene die Quadratur des Kreises, an der wir bei Archimedes das Exhaustionsverfahren kennen gelernt haben. Der Kreisumfang, sagt Kepler, hat unendlich viele Teile. Jedes dieser Teilchen ist als Basis eines gleichschenkligen Dreiecks anzusehen. Wir erhalten so unendlich viele Dreiecke, die sämtlich mit ihren Spitzen im Mittelpunkte des Kreises liegen. Werden nun die sämtlichen Grundlinien, deren Summe gleich der Peripherie ist, auf einer Geraden aneinander gefügt und mit dem Mittelpunkte des Kreises verbunden, so erhalten wir ein aus unendlich vielen Dreieckchen bestehendes größeres Dreieck, dessen Inhalt gleich dem des Kreises ist.
Auf die gleiche Weise wird der Inhalt der Kugel berechnet. »Sie enthält«, sagt Kepler, »der Möglichkeit nach gleichsam unendlich viele Kegel, deren Grundflächen sozusagen Punkte sind, während die Spitzen im Mittelpunkte der Kugel zusammenstoßen.«
Eins der lehrreichsten Beispiele für Keplers Verfahren ist seine Kubatur des Ringes (s. Abb. 53). Dieser wird zunächst durch Ebenen, welche durch die Achse A gehen, in unendlich viele Scheibchen zerlegt. Diese Scheibchen sind aber nicht überall gleich dick, sondern sie sind, von ihrer eigenen Mitte aus gerechnet,[S. 168] nach der Achse A zu dünner und nach der entgegengesetzten Richtung dicker. Diese Unterschiede gleichen sich aber aus, und infolgedessen ist der Rauminhalt des Ringes gleich dem Inhalt eines Zylinders, dessen Grundfläche mit einer Schnittfläche des Ringes zusammenfällt, während seine Höhe gleich dem Kreise ist, den der Mittelpunkt F dieser Schnittfläche bei ihrer Rotation um die Achse A beschreibt.
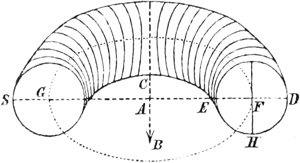
Zu den wenigen, von den Alten betrachteten Rotationskörpern fügte Kepler eine Fülle von neuen, so daß die Gesamtzahl der von ihm betrachteten Körper sich auf 92 beläuft. Diese Mannigfaltigkeit ergab sich, indem er geradlinige Figuren und die vier Kegelschnitte um Durchmesser, Sehnen, Tangenten oder außerhalb dieser Kurven gelegene Achsen rotieren ließ (s. Abb. 54). Die entstandenen Körper benannte Kepler oft nach Früchten. So entstand sein »Apfel«, wenn ein Kreisabschnitt, der größer als der Halbkreis ist, um seine Sehne rotiert299. War der rotierende Kreisabschnitt dagegen kleiner als der Halbkreis, so nannte er den entstandenen Körper »Zitrone«.
Die mathematische Strenge eines Euklid und Archimedes vermochte Kepler bei seinen Ableitungen nicht zu erreichen. Dazu bedurfte es der weiteren Entwicklung der Infinitesimalmethode, die er erst begründete. In manchen Fällen mußte er sich mit Wahrscheinlichkeitsschlüssen begnügen, oder er verfehlte gar die richtige Lösung des vorliegenden Einzelfalles.
Kepler hatte sich in seiner »Doliometrie« nicht nur die Aufgabe gestellt, den Inhalt von Fässern und anderen Rotationskörpern zu berechnen, sondern er wollte zugleich untersuchen, welche Form des Fasses die zweckmäßigste sei, d. h. beim geringsten Verbrauch[S. 169] an Material möglichst viel fassen könne. Ein Problem von der Art des zuletzt erwähnten hat man als ein isoperimetrisches bezeichnet, und wir werden erfahren, daß auch in späteren Perioden derartige Probleme für die Entwicklung der höheren Analysis von der allergrößten Wichtigkeit gewesen sind. Als Beispiel unter Keplers hierher gehörigen Betrachtungen sei der Satz erwähnt, daß der Würfel das größte Parallelepipedon ist, das in eine Kugel einbeschrieben werden kann300.
Kepler bemerkte auch schon, daß die Maximalwerte dadurch gekennzeichnet sind, daß in ihrer Nähe die Veränderungen einer Funktion gleich Null werden. Ist z. B. MP (Abb. 55) die größte Ordinate der Kurve AMB, so ist die Zu- und Abnahme von MP bei unendlich kleiner paralleler Verschiebung gleich Null. Kepler zeigte durch diesen für die Theorie der Maxima und Minima grundlegenden Satz, wenn er ihn auch noch nicht zu beweisen vermochte, wie tief er auch nach dieser Seite in die Infinitesimalbetrachtungen eingedrungen war. In Keplers Worten lautet der Satz: »An solchen Stellen, wo der Übergang von einem kleineren zum größten und wieder zum kleineren stattfindet, ist der Unterschied immer bis zu einem gewissen Grade unmerklich.«
Wenig später als Kepler nahm der Italiener Cavalieri301 das Problem der Quadratur und Kubatur gleichfalls nach einer von der Mathematik der Alten abweichenden Methode in Angriff. Dies geschah 1635 in seiner »Geometrie der Indivisibilien«302. Eine klare Definition des Wortes »Indivisibilien«, d. h. die »Unteilbaren«, hat Cavalieri nicht gegeben. Sein Verfahren, die Flächen auf Linien und die Körper auf Flächen zurückzuführen, hat auch wohl das Mißverständnis hervorgerufen, als ob Cavalieri die Flächen als die Summen unendlich vieler Parallelen und die[S. 170] Körper als die Summen von Flächen auffassen wollte, und infolgedessen Widerspruch erregt. Cavalieri weiß aber sehr wohl, daß die Summe aller parallelen Sehnen einer geschlossenen Fläche unendlich und daß das Verhältnis zwischen zwei solchen Summen unbestimmt ist. Besitzen dagegen die zahlreichen parallelen Sehnen, welche durch zwei Flächen gelegt werden, die von zwei Parallelen eingeschlossen sind, gleichen Abstand, so erhält das Verhältnis der Sehnensummen einen Wert, der sich mit der Vermehrung der Sehnen einer bestimmten Grenze nähert. Und zwar entspricht dies Verhältnis dem der beiden Flächen, welche durch die Sehnen zerteilt werden. Ein einfaches Beispiel möge das Gesagte erläutern. Man errichte über der Grundlinie eines Dreiecks ein Rechteck von gleicher Höhe und ziehe dann in beiden Figuren eine Anzahl Linien parallel zur Grundlinie in gleichen Abständen. Dann wird die Summe der Strecken im Dreieck halb so groß sein wie die Summe der Strecken im Rechteck. Daraus schließt Cavalieri, daß auch die Flächen im Verhältnis von 1 : 2 stehen.
Nach demselben Verfahren ergibt sich, daß eine Ellipse und ein Kreis, dessen Durchmesser mit einer Achse der Ellipse zusammenfällt, sich der Fläche nach verhalten wie die andere Achse der Ellipse zum Kreisdurchmesser.
Wird Cavalieris Methode auf körperliche Gebilde übertragen, so sind statt der Linien parallele Ebenen in gleichen Abständen zu wählen. Schneiden diese Ebenen die Körper in Flächen, die in einem gegebenen Verhältnis stehen, so gilt für die Volumina der Körper das gleiche Verhältnis. Noch heute trägt dieser Satz bekanntlich den Namen Cavalieris. Eingeschränkt auf inhaltsgleiche Gebilde lautet er: Gebilde der Ebene sowie des Raumes sind inhaltsgleich, wenn die in gleicher Höhe geführten Schnitte gleiche Strecken bzw. Flächen ergeben.
Gegenüber der Methode Keplers, der sich bestimmte Aufgaben stellte, besaß die Methode Cavalieris den Vorzug größerer Allgemeingültigkeit und abstrakterer Behandlung. Trotz des Widerspruches, den beide Männer fanden, war die von ihnen eingeführte Infinitesimalbetrachtung die wertvollste Idee, die jemals die Mathematik bereichert hat. Erweisen sollte sich ihre Fruchtbarkeit zwar erst nach der Erfindung der analytischen Geometrie, aus deren Verknüpfung mit der neuen Betrachtungsweise die Differential- und Integralrechnung als das wichtigste mathematische Hilfsmittel der neueren Naturforschung hervorging.
Unter den wissenschaftlichen Gegnern Keplers und Cavalieris ist besonders Guldin zu nennen. Er befaßte sich in einem umfangreichen Werke mit der Bestimmung der Schwerpunkte von Kurven, Flächen und Körpern und zwar eingehender, als es bisher geschehen war303. Fußend auf einem Satz, der sich bei Pappus findet, ging Guldin gleichfalls zu Inhaltsbestimmungen über. Der Pappus-Guldinsche Satz, der heute noch als die Guldinsche Regel bezeichnet wird, besagt, daß der Rauminhalt eines Rotationskörpers gleich dem Produkt aus der erzeugenden Fläche und dem Wege ihres Schwerpunktes ist.
Einen einwandfreien Beweis dieses Satzes vermochte Guldin nicht zu geben. Seine Richtigkeit folgerte er vielmehr aus dem Umstande, daß man mit Hilfe dieser Regel zu den gleichen Ergebnissen gelangt, die sich auch auf anderen Wegen finden lassen. Seine Beispiele sind oft dieselben, die Kepler behandelt hat. Während aber Keplers, von Guldin als unwissenschaftlich bekämpfte Methode den Keim der höheren Mathematik enthielt, ist Guldins Verfahren ohne Einfluß auf die Weiterentwicklung dieser Wissenschaft geblieben, zumal die Quadratur der gegebenen Figur und die Bestimmung ihres Schwerpunktes häufig weit schwieriger sind, als die direkte Kubatur des betreffenden Rotationskörpers304.
Einen weiteren Schritt auf dem Gebiete der Infinitesimalbetrachtungen bedeutet die »Arithmetik des Unendlichen« des Engländers Wallis305 (1655). Wallis wurde durch die Untersuchungen Cavalieris angeregt, sich mit Quadraturen und Kubaturen zu beschäftigen. Sie bilden den wesentlichen Inhalt seiner »Arithmetik des Unendlichen«. Aus dem Titel des Werkes ist schon ersichtlich, daß Wallis im Gegensatz zu Cavalieri, der seine Ableitungen geometrisch zu gestalten suchte, vorzugsweise rechnerisch verfuhr. Dies gelang ihm, indem er die analytische Methode des Descartes auf die infinitesimale Betrachtungsweise Keplers und Cavalieris übertrug. Ob Wallis mit der Doliometrie Keplers bekannt war, ist allerdings zweifelhaft306.
Wallis zerlegt z. B. eine Fläche, um deren Quadratur es sich handelt, durch unendlich viele parallele Ordinaten in eine unendlich große Zahl von unendlich schmalen Parallelogrammen und sucht deren Summe zu ermitteln. Dabei bedient er sich der noch heute üblichen Form des Grenzüberganges.
Die Erweiterung dieser von Kepler, Cavalieri und anderen geschaffenen Grundlagen einer neuen, höheren Mathematik zu einem allgemeinen, für die Fortentwicklung der Naturwissenschaft sowohl wie der Technik unentbehrlichen Hilfsmittel ist insbesondere das Werk von Newton und von Leibniz.
Durch seine Untersuchungen über unendliche Reihen war Newton zu einer allgemeineren Lösung der Tangentenaufgabe gelangt, mit der sich schon Fermat und Descartes beschäftigt hatten. Newton veröffentlichte sein Verfahren zunächst nicht, sondern setzte seit 1669 mehrere Personen, mit denen er in wissenschaftlichem Verkehr stand, davon in Kenntnis. Durch einen Brief des Sekretärs der Royal-Society307 erfuhr auch Leibniz davon. Diesen Brief empfing Leibniz jedoch erst 1677. Er antwortete noch in demselben Jahre unter Darlegung einer Methode, die zum gleichen Ziele führe und machte sie im Jahre 1684 und 1686 bekannt. In der Schrift vom Jahre 1684308 entwickelte er die Prinzipien der Differentialrechnung. Er bezeichnete es als ihre Aufgabe, den unendlich kleinen Zuwachs zu bestimmen, den eine Funktion f(x) erfährt, wenn sich die Variable x unendlich wenig ändert. Jenen unendlich kleinen Zuwachs nannte Leibniz das Differential der Funktion. Er bezeichnete ihn mit d.
In der zweiten Schrift309 entwickelte Leibniz die Prinzipien der Integralrechnung. Er stellte sich darin die Aufgabe, umgekehrt aus dem unendlich kleinen Zuwachs die Funktion zu finden, ein Verfahren, das man als Integration bezeichnet. Leibniz führte für die gesuchte Funktion das Zeichen ∫ (Integral) ein. Auch erkannte er schon den Zusammenhang, in dem das Integrationsverfahren mit der Quadratur und mit der Kubatur steht.
Bald nach diesen Veröffentlichungen erschienen die »Prinzipien« (1687), in denen Newton sich der geometrischen Einkleidung seiner Beweise bediente. So kam es, daß sich die von[S. 173] Leibniz erfundene Methode rasch ausbreitete, während diejenige Newtons fast unbekannt blieb und vollständig erst nach seinem Tode310 veröffentlicht wurde. Er nannte sie Methode der Fluxionen. Die unendlich kleinen Größen, mit denen Leibniz operiert, ersetzt Newton durch seine verschwindenden Größen. Das Neue ist bei Newton vor allem der Begriff der Grenze. Er versteht darunter den Wert, dem sich die gleichsam fließenden (daher der Ausdruck Fluxionen) Größen immer mehr nähern.
Erwähnt sei noch, daß im Jahre 1699 ein heftiger Prioritätsstreit entbrannte. Er wurde entfacht durch die Bemerkung eines Mathematikers311, daß Leibniz sein Verfahren wahrscheinlich Newton entlehnt habe. Leibniz war daraufhin so unvorsichtig, in einer anonymen Schrift Newton des Plagiats zu beschuldigen. Eine Aussöhnung fand nicht statt. Leibniz hat bis zu seinem Tode (1716) sehr unter diesem Streit gelitten. Newton hat in seinen »Prinzipien« anerkannt, daß Leibniz auf die gleiche Methode wie er gekommen sei. Erst in der nach Newtons Tode erschienenen Auflage ist die Bemerkung fortgelassen.
Daran, daß Newton die Priorität gebührt, ist nicht zu zweifeln, wie auch Leibniz wohl die Anregung zu seiner Entdeckung durch Newton empfangen hat. Vor allem hat Leibniz das Verdienst, die neue Methode zuerst bekanntgegeben und durch den von ihm geschaffenen Algorithmus ganz besonders zu ihrer Ausbreitung beigetragen zu haben.
Die tiefere Begründung der Infinitesimalmethode erfolgte erst durch Carnot312, den großen Carnot der französischen Revolution, dessen Neffe grundlegende Untersuchungen auf dem Gebiete der Wärmelehre anstellte (s. Bd. III ds. Werkes). Um die mathematische Strenge des Verfahrens hat sich Cauchy das größte Verdienst erworben. Er entschied sich für die von Newton begründete Methode der Grenzwerte, die an Klarheit und Schärfe von keiner anderen erreicht wird.
Wie die Mathematik, so ist auch die Philosophie auf die Entwicklung der Naturwissenschaften von großem Einfluß gewesen. Alle drei entspringen ja der gleichen Quelle, nämlich dem uns innewohnenden Triebe, uns gegen die geistige Umwelt einzustellen. Bei der Philosophie erweitert sich dieser Trieb dahin, auch das Verhältnis der Umwelt zum denkenden und forschenden Subjekt zu ergründen. Wie sich die Mathematik, die Philosophie und die Naturwissenschaften seit dem Altertum gegenseitig bedingt haben, wurde in früheren Abschnitten gezeigt. Im Anfange war die Berührung eine so innige, daß gewöhnlich ein und derselbe Mann Philosoph, Mathematiker und Naturforscher war. Man braucht nur an Thales, Platon und Aristoteles zu erinnern. Später setzte die Spezialisierung ein. Männer wie Archimedes und Heron haben sich schwerlich eingehender mit philosophischen Fragen beschäftigt, wenigstens erkennen wir es nicht aus ihren Werken. Auch die Mathematik wurde vielen ein Sondergebiet, das sich von den übrigen loslöste und als reine Mathematik seine eigenen Wege ging. Dagegen ist die Vereinigung des naturwissenschaftlichen Forschens mit mathematischem Denken durch alle Zeiten erhalten geblieben. Die Astronomie war seit den ersten Anfängen angewandte Mathematik, die Physik war es, sobald sie sich mechanischen Problemen zuwandte, und die übrigen Zweige der Naturwissenschaft erhoben sich erst in dem Maße auf eine Stufe, die als wissenschaftlich bezeichnet werden kann, in dem sie der Mathematik und der auf ihr beruhenden Mechanik ihre Tore öffneten.
Trotz der engen Beziehungen, die zwischen den Naturwissenschaften, der Mathematik und der Philosophie herrschen und jederzeit vorhanden waren, haben sich diese drei Wissenschaften keineswegs stets gegenseitig gefördert. Selbst die Mathematik konnte die Entwicklung der Naturwissenschaften hemmen, indem sie letztere[S. 175] mit geometrischen und Zahlenspekulationen überwucherte, anstatt ihnen lediglich bei der Ausbildung des messenden Verfahrens behilflich zu sein. Geradezu unheilvoll ist mitunter der Einfluß der Philosophie auf die Naturwissenschaft gewesen. Letztere hatte am meisten, erstere am wenigsten festen Boden unter den Füßen. Die Philosophie konnte daher besonders leicht auf Abwege geraten. Das ist bis in die neueste Zeit geschehen, wie uns die Betrachtungen über den Einfluß der während der ersten Hälfte des 19. Jahrhunderts herrschenden Naturphilosophie zeigen werden. In Deutschland konnten die Naturwissenschaften damals erst wieder aufblühen, nachdem sie sich von der zeitgenössischen Philosophie losgelöst hatten. Eine ähnliche Befreiung aus den Fesseln der Philosophie mußte auch dem Aufblühen der Naturwissenschaften zu Beginn des 17. Jahrhunderts vorhergehen. Bis dahin reicht für die Philosophie das Zeitalter der Scholastik. Sie erblickte ihre Aufgabe in der Vermittlung zwischen Wissen und Glauben. Anfangs galt ihr das Dogma als unerschütterliche Wahrheit und Aristoteles als die Hauptquelle alles Wissens. Zwischen beiden zu vermitteln, erforderte einen großen Aufwand an Spitzfindigkeit. Eine solche war auch der Grundsatz, daß etwas vom Standpunkt des Dogmas aus wahr, mit der Vernunft aber unvereinbar sein könne. Dieser Grundsatz wurde von der Kirche sehr befehdet, da er schon ein Streben der Philosophie bekundete, sich von den Fesseln der Kirche zu befreien. Dieses Streben führte schließlich dahin, daß die Philosophie selbständig wurde, und daß der durch das scholastische Verfahren rege gewordene Geist des Prüfens und des Zweifelns endlich mit allen Voraussetzungen brach. Diese Erneuerung begegnet uns bei Bacon und bei Descartes.
Von Bacon und seiner Stellung einerseits zur Scholastik, andererseits zu der in seinem Zeitalter auch ohne sein Zutun sich entwickelnden experimentellen Naturforschung war schon die Rede. Wir wenden uns jetzt Descartes als dem eigentlichen Begründer der neueren Philosophie zu. Seine großen Verdienste um die Mathematik und um die Lösung manches naturwissenschaftlichen Problems haben uns bereits beschäftigt, auch werden wir ihnen noch an anderen Stellen begegnen313.
Es wird hier, sowie in den folgenden Abschnitten dieses Kapitels von einem Hineinbeziehen der Philosophie in ihrem ganzen Umfange abgesehen. Der Ausgangspunkt der Cartesianischen Philosophie ist nämlich das Verhältnis des Menschen zu einem vernünftigen Urheber der Welt. Sie ist also ihrem Wesen nach dualistisch und überschreitet insofern die Grenzen der naturwissenschaftlichen Forschung. Für letztere kommt die Philosophie nur insoweit in Betracht, als sie Naturphilosophie ist. Mit ihren Prinzipien hat Descartes sich gleichfalls eingehend beschäftigt. Sie betreffen das Wesen der Materie und der Kraft, sowie ihr Verhältnis zur Beseelung. Die philosophische Erörterung dieser Begriffe ist von einer tieferen Erfassung der naturwissenschaftlichen Probleme untrennbar. In dieser Erörterung wollen wir den Naturphilosophen folgen, die, zu Beginn der Neuzeit, häufig auch Naturforscher waren. Dies gilt besonders von Descartes.
In seinen »Prinzipien der Philosophie« sucht er, sämtliche Naturerscheinungen aus den Begriffen Materie und Bewegung abzuleiten. Als das Wesen der Materie betrachtet er die Ausdehnung. »Ich gestehe«, sagt er, »daß ich keine andere Materie anerkenne als jene, welche die Mathematiker Quantität nennen. An dieser betrachtete ich nichts anderes als Teilung, Gestalt und Bewegung. Ferner lasse ich nichts gelten, was nicht aus allgemeinen Begriffen, über deren Wahrheit kein Zweifel besteht, so sicher gefolgert werden kann, daß es als mathematisch bewiesen anzusehen ist. Da sich auf diese Weise alle Naturerscheinungen erklären lassen, so halte ich andere Prinzipien weder für zulässig, noch für wünschenswert.«
Nach Descartes ist jeder Raum von Materie erfüllt. Trotzdem nimmt er kleine Teilchen an, aus deren Gestalt, Größe und Bewegung die Naturerscheinungen zu erklären seien. Auch Demokrit hatte solche Teilchen angenommen, die er für unteilbar und für schwer hielt. Demokrit hatte ferner ein Leeres vorausgesetzt. Nach Descartes dagegen ist ein Vakuum unmöglich. Ferner sind die Teilchen, aus denen der Stoff besteht, nach Descartes weiter teilbar, auch besitzen sie keine anziehende Kraft, keine Schwere.
»Wenn ich«, sagt Descartes, »den Körperteilchen eine bestimmte Gestalt, Größe und Bewegung beilege, obgleich ich zugeben muß, daß diese Teilchen nicht wahrnehmbar sind, so wird man vielleicht fragen, woher ich denn jene Eigenschaften kenne.« Seine Antwort lautet, zunächst entsprächen sie den einfachsten[S. 177] Prinzipien, die er bei seinen Überlegungen in Betracht gezogen habe. Ferner genügten seine Ableitungen dem tatsächlichen Verhalten der Körper, was wiederum für die Richtigkeit seiner Voraussetzungen bürge.
Die Erklärung der Erscheinungen aus den Bewegungen kleinster Teilchen ist somit das Ziel, das Descartes für die Naturwissenschaften aufgestellt hat. Dieses Ziel sucht er durch Deduktionen aus wenigen Prinzipien nach dem Muster der Mathematik zu erreichen. Descartes' Auffassung des Naturganzen als eines Mechanismus, aus dem er sowohl die anorganische wie die organische Welt erklären wollte, steht im schroffsten Gegensatze zu der vor ihm herrschenden, aristotelisch-scholastischen Weltanschauung, zumal Descartes den in dieser herrschenden Zweckbegriff vollständig aus seinem System verbannte. In diesem Punkte berührt er sich mit Gassendi314. Nur daß letzterer auf die Atomistik des Altertums, insbesondere die Lehren Epikurs, zurückgreift, während Descartes die Unteilbarkeit der materiellen Teilchen und das Vorhandensein des leeren Raums nicht anerkennt. Auch darin stimmen Descartes und Gassendi überein, daß sie jede Wirkung der Körper aufeinander auf den Stoß bewegter Materie zurückführen und alle Sinnesqualitäten auf die Größe, die Gestalt und die Bewegung der materiellen Teilchen (der Korpuskeln bei Descartes und der Atome bei Gassendi).
Lag auch ein berechtigtes Streben in dem Versuche, zu wenigen umfassenden Prinzipien zu gelangen, so bestand doch darin wieder eine Gefahr, daß diese Prinzipien nicht induktiv gewonnen, sondern a priori aufgestellt waren. Dadurch erschien die experimentelle Forschung bedroht. Zwar verwirft Descartes das Experiment nicht, doch steht es ihm, verglichen mit dem Denken, an zweiter Stelle. Mit dieser Einschätzung des Experimentes[S. 178] steht die Haltung in Einklang, die Descartes Galilei gegenüber einnahm. In einem Briefe an Mersenne schreibt er, er sehe in Galileis Schriften nichts, um das er ihn beneide und fast nichts, das er als das Seinige betrachtet wissen möchte. In diesem ablehnenden Verhalten gegen die Ergebnisse der zeitgenössischen exakten Naturforschung berührt sich Descartes in gewissem Grade mit Bacon.
Die Verbindung der Naturwissenschaft mit der Philosophie, wie sie sich zur Zeit der Erneuerung beider Wissenschaften bei Descartes und Bacon vollzog, erwies sich somit für die exakte Wissenschaft als wenig förderlich. Weder der vage Empirismus Bacons vermochten die Methode der Forschung zu begründen, noch vermochten es die Spekulationen eines Descartes. Nicht die Philosophie hat den Naturwissenschaften ihre Methode vorgezeichnet. Die Methode der letzteren ist vielmehr unabhängig von den herrschenden Lehren der Philosophie entstanden, um sich langsam aber sicheren Schrittes dem Ziele zu nähern, das die Spekulation in kühnem Fluge vergeblich zu erreichen suchte. In ihren Keimen tritt uns die Methode der neueren Naturwissenschaft schon im Verlauf des 16. Jahrhunderts entgegen. Ihr Aufbau erfolgte vor allem durch Galilei, dem Descartes vorwarf, er habe, ohne die ersten Ursachen der Natur zu betrachten, nur die Gründe einiger besonderen Wirkungen gesucht und ohne Fundament gebaut. Die exakte Forschung sah sich also gleich in ihrem Anfange von einer Philosophie bedroht, die vor keinem Problem zurückschreckte, so daß Huygens sagen konnte: »Es scheint, daß Descartes über alle Gegenstände der Physik entscheiden will, unbekümmert darum, ob er wahr spricht oder nicht«315.
Die Betrachtungen, denen Descartes sich überließ, mußten in einer Zeit, in der die Scheidung zwischen dem Erreichbaren und dem, was stets Problem bleibt, noch nicht zum Bewußtsein gekommen war, von bestrickendem Reiz sein. Fragen über das Wesen der Materie, die Aggregatzustände, die Ursache der Schwere standen im Vordergrunde. Atomistik und Korpuskulartheorie sollten über sie entscheiden. An Gassendi schloß sich Huygens an, der gleichfalls einer strengen Atomistik huldigte, während Boyle, Hooke, Borelli sich mehr den physikalischen Theorien[S. 179] des Descartes zuneigten. So bedeutend der Unterschied der Lehren von Gassendi und Descartes auch ist, so stimmen sie doch darin überein, daß sie alle Erscheinungen aus den Bewegungen der Materie und dem Stoß ihrer Teilchen zu erklären und dadurch ein anschauliches Bild der Naturvorgänge zu geben suchen. Druck, Stoß und Zug vermöge hakenförmiger Verbindungen bilden die Begriffe, mit denen man arbeitete. Der Begriff des Atoms, wie er von Gassendi aus dem Altertum übernommen worden war, schließt innere Kräfte vollständig aus. Die Atome Gassendis, sowie die Korpuskeln Descartes' sind von Anfang an mit Bewegung begabt. Alle Wirkung ist letzten Endes eine Übertragung der Bewegung in Berührungsnähe. Wie es bei den Alten besondere Atome für die einzelnen Empfindungen gab (Bd. I, S. 72), so gibt es bei Gassendi besondere Wärmeatome. Sie sind zwar nicht an sich warm, sondern sie erregen durch ihre Gestalt, durch ihre Größe und ihre Bewegung die Wärme. Die Cartesianer nahmen auch hier zur materia subtilis die Zuflucht. Auch Huygens nahm eine solche zur Erklärung der Wärme an.
Abweichend von diesen Ansichten gewann indessen auch schon frühzeitig die Annahme Verbreitung, daß die Wärme eine bloße Bewegung der kleinsten Teilchen sei, die sich mechanisch in den Körpern erzeugen lasse. Besonders Hooke und Locke traten für diese Ansicht ein. Durch den Mechanismus, den Gassendi und Descartes einführten, wurden die verborgenen Qualitäten der Scholastiker und alle Sympathien und Antipathien aus der Naturwissenschaft verbannt und die Bewegung der Himmelskörper wie der Fall auf der Erde auf die Stoßwirkung kleinster Teilchen zurückgeführt. Der Satz, daß ein Körper nur dort wirken könne, wo er sei, galt als Axiom. Nur vereinzelt tauchten Ansichten auf, welche der Materie eine anziehende Kraft beilegten, so bei Kepler und bei Gilbert. Bacon äußert sich darüber folgendermaßen: »Bei den Lichtstrahlen, den Tönen, der Wärme und einigen anderen in die Ferne wirkenden Dingen ist es wahrscheinlich, daß die zwischen befindliche Materie disponiert und alteriert wird und daß für die Übertragung der Wirkung ein geeignetes Medium erforderlich ist316.« Die magnetische Kraft läßt sich indes nach Bacon durch eine Mitwirkung des Mediums nicht erklären und Mersenne berichtet bereits317, daß viele die Schwere nicht[S. 180] wie Descartes auf einen Druck, sondern auf eine anziehende Kraft der Erde zurückführen wollten. Bei Roberval findet sich dann die bestimmte Vorstellung318, daß jedem einzelnen Teilchen der Materie eine anziehende Kraft als wesentliche Eigenschaft beizulegen sei. Und mehr als vierzig Jahre später schreibt Borelli319, daß man sehr häufig der Annahme einer anziehenden Kraft begegne. Borelli wendet sich lebhaft dagegen, freilich nur um durch einen motus spontaneus, der dem Eisen und dem Magneten, sowie den schweren Körpern innewohne, den Magnetismus und die Gravitation zu erklären. So wurde allmählich der Begriff einer Anziehung in die Ferne eine den Physikern geläufige Vorstellung.
Aus den Spekulationen über die Materie erwuchsen solche über den Kraftbegriff. Descartes hatte das Wesen der Materie in die Ausdehnung gesetzt. Daneben schreibt er nach dem Vorgange Keplers320 der Materie Trägheit zu, vermöge deren sie einer Veränderung des Zustandes der Ruhe oder der Bewegung widerstehe321. Dazu fügten Boyle322 und Huygens323 die Undurchdringlichkeit als eine weitere wesentliche Eigenschaft, während Hooke324 die Undurchdringlichkeit auf eine vibrierende Bewegung der kleinsten Teilchen zurückführte. Auch Huygens bemerkt, er sei nicht der Ansicht des Descartes, der das Wesen der Materie in die Ausdehnung setze. Man müsse vielmehr noch »la dureté parfaite, qui rend le corps impénétrable« hinzufügen. Locke schlug später statt des negativen Ausdrucks der Undurchdringlichkeit die positive Bezeichnung solidity vor325. Hooke macht übrigens eine Bemerkung über das Verhältnis von Materie und Kraft, die, wie so manches, sich der Beachtung entzogen hat. »Ich setze voraus«, sagt er, »daß alle Dinge, welche zu Objekten[S. 181] unserer Sinne werden, aus Materie und Kraft zusammengesetzt sind. Wir nehmen diese gegenwärtig als distinkte Wesenheiten an, obschon sich später vielleicht finden wird, daß sie nur verschiedene Auffassungen ein und desselben Wesens sind.«
Durch die Bewegung ließ Descartes die ursprünglich einheitliche Materie sich in drei Elemente teilen, die sich durch den verschiedenen Grad der Feinheit unterscheiden sollten. Aus den gröbsten sollten nach ihm die Erde, die Planeten und die Kometen gebildet sein, aus feineren die Fixsterne und die Sonne, und aus den allerfeinsten der den Weltraum ausfüllende Stoff, auf dessen Wirbelbewegung der Kreislauf der Planeten beruhe. Dieser subtile Stoff erfüllt nach Descartes' Vorstellung auch die Zwischenräume zwischen den groben Teilchen, welche die irdische Materie zusammensetzen. Er vermittelt ferner, da er sozusagen allgegenwärtig ist, die Fortpflanzung des Lichtes. Diese Vorstellung ist in die neuere Physik übergegangen. Die Unterscheidung nach dem Grad der Feinheit, die den Keim zu der späteren Trennung in wägbare und unwägbare Materie bildete, lieferte der cartesianischen Physik das Mittel, nicht nur die Gravitation und die Schwere, sondern auch Kohäsion, Adhäsion, Wärme, Licht, Elektrizität, die Aggregatzustände usw., mechanisch durch die Wirbelbewegung oder den Stoß einer materia subtilis zu erklären. Hierbei wurde später, namentlich durch Huygens, Hooke, Daniel Bernoulli und Euler für jedes der aufgezählten Phänomene eine besondere materia subtilis angenommen, woraus dann die Lehre von den Imponderabilien entstanden ist. Den festen Aggregatzustand führte Descartes auf die Ruhe der Teilchen zurück. Anders Hooke, der die mechanische Theorie der Wärme vorwegnahm, indem er bemerkte: »Daß die Teilchen aller Körper, so fest sie auch sein mögen, doch vibrieren, dazu braucht es meines Erachtens keinen anderen Beweis als den, daß alle Körper einen gewissen Grad Wärme in sich haben und daß noch niemals ein absolut kalter Körper gefunden ist«326.
Hooke, der für die feine Materie den Namen Äther einführte327, läßt den ganzen Weltraum von dieser Substanz erfüllt sein. In ihr sind die übrigen Körper gleichsam aufgelöst. Statt der Wirbelbewegungen des Descartes schreibt Hooke dem[S. 182] Äther eine vibrierende Bewegung zu. Ausführlich erklärt er aus ihr die Erscheinungen der Gravitation und des Lichtes. Die weitere Ausbildung der Ätherhypothese erfolgte besonders durch Huygens.
Die von Descartes und seinen Nachfolgern geschaffene Lehre vom Weltmechanismus erhielt dadurch einen gewissen Abschluß, daß sich die Quantität der Materie und die Quantität der Bewegung unveränderlich erhalten sollten328. Der Keim zu dieser Anschauung findet sich schon bei Epikur. Er weist darauf hin, daß es keinen Ort außerhalb des Universums gebe, wohin ein Teilchen der Materie zu entfliehen, und von wo eine neue Kraft in das Universum einzudringen vermöge329. Auch diesen Satz übernahm Gassendi mit dem System Epikurs und drückt ihn in folgenden Worten aus: »Wenn die Körper in den Zustand der Ruhe übergehen, so geht die eingeborene Kraft der Atome nicht verloren, sondern sie wird nur gehemmt. Auch wird die Kraft nicht erzeugt, wenn die Körper anfangen sich zu bewegen. Sie erlangt vielmehr nur ihre Freiheit wieder. Es bleibt nämlich soviel Trieb (impetus) beständig in den Körpern, wie von Anfang an vorhanden gewesen ist330.«
Diesen Ausführungen entspricht Descartes' Behauptung, daß sich das Bewegungsquantum erhalte. Sie bildet den Ausgangspunkt jener Forschungen, die schließlich die volle Gültigkeit des Prinzips der Erhaltung der Energie gezeitigt haben.
Wir haben bisher die Cartesianische Philosophie nur insoweit betrachtet, als sie auf die Erklärung des Weltgeschehens hinauslief. Neben der körperlichen Welt, die Descartes aus rein mechanischen Prinzipien erklären zu können glaubte, erkannte er indessen als gleich wirklich eine geistige Welt an. Beide Welten haben indessen nach Descartes nichts miteinander gemein.
Wie dieser völlige Dualismus überwunden wurde, kann hier nur angedeutet werden. Den ersten Schritt tat Hobbes331, indem[S. 183] er auch die seelischen Vorgänge aus den Bewegungsgesetzen der Mechanik zu erklären suchte und damit die materialistische Richtung der Naturphilosophie begründete. Die wichtigste Konsequenz der Auffassung von Hobbes bestand darin, daß es nach ihr keinen freien Willen gibt.
Über den einseitigen Dualismus und den nicht weniger einseitigen Materialismus hinaus hat dann Spinoza332 das Denken geführt. Nach ihm gibt es nur eine wirkliche Substanz. Spinoza braucht für sie den herkömmlichen Namen Gott. Diese absolute und unendliche Substanz ist Ursache ihrer selbst und aller Dinge. Gott und Natur sind somit identisch. Das Geistige und das Körperliche sind nur Modi, d. h. nur verschiedene Erscheinungsformen der nämlichen Substanz. Sie hängen in der Weise zusammen, daß jedem physischen ein seelischer Vorgang entspricht, die Natur also geistig-körperlich ist. Wie sich auf diesen philosophischen Grundvorstellungen die moderne, nach naturwissenschaftlicher Methode arbeitende Psychophysik entwickelt hat, kann erst gegen den Schluß des vorliegenden Werkes dargelegt werden.
Trotz der zahlreichen Anregungen, welche die neuere Naturwissenschaft durch die ihr parallel verlaufende Entwicklung der Philosophie empfing, verhielten sich die großen Naturforscher ihr gegenüber im allgemeinen ablehnend, weil sie ihre Aufgabe in ihnen näher liegenden Dingen erblickten.
Newtons Wort »Hypotheses non fingo« (Hypothesen erdichte ich nicht) war eine entschiedene Absage gegenüber den Spekulationen der Cartesianischen Physik. »Alles, was nicht aus den Erscheinungen folgt,« sagt Newton, »ist eine Hypothese. Solche dürfen nicht in die Experimentalphysik aufgenommen werden. In[S. 184] dieser leitet man die Sätze aus den Erscheinungen ab und verallgemeinert sie durch Induktion333«. Es galt dem Überwuchern der Hypothesen Einhalt zu gebieten und anstatt an dem luftigen Gebäude der Cartesianischen Naturphilosophie weiter zu bauen, die wahren Gesetze der Natur zu entdecken. Nachdem man die scholastische Lehre von den substantiellen Formen und den verborgenen Eigenschaften aufgegeben hatte, waren, wie Newton forderte, die Erscheinungen der Natur auf mathemathische Prinzipien zurückzuführen. Darin erblickte er seine Hauptaufgabe. Sie lautet: Mechanische Erklärung aller Naturerscheinungen unter Zurückgehen auf die Kräfte.
An dem Begriff der Kraft, wie er von Newton verwendet wird, zeigt sich am deutlichsten der fundamentale Unterschied der alten und der neueren Physik. In diesem Begriff liegt ferner der Hauptanlaß zu der Opposition, die Newtons System fand, sowie der Grund zu den Verirrungen, denen viele Nachfolger Newtons anheimfielen. Auf Druck und Stoß als die unserer sinnlichen Anschauung geläufigen Vorstellungen reduzierte sich die Mechanik der Korpuskularphilosophie. Newton dagegen führte den Begriff der Kraft als »causa mathematica« ein. Die »causa physica« bleibt dabei unbestimmt. »Die physischen Ursachen und den Sitz der Kräfte ziehe ich nicht in Betracht«, sagt Newton. Nur unter dem mathematischen Bilde der Abhängigkeit wird der Kausalzusammenhang der Naturerscheinungen dargelegt. Newton kommt es lediglich darauf an, die Gesetze der Bewegungen zu ermitteln. Wiederholt erklärt er, daß er nur in diesem Sinne von Kräften rede. »Die Benennungen Anziehung, Stoß, Hinneigung gegen den Mittelpunkt«, heißt es in den Prinzipien334, »nehme ich an, indem ich diese Kräfte nicht im physischen, sondern nur im mathematischen Sinne betrachte. Man möge daraus nicht etwa schließen, daß ich die physische Ursache erklären will oder daß ich den Mittelpunkten wirkliche Kräfte beilege, indem ich sage, die Mittelpunkte zögen an«335. Wenn Newton die Zentripetalkräfte als Anziehungen bezeichnet, so bemerkt er sogleich, daß sie, rein physikalisch betrachtet, vielleicht richtiger Anstöße genannt werden müßten336. Dieser Auffassung entsprechend hat Newton sich wiederholt[S. 185] gegen eine Wirkung in die Ferne, sowie gegen die Annahme erklärt, daß die Schwere eine wesentliche Eigenschaft der Materie sei. So schreibt er: »Es ist unbegreiflich, daß Materie ohne die Vermittlung von irgend etwas, was nicht materiell ist, andere Materie beeinflussen könnte, wie es der Fall sein müßte, wenn die Schwere eine wesentliche, inhärierende Eigenschaft der Materie wäre. Daß ein Körper auf einen anderen aus der Entfernung durch den leeren Raum wirken könnte ohne die Vermittlung von etwas anderem, halte ich für eine große Ungereimtheit. Die Schwere muß durch ein beständig nach bestimmten Gesetzen wirkendes Agens verursacht werden«337. Ob aber dieses Agens materiell oder immateriell ist, darüber will Newton keine Entscheidung treffen. In einem Briefe Newtons an Boyle338 wird die Ursache der Schwere auf den Äther zurückgeführt. Doch bemerkt Newton am Schlusse: »Ich habe so wenig Geschmack an solchen Dingen, daß ich schwerlich die Feder dazu ansetzen würde, wenn mich nicht Ihre Aufforderung dazu bewogen hätte«. Entgegen der von Newton gegebenen Definition der Kraft als »causa mathematica« und trotz seiner Warnung, die Schwere als eine wesentliche Eigenschaft der Materie zu betrachten, wurde für die Nachfolger Newtons die unvermittelte Fernwirkung (actio in distans) Tatsache.
Diese Auffassung wurde durch Roger Cotes, der 1713 die Vorrede zur zweiten Ausgabe der »Prinzipien« verfaßte, und durch Roberval vertreten. Letzterer erklärte die Attraktion als eine allgemeine Eigenschaft des Stoffes und schrieb diese Kraft ausdrücklich jedem einzelnen Teilchen zu. Allmählich wurde dann diese Vorstellung zu einer nicht nur den Philosophen, sondern auch den Physikern geläufigen. Anfangs zwar machte sich von mehreren Seiten Widerspruch geltend. Hatte man in der Cartesianischen Physik die Bewegungen der Gestirne sowie den Fall der Körper auf der Erde durch die Wirbelbewegung einer materia subtilis auf rein mechanische Ursachen zurückzuführen gesucht, so erblickte man in der Attraktion der Newtonianer eine Rückkehr zu der scholastischen Lehre von den okkulten Qualitäten. Diese Stellung nahmen unter anderen Johann Bernoulli339 und Huygens340 ein. Obgleich Huygens die Vorzüge des Newtonschen[S. 186] Systems vor dem Cartesianischen anerkannte, erklärte er, daß »eine Attraktion nicht aus den Prinzipien der Mechanik erklärt werden könne.« Auch Leibniz wandte sich gegen die Anziehung in die Ferne, während Daniel Bernoulli zu den Newtonianern hinüberschwenkte und auch Euler mit sich zu ziehen suchte. Er schreibt an diesen: »Konnte Gott eine Seele erschaffen, deren Natur uns unbegreiflich ist, so konnte er auch der Materie eine allgemeine Anziehung verleihen«341. Euler lehnte indessen die Attraktionshypothese ab; er ließ sie zwar als Arbeitshypothese gelten, wenngleich sie »mit der Physik gänzlich unvereinbar«342 sei.
Der Kampf zwischen den Cartesianern und den Newtonianern bietet, abgesehen von seiner geschichtlichen Bedeutung, ein besonderes Interesse, indem sich hier an der Schwelle der neueren Zeit an einem glänzenden Beispiele dartun läßt, wie hinderlich für den ersprießlichen Fortschritt der Wissenschaft, sich jedes Übermaß an Spekulation erweist. Die Aufgabe, die Descartes der Physik gestellt hatte, nämlich eine mechanische Erklärung der Naturerscheinungen zu geben, wurde von Newton dadurch ihrer Lösung näher gebracht, daß er auf dem dornenvollen Wege der Forschung die Gesetze der Natur enthüllte, während die Cartesianer den mühelosen Weg der Spekulation verfolgten, ohne zu Ergebnissen von Wert zu gelangen. Unter Lossagung von allen spekulativen Elementen, die so weit ging, daß er der Hypothese nur geringen Wert beilegte, erblickte Newton den obersten Grundsatz der Naturforschung darin, die Naturgesetze in den Tatsachen zu suchen und da abzubrechen, wo sich unlösbare Probleme zeigen. Auf diese Weise gelangte durch Newton, entgegen der spekulativen Richtung der Cartesianischen Physik, die empirisch-mathematische Methode zur vollen Geltung. Ihr verdankt die Wissenschaft den raschen Aufschwung, den sie unter den Nachfolgern Newtons nahm.
Sein entschlossenes Eintreten für die richtige Methode in einer Zeit, in welcher die Naturphilosophie die besten Köpfe gefangen nahm, bildet einen Wendepunkt in der Entwicklung der Naturwissenschaften. Nicht minder bezeichnen die Ergebnisse, zu denen Newton durch eben diese Methode gelangte, den Anfang einer neuen Aera.
Auch der Begriff der Materie erfuhr eine Umwandlung und zwar durch Leibniz. Dieser bestritt die Ansicht des Descartes, daß das Wesen der Materie allein in der Ausdehnung beruhe. Es genüge auch nicht, daß man später der Materie die Eigenschaft der Undurchdringlichkeit beigelegt habe. Das seien lediglich passive Eigenschaften343. Zu der Ausdehnung und der Undurchdringlichkeit müsse man zur Kennzeichnung des Wesens der Materie die Kraft hinzufügen. Dieses aktive Prinzip besitzt nach Leibniz auch die Fähigkeit des Perzipierens. Aus dieser Auffassung entsprang die von ihm herrührende Lehre von den Monaden. So sehr auch bei Leibniz metaphysische Spekulationen, denen wir hier nicht folgen können, in den Vordergrund treten, so unumwunden spricht er sich doch dahin aus, daß für alle Vorgänge der materiellen Welt nur eine rein mechanische Erklärung zulässig sei.
Außer der Attraktion nahmen die Newtonianer auch eine abstoßende Kraft an. Und zwar galten ihnen beide als physikalische Kräfte, während sie für Newton nur »causae mathematicae« waren. Newton hatte in den »Prinzipien« zur Erklärung der Konstitution eines elastischen Fluidums die Hypothese von der Repulsivkraft der Teilchen aufgestellt. Daraus entsprang bei den späteren Physikern die Ansicht, daß die Repulsivkraft der Gasmolekeln eine von Newton bewiesene physikalische Wahrheit sei.
Auch die Frage nach der Konstanz der Materie wurde von neuem erörtert. Während der Satz von der Unzerstörbarkeit des Stoffes trotz allen Wechsels, den der Begriff der Materie erfuhr, nicht ernstlich angezweifelt wurde und das Fundament der in diesem Zeitalter entstehenden wissenschaftlichen Chemie bildete, ist der Grundpfeiler der neueren Physik, der Satz von der Erhaltung der Energie erst von Leibniz scharf formuliert, aber erst viel später in seiner vollen Bedeutung anerkannt worden. Descartes hatte ja den Satz aufgestellt, daß die Quantität der Bewegung im Universum konstant bleibe. Huygens wies dagegen in einem Zusatze zu den Stoßgesetzen elastischer Körper darauf hin344, daß die Bewegungsgröße zweier Körper beim Zusammenstoß sich vermehren oder vermindern könne. Nur die algebraische Summe der Bewegungsgrößen bleibe vor und nach dem Stoße gleich. Huygens zeigte ferner, daß die Summen der beiden Produkte aus den Massen in die Quadrate ihrer Geschwindigkeiten vor[S. 188] und nach dem Stoße gleich groß sind. Damit war zum ersten Male das Prinzip der Erhaltung der lebendigen Kräfte klar ausgesprochen. Descartes hatte das Produkt mv als Kräftemaß betrachtet. Hooke suchte bereits 1669 zu zeigen, daß die Kraft eines bewegten Körpers dem Quadrate von v proportional ist345. Zehn Jahre später gelangt er zu folgendem Ausdruck: »Wird ein Körper mit einem gewissen Geschwindigkeitsgrade durch ein bestimmtes Kraftquantum bewegt, so erfordert dieser Körper vier mal so viel Kraft, um zweimal, und neunmal so viel Kraft, um dreimal so schnell bewegt zu werden usw. Dies gilt nicht nur für die Bewegung von Kugeln und Pfeilen, die abgeschossen werden, sondern auch für vibrierende Körper, für Sprungfedern, für senkrecht oder schräg fallende Körper, kurz für sämtliche Bewegungen, wenn man nur von dem Widerstand des Mediums dabei absieht«.
Wir sind mit diesen Betrachtungen von der bloßen Spekulation wieder bei dem Gebiet der Tatsachen angelangt und werden in einem späteren Abschnitt die hier nur angedeuteten Keime der theoretischen Physik in ihrer Entwicklung verfolgen. Zunächst wenden wir uns den weiteren Ergebnissen der experimentellen Forschung zu, da nur mit ihrer Hilfe ein Eindringen in die Zusammenhänge möglich war.
Der erste, der sich nach dem Wiederaufleben der Wissenschaften eingehender mit der Mechanik der Flüssigkeiten beschäftigte, war der Niederländer Stevin.
Simon Stevin (Stevens) wurde 1548 in Brügge geboren und bekleidete die Stelle eines Oberaufsehers der Land- und Wasserbauten in Holland. Er starb 1620 in Leyden. Stevin und Galilei haben ihre Untersuchungen unabhängig voneinander ausgeführt. Fast zur selben Zeit, als Galilei die Grundlagen der Mechanik schuf, »feierte die archimedische, rein statische Methode ihren letzten Triumph«346 durch Stevin. Letzterer machte seine Methoden und Entdeckungen in einer Schrift bekannt, die er »Prinzipien des Gleichgewichts« betitelte und 1586 veröffentlichte347. Nach seinem Tode wurde eine Sammlung seiner Schriften in französischer Sprache herausgegeben348.
Stevin hat sich sowohl um die Statik der festen wie der flüssigen Körper hervorragend verdient gemacht und das Prinzip der virtuellen Verschiebungen gekannt, allerdings, ohne es wie Galilei auf die flüssigen Körper auszudehnen. Stevin verwendet das Prinzip bei der Untersuchung der Rollen und Rollenverbindungen (lose Rolle, Flaschenzug, Potenzflaschenzug) und findet, daß an ihnen Gleichgewicht herrscht, wenn die Produkte aus den Gewichten und den entsprechenden Wegen oder, was auf dasselbe hinausläuft, Geschwindigkeiten auf beiden Seiten gleich sind.
Durch eine originelle Betrachtung gelangt Stevin dann zu den Gleichgewichtsbedingungen, die für die schiefe Ebene gelten, und zum Satz vom Parallelogramm der Kräfte. Seine Betrachtung, die weniger einen Beweis als eine intuitive Art des Erkennens bedeutet, läuft auf folgendes hinaus: Stevin denkt sich um das[S. 190] Dreieck ABC, dessen Grundlinie wagerecht verläuft, eine Kette geschlungen, die aus gleichschweren Gliedern besteht (Abb. 56) und ohne jede Reibung um das Dreieck bewegt werden kann. Eine solche Kette muß im Gleichgewicht sein, da sie sich sonst ja unaufhörlich bewegen würde. Das Gleichgewicht kann auch keine Störung erleiden, wenn man die beiden gleichschweren, symmetrischen Teile SL und VK, die sich unter der Basis des Dreiecks befinden, ganz fort läßt. Somit vermag das kürzere Kettenstück über BC dem längeren über AB das Gleichgewicht zu halten. Die Gewichte der Kettenstücke verhalten sich aber, da ihre Glieder gleiche Abstände besitzen und gleich schwer sind, wie die Seiten AB und BC. Es folgt also aus dieser Betrachtung der Satz, daß zwei Gewichte auf den schiefen Ebenen AB und BC im Gleichgewichte stehen, wenn sie sich wie die Längen dieser Ebenen verhalten.
Steht BC senkrecht zu AB, so haben wir das einfachere Gesetz für die schiefe Ebene, daß sich die Kraft zur Last wie die Höhe zur Länge verhält.
Indem Stevin das Gewicht auf der schiefen Ebene in einen zur schiefen Ebene parallelen und einen dazu senkrechten Teil zerlegte, gelangte er zu dem Satz vom Parallelogramm der Kräfte, allerdings in seiner Beschränkung auf statische Verhältnisse. Er selbst war von dem Ergebnis seines Nachdenkens und seiner Versuche so überrascht, daß er in den Ruf ausbrach: »Hier ist ein Wunder und doch kein Wunder«349!
Das größte Verdienst hat sich Stevin dadurch erworben, daß er die wichtigsten Sätze der Hydrostatik auffand. So rührt von ihm der Nachweis des hydrostatischen Paradoxons her350, d. h. des Satzes, daß der Bodendruck einzig von der Größe der gedrückten[S. 191] Fläche und der Höhe der Flüssigkeitssäule und nicht von der Gestalt des Gefäßes abhängt. Stevin führte diesen Nachweis durch einen Versuch (Abb. 57), den er mit folgenden Worten schildert: ABCD ist ein mit Wasser gefülltes Gefäß, in dessen Boden sich eine runde Öffnung EF befindet, die mit einer hölzernen Scheibe GH bedeckt ist. IRL ist ein zweites Gefäß von derselben Höhe wie das vorige und mit einer gleichgroßen Öffnung im Boden. Diese Öffnung sei gleichfalls durch eine Holzscheibe OP von demselben Gewicht wie die vorige geschlossen. Man findet dann durch den Versuch, daß die Scheiben nicht emporsteigen, sondern gegen die Öffnungen gepreßt werden; und zwar werden sie denselben Druck empfangen. Dies läßt sich nachweisen, indem man die gleichen Gewichte T und S anbringt, die ebenso schwer sind wie die über der Scheibe GH befindliche Wassersäule ERQF351.
Auf diese Weise, bemerkt Stevin, könne 1 Pfund Wasser in einer engen Röhre gegen einen Verschluß in einem weiten Gefäß wohl einen Druck von 100000 Pfund ausüben. Damit war ein Gedanke ausgesprochen, auf den die spätere Erfindung der hydraulischen Presse zurückzuführen ist.
Den aufwärts gerichteten Druck in Flüssigkeiten wies Stevin nach, indem er eine Metallplatte G (siehe Abbildung 58) gegen die beiderseits offene Röhre EF legte und das von der Platte verschlossene Ende in das Wasser hinabsenkte. Es zeigte sich, daß die Platte nicht abfällt, sondern durch den aufwärts gerichteten Druck der Flüssigkeit gegen die Röhre gepreßt wird352.
Handelt es sich bei Stevin um die Bestimmung des Druckes, den ein Stück der Seitenwand eines mit Wasser gefüllten Gefäßes auszuhalten hat353, so zerlegt Stevin dieses Stück durch horizontal verlaufende Linien in eine Summe von kleinen Rechtecken. Das oberste Stück (Abb. 59) empfängt einen Druck, der größer ist als der Druck eines Wasserprismas von der Grundfläche g und der Höhe h, indes geringer als der Druck eines Prismas von der gleichen Grundfläche und der Höhe h1. Dieselbe Betrachtung ergibt sich für alle übrigen Rechtecke. Stevin erhält dann durch Summierung einen Gesamtdruck, der zu groß, und durch eine zweite Summierung einen Gesamtdruck, der zu klein ist. Beide Summen nähern sich, wenn man die Streifen immer schmäler nimmt, dem gleichen Grenzwert.
Endlich untersuchte Stevin noch die Gleichgewichtsbedingungen schwimmender Körper. Er fand, daß bei solchen ihr Schwerpunkt und der Schwerpunkt der verdrängten Wassermasse in einer Vertikalen liegen. Auch schwimmt ein Körper nach Stevin nur dann stabil, wenn sein Schwerpunkt unter dem Schwerpunkt der verdrängten Wassermasse liegt. Und zwar schwimme er um so stabiler, je tiefer der Schwerpunkt des Körpers sich unter dem Schwerpunkt der verdrängten Flüssigkeit befinde.
Auch Galileis Schüler dehnten ihre Untersuchungen auf die Mechanik der Flüssigkeiten und der Gase aus. Vor allem ist hier Galileis hervorragendster Schüler Torricelli zu nennen.
Evangelista Torricelli wurde 1608 als Sproß eines vornehmen Geschlechtes in Faenza geboren. Im Alter von 20 Jahren kam er nach Rom, wo er Schüler des Mathematikers Castelli wurde. Castelli hatte vorher in Pisa gelehrt und war seitdem[S. 193] Galileis eifriger Anhänger und Freund, der seine eigenen Schüler mit dem Geiste und dem Streben des großen Begründers der neueren Naturforschung zu erfüllen suchte. Auf besonders fruchtbaren Boden gelangten die neuen Gedanken bei Torricelli. Nach dem Erscheinen der »Unterredungen«, des grundlegenden Werkes über die Mechanik354 verfaßte Torricelli eine Schrift über den gleichen Gegenstand, in der er einige der von Galilei gefundenen Bewegungsgesetze auf eine eigene Art zu beweisen suchte. Diese Schrift gelangte einige Jahre später in die Hände des großen, mittlerweile völlig erblindeten Meisters und rief in ihm den Wunsch hervor, die junge bedeutende Kraft, die sich ihm offenbart hatte, an sich zu fesseln. So kam denn Torricelli nach Florenz und verfaßte dort unter der Leitung Galileis eine Fortsetzung der »Unterredungen«, die später durch Viviani veröffentlicht wurde355. Die gemeinsame Arbeit Galileis und Torricellis dauerte indessen nur wenige Monate. Dann wurde ihr durch den Tod des Meisters ein Ziel gesetzt. Torricelli wirkte in Florenz im Geiste Galileis weiter, bekleidet mit den Ämtern und Würden des Meisters, bis ihn im Jahre 1647 ein früher Tod ereilte.
Die wichtigste wissenschaftliche Tat Torricellis bestand darin, daß er neben der von Galilei begründeten Dynamik der festen Körper eine Dynamik der flüssigen Körper schuf. Dies geschah in einer im Jahre 1644 erschienenen Abhandlung über ausströmende Flüssigkeiten356, die für das Gebiet der Hydrodynamik grundlegend geworden ist. Torricelli wies nach, daß ein Strahl, der aus einem mit Flüssigkeit gefüllten Behälter seitlich heraustritt, die Form einer Parabel annimmt. Ferner zeigte er, daß die Geschwindigkeit der Flüssigkeit, und mithin auch die ausfließende Menge, zu der Höhe der über der Ausflußöffnung befindlichen Säule in einem bestimmten Verhältnis steht. Für die vierfache Höhe ergab sich die doppelte, für die neunfache dagegen die dreifache Geschwindigkeit, d. h. die Geschwindigkeiten verhalten sich wie die Quadratwurzeln aus den Druckhöhen357.
Da den Geschwindigkeiten die Ausflußzeiten entsprechen, so folgt aus dem erwähnten Gesetz, daß die Zeiten, in denen gleiche Gefäße durch gleich große Öffnungen sich leeren, sich wie die Quadratwurzeln aus den Höhen der über den Öffnungen befindlichen Flüssigkeitsmengen verhalten.
Befindet sich die Ausflußöffnung in dem horizontalen Boden des Gefäßes, so ergibt sich nach Torricelli, daß die Ausflußmengen für gleiche Zeiten wie die ungeraden Zahlen abnehmen. Beträgt z. B. die für das Ausfließen erforderliche Gesamtzeit 6 Sekunden, und setzt man die in der letzten Sekunde ausfließende Menge gleich 1, so betragen die Ausflußmengen in der 5., 4., 3.... Sekunde 3, 5, 7 ...
Auch die Dynamik der festen Körper wurde durch Torricelli weiter ausgebaut. So hat er sich mit der Wurfbewegung beschäftigt und gezeigt, daß die Wurfweite für den Neigungswinkel 45° + α gleich derjenigen für den Winkel 45° - α ist.
Am bekanntesten ist Torricelli durch die Erfindung des Quecksilberbarometers geworden. Anknüpfend an die von Galilei erwähnte Beobachtung358, daß Wasser dem Kolben einer Pumpe nur bis zu einer gewissen Höhe (10 m) folgt, untersuchte Torricelli, wie weit wohl Quecksilber, das etwa 14mal so schwer wie Wasser ist, von dem vermeintlichen Horror vacui emporgehoben wird. Der auf Torricellis Veranlassung von Viviani angestellte Versuch zeigte, wie Torricelli vorausgesagt, daß die Steighöhe des Quecksilbers in demselben Verhältnis geringer ist, wie sein spezifisches Gewicht größer als dasjenige des Wassers ist. Beide Forscher führten im Jahre 1643 den Versuch in der in Abb. 60 dargestellten Weise aus. Sie nahmen ein Rohr von zwei Ellen Länge, füllten es mit Quecksilber und kehrten es in einem mit Quecksilber gefüllten Behälter um, indem sie das offene Ende des Rohres verschlossen. Nachdem der Verschluß aufgehoben war, sank das Quecksilber bis zu einer Höhe von 1½ Ellen herab und blieb dort in der Schwebe. Das Vakuum, das sich hierbei über dem Quecksilber bildet, wurde in der Folge als die Torricellische Leere bezeichnet. Der Apparat selbst ist ein Barometer, da die Höhe der Quecksilbersäule der Größe des Luftdruckes entspricht. Die[S. 195] Schwankungen, die man an diesem Instrument beobachtet, erklärte Torricelli aus den Änderungen des Luftdrucks. Die Lehre vom Horror vacui war jedoch dermaßen eingewurzelt, daß erst die überzeugende Kraft, die den Versuchen Pascals und Guerickes innewohnte, jenes unrichtige Prinzip aus der Physik verschwinden ließ.
Über die Versuche, welche die Accademia del Cimento mit dem Barometer, sowie über Vorgänge im Vakuum anstellte, wurde schon an früherer Stelle berichtet359.
Erst dem Franzosen Pascal, einem scharfsinnigen Kopf, der sich auch durch seine gegen die Jesuiten gerichteten »Lettres provinciales« einen Namen in der französischen Literatur erworben hat, gelang es, die Frage, ob ein Horror vacui oder der Luftdruck die Flüssigkeiten in der Schwebe hält, durch einen entscheidenden Versuch zu lösen.
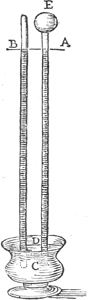
Pascal wurde 1623 in Clermont geboren. Sein Vater zog bald darauf nach Paris und verkehrte dort mit bedeutenden Gelehrten wie Roberval und Mersenne. Dadurch fand das in dem jungen Pascal frühzeitig sich regende mathematische Talent die erste Nahrung. Es wird erzählt, daß Pascal, bevor er mathematischen Unterricht genossen, den Satz von der Winkelsumme im Dreieck fand und als Zehnjähriger eine Abhandlung über den Klang verfaßte. Dazu soll ihn die Beobachtung veranlaßt haben, daß ein zum Tönen gebrachtes Trinkglas bei der Berührung verstummt. Gewiß ist, daß Pascal mit 16 Jahren ein Buch von wissenschaftlichem Wert über die Kegelschnitte schrieb und dadurch die Aufmerksamkeit von Descartes auf sich lenkte.
Pascals Verdienste sind besonders auf dem Gebiete der Mathematik zu suchen. Allzu angestrengte Tätigkeit untergrub[S. 196] seine wenig feste Gesundheit schon im jugendlichen Alter. Er wurde schließlich religiös-schwermütig und starb 1662 im Alter von 39 Jahren.
Die Kunde von Torricellis Versuch gelangte durch Mersennes ausgedehnten Briefwechsel nach Frankreich361. Pascal wiederholte den Versuch mit Quecksilber und mit Wasser, das er in 40 Fuß lange Röhren einschloß, hielt aber zunächst an der Lehre vom Horror vacui fest. Als jedoch Torricellis Erklärung in Frankreich bekannt wurde, stimmte er ihr lebhaft zu, erkannte aber, daß es noch eines entscheidenden Versuches bedürfe. Dieser Versuch Pascals362 bestand darin, das Torricellische Vakuum mehrere Male an einem Tage in derselben Röhre und mit demselben Quecksilber hervorzurufen, und zwar das eine Mal am Fuße, das andere Mal auf dem Gipfel eines Berges, um zu prüfen, ob die Höhe des in der Röhre schwebenden Quecksilbers in beiden Fällen dieselbe oder verschieden sei363. War nämlich die Quecksilbersäule auf dem Gipfel kürzer als am Fuße des Berges, so mußte daraus geschlossen werden, daß der Luftdruck es ist, der das Quecksilber in der Schwebe hält. »Es ist leicht ersichtlich«, sagt Pascal, »daß am Fuße des Berges eine größere Luftmenge einen Druck ausübt als auf dem Gipfel, während kein Grund vorliegt, daß die Natur in der unteren Region einen größeren Abscheu vor der Leere empfinden sollte als in der oberen.«
Der Versuch, den Pascal nicht selbst anstellte, sondern durch seinen Schwager Périer auf dem Gipfel des 4300 Pariser Fuß hohen Puy de Dôme ausführen ließ, entsprach ganz dieser Erwartung. Périer stellte am Fuße des Berges in Clermont in zwei Gefäßen das Vakuum her. Es zeigte sich, daß das Quecksilber in beiden Röhren dieselbe Höhe von 26 Zoll 3½ Linien hatte. Darauf ließ er eine Röhre in ihrem Gefäße, ohne den Versuch zu unterbrechen; er merkte die Höhe der Quecksilbersäule auf dem Glase an und bat jemanden, sorgfältig und unausgesetzt während des ganzen Tages darauf zu achten, ob eine Änderung einträte. Mit dem zweiten Apparat begab er sich in Begleitung[S. 197] mehrerer Personen auf den Gipfel des Puy-de-Dôme und stellte dort, 500 Toisen oberhalb des ersten Ortes, in der gleichen Art denselben Versuch an, den er vorher am Fuße gemacht hatte. Es zeigte sich, daß die Höhe der Quecksilbersäule jetzt nur noch 23 Zoll und 2 Linien betrug, während sie in Clermont gleichzeitig in der gleichen Röhre 26 Zoll 3½ Linien betragen hatte, so daß der Unterschied bei diesen Versuchen sich auf 3 Zoll 1½ Linien belief. Dies erfüllte alle mit Bewunderung und Erstaunen.
Später stellte Périer beim Abstieg denselben Versuch mit den gleichen Apparaten an und zwar 150 Toisen oberhalb Clermonts. Dort fand er, daß die Höhe der Quecksilbersäule 25 Zoll betrug. »Dies verschaffte uns«, schrieb Périer, »keine geringe Genugtuung, da wir sahen, daß die Höhe der Quecksilbersäule sich mit der Höhe des Ortes verminderte.«
Nach Clermont zurückgekehrt, fand er dort an dem Apparat, den er unverändert zurückgelassen, denselben Stand der Quecksilbersäule wie bei seinem Aufbruch, nämlich 26 Zoll 3½ Linien. Die Person, die zur Beobachtung zurückgeblieben war, berichtete, daß während der ganzen Zeit darin keine Änderung eingetreten sei.
Am folgenden Tage wurde Périer der Vorschlag gemacht, denselben Versuch am Fuße und auf der Spitze des höchsten Turmes Clermonts zu wiederholen, um zu erproben, ob in diesem Falle ein Unterschied bemerkbar sei. Auch dieses Mal fand er einen Unterschied in der Höhe der Quecksilbersäule, der sich allerdings nur auf wenige Linien belief.
Außer seinem Bergexperiment ersann Pascal noch einen zweiten Versuch, um den Luftdruck als die Ursache des Torricellischen Phänomens nachzuweisen. Er verband mit der beiderseits offenen Röhre ab die U-förmig gebogene Röhre cd. Die Stücke ab und cd hatten jedes die Länge der für den Torricellischen Versuch gebräuchlichen Röhre, d.h. sie waren jedes etwa einen Meter lang, und das Ganze stellte sich als ein Übereinander zweier Torricellischen Röhren dar. Die verbundenen Röhren wurden darauf ganz mit Quecksilber gefüllt und mit dem Ende a in Quecksilber getaucht, während man a und b mit den Fingern geschlossen hielt. Öffnete Pascal darauf a allein, so[S. 198] fiel das Quecksilber in cd ganz in den unteren Teil der oberen U-Röhre, bis es in beiden Schenkeln im gleichen Niveau stand. Gleichzeitig sank das Quecksilber in der Röhre ab bis zum herrschenden Barometerstande, und der Finger bei b wurde durch den äußeren Luftdruck fest gegen die Öffnung gepreßt. Es war also damit dasselbe erreicht, als ob man für das obere Barometer den Druck der äußeren Luft gänzlich entfernt hätte. Öffnete man nämlich jetzt b, so stieg das Quecksilber im oberen Barometer cd auf den gewöhnlichen Stand, gleichzeitig aber sank es in ab ganz herab.
Pascal unternahm es darauf, die Statik der gasförmig-flüssigen und der, hinsichtlich des Druckes ähnlichen Gesetzen folgenden tropfbar-flüssigen Körper, in einer Abhandlung darzustellen. Sie nimmt infolge ihrer klaren Fassung und ihrer überzeugenden Versuche einen hervorragenden Platz unter den physikalischen Schriften des 17. Jahrhunderts ein und führt den Titel364 »Abhandlung über das Gleichgewicht der Flüssigkeiten«. Sie erläutert zunächst, welche Fülle alltäglicher Erscheinungen als Wirkungen des Luftdruckes aufzufassen sind. So wird das Saugen, Schröpfen, Pumpen, Heben usw., irrtümlicherweise aber auch die Adhäsion geschliffener Platten auf ihn zurückgeführt. Der bedeutendste Schritt, den Pascal tat, ist die Erkenntnis, daß die durch den Luftdruck und die durch den Druck einer tropfbaren Flüssigkeit hervorgerufenen Erscheinungen einander völlig entsprechen. Als Beispiel für die Art, wie Pascal den experimentellen Nachweis führte, wählen wir seinen Versuch, das Fließen des Hebers durch den Wasserdruck hervorzurufen. Er tauchte die gabelförmig gestaltete, an allen drei Enden offene Röhre abc mit den Schenkeln a und b in Quecksilbergefäße, die sich unter Wasser befanden (Abb. 62). War das Wassergefäß, in das die ganze Vorrichtung hinabgesenkt wurde, hinreichend tief, so stieg das Quecksilber, bis sich die Säulen vereinigten; und von diesem Augenblicke an floß es von dem höher gelegenen Gefäße d infolge des vorhandenen Druckunterschiedes nach dem tieferen Gefäße e.
Für die Hydrostatik hatten zwar Galilei und ganz besonders Stevin neue Grundlagen geschaffen, doch hat Pascal denselben Gegenstand unabhängig von jenen mit großer Klarheit und unter Hervorkehrung wesentlich neuer Gesichtspunkte behandelt. Pascal gründet seine hydrostatischen Untersuchungen auf den Satz, daß sich der Druck in Flüssigkeiten nach allen Seiten gleichmäßig fortpflanzt. Ferner wendet er nach dem Vorgange Galileis das Prinzip der virtuellen Geschwindigkeiten oder Verschiebungen auf die Hydrostatik an; doch bekundet Pascals Auffassung einen wesentlichen Fortschritt. Er betrachtet jede Flüssigkeit, die von festen Körpern begrenzt wird, als eine Maschine, an der die Kräfte, wie an dem Hebel und den anderen einfachen Maschinen, nach bestimmten Verhältnissen ins Gleichgewicht gesetzt werden. Betrachten wir z. B. mit Pascal zwei kommunizierende, durch Kolben abgeschlossene Gefäße. Die Kolben seien durch Gewichte belastet, die den Oberflächen proportional sind. In diesem Falle ist Gleichgewicht vorhanden. Es sind nämlich bei jeder Verschiebung dieses Systems die nach den entgegengesetzten Richtungen geleisteten Arbeiten einander gleich. Oder, um die Beziehung zur Mechanik der festen Körper hervortreten zu lassen, für die das Prinzip der virtuellen Geschwindigkeiten zuerst entwickelt wurde: die geschilderte hydrostatische Vorrichtung entspricht in ihrer Wirkungsweise vollkommen einem Hebel mit zwei ungleichen Armen. »Man muß«, sagte Pascal, »bewundern, daß sich in dieser neuen Maschine«, nämlich in der von einem Gefäß und zwei verschiebbaren Kolben begrenzten Flüssigkeit, »jene beständige Ordnung wieder findet, die für den Hebel, die Rolle usw. gilt, daß sich nämlich die Wege umgekehrt wie die Kräfte verhalten. Dies kann man sogar als die wahre Ursache jener Wirkung betrachten. Denn offenbar ist es dasselbe, ob man 100 Pfund Wasser einen Zoll Weges oder ein Pfund Wasser einen Weg von 100 Zoll zurücklegen läßt«365.
Erwähnt sei noch, daß Pascal im Anschluß an sein Bergexperiment das Barometer als Instrument zum Messen von Höhen in Vorschlag brachte und das Gewicht der gesamten Atmosphäre auf 8 Trillionen Pfund berechnete.
Auch die atmosphärischen Bewegungen wurden, nachdem der Luftdruck als die Ursache zahlreicher physikalischer Erscheinungen erkannt war, auf Gleichgewichtsstörungen dieses Druckes zurückgeführt.[S. 200] Torricelli war der erste, der aus diesem physikalischen Prinzip die Luftströmungen zu erklären suchte366. Er nahm an, daß zwischen Gegenden verdünnter und solchen dichterer Luft ein Ausgleich durch eine Strömung stattfinde, die sich uns als Wind bemerkbar mache. Als ein Beispiel hierfür galt ihm die besonders in Italien auffallende Erscheinung, daß an warmen Frühlingstagen ein kühler Wind aus den Pforten größerer Kirchen hervorbricht. »Die Luft«, so lautet seine Erklärung, »ist in großen Gebäuden um diese Zeit bedeutend kühler und schwerer, als die Luft in ihrer Umgebung. Daher fließt sie an der Pforte heraus, wie Wasser es tun würde, wenn man es in das Gebäude eingeschlossen hätte und dann plötzlich eine seitliche Öffnung herstellte.«
Die bedeutendste Förderung empfing die Physik der Gase durch die Versuche, die Guericke mit Hilfe der von ihm erfundenen Luftpumpe anstellte. Die neuere, das Experiment in den Vordergrund stellende Richtung der Naturwissenschaft hatte in Deutschland vor Guericke wenig Beachtung gefunden. Ein Mann wie Kepler gelangte nicht einmal dazu, die Ergebnisse seines Nachdenkens, sofern sie das Bild auf der Netzhaut und die Konstruktion des astronomischen Fernrohrs betrafen, durch den Versuch nachzuprüfen. In Guericke tritt uns dagegen ein Experimentator ersten Ranges entgegen. Als solchen haben wir ihn zu würdigen, nicht nach seiner Begabung zur Entwicklung theoretischer und philosophischer Vorstellungen. In dieser Hinsicht mag sogar das Urteil eines Leibniz, daß Guericke kein Naturforscher ersten Ranges sei, berechtigt sein. Andererseits übertraf Guericke durch folgerichtiges Denken die Mehrzahl seiner Zeitgenossen. Indem sie an die Stelle verschwommener Vorstellungen die scharfe Logik der neueren Naturwissenschaft setzten, haben Guericke und geistesverwandte Männer, die in den nördlichen Ländern Europas bald in größerer Zahl erstanden, der wahren, auf die Ergebnisse der exakten Forschung sich gründenden Philosophie erst die Wege geebnet. In Anbetracht dieser Bedeutung Guerickes wird es sich rechtfertigen, wenn wir zunächst bei seinem Leben verweilen, dessen Schilderung, wie die Biographien[S. 201] Galileis und Keplers, zugleich einen Schluß auf die Zustände des 17. Jahrhunderts gestattet.
Otto von Guericke367 wurde am 20. November 1602 in Magdeburg als Sprößling einer Patrizierfamilie geboren368. Er studierte zunächst Rechtsgelehrsamkeit. Später befaßte er sich mit Mathematik, Mechanik und Befestigungslehre. An seine Studienjahre schloß sich eine Reise nach Frankreich und England an. Nach dieser Vorbereitung trat Guericke in das Ratskollegium seiner Vaterstadt ein. Durch das Unglück, das der dreißigjährige Krieg über Magdeburg brachte, wurde auch Guericke schwer betroffen. Als die Horden Tillys im Jahre 1631 plündernd und mordend in die Stadt eindrangen, vermochte Guericke kaum das nackte Leben zu retten. Durch seine Kenntnisse in den Ingenieurwissenschaften gelang es ihm, sich eine neue Existenz zu gründen. So war er nach der Zerstörung Magdeburgs in verschiedenen Städten Deutschlands mit der Anlage von Befestigungen betraut, einer Tätigkeit, in der jene Zeit die wichtigste Aufgabe der Technik erblickte. Diese Arbeit hatte das Gute im Gefolge, daß Guericke dazu überging, die Mittel der Ingenieurmechanik auf die Lösung wissenschaftlicher Aufgaben anzuwenden. Leider ist wenig über die allmähliche Ausreifung und Durchführung seiner Experimentaluntersuchungen bekannt geworden. Selbst über die Zeit der Erfindung der Luftpumpe konnten genauere Daten nicht ermittelt werden369. Als endgültige Form der von Guericke erfundenen Luftpumpe ist diejenige zu betrachten, die er in seinem Werke beschreibt und abbildet. Die Abbildung ist auf S. 205 dies. Bds. wiedergegeben.
Später kehrte Guericke nach Magdeburg zurück, um sich am Wiederaufbau der Stadt zu beteiligen. Unter seiner Leitung wurden die Festungswerke und die von den Kaiserlichen zerstörte Elbbrücke wieder hergestellt. Für Guericke folgte dann zunächst eine ruhige Zeit, während er später nach seiner Ernennung zum Bürgermeister mit Geschäften überhäuft war. So finden wir ihn als Vertreter Magdeburgs auf dem Friedenskongreß in Osnabrück, dann wieder am Hofe in Wien oder auf dem Reichstage zu Regensburg.[S. 202] Dort zeigte er dem Kaiser und den versammelten Ständen im Jahre 1654 seine Luftpumpe und den so berühmt gewordenen Versuch mit den Magdeburger Halbkugeln.
In Anbetracht des Umstandes, daß Guerickes Versuche jahrelange Mühen und bedeutende Kosten erforderten – sein Sohn hat sie auf 20000 Taler beziffert – hat die Annahme etwas für sich, daß diese Versuche in das Jahrzehnt von 1635–1645 fallen.
Die erste Veröffentlichung über die Luftpumpe und die von Guericke angestellten Versuche rührt von dem Würzburger Professor Kaspar Schott her. Dieser befaßte sich im Auftrage seines Landesherrn mit der Wiederholung jener Versuche, ohne sich jedoch von der durch Guericke mit Nachdruck bekämpften Lehre vom Horror vacui freimachen zu können.
Kaspar Schott wurde 1608 in der Nähe von Würzburg geboren und starb dort 1666 als Professor der Physik und Mathematik. Er gehörte der alten, damals in Deutschland herrschenden Schule von Physikern an, die noch in einem Wust philologischer und philosophischer Gelehrsamkeit steckten und außerstande waren, den von Galilei eingeschlagenen Weg der induktiven Naturforschung zu beschreiten. Dazu kam bei Schott und seinen Geistesverwandten eine große Abhängigkeit von religiösen Dogmen. In jeder neuen Entdeckung witterten sie Gefahr für die herrschende Philosophie und die Kirche. Auch Schott eifert gegen die Vertreter der neueren Naturwissenschaft, die er spöttisch als »neotericos philosophastros«370 bezeichnet und denen er vorwirft, sie wollten aus dem sogenannten leeren Raum vieles schließen, was vom Standpunkte der Philosophie töricht und in bezug auf den orthodoxen Glauben gefährlich sei. Trotzdem hat sich Schott ein gewisses Verdienst um die Belebung der naturwissenschaftlichen Forschung in Deutschland, erworben, weil er, ähnlich wie Mersenne in Frankreich, mit zahlreichen Forschern in schriftlichem Verkehr stand und dadurch zur raschen Verbreitung neuer Beobachtungen und Entdeckungen beitrug, Probleme aufwarf und Streitfragen in Fluß hielt. So war er auch der erste, durch den die Gelehrten von Guerickes Erfindungen und Entdeckungen ausführlichere Kenntnis erhielten. Dies geschah durch Schotts Mechanik der Flüssigkeiten und der Gase (Mechanica hydraulico-pneumatica) vom Jahre 1657. Schott wurde zu seiner Veröffentlichung über die Magdeburgischen Versuche durch den Kurfürsten[S. 203] Johann Philipp von Mainz, der zugleich Bischof von Würzburg war und Guerickes Versuche 1654 in Regensburg gesehen hatte, veranlaßt. Welches Staunen die neuen, heute als etwas Alltägliches erscheinenden Vorgänge bei den Zeitgenossen verursachten, geht aus Schotts Vorrede zu seinen einige Jahre später erschienenen »Technischen Merkwürdigkeiten« (Technica curiosa 1664) hervor. Schott sagt dort über die Magdeburger Wunderdinge: »Ich trage kein Bedenken zu bekennen, daß ich auf diesem Gebiete nichts Bewunderungswürdigeres gesehen habe. Auch meine ich, daß die Sonne niemals Ähnliches, geschweige denn Wunderbareres seit der Erschaffung der Welt beschien.«
Ursprünglich hatte Guericke nicht die Absicht, über seine Erfindungen und Entdeckungen zu schreiben, doch zwang ihm der Widerspruch, den er fand, endlich die Feder in die Hand. So entstand das im Jahre 1663 vollendete, indes erst 1672 erschienene umfangreiche Werk »Über den leeren Raum«371. Der weitaus wichtigste Teil desselben ist das dritte, »Über eigene Versuche« betitelte Buch. Es ist eine der wichtigsten und lehrreichsten älteren Monographien über einen physikalischen Gegenstand372.
Infolge philosophischer Streitigkeiten über den leeren Raum war in Guericke der Wunsch entstanden, die Frage, ob ein Vakuum möglich sei, durch Versuche zu beantworten. Denn die Gewandtheit im Disputieren gelte nichts auf dem Gebiete der Naturwissenschaften373. Wir erfahren aus der von ihm gegebenen Darstellung zunächst von seinen Bemühungen, ein Faß zu evakuieren374. Es wurde mit Wasser gefüllt und wohl verpicht, so daß die Luft nicht einzudringen vermochte. Am unteren Teile des Fasses wurde eine Messingspritze als Pumpe angebracht, mit deren Hilfe man das Wasser herausziehen konnte. Letzteres, schloß Guericke, müsse vermöge seiner Schwere herabsinken und über sich einen leeren Raum zurücklassen. An der Spritze hatte Guericke zwei Ventile[S. 204] angebracht, von denen das eine den Eintritt des Wassers aus dem Faß in die Spritze, das andere den Abfluß nach außen vermittelte.
Die Bemühungen, das so hergerichtete Faß luftleer zu machen, scheiterten jedoch an der Porosität des Holzes. Selbst als Guericke das Faß, um das Eindringen der Luft zu verhindern, in einen größeren, mit Wasser gefüllten Behälter einschloß, mißlang der Versuch, Das Wasser wurde zwar aus dem kleineren Faß herausgezogen, trotzdem fand sich letzteres nach einiger Zeit zum Erstaunen aller Zuschauer zum Teil mit Wasser, zum Teil mit Luft gefüllt. Diese Stoffe waren durch die Poren des Holzes eingedrungen.
Nachdem die Porosität des Holzes als die Ursache des Mißerfolges erkannt war, wählte Guericke für sein Vorhaben eine kupferne Kugel. Er verband sie mit einer Spritze, wie er sie bei den vorhergehenden Versuchen benutzt hatte. Anfangs ließ sich der Stempel leicht bewegen; bald wurde dies aber immer schwieriger. Als nun Guericke glaubte, es sei nahezu alle Luft herausgeschafft, wurde die Metallkugel plötzlich mit lautem Knall und zu aller Schrecken zerknittert. Guericke schrieb diesen Vorfall dem Umstände zu, daß sich an der Kugel wahrscheinlich eine flache Stelle befunden hatte, die den Druck der umgebenden Luft nicht auszuhalten vermochte. Als der Metallarbeiter eine vollkommen runde Kugel hergestellt hatte, gelang der Versuch. Zum Beweise, daß die Kugel vollständig evakuiert war, diente der Umstand, daß aus dem nach außen führenden Ventil der Spritze endlich keine herausgezogene Luft mehr entwich.
Öffnete man dann den Hahn der Kugel, so drang die Luft mit großer Gewalt in sie ein. Brachte man dabei das Gesicht an den Hahn, so wurde einem der Atem benommen, ja man konnte die Hand nicht über den Hahn halten, ohne daß sie mit Heftigkeit angezogen wurde.
Nach diesem so glänzend gelungenen Versuch baute Guericke eine verbesserte Luftpumpe, die folgende Einrichtung aufwies (siehe Abb. 63)375. Ein Dreifuß wurde mit Schrauben am Boden[S. 205] befestigt. Zwischen seinen Füßen wurde in passender Höhe der Stiefel der Pumpe angebracht, deren Kolben durch den Hebel wu bewegt wurde. Der obere, deckelförmige Teil der Luftpumpe ist in Fig. IV abgebildet. Er trägt eine Röhre n, in welche der[S. 206] Hahn des Rezipienten gesteckt wird. Unter dieser Röhre befindet sich ein Lederventil, das sich bei der Abwärtsbewegung des Kolbens öffnet und die Luft aus dem Rezipienten in den Stiefel treten läßt. Durch das äußere Ventil z (Fig. IV) entweicht die Luft beim Aufwärtsbewegen des Kolbens. Das trichterförmige Gefäß xx wird nach der Verbindung und dem Abdichten aller Teile mit Wasser gefüllt, um das Wiedereindringen von Luft nach Möglichkeit zu verhindern. Aus demselben Grunde wird das untere Ende des Stiefels in einen Wasserbehälter (Fig. VI) getaucht.
Guericke erkannte bald, daß die Luft nicht etwa infolge ihrer Schwere aus dem Rezipienten in den Kolben gelangt, wie er anfänglich voraussetzte, sondern infolge ihrer Expansivkraft. Da letztere gegen das Ende der Evakuierung indessen nicht mehr groß genug war, um das unter der Röhre n befindliche Ventil zu bewegen, brachte er noch ein Röhrchen m mit einem kleinen Stempel an, der die Bewegung des Ventils unabhängig von der Elastizität der Luft gestattete.
Als Guericke eines Tages in den entleerten Rezipienten vermittelst einer Röhre Wasser aus einem Kübel steigen ließ, der am Boden des Zimmers stand, kam er auf den Gedanken, zu untersuchen, wie weit wohl bei diesem Versuch der Rezipient von dem Kübel entfernt sein könne. Er verlängerte daher die Röhre, so daß sie aus dem zweiten Stockwerk seines Hauses durch das Fenster bis auf den Boden des Hofes reichte. Nachdem dann ein Gefäß mit Wasser darunter gesetzt war, öffnete er den Rezipienten. Das Wasser stieg darauf, seiner Schwere entgegen, nichtsdestoweniger in das entleerte Gefäß empor. Bei einer Wiederholung des Versuches unter Anwendung einer längeren Röhre stieg das Wasser sogar bis in das dritte Stockwerk. Erst nachdem Guericke sich mit seinem Rezipienten in den vierten Stock begeben hatte, nahm er wahr, daß kein Wasser mehr in das Gefäß gelangte, sondern daß es in der Röhre in der Schwebe blieb.
Abb. 64, welche eine Wiedergabe der X. Tafel des Guerickeschen Werkes ist, enthält auf der rechten Seite das Wasserbarometer. mm ist der Kübel, i der Rezipient, bg die aus vier Stücken zusammengesetzte Röhre. Jedes Stück besaß am oberen Ende eine napfförmige Erweiterung, in die nach dem Zusammenfügen zum besseren Abdichten Wasser gegossen wurde. Die Rohrstücke[S. 207] bestanden aus Messing, so daß sich die Steighöhe nicht genau ermitteln ließ. Es war daher nötig, an der Stelle, wo sich das in der Schwebe befindliche Wasser vermuten ließ, eine Glasröhre vermittelst Kitt gut schließend einzuschalten und den Versuch von neuem anzustellen. Als jetzt der Hahn des Rezipienten geöffnet[S. 208] wurde, sah Guericke das Wasser eindringen, einige Male in der Glasröhre auf und niederschwanken, endlich aber zur Ruhe kommen. Jetzt ließ sich die Stelle, bis zu der das Wasser gestiegen war, genau feststellen. Guericke merkte diese Stelle an und ließ von hier ein Lot bis zum Boden des Hofes hinab. Die Länge des Lotes fand er gleich etwa 19 Magdeburger Ellen.
Fortgesetzte Beobachtungen an diesem Apparat ließen Guericke alsbald Schwankungen in der Höhe der Wassersäule entdecken. Das Wasser stand nämlich mitunter um mehrere Handbreit höher und dann wieder um soviel tiefer. Um diese Schwankungen besser zu verfolgen, brachte Guericke eine aus Holz geschnitzte Figur in die Röhre, die mit dem Wasser auf- und niederstieg und dabei auf eine an der Röhre angebrachte Skala wies (Fig. 10, IV). Aus diesen Schwankungen, von denen Pascal nachwies, daß sie in viel beträchtlicherem Maße beim Durchschreiten verschiedener Niveaus der Atmosphäre eintreten (s. S. 197), schlossen beide Forscher, daß nicht der Horror vacui, sondern eine äußere Ursache, der Luftdruck nämlich, das Steigen der Flüssigkeiten hervorruft. »Wenn das Emporsteigen infolge des Abscheus vor dem leeren Raum geschähe,« meint Guericke, »so müßte das Wasser entweder bis zu einer beliebigen Höhe dem Vakuum folgen oder immer in ein- und derselben Höhe stehen bleiben. Daß aber die Höhe sich ändert, ist das sicherste Zeichen dafür, daß nicht nur das Emporsteigen, sondern auch die Schwankungen des Wassers von einer äußeren Ursache herrühren. Seine Höhe hängt also nicht von dem Abscheu der Natur vor dem leeren Raume ab, sondern von dem Gleichgewicht zwischen dem Druck der Wassersäule und dem Luftdruck.«
Ferner entging es Guericke nicht, daß zwischen den von ihm entdeckten Schwankungen der Wassersäule und den Witterungserscheinungen ein gewisser Zusammenhang besteht. Über eine Wettervorhersage berichtet er mit folgenden Worten: »Ich habe mit Bestimmtheit, als im vergangenen Jahre jener ungeheure Sturm stattfand, eine besondere, außerordentliche Veränderung der Luft wahrgenommen. Sie war so leicht im Vergleich zu sonst geworden, daß der Finger des Männchens bis unter den äußersten, an der Glasröhre angebrachten Punkt herabstieg. Als ich dies sah, teilte ich den Umstehenden mit, es sei ohne Zweifel irgendwo ein großes Unwetter ausgebrochen. Und kaum waren zwei Stunden verflossen, als der Orkan in unsere Gegend einbrach.«
Das Nächstliegende war, daß Guericke eine abgeschlossene Luftmenge wog, indem er den Gewichtsunterschied zwischen dem mit Luft gefüllten und dem luftleeren Rezipienten feststellte376. Von einem hervorragenden Beobachtungsvermögen zeugt es, daß ihm die geringen, durch die Änderungen des aërostatischen Auftriebs veranlaßten Schwankungen im Gewichte des evakuierten Rezipienten nicht entgingen. Die 3. Abbildung seiner X. Kupfertafel377 erläutert den betreffenden Versuch. Der leergepumpte Rezipient L wurde mit einem an Rauminhalt viel kleineren Metallkörper ins Gleichgewicht gebracht. Als Guericke diese Vorrichtung längere Zeit beobachtete, fand er, daß der Rezipient bald höher, bald tiefer stand. Er bemerkt hierzu ganz richtig, daß beim Eintauchen des ganzen Apparates in Wasser der Rezipient in diesem dichteren Medium viel leichter erscheinen und erheblich in die Höhe steigen müsse. Sein Apparat lieferte also den Nachweis, daß das unter dem Namen des Auftriebs bekannte und schon von Archimedes erforschte Verhalten auch für gasförmige Medien gilt.
Auf Grund der von ihm gefundenen Tatsache, daß die Luft denselben Druck ausübt wie eine 19 Magdeburger Ellen (10 m) hohe Wassersäule, zeigt Guericke378, wie man den Druck eines beliebigen Luftzylinders berechnen kann. In dem Fall, daß der Durchmesser des Zylinders 2/3 Ellen beträgt, findet er für ihn einen Druck von 2687 Pfund. Um diesen außerordentlichen Druck recht augenfällig zu zeigen, verfuhr er folgendermaßen: Er ließ zwei Halbkugeln aus Kupfer von etwa 2/3 Magdeburger Ellen Durchmesser so herrichten, daß sie gut aufeinander paßten. Die eine Halbkugel wurde mit einem Ventil versehen, mit dessen Hilfe die im Innern der Kugel befindliche Luft herausgezogen werden konnte. Die Schalen besaßen ferner eiserne Ringe, um Pferde daran zu spannen. Ferner ließ Guericke einen Ring aus Leder herstellen, der gut mit Wachs und Öl durchtränkt war, so daß er keine Luft durchließ.
Die Schalen wurden, nachdem der Lederring zwischen sie gebracht war, aufeinander gelegt und darauf die Luft schnell herausgepumpt.[S. 210] Die beiden Schalen wurden dadurch von dem Drucke der äußeren Luft so fest zusammengepreßt, daß sechzehn Pferde sie nur mit Mühe voneinander reißen konnten. Ließ man jedoch durch Öffnen des Hahnes die Luft wieder eintreten, so konnten die Halbkugeln schon mit den Händen getrennt werden.
Fast alle Luftpumpenversuche, die im heutigen Physikunterrichte gezeigt werden, rühren von Guericke her. So wies er nach, daß der Schall sich im Vakuum nicht fortpflanzt, während das Licht ungehindert hindurchgeht. Tiere starben in seinem entleerten Rezipienten nach kurzer Zeit. Fische mit allseitig geschlossener Schwimmblase schwollen darin infolge der Expansion der Luft stark an, während bei solchen Fischen, deren Schwimmblase einen Ausführungsgang nach dem Schlunde besitzt, die eingeschlossene Luft infolge der gleichen Ursache zum Teil entwich. Guericke zeigte ferner, daß das Feuer im Vakuum erlischt. Er bestätigte auch die Beobachtung, daß bei der Verbrennung Luft verzehrt wird. Eine Kerze, die in einem geschlossenen Rezipienten brannte, erlosch nämlich, sobald ein Teil der Luft verbraucht war379. Bei der Erörterung dieses Versuches zeigt Guericke, wie klar er urteilt. Zunächst wirft er die Frage auf, warum das Erlöschen eintritt, bevor die ganze Luftmenge aufgezehrt ist. Als Grund dafür gibt er an, daß die Luft durch die Produkte der Verbrennung verunreinigt werde. Die weitere Frage, ob das Feuer die Luft in der Weise verzehrt, daß es letztere vernichtet, oder ob es die Luft in einen anderen Stoff verwandelt, entscheidet Guericke in letzterem Sinne. Doch sei der Stoff so fein, daß man ihn nicht wahrnehmen könne.
Über die Ursache des Luftdrucks äußert sich Guericke mit folgenden Worten: »Einige verlegen die Ursache in die von allen Seiten kommenden Strahlen der Sterne. Wäre dies der Fall, so müßte indessen auch die Erdkugel diesen Druck empfangen und ihm Widerstand leisten. Wenn aber zwei Körper einander drücken, so wird ein zwischen ihnen befindlicher Gegenstand von beiden Seiten denselben Druck erleiden. Daraus würde notwendig folgen, daß die oberen Teile der Luft in gleichem Maße gedrückt werden, wie die unteren, was aber durch die Versuche widerlegt wird.«
»Da die untere Luft stärker zusammengedrückt ist als die obere, und man dies nicht erst auf hohen Bergen, sondern schon[S. 211] auf Türmen wahrnimmt380, so folgt daraus, daß die Luft sich nicht weit von der Oberfläche der Erde erstreckt, sondern daß ihre Höhe, verglichen mit der großen Entfernung der Sterne, nur gering ist.«
Um die Fortpflanzung des Schalles im Vakuum zu prüfen, hatte Berti in Rom im Jahre 1647 einen Apparat ersonnen, der große Ähnlichkeit mit Guerickes Wasserbarometer besaß. Berti errichtete an seinem Hause eine Röhre von 100 Fuß Länge. An ihrem oberen Ende verband er sie luftdicht mit einem Gefäß, in dem sich ein Schlagwerk befand. Der ganze Apparat wurde durch eine obere Öffnung mit Wasser gefüllt. Diese Öffnung wurde dann luftdicht geschlossen, worauf das untere Ende der Röhre, das in Wasser tauchte, geöffnet wurde. Das Wasser sank und in dem Gefäß entstand ein leerer Raum. Trotzdem gab das Schlagwerk, das vermittelst eines Magneten in Bewegung gesetzt wurde, einen Ton. Hieraus leiteten Berti und Schott, der über den geschilderten Versuch berichtete, einen Einwurf gegen die Möglichkeit des Vakuums her. Guericke und nach ihm Boyle zeigten jedoch, daß, bei Vermeidung aller Fehler, Gefäße derart evakuiert werden können, daß der Schall sich in ihnen nicht oder kaum noch fortpflanzt381. So hing Guericke das Schlagwerk an einem Faden auf, um die Fortpflanzung des Schalles durch die feste Materie des Rezipienten nach Möglichkeit zu verhindern.
Mit dem von Torricelli erfundenen Verfahren, ein Vakuum über Quecksilber herzustellen, wurde Guericke erst 1654 auf dem Reichstage zu Regensburg382 bekannt. – Auch um die Elektrizitäts-, die Wärmelehre und die Mechanik hat sich Guericke Verdienste erworben. Doch ist davon an anderer Stelle die Rede.
Als die Kunde von der Erfindung Guerickes nach England gelangt war, machte sich dort Boyle an die Herstellung einer Luftpumpe, die in mehrfacher Hinsicht diejenige Guerickes übertraf.[S. 212] Im Jahre 1660 veröffentlichte Boyle seine »Neuen Versuche«383, die sich zum Teil mit den »magdeburgischen« deckten, zum Teil aber wirklich »neu« waren. Erwähnt sei die Beobachtung, daß erwärmtes Wasser im Vakuum kocht, womit die Abhängigkeit des Siedepunktes von dem auf der Flüssigkeit lastenden Druck erwiesen war.
Boyle war auch der erste, der die einfache Beziehung erkannte, die zwischen dem Druck und dem Volumen eines Gases besteht. Er schloß 12 Kubikzoll Luft durch Quecksilber in dem kürzeren Schenkel einer U-förmig gebogenen Röhre ab (siehe Abb. 65). In dem Maße, in dem Quecksilber in den längeren offenen Schenkel gegossen wurde, verringerte sich das Volumen der abgesperrten Luft. Bei einem Drucke von zwei Atmosphären nahm sie nur noch sechs Kubikzoll, bei drei Atmosphären vier Kubikzoll (ein Drittel des ursprünglichen Volumens) ein, oder, wie Boyle es aussprach, die Luft verdichtete sich im Verhältnis der zusammendrückenden Kräfte.
Dieses Grundgesetz der Aëromechanik385 wurde geraume Zeit später durch den Franzosen Mariotte (1620–1684) selbständig aufgefunden und klarer ausgesprochen als von Boyle. Eine vortreffliche Darstellung seiner Entdeckung gab Mariotte in der »Abhandlung über die Natur der Luft«386. Mariotte tauchte ein Barometer in hinreichend tiefes, klares Wasser, und bemerkte, daß eine Wassersäule von 14 Zoll Höhe ein Steigen des Quecksilbers um einen Zoll bewirkt. »Offenbar rührt dies«, sagt Mariotte, »daher, daß das spezifische Gewicht des Quecksilbers 14mal größer ist als dasjenige des Wassers.« Wenn das Quecksilber im Barometer 28 Zoll hoch stehe, so gehe daraus hervor,[S. 213] daß diese Quecksilbersäule gerade so viel wiege wie eine Luftsäule von gleicher Grundfläche, die sich von der Oberfläche des in dem Gefäße befindlichen Quecksilbers bis zur Grenze der Atmosphäre erstrecke.
Eine zweite Eigenschaft der Luft bestehe darin, daß sie außerordentlich verdichtet und ausgedehnt werden könne, dabei aber immerfort einen Druck ausübe, wodurch die Luft die Körper, die sie einschließen, zurückstoße oder zurückzustoßen strebe. Während die meisten anderen Spannkräfte allmählich abnehmen, bemerke man nie, daß dies bezüglich der Spannung der Luft der Fall sei. So komme es vor, daß lange Zeit geladene Windbüchsen dasselbe leisteten, als ob sie soeben geladen wären. Daß die Luft im Verhältnis zur Steigerung des Druckes, der auf ihr lastet, verdichtet wird, zeigte Mariotte wie Boyle vermittelst einer U-förmig gebogenen Röhre. Er wies auch darauf hin, daß der kürzere Schenkel dieser Röhre, wenn der Beweis gelingen soll, überall gleich weit sein müsse, während dies für den längeren Schenkel nicht erforderlich sei.
Daß das Volumen der Luft dem Drucke auch dann umgekehrt proportional ist, wenn wir den Druck vermindern, bewies Mariotte auf folgende Weise. Er schloß in einem Barometerrohr Quecksilber und Luft ab und machte den Torricellischen Versuch. Das Quecksilber sank dann. »Indem es fällt«, sagt Mariotte, »dehnt die im Innern der Röhre befindliche Luft sich aus. Infolgedessen ist ihre Spannung geringer. Ein Teil des Quecksilbers bleibt in der Röhre. Und zwar wird die Höhe der Quecksilbersäule von der Dichte der eingeschlossenen Luft abhängen. Das Quecksilber, das in der Röhre schweben bleibt, hebt den Rest des Luftdrucks auf, so daß sich ein Gleichgewichtszustand bildet zwischen dem Drucke der Atmosphäre einerseits und dem Drucke der Quecksilbersäule, vermehrt um die Spannung der eingeschlossenen Luft andererseits.« Wenn die Luft im Verhältnis des Druckes, der auf ihr lastet, ihr Volumen verändert, so muß, schloß Mariotte richtig bei einem Versuche, bei dem das Quecksilber in der Röhre 14 Zoll hoch steht, die eingeschlossene Luft die doppelte Ausdehnung besitzen wie vorher, vorausgesetzt, daß zur selben Zeit ein Barometer ohne Luft eine Quecksilberhöhe von 28 Zoll anzeigt.
Um zu zeigen, daß es sich so verhält, machte Mariotte folgende Probe. Er bediente sich einer Röhre von 40 Zoll Länge und füllte 27½ Zoll Quecksilber hinein, so daß sich 12½ Zoll Luft darin befanden. Nachdem die Röhre umgedreht und[S. 214] 1 Zoll tief in das Quecksilber des Gefäßes getaucht war, fiel das Quecksilber beim Fortnehmen des Fingers und blieb nach einigen Schwankungen in einer Höhe von 14 Zoll stehen. Die eingeschlossene Luft nahm jetzt 25 Zoll387 ein, hatte also ihr Volumen verdoppelt, da sich vor dem Versuche nur 12½ Zoll Luft in der Röhre befanden. War also der Druck auf die Hälfte vermindert, so hatte sich das Volumen der Luft verdoppelt.
Die Idee des Aneroidbarometers begegnet uns zuerst bei Leibniz. Er schreibt: »Ich glaube, daß man ein Barometer ohne Quecksilber nach Art eines wohl verschlossenen Blasebalgs oder nach Art einer Pumpe herstellen kann«388. In einem Briefe an Johann Bernoulli finden sich folgende Ausführungen über diesen Gegenstand: »Ich habe zuweilen an ein tragbares Barometer gedacht, das in einen, einer Uhr ähnlichen, kleinen Behälter eingeschlossen werden könnte. Quecksilber soll dabei nicht zur Verwendung kommen, sondern eine Art Blasebalg, den das Gewicht der Luft zusammenzudrücken sucht, während er durch die Kraft einer elastischen Feder Widerstand leistet.« Zu einer brauchbaren Ausführung dieses Gedankens kam es erst um die Mitte des 19. Jahrhunderts389.
Von einem Zeitalter, das sich mit solcher Energie und mit solchem Erfolge der experimentellen Forschung zuwandte, wie das 17. Jahrhundert, ließ sich erwarten, daß auch die Chemie um manche wichtige Entdeckung bereichert würde, wenn auch diese Wissenschaft erst weit später diejenige Stufe einnahm, auf die ihre ältere Schwester, die Physik, durch Galilei und seine Zeitgenossen gelangt war.
Wir verließen die Chemie an einem Punkte ihrer Entwicklung, an dem eine wesentliche Änderung ihrer ganzen Richtung eintrat. Ihr bisheriges Ziel, den Stein der Weisen und mit dessen Hilfe Gold zu bereiten, trat nämlich im Verlauf des 16. Jahrhunderts immer mehr gegen dasjenige zurück, Präparate zur Heilung von Krankheiten herzustellen. Diese unter dem Namen der Iatrochemie bekannte Richtung der Chemie erreichte ihren Höhepunkt in van Helmont. Begründet war die Iatrochemie durch Paracelsus, mit dessen Leben und Wirken wir schon bekannt geworden sind390. Paracelsus pries in übertriebenem Maße die Heilwirkung anorganischer Verbindungen, während Libavius, der uns wie van Helmont in diesem Abschnitt beschäftigen wird, eine vermittelnde Stellung einnahm. Alle drei standen, obgleich sie der Chemie neue Ziele wiesen, noch mit einem Fuße im alchemistischen Zeitalter.
Johann Baptist van Helmont entstammte einem vornehmen niederländischen Geschlecht. Er wurde 1577 in Brüssel geboren391 und widmete sich zunächst der Theologie. Da diese ihn nicht[S. 216] befriedigte, wandte er sich der Heilkunde zu. Auch hier geriet er mit den hergebrachten, Galen entstammenden Dogmen in einen Widerspruch, aus dem ihn erst die neue, auf chemischer Grundlage errichtete Lehre des Paracelsus befreite. Van Helmont verzichtete auf eine glänzende Laufbahn, die sich ihm durch äußere Verhältnisse wohl eröffnet hätte. Er zog es vor, sich in der Stille seines Laboratoriums ganz der Forschung zu widmen.
Als besonderes Verdienst hat man es van Helmont angerechnet, daß er zum ersten Male die Verschiedenartigkeit der luftförmigen Körper hervorgehoben, sowie den Begriff und die Bezeichnung »Gas« eingeführt habe392. Vor ihm hatte man trotz ihrer großen Unterschiede Wasserstoff, Schwefeldioxyd, Kohlendioxyd und atmosphärische Luft für wesentlich ein und dasselbe gehalten. Am genauesten hat van Helmont das Kohlendioxyd untersucht. Er zeigte, daß dieses Gas sich aus Kalkstein, sowie aus Pottasche durch Übergießen mit Säuren entwickeln läßt und daß es mit dem Verbrennungsprodukt der Kohle identisch ist. Auch daß sich Kohlendioxyd in Mineralwässern findet und bei der Gärung entsteht, war ihm bekannt393.
Die Erkenntnis, daß es in der Chemie kein eigentliches Entstehen und Vergehen gibt, regte sich gleichfalls schon bei van Helmont. So lehrte er, daß Kupfer, das aus dem blauen Vitriol durch Zusatz von Eisen abgeschieden wird, nicht etwa neu entstanden sei. Auch das Silber läßt er in seinen Salzen fortbestehen. Trotz alledem beschäftigte ihn das alchemistische Problem; ja, dieses gewann infolge des Ansehens, das van Helmont genoß, sogar erhöhte Beachtung.
Um den Stein der Weisen, die Materia prima, zu gewinnen, schmolzen, kochten und mischten die Alchemisten alle Stoffe, auf die man nur verfallen konnte. »Durchprobiert«, sagt ein hervorragender Schilderer der alchemistischen Bestrebungen394, »wurde, was auf der Erde vorkommt, was sie in ihren Tiefen birgt und was auf sie herabfällt.« Man untersuchte auch Pflanzensäfte und Tiersekrete, wie Milch und Speichel, Fäces und Harn. Auf diese[S. 217] Weise wurde zwar nicht die Materia prima gefunden, aber manche wertvolle Beobachtung gemacht, vor allem wurde die Beschäftigung mit der Natur in den Mittelpunkt des menschlichen Tuns und Denkens gerückt. War man doch bis dahin in mystischen und religiösen Vorstellungen nicht selten so befangen, daß jede Beschäftigung mit natürlichen Vorgängen als sündhaft, mindestens aber als niedrig betrachtet wurde. Wenn es auch der experimentellen Forschungsweise an Mitteln und den richtigen Methoden noch sehr gebrach, so wurde doch der Boden für eine höhere, eigentlich wissenschaftliche Tätigkeit auf solche Weise vorbereitet und manche wichtige, wenn auch mehr zufällige Entdeckung gemacht. So führte das von den Alchemisten geübte Kochen, Glühen und Destillieren aller möglichen Stoffe, welche die zur Darstellung des Goldes notwendige Materia prima geben sollten, im 17. Jahrhundert zur Entdeckung des Phosphors durch den Hamburger Kaufmann Brand395. Dieser ließ sich bei seinen Versuchen von dem Gedanken leiten, daß die im Organismus tätige Lebenskraft, die so Wunderbares bewirke, imstande sein müsse, die Metalle zu verwandeln. Er unterwarf daher den beim Eindampfen von Harn erhaltenen Rückstand der trockenen Destillation. Dabei wurden die phosphorhaltigen Verbindungen des Harns durch den in der organischen Materie enthaltenen Kohlenstoff reduziert. Das auf solche Weise396 im Jahre 1669 erhaltene Element Phosphor erregte wegen seiner überraschenden Eigenschaften das größte Aufsehen.
Von Interesse sind auch die Beziehungen des Philosophen Leibniz, der über die Erfindung des Phosphors ausführlich berichtete, zu den alchemistischen Bestrebungen seiner Zeit397. Leibniz war, als er in Altdorf studierte, Mitglied der Nürnberger hermetischen Gesellschaft. Die Stellung, die er jedoch den Übertreibungen der Alchemisten gegenüber einnahm, geht aus folgenden, für das Gelehrtendeutsch jener Zeit charakteristischen Worten des großen Philosophen hervor:
»Die Laboranten, Charlatans, Marktschreier, Alchymisten und andere Vaganten und Grillenfänger sind gemeiniglich Leute von[S. 218] großem Ingenio, bisweilen auch Experienz, nur daß die disproportio ingenii et indicii, oder auch bisweilen die Wollust, die sie haben, sich in ihren eitelen Hoffnungen zu unterhalten, sie ruiniert und in Verderben und in Verachtung bringet. Gewißlich, es weiß bisweilen ein solcher Mensch mehr aus der Erfahrung und Natur gewonnene Realitäten, als mancher in der Welt hochangesehene Gelehrte, der seine aus den Büchern zusammen gelesene Wissenschaft mit Eloquenz, Adresse und anderen politischen Streichen zu schmücken und zu Markt zu bringen weiß, dahingegen der andere mit seiner Extravaganz sich verhaßt oder verächtlich macht. Daran sich aber verständige Regenten in einer wohlbestellten Republique nicht kehren, sondern sich solcher Menschen bedienen, ihnen gewisse regulierte Employ und Arbeit geben und dadurch sowohl ihr als ihrer Talente Verderben verhüten können.« (Klopp, die Werke von Leibniz. Bd. I. S. 143.)
Auch König Friedrich I. von Preußen hatte seinen Goldmacher, den Grafen Cajetan, einen Italiener, der ihm versprach, in wenigen Wochen für sechs Millionen Taler Gold zu machen. Als sich die Hoffnung des Königs nicht erfüllte, ließ er den »Grafen« aufknüpfen. Vorher hatte dieser dem Kurfürsten von Bayern und dem Kaiser große Summen durch ähnliche Versprechungen abzuschwindeln verstanden.
Im 17. Jahrhundert begegnet uns auch die Umkehrung der bisherigen Aufgabe der Alchemie. Anstatt Gold zu schaffen, wollte man gegebenes Gold zerstören oder, wie man sich ausdrückte, »aus seinem Wesen setzen«. Es erschien eine Schrift unter dem Titel »Sol sine veste oder dreißig Experimente, dem Gold seinen Purpur auszuziehen«398. Als eine solche Zerstörung des Goldes wurde z. B. die eigentümliche feinste Verteilung des Goldes im Glasfluß aufgefaßt. Selbst Kunkel glaubte, das Gold, das die Farbe des Rubinglases bewirkt, sei aus seinem Wesen gesetzt, d. h. nicht mehr als Gold vorhanden.
Bei den Stoffverwandlungen spielte auch die Lehre, daß das Wasser der Hauptbestandteil aller Stoffe sei, eine Rolle. Diese Ansicht war bei van Helmont jedoch kein bloßes Philosophem wie bei Thales. Sie stützte sich vielmehr auf, wenn auch irrtümlich gedeutete, Beobachtungen und Versuche. Van Helmont hatte z. B. 200 Pfund Erde in einem irdenen Gefäße abgewogen und in dieses eine 5 Pfund schwere Weide gepflanzt. Letztere[S. 219] wurde nur mit Regenwasser begossen. Nach Verlauf von 5 Jahren wog die Weide 170 Pfund, während das Gewicht der Erde nur um wenige Unzen abgenommen hatte. Die Gewichtszunahme der Weide schrieb van Helmont, da er die Rolle des atmosphärischen Kohlenstoffs noch nicht kannte, allein dem Wasser zu.
Im Zeitalter der Iatrochemie sind sehr wahrscheinlich auch die Schriften entstanden, die früher Basilius Valentinus (er sollte um 1450 gelebt haben) zugeschrieben wurden. Zu Beginn des 17. Jahrhunderts gab nämlich Thölde, Ratskämmerer zu Frankenhausen, eine Anzahl alchemistischer Schriften heraus. Die Titel der wichtigeren lauten: »Triumphwagen Antimonii« und »Vom großen Stein der uralten Weisen«. Diese Schriften gaben den alchemistischen Bestrebungen, die ihren Höhepunkt damals schon überschritten hatten, wieder Anregung. Nach neueren Untersuchungen beruhen sie indessen auf einer literarischen Fälschung ganz eigener Art. Sind auch die Einzelumstände dieser Fälschung noch nicht genügend aufgeklärt, so ist doch so viel gewiß, daß die unter dem Namen des Basilius Valentinus gehenden Schriften nicht von einem im 15. Jahrhundert lebenden Mönche dieses Namens herrühren, sondern erst gegen das Ende des 16. oder zu Beginn des 17. Jahrhunderts verfaßt wurden.
Die Aufnahme zahlreicher anorganischer Verbindungen unter die Heilmittel rief anfangs manchen und gewiß sehr oft berechtigten Widerstand hervor. In Heidelberg z. B. ließ die medizinische Fakultät noch bis zur Mitte des 17. Jahrhunderts diejenigen, denen sie die Doktorwürde verlieh, schwören, daß sie niemals von Antimon- und Quecksilberpräparaten in ihrer ärztlichen Praxis Gebrauch machen wollten. Ein ähnliches Verbot bestand auch in Paris.
Zwischen den Paracelsisten und den Anhängern der älteren Heilkunde suchte besonders Libavius zu vermitteln. Andreas Libavius wurde in Halle geboren399. Er studierte Medizin, Geschichte und Sprachwissenschaften und starb im Jahre 1616 als Direktor des Gymnasiums zu Coburg. Libavius war der namhafteste deutsche Chemiker seiner Zeit. Wir verdanken ihm das erste Lehrbuch der Chemie, seine 1595 erschienene Alchymia, mit dem wir uns etwas näher befassen wollen. Wie schon der Titel sagt und wie die ersten Sätze des Buches lehren, war Libavius ein erklärter Anhänger der Alchemie. Sie ist für ihn die Kunst,[S. 220] die Magisterien, d. h. die Stoffe, die zur Metallverwandlung dienen, zu erzeugen und die reinen Grundbestandteile aus ihren Mischungen abzuscheiden400. Als Grundbestandteile oder Prinzipien unterscheidet auch er Mercurius, Sal und Sulphur. Der zweite Teil der »Alchymia« des Libavius ist das eigentliche Lehrbuch der Chemie, da sich darin im wesentlichen eine Darstellung der zu seiner Zeit bekannten chemischen Tatsachen und die Grundzüge einer Dokimasie (Probierkunst) finden. Die Überschriften der einzelnen Abschnitte lauten:
Als solche werden aufgezählt: Quecksilber, Wismut, Antimon, Schwefel und Arsen.
Libavius untersuchte die schon lange vor ihm bekannten Bleisalze, Bleizucker und Bleiessig, genauer und brachte sie als Heilmittel in Vorschlag. Er vereinfachte die Darstellung der Schwefelsäure und wies nach, das die aus Alaun, Vitriol oder Schwefel erzeugte Säure ein und dieselbe Substanz ist.
Wie der gleichzeitig lebende Agricola bemühte sich Libavius auch, Mittel und Wege anzugeben, um in den Erzen und den metallischen Präparaten den Metallgehalt nachzuweisen. Beide begründeten die, durch hüttenmännische Erfahrungen allerdings seit alters vorbereitete, metallurgische Probierkunst (Dokimasie). So legte sich Libavius die Frage vor, wieviel Gold anderen Metallen, wie dem Silber, dem Blei oder dem Quecksilber beigemengt sei, wie man den Silbergehalt der Bleiglätte ermitteln könne usw. Von besonderem Werte ist das Buch des Libavius noch dadurch, daß es eine genaue Beschreibung der gegen den Ausgang des 16. Jahrhunderts üblichen chemischen Apparate und Vorrichtungen enthält. Neben der Wärme suchte man z. B. auch das Licht als chemisches Agens zu verwerten, wovon uns die Abbildungen des Libavius eine Vorstellung geben.
Eine große Förderung erfuhr die Chemie in Deutschland durch das Emporblühen der Gewerbe. Als der wichtigste Vertreter der infolgedessen als besonderer Wissenszweig aufkommenden angewandten Chemie begegnet uns Glauber. Johann Rudolf Glauber (1604–1668) bereicherte die anorganische Chemie um eine Reihe von Entdeckungen, die zumeist die Chlorverbindungen betreffen. Auf dieses Gebiet wurde Glauber dadurch geführt, daß er die Darstellung der Salzsäure durch Einwirkung von Schwefelsäure auf Kochsalz kennen lernte. Ganz entsprechend stellte er auch die Salpetersäure aus Salpeter und Schwefelsäure her. Das dabei auftretende Natriumsalz der Schwefelsäure ist nach ihm Glaubersalz genannt worden401. Das Chlor soll Glauber gleichfalls schon gekannt haben. Vor Glauber hatte man die Chloride aus den Metallen hergestellt, indem man letztere mit Sublimat (Quecksilberchlorid) erhitzte. Infolgedessen war man zu der irrtümlichen Annahme gelangt, daß in den Chlorverbindungen der Metalle Quecksilber enthalten sei. Glauber lehrte dagegen, sie seien Verbindungen der Metalle mit Salzsäure. Er traf damit zwar auch noch nicht das Richtige, da es sich nur um den einen Bestandteil der Salzsäure, das Chlor, handelt, dessen Reindarstellung erst Scheele gelang. Die Chloride, die Glauber untersucht und beschrieben, zum Teil auch als erster reiner dargestellt hat, sind Zinn- und Zinkchlorid, Eisenchlorid, Chlorblei, Arsen- und Kupferchlorür. Auch das Chlorsilber und seine Entstehung aus Silberlösung durch Zusatz von Salzsäure wurde damals bekannt. Ferner gelang Glauber die Darstellung des als vulkanisches Produkt schon lange bekannten Salmiaks durch die Einwirkung der Salzsäure auf das unter dem Namen »flüchtiges Laugensalz« bekannte kohlensaure Ammoniak. Letzteres hatten die Alchemisten früherer Jahrhunderte durch Destillation von gefaultem Harn gewonnen.
Man kann sich denken, welche Umwälzung, aber auch welchen Mißbrauch, all diese Präparate, die in der übertriebensten Weise und mit der größten Geheimnistuerei angepriesen wurden, auf dem Gebiete der Heilkunde hervorriefen. Insbesondere war man bemüht, neue Arsen-, Antimon- und Quecksilberpräparate herzustellen[S. 222] und für Heilzwecke zu benutzen. So lernte man antimonsaures Kalium und einige weinsaure Salze kennen. Die Einwirkung von Antimonoxyd auf Weinstein lieferte den Brechweinstein, der gleichfalls für den Arzneischatz sofort die größte Bedeutung erlangte. Es ist begreiflich, daß das wissenschaftliche Interesse an den beobachteten Vorgängen und Verbindungen der medizinischen Bedeutung gegenüber immer mehr überwog, so daß das Ziel der Chemie verschoben wurde. Aus einem bloßen Zweige der Heilkunde erwuchs auf diese Weise, ganz ähnlich, wie es der Zoologie und der Botanik ergangen war, die reine Wissenschaft, die ihren Gegenstand, losgelöst von allen Nützlichkeitsbestrebungen, um seiner selbst willen zu erforschen bemüht ist.
Ein wissenschaftliches Ergebnis der experimentellen Arbeiten Glaubers war z. B. das klarere Hervortreten des Begriffes der chemischen Verwandtschaft. So braucht Glauber, wenn er von der Befreiung des Ammoniaks aus Salmiak durch die Einwirkung von Kalk handelt402, den Ausdruck, der eine Bestandteil des Salmiaks »liebe den Kalk mehr als der andere und werde auch von dem Kalke mehr geliebt«. Auch die doppelte Verwandtschaft ist ein Begriff, der in seinen Anfängen bis auf Glauber zurückgeht. So führte er aus, daß aus Quecksilberchlorid und Schwefelantimon durch wechselseitigen Austausch der Bestandteile Schwefelquecksilber und Antimonchlorid hervorgehen. Um eine Probe der damals herrschenden Ausdrucksweise zu geben, sei hier diese Umsetzung in Glaubers Sprache unter Hinzufügung der heutigen Formeln beschrieben: »Wenn der Mercurius sublimatus (HgCl2) mit Antimonio (Sb2S3) vermischt die Hitze empfindet, so greifen die Spiritus (Cl), die bei dem Mercurio sublimato sein, den Antimonium (Sb2S3) lieber an und lassen den Mercurium (Hg) wieder fallen, und geht also ein dick Oleum (SbCl3) über. Der Sulphur antimonii (S) aber konjugiert sich mit dem Mercurio vivo (Hg) und gibt einen Zinnober (HgS), der im Halse der Retorte bleibt«403.
Die ursprüngliche Vorstellung, daß ähnliche Stoffe mit einander verwandt seien, wich der richtigen Erkenntnis, daß gerade die verschiedenartigsten Stoffe das größte Vereinigungsbestreben haben. Am deutlichsten sprach es Hermann Boerhaave (1668–1738) aus, daß gerade nicht verwandte Stoffe die Kraft besitzen, die man[S. 223] als chemische Verwandtschaft oder Affinität bezeichnet, ein Wort, das uns schon bei Albertus Magnus begegnet.
Als überzeugter Anhänger der Alchemie kann Glauber nicht mehr gelten. Er sagt von ihr: »Wer Zeit und Gelegenheit haben mag, solche Arbeiten im großen anzustellen, dem ist es nicht gewehrt, zu versuchen, ob Nutzen damit zu erlangen ist«. Auch bekennt er, daß er selbst nicht den geringsten Erfolg »in Verbesserung der Metalle« gehabt habe.
Glaubers Hauptwerk führt den Titel »Novi furni philosophici«. Es erschien zuerst im Jahre 1648 unter der deutschen Bezeichnung »Beschreibung einer Destillierkunst«. Über Glaubers Verfahren sei auf Grund seiner dort gegebenen Darstellung noch einiges mitgeteilt. Das Kapitel, das von der Salzsäure handelt, überschreibt er: »Wie man einen Spiritus salis destillieren soll«. Die Vorschrift lautet: »Man nimmt gewöhnliches Kochsalz und mischt Vitriol oder Alaun darunter. Diese Mischung bringt man über glühende Kohlen. Der davon ausgehende Spiritus wird in einem Rezipienten verdichtet (siehe Abb. 66). Nun könnte jemand sagen, daß dieser Spiritus salis nicht rein sei,[S. 224] denn der Spiritus des Vitriols oder des Alauns gehe auch mit über. Darauf antworte ich, daß dies nicht der Fall ist. Ich habe nämlich häufiger Vitriol oder Alaun für sich in den Ofen gebracht. Dann ist gar kein Spiritus gekommen. Die Ursache ist die, daß der Spiritus des Vitriols oder des Alauns nicht emporsteigt, sondern im Ofen verbrennt.« Die Abbildung seines Ofens erläutert Glauber, wie folgt: A ist der Ofen mit seinem eingemauerten eisernen Destilliergefäß, daran ein Rezipient akkommodiert ist. C zeigt die Gestalt des Destilliergefäßes, und D läßt erkennen, wie »es inwendig anzusehen ist«.
Der nächste Abschnitt handelt von der Verwendung der Salzsäure (De usu Spiritus salis). Glauber preist sie als »eine herrliche Medizin für den innerlichen und den äußerlichen Gebrauch«, als Lösungsmittel für alle Mineralien und Metalle »excepta Luna« d. h. mit Ausnahme des Silbers. Im Haushalt soll die Salzsäure an die Stelle von Essig treten, da Fleisch, Geflügel und anderes mit Salzsäure zubereitet »viel lieblicher schmecke«.
Die weiteren Vorschriften Glaubers beziehen sich auf die Darstellung von Schwefelsäure, Salpetersäure und Königswasser, sowie deren Verwendung. Durch Destillation von Vitriol erhält er die Schwefelsäure als »ein schweres Oleum, das man mit starkem Feuer vertreiben und rektifizieren kann, wodurch es klar wird«. Mit diesem »korossiven Oleum Vitrioli« könne man auch etliche Metalle solvieren und in ihre Vitriole umwandeln, so Eisen und Zink. Man müsse jedoch Wasser hinzufügen, da das Oleum sonst nicht angreife.
Die Verwendung zu Heilzwecken spielt auch hier eine Rolle, so soll die Wärme, die sich bei der Einwirkung der Säure auf Eisen entwickelt, Krankheiten zu heilen vermögen.
Vom Spiritus Nitri (Salpetersäure) heißt es, er werde zwar in fast allen Apotheken gefunden, aber in der Heilkunde nicht viel gebraucht. Aqua regis (Königswasser) endlich bereitet Glauber, indem er in gläsernen Retorten Kochsalz in Salpetersäure auflöst.
In einem zweiten, »Teutschlands Wohlfahrt« betitelten Werke suchte Glauber die Bedeutung der Chemie für die Volkswirtschaft darzutun. »Dieses Werk«, sagt er in seiner Einleitung, »mit dem ich meinem Vaterlande zu dienen mir vorgenommen, besteht in Offenbarung der in Deutschland verborgenen großen Schätze, die zwar bisher auch sind gewonnen worden, aber nicht, wie es wohl hätte sein sollen und können. Z. B. läßt sich das Holz, so[S. 225] doch liegt und verdirbt, zu Salpeter machen, um den Feinden damit die Spitze zu bieten. In künftigen großen Landsterben werden sich ferner durch Konzentrieren der Mineralien und Metalle gute Medikamente bereiten lassen.«
Sehr gefördert wurde die Chemie während des 17. Jahrhunderts durch die Arbeiten Boyles. Robert Boyle wurde im Jahre 1626 geboren. Er studierte in Oxford und in Genf und lebte von 1668 an in London, wo er mit Newton, Hooke und anderen hervorragenden Gelehrten die Royal Society gründete. Der gemeinsame Grundzug dieser Männer war der, daß sie sich bei ihren, im Geiste echter Forschung ausgeführten Arbeiten lediglich von dem Streben nach Naturerkenntnis und von keinerlei Nebenabsichten leiten ließen. Boyle war der erste, der die wahre Aufgabe der Chemie in der Erkenntnis der Zusammensetzung der Körper erblickte. »Die Chemiker« sagt er404, »haben sich bisher durch enge Prinzipien, die der höheren Gesichtspunkte entbehrten, leiten lassen. Sie erblickten ihre Aufgabe in der Bereitung von Heilmitteln und in der Verwandlung der Metalle. Ich habe versucht, die Chemie von einem ganz anderen Gesichtspunkte aus zu behandeln, nicht als Arzt, noch als Alchemist, sondern als Naturphilosoph«. Er habe, fährt er fort, den Plan für eine chemische Philosophie gezeichnet, die er durch seine Versuche und Beobachtungen zu vervollständigen hoffe. Den Menschen müsse der Fortschritt der Wissenschaft mehr am Herzen liegen als ihre engeren Interessen. Der Welt würde dadurch der größte Dienst geleistet, daß man Versuche anstelle, Beobachtungen sammle und keine Theorie aufstelle, ohne zuvor die in Betracht kommenden Erscheinungen geprüft zu haben.
Mit der Aufstellung dieser Gesichtspunkte begann für die Chemie ein neues Zeitalter. Indem Boyle als letzte Bestandteile, als Elemente im Sinne der heutigen Wissenschaft, diejenigen Stoffe ansprach, die keiner weiteren Zerlegung fähig sind, war das Schicksal der aristotelischen Elemente (Feuer, Erde, Luft und Wasser), sowie der Prinzipien der Alchemisten (Salz, Schwefel und Quecksilber) besiegelt. Auch der Unterschied zwischen mechanischer Mischung und chemischer Verbindung wurde von Boyle zum ersten[S. 226] Male scharf hervorgehoben. Als charakteristisch für die Verbindungen stellte er das Verschwinden der Eigenschaften der Bestandteile bin.
Anknüpfend an van Helmont destillierte Boyle Regenwasser aus Glasgefäßen. Er fand stets einen Rückstand und glaubte damit gleichfalls bewiesen zu haben, daß sich das Wasser in erdige Bestandteile verwandeln lasse. Erst durch Lavoisier und Scheele wurde der wahre Sachverhalt aufgeklärt und die Ansicht, daß das Wasser eine derartige Umwandlung erfahren könne, als unhaltbar nachgewiesen. Ein zweiter wichtiger Versuch, an den Lavoisier bei der Begründung der neueren Chemie anknüpfte, betrifft die Verkalkung (Oxydation) der Metalle beim Erhitzen an der Luft. Boyle schmolz Zinn und Blei und wies nach, daß der erhaltene Metallkalk schwerer ist als das Metall405. Um dies zu erklären, nahm er aber an, daß ein aus dem Feuer stammender Stoff das Gefäß, in dem die Schmelzung vor sich geht, durchdringe und sich mit dem Metall verbinde. Ein ähnlicher hypothetischer, von Lavoisier später als unhaltbar erkannter Stoff, das Phlogiston, das bei der Verbrennung entweichen sollte, erhielt bei den auf Boyle folgenden Chemikern eine solche Bedeutung, daß das von Boyle bis Lavoisier reichende Zeitalter der Chemie das phlogistische genannt wird.
Durch die Forschungen Boyles, dem seine Landsleute den Beinamen des großen Experimentators gegeben haben, wurde auch die analytische Chemie begründet. Bisher hatte man sich bei qualitativen Untersuchungen wesentlich auf das sogenannte trockene Verfahren beschränkt, das heute noch bei der Vorprüfung, sowie bei der Bestimmung von Mineralien Anwendung findet. Boyle lehrte die in Lösung gebrachte Substanz mit Hilfe flüssiger Reagentien untersuchen, indem er aus der Entstehung und der Beschaffenheit von Niederschlägen auf die Zusammensetzung des zu untersuchenden Stoffes schloß. So wies er Salzsäure mittelst Silberlösung und Schwefelsäure durch Kalksalze nach. Er fällte Eisen durch Galläpfeltinktur406 und bediente sich zum Nachweise der Säuren mit Pflanzensäften gefärbter Papiere, alles Verfahrungsarten, die auch heute noch im Gebrauch sind.
In das Zeitalter Boyles fällt auch eine Vorwegnahme der antiphlogistischen Lehre durch den englischen Arzt John Mayow,[S. 227] dessen Verhältnis zu Lavoisier etwa dasselbe ist wie auf astronomischen Gebiete dasjenige Aristarchs zu Koppernikus.
John Mayow wurde im Jahre 1643 in London geboren. Er widmete sich der Heilkunst, die er in dem kleinen Badeorte Bath ausübte. Zur Beschäftigung mit der Chemie wurde er dadurch geführt, daß er die Heilquelle von Bath untersuchte. Später wurde Mayow Mitglied der Royal Society. Bald darauf (1679) starb er in noch jugendlichem Alter in London. Mayow war gleich vielen Forschern seines Zeitalters ein eifriger Anhänger der Philosophie des Descartes, dessen Werke ihn zur mechanistischen Erklärung der Naturvorgänge angeregt hatten. Seine wichtigsten Untersuchungen und Betrachtungen legte Mayow in seinem »Tractatus quinque« genannten Werke nieder. Den für die Entwicklung der Chemie bedeutendsten Abschnitt dieser Schrift bilden die in deutscher Übersetzung erschienenen »Untersuchungen über den Salpeter und den salpetrigen Luftgeist, das Brennen und das Atmen«407. Leider fanden die Arbeiten Mayows nicht die verdiente Beachtung. Sie gerieten infolgedessen schließlich in Vergessenheit. Es erging ihnen ähnlich wie später den botanischen Arbeiten Sprengels, die trotz ihrer außerordentlichen Bedeutung gleichfalls ein Jahrhundert ruhten. Erst nach der Entdeckung des Sauerstoffs und nach der Begründung der antiphlogistischen Theorie durch Lavoisier wurde von deutscher und englischer Seite darauf hingewiesen, daß schon Mayow das wahre Wesen der Verbrennung und der Atmung erkannt habe. Hätte Mayow größere Beachtung gefunden und länger gelebt, um seine Lehre fester zu begründen, so wäre die chemische Wissenschaft schwerlich ein Jahrhundert in der irrigen Phlogistontheorie befangen geblieben. Man muß nämlich erwägen, daß die Gewichtszunahme, welche die Metalle beim Erhitzen an der Luft erfahren, im 17. Jahrhundert schon von mehreren Seiten, wie von Hooke, Boyle und Rey, festgestellt worden war. Rey war es auch, der diese Erscheinung auf den Zutritt der Luft zu den Metallen zurückführte. Und Hooke, der so oft mit seinen knappen Bemerkungen das Richtige traf und ja auch die Gravitationstheorie vorwegnahm, gab in seiner Mikrographie (1665) eine Verbrennungstheorie, die gleichfalls schon den Keim der antiphlogistischen Lehre enthielt. Hooke nahm nämlich an, daß in der Luft und[S. 228] im Salpeter ein Stoff enthalten sei, der auf die brennbaren Körper wirke.
Von der Untersuchung des Salpeters geht auch Mayow aus. Dieser wunderbare Stoff, meinte er, sei berufen, in der Wissenschaft ebensoviel Lärm wie im Kriege zu verursachen. Als Bestandteile des Salpeters lehre seine Entstehung und seine Zerlegung einen sauren Salpetergeist (wie er die Salpetersäure nannte) und eine alkalische Substanz kennen. Gieße man nämlich die durch Destillation aus dem Salpeter erhaltene Säure auf ein geeignetes alkalisches Salz, so bilde sich der Salpeter mit all seinen bekannten Eigenschaften von neuem. Auch der natürliche Salpeter entstehe durch die Einwirkung von Salpetergeist auf alkalische Salze des Bodens; doch dürfe man nicht annehmen, daß der Salpetergeist, d. h. die Salpetersäure, als solcher in der Luft enthalten sei. Vielmehr sei in der Luft nur ein Teil dieses Geistes enthalten, nämlich die salpetrige Luftsubstanz. Letztere unterhalte die Verbrennung und die Atmung. Sie ist also mit dem Sauerstoff der Antiphlogistiker völlig identisch.
Es verdiene auch Erwähnung, bemerkt Mayow, daß Antimon durch Verkalkung an Gewicht zunehme408. Es sei schwer einzusehen, woher diese Gewichtszunahme rühre, wenn nicht von den mit dem Metall sich verbindenden Luftteilchen. »Ich weiß sehr wohl«, fügt er hinzu, »daß nach der gewöhnlichen Meinung die Verkalkung des Antimons in der Entfernung seines Schwefels bestehen soll. Trotzdem bin ich geneigt zu glauben, daß diese Ansicht kaum die Wahrheit trifft«.
Der Hauptzweck der Atmung besteht nach Mayow darin, gewisse, dem tierischen Leben unentbehrliche Teilchen aus der Luft den Lungen zuzuführen und sie mit dem Blute auf das innigste zu vermischen. Er habe, sagt Mayow, Versuche angegeben, welche zeigten, daß die von den Lungen ausgeatmete Luft gewisser Teilchen beraubt sei, wobei sie gleichzeitig eine Volumverminderung erfahren habe. Letztere werde dadurch hervorgerufen, daß der Luft die salpetrigen Luftteilchen (d. h. der Sauerstoff) entzogen wurden.
Mayow legt sich sodann die Frage vor, welche Aufgabe der in das Blut gelangende Sauerstoff im Organismus zu erfüllen habe und findet auch hierauf eine im ganzen richtige Antwort. »Ich huldige der Ansicht« bemerkt er, »daß sowohl bei den Tieren als[S. 229] auch bei den Pflanzen der salpetrige Luftgeist die Hauptquelle des Lebens und der Bewegung ist«. Auch die Körperwärme könne man nicht etwa auf eine in den Gelenken stattfindende Reibung zurückführen. Sie rühre vielmehr gleichfalls von der Wirkung des Sauerstoffes auf das Blut her, in dem brennbare Stoffe in Menge vorhanden seien. Daß das Blut bei seinem Eintritt in die Lunge dunkelrot, und beim Verlassen hellrot ist, war eine Mayow bekannte, durch die Erfahrung längst ermittelte Tatsache. Daß es sich hierbei um eine chemische Einwirkung der Luft auf das Blut handelt, geht ihm daraus hervor, daß venöses, der Luft ausgesetztes Blut an der Oberfläche hellrot wird, während die unteren Schichten dunkelrot bleiben.
Im Lichte der von Mayow entwickelten Theorie der Atmung gewannen also auch verwandte Gebiete der Physiologie, wie die Tätigkeit und das Zusammenwirken der Atmungs- und der Kreislauforgane, an Klarheit. Auch darauf wies Mayow hin, daß beim Fötus an die Stelle der Atmung die Versorgung mit Sauerstoff durch das arterielle, an Sauerstoff so reiche Blut der Mutter tritt.
Die von Mayow ausgesprochenen Ansichten waren nicht etwa lediglich glückliche Einfälle, sondern das Ergebnis oft sehr sinnreich ausgedachter Versuche. Eins der schönsten Beispiele, und wohl eine der ersten gasometrischen Untersuchungen, ist folgendes: Man bringe einen Stab in der Weise, wie es die Abbildung 67 zeigt, in einem Glasgefäße an. An diesen Stab hänge man einen glasierten, mit Salpetersäure (Salpetergeist nennt sie Mayow) gefüllten Topf. Dicht über den Topf wird an einem Faden ein Bündel von Eisenstückchen befestigt. Der Faden wird zunächst über den Stab und dann unter den Rand des Gefäßes hinaus geführt (siehe Abb. 67), so daß man das Eisenbündel in die Säure tauchen und wieder herausziehen kann. »Nachdem«, fährt Mayow fort, »die durch Berührung mit den Händen erwärmte Luft sich abgekühlt hat und die Höhe des inneren Wasserspiegels angemerkt worden ist, lasse man die Eisenstücke in die Säure gleiten«. Es entstand eine lebhafte Einwirkung, und das innere[S. 230] Niveau wurde durch die entwickelten Dämpfe zunächst herunter gedrückt. Nachdem die Reaktion einige Zeit gedauert, zog Mayow das Eisen wieder empor. Jetzt stieg das Wasser über den ursprünglichen Stand hinaus, wobei »ein Viertel des von der Luft ursprünglich erfüllten Raumes von dem Wasser eingenommen wurde«. Diese Raumverminderung wird ganz richtig auf die Fortnahme des Sauerstoffes oder, wie Mayow sagt, der salpetrigen Luftteilchen zurückgeführt409. »In der Tat«, sagt er, »erfährt hier die Luft eine Verminderung auf ganz dieselbe Weise wie bei der Verbrennung«. Das ein Jahrhundert später erfundene Eudiometer beruht auf derselben Wechselwirkung zwischen den aus der Salpetersäure entstehenden Gasen und dem Sauerstoff der Luft410.
Wir haben in einem früheren Abschnitt die ersten Ansätze zur Neubegründung der organischen Wissenschaften kennen gelernt. Das wichtigste Ergebnis auf dem Gebiete der Botanik waren die Entstehung der Kräuterbücher (Bock und Brunfels), die Anlage der ersten botanischen Gärten und Herbarien, sowie die Ausdehnung der Florenkenntnis auf die neuentdeckten außereuropäischen Länder. Gleichzeitig erfolgte die Neubegründung der Zoologie durch die umfassenden Werke eines Gesner und eines Aldrovandi. Wotton verbesserte die Systematik, während Vesal die Grundlagen der neueren Anatomie errichtete.
In der Pflege der Botanik zeichneten sich neben den Deutschen besonders die Niederländer aus. War doch die Anregung, welche diesem Volksstamm durch den Handel und die Entdeckungsreisen auf naturhistorischem Gebiete zuteil wurde, nicht gering. Auch standen schon damals der Gartenbau und die Blumenzucht in den Niederlanden in hoher Blüte. Als der größte Botaniker des 16. Jahrhunderts gilt Carolus Clusius in Antwerpen (1525–1609). Er war eine Zeitlang mit der Verwaltung der kaiserlichen Gärten in Wien betraut und fand dadurch Gelegenheit, auch Ungarn naturhistorisch zu durchforschen. Clusius starb als Professor der Naturgeschichte in Leyden im Jahre 1609, nachdem er die Botanik um eine derartige Fülle neuer Arten bereichert hatte, wie niemand vor und nach ihm. Die Frucht seines Aufenthalts in Österreich-Ungarn war eine Flora von Osteuropa411. Von Augsburg hatte er mit Angehörigen des Hauses Fugger eine Reise[S. 232] durch Frankreich, Spanien und Portugal unternommen. Das Ergebnis dieser Reise war ein floristisches Werk über die pyrenäische Halbinsel412. Außerdem hat Clusius als einer der ersten die Pflanzen Indiens und der Levante beschrieben413. Er hat die neuen Arten auch vortrefflich abgebildet.
Clusius konnte sein Vorhaben nur mit Unterstützung von zahlreichen Forschern und Reisenden vollbringen. Unter seinen Mitarbeitern ist vor allem der Niederländer Lobelius zu nennen. Er wurde 1538 geboren und starb 1616 in England, wo er die königlichen Gärten verwaltete.
Bei Lobelius tritt das Gefühl für die natürliche Verwandtschaft schon sehr deutlich hervor. So bilden die Gräser, die Liliaceen, die Orchideen, die Kreuzblüter, die Doldengewächse, die Schmetterlings- und die Lippenblüter bei ihm schon deutlich erkennbare Gruppen.
Während man sich im 16. Jahrhundert in Mitteleuropa vorzugsweise der umgebenden Pflanzenwelt zuwandte, bemühten sich die Italiener um diese Zeit in erster Linie um die Erklärung der alten botanischen Schriften. Da sie aber merkten, daß bei Dioskurides und Plinius nur ein geringer Bruchteil der in Italien vorkommenden Pflanzen erwähnt wird, wandten auch sie sich zumal in Norditalien der Erforschung der heimatlichen Flora zu. Hier waren es besonders die südlichen Kalkalpen, die durch ihren außergewöhnlichen Pflanzenreichtum die Aufmerksamkeit von Apothekern, Ärzten und anderen der Botanik obliegenden Männern auf sich zogen. So entstanden mehrere Monographien, die sich ausschließlich mit der Flora des an Pflanzen so reichen Monte Baldo, eines östlich vom Gardasee gelegenen Kalkgebirges, beschäftigten.
Einer der hervorragendsten unter den italienischen Botanikern des 16. Jahrhunderts war Mattioli (1501–1577). Er wußte wie kein anderer den Dioskurides zu kommentieren und »mit seltener Spürkraft die Pflanzen der Alten zu erraten«414. Mattioli war auch ein scharfer Beobachter und eifriger Sammler, der die Wissenschaft um die Kenntnis zahlreicher neuer Arten bereicherte.
Das Bestreben, an die Stelle der anfangs üblichen alphabetischen eine natürliche Anordnung zu setzen, fand eine Fortsetzung[S. 233] bei Bauhin, in dem die erste Periode der neueren Botanik ihren Gipfel erreichte.
Kaspar Bauhin wurde 1550 als Sohn eines Arztes in Basel geboren. Er verbrachte einen Teil seiner Studienzeit in Padua und durchforschte die Flora von Deutschland, Italien und Frankreich. Ganz davon abgesehen, daß Bauhin zahlreiche neue Arten entdeckte, besteht sein großes Verdienst in der Durchführung der erschöpfenden Artdiagnose, der Einführung der binären Nomenklatur, der Anordnung der Pflanzen nach ihrer Ähnlichkeit, und endlich der Entwirrung der zahllosen Synonyme.
Wir beginnen mit dem letzten Punkte. Seit dem Wiederaufleben der Botanik waren in allen Teilen Europas und in den entdeckten außereuropäischen Ländern neue Pflanzen bekannt geworden, die an Zahl die von den Alten beschriebenen Pflanzen bei weitem übertrafen. Die Benennung dieser neuen Pflanzen war aber ohne einheitliche Gesichtspunkte und zum Teil unter ganz willkürlicher Verwertung der alten Pflanzennamen erfolgt. Ja, derselben Art waren von den verschiedenen Schriftstellern häufig auch verschiedene Namen beigelegt, und die gleichen Namen für verschiedene Arten gebraucht worden. Die Verwirrung war also eine schlimme und drohte jeden gesunden Fortschritt der Wissenschaft, für die der Name keineswegs »Schall und Rauch« ist, zu untergraben. Diesem unhaltbaren Zustande machte Bauhin durch sein in vierzigjähriger, mühevoller Arbeit entstandenes Werk über die Pflanzensynonyme ein Ende415. In ihm wies er für alle ihm bekannten, etwa 6000 Arten die von den verschiedenen Botanikern gebrauchten Namen nach und schuf damit für die botanische Literatur das vollständigste Synonymenwerk, das noch heute für den Systematiker wichtig ist. »Gewiß kein kleines Lob, das einem Buche nach 250 Jahren noch gespendet werden kann«416.
Auf solche Weise brachte Bauhin nicht nur Ordnung in die gelehrten Arbeiten seiner Vorgänger, sondern er beugte auch durch die vorbildliche Art, wie er selbst die Pflanzen benannte und beschrieb, dem Einreißen einer neuen Verwirrung vor. Die Beschreibung der Pflanzen wurde nämlich von ihm zu der Kunst ausgebildet, in wenigen Zeilen erschöpfende, die Wiedererkennung leicht ermöglichende Diagnosen zu geben. Jede von[S. 234] ihnen berücksichtigte in aller Kürze sämtliche Teile der Pflanze. Die Form, die Größe, die Verzweigung der Wurzel und des Stengels, die Gestalt der Blätter, die Beschaffenheit der Blüte, der Frucht und des Samens: alles wurde in knappen, treffenden Worten aufgeführt, ohne den Raum von etwa 20 Zeilen zu überschreiten. Ferner wurden Arten und Gattungen bei ihm scharf und bewußt unterschieden. Jede Art erhielt eine meist aus zwei Wörtern bestehende Benennung, die als Gattungs- und als Speziesnamen gelten können. Die binäre Nomenklatur, um deren Durchführung sich später Linné so große Verdienste erworben hat, ist also auf Bauhin zurückzuführen.
Endlich tritt bei Bauhin in seinem Synonymenwerk die Anordnung nach der Ähnlichkeit in den gesamten Merkmalen, nach natürlichen Familien würden wir heute sagen, noch mehr wie bei Lobelius hervor, ohne daß jedoch die so erhaltenen Gruppen benannt oder deutlich voneinander getrennt worden wären. Auch Bauhin beginnt mit den Gräsern, die er für die einfachsten Blütenpflanzen hielt. Es folgen die Liliengewächse, die wichtigsten Familien der krautartigen Pflanzen und endlich die Bäume. Die Sonderstellung der Farnkräuter vermochte Bauhin so wenig wie Lobelius zu erkennen. Auch fehlt es nicht an Zusammenstellungen, die uns heute als große Irrtümer erscheinen. So bringt Bauhin z. B. die phanerogamen Wasserlinsen mit den Moosen, und die Schwämme mit den Meeresalgen in Verbindung. Andererseits dürfen wir ihm solche Fehler nicht zu sehr anrechnen, weil das Verhältnis der Kryptogamen zu den Phanerogamen erst Jahrhunderte nach Bauhin seine Aufklärung gefunden hat und die Natur der Pflanzentiere erst im 18. Jahrhundert durch Trembley enthüllt wurde.
Während das induktive Verfahren, dessen Ansätze uns in den Kräuterbüchern begegnen, zu einer wenn auch noch mangelhaften natürlichen Systematik führte, ging man in Italien bei der Neubegründung der Botanik vielfach noch in aristotelischer Weise von vorher getroffenen Einteilungsprinzipien aus. Hier suchte Caesalpin den immer mehr anschwellenden Artenreichtum zu bewältigen, indem er seiner Anordnung insbesondere die Beschaffenheit der Früchte zugrunde legte. Diese Richtung der einseitig künstlichen Systematik[S. 235] wurde in der Folge zunächst zur herrschenden, weil sie dem Bedürfnis der Praxis besser entsprach als die noch unvollkommene natürliche Gruppierung, die für die Wissenschaft jedoch einen höheren Wert besitzt. Wir werden später Linné als denjenigen kennen lernen, dem das von Caesalpin erstrebte Werk gelang. Linné erwies diesem seinem Vorgänger auch alle Anerkennung, indem er ihn als den ersten wahren Systematiker bezeichnete.
Das botanische Hauptwerk des Andrea Caesalpino417 erschien 1583 unter dem Titel: De plantis libri XVI. Caesalpin liefert darin zwar auch Beschreibungen einzelner Pflanzen, er geht aber nach zwei Richtungen über die Verfasser der Kräuterbücher hinaus. Einmal beschränkt er sich nicht wie jene auf die Schilderung des allgemeinen Habitus einer Pflanze, sondern er untersucht die einzelnen Pflanzenteile genau und berücksichtigt dabei besonders die Fruktifikationsorgane. Zweitens begegnet uns bei Caesalpin eine denkende, philosophische Betrachtung der Pflanze im allgemeinen und ihrer Natur. Die Grundzüge der theoretischen Botanik, zu denen er auf diese Weise in der Einleitung zum ersten Buche seines Werkes gelangte, sind indessen in überwiegend aristotelischem Sinne abgefaßt. Da die Pflanze ausschließlich jene Art von Seele besitze, durch welche die Ernährung, das Wachstum und die Fortpflanzung erfolge, so begnüge sie sich mit viel einfacheren Werkzeugen als das Tier, dem außerdem noch Bewegung und Empfindung zukomme. Die Tätigkeit der Pflanzenseele bestehe darin, durch die Ernährung das Einzelwesen und durch die Fortpflanzung die Art zu erhalten. Daher seien der Pflanze zwei Teile verliehen, die Wurzel, durch die sie die Nahrung aufnehme, und der Stengel, der die Frucht erzeuge. Für die niederen Pflanzen, wie die Pilze und die Flechten, an denen Caesalpin noch keine Fortpflanzungsorgane wahrzunehmen vermochte, nimmt er mit Aristoteles die Urzeugung (Generatio spontanea) an. Sie entständen durch Fäulnis und brauchten sich daher nur zu ernähren und zu wachsen. Sie seien Mitteldinge zwischen der unorganischen Natur und den vollkommenen Pflanzen, wie es ja auch Übergangsstufen zwischen den letzteren und den Tieren gebe.
Der Einfluß, den Caesalpin auf die Entwicklung der Botanik im 17. und 18. Jahrhundert ausgeübt hat, ist nicht zu unterschätzen.[S. 236] Das von ihm begründete Lehrgebäude wurde durch Linné vollendet und damit die Entwicklung der künstlichen Systematik im wesentlichen zum Abschluß gebracht.
In das 17. Jahrhundert fallen auch die ersten Schritte zur Begründung einer wissenschaftlichen Morphologie der Pflanzen. Als ihr Hauptvertreter ist der Deutsche Joachim Jungius zu nennen. Von dem Lebensgange dieses Mannes (1587–1657) und seiner Bedeutung für die allgemeine Geisteskultur seines Zeitalters wird an späterer Stelle noch gehandelt werden. Sein Bestreben, Besseres an die Stelle des scholastischen Wortkrams zu setzen, der im 17. Jahrhundert sich in Deutschland breit machte, war besonders auf botanischem Gebiete von Erfolg begleitet. Ein gewaltiger handschriftlicher Nachlaß418 zeugt davon, daß sich die Reformbestrebungen des Jungius auf das gesamte Gebiet der Naturlehre erstreckten. Mit logischer Klarheit, gestützt auf Demokrits Atomistik und ausgestattet mit einem scharfen Beobachtungsvermögen, hat Jungius erfolgreich an der Erneuerung der Wissenschaften gearbeitet. Sein Einfluß hätte noch größer sein können, wenn er sich nicht auf Vorträge, Diktate und schriftliche Aufzeichnungen beschränkt hätte. Zum Glück erging es ihm nicht wie ein Jahrhundert vorher Lionardo da Vinci, der auch fast nichts von seinen wertvollen Aufzeichnungen veröffentlicht und infolgedessen auf die Entwicklung der Wissenschaften einen viel zu geringen Einfluß ausgeübt hat. Während die Manuskripte Lionardos erst gegen das Ende des 18. Jahrhunderts zugänglich gemacht wurden, kamen wichtige botanische Schriften des Jungius bald nach seinem Tode durch Vermittlung seiner Schüler an das Licht der Öffentlichkeit. Sie fanden nicht nur in der Heimat, sondern auch in England durch Ray und in Schweden durch Linné die ihnen gebührende Beachtung.
Durch sein botanisches Hauptwerk419 wirkte Jungius nach zwei Richtungen. Zunächst schuf er eine wissenschaftliche Terminologie, die so geeignet war, daß sie zum Teil sich bis auf den heutigen Tag erhalten hat. So sind, um ein Beispiel zu erwähnen, die noch heute für die verschiedenen Blütenstände gebräuchlichen[S. 237] Ausdrücke wie spica, panicula, umbella, corymbus, sowie ihre genauere Definition auf Jungius zurückzuführen. Auch Linné hat sich hinsichtlich der Nomenklatur an Jungius angeschlossen. Jungius war es ferner, der zuerst auf die Formwandlungen hinwies, welche die Blätter eines Stengels mit ihrer Entfernung vom Erdboden erfahren. Auch die einfachen und die vorher oft mit Zweigen verwechselten zusammengesetzten Blätter wurden von ihm deutlich unterschieden und benannt.
Sehr ausführlich hat Jungius auch die Gestalt der Blüte behandelt, obgleich ihm das Wesen der Sexualität noch verborgen blieb. Die Klarstellung der morphologischen Grundbegriffe bedingte auch eine bessere Anordnung der Pflanzen. Geruch, Geschmack, medizinische Wirkungen, Farbe und andere nebensächliche Charaktere wurden von Jungius als wertlos für die Anordnung erachtet. Auch die bis dahin immer noch anzutreffende Einteilung in Bäume, Sträucher und Kräuter wurde von ihm als nichtig zurückgewiesen.
Im einzelnen gestaltete Jungius das Pflanzensystem übersichtlicher, indem er für zahlreiche, früher getrennt aufgeführte Pflanzen die Zusammengehörigkeit nach ihrem gesamten Habitus nachwies und Regeln für die Benennung der Pflanzen aufstellte.
Die von Bauhin und Jungius entwickelten Grundsätze fanden zunächst in England fruchtbaren Boden, wo sie Morisons und Rays Bemühungen um den Ausbau der systematischen Botanik förderten420.
Morison unterzog das System Bauhins, wie dieser es in seinem »Pinax« niedergelegt hatte, einer gründlichen Durchsicht und zeigte, welche Pflanzen dort einen unrichtigen Platz einnahmen. Ferner war er der erste Botaniker, der eine größere Pflanzengruppe, und zwar die Umbelliferen, einer eingehenden, monographischen Bearbeitung unterwarf421. Die Doldengewächse wurden in dieser Arbeit nach der Beschaffenheit der Früchte in eine Reihe von Unterabteilungen zerlegt.
In Morisons Fußstapfen trat der auch als Zoologe bekannt gewordene John Ray422. Er stellte in einem umfangreichen Werke423 ähnlich wie Bauhin den gesamten, bis dahin geschaffenen Inhalt der botanischen Wissenschaft zusammen. Die morphologischen[S. 238] Teile behandelte er im engsten Anschluß an Jungius. In seinem System kommen zum ersten Male die großen natürlichen Gruppen des Pflanzenreichs zum Ausdruck. Er beginnt mit den unvollkommenen Pflanzen (Imperfectae), den Pilzen, Moosen, Farnkräutern und unterseeischen Pflanzen. Zu letzteren werden neben den Tangen auch die Pflanzentiere gerechnet. Die blühenden Pflanzen teilt Ray in die zweisamenlappigen (Dikotyledonen) und die einsamenlappigen Gewächse (Monokotyledonen). Von letzteren werden die Gräser mit besonderer Ausführlichkeit behandelt und nach ihrem Gesamteindruck systematisch weiter gegliedert.
Den Monokotylen werden auch die Palmen, die Liliengewächse und die Orchideen zugewiesen. Die natürlichen Gruppen der Labiaten und der Schmetterlingsblüter hatte man schon früher erkannt. Mehr oder minder deutlich treten jetzt auch die Kreuzblüter, die Rubiaceen, die Rauhblätterigen, die Korbblüter und andere, dem natürlichen System entsprechende Gruppen zutage. Die Einteilung im einzelnen blieb indessen recht mangelhaft, da es noch zu sehr an leitenden Gesichtspunkten fehlte.
Hatten Morison und nach ihm Ray in der Beschaffenheit der Früchte ein systematisches Merkmal von hervorragender Wichtigkeit erblickt, so legte der Deutsche Rivinus424 den größten Wert auf die Zahl und den Zusammenhang der Kronenblätter. Bei Rivinus begegnet uns auch schon der von Linné später durchgeführte Grundsatz, den Gattungsnamen bei jeder Art zu wiederholen und letztere durch ein hinzugefügtes Adjektiv auszudrücken.
In Frankreich fand in diesem, Linné vorhergehenden Stadium der Botanik diese Wissenschaft ihren hervorragendsten Vertreter in Tournefort425. Sein System bedeutete insofern einen Rückschritt, als es die von Ray erkannten, großen, natürlichen Gruppen der Kryptogamen, Monokotylen und Dikotylen nicht zum Ausdruck brachte. Für die Einteilung der Blütenpflanzen war, wie bei Rivinus, die Beschaffenheit der Blumenkrone maßgebend. Danach wurden blumenblattlose (apetale) und petaloide Pflanzen unterschieden. Letztere zerfielen in einblätterige (monopetale) und vielblätterige (polypetale) Pflanzen. Zu den monopetalen rechneten z. B. die Glockenblumengewächse und die Lippenblüter mit ihren[S. 239] aus einem Stück bestehenden Kronen, zu den Polypetalen dagegen Kreuzblüter, Rosengewächse, Schmetterlingsblüter usw.
Die 22 Klassen, zu denen Tournefort unter gleichzeitiger Verwertung der so unbestimmten Begriffe Bäume, Sträucher und Kräuter gelangte, zerfielen in Gruppen. Soweit es sich um petaloide Pflanzen handelte, wurden diese Gruppen nach der Beschaffenheit der Kronen gebildet. So wurden bei den Lippenblütern solche mit gerader, helmartiger und löffelförmiger Oberlippe unterschieden. An diese reihten sich die Lippenblüter ohne Oberlippe. Tournefort schuf also ein künstliches System, d. h. ein solches, das auf der Beschaffenheit eines willkürlich herausgegriffenen Organs, und zwar der Krone, beruhte. Es blieb während der ersten Jahrzehnte des 18. Jahrhunderts das herrschende. Dann wurde es durch Linnés künstliches System, das sich auf die Beschaffenheit der Staubgefäße gründete, abgelöst. Tournefort selbst hatte den Staubgefäßen nur geringe Bedeutung beigelegt, indem er sie als bloße Absonderungsorgane betrachtete.
Man hat Tournefort wohl das Verdienst zugeschrieben, daß er den Begriff der Gattung festgestellt habe. Gattungs- und Artbegriff haben sich indessen seit dem Wiederaufblühen der Botanik durch Einzelbeschreibung und Vergleich ganz allmählich herausgebildet. Bauhin trug diesen Begriffen ferner schon lange vor Tournefort durch seine Art der Namengebung Rechnung. Beide Begriffe nahmen allerdings an Bestimmtheit zu, je mehr man die wesentlichen von den unwesentlichen Merkmalen unterscheiden lernte und erkannte, daß die Zusammengehörigkeit zu einer Gattung nicht durch die Übereinstimmung eines einzigen, sondern der Mehrzahl der wesentlichsten Teile bestimmt ist. Als solche wurden immer mehr die Fortpflanzungsorgane erkannt.
Weniger fest stand der Artbegriff, weil man bei seiner Aufstellung mitunter allzu veränderliche Abwandlungen berücksichtigte und Spielarten von echten Arten noch nicht zu unterscheiden wußte. Zu dieser Frage äußerte sich auch Leibniz, indem er dem einseitig systematischen Standpunkte einzelner Botaniker eine recht zutreffende, im Einklang mit dem natürlichen Systeme stehende Bemerkung entgegenhielt. Anlaß dazu gab ihm die Äußerung eines deutschen Botanikers, die für das System verwertbaren Merkmale seien nicht den Blüten, sondern den Wurzeln zu entnehmen. Leibniz bemerkte dazu426, man müsse die Merkmale aller Teile[S. 240] berücksichtigen. Dabei sei aber zu beachten, daß der Zweck des Pflanzenlebens die Erhaltung des Einzelwesens und der Art sei. Deshalb müsse man beim Aufbau des Systems denjenigen Teilen den Vorzug geben, die zu diesen Zwecken in engster Beziehung ständen.
Verfehlt wäre es jedoch in diesem und in anderen, ähnlichen Fällen solchen gelegentlichen treffenden Äußerungen einen für den Gang der Wissenschaft entscheidenden Wert beizulegen und Leibniz z. B., wie es wohl geschehen ist, zu den Mitbegründern der Sexualtheorie und des darauf begründeten Systems zu zählen.
Eine ähnliche Entwicklung, wie sie die Botanik nach dem Wiederaufleben der Wissenschaften erfuhr, begegnet uns auf dem Gebiete der Zoologie. Auch hier knüpfte man zunächst an die Alten an; darauf begab man sich an die Beobachtung und die Beschreibung der zugänglichen Tierformen, und schließlich erwuchsen aus den Einzelbeschreibungen umfangreiche zoographische Sammelwerke. Als Repräsentanten dieser Richtung haben wir besonders Gesner und Aldrovandi kennen gelernt. Wie die Pflanzenkenntnis so wurde auch die Kenntnis der Tierformen durch die geographischen Entdeckungen außerordentlich erweitert. Um die Mitte des 17. Jahrhunderts begegnen uns z. B. schon besondere Werke über die Faunen Brasiliens und Ostindiens.
Auf die Periode des Sammelns folgte diejenige des Ordnens. Auch in dieser Hinsicht läuft die Entwicklung der Zoologie derjenigen der Botanik parallel. Ja, es sind zum Teil dieselben Männer, die im 17. Jahrhundert sich der Systematik des Tier- und Pflanzenreiches widmen. Dies gilt auch von dem größten Systematiker auf dem Gebiete der Zoologie des 17. Jahrhunderts, dem Engländer Ray.
John Ray wurde 1628 in Essex geboren. Er durchforschte die Tier- und Pflanzenwelt Großbritanniens, Deutschlands, Frankreichs und Italiens, war Mitglied der Royal-Society und starb im Jahre 1705. Nach der Herausgabe mehrerer botanischer Werke427 schuf er ein für die systematische Zoologie grundlegendes Werk in seiner Synopsis vom Jahre 1693. Ray teilt darin die Tierwelt in Wirbeltiere und in Wirbellose ein, wie es schon Aristoteles[S. 241] getan. Er bedient sich sogar der aristotelischen Bezeichnungen »Bluttiere« und »Blutlose«. Die Wirbeltiere zerfallen nach Ray in Lungenatmer und Kiemenatmer (Fische). Die Lungenatmer werden in Lebendiggebärende und Eierlegende (Vögel) eingeteilt. Auch der Bau des Gefäßsystems wird verwertet, indem die eierlegenden Lungenatmer mit nur einem Herzventrikel zu einer besonderen Gruppe zusammengefaßt werden. Für die Bildung von Unterabteilungen werden der Bau des Gebisses und die Beschaffenheit der Gliedmaßen verwertet. So begegnen uns Nagetiere (Hasenartige), Krallentiere, die Ein-, Zwei- und Vierhufer (Nashorn und Nilpferd). Nach ähnlichen Gesichtspunkten werden die Vögel gruppiert, sodaß auch hier die Grundlagen der späteren Einteilung geschaffen wurden. Die Wirbellosen zerfallen bei Ray in Weichtiere, Krustentiere (Krebse), Schaltiere (Muscheln und Schnecken) und Insekten. Letztere hat er am eingehendsten bearbeitet. Er begreift darunter alle mit Einschnitten versehenen Tiere.
Was Ray auf dem Gebiete der zoologischen Systematik geschaffen, bildete die unmittelbare Grundlage des Linnéschen Systems, das uns an späterer Stelle beschäftigen wird. Auch in der scharfen Erfassung des Artbegriffs war Ray ein Vorläufer Linnés. »Formen, die der Species nach verschieden sind«, heißt es bei Ray428, »behalten diese ihre spezifische Natur beständig, und es entsteht die eine nicht aus dem Samen einer anderen.« Ray huldigte indessen noch keineswegs der starren Auffassung des Artbegriffes, der uns bei den Systematikern des 18. Jahrhunderts begegnet. Denn er fügt seiner Erklärung429 folgende Einschränkung hinzu: »Nun ist aber dieses Zeichen der spezifischen Übereinstimmung, obschon ziemlich konstant, doch nicht beständig und untrüglich«.
Das 17. Jahrhundert war indessen für die Zoologie und die Botanik nicht etwa ein Zeitalter der bloßen Systematik. Es kam vielmehr als zweites, besonders wichtiges Moment hinzu, daß die beschreibenden Naturwissenschaften unter den Einfluß der seit Galilei emporblühenden exakten physikalischen Forschung gerieten. Dies führte zur Anwendung besonderer Hilfsmittel, z. B. des Mikroskops, auf die Erforschung der Lebewesen. Die Blicke der Zoologen und der Botaniker wurden dadurch mehr als bisher auf den inneren Bau der Organismen und die kleinsten Lebewesen gelenkt.[S. 242] Ja, es erschloß sich den erstaunten Blicken eine neue Welt, die bis dahin, der Kleinheit ihrer Formen wegen, den Sinnen ganz verborgen geblieben war. Die Berührung mit der physikalischen Forschung führte aber nicht nur zur Benutzung technischer Hilfsmittel, sondern es wurde auch die Methode der neueren physikalischen Forschung, der messende Versuch, auf die Erscheinungen der Tier- und Pflanzenwelt angewandt. Von Einfluß war in dieser Hinsicht auch der Hauptzug der neueren, mit Descartes anhebenden Philosophie, die alles Geschehen auf die Grundgesetze der Mechanik zurückzuführen suchte und selbst die Organismen nach der körperlichen Seite als bloße Maschinen betrachtete. So entstand im 17. Jahrhundert die biomechanische Richtung, als deren Hauptvertreter wir Borelli kennen lernen werden. Die hier nur angedeuteten, auf den Einfluß der Physik zurückzuführenden Fortschritte der biologischen Wissenschaften sollen in besonderen Abschnitten behandelt werden, nachdem wir zunächst das Emporblühen der anorganischen Wissenschaften während der auf Galileis Zeitalter folgenden Newton-Huygens-Periode kennen gelernt haben.
Während der ersten Hälfte des 17. Jahrhunderts lag der Schwerpunkt der wissenschaftlichen Arbeit auf dem Gebiete der Mechanik. Erst nachdem man die Gesetze festgestellt hatte, die das Verhalten der festen, flüssigen und gasförmigen Körper regeln, war eine Grundlage für die weitere Erforschung alles Geschehens geschaffen. Den Versuch einer mechanischen Erklärung aller Naturerscheinungen unternimmt das nachfolgende Zeitalter, dessen bedeutendste Tat die Begründung der Mechanik des Himmels durch Newton ist.
Galilei hatte in einem an Kepler gerichteten Briefe die Befürchtung ausgesprochen, daß auf den das 17. Jahrhundert kennzeichnenden wissenschaftlichen Aufschwung vielleicht eine Zeit des Stillstandes eintreten werde. War doch auf die Blüteperiode der griechischen Wissenschaft eine Brache von vielen Jahrhunderten gefolgt. Diese Befürchtung Galileis erwies sich als grundlos. Die Wissenschaft war zu einem Gemeingut der zivilisierten Menschheit geworden; sie war nicht mehr an das Schicksal eines Volkes gebunden. Während auf dem Boden Italiens rückwärts gerichtete Bestrebungen ihren Fortschritt hemmten, gelangte sie zunächst vornehmlich in England, in den Niederlanden und in Frankreich zur Entfaltung. Günstig beeinflußt wurden die Naturwissenschaften durch den Fortschritt der Mathematik, insbesondere durch die Begründung der analytischen Geometrie und der Infinitesimalrechnung. Eine zu weit gehende Arbeitsteilung, wie sie heute, nicht ohne Gefahr für die Wissenschaft, Platz gegriffen, bestand damals noch nicht. So sehen wir die hervorragendsten Philosophen und Mathematiker – es sei nur an Descartes430 und[S. 244] Leibniz erinnert – eifrig an der Lösung naturwissenschaftlicher Aufgaben mitarbeiten. Die neuere Philosophie zeigte sich von dem Bestreben beseelt, mit allen hergebrachten Anschauungen zu brechen und ihre Probleme vom Standpunkt der Voraussetzungslosigkeit in Angriff zu nehmen. Dies Bestreben erwies sich auch für das naturwissenschaftliche Gebiet als überaus fruchtbringend. Von nachhaltigem Einfluß auf das letztere ist insbesondere der englische Philosoph John Locke (1632–1704) gewesen, dessen gründliche Untersuchungen über das Erkenntnisvermögen den modernen Realismus ins Leben gerufen haben.
Es ist bemerkenswert, eine wie hohe Wertschätzung die Mathematik in ihrer Anwendung auf die Naturwissenschaften erfuhr. Mathematik und mathematische Physik waren im Verein mit der aus den scholastischen Banden befreiten Philosophie zum Inbegriff aller Wissenschaften, ja sozusagen zu einem neuen Evangelium geworden. Sie wurden sogar zu einem Bestandteil der höfischen Bildung. Vornehme Frauen umgaben sich mit Philosophen und Mathematikern anstatt wie früher mit Dichtern und Sängern. Wie im Zeitalter der Renaissance die Begeisterung für die Antike, so galt während des 17. Jahrhunderts eine nicht geringere Begeisterung für die exakten Wissenschaften und die ihr geistesverwandte neuere Philosophie als ein Ersatz für das religiöse Leben der vergangenen Jahrhunderte. Eine solche Strömung zeitigte als erfreulichste Erscheinung die Gründung der großen nordeuropäischen Akademien.
Nach dem Vorbilde der Accademia del Cimento entstanden nämlich auch in den nördlichen Ländern Europas gelehrte Gesellschaften, die, gefördert durch reiche Mittel sowie durch die Gunst der Monarchen, für die weitere Entwicklung von großer Bedeutung wurden. Den wesentlichsten Vorteil derartiger Vereinigungen hat einmal Laplace mit folgenden Worten gekennzeichnet: »Während der einzelne Gelehrte sich leicht dem Dogmatisieren hingibt, führt in einer gelehrten Gesellschaft der Zusammenprall dogmatischer Ansichten sehr bald zu ihrer Zerstörung. Der Wunsch, sich gegenseitig zu überzeugen, ruft ferner unter den Mitgliedern die Übereinkunft hervor, nichts anderes als die Ergebnisse der Beobachtung und Rechnung anzunehmen«431.
In der Pflege dieses Geistes zeichneten sich vor allem die unter Ludwig XIV. im Jahre 1666 ins Leben gerufene Pariser[S. 245] Akademie, sowie die um dieselbe Zeit entstandene Royal Society432 in London aus. Und während des 18. Jahrhunderts, besonders im Fridericianischen Zeitalter, erlangte die durch Leibniz ins Leben gerufene Preußische Akademie der Wissenschaften eine ähnliche Bedeutung.
Die Geschichte dieser Akademien zeigt uns mehr als der Lebens- und Entwicklungsgang des einzelnen Forschers die Wissenschaft in ihrer Abhängigkeit von dem gesamten Kulturzustande und der politischen Gestaltung Europas. Wir wollen daher bei dieser Erscheinung, die uns die neuere Geschichte der Wissenschaften bietet, noch etwas verweilen.
In der Zeit vor der Begründung der großen Akademien erwarb sich der Jesuit Mersenne (1588–1648) dadurch ein besonderes Verdienst, daß er durch eine umfangreiche Korrespondenz den Austausch an Erfahrungen und Gedanken zwischen den einzelnen Gelehrten besorgte. Mersennes Briefwechsel, der ein reiches Material für die Geschichte der Wissenschaften darstellt, wird in der Nationalbibliothek zu Paris aufbewahrt433. In demselben Sinne wie Mersenne wirkte in Deutschland ein anderer Jesuit, der Pater Kaspar Schott. Die Rolle solcher Männer übernahmen mit der Gründung der erwähnten Akademien die Sekretäre dieser Gesellschaften.
Die Royal Society wurde von einer Anzahl englischer Forscher im Jahre 1645 ins Leben gerufen, um, wie die Stifter sagten, in der Unterhaltung über naturwissenschaftliche Gegenstände Trost über das Elend des Landes zu suchen. Die Geschichte der Royal Society ist ein wichtiges Stück der Geschichte der Wissenschaften überhaupt. Der Gedanke, ein von jedem Nebenzwecke unabhängiges wissenschaftliches Institut zu gründen und es mit allen Mitteln zu versehen, ging in England von Francis Bacon aus. Er hat diesen Gedanken in seiner neuen Atlantis geäußert und sein Ideal als das Haus Salomos bezeichnet. Auch der König wurde für diesen Plan gewonnen; er sicherte der Vereinigung, zu deren Begründern Boyle und Wren zählten, seinen besonderen Schutz zu und verlieh ihr Korporationsrechte, sowie den Titel einer königlichen Gesellschaft434.[S. 246] Das Ziel dieser Vereinigung war zwar, das schon von Bacon gewünschte System der Wissenschaften zu errichten. Man erkannte aber, daß dazu zunächst eine sichere Grundlage durch die rein empirische Erforschung der Tatsachen ohne Rücksicht auf irgend welche Theorien geschaffen werden müsse. Man war also in den für die Naturwissenschaften interessierten Kreisen Englands von demselben Geiste ergriffen, der die Mitglieder der Accademia del Cimento beseelte und durch sie schon so bedeutende Erfolge gezeitigt hatte.
Das Hauptgewicht wurde nicht auf Vorträge, sondern auf Versuche und Demonstrationen gelegt, welche die Entdecker neuer Gesetze und Tatsachen im Beisein von Mitgliedern der Akademie zu wiederholen hatten. Unter diesen Mitgliedern waltete zunächst das medizinische Element vor. Daher kam es, daß man sich in den ersten Jahren besonders mit der Nachprüfung der Harveyschen Lehre vom Blutkreislauf befaßte und manche neue Stütze für diese Lehre beibrachte. Boyle stellte im Schoße der Royal Society seine Versuche über die Atmung an. Andere Forscher nahmen Zergliederungen von Organismen vor. Kurz, dem unmittelbaren Zeugnis der Sinne wurde eine entscheidende Bedeutung eingeräumt und manche irrige Meinung, ja mancher Aberglauben dadurch beseitigt. Die Gesellschaft beschränkte sich indessen nicht auf den Verkehr der Mitglieder unter sich, sie trat auch mit bedeutenden auswärtigen Gelehrten in Verbindung. Den umfangreichen schriftlichen Verkehr, der dazu nötig war, leitete in den ersten Jahren ein Deutscher namens Oldenburg, der die Stelle eines Sekretärs der Akademie einnahm435.
Leeuwenhoek, Malpighi und viele andere richteten die ersten Mitteilungen über ihre Entdeckungen an die Royal Society. Letztere unterstützte nämlich wissenschaftliche Unternehmungen, auch wenn sie von Ausländern ausgingen, in freigebiger Weise. So ließ sie Malpighis große Abhandlung über den Seidenschmetterling auf ihre Kosten drucken und mit Kupfertafeln ausstatten.
Die Veröffentlichungen der Royal Society führten die Bezeichnung Philosophical Transactions436. Sie erschienen seit dem[S. 247] Jahre 1664 und bildeten durch ihre Berichte und ihre Abhandlungen die wichtigste Quelle für die Entwicklung, welche die Wissenschaften im Verlauf der letzten Jahrhunderte genommen haben.
Seit ihrer Begründung stand für die Royal Society die Astronomie im Mittelpunkte des Interesses. Dieses wurde besonders durch die lebhafte Anteilnahme genährt, die Karl II. ihrer nautischen Anwendung wegen für die Astronomie empfand. Auf das Zusammenwirken des Königs und der Gesellschaft, der auch der königliche Astronom angehörte, ist die Gründung der Sternwarte in Greenwich zurückzuführen. Unter den übrigen wissenschaftlichen Aufgaben, mit denen man sich um die Mitte des 18. Jahrhunderts beschäftigte, standen obenan die Probleme der Mechanik, der Ausbau der Lehre von der Bewegung zu einem zusammenhängenden, auf wenige Axiome sich gründenden System. Dem Verdienste der Royal Society, das vor allem darin bestand, die wissenschaftlichen Aufgaben ihrer Zeit zu erkennen und deren Lösung stets wieder in Anregung zu bringen, gesellte sich das besondere Glück zu, daß in ihrem Schoße der Genius erstand, der diese Fragen einer umfassenden Lösung entgegenführte. Dieses Genie, das bedeutendste Mitglied der Royal Society, war Newton. In ihm finden nämlich die beiden Hauptstämme der neueren Naturwissenschaft, die Astronomie in der Gestalt, die Kepler ihr gegeben, und die Mechanik, wie sie aus dem Haupte Galileis hervorging, ihren Zusammenschluß und ihre Fortentwicklung.
Wie die Royal Society, so ging auch die Pariser Akademie der Wissenschaften, die 1666 unter Ludwig XIV. durch Colbert ins Leben gerufen wurde, aus dem Bedürfnis einiger Forscher hervor, die sich zwanglos zusammenfanden. Es war das der Kreis, der sich schon Jahrzehnte vor der Gründung der Akademie um Mersenne437 versammelte.
Die Pariser Akademie der Wissenschaften438 entwickelte sich noch im 17. Jahrhundert zu einer der Royal Society ebenbürtigen Einrichtung. Beide Akademien gaben in regelmäßiger Folge Druckschriften heraus, in denen die bedeutendsten Arbeiten der einheimischen aber auch fremder Gelehrter veröffentlicht wurden.
Während der Revolution wurde die Pariser Akademie der Wissenschaften zunächst (1793) aufgehoben, indes schon 1795 wieder eingerichtet. Ihre endgültige Einrichtung empfing sie nach der Beendigung des Revolutionszeitalters (im Jahre 1816). Sie zählt statutengemäß 65 Mitglieder und zerfällt in 11 Abteilungen, nämlich in eine solche für Mathematik, Mechanik, Astronomie, Geographie, Physik, Chemie, Mineralogie, Botanik, Agrikultur, Zoologie einschließlich Anatomie, Heilkunde.
An die Royal Society und die Pariser Akademie haben sich im 18. Jahrhundert eine größere Zahl von ähnlichen Forschungsinstituten angeschlossen. Die wichtigsten unter ihnen sind die folgenden: Berlin (1700), Petersburg (1725), Stockholm (1739), München (1759). Die Münchener Akademie verdient besondere Anerkennung für die Verdienste, die sie sich um die Geschichte der Wissenschaften erworben hat439.
Bevor wir uns mit dem Lebensgange und den Taten Newtons befassen, wollen wir einen Blick auf Deutschland werfen, das während des 17. Jahrhunderts in Leibniz einen dem englischen Forscher zwar nicht ebenbürtigen, ihn an Vielseitigkeit aber übertreffenden Führer besaß, in dem die aus der Renaissance, der Reformation und der exakten Wissenschaft hervorquellenden Kräfte, wie in keinem anderen, in die Erscheinung traten. Daneben ist Jungius zu nennen, in dem sich während der ersten Hälfte des 17. Jahrhunderts das Streben nach einer Erneuerung der Wissenschaften verkörperte. Auch in dem Bemühen, die der freien Forschung sich widmenden Kräfte zu gemeinsamer Tätigkeit anzuspornen, müssen wir Jungius als einen Vorläufer von Leibniz bezeichnen.
Joachim Jungius wurde im Jahre 1587 in Lübeck geboren. Er widmete sich der Heilkunde und hielt sich einige Jahre in Italien auf, wo er mit den botanischen Forschungen Caesalpins bekannt und mit dem Geiste der in Italien aufblühenden neueren Naturwissenschaft erfüllt wurde. Nach Deutschland zurückgekehrt, nahm er dort den Kampf gegen die Scholastik auf und suchte gleichgesinnte Männer um sich zu scharen. Von diesem Bestreben geleitet, gründete Jungius 1622 in Rostock die erste deutsche Gesellschaft, welche die Pflege der Mathematik und die Erforschung der Natur als ihre wichtigste Aufgabe bezeichnete. Ihr Zweck sollte darin bestehen, »die Wahrheit aus[S. 249] der Vernunft und der Erfahrung zu erforschen, die Wissenschaften von der Sophistik zu befreien und durch Erfindungen zu vermehren«. Von den Erfolgen, die Jungius selbst in der gewollten Richtung aufzuweisen hatte, wird an anderer Stelle die Rede sein440.
Neben der Rostocker Gesellschaft verdient auch die etwas später (1652) auf deutschem Boden entstandene Kaiserlich Leopoldinische Akademie genannt zu werden. Sie gibt seit dem Jahre 1672 Abhandlungen meist naturgeschichtlichen Inhalts heraus, hat aber für das wissenschaftliche Leben in Deutschland keine ihrem stolzen Namen entsprechende Bedeutung gewonnen. Dies lag daran, daß der Sitz dieser Akademie häufig wechselte und daß ihre Mitglieder über das ganze Land zerstreut lebten. Damit fiel das fruchtbarste Moment, der häufige persönliche Gedankenaustausch zwischen den Mitgliedern fort. Auch der Umstand, daß die einzelnen deutschen Länder (Preußen, Bayern) in ihren Hauptstädten Akademien unterhielten, ließ eine allgemeine deutsche Akademie, wie es die Leopoldinische sein wollte, nicht erstarken.
Der Gedanke, den Jungius und die Gründer der Leopoldinischen Akademie wenn auch nur in bescheidenem Maße verwirklichten, lebte in Leibniz wieder auf, als er während seines mehrjährigen Aufenthaltes in Paris den außerordentlichen Nutzen einer großen, vom Staate in freigebiger Weise geförderten Vereinigung gelehrter Forscher kennen gelernt hatte. Leibniz bot seinen ganzen Eifer und seine Beredsamkeit auf, um eine ähnliche Einrichtung für Deutschland ins Leben zu rufen.
Dies geschah in seiner von mehreren Entwürfen begleiteten Consultatio vom Jahre 1672441. Die Grundsätze, die Leibniz darin entwickelte, sind in Kürze die folgenden: Alle Kräfte müssen sich vereinigen, um tiefer in die Natur einzudringen. Zunächst sind deshalb die einfacheren gelösten und die schwierigeren ungelösten Probleme übersichtlich zusammenzustellen, um der Forschung Ziel und Richtung zu geben. Die von einer solchen Neubelebung zu erwartenden Ergebnisse sind der Allgemeinheit[S. 250] zugänglich zu machen, damit sie auch für die Bildung und das Leben Früchte zeitigen können. Deshalb sollte sich die zu gründende Akademie in ihren Veröffentlichungen der deutschen Sprache bedienen. Scharf und zutreffend urteilt bei dieser Gelegenheit schon Leibniz über den Wert der einseitig klassischen Bildung und die übertriebene Wertschätzung der grammatisch-philologischen Schulung, wenn er sagt: »Wir nötigen unsere Jugend dazu, zuerst die Herkulesarbeit der Bezwingung verschiedener Sprachen zu leisten, wodurch oft die Schärfe des Geistes abgestumpft wird, und verurteilen alle, welche die Kenntnis des Lateinischen entbehren, zur Unwissenheit«. Die Befürchtung, daß durch das Aufgeben der alten Sprachen als allgemeines Bildungsmittel das altsprachliche Studium in Verfall kommen werde, weist Leibniz mit vollem Recht zurück. Niemals werde der Theologe das Griechische oder der Jurist das Lateinische entbehren wollen, noch der Geschichtsforscher sich den Zugang zu den Quellen versperren lassen.
Die Anregungen, welche die Consultatio brachte, waren zunächst ohne Erfolg. Leibniz wurde dadurch recht deutlich daran erinnert, daß es wohl ein Frankreich, aber kein Deutschland gab. Er ließ jedoch seinen Plan nicht fallen, an dessen Verwirklichung er die Hoffnung knüpfte, daß die deutsche Wissenschaft bald die der anderen Nationen überflügeln werde. Was sich nicht für das Deutsche Reich ins Leben rufen ließ, war vielleicht in einem der Einzelstaaten, die das Reich in seinem lockeren Gefüge zusammensetzten, möglich. Und so richtete er denn in dieser, ihm wie keine andere am Herzen liegenden Sache seine Aufmerksamkeit auf den mächtigsten deutschen Staat, auf das emporstrebende Brandenburg-Preußen. Ein äußerer Umstand kam Leibniz zu Hilfe. Der Kurfürst Friedrich III. von Brandenburg vermählte sich mit der hannoverschen Prinzessin Sophie Charlotte. An dieser hatte Leibniz, der nach seiner Rückkehr aus Paris in hannoversche Dienste getreten war, eine begeisterte Schülerin gefunden. Die Beziehungen zwischen der neuen Kurfürstin und ihrem früheren Lehrer erhielten in einem regen Briefwechsel ihre Fortsetzung, und der wichtigste Gegenstand dieses Briefwechsels war der alte Leibniz'sche Plan, in Deutschland, und zwar jetzt in Berlin, eine der französischen Akademie der Wissenschaften ebenbürtige Schöpfung ins Leben zu rufen. Leibniz wies besonders darauf hin, daß Preußen auf dem Gebiet der praktischen Künste Kraft gewinnen müsse. Denn bei dem Kampf und Wettbewerb[S. 251] der Völker werde die zivilisierteste und gewerbreichste Nation den Sieg davontragen. Die Akademie sollte eins der Mittel sein, dem protestantischen Deutschland unter Preußens Führung durch die Anwendung der Wissenschaften auf Landwirtschaft und Gewerbe einen inneren, friedlichen Machtzuwachs zu verleihen.
Nach langem Harren und Mühen drang Leibniz endlich in Berlin mit seinen Vorschlägen durch. Am 19. März des Jahres 1700 befahl der Kurfürst, eine »Académie des Sciences und ein Observatorium in Berlin zu etablieren.« Ein Vierteljahrhundert hatte es also gewährt, bis der erste, von Leibniz in seiner Consultatio entwickelte Vorschlag in die Tat umgesetzt worden war. Leibniz wurde nach Berlin berufen und an die Spitze der Akademie gestellt. Im übrigen entsprachen die zur Verfügung gestellten Mittel zunächst in keiner Weise der Größe des von Leibniz entwickelten Planes. Der ganzen Sinnesart Friedrich Wilhelms I., der etwa ein Jahrzehnt nach der Begründung der Akademie den Thron bestieg, entsprach es nicht, gelehrte Einrichtungen zu fördern. Dieser König, dem Preußen im übrigen so vieles verdankt, verkannte, ja verhöhnte sogar die Akademie und ihre Einrichtungen. Die einzige Wissenschaft, die er achtete, und förderte, war die Chemie, die während seiner Regierungszeit in Preußen einige hervorragende Vertreter, wie Stahl und Pott, besaß.
Mit einem Schlage änderten sich die unter Friedrich Wilhelm I. bestehenden Verhältnisse, als sein großer Sohn die Regierung übernahm und mit ihm »die Wissenschaften und die Künste auf den Thron stiegen«. Schon als Kronprinz hatte Friedrich II. den Plan gefaßt, die Akademie der Wissenschaften zu neuem Leben zu erwecken. Er hatte sogar in Europa nach geeigneten Gelehrten Ausschau gehalten, die er nach seiner Thronbesteigung durch die Akademie an Preußen zu fesseln wünschte. Seine Aufmerksamkeit richtete sich zunächst auf Maupertuis und Wolf. Maupertuis galt seinen Zeitgenossen als einer der hervorragendsten Vertreter der Astronomie sowie der mathematischen Physik. Wolf dagegen genoß als Philosoph das größte Ansehen. Friedrich glaubte, daß diese beiden Männer berufen seien, Newton und Leibniz zu ersetzen. Die Geschichte hat sie jedoch weit geringer einschätzen müssen. Wolf nahm die Berufung nach Berlin nicht an. Er hatte in Preußen schlechte Erfahrungen gemacht. Während er in Halle die Professur der Philosophie bekleidete, hatten seine theologischen Amtsgenossen ihn der Irreligiosität beschuldigt und[S. 252] damit erzielt, daß Wolf bei Strafe des Stranges binnen 48 Stunden das Land verlassen mußte. Wolfs Verdienst um die Philosophie beschränkte sich im wesentlichen darauf, daß er die Leibniz'schen Lehren weiter ausbaute und für ihre Verbreitung sorgte. Dabei bediente er sich – und das ist ein bahnbrechendes Verdienst gewesen – der von Leibniz gegebenen Anregung gemäß der deutschen Sprache.
Maupertuis dagegen folgte dem Rufe des Königs und wurde 1742 zum Direktor der Akademie ernannt. Ein Jahr vorher war auch der große Euler für sie gewonnen worden. Die ersten Jahrzehnte der Fridericianischen Zeit waren für die Preußische Akademie der Wissenschaften die bedeutendsten. Maupertuis verstand es, hervorragende Männer als wirkliche oder auswärtige Mitglieder in ihr zu vereinigen. Die Preußische Akademie war damals, und das ist ihr schönster Ruhmestitel gewesen, eine Freistätte für die vom Fanatismus oder vom Absolutismus aus anderen Ländern vertriebenen Gelehrten und eine Burg gegenüber der Unduldsamkeit der Kirche442. Was ihre Mitglieder, unter denen neben den erwähnten noch Lagrange, Lambert und Marggraf genannt seien, für die Wissenschaft geleistet haben, bleibt späteren Abschnitten vorbehalten.
Unter den Mitteln, deren sich die Akademien zur Erreichung ihrer Zwecke bedienten, standen die Preisaufgaben obenan. An ihrer Lösung beteiligten sich in regem Wetteifer die besten Kräfte. Sie waren gleichsam, wie der Historiograph der Preußischen Akademie der Wissenschaften sich ausdrückt, die Hebel, durch die Jahr für Jahr die Wissenschaften um eine Stufe gehoben wurden. Der Fragestellung, in welcher der Geist und das Geschick der betreffenden Akademie zum Ausdruck kam, blickte man fast mit der gleichen Spannung entgegen wie der Verkündigung des Preises.
Die von Seiten der Akademien herausgegebenen Berichte fanden eine wertvolle Ergänzung in anderen periodisch erscheinenden wissenschaftlichen Veröffentlichungen. Unter ihnen sind besonders die Acta Eruditorum zu nennen. Sie erschienen seit dem Jahre 1682 in Leipzig und enthalten viele mathematische und physikalische Abhandlungen, daneben aber auch solche aus allen anderen Wissensgebieten. Leibniz, Tschirnhausen und viele andere Männer von Bedeutung gehörten zu ihren Mitarbeitern.[S. 253] Der letzte Band ist 1776 erschienen. In dem Maße, in dem für die einzelnen Zweige der Naturwissenschaft besondere Zeitschriften ins Leben gerufen wurden, verloren die »Acta Eruditorum« an Wert und gingen endlich (1776) ein.
Auch durch die im 18. Jahrhundert herrschende Sitte, daß sich die Mitglieder der verschiedenen Akademien gegenseitig Probleme vorlegten, wurde die Wissenschaft gefördert, doch entstanden hierbei nicht selten durch nationale Eifersucht geschürte Streitigkeiten, die sich namentlich zwischen den Deutschen und den Engländern geltend machten. Solche Streitigkeiten waren mitunter recht unerquicklich. Im ganzen genommen, haben sie der Wissenschaft aber nicht geschadet.
Nachdem wir den allgemein geschichtlichen, kulturhistorischen und naturphilosophischen Hintergrund kennen gelernt haben, von dem sich die gewaltige Forschergestalt Newtons abhebt, gehen wir zur Schilderung seiner Lebensarbeit und seiner Persönlichkeit über.
Isaak Newton443 wurde am 4. Januar 1643 in Woolsthorpe, einem in der Grafschaft Lincolnshire gelegenen Dorfe, geboren, ein Jahr, nachdem Galilei die Augen geschlossen hatte und hundert Jahre nach dem Tode des Koppernikus. Sein Vater, der dort Landwirtschaft betrieb, war einige Monate vor der Geburt des Sohnes gestorben. Die Mutter hegte den Wunsch, daß letzterer das kleine Besitztum, das sie ihr eigen nannte, später übernehmen möchte. Newton wurde auf die Schule zu Grantham, einem wenige Meilen von Woolsthorpe entfernten Städtchen, geschickt. Seine Lernbegierde war zunächst gering. Mit besonderem Eifer beschäftigte er sich mit der Herstellung mechanischer Vorrichtungen. So entstanden Windmühlen, Sonnen- und Wasseruhren usw. Auch in anderer Hinsicht zeigte sich die Eigenart Newtons, der an den Spielen seiner Jugendgefährten nur geringen Anteil nahm.
Als der Knabe mit 14 Jahren auf das kleine Gut der Mutter zurückkehrte, dessen Bewirtschaftung er übernehmen sollte, zeigte es sich, daß er für die Geschäfte des praktischen Lebens keine rechte Neigung besaß. Auf Anraten und unter Beihilfe seines Oheims, der ihn hinter einer Hecke, mit dem Lesen eines geometrischen Buches beschäftigt, gefunden hatte, wurde Newton deshalb nach Grantham zurückgeschickt. Mit 17 Jahren bezog[S. 255] er die Universität Cambridge. Hier studierte er zunächst die mathematischen Werke der Alten, insbesondere die Geometrie Euklids. Darauf fesselten ihn die Arbeiten der neueren Schriftsteller. Er las die mathematischen Schriften des Descartes, die Arithmetik von Wallis444, welche die Keime der später von Newton und Leibniz erfundenen Infinitesimalrechnung enthält, und die Dioptrik Keplers. An alle Arbeiten anderer trat er jedoch mit einer Selbständigkeit des Denkens heran, wie sie nur hervorragende Geister auszeichnet. Eigene mathematische Untersuchungen leiteten ihn schon während seiner Studienzeit zur Auffindung des allgemeinen binomischen Lehrsatzes. Auch nahm er, bereits bevor er in Cambridge als letzten akademischen Grad die Magisterwürde erlangt hatte, das Gravitationsproblem in Angriff. Ihn leitete dabei der fruchtbare Gedanke, die Identität der Schwere und der von der Erde auf den Mond wirkenden Kraft nachzuweisen. Indes gelangte er damals noch nicht zum Ziele, weil ihm die, seiner Rechnung zugrunde zu legenden Abmessungen der Erde nicht hinreichend genau bekannt waren. Die später zu besprechende Gradmessung Picards verschaffte endlich seiner Ableitung die richtigen Unterlagen, so daß erst 16 Jahre später jener Gedanke als zutreffend bewiesen werden konnte.
In den Beginn der wissenschaftlichen Tätigkeit Newtons fällt seine erste Beschäftigung mit der Optik. Wie auf Galilei, so wurde auch auf Newton die Mitwelt zuerst infolge seiner Verdienste um die Erfindung, beziehungsweise die Verbesserung des Fernrohrs aufmerksam. Man hatte bemerkt, daß zwei Eigenschaften der Glaslinsen der Vervollkommnung dieses Instrumentes im Wege standen. Einmal wurden parallel einfallende Strahlen nicht genau in einem Punkte vereinigt; zweitens machten sich an den Bildern farbige Ränder bemerkbar. Beide Erscheinungen sind unter dem Namen der sphärischen und der chromatischen Abweichung bekannt. Da die letztere an den durch[S. 256] Hohlspiegel erzeugten Bildern nicht auftritt, so brachte Newton die von mehreren Seiten445 geäußerte Idee eines Spiegelteleskops zur Ausführung (s. Abb. 68). Das durch einen sphärischen Hohlspiegel (aqsb) erzeugte Bild wurde von einem schräg gestellten Planspiegel (fg) seitwärts reflektiert und durch eine in der Seitenwand angebrachte Linse (h) betrachtet (siehe Abb. 69).
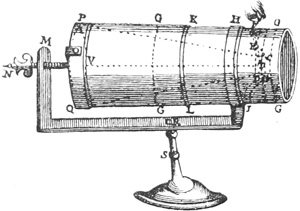
Das erste, im Jahre 1668 verfertigte Spiegelteleskop war nur 5 Zoll lang. Man war jedoch imstande, damit die Monde Jupiters, sowie die Lichtgestalten der Venus zu erkennen. Einige Jahre später447 sandte Newton ein zweites, größeres Instrument an die Royal Society. Es fand deren Beifall und erregte auch die Bewunderung des[S. 257] Hofes. Dieses Instrument wird noch heute in der Bibliothek jener Gesellschaft aufbewahrt. Es trägt die Inschrift:
Invented by Sir Isaac Newton
and made with his own hands.
1671.
Das Verdienst des genialen Erfinders, der seit dem Jahre 1662 die Professur der Mathematik in Cambridge bekleidete, wurde dadurch anerkannt, daß man ihn in die Royal Society aufnahm, deren Vorsitz er in späteren Jahren führte.
Eine kurze Erwähnung verdient auch der Spiegelsextant. Sein Erfinder ist John Hadley. Nach Maskelyne448 hat sich schon Newton mit der Idee befaßt, für die Beobachtung von Monddistanzen einen Spiegeloktanten herzustellen. Die Beschreibung eines brauchbaren Spiegelmeßapparats, der alle älteren, bisher von den Seefahrern benutzten Winkelmeßinstrumente verdrängte, veröffentlichte Hadley im Jahre 1731449. Seine Abbildung stellt einen Oktanten mit einem senkrecht zur Mittellinie gerichteten Fernrohr dar. Vor dem Fernrohr befindet sich der feste, und links davon der auf einer beweglichen Alhidade angebrachte Spiegel. Vor diesem kann ein Blendglas (ganz links in der Abbildung) gedreht[S. 258] werden. An Stelle des in Grade und Minuten geteilten Oktanten setzte man den Sextanten, von dem das Instrument seinen Namen erhielt.
Von nicht geringerem Belang als jene, in erster Linie der Praxis dienenden Erfolge war die Förderung, welche die theoretische Optik durch Newton erfuhr. Mit der Brechung des Lichtes hatten sich schon die Alten, sowie unter den Neueren besonders Kepler und Snellius befaßt. Eine Vertiefung von großer Tragweite erlangte dieses Problem, als Newton sein Augenmerk auf die bis dahin kaum weiter verfolgte Erscheinung der Farbenzerstreuung richtete. Sämtliche grundlegenden Versuche, welche dieses Gebiet betreffen und die ihn seit dem Jahre 1666 beschäftigten, rühren von ihm her. Eine zusammenfassende Darstellung gab Newton in seinen drei Büchern über die Optik450. Newton beginnt das erste Buch mit der Versicherung, daß er die Eigenschaften des Lichtes nicht durch Hypothesen erklären, sondern daß er sie nur aufdecken und durch Versuche und Rechnung klarstellen wolle. Diesem Vorsatz ist er nicht immer treu geblieben, sondern durch das ganze Werk zieht sich die Auffassung, daß wir es in dem Licht mit einer feinen, aus gesonderten Teilchen bestehenden Materie zu tun haben, die von den leuchtenden Körpern ausgestoßen wird. Newtons Ansicht ist unter dem Namen der Emanations- oder Emissionstheorie bekannt geworden und hat die Wissenschaft bis in das 19. Jahrhundert hinein beherrscht.
Den Ausgangspunkt der Untersuchung bildete der Nachweis, daß Licht verschiedener Farbe einen verschiedenen Grad der Brechbarkeit besitzt. In einem dunklen Zimmer brachte Newton hinter einer kleinen Öffnung ein Glasprisma an. Letzteres lenkte den Lichtstrahl, der durch die Öffnung eindrang, ab und rief auf der gegenüberliegenden Wand des Zimmers ein Spektrum hervor. Die Achse des Prismas war senkrecht zu den einfallenden Lichtstrahlen gerichtet. Als Newton das Prisma um diese Achse[S. 259] drehte, sah er das Spektrum zuerst hinab- und dann wieder hinaufsteigen. Zwischen der Ab- und Aufwärtsbewegung, in dem Augenblicke, als das Bild still zu stehen schien, also das Minimum der Ablenkung stattfand, stellte er das Prisma fest. Nun ließ er das gebrochene Licht senkrecht auf einen Bogen weißen Papieres MN fallen, der auf der gegenüberliegenden Wand des Zimmers angebracht war, und beobachtete die Gestalt und die Größe des dort entstandenen Spektrums (Abb. 71). Letzteres war rot in seinem am wenigsten gebrochenen Ende T, violett in dem am stärksten abgelenkten Ende P. Darauf wurden in den Weg des Lichtstrahls zwei Bretter (Abb. 72) DE und de mit Öffnungen bei G und g gestellt. Durch G. ging nur ein Teil des gebrochenen Lichtes, während der Rest aufgefangen wurde. Zwölf Fuß von dem ersten Brette entfernt, befestigte Newton das zweite Brett de (Abb. 72) in der Weise, daß wieder nur ein Teil des gebrochenen Lichtes,[S. 260] das durch G gelangt war, das Loch g in jenem zweiten Brette passieren konnte. Unmittelbar hinter dem zweiten Brette de brachte er dann ein anderes Prisma abc an, welches das die Öffnung g passierende Licht ablenken sollte. Indem er nun das erste Prisma ABC langsam um seine Achse hin- und herdrehte, bewirkte er, daß das Spektrum sich auf- und abbewegte, so daß alle Teile desselben nacheinander auf das Prisma abc fallen mußten. Gleichzeitig merkte Newton die Stellen auf der gegenüberliegenden Wand NM (Abb. 72) an, auf welche die Lichtstrahlen nach ihrem Durchgänge durch das zweite Prisma abc gelangten. Aus der verschiedenen Höhe dieser Stellen fand er, daß die Strahlen stärkster Brechbarkeit, die den blauen Teil des Spektrums bilden, stärker gebrochen werden, als das rote Licht. Trat nämlich der untere rote Teil des Spektrums durch die Öffnung g, so gelangte dieses Licht zu einer tieferen Stelle M der Wand. Wurde dagegen der obere blaue Teil des Spektrums durch dieselbe Öffnung g geworfen, so gelangte der betreffende Strahl zu der höheren Stelle N. Die dazwischen befindlichen Teile des Spektrums endlich fielen nach dem Passieren der Öffnung g zwischen M und N auf die Wand (Abb. 72).
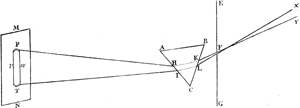

Diesem Versuch wurde von Newton eine solch entscheidende Bedeutung beigelegt, daß er ihn als Experimentum crucis, d. h. als einen am Kreuzwege entscheidenden Versuch, bezeichnet hat. Das Wort ist der bei Bacon üblichen, an Bildern so reichen Terminologie entnommen.
Durch Vereinigung sämtlicher Spektralfarben ließ sich das weiße Sonnenlicht in seiner vollen Ursprünglichkeit wieder herstellen. Newton zeigte dies durch folgenden Versuch.
ABC abc (Abb. 73) stellt ein Prisma vor, das in ein dunkles Zimmer fallendes Sonnenlicht so brach, daß es auf die Linse MN fiel und darauf bei pqrst die bekannten Spektralfarben erzeugte. Die divergierenden Strahlen gelangten dann vermöge der Brechung durch die Linse nach X und erzeugten dort durch Mischung sämtlicher Farben einen weißen Lichtstrahl.
Darauf wurde ein zweites Prisma DEG deg parallel dem ersten in X aufgestellt, um das weiße Licht aufwärts nach Y zu brechen (Abb. 73). Die Brechungswinkel der Prismen und ihre Abstände von der Linse waren gleich, so daß die Strahlen, die nach X zu konvergierten und, ohne eine dort stattfindende Brechung, sich daselbst hätten schneiden und hierauf wieder divergieren müssen, durch das zweite Prisma parallel gemacht wurden. War letzteres[S. 261] der Fall, so setzten diese Strahlen wieder einen weißen Lichtstrahl zusammen, und man konnte sämtliche Versuche mit diesem Strahle XY anstellen, die vorher im direkten Sonnenlicht gemacht waren. Durch Auffangen irgend einer Spektralfarbe pqrst vor der Linse MN ließ sich zeigen, daß die durch Versuche mit dem Strahl XY erzeugten Farben keine anderen waren, als diejenigen, die den Strahlen entsprachen, aus denen XY zusammengesetzt wurde. Daraus war ersichtlich, daß die Farben nicht durch irgend eine, infolge der Brechung und der Reflexion bewirkte Veränderung des Lichtes sich erst bilden, sondern daß sie aus der Trennung und der Zusammensetzung von Strahlen hervorgehen, von denen jeder eine gewisse Farbe besitzt.
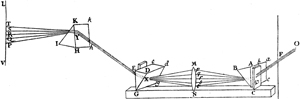
Um die Ursache der Körperfarben zu erkunden, brachte Newton verschiedene Gegenstände in den Strahl XY (Abb. 73) und fand, daß sie dort sämtlich in der Farbe erschienen, die sie bei Tageslicht besitzen. So zeigte z. B. Zinnober in dem Lichtstrahl XY dieselbe Farbe wie im Tageslicht. Wenn man bei der Linse MN die grünen und die blauen Strahlen auffing, wurde seine rote Farbe noch voller und lebhafter. Beseitigte man aber diejenigen Lichtstrahlen, welche die rote Farbe hervorrufen, so erschien der Zinnober nicht mehr rot, sondern er war gelb oder grün oder von anderer Farbe, entsprechend den Strahlenarten, die auf ihn fielen. Setzte Newton Zinnober und Ultramarin nebeneinander dem homogenen roten Lichte aus, so erschienen beide rot. Zinnober zeigte jedoch ein helles, glänzendes, Ultramarin dagegen ein schwaches dunkles Rot. Im homogenen blauen Licht erschienen[S. 262] dagegen beide Stoffe blau. Diesmal erglänzte aber Ultramarin in einem kräftigen, glänzenden Blau, während Zinnober nur eine schwache, dunkelblaue Farbe aufwies. Aus diesen Versuchen schloß Newton, daß die Farben daher rühren, daß die Körper je nach ihrer Art die einen oder die anderen Strahlenarten vorwiegend reflektieren. Die Veilchen reflektieren die brechbarsten Strahlen am meisten und haben daher ihre Farbe. Und so ist es nach Newton bei allen übrigen Körpern. Jeder wirft die Strahlen der ihm eigentümlichen Farbe in größerer Menge zurück als die anderen und hat seine Farbe dadurch, daß die ersteren in dem von ihm reflektierten Lichte überwiegen. Streng genommen sind also die Körper, wie Newton hervorhebt, nicht gefärbt, sondern sie besitzen eine gewisse Kraft, die Empfindung dieser oder jener Farbe zu erregen. Wie der Schall einer Glocke nichts anderes ist, als eine zitternde Bewegung des tönenden Körpers, die sich auf die Luft überträgt und unser Empfindungsorgan erregt, so sind auch »die Farben an den Objekten nichts weiter als ihre Fähigkeit, diese oder jene Strahlenart zu reflektieren. Und in den Strahlen ist wiederum nichts anderes als die Fähigkeit, diese Bewegung bis in unser Empfindungsorgan zu verbreiten. In letzterem endlich entsteht die Empfindung dieser Bewegungen in Gestalt von Farben«.
Ohne Zweifel bedeutet die Farbentheorie Newtons einen der größten Fortschritte der Optik. Man muß sich vergegenwärtigen, daß die Lehre des Aristoteles, nach der die Farben aus einer Mischung von Weiß und Schwarz, von Licht und Finsternis hervorgehen, im 17. Jahrhundert noch in voller Geltung war. Selbst Kepler wurde von dieser aristotelischen Auffassung beherrscht454 und de Dominis äußerte sich in seiner so hervorragenden optischen Schrift vom Jahre 1611, mische man dem Lichte etwas Dunkles hinzu, ohne jedoch das ganze Licht zu verhindern oder auszulöschen, so entständen die Farben455. Z. B. erscheine ein Feuer rot, weil der Rauch, den es mit sich führt, es verdunkle.
Nachdem Newton die verschiedene Brechbarkeit der Strahlenarten nachgewiesen hatte, mußte sich die Frage erheben, ob das ohne Rücksicht auf die Farbenlehre von Snellius aufgestellte Gesetz, daß der Sinus des Einfallwinkels zum Sinus des Brechungswinkels in einem bestimmten Verhältnis steht, für jede einzelne Strahlengattung gültig ist. Es sei sehr glaublich, meinte Newton, daß es sich so verhalte, weil die Natur immer gleichförmige Gesetze befolge. Ein experimenteller Nachweis456 war indessen doch erwünscht, und wurde von Newton auch erbracht. Brechung und Farbenerzeugung hielt Newton auf Grund dieser Versuche für zwei stets miteinander verknüpfte Vorgänge. Daher hielt er sich auch für überzeugt, daß es kein Mittel gäbe, den Fehler der chromatischen Abweichung zu beseitigen.
Die Unvollkommenheit der Fernrohre wurde vor Newton ausschließlich der sphärischen Gestalt der Gläser zugeschrieben. Nach ihm entsteht der größte Fehler dadurch, daß Strahlen verschiedener Brechbarkeit nicht nach einem Punkt konvergieren. Die Untersuchung hatte nämlich ergeben, daß für Strahlen, die von einem weit entfernten leuchtenden Punkte kommen, der Brennpunkt der brechbarsten Strahlen, verglichen mit demjenigen der am wenigsten brechbaren Strahlen, ungefähr um den 28. Teil der mittleren Brennweite näher bei der Linse liegt. Trotz dieser Erkenntnis erhob sich ein Wettkampf zwischen dem dioptrischen Fernrohr und dem Spiegelteleskop. Man suchte den Fehler des ersteren nämlich dadurch zu verringern, daß man der Objektivlinse eine sehr mäßige Krümmung und dementsprechend eine bedeutende Brennweite gab. Das Fernrohr nahm infolgedessen immer größere Abmessungen an. Schließlich verzichtete man nach einem von Huygens herrührenden Vorschlage auf eine feste Verbindung der beiden Linsen. Es entstand das sogenannte Luftfernrohr (Abb. 74), bei dem die Objektivbrennweite auf 2 Meter gesteigert war. Auch der Reflektor erreichte später infolge der Bemühungen Wilhelm Herschels die ansehnliche Länge von 40 Fuß457. Wie die durch Euler angebahnte Erfindung der achromatischen Linse dem Refraktor endlich zum Siege verhalf458 und das Irrtümliche der[S. 264] Newton'schen Voraussetzung aufdeckte, wird der Gegenstand späterer Betrachtungen sein.
Eine weitere Folge von Newtons Spektraluntersuchungen war seine Theorie vom Regenbogen, durch die ein Jahrtausende altes Rätsel gelöst wurde. Aristoteles hatte den Regenbogen aus der Spiegelung zu erklären gesucht, während ihn die arabischen Optiker auf die Brechung des Lichtes zurückführten. Nachdem dann Snellius sein Gesetz gefunden, vermochten Descartes und de Dominis die Erscheinung theoretisch und experimentell soweit zu analysieren, daß nur noch das Auftreten der Farben zu erklären blieb. Dies geschah durch Newton. Die seiner »Optik« entnommene Abb. 75 stellt den inneren und den äußeren[S. 265] Regenbogen, sowie den Gang der Lichtstrahlen durch Tropfen dar, die sich im roten F und im violetten Teile E befinden459. Man erkennt, daß im innern Bogen eine einmalige, im äußern dagegen eine doppelte Reflexion an der Wand der Tropfen stattfindet. Letzteres hatte schon Descartes angenommen, um zu erklären, daß der äußere Bogen lichtschwächer ist. Newton zeigte nun, wie von dem Tröpfchen E, dessen Winkelabstand von dem gemeinschaftlichen, in der Verlängerung der Linie OP liegenden Mittelpunkt der beiden Bögen 40° 17ʹ beträgt, der violette Teil des Spektrums nach dem Auge O des Beobachters gelangt. OP ist die Linie, welche die Sonne mit dem Auge verbindet. Der Tropfen F dagegen, dessen Abstand von dem Punkte, wo OP das Himmelsgewölbe schneidet, 42° 2ʹ beträgt, wird Strahlen geringerer Brechbarkeit zum Auge senden, wie aus der Abbildung ohne weiteres ersichtlich ist. Diejenige ringförmige Zone, in der sich der Tropfen F befindet, muß deshalb rot erscheinen. Im äußeren Bogen kehrt sich das Verhältnis um. Der Tropfen H sendet den stärker abgelenkten, violetten Teil des Spektrums zum Auge, während das Rot von der inneren, durch den Tropfen G repräsentierten Zone erzeugt wird.
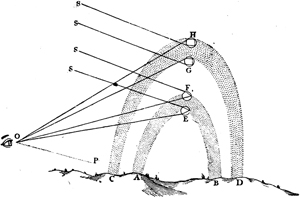
Den experimentellen Nachweis lieferte Newton nach dem Vorgange von Descartes und de Dominis461, indem er eine[S. 266] mit Wasser gefüllte Glaskugel in die Sonne hing und die Kugel hob und senkte, so daß der Winkel zwischen dem Sonnenstrahl und der die Glaskugel mit dem Auge verbindenden Linie die verschiedensten Werte durchlief. Betrug dieser Winkel etwa 42°, so sah man an der unteren, von der Sonne abgewendeten Seite der Kugel ein lebhaftes Rot. Ließ man die Kugel herab, so daß der Winkel um einige Grade kleiner wurde, so erschienen an Stelle des Rot nach und nach Gelb, Grün und Blau. Wurde die Kugel hinaufgezogen, so erschien bei einem Winkel von 51° das Rot auf der oberen, der Sonne zugekehrten Seite. Die übrigen Farben erschienen nacheinander, wenn man den Winkel allmählich durch weiteres Emporziehen der Kugel um einige Grade vergrößerte.
Im Verlauf des 17. Jahrhunderts waren mehrere, bisher unbekannte Erscheinungen in den Gesichtskreis der Physiker getreten. Bartholin hatte die Doppelbrechung am isländischen Kalkspat, Grimaldi die Beugung des Lichtes entdeckt, während Hooke sich zuerst mit den Farben dünner Blättchen beschäftigte. Dadurch waren neue Aufgaben auf dem Gebiete der Optik gegeben. Zwar blieb die theoretische Lösung dieser Aufgaben einem späteren Zeitalter vorbehalten; ihre experimentelle Erforschung hat indes Newton gleichfalls in erheblichem Maße gefördert.
Der italienische Mathematiker Grimaldi (1618–1663) hatte seine Beobachtungen über die Natur des Lichtes in einem Werk zusammengefaßt, das im Jahre 1665, zu jener Zeit, als Newton seine Untersuchungen begann, veröffentlicht wurde. In diesem Werke findet sich nicht nur die erste Beschreibung des durch ein Prisma erzeugten Sonnenspektrums462, es wird darin auch über merkwürdige Erscheinungen berichtet, die später mit dem Namen der Diffraktion und der Interferenz belegt wurden. Die für die Theorie des Lichtes grundlegenden Versuche Grimaldis wurden schon in einem früheren Abschnitt geschildert463.
Die ersten Anhänger einer die Allverbreitung eines außerordentlich elastischen Mediums voraussetzenden Wellentheorie waren außer Grimaldi, der die Wahrheit nur dunkel ahnte,[S. 267] Hooke und Huygens. Letzterer hat die Undulationstheorie, wie wir später sehen werden, besonders klar entwickelt464 und gilt mit Recht als ihr eigentlicher Begründer. Manche Äußerungen Newtons weisen darauf hin, daß er der Wellentheorie durchaus nicht jede Berechtigung absprach. Dennoch sah er sich veranlaßt, seine eigenen Erklärungen auf die Annahme zu stützen, daß das Licht ein Stoff sei, der von den leuchtenden Körpern ausgesandt wird. Während nämlich beide Lehren, die Undulationstheorie, sowie die von Newton begründete Emissionstheorie, die Erscheinungen der Reflexion und der Brechung zu deuten vermochten, war die erstere in der Fassung, die Huygens ihr gegeben, noch nicht imstande, das Auftreten der Farben zu erklären.
Nach der Annahme Newtons gibt es Lichtteilchen verschiedener Größe. Trifft ein Strahl des weißen Lichtes, in dem alle Größen vertreten sind, in schräger Richtung auf einen durchsichtigen Körper, so werden die kleinsten, das Violett ausmachenden Teilchen durch eine von den Partikeln des Körpers ausgehende Anziehung in höherem Grade aus ihrer Richtung abgelenkt als die gröberen, die rote Farbe bedingenden. Zwischen beiden Ablenkungen finden alle Übergänge statt, und so entsteht nach Newton das zusammenhängende Farbenband des Spektrums. Um die Beugung und die gleich zu besprechenden Farben dünner Blättchen zu erklären, mußte Newton dem Lichtstoff wieder neue Eigenschaften beilegen, so daß seine Hypothese mit jeder neu hinzutretenden Erscheinung verwickelter wurde, ein Umstand, der von vornherein nicht gerade zu ihren Gunsten sprach. Gestützt auf das große Ansehen ihres Urhebers hat sich die Emissionstheorie dennoch, obgleich von verschiedenen Seiten, insbesondere von Euler465, auf ihre Schwächen hingewiesen wurde, durch das ganze 18. Jahrhundert und darüber hinaus behauptet.
Ein weiteres Feld für optische Untersuchungen hatten Hookes Arbeiten über die Farben dünner Blättchen erschlossen. Robert Hooke wurde 1635 auf der Insel Wight geboren und starb im Jahre 1703 in London. Er war Mitglied der Royal Society und zeichnete sich durch große Vielseitigkeit aus, die ihn leider von dem beharrlichen Verfolgen eines Grundgedankens abzog. An Hookes Bemerkungen über die Natur des Lichtes knüpfte[S. 268] später Huygens die ausführliche Darstellung der Undulationstheorie an.
Hookes Untersuchungen, die zu denjenigen Newtons hinüberleiten, finden sich in seiner Mikrographie466, einem Werke, das auch in naturgeschichtlicher Hinsicht wichtig ist, weil darin die ersten Beobachtungen über den zelligen Bau der Pflanzen mitgeteilt werden. »Dicke Glimmerblättchen«, heißt es dort467, »sind farblos. Mache ich sie durch Spaltung immer dünner, so zeigt sich zuletzt jedes Blättchen schön gefärbt; dringt in die Spalten Luft ein, so zeigen sich Regenbogenfarben. Beim Zusammenpressen von Glasplatten entstehen Erscheinungen der gleichen Art«. Sehr dünn geblasenes Glas, angelassener Stahl, überhaupt sehr dünne durchsichtige Körper, die auf reflektierenden Körpern von anderer brechender Kraft liegen, bringen dieselben Farben hervor. Hooke führt die Entstehung dieser Farben auf eine »Verwirrung« der an den Grenzflächen der dünnen Schicht reflektierten Schwingungen zurück. Die Teilchen jedes leuchtenden Körpers seien in größerer oder geringerer Bewegung. Manche Stoffe würden durch Stoß oder Reibung leuchtend. Man müsse daher annehmen, daß das Licht in feinen Vibrationen bestehe, und daß nur solche Körper durchsichtig seien, welche diese Bewegung aufnehmen und fortleiten könnten. Das Zustandekommen der Interferenzfarben erläutert obenstehende, dem Werke Hookes entnommene Abbildung. (Siehe Abbildung 76.) Fällt danach ein Lichtstrahl, dem[S. 269] Hooke einen gewissen Durchmesser beilegt, auf eine dünne durchsichtige Platte, so wird ein Teil des Strahles gleich an der ersten Oberfläche zurückgeworfen. Ein anderer Teil dringt in die Platte ein und wird dann an der unteren Grenzfläche reflektiert, um endlich, abermals gebrochen und dem zuerst reflektierten Teile parallel, aus der Platte wieder auszutreten. Da nun das Licht zu seiner Fortpflanzung Zeit gebraucht, so werden die beiden Teile, in die der Strahl zerlegt ist, nicht gleichzeitig von der ersten Fläche zurückgehen. Durch dieses Nacheinander werden nach Hooke auf der Netzhaut die Farben hervorgerufen. Rot ist danach der Eindruck, den das Licht erzeugt, wenn der stärkere, an der ersten Oberfläche reflektierte Teil vorangeht und der schwächere folgt. Beim Blau ist es umgekehrt. Letzteres entsteht bei der Interferenz, wenn das schwächere, aus der Platte kommende Licht mit dem Teil eines nachfolgenden Lichtstrahls zusammentrifft, der an der oberen Fläche reflektiert wird. Der schwächere Teil kann dann vorangehen und der einheitlich empfundene Lichtstrahl die Empfindung von Blau hervorbringen. Blau und Grün sind für Hooke die Grundfarben. Aus ihrer Mischung entstehen die übrigen. Bei aller Unzulänglichkeit der Hooke'schen Theorie ist doch ihr Grundgedanke, die Farben dünner Blättchen durch die Interferenz zweier an den Oberflächen reflektierten Strahlen entstehen zu lassen, in die heutige theoretische Optik übergegangen. Sein Mühen, Beziehungen zwischen der Dicke der die Interferenzerscheinungen veranlassenden Schicht und den erzielten Wirkungen zu finden, blieb jedoch erfolglos.
»Eins, was von größter Wichtigkeit für diese Hypothese zu sein scheint«, sagt Hooke über diesen Punkt, »nämlich die Bestimmung der Dicke der Platten, die für das Eintreten jener Farbenerscheinungen notwendig ist, habe ich vielfach vergeblich auszuführen versucht. So außerordentlich dünn sind jene Platten und so unvollkommen unsere Mikroskope, daß alle meine Bemühungen in dieser Beziehung erfolglos gewesen sind.«
An diesem Punkte setzten die Untersuchungen Newtons ein, die er im zweiten Buche seiner Optik zusammenfaßt. Um die Reihenfolge der Farben genauer zu ermitteln, legte Newton die Linse eines Teleskops auf eine ebene Glasfläche. Es entstanden die den Farben dünner Blättchen entsprechenden »Newtonschen Ringe«, die im einfachen Lichte nur in einer Folge von hell und dunkel bestehen, während das auf die Platte fallende Sonnenlicht die Spektralfarben hervorruft.
In der Nähe der Berührungsstelle, die selbst vollkommen durchsichtig und farblos ist, bemerkte Newton die Farbenringe in der Reihenfolge Violett, Blau, Grün, Gelb, Rot. Und diese Folge wiederholte sich, bis die Farben immer schwächer wurden und nach der vierten Folge etwa in Weiß übergingen. Auch aus diesem Ineinanderfließen schloß er, daß das weiße Licht eine Mischung aller Farben sei.
Aus der Krümmung der Linse und dem Abstand der Ringe vom Berührungspunkte berechnete Newton die jeder Farbe entsprechende Tiefe der Luftschicht. Für das Gelb eines jeden Farbenringes verhielten sich die betreffenden Werte wie 1 : 3 : 5 : 7 ... während für die zwischen den gelben Zonen liegenden dunklen Partien die Durchmesser der Schicht dem Verhältnis 2 : 4 : 6 ... entsprachen. Es ergab sich somit auf Grund der Messungen und Berechnungen das einfache Gesetz, daß die den hellen und den dunklen Stellen entsprechenden Tiefen des vom Glase eingeschlossenen Mediums sich wie die natürlichen Zahlen verhalten468.
Newtons weitere Bemühungen bestanden darin, eine Analogie zwischen den dauernden Farben der natürlichen Körper und den Farben dünner durchsichtiger Blättchen darzutun. Dies geschah, indem er die Oberflächen der Körper als dünne Platten auffaßte, da alle Körper bis zu einem gewissen Grade durchsichtig seien.
Wie den Betrachtungen Hookes verhielt sich Newton auch den Versuchen Grimaldis gegenüber. In beiden Fällen ergänzte er die Arbeiten seiner Vorgänger durch genaue Messungen und lieferte dadurch wertvolles Material zur festeren Begründung der Theorie, die später an die Stelle seiner eigenen, unzutreffenden Ansichten über die Natur des Lichtes treten sollte.
Das dritte Buch der Optik enthält außer einer Nachprüfung und Erweiterung der Grimaldischen Versuche über die Beugung des Lichtes eine Anzahl von Betrachtungen, die Newton »Fragen« (Queries) genannt hat. In diesen »Fragen« bringt er das zur Sprache, was er den Forschern zur Prüfung durch weitere Beobachtungen und Versuche überlassen wollte. Newton wünschte nämlich aus seinem Lehrgang der Optik dasjenige auszuscheiden, worüber er mit sich selbst noch nicht ins Reine gekommen war. So wird die Frage aufgeworfen, ob das Licht nicht die Körper dadurch erwärme, daß es die Körperteilchen in eine vibrierende[S. 271] Bewegung versetze469. Daß erhitzte Körper Licht aussenden, scheint ihm wiederum von einer vibrierenden Bewegung ihrer Teilchen herzurühren470. In den Belegen, die Newton für diese Meinung beibringt, werden allerdings Erscheinungen zusammengestellt, für die sich im weiteren Verlaufe der Forschung die verschiedensten Ursachen ergeben haben. So sagt Newton, es leuchte Meerwasser beim Sturm, Quecksilber, wenn es im Vakuum geschüttelt werde, der Rücken einer Katze, wenn man ihn im Dunklen streichle. Ferner leuchte Phosphor beim Reiben und Eisen, wenn es rasch mit dem Hammer bearbeitet werde. Setze man eine Glaskugel in rasche Umdrehung, so leuchte sie an der Stelle, gegen die man die Handfläche presse.
Weiter wird gefragt, ob nicht die Empfindung verschiedener Farben etwa dadurch erregt werde, daß das Licht Schwingungen von verschiedener Größe mache, etwa so, wie die Schwingungen der Luft je nach ihrer Verschiedenheit die Empfindung der Töne erregen. Allerdings dachte sich Newton diese Schwingungen als longitudinale Schwingungen in dem Strome der materiellen Lichtkörperchen. – Newton verläßt also auch hier den Boden seiner Theorie nicht. Ja er ist sogar der Ansicht, daß sich die festen Körper und das Licht ineinander umwandeln lassen471.
In einer seiner »Fragen«, die er an das Verhalten des Lichtes zum Doppelspat anknüpft, ist der Ursprung des Namens »Polarisation« zu suchen. »Sieht nicht«, sagt Newton472, »die ungewöhnliche Brechung im isländischen Kristall gar sehr danach aus, als käme sie durch eine Art anziehender Kraft zustande, die nach gewissen Seiten hin sowohl den Strahlen als den Kristallteilchen innewohnt?« Die den Strahlen innewohnende Kraft sollte derjenigen der Kristallteilchen ebenso entsprechen wie sich die »Pole zweier Magnete entsprechen«. Wie ferner der Magnetismus verstärkt oder geschwächt werden oder ganz fehlen könne, so sei auch die Kraft, die senkrecht einfallenden Lichtstrahlen zu brechen, größer im Doppelspat, kleiner im Bergkristall und endlich in anderen Körpern gar nicht vorhanden.
Dieser Gedanke Newtons wurde ein Jahrhundert nachher von Malus, als er die Polarisation durch Reflexion entdeckte, wieder[S. 272] aufgenommen. Und das Wort »Polarisation«, das zur Bezeichnung der »Seitlichkeit« gewisser Lichtstrahlen gewählt war, wurde später auch von den Anhängern der Wellenlehre gebraucht.
Im Anschluß an seine »Fragen« entwickelte Newton, gleichfalls in hypothetischer Form, die Grundzüge der Emissions- oder Emanationstheorie. Nach dieser bestehen die Lichtstrahlen aus sehr kleinen Körperchen, die von den leuchtenden Substanzen ausgesandt werden. Solche Körper werden sich durch ein gleichförmiges Medium in geraden Linien fortbewegen. Durchsichtige Substanzen werden aus der Entfernung auf sie wirken, indem sie sie brechen, zurückwerfen und beugen. Um die Verschiedenheit in den Farben und in den Graden der Brechbarkeit zu erklären, genügt die Annahme, daß die Lichtstrahlen aus Körperchen verschiedener Größe bestehen, von denen die kleinsten das Violett erzeugen, die übrigen in dem Maße, in dem sie größer werden, das Blau, Grün, Gelb und Rot hervorrufen und immer schwerer abgelenkt werden.
Am meisten tritt die Schwäche der Emissionstheorie dort hervor, wo es sich um Interferenzerscheinungen handelt. Die Annahme periodisch wiederkehrender Anwandlungen leichterer Reflexion und leichteren Durchganges, die Newton hier machte, kann den Rang einer mechanischen Erklärung nicht beanspruchen. Ähnliche Schwierigkeiten bereitete die Doppelbrechung im isländischen Kalkspat. Newton meinte indes, sie müsse gleichfalls durch eine Art anziehender Kraft zustande kommen, die nach gewissen Seiten hin sowohl den Strahlen als den Kristallteilchen innewohne. Es sei aber schwer zu begreifen, wie die Lichtstrahlen nach zwei Seiten hin eine Kraft äußern könnten, wenn sie nicht aus Korpuskeln beständen.
Obgleich Newton selbst sich durchaus nicht entschieden zugunsten der einen oder der anderen der in dem Anhang zur Optik erörterten Theorien entschieden hatte, wurde von seinen Schülern und Anhängern der Emanationstheorie der Wert eines durch die Autorität des Meisters gestützten Dogmas beigelegt. Was Newton nur bezweifelte, wurde verworfen, was er dagegen für wahrscheinlich hielt, wurde als vollkommen sicher erachtet. So wurde er durch seine Schule zum Vater der Emanationstheorie473, während er doch immer seine Neutralität gegenüber jeder Hypothese betont hatte. Diese Theorie setzte sich so unerschütterlich in den Köpfen[S. 273] fest, daß abweichende, von Huygens, Euler und Christian Wolf geäußerte Ansichten gar keine Beachtung fanden. Scheu und Ehrfurcht gegenüber Newton hielt die meisten Physiker des 18. Jahrhunderts davon ab, auch nur den leisesten Zweifel in die Richtigkeit der Emanationstheorie zu setzen. »Es ist wirklich ein trüber Fleck in der Geschichte der Physik«, sagt einer ihrer Darsteller474, »und ein schlagender Beweis dafür, wie schädlich die Autorität eines großen Geistes auf die nachfolgenden Zeitalter wirken kann, wenn sie sich soweit steigert, daß dadurch die unbefangene Forschung unterdrückt wird.«
Seinen Höhepunkt erreichte Newtons Schaffen, als er den im Jahre 1666 erfolglos angestellten Versuch, die Bewegung der Himmelskörper aus den Gesetzen der Mechanik zu erklären, wieder aufnahm. Anlaß hierzu bot ihm die im Jahre 1682 an ihn gelangte Mitteilung, daß Picard in Frankreich wesentlich andere Abmessungen für die Erdkugel erhalten habe, als man in England zur Zeit Newtons annahm. Jean Picard (1620–1682), ein Mitglied der französischen Akademie, hatte noch unter der Voraussetzung, daß die Erde die Gestalt einer Kugel besitze, eine Gradmessung durch Triangulation zwischen Amiens und Malvoisine ausgeführt475. Bei dieser Messung kamen zum erstenmal mit Fernrohren versehene Winkelmeßinstrumente in Anwendung. Picard hatte für den Breitengrad den Wert von 70 englischen Meilen oder 57060 Toisen476 gefunden, während Newton, der die von Snellius im Jahre 1617 ausgeführte Messung nicht kannte477, bei[S. 274] seiner 1666 angestellten Rechnung 60 englische Meilen für den Breitengrad zu Grunde gelegt hatte.
Die mittlere Entfernung des Mondes war hinlänglich genau bekannt. Newton nahm sie zu 60 Erdhalbmessern an. Das Stück, um das der Mond in einer Minute infolge der auf ihn wirkenden Zentripetalkraft von der Tangente seiner Bahn abgelenkt wird, ergab sich aus diesen Daten gleich 15 Fuß478. Unter der im Jahre 1666 gemachten Annahme hatte die Rechnung 13½ Fuß ergeben, ein Wert, der keine einfache Beziehung zu dem an der Oberfläche der Erde von einem frei fallenden Körper in einer Minute durchlaufenen Wege erkennen ließ. Letzterer beträgt 5400 = 60 · 60 · 15 Fuß. Er ist also im Verhältnis des Quadrates der Entfernung größer als die zum Erdzentrum gerichtete Bewegung des Mondes, und in demselben Maße ist es daher auch die auf den fallenden Körper wirkende Kraft. Die Zentripetalkraft ergab sich folglich als mit der Schwere identisch, wenn man für die letztere voraussetzte, daß ihre Abnahme dem Quadrate der Entfernung entspricht. Damit war ein Gesetz von der größten Allgemeingültigkeit aufgefunden, das man mit Recht als das Weltgesetz bezeichnet hat.
Als Newton die soeben mitgeteilte Folgerung zog, ergriff ihn eine solche Erregung, daß er einen Freund bitten mußte, die Rechnung zu Ende zu führen. Was schon Anaxagoras vorgeahnt hatte, als er aussprach, wenn die Schwungkraft des Mondes aufhöre, so müsse dieser zur Erde fallen wie der Stein aus der Schleuder; was bei Kepler und bei Hooke mit wachsender Deutlichkeit hervortrat: das stand mit einem Schlage klar vor dem Geiste Newtons. Auf die glückliche Entdeckung des Augenblicks folgten dann Jahre mühevollster Arbeit. Galt es doch, die Richtigkeit des gefundenen Prinzips durch seine Anwendung auf sämtliche astronomischen Erscheinungen zu erweisen. Die Untersuchung[S. 275] wurde auf die Planeten, die Jupitermonde, die Erscheinung der Ebbe und Flut, ja selbst auf die Kometen ausgedehnt. Überall ergab sich die Bestätigung des Gravitationsgesetzes, nach dem die anziehende Kraft den Massen direkt und dem Quadrate der Entfernung umgekehrt proportional ist. So entstanden die »Mathematischen Prinzipien der Naturwissenschaft«, durch welche Newton die Erklärung des Weltmechanismus aus seiner Gravitationstheorie zu einem vorläufigen Abschluß brachte479.
In seiner Schrift über die Bewegung der Erde480 streifte Hooke schon an die Entdeckung des Gravitationsgesetzes. »Ich werde«, heißt es dort, »ein Weltsystem entwickeln, das in jeder Beziehung mit den bekannten Regeln der Mechanik übereinstimmt. Dies System beruht auf drei Annahmen: Erstens, daß alle Himmelskörper ohne Ausnahme eine gegen ihren Mittelpunkt gerichtete Anziehung oder Schwerkraft besitzen, wodurch sie nicht bloß ihre eigenen Teile, sondern auch alle innerhalb ihrer Wirkungssphäre befindlichen Himmelskörper anziehen. Die zweite Voraussetzung ist die, daß alle Körper, die in eine geradlinige und gleichförmige Bewegung versetzt werden, sich so lange in gerader Linie fortbewegen, bis sie durch irgendeine Kraft abgelenkt und in die Bahn gezwungen werden, die einem Kreise, einer Ellipse oder einer anderen, nicht so einfachen, krummen Linie entspricht. Nach der dritten Annahme sind die anziehenden Kräfte um so stärker, je näher ihrem Sitz der Körper ist, auf den sie wirken. Welches die verschiedenen Grade der Anziehung sind, habe ich noch nicht durch Versuche feststellen können. Aber es ist ein Gedanke, der, wenn er weiter verfolgt wird, den Astronomen in den Stand setzen muß, alle Bewegungen der Himmelskörper nach einem gewissen Gesetze zu bestimmen.« An diese Ausführungen wird der Wunsch geknüpft, daß jemand diesen Gedanken verfolgen möge, da der Verfasser durch andere Dinge zu sehr in Anspruch genommen sei.
Die Gravitationsmechanik stellt sich im wesentlichen als eine Fortbildung der von Galilei aufgefundenen Sätze über den Wurf dar. Am klarsten geht dieser Zusammenhang aus der folgenden,[S. 276] von Newton selbst gegebenen Darstellung hervor481: »Daß durch die Zentralkräfte die Planeten in ihren Bahnen erhalten werden können, ersieht man aus der Bewegung der Wurfgeschosse. Ein geworfener Stein wird, indem auf ihn die Schwere wirkt, vom geraden Wege abgelenkt und fällt, indem er eine krumme Linie beschreibt, zuletzt zur Erde. Wird er mit größerer Geschwindigkeit geworfen, so fliegt er weiter fort. Und so könnte es geschehen, daß er einen Bogen von 10, 100, 1000 Meilen beschriebe und zuletzt über die Grenzen der Erde hinausginge und nicht mehr zurückfiele. Es bezeichne (Abb. 77) AFB die Oberfläche der Erde, C ihren Mittelpunkt und VD, VE, VF krumme Linien, die ein von der Spitze V eines sehr hohen Berges in horizontaler Richtung und mit wachsender Geschwindigkeit geworfener Körper beschreibt. Damit der Widerstand der Luft nicht in Rechnung gestellt zu werden braucht, wollen wir sie uns ganz fortgenommen denken. Auf dieselbe Weise, wie der mit zunehmender Geschwindigkeit geworfene Körper die Bögen VD, VE und VF beschreibt, wird er endlich, wenn die Geschwindigkeit noch weiter vergrößert wird, über den Umfang der Erde fortgehen und zu dem Berge, von dem aus er geworfen wurde, zurückkehren482. Da nach den Sätzen, die von der Zentrifugalkraft handeln483, die Geschwindigkeit bei der Rückkehr zum Berge nicht kleiner als beim Ausgange sein kann, so muß der Körper fortfahren, sich in derselben Weise um die Erde herumzubewegen. Denken wir uns Körper aus höheren Punkten in horizontaler Richtung fortgeworfen, und zwar aus Punkten, die 10 Meilen, 100 Meilen oder ebensoviele Halbmesser über der Oberfläche der Erde liegen, so werden diese Körper, je nach ihrer Geschwindigkeit und nach der in den einzelnen Punkten[S. 277] herrschenden Anziehung, Kurven beschreiben, die entweder konzentrisch oder exzentrisch sind. In diesen Bahnen werden sie fortfahren, nach der Weise der Planeten den Weltraum zu durchwandern.«
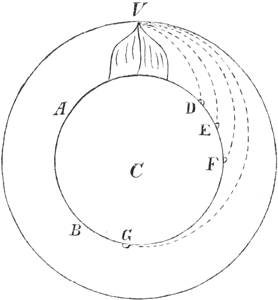
Die hier gegenüber der Betrachtung Galileis eingetretene Erweiterung besteht also darin, daß die Richtung der auf den Körper konstant wirkenden Kraft sich stetig ändert, während sie im anderen Falle485 die gleiche bleibt.
Newton begründete mit seinem Werk die neuere mathematische Physik; und die »Prinzipien« sind zwar nicht dem Umfange, wohl aber der Methode nach das erste Lehrbuch dieses Gebietes.
Die Bedeutung der »Prinzipien« für die Entwicklung nicht nur der Mechanik und der Astronomie, sondern aller übrigen Zweige der Naturwissenschaft ist so groß, daß wir diesem Werke eine etwas eingehendere Betrachtung widmen müssen.
Newton beginnt mit einer Reihe von Definitionen und Gesetzen, die teils neu sind, teils zum ersten Male mit der nötigen Klarheit von ihm ausgesprochen werden. Die wichtigsten lauten486:
Um verwickeltere Bewegungsaufgaben zu lösen, genügte die von den Alten geschaffene mathematische Methode nicht mehr. In der Dynamik waren veränderliche, »fließende« Größen und die momentanen Veränderungen, die ihr Verhältnis erleidet, in Rechnung zu ziehen. Newton befand sich, als er die »Prinzipien« schrieb, schon im Besitze einer von ihm erfundenen, als Fluxionsrechnung bezeichneten Methode, die speziell für die Mechanik geschaffen war und der soeben ausgesprochenen Forderung genügte. Newton gibt an mehreren Stellen seines Werkes, allerdings nur kurze, lückenhafte Abrisse dieser Methode. Seltsamerweise zieht er aber bei der Lösung der Bewegungsaufgaben die alte, geometrisch-synthetische Art der Darstellung vor, obgleich er, wie er später selbst angab, auf analytischem Wege zu seinen Resultaten gelangt war.
Nachdem er die mechanischen Grundbegriffe, wie wir an einigen Beispielen gesehen haben, formuliert und seine mathematische Methode auseinandergesetzt, wendet sich Newton seiner eigentlichen Aufgabe zu, nämlich der Bestimmung der Zentralkräfte. Zunächst beweist er in der noch heute üblichen Weise, daß die Bahnen von Körpern, die sich unter dem Einfluß einer Zentripetalkraft bewegen, in festen Ebenen liegen, und daß die von den Radien beschriebenen Flächen den Zeiten proportional sind. Es möge wenigstens die Newtons Beweis zugrunde liegende Konstruktion hier Platz finden (Abb. 78).
Auf diesen Satz folgt seine Umkehrung, daß nämlich jeder Körper, der sich in einer festen Fläche so bewegt, daß die Leitstrahlen in gleichen Zeiten gleiche Flächen beschreiben, unter der Wirkung einer Zentripetalkraft steht.
Newton geht dann zu der Bewegung der Körper in Kegelschnitten über, deren einer Brennpunkt das Kraftzentrum ist.[S. 279] Er betrachtet zuerst den für die Planetenbewegung wichtigsten Fall, daß der Körper sich in einer Ellipse bewegt, und sucht das Gesetz der nach ihrem Brennpunkt gerichteten Zentralkraft zu ermitteln. Es ergibt sich, daß die gesuchte Kraft dem Quadrate des Radius vector umgekehrt proportional ist. Dasselbe Gesetz wird dann auch für die Parabel und für die Hyperbel dargetan. In einem besonderen Abschnitt werden die anziehenden Kräfte sphärischer Körper erörtert. Ihre Gesamtanziehungen werden aus den Einzelanziehungen der Teilchen abgeleitet, die den Körper zusammensetzen. Newton findet, daß die Wirkung einer homogenen Vollkugel auf einen außerhalb befindlichen Punkt der Masse direkt und dem Quadrat des Abstandes vom Mittelpunkt der Kugel umgekehrt proportional ist. Dagegen ergibt sich, daß die Wirkung der Vollkugel auf einen inneren Punkt der Entfernung dieses Punktes vom Mittelpunkte entspricht. Die Anziehungen endlich, die zwei Kugeln aufeinander ausüben, verhalten sich wie die Massen der anziehenden Kugeln und umgekehrt wie die Quadrate der Entfernungen der Mittelpunkte.
Nachdem Newton in den beiden ersten Büchern seines fundamentalen Werkes die allgemeinen Gesetze der Bewegung, einschließlich der Bewegungen der Flüssigkeiten entwickelt, bringt er im dritten Buche die Anwendung dieser Gesetze auf das Weltsystem.
Newton zeigt, daß sowohl das zweite wie auch das dritte Keplersche Gesetz aus dem allgemeinen Gesetze, das die Anziehung regelt, gefolgert werden können. Es wird ferner dargetan, daß alle Monde gegen ihre Planeten und alle Planeten gegen die Sonne gravitieren, sowie daß sich die Bewegungen dieser Körper durch Zentralkräfte regeln, die den Massen direkt und dem Quadrate der Entfernung umgekehrt proportional sind. Das Newtonsche Gesetz gilt somit für den ganzen Weltraum. Es ist das schon so lange erstrebte, mehr oder minder deutlich von anderen vorgeahnte, von Newton dagegen erst in voller Klarheit enthüllte Weltgesetz.
Auf die Erkenntnis dieses allgemeinsten Gesetzes folgt wieder die Ableitung der Einzelheiten, wie der planetarischen Störungen, der Ungleichheiten der Mondbewegung, der Ebbe und Flut des Meeres usw. »Alle Planeten«, sagt Newton, »sind gegeneinander schwer, daher werden z. B. Jupiter und Saturn sich in der Nähe ihrer Konjunktion anziehen und ihre Bewegungen wechselseitig merklich stören. Ebenso wird die Sonne die Bewegung des Mondes[S. 280] stören, und Sonne und Mond das Meer beeinflussen.« Die Ableitung der gedachten Erscheinungen, die bisher jeder mechanischen Erklärung gespottet hatten, aus dem Gravitationsgesetz machte nicht geringe Schwierigkeiten. Sie völlig zu heben, war Newton noch nicht imstande, weil er sich auf die anziehenden Kräfte von Körpern sphärischer Gestalt beschränkte. Doch ist es ihm gelungen, in der Hauptsache den Zusammenhang und die Begründung des Weltsystems aus seinem Gesetze abzuleiten.
Daß die Gezeiten wohl auf eine kosmische Anziehung zurückzuführen seien, hatte schon Kepler ausgesprochen. Er betrachtete Ebbe und Flut als einen Beweis dafür, daß sich die anziehende Kraft des Mondes bis zur Erde erstrecke. Selbst im Altertum begegnet uns schon diese Ansicht. Ja, Seneca erwähnt sogar, daß sich bei Springfluten außer der Kraft des Mondes auch die der Sonne bemerkbar mache487.
Von diesen Vermutungen bis zur Begründung der Gesetze einer Erscheinung und bis zum Nachweise, daß die Tatsachen im allgemeinen diesen Gesetzen entsprechen, war indessen ein großer Fortschritt. Ihn herbeigeführt zu haben, ist eins der wesentlichsten Verdienste Newtons. Auf ihn konnten sich später Euler und Laplace stützen und die Gezeitentheorie im 17. Jahrhundert zu einem gewissen Abschluß bringen488. Der Kernpunkt der Newtonschen Theorie ist der Satz, daß das Wasser auf der dem Monde zugekehrten Seite der Erde stärker angezogen wird als auf der vom Monde abgewandten Seite, so daß es dort der Erde gegenüber, die ja auch zum Monde gravitiert oder sozusagen nach ihm hinfällt, zurückbleibt. Die Folge ist, daß zwei Flutwellen entstehen. Das Ansteigen des Wassers auf der dem Monde zugekehrten Seite erschien ja auch vor Newton begreiflich. Das Zustandekommen der zweiten Welle und manche Einzelheit der Flutbewegung wurde jedoch erst durch ihn erklärt.
An die Gravitationslehre anknüpfend, wollen wir noch die Ansichten erwähnen, die Newton sich nach dem Vorgange von Descartes und Gassendi über die Konstitution der Materie gebildet hatte. Er hielt es für das Wahrscheinlichste, daß sie aus festen, undurchdringlichen, beweglichen Partikeln bestehe. Da die Naturkörper, z. B. das Wasser, in ihren Eigenschaften unveränderlich seien, so müßten die Partikeln, aus denen sie beständen,[S. 281] weder abgenutzt noch zerstört werden können. Der Wandel der körperlichen Dinge sei ausschließlich in die Trennungen, Vereinigungen und Bewegungen jener unveränderlichen Teilchen zu verlegen. Diese Veränderungen sollten aus aktiven Prinzipien folgen, zu denen Newton die Schwerkraft rechnet.
Den Begriff der anziehenden Kraft (als causa mathematica) übertrug Newton auch auf die Erscheinungen der Kohäsion, der Adhäsion, der chemischen Verbindung usw. »Ich möchte«, sagte er, »aus der Kohärenz der Körper schließen, daß auch deren kleinste Teilchen sich gegenseitig anziehen durch eine Kraft, die auf kleine Entfernungen hin auch die chemischen Wirkungen hervorbringt«489. Er betont aber, daß diese Prinzipien nicht mit den verborgenen Qualitäten der Aristoteliker verwechselt werden dürften, sondern allgemeine Naturgesetze seien. Die Wahrheit dieser Prinzipien werde uns aus den Erscheinungen deutlich, wenn ihre Ursachen bis jetzt auch nicht entdeckt worden seien. Der Unterschied ist also der, daß die Aristoteliker annahmen, die Wirkungen der Dinge entsprängen unbekannten Eigenschaften, die sich weder entdecken noch klarstellen ließen. Damit war natürlich jeder Fortschritt in der Naturerkenntnis gehemmt. Die neuere, durch Newton vertretene Richtung erkannte es dagegen als einen großen Fortschritt, aus den Erscheinungen allgemeine Prinzipien der Bewegung herzuleiten und dann zu zeigen, wie aus solchen Prinzipien die Eigenschaften und Wirkungen der körperlichen Dinge folgen, wenn auch die Ursache jener Prinzipien selbst unbekannt bleibt. Das war der Grundgedanke, der Newton bei seinen Forschungen leitete; und in diesem Sinne ist auch sein oft erwähnter Ausspruch: »Hypothesen ersinne ich nicht« zu verstehen. Die gleiche Beschränkung wie Newton hatte sich Galilei auferlegt. »Die Ursache der Gesetze freifallender Körper ist kein notwendiger Teil unserer Untersuchung«, sagt dieser. »Für uns genügt es, die Eigenschaften dieser Bewegung unter der Voraussetzung eines einfachen Gesetzes kennen zu lernen.«
Newtons Weltanschauung war indessen keine rein materialistische. Es erscheint ihm durchaus unphilosophisch, anzunehmen, die Welt sei allein durch die Wirkung der Naturgesetze aus dem[S. 282] Chaos entstanden. Die wundervolle Gesetzmäßigkeit im Planetensystem z. B. könne nicht aus einem blinden Walten hervorgegangen sein, sondern sie entspräche einer bestimmten Sorgfalt und Anordnung. Wir werden später sehen, daß das 18. Jahrhundert Newton hierin nicht beipflichtete, und daß ein Kant und ein Laplace versucht haben, den Aufbau des Planetensystems auf rein mechanisch wirkende Ursachen zurückzuführen.
Aber auch abgesehen von diesen, auf einen teleologischen Standpunkt Newtons hindeutenden Erwägungen ist seine Auffassung des Weltganzen eine dualistische. Er nimmt an, daß eine geistige Substanz alle Körper durchdringe und in ihnen enthalten sei. »Durch die Kraft dieser geistigen Substanz«, sagt er490, »ziehen sich die Teilchen der Körper wechselseitig an«. Durch diese Kraft wirken sie aber auch auf die größte Entfernung. Aus den Vibrationen der geistigen Kraft scheint ihm auch die Tätigkeit des Gehirns und die Wirkung dieses Organs auf die Nerven und die Muskeln erklärlich. Daß Newton außerdem in den »Prinzipien« Betrachtungen über das Wesen Gottes anstellt, als den er nicht etwa die Weltseele gelten lassen will, steht außer Zusammenhang mit seinem, im übrigen so wohl gefügten, Lehrsystem.
Newtons Lehre vermochte sich, zumal in Frankreich und in Deutschland, nur langsam Bahn zu brechen, da die zeitgenössischen Astronomen, noch mehr aber die Physiker, zu sehr in der von Descartes herrührenden Wirbeltheorie befangen waren. Letzterer, der als Begründer der neueren Philosophie das größte Ansehen genoß, und dessen Bemühen um die Formulierung des Brechungsgesetzes, um die Theorie des Regenbogens, sowie um die Begründung der analytischen Geometrie alle Anerkennung verdiente, dachte sich die Planeten in kreisenden Ätherströmen schwimmend, in deren Mitte sich die Sonne befinden sollte. Eine Wirkung in die Ferne schien den Anhängern der Cartesianischen Physik ganz unannehmbar491.
Aus Newtons Schriften geht nicht mit Sicherheit hervor, ob er sich die Wirkung in die Ferne als eine unvermittelte oder als eine vermittelte dachte. Anfangs war Newton zu der Annahme geneigt, daß die Bewegungen der Gestirne aus mechanischen Prinzipien zu erklären seien. Später sah er jedoch davon ab, da er sich außerstande fühlte, den Grund der Schwere aus den Erscheinungen abzuleiten. In der Vorrede zur zweiten Ausgabe der »Prinzipien« von 1713 wird die Gravitation denn auch als eine »causa simplicissima« hingestellt, für die es keine mechanische Erklärung gebe. Jene Vorrede hat indessen Newtons Freund Cotes (Prof. d. Astronomie in Cambridge) verfaßt, und man darf die darin geäußerten Ansichten nicht ohne weiteres auf Newton übertragen. Dafür, daß Newton ein materielles Agens durchaus nicht etwa für ganz ausgeschlossen hielt, spricht nämlich folgende von ihm herrührende Bemerkung: »Daß die Gravitation eine inhärente Eigenschaft der Materie sei, derart, daß ein Körper auf einen anderen aus der Ferne und durch den völlig leeren Raum ohne die Vermittlung von irgend etwas anderem wirke, erscheint mir als eine große Absurdität. Ich kann mir nicht vorstellen, daß jemand, der fähig ist, philosophisch zu denken, in sie verfallen kann.«
Jedenfalls ist also die Annahme einer durch das Medium erfolgenden Wirkung nicht erst im 19. Jahrhundert durch Faraday entstanden. Sie hat vielmehr schon im 18. Jahrhundert namhafte Vertreter gefunden. Auch Kepler hat sich lange vor Newton gegen die Möglichkeit einer »actio in distans« ausgesprochen und eine die Schwere bedingende Strahlungsenergie angenommen, die sich wie das Licht durch den Raum ausbreiten und alle Körper durchdringen sollte492. Der große deutsche Philosoph Leibniz nahm eine vermittelnde Stellung ein. Viel weniger als er konnte sich Huygens mit der Newtonschen Kraftidee befreunden493. Er bemühte sich deshalb, auf Cartesianischer Grundlage die Schwerkraft, für die er das Newtonsche Gesetz nicht etwa in Abrede stellte, mechanisch zu erklären. Seine Ansichten, auf die wir in dem nächsten Abschnitt zurückkommen, entwickelte er im Jahre 1690 als Anhang zu seinem Werke über das Licht.
Allmählich gelangte die Newtonsche Gravitationsmechanik indessen doch zur allgemeinen Anerkennung. In Frankreich, wo man besonders lange an Descartes festhielt, wurde der neuen[S. 284] Lehre erst durch Voltaire und Maupertuis Bahn gebrochen. Das Gravitationsgesetz wurde zwar als richtig anerkannt, um so energischer bekämpfte man die Annahme der in die Ferne wirkenden Kraft, der »Zentripetalkraft« Newtons, und suchte durch ein modifiziertes Wirbelsystem die kosmischen Erscheinungen zu erklären. Auch durch den Stoß von Molekeln, die sich im Weltraum bewegen sollten, suchte man die Gravitation auf ein anschauliches Prinzip zurückzuführen494. Indes hundert Jahre später waren es gerade die Franzosen, vor allem ihr großer Astronom Laplace, die das von Newton in den gröberen Zügen ausgearbeitete System bis in alle Einzelheiten vollendet haben.
Zu jener Zeit, als die »Prinzipien« erschienen, bekleidete Newton immer noch die Professur der Mathematik in Cambridge, deren kärgliche Besoldung nur den bescheidensten Ansprüchen genügte. Dazu traf ihn das Unglück, daß ein Teil seiner wertvollen Aufzeichnungen verbrannte. Newton wurde dadurch so bekümmert, daß man eine Geistesstörung befürchtete. Diese äußeren Verhältnisse wurden mit einem Schlage durch Newtons Ernennung zum königlichen Münzmeister geändert. Seitdem wohnte er, im Alter mit Ehren überhäuft, bald in der Hauptstadt, bald auf einem Landsitz in der Nähe, bis ein Steinleiden am 31. März des Jahres 1727 seinem, an wissenschaftlichen Erfolgen so überaus reichen Leben ein Ende bereitete.
Newton war trotz seiner außerordentlichen Bedeutung ein bescheidener, stiller Gelehrter. »Ich weiß nicht«, sprach er einst, »wie ich der Welt erscheine. Mir selbst aber komme ich vor wie ein Knabe, der am Meeresufer spielt und sich damit belustigt, dann und wann einen glatten Kiesel oder eine schönere Muschel als gewöhnlich zu finden, während der große Ozean der Wahrheit unerforscht vor mir liegt.«
Newton wurde in der Westminsterabtei, der Stätte, wo Englands große Männer ruhen, unter Ehrenbezeugungen beigesetzt, wie sie sonst nur verstorbenen Mitgliedern des königlichen Hauses erwiesen werden. Das Denkmal, das seinen Staub bedeckt, trägt einen in lateinischer Sprache verfaßten Nachruf. Er lautet in deutscher Übersetzung:
Hier ruht
Sir Isaac Newton,
Der mit fast göttlicher Geisteskraft
Der Planeten Bewegung und Gestalten,
Die Bahnen der Kometen und die Gezeiten des Ozeans
Mit Hilfe seiner mathematischen Methode
Zuerst erklärte.
Er ist es, der die Verschiedenheiten der Lichtstrahlen,
Sowie die daraus entspringenden Eigentümlichkeiten der Farben,
Die niemand vorher auch nur vermutete, erforscht hat.
Als der Natur, der Altertümer und der Heiligen Schrift
Fleißiger, scharfsinniger und getreuer Deuter,
Verherrlichte er die Majestät des allmächtigen Schöpfers in seiner Philosophie.
Die vom Evangelium geforderte Einfalt bewies er durch seinen Wandel.
Mögen die Sterblichen sich freuen, daß unter ihnen wallte
Eine solche Zierde des Menschengeschlechts.
Geboren am 25. Dezember 1642, gestorben am 20. März 1727495.
Aus der Schar der zeitgenössischen Forscher ragte wohl niemand so weit an Newton heran wie der schon wiederholt erwähnte Niederländer Huygens, den Newton selbst Summus Hugenius nannte. Auch Huygens stand auf den Schultern Galileis. Seine Tätigkeit erstreckte sich auf dieselben Wissensgebiete, auf denen Newton bahnbrechend wirkte, auf die Optik und die Mechanik; und wo zwischen beiden Forschern Meinungsverschiedenheiten entstanden, hat deren Klärung nur Fortschritte gezeitigt.
Christiaan Huygens wurde am 14. April des Jahres 1629 im Haag geboren. Ausgestattet mit einer mathematischen Begabung, die frühzeitig Bewunderung erregte, zeichnete ihn außerdem ein hervorragendes Geschick für die praktische Bewältigung mechanischer Probleme aus. Wie auf Galilei und auf Newton, so ist auch auf ihn die Mitwelt zuerst durch seine astronomischen Entdeckungen aufmerksam geworden. Die von Galilei am Saturn beobachtete, rätselhafte Erscheinung, die Galilei für eine Verdreifachung dieses Gestirns angesehen hatte496, erfuhr nämlich durch Huygens die richtige Deutung. Vor ihm hatten sich Grimaldi und besonders Hevel mit der Deutung des rätselhaften Aussehens dieses Planeten beschäftigt. Grimaldi hatte den Eindruck, als ob Saturn mit zwei Henkeln versehen sei, während Hevel für das veränderliche Aussehen des Planeten einen periodischen Wechsel innerhalb eines bestimmten Zeitraums nachwies.
Huygens dagegen erkannte vermittelst der vorzüglichen, von ihm verfertigten Refraktoren, daß es sich hier weder um eine Verdreifachung handeln könne, noch um zwei Henkel, die spätere Beobachter zu sehen glaubten; sondern er erblickte den Saturn von einem freischwebenden Ringe umgeben, wie es uns die dem Werke über das System des Saturn497 entnommene Abbildung 81 erkennen läßt.
Huygens machte diese Entdeckung im Jahre 1655. Er veröffentlichte sie zunächst nach damaliger Sitte in Form eines Änigmas. Es lautete:
a7 c5 d1 e5 g1 h1 i7 l1 m2 n9 o4 p2 q1 r2 s1 t5 u5.
In diesem Ausdruck bedeuten die Ziffern, wie oft der betreffende Buchstabe in der Lösung vorkommt. Letztere war: Saturnus cingitur[S. 288] annulo tenui, plano, nusquam cohaerente et ad eclipticam inclinato498.
Huygens durfte mit Recht von einem System des Saturn reden, da er auch den sechsten und größten der ihn umkreisenden Monde gefunden hatte499. Er verfolgte diesen neuen Weltkörper lange Zeit und fand, daß er in 16 Tagen seinen Umlauf um den Saturn vollendet.
Der von Huygens entdeckte Mond des Saturn war der erste500 der vielen kleinen Begleiter dieses Planeten, den ein menschliches Auge erblickte; deshalb war auch diese Entdeckung Huygens' eine wesentliche Bereicherung unserer Kenntnis des Planetensystems.
Fast zur selben Zeit, als die Entdeckung des Saturnringes erfolgte, wurde Huygens auf die später zu besprechende Erfindung der Pendeluhr geleitet501. Durch diese Leistungen war er schon, bevor er das 30. Lebensjahr erreicht und noch ehe er seine für die Mechanik und die Optik grundlegenden Werke veröffentlicht hatte, zu einer Berühmtheit von europäischem Rufe geworden.
Als daher Colbert die französische Akademie der Wissenschaften errichtete, war es das Erste, daß er den niederländischen Forscher an sie berief. Huygens leistete der Ernennung Folge und blieb von 1666 bis 1681 eine Zierde des neubegründeten Instituts. Da jedoch in Frankreich die Verfolgungen der Protestanten einen bedrohlichen Charakter annahmen, kehrte er noch vor der Aufhebung des Ediktes von Nantes in die Vaterstadt zurück, obgleich man ihm selbst volle Religionsfreiheit zugesichert hatte. Er starb am 8. Juni 1695.
Huygens' Hauptverdienst um die Optik besteht in dem Ausbau der Wellentheorie des Lichtes. Angeregt wurden seine Betrachtungen einerseits durch die Spekulationen Descartes' und Hookes502, von denen der letztere das Licht gleichfalls als eine Wellenbewegung ansprach, ohne jedoch seine Ansichten ausführlicher[S. 289] zu begründen; andererseits durch die Entdeckung der Doppelbrechung, sowie der Fortpflanzungsgeschwindigkeit des Lichtes503. Mit dem Problem, diese Geschwindigkeit gleich derjenigen des Schalles zu messen, hatte sich schon Galilei befaßt. Er war indes, wie man es bei der Anwendung einfacher Lichtsignale nicht anders erwarten konnte, zu keinem Ergebnis gelangt. Descartes' Meinung ging dahin, daß zwar nichts Stoffliches von den leuchtenden Körpern in unser Auge gelange; indessen sei das Licht keine Bewegung, sondern vielmehr ein Streben nach Bewegung. Und dieses Streben beanspruche, als etwas gänzlich Unkörperliches, zu seiner Fortpflanzung keine Zeit. Descartes war der Erste, der die Frage durch astronomische Gründe zu entscheiden suchte. Braucht das Licht, so schloß er, zu seiner Ausbreitung Zeit, dann kann die Verfinsterung des Mondes durch die Erde nicht in demselben Augenblicke eintreten, in dem sich die Erdkugel zwischen Mond und Sonne schiebt. Nun zeigen aber die Beobachtungen, daß die Mondfinsternis in eben diesem Augenblicke beginnt. Die Fortpflanzung des Lichtes kann also keine Zeit beanspruchen. Demgegenüber bemerkte Huygens, daß die Betrachtungen, die Descartes anstellte, wohl eine sehr schnelle, keineswegs aber eine augenblickliche Fortpflanzung des Lichtes beweisen. Wenn letzteres z. B. den Weg von der Erde zum Monde innerhalb zehn Sekunden zurücklege, so würde dies bei der astronomischen Beobachtung nicht leicht wahrzunehmen sein.
Descartes war es auch, der zuerst die alte pseudo-aristotelische Ansicht von der Entstehung der Farben aus einer Mischung von Hell und Dunkel durch eine auf mechanischen Prinzipien beruhende Erklärung zu ersetzen suchte, während Huygens von einer Erklärung der Farben gänzlich absah.
Huygens' Voraussetzung, daß das Licht zu seinem Wege Zeit gebrauche, hatte erst wenige Jahre vor der Veröffentlichung seiner Wellentheorie ihre Bestätigung gefunden504. Dies geschah durch die Beobachtungen, die der dänische Mathematiker Olaf Römer505 an dem innersten Jupitertrabanten anstellte. Letzterer[S. 290] bewegt sich in etwa 42½506 Stunden um den Zentralkörper und tritt nach jedesmaligem Ablauf dieses Zeitraums aus dem Schatten des Jupiter heraus. Huygens gibt in seiner Abhandlung folgenden Bericht über die von Römer angestellten Beobachtungen und Folgerungen: A (Abb. 82) sei die Sonne, BCDE die jährliche Bahn der Erde, F der Jupiter und GN die Bahn des nächsten seiner Begleiter. Bei H möge dieser aus dem Schatten des Jupiter treten. Setzt man nun voraus, daß dies geschah, während die Erde sich im Punkte B befand, so müßte man, wenn die Erde an derselben Stelle bliebe, nach Ablauf von 42½ Stunden einen ebensolchen Austritt beobachten. Wenn die Erde beispielsweise während 30 Umläufe des Mondes immer in B verharrte, so würde man ihn gerade nach 30 · 42½ Stunden wieder aus dem Schatten hervorkommen sehen. Während dieser Zeit hat sich indes die Erde nach C bewegt, indem sie sich mehr und mehr von dem Jupiter entfernt, der infolge seiner langen Umlaufszeit seine Stellung wenig verändert. Daraus folgt, daß, wenn das Licht für seine Fortpflanzung Zeit gebraucht, das Auftauchen des kleinen Mondes in C später bemerkt werden wird, als dies in B geschehen wäre. Man muß nämlich zu der Zeit von 30 · 42½ Stunden noch diejenige hinzufügen, die das Licht gebraucht, um den Weg MC, nämlich den Unterschied der Strecken CH und BH zu durcheilen. Ebenso wird man, wenn die Erde von D nach E gelangt und sich somit dem Jupiter nähert, das Eintreten des Mondes G in den Schatten bei E früher beobachten müssen, als dies geschehen würde, wenn die Erde in D geblieben wäre. Römers Beobachtungen und[S. 291] Berechnungen ergaben, daß das Licht ungefähr 11 Minuten gebraucht, um den Halbmesser der Erdbahn zu durchlaufen. Spätere Messungen haben diesen, in Anbetracht der großen Strecke sehr geringen Wert sogar auf 8 Minuten herabgesetzt. Die Lichtgeschwindigkeit ist demnach nicht das 600000fache derjenigen des Schalles, wie Huygens angab, sondern nahezu das 900000fache.
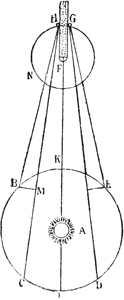
Wenn das Licht zu seinem Wege Zeit gebraucht, so folgt daraus nach Huygens, daß es sich wie der Schall in kugelförmigen Flächen oder Wellen ausbreitet. Indessen hebt er einen wichtigen Unterschied hervor. Während nämlich der Schall durch die plötzliche Erschütterung des ganzen Körpers oder eines beträchtlichen Teiles eines solchen hervorgebracht wird, muß die Lichtbewegung von jedem Punkte des leuchtenden Gegenstandes ausgehen, damit man alle seine Teile wahrnehmen kann.
Um das Licht zu erklären, nimmt Huygens ferner an, die leuchtenden Körper seien aus sehr kleinen Teilchen zusammengesetzt, die sich heftig bewegen und gegen die umgebenden, noch viel kleineren den Raum erfüllenden Teilchen stoßen. »Die Bewegung dieser Teilchen, die das Licht verursachen«, fügt er hinzu, »muß viel schneller und heftiger sein als diejenige der Körper, die den Schall bewirken, denn wir sehen, daß die zitternde Bewegung eines tönenden Körpers ebenso wenig imstande ist, Licht zu erzeugen, wie die Bewegung der Hand in der Luft Schall hervorzubringen vermag.«
Die Materie, in der die von den leuchtenden Körpern ausgehende Bewegung sich ausbreitet, nennt Huygens »Äther«. Sie könne nicht dieselbe sein, wie diejenige, die zur Ausbreitung des Schalles diene. Denn man finde, daß letztere nichts anderes ist, als die Luft, und daß, wenn man die Luft wegnimmt, die andere, dem Lichte dienende Substanz zurückbleibt. Es muß also, schließt Huygens, ein von der Luft verschiedener Stoff, eben der Äther, vorhanden sein. Dieser erfüllt den unendlichen Himmelsraum und den Raum zwischen den wägbaren Teilchen der Körper. Er ist nicht schwer und somit nicht dem Gesetz der Gravitation unterworfen.
Aus seiner Äthertheorie erklärte Huygens auch die Adhäsion sowie die Kapillarität. Er war anfangs geneigt, beide auf den Druck der Luft zurückzuführen. Versuche mit der Luftpumpe ergaben ihm jedoch, daß die Erscheinungen im Vakuum dieselben bleiben. Darauf erklärte er die Adhäsion, die Kapillarität und verwandte Erscheinungen aus dem Druck einer materia subtilis, auf die er auch das Licht zurückführte.
Um die so außerordentlich rasche Fortpflanzung des Lichtes zu verstehen, legt Huygens den Ätherteilchen drei Eigenschaften bei. Sie sind äußerst klein, weit kleiner als die Luftteilchen; sie sind ferner sehr hart, gleichzeitig aber äußerst elastisch. Nimmt man nämlich eine Anzahl gleich großer Kugeln aus sehr hartem und gleichzeitig sehr elastischem Stoff, etwa Stahl, und ordnet sie in gerader Linie so an, daß sie sich berühren, so wird, wenn eine gleiche Kugel gegen die erste Kugel dieser Reihe stößt, die Bewegung wie in einem Augenblicke bis zur letzten gelangen. Diese trennt sich darauf von der Reihe, ohne daß man bemerkt, daß die übrigen sich bewegt hätten. Die Kugel, die den Stoß ausgeübt hat, bleibt sogar unbeweglich mit den übrigen vereint508. Es offenbare sich hierin ein Bewegungsübergang von außerordentlicher Geschwindigkeit, die umso größer sei, je größere Härte und Elastizität die Substanz der Kugeln besitze. Darin, daß der Äther als flüssiger Körper sich in beständiger Bewegung befinden muß, weil die Bewegung der übrigen Materie in ihm vor sich geht, erblickt Huygens keine Schwierigkeit. Die Fortpflanzung der Ätherwellen besteht nämlich nach ihm nicht in der Fortbewegung der Ätherteilchen, sondern in einer geringen Erschütterung, die sich trotz der ihre gegenseitige Lage verändernden Bewegung auf die umgebenden Teilchen übertragen müsse. Was den Ursprung dieser Wellen und die Art ihrer Fortpflanzung anbetrifft, fährt Huygens fort, so folgt aus dem Vorausgeschickten, daß jede kleine Stelle eines leuchtenden Körpers, wie der Sonne, einer Kerze oder einer glühenden Kohle, Wellen erzeugt, deren Mittelpunkt diese Stelle ist. Sind z. B. in einer Kerzenflamme A, B, C (Abb. 83) verschiedene Punkte, dann stellen die um jeden dieser Punkte beschriebenen konzentrischen Kreise die Wellen dar, die von den Punkten ausgehen.
Auch darin, daß eine Menge von Wellen sich durchkreuzen, ohne sich gegenseitig aufzuheben, liegt für Huygens nichts Unbegreifliches. Könne doch dasselbe Stoffteilchen mehrere Wellen[S. 293] fortpflanzen, die von verschiedenen oder sogar von entgegengesetzten Seiten kommen. Und zwar geschehe dies nicht nur, wenn das Teilchen durch rasch aufeinanderfolgende Stöße, sondern auch, wenn es durch Stöße getroffen werde, die in demselben Augenblicke darauf wirken. Als Beweismittel führt Huygens den schon oben erwähnten, aus elastischen Kugeln bestehenden Apparat ins Feld. Wenn man nämlich gegen die ruhenden Kugeln von entgegengesetzten Seiten in demselben Augenblicke gleich große Kugeln A und D stoße (Abb. 84), so werde man jede Kugel mit derselben Geschwindigkeit, die sie beim Aufprall hatte, zurückschnellen und die ganze Reihe an ihrer Stelle verharren sehen, obgleich die Bewegung vollständig und zwar zweimal durch sie hindurchgegangen sei. Zwar könne es unglaublich erscheinen, daß die durch die Bewegung so kleiner Körperchen hervorgebrachten Wellen sich auf so ungeheure Entfernungen fortzupflanzen vermögen, wie von der Sonne oder den Fixsternen bis zur Erde. Doch auch dies Bedenken weiß Huygens zu beseitigen. Wenn sich nämlich auch die Kraft dieser Wellen in dem Maße abschwäche, in dem sich die Wellen von ihrem Ursprünge entfernen, so müsse man doch erwägen, daß in einer großen Entfernung vom leuchtenden Körper eine Unzahl von Wellen sich vereinigen. »Die unendliche Zahl von Wellen, die in demselben Augenblicke von allen Punkten eines Fixsternes, etwa eines so großen wie die Sonne, herkommen, bilden nur eine einzige Welle, die auch genügend Kraft besitzen wird, um auf unsere Augen Eindruck zu machen.«
Hinsichtlich der Fortpflanzung dieser Wellen sei ferner zu bedenken, daß jedes Teilchen des Stoffes, in dem eine Welle sich ausbreitet, nicht nur dem nächsten Teilchen, das in der von dem leuchtenden Punkte aus gezogenen geraden Linie liegt, seine Bewegung mitteilen muß, sondern auch allen übrigen, die es berühren und die sich seiner Bewegung widersetzen. Daher muß sich um jedes Teilchen eine Welle bilden, deren Mittelpunkt dieses Teilchen ist. Wenn also DCF (s. Abb. 85) eine Welle sei, die von dem leuchtenden Punkte A als Zentrum ausgegangen ist, so werde das Teilchen B, das zu den von der Kugel DCF umschlossenen gehört, seine die Welle DCF in C berührende besondere Welle KCL in demselben[S. 294] Augenblicke gebildet haben, in dem die von A ausgesandte Hauptwelle in DCF angelangt sei. Ferner sei klar, daß die Welle KCL die Welle DCF eben nur in dem Punkt C berühre, d. h. in demjenigen, der auf der durch AB gezogenen Graden liegt. Auf dieselbe Weise bilde jedes andere Teilchen innerhalb der Kugel DCEF wie bbdd usw. seine eigene Welle. Jede dieser Wellen sei indessen nur unendlich klein im Vergleich zur Welle DCEF, zu deren Bildung alle übrigen mit demjenigen Teile ihrer Oberfläche beitragen, der von dem Mittelpunkte A am weitesten entfernt sei. Ferner könne der Wellenteil BG (Abb. 85), der den leuchtenden Punkt A zum Mittelpunkt hat, sich nur bis zu dem von den Geraden ABC und AGE begrenzten Bogen CE ausbreiten. Obgleich nämlich die Einzelwellen, welche durch die im Raume CAE enthaltenen Teilchen erzeugt werden, auch außerhalb dieses Raumes sich ausbreiten müßten, so träfen sie doch nirgends sonst, als eben nur in dem Bogen CE, im nämlichen Augenblicke zusammen, um eine die Bewegung abgrenzende Welle zu bilden. Hierin liegt für Huygens auch der Grund, weshalb sich das Licht, sofern seine Strahlen nicht zurückgeworfen oder gebrochen werden, nur in geraden Linien fortpflanzt, so daß es einen Gegenstand nur dann beleuchtet, wenn der Weg von seiner Quelle bis zu diesem Gegenstande längs solcher Linien offen steht. Wenn beispielsweise eine durch undurchsichtige Körper begrenzte Öffnung BG vorhanden wäre, so würden die von dem Punkte A kommenden Wellen immer durch die Geraden BC und GE begrenzt sein, da diejenigen Teile der Einzelwellen, die sich über BC und GE hinaus ausbreiten, zu schwach seien, um daselbst Licht hervorzubringen.
Die Erscheinungen der Reflexion und der Brechung vermag Huygens aus seinem soeben entwickelten Prinzip ohne Schwierigkeiten abzuleiten. AB sei eine ebene Fläche (Abb. 86), AC ein Teil einer Lichtwelle, deren Mittelpunkt soweit entfernt sei, daß AC als gerade Linie betrachtet werden kann. Die Einzelwellen, die von den Punkten KKK ausgehen, werden dann in einem bestimmten Augenblicke durch die gemeinschaftliche Tangente BN begrenzt. Aus der Figur (Abb. 86) ersieht man, daß die Winkel[S. 295] CBA und NAB gleich sind, somit das Reflexionsgesetz bewiesen ist509.
Ebenso leicht erklärt Huygens aus seinem Prinzip die einfache Brechung, unter der Voraussetzung, daß das Licht in den durchsichtigen Körpern eine Verminderung seiner Geschwindigkeit erleidet. Daß die Körper keine kontinuierliche Masse bilden, sondern aus nebeneinander gelagerten Teilchen bestehen, schließt Huygens daraus, daß der Magnetismus und die Schwerkraft, die für ihn materieller Natur sind, durch feste Körper hindurch wirken. Die verbleibenden Zwischenräume sollen durch die Teilchen des Äthers ausgefüllt sein. Beim Durchgang des Lichtes durch Körper seien aber nicht nur die Äther-, sondern auch die Körperteilchen in Bewegung und aus der geringeren Elastizität der letzteren erkläre sich die Verlangsamung der Lichtwellen510. Es erhebt sich nun die Frage, weshalb nicht alle Körper durchsichtig sind, da doch der Äther ihre Poren erfüllt. Huygens begegnet dieser Schwierigkeit durch die Annahme, daß gewisse Körperteilchen dem Äther gegenüber nachgiebig seien, ihre Gestalt unter dem Druck des Äthers verändern und so die Bewegung des Äthers vernichten.
Wir sehen, wie Huygens die von der neueren Philosophie, insbesondere von Descartes begründete Korpuskulartheorie auszubauen und den Zwecken der Naturerklärung dienstbar zu machen suchte. Huygens nahm in der Entwicklung dieser Theorie eine abschließende Stellung ein, indem er ihr den Wert einer wissenschaftlichen, die Grundsätze der Kinetik benutzenden Betrachtungsweise zu verleihen wußte. Sehen wir nun, wie Huygens das Verhalten des Lichtstrahls beim Eindringen in durchsichtige Körper aus seinen Prinzipien erklärt.
AB (Abb. 87) sei die Grenze des durchsichtigen Körpers, AC ein Wellenteil einer Lichtquelle, die soweit entfernt ist, daß[S. 296] AC als gerade Linie angenommen werden kann. Es mögen sich ferner die Geschwindigkeiten außerhalb und innerhalb des Körpers wie 3 : 2 verhalten. Dann wird sich in der Zeit, die das Licht gebraucht, um von C nach B zu gelangen, um A in dem Körper eine Welle gebildet haben, die durch BN begrenzt wird, und zwar wird das Stück AN nach der Voraussetzung zwei Drittel von AG sein. Indessen auch um die Punkte KKK bilden sich Einzelwellen, die durch Kreise dargestellt werden, deren Halbmesser zwei Drittel der entsprechenden Verlängerungen KM, KM, KM betragen. Alle diese Kreise haben nun BN als gemeinschaftliche Tangente. Letztere begrenzt die Bewegung und ist somit die Fortsetzung der Welle AC für den Augenblick, in dem sie von C nach B gelangt ist. Die Lichtgeschwindigkeiten CB und AN, die für diesen Fall = 3 : 2 angenommen wurden, verhalten sich auch wie der Sinus von EAD zum Sinus von FAN, so daß die Konstruktion mit dem Brechungsgesetz in vollkommenem Einklang steht.
Weit größere Schwierigkeiten machte es, aus dem Prinzip der Elementarwellen die um die Mitte des 17. Jahrhunderts am isländischen Spat entdeckte Doppelbrechung abzuleiten. Die betreffende Untersuchung von Huygens bildet, wie sein Herausgeber sich ausdrückt, den Glanz- und Mittelpunkt des ganzen Werkes und ist ein unübertroffenes Muster des Zusammenwirkens experimenteller Forschung und scharfsinniger Analyse.
Huygens war bei dem Aufsehen, das Bartholins Schrift über den Doppelspat511 erregt hatte, zu seiner Untersuchung geradezu gezwungen, weil die neuentdeckte, wunderbare Erscheinung seine Erklärung der gewöhnlichen Brechung umzustürzen schien. Das Ergebnis war, daß sich die Doppelbrechung auf das gleiche[S. 297] Grundgesetz zurückführen und somit zur Bestätigung desselben verwerten ließ.
Huygens begab sich zunächst an eine Nachprüfung der von Bartholin gefundenen Ergebnisse. Die Winkel C, D (Abb. 88) des Rhomboeders fand er gleich 101° 52ʹ, die Winkel A, B dagegen gleich 78° 8ʹ.
Um die Form, die Spaltbarkeit und weiterhin auch die optischen Eigenschaften des Doppelspats zu erklären, unternahm Huygens einen für die weitere Entwicklung der mineralogischen Wissenschaft sehr wichtigen Schritt. Er stellte sich nämlich vor, daß der Kristall aus kleinsten Teilchen zusammengesetzt sei. Indem er dann weiter über die Form und die Lagerung dieser Teilchen gewisse Annahmen machte, gelang es ihm, aus diesen Annahmen die beobachteten Erscheinungen abzuleiten. Huygens nahm an, die Teilchen des Kristalles seien Sphäroide, wie sie aus der Umdrehung einer Ellipse um ihre kleinere Achse hervorgehen. Stehen die Achsen dieser Sphäroide in einem bestimmten Verhältnis und setzt man eine größere Zahl solcher Sphäroide in der in Abb. 89 angegebenen Weise zusammen, so ergibt sich die aus der Beobachtung gefundene Form mit den an ihr gefundenen Winkel- und Spaltungsverhältnissen. Wären nämlich die Sphäroide durch ein Bindemittel (im Modell könnte man die in der Natur zwischen den Sphäroiden wirkenden Anziehungen durch Zusammenleimen ersetzen) verbunden, so würde sich der aus ihnen aufgebaute Körper nach Flächen spalten, welche den die Ecken bildenden Flächen parallel sein müßten. Jedes Sphäroid würde sich nämlich von nur drei Sphäroiden der benachbarten Schicht losreißen, während es sich doch von sechs Sphäroiden trennen müßte, um die Schicht zu verlassen, der es selbst angehört.
Da Huygens die Entdeckung machte, daß auch der Bergkristall das Licht doppelt bricht, nahm er für dieses Mineral einen[S. 298] ähnlichen Aufbau an. Derartige Betrachtungen über den regelmäßigen Bau der Kristalle aus gleichartigen Teilchen von bestimmter Form sind, wie wir sehen werden, im 19. Jahrhundert durch Hauy wieder aufgenommen und auf sämtliche Kristallformen ausgedehnt worden.
Über die Entdeckung der viel weniger auffallenden Doppelbrechung des Bergkristalls teilt Huygens mit, er habe aus dem Material nach verschiedenen Richtungen Prismen schneiden und diese gut polieren lassen. Als er durch solche Prismen nach einer Kerzenflamme blickte, erschien sie ihm doppelt. Jetzt war auch die Tatsache aufgeklärt, daß sich Linsen aus dem so durchsichtigen Bergkristall für Fernrohre von einiger Länge als unbrauchbar erwiesen hatten.
Wie die Form und die Spaltbarkeit des Doppelspats durch die Annahme kleiner Sphäroide verständlich wird, so lassen sich die optischen Eigenschaften nach Huygens aus sphäroidischen Lichtwellen erklären, die in ihrer Lage mit den Körperteilchen übereinstimmen, so daß der Aufbau des Kristalls als die Ursache sämtlicher geometrischen und physikalischen Eigenschaften erscheint512. Es würde indessen zu weit führen, wenn wir den Gang dieser Untersuchung eingehender verfolgen wollten. Es genügt hier, die Fortpflanzung in sphäroidischen Wellen für das Licht zu betrachten, das senkrecht auf die Fläche des Kristalles trifft und trotzdem abgelenkt wird. Solche Wellen werden sich bilden, wenn sich das Licht »in der einen Richtung etwas schneller als in der anderen ausbreitet.« AB (Abb. 90) sei die Grenze zwischen dem Kristall und der Luft, RC sei ein Wellenteil des Lichtes. Der Strahl treffe den Kristall in AKkkB. Von diesen Punkten gehen aber nicht, wie es sonst die Regel ist, halbkugelförmige,[S. 299] sondern halbsphäroidische Einzelwellen aus, deren große Achsen, wie VAX, gegen die Ebene AB geneigt sind. Um Punkt A wird sich nach Ablauf eines gewissen Zeitteilchens ein halbes Sphäroid SVNT gebildet haben, das die vom Punkte A ausgehende Einzelwelle darstellt. Um die Punkte K, k, k, B bilden sich in derselben Zeit gleiche und ähnlich wie SVNT liegende Einzelwellen, deren gemeinsame Tangente NQ analog der früheren Betrachtungsweise wieder die in dem Kristall befindliche Fortsetzung der Welle RC ist, denn diese Linie begrenzt in demselben Augenblicke die Bewegung, die von der auf AB treffenden Welle RC herrührt. Diese gemeinsame Tangente NQ ist zwar AB parallel und an Länge gleich, sie liegt aber nicht AB genau gegenüber. »Jetzt verstand ich«, sagt Huygens, »daß die an der Öffnung AB anlangende Welle RC fortfährt, sich von dort zwischen den Parallelen AN und BQ fortzupflanzen.«
Wie Huygens dann die Lage und das Achsenverhältnis der Sphäroide ergründet und unter der Annahme halbsphäroidischer Einzelwellen durch eine Tangentenkonstruktion ähnlich derjenigen, die wir in Abb. 87 kennen gelernt haben, den Gang des außergewöhnlichen Strahles für schräg einfallendes Licht findet, muß in seiner Abhandlung selbst nachgesehen werden513.
Aus der Konstruktion ergibt sich außer der zuerst betrachteten Anomalie, daß senkrecht auffallendes Licht gebrochen wird, auch die Notwendigkeit, daß es schräg einfallende Strahlen geben muß, welche durch den Doppelspat hindurchgehen, ohne eine Brechung zu erleiden. In Übereinstimmung mit der Rechnung zeigte die Erfahrung, daß sich so der Strahl verhält, der die Fläche des Kristalls unter einem Winkel von 73° 20ʹ trifft514. Kurz, Huygens fand, daß jede Erscheinung, die er aus seiner Hypothese abzuleiten vermochte, mit der Beobachtung übereinstimmte, ein »nicht gering zu veranschlagender Beweis« für die Richtigkeit seiner Voraussetzungen.
Nachdem Huygens seine Untersuchungen der optischen Eigenschaften des Doppelspats bis zu diesem Punkte gefördert[S. 300] hatte, entdeckte er noch »eine wunderbare Erscheinung«, die er aus seiner Theorie nicht abzuleiten vermochte, nämlich die Polarisation des Lichtes durch Doppelbrechung. Er beschreibt diese Entdeckung in folgender Weise: »Nimmt man zwei Stücke des Kristalls und legt sie (Abb. 91) so aufeinander, daß alle Seiten des einen denjenigen des anderen parallel sind, so wird der Strahl AB, der in dem ersten Stück in die beiden Strahlen BD und BC zerlegt wird, beim Eintritt in das zweite Stück sich nicht noch einmal spalten. Es wird vielmehr der von der regelmäßigen Brechung herrührende Strahl DG noch eine regelmäßige Brechung, der außergewöhnliche Strahl CE eine unregelmäßige Brechung erleiden (Abb. 91). Dies geschieht immer, wenn die Hauptschnitte beider Rhomboeder in ein und derselben Ebene liegen, auch wenn die Seitenflächen der Rhomboeder gleichzeitig gegeneinander geneigt sind.«
Ordnete Huygens die beiden Kristalle dann in der Weise an, daß ihre Hauptschnitte sich rechtwinklig schnitten (Abb. 92), so erlitt der gewöhnliche Strahl ABDG in dem zweiten Kristall nur die eine, aber außergewöhnliche Brechung GH, der außergewöhnliche Strahl aber nur die eine, und zwar gewöhnliche Brechung EF.
In allen Zwischenstellungen endlich teilten sich die Strahlen beim Eintritt in den unteren Kristall von neuem in je zwei, so daß aus dem ursprünglich einzigen Strahl AB vier Strahlen entstanden. Diese vier Strahlen sind, wie Huygens fand, je nach der Stellung[S. 301] der Kristalle bald von gleicher, bald von verschiedener Helligkeit, jedoch so, daß sie »alle zusammen anscheinend nicht mehr Licht enthalten, als der eine Strahl AB.«
Wenn Huygens sich auch nicht an eine Erklärung dieser von ihm herrührenden, höchst wichtigen Entdeckung heranwagt, so macht er doch darüber eine sehr zutreffende Bemerkung, welche denen, die sich später mit dem Problem beschäftigten, einen wertvollen Fingerzeig bot. Huygens meint nämlich, die Lichtwellen erhielten offenbar bei ihrem Durchgang durch den ersten Kristall eine gewisse Anordnung, durch die ihr Verhalten in dem zweiten Kristall bestimmt werde. Welcher Art aber die Anordnung sei, dafür habe er keine befriedigende Erklärung finden können. Die von Huygens als Polarisation bezeichnete Erscheinung blieb als vereinzelte Sonderbarkeit fast unbeachtet, bis Malus nach mehr als einem Jahrhundert fand, daß das Licht auch durch Reflexion polarisiert werden kann515. Die Polarisation mußte solange jedem Erklärungsversuche widerstreben, als man mit Huygens annahm, daß die Lichtschwingungen gleich denjenigen des Schalles longitudinal seien. Erst nachdem man diese Annahme aufgegeben, gelang der Undulationstheorie, wie uns die weitere Entwicklung lehren wird, die Erklärung sämtlicher optischen Erscheinungen.
Auch auf eine Erklärung der Farben hat Huygens verzichtet. Ihre Entstehung wird in seiner Abhandlung nirgends gestreift. Dieser Umstand hat viel dazu beigetragen, daß die Wellentheorie zunächst der Emissionstheorie ihre Herrschaft nicht streitig zu machen vermochte. Die, wenige Jahre vor der Entstehung seiner Abhandlung von Grimaldi (1665) entdeckte, Beugung des Lichtes scheint Huygens damals noch nicht gekannt zu haben, da er sie nirgends erwähnt.
Descartes war der erste Physiker, der eine Farbenlehre schuf, die von der bisher gültigen Meinung des Aristoteles516, nach der die Farben durch Mischung von Licht und Dunkelheit entstehen sollten, abwich. Für ihn enthält der kosmische Raum eine außerordentlich feine Materie, die auch die Zwischenräume der aus gröberem Stoff gebildeten, unseren Sinnen sich offenbarenden Materie ausfüllt. Dieser feine Stoff befindet sich nach Descartes als Ganzes und auch in seinen einzelnen Teilchen in einer rotierenden[S. 302] Bewegung. Die großen Wirbel sind die Ursache der Planetenbewegung, während die verschieden großen Teilrotationen die Verschiedenartigkeit der Farben bedingen. Der Lichtstrahl selbst besteht nur in einem Druck auf die den kosmischen Raum erfüllenden Elementarteilchen, und ein solcher Druck braucht, weil er ja nur Tendenz zur Bewegung und nicht Bewegung selbst ist, zu seiner Fortpflanzung keine Zeit. Das Auge empfindet diesen Druck als Licht, und als Farben die Rotationsbewegung der Elementarteilchen, die unter dem Einfluß dichter optischer Medien überdies Änderungen erleidet, welche zum Zustandekommen des Spektrums führen. Der stärksten Rotation der kugelförmigen Teilchen entspricht das Rot, der schwächsten das Violett.
Descartes' Theorie fand zwar keine Annahme. Sie erregte aber als der erste Versuch, das Licht und die Farben mechanisch zu erklären die Aufmerksamkeit aller zeitgenössischen Physiker. Auch Boyle und Newton haben sich mit ihr auseinander gesetzt.
Von gleicher Bedeutung wie seine Leistungen auf dem Gebiete der Optik waren Huygens' Arbeiten auf dem Felde der Mechanik, wenn es sich auch hier nur um ein Fortbauen auf den von Galilei herrührenden Grundlagen handeln konnte. Knüpfte Newton an Galileis Untersuchungen über den Wurf an, so entwickelte Huygens die Theorie des Pendels, für das der große Meister nur die fundamentalen Gesetze aufgefunden hatte, bis in alle Einzelheiten. Dabei wandte er in seinem 1673 erschienenen Werke über die Pendeluhr517, das den »Prinzipien« Newtons als ebenbürtig an die Seite gestellt werden kann, die Geometrie in solch bewunderungswürdiger Weise auf mechanische Probleme an, daß Newton sehr wahrscheinlich durch die Mustergültigkeit der Huygens'schen Darstellung bewogen wurde, sich in dem genannten Hauptwerk gleichfalls geometrischer Beweise zu bedienen,[S. 303] anstatt der höheren Analysis, in deren Besitz er sich damals schon befand, den Vorzug einzuräumen518.
Die Frage der Einführung eines genauen Zeitmaßes war im Verlauf des 17. Jahrhunderts, in dem so große Dinge auf den Gebieten der Astronomie und der Physik geschahen, zu einer brennenden geworden. Der weitere Fortschritt dieser Wissenschaften mußte wesentlich von der Einführung eines solchen abhängen. Wir sahen, daß noch Galilei sich bei seinen Fallversuchen einer Art Wasseruhr bediente519. Da Galilei mit Hilfe dieser Vorrichtung die Schwingungsdauer eines und desselben Pendels als konstant erwies, so mußte er auf den Gedanken kommen, sich dieses so viel einfacheren Mittels als Zeitmaß zu bedienen. Galilei hatte sogar die Idee, das Pendel mit einem Zählwerk zu verbinden520. Es kam nur noch darauf an, den wiederholten Anstoß seitens der Hand, den die von Galilei ersonnene Vorrichtung erforderte, durch eine automatisch wirkende Einrichtung zu ersetzen. Hierin besteht die Erfindung des großen Huygens, auf die er 1667, im 28. Jahre seines Lebens, ein Patent nahm521.
Während man sich im Altertum, sowie im früheren Mittelalter nur der Sonnen- und der Wasseruhren bedient hatte, kamen seit dem 11. Jahrhundert Räderuhren mit Gewichten auf. Später wurden diese Uhren mit einem Schlagwerk in Verbindung gesetzt. In der zweiten Hälfte des 14. Jahrhunderts gab es derartige Turmuhren schon in vielen Städten. Ihre Regulierung erfolgte durch Windflügel, wie sie noch heute bei den Spielwerken gebräuchlich sind, oder durch eine horizontale, mit Gewichten beschwerte Stange. Ihr Gang war jedoch so ungenau, daß ein Wärter ihn überwachen und nach der Sonne und den Sternen regeln mußte.
Die nachstehende Abbildung zeigt uns die älteste der noch vorhandenen Turmuhren. Sie hat von 1348–1872 in Dover die Stunden angegeben. Das nicht mit abgebildete Gewicht hängt am Seile a und dreht zunächst das Zahnrad b. Dieses setzt vermittelst des Zahngetriebes das Sperrad c in Bewegung, das seinerseits mit der senkrechten Achse d eines Horizontalpendels in Verbindung steht. Letzteres wird durch Laufgewichte zu schnellerem oder langsamerem Schwingen veranlaßt und erhält seinen Antrieb durch zwei an seiner Achse d befindliche Platten, die um den Durchmesser des Sperrades von einander entfernt sind und abwechselnd in dessen Zähne eingreifen.
Deutschlands berühmteste Uhr war die im Jahre 1574 eingeweihte astronomische Uhr im Straßburger Münster522. Sie war mit einem Himmelsglobus verbunden (er befindet sich noch in Straßburg). Dahinter befand sich ein immerwährender Kalender.[S. 305] Ein Astrolabium zeigte den jeweiligen Stand der Planeten im Tierkreise an usw. Manches davon ist erhalten geblieben523.
Für astronomische Beobachtungen hat zuerst Walther in Nürnberg im Jahre 1484 eine Räderuhr konstruiert und benutzt. Hausuhren mit Schlagwerk kamen um die Mitte des 16. Jahrhunderts auf. Auch Taschenuhren waren damals schon häufiger anzutreffen. Sie werden auf Peter Henlein in Nürnberg zurückgeführt, der das Gewicht durch eine Feder ersetzte (1505). Ein Zeitgenosse schreibt darüber: »Er machte kleine Uhren mit vielen Rädern. Diese Uhren können im Geldbeutel getragen werden.« Wegen ihrer Form nannte man sie Nürnberger Eier.
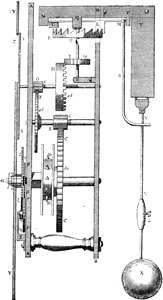
Die dem Werke des Huygens entnommene Abbild. 94 zeigt die von ihm erfundene Pendeluhr. Sie besteht in der Verbindung eines horizontalen, gezähnten Rades K mit einer horizontalen Achse, deren Schaufeln LL abwechselnd zwischen die Zähne eingreifen. Über D ist eine Schnur gewickelt,[S. 306] die das Gewicht trägt. Die heute gebräuchliche Ankerhemmung wurde erst später erfunden525.
Galilei hatte die Analogie der Pendelbewegung mit dem Fall über die schiefe Ebene nachgewiesen. Huygens verallgemeinerte diese Betrachtung, indem er den Fall durch eine beliebige Kurve auf eine Folge von Bewegungen auf geneigten Ebenen zurückführte. Er fand, daß unter den von ihm untersuchten Linien eine vorhanden war, in der die Fallbewegung im luftleeren Raum vollkommen isochron verläuft. Es war dies nicht der Kreisbogen, für den Galilei die Isochronie der Schwingungen nachgewiesen zu haben glaubte, sondern die Cykloide. Der tiefste Punkt B der Cykloide ABC (siehe Abb. 95) wird nämlich, wenn ein Körper in dieser Kurve fällt, stets in derselben Zeit erreicht, von welchem der zwischen A und B gelegenen Punkte aus die Bewegung auch beginnen mag526.
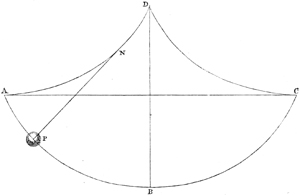
Dieses Ergebnis seiner mathematischen Untersuchung wußte Huygens auch praktisch zu verwerten. Um dem Pendel anstatt der Kreis- die Cykloidenbewegung zu erteilen, kam es darauf an, daß der Faden, der bei dem Kreispendel in jeder Stellung eine gerade Linie bildet, gezwungen wird, sich an eine Kurve von bestimmter[S. 307] Gestalt anzuschmiegen. Die Untersuchung ergab, daß diese Kurve gleichfalls eine Cykloide sein muß. In der Abb. 95 stimmen dementsprechend die Cykloidenstücke AD und CD mit den Stücken AB und BC überein. Abb. 96 zeigt uns die von Huygens für sein Cykloidenpendel vorgeschlagene Einrichtung. Sie besitzt zwei feste, cykloidisch gekrümmte Backen, denen sich der obere fadenförmige Teil des Pendels anschmiegt. Anwendung hat das Cykloidenpendel selten gefunden, da das Kreispendel nach Einführung der Ankerhemmung und bei Anwendung kleiner Ausschläge den hinsichtlich der Genauigkeit des Ganges zu stellenden Anforderungen genügend entspricht.
Die Taschenuhr versah Huygens (siehe Abb. 97) mit der noch jetzt gebräuchlichen Unruhe528. Ferner entwickelte er die Theorie des konischen oder Zentrifugalpendels529, das in einem horizontalen, vollen Kreise schwingt, während gleichzeitig der Faden die Kegelfläche beschreibt, eine Vorrichtung, die später Watt als Regulator der von ihm verbesserten Dampfmaschine verwendet hat.
Fügen wir noch hinzu, daß Huygens die Länge des Sekundenpendels zum erstenmal genauer bestimmte (er fand sie gleich 3,0565 Pariser Fuß), daß er ferner die Formel für die Pendelbewegung531 und aus ihr die Beschleunigung für den freien Fall ableitete, so erkennen wir, mit welcher Fülle neuer Entdeckungen die Wissenschaft durch ihn bereichert wurde.
Die Beschleunigung g für den freien Fall oder die Acceleration der Schwerkraft ergab sich, indem man in die Pendelformel t = π√(l/g) für l die Werte für das Sekundenpendel (t = 1 und l = 3,0565) einsetzte und sie dann nach g auflöste: 1 = π√(3,0565/g); g = π2 · 3,0565 = 30,1666 Pariser Fuß, wofür Huygens 30 Fuß 2 Zoll setzte.
Den Wert, den Huygens in Paris für die Länge des Sekundenpendels ermittelt hatte, brachte er als Einheit für das Längenmaß in Vorschlag, ohne jedoch den Beifall seiner Zeitgenossen zu finden.
Huygens hat sich nicht damit begnügt, die Wirkungen der Schwerkraft zu erforschen, er hat sie auch, wie das Licht, mechanisch zu erläutern gesucht532. Die Schwere darf man nach ihm nicht auf eine »Eigenschaft« oder Neigung zurückführen wollen, sondern sie ist, wie jeder Vorgang in der Natur, aus der Bewegung zu erklären. Huygens knüpft an Descartes an, der die Schwere aus der Bewegung einer um die Erde kreisenden Materie zu begreifen gesucht hatte. Die Schwere, sagt Huygens, wirke auf eine so geheime Weise, daß die Sinne nichts darüber zu entdecken vermöchten. Früher habe man diese Wirkungen inhärenten[S. 309] Eigenschaften (Qualitäten) der Körper zugeschrieben. Dies heiße jedoch nicht die Ursachen auseinandersetzen, sondern dunkle Prinzipien unterschieben. Descartes dagegen habe erkannt, daß man die physikalischen Vorgänge auf Begriffe zurückführen müsse, die unsere Fassungskraft nicht übersteigen. Als solche gelten Descartes und Huygens die qualitätslose Materie und ihre Bewegung.
Huygens ging dabei von folgendem Experiment aus. Er bedeckte den Boden eines zylindrischen Gefäßes mit kleinen Stückchen eines festen Körpers (z. B. Siegellack). Dann füllte er es zum Teil mit Wasser und ließ es mit Hilfe einer Zentrifugalmaschine um die Achse rotieren. Hielt er die Maschine und damit das Gefäß plötzlich an, so rotierte das Wasser noch einige Zeit. Dabei zeigte es sich, daß die Siegellackstückchen nach dem Mittelpunkt des Bodens getrieben wurden. Wie das Wasser in dem Gefäß, so rotiert nach Huygens um die Erde eine »Äthermaterie«, deren Flüssigkeitsgrad man sich unvergleichlich viel größer vorstellen müsse als denjenigen, den wir beim Wasser bemerken. Befänden sich in dieser flüssigen Materie gröbere Körper, so würden sie, wie der Versuch es zeige, nicht der raschen Bewegung jener Materie folgen, sondern nach dem Zentrum der Bewegung gestoßen. Die Schwere sei also »die Wirkung des Äthers, der sich um den Erdmittelpunkt bewegt und sich von diesem Zentrum zu entfernen und an seine Stelle diejenigen Körper zu drängen sucht, welche dieser Bewegung nicht folgen.«
Auf die hier von Huygens entwickelten Vorstellungen gehen im Grunde genommen auch die neueren Bestrebungen zurück, die Gravitation mechanisch zu erklären.
Huygens' Bedeutung ist hiermit bei weitem noch nicht erschöpft. Die bisher gestreiften Leistungen auf dem Gebiete der Mechanik waren nämlich entweder praktischer Art, oder sie bestanden in der Betrachtung des einfachen Pendels, worunter ein materieller Punkt verstanden wird, der an einem gewichtslosen Faden schwingt. Bald nachdem die Untersuchungen Galileis in den nördlichen Ländern Europas bekannt geworden waren, hatte ein französischer Gelehrter533 die Frage aufgeworfen, nach[S. 310] welchen Gesetzen denn die Schwingungen beliebig gestalteter Körper vor sich gingen. Descartes und andere scharfsinnige Mathematiker, darunter auch der damals 17 Jahre alte Huygens, nahmen das Problem in Angriff, ohne eine Lösung finden zu können. Descartes gab zwar eine schärfere Formulierung. »Wie es einen Schwerpunkt in allen frei herabfallenden Körpern gibt«, sagt er, »so haben alle Körper, die sich vermöge der Schwere um irgend einen Punkt bewegen, einen Agitationspunkt; und alle Körper, bei denen dieser Agitationspunkt gleich weit vom Aufhängepunkt entfernt ist, machen ihre Hin- und Hergänge in derselben Zeit«. Die Bestimmung dieses Agitations-, Oszillations- oder Schwingungsmittelpunktes gelang erst viel später Huygens, der seine Methode, 27 Jahre, nachdem die Frage aufgeworfen war, in seinem Werke über die Pendeluhr bekannt gab.
Man nehme außer dem materiellen Punkt, der das einfache Pendel bildet, auf der Pendellinie noch einen zweiten Punkt an, der mit dem ersten in fester Verbindung steht (siehe Abb. 98). Sucht man nun die Länge ox desjenigen einfachen Pendels zu bestimmen, das die gleiche Schwingungszeit wie das System ab besitzt, so hat man das Problem des Schwingungsmittelpunktes in seiner einfachsten Form. Der Punkt b wird durch a gehemmt, a durch b dagegen beschleunigt. Mithin wird der Punkt b langsamer und der Punkt a schneller schwingen, als sie es für sich allein tun würden, und es muß zwischen b und a einen Punkt geben, der die gleiche Schwingungszeit besitzt wie das System ab.
Es entsteht nun die Frage, wie sich bei einem physischen, aus unendlich vielen Massenteilchen zusammengesetzten Pendel die Bewegungen der untereinander in fester Verbindung stehenden Teile zu einer Gesamtbewegung vereinigen. Die Lösung dieses Problems des physischen oder zusammengesetzten Pendels ist ohne Frage die bedeutendste Leistung, die Huygens auf dem Gebiete der theoretischen Mechanik vollbrachte. Er widmet dem Problem den vierten Teil seines großen Werkes. Vorausgeschickt sind einige Erklärungen, darunter vor allem die Definition des Schwingungsmittelpunktes. Sie lautet: »Als Schwingungs- oder Oszillationszentrum einer beliebigen Figur wird derjenige Punkt[S. 311] auf der Schwerelinie bezeichnet, der soweit von der Schwingungsachse entfernt ist, wie die Länge des einfachen Pendels beträgt, das die gleiche Schwingungsdauer wie die Figur besitzt534.« Man kann sich also in diesem Punkte die Masse des schwingenden Körpers ebenso konzentriert denken, wie in dem Schwerpunkt die Masse des ruhenden Körpers. Auch in dem Oszillationspunkt sind nämlich die verschiedenen, auf die Teile des Pendels während seiner Schwingung wirkenden Kräfte zu einer Resultierenden vereinigt, wie während der Ruhelage die parallel gerichteten Schwerkräfte sich zu einer Resultierenden zusammensetzen, die durch einen Punkt des ganzen Systems geht, den wir deshalb als Schwerpunkt bezeichnen. Die Lösung dieses verwickelten Problems gelang Huygens auf Grund eines von ihm aufgestellten Prinzips, das sich sowohl hier als auch in der Folge als eins der allerwichtigsten erwiesen hat. Es lautet in der Fassung seines Begründers: »Wenn irgendwelche schwere Körper vermöge der auf sie wirkenden Schwerkraft sich in Bewegung setzen, so kann ihr gemeinsamer Schwerpunkt nicht höher steigen, als er sich zu Beginn der Bewegung befand«535. Huygens erläutert dies Prinzip am Pendel, indem er sagt, nach der Entfernung der Luft und jedweden anderen Hindernisses müsse der Schwerpunkt des bewegten Pendels beim Herabfallen und Emporsteigen stets gleiche Bogen durchlaufen. Damit ist für ihn zugleich die Möglichkeit des Perpetuum mobile, d. h. einer Erzeugung von Kraft ohne einen entsprechenden Aufwand widerlegt. Eine solche Erzeugung aus dem Nichts würde nämlich statthaben, wenn die Masse höher stiege, als sie zuvor herabgefallen ist.
Aus den Fallgesetzen war bekannt, daß die Höhe, welche die Masse beim Emporsteigen erreicht, proportional ist dem Quadrate der Geschwindigkeit, die sie beim Herabfallen erlangt. Die Geschwindigkeiten der Massenteilchen des Pendels sind aber den Abständen dieser Teilchen von der Drehungsachse proportional. Mit Hilfe dieser Sätze gelingt Huygens die allgemeine Lösung des Problems vom Schwingungsmittelpunkt. »Man findet seine Entfernung von der Drehachse«, sagt er, »indem man die Summe der Produkte der Massen mit den Quadraten der Abstände von der Drehungsachse durch das Produkt aus der Summe dieser Massen und ihren Abständen von der Drehungsachse dividiert.« Zur Erläuterung diene die Abb. 99. Eine Reihe von materiellen Punkten B, C, D ..., deren Massen m1 m2 m3 sind, seien zu einem Massensystem verbunden. Ihre Entfernungen von der Drehungsachse A seien a1, a2, a3 ... Dann ist nach dem von Huygens gefundenen Satze die Entfernung z des Schwingungspunktes O vom Aufhängepunkt A:
z = (m1a12 + m2a22 + m3a32 ...)/(m1a1 + m2a2 + m3a3 ...)
oder kürzer ausgedrückt:
z = (∑ (ma2))/(∑ ma)
Nachdem dann Euler für das Produkt aus der Masse und dem Quadrat ihrer Entfernung von der Drehungsachse die Bezeichnung »Trägheitsmoment« eingeführt hatte, lautete der Satz von Huygens in der noch heute üblichen Fassung: Man erhält die Entfernung des Schwingungspunktes von der Drehachse eines physischen Pendels, wenn man die Summe der Trägheitsmomente durch die Summe der statischen Momente dividiert.
Der von Huygens ausgesprochene Satz, daß der gemeinschaftliche Schwerpunkt miteinander verbundener, als Ganzes aber isolierter Massen nicht höher steigen kann, als er zuvor durch den Fall herabgesunken ist, wurde später von Johann Bernoulli als ein allgemeines Naturgesetz hingestellt und das »Prinzip von der Erhaltung der lebendigen Kräfte« genannt. Der letztere Ausdruck stammt wieder von Leibniz her, der unter lebendiger Kraft das Produkt aus der Masse und dem Quadrate der Geschwindigkeit[S. 313] verstand und über den im Weltall vorhandenen Kräftevorrat gleichfalls schon Betrachtungen anstellte.
Auf die Ableitung der Hauptsätze folgt die Bestimmung des Schwingungsmittelpunktes für einige geometrische Figuren. Auch darauf machte schon Huygens aufmerksam, daß sich die Schwingungszeit eines Pendels nicht ändert, wenn man es im Schwingungsmittelpunkte aufhängt, und daß in diesem Falle der Punkt, der vorher Aufhängepunkt war, zum Schwingungsmittelpunkte wird. Von ihm rührt also die Idee des Reversionspendels her, das erst im 19. Jahrhundert für die genauere Bestimmung der Länge des Sekundenpendels so wichtig geworden ist.
Am Schlusse seines Werkes über die Pendeluhr bringt Huygens noch die wichtigsten Sätze über die Zentrifugalkraft. Auch hier handelt es sich um eine Erweiterung der Galilei'schen Lehre von der Pendelbewegung. Wird ein Körper, der sich im Zustande der geradlinigen und gleichförmigen Bewegung befindet, in eine kreisförmige Bahn gezwungen, so übt er einen vom Zentrum dieses Kreises fortgerichteten Zug aus, dem entweder durch den gleichen Gegendruck oder durch die Spannung eines den Körper und das Zentrum verbindenden Fadens das Gleichgewicht gehalten werden muß. Huygens lieferte den Beweis, daß die Zentrifugalkraft wie das Quadrat der Geschwindigkeit zunimmt und in dem Verhältnis kleiner wird, wie der Radius wächst.
Eine ausführliche Abhandlung, die Huygens über die Zentrifugalkraft geschrieben, wurde erst nach seinem Tode veröffentlicht. Sie führt den Titel Tractatus de vi centrifuga und ist neuerdings in deutscher Übersetzung herausgegeben worden536. Als sie zuerst im Jahre 1703 erschien, hatte Newton die Lehre von der Zentrifugalkraft schon von einem viel allgemeineren Standpunkt aus entwickelt und sich dabei nicht wie Huygens auf die Kreisbewegung beschränkt, sondern die Untersuchung dieses Problems auf die elliptische Bewegung der Himmelskörper ausgedehnt.
Das Ergebnis der von Huygens über die Zentrifugalkraft geführten Untersuchung läßt sich durch zwei Sätze ausdrücken, aus denen man sämtliche für diese Kraft in Betracht kommenden[S. 314] Umstände ableiten kann. Bezeichnet man nämlich die Geschwindigkeit des im Kreise sich bewegenden Körpers mit v, seine Masse mit m und den Halbmesser des Kreises mit r, so ist die Zentrifugalkraft:
P = mv2/r
Da ferner v gleich dem Verhältnis des Weges 2rπ zur Zeit t ist, so ist auch
P = m4rπ2/t2
Die Formel P = (mv2)/r ist der kürzeste Ausdruck der beiden in der Abhandlung vorangestellten Lehrsätze, die Huygens, wie folgt, ausspricht:
Huygens untersucht dann, wie groß die Geschwindigkeit eines Körpers sein muß, wenn die auf ihn wirkende Zentrifugalkraft die Schwere aufheben soll. Er erörtert ferner die infolge der Pendelbewegung auftretende Zentrifugalkraft und findet beispielsweise537, daß ein einfaches Pendel, dessen Masse = 1 gesetzt wird, nach Ablauf der größten seitlichen Schwingung, d. h. nachdem es durch den ganzen Quadranten des Kreises gefallen und im tiefsten Punkte angekommen ist, mit einer dreimal so großen Kraft an seinem Faden zieht, als wenn es ruhend an ihm hängt538. Am eingehendsten betrachtet er endlich den Fall, daß »an Fäden aufgehängte Körper so rotieren, daß sie horizontale Kreisperipherien durchlaufen, während das andere Fadenende unbewegt bleibt«. Er findet, daß sich die Kräfte, welche die Fäden spannen, bei zwei[S. 315] Zentrifugalpendeln (Abb. 100) von gleichem Gewicht, aber ungleichen Fadenlängen, bei gleicher Höhe der Kegel wie die Fadenlängen verhalten. Bezüglich der übrigen bei der Bewegung des Zentrifugalpendels obwaltenden Verhältnisse muß auf die Lehrsätze VIII-XIV der Huygens'schen Abhandlung hingewiesen werden.
Unter den Versuchen, die Huygens über die Zentrifugalkraft anstellte, sind ihrer Bedeutung wegen besonders die folgenden hervorzuheben. Er ließ einen ganz mit Wasser gefüllten Behälter, in den er zuvor einige Holzkugeln gebracht hatte, um seine Achse rotieren. Die Holzkugeln eilten dann auf die Achse zu, ein Beweis, daß die Zentrifugalkraft von dem spezifischen Gewicht der rotierenden Körper abhängig ist. Der Versuch wird heute in der Weise ausgeführt, daß man Holzkugeln in die Röhren RR des in Abbildung 101 skizzierten Apparates bringt. Sind die Röhren mit Luft gefüllt, so entfernen sich die Kugeln von der Achse und laufen, wenn die Drehung hinreichend schnell erfolgt, bergan. Füllt man die Röhren dagegen vollständig mit Wasser, so bewegt sich das spezifisch leichtere Holz nach der Achse hin. Das Hinablaufen der Holzkugeln in der mit Wasser gefüllten Röhre erregt zunächst Verwunderung. Die Technik hat sich dies Verhalten bekanntlich zunutze gemacht, um mittelst Zentrifugen die wässrigen Bestandteile der Milch von den darin schwimmenden, spezifisch leichteren Buttertröpfchen zu trennen.
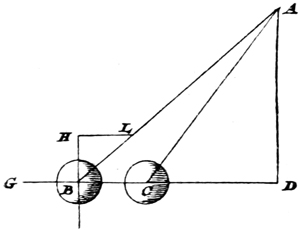
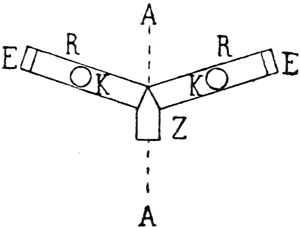
Den zweiten Versuch stellte Huygens mit einer Tonkugel an, indem er sie in rasche Drehung versetzte. Die Zentrifugalkraft wirkt auf jeden, außerhalb der Drehachse gelegenen Punkt[S. 316] eines rotierenden Körpers. Ist die Verbindung keine starre, besteht der Körper z. B. aus einem plastischen Stoff, so werden, schloß Huygens, infolge der mit der Entfernung von der Achse wachsenden Zentrifugalkräfte Formveränderungen eintreten. Zum Beweise des Gesagten wurde eine Tonkugel auf eine durch ihren Mittelpunkt gehende Achse gesteckt und in Drehung versetzt. Die Kugel nahm darauf die Form eines an den Polen abgeplatteten Sphäroids an. Durch diesen Versuch und die vorausgehenden Überlegungen vermochte Huygens die von ihm beobachtete Abplattung des Jupiter zu deuten. Sie erschien ihm als das sicherste Zeichen dafür, daß dieser Planet, ähnlich wie die Erde, eine Rotationsbewegung besitzt. Dann war aber auch, schloß Huygens, die allen bisherigen Gradmessungen zugrunde liegende Ansicht von der Kugelgestalt der Erde vermutlich eine irrige. Rotiert nämlich die Erde, und ist sie kein absolut starrer Körper, so muß sie gleichfalls von der Kugelgestalt abweichen. Die von Huygens angestellte Berechnung ergab für unseren Planeten eine Abplattung von 1 : 587. Newton, der sich mit derselben Frage beschäftigte, fand auf theoretischem Wege ein Resultat, das den Ergebnissen späterer Messungen besser entsprach. Der von ihm berechnete Wert betrug 1 : 229.
Diese Untersuchungen der beiden großen Mathematiker sollten durch eine merkwürdige Beobachtung, die zugleich auf die Wichtigkeit der Pendeluhr das hellste Licht warf, ihre Bestätigung finden. Der französische Astronom Jean Richer stellte im Jahre 1672 auf der in der Nähe des Äquators gelegenen Insel Cayenne astronomische Messungen an. Dabei fiel ihm auf, daß seine von Paris mitgenommene Uhr täglich um 2 Minuten zurückblieb. Als er das Pendel um 5/4 Linien541 verkürzte, zeigte die Uhr wieder einen richtigen Gang. Nach Paris zurückgebracht, ging sie indes zu schnell, bis dem Pendel seine ursprüngliche Länge wiedergegeben wurde. Huygens erklärte diese Erscheinung als eine Folge der mit der Annäherung an den Äquator zunehmenden Schwungkraft, welche der Schwere entgegenwirkt und unter dem Äquator 1/289 der Schwere zu Paris beträgt542. Würde demnach, führt Huygens aus, die Erde 17mal so schnell rotieren (172 = 289), so würde die Schwere durch die Schwungkraft völlig aufgehoben werden, so daß[S. 317] bei einer weiteren Steigerung der letzteren die am Äquator befindlichen Körper sich von der Erde fortbewegen müßten.
Eine Berechnung Newtons ergab zwar für die Schwungkraft gleichfalls den von Huygens gefundenen Wert. Während letzterer aber noch annahm, daß die Schwere auf der ganzen Erde die gleiche sei, und daß die Änderungen in der Länge des Sekundenpendels ausschließlich durch die wechselnde Größe der Schwungkraft bedingt würden, zeigte Newton, daß die Schwere, auch wenn man von der Zentrifugalkraft völlig absieht, einen veränderlichen Wert besitzt und mit der Annäherung an den Äquator abnimmt. Für die Notwendigkeit einer Verkürzung des Pendels an Orten geringerer geographischer Breite ergaben sich somit zwei Ursachen, die Verminderung der Schwere und das Anwachsen der, einen Teil der letzteren aufhebenden, Zentrifugalkraft.
Die Mehrzahl der französischen Gelehrten verhielt sich diesen Ergebnissen gegenüber ablehnend. Man war zunächst geneigt, die von Richer beobachtete Erscheinung auf den Einfluß der Wärme zurückzuführen. Newton hatte diesen Einfluß als zwar meßbar, aber sehr geringfügig, angenommen, da eine 3 Fuß lange Eisenstange während des Winters nur um 1/6 Linie kürzer sei als im Sommer. Auch gegen die Lehre, daß die Erde ein an den Polen abgeplattetes Sphäroid sei, erhob sich in Frankreich Widerspruch. Dominique Cassini (1625–1712), der Direktor der im Jahre 1667 gegründeten Pariser Sternwarte, für dessen ausgezeichnetes Beobachtungsvermögen die Entdeckung von vier Saturnmonden543, sowie der Rotation des Jupiter sprachen, glaubte nämlich aus den Resultaten neuerer Gradmessungen schließen zu dürfen, daß die Erde eher ein längliches Sphäroid sei, anstatt an den Polen eine Abplattung aufzuweisen. Die Newtonianer nahmen indes die Beobachtungen an dem Jupiter, der entsprechend seiner auffallend raschen Umdrehung544 eine starke Abplattung an den Polen zeigt, als einen Analogiebeweis für ihre außerdem durch die oben erwähnten theoretischen Gründe gestützte Ansicht in Anspruch.
Dieser Streit setzte sich bis über das Zeitalter Newtons hinaus fort. Endlich sahen sich die französischen Gelehrten veranlaßt, ihn durch genauere Gradmessungen zum Austrag zu bringen. Das Ergebnis war die Richtigkeit der Voraussetzung Newtons, dessen[S. 318] System nunmehr auch in Frankreich einen vollständigen Sieg errang. Wir werden uns mit dieser Lösung des Problems bei der Betrachtung des auf die Newton-Huygensperiode folgenden Zeitraumes, in dem auch die erste genauere Feststellung der Abmessungen unseres Sonnensystems gelang, zu beschäftigen haben545.
Auf das Gesetz von der Erhaltung der lebendigen Kräfte wurde Huygens nicht nur, wie wir oben gesehen haben, durch die Erforschung der Pendelbewegung geführt, sondern er gelangte zu diesem Grundgesetz gleichfalls durch die von ihm und einigen ihm nahestehenden Physikern in Angriff genommene Untersuchung des Stoßes. Eine Theorie des Stoßes gab es während der ersten Hälfte 17. Jahrhunderts noch nicht. Galilei hatte in seinen »Unterredungen« dem Stoßproblem zwar einen besonderen Abschnitt gewidmet; leider ist dieser aber unvollendet geblieben. Soviel ist gewiß, daß Galilei hier über allgemeinere Überlegungen nicht hinausgekommen ist546. Auch Descartes' Bemühungen, die Gesetze des Stoßes zu ergründen, waren erfolglos geblieben. Aus diesem Grunde stellte im Jahre 1668 die Royal Society ihren Mitgliedern die Aufgabe, die angedeutete, in der Mechanik noch bestehende Lücke auszufüllen. Infolgedessen entstanden die Abhandlungen, die Wallis, Wren und Huygens kurze Zeit nach der an sie ergangenen Aufforderung über die Theorie des Stoßes veröffentlichten.
John Wallis wurde 1616 in einem kleinen Orte der Grafschaft Kent geboren und bekleidete seit 1649 die Professur der Mathematik in Oxford547. Sein Hauptverdienst ist seine Mitwirkung an der Begründung der höheren Mathematik. Die von Cavalieri und von Wallis herrührenden Vorarbeiten haben Newton und Leibniz den Weg zur Erfindung der Infinitesimalrechnung geebnet. Wallis war 1650 mit Cavalieris548 »Indivisibilien« bekannt geworden. Er ließ auf dieses Werk im Jahre 1655 seine »Arithmetica infinitorum« folgen549, in der Quadraturen durch Zerlegen[S. 319] eines Flächenstückes in unendlich viele schmale Parallelogramme und deren Summierung ausgeführt werden.
Wallis war der erste von den drei Begründern der Theorie des Stoßes, der seine Abhandlung der Royal Society vorlegte. Sie erschien im Jahre 1668 und führt den Titel: A summary Account given by Dr. John Wallis of the general laws of motion550.
Wallis betrachtet den Stoß unelastischer Körper, und zwar den zentralen Stoß, bei dem sich die Körper auf einer, ihre Schwerpunkte verbindenden, geraden Linie bewegen. Für seine Ableitung verwendet er den schon bei Descartes vorkommenden Begriff der Bewegungsgröße. Die Massen der zusammenstoßenden Körper seien m und m1. Die Geschwindigkeiten seien v und v1. Die Geschwindigkeit, welche die Masse m + m1 nach dem Stoß besitzt, sei dagegen u. Dann besteht, wie Wallis fand, die Gleichung u = (mv + m1v1)/(m + m1) für die gleichgerichtete und u = (mv - m1v1)/(m + m1) für die entgegengesetzt gerichtete Bewegung.
Der Zweite, der sich auf Veranlassung der Royal Society mit der Erforschung der Stoßgesetze befaßte, war der als Baumeister berühmte Christoph Wren, dem London mehr als 60 öffentliche Gebäude und den Plan für seinen Wiederaufbau nach dem großen Brande vom Jahre 1666 verdankte. Wren wurde 1632 geboren und starb im Jahre 1723. Er gehörte zu den Gründern der Royal Society.
Wren fand durch Versuche mit pendelnden Körpern die Sätze für den Stoß elastischer Körper, ohne die dazu gehörenden Ableitungen geben zu können. Auch Huygens veröffentlichte wenige Monate nach Wren die Gesetze für den zentralen Stoß elastischer Körper ohne Beweise (im Februar des Jahres 1669). Die von Wren und von Huygens gefundenen Ergebnisse lassen sich in folgende Formeln einkleiden. Sind m und m1 die stoßenden Massen, v und v1 die Geschwindigkeiten vor, u und u1 die Geschwindigkeiten nach dem Stoß, ist ferner e der Elastizitätskoeffizient, so ist:
u = (mv + m1v1 - e(v - v1)m1)/(m + m1)
u1 = (mv + m1v1 + e(v - v1)m)/(m + m1).
Huygens hat später die Lehre vom Stoß ausführlicher und mit Beweisen entwickelt. Die betreffende Abhandlung erschien aber erst acht Jahre nach seinem Tode in lateinischer Sprache. Sie wurde neuerdings in deutscher Übersetzung herausgegeben551. Mit dem Inhalt dieser grundlegenden Arbeit des großen Forschers wollen wir uns etwas näher befassen.
Obgleich Huygens nirgends von vollkommener Elastizität spricht, setzt er sie dennoch stets voraus. Es geht dies aus der zweiten von den drei, seinen Lehrsätzen vorangestellten, Voraussetzungen hervor. Sie lautet: »Wenn zwei gleiche Körper mit gleichen Geschwindigkeiten aus entgegengesetzter Richtung und direkt sich treffen, so prallt jeder von beiden mit derselben Geschwindigkeit zurück, mit der er kam.« Die andere Voraussetzung ist das Beharrungsgesetz und die dritte das wichtige, von Huygens aufgestellte und in seiner Schrift zur konsequenten Durchführung gebrachte Axiom der relativen Bewegung. Nach diesem Axiom ist die Bewegung der Körper und die Gleichheit oder Verschiedenheit der Geschwindigkeiten relativ aufzufassen, d. h. im Hinblick auf andere Körper, die als ruhend betrachtet werden, wenn sie auch vielleicht in einer anderen, gemeinsamen Bewegung begriffen sind. Huygens erläutert z. B. den Fall, daß der Insasse eines fahrenden Schiffes zwei gleiche Kugeln in der Fahrtrichtung mit gleicher Geschwindigkeit aufeinanderprallen läßt. Für ihn werden sie dann mit gleicher Geschwindigkeit voneinander zurückprallen. Für einen am Lande stehenden Zuschauer muß indessen, wenn die Geschwindigkeit der Kugeln gleich derjenigen des Schiffes ist, die eine Kugel nach dem Stoße unbewegt bleiben, während die andere mit einer Geschwindigkeit zurückprallt, die doppelt so groß ist als die ihr von dem Passagier erteilte Geschwindigkeit.
Die Sätze, welche Huygens entwickelt, behandeln durchweg den zentralen Stoß. Da indessen das Verhältnis der Massen und der Geschwindigkeiten geändert wird, so ergibt sich für seine Betrachtungen eine Mannigfaltigkeit von Fällen. Einige der wichtigsten[S. 321] mögen hier hervorgehoben werden. »Wenn auf einen ruhenden Körper ein anderer gleicher Körper stößt, so wird dieser nach der Berührung ruhen, für den ruhenden aber wird dieselbe Geschwindigkeit gewonnen werden, die der stoßende besaß.«
Dieser Satz ist ein besonderer Fall des folgenden: »Wenn zwei gleiche, mit ungleichen Geschwindigkeiten bewegte Körper zusammenstoßen, so werden sie sich nach dem Stoße mit vertauschten Geschwindigkeiten bewegen.«
In diesem, besonders aber in dem berühmten elften, von Huygens aufgestellten Satze, kommt das umfassende Prinzip zum Ausdruck, daß die gesamte Bewegungsenergie beim Stoße vollkommen elastischer Körper unverändert bleibt.
Der elfte Satz lautet: Beim wechselseitigen Stoß zweier Körper ist die Summe der Produkte aus den Massen mit den Quadraten ihrer Geschwindigkeiten vor und nach dem Stoße gleich. Jenes Produkt wurde seit Leibniz als lebendige Kraft bezeichnet. In dem Satz von Huygens (1669) wird somit zum ersten Male das umfassendste Gesetz der Mechanik, das Gesetz von der Erhaltung der lebendigen Kraft, zum Ausdruck gebracht. Eine philosophische Andeutung dieses Grundgesetzes findet sich zwar schon bei Epikur, dessen Ansichten über das Kräftespiel des Universums Lucretius Carus in poetische Formen kleidete552. In seiner vollen Bedeutung konnte es erst später erkannt werden, nachdem man die Wärme als eine besondere Art der Bewegung kennen gelernt hatte. Einen Ausdruck für die Allgemeingültigkeit des Gesetzes finden wir jedoch schon bei Leibniz, wenn er sich folgendermaßen ausspricht: »Das Universum ist ein System von Körpern, die mit anderen nicht kommunizieren. Daher erhält sich in ihm immer dieselbe Kraft«553. Auch was beim Stoß die kleinsten Teilchen an Kraft absorbieren, bemerkt Leibniz an anderer Stelle, sei für das Universum nicht verloren554.
Den Ausgangspunkt für diese von Leibniz angestellten Betrachtungen bildete eine Behauptung des Descartes, die Leibniz als irrtümlich bekämpfte. Descartes hatte nämlich für die Kraftmessung[S. 322] das Produkt aus Masse und Geschwindigkeit, das sogenannte Bewegungsquantum, gewählt und behauptet, die Summe der Bewegungsquanten müsse für das Universum konstant bleiben. Hiergegen wandte sich Leibniz in seiner Abhandlung vom Jahre 1686, deren vollständiger, sehr bezeichnender Titel folgendermaßen lautet555: Kurzer Nachweis des bemerkenswerten Irrtums des Descartes und anderer bezüglich eines Naturgesetzes, demzufolge, wie sie annehmen, durch Gott immer dasselbe Quantum an Bewegung sich erhalte556.
Leibniz suchte seinen Gegner zu widerlegen, indem er einen anderen, und zwar richtigen Satz des letzteren mit Hilfe der von Galilei erkannten Fallgesetze auf einen neuen Ausdruck brachte557. Descartes hatte nämlich den richtigen Gedanken, die Größe der Kraft durch das Produkt von Gewicht und Erhebung auszudrücken. Daraus ergab sich, weil nach den Fallgesetzen die Erhebungen den Quadraten der beim Beginn des Aufsteigens vorhandenen Anfangsgeschwindigkeiten proportional sind, daß die Wirkungsgröße dem Produkt aus Gewicht und Geschwindigkeitsquadrat und nicht dem Produkt aus Gewicht und Geschwindigkeit proportional ist. Leibniz beging insofern noch einen Irrtum, als er das Produkt mv2 als den Ausdruck für die Arbeitsfähigkeit ansah, während der tatsächliche Wert mv2/2 ist.
Freilich war Leibniz das Verhältnis zwischen potentieller und kinetischer Energie wie auch die Äquivalenz der Naturkräfte noch unbekannt, obgleich er mit vielen seiner Zeitgenossen die Ansicht teilte, daß die Wärme in einer Bewegung der kleinsten Teilchen bestehe. Er gibt sogar ein bezeichnendes Bild von dem Übergang der Massenbewegung in Molekularbewegung, indem er[S. 323] diesen Übergang mit dem Wechseln eines größeren Geldstückes in Scheidemünze vergleicht558.
Wir wollen von dem Standpunkt, den Leibniz in dieser Frage gewonnen, noch einen kurzen Blick vor- und rückwärts tun. Auf die Anklänge bei Epikur haben wir schon hingewiesen. Voltaire konnte daher im Hinblick auf den bei Descartes wieder aufkeimenden Gedanken sagen, sein Landsmann habe nur eine alte Chimäre Epikurs erneuert559. Newton hat sich um die Einführung des Prinzips von der Erhaltung der Kraft in die Dynamik keine Verdienste erworben, insbesondere war er weit davon entfernt, Anschauungen über die Abgeschlossenheit und den Kräftevorrat des Universums zu entwickeln, wie sie uns bei Leibniz begegnen. Dies kommt auch in dem von Leibniz herrührenden Worte zum Ausdruck, die göttliche Maschine Newtons, d. h. das Universum, wie er es sich dachte, sei nach Newtons eigener Annahme so unvollkommen, daß es von Zeit zu Zeit ausgebessert werden müsse.
Aus den Stoßgesetzen hatte sich ergeben, daß die Quantität der Bewegung nicht konstant ist, und Newton hatte daraus geschlossen, daß, entgegen der Behauptung Descartes', das Bewegungsquantum daher auch für das Weltall nicht konstant sein könne. Es seien zwei Prinzipien nötig, eins, um die Körper in Bewegung zu setzen, und ein anderes, um die Bewegung zu erhalten. Dagegen wandte sich Joh. Bernoulli: Wenn Newton die wahre Bedeutung des Prinzips der Erhaltung der lebendigen Kräfte erkannt hätte, so würde er nicht zwei verschiedene Prinzipien aufgestellt haben. Dasselbe Prinzip nämlich, durch das die Bewegung mitgeteilt werde, bewirke auch, daß die Bewegung sich erhalte, und zwar nicht im Verhältnis der Quantität der Bewegung, sondern im Verhältnis der lebendigen Kräfte, woraus hervorgehe, daß die Bewegung in der Welt niemals verloren gehen könne560.
Wie Joh. Bernoulli, so betonte auch Leibniz, daß die Summe der Kräfte in der Welt erhalten bleibe. Die Kraft vermindere[S. 324] sich nicht, da kein Körper seine Kraft verliere, ohne sie auf einen anderen zu übertragen. Ebensowenig vermehre sich die Kraft, da keine Maschine, also auch die Welt nicht, ohne äußeren Impuls Kraft aus sich erzeugen könne.
Mit dem Prinzip von der Erhaltung der Kraft haben sich unter Huygens' Nachfolgern während des 18. Jahrhunderts besonders Johann und Daniel Bernoulli beschäftigt.
Am meisten Beachtung verdienen die Ausführungen, die Daniel Bernoulli im Jahre 1750 über diesen Gegenstand veröffentlichte561. Bei den Betrachtungen, die wir bei Huygens und bei Leibniz antreffen, handelt es sich um die lebendigen Kräfte, die durch eine gleichförmige, sich selbst parallel bleibende Schwerkraft erzeugt werden. Daniel Bernoulli untersucht den Fall, daß die Zentren ihren Ort verändern, und beispielsweise die Körper sich gegenseitig nach dem Newtonschen Gesetze anziehen. Zunächst seien es zwei Körper. Ihre Massen seien M und m und ihre Entfernung a. Die Körper sind frei beweglich, so daß sie sich einander nähern können. Bernoulli beweist dann, daß die Summe ihrer lebendigen Kräfte unverändert fortbesteht, wie auch die beiden Körper aus ihrer anfänglichen Entfernung a in eine neue x übergehen. Darauf dehnt Bernoulli die Untersuchung auf drei und weiter auf beliebig viele Körper aus und zeigt, daß auch für sie das gleiche Gesetz gilt, gleichgültig, welche Bahnen die einzelnen Körper auch beschreiben mögen. »Die Natur«, so schließt er, »verleugnet niemals das große Gesetz von der Erhaltung der lebendigen Kräfte«. Bernoulli war es also, der dieses Gesetz zu seiner heutigen allgemeinen Bedeutung erhoben hat562.
Daniel Bernoulli zerstreute den metaphysischen Nebel, der sich um das Prinzip der Erhaltung der lebendigen Kraft verbreitet hatte. Um jeden Anstoß zu vermeiden, zieht er die Bezeichnung vor: »Gleichheit zwischen dem aktuellen Herabsteigen und dem potentiellen Aufsteigen« und knüpft damit direkt an Huygens an.
Johann Bernoulli563 sagt: »Wir schließen, daß jede lebendige Kraft ihre bestimmte Quantität hat, von der nichts verloren gehen[S. 325] kann, was sich nicht in dem ausgegebenen Effekte wiederfindet. Hieraus folgt, daß die lebendige Kraft sich immer erhält, so daß diejenige, die sich vor der Aktion in einem oder mehreren Körpern befand, nach der Aktion in dem einen oder den anderen Körpern sich vorfindet, wenn nicht ein Teil von ihr in dem ersten Körper oder in dem System zurückgeblieben ist. Das ist es, was ich die »Erhaltung der lebendigen Kräfte« nenne.« Dieses allgemeine Naturgesetz sei auch da gültig, wo scheinbar eine Abweichung stattfinde. »Wenn nämlich die Körper nicht vollkommen elastisch sind, so scheint ein Teil der lebendigen Kräfte beim Zusammendrücken ohne Rückkehr in den früheren Zustand verloren zu gehen. Wir müssen uns aber vorstellen, daß dieses Zusammendrücken der Kompression einer elastischen Feder entspricht, die durch ein Band (Sperrvorrichtung) verhindert wird, sich wieder auszudehnen und auf diese Art die lebendigen Kräfte, die sie von dem auf sie treffenden Körper empfangen, nicht zurück gibt, sondern in sich zurück behält, so daß ein Verlust an Kraft nicht stattfindet.« Dies ist für Johann Bernoulli eine Denknotwendigkeit, denn jedermann betrachte es als ein Axiom, daß keine wirkende Ursache verloren gehen kann, weder als Ganzes noch als Teil, ohne einen dem Verluste gleichen Effekt zu bewirken. Ähnlich wie Johann äußert sich Daniel Bernoulli564. Beide waren also dem Ziele nahe, den Übergang von Massenbewegung zur Molekularbewegung und das mechanische Äquivalent der Wärme zu finden.
Was in dieser und der nächst folgenden Periode fehlte, waren sichere numerische Daten. Mit Recht wies Diderot darauf hin565, daß man zu einer Kenntnis der Korrelation der Naturkräfte erst gelangen werde, wenn der experimentelle Teil der Physik weiter vorgeschritten sei.
Da das Prinzip der Erhaltung der Energie auf die Mechanik beschränkt blieb, und es nicht gelang, es für alle Gebiete der Physik durchzuführen, geriet es fast in Vergessenheit, so daß selbst Kant, obgleich er eine Schrift über die Schätzung der lebendigen Kräfte veröffentlichte, das Prinzip nicht erwähnte.
Erst durch die neuere umfassendere Begründung des Prinzips von der Erhaltung der Energie ist der Zusammenhang zwischen den einzelnen Zweigen der Physik gewonnen und damit die Mechanik zur Grundlage für alle übrigen Zweige der Physik gemacht worden.
Auffallend ist, wie erwähnt, daß auch Kant bei seinen Betrachtungen über das Weltall und den Weltbildungsprozeß nirgends auf das Prinzip von der Erhaltung der Kraft Bezug nahm. Dagegen lehrte er in seinen »Metaphysischen Anfangsgründen der Naturwissenschaft« die Unveränderlichkeit der Quantität der Materie566. Die Ausdehnung des Prinzips, von der Dynamik, für die es zunächst erkannt war, auf sämtliche Naturvorgänge, erfolgte erst in der Mitte des 19. Jahrhunderts durch Mayer, Joule und Helmholtz. Das Verhältnis dieser Männer zu Daniel Bernoulli läßt sich mit demjenigen vergleichen, das zwischen Koppernikus und Aristarch besteht.
Unter den Zeitgenossen Newtons ragte neben Huygens der Franzose Mariotte hervor, wenn er auch den beiden zuerst genannten Forschern an Bedeutung erheblich nachstand. Mariotte wurde 1620 geboren und trat 1666, also im Jahre ihrer Gründung, in die Pariser Akademie der Wissenschaften ein. Er starb in Paris am 12. Mai des Jahres 1684. Mariotte arbeitete besonders auf den Gebieten der Mechanik, der Optik und der Wärmelehre567. Sein Verdienst um die ihm und Boyle gelungene Auffindung des Grundgesetzes der Aëromechanik haben wir schon an früherer Stelle hervorgehoben. Mariotte veröffentlichte seine Entdeckung dieses Grundgesetzes im Jahre 1676, sechzehn Jahre später als Boyle, in einer »Essai sur la nature de l'air« betitelten Abhandlung568. Wenn sein Verdienst auch dadurch, daß Boyle die Priorität gebührt, verringert wird, so war doch Mariotte der erste, der aus diesem Gesetz die Abhängigkeit des Luftdrucks von der Höhe zu ermitteln suchte und so die barometrische Höhenmessung begründete. Der Weg, den Mariotte hierbei einschlug, war zwar der richtige, doch gelang es erst Deluc, eine brauchbare hypsometrische Formel abzuleiten.
Die Hydromechanik bereicherte Mariotte durch seinen »Traité du mouvement des eaux et des autres fluides«. Die Schrift erschien 1686569 und handelt besonders von dem Ausfluß und der[S. 327] dabei auftretenden Reibung, aus der Mariotte manchen Widerspruch zwischen Theorie und Erfahrung erklärte. In dieser Abhandlung hat er auch die bekannte, nach ihm Mariottesche Flasche genannte Vorrichtung beschrieben, die es ermöglicht, eine Flüssigkeit unter konstantem Druck ausfließen zu lassen. Ferner gab er hier die erste Formel der Berechnung der Wandstärke für zylindrische Röhren, die einen Druck von innen erfahren, erörterte die Bewegung des Wassers in solchen Röhren, die Stoßwirkung von Flüssigkeiten, die Springhöhe von Fontänen und manche andere für Wissenschaft und Technik gleich wichtige Frage. Die Veranlassung zu seinen Untersuchungen über Hydrostatik und Hydrodynamik sollen ihm die prächtigen Wasserwerke zu Versailles gegeben haben570. Auch mit der Mechanik der festen Körper hat sich Mariotte beschäftigt. In einer Abhandlung571 vom Jahre 1677 untersuchte er den Stoß und beschrieb eine Vorrichtung, um die von ihm und anderen (insbesondere von Wren) gefundenen Gesetze experimentell nachzuweisen. Sie besteht aus einer Anzahl Elfenbeinkugeln, die sich berühren und so aufgehängt sind, daß ihre Mittelpunkte in einer horizontalen geraden Linie liegen572.
In der Optik ist Mariotte durch die Entdeckung des »blinden Flecks« im Auge bekannt geworden. Er machte der Pariser Akademie darüber im Jahre 1666 folgende Mitteilung: »Ich hatte bei anatomischen Untersuchungen von Menschen und Tieren oft beobachtet, daß der Sehnerv nicht genau der Pupille gegenüber in den Augapfel eintritt, sondern etwas höher und mehr nach der Nase hin. Um daher die von einem Gegenstande kommenden Lichtstrahlen auf den Sehnerven meines Auges fallen zu lassen und zu untersuchen, was dann geschähe, befestigte ich auf einem dunklen Hintergrund, etwa in der Höhe meiner Augen, eine kleine Scheibe aus weißem Papier, die mir zum Fixieren dienen sollte. Ferner brachte ich eine zweite Scheibe rechts von der ersten, aber etwas tiefer und etwa 2 Fuß davon entfernt an, so daß sie auf den Sehnerven meines rechten Auges wirken konnte, während ich das linke geschlossen hielt. Ich stellte mich der ersten Scheibe gegenüber und entfernte mich allmählich, indem ich sie immer im Auge behielt. Als ich mich etwa neun Fuß entfernt hatte, verschwand die zweite Scheibe, die etwa 4 Zoll Durchmesser besaß,[S. 328] vollständig. Dies ließ sich nicht etwa aus der seitlichen Lage der zweiten Scheibe erklären, denn ich bemerkte andere Gegenstände, die sich noch mehr seitlich befanden, so daß ich hätte glauben können, man habe die zweite Scheibe entfernt. Doch erblickte ich sie sofort wieder, sobald ich die Stellung meines Auges ein wenig veränderte. Sobald ich dann wieder die erste Scheibe ins Auge faßte, verschwand die zweite, zur Rechten befindliche Scheibe sofort wieder. Ich machte dann denselben Versuch, indem ich meine Entfernung von den Scheiben, gleichzeitig aber, und zwar im selben Verhältnis, deren Abstand voneinander änderte. Ich stellte ihn ferner mit dem linken Auge an, indem ich das rechte geschlossen hielt. Zuvor hatte ich die zweite Scheibe, links von meinem Fixierpunkte (der ersten Scheibe nämlich) anbringen lassen. Auf solche Weise stellte ich fest, daß es sich unzweifelhaft um einen Sehfehler handelt, der den Sehnerven (richtiger seine Eintrittstelle) betrifft. Das Überraschende ist, daß, wenn man auf diese Weise eine auf hellem Grunde befindliche schwarze Papierscheibe verschwinden sieht, man nicht etwa irgend welchen Schatten oder eine dunkle Stelle dort erblickt, wo sich das Papier befindet. Der Hintergrund erscheint vielmehr in seiner ganzen Ausdehnung weiß«573. Der Versuch erregte das größte Aufsehen. Die Royal Society wiederholte ihn 1668 sogar in Gegenwart des Königs. Mariotte kam zu dem unrichtigen Schluß, daß nicht die Netzhaut, sondern die darunter liegende Aderhaut der Sitz des Sehvermögens sei.
Ein Verdienst um die Optik erwarb sich Mariotte auch durch seine Erklärung der um Mond und Sonne mitunter auftretenden Höfe, sowie der Nebenmonde und der Nebensonnen. Seine Theorie über die Entstehung der einen Durchmesser von 23 Graden besitzenden Höfe gilt im wesentlichen auch heute noch. Er erklärt die Erscheinung durch die Annahme, daß in den höheren Regionen prismatische Eisnadeln schweben, in denen das Licht eine zweimalige Brechung und eine Reflexion erleidet. Das Beweisverfahren ist demjenigen ähnlich, das Descartes zur Erklärung des Regenbogens aus der in den Wassertropfen stattfindenden Brechung und Spiegelung anwendet. Da die Eisnadeln in allen denkbaren Lagen die Luft zwischen dem Auge des Beobachters und der Sonne oder dem Mond erfüllen, so muß auch immer eine genügende Anzahl von Nadeln vorhanden sein, deren Achse senkrecht[S. 329] zur Verbindungslinie des Auges mit dem Himmelskörper steht. Für diese Stellung der Nadeln ergibt aber die Berechnung den beobachteten Winkel von 23 Graden.
Auf dem Gebiet der Wärmelehre verdanken wir Mariotte wichtige Beobachtungen, die Licht über die Wärmestrahlung verbreiten. Er wies z. B. nach, daß die Sonnenstrahlen das Glas fast ungeschwächt durchdringen, während die Wärme des Kaminfeuers dadurch fast ganz zurückgehalten wird. Mariotte bediente sich dazu eines Brennspiegels, der vor einem Kaminfeuer in seinem Fokus eine unerträgliche Hitze erzeugte. Letztere verminderte sich sehr, wenn eine Glasplatte zwischen den Kamin und den Spiegel gebracht wurde. Berühmt ist ferner Mariottes Versuch, Schießpulver mit einer aus Eis gebildeten Linse zu entzünden. Er beschreibt ihn mit folgenden Worten574: »Mehrere Personen haben versucht, Brennspiegel aus Eis herzustellen, indessen hat dies seine Schwierigkeiten. Um vollkommen reines Eis herzustellen, ließ ich klares Wasser eine halbe Stunde kochen und trieb so alle Luft heraus. Dies Wasser ließ ich zu einer Platte gefrieren, die einige Zoll dick war. Sie enthielt keine Blase und war vollkommen durchsichtig. Ein Stück dieser Eisplatte brachte ich dann in ein kleines, sphärisch ausgehöhltes Gefäß und ließ das Eis darin unter wiederholtem Umwenden so lange schmelzen, bis es auf beiden Seiten die sphärische Form des Gefäßes angenommen hatte. Dann ergriff ich das Eisstück an den Rändern, wobei ich mich eines Handschuhes bediente, und brachte es in die Sonne. In kurzer Zeit vermochte ich mit Hilfe einer solchen, aus Eis verfertigten Linse Schießpulver zu entzünden, das ich in ihren Brennpunkt gebracht hatte.«
Das Wesen der Wärme erblickten die meisten im 17. Jahrhundert zumal nach der Wiederbelebung der atomistischen Lehre durch Gassendi, in besonderen Wärmeatomen, wie man auch für das Licht eigene Atome annahm. Wenn Gassendi sagt, daß die Wärme eindringt, auflöst usw., so versteht er darunter, daß bestimmte Atome, die nicht etwa selbst warm sind, in die Körper eindringen, durch sie hindurchgehen, sie auseinandertreiben usw. Die Wärmeatome betrachtete man als sehr klein, rund und mit lebhafter Bewegung begabt. Diese Eigenschaften sollten sie befähigen, in die Poren aller Körper einzudringen.
Daß man es in der Wärme mit einem Bewegungszustand zu tun haben könne, wurde nur vereinzelt und ohne tiefere wissenschaftliche[S. 330] Begründung ausgesprochen. Immerhin bestand ein Gegensatz der Meinungen, zumal nachdem Daniel Bernoulli und Euler zu Beginn des 18. Jahrhunderts Ansichten über die Natur der Wärme entwickelt hatten, die von den herrschenden abwichen. Auch eine Preisaufgabe, welche die Akademie der Wissenschaften zu Paris im Jahre 1736 »über das Wesen des Feuers und seine Fortpflanzung« gestellt hatte, wurde im Sinne der Materialität der Wärme beantwortet. Im übrigen konnte die Frage nach der Ausbreitung des Feuers bei dem damaligen Stande der Physik und der Chemie keine Lösung finden. Wenig später hat auch Kant zu dieser Frage Stellung genommen575. Nach ihm ist »der Stoff des Feuers ein elastischer Stoff, der die Elemente der Körper zusammenhält. Seine wellenförmige oder zitternde Bewegung ist das, was man Wärme nennt«.
Was uns im 17. und 18. Jahrhundert auf dem Gebiet der Wärmetheorie begegnet, bestand somit vorzugsweise aus Hypothesen und Vergleichen. Dagegen fehlte es an der genügenden Stütze durch Versuche und Messungen.
Im Zusammenhange mit der Wärmelehre wurde auch die Meteorologie gefördert. So verglich Mariotte z. B. die Niederschlagsmenge mit dem aus einem Stromgebiet abfließenden Wasserquantum. Seine Berechnungen stellte er für die Seine an, deren Gebiet er auf 3000 französische Quadratmeilen schätzte. Die jährliche Regenhöhe betrug nach den damals angestellten Messungen 15 Zoll, was eine Wassermenge von mehr als 600 Millionen Kubikfuß ergab, während die Seine nur etwa 100 Millionen Kubikfuß, also 1/6 des gesamten Niederschlags, fortführt. Diese Berechnung würde zwar heute keinen Anspruch auf Genauigkeit mehr erheben können. Auch konnte Mariotte kaum ahnen, wie wichtig solche Ermittlungen, zu denen er den Weg gewiesen, für spätere, auf eine wirtschaftlichere Ausnutzung des Wasserreichtums gerichtete Bestrebungen sein würden.
Noch engere Beziehungen als zwischen Newton und Huygens bestanden zwischen dem unvergleichlichen englischen Forscher und seinem jüngeren Landsmann Halley, der zu Newton in[S. 331] einem ähnlichen Verhältnis stand, wie ein halbes Jahrhundert früher Torricelli zu Galilei.
Edmund Halley wurde 1656 in der Nähe von London geboren. Seine Neigung für die Mathematik und die Physik zeigte sich wie bei Newton sehr früh. Als 15jähriger Schüler widmete er sich schon der Verfertigung von Apparaten und Beobachtungen über den Erdmagnetismus. Halley studierte in Oxford und veröffentlichte mit 20 Jahren seine erste Abhandlung in den Philosophical Transactions. Sie betraf die Exzentrizität der Planetenbahnen. Im selben Alter wußte er vornehme Gönner dafür zu gewinnen, daß man ihn mit dem Auftrage, einen Fixsternkatalog des südlichen Himmels herzustellen, nach St. Helena schickte. Die Kosten für diese Expedition übernahm die Ostindische Kompagnie. Der Katalog, der etwa 360, in Europa nicht sichtbare, Sterne enthielt, erschien 1679576 und trug Halley die Mitgliedschaft der Royal Society ein, in der er ein Jahr vor der Veröffentlichung seiner Arbeit, als 22jähriger, aufgenommen wurde. Nach seiner Rückkehr wurde Halley durch die Erscheinung der großen Kometen von 1680 und 1682 angeregt, sich der Erforschung dieser Himmelskörper zu widmen. Zunächst galt es noch, eine Methode zu finden, um aus einer Reihe von Beobachtungen die Bahn eines Kometen zu bestimmen. Zu diesem Zwecke trat Halley im Jahre 1684 mit Newton in Verbindung. Letzterer setzte ihn von seinem, später am Schlusse der Prinzipien veröffentlichten Konstruktionsverfahren in Kenntnis. Dabei gewann Halley auch Einblick in die übrigen Vorarbeiten zu Newtons großem Werke, das dieser, wie Koppernikus seine »Kreisbewegungen«, jahrelang nicht zum Abschluß und zur Kenntnis der Mitwelt brachte, um immer noch kleine Unvollkommenheiten zu beseitigen. Dem Drängen Halleys, der Newton das Werk förmlich abringen mußte und den Druck besorgte, ist es zu danken, daß die »Prinzipien« endlich im Jahre 1688 erschienen.
Nach der von Newton geschaffenen Theorie berechnete Halley aus den vorhandenen Beobachtungen die Bahnen von 24 Kometen, die in den Jahren 1337 bis 1608 erschienen waren. Der früheren Annahme entgegen, daß man es in diesen Weltkörpern durchweg mit fremden Eindringlingen ganz unbekannter Herkunft zu tun habe, die auf ihrem parabolischen Wege dem Sonnensystem einen kurzen Besuch abstatteten, machte Halley die überraschende[S. 332] Entdeckung, daß gewisse Kometen Glieder unseres Systems sind und sich wie die Planeten in elliptischen, wenn auch sehr langgestreckten Bahnen um die Sonne bewegen. Diese Entdeckung machte er an dem Kometen des Jahres 1682. Die Berechnung ergab nämlich für diesen und die 1607 und 1531 erschienenen Kometen fast die gleichen Elemente577. War die Annahme Halleys, daß es sich hier um dasselbe Gestirn handle, das sich innerhalb 75 Jahren in elliptischer Bahn um die Sonne bewege, zutreffend, so war eine neue Wiederkehr im Jahre 1759 zu erwarten. Diese einzigartige Vorhersage, der im 19. Jahrhundert die Entdeckung des Neptun durch Leverrier an die Seite zu stellen ist, traf auch ein. Der Komet erschien 1835 nach weiteren 75 Jahren und wurde auch im Jahre 1910 beobachtet. Die Erscheinung des Halleyschen Kometen ist später bis zu dem Beginn unserer Zeitrechnung zurück verfolgt worden. Eine periodische Wiederkehr hat Halley ferner für den Kometen von 1680, wohl den größten der je beobachtet wurde – sein Schweif war 70 Grad lang – wahrscheinlich gemacht. Die Umlaufszeit beträgt für diesen Kometen nach Halleys Annahme 575 Jahre. Die Richtigkeit dieser Annahme würde also erst durch eine Wiederkehr im Jahre 2255 ihre Bestätigung finden können.
Halley hat auch zuerst die Meteore mit den Kometen in Parallele gebracht, indem er für sie gleichfalls einen kosmischen Ursprung annahm. Früher hatten sie für atmosphärische Erscheinungen gegolten. Aus den Beobachtungsdaten, die für ein 1708 in England gesehenes Meteor vorlagen, ergab sich eine solche Höhe für das Aufleuchten der Feuerkugel, daß Halley zu der erwähnten Annahme geführt wurde. Er drang indessen mit seiner Ansicht nicht durch, und es blieb Chladni vorbehalten, endgültig die Lehre zur Anerkennung zu bringen, daß wir es in den Meteoren und in den Sternschnuppen mit kosmischen Gebilden zu tun haben578.
Halleys weitere astronomische Tätigkeit fällt vorzugsweise in die erste Hälfte des 18. Jahrhunderts. Sie wird in einem späteren, die Astronomie dieses Zeitraums behandelnden Abschnitt geschildert werden. Als Physiker hat sich Halley auf dem Gebiete[S. 333] der Optik, des Magnetismus und der Wärmelehre sehr verdient gemacht.
Wir haben erfahren, mit welchen Schwierigkeiten Kepler bei der Begründung der Dioptrik zu kämpfen hatte, weil ihm die Kenntnis des Brechungsgesetzes und einer Formel für die Brenn- und Vereinigungsweiten der Linsen noch fehlte. Die Feststellung dieser Formel gelang, nachdem eine Regel für die Berechnung der Brennweiten sphärischer Gläser von Cavalieri aufgefunden war579, in allgemein gültiger Weise erst Halley im Jahre 1693580. Seine dioptrische Fundamentalformel läßt sich auf die bekannte einfache Form 1/f = 1/a + 1/b bringen, worin f die Brennweite, a und b Gegenstands- und Bildweite bedeuten. Sie gilt nicht nur für sphärische Linsen, sondern auch für sphärisch gekrümmte Spiegel581.
Eine andere wichtige Formel, deren Ableitung wir Halley verdanken582, ist die von Mariotte vergeblich gesuchte Formel für die barometrische Höhenmessung. Der Weg, den Halley dabei einschlug, ist der folgende: Nach dem Boyleschen Gesetze verhalten sich die Volumina einer Luftmasse umgekehrt wie die Drucke oder v : v1 = p1 : p. Ebenso verhalten sich aber auch die Koordinaten einer Hyperbel, wenn wir ihre Asymptoten als Ordinaten- und[S. 334] Abszissenachse wählen. Es ist nämlich (s. Abb. 102) OP : OQ = QB : PA. Stellen somit OP, OQ und OR die Drucke vor, so sind PA, QB und RC die zugehörigen Volumina der betreffenden Luftmasse. Für die Volumina können wir die Höhen setzen, da in einer zylindrischen oder prismatischen Luftschicht, die sich von der Erde bis zur Grenze der Atmosphäre erstreckt, die Grundflächen für alle Teilschichten dieselben bleiben. Nun ist aber die Gesamthöhe aller Luftschichten zwischen zwei Stellen, denen der Barometerstand OS und OR zukommt, gleich der Fläche RCDS. Ferner verhalten sich bei der zugrunde gelegten Hyperbel die Flächen
RCDS : QBCR = log(OS/OR) : log(OR/OQ).
Daraus folgt, da die Flächenräume die Höhen und die Abszissen die Barometerstände vorstellen,
H = A log(B/b).
A bedeutet eine Konstante, deren Wert Halley aus dem Verhältnis der Dichten von Luft und Quecksilber bestimmte. Dies ist die Barometerformel in ihrer einfachsten Form und ohne Berücksichtigung der Temperatur. Der erste, der sich dieser logarithmischen Formel bei Höhenmessungen bediente, war Bouguer während seiner mit Condamine unternommenen Gradmessung in Peru.
Halleys Verdienste um die Mathematik können hier nur ganz kurz gestreift werden. Erwähnt seien einige Arbeiten, die eine konstruktive Auflösung der kubischen und der biquadratischen[S. 335] Gleichungen unter Anwendung der Kegelschnitte brachten583. Wichtig ist auch Halleys etwas später (1695) erschienene Abhandlung über die Berechnung der Logarithmen584. Sie enthält unter anderem eine bis auf 60 Dezimalen durchgeführte Berechnung des Moduls des Briggschen Logarithmensystems585. Auch durch seine Apollonios-Ausgabe vom Jahre 1710 erwarb sich Halley hervorragende Verdienste. Da nur die ersten vier Bücher, die Apollonios über die Kegelschnitte geschrieben, in griechischer Sprache auf uns gekommen sind, während vom fünften, sechsten und siebenten Buche nur eine arabische Übersetzung zu Gebote stand, so war Halley, um seine Aufgabe zu lösen, zur Erlernung der arabischen Sprache gezwungen. Letztere beherrschte er bald in solchem Maße, daß er Verbesserungsvorschläge zu arabischen Texten machen konnte, welche die Bewunderung der Orientalisten erregten.
Etwas eingehender betrachten müssen wir Halleys Anwendung der Mathematik auf ein biologisches und sozialpolitisches Problem, nämlich auf die Ermittlung der Lebenswahrscheinlichkeiten, ein Problem, das für die gegen das Ende des 17. Jahrhunderts in England und in Holland aufkommende Rentenversicherung von größter Bedeutung war. Die betreffende Arbeit Halleys erschien 1693586 unter dem Titel: Eine Schätzung des Sterblichkeitsgrades, gegründet auf eine Statistik der Geburts- und Sterbefälle. Halleys Schrift enthält für jene Zeit ganz neue, die Sterblichkeit betreffende Entwicklungen und bringt eine solche Fülle der fruchtbarsten Gedanken, daß man sie als grundlegend für diesen Teil der Sozialwissenschaft betrachten muß587.
Erwähnt sei gleich an dieser Stelle, daß sich mit dem weiteren Ausbau der von Halley gegebenen Grundzüge dieses Gebietes der französische Mathematiker Moivre588 und in Deutschland besonders Süßmilch beschäftigt haben. Süßmilchs Werk erschien 1741 unter dem Titel: Die göttliche Ordnung in den Veränderungen des menschlichen Geschlechtes aus der Geburt, dem Tode und der[S. 336] Fortpflanzung erwiesen. Die Schrift Süßmilchs ist gleichfalls ein für die statistische Wissenschaft grundlegendes und unentbehrliches Werk, da es die Vorarbeiten Halleys und andere Forschungen dieses Gebietes vereinigt589.
Wir kehren nach dieser kurzen Abschweifung zu Halley zurück, dessen wissenschaftlicher Werdegang, je weiter man ihn verfolgt, um so mehr Bewunderung hervorruft. Halley hatte sich seit frühester Jugend mit den Erscheinungen des Erdmagnetismus befaßt, und es war sein Lieblingswunsch, diese Erscheinungen auch in den Tropen eingehender zu erforschen. Sein Gedanke, von dem man sich Vorteile für die Nautik versprach, fand Anklang, und Halley wurde auf Kosten der Regierung zum Führer von zwei Expeditionen ernannt, auf denen er während der Jahre 1698 bis 1700 das tropische Amerika, mehrere Inselgruppen und Küstenpunkte Afrikas und Ostindiens besuchte. Das Ergebnis dieser Reisen, die sich in südlicher Richtung bis zum 53. Breitengrad erstreckten, war die erste Deklinationskarte. Sie ist das Muster für alle späteren Deklinationskarten gewesen und ist noch heute für das Studium der säkularen Schwankungen der Deklination von Wert.
Halleys Karte erschien 1701 unter dem Titel: A general chart, showing at one view the variation of the compass590. Sein Verfahren, die in zahlreichen Einzelbeobachtungen gewonnenen Ergebnisse übersichtlich zu machen, bestand darin, daß er die Punkte gleicher Deklination verband und dadurch eine graphische Darstellungsweise einführte, die seitdem Gemeingut der Wissenschaft geworden ist. Für die nach Halleys Verfahren entstehenden Linien gleicher Abweichung kam die Bezeichnung Isogonen in Aufnahme.
Daß die magnetische Deklination an einem und demselben Orte säkularen Schwankungen unterliegt, war schon seit längerer Zeit bekannt591. Einige Jahrzehnte nach dem Erscheinen der Halleyschen Karte wurden auch die kleinen täglichen Schwankungen entdeckt592.
Halley war auch der erste, der die Erscheinung des Nordlichts mit dem Erdmagnetismus in Beziehung brachte. Er beobachtete[S. 337] nämlich, daß die westliche Abweichung des Nordlichts dieselbe Größe wie die westliche Abweichung der Magnetnadel besitzt. Die Erkenntnis dieser Tatsache war von hervorragender Wichtigkeit, wenn auch der von Halley daran geknüpfte Versuch, das Nordlicht zu erklären, mißlang593.
Wie kaum anders zu erwarten, hat Halley als Leiter mehrerer nautischer Unternehmungen sich auch Verdienste um die Meereskunde erworben. Er verbesserte die Taucherglocke, beschrieb eine Taucherkappe und machte, als er sich selbst bis zu einer beträchtlichen Tiefe ins Meer hinabließ, die Beobachtung, daß das Meerwasser grünes Licht zurückwirft, das komplementäre rote dagegen durchläßt, so daß z. B. seine Hände ihm in größerer Meerestiefe ganz rot erschienen. Auch die Regelmäßigkeit der Passat- und der Monsunwinde regten das Nachdenken Halleys an, doch blieben seine Erklärungen hier unzulänglich.
Da Halley die Entstehung der Winde auf die ungleichmäßige Erwärmung der Luft zurückführte, kann es nicht wundernehmen, daß er sich auch mit den Methoden der Wärmemessung befaßte. Er kannte die Konstanz des Siedepunktes von Flüssigkeiten und brachte als oberen Fixpunkt den Siedepunkt des Alkohols in Vorschlag. Als unteren Fixpunkt empfahl er die Temperatur tiefer Keller. Auch stellte er Messungen über die Ausdehnung an, die Wasser und Quecksilber beim Erwärmen erfahren.
Nachdem Halley seine Expeditionen, die er als englischer Flottenkapitän befehligte, vollendet hatte, wurde er zum Professor der Geometrie in Oxford ernannt. Daneben bekleidete er die Stelle des Sekretärs der Royal Society. Nach dem Tode Flamsteeds übernahm er im Jahre 1721 die Leitung der Sternwarte zu Greenwich. Auf diesem Posten blieb er bis zu seinem Tode (1742). Auf die hervorragenden Verdienste, die Halley sich um die Förderung der Astronomie erworben, kann erst in einem späteren Abschnitt, der sich mit der Entwicklung dieser Wissenschaft während des 18. Jahrhunderts beschäftigt, näher eingegangen werden594.
Wir haben an einer früheren Stelle erwähnt, daß sich Cassini an der Streitfrage beteiligte, welches die genauere Gestalt der Erde sei. Da uns in Cassini einer der hervorragendsten astronomischen[S. 338] Beobachter des Newtonschen Zeitalters begegnet, wollen wir auch bei seinen Lebensschicksalen und Verdiensten etwas verweilen.
Giovanni Domenico (Dominique) Cassini wurde 1625 in der Nähe von Nizza geboren. Im Alter von 25 Jahren wurde er an Stelle Cavalieris zum Professor in Bologna ernannt. Cassinis erste astronomische Entdeckung bestand darin, daß er (1665) die Rotationszeit des Jupiter zu 9 Stunden und 56 Minuten bestimmte. In den folgenden Jahren dehnte Cassini seine Untersuchungen über die Rotation auf Mars und Venus aus. Er fand für diese beiden Planeten die Zeit einer Umdrehung gleich 24h 37m, beziehungsweise 23h 21m.
Um jene Zeit hatte Colbert die französische Akademie der Wissenschaften ins Leben gerufen und die Pariser Sternwarte errichtet. Gleich Huygens wurde nun auch Cassini zum Mitglied der Akademie ernannt und 1669 nach Paris berufen, um dort als königlicher Astronom die Leitung der Sternwarte zu übernehmen. In dieser Stellung blieb er über 40 Jahre. Er starb im Jahre 1712.
Die Berufung nach Paris hatte Cassini vor allem seiner Berechnung von Tafeln für die Jupitermonde zu verdanken595. Er löste damit eine Aufgabe, mit der sich, wie wir schon erfuhren, Galilei während seiner letzten Lebensjahre beschäftigt hatte596.
Erheblich bereichert wurde unsere Kenntnis des Planetensystems dadurch, daß Cassini dem ersten, von Huygens entdeckten Saturnmonde die Entdeckung von vier weiteren Trabanten des Saturns anreihte. Er nannte sie zu Ehren Ludwigs XIV. Sidera Ludovicea597.
Die Beobachtungen über die Jupitermonde setzte Cassini, um seine in Bologna erhaltenen Tafeln zu verbessern, in Paris fort. Hierbei fand er in Olaf Römer einen Mitarbeiter. Römer blieb es vorbehalten, bei dieser Tätigkeit auf eine der größten Entdeckungen zu stoßen. Bei der Bewegung der Monde ergaben sich nämlich gewisse Ungleichmäßigkeiten, die schon Cassini auf die Vermutung brachten, »daß das Licht einige Zeit gebrauche, um von einem der Jupitermonde zu uns zu gelangen«. Cassini gab jedoch diese Ansicht wieder auf, während Römer an ihr festhielt und, wie wir an anderer Stelle sahen598, den Nachweis für ihre Richtigkeit erbrachte.
Cassini gebührt auch das Verdienst, in Gemeinschaft mit einem jüngeren, ihm als Hilfsarbeiter zugewiesenen Astronomen599 die ersten umfassenderen Beobachtungen über das noch immer rätselhafte Tierkreis- oder Zodiakallicht angestellt zu haben. Der merkwürdige, während der Dämmerung mitunter sich zeigende kegelförmige Lichtschimmer, den wir mit diesem Namen bezeichnen, war schon den Arabern aufgefallen. In der europäischen Literatur begegnet uns die erste deutliche Beschreibung im Jahre 1661600.
Cassinis Beobachtungen über das Zodiakallicht wurden während des Zeitraums von 1683–1688 angestellt. Aus ihnen ging hervor, daß die Lichterscheinung der jährlichen Bewegung der Sonne folgt. Den Ursprung der Erscheinung verlegten Cassini und sein Mitarbeiter in einen Ring von kleinen, das Licht reflektierenden Körpern, welche die Sonne umkreisen.
Den Erfolgen gegenüber, die Cassini als beobachtender Astronom zu verzeichnen hatte, sind seine Leistungen um die Fortbildung der Theorie nur unbedeutend. Cassini stand, indem er in den Anschauungen von Descartes beharrte, den Neuerungen auf diesem Gebiete sogar ablehnend gegenüber. Ein Sohn, ein Enkel und ein Urenkel Cassinis haben sich gleichfalls als Astronomen einen Namen gemacht601.
Neben der Optik und der Mechanik, deren Fortschritte in Verbindung mit einer Weiterentwicklung der mathematischen Wissenschaft die Astronomie während der Newton-Huygens-Periode ganz außerordentlich gefördert haben, wurden die übrigen Zweige der Physik nicht in gleichem Maße berücksichtigt. Auf dem Gebiete der Elektrizitätslehre ist kaum eine nennenswerte Entdeckung zu verzeichnen; hier sollte der weitere Ausbau insbesondere dem 18. Jahrhundert vorbehalten bleiben. Dazu kam, daß das wissenschaftliche Streben in Italien nachließ, und Deutschland in seiner Mitarbeit trotz der Entwicklung, welche die experimentelle Technik durch die Arbeiten Guerickes erfahren hatte, zurückblieb. Dieses Land litt unter den Folgen des dreißigjährigen Krieges. Es war verarmt und zerrüttet, während die Wissenschaften auf dem Punkte angelangt waren, wo sie zu ihrer Fortentwicklung nicht nur der moralischen, sondern auch der materiellen Unterstützung weiterer Kreise bedurften. Statt dessen wandten die Machthaber Deutschlands in ihrer steten Geldbedürftigkeit immer noch dem alchemistischen Problem ihr Interesse zu und spendeten für dessen Lösung Mittel, die eines besseren Zweckes würdig gewesen wären602.
Unter den wenigen Deutschen, die während der zweiten Hälfte des 17. Jahrhunderts sich größere Verdienste um die Förderung der Wissenschaften erwarben, sind vor allem Tschirnhausen und Leibniz zu nennen. Ehrenfried Walter Graf von Tschirnhausen (auch Tschirnhaus) wurde 1651 in der Nähe von Görlitz geboren. Er gehört gleich Hevel und Guericke zur Klasse der reichen Privatleute, die sich im 17. Jahrhundert, angeregt durch die Erfolge der induktiven Forschungsweise, aus Liebhaberei den exakten Wissenschaften zuwandten. Tschirnhausen studierte in Leyden, wo Medizin und Naturwissenschaften im 17. Jahrhundert eine ganz hervorragende Pflegstätte besaßen. Er machte dann ausgedehnte Reisen, unterhielt persönliche Beziehungen zu Leibniz und Spinoza, war auswärtiges Mitglied der französischen Akademie der Wissenschaften und starb 1708 in Dresden. Tschirnhausen verwandte wie Guericke bedeutende Summen auf die[S. 341] Verfertigung physikalischer, insbesondere optischer Apparate. Seine aus Kupfer hergestellten Hohlspiegel, deren größter noch heute eine Sehenswürdigkeit bildet, erreichten einen Durchmesser von 3 und eine Brennweite von 2 Ellen. Sie waren imstande, einen Taler innerhalb 5 Minuten zu schmelzen, brachten jedoch keine merkliche Erwärmung hervor, als man mit ihrer Hilfe das Licht des Mondes sammelte. Tschirnhausens Linsen besaßen bis 80 cm Durchmesser603. Eine von ihnen gelangte nach Florenz und ward zu den Versuchen benutzt, die man dort im Jahre 1695 über die Verbrennlichkeit des Diamanten anstellte. Im Brennpunkt dieser Linse, die Porzellan und Bimsstein zum Schmelzen brachte, verbrannte ein Diamant von 140 Gran Gewicht innerhalb einer halben Stunde.
Durch seine Experimente mit Brennspiegeln wurde Tschirnhausen auch zu theoretischen Untersuchungen auf dem Gebiete der Optik veranlaßt. Sie betrafen die katakaustische oder Brennlinie, d. h. diejenige Kurve, welche durch die Reflexion der in den Hohlspiegel fallenden Strahlen dadurch hervorgerufen wird, daß diese Strahlen nicht denselben Punkt der optischen Achse treffen. Die katakaustische Linie ist mit anderen Worten der geometrische Ort der Durchschnittspunkte je zweier benachbarter, reflektierter Strahlen. In der nebenstehenden Abb. 103 finde in AFE die Reflexion parallel einfallender Strahlen statt. Der Strahl DF werde in der Richtung FG zurückgeworfen. Ein DF benachbarter Strahl erzeugt einen von FG nur wenig abweichenden reflektierten Strahl. Beide schneiden sich in G. Die Schnittpunkte sämtlicher reflektierten Strahlen liegen auf der Kurve EGB, der katakaustischen Linie, für welche die reflektierten Strahlen somit eine einhüllende Schar von Tangenten bilden.
Tschirnhausens Satz über die Brennlinie besagt nun, daß ihr Stück EG der Summe der beiden Strahlen DF und FG gleich[S. 342] ist. Ausführlicher haben sich mit der Katakaustika und der infolge der Brechung erzeugten Diakaustika Johann und Jakob Bernoulli beschäftigt.
Tschirnhausen veröffentlichte seine Arbeiten größtenteils in den »Acta Eruditorum«, einer Zeitschrift, die für Deutschland etwa diejenige Bedeutung besaß, die den Philosophical Transactions der Engländer zukommt. Die Acta Eruditorum sind die älteste gelehrte Zeitschrift, die auf deutschem Boden entstand. Näheres über sie enthält der einleitende Abschnitt dieses Bandes.
Aller Wahrscheinlichkeit nach gebührt Tschirnhausen auch das Verdienst, als erster in Europa Porzellan hergestellt zu haben. Als Erfinder des europäischen Porzellans wird zwar häufig der Alchemist Böttger genannt, der Tschirnhausen bei seinen Versuchen zur Hand ging und sich die Ehre der Erfindung beizulegen wußte. Trotzdem galt während des 18. Jahrhunderts Tschirnhausen, und zwar wohl mit Recht, als der eigentliche Erfinder des sächsischen Porzellans. Erst als Böttgers Verdienste in einer umfangreichen Biographie604 hervorgehoben wurden, geriet Tschirnhausen in Vergessenheit. Die neuesten, quellenmäßigen Untersuchungen605 haben diesen »durch den Biographen Böttgers bewirkten, merkwürdigen Personenwechsel in der Erfindungsgeschichte des Porzellans« aufgeklärt606. Nach diesen Feststellungen hat Tschirnhausen sich schon um die Darstellung des Porzellans bemüht, als Böttger kaum 10 Jahre alt war. Bekanntlich hielt August der Starke Böttger gefangen, weil dieser sein Versprechen, Gold zu machen, nicht erfüllt hatte. Tschirnhausen hatte Zugang zu Böttger und regte ihn an, anstatt der unfruchtbaren alchemistischen Bemühungen unter seiner Leitung die Herstellung von Porzellan zu versuchen. Diese Versuche glückten im Jahre 1707. Ein Jahr später starb Tschirnhausen, und Böttger, der allein um das Verfahren wußte, spielte sich als dessen Erfinder auf.
Ein Mann, den wir schon des öfteren erwähnten, dessen Bedeutung für die Philosophie, die Mathematik und alle Zweige der theoretischen und angewandten Naturwissenschaften sich in den wenigen Zeilen, die wir ihm hier widmen können, nicht erschöpfend darstellen läßt, war Leibniz. Man hat ihn als den Aristoteles des 17. Jahrhunderts bezeichnet. Allerdings begegnet uns in[S. 343] Leibniz eine polyhistorische Gelehrsamkeit verbunden mit einer Selbständigkeit des Denkens, wie sie kaum wieder gefunden werden. Während diese Geistesanlage Aristoteles zu einer systematischen Bearbeitung der Philosophie und der Naturwissenschaften führte, blieb die Tätigkeit, die Leibniz entfaltete, allzusehr zersplittert. Selbst wichtige philosophische Schriften, wie die Theodicee und die Monadologie, verfaßte er, um sich mit hohen Persönlichkeiten über die Grundfragen der Philosophie auseinandersetzen. Und noch mehr tragen die übrigen Veröffentlichungen, die sich auf alle Gebiete menschlichen Denkens und Handelns erstrecken, den Charakter unter sich in nur geringem inneren Zusammenhange stehender Gelegenheitsschriften.
Gottfried Wilhelm Leibniz wurde am 21. Juni 1646 in Leipzig geboren, wo sein Vater ein akademisches Lehramt bekleidete. Über den Entwicklungsgang, den Leibniz während der ersten Jahrzehnte seines Lebens nahm, hat er selbst ausführliche Mitteilungen hinterlassen607. Er lernte als Knabe Lateinisch ohne Mithilfe eines Lehrers. Überhaupt war er in den meisten Dingen Autodidakt, dabei aber stets begierig, »alle Dinge tiefer zu durchdringen und Neues zu finden«. Da ihm die Bibliothek seines Vaters zur Verfügung stand, lernte er sehr früh die alten Schriftsteller, besonders Aristoteles, kennen. Er las auch scholastische Schriften. Durch das Studium der Cartesischen Werke fand in ihm die Wandlung von der teleologischen Weltanschauung zur Erfassung des Kausalitätsprinzips statt. Leibniz bekennt in einem späteren Schreiben, erst als er die Schule verlassen habe, sei er mit den Schriften der neueren Philosophen bekannt geworden. Er erinnere sich, daß er damals als fünfzehnjähriger Knabe spazieren ging und überlegte, ob er in der scholastischen Betrachtungsweise beharren solle. »Endlich siegte die mechanische Theorie und brachte mich dazu, die mathematischen Wissenschaften zu studieren.«
Mit fünfzehn Jahren bezog Leibniz die Universität seiner Vaterstadt. Sein Fachstudium war die Rechtsgelehrsamkeit. Nach dessen Beendigung wollte man ihn »seiner Jugend wegen« nicht zur Promotion zulassen. Aus diesem Grunde erwarb er (1666) die Doktorwürde in Altdorf, wo ihm seines hervorragenden Wissens und seiner Beredtsamkeit wegen sofort eine Professur angeboten wurde. Leibniz schlug sie aus und ging nach Nürnberg. Dort trat er mit der alchemistischen Gesellschaft der Rosenkreuzer[S. 344] in Beziehung. Er war ein Jahr im Dienste dieser Gesellschaft tätig und hatte alchemistische Werke zu exzerpieren, die Korrespondenz zu führen usw. Wenn sich auch Leibniz nicht an der Lösung alchemistischer Probleme beteiligte, so bewahrte er ihnen doch stets ein lebhaftes theoretisches Interesse608. Von den praktischen Zielen der Alchemisten will er nichts wissen. Er wünscht sogar in einer im späteren Alter abgefaßten Schrift609, daß die künstliche Erzeugung von Gold und Silber, wenn sie gelingen sollte, um des gemeinen Besten willen unterdrückt werden möge. Erstrebenswert erschien ihm dagegen, »aus dem Golde die Quintessenz herauszuziehen, wie aus dem Wein den Weingeist, und mit dieser Quintessenz ein anderes Metall in Gold zu verwandeln.« Das würde zwar nichts einbringen, sondern eher etwas kosten, es würde aber die Naturerkenntnis fördern. Resigniert fügt er jedoch hinzu, auch die Verwirklichung dieser letzten Aufgabe sei nicht wahrscheinlich.
Nachdem Leibniz Nürnberg verlassen hatte, trat er in den Dienst des Kurfürsten von Mainz, der sich für Guerickes Versuche so lebhaft interessierte610. Von Mainz wurde Leibniz in diplomatischer Sendung 1672 nach Paris geschickt. Es galt, Ludwig XIV. zu einem Zuge nach Ägypten zu bewegen, um dadurch Deutschland vor den Eroberungsgelüsten dieses Königs zu bewahren. Der Gedanke einer solchen Expedition rührte von Leibniz her und wurde dem Könige in einer von dem deutschen Philosophen ausgearbeiteten Denkschrift unterbreitet. Blieben diese diplomatischen Bemühungen auch ohne Erfolg, so war der Aufenthalt in Paris für Leibniz doch von großer Bedeutung. Er wurde hier mit vielen bedeutenden Männern, vor allem mit Huygens bekannt. Durch den persönlichen Einfluß dieses Mannes und durch das Studium des Huygensschen Werkes über die Pendeluhr wurde das Interesse, das Leibniz der Mathematik und der Mechanik schon früher entgegengebracht hatte, von neuem entfacht. Auf die bereits in Nürnberg gemachte Erfindung der Rechenmaschine folgte diejenige der Differentialrechnung. Beide Erfindungen, sowie der sich an die zweite anknüpfende Prioritätsstreit mit Newton haben uns an anderer Stelle beschäftigt.
Von Paris kehrte Leibniz 1676 über London nach Deutschland zurück. Er wurde Bibliothekar in Hannover, wo er den[S. 345] größten Teil seines Lebens zugebracht hat. Das von Leibniz geschaffene philosophische System erregte das besondere Interesse von Sophie Charlotte, der Großmutter Friedrichs des Großen, der Leibniz nachrühmte, er habe allein eine ganze Akademie vorgestellt. Sophie Charlotte bewog ihren Gemahl, den späteren König Friedrich I., auf den von Leibniz ausgehenden Vorschlag hin im Jahre 1700 in Berlin eine Akademie, die »Societät der Wissenschaften«, zu errichten. Leibniz wurde deren erster Präsident. Auch zur Errichtung der Petersburger Akademie hat Leibniz durch seine persönliche Einwirkung auf Peter den Großen die Anregung gegeben611. In gleichem Sinne hat er in Dresden und in Wien gewirkt. Durch diese Veranstaltungen sollte nach seinem Plane die Wissenschaft nicht nur gefördert, sondern auch zum Gemeingut gemacht werden. Die Aufklärung der Mitwelt war vor allem das Ziel des großen Philosophen, und auf diesem Wege folgten ihm während des 18. Jahrhunderts Männer wie Christian Wolf, der die Leibnizsche Philosophie popularisierte, Basedow, dessen Verdienste auf dem Gebiete des Erziehungswesens liegen, ja selbst ein Lessing und ein Herder.
Leibniz starb in Hannover am 14. November 1716. Es mag bei der Erwähnung seines Todes ein bedauerlicher Zug früherer deutscher Art nicht unberührt bleiben. Von Leibniz berichtet der Chronist, »man habe ihn eher wie einen Wegelagerer begraben, denn wie einen Mann, der eine Zierde seines Vaterlandes gewesen«. Vom Hofe erschien niemand, kein Geistlicher geleitete den Sarg. Als dagegen ein Jahrzehnt später Newton in der Westminsterabtei beerdigt wurde, trugen der Lord-Oberkanzler und Herzöge das Leichentuch. Solche Gegensätze verdienen zur Mahnung für kommende Geschlechter erwähnt zu werden. Selbst die Pariser Akademie ehrte Leibniz durch eine Gedenkfeier, während die Berliner von dem Tode ihres Begründers und bedeutendsten Mitgliedes keine Notiz nahm!
Den Ausgangspunkt für die Darstellung der meisten chemischen Verbindungen bilden die Mineralien. In dem Maße, wie eine wissenschaftlichen Zielen zustrebende Chemie emporwuchs, trat dem praktischen Interesse an den Mineralien, von dem Agricola z. B.612 noch vorzugsweise geleitet wurde, das wissenschaftliche an die Seite. Es erhob sich die Frage nach der Zusammensetzung und der Entstehung nicht nur der Mineralien, sondern der starren Erdrinde überhaupt. Um die Beantwortung dieser Frage hat sich niemand während des 17. Jahrhunderts mit gleichem Scharfsinn und mit gleichem Erfolge bemüht wie Steno.
Nikolaus Steno oder Stenon wurde 1631 in Kopenhagen geboren. Er widmete sich in Paris dem Stadium der Medizin und war in den sechziger Jahren des 17. Jahrhunderts Leibarzt am Hofe in Florenz. Im Jahre 1672 kehrte Steno auf Wunsch seines Königs nach Kopenhagen zurück, um dort eine Professur für Anatomie zu übernehmen. Er verließ jedoch sein Vaterland bald wieder, da er dort seiner religiösen Überzeugung wegen angefeindet wurde, und starb, nachdem er sich an verschiedenen Orten Deutschlands aufgehalten, im Jahre 1687 in Schwerin. Sein Leichnam wurde auf Wunsch der Mediceer nach Florenz übergeführt und in St. Lorenzo beigesetzt.
Steno befaßte sich eingehend mit der Erforschung der Bodenverhältnisse Toskanas. Die Frucht dieser Untersuchungen war eine Arbeit, die zum erstenmal die Grundlagen der geologischen Wissenschaft in klarer, durch Profile erläuterter Darstellung entwickelte, während die Literatur vor Steno nur vereinzelt zutreffende Bemerkungen über geologische Dinge enthält613.
Zunächst bemühte sich Steno darzutun, daß weder die Mineralien noch die Schichten, welche die Gebirge zusammensetzen, erschaffene, von Anbeginn vorhandene Naturkörper sind, als die sie im Gegensatz zu der vergänglichen Tier- und Pflanzenwelt wohl der naiven Betrachtung erscheinen. Wie sehr diese in geologischen Dingen zur Zeit Stenos noch vorherrschte, erkennt man daraus, daß er sich ausdrücklich gegen die Meinung wendet, die Berge seien nach Art der Pflanzen gewachsen, oder sie seien mit dem Knochengerüst der Tiere zu vergleichen.
Die Mineralien, deren am Bergkristall, Schwefelkies, Eisenglanz und Diamant auftretende Formen Steno beschrieb, wachsen nach ihm durch Ansatz von außen. Der Ansatz geschehe indessen nicht auf allen Flächen gleichmäßig. Die Folge seien Verzerrungen der mathematischen Form, während die Neigung der begrenzenden Flächen stets dieselbe bleibe.
Steno machte diese Beobachtungen besonders am Bergkristall, einem Mineral, das seit den ältesten Zeiten der auffallenden Form und der Größe seiner Kristalle, sowie seiner Durchsichtigkeit wegen die Aufmerksamkeit auf sich gelenkt hatte. Steno tritt der Meinung entgegen, daß der Bergkristall durch Kälte oder im Feuer entstanden oder gar im Anbeginn der Welt geschaffen sei. Kristalle sind nach seiner Meinung aus Lösungen hervorgegangen und können durch geeignete Mittel wieder in Lösung übergeführt werden. Darauf weisen, wie er ausführt, auch die verschiedenfarbigen Schichten hin, aus denen die Kristalle mitunter zusammengesetzt sind. Zum Beweise seiner Ansicht läßt Steno verschiedene Salze, wie Vitriol und Alaun, aus einer Lösung kristallisieren und findet hierbei ähnliche Erscheinungen, wie sie an Mineralien auftreten. Nicht nur die Schichtung und die Verzerrungen der Form, sondern[S. 348] auch die treppenförmigen Absätze, die Einschlüsse von Flüssigkeiten usw. erklärt Steno aus der Bildungsweise der Kristalle. Die verschiedene Ausdehnung der Flächen unter Beibehaltung der Winkel erläutert er durch die hier wiedergegebenen, sehr lehrreichen Abbildungen der Quer- und Längsschnitte durch verschiedenartig ausgebildete Bergkristalle (Abb. 104 u. 105). Steno hat also schon das Grundgesetz der Mineralogie, das Gesetz von der Konstanz der Kantenwinkel, klar ausgesprochen, wenn es auch in seiner Allgemeingültigkeit erst in dem nachfolgenden Jahrhundert von Romé de l'Isle erkannt wurde.
Die Erscheinung, daß die Prismenflächen des Bergkristalls quergestreift sind, erklärt Steno durch die Annahme, daß solche Flächen durch Aggregation zahlreicher Pyramiden entständen, die sich in der Längsrichtung des Kristalles aneinander gereiht hätten.
Während die Mineralien aus wässerigen Lösungen auskristallisieren, ein Vorgang, den Steno aus einer Art magnetischer Kraft erklären wollte, sind die Felsschichten nach ihm durch Absatz vorher im Wasser schwebender Teilchen entstanden. Letztere haben, dem Gesetz der Schwere zufolge, Schichten von ursprünglich horizontaler Lage gebildet. Für den Absatz aus dem Wasser spricht nach Steno auch die Tatsache, daß die niedersinkenden Teilchen sich den Körpern, die sie einschließen, genau angepaßt haben und ihre kleinsten Höhlungen ausfüllen.
Jeder Wechsel in der Beschaffenheit des Gesteinsmaterials, das die Schichten zusammensetzt, weist nach ihm auf eine Änderung der Entstehungsbedingungen hin. Sei es, daß die Flüssigkeit, aus der die Schichten sich bildeten, dem periodischen Wechsel der Jahreszeiten unterworfen war, oder daß sich ihre Zusammensetzung änderte.
Enthält eine Schicht Seesalz, sowie Überreste von Meeresbewohnern, so muß man annehmen, daß sich das Meer einst dort befand, wo wir die Schicht jetzt antreffen. Entweder stand das[S. 349] Meer einst höher, oder das Land hat sich gesenkt. Aus Abdrücken von Gräsern und Binsen, Versteinerungen von Baumstämmen usw. ist auf den terrestrischen Ursprung derjenigen Schicht, in der solche Überreste enthalten sind, zu schließen. Derartige Bildungen rühren von der Überschwemmung eines Flusses oder dem Hereinbrechen eines Bergstromes her.
Mit außerordentlicher Klarheit entwickelt Steno ferner eine allgemeine Schichtenlehre (Stratigraphie), deren Grundzüge wir hier nach seinen Angaben gleichfalls kurz skizzieren wollen. Die Bildung jeder Schicht setzt eine feste Unterlage voraus. Die oberen Schichten sind daher ihrer Entstehung nach jünger als die unteren. Jede Schicht wird von zwei parallelen Ebenen eingeschlossen und besaß ursprünglich, weil sie sich aus einer Flüssigkeit niederschlug, eine horizontale Lage. Jede Schicht muß aber auch seitlich begrenzt sein, wenn man nicht Grund zu der Annahme hat, daß sie sich über die ganze Erdkugel erstreckt. Wo man einer Schicht begegnet, muß man daher entweder ihre Fortsetzung finden, oder andere feste Körper, die ihre weitere Ausdehnung verhinderten614.
Wenn man heute senkrechte oder geneigte, ja selbst gebogene Schichten antrifft, führt Steno weiter aus, so sind sie erst nachträglich durch die gebirgsbildenden Kräfte aus der ursprünglich horizontalen Lage in ihre jetzige gebracht worden. Auf eine gewaltsame Unterbrechung einer ursprünglich ein Ganzes bildenden Schicht weise auch der Umstand hin, daß man an den einander gegenüber befindlichen Anhängen der Gebirge häufig abgebrochene Schichten finde, die in ihrer Substanz und in ihrem Aussehen völlige Übereinstimmung zeigen.
Die Gebirgsbildung selbst wird auf zwei Kräfte zurückgeführt, die aus dem Erdinnern heraus wirkende vulkanische Kraft und die Tätigkeit des Wassers, das in Gestalt des Regens und der Flüsse die durch den Wechsel von Wärme und Kälte zerbrochenen Schichten durchziehe und die Oberfläche der Erde gestalten helfe.
Nicht richtig gedeutet werden die Kohlenlager. Sie werden nämlich auf durch Wasser gelöschte Waldbrände zurückgeführt.
Steno unterschied, wie ihm A. v. Humboldt615 nachrühmt, zum erstenmal diejenigen Felsschichten, die schon vor der Tier- und Pflanzenwelt vorhanden waren und infolgedessen keine organischen[S. 350] Überreste einschließen, von den späteren Schichten, die jenen aufgelagert und mit organischen Resten angefüllt sind. »Er ließ für den Boden Toskanas nach Art unserer heutigen Geologen sechs große Naturepochen zu, innerhalb deren das Meer periodisch das feste Land überschwemmte oder sich in seine alten Grenzen zurückzog«616.
In der ältesten Zeit habe das Meer die gesamte Erde bedeckt und diejenigen Schichten gebildet, die heute den Kern und die höchsten Kämme der Gebirge bilden. Daß diese Schichten keine Versteinerungen führen, beweise, daß das Urmeer noch keine Bewohner gehabt habe. Dann erfolgte die Bildung von Festland, und in der dritten Periode setzte die Gebirgsbildung ein.
Daß die Schichten nur selten ihre ursprünglich horizontale Lage beibehielten, sondern in der Regel in geneigter, ja selbst in senkrechter Stellung angetroffen werden, führt Steno auf zwei Ursachen zurück. Entweder wurden die Schichten durch Stöße zertrümmert, die aus der Tiefe kamen, oder es erfolgte ein Einsturz, indem die unteren Schichten durch die Tätigkeit des Wassers fortgeführt, und so die oberen ihrer Stütze beraubt wurden.
In der vierten Periode fand eine neue Überflutung statt, und es bildeten sich infolgedessen die Versteinerungen führenden Schichten. Dann trat der Boden wieder aus der Wasserbedeckung hervor, und in der letzten (sechsten) Periode erhielten die Gebirge durch die erodierende Tätigkeit des Wassers und infolge vulkanischer Ausbrüche ihre heutige Gestalt, während sich an den Flußmündungen und im Meere neue Sedimente bildeten. Infolge der mannigfachen durch vulkanische Hebung oder durch Einsturz hervorgerufenen Schichtenstörungen hatten sich Spalten gebildet, in denen sich Mineralien absetzten. Diese Darstellung der Erdgeschichte wußte Steno durch schematische, die Bodenverhältnisse Toskanas betreffende Zeichnungen zu erläutern, in denen uns die ersten geologischen Profile begegnen.
Steno hat seine Ansichten über die Entwicklung der Erde mit der biblischen Schöpfungsgeschichte möglichst in Einklang zu bringen gesucht. Wäre er gänzlich frei von allen Nebenrücksichten an seinen Gegenstand herangetreten, so würden die Ergebnisse seiner Forschungen das Wesen der geologischen Veränderungen noch klarer widergespiegelt haben. Nichtsdestoweniger verdient Steno den schönen Ruhmestitel, daß er seiner Zeit weit vorauseilte[S. 351] und Entdeckungen machte, die erst Jahrhunderte nach seinem Tode ihren Platz unter den anerkannten wissenschaftlichen Wahrheiten finden sollten.
Zu den ersten Schriften, die sich mit dem inneren Bau und der Entstehung der Erde befaßten, gehört Kirchers »Unterirdische Welt«617, ein Werk, dessen Bedeutung darin besteht, daß es die erste, allerdings noch mit vielen Mängeln behaftete physikalische Erdbeschreibung ist.
Kirchers Buch entsprang weniger dem Forschungstriebe als der polyhistorischen, oft mit Kritiklosigkeit verbundenen Gelehrsamkeit seines Verfassers. Die vulkanischen Erscheinungen wurden jedoch auf Grund eigener, in Mittelitalien, Sizilien und auf den liparischen Inseln angestellter Beobachtungen geschildert. Von besonderem Wert sind die den Vulkanismus betreffenden Abschnitte dadurch, daß Kircher es unternimmt, alle geschichtlich bekannt gewordenen Ausbrüche der südeuropäischen Vulkane, sowie die historisch verbürgten Umgestaltungen der Meeresküsten aufzuzählen. Ein phantastisches Gemälde ist Kirchers Schilderung des Erdinnern. Er stellt sich letzteres als von zwei Systemen verzweigter Kanäle durchzogen vor. In dem einen System bewegt sich eine glutflüssige Masse, die in den Vulkanen zutage tritt; das andere System wird dagegen vom Meere aus mit Wasser versorgt und speist die Quellen. Eingehender werden die Bodenbestandteile beschrieben. Die Versteinerungen, die sich in den Schichten der Erdrinde finden, werden nur zum Teil auf frühere Lebewesen zurückgeführt, manches wird aus einer plastischen Kraft der unorganischen Materie erklärt. Erwähnenswert ist noch, daß sich bei Kircher die ersten Angaben über die mit dem Eindringen in das Erdinnere verknüpfte stetige Zunahme der Temperatur finden. Er verdankte diese Angaben den Bergleuten.
Auch Descartes und Leibniz beschäftigten sich mit der Frage nach der Natur und der Entstehung unseres Planeten. Descartes entwickelt seine Anschauungen über das Weltsystem[S. 352] und die Physik der Erde im zweiten Teile seines Hauptwerkes618, nachdem er zuvor die Prinzipien der Erkenntnistheorie und der Mechanik dargestellt. Die Erde und die übrigen Planeten waren nach ihm ursprünglich glühende Sonnen. Infolge der Abkühlung bildete sich eine starre Rinde. Diese enthält die leichteren Bestandteile des Erdkörpers, während sich die schwereren Stoffe um den Mittelpunkt sammelten619. Infolge des Zerbrechens der Rinde entstanden Meere und Festländer, Berge und Täler.
Die Erdbeben führte Descartes auf die Wirkung einer noch im Innern vorhandenen flüssigen Masse zurück. Er gelangte also schon zu ähnlichen Anschauungen, wie sie die moderne Geologie auf Grund eines viel eingehenderen Studiums der geologischen Vorgänge entwickelt hat. Dieses Verdienst des Descartes um die Begründung der Kosmologie und der Geologie ist neuerdings in Frankreich besonders gewürdigt worden620.
Ähnliche Ansichten, wie die soeben entwickelten, äußerte einige Jahrzehnte später der große deutsche Philosoph Leibniz in seiner »Protogaea«. Neben mancher phantastischen Vorstellung enthält diese Schrift zahlreiche treffende Bemerkungen. Leibniz nimmt an, die Planeten seien aus der Sonne hervorgegangen und daher ursprünglich glühend flüssig gewesen. Durch Abkühlung hätten sich zuerst auf der geschmolzenen Masse schwimmende Schlacken gebildet, wie sie noch heute auf der Sonne entständen und unseren Augen als Sonnenflecken sich bemerkbar machten. Endlich sei eine zusammenhängende, erkaltete Rinde entstanden, während die Hitze im Innern aufgespeichert blieb. Infolge der Abkühlung verdichtete sich auch das Wasser, das im Urzustande der Erde Dampfform besaß. Auf diese Weise entstand das Urmeer als eine Lösung der an der erkalteten Oberfläche befindlichen Salze. Die glasartige Grundmasse der Erde wurde in der folgenden Periode teils durch die lösende Kraft und die Bewegung des Wassers, teils durch die vereinte Wirkung von Salzen und Hitze auf mancherlei Art zerfressen und zerstört, so daß sich die obere Schicht dieser Grundmasse in Schlamm verwandelte. Indem sich die erkaltete Rinde zusammenzog, entstanden Sprünge, Erhöhungen[S. 353] und Vertiefungen. Die von den bergigen Erhöhungen abfließenden Gewässer führten Schlamm mit sich und bildeten neue Gesteinsschichten. Die Gesteine haben nach Leibniz also einen doppelten Ursprung; teils entstanden sie aus dem Schmelzfluß, teils wuchsen sie, nach der Zerteilung im Wasser, wieder zusammen. Durch die Spalten der Rinde drang das Wasser auch in das noch jetzt glutflüssige Erdinnere und rief dort einen Kampf hervor, der sich noch heute in den Vulkanausbrüchen und den Erdbeben äußert.
Die Versteinerungen führt Leibniz auf frühere Lebewesen zurück621. Ausführlich bespricht er die Fischabdrücke des Mansfelder Kupferschiefers, wie denn überhaupt die »Protogaea« wohl als die Frucht seiner Beschäftigung mit dem Bergbau des Harzes zu betrachten ist, zu der ihm seine amtliche Stellung in Hannover den Anlaß bot. Die Erklärung, die Leibniz über die Entstehung der Mansfelder Fischabdrücke gab, kann auch heute noch als im wesentlichen zutreffend gelten.
»Die meisten«, sagt er, »nehmen behufs Erklärung ihre Zuflucht zu dem Spiele der Natur, einem leeren Worte. Sie nehmen an, die große Baumeisterin Natur ahme gleichsam im Scherze Zähne und Knochen der Tiere nach. Die Übereinstimmung jener Fischzeichnungen mit wirklichen Fischen ist indessen so groß, daß die Flossen und Schuppen haarscharf abgedruckt sind. Ja, man sieht an einem Orte so viel Abdrücke, daß man hier eine andere Ursache vermuten muß als das Spiel des Zufalls. Wie wäre es zum Beispiel, wenn wir annähmen, es sei ein großer See mit seinen Fischen entweder durch ein Erdbeben oder durch die Wirkung des Wassers mit Erde gefüllt worden? Diese Erde wird, als sie zu Stein wurde, in die weiche Masse eingedrückte Spuren behalten haben, die später, als die tierischen Überreste längst vergangen waren, mit Erz622 ausgefüllt sind. Es ist möglich, daß[S. 354] diese metallische Materie, die in dem ganzen Schlamm verteilt war, durch die Wärme verflüchtigt wurde und in die Höhlungen eindrang, die der Fisch zurückließ. Wir finden etwas ähnliches bei den Goldschmieden. Sie überziehen eine Spinne oder ein anderes Tier mit einem Stoff, der am Feuer hart wird. Alsdann schaffen sie die Asche des Tieres aus diesem Gerüst durch hineingelassenes Quecksilber heraus. Anstelle des letzteren gießen sie endlich durch dieselbe Öffnung Silber hinein. So erhält man ein silbernes Tier, dessen Ähnlichkeit mit dem lebenden Geschöpf erstaunlich ist.«
Überzeugt von der Neuheit und der Wichtigkeit seines Gegenstandes, sagt Leibniz, seine Ausführungen wären zwar nur ein Versuch; doch sei in ihnen der Same zu einer neuen Wissenschaft enthalten. Die Nachwelt werde alles besser feststellen können, wenn sie die Arten der Erdschichten und ihren Verlauf erforschen werde. Die bisherige Vernachlässigung dieser so wichtigen Aufgabe entlockt ihm den unwilligen Ausruf: »Oft ärgere ich mich über die menschliche Faulheit, welche die Augen nicht öffnet, noch die offenkundige Wissenschaft in Besitz nehmen mag.« Das 17. Jahrhundert war eben das Zeitalter, in dem die Menschheit erst eifriger in dem Buche der Natur zu lesen begann.
Zu bemerkenswerten Ansichten gelangte auch Hooke623. Er lehrte, daß die Versteinerungen, die man in früheren Jahrhunderten für Naturspiele oder für bloße Ansätze einer in der Erde waltenden schöpferischen Kraft gehalten hatte, aus dem Tier- und Pflanzenreiche stammen. Hooke erklärte, die Versteinerungen seien wertvollere Dokumente als Manuskripte und Münzen, da sie nicht gefälscht werden könnten, und fordert, aus dem Auftreten der Versteinerungen die Geschichte der Erde zu enträtseln. Auch über den Versteinerungsprozeß selbst äußerte Hooke manche zutreffende Ansicht.
Er suchte ferner darzutun, daß die Petrefakten Englands zum größten Teile ausgestorbenen Gattungen angehören und am meisten mit noch heute lebenden exotischen Formen übereinstimmen. Daraus zog er den Schluß, England müsse sich in früheren Zeiträumen der geologischen Entwicklung unter dem Meere einer heißen Zone befunden haben. Ferner wurden die Knochen großer[S. 355] Vierfüßer, die man vorher als Beweise für das frühere Vorhandensein von Riesen angesehen hatte, als Überreste von Individuen der Gattung Elephas gedeutet624.
An die Beobachtungen schlossen sich auch schon geologische Versuche an. So bemühte man sich, die unterirdische Wärme als eine Folge chemischer Vorgänge nachzuweisen, eine Auffassung, die in unseren Tagen wieder ihre Verfechter gefunden hat. Ein französischer Forscher625 ahmte z. B. einen Vulkan dadurch nach, daß er ein feuchtes Gemenge von Schwefel und Eisen vergrub. Diese Masse erhitzte sich unter dem Einflusse des aus der Luft hinzutretenden Sauerstoffs so sehr, daß eruptionsartige Erscheinungen unter Zerbersten der Bedeckung vor sich gingen.
Für die Begründung der neueren Mineralogie im 17. Jahrhundert ist es bezeichnend, daß genauere Beobachtungen an einzelnen, besonders auffallenden Mineralien gemacht wurden, ohne daß man dazu überging, die gewonnenen Ergebnisse auf die übrigen auszudehnen. Ein vergleichendes mineralogisches Studium blieb einem späteren Zeitalter vorbehalten. Steno hatte seine Forschungen insbesondere am Bergkristall angestellt. Ein anderes Mineral, das im 17. Jahrhundert die Aufmerksamkeit der Naturkundigen in hohem Grade auf sich lenkte, war der isländische Doppelspat. Durch dänische Kaufleute gelangte dieses Mineral in die Hände Bartholins, der ihm die eingehendste Untersuchung widmete.
Erasmus Bartholinus, der Entdecker der Doppelbrechung, wurde 1625 in Dänemark geboren. Er studierte Medizin, bereiste das westliche Europa und Italien und wurde 1656 Professor der Mathematik in Kopenhagen. Er starb 1698.
Bartholin schrieb einige mathematische und astronomische Werke; er ist aber besonders durch seine Schrift über den isländischen Doppelspat und dessen optische Eigenschaften bekannt geworden626. Die Schrift enthält eine Monographie über das erwähnte Mineral, die so eingehend und genau ist, daß man in Anbetracht der Bartholin zu Gebote stehenden Hilfsmittel und Vorarbeiten[S. 356] nicht mehr erwarten kann. Bartholin beschränkt sich nicht auf eine bloße Beschreibung der Kristallform, sondern er mißt die an den begrenzenden Flächen auftretenden Winkel, deren Werte er gleich 101° und 79° ermittelt. Er zeigt, daß von den beiden Bildern, die man durch den Doppelspat erblickt, das eine sich beim Drehen des Kristalls bewegt, während das andere still steht; daß man aber in gewisser Richtung nur ein Bild wahrnimmt. Bartholin weist ferner nach, daß das Auftreten von zwei Bildern nicht etwa durch eine Spiegelung, sondern durch ein ganz ungewöhnliches Verhalten hervorgerufen werde, indem das feste Bild durch eine gewöhnliche, das bewegliche dagegen durch eine außergewöhnliche Brechung entstehe. Das Gesetz der letzteren vermochte Bartholin nicht zu ermitteln, auch entging ihm die Polarisation des durch den Kalkspat gegangenen Lichtes. Ihre Entdeckung blieb Huygens vorbehalten627.
Die weitere Untersuchung Bartholins betraf die physikalische und die chemische Natur des Doppelspats. Es zeigte sich, daß der Kristall, mit Tuch gerieben, wie der Bernstein, Strohhalme und andere leichte Körper anzieht, daß er unter Wasser seine Glätte allmählich verliert, mit Scheidewasser aufbraust, durch starke Hitze in Kalk verwandelt wird. Kurz, der Doppelspat wurde genauer untersucht, als es bis dahin mit irgend einem anderen Mineral geschehen war. Daß die Arbeit Bartholins den großen Physiker Huygens zu einer Nachuntersuchung des Doppelspats und zu wichtigen Betrachtungen über die Natur des Lichtes anregte, ist der Gegenstand eines früheren Abschnitts gewesen. Huygens hat auch seinen Landsmann Leeuwenhoek veranlaßt, eine monographische Abhandlung über ein anderes Mineral, den Gips, zu liefern628. Leeuwenhoek machte durch diese Arbeit auf mehrere wichtige mineralogische Tatsachen aufmerksam. Er wies darauf hin, daß die Spaltbarkeit gewissen Gesetzen folgt, und daß beispielsweise die Winkel der durch Spaltung aus dem Gips erhaltenen rhomboidischen Tafeln 112° und 68° (genauer 113° 46ʹ und 66° 14ʹ) betragen. Ferner zeigte er, daß das beim Glühen aus dem Gips entweichende Wasser ein Fünftel vom Gewicht des Minerals ausmacht. Er brachte ferner Gips in Lösung, indem er das gebrannte Mineral mit Wasser übergoß und nachwies,[S. 357] daß sich aus dieser Lösung beim Verdunsten des Wassers Kristalle ausscheiden. Diese Versuche veranlaßten ihn auch, über die Bildung der Mineralien im Innern der Erde Betrachtungen anzustellen. Sie enthalten indessen wenig Zutreffendes.
Eine größere Summe von Erfahrungen und Beobachtungen lag bezüglich der Edelsteine vor. Auch ihnen wurde eine monographische Bearbeitung zuteil. Und zwar geschah dies durch den in erster Linie als Physiker bekannten Robert Boyle629. Auch er gelangte zu dem Ergebnis, daß die Mineralien sich aus dem flüssigen Zustande gebildet hätten, und zwar in derselben Weise, wie Salze in Kristallform aus der Lösung ausgeschieden würden. Für diese Ansicht führt Boyle einige bemerkenswerte Gründe an630. So habe man Bergkristall und andere Mineralien mit flüssigen Einschlüssen gefunden. Ferner sei die Farbe der meisten Edelsteine durch Beimengungen hervorgerufen, die in der Regel durch die ganze Masse gleichmäßig verteilt seien, mitunter aber stellenweise oder gänzlich fehlten. Auch daß die Mineralien, wie die aus wässeriger Lösung entstandenen Salze, spaltbar seien, spreche für die gleiche Art der Entstehung.
Boyle wies ferner darauf hin, daß es auch eine Kristallisation aus dem Schmelzfluß gebe; er untersuchte diesen Vorgang genauer, und zwar am Wismut, prüfte auch den Einfluß der durch rasche Abkühlung beschleunigten Kristallisation auf die Beschaffenheit der Kristalle, wies im Granat durch die Analyse und durch die Wirkung des Magneten einen Eisengehalt nach, und bestimmte das spezifische Gewicht vieler Mineralien. Kurz, er bereicherte die mineralogische Wissenschaft um eine nennenswerte Summe von Einzelkenntnissen, sodaß er neben Steno und Bartholin als einer ihrer Begründer genannt werden kann.
Zu der Zeit, als Boyle sich bemühte, die Mineralogie und die Chemie auf eine wissenschaftliche Grundlage zu erheben, waren die deutschen Chemiker Kunkel und Becher noch in alchemistischen Vorstellungen befangen. Kunkel (1630 bis 1702) hat indes, trotz der Irrigkeit seiner Ansichten, die Chemie durch zahlreiche Beobachtungen bereichert.
Eine der wichtigsten chemischen Entdeckungen des 17. Jahrhunderts war diejenige des Phosphors631. Sie erfolgte durch Brand (1669). Dieser hielt sein Verfahren zuerst geheim. Auf Grund einiger Andeutungen gelang Kunkel jedoch gleichfalls die Darstellung, so daß er einige Jahre nach der Entdeckung des Phosphors das neue Element dem Großen Kurfürsten zeigen konnte. Letzterer ernannte ihn zum Leiter eines alchemistischen Laboratoriums, das er gleich manchen anderen Fürsten des 17. Jahrhunderts unterhielt.
Becher (1635–1682) hielt sich wie Kunkel zeitweilig auch als Alchemist an deutschen Höfen auf. Er und der etwas später lebende Stahl632 sind die Begründer der Phlogistontheorie, die trotz ihrer damals schon von manchem als irrig erkannten Voraussetzungen die Chemie fast des gesamten 18. Jahrhunderts beherrscht hat.
Daß die Aufstellung eines den Tatsachen entsprechenden Systems der Chemie soviel später als die Begründung der Mechanik erfolgte, ist darauf zurückzuleiten, daß die Chemie eine vorwiegend induktiv verfahrende Wissenschaft ist, und sich der deduktiven Behandlung erst in unseren Tagen zu erschließen beginnt. Was den Fortschritt der physikalischen Zweige, insbesondere der Optik und der Mechanik, so ungemein gefördert hat, war die innige Verbindung und die gegenseitige Unterstützung der induktiven und der deduktiven Forschungsweise von den ersten Schritten auf diesen Gebieten an. Die Grundlagen einer chemischen Theorie zu schaffen, war bei weitem schwieriger, weil die chemischen Vorgänge nicht unmittelbar in die Sinne treten, sondern erst durch eine lange, mühevolle Verknüpfung der Ergebnisse experimenteller Forschung erschlossen werden müssen. Die Chemie hatte indes seit Boyle, Becher und Stahl ihre wahre Aufgabe darin erkannt, die stofflichen Veränderungen auf dem Wege des Experiments zu erforschen. Insbesondere galt es, die so mannigfachen Wandlungen der Materie, die mit der Verbrennung Hand in Hand gehen, auf ein einziges Prinzip zurückzuführen. Als solches glaubten Becher und Stahl eine in den brennbaren Körpern angenommene Materie, die Stahl als Phlogiston bezeichnete, erkannt[S. 359] zu haben. Der Verbrennungsprozeß sollte in dem Entweichen dieses Phlogistons bestehen. Der brennbare Körper mußte folglich eine Verbindung von Phlogiston mit dem gleichfalls schon in der Substanz enthaltenen Verbrennungsprodukt sein. Je weniger Verbrennungsprodukt, desto reicher war der ursprüngliche Körper an Phlogiston. Kohle, die nur eine geringe Menge Asche hinterläßt, war demnach nahezu reines Phlogiston. Wurde Zink verbrannt, so zerfiel es in seine Bestandteile Zinkweiß und Phlogiston. Die Wiedergewinnung des Zinks aus dem Zinkoxyd durch Erhitzen mit Kohle bestand in einer Zuführung des in der letzteren enthaltenen Phlogistons. So gelang es in leichtfaßlicher Weise, nicht nur die Vorgänge der Oxydation und der Reduktion, sondern auch die der Atmung und der Verwesung auf ein Prinzip zurückzuführen. Die mit der Phlogistontheorie unvereinbare, für manche Fälle schon bekannte Tatsache, daß das Gewicht des Verbrennungsproduktes dasjenige der unverbrannten Substanz übertrifft, wurde nicht weiter beachtet. Obgleich von einem unrichtigen Grundsatz geleitet, haben die Phlogistiker des 18. Jahrhunderts, unter denen sich Experimentatoren ersten Ranges wie Scheele, Priestley und Marggraf befanden, die Chemie in hohem Grade gefördert. Durch ihr Bemühen, in dem sie Baustein auf Baustein zusammentrugen, zwar ohne sie in richtiger Weise ordnen zu können, haben sie selbst den Sturz der Phlogistontheorie herbeigeführt und dem Manne, dessen Scharfsinn wir die logische Verknüpfung der zahllosen chemischen Einzelbeobachtungen verdanken, dem Franzosen Lavoisier, erst sein Werk ermöglicht.
Insbesondere wollen wir hier Marggrafs gedenken, der um die Mitte des 18. Jahrhunderts in Berlin als eine Zierde der dortigen Akademie der Wissenschaften wirkte. Diese Gesellschaft besaß um jene Zeit eine Reihe vortrefflicher Chemiker in ihrer Mitte, so daß ihr Präsident Maupertuis Friedrich dem Großen mit Recht sagen konnte: »Unsere Chemiker stechen alle Chemiker Europas aus«633.
Andreas Sigismund Marggraf wurde 1709 in Berlin geboren. Durch seinen Vater, der eine Apotheke besaß, wurde er der Pharmazie zugeführt. Von den Hilfswissenschaften dieses[S. 360] Gebietes fesselte ihn die Chemie in solchem Grade, daß er sich ihr ausschließlich widmete. Nach Beendigung seiner Studien, denen er auf der Universität Halle und auf der Bergschule zu Freiberg oblag, kehrte er nach Berlin zurück, um sich ausschließlich mit chemischen und mineralogischen Forschungen zu befassen. Er wurde Mitglied der Akademie und später Direktor der naturwissenschaftlichen Abteilung dieses Instituts, in dessen Abhandlungen während der Jahre 1747–1779 die Arbeiten Marggrafs veröffentlicht wurden. Diese haben zahlreiche Punkte der anorganischen und der organischen Chemie, sowie der Mineralogie aufgehellt. Die von Marggraf gewonnenen Ergebnisse wurden dadurch erzielt, daß er die Analyse besonders auf nassem Wege ausübte und dies Verfahren durch manche Hilfsmittel ausbaute. Auch wird ihm nachgerühmt, daß er der erste war, der sich bei chemischen Untersuchungen des Mikroskops bediente.
Auf die Ergebnisse seiner analytischen Forschungen werden wir zum Teil noch bei der Besprechung der mineralogischen Fortschritte zurückkommen. Hier sei nur hervorgehoben, daß er die Bittererde634 und die Tonerde635 als besondere von der Kalkerde durchaus verschiedene Substanzen erkannte. Marggraf zeigte ferner, daß der Gips eine Verbindung von Kalkerde, Schwefelsäure und Wasser ist; er erkannte die Zusammensetzung von Alaun und von Urinsalz, in welchem er Phosphorsäure und flüchtiges Alkali entdeckte. Zahlreiche Untersuchungen über den Phosphor, seine Darstellung und seine Verbindungen rühren von Marggraf und seinen Schülern her. Vor allem wurde die Phosphorsäure genauer untersucht636. Marggraf stellte sie entweder durch Kochen von Phosphor mit Salpetersäure oder durch Verbrennen des Phosphors her. Dabei entging ihm nicht, daß die entstandene Phosphorsäure mehr wog als der in die Verbindung eingehende Phosphor, eine Tatsache, die eigentlich Marggrafs Anschauungen hätte erschüttern müssen, da sie der phlogistischen Theorie, nach der die[S. 361] Verbrennung in dem Entweichen einer Materie bestehen sollte, durchaus widersprach. Es zeigte sich indessen an ihm die so häufige Erscheinung, daß gerade der Fachmann oft am wenigsten geneigt ist, liebgewordene Theorien, auf denen er das ganze System seines Wissens aufgebaut hat, einer umwälzenden, neuen Anschauung zu opfern.
Marggraf hat noch die Anfänge der antiphlogistischen Lehre miterlebt, ist aber trotzdem Phlogistiker geblieben. Dieses hartnäckige Festhalten an einem Irrtum schmälert Marggrafs Verdienste um die Wissenschaft indessen nicht wesentlich, da sie sich bis zu einem gewissen Grade unabhängig von dem Wechsel der Theorien, aus festgefügten Tatsachen aufbaut. Marggraf hat übrigens nicht nur das Mikroskop, sondern auch die Wage in die Chemie eingeführt, ein Verdienst, das man gewöhnlich ausschließlich Lavoisier zuschreibt. Er fällte z. B. Silberlösung mit Kochsalz und verglich das Gewicht des gelösten Silbers mit demjenigen des Silberchloridniederschlages. In solchen und in ähnlichen Versuchen, die gleichzeitig in Schweden Bergman637 anstellte, begegnen uns die Anfänge der quantitativen Analyse, d. h. des Verfahrens, die Stoffe nicht nur isoliert zu wägen, sondern sie in Form von unlöslichen Verbindungen bekannter Zusammensetzung abzuscheiden und deren Gewicht zu ermitteln.
Groß ist auch die Förderung, welche die technische Chemie durch Marggraf erfuhr. Er lehrte neue Metallegierungen kennen, verbesserte die hüttenmännische Gewinnung des Zinks, das seitdem in größerer Menge der Industrie zu Gebote stand, vor allem aber lehrte er, den Zucker aus einheimischen Pflanzen darstellen. Über diese Entdeckung, deren Tragweite Marggraf wohl geahnt hat, berichtet er in den Abhandlungen der Akademie vom Jahre 1747638 unter der Überschrift: »Chemische Versuche angestellt in der Absicht, wirklichen Zucker aus verschiedenen, in unseren Gegenden wachsenden Pflanzen herzustellen«. Unter den Pflanzen, aus deren Wurzeln er reinen Zucker dargestellt hat, hebt er besonders die Runkelrübe hervor. »Man erkennt«, schließt er seine Abhandlung, »welche praktischen Anwendungen man von diesen Versuchen machen kann. Man wird sich anstatt des teuren Rohrzuckers oder eines schlechten Sirups in Zukunft des Zuckers unserer Pflanzen bedienen können.« Marggraf war sich darüber[S. 362] vollkommen klar, daß es sich hier nicht um einen dem Rohrzucker nur ähnlichen Stoff, sondern um das Vorkommen des Rohrzuckers selbst in dem Saft der Runkelrübe handelte.
Technisch ausgestaltet wurde die Gewinnung des Zuckers aus Rüben durch Marggrafs Schüler Achard. Eigentlich lebensfähig wurde das Verfahren aber erst, nachdem Napoleon durch seine Zollschranken die Einfuhr von Kolonialzucker nach dem europäischen Kontinent unterbunden hatte. Dadurch sah die chemische Industrie sich gezwungen, an die Beschaffung eines Ersatzmittels zu denken. Der große Aufschwung der Rübenzuckerfabrikation datiert indessen erst seit etwa dem Jahre 1825.
Schon im 16. Jahrhundert hatten sich die Zoologen nicht mehr auf die bloße Beschreibung der äußeren Form und eine im wesentlichen hierauf begründete Systematik beschränkt, sondern begonnen, auch das Innere des tierischen Organismus, sowie seine Entwicklung zu erforschen. In weit höherem Maße gilt dies von dem 17. Jahrhundert, dem Zeitalter, in dem sich durch das Mikroskop nicht nur die feineren Formverhältnisse des Tierkörpers erschlossen, sondern in dem auch die ohne eine Verschärfung der Sinnesorgane gar nicht mögliche Anatomie der Pflanzen begründet wurde. Der Richtung jener Zeit entsprechend, die auf ein Zurückführen der in der Natur obwaltenden Vorgänge auf physikalische Grundsätze abzielte, regte sich auch das Bestreben, die Funktionen des lebenden Organismus aus der Mechanik zu erklären. Kurz, es begegnen uns in diesem Zeitalter die Anfänge desjenigen, mehr durch seine Methode als durch den Gegenstand gekennzeichneten Wissenszweiges, den wir als Biologie im weiteren Sinne bezeichnen.
Die größte Errungenschaft auf diesem Gebiete ist die von dem Engländer Harvey (1578–1658) begründete Lehre von dem Kreislauf des Blutes. Die seit Vesal emporblühende Anatomie hatte eine Reihe von Tatsachen zutage gefördert, die sich mit den herrschenden Ansichten Galens639 nicht vereinigen ließen. So waren die für Galens Lehre so wichtigen Annahmen, daß die Herzscheidewand porös sei und die Arterien Luft führten, endgültig widerlegt worden. Auch hatte man die Klappen des Herzens gründlich untersucht und ferner die Klappen in den Venen gefunden, von denen Galen noch keine Kenntnis besaß. Fabricio, der 1570 die Venenklappen entdeckte, hatte schon[S. 364] über ihren Zweck nachgedacht und war zu der Ansicht gelangt, sie hätten die Aufgabe, Unregelmäßigkeiten auszugleichen, welche die Blutbewegung durch die Bewegung der Gliedmaßen erleiden könnte. Die wahre Bedeutung der Klappen erkannte er also noch nicht. Dazu bedurfte es erst der großen Tat eines Harvey. Endlich hat noch ein gelehrter Arzt, Serveto, der als ein Opfer Calvins in Genf verbrannt wurde, schon im Jahre 1540 darauf hingewiesen, daß das Blut durch die Lungenschlagader vom Herzen nach der Lunge geführt werde. Hier ändere es durch die Vermischung mit der Luft seine Farbe und komme durch die Lungenvenen zum linken Herzen zurück. Damit war das Prinzip des Lungen- oder des kleinen Kreislaufs erkannt. Bestätigt wurde Servetos Lehre, wenn auch nicht von ihm selbst, durch Experimente an Tieren, mit denen sich auch Vesal befaßt hat640. All diese Entdeckungen hatten indessen nur bei einigen aufgeklärten Forschern Zweifel an Galens Lehre hervorgerufen. Richtige Anschauungen konnten nämlich kaum aufkommen, so lange man an dem mystischen Pneuma des griechischen Arztes festhielt.
Erst durch Harveys über 20 Jahre sich erstreckende Bemühungen wurde über das bisher so dunkle, von Widersprüchen beherrschte Gebiet volles Licht verbreitet. Dies war nur dadurch möglich, daß Harvey, der nicht umsonst bei den Italienern in die Schule ging, zwei Grundsätze in sich verkörperte, die durch Galilei und seine Jünger als die Leitsterne alles naturwissenschaftlichen Forschens zur Geltung gekommen waren, nämlich die Befreiung von hergebrachten, durch die Autorität des Altertums gestützten Meinungen und die Befolgung des experimentellen Verfahrens. Darin, daß Harvey diese Grundsätze der neueren Naturwissenschaft in die Physiologie einführte, liegt eine nicht geringere Bedeutung als in den Ergebnissen seiner Forschung selbst.
Zwar dürfen wir nicht erwarten, daß die Befreiung von den Anschauungen, die bis dahin gegolten, und das Einlenken in neue Bahnen mit einem Male und völlig gelungen wäre. Auch die größten Neuerer bleiben in mancher Hinsicht, wie wir es auch bei Galilei, Gilbert und Kepler gesehen haben, Kinder ihrer Zeit. So war das Ansehen, das Galen genoß, selbst bei Harvey noch so groß, daß er fast ein Jahrzehnt nach seiner Entdeckung[S. 365] verstreichen ließ, ehe er sie in seinem »anatomischen Übungsstück über die Bewegung des Herzens und des Blutes« bekannt zu geben wagte641.
William Harvey wurde 1578 geboren. Er studierte in Cambridge Medizin und ging 1598 nach Padua, wo er Schüler des soeben genannten bedeutenden Anatomen Fabricio ab Aquapendente wurde. Nach seiner Rückkehr wirkte er zunächst als Arzt und später als Professor der Anatomie in London. Seine Lehre vom Kreislauf des Blutes begründete er schon 1619. Veröffentlicht wurde sie indessen erst ein Jahrzehnt später (1628), nachdem Harvey durch Vivisektionen ein umfangreiches Beweismaterial gesammelt hatte. Bald darauf ernannte ihn Karl I. zu seinem Leibarzt. Als solcher war er gezwungen, während des Bürgerkrieges den König auf seinen Zügen zu begleiten642. Harvey starb im Jahre 1658.
Als neu enthält die Lehre Harveys folgende Punkte: Das Herz verhält sich wie ein Muskel. Es wird beim Zusammenziehen härter und blässer und stößt das Blut, das passiv aufgenommen wird, von sich. Das bei der Systole (Zusammenziehung) des Herzens fortgetriebene Blut gelangt in die Arterien, die sich also in der Diastole (im Zustande der Ausdehnung) befinden, wenn sich das Herz zusammenzieht. Aus den Verzweigungen der Arterien tritt das Blut in die Venen über und strömt in diesen zum Herzen zurück, so daß dieses in einer bestimmten Zeit von der ganzen Masse des Blutes durchflossen wird.
Um die Mitte des 17. Jahrhunderts wurde auch der alte Irrtum beseitigt, daß sich das Blut in der Leber bilde. Dies geschah durch die Entdeckung des in das Venensystem einmündenden Ductus thoracicus643, dessen Zusammenhang mit den Lymphgefäßen des Darmes man fast gleichzeitig auffand. Erst hierdurch wurde der »Kreis der die Lehre Harveys ergänzenden Entdeckungen geschlossen«644.
Da die Klappen auch in den horizontal verlaufenden Venen der Vierfüßler vorhanden sind, so können sie nicht den von[S. 366] Fabricio behaupteten Zweck haben, den Sturz des Blutes zu mäßigen, sondern es liegt ihnen ob, den Rückfluß aus den Ästen, die das venöse Blut zum Herzen führen, in die Verzweigungen, in denen das Blut sich sammelt, zu verhindern. Während das arterielle System von der linken Herzkammer gespeist wird, befördert die Kontraktion der rechten Kammer das venöse Blut durch den schon von Serveto gelehrten kleinen Kreislauf zunächst in die Lungen. Dort erleidet es durch die atmosphärische Luft eine Farbenveränderung, über deren Natur Harvey nicht ins klare kommen konnte, weil ihm die Einsicht in die chemische Rolle der Luft noch fehlte. Der kleine Kreislauf findet dadurch seinen Abschluß, daß das Blut von der Lunge zum Herzen zurückströmt. All diese Feststellungen erfolgten, aus genauer anatomischer Untersuchung, gestützt durch Experimente an höheren und niederen Tieren. Trotz aller Gründlichkeit und Klarheit fand Harveys Arbeit, wie alles, was den eingewurzelten Meinungen widerspricht, zunächst lebhafte Anfeindung. Einer der ersten, welcher der neuen Lehre Geltung verschaffte, war Descartes. Dieser wurde mit dem Inhalt der Harvey'schen Schrift durch den vielgeschäftigen Mersenne bekannt und gab in seinem »Discours de la méthode«, auf Grund der Harvey'schen Entdeckungen, selbst eine ausführliche Darstellung der Lehre vom Blutkreislauf645.
Nachdem diese Lehre Anerkennung gefunden, galt es, eine Reihe von Einzelfragen zu entscheiden. Der Verlauf der gröberen Äste des Gefäßsystems wurde durch das bald aufkommende Verfahren der Injektion eingehender festgestellt, als dies durch bloßes Zerschneiden der Leichen möglich war. In seinen Anfängen reicht dies Verfahren freilich viel weiter zurück. Seine Erfindung wird Sylvius zugeschrieben, der während der ersten Hälfte des 16. Jahrhunderts lebte und auch schon auf die Venenklappen hinwies. Zur Erforschung der feinsten Verzweigungen der Gefäße wandten zuerst Malpighi (1661) und später Leeuwenhoek das Mikroskop an. Die anfangs bestehende Meinung, daß die feineren Äste der Arterien das Blut in die Gewebe ergössen, und die Venen es mit ihren äußersten Enden wieder aufsögen, wurde durch den Nachweis eines zarten, die Arterien mit den Venen verbindenden Netzes von Kapillargefäßen wesentlich berichtigt. Gleichzeitig entdeckten beide Forscher die in dem Blute schwimmenden, roten Körperchen.
Des weiteren erhob sich die Frage nach der Entstehung des Blutes. Galen hatte angenommen, daß das Blut in der Leber bereitet werde und von dort in die obere Hohlvene gelange, die mit der Leber durch eine Abzweigung in Verbindung steht. Das Material für die Blutbereitung mußte aber doch in letzter Linie aus dem Nahrungssaft stammen. Die anatomischen Elemente, welche den Darm mit dem Blutgefäßsystem in Verbindung setzen, vermochte man indessen erst um die Mitte des 17. Jahrhunderts zu erkennen. Es erfolgte646 der Nachweis, daß die schon vor Harvey in der Wand des Darmes entdeckten Chylusgefäße sämtlich in einen gemeinsamen Gang, den Ductus thoracicus, eintreten und ihren Inhalt durch diesen in die linke Schlüsselbeinvene ergießen647. An die Entdeckung und die richtige Deutung der Chylusgefäße reihte sich diejenige des Lymphgefäßsystems648. Erst jetzt ließ sich auf die Frage, welche Rolle die einzelnen Organe und Organsysteme bei der Blutbereitung spielen, eine zunächst wohl befriedigende, die chemisch-physiologische Seite indes noch gar nicht berührende Antwort geben.
Ähnliche Schwierigkeiten erhoben sich, als man nach einer Erklärung für die sich stets und rhythmisch wiederholende Herzbewegung suchte. Nach Galen wurden die Herzkammern passiv ausgedehnt, indem das Blut unter dem Einfluß der Wärme, deren Sitz Galen und Aristoteles ins Herz verlegten, sich ausdehnen und gleichsam aufbrausen sollte. Die neue Lehre erblickte dagegen die Ursache der Blutbewegung in der Zusammenziehung des muskulösen Herzens. Was veranlaßte aber diese Zusammenziehung? Descartes glaubte, das einströmende Blut wirke als Reiz auf den Herzmuskel. Diese Ansicht wurde durch Experimente widerlegt. Entfernte man z. B. das Herz aus der Brust eines lebenden Tieres, so dauerten die Kontraktionen noch lange fort. Sie ließen sich sogar, nachdem sie gänzlich aufgehört hatten, durch leichte Reize wieder anregen. Um die Frage nach dem Impuls des Herzens beantworten zu können, mußten spätere Zeitalter erst eingehende Untersuchungen über die Herzinnervation und deren Zusammenhang mit dem übrigen Nervensystem anstellen.
Nachdem Harvey und schon vor ihm Serveto nachgewiesen hatten, daß das Blut in einem zweiten, kleineren Kreislauf durch die Lungen geführt wird, wandte man sich der Erforschung auch dieser Organe mit erhöhtem Eifer zu. Wieder war es Malpighi, dessen Untersuchungen auch hier die Grundlage geschaffen haben. Er wies (1661) nach, daß die Lungen ein doppeltes Röhrenwerk darstellen, indem die Verästelungen der Luftröhren in feinen Bläschen endigen, die von den Blutgefäßen umsponnen werden.
Aus den erwähnten Untersuchungen Malpighis über den Bau der Lunge und über die Kapillargefäße geht zur Genüge hervor, daß für die Physiologie das Mikroskop etwa dieselbe Bedeutung besitzt, die für die Astronomie dem Fernrohr zukommt. Dem Mikroskop hatte man, obgleich es früher erfunden wurde als das Fernrohr, zunächst ein weit geringeres Interesse entgegengebracht. Selbst Leeuwenhoek, der in der zweiten Hälfte des 17. Jahrhunderts die Erforschung kleinster Lebewesen außerordentlich förderte, verwandte dazu einfache, bikonvexe Linsen aus besonders feinem Glase. Er erzielte mit ihnen eine 160fache lineare Vergrößerung. Solche Linsen, deren sich auch Huygens bediente, waren nur stecknadelkopfgroß. Ihr Gebrauch erforderte große Geschicklichkeit und ein hervorragendes Sehvermögen. Letzteres, sowie die Sorgfalt im Beobachten, wurden durch die Verwendung des Mikroskops in solchem Maße gesteigert, daß auch das unbewaffnete Auge Dinge wahrnehmen lernte, die sich früher der Beobachtung entzogen hatten.
Erst verhältnismäßig spät erhielt das Instrument denjenigen Grad der Vollendung, der es zu wissenschaftlichen Untersuchungen geeignet machte. Man suchte eine stärkere Vergrößerung und eine geringere Farbenzerstreuung dadurch herbeizuführen, daß man das Objektiv und das Okular, die bisher nur aus je einer Linse bestanden, aus zwei Linsen zusammensetzte. Ferner ersann man Beleuchtungsvorrichtungen, wofür uns die Abbildung Hookes ein Beispiel gibt. (Siehe Abb. 106.)
Um den Zeitgenossen die Brauchbarkeit seines Mikroskops zu beweisen, veröffentlichte Hooke im Jahre 1667 seine »Micrographie oder Beschreibung kleiner Gegenstände«. Eine Beteiligung an der Lösung biologischer Probleme lag weniger in der Absicht dieses Forschers; trotzdem machte er eine Entdeckung von der weitgehendsten Bedeutung, indem er die Aufmerksamkeit auf den[S. 369] zelligen Bau der Pflanzen richtete. Hooke bildete ferner den Stachel der Biene ab, dessen Widerhaken deutlich zu erkennen sind. Auch die Häkchen, welche die feinsten Äste der Federn verbinden, sind in der Mikrographie dargestellt; wie sich denn überhaupt der Verfasser dieses Werkes mit einer fast kindlich zu nennenden Wißbegierde mit allem beschäftigt, was sich ihm zufällig darbot.
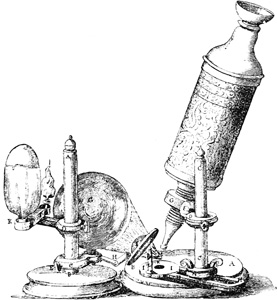
Auch die Mitglieder der Accademia del Cimento befaßten sich nicht ausschließlich mit rein physikalischen Problemen. Sie zeigten sich vielmehr bestrebt, in Galileis Sinne die Methode des großen Meisters auf alle Gebiete der Naturwissenschaften auszudehnen. In dieser Hinsicht ist vor allem Borelli zu nennen.
Giovanni Alfonso Borelli wurde 1608 in Neapel geboren. Er studierte Mathematik und Philosophie und war an verschiedenen Orten Italiens als Lehrer und vielseitiger Forscher tätig. Malpighi[S. 370] zählte zu seinen Schülern. In Florenz war Borelli als eins der eifrigsten Mitglieder der Accademia del Cimento an physikalischen Untersuchungen beteiligt650. Nach der Auflösung der Florentiner Akademie hielt er sich in Rom auf. Seine bedeutendste Arbeit handelt von der Bewegung der Tiere.
Borelli hat durch diese Schrift651 der Physiologie die wertvollsten Dienste geleistet, indem er die Grundsätze der Mechanik auf die Physiologie anwenden lehrte. Er zeigte z. B., daß beim Zusammenwirken der Muskeln und der Knochen letztere als Wurfhebel dienen, d. h. als einarmige Hebel, bei denen die in den Muskeln tätige Kraft an dem kleineren Hebelarm angreift. In der durch Abb. 107 erläuterten Stellung des Armes wird sich z. B. der Muskelzug, welcher der Last R das Gleichgewicht hält, zu dieser Last entsprechend dem Hebelgesetz wie die Strecke OK zur Strecke OJ verhalten. Der von dem zweiköpfigen Armmuskel CF, dem Biceps, ausgeübte Zug muß also die in B wirkende Last bedeutend übertreffen. Borelli berechnete, daß sämtliche Muskeln des Armes, wenn er horizontal gehalten und an den Fingern mit 10 Pfund belastet wird, einen Zug ausüben, der viele Male größer ist als das Gewicht.
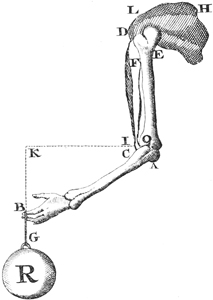
Auch die Mechanik des Gehens, Laufens, Springens, Schwimmens und Fliegens wurde durch Borelli einer solch vortrefflichen physikalischen Untersuchung unterworfen, daß erst die neueste Zeit durch die Gebrüder Weber Besseres geleistet hat. Abb. 108 zeigt uns das Verfahren, das Borelli zur Ermittlung des Schwerpunktes[S. 371] einschlug653. Welche Bedeutung gerade die Lage dieses Punktes und die Art, wie er unterstützt wird, bei dem Zustandekommen der einzelnen Bewegung besitzt, wurde von Borelli besonders eingehend untersucht. Wie groß der Fortschritt in der richtigen Auffassung der Mechanik des Körpers war, läßt sich ermessen, wenn man berücksichtigt, daß das Fleisch bis zum Beginn des 17. Jahrhunderts entweder als bloßes Füllmaterial oder als Organ des Gefühls und des Tastens betrachtet wurde. Erst jetzt begann man auf die Verkürzung der Muskeln beim Zustandekommen der Bewegungen zu achten. Borelli suchte diese Verkürzung aus einer Art von Elastizität des Muskels begreiflich zu machen. Vor allem aber hob er hervor, daß dieser Vorgang wieder von der Tätigkeit der Nerven abhängig sei. Manches von dem, was die Neuzeit hier wieder kennen lernte, war schon dem Altertum, besonders Galen, bekannt (siehe z. B. Bd. I S. 235).
Auch die Atembewegung untersuchte Borelli. Er erkannte, welche Rolle die Zwischenrippenmuskeln bei der das Einatmen bedingenden Erweiterung des Brustkastens spielen, daß das Ausatmen mehr passiv durch ein Erschlaffen jener Muskeln vor sich geht, und daß vor allem die Lunge selbst bei diesem ganzen Vorgang sich durchaus passiv verhält, indem sie der Bewegung der Muskulatur nur folgt. Auf die Bedeutung, die das Zwerchfell neben der Rippenmuskulatur für die Atembewegung besitzt, wurde erst von einem Schüler Borellis hingewiesen654.
Für die Anatomie und für die Physiologie der höheren Tiere waren Malpighis Forschungen über die Drüsengewebe von Bedeutung. Während z. B. manche seiner Zeitgenossen die Galle noch in der Gallenblase entstehen ließen, verlegte Malpighi mit aller Bestimmtheit die Absonderung dieses Sekretes in die Leber. Seine Untersuchung der äußeren Haut als wichtigstem Tastorgan lehrte die unter der Oberhaut befindliche Schleimschicht kennen, die noch heute Malpighis Namen führt.
Der anatomische Bau und die Funktion der Drüsen wurde von Malpighi zum ersten Male richtig gedeutet. Er erkannte, daß diese Organe der Hauptsache nach aus kleinen Bläschen (Zellen) bestehen, die in die Ausführungsgänge eine Flüssigkeit von besonderer Art und Wirkung ergießen.
Es gibt kaum einen Teil der Anatomie oder der Physiologie, den Malpighi nicht durch grundlegende Lehren bereichert hätte. Wie über den Bau der Lunge, so verdanken wir ihm auch über den Bau der Nieren655 und der Körperhaut die wichtigsten Entdeckungen. Malpighi verfolgte die Harnkanälchen und zeigte, wie sie in der Niere zu pyramidenförmigen Bündeln zusammentreten. Er untersuchte ferner den Verlauf der Gefäße innerhalb der Niere, entdeckte die nach ihm benannten Nierenkörperchen und wies nach, daß sie mit den Harnkanälchen in Verbindung stehen. An diese anatomischen Befunde schlossen sich Versuche an, durch die Malpighi feststellte, daß der Urin aus dem Nierenbecken durch die Harnleiter in die Harnblase geleitet wird.
Malpighis Forschungen über die Körperhaut gipfelten in der Entdeckung, daß der Tastsinn in gewissen, unter der Epidermis liegenden Papillen lokalisiert ist.
Eine ganz wesentliche Bereicherung erfuhr die Zoologie im 17. Jahrhundert durch die Erschließung der Welt des Kleinen mit Hilfe des einfachen und des zusammengesetzten Mikroskops.
Man wird jetzt mit Lebewesen näher bekannt, denen man bisher ihrer geringen Körpergröße wegen kaum oder gar nicht Beachtung geschenkt hat. Mit Erstaunen und Bewunderung erkennt man, daß ihr Inneres, das dem unbewaffneten Auge als eine gleichartige Masse erscheint, einen Bau aufweist, der in seiner Art demjenigen der höheren Tiere durchaus nicht nachsteht. Der Ausspruch des Plinius »Natura in minimis maxima« wird jetzt erst als wahr erkannt. Geleitet von dem Zweckmäßigkeitsbegriff sucht man nach einem Verständnis für das Geschaute.
In der Überzeugung, daß der Schöpfer alles planvoll eingerichtet habe und in seinen Werken zu erkennen sei, sehen wir Swammerdam seine mühevollen Untersuchungen über den Bau und die Entwicklung der Insekten vollbringen.
Jan Swammerdam wurde am 12. Februar 1637 in Amsterdam geboren. Sein Vater war Apotheker und besaß ein hervorragendes Interesse für Naturalien. Er hatte in einem Zeitraum von 50 Jahren eine reiche Sammlung zusammengebracht. Der heranwachsende Sohn wurde mit ihrer Instandhaltung betraut und gewann infolgedessen einen unbezwinglichen Hang zur Naturforschung. Boerhaave erzählt, der Knabe sei allen Tierchen seiner Umgebung nachgegangen und habe Luft und Wasser, Felder, Wiesen, Sandberge, Kräuter usw. nach ihnen durchsucht, um Eier, Nahrung, Wohnung und Krankheiten kennen zu lernen. Als er später (von 1661 ab) in Leyden sich dem Studium der Medizin hingab, schloß Swammerdam sich besonders eng an seinen Lehrer[S. 374] der Anatomie656 an. Nach Beendigung seiner Studien ging er jedoch nicht dem ärztlichen Berufe nach, sondern verwendete die erworbenen anatomischen Kenntnisse auf die Zergliederung der kleinsten Lebewesen, deren äußere Form und Lebensgewohnheiten ihn während seiner Knabenzeit schon in solch hohem Grade gefesselt hatten.
In Leyden lernte Swammerdam auch den hervorragenden dänischen Forscher Nicolaus Steno kennen, der später in Toskana weilte und dort die Grundlagen der Geologie schuf657. Der Großherzog von Toskana, der sich 1668 in Holland aufhielt, wurde damals auch mit Swammerdam bekannt und besichtigte dessen Sammlungen. »Nichts verwunderte den Großherzog so sehr«, erzählt Boerhaave in seiner Schilderung des Lebens Swammerdams, »als daß letzterer zeigte, wie ein Falter zusammengerollt in einer Puppe steckt. Aus dieser nahm ihn Swammerdam mit unglaublicher Geschicklichkeit und mit unbegreiflich feinen Werkzeugen heraus, um dem Fürsten die verwickelten Teile des Insekts auf das deutlichste auseinanderzusetzen«. Der Großherzog bot Swammerdam für seine Sammlung 12000 Gulden und knüpfte an dieses Anerbieten die Bedingung, daß der Forscher an den toskanischen Hof kommen und dort die Sammlung verwalten und bereichern sollte. Leider schlug Swammerdam dieses Anerbieten, sowie jede andere Anstellung aus. Er starb, kränklich und verarmt, im Jahre 1680.
Seinen Fleiß im Nachspüren nennt Boerhaave658 mehr als menschlich. Sobald ihm die Sonne hinreichendes Licht spendete, begann er unter freiem Himmel seine feinen Präparate zu betrachten. Während der Abend- und der Nachtstunden wurde beschrieben und gezeichnet. Bei der Untersuchung benutzte er Gläser von sehr verschiedener Schärfe. Der betreffende Gegenstand wurde zuerst bei schwacher Vergrößerung untersucht, dann betrachtete er ihn mit immer kleineren Linsen. Die Scheren, Messer und Lanzetten, deren sich Swammerdam bediente, waren so klein, daß er sie unter dem Vergrößerungsglase schleifen mußte. Um den Verlauf der zarten Gefäße zu verfolgen, blies er sie mit Hilfe feiner gläserner Röhren auf, oder er füllte sie mit gefärbten Flüssigkeiten.[S. 375] Auf solche Weise pflegte er die Gedärme einer Biene so deutlich zu zeigen, wie man es bisher nur an größeren Tieren zu tun vermochte. Swammerdams zootomische Arbeiten erstreckten sich auch auf die Weichtiere (z. B. die Weinbergsschnecke und die Sepie), sowie die Amphibien. Der Bau und die Entwicklung des Frosches wurden von ihm mit einer so weitgehenden Genauigkeit untersucht, daß Swammerdams Befunde über den Bau der Urogenitalorgane erst durch Arbeiten des 19. Jahrhunderts ihre Bestätigung gefunden haben659.
Unter den zahlreichen Kunstgriffen, die Swammerdam in die Anatomie einführte, seien noch folgende erwähnt. Er benutzte saure Flüssigkeiten, welche den zarten Teilen bei längerer Einwirkung größere Festigkeit und Härte verliehen. Um das, manche Organsysteme einhüllende, den Einblick in die Form und den Zusammenhang der Teile hindernde Fett zu entfernen, wandte er als Lösungsmittel Terpentinöl an. Mitunter verwandte er ganze Tage darauf, das Fett aus einer Raupe zu entfernen. Zum Injizieren bediente er sich nicht nur gefärbter Flüssigkeiten, sondern er benutzte zu diesem Zwecke auch geschmolzenes Wachs. Auch den Kunstgriff, kleinere Tiere unter Wasser zu zerlegen, so daß die voneinander gelösten Teile ins Flottieren kamen und sich so leichter trennen und verfolgen ließen, hat Swammerdam in die anatomische Technik eingeführt.
Wenden wir uns Swammerdams Untersuchungen der niederen Tierwelt im einzelnen zu, so ist vor allem seine Abhandlung über den Bau und die Entwicklung der Bienen zu nennen. Nach einem Ausspruch Boerhaaves, der Swammerdams Schriften unter dem Titel »Bibel der Natur« herausgab, ist das Buch über die Bienen ein Werk, das bis auf jene Zeiten nicht seinesgleichen gefunden hatte. Nach Boerhaave ist es im Anfange der 70er Jahre des 17. Jahrhunderts entstanden. Swammerdam, dessen Augen durch die unermüdliche Anstrengung schließlich »ganz stumpf« geworden seien, habe sich daran »zu schanden« gearbeitet.
Um von der Forschungsweise Swammerdams und den Ergebnissen seiner Untersuchungen einen Begriff zu geben, sei einiges aus dieser, für die Entwicklung der Zootomie so wichtigen Abhandlung über die Biene mitgeteilt.
Zunächst werden die drei Formen, die Männchen, die Weibchen und die Arbeitsbienen, genau beschrieben und ihre Lebensweise geschildert.[S. 376] Dann folgt die Beschreibung der inneren Organe. Das obere und das untere Schlundganglion werden als Gehirn und kleines Gehirn unterschieden. Von letzterem geht nach Swammerdams Entdeckung das Mark aus. Es zieht sich durch den ganzen Körper, indem es in gewissen Abständen knotige Verdickungen bildet, aus denen die feineren Nerven hervorsprießen.
In der Brust erblickt Swammerdam die Muskeln der Flügel und der Beine, sowie die Luftröhren. Im Hinterleibe findet er die Speiseröhre, die sich durch die Brust erstreckt, den Magen, die dünnen und die dicken Gedärme, sowie besondere, zum Darm gehörende Drüsen und die Atmungswerkzeuge mit ihren Bläschen und Luftröhren. Das Herz erblickt er gleichfalls, sowie eine Menge Fett und die Muskeln, die unter den Ringen liegen und sie bewegen.
Sehr genau wird die Entwicklung der Biene von dem Verlassen des Eies an beschrieben. Und zwar beschränkt sich Swammerdam nicht etwa auf die Veränderungen, welche die äußere Form erleidet, sondern er geht auf das Wachstum der inneren Organe ein und gelangt dadurch als erster zu einer klaren Auffassung der bis dahin in ihrem Wesen so sehr verkannten Metamorphose der Insekten.
Vor der Zergliederung brachte er die zu untersuchenden Tiere in farbige Flüssigkeiten. Auf die Weise bekam er Teile zu sehen, die sonst nicht oder nicht deutlich genug hervortreten. Öffnete er die Bienenlarve auf der Rückenseite, so quoll ihm nach seiner Schilderung eine Flüssigkeit entgegen, die aus den verletzten Adern und dem Herzen kam. Unter der Haut traf er die Muskeln, welche die Ringe des Leibes bewegen; darauf kam das Fett zum Vorschein und in dem Fett, mitten auf dem Rücken, das Herz als eine lange, den ganzen Rücken bis zum Kopf durchziehende und Gefäße nach allen Richtungen aussendende Röhre. Im weiteren Verlaufe der Zergliederung erblickte er unter dem Herzen den mit unzählig vielen Luftröhren umflochtenen Magen (s. Abb. 109). Er fand ihn fleischig und mit einer gelben Substanz gefüllt. Hinten am Magen (d) zeigten sich vier Gefäßchen (e). Es waren die Malpighischen Gefäße, die später in weit größerer Zahl auftreten und für harnabsondernde Organe gelten, während ihnen früher wohl die Funktion der Leber, also eine Art Gallenbereitung, zugeschrieben wurde. Swammerdam selbst sagt von ihnen, er habe ihre Aufgabe nicht erraten können, doch nach langer, unverdrossener Mühe festgestellt, daß diese Gefäße an den Enden geschlossen sind.
Auf jeder Seite der Bienenlarve wies Swammerdam zehn Atmungsöffnungen nach. Er erkannte auch, daß sämtliche Luftröhren, die in den Körper führen, unter sich verbunden sind, und zwar geschehe dies durch eine Röhre, die von der einen Öffnung zur nächsten, von dieser zur dritten und so fort durch den ganzen Körper ziehe. »Der Bau dieser Luftröhren«, ruft er aus, »ist wunderbar, ja sehr wunderbar; sie bestehen insgesamt aus dicht nebeneinander befindlichen Ringen, welche durch sehr dünne Häutchen miteinander verbunden sind. Die Luftröhren stehen immer offen, wie bei uns Menschen und den höheren Tieren. Auch ist bezüglich der Luftröhren noch zu bemerken, daß sie alle Teile des Körpers, selbst das Gehirn und das Auge durchsetzen, wie ich noch näher bei der Zergliederung dieses unergründlichen Kunst- und Meisterstückes des großen Baumeisters zeigen werde.«
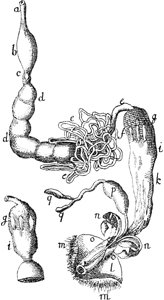
b Saugmagen; d Magen; e Malpighi'sche Gefäße; p Giftblase; q Giftdrüsen; i Mastdarm; m Teile des letzten Bauchringes.
Swammerdam beobachtete auch, daß die Häutung sich bis auf diese zarten Luftröhren erstreckt. Es würden nämlich bei diesem Vorgange ganze Adern und Röhren ausgestoßen, so daß die im Innern abgestreiften Luftröhren in der ihnen eigentümlichen Lage und Gestalt zum Leibe hervordrängen. Desgleichen häute sich auch der Magen, der Mund und das Ende des Darmes; doch sei dies schwierig zu beobachten. Auffällig sei auch, daß, nachdem der Wurm zum Püppchen geworden, alle Gliedmaßen, Flügel, Fühler und Freßwerkzeuge Luftröhren besäßen, die beim Ausstrecken dieser Teile mit Luft gefüllt würden und zur Ausdehnung der Glieder das Ihrige beitrügen.
Mit der Schärfe und Sorgfalt der Beobachtung, die sich in den mitgeteilten Ergebnissen der Untersuchungen Swammerdams ausspricht, steht die klare, vorurteilsfreie Auffassung, welche dieser Forscher den Naturerscheinungen entgegenbringt, im Einklang. Durch Swammerdam, sowie den gleichzeitig lebenden Italiener Redi wurde die seit jeher in den Köpfen der Gelehrten wie der Ungelehrten spukende Ansicht von der Urzeugung niederer Tiere, wenn auch nicht gänzlich beseitigt, so doch für zahlreiche Fälle widerlegt. Wie in früheren Jahrhunderten verschanzte sich nämlich auch im 18. die Unwissenheit stets wieder hinter dieser Irrlehre. Harvey, der in seiner Schrift über die Erzeugung der Tiere660 Hervorragendes geleistet und das Wort »Ex ovo omnia« an ihre Spitze gestellt hatte, besaß durchaus keine klaren Vorstellungen über die Entwicklung der Insekten und der übrigen niederen Tiere. »Einige Geschöpfe«, sagt er, »werden aus einem schon fertigen Stoffe vollends gebildet und aus einer Gestalt in die andere verändert. Alle Teile werden zugleich durch eine Verwandlung geboren und unterschieden. So geschieht die Zeugung der Insekten661.« Harvey zeigte sich in der Behandlung dieser Frage also noch ganz von der Überlieferung, sowie der landläufigen Auffassung beeinflußt, für die schon mit dem Worte »Verwandlung« der Irrtum eng verknüpft war. Welch sonderbare Vorstellungen man mit diesem Worte verband, geht auch aus folgenden Ausführungen Harveys hervor: »Durch die Verwandlung erhalten die Tiere eine Gestalt wie durch ein eingedrücktes Siegel. Bei solchen Tieren aber, welche durch Wachstum entstehen, bringt die Bildungskraft andere und anders geordnete Teile nacheinander hervor662.« Wenn man bedenkt, daß einer der hervorragendsten Anatomen des 17. Jahrhunderts solche Anschauungen hegte, ein Mann, der selbst heute wohl noch auf Grund des oben erwähnten Wortes als ein Bekämpfer der Lehre von der Urzeugung betrachtet wird663, so erscheint die Bedeutung Swammerdams erst in vollem Lichte. Wo der letztere das Wort Verwandlung gebraucht, will er darunter nichts anderes verstanden wissen, als eine langsame,[S. 379] auf natürliche Weise vor sich gehende Gestaltung der Gliedmaßen, die unter der ursprünglichen Hülle stattfindet und sich daher der unmittelbaren Beobachtung entzieht, bis die neue Form die alte Haut plötzlich zersprengt.
Swammerdam hält es für ausgemacht, daß in der ganzen Natur keine Urzeugung, sondern nur Fortpflanzung stattfindet, und daß jedes wirbellose Tier aus einem Ei hervorkommt, das ein anderes Tier derselben Art gelegt hat. Zwar ist es ihm nicht möglich, für alle Fälle diese Ansicht durch die Beobachtung zu erweisen. Das von ihm beigebrachte Material ist indes umfangreich genug, um diese Verallgemeinerung zu rechtfertigen. Dazu tritt der von ihm geführte Analogiebeweis durch die Aufdeckung einer von den Anhängern der Urzeugung nicht vermuteten Feinheit im inneren Bau der niederen Tiere. »Alle Züge des Apelles«, sagt Swammerdam in seiner Anatomie des Nashornkäfers664, »sind gegen die zarten Striche der Natur nur grobe Balken. Alles künstliche Gewebe der Menschen muß sich vor einer einzigen Trachee verkriechen. Wer will sie abbilden? Welcher Witz vermag sie zu beschreiben? Welcher Fleiß kann sie hinlänglich untersuchen?« Da also die Organe der Insekten sich als ebenso vollendet, zweckmäßig und kunstvoll gearbeitet erweisen wie diejenigen der allergrößten Geschöpfe, so konnten jene Wesen auch unmöglich, wie die Anhänger der Urzeugung wollten, durch einen zufälligen Zusammenfluß von Stoffen entstanden sein, sondern sie mußten sich gleich den höheren Tieren durch elterliche Zeugung gebildet haben.
Indem Swammerdam bei den Insekten die Verschiedenheiten in der Entwicklung hervorhob, schuf er zugleich die Grundlage für die heutige Systematik dieser Tierklasse. Der erste Fall besteht nach ihm darin, daß das Tier, in allen seinen Gliedmaßen vollkommen ausgebildet, das Ei verläßt. Als ein Beispiel dieser Gruppe wird die Laus genauer untersucht. Bei dem zweiten Typus findet nach dem Verlassen des Eies nur noch ein allmähliches Heranwachsen der Flügel statt, ein Ruhezustand (Puppenstadium) tritt nicht ein. Swammerdam schildert diesen Fall bei der Libelle. Bienen, Ameisen und Käfer kommen unentwickelt aus dem Ei hervor und erhalten die vollkommene Gestalt durch allmähliche Ausbildung der Gliedmaßen unter der Haut. »Endlich«, sagt Swammerdam, »treten alle Glieder, nachdem die Haut abgestreift[S. 380] ist, hervor. Der Vorhang, der soviel Irrungen unter den Gelehrten angestiftet hat, wird sozusagen fortgezogen.«
Wie erstaunte aber unser Forscher, als einmal aus vier Puppen eines Tagschmetterlings anstatt des erwarteten Falters zahlreiche, kleine, geflügelte Insekten hervorbrachen! Eine Erklärung dieser merkwürdigen Erscheinung konnte erst später erfolgen, als man das geheimnisvolle Treiben der Schlupfwespen kennen gelernt hatte. Diese legen bekanntlich ihre Eier in die Larven anderer Kerbtiere, so daß die Puppe von der sich entwickelnden jungen Brut, die endlich die Haut durchbricht, aufgezehrt wird.
Einen Bundesgenossen, der auf dem Wege des planmäßigen Versuches gleichfalls zur Erschütterung der Lehre von der Urzeugung beitrug, fand Swammerdam in dem Italiener Redi665. Dieser lieferte in einer 1668 erschienenen Schrift, die er »Versuche betreffend die Erzeugung der Insekten« betitelte, den Nachweis, daß in den von ihm untersuchten Fällen vermeintlicher Urzeugung die Insekten nicht aus faulenden Stoffen, sondern aus Eiern entstanden, welche Tiere derselben Art vorher in jene Stoffe gelegt hatten. In richtiger Vorahnung der Erkenntnis einer späteren Zeit bemerkt Swammerdam hierzu, kein Tier werde durch Fäulnis erzeugt, sondern es werde umgekehrt die Fäulnis erst durch die Tiere verursacht.
Am bekanntesten ist Redis Versuch, durch den er die Entstehung der Fleischmaden auf Fliegeneier zurückführte. Wurde nämlich das Fleisch mit einem feinen Netz bedeckt, das die Fliegen an der Ablage der Eier hinderte, so traten auch keine Maden auf.
Auch für einige parasitische Würmer lieferte Redi den Nachweis, daß sie durch Zeugung entstehen. Trotzdem fand die Lehre von der Urzeugung immer wieder der Forschung noch zu sehr verschlossene Gebiete, wo sie ihr Dasein bis in die neueste Zeit hinein weiter fristen konnte. Über Redi sei noch erwähnt, daß er sich auch um die Anatomie der Schlangen, des Zitterrochens und der Vögel Verdienste erworben hat. Seine Untersuchung des Vogelkörpers erstreckte sich besonders auf die Luftsäcke, die von der Lunge aus der Luft einen Zutritt bis in die Knochen gestatten.
Der hervorragendste Forscher auf den Gebieten der Anatomie, der Physiologie und der Entwicklungsgeschichte, den das Italien des 17. Jahrhunderts hervorbrachte, war Marcello Malpighi666 (1628 bis 1694), ein Schüler und Freund Borellis. Seine Verdienste um die Einführung des Mikroskops in das naturwissenschaftliche Studium, sowie um die Begründung der Anatomie der Pflanzen wurden schon gewürdigt. Malpighi machte von Swammerdams Erfindung der Injektion, d. h. der Erfüllung feiner Gefäße mit gefärbten Flüssigkeiten oder erstarrenden Massen (z. B. geschmolzenem Wachs) ausgedehnten Gebrauch. Gleich dem niederländischen Forscher, der die Hoffnung aussprach, daß man durch das Studium der Insekten zu den Gründen der Zeugung anderer Tiere gleichsam hinaufsteigen werde, läßt Malpighi sich von dem richtigen Gedanken leiten, durch die Erforschung der niederen Formen ein tieferes Verständnis des Baues der höheren Tiere anzubahnen, ein Gedanke, der ihn zur Beschäftigung mit den Pflanzen, als den einfachsten Organismen, geführt hatte. So lieferte Malpighi eine für jene Zeit mustergültige Arbeit über den Seidenschmetterling667, dessen Anatomie und Entwicklung er eingehend untersuchte. Diese Arbeit enthält die erste Beschreibung des Rückengefäßes und des Nervensystems der Insekten, sowie der Spinndrüsen und der nach ihrem Entdecker genannten Blindsäcke, die Swammerdam später auch in der Biene nachwies668.

Die Abb. 110 (s. vorige Seite) gibt uns Malpighis Zeichnung des bauchständigen zentralen Nervenstranges wieder. Malpighi unterschied an ihnen 13 Nervenknoten. Von diesen aus verfolgte er die Nervenstränge bis in ihre einzelnen Verzweigungen. Er zeigte z. B., daß von den Knoten I, I aus Nerven nach den Augen und nach den Freßwerkzeugen geschickt werden. Die Knoten GG befinden sich nach seiner Schilderung zwischen den beiden vordersten Öffnungen des Tracheensystems. Dann treten die beiden Nervenstränge in O weit auseinander und bilden auf diese Weise den Schlundring. M endlich bezeichnet die letzten feinen Verzweigungen des ganzen Stranges.
Die erste Figur der Tafel II (siehe Abb. 111) zeigt uns, mit welcher Genauigkeit Malpighi den Lauf der von den paarweis sich gegenüberstehenden Öffnungen (Stigmen) 1–9 (Abb. 110) ausgehenden Tracheen verfolgt hat. Die Figur stellt die feinsten Tracheenverzweigungen dar, die einen Nervenknoten versorgen. Wenn man sich vergegenwärtigt, welch winziges Gebilde ein solcher Knoten ist, so muß man nicht nur die Sorgfalt des Forschers anerkennen, sondern auch die Güte, die das Mikroskop innerhalb eines verhältnismäßig so kurzen Zeitraums erreicht hatte. Die große, obere Trachee PD, deren Spiralwindungen zu erkennen sind, verbindet zwei einander gegenüber befindliche Stigmen. Sie sendet Äste, die in die feinsten Verzweigungen auslaufen, nach dem benachbarten Nervenknoten. Den übrigen Knoten und dem sie verbindenden Mark, sowie allen übrigen Geweben wird in entsprechender Weise Luft zugeführt.
In Malpighis Arbeit über den Seidenschmetterling werden auch die Verdauungsorgane und der Fortpflanzungsapparat beschrieben. Ferner sucht Malpighi die Veränderungen festzustellen, welche die einzelnen Organsysteme während der verschiedenen Entwicklungsstufen des Insekts durchlaufen.
Ein Gegenstück zur Entwicklungsgeschichte des Seidenschmetterlings lieferte Malpighis Untersuchung der Entstehung eines Wirbeltieres, nämlich des Hühnchens im Ei. Es wird damit ein Problem wieder aufgenommen, das schon Aristoteles und den der vorigen Periode angehörenden Fabricio beschäftigt hatte. Auch zur Bewältigung dieser Aufgabe, die erst im 19. Jahrhundert, seitdem v. Baer die Embryologie zur wichtigsten Grundlage der zoologischen Forschung erhob, einer befriedigenden Lösung entgegengeführt wurde, hat Malpighi zum erstenmal die Hilfe des Mikroskops in Anspruch genommen. Insbesondere wurde die Entstehung der Wirbelsäule, sowie der Gehirnabteilungen am Hühnchen verfolgt.
Wir wollen auch bei dieser Abhandlung, die Malpighi »Über das bebrütete Ei« betitelte und 1672 herausgab, einen Augenblick verweilen, da sie die Grundlage für alle weiteren entwicklungsgeschichtlichen Arbeiten geworden ist. Der Wert der Abhandlung wird dadurch noch erhöht, daß Malpighi ihr eine größere Zahl (59) vortrefflicher Abbildungen beigegeben hat. Die zweite Tafel, welche die Entstehung der Wirbelsäule und der Gehirnanlagen erkennen läßt, ist in nachstehender Abbildung 112 wiedergegeben. In Fig. VIII erblicken wir eine Furche, die Primitivrinne oder nach Malpighis Bezeichnung die Carina. A ist als Kopfende, dem sich die erste Andeutung des Halses ansetzt, und D, D sind als die Wirbelanlagen zu erkennen.
In Fig. XI zeigt uns Malpighi, daß am Grunde der Rinne sich das Rückenmark (C) bildet, dem in der Kopfgegend einige blasenartige Auftreibungen (Vesiculae cerebri nennt sie Malpighi) anhängen. Wie sich die Rinne allmählich schließt und mit ihren Rändern verwächst, zeigt Fig. XVII. Die untere Abbildung stellt die Umgebung der embryonalen Anlagen dar. Wir erkennen aus Malpighis Zeichnung den Sack F und mehrere Zonen, von denen er die Zone H Area umbilicalis nennt.
In Fig. XVII erscheint zuerst die Anlage des Herzens (D) als
ein einfaches Rohr. Gleichzeitig bemerkt man (Fig. XVIII) auf[S. 384]
[S. 385]
der als Area umbilicalis bezeichneten Zone zahlreiche Gefäße, die
bei B dargestellt sind (Abb. 113). Diese Gefäße sehen, wie Malpighi
beobachtete, zuerst gelblich aus, nehmen aber bald eine
rötliche Farbe an.
Fig. XIX (siehe Abbildung
112) stellt
das Erscheinen der
Augen (A) zu beiden
Seiten der Hirnanlage
dar.
Man muß Malpighi das große Verdienst zuerkennen, daß er eine fast den ganzen Gang der Entwicklung des Embryos umfassende Darstellung gegeben hat, die in vielen Punkten durch spätere Untersuchungen vollste Bestätigung fand, und grundlegend für die weitere Bearbeitung der Embryologie geworden ist670.
Zu einer genaueren Untersuchung des Nervensystems, insbesondere des Gehirns, erwiesen sich die Mikroskope, mit denen Malpighi seine Forschungen anstellte, noch nicht als ausreichend. So faßte er z. B. die Nerven als hohle Röhren und das Gehirn als ein drüsenartiges Organ auf. Diese Sinnestäuschungen führten auf dem Gebiete der Physiologie und der so eng mit ihr verknüpften Psychologie zu sonderbaren Irrlehren. Man nahm z. B. an, daß feine, flüssige Absonderungen im Gehirne abgeschieden und als Lebensgeister (Spiritus animales) durch die Nerven in einer dem Kreislauf des Blutes ähnlichen Bewegung, dem ganzen Körper zugeführt würden.
Während die zuletzt genannten Mikroskopiker dieses Zeitraumes bei ihren Forschungen planmäßig zu Werke gingen, entsprangen die Untersuchungen Leeuwenhoeks mehr der Liebhaberei als einem Streben nach Vertiefung in den Gegenstand. Leeuwenhoek eröffnet die Reihe jener Männer, die insbesondere während des 18. Jahrhunderts eifrig mikroskopierten, um »ihr Gemüt und ihre Augen zu ergötzen«671. Doch ist ihm eine Fülle mikroskopischer Funde zu verdanken. Seine sich über 50 Jahre erstreckenden Beobachtungen hat er in einer Reihe von Briefen mitgeteilt, die später zu einem Werke vereinigt wurden672.
Anton van Leeuwenhoek wurde 1632 in Delft geboren. Er wurde zum Kaufmannsstande bestimmt, wandte sich aber, ohne eine wissenschaftliche Ausbildung erlangt zu haben, der Verfertigung von Linsen und der Erschließung der gesamten bisher unsichtbaren Welt des Kleinen zu. Seine Abhandlungen über die entdeckten Naturwunder sandte er an die Royal Society, die sie in den Philosophical Transactions veröffentlichte. Die erste dieser Abhandlungen datiert vom Jahre 1673. Das Werk, in dem er sämtliche Abhandlungen vereinigte, erschien zuerst in holländischer Sprache. Leeuwenhoek verstand nämlich kein Latein. Von 1695–1719 wurde es unter dem Titel »Arcana naturae ope microscopiorum detecta« (Geheimnisse der Natur mit Hilfe der Mikroskope entdeckt), in vier starken Bänden und durch viele Abbildungen erläutert, herausgegeben. Die Royal Society machte Leeuwenhoek zu ihrem Mitgliede. Er starb im Alter von 90 Jahren (1723) zu Delft, wo ihm ein prächtiges Denkmal errichtet wurde.
Am bekanntesten ist Leeuwenhoek durch seine 1675 erfolgte Entdeckung der Aufgußtierchen geworden, von denen er eine Anzahl Formen beschrieb. Er sah und beschrieb auch die Rädertiere. Die Mängel, die seinen Hilfsmitteln noch anhaften, verleiteten ihn, den Infusorien Organe und Verrichtungen (wie die Begattung) zuzuschreiben, die bei ihnen nicht vorkommen. Leeuwenhoek entdeckte die Infusorien nach seiner Schilderung in Aufgüssen und im Schleime des Mundes. Über letzteren berichtet er folgendes673: »Ich untersuchte die weiße Masse, die sich zwischen[S. 387] den Zähnen bildet und mischte sie mit Regenwasser, in dem sich keine Tierchen befanden. Ich nahm dann zu meiner großen Verwunderung wahr, daß sich in der erwähnten Masse viele, sehr kleine Geschöpfe befanden, die sich in der ergötzlichsten Weise bewegten.« Zur Erläuterung des Gesagten diene nebenstehende Abbildung 114 Leeuwenhoeks, die offenbar Bazillen und Aufgußtierchen darstellt.
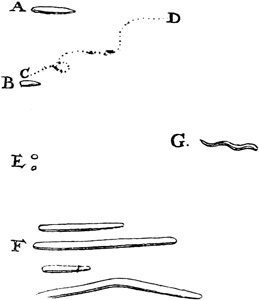
Im Zusammenhang mit diesem Nachweis mikroskopisch kleiner Organismen im lebenden Körper entstand schon im 17. Jahrhundert eine, allerdings noch sehr phantastische und den Kausalzusammenhang noch kaum berücksichtigende, Lehre von den organisierten Krankheitserregern (dem Contagium animatum)675. Während des 18. Jahrhunderts gewann durch die weitere Ausdehnung der mikroskopischen Forschung die Vermutung, daß ein ursächlicher Zusammenhang zwischen gewissen Krankheiten und niederen Organismen besteht, mehr und mehr festen Boden, bis dann im 19. Jahrhundert die Lehre vom Contagium animatum zu einem fest begründeten Bestandteil der Pathologie nicht nur des Menschen, sondern auch der höheren Tiere und Pflanzen wurde.
Auch die Zellen der Hefe hat Leeuwenhoek (1680) wahrgenommen, ohne sie jedoch als Organismen zu deuten.
Er bemerkte ferner die Blutkörperchen und das bekannte wunderbare Schauspiel der Zirkulation des Blutes in dem Körper der Froschlarven. »Als ich den Schwanz dieses Würmchens untersuchte«, so berichtet er, »nahm ich ein Schauspiel wahr, das alles übertraf, was ich bisher beobachtet habe. Ich sah nicht nur das Blut durch die feinsten Gefäße von der Mitte des Schwanzes zu den äußeren Teilen strömen, sondern jedes Gefäß machte eine Biegung und beförderte das Blut wieder zur Mitte des Schwanzes zurück, damit es von neuem zum Herzen ströme«676. Leeuwenhoek bemerkte[S. 388] auch die Knospung der Süßwasserpolypen, sowie die parthenogenetische Fortpflanzung der Blattläuse, die er mit folgenden Worten schildert: »Die von mir entdeckte Art der Fortpflanzung dieser Geschöpfe erschien mir merkwürdiger als irgend eine der bisher bekannt gewordenen. Vergebens suchte ich nach Eiern oder Männchen. Endlich beschloß ich, die größeren von ihnen aufzuschneiden, damit ich Eier aus ihrem Körper erhielt. An Stelle der Eier zog ich jedoch voll Verwunderung kleine Tierchen hervor, die in ihrem Aussehen den Muttertieren so ähnlich waren wie ein Ei dem andern. Nicht nur eins, sondern wohl vier zog ich vollkommen ausgebildet aus demselben Körper677 hervor.«
Leeuwenhoek beobachtete auch, daß die Ameisen gern die Blattläuse aufsuchen, glaubte aber, daß letztere von den Ameisen verzehrt würden, während diese ja nur den von den Blattläusen ausgeschiedenen, als Honigtau bezeichneten Saft genießen. Für den Honigtau, von dem man bisher annahm, daß er aus der Luft auf die Blätter gelange, wies Leeuwenhoek den tierischen Ursprung nach.
Die grundlegenden Entdeckungen, die Leeuwenhoek über den mikroskopischen Bau des Menschen und der höheren Tiere machte, sind so zahlreich, daß sie hier nicht alle erwähnt werden können. Er erkannte den faserigen Bau der Nerven, beging allerdings den Irrtum, die Nervenfaser für hohl zu halten. Ferner erfuhr die Anatomie des Auges die größte Erweiterung durch Leeuwenhoeks mikroskopische Untersuchung dieses so oft schon vor ihm durchforschten Organs. Er fand, daß die Linse aus elastischen Fasern zusammengesetzt ist, die mehrere Schichten bilden, so daß dieser Teil des Auges in drei Teile gespalten werden kann. Auch für die Hornhaut wies Leeuwenhoek die faserige Beschaffenheit und das Vorhandensein eines epithelialen Überzugs nach. Ferner machte er am Auge noch die wichtige Beobachtung, daß die Netzhaut, der er eine genauere Beschreibung widmet, eine Stäbchenschicht enthält, wenigstens finden wir bei ihm die erste Andeutung einer solchen678. Am Insektenauge wies Leeuwenhoek[S. 389] die Zusammensetzung aus zahlreichen Facetten nach. Er entdeckte ferner die Schuppen der Oberhaut, die Röhrchen in der Zahnsubstanz und zahllose andere Einzelheiten.
Nachdem im Jahre 1677 der in Leyden studierende Deutsche Ludwig Ham die wunderbare Entdeckung gemacht hatte, daß der menschliche Samen selbständig sich bewegende Gebilde enthält, die man Samentierchen nannte, bestätigte Leeuwenhoek diese Beobachtung. Er beschränkte sich aber nicht auf diesen einzelnen Fall, sondern dehnte die Frage nach dem Vorkommen ähnlicher Gebilde über das gesamte Tierreich aus und vermochte bei allen Klassen das Vorhandensein von Samenfäden nachzuweisen. Dadurch erhielt die von Harvey begründete Lehre von der Evolution eine wesentliche Umgestaltung. Leeuwenhoek glaubte nämlich, daß in den Samenfäden die Anlage des Embryos enthalten sei, und daß den weiblichen Geschlechtsorganen etwa die Rolle von Brutbehältern zukäme.
Endlich sei hervorgehoben, daß Leeuwenhoek als erster die Querstreifung der willkürlichen Muskeln bemerkte. Die obenstehende Abb. 115 zeigt seine Darstellung einiger Muskelfasern des Herzens, welche die Eigentümlichkeit besitzen, sich netzartig[S. 390] zu verzweigen, während die gewöhnlichen Fasern parallel laufen679.
Die größte Bewunderung hat es erregt, daß Leeuwenhoek eine gewaltige Summe verhältnismäßig oft recht schwieriger Beobachtungen nicht mit dem zusammengesetzten, sondern mit dem einfachen Mikroskop gemacht hat, obgleich Robert Hooke dem erstgenannten Hilfsmittel schon um 1660 eine für wissenschaftliche Arbeiten ganz geeignete Form gegeben hatte. Mit seinen einfachen bikonvexen Linsen, die Leeuwenhoek mit unübertrefflicher Geschicklichkeit anzufertigen wußte, erreichte er eine 160fache lineare Vergrößerung. Nach seinem Tode gelangten diese Vergrößerungsgläser in den Besitz der Royal Society. Mit solch einfachen Hilfsmitteln ließen sich die erwähnten Funde nur machen, wenn das Auge des Beobachters von außergewöhnlicher Schärfe und gut geschult war, und wenn sich dazu noch eine ganz außerordentliche Geschicklichkeit und Ausdauer gesellten. Bezüglich der Abbildungen Leeuwenhoeks ist allerdings mit Recht bemerkt worden, daß sie mit den von Malpighi und anderen Forschern jener Zeit herrührenden Abbildungen den Vergleich nicht aushalten.
Diese Musterung der Erfolge eines Steno, Grew, Malpighi, Swammerdam und Leeuwenhoek lehrt, daß in der zweiten Hälfte des 17. Jahrhunderts der gewaltige Anstoß, der mit der Begründung der Dynamik anhob und darauf die gesamte Physik und Astronomie ergriff, auch auf die übrigen Gebiete der Naturwissenschaften seine Wirkung übte, so daß überall neue Grundlagen geschaffen wurden. Auf diesen hat das nachfolgende 18. Jahrhundert während des größten Teiles seines Verlaufes in ruhiger Entwicklung weiter gebaut. Erst gegen das Ende des 18. Jahrhunderts trat von neuem ein Umschwung auf fast allen Gebieten ein. Er kennzeichnet den Beginn der neuesten und letzten Periode in der Entwicklung der Wissenschaften, die uns nicht nur unmittelbar in die Geschehnisse des Tages hinüberleitet, sondern auch zahlreiche Keime künftiger Verallgemeinerungen, Entdeckungen und Erfindungen in sich birgt.
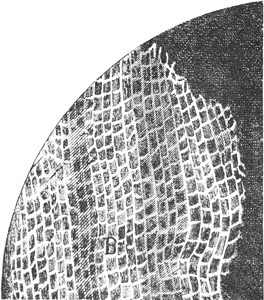
Hooke, dessen Verdienst um die Verbesserung des Mikroskops wir kennen gelernt haben, war der erste, der den zelligen Bau der Pflanzen entdeckte, ohne indes im entferntesten die Bedeutung des Gesehenen zu ahnen. Als er den dünnen Schnitt eines Flaschenkorkes betrachtete, erblickte er zahlreiche, durch Wände getrennte Räume, denen er die bis auf den heutigen Tag für die Elementarorgane des Tier- und Pflanzenkörpers gebliebene Bezeichnung »Zellen« gab. Er berechnete, daß 1200 Millionen solcher Zellen auf einen Kubikzoll Kork kommen. Die nebenstehende Abb. 116 ist eine Wiedergabe des ältesten Bildes, das den zelligen Bau einer pflanzlichen Substanz darstellt681. Die gleiche Art des inneren Gefüges wies Hooke für das Mark des Hollunders, sowie für das Holz verschiedener Pflanzen nach. Dabei entging es ihm nicht, daß die Zellen oft langgestreckt und im[S. 392] frischen Zustande mit Saft gefüllt sind. Hooke bemerkte manche weitere Einzelheit. So beschreibt er die Spiralgefäße des Holzes, die Brennhaare der Nesseln, deren Saft er als die Ursache des Brennens erkannte682, den Bau der Schimmelpilze usw.
Nur gelegentliche Entdeckungen über den inneren Bau der Pflanzen machte Leeuwenhoek, dessen Verdienste um die mikroskopische Erforschung des Tierleibes wir im vorigen Abschnitt kennen gelernt haben. So entdeckte Leeuwenhoek die Tüpfel auf den im Holz verlaufenden Gefäßen. Die merkwürdige Erscheinung richtig zu deuten, gelang erst im 19. Jahrhundert. Leeuwenhoek war auch der erste, der auf das Vorkommen von Kristallen im Innern der Pflanze hinwies.
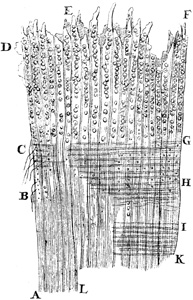
Seine nebenstehend wiedergegebene Abbildung (Abb. 117) stellt die Tüpfel der Holzfasern und der Markstrahlen einer Kiefer dar. Die Tüpfel der Markstrahlen hielt er für Öffnungen. Auch die Natur der gehöften Tüpfel verkannte er gänzlich. Er sagt darüber folgendes684: »Die Abbildung zeigt uns etwas vom Holz der Kiefer, das ich so fein wie möglich der Länge nach spaltete. Infolge der Feinheit des Splitterchens nahm das Auge deutlich zahlreiche Kügelchen wahr, die in den Zellen des Holzes (in tubis ligneis) lagen. Der Anblick ist sehr überraschend, nicht nur wegen der vollkommenen Rundung dieser Kügelchen, sondern auch weil in[S. 393] ihnen mitunter ein heller Fleck erscheint. Diese Kügelchen sind meiner Ansicht derjenige Stoff, den wir als Harz bezeichnen.«
Die ersten planmäßigen, pflanzenanatomischen Untersuchungen sollten nicht lange auf sich warten lassen. Sie erfolgten durch Nehemia Grew, einen Landsmann Hookes, und den als Anatomen und Physiologen hervorragenden Italiener Malpighi. Beide Männer legten die Ergebnisse ihrer Forschungen fast gleichzeitig (im Jahre 1671) der Royal Society vor. Eine ausführliche Darstellung gaben sie in zwei umfangreichen, erst mehrere Jahre später veröffentlichten Werken685.
Die von Grew und Malpighi unabhängig voneinander angestellten Untersuchungen verfolgen nicht etwa schon das Ziel, die Zelle, deren Inhalt man erst viel später seinem Wesen nach verstehen lernte, als das Grundorgan aller Pflanzenteile nachzuweisen. Neben der Beschreibung der mit bloßem Auge nur unvollkommen sichtbaren, äußeren Pflanzenteile, insbesondere der Blütenorgane, Knospenanlagen, Früchte, Samen usw., beschränken sie sich vielmehr auf die Darstellung grob anatomischer Verhältnisse. Die ganze Untersuchung läuft mehr auf eine Zergliederung der Organe in die einzelnen Gewebe hinaus, als auf den Nachweis der Gewebselemente und deren gesetzmäßige Verknüpfung. Das Verfahren ist also das analytische. Als Elemente der Gewebe werden Fasern und Zellen unterschieden.
Nehemia Grew wurde 1628 als der Sohn eines Geistlichen in England geboren. Er widmete sich dem ärztlichen Beruf, daneben aber pflanzenanatomischen Untersuchungen. Grew bekleidete als Mitglied der Royal Society das Amt ihres Sekretärs. Er starb im Jahre 1711.
Grews »Anatomie der Pflanzen« zeugt von einer hervorragenden Geschicklichkeit im Mikroskopieren und von einem ganz außerordentlichen Beobachtungsvermögen. Will man die Bedeutung dieses Buches würdigen, so muß man erwägen, daß Grew keinen Vorgänger auf dem von ihm durchforschten Gebiete hatte, sondern[S. 394] nur vereinzelte, dazu meist unrichtig gedeutete Beobachtungen vorfand. Daher konnte sein Buch noch in neuerer Zeit wegen der klaren Anschauung, die es vermittelt, Anfängern zur ersten Orientierung von berufenster Seite empfohlen werden686. Die folgenden Abschnitte mögen aus dem Inhalt des großen, unsterblichen Werkes einiges wiedergeben.
Neben dem Grund- oder Füllgewebe, für das Grew das noch jetzt gebräuchliche Wort »Parenchym« einführte, unterschied er drei Arten von Fasern, die Spiralröhren, die Faserzellen und die Saftgänge (milk vessels). Nicht verdickte Teile der Zellwände hatten die ersten Beobachter wohl für Löcher gehalten, durch welche die Saftbewegung vor sich gehe. Grew widerlegte diese Ansicht und zeigte, daß es sich hier nicht um Öffnungen handle, sondern daß das Parenchym am besten mit dem Schaum auf Flüssigkeiten verglichen werden könne. Der von Grew herstammende Ausdruck »Gewebe« für alle aus gleichartigen Elementen bestehenden Zellvereinigungen ist wie der Ausdruck »Parenchym« in die heutige Terminologie übergegangen. Die zuerst damit verknüpfte Vorstellung, daß das Innere der Pflanze mit einem künstlichen Gewebe, einem Spitzengewebe etwa, verglichen werden könne, hat sich allerdings als unzutreffend erwiesen.
Grew bemerkte auch die Spaltöffnungen der Blattoberhaut. Diese wichtige Entdeckung leitete ihn auf die Vorstellung, daß die Blätter den Verkehr des Pflanzeninnern mit der Außenwelt, also das Ein- und Ausatmen, besorgen. Allerdings war die Chemie im 17. Jahrhundert noch zu wenig entwickelt, um den Verlauf dieses Stoffaustausches näher festzustellen.
Da Grew sich stets bemühte, das Gesehene physiologisch zu deuten, so kann es nicht Wunder nehmen, daß er bei der mikroskopischen Untersuchung der Blütenteile auch auf die Frage nach der Sexualität der Pflanze geführt wurde. Er bejahte diese wichtige Frage, die zehn Jahre nach ihm in Deutschland durch Camerarius687 gleichfalls im bejahenden Sinne entschieden wurde. Grews Ausführungen über diesen Punkt lauten etwa folgendermaßen. In der Blume befinde sich ein Samen erzeugender Teil, die Staubgefäße, und ein dem Eierstock entsprechender Teil. Letzterer werde durch die Kügelchen, die sich in den Staubgefäßen befänden und dem Samen der Tiere gleichwertig seien, befruchtet.[S. 395] Die Pflanze sei also ein Zwitter688. Trotz dieser, dem Wesen der Sache nahekommenden Vorstellung gebührt die Priorität der Entdeckung Camerarius, weil dieser die Notwendigkeit des Zusammenwirkens von Staubgefäß und Stempel zum Zwecke der Befruchtung zuerst durch einwandfreie Versuche erhärtete.
Neben Grew ist vor allem der Italiener Malpighi unter den Begründern der Phytotomie zu nennen. Marcello Malpighi wurde am 10. März des Jahres 1628 in der Nähe von Bologna geboren. Er studierte in Pisa, wo er mit dem zwanzig Jahre älteren Borelli, der ihn unterrichtete, ein enges Freundschaftsbündnis einging. Borelli war eins der hervorragendsten Mitglieder der Accademia del Cimento, die im Geiste Galileis die Erforschung der Natur durch ausgedehnte Anwendung des Experiments erstrebte. Borelli war es, der die neue Forschungsweise auf das Gebiet des organischen Lebens ausdehnte, und auf diesem Wege folgte ihm in Italien Malpighi. Nach Beendigung seiner medizinischen Studien beschäftigte sich dieser besonders mit anatomischen Untersuchungen. Im Jahre 1656 wurde er Professor der Medizin in Bologna. Mit wenigen Unterbrechungen lehrte er dort bis 1691. In diesem Jahre ernannte ihn der Papst zu seinem Leibarzt. Infolgedessen siedelte Malpighi nach Rom über, wo er im Jahre 1694 starb.
Malpighi689 weist insbesondere auf die große Verbreitung der Spiralröhren hin (Abb. 118). Überall wird die Frage nach der Funktion der beschriebenen Elemente mit den anatomischen Befunden verknüpft. Die Physik und insbesondere die Chemie waren indes noch nicht imstande, der Pflanzenphysiologie ihre unentbehrliche Hilfe zu gewähren, so daß die Fragen nach der Saftbewegung und der Ernährung, obwohl sie im Mittelpunkte des Forschens standen, keine Lösung finden konnten. Malpighi, der sogar eine derjenigen des Darmes ähnliche Bewegung der Spiralröhren690 wahrgenommen haben wollte, gelangte immerhin zu der für die weitere Entwicklung der Ernährungsphysiologie grundlegenden Erkenntnis,[S. 396] daß die Blätter diejenigen Organe sind, welche die Nahrung der Pflanzen bereiten. Auch zeigte er, daß das Produkt der Assimilation von hier aus in die übrigen Teile des Organismus gelangt und dort entweder zunächst aufgespeichert oder sofort zum Wachstum gebraucht wird.
Malpighis Werk beginnt mit einer genial entworfenen Skizze über den Bau und die Verrichtungen der pflanzlichen Organe. Er nennt diesen Abschnitt Anatomes plantarum idea. Was er bringt, ist im wesentlichen dasjenige, was er schon im Jahre 1671, um sich die Priorität zu sichern, der Royal Society unterbreitet hatte, welcher der italienische Forscher seit 1669 als auswärtiges Mitglied angehörte. Dann folgt die durch nicht weniger als 93 Tafeln unterstützte ausführliche Darstellung.
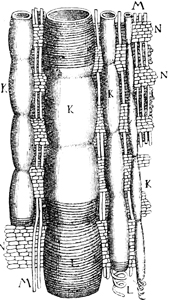
Von besonderem Werte ist es, zu erfahren, wie bei Malpighi und denjenigen seiner Zeitgenossen, in denen der Geist der neueren Naturwissenschaft lebte, der Bruch mit der bisherigen Art der Forschung zum Ausdruck kam. Die Kriege und die staatlichen Veränderungen haben nach Malpighis Ansicht die Entwicklung der Wissenschaften nicht so ungünstig beeinflußt wie die verkehrte Art des Studiums. Bisher habe man nämlich die Wissenschaften stets in ihrem ganzen Umfang durchmessen und sie als etwas Fertiges betrachtet, anstatt sich der andauernden und genauen Durchforschung eines begrenzten Gebietes zu widmen. Auch er habe sich in der Begeisterung seiner Jugend gleich an die Anatomie der höheren Tiere gewagt. Da ihm indessen vieles dunkel geblieben sei, so sei er auf den Gedanken gekommen, das Wesen der Dinge durch Analogien zu erschließen und die schwierigeren Erscheinungen durch Vermittlung der einfacheren, leichter verständlichen zu erforschen. So sei er zur Untersuchung der Insekten geschritten, um den Körperbau der vollkommneren Tiere zu begreifen. Aber auch auf diesem Gebiete seien ihm die Schwierigkeiten noch zu groß erschienen; deshalb habe er sich[S. 397] zunächst an die Erforschung der Pflanzen begeben, um nach eingehender Beschäftigung mit ihnen seine Schritte wieder zurück zu wenden und über die Stufe der Pflanzenwelt den Weg zu den früheren Problemen zu finden. Eigentlich, meint er mit Recht, hätte er zur Erklärung des Organischen von der Erforschung der Mineralien oder gar der Elemente ausgehen müssen. Ein solches Unternehmen würde jedoch seine Kräfte überstiegen haben.
Malpighi untersucht dann besonders die Anatomie des Stammes, während er sich bezüglich der Blätter und der Blüten mehr auf die makroskopischen oder grob anatomischen Verhältnisse beschränkt. Der äußerste Teil der Pflanze ist eine Haut, die aus Säckchen (Zellen) besteht. Sie werden im Alter entleert und stellen eine trockne Oberschicht dar. Darunter kommen netzartig verschlungene Fasern zum Vorschein, zwischen denen jedoch wieder längliche Säckchen auftreten, die in horizontaler Richtung gegen das Holz verlaufen. Ähnlich fand er das Holz aus längs verlaufenden Fasern und Spiralröhren zusammengesetzt, deren Maschen von horizontal verlaufenden Schlauchbündeln durchsetzt sind. Unklar blieb ihm der Ursprung der Holz- und Rindenschichten aus dem zwischen beiden liegenden Bildungsgewebe, dem Cambium. Malpighi läßt die Holzlagen aus den innersten Schichten der Rinde hervorgehen, ein Irrtum, der sich in der Pflanzenanatomie bis in die ersten Jahrzehnte des 19. Jahrhunderts hinein erhalten hat. Häufig war ihm der Gedanke gekommen, daß in der faserigen Rinde die Anlagen, aus denen jedes Jahr der Holzzylinder vergrößert werde, zusammengedrängt schon vorher existieren, wie es bei den Schmetterlingen für mehrere Teile vorkomme, die an der Raupe und der Puppe noch nicht sichtbar seien. Es begegnet uns also schon hier ein Anklang an die später soviel umstrittene Lehre von der Evolution in der Anlage präexistierender, für die Beobachtung aber noch nicht vorhandener Organe, eine Lehre, die, wie wir sehen werden, zu den ungereimtesten Konsequenzen führte. Sehr wertvoll war es, daß Malpighi den ununterbrochenen Zusammenhang der Gewebeschichten gleich bei der Begründung der Anatomie der Pflanzen erkannte und in solch treffender Weise hervorhob, daß einige seiner zusammenfassenden Ausführungen hier Platz finden mögen: »Die Wurzeln«, sagt Malpighi, »sind bei den Bäumen ein Teil des Stammes, der sich in der Erde verzweigt und endlich sich in haarfeine Fäden auflöst. Die feinen Röhren, die im Boden getrennt verlaufen, sammeln sich nach und nach zu Bündeln und treten[S. 398] endlich zu einem einzigen großen Zylinder, dem Stamm, zusammen. Dieser streckt dann infolge der wieder eintretenden Trennung der Röhren am anderen Ende seine Äste aus, bis die Röhrenbündel durch immer weitere Teilung in den Blättern ihre letzte Begrenzung finden.«
Die ausführliche Darstellung Malpighis ist nur in ihren ersten Abschnitten, die von der Rinde und dem Stamme handeln, anatomischen Inhalts. In den späteren Abschnitten werden morphologische Dinge wie die Knospenlage, die Teile der Blüten, Haare, Stacheln, Ranken usw. beschrieben. Das Hauptinteresse Malpighis wendet sich der Fortpflanzung und ihren Organen zu. Hier zeigt sich besonders sein Bemühen eine Analogie zwischen den tierischen und pflanzlichen Erscheinungen nachzuweisen. Er gelangt zu dem Ergebnis, daß der Samen der Pflanzen ein Ei ist, das den aus den wesentlichen Teilen der Pflanze bestehenden Embryo einschließt und jahrelang entwicklungsfähig bleibt. Unter dem Drucke der eindringenden Feuchtigkeit entfalten sich die Teile, und das Pflänzchen wird zum Keimling. Die Keimblätter haben, wie Malpighi gleichfalls erkannte, die Aufgabe, dem Keimling seine erste Nahrung zu liefern. Borelli bestritt dies; und durch diesen Widerspruch wurde Malpighi dazu veranlaßt, den Keimlingsvorgang einiger Pflanzen, wie des Lorbeers und der Dattelpalme, recht genau zu untersuchen und durch Abbildungen zu erläutern. Schon früher hatte er die Keimungsgeschichte von Ricinus verfolgt und in 20 Abbildungen dargestellt. Über den Vorgang der Befruchtung und das Wesen des Blütenstaubs blieb Malpighi indessen noch völlig im Dunkeln. Staubgefäße und Blütenblätter haben seiner Ansicht nach die Aufgabe, eine Art Reinigung und Läuterung des Saftes vorzunehmen, aus dem sich der Samen bilden soll. Die Tatsache, daß sich an den Blütenblättern oft Sekrete absondern, deren Bedeutung für den Bestäubungsvorgang Malpighi noch nicht kannte, hat ihn auf jene ganz unzutreffende Ansicht geführt. Ja, er geht soweit, in der Absonderung des Nektars einen Vorgang zu erblicken, welcher der Menstruation der höheren Tiere analog sei. Diese habe nämlich auch die Aufgabe, alle Substanzen, die das Empfängnisorgan irgendwie beeinträchtigen könnten, fortzuschaffen, damit der Rest des gereinigten Blutes, das im Uterus verbleibe, leichter befruchtet und dem Wesen des Tieres angepaßt werden könne. Man erkennt, auf wie verkehrte Vorstellungen das Bestreben führen kann, überall Analogien aufzuweisen und hierin die Hauptaufgabe der Naturerklärung zu erblicken. Es ist in[S. 399] dieser Hinsicht auch auf späteren Stufen der Wissenschaft oft gefehlt und weit über das Ziel hinausgeschossen worden. Selbst heute spielen die falschen Analogien noch eine verhängnisvolle Rolle. Es ist gerade die Geschichte der Wissenschaften, die uns immer wieder zu äußerster Vorsicht in dieser Beziehung mahnt.
Die von Malpighi und Grew begründete Anatomie der Pflanzen wurde zunächst nicht weiter ausgebaut. Die Physiologen und vor allem die Systematiker der nachfolgenden Periode glaubten dieses Zweiges der botanischen Wissenschaft entraten zu können. Auch besaß das Mikroskop noch nicht diejenige Vollendung, die es zur Aufhellung feinerer anatomischer Einzelheiten befähigt hätte. So kam es, daß der Ausbau des in der zweiten Hälfte des 17. Jahrhunderts erschlossenen Gebietes erst zu Beginn des 19. Jahrhunderts anhub, um dann in rascher Folge zu Ergebnissen zu führen, die das Gesamtbild der Botanik wesentlich verändert und dazu beigetragen haben, daß sie auf den Rang einer induktiven Wissenschaft erhoben worden ist.
Die hervorragendste Entdeckung, die das 17. Jahrhundert auf dem Gebiete der Pflanzenphysiologie zeitigte, war der Nachweis der Sexualität der Pflanzen. Eine Vorahnung treffen wir schon im Altertum. So berichtet Theophrast über ein beim Feigenbaum angewandtes, als Kaprifikation bezeichnetes Verfahren, das auf die Erzielung besserer Früchte hinausläuft. Man hatte seit alters beobachtet, daß auf der wilden Feige (Caprificus) eine Gallwespe (Cynips psenes, L.) lebt, durch deren Stich die Früchte an Saft, an Zuckergehalt und Größe zunehmen. Aus diesem Grunde hing man angestochene wilde Feigen an die in den Gärten gezogenen Feigenbäume, damit die ausschlüpfenden Insekten deren Früchte in der gleichen günstigen Weise beeinflussen sollten691. Theophrast wies darauf hin, daß die Insekten hier nicht den Ansatz der Früchte hervorrufen, sondern nur ihr Reifen befördern. Der Vorgang besaß also mit dem an der Dattelpalme beobachteten692 eine nur äußerliche Ähnlichkeit.
Die Unterscheidung zwischen weiblichen und männlichen Pflanzen, d. h. in fruchttragende und solche, die keine Früchte[S. 400] hervorbringen, lag zur Zeit des Aristoteles und Theophrast wohl schon im Sprachgebrauch. Auf eine Kenntnis des Befruchtungsvorganges darf man daraus jedoch nicht schließen. Als besondere Arten der Vermehrung berücksichtigte Theophrast auch das Aussetzen von Ablegern, das Pfropfen und das Okulieren, wobei die Pflanze dem Pfropfreis sozusagen als Boden diene693. Die Sexualität der Pflanzen auf dem Wege des Versuches sicher nachgewiesen zu haben, ist das Verdienst des Tübinger Professors Camerarius.
Rudolf Jakob Camerarius wurde 1665 in Tübingen geboren und starb dort 1721. Im Jahre 1688 wurde er Professor und Direktor des botanischen Gartens in Tübingen.
Wenn die Botaniker des 16. und 17. Jahrhunderts von männlichen und weiblichen Pflanzen redeten, so geschah es nur in bildlichem Sinne, um dadurch eine oft nicht verkennbare Verschiedenheit im ganzen Aussehen zu bezeichnen. Caesalpin und Malpighi nahmen an, daß die Entstehung des Samens ein der Knospenbildung entsprechender Vorgang sei. Den Staubgefäßen und den Blumenblättern fiel nach ihrer Meinung die Aufgabe zu, einen Teil der Feuchtigkeit an sich zu ziehen, damit in den übrigen Teilen der Blüte ein umso reinerer Saft zur Bildung des Samens zurück bleibe.
Camerarius ging dagegen von der Beobachtung aus, daß ein nur Früchte tragender Maulbeerbaum, in dessen Nähe sich kein Blütenstaub erzeugendes Exemplar befindet, taube, hohle, zur Keimung unfähige Samen hervorbringt. Er entschloß sich darauf, das Verhältnis, in dem die verschiedenartig gestalteten Individuen derselben Pflanzenart zueinander stehen, auf dem einzig Erfolg versprechenden Wege des Versuches zu erkunden. Camerarius wählte dazu eine der gemeinsten zweihäusigen Pflanzen, das jährige Bingelkraut (Mercurialis annua). Brachte er von diesem die reifen, keimfähigen Samen in den Boden, so sah er zweierlei Pflanzen aus ihnen hervorgehen, die im allgemeinen einander ähnlich waren und auch gleich benannt werden. Doch bemerkte er, daß die einen nur Staubgefäße hervorbringen und gänzlich ohne Frucht und Samen bleiben, während die anderen Früchte tragen, dafür aber der Blumenblätter und der Staubbeutel entbehren. Sonderte er nun die fruchtbringenden Exemplare des Bingelkrauts von den Blütenstaub erzeugenden völlig ab, so entstanden zwar Samen, sie[S. 401] waren aber nicht keimfähig. Darauf ging er zu Versuchen mit solchen Pflanzen über, die Staubgefäß- und Stempelblüten auf demselben Individuum erzeugen. Wurden z. B. bei Ricinus und Mais die Staubgefäßblüten entfernt, bevor die Antheren zur Entwicklung gelangt waren, so erhielt er in keinem Falle reife Samen. Camerarius beschreibt diese Versuche mit folgenden Worten: »Als ich beim Ricinus die runden, Blütenstaub erzeugenden Knospen vor der Entfaltung der Staubbeutel entfernt und das Auftreten neuer derartiger Knospen sorgfältig verhindert hatte, erhielt ich aus den vorhandenen unverletzten Samenanlagen niemals Samen, sondern ich sah die tauben Samenhäute herabhängen und schließlich verwelkt und verschrumpft untergehen. Ähnlich verhielt es sich beim Mais. Nachdem ich den Schopf (der die Staubgefäßblüten enthält) rechtzeitig abgeschnitten hatte, erschienen zwei Kolben, die gänzlich des Samens entbehren, so daß eine große Zahl leerer Samenhäute vorhanden war«. »Es erscheint daher gerechtfertigt«, schließt Camerarius, »den Antheren die Bedeutung von männlichen Geschlechtsorganen beizulegen, in denen der Same, jenes Pulver nämlich, ausgeschieden wird. Ebenso ist einleuchtend, daß der Fruchtknoten mit seinem Griffel das weibliche Geschlechtsorgan der Pflanze darstellt«694.
Camerarius verhehlte sich durchaus nicht die Schwierigkeiten, die damals noch dieser Theorie anhafteten. So mußten ihm die Schachtelhalme und die Bärlappgewächse als Pflanzen erscheinen, welche Staubbeutel besitzen und dennoch keine Samen erzeugen. Bei diesen Pflanzen, meint Camerarius, sei der männliche Samen reichlich vorhanden. Aber, fährt er fort, es entspricht ihm kein weibliches Geschlecht, denn es fehlen die Griffel, die Samenbehälter, die Samen. Eine Lösung dieses scheinbaren Widerspruchs brachte erst das 19. Jahrhundert durch die Aufhellung der Keimungsvorgänge der beiden, heute als Equiseten und Lykopodien bezeichneten Pflanzengruppen. Camerarius zieht sich damit aus der ihm sich bietenden Schwierigkeit, daß er die erwähnten Pflanzengruppen zu den unvollkommenen (kryptogamen) Pflanzen rechnet, deren Ursprung und Vermehrung noch dunkel sei.
Mißlungene Versuche mit dem Hanf brachten Camerarius dazu, die Frage aufzuwerfen, ob nicht die Griffel einer Pflanze durch den Pollen einer anderen bestäubt werden könnten, kurz, ob auch im Pflanzenreiche eine Bastardbildung möglich sei. Er erzählte, er habe drei junge Pflanzen des weiblichen Hanfes vom Felde in den Garten verpflanzt und darauf geachtet, daß sie von keiner Blüte einer benachbarten männlichen Pflanze ihrer Art bestäubt werden konnten. Trotzdem brachten die weiblichen Hanfpflanzen viele fruchtbare Körner hervor, ein unerwarteter Ausgang, der Camerarius zunächst sehr verdroß, dann aber auf folgende Überlegung brachte. Entweder seien die weiblichen Pflanzen zu spät aus dem Bereiche der männlichen entfernt worden, von denen einige vielleicht schon ihren Staub verstreut hätten. Es sei aber auch möglich, daß in dem Garten Pflanzen anderer Art, die dort in Menge vorhanden gewesen, die befruchtungsbedürftigen, weiblichen Hanfpflanzen bestäubt hätten. Zweifle doch niemand daran, daß im Tierreich ein Weibchen von dem Männchen einer anderen Art befruchtet werden könne. Neu sei allerdings die Frage, ob eine weibliche Pflanze von der männlichen einer anderen Art befruchtet werden könne, der weibliche Hanf z. B. von dem männlichen Hopfen. Die Entscheidung, die der Lehre von der Sexualität der Pflanzen eine wertvolle Stütze verliehen hätte, blieb allerdings einer späteren Zeit und einem anderen Forscher vorbehalten695.
Ließ sich auch die geschlechtliche Differenzierung der Pflanzen nachweisen, so war eine Einsicht in die Art des Befruchtungsvorganges damit noch nicht gewonnen. Zur Lösung dieser Frage, meint Camerarius, wäre es sehr zu wünschen, daß man von den Mikroskopikern erführe, was die Körnchen der Staubbeutel enthalten, wie weit sie in den weiblichen Apparat eindringen, ob sie unversehrt an den Ort kommen, wo ihre Vereinigung mit den Samenknospen stattfindet, und was dabei aus ihnen austritt.
Die Aufhellung dieser Verhältnisse sollte, wie wir später sehen werden, erst im 19. Jahrhundert gelingen. Camerarius hielt es noch für selbstverständlich, daß in jenem häufigsten Falle, in dem Staubgefäße und Stempel in einer Blüte vereinigt sind, die Befruchtung zwischen diesen, nahe benachbarten Teilen stattfinde, während doch in der Tat in der Natur, wie spätere Untersuchungen gezeigt haben, alle erdenklichen Veranstaltungen vorhanden sind, um eine Selbstbefruchtung der Zwitterblüten zu verhindern. Einen der[S. 403] Vereinigung der Geschlechter in den Zwitterblüten entsprechenden Hermaphroditismus hatte der zur Zeit des Camerarius lebende Swammerdam im Tierreich, und zwar an den Schnecken, aufgefunden. Camerarius erwähnt diese Beobachtung und bemerkt dazu, daß dieser Fall, der im Tierreich eine Seltenheit bedeute, bei den Pflanzen eben die Regel sei. Gleichzeitig wundert er sich darüber, daß die Schnecken sich nicht selbst befruchten, während dies doch, wie er annimmt, bei den Pflanzen der Fall sei.
Den Schluß der Schrift des Camerarius bildet eine, mit Goethes Metamorphose der Pflanze in Parallele zu stellende, lateinische Ode, deren Verfasser nicht bekannt ist. Sie enthält die Grundzüge der neuen Lehre und schließt mit den Worten:
Bestätigt seh'n wir jetzt mit Verwunderung
Für Tier' und Pflanzen gleiche Geschlechtlichkeit!
Was lebt, was Nachkommen hervorbringt,
Alles entsteht auf dieselbe Weise.
O mächt'ge Kraft des Geistes, die Du entdeckt
Zuerst so Großes, was durch Jahrhunderte
Verborgen war; wer der Natur sich
Weihte, ihn möge Dein Ruhm begeistern.
O hehre Allmacht, die Du die Welt erschufst,
Du sorgst, die Ordnung, welche Du eingesetzt,
In der Natur stets zu erhalten,
Liebst zu verjüngen die alte Schöpfung.
Linné, der bald darauf die Systematik durch die Errichtung seines auf die Sexualität gegründeten Systems zu einem vorläufigen Abschluß brachte, fußte, was diese Grundlage anbetraf, wesentlich auf Camerarius, wenn dessen Lehre durch ihn auch keine nennenswerte Fortbildung erfuhr. Letzteres geschah erst durch die Untersuchungen Koelreuters, die späterer Besprechung vorbehalten bleiben.
Die von Galilei, Newton, Huygens und anderen ausgeübte Methode, welche durch die Verknüpfung des Versuchs mit dem mathematischen Beweisverfahren zum Auffinden der Naturgesetze führt, blieb während des 18. Jahrhunderts, wie zur Zeit ihrer Schöpfer, im wesentlichen auf die Astronomie und die Mechanik beschränkt. Auch galt es, während dieses Zeitraumes die von Newton696 und Leibniz697 ins Leben gerufene höhere Analysis zur Bewältigung derjenigen großen Aufgaben geeignet zu machen, die zunächst auf den Gebieten der Mechanik, der Optik und der Akustik einer Lösung harrten.
Daß die höhere Mathematik im Verlauf des 18. Jahrhunderts zu dem »Riesenschwerte« des Astronomen und Physikers und später des modernen Naturforschers überhaupt wurde, ist vor allem den Mitgliedern der Familie Bernoulli und Leonhard Euler zu verdanken. Der älteste und zugleich einer der bedeutendsten unter den zahlreichen großen Mathematikern dieser Familie ist Jakob Bernoulli (1654–1705). Er ist als einer der wichtigsten Bahnbrecher auf den Gebieten der Infinitesimalrechnung, der Reihenlehre, Kombinationslehre und Wahrscheinlichkeitsrechnung zu nennen698. Jacob Bernoulli beschäftigte sich mit den beiden zuletzt genannten Gegenständen seit etwa 1680. Sein großes Werk, in dem er die[S. 405] eigenen und die Forschungen anderer Mathematiker über Kombinatorik und Wahrscheinlichkeitsrechnung zusammenfaßte, erschien jedoch erst einige Jahrzehnte später699. Es enthält auf dem Gebiete der ersteren, und zwar in der noch heute üblichen Form, so ziemlich alles, was den Bestand dieser Disziplin ausmacht700. Bei weitem der wichtigste Abschnitt des Werkes ist der letzte701. Bernoulli stellte sich darin die Aufgabe, die Wahrscheinlichkeitsrechnung auf »bürgerliche, sittliche und wirtschaftliche Verhältnisse« anzuwenden. Im Hinblick auf die ganz neuen Bahnen, welche damit diesem Zweige der Mathematik gewiesen werden, ist es doppelt bedauerlich, daß dieser Abschnitt unvollendet geblieben ist. Die Wahrscheinlichkeit wird als ein Grad der Gewißheit erklärt, der sich von der Gewißheit selbst wie ein Teil vom Ganzen unterscheidet. Besteht die absolute Gewißheit (a oder 1) aus 5 Wahrscheinlichkeiten (oder Teilen), von denen 3 für das Eintreten eines Ereignisses und zwei dagegen sprechen, so besitzt das Ereignis 3/5a oder 3/5 der Gewißheit.
Die Untersuchung gipfelt in dem Bernoullischen Theorem702, das man auch das Gesetz der großen Zahlen genannt hat. Das Theorem betrifft die Frage, ob durch Vermehrung der Beobachtungen, oder durch fortgesetzte Häufung der Einzelfälle, die Wahrscheinlichkeit dafür wächst, daß die Zahl der günstigen zur Zahl der ungünstigen Fälle schließlich das wahre Verhältnis erreicht. Bernoulli formuliert das Problem und bejaht es auf Grund eines mathematischen Beweisverfahrens. Sehr treffend bemerkt er, die Aufgabe habe sozusagen ihre Asymptote, indem, auch bei beliebiger Vermehrung der Beobachtungen, ein bestimmter Grad von Wahrscheinlichkeit, das wahre Verhältnis der Fälle gefunden zu haben, nicht überschritten werden könne.
Als Beispiel wählt Bernoulli eine zugedeckte Urne, in der sich ohne unser Vorwissen 3000 weiße und 2000 schwarze Steine befinden. Durch häufiges Ziehen und jedesmaliges Zurücklegen der Steinchen in die Urne wird man mit immer größerer, schließlich mit an Gewißheit grenzender Wahrscheinlichkeit das Verhältnis 3 : 2 ermitteln,[S. 406] indem dieser Wert mit der Häufung der Fälle in immer engere Grenzen eingeschlossen wird. Wir sind daher, sagt Bernoulli, gezwungen, bei allen Geschehnissen eine gewisse Notwendigkeit anzuerkennen. Würde man nämlich alle Ereignisse durch alle Ewigkeit hindurch beobachten, so würde schließlich die Wahrscheinlichkeit in volle Gewißheit übergehen. Man müsse also bei noch so zufällig erscheinenden Dingen doch eine Notwendigkeit annehmen und zu dem Schlüsse kommen, daß alles in der Welt in bestimmter Gesetzmäßigkeit vor sich gehe.
Jacob Bernoullis Arbeiten über unendliche Reihen703 sind darauf zurückzuführen, daß sie häufig ein Mittel bieten, um zu einer Lösung von Integrationsaufgaben zu gelangen. Deshalb hatten sich schon die Begründer der Infinitesimalrechnung, Wallis und Newton, mit der Entwicklung von Funktionen in unendliche Reihen befaßt704. So hatte Wallis die Fläche zwischen der Hyperbel und ihren Asymptoten durch eine unendliche Reihe dargestellt. Man findet bei ihm auch schon die Reihe der reziproken Quadratzahlen:
1/(12) + 1/(22) + 1/(32) + ...,
deren Summierung jedoch erst Euler vollzog.
Die erste Integration mit Hilfe der Reihenentwicklung gelang Nikolaus Mercator (1668) bei seiner Quadratur der gleichseitigen Hyperbel705. Auch Leibniz hat sich mit der Summation einiger unendlichen Reihen befaßt, die auf die Ermittlung von π hinauslaufen. In ihren ersten Anfängen geht die Lehre von den unendlichen Reihen sogar auf Euklid und Archimedes zurück. Die eigentliche Begründung der Theorie der unendlichen Reihen erfolgte jedoch erst durch Newton, den Entdecker der allgemeinen Binomialformel. Für ganzzahlige positive Exponenten, die eine[S. 407] endliche Reihe ergeben, war die Entwicklung der Formel (a + b)n schon lange vor Newton bekannt.
Auf Jacob Bernoullis Arbeiten über unendliche Reihen kann hier nicht näher eingegangen werden. Die Ergebnisse verdienen hier nur insoweit Erwähnung, als sie zur angewandten Mathematik hinüberleiten. So gelang es Bernoulli, die Beziehung zwischen den Koordinaten der elastischen Kurve durch eine Reihe auszudrücken, die Parabel und die logarithmische Linie mit Hilfe einer solchen zu rektifizieren, und anderes mehr706.
Von Jacob Bernoulli und seinem Bruder Johann wurde die Aufmerksamkeit der Mathematiker auch wieder auf die für die Physik besonders wichtigen Maxima- und Minimaaufgaben gelenkt und durch die Behandlung der sogenannten isoperimetrischen Probleme ein Grund geschaffen, auf dem später Euler, Lagrange und andere die Variationsrechnung errichten konnten.
Die isoperimetrischen Probleme handeln von Kurven, die gewissen Maxima- und Minimabedingungen genügen. Das älteste dieser Probleme lautet: Welche unter allen isoperimetrischen Kurven schließt die größte Fläche ein? Schon das Altertum beantwortete diese Frage dahin, daß die verlangte Kurve der Kreis sei707.
Das erste isoperimetrische Problem, mit dem sich Johann Bernoulli beschäftigte, betrifft die Brachystochrone, die Linie des kürzesten Falles708. Johann Bernoulli formulierte dies Problem mit folgenden Worten: »Zwei gegebene Punkte, die verschiedenen Abstand vom Erdboden haben und nicht senkrecht übereinander liegen, sollen durch eine Kurve verbunden werden, auf der ein beweglicher Körper, vom oberen Punkte ausgehend, vermöge seiner Schwere in der kürzesten Zeit zum unteren Punkte gelangt«. Nachdem er die Lösung gefunden, forderte er nach damaliger Sitte »die scharfsinnigsten Mathematiker des ganzen Erdkreises«[S. 408] auf, gleichfalls die Aufgabe zu lösen. Leibniz gelang dies noch am nämlichen Tage, an dem er davon Kenntnis erhielt. Auch Newton und Jacob Bernoulli fanden übereinstimmend die Lösung, daß die Zykloide die gesuchte Kurve sei. Die Verwunderung war umso größer, als Huygens diese Kurve schon als diejenige erkannt hatte, in der die Fallbewegung von allen Punkten aus dieselbe Zeit beansprucht. Er hatte ihr aus diesem Grunde den Namen »Tautochrone« beigelegt. So zeige, sagt Jacob Bernoulli in der Bekanntgabe seiner Lösung709, eine Kurve, die von so vielen Mathematikern untersucht worden sei, daß an ihr nichts mehr zu erforschen übrig schien, plötzlich eine ganz neue Eigenschaft.
Die beiden älteren Bernoulli errichteten in erster Linie auf den geschaffenen Grundlagen das Gebäude der Differential- und Integralrechnung.
Eine Auswahl aus seinen Vorlesungen über die Methoden der Integralrechnung schrieb Johann Bernoulli in den Jahren 1691 und 1692 nieder710. Ein von ihm herrührendes Werk über die Differentialrechnung scheint verloren gegangen zu sein. Johann und Jacob Bernoulli ist es besonders zu danken, daß sich das von Leibniz gefundene Verfahren der Infinitesimalrechnung rasch einbürgerte.
Johann Bernoulli beginnt nach einigen allgemeinen Betrachtungen mit der Quadratur von Flächen und der Rektifikation von Kurven. Danach wendet er sich physikomechanischen Problemen zu, z. B. den zuerst von Tschirnhausen eingehender untersuchten kaustischen Linien, und der Kettenlinie. Später sehen wir Daniel Bernoulli vorzugsweise damit beschäftigt, schwierige mechanische Probleme, bei denen die von Huygens und selbst noch von Newton in seinen »Prinzipien« befolgte geometrische Methode keine Aussicht auf Erfolg bot, vermöge des neuen Hilfsmittels zu bewältigen. Daniel Bernoulli ist daher als der Hauptbegründer desjenigen Wissenszweiges zu nennen, den man als mathematische[S. 409] Physik bezeichnet. Er führte in die Mechanik das Prinzip von der Erhaltung der Kraft ein, das schon Huygens bei seinen Untersuchungen über das zusammengesetzte Pendel vorgeschwebt hat, und brachte dieses Prinzip bei seinen Arbeiten über die Bewegung flüssiger Körper überall zur Anwendung (Hydrodynamik 1738)711. Huygens hatte es dahin ausgesprochen, daß ein frei fallender Körper, wie immer man seine Bewegungsrichtung ändert, nur bis zur ursprünglichen Höhe wieder emporsteigen kann, da die Wirkung der Ursache gleichwertig sei. Aus diesem Grunde hatte Huygens auch die Möglichkeit eines Perpetuum mobile bestritten. Obgleich Daniel Bernoulli712 die große Bedeutung des Prinzips von der Erhaltung der Kraft wohl ahnte, blieb es doch dem 19. Jahrhundert vorbehalten, es in seiner Allgemeingültigkeit nachzuweisen und die gesamte Naturlehre darauf zu begründen.
Zu den mechanischen Vorgängen, mit denen sich das 18. Jahrhundert beschäftigte, gehörten auch der Fall und der Wurf. Galilei hatte zwar die Theorie dieser Bewegungen entwickelt und damit für die Mechanik eine neue Ära eröffnet. Er hatte jedoch von einem sehr wesentlichen Faktor, dem Luftwiderstande, abgesehen, nicht etwa weil er die Wichtigkeit dieses Faktors nicht kannte, sondern weil sich Galilei die erwähnte Beschränkung noch auferlegen mußte.
Ein Gesetz für den Widerstand, den Flüssigkeiten und Gase auf bewegte Körper ausüben, stellte zuerst Newton auf. Er gelangte zu der Annahme, daß der Widerstand des Mediums für ein und denselben Körper dem Quadrate der Geschwindigkeit proportional sei. Auf Newtons Veranlassung wurden Versuche angestellt, um das Gesetz zu prüfen. Es erwies sich auch für mittlere Geschwindigkeiten als gültig.
Die Bahn, die ein geworfener Körper unter dem Einfluß des Luftwiderstandes beschreibt, suchte zuerst Johann Bernoulli zu bestimmen. Es ergab sich jedoch, daß die mathematische Analyse zur Bewältigung dieser Aufgabe nicht imstande war, und daß eine angenäherte Lösung des ballistischen Problems sich nur durch die Vereinigung von Versuch und Rechnung erhoffen ließ. Am erfolgreichsten in dieser Richtung war die Arbeit von Robins713, die Euler unter dem Titel »Neue Grundsätze der Artillerie«714 in deutscher Sprache herausgab. Robins zeigte, daß Newtons Gesetz nur für geringe Geschwindigkeiten gilt, daß aber mit größeren Geschwindigkeiten der Widerstand weit stärker wächst, als jenes Gesetz angibt.
Um die Geschwindigkeit des Geschosses in irgend einem Punkte der Wurfbahn bestimmen zu können, konstruierte Robins sein »ballistisches Pendel«. Ein Körper von bedeutendem Gewicht wurde so aufgehängt, daß er pendeln konnte. Schoß man eine Kugel gegen diesen Körper, so ließ sich aus dem Gewicht, den Dimensionen und dem Ausschlag des Pendels die Geschwindigkeit der Kugel den Stoßgesetzen gemäß berechnen. Nach dem Stoß besitzen nämlich das Pendel, dessen Masse M, und die Kugel, deren Masse m und deren Geschwindigkeit im Augenblicke des Zusammentreffens v sei, die gleiche Geschwindigkeit V. Gemäß den Stoßgesetzen ist aber
mv = (M + m)V.
Daraus folgt, daß
v = (M + m)/m · V ist715.
Mit dem Einfluß des Widerstandes, den Gase und Flüssigkeiten der Bewegung entgegensetzen, haben sich die theoretische und die Experimentalphysik seit Bernoulli und Robins immer wieder beschäftigt, ohne indes bei der Kompliziertheit der in Betracht kommenden Umstände bisher zu einem abschließenden Ergebnis zu gelangen.
Fast noch übertroffen wurden die Leistungen Daniel Bernoullis durch diejenigen Eulers. Leonhard Euler wurde am 15. April des Jahres 1707 in Basel geboren und war ein Schüler des daselbst ein Lehramt bekleidenden Johann Bernoulli. Auf[S. 411] die Empfehlung Daniel Bernoullis hin kam Euler mit 20 Jahren an die Akademie zu Petersburg. Bezeichnend für seine ungewöhnliche mathematische Befähigung ist Folgendes. Als es galt, gewisse astronomische Tafeln zu berechnen, erklärten die Mathematiker der Akademie, hierzu einer Frist von einigen Monaten zu bedürfen. Euler dagegen erbot sich, jene Tafeln in drei Tagen fertig zu stellen, und hielt auch Wort. Doch hatte er diese Leistung mit dem Verluste eines Auges zu bezahlen, das er infolge einer durch die Überanstrengung herbeigeführten Krankheit einbüßte. Im Jahre 1741 berief Friedrich der Große durch ein aus dem Feldlager stammendes Schreiben Euler an die Preußische Akademie der Wissenschaften. Volle 25 Jahre arbeitete er als eine Zierde dieser Gesellschaft in der Residenz der Preußischen Könige an dem Ausbau der neueren Mathematik. Dabei entfaltete der große Mann eine beispiellose Produktivität. Allein in den Jahrbüchern der Berliner Akademie veröffentlichte er 121, zum[S. 412] Teil sehr umfangreiche, Abhandlungen716. Nach Maupertuis' Tode leitete Euler die Akademie. Schließlich traten aber Zerwürfnisse ein, die Euler veranlaßten, sein Verhältnis zur Berliner Akademie zu lösen und, einer Aufforderung Katharinas der Zweiten folgend, nach Petersburg zurückzukehren. An seine Stelle trat in die Berliner Akademie als würdiger Nachfolger Lagrange ein. Trotzdem Euler bald darauf völlig erblindete, erlahmte seine wissenschaftliche Tätigkeit nicht. Noch wenige Stunden vor seinem am 7. September 1783 erfolgten Tode war er damit beschäftigt, die Bewegung des in demselben Jahre erfundenen Luftballons zu berechnen.
Bevor wir uns Eulers Arbeiten auf den Gebieten der mathematischen Physik und der Astronomie zuwenden, haben wir ihn als das kennen zu lernen, was er in erster Linie war, nämlich als Mathematiker. Gibt es doch keinen Zweig der reinen Mathematik, der ihm nicht eine außerordentliche Förderung verdankte717. Er war es, der die Bemühungen Vietas zum Abschluß brachte und die Algebra zu einer »internationalen mathematischen Kurzschrift« gestaltete718. In seiner »Einführung in die Analysis des Unendlichen« vom Jahre 1748719 gab er eine umfassende Erörterung der Kurven, welche durch die allgemeine Gleichung zweiten Grades definiert werden. Während er dadurch die analytische Geometrie förderte, verstand er es andererseits, den höheren Kalkül von beengenden geometrischen Fesseln loszulösen und ihn zu einer selbständigen Disziplin zu gestalten. Euler vor allem gelang ferner die scharfe Erfassung des Funktionsbegriffes, dem die ersten Kapitel der »Introductio« gelten, jenes Begriffes, den man wohl zu den wichtigsten Schöpfungen der neueren Mathematik gerechnet hat720.[S. 413] Im Anschluß an Bernoullis Untersuchungen über isoperimetrische Probleme erfand Euler als einen besonderen Teil der höheren Analysis die Variationsrechnung.
Während Johann Bernoulli über die isoperimetrischen Probleme sich dahin geäußert hatte, daß man wohl vergebens nach einem allgemeinen Verfahren für ihre Lösung suchen werde, unternahm Euler die ersten Schritte zur Ausbildung einer »Methode, Kurven zu finden, denen eine Eigenschaft im höchsten oder geringsten Grade zukommt.« Eine Auswahl geeigneter Abschnitte der betreffenden umfangreichen Schrift Eulers wurde neuerdings in deutscher Übersetzung veröffentlicht721. Ein näheres Eingehen auf den Inhalt des gewöhnlich als »Methodus inveniendi« bezeichneten Hauptwerkes von Euler ist hier nicht am Platze722. Bemerkt sei nur, daß die von Euler befolgte Methode wesentlich geometrisch ist, wodurch die Behandlung der einfacheren Probleme sehr klar und durchsichtig wird. Euler hat sein Verfahren als Variationsrechnung bezeichnet und es mit folgenden Worten erläutert. »Die Variationsrechnung ist die Methode, die Änderung aufzufinden, die ein aus beliebig vielen Veränderlichen zusammengesetzter Ausdruck erleidet, wenn man entweder alle oder nur einige Variabeln sich ändern läßt«723.
In einem Anhang zu dem Werke »Methodus inveniendi« setzt Euler die Bedeutung, welche die in diesem vorgetragenen Lehren für die Lösung physikalischer Probleme besitzen, des Näheren auseinander. Er meint, »es geschehe nichts in der Natur, dem nicht irgendein Verhältnis des Maximums oder des Minimums zu Grunde liege«. Daraus ergibt sich für die Forschung ein direktes und ein indirektes Verfahren. Das eine führt zur Bestätigung des anderen, wodurch ein hoher Grad von Gewißheit verbürgt wird. Handelt es sich z. B. darum, die Krümmung eines an den beiden Enden aufgehängten Seiles festzustellen, so geschieht dies entweder direkt, indem man die Wirkungen untersucht, welche die Schwere auf das Seil ausübt. Oder man bedient[S. 414] sich der Methode der Maxima und Minima und erörtert mit ihrer Hilfe, welche Gestalt das Seil annehmen muß, damit sein Schwerpunkt in die möglichst tiefe Lage gelangt. Auf beiden Wegen erhält man ein und dieselbe Kurve, die Kettenlinie, die der Parabel sehr ähnlich sieht724.
Von der Kettenlinie, bei welcher die Elastizität keine Rolle spielt, ging man zur Untersuchung derjenigen Kurven über, die ein elastisches Band unter der Einwirkung von Kräften annimmt. Die hierbei entstehenden Gestalten waren längst bekannt. Jedermann kennt z. B. die in Abb. 120 dargestellte Form, die ein aus Fischbein oder Stahl hergestellter Streifen annimmt, wenn wir an den Endpunkten A und C zwei Kräfte in den Richtungen AD und CD wirken lassen, und der Streifen in B festgehalten wird.
Von der Untersuchung der elastischen Kurven, bei denen die Theorie der Maxima und Minima gleichfalls eine Rolle spielt, ging man zu den Schwingungen elastischer Bänder über. Der erste, der sich mit diesen Problemen eingehender befaßte, war Daniel Bernoulli. Wird die schwingende Bewegung hinreichend schnell, so wird durch sie ein Ton hervorgerufen, dessen Natur sich mit Hilfe von Experimenten untersuchen läßt. So vermochte man auf physikalischem Wege das Ergebnis der mathematischen Analyse zu bestätigen und tiefer in das Wesen der elastischen Körper einzudringen. Auch dies geschah besonders durch Euler. Er unterschied dabei verschiedene Fälle, z. B. das Verhalten eines elastischen Bandes, das an einem Ende befestigt ist, oder desjenigen, das an beiden Endpunkten festgehalten wird. Bei diesen Untersuchungen sonderte Euler die Schwingungen von Körpern, die erst infolge ihrer Spannung elastisch sind (elastische Saite) von[S. 415] den Schwingungen an sich elastischer Bänder725. Die Töne, die dadurch hervorgerufen werden, hat besonders Chladni in seiner »Akustik«726 untersucht und mit den mathematisch gefundenen Ergebnissen Eulers in guter Übereinstimmung gefunden.
Eine der frühesten Arbeiten Eulers auf dem Gebiete der angewandten Mathematik betrifft die von Newton gegebene Theorie der Gezeiten727. Die Pariser Akademie der Wissenschaften hatte bei der Wichtigkeit des Gegenstandes zu Beginn des 18. Jahrhunderts zahlreiche Flutbeobachtungen in den französischen Häfen anstellen lassen. Dabei hatte sich gezeigt, daß man diese Beobachtungen nur zum Teil aus Newtons Theorie erklären konnte. Die Akademie schrieb deshalb im Jahre 1740 Preise über diese Frage aus. Unter den gekrönten Arbeiten befanden sich auch diejenigen von Euler und Bernoulli. Es gelang, auf der durch Newton geschaffenen Grundlage, mit Hilfe der höheren Analysis manche Umstände in Rechnung zu ziehen, die bei den Gezeiten mitwirken, so daß z. B. das Zurückbleiben der Flutwelle hinter der Kulmination des Mondes bestimmt werden konnte.
Auch die Lösung einer zweiten, für die Nautik sehr wichtigen Aufgabe, an der sich Galilei in seinen letzten Lebensjahren vergebens abgemüht hatte, des Problems der Längenbestimmung, blieb Euler vorbehalten. Galilei und das Altertum hatten ihren Berechnungen gewisse astronomische Erscheinungen, wie die Verfinsterungen der Jupitermonde oder die viel seltener vorkommenden Mondfinsternisse, zugrunde gelegt. Schon vor Galilei erfolgten neue Vorschläge, deren Durchführung die endliche Lösung des so lange schwebenden Problems herbeiführen sollte. Da der Mond infolge seiner Bewegung um die Erde seinen Ort rasch ändert, kann der Abstand des Mondes von bestimmten Fixsternen, der von Minute zu Minute ein anderer ist, zum Vergleich der Ortszeiten und damit zur Längenbestimmung dienen. Es würde dazu nur eine Tabelle erforderlich sein, die für einen bestimmten Ort der Erde die Abstände des Mondes für die einzelnen Tage, Stunden und Minuten angibt. Wird dann die betreffende Distanz an dem Orte der Beobachtung zu einer anderen Tageszeit gemessen, so läßt sich aus dem Unterschiede der Zeiten der Längenunterschied[S. 416] berechnen728. Ein zweites in Vorschlag gebrachtes Verfahren729 beruht auf der Anwendung genauer Chronometer, die während der ganzen Dauer der Reise die Zeit desjenigen Ortes angeben, den man zum Ausgangspunkte für die Längenbestimmung gewählt hat. Die Verwirklichung dieser beiden Vorschläge wurde lebhaft angestrebt, nachdem im Jahre 1713 das englische Parlament einen Preis von 20000 Pfund für die praktische Lösung des Längenproblems ausgesetzt hatte.
Da die Bewegung des Mondes von den anziehenden Kräften der Erde und der Sonne abhängt, war sie weit schwieriger zu ermitteln als diejenige der Planeten. Noch zur Zeit Newtons betrug der Fehler bei der Vorausbestimmung einer Mondfinsternis mitunter eine Stunde und mehr. Auf Grund der Berechnungen Eulers730 und eigener Beobachtungen brachte der Astronom Tobias Mayer731 in Göttingen um die Mitte des 18. Jahrhunderts Mondtafeln zuwege, die für Längenbestimmungen genügten. Die Witwe Mayers, sowie auch Euler erhielten daher einen Teil des Preises.
Ein hinlänglich genau gehendes Chronometer lieferte im Jahre 1758 der Uhrmacher John Harrison. Dieses wies nach einer vier Monate dauernden Fahrt einen Fehler von nur etwa zwei Minuten auf. Durch fortgesetzte Bemühungen wurde dieser Fehler noch weiter herabgemindert, worauf Harrison die Hälfte der vom Parlamente ausgesetzten Summe erhielt. Um die Länge des Pendels dem Einfluß der Temperaturschwankungen zu entziehen, verfertigte Harrison 1725 nach dem Vorgange Grahams Rost- oder Kompensationspendel, indem er Metalle von verschiedenen Ausdehnungskoeffizienten, wie Messing und Eisen, vereinigte. Graham (1675–1751) hatte zu diesem Zwecke die sogenannte Quecksilberkompensation erfunden.
Verwickelte, nur mit Hilfe der höheren Analysis zu lösende Probleme boten die Schallerscheinungen dar. Euler untersuchte nicht nur die Schwingungen von Saiten und Stäben732, sondern er bestimmte auch die Grenzen der Hörbarkeit. Seinen Versuchen gemäß fallen sie etwa mit den Schwingungszahlen 20 und 7000[S. 417] zusammen. Überhaupt erwarb sich Euler große Verdienste um eine wissenschaftliche Behandlung der Musik. Indessen hatte es schon weit früher (um 1700) Sauveur unternommen, aus der Musik ein Objekt der naturwissenschaftlichen Forschung zu machen733. Bei Sauveur begegnet uns die später auch von Euler vertretene Ansicht, daß die Konsonanz auf ein einfaches Schwingungsverhältnis zurückzuführen sei, das vom Gehörorgan leicht aufgefaßt wird. Töne, deren Schwingungszahlen sich wie 5 : 6 verhalten, werden nach Sauveur nicht mehr als konsonierend empfunden. Den Wert 5 : 6 betrachtet er als die Grenze der Konsonanz.
Das Hauptverdienst Sauveurs besteht darin, daß er bestrebt war, in die musikalisch-akustische Untersuchung überall das quantitative Verfahren einzuführen. Sauveur machte auch schon die Beobachtung, daß eine schwingende Saite außer ihrem Grundton zugleich Obertöne erkennen läßt. Dies beruht darauf, daß die Saite entweder ungeteilt schwingt (Abb. 121, I), oder daß sie mehrere Teilschwingungen vollzieht (Abb. 121, II), oder endlich, daß sie gleichzeitig als Ganzes und daneben in ihren Teilen Schwingungen macht (Abb. 121, III). Die so entstehenden höheren Töne nennt man Flageolett- oder Obertöne. Sie lassen sich nur durch besondere Vorkehrungen ausschließen. Gewöhnlich tritt der Schwingungszustand III ein. Das geschilderte Verhalten wurde schon im Jahre 1674734 entdeckt, jedoch von Sauveur unabhängig davon aufgefunden und genauer verfolgt735. Sauveur benutzte[S. 418] für seine Untersuchung ein Monochord. Er rief an einer Saite ihren Grundton hervor. Darauf berührte er sie an gewissen Stellen.
c b cʹ
a–––––––––––––––––––––aʹ
Geschah dies in b, so erhielt er die Oktave, geschah es in c, so hörte man die zweite Oktave. Zur Untersuchung des Schwingungszustandes führte Sauveur das noch heute gebräuchliche Verfahren ein. Er setzte z. B. auf b, c, cʹ schwarze Papierreiterchen, und auf die genau dazwischen liegenden Punkte weiße. Brachte er dann die Saite zum Tönen, indem er sie gleichzeitig in c berührte, so blieben die schwarzen Reiter sitzen, während die weißen abflogen. Die Punkte b, c, cʹ, die in Ruhe bleiben, nannte Sauveur Knoten, die dazwischen liegenden schwingenden Teile Bäuche, Bezeichnungen, die bis auf den heutigen Tag üblich geblieben sind.
Wie die Obertöne, deren Bedeutung für das Zustandekommen dessen, was wir Klangfarbe nennen, Helmholtz später untersucht hat, so wurde auch die unter dem Namen der »Schwebung« bekannte Erscheinung durch Sauveur wissenschaftlich erklärt. Es war den Orgelbauern schon längst aufgefallen, daß das Ohr in regelmäßiger Folge eigentümliche Stöße wahrnimmt, wenn zwei Pfeifen angeblasen werden, deren Töne sich nur wenig voneinander unterscheiden. Sauveur hat diese Stöße (er nannte sie battements, Schläge) aus dem Zusammentreffen von Schwingungen erklärt, die sich als ein jedesmaliges Anschwellen des Tones bemerkbar machen. Besteht z. B. ein Ton aus neun Schwingungen für eine gewisse Zeit, während ein gleichzeitig stattfindender Ton durch zehn Schwingungen während derselben Zeit hervorgerufen wird, so werden nach Ablauf dieser Zeit jedesmal die Schwingungen zusammenfallen. In diesem Augenblick wird der Ton am stärksten erscheinen, dann wieder abschwellen, um nach Ablauf derselben Zeit von neuem verstärkt zu sein. Sauveur benutzte dies Verhalten, um die Schwingungszahl eines Tones zu ermitteln, indem er ihn gleichzeitig mit einem Ton von bekannter Schwingungszahl erklingen ließ und die Anzahl der in einer Sekunde stattfindenden Schwebungen feststellte736.
Infolge der Zurückführung der akustischen Vorgänge auf die Schwingungen elastischer Körper und Medien mußte sich dem schon von Huygens unternommenen Versuch, die Lichtphänomene aus denselben Prinzipien zu erklären, Aussicht auf Erfolg darbieten. So sehen wir denn Euler eifrig bemüht, die Analogie der Schall- und Lichterscheinungen darzutun. Nachdem er alle Schwächen der Emanationstheorie Newtons, die er für geradezu vernunftwidrig erklärte, nachgewiesen hatte, entwickelte er seine eigenen Ansichten vom Äther und vom Licht. Euler geht, wie vor ihm Huygens, von der Annahme aus, daß der Raum zwischen den Himmelskörpern mit einer äußerst feinen Materie, dem Äther, erfüllt sei. Letzterer sei eine Flüssigkeit wie die Luft, aber unvergleichlich viel feiner und verteilter, da die Himmelskörper ihn durchschneiden, ohne in ihm einen merklichen Widerstand zu finden. Ferner besitze der Äther das Vermögen, sich nach allen Richtungen auszubreiten und jeden leeren Raum auszufüllen. Infolgedessen finde er sich nicht nur in den höheren Regionen, sondern er durchdringe die Atmosphäre und dringe auch in die Zwischenräume aller irdischen Körper ein.
Da die Luft infolge entsprechender Eigenschaften geeignet sei, die Erzitterungen der tönenden Körper aufzunehmen und sie nach allen Richtungen fortzupflanzen, worin ja der Schall bestehe, so sei es natürlich, daß der Äther unter ähnlichen Umständen Erschütterungen empfangen und sie nach allen Richtungen und auf viel größere Entfernungen vermitteln werde. Diese Erzitterungen des Äthers bewirken nach Euler das Licht. In Wirklichkeit komme also nichts Stoffliches von der Sonne zu uns, ebensowenig wie von einer Glocke, wenn ihr Geläut unser Ohr trifft. Man brauche daher auch nicht zu befürchten, daß die Sonne, indem sie Licht spendet, die geringste Einbuße an Substanz erleide. Den scheinbaren Widerspruch, der darin liegt, daß die irdischen Lichtquellen sich doch augenscheinlich verzehren, erklärte Euler ganz richtig daraus, daß diese Lichtquellen nicht nur leuchten, sondern auch Rauch und Ausdünstungen abgeben. Könnte man, sagt Euler, diesen Rauch und diese Ausdünstungen aufheben, so würde das bloße Leuchten keine Verminderung mit sich bringen. Als Beweis dafür gilt ihm die Erscheinung, daß Quecksilber, das man in einer evakuierten Röhre schüttelt, in den leuchtenden Zustand versetzt wird, ohne an Substanz einzubüßen.
Daß sich die Zahl der Ätherschwingungen je werde ermitteln lassen, bezweifelte Euler. Das Sonnenlicht soll deshalb weiß erscheinen, weil es in Ätherschwingungen von jeder Zahl bestehe. Bei der Brechung spalte sich das weiße Licht in Wellen von verschiedener Länge; diese rufen nach ihrer Trennung die einfachen Farben hervor. Um die Körperfarben zu erklären, vergleicht Euler die Teilchen der Körper mit gespannten Saiten. Wie diese durch Töne, die ihrem Grundton entsprechen, in Schwingungen versetzt werden, ebenso verhalten sich die Körperteilchen, je nach dem Grade ihrer Elastizität, gegenüber den Schwingungen des Äthers. Ein Körper erscheint uns rot, wenn seine Teilchen eine bestimmte, dem roten Licht entsprechende Zahl von Schwingungen mitmachen. Weiß erscheint der Körper, wenn seine Teilchen vermöge ihres Spannungszustandes auf alle Schwingungen abgestimmt sind, die das Sonnenlicht enthält; schwarz erscheint er, wenn er nicht mitschwingt.
Aus dem Gesagten erkennen wir, daß Euler den Vorstellungen, die sich später aus der Undulationstheorie über das Zustandekommen der Farben entwickelt haben, sehr nahe gekommen ist. Trotz aller Klarheit, mit welcher er seine Anschauungen über die Natur des Lichtes in den Briefen an eine deutsche Prinzessin737 vorträgt, sowie seiner in den Denkschriften der Berliner Akademie gegebenen wissenschaftlichen Begründung dieser Anschauungen, blieb die von Newton herrührende Emanationstheorie unerschüttert. Was dem bloßen, gleichfalls von einem theoretischen Standpunkte aus erfolgenden Bekämpfen einer irrigen Hypothese nicht gelang, hat die spätere Entdeckung neuer Tatsachen sofort herbeigeführt. Solchen gegenüber konnte eine Hypothese, die sich nicht mit ihnen in Einklang bringen ließ, keinen Stand halten.
Auch um die Berichtigung eines anderen Irrtums Newtons machte Euler sich verdient. Ersterer hatte die Beseitigung der chromatischen Abweichung für unmöglich erklärt, da die Brechung des Lichtes stets mit einer Farbenzerstreuung verbunden sei. Infolgedessen hielt man die Vervollkommnung der dioptrischen Fernröhre für ausgeschlossen und wandte sich gleich Newton vorzugsweise der Verfertigung von Spiegelteleskopen zu, die gegen das Ende des 18. Jahrhunderts durch Wilhelm Herschel einen hohen Grad der Vollendung erreichten. Der Ansicht Newtons gegenüber wies nun Euler im Jahre 1747 darauf hin, daß im Baue[S. 421] unseres Auges das von Newton für unlösbar gehaltene Problem doch gelöst sei, da die auf der Netzhaut erzeugten Bilder den Fehler der chromatischen Abweichung nicht besäßen. Da beim Auge in verschiedenem Grade brechende Medien, wie die Substanz der Hornhaut, die Linse und der Glaskörper, bei der Bilderzeugung zusammenwirken, so kam Euler auf den Gedanken, mit dem Glase einen zweiten Stoff in entsprechender Weise zu verbinden und dadurch die Farbenzerstreuung zu beseitigen. Euler suchte dieses zu erreichen, indem er seine Objektivgläser, wie es die nebenstehende Abb. 122 erläutert, aus Glas und Wasser zusammensetzte. Das Verfahren bot zwar in der Ausführung Schwierigkeiten, zeigte aber immerhin die Richtigkeit der Eulerschen Folgerungen, da die Bilder, wenn sie auch nicht die gewünschte Schärfe besaßen, doch frei von dem gedachten Fehler waren.
Angeregt durch diese Untersuchung Eulers kam zehn Jahre später der Optiker Dollond738 auf den Gedanken, anstatt Glas und Wasser zwei Glassorten von ungleichem Brechungsvermögen zu wählen. Zunächst verfertigte er Kron- und Flintglasprismen von verschiedenen Brechungswinkeln. Beim Prüfen dieser Prismen ergaben sich Zusammenstellungen, bei denen der hindurchgegangene Strahl keine Farbenzerstreuung mehr aufwies und doch noch, wenn auch in geringerem Grade, gebrochen wurde. Nachdem sich auf solche Weise der Gedanke als durchführbar erwiesen, ging Dollond zu seiner praktischen Verwertung über. Er setzte Linsen aus zwei Stücken zusammen, von denen das eine aus Kron-, das andere aus Flintglas bestand. Auch hierbei wurde die zweckmäßigste Vereinigung durch Ausprobieren bewerkstelligt. Damit war das achromatische Fernrohr erfunden, das durch Dollonds Sohn und insbesondere im Beginn des 19. Jahrhunderts durch Joseph Fraunhofer einen solchen Grad der Vollendung erhielt, daß der während des 18. Jahrhunderts herrschende Reflektor das Feld räumen mußte739.
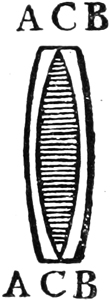
Auch mit einem wichtigen Problem der angewandten Mechanik hat sich Euler beschäftigt. Im Jahre 1750 hatte Segner das nach ihm benannte Wasserrad erfunden741. Dies veranlaßte Euler, eine »Vollständigere Theorie der Maschinen, die durch die Reaktion des Wassers in Bewegung gesetzt werden«, zu entwickeln742. Die Arbeiten von Segner und Euler sind für den Bau der horizontalen Wasserräder (Turbinen) grundlegend gewesen. Die soeben erwähnte Abhandlung Eulers wird selbst heute noch als nur wenig veraltet betrachtet743. Euler löst in ihr die Aufgabe, die Leistung einer hydraulischen Maschine zu finden, die für ein gegebenes Gefälle und einen bestimmten Wasserverbrauch gebaut ist. Ferner wird an einer Reihe von Beispielen gezeigt, wie man für gewisse Bedingungen die größtmögliche Leistung der Turbine berechnen kann.
Der Weg zu der dem 18. Jahrhundert gelungenen, vorläufig abschließenden Gestaltung der Mechanik führt von den Bernoullis und Euler über d'Alembert zu Lagrange, dem großen Analytiker, dem jener Abschluß vorbehalten blieb. Die durch Euler repräsentierte, ältere Generation begnügte sich mit der Lösung zahlreicher, isolierter Aufgaben aus allen Teilen der angewandten Mathematik. Für jedes Problem mußte man daher einen neuen Weg, für jede Aufgabe besondere Kunstgriffe suchen, so daß nur die hervorragendsten mathematischen Talente sich auf dem Gebiete der Mechanik betätigen konnten. Durch d'Alembert und in noch höherem Grade durch Lagrange wurde dieser Mangel beseitigt, indem sie die allgemeinen Sätze fanden, die auf ganze Gruppen von mechanischen Aufgaben anwendbar sind. D'Alembert war es, der diese »Formgebung« der Mechanik einleitete, während Lagrange sie vollendete744. Diese Bedeutung d'Alemberts rechtfertigt es, daß wir nicht nur seinem Hauptwerk, sondern auch seinem Lebensgang eine kurze Darstellung zuteil werden lassen, zumal seine Beziehungen zu den philosophischen Bestrebungen der Aufklärungsperiode von besonderem Interesse sind.
D'Alemberts Lebensumstände waren ganz außergewöhnliche. Zu der Zeit, als in Frankreich der berüchtigte Herzog von Orleans die Regentschaft führte, fand man auf den Stufen einer Kirche ein ausgesetztes Kind, das der Frau des Handwerkers Alembert zum Aufziehen übergeben wurde. Erst als dieses Kind zum Manne geworden, der sich unter dem Namen d'Alembert einen geachteten Namen geschaffen hatte, wurde der Schleier, der seine Herkunft verbarg, gelüftet. Es stellte sich nämlich heraus, daß seine Mutter eine Frau war, in deren Salon hervorragende Schriftsteller, vornehme Militärs und Kleriker, darunter der spätere Papst Benedikt XIV., verkehrten. Mit 12 Jahren wurde d'Alembert in ein Collège aufgenommen. Er studierte Theologie, die Rechte und Medizin, bis er sich schließlich mit ausgesprochener Neigung der Philosophie und den mathematischen Wissenschaften zuwandte.
D'Alembert wurde Mitglied der Pariser und der Berliner Akademie. Den glänzenden Verlockungen, durch die ihn Friedrich der Große und Katharina II. an sich zu fesseln suchten, widerstand er. Er blieb in Frankreich und starb dort im Jahre 1783.
Seine grundlegende »Abhandlung über Dynamik« veröffentlichte d'Alembert im Alter von 26 Jahren (1743)745. Sie bedeutet einen Markstein in der Entwicklung der Mechanik, weil sie für die Bewegung der Körper ein ebenso einfaches Grundprinzip aufstellte, wie man es für das Gleichgewicht in dem Prinzip der virtuellen Geschwindigkeiten besaß.
Die Ableitung des d'Alembert'schen Prinzips geht auf das Problem des zusammengesetzten Pendels zurück. Offenbar ist ein solches nichts anderes als ein Hebel, der sich in Bewegung befindet. An einem solchen werden die auf jeden Massenpunkt wirkenden Kräfte bekanntlich in zwei Bestandteile zerlegt, von denen die einen sich gegenseitig aufheben, zur Bewegung also nicht beitragen, während die anderen im Gegensatz zu jenen »verlorenen«, sich das Gleichgewicht haltenden Kräften dem System die Bewegung erteilen. Derjenige Massenpunkt, an dem weder Verlust noch Gewinn stattfindet, ist der uns aus früheren Betrachtungen bekannte Schwingungsmittelpunkt. Auch d'Alembert behandelt als typischen Fall für sein Prinzip eine an einem Ende befestigte und im übrigen mit verschiedenen Körpern beschwerte Stange,[S. 424] also ein System, das sich gleichfalls als ein zusammengesetztes Pendel oder ein in Bewegung begriffener Hebel betrachten läßt. Dann zerlegt er, wie es schon vor ihm Jakob Bernoulli bei der Untersuchung des zusammengesetzten Pendels getan, die wirkenden Kräfte in diejenigen, die im Gleichgewicht sein müssen, und in diejenigen, welche die Bewegung hervorrufen. In dieser Art der Betrachtung liegt das Wesen von d'Alemberts Prinzip, das in seiner allgemeinen Fassung folgendermaßen lautet: Werden einem System von materiellen Punkten oder Körpern Bewegungen mitgeteilt, die infolge der wechselseitigen Verbindung der Punkte oder Körper eine Abänderung erfahren, so findet man die resultierenden Bewegungen auf folgende Weise. Man zerlege die jedem Körper mitgeteilten Bewegungen in je zwei andere a, α; b, β; c, γ ... derart, daß die Körper, wenn man ihnen nur die Bewegungen a, b, c beigelegt hätte, diese Bewegungen hätten bewahren können, ohne sich gegenseitig zu hindern; und daß, wenn man ihnen nur die Bewegungen α, β, γ ... eingeprägt hätte, das System in Ruhe geblieben wäre. Dann werden a, b, c ... die Bewegungen sein, welche diese Körper infolge ihrer Wechselwirkung annehmen.
Zahlreiche Anwendungen seines Prinzips hat d'Alembert im dritten Abschnitt seiner Abhandlung geboten746. Ferner gelang es ihm, die Theorie der Bewegung der Flüssigkeiten auf sein Prinzip zurückzuführen747. D'Alembert huldigte der zu seiner Zeit verbreiteten Ansicht, daß die Prinzipien der Mechanik beweisbar seien. Die Scheinbeweise, die er bringt, laufen indessen nur darauf hinaus, daß der behauptete Satz wahr sei, weil für das Gegenteil kein genügender Grund vorliege. Ein Zweifel hinsichtlich des Wesens der mechanischen Prinzipien spricht sich indessen schon in der zu jener Zeit gestellten Preisfrage der Berliner Akademie aus, »ob die Gesetze von notwendiger oder nur erfahrungsmäßiger Wahrheit seien«. D'Alemberts Satz führt offenbar die Aufgaben der Dynamik auf Gleichgewichtsuntersuchungen und die dabei gewonnenen Erfahrungen zurück. Der Satz macht die Erfahrung nicht etwa überflüssig. Er hat den »Wert einer Schablone« zur bequemen Lösung von Aufgaben. Er fördert »nicht so sehr das Durchblicken der Vorgänge, als ihre praktische Bewältigung«748.
Bevor wir näher auf die weitere Entwicklung der Physik eingehen, wollen wir uns mit dem Manne beschäftigen, der an Eulers Stelle trat und das Werk dieses Meisters fortgeführt hat. Das war Lagrange. Ihm und Euler ist es gelungen, anstatt des synthetischen Verfahrens früherer Jahrhunderte in allen Zweigen der reinen und der angewandten Mathematik, das rechnerische, analytische Verfahren zur Durchführung zu bringen.
Lagrange ist sowohl in amtlicher als in wissenschaftlicher Beziehung als der Nachfolger Eulers zu bezeichnen. Er wurde nämlich nach dem Fortgange Eulers (1766) in die Preußische Akademie der Wissenschaften aufgenommen und wirkte bis zum Tode Friedrichs des Großen (1786) in Berlin. Ein besserer Ersatz für Euler war nicht zu finden. An Bedeutung für die Weiterentwicklung der Mechanik trat Lagrange gegen Euler nicht zurück, so daß die Preußische Akademie sich rühmen kann, fast ein halbes Jahrhundert die beiden größten Meister dieser Wissenschaft zu den Ihren gezählt zu haben.
Wie sehr die staatliche Fürsorge den Fortschritt der Wissenschaften mitunter beeinflußt hat, das zeigt vor allem das Preußen Friedrichs des Großen. Unter dem rauhen, jedes wissenschaftlichen Sinnes baren Vater dieses Monarchen hatte die Preußische Akademie, in der sich während des späteren Verlaufs des 18. Jahrhunderts das regste geistige Leben verkörperte, ein geradezu klägliches Dasein gefristet. Der König hatte für die Gelehrten seines Staates kaum etwas anderes übrig als Spott. Der kulturelle und der politische Fortschritt Preußens wären unterblieben, wenn die Wissenschaften dort auch weiterhin eine so geringe Beachtung gefunden hätten wie zur Zeit Friedrich Wilhelms I. Was dieser versäumte, hat jedoch sein großer Sohn vollauf wieder ausgeglichen. Und zwar geschah dies nicht nur durch äußere Mittel, sondern vor allem durch die persönliche Anteilnahme und das stete Wohlwollen, das er den Gelehrten entgegenbrachte, sowie durch den Schutz, den er ihnen allen reaktionären Strömungen gegenüber bot. Wenn man sich die Entdeckungen und die Arbeiten vergegenwärtigt, welche die Mathematiker, Astronomen, Physiker, Chemiker, Anatomen und Botaniker der Preußischen Akademie während der Fridericianischen Periode geleistet haben, so muß man dem Historiker749 dieser Akademie darin recht geben, daß sie in Hinsicht auf die Naturwissenschaften zu jener Zeit von keiner[S. 426] anderen Akademie übertroffen worden sei. Man darf indessen nicht vergessen, daß ihre hervorragendsten Mitglieder Ausländer waren. Doch kehren wir zu Lagrange zurück.
Joseph Louis Lagrange wurde am 25. Januar 1736 in Turin geboren. Sein Vater stammte aus Frankreich; dieser geriet in Turin in solch mißliche Verhältnisse, daß der junge Lagrange, der Jüngste unter elf Geschwistern, frühzeitig auf seine eigene Kraft angewiesen war. Lagrange hat diesen Umstand später oft als ein Glück bezeichnet. Er meinte, hätte er Vermögen gehabt, so würde er die Mathematik nicht geliebt, vielleicht nicht einmal kennen gelernt haben. So sehen wir ihn, kaum 19 Jahre alt, bereits als Lehrer der Mathematik an einer Artillerieschule unterrichten, wo er jünger als ein Teil seiner Schüler war. Mit Euler und d'Alembert wurde Lagrange dadurch bekannt, daß er sich gleich den genannten großen Mathematikern mit dem damals so viel erörterten Problem der Saitenschwingungen befaßte. Zu einer Berühmtheit wurde Lagrange, als er mit 28 Jahren (1764) den großen mathematischen Preis der Pariser Akademie für eine Arbeit über die Libration des Mondes750 erhielt. Bei dieser Untersuchung hat er zum ersten Male das Prinzip der virtuellen Geschwindigkeiten751 angewandt, das er an die Spitze der analytischen Mechanik stellte. Nach Berlin war Lagrange durch Vermittlung d'Alemberts gekommen, den Friedrich der Große zunächst und zwar vergeblich um die Übernahme der bisher von Euler verwalteten Stelle zu gewinnen suchte. Nach dem Tode des großen Königs wurde Lagrange der Aufenthalt in Berlin durch einen Minister aber derartig verleidet, daß er nach Paris zurückkehrte, wo ihm durch Vermittlung der Königin freie Wohnung im Louvre angewiesen wurde. In Paris veröffentlichte er im Jahre 1788 sein Hauptwerk, die Mécanique analytique. Da Lagrange im öffentlichen Leben nicht hervortrat, so wurde er durch die Wirren der Revolutionszeit auch nur wenig behelligt. Er wirkte während dieses Zeitabschnittes an der École Polytechnique und war auch in der Kommission tätig, die 1792 mit der Festsetzung des neuen Maßsystems beauftragt wurde. Napoleon, der größte Förderer der exakten Wissenschaften, den die Geschichte kennt, überhäufte ihn mit Ehren und nannte ihn, halb im Scherz, halb aus Bewunderung, »La haute pyramide des sciences mathématiques«.[S. 427] Lagrange starb am 10. April des Jahres 1813 und wurde im Pantheon bestattet. Seine Bedeutung hat Laplace in einem Nachruf mit folgenden Worten gekennzeichnet: »Lagrange hat gleich Newton in höchstem Maße die glückliche Kunst besessen, die allgemeinen Prinzipien zu entdecken, die das Wesen der Wissenschaft ausmachen. Diese Kunst verstand er mit einer seltenen Eleganz in der Entwicklung der abstraktesten Theorien zu verbinden.«
Wir beschäftigen uns zunächst mit dem Anteil, den Lagrange an der Entwicklung der reinen Mathematik genommen hat. Auf diesem Gebiete setzte er die Arbeit der Bernoulli und Eulers fort. Nur erwähnt seien Lagranges Zusätze zu Eulers Elementen der Algebra. Sie beziehen sich auf das Gebiet der unbestimmten oder diophantischen Analysis, dem Euler den letzten Teil seines Werkes widmete. Diese Untersuchungen gehören der reinen Mathematik an und stehen mit der Entwicklung der Naturwissenschaften in einem nur lockeren Zusammenhange. Sie haben aber in der neuesten Zeit die Grundlage für die Theorie der algebraischen Zahlen gebildet und sind aus diesem Grunde vor kurzem durch eine deutsche Übersetzung zugänglicher gemacht worden752.
Mit den unbestimmten Gleichungen befaßt sich Lagrange auch in einer für dieses Gebiet grundlegenden Abhandlung vom Jahre 1768753. Er bewältigt darin die Aufgabe, alle unbestimmten Gleichungen zweiten Grades mit zwei Unbekannten durch ganze Zahlen zu lösen. Der Versuch, solche Gleichungen zu lösen, reicht weit in der Geschichte der Mathematik zurück. Fermat gelang die Lösung, doch hat er sein Verfahren nicht bekannt gegeben. Es blieb daher Lagrange vorbehalten, ein allgemeines Verfahren zu entwickeln und zu beweisen, daß jene Gleichungen stets in ganzen Zahlen lösbar sind. Da sich nun jede Gleichung zweiten Grades mit zwei Unbekannten auf die einfache Form[S. 428] A = x2 + By2 bringen läßt, so war das Problem in seiner Allgemeinheit gelöst.
Gleichfalls an Euler anknüpfend, hat Lagrange ferner die Theorie der partiellen Differentialgleichungen mitbegründet. Wird eine Gleichung y = f(x) differenziert, so läßt sich aus der entstandenen Differentialgleichung durch Integration die ursprüngliche Gleichung wiederherstellen. Eine solche Integration ist jedoch nicht für jede beliebige Differentialgleichung möglich. Es galt daher, ein Kennzeichen für die Integrierbarkeit einer Differentialgleichung zu finden, und diese Aufgabe löste Euler für solche Gleichungen erster Ordnung schon 1734. Später dehnte er mit Erfolg diese Untersuchungen auf Differentialgleichungen höherer Ordnung aus. Zu einer allgemeinen Theorie für dieses Gebiet ist Euler allerdings nicht gelangt, sondern er beschränkte sich auf die Durchführung zahlreicher besonderer Fälle von Integrationen. Die allgemeine Lösung des Problems blieb Laplace und den Mathematikern des 19. Jahrhunderts (Pfaff, Cauchy und anderen) vorbehalten.
Die Abhandlungen von Lagrange, welche die Lehre von der Integration der Differentialgleichungen förderten, fallen in den Zeitraum von 1772–1785. Seine Untersuchung vom Jahre 1772 »Über die Integration der partiellen Differentialgleichungen erster Ordnung« wurde auch in deutscher Übersetzung zugänglich gemacht754. Eine vollständige Integrationsmethode für lineare partielle Differentialgleichungen mit beliebig vielen Veränderlichen fand Lagrange indessen erst sieben Jahre später, nachdem er sich dem durch Eulers Untersuchungen gestellten Problem zugewandt hatte.
Mit Lagrange begann auch eine neue Epoche in der Behandlung der Maxima- und Minimaaufgaben. Der Fortschritt bestand darin, daß er die analytische Bewältigung der hierher gehörigen Probleme ins Auge faßte, während die Bernoulli und Euler vorzugsweise geometrisch verfuhren. Die hierbei befolgte Methode von Lagrange bestand in einer engen Verbindung der Differential- mit der Integralrechnung und wurde von Euler mit dem besonderen Namen der »Variationsrechnung« belegt. Die grundlegende Abhandlung von Lagrange für diesen Teil der höheren Analysis erschien im Jahre 1762755.
Wie die Isoperimeterprobleme756 seit dem Altertum behandelt und insbesondere durch Fermat gefördert wurden, haben wir an früherer Stelle757 erfahren. Während des 18. Jahrhunderts waren es zunächst die Bernoulli und Euler, die sich mit diesen Problemen befaßten. In seiner epochemachenden Abhandlung vom Jahre 1762 löste Lagrange in seiner Allgemeinheit das Problem, für eine Integralformel ∫Z, in der Z eine bestimmte Funktion der Variabeln x, y, z und ihrer Differentiale bezeichnet, diejenige Relation zu finden, welche diese Variabeln unter sich haben müssen, damit ∫Z ein Maximum oder ein Minimum wird. Dann wendet er sich zur Erläuterung seiner Methode der Brachystochrone zu, einer Kurve, die in der Geschichte der Mathematik ihre besondere Bedeutung besitzt, weil sie den Untersuchungen der Bernoulli über isoperimetrische Probleme zum Ausgangspunkt gedient hat758.
Eine Vereinfachung und Vervollständigung der Variationsrechnung hat Lagrange in einer Abhandlung759 vom Jahre 1770 und vor allem in seiner »Analytischen Mechanik« (1788) gegeben. Auch Legendre und später Jacobi haben wertvolle Beiträge zur weiteren Ausgestaltung des für die mathematische Physik so wichtigen Verfahrens geliefert760.
Lagrange war es vorbehalten, die Mechanik in ein System zu bringen und durch die Verbindung des Prinzips der virtuellen Geschwindigkeiten mit dem Satze von d'Alembert diejenige Gleichung abzuleiten, die er selbst als die dynamische Grundformel bezeichnete, weil sich danach »die Bewegung irgend eines Systems von Körpern regelt«761. Durch diese Leistung Lagranges ist seine »Mécanique analytique« vom Jahre 1788 zum Fundament[S. 430] der neueren Mechanik geworden und zu einer Bedeutung gelangt, die derjenigen, die Newtons »Prinzipien« für das vorhergehende Zeitalter besaßen, fast gleichkommt. Ein wesentlicher Unterschied zwischen Newton und Lagrange besteht indessen darin, daß Newton seine Sätze an der Figur entwickelte und somit rein geometrisch (synthetisch) verfuhr, während Lagrange und sein Vorgänger Euler auf dem Gebiete der Mechanik die analytische oder rechnende Methode begründeten. Das Bestreben dieser Analytiker lief darauf hinaus, zu möglichst umfassenden Formeln zu gelangen, welche die Behandlung der zahlreichen Einzelfälle nach dem gleichen Schema ermöglichen und sie dadurch erleichtern. In diesem Sinne ist Lagranges analytische Mechanik wohl als eine der großartigsten Leistungen für die Ökonomie des Denkens bezeichnet worden762.
Für die Statik leitete Lagrange die allgemeine Formel für das Gleichgewicht eines beliebigen Systems von Kräften aus dem Prinzip der virtuellen Verschiebungen ab. Wirken auf eine Anzahl von Massenpunkten, die zu einem System verbunden sind, die Kräfte P1, P2, P3 ... und sind die entsprechenden virtuellen Verschiebungen p1, p2, p3 ..., so herrscht in dem System Gleichgewicht, wenn P1p1 + P2p2 + P3p3 + ... = 0 ist. Der kürzeste Ausdruck für diese Grundformel der Statik lautet:
∑Pp = 0.
Bezieht man die Massenpunkte auf ein rechtwinkliges Koordinatensystem und zerlegt jede Kraft in ihre parallel zu den Koordinatenachsen wirkenden Komponenten, so lautet die Formel:
∑(Xdx + Ydy + Zdz) = 0.
Die Komponenten für die einzelnen Massenpunkte sind X1Y1Z1, X2Y2Z2 usw. Ferner sind die virtuellen Verschiebungen für die zuletzt erwähnte Formel, gleichfalls parallel den Achsen zerlegt, dx1dy1dz1, dx2dy2dz2 usw.
Die Ableitung der Grundformel für die Dynamik aus dem Prinzip der virtuellen Geschwindigkeiten in Verknüpfung mit dem Satz von d'Alembert gestaltet sich folgendermaßen. Es seien m1m2m3 ... die Massenpunkte, x1y1z1, x2y2z2 ... die zugehörigen Koordinaten, und X1Y1Z1, X2Y2Z2 ... wieder die Kraftkomponenten. Da die Massenpunkte unter sich verbunden sind, so führen[S. 431] sie Bewegungen aus, welche durch die Kräfte m1d2x1/(dt2), m1d2y1/(dt2), m1d2z1/(dt2) ... an den nicht miteinander verbundenen Massen hervorgerufen werden können. Diese Kräfte und die angreifenden Kräfte X, Y, Z ... stehen nach d'Alemberts Prinzip im Gleichgewicht. Wendet man darauf das Prinzip der virtuellen Verschiebungen an, so ergibt sich die Formel:
Σm(d2x/(dt2)δx + d2y/(dt2)δy + d2z/(dt2)δz) = Σm(Xδx + Yδy + Zδz).
Dafür kann man auch schreiben:
Σ{m(X - d2x/(dt2))δx + m(Y - d2y/(dt2))δy + m(Z - d2z/(dt2))δz} = 0.
Die Grundformeln der analytischen Mechanik geben uns nicht etwa neue Aufschlüsse über die Natur der mechanischen Vorgänge, sondern sie bauen sich auf schon bekannten Prinzipien auf. Was sie bieten, ist die Möglichkeit, mit ihrer Hilfe auf rechnerischem Wege zur Bewältigung der Einzelfälle dieser Wissenschaft zu gelangen763. Die Vervollkommnung, welche die analytische Mechanik seit Lagrange durch Poisson, Green, Hamilton, Gauß, Helmholtz und andere Forscher erfuhr, hing daher von der weiteren Entwicklung des Kalküls ab.
Durch seine »Analytische Mechanik« förderte Lagrange nicht nur die mathematische Physik, sondern vor allem auch die theoretische Astronomie. Um letztere machte sich Lagrange außerdem noch durch eine Reihe von Abhandlungen verdient, unter denen sein »Versuch einer neuen Methode, um das Problem der drei Körper zu lösen« besondere Erwähnung verdient764.
Die Abweichungen, die ein Planet in seiner elliptischen Bahn um den Zentralkörper durch den Einfluß eines dritten Weltkörpers erfährt, hatte Newton noch nicht in Rechnung ziehen können. Die ersten, denen dies für besondere Fälle gelang, waren Clairaut und Euler. Nach ihnen haben sich um die Bewältigung dieses Problems Lagrange und ganz besonders Laplace verdient gemacht. War man auch nicht imstande, eine völlig befriedigende Theorie zu finden, so erkannte man doch, daß auch unter dem Einfluß eines dritten Körpers eine elliptische Bewegung stattfindet,[S. 432] bei der jedoch die Elemente der Ellipse sehr langsamen (säkularen) Änderungen unterworfen sind. Da also im Verlaufe langer Zeiträume periodisch derselbe Zustand wieder eintritt, so erschien die Stabilität des Sonnensystems gesichert.
Endlich sei noch erwähnt, daß Lagrange die mathematische Analyse auch in den Dienst der Kartographie gestellt hat. Der erste, der die Theorie dieser Disziplin unter allgemeine Gesichtspunkte zu bringen suchte, war bekanntlich Lambert765. Er stellte sich die Aufgabe, die Lage der Längen- und Breitenkreise so zu bestimmen, daß alle auf der Karte vorkommenden Winkel den betreffenden Winkeln auf der Erdkugel gleich sind. Dieselbe Aufgabe beschäftigte auch Euler766. Während Lambert und Euler sich noch auf bestimmte Projektionsarten beschränkten, suchte Lagrange der Theorie eine größere Allgemeinheit zu geben, indem er alle Fälle in Betracht zog, in welchen die Meridiane und die Parallelkreise durch Kreise wiedergegeben werden767.
Die Ausdehnung der mathematischen Analyse auf sämtliche Gebiete der Naturwissenschaft kam im 18. Jahrhundert nicht nur der reinen und der angewandten Mechanik, sondern auch der Optik und der so lange vernachlässigten Akustik zugute.
Die Optik war bis auf Keplers und Scheiners Zeit eine vorwiegend geometrische Wissenschaft gewesen. Scheiner errichtete die Grundlagen für die physiologische Optik. Eine bemerkenswerte Erweiterung der Theorie des Sehens unter Berücksichtigung der physiologischen und der physikalischen, insbesondere der quantitativen Seite, erfolgte um die Mitte des 18. Jahrhunderts durch Lambert, den wir als den Begründer der Photometrie bezeichnen müssen. Lambert erschöpfte dies Gebiet in einer Weise, daß seit dem Erscheinen seines großen, diesen Wissenszweig behandelnden Hauptwerkes768 nur wenige die Photometrie betreffende[S. 433] Fragen aufgeworfen und erörtert worden sind, die er nicht schon behandelt oder gestreift hätte.
Johann Heinrich Lambert wurde am 26. August des Jahres 1728 zu Mülhausen im Elsaß als Sohn eines armen Handwerkers geboren. Da es an Mitteln fehlte, um den hochbegabten Knaben, dem Rate seiner Lehrer entsprechend, studieren zu lassen, war Lambert zunächst gezwungen, das Schneiderhandwerk zu erlernen. Seiner schönen Handschrift verdankte er dann eine Anstellung als Schreiber. Zunächst war er als solcher in einem Eisenwerk, später bei einem Professor der Rechtswissenschaft in Basel tätig. Letzterer ließ ihm einen Teil des Tages zur wissenschaftlichen Weiterbildung frei, und so vermochte es Lambert, die Lücken seiner Bildung auszufüllen. Sein Gönner verschaffte ihm darauf eine Stelle als Erzieher in einem gräflichen Hause. Hier und in den Jahren, die er mit seinen Zöglingen auf der Universität verlebte, fand Lambert Muße, sich eingehender mit wissenschaftlicher Arbeit zu befassen. Sein Interesse war besonders der Astronomie zugewandt. Aus dem Bestreben, gewisse astronomische Fragen zu lösen, entsprang auch seine Beschäftigung mit der Lehre vom Licht. Bald nachdem Lambert seine Tätigkeit als Erzieher aufgegeben hatte, erschienen rasch nacheinander seine drei Hauptwerke, nämlich die Photometrie (1760), eine Abhandlung über den Lauf der Kometen und seine kosmologischen Briefe (1761). Lambert war dadurch als kaum Dreißigjähriger mit einem Schlage zu einer europäischen Berühmtheit geworden. Auch als Philosoph gewann der vielseitige Mann einen solch hervorragenden Ruf, daß Kant ihn für einen der ersten unter seinen Zeitgenossen hielt769. Kant schrieb an Lambert, er halte ihn für das größte Genie Deutschlands und für den geeigneten Mann, die Philosophie zu reformieren. Er selbst wolle keine Zeile in seinen Werken stehen lassen, die Lambert nicht deutlich finde. Die Bemühungen der Petersburger Akademie um Lambert wurden dadurch vereitelt, daß ihn die Berliner Akademie zum Mitglied ihrer physikalischen Klasse mit einem Jahresgehalt von 500 Talern[S. 434] ernannte. Lambert stand in regem wissenschaftlichen Verkehr mit Euler und Lagrange. Er starb am 25. September 1777. Sein frühzeitiger Tod wird darauf zurückgeführt, daß er durch übermäßiges Arbeiten seine Gesundheit untergrub.
Über Lambert besitzen wir folgende Charakterzeichnung: »Er war gleichgültig gegen alles, was das Leben schön und behaglich macht. Sein Kopf arbeitete unbehelligt durch Leidenschaften wie eine schwer zum Stehen zu bringende Maschine. Dabei war er harmlos und naturwüchsig. In der Mathematik stand Lambert nicht auf der Höhe von Euler und Lagrange. In der Astronomie war er kein Herschel, in der Physik kein Newton. In der Philosophie gebrach es ihm an Leibnizens Fülle und Beweglichkeit und an Kants bohrendem Tiefsinn. Aber, daß er alle vier Disziplinen mit grundlegenden und fortbildungsfähigen Arbeiten befruchtete, macht ihn doch den Größten ähnlich.«
Auf dem Gebiete der Photometrie war vor Lambert nur wenig geschehen. Kepler hatte zwar den Hauptsatz, daß die Lichtstärke mit dem Quadrate der Entfernung abnimmt, geometrisch abgeleitet, zu Versuchen, die Lichtstärken verschiedener leuchtender Körper zu vergleichen, war indessen erst Huygens übergegangen. Das erste wirkliche Photometer hatte dann der Franzose Bouguer (1698 bis 1758) geschaffen. Es bestand aus zwei durchscheinenden Schirmen, die sich in den Öffnungen OO1 (s. Abb. 123) befanden. Damit das Licht der beiden Lichtquellen sich nicht vermischen konnte, war zwischen den beiden Öffnungen nach der Seite der Flammen eine Scheidewand (F) angebracht. Die Lichtquelle, deren Stärke zu messen war, wurde verschoben, bis dem vor OO1 befindlichen Auge die transparenten, in OO1 befindlichen Schirme gleich hell erschienen.
Bouguer verfaßte auch ein Werk über die Photometrie, das 1760, also gleichzeitig mit Lamberts, denselben Gegenstand betreffender Schrift erschien, von Lambert also nicht berücksichtigt werden konnte770. Es läßt sich begreifen, daß die Verdienste Bouguers[S. 435] und Lamberts um die Begründung des neuen Wissenszweiges gegeneinander abgewogen wurden, und es hat nicht an Stimmen gefehlt, die Lambert gegenüber Bouguer zu verkleinern suchten771. Anerkannt muß werden, daß der französische den deutschen Forscher in der Anstellung sinnreicher und sorgfältiger Versuche übertraf, während Lambert bei seinen experimentellen Untersuchungen sogar mit einer gewissen Nachlässigkeit verfuhr. Bestand doch sein ganzes Instrumentarium nur aus drei kleinen Spiegeln, zwei Linsen, einigen Glasplatten und einem Prisma. Andererseits gebührt Lambert das Verdienst, die Begriffe und das System der Photometrie geschaffen zu haben. Während Bouguer sich an Beobachtungen hält und aus ihnen nicht mehr folgert, als sich streng genommen daraus folgern läßt772, weiß Lambert jedem Problem eine, bis zum Ziel gelangende, mathematische Lösung zu geben. Allerdings war dies mitunter nur auf Grund einer so weit gehenden Vereinfachung der Voraussetzungen möglich, daß das Ergebnis der Rechnung nur als eine rohe Annäherung an die wirklichen Verhältnisse betrachtet werden durfte. Daß der Franzose, wie wir hervorhoben, die Beobachtung und die genaue Messung, der Deutsche dagegen die Begriffsbestimmung und die Ableitung, unbeschadet mangelhafter Empirie, in den Vordergrund stellt, war kein Zufall, sondern entsprach der Eigenart französischen und deutschen Geistes. Ein ähnliches Verhältnis waltete im 18. Jahrhundert zwischen den englischen und den deutschen Geisteserzeugnissen. Daß die Deutschen die Vorzüge der westeuropäischen Forschungsweise sich anzueignen und mit den eigenen Vorzügen zu verbinden wußten, hat dem Deutschland des 19. und 20. Jahrhunderts die führende Rolle auf manchen Gebieten der Naturwissenschaften eingebracht.
Nach diesen allgemeinen Bemerkungen und der Eingliederung Lamberts in die Reihe seiner Zeitgenossen773 wenden wir uns seiner Photometrie zu, einem Werke, das, wie sein Herausgeber hervorhebt, für den Astrophysiker ebenso unentbehrlich ist, wie für den Astronomen Laplaces Mécanique céleste774.
Lambert beginnt mit einer Betrachtung der Grundbegriffe der Photometrie. Gerade dasjenige, meint er, sei unserer Einsicht am meisten verschlossen, was der sinnlichen Wahrnehmung fortwährend begegne. Dafür stelle die Theorie des Lichtes ein ausgezeichnetes Beispiel dar. Daß diese nicht genüge, könne man schon daraus schließen, daß zwei so verschiedene Hypothesen wie diejenige von Newton und Euler (richtiger Huygens) zur Erklärung der Erscheinungen angewendet würden. Die erstere liege dem Verständnis näher, doch entspreche Eulers Theorie wohl mehr der Natur der Sache. Lambert knüpft daran einen oft wiederholten Ausspruch über die Beurteilung von Hypothesen. Seine Worte lauten: »Unter die vornehmsten und sichersten Kriterien dafür, daß eine Hypothese sich der Wahrheit nähert, muß man den Fall nehmen, wenn man aus ihrem Lehrgebäude den Eintritt neuer Erscheinungen vorhersehen und wenn man Sätze daraus folgern kann, denen die zu diesem Zwecke angestellten Versuche beipflichten«775. Diese Prüfung sollte erst weit später zugunsten der von Huygens und Euler vertretenen Wellentheorie entscheiden776.
Da es für photometrische Untersuchungen kein absolutes Maß gibt, sondern stets ein sehr subjektiver Faktor, das Urteil des Auges nämlich, in Betracht gezogen werden muß, macht Lambert die Voraussetzung, daß »eine Erscheinung stets dieselbe ist, so oft dasselbe Auge auf die gleiche Weise affiziert wird«. Das Auge sei bei verschiedenen Helligkeitsgraden zwar nicht imstande, zu entscheiden, um wieviel der eine größer sei als der andere, doch müsse man voraussetzen, daß das Auge über die Gleichheit zweier Helligkeitsgrade entscheiden könne. Nur durch die Verknüpfung dieses Axioms mit den schon aus geometrischen Überlegungen folgenden Prinzipien der Photometrie könne man zu einem Ausbau dieses Teils der Optik gelangen.
Von solchen Prinzipien hob Lambert außer dem Satze von der Abnahme des Lichtes mit dem Quadrate der Entfernung noch zwei besonders hervor. Das erste lautet: »Wird dieselbe Fläche einmal von m, das andere Mal von n Lichtquellen beleuchtet, von denen jede dieselbe Intensität besitzt und ihr Licht unter völlig gleichen Umständen nach der Fläche sendet, so verhalten sich die Helligkeitsgrade wie m : n.« Die Beleuchtung eines Blattes ist[S. 437] also um so stärker, je größer die Anzahl der leuchtenden Kerzen ist, vorausgesetzt, daß diese gleich hell sind, die gleiche Entfernung vom Blatte und die gleiche Größe besitzen777.
Der dritte, wichtigste Grundsatz sprach aus, daß die Helligkeit in demselben Verhältnis abnimmt wie der Sinus des Neigungswinkels. Der geometrische Beweis, den Lambert hierfür bringt (Photometrie § 53), ist in alle Lehrbücher der Physik übergegangen. Lambert begnügte sich nicht mit dem theoretischen Beweise dieser Sätze, sondern er suchte auch durch geeignete Versuche ihre gegenseitige Abhängigkeit darzutun und ihnen auf diese Weise eine noch größere Sicherheit zu verleihen.
Das nächste Kapitel beschäftigt sich mit der Messung und der Stärke des direkten Lichtes. Für zahlreiche Einzelfälle wird die Lichtmenge oder die Erleuchtungskraft berechnet, die von verschieden gestalteten Flächenstücken ausgeht. Das von Lambert benutzte Photometer stimmte mit dem nach Rumford benannten ziemlich überein. Lamberts Verfahren bestand darin, daß er die Helligkeit zweier Flächenstücke verglich, von denen das eine durch eine bestimmte Lichtquelle, das andere durch eine Lichtquelle, deren Stärke ermittelt werden sollte, beleuchtet wurde. Die Einrichtung geht aus Fig. 2 der Photometrie (s. Abb. 124) hervor.
In K und A befinden sich die beiden Lichtquellen, die verglichen werden sollen. BDCEFG sei eine weiße, ebene Fläche; vor dieser ist über HI ein undurchsichtiger, Schatten spendender Schirm aufgestellt. Der von der Lichtquelle bei A herrührende Schatten bedeckt den Teil DFEC der weißen Fläche, während der von K ausgehende Schatten auf DFGB fällt. Auf diese Weise wird der vordere Teil der Fläche DFGB nur von der[S. 438] Lichtquelle in A, der hintere Teil DFEC nur von den von K kommenden Strahlen beleuchtet. Die eine Lichtquelle wird dann so lange bewegt, bis die weiße Fläche zu beiden Seiten der Linie DF gleich hell erscheint.
Auf das Kapitel, das sich mit dem direkten Lichte beschäftigt, folgt ein anderes über die Reflexion des Lichtes durch dunkle Körper778. Ferner wird von der durch zerstreutes Licht erzeugten Helligkeit der durchsichtigen Körper, insbesondere der irdischen Atmosphäre gehandelt und eine Formel für die Extinktion des Lichtes auf seinem Wege durch die Atmosphäre abgeleitet (Photometrie § 878 bis 882). Im Anschluß hieran wird die Dämmerung untersucht und die Höhe der Atmosphäre unter gewissen einfachen Annahmen berechnet.
Der sechste Teil des Lambertschen Werkes enthält die Grundzüge der Astrophotometrie. Es wird darin die Theorie der Lichtstärke des Mondes und der Hauptplaneten entwickelt. Den Schluß bildet eine experimentelle und theoretische Erörterung über die Intensität des heterogenen und des relativen Lichtes, worunter die Farben und der Schatten verstanden sind.
Auf den Gang der Untersuchung kann hier nicht näher eingegangen werden, doch sei hier einiges über die Ergebnisse mitgeteilt. Nach Lambert entspricht die Absorption des Lichtes beim senkrechten Durchgang durch die Atmosphäre dem Verhältnis 100 : 59779. Für die mittlere Helligkeit des Vollmondes zu derjenigen der Sonne wird das Verhältnis 1 : 277000 ermittelt, und die mittlere Helligkeit des Vollmondes zu zwei Dritteln der mittleren Zentralhelligkeit bestimmt. Letztere wird dann auch für die Planeten aus der Zentralhelligkeit der Erde nach dem ersten von Kepler ausgesprochenen Grundsatz der Photometrie berechnet.
Während die Mechanik und die Optik seit den Zeiten Galileis von seiten aller hervorragenden Physiker gefördert wurden, blieb das Gebiet der Akustik zunächst vernachlässigt. Newton hatte zwar in seinen »Prinzipien« eine Formel für die Fortpflanzungsgeschwindigkeit des Schalles abgeleitet. Die experimentellen Bestimmungen dieser wichtigen Konstante schwankten jedoch zwischen[S. 439] 1071 und 1255 Pariser Fuß. Die Berechnung aus Newtons Formel ergab den noch geringeren Wert von 906 Fuß. Dieser Widerspruch zwischen Theorie und Erfahrung bewog die Mathematiker, sich mehr als bisher der Akustik zuzuwenden. Zunächst prüften Euler und bald darauf Lagrange die Newtonsche Formel, ohne jedoch zu einer Lösung des bestehenden Widerspruchs gelangen zu können. Daniel Bernoulli wandte sich besonders der Untersuchung der Luftschwingungen in den Orgelpfeifen zu780. Er sowie Euler lieferten ferner Untersuchungen über die Schwingungen von Saiten und Stäben. Die Abhandlungen, die Euler, Lagrange, Bernoulli, d'Alembert u. a. über diesen Gegenstand veröffentlichten, besitzen indessen mehr mathematischen als physikalischen Wert. Der erste, der den akustischen Problemen durch eine erfolgreiche Vereinigung von Experiment und mathematischer Analyse gerecht zu werden vermochte, war Chladni.
Ernst Florens Friedrich Chladni wurde als Sohn eines Professors der Rechte am 30. November 1756 in Wittenberg geboren. Er studierte zunächst gleichfalls die Rechte, wandte sich aber später mit großer Vorliebe den Naturwissenschaften und der Musik zu. Die Beschäftigung mit der letzteren veranlaßte ihn zum Lesen akustischer Schriften. Da ihm diese indessen nur sehr unvollkommene Aufschlüsse gaben, ging er zu eigenen Untersuchungen über.
Vor Chladni hatte man sich ausschließlich mit den Quer- oder Transversalschwingungen von Saiten befaßt. Chladni entdeckte, daß an Saiten und insbesondere an Stäben auch Longitudinalschwingungen und drehende Schwingungen hervorgerufen werden können781.
Um Longitudinalschwingungen zu erhalten, wurden die Stäbe festgehalten und der Länge nach gestrichen. Chladni benutzte dazu besonders Glasröhren. Zum Hervorrufen der Töne bediente er sich eines mit Smirgel bestreuten Tuches, das er mit der Hand den Stab entlang rieb. Bei mittlerer Länge des Stabes waren die Töne sehr hoch. Sie standen ferner in keinem bestimmten Verhältnis zu den an demselben Stab durch transversale Schwingungen erzeugten Tönen.
Auf die Longitudinalschwingungen von Stäben, die Chladni beschrieb (Über die Longitudinalschwingungen der Saiten und Stäbe, Erfurt 1796) gründete er die Erfindung einiger neuer Musikinstrumente, des Euphons und des Klavizylinders.
Das Euphon bestand aus Glasstäben, die auf Eisenstäben ruhten und mit angefeuchteten Fingern gerieben wurden. Beim Klavizylinder bestanden die Stäbe aus Holz; sie wurden durch eine Tastatur gegen einen rotierenden feuchten Glaszylinder gepreßt. Beide Instrumente gaben einen sanften, anhaltenden, langsam an- und abschwellenden Ton. Sie haben indessen keine Verbreitung gefunden.
Das Studium der Longitudinalschwingungen führte Chladni auch zu einer Berechnung der Fortpflanzungsgeschwindigkeit des Schalles in festen Körpern. Er fand sie weit größer als die Schallgeschwindigkeit in der Luft. Wählte er letztere als Einheit, so ergab sich diejenige für
| Zinn | gleich | 7,5 |
| Silber | » | 9 |
| Kupfer | » | 12 |
| Eisen | » | 17 |
| Glas | » | 17. |
Eine direkte Messung der Schallgeschwindigkeit in einem Metall hat einige Jahrzehnte später Biot vorgenommen. Er stellte sie an gußeisernen Röhren an, die auf eine längere Strecke verbunden waren. Wurde die so entstandene, sehr lange metallische Leitung an einem Ende angeschlagen, so nahm man den Ton zuerst durch das Metall und später durch die Luft wahr. Aus der Zeitdifferenz ergab sich für Gußeisen eine Fortpflanzungsgeschwindigkeit des Schalles von etwa 3500 Metern.
Chladni untersuchte auch die Geschwindigkeit in verschiedenen Gasen. Über die Stärke des Schalles in den Gasarten hatte schon Priestley Versuche angestellt. Er hatte gefunden, daß der Schall in Wasserstoff fast so schwach ist wie im Vakuum, während er in Sauerstoff und in Kohlensäure stärker ist als in der atmosphärischen Luft. Eine direkte Messung in den verschiedenen Gasarten vermochte Chladni nicht vorzunehmen. Sein Verfahren bestand darin, daß er Orgelpfeifen in verschiedenen Gasen ertönen ließ. Da hier die Schwingungszahl und somit die Höhe der Töne zu der Fortpflanzungsgeschwindigkeit in einem mathematisch bestimmten Verhältnis steht, ließ sich aus der Verschiedenheit der Tonhöhe, welche dieselbe Pfeife in verschiedenen[S. 441] Gasen aufwies, die Fortpflanzungsgeschwindigkeit des Schalles für jedes Gas ermitteln. Direkte Messungen hat später Regnault in Wasserleitungsröhren vorgenommen, die mit verschiedenen Gasen gefüllt waren. Sie ergaben, daß Chladnis Ableitungen im allgemeinen zutreffend sind.
Ein ganz neues Gebiet wurde von Chladni dadurch erschlossen, daß er sich der experimentellen und der mathematischen Untersuchung schwingender Platten zuwandte. Ausführlich berichtete er darüber 1787 in einer Schrift, die den Titel »Entdeckungen über die Theorie des Klanges« führt. Besonderes Aufsehen erregte er durch die Art, wie er die Schwingungen der Platten vermittelst der nach ihm genannten Chladnischen Klangfiguren sichtbar machte. Auf sein Verfahren wurde er durch die Lichtenbergschen Staubfiguren geführt. Sie entstehen, wenn fein gepulverte Körper, wie Schwefelblumen oder Mennige, auf Platten gebracht werden und man auf sie die Elektrizität überspringen läßt. Die Art, wie sich das Pulver lagert, läßt erkennen, ob die Elektrizität positiv oder negativ war.
War der überspringende Funke positiv, so ordnete sich das Pulver zu eigentümlichen Strahlen, war er negativ, so entstanden wolkenartige Gebilde. Als Chladni diese Versuche wiederholte, kam ihm plötzlich der Gedanke: Sollte sich nicht auf ebenen Scheiben, sobald sie klingen und etwas Sand darauf gestreut wird, eine Figur bilden, die den betreffenden Ton kennzeichnet und so gleichsam sichtbar macht.
Um auf diese Weise den akustischen Zustand einer Platte festzustellen, befestigte Chladni sie in horizontaler Lage an einer oder mehreren Stellen, strich sie unter rechtem Winkel mit einem Violinbogen und streute gleichzeitig Sand hinauf. Letzterer ordnet sich dann in den bekannten regelmäßigen Figuren an, indem er »von den schwingenden Stellen heruntergeworfen wird und auf den nicht schwingenden Stellen ruhig liegen bleibt.« Chladni erkannte daraus, daß »die natürliche Gestalt des Körpers durch die elastischen Flächenkrümmungen, ebenso in gewissen Linien durchschnitten wird, wie dieses bei den krummen Schwingungslinien der Saiten in gewissen Punkten geschieht, und daß zwei Stellen, die durch eine solche feste Linie voneinander gesondert sind, stets nach entgegengesetzten Richtungen schwingen«.
Die folgenden, dem Werke Chladnis entnommenen 4 Figuren zeigen uns, wie eine quadratische Platte schwingt, wenn sie in verschiedener Weise festgehalten und gestrichen wird.
Fig. 87 erscheint, wenn die Scheibe in der Mitte gehalten und an einer Ecke gestrichen wird. Diese Schwingungsart gibt den tiefsten Ton.
Fig. 88 entsteht, wenn man die Scheibe wieder in der Mitte befestigt, aber in der Mitte einer Seite streicht.
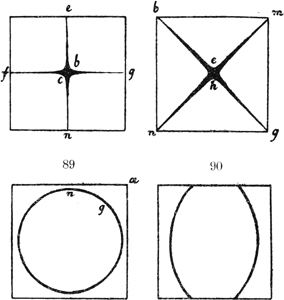
Der Ton ist dann nicht derselbe wie vorher, sondern etwa um eine Quinte höher.
Fig. 89, die leicht in 90 übergeht, erhält man, wenn die Scheibe bei n oder g gehalten und bei a gestrichen wird. Der Ton ist wieder etwas höher als der vorige.
Chladni zeigte, daß man durch Festhalten mehrerer Stellen und Abwechseln ihrer Lage eine ganz außerordentliche Mannigfaltigkeit von Schwingungszuständen und diesen entsprechenden Klangfiguren hervorrufen kann. Sie könnten, meint er, den Tapeten- und Kattunfabrikanten genug Stoff zur Bereicherung ihrer Muster geben. Die Klangfiguren fesselten das Interesse aller Kreise in hohem Grade, da Chladni, der kein Amt bekleidete, sie an vielen Orten in akustischen Vorträgen, durch die er seinen Lebensunterhalt erwarb, vorführte783.
Außer den erwähnten Schriften Chladnis ist noch sein zusammenfassendes Werk, »Die Akustik«, zu erwähnen784. In seinen neuen Beiträgen zur Akustik vom Jahre 1817 ermittelte Chladni die obere Grenze der Hörbarkeit von Tönen zu 22000 Schwingungen in der Sekunde.
Chladnis Verdienst um die Aufklärung der Natur der Meteore wird an anderer Stelle gewürdigt werden. Er starb in Breslau am 3. April des Jahres 1827.
Über den Stand der gesamten Experimentalphysik des 18. Jahrhunderts geben die großen Werke von Desaguliers, s'Gravesande und Musschenbroek Auskunft. Die genaueren Titel dieser mehr als bloß historisches Interesse erregenden Werke finden sich in der Literaturübersicht am Schluß des vierten Bandes. Sie befassen sich in erster Linie mit Gegenständen der angewandten Mathematik und haben dazu beigetragen, die Wissenschaft jener Zeit von der oft überwuchernden Spekulation immer wieder auf den sicheren Boden des Experiments zurückzuführen. Desaguliers beschäftigt sich besonders mit der Mechanik und dem Maschinenwesen. Bei s'Gravesande fallen dagegen die zahlreichen Untersuchungen aus dem Gebiete der Hydrostatik und der Hydrodynamik auf, während Musschenbroek, angeregt durch die Versuche der Florentiner Akademie, zahlreiche Versuche über die Wärme anstellte.
Die Astronomie wurde während des 18. Jahrhunderts immer mehr zum Vorbild, dem die übrigen Naturwissenschaften, vor allem die Physik, nachzueifern strebten. In der Vollendung der Methoden, sowie bezüglich der Sicherheit der Resultate, zu denen die Astronomie gelangte, reichte jedoch kein anderer Zweig an sie heran.
Neben dem Wettkampf zwischen dem dioptrischen Fernrohr und dem Reflektor beschäftigten die Astronomen des 18. Jahrhunderts noch zwei wichtige Fragen, welche die vorhergehende Periode aufgeworfen hatte. Sie betrafen die Abweichung der Erde von der Kugelgestalt und die Bestimmung der Sonnenparallaxe aus den 1761 und 1769 wieder zu erwartenden Vorübergängen der Venus. Um die von Newton und Huygens herrührende Annahme, daß die Erde ein an den Polen abgeplattetes Rotationsellipsoid sei785, auf ihre Richtigkeit zu prüfen, waren genaue Gradmessungen in der Nähe eines Pols und des Äquators erforderlich. War, der Theorie Newtons gemäß, die Krümmung in der Nähe der Pole eine geringere, so mußte sich hier für den Breitengrad eine größere Strecke ergeben als für eben dieses Maß in der Nähe des Äquators. Zur Entscheidung dieser Frage sandte die französische Regierung in den Jahren 1735 und 1736 Expeditionen nach Peru und Lappland. Die erstere, die von Bouguer786 und de la Condamine787 geleitet wurde, maß den Abstand zwischen zwei nördlich und südlich vom Äquator gelegenen Orten und fand für den Grad 56734 Toisen. Die von Maupertuis788 geführte zweite Expedition[S. 445] stellte ihre Messungen in der Nähe des Tornea unter dem 66. Grade nördlicher Breite an. Das von dieser Expedition gefundene Ergebnis belief sich auf 57438 Toisen789, war also um 704 Toisen größer als das am Äquator erhaltene, während sich für die Breite von 45° ein zwischen diesen beiden Größen liegender Wert von 57012 Toisen ergab. Die von Newton und Huygens aufgestellte Ansicht über die Gestalt der Erde hatte somit ihre Bestätigung erfahren. Nach de la Condamine ergaben diese Messungen, daß sich die Erdachse zum Durchmesser des Äquators wie 299 : 300 verhält, während Newton auf rechnerischem Wege das Verhältnis 288 : 289 gefunden hatte.
Zu den Männern, die Maupertuis auf seiner Lapplandexpedition begleiteten, gehörte der damals erst 23 Jahre alte Clairaut, der zu den größten Mathematikern Frankreichs zählt790. Ihm verdankt man die bedeutendste theoretische Untersuchung über die Gestalt der Erde791.
Clairauts Arbeit wurde besonders dadurch veranlaßt, daß die beiden Gradmessungen zwar die Richtigkeit der von Newton und Huygens vertretenen Annahme bewiesen, daß sich aber die Abplattung als nahezu doppelt so groß herausstellte, wie sie nach der Theorie hätte sein sollen. Clairaut ging davon aus, daß die Gestalt der Erde, abgesehen von den sehr geringen, als Berg und Tal in die Erscheinung tretenden Unregelmäßigkeiten, von den Gesetzen[S. 446] der Hydrostatik abhängen muß. Die Ausmessung der Erde könne daher nur dasselbe ergeben, wie wenn die Messungen auf einer festgewordenen Flüssigkeit ausgeführt wären, die vorher eine dem Gleichgewicht entsprechende Gestalt angenommen hätte. An dem damit gegebenen Problem, die Gestalt der Erde aus den hydrostatischen Gesetzen abzuleiten, hat sich die mathematische Hydrostatik recht eigentlich erst entwickelt792.
Die Anfangsgründe der Lehre vom Gleichgewicht der Flüssigkeiten rühren besonders von Newton und von Huygens her. Huygens hatte ausgesprochen, daß eine flüssige Masse nur dann in Ruhe ist, wenn ihre Oberfläche ein Niveau darstellt, d. h. wenn sie überall lotrecht zu den Kraftresultanten verläuft. Newton dagegen führte den Gleichgewichtszustand auf den Druck zurück, der in Flüssigkeitssäulen herrscht, die von der Oberfläche zum Kraftzentrum reichen. Clairaut endlich stellte ein umfassenderes Prinzip an die Spitze. Es spricht aus, daß eine flüssige Masse nur dann im Gleichgewicht sein kann, wenn die an allen Stellen eines beliebig geformten Kanals auftretenden Kräfte sich gegenseitig aufheben. Diesen Kanal kann man sich so entstanden denken, daß die übrige Masse der Flüssigkeit fest wird. Der Kanal kann ferner an der Oberfläche münden, in der Oberfläche selbst verlaufen oder auch in sich zurückkehren (Abb. 126). Von diesem Prinzip des beliebigen Kanals ausgehend, gelangte Clairaut zu den partiellen Differentialgleichungen für das Gleichgewicht der Flüssigkeiten. Besteht nämlich für jeden beliebigen Kanal Gleichgewicht, so ist offenbar auch die ganze Flüssigkeitsmasse im Zustande des Gleichgewichts.
Bei der Verwendung hydrostatischer Untersuchungen zur Erklärung der Gestalt der Erde beschränkte sich Newton auf eine homogene Masse. Für eine solche hatte Newton das Achsenverhältnis gleich 230 : 231 berechnet. Clairaut dehnte dagegen die Untersuchung auf den Fall aus, daß die Dichte der Schichten[S. 447] sich mit der Annäherung an das Zentrum ändert. Auf die Einzelheiten dieser Untersuchung und das daraus sich ergebende »Clairautsche Theorem«793 kann hier nicht näher eingegangen werden, da es sich um einen Gegenstand der höheren Analysis handelt.
Clairaut gehörte auch zu den ersten, die den höheren Kalkül auf die Theorie der Mondbewegung anwandten. Dazu bedurfte es einer Erörterung des Problems der drei Körper794, um dessen angenäherte Lösung sich außer Clairaut besonders d'Alembert, Euler, Lagrange und Laplace verdient gemacht haben.
Erwähnt sei noch, daß sich in Clairauts »Theorie der Erdgestalt« schon der Grundgedanke der Lehre von der Kraftfunktion oder dem Potential findet, mit deren Weiterentwicklung sich besonders Green, Laplace und Gauß beschäftigt haben795.
Weit genauer als diejenige Gradmessung, an der Clairaut sich beteiligte, war eine zweite, gegen das Ende des 18. Jahrhunderts vorgenommene. In diesem Falle handelt es sich nicht um eine vergleichende, aus rein wissenschaftlichen Gründen stattgefundene Messung, sondern um eine solche, die darauf abzielte, den genauen Wert einer den Maßen und Gewichten zugrunde zu legenden Naturkonstante zu ermitteln.
Der Wunsch, ein einheitliches Maß- und Gewichtssystem zu besitzen, war schon im 14. Jahrhundert mit dem Emporblühen des Handels rege geworden. Man empfand immer deutlicher, daß die bestehenden Unterschiede keinerlei Vorteil boten, sondern nur zu Mißbräuchen, Bedrückungen und Betrügereien Anlaß gaben. Die Bemühungen, hier Besserung zu schaffen, scheiterten schon an dem Widerstande der Fürsten und Prälaten. Es war daher eine der ersten Forderungen der Revolutionsmänner, die zahlreichen, in Frankreich wie in allen anderen Ländern bestehenden Maße durch ein gemeinsames, der Natur entlehntes Längenmaß zu ersetzen, und dieses als Grundlage für die Hohlmaße und die Gewichte festzulegen.
Als solches hatte schon 1670 ein Franzose796 die Minute eines Längengrades vorgeschlagen. Fast zur selben Zeit brachte Huygens in seinem Werke über die Pendeluhr (1673) das Sekundenpendel als Längeneinheit in Vorschlag. Huygens wünschte den dritten Teil des Sekundenpendels als Stundenfuß in allgemeinen Gebrauch genommen zu sehen. Bald darauf entdeckte man jedoch die Abhängigkeit der Länge des Sekundenpendels von der geographischen Breite. Aus diesem Grunde wurde die von Huygens ausgehende Anregung nicht weiter verfolgt.
Im Jahre 1790 wurde die Angelegenheit in der konstituierenden Nationalversammlung behandelt. Letztere beschloß, die Länge, welche das Sekundenpendel unter dem 45. Breitengrade besitzt, als Maßeinheit zu wählen und beauftragte eine Kommission, in der sich die bedeutendsten französischen Gelehrten (wie Laplace, Lagrange, Monge und Borda) befanden, das Erforderliche in die Wege zu leiten. Ein weiterer Beschluß lief darauf hinaus, auch die englische Regierung für das Vorhaben zu gewinnen, und die französische Kommission durch eine von der Royal Society in London gewählte zu ergänzen. Man verwarf den Vorschlag, als Längenmaß das Sekundenpendel festzusetzen, weil dieses wieder durch eine andere Größe, nämlich die Zeit und ihre willkürliche Einteilung in Sekunden, bedingt sei. Die Kommission schlug deshalb vor, den Meridianquadranten möglichst genau zu messen und seinen zehnmillionsten Teil als die gewünschte Einheit anzunehmen.
Veranlaßt durch diese Verhandlungen und Beschlüsse entstanden zwei Arbeiten, von denen die eine auf eine möglichst genaue Bestimmung des Sekundenpendels hinauslief. Die andere schuf die Grundlage des metrischen Systems. Sie bestand in der Messung eines von Dünkirchen bis Barcelona reichenden Meridianbogens797.
Die Pendelmessungen währten vom Juni bis zum August 1792. Sie erfolgten unter Anwendung aller Kautelen und mit der größten[S. 449] Genauigkeit nach der Methode der Koinzidenzen. Das Verfahren beruhte darauf, daß die Schwingungen des Pendels einer astronomischen Uhr mit den Schwingungen des zu messenden Pendels verglichen wurden. Uhr und Pendel waren durch einen Glaskasten vor Luftbewegungen geschützt. Das Pendel bestand aus einem dünnen Platindraht und einer Platinkugel von etwa 161/6 Linien Durchmesser. Sie war auf eine besondere Art befestigt798 und die Aufhängevorrichtung wurde so eingerichtet, daß sie auf die Schwingungsdauer des Pendels keinen Einfluß hatte. Die Beobachtung nach der Methode der Koinzidenzen, deren sich Borda zuerst bediente, geschieht folgendermaßen: Man läßt beide Pendel schwingen und beobachtet die Durchgänge durch das Gesichtsfeld eines in die Richtung DD, eingestellten Fernrohrs. Man bestimmt zunächst den Zeitpunkt, in dem beide Pendel gleichzeitig durch das Gesichtsfeld gehen (eine Koinzidenz). Da die Pendel nicht gleich lang sind, so wird bei der nächsten Schwingung das eine Pendel schon ein wenig vorangeeilt sein, und die nächste Koinzidenz wird eintreten, sobald das etwas rascher schwingende Pendel eine volle Schwingung mehr gemacht hat als das andere. Je mehr Koinzidenzen man unter jedesmaliger Feststellung der von einer Koinzidenz bis zur anderen verflossenen Zeit ermittelt, desto genauer wird die experimentelle Grundlage für die sich anschließenden Berechnungen sein. Zunächst galt es, aus der Beobachtung der Koinzidenzen die Zahl der Schwingungen zu bestimmen, die das Pendel in einem Tage mittlerer Sonnenzeit macht. Dann mußten alle erforderlichen Korrekturen vorgenommen werden, um die Entfernung des Aufhängepunktes bis zum Schwingungsmittelpunkt zu finden. Endlich galt es, aus dieser reduzierten[S. 450] Entfernung und der Zahl der Schwingungen, die das benutzte Pendel an einem Tage macht, die Länge des Sekundenpendels zu berechnen. Sie ergab sich für Paris (48° 50ʹ 14ʺ n. Br.) gleich 440,5593 Linien. Daraus folgt für die Beschleunigung g der Wert 9,80882 m799.
Wir wenden uns jetzt der zweiten, durch den Wunsch nach einem einheitlichen Maß veranlaßten Messung zu. Sie wurde besonders im Anfange durch die Wirren der Revolution in hohem Grade gestört und nahm eine Reihe von Jahren in Anspruch. Man muß die Kühnheit, die Ausdauer und das Geschick bewundern, womit ein solches Riesenwerk in einer Zeit ins Werk gesetzt und durchgeführt wurde, in der das Land unter Greueltaten litt, von Feinden bedroht war und keine festbegründete, staatliche Ordnung besaß. Durch ein Gesetz vom 1. August 1793 wurde die Länge des Meters vorläufig auf 443,443 Linien festgesetzt unter der Voraussetzung, daß das zu erwartende Ergebnis der Gradmessung nicht wesentlich hiervon abweichen werde.
Über dieses Ergebnis konnte die Kommission für Maß und Gewicht erst mehrere Jahre später berichten. Das durch geodätische Bestimmungen gefundene, als Meter bezeichnete Maß belief sich auf 443,296 Linien (3 Fuß 11,296 Linien). Das provisorische Maß war also um 0,146 Linien, d. h. um etwa 1/3 mm länger als das durch die Gradmessung ermittelte Meter. Darauf wurde die Einheit des Gewichtes im dezimalen metrischen System bestimmt. Es ergab sich, daß das Kubikdezimeter destillierten Wassers von größter Dichte im leeren Raum 18827,15 Gran wog800. Die so erhaltenen, sehr genau gearbeiteten, aus Platin verfertigten Normalmaße (ein Meter und ein Kilogramm) wurden am 22. Juni 1799 im Staatsarchiv hinterlegt. Sie werden dort mit größter Sorgfalt aufbewahrt und nur selten zur Verifizierung gebraucht, da für diesen Zweck von ihnen entnommene Maße dienen.
Es konnte nicht ausbleiben, daß man später Fehler in der Bestimmung des Gradbogens entdeckte. Eine 1840 unternommene Berechnung ergab für das Meter 3 Fuß 11,375 Linien. Danach ist ein Meridianquadrant nicht 10000000, sondern 10000856 mal so groß, wie der in Paris aufbewahrte étalon primitif. Man beschloß aber, an letzterem festzuhalten, »weil man auf dem eingeschlagenen Wege doch nicht in aller Strenge zu einem natürlichen Maße gelangen« könne.
Wie das Ergebnis dieser zu den denkwürdigsten wissenschaftlichen Untersuchungen zählenden Gradmessung, so ist auch ihre Ausführung von Interesse. Übertraf sie doch alle früheren an Umfang und Genauigkeit. Die äußersten Punkte des gemessenen Bogens waren Dünkirchen (51° 2ʹ 10,5ʺ n. Br.) und ein Turm (41° 21ʹ 44,8ʺ n. Br.) in der Nähe von Barcelona. Die Länge dieses Bogens betrug also 9° 40ʹ 25,7ʺ. Seine Mitte lag unter 49° 11ʹ 58ʺ. Da man die Mitte des Bogens möglichst unter 45° n. Br. zu haben wünschte, dehnte man die Triangulationen später (1806) weiter nach Süden bis zur Insel Formentera aus. Der Bogen erhielt dadurch eine Länge von 12° 22ʹ 13,44ʺ. Seine Mitte fällt unter 44° 51ʹ 2,83ʺ.
Der Triangulation wurden zwei Standlinien zugrunde gelegt. Die eine in der Nähe von Paris war 6075,9 Toisen lang, die andere in der Nähe der spanischen Grenze (Perpignan) besaß eine Länge von 6006,25 Toisen und diente zur Kontrolle. Ausgemessen wurden diese Standlinien mit Platinstangen, die unter der Aufsicht von Borda mit der größten Sorgfalt verfertigt waren. Besondere Vorkehrungen dienten dazu, um die jeweils herrschende Temperatur bei der Benutzung dieser Stangen in Betracht zu ziehen usw. In wissenschaftlicher Hinsicht hatte die Messung das bemerkenswerte Ergebnis, daß die Erde kein regelmäßiges Rotationsellipsoid vorstellt, daß also kein Meridianquadrant genau gleich dem anderen ist. Auch eine zur selben Zeit in England unternommene Gradmessung kleineren Umfangs, die aber mit größter Genauigkeit durchgeführt wurde, ergab die gleiche Anomalie. Um also wenigstens annähernd die Gestalt der Erde zu bestimmen, mußte man die Ergebnisse aller an den verschiedenen Orten der Erde vorgenommenen Gradmessungen zusammenfassen und nach der Methode der kleinsten Quadrate diejenige Gestalt daraus berechnen, die der wahren Gestalt der Erde am nächsten kommt. Diese Aufgabe, mit der sich schon Bessel beschäftigte, suchte das im Jahre 1886 gegründete Unternehmen der internationalen Erdmessung[S. 452] zu lösen. Das Ergebnis, zu dem man seitdem vorgedrungen ist, läuft darauf hinaus, daß die Erde keine regelmäßige mathematische Gestalt besitzt. Sie bildet zwar eine nach außen überall konvexe Fläche, zu deren Bestimmung indessen die geodätische Untersuchung nur vorzudringen vermag, wenn sie sich mit der systematisch durchgeführten Schweremessung verbindet. Man hat sie als Geoid bezeichnet und bringt sie mit dem Normalellipsoid in der Art in Verbindung, daß die Abweichungen zwischen diesem und dem Geoid durch trigonometrische Messung, geodätisches Nivellement und Schweremessung ermittelt werden, um auf diese Weise immer genaueren Aufschluß über die wahre Gestalt der Erde zu erlangen.
In der Periode, die wir schildern, wurden auch die Entfernung und die Größe der Sonne, sowie die Abmessungen des Planetensystems nach ihrem absoluten Werte bestimmt, und damit Aufgaben gelöst, die der Astronomie seit der Zeit Aristarchs vorgeschwebt hatten.
Edmund Halley (1656–1742), ein jüngerer Zeitgenosse Newtons, dessen Verdienste um die Fortbildung der Physik, der Astronomie und der physikalischen Geographie wir kennen gelernt haben, war gelegentlich eines von ihm beobachteten Vorüberganges Merkurs vor der Sonne auf den Gedanken gekommen, einen derartigen Vorgang zur Bestimmung der Sonnenparallaxe zu verwerten, d. h. desjenigen Winkels, unter dem der Erdhalbmesser von der Sonne aus erscheint.
Halley machte seinen Vorschlag in zwei Abhandlungen, die 1693 und 1716 in den Philosophical Transactions erschienen. Ihre Titel lauten: »Über die sichtbare Konjunktion der unteren Planeten mit der Sonne«801 und »Ein besonderes Verfahren, durch das die Parallaxe der Sonne mit Hilfe der vor der Sonnenscheibe zu erblickenden Venus sicher bestimmt werden kann«802. Halleys Vorschlag ging dahin, von mehreren entfernten Stellen der Erde aus die Durchgangszeiten eines der unteren Planeten, d. h. die Zeiten ihres Vorüberganges vor der Sonnenscheibe zu beobachten.
Bei einem Merkur- oder Venusdurchgang beschreiben nämlich die genannten Planeten auf der Sonnenscheibe Sehnen, deren Lage und Größe je nach dem Orte, den der Beobachter auf der Erde einnimmt, verschieden ist. Infolgedessen ist auch die Zeit eines und desselben Vorüberganges für die einzelnen Beobachtungsstationen von verschiedener Dauer. Wie aus Abb. 128 ersichtlich ist, steht die Entfernung cd der Sehnen ef und gh zu den Abständen der drei Weltkörper und dem durch Messungen auf der Erde seiner absoluten Größe nach bekannten Stück ab in einer gewissen Beziehung, so daß sich aus den Ergebnissen der Beobachtung eines Venusdurchganges die Größe und die Entfernung der Sonne berechnen läßt803.
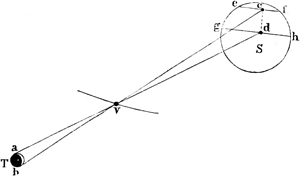
Halley selbst war es nicht mehr vergönnt, seinen Vorschlag ins Werk zu setzen, da Vorübergänge der Venus seltene Ereignisse sind und sich seit seinem Tode erst viermal wiederholt haben, nämlich in den Jahren 1761, 1769, 1874 und 1882. Sowohl für das Jahr 1761 als auch für 1769 wurden Expeditionen ausgesandt. Insbesondere waren daran England, Frankreich und Rußland beteiligt. Aus dem an der Hudsonbay, in Lappland, auf Tahiti usw. angestellten Beobachtungen berechnete der französische Astronom Delalande eine Parallaxe von 8,5–8,6 Sekunden. Da der mittlere scheinbare Durchmesser der Sonne sich auf 31ʹ 37ʺ = 1897 Sekunden beläuft, so ergibt sich aus dieser Bestimmung Delalandes, daß der Sonnendurchmesser denjenigen der Erde nahezu um das 113fache übertrifft, oder daß das Volumen der Sonne 1400000mal so groß ist wie dasjenige der Erde. Für die halbe große Bahnachse ergab sich ein Wert von 20682000 geographischen Meilen. Eine sorgfältige Neuberechnung der Sonnenparallaxe[S. 454] nach den 1761 gewonnenen Daten veröffentlichte später Encke (1822). Er fand den Wert der Parallaxe gleich 8,53 Sekunden.
Sind die Größenverhältnisse des Systems bekannt, so läßt sich durch eine ähnliche Schlußfolgerung, wie diejenige, die Newton auf die Entdeckung des Gravitationsgesetzes führte805, die Kraft ermitteln, mit der ein Körper in der Nähe der Sonnenoberfläche angezogen wird. Delalande fand, daß diese Kraft 29mal die Anziehung der Erde übertrifft, so daß ein frei fallender Körper auf der Sonne in der ersten Sekunde 29 × 15,09 = 434 Pariser Fuß zurücklegt. Die neueren Bestimmungen haben für die Sonnenparallaxe 8,88ʺ ergeben, wodurch sich der Abstand der Erde von der Sonne auf rund 20000000 geographische Meilen (148,6 Millionen Kilometer) vermindert, und auch die übrigen Werte entsprechende Änderungen erfahren.
Von außerordentlicher Tragweite war Halleys Beobachtung, daß die Fixsterne ihre gegenseitige Stellung ändern. Er machte sie am Aldebaran, Arktur und Sirius, für die nach seinen Angaben diese, als Eigenbewegung bezeichnete Änderung sich seit den Zeiten des Ptolemäos auf die beträchtliche Größe von etwa einem halben Grad belief806.
Newton hatte auf theoretischem Wege nicht nur die Abplattung, sondern auch die Dichte unseres Weltkörpers ermittelt. Die Bestimmung der ersteren und der sich daran anknüpfende Streit hatte die Aussendung der Expeditionen nach Lappland und nach Quito zur Folge gehabt. In Quito machte Bouguer807 eine Entdeckung, welche die Handhabe bot, um auch die Newtonsche Berechnung der Erddichte zu verifizieren. Bouguer fand nämlich, daß infolge der Anziehung des Chimborazo das Bleilot um 7–8ʺ von der senkrechten Lage abwich. Diese Beobachtung veranlaßte den Engländer Maskelyne (1732–1811), derartige Untersuchungen an einem nach Volumen und Dichte bekannten Berge anzustellen, um aus der Größe jener Abweichung und der Masse, die sie hervorruft, die unbekannte Masse der Erde auf Grund des Newtonschen Gravitationsgesetzes zu berechnen808.
Maskelyne wählte für seine im Jahre 1774 angestellten Messungen einen steilen, regelmäßig geformten Granitberg Schottlands. Die Dichte dieses Berges wurde auf Grund mehrerer, an verschiedenen Stellen entnommener Proben zu 2,5 gefunden, und aus diesem Wert und dem Rauminhalt des Berges die gesamte auf das Pendel wirkende Masse berechnet. Die Ablenkung selbst wurde dann in der Weise bestimmt, daß die Polhöhe nördlich und südlich von dem Berge gemessen wurde (siehe Abb. 129). Eine auf Grund der so gewonnenen Daten angestellte Rechnung ergab für die Erde als mittlere Dichte 4,71. Letztere ist danach etwa doppelt so groß wie diejenige des Granits, eines Gesteins, mit dem die meisten Substanzen, welche die starre Erdkruste zusammensetzen, hinsichtlich ihrer Dichte nahezu übereinstimmen.
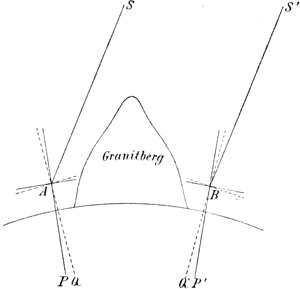
Der Abstand der durch A und B gezogenen Breitenkreise betrug 4364,4 Fuß. Dementsprechend hätten die Lote AP und BPʹ, wenn der Berg nicht vorhanden gewesen wäre, einen Winkel von 42,92 Sekunden bilden müssen, und dieser Winkel wäre gleich der Differenz der Polhöhen gewesen. Die astronomischen Beobachtungen ergaben jedoch eine Polhöhendifferenz von 54,6ʺ. Der Unterschied von 11,6 Sekunden ist durch eine Verminderung der Polhöhe bei A um den Winkel PAQ und eine Vermehrung bei B um PʹBQʹ hervorgerufen. PAQ + PʹBQʹ = doppelte Ablenkung = 11,6 Sekunden.
Durch die Lösung derartiger Aufgaben trat die Astronomie in eine immer engere Beziehung zur Physik der Erde. Aber auch die reine Physik sollte durch die Bewältigung eines astronomischen Problems eine wichtige Förderung erhalten. Im 17. Jahrhundert[S. 456] hatte Römer auf astronomischem Wege eine physikalische Konstante, die Fortpflanzungsgeschwindigkeit des Lichtes nämlich, festgestellt. Jetzt bot sich eine andere Gelegenheit, dieselbe Größe zu ermitteln und infolge der Übereinstimmung der auf verschiedenen Wegen erhaltenen Ergebnisse zu einem höheren Grade der Gewißheit zu gelangen.
Seit dem Bekanntwerden des koppernikanischen Systems war seinen Anhängern die Aufgabe gestellt, den Umlauf der Erde um die Sonne durch den Nachweis einer entsprechenden, scheinbaren, jährlichen Bewegung der Fixsterne darzutun. In Abb. 130 bedeute ABCD die Erdbahn, S sei ein Stern, der sich in der Ebene der Ekliptik befinde. Steht nun der Durchmesser CA der Erdbahn zu dem Abstand ES des Sternes in einem nicht zu kleinen Verhältnis, so wird der Fixstern im Verlaufe eines Jahres am Himmel die scheinbare Bewegung SʹSʺSʹ erkennen lassen. Beobachtungen an einem außerhalb der Ekliptik gelegenen Fixstern werden für diesen als scheinbare Bahn eine Kurve ergeben, deren Gestalt der von dem Sterne aus beobachteten Bahn der Erde genau entspricht809. Der Winkel CSE, unter dem von dem Sterne aus der Halbmesser der Erdbahn erscheint, wird die jährliche Parallaxe des Sternes genannt. Tycho, der hinsichtlich der Genauigkeit seiner Messungen alle Vorgänger übertraf, mühte sich vergeblich ab, eine solche Parallaxe am Polarstern nachzuweisen, und erklärte insbesondere aus diesem Grunde dem koppernikanischen System seine Gegnerschaft. Letzteres war trotzdem zur unbestrittenen Herrschaft gelangt, ohne daß der geforderte, unmittelbare Nachweis der Umlaufbewegung bisher erbracht worden wäre.
Da die Schärfe der astronomischen Beobachtung seit den Zeiten Tychos sich vervielfältigt hatte810, so nahmen Hooke und[S. 457] Cassini das alte Problem wieder auf. Ersterer wählte für seine Messungen den in der Nähe des Nordpols der Ekliptik befindlichen Stern γ Draconis und wies nach, daß dieser Himmelskörper tatsächlich seine Stellung innerhalb eines Vierteljahres um 25 Sekunden ändert.
James Bradley (1692–1763), der nach dem Tode Halleys811 zum Direktor der Sternwarte zu Greenwich ernannt worden war, stellte während der Jahre 1725–1728 zu dem gleichen Zwecke zahlreiche Beobachtungen an. Neben γ Draconis zog er indes auch andere Fixsterne in Betracht, die in der Ekliptik selbst oder zwischen dem Pole und der Ebene der Ekliptik liegen. Seine Beobachtungen ließen scheinbare Bewegungen erkennen, die zwar den Beweis für eine Bewegung der Erde um die Sonne lieferten, indes doch nicht als parallaktische betrachtet werden konnten. Während nämlich γ Draconis im Laufe eines Jahres eine nahezu kreisförmige Bahn von 40ʺ Durchmesser beschrieb, durchliefen die in der Ekliptik gelegenen Sterne in demselben Zeitraum zweimal eine Linie, die unter demselben Winkel von 40ʺ gesehen wurde. Zwischen der Ebene und den Polen der Ekliptik befindliche Sterne endlich legten unterdessen Ellipsen zurück, deren große Achsen wieder 40ʺ maßen und der Ebene der Ekliptik parallel waren, während der Wert der kleinen Achsen zwischen 0ʺ und 40ʺ schwankte, je nachdem der betreffende Stern der Ekliptik oder ihrem Pole näher gelegen war812. Um diese scheinbaren Bewegungen auf eine Parallaxe zurückzuführen, hätte man, da in allen Fällen derselbe Wert von 40ʺ wiederkehrt, zunächst annehmen müssen, daß sämtliche Fixsterne gleich weit von der Erde entfernt seien. Dieser an sich schon unwahrscheinlichen Annahme widersprach aber die Tatsache, daß in B und D (siehe Abb. 130) der Stern nicht an demselben Orte gesehen wurde, wie es bei der parallaktischen Bewegung doch der Fall sein müßte. Bradley fand nämlich, daß, wenn die Erde sich in D befindet und sich in der Richtung Dd bewegt, der Stern nach Sʹ verschoben erscheint. Befindet sich die Erde dagegen in B, wo ihre Bewegungsrichtung die entgegengesetzte ist, so findet die Verschiebung nach Sʺ statt. In beiden Fällen erreicht der Wert dieser Verschiebung 20ʺ, während in C und A, wo die Bewegungsrichtung der Erde mit derjenigen des von dem Fixstern kommenden Lichtes übereinstimmt, der[S. 458] Stern, falls er in der Ebene der Ekliptik liegt, an seinem wahren Orte gesehen wird.
Zur Erklärung dieser auffallenden Erscheinung soll Bradley durch eine alltägliche Beobachtung gelangt sein. Er bemerkte nämlich bei einer Bootfahrt, daß die Fahne die Windrichtung wirklich angibt, wenn der Lauf des Schiffes mit der Richtung des Windes übereinstimmt. Änderte man dagegen den Kurs, so nahm die Fahne die Stellung an, die sich als abhängig von den Richtungen und den Geschwindigkeiten des Windes und des Bootes erwies. Pflanzt sich, so folgerte Bradley, das Licht mit endlicher Geschwindigkeit fort, so muß sich letztere mit derjenigen der Erde zusammensetzen. Abb. 131 stellt das Parallelogramm dieser Geschwindigkeiten dar.
Zu der Zeit, in der sich die Erde in den Stellungen B und D (Abb. 130) befindet, beträgt ihre durch das Stück ab (Abb. 131) wiedergegebene Geschwindigkeit, wie überall auf ihrer Bahn, etwa 4 Meilen. Die Aberration erreicht dann ihren größten Wert von 20ʺ, der dem Winkel acb beizulegen ist. In diesem Falle verhält sich bc zu ab wie die Geschwindigkeit des Lichtes zu derjenigen der Erde. Ist der eine dieser Werte bekannt, so ist der andere durch eine einfache Beziehung gegeben813. Bradley erhielt so für die Fortpflanzungsgeschwindigkeit des Lichtes, fast in Übereinstimmung mit dem von Römer gefundenen Ergebnis, den Wert von 40000 Meilen. Beide auf astronomischem Wege erhaltenen Bestimmungen fanden um die Mitte des 19. Jahrhunderts eine Bestätigung durch terrestrische, nach rein physikalischer Methode angestellte Messungen.
Bei Newton und den auf ihn folgenden Astronomen war das Hauptinteresse auf das Planetensystem gerichtet, für das die Gravitationsmechanik zunächst noch zahlreiche Probleme bot. Mit den Kometenbahnen hatte sich zwar Newton in seinen Prinzipien auch beschäftigt, doch war die von ihm geschaffene Methode noch[S. 459] sehr unvollkommen. Weitere Untersuchungen auf diesen Gebieten unternahmen Euler und ganz besonders Lambert. Hatte Kepler für diese Himmelskörper noch eine geradlinige Bewegung angenommen, so lieferte Newton den Nachweis, daß es sich auch hier um Kegelschnitte handle. Er lehrte ferner, durch Konstruktion aus drei Positionen die parabolische Bahn ermitteln, ein Verfahren, dessen sich besonders Halley mit Erfolg bediente.
Grundlegende, geradezu klassische Arbeiten über die Bestimmung der Kometenbahnen rühren von Lambert her, mit dessen Lebensgang und Verdiensten um die Physik wir schon im vorigen Abschnitte bekannt geworden sind814. Lamberts Ziel bestand, wie er in seiner Vorrede hervorhebt, darin, die Bahn des Kometen auf Grund von drei Beobachtungen, aus den Eigenschaften der Kegelschnitte vollständig zu ermitteln. Von besonderer Wichtigkeit ist Lamberts Satz815, daß die Zeit, die zum Durchlaufen eines Kurvenstücks erforderlich ist, aus der Sehne und den beiden Vektoren ermittelt werden kann. Für die Parabel hatte diesen Satz schon Euler gefunden816. Er erkannte jedoch noch nicht seine Bedeutung und hat ihn nicht bei seinen Arbeiten über die Bahnbestimmung benutzt, während Lambert ihn auf hyperbolische Bahnen ausdehnte.
Nachdem Lambert die Bewegung der Kometen erörtert hat, befaßt er sich mit dem Verfahren, eine parabolische Kometenbahn aus den Beobachtungen zu bestimmen. Genauer lautet das Problem, das er sich stellt, folgendermaßen817: Gegeben sind drei geozentrische Örter eines in einer Parabel sich bewegenden Kometen; man soll Lage und Größe der Bahn ermitteln. Die Lösung führte ihn auf eine Gleichung 6. Grades. Werden Lamberts Ausdrücke nach einer kleinen Berichtigung entwickelt, so gibt seine Methode ein brauchbares Verfahren818.
Unabhängig von Kant hat Lambert ferner Ansichten über den Bau des Weltalls entwickelt, die mit den Ergebnissen der neueren Forschung in Einklang stehen. Es geschah dies in seiner[S. 460] 1761 erschienenen Schrift »Kosmologische Briefe über die Einrichtung des Weltbaus«. Lambert unterscheidet darin Weltsysteme erster, zweiter und dritter Ordnung. Ein System erster Ordnung bilden die Sonne und jeder Fixstern, da alle Fixsterne als Zentren von ebensoviel Scharen von Planeten und Kometen aufzufassen sind.
Das Sonnensystem kreist mit zahlreichen benachbarten Sonnensystemen um einen gemeinschaftlichen Schwerpunkt. Das Ganze betrachtet Lambert als ein System zweiter Ordnung. Aus solchen setzt sich endlich die Milchstraße als eine Scheibe, deren Durchmesser nach vielen tausend Siriusweiten zählt, zusammen. Vielleicht sei, meint Lambert, auch hiermit die Gliederung zu immer umfassenderen Gruppen nicht abgeschlossen, doch übersteige eine Fortsetzung dieser Betrachtung unser Fassungsvermögen.
Die etwa drei Jahrzehnte (1718) vor der Herausgabe der Kosmologischen Briefe durch Bradley entdeckte Eigenbewegung der Fixsterne würde sich, diesen Ausführungen Lamberts entsprechend, aus zwei Bewegungen zusammensetzen, der Bewegung der Sterne selbst und der von Lambert vorgeahnten Bewegung unseres Sonnensystems. »Es wird später möglich werden«, sagt Lambert, »diese beiden Komponenten zu trennen und die Richtung anzugeben, nach der sich unsere Sonne bewegt.« Diese Voraussage sollte, wie wir in einem späteren Abschnitt sehen werden, schon einige Jahrzehnte später (1781) durch Herschel in Erfüllung gehen.
Ganz Hervorragendes hat Lambert auch auf einem Nebengebiet der Astronomie, auf dem Gebiete der Kartographie, geleistet, so daß man für dieses mit dem Erscheinen von Lamberts Schrift über Land- und Himmelskarten wohl eine neue Epoche datiert hat. Die Schrift ist mit Anmerkungen versehen von neuem herausgegeben worden819. Ihr erstes Erscheinen fiel in das Jahr 1772.
Der in die zweite Hälfte des 18. Jahrhunderts fallende große Aufschwung der Kartographie hing mit dem Einsetzen der wissenschaftlichen[S. 461] Entdeckungsreisen (Cook) und mit genaueren topographischen Landesaufnahmen zusammen. So entstand (1750 bis 1793) auf Grund einer großen genauen Landesvermessung Cassinis Carte géométrique de la France. Sie umfaßte 184 Blätter im Maßstab von 1 : 86400 und diente für die Karten der übrigen Länder als Muster820. In gleichem Maße epochemachend war die erwähnte Schrift Lamberts.
Zwar fehlte es vor Lambert nicht an Untersuchungen über einzelne Entwerfungsarten. Ihm gebührt jedoch das Verdienst, daß er zuerst die allgemeinen Grundsätze, die bei der Kartenprojektion in Betracht kommen, aufstellte und als erster diejenigen Forderungen erörterte, die das Kartenbild zu erfüllen hat. Im Verfolg dieser Aufgaben kam Lambert auch auf mehrere neue Projektionsarten, die noch heute im Gebrauch sind. Es sind dies vor allem die winkeltreue und flächentreue Kegelprojektion821.
Mit demselben Gegenstande hat sich einige Jahre später auch Leonhard Euler beschäftigt. Ihm hatte auch die sphärische Trigonometrie um die Mitte des 18. Jahrhunderts Fortschritte zu verdanken, die in erster Linie der Astronomie zugute kamen. Eulers Abhandlungen über Kartenprojektion822 gehen über die Behandlung, die Lambert dem gleichen Gegenstande widmete, weit hinaus und leiten andererseits zu den Untersuchungen über, die Lagrange und später Gauß823 über die konforme Abbildung von Flächen auf anderen Flächen angestellt haben.
Die erste Arbeit Eulers handelt von der Abbildung der Kugelfläche in einer Ebene, und zwar behandelt Euler nicht nur die früheren Projektionen, bei denen die einzelnen Punkte der Kugelfläche nach den Gesetzen der Perspektive so auf eine Ebene projiziert werden, wie sie dem Beobachter von einem bestimmten[S. 462] Punkte aus erscheinen, sondern er faßt seine Aufgabe in weiterem Sinne auf und zeigt, wie die Punkte der Kugelfläche nach einem beliebigen Gesetz in einer Ebene dargestellt werden können.
Unter anderem werden die Bedingungen der Mercator'schen Projektionsart entwickelt und dargetan, daß für diese die kleinsten Teile der Oberfläche ihren Bildern in der Ebene ähnlich sind, also das Prinzip der Konformität oder Winkeltreue gewahrt ist. Euler zeigte ferner, daß der größte Vorteil, den derartige Karten den Seefahrern gewähren, darin besteht, daß die loxodromischen Linien, d. h. die Kurven, die sämtliche Meridiane unter dem gleichen Winkel schneiden, bei dieser Projektionsart als gerade Linien erscheinen. Jede gerade Linie schneidet nämlich alle Meridiane der Karte, die ja bei Mercators Projektion einander parallel sind, unter demselben Winkel.
Auch die bekannte Abbildung der Erdhalbkugeln im Innern von Kreisen, deren Mitte der Pol einnimmt, während die Meridiane und die Parallelkreise sich senkrecht schneiden, wird von Euler aus den von ihm aufgestellten allgemeinen Gleichungen abgeleitet und gezeigt, daß auch für diese Projektionsart alle sehr kleinen, auf der Kugel beliebig angenommenen Figuren durch ähnliche Figuren in der Ebene wiedergegeben werden.
In der zweiten Abhandlung wird ein für die Darstellung besonders häufiger, flächentreuer Entwurf aus den allgemeinen Bedingungen erörtert, der Entwurf nämlich, bei dem die Meridiane und die Parallelkreise als Kreise erscheinen.
Die letzte Abhandlung endlich erörtert die Projektionsart, die De Lisle seiner Karte des russischen Reiches zugrunde gelegt hat824, und zeigt, wie man die Fehler einer solchen nach De Lislescher Projektion entworfenen Karte möglichst verringern kann. Die genannte Projektionsart ist eine konische, d. h. ein Teil der Kugelzone wird derart auf einen Kegel übertragen, daß den Meridianen gerade Linien, den Parallelkreisen der Kugel aber parallele Kreise auf dem Mantel des Kegels entsprechen.
Nicht minder groß sind die Verdienste, die sich Euler um die wichtigste Hilfswissenschaft der Astronomie, die Trigonometrie, erworben hat. In seiner ersten Abhandlung über diesen Gegenstand[S. 463] (1753) stellte er sich die Aufgabe, wichtige Sätze der sphärischen Trigonometrie nach der Methode der größten und kleinsten Werte abzuleiten825.
Etwaige Bedenken gegen die Ableitung der sphärischen Trigonometrie aus den Regeln der Infinitesimalrechnung werden von Euler zurückgewiesen. Es sei immer von Nutzen, auf verschiedenem Wege dieselben Wahrheiten zu erreichen, weil aus diesem Verfahren sich stets neue Gesichtspunkte ergeben würden. Zur Notwendigkeit wurde aber die Anwendung der neuen Methode hier wie in allen übrigen Fällen, wenn man ein Problem ganz allgemein lösen wollte. Die bisher übliche Betrachtungsweise war auf das ebene und das sphärische Dreieck beschränkt. Wollte man dagegen Dreiecke untersuchen, die auf einer beliebigen, z. B. einer konoidischen oder sphäroidischen Fläche dadurch entstehen, daß man drei Punkte durch drei kürzeste, der betreffenden Oberfläche angehörende Linien verbindet, so war damit ein Problem gegeben, das sich nur mit den Mitteln der höheren Mathematik lösen ließ. Die Wichtigkeit einer solchen Begründung der Trigonometrie auf einer allgemeinen Auffassung leuchtet ein, wenn man bedenkt, daß die Messungen der Geodäten nicht auf einer Kugel, sondern, wie Euler hervorhebt, auf einer sphäroidisch gestalteten Fläche geschehen. Wenn man die bei den Triangulationen erforderlichen Dreiecke recht groß wähle, so müsse man auf diesen Umstand auch Rücksicht nehmen. In der erwähnten Abhandlung leitet Euler nur die Formeln für die Kugeloberfläche mit Hilfe der Infinitesimalrechnung ab. Für andere Flächen, wie das Sphäroid (Umdrehungsellipsoid), wird diese Trigonometrie der kürzesten Linien (der Name sphärische Trigonometrie paßt ja nur für die Kugel) in einer späteren Arbeit behandelt826. Auch darauf wies Euler hin, daß die ebene Trigonometrie aus der sphärischen hervorgeht, wenn man den Radius der Kugel unendlich groß werden läßt827. Sehr glücklich war sein Gedanke, die Seiten eines Dreiecks mit a, b, c und die entsprechenden Gegenwinkel mit A, B, C zu bezeichnen. Die trigonometrischen Formeln wurden dadurch viel übersichtlicher und neue Beziehungen weit leichter[S. 464] als bisher entdeckt828. Die trigonometrischen Formeln, die wir heute benutzen, hat Euler mit Ausnahme der Gaußschen Formeln829 infolgedessen besonders klar dargestellt, teilweise auch zum ersten Male abgeleitet830.
Wesentlich bedingt durch die Fortschritte der Physik und der Chemie entwickelten sich im 18. Jahrhundert die Mineralogie und die Geologie auf der in der vorhergehenden Epoche vor allem durch Steno geschaffenen Grundlage weiter.
Die von Agricola begründete Lehre von den äußeren Kennzeichen bildete bei Linné zwar noch den Kernpunkt der mineralogischen Wissenschaft. Doch dürfen wir nicht vergessen, daß Linné auf diesem Gebiete kein Forscher war, sondern die Mineralien nur seinem alles umfassenden Natursystem anzugliedern suchte. Seine Begriffsbestimmungen erhoben sich kaum über die von Agricola aufgestellten; sie waren sogar weniger verständlich, da bei Linné Erläuterungen durch Beispiele, wie sie Agricola gegeben, fehlten831.
Linné berücksichtigte die äußere Gestalt (würflig, säulenförmig, pyramidal), die Oberfläche (rauh, glatt), die innere Struktur (körnig, faserig, blätterig), die Härte (am Stahl funkend, läßt sich schneiden, schreibt) und endlich das optische Verhalten (durchsichtig, gefärbt usw.). Der Kristallform schenkte man zu jener Zeit noch geringe Aufmerksamkeit. Linné suchte die an den Mineralien vorkommenden Formen auf einige bekannte Salze (Kochsalz, Salpeter, Alaun, Vitriol) zurückzuführen. Dies war ein vergebliches Bemühen, zumal Linné sich von der sonderbaren Vorstellung leiten ließ, daß dasjenige Salz, mit dem ein Mineral in seiner Kristallform übereinstimmt, auch die Ursache für die Form des Minerals sei.
Erst im 18. Jahrhundert gelangte man allgemeiner zu der Auffassung, daß man es in den Mineralien mit Verbindungen zu[S. 466] tun habe und begann sie nach ihrer Zusammensetzung einzuteilen. Ein nach diesem Gesichtspunkt durchgeführtes System konnte sich indessen im 18. Jahrhundert wegen des unfertigen Zustandes der Chemie noch nicht entwickeln. Durch das Handinhandgehen der Mineralogie mit der Chemie wurden aber im 18. Jahrhundert die wichtigen Grundlagen für die Mineralchemie geschaffen. Die größten Verdienste um diesen Wissenzweig haben sich die schwedischen Forscher Cronstedt (1722–1765) und Bergman (1735–1784) erworben.
Dem wichtigsten Instrument zur chemischen Untersuchung der Mineralien, dem Lötrohr, begegnet man gelegentlich schon im 17. Jahrhundert. Seine ausgedehnte, mit zahlreichen Kunstgriffen verknüpfte Anwendung verdankt man indessen Cronstedt. Er lehrte auf einem Stück Kohle eine kleine Probe des zu untersuchenden Minerals durch Hinaufblasen der Flamme und die Anwendung von Flußmitteln all den chemischen Prozessen unterwerfen, denen die Erze beim Hüttenbetriebe im Schmelzofen unter der Wirkung des Gebläses ausgesetzt sind. Dabei läßt aber die Behandlung der kleinen Probe hinsichtlich der Zusammensetzung des Minerals weit mehr erkennen als die hüttenmännischen Prozesse, weil letztere der unmittelbaren Beobachtung viel weniger zugänglich sind. Arsen und Schwefel werden vor dem Lötrohr an dem Geruch ihrer bei der Verbrennung entstehenden Oxyde, Antimon am Beschlage erkannt. In der reduzierenden Flamme werden Blei, Silber, Kupfer, Eisen usw. abgeschieden832. Insbesondere achtete Cronstedt auf die Färbung der Flußmittel, die er der Probe vor dem Schmelzen zusetzte. Als Flußmittel gebrauchte er Borax, der z. B. durch Kobalt blau, durch Kupfer grün und durch Braunstein violett gefärbt wird, ferner dienten ihm als Ersatz für Borax in geeigneten Fällen Soda und Phosphorsalz833.
Der Schmelzfluß wurde auf der Kohle hergestellt, seine Herstellung am Platindrahte erfolgte erst später, nachdem der Gebrauch des Platins allgemeiner geworden war834. Ließ sich das Lötrohr auch für die quantitative Untersuchung der Mineralien nicht verwerten, so wurde es doch auf die geschilderte Weise in der Hand Cronstedts zu einem Hilfsmittel, das der Mineralchemie ebenso wertvolle Dienste leistete, wie sie die Kristallographie der Anwendung des Goniometers verdankt.
Um das weitere Eindringen in die chemische Natur der Mineralien zu ermöglichen, mußte sich zu dem Lötrohrverfahren, oder der Untersuchung auf trockenem Wege, die Analyse des in den löslichen Zustand übergeführten Minerals gesellen. Nur auf diesem Wege ließen sich genauere Ermittlungen anstellen. Diesen Weg erschlossen zu haben, ist vor allem dem schwedischen Chemiker Bergman zu danken. Seine Verdienste um den Ausbau der qualitativen und der Gewichtsanalyse werden jedoch an anderer Stelle besprochen werden. Wir haben es hier nur mit der von Bergman geübten Anwendung dieser Methode auf die Mineralien zu tun. Hatte er das Mineral, das zuerst aufs feinste gepulvert, gegebenenfalls auch durch Schmelzen mit Pottasche »aufgeschlossen« wurde, in einer Säure gelöst, so begann die qualitative Untersuchung durch Reagentien, die größtenteils noch heute gebraucht werden. Dann folgte die quantitative Bestimmung. Ihre Ergebnisse werden jedoch aus zwei Gründen recht ungenau. Einmal waren die Methoden der Gewichtsanalyse noch zu unvollkommen; ferner waren mitunter die Bestandteile der Mineralien, die Bergman untersuchte, noch nicht sämtlich bekannt. So erblickte er im Rubin, der nur aus Tonerde besteht (Al2O3), eine Verbindung dieses Oxyds mit Kieselerde. Hyazinth dagegen, der aus Kiesel- und Zirkonerde zusammengesetzt ist, wurde für eine Verbindung von Kieselerde mit Ton- und Kalkerde angesehen, weil Bergman die Zirkonerde noch nicht als eigentümliche Substanz erkannt hatte. Dies geschah erst durch Klaproth (1789), der sich ganz besonders bemühte, die Mineralchemie im Anschluß an Bergman weiter auszubauen. Das Ergebnis der Bemühungen von Scheele, Bergman, Klaproth und anderen Chemikern des 18. Jahrhunderts, die ihre Wissenschaft mit der Mineralogie zu verknüpfen strebten, bestand darin, daß Werner, der zwar selbst kein Chemiker war, aber die Wichtigkeit der Zusammensetzung der Mineralien zu würdigen wußte, noch vor Ablauf des 18. Jahrhunderts ein mineralogisches System nach chemischen Gesichtspunkten aufstellte.
Die Gruppierung der Mineralien nach »inneren Kennzeichen« war zwar schon früher versucht worden835. Doch war der Erfolg naturgemäß nur gering, solange nicht die Mineralanalyse der[S. 468] Systematik die Wege geebnet hatte, und bevor man nicht eine Scheidung zwischen Mineralien, Gesteinen und Versteinerungen durchzuführen wußte. Ein kurzer Überblick über das System Werners lehrt uns am besten den Standpunkt kennen, den die mineralogische Systematik gegen das Ende des 18. Jahrhunderts eingenommen hatte.
In die erste Klasse wurden die in Wasser unlöslichen Oxyde der Nichtmetalle und die Silikate der Leichtmetalle, die selbst noch der Entdeckung harrten, gestellt. So begegnet uns in dieser Klasse, zu der übrigens auch der Diamant gerechnet wurde, das den Quarz (SiO2) und viele Silikate umfassende Kieselgeschlecht. An dieses reihten sich das Tongeschlecht mit Korund (Al2O3), Feldspat, Glimmer, die ja beide Tonerde enthalten, und einige scheinbar homogene und daher noch als Mineralien betrachtete Gesteine, wie Basalt und Tonschiefer.
Als Salze (II. Klasse) werden in Wasser lösliche, dem Kochsalz ähnliche Mineralien zusammengefaßt, wie Alaun, Salpeter und Salmiak. Dann folgen als III. Klasse die brennbaren Mineralien (Schwefel, Bernstein, Steinkohle usw.).
Am besten bestimmt ist die IV. und letzte Klasse. Sie umfaßt die Schwermetalle und ihre Verbindungen. Eingeteilt wird sie in die silberhaltigen Erze (das Silbergeschlecht), die kupferhaltigen, bleihaltigen usw. Auf die Elemente, mit denen die Schwermetalle verbunden sind, wird bei dieser Einteilung kein Gewicht gelegt. So umfaßt das Eisengeschlecht etwa folgende Mineralspezies:
| 1. Gediegenes Eisen | Fe |
| 2. Schwefelkies | FeS2 |
| 3. Magneteisenstein | Fe3O4 |
| 4. Eisenglanz | Fe2O3 |
| 5. Spateisenstein | FeCO3 usw. |
Zu einem ähnlichen Mineralsystem war man um 1800 auch in Frankreich gelangt836. Diese Systeme mußten sich indessen in dem Maße, in dem man in die chemische Zusammensetzung der Mineralien eindrang, als unzulänglich erweisen. Schwefelkies, Eisenglanz und Eisenspat z.B. waren, trotzdem sie alle drei Eisen enthalten, in chemischer Hinsicht drei verschiedenen Gruppen zuzuweisen. Ferner griff auch die Erkenntnis Platz, daß die chemische Konstitution in manchen Fällen für die Krystallform bestimmend[S. 469] ist. Damit waren die wichtigsten Gesichtspunkte gegeben, nach denen sich die Systematik im 19. Jahrhundert, wie wir sehen werden, weiter entwickeln sollte.
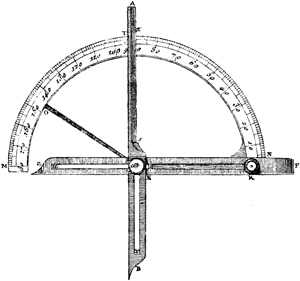
GF und AB sind zwei Lineale, deren Abschnitte GC und BC je nach der Größe des zu messenden Objektes verlängert oder verkürzt werden können. MTN trägt den Gradbogen, AB wird um C gedreht. OC dient zur Stütze des Gradbogens. AB wird gedreht, bis die Schenkel BC und CG den, sich schneidenden Kristallflächen genau anliegen. Der Kantenwinkel läßt sich dann auf dem Gradbogen ablesen.
Aus dem Bedürfnisse, die Mineralien auch ohne eingehendere chemische Analyse zu bestimmen, entspringt die Kennzeichenlehre, die insbesondere auf der Verwendung des 1758 von Cronstedt eingeführten Lötrohrs beruht. Borax, Phosphorsalz und andere noch heute zur raschen Bestimmung gebräuchliche Hilfsmittel kommen in Aufnahme. Auch die Farbe und die Spaltbarkeit werden als wichtige Kennzeichen verwertet. Ebenso wird das spezifische Gewicht berücksichtigt, doch begnügt man sich zunächst mit dem bloßen Abschätzen des letzteren. Eine größere Beachtung fand diese physikalische Konstante erst, nachdem in Nicholsons Senkwage838 ein bequemes Mittel zur raschen Bestimmung des spezifischen Gewichtes an die Hand gegeben war. Seitdem Steno auf die Konstanz der Winkel hingewiesen hatte, wandte man sich auch mit wachsendem Interesse dem an den Mineralien in die Erscheinung tretenden Formenreichtum zu. Dem französischen Forscher de l'Isle839 gelang es, die von Steno nur für einige Fälle nachgewiesene[S. 470] Regel in ihrer Allgemeingültigkeit zu erkennen. Als Meßinstrument bediente er sich hierbei des von seinem Gehilfen840 erfundenen Anlegegoniometers (s. Abb. 132 auf der vorigen Seite).
In seiner »Urgeschichte« hatte Leibniz mit Nachdruck als Vorbedingung für die weitere Entwicklung der Geologie die gründliche Untersuchung der Beschaffenheit und des Verlaufs der Erdschichten gefordert. An die Lösung dieser Aufgabe machte sich unter hervorragender Beteiligung Deutschlands das 18. Jahrhundert. Das Interesse für die geologischen Kräfte wurde in diesem Zeitraum auch durch zwei außergewöhnliche, elementare Vorgänge in hohem Grade angeregt, nämlich durch die Entstehung einer vulkanischen Insel (Santorin) inmitten des ägäischen Meeres und durch das furchtbare Erdbeben von Lissabon. Insbesondere das letztere rief eine wahre Flut von Schriften hervor841. Unter anderen hat sich auch Immanuel Kant mit diesem Naturereignis und seiner Ursache eingehend beschäftigt842.
An die Entstehung von Santorin und die Bildung des Monte Nuovo bei Pozzuoli knüpfte Moro843 seine Theorien über die Entstehung der Erde an. Moro unterscheidet die ursprünglichen Gesteine von den sekundären, geschichteten und läßt alle Inseln, Kontinente und Gebirge durch vulkanische Hebung entstehen. Auch Moros Landsmann Vallisneri844 suchte die geologischen Erscheinungen auf natürliche Ursachen zurückzuführen. Er untersuchte845 die marinen Ablagerungen, die sich zu beiden Seiten des Apennin befinden und wies die Verbreitung derartiger Ablagerungen auch für die übrigen europäischen Länder nach. So kam er zu der Erkenntnis, daß das heutige Festland früher Meeresboden gewesen sei, und daß sich die Versteinerungen führenden Schichten dereinst durch allmählichen Absatz bildeten und gleichzeitig die Überreste abgestorbener Organismen, unsere heutigen Petrefakten, einhüllten.
Während man anfangs alle leblosen Körper, die der Schoß der Erde birgt, unter dem Namen »Fossilien« vereinigte, gelangte man im Laufe des 18. Jahrhunderts dazu, die Versteinerungen und die Felsarten von den eigentlichen, dem Auge gleichartig erscheinenden Mineralien zu trennen. Von jetzt an traten Versteinerungslehre und Geognosie der Mineralogie als selbständige Wissenzweige zur Seite. Mit großem Eifer wandte man sich in allen Kulturländern diesen neu erschlossenen Forschungsgebieten zu und begab sich an das gründliche Studium von Naturkörpern, denen man bisher neben der Tier- und Pflanzenwelt nur geringe Beachtung gezollt hatte. An den Universitäten wurden neue Lehrstühle errichtet. Gleich den Botanikern und den Zoologen unternahmen jetzt auch Geologen Reisen zur Erforschung fremder Länder. Besondere Schulen wurden gegründet; so verdanken die Bergakademie in Freiberg und die École de mines in Paris ihren Ursprung der geschilderten Bewegung. Die erstere der genannten Anstalten gelangte rasch zu europäischer Berühmtheit durch die Tätigkeit eines Mannes, mit dem wir uns zunächst befassen müssen. Es ist dies der Deutsche Werner, der sich um die Kennzeichenlehre und die Geognosie besonders verdient gemacht hat. Bevor wir uns ihm zuwenden, müssen wir uns mit zwei anderen deutschen Geologen beschäftigen, die für Werners wissenschaftliche Tätigkeit die Grundlagen schufen, indem sie die geologische Spekulation beiseite setzten und eine gründliche, voraussetzungslose Durchforschung der Erdschichten unternahmen. Diese Männer waren Lehmann und Füchsel.
Lehmann846, der in Berlin und später in Petersburg Mineralogie und Chemie lehrte, veröffentlichte als das Ergebnis zahlreicher Beobachtungen die erste genauere Untersuchung über die Zusammensetzung und die Lagerung der geschichteten Gebirgsglieder847. Er unterscheidet sie als »Flözgebirge« von den »Ganggesteinen«, die früher entstanden seien und sich »in die ewige Teufe fortsetzen«. Bezeichnend ist nun, daß die ersten deutschen Geologen, die sich nicht auf Spekulationen beschränkten, sondern sich an die Erforschung der tatsächlichen Verhältnisse begaben, die Erdrinde ihrer Hauptmasse nach, den Granit und Basalt eingeschlossen, aus dem Wasser entstehen ließen, während man in Italien unter dem unmittelbaren Eindruck des Vulkanismus alles[S. 472] auf diese Kraft zurückzuführen suchte und selbst geschichtete Gesteine als Eruptionsprodukte betrachtete, wie es vor allem Moro tat.
Lehmanns Arbeit gründet sich, wie die Betrachtungen von Leibniz und die eingehenderen Untersuchungen Füchsels, besonders auf die geologische Natur des Mansfelder, durch den Bergbau seit alters aufgeschlossenen Bodens. Lehmann unterscheidet 30 verschiedene Schichten und bedient sich dabei zum Teil noch heute üblicher Bezeichnungen, wie der Ausdrücke Zechstein, Kupferschiefer, Rottotliegendes.
Von dem zweiten Vorläufer Werners, dem Arzt Füchsel, rührt die erste scharf ausgeprägte Terminologie her. Von besonderer Wichtigkeit ist die durch ihn erfolgte Aufstellung des Begriffes »Formation«. »Jeder einzelne Niederschlag«, sagt Füchsel, »bildet eine Erdschicht oder Bank. Aber es gibt gewisse Folgen von Schichten, die unter gleichen Verhältnissen unmittelbar nacheinander entstanden sind; solche Reihen bilden zusammen das, was wir eine Formation nennen, und eine solche Formation bezeichnet eine Epoche in der Geschichte der Erde«. Die einzelnen Formationen kennzeichnete Füchsel durch das Vorhandensein von eigentümlichen Versteinerungen, den Leitfossilien.
G. Ch. Füchsel wurde 1722 in Ilmenau geboren und wirkte als Arzt in Rudolstadt. Dort starb er 1773. Über seine geologischen Arbeiten schrieb er in seiner »Historia terrae et maris ex historia Thuringiae per montium descriptionem erecta 1762«.
Er unterschied für Thüringen folgende neun Formationen:
Füchsel stellte auch als erster in Deutschland eine geologische Karte der von ihm durchforschten Gegend her. Auch wußte er seine Beschreibungen durch deutliche Profile zu unterstützen.[S. 473] Seine Veröffentlichungen wurden zwar der Allgemeinheit wenig bekannt, doch sind sie es, auf die Werner, der Linné der Geologie, sich insbesondere stützte.
Die gleichen Bestrebungen wie in Deutschland begegnen uns im 18. Jahrhundert in Frankreich. Dort untersuchte Guettard das Pariser Becken und gelangte zu dem Schlusse, daß dieses einst von Wasser bedeckt gewesen und durch die im Lauf der Zeit zu festem Gestein gewordenen Ablagerungen einmündender Flüsse ausgefüllt worden sei. Die Berge der Auvergne, wie den Puy de Dôme und den Mont Dore, erkannte Guettard als erloschene Vulkane.
Guettards848 Schrift über die Vulkane der Auvergne ist für die Entwicklung der Geologie von großer Bedeutung gewesen, da sie den Blick der Geologen von den nur sporadisch vorkommenden tätigen Vulkanen auf die außerordentliche Bedeutung des Vulkanismus für längst abgelaufene Perioden der Erdgeschichte lenkte849. Daß die Kegel der Auvergne einst tätige Vulkane waren, schloß Guettard aus den lavaartigen Gesteinen und den Bimssteinmassen, die sich dort zeigen. Für den Basalt nahm er seiner scheinbar kristallinischen Regelmäßigkeit wegen den vulkanischen Ursprung nicht an. Er hielt ihn vielmehr für eine Kristallisation aus einer wässrigen Lösung. Erst ein jüngerer Zeitgenosse und Landsmann Guettards erkannte die wahre Natur des Basalts. Dies war Desmarest850. Er zeigte, daß der Basalt oft deutlich auf vulkanischer Asche lagert, daß er mitunter auch von dieser bedeckt wird oder allmählich in Lava übergeht. Wieder an anderen Stellen fand er den Basalt stromartig geflossen, so daß an seiner ursprünglich feurig-flüssigen Beschaffenheit nicht mehr gezweifelt werden konnte. Die gleiche Entstehungsart machte Desmarest auch für die älteren Massengesteine (Granit und Porphyr) wahrscheinlich.
Im Jahre 1746 veröffentlichte Guettard eine geognostische Karte, die den Aufbau Frankreichs, Englands und eines Teiles[S. 474] von Mitteleuropa zur Darstellung brachte. Diese Karte gibt nicht nur über das Vorkommen von Gesteinen und Mineralien Auskunft, sondern es sind auf ihr auch die wichtigsten Bergwerke und Mineralquellen, sowie Fundorte von Versteinerungen verzeichnet, so daß sie noch heute mit Vorteil gebraucht werden kann851.
Später vereinigte sich Guettard mit Lavoisier in der Absicht, gemeinschaftlich mit diesem einen mineralogisch-geognostischen Atlas von Frankreich herauszugeben. Es erschienen auch eine größere Anzahl von Blättern, doch blieb das Unternehmen unvollendet.
Eine eigenartige Stellung in der Geschichte der Geologie nimmt Buffon, der geistreichste Naturforscher des 18. Jahrhunderts, ein. Buffon852 (1707–1788), dessen Lebens- und Entwicklungsgang an anderer Stelle geschildert werden soll, hat die Geologie weniger durch neue Beobachtungen bereichert, sondern durch die Art, wie er die bis dahin bekannt gewordenen Tatsachen zusammenzufassen und mit neuen Gedanken zu verknüpfen wußte. Er hat die Geologie mit einer vor ihm nicht anzutreffenden Klarheit als die in langen Zeiträumen sich abspielende Geschichte unseres Planeten dargestellt. Die Planeten sind nach ihm aus der Sonne hervorgegangen. Die Loslösung der Planeten vom Zentralkörper erfolgte nach der allerdings unhaltbaren Hypothese Buffons durch den Zusammenstoß der Sonne mit einem Kometen.
Um ein Urteil über die Dauer der gesamten Erdgeschichte zu gewinnen, stellte Buffon zahlreiche Versuche über die Abkühlung glühender Kugeln von verschiedenem Durchmesser an. Aus den Ergebnissen dieser Versuche berechnete er, daß sich die Erdkugel in etwa 75000 Jahren von ihrer anfänglichen bis zu ihrer heutigen Temperatur abgekühlt habe. Es ergaben sich daraus für die einzelnen Perioden der Erdgeschichte Zeiträume853, die heute als viel zu gering erscheinen. Während des ersten Zeitraums, den Buffon auf 35000 Jahre bemessen zu dürfen glaubte, schieden sich infolge einer unregelmäßigen Zusammenziehung der äußeren Rinde die Festlandsmassen von den Meeresbecken. Aus[S. 475] der gleichen Ursache und durch Gasentwicklung im Innern des Erdkörpers entstand das Urgebirge. Während anfangs das Wasser die Erde als eine Dunstmasse umgab, verdichtete es sich mit der fortschreitenden Abkühlung. Die dritte Periode beginnt daher mit der Entstehung des Urmeeres, aus dem nur die Gipfel der Urgebirge hervorragten. Das heiße Wasser des Urmeeres besaß in hohem Grade die Fähigkeit, feste Bestandteile der Erdoberfläche zu zersetzen und aufzulösen. Allmählich sonderten sich aus dieser Lösung diese Bestandteile als Ton, Schiefer und Sand in parallelen, dem Urgebirge auf- und angelagerten Schichten wieder ab. Das Meer bevölkerte sich schließlich infolge der weiteren Abkühlung mit lebenden Wesen, deren Gehäuse gleichfalls zur Bildung von Schichten beitrugen. Die fortschreitende Änderung der Lebensbedingungen bewirkte, daß auch die Lebewelt ihren Charakter ununterbrochen durch das Aussterben von Arten und die Entstehung neuer Arten änderte. Aus den Überresten zusammengesetzter Pflanzen entstanden in dieser Periode auch die Steinkohlen führenden Schichten.
Während der nächsten (vierten) Periode entwickelte sich durch das Eindringen größerer Wassermengen in das heiße Erdinnere eine gewaltige vulkanische Tätigkeit, durch welche der bisherige Aufbau der Erdkruste sehr gestört und die Lage der Schichten in mannigfacher Weise geändert wurde. Die heutigen Eruptionen und Erdbeben betrachtet Buffon als die verhältnismäßig unbedeutenden Nachwehen des gewaltigen Kampfes der Elemente, der in jener Periode stattfand.
Im folgenden Zeitraum näherten sich die irdischen Zustände den heutigen. Gewaltige Landsäugetiere entstanden unter höheren Breiten zu einer Zeit, als die Lebensbedingungen in der Nähe der heißen Äquatorialzone noch ungünstig waren. Die Flora und die Fauna drangen daher von den Polargegenden allmählich in die niederen Breiten vor, während in der Verteilung von Wasser und Land nur noch geringe Änderungen stattfanden. So löste sich in dieser, mit dem Erscheinen des Menschen ihren Abschluß findenden Periode Großbritannien von Frankreich. Es entstand die Ostsee, und in den außereuropäischen Teilen der Erde fanden ähnliche Verschiebungen statt, zu denen Buffon die Entstehung der Sundainseln und der Antillen aus Teilen der benachbarten Festländer rechnet.
Es ist ein Reichtum von neuen Gedanken, die uns in Buffons Darstellung der Epochen der Natur begegnen, Gedanken, die in[S. 476] ihrer ganzen Bedeutung zum Teil erst spätere Generationen gewürdigt haben.
Während Buffon wie kein anderer Forscher des 18. Jahrhunderts die Geologie als Ganzes darzustellen wußte, bemühten sich andere Männer die Grundlagen dieser Wissenschaft durch eindringende Beobachtung der Einzeltatsachen immer mehr zu befestigen. Unter ihnen sind zu nennen: Pallas als Erforscher außereuropäischer Länder, Saussure wegen seiner Begründung des wissenschaftlichen Alpinismus, und Werner, der die von Lehmann und Füchsel begonnene, genauere Erforschung der einzelnen Formationsglieder fortsetzte.
Pallas854 wurde 1741 in Berlin geboren. Er studierte Medizin und Naturwissenschaften und wurde in noch jugendlichem Alter an die Petersburger Akademie berufen und von Katharina II. mit der Leitung einer Forschungsreise nach Sibirien betraut (1768–1774). Nach seiner Rückkehr veröffentlichte er ein Reisewerk über das nördliche Asien, das alle bisher erschienenen Reisewerke in bezug auf Reichtum an neuen Beobachtungen übertraf. Pallas starb 1811 in Berlin.
Das Hauptergebnis seiner Durchforschung Sibiriens war die Beobachtung, daß der Boden dieses Landes in seinen oberflächlichen, aus Ton, Mergel und Pflanzenresten bestehenden Teilen mit den Knochen großer Landsäugetiere förmlich durchsetzt ist. Die Erklärung, die Pallas hierfür gab, war wenig stichhaltig. Sie hat trotzdem der phantastischen, bald darauf von Cuvier aufgestellten Katastrophentheorie als Grundlage gedient: Aus dem vulkanischen Charakter der Südsee, die ihm »über einem einzigen vulkanischen Gewölbe zu stehen« schien und aus der Beschaffenheit der sibirischen Ebene folgerte Pallas nämlich, die Gewässer des Stillen Ozeans seien durch vulkanische Kraft nach den Polen gedrängt worden und hätten zahllose Pflanzen und Tiere der tropischen Länder dorthin geschwemmt und im Schutt der Gebirge begraben.
Kamen die Forschungen von Pallas auch in erster Linie der Zoologie, der Botanik und der Völkerkunde zugute, so ist doch auch in geologischer Beziehung manche genaue Beobachtung und treffende Ansicht auf ihn zurückzuführen. Die Meinung[S. 477] Buffons, daß das Urmeer fast bis zu den Gipfeln der ältesten Gebirge gereicht habe, wies Pallas zurück. Nach ihm fand die Erhebung der geschichteten Gesteine bis weit über das Niveau des Meeres hinaus durch vulkanische Kräfte statt. Pallas verstand es, aus der Störung der Schichten und ihren Lagerungsverhältnissen Schlüsse auf das Alter der Gebirge zu ziehen und z. B. begreiflich zu machen, daß die Alpen einem relativ jungen gebirgsbildenden Vorgang ihren Ursprung verdanken.
Fast ausschließlich der Erforschung der Alpen widmete sich Horace Benedicte de Saussure in vieljähriger, mühevoller Tätigkeit. Saussure wurde 1740 in Genf geboren und bekleidete dort eine Professur. Im Jahre 1787 führte er zu wissenschaftlichen Zwecken die erste Besteigung des Montblanc aus855. Er starb 1799. Als Ergebnis seiner alpinistischen Untersuchungen, die sich nicht nur auf die geognostischen, sondern auch auf die biologischen, meteorologischen und physikalischen Verhältnisse des Hochgebirges erstrecken, veröffentlichte er ein umfangreiches Werk856.
Saussure erkannte, daß der Kern der Alpen aus Urgestein (insbesondere Granit) besteht, und daß sich an diese Gesteine geschichtete, zunächst auch noch versteinerungslose Gebirgsglieder anlehnen. Hervorzuheben ist, daß Saussure, obgleich er die wissenschaftliche Erforschung der Gletscher begann, die Findlingsblöcke und andere glaziale Gebilde doch nicht als solche erkannte, sondern sie im Sinne der Katastrophentheorie als Zeugen plötzlich auftretender Gewalten, z. B. eines Zusammenbruchs von Gebirgsmassen, auffaßte. Wertvoll war dagegen sein Nachweis, daß die Westalpen nicht durch vulkanische Tätigkeit gehoben sein können, da sich nirgends Spuren einer solchen finden. Über die eigentliche Ursache der Gebirgsbildung blieb er jedoch die Auskunft schuldig.
Erwähnt sei noch, daß Saussure seine geologischen Arbeiten mit solchen über die Schneegrenze, über die Wärmezunahme im Erdinnern und die Verbreitung der Pflanzenwelt nach Höhenzonen zu verknüpfen wußte. In letzterer Hinsicht hat er den pflanzenklimatologischen Untersuchungen vorgearbeitet, die später v. Humboldt am Pik von Teneriffa und in Südamerika anstellte.
In dem Maße, wie die Kenntnis der Gesteins- oder Gebirgsarten wuchs, nahm die bei ihrer Anordnung und Benennung einreißende Verwirrung zu. Diesem Zustande machte Werners erstes systematisches Lehrbuch der Geognosie ein Ende. Es erschien im Jahre 1787 und führt den Titel: »Kurze Klassifikation und Beschreibung der verschiedenen Gebirgsarten«.
Abraham Gottlob Werner wurde am 25. September 1750 in einem kleinen Orte der Oberlausitz geboren. Sein Vater verwaltete ein Eisenhüttenwerk und besaß eine Mineraliensammlung, die den Knaben in hohem Grade fesselte. Seit dem Jahre 1775 bekleidete Werner ein Lehramt an der Bergakademie in Freiberg857.
In den von ihm vertretenen Gebieten nahm er bald eine ähnliche Stellung ein, wie sie um dieselbe Zeit Linné in der Reihe der Botaniker und Zoologen besaß. Beide Männer wirkten vorzugsweise als Lehrer und Systematiker. Sie verstanden es, für ihre Wissenschaft zu begeistern und ihr Jünger zuzuführen, während die durch eigenes Forschen aufgefundenen Ergebnisse sich in bescheideneren Grenzen hielten. Bei Werner, wie bei Linné, entwickelte sich ferner eine gewisse Einseitigkeit, wodurch der weitere Ausbau der Wissenschaft bei dem Ansehen, das beide Männer genossen, mitunter ungünstig beeinflußt worden ist.
Da Werners Buch über die Fossilien858 sich besonders eignet, um mit dem Standpunkt, den die Mineralogie im 18. Jahrhundert einnahm, bekannt zu machen, da es ferner, wie selten eine Schrift, den Fortschritt dieser Wissenschaft bedingt hat, so sei aus seinem Inhalt hier noch einiges mitgeteilt.
Unter Fossilienkunde versteht Werner das, was wir heute als Mineralogie bezeichnen. Sie ist ihm nicht nur ihres Nutzens wegen von besonderer Wichtigkeit, sondern auch, weil auf ihr die »Lehre von den Gebirgen« (Petrographie) und die »mineralogische Geographie« (Geologie) beruhen.
Als den Begründer der neueren Mineralogie haben wir den Deutschen Agricola (Bauer) kennen gelernt859. In den auf Agricola folgenden zwei Jahrhunderten waren die Fortschritte dieser[S. 479] Wissenschaft jedoch gering. Ein erneutes Aufblühen begann um 1730, also etwa 40 Jahre vor dem epochemachenden Auftreten Werners. Zwischen den Mineralogen des 18. Jahrhunderts war eine gewisse Scheidung eingetreten. Die einen gründeten ihre Wissenschaft ausschließlich auf die äußeren Kennzeichen der Mineralien, während andere die wichtigste Aufgabe in der Zerlegung der Mineralien in ihre Bestandteile erblickten. Eine vermittelnde Richtung wollte Gruppen von Mineralien nach ihrer chemischen Zusammensetzung bilden. Für die Bestimmung der Mineralspezies innerhalb dieser Gruppen sollten aber die äußeren Kennzeichen maßgebend sein860. Werner dagegen hielt es für das Natürlichste, die systematische Gliederung des Mineralreichs ausschließlich nach der chemischen Zusammensetzung vorzunehmen, weil auf ihr die wesentlichste Verschiedenheit der Mineralien beruhe. Wenn sein Buch trotzdem in erster Linie von den Kennzeichen handelt, so liegt darin kein Widerspruch. »Denn«, sagt Werner, »die Mineralien in ein System bringen und nach Mitteln suchen, um die einzelnen Mineralspezies rasch und sicher zu erkennen, sind zwei verschiedene Dinge.« Zudem war die Chemie noch zu unentwickelt, um für das von Werner gewünschte System schon eine ausreichende Grundlage zu geben. Es lag daher näher, zunächst die Lehre von den äußeren Kennzeichen der Mineralien durch eingehende Erforschung und scharfe Begriffsbestimmung zu vervollkommnen. Hierin bestand denn auch vor allem Werners Reformwerk. Recht treffend bemerkt er, er wolle lieber die Mineralien schlecht geordnet und gut beschrieben als gut geordnet und schlecht beschrieben haben.
Werner unterscheidet äußere, innere und physikalische Kennzeichen. Die inneren oder chemischen Kennzeichen sind ihm zwar die wichtigsten, indes aus verschiedenen Gründen unbequem. Ihre Ermittlung erfordere viele Vorkehrungen und setze voraus, daß der Mineraloge gleichzeitig ein geschickter Chemiker sei. Bei der chemischen Untersuchung gehe ferner die Substanz verloren, da man sie zerlegen müsse. Unter den physikalischen Kennzeichen versteht Werner das Verhalten der Mineralien gegen andere Körper, insbesondere das magnetische und elektrische Verhalten. Da dieses keine große Rolle spielt, so bleiben als wichtigste die äußeren, durch unsere Sinne wahrnehmbaren Kennzeichen übrig.
Am ausführlichsten behandelt Werner die Farbe. Sie sei zwar allein nicht hinreichend, um die Mineralien zu unterscheiden, das seien aber alle übrigen Eigenschaften einzeln genommen auch nicht. Nur die Summe aller Eigenschaften bestimme den Begriff eines Minerals861. Werner unterscheidet acht Hauptfarben: Weiß, Grau, Schwarz, Blau, Grün, Gelb, Rot und Braun. Für jede Hauptfarbe werden, unter Anführung eines typischen Minerals, eine Anzahl Abstufungen unterschieden. Beim Gelb z. B.:
Jede dieser Abstufungen wird nicht nur durch ein oder mehrere Beispiele gekennzeichnet, sondern außerdem noch genau beschrieben. Goldgelb, sagt Werner z. B., ist eine metallische, hohe, gelbe Farbe, in der keine Beimischung einer anderen wahrzunehmen ist.
Werner schuf auch die für die äußere Gestalt (den Habitus) noch heute üblichen Bezeichnungen, indem er Ausdrücke wie »derb, eingesprengt, angeflogen, gestrickt, dendritisch« usw. so scharf umschrieb, daß sie für eine wissenschaftliche Terminologie zweckdienlich waren.
Die Kristallform findet zwar schon eine ausgedehntere Berücksichtigung, doch ist Werner von einer wissenschaftlichen Kristallographie noch weit entfernt. Er unterscheidet eine Reihe von Grundgestalten, wie die Säule, die Pyramide, die Tafel, die Achtflächner (Würfel und Rhomboeder), und beschreibt, wie sie durch Abstumpfung, Zuschärfung und Zuspitzung verändert werden. Abgestumpft nennt er z. B. einen Kristall, wenn »einige oder alle« Ecken oder Kanten wie abgeschnitten sind. Daß am Bleiglanz und am Kalkspat ein großer Formenreichtum vorkommt, wird nur nebenbei erwähnt862. Auch geht aus Werners Beschreibungen hervor, daß er charakteristische Formen, wie das Pentagondodekaeder am Schwefelkies, ebensowenig näher untersucht hat wie seine Vorgänger863.
Wie gering auf dem Gebiete der Naturbeschreibung noch das Bedürfnis nach wissenschaftlicher Genauigkeit war, geht aus der ganzen Art hervor, wie Werner das so wichtige, die größten[S. 481] Verschiedenheiten aufweisende Kennzeichen der »Schwere« berücksichtigt. Von der so einfachen Bestimmung des spezifischen Gewichtes mittels der hydrostatischen Wage heißt es864: »Dieser Versuch ist in der Mineralogie unbrauchbar. Denn wie ist es möglich, die dazu nötigen Werkzeuge gleich bei der Hand zu haben, und in welchem Kabinett würde es einem Mineralogen erlaubt sein, mit den Erzstufen dergleichen Versuche anzustellen? Hier müssen wir uns unserer Gliedmaßen bedienen, indem wir das Mineral in die Höhe heben. Unser Gefühl muß uns dann sagen, wie groß, unter Bemessung des räumlichen Umfangs, den wir nach Augenmaß beurteilen, die verhältnismäßige Schwere ist.« Einem derartigen noch ganz unwissenschaftlichen Verfahren entspricht es denn auch, wenn Werner sich bei seinen Beschreibungen der Angaben leicht, nicht sonderlich schwer, schwer und außerordentlich schwer, bedient.
Nur ganz nebenher wird auch das chemische Verhalten herangezogen. So empfiehlt Werner den Nachweis von Kupfer durch Ammoniak (blaue Farbe der Lösung), das Betupfen mit Säure, um kohlensaure Salze nachzuweisen, usw.
Zum Schluß sei als ein Beispiel, wie Werner die Mineralogie darstellt, seine Beschreibung von Fraueneis (Gips) hierhergesetzt:
Mag uns auch heute das von Werner Geschaffene nur dürftig erscheinen, sein Reformwerk hatte doch den glänzendsten Erfolg und bewirkte, daß die Mineralogie schon unter seinen Schülern (Breithaupt, Weiß u. a.) eine achtunggebietende Stelle einnahm.
Als Geognosie bezeichnet Werner »die Wissenschaft, die uns den festen Erdkörper überhaupt kennen lehrt, und uns mit den verschiedenen Lagerstätten der Fossilien, aus denen die Erde besteht, und mit ihrer Erzeugung und ihrem Verhalten gegeneinander bekannt macht«. Obgleich durch verschiedenartige Zusammenstellung der Mineralien, von denen schon Werner über 200 kannte, sich eine unbegrenzte Zahl von Mischungen ergeben würde, fand sich, daß die Verschiedenheit der Gebirgsarten durchaus nicht ins Unendliche geht und daß die meisten sehr charakteristisch und leicht bestimmbar sind. »Es ist wahrscheinlich«, sagt Werner, »daß wir den größten Teil der Gebirgsarten schon kennen, da diejenigen der entferntesten Länder insgemein mit den uns bekannten übereinstimmen«865. Sämtliche Arten werden sodann in fünf Gruppen eingeteilt, die Werner als Urgebirge, Übergangsgebirge, Flözgebirge, aufgeschwemmtes Gebirge und vulkanische Gesteine unterscheidet.
Zu der ersten Gruppe werden Granit, Gneiß und Glimmerschiefer gerechnet. »Uranfänglich« nennt Werner diese Gesteine, weil sie gleichsam den Kern der Gebirge vorstellen und sich in das Innere der Erde erstrecken. Auch der Mangel an Versteinerungen ist ihm charakteristisch für diese Bildungen. Erst im Übergangsgebirge, das vorzugsweise aus Tonschiefer und Grauwacke besteht, begegnen uns die ersten Versteinerungen.
Als Flözgebirge bezeichnet Werner Muschelkalk, Sandstein, rotes Totliegendes, Basalt, Steinkohle, Steinsalz und Gips. Es ist ihm wahrscheinlich, daß diese Gesteine aus Gliedern der älteren Gruppe hervorgegangen sind, die ihrerseits wieder durch Kristallisation aus wäßriger Lösung entstanden sein sollten. Eigentümlich ist ihm für das Flözgebirge das Vorhandensein von meist zahlreichen Versteinerungen, sowie die Erscheinung, daß seine Gesteine innerhalb desselben Gebirgsstocks in der Regel in Lagen miteinander abwechseln, während ein uranfängliches Gestein an dem Aufbau eines Gebirges ausschließlich oder doch auf weite Erstreckung beteiligt sei.
Die Verwitterungsprodukte der genannten Gesteine endlich werden als aufgeschwemmtes Gebirge bezeichnet, das entweder als Seifen aus Kiesel und Sand die Täler füllt, oder die alles bedeckende Schicht des niedrigen Landes bildet.
Die Anschauungen, welche Werner über die Natur und den Ursprung der vulkanischen Gesteine entwickelte, haben dem Fortschreiten der geologischen Wissenschaft gegenüber keinen Stand halten können. Er betrachtete sie nämlich als jüngste Produkte, die aus den sedimentären Gesteinen durch die Wirkung brennender Kohlenflöze umgeschmolzen seien. Von dem Basalt, dessen feurig-flüssiger Ursprung durch die Untersuchungen französischer Geologen als zweifellos dargetan worden war, behauptete Werner, das Gestein sei sedimentär; es habe einst ein weit verbreitetes Lager ausgemacht, das größtenteils wieder zerstört worden sei und die zerstreuten Basaltkuppen als Überreste zurückgelassen habe.
Diese Ansicht Werners wurde von einem seiner Schüler866 angegriffen, und alsbald erhob sich in Deutschland eine erbitterte wissenschaftliche Fehde zwischen den Anhängern Werners, den »Neptunisten«, und ihren Gegnern, den »Vulkanisten«. Es ist bekannt, daß auch Goethe, wie aus zahlreichen Stellen seiner Werke hervorgeht, an dieser Streitfrage lebhaften Anteil nahm.
Auch die neue, von Pallas und Saussure verfochtene Lehre, daß die Gebirge und ausgedehnte Teile der Erdoberfläche emporgehoben worden seien, bekämpfte Werner. Nach seiner Meinung änderte sich das Niveau des Weltmeeres; indem die gewaltigen Wassermassen von den Kontinenten abflössen, schufen sie durch ihre erodierende Tätigkeit die Unebenheiten der Erdoberfläche, ein Irrtum, der gleichfalls durch einen Schüler Werners, den hervorragenden Geologen von Buch, widerlegt wurde.
Die erwähnten Einseitigkeiten und Irrtümer erklären sich besonders aus dem Umstande, daß Werner seine Lehren auf Beobachtungen aufbaute, die sich auf das Erzgebirge und die angrenzenden Teile von Böhmen und Sachsen beschränkten, während die französischen Geologen und die jüngere, von Werner vorgebildete Generation deutscher Forscher zunächst Italien und bald darauf auch das übrige Europa und die außereuropäischen Erdteile geologisch untersuchten und mit der Ausdehnung des Gesichtskreises zu allgemeineren und richtigeren Ansichten kamen. Werners Verdienst war trotzdem nicht gering. Es besteht für die Geologie[S. 484] wie für die Mineralogie darin, eine »feste Terminologie eingeführt und dadurch eine klare Darstellung der Beobachtungen ermöglicht zu haben«867.
Bevor wir uns den jüngeren Geologen zuwenden, müssen wir uns mit dem Manne befassen, der am meisten zum Sturz der einseitig »neptunistischen« Lehre Werners beigetragen hat. Es ist das James Hutton. Er wurde 1726 in Edinburg geboren, studierte in seiner Vaterstadt und in Paris, wirkte als Privatgelehrter und starb 1797. Hutton war ein unvergleichlicher Beobachter und ein nüchterner scharfer Denker. Seine streng induktiv begründeten geologischen Ansichten entwickelte er zuerst im Jahre 1785. Ausführlich legte er sie in der 1795 erschienenen »Theorie der Erde« dar868.
Seine Beobachtungen stellte Hutton in England, Frankreich und vor allem in Schottland an. Dort untersuchte er im Grampiangebirge die Grenze zwischen dem Granit und den benachbarten Gesteinen. Dabei machte er die wichtige Entdeckung, daß von einem Granitstock mitunter Gänge ausgehen, die das Nebengestein durchsetzen, und letzteres an den Stellen, wo der Granit es berührt, oft wesentlich verändern. Hutton schloß hieraus, daß der Granit und der sich ähnlich verhaltende Porphyr eruptiv und jünger als die durchsetzten Schichten seien. Er beobachtete ferner, daß die von ihm als ursprünglich feurig-flüssig angesehenen Gesteine sich mitunter zwischen die Schichten sedimentärer Gesteine ergossen haben und daher irrtümlich für flözartige Bildungen angesehen wurden.
Zu erklären blieb noch der Unterschied, den Granit, Porphyr und Basalt gegenüber den eigentlichen, porösen und meist kein deutliches kristallinisches Gefüge aufweisenden Laven der noch tätigen Vulkane besitzen. Die Schwierigkeit wurde dadurch gehoben, daß zu jener Zeit die experimentelle Geologie einsetzte und Beweise für die Richtigkeit der Huttonschen Lehre brachte. James Hall, ein Landsmann Huttons und der Begründer des geologischen Versuchs, zeigte, daß die Laven des Vesuvs, wenn man sie schmilzt und langsam erstarren läßt, kristallinische Massen ergeben, deren Gefüge von den Bedingungen dieses Versuches abhängt. Die Ansicht der Neptunisten, daß eine kristallinische Beschaffenheit[S. 485] stets auf eine Ausscheidung aus wäßriger Lösung hindeute, war dadurch als Irrtum nachgewiesen. Ferner erwies Hall auf experimentellem Wege die Richtigkeit der Ansicht Huttons, nach welcher der hohe Druck, unter dem sich manche Gesteine im Erdinnern bilden, die Beschaffenheit ihres Gefüges bedinge. Hall schmolz z. B. Kreide in geschlossenen Gefäßen, so daß eine Zersetzung in Kalk und Kohlensäure nicht eintreten konnte. Auch in diesem Falle war das Erstarrungsprodukt körnig kristallinisch und mit dem Marmor völlig identisch869. Die älteren, unter Druck und langsam aus dem Schmelzfluß erstarrten Massengesteine wurden fortan als plutonische Gesteine bezeichnet.
Weit vorangeeilt war Hutton seinen der Katastrophenlehre huldigenden Zeitgenossen durch die Gesamtauffassung, die er sich vom geologischen Geschehen gebildet hatte. Er zeigte sich nämlich schon von den beiden Grundvorstellungen beherrscht, die erst seit Lyell Gemeingut der Geologen geworden sind870. Hutton lehnt nämlich den Gedanken, daß es sich in der Entwicklung der Erde um Katastrophen oder gar um übernatürliche Kräfte gehandelt habe, entschieden ab und sucht die Tatsachen aus den bekannten, noch heute wirkenden Kräften zu erklären. Da deren Wirkungen innerhalb der kurzen der Beobachtung zugänglichen Zeit aber nur geringfügig sein kann, so nahm Hutton zweitens die Vorstellung bedeutender Zeiträume zuhilfe, innerhalb welcher die Wirkungen der geologischen Kräfte sich zu großen Gesamtwirkungen summieren mußten.
Hinsichtlich der geschichteten Gesteine entwickelte Hutton gleichfalls Ansichten, die sich im wesentlichen mit den heutigen geologischen Anschauungen decken. Für diese Gesteine nahm er einen doppelten Ursprung an. Sie entstanden auf dem Grunde der Gewässer als Sand- oder Tonschichten aus dem Material, das sich durch die Zertrümmerung des festen Landes bildete. Jene Schichten wechseln mit Kalksteinen ab, die ihrerseits aus den Schalen der Meeresbewohner hervorgingen. An die Oberfläche[S. 486] gelangten die sedimentären Gesteine nicht etwa durch das Sinken des Meeresspiegels, wie manche der älteren Geologen annahmen, sondern die vulkanische Hitze bewirkte eine teilweise Hebung der Erdkruste. Unter dem Einfluß dieser Hitze sollten sich auch die Sedimente verfestigt haben, eine Ansicht, der die neuere Geologie allerdings nicht in ihrem ganzen Umfange beipflichtet. Die Hutton'sche Schule hat auch die erodierende Tätigkeit des Wassers in vortrefflicher Weise gewürdigt und zuerst auf die gestaltende und transportierende Wirkung des Gletschereises hingewiesen871.
Sollte das Studium der Gebirgsglieder Licht über die Entwicklungsgeschichte der Erde verbreiten, so mußte die Aufmerksamkeit sich in steigendem Maße den Einschlüssen der Gesteine, den Versteinerungen, zuwenden. Die alte, verbreitete Meinung, man habe es in diesen mit Naturspielen oder mit den Überresten der Sintflut zu tun, wich allmählich der Erkenntnis, daß die Fossilien Zeugnis von vergangenen Tier- und Pflanzenwelten ablegen. So entstand die Paläontologie, die vereint mit der gleichfalls im 18. Jahrhundert sich entwickelnden Geognosie, die Grundlage für die geologische Wissenschaft des 19. Jahrhunderts bilden sollte. Es entstanden Schriften über die fossilen Pflanzen, wie das Werk Scheuchzers872. Und im Jahre 1755 erschien in Deutschland ein größeres, systematisches Werk paläontologischen Inhalts, das sich den großen naturhistorischen Werken der Botaniker und der Zoologen dieses, sowie des verflossenen Zeitraums als ebenbürtig an die Seite stellen konnte873.
Der Schweizer Scheuchzer (1672–1733) war der Hauptvertreter der »Diluvianer«, die alle Versteinerungen als Zeugnisse für die Sintflut betrachteten. Einen im Kalkschiefer zu Oeningen gefundenen Abdruck, den Cuvier später einem Riesensalamander (Andrias Scheuchzeri) zuschrieb, hielt Scheuchzer für den »homo diluvii testis«, das »Beingerüst eines verruchten Menschenkindes,[S. 487] um dessen Sünde willen das Unglück über die Welt hereingebrochen.«
Der Verfasser des erwähnten paläontologischen Hauptwerkes war der Nürnberger Sammler und Maler Knorr874. Unterstützt durch den Jenenser Professor Walch gab Knorr ein mit hunderten von kolorierten Tafeln versehenes Werk heraus, das für die Versteinerungskunde grundlegend gewesen ist. Die Erläuterungen der Tafeln rühren von Walch her und gelten als Muster gründlicher Gelehrsamkeit, während man die Herstellung der zahlreichen Tafeln stets als Zeugnis eines bewunderungswürdigen Fleißes betrachten wird. Der reiche Inhalt kann nur angedeutet werden; er betrifft die fossilen Fische, Krebse, Seelilien (Crinoideen), Ammoniten, Nautiliden, Muscheln, Schnecken, Brachiopoden, Schwämme, Korallen, Belemniten usw. Am vortrefflichsten ist der Abschnitt über die für das Silur charakteristische Krebstiergruppe der Trilobiten. Aus dem Pflanzenreiche werden die fossilen Hölzer und die Steinkohlenpflanzen genau beschrieben. Der Wert des Werkes wird dadurch erhöht, daß es die vollständigsten und zuverlässigsten Angaben über die gesamte frühere Literatur enthält.
Werner und seine Schüler hatten ihr Augenmerk in erster Linie auf die Zusammensetzung und die Lagerung der Gebirgsglieder gerichtet und den Versteinerungen nur geringe Aufmerksamkeit gezollt. Das Werk von Knorr und Walch hatte sich dagegen auf genaues Beschreiben beschränkt. Erst seit dem Ende des 18. Jahrhunderts lernte man nach und nach die Versteinerungen als geschichtliche Denkmäler schätzen und ihr Verhältnis zur gegenwärtigen Lebewelt begreifen. Die Blattabdrücke der steinkohlenführenden Schichten z. B. hatten die älteren Geologen auf tropische Gewächse zurückgeführt. Und es erschien fast als ein Wagnis, daß 1784 ein Geologe875 erklärte, die betreffenden Überbleibsel hätten nichts mit jetzt lebenden Pflanzen zu tun, sondern seien auf gänzlich ausgestorbene Arten zurückzuführen.
Ähnlich änderten sich die Ansichten über die Versteinerungen tierischen Ursprungs. Große fossile Knochen von Säugern hatte man zwar seit dem Altertum schon hin und wieder ausgegraben. Erwähnung finden derartige Funde z. B. bei Plinius und später bei Athanasius Kircher. Wissenschaftliches Interesse erregten sie indessen erst im 18. Jahrhundert, als sich ihre Häufigkeit auffallend[S. 488] mehrte, und man sich nicht mehr mit der Fabel begnügte, daß es sich hier um untergegangene Riesengeschlechter handle. Im Jahre 1700 entdeckte man bei Cannstatt fossile Knochen, unter denen sich viele Elephantenzähne befanden, und etwa 100 Jahre später konnte Blumenbach mehrere hundert Stellen angeben, an denen man in Deutschland Überreste eines vorweltlichen Elefanten gefunden hatte, den Blumenbach als Elephas primigenius (Mammut) von den lebenden Arten dieser Gattung unterschied. Die ersten Nachrichten über Mammutreste in Sibirien stammen aus dem Jahre 1725, und gegen das Ende des 18. Jahrhunderts wies Pallas876 nach, daß der Boden des nördlichen Asiens mit den Überresten des Mammuts förmlich durchsät sei.
Ähnliche, von gewaltigen Landsäugern herrührende Funde machte man während des 18. Jahrhunderts in Amerika. Aus Resten, die man im nördlichen Teile dieses Kontinents entdeckte, gelang es, das Skelett des Mastodons wieder herzustellen; und im Jahre 1789 kam das vollständige, in den Pampas ausgegrabene Skelett eines riesigen Geschöpfes nach Europa. Das ausgestorbene Tier, dem es angehörte, wurde unter dem Namen Megatherium (Riesenfaultier) beschrieben. Um dieselbe Zeit bemerkte man im Pariser Gips zum ersten Male fossile Knochen von Vögeln.
Ein ganz neuer Geist wurde der Paläontologie eingehaucht, als Cuvier sie mit der Zoologie und mit der vergleichenden Anatomie in die engste Verbindung brachte. Wie auf diese Weise die Versteinerungskunde sich aus der bloßen Naturbeschreibung zu einer induktiv verfahrenden, modernen Wissenschaft entwickelte, bleibt späterer Darstellung vorbehalten.
Die Ergebnisse der neueren Philosophie, sowie der neueren Naturwissenschaft übten einen Einfluß auf das allgemeine Denken aus, der sich seit dem Beginn des 18. Jahrhunderts in wachsendem Maße geltend machte und wiederum eine Rückwirkung auf das wissenschaftliche Denken äußerte. Die Wurzeln dieser unter dem Namen der »Aufklärung« bekannten Erscheinung sind in England zu suchen. Von dort aus pflanzte sie sich nach Frankreich fort, um schließlich auch in Deutschland und den übrigen europäischen Ländern ihren Widerhall zu finden. Das Ziel der Aufklärung war die Befreiung von den kirchlichen Dogmen und anderen Vorurteilen, denen sich Galilei, Descartes und Huygens noch gebeugt hatten, während seit dem Anfang des 18. Jahrhunderts Philosophie und Forschung auf der ganzen Linie mehr oder weniger offen im bewußten Gegensatz zur herrschenden kirchlichen Lehre standen. Daß die Kirche dem Geiste der neuen Zeit sich nicht anpaßte, ja ihn sogar, wo sie es konnte, in Fesseln schlug, erregte den Widerspruch der Gelehrten und der Gebildeten. In England knüpfte diese geistige Revolution vor allem an die Lehren Lockes an. Ihr Führer war der Ire John Toland (1670–1722). Die Schriften Tolands und seiner Anhänger haben Holbach und Diderot, die für ihre Übersetzung sorgten, sowie andere französische Aufklärer angeregt. Vor allem war es Voltaire, der auf den Spuren Tolands und seiner Jünger wandelte und, wie sie, veraltete Anschauungen und Gebräuche mit allen Waffen des Geistes bekämpfte. Tolands Einfluß erstreckte sich so weit, daß wir ihn auch als den Vater des neueren Monismus betrachten müssen877. Gleich sein erstes Werk, das er im Jahre 1696 anonym erscheinen ließ, erregte ungeheures Aufsehen. »Nur wer das Erscheinen des ‚Leben Jesu‛ von Strauß[S. 490] erlebt hat, kann sich hierüber eine annähernde Vorstellung machen«878. Toland suchte darzutun, daß die Lehren des Evangeliums, richtig gedeutet, nichts enthalten, was nicht mit der Vernunft vereinbar ist. Das Buch (Christianity not mysterious) gilt noch heute als die Grundlage des »Deismus«. Danach offenbart sich Gott nicht durch Wunder, sondern er wirkt nur innerhalb der Naturgesetze. Die Verfechter dieser Ansicht nannten sich Freidenker (free-thinker), ein Wort, das ja noch in der Jetztzeit seine Geltung hat.
Die Kirche verhielt sich gegen Toland genau so, wie hundert Jahre vor ihm, gegen Galilei. Sie brachte es fertig, daß im irischen Parlament der Beschluß gefaßt wurde, Tolands Buch öffentlich zu verbrennen. Es wurde sogar vorgeschlagen, nicht nur das Buch, sondern auch den Verfasser den Flammen zu überliefern. Toland entzog sich seinen Verfolgern durch die Flucht. Später begab er sich auf Einladung der Königin Sophie Charlotte nach Berlin. Dort verkehrte er in dem gelehrten Kreise, den die Königin um sich versammelte, und dem auch Leibniz angehörte. Briefe, die Toland später an die Königin richtete, erschienen unter dem Titel: Letters to Serena (London 1704). In diesen Briefen suchte er nachzuweisen, daß die geistigen Vorgänge nur als Tätigkeitsformen der Materie zu betrachten sind. Kann die Materie denken? und Wie kommt Bewegung in die Materie? Das sind die wichtigsten Fragen, die Toland beschäftigen. Die allgemeine Ursache der Bewegung ist nach Descartes Gott, der die Materie zugleich mit der Bewegung geschaffen hat. Wie heute das Verhältnis von Materie und Energie, so bildete damals das Verhältnis von Materie und Bewegung den Hauptgegenstand der naturphilosophischen Untersuchungen. Die Ruhe betrachtete Toland nur als einen Grenzfall, in dem zwei gleichstarke, entgegengesetzt gerichtete Bewegungen einander aufheben. Undurchdringlichkeit, Ausdehnung und Aktion sind nach ihm nicht drei verschiedene Dinge; sie entspringen nur verschiedenen Betrachtungsweisen eines und desselben Dinges. Descartes hatte das Wesen der Materie in der Ausdehnung erblickt; Huygens hatte ihr außerdem als nicht minder wesentlich die Undurchdringlichkeit zugeschrieben. Aktion endlich ist vielleicht im Tolandschen Sinne schon eine Vorahnung von dem, was die heutige Physik als Erhaltung der Kraft bezeichnet. Tolands Auffassung läßt sich[S. 491] im Sinne moderner Naturauffassung dahin präzisieren, daß es weder Kraft noch Materie gibt, sondern daß beide von verschiedenen Standpunkten aus aufgenommene Abstraktionen der Dinge sind.
Das Prinzip von der Erhaltung der Kraft gelangt bei ihm, wenn auch in philosophischer Fassung, in folgenden Worten zum Ausdruck: »Sowie die einzelnen Körper nur die verschiedenen Modifikationen der Materie und in ihr sämtlich enthalten sind, so sind alle einzelnen Bewegungen der Materie nur die verschiedenen Äußerungen der allgemeinen Aktion, die ebensowenig wie die Materie vermehrt noch vermindert werden kann«879.
Dies Prinzip läßt sich in seinen Vorahnungen also rückwärts über Toland, Leibniz, Descartes, Gassendi bis ins Altertum, wo wir es bei Epikur als schon bekannt antreffen, zurückverfolgen. Bei Descartes lautet die Fassung, daß Gott nicht nur die Menge der Materie, sondern auch die Summe der in der Welt vorhandenen Bewegung konstant erhalte, wobei Descartes als das Maß der Kraft das Produkt von Masse und Geschwindigkeit bezeichnete880.
In Frankreich wirkte der Geist der Aufklärungsperiode besonders in Männern wie d'Alembert, Holbach und Voltaire. Unter ihnen nahm d'Alembert die hervorragendste Stellung als Naturforscher ein. Er war sehr vielseitig begabt und bildete den Mittelpunkt einer Vereinigung, die sich später zu dem so bekannt gewordenen Holbachschen Zirkel erweiterte. D'Alembert würdigte gleich der Mehrzahl der französischen Gelehrten jener Zeit neben der Arbeit nichts so sehr als die geistig angeregte Unterhaltung, die in den Salons von Damen der Gesellschaft und des Hofes in Fluß gehalten wurde. Hat doch in keinem Lande die Frau eine so weitgehende Einwirkung auf die Politik, auf Kunst und Wissenschaft ausgeübt wie gerade in Frankreich. Und man kann sagen, daß diese mehr mittelbare Anregung der Wissenschaft nicht zum Nachteil gereicht, sondern die französischen Gelehrten in ihrer klaren, leicht verständlichen Ausdrucksweise gefördert hat.
In Gemeinschaft mit Diderot gab d'Alembert die berühmte Enzyklopädie heraus, die den beiden Männern und ihrem für die Aufklärung wirkenden Anhang den Namen der Enzyklopädisten eintrug. D'Alembert übernahm den mathematischen Teil dieses[S. 492] Werkes, das in alphabetischer Folge alle bis zur Mitte des 18. Jahrhunderts erworbenen Kenntnisse übermitteln sollte. Der Mathematik und den Naturwissenschaften wurde der erste Platz eingeräumt und betont, daß auf die alten Sprachen und die Altertumswissenschaft nicht viel Gewicht zu legen sei. Schoß man auch über das Ziel hinaus, so machte sich hierin doch eine gesunde Reaktion gegen die Überschätzung geltend, welche die »Humaniora« als Bestandteile der allgemeinen Bildung genossen haben und sehr häufig auch heute noch beanspruchen. Zu weit ging d'Alembert besonders darin, daß er das Verdienst der Alten um die Entwicklung der Mathematik und der Naturwissenschaften sehr gering einschätzte.
Neben Diderot und d'Alembert sind besonders Holbach, Lamettrie881 und Helvetius zu nennen. Holbach wurde 1723 in der Pfalz geboren und starb 1789 in Paris. Er arbeitete gleichfalls an der großen Enzyklopädie und ist besonders durch sein »System der Natur« bekannt geworden882. Diese Schrift sowie diejenige des Helvetius (1715–1771) über den Geist bedeuten den Höhepunkt der materialistischen Weltanschauung und sind von größtem Einfluß auf das geistige Leben des Zeitalters der Aufklärung gewesen.
Im »System der Natur« wird alles Geschehen allein auf Materie und Bewegung zurückgeführt. An die Stelle der Teleologie wird auch auf seelischem Gebiete überall das rein mechanische Wirken gesetzt. Die Moral wird aus dem physisch zu erklärenden Instinkt hergeleitet.
Über das Verhältnis des Menschen zur Natur äußert sich Holbach in folgenden Worten: »Die Menschen werden sich jederzeit um die Wahrheit bringen, wenn sie die Erfahrung für selbstgeschaffene Systeme hingeben. Der Mensch ist ein Geschöpf der Natur; in ihr wurzelt er, ihren Gesetzen ist er unterworfen; ihrer kann er sich nicht entschlagen; selbst im Denken kann er nicht aus ihr heraustreten. Für ein von der Natur gebildetes, durch sie bestimmtes Wesen gibt es nichts jenseits des großen Ganzen, unter dessen Einflüssen es steht. Wesen, die man jenseits der Natur setzt, sind jederzeit Geschöpfe unserer Einbildungskraft.
Der Mensch höre also auf, außerhalb der Welt Wesen zu suchen und von ihnen ein Glück zu erwarten, das die Natur ihm[S. 493] versagt. Er lerne vielmehr eben diese Natur und ihre Gesetze kennen. Dann wende er das Beobachtete auf seine eigene Glückseligkeit an, mit stiller Unterwerfung unter die Gesetze, denen er sich nicht entziehen kann.
Offenbar ist es ein Mißbrauch, wenn man dem Menschen ein physisches und ein moralisches Sein beilegt. Der Mensch ist ein rein physisches Wesen und seine moralische Existenz ist nur eine besondere Seite seines physischen Seins. Seine sichtbaren Handlungen sowohl wie seine inneren Erregungen sind natürliche Folgen seines eigentümlichen Mechanismus und der Eindrücke, die er von Wesen seiner Umgebung erhält.«
Auf die philosophische Unhaltbarkeit dieser Lehren hat schon Voltaire hingewiesen. Ihren unumwundensten Ausdruck fanden sie in Lamettries Buch, Der Mensch eine Maschine883.
Hiermit endet unsere Betrachtung der naturwissenschaftlichen Errungenschaften desjenigen Zeitalters, das vom Wiederaufleben der Wissenschaften bis zu dem gegen das Ende des 18. Jahrhunderts einsetzenden Umschwung reicht. Wir gedachten auch der geistigen Strömungen, die neben der geschilderten Entwicklung einhergingen, sie bedingten und durch sie bedingt wurden. Der nächste und der Schlußband sollen das Emporblühen der Naturwissenschaften in der mit jenem Umschwung anhebenden neuesten Zeit bis zu den Problemen des Tages schildern.
| Figur | aus | |
| 1. | Mikroskop aus zwei Sammellinsen | Gerland u. Traumüller, Geschichte d. physikalisch. Experimentierkunst. Leipzig, W. Engelmann. 1899. Abb. 109. |
| 2. | Keplers Konstruktion des astronomischen Fernrohrs | Keplers Dioptrik (Ostwalds Klassiker Nr. 144. S. 38). |
| 3. | Keplers Abbildung zur Erläuterung des holländischen Fernrohrs | Keplers Dioptrik (Ostwalds Klassiker Nr. 144. S. 59). |
| 4. | Keplers Teleobjektiv | Keplers Dioptrik (Ostwalds Klassiker Nr. 144. S. 60). |
| 5. | Galileis Erklärung der Gezeiten | Dialog, Ausg. v. Strauß. S. 446. |
| 6. | Galileis Versuch, den Widerstand des Vakuums zu messen | Ostwalds Klassiker Nr. 11. S. 70. |
| 7. | Galilei ermittelt das Gesetz der gleichförmig beschleunigten Bewegung | Ostwalds Klassiker Nr. 24. S. 21. |
| 8. | Galilei untersucht die Bewegung auf der schiefen Ebene | Ostwalds Klassiker Nr. 24. S. 40. |
| 9. | Galileis Versuch, der später auf das Gesetz von der Erhaltung der Kraft geführt hat | Ostwalds Klassiker Nr. 24. S. 19. |
| 10. | Zur Erklärung der Isochronie der Pendelschwingungen. | |
| 11. | Kreis und Zykloide als Bahnen des schwingenden Körpers. | |
| 12. | Galilei verbindet das Pendel mit einem Zählwerk | Gerland u. Traumüller, Geschichte d. physik. Experimentierkunst. 1899. S. 120. |
| 13. | Galileis Entwurf einer Pendeluhr | Zeitschrift f. Instrumentenkunde. 1868. S. 79. |
| 14. | Galileis Ableitung der Wurfkurve | Ostwalds Klass. Nr. 24. Fig. 108. |
| 15. | Ableitung des Hebelgesetzes aus dem Prinzip der virtuellen Geschwindigkeiten | M. Rühlmann, Gesch. d. techn. Mechanik. 1885. Abb. 13. |
| 16. | Galilei wendet das Prinzip der virtuellen Geschwindigkeiten auf die schiefe Ebene an | E. Mach, Die Mechanik in ihrer Entwicklung. 1883. Fig. 40 (S. 47). |
| 17. | Galileis Versuch über Kräftebeziehungen in einem System von Körpern | E. Mach, Die Mechanik in ihrer Entwicklung. 1883. S. 157. |
| 18. | Galilei vergleicht die Bruchfestigkeit hohler und massiver Zylinder | Ostwalds Klass. Nr. 11. Fig. 37. |
| 19. | Galilei untersucht die Bruchfestigkeit eines Balkens | Rühlmann, Vorträge über Gesch. der techn. Mechanik. Leipzig 1885. Fig. 12. |
| 20. | Galilei untersucht die Bruchfestigkeit von Prismen | Ostwalds Klass. Nr. 11. Fig. 18. |
| 21. | Galileis Thermoskop | Gerland u. Traumüller, Geschichte d. physik. Experimentierkunst. 1899. S. 116. |
| 22. | Das in den Abhandlungen der Accademia del Cimento dargestellte Gefäßbarometer | Musschenbroek, Tent. MDCCLVI Tab. IX. Fig. 3. |
| 23. | Vorrichtung für Versuche im Vakuum | desgl. |
| 24. | Durch Kapillarwirkung hervorgerufene Bewegungen. | |
| 25. | Guerickes Thermoskop | Guerickes »Experimenta nova«. Cap. 37. |
| 26. | Drebbels Thermoskop. | |
| 27. | Das i. d. Abhandlungen der Accademia del Cimento dargestellte Thermometer | Musschenbroek, Tentamina Tab. I. Fig. 1. |
| 28. | Versuch der Akademiker über die Zusammendrückbarkeit des Wassers | desgl. |
| 29. | Grimaldis Nachweis der Beugung des Lichtes | Grimaldi, Physico-Mathesis de lumine, coloribus et iride. Bologna 1665. |
| 30. | Grimaldi beobachtet die Beugung an einem Lichtkegel | desgl. |
| 31. | Grimaldi entdeckt die Interferenz des Lichtes | desgl. |
| 32. | Die Pole eines kugelförmigen Magneten aufzufinden | Gilbert, Physiologia nova de magnete, magneticisque corporibus et de magno magnete tellure. London 1600. |
| 33. | Die Teilung eines Magneten | desgl. |
| 34. | Gilbert untersucht die Stellung eines kleineren Magneten zu seiner Terella | desgl. |
| 35. | Gilberts Versuche m. armierten Magneten | desgl. |
| 36. | Guerickes Elektrisiermaschine | Otto v. Guericke, De vacuo spatio 1672. Tafel XVIII. Fig. 5. |
| 37. | Keplers Bild | Günther, Kepler u. Galilei. |
| 38. | Keplers Konstruktion der Planetensphären | Keplers Mysterium cosmographicum de admirabili proportione orbium coelestium. Tübingen 1596. (Opera omnia. Bd. I.) |
| 39. | Keplers Konstruktion der Planetensphären | desgl. |
| 40. | Tychos Riesenquadrant | Tychos Astronomiae instauratae Mechanica. 1602. |
| 41. | Tychos Distanzenmesser | desgl. |
| 42. | Tychos Azimutalquadrant | Tychonis Brahe, De mundi aetherei recentioribus phaenomenis. Prag 1603. 2. Buch. Abbildung auf S. 463. |
| 43. | Tychos System | Guericke, De vacuo spatio. Buch I. Abb. III. |
| 44. | Erläuterung des zweiten Keplerschen Gesetzes. | |
| 45. | Kepler erblickt einen Sonnenflecken | Kepler, Opera omnia (ed. Frisch). Bd. II. S. 805. |
| 46. | Keplers Verfahren, den Brechungswinkel zu bestimmen | Keplers Dioptrik. Opera omnia Bd. II. S. 528. |
| 47. | Snellius entdeckt das Brechungsgesetz. | |
| 48. | Ableitung des Brechungsgesetzes. | |
| 49. | Kepler beweist, daß eine Linse umgekehrte Bilder liefert | Keplers Dioptrik. (Ostwalds Klassiker Nr. 144. Fig. 11.) |
| 50. | Hevels Abbildung des Mondes | Hevels Selenographie. 1647. Tafel 23. |
| 51. | Das Reflexionsgesetz, erklärt aus dem Prinzip der kleinsten Wirkung. | |
| 52. | Fermat erklärt das Brechungsgesetz aus dem Prinzip der kleinsten Wirkung. | |
| 53. | Keplers Kubatur des Ringes | Opera omnia (ed. Frisch) Bd. IV, p. 575. (Ostwalds Klassiker Nr. 165. S. 7.) |
| 54. | Keplers Rotationskörper, den er Apfel nannte | Keplers Doliometrie. (Ostwalds Klassiker Nr. 165. S. 7.) |
| 55. | Keplers Untersuchung der größten und kleinsten Werte. | |
| 56. | Stevins Ableitung der Gleichgewichtsbedingung für die schiefe Ebene | Stevin, Beghinselen der Weegkonst. Leyden 1586. |
| 57. | Stevins Nachweis des hydrostatischen Paradoxons | Stevins Werke. Leyden 1634. S. 499. Fig. 4. |
| 58. | Stevins Nachweis des aufwärts gerichteten Druckes | Stevins Werke. Leyden 1634. S. 500. Fig. 2 u. 3. |
| 59. | Stevins Ableitung des Seitendruckes. | |
| 60. | Torricellis Versuch. Torricelli, Esperienza del Argento Vivo | 7. Heft der »Neudrucke«, herausgegeben von Prof. Dr. G. Hellmann, Berlin 1897. |
| 61. | Pascals Abänderung des Torricelli'schen Versuches | Mach, Die Mechanik in ihrer Entwicklung. Fig. 83. |
| 62. | Pascals durch den Druck des Wassers in Tätigkeit gesetzter Hebel | Mach, Die Mechanik in ihrer Entwicklung. Fig. 82. |
| 63. | Guerickes Luftpumpe | Wiedergabe der 6. Tafel von Guerickes De vacuo spatio. |
| 64. | Guerickes Wasserbarometer | Wiedergabe der 10. Tafel von Guerickes De vacuo spatio. |
| 65. | Boyles Versuch, eine Beziehung zwischen dem Druck und dem Volumen eines Gases zu finden | Boyle, Opera varia. 1680. S. 38. Fig. 5. |
| 66. | Glaubers Destillierofen | Glauber, Beschreibung einer Destillierkunst. 1648. |
| 67. | Mayows Analyse der Luft | Ostwalds Klass. Nr. 125. Fig. 3. |
| 68. | Ansicht von Newtons Spiegelteleskop | Abbildung aus den Philos. Transactions von 1672. |
| 69. | Newtons schematische Zeichnung seines Spiegelteleskops | Newtons Optik. 1721. 1. Buch. 1. Teil. Tafel 5. Fig. 29. |
| 70. | Hadleys Spiegeloktant | Abbildung aus den Philos. Transactions von 1732. |
| 71. | Newton untersucht das Spektrum | Newtons Optik. I. Tafel III. Abb. 13. |
| 72. | Newtons Nachweis, daß die Spektralfarben verschieden brechbar sind | Newtons Optik. I. Tafel IV. Abb. 18. |
| 73. | Newton vereinigt die Spektralfarben zu weißem Licht | Newtons Optik. II. Tafel IV. Abb. 16. |
| 74. | Das Luftfernrohr | nach Huygens. |
| 75. | Newton erklärt das Zustandekommen des Regenbogens | Newton Optics. London 1721. Book I. Part. II. Tab. IV. Fig. 15. |
| 76. | Hooke erklärt die Interferenz | Hookes Micrographia. |
| 77. | Newtons Ableitung der Zentralbewegung aus der Wurfbewegung | Newtons Principien (Ausgabe von Wolfers). Fig. 213. |
| 78. | Newtons Satz über die Zentralbewegung | a. a. O. (1872). Fig. 15. |
| 79. | Newtons Bild. | |
| 80. | Huygens' Bild. | |
| 81. | Huygens' Darstellung des Saturnringes | Christiani Hugenii Systema Saturnium. Haag 1659. |
| 82. | Römer berechnet die Geschwindigkeit des Lichtes | Huygens, Abhandlung über das Licht. Fig. 2 (Ostwalds Klassiker Nr. 20. S. 14). |
| 83. | Die Fortpflanzung des Lichtes | a. a. O. Abb. auf S. 21. |
| 84. | Huygens erklärt die Fortpflanzung des Lichtes | a. a. O. Abb. auf S. 22. |
| 85. | Erläuterung des Huygens'schen Prinzips | a. a. O. Abb. auf S. 23. |
| 86. | Huygens erklärt die Reflexion des Lichtes | a. a. O. Abb. auf S. 26. |
| 87. | Huygens leitet aus seinem Prinzip das Brechungsgesetz ab | a. a. O. Abb. auf S. 36. |
| 88. | Huygens untersucht den Doppelspat | a. a. O. Abb. auf S. 50. |
| 89. | Huygens erläutert den Aufbau des Doppelspats | |
| 90. | Huygens erklärt die Doppelbrechung | a. a. O. Abb. auf S. 57. |
| 91. u. 92. | Huygens entdeckt die Polarisation durch Doppelbrechung | Wilde, Geschichte d. Optik, Bd. II. Tafel II. Fig. 33. |
| 93. | Turmuhr aus dem 14. Jahrhundert | Gerland u. Traumüller, Geschichte d. physik. Experimentierkunst. Fig. 75. |
| 94. | Huygens' Abbildung der von ihm erfundenen Pendeluhr | Christiani Hugenii, Horologium oscillatorium. 1673. S. 4. Fig. 1. |
| 95. | Huygens beweist, daß die Schwingungen in der Cykloide isochron erfolgen | Horologium oscillatorium. Figur auf S. 12. |
| 96. | Huygens' Cykloidenpendel | Huygens, Horologium oscillatorium. S. 4. Fig. 2. |
| 97. | Huygens' Unruhe | Huygens, Opera varia. Bd. I. |
| 98. | Das Problem des Schwingungsmittelpunktes | |
| 99. | Huygens löst das Problem des Schwingungsmittelpunktes | Rühlmann, Geschichte der techn. Mechanik. S. 95. Abb. 19. |
| 100. | Huygens untersucht die Bewegung des Zentrifugalpendels | Ostwalds Klass. Nr. 138. Fig. 21. |
| 101. | Huygens zeigt, daß sich bewegliche Körper unter dem Einfluß der Zentrifugalkraft nach den spezifischen Gewichten ordnen | E. Mach, Die Mechanik in ihrer Entwicklung. Fig. 106. |
| 102. | Halleys Ableitung der barometrischen Höhenformel | |
| 103. | Tschirnhausens Satz über die katakaustische Linie | Cantor, Vorlesungen z. Geschichte d. Mathematik. Bd. III. S. 142. |
| 104. | Stenos Zeichnungen von Längsschnitten durch Bergkristalle | v. Kobell, Geschichte der Mineralogie. S. 18. |
| 105. | Stenos Zeichnungen von Querschnitten durch Bergkristalle | desgl. |
| 106. | Hookes zusammengesetztes Mikroskop | Hookes Micrographia. Schem. I. Fig. 5 u. 6. |
| 107. | Borelli erläutert die Wirkung des zweiköpfigen Armmuskels | Borelius, De motu animalium. Leyden 1685. Tab. III. Fig. 2. |
| 108. | Borelli ermittelt den Schwerpunkt eines Menschen | Borelius, De motu animalium. Leyden 1685. Fig. 12. |
| 109. | Swammerdams Zeichnung des Darmkanals der Biene | Swammerdam, Bibel der Natur. Tafel XVIII. Fig. 1. |
| 110. | Malpighis Darstellung des Nervensystems vom Seidenschmetterling | Malpighi, De Bombycibus. Tab. VI. Fig. 1 u. 2. |
| 111. | Malpighi untersucht die Verbindung eines Nervenknotens mit dem Tracheensystem | desgl. |
| 112. | Malpighis Darstellung der Entwicklung eines Wirbeltieres | Malpighi, De ovo incubato. Taf. II. |
| 113. | Malpighis Darstellung der Entwicklung eines Wirbeltieres | desgl. |
| 114. | Leeuwenhoeks Abbildung von Infusorien | Leeuwenhoek, Arcana naturae. 1695. Bd. I. S. 42. |
| 115. | Leeuwenhoeks Darstellung der Muskelfasern des Herzens | Leeuwenhoek, Arcana naturae. 1695. Bd. I. S. 447. |
| 116. | Die älteste Abbildung, welche den zelligen Bau der Korksubstanz darstellt | Hooke, Micrographia. Schem. XI. Fig. 1. |
| 117. | Leeuwenhoek bildet die einfachen und die gehöften Tüpfel der Holzfasern einer Kiefer ab | Arcana naturae. Bd. I. S. 315. |
| 118. | Malpighis Darstellung eines Längsschnittes durch das Holz der Rebe | Malpighi, Die Anatomie der Pflanzen, bearb. v. M. Möbius, (Ostwalds Klass. Nr. 120. S. 31.) |
| 119. | Eulers Bild. | |
| 120. | Eine der von Euler untersuchten elastischen Kurven. | |
| 121. | Schwingende Saiten. | |
| 122. | Eulers aus Glas und Wasser zusammengesetztes Objektivglas | Eulers Briefe an eine deutsche Prinzessin. Leipzig 1773. Bd. III. Abb. auf S. 299. |
| 123. | Bouguers Photometer | Wilde, Gesch. d. Optik. II. Teil. 3. Tafel. |
| 124. | Lamberts Photometer | Lambert, Photometrie. (Ostwalds Klassiker Nr. 31. Fig. 2.) |
| 125. | Chladni'sche Klangfiguren | Chladni, Entdeckungen über die Theorie des Klanges. Taf. VIII. Fig. 87–90. |
| 126. | Erläuterung des Clairaut'sehen Kanalprinzips. | |
| 127. | Die Bestimmung der Länge des Sekundenpendels. | |
| 128. | Halleys Bestimmung der Sonnenparallaxe | J. Müller, Lehrbuch d. kosmischen Physik. 5. Aufl. 1894. Fig. 97. |
| 129. | Maskelyne und Hutton bestimmen die Dichte der Erde. | |
| 130. | Bradley entdeckt die Aberration. | |
| 131. | Bradleys Erklärung der Aberration. | |
| 132. | Das von Romé de l'Isle gebrauchte Anlegegoniometer | Hauy, Traité de Minéralogie. 1801. Bd. V, p. VIII. Fig. 77. |
A.
B.
C.
D.
E.
F.
G.
H.
I.
J.
K.
L.
M.
N.
O.
P.
Q.
R.
S.
T.
U.
V.
W.
Z.
Zu S. 88, Anm. 2: Vgl. K. Meyer, Die Entwicklung des Temperaturbegriffs im Laufe der Zeiten. Nr. 48 der Sammlung »Die Wissenschaft«, Verlag von Vieweg, Braunschweig.
Zu S. 119: Zu den Ausführungen Keplers bemerkt E. Wiedemann: »Faraday hat einmal meinem Vater gesagt, wenn man wüßte, was er alles versucht habe, so würde man ihn für verrückt halten.«
Zu S. 121: Der Ehrensaal des Deutschen Museums in München birgt eine Rekonstruktion der »Uranienborg« nebst den von Tycho benutzten Instrumenten in der Größe 1 : 10.
Zu S. 129: Unter den Gegnern des Hexenwahns ist auch der Jesuit Spee (1591–1635) zu nennen, der sich durch seine geistlichen Lieder einen Namen in der Literaturgeschichte erworben hat (Wü).
E. Wiedemann bemerkt zu diesem Punkt: Ob wir dank der Telepathie nicht bald wieder Hexenprozesse haben werden? Wir sind auf dem besten Wege dazu! Sobald die Telepathie geglaubt wird, gibt es auch Hexen!
Zu S. 141: Das Problem des Sonnenbildes wurde schon von Kamâl al Dîn gelöst (Wi).
Zu S. 143 oben: Alhazen war schon bekannt, daß das Verhältnis zwischen dem Einfalls- und dem Brechungswinkel nicht konstant ist (Wi).
Zu S. 145 Mitte: Auch Alhazen war mit der am sphärischen Hohlspiegel auftretenden Abweichung schon bekannt (Wi).
Zu S. 145 unten: Der Gedanke, den Linsen eine hyperbolische Form zu geben, begegnet uns nach den neuesten Untersuchungen, welche die großen Verdienste der Araber um die Entwicklung der Optik dargetan haben, schon bei Kamâl al Dîn (Wi).
Zu S. 150, Anm. 3: Siehe auch S. Günther, Vergleichende Mond- und Erdkunde (Vieweg, Die Wissenschaft) (Wü).
Zu S. 174 (4. Zeile): Es muß heißen »uns gegen die Umwelt geistig einzustellen« statt »uns gegen die geistige Umwelt einzustellen«.
Zu S. 201: Ein prächtiges Ölbild Otto v. Guerickes befindet sich im Ehrensaal des Deutschen Museums zu München.
Zu S. 207: Der Saal für Mechanik im Deutschen Museum zu München enthält außer der Originalluftpumpe Guerickes auch Nachbildungen des Baroskops (Abb. 64 unten).
Zu S. 265: Nach E. Wiedemann finden sich auch bei Kamâl al Dîn schon richtige Vorstellungen über das Zustandekommen des Regenbogens.
Zu S. 282: Zu dem zweiten Absatz ist zu bemerken, daß dies Verhalten Newtons für seine ganze Denkungsart bezeichnend ist (Wi).
Zu S. 338: Herrn Prof. Dr. Plaßmann (Münster i. W.) verdanke ich folgende Mitteilung über die Entdeckung der Saturnmonde:
In neuerer Zeit wurden zwei weitere Monde auf photographischem Wege entdeckt. Nach dem Abstände von dem Hauptplaneten (gemessen von dessen Mittelpunkt und in Teilen seines Äquatorradius) lassen sich die 10 Monde folgendermaßen ordnen:
| Satellit | Entdecker – Zeit | Abstand |
| Mimas | W. Herschel 1789 | 3,1 |
| Enceledus | " " " | 3,9 |
| Tethys | D. Cassini 1684 | 4,9 |
| Dione | " " " | 6,2 |
| Rhea | " " 1672 | 8,7 |
| Titan | Chr. Huygens 1655 | 20,2 |
| Themis | W. H. Pickering 1904 | 24,2 |
| Hyperion | W. Cr. Bond 1848 | 24,5 |
| Japetus | D. Cassini 1671 | 58,9 |
| Phoebe | W. H. Pickering 1898 | 214,4 |
Zu S. 432: Mit physiologischer Optik hatten sich schon Ptolemäos und vor allem Ibn al Haitam befaßt (Wi). Siehe Bd. I dieses Werkes.
Zu S. 491: Hier wie an früheren Stellen decken sich die modernen Anschauungen nicht etwa vollkommen mit den älteren. Das Prinzip der Erhaltung der Kraft (richtiger der Energie) konnte erst in Verknüpfung mit dem Arbeitsbegriff aufgestellt werden. (Auf Grund einer Bemerkung von E. Wiedemann.)
[1] Kugler, Astronomische und meteorologische Finsternisse. (Zeitschr. d. deutschen morgenländ. Gesellschaft 1902. S. 60.)
[2] Besonders K. F. Ginzels Berechnungen der Sonnenfinsternisse für Rom, Athen, Memphis und Babylon für den Zeitraum von 900 v. Chr. bis 600 n. Chr.
[3] Das Wort hat also eine von seiner heutigen ganz abweichende Bedeutung.
[4] v. Lippmann, Abhandlungen und Vorträge zur Geschichte der Naturwissenschaften. Leipzig 1906. S. 142.
[5] L. v. Ranke, Englische Geschichte. I, 4.
[6] Näheres hierüber siehe an späterer Stelle.
[7] Nach den Niederlanden weist auch die älteste Kunde über die Laterna magica. Vgl. F. P. Liesegang, Christian Huygens und die Erfindung der Zauberlaterne. (Deutsche opt. Wochenschrift 1919. S. 152 u. 165.)
[8] Siehe darüber: Servus, Die Geschichte des Fernrohrs bis auf die neueste Zeit. Berlin 1886. Petri, Das Mikroskop von seinen Anfängen bis zu seiner jetzigen Vervollkommnung. Berlin 1896. M. v. Rohr, Die optischen Instrumente (Leipzig, Teubner, 1906), sowie v. Rohrs Abhandlungen in der optischen Wochenschrift.
[9] Die betreffende Bibelstelle lautet: Wiederum führte ihn der Teufel auf einen hohen Berg und zeigte ihm alle Reiche der Welt und ihre Herrlichkeit.
[10] Heller, Gesch. d. Phys. I. 384.
Den der Erfindung zu Grunde liegenden Gedanken hat Porta in seiner Magia naturalis angedeutet, jedoch ohne daß ihm die Ausführung gelungen wäre. Es heißt dort: »Konkave Linsen lassen ferne Gegenstände, konvexe nahe sehr deutlich wahrnehmen. Wenn man beide Linsenarten richtig zusammenzusetzen wüßte, so würde man ferne wie nahe Gegenstände deutlich sehen«.
[11] Nach dem Zeugnis des belgischen Gesandten Borelius. Das betreffende, lateinisch verfaßte Schriftstück findet sich in Wildes Geschichte der Optik I. 147. wiedergegeben.
[12] Wilde, Geschichte der Optik. Bd. I. 150.
In Middelburg wird noch heute ein Mikroskop gezeigt, das Jansen verfertigt haben soll. Es befindet sich im Besitz der dortigen wissenschaftlichen Gesellschaft. Über dieses und andere Mikroskope von historischem Interesse siehe den Bericht von R. Biedermann über die Ausstellung im South Kensington Museum. Berlin 1877. S. 945.
[13] Gerland und Traumüller, Geschichte der physikalischen Experimentierkunst. Leipzig. W. Engelmann. 1899. Abb. 109.
[14] Wolff, Gesch. d. Astronomie. S. 359.
[15] Heller, Geschichte der Physik I. 386.
[16] Galilei, Sidereus nuntius, 1610. Le opere di Galileo Galilei, Ed. naz. Vol. III. Parte prima. p. 60. Firenze 1892.
[17] Johannis Kepleri Dioptrice. 1611. Kepleri Opera omnia (ed. Frisch) II. 515 ff.
[18] Dioptrice, Problema LXXXVI. Duobus convexis majora et distincta praestare visibilia, sed everso situ.
[19] Ostwalds Klassiker Bd. 144. S. 49.
[20] Keplers Dioptrik, 89. Problem; es lautet: Tribus convexis erecta et distincta et majora praestare visibilia.
[21] Wie er in seinem »Rosa Ursina« betitelten Werke mitteilt. Siehe an späterer Stelle.
[22] Ostwalds Klassiker. 144. (Keplers Dioptrik oder Schilderung der Folgen, die sich aus der unlängst gemachten Erfindung der Fernrohre für das Sehen und die sichtbaren Gegenstände ergeben. 1611. Übersetzt von F. Plehn. Leipzig, W. Engelmann, 1904). S. 61.
[23] Ostwalds Klassiker, 144. S. 72.
[24] Christoph Scheiner wurde im Jahre 1575 in einem kleinen schwäbischen Orte geboren. Mit 20 Jahren trat er in den Jesuitenorden ein. Er lehrte Mathematik in Ingolstadt und Rom und starb 1650 als Rektor eines Jesuitenkollegiums.
[25] Näheres darüber siehe an späterer Stelle.
[26] Humboldt, Kosmos III. 383.
[27] Rosa ist ein symbolischer Name für die Sonne. Das Adjektiv Ursina weist darauf hin, daß Scheiner das Buch einem Herzog von Orsini widmete, der ihn bei seinen Untersuchungen unterstützt hatte.
[28] Scheiner, Oculus, hoc est fundamentum opticum. 1619.
[29] Scheiner, Oculus, Liber III. Pars I. Cap. VI. Refractio radii visorii ex aëre in tunicam Corneam. VII. Refractio e Cornea in humorem Aqueum. Cap. VIII. Densitas humorum oculi comparata. Cap. IX. Refractio radii ex Aqueo humore in Crystallinum. Cap. X. Refractio crystallino humore in Vitreum. Cap. XI. Refractio e Vitreo humore in tunicam Retinam.
[30] Libri, Histoire des sciences mathématiques en Italie. Bd. III. S. 201.
[31] In seinen Galilei-Studien handelt E. Wohlwill von zahlreichen, das Leben Galileis betreffenden Einzelheiten (Mitteilungen zur Gesch. der Med. u. Naturwissensch.). Wohlwill unternimmt darin auch die Nachprüfung mancher Angaben der Biographen Galileis. Als erster unter diesen ist Niccolo Gherardini zu nennen. Er hatte Galilei 1633 kennen gelernt und gab 15 Jahre nach Galileis Tode die erwähnte Biographie heraus. Auch einem Schüler Galileis, Vincenzio Viviani, verdanken wir eine Schilderung des Lebens seines Meisters. Ihr Titel lautet: Raconto istorico della vita di Galileo Galilei.
Eine von Wohlwill unternommene Würdigung der Galilei-Biographie Vivianis hat ergeben, daß die Angaben Vivianis nur mit Vorsicht aufzunehmen sind. Vivianis Darstellung zeigt, wie manche von Schülern herrührende Biographien, den Fehler, daß die Objektivität der Darstellung unter der pietätvollen Gesinnung des Schriftstellers leidet. Wohlwill kommt zu dem Ergebnis, daß die Angaben Vivianis, für die eine Bestätigung durch anderweitige Zeugnisse fehlt, als hinreichend beglaubigte Daten nicht angesehen werden können. Zu weit scheint Wohlwill zu gehen, wenn er Viviani absichtliche Fälschungen vorwirft und z. B. annimmt, er habe Galilei die Erfindung der Pendeluhr zugeschrieben, während Viviani sie sehr wahrscheinlich selbst erfunden habe.
[32] Forschungen über die Vorgänger Galileis hat P. Duhem angestellt. Siehe darüber auch den I. Band.
[33] Galilei, Opere complete ed. Alberi, VI. 11–12.
[34] Allerdings nicht allein wegen seiner Anhängerschaft an Koppernikus.
[35] Verbürgt ist dies nicht. Nach neueren Untersuchungen handelt es sich sogar wohl nur um eine Erfindung, mit der man Galilei einen besonderen Nimbus zu verleihen bezweckte. – Nach Wohlwill (Galilei-Studien in den Mitteil. zur Gesch. d. Med. u. Naturwissensch. Bd. IV. N. 27. S. 247) ist Gustav Adolf sogar niemals in Italien gewesen.
[36] Galilei sah zuerst drei Trabanten. Das war am 7. Januar 1610; einige Tage später erblickte er alle vier. Darauf verfolgte er ihre Bewegungen mehrere Monate sehr genau. Zu Ehren seines Herrscherhauses nannte Galilei die Jupitermonde die »Mediceischen Gestirne«. Gegen Ende des Jahres 1610 entdeckte Galilei die Lichtgestalten der Venus.
[37] Aus Fabronis »Lettere inedite d'uomini illustri, Florenz 1773«, übersetzt von C. J. Jagemann. Siehe Geschichte des Lebens und der Schriften des Galilei von C. J. Jagemann, Weimar 1783.
[38] Nach A. B. Hanschmann, Bernhard Palissy als Vater der induktiven Wissenschaftsmethode. Leipzig 1903. S. 145.
[39] Sidereus nuntius. Venedig 1610. Diese Schrift findet sich im dritten Bande der Alberischen Gesamtausgabe der Werke Galileis.
[40] So zählte er im Sternenbilde der Plejaden 40 Sterne, während das unbewaffnete Auge nur 6 erkennt. Den Mond, den die Aristoteliker für eine Scheibe hielten, erblickte er als eine Welt gleich der unsrigen mit Gebirgen und Tälern. Er war sogar imstande, die Höhe der Mondberge aus der Länge ihres Schattens zu berechnen.
[41] Fabricius und Scheiner.
[42] Siehe weiter unten bei Kepler.
[43] Gerhard Berthold, Der Magister Johann Fabricius und die Sonnenflecken. Leipzig 1894.
[44] De maculis in sole observatis. Wittenberg 1611. Ein Neudruck des sehr seltenen lateinischen Originals findet sich in der erwähnten Schrift von G. Berthold.
[46] An Marcus Welser. Die Briefe waren vom November und Dezember des Jahres 1611 datiert und mit dem Pseudonym »Apelles latens post tabulam« unterzeichnet.
[47] In der von Moritz Carriere gegebenen Übersetzung. Siehe Carriere, Die philosophische Weltanschauung der Reformationszeit. Stuttgart und Tübingen 1847. S. 139.
[48] Dialog über die beiden hauptsächlichsten Weltsysteme, das Ptolemäische und das Koppernikanische, von Galileo Galilei. Aus dem Italienischen übersetzt und erläutert von Emil Strauß. Leipzig B. G. Teubner 1891. Der Titel des Originals lautet: Dialogo de Galileo Galilei sopra i due massimi sistemi del mondo, Tolemaico e Copernicano. MDCXXXII.
[49] Wie in so vielen Fällen, war die »Schule« weit beschränkter und engherziger als der Meister, und vieles, was sie als »aristotelisch« zu lehren vorgab, hat Aristoteles selbst teils gar nicht behauptet, teils nicht als Dogma hingestellt! Vgl. v. Lippmann, Abhandl. u. Vorträge, Bd. 2, S. 153 (über Aristoteles).
[50] Ausgabe von Strauß S. 37.
[51] Dialog, S. 57.
[52] Dialog (Ausgabe von Strauß) S. 81.
[53] Es geschieht dies im zweiten »Tag« des Dialogs.
[54] Dialog (Ausgabe von Strauß). S. 209.
[55] Dialog (Strauß). S. 382.
[56] Dialog. 4. Tag.
[57] Gleich 1200 Erdhalbmessern statt 23000.
[58] Dialog, Ausgabe von Strauß. S. 446.
[59] Es ist daher zu begrüßen, daß es durch eine mit den nötigen Erläuterungen versehene Übersetzung dem deutschen Leser zugänglicher gemacht wurde. Sie erschien 1891 bei B. G. Teubner: E. Strauß, Dialog über die beiden hauptsächlichsten Weltsysteme von Galileo Galilei.
[60] Siehe S. 26 dies. Bds.
[61] Es sei verwiesen auf Gebler, Galileo Galilei und die Römische Kurie. Nach authentischen Quellen dargestellt. Stuttgart 1876–1880, sowie auf Wohlwill, der Inquisitionsprozeß des Galileo Galilei. Berlin 1870. Eine neuere Biographie veröffentlichte Wohlwill unter dem Titel: Galilei und sein Kampf für die Koppernikanische Lehre. 1909. Hamburg. L. Voss.
[62] Riccioli, Almagestum novum, lib. IX.
[63] Siehe auch G. Bertholds in der Zeitschrift für Geschichte der Mathematik (1897) erschienene Notiz: Über den angeblichen Ausspruch Galileis »Eppur si muove«.
[64] Seine Mitteilung über diese Entdeckung datiert vom 20. Februar 1637.
[65] Hevels Selenographie, Danzig 1647.
[66] Er hatte sich deswegen 1616 mit Philipp III. von Spanien vergeblich in Verbindung gesetzt (S. Jagemann. Geschichte des Lebens und der Schriften des G. Galilei. 1783. S. 146).
[67] Heller, Geschichte der Physik, I. 366.
[68] Unterredungen und mathematische Demonstrationen über zwei neue Wissenszweige von Galileo Galilei. Aus dem Italienischen übersetzt und herausgegeben von A. v. Oettingen. Leipzig. Verlag von Wilhelm Engelmann 1890. Ostwalds Klassiker der exakten Wissenschaften Nr. 11, 24 u. 25. Der Originaltitel lautet: Discorsi e dimostrazioni matematiche intorno a due nuove scienze. Leyden 1638.
[69] S. Bd. I. S. 430.
[70] Galilei, Unterredungen und mathematische Demonstrationen, Dritter und vierter Tag. Ostwalds Klassiker Nr. 24. S. 3
[71] Dieser Schluß war nicht zulässig. Welche Rolle hier der Luftdruck spielt, war Galilei allerdings noch unbekannt.
[72] Ostwalds Klassiker Nr. 11. S. 70.
[73] Ostwalds Klassiker Nr. 11. S. 71.
[74] Ostwalds Klassiker Nr. 11. S. 72.
Daß die Luft schwer sei, wurde auch schon im Altertum angenommen. Auch Lionardo da Vinci und Cardano schrieben der Luft Gewicht zu. Cardano stellte das Problem, »das Verhältnis der Dichte des Wassers zu derjenigen der Luft durch Wägung zu finden.« Er hielt die Luft für 50mal so leicht wie Wasser.
[75] Galilei gibt nämlich an (Ostwalds Klassiker Nr. 11, Seite 72), sie sei gegen 400mal leichter, während sie tatsächlich 773mal so leicht ist.
[76] Rafaelo Caverni, Storia del metodo sperimentale in Italia. Tomo IV. p. 269 u. f. Firenze 1895.
[77] Commentaria in Aristotelem Graeca, edita consilio et auctoritate Academiae literarum regiae Borussicae Vol. XVII. Philoponi in physicorum libros quinque posteriores. Ed. Hieronymus Vitelli, Berolini 1888, p. 683.
[78] Viviani in seinem Bericht über das Leben Galileis, der 1654 geschrieben, aber erst 1717 veröffentlicht wurde. Galilei selbst hat diese Versuche in seinen Schriften nicht erwähnt, daraus glaubt Wohlwill schließen zu dürfen, daß es sich hier nur um eine der in der Geschichte der Wissenschaften so häufigen Legenden handelt (Mitteilungen zur Geschichte der Medizin und der Naturwissenschaften IV, 2. 1905). Daß übrigens Galilei die Angaben des Aristoteles durch Fallversuche widerlegt hat, geht aus seiner in den »Unterredungen« gegebenen Darstellung zur Genüge hervor. Ob diese Versuche vom Turme zu Pisa oder von einem anderen hohen Gebäude vorgenommen wurden, ist im Grunde ohne Bedeutung.
[79] Mach, Die Mechanik in ihrer Entwicklung. Leipzig 1883. S. 133.
[80] Siehe die Mitteilungen z. Gesch. d. Medizin u. d. Naturwiss. XIV. Bd. S. 181.
[81] Dialog, Ausgabe von Strauß, S. 237.
[82] Galilei braucht hierfür die Ausdrücke impeto, energia und momento del descendere.
[83] Ostwalds Klassiker Nr. 24. S. 30.
[84] Ostwalds Klassiker Nr. 24. S. 25.
[85] Ostwalds Klassiker Nr. 24. S. 35.
[86] Ostwalds Klassiker Nr. 11. S. 75.
[87] Den Isochronismus der Pendelschwingungen entdeckte Galilei bereits 1582 während seiner Studienzeit in Pisa.
[88] Näheres siehe bei Gerland und Traumüller, Geschichte der physikalischen Experimentierkunst, Leipzig 1899, S. 120 u. f.
[89] Näheres berichtet darüber A. Kistner in den Mitteilungen zur Geschichte d. Medizin u. d. Naturw. Bd. XIV. S. 240.
[90] Näheres findet sich in der Abhandlung E. Gerlands, Über die Erfindung der Pendeluhr. Bibl. math. III. Folge, Bd. V. S. 234.
[91] Zeitschrift für Instrumentenkunde 1888. S. 79.
Die Zeichnung stellt die erste Idee der Anwendung des Pendels auf die Uhr dar. Sie wurde nach den Angaben Galileis, der damals schon blind war, von seinem Sohne und von seinem Schüler Viviani angefertigt. Näheres siehe im Bericht über die Ausstellung im South-Kensington Museum. Berlin 1877. S. 411 u. f.
[92] Ostwalds Klassiker Nr. 11. S. 84.
[93] S. Bd. I. S. 430.
[94] Näheres über die Entdeckung dieses Prinzips siehe bei E. Wohlwill, Die Entdeckung des Beharrungsgesetzes (Zeitschrift für Völkerpsychologie und Sprachwissenschaft. Bd. XIV u. XV.)
[95] P. Tannery, Galilée et les principes de la dynamique.
Siehe auch die Jahrbücher über die Fortschritte der Mathematik, Jahrgang 1901.
[96] Rosenberger, Geschichte der Physik B. II. S. 227.
[97] Der analytische Ausdruck für diese Kurve lautet: y2 = 2px. Für zwei Punkte x_{ʹ}y_{ʹ} und x_{ʺ}y_{ʺ} erhalten wir y_{ʹ}2 = 2px_{ʹ} und y_{ʺ}2 = 2px_{ʺ}. Die Division der beiden Gleichungen ergibt das oben ausgesprochene Gesetz: x_{ʹ} : x_{ʺ} = y_{ʹ}2 : y_{ʺ}2.
[98] Galileis Unterredungen und mathematische Demonstrationen. Siehe Ostwalds Klassiker Nr. 24. Fig. 108.
[99] Ostwalds Klassiker Nr. 24. S. 107.
[100] Ostwalds Klassiker Nr. 24. S. 119. Mit dem Problem der Kettenlinie befaßten sich Huygens, Leibniz und Johann Bernoulli. Die erste Lösung erfolgte 1690 durch Jakob Bernoulli (Acta Eruditorum, Mai 1690).
[101] Ostwalds Klassiker Nr. 24. S. 90 u. 91. Über die Ausführung dieses Versuches durch die Florentiner Akademie siehe an späterer Stelle dies. Bds.
[102] Benjamin Robins, New principles of gunnery. London 1742. Näheres siehe an späterer Stelle.
[103] Eingehender hat man diese Fragen erst in der neuesten Zeit untersucht.
[104] Es ist hier der moderne Ausdruck gebraucht.
[105] Mach, Die Mechanik in ihrer Entwicklung. 1883. S. 47.
[106] Aristoteles, Mechan. Probleme (Poselger). Hannover 1881. S. 34. Näheres über den vermutlichen Verfasser dieser Schrift findet sich auf S. 128 des ersten Bandes.
[107] Ostwalds Klassiker Nr. 25. S. 43. (Galilei, Unterredungen und mathematische Demonstrationen, fünfter und sechster Tag).
[108] Mach, Die Mechanik in ihrer Entwicklung. 1883. Fig. 157.
[109] M. Rühlmann, Vorträge über Geschichte der technischen Mechanik. Leipzig 1885. Fig. 12.
[110] Discorso intorno alle cose che stanno in su l'acqua o che in quelle.
[111] Nelli, Vita I. p. 62. Das Patent datiert vom Jahre 1594 (Libri, l'histoire des mathématiques en Italie. IV. S. 197).
[112] Nelli. Vita e commercio letterario di Galileo Galilei. Vol. I. Losanna 1793. S. 72.
[113] Traumüller und Gerland, Geschichte der physikalischen Experimentierkunst. Leipzig 1899. S. 116.
[114] Der Vorschlag rührte von Galileis Freund Sagredo her.
[115] Sanctorius, Professor der Medizin in Padua.
[116] Harmonicorum libri XII. Paris 1636.
[117] Ostwalds Klassiker Nr. 11. S. 86.
[118] Z. B. Schwenter (Bd. I, S. 424).
[119] Siehe an späterer Stelle.
[120] »Dialog« Ausg. von Strauß S. 418–434 und an anderen Stellen.
[121] Dialog (Strauß) S. 70.
[122] Dialog (Strauß) S. 278.
[123] Dialog (Strauß) S. 424.
[124] Le opere di Galileo Galilei, Florenz 1842–1856. Sie rührt von Alberi her.
[125] Favaro, Le Opere di Galileo Galilei. Edizione nazionale sotto gli auspicie di Sua Maestà il Re d'Italia. Firenze 1890 u. f.
E. Wiedemann nennt diese Nationalausgabe mit Recht »eins der schönsten Denkmäler, das je Nationen einem ihrer großen Gelehrten gesetzt haben«.
[126] Die Briefe an und von Kepler erschienen 1672 unter dem Titel Epistolae Joannis Kepleri et Math. Berneggeri mutuae. Sie sind im 1. Bande der von Ch. Frisch besorgten großen Ausgabe der Keplerschen Werke zum Teil abgedruckt.
[127] Näheres über Bernegger und sein Verhältnis zu Galilei hat Eilhard Wiedemann in den Berichten der physik. mediz. Sozietät in Erlangen (Bd. 36, 1904) unter dem Titel, »Studien zur Geschichte Galileis« bekannt gegeben.
[128] Die erste naturwissenschaftliche Gesellschaft rief Porta 1560 in Neapel ins Leben. Sie hieß Academia secretorum naturae und bestand nur kurze Zeit. Im Jahre 1603 wurde die Accademia dei Lyncei (Akademie der Lüchse) in Rom gegründet. Sie hatte neben der Förderung der Naturwissenschaften künstlerische und literarische Ziele im Auge. Noch mehr galt dies von der Accademia della Crusca.
[129] Eins ihrer Mitglieder (Antonio Oliva) fiel in Rom der Inquisition in die Hände. Um der Tortur zu entgehen, nahm er sich durch einen Sturz aus dem Fenster seines Gefängnisses das Leben.
[130] In den Saggi di naturali esperienze fatte nell' Accademia del Cimento, Florenz, 1667. Im Jahre 1731 wurden die »Saggi« in lateinischer Übersetzung von Musschenbroek herausgegeben: Tentamina experimentorum naturalium captorum in Accademia del Cimento.
[131] Musschenbroek, Tentamina experimentorum captorum in Accademia del Cimento. MDCCLVI. Tab. IX. Fig. 3.
[132] Abbildung aus Musschenbroeks Bericht über die Versuche der Accademia del Cimento.
[133] De vi repercussionis et motionibus naturalibus a gravitate pendentibus. Reggio 1670. Angestellt hatte Borelli die in diesem Werk beschriebenen Versuche schon im Jahre 1655.
[134] Siehe Bd. II an spät. Stelle.
[135] Sie rührt von Clairaut her und findet sich im 189. Bande von Ostwalds Klassikern S. 60 u. f. auseinandergesetzt.
[136] Guericke, Experimenta nova ut vocantur Magdeburgica, Cap. 37.
[137] Cornelius Drebbel wurde geboren zu Alkmar 1672. Nach einem wechselvollen Leben gelangte er nach England an den Hof Jakobs I. Dort starb er 1634. Drebbel war ein Physiker von dem Schlage Portas und Kirchers. Seine magisch-physikalischen Versuche beschrieb er in seinem Traktat von der Natur der Elemente.
[138] Über Drebbels Apparat, sowie über die Vorgeschichte des Thermometers im allgemeinen hat E. Wohlwill in den Mitteilungen zur Geschichte der Medizin und der Naturwissenschaften berichtet. Jahrg. 1902. Heft 1–4.
[139] In seiner Abhandlung »Neue Beiträge zur Vorgeschichte des Thermometers« macht Wohlwill es wahrscheinlich, daß die Erfindung dieses Instrumentes in den Niederlanden ganz unabhängig von derjenigen in Italien erfolgte. (Mitteilungen zur Geschichte der Medizin und Naturwissenschaften. 1902. Nr. 4.)
[140] Musschenbroek, Tentamina. Tab. I. Fig. 1.
[141] Renaldini, Philosophia naturalis. 1694. III, 276. Nach Gerland hat Huygens zum erstenmal, und zwar schon 1665, den Vorschlag gemacht, den Schmelzpunkt und den Siedepunkt des Wassers als Fundamentalpunkte zu benutzen (Zeitschrift für Instrumentenkunde XIII, 390. 1893.)
[142] Abschn. III der Abhandlungen der Accademia del Cimento. Florenz 1667.
[143] E. v. Lippmann, Abhandlungen und Vorträge zur Geschichte der Naturwissenschaften. Leipzig 1906.
[144] Abschnitt IV der »Saggi«.
[145] Abbildung aus Musschenbroek: Tentamina experimentorum naturalium captorum in Accademia del Cimento.
[146] Gerland, Beiträge zur Geschichte der Physik. Leopoldina. Halle 1882.
[147] Eines dieser Instrumente befindet sich noch heute im physikalischen Museum zu Florenz.
[148] Benzenberg, Versuche über das Gesetz des Falles, über den Widerstand der Luft und über die Umdrehung der Erde. Dortmund 1804. S. 101.
[149] Bologna 1665.
[150] l. c. S. 235 u. f.
[151] Physico-Mathesis, s. S. 2.
[152] Physico-Mathesis, S. 8.
[153] Physico-Mathesis, Propos. XXII.
[154] Physico-Mathesis, Propos. XXIV. S. 231.
[155] Ostwalds Klassiker Nr. 43.
[156] Grimaldi, Physico-Mathesis. Propos. XLII.
[157] Im ersten Buche seiner Physico-Mathesis sucht Grimaldi in 60 Propositionen darzutun, daß das Licht eine Substanz sei, im zweiten spricht er sich in einer Reihe von Propositionen für die Akzidentalität des Lichtes, also für das Gegenteil aus.
[158] Rosenberger, Newton und seine Prinzipien. S. 27.
[159] L. v. Ranke, Englische Geschichte im 17. Jahrhundert, I, 324.
[160] Ein Ausspruch Bacons: »Scientia est potentia.«
[161] Gilbert, Physiologia nova de magnete magneticisque corporibus et de magno magnete tellure, London 1600. Auch in Deutschland erschienen mehrere Ausgaben, so in Stettin 1628 und 1633, sowie in Frankfurt a. M. 1629. Eine biographische Skizze über Gilbert veröffentlichte F. M. Feldhaus. Winters Universitätsbuchhandlung. Heidelberg 1904.
[162] Nach anderen Angaben 1544. Siehe Mitteilungen z. Gesch. d. Mediz. und Naturw. 1904. (Bd. III; Heft 1 u. 2.) S. 115.
[163] Ein auf Deutsch schlecht wiederzugebendes Diminutiv von Terra, die Erde.
[164] Über Petrus Peregrinus siehe auch Bd. I. S. 353. Seine Schrift wurde durch G. Hellmann von neuem herausgegeben. Siehe Nr. 10 der von diesem veröffentlichten Neudrucke von Schriften über Meteorologie. Nr. 10 bringt unter dem Titel »Rara Magnetica« die seltensten und wichtigsten Abhandlungen über den Erdmagnetismus aus der ersten bis Gilbert reichenden Periode.
[165] Gilbert, De magnete, Buch II, Kapitel II.
[166] Über die Verwendung der Magnetnadel bei der Anlage von Gruben berichtet Agricola (1490–1555) in seinem Werke De re metallica.
[167] Gilbert, De magnete, I, 1. Diese Messung rührt von Robert Norman her. Die erste, jedoch sehr ungenaue Beobachtung der Inklination erfolgte im Jahre 1544 durch den Deutschen Georg Hartmann.
[168] Gilbert, De magnete. Lib. II. Cap. VI.
[169] Gilbert, De magnete II, Cap. IV.
[170] Ähnliche Gedanken wie bei Gilbert begegnen uns auch bei Descartes, und man kann annehmen, daß dieser seine Wirbeltheorie unter dem Einfluß von Gilberts Lehren entwickelt hat (M. L. Hoppe, Die Abhängigkeit der Wirbeltheorie des Descartes von Gilberts Lehre vom Magnetismus. Halle a. S. 1914).
[171] Solche Versuche stellte auch schon Galilei an. Siehe S. 77 dies. Bds.
[172] Gilbert, De magnete. Cap. XX.
[173] Otto von Guericke, De vacuo spatio. 1672. Tafel XVIII. Fig. 5.
[174] Hoppe, Geschichte der Elektrizität. Leipzig 1884, S. 5.
[175] Bacon, Novum organon. 1610. Übersetzt und erläutert von J. H. v. Kirchmann, Berlin, 1870.
[176] Telesio (Bernardinus Telesius) schrieb in der Vorrede zu diesem naturphilosophischen Buch, er könne nicht begreifen, daß so viele ausgezeichnete Männer sich durch die Jahrhunderte mit der aristotelischen Physik zufriedengegeben hätten. Er gründete eine Vereinigung, die sich die Aufgabe stellte, die Natur zu ergründen und die Philosophie des Aristoteles zu beseitigen. Diese Vereinbarung wurde durch die Kurie aufgelöst.
Nach Telesio gibt es nur drei Prinzipien, ein völlig passives, den Stoff, und zwei bewegende, die Wärme und die Kälte. Erstere dehnt den Stoff aus, letztere zieht ihn zusammen. Die experimentelle Erforschung der Natur hat Telesio nicht gefördert. Sein Verdienst ist, daß er die Menschheit vom Autoritätsglauben freizumachen suchte.
[177] Näheres über ihn und seine Beziehung zu Bacon findet man in dem Buche von A. B. Hanschmann, Bernhard Palissy als Vater der induktiven Wissenschaftsmethode. Leipzig 1903.
Über Palissy siehe auch Bd. I dies. Werkes S. 438, 444, 445.
[178] L. v. Ranke, Englische Geschichte. Bd. II. S. 135.
[179] Siehe Draper, Geschichte der geistigen Entwicklung Europas. Leipzig 1841. S. 527 u. f.
[180] Novum organum scientiarum. Lugd. Bat. 1645. Kap. 48, S. 366.
[181] Eine scharfe, aber in mancher Hinsicht gerechte Beurteilung Bacons rührt von Liebig her (Ueber Bacon und die Methode der Naturforschung, München 1863): »Bacons Urteil über Gilbert und Coppernikus ist sein eigenes wissenschaftliches Todesurteil. Die Tatsachen, die Gilbert entdeckte, hielt Bacon für Fabeln (Nov. Organ. II. Aph. 48) und Coppernikus erklärt er für einen Schwindler (Glob. intell. Cap. VI).« Das Vernichtende für Bacon ist, daß er beide verurteilt, weil er ihrer Forschungsmethode die Berechtigung abspricht. (Nov. Org. I. Aph. 64.) Liebig hat es von philosophischer Seite an Entgegnungen zugunsten Bacons nicht gefehlt. Das zutreffende Urteil ist auf der mittleren Linie zu finden, der die Darstellung des vorliegenden Werkes gefolgt ist. Vgl. v. Lippmann in »Abhandl. u. Vorträge« Bd. I: Bacon.
[182] Die gleiche Forderung ist oft und lange vor Comenius erhoben worden. Es kam aber vor allem darauf an, wie Galilei sich ausdrückt, die »Sprache und die Schriftzeichen verstehen zu lernen, worin dieses Buch geschrieben ist. Erst dann könne es verstanden werden«.
Auch die übliche Art der philologischen Ausbildung wurde angegriffen. Gegen sie wandte sich besonders der geistreiche Montaigne (1533–1592), der zu dem Urteil gelangte, daß der Zögling durch das jahrelange Studium der griechischen und der lateinischen Sprache »dummer werde, als er war, da er von Hause fortging«.
[183] Der gregorianische Kalender schaltet somit in 400 Jahren 97 Tage ein; sein Fehler beträgt für diesen Zeitraum nur 0,122 Tage.
[184] Die evangelischen Stände des Deutschen Reiches nahmen den gregorianischen Kalender 1700 an. England folgte erst 1752, während die griechisch-katholische Kirche sich bis auf den heutigen Tag ablehnend verhalten hat.
[185] Rosa Ursina sive sol ex admirando facularum et macularum suarum phaenomeno varius. 1630.
[186] Kästner, Geschichte der Mathematik. IV. S. 247.
[187] Siehe Günther, Kepler u. Galilei. E. Hofmann & Co., Berlin. 1896.
[188] Siehe Dannemann, Aus der Werkstatt großer Forscher. 3. Auflage, Abschnitt 12. Es handelt sich um den Halleyschen Kometen.
Eine volkstümliche Darstellung der Lehren Keplers bringt das Buch L. Günthers, Die Mechanik des Weltalls. Leipzig 1909.
[189] Breitschwerdt, J. Keplers Leben und Wirken. 1831. S. 71.
[190] Prodromus dissertationum cosmographicarum continens Mysterium cosmographicum de admirabili proportione orbium coelestium a Joanne Keplero. Tübingen 1596.
[191] Ein Bild des Lebens und Schaffens Tychos hat J. E. L. Dreyer geliefert: Tycho Brahe, ein Bild wissenschaftlichen Lebens und Arbeitens im 16. Jahrhundert. Autorisierte deutsche Übersetzung von M. Bruns. XII, 434 S. Karlsruhe, 1894.
[192] Friedrich II.
[193] Namens Hven.
[194] Nach Tychos »Mechanica«. 1602.
[195] Brief an Rothmann vom 24. 11. 1589. Tychonis Brahe, epistolarum astronomicarum libri. 1610.
[196] Bei Annahme des koppernikanischen Systems nämlich.
[197] Siehe den 66. Abschnitt von Dannemann, Aus der Werkstatt großer Forscher. Leipzig, W. Engelmann. 1908.
[198] Tycho Brahe, De mundi aetherei recentioribus phaenomenis. Liber secundus. Prag 1603. Figur auf S. 463.
[199] Im Jahre 1587.
[200] 1588.
[201] Laplace sagt in seiner Darstellung des Weltsystems (Ausgabe von Hauff), der Name aller derjenigen, welche ihre Gewalt mißbrauchten, um die Fortschritte der Vernunft aufzuhalten, müsse der Verwünschung aller Zeitalter preisgegeben werden. Als Tychos größten Widersacher nennt Laplace (Bd. II, S. 278) den dänischen Minister Walchendorp.
[202] Guericke, De vacuo spatio. lib. I. Icon. III.
[203] De motibus stellae Martis, Pars Secunda, Cap. 7.
[204] Siehe Johannes Frischauf, Grundriß der theoretischen Astronomie und der Geschichte der Planetentheorien. Leipzig, W. Engelmann. 1903.
[205] De motibus stellae Martis. Prag 1609, Opera omnia ed. Frisch. III. 135 ff.
[206] Am 24. Oktober 1601.
[207] Die Hexenverfolgungen haben mit dem Ende des 15. Jahrhunderts mehr als zweihundert Jahre wie die Pest gewirkt. Näheres siehe bei Binz, Doktor Johann Weyer, ein rheinischer Arzt, der erste Bekämpfer des Hexenwahns. Berlin 1896. Das Unheil ging von der Kirche aus. Seine Ausrottung erfolgte durch die der Naturwissenschaft zu verdankende Aufklärung. Als Beweis für die Verblendung jener Zeit mögen folgende Zeilen eines berühmten Theologen dienen. Sie sind einem Buche entnommen, daß auf Befehl Joachims von Brandenburg verfaßt wurde. Es heißt dort von den Hexen: »Kein Glied ist an unserem Körper, dem sie nicht schaden können. Meist machen sie die Menschen besessen und lassen sie von den Dämonen kreuzigen. Mit letzteren treten sie sogar in fleischliche Verbindung. Kein Ort ist so klein, wo man nicht eine Hexe findet. Aber selten findet sich ein Inquisitor«. Daß sich letztere auf kirchliches Geheiß bald einstellten, beweist die Tatsache, daß allein in der Gegend von Bormio die von Innocenz VIII. eingesetzten Inquisitoren in einem Jahre 41 Hexen verbrannten.
[208] Tabulae Rudolphinae. Ulm 1627. Opera omnia (ed. Frisch), VI. 661.
[209] Bürgi, ein Schweizer (1552–1632), und Napier oder Neper, ein Schotte (1550–1617), machten die so wichtige Erfindung der Logarithmen unabhängig voneinander. Bürgi war zuerst Gehilfe an der vom Landgrafen von Hessen unterhaltenen Sternwarte zu Cassel. Später leitete er diese Sternwarte, trat aber bald nach dem Tode seines fürstlichen Gönners in den Dienst Rudolfs des Zweiten über und wurde so zum Mitarbeiter Keplers.
[210] De motibus stellae Martis, Cap. 59 (Opera, edit. Frisch, Bd. III).
[211] Opera omnia (ed. Frisch) I. 106.
[212] »Harmonices mundi« lib. V.
[213] Opera omnia V. 279.
[214] Da sich die Massen bei gleicher Dichte wie die Volumina verhalten. In Wahrheit beträgt das Volumen der Erde etwa das 50fache von dem des Mondes, während sich die Dichten beider Weltkörper wie 1 : 0,6 verhalten. Die betreffende Stelle findet sich in Keplers Astronomia nova (Opera omnia III, 151).
[215] Nach einem von Kästner in seiner Geschichte der Mathematik Bd. IV. 360 mitgeteilten Auszug der Epitome astronomicae copernicanae Keplers.
[216] Joannis Kepleri Phaenomenon singulare seu Mercurius in sole. Leipzig 1609. (Opera omnia, ed. Frisch. II, 793.)
[217] In Einhards Vita Caroli Magni (herausgegeben von Jaffé 1876) wird berichtet, der Merkur sei im April des Jahres 807 »quasi parva macula nigra« vor der Sonnenscheibe gesehen worden.
[218] Opera omnia, II, S. 805.
[219] Durch Dr. G. Berthold.
[220] Siehe das Vorwort zu der erwähnten Ausgabe Dr. Bertholds. Über Keplers Stellung zur Astrologie siehe auch S. 115 dieses Bandes.
[221] Der Prediger David Fabricius war nicht etwa ein Mann, der sich mit der Astronomie nur oberflächlich aus Liebhaberei befaßte, sondern er hat nach Tycho Brahes Tode die erste Stelle unter den beobachtenden Astronomen eingenommen. So urteilt wenigstens Kepler, mit dem Fabricius in regem Briefwechsel stand. Für die Bestimmung der Marsbahn hat Kepler durch Fabricius viel wertvolles Material erhalten. David Fabricius gehörte auch zu den ersten, die das Fernrohr zu astronomischen Zwecken benutzten. Wahrscheinlich brachte es ihm sein Sohn Johann, der sich 1610 als Student der Medizin in Leyden aufhielt, aus Holland mit. Mit einem solchen Fernrohr entdeckte Johann Fabricius im elterlichen Hause die Sonnenflecken. Er stellte darauf unter Aufsicht seines Vaters eine Reihe von Beobachtungen zusammen und veröffentlichte deren Ergebnis in einer Schrift, die 1611 unter dem Titel »De Maculis in sole observatis« (Von den Sonnenflecken) erschien. (Näheres darüber siehe Bd. II. S. 26.)
[222] Erschienen 1618–1621 in Linz und Frankfurt; Opera omnia VI, 113 u. f.
[223] Somnium Kepleri von Ludwig Kepler dem Sohne. Frankfurt 1634. Eine deutsche, mit Erläuterungen versehene Ausgabe besorgte L. Günther, Leipzig, B. G. Teubner. 1898.
[224] Günther hat auch diese Anmerkungen übersetzt und erläutert. L. Günther, Keplers Traum vom Monde. Leipzig 1898.
[225] Günther, Keplers Traum. S. 129 u. f.
[226] A. a. O. S. 174.
[227] Siehe auch H. Hankel, Die Entwicklung der Mathematik. Tübingen 1869. S. 26.
[228] Ad Vitellionem Paralipomena. Frankfurt 1604 (Gesamtausgabe von Frisch II, 119).
[229] Johannis Kepleri Dioptrice. Augsburg 1611 (Gesamtausgabe von Frisch II. 515). – Keplers Dioptrik wurde neuerdings von Plehn in deutscher Übersetzung als Band 144 von Ostwalds Klassikern der exakten Wissenschaften herausgegeben (Leipzig, Verlag von Wilhelm Engelmann, 1904).
[230] Siehe S. 133 ds. Bds.
[231] Ad Vitellionem Paralip. Cap. I, Prop. IX. (Edit. Frisch. II, 113).
[232] Der vollständige Titel lautet: Ad Vitellionem Paralipomena, quibus Astronomiae pars optica traditur. Frankfurt 1604. Ausgabe von Frisch II. 119–397.
Der Pole Vitello (Vitellio) lebte um 1270. Er war also ein Zeitgenosse Roger Bacons. Vitello hat seine Optik, die im wesentlichen in einer Wiedergabe der Lehren Alhazens besteht, in Italien verfaßt. Sie erschien wiederholt gedruckt. Am bekanntesten ist die Ausgabe von Risner (Basel, 1572).
[233] Letzteres wird damit begründet, daß das Licht nichts Stoffliches sei (quia lux materia caret).
[234] Sicut se habent sphaericae superficies, quibus origo lucis pro centro est, amplior ad angustiorem: ita se habet fortitudo seu densitas lucis radiorum in angustiori ad illam in laxiori sphaerica superficie.
[235] Dies geschah durch Harriot, Epist. ad Keplerum scriptae; ed. Hanschii, 233; 1606. Siehe auch Wilde, Geschichte der Optik. I. 190.
[236] Ad Vitellionem. cap. 2. Opera omnia II. 153. – Einen Überblick über den Inhalt dieses Werkes, das die optischen Grundlagen der Astronomie entwickelt, gibt F. Plehn im Archiv für Optik. I. Bd. S. 75 u. f. 1908.
[237] Wilde, Geschichte der Optik. I. 188.
[238] Poggendorff, Geschichte der Physik. S. 167.
[239] Johannis Kepleri Dioptrice 1611. Opera omnia II. S. 515–567.
[240] Johannes Keplers Dioptrik oder Schilderung der Folgen, die sich aus der unlängst gemachten Erfindung der Fernrohre für das Sehen und die sichtbaren Gegenstände ergeben. 1611. Übersetzt und herausgegeben von Ferdinand Plehn. Ostwalds Klassiker der exakten Wissenschaften. Nr. 144. Leipzig, Verlag von W. Engelmann. 1904.
[241] Keplers Dioptrice, Figur zu Problema IV (Editio Frisch II, 528).
[242] Dioptrice, XIII. Propositio (Edit. Frisch II, 530): Nullus radius, qui intra corpus crystalli super unam ejus superficiem plus 42° inclinatur a vertice, potent illam superficiem penetrare.
[243] Dioptrik, Lehrsatz XII.
[244] Das Komplement des 42° betragenden Brechungswinkels.
[245] Der von Snellius gefundene Ausdruck läßt sich leicht in den gebräuchlichen umwandeln. Man geht von der oben gegebenen Abb. 47 aus und schlägt um C einen Kreis mit CA als Einheit (siehe Abb. 48). Dann ist sin α (Einfallsw.) = DE und sin β (Brchsw.) = AF, ferner ist AC : CB = sin (180 - α) : sin β = sin α : sin β = DE : AF. Ist nun AC : CB konstant, und zwar für Luft und Wasser = 3 : 2, so gilt dasselbe von sin α : sin β, da wir diesen Ausdruck gleich AC : CB gefunden haben.
[246] Descartes Dioptrik, Kapitel 2. Näheres über Descartes' Anteil an der Entdeckung des Brechungsgesetzes siehe in der bezüglichen Abhandlung von P. Kramer (Abhandlungen zur Geschichte der Mathematik. 4. Heft. 1882), sowie in der Abhandlung von H. Wieleitner »Das Brechungsgesetz bei Descartes und Snellius« (Natur und Kultur, 13. Jahrgang. S. 403–406).
[247] Lehrsatz XXXIX.
[248] Siehe auch Wilde, Geschichte der Optik. Berlin 1838. Bd. I. S. 201.
[249] Die Ähnlichkeit des Auges mit der Dunkelkammer findet man zuerst bei Lionardo da Vinci erwähnt. Porta, dem wir die erste abendländische Beschreibung der Dunkelkammer verdanken, betrachtete die hintere Wand des Auges als einen Hohlspiegel, von dem aus das Licht nach der Mitte des Auges gelange, um dort wahrgenommen zu werden.
Der Nachweis, daß die Linse des Auges ein Bild auf die Netzhaut wirft, erfolgte indessen schon vor Scheiner (Arauzi 1587). Das Auge eines Tieres wurde auf der hinteren Seite mit einem Ausschnitt versehen. In diesem Ausschnitt fing man das Bild eines vor dem Auge befindlichen Lichtes auf. E. Pergens, Geschichtliches über das Netzhautbildchen und den Optikuseintritt. Klinisches Monatsblatt für Augenheilkunde. Bd. 42, I. S. 137–143.
[250] In Vitellionem Paralipomena. Cap. V.
[251] Ostwalds Klassiker Nr. 144 (Dioptrik), S. 26–34.
[252] Siehe an späterer Stelle dieses Werkes.
[253] Dioptrik, Lehrsatz 62.
[254] Wilde, Geschichte der Optik, I. S. 199.
[255] Hirschberg, Die Optik der alten Griechen. Zeitschr. f. Psychologie und Physiol. d. Sinnesorgane. Bd. XVI. S. 350. Siehe auch Bd. I ds. Werkes S. 267.
[256] Ad Vitellionem Paralipomena. Frankfurt 1604. Cap. V. Propos. XXVIII (Edit. Frisch II, 255.)
[257] Kepler, Dioptrice LXIV, Propositio. (Ed. Frisch II, 540.)
[258] Siehe Wilde, Geschichte der Optik I, 254.
[259] Siehe S. 14 u. f. ds. Bds.
[260] Siehe Ostwalds Klassiker d. exakt. Wiss. Nr. 20, S. 12 u. 13.
[261] Hevelius, eigentlich Hewelke.
[262] Selenographia seu descriptio lunae et macularum ejusdem.
[263] Wolf, Geschichte der Astronomie. S. 396.
[264] Näheres über das mutmaßliche Schicksal dieser Briefe siehe in Poggendorffs Geschichte der Physik. S. 448.
[265] Eine englische Ausgabe besorgte Newton (Cambridge 1681).
[266] In seiner Pratique d'Arithmétique. Leyden 1585.
[267] In seiner Pratique d'Arithmétique.
[268] Zuerst in dem Rechenbuch des Johannes Widmann von Eger, das 1489 in Leipzig erschien. Erwähnt seien auch die Rechenbücher von Adam Riese, dessen Verdienst um die Kunst des Rechnens ja sprichwörtlich geworden ist. Die Rechenbücher Adam Rieses haben wissenschaftlich keine Bedeutung; sie waren aber praktisch recht brauchbar und sehr verbreitet. Über die Species, die Progressionen, die Bruchrechnung und die Regel de tri gehen sie kaum hinaus. Adam Riese (1492–1559) war Bergbeamter in Annaberg und leitete gleichzeitig eine Schule, in der er besonders das Rechnen lehrte.
[269] Cantor, Geschichte der Mathematik. Bd. II. S. 479.
[270] Anfänge hierzu finden sich schon bei Aristoteles.
[271] Cantor, Geschichte der Mathematik. Bd. II. S. 581.
[272] Näheres siehe Cantor II. S. 718.
[273] Suter, Geschichte d. mathem. Wissenschaften. Bd. II. S. 19.
[274] O. Stolz, Größen und Zahlen. Leipzig 1891. S. 11.
[275] Scipione del Ferro, 1508.
[276] Tropfke I. S. 285.
[277] Luigi Ferrari, 1522–1565.
[278] Gauß 1799 und Abel 1824.
[279] Veröffentlicht in Descartes' »Geometrie« im Jahre 1634. Eine deutsche Bearbeitung des Werkes lieferte Schlesinger. Berlin 1894.
[280] Cantor, Geschichte der Mathematik. Bd. II. S. 780.
[281] Cantor II. S. 605.
[282] Über Euklids drei Bücher Porismen siehe Cantor I. S. 239 u. f. Vielleicht hängt der Ausdruck mit πείρω, ich forsche, zusammen; jedenfalls verstand man darunter einen Satz, der ein neues Problem anregte und einschloß. (Cantor I. S. 291.)
[283] Fermat entwickelte seine analytisch-geometrische Methode in seiner Schrift: »Ad locos planos et solidos isagoge«. Die ihm Descartes gegenüber zugeschriebenen Prioritätsansprüche sind schwer zu entscheiden, weil Fermat sich zumeist darauf beschränkte, die Ergebnisse seiner Forschungen in Paris lebenden Mathematikern (besonders Mersenne) brieflich mitzuteilen. Seine Werke und ein großer Teil seiner Briefe wurden erst längere Zeit nach seinem Tode veröffentlicht. Fermat, Varia opera. Tolosae 1679.
[284] Elemente VI. 27.
[285] Bei Regiomontan begegnet uns z.B. die Aufgabe, festzustellen, von welchem Punkte der Erdoberfläche eine 10 Fuß lange senkrechte Stange, die 4 Fuß über dem Boden endigt, am größten erscheint. Eine Lösung hat Regiomontan indessen nicht gegeben. Im 16. Jahrhundert (bei Tartaglia) begegnet uns ferner die Aufgabe, eine bestimmte Zahl so zu teilen, daß das Produkt dieser Teile multipliziert mit ihrer Differenz den größten Wert hat.
[286] Methodus ad disquirendum maximum et minimum (Fermat, Opera varia S. 63 u. f.). Fermat wandte seine Methode schon 1629, also lange vor dem Erscheinen des Descartes'schen Werkes an. (Cantor II. S. 782.)
[287] de la moindre action.
[288] Der Gedanke findet sich bei Pappus. S. auch Mach, Die Mechanik in ihrer Entwicklung. S. 397.
[289] Dühring, Kritische Geschichte der allgemeinen Prinzipien der Mechanik. Berlin 1873. S. 290.
[290] Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes; neuerdings in Ostwalds Klassikern Nr. 46 in deutscher Übersetzung erschienen. Leipzig, W. Engelmann. 1894.
[291] Les lois du mouvement et du repos, déduites d'un principe métaphysique. Histoire de l'Académie de Berlin 1746. p. 290.
[292] Siehe den 8. Abschnitt des III. Bandes.
[293] Archimedes (ed. Nizze) Seite 12–23. Siehe auch: Dannemann, Die Naturwissenschaften in ihrer Entwicklung. Bd. I. S. 164 u. f.
[294] A. a. O. S. 163.
[295] De motibus stellae Martis: Cap. 59, 5. Opera Kepleri (ed. Frisch) III, 401.
[296] Zeuthen, Geschichte der Mathematik im 16. und 17. Jahrhundert. Leipzig, B. G. Teubner. 1903. S. 255.
[297] Nova Stereometria Doliorum vinariorum. Linz 1615. Opera omnia (ed. Frisch) IV, 555. Unter dem Titel »Neue Stereometrie der Fässer« aus dem Lateinischen übersetzt und herausgegeben von R. Klug. Bd. 165 von »Ostwalds Klassikern der exakten Wissenschaften«. Leipzig, W. Engelmann. 1908.
[298] Opera omnia IV. 575.
[299] Opera Kepleri IV, 584–585.
[300] Kepleri Opera omnia (ed. Frisch) IV, 607–609.
[301] Bonaventura Cavalieri wurde 1598 in Bologna geboren. Er war Schüler und später Freund Galileis. Nachdem Cavalieri in Bologna als Professor der Mathematik gewirkt hatte, starb er dort im Jahre 1647.
[302] Geometria indivisibilibus continuorum nova quadam ratione promota.
[303] Das Werk Guldins erschien 1635–1641 unter dem Titel Centrobaryca. Paul Guldin wurde 1577 in St. Gallen geboren; er war Jesuit und wirkte als Lehrer der Mathematik in Rom und an anderen Orten. Guldin starb 1643.
[304] Gerhard, Geschichte der Mathematik in Deutschland. S. 130.
[305] Arithmetica infinitorum sive nova methodus inquirendi in curvilineorum quadraturam 1655. John Wallis wurde 1616 in einem kleinen Orte der Grafschaft Kent geboren und wirkte als Professor der Mathematik in Oxford. Er gehört zu den Begründern der Royal Society und starb im Jahre 1703.
[306] Cantor, Geschichte der Mathematik. II. S. 822.
[307] Der Brief wurde im Oktober 1674 an Leibniz gesandt.
[308] Nova methodus pro maximis et minimis itemque tangentibus... (Acta eruditorum 1684).
[309] De geometria recondita et analysi indivisibilium atque infinitorum. Acta eruditor. 1686.
[310] Method of fluxions. London 1736. Geschrieben hatte Newton dieses Werk schon 1671.
[311] Fatio de Duillier.
[312] Réflexions sur la metaphysique du calcul. infinitesimal 1797.
[313] René Descartes (Cartesius) wurde 1596 in der Touraine geboren und starb 1650 in Stockholm, wohin er durch die Königin Christine von Schweden berufen worden war. Vorher hatte er nach einer unsteten Jugend viele Jahre in Holland gelebt.
[314] Pierre Gassendi, geboren 1592 in der Provence, gestorben in Paris im Jahre 1655, ist der Erneuerer der atomistischen Lehre Epikurs. Über das Verhältnis Epikurs zu Demokrit siehe Bd. I. S. 75. Nach Gassendi wurde eine bestimmte Anzahl von Atomen geschaffen. Sie sind der Urgrund aller Dinge. Außer den Elementen bestehen daher auch das Licht, die Wärme usw. aus Atomen. Sie sind unteilbar, von bestimmter Größe und Gestalt, schwer, absolut hart und undurchdringlich. Zwischen den Atomen befindet sich der leere Raum. Kurz, in den Grundzügen und mit nur geringen Abänderungen entwickelt Gassendi in seiner Physica corpuscularis die zuerst von Demokrit aufgestellten Lehren der materialistischen Weltanschauung. (Näheres siehe bei Lange in seiner Geschichte des Materialismus und Kritik seiner Bedeutung für die Gegenwart. 1882. S. 184 u. f.)
[315] Brief von Huygens an Leibniz vom 11. Juli 1692. Chr. Hugenii exercitationes mathem. ed. Uylenbroek. Hag. Com. 1833. I, 136.
[316] Novum organum. Lugd. Bat. 1645. Lib. II. Art. 37. p. 294.
[317] Cogitata physico-mathematica. Parisiis 1644. p. 21.
[318] Aristarchus Samius, de mundi systemate Parisiis 1644, p. 2. Vgl. J. C. Fischer, Geschichte der Physik. 1801. Bd. I. S. 272.
[319] De motionibus naturalibus. Lugd. Bat. 1686. c. VI. p. 166.
[320] Epitome astronomiae. 1621. Lib. IV. p. 510. Leibniz macht an verschiedenen Stellen darauf aufmerksam, daß zuerst Kepler diesen Begriff einer Trägheit eingeführt habe. Ansätze zu ihm finden sich nach v. Lippmann schon bei Aristoteles.
[321] Principia philosophiae 1677. P. II. § 43. p. 41.
[322] Boyle, Origo formarum et qualitatum. 1669. p. 50.
[323] Huygens, Discours sur la cause de la pésanteur 1690. p. 162.
[324] Hooke, De potentia restitutiva. 1678. p. 7.
[325] Locke, An essay concerning human understanding. London 1731. V. I. Book II. p. 87.
[326] Micrographia, London 1665. p. 16.
[327] Micrographia, 1665. p. 12.
[328] Descartes, Principia philosophiae. 1677. P. II. § 36. p. 37.
[329] T. Lucretii Cari, De rerum natura libri sex. II. v. 294–307. Vgl. G. Berthold, Notizen zur Geschichte des Prinzips der Erhaltung der Kraft (Ber. d. Kgl. Akad. d. Wiss. z. Berlin. 1875. S. 57, sowie Bd. I des vorliegenden Werkes S. 241).
[330] Animadversiones in X. libr. Diogenis Laertii 1675. V. I. p. 241.
[331] Der Engländer Thomas Hobbes (1632–1679) suchte gleich Descartes alle Vorgänge auf die Bewegung kleiner Teilchen zurückzuführen. Die Bewegung pflanzt sich dadurch fort, daß sich das Medium bewegt. Eine unvermittelte Wirkung in die Ferne gibt es nicht. Dies alles kennzeichnet die Philosophie des Hobbes als materialistisch. Gleichzeitig ist sie sensualistisch, indem sie alle Begriffe auf die Wirkung der Sinnesorgane zurückführt. Bekannt ist der Satz, durch den Hobbes dies folgendermaßen ausdrückt: »Nihil est in intellectu, quod non prius fuerit in sensu«. Dieser Satz wird irrtümlich mitunter Locke zugeschrieben.
[332] Spinoza (1632–1677) stammt von portugiesischen Juden, die nach Amsterdam geflüchtet waren, um den Verfolgungen der Inquisition zu entgehen. Die jüdische Gemeinde verhielt sich gegen Spinoza nicht weniger intolerant, da sie ihn seiner religiösen Ansichten wegen durch Meuchelmord aus dem Wege zu räumen suchte und schließlich ausstieß. Spinoza erwarb sich seinen Lebensunterhalt durch das Schleifen optischer Gläser. Er wurde durch seine philosophischen Schriften als Fortsetzer des cartesianischen Systems bekannt und erhielt einen Ruf nach Heidelberg, den er aber ausschlug, weil er die Freiheit der Forschung nicht als gesichert ansah.
[333] Newton. Philosophiae naturalis principia mathematica 1723. Lib. III. Scholium generale p. 484.
[334] Philosophiae natur. princ. math. 1723. S. 5.
[335] a. a. O. S. 147.
[336] a. a. O. S. 173.
[337] Auszug aus dem Briefe Newtons an Bentley v. 25. II. 1692; abgedruckt bei S. Horsley, J. Newtoni op. omn. Lond. 1782. IV. p. 438.
[338] Horsley l. c. p. 394.
[339] Opera omnia; Lausanne 1742. III. 138.
[340] Diss. de causa gravitatis. Chr. Hugenii op. reliqua. 1728. I. 121. 125.
[341] P. H. Fuß, correspondance math. et physique. St. Petersburg 1843. T. II p. 550.
[342] Nov. act. Petrop. 1779. T. III. P. I. p. 162.
[343] Opera philosophica, ed. Erdmann. 1820. p. 466.
[344] Journal des savants. 1669. S. 23.
[345] Th. Birsch, The history of the Royal Society. Lond. 1756. Bd. II. S. 337.
[346] Rosenberger, Geschichte der Physik. II. 131.
[347] De Beghinselen der Weegkonst. Leyden 1586.
[348] Les [oe]uvres mathématiques de Simon Stevin. Leyden 1634.
[349] Wonder en is gheen Wonder.
[350] Stevins Werke, Seite 499. V. Buch der Statik.
[351] Stevins Werke, S. 499, Fig. 4.
[352] Stevins Werke, S. 500, Fig. 2 u. 3.
Beide Nachweise gehören bekanntlich zum festen Bestand des heutigen Physikunterrichts, der sich dazu derselben Apparate wie Stevin bedient.
[353] Stevins Werke, Les [oe]uvres mathématiques de Simon Stevin, herausgegeben von Girard, Leyden 1634. Des éléments hydrostatiques; Théorème IX. p. 488–491. Die betreffende Untersuchung hat Stevin im Jahre 1608 veröffentlicht (S. Cantor, Geschichte der Mathematik. II. 533).
[354] Galileis Discorsi erschienen 1638.
[355] Viviani, Della scienza universale delle proporzioni.
[356] Opera geometrica. Florenz 1644, 3. Abschnitt: De motu gravium naturaliter descendentium.
[357] v = √(2gh), v1 = √(2gh1), v : v1 = √h : √h1. Mit der Formel v = √(2gh) war Torricelli noch nicht bekannt; sie rührt von Johann und Daniel Bernoulli her. Bei Torricelli ist v = A · √h, worin h die Höhe und A eine Konstante bedeutet.
[358] Siehe Ostwalds Klassiker Nr. 11. S. 17.
[359] Siehe S. 82 u. 83 dies. Bds.
[360] Siehe das 7. Heft der »Neudrucke von Schriften und Karten über Meteorologie u. Erdmagnetismus«, hrsg. von Prof. Dr. G. Hellmann: Evangelista Torricelli, Esperienza dell'Argento Vivo. Berlin. A. Asher & Co. 1897.
[361] Torricelli hatte zuerst Ricci in Rom darüber geschrieben und dieser Mersenne berichtet.
[362] Zu dem Descartes Pascal angeregt haben will.
[363] Blaise Pascal, Récit de la grande expérience de l'équilibre des liqueurs, Paris 1648. Neuerdings erschienen als 2. Heft der »Neudrucke von Schriften und Karten über Meteorologie und Erdmagnetismus«, herausgegeben von Professor Dr. G. Hellmann. Berlin, A. Asher & Co.
[364] Traité de l'équilibre des liqueurs et de la pesanteur de la masse de l'air. Paris 1663. Verfaßt wurde diese Abhandlung schon im Jahre 1653.
[365] Pascal, Oeuvres III. p. 86–86.
[366] In seinen akademischen Vorlesungen (lezioni academiche), die 1715 in Florenz erschienen, und zwar in der 7. Vorlesung.
[367] Eine ausführliche Biographie lieferte F. W. Hoffmann unter dem Titel: O. v. Guericke, ein Lebensbild aus der Geschichte des 17. Jahrhunderts.
[368] Er starb am 11. Mai 1686 in Hamburg.
[369] Siehe die betreffenden Abhandlungen G. Bertholds in den Annalen der Physik und Chemie Bd. 20. 1883, Bd. 54. 1895, sowie in den Verhandlungen der Akademie der Wissenschaften zu Stockholm 1895. Nr. 1.
[370] Mechanica hydraulico-pneumatica, S. 307.
[371] Ottonis de Guericke Experimenta nova (ut vocantur) Magdeburgica de Vacuo Spatio. Amsterdam 1672
[372] Aus dem Lateinischen übersetzt und mit Anmerkungen herausgegeben von Friedrich Dannemann. Leipzig, Verlag von Wilhelm Engelmann, 1894 (59. Bd. von Ostwalds Klassikern der exakten Wissenschaften).
Einige wichtige Kapitel des »Über eigene Versuche« betitelten Buches bilden mit den erforderlichen Erläuterungen den 17. Abschnitt des Werkes von Dannemann, Aus der Werkstatt großer Forscher. Leipzig, W. Engelmann 1908.
[373] Auf der ersten Seite der Vorrede seines Werkes de Vacuo Spatio.
[374] Ostwalds Klassiker Nr. 59. S. 11.
[375] Eine der von Guericke gebauten Luftpumpen sowie seine Magdeburger Halbkugeln befinden sich jetzt im Deutschen Museum von Meisterwerken der Naturwissenschaft und der Technik in München. Die Zeit der Erfindung der Luftpumpe wird auf 1647–49 oder 1651–52 angesetzt. Ob mit Recht, bleibt dahingestellt. Siehe F. Poske, Zum Gedächtnis Otto von Guerickes. Verhandl. d. Deutschen physikal. Gesellsch. IV (1902). Nr. 16.
Eine andere Luftpumpe gelangte 1676 nach Stockholm. Dort diente sie Jahrzehnte zur Anstellung von Versuchen. Als noch vorhanden wurde sie zuletzt im Jahre 1734 nachgewiesen. Neuere Nachforschungen nach dieser Originalluftpumpe Guerickes blieben zunächst ohne Erfolg (Berthold in Poggend. Annalen. 1895. S. 726). Vor kurzem (1917) hat sie sich aber in den Sammlungen der Universität Lund wiedergefunden. Über die noch erhaltenen Luftpumpen und Nebenapparate Guerickes, sowie die ersten englischen und niederländischen Luftpumpen gibt der »Bericht über die Ausstellung wissenschaftlicher Apparate im South Kensington Museum« (Berlin 1877. S. 158 u. f.) Auskunft.
[376] Magdeburgische Versuche Kapitel XXII. Siehe 59. Bd. von Ostwalds Klassikern der exakten Wissenschaften S. 66.
[377] Siehe S. 207.
[378] Siehe Ostwalds Klassiker Nr. 59. S. 66.
[379] Ostwalds Klassiker Nr. 59. S. 45.
[380] Pascal hatte dies aus der Verkürzung der Quecksilbersäule des Barometers gefolgert (siehe S. 197 d. Bds.). Guericke verschloß einen Rezipienten am Fuße eines Kirchturms und begab sich mit ihm auf die Spitze desselben. Wurde der Hahn jetzt gedreht, so trat Luft aus, während Luft in den Rezipienten hineindrang, wenn man ihn auf der Spitze des Turmes verschloß und am Fuße wieder öffnete. Guericke, De vacuo spatio. III. Buch, 30. Kap.
[381] Ostwalds Klassiker Nr. 59. Kap. XV.
[382] Ostwalds Klassiker Nr. 59. S. 108.
[383] New experiments, Physico-Mechanical, touching the Spring of the Air and its Effects made in the most part in a new pneumatical engine. Oxford 1660. Ein Jahr später erschien eine lateinische Übersetzung unter dem Titel: Nova experimenta de vi aeris elastica.
[384] R. Boyle, Opera varia. Genevae 1680. S. 38. Fig. 5.
[385] Mitgeteilt von Boyle in seiner Schrift gegen Linus, Defensio contra Linum London 1662. Cap. V. Opera Varia. Genf 1680. S. 42 ff.
[386] Mariotte, Essai sur la nature de l'air. 1679. Die wichtigsten Abschnitte enthält Dannemann, Aus der Werkstatt großer Forscher. S. 104 u. f.
[387] 40–1–14.
[388] Leibnizens und Huygens' Briefwechsel mit Papin. Herausgegeben von Gerland. Berlin 1881. S. 222.
[389] Durch Vidi. Poggendorffs Annalen. 1848. Bd. 73. S. 620.
[390] Siehe Bd. I S. 434.
[391] Dort ist er 1644 auch gestorben.
[392] Eine sehr ausführliche Geschichte des Namens »Gas« bringt v. Lippmann im II. Bande seiner Abhandlungen u. Vorträge. S. 361–394. Veit u. Co. Leipzig 1913.
[393] Van Helmonts Schriften hat sein Sohn unter dem Titel »Ortus medicinae vel opera et opuscula omnia« im Jahre 1648 herausgegeben.
[394] H. Kopp, Die Alchemie in älterer und neuerer Zeit, Heidelberg 1886. Bd. I. S. 8.
[395] Leibniz, Historia inventionis phosphori. Miscellanea Berolinensia 1710. T. 1. p. 91.
[396] Ein Jahrhundert später (1776) zeigte Gahn, daß sich Phosphor aus kalzinierten Knochen darstellen läßt, indem man den beim Eindampfen der Knochen mit Schwefelsäure erhaltenen Rückstand mit Kohle destilliert.
[397] H. Peters, Leibniz in seiner Beziehung zur Chemie und den anderen Naturwissenschaften. Chemikerzeitung 1901. Nr. 81 u. 82.
[398] J. C. Orchall, Augsburg 1684.
[399] Das Geburtsjahr ist nicht bekannt.
[400] Alchemia est ars perficiendi magisteria et essentias puras e mistis separato corpore extrahendi.
[401] Es wurde auch als Wundersalz (Sal mirabile) bezeichnet und fand in der Heilkunde bald ausgedehnte Anwendung.
[402] 2NH4Cl + CaO = CaCl2 + 2NH3 + H2O.
[403] In der heutigen Formelsprache würde dieser Vorgang durch folgende Gleichung wiederzugeben sein:
3HgCl2 + Sb2S3 = 2SbCl3 + 3HgS.
[404] In seinem Preliminary discourse.
[405] E. Bloch, Boyles Anschauungen über die Metallverkalkung. Chemikerzeitung. 1915. S. 481–486.
[406] Nach v. Lippmann kannte diese Reaktion schon Plinius.
[407] Ostwalds Klassiker der exakten Wissenschaften Nr. 125. Leipzig, W. Engelmann. 1901.
[408] Dies hatte man seit 1600 schon wiederholt vor Mayow beobachtet.
[409] Ostwalds Klassiker Nr. 125. S. 15.
[410] Siehe den 19. Abschnitt des 3. Bandes.
[411] Rariarum stirpium per Pannoniam, Austriam et alias provincias observatarum historia. Antwerpen 1583.
[412] Rariarum stirpium per Hispanias observatarum historia. Antwerpen 1576.
[413] Exoticorum libri 10. Antwerpen 1605.
[414] Sprengel, Geschichte der Botanik. I. 294.
[415] Pinax theatri botanici. Basel 1623.
[416] Sachs, Geschichte der Botanik. S. 37.
[417] Er wurde 1519 in Arezzo geboren, war ein Schüler des (Bd. I. S. 458) erwähnten Luca Ghini und starb 1603.
[418] Emil Wohlwill, Joachim Jungius. Mit Beiträgen zu Jungius' Biographie und zur Kenntnis seines handschriftlichen Nachlasses. Hamburg 1888.
[419] Isagoge phytoscopica. 1678.
[420] Robert Morison wurde 1620 in Aberdeen geboren. Er starb 1683.
[421] Plantarum umbelliferarum distributio nova. 1672.
[422] Er wurde 1628 in Essex geboren und starb 1705.
[423] Historia plantarum. 1686–1704.
[424] Latinisiert für Bachmann (1652–1725).
[425] Tournefort (1656–1708) wurde in der Provence geboren. Er wirkte als Professor am Jardin des Plantes und durchforschte die Flora in Griechenland, Nordafrika und Kleinasien, Ländern, welche der Botanik des Altertums wegen immer noch eine besondere Anziehungskraft ausübten.
[426] Sprengel, Geschichte der Botanik. II. 157.
[427] Historia plantarum (1686) und Methodus plantarum nova (1682).
[428] Historia plantarum. Bd. I. 1886. S. 40.
[429] a. a. O. S. 42.
[430] Karl Jungmann, Die Weltentstehungslehre des Descartes. Bd. 54 der Berner Studien zur Philosophie und ihrer Geschichte. Herausgegeben von Ludwig Stein. Bern, Buchdruckerei Scheitlin, Spring & Co., 1907. 51 Seiten.
[431] Laplace, Précis de l'histoire de l'astronomie. Paris 1821. p. 99.
[432] Die Royal Society veröffentlichte ihre Arbeiten seit dem Jahre 1665 unter dem Titel »Philosophical Transactions«.
[433] Siehe auch P. Tannery, Les sociétés savantes et l'histoire des sciences. Paris, 1906.
[434] Weld, History of the Royal Society, und v. Ranke, Englische Geschichte. V. 165. Die Verleihung der Korporationsrechte erfolgte am 10. Juli 1662.
[435] Heinrich Oldenburg war im Jahre 1626 in Bremen geboren und als Konsul seiner Vaterstadt nach England gekommen. Nach Verlust seiner Stelle zog er als Hofmeister eines jungen Lords nach Oxford. Dort wurde er mit Mitgliedern der Royal Society bekannt, die ihm seiner Sprachkenntnisse wegen das Amt eines Sekretärs anvertrauten.
[436] Zeitweilig führten sie den Titel Philosophical Collection. Die Gesellschaft selbst übernahm die Herausgabe erst vom 47. Bande (1753) ab.
[437] Über ihn und seine Bedeutung für die Förderung der Wissenschaften wurde an anderer Stelle (s. S. 245) schon berichtet.
[438] Nicht zu verwechseln mit der schon vor ihr gegründeten französischen Akademie, die wie die Accademia della Crusca in Rom, der Pflege der französischen Sprache diente.
[439] Siehe den ersten Abschnitt des IV. Bandes.
[440] Jungius wirkte eine Zeitlang als Rektor des Johanneums in Hamburg. Er starb nach einem vielbewegten Leben 1667. Siehe auch Guhrauer, Joachim Jungius und sein Zeitalter. Tübingen 1850.
[441] Der vollständige Titel lautet in der Übersetzung: Vorschlag, die Naturforschung ihres Nutzens wegen zu fördern und zu diesem Zwecke eine Deutsche Gesellschaft zu gründen, deren Aufgabe es sein würde die nutzbringenden Künste und Wissenschaften in unserer Sprache zu beschreiben und den Ruhm des Vaterlandes zu mehren.
[442] Harnack, Geschichte der preußischen Akademie der Wissenschaften, Berlin 1901. S. 243.
[443] Eine ausführliche Biographie Newtons verfaßte Brewster: Life of Newton. London 1831. Übersetzt von B. M. Goldberg. Leipzig 1833. Neu bearbeitet erschien dies Werk unter dem Titel: Memoirs of the Life, Writings and Discoveries of Sir Isaac Newton. Edinburg. 2 Bde. 1855. 2. Aufl. 1860. Siehe auch Snell, Newton und die mechanische Naturwissenschaft. Dresden u. Leipzig 1843.
[444] Wallis, Arithmetica infinitorum sive nova methodus inquirendi in curvilineorum quadraturam. 1655. Wallis beschäftigte sich darin wie Cavalieri in seinen »Indivisibilien« vorzugsweise mit Quadraturen und Kubaturen, verfuhr, anknüpfend an Descartes, aber mehr rechnerisch, während Cavalieri seine Ableitungen so geometrisch als irgend möglich zu gestalten trachtete (siehe auch Cantors Geschichte der Mathematik II, 822).
[445] Zucchi 1616. Siehe Nicolai Zucchii Optica philosophica. Leyden 1652. Die bezügliche Stelle wird von Wilde in seiner Geschichte der Optik, Bd. I. Seite 308 angegeben. Zucchi machte auch, wie er an dieser Stelle mitteilt, den entsprechenden Fundamentalversuch, indem er das Licht mit einem Hohlspiegel auffing und gleichzeitig eine Konkavlinse in passender Entfernung ans Auge brachte. Er wird deshalb von Wilde schon als der Erfinder des Spiegelteleskops bezeichnet (Wilde I, 308). Gregory beschränkte sich in seiner Optica promota vom Jahre 1663 (Seite 92 u. f.) auf den bloßen Vorschlag, das durch zwei Spiegel erzeugte Bild durch eine Linse zu betrachten. Die Ausführung dieses Gregory'schen Teleskops erfolgte erst ein Jahrzehnt später (1774) durch Hooke. Siehe die schematische Zeichnung in Wüllners Lehrbuch der Experimentalphysik II, 344.
[446] Aus den Philos. Transactions von 1672.
[447] 1672.
[448] Philos. Transact. 1742. S. 155.
[449] Philos. Transact. 1731. S. 147 u. f.
[450] Optics or a treatise of the reflections, refractions, inflections and coulours of light. London 1704. – Newtons Optik wurde als 96. und 97. Band von Ostwalds Klassikern der exakten Wissenschaften übersetzt und herausgegeben von W. Abendroth. W. Engelmann, Leipzig. 1898. – Es ist dies die erste deutsche Übersetzung. Neben vier englischen Auflagen gibt es sechs lateinische und drei französische Ausgaben.
[451] Newtons Optik. I. Tafel III. Abb. 13.
[452] Newtons Optik. I. Tafel IV. Abb. 18.
[453] Newtons Optik, II. Taf. IV. Abb. 16.
[454] Opera omnia (ed. Frisch) II. 119 u. f.
[455] De radiis visus et lucis in vitris perspectivis et iride Tractatus Marci de Dominis, Venedig 1611.
De Dominis (1566–1624) war Kleriker und erlitt ein ähnliches Schicksal wie Giordano Bruno. Er geriet mit den katholischen Lehren in Widerspruch, wurde von der Inquisition gefangen gesetzt und starb in dem Kerker der Engelsburg, wahrscheinlich an Gift.
Nach v. Lippmann entstammt die Lehre, daß die Farben eine Mischung von Weiß und Dunkel seien, pseudo-aristotelischen Schriften.
[456] Näheres siehe Newtons Optik (Ostwalds Klassiker Bd. 96 S. 50 u. f.) sowie Wilde, Geschichte der Optik. II. S. 44 u. f.
[457] Der Spiegel hatte einen Durchmesser von 4 Fuß und wog 2000 Pfund. Herschel lieferte eine Beschreibung dieses Fernrohrs in den Philos. Transact. 1795, II, pag. 347. Das Teleskop des Earl of Rosse vom Jahre 1845 besaß sogar eine Länge von 16,6 und einen Spiegeldurchmesser von 1,82 m.
[458] Für bestimmte Zwecke (photographische Aufnahmen) werden auch jetzt noch gewaltige Reflektoren von über 2 m Öffnung benutzt.
[459] Bzw. in G (rot) und in H (violett) beim äußeren Bogen.
[460] Ostwalds Klassiker. Bd. 96. S. 130.
[461] Jesuit, von 1566–1624 lebend. Er wurde von der Inquisition seiner freieren religiösen Auffassung wegen eingekerkert.
[462] Grimaldi, Physico-Mathesis de lumine, coloribus et iride. Bologna 1665. S. 235 u. f.
[463] Siehe S. 92 u. f.
[464] Huygens, Abhandlung über das Licht. Nr. 20 von Ostwalds Klassikern der exakten Wissenschaften.
[465] Dannemann, Aus der Werkstatt großer Forscher. Leipzig 1908. Abschnitt 34.
[466] Hooke, Micrographia or some philosophical descriptions of minute bodies. London 1665.
[467] Micrographia, Observat. IX: Of the Colours observable in Muscovy Glass and other thin Bodies.
[468] Newton, Optice, Lib. II. Pars 1. Observatio VI. S. 149 der Clarkeschen Ausgabe von 1740.
[469] Frage 5. (Ostwalds Klassiker. Nr. 97. S. 101.)
[470] Frage 8. (Ostwalds Klassiker. Nr. 97. S. 101.)
[471] Frage 30. (Ostwalds Klassiker. Nr. 97. S. 124.)
[472] Frage 29. (Ostwalds Klassiker. Nr. 97. S. 123.)
[473] Rosenberger, Newtons Prinzipien. S. 329.
[474] Poggendorff, Geschichte der Physik. S. 645.
[475] Picard, La mésure de la terre. Paris 1671.
[476] 1 Toise = 6 frz. Fuß = 1,949 m.
[477] Sie hatte für den Breitengrad 55972 Toisen ergeben. Snellius verfuhr folgendermaßen. Er bestimmte die Polhöhe von Alkmaar zu 52° 40,5ʹ, diejenige von Bergen op Zoom zu 51° 29ʹ. Der Abstand der durch beide Orte gehenden Parallelkreise ergab sich daraus zu 1° 11,5ʹ. Die Messung dieses Abstandes ergab 55072 Toisen für den Grad. Bei dieser Messung wurde zum erstenmal das Verfahren der Triangulation angewandt (De terrae ambitu a Willebrordo Snellio, Leyden 1617), indem Snellius von einer festen, äußerst genau gemessenen Standlinie oder Basis ausging und von dieser aus durch Winkelmessung ein Netz von Dreiecken bestimmte. Als einige Jahre nach seiner ersten Messung die Umgegend von Leyden überschwemmt wurde und überfror, benutzte er diese Gelegenheit, um nochmals eine Ausgangslinie möglichst genau zu messen.
Willibrord Snellius, in Leyden 1591 geboren und dort als Universitätslehrer 1626 gestorben, ist uns bei früherer Gelegenheit als der Entdecker des Brechungsgesetzes bekannt geworden. Von ihm rührt auch das trigonometrische Verfahren des »Rückwärtseinschneiden« her, das fälschlich wohl dem Franzosen Pothenot zugeschrieben wird. Die hier kurz geschilderte Tätigkeit dieses hervorragenden Geometers war es also, die Newton die Lösung des größten naturwissenschaftlichen Problems, das je den Menschengeist beschäftigte, ermöglicht hat.
[478] Genau gleich 15ʹ 1ʺ 14/9ʺ. Siehe Newtons Prinzipien (Ausgabe von Wolfers) S. 386.
[479] Philosophiae naturalis principia mathematica, London 1687. Übersetzt von Wolfers, Berlin 1872. Siehe auch Ferd. Rosenberger: Isaac Newton und seine physikalischen Prinzipien. Ein Hauptstück aus der Entwicklungsgeschichte der modernen Physik. Leipzig 1895.
[480] Hooke, An attempt to prove the motion of the earth, London 1674. S. 27 und 28.
[481] Newtons Prinzipien (ed. Wolfers), S. 515.
[482] Dies würde geschehen, wenn die Geschwindigkeit 21000ʹ für die Sekunde beträgt.
[483] Newtons Prinzipien. I. Buch. § 13.
[484] Newtons Prinzipien (ed. Wolfers), Fig. 213.
[486] Siehe auch die »Begriffsbestimmungen und Leitsätze« aus Newtons mathematischen »Prinzipien der Naturphilosophie«, die im ersten Teil des 191. Bandes von Ostwalds Klassik. d. exakt. Wissensch. zusammengestellt sind (Leipzig, W. Engelmann, 1914).
[487] Seneca, Nat. Quaest. III, 28.
[488] Näheres darüber siehe im III. Bande.
[489] Optik, Frage 31.
[490] Newtons Prinzipien III. 5. Abschnitt.
[491] Den Gegensatz zwischen den Newtonianern und den Cartesianern verspottete Voltaire einst mit folgenden Worten: »Wenn ein Franzose in London ankommt, so findet er einen großen Unterschied. In Paris verließ er die Welt ganz voll von Materie, in London findet er sie völlig leer. In Paris sieht er das Universum von ätherischen Wirbeln erfüllt, während in London unsichtbare Kräfte ihr Spiel treiben. Dort ist es der Druck des Mondes, der Ebbe und Flut bewirkt, während in England das Meer gegen den Mond gravitiert und alles durch den Zug verrichtet wird.«
[492] E. Hoppe, Zur Geschichte der Fernwirkung. Programm des Wilhelmgymnasiums, Hamburg 1901.
[493] Rosenberger, Newtons Prinzipien. S. 234.
[494] Ausführlicher wurde das System der corpuscules ultramondaines von Le Sage entwickelt (Prévost, Deux traités de physique mécanique, Genève et Paris, 1818).
[495] Nach dem gregorianischen Kalender am 5. Januar 1643 und am 31. März 1727.
[496] Siehe S. 24.
[497] Christiani Hugenii Systema Saturnium. Haag 1659.
[498] Saturn wird von einem dünnen, ebenen, freischwebenden Ringe umgeben, der zur Ekliptik geneigt ist.
[499] Die übrigen Saturnmonde wurden später von Cassini, Herschel u. a. entdeckt.
[500] Der Reihenfolge nach, wie oben erwähnt, der sechste Mond.
[501] Das Patent, das er auf seine Erfindung nahm, datiert vom 16. Juni 1657.
[502] Siehe S. 96.
[503] Siehe S. 290.
[504] Siehe Dannemann, Aus der Werkstatt großer Forscher, S. 96.
[505] Olaf oder Olof Römer wurde am 25. September 1644 zu Arhuus geboren und starb am 19. September 1710 in Kopenhagen. Die erwähnten Beobachtungen stellte er 1672–1676 auf der Pariser Sternwarte an. Sein Bericht an die Pariser Akademie datiert vom 22. November 1675. (Anc. Mémoires, Paris. Tome I et X.)
[506] 42 Stunden 27 Minuten 33 Sekunden.
[507] Chr. Huygens, Abhandlung über das Licht. Fig. 2. Siehe Ostwalds Klassiker der exakten Wissenschaften Nr. 20, S. 14.
Die Abhandlung über das Licht (Traité de la lumière) erschien im Jahre 1690 in Leyden, zusammen mit der Untersuchung über die Ursache der Schwere (Discours de la Cause de la Pesanteur). Die Arbeit über das Licht entstand schon in Paris um 1678. Dadurch, daß Huygens 1681 Frankreich der Mißhandlung seiner Glaubensgenossen wegen verließ, wurde die Herausgabe bis zum Jahre 1690 verzögert. Eine lateinische Übersetzung wurde 1728 von s'Gravesande unter dem Titel »Tractatus de Lumine« herausgegeben.
[508] Dieser in vielen Lehrbüchern der Physik beschriebene Apparat (z. B. Wüllner, Lehrbuch der Experimentalphysik, III. Aufl. Bd. I, Fig. 66) zum Nachweis der Gesetze des Stoßes wurde von Mariotte angegeben. (Traité de la percussion ou du choc des corps. Paris 1677.)
[509] Ostwalds Klassiker Nr. 20. S. 26.
[510] Ostwalds Klassiker Nr. 20. S. 34.
[511] Experimenta crystalli islandici disdiaclastici, quibus mira et insolita refractio detegitur. Havniae 1669.
[512] Huygens hatte wie Bartholin gefunden, daß Licht, das in einen Doppelspatkristall eindringt, im allgemeinen zwei Brechungen erleidet, von denen die eine dem von Snellius gefundenen Gesetze folgt, nach dem der Sinus des Einfallswinkels zum Sinus des Brechungswinkels in einem bestimmten Verhältnis steht. Dies Verhältnis ermittelten Bartholin und Huygens übereinstimmend gleich 5 : 3. Es blieb für alle Neigungen stets dasselbe, während sich dies Verhältnis für den zweiten, außergewöhnlichen Strahl mit der Neigung des einfallenden Strahles änderte. Um das Auftreten beider Strahlen zu erklären, mußte Huygens annehmen, daß sich ein Teil des Lichtes nach dem Eintreten in den Kristall in kugelförmigen Wellen fortpflanze, ein anderer dagegen in sphäroidischen. Ferner galt es, für den durch letztere bewirkten Strahl ein dem von Snellius ermittelten analoges Gesetz zu finden, was Bartholin nicht vermocht hatte.
[513] Ostwalds Klassiker Nr. 20. S. 61.
[514] Ostwalds Klassiker Nr. 20. S. 65.
[515] Siehe an späterer Stelle dieses Werkes.
[516] Nach heutiger Annahme ist die aristotelische Schrift »Über die Farben« nicht echt-aristotelisch, entstammt aber der Schule des Philosophen. S. auch Wilde, Gesch. d. Optik. I. S. 8 u. f.
[517] Horologium oscillatorium sive de motu pendulorum. Paris 1673. Eine Besprechung der einzelnen Teile dieses Werkes bringt eine Abhandlung von A. Heckscher in den Mitteilungen z. Gesch. d. Med. u. d. Natw. XIV. Bd. S. 97. In deutscher Übersetzung wurde es von A. Heckscher und A. v. Oettingen als 192. Band von Ostwalds Klassikern der exakten Wissenschaften, unter dem Titel »Die Pendeluhr« herausgegeben. Leipzig, W. Engelmann, 1913. Huygens erste Pendeluhr wird noch heute im physikalischen Kabinett der Universität Leyden aufbewahrt.
[518] Im Besitze der Grundzüge seines unter dem Namen der Fluxionsrechnung bekannt gewordenen analytischen Verfahrens befand sich Newton schon im Jahre 1666. Siehe Cantor, Geschichte der Mathematik. Bd. III. S. 150 u. f.
[519] Siehe S. 52 ds. Bds.
[520] Das von Viviani herrührende Modell dieser Vorrichtung existiert noch im Galilei-Museum zu Florenz. Siehe Günther, Vermischte Untersuchungen zur Geschichte der mathematischen Wissenschaften. 1876. Seite 316.
[521] Die Erteilung von Erfindungspatenten ist eine neuzeitliche Einrichtung. Ihre Ausbreitung gehört dem 19. Jahrhundert an. Die Anfänge des Patentwesens reichen jedoch bis ins 17. Jahrhundert zurück. Das erste Patentgesetz wurde 1624 in England durch Jakob I. bestätigt. Während der ersten hundert Jahre wurden in England im ganzen nur etwa 300 Patente erteilt. In Frankreich setzte die Patentgesetzgebung im Jahre 1791 und in Preußen 1815 ein.
[522] Siehe über sie die Arbeit von W. Schmidt in den Abhandlungen zur Geschichte der Mathematik. 8. Heft (1898). S. 177.
[523] Siehe die der Arbeit Schmidts beigegebene Photographie.
[524] Christiani Hugenii, Horologium oscillatorium. Paris MDCLXXIII. pag. 4. Fig. 1.
[525] Der Londoner Uhrmacher Clement erfand die Ankerhemmung im Jahre 1680.
[526] Horologium oscillatorium, Pars II.
[527] Horologium oscillatorium. Fig. auf S. 12.
[528] Diese Erfindung wurde veröffentlicht im Journal des savants vom 25. Februar 1675.
[529] Horologium oscillatorium, Pars 5. Eine zusammenfassende Arbeit über die Geschichte der Erfindung der Pendeluhr lieferte E. Gerland in Wiedemanns Annalen, Bd. 4, Seite 585–613.
Gerland schreibt Galilei das Verdienst zu, die Pendeluhr schon 1641, also 15 Jahre vor Huygens erfunden zu haben. Beide Männer seien unabhängig voneinander auf sie gekommen. Von Galileis Apparat existiert jedoch nur ein Entwurf. Er ist zehn Jahre nach Galileis Tode nur unvollkommen zur Verwirklichung gelangt. (Siehe Gerland und Traumüller, Geschichte der physikalischen Experimentierkunst. S. 121 und S. 57 des vorlieg. Bandes.)
[530] Horologium oscillatorium. pag. 4. Fig. II.
[531] t = π√(l/g).
[532] Dies geschah in der »Abhandlung über die Ursache der Schwere« (Discours de la cause de la pesanteur), die 1690 als Anhang zu der Abhandlung über das Licht erschien und von R. Mewes deutsch herausgegeben wurde (A. Friedländer, Berlin 1893).
[533] Der mit den hervorragendsten Männern seiner Zeit in Briefwechsel stehende Pater Mersenne (1588–1648).
[534] Centrum oscillationis vel agitationis figurae cujuslibet, dicatur punctum in linea centri, tantum ab axe oscillationis distans, quanta est longitudo penduli simplicis quod figurae isochronum sit.
[535] Si pondera quodlibet, vi gravitatis suae, moveri incipiant, non posse centrum gravitatis ex ipsis compositae altius, quam ubi incipiente motu reperiebatur, ascendere.
Diesen Satz benutzt Huygens, um die Unmöglichkeit des Perpetuum mobile nachzuweisen. Er erklärt es für »mechanisch« unmöglich. Huygens hatte indessen noch nicht erkannt, daß das Prinzip der Erhaltung der Kraft für sämtliche Naturkräfte gilt. So sagt er in einem Briefe an Leibniz ausdrücklich, ein Perpetuum mobile sei zwar mechanisch unmöglich, doch bestehe einige Hoffnung, ein solches physico-mechanisch zu konstruieren, z. B. mit Hilfe eines Magneten. Dagegen hatte Mersenne bereits 1644 die Möglichkeit eines Perpetuum mobile überhaupt in Abrede gestellt, und die auf dessen Konstruktion gerichteten Bestrebungen mit dem Suchen nach dem Stein der Weisen verglichen. Cogitata physico-mechanica. 1644. S. 224.
[536] Von Felix Haushofer im 138. Bande von Ostwalds Klassikern der exakten Wissenschaften. W. Engelmannn, Leipzig 1903.
[537] Ostwalds Klassiker Nr. 138. S. 158.
[538] Im tiefsten Punkte ist nämlich, da dann die durchfallene Strecke = l ist, v = [sqrt](2gl) und die Zentrifugalkraft P = v2/l = 2gl/l = 2g. Dazu kommt die Schwere g, so daß (für m = 1) die gesamte Zugkraft = 3g ist.
[539] Ostwalds Klassiker Nr. 138, Fig. 21.
[540] Mach, Mechanik. Fig. 106.
[541] Newtons Prinzipien (übers. von Wolfers) S. 406.
[542] D. h. unter Berücksichtigung der in Paris gleichfalls durch die Zentrifugalkraft hervorgerufenen Verminderung der Schwere. Siehe auch die über diesen Gegenstand von Newton in seinen Prinzipien der Naturlehre (ed. Wolfers) S. 401 angestellten Berechnungen.
[543] Cassini entdeckte in den Jahren 1671 bis 1684 den dritten, vierten, fünften und achten Mond des Saturn.
[544] Cassini bestimmte deren Dauer zu 9 Stunden 56 Minuten; die Abplattung des Jupiter beträgt 1/14.
[545] Siehe an späterer Stelle dieses Bandes.
[547] Er starb dort im Jahre 1703.
[549] Wallis, Opera mathematica I, 355–478. Der vollständige Titel lautet: Arithmetica infinitorum sive nova methodus inquirendi in curvilineorum quadraturam.
[550] Sie wurde in lateinischer Sprache im darauf folgenden Jahre in den Philosophical Transactions veröffentlicht.
[551] Christian Huygens, »Über die Bewegung der Körper durch den Stoß«, als 138. Band I. Teil von Ostwalds Klassikern der exakten Wissenschaften herausgegeben von Felix Hausdorff. Leipzig, Verlag von W. Engelmann, 1903. Diese Abhandlung von Huygens erschien unter dem Titel »Tractatus de motu corporum ex percussione« im Jahre 1703 (Opuscula posthuma).
[552] S. Bd. I dieses Werkes, S. 241. Danach haben die Atomisten die Konstanz der Materie und der Kraft damit begründet, daß es keinen Ort außerhalb des Weltalls gäbe, wohin ein Teilchen der Materie entfliehen, oder von wo eine neue Kraft in das Universum einzudringen vermöge.
[553] Leibniz, Mathematische Schriften. Herausgegeben von Gerhardt. Halle 1860. II. Abt. Bd. II. S. 434.
[554] Ausgabe von Pertz-Gerhardt. Bd. VI. S. 231.
[555] Brevis demonstratio etc. (Acta eruditorum 1686. S. 163.)
[556] Der Kampf wogte bis 1691 zwischen Leibniz einerseits und Papin und anderen Cartesianern andererseits hin und her. Dann beteiligten sich auch die Engländer (Briefwechsel zwischen Clarke und Leibniz) daran. J. Bernoulli war zuerst gegen Leibniz, trat dann aber auf seine Seite. In diesen Streit mischten sich schließlich die Gelehrten aller Länder Europas. Endgültig entschieden wurde er erst 1743 durch d'Alembert. Dieser erklärte, daß der ganze Streit nur auf eine leere metaphysische Diskussion oder auf einen Wortstreit hinauslaufe. D'Alembert, Traité de dynamique. 1743. Vorrede S. 21.
[557] Dühring, Kritische Geschichte der allgemeinen Prinzipien der Mechanik. S. 230.
[558] Opera philosophica S. 775.
[559] H. Berthold, Notiz zur Geschichte des Prinzips der Erhaltung der Kraft (Chem. Zentralbl. VII, 7. 1876).
[560] Opera omnia III. S. 253.
[561] Daniel Bernoulli, Bemerkungen über eine allgemeinere Fassung des Satzes von der Erhaltung der lebendigen Kraft. Berlin 1750. Aus dem Französischen übersetzt und veröffentlicht im 191. Bande von Ostwalds Klassikern. Leipzig, W. Engelmann. 1914.
[562] Siehe auch Jacobis Vorlesungen über Dynamik, herausgegeben von E. Lottner, Berlin 1884. S. 19.
[563] De vera ratione virium vivarum. Acta erudit. 1735. 240.
[564] Hydrodynamica 1738. Sectio I. § 20. S. 12.
[565] Pensées sur l'interprétation de la nature 1754. § 45. p. 61.
[566] Siehe A. Stadler, Kant und das Prinzip von der Erhaltung der Kraft. (Philosoph. Monatshefte Bd. XV. Leipzig 1879.)
[567] Eine Sammlung seiner Werke erschien 1717 in Leyden: [OE]uvres de Mariotte, divisées en deux tomes.
[568] [OE]uvres de Mariotte. Bd. I. S. 149 u. f.
[569] [OE]uvres de Mariotte. Bd. II. S. 322 u. f.
[570] Poggendorff, Geschichte der Physik. S. 493.
[571] Traité de la percussion ou choc des corps. Paris 1677. [OE]uvres, Bd. 1. S. 3 u. f.
[573] Mariotte, [OE]uvres. Bd. II. S. 496.
[574] [OE]uvres de Mariotte. Bd. II. S. 607.
[575] I. Kant, Einige kurz gefaßte Bemerkungen über das Feuer. Königsberg 1755.
[576] Catalogus stellarum australium, seu supplementum catalogi Tychonici.
[577] Eine Zusammenstellung der Elemente findet sich in Wolffs Geschichte der Astronomie. S. 702. Der Halleysche Komet flößte bei seinem Erscheinen im Jahre 1456 während der Belagerung von Belgrad Türken und Christen Schrecken ein.
[578] Siehe an späterer Stelle (Bd. III).
[579] Im Jahre 1647. Siehe Wilde, Geschichte der Optik. I. 272.
[580] Philos. Transactions von 1693.
[581] Den von Halley geführten Beweis dieser Formel enthält Wildes Geschichte der Optik. I. 275 u. f.
[582] Philos. Transactions 1686. Discourse of the rule of the decrease of the height of the mercury in the barometer, according as places are elevated above the surface of the earth.
Abb. 102 ist der Abhandlung Halleys entnommen (Philos. Transact. 1686, S. 79). Für die Höhen, die einem gemessenen Barometerstand entsprechen, berechnete Halley folgende Tabelle:
| Barometerstand in Zollen | Höhe in Fuß |
| 30 | 0 |
| 29 | 915 |
| 28 | 1862 |
| 27 | 2844 |
| 26 | 4922 |
| 20 | 10947 |
| 15 | 18715 |
| 10 | 29662 |
| 5 | 48378 |
| 1 | 91831 |
[583] Cantor, Geschichte der Mathematik. III. S. 114 u. 115.
[584] Cantor III. S. 80–82.
[585] Cantor III. S. 363.
[586] Philos. Transactions XVII 596–610. An Estimate of the Degrees of the Mortality of Mankind, drawn from curious Tables of the Births and Funerals at the City of Breslaw with an Attempt to ascertain the Price of Annuities upon Lives.
[587] Cantor, Geschichte der Mathematik. Bd. III. S. 45–47.
[588] Cantor III. S. 343.
[589] Cantor, Geschichte der Mathematik. III. S. 616.
[590] Übersichtliche Karte, die mit einem Blick die Deklination der Magnetnadel erkennen läßt.
[591] Die Entdeckung dieser Erscheinung erfolgte durch E. Gunter 1622.
[592] Graham, Observations made on the variation of the horizontal needle at London. 1722–23.
[593] Heller, Geschichte der Physik. II. S. 308.
[594] Siehe an späterer Stelle dieses Bandes.
[595] Ephemerides Bononienses Mediceorum Siderum. Bologna 1668.
[597] Die vier Jupitermonde hatte Galilei gleichfalls zu Ehren seines fürstlichen Gönners als Sidera Medicea bezeichnet.
Nach der Zeit ihrer Entdeckung lassen sich die Saturnmonde in folgende Reihe bringen:
| Huygens | entdeckte | den | 6. | Mond | im | Jahre | 1655, |
| Cassini | " | " | 8. | " | " | " | 1671, |
| " | " | " | 5. | " | " | " | 1672, |
| " | " | " | 4. | " | " | " | 1684, |
| " | " | " | 3. | " | " | " | 1684, |
| Herschel | " | " | 1. | " | " | " | 1789, |
| " | " | " | 2. | " | " | " | 1789, |
| Bond | " | " | 7. | " | " | " | 1848. |
Dazu kamen 1898 und 1904 noch zwei weitere Monde. (Siehe den Anhang.)
[599] Nicolaus Fatio, geboren 1664 in Basel.
[600] Sie rührt von dem Engländer Childrey her und wurde von ihm in seiner Britannia Baconica veröffentlicht.
[601] Jacques Cassini 1677–1756.
César François Cassini de Thury 1714–1784.
Jacques Dominique Cassini de Thury 1748–1845.
Letzterer leitete die Pariser Sternwarte bis 1793.
[602] Lehrreich ist in dieser Hinsicht die Geschichte Böttgers, des angeblichen Erfinders des Porzellans. Siehe dessen Biographie von Engelhardt. Siehe ferner S. 342.
[603] Siehe Gerland: Beiträge zur Geschichte der Physik. Leopoldina, Halle 1882. Eine Linse von 4,34 m Brennweite befindet sich in Kassel. Sie ist jedoch voll von Schlieren.
[604] Von K. A. Engelhardt.
[605] Von Peters.
[606] Siehe das Referat Diergarts in den Mitteilungen zur Geschichte der Medizin und der Naturwissenschaften. Bd. V. S. 534.
[607] Vita a se ipso breviter delineata (kurze Selbstbiographie).
[608] Kopp, Geschichte der Alchemie. Bd. I. S. 233.
[609] Miscellanea Berolinensia. Berolini 1710. S. 16 ff.
[610] Siehe S. 203.
[611] Die Eröffnung der Petersburger Akademie fand zwar erst nach Peters Tode statt.
[612] Siehe Bd. I. S. 437.
[613] Steno, De solido inter solidum naturaliter contento. Florenz 1669. Ein von Élie de Beaumont herrührender Auszug dieser Schrift findet sich in den »Annales de sciences naturelles«. XXV. p. 337.
[614] Annales des sciences naturelles. XXV. S. 347.
[615] Humboldt, Essai géognostique. Paris 1823. pag. 38.
[616] Humboldt a. a. O.
[617] Athanasius Kircher Mundus subterraneus, in quo universae naturae majestas et divitiae demonstrantur. 2 vol. fol. Amsterdam 1664.
Der gelehrte Jesuit Kircher wurde 1602 in der Nähe von Eisenach geboren. Er wirkte als Lehrer der Mathematik in Rom, wo er das Museum Kircherianum gründete, und starb dort 1680.
[618] Principia philosophiae. 1644.
[619] Descartes unterschied drei Grundstoffe, die in der Sonne, im Weltraum und auf der Erde vertreten sein sollten. Siehe E. Bloch, Die chemischen Theorien bei Descartes und den Kartesianern (Isis, 1914. S. 590–635).
[620] G. Daubrée, Descartes l'un des créateurs de la Cosmologie et de la Géologie. Paris 1880.
[621] Man vergleiche dazu Bd. I S. 260, 380, 443, 445.
[622] Auch die heutigen Geologen nehmen an, daß die Mansfelder Schiefer aus dem feinen Schlamme einer mit Fischen reich bevölkerten Meeresbucht entstanden sind. Dieser Bucht wurden schwefelsaure Salze von Kupfer, Eisen und Silber zugeführt. Die Fische starben infolgedessen und sanken in den Schlamm. Der Reichtum an tierischer, in Zersetzung begriffener Substanz machte den aus diesem Schlamm hervorgehenden Schiefer bituminös (pechhaltig). Gleichzeitig wirkte die organische Substanz reduzierend auf jene schwefelsauren Metallsalze. Diese wurden infolgedessen in Schwefelmetalle (Erze) verwandelt, die den Kupferschiefer durchsetzen und insbesondere die Stellen überziehen, an denen sich einst die verwesenden Fischkörper befanden.
[623] Hooke, Lectures on Earthquakes, 1688.
[624] Dies geschah durch Langmantel im Jahre 1688.
[625] N. Lemery.
[626] Experimenta Crystalli Islandici Disdiaclastici, quibus mira et insolita refractio detegitur. Havniae 1669.
[627] Siehe S. 301.
[628] Arcana naturae detecta ab Antonio van Leeuwenhoek. 1695. p. 124.
[630] Specimen de Gemmarum origine et virtutibus, auctore Roberto Boyle. 1673.
[631] Siehe S. 217 dies. Bds.
[632] Georg Ernst Stahl wurde 1660 in Ansbach geboren und war Professor der Medizin und der Chemie in Halle. Von 1716 bis zu seinem Tode (1734) wirkte er in Berlin.
[633] Außer Marggraf und seinem Schüler Achard sind von den Berliner Chemikern noch Neumann und Pott zu nennen. Casper Neumann (1683–1737) war Professor an der medizinischen Bildungsanstalt zu Berlin. Sein Nachfolger war Johann Heinrich Pott (1692–1777). Ersterer hat sich um die Analyse, letzterer um die Mineralchemie Verdienste erworben.
[634] 1760. Vgl. v. Lippmann, »Abhandl. u. Vorträge«. Bd. I: Marggraf.
[635] 1754. Vgl. v. Lippmann, »Abhandl. u. Vorträge«. Bd. I: Marggraf.
[636] Einige von Marggrafs Arbeiten über den Phosphor wurden im 187. Bande von Ostwalds Klassikern veröffentlicht (W. Engelmann, Leipzig 1912). Insbesondere die erste der dort veröffentlichten Abhandlungen, die 1743 in den Miscellanea Berolinensia (VII, 324–344) erschien, ist von epochemachender Bedeutung, weil durch sie der Phosphor des Geheimnisvollen entkleidet wurde, das ihn seit seiner Entdeckung umgab (Ostwalds Klassiker Nr. 187. S. 43).
[637] Siehe an späterer Stelle.
[638] Siehe a. a. O. S. 79–90.
[639] Siehe Bd. I dieses Werkes. S. 179.
[640] John Hemmeter, Michael Servetus. Discoverer of the Pulmonary Circulation. His Life and Work. Janus. S. 331–364 mit 9 Tafeln.
[641] Exercitatio anatomica de motu cordis et sanguinis in animalibus. Francof. 1628.
[642] West, Harvey and his times. London 1874.
[643] So lautet der anatomische Name des großen Gefäßes, das den in den Lymphgefäßen des Magens und des Darmes bereiteten Milch- oder Speisesaft (Chylus) dem Blutstrom zuführt.
[644] Haeser, Geschichte der Medizin. Bd. II. S. 277.
[645] Siehe auch K. Lasswitz, Geschichte der Atomistik. II. S. 84.
[646] Durch Jean Pecquet.
[647] Siehe auch S. 365, Anm. 3.
[648] Sie erfolgte durch den schwedischen Arzt Olaf Rudbeck im Jahre 1651.
[649] Hooke, Micrographia. Schem. I, Fig. 5/6.
[650] Borelli erfand den Heliostaten, indem er einem Spiegel durch ein Uhrwerk eine solche Bewegung gab, daß die Sonnenstrahlen immer nach derselben Richtung zurückgeworfen werden.
[651] Borelius, De motu animalium. Rom 1680, Leyden 1685.
[652] Borelius, De motu animalium. Leyden 1685. Tab. III. Fig. 2.
[653] De motu animalium. Tab. X. Fig. 12.
[654] Lorenzo Bellini. Die insbesondere durch Borelli ins Leben gerufene Schule wird wohl als die iatrophysische bezeichnet.
[655] Malpighi, Opera omnia. London 1697. B. II. S. 87: De renibus.
[656] Jan van Hoorne. Er war der erste, der die Bedeutung der Ovarien für die Entstehung des Embryos erkannte. Siehe Hirsch, Geschichte der medizinischen Wissenschaften, S. 120.
[657] Siehe S. 346.
[658] Boerhaave (1668–1738) war Professor der Chemie und der Botanik in Leyden.
[659] Siehe Carus, Geschichte der Zoologie. München 1872. S. 403.
[660] Harvey, Exercitationes de generatione animalium. London 1651.
[661] De gener. animal. XLV. Leydener Ausgabe vom Jahre 1737. Seite 161.
[662] A. a. O. Seite 162 und 163.
[663] Siehe auch »Harvey, Über die Erzeugung der Tiere« von W. Preyer. Zeitschrift Kosmos, II. Jahrgang. Seite 396.
[664] Bibel der Natur. 1752. Seite 126.
[665] Francesco Redi (1618–1676). Arzt in Florenz und Mitglied der Accademia del Cimento.
[666] Professor der Medizin in Bologna, später Leibarzt von Papst Innocenz XII.
[667] Malpighi, Opera omnia, London 1686.
[668] Siehe S. 376.
[669] Malpighi, De Bombycibus. Tab. VI. Fig. 2.
[670] A. Hirsch, Geschichte der medizinischen Wissenschaften. 1893. S. 122.
[671] Ledermüller, Mikroskopische Gemüts- und Augenergötzungen. 1763.
[672] Leeuwenhoek, Arcana naturae. Delphis Batavorum 1695–1719.
[673] Arcana naturae Bd. I. S. 42.
[674] Arcana naturae. Bd. I. S. 42.
[675] Hirsch, Geschichte der Medizin. S. 493.
[676] Arcana naturae. 1695. Bd. I. S. 173.
[677] Arcana naturae, 1695, Bd. I. Brief 90. Die nähere Aufklärung über dies Verhalten der Blattläuse gab Bonnet im 1. Bande seiner Insektologie. Paris 1745.
[678] Hirsch, Geschichte der Medizin. S. 115.
[679] Abbildung aus Leeuwenhoeks Arcana naturae, 1695. Bd. I. Seite 447.
[680] Hookes »Micrographia«, Schem. XI, Fig. 1.
[681] Hooke, Micrographia or some physiological descriptions of minute bodies. London 1667. pg. 112 (Observat. XVIII).
[682] Micrographia. S. 143.
[683] Arcana naturae. Bd. I. S. 315.
[684] Arcana naturae. Bd. I. S. 318.
[685] Malpighi, Anatome plantarum. 1675. Grew, The anatomy of plants. 1682. Fol. mit 83 Kupfertafeln.
Siehe Marcellus Malpighi, Die Anatomie der Pflanzen, bearbeitet von M. Möbius. Ostwalds Klassiker der exakten Wissenschaften. Nr. 120. S. 31. Leipzig, Verlag von Wilhelm Engelmann, 1901.
[686] Sachs, Geschichte der Botanik. S. 259.
[687] Siehe S. 399.
[688] The anatomy of plants. S. 172.
[689] Siehe Marcellus Malpighi, Die Anatomie der Pflanzen, bearbeitet von M. Möbius. Ostwalds Klassiker der exakten Wissenschaften. Nr. 120. S. 31. Leipzig, Verlag von Wilhelm Engelmann, 1901.
[690] Die Spiralröhren bestehen nach Malpighi aus einem zarten Streifen von geringer Breite, der spiralig verläuft und an den äußeren Rändern zusammenhängt. »Findet ein Zerreißen statt, so zerfällt das Spiralband nicht in einzelne Ringe, wie es bei der Trachee der höheren Tiere der Fall ist, sondern es entsteht ein langes Band« (Ostwalds Klassiker 120. S. 7).
[691] Das Verfahren ist noch heute in Gebrauch.
[692] Siehe Bd. I dieses Werkes, S. 145.
[693] Theophrast, Von den Ursachen der Pflanzen. I, 6.
[694] Camerarius, De sexu plantarum epistola, datiert vom 25. August 1694. Herausgegeben von J. G. Gmelin, Tübingen 1749. Eine Ausgabe in deutscher Übersetzung veranstaltete M. Möbius. Ostwalds Klassiker der exakten Wissenschaften. Nr. 105. Leipzig, Verlag von Wilhelm Engelmann, 1899. Siehe auch Dannemann, Aus der Werkstatt großer Forscher, 3. Aufl., Abschnitt 27.
[695] Koelreuter, siehe an späterer Stelle.
[696] Newton, Abhandlung über die Quadratur der Kurven (1704). Aus dem Lateinischen übersetzt von G. Kowalewski. Band 164 von Ostwalds Klassikern der exakten Wissenschaften. Leipzig, Verlag von W. Engelmann. 1908.
[697] Leibniz, Über die Analysis des Unendlichen. Aus dem Lateinischen übersetzt von G. Kowalewski. Band 162 von Ostwalds Klassikern der exakten Wissenschaften. Leipzig, Verlag von Wilhelm Engelmann. 1908.
[698] Siehe auch S. 165.
[699] Ars conjectandi (Wahrscheinlichkeitsrechnung) von Jakob Bernoulli. Basel 1713. Als 107. und 108. Bd. von Ostwalds Klassikern in deutscher Übersetzung herausgegeben von R. Haussner. Leipzig, Verlag von Wilhelm Engelmann. 1899.
[700] Tropfke, Geschichte der Elementarmathematik. Bd. II. 354.
[701] Ostwalds Klassiker Nr. 108. S. 71 u. f.
[702] Ostwalds Klassiker Nr. 108. S. 104.
[703] Sie entstanden in der Zeit von 1689 bis 1704 und bilden den Inhalt des 171. Bandes von Ostwalds Klassikern der exakten Wissenschaften. Leipzig, W. Engelmann. 1904. Die Übersetzung und die Herausgabe erfolgten durch G. Kowalewski.
[704] Wallis in seiner Arithmetica infinitorum (1655) und Newton in seiner Methodus fluxionum.
[705] Ostwalds Klassiker. Bd. 171. S. 110.
Nicolaus Mercator (nicht mit dem hundert Jahre vor ihm lebenden Gerhard zu verwechseln) wurde 1640(?) in Holstein geboren. Er war Mitglied der Royal Society und starb 1687. Seine mathematischen Untersuchungen wurden besonders durch Wallis' Arithmetica infinitorum (1655) angeregt.
[706] Von neueren Untersuchungen über Reihen seien noch diejenigen von Paul du Bois Reymond erwähnt, weil sie Aufnahme in die Sammlung Ostwalds gefunden haben; P. du Bois Reymond, Über unendliche und trigonometrische Reihen. Als 185. Band von Ostwalds Klassikern herausgegeben. Leipzig, W. Engelmann. 1912.
P. du Bois Reymond, Über die Darstellung der Funktionen durch trigonometrische Reihen. Als 186. Bd. von Ostwalds Klassikern herausgegeben. Leipzig, W. Engelmann. 1912.
[707] Pappus, V. 2.
[708] Abhandlungen über Variationsrechnung: Ostwalds Klassiker Nr. 46, S. 3–13. Leipzig, W. Engelmann. 1894.
[709] Ostwalds Klassiker der exakten Wissenschaften. Bd. 46. S. 14–20. Leipzig, W. Engelmann. 1894.
[710] Siehe Johann Bernoulli, Die erste Integralrechnung. Aus dem Lateinischen übersetzt und als Bd. 194 von Ostwalds Klassik. d. exakt. Wiss. herausgegeb. von G. Kowalewski. Leipzig, W. Engelmann. 1914.
[711] Hydrodynamica seu de viribus et motibus fluidorum commentarii 1738.
[712] Jacob Bernoulli (1654–1705), Johann Bernoulli (1667–1748), Bruder des vorigen. Daniel Bernoulli (1700–1802), Sohn von Johann Bernoulli.
Die Familie Bernoulli gilt als ein Beispiel dafür, daß sich das so seltene mathematische Talent in einer Familie vererben kann. Dies Beispiel ist allerdings wohl einzig in seiner Art. Acht Mitglieder der Familie Bernoulli waren bedeutende Mathematiker, darunter sind die drei obigen, so oft erwähnten als Mathematiker ersten Ranges bekannt. Die Bernoulli stammen aus Antwerpen, von wo ein Jacob Bernoulli nach Frankfurt auswanderte, um sich den Verfolgungen des Herzogs Alba zu entziehen. Einer seiner Enkel wurde 1622 Bürger der Stadt Basel. Der mathematische Lehrstuhl der Universität Basel war länger als ein Jahrhundert von einem Bernoulli besetzt.
[713] Robins, New Principles of gunnery. London. 1742.
[714] Berlin, 1745.
[715] Diese Formel gilt, wenn wir das Pendel als ein einfaches betrachten.
[716] Die Zahl sämtlicher von Euler veröffentlichten Abhandlungen wird auf 700 veranschlagt. Daneben verfaßte er 45 Bände selbständiger Werke. Eine Ausgabe sämtlicher von Euler herrührenden Schriften würde etwa 2000 Druckbogen umfassen.
[717] Eulers »Einführung in die Analysis des Unendlichen« und seine »Anleitung zur Differential- und Integralrechnung« gelten noch heute als vorzügliche Lehrbücher der höheren Mathematik. So viele Werke seitdem über denselben Gegenstand geschrieben sind, »sie sind fast alle mehr oder weniger Variationen des von Euler behandelten Themas« (F. Radio in L. Euler S. 16).
[718] Tropfke, Geschichte der Elementarmathematik. Bd. I. S. 127.
[719] Introductio in analysin infinitorum.
[720] H. Hankel, Die Entwicklung der Mathematik in den letzten Jahrhunderten. S. 15.
[721] Durch P. Stäckel im 46. Band von Ostwalds Klassikern. Leipzig. W. Engelmann. 1894. Eulers Werk erschien 1744. Der vollständige Titel lautet: Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti.
[722] Eine Inhaltsübersicht gibt Cantor im III. Bande seiner Geschichte der Mathematik. S. 830–840.
[723] Leonhard Euler, Vollständige Anleitung zur Integralrechnung. Ausgabe von Salomon. Bd. III. S. 392.
[724] Über das Problem der Kettenlinie bei Galilei, der es noch nicht zu lösen vermochte, und Huygens, Leibniz, sowie den Gebrüdern Bernoulli s. S. 61, Anm. 2.
[725] L. Euler, Von den elastischen Kurven (1744). Einen Neudruck der Abhandlung enthält Nr. 175 der Sammlung »Ostwalds Klassiker der exakten Wissenschaften«.
[727] Siehe S. 280.
[728] Diese Methode wurde schon von Apian (1495–1552) in dessen Kosmographie (§ 5) empfohlen.
[729] Herrührend von Gemma Frisius (1508–1555).
[730] Novae et correctae tabulae ad loca Lunae computanda. Berlin 1746.
[731] Novae tabulae motuum Solis et Lunae. 1752.
[732] Siehe S. 414.
[733] E. Mach, Zur Geschichte der Akustik (E. Machs Vorlesungen. IV. Leipzig, J. A. Barth. 1896). Sauveurs akustische Abhandlungen finden sich in den Mém. de Paris von 1701.
[734] Durch Noble und Pigot, die in den Philos. Transactions vom Jahre 1677 darüber berichteten.
[735] Descartes, der sich mit Mersenne über das Verhalten schwingender Saiten unterhielt, hat schon vermutet, daß die Saiten Teilschwingungen vollziehen, und daß dadurch ihr Ton beeinflußt wird.
[736] Wurde ein Ton z. B. durch 36 Schwingungen in der Sekunde hervorgerufen, und ergaben sich für einen zweiten, etwas höheren Ton vier Stöße in der Sekunde, so beruhte dieser auf 40 Schwingungen, entsprechend dem oben gegebenen Beispiel. Bemerkt sei noch das Kuriosum, daß Sauveur ganz unmusikalisch war und seine Untersuchungen nur unter Mitwirkung von Musikern anzustellen vermochte.
[737] Siehe Dannemann, »Aus der Werkstatt«, 3. Aufl., Abschnitt 34.
[738] Geboren 1706 in der Nähe von London.
[739] Von Dollonds Fernrohren befinden sich noch mehrere im Besitz der Petersburger Akademie der Wissenschaften. Dollond hatte sie für die russische Expedition zur Beobachtung des Venusdurchgangs vom Jahre 1769 geliefert.
[740] Eulers Briefe an eine deutsche Prinzessin. Leipzig 1773. Bd. III. Abbildung auf S. 299.
[741] J. A. Segner (1704–1777), Programma, quo theoriam machinae cujusdam hydraulicae praemittit. Gött. 1750.
[742] Als 182. Band von »Ostwalds Klassiker der exakten Wissenschaften« erschienen. Leipzig, W. Engelmann. 1911.
[743] Ostwalds Klassiker Nr. 182. S. 71.
[744] Dühring, Prinzipien der Mechanik. § 162.
[745] Abhandlung über Dynamik (Traité de dynamique) von d'Alembert. Übersetzt und als Bd. 106 von Ostwalds Klassikern herausgegeben von A. Korn. Leipzig, W. Engelmann. 1899.
[746] Ostwalds Klassiker Bd. 106. S. 71 u. f.
[747] D'Alembert, Traité de l'équilibre et du mouvement des fluids. Paris 1744.
[748] E. Mach, Die Mechanik in ihrer Entwicklung. 1883. S. 335.
[749] Harnack, Geschichte der Preußischen Akademie der Wissenschaften.
[750] Siehe S. 41 dies. Bandes.
[751] Siehe S. 62 dies. Bandes.
[752] J. L. Lagranges Zusätze zu Eulers Elementen der Algebra. Als 103. Band von Ostwalds Klassikern der exakten Wissenschaften herausgegeben von A. J. v. Öttingen und H. Weber. Leipzig, Verlag von W. Engelmann. 1898.
[753] J. L. Lagrange, Über die Lösung der unbestimmten Probleme zweiten Grades. Aus dem Französischen übersetzt und als 146. Band von Ostwalds Klassikern herausgegeben von Eugen Netto. Leipzig, W. Engelmann. 1904.
[754] Durch G. Kowalewski im 113. Band von Ostwalds Klassikern der exakten Wissenschaften. Leipzig, Verlag von W. Engelmann. 1900.
[755] Lagrange, Versuch einer neuen Methode, um die Maxima und Minima unbestimmter Integralformeln zu bestimmen. Im 47. Bande von Ostwalds Klassikern herausgegeben von P. Stäckel. Leipzig, W. Engelmann. 1894.
[756] Ein anderer Ausdruck für Maxima- und Minimaaufgaben.
[757] Siehe S. 159 dies. Bandes.
[759] Lagrange, Über die Methode der Variation. 1770. Im 47. Bande von Ostwalds Klassikern herausgegeben von P. Stäckel. Leipzig, W. Engelmann. 1894.
[760] Die betreffenden Arbeiten von Legendre und Jacobi hat P. Stäckel gleichfalls im 47. Bande von Ostwalds Klassikern veröffentlicht.
[761] Mec. analyt. Partie II, Sect. II.
[762] E. Mach, Die Mechanik in ihrer Entwicklung. Leipzig 1897. S. 458.
[763] Mach, a. a O. S. 471.
[764] Essai d'une nouvelle méthode pour résoudre le problème des trois corps. Paris 1788.
[765] Siehe Ostwalds Klassiker. Bd. 54.
[766] Siehe Ostwalds Klassiker. Bd. 93.
[767] J. L. de Lagrange, Über die Konstruktion geographischer Karten (1779). Im 55. Bande von Ostwalds Klassikern der exakten Wissenschaften herausgegeben von A. Wangerin. Leipzig, W. Engelmann. 1894.
[768] Lambert, Photometria sive de mensura et gradibus luminis, colorium et umbrae, 1760. Das Werk wurde als 31., 32. und 33. Band von Ostwalds Klassikern d. exakten Wissensch. übersetzt und mit zahlreichen Anmerkungen herausgegeben von E. Anding. Leipzig, Verlag von W. Engelmann. 1892.
[769] Lamberts philosophische Werke verdienen deshalb besondere Beachtung, weil sie aus dem Bestreben hervorgegangen sind, die Mathematik und die exakte Beweisführung auf dem Gebiete der Philosophie zur Geltung zu bringen. Ihre Titel lauten: 1. Neues Organon oder Gedanken über die Erforschung und Bezeichnung des Wahren und dessen Unterscheidung von Irrtum und Schein. Leipzig 1764. 2. Architektonik oder Theorie des Einfachen und Ersten in der philosophischen und mathematischen Erkenntnis. Riga 1771.
[770] Bouguer, Traité d'optique sur la gradation de la lumière. Ouvrage posthume. Paris 1760.
[771] Siehe darüber Zöllners Photometrische Untersuchungen.
[772] Zöllner, Photometrische Untersuchungen. S. 27 u. f.
[773] Über die Beziehung von Lamberts Photometrie zum neueren Standpunkte der Wissenschaft handelt G. Recknagels gekrönte Preisschrift: Lamberts Photometrie. München 1861.
[774] Ostwalds Klassiker Nr. 33. S. 63.
[775] Ostwalds Klassiker Nr. 31. S. 5.
[776] Durch die Entdeckung der konischen Refraktion.
[777] Ostwalds Klassiker. Bd. 31. S. 21. Auf diesen Grundsatz hatte auch schon Euler hingewiesen.
[778] Ostwalds Klassiker. Bd. 32. S. 1 u. f.
[779] Ostwalds Klassiker. Bd. 32. S. 71.
[780] Dan. Bernoulli, Sur le son et sur les tons des tuyaux d'orgues Mém. de Paris. 1762.
[781] Über die drehenden Schwingungen eines Stabes berichtete Chladni in den neuen Schriften der naturforschenden Freunde in Berlin. II. Bd. 1799.
[782] Chladni, Entdeckungen über die Theorie des Klanges. 1787. Taf. VIII. Fig. 87–90.
[783] Chladni wurde von Napoleon, der den Ergebnissen der physikalischen Forschung das größte Interesse entgegenbrachte, ehrenvoll aufgenommen. Napoleons Ausspruch: »Chladni läßt uns die Töne sehen«, machte die Runde durch die ganze gebildete Welt. Siehe J. Ebstein »Aus Chladnis Leben und Wirken« (Mitteilungen zur Geschichte der Med. und der Naturw., IV. Bd. Nr. 3 (1905), S. 438 u. f.). Ebsteins Abhandlung enthält 18 bisher ungedruckte Briefe Chladnis. Chladni hat die Aufnahme, die er bei den französischen Gelehrten und am Hofe Napoleons fand, ausführlich geschildert (in der musikalischen Zeitschrift »Cäcilia«). Er hielt sich in Paris fast 1½ Jahre auf (1808–1810). Im Jahre 1809 wurde er durch Laplace und Berthollet dem Kaiser vorgestellt, um seine Versuche zu zeigen und seinen Klavizylinder vorzuführen. Der Besuch dauerte mehrere Stunden. Am anderen Tage wurde Chladni eine Gratifikation von 6000 Frank gesandt. Napoleon zeigte sich auf dem Gebiete der Akustik gut bewandert. Er wußte recht wohl, daß man noch nicht imstande sei, Flächen so dem Kalkül zu unterwerfen wie Kurven. Er setzte daher 3000 Frank als Preis für eine mathematische Theorie der Flächenschwingungen aus, auf denen die Chladnischen Figuren beruhen.
[784] Chladni, Die Akustik. Leipzig 1802.
[785] Siehe S. 316 ds. Bds.
[786] Pierre Bouguer wurde im Jahre 1698 in der Bretagne geboren und starb 1758.
[787] Charles Maria de la Condamine wurde 1701 in Paris geboren und starb im Jahre 1774.
[788] Pierre de Maupertuis wurde 1698 zu St. Malo geboren und trat im Jahre 1731 in die Akademie ein. Zehn Jahre später berief ihn Friedrich der Große nach Berlin und ernannte ihn zum Präsidenten der dortigen Akademie. Während er diese Stellung bekleidete, hat Maupertuis wissenschaftlich wenig geleistet; um so größeres Aufsehen erregte sein Streit mit Voltaire, der die Entfremdung zwischen dem letzteren und dem Könige zur Folge hatte. 1753 kehrte Maupertuis nach Paris zurück. Er starb im Jahre 1759.
[789] 1 Toise = 1,949 m.
[790] Alexis Claude Clairaut (Clairault) wurde 1713 in Paris geboren. Sein Vater war dort Lehrer der Mathematik. Er förderte seinen Sohn, der einen ganz außergewöhnlichen Fall frühreifen mathematischen Talentes darbot, in solchem Grade, daß der junge Clairaut schon in seinem 13. Lebensjahre der Pariser Akademie eine Arbeit vorlegte, in der mehrere Kurven mit den Hilfsmitteln der Infinitesimalrechnung diskutiert waren. Mit 16 Jahren reichte Clairaut der Akademie eine Abhandlung ein, von welcher der Berichterstatter sagte, die geschicktesten Mathematiker würden es sich zur Ehre anrechnen, Verfasser dieser Schrift zu sein. (Näheres darüber siehe bei Cantor, Gesch. d. Math. III. 1901. S. 779.) Clairaut starb 1765 in Paris.
[791] Clairaut, Théorie de la Figure de la Terre, tirée des Principes de l'Hydrostatique. Paris 1743. Eine deutsche Ausgabe erschien als 189. Band von Ostwalds Klass. d. exakt. Wiss. Leipzig, W. Engelmann. 1913.
[792] Mach, Die Mechanik in ihrer Entwicklung, historisch-kritisch dargestellt. 1901. S. 428 u. f.
[793] Dieser Satz besagt, daß bei einem kugelähnlichen Sphäroid die Schwere von dem Gesetz, nach dem sich die innere Dichtigkeit ändert, unabhängig ist. Er lautet:
g_{φ} = g0(1 + sin2φ(5/2 f/g0 - α)).
In dieser Formel bedeutet α die Abplattung, g0 und gφ die Beschleunigung am Äquator, bzw. unter der Breite φ, und f die Zentrifugalkraft am Äquator.
[794] Siehe Bd. II S. 374.
[795] Siehe Bd. III Abschnitt 20.
[796] Gabriel Mouton (1618–1694), Observationes diametrorum solis et lunae apparentium, medianarumque. pag. 427.
[797] Der Bericht über diese, von Méchain und Delambre ausgeführte Messung erschien in drei Bänden in Paris in den Jahren 1806 bis 1810. Eine Auswahl wurde übersetzt und herausgegeben im 181. Bande von Ostwalds Klassikern der exakten Wissenschaften. Dieser enthält auch die von Borda und Cassini verfaßte Abhandlung über die Länge des Sekundenpendels. Leipzig, W. Engelmann. 1911.
[798] Um sie gegen Kugeln aus anderen Substanzen leicht auswechseln zu können und auf diese Weise zu zeigen, daß der Wert von g für alle Substanzen der gleiche sei.
[799] Bessel wiederholte die Bestimmung (Untersuchungen über die Länge des einfachen Sekundenpendels. 1826. S. Bd. IV dies. Werkes). Er bediente sich gleichfalls der Methode der Koinzidenzen und fand für Königsberg die Länge gleich 440,8179 Linien, sowie für die entsprechende Beschleunigung g = 9,81443 m. Kater bestimmte (1818) mit Hilfe des Reversionspendels g zu 9,80804 m unter der Breite von London und auf den Meeresspiegel reduziert. Kater, Experiments for determining the length of the pendulum vibrating seconds in the latitude of London (Phil. Trans. 1818. Näheres siehe im IV. Bande).
[800] Ostwalds Klassiker Nr. 181. S. 186.
[801] De visibili conjunctione inferiorum planetarum cum Sole.
[802] Methodus singularis, qua Solis parallaxis ope. Veneris intra Solem conspiciendae tuto determinari poterit.
[803] Da sich die Abstände der Erde und der Venus von der Sonne wie 1 : 0,723 verhalten, so ergibt sich die Proportion cd : ab = 0,723:(1 - 0,723), woraus folgt, daß das zunächst gesuchte Stück cd = 2,6ab ist.
[804] Joh. Müllers Lehrbuch der kosmischen Physik, 5. Aufl. Braunschweig 1894, Fig. 97.
[805] Siehe S. 274 d. Bds.
[806] Philosophical Transactions von 1718.
[808] Maskelyne, An account of observations made on the mountain Shehallien for finding its attraction. Philosophical Transactions for the year 1795 (Vol. LXV), pg. 500. Nevil Maskelyne wurde 1732 in London geboren und starb 1811 in Greenwich als Astronom der dortigen Sternwarte. Im Jahre 1761 beobachtete er den Durchgang der Venus von St. Helena aus. Ferner war er Begutachter der Ansprüche Harrisons und Mayers an den großen Preis, den die englische Regierung für die Lösung des Längenproblems ausgesetzt hatte. (Siehe S. 416.)
[809] Siehe Dannemann, Aus der Werkstatt großer Forscher, S. 354.
[810] Die Instrumente gaben damals schon einzelne Sekunden an, während die Genauigkeit sich zur Zeit Tychos nur auf Minuten belief.
[811] Halley starb im Jahre 1742.
[812] Bradley, Account of a new discovered motion of the fixed stars (Phil. Transact. 1728).
[813] bc/ab = cotg 20ʺ; bc = ab · cotg 20ʺ
[814] J. H. Lamberts Abhandlungen zur Bahnbestimmung der Kometen erschienen 1761, 1771 und 1772. Sie wurden neuerdings von J. Bauschinger als 133. Band von Ostwalds Klassikern der exakten Wissenschaften herausgegeben. Leipzig, W. Engelmann. 1902.
[815] Ostwalds Klassiker Nr. 133. S. 36.
[816] Miscell. Berol. Tom. VII. pag. 20.
[817] Ostwalds Klassiker Nr. 133. S. 65.
[818] Ostwalds Klassiker Nr. 133. S. 141.
[819] J. H. Lambert, Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelskarten. Herausgegeben von A. Wangerin als 54. Band von Ostwalds Klassikern der exakten Wissenschaften. Leipzig, Verlag von W. Engelmann. 1894.
[820] Ein entsprechendes Unternehmen war für Mitteleuropa die Reymannsche Karte, von der 1806 die ersten 6 Sektionen erschienen. Die Karte wuchs bis 1874 auf 405 Blätter (1 : 200000). Dann ging sie in den Besitz des preußischen Generalstabs über, der den Umfang auf 796 Blätter erweiterte.
[821] Das Nähere hierüber siehe in Ostwalds Klassikern Bd. 54. S. 24 u. 67.
[822] Sie wurden 1777 in den Berichten der Petersburger Akademie der Wissenschaften veröffentlicht und, übersetzt und erläutert, von A. Wangerin als 93. Band von Ostwalds Klassikern wieder herausgegeben. Leipzig, W. Engelmann. 1898.
[823] Über Kartenprojektion. Abhandlungen von Lagrange (1779) und Gauß (1822). Ostwalds Klassiker der exakten Wissenschaften. Bd. 55. Leipzig, W. Engelmann. 1894.
[824] Die Projektionsart rührt nicht von De Lisle, sondern von Mercator her, der sie schon 1585 benutzt hat.
[825] L. Euler, Grundlage der sphärischen Trigonometrie, im 73. Bande von Ostwalds Klassikern in deutscher Übersetzung herausgegeben von E. Hammer. Leipzig, Verlag von W. Engelmann. 1896.
[826] Elemente der sphäroidischen Trigonometrie. Abhandlungen d. Berliner Akademie. 1753. IX. 268–293.
[827] Tropfke, Geschichte der Elementarmathematik. II. S. 295.
[828] Zum Vergleich mögen Eulers Schreibweise und die damals übliche Schreibweise des pythagoräischen Satzes für jedes beliebige ebene Dreieck hier Platz finden:
a2 = b2 + c2 - 2bc cos A
und
BCq = ABq + ACq - 2AB × AC × (Cosin BAC)/(sin. tot.).
[829] Sie wurden 1807 und 1808 durch Mollweide und durch Delambre bekannt gegeben.
[830] L. Euler, Allgemeine sphärische Trigonometrie in kurzer und durchsichtiger Entwicklung von den einfachsten Voraussetzungen ausgehend. Im 73. Bande von Ostwalds Klassikern übersetzt und herausgegeben von H. Hammer. Leipzig, W. Engelmann. 1896.
[831] Caroli a Linné, Systema naturae. 1768. Bd. III. S. 29 u. f.
[832] Die Natur dieses Vorganges konnte sich erst später durch die antiphlogistische Lehre enthüllen.
[833] Natriumammoniumhydrophosphat, das man damals aus Harn darstellte.
[834] Als Blech und Draht kam Platin erst seit 1772 in den Handel.
[835] Wallerius, 1768.
[836] Hauy, 1801.
[837] Hauy, Traité de Minéralogie. 1801. Bd. V, p. VIII, Fig. 77.
[838] W. Nicholson (1753–1815). Description of a new instrument of measuring the specific gravities of bodies. (Mem. Manchest. Soc. II. 1787.)
[839] Romé de l'Isle (1736–1790). Cristallographie ou description des formes propres à tous les corps du règne minéral. Paris 1783.
[840] Namens Carangeot.
[841] Zittel, Geschichte der Geologie und der Paläontologie. S. 64.
[842] Kant, Geschichte der Naturbeschreibung des Erdbebens vom Jahre 1755. Die kleine Schrift erschien 1756.
[843] Lazzaro Moro, 1687–1740.
[844] Antonio Vallisneri (1661–1730) war Professor in Padua.
[845] A. Vallisneri, Dei corpi marini che sui monti si trovano. Venezia 1721.
[846] J. G. Lehmann war Professor der Chemie und Mineralogie in Berlin. Er starb 1767.
[847] J. G. Lehmann, Versuch einer Geschichte der Flözgebirge. Berlin 1756.
[848] Jean Etienne Guettard wurde 1715 geboren und war Verwalter einer naturgeschichtlichen Sammlung. Er machte zahlreiche Reisen und starb 1786 in Paris.
[849] Mém. Acad. roy. des Sciences pour 1702. S. 27. Sur quelques montagnes de la France qui ont été Volcans.
[850] Nicolas Desmarest, 1725 geboren und 1815 als Leiter der Porzellanfabrik zu Sèvres gestorben. Er reiste viele Jahre, um Frankreich und Italien geologisch zu durchforschen.
[851] Zittel, Geschichte der Geologie. S. 56.
[852] George Louis Leclerc de Buffon.
[853] Buffon, Epoques de la Nature. 1778.
[854] Simon Peter Pallas.
[855] De Saussure, Rélation d'un voyage à la cime du Montblanc en août 1787. Er ermittelte die Höhe des Montblanc zu 2426 Toisen. Vorher hatte ein Führer den Montblanc erstiegen und dadurch Saussures Expedition ermöglicht.
[856] Voyage dans les Alpes. 1779–1796. 4 Bde.
[857] Ein Jahr vorher war sein erstes Werk unter dem Titel »Von den äußerlichen Kennzeichen der Fossilien« erschienen.
[858] Werner, Von den äußerlichen Kennzeichen der Fossilien.
[859] Georgius Agricola, De natura fossilium. Basileae 1546.
[860] Wallerius, De systematibus mineralogicis et systemate mineralogico rite condendo. 1768.
[861] Werner, a. a. O. S. 89.
[862] Werner, Von den äußeren Kennzeichen der Mineralien. S. 197.
[863] v. Kobell, Geschichte der Mineralogie. S. 93.
[864] Werner, a. a. O. S. 274.
[865] Werner, a. a. O. in der Einleitung.
[866] Er hieß K. W. Voigt und sammelte in der Rhön eine große Anzahl von Beobachtungen, die auf das Deutlichste gegen den neptunischen Ursprung des Basalts sprachen.
[867] Zittel, Geschichte der Geologie. S. 90.
[868] J. Hutton, Theory of the Earth. Edinburg 1795. 2 Bände. Ein Auszug in deutscher Sprache erschien im 6. Bande von Voigts Magazin der Physik.
[869] Die von Hall benutzten Vorrichtungen, sowie die mit ihnen in den Jahren 1787–1805 erzielten geologischen Präparate werden im Museum der Geologischen Gesellschaft zu London aufbewahrt. Es befinden sich darunter Porzellanröhren, in denen Kreide unter Druck geschmolzen wurde, sowie Proben von Basalt und Lava, die geschmolzen und unter verschiedenen Bedingungen abgekühlt wurden, usw.
[870] Beide Anschauungen vertritt nach dem Vorgange Demokrits schon Aristoteles. Siehe Bd. I S. 124 u. f.
[871] John Playfair (Schüler Huttons, lebte von 1748–1819), Illustration of the Huttonian Theory. 1802.
[872] Scheuchzer, Herbarium diluvianum. 1721.
[873] Knorrs mit 300 vortrefflichen Kupfertafeln versehenes Werk vom Jahre 1755, das unter dem Titel »Sammlung von Merkwürdigkeiten der Natur und Altertümern des Erdbodens« in Nürnberg erschien.
[874] Georg Wolfgang Knorr, 1706–1761.
[875] G. A. Suckow, Näheres siehe Zittel, Geschichte der Geologie. S. 214.
[877] Dr. G. Berthold, John Toland und der Monismus der Gegenwart. Heidelberg 1876, Carl Winter.
[878] A. a. O. S. 5.
[879] Siehe die Bemerkung in den Zusätzen.
[880] Principia philosophiae. 1677. P. II. § 36. Es wird also irrtümlicherweise die Bewegungsgröße für konstant gehalten.
[881] Richtig lautet der Name La Métherie.
[882] Système de la nature ou des lois du monde physique et morale. 1770.
[883] Siehe auch E. du Bois-Reymond, Lamettrie. Berlin 1875. Verlag von A. Hirschwald. Eine deutsche Ausgabe des Systems der Natur erschien 1841 in Leipzig.
[884] Sie rühren zum großen Teile von E. Wiedemann (Wi) und J. Würschmidt (Wü) her. Die Bemerkungen E. v. Lippmanns konnten sämtlich im Text Platz finden.
Des Verfassers Grundriß einer Geschichte der Naturwissenschaften hat in zweiter Auflage G. W. A. Kahlbaum (I, 160 und III, 75) in anerkennendster Weise besprochen und zugleich die Gefühle ausgesprochen, die angesichts der Erfolge dieses Werkes jeden Historiker der Naturwissenschaften beseelen müssen. Aus den gleichen Gründen begrüßen wir es heute freudigst, daß unser Gesellschaftsmitglied und Mitarbeiter den zweiten Teil dieses Buches zu einem vierbändigen Werke ausgestalten will und davon bereits den ersten Band vorzulegen vermag.
(H. Stadler in den Mitteilungen zur Geschichte der Medizin und der Naturwissenschaften, Bd. X, 2. Heft.)
Der soeben erschienene 2. Band dieses großen Werkes behandelt die Zeit von Galilei bis zur Mitte des 18. Jahrhunderts, also jene Epoche, in welcher die Grundlagen der neueren Naturwissenschaften gelegt wurden. Auch in diesem Bande hat sich der Verfasser mit Erfolg bemüht, eine Darstellung zu schaffen, die nicht nur dem Historiker dient, sondern für jeden anregend ist, der sich überhaupt für die Naturwissenschaft interessiert.
(Kölnische Zeitung, 20. Februar 1911.)
Ähnlich wie Cantors Vorlesungen über Geschichte der Mathematik ein »standard work« allerersten Ranges bleiben werden, so wird auch Dannemanns Werk von bleibendem Wert sein, das für den Geschichtsforscher wie für den Mediziner, für den Lehrer wie für den Techniker großen Nutzen haben und dessen Lektüre für jeden, der sich für die Naturwissenschaften interessiert, eine Quelle hohen Genusses bilden wird.
(Monatsschrift für höhere Schulen, 1911, 6. Heft.)
Besonders dankenswert erscheint, wie Dannemann in allen diesen Wissenschaften die verbindenden großen Gedanken herauszuschälen weiß, die im hohen Maße geeignet sind, die Vertreter der einzelnen naturwissenschaftlichen Disziplinen vor Einseitigkeit zu bewahren.
(Ärztliche Rundschau, 1910, XX. Jahrgang, Nr. 47.)
Für die Hebung der Kultur unseres Volkes kann dieses Buch, das die Wissenschaft und ihre Erfolge als etwas Werdendes vorstellt, von größtem Nutzen sein, da es die Erfolge fortschrittlichen Denkens gegenüber den Schwächen dogmatischer Gesinnung aufs deutlichste vergegenwärtigt.
(Prometheus, 26. November 1910, XXII. Jahrgang.)
L'ouvrage me paraît excellent; il a d'ailleurs une qualité inappréciable; c'est de n'avoir pas d'équivalent.
(Revue générale des Sciences. Paris 15. III. 1912.)
Das Gesamtwerk, dessen Inhalt durch gute Register und Literaturverzeichnisse übersichtlich zusammengehalten wird, liegt nun, auch in äußerlich schönem Gewande, vollständig vor; es gehört fraglos zu den besten, bestgeschriebenen, originellsten und nutzbringendsten der neueren naturwissenschaftlichen Literatur und ist mehr als jedes andere geeignet, den immer unheilvoller hervortretenden Folgen der völligen Zersplitterung unter den Naturforschern abzuhelfen und deren allgemeine Fortbildung wieder zu heben. Es gereicht dem Verfasser zur Ehre, nicht minder aber auch der ganzen deutschen Literatur.
(Prof. Dr. E. O. von Lippmann in der Chemiker-Zeitung 1913.)
Seit Jahren empfehle ich meinen Hörern in der einführenden Vorlesung über experimentelle Chemie das Dannemannsche ausgezeichnete, noch nicht nach Gebühr verbreitete Werk »Die Naturwissenschaften in ihrer Entwicklung und in ihrem Zusammenhange«.
(Dr. A. Stock, Prof. a. d. Univ. Berlin und am Kaiser-Wilh.-Inst. Dahlem, in d. Monatsschrift f. d. chem. u. biol. Unterr. 1920.)
Aus den Besprechungen des ersten Bandes der zweiten Auflage.
So steht das Werk in seiner verjüngten Gestalt zweifellos auf der Höhe und kann jedem, der sich für die Geschichte der Naturwissenschaften interessiert, aufs beste empfohlen werden.
(Süddeutsche Zeitung, 23. Dezember 1920.)
Das Werk wird dem Lehrer einer höheren Schule Gelegenheit geben, sich ohne zu große Mühe über alle Punkte zu vergewissern, die er in seinem Unterricht zu verwerten beabsichtigt. Es wird aber zugleich auch dem Lehrer der Hochschule als wertvoller Handweiser für eine Reihe von akademischen Vorträgen über das Gesamtgebiet der Naturwissenschaften willkommen sein. Und mit dem Verfasser hofft der Unterzeichnete, daß recht bald schon das Bedürfnis derartiger Vorträge von allen unseren hohen Schulen anerkannt werden möchte.
(S. Günther in der D. Lit.-Ztg. v. 11. u. 25. September 1920.)
Von dem Verfasser erschienen ferner:
Leitfaden für die Übungen im chemischen Unterricht der oberen Klassen höherer Lehranstalten. 6. Aufl. B. G. Teubner, Leipzig 1920.
Aus der Werkstatt großer Forscher. 430 Seiten. 3. Aufl. Leipzig 1908. Wilhelm Engelmann.
Gebunden M. 13.50 einschließl. V.-T.-Z.
»Es sei jeder, der sich bisher noch nicht mit diesem vortrefflichen Werke bekannt gemacht hat, darauf hingewiesen, die sehr wertvolle Bekanntschaft nicht länger hinauszuschieben.«
(Prof. Dr. Wilh. Ostwald.)
Naturlehre für höhere Lehranstalten, auf Schülerübungen gegründet. Hannover 1908. Hahnsche Buchhandlung.
»Der Verfasser hat so alle Momente vereinigt, die zur Erteilung eines zeitgemäßen Unterrichts von Belang sind und zwar so, daß zu dem neuen Plane ein Übergang von dem bestehenden her möglich ist.«
(Deutsche Literaturzeitung, 1909, Nr. 5.)
Handbuch für den physikalischen Unterricht. J. Beltz, Langensalza 1919.
»Was in diesem Buche gesagt wird, faßt alle lebenskräftigen Reformgedanken der letzten Jahre in geschickter Weise zusammen.«
(R. Winderlich, i. d. Ztschr. f. d. math. u. naturw. Unterr.)
VERLAG VON WILHELM ENGELMANN IN LEIPZIG
Logarithmisch-trigonometrische Tafeln mit 8 Dezimalstellen.
Enthaltend die Logarithmen aller Zahlen von 1–200000 und die Logarithmen der trigonometrischen Funktionen für jede Sexagesimalsekunde des Quadranten. Mit Unterstützung der Preußischen Akademie der Wissenschaften in Berlin und der Akademie der Wissenschaften in Wien. Neu berechnet und herausgegeben von Professor Dr. J. Bauschinger und Professor Dr. J. Peters. 2 Bände. Lex.-8.
M. 78.–
Aus den Besprechungen:
»... Mit ... hat die Tafelliteratur erstklassige Bereicherungen erfahren, die von bleibendem Wert sind und für die Erstellung von Tabellensammlungen vorbildlich sein sollten ...«
(Archiv der Mathematik und Physik.)
Zur Geschichte der astronomischen Meßwerkzeuge von Purbach bis Reichenbach 1450–1830 von Joh. A. Repsold. 1. Band. Mit 171 Abbildungen (VIII und 132 Seiten gr. 8).
M. 24.–
Aus den Besprechungen:
»Das Buch, das sich überall als eine reiche Quelle der Belehrung über die Zweckdienlichkeit und die sachgemäße Verwendung der Instrumente, sowie über die Vorteile und Nachteile der einzelnen Konstruktionen darbietet, wird gewiß nicht verfehlen, einen dauernden, großen Nutzen für die Wissenschaft zu stiften.«
(Astronomische Nachrichten, Bd. 177, Nr. 6.)
»Ein höchst interessantes, lehrreiches Werk ist es, das der Verfasser, der wie kein anderer dazu berufen war, es zu schreiben, den Mechanikern und Astronomen darbietet.«
(Zeitschrift für Instrumentenkunde. XXVIII. Jahrg., Sept. 1908.)
Vorstehende Preise einschließlich Verleger-Teuerungszuschlag.
Bei der Transkription vorgenommene Änderungen und weitere Anmerkungen:
In "»Stellt man nun zwischen das Auge und dieses undeutliche Bild, und zwar nahe dahinter eine zweite Sammellinse OP, so wird letztere die von D und F kommenden Strahlen konvergent und das Bild dadurch deutlich machen.« Auch wird dieses durch das Okular erzeugte Bild, wie Kepler dartut, größer erscheinen als das Bild das »die dem Auge nächststehende Linse (OP) von der entfernteren Linse (AB) erhalten hatte«[2]." erstes öffnendes und zweites schließendes Anführungszeichen ergänzt.
In "Ließ Grimaldi durch die Öffnungen CD und GH (siehe Abb. 30) einen Lichtkegel fallen, der von dem Schirm IK aufgefangen wurde, so besaßen die Grundflächen dieses Kegels nicht den Durchmesser NO, den die geometrische Konstruktion auf Grund der geradlinigen Fortpflanzung des Lichtes fordert, sondern einen größeren Durchmesser IK." stand "angefangen" statt "aufgefangen", und "JK" statt "IK" (Text wurde Abbildung 30 angepasst).
In "Auf dieses Gebiet wurde Glauber dadurch geführt, daß er die Darstellung der Salzsäure durch Einwirkung von Schwefelsäure auf Kochsalz kennen lernte" stand "lehrte" statt "lernte".
In "Ferner könne der Wellenteil BG (Abb. 85), der den leuchtenden Punkt A zum Mittelpunkt hat, sich nur bis zu dem von den Geraden ABC und AGE begrenzten Bogen CE ausbreiten." stand "dem Graden" statt "den Geraden".
In "z = (m1a12 + m2a22 + m3a32 ...)/(m1a1 + m2a2 + m3a3 ...)": Tiefergestellte 1 an der Variable a im Formelteil m1a12 hinzugefügt.
In "Σ{m(X - d2x/(dt2))δx + m(Y - d2y/(dt2))δy + m(Z - d2z/(dt2))δz} = 0." stand im mittleren Formelteil der Partikel "δy" in der Klammer.
Fußnote 97: In x_{ʹ} : x_{ʺ} = y_{ʹ}2 : y_{ʺ}2 wurde der Strich hinter dem x im ersten Formelteil ergänzt.
***END OF THE PROJECT GUTENBERG EBOOK DIE NATURWISSENSCHAFTEN IN IHRER ENTWICKLUNG UND IN IHREM ZUSAMMENHANGE, II. BAND***
******* This file should be named 54127-h.htm or 54127-h.zip *******
This and all associated files of various formats will be found in:
http://www.gutenberg.org/5/4/1/2/54127
Updated editions will replace the previous one--the old editions will be renamed.
Creating the works from print editions not protected by U.S. copyright law means that no one owns a United States copyright in these works, so the Foundation (and you!) can copy and distribute it in the United States without permission and without paying copyright royalties. Special rules, set forth in the General Terms of Use part of this license, apply to copying and distributing Project Gutenberg-tm electronic works to protect the PROJECT GUTENBERG-tm concept and trademark. Project Gutenberg is a registered trademark, and may not be used if you charge for the eBooks, unless you receive specific permission. If you do not charge anything for copies of this eBook, complying with the rules is very easy. You may use this eBook for nearly any purpose such as creation of derivative works, reports, performances and research. They may be modified and printed and given away--you may do practically ANYTHING in the United States with eBooks not protected by U.S. copyright law. Redistribution is subject to the trademark license, especially commercial redistribution.
To protect the Project Gutenberg-tm mission of promoting the free distribution of electronic works, by using or distributing this work (or any other work associated in any way with the phrase "Project Gutenberg"), you agree to comply with all the terms of the Full Project Gutenberg-tm License available with this file or online at www.gutenberg.org/license.
1.A. By reading or using any part of this Project Gutenberg-tm electronic work, you indicate that you have read, understand, agree to and accept all the terms of this license and intellectual property (trademark/copyright) agreement. If you do not agree to abide by all the terms of this agreement, you must cease using and return or destroy all copies of Project Gutenberg-tm electronic works in your possession. If you paid a fee for obtaining a copy of or access to a Project Gutenberg-tm electronic work and you do not agree to be bound by the terms of this agreement, you may obtain a refund from the person or entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be used on or associated in any way with an electronic work by people who agree to be bound by the terms of this agreement. There are a few things that you can do with most Project Gutenberg-tm electronic works even without complying with the full terms of this agreement. See paragraph 1.C below. There are a lot of things you can do with Project Gutenberg-tm electronic works if you follow the terms of this agreement and help preserve free future access to Project Gutenberg-tm electronic works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation" or PGLAF), owns a compilation copyright in the collection of Project Gutenberg-tm electronic works. Nearly all the individual works in the collection are in the public domain in the United States. If an individual work is unprotected by copyright law in the United States and you are located in the United States, we do not claim a right to prevent you from copying, distributing, performing, displaying or creating derivative works based on the work as long as all references to Project Gutenberg are removed. Of course, we hope that you will support the Project Gutenberg-tm mission of promoting free access to electronic works by freely sharing Project Gutenberg-tm works in compliance with the terms of this agreement for keeping the Project Gutenberg-tm name associated with the work. You can easily comply with the terms of this agreement by keeping this work in the same format with its attached full Project Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern what you can do with this work. Copyright laws in most countries are in a constant state of change. If you are outside the United States, check the laws of your country in addition to the terms of this agreement before downloading, copying, displaying, performing, distributing or creating derivative works based on this work or any other Project Gutenberg-tm work. The Foundation makes no representations concerning the copyright status of any work in any country outside the United States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate access to, the full Project Gutenberg-tm License must appear prominently whenever any copy of a Project Gutenberg-tm work (any work on which the phrase "Project Gutenberg" appears, or with which the phrase "Project Gutenberg" is associated) is accessed, displayed, performed, viewed, copied or distributed:
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.
1.E.2. If an individual Project Gutenberg-tm electronic work is derived from texts not protected by U.S. copyright law (does not contain a notice indicating that it is posted with permission of the copyright holder), the work can be copied and distributed to anyone in the United States without paying any fees or charges. If you are redistributing or providing access to a work with the phrase "Project Gutenberg" associated with or appearing on the work, you must comply either with the requirements of paragraphs 1.E.1 through 1.E.7 or obtain permission for the use of the work and the Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or 1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted with the permission of the copyright holder, your use and distribution must comply with both paragraphs 1.E.1 through 1.E.7 and any additional terms imposed by the copyright holder. Additional terms will be linked to the Project Gutenberg-tm License for all works posted with the permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm License terms from this work, or any files containing a part of this work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this electronic work, or any part of this electronic work, without prominently displaying the sentence set forth in paragraph 1.E.1 with active links or immediate access to the full terms of the Project Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary, compressed, marked up, nonproprietary or proprietary form, including any word processing or hypertext form. However, if you provide access to or distribute copies of a Project Gutenberg-tm work in a format other than "Plain Vanilla ASCII" or other format used in the official version posted on the official Project Gutenberg-tm web site (www.gutenberg.org), you must, at no additional cost, fee or expense to the user, provide a copy, a means of exporting a copy, or a means of obtaining a copy upon request, of the work in its original "Plain Vanilla ASCII" or other form. Any alternate format must include the full Project Gutenberg-tm License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying, performing, copying or distributing any Project Gutenberg-tm works unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing access to or distributing Project Gutenberg-tm electronic works provided that
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm electronic work or group of works on different terms than are set forth in this agreement, you must obtain permission in writing from both the Project Gutenberg Literary Archive Foundation and The Project Gutenberg Trademark LLC, the owner of the Project Gutenberg-tm trademark. Contact the Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable effort to identify, do copyright research on, transcribe and proofread works not protected by U.S. copyright law in creating the Project Gutenberg-tm collection. Despite these efforts, Project Gutenberg-tm electronic works, and the medium on which they may be stored, may contain "Defects," such as, but not limited to, incomplete, inaccurate or corrupt data, transcription errors, a copyright or other intellectual property infringement, a defective or damaged disk or other medium, a computer virus, or computer codes that damage or cannot be read by your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right of Replacement or Refund" described in paragraph 1.F.3, the Project Gutenberg Literary Archive Foundation, the owner of the Project Gutenberg-tm trademark, and any other party distributing a Project Gutenberg-tm electronic work under this agreement, disclaim all liability to you for damages, costs and expenses, including legal fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE PROVIDED IN PARAGRAPH 1.F.3. YOU AGREE THAT THE FOUNDATION, THE TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a defect in this electronic work within 90 days of receiving it, you can receive a refund of the money (if any) you paid for it by sending a written explanation to the person you received the work from. If you received the work on a physical medium, you must return the medium with your written explanation. The person or entity that provided you with the defective work may elect to provide a replacement copy in lieu of a refund. If you received the work electronically, the person or entity providing it to you may choose to give you a second opportunity to receive the work electronically in lieu of a refund. If the second copy is also defective, you may demand a refund in writing without further opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth in paragraph 1.F.3, this work is provided to you 'AS-IS', WITH NO OTHER WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO WARRANTIES OF MERCHANTABILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied warranties or the exclusion or limitation of certain types of damages. If any disclaimer or limitation set forth in this agreement violates the law of the state applicable to this agreement, the agreement shall be interpreted to make the maximum disclaimer or limitation permitted by the applicable state law. The invalidity or unenforceability of any provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the trademark owner, any agent or employee of the Foundation, anyone providing copies of Project Gutenberg-tm electronic works in accordance with this agreement, and any volunteers associated with the production, promotion and distribution of Project Gutenberg-tm electronic works, harmless from all liability, costs and expenses, including legal fees, that arise directly or indirectly from any of the following which you do or cause to occur: (a) distribution of this or any Project Gutenberg-tm work, (b) alteration, modification, or additions or deletions to any Project Gutenberg-tm work, and (c) any Defect you cause.
Project Gutenberg-tm is synonymous with the free distribution of electronic works in formats readable by the widest variety of computers including obsolete, old, middle-aged and new computers. It exists because of the efforts of hundreds of volunteers and donations from people in all walks of life.
Volunteers and financial support to provide volunteers with the assistance they need are critical to reaching Project Gutenberg-tm's goals and ensuring that the Project Gutenberg-tm collection will remain freely available for generations to come. In 2001, the Project Gutenberg Literary Archive Foundation was created to provide a secure and permanent future for Project Gutenberg-tm and future generations. To learn more about the Project Gutenberg Literary Archive Foundation and how your efforts and donations can help, see Sections 3 and 4 and the Foundation information page at www.gutenberg.org.
The Project Gutenberg Literary Archive Foundation is a non profit 501(c)(3) educational corporation organized under the laws of the state of Mississippi and granted tax exempt status by the Internal Revenue Service. The Foundation's EIN or federal tax identification number is 64-6221541. Contributions to the Project Gutenberg Literary Archive Foundation are tax deductible to the full extent permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is in Fairbanks, Alaska, with the mailing address: PO Box 750175, Fairbanks, AK 99775, but its volunteers and employees are scattered throughout numerous locations. Its business office is located at 809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887. Email contact links and up to date contact information can be found at the Foundation's web site and official page at www.gutenberg.org/contact
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
gbnewby@pglaf.org
Project Gutenberg-tm depends upon and cannot survive without wide spread public support and donations to carry out its mission of increasing the number of public domain and licensed works that can be freely distributed in machine readable form accessible by the widest array of equipment including outdated equipment. Many small donations ($1 to $5,000) are particularly important to maintaining tax exempt status with the IRS.
The Foundation is committed to complying with the laws regulating charities and charitable donations in all 50 states of the United States. Compliance requirements are not uniform and it takes a considerable effort, much paperwork and many fees to meet and keep up with these requirements. We do not solicit donations in locations where we have not received written confirmation of compliance. To SEND DONATIONS or determine the status of compliance for any particular state visit www.gutenberg.org/donate.
While we cannot and do not solicit contributions from states where we have not met the solicitation requirements, we know of no prohibition against accepting unsolicited donations from donors in such states who approach us with offers to donate.
International donations are gratefully accepted, but we cannot make any statements concerning tax treatment of donations received from outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation methods and addresses. Donations are accepted in a number of other ways including checks, online payments and credit card donations. To donate, please visit: www.gutenberg.org/donate
Professor Michael S. Hart was the originator of the Project Gutenberg-tm concept of a library of electronic works that could be freely shared with anyone. For forty years, he produced and distributed Project Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed editions, all of which are confirmed as not protected by copyright in the U.S. unless a copyright notice is included. Thus, we do not necessarily keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility: www.gutenberg.org
This Web site includes information about Project Gutenberg-tm, including how to make donations to the Project Gutenberg Literary Archive Foundation, how to help produce our new eBooks, and how to subscribe to our email newsletter to hear about new eBooks.