*** START OF THE PROJECT GUTENBERG EBOOK 63884 ***

Please see the Transcriber’s Notes at the end of this text.

Latest Conjuring
By WILL GOLDSTON
The Latest and Best Book Published

A Few Principal Items—

Chapter I.—Latest tricks with and without apparatus, many published for the first time. Illustrated.

Chapter II.—Every new and startling illusion accurately explained with illustrations.

Chapter III.—Latest methods for performing the “Mystic Kettle” that boils on ice, including the “Magic Kettle,” the most remarkable utensil to hold liquor. This little kettle can produce almost any drink from milk to whisky. Illustrated.

Chapter IV.—Correct methods to escape from Handcuffs, Leg-irons, Rope, Iron Collars, Padlocks, Sacks, Iron Trunks, Wooden Boxes, Barrels, Iron Cages. Illustrated.

Chapter V.—Hand Shadows and how to work them. Illustrated.

Without a doubt the greatest and cheapest book ever
published on Magic.

Order Immediately to Avoid Disappointment

Handsomely Bound in Cloth, 2/-
Post Free, 2/3

The Secrets of Magic
By WILL GOLDSTON

Over 100 pages and as many illustrations. This up-to-date work, describing only the latest secrets and effects in conjuring, also contains biographies of leading magicians.

This book is in its 4th Edition, and is without doubt a very useful book, as it contains many valuable tricks and illusions never before divulged.

Cloth Bound. Price 2/6. Postage 3d.

A. W. GAMAGE, Ltd

HOLBORN

LONDON, E.C.

THE TWENTIETH CENTURY
STANDARD PUZZLE
BOOK

THREE PARTS IN ONE VOLUME

EDITED BY
A. CYRIL PEARSON, M.A.

AUTHOR OF
‘100 Chess Problems,’ ‘Anagrams, Ancient and Modern,’ etc.

PROFUSELY ILLUSTRATED

SECOND IMPRESSION

LONDON
GEORGE ROUTLEDGE & SONS, LTD.
NEW YORK: E. P. DUTTON & CO.

Also in Three Parts

III.—Magic Squares, Picture Puzzles, Enigmas, Charades, Riddles, Conundrums, Nuts to Crack, Solutions.

III.—Optical Illusions, Freaks of Figures, Chess Cameos, Science at Play, Curious Calculations, Word and Letter Puzzles, Solutions.

III.—Word Puzzles, Missing Words, Letter Puzzles, Anagrams, Picture Puzzles, Palindromes, Solutions.

Also by the same Author

Pictured Puzzles and Word Play. Profusely Illustrated. Crown 8vo. Cloth.

PART I.

	PAGE
Magic Squares, Puzzles, Tricks, Enigmas	I-1
Charades, Etc.	I-80
Riddles and Conundrums	I-104
Nuts to Crack	I-115
Solutions	I-148

[I-1]

MAGIC SQUARES

No. I.—FOUR HUNDRED YEARS OLD!

In Albert Dürer’s day, as in Milton’s, “melancholy” meant thoughtfulness, and on this ground we find on his woodcut, “Melancholia, or the Genius of the Industrial Science of Mechanics,” a very early instance of a Magic Square, showing that Puzzles had a recognised place in mental gymnastics four hundred years ago.

[I-2]

No. II.—A SIMPLE MAGIC SQUARE

Much time was devoted in olden days to the construction and elaboration of Magic Squares. Before we go more deeply into this fascinating subject, let us study the following pretty and ingenious method of making a Magic Square of sixteen numbers, which is comparatively simple, and easily committed to memory:—

1	15	14	4
12	6	7	9
8	10	11	5
13	3	2	16

Start with the small square at the top left-hand corner, placing there the 1; then count continuously from left to right, square by square, but only insert those numbers which fall upon the diagonals—namely, 4, 6, 7, 10, 11, 13, and 16.

Then start afresh at the bottom right-hand corner, calling it 1, and fill up the remaining squares in order, from right to left, counting continuously, and so placing in their turn 2, 3, 5, 8, 9, 12, 14, and 15. Each row, column, diagonal, and almost every cluster of four has 34 as the sum of its numbers.

[I-3]

No. III.—ANOTHER MAGIC SQUARE

1	20	16	23	5
15	7	12	9	22
24	18	13	8	2
4	17	14	19	11
21	3	10	6	25

In this Magic Square the rows, columns, and diagonals add up to 65, and the sum of any two opposite and corresponding squares is 26.

ENIGMAS

1
A MYSTIC ENIGMA

He stood himself beside himself
And looked into the sea;
Within himself he saw himself,
And at himself gazed he.
Now when himself he saw himself
Within himself go round,
Into himself he threw himself,
And in himself was drowned.
Now if he had not been himself,
But other beast beside,
He would himself have cut himself
Nor in himself have died.

Solution

[I-4]

No. IV.—A NEST OF CENTURIES

22	47	16	41	10	35	4
5	23	48	17	42	11	29
30	6	24	49	18	36	12
13	31	7	25	43	19	37
38	14	32	1	26	44	20
21	39	8	33	2	27	45
46	15	40	9	34	3	28

The numbers in this Magic Square of 49 cells add up in all rows, columns, and diagonals to 175. The four corner cells of every square or rectangle that has cell 25 in its centre, and cells 1, 7, 49, 43, add up to 100.

2

One morning Chloe, to avoid the heat,
Sat in a corner of a shady seat.
Young Strephon, on the self-same errand bound,
This fairest flower of all the garden found.
Her peerless beauty set his heart aflame,
Three monosyllables expressed his aim.

At a respectful distance he conversed
About the weather; then became immersed
In other topics, lessening the while
The space between them, heartened by her smile.
The same three simple words, now joined in one,
Expressed their happy state at set of sun.

Solution

[I-5]

No. V.—THE MAKING OF A MAGIC SQUARE

An ideal Magic Square can be constructed thus:

Place 1, 2, 3, 4, 5 in any order in the five top cells, set an asterisk over the third column, as shown in the diagram; begin the next row with this figure, and let the rest follow in the original sequence; continue this method with the other three rows.

Preparatory Square No. 1.

		*
1	3	5	2	4
5	2	4	1	3
4	1	3	5	2
3	5	2	4	1
2	4	1	3	5

Preparatory Square No. 2.

			*
5	15	0	10	20
10	20	5	15	0
15	0	10	20	5
20	5	15	0	10
0	10	20	5	15

Make a similar square of 25 cells with 0, 5, 10, 15, 20, as is shown in No. 2, placing the asterisk in this case over the fourth column of cells, and proceeding as before, in an unchanging sequence. Using these two preparatory squares, try to form a Magic Square in which the same number can be counted up in forty-two different ways.

Solution

[I-6]

No. VI.—ANOTHER WAY TO MAKE A MAGIC SQUARE

Here is one of many methods by which a Magic Square of the first twenty-five numbers can readily be made.

				1
			2		6
		3	20	7	24	11
	4	16	8	25	12	4	16
5		9	21	13	5	17		21
	10	22	14	1	18	10	22
		15	2	19	6	23
			20		24
				25

This is done by first placing the figures from 1 to 25 in diagonal rows, as is shown above, and then introducing the numbers that are outside the square into it, by moving each of them five places right, left, up, or down. A Magic Square is thus formed, the numbers of which add up to 65 in lines, columns and diagonals, and with the centre and any four corresponding numbers on the borders.

[I-7]

No. VII.—A MONSTER MAGIC SQUARE

Here is what may indeed be called a Champion Magic Square:—

23	464	459	457	109	111	108	110	132	133	130	131	373	371	357	356	372	382	370	335	30	22
25	41	436	435	433	432	196	195	241	242	200	225	284	287	246	245	288	261	51	58	47	460
27	45	13	474	469	467	82	81	72	90	91	83	401	400	396	398	399	397	20	12	440	458
461	55	15	34	450	449	447	446	156	157	180	181	326	327	306	307	44	37	33	470	430	24
456	56	17	42	3	484	479	477	66	65	68	67	422	421	416	415	10	2	443	468	429	29
137	428	471	41	5	127	126	125	361	362	363	364	365	366	118	117	116	480	444	14	57	348
153	431	466	31	7	347	148	338	339	145	143	342	142	344	345	139	138	478	454	19	54	332
154	439	98	453	481	325	161	169	168	318	319	320	321	163	162	324	160	4	32	387	46	331
384	266	407	445	476	292	293	191	190	299	298	297	186	185	184	302	193	9	40	78	219	101
383	268	406	442	424	270	280	272	273	211	210	209	208	278	279	205	215	61	43	79	217	102
379	265	392	172	60	248	227	250	251	230	232	231	233	256	257	258	237	425	313	93	220	106
378	267	391	173	59	226	249	228	229	252	254	253	255	234	235	236	259	426	312	94	218	107
351	282	405	176	74	204	214	206	207	277	276	275	274	212	213	271	281	411	309	80	203	134
350	263	390	177	73	182	192	301	300	189	187	188	296	295	294	183	303	412	308	95	222	135
334	199	77	330	423	171	315	323	322	164	165	166	167	317	316	170	314	62	155	408	286	151
333	216	96	311	413	149	346	147	146	340	341	144	343	141	140	337	336	72	174	389	269	152
100	221	76	310	414	369	359	360	124	123	122	121	120	119	367	368	358	71	175	409	264	385
99	223	75	291	483	1	6	8	419	420	417	418	63	64	69	70	475	482	194	410	262	386
104	202	97	452	35	36	38	39	329	328	305	304	159	158	179	178	441	448	451	388	283	381
105	238	473	11	16	18	403	404	393	395	394	402	84	85	89	87	86	88	465	472	247	380
136	438	49	50	52	53	289	290	244	243	285	260	201	198	239	240	197	224	434	427	437	349
463	21	26	28	376	374	377	375	353	352	355	354	112	114	128	129	113	103	115	150	455	462

Its 484 cells form, as they are numbered, a Magic Square, in which all rows, columns, and diagonals add up to 5335, and it is no easy matter to determine in how many other symmetrical ways its key-number can be found.

When the cells outside each of the dark border lines are removed, three other perfect Magic Squares remain.

Collectors should take particular note of this masterpiece.

[I-8]

No. VIII.—A NOVEL MAGIC SQUARE

A Magic Square of nine cells can be built up by taking any number divisible by 3, and placing, as a start, its third in the central cell. Thus:—

28	29	24
23	27	31
30	25	26

Say that 81 is chosen for the key number. Place 27 in the centre; 28, 29, in cells 1, 2; 30 in cell 7; 31 in 6; and then fill up cells 3, 4, 8, and 9 with the numbers necessary to make up 81 in each row, column, and diagonal.

Any number above 14 that is divisible by 3 can be dealt with in this way.

3

Enriched I am with much that’s fat,
Yet money I possess not;
Enlightening all who come to me,
True wisdom I express not.
I may be wicked, but protest
That sinful none have found me;
Though I destroy myself to be
Of use to those around me.

Solution

[I-9]

No. IX.—TWIN MAGIC SQUARES

Among the infinite number of Magic Squares which can be constructed, it would be difficult to find a more remarkable setting of the numbers 1 to 32 inclusive than this, in which two squares, each of 16 cells, are perfect twins in characteristics and curious combinations.

1	8	29	28	11	14	23	18
30	27	2	7	21	20	9	16
4	5	32	25	10	15	22	19
31	26	3	6	24	17	12	13

There are at least forty-eight different ways in which 66 is the sum of four of these numbers. Besides the usual rows, columns, and diagonals, any square group of four, both corner sets, all opposite pairs on the outer cells, and each set of corresponding cells next to the corners, add up exactly to 66.

4

Of Spanish extraction, my hue
Is as dark as a negro can be;
I am solid, and yet it is true
That in part I am wet as the sea,
My second and first are the same
In all but condition and name;
My second can burst
The abode of my first,
And my whole from the underground came.

Solution

[I-10]

No. X.—A BORDERED MAGIC SQUARE

Here is a notable specimen of a Magic Square:—

4	5	6	43	39	38	40
49	15	16	33	30	31	1
48	37	22	27	26	13	2
47	36	29	25	21	14	3
8	18	24	23	28	32	42
9	19	34	17	20	35	41
10	45	44	7	11	12	46

The rows, columns, and diagonals all add up to exactly 175 in the full square. Strip off the outside cells all around, and a second Magic Square remains, which adds up in all such ways to 125.

Strip off another border, as is again indicated by the darker lines, and a third Magic Square is left, which adds up to 75.

5
AN OLD ENIGMA
By Hannah More

I’m a strange contradiction: I’m new and I’m old,
I’m sometimes in tatters and sometimes in gold,
Though I never could read, yet letter’d I’m found,
Though blind I enlighten, though free I am bound.

I’m English, I’m German, I’m French, and I’m Dutch;
Some love me too dearly, some slight me too much.
I often die young, though I sometimes live ages,
And no Queen is attended by so many pages.

Solution

[I-11]

No. XI.—A LARGER BORDERED MAGIC SQUARE

Here is another example of what is called a “bordered” Magic Square:—

5	80	59	73	61	3	63	12	13
1	20	55	30	57	28	71	26	81
4	14	31	50	29	60	35	68	78
76	58	46	38	45	40	36	24	6
7	65	33	43	41	39	49	17	75
74	64	48	42	37	44	31	18	8
67	10	47	32	53	22	51	72	15
66	56	27	52	25	54	11	62	16
69	2	23	9	21	79	19	70	77

These 81 cells form a complete magic square, in which rows, columns, and diagonals add up to 369. As each border is removed fresh Magic Squares are formed, of which the distinctive numbers are 287, 205, and 123. The central 41 is in every case the greatest common divisor.

[I-12]

No. XII.—A CENTURY OF CELLS

Can you complete this Magic Square, so that the rows, columns, and diagonals add up in every case to 505?

91	2	3	97	6	95	94	8	9	100
20				16	15				81
21				25	26				30
60				66	65				41
50	49	48	57	55	56	54	43	42	51
61	59	58	47	45	46	44	53	52	40
31				35	36				70
80				75	76				71
90				86	85				11
1	99	98	4	96	5	7	93	92	10

We have given you a substantial start, and, as a further hint, as all the numbers in the first and last columns end in 0 or 1, so in the two next columns all end in 2 or 9, in the two next in 3 or 8, in the two next in 4 or 7, and in the two central columns in 5 or 6.

Solution

6
HALLAM’S UNSOLVED ENIGMA

I sit on a rock while I’m raising the wind,
But the storm once abated I’m gentle and kind.
I’ve Kings at my feet, who await but my nod
To kneel in the dust on the ground I have trod.
Though seen to the world, I am known to but few,
The Gentile detests me, I’m pork to the Jew.
I never have passed but one night in the dark,
And that was with Noah alone in the ark.
My weight is three pounds, my length is a mile.
And when I’m discovered you’ll say, with a smile,
That my first and my last are the pride of this isle.

Solution

[I-13]

No. XIII.—A SINGULAR MAGIC SQUARE

In this Magic Square, not only do the rows, columns, and diagonals add up to 260, but this same number is produced in three other and quite unusual ways:—

18	63	4	61	6	59	8	41
49	32	51	14	53	12	39	10
2	47	36	45	22	27	24	57
33	16	35	46	21	28	55	26
31	50	29	20	43	38	9	40
64	17	30	19	44	37	42	7
15	34	13	52	11	54	25	56
48	1	62	3	60	5	58	23

(1) Each group of 8 numbers, ranged in a circle round the centre; there are six of these, of which the smallest is 22, 28, 38, 44, 19, 29, 35, 45, and the largest is 8, 10, 56, 58, 1, 15, 49, 63. (2) The sum of the 4 central numbers and 4 corners. (3) The diagonal cross of 4 numbers in the middle of the board.

[I-14]

No. XIV.—SQUARING THE YEAR

On another page we give an interesting Magic Square of 121 cells based upon the figures of the year 1892. Here, in much more condensed form, is one more up to date.

637	630	635
632	634	636
633	638	631

The rows, columns, and diagonals of these nine cells add up in all cases to the figures of the year 1902.

The central 634 is found by dividing 1902 by its lowest factor greater than 2, and this is taken as the middle term of nine numbers, which are thus arranged to form a Magic Square.

7
RANK TREASON
By an Irish Rebel, 1798

The pomps of Courts and pride of Kings
I prize above all earthly things;
I love my country, but the King
Above all men his praise I sing.
The royal banners are displayed,
And may success the standard aid!

I fain would banish far from hence
The “Rights of Men” and “Common Sense;”
Confusion to his odious reign,
That Foe to princes, Thomas Payne.
Defeat and ruin seize the cause
Of France, its liberties and laws!

Where does the treason come in?

Solution

[I-15]

No. XV.—SQUARING ANOTHER YEAR

The following square of numbers is interesting in connection with the year 1906.

A	B	C	D
476	469	477	484
E	F	G	H
483	478	470	475
I	J	K	L
471	474	482	479
M	N	O	P
480	481	473	472

Add	the rows	—	ABCD, EFGH, IJKL, MNOP.
or	the squares	—	ABEF, CDGH, IJMN, KLOP.
or	semi-diagonals	—	AFIN, BEJM, CHKP, DGLO,
or	semi-diagonals	—	AFCH, BEGD, INKP, MJOL.

and the sum, in every case, is 1906. [I-16]

No. XVI.—MANIFOLD MAGIC SQUARES

Here is quite a curious nest of clustered Magic Squares, which is worth preserving:—

2	13	24	10	16	2	13	24	10	16	2
9	20	1	12	23	9	20	1	12	23	9
11	22	8	19	5	11	22	8	19	5	11
18	4	15	21	7	18	4	15	21	7	18
25	6	17	3	14	25	6	17	3	14	25
2	13	24	10	16	2	13	24	10	16	2
9	20	1	12	23	9	20	1	12	23	9
11	22	8	19	5	11	22	8	19	5	11
18	4	15	21	7	18	4	15	21	7	18
25	6	17	3	14	25	6	17	3	14	25
2	13	24	10	16	2	13	24	10	16	2
9	20	1	12	23	9	20	1	12	23	9
11	22	8	19	5	11	22	8	19	5	11

Every square of every possible combination of 25 of these numbers in their cells, such as the two with darker borders, is a perfect Magic Square, with rows, columns, and diagonals that add up in all cases to 65.

8
AN ENIGMA FOR CHRISTMAS HOLIDAYS

Formed half beneath and half above the earth,
We owe, as twins, to art our second birth.
The smith’s and carpenter’s adopted daughters,
Made upon earth, we travel on the waters.
Swifter we move as tighter we are bound,
Yet never touch the sea, or air, or ground.
We serve the poor for use, the rich for whim,
Sink if it rains, and if it freezes swim.

Solution

[I-17]

No. XVII.—LARGER AUXILIARY MAGIC SQUARES

A very interesting method of constructing a Magic Square is shown in these three diagrams:—

1	2	3	4	5	6	7	8	9	10	11
3	4	5	6	7	8	9	10	11	1	2
5	6	7	8	9	10	11	1	2	3	4
7	8	9	10	11	1	2	3	4	5	6
9	10	11	1	2	3	4	5	6	7	8
11	1	2	3	4	5	6	7	8	9	10
2	3	4	5	6	7	8	9	10	11	1
4	5	6	7	8	9	10	11	1	2	3
6	7	8	9	10	11	1	2	3	4	5
8	9	10	11	1	2	3	4	5	6	7
10	11	1	2	3	4	5	6	7	8	9

0	11	22	33	44	55	66	77	88	99	110
33	44	55	66	77	88	99	110	0	11	22
66	77	88	99	110	0	11	22	33	44	55
99	110	0	11	22	33	44	55	66	77	88
11	22	33	44	55	66	77	88	99	110	0
44	55	66	77	88	99	110	0	11	22	33
77	88	99	110	0	11	22	33	44	55	66
110	0	11	22	33	44	55	66	77	88	99
22	33	44	55	66	77	88	99	110	0	11
55	66	77	88	99	110	0	11	22	33	44
88	99	110	0	11	22	33	44	55	66	77

1	13	25	37	49	61	73	85	97	109	121
36	48	60	72	84	96	108	120	11	12	24
71	83	95	107	119	10	22	23	35	47	59
106	118	9	21	33	34	46	58	70	82	94
20	32	44	45	57	69	81	93	105	117	8
55	56	68	80	92	104	116	7	19	31	43
79	91	103	115	6	18	30	42	54	66	67
114	5	17	29	41	53	65	77	78	90	102
28	40	52	64	76	88	89	101	113	4	16
63	75	87	99	100	112	3	15	27	39	51
98	110	111	2	14	26	38	50	62	74	86

It will be noticed that each row after the first, in the two upper auxiliary squares, begins with a number from the same column in the row above it, and maintains the same sequence of numbers. When the corresponding cells of these two squares are added together, and placed in the third square, a Magic Square is formed, in which 671 is the sum of all rows, columns, and diagonals.

[I-18]

No. XVIII.—SQUARING BY ANNO DOMINI

Here is a curious form of Magic Square. The year 1892 is taken as its basis.

112	124	136	148	160	172	184	196	208	220	232
147	159	171	183	195	207	219	231	122	123	135
182	194	206	218	230	121	133	134	146	158	170
217	229	120	132	144	145	157	169	181	193	205
131	143	155	156	168	180	192	204	216	228	119
166	167	179	191	203	215	227	118	130	142	154
190	202	214	226	117	129	141	153	165	177	178
225	116	128	140	152	164	176	188	189	201	213
139	151	163	175	187	199	200	212	224	115	127
174	186	198	210	211	223	114	126	138	150	162
209	221	222	113	125	137	149	161	173	185	197

Within this square 1892 can be counted up in all the usual ways, and altogether in 44 variations. Thus any two rows that run parallel to a diagonal, and have between them eleven cells, add up to this number, if they are on opposite sides of the diagonal.

9

The sun, the sun is my delight!
I shun a gloomy day,
Though I am often seen at night
To dart across the way.
Sometimes you see me climb a wall
As nimble as a cat,
Then down into a pit I fall
Like any frightened rat.
Catch me who can—woman or man—
None have succeeded who after me ran.

Solution

[I-19]

No. XIX.—A MAGIC SQUARE OF SEVEN

						1
					8		2
				15		9		3
			22	47	16	41	10	35	4
		29	5	23	48	17	42	11	29	5
	36		30	6	24	49	18	36	12		6
43		37	13	31	7	25	43	19	37	13		7
	44		38	14	32	1	26	44	20		14
		45	21	39	8	33	2	27	45	21
			46	15	40	9	34	3	28
				47		41		35
					48		42
						49

This Magic Square of 49 cells is constructed with a diagonal arrangement of the numbers from 1 to 49 in their proper order. Those that fall outside the central square are written into it in the seventh cell inwards from where they stand. It is interesting to find out the many combinations in which the number 175 is made up.

10
WHAT MOVED HIM?

I grasped it, meaning nothing wrong,
And moved to meet my friend,
When lo! the stalwart man and strong
At once began to bend.
The biped by the quadruped
No longer upright stood,
But bowed the knee and bent his head
Before the carved wood.

Solution

[I-20]

No. XX.—CURIOUS SQUARES

These are two interesting Magic Squares found on an antique gong, at Caius College, Cambridge:—

6	13	8
11	9	7
10	5	12

7	14	9
12	20	8
11	6	13

In the one nine numbers are so arranged that they count up to 27 in every direction; and in the other the outer rows total 30, while the central rows and diagonals make 40.

11
RINGING THE CHANGES

My figure, singular and slight,
Measures but half enough at sight.
I rode the waters day and night.
I tell the new in Time’s quick flight,
Or how old ages rolled in might.
Cut off my tail, it still is on!
Put on my head, and there is none!

Solution

[I-21]

No. XXI.—A MOORISH MAGIC SQUARE

Among Moorish Mussulmans 78 is a mystic number.

40	10	20	8
7	21	9	41
12	42	6	18
19	5	43	11

Here is a cleverly-constructed Magic Square, to which this number is the key.

The number 78 can be arrived at in twenty-three different combinations—namely, ten rows, columns, or diagonals; four corner squares of four cells; one central square of four cells; the four corner cells; two sets of corresponding diagonal cells next to the corners; and two sets of central cells on the top and bottom rows, and on the outside columns.

[I-22]

No. XXII.—A CHOICE MAGIC SQUARE

Here is a Magic Square of singular charm:—

31	36	29	76	81	74	13	18	11
30	32	34	75	77	79	12	14	16
35	28	33	80	73	78	17	10	15
22	27	20	40	45	38	58	63	56
21	23	25	39	41	43	57	59	61
26	19	24	44	37	42	62	55	60
67	72	65	4	9	2	49	54	47
66	68	70	3	5	7	48	50	52
71	64	69	8	1	6	53	46	51

The 81 cells of this remarkable square are divided by parallel lines into 9 equal parts, each made up of 9 consecutive numbers, and each a Magic Square in itself within the parent square. Readers can work out for themselves the combinations in the larger square and in the little ones.

12
CANNING’S ENIGMA

There is a noun of plural number,
Foe to peace and tranquil slumber.
Now almost any noun you take
By adding “s” you plural make.
But if you add an “s” to this
Strange is the metamorphosis.
Plural is plural now no more,
And sweet what bitter was before.

Solution

[I-23]

XXIII.—THE TWIN PUZZLE SQUARES

1	2	3		2	3


	5	6	4	5


7	8		7	8	9

Fill each square by repeating two of its figures in the vacant cells. Then rearrange them all, so that the sums of the corresponding rows in each square are equal, and the sums of the squares of the corresponding cells of these rows are also equal; and so that the sums of the four diagonals are equal, and the sum of the squares of the cells in corresponding diagonals are equal.

Solution

13

There is an old-world charm about this Enigma:—

In the ears of young and old
I repeat what I am told;
And they hear me, old and young,
Though I have no busy tongue.
When a thunder-clap awakes me
Not a touch of terror takes me;
Yet so tender is my ear
That the softest sound I fear.
Call me not with bated breath,
For a whisper is my death.

Solution

[I-24]

No: XXIV.—MAGIC FRACTIONS

Here is an arrangement of fractions which form a perfect Magic Square:—

38	512	524
16	13	12
1124	14	724

If these fractions are added together in any one of the eight directions, the result in every case is unity. Thus ³⁄₈ + ¹⁄₃ + ⁷⁄₂₄ = 1, ¹⁄₆ + ¹⁄₃ + ¹⁄₂ = 1, and so on throughout the rows, columns, and diagonals.

14
“DOUBLE, DOUBLE, TOIL AND TROUBLE!”

“By hammer and hand
All arts do stand”—
So says an ancient saw;
But hammer and hand
Will work or stand
By my unwritten law.
Behold me, as sparks from the anvils fly,
But fires lie down at my bitter cry.

Solution

[I-25]

No. XXV.—MORE MAGIC FRACTIONS

We are indebted to a friend for the following elaborate Magic Square of fractions, on the lines of that on the preceding page.

1980	720	140	1180	14
1340	18	980	940	1780
110	780	15	516	310
316	740	2380	1140	340
320	2180	38	120	1380

The composer claims that there are at least 160 combinations of 5 cells in which these fractions add up to unity, including, of course, the usual rows, columns, and diagonals.

15

Two brothers wisely kept apart,
Together ne’er employed;
Though to one purpose we are bent
Each takes a different side.

We travel much, yet prisoners are,
And close confined to boot,
Can with the fleetest horse keep pace,
Yet always go on foot.

Solution

[I-26]

No. XXVI.—A MAGIC OBLONG

On similar lines to Magic Squares, but as a distinct variety, we give below a specimen of a Magic Oblong.

1	10	11	29	28	19	18	16
9	2	30	12	20	27	7	25
24	31	3	21	13	6	26	8
32	23	22	4	5	14	15	17

The four rows of this Oblong add up in each case to 132, and its eight columns to 66. Two of its diagonals, from 10 to 5 and from 28 to 23, also total 66, as do the four squares at the right-hand ends of the top and bottom double rows.

16

My name declares my date to be
The morning of a Christian year;
And motherless, as all agree,
And yet a mother, too, ’tis clear.
A father, too, which none dispute,
And when my son comes I’m a fruit.
And, not to puzzle overmuch,
’Twas I took Holland for the Dutch.

Solution

17

My head is ten times ten,
My body is but one.
Add just five hundred more, and then
My history is done.
Although I own no royal throne,
Throughout the sunny South in fame I stand alone.

Solution

[I-27]

No. XXVII.—A MAGIC CUBE

Much more complicated than the Magic Square is the Magic Cube.

First Layer from Top.

121	27	83	14	70
10	61	117	48	79
44	100	1	57	113
53	109	40	91	22
87	18	74	105	31

Second Layer from Top.

2	58	114	45	96
36	92	23	54	110
75	101	32	88	19
84	15	66	122	28
118	49	80	6	62

Third Layer from Top.

33	89	20	71	102
67	123	29	85	11
76	7	63	119	50
115	41	97	3	59
24	55	106	37	93

Fourth Layer from Top.

64	120	46	77	8
98	4	60	111	42
107	38	94	25	51
16	72	103	34	90
30	81	12	68	124

Lowest Layer.

95	21	52	108	39
104	35	86	17	73
13	69	125	26	82
47	78	9	65	116
56	112	43	99	5

Those who enjoy such feats with figures will find it interesting to work out the many ways in which, when the layers are placed one upon another, and form a cube, the number 315 is obtained by adding together the cell-numbers that lie in lines in the length, breadth, and thickness of the cube.

18

Sad offspring of a blighted race,
Pale Sorrow was my mother;
I’ve never seen the smiling face
Of sister or of brother.

Of all the saddest things on earth,
There’s none more sad than I,
No heart rejoices at my birth.
And with a breath I die!

Solution

[I-28]

No. XXVIII.—A MAGIC CIRCLE

The Magic Circle below has this particular property:—

			32
		61		94
	52				38
191						4
28						193
	26				44
		98		67
			16

The 14 numbers ranged in smaller circles within its circumference are such that the sum of the squares of any adjacent two of them is equal to the sum of the squares of the pair diametrically opposite.

19

Add a hundred and nothing to ten,
And the same to a hundred times more,
Catch a bee, send it after them, then
Make an end of a fop and a bore.

Solution

[I-29]

No. XXIX.—MAGIC CIRCLE OF CIRCLES

We have had some good specimens of Magic Squares. Here is a very curious and most interesting Magic Circle, in which particular numbers, from 12 to 75 inclusive, are arranged in 8 concentric circular spaces and in 8 radiating lines, with the central 12 common to them all.

								62	73
								24	15
								71	64
								17	22
								69	66
								19	20
								60	75
								26	13
57	31	48	38	50	36	59	29	12		74	12	67	21	65	23	72	14
46	40	55	33	53	35	44	42			16	27	68	18	70	16	63	25
								45	58
								43	28
								52	51
								34	37
								54	49
								32	39
								47	56
								41	30

The sum of all the numbers in any of the concentric circular spaces, with the 12, is 360, which is the number of degrees in a circle.

The sum of the numbers in each radiating line with the 12, is also 360.

The sum of the numbers in the upper or lower half of any of the circular spaces, with half of 12, is 180, the degrees of a semi-circle.

The sum of any outer or inner four of the numbers on the radiating lines, with the half of 12, is also 180.

[I-30]

No. XXX.—THE UNIQUE TRIANGLE

In the following triangle, if two couples of the figures on opposite sides are transposed, the sums of the sides become equal, and also the sums of the squares of the numbers that lie along the sides. Which are the figures that must be transposed?

			5
		4		6
	3				7
2		1		9		0

Solution

20

They did not climb in hope of gain,
But at stern duty’s call;
They were united in their aim,
Divided in their fall.

Solution

21

Forsaken in some desert vast,
Where never human being dwelt,
Or on some lonely island cast,
Unseen, unheard, I still am felt.

Brimful of talent, sense, and wit,
I cannot speak or understand;
I’m out of sight in Church, and yet
Grace many temples in the land.

Solution

[I-31]

No. XXXI.—MAGIC TRIANGLES

Here is a nest of concentric triangles. Can you arrange the first 18 numbers at their angles, and at the centres of their sides, so that they count 19, 38, or 57 in many ways, down, across, or along some angles?

This curiosity is found in an old document of the Mathematical Society of Spitalfields, dated 1717.

Solution

22

Allow me, pray, to go as first,
And then as number two;
Then after these, why, there you are,
To follow as is due.

But lest you never guess this queer
And hyperbolic fable,
Pray let there follow after that
Whatever may be able.

Solution

[I-32]

No. XXXII.—TWIN TRIANGLES

The numbers outside these twin triangles give the sum of the squares of the four figures of the adjacent sides:—

			7
		2		3
135						99
	9				5
1		8		6		4
			117
			*
			137
6		4		2		9
	5				1
119						155
		7		8
			3

The twins are also closely allied on these points:—

18 is the common difference of 99, 117, 135, and of 119, 137, 155.

19 is the sum of each side of the upper triangle.

20 is the common difference of any two sums of squares symmetrically placed, both being on a line through the central spot.

21 is the sum of each side of the lower triangle.

10 is the sum of any two figures in the two triangles that correspond.

254 is the sum of 135, 119, of 117, 137, and of 90, 155.

By transposing in each triangle the figures joined by dotted lines, the nine digits run in natural sequence.

[I-33]

No. XXXIII.—A MAGIC HEXAGON

We have dealt with Magic Squares, Circles, and Triangles. Here is a Magic Hexagon, or a nest of Hexagons, in which the numbers from 1 to 73 are arranged about the common centre 37.

						1		5		6	70	60		59		58
					63												8
				62				19		53	46	22		45				9
			61				20								24				64
		2				48				31	42	38				49				57
	3				47				39				40				44				56
67				51				41			37			33				23				7
	66				50				34				35				54				11
		65				25				36	32	43				26				12
			10				30								27				13
				17				29		21	28	52		55				72
					18												71
						16		69		68	4	14		15		73

Each of these Hexagons always gives the same sum, when counted along the six sides, or along the six diameters which join its corners, or along the six which are at right angles to its sides. These sums are 259, 185, and 111.

23

When I am in, its four legs have no motion;
When I am out, as fish it swims the ocean.
Then, if transposed, it strides across a stream,
Or adds its quality to eyes that gleam.

Solution

[I-34]

No. XXXIV.—MAGIC HEXAGON IN A CIRCLE

Inscribe six equilateral triangles in a circle, as shown in this diagram, so as to form a regular hexagon.

Now place the nine digits round the sides of each of the triangles, so that their sum on each side may be 20, and so that, while there are no two triangles exactly alike in arrangement, the squares of the sums on the other sides may be alternately equal.

Solution

24
A PERSONAL ENIGMA

We can but see his sad reverse,
And while we say alas!
We hail his work so keen and terse,
With just a touch of gas.

Solution

[I-35]

No. XXXV.—A MAGIC CROSS

There are 33 different combinations of four of the numbers in the cells of this magic cross which total up in each case to 26.

	1	12
9	8	5	4
2	7	6	11
	10	3

Those who care to work them out on separate crosses will find that there is a very regular correspondence in the positions which the numbers occupy.

25

What boy can live on with a prospect of age,
If you cut off his head at an early stage?

Solution

26
By Lord Macaulay

Here’s plenty of water, you’ll all of you say;
And minus the h a thing used every day;
And here is nice beverage; put them together—
What is it with claws, but with never a feather?

Solution

[I-36]

No. XXXVI.—A CHARMING PUZZLE

Here is quite a charming little puzzle, which is by no means easy of accomplishment:—

✦	✦	✦
✦	✦	✦
✦	✦	✦

Start from one of these nine dots, and without taking the pen from the paper draw four straight lines which pass through them all. Each line, after the first, must start where the preceding one ends.

Solution

27
A BROKEN TALE

The deil jumped
the clouds so high
That he bounded almost
right
the sky.
the trees
gates and fields and
He dodged with his tail
dragging
all these,
But, alas! made a terrible
bl,
For a twist in his tail
a rail,
hooked
And broke that appendage
as.

Solution

[I-37]

No. XXXVII.—LEAP-FROG

Place on a chess or draught-board three white men on the squares marked a, and three black men on the squares marked b.

The pieces marked a can only move one square at a time, from left to right, and those marked b one square at a time, from right to left, on to unoccupied squares; and any piece can leap over one of the other colour, on to an unoccupied square. What is the least number of moves in which the positions of the white and the black men can be reversed, so that each square now occupied by a white is occupied by a black, and each now occupied by a black holds a white piece?

Solution

28

To a word of assent join the first half of fright,
Then add what will never be seen in the night.
By such a conjunction we quickly attain
What most men have seen, but can’t see again.

Solution

29

My first is stately, proud, and grave,
My next will guard your treasure;
My whole, a slow but sturdy slave,
Will wait upon your pleasure.

Solution

[I-38]

No. XXXVIII.—SORTING THE COUNTERS

In the upper row of this diagram four white and four black counters are placed alternately.

It is possible, by moving these counters two at a time, to arrange them in four moves as they stand on the lower row. Can you do this? Draughtsmen are handy for solving this puzzle, on a paper ruled as above.

Solution

30

I am a word of letters six,
First link me with your mind;
Then shuffle me, and lo! I mix
With grief of noisy kind.
Shake me again, and you may fix
A cloak that hangs behind.

Solution

31

We are of use to every man
In walking, riding, rambling;
We join the gambols of the knave,
And play the knave in gambling!

Solution

[I-39]

No. XXXIX.—A TRANSFORMATION

Take five wooden matches, and bend each of them into a V. Place them together, as is shown in the diagram, so that they take the form of an asterisk, or a ten-pointed star.

Lay them on some smooth surface, and without touching them transform them into a star with five points.

Solution

32

Strange that a straggling tiresome weed
Will change its meaning quite,
And turn into a sign of grief
If we transpose it right;
And, stranger still, transposed again
Will tell of ease from grief or pain.

Solution

33

Find me two English verbs that ever
In a united state will blend,
Let one say “join,” the other “sever,”
While I divide them to the end.

Solution

[I-40]

No. XL.—DOMINO BUILDING

It is possible, with plenty of patience, to build up a whole set of dominoes, so that they are safely supported on only two stones set up on end.

This, which might well seem impossible, is done by placing, as a foundation, dominoes in the positions indicated by dotted lines. The arch is then carefully constructed, as shown in the diagram, and for the finish the four stones between the two foundation arches are drawn out, and placed in pairs on end above, and finally, with the utmost care, the other four are drawn away, and built in on the top. Thus the stones indicated by the dotted lines at the base take their place within the dotted lines above.

[I-41]

No. XLI.—FAST AND LOOSE

This diagram represents a shallow box, on the bottom of which twelve counters or draughtsmen are lying loose.

How can they be readjusted so that they will wedge themselves together, and against the side of the box, and it can be turned upside down without displacing them?

Solution

34

Taken entire
I’m full of fire.
With head away
A tax I pay.
If tail you bar
I turn from tar.
Headless again,
With tail restored.
Goddess of pain,
I sow discord.

Solution

[I-42]

No. XLII.—MAZY PROGRESS.

The diagram below is an exact reproduction of an old-fashioned maze, cut in the ground near Nottingham. It is eighteen yards square, and the black line represents the pathway, which is 535 feet in length.

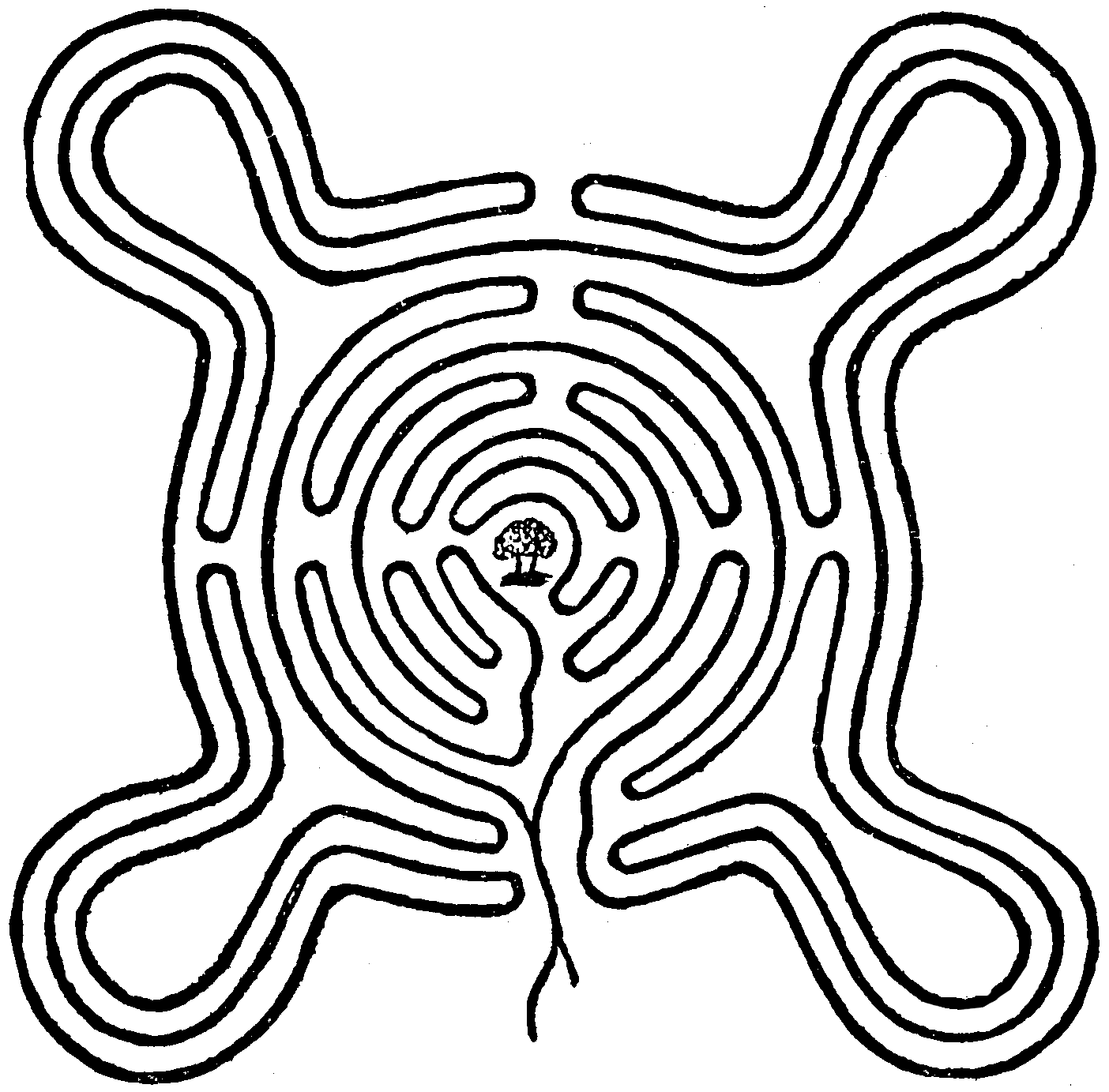
The point of this convoluted path is not so much to puzzle people, as to show how much ground may be covered without diverging far from a centre, or going over the same ground twice. As we advance along the line there are no obstructions, and we find ourselves, after passing over the whole of it, on the spot whence we set out.

35

Thrice three pins in shining line
Mary meant to fix;
Why did Mary turn the nine
Into thirty-six?

Solution

[I-43]

No. XLIII.—FOR CLEVER PENCILS

Start at A, and trace these figures with one continuous line, finishing at B.

You must not take your pencil from the paper, or go over any line twice.

Solution

36

A ring and a wing and three-fourths of a fog,
Will bring to your view a most obstinate dog.

Solution

37

Add fifty-seven to two-thirds of one,
Then take a fiddle,
And it will help to show you what is done,
To make this riddle.

Solution

38

I am a fish so neat and clever,
In pools and crystal streams I play,
To find me out my name you sever
As near the middle as you may.

Solution

[I-44]

No. XLIV.—TEST AND TRY

Those who have not seen it will find some real fun in the following little experiment. Fix three matches as shown in the diagram, light the cross match in the middle, and watch to see which of the ends will first catch fire, or what will happen.

39

I stand stock still, let who will hurry,
You cannot put me in a flurry,
Nor stir my stumps, for all your worry.

I am in haste, let none delay me
As fleetest couriers convey me.
You must transpose me ere you stay me.

Solution

40

Two to one, in case we hide,
You will find us in our site;
We are harmless side by side,
Parted we prepare to bite.
When united we divide,
When divided we unite.

Solution

[I-45]

No. XLV.—A CURIOUS PHENOMENON

Equal volumes of alcohol and water, when mixed, occupy less space than when separate, to the extent indicated in this picture:

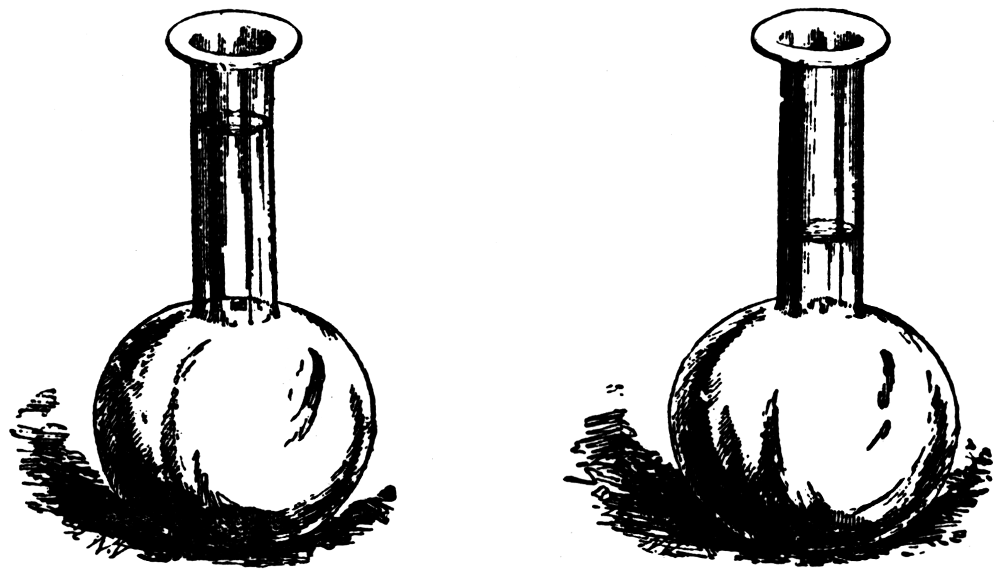
If the sum of the volume of the two separate liquids is 100, the volume of the mixture will be only 94. It is thought that the molecules of the two liquids accommodate themselves to each other, so as to reduce the pores and diminish the volume of the mixture.

41

Cut off my head, I’m every inch a king,
A warrior formed to deal a heavy blow;
Halve what remains, my second is a thing
Which nothing but my third can e’er make go.
My whole will vary as you take your line,
This less than human, that way all divine.

Solution

42

One half of me in solid earth you find,
The other half in ocean’s ample bed:
When in my whole we see these parts combined,
The earth remains, but all the sea is fled.

Solution

[I-46]

No. XLVI.—A HOME-MADE MICROSCOPE

The simplest and cheapest of all microscopes can easily be made at home. The only materials needed are a thin slip of glass, on to which one or two short paper tubes, coated with black sealing wax, are cemented with the wax, a small stick, and a tumbler half full of water.

Water is dropped gradually by aid of the stick into the cells, until lenses are formed of the desired convexity, and objects held below the glass will be more or less magnified.

43

Not ever changed unless unchanged,
Nor hanged unless beheaded;
Quick eyes may find in me arranged
Almost an angel bedded.

Solution

[I-47]

No. XLVII.—A PRETTY EXPERIMENT

For this curious experiment a glass bottle or decanter about half full of water and a sound stalk of straw are needed.

Bend the straw without breaking it, and put it, as is shown, into the bottle, which can then be lifted steadily and safely by the straw, if it is a sound one.

44
“WHAT THE DICKENS IS HIS NAME?”
Merry Wives of Windsor.

A Russian nobleman had three sons. Rab, the eldest, became a lawyer, his brother Mary was a soldier, and the youngest was sent to sea. What was his name?

Solution

[I-48]

No. XLVIII.—A BOTTLED BUTTON

The button in a clear glass bottle, as is shown below, hangs attached by a thread to the cork, which is securely sealed at the top.

How can you sever the thread so that the button falls to the bottom without uncorking or breaking the bottle?

Solution

45
A NEW “LIGHT BRIGADE”

Six before six before
Five times a hundred;
This must be brilliant, or
Solvers have blundered.

Solution

[I-49]

No. XLIX.—CLEARING THE WAY

Here is a pretty trick which requires an empty bottle, a lucifer match, and a small coin.

Break the wooden match almost in half, and place it and the coin in the position shown above. Now consider how you can cause the coin to drop into the bottle, if no one touches it, or the match, or the bottle.

Solution

46

Scorned by the meek and humble mind,
And often by the vain possessed,
Heard by the deaf, seen by the blind,
I give the troubled spirit rest.

Solution

47

To fifty for my half append
Two-thirds of one;
The other third my whole will end
When you have done.

Solution

[I-50]

No. L.—IS WATER POROUS?

Our belief that two portions of matter cannot occupy the same space at the same time is almost shaken by the following experiment:

If we introduce slowly some fine powdered sugar into a tumblerful of warm water a considerable quantity may be dissolved in the water without increasing its bulk.

It is thought that the atoms of the water are so disposed as to receive the sugar between them, as a scuttle filled with coal might accommodate a quantity of sand.

48
A DOUBLE SHUFFLE

See, the letters that I bring
Change their meaning quite;
Spell a hard and heavy thing,
Spell a soft and light.

Solution

[I-51]

No. LI.—A TEST OF GRAVITY

Set a stool, as is shown in the diagram below, about nine or ten inches from the wall.

Clasp it firmly by its two side edges, plant your feet well away from it, and rest your head against the wall. Now lift the stool, and then try, without moving your feet, to recover an upright position.

It will be as impossible as it is to stand on one leg while the foot of that leg rests sideways against a wall or door.

[I-52]

No. LII.—BILLIARD MAGIC

Place a set of billiard balls as is shown in the diagram, the spot ball overhanging a corner pocket, and the red and the plain white in a straight line with it, leaving an eighth of an inch between the balls.

How can you pot the spot white with the plain white, using a cue, and without touching, or in any way disturbing, the red ball? There is not room to pass on either side between the red ball and the cushion.

Solution

[I-53]

No. LIII.—THE NIMBLE COIN

Prepare a circular band of stiff paper, as is shown in the diagram, and balance it, with a coin on the top, on the lip of a bottle.

How can you most effectively transfer the coin into the bottle?

Solution

49
AN ENIGMA BY MUTATION

Search high or low, you’d find me where you list;
For not a place without me can exist.
I lose my head, and, seen with shoulders fair,
Become the very fairest of the fair.
Again I lose it, and, like some staunch hound,
The first and best amongst a pack am found.
And if at first both head and tail I lose
I am a portion such as all would choose.

Solution

[I-54]

No. LIV.—HIT IT HARD!

Place a strip of thin board, or a long wide flat ruler, on the edge of a table, so that it just balances itself, and spread over it an ordinary newspaper, as is shown in the illustration.

You may now hit it quite hard with your doubled fist, or with a stick, and the newspaper will hold it down, and remain as firmly in its place as if it were glued to the table over it. You are more likely to break the stick with which you strike than to displace the strip of wood or the paper. Try the experiment.

50
AN ENIGMA BY SWIFT

We are little airy creatures
All of different voice and features.
One of us in glass is set,
One of us is found in jet.
Another you may see in tin,
And the fourth a box within.
If the others you pursue
They can never fly from you.

Solution

[I-55]

No. LV.—THE BRIDGE OF KNIVES

Here is an after-dinner balancing trick, which it is well to practise with something less brittle than the best glass:—

It will be seen that the blades of the knives are so cunningly interlaced as to form quite a firm support.

51
A MEDLEY

Twice six is six, and so
Six is but three;
Three is just five you know,
What can we be?
Would you count more of us,
Nine are but four of us,
Ten are but three.

Solution

[I-56]

No. LVI.—DIFFERENT DENSITIES

Here is a pretty little experiment, which shows the effect of liquids of different densities.

Drop an egg into a glass vessel half full of water, it sinks to the bottom. Drop it into strong brine, it floats. Introduce the brine through a long funnel at the bottom of the pure water, and the water and the egg will be lifted, so that the egg floats between the water and the brine in equilibrium. The egg is denser than the water, and the brine is denser than the egg.

52
THE MISSING LINK

A friend to all the human race
From emperor to peasant,
None is more missed when out of place,
More opportune when present.

Obedient to the general will
I yield to due control;
And yet the public twist me, till
They put me in a hole!

Solution

[I-57]

No. LVII.—COLUMBUS OUTDONE

Here is a very simple and effective little trick. Offer to balance an egg on its end on the lip of a glass bottle.

The picture shows how it is done, with the aid of a cork and a couple of silver forks.

(From “La Science Amusante”).

53

Two words of equal length we here indite,
Which hold a famous father and his mate.
Embracing five, with fifty left and right,
The mother, looking both ways, keeps things straight.

Her husband, following a thousand quite,
With them has changed his sex, a funny fate,
And if this lady lose her head, she might,
Being a man, oppose the water-rate.

Solution

[I-58]

No. LVIII.—WHAT WILL HAPPEN?

The boy in this picture is blowing hard against the bottle, which is between his mouth and the candle flame.

What will happen?

Solution

54

In marble walls as white as milk,
Lined with a skin as soft as silk,
Within a fountain crystal clear
A golden apple doth appear.
No doors are there to this stronghold,
Yet thieves break in, and steal the gold.

Solution

[I-59]

No. LIX.—THE FLOATING NEEDLE

Here is a simple way to make a needle float on water:—

Fill a wineglass or tumbler with water, and on this lay quite flat a cigarette paper; place a needle gently on this, and presently the paper will sink, and the needle will float on the water.

55

A one-syllable adjective I,
Indeterminate, misty, obscure:
Reduce me by five, and then try
How you like my attacks to endure.

I’m now a two-syllable noun,
My victims are hot and are cold;
In country more rife than in town,
I’m not such a pest as of old.

Solution

[I-60]

No. LX.—VIS INERTIÆ

Here is a pile of ten draughtsmen—one black among nine white.

If I take another draughtsman, and with a strong pull of my finger send it spinning against the column, what will happen?

Solution

56
DR. WHEWELL’S ENIGMA

A headless man had a letter to write,
He who read it had lost his sight.
The dumb repeated it word for word,
And deaf was the man who listened and heard.

Solution

57
AN ENIGMA FOR MOTORISTS

I am rough, I am smooth,
I am wet, I am dry;
My station is low,
My title is high.
The King my lawful master is,
I’m used by all, though only his.

Solution

[I-61]

No. LXI.—CUT AND COME AGAIN

How long would it take to divide completely a 2 ft. block of ice by means of a piece of wire on which a weight of 5 lb. hangs?

Solution

58

Without a dome, we are within a dome;
Homeless and roofless, we have roof and home.
Though frequent streams may flood our base and roof,
We rest unharmed, and always waterproof.

Solution

59

I’m the most fearful of fates upon earth,
Cut off my head and bright moments have birth,
Lop off my shoulders, and riddle my riddle;
Anything seems to be found in my middle.

Solution

[I-62]

No. LXII.—WHERE WILL IT BREAK?

When weak cords of equal strength are attached to opposite parts of a wooden or metal ball which is suspended by one of them, a sharp, sudden pull will snap the lower cord before the movement has time to affect the ball; but a gentle, steady pull will cause the upper cord to snap, as it supports the weight below it.

60

I may be safe when honest ways prevail,
With no unworthy tricks or jobbery.
Cut off my head and fix it to my tail,
And I become at once rank robbery.

Solution

[I-63]

No. LXIII.—CATCHING THE DICE

Hold a pair of dice, and a cup for casting them, in one hand as is shown in the diagram.

Now, holding the cup fast, throw up one of the dice and catch it in the cup. How can you best be sure of catching the other also in the cup?

Solution

61

Here is a metrical Enigma, which appeals with particular force to all married folk, and to our cousins in America:

This is of fellowship the token,
Reverse it, and the bond is broken.

Solution

[I-64]

No. LXIV.—WILL THEY FALL?

Build up seven dominoes into a double arch, as is shown in the diagram below, and place a single domino in the position indicated.

Now put the fore-finger carefully through the lower archway, and give this domino quite a smart tip up by pressing on its corner. What will happen if this is done cleverly? Try it.

Solution

62

A monk in a moment, by violence heated,
Endangered the peace of his soul.
To atone for my second, my first he repeated
Just ten times a day on my whole.

Solution

[I-65]

No. LXV.—A TRANSPOSITION

Place three pennies in contact in a line as is shown below, so that a “head” is between two “tails.”

Can you introduce the coin with a shaded surface between the other two in a straight line, without touching one of these two, and without moving the other?

Solution

63

Two syllables this word contains:
Reverse them and then what remains?

With cap and pipe and goggles too
The comics hold him up to view,
Reverse his parts you would declare
A dog should not be quartered there.

Solution

64

Though I myself shut up may be,
My work is to set prisoners free.
No slave his lord’s commands obeys
With more insinuating ways.
All find me handy, sharp, and bright,
Where men in wit and wine delight;
While many keep me for their ease,
And turn and twist me as they please.

Solution

[I-66]

No. LXVI.—COIN COUNTING

Place ten coins in a circle, as is shown in this diagram, so that on all of them the king’s head is uppermost.

Now start from any coin you choose, calling it 1, the next 2, and so on, and turn the fourth, so that the tail is uppermost. Start again on any king’s head, and again turn the fourth, and continue to do this until all but one are turned.

Coins already turned are reckoned in the counting, but the count of “four” must fall on an unturned coin.

Can you find a plan for turning all the coins but one in this way without ever failing to count four upon a fresh spot, and to start on an unturned coin?

Solution

[I-67]

No. LXVII.—THE BALANCED CORK

The diagram below shows how, using one hand only, and grasping a bottle of wine by its body, the contents can be poured out without cutting or boring the cork, or altogether removing it from the bottle.

65

Transformed by art, and fond of port,
I blister in the sun;
But when I turn, and face the sport,
Away full tilt I run;
For if I double I am caught,
And that can be no fun.

Solution

66

A man without eyes saw plums on a tree,
He neither took plums nor plums left he.

Solution

[I-68]

No. LXVIII.—NUTS TO CRACK

A sharply-pointed knife with a heavy handle is stuck very lightly into the lintel of a door, and the nut that is to be cracked is placed under it, so that when the knife is released by a touch the nut is cracked.

What simple and certain plan can you suggest for making sure that the knife shall hit the nut exactly in the middle without fail?

Solution

67
A SINGULAR ENIGMA

Strange paradox! though my two halves are gone,
I still remain an undivided whole.
But were I double what I am, though one,
I then should be but half, upon my soul!

Solution

[I-69]

No. LXIX.—THE FLOATING CORKS

If we throw an ordinary wine cork into a tub of water it will naturally float on its side. It is, however, possible to arrange a group of seven such corks, without fastening them in any way, so that they will float in upright positions.

Place them together, as is shown in the illustration, and, holding them firmly, dip them under the water till they are well wetted. Then, keeping them exactly upright, leave go quietly, and they will float in a compact bunch if they are brought slowly to the surface.

68
A PARADOX

I start with five thousand, and take nothing off,
Yet really in doing so nine-tenths I doff;
And it proves with no strain upon numbers or reason,
That the smaller are larger in size and in season.

Solution

[I-70]

No. LXX.—A LIGHT, STEADY HAND

As an exercise of patience and dexterity, try to balance a set of dominoes upon one that stands upon its narrow end:—

This is no easy matter, but a little patience will enable us to arrange the stones in layers, which can with care be lifted into place and balanced there.

69

With letters three indite my name,
Add one to show what I became,
Or try to tell what brought me fame.

Solution

[I-71]

No. LXXI.—WHAT IS THIS?

We expect to puzzle our readers completely by this diagram:—

It is simply the enlargement by photography of part of a familiar picture.

Solution

70

Eight letters respond to the quest
Of all for enjoyment athirst;
Two articles lead to the rest,
And the last of the rest is the first.

Solution

71

When letters five compose my name
I’m seldom seen but in a flame.
Take off one letter, then you see
That winter is the time for me.
Another take, and I appear
What many must be year by year.

Solution

[I-72]

No. LXXII.—TAKING THE GROUND FROM UNDER IT

Place a strip of smooth paper on a table so that it overhangs the side, as is shown in the diagram. Stand a new penny steadily on edge upon the paper.

Take hold of the paper firmly, and give it a smart, steady pull. If this is properly done it will leave the penny standing unmoved in its place.

72

A shining wit pronounced of late
That water in a freezing state
Is like an acting magistrate.
What was the quibble in his pate?

Solution

73

By something formed I nothing am,
Yet anything that you can name.
In all things false, yet ever true,
And still the same but never new;
Like thought I’m in a moment gone,
Nor can I ever be alone.

Solution

[I-73]

No. LXXIII.—A READY RECKONER

Two men, standing on the bank of a broad stream, across which they could not cast their fishing lines, could not agree as to its width. A bet on the point was offered and accepted, and the question was presently decided for them by an ingenious friend who came along, without any particular appliances for measurement.

He stood on the edge of the bank, steadied his chin with one hand, and with the other tilted his cap till its peak just cut the top of the opposite bank.

Then, turning round, he stood exactly where the peak cut the level ground behind him, and, by stepping to that spot, was able to measure a distance equal to the width of the stream.

74

When you and I together meet,
Then there are six to see and greet.
If I and you should meet once more,
Our company would be but four.
And when you leave me all alone
I am a solitary one.

Solution

[I-74]

No. LXXIV.—THE CLIMBING HOOP

Paste or pin together the ends of a long strip of stiff paper so as to form a hoop, and place on the table a board resting at one end upon a book. Challenge those in your company to make the hoop run up the board without any impulse.

They must of course fail, but you can succeed by secretly fastening with beeswax a small stone or piece of metal inside the hoop, as is indicated in the diagram.

75

Invisible yet never out of sight,
I am indeed a centre of delight.
In quiet times I help to make things right,
Yet act as second in the fiercest fight.

Solution

[I-75]

No. LXXV.—THE SEAL OF MAHOMET

This double crescent, called the Seal of Mahomet, from a legend that the prophet was wont to describe it on the ground with one stroke of his scimitar, is to be made by one continuous stroke of pen or pencil, without going twice over any part of it.

Solution

76

Though I mingle with thieves,
And with all that deceives,
And never keep clear of depravity
Though possessed by a devil,
Or seen in a revel,
I do keep my centre of gravity.

Solution

77

There’s not a bird that cleaves the sky
With crest or plume more gay than I,
Yet guess me by this token:
That I am never seen to fly
Unless my wings are broken.

Solution

[I-76]

No. LXXVI.—MOVE THE MATCHES

Arrange 15 matches thus—

Remove 6 and what number will be left?

Solution

78

Split into three and mixed,
With Dives I am found.
Split into two and fixed
On four legs, flat or round.
In my most kindly sense unbroken,
Warm hearts and helpers I betoken.

Solution

79

I am high, I am low,
I am thick, I am thin,
I can keep out the snow,
But may let the rain in.

Solution

80
HIDDEN FRUIT

Go range through every clime, where’er
The patriot muse appears
He deeds of valour antedates,
His ban an army fears.

By midnight lamp each poet soul
Is plumed for flight sublime;
Pale monarch moon and shining stars
Witness his glowing rhyme!

Incited by the muse man goes
To grapple with his wrongs;
The poet cares not who makes laws,
If he may make the songs.

Can you discover ten fruits in these lines?

Solution

[I-77]

No. LXXVII.—LINES ON AN OLD SAMPLER

When I can plant with seventeen trees
Twice fourteen rows, in each row three;
A friend of mine I then shall please,
Who says he’ll give them all to me.

Solution

81

The last of you before the end
Close to an inn we first must find,
If nothing follows all will tend
To hints that rankle in the mind.

Solution

[I-78]

No. LXXVIII.—DOMINO DUPLICITY

By the following ingenious arrangement of the stones a set of dominoes appears to be unduly rich in doublets:—

It will be noticed that the charm of this arrangement is that the whole figure contains a double set of quartettes, on which the pips are similar.

82

Many men of many minds,
Many birds of many kinds,
Some are dun, and some are gray—
Which is this one? tell me, pray!
See him where the water shines,
But not perching on the pines.

Solution

[I-79]

No. LXXIX.—MORE DOMINO DUPLICITY

This again shows how the stones can be placed so that an ordinary set of dominoes seems to be unduly rich in doublets.

83

We know how, by the addition of a single letter, our cares can be softened into a caress; but in the following Enigma a still more contradictory result follows, without the addition or alteration of a letter, by a mere separation of syllables:—

None can locate the subject of my riddle.
For all the world would seek its place in vain;
Cut it asunder almost in the middle,
And in our very midst its place is plain.

An aching void, an absolute negation,
Into the opposite extreme it breaks;
With just a gap to mark their new relation
Each letter still the same position takes.

Solution

[I-80]

No. LXXX.—TWO MORE PATTERNS

Here are two more perfect arrangements of a set of dominoes in quartettes, so that the pips and blanks are similarly grouped and repeated:—

CHARADES

1
SIR WALTER SCOTT’S CHARADE

Sir Hilary fought at Agincourt,
Sooth! ’twas an awful day
And though in olden days of sport
The rufflers of the camp and court
Had little time to pray,
’Tis said Sir Hilary muttered there
Two syllables by way of prayer.

“My first to all the brave and proud
Who see to-morrow’s sun;
My next with her cold and quiet cloud
To those who find a dewy shroud
Before the day is won.
And both together to all bright eyes
That weep when a warrior nobly dies!”

Solution

[I-81]

No. LXXXI.—COUNTING THEM OUT

Arrange twelve dominoes as is shown in this diagram, and start counting in French from the double five, thus u, n, un; remove the stone you thus reach, which has one pip upon it, and start afresh with the next stone, d, e, u, x, deux; this brings you to the stone with two pips; then t, r, o, i, s, trois, brings you to that with three, and so on until douze brings you to twelve.

Always remove the stone as you hit upon each consecutive number.

Now who can re-arrange these same stones so that a similar result works out in English, thus—o, n, e, one (remove the stone), t, w, o, two, and so on throughout?

Solution

2
A FAMILY CHARADE

A man with fourscore winters white
Sat dozing in his chair;
His frosted brow was quite my first,
Crowned with its silver hair.

My whole, when playing at his feet,
Sly glances upward stole;
My second, standing at his side,
Was father of my whole.

Solution

[I-82]

No. LXXXII.—TRICKS WITH DOMINOES

In this diagram the word EACH is formed by the use of a complete set of stones, placing every letter in proper domino sequence.

There are also the same number of pips in each letter. Can you construct another English word under the same conditions? As a hint, the word that we have in mind is plural.

Solution

3

Upon my face is not a single hair,
Although my beard uncut is growing there.
Men call me Shelley, though I can’t converse,
To me all tongues alike would be a curse.
I in my house must night and day abide,
And though quite well must keep my bed, outside.
For me no bell shall toll a funeral knell,
I’m doomed, like Shelley, dead to have no shell.

Solution

4

This amusing Charade is from the pen of a wise and witty Irish Bishop:—

True to the trumpet call of fame and duty
The soldier arms, and hastens to depart;
Nor casts one look behind, though love and beauty
Whisper my first in tones that thrill his heart.

The war is o’er, with wealth and honour laden
The hero seeks the well-remembered Hall:
He woos and wins the unreluctant maiden,
And bids my second o’er her blushes fall.

He takes her hand—a mist of rapture thickens
Before her eyes. Such bliss succeeding pain
O’ertasks her strength, and fainting nature sickens,
Until my whole is rudely snapt in twain.

Solution

[I-83]

No. LXXXIII.—THE HOUR GLASS

This very beautiful specimen of a knight’s tour on the chess-board takes its name from the figure formed by the tracery at its centre.

An endless number of symmetrical patterns of varied design can be formed, by a knight’s consecutive moves, with patience and ingenuity.

[I-84]

No. LXXXIV.—A STAR’S TOUR

Here is a pretty and very regular specimen of a knight’s tour on the chess board.

It is one of many variations which produce in the tracery a central star.

5
MAKE IT KNOWN

My first she was a serving maid,
Who went to buy some tea;
How much she bought my second tells,
As all may plainly see.

Now when the answer you have found
Tell it to others too;
My whole will then to maids and men
Explain what ’tis you do.

Solution

[I-85]

No. LXXXV.—THE MARBLE ARCH

Here is a remarkably symmetrical specimen of a knight’s tour on the chess board.

It takes its name from the central archway, which this arrangement forms.

6

My fourth is just ten times my first
When that takes on my second;
My third and second when reversed
Double my first are reckoned.
All this is empty, though my pen
So full may seem to show it;
Reverse my first and second, then
My whole becomes a poet.

Solution

7

O’er distant hills the rising moon
The evening mist dispersed:
And beaming radiant in the sky
She plainly showed my first.

A horseman guided by her light,
Approached with headlong speed
And as he rode my second said
To urge his flagging steed.

His lady waited at the gate,
Though trysting hour was past.
She was my whole, because her lord
Was then my third and last.

Solution

[I-86]

No. LXXXVI.—ANOTHER TOUR AMONG STARS

In No. LXXXIV we gave a pretty illustration of a knight’s tour, with a central star.

Here is a good course which shows in its symmetrical tracery a pair of stars.

[I-87]

No. LXXXVII.—THE WINDMILL

Among the countless fanciful variations of the knight’s tour that are possible, some have been so designed that more than a merely symmetrical pattern is involved.

Here is, for example, an excellent suggestion of the sails of a windmill with their central fittings.

8
A TROPICAL CHARADE

My first’s a liquid or a solid snare,
My all is hot, or in a maiden’s hair;
My second just a track.
Transpose my first, and they will both declare
My all is now a black.

Solution

[I-88]

No. LXXXVIII.—LAZY TONGS

Here is a very distinctive specimen of the knight’s tour, in which the design reminds us of the old-fashioned lazy-tongs, which stretched out and then back, by opening or shutting their handles on finger and thumb.

9
A FLORAL CHARADE

My first must be below the ground,
To do its proper duty;
Within my second may be found
Chaps that can boast no beauty;
Some simple garden holds the two combined,
Old-fashioned emblem of a candid mind.

Solution

[I-89]

No. LXXXIX.—CHESS ARITHMETIC

This beautiful symmetrical knight’s tour involves in its accomplishment a pretty problem in arithmetic:—

If we follow the course of the knight step by step, and number consecutively the squares on which it rests at each move, we find that there is a constant difference of 32 between the numbers on any two of these squares that correspond in position on opposite sides of the central line.

10

My first can be no joke to crack,
My second I adore;
Reverse her name, and you will see
Just what that maiden is to me.
My whole is grown where boys are black
Upon a sultry shore.

Solution

[I-90]

No. XC.—A SHORT KNIGHT’S TOUR

This short symmetrical knight’s tour can be tested on a corner of the chessboard:—

The knight can start from any square, and, taking the course indicated, return on the twentieth move to the starting point.

11
By George Canning

Though weak my first is reckoned,
And game made of my second;
Yet both bade hosts defiance
When joined in close alliance.

Solution

12

As Lubin did my first, and, scythe in hand,
Espied his Phyllis by the hedgerow stand,
He called out to my next, in cheery tones and clear,
“Tell me, sweet all, you’ll fetch a pot of beer.”

Solution

[I-91]

No. XCI.—THE STOLEN PEARLS

A dishonest jeweller, who had a cross of pearls to repair for a lady of title, on which nine pearls could be counted from the top, or from either of the side ends to the bottom, kept back two of the pearls, and yet contrived to return the cross re-set so that nine pearls could still be counted in each direction, as at first. How was this done?

Solution

13
A WORD OF WARNING

Says William to his thriftless wife,
“To first unless you try,
Your wasteful ways will spoil our life.”
Her’s is a curt reply.

Second and third her answer give;
Full soon their fortunes fall,
Each of the hapless pair must live
And wander as my all.

Solution

[I-92]

14
A FINE CHARADE BY PRAED

Come from my first, ay, come;
The battle dawn is nigh,
And the screaming trump and the thundering drum
Are calling thee to die.
Fight, as thy father fought,
Fall, as thy father fell:
Thy task is taught, thy shroud is wrought,
So forward and farewell!

Toll ye my second, toll;
Fling high the flambeau’s light,
And sing the hymn for a parted soul
Beneath the silent night.
The helm upon his head,
The cross upon his breast,
Let the prayer be said, and the tear be shed
Now take him to his rest!

Call ye my whole, go call
The lord of lute and lay,
And let him greet the sable pall
With a noble song to-day.
Ay, call him by his name,
No fitter hand may crave
To light the flame of a soldier’s fame
On the turf of a soldier’s grave!

Solution

15

My first has cause in dread to hold
The foggy month November.
My next, when given to knights of old
Was held to mean “remember!”

Solution

[I-93]

16

With one line many do my first,
With two it can but meet;
My second, as its breakers burst,
Around my whole may beat.

Solution

17

She was my first; one happy day
She was my second,
And shewed my all. Now can you say
How this is reckoned?

Solution

18

My first it may a seaman save,
Or cause a fighter’s fall;
My next reminds us of the wave,
Or of unseemly brawl.
My whole is rather pert than brave,
And like a rubber ball.

Solution

19

Seen with a stolen spoon, my first was reckoned
Bad as my whole in moral tone.
Whether a number or alone my second
Touched by my third is turned to stone.

Solution

20
NOT A CATECHISM

My first a friend, companion, guide,
Is loving, staunch, and cheery;
My second has a cleansing side,
My third denotes a theory.
My whole, good luck! is held by few
To bore and make us weary.

Solution

[I-94]

21

My first is an insect,
My second a border;
My whole puts the face
Into tuneful disorder.

Solution

22

My first seldom crosses your path,
Though wheels and a body it hath;
My next from a clown
Much applause will bring down,
My whole was Goliath of Gath.

Solution

23

My first he sat upon my whole
And used it as my second.
His halves akin in Latin and
In English may be reckoned.

Solution

24
A PHONETIC FLORAL CHARADE

My first comes often to our mind
When for a saint we look.
My second sees the greetings kind
Of Bobby and the cook.
My whole in hothouse you may find,
Or pictured in a book.

Solution

25

Man cannot live without my first,
By day and night ’tis used;
My second is by all accursed,
By day and night abused.
My whole is never seen by day,
And never used by night,
’Tis dear to friends when far away,
But hated when in sight.

Solution

[I-95]

26
BY AN OXFORD OAR

I am my first, my second thou mayest be
In classic shades, where gently roll
The crystal waters of my whole
To seek the sea.

Solution

27

My first is worn by night and day,
And very useful reckoned;
London, or Bath, or Bristol may
With truth be styled my second.
Now if you cannot find me out
You lack my whole without a doubt.

Solution

28

My first now marks the soldier’s face,
Who was my next’s defender;
But when my whole attacked the place
It drove him to surrender.

Solution

29

My first is away from Paris, and may
Come round with a rap at your portal;
My second is Spanish, but quickly will vanish
If it turns to a nod from a mortal.

Solution

30

Often my first a B begins,
One always starts my second.
My all, though free from grosser sins,
Of little worth is reckoned.

Solution

31

My first is a kind of butter,
My second is a sort of cutter;
My whole, whether smaller or larger,
Was always a kind of charger.

Solution

[I-96]

32

My first is but lately promoted
To a place in our language, and quoted.
My second it lives in the sea.
On the hill-tops it flourishes free.
My whole I should certainly call
A delectable dainty for all.

Solution

33
AN ENIGMA-CHARADE

Take in my first, and you will find
It helps you to make up your mind.
Write to my second, and behold
You see into the secret told.

Solution

34
A QUAINT CHARADE
By Charles James Fox

My first is expressive of no disrespect,
But I never call you by it when you are by;
If my second you still are resolved to reject,
As dead as my whole I shall presently lie.

Solution

35

My first reversed will plainly show
An apple in its embryo.
Reverse my second, and we see
That which in sight can never be.
Replace them both, and write me down
Six letters that will spell a town.

Solution

36

My first is equal to the rest,
My second not so much;
My whole is better than the best,
Beyond compare nonsuch.

Solution

[I-97]

37
AN ITALIAN POET’S LOVE SONG

Hear me, my all: oh, be my first!
My second is a single;
If you say yes, then in my third
Our happy lives shall mingle.

Solution

38
A PARADOX

My first a simple verb, or half a verb, may be;
Almost the same my next, or half the same, we see.
My whole may weigh a ton or more, and yet be light,
Dull, and bereft of motion; swift, exceeding bright.

Solution

39

My first is found in fruit,
You take it for my second;
My whole in church to suit
Attentive ears is reckoned.

Solution

40

My first is frugal, lean, and thin,
My second leads to eve,
My whole is hidden by a skin,
But not of sheep or beeve.

Solution

41
VERY PERSONAL

My first to us may point ’tis clear,
And what I say is true, sir!
My next to her your thoughts will steer,
My whole it is in view, sir!

Solution

[I-98]

42

My second in my first can speed
Across United States;
My third from Q’s pen we can read,
My whole has water-rates;
My first and second drive my first along,
My third and second drive a mind all wrong.

Solution

43

To puzzle solvers can I shine,
And so my first is writ.
With this my second did combine
To make a happy hit.
My whole, with both fixed in a line
Firm as I can, did fit.

Solution

44
A RUSTIC CHARADE

My first and second are my third,
My third my first and second may be;
My whole, if right you read the word,
May never have a wife or baby.

Solution

45

Let my second cut my first
Into slices thin;
Seek in Shakespeare for my whole,
Injured by his kin.

Solution

46
A FIRM GRIP

I may give you my first with my second,
Or my second may give with my first;
The one act as friendly is reckoned,
The other will rank with the worst.
If my whole through my second creeps over my first,
It will cling as a bond that no effort can burst.

Solution

[I-99]

47

My first is called a sin in name,
My third its simple cure;
My second puts an end to fame,
My whole in ease is sure.

Solution

48

In my first ’tis sweet to tarry
’Mid my second’s realms of bliss.
In the two, though none can marry,
All are subject to a kiss.

Solution

49

My first, which washes half a nation’s gums,
From foreign climes within my second comes:
And though, my whole, thine is no teacher’s part,
Thou art not science, but thou teachest art!

Solution

50

My first on country hedges grows,
My next is found in garden rows,
My third to make it more transpose,
My whole is one of London’s shows.

Solution

51

My first the best solver can never find out,
My second is looked for in vain;
My third may hide all from our view round about,
My whole must be weak, or in pain.

Solution

52
SORROW’S ANTIDOTE

My first does affliction denote,
Which my second is destined to bear;
My whole is the sweet antidote
That affliction to soothe and to share.

Solution

[I-100]

53

I see a sign of music not reversed, and then
My second and my third both pass beyond my ken.

Solution

54

My first has my second my third his mouth;
My whole was a tribe in the sunny south.

Solution

55
“QUOD” ERAT DEMONSTRANDUM

My second makes my ending,
My first is its reverse;
My whole bad men is sending
From court to quarters worse.

Solution

56

My first, though won and never lost,
Reversed is now before ye:
My second turns as red as blood
Upon a field of glory.
My whole is plain, yet you’ll confess
It is a wonder if you guess.

Solution

57

I get my second when I take my first,
And then my upright character is lost;
My whole gives quarters to a rat reversed,
Or is a refuge for the tempest tost.

Solution

58

My first is almost a cropper;
My second is often a propper;
My whole was entirely a whopper.

Solution

[I-101]

59
A FLORAL CHARADE

My first by poet’s eye was seen
Sad watching at the gates of heaven.
My next in tints of tender green
By Dickens with quaint art was given.

Solution

60

My first is nothing but a name
My second is more small;
My whole is of such slender fame
It has no name at all.

Solution

61

When second is of whole a fourth,
And first a fifth of second,
Then first by second multiplied
To make my whole is reckoned.

Solution

62
A CHARADE WITH A MORAL

My first is black, my second red,
My whole no man should take to bed.

Solution

63

My first upon their prey can dart,
My next can ne’er be down;
My whole performs a saucy part
In country or in town.

Solution

64

My first makes hills unpleasant
To every cyclist’s wheel.
My next is where they take you to
If in the streets you steal.
My whole is what I most dislike
When in the dumps I feel.

Solution

[I-102]

65

My first is the voice of heart-sorrows or joys,
My second, bar one, have been all of them boys,
My whole is made ill by the harsh raven’s noise.

Solution

66
QUITE SELF-CONTAINED

My first is in my second,
My third contains an ass;
And when my whole is reckoned
You see it is in glass.

Solution

67

Safe on Lucinda’s arm my first may rest,
And raise no tumult in Alonzo’s breast.
My second can the want of legs supply
To those that neither creep, nor walk, nor fly;
My whole is rival to the fairest toast,
And when most warmly welcomed suffers most.

Solution

68

My second, my first can control,
If his understanding is reckoned.
My second may not be my whole,
But my whole must be always my second.

Solution

69
AN OLD COCKNEY CHARADE

My first’s a little thing that hops,
My second comes with summer crops,
My whole is good with mutton chops.

Solution

70
A STRIKING CHARADE

My first I gently strike, and lo!
It soon becomes my second.
Indeed if this should not be so
My whole it is not reckoned.

Solution

[I-103]

71
PLANTING PEAS

“I think,” said Ted, “it will be wise
To set the peas this way;
For here they will face friendly skies,
And sun shines all the day.”

“Your first is good,” the gardener said,
“Peas thrive in sun and shower;
So now, good second, dig the bed
Where all can see them flower.”

Can you fit a word of two syllables to this Charade?

Solution

72

My first is found where wit and wine
Combine to grace the festal board;
My second where sad captives pine,
In dungeon of some tyrant lord.
My whole is ready for the doomed,
Twice tried by fire ere once consumed.

Solution

73
A BRAIN TWISTER

My first is half my second
And my third is half my first
My second and my third are good
To quench a mighty thirst.

Solution

[I-104]

RIDDLES AND CONUNDRUMS

1.

Woman is my end, was my beginning, and you will find her in my midst.

Solution

2

I am an uncle, but it is not nice
To be saluted as an uncle twice.

Why not?

Solution

3.

If a tailor and a goose are on the top of the Monument, which is the quickest way for the tailor to get down?

Solution

4.

My first is almost all, so is my second, and also my whole?

Solution

5

Those who have me do not desire me,
And yet they never wish to lose me,
Those who gain me have me no longer.

Solution

6.

Why may a barrister’s fees be said to be cheap?

Solution

7

Two brothers are we, great burdens we bear,
By which we are heavily prest:
We are full all the day to endure wear and tear,
But empty when able to rest.

Solution

[I-105]

8.

Peter Portman was so proud of his small feet that a wag started the following riddle: “Why are Portman’s feet larger than any others in his club?”

Solution

9

There is a word of letters four,
Take two away, and four remain;
Take three away, and five before
Your eyes you see as plain as plain.

Solution

10

To one syllable adjusted,
Running on the ground,
I have two, no longer trusted,
If you turn me round.

Solution

11.

Why is a raven like a writing desk?

Solution

12.

What do they do with peaches in California?

Solution

13.

What is the utmost effort ever made by a piebald horse at a high jump?

Solution

14

“In my first my second sat,
Then my third and fourth I ate.”

Under my first my second stood,
That’s your riddle: mine’s as good!

Solution

15.

What are the differences between a gardener, a billiard-marker, a precise man, and a verger?

Solution

16.

Which can see most, a man with two eyes, or a man with one?

Solution

[I-106]

17.

When you do not know the time, and “ask a policeman” what o’clock it is, why are you like the Viceroy of India?

Solution

18.

What is the question to which “yes” is the only possible reply?

Solution

19.

What is that which will go up a pipe down, but will not go down a pipe up; or will go down a pipe down, but not up a pipe up, and yet when it has gone up a pipe or down a pipe, will go up or down?

Solution

20.

Why was London for many years a wonderful place for carrying sound?

Solution

21.

Why is a motor-car like swimming fish?

Solution

22.

Who can decipher this?

1/6d. me a bloater.

Solution

23.

Why is a moth flying round a candle like a garden-gate?

Solution

24

To half a dozen add half a score,
And you will plainly see
Just twenty, neither less nor more—
Now say, how can this be?

Solution

25.

If I caught a newt why would it be a small one?

Solution

26.

How can a lawyer’s fee be paid with only a threepenny piece?

Solution

27.

When does the cannon ball?

Solution

[I-107]

28.

Why should children go to bed soon after tea?

Solution

29.

Which may weigh the most, Scotsmen or Irishmen?

Solution

30.

Why cannot we have our hair cut?

Solution

31.

Divide a hundred and fifty by half of ten, add two-thirds of ten, and so you will find a town.

Solution

32.

The following riddle is from the pen and fertile brain of Archbishop Whately, who, it is said, offered in vain £50 for its solution:—

When from the Ark’s capacious round
Mankind came forth in pairs,
Who was it that first heard the sound
Of steps upon the stairs?

Solution

33.

If Moses was the son of Pharaoh’s daughter, who was the daughter of Pharaoh’s son?

Solution

34.

I am a word of three syllables, and in all my fulness I represent woman. Rob me of five letters and I am a man. Take away but four, I am woman again. Remove only three, and I resume my manhood. What am I?

Solution

35.

A cyclist on a night journey punctures his tyre, and finds that he has forgotten his outfit for repairs. After wheeling the disabled machine uphill for about two miles he registers a vow. What is it?

Solution

36

Some more than the mere whole my whole contains;
Remove that whole, and some of it remains!

Solution

[I-108]

37.

Why were Younghusband’s pack-horses in Thibet like up-to-date motor cars?

Solution

38

The public credit and the public shame
Differ in everything except in name.

Solution

39.

Why is a telescope like a miser?

Solution

40.

If I were in the sun, and you were out of it, what would it be?

Solution

41

I’m a word of four letters akin to the snow,
Just half of my first my third letter will show.
One fifth of my fourth my first you may call,
Of my second ’tis best to say nothing at all.

Solution

42.

What is the chief and most natural thing for politicians to desire to do when for the time they are out in the cold, awaiting a change of Government?

Solution

43.

I am long lasting, beginning at my end, ending with no beginning, and my end and my beginning between them will bring you to an end.

Solution

44

With both feet crossed sit steady on a stool,
Then uncross one, and try to find a fool.

Solution

A RABBIT RUN

45. How far can a rabbit run into a square wood, with sides that each measure a mile, if it keeps on a straight course and does not break cover?

Solution

[I-109]

46

Often talked of, never seen,
Ever coming, never been,
Daily looked for, never here,
Still approaching in the rear.
Thousands for my presence wait,
But, by the decree of Fate,
Though expected to appear
They will never see me here.

Solution

47.

I received my first because I was rash enough to say my second to my third, when seeking re-election at my whole.

Solution

48

How is it, in this charming weather,
You and I can’t lunch together?

Solution

49

With a head, and without a head,
With a tail, and without a tail,
With a head without a tail,
With a tail without a head,
With a head and tail,
Without a head and tail.

Solution

50.

“Ask me another,” she said, when he pressed her to name the happy day. “I will,” he replied. “Why is the letter ‘d’ like the answer which I seek from you?”

Solution

51
SWIFT’S RIDDLE

Two thirds of an ass, and a hole in the ground,
Will dress you a dinner worth many a pound.

Solution

[I-110]

TOM HOOD’S RIDDLE

52. Here is a riddle for which Tom Hood was responsible. Can you solve it?

Twice to thine,
Once to mine,
With Congou make a gift divine.

Solution

53.

Hold up your hand and you will see what you never have seen, never can see, and never will see. What is this?

Solution

54.

Can you tell the difference between the Emperor of Russia and an ill-shod beggar?

Solution

55.

Why did Eden Philpotts?

Solution

56.

We have heard much of man’s imagined connection with the monkey, through some missing link. What evidence can we gather from early records of, at any rate, some verbal kinship with the patient ass?

Solution

57.

My first is gold, my second is silver, my third is copper, and my whole is tin.

Solution

58.

What is highest when its head is off?

Solution

59.

What word is there of six letters which can be so read that it claims to be spelt with only one?

Solution

60.

If a good oyster is a native, what is a bad one?

Solution

61.

Why is John Bright?

Solution

62.

If I walk into a room full of people, and place a new penny upon the table in full view of the company, what does the coin do?

[I-111]

Solution

63.

Jones, who had made it, and put it into his waistcoat pocket, lost it. Brown picked it up, and lighted his cigar with it. Then they both went to the train in it, and ran all the way.

Solution

64.

Why cannot a deaf and dumb man tickle nine people?

Solution

65.

When did “London” begin with an l and end with an e?

Solution

66.

I sent my second to my first, but many a whole passed before he came back to me.

Solution

67.

Which weighs most, the new moon or the full moon?

Solution

68.

Here is a puzzle which is unique and most remarkable, and which seems to be impossible, though it is absolutely sound:—

There is an English word of more than two letters, of which “la” is the middle, is the beginning, and is the end, though there is but one “a” and one “l” in the word. What is it?

Solution

69.

Why is a bee like a rook?

Solution

70
A DARK REBUS

O
B e D

Solution

71
A MONKEY PUZZLER

If a monkey is placed before a cross, why does it at once get to the top?

Solution

[I-112]

72
A RIDDLE BY COWPER

I am just two and two, warm and cold,
And the parent of numbers untold;
Lawful, unlawful, duty, fault,
Often costly, worthless bought.
A priceless boon, a matter of course,
Willingly yielded, taken by force.

The answer has been defined as “two heads and an application.”

Solution

HOW’S THAT, UMPIRE?

73. How can the Latin exhortation “Macte!” which may be roughly rendered “Go on and prosper!” be applied at cricket to a batsman at a critical moment?

Solution

BY TAPE MEASUREMENT

74. Are you good at topography? If so, can you discover and locate, from this description of its surroundings, a town within 30 miles of London?

Half an inch before the trees, and half a foot and half a yard after them, lead us to an English town.

Solution

75.

We know how, by the addition of a single letter, our cares can be softened into a caress; but in the following enigma a still more contradictory result follows, without the addition or alteration of a letter, by a mere separation of syllables:—

None can locate the subject of my riddle,
For all the world would seek its place in vain;
Cut it asunder almost in the middle,
And in our very midst its place is plain.
[I-113]

An aching void, an absolute negation,
Into the opposite extreme it breaks;
With just a gap to mark their new relation
Each letter still the same position takes.

Solution

76. MULTUM IN PARVO

What two letters describe in nine letters the position of one who has been left alone in his extremity?

Solution

77. A CHANGE OF SEX

“Oh! would I were a man,” cried a schoolmistress, “that I might always teach boys.”

We boys overheard her, and placed her with us. What did we thus turn her into?

Solution

78. A STRIKING MATCH PUZZLE

How can you make a Maltese cross with less than twelve unbent and unbroken matches?

Solution

79

Have we any reason to suppose that in very early times there were less vowels than we have now?

Solution

80. A FRENCH RIDDLE

As Susette was sitting in the cool shadow of an olive grove at Mentone, Henri came up and said to her, with his best bow, “Je sais que vous n’avez pas mon premier, mais que vous êtes mon second, et je vous donnerai mon tout!” What did he hold out to her?

Solution

81

On a church close to an old ruined priory, near Lewes, there is a weathercock in the shape of a fish, probably an emblem of the faith. What moral lesson does this relic of early days convey to us?

Solution

[I-114]

82

Take five from half of ten,
Set fifty in the middle,
Add twice five hundred then
To finish up the riddle,
And make it with your pen
As fit as any fiddle.

Solution

83. A PARADOX

“For the want of water we drank water, and if we had had water we should have drank wine.”

Who can have said this, and what did they mean?

Solution

84. WHAT IS IT?

The poor have two, the rich have none,
Millions have many, you have one.

Solution

85

A thousand and one,
And a sixth part of twenty;
Some may have none,
But others have plenty!

Solution

86. GREAT SCOTT!

“Charge, Chester, charge! on, Stanley, on!”
Were the last words of Marmion.
Now, had I been in Stanley’s place
When Marmion urged him to the chase,
You would have thought, unless you knew,
That Scottish fray was Irish stew!

Shade of Sir Walter! What does all this mean?

Solution

87

I may be half of ten,
I may be nearly nine;
If eight contains me then
Two-thirds of six are mine.
A third of one, a fourth of four,
I am an eighth of many more.

Solution

[I-115]

88. QUITE A BEATITUDE

Let her be, or beat her,
Give her little ease;
Then in safety seat her
All among the bees.

Solution

89

Sharpen your wits till they are keen,
Then see if you can guess
What word it is that I have seen,
And spell it with an s!

Solution

90. RATHER PERSONAL

Take part of a foot,
And with judgment transpose.
You will find that you have it
Just under your nose.

Solution

NUTS TO CRACK

CRAZY LOGIC

1. Can you prove, by what we may call crazy logic, that madman is equal to madam?

Solution

A BIT OF BOTANY

2. A rat with its teeth in the webbed feet of its prey was what the squirrel saw one summer’s day, when he ran down from the tree-tops for a cool drink in the pond below his nest. Can you find out from this the name of the water-plant that was floating in the shade?

Solution

[I-116]

SIX SUNKEN ISLANDS

3. He set down the answer to that sum at random.

By bold policy Prussia became a leading power.

A great taste for mosaic has arisen lately.

The glad news was swiftly borne over England.

At dusk, year after year, the old man rambled home.

The children cried, hearing such dismal tales.

In each of these lines the name of an island is buried.

Solution

BURIED GEOGRAPHICAL NAMES

4. We could hide a light royal boat with a man or two; the skipper, though, came to a bad end.

In this short sentence seven geographical names are buried, formed by consecutive letters, which are parts always of more than one word. Can you dig them out?

Solution

A TRANSPOSITION

5. What can you make of this? The letters are jumbled, but the words are in due order.

Eltsheothwoedlaniscimtyyesrmh
Tsihptsnrtoniaisoetcra;
Ndaothetdandartssdensitemeb
Ehcatreeltnisitlpace.

Solution

6
ALL IN A ROW

Three little articles all in a line
Lead to a thousand, expressing,
If with another all these you combine
What can be never a blessing.

Solution

[I-117]

7
ASK A POLICEMAN

Ask a policeman, possibly he knows,
In uniformed array.
If not, an added letter plainly shows
How little he can say.

Solution

8
RULING LETTERS

We rule the world, we letters five,
We rule the world, we do;
And of our number three contrive
To rule the other two.

Solution

MIND YOUR STOPS

9. How would you punctuate the following sentence?

Maud like the pretty girl that she was went for a walk in the meadows.

Solution

10. ANSWER BY ECHO

What were they who paid three guineas
To hear a tune of Paganini’s?

Solution

11. BREAKING A RECORD

Only eight different letters are used in the construction of this verse:—

Sad as the saddest end is his,
He hath insensate died.
He sinned, and that his Satan is
That standeth at his side.

Wishing to break this record, we have put together a rhyming verse of similar length, in which only five letters are used. They are these:

[I-118]

(18 times) eeeeeeeeeeeeeeeeee.
(20 times) nnnnnnnnnnnnnnnnnnnn.
(18 times) tttttttttttttttttt.
(16 times) iiiiiiiiiiiiiiii.
(15 times) sssssssssssssss.

Solution

12. A CATCH SENTENCE

If is is not is and is not is is what is it is not is and what is it is is not if is not is is? Can you punctuate this so that it has meaning?

Solution

13. CATCHING A HINT

Passing one day by train through a station I caught sight of two words upon a large advertisement, which seemed cut out for puzzle purposes; and before long I had framed the following riddle:

Bisect my first, transpose its first half, and between this and its second half insert what remains if you take my second from my first. The result is as good to eat as my first and second are to drink.

Solution

14. IS IT GRAMMAR?

It is difficult at first sight to grasp the meaning of this apparently simple sentence:—“Time flies you cannot they pass at such irregular intervals.” How does it read?

Solution

15. ROYAL MEMORIES

In Queen Victoria’s Jubilee year I went to the South Kensington Museum. As I entered, looking at my watch, I thought of the good Queen. After some hours of quiet enjoyment I came away, again looking at my watch, and was reminded that the Prince Consort was not alive to share the Jubilee joys. At what time, and for how long was I in the Museum?

Solution

[I-119]

16. A SEASONABLE MOTTO

CCC SAW

Solution

17. AN OLD LATIN LEGEND

AMANS TAM ERAT
HI DESINT HERO
AD DIGITO UT MANDO

What is the interpretation?

Solution

18. THINGS ARE NOT WHAT THEY SEEM

Does the following statement imply that there is a curative virtue in rose-coloured rays?

“I know that roseate hues preserve.”

Solution

19. DOCTOR FELL

“Keep the patients warm and quiet;
Solids are not well;
Let all sops be now their diet,”
So said Doctor Fell.

To what objection was this diet open?

Solution

20. DISLOCATED WORDS

These thirty-six letters form an English sentence:—

SAR BAB SAR BAB SAR BAB
SAR BAB SAR BAB SAR ARA

What can it be?

Solution

[I-120]

21. BROAD WILTSHIRE

“Igineyvartydreevriswutts.”

Can you interpret this sentence, spoken by a sturdy farmer in the corn market?

Solution

22. FIND A RHYME

Try to find a rhyme to Chrysanthemum.

Solution

23. ABOUT THE EGGS

Did you hear that pathetic tale of the three eggs?

Solution

24. AN ANCIENT LEGEND

Doun tooth ers
A sy
Ouw ould bed
One by.

Solution

25. A FAMILY PARTY

HERE LIE

Two grandmothers, and their two granddaughters;
Two husbands, and their two wives;
Two fathers, and their two daughters;
Two mothers, and their two sons;
Two maidens, and their two mothers;
Two sisters, and their two brothers;
Yet but —— in all lie buried here.

How many does the —— represent?

Solution

26. A SIMPLE CHARM

A superstitious couple in the country who heard mysterious noises at night in their house, sought the advice of a “wise woman” in the neighbourhood. She gave them on paper the following charm, which would, she assured them, counteract their evil star, and solve the mystery:—

ground
turn evil star.

What was its significance?

[I-121]

Solution

27. MADE IN FRANCE

We are five varied vowels of foreign sound,
Supported by one consonant between us.
Three letters now in four, where may be found
Another trio, quite a silly genus.

Solution

28. A PARADOX

What in his mind no man can find
Four symbols will display;
But only one remains behind
If one we take away.

Solution

29. THE BARBER’S JOKE

A barber placed prominently in his window the following notice:—

What do you think
I will shave you for nothing and give you a drink.

Attracted by this, a man went into the shop, and was shaved, but instead of receiving any liquid refreshment, he was surprised by a demand for the usual payment.

What was the barber’s explanation?

Solution

30. A FLIGHT OF FANCY

GENUI NE JAM
A
ICARUM.

This label, said to have been found among the ruins of old Rome, seems to bear a very early reference to the birth of Icarus, the flying man; or perhaps to some flying machine named after him, but not yet perfected. Can this be so?

Solution

[I-122]

31. A SPELL

Two c’s, an h, an n, a p,
Three a’s, a u, an i, an e,
Tell us what English word are we?

Solution

32. JOHNSON’S CAT

Johnson’s cat went up a tree,
Which was sixty feet and three;
Every day she climbed eleven,
Every night she came down seven.
Tell me, if she did not drop,
When her paws would touch the top.

Solution

33. THE EXPANDING NINES

Some of us may perhaps remember Titania’s promise to Bottom in A Midsummer Night’s Dream:

“I have a venturous fairy, that shall seek
The squirrel’s hoard, and fetch thee new nuts.”

Here is a little puzzle so fresh and curious that it will tempt the fancy of those who find it added to our hoard:

A third of six behind them fix,
A third of six before;
Thus make two nines, when all combines,
Exactly fifty-four.

Solution

34. ACROSS THE MOAT

Form a square with four matches. Outside this, at an equal distance all round, form another square with twelve matches, just so far away that the space between them cannot be spanned by a match. With two matches only, form a firm bridge from the outer to the inner square.

[I-123]

Solution

35. IS IT BANTING?

We start when the ninth hour is past,
Then there’s an end of you.
A vengeful goddess shows at last
What antifat will do.

Solution

36. QUITE A FAMILY PARTY

The telephone-bell roused Mrs P.W. from her after-luncheon nap, and her husband’s voice came to her ears, from his office in the city:—“I am bringing home to dinner my father’s brother-in-law, my brother’s father-in-law, my father-in-law’s brother, and my brother-in-law’s father.”

“Right!” she replied, knowing his quaint ways, “I shall be prepared.” For how many guests did she provide?

Solution

37. THE WILY WAYFARER

“Give me as much money as I have in my hand,” said Will Slimly to the landlord of a country inn, “and I will spend sixpence with you.” This was done, and repeated twice with the cash that was still in hand, and then the traveller was penniless. How much had he at first, and how much did the landlord contribute to Will’s refreshment?

Solution

38. A CLEVER CONSTRUCTION

How can four triangles of equal size be formed with six similar matches?

Solution

39. A KNOTTY POINT

When first the marriage knot was tied
Between my wife and me,
My age as oft repeated hers
As three times three does three;
[I-124]

But when ten years and half ten years
We man and wife had been,
Her age came then as near to mine
As eight does to sixteen.
What age was hers, what age was mine,
When we were wed, from this divine.

Solution

40. A DIVISION SUM

“Take this half-crown,” said the vicar at a village festival, “and divide it equally between those two fathers and their two sons, but give nothing of less value than a penny to either of them.”

The schoolboy, who was a sharp lad, changed the half-crown, and divided it equally among them. How was this possible?

Solution

41. A CROOKED ANSWER

Tom (yawning) to Nell—“I wish we could play lawn-tennis!”

Nell (annoyed).—“Odioso ni mus rem. Moto ima os illud nam?”

Can you make head or tail, in Latin or in English, of her reply?

Solution

42. THE PEELER’S SMILE

Two policemen stood behind a hedge, watching for motor-car scorchers. One looked up the road, the other looked down it, so as to command both directions.

“Bill,” said one, without turning his head, “what are you smiling at?” How could he tell that his mate was smiling?

Solution

[I-125]

43. THE NIMBLE NINES

Twenty-seven with three nines
You and I can score;
Anyone one on other lines
Can extend them more.
Who can write them to be seen
Equal only to sixteen?

Solution

44. A TRYING SENTENCE

That that is is that that is not is not is not that it it is.

Solution

45. SHORT AND SWEET

What is this?

ALLO.

Solution

46. SUPPLY THE CONSONANTS

An English Proverb

ieaoaaaeaai

Solution

47. IT LOOKS BLACK

| | | | | | | | | | | | |

Add thirteen more strokes, and make—what?

Solution

48. THE CORONER’S CHOICE

Can a coroner, after signing his name, write his official position in more ways than one?

Solution

HOW MANY PIPS?

Here is a good and simple card trick. Ask anyone to choose three cards from a pack, and to place them face downwards on the table. Then, beginning to count with the number of pips[I-126] on each card laid down, let him place other cards upon these, one heap at a time, until in every case he counts up to 15, adding mentally 1 as he places down each card.

When he has completed the three heaps, take from him the remaining cards, and count them. Their number, less 4, will always be the number of pips on the three chosen cards. An ace counts 11, and a court card 10.

Thus, if he has chosen a 7, a 10, and an ace (11), he must cap these with 8, 5, and 4 cards respectively. There will then be 32 cards left, and 32 - 4 = 28, which is the sum of 7, 10, and 11.

ROUND THE MONKEY

Now for a few words about an old friend, familiar to most of us. If a monkey sits on a post holding one end of a string, and continually moves to face a man who holds the other end, and who walks round the post, does that man walk round the monkey?

R. A. Proctor, the astronomer, treated the question thus, some years ago in Knowledge:—“In what way does going round a thing imply seeing every side of it? Suppose a man shut his eyes, would that make any difference? Or suppose the man stood still, and the monkey turned round, so as to show the man its front and back, would the stationary man have gone round the monkey?”

We commend this ancient and puzzling subject of controversy to our readers. Our own opinion is that the man does walk round the monkey, in the commonly accepted meaning of the words, but “who shall decide when doctors disagree?”

[I-127]

BURIED ANIMALS

Here are a few cleverly buried animals:

“Come hither, mine friend,” said the monk, eyeing him kindly, “be a very good boy, step through the furze bravely, and seek the lost riches.”

Ermine; monkey; beaver; zebra; ostrich.

We, as electricians, proclaim the electric motor cab a boon to London.

Weasel; baboon.

QUESTIONS WELL ANSWERED

What could not the cruet stand?
Seeing an apostle spoon.

Why did the barmaid champagne?
Because the stout porter bitter.

A TABLE OF AFFINITY

When it was reported that M. de Lesseps and his son were to marry sisters, the Rappel suggested these possible complications. Lesseps the younger will be his father’s brother-in-law, and his wife will be her own sister’s sister-in-law.

If Lesseps the elder has a son, and Lesseps the younger has a daughter, and these marry, then the daughter of Lesseps the younger will be her father’s sister-in-law, and the son of Lesseps the elder will be the son-in-law of his brother. The son of the second marriage will have two grandfathers, Lesseps the elder and the younger, so that old Lesseps will become his own son’s brother.

[I-128]

MARY QUITE CONTRARY

Mary had a little lamb,
With feet as black as soot;
And into Mary’s bread and milk
He put his little foot.
Now Mary was an honest girl,
And scorned a hollow sham;
So the one word that Mary said
Was mother to the lamb!

MACARONIC VERSE

Latin

“Is acer,” sed jacto his mas ter at te,
“Cantu passus sum jam?” “Notabit,” anser de;
“Mi jam potis empti, solis tento me,
For uva da lotas i vere vel se!”

English

“I say, sir,” said Jack to his master at tea,
“Can’t you pass us some jam?” “Not a bit,” answered he,
“My jam pot is empty, so listen to me,
For you’ve had a lot as I very well see!”

HAM SANDWICHES

We most of us know the good old double-barrelled riddle, “Why need we never starve in the desert?” “Because of the sand which is there.” “How did the sandwiches get there?” “Ham settled there, and his descendants bred and mustered.” This clever metrical solution is by Archbishop Whately:—

[I-129]

A traveller o’er the desert wild
Should ne’er let want confound him,
For he at any time can eat
The sand which is around him.
It might seem strange that he should find
Such palatable fare,
Did we not know the sons of Ham
Were bred and mustered there.

A GOOD MOTTO

We know that Latin motto, with its clever double meaning, suggested for a retired tobacconist, “Quid rides”—why do you smile?—or quid rides. Here is another, proposed many years ago, for a doctor of indifferent repute:—

Take some device in your own way,
Neither too solemn, nor too gay;
Three ducks suppose, white, grey, and black,
And let your motto be “Quack! Quack!”

ON ONE NOTT

There was a man who was Nott born,
His sire was Nott before him;
He did Nott live, he did Nott die,
His tombstone was Nott o’er him.

ON JOHN SO

So died John So,
So, so, did he so?
So did he live, and So did he die,
So, so, did he so?
So let him lie!

[I-130]

STRANGE SIGHTS

The importance of proper punctuation is very happily illustrated by the following lines:—

I saw a peacock with a fiery tail
I saw a blazing comet pour down hail
I saw a cloud enwrapped with ivy round
I saw an oak tree swallow up a whale
I saw the boundless sea brimful of ale
I saw a Venice glass fifteen feet deep
I saw a well full of mens’ tears that weep
I saw wet eyes among the things that I saw
Were no sore eyes nor any other eye-sore.

A QUAINT INSCRIPTION

There is a curiously constructed inscription over the door of the cloister of the Convent of the Carmelites at Caen, which runs thus:—

D		di		Si		scap		ac		ab as
	um		vus		mon		ulare		cepit		tris.
T		sæ		Dæ		ul		in		in an

The lines are in honour of one Simon Stock of that order, and they may be freely rendered:—

W		ho		Si		first beg		pr
	hen		ly		mon		an his		eaching.
T		wi		De		howled to sc		t

NONSENSE VERSE
IMPROMPTU, BY AN OLD DIVINE

If down his throat a man should choose
In fun to jump or slide,
He’d scrape his shoes against his teeth,
Nor soil his own inside.
Or if his teeth were lost and gone,
And not a stump to scrape upon,
He’d see at once how very pat
His tongue lay there by way of mat,
And he would wipe his feet on that!

[I-131]

EDGAR POE’S RIDDLE

Edgar A. Poe addressed the following puzzle-valentine to a lady, adding, “You will not read the riddle, though you do the best you can do:”—

For her this rhyme is penned whose luminous eyes,
Brightly expressive as the twins of Leda,
Shall find her own sweet name, that nestling lies
Upon the page, enwrapped from every reader.
Search narrowly the lines—they hold a treasure
Divine—a talisman—an amulet
That must be worn at heart. Search well the measure.

The first letter of the first line, the second of the second, the third of the third, and so on spell the lady’s name—Frances.

AN ILLUSION OF TYPE

A curious optical illusion is illustrated by printing a row of ordinary capital letters and figures which are symmetrical, thus:—

SSSSSXXXXX3333388888

If we glance at them casually it does not strike us that their upper parts are smaller than the lower, but if we turn the paper upside down we are at once surprised to see how marked the difference really is.

AN EXCHANGE OF COMPLIMENTS

At a tavern one night
Messrs More, Strange, and Wright
Met, good cheer and good thoughts to exchange.
Says More, “Of us three
The whole town will agree
There is only one knave, and that’s Strange!”

[I-132] “Yes,” says Strange, rather sore,
“I’m sure there’s one More,
A most terrible knave, and a bite,
Who cheated his mother,
His sister, and brother.”
“Oh yes,” replied More, “that is Wright!”

ΗΚΙΣΤΑ ΛΙΨ
HE KISSED HER LIPS

(According to the daily Press, a good old-fashioned kiss lately lost favour in some quarters.)

Though a billiard player’s miss
Cannot meet or make a kiss;
Though a modern school of misses
Be not in the cue for kisses;
Chloe’s lips are not amiss,
Kismet! I have met a kiss.

QUESTIONS WELL ANSWERED

We must not fail to register these two Questions Well Answered, which it is hard to match for excellence:—

Q.—Why did the fly fly?

A.—Because the spider spied her!

And

Q.—Why did the lobster blush?

A.—Because it saw the salad dressing!

The following puzzling lines were the outburst of the wanton wit of a lover, in his effort to play off one lady against another, and so retain two strings to his bow:—

I don’t want the one that I don’t want to know
That I want the one that I want;
But the one that I do want wants me to go
And give up the one I don’t want.

[I-133] Why I don’t want the one that I don’t want to know
That I want the one that I want,
Is because, if the one that I want can’t be so,
I shall want the one I don’t want.

Charles Lamb was responsible for the following ingenious perversion of words, when the Whig associates of the Prince Regent were sore at not obtaining office:—

Ye politicians tell me pray
Why thus with woe and care rent?
This is the worst that you can say,
Some wind has blown the wig away,
And left the hair apparent!

We may assume that this was the germ of the riddle “What is the difference between the Prince of Wales, a bald-headed man, and a monkey?” One is the heir-apparent, the second has no hair apparent, and the third is a hairy parent.

GRAMMAR OF A SORT

When is whiskey an adverb?
When it qualifies water.
When does a cow become a pronoun?
When it stands for Mary.

Can the conjunction “and” be used otherwise than as a connecting link?

Yes, as in the puzzle sentence, “It was and I said not or,” which, if no comma is placed after “said,” no one can read easily at sight.

A TONGUE TWISTER

The tragedy “William Tell” was to be played many years ago at the old Drury Lane Theatre, and an actor, familiarly known as Will, asked[I-134] the exponent of the part of Tell, on the eve of its production, whether he thought the play would tell with the critics and the public.

The following question and answer passed between them, in which only two different words were used, in an intelligible sequence of twenty-five words:—

Will.—“The question has arisen Tell, ‘will Will Tell tell?’ Will Tell tell Will ‘will Will Tell tell?’”

Tell.—“Tell will tell Will ‘will Will Tell tell?’ ‘Will Tell will tell!’”

THE LADY AND THE TIGER

Many of our readers will enjoy this very clever rendering of a well-known Limerick:—

There was a young lady of Riga,
Who smiled as she rode on a tiger.
They returned from the ride
With the lady inside,
And the smile on the face of the tiger!

Puella Rigensis ridebat,
Quam tigris in tergo vehebat;
Externa profecta,
Interna revecta,
Sed risus cum tigre manebat!

ANOTHER TONGUE TWISTER

Six sieves of sifted thistles,
Six sieves of unsifted thistles,
And six thistle sifters.

To be repeated six times rapidly and articulately.

NOVEL DEFINITION OF A MAN’S HAT

Darkness that may be felt.

[I-135]

IS IT LATIN?

The following cryptic notice was posted recently on the green baize notice-board of a West-End Club:—

O nec ango in ab illi
Ardor pyram id contestata
Potor ac an non.
Si deis puto nat times
Ora res tu sed.

For some time its message was a mystery, until the sharp eyes of a member deciphered in what seemed to be real Latin, and was made up of Latin words, this English sentence, appropriate to the place:—“One can go in a billiard or pyramid contest at a pot or a cannon. Side is put on at times, or a rest used.”

FOR THE CHILDREN

A QUESTION

How much wood would a wood-chuck chuck,
If a wood-chuck could chuck wood?

THE REPLY

The wood that a wood-chuck would chuck
Is the wood that a wood chuck could chuck,
If the wood-chuck that could chuck would chuck,
Or a wood-chuck could chuck wood!

A QUAINT CONCEIT

The Capitol was saved of old
By geese with noisy bill;
More sage than silly, birds so bold
Should have a mission still.

Time was when roving on the loose,
A goose would raise my dander;
But now I feel each proper goose
Should have her propaganda!

[I-136]

A LACK OF HOPS!

A man fond of his joke, and speaking of Lenten fare to a friend in a letter, wrote:—

I had a fish
In a dish
From an Archbish——

leaving it to his ingenuity to complete the broken line. The reply was a clever solution to the puzzle:—

I had a fish
In a dish
From an Archbish——
’Op is not here
For he gave me no beer!

FOR THE CHILDREN

The following simple calculation will be amusing to children:—If an even number of coins or sweets are held in one hand, and an odd number in the other, let the holder multiply those in the right hand by 2, and those in the left hand by 3, and add together the two results. If this is an even quantity the coins or sweets in the right hand are even, and in the left odd; if it is odd the contrary is the case.

PETER PIPER’S WIFE

(To be read or said rapidly.)

Betty bit a bit o’ butter,
Bitter bit!
But a better bit o’ butter
Betty bit!

[I-137]

PHONETIC VERSE
“A haunt each mermaid knows”

Eh horn teach myrrh made nose,
Buy seize wear awl groat ales;
Hear chilled wrens port inn rose,
Seek your gain steals oar wails.

Sum son there yell oh hare,
Sums whim threw sigh leant baize;
Sow form sand fay says fare
Shy never knight sand daze.

PORSON’S EPIGRAM

Porson wrote a Latin epigram on a Fellow of one of the Colleges who always pronounced the a of Euphrates short. This was wittily translated thus:—

With fear on the Euphrates shore
The wild waves made him shiver.
But he thought to pass more quickly o’er,
So he abridged—the river!

ALL THE ALPHABET

All the letters of the alphabet are used in these lines, which have such an easy flow:—

“God gives the grazing ox his meat,
And quickly hears the sheep’s, low cry.
But man, who tastes his finest wheat,
Should joy to lift His praises high.”

A FRENCH TONGUE TWISTER

A French mother, as she gives to her child a cup of tea to allay its cough, says:—

“Ton thé t’a-t-il oté ta toux?”
(Thy tea, has it removed thy cough?)

This sentence, repeated rapidly, is warranted to tire the nimblest tongue.

[I-138]

QUEER QUESTIONS AND QUAINT REPLIES

Why does the cannon ball?
Because the Vickers Maxim
(the vicar smacks him!)
Why is the river Itchen?
Because there is a current in its bed.

WAS IT SCANDAL?

Dick and Harry meet in a dim hotel passage:—

Dick.—Did you hear that story about No. 288?

Harry (all ears).—No; what was it?

Dick.—Oh, it’s too gross, too gross entirely!

Harry.—Tell away. I’ll try to stand it.

Dick.—Well; 288 is two gross, isn’t it?

AN INCONSEQUENT ECHO

Byron in his “Bride of Abydos” is responsible for the following strangely inconsequent echo:—

Hark to the hurried question of Despair,
“Where is my child?” and Echo answers,
“Where?”

A well-conducted echo would assuredly have seconded the cry of Despair by repeating the final syllables “my child!”

AN APPROPRIATE ANSWER

Why did the Razorbill raise her bill?
To let the sea urchin see her chin!

CRICKET LATIN

Bene audax.
Well bowled!

[I-139]

MACARONIC VERSE

Here is a modern specimen of Macaronic verse:—

Luce metat ipse sutor
(Cantas Orci madentes!)
“Qua forum an empti putor
Potor tria quarto pes!”

Which reads into English thus:—

Lucy met a tipsy suitor
(Can’t a saucy maiden tease!)
“Quaff o’ rum an empty pewter
Pot, or try a quart o’ peas!”

MACARONIC PROSE

LATIN

Puris agem, suetis a sylva bella vi olet indue mos is pura sueta far, amar vel verre ex que sit.

ENGLISH READING

Pure is a gem, sweet is a silver bell, a violet in dewy moss is purer, sweeter far, a marvel very exquisite.

THE LONG AND THE SHORT OF IT

These quaint lines were once addressed to a very tall barrister, named Long, when he was briefless:—

“Longè longorum longissime, Longe, virorum,
Dic mihi, te quæso, num Breve quicquid habes?”

MOORE’S RIDDLE

Thomas Moore, the poet, is responsible for the following rude riddle, and its reply:—

[I-140]

Why is a pump like Viscount Castlereagh?

Because it is a slender thing of wood,
That up and down its awkward arms doth sway,
And coolly spout, and spout, and spout away,
In one weak, washy, everlasting flood!

BIGGAR AND BIGGER

Mrs Biggar had a baby. Which was the bigger? The baby was a little Biggar!

Which was the bigger, Mr Biggar or the baby? Mr Biggar was father Biggar!

Mr Biggar died; was the baby then bigger than Mrs Biggar? No, for the baby was fatherless!

MAGIC CARD SQUARE

Place the sixteen court cards from an ordinary pack in the form of a square, so arranged that no row, no column, and neither of the diagonals shall contain more than one card of each suit, and one of each rank.

As the solution presents no difficulty, but merely calls for patience and attention, we will leave it to the ingenuity of our readers.

THE ANNO DOMINI PUZZLE

A Scottish tradesman had made, as he supposed, about £4,000, but his old clerk produced a balance-sheet which plainly showed £6,000 to his credit. It came upon the old gentleman as quite a disappointing shock when presently the puzzle was solved by the discovery that in the addition the year of Our Lord had been taken into account!

[I-141]

A PUBLIC SINK

The following ingenious play upon words dates from the days when a promise was made that the Thames pollution should cease in five years:—

In shorter time, kind sir, contrive
To purify our drink;
For while your figure is a Five
Our river is a Cinq!

ENGLISH AS SHE IS SPOKE

“Mr Smith presents his compliments to Mr Brown, and I have got a hat that is not his, and he has got a hat that is not yours, so no doubt they are the expectant ones!”

PICKING FROM PUNCH

This play upon words appeared many years ago in the pages of Punch, and is worth preserving:—

To win the maid the poet tries,
And sonnets writes to Julia’s eyes.
She likes a verse, but, cruel whim,
She still remains averse to him.

FRENCH ALLITERATION

“Si six scies scient six cigares, six cent six scies scient six cent six cigares.”

To be said trippingly without a trip.

If 6 saws cut 6 cigars, 606 saws cut 606 cigars.

MIND YOUR STOPS!

Here is a good illustration of the nonsense that may easily result from the misuse of punctuation:—

Every lady in the land
Has twenty nails on each hand;
Five and twenty on hands and feet,
This is true without deceit.

[I-142]

A NOVEL DERIVATION

“Yes,” said an Eton captain of the boats to his uncle, the admiral, “I can quite believe that the British Jack Tar takes his name from that Latin verb, which is so suggestive of a life on the ocean wave, jactari, to be tossed about.”

AN AERATED BISHOP

A bishop of Sodor and Man found himself entered in the visitor’s book of a French hotel as “L’évêque du siphon et de l’homme!”

A HAPPY THOUGHT

They cannot be complete in aught
Who are not humourously prone;
A man without a merry thought
Can hardly have a funny bone.

OUGH!

Though the tough cough and hiccough
Make me hoarse,
Through life’s dark lough I plough
My patient course.

CUM GRANO SALIS

I know Eno, you know too,
Fact is we all three know.
We know Eno, he knows you.
You know I know Eno!

OLD AND SOUND ADVICE

Nicholas, 1828.

He who a watch would wear
This must he do;
Pocket his watch, and watch
His pocket too!

[I-143]

COLD-DRAWN CONCLUSIONS

Why is a lame dog like a blotting-pad?

A lame dog is a slow pup.

A slope up is an inclined plane.

An ink-lined plane is a blotting-pad!

THE LAST OF MARY

Mary had a little lamp,
Filled with benzoline;
Tried to light it at the fire,
Has not since benzine!

A BURIED WORD

It is difficult to imagine that the very incarnation of what is wild and forbidding is buried in those words of peace and promise, “On Christmas Eve you rang out Angel peals,” until we find in them the consecutive letters “ourangoutang!”

EVE’S APPLE

How many apples were eaten by Adam and Eve? We know that Eve 81, and that Adam 812, total 893. But Adam 8142 please his wife, and Eve 81242 please Adam, total 89,384. Then again Eve 814240 fy herself, and Adam 8124240 fy himself, total 8,938,480!

U C I D K
(You see I decay!)

“Surely, good sir, you follow me?
It is as plain as A B C.”
“Repeat it in a treble clef,
For I am rather D E F!”

[I-144]

BURIED BY ACCIDENT

Quite unconscious that he was burying a cat in his melodious lines Moore wrote:—

“How sweet the answer Echo makes
To music at night...!”

A LAWYER’S PROPOSAL

Fee simple and the simple fee,
And all the fees in tail,
Are nothing when compared with thee,
Thou best of fees, fe-male!

A BROAD GRIN

“Sesquipedalia verba,” words a foot and a half long, were condemned by Horace in his “Ars Poetica.” Had he known English, what would he have said of “smiles,” a word so long that there is a mile between its first and last letters?

SWISS HUMOUR

A Swiss lad asked me, as I stopped quite breathless on an Alpine height, “Do you prefer ‘monter’ to ‘descendre?’” I declared a preference for downhill, but he most convincingly replied, “I prefer ‘mon thé’ to ‘des cendres!’” (my tea to cinders).

QUESTIONS WELL ANSWERED

Why did the penny stamp?
Because the threepenny bit.
Why did the sausage roll?
Because it saw the apple turn-over.

[I-145]

MEN OF LETTERS

A budding author something new
Submitting, signed himself X Q.
The editor the essay read,
And begged he might be X Q Z!

PUZZLES ON THE PAVEMENT

An angry street arab, who seems to have caught the infection of our letter puzzles, was heard recently to call out to a gutter-snipe, “You are a fifty-one ar!” (LIAR.)

PHONETIC ANSWERS

Why may you pick an artist’s pocket?—Because he has pictures.

What is the solace for a mind deprest?—Deep rest.

A FLIGHT OF FANCY

There was a man from Yankeeland
Who round a walnut tree
Did run so fast—that lissome man—
His own back he could see!

BURNS IN SABOTS

“Guigne a beau de qui sabot de
Nid a beau de t’elle?”

DOG LATIN

Here are all the elements of a rat hunt, expressed in Latin words:—“Sit stillabit,” sed amanto hiscat, “sta redde, sum misi feror arat trito unda minus, solet me terna ferret in micat.” They read into English, if differently pointed, thus:—Sit still a bit, said a man to his cat, stay ready, some mice I fear, or a rat try to undermine us, so let me turn a ferret in, my cat.

[I-146]

EARLY RITUAL

It is said that at first Adam thought Eve angelical, but there came a time when they both took to vestments.

LEST WE FORGET

If a man says that he forgets what he does not wish to remember, does he mean to say that he does not remember what it is that he wishes to forget; or that he is able to forget that which he does not wish to remember?

QUAINT ANGLO-FRENCH QUESTION AND REPLY

Pas qu’il ma, ou qu’il pas?

Marwood!

SOME POPULAR DEFINITIONS

Cricket.	Lawn Tennis.	Football.
Lords	Ladies	Legs
Stumps	Jumps	Bumps.

REAL DOG LATIN

Pax in bello.
The dogs of war.

A QUAINT EPITAPH

Here in S X I lies.
Killed by X S I dies.

A PHONETIC REPLY

What is the French for teetotaler?—Thé tout à l’heure!

[I-147]

A FREE RENDERING

Varietas pro Rege.
Change for a sovereign!

A FREE TRANSLATION

“Splendide mendax.”
Lying in State.

A WORD AND A BLOW

When Dunlop, in playful mood, said that no one could make a good pun on his name, a smart bystander at once exclaimed, “Lop off the end, and the thing is done!”

DOG LATIN (FOR SCHOOLBOYS)

Mitte meos super omnes ad candam aut esse homines mortui.

The Dog Latin may be rendered thus: “Send my overalls to the tailor to be mended.”

HIS L. E. G.

Some printer’s devil must have been at work when the proof-reader found “The Legend of the Cid,” set up in type as “The leg end of the Kid!”

[I-148]

SOLUTIONS

No. V.—THE MAKING OF A MAGIC SQUARE

The perfect Magic Square, for which we have given the construction of two preparatory squares, is formed by placing one of these over the other, so that the numbers in their corresponding cells combine, as is shown below.

Preparatory Square No. 1.

		*
1	3	5	2	4
5	2	4	1	3
4	1	3	5	2
3	5	2	4	1
2	4	1	3	5

Preparatory Square No. 2.

			*
5	15	0	10	20
10	20	5	15	0
15	0	10	20	5
20	5	15	0	10
0	10	20	5	15

The Perfect Magic Square.

6	18	5	12	24
15	22	9	16	3
19	1	13	25	7
23	10	17	4	11
2	14	21	8	20

No less than 57,600 Magic Squares can be formed with twenty-five cells by varying the arrangement of these same figures, but not many are so perfect as our specimen, in which sixty-five[I-149] can be counted in forty-two ways. These comprise each horizontal row; each perpendicular row; main diagonals; blended diagonals from every corner (such as 6, with 14, 17, 25, 3; or 15, 18, with 21, 4, 7); centre with any four equidistant in outer cells; any perfect St George’s cross (such as 18, 22, 1, 15, 9); and any perfect St Andrew’s cross (such as 6, 22, 13, 5, 19).

Back to Description

No. XII.—A CENTURY OF CELLS

Here is the solution of the ingenious Magic Square of 100 cells with 36 cells unfilled. The rows, columns, and diagonals all add up to 505.

91	2	3	97	6	95	94	8	9	100
20	82	83	17	16	15	14	88	89	81
21	72	73	74	25	26	27	78	79	30
60	39	38	64	66	65	67	33	32	41
50	49	48	57	55	56	54	43	42	51
61	59	58	47	45	46	44	53	52	40
31	69	68	34	35	36	37	63	62	70
80	22	23	24	75	76	77	28	29	71
90	12	13	87	86	85	84	18	19	11
1	99	98	4	96	5	7	93	92	10

Notice that the top and bottom rows contain all the numbers from 1 to 10 and from 91 to 100; the two rows next to these range from 11 to 20 and from 81 to 90; the two next from 21 to 30 and from 71 to 80; the two next from 31 to 39 and 60 to 70, excluding 61, but including 41; and the two central rows the numbers run from 42 to 59, with 40 and 61.

Back to Description

[I-150]

No. XXIII.—TWIN PUZZLE SQUARES

The following diagram shows how the twin Magic Squares are evolved from our diagram:—

1	5	6	2	3	7


2	6	7	3	4	8


3	7	8	4	5	9

The sums of the corresponding rows in each square are now equal, and the sums of the squares of the corresponding cells of these rows are equal. The sums of the four diagonals are also equal, and the sum of the squares of the cells in corresponding diagonals are equal. The sum of any two numbers symmetrically placed with respect to the connecting link between the 7 and the 3 is always 10.

Back to Description

No. XXX.—THE UNIQUE TRIANGLE

The figures to be transposed in triangle A are 9 and 3 and 7 and 1.

			5
		4		6
	3				7
2		1		9		8

			5
		4		6
	9				1
2		7		3		8

Then in triangle B, the sum of the side is in each case 20, and the sums of the squares of the numbers along the sides is in each case 126.

Back to Description

[I-151]

No. XXXI.—MAGIC TRIANGLES

The subjoined diagram shows the order in which the first 18 numbers can be arranged so that they count 19, 38, or 57 in many ways, down, across, or along some angles, 19 in 6 ways, 38 in 12, and 57 in 14 ways.

Thus, for examples—

7	+	12	=	14	+	5	=	4	+	15	=	19
7	+	11	+	14	+	6		———			=	38
7	+	14	+	4	+	5	+	12	+	15	=	57

Back to Description

No. XXXIV.—MAGIC HEXAGON IN A CIRCLE

The figures in the Magic Hexagon must be arranged as is shown in this diagram:—

[I-152]

									126
				5		2		7		3		8		5
			8		2		4				6		3		7
114																		114
		4				6		9		1		8				2
	3		1		9		7		5		4		1		9		6
	1		3		7		9		8		6		7		3		4
		8				2		3		9		1				9
126																		126
			6		4		4				1		8		2
				5		5		6		7		2		5
									114

It will be seen that the sum of the four digits on each side of each triangle is twenty, and that, while their arrangements vary, the total of the added squares of the numbers on the alternate sides of the hexagon are equal.

Back to Description

No. XXXVI.—A CHARMING PUZZLE

✦	✦	✦
✦	✦	✦
✦	✦	✦

To pass through these nine dots with four continuous straight lines, start at the top right-hand[I-153] corner, and draw a line along the top of the square and beyond its limits, until its end is in line with the central dots of the side and base. Draw the second line through these, continuing it until its end is below and in line with the right-hand side of the square; draw the third line up to the starting-point, and the fourth as a diagonal, which completes the course.

Back to Description

No. XXXVII.—LEAP-FROG

On a chess or draught-board three white men are placed on squares marked a and three black men on squares marked b in the diagram—

a	a	a		b	b	b
1	2	3	4	5	6	7

Every a can move from left to right one square at a time, and every b from right to left, and any piece can leap over one of another colour on to an unoccupied square. They can reverse their positions thus:—

If we number the cells or squares consecutively, and notice that at starting the vacant cell is No. 4, then in the successive moves the vacant cells will be 3, 5, 6, 4, 2, 1, 3, 5, 7, 6, 4, 2, 3, 5, 4. Of the moves thus indicated six are simple, and nine are leaps.

Back to Description

No. XXXVIII.—SORTING THE COUNTERS

The counters are changed in four moves only, moving two at a time as follows:—

[I-154]

Move	2 and 3	to	9 and 10.
„	5 and 6	to	2 and 3.
„	8 and 9	to	5 and 6.
„	1 and 2	to	8 and 9.

Back to Description

No. XXXIX.—A TRANSFORMATION

To change the ten-pointed star of wooden matches into one of five points without touching it, let a little water fall into the very centre, as it lies on quite a smooth surface, and in a few moments, under the action of the water, it will gradually assume the shape shown in the second diagram, of a five-pointed star.

This is a very simple and effective after-dinner trick. Small matches move best.

Back to Description

[I-155]

No. XLI.—FAST AND LOOSE

The twelve counters or draughtsmen lying loosely at the bottom of a shallow box can be arranged so that they wedge themselves together and against the side thus:—

Temporary centre

Place one for the moment in the centre, and six round it. Hold these firmly in their places with the left hand, and fix the other five round them, as is shown in the diagram. Then remove the temporary centre, and fill in with it the vacant place. All will then be in firm contact, and the box may be turned upside down without displacing them.

Back to Description

[I-156]

No. XLIII.—FOR CLEVER PENCILS

This diagram, shows how a continuous course is possible without taking pencil from paper, or going twice over any line.

We have purposely left spaces wide enough to make the solution perfectly clear.

Back to Description

No. XLVIII.—A BOTTLED BUTTON

The diagram below shows how the thread within the bottle is severed so that the button[I-157] falls, without uncorking the bottle or breaking it.

Nothing is needed but a lens to focus the rays of the sun, which pass through the glass without heating it, and burn the thread.

Back to Description

No. XLIX.—CLEARING THE WAY

In order to cause the coin to fall into the bottle without touching coin, match, or bottle, let a drop or two of water fall upon the bent middle of the match.

Very soon, under the action of the water, the two ends of the match will open out so that the coin which was resting on them falls between them into the bottle.

Back to Description

[I-158]

No. LII.—BILLIARD MAGIC

The diagram we give below shows the ingenious trick by which the plain white, if struck gently with a cue, will, aided by the tumbler, pot the spot white ball without in any way disturbing the red.

The balls to start with are an eighth of an inch apart, and there is not room for a ball to pass between the cushions and the red. Place the tumbler close to spot white.

Back to Description

[I-159]

No. LIII.—THE NIMBLE COIN

The most effective way to transfer the coin from the top of the circular band of paper into the bottle is to strike a smart blow with a cane, or any small stick, on the inside of the paper band. There is not time for the coin to be influenced in the same direction, and it falls plumb into the neck of the bottle.

Back to Description

No. LVIII.—WHAT WILL HAPPEN?

When the boy shown in this picture blows hard at the bottle which is between his mouth and the candle flame, the divided air current[I-160] flows round the bottle, reunites, and extinguishes the flame.

Back to Description

No. LX.—VIS INERTIÆ

If, by a strong pull of my finger, I launch the draughtsman that is on the edge of the table against the column of ten in front of it, the black man, which is just at the height to receive the full force of the blow, will be knocked clean out of its place, while the others will not fall. This is another illustration of the vis inertiæ.

Back to Description

[I-161]

No. LXI.—CUT AND COME AGAIN

A block of ice would never be divided completely by a loop of wire on which hangs a 5 ℔ weight. For as the wire works its way through, the slit closes up by refreezing, and the weight falls to the ground with the wire, leaving the ice still in a single block.

Back to Description

No. LXIII.—CATCHING THE DICE

It is quite easy to throw the upper of this pair of dice into the air and catch it in the cup, but the other is more elusive. As you throw it upward with sufficient force you will also throw[I-162] the die that has been already caught out of the cup.

The secret of success lies in dropping the hand and cup rapidly downwards, quitting hold at the same moment of the die, which then falls quietly into the cup held to receive it.

Back to Description

No. LXIV.—WILL THEY FALL?

When the single domino shown in the diagram in front of the double archway, is quite smartly tipped up by the forefinger carefully inserted through the lower arch, the stone which lies flat below another is knocked clean out, while[I-163] none of the other stones fall, another practical illustration of vis inertiæ.

For this very curious trick, club dominoes, thick and large, should be used. Some patience and experience is needed, but success at last is certain.

Back to Description

No. LXV.—A TRANSPOSITION

You will be able to place the shaded coin between the other two in a straight line without touching one of these, and without moving the other, if you place a finger firmly on the king’s head and then move the shaded coin an inch or[I-164] two to the right, and flick it back against the coin you hold. The other “tail” coin will then spring away far enough to allow the space that is required.

Back to Description

No. LXVI.—COIN COUNTING

After reaching and turning the coin which you first call “four,” miss three coins, and begin then a fresh set of four; repeat this process to the end.

Back to Description

No. LXVIII.—NUTS TO CRACK

Hold a cup of water so that it will wet the handle of the knife, then remove it, and place the nut exactly on the spot where the drop of water falls from the handle.

Back to Description

No. LXXI.—WHAT IS THIS?

The photographic enlargement is simply a much magnified reproduction of Mr Chamberlain’s eye and eyeglass, exactly as they appear in the picture which we give below, taken from[I-165] its negative. A strong condensing lens will reproduce the original effect, which can also be obtained by holding the enlargement at a distance.

Back to Description

[I-166]

No. LXXV.—THE SEAL OF MAHOMET

This double crescent may be drawn by one continuous line, without passing twice over any part, by starting at A, passing along the curve AGD, from D along DEB, from B along BFC, and from C along CEA.

Back to Description

No. LXXVI.—MOVE THE MATCHES

If fifteen matches are arranged thus—

and six are removed, ten is the number that remains, thus—

or one hundred may remain, thus:—

Back to Description

[I-167]

No. LXXVII.—LINES ON AN OLD SAMPLER

This diagram shows the arrangement in which seventeen trees can be planted in twenty-eight rows, three trees in each row:—

Back to Description

No. LXXXI.—COUNTING THEM OUT

Here is an arrangement of dominoes which enables us to count out the first twelve numbers, one after the other, by their spelling:—

Start with the double five, and, touching each stone in turn, say o, n, e, one; remove the stone with one pip, and go on, t, w, o, two; remove[I-168] the two, and say t, h, r, e, e, three, and so on till you reach at last the twelve.

Playing cards can be used, counting knave, queen, as eleven, twelve. It makes quite a good trick if you place the cards face downwards in the proper order, and then, saying that you will call up each number in turn, move the cards one at a time to the other end, spelling out each number as before, either aloud or not, and turning up and throwing out each as you hit upon it. If you do not call the letters aloud it adds to the mystery if you are blindfolded.

Back to Description

No. LXXXII.—TRICKS WITH DOMINOES

This is the other combination of stones and their pips which fulfils the conditions, and forms the word AGES.

In both cases a complete set of stones is used, which are arranged in proper domino sequence, and everyone of the eight letters carries exactly forty-two pips.

Back to Description

[I-169]

No. XCI—THE STOLEN PEARLS

The dishonest jeweller reset the pearls in a cross so that its arms were a stage higher up. It will be seen that by this arrangement nine pearls can still be counted in each direction.

Back to Description

ENIGMAS

1. Self-assassin, a neddy. Saw an ass in an eddy!

Back to Enigma

2. To get her: Together.

3. A candle.

4. Liquorice.

5. A book.

6. One solver proposes raven, croaking before a storm; once an object of worship; seldom seen; forbidden in Leviticus as food; alone with Noah when its mate was sent forth; weighing about 3 lbs; the name of a small South Carolina island, having as its first and last letters R and N; the Royal Navy.

Another finds in K the key, as that letter with no ar is alone in ark. With much ingenuity he shows that the last line calls for a second letter,[I-170] and that the letters K and G can be traced throughout almost all Hallam’s “lights;” Kilogram being nearly 3 lbs., and Knot a mile; while either K.G. (Knight of the Garter) or King would fit the final line.

Back to Enigma

7. The lines become “rank treason” if the corresponding lines of the two stanzas are read together, thus:—

The pomps of Courts and pride of Kings
I fain would banish far from hence,

and so on throughout.

8. A pair of skates.

9. A shadow.

10. A chair.

11. The changes that are rung are one, eno, Noe, neo, eon, on, none.

12. Cares, caress.

13. Echo.

14. Strike.

15. A pair of spurs.

16. A.D.A.M.; Adam; a dam; Adam; a damson; a dam.

Back to Enigma

17. The CID, the Castilian hero whose fame was at its height in the middle of the eleventh century.

18. A sigh.

19. Coxcomb.

20. Jack and Jill.

21. A man’s felt hat.

Back to Enigma

22. Measurable.

Back to Enigma

23. Chair, char, arch.

Back to Enigma

24. Sala (G.A.S.), which reversed is alas.

Back to Enigma

25. Page, (p)age.

Back to Enigma

26. C (sea), A (hay), T (tea).

Back to Enigma

27. A BROKEN TALE

The deil jumped over the clouds so high
That he bounded almost right over the sky.
Over gates and fields, and under the trees
He dodged, with his tail dragging over all these,
But, alas! made a terrible blunder,
For a twist in his tail hooked under a rail,
And broke that appendage asunder.

Back to Enigma

28. Yesterday. Most excludes Adam, and ter is half of terror.

Back to Enigma

[I-171]

29. Donkey.

Back to Enigma

30. Mental, lament, mantle.

Back to Enigma

31. His heels.

Back to Enigma

32. Tares, tears, a rest.

Back to Enigma

33. Connecticut.

Back to Enigma

34. Grate, rate, rat, ate.

Back to Enigma

35. Mary, in fanciful mood, on her thirty-sixth birthday, decorated her pincushion thus—XXXVI.

Back to Enigma

36. Opinionist.

Back to Enigma

37. Violin (LVII + on).

Back to Enigma

38. Trout (tr—out).

Back to Enigma

39. Post—stop.

Back to Enigma

40. A pair of scissors in a case.

41. Dog.

42. Mainland.

43. Changed.

44. The name of the Russian nobleman’s third son, the boy who went to sea, was Yvan. As the name of the eldest, Rab, who became a lawyer, was Bar reversed, and that of the soldier son Mary was Army as an anagram, so Yvan’s name resolves itself into Navy, his profession.

45. VIVID.

46. Nothing.

47. London.

48. Rock, cork.

49. Place, lace, ace, lac.

Back to Enigma

50. a, e, i, o, u, y.

Back to Enigma

51. The solution of the enigma which begins:—

“Twice six is six, and so
Six is but three;
Three is just five you know,
What can we be?”

is the number of letters of the alphabet used in spelling a number. Thus twice six, or twelve, is composed of six letters, and so on.

52. A button.

53. LEVEL—MADAM.

54. An egg.

55. Vague.

56.

A headless man had a letter to write,
(The letter O, i.e. nothing.)
He who read it had lost his sight,
(He read nothing.)
[I-172] The dumb repeated it word for word,
(He said nothing.)
And deaf was he who listened and heard.
(He heard nothing.)

Back to Enigma

57. Highway.

Back to Enigma

58. A set of false teeth.

Back to Enigma

59. The “fearful fate” enigma is slaughter; cut off its head and we have laughter; lop off its shoulders and we find aught.

Back to Enigma

60. Speculation—peculations.

Back to Enigma

61. The word “united” is “of fellowship the token,” and the requirement “reverse it, and the bond is broken” refers only to the two central letters. When this is reversed the word “untied” is formed.

62. Average.

63. German—manger.

64. Corkscrew.

65. Tar is transformed by Art, and as a sailor is fond of port, and blisters in the sun. When it turns to run it becomes Rat, and when it doubles it is Tartar, and is caught.

Back to Enigma

66.

A man with one eye two plums must have seen,
One perfectly ripe, the other quite green.
The former he took, and ate it with pleasure,
The other he left to ripen at leisure.

Back to Enigma

67. A widower who has lost two wives.

Back to Enigma

68. The grape-vine on the Marquis of Breadalbane’s estate, Killin, N.B., which bears more than 5000 bunches of grapes, of which only 500, properly thinned out, are allowed to mature, so that the fewer and smaller bunches bear finer fruit.

Back to Enigma

69. Poe, poet, poetry.

Back to Enigma

70. Theatres. The articles the and a lead on to the other four letters tres, and these form the word rest, if the t is transferred to the end.

Back to Enigma

71. Scold, cold, old.

Back to Enigma

72. Justice, (just—ice).

Back to Enigma

73. A shadow.

Back to Enigma

74. VI., IV., I.

Back to Enigma

[I-173]

75. The letter I.

Back to Enigma

76. The letter V.

Back to Enigma

77. An army.

Back to Enigma

78. A rich table; chair, table; charitable.

Back to Enigma

79. High-low.

Back to Enigma

80. Orange, pear, date, banana, peach, plum, lime, lemon, mango, apple.

Back to Enigma

81. Innuendo.

Back to Enigma

82. Snipe, of which pines is an exact anagram.

Back to Enigma

83.

None can locate the subject of my riddle,
For all the world would seek its place in vain,
Cut it asunder almost in the middle,
And in our very midst its place is plain

is solved by nowhere, now here.

Back to Enigma

CHARADES

1. Good-night (knight).

2. Grandson.

3. Oyster.

4. Stay-lace.

5. Ann—ounce.

6. VOID, OVID.

7. Disconsolate (disc—on—so—late).

Back to Charade

8. Ginger—Nigger. (G.E.R. Great Eastern Railway).

Back to Charade

9. Honesty (hone, below the razor).

Back to Charade

10. Nutmeg.

Back to Charade

11. Waterloo.

Back to Charade

12. Whether (whet—her).

Back to Charade

13. Mendicant (mend I can’t).

14. Campbell.

15. Foxglove.

16. Anglesea.

17. Shewed.

18. Sparrow, often a gutter percher!

Back to Charade

19. Dishonest (dish—one—st).

Back to Charade

20. Dogmatism.

Back to Charade

21. Anthem.

Back to Charade

22. Gigantic (gig—antic).

Back to Charade

23. Toad (ad is Latin for to).

Back to Charade

24. Cineraria (sinner—area).

Back to Charade

25. Ignis—fatuus, or Will-o’-the-wisp (ignis, fire—fatuus, a fool).

Back to Charade

[I-174]

26. Isis (sis in Latin, thou mayest be).

27. Capacity.

28. Scarcity.

29. Pardon.

30. Humbug.

31. Ramrod.

32. Dumpling.

33. Into.

34. Herring.

35. Dublin (bud—nil).

Back to Charade

36. Peerless.

Back to Charade

37. Beatrice.

Back to Charade

38. Beam—be is half of the word verb, am is half of same, and be and am are similar in sense.

39. Pulpit.

40. Spare—rib.

41. Usher.

42. The ship Carmania.

43. Candid.

44. Husbandman.

45. Hamlet.

46. Handcuff.

47. Sinecure.

48. Infancy.

49. Teachest.

50. Hippodrome.

51. Invalid.

52. Woman.

53. Kensington.

54. Benjamin.

55. Stipendiary.

56. Wonder.

57. Cabin.

58. Falstaff.

59. Periwinkle.

60. Nameless.

61. Fourscore.

62. Hatred.

63. Catsup.

64. Molestation.

65. Omen.

66. Isinglass.

67. Muffin.

68. Footman.

69. Sparrow-grass.

70. Matchless.

71. Planted.

72. Toast-rack.

73. Half-and-half, if properly punctuated.

Back to Charade

RIDDLES AND CONUNDRUMS

1. Washerwoman.

Back to Riddle

“Call me an uncle, then you speak me fair,
Call me an uncle-an uncle if you dare!”

Back to Riddle

3. Pluck the goose.

Back to Riddle

4. Also.

[I-175]

Back to Riddle

5. A lawsuit.

Back to Riddle

6. Because they are bargains.

Back to Riddle

7. A pair of shoes.

Back to Riddle

8. Because whenever he goes out he can put his portmanteaux (Portman toes) into his boots.

Back to Riddle

9. FIVE.

Back to Riddle

10. Rail—liar.

Back to Riddle

11. Because it slopes with a flap!

Back to Riddle

12. In California they eat all the peaches they can, and can all they can’t!

Back to Riddle

13. The utmost effort ever made by a piebald (or by any) horse at a high jump is four feet from the ground!

Back to Riddle

14. Insatiate (in—sat—I—ate).

The clever couplet—

Under my first my second stood.
That’s your riddle: mine’s as good!

was intended to point out that the enigma

In my first my second sat,
Then my third and fourth I ate

was understood, and to frame at the same time a fresh one of similar sort.

Back to Riddle

15. A gardener minds his peas, a billiard-marker his cues, a precise man his p’s and q’s, and a verger his keys and pews.

Back to Riddle

16. A man with one eye can see more than a man with two, for in addition to all else he can see the other man’s two eyes, which can only see his one.

Back to Riddle

17. When you ask a policeman what o’clock it is, you are like the Viceroy of India, because you are as king for the time.

Back to Riddle

18. “What does Y E S spell?” is the question to which “yes” is the only possible reply.

Back to Riddle

19. An umbrella.

Back to Riddle

20. London for many years was a wonderful place for sound, for you could laugh at 5 p.m. at Waterloo Junction, and by walking briskly across[I-176] the river be in time for the late Echo at Charing Cross.

Back to Riddle

21. Because it may be smelt!

Back to Riddle

22. The full reading of “1s. 6d. me a bloater” is “Bob Tanner sent me a bloater.”

Note.—If any solver should ask, “But where is the ‘sent’?” we reply, “The scent was in the bloater!”

Back to Riddle

23. The solution of the prime conundrum “Why is a moth flying round a candle like a garden gate?” is—Because if it keeps on it singes its wings (its hinges it swings).

Back to Riddle

24. (Twe)lve—twe(nty) = twenty.

Back to Riddle

25. Because it would be my newt (minute).

Back to Riddle

26. The steps by which, in paying my debt to a lawyer, a threepenny piece swells to the needed six and eightpence are these:—

Three pence is one and two pence;
One and two pence is fourteen pence;
Fourteen pence is six and eight pence!

Back to Riddle

27. When the Vickers Maxim (vicar smacks him).

Back to Riddle

28. Children should go to bed soon after tea because when “t” is taken away night is nigh.

Back to Riddle

29. Scottish may be lighter than Irish men, for while Irishmen may be men of Cork, Scotsmen may be men of Ayr.

Back to Riddle

30. Because barbers do not cut hair any longer!

Back to Riddle

31. Colenso.

Back to Riddle

32. This is Archbishop Whately’s riddle, and a solution, suggested long after his offer of £50 had expired:—

When from the Ark’s capacious round
Mankind came forth in pairs,
Who was it that first heard the sound
Of boots upon the stairs?
[I-177]

To him who cons the matter o’er,
A little thought reveals,
He heard it first who went before
Two pairs of soles and eels!

Back to Riddle

33. If Moses was the son of Pharaoh’s daughter, he was the daughter of Pharaoh’s son.

Back to Riddle

34. The word of three syllables which represents woman or man alternately by three contractions is heroine—hero—her—he.

Back to Riddle

35. Solution to-morrow!

Back to Riddle

36. Wholesome.

Back to Riddle

37. They were jolly well tired!

Back to Riddle

38. The stocks.

Back to Riddle

39. Because it makes a far—thing present.

Back to Riddle

40. If I were in the sun, and you were out of it, it would be a sin.

Back to Riddle

41. COLD.

Back to Riddle

42. Take off—ice.

Back to Riddle

43. Enduring.

Back to Riddle

44. Uncross the “t” of “a foot,” and it becomes “a fool.”

Back to Riddle

45. A rabbit can run into a square wood with sides that each measures a mile, keeping always in a straight line, until it reaches the middle of the wood, when it must begin to run out of it!

Back to Riddle

46. To-morrow.

Back to Riddle

47. Scar—bo—rough.

Back to Riddle

48.

Though I in time for lunch may be,
U cannot come till after T.

Back to Riddle

49. A wig.

Back to Riddle

50. Because we cannot be wed without it.

Back to Riddle

51. A spit.

Back to Riddle

52. Wit (double you—I—tea).

Back to Riddle

53. Holding up your hand you will see what you never have seen, never can see, and never will see—namely, the little finger as long as the finger next to it!

Back to Riddle

54. The Emperor of Russia issues manifestoes.[I-178] An ill-shod beggar manifests toes without his shoes!

Back to Riddle

55. To show Walsham How a good bishop is made.

Back to Riddle

56. There was certainly a tribe of Man—asses.

Back to Riddle

57. L. s. d.

Back to Riddle

58. A pillow.

Back to Riddle

59. Abused (a—b—used).

Back to Riddle

60. A settler.

Back to Riddle

61. Because John Burns.

Back to Riddle

62. It looks round!

Back to Riddle

63. A minute.

Back to Riddle

64. A deaf and dumb man cannot tickle nine persons, because he can only gesticulate (just tickle eight!).

Back to Riddle

65. London always began with an l, and end always began with an e!

Back to Riddle

66. Season.

Back to Riddle

67. The new moon, for the full moon is much lighter.

Back to Riddle

68. Island (la is the middle, is is the beginning, and is the end!).

Back to Riddle

69. Because! (bee caws).

Back to Riddle

70. The reading of the Dark Rebus

O
B e D

is—a little blackie in bed with nothing over him.

Back to Riddle

71. If a monkey is placed before a cross it at once gets to the top, for APE is then APEX.

Back to Riddle

72. The answer to this riddle, defined as “two heads and an application,” is a kiss.

Back to Riddle

73. The Latin expression of encouragement “macte” may be applied in its English equivalent in-crease to a batsman when an umpire says of him “not out” after a risky run.

Back to Riddle

74. The place which answers to the description “Half an inch (ch) before the trees (elms), half[I-179] a foot (fo), and half a yard (rd) after them leads us to an English town,” is Chelmsford.

Back to Riddle

75. The subject of the riddle, which none can locate, is nowhere. Cut asunder almost in the middle, it breaks into the opposite extreme, and becomes now here!

Back to Riddle

76. The two letters which in nine letters describe the position of one who has been left alone in his extremity are a b and one d. Abandoned.

Back to Riddle

77. Usher (us—her).

Back to Riddle

78. You can make a Maltese cross with less than twelve unbent and unbroken matches, by striking only one match and dropping it down his back. If the first fails, try another!

Back to Riddle

79. We may suppose that there were less vowels than we have now in the early days of Noe, when u and i were not there.

Back to Riddle

80. An orange (or—ange).

Back to Riddle

81. The moral taught to us by the old emblem of a weathercock in the shape of a fish on a church near Lewes is, “It is vain to aspire!”

Back to Riddle

82. FIDDLE.

Back to Riddle

83. The words “for the want of water we drank water, and if we had had water we should have drank wine,” were spoken by the crew of a vessel that could not cross the harbour bar for want of water, and who had no wine on board.

Back to Riddle

84.

The poor have two, the rich have none,
Millions have many, you have one,

is solved by O.

Back to Riddle

85. Money.

Back to Riddle

86. Had I been in Stanley’s place when Marmion cried “On, Stanley, on!” the resulting word on-i-on would have made the Scottish fray seem more like Irish stew.

Back to Riddle

87. The figure O.

[I-180]

Back to Riddle

88.

Let her be, or beat her,
Give her little ease;
Then in safety seat her
All among the bees,

is solved by A Queen Bee. The Bee is made up of the letter b, in Greek called beta, and two little es.

Back to Riddle

89. Its.

Back to Riddle

90. Inch—chin.

Back to Riddle

NUTS TO CRACK

1. CRAZY LOGIC

Can you prove that madman = madam is solved thus:—

A madman is a man beside himself. Therefore a madman = two men.

Madam is a woman. Woman is double you O man (w-o-man). Therefore madam = two men.

And as things which are equal to the same are equal to one another, therefore madman = madam.

Q. E. D.
(Quite easily Done.)

Back to Description

2. A BIT OF BOTANY

The water-plant is the Frogbit, which floats and spreads on the surface of ponds and pools.

Back to Description

3. The six islands buried in the lines—

He set down the answer to that sum at random.

By bold policy Prussia became a leading power.

A great taste for mosaic has arisen lately.

The glad news was swiftly borne over England.

At dusk, year after year, the old man rambled home.

The children cried, hearing such dismal tales.

are Sumatra, Cyprus, Formosa, Borneo, Skye, Malta.

Back to Description

4. The seven geographical names “buried” in the sentence, “We could hide a light royal[I-181] boat with a man or two; the skipper, though, came to a bad end,” are Deal, Troy, Witham, Esk, Perth, Baden, Aden.

Back to Description

5. The jumbled letter lines read thus:—

Let those who deal in mystic rhymes
This transposition trace;
And to The Standard send betimes
Each letter in its place.

Back to Description

Three little articles all in a line
Lead to a thousand, expressing,
If with another all these you combine,
What can be never a blessing—

is solved by ANATHEMA (an-a-the-M-a).

Back to Description

Ask a policeman, possibly he knows
In uniformed array
If not, an added letter plainly shows
How little he can say—

is solved by adding n to uniformed—uninformed.

Back to Description

8. The Ruling letters in:—

We rule the world, we letters five,
We rule the world, we do!
And of our number three contrive
To rule the other two—

are B. U. T. (beauty), and Y. Z. (wise head).

Back to Description

9. Many might punctuate the sentence, “Maud like the pretty girl that she was went for a walk in the meadows” by merely putting a full stop at the end of it. But why not make a dash after Maud?

Back to Description

10. The answer by Echo to

What were they who paid three guineas
To hear a tune of Paganini’s

is Pack o’ ninnies!

Back to Description

11. The verse in which only five different letters are used is—

[I-182]

It is nineteen tennis nets,
Nine in tents in tints intense.
Ten sent in inset in sets,
See it, test it, it is sense!

Back to Description

12. The catch sentence: “If is is not is and is not is is what is it is not is and what is it is is not if is not is is?” becomes intelligible if it is punctuated thus: If “is” is not “is,” and “is not” is “is,” what is it “is not” is, and what is it “is” is not, if “is not” is “is?”

Back to Description

13. The words on the placard were PALE ALE, and these through the steps described become PA-LE AP-LE, APPLE.

Back to Description

14. The reading of “Time flies you cannot they pass at such irregular intervals,” is as though it ran “You cannot time flies, they pass at such irregular intervals.”

Back to Description

ROYAL MEMORIES

15. I was reminded of Queen Victoria as I entered the South Kensington Museum at five minutes to one, because I noticed that the hands of my watch were so placed as to represent a very perfect V.

When I left the building it was twenty-five minutes and forty-five seconds to six, and then the hands, with the help of the seconds hand which crossed it, formed a very perfect A, and so reminded me of Prince Albert.

Back to Description

16. The solution of

CCC SAW

is “the season was backward.”

Back to Description

[I-183]

17. THE OLD LATIN LEGEND

AMANS TAM ERAT
HI DESINT HERO
AD DIGITO UT MANDO

reads off into excellent English thus:—

“A man’s tame rat hides in the road; dig it out man, do!”

Back to Description

18. The statement “I know that roseate hues preserve” does not imply that there is any curative virtue in rose-coloured rays, but asserts “I know that Rose ate Hugh’s preserve!”

Back to Description

19. The following exception was taken to Dr Fell’s diet for the sick of all sops:—

“Sure the doctor’s wits are failing,”
Cried a saucy wag.
“Allsopp’s ale the sick and ailing
To their bier will drag.”

Back to Description

20. The English dislocated sentence formed by these thirty-six letters:—

SAR BAB SAR BAB SAR BAB
SAR BAB SAR BAB SAR ARA

is, “A bar as a barb bars Barbara’s Barabbas.”

Back to Description

21. The Wiltshire farmer’s sentence—

“Igineyvartydreevriswutts”

when interpreted runs, “I gave him forty-three for his oats.”

Back to Description

22. Here is a tolerable rhyme to Chrysanthemum:—

Through gardens where appear
Beds of chrysanthemum,
We pass at eve to hear
Our choir their anthem hum.

Back to Description

23. This was, in brief, the pathetic tale of the three eggs—“Two bad!”

Back to Description

[I-184]

24. THE ANCIENT LEGEND

Doun tooth ers
A sy
Ouw ould bed
One by.

reads thus:—“Do unto others as you would be done by.”

Back to Description

25. There were but six persons in the vault which contained two grandmothers and their two grand-daughters; two husbands and their two wives; two fathers and their two daughters; two mothers and their two sons; two maidens and their two mothers; two sisters and their two brothers. Two widows had each one son, and each married the son of the other, and had a daughter by the marriage.

Back to Description

26. The supposed charm—

ground
turn evil star

given by the wise woman to a nervous couple, to counteract their evil star, and account for mysterious noises, is merely “Rats live underground,” turn being a direction to the solver.

Back to Description

27. The word composed of five varied vowels of foreign sound, with but one consonant between them, is oiseau, the French for bird. The three letters which flow in four are eau, water, which flows in the River Oise, and the other trio spell oie, a goose, which is found therein.

Back to Description

28. The Paradox—

What in his mind no man can find
Four symbols will display;
But only one remains behind
If one we take away—

is solved by Bone.

Back to Description

[I-185]

29. The barber who had placed in his window the notice—

“What do you think
I will shave you for nothing and give you a drink”

explained, to the man who expected a free shave and a cool drink, that the interpretation was really this:—“What? Do you think I will shave you for nothing, and give you a drink?”

Back to Description

30. The curious Latin label—

GENUI NE JAM
A
ICARUM.

has no reference to Icarus, or to flying machines. Its proper place was on a cask of “Genuine Jamaica Rum.”

Back to Description

31. The puzzle word is ipecacuanha.

Back to Description

32.

Johnson’s cat went up a tree,
Which was sixty feet and three;
Every day she climbed eleven,
Every night she came down seven.
Tell me, if she did not drop,
When her paws would touch the top—

is solved thus:—As each day and night the cat climbed up eleven feet, and came down seven, the daily upward gain was four feet, and thirteen days would bring her fifty-two feet up the tree. Then on the fourteenth day she mounted the remaining eleven feet, and was at the top, so that no coming down seven feet is to be taken into account, and she attains her place in fourteen days.

Back to Description

33.

A third of six behind them fix,
A third of six before;
Thus makes two nines, when all combines,
Exactly fifty-four—

[I-186]

is solved:—

IX NINE (the two nines.)

IX NINES = 54.

(S is a third of six) S

Back to Description

34. To bridge the moat, or space between the two squares which one match cannot span, place one match across one of the corners of the outer square, and the other from this to the inner square.

Back to Description

35.

We start when the ninth hour is past,
Then there’s an end of you.
A vengeful goddess shows at last
What Antifat will do—

is solved by attenuate (at ten-u-Ate, goddess of vengeance).

Back to Description

36. Mrs P.W. had only one guest to provide for. Her husband had invited his father’s brother-in-law, Jones, who was his brother’s father-in-law, because Mr P.W.’s brother had married Jones’ daughter, and his father-in-law’s brother, because he had himself married Jones’ niece, and also his brother-in-law’s father, as Mr P.W.’s sister married Jones’ son.

Back to Description

37. This sharp customer started with fivepence farthing, and gradually extracted from the landlord’s pocket a shilling and three farthings towards the eighteenpence which he spent in refreshments.

Back to Description

38. To form four triangles of equal size with six similar matches, place three of them in a triangle on the table, and hold or balance the other three above these, so as to form the skeleton of a pyramid.

Back to Description

39. The following couplet solves this question:—

Forty-five-years I had seen
When my bride was but fifteen

Back to Description

[I-187]

40. The lad gave tenpence each to a grandfather, his son, and his grandson.

Back to Description

41. Nell’s reply to Tom, when he said, with a yawn, “I wish we could play lawn-tennis!” “Odioso ni mus rem. Moto ima os illud nam,” was not Latin, but good sound English. Read each word in its order backwards, and you have-- “Oh! so do I in summer. Oh, Tom! am I so dull, I man?”

Back to Description

42. The policeman who was looking up the road for motor-car scorchers was able to see that his mate, who was looking down the road, was smiling, because they stood face to face.

Back to Description

43.

Twenty-seven with three nines
You and I can score;
Anyone on other lines
Can extend them more.
Who can write them to be seen
Equal only to sixteen?—

is solved thus:—Two of the three nines are reversed, and then

966 = 16.

Back to Description

44. The trying sentence, “that that is is that that is not is not is not that it it is,” is cleared thus by proper punctuation:—That that is, is; that that is not, is not. Is not that it? It is.

Back to Description

45. A L L O is “Nothing after all.”

Back to Description

46. The proverb with missing consonants is—Give a dog a bad name and hang him.

Back to Description

47. If to the thirteen upright strokes—

| | | | | | | | | | | | |

thirteen more are added, the word HOTTENTOT may be formed.

Back to Description

48. A coroner could, after signing his name, write down his official position with c or one r.

Back to Description

PART II.

	PAGE
Optical Illusions	II-1
Freaks of Figures	II-20
Chess Cameos	II-26
Science at Play	II-58
Curious Calculations	II-114
Word and Letter Puzzles	II-147
Solutions	II-167

[II-1]

OPTICAL ILLUSIONS

No. I.—SWALLOWED!

Take a small card and place it on its longer edge upon the dotted line. Now set the picture in a good light on the table, and let your head drop gradually towards the card until you almost touch it with your nose. You will see the bird fly into the jaws of the snake!

AMUSING PROBLEMS

THE CARPENTER’S PUZZLE

1. A carpenter was called in to mend a hole in a wooden floor. The gap was two feet wide, and twelve feet long, while the only board at hand was three feet wide, and eight feet long.

This had been put aside as useless, but, on catching sight of it, the carpenter ran his rule over it and said that he could make a perfect fit, and cover all the hole by cutting the board into two pieces. How did he do this?

Solution

[II-2]

No. II.—AN ILLUSION OF ROTATION

This most interesting optical illusion was devised by Professor Thompson some years ago:—

If the illustration is moved by hand in a small circle on the level, with such motion as is given in rinsing out a bowl, the circles of the larger diagram will seem to revolve in the direction in which the paper is moved, while the cogs of the smaller diagram will apparently turn slowly in the opposite direction.

[II-3]

No. III.—WHIRLING WHEELS

Here is another combination of the clever illusion of the whirling wheels.

If a rapid rotating motion is given to the diagram, each circle will seem to revolve, and the cog wheel in the centre will appear to move slowly round in the opposite direction.

GOLDEN PIPPINS

2. A man leaves an orchard of forty choice apple trees to his ten sons. On the first tree is one apple, on the second there are two, on the third three, and so on to the fortieth, on which there are forty.

Each son is to have four of the trees, and on them an equal number of the apples. How can they thus apportion the trees, and how many apples will each son have? Here is one way:—

1	2	3	4	5	6	7	8	9	10
20	19	18	17	16	15	14	13	12	11
21	22	23	24	25	26	27	28	29	30
40	39	38	37	36	35	34	33	32	31
82	82	82	82	82	82	82	82	82	82

Can you find another perfect solution?

Solution

[II-4]

No. IV.—AN ILLUSION OF MOTION

We call very particular attention to this fascinating illustration of the fact that the mind and eye may receive and register false impressions under quite simple conditions:—

Hold this at rather more than reading distance, upright, and move it steadily up and down. The dark line will soon seem to slide up and down upon the perpendicular line. It will be better seen if drawn to pattern on a card.

[II-5]

No. V.—ARE THEY PARALLEL?

As the eye falls upon the principal lines of this interesting diagram, an immediate impression is formed that they are not parallel.

This, however, is a most curious illusion, created in the mind entirely by the short sloping lines, as is found at once by the simple test of measurement.

AN AWKWARD FIX

3. With no knowledge of the surrounding district, I was making my way to a distant town through country roads, guided by the successive sign-posts that were provided.

Coming presently to four cross-roads I found to my dismay that some one had in mischief uprooted the sign-post and thrown it into the ditch. In this perplexing fix how could I find my way? A bright thought struck me. What was it?

Solution

LINKED SWEETNESS LONG DRAWN OUT

4. As I stood on the platform at a quiet country station, an engine, coming along from my left at thirty miles an hour, began to whistle when still a mile away from me. The shrill sound continued until the engine had passed a mile and a half to my right. For how long was I hearing its whistle?

Solution

[II-6]

No. VI.—ILLUSION OF LENGTH

In this curious optical illusion the lines are exactly equal in length.

The eye is misled by the effect which the lines drawn outward and inward at their ends produce upon the mind and sight.

ELASTIC QUARTERS

In room marked A two men were placed,
A third he lodged in B;
The fourth to C was next assigned,
The fifth was sent to D.
In E the sixth was tucked away,
F held the seventh man;
For eighth and ninth were G and H,
Then back to A he ran.
Thence taking one, the tenth and last,
He lodged him safe in I;
Thus in nine rooms ten men found place,
Now can you tell me why?

Solution

EXCLUDED DAYS

6. Are there any particular days of the week with which no new century can begin?

Solution

[II-7]

No. VII.—ILLUSION OF HEIGHT

These straight lines, at right angles to each other, are, though they do not seem to be, exactly equal in length.

This and similar illusions are probably due to the variation of the vague mental standard which we unconsciously employ, and to the fact that the mind cannot form and adhere to a definite scale of measurement.

DRIVING POWER

7. Why has a spliced cricket bat such good driving power? and why is the “follow through” of the head of a golf club so telling in a driving stroke?

Solution

THE BUSY BOOKWORM

8. On my bookshelf in proper order stand two volumes. Each is two inches thick over all, and each cover is an eighth of an inch in thickness. How far would a bookworm have to bore in order to penetrate from the first page of Vol. I. to the last page of Vol. II.?

Solution

[II-8]

No. VIII.—ILLUSION OF DIRECTION

Can you decide at a glance which of the two lines below the thick band is a continuation of the line above it?

Make up your mind quickly, and then test your decision with a straight edge.

A TERRIBLE TUMBLE

9. From what height must a man fall out of an airship—screaming as he goes overboard—so as to reach the earth before the sound of his cry?

N.B.—Resistance of the air, and the acoustical fact that sound will not travel from a rare to a dense atmosphere, are to be disregarded.

Solution

IN A PREDICAMENT

10. Imagine a man on a perfectly smooth table surface of considerable size, in a vacuum, where there is no outside force to move him, and there is no friction. He may raise himself up and down, slide his feet about, double himself up, wave his arms, but his centre of gravity will be always vertically above the same point of the surface.

How could he escape from this predicament, if it was a possible one?

Solution

[II-9]

No. IX.—THINGS ARE NOT WHAT THEY SEEM

It is difficult, even after measurement, to believe that these figures are of the same size.

But they will stand the test of measurement.

A CLIMBING MONKEY

11. A rope passes over a single fixed pulley. A monkey clings to one end of the rope, and on the other end hangs a weight exactly as heavy as the monkey. The monkey presently starts to climb up the rope. Will he succeed?

Solution

GAINING GROUND

12. Seeing that the tension on a pair of traces tends as much to pull the horse backward as it does to pull the carriage forward, why do the traces move on at all?

Solution

[II-10]

No. X.—THE SHIFTING BRICK

A very curious and interesting form of optical illusion is well illustrated by what may be called “the shifting brick.”

The central brick, drawn to show all its edges, as though it were made of glass, will assume the form indicated by one or other of the smaller bricks at its right and left, according to the way in which the eyes accommodate themselves for the moment to one pattern or to the other. If you do not see this at first, look steadily for awhile at the pattern you desire.

ASK A CYCLIST

13. Why does a rubber tyre leave a double rut in dust, and a single one in mud?

Solution

TODHUNTER’S UNIQUE PUZZLE PROBLEM

14. If two cats, on opposite sides of a sharply sloping roof, are on the point of slipping off, which will hold on the longest?

Solution

[II-11]

No. XI.—AN ILLUSION WITH COINS

If you place four coins in the positions shown at the top of this diagram, and attempt, or challenge some one to attempt, without any measuring, to move the single coin down in a straight line until the spaces from C to D on either side exactly equal the distance from A to B—

It must drop as far as is shown here, which seems to the unaided eye to be too far.

This excellent illusion can be shown as an after-dinner trick with four napkin-rings.

[II-12]

No. XII.—THE FICKLE BARREL

Here is another excellent optical illusion. Look attentively at the diagram below, and notice in which direction you apparently look into it, as though it were an open cask.

Now shake the paper, or move it slightly, and you will find, more often than not, that you seem to see into it in quite the opposite direction.

HEADS I WIN!

15. I hold a penny level between my finger and thumb, and presently let it fall from the thumb by withdrawing my finger. It makes exactly a half-turn in falling through the first foot. If it starts “heads,” how far must it fall to bring it “heads” to the floor?

Solution

HE DID IT!

16. “They call these safety matches,” said Funnyboy at his club one day, “and say that they strike only on the box. Don’t believe it! I can strike them quite easily on my boot.”

No sooner said than done. He took out a match, struck it on his boot, and—phiz!—it was instantly alight. The box was handed round, and match after match was struck by the bystanders on their boots, but not one of them could succeed.

“You don’t give the magic touch,” said Funnyboy, as he gaily struck another. How did he do it?

Solution

[II-13]

No. XIII.—A STRANGE OPTICAL ILLUSION

How many cubes can you see as you look at the large diagram? The two smaller ones should be looked at first alternately, and they will assist the eye to see at one time six, and at another time seven, very distinct cubes.

[II-14]

No. XIV.—A CIRCULAR ILLUSION

This curious optical illusion is not easily followed by eye to the finish of the several lines.

Each short line is, in fact, part of the circumference of a circle, and the circles when completed will be found to be accurately concentric. It would seem at first sight that the lines are taking courses which would eventually meet at some point common to them all.

A CYCLE SURPRISE

17. We commend this curious point to the special attention of cyclists:—

A bicycle is stationary, with one pedal at its lowest point. If this bicycle is lightly supported, and the bottom pedal is pulled backward, what will happen?

Solution

[II-15]

No. XV.—THE GHOST OF A COIN

A most remarkable optical illusion is produced by the blending of the dark and light converging rays of this diagram. Stand with your back to the light, hold the page, or better still, the diagram copied on a card, by the lower right-hand corner, give it a continuous revolving movement in either direction, and the visible ghost of a silver coin, sometimes as large as sixpence, sometimes as large as a shilling, will appear! Where can it come from?

ROUGH AND READY

18. A merchant has a large pair of scales, but he has lost his weights, and cannot at the moment replace them. A neighbour sends him six rough stones, assuring him that with them he can weigh any number of pounds, from 1 to 364. What did each stone weigh?

Solution

[II-16]

No. XVI.—A TAME GOOSE

Here is a pretty form of our first illusion:—

Place the edge of a card on the dotted line, look down upon it in a good light, and, as you drop your face till it almost touches the card, you will see the goose move towards the sugar in the little maiden’s hand.

REJECTED ADDRESSES

19. A wheel is running along a level road, and a small clot of mud is thrown from the hindermost part of the rim. What happens to it? Does it ever renew its acquaintance with the wheel that has thus rejected it?

Solution

[II-17]

No. XVII.—ILLUSION OF LENGTH

Here is another method by which an optical illusion of length is very plainly shown:—

Judged by appearances, the line A B in the larger figure is considerably longer than the line A B below it, but tested by measurement they are exactly equal.

THE CARELESS CARPENTER

20. A village carpenter undertook to make a cupboard door. When he began to put it in its place it was too big, so he took it back to his workshop to alter it. Unfortunately he now cut it too little. What could he do? He determined to cut it again, and it at once became a good fit. How was this done?

Solution

[II-18]

No. XVIII.—PERPENDICULAR LINES

Here is another excellent illustration that seeing is not always believing.

No one could suppose at first sight that these four lines are perfectly straight and parallel, but they will stand the test of a straight edge. The divergent rays distract the vision.

BY THE COMPASS

21. If from the North Pole you start sailing in a south-westerly direction, and keep a straight course for twenty miles, to what point of the compass must you steer to get back as quickly as possible to the Pole?

Solution

[II-19]

No. XIX.—ILLUSION OF PERSPECTIVE

The optical illusion in the picture which we reproduce is due to the defective drawing of the two men on the platform. In actual size upon the paper the further man looks much taller than the other.

Measurement, however, shows the figures to be exactly of a height. This illusion is due to the fact that the head of the further man is quite out of perspective. If he is about as tall as the other, and on level ground, both heads should be about on the same line. As drawn, he is, in fact, a monster more than eight feet high.

DICK IN A SWING

22. If Dick, who is five feet in height, stands bolt-upright in a swing, the ropes of which are twenty feet long, how much further in round numbers do his feet travel than his head in describing a semi-circle?

Solution

[II-20]

No. XX.—OUR BLIND SPOT

Here is an excellent and very simple illustration of a well-known optical curiosity:—

Hold this picture at arm’s length in the right hand, hold the left hand over the left eye, and draw the picture towards you gradually, looking always at the black cross with the right eye. The black disc will presently disappear, and then come into sight again as you continue to advance the paper.

A POSER

23. Can you name nine countries in Europe of which the initial letters are the same as the finals?

Solution

FREAKS OF FIGURES

A HANDY SHORT CUT

Here is a delightfully simple way in which market gardeners, or others who buy or sell weighty produce, can check their invoices for potatoes or what not.

Say, for example, that a consignment weighs 6 tons, 10 cwts., 1 qr. Then, since 20 cwts. are to a ton as 20s. are to a pound, and each quarter would answer on these lines to 3d., we can at once write down £6 10s. 3d., as the price at £1 the ton. On this sure basis any further calculation is easily made.

[II-21]

No. XXI.—THE PERSISTENCE OF VISION

HOW TO SEE THE GHOST

Look steadily, in a good light, for thirty seconds at the cross in the eye of the pictured skull; then look up at the wall or ceiling, or look fixedly at a sheet of paper for another thirty seconds, when a ghost-like image of the skull will be developed.

NOT SO FAST!

A gardener, when he had planted 100 trees on a line at intervals of 10 yards, was able to walk from the first of these to the last in a few seconds, for they were set on the circumference of a circle!

[II-22]

No. XXII.—THE PERSISTENCE OF VISION

Here is another example of what is known as the persistence of vision:—

Look fixedly for some little time at this grotesque figure, then turn your eyes to the wall or ceiling, and you will in a few seconds see it appear in dark form upon a light ground.

A PUZZLE NUMBER

The sum of nine figures a number will make,
Of which just a third will remain
If fifty away from the whole you should take,
Thus turning a loss to a gain.

It needs something more than mere arithmetic to discover that the solution to this puzzle is XLV, the sum of the nine digits, for if the L is removed, XV, the third of XLV, remains.

[II-23]

No. XXIII.—ANOTHER PARALLEL FREAK

Here is another curious illusion:—

The four straight lines are perfectly parallel, but the contradictory herring-bones disturb the eye.

THE MAGIC OF FIGURES

If our penny had been current coin in the first year of the Christian era, and had been invested at compound interest at five per cent., it would have amounted in 1905 to more than £132,010,000,000,000,000,000,000,000,000,000,000,000.

This gigantic sum would afford an income of £101,890,000,000,000,000,000 every second to every man, woman, and child in the world, if we take its population to be 1,483,000,000 souls!

Absurdly small in contrast to these startling figures is the modest eight shillings which the same penny would have yielded in the same time at simple interest.

[II-24]

No. XXIV.—ILLUSION OF LENGTH

Here in another form is shown the illusion of length.

At first sight it seems that the two upright lines are distinctly longer than the line that slopes, but it is not so.

WHAT IS YOUR AGE?

Here is a neat method of discovering the age of a person older than yourself:—

Subtract your own age from 99. Ask your friend to add this remainder to his age, and then to remove the first figure and add it to the last, telling you the result. This will always be the difference of your ages. Thus, if you are 22, and he is 35, 99 - 22 = 77. Then 35 + 77 = 112. The next process turns this into 13, which, added to your age, gives his age, 35.

[II-25]

No. XXV.—THE HONEYCOMB ILLUSION

In this diagram one hundred and twenty-one circular spots are grouped in a diamond.

If we half close our eyes, and look at this through our eye-lashes, we find that it takes on the appearance of a section of honeycomb, with hexagonal cells.

MULTIPLICATION NO VEXATION

Here is a ready method for multiplying together any two numbers between 12 and 20.

Take one of the two numbers and add it to the unit digit of the other. Beneath the sum thus obtained, but one place to the right, put the product of the unit digits of the two original numbers.

The sum of these new numbers is the product of the numbers that were chosen. Thus:—

19 × 13.	(19 + 3)	=	22
(9 × 3)		=	27
			247

[II-26]

No. XXVI.—CHESS CAMEO
By Dr Gold
A Chess Joke

BLACK

WHITE

Black has made an illegal move. He must replace this, and move his king as the penalty. White then mates on the move.

Solution

[1]SHOT IN A PYRAMID

Here is a method for determining the total number of balls in a solid pyramid built up on a square base:—

Multiply the number of shot on one side of the base line by 2, add 3, multiply by the number on the base line, add 1, multiply again by the number on the base, and finally divide by 6. Thus, if the base line is 12—

12 × 2 + 3 = 27; 27 × 12 + 1 = 325; 325 × 12 = 3900; and 3900 ÷ 6 = 650, which is the required number.

[1] N.B.—This title does not imply a tragedy.

[II-27]

No. XXVII.—CHESS CAMEO
By A. Cyril Pearson
A Chess Puzzle

BLACK

WHITE

White might have given mate on the last move. White now to retract his move, and mate at once.

Show by analysis the mating position.

Solution

[II-28]

No. XXVIII.—CHESS CAMEO
By J. G. Campbell
A very Clever Device

BLACK

WHITE

White to play and draw.

Solution

COMIC ARITHMETIC

“Now, boys,” said Dr Bulbous Roots to class, “you shall have a half-holiday if you prove in a novel way that 10 is an even number.”

Next morning, when the doctor came into school, he found this on the blackboard:—

	SIX	=	6
	SIX	=	9
By subtraction	S	=	-3
	SEVEN	=	7
	S	=	-3
Therefore	SEVEN	=	10

Q. E. D.
(Quite easily done!)

The half-holiday was won.

[II-29]

No. XXIX.—CHESS CAMEO
By E. B. Cook
A Fine Example

BLACK

WHITE

White to play, and draw.

Solution

[II-30]

No. XXX.—CHESS CAMEO
By A. F. Mackenzie
A Prize Problem

BLACK

WHITE

White to play, and mate in two moves.

There are twelve variations in this beautiful problem.

Solution

MAGIC MULTIPLICATION

It will interest all who study short cuts and contrivances to know that a novice at arithmetic who has mastered simple addition, and can multiply or divide by 2, but by no higher numbers, can, by using all these methods, multiply any two numbers together easily and accurately.

This is how it is done:—

Write down the numbers, say 53 and 21, divide one of them by 2 as often as possible, omitting remainders, and multiply the other by 2 the same number of times; set these down side by side, as in the instance given below, and wherever there is an even number on the division side, strike out the corresponding number on the multiplication side. Add up what remains on that side, and the sum is done. Thus:—

53	21)
26	(42)
13	84)
6	(168)
3	336)
1	672)
	1113)

which is 53 multiplied by 21.

[II-31]

No. XXXI.—CHESS CAMEO
By A. W. Galitzky
A Prize Problem

BLACK

WHITE

White to play, and mate in two moves.

Solution

[II-32]

No. XXXII.—CHESS CAMEO
By S. Loyd

BLACK

WHITE

White to play, and mate in two moves.

Solution

[II-33]

No. XXXIII.—CHESS CAMEO
By B. G. Laws
A Prize Problem

BLACK

WHITE

White to play, and mate in two moves.

Solution

PERFECT NUMBERS

The following particulars about a very rare property of numbers will be new and interesting to many of our readers:—

The number 6 can only be divided without remainder by 1, 2, and 3, excluding 6 itself. The sum of 1 + 2 + 3 is 6. The only exact divisors of 28 are 1, 2, 4, 7, and 14, and the sum of these is 28; 6 and 28 are therefore known as perfect numbers.

The only other known numbers which fulfil these conditions are 496; 8128; 33,550,336; 8,589,869,056; 137,438,691,328; and 2,305,843,008,139,952,128. This most remarkable rarity of perfect numbers is a symbol of their perfection.

[II-34]

No. XXXIV.—CHESS CAMEO
By Emil Hoffmann

BLACK

WHITE

White to play, and mate in two moves. There are no less than twelve variations!

Solution

[II-35]

No. XXXV.—CHESS CAMEO
By J. Pospicil
A Prize Problem

BLACK

WHITE

White to play, and mate in two moves.

Solution

AMICABLE NUMBERS

Somewhat akin to perfect numbers are what are known as amicable numbers, of which there is a still smaller quantity in the realm of numbers.

The number 220 can be divided without remainder only by 1, 2, 4, 5, 10, 11, 22, 44, 55, and 110, and the sum of these divisors is 284. The only divisors of 284 are 1, 2, 4, 71, and 142, and the sum of these is 220.

The only other pairs of numbers which fulfil this curious mutual condition, that the sum of the divisors of each number exactly equals the other number, are 17,296 with 18,416, and 9,363,584 with 9,437,056. No other numbers, at least below ten millions, are in this way “amicable.”

[II-36]

No. XXXVI.—CHESS CAMEO
By H. J. C. Andrews
A Prize Problem

BLACK

WHITE

White to play, and mate in two moves.

Solution

[II-37]

No. XXXVII.—CHESS CAMEO
By Alfred de Musset
A Gem of the First Water

BLACK

WHITE

White to play, and mate in three moves.

Solution

A SWARM OF ONES

1	×	9	+	2	=	11
12	×	9	+	3	=	111
123	×	9	+	4	=	1111
1234	×	9	+	5	=	11111
12345	×	9	+	6	=	111111
123456	×	9	+	7	=	1111111
1234567	×	9	+	8	=	11111111
12345678	×	9	+	9	=	111111111

[II-38]

No. XXXVIII.—CHESS CAMEO
By Frank Healey
A Masterpiece

BLACK

WHITE

White to play, and mate in three moves.

Solution

DIVINATION BY FIGURES

There is a pleasant touch of mystery in the following method of discovering a person’s age:—Ask any such subjects of your curiosity to write down the tens digit of the year of their birth, to multiply this by 5, to add 2 to the product, to multiply this result by 2, and finally to add the units digit of their birth year. Then, taking the paper from them, subtract the sum from 100. This will give you their age in 1896, from which their present age is easily determined.

[II-39]

No. XXXIX.—CHESS CAMEO
By Frank Healey
The “Bristol Prize Problem”

BLACK

WHITE

White to play, and mate in three moves.

Solution

FUR AND FEATHERS

As I came in after a day among the birds and rabbits, the keeper asked me—“Well, sir, what sport?” I replied, “36 heads and 100 feet.” It took him some time to calculate that I had accounted for 22 birds and 14 rabbits.

[II-40]

No. XL.—CHESS CAMEO
By J. E. Campbell
Splendid Strategy

BLACK

WHITE

White to play, and mate in three moves.

Solution

JUGGLING WITH THE DIGITS

The nine digits can be arranged to form fractions equivalent to

13 14 15 16 17 18 19

thus:—

582317469 = 13 795631824 = 14 297314865 = 15 294317658 = 16 527436918 = 17 932174568 = 18 836175249 = 19

[II-41]

No. XLI.—CHESS CAMEO
By W. Grimshaw

BLACK

WHITE

White to play, and mate in three moves.

Solution

[II-42]

No. XLII.—CHESS CAMEO
By S. Loyd

BLACK

WHITE

White to play, and mate in three moves.

Solution

A MOTOR PROBLEM

This motor problem will be new and amusing to many readers:—

Let m be the driver of a motor-car, working with velocity v. If a sufficiently high value is given to v, it will ultimately reach pc. In most cases v will then = o. For low values of v, pc may be neglected; but if v be large it will generally be necessary to square pc, after which v will again assume a positive value.

By a well-known elementary theorem, pc + lsd = (pc)², but the squaring may sometimes be effected by substituting x³ (or × × ×) for lsd. This is preferable, if lsd is small with regard to m. If lsd be made sufficiently large, pc will vanish.

Now if jp be substituted for pc (which may happen if the difference between m and pc be large) the solution of the problem is more difficult. No value of lsd can be found to effect the squaring of jp, for, as is well-known, (jp)² is an impossible quantity.

[II-43]

No. XLIII.—CHESS CAMEO
By J. G. Campbell

BLACK

WHITE

White to play, and mate in three moves.

Solution

[II-44]

No. XLIV.—CHESS CAMEO
By Frank Healey

BLACK

WHITE

White to play, and mate in three moves.

Solution

A NEAT METHOD OF DIVISION

To divide any sum easily by 99, cut off the two right-hand figures of the dividend and add them to all the others. Set down the result of this in line below, and then repeat this process until no figures remain on the left to be thus dealt with.

Now draw a line down between the tens and hundreds columns, and add all up on the left of it, thus:—

8694		32		120		78
87		26		1		98
1		13				99
		14		121	and	99	over.
8782	and	14	over.	In other words, 122.

The last number on the right of the lines shows always the remainder. If this should appear as 99 (as in the second example above), add one to the number on the left.

[II-45]

No. XLV.—CHESS CAMEO
By Blumenthal and Kund

BLACK

WHITE

White to play, and mate in three moves.

Solution

[II-46]

No. XLVI.—CHESS CAMEO
By A. F. Mackenzie
A Prize Problem

BLACK

WHITE

White to play, and mate in three moves.

Solution

A SMART SCHOOLBOY

The question, “How many times can 19 be subtracted from a million?” was set by an examiner, who no doubt expected that the answer would be obtained by dividing a million by 19. One bright youth, however, filled a neatly-written page with repetitions of

1,000,000	1,000,000	1,000,000
19	19	19
999,981	999,981	999,981

and added at the foot of the page, “N.B.—I can do this as often as you like.”

There was a touch of unintended humour in this, for, after all, the boy gave a correct answer to a badly worded question.

[II-47]

No. XLVII.—CHESS CAMEO
By A. Cyril Pearson

BLACK

WHITE

White to play, and mate in three moves.

Solution

[II-48]

No. XLVIII.—CHESS CAMEO
By Frank Healey
Quite a Gem

BLACK

WHITE

White to play, and mate in three moves.

Solution

LEWIS CARROLL’S SHORT CUT

Here is a very smart and very simple method of dividing any multiple of 9 by 9, from the fertile brain of Lewis Carroll:—Place a cypher over the final figure, subtract the final figure from this, place the result above in the tens place, subtract the original tens figure from this, and so on to the end. Then the top line, excluding the intruded cypher, gives the result desired. Thus:—

36459 ÷ 9 = 4051,0 36459 = 4051.

[II-49]

No. XLIX.—CHESS CAMEO
By A. Bayersdorfer

BLACK

WHITE

White to play, and mate in three moves.

Solution

ANOTHER FREAK OF FIGURES

1	×	8	+	1	=	9
12	×	8	+	2	=	98
123	×	8	+	3	=	987
1234	×	8	+	4	=	9876
12345	×	8	+	5	=	98765
123456	×	8	+	6	=	987654
1234567	×	8	+	7	=	9876543
12345678	×	8	+	8	=	98765432
123456789	×	8	+	9	=	987654321

[II-50]

No. L.—CHESS CAMEO
By J. Dobrusky

BLACK

WHITE

White to play, and mate in three moves.

Solution

DIVINATION BY NUMBERS

Here is one of the methods by which we can readily discover a number that is thought of. The thought-reader gives these directions to his subject: “Add 1 to three times the number you have thought of; multiply the sum by 3; add to this the number thought of; subtract 3, and tell me the remainder.” This is always ten times the number thought of. Thus, if 6 is thought of—6 × 3 + 1 = 19; 19 × 3 = 57; 57 + 6 - 3 = 60, and 60 ÷ 10 = 6.

[II-51]

No. LI.—CHESS CAMEO
By Konrad Bayer

BLACK

WHITE

White to play, and mate in three moves.

Solution

COINCIDENCES

Here is a curious rough rule for remembering distances and sizes:—

The diameter of the earth multiplied by 108 gives approximately the sun’s diameter. The diameter of the sun multiplied by 108 gives the mean distance of the earth from the sun. The diameter of the moon multiplied by 108 gives the mean distance of the moon from the earth.

[II-52]

No. LII.—CHESS CAMEO
By J. Berger

BLACK

WHITE

White to play, and mate in three moves.

Solution

PERSONAL ARITHMETIC

Says Giles, “My wife and I are two,
Yet faith I know not why, sir.”
Quoth Jack, “You’re ten, if I speak true,
She’s one, and you’re a cypher!”

[II-53]

No. LIII.—CHESS CAMEO
By H. F. L. Meyer

BLACK

WHITE

White to play, and mate in three moves.

Solution

DIVISION BY SUBTRACTION

Here is a curious and quite uncommon method of dividing any multiple of 11 by 11.

Set down the multiple of 11, place a cypher under its last figure, draw a line, and subtract, placing the first remainder under the tens place. Subtract this from the next number in order, and so on throughout, adding in always any number that is carried. Thus:—

363	56408	375034
0	0	0
33	5128	34094

[II-54]

No. LIV.—CHESS CAMEO
By Frank Healey

BLACK

WHITE

White to play, and mate in three moves.

Solution

LUCK IN ODD NUMBERS

Perhaps the old saying, “there is luck in odd numbers,” may have some connection with the curious fact that the sum of any quantity of consecutive odd numbers, beginning always with 1, is the square of that number. Thus:—

1 + 3 + 5	=	9	=	3	×	3.
1 + 3 + 5, etc., up to 17	=	81	=	9	×	9.
1 + 3 + 5, etc., up to 99	=	2500	=	50	×	50.

[II-55]

No. LV.—CHESS CAMEO
By Frank Healey

BLACK

WHITE

White to play, and mate in three moves.

Solution

THE VERSATILE NUMBER

In the number 142857, if the digits which belong to it are in succession transposed from the first place to the end, the result is in each case a multiple of the original number. Thus:—

285714	=	142857	×	2
428571	=	142857	×	3
571428	=	142857	×	4
714285	=	142857	×	5
857142	=	142857	×	6

[II-56]

No. LVI.—CHESS CAMEO
By J. E. Campbell

BLACK

WHITE

White to play, and mate in three moves.

Solution

A PARADOX

By the following simple method, a plausible attempt is made to prove that 1 is equal to 2:—

Suppose that a = b, then

ab		=	a²
∴	ab - b²	=	a² - b²
∴	b(a - b)	=	(a + b)(a - b)
∴ b		=	a + b
∴ b		=	2b
∴ 1		=	2

This process only proves in reality that 0 × 1 = 0 × 2, which is true.

[II-57]

No. LVII.—CHESS CAMEO
Double First Prize
By A. Cyril Pearson

BLACK

WHITE

White to play, and mate in four moves.

Solution

QUICK CALCULATION

Few people know a very singular but simple method of calculating rapidly how much any given number of pence a day amounts to in a year. The rule is this:—Set down the given number of pence as pounds; under this place its half, and under that the result of the number of original pence multiplied always by five. Take, for example, 7d a day:—

£7	0	0
3	10	0
	2	11
£10	12	11

The reason for this is evident as soon as we remember that the 365 days of a year may be split up into 240, 120, and 5, and that 240 happens to be the number of pence in a pound.

[II-58]

SCIENCE AT PLAY

No. LVIII.—THE GEARED WHEELS

A small wheel with ten teeth is geared into a large fixed wheel which has forty teeth. This small wheel, with an arrow mark on its highest cog, is revolved completely round the large wheel. How often during its course is the arrow pointing directly upwards? Here is a diagram of the starting position.

Solution

[II-59]

No. LIX.—ADVANCING BACKWARDS

Here is a most curious and interesting question:—When an engine is drawing a train at full speed from York to London, what part of the train at any given moment is moving towards York?

At any time, when the engine is drawing a train at full speed from York to London, that part of the flange of each wheel which is for the moment at its lowest is actually moving backwards towards York.

For any point, such as A, on the circumference of the tyre, describes in running along a series of curves, as shown by full lines in the diagram; and any point, B, on the outer edge of the flange, follows a path shown by the dotted curves.

If these lines are followed round with a pencil in the direction of the arrows, it will be found that the point on the flange actually moves backwards as it passes below the track, while the point A, as it completes each curve, is at rest for the instant on the track, just before it starts afresh. The speed of the train does not affect these very curious facts.

[II-60]

No. LX.—THE FIFTEEN BRIDGES

In the subjoined diagram A and B represent two islands, round which a river runs as is indicated, with fifteen connecting bridges, that lead from the islands to the river’s banks.

Can you contrive to pass in turn over all these bridges without ever passing over the same one twice?

Solution

ARRANGING THE DIGITS

In a school where two boys were taught to think out the bearings of their work, a sharp pupil remarked that 100 is represented on paper by the smallest digit and two cyphers, which are in themselves symbols of nothing. The master, quick to catch any signs of mental activity, took the opportunity to propound to his class the following ingenious puzzle:—How can the sum of 100 be represented exactly in figures and signs by making use of all the nine digits in their reverse order? This is how it is done:—

9 × 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 100.

Another ingenious method of using the nine digits, so that by simple addition they sum up to exactly 100, and each is used once only, is this:—

15 + 36 + 47 = 98 + 2 = 100

Here is another arrangement by which the nine digits written in their inverse order can be made to represent exactly 100:—

98 - 76 + 54 + 3 + 21 = 100.

Here is yet another way of arriving at 100 by using each of the digits, this time with an 0:—

40¹⁄₂
59³⁸⁄₇₆
100

[II-61]

No. LXI.—LOOPING THE LOOP

Here is quite a pretty scientific experiment, which any one of a handy turn can construct and arrange:—

The spiral track is formed of two wires bent, and connected by curved cross-pieces. The upper twist is turned so that the ball starts on a horizontal course.

During the accelerated descent the ball acquires momentum enough to keep it on the vertical track, held outwardly against the wires by centrifugal force.

Convenient proportions are: height of spiral two feet, diameter six inches, and wire rails three-quarters of an inch apart.

[II-62]

No. LXII.—A MECHANICAL BIRD

A close approach to an ideal flying machine can be made with a little ingenuity. Two Y-shaped standards, secured to the backbone rod, support two wires which carry wings of thin silk, provided with light stays, and connected at their inner corners with the backbone by threads.

Rubber bands are attached to a loop on the inner end of the crank shaft, and secured to a post at the rear. These are twisted by turning the shaft with the cross wire, and when the tension is released the wings beat the air and carry the bird forward. It is known as Penaud’s mechanical bird, and has been sold as an attractive toy.

[II-63]

No. LXIII.—LINE OF SWIFTEST DESCENT

A simple apparatus constructed on the lines of this illustration will give an interesting proof of the laws which govern falling bodies on an inclined plane or on a curved path.

In the case of the inclined plane the ball is governed by the usual law which controls falling bodies. In that of the concave circular curve, as it is accelerated rapidly at the start, it makes its longer journey in quicker time. In the case of the cycloidal curve it acquires a high velocity. This curve has therefore been called “the curve of swiftest descent,” as a falling body passes over it in less time than upon any path except the vertical.

[II-64]

No. LXIV.—A CENTRIFUGAL RAILWAY

Here is another very simple and pretty illustration of the natural forces which come into play in “looping the loop.”

This scientific toy on a small scale may be easily made, if care is taken that the height of the higher end of the rails is to the height of the circular part in a greater ratio than 5 to 4.

A ball started at the higher end follows the track throughout, and at one point is held by centrifugal force against the under side of the rails, against the force of gravity.

[II-65]

No. LXV.—A QUESTION OF GRAVITY

If a ball is fired point blank from a perfectly horizontal gun, and travels half a mile over a level plain before it touches ground, and another similar ball is at the same moment dropped from the same height by some mechanical means, the two balls will touch ground simultaneously. The flight, however long, of one through the air has no influence upon the force of gravity, which draws it earthward at the same resistless rate as it draws the other that is merely dropped.

A SHORT CUT

A quick method of multiplying any number of figures by 5 is to divide them by 2, annexing a cypher to the result when there is no remainder, and if there is any remainder annexing a 5. Thus:—

464 × 5 = 2320; 464 ÷ 2 = 232, annex 0, = 2320.
753 × 5 = 3765; 753 ÷ 2 = 376, annex 5, = 3765.

[II-66]

No. LXVI.—A DUCK HUNT

A duck begins to swim round the edge of a circular pond, and at the same moment a water spaniel starts from the middle of the pond in pursuit of it.

If both swim at the same pace, how must the dog steer his course so that he is sure in any case to overtake the duck speedily?

Solution

THE MAGIC OF DATES

Louis Napoleon, Emperor 1852

	1852		1852		1852
date	1	date	1	date	1
of	8	of	8	of	8
his	0	Empress’s	2	their	5
birth	8	birth	6	marriage	3
	1869		1869		1869

Thus, by a most remarkable series of coincidences, the principal dates of the Emperor and Empress of the French added, as is shown above, to the year of the Emperor’s accession, express in each instance the year before his fall.

[II-67]

No. LXVII.—GEOMETRY WITH DOMINOES

In this domino diagram we have a pretty and practical proof that the squares of the sides containing the right angle in any right-angled triangle are together equal to the square of the side opposite to the right angle.

Each stone forms two squares, and it is easily seen that the number of squares which make up the whole square on the line opposite the right angle are equal to the number of those which make up the two whole squares on the lines which contain that angle.

A second point to be noticed is that the number of pips on the large square are equal to the number on the other two squares combined, an arrangement of the stones which forms quite a game of patience to reproduce, if this pattern is not at hand.

[II-68]

No. LXVIII.—TO COLOUR MAPS

Four colours at most are needed to distinguish the surfaces of separate districts on any plane map, so that no two with a common boundary are tinted alike.

On this diagram A, B, and C, are adjoining districts, on a plane surface, and X borders, in one way or another, upon each.

It is clearly impossible to introduce a fifth area which shall so adjoin these four districts as to need another tint.

A FREAK OF FIGURES

Here is another freak of figures:—

9	×	1	-	1	=	8
9	×	21	-	1	=	188
9	×	321	-	1	=	2888
9	×	4321	-	1	=	38888
9	×	54321	-	1	=	488888
9	×	654321	-	1	=	5888888
9	×	7654321	-	1	=	68888888
9	×	87654321	-	1	=	788888888
9	×	987654321	-	1	=	8888888888

[II-69]

No. LXIX.—THE TETHERED BIRD

A bird made fast to a pole six inches in diameter by a cord fifty feet long, in its flight first uncoils the cord, keeping it always taut, and then recoils it in the reverse direction, rewinding the coils close together. If it starts with the cord fully coiled, and continues its flight until it brings up against the pole, how far does it fly in its double course?

Solution

STRIKE IT OUT

Ask a person to write down in a line any number of figures, then to add them all together as units, and to subtract the result from the sum set down. Let him then strike out any one figure, and add the others together as units, telling you the result.

If this has been correctly done, the figure struck out can always be determined by deducting the final total from the multiple of 9 next above it. If the total happens to be a multiple of 9, then a 9 was struck out.

[II-70]

No. LXX.—THE MOVING DISC AND THE FLY

A fly, starting from the point A, just outside a revolving disc, and always making straight for its mate at the point B, crosses the disc in four minutes, while the disc is revolving twice. What effect has the revolution of the disc on the path of the fly?

Solution

A MAGIC SQUARE

This Magic Square is so arranged that the product of the continued multiplication of the numbers in each row, column, or diagonal is 4096, which is the cube of the central 16.

8	256	2
4	16	64
128	1	32

[II-71]

No. LXXI.—A SHUNTING PUZZLE

The railway, D E F, has two sidings, D B A and F C A, connected at A. The rails at A, common to both, are long enough to hold a single wagon such as P or Q, but too short to admit the whole of the engine R, which, if it runs up either siding, must return the same way.

How can the engine R be used to interchange the wagons P and Q without allowing any flying shunts?—From Ball’s Mathematical Recreations.

Solution

[II-72]

No. LXXII.—A CURIOUS FACT

It is a little known and very interesting fact that an equilateral triangle can easily be drawn by rule of thumb in the following way:—Take a triangle of any shape or size, and on each of its sides erect an equilateral triangle. Find and join the centres of these, and a fourth equilateral triangle is always thus formed, as shown by the dotted lines.

These centres are centres of gravity, and they are symmetrically distributed around the centre of gravity of the original triangle.

The figure formed by joining them must therefore be symmetrical, and, as in this case, it is a triangle, it must be always equilateral.

[II-73]

No. LXXIII.—TRY THIS EXPERIMENT

There can be no better instance of how the eye may be deceived than is so strikingly afforded in these very curious diagrams:—

The square which obviously contains sixty-four small squares, is to be cut into four parts, as is shown by the thicker lines. When these four pieces are quite simply put together, as shown in the second figure, there seem to be sixty-five squares instead of sixty-four.

This phenomena is due to the fact that the edges of the four pieces, which lie along the diagonal A B, do not exactly coincide in direction. In reality they include a very narrow diamond, not easily detected, whose area is just equal to that of one of the sixty-four small squares.

FIGURES IN SWARMS

Very curious are the results when the nine digits in reverse order are multiplied by 9 and its multiples up to 81. Thus:—

9	8	7	6	5	4	3	2	1	×	9	=		8	8	8	8	8	8	8	8	8	9
									×	18	=	1	7	7	7	7	7	7	7	7	7	8
									×	27	=	2	6	6	6	6	6	6	6	9	9	7
									×	36	=	3	5	5	5	5	5	5	5	5	5	6
									×	45	=	4	4	4	4	4	4	4	4	4	4	5
									×	54	=	5	3	3	3	3	3	3	3	3	3	4
									×	63	=	6	2	2	2	2	2	2	2	2	2	3
									×	72	=	7	1	1	1	1	1	1	1	1	1	2
									×	81	=	8	0	0	0	0	0	0	0	0	0	1

It will be seen that the figures by which the reversed digits are multiplied reappear at the beginning and end of each result except the first, and that the figures repeated between them are to be found by dividing the divisors by 9 and subtracting the result from 9. Thus, 54 ÷ 9 = 6, and 9 - 6 = 3.

[II-74]

No. LXXIV.—A TRIANGLE OF TRIANGLES

In this nest of triangles there are no less than six hundred and fifty-three distinct triangles of various shapes and sizes.

[II-75]

No. LXXV.—PHARAOH’S SEAL

In a chamber of the Great Pyramid an ancient Egyptian jar was found, marked with the device now known as Pharaoh’s seal.

Can you count the number of triangles or pyramids, of many sizes, but all of similar shape that are expressed on it? Solvers should draw the figure on a larger scale.

Solution

MAKING CUBES

It is interesting to note that the repeated addition of odd numbers to one another can be so arranged as to produce cube numbers in due sequence. Thus:—

1	=	1 × 1 × 1
3 + 5	=	2 × 2 × 2
7 + 9 + 11	=	3 × 3 × 3
13 + 15 + 17 + 19	=	4 × 4 × 4
21 + 23 + 25 + 27 + 29	=	5 × 5 × 5

and so on, to any extent.

[II-76]

No. LXXVI.—ROUND THE GARDEN

In a large old-fashioned garden walks were arranged round a central fountain in the shape of a Maltese cross.

If four persons started at noon from the fountain, walking round the four paths at two, three, four and five miles an hour respectively, at what time would they meet for the third time at their starting-point, if the distance on each track was one-third of a mile?

Solution

A NICE SHORT CUT

When the tens of two numbers are the same, and their units added together make ten, multiply the units together, increase one of the tens by unity, and multiply it by the other ten. The result is the product of the two original numbers, if the first result follows the other. Thus:—

43 × 47 = 2021.

[II-77]

No. LXXVII.—A JOINER’S PUZZLE

Can you cut Fig. A into two parts, and so rearrange these that they form either Fig. B or Fig. C?

The two parts of A must not be turned round to form B or C, but must retain their original direction.

Solution

A CALCULATION

Coal may fail us, but we can never run short of material for “words that burn.” It has been calculated that if a man could read 100,000 words in an hour, and there were 4,650,000 men available, they could not pronounce the possible variations which could be formed from the alphabet in 70,000 years!

A PARADOX

It is possible, in a sense, by the following neat method, to take 45 from 45, and find that 45 remains:—

987654321	=	45.
123456789	=	45.
864197532	=	45.

[II-78]

No. LXXVIII.—THE BROKEN OCTAGON

Cut out in stiff cardboard four pieces shaped as Fig. 1, four as Fig. 2, and four as Fig. 3, taking care that they are all exactly true to pattern in shape and proportion to one another.

Now see whether you can put the twelve pieces together so as to form a perfect octagon.

Solution

PROPERTIES OF SEVEN

Here is a proof that 7, if it cannot rival the mystic 9, has quaint properties of its own:—

	1	5	8	7	3	×	7	=	1	1	1	1	1	1
	3	1	7	4	6	×	7	=	2	2	2	2	2	2
	4	7	6	1	9	×	7	=	3	3	3	3	3	3
	6	3	4	9	2	×	7	=	4	4	4	4	4	4
	7	9	3	6	5	×	7	=	5	5	5	5	5	5
	9	5	2	3	8	×	7	=	6	6	6	6	6	6
1	1	1	1	1	1	×	7	=	7	7	7	7	7	7
1	2	6	9	8	4	×	7	=	8	8	8	8	8	8
1	4	2	8	5	7	×	7	=	9	9	9	9	9	9

A SWARM OF EIGHTS

Here is an arithmetical curiosity:—

9	×	9								+	7	=	8	8
9	×	9	8							+	6	=	8	8	8
9	×	9	8	7						+	5	=	8	8	8	8
9	×	9	8	7	6					+	4	=	8	8	8	8	8
9	×	9	8	7	6	5				+	3	=	8	8	8	8	8	8
9	×	9	8	7	6	5	4			+	2	=	8	8	8	8	8	8	8
9	×	9	8	7	6	5	4	3		+	1	=	8	8	8	8	8	8	8	8
9	×	9	8	7	6	5	4	3	2	+	0	=	8	8	8	8	8	8	8	8	8

[II-79]

No. LXXIX.—AT A DUCK POND

A farmer’s wife kept a pure strain of Aylesbury ducks for market on a square pond, with a duck-house at each corner. As trade grew brisk she found that she must enlarge her pond. An ingenious neighbour undertook to arrange this without altering the shape of the pond, and without disturbing the duck-houses. What was his plan?

Solution

STRANGE SUBTRACTION

It would seem impossible to subtract 69 from 55, but it can be arranged thus, with six as a remainder:—

SIX	IX	XL
IX	X	L
S	I	X

[II-80]

No. LXXX.—ALL ON THE SQUARE

Cut out in cardboard twenty triangular pieces exactly the size and shape of this one, and try to place them together so that they form a perfect square.

Solution

ANOTHER MYSTIC NUMBER

The decimal equivalent of ¹⁄₁₃ is .076923. This (omitting the point), multiplied by 1, 3, 4, 9, 10, or 12, yields results in which the same figures appear in varied order, but similar sequence, and multiplied by 2, 5, 6, 7, 8, or 11, it yields a different series, with similar characteristics. Thus:—

76923	×	1	=	76923	76923	×	2	=	153846
	×	3	=	230769		×	5	=	384615
	×	4	=	307692		×	6	=	461538
	×	9	=	692307		×	7	=	538461
	×	10	=	769230		×	8	=	615384
	×	12	=	923076		×	11	=	846153

DON’T BUY IT TO TRY IT

A kaleidoscope cylinder contains twenty small pieces of coloured glass. As we turn it round, or shake it, so as to make ten changes of pattern every minute, it will take the inconceivable space of time of 462,880,899,576 years and 360 days to exhaust all the possible symmetrical variations. (The 360 days is good!)

[II-81]

No. LXXXI.—PINS AND DOTS

Here is an amusing little exercise for the ingenuity of our solvers.

Take six sharp pins, and puzzle out how to stick them into six of the black dots, so that no two pins, are on the same line, in any direction, vertical, horizontal, or diagonal.

Solution

[II-82]

No. LXXXII.—A TRICKY COURSE

The middle of a large playground was paved with sixty-four square flagstones of equal size, which are numbered on this diagram from one to sixty-four.

1	9	17	25	33	41	49	57
2	10	18	26	34	42	50	58
3	11	19	27	35	43	51	59
4	12	20	28	36	44	52	60
5	13	21	29	37	45	53	61
6	14	22	30	38	46	54	62
7	15	23	31	39	47	55	63
8	16	24	32	40	48	56	64

One of the schoolmasters, who had a head for puzzles, took his stand upon the square here numbered 19, and offered a prize to any boy who, starting from the square numbered 46, could make his way to him, passing through every square once, and only once. It was after many vain attempts that the course was at last discovered. Can you work it out?

Solution

[II-83]

No. LXXXIII.—FOR THE CHILDREN

Place twelve draughtsmen, or buttons, in a square, so that you count four along each side of it, thus:—

Now take the same men or buttons, and arrange them so that they form another square, and you can count five along each side of it.

Solution

A GAME OF NINES

Here is a good specimen of the eccentricities and powers of numbers:—

153846	×	13	=	1999998
230769	×	13	=	2999997
307692	×	13	=	3999996
384615	×	13	=	4999995
461538	×	13	=	5999994
538461	×	13	=	6999993
615384	×	13	=	7999992
692307	×	13	=	8999991

[II-84]

No. LXXXIV.—TELL-TALE TABLES

She was quite an old maid, and her age was a most absolute secret. Determined to discover it, her scapegrace nephew, on Christmas Eve, produced these tables, and asked her with well simulated innocence on which of them she could see the number of her age.

1	23	45	2	23	46	16	27	54
3	25	47	3	26	47	17	28	55
5	27	49	6	27	50	18	29	56
7	29	51	7	30	51	19	30	57
9	31	53	10	31	54	20	31	58
11	33	55	11	34	55	21	48	59
13	35	57	14	35	58	22	49	60
15	37	59	15	38	59	23	50	61
17	39	61	18	39	62	24	51	62
19	41	A	19	42	B	25	52	C
21	43	A	22	43	B	26	53	C

8	27	46	4	23	46	32	43	54
9	28	47	5	28	47	33	44	55
10	29	56	6	29	52	34	45	56
11	30	57	7	30	53	35	46	57
12	31	58	12	31	54	36	47	58
13	40	59	13	36	55	37	48	59
14	41	60	14	37	60	38	49	60
15	42	61	15	38	61	39	50	61
24	43	62	20	39	62	40	51	62
25	44	D	21	44	E	41	52	F
26	45	D	22	45	E	42	53	F

From her answer he was able to calculate that the old lady was fifty-five.

The tell-tale tables disclosed her age thus:—As it appeared in tables A, B, C, E, and F, he added together the numbers at the top left-hand corners, and found the total to be fifty-five. This rule applies in all cases.

[II-85]

No. LXXXV.—A PAPER PUZZLE

Of the many paper-cutting tricks which appeal to us none is more simple and attractive than this:—

Take a piece of paper, say 5 inches by 3 inches, but any oblong shape and size will do, and after folding it four times cut it lengthways up the centre. Unfold the pieces, and to your surprise you will find a perfect cross and other pieces in pairs of the shapes shown above. The puzzle is how to fold the paper.

The paper must be folded first so that B comes upon C, then so that A comes upon D, then from D to C, and lastly from E to C. If it is now cut lengthways exactly along the centre the figures shown on the original diagram will be formed, which resemble a cross and lighted candles on an altar.

[II-86]

No. LXXXVI.—A HOME-MADE PUZZLE

Take a thin board, about eight inches square, and mark it out into thirty-six equal parts; bore a hole in the centre of each part, and then fit in a small wooden peg, leaving about a quarter inch above the surface, as is shown in Fig. 1, the section below the diagram.

Prepare thirty-six pieces of white or coloured cardboard of the length A to B, and place them over the pegs in any direction in which they will fit so as to form some such symmetrical pattern as is given on the second diagram, putting two holes only on each peg. Chess-players will see that this is the regular knight’s move.

Quite a number of beautiful[II-87] designs can be thus formed, and those who have not the means at hand for making a complete set can enjoy the puzzle by merely marking out thirty-six squares, and drawing lines from centre to centre of the exact length from A to B, with black or coloured pencils.

No. LXXXVII.—LOYD’S MITRE PROBLEM

Divide this figure into four similar and equal parts.

Solution

A PRETTY PROBLEM

The solution of the pretty little problem: place three twos in three different groups, so that twice the first group, or half the third group equals the second group, is this:—

22 + 2 = 12 2 - 22 = 1 2 + 22 = 2

[II-88]

No. LXXXVIII.—CONTINUOUS LINES

The following figure, which represents part of a brick wall, cannot be marked out along all the edges of the bricks in less than six continuous lines without going more than once over the same line:—

Here, in strong contrast to the simple figure given above, which could not be traced without lifting the pen six times from the paper, is an intricate design, the lines of which, on the upper or on the lower half, can be traced without any break at all.

The general rule that governs such cases is, that where an uneven number of lines meet a fresh start has to be made. In the diagram now given the only such points are at the extremities of the upper and lower halves of the figure at A and X. At all other points two, or four, or six lines converge, and there is no break of continuity in a tracing of the figure.

[II-89]

No. LXXXIX.—CUT OFF THE CORNERS

Can you suggest quite a simple and practical way to fix the points on the sides of a square which will be at the angles of an octagon formed by cutting off equal corners of the square, as shown below?

Solution

MYSTIC FIGURES

Very interesting and curious are the properties of the figures 142857, used in varied order but always in similar sequence, in connection with 7 and 9:—

1	4	2	8	5	7	×	7	=		9	9	9	9	9	9	÷	9	=	1	1	1	1	1	1
2	8	5	7	1	4	×	7	=	1	9	9	9	9	9	8	÷	9	=	2	2	2	2	2	2
4	2	8	5	7	1	×	7	=	2	9	9	9	9	9	7	÷	9	=	3	3	3	3	3	3
5	7	1	4	2	8	×	7	=	3	9	9	9	9	9	6	÷	9	=	4	4	4	4	4	4
7	1	4	2	8	5	×	7	=	4	9	9	9	9	9	5	÷	9	=	5	5	5	5	5	5
8	5	7	1	4	2	×	7	=	5	9	9	9	9	9	4	÷	9	=	6	6	6	6	6	6

[II-90]

No. XC.—THE FIVE TRIANGLES

The subjoined diagram shows how a square with sides that measure each 12 yards can be divided into five triangles, no two of which are of equal area, and of which the sides and areas can be expressed in yards by whole numbers:—

The areas of these triangles are 6, 12, 24, 48, and 54 square yards respectively, and the sum of these, 144 square yards, is the area of the square.

CURIOUS COINCIDENCES

Our readers may remember the remarkable fact that the figures of the sum, £12, 12s. 8d., when written thus, 12,128, exactly represent the number of farthings it contains. Now this, so far as we know, is the only instance of the peculiarity, but there are at least five other cases which come curiously near to it. They are these:—

£	s.	d.
9	9	6		=	9096	farthings
6	6	4		=	6064	„
3	3	2		=	3032	„
10	10	6	¹⁄₂	=	10106	„
13	13	8	¹⁄₂	=	13138	„

[II-91]

No. XCI.—PLACING A LADDER

If a ladder, with rungs 1 foot apart, rests against a wall, and its thirteenth rung is 12 feet above the ground, the foot of the ladder is 25 feet from the wall.

Proof.—Drop a perpendicular from A to B. Then, as A B C is a right angle, and the squares on A C, A B, are 169 feet and 144 feet, the square on C B must be 25 feet, and the length of C B is 5 feet. We thus move 5 feet towards the wall in going 13 feet up the ladder, and in mounting 65 feet (five times as far) we must cover 25 feet.

[II-92]

No. XCII.—GRACEFUL CURVES

A prettily ingenious method of dividing the area of a circle into quarters, each of them a perfect curve, with perimeter (or enclosing line) equal to the circumference of the circle, and with which four circles can be formed, is clearly shown by the subjoined diagrams:—

NIGHTS AT A ROUND TABLE

The host of a large hotel at Cairo noticed that his Visitors’ Book contained the names of an Austrian, a Brazilian, a Chinaman, a Dane, an Englishman, a Frenchman, a German, and a Hungarian. Moved by this curious alphabetical list, he offered them all free quarters and the best of everything if they could arrange themselves at a round dining-table so that not one of them should have the same two neighbours on any two occasions for 21 successive days.

The following is one of many ways in which this arrangement can be made, and it seems to be the simplest of them all.

Number the persons 1 to 8; and for our first day set them down in numerical order except that the two centre ones (4 and 5) change places:

(1st day)—

Keep the 1 and the 7 unaltered but double each of the other numbers. When the product is greater than 8, divide by 7, and only set down the remainder. Thus we get:

(8th day)—

(Here the fourth figure 3 is 5 × 2 ÷ 7, giving remainder 3, and so on.)

Repeat this operation once more:

(15th day)—

To fill in the intermediate days we have only to keep 1 unchanged and let the remaining numbers run downwards in simple numerical order, following 8 with 2, 2 with 3, and so on. Thus:—

1st day—	1	2	3	5	4	6	7	8
2nd day—	1	3	4	6	5	7	8	2
3rd day—	1	4	5	7	6	8	2	3
4th day—	1	5	6	8	7	2	3	4
5th day—	1	6	7	2	8	3	4	5
6th day—	1	7	8	3	2	4	5	6
7th day—	1	8	2	4	3	5	6	7
8th day—	1	4	6	3	8	5	7	2
9th day—	1	5	7	4	2	6	8	3
10th day—	1	6	8	5	3	7	2	4
11th day—	1	7	2	6	4	8	3	5
12th day—	1	8	3	7	5	2	4	6
13th day—	1	2	4	8	6	3	5	7
14th day—	1	3	5	2	7	4	6	8
15th day—	1	8	5	6	2	3	7	4
16th day—	1	2	6	7	3	4	8	5
17th day—	1	3	7	8	4	5	2	6
18th day—	1	4	8	2	5	6	3	7
19th day—	1	5	2	3	6	7	4	8
20th day—	1	6	3	4	7	8	5	2
21st day—	1	7	4	5	8	2	6	3

This completes the schedule. It will be found on examination that every number is between every pair of the other numbers once, and once only.

In order to reduce our first-day ring to exact numerical order we have only to interchange the numbers 4 and 5 throughout. The first three lines for example would then become:

1	2	3	4	5	6	7	8
1	3	5	6	4	7	8	2
1	5	4	7	6	8	2	3,	etc.

or, by putting letters for figures,

A	B	C	D	E	F	G	H
A	C	E	F	D	G	H	B
A	E	D	G	F	H	B	C,	etc.

An arrangement of the guests is thus arrived at for twenty-one successive days, so that not one of them has the same two neighbours on any two occasions.

[II-93]

No. XCIII.—MAKING MANY SQUARES

Can you apply the two oblongs drawn below to the two concentric squares, so as to produce thirty-one perfect squares?

Solution

No. XCIV.—CUT ACROSS

Take a piece of cardboard in the form of a Greek cross with arms, as shown here, and divide it by two straight cuts, so that the pieces when reunited form a perfect square.

Solution

No. XCV.—A PRETTY PUZZLE

The diagrams which we give below show how a hollow square can be formed of the pieces of three-quarters of another square from which a corner has been cut away:—

[II-96]

No. XCVI.—A FIVE-FOLD SQUARE

The subjoined diagram shows how a square of paper or cardboard may be cut into nine pieces which, when suitably arranged, form five perfect squares.

THE SOCIABLE SCHOOLGIRLS

On how many days can fifteen schoolgirls go out for a walk so arranged in rows of three, that no two are together more than once?

Fifteen schoolgirls can go out for a walk on seven days so arranged in rows of three that no two are together more than once.

It is said, on high authority, that there are no less than 15,567,522,000 different solutions to this problem. Here is one of them, given in Ball’s Mathematical Recreations, in which k stands for one of the girls, and a, b, c, d, e, f, g, in their modifications, for her companions on the seven different days:—

Sunday	Monday	Tuesday	Wednesday	Thursday	Friday	Saturday
ka₁a₂	kb₁b₂	kc₁c₂	kd₁d₂	ke₁e₂	kf₁f₂	kg₁g₂
b₁d₁f₁	a₁d₂e₂	a₁d₁e₁	a₂b₂c₂	a₂b₁c₁	a₁b₂c₁	a₁b₁c₂
b₂e₁g₁	a₂f₂g₂	a₂f₁g₁	a₁f₂g₁	a₁f₁g₂	a₂d₂e₁	a₂d₁e₂
c₁d₂g₂	c₁d₁g₁	b₁d₂f₂	b₁e₁g₂	b₂d₁f₂	b₁e₂g₁	b₂d₂f₁
c₂e₂f₂	c₂e₁f₁	b₂e₂g₂	c₁e₂f₁	c₂d₂g₁	c₂d₁g₂	c₁e₁f₂

It is an excellent game of patience, for those who have time and inclination, to place the figures 1 to 15 inclusive in seven such columns, so as to fulfil the conditions.

[II-97]

No. XCVII.—THE THREE CROSSES

It is possible from a Greek cross to cut off four equal pieces which, when put together, will form another Greek cross exactly half the size of the original, and by this process to leave a third Greek cross complete.

This is how to do it:—

Bisect C D at N, F G at O, K L at P, and B I at Q.

Join N H, O M, P A, Q E, intersecting at R, S, T, U.

Bisect A R at V, E S at W, T H at X, and M U at Y.

Join V Q, N Y, W P, O X, N W, V O, Q X, Y P.

Carefully cut out from the original Greek cross the newly-formed Greek cross, and the odd pieces from around it can be arranged to form another Greek cross.

[II-98]

No. XCVIII.—THE HAMMOCK

The greatest number of plane figures that can be formed by the union of ten straight lines is thirty-six.

The two equal lines at right angles are first drawn, and each is divided into eight equal parts. The other eight straight lines are then drawn from a to a, from b to b, and so on, until the hammock-shaped network of thirty-six plane figures is produced.

[II-99]

No. XCIX.—CUTTING A CRUMPET

It will be seen on the diagram below that seven straight vertical cuts with a table-knife will divide a crumpet into twenty-eight parts.

BALANCE THE SCALES

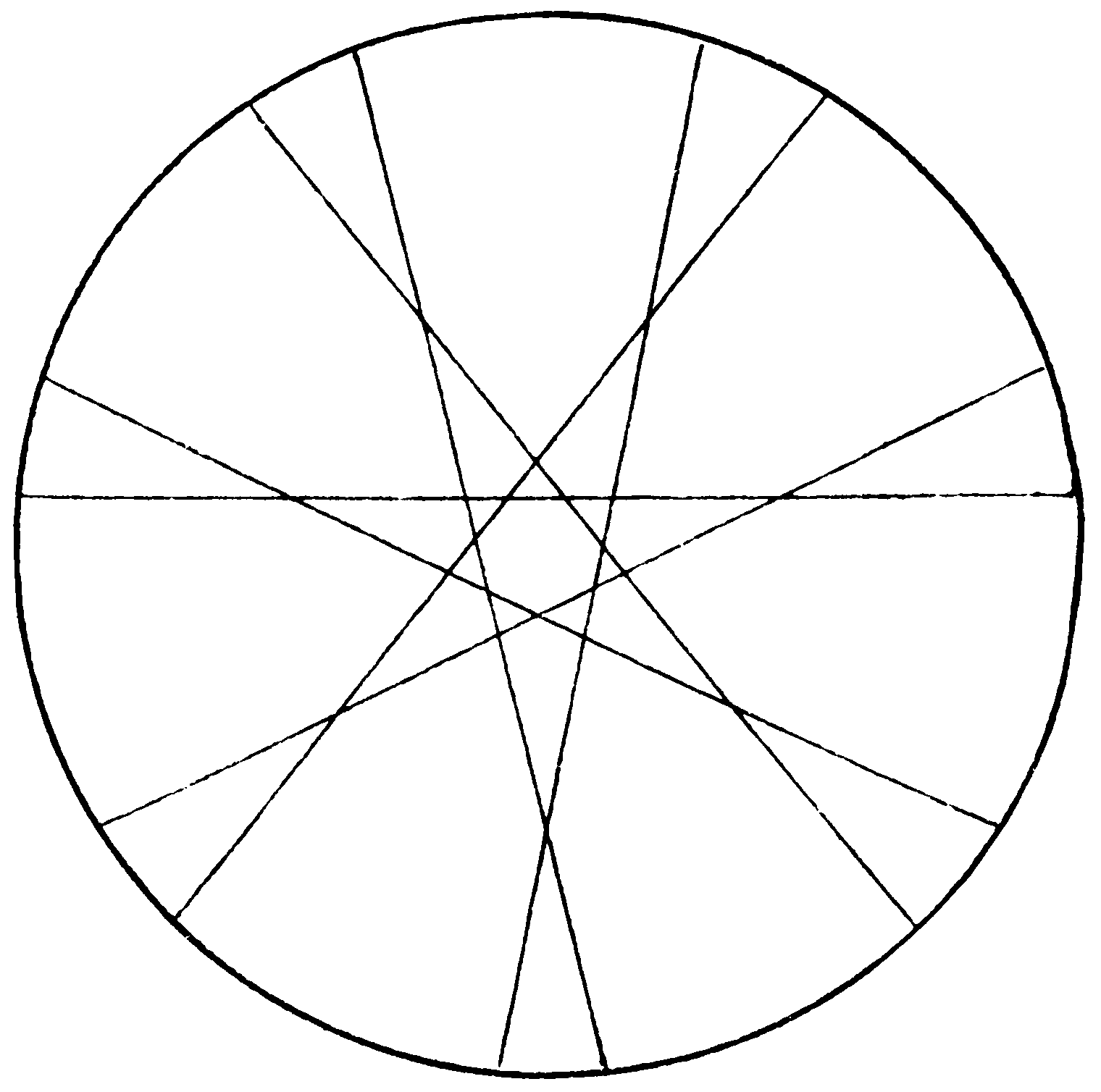
The nine digits can be so adjusted as to form an equation, or, if taken as weight, to balance the scales. Thus:—

9, 6¹⁄₂ = 3, 5, 7⁴⁄₈

TRUE STRETCHES OF IMAGINATION

How large is the sea? This is a bold big question, and any possible answer involves a considerable stretch of the imagination. Here is a startling illustration of its vast volume:—

If the water of the sea could be gathered into a round column, reaching the 93,000,000 miles which separate us from the sun, the diameter of this column would be nearly two miles and a half!

It is perhaps even more difficult to realise that this mighty mass of waters could be dissipated in a few moments, if the column we have imagined could become ice, and if the entire heat of the sun could be concentrated upon it. All would be melted in one second of time, and converted into steam in eight seconds!

[II-100]

No. C.—TO MAKE AN ENVELOPE

Many of our readers may be glad to know an easy way to make an envelope of any shape or size.

This diagram speaks for itself. When the lines A B, A C, D B, D C have been drawn, the corners of the rectangle, H E G F, are folded over, as shown by the dotted lines, after the corners have been rounded, and the margins touched with gum.

[II-101]

No. CI.—SQUARING AN OBLONG

The diagrams below will show how a piece of paper, 15 inches long and 3 inches wide, can be cut into five parts, and rearranged to form a perfect square.

A PLAGUE OF BLOW-FLIES

The following astounding calculation is answer enough to a question put by one of the authors of “Rejected Addresses:”—“Who filled the butchers’ shops with big blue flies?”

A pair of blow-flies can produce ten thousand eggs, which mature in a fortnight. If every egg hatches out, and there are equal numbers of either sex, which forthwith increase and multiply at the same rapid rate, and if their descendants do the like, so that all survive at the end of six months, it has been calculated that, if thirty-two would fill a cubic inch of space, the whole innumerable swarm would cover the globe, land and sea, half a mile deep everywhere.

[II-102]

No. CII.—BY RULE OF THUMB

Here is quite a neat way to make an equilateral triangle without using compasses:—

Take a piece of paper exactly square, which we will call A B C D, fold it across the middle, so as to form the crease E F; unfold it, and fold it again so that the corner D falls upon the crease E F at G, and the angle at G is exactly divided. Again unfold the square, and from G draw the straight lines G C and G D. Then G C D is the equilateral triangle required.

THE VALUE OF A FRENCHWOMAN

How can we be sure that the value of a Frenchwoman is just 1 franc 8 centimes?

We can be sure that the exact value of a Frenchwoman is 1 franc 8 centimes, for

	Two Frenchwomen	=	Deux Françaises.
	Deux Françaises	=	deux francs seize. (2 francs 16).
Therefore,	One Frenchwoman	=	1 franc 8!

[II-103]

No. CIII.—CLEARING THE WALL

If a 52-feet ladder is set up so as just to clear a garden wall 12 feet high and 15 feet from the building, it will touch the house 48 feet from the ground.

Our diagram shows this, and also, by a dotted line, the only other possible position in which it could fulfil the conditions, if it were then of any practical use.

A BURDEN OF PINS

If one pin could be dropped into a vessel this week, two the next, four the next, and so on, doubling each time for a year, the accumulated quantity would be 4,503,599,627,370,495, and their weight, if we reckon 200 pins to the ounce, would amount to 628,292,358 tons, a full load for 27,924 ships as large as the Great Eastern, whose capacity was 22,500 tons.

[II-104]

No. CIV.—MEMORIES OF EUCLID

When at the signpost which said “To A 4 miles, to B 9 miles” on one arm, and on the other “To C 3 miles, to D —— miles,” and the boy whom I met could only tell me that the farm he worked at was equidistant from A, B, C, and D, and nearer to them than to the signpost, and that all the roads ran straight, I found, thanks to memories of Euclid, that I was 12 miles from D.

Since B A and D C intersect outside the circle at the signpost E,

therefore	A E × E B = C E × E D.
but	A E × E B = 4 × 9 = 36,
therefore	C E × E D = 36,
and	C E = 3, therefore E D = 12.

Q.E.D.

[II-105]

No. CV.—A TRANSFORMATION

This seems to be quite a poor attempt at a Maltese cross, but there is method in the madness of its make.

It is possible by two straight cuts to divide this uneven cross into four pieces which can be arranged together again so that they form a perfect square. Where must the cuts be made, and how are the four pieces rearranged?

Solution

BREVITY IS THE SOUL OF WIT

We all remember that splendidly terse message of success sent home to the authorities by Napier when he had conquered the armies of Scinde—“Peccavi!” (I have sinned).

History had an excellent opportunity for repeating itself when Admiral Dewey defeated the Spaniel fleet, for he might have conveyed the news of his victory by the one burning word—“Cantharides”—“The Spanish fly!”

[II-106]

No. CVI—SHIFTING THE CELLS

In the diagram below a square is subdivided into twenty-five cells.

Can you, keeping always on the straight lines, cut this into four pieces, and arrange these as two perfect squares, in which every semicircle still occupies the upper half of its cell?

Solution

A HOME-MADE MICROSCOPE

The following very simple recipe for a home-made microscope has been suggested by a Fellow of the Royal Microscopical Society:—

Take a piece of black card, make a small pinhole in it, put it close to the eye, and look at some small object closely, such as the type of a newspaper. A very decided magnifying power will be shown thus.

[II-107]

No. CVII.—IN A TANGLE

Where on this diagram must we place twenty-one pins or dots so that they fall into symmetrical design and form thirty rows, with three in each row?

Solution

ON ALL FOURS

Those who are fond of figures will find it a most interesting exercise to see how far they are able to represent every number, from one up to a hundred, by the use of four fours. Any of the usual signs and symbols of arithmetic may be brought into use. Here are a few instances of what may thus be done:—

3 = 4 + 4 + 44; 9 = 4 + 4 + 44;

36 = 4(4 + 4) + 4; 45 = 44 + 44;

52 = 44 + 4 + 4; 60 = 4 × 4 × 4 - 4.

[II-108]

No. CVIII.—STILL A SQUARE

This figure, which now forms a square, and the quarter of that square, can be so divided by two straight lines that its parts, separated and then reunited, form a perfect square. How is this done?

Solution

A MAGIC SQUARE

Here we have arranged five rows of five cards each, so that no two similar cards are in the same lines. Counting the ace as eleven, each row, column, and diagonal adds up to exactly twenty-six.

After you have looked at this Magic Square, and set it out on the table, shuffle the cards, and try to re-arrange them so as to give the same results.

[II-109]

No. CIX.—A TRANSFORMATION

Cut a square of paper or cardboard into seven such pieces as are marked in this diagram.

Can you rearrange them so that they form the figure 8.

Solution

A SECRET REVEALED

There are several ways in which strange juggling with figures and numbers is to be done, but none is more curious than this:—

Ask someone, whose age you do not know, to write down secretly the date and month of his birth in figures, to multiply this by 2, to add 5, to multiply by 50, to add his age last birthday and 365. He then hands you this total only from this you subtract 615. This reveals to you at a glance his age and birthday.

Thus, if he was born April 7 and is 23, 74 (the day and the month) × 2 = 148; 148 + 5 = 153; 153 × 50 = 7650; 7650 + 23 (his age) = 7673; and 7673 + 365 = 8038. If from this you subtract 615, you have 7423, which represents to you the seventh day of the fourth month, 23 years age! This rule works out correctly in all cases.

[II-110]

No. CX.—TO MAKE AN OBLONG

Cut out in stiff paper or cardboard two pieces of the shape and size of the small triangle, and four pieces of the shapes and sizes of the other three patterns—fourteen pieces in all.

The puzzle is to fit these pieces together so that they form a perfect oblong.

Solution

SLEEPERS THAT SLIP AND SLEEP

Here is a string of sentences, which may be used as stimulating mental gymnastics when we leave the “Land of Nod.”

A sleeper runs on sleepers, and in this sleeper on sleepers sleepers sleep. As this sleeper carries its sleepers over the sleepers that are under the sleeper, a slack sleeper slips. This jars the sleeper and its sleepers, so that they slip and no longer sleep.

DAYS THAT ARE BARRED

Clever calculation has established a fact which we shall not be able to verify by personal experience. Whatever else may happen, the first day of a century can never fall on Sunday, Wednesday, or Friday.

[II-111]

No. CXI.—SQUARES ON THE CROSS

On this cross there are seventeen distinct and perfect squares marked out at their corners by asterisks.

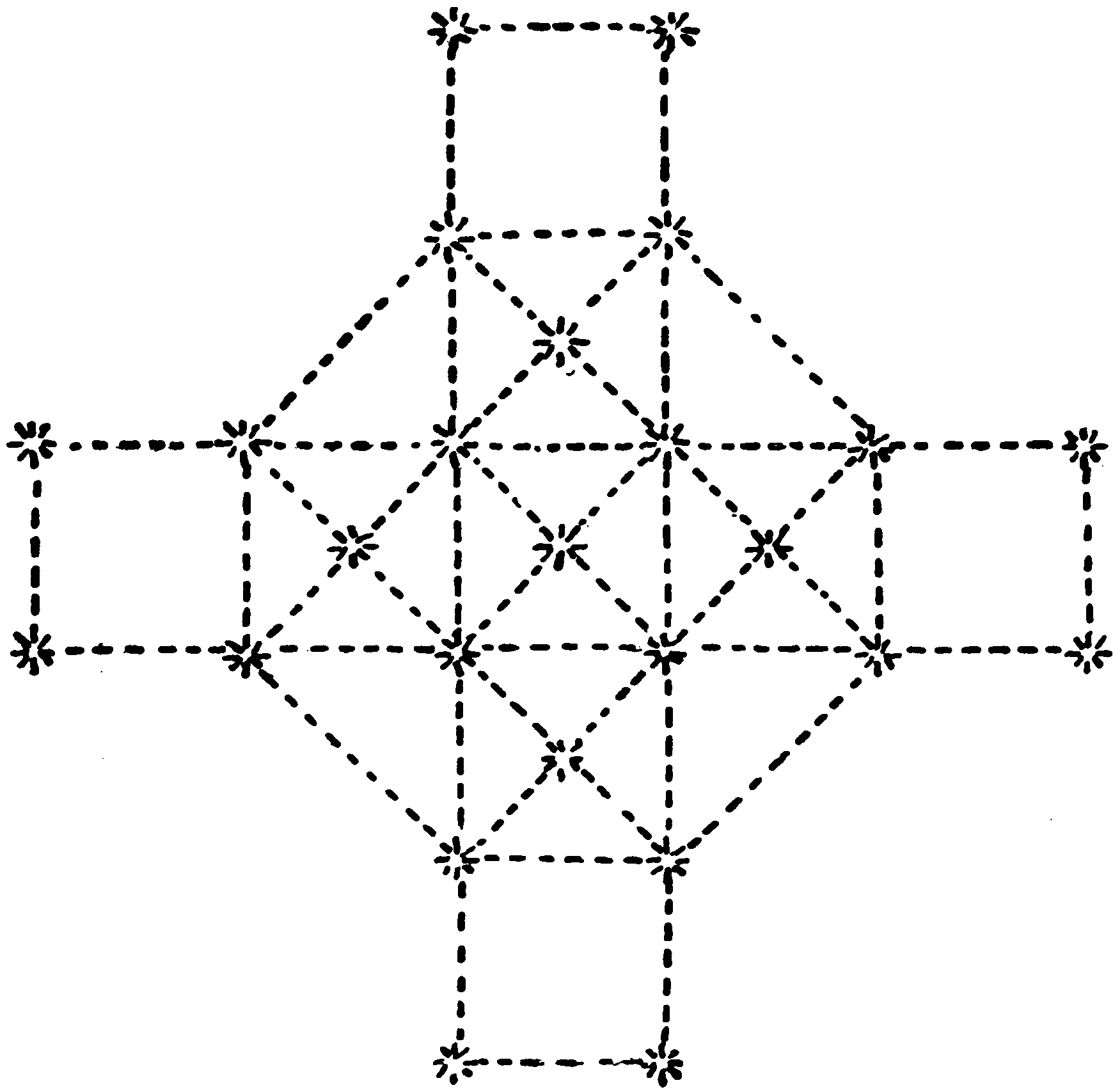
How few, and which, of these can you remove, so that not a single perfect square remains?

Solution

STANDING ROOM FOR ALL

On a globe 2 feet in diameter the Dead Sea appears but as a small coloured dot. If it were frozen over there would be standing room on its surface for the whole human race, allowing 6 square feet for each person; and if they were all suddenly engulfed, it would merely raise the level of the lake about 4 inches.

[II-112]

No. CXII.—A CHINESE PUZZLE

Here is quite a good exercise for ingenious brains and fingers. Cut a piece of stiff paper or cardboard into such a right-angled triangle as is shown below.

Can you divide this into only three pieces, which, when rearranged, will form the design given as No. 2?

Solution

A DEAL IN ROSES

I sent an order for dwarf roses to a famous nursery-garden, asking for a parcel of less than 100 plants, and stipulating that if I planted them 3 in a row there should be 1 over; if 4 in a row 2 over; if 5 in a row 3 over, and if 6 in a row 4 over, as a condition for payment.

The nurseryman was equal to the occasion, charged me for 58 trees, and duly received his cheque.

[II-113]

No. CXIII.—FIRESIDE FUN

This puzzle is not so easy of solution as it may seem at first sight.

Take a counter, or a coin, and place it on one of the points; then push it across to the opposite point, and leave it there. Do this with a second counter or coin, starting on a vacant point, and continue this process until every point is covered, as we place the eighth counter or coin on the last point.

Solution

A NOVEL EXERCISE

“Write down,” said a schoolmaster, “the nine digits in such order that the first three shall be one third of the last three, and the central three the result of subtracting the first three from the last.”

The arrangement which satisfies these conditions is, 219, 438, 657.

[II-114]

CURIOUS CALCULATIONS

1.

There is a sum of money of such sort that its pounds, shillings, and pence, written down as one continuous number, represent exactly the number of farthings which it contains. What is it?

Solution

THE SLIP CARRIAGE

2. If on a level track a train, running all the time at 30 miles an hour, slips a carriage, which is uniformly retarded by the brakes, and which comes to rest in 200 yards, how far has the train itself then travelled?

Solution

3.

A traveller said to the landlord of an inn, “Give me as much money as I have in my hand, and I will spend sixpence with you.” This was done, and the process was twice repeated, when the traveller had no money left. How much had he at first?

Solution

4.

How can we obtain eleven by adding one-third of twelve to four-fifths of seven?

Solution

FILL IN THE GAPS

5. Can you replace the missing figures in this mutilated long division sum?

2	1	5	)	*	7	*	9	*	(	1	*	*
				*	*	*
				*	5	*	9
				*	5	*	5
						*	4	*
						*	*	*

Solution

[II-115]

6.

I buy as many heads of asparagus in the market as can be contained by a string 1 foot long. Next day I take a string 2 feet long, and buy as many as it will gird, offering double the price that I have given before. Was this a reasonable offer?

Solution

ALIKE FROM EITHER END

7. As “one good turn deserves another,” first reverse me, then reverse my square, then my cube, then my fourth power. When all this is done no change has been made. What am I?

Solution

THE SEALED BAGS

8. How can a thousand pounds be so conveniently stored in ten sealed bags that any sum in pounds from £1 to £1000 can be paid without breaking any of the seals?

Solution

9.

This is at once a problem and a puzzle:—

Though you twist and turn me over,
Yet no change can you discover.
Take me thrice, and cut in twain,
You will find but one remain.

Solution

10.

Three gamblers, when they sit down to play, agree that the loser shall always double the sum of money that the other two have before them. After each of them has lost once, it is found that each has eight sovereigns on the table. How much money had each at starting?

Solution

FIND THE MULTIPLIER

11. When Tom’s back was turned, the boy sitting next to him rubbed out almost all his[II-116] sum. Tom could not remember the multiplier, and only this remained on his slate—

		3	4	5
			.	.
	.	.	.	.
.	.	.	.
.	.	7	6	.

Can you reconstruct the sum?

Solution

JUGGLING WITH THE DIGITS

12. The sum of the nine digits is 45. Can you hit upon other arrangements of 1, 2, 3, 4, 5, 6, 7, 8, 9, writing each of them once only, which will produce the same total. Of course fractions may be used.

Solution

A BRAIN TWISTER

13. The combined ages of Mary and Ann are forty-four years. Mary is twice as old as Ann was when Mary was half as old as Ann will be when Ann is three times as old as Mary was when Mary was three times as old as Ann. How old, then, is Mary?

Solution

14.

Mr Oldboy was playing backgammon with his wife on the eve of his golden wedding, and could not make up his mind whether he should leave a blot where it could be taken up by an ace, or one which a tré would hit.

His grandson, at home from Cambridge for the Christmas vacation, solved the question for him easily. What was his decision?

Solution

[II-117]

“ASK WHERE’S THE NORTH?”—Pope.

15. I am aboard a steamer, anchored in a bay where the needle points due north, and exactly 1200 miles from the North Pole. If the course is perfectly clear, and I steam continuously at the rate of 20 miles an hour, always steering north by the compass needle, how long will it take me to reach the North Pole?

Solution

16.

Three persons, A, B, and C, share twenty-one wine casks of equal capacity, of which seven are full, seven are half full, and seven are empty. How can these be so apportioned that each person shall have an equal number of casks, and an equal quantity of wine, without transferring any of it from cask to cask?

Solution

17.

A hungry mouse, in search of provender, came upon a box containing ears of corn. He could carry three ears home at a time, and only had opportunity to make fourteen journeys to and fro. How many ears could he add to his store?

Solution

18.

Take exactly equal quantities of lard and butter; mix a small piece of the butter intimately with all the lard. From this blend take a piece just as large as the fragment removed from the butter, and mix this thoroughly with the butter. Is there now more lard in the butter or more butter in the lard?

Solution

WHERE IS THE FALLACY?

19. Here is an apparent proof that 2 = 3:—

4 - 10 = 9 - 15

4 - 10 + ²⁵⁄₄ = 9 - 15 + ²⁵⁄₄

and the square roots of these:—

2 - ⁵⁄₂ = 3 - ⁵⁄₂

therefore 2 = 3.

[II-118]

Solution

PARCEL POST LIMITATIONS

20. Our Parcel Post regulations limit the length of a parcel to 3 feet 6 inches, and the length and girth combined to 6 feet. What is the largest parcel of any size that can be sent through the post under these conditions?

Solution

21.

How can we show, or seem to show, that either four, five, or six nines amount to one hundred?

Solution

TEST YOUR SKILL

22. Can you arrange nine numbers in the nine cells of a square, the largest number 100, and the least 1, so that the product by multiplication of each row, column and diagonal is 1000?

Solution

CATCHING CRABS

23. Seven London boys were at the seaside for a week’s holiday, and during the six week-days they caught four fine crabs in pools under the rocks, when the tide was out at Beachy Head.

Hearing of this, the twenty-one boys of a school in the neighbourhood determined to explore the pools; but with the same rate of success they only caught one large crab. For how long were they busy searching under the seaweed?

Solution

SETTING A WATCH

24. On how many nights could a watch be set of a different trio from a company of fifteen soldiers, and how often on these terms could one of them, John Pipeclay, be included?

Solution

“IMPERIAL CÆSAR”

25. If Augustus Cæsar was born on September 23rd, B.C. 63, on what day and in what year did he celebrate his sixty-third birthday, and by what five-letter symbol can we express the date?

Solution

[II-119]

26.

A was born in 1847, B in 1874. In what years have the same two digits served to express the ages of both, if they are still living?

Solution

THIS SHOULD “AMUSE”

27.

A hundred and one by fifty divide,
To this let a cypher be duly applied;
And when the result you can rightly divine,
You find that its value is just one in nine.

Solution

OVER THE FERRY

28. A man started one Monday morning with money in his purse to buy goods in a neighbouring town. He paid a penny to cross the ferry, spent half of the money he then had, and paid another penny at the ferry on his return home.

He did exactly the same for the next five days, and on Saturday evening reached home with just one penny in his pocket. How much had he in his pocket on Monday before he reached the ferry?

Solution

THE MEN, THE MONKEY, AND THE MANGOES

29. Three men gathered mangoes, and agreed that next day they would give one to their monkey and divide the rest equally. The first who arrived gave one to the monkey, and then took his proper share; the second came later and did likewise, and the third later still, neither knowing that any one had preceded him. Finally they met, and, as there were still mangoes, gave one to the monkey, and shared the rest equally. How many mangoes at least must there have been if all the divisions were accurate?

Solution

[II-120]

30.

I look at my watch between four and five, and again between seven and eight. The hands have, I find, exactly changed places, so that the hour-hand is where the minute-hand was, and the minute-hand takes the place of the hour-hand. At what time did I first look at my watch?

Solution

A LARGE ORDER

31. There is a number consisting of twenty-two figures, of which the last is 7. If this is moved to the first place, the number is increased exactly sevenfold. Can you discover this lengthy number?

Solution

32.

A farmer borrowed from a miller a sack of wheat, 4 feet long and 6 feet in circumference. He sent in repayment two sacks, each 4 feet long and 3 feet in circumference. Was the miller satisfied?

Solution

THE FIVE GAMBLERS

33. Five gamblers, whom we will call A, B, C, D, and E, play together, on the condition that after each hazard he who loses shall give to all the others as much as they then have in hand.

Each loses in turn, beginning with A, and when they leave the table each has the same sum in hand, thirty-two pounds. How much had each at first?

Solution

34.

Knowing that the square of 87 is 7569, how can we rapidly, without multiplication, determine in succession the squares of 88, 89, and 90?

Solution

NOT WHOLE NUMBERS

35.

Two numbers seek which make eleven,
Divide the larger by the less,
The quotient is exactly seven,
As all who solve it will confess.

Solution

[II-121]

AN AMPLE CHOICE

36. If there are twenty sorts of things from which 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 different selections can be made, how many of each sort are there?

Solution

37.

Three women, with no money, went to market. The first had thirty-three apples, the second twenty-nine, the third twenty-seven. Each woman sold the same number of apples for a penny. They all sold out, and yet each received an equal amount of money. How was this?

Solution

SIMPLE SUBTRACTION

38.

Take five from five, oh, that is mean!
Take five from seven, and this is seen.

Solution

39.

If a bun and a half cost three halfpence, how many do you buy for sixpence?

Solution

40.

How many times in a day would the hands of a watch meet each other, if the minute-hand moved backward and the hour-hand forward?

Solution

41.

How can half-a-crown be equally divided between two fathers and two sons so that a penny is the coin of smallest value given to them?

Solution

SIZE AND SPEED

42. If the number of the revolutions of the wheel of a bicycle in six seconds is equal to the number of miles an hour at which it is running, what is the circumference of the wheel?

Solution

43.

Hearing a clock strike, and being uncertain of the hour, I asked a policeman. He had a turn for figures, and replied: “Take half, a third, and a fourth of the hour that has just struck, and the total will be one larger than that hour.” What o’clock was it?

Solution

[II-122]

AFTER LONG YEARS

44.

If cash is lent at five per cent.
To those who choose to borrow,
How soon shall I be worth a pound
If I lend a crown to-morrow?

Solution

ON THE JUMP

45. If I jump off a table with a 20-lb. dumb-bell in my hand, what is the pressure upon me of its weight while I am in the air?

Solution

AT A BAZAAR

46. In charitable mood I went recently to a bazaar where there were four tents arranged to tempt a purchaser. At the door of each tent I paid a shilling, and in each tent I spent half of the money remaining in my purse, giving the door-keepers each another shilling as I came out.

It took my last shilling to pay the fourth door-keeper. How much money had I at first, and what did I spend in each tent?

Solution

OUT IN THE RAIN

47. Rain is falling vertically, at a speed of 5 miles an hour. I am walking through it at 4 miles an hour. At what angle to the vertical must I hold my umbrella, so that the raindrops strike its top at right angles?

Solution

A MONKEY PUZZLER

48. The following interesting problem, translated from the original Sanscrit, is given by Longfellow in his “Kavanagh”:—

“A tree, 100 cubits high, is distant from a well 200 cubits. From the top of this tree one monkey descends, and goes to the well.[II-123] Another monkey leaps straight upwards from the top, and then descends to the well by the hypotenuse. Both pass over an equal space. How high does the second monkey leap?”

Solution

49.

A steamboat 105 miles east of Tynemouth Lighthouse springs a leak. She puts back at once, and in the first hour goes at the rate of 10 miles an hour.

More and more water-logged, she decreases her speed each succeeding hour at the rate of one-tenth of what it has been during the previous hour. When will she reach the lighthouse?

Solution

50.

If a hen and a half lays an egg and a half in a day and a half, how many eggs will twenty-one hens lay in a week?

Solution

51.

If the population of Bristol exceeds by two hundred and thirty-seven the number of hairs on the head of any one of its inhabitants, how many of them at least, if none are bald, must have the same number of hairs on their heads?

Solution

52.

A benevolent uncle has in his pocket a sovereign, a half-sovereign, a crown, a half-crown, a florin, a shilling, and a threepenny piece. In how many different ways can he tip his nephew, using only these coins, and how is this most easily determined?

Solution

53.

Here is a prime problem, in more senses than one, which will tax the ingenuity of our solvers:—I am a prime number of three figures. Increased by one-third, ignoring fractions, I become a square number. Transpose my first[II-124] two figures and increase me by one-third, and again I am a square number. Put my first figure last, and increase me by one-third, and I am another square number. Reverse my three figures, and increase as before by one-third, and for a fourth time I become a square number. What are my original figures?

Solution

54.

In how many different ways can six different things be divided between two boys?

Solution

55.

What is quite the highest number that can be scored at six card cribbage by the dealer, if he has the power to select all the cards, and to determine the order in which every card shall be played?

Solution

COVERING THE WALLS

56. A fanciful collector, who bought pictures with more regard to quantity than quality, gave instructions that the area of each frame should exactly equal that of the picture it contained, and that the frames should be of the same width all round.

At an auction he picked up a so-called “old master,” unframed, which measured 18 inches by 12 inches. What width of frame will fulfil his conditions?

Solution

A FAMILY REGISTER

57. Our family consists of my mother, a brother, a sister, and myself. Our average age is thirty-nine. My mother was twenty when I was born; my sister is two years my junior, and my brother is four years younger than she is. What are our respective ages?

Solution

[II-125]

58.

A spider in a dockyard unwittingly attached her web to a mechanical capstan 1 foot in diameter, at the moment when it began to revolve. To hold her ground she paid out 73 feet of thread, when the capstan stopped, and she found herself drained of silk.

To make the best of a bad job she determined to unwind her thread, walking round and round the capstan at the end of the stretched thread. When she had gone a mile in her spiral path she stopped, tired and in despair. How far was she then from the end of her task?

Solution

59.

A mountebank at a fair had six dice, each marked only on one face 1, 2, 3, 4, 5, or 6, respectively. He offered to return a hundredfold any stake to a player who should turn up all the six marked faces once in twenty throws. How far was this from being a fair offer?

Solution

CATS’-MEAT FOR DOGS

60.

If ninety groats for twenty cats
Will furnish three weeks’ fare,
How many hounds for forty pounds,
Less one, may winter there?

Just ninety days and one assume
The winter’s space to be;
And note that what five cats consume
Will serve for dogs but three.

(A groat = 4d.)

Solution

61.

Two wineglasses of equal size are respectively half and one-third full of wine. They are filled up with water, and their contents are then mixed. Half of this mixture is finally poured back into one of the wineglasses. What part of this will be wine and what part will be water?

Solution

[II-126]

62.

A legend goes that on a stout ship on which St Peter was carried with twenty-nine others, of whom fourteen were Christians and fifteen Jews, he so arranged their places, that when a storm arose, and it was decided to throw half of the passengers overboard, all the Christians were saved. The order was that every ninth man should be cast into the sea. How did he place the Christians and the Jews?

Solution

A PROLIFIC COW

63. Farmer Southdown was the proud possessor of a prize cow, which had a fine calf every year for sixteen years. Each of these calves when two years old, and their calves also in their turn, followed this excellent example. How many head did they thus muster in sixteen years?

Solution

64.

A shepherd was asked how many sheep he had in his flock. He replied that he could not say, but he knew that if he counted them by twos, by threes, by fours, by fives, or by sixes, there was always one over, but if he counted them by sevens, there was no remainder. What is the smallest number that will answer these conditions?

Solution

READY RECKONING

65. If a number of round bullets of equal size are arranged in rows one above another evenly graduated till a single bullet crowns the flat pyramid, how can their number be readily reckoned, however long the base line may be?

Solution

[II-127]

THE TITHE OF WAR

66.

Old General Host
A battle lost,
And reckoned on a hissing,
When he saw plain
What men were slain,
And prisoners, and missing.

To his dismay
He learned next day
What havoc war had wrought;
He had, at most,
But half his host
Plus ten times three, six, ought.

One-eighth were lain
On beds of pain,
With hundreds six beside;
One-fifth were dead,
Captives, or fled,
Lost in grim warfare’s tide.

Now, if you can,
Tell me, my man,
What troops the general numbered,
When on that night
Before the fight
The deadly cannon slumbered?

Solution

[II-128]

67.

A farmer sends five pieces of chain, of three links each, to be made into one continuous length. He agrees to pay a penny for each link cut, and a penny for each link joined. What was the blacksmith entitled to charge if he worked in the best interest of the farmer?

Solution

68.

In a parcel of old silver and copper coins each silver piece is worth as many pence as there are copper coins, and each copper coin is worth as many pence as there are silver coins, and the whole is worth eighteen shillings. How many are there of each?

Solution

A FEAT WITH FIGURES

69. Take the natural numbers 1 to 11, inclusive, and arrange them in five groups, not using any of them more than once, so that these groups are equal. Any necessary signs or indices may be used.

Solution

HOW OLD WAS JOHN?

70. John Bull passed one-sixth of his life in childhood and one-twelfth as a youth. When one-seventh of his life had elapsed he had a son who died at half his father’s age, and John himself lived on four years more. How old was he at the last?

Solution

FIGURE IT OUT

71. There are two numbers under two thousand, such that if unity is added to each of them, or to the half of each, the result is in every case a square number. Can you find them?

Solution

72.

A cheese in one scale of a balance with arms of unequal length seems to weigh 16 lbs. In the other scale it weighs but 9 lbs. What is its true weight?

Solution

[II-129]

“DIVISION IS AS BAD!”

73. Can you divide 100 into two such parts that if the larger is divided by the lesser the quotient is also 100?

Solution

74.

I have marbles in my two side pockets. If I add one to those in the right-hand pocket, and multiply its increased contents by the number it held at first, and then deal in a similar way with those in the other pocket, the difference between the two results is 90. If, however, I multiply the sum of the two original quantities by the square of their difference, the result is 176. How many marbles had I at first in each pocket?

Solution

A SURFEIT OF BRIDGE

75. A friendly circle of twenty-one persons agreed to meet each week, five at a time, for an afternoon of bridge, so long as they could do so without forming exactly the same party on any two occasions.

As a central room had to be hired, it was important to have some idea as to the length of time for which they would require it. How long could they keep up their weekly meetings?

Solution

76.

A herring and a half costs a penny and a half; what is the price of a dozen?

Solution

77.

What sum of money is in any sense seen to be the double of itself?

Solution

COMIC ARITHMETIC

78. At the close of his lecture upon unknown quantities, Dr Bulbous Roots, in playful mood, wrote this puzzle on his blackboard:—

[II-130]

Divide my fifth by my first and you have my fourth; subtract my first from my fifth and you have my second; multiply my first by my fourth followed by my second, and you have my third; place my second after my first and you have my third multiplied by my fourth. What am I?

Solution

DROPPED THROUGH THE GLOBE

79. If we can imagine the earth at a standstill for the purpose of our experiment, and if a perfectly straight tunnel could be bored through its centre from side to side, what would be the course of a cannon ball dropped into it from one end, under the action of gravity?

Solution

LOVE LETTERS

80.

A lady to her lover cried,
“How many notes have you of mine?”
“Six more I’ve sent,” the youth replied,
“Than I have had of thine.”

“But if from one pound ten you take
The pennies we on stamps have spent,
One eighth their cost you thus will make.”
How many had they had and sent?

Solution

81.

A man, on the day of his marriage, made his will, leaving his money thus:—If a son should be born, two-thirds of the estate to that son and one-third to the widow. If a daughter should be born, two-thirds to the widow and one-third to that daughter. In the course of time twins were born, a boy and a girl. The man fell sick and died without making a fresh will. How ought his estate to be divided in justice to the widow, son, and daughter?

Solution

[II-131]

82.

My carpet is 22 feet across. My stride, either backwards or forwards, is always 2 feet, and I make a stride every second. If I take three strides forwards and two backwards continuously until I cross the carpet, how long does it take me to reach the end of it?

Solution

NO TIME TO BE LOST

83. A merchant at Lisbon has an urgent business call to New York. Taking these places to be, as they appear on a map of the world, on the same parallel of latitude, and at a distance measured along the parallel, of some 3600 miles, if the captain of a vessel chartered to go there sails along this parallel, will he be doing the best that he can for the impatient merchant?

Solution

ROUND THE ANGLES

84. Two schoolboys, John and Harry, start from the right angle of a triangular field, and run along its sides. John’s speed is to Harry’s as 13 is to 11.

They meet first in the middle of the opposite side, and again 32 yards from their starting point. How far was it round the field?

Solution

AN ECHO FROM THE PAST

85. The following question is given and spelt exactly as it was contributed to a puzzle column by “John Hill, Gent.,” in 1760:—

“A vintner has 2 sorts of wine, viz. A and B, which if mixed in equal parts a flagon of mixed will cost 15 pence; but if they be mixed in a sesqui-alter proportion, as you should take two flagons of A as often as you take three of B, a flagon will cost 14 pence. Required the price of each wine singly.”

Solution

[II-132]

PROMISCUOUS CHARITY

86. A man met a beggar and gave him half the money he had in his pocket, and a shilling besides. Meeting another he gave him half of what was left and two shillings, and to a third, he gave half of the remainder and three shillings. This left a shilling in his pocket. How much had he at first?

Solution

87.

A young clerk wishes to start work at an office in the City on January 1st. He has two promising offers, one from A of £100 a year, with a yearly rise of £20, the other from B of £100 a year with a half-yearly rise of £5. Which should he accept, and why?

Solution

HOW CAN I PAY MY BILL?

88. I have an abundance of florins and half-crowns, but no other coins. In how many different ways can I pay my tailor £11, 10s. without receiving change?

Solution

89.

A monkey climbing up a greased pole ascends 3 feet and slips down 2 feet in alternate seconds till he reaches the top. If the pole is 60 feet high, how long does it take him to arrive there?

Solution

“SAFE BIND, SAFE FIND”

90. Old Adze, the village carpenter, who kept his tools in an open chest, found that his neighbours sometimes borrowed and forgot to return them.

To guard against this, he secured the lid of the chest with a letter lock, which carried six revolving rings, each engraved with twelve different letters. What are the chances against any one discovering the secret word formed by a letter on each ring, which will open the lock, and be the only key to the puzzle?

Solution

[II-133]

91.

Five merry married couples happened to meet at a Swiss hotel, and one of the husbands laughingly proposed that they should dine together at a round table, with the ladies always in the same places so long as the men could seat themselves each between two ladies, but never next to his own wife. How long would their nights at the round table be continued under these conditions?

Solution

SOUNDING THE DEPTH

92. In calm water the tip of a stiff rush is 9 inches above the surface of a lake. As a steady wind rises it is gradually blown aslant, until at the distance of a yard it is submerged. Can you decide from these data the depth of the water in which the rush grows?

Solution

AMINTA’S AGE

93.

If to Aminta’s age exact
Its square you add, and eighteen more,
And from her age its third subtract,
And to the difference add three score,
The latter to the former then
Will just the same proportion bear
As eighteen does to nine times ten.
Can you Aminta’s age declare?

Solution

ONE FOR THE PARROT

94. A bag of nuts was to be divided thus among four boys:—Dick took a quarter, and finding that there was one over when he made the division, gave it to the parrot. Tom dealt in exactly the same way with the remainder, as did Jack and Harry in their turns, each finding one nut from the reduced shares to spare for the[II-134] parrot. The final remainder was equally divided among the boys, and again there was one for the bird. How many nuts, at the lowest estimate, did the bag contain?

Solution

95.

Here is an easy one:—

If five times four are thirty-three,
What will the fourth of twenty be?

Solution

96.

What fraction of a pound, added to the same fraction of a shilling, and the same fraction of a penny, will make up exactly one pound?

Solution

MENTAL ARITHMETIC

97. “Now, boys!” said Dr Tripos, “I think of a number, add 3, divide by 2, add 8, multiply by 2, subtract 2, and thus arrive at twice the number I thought of.” What was it?

Solution

98.

Two club friends, A and B, deposit similar stakes with C, and agree that whoever first wins three games at billiards shall take the whole of them. A wins two games and B wins one. Upon this they determine to divide the stakes in proper shares. How must this division be arranged?

Solution

99.

Not so simple as it sounds is the following compact little problem:—If I run by motor from London to Brighton at 10 miles an hour, and return over the same course at 15 miles an hour, what is my average speed?

Solution

100.

“I can divide my sheep,” says Farmer Hodge, who from his schooldays had a turn for figures, “into two unequal parts, so that the larger part added to the square of the smaller part shall be equal to the smaller part added to the square of the larger part.”

How many sheep had the farmer?

Solution

[II-135]

A HELPFUL BURDEN

101. The following question was proposed in an old book of Mathematical Curiosities published more than a hundred years ago:—

“It often happens that if we take two horses, in every respect alike, yet, if both are put to the draught, that horse which is most loaded shall be capable of performing most work; so that the horse which carries the heavier weight can draw the larger load. How is this?”

Solution

102.

In the king’s treasury were six chests. Two held sovereigns, two shillings, and two pence, in equal numbers of these coins. “Pay my guard,” said the king, “giving an equal share to each man, and three shares to the captain; give change if necessary.” “It may not be possible,” replied the treasurer, “and the captain may claim four shares.” “Tut, tut,” said the king, “it can be done whatever the amount of the treasure, and whether the captain has three shares or four.”

Was the king right? If so, how many men were there in the guard?

Solution

NUTS TO CRACK

103. I bought a parcel of nuts at forty-nine for twopence. I divided it into two equal parts, one of which I sold at twenty-four, the other at twenty-five for a penny. I spent and received an integral number of pence, but bought the least possible number of nuts. How many did I buy? What did they cost? What did I gain?

Solution

MONEY MATTERS

104. My purse contained sovereigns and shillings. After I had spent half of its contents there were as many pounds left as I had shillings at first. With what sum did I start?

Solution

[II-136]

A DELICATE QUESTION

105. A lady was asked her age in a letter, and she replied by postcard thus:—

If first my age is multiplied by three,
And then of that two-sevenths tripled be,
The square root of two-ninths of this is four,
Now tell my age, or never see me more!

What was her age?

Solution

106.

If cars run at uniform speed on the twopenny tube, from Shepherd’s Bush to the Bank at intervals of two minutes, how many shall I meet in half an hour if I am travelling from the Bank to Shepherd’s Bush?

Solution

PAYMENT BY RESULTS

107. What would it cost me to keep my word if I were to offer my greengrocer a farthing for every different group of ten apples he could select from a basket of a hundred apples?

Solution

108.

If the minute-hand of a clock moves round in the opposite direction to the hour-hand, what will be the real time between three and four, when the hands are exactly together?

Solution

109.

Two monkeys have stolen some filberts and some walnuts. As they begin their feast they see the owner of the garden coming with a stick. It will take him two and a half minutes to reach them. There are twice as many filberts as walnuts, and one monkey finishes the walnuts at the rate of fifteen a minute in four-fifths of the time and bolts. The other manages to finish the filberts just in time.

If the walnut monkey had stopped to help him till all was finished, when would they have got away if they ate filberts at equal rates?

Solution

[II-137]

110.

A cashier, in payment for a cheque, gives by mistake pounds for shillings and shillings for pounds. The receiver spends half-a-crown, and then finds that he has twice as much as the cheque was worth. What was its value?

Solution

111.

What five uneven figures can be added together so as to make up 14?

Solution

112.

Three posts which vary in value are vacant in an office. In how many ways can the manager fill these up from seven clerks who apply for the appointments?

Solution

113.

“It is now ⁵⁄₁₁ of the time to midnight,” said the fasting man, who began his task at noon. What time was it?

Solution

A STRIKING TIME

114. If a clock takes six seconds to strike six how long will it take to strike eleven?

Solution

WHAT ARE THE ODDS?

115. How would you arrange twenty horses in three stalls so as to have an odd number of horses in each stall?

Solution

116.

Here is a pretty little problem, which has at any rate an Algebraic form, and is exceedingly ingenious:—

Given a, b, c, to find q.

Solution

WHEN WAS HE BORN?

117. Tom Evergreen was asked his age by some men at his club on his birthday in 1875. “The number of months,” he said, “that I have lived are exactly half as many as the number which denotes the year in which I was born.” How old was he?

Solution

[II-138]

118.

Draw three circles of any size, and in any position, so long as they do not intersect, or lie one within another. How many different circles can be drawn touching all the three?

Solution

119.

We have seen that the nine digits can be so dealt with, using each once, as to add up to 100. How can 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 be arranged so that they form a sum which is equal to 1?

Solution

120.

How is it possible, by quite a simple method, to find the sum of the first fifty numbers without actually adding them together?

Solution

121.

Two tram-cars, A and B, start at the same time. A runs into a “lie by” in four minutes, and waits there five minutes, when B meets and passes it. Both complete the whole course at the same moment. In what time can A complete it without a rest?

Solution

A CURIOUS DEDUCTION

122. Take 10, double it, deduct 10, and tell me what remains.

Solution

123.

The average weight of the Oxford crew is increased by 2 lbs., when one of them, who weighs 12 stone, is replaced by a fresh man. What is the fresh man’s weight?

Solution

ASK ANY MOTORIST

124. A motor car is twice as old as its tyres were when it was as old as its tyres are. When these tyres are as old as the car is now, the united[II-139] ages of car and tyres will be two years and a quarter. What are their respective ages now?

Solution

125.

A and B on the edge of a desert can each carry provisions for himself for twelve days. How far into the desert can an advance be made, so that neither of them misses a day’s food?

Solution

126.

A bottle of medicine and its cork cost half-a-crown, but the bottle and the medicine cost two shillings and a penny more than the cork. What did the cork cost?

Solution

IN A FIX

127. A boat’s crew are afloat far from land with no sail or oars. How can they, without making any use of wind or stream, and without any outside help, regain the shore by means of a coil of rope which happens to be at hand.

Solution

128.

What is the largest sum in silver that I can have in my pockets without being able to give change for a half-sovereign.

Solution

129.

I have apples in a basket. Without cutting an apple I give half of the number and half an apple to one person; half of what then remains and half an apple to another, and half of what are still left and half an apple to a third. One apple now remains in the basket. How many were there at first?

Solution

A QUEER DIVISION

130.

A third of twelve divide
By just a fifth of seven;
And you will soon decide
That this must give eleven.

Solution

[II-140]

131.

A motor goes 9 miles an hour uphill, 18 miles an hour downhill, and 12 miles an hour on the level. How long will it take to run 50 miles and return at once over the same course?

Solution

132.

In firing at a mark A hits it in two out of three shots, B in three out of four, and C in four out of five. The mark was hit 931 times. If each fired the same number of shots, how many hits did each make, and how many shots were fired?

Solution

133.

If a cat and a dog, evenly matched in speed, run a race out and back over a course 75 yards in all, and the dog always takes 5 feet at a bound and the cat 3 feet, which will win?

Solution

IN A FOG

134. In a fog a man caught up a wagon going in the same direction at 3 miles an hour. If the wagon was just visible to him at a distance of 55 yards, and he could see it for five minutes, at how many miles an hour was he walking?

Solution

135.

Three horses start in a race. In how many different ways can they be placed by the judge?

Solution

NEW ZEALAND FOOTBALL

136. The New Zealanders, winning a match against Oxbridge, scored 34 points, from tries and tries converted into goals.

If every try had been converted they would have made four-fifths of the maximum which a score of 34 points from tries and goals can yield.

What is this maximum, and what was their actual score?

Solution

[II-141]

137.

What is the smallest number, of which the alternate figures are cyphers, that is divisible by 9 and by 11?

Solution

138.

Here is an interesting little problem:—A, with 8d. in his hand, meets B and C, who have five and three loaves respectively. In hungry mood they all agree to share the loaves equally, and to divide the money fairly between B and C. How much does each receive?

Solution

THE MONEY-BOXES

139. When four money-boxes, containing pennies only, were opened and counted, it was found that the number in the first with half those in all the others, in the second with a third of all the others, in the third with a fourth of all the others, and in the fourth with a fifth of all the others, amounted in each case to 740. How much money did the boxes contain, and how was it divided?

Solution

140.

Two steamers start together to make a trip to a far-off buoy and back. Steamer A runs all the time at 10 miles an hour. Steamer B does the passage out at 8 miles an hour, and the return at 12 miles. Will they regain port together?

Solution

141.

A golf player has two clubs mended in London. One has a new head, the other a new leather face. The head costs four times as much as the face. At St Andrews it costs five times as much, and the leather face at St Andrews is half the London price. Including a shilling for a ball he pays twice the St Andrews charges for these repairs. What is the London charge for each?

Solution

[II-142]

FROM TWO WRONGS TO MAKE A RIGHT

142. Two children were asked to give the total number of animals in a pasture, where sheep and cattle were grazing. They were told the numbers of sheep and of cattle, but one subtracted, and gave 100 as the answer, and the other arrived at 11,900 by multiplication. What was the correct total?

Solution

THE STONE CARRIER

143. Fifty-two stones are placed at intervals along a straight road. The distance between the first and the second is 1 yard, between the second and the third it is 3 yards, between the next two 5 yards, and so on, the intervals increasing each time by 2 yards.

How far would a tramp have to travel to earn five shillings promised to him when he had brought them one by one to a basket placed at the first stone?

Solution

144.

On a division in the House of Commons, if the Ayes had been increased by fifty from the Noes, the motion would have been carried by five to three. If the Noes had received sixty votes from the Ayes, it would have been lost by four to three. Did the motion succeed? How many voted?

Solution

A WATCH PUZZLE

145. How many positions are there on the face of a watch in which the places of the hour and minute-hands can be interchanged so as still to indicate a possible time?

Solution

CRICKET SCORES

146. In a cricket match the scores in each successive innings are a quarter less than in the preceding innings. The match was played out, and the side that went in first won by fifty runs. What was the complete score?

Solution

[II-143]

HOW HIGH CAN YOU THROW?

147. A boy throws a cricket ball vertically upwards, and catches it as it falls just five seconds later. How high from his hands does the ball go?

Solution

MEASURE THE CARPET

148. It may be said of a section of the gigantic carpet at Olympia that had it been 5 feet broader and 4 feet longer it would have contained 116 more feet; but if 4 feet broader and 5 longer the increase would have been but 113 feet. What were its actual breadth and length?

Solution

149.

In estimating the cost of a hundred similar articles, the mistake was made of reading pounds for shillings and shillings for pence in each case, and under these conditions the estimated cost was £212 18s. 4d. in excess of the real cost. What was the true cost of the articles?

Solution

SQUARES IN STREETS

150. The square of the number of my house is equal to the difference of the squares of the numbers of my next door neighbour’s houses on either side.

My brother, who lives in the next street, can say the same of the number of his house, though his number is not the same as mine. How are our houses numbered?

Solution

151.

Two men of unequal strength are set to move a block of marble which weighs 270 lbs., using for the purpose a light plank 6 feet long. The stronger man can carry 180 lbs. How must the block be placed so as to allow him just that share of the weight?

Solution

[II-144]

152.

A man has twenty coins, of which some are shillings and the rest half-crowns. If he were to change the half-crowns for sixpences and the shillings for pence he would have 156 coins. How many shillings has he?

Solution

COUNT THE COINS

153. Some coins are placed at equal distances apart on a table, so that they form the sides of an equilateral triangle.

From the middle of each side as many are then taken as equal the square root of the number on that side, and placed on the opposite corner coin. The number of coins on each side is then to the original number as 5 is to 4. How many coins are there in all?

Solution

PUTTING IN THE POSTS

154. A gardener, wishing to fence round a piece of ground with some light posts, found that if he set them a foot apart there would be 150 too few, but if placed a yard apart there would be 70 to spare. How many posts had he?

Solution

155.

A gives B £100 to buy 100 animals, which must be cows at £5 each, sheep at £1, and geese at 1s. How many of each sort can he buy?

Solution

156.

John is twice as old as Mary was when he was as old as Mary is. John is now twenty-one. How old is Mary?

Solution

157.

In a cricket match A made 35 runs; C and D made respectively half and one-third as many as B, and B’s score was as much below A’s as C’s was above D’s. What did B, C, and D each score?

Solution

[II-145]

SETTLED BY REMAINDERS

158. What is the least number which, divided by 2, 3, 4, 5, 6, 7, 8, 9, or 10, leaves respectively as remainders 1, 2, 3, 4, 5, 6, 7, 8, and 9?

Solution

TABLE TURNING

159. A square table stands on four legs, which are set at the middle point of its sides. What is the greatest weight that this table can uphold upon one of its corners?

Solution

BRIBING THE BOYS

160. Well pleased with the inspector’s report, the rector of a country parish came into his school with 99 new pennies in his pocket, and said that he would give them to the five boys in Standard VII. if they could, within an hour, show him how to divide them so that the first share should exceed the second by 3, be less than the third by 10, be greater than the fourth by 9, and less than the fifth by 16. What was the answer which would satisfy these conditions?

Solution

SHEEP-STEALING

161. Some Indian raiders carried off a third of a flock of sheep, and a third of a sheep. Another party took a fourth of what remained, and a fourth of a sheep. Others took a fifth of the rest and three-fifths of a sheep. What was the number of the full flock, if there were then 409 left?

Solution

162.

Three boys begin to fill a cistern. A brings a pint at the end of every three minutes, B a quart every five minutes, and C a gallon every seven minutes. If the cistern holds fifty-three gallons, in what time will it be filled, and who will pour in the last contribution?

Solution

[II-146]

ESTIMATE OF AGE

163. A man late in the last century said that his age was the square root of the year in which he was born. In what year did he say this?

Solution

A DEAL IN CHINA

164. A dealer in Eastern curios sold a Satzuma vase for £119, and on calculation found that the number which expressed his profit per cent. expressed also the cost price in pounds of the vase. What was this number?

Solution

165.

What is the chance of throwing at least one ace in a single throw with a pair of dice?

Solution

166.

A thief starts running from a country house as fast as he can. Four minutes later a policeman starts in pursuit. If both run straight along the road, and the policeman gets over the ground one-third faster than the thief, how soon will he catch him?

Solution

167.

Twenty-seven articles are exposed for sale on one of the stalls of a bazaar. What choice has a purchaser?

Solution

VERY PERSONAL

168. “How old are you, dad?” said Nellie on her birthday, as her father gave her as many shillings as she was years old. His answer was quite a puzzle for a time, but with the help of her schoolfellows Nellie worked it out.

This is what he said:—

“I was twice as old as you are
The day that you were born.
You will be just what I was then
When fourteen years are gone.”

How old was Nellie, and how old was her dad?

Solution

[II-147]

WORD AND LETTER PUZZLES

A MAGIC COCOON

This Magic Cocoon is so cleverly spun that the word can be traced and read in many ways.

					N
				N	O	N
			N	O	O	O	N
		N	O	O	C	O	O	N
	N	O	O	C	O	C	O	O	N
N	O	O	C	O	C	O	C	O	O	N
	N	O	O	C	O	C	O	O	N
		N	O	O	C	O	O	N
			N	O	O	O	N
				N	O	N
					N

How many readings can you discover starting from one or other of the Cs, and passing up and down or sideways, but not diagonally, and never over the same letter twice in a reading? There are 756!

THE CHRONOGRAM

The Chronogram, severely classed by Addison as “a species of false wit” is a sentence in which the salient letters represent in Roman numerals some particular year. A good English specimen is this: “My Day Closed Is In Immortality.” The capital letters in these words give MDCIII., or 1603, the year in which Queen Elizabeth died.

[II-148]

A FRENCH CHRONOGRAM

The battle-cry at Montlhéry in 1465 was:—“à CheVaL, à CheVaL, gendarMes, à CheVaL!” Taking the letters printed in capitals—

M	=	1000
CCC	=	300
LLL	=	150
VVV	=	15
we have the date of the battle		1465

A NOTABLE CHRONOGRAM

QVI CHRISTI IAVDES CANTANT
SANCTÆ PASSIONIS SVÆ VIRTVTE
IN IPSO ET PATRE VNVM SINT.

This curious inscription is placed over the organ at Ober Ammergau. Add together its Roman numerals and they give the date at which the organ was dedicated. The English of it is:—

May those who sing the praises of Christ be by virtue of His Sacred Passion one in The Father and in Himself.

A PERFECT CHRONOGRAM

On a damaged inscription to Bishop Berkeley in Winchester Cathedral are the words—VIXI, LVXI—I have lived, I have shone. Added together in their values as Roman numerals the letters of these two words give his age exactly at his death—eighty-three.

[II-149]

A PRIZE MOTTO

On the return of the C.I.V. from the Boer War a prize was offered by Truth for the best motto appropriate to them. This was to consist of three words of which the first must begin with C the second with I and the third with V.

The prize was taken by the following Latin motto which is singularly happy both in construction and in meaning:—

CIVI	IVI	VICI
I roused	I went	I won.

The sequence of events is perfect; no letters but C.I.V. are used and the motto is a palindrome if read by syllables.

THE MUSICAL SCALE

As in olden days some of the Psalms and other writings were constructed in acrostic form, so in the Middle Ages even serious writers would juggle with letters, as though they felt that such tricky methods were an aid to memory.

It was in this spirit that Guido Aretino, a Benedictine monk of Tuscany in 1204, gave names to the notes used in the musical scale from the first syllables of the lines of a Latin hymn. “Ut” is still used in France, though we and the Italians have substituted “do.”

UT queant laxis	REsonare fibris,
MIra gestorum	FAmuli tuorum,
SOLve polutis	LAbii reatis
O Pater alme!

ALL THE ALPHABET!

Many of us know that there is a long verse in the Book of Ezra in which all the letters of the[II-150] alphabet are used, taking “j” as “i” (Ezra vii., v. 21).

This very curious coincidence also occurs in a comparatively short sentence in “The Beth Book,” by Sarah Grand:—“It was an exquisitely deep blue just then, with filmy white clouds drawn up over it like gauze;” and here “j” is itself in evidence.

APT ALLITERATION

Schopenhauer, the famous German philosopher, who was a confirmed bachelor and misogynist, was compelled while living at Frankfort to support an old lady who had been crippled by his violence. When her death came as a welcome relief to him, he composed the following clever epitaph:—

Obit anus,
Abit onus.

which by the interchange of two letters pictured the position. It may be freely rendered:—

Old lady dies,
My burden flies.

A DOUBLE SEQUENCE

The following clever composition, which appeared in the pages of Truth, contains a double sequence of words, which increase a letter at a time, the same letters appearing in varied order until at last “o” culminates in thornless, and “a” in restrainest. It is quite a remarkable tour-de-force.

O lack-a-day! at eve we sat,
One star had lit its lamps on high.
We did not note the circling bat,
Start from the stone when flitting nigh.
For the strait gate of honest doubt
Shut off the thrones of Love and Gain;
[II-151] We dreamed not, as we mourned without,
That Time’s swift transit shortens pain.
O Thou, Who trainest souls to shine,
Though once we craved a thornless lot,
This gracious truth we now divine:
The bruised reed Thou strainest not;
But by restraints, that gently tame;
Restrainest Passion’s kindling flame.

THE REIGN OF TERROR

During the Reign of Terror, France and her people and position were thus alphabetically described:—

Le peuple Français	A B C.	(abaissé).
La gloire nationale	F A C.	(effacée).
Les places fortes	O Q P.	(occupées).
Quarante trois députés	C D.	(cédés).
L’armée	D P C.	(dépaysée).
Les ministres	A J.	(agés).
La liberté	O T.	(ôtée).
La charte	L U D.	(éludée).

SEE-SAW

This elaborate method of piling up no less than seven consecutive “thats,” so that they make tolerable sense, was told to his boys during school-time by Dr Moberly, then headmaster of Winchester, and afterwards Bishop of Salisbury, just fifty years ago:—

I saw that C saw.

C saw that that I saw.

I saw that that that C saw was so.

C saw that, that that that I saw was so.

I saw that, that that that that C saw was so.

C saw that that, that that that that I saw was so.

I saw that that, that that that that that C saw was so.

[II-152]

FOR A ROMAN HOLIDAY

If the Roman ladies and children, at their equivalent for Christmas, amused themselves by acting verbal charades, an excellent word was at their disposal, “sustineamus”—“let us endure,” which can be broken up exactly into sus, tinea, mus—a sow, a moth, a mouse.

A WORD SQUARE

1. Can you complete this word square, so that its four words read alike from top to bottom and from left to right?

*	E	*	*
E	*	*	*
*	*	*	E
*	*	E	*

Solution

ANOTHER WORD SQUARE

2. Can you fill in this word square?

C	*	*	C	*	E
*	N	U	*	E	S
*	U	*	E	S	*
C	*	E	*	S	*
*	E	S	*	*	E
E	*	T	E	*	*

Solution

DUPLICATE LETTERS

3. In this sentence, when complete,

So * * * * AG * * * * LATI * * * * X * * * * ITH

each group of four missing letters contains two pairs of letters which are alike. Can you on these lines complete the sentence?

[II-153]

Here is a similar sentence by way of illustration:

T * * * * M * * * * TERTAIN * * * * MUND,

which becomes when filled in—

Two women entertained Edmund.

Solution

ANOTHER WORD SQUARE

4. Can you complete this word square by substituting letters for the dots?

W	*	*	*	E
*	*	T	*	*
*	T	O	N	*
*	*	N	*	*
E	*	*	*	T

Solution

WORD BUILDING

5. What word can be made with these?

L S D U D O D U D.

Solution

6.

A lovelorn youth consulted a married lady on his condition, and was asked by her on a slip of paper:—

“Loruve?”

When he had deciphered this, and had answered in the affirmative, she handed to him another slip, on which this advice was written:—

		L
“Prove	A		F	and ensure success.”
		D

What did it all mean?

Solution

A DOUBLE ACROSTIC

Saint of Spain, whose daily word
Twenty years hath London heard!
[II-154] Sweet days, elastic metal, motion sharp.
My halls once echoed to an Irish harp.
The “son of sorrow,” honourable of yore.
Dread goddess, loosing the loud dogs of war.
Time’s atom—total of eternities.
This name an insect bears, a patriot bore.
“So do, yet hear me,” said Themistocles.

Solution

ANOTHER WORD SQUARE

8. Can you complete this word square?

*	M	*	N	*	S
M	*	N	*	O	*
*	N	*	B	*	E
N	*	B	*	L	*
*	O	*	L	*	R
S	*	E	*	R	*

Solution

A FRENCH ORACLE

9. A spruce young Frenchman at a fête consulted a modern oracle as to how he could best please the ladies. This was the mystic response:—

MEC DO BIC.

Can you interpret it?

Solution

A QUAINT EQUATION

10. In our young days we have often wrestled with vulgar fractions, but apart from Algebra we have had no serious concern with any in which letters take the place of figures. A specimen of this sort, not known to science, is the following curiosity:—

m ot y = mo.

Solution

[II-155]

11.

The puzzle in Truth was recently founded upon “ourang-outang,” which had been cleverly buried. We will give a few of the best results. This is one:—

Poor wretch! a moisture filled his eye,
“Do not rebuff a lonely boy,”
Said he, “If ere I sink and die
Your smile—O! pardon will be joy!”

Another is:—

Though I jump, and row, and run,
Cap or cup I never won.

What animals are buried in these lines?

Solution

LIKE A PEACOCK’S TAIL

12.

Fourteen letters here we fix,
Vowels only two are spoken;
All together these we mix
Into what can not be broken.

Solution

A WEIRD WORD

13. There is an English word of thirteen letters in which the same vowel occurs four times, the same consonant six times, another consonant twice, and another once. Can you hit upon it?

Solution

A CONDENSED PROVERB

14. Though brevity is said to be the soul of wit, we are too often flooded nowadays with a superabundance of words.

Here is an attempt at modest condensation. A familiar English proverb is quite clearly expressed to the solver’s seeing eyes in this brief phrase:—

WE IS DO

What is the proverb?

[II-156]

Solution

ANOTHER WORD SQUARE

15. Can you complete this word square?

W	*	*	*	*	S
*	R	*	*	R	*
*	*	O	R	*	*
*	*	R	M	*	*
*	R	*	*	N	*
S	*	*	*	*	M

Solution

CAN YOU DECIPHER IT?

16. The following puzzle lines are attributed to Dr Whewell:—

			O	O	N	O	O.
U	O	A	O	O	I	O	U
O	N	O	O	O	O	M	E	T	O	O.
U	O	A	O	I	D	O	S	O
I	O	N	O	O	I	O	U	T	O	O!

Solution

A BROKEN DIAMOND

17. Can you fill in the vacancies in this diamond?

				P
			F	O	*
		C	*	R	*	*
	F	*	*	C	*	*	*
P	O	R	C	E	L	A	I	N
	R	*	*	L	*	*	*
		S	*	A	*	*
			S	I	*
				N

Its words must read alike from left to right and from top to bottom.

[II-157]

Solution

WHAT IS THIS?

18.

Tan HE Edsa VEN in
It N Gja SmeTs AsgN
aD Az Rett De.

Solution

A PHONETIC JOURNEY

19. I can travel first-class on the Great Eastern Railway from 2 2 2 2 2 2 2 2 4 4 4 4 4 5 0 0. What is the cost of my journey, and its length in time?

Solution

A CURIOUS OLD INSCRIPTION

20.

Seogeh sreve ereh wcisume vahl
Lah sehs se otreh nos llebdnas
Regni freh nos gnires rohyer
Ganoed iryd ale nifae esots sorcy
Rub nabot es rohk co caed ir.

Can you decipher it?

Solution

IRISH STEW AT SIMPSON’S

21. I wrote the following note recently:—

Dear Jack,—Meet me at Simpson’s to-morrow at 1.30. We will sample their excellent Irish stew. Here are some catchwords that will remind you of the invitation:—

Join me at and
Join me at ai
Join me at as

Why should they remind him of it?

Solution

ENGLISH AS SHE IS SPELT!

22. This was the exact text of a letter sent to the master of an English village school by a labourer as an excuse for his boy’s absence:—

“Cepatomtogoatatrin”

Can you decipher it?

[II-158]

Solution

A DOUBLE ACROSTIC

23. This double Acrostic will afford an easy exercise in mental gymnastics for those to whom such pastime appeals:—

Now we are fain
To rack your brain.

1. More fit for babes and sucklings than for you.

2. Robbed of externals this is very true.

3. Diminutive in measure and in weight.

4. Pen-name of one a true pen potentate.

5. A palindrome quite plain is here in sight.

6. Sans head and tail it also yields this light.

7. Here is in short what anyone may write.

Solution

FIND THE PROVERB

24.	c	e	f	h	i	m	n	o	r	s	t	v	y
	3	2	2	2	7	1	1	2	6	5	8	3	9
		4		4	1		2	1		6	1
		3			1		5	8		2	3
		5			7		9				6
		4

The letters with ones under them are the first letters of words, those with twos under them are second letters of words, and so on.

Solution

A PUZZLE WILL

25. Having occasion to make a few slight additions to my will, I called in my lawyer to arrange the matter. How far forward did the instructions contained in the following lines carry him in his work?

Set down a hundred in my will,
Add nothing to the text;
Five hundred now a space may fill,
And one be added next.

[II-159]

Another hundred write as well,
And yet another one;
Then fifty more, and try to tell
The deed that now is done.

Solution

ANOTHER WORD SQUARE

26. Can you complete this word square?

*	D	*	*	O	*
D	*	*	I	*	E
*	S	*	A	*	D
T	*	A	*	A	*
*	R	*	A	*	E
R	*	D	*	E	*

Solution

MUSICAL EPITAPHS

27. Over the grave of a French musician, who was choked by a fish bone, the following epitaph was inscribed in notes of music:—A. G. A. E. A.

Over the porch of the house of Gustave Doré these musical notes were placed on a tablet:—C. E. B. A. C. D.

What do these inscriptions signify?

Solution

QUITE TOO TOO

28. “Where can we meet to-morrow?” said Jack Spooner to his best girl.

“We will go,” she replied, “at 222222222222 LEY STREET.”

When and where did they meet?

Solution

A BROKEN WORD

29. What does this spell?

CT T T T T T T T T T

[II-160]

Solution

CONTRADICTORY TERMS

30. What English word is it which may be so treated as to affirm or disallow the use of its own initial or final letter?

Solution

PRINTERS’ PIE

31. Can you arrange these letters

E I O O O U
B C N N R R S S

so that they form the title of a book well-known to boys?

Solution

FILL IN THE GAPS

32. Keeping these letters in their present order make a sensible sentence by inserting among them as often as is necessary another letter, which must be in every case the same.

A DEN I I CAN DOCK.

Solution

DISTORTED SHAKESPEARE

33. Here is a well-known quotation from Shakespeare, which seems to need some straightening out:—

OXXU8 MAAULGIHCTE

NOR

Solution

A PHONETIC NIGHTMARE

34. Here, as an awful warning to those who are ready to accept the definition of English spelling given by a former headmaster of Winchester—“Consonants are interchangeable, and vowels do not count”—is a common English word of twelve letters, in “linked sweetness long drawn out.”

Iewkngheaurrhphthewempeighghtips.

Can you decipher it?

[II-161]

Solution

ANOTHER WORD SQUARE

35. Can you, by filling in letters, complete this word square so that it shall read alike across and from top to bottom?

*	A	*	*
A	*	*	A
*	E	*	*
*	A	*	E

Solution

A QUAINT INSCRIPTION

36. The following curious inscription may be seen on a card hanging up in the bar of an old riverside inn in Norfolk:—

THEM * ILL * ERSLEA * VET * HEMI
LLT * HEW * HER * RYMEN * LOW
ERTH * EIRS * AILTH * EMA
LTS * TER * SLE * AVET * HE * KI
LN * FORAD * ROPO * FTH
EWHI * TESW * AN * SALE.

Can you decipher it?

Solution

A POET’S PI

37.

TONDEBNIOTOCHUMFOARYHUR
OTDIRECTTHAWHOTERSOFKLSYA;
TIKATESTUBALIGHTSTILLETRUFLYR
OTBOWLALLNEFESLEAVARFWYAA.

In this printer’s pie the words are in their proper sequence, but the letters are tangled.

Solution

BURIED PLACES

38. In the following short sentences five names of places are buried—that is to say, the letters which spell them in proper order form parts of[II-162] more words than one. Thus, for example “Paris” might be buried in the words “go up a rise:”

“The men could ride all on donkeys, the skipper, though, came to a bad end.”

When you have discovered these places, try to find out what very unexpected word of more than four letters is buried in the sentence, “On Christmas Eve you rang out angel peals.”

Solution

TREASON CONDONED

39. According to an old poet, Sir John Harrington (1561-1612):—

“Treason doth never flourish; what’s the reason?
For if it prosper none dare call it treason!”

The classic lines may possibly have been the germ of the flippant modern riddle, “Why is it no offence to conspire in the evening?”

Solution

A BIT OF BOTANY

40.

Inscribe an m above a line
And write an e below,
This woodland flower is hung so fine
It bends when zephyrs flow.

Solution

A PIED PROVERB

41. The following letters, if they are properly rearranged, will fall into the words which form a popular proverb:—

A A E E G G H I L L M N N N O O O O R R S S S S T T

Can you place them in position?

Solution

A DROP LETTER PUZZLE

42. Can you fill in the gaps of this proverb?

E**t* *e*s**s *a*e *h* *o** **i*e.

[II-163]

Solution

MULTUM IN PARVO

43. There is an English word of five syllables which has only eight letters, five of them vowels—an a, an e, twice i, and y. What are its consonants?

Solution

DOUBLETS

44. Can you turn TORMENT to RAPTURE, using four links, changing only one letter each time, and varying the order of the letters?

Solution

A PIED PROVERB

45. Can you arrange these letters so that they form a sentence of five words?

a a c e e e f f h h i i i i i m n n o o o p r r s s t t t t t.

The result is a well-known English proverb.

Solution

WHAT CAN IT BE?

46. Add one letter, and make this into a sensible English sentence:—

G D L D P R T F R R T H D X X F R D D N S

Solution

OUT OF PROPORTION

47.

One vowel in an English word is found,
Which by eight consonants is hedged around.

Solution

48.

Can you form an English word with these letters?

A A A A A B B N N I I R S S T T.

Solution

49.

What is this? It is found in Shakespeare:—

K I N I.

Solution

ALPHA BETA

50. There are two English words which contain each of them ten letters, and six of these are a, b, c, d, e, f, the first six letters of the alphabet. Can you build up either or both of them without looking at the solution?

Solution

[II-164]

SHIFTING NUMBERS

51.

Of a band of true kinsmen I stand at the head,
Who, to keep themselves warm, cluster three in a bed.
Put four into gaol and their number has risen,
So that six can be counted together in prison.
Take the six and recount them, they dwindle to three;
Count again, and a change into five you will see.
With no number from one to one hundred I mix,
Yet with five of my mates I am seen to make six.

Solution

AN IMPUDENT PRODIGAL

52. The prodigal son of a wealthy colonial farmer received a letter from his father, to suggest that a considerable part of his inheritance should be safeguarded before he squandered it. His reply ran thus:—“Dear dad, keep 1000050.” As such a sum, even in dollars, was out of the question, the father was completely puzzled.

What did the prodigal mean?

Solution

BURIED POETS

53. The names of eight famous British poets are buried in these lines, that is to say, the letters that spell the names form in their proper order parts of different words:—

The sun is darting rays of gold
Upon the moor, enchanting spot,
Whose purpled heights, by Ronald loved,
Up open to his Shepherd cot.
[II-165]

And sundry denizens of air
Are flying, aye, each to his nest;
And eager make at such an hour
All haste to reach the mansions-blest.

Can you dig them up?

Solution

A FATEFUL LETTER

54. When A. B. gave up the reins of government, and C. B. took office in his place, it was found that their political positions could be exactly described by two quite common English verbs, which differ only in this, that the one is longer by one letter than the other, while the rest of the letters are the same, and in the same order. What are these two verbs?

Solution

A PRIZE REBUS

55. The following is a prize Rebus:—

done
mutt
and
i
you make me

a glutt
T. c. d.

Solution

A LETTER TANGLE

56.

First a c and a t, last a c and a t,
With a couple of letters between,
Form a sight that our eyes are delighted to see,
Unless in their sight it is seen.

Solution

A TRANSPOSITION

57.

Cut off my tail and set it at my head,
What was an island is a little bear instead.

Solution

[II-166]

A REBUS

T S.

58. What English word do these two letters indicate? There are two possible solutions of equal merit.

Solution

A PHONETIC PHRASE

59. How can we read this?

I N X I N X I N.

Solution

A GOOD END

60.

IFS

Solution

[II-167]

SOLUTIONS

CHESS CAMEOS

No. XXVI

Black has made the false move Kt from Q sq to Kt 3. When this is replaced, and the king is moved as the proper penalty, White mates at once with one or other of the Knights.

Back to Cameo

No. XXVII

Replace the White Kt at B 7, and a Black Pawn at K 4; then P takes P en pas. Mate.

ANALYSIS AND PROOF

It can be proved that Black’s last move must have been P from K 2 to K 4, so that White may take the P en pas.

The Black King cannot have moved from any occupied square.

(The White Kt now occupies B 7.)

Nor from Kt 3 or 4, as both are now doubly guarded, so that he cannot have moved out of a check.

(The White Kt now helps to guard Kt 5.)

Nor can he have moved from K 2, as the White P on Q 6 cannot have moved to give check.

No other P can have moved.

The K P cannot have moved from K 3, became of the position of the White King.

Therefore Black’s last move must have been P from K 2 to K 4, which White can take en pas giving Mate.

Back to Cameo

[II-168]

No. XXVIII

B—Q 2P—R 7 B—R 5P—R 7 becomes Q P—Kt 4any White hasno move.

The way in which the B runs to earth and is shut in is most ingenious. Black with the new Q cannot anyhow give White a move.

Back to Cameo

No. XXIX

R—Kt 7, ch.K moves R—Kt 5P becomes Q R—B 5, ch.Q × R, stalemate.

Back to Cameo

No. XXX

B—Kt 8.

Back to Cameo

No. XXXI

B—R 4.

Back to Cameo

No. XXXII

B—R sq.

Back to Cameo

No. XXXIII

B—Q 4.

Back to Cameo

No. XXXIV

B—B sq.

Back to Cameo

No. XXXV

K—R 4.

Back to Cameo

No. XXXVI

Kt—Kt’s 6.

Back to Cameo

No. XXXVII

R—Kt 5Kt × R Kt—B 6Kt—B 6 ch. Kt × Kt mate

Back to Cameo

No. XXXVIII

Kt—R 7B moves Q—KB 8B returns Q—R 8 mate.

Any other move of the Kt would impede the movements of the Q.

Back to Cameo

No. XXXIX

R—R sq.B moves. Q—Kt sq.B returns. Q to Kt sq. mate.

[II-169]

Back to Cameo

No. XL

This beautiful problem is solved by:—

Q—Kt 6P × Q K—B 2any mates accordingly.

Kt—K 3 R—B 3any mates accordingly.

Back to Cameo

No. XLI

R—R 2.B × Kt Q—R sq.any Q mates.

B—Q sq. Kt—QB 8,any Q or Kt mates.

B elsewhere Kt—QB 6,any Q or Kt mates.

Back to Cameo

No. XLII

Kt—Kt 4, dis. ch.K—R 8. Q—KR 2, ch.P × Q. Kt—B 2, mate.

There are other variations.

Back to Cameo

No. XLIII

B—Kt sq.P × Kt, Q—QR7,K × Kt. Q mates.

If K × Kt, Q × P, and mates next move.

Back to Cameo

No. XLIV

K—Q 7,K moves R—Q 5,K × R Q mates.

Back to Cameo

No. XLV

R—Q 8K moves Q × P, ch.K × Q B mates.

B moves Q—K 7any Q mates.

Back to Cameo

[II-170]

No. XLVI

B—B 6K × R Q—Q 7, ch.K × Q R mates.

B × R R—B 6, ch.K × P Q mates.

There are other variations.

Back to Cameo

No. XLVII

Q—R 8Kt × Q Kt—B 6any mates accordingly.

Back to Cameo

No. XLVIII

B—Kt 8B—K Kt 2 Q × B, ch.Kt—K 4 Q—QR 7, mate.

B—B 3 Q—Q 2, ch.K moves P mates.

Back to Cameo

No. XLIX

B—Kt 2K—K 4 Q—K 3 ch.any mates.

There are other variations.

Back to Cameo

No. L

Q—KR 2K—B 3 or B4 Q—Q 6, ch.Q × Q Kt—K 5. double ch. mate.

There are other variations.

Back to Cameo

No. LI

R—QR sq.P moves R—R 2P × R P mates.

Back to Cameo

[II-171]

No. LII

Q—B sq.P—K 7 Q × BP ch.K—Q 3 Q mates.

K—Q 2 Q × BP ch.K—B 3 Q mates.

There are other variations.

Back to Cameo

No. LIII

B—R 8K—R 2 Q—QR sq.K moves Q—Q Kt. 7, mate.

Back to Cameo

No. LIV

Q—R 5B × Q or B—B 2 Kt—Kt 5any Kt mates.

Back to Cameo

No. LV

K—Kt 7Kt—B 3 Q—Q 5, ch.Kt × Q Kt. mates.

P—K 3 Q—B 8, ch.K moves Q mates.

Back to Cameo

No. LVI

R—Kt 6P moves B—Kt 4P × B R × P mate.

Back to Cameo

No. LVII

Kt from R 3—Kt 5P × Kt B—B 4P × B P—Q 4 ch.P × P en pas R—B 5 mate.

R × B R—Kt 5 ch.any mates accordingly.

and if

Q—K 6 Kt—Q 6Q—Kt 3 R—B 5 ch.Q × R Kt—B 7 mate.

Back to Cameo

[II-172]

SCIENCE AT PLAY

No. LVIII.—THE GEARED WHEELS

The arrow head at the top of a small wheel with ten teeth, which is geared into and revolved round a large fixed wheel with forty teeth, will point directly upwards five times in its course round the large wheel. Four of these turnings are due to the rotation of the small wheel on its own axis, and one of them results from its revolution round the large wheel.

Back to Description

No. LX.—THE FIFTEEN BRIDGES

It is possible to pass over all the bridges which connect the islands A and B and the banks of the surrounding river without going over any of them twice.

The course can be shown thus, using capital letters for the different regions of land, and italics for the bridges:—Ea Fb Bc Fd Ae Ff Cg Ah Ci Dk Am En Ap Bq ElD.

This order of the bridges can, of course, be reversed.

Back to Description

No. LXVI.—A DUCK HUNT

In order that a spaniel starting from the middle of a circular pond, and going at the same pace as a duck that is swimming round its edge, shall be sure to catch it speedily, the dog must always keep in the straight line between the duck and the centre of the pond.

The duck can never gain an advantage by turning back, and if it swims on continuously in a circle it will be overtaken when it has passed through a quarter of the circumference, for the dog will in the same time have described a semi-circle whose diameter is the radius of the pond, ending at the point where the duck is caught.

Back to Description

[II-173]

No. LXIX.—THE TETHERED BIRD

When a bird tethered by a cord 50 feet long to a post 6 inches in diameter uncoils the full length of the cord, and recoils it in the opposite direction, keeping it always taut, it flies 10,157 feet, or very nearly 2 miles, in its double course.

To avoid possible misunderstanding, we point out that, in order to pass from the uncoiling to the recoiling position, the bird must fly through a semicircle at the end of the fully extended cord.

Back to Description

No. LXX.—THE MOVING DISC AND THE FLY

When a fly, starting from the point A, just outside the revolving disc, and always making straight for its mate at the point B, crosses the disc in four minutes, during which time the disc[II-174] is turning twice, the revolution of the disc has a most curious and interesting effect on the path of the fly.

The fly is a quarter of a minute in passing from the outside circle to the next, during which the disc has made an eighth of a revolution, and the fly has reached the point marked 1. The succeeding points up to 16 show the position of the fly at each quarter of a minute, until, by a prettily repeated curve, B is reached.

Back to Description

No. LXXI.—A SHUNTING PUZZLE

The following method enables the engine R to interchange the positions of the wagons, P and Q, for either of which there is room on the straight rails at A, while there is not room there for the engine, which, if it runs up either siding, must return the same way:—

1. R pushes P into A. 2. R returns, pushes Q up to P in A, couples Q to P, draws them both out to F, and then pushes them to E. 3. P is now uncoupled, R takes Q back to A, and leaves it there. 4. R returns to P, pulls P back to C, and leaves it there. 5. R, running successively through F, D, B, comes to A, draws Q out, and leaves it at B.

Back to Description

No. LXXV.—PHARAOH’S SEAL

It is quite puzzling to decide how many similar triangles or pyramids are expressed on the seal of Pharaoh. There are in fact 96.

Back to Description

No. LXXVI.—ROUND THE GARDEN

The four persons who started at noon from the central fountain, and walked round the four[II-175] paths at the rates of two, three, four, and five miles an hour would meet for the third time at their starting point at one o’clock, if the distance on each track was one-third of a mile.

Back to Description

No. LXXVII.—A JOINER’S PUZZLE

This diagram shows how to divide Fig. A into two parts, and so rearrange these that they form either Fig. B or Fig. C, without turning either of the pieces.

Cut the five steps, and shift the two pieces as is shown.

Back to Description

No. LXXVIII.—THE BROKEN OCTAGON

The Broken Octagon is repaired and made perfect if its pieces are put together thus:—

Back to Description

[II-176]

No. LXXIX.—AT A DUCK POND

The pond was doubled in size without disturbing the duck-houses, thus:—

Back to Description

No. LXXX.—ALL ON THE SQUARE

This is a perfect arrangement:—

Back to Description

No. LXXXI.—PINS AND DOTS

The pins may be placed thus:—

On the third dot in the top line; on the sixth[II-177] dot in the second line; on the second dot in the third line; on the fifth dot in the fourth line; on the first dot in the fifth line; on the fourth dot in the sixth line.

Back to Description

No. LXXXII.—A TRICKY COURSE

To trace this course draw lines upon the diagram from square 46 to squares 38, 52, 55, 23, 58, 64, 8, 57, 1, 7, 42, 10, 13, 27, and 19. This gives fifteen lines which pass through every square only once.

Back to Description

No. LXXXIII.—FOR THE CHILDREN

Make a square with three on every side, and place the remaining four one on each of the corner men or buttons.

Back to Description

[II-178]

No. LXXXVII.—LOYD’S MITRE PROBLEM

The figure given is thus divided into four equal and similar parts:—

Back to Description

No. LXXXIX.—CUT OFF THE CORNERS

A very simple rule of thumb method for striking the points in the sides of a square, which will[II-179] be at the angles of an octagon formed by cutting off equal corners of the square, is to place another square of equal size upon the original one, so that the centre is common to both, and the diagonal of the new square lies upon a diameter of the other parallel to its side.

Back to Description

No. XCIII.—MAKING MANY SQUARES

The subjoined diagram shows how the two oblongs, applied to the two concentric squares, produce 31 perfect squares, namely, 17 small ones, one equal to 25 of these, 5 equal to 9, and 8 equal to 4.

Back to Description

No. XCIV.—CUT ACROSS

The Greek Cross can be divided by two straight cuts, so that the resulting pieces will form a[II-180] perfect square when re-set, as is shown in these figures:—

Back to Description

No. CV.—A TRANSFORMATION

The diagram which is given below shows how the irregular Maltese Cross can be divided by two straight cuts into four pieces, which form when properly rearranged, a perfect square.

Back to Description

No. CVI.—SHIFTING THE CELLS

The following diagram shows by its dark lines how the whole square can be cut into four pieces, and these arranged as two perfect squares in which every semicircle still occupies the upper half of its cell.

One piece forms a square of nine cells, and it[II-181] is easy to arrange the other three pieces in a square of sixteen cells by lifting the three cells and dropping the two.

Back to Description

No. CVII.—IN A TANGLE

It will be seen, on the subjoined diagram, how[II-182] twenty-one counters or coins can be placed on the figure so that they fall into symmetrical design, and form thirty rows, with three in each row.

Back to Description

No. CVIII.—STILL A SQUARE

In order that a square and an additional quarter may be divided by two straight lines so that their parts, separated and then reunited, form a perfect square, lines must be drawn from the point A to the corners B and C. Draw the figure on paper, cut through these lines, and you will find that the pieces can be so reunited that they form a perfect square.

Back to Description

No. CIX.—A TRANSFORMATION

The diagram below shows how the seven parts of the square can be rearranged so that they form the figure 8.

Back to Description

[II-183]

No. CX.—TO MAKE AN OBLONG

Here is an oblong formed by piecing together two of the smaller triangles, and four of each of the other patterns—

Here is another:—

Back to Description

No. CXI.—SQUARES ON THE CROSS

This diagram shows how every indication of the seventeen squares is broken up by the removal[II-184] of seven of the asterisks which mark their corners.

Those surrounded by circles are to be removed.

Back to Description

No. CXII.—A CHINESE PUZZLE

The dotted lines on the triangular figure show[II-185] how a piece of cardboard cut to the shape of Fig. 1 can be divided into three pieces, and rearranged so that these form a star shaped as in Fig. 2.

Back to Description

No. CXIII.—FIRESIDE FUN

To solve this puzzle slip the first coin or counter from A to D, then the others in turn from F to A, from C to F, from H to C, from E to H, from B to E, from G to B, and place the last on G. It can only be done by a sequence of this sort, in which each starting point is the finish of the next move.

Back to Description

AMUSING PROBLEMS

1. THE CARPENTER’S PUZZLE

The carpenter cleverly contrived to mend a hole 2 feet wide and 12 feet long, by cutting the board which was 3 feet wide and 8 feet long, as[II-186] is shown in Fig. 1, and putting the two pieces together as is shown in Fig. 2.

Back to Problem

2. GOLDEN PIPPINS

Here is another solution:—

1	3	5	7	9	11	13	15	17	19
39	37	35	33	31	29	27	25	23	21
2	4	6	8	10	12	14	16	18	20
40	38	36	34	32	30	28	26	24	22
82	82	82	82	82	82	82	82	82	82

Back to Problem

3. AN AWKWARD FIX

I was able to find my way in a strange district, when the sign-post lay uprooted in the ditch, without any difficulty. I simply replaced the post in its hole, so that the proper arm, with its lettering, pointed the way that I had come, and then, of necessity, the directions of the other arms were correct.

Back to Problem

4. LINKED SWEETNESS LONG DRAWN OUT

The train was whistling for 5 minutes. Sound travels about a mile in 5 seconds, so the first I heard of it was 5 seconds after it began. Its last sound reached me 7¹⁄₂ seconds after it ceased, so I heard the whistle for 5 minutes, 2¹⁄₂ seconds.

Back to Problem

5.

These quarters were not so elastic as they are made to appear. In good truth, considering that the second man who was placed in A was afterwards removed to I, no real second man was provided for at all.

Back to Problem

[II-187]

6.

The first day of a new century can never be Sunday, Wednesday, or Friday. The cycle of the Gregorian calendar is completed in 400 years, after which all dates repeat themselves.

As in this cycle there are only four first days of a century, it is clear that three of the seven days of the week must be excluded. Any perpetual calendar shows that the four which do occur are Monday, Tuesday, Thursday, and Saturday, so that Sunday, Wednesday, and Friday are shut out.

A neat corollary to this proof is that Monday is the only day which may be the first, or which may be the last, day of a century.

Back to Problem

7.

A cricket bat with spliced handle has such good driving power, because the elasticity of the handle allows the ball to be in contact with the blade of the bat for a longer time than would otherwise be possible.

With similar effect the “follow through” of the club head at golf maintains contact with the ball, when it is already travelling fast.

Back to Problem

8.

When two volumes stand in proper order on my bookshelf, each 2 inches thick over all, with covers ¹⁄₈ of an inch in thickness, a bookworm would only have to bore ¹⁄₄ of an inch, to penetrate from the first page of Vol. I, to the last page of Vol. II, for these pages would be in actual contact if there was no binding. This very pretty and puzzling question combines in its solution all the best qualities of a clever catch with solid and simple facts.

Back to Problem

9.

A man would have to fall from a height of nearly 15 miles to reach earth before the sound of his cry as he started. The velocity of sound is constant, while that of a falling body is continually accelerated. At first the cry far outstrips[II-188] the falling man, but he overtakes and passes through his own scream in about 14¹⁄₂ miles, for his body falls through the 15 miles in 70 seconds, and sound travels as far in 72 seconds. Air resistance, and the fact that sound cannot pass from a rare to a dense atmosphere, are disregarded in this curious calculation.

Back to Problem

10.

A man on a perfectly smooth table in a vacuum, and where there was no friction, though no contortions of his body would avail to get away from this position, could escape from the predicament by throwing from him something which he could detach from his person, such as his watch or coat. He would himself instantly slide off in the opposite direction!

Back to Problem

11.

The monkey clinging to one end of a rope that passes over a single fixed pulley, while an equal weight hangs on the other end, cannot climb up the rope, or rise any higher from the ground.

If he continues to try to climb up, he will gradually pull the balancing weight on the other end of the rope upwards, and the slack of the rope will drop below him, while he remains in the same place.

If, after some efforts, he rests, he will sink lower and lower, until the weight reaches the pulley, because of the extra weight of rope on his side, if friction is disregarded.

Back to Problem

12.

Though the tension on a pair of traces tends as much to pull the horse backward as it does to pull the carriage forward, it is the initial pull from slack to taut which sets the traces in motion; and this, once started, must continue indefinitely until checked by a counter pull.

Back to Problem

13.

Some say that a rubber tyre leaves a double[II-189] rut in dust and a single one in mud, because the air, rushing from each side into the wake of the wheel, piles up the loose dust. Others hold that the central ridge is caused by the continuous contraction of the tyre as it passes its point of contact with the road.

A correspondent, writing some years ago to “Knowledge,” said:—“It is our old friend the sucker. The tyre being round, the weight on centre of track only is great enough to enable the tyre to draw up a ridge of dust after it.”

Back to Problem

14.

If two cats on a sloping roof are on the point of slipping off, one might think that whichever had the longest paws (pause) would hold on best. Todhunter, in playful mood, saw deeper into it than that, and pronounced for the cat that had the highest mew, for to his mathematical mind the Greek letter mu was the coefficient of friction!

Back to Problem

15.

If a penny held between finger and thumb, and released by withdrawing the finger, starts “heads” and makes half a turn in falling through the first foot, it will be “heads” again on reaching the floor, if it is held four feet above it at first.

Back to Problem

16. HE DID IT!

Funnyboy had secretly prepared himself for the occasion by rubbing the chemical coating from the side of the box on to his boot.

Back to Problem

17. THE CYCLE SURPRISE

If a bicycle is stationary, with one pedal at its lowest point, and that pedal is pulled backwards, while the bicycle is lightly supported, the bicycle will move backwards, and the pedal relatively to the bicycle, will move forwards. This would be quite unexpected by most people, and it is well worth trying.

Back to Problem

[II-190]

18.

The rough stones, by which any number of pounds, from 1 to 364, can be weighed, are respectively 1 ℔., 3 ℔s., 9 ℔s., 27 ℔s., 81 ℔s., and 243 ℔s. in weight.

Back to Problem

19.

If we disregard the resistance of the air, a small clot of mud thrown from the hindermost part of a wheel would describe a parabola, which would, in its descending limb, bring it back into kissing contact with the wheel which had rejected it.

Back to Problem

20. THE CARELESS CARPENTER

When the carpenter cut the door too little, he did not in fact cut it enough, and he had to cut it again, so that it might fit.

Back to Problem

21.

If from the North Pole you start sailing in a south-westerly direction, and keep a straight course for twenty miles, you must steer due north to get back as quickly as possible to the Pole, if, indeed, it has been possible to start from it in any direction other than due south.

Back to Problem

22. DICK IN A SWING

Dick’s feet will travel in round numbers nearly 16 feet further than his head, or to be exact, 15·707,960 feet.

Back to Problem

23. A POSER

The initial letters of Turkey, Holland, England, France, Italy, Norway, Austria, Lapland, and Spain spell, and in this sense are the same as, “the finals.”

Back to Problem

CURIOUS CALCULATIONS

1.

The only sum of money which satisfies the condition that its pounds, shillings, and pence written down as a continuous number, exactly give the number of farthings which it represents, is £12, 12s., 8d., for this sum contains 12,128 farthings.

Back to Description

[II-191]

2.

If, when a train, on a level track, and running all the time at 30 miles an hour, slips a carriage which is uniformly retarded by brakes, and this comes to rest in 200 yards, the train itself will then have travelled 400 yards.

The slip carriage, uniformly retarded from 30 miles an hour to no miles an hour, has an average speed of 15 miles an hour, while the train itself, running on at 30 miles an hour all the time, has just double that speed, and so covers just twice the distance.

Back to Description

3.

The traveller had fivepence farthing when he said to the landlord, “Give me as much as I have in my hand, and I will spend sixpence with you.” After repeating this process twice he had no money left.

Back to Description

4.

This is the way to obtain eleven by adding one-third of twelve to four-fifths of seven—

TW(EL)VE + S(EVEN) = ELEVEN

Back to Description

5.

Here is the completed sum:—

2	1	5	)	*	7	*	9	*	(	1	*	*	2	1	5	)	3	7	1	9	5	(	1	7	3
				*	*	*											2	1	5
				*	5	*	9										1	5	6	9
				*	5	*	5										1	5	0	5
						*	4	*											6	4	5
						*	*	*											6	4	5

The clue is that no figure but 3, when multiplied into 215, produces 4 in the tens place.

Back to Description

6.

If I attempt to buy as many heads of asparagus as can be encircled by a string 2 feet long for double the price paid for as many as half[II-192] that length will encompass, I shall not succeed. A circle double of another in circumference is also double in diameter, and its area is four times that of the other.

Back to Description

7.

If, when you reverse me, and my square, and my cube, and my fourth power, you find that no changes have been made, I am 11, my square is 121, my cube 1331, and my fourth power 14641.

Back to Description

8.

A thousand pounds can be stored in ten sealed bags, so that any sum in pounds up to £1,000 can be paid without breaking any of the seals, by placing in the bags 1, 2, 4, 8, 16, 32, 64, 128, 256, and 489 sovereigns.

Back to Description

9.

It is the fraction ⁶⁄₉ which is unchanged when turned over, and which, when taken thrice, and then divided by two becomes 1.

Back to Description

10.

When the three gamblers agreed that the loser should always double the sum of money that the other two had before them, and they each lost once, and fulfilled the conditions, remaining each with eight sovereigns in hand, they had started with £13, £7, and £4 as the following table shows:—

	A	B	C
	£	£	£
At starts	13	7	4
When A loses	2	14	8
When B loses	4	4	16
When C loses	8	8	8

Back to Description

[II-193]

11.

Tom’s sum, which his mischievous neighbour rubbed almost out, is reconstructed thus:—

		3	4	5			3	4	5
			*	*				3	7
	*	*	*	*		2	4	1	5
*	*	*	*		1	0	3	5
*	*	7	6	*	1	2	7	6	5

Back to Description

12.

Here are two other arrangements of the nine digits which produce 45, their sum; each is used once only:—

5 × 8 × 9 × (7 + 2)1 × 3 × 4 × 6 = 45

7² - 5 × 8 × 93 × 4 × 6 + 1 = 45

Back to Description

13.

If, when the combined ages of Mary and Ann are 44, Mary is twice as old as Ann was when Mary was half as old as Ann will be when Ann is three times as old as Mary was when Mary was three times as old as Ann, Mary is 27¹⁄₂ years old, and Ann is 16¹⁄₂.

For, tracing the question backwards, when Ann was 5¹⁄₂ Mary was 16¹⁄₂. When Ann is three times that age she will be 49¹⁄₂. The half of this is 24³⁄₄, and when Mary was at that age Ann was 13³⁄₄. Mary’s age, by the question, was twice this, or 27¹⁄₂.

Back to Description

14.

It is safer at backgammon to leave a blot in the tables which can be taken by an ace than one which a three would hit. In either the case of an actual ace or a three the chance is one in[II-194] eleven; but there are two chances of throwing deuce-ace, the equivalent of three.

Back to Description

15.

If I start from a bay, where the needle points due north, 1200 miles from the North Pole, and the course is perfectly clear, I can never reach it if I steam continuously 20 miles an hour, steering always north by the compass needle. After about 200 miles I come upon the Magnetic Pole, which so affects the needle that it no longer leads me northward, and I may have to steer south by it to reach the geographical Pole.

Back to Description

16.

The 21 casks, 7 full, 7 half full, and 7 empty, were shared equally by A, B, and C, as follows:—

	Full cask.	Half full.	Empty.
A	2	3	2
B	2	3	2
C	3	1	3
or—
A	3	1	3
B	3	1	3
C	1	5	1

Thus each had 7 casks, and the equivalent of 3¹⁄₂ caskfuls of wine.

Back to Description

17.

The foraging mouse, able to carry home three ears at a time from a box full of ears of corn, could not add more than fourteen ears of corn to its store in fourteen journeys, for it had each time to carry along two ears of its own.

Back to Description

18.

If, with equal quantities of butter and lard, a small piece of butter is taken and mixed into all the lard, and if then a piece of this blend of similar size is put back into the butter, there[II-195] will be in the end exactly as much lard in the butter as there is butter in the lard.

Back to Description

19.

The fallacy of the equation—

4 - 10 = 9 - 15
4 - 10 + ²⁵⁄₄ = 9 - 15 + ²⁵⁄₄

and the square roots of these—

2 - ⁵⁄₂ = 3 - ⁵⁄₂
therefore 2 = 3

is explained thus:—The fallacy lies in ignoring the fact that the square roots are plus or minus. In the working we have taken both roots as plus. If we take one root plus, and the other minus, and add ⁵⁄₂, we have either 2 = 2, or 3 = 3.

Back to Description

20.

The largest possible parcel which can be sent through the post under the official limits of 3 feet 6 inches in length, and 6 feet in length and girth combined, is a cylinder 2 feet long and 4 feet in circumference, the cubic contents of which are 2⁶⁄₁₁ cubic feet.

Back to Description

21.

We can show, or seem to show, that either four, five, or six nines amount to 100, thus:—

99⁹⁄₉ = 100

IX
IX
IX
IX
IX
100

9 × 9 + 9 + 9⁹⁄₉ = 100

Back to Description

22.

This is the magic square arrangement, so[II-196] contrived that the products of the rows, columns, and diagonals are all 1,000.

50	1	20
4	10	25
5	100	2

Back to Description

23.

If seven boys caught four crabs in the rock-pools at Beachy Head in six days, the twenty-one boys who searched under the seaweed and only caught one crab with the same rate of success were only at work for half a day.

Back to Description

24.

A watch could be set of a different trio from a company of fifteen soldiers for 455 nights, and one of them, John Pipeclay, could be included ninety-one times.

Back to Description

25.

If Augustus Cæsar was born September 23, B.C. 63, he celebrated his sixty-third birthday on September 23, B.C. 0; or, writing it otherwise, September 23, A.D. 0; or again, if we wish to include both symbols, B.C. 0 A.D. It is clear that his sixty-second birthday fell on September 23, B.C. 1, and his sixty-fourth on September 23, A.D. 1, so that the intervening year may be written as above.

Back to Description

26.

The difference of the ages of A and B who were born in 1847 and 1874, is 27, or 30 - 03. Hence, when A was 30 B was 03. And A was 30 in 1877. Eleven years later A was 41 and B 14, and eleven years after that A was 52 and B 25. Thus the same two digits served to express the[II-197] ages of both in 1877, 1888, and 1899. This can only happen in the cases of those whose ages differ by some multiple of nine.

Back to Description

27

A hundred and one by fifty divide,
To this let a cypher be duly applied;
And when the result you can rightly divine,
You find that its value is just one in nine—

is solved by CLIO, one of the nine Muses.

Back to Description

28.

The man who paid a penny on Monday morning to cross the ferry, spent half of what money he then had left in the town, and paid another penny to recross the ferry, and who repeated this course on each succeeding day, reaching home on Saturday evening with one penny in his pocket, started on Monday with £1 1s. 1d. in hand.

Back to Description

29.

When the three men agreed to share their mangoes equally after giving one to the monkey, and when each helped himself to a third after giving one to the monkey, without knowing that anyone had been before him, and they finally met together, gave one to the monkey, and divided what still remained, there must have been at least seventy-nine mangoes for division at the first.

Back to Description

30.

If, after having looked at my watch between 4 and 5, I look again between 7 and 8, and find that the hour and minute-hands have then exactly changed places, it was 36¹²⁄₁₃ minutes past 4 when I first looked. At that time the hour-hand would be pointing to 23¹⁄₁₃ minutes on the dial, and at 23¹⁄₁₃ minutes past 7 the hour hand would be pointing to 36¹²⁄₁₃ minutes.

Back to Description

31.

The number consisting of 22 figures, of[II-198] which the last is 7, which is increased exactly sevenfold if this 7 is moved to the first place, is 1,014,492,753,623,188,405,797.

Back to Description

32.

The two sacks of wheat, each 4 feet long and 3 feet in circumference, which the farmer sent to the miller in repayment for one sack 4 feet long and 6 feet in circumference, far from being a satisfactory equivalent, contained but half the quantity of the larger sack, for the area of a circle the diameter of which is double that of another is equal to four times the area of that other.

Back to Description

33.

The five gamblers, who made the condition that each on losing should pay to the others as much as they then had in hand, and who each lost in turn, and had each £32 in hand at the finish, started with £81, £41, £21, £11, and £6 respectively.

Back to Description

34.

If we know the square of any number, we can rapidly determine the square of the next number, without multiplication, by adding the two numbers to the known square. Thus if we know that the square of 87 is 7569,

then the square of 88 = 7569 + 87 + 88 = 7744;
so too the square of 89 = 7744 + 88 + 89 = 7921;
and the square of 90 = 7921 + 89 + 90 = 8100.

Back to Description

35.

The two numbers which solve the problem—

Two numbers seek which make eleven,
Divide the larger by the less,
The quotient is exactly seven,
As all who find them will confess—

are 1³⁄₈ and 9⁵⁄₈, for 1³⁄₈ + 9⁵⁄₈ = 11, and ⁷⁷⁄₈ ÷ ¹¹⁄₈ = 7.

Back to Description

36.

There must be nine things of each sort, in order that 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9[II-199] different selections may be made from twenty sorts of things.

Back to Description

37.

The women who had respectively 33, 29, and 27 apples, and sold the same number for a penny, receiving an equal amount of money, began by selling at the rate of three a penny. The first sold ten pennyworth, the second eight pennyworth, and the third seven pennyworth.

The first had then left three apples, the second five, and the third six. These they sold at one penny each, so that they received on the whole—

The first	10d.	+	3d.	=	13d.
The second	8d.	+	5d.	=	13d.
The third	7d.	+	6d.	=	13d.

Back to Description

38.

The puzzle—

Take five from five, oh, that is mean!
Take five from seven, and this is seen—

is solved by fie, seen.

Back to Description

39.

If a bun and a half cost three halfpence, it is plain that each bun costs a penny, but, by general custom, you buy seven for sixpence.

Back to Description

40.

The hands of a watch would meet each other twenty-five times in a day, if the minute-hand moved backwards and the hour-hand forwards. They are, of course, together at starting.

Back to Description

41.

The only way in which half-a-crown can be equally divided between two fathers and two sons, so that a penny is the smallest coin made use of, is to give tenpence each to a grandfather, his son, and his grandson.

Back to Description

42.

If the number of the revolutions of a bicycle wheel in six seconds is equal to the number of miles an hour at which it is running, the circumference of the wheel is 8⁴⁄₅ feet.

Back to Description

43.

The hour that struck was twelve o’clock.

Back to Description

[II-200]

44.

Sixty years.

Back to Description

45.

If I jump off a table with a 20lb dumb-bell in my hand there is no pressure upon me from its weight while I am in the air.

Back to Description

46.

If at a bazaar I paid a shilling on entering each of four tents, and another shilling on leaving it, and spent in each tent half of what was in my pocket, and if my fourth payment on leaving took my last shilling, I started with 45s., spending 22s. in tent 1, 10s. in tent 2, 4s. in tent 3, and 1s. in tent 4, having also paid to the doorkeepers 8s.

Back to Description

47.

When rain is falling vertically at 5 miles an hour, and I am walking through it at 4 miles an hour, the rain drops will strike the top of my umbrella at right angles if I hold it at an angle of nearly 39 degrees.

As I walk along, meeting the rain, the effect is the same as it would be if I was standing still, and the wind was blowing the rain towards me at the rate of 4 miles an hour.

Back to Description

48.

When one monkey descends from the top of a tree 100 cubits high, and makes its way to a well 200 yards distant, while another monkey, leaping upwards from the top, descends by the hypotenuse to the well, both passing over an equal space, the second monkey springs 50 cubits into the air.

Back to Description

49.

The steamboat which springs a leak 105 miles east of Tynemouth Lighthouse, and, putting back, goes at the rate of 10 miles an hour the first hour, but loses ground to the extent in each succeeding hour of one-tenth of her speed in the previous hour, never reaches the lighthouse, but goes down 5 miles short of it.

Back to Description

[II-201]

50.

Twenty-one hens will lay ninety-eight eggs in a week, if a hen and a-half lays an egg and a-half in a day and a-half. Evidently one egg is laid in a day by a hen and a-half, that is to say three hens lay two eggs in a day. Therefore, twenty-one hens lay fourteen eggs, in a day, or ninety-eight in a week.

Q. E. D. (Quite easily done!)

Back to Description

51.

If the population of Bristol exceeds by 237 the number of hairs on the head of anyone of its inhabitants that are not bald, at least 474 of them must have the same number of hairs on their heads.

Back to Description

52.

In tipping his nephew from seven different coins, the uncle may give or retain each, thus disposing of it in two ways, or of all in 2 × 2 × 2 × 2 × 2 × 2 × 2 ways. But as one of these ways would be to retain them all, there are not 128, but only 127 possible variations of the tip.

Back to Description

53.

The prime number which fulfils the various conditions of the question is 127. Increased by one-third, excluding fractions, it becomes 169, the square of 13. If its first two figures are transposed, and it is increased by one-third, it becomes 289, the square of 17. If its first figure is put last, and it is increased by one-third, it becomes 361, the square of 19. If, finally, its three figures are transposed, and then increased by one-third, it becomes 961, the square of 31.

Back to Description

54.

Six things can be divided between two boys in 62 ways. They could be carried by two boys in 64 ways (2 × 2 × 2 × 2 × 2 × 2), but they are not divided between two boys if all are given to one, so that two of the 64 ways must be rejected.

Back to Description

[II-202]

55.

The highest possible score that the dealer can make at six cribbage, if he is allowed to select the cards, and to determine the order of play, is 78. The dealer and his opponent must each hold 3, 3, 4, 4, the turn-up must be a 5, and crib must have the knave of the suit turned up, and 5, 5, 5. It will amuse many of our readers to test this with the cards.

Back to Description

56.

The picture frame must be 3 inches in width all round, if it is exactly to equal in area the picture it contains, which measures 18 inches by 12 inches.

Back to Description

57.

If my mother was 20 when I was born, my sister is two years my junior, and my brother is four years younger still, our ages are 56, 36, 34, and 30.

Back to Description

58.

The spider in the dockyard, whose thread was drawn from her by a revolving capstan 1 foot in diameter, until 73 feet of it were paid out, after walking for a mile round and round the capstan at the end of the stretched thread in an effort to unwind it all, had, when she stopped in her spiral course, 49 more feet to walk to complete her task.

Back to Description

59.

The mountebank at a fair, who offered to return any stake a hundredfold to anyone who could turn up all the sequence in twenty throws of dice marked each on one face only with 1, 2, 3, 4, 5, or 6, should in fairness have engaged to return 2332 times the money; for of the 46,656 possible combinations of the faces of the dice, only one can give the six marked faces uppermost. Thus the chance of throwing them all at one throw is expressed by ¹⁄₄₆₆₅₆, and in twenty throws by about ¹⁄₂₃₃₂.

Back to Description

[II-203]

60.

If 90 groats (each = 4d.) feed twenty cats for three weeks, and five cats consume as much as three dogs, seventy-two hounds can be fed for £39 in a period of ninety-one days.

Back to Description

61.

When equal wine-glasses, a half and a third full of wine, are filled up with water, and their contents are mixed, and one wine-glass is filled with the mixture, it contains ⁵⁄₁₂ wine and ⁷⁄₁₂ water.

Back to Description

62.

The arrangement by which St Peter is said to have secured safety for the fifteen Christians, when half of the vessel’s passengers were thrown overboard in a storm, is as follows:—

XXXXIIIIIXXIXXXIXIIXXIIIXIIXXI

Each Christian is represented by an X, and if every ninth man is taken until fifteen have been selected, no X becomes a victim.

Back to Description

63.

If Farmer Southdown’s cow had a fine calf every year, and each of these, and their calves in their turn, at two years old followed this example, the result would be no less than 2584 head in sixteen years.

Back to Description

64.

The number of the flock was 301. This is found by first taking the least common multiple of 2, 3, 4, 5, 6, which is 60, and then finding the lowest multiple of this, which with 1 added is divisible by 7. This 301 is exactly divisible by 7, but by the smaller numbers there is 1 as remainder.

Back to Description

[II-204]

65.

The rule for determining easily the number of round bullets in a flat pyramid, with a base line of any length, is this:—

Add a half to half the number on the base line, and multiply the result by the number on that line. Thus, if there are twelve bullets as a foundation—

12 + ¹⁄₂ = ¹³⁄₂; and ¹³⁄₂ × ¹²⁄₁ = 78.

The same result is reached by multiplying the number on the base line by a number larger by one, and then halving the result. Thus—

12 × 13 = 156, 156 ÷ 2 = 78.

Back to Description

66.

We can gather from the lines—

Old General Host
A battle lost,
And reckoned on a hissing,
When he saw plain
What men were slain,
And prisoners, and missing.

To his dismay
He learned next day
What havoc war had wrought;
He had, at most,
But half his host
Plus ten times three, six, ought.

One-eighth were lain
On beds of pain,
With hundreds six beside;
One-fifth were dead,
Captives, or fled,
Lost in grim warfare’s tide.

Now, if you can,
Tell me, my man,
[II-205] What troops the general numbered,
When on that night
Before the fight
The deadly cannon slumbered?

that old General Host had an army 24,000 strong.

Back to Description

67.

When the farmer sent five pieces of chain of 3 links each, to be made into one continuous length, agreeing to pay a penny for each link cut, and a penny for each link joined, the blacksmith, if he worked in the best interest of the farmer, could only charge sixpence: for he could cut asunder one set of 3 links, and use these three single links between the other four sets.

Back to Description

68.

If, in a parcel of old silver and copper coins, each silver piece is worth as many pence as there are copper coins, and each copper coin is worth as many pence as there are silver coins, there are eighteen silver and six copper coins, when the whole parcel is worth eighteen shillings.

Back to Description

69.

These are five groups that can be arranged with the numbers 1 to 11 inclusive, so that they are all equal:—

(8² - 5² + 1) = (11² - 9²) = (7² - 3²) = (6² + 2²) = 4(10).

Back to Description

70.

John Bull, under the conditions given, lived to the age of eighty-four years.

Back to Description

71.

The two numbers to each of which, or to the halves of which, unity is added, forming in every case a square number, are 48 and 1680.

Back to Description

72.

The true weight of a cheese that seemed to weigh 16 ℔s. in one scale of a balance with arms of unequal length, and only 9℔s. in the other, is 12℔. This is found by multiplying the 16 by the 9, and finding the square root of the result.

Back to Description

[II-206]

73.

The two parts into which 100 can be divided, so that if one of them is divided by the other the quotient is again exactly 100 are 99¹⁄₁₀₁ and ¹⁰⁰⁄₁₀₁.

Back to Description

74.

If, with marbles in two pockets, I add one to those in that on the right, and then multiply its contents by the number it held at first, and after dealing in a similar way with those on the left, find the difference between the two results to be 90; while if I multiply the sum of the two original quantities by the square of their difference the result is 176, I started with twenty-three in the right-hand pocket and twenty-one in the other.

Back to Description

75.

The circle of twenty-one friends who arranged to meet each week five at a time for Bridge so long as exactly the same party did not meet more than once, and who wished to hire a central room for this purpose, would need it for no less than 20,349 weeks, or more than 390 years, to carry out their plan.

Back to Description

76.

If a herring and a half costs (not cost) a penny and a half, the price of a dozen such quantities is eighteenpence.

Back to Description

77.

The sum of money which in a sense appears to be the double of itself is 1s. 10d., for we may write it one and ten pence or two and twenty pence.

Back to Description

78.

The “comic arithmetic” question set by Dr Bulbous Roots—

Divide my fifth by my first, and you have my fourth; subtract my first from my fifth, and you have my second; multiply my first by my fourth followed by my second, and you have my third; place my second after my first, and you have my third multiplied by my fourth—is solved by COMIC.

Back to Description

[II-207]

79.

If the earth could stand still, and a straight tunnel could be bored through it, a cannon ball dropped into it, if there is no air or other source of friction, would oscillate continually from end to end.

Taking air into account, the ball would fall short of the opposite end at its first lap, and in succeeding laps its path would become shorter and shorter, until its initial energy was exhausted, when it would come to rest at the centre.

Back to Description

80.

He sent 163. She sent 157.

Back to Description

81.

When twins were born the estate was properly divided thus:—

Taking the daughter’s share as	1
The widow’s share would be	2
And the son’s share	4
Total	7	shares.

So the son takes four-sevenths, the widow two-sevenths, and the daughter one-seventh of the estate.

Back to Description

82.

If each of my strides forwards or backwards across a 22 feet carpet is 2 feet, and I make a stride every second; and if I take three strides forwards and two backwards until I cross the carpet, I reach the end of it in forty-three seconds. In three steps I advance 6 feet. Then in two steps I retrace 4 feet, thus gaining only 2 feet in five steps, i.e., in five seconds. I therefore advance 16 feet in forty seconds, and three more strides cover the remaining 6 feet.

Back to Description

83.

If the captain of a vessel chartered to sail from Lisbon to New York, which appear on a map of the world to be on the same parallel of latitude, and which are, along the parallel,[II-208] about 3600 miles apart, takes his ship along this parallel, he will not be doing his best for the impatient merchant who has had an urgent business call to New York.

The shortest course between the two points is traced by a segment of a “great circle,” having its centre at the centre of the earth, and touching the two points. This segment lies wholly north of the parallel, and is the shortest possible course.

Back to Description

84.

When John and Harry, starting from the right angle of a triangular field, run along its sides, and meet first in the middle of the opposite side, and again 32 yards from their starting point, if John’s speed is to Harry’s as 13 to 11, the sides of the field measure 384 yards.

Back to Description

85.

If two sorts of wine when mixed in a flagon in equal parts cost 15d., but when mixed so that there are two parts of A to three of B cost 14d., a flagon of A would cost 20d., and a flagon of B 10d.

Back to Description

86.

If, when a man met a beggar, he gave him half of his loose cash and a shilling, and meeting another gave him half what was left and two shillings, and to a third half the remainder and three shillings, he had two guineas at first.

Back to Description

87.

The clerk who has two offers of work from January 1, one from A of £100 a year, with an annual rise of £20, and the other from B of £100 a year, with a half-yearly rise of £5, should accept B’s offer.

The half-yearly payments from A (allowing for the rise), would be 50, 50, 60, 60, 70, 70, etc., etc.; and from B they would be 50, 55, 60, 65, 70, 75, etc., etc., so that B’s offer is worth £5 a year more than A’s always.

Back to Description

[II-209]

88.

If I have a number of florins and half-crowns, but no other coins, I can pay my tailor £11, 10s. in 224 different ways.

This can be found thus by rule of thumb: Start with 0 half-crowns and 115 florins. Then 4 half-crowns and 110 florins. Add 4 half-crowns and deduct 5 florins each time till 92 half-crowns and 0 florins is reached.

Back to Description

89.

The monkey climbing a greased pole, 60 feet high, who ascended 3 feet, and slipped back 2 feet in alternate seconds, reached the top in 1 minute, 55 seconds, for he did not slip back from the top.

Back to Description

90.

When Adze, the carpenter, secured his tool-chest with a puzzle lock of six revolving rings, each engraved with twelve different letters, the chances against any one discovering the secret word formed by a letter on each ring was 2,985,983 to 1; for the seventy-two letters may be placed in 2,985,984 different arrangements, only one of which is the key.

Back to Description

91.

The five married couples who arranged to dine together in Switzerland at a round table, with the ladies always in the same places, so long as the men could seat themselves each between two ladies, but never next to his own wife, were able under these conditions to enjoy thirteen of these nights at the round table.

Back to Description

92.

If in a calm the tip of a rush is 9 inches above the surface of a lake, and as the wind rises it is gradually blown aslant, until at the distance of a yard it is submerged, it is growing in water that is 5 feet 7¹⁄₂ inches deep.

Back to Description

[II-210]

93.

Aminta was eighteen.

Back to Description

94.

When Dick took a quarter of the bag of nuts, and gave the one over to the parrot, and Tom and Jack and Harry dealt in the same way with the remainders in their turns, each finding a nut over from the reduced shares for the bird, and one was again over when they divided the final remainder equally, there were, at the lowest estimate, 1021 nuts in the bag.

Back to Description

95.

Eight and a quarter is the answer to the nonsense question—

If five times four are thirty-three,
What will the fourth of twenty be?

Back to Description

96.

The similar fraction of a pound, a shilling, and a penny which make up exactly a pound are as follows:—

		s.	d.
²⁴⁰⁄₂₅₃ of £1 =		18	11	¹⁶⁹⁄₂₅₃
²⁴⁰⁄₂₅₃ of 1s. =			11	⁹⁷⁄₂₅₃
²⁴⁰⁄₂₅₃ of 1d. =				²⁴⁰⁄₂₅₃
	£1	0	0

Back to Description

97.

When Dr Tripos thought of a number, added 3, divided by 2, added 8, multiplied by 2, subtracted 2, and thus arrived at double the number, he started with 17.

Back to Description

98.

When A and B deposited equal stakes with C, and agreed that the one who should first win three games of billiards should take all, but consented to a division in proper shares when A had won two games and B one, it was evident that if A won the next game all would go to him,[II-211] while if he lost he would be entitled to one half. One case was as probable as the other, therefore he was entitled to half of these sums taken together; that is, to three quarters of the stakes, and B to a quarter only.

Back to Description

99.

The average speed of a motor which runs over any course at 10 miles an hour, and returns over the same course at 15 miles an hour, is 12 miles an hour, and not 12¹⁄₂, as might be imagined. Thus a run of 60 miles out takes, under the conditions, six hours, and the return takes four hours; so that the double journey of 120 miles is done in ten hours, at an average speed of 12 miles an hour.

Back to Description

100.

Farmer Hodge, who proposed to divide his sheep into two unequal parts, so that the larger part added to the square of the smaller part should equal the smaller part added to the square of the larger part, had but one sheep.

Faithful to his word, he divided this sheep into two unequal parts, ²⁄₃ and ¹⁄₃, and was able to show that ²⁄₃ + ¹⁄₉ = ⁷⁄₉, and that ¹⁄₃ + ⁴⁄₉ = ⁷⁄₉. He was heard to declare further, and he was absolutely right, that no number larger than 1 can be so divided as to satisfy the conditions which he had laid down.

The fact that sheep is both singular and plural, adds much to the perplexing points of this attractive problem.

Here is a very simple proof that the number must be 1:—

Let	a + b	=	no. of sheep
then	a² + b	=	b² + a
	a² - b²	=	a - b
or	(a + b)(a - b)	=	a - b
therefore	a + b	=	1.

Back to Description

[II-212]

101.

A horse that carries a load can draw a greater weight up the shaft of a mine than a horse that bears no burden. The load holds him more firmly to the ground, and thus gives him greater power over the weight he is raising from below.

Back to Description

102.

In the six chests, of which two contained pence, two shillings, and two pounds, there must have been at least the value of 506 pence. This can be divided into 22 (or 19 + 3) shares of 23d. each, or 23 (19 + 4) shares of 22d. each. Evidently then the treasure can be divided so that 19 men have equal shares, while their captain has either 3 shares or 4 shares.

Back to Description

103.

If I bought a parcel of nuts at 49 for 2d., and divided it into two equal parts, one of which I sold at 24, the other at 25 a penny; and if I spent and received an integral number of pence, but bought the least possible number of nuts, I bought 58,800 nuts, at a cost of £10, and I gained a penny.

Back to Description

104.

When, with a purse containing sovereigns and shillings, after spending half of its contents, I found as many pounds left as I had shillings at first, I started with £13, 6s.

Back to Description

105.

When the lady replied to a question as to her age—

If first my age is multiplied by three,
And then of that two-sevenths tripled be,
The square root of two-ninths of this is four;
Now tell my age, or never see me more—

she was 28 years old.

Back to Description

106.

If cars run, at uniform speed, from Shepherd’s Bush to the Bank, at intervals of two minutes, and I am travelling at the same[II-213] rate in the opposite direction, I shall meet 30 in half-an-hour, for there are already 15 on the track approaching me, and 15 are started from the other end during my half hour’s course.

Back to Description

107.

If it was possible to carry out my offer of a farthing for every different group of apples which my greengrocer could select from a basket of 100 apples, he would be entitled to the stupendous sum of £18,031,572,350 19s. 2d.

Back to Description

108.

If the minute-hand of a clock moves round between 3 and 4 in the opposite direction to the hour-hand, the hands will be exactly together when it is really 41⁷⁄₁₃ minutes past 3.

Back to Description

109.

If the walnut monkey had stopped to help the other, and they had eaten filberts at equal rates, they would have escaped in 2¹⁄₄ minutes.

Back to Description

110.

The value of the cheque, for which the cashier paid by mistake pounds for shillings, was £5, 11s. 6d. The receiver to whom £11, 5s. 6d. was handed, spent half-a-crown, and then found that he had left £11, 3s., just twice the amount of the original cheque.

Back to Description

111.

The number 14 can be made up by adding together five uneven figures thus:—11 + 1 + 1 + 1. It will be seen that although only four numbers are used, 11 is made up of two figures.

Here is another, and quite a curious solution, 1 + 1 + 1 + 1 = 4, and with another 1 we can make up 14!

Back to Description

112.

A business manager can fill up three vacant posts of varying value from seven applicants in 210 different ways. For the first[II-214] post there would be a choice among 7, for the second among 6, and for the third among 5, so that the possible variations would amount to 7 × 6 × 5 = 210.

Back to Description

113.

If the fasting man, who began his task at noon, said it is now ⁵⁄₁₁ of the time to midnight, he spoke at 3.45 p.m., meaning that ⁵⁄₁₁ of the remaining time till midnight had elapsed since noon.

Back to Description

114.

If a clock takes six seconds to strike 6, it will take 12 seconds to strike 11, for there must be ten intervals of 1¹⁄₅ seconds each.

Back to Description

115.

Twenty horses can be arranged in three stalls, so that there is an odd number in each, by placing one in the first stall, three in the second, and sixteen (an odd number to put into any stall!) in the third.

Back to Description

116.

The little problem, “Given a, b, c, to find q,” is solved, without recourse to algebra, thus: a, b, c, = c, a, b; take a cab and go over Kew Bridge, and you find a phonetic Q!

Back to Description

117.

Tom Evergreen was 75 years old when he was asked his age by some men at his club in 1875, and said—“The number of months that I have lived are exactly half as many as the number which denotes the year in which I was born.”

Back to Description

118.

Eight different circles can be drawn. A circle can have one of the three inside and two outside in three ways, or one outside and three inside in three ways (each of the three being inside or outside in turn), or all three may be inside, or all three may be outside, the touching circle.

Back to Description

[II-215]

119.

The way to arrange 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, so that used once each they form a sum which is equal to 1 is this:—

3570 + 148296 = 1

Back to Description

120.

The sum of the first fifty numbers may be found without any addition thus:—The first fifty numbers form twenty-five pairs of fifty-one each (1 + 50, 2 + 49, etc., etc.), and 51 × 25 is practically 51 × 100 ÷ 4 = 1275.

Back to Description

121.

The tramcar A, which started at the same time as B, but ran into a “lie by” in four minutes, and waited there five minutes till B came along, when they completed their courses at the same moment in opposite directions, could have run the whole distance in ten minutes.

Back to Description

122.

What remains will be 8 if we take 10 and double it by writing one 10 over another so as to form 18, and then deduct 10.

Back to Description

123.

If the average weight of the Oxford crew is increased by 2℔s., when one of them who weighs 12 stone, is replaced by a fresh man, the weight of that substitute is 13 stone 2℔s.

Back to Description

124.

If a motor-car is twice as old as its tyres were when it was old as its tyres are, and if, when these tyres are as old as the car itself is now, their united ages will be 2¹⁄₄ years, the car is now 12 months old, and the tyres have had 9 months’ wear.

Back to Description

[II-216]

125.

A and B, who could each carry provisions for himself for twelve days, started to penetrate as far as possible into a desert, on the understanding that neither of them should miss a day’s food. After an advance of four days, each had provisions still for eight days. One gave four portions of his store to his companion, which did not overload him, and returned with the other four. His comrade was then able to advance another four days’ journey, and still have rations for the eight days’ return. Thus the furthest possible penetration into the desert under the conditions was an eight days’ march.

Back to Description

126.

If, when a bottle of medicine and its cork cost half-a-crown, the bottle and the medicine cost two and a penny more than the cork, the cork cost twopence half-penny.

Back to Description

127.

A boat’s crew far from land, with no sail or oars, and with no assistance from wind or stream, or outside help of any kind, can regain the shore by means of a coil of rope. Motion is given to the boat by tying one end of the rope to the after thwart, and giving the other end a series of violent jerks in a direction parallel to the keel. This curious illustration of mechanical principles is from “Ball’s Mechanical Recreations.” (Macmillan.)

Back to Description

128.

It will be found that after a crown and as many four-shilling pieces as possible have been crammed into our pockets, there would still be room for one sixpence and one threepenny-piece in some corner or cranny. We can, therefore, have one crown, one sixpence, one threepenny-piece, and as many four-shilling pieces as our pockets will hold, and yet be unable to give change for a half-sovereign.

Back to Description

[II-217]

129.

There were fifteen apples in the basket. Half of these and half an apple, i.e., eight were first given, then half the remainder and half an apple, i.e., four, then on similar lines two, leaving one in the basket.

Back to Description

130.

The Queer Division—

A third of twelve divide
By just a fifth of seven;
And you will soon decide
That this must give eleven—

is solved by LV ÷ V, or 55 ÷ 5 = 11.

Back to Description

131.

A motor that goes 9 miles an hour uphill, 18 miles an hour downhill, and 12 miles an hour on the level, will take 8 hours and 20 minutes to run 50 miles out and return at once over the same course.

Back to Description

132.

The number of shots fired at a mark was 420 each by A, B, and C. A made 280 hits, B 315, and C 336.

Back to Description

133.

If a dog and a cat, evenly matched in speed, run a race out and back over a course of 75 yards in all, and the dog always takes 5 feet at a bound, and the cat 3 feet, the cat will win, because at the turning point the dog overleaps the half distance more than the cat does, and so has a longer run in.

Back to Description

134.

When a man caught up a wagon going at 3 miles an hour, which was just visible to him in a fog at a distance of 55 yards, and which he saw for five minutes before reaching it, he was walking at the rate of 3³⁄₈ miles an hour.

Back to Description

[II-218]

135.

Three horses, A B C, can be placed after a race in thirteen different ways, thus:—A B C, A C B, B A C, B C A, C A B, C B A, or A B C as a dead heat; or A B, A C, or B C equal for the first place; or A first with B C equal seconds; or B first with A C equal seconds; or C first with A B equal seconds.

Back to Description

136.

The 34 points scored against Oxbridge by the New Zealanders can be made up in two ways, either by 8 tries and 2 converted tries, or by 3 tries and 5 converted tries.

The highest possible score on these lines is 10 tries converted, equalling 50 points, and as the New Zealanders’ score, if all tries are converted, becomes four-fifths of this, their actual score was 3 tries and 5 converted into goals.

Back to Description

137.

The smallest number, of which the alternate figures are cyphers, which is divisible by 9 and by 11 is 909090909090909090909!

Back to Description

138.

Our problem in which it is stated that A with 8d. met B and C with five and three loaves, and asked how the cash should be divided between B and C, if all agreed to share the loaves. Now each eats two loaves and two-thirds of a loaf, and B gives seven-thirds of a loaf to A, while C gives him one-third of a loaf. So B receives 7d. and C 1d.

Back to Description

139.

When, on opening four money-boxes containing pennies only, it was found that those in the first with half of all the rest, those in the second with a third of the others, those in the third with a fourth, and those in the fourth with a fifth of all the rest, amounted in each case to 740, the four boxes held £6. 1s. 8d., and the numbers of pennies were 20, 380, 500, and 560.

Back to Description

[II-219]

140.

If two steamers, A and B, start together for a trip to a distant buoy and back, and A steams all the time at ten knots an hour, while B goes outward at eight knots and returns at twelve knots an hour, B will regain port later than A, because its loss on the outward course will not have been recovered on the run home.

Back to Description

141.

If in London a new head to a golf club costs four times as much as a new leather face, while at St Andrews it costs five times as much, and if the leather face costs twice as much in London as in St Andrews, and if, including a shilling paid for a ball, the charges in London were twice as much as they would have been at St Andrews, the London cost of a new head is four shillings, and of a leather face a shilling.

Back to Description

142.

When two children were asked to give the total number of sheep and cattle in a pasture, from the number of each sort, and one by subtraction answered 10, while the other arrived at 11,900 by multiplication, the true numbers were 170 sheep, 70 cattle, 240 in all.

Back to Description

143.

If a man picks up one by one fifty-two stones, placed at such intervals on a straight road that the second is a yard from the first, the third 3 yards from the second, and so on with intervals increasing each time by 2 yards, and bring them all to a basket placed at the first stone, he has to travel about 52 miles, or, to be quite exact, 51 miles, 1292 yards.

Back to Description

144.

When, in the House of Commons, if the Ayes had been increased by 50 from the Noes, the motion would have been carried by 5 to 3;[II-220] and if the Noes had taken 60 votes from the Ayes it would have been lost by 4 to 3, the motion succeeded; 300 voted “Aye,” and 260 “No.”

Back to Description

145.

There are 143 positions on the face of a watch in which the places of the hour and minute-hands can be interchanged, and still indicate a possible time. There would be 144 such positions but for the fact that at twelve o’clock the hands occupy the same place.

Back to Description

146.

If in a cricket match the scores in each successive innings are a quarter less than in the preceding innings, and the side which goes in first wins by 50 runs, the complete scores of the winners are 128 and 72, and of the losers 96 and 54.

Back to Description

147.

When a ball is thrown vertically upwards, and caught five seconds later, it has risen 100 feet. It takes the same time to rise as to fall, and when a body falls from rest, it travels a number of feet represented by sixteen times the square of the time in seconds.

Hence comes the rule that the height in feet of a vertical throw is found by squaring the time in seconds of its flight, and multiplying by four.

Back to Description

148.

The carpet which, had it been 5 feet broader and 4 feet longer, would have contained 116 more feet, and if 4 feet broader and 5 longer 113 more, was 12 feet long and 9 feet broad.

Back to Description

149.

When, in estimating the cost of a hundred similar articles, shillings were read as pounds, and pence as shillings, and the estimated cost was in consequence £212, 18s. 4d. in excess of the real cost, the true cost of each article was 2s. 5d.

[II-221]

Back to Description

150.

If the square of the number of my house is equal to the difference of the squares of the numbers of my next door neighbours’ houses, and if my brother in the next street can say the same of his house, though its number is not the same as that of mine, our houses are numbered 8 and 4. In my street the even numbers are all on one side, in my brother’s street they, run odd and even consecutively, and so 8² = 10² - 6², and 4² = 5² - 3².

Back to Description

151.

When two men of unequal strength have to move a block which weighs 270 ℔s., on a light plank 6 feet long, if the stronger man can carry 180 ℔s., the block must be placed 2 feet from him, so that he may have that share of the load.

Back to Description

152.

If a man who had twenty coins, some shillings, and the rest half-crowns, were to change the half-crowns for sixpences, and the shillings for pence, and then found that he had 156 coins, he must have had eight shillings at first.

Back to Description

153.

If, when coins are placed on a table at equal distances apart, so as to form sides of an equilateral triangle, and when as many are taken from the middle of each side as equal the square root of the number on that side, and placed on the opposite corner, the number on each side is then to the original number as five is to four, there are forty-five coins in all.

Back to Description

154.

When the gardener found that he would have 150 too few if he set his posts a foot apart, and seventy to spare if he set them at every yard, he had 180 posts.

Back to Description

[II-222]

155.

In order to buy with £100 a hundred animals, cows at £5, sheep at £1, and geese at 1s. each, the purchaser must secure nineteen cows, one sheep, and eighty geese.

Back to Description

156.

If John, who is 21, is twice as old as Mary was when he was as old as Mary is, Mary’s age now is 15³⁄₄ years.

Back to Description

157.

If in a cricket match A makes 35 runs, and C and D make respectively half and a third of B’s score, and if B scores as many less than A as C scores more than D, B made 30, C 15, and D 10 runs.

Back to Description

158.

The least number which, divided by 2, 3, 4, 5, 6, 7, 8, 9, or 10, leaves remainders 1, 2, 3, 4, 5, 6, 7, 8, 9, is 2519, their least common multiple less 1.

Back to Description

159.

A square table standing on four legs, which are set at the middle points of its sides, can at most uphold its own weight upon one of its corners.

Back to Description

160.

The division of ninety-nine pennies, so that share 1 exceeds share 2 by 3, is less than share 3 by 10, exceeds share 4 by 9, and is less than share 5 by 16, is 17, 14, 27, 8, and 33.

Back to Description

161.

If Indians carried off a third of a flock and a third of a sheep, and others took a fourth of the remainder and a fourth of a sheep, and others a fifth of the rest and three-fifths of a sheep, and there were then 409 left, the full flock was 1025 sheep.

[II-223]

Back to Description

162.

When a cistern which held fifty-three gallons was filled by three boys, A bringing a pint every three minutes, B a quart every five minutes, and C a gallon every seven minutes, it took 230 minutes to fill it, and B poured in the final quart, A and C coming up one minute too late to contribute at the last.

Back to Description

163.

A man who said, late in the last century, that his age then was the square root of the year in which he was born, was speaking in the year 1892.

Back to Description

164.

If when a dealer in curios sold a vase for £119, his profit per cent., and the cost price of the vase, were expressed by the same number, it had cost him £70.

Back to Description

165.

The chance of throwing at least one ace in a single throw with a pair of dice is ¹¹⁄₃₆, for there are five ways in which each dice can be thrown so as not to give an ace, so that twenty-five possible throws exclude aces. Hence the chance of not throwing an ace is ²⁵⁄₃₆, which leaves ¹¹⁄₃₆ in favour of it.

Back to Description

166.

The policeman who ran after a thief starting four minutes later, and running one-third faster, if they both ran straight along the road, caught him in twelve minutes.

Back to Description

167.

At a bazaar stall, where twenty-seven articles are exposed for sale, a purchaser may buy one thing or more, and the number of choices open to him is one less than the continued product of twenty-seven twos, or 134217727.

Back to Description

[II-224]

VERY PERSONAL

168. When Nellie’s father said:—

I was twice as old as you are
The day that you were born.
You will be just what I was then
When fourteen years are gone—

he was 42, and she was 14.

Back to Description

WORD AND LETTER PUZZLES

1.

The word square is completed thus:—

M	E	A	D
E	D	G	E
A	G	U	E
D	E	E	D

Back to Puzzle

2.

The word square filled in is:—

C	I	R	C	L	E
I	N	U	R	E	S
R	U	D	E	S	T
C	R	E	A	S	E
L	E	S	S	E	E
E	S	T	E	E	M

Notice the curious diagonal of E’s.

Back to Puzzle

3.

In the incomplete sentence,

SO * * * * AG * * * * LATI * * * * X * * * * ITH

the duplicate letters are filled in thus:—

SOME MEAGRE RELATIVE VEXED EDITH

The two last letters of each word are repeated as the two first of the word that follows.

Back to Puzzle

[II-225]

4.

The word square is completed thus:—

W	A	S	T	E
A	C	T	O	R
S	T	O	N	E
T	O	N	I	C
E	R	E	C	T

Back to Puzzle

5.

By twice building up two Ds into a B we make BULBOUS.

Back to Puzzle

6.

The question put on paper to the love-lorn youth, “Loruve?” is, when interpreted, “Are you in love?” and the advice given to him on another slip, “Prove L A FD and ensure success,” reads into, “Prove a fond lover, and ensure success” (a f on d l over).

Back to Puzzle

7. DOUBLE ACROSTIC
ST. JAMES’ GAZETTE

S	prin	G
T	ar	A
J	abe	Z
A	t	E
M	omen	T
E	mme	T
S	trik	E

Back to Puzzle

8.

The completed word square is—

A	M	E	N	D	S
M	I	N	I	O	N
E	N	A	B	L	E
N	I	B	B	L	E
D	O	L	L	A	R
S	N	E	E	R	S

Back to Puzzle

[II-226]

9.

The oracular response to a young Frenchman at a fête, who inquired how he could best please the ladies—

MEC DO BIC

conceals this sage advice—

Aimez, cédez, obéissez!
Love, yield, obey!

Back to Puzzle

10.

The solution to our Letter Fraction Problem is of a verbal character. The original statement

m ot y = mo

is dealt with thus:—

m on ot on y = mo not on y, and so the word monotony solves the equation.

Back to Puzzle

11.

The buried beasts are chamois, buffalo, heifer, and leopard; and when the Oxford athlete cries—

“Though I jump and row and run,
Cap or cup I never won”

he introduces us to a porcupine.

Back to Puzzle

12.

The lines—

Fourteen letters here we fix,
Vowels only two are spoken;
All together these we mix
Into what can not be broken—

is solved by indivisibility, which has many an i, like a peacock’s tail.

Back to Puzzle

13.

The English word of thirteen letters in which the same vowel occurs four times, the same consonant six times, another twice, and another once, is Senselessness.

Back to Puzzle

14.

The condensed proverb “WE IS DO” reads at its full length as “Well begun is half done.”

Back to Puzzle

[II-227]

15.

This is the completed word square:—

W	A	S	H	E	S
A	R	T	E	R	Y
S	T	O	R	M	S
H	E	R	M	I	T
E	R	M	I	N	E
S	Y	S	T	E	M

Back to Puzzle

16.

Dr Whewell’s puzzle lines—

			O	O	N	O	O.
U	O	A	O	O	I	O	U
O	N	O	O	O	O	M	E	T	O	O.
U	O	A	O	I	D	O	S	O
I	O	N	O	O	I	O	U	T	O	O!

read thus:—

OH SIGH FOR NO CIPHER

You sigh for a cipher, O, I sigh for you,
Sigh for no cipher, O sigh for me too.
You sigh for a cipher, I decipher so,
I sigh for no cipher, I sigh for you too!

Back to Puzzle

17.

This is the completed diamond:—

				P
			P	O	R
		C	O	R	E	S
	F	O	R	C	E	P	S
P	O	R	C	E	L	A	I	N
	R	E	F	L	E	C	T
		S	P	A	C	E
			S	I	T
				N

Back to Puzzle

18.

The medley—

Tan HE Edsa VEN in
It N Gja SmeTs AsgN
aD Az Rett De

is read by taking first the capitals in their order, and then the small type. It comes put out as “The Evening Standard and Saint James’s Gazette.”

Back to Puzzle

[II-228]

19.

The statement, I can travel first-class on the G.E.R. from 2222222244444500, reads into—from 22 to 2 to 22 to 4 for 44 4d; or, in plain terms, from 1.38 to 3.38 for 14s. 8d. This works out at about 3d. a mile, the usual allowance for first-class, for two hours, at about 29 miles an hour.

Back to Puzzle

20. A CURIOUS OLD INSCRIPTION

Read the inscription backwards, and it resolves itself into the lines familiar to us in our childhood:—

Ride a cock horse to Banbury Cross
To see a fine lady ride on a grey horse.
Rings on her fingers and bells on her toes,
She shall have music wherever she goes!

Back to Puzzle

21.

The reason why the invitation to Jack to sample the Irish stew at Simpson’s was to be kept in mind by the catch words—

Join me at and
Join me at ai
Join me at as

is because if you join me and at, and note that and is on i, which is on s, you arrive at the suggestive sentence—meat and onions.

Back to Puzzle

22.

The labourer’s quaint letter, which ran “Cepatomtogoatatrin,” was, in plainer English, “Kept at home to go a tatering.”

Back to Puzzle

23.

Our double acrostic comes out thus:—

Problem—Puzzles

P	a	P
(T) R		U (E)
O		Z
B	o	Z
L	eve	L
E	v	E
M		S

Back to Puzzle

[II-229]

24.

The Hidden Proverb is—

“Necessity is the mother of invention.”

Back to Puzzle

25.

The “deed done” in our Will puzzle is the making in Roman numerals of “Codicil.” The lawyer was to set down, a hundred, to add nothing, to set down five hundred, then one, then another hundred, and then one more, and, finally, fifty, and accordingly he wrote upon the parchment the one word CODICIL.

Back to Puzzle

26.

The word square is—

E	D	I	T	O	R
D	E	S	I	R	E
I	S	L	A	N	D
T	I	A	R	A	S
O	R	N	A	T	E
R	E	D	S	E	A

Back to Puzzle

27.

The notes of music A. G. A. E. A. over the grave of a French musician, who was choked by a fish bone, are in the French notation, “La sol la mi la,” which reads into “La sole l’a mis 1à.”

Similarly the inscription over the porch of Gustave Doré’s house C. E. B. A. C. D. is equivalent to “Do, mi, si, la, do, re,” which may be taken to represent “Domicile à Doré.”

Back to Puzzle

28.

When his best girl said to Jack Spooner, “We can go to-morrow at 222222222222 LEY STREET,” he understood her to mean, “We can go to-morrow, at two minutes to two, to two twenty-two, to 222 Tooley Street.”

Back to Puzzle

29

CT T T T T T T T T T spells contents (c on ten ts!).

Back to Puzzle

[II-230]

30.

We can treat the word disused so as to affirm or to disallow the use of its initial or final d, for we can write it d is used, or disuse d!

Back to Puzzle

31.

The title of the book shaken up into

E I O O O U
B C N N R R S S

is “Robinson Crusoe.”

Back to Puzzle

32.

If the letter M only is inserted in the proper places in the line—

A DEN I I CAN DOCK

it will read: Madmen mimic and mock.

Back to Puzzle

33.

The quotation from Shakespeare—

OXXU8 MAAULGIHCTE

NOR

is by interpretation:—“Nothing extenuate, nor set down aught in malice.”

Back to Puzzle

34.

The phonetic nightmare—

Ieukngheaurrhphthewempeighghteaps—

is merely the word unfortunates. It can be justified thus by English spelling of similar sound taken letter by letter:—

u—iew in view; n—kn in know; f—gh in tough; o—eau in beau; r—rrh in myrrh; t—phth in phthisis; u—ewe; n—mp in comptroller; a—eigh in neigh; t—ght in light; e—ea in tea; and s—ps in psalm.

Back to Puzzle

35.

The word square is completed thus:—

F	A	R	M
A	R	E	A
R	E	N	T
M	A	T	E

Back to Puzzle

[II-231]

36. A QUAINT INSCRIPTION

The millers leave the mill,
The wherrymen lower their sail;
The maltsters leave the kiln,
For a drop of the White Swan’s ale.

Back to Puzzle

37. A POET’S PI

TONDEBNIOTOCHUMFOARYHUR
OTDIRECTTHAWHOTERSOFKLSYA;
TIKATESTUBALIGHTSTILLETRUFLYR
OTBOWLALLNFESLEAVARFWYAA

is disentangled thus:—

Don’t be in too much of a hurry
To credit what other folks say;
It takes but a slight little flurry
To blow fallen leaves far away.

Back to Puzzle

38. BURIED PLACES

The five buried places are Deal, London, Esk, Perth, and Baden. The word is Ourangoutang.

Back to Puzzle

39.

It is no offence to conspire in the evening, because what is treasonable is reasonable after t!

Back to Puzzle

40.

The bit of botany—

Inscribe an m above a line,
And write an e below,
This woodland flower is hung so fine
It bends when zephyrs blow—

is solved by, me, an em on e, the delicately hung wind-flower.

Back to Puzzle

[II-232]

41. A PIED PROVERB

The pied proverb, is “A rolling stone gathers no moss.”

Back to Puzzle

42.

The Drop Letter Proverb—

E..t. .e.s..s .a.e .h. .o.. ..i.e, is—Empty vessels make the most noise.

Back to Puzzle

43.

The English word of five syllables, which has eight letters, five of them vowels—namely an a, an e, twice i, and y—is Ideality.

Back to Puzzle

44.

TORMENT may be turned into RAPTURE, using four links, changing only one letter each time, and varying the order of the letters, thus: TORMENT, portent, protest, pratest, praters, RAPTURE.

Back to Puzzle

45.

The pied sentence—

a a c e e e f f h h i i i i i m n n o o o p r r s s t t t t t

can be cast into the proverb—

“Procrastination is the thief of time.”

Back to Puzzle

46.

The English sentence, when the letter o is added, reads:—

“Good old port for orthodox Oxford dons.”

Back to Puzzle

47

One vowel in an English word is found,
Which by eight consonants is hedged around—

is solved by Strengths.

Back to Puzzle

48.

The letters AAAAABBNNIIRSSTT form the word Antisabbatarians.

Back to Puzzle

[II-233]

49.

The quotation from Shakespeare,

KINI

stands for “A little more than kin, and less than kind.”

Back to Puzzle

50.

The two English words which have the first six letters of the alphabet among their ten letters are fabricated and bifurcated.

Back to Puzzle

51. SHIFTING NUMBERS

The letter A stands at the head of the letters of the alphabet. For bed 3 of these are used; for goal, 4; for prison, 6; for six, 3; for three, 5. The letter A is not used in the spelling of the name of any number from 1 to 100, but it makes up, with the other vowels, the number 6.

Back to Puzzle

52.

The prodigal’s letter to his father, “Dear Dad, keep 1000050,” in reply to a suggestion for safeguarding some of his prospects, was written in playful impudence; and its interpretation is, “Dear Dad, keep cool!” for the figures in Roman numerals are COOL.

Back to Puzzle

53. BURIED POETS

The poets’ names buried in the lines—

The sun is darting rays of gold
Upon the moor, enchanting spot;
Whose purpled heights, by Ronald loved,
Up open to his Shepherd cot.

And sundry denizens of air
Are flying, aye, each to his nest;
And eager make at such an hour
All haste to reach the mansions blest.

are Gray, Moore, Byron, Pope, Dryden, Gay, Keats, and Hemans.

Back to Puzzle

[II-234]

54.

When A. B. gave up the reins of government, and C.B. took office in his place, the two verbs, similar in all respects, except that the one is longer by one letter than the other, which expressed the change, were resigns—reigns.

Back to Puzzle

55

Underdone mutton and onion make between you and me,
A glutton a little seedy after a capital tea.

Back to Puzzle

56

First a c and a t, last a c and a t,
With a couple of letters between,
Form a sight that our eyes are delighted to see,
Unless in their sight it is seen—

is solved by Cataract. The first line reads, First a c and a t, last a c and a t, that is cat and act.

Back to Puzzle

57.

Cuba.

Back to Puzzle

58.

The Rebus T S is solved by the words tones and tans, t before one s, or t before an s.

Back to Puzzle

59.

The phonetic phrase—

INXINXIN—

is, Ink sinks in!

Back to Puzzle

A GOOD END

60. Finis (F IN IS).

Back to Puzzle

PART III.

	PAGE
Word Puzzles, Missing Words, Letter Puzzles	1
Anagrams, Picture Puzzles	48
Palindromes	108
Solutions	111

[III-1]

WORD PUZZLES

No. I—AN EARLY CRYPTOGRAM

The use of some sort of grille was not uncommon in olden days among the many methods then employed for secret correspondence. Here is an early and interesting specimen:—

VENITE PAUPERES

An important despatch would appear to be a mere confusion of letters, until it fell into the right hands, and this perforated key was laid over it, when the intended instructions were at once revealed, and read in the openings of the tracery.

[III-2]

No. II.—A MANIFOLD MONOGRAM

Here, by seven straight lines and one circle, a manifold monogram is formed.

Within its borders we find a circle, a square, a parallelogram, a triangle, the vowels a, e, i, o, u; the consonants, C, D, H, K, L, M, T, W; and other forms and figures.

MISSING WORDS

1. PICKING AND STEALING

What tempting ...... beguiled the boy to sample
Fruit that hung ...... on the parson’s trees?
...... upon ...... shall make him an example
When the stern ...... has brought him to his knees.

The missing words are spelt with the same six letters.

Solution

[III-3]

No. III.—A BOOK AND ITS AUTHOR

What well-known book and its author may be represented thus:—

Solution

2. A SWARM OF MISSING WORDS

No less than eight different words, spelt with the same six letters, are available to fill the gaps in the following lines:—

Man of the dark room, ...... none I find
Upon these ...... of likeness to my features.
...... then nought, O man of evil mind,
Who ...... thus to libel fellow-creatures?
Evil thus done ...... upon the doer,
The ...... in thy conduct, Sir, are many;
...... thy life, and let thy crimes be fewer,
Or all thy ...... of good won’t fetch a penny!

Solution

[III-4]

No. IV.—ON THE SHUTTERS

Upon the shutters of a barber’s shop the following legend was painted in bold letters:—

No.
John Mar
in atten
from 8 a.m.
Barber
Hair C
The bald cry a
for hi
as displayed
which make hair g
Closes

I
shall
dance
daily
and
utter
loud
s creams
in this window
listen
after 8 p.m.

One evening about 8.30, when it was blowing great guns, quite a crowd gathered round the window, and seemed to be enjoying some excellent joke. What was amusing them when one shutter blew open?

Solution

3. NO HEART!

False Kate! ... .... . ...... ’s nest,
.. ..... the Upas tree,
I will not budge, ... .... to rest,
.. .... . coward be.

No, not .... ... enough their sting
To drive me back to thee;
None swifter meet thy beckoning
.... ... the hills I flee.

... .... frosts less my love would quell.
Rather than seek thy side,
Of ... .... horse I love so well
I’ll ... .... hoofs and hide!

The number of letters in each word of the missing phrases is indicated by dots, and the seven letters in each case are those that spell also “no heart,” which we give as a title and clue.

Solution

[III-5]

No. V.—A PHONETIC MAXIMUM

How far phonetic spelling may be pushed, is illustrated by the following swarm of variations given in a book published at Enfield in 1829:—

Scissars	—	ers	—	irs	—	ors	—	urs	—	yrs
Scisars	—	„	—	„	—	„	—	„	—	„
Sciszars	—	„	—	„	—	„	—	„	—	„
Scizars	—	„	—	„	—	„	—	„	—	„
Scizscars	—	„	—	„	—	„	—	„	—	„
Scizzars	—	„	—	„	—	„	—	„	—	„

Or the word may start with Sis, Siss, Siz, Sys, Syss, Syzz, Syzs, Syz, Cis, Ciss, Ciz, Cisz, Cysz, Cyz, Cyzz. By substituting “z” for the final “s” we may double the number, and reach a total of 1224.

4. UNNATURAL HISTORY

’Neath ...... Indian seas fierce battles spread
’Twixt ...... hermit-crabs and other shellfish!
With horrid ...... when their foes are dead,
These crabs declare their shells ......, so selfish!

Each missing word has the same six letters.

Solution

[III-6]

No. VI.—SOLVITUR AMBULANDO

On this chequered floor, paved with slabs each a foot square, the palindrome word ROTATOR can be traced in various ways.

If a man walks over it, taking one slab at every step, and never lengthening his strides, how many steps will he take in tracing every possible variation of the word, and how many such variations are there?

Solution

[III-7]

No. VII.—A CURIOUS CHRONOGRAPH

A bachelor clergyman, whose initials were I.E.V., had built a fernery with the profits of his tracts on the deceased wife’s sister question. He dated it on a mural tablet thus:—


	My LateVVIfe’ssIsterbVILtthIs VVaLL; bVT I In trVth neVer VVeD any VVIfe at aLL, nor VVont forsooth, saIth I. e. V.

If the Roman numerals are extracted from this inscription, and added together, they amount to 1884, the desired date.

5

Though ——— secure and ——— in his cage,
Our Polly, when ———, will fly into a rage.

Each missing word has the same six letters.

Solution

6

All courtly honours are but light
As grains that from a ——— fly;
And he who wears the ——— bright
May haply in a ——— die.

The missing words are spelt with the same six letters.

Solution

7

I’d rather from a ——— eat,
I give my sacred word,
Than dine in slums where ——— meet,
And ——— pedlars herd.

Each missing word has the same six letters.

Solution

[III-8]

No. VIII.—AN OLD SAMPLER

In the drawer of a cabinet that had belonged to my grandmother I came upon an old sampler, beautifully worked in scarlet cross-stitch. Its very curious legend runs as follows:—


		AL. IT.
	T.L	EW. O. MA!
	N.T.	Ho! UGH. AVE. Ryli.
	T.T.	Let. Hi! N.G.I.
	S.S.	We. Et. Erf. Art. Ha!
	N.S.	Ug. Ara. N.D.F. Lo!
	W.E.	R.S.T. Ha! TB.
	L.O.	O! Mins. Pri.
		N. G.

Solution

8

A much married ....... of Cadiz
Once ....... some riotous ladies.
To ....... him they chucked
A ......., but he ducked,
Which ....... these rude ladies of Cadiz.

The five missing words are spelt with the same seven letters.

Solution

9. THE LASS AND HER LOVER

A lass and her lover were ——— by the sky
Not to ——— too far where no shelter was nigh.
She lingered behind, and —— — old church,
St. ——— by name, and was left in the lurch.

She tried a short cut through a park on the grass,
But sternly the ——— forbade her to pass;
Then helplessly stood the disconsolate maid,
When the lad she was soon to —— —— to her aid.

The missing words are spelt with the same six letters.

Solution

[III-9]

No. IX.—THE LANDLORD’S PUZZLE

The following curious Missing Words Puzzle is to be seen on a card which hangs in the bar of an inn in the Isle of Man:—

I had both—	by both I set great store	and a—
I lent my—	and took his word therefor;	to my—
I asked my—	and nought but words I got.	from my—
I lost my—	for sue him I would not.	and my—

At length with—	which pleased me very well,	came my—
I had my—	away quite from me fell:	but my—
If I’d both—	as I have had before,	and a—
I’d keep my—	and play the fool no more.	and my—

It is to be read thus:—

I had both money and a friend, by both I set great store,
I lent my money to my friend, and took his word therefor,

and so on to the end.

10

When ———— smiles, and sunbeams play
On flowers that ———— and deck the green,
———— can match the scene so gay
———— they crown the May-day queen?

The missing words are spelt with the same seven letters.

Solution

11

’Tis said of William, while his forces rested
On Albion’s ———, when Harold had been bested,
He made the ——— of his ——— fuse
Saxon spear-heads, to fashion into shoes.

Each missing word has the same six letters.

Solution

[III-10]

No. X.—DECAPITATED WORDS

The decapitated words are in italics:—

The ship rode in an eastern bay,
Asleep astern the master lay,
A stern and rugged man was he,
And, like a tern, at home at sea.
Like swooping ern he caught his prey
Whene’er an R.N. came his way;
But while due N. the needle kept
He in his cabin lay and slept.

The ern, or erne, is the sea-eagle.

12

Happiness, brighter than ———, is dead;
Life’s battle, sterner and ——— now,
Heals the sore ——— that love left as it fled,
——— remembrance of long broken vow!

The missing words are spelt with the same six letters.

Solution

13. AN AUTHOR’S EPIGRAM

Press critics fall on me like sharks;
“A shameless ....... of odds and ends,
No ....... original,” and more remarks
In adverse mood. But stay, my friends,
He ....... best who hath his record clean;
My faults are published, yours are yet unseen!

The missing words have the same seven letters.

Solution

14

...... are his ......, fashion-forms of grace
In ...... deftly hinted.
...... soft as ......, crowned by Beauty’s face,
In ...... hues are tinted.

The six missing words are spelt with the same six letters.

Solution

[III-11]

No. XI.—AN ANCIENT ANAGRAM

On the front of a church, in the Largo Remedios, at Braga, in Portugal, there is an inscription which, with its letter-perfect Anagram, runs as follows:—


	BEATUS IOANNES MARCUS
	CHRISTI DOMINI DISCIPULUS

	ANAGRAM

	IS IN MUNDO PIUS EST MEDICUS
	TUIS INCOLIS, BRACHARA

which may be rendered—“Blessed John Mark, disciple of Christ the Lord.” He in this world is the holy healer of thy people Braga!

15

When Kate — ——— —— —— displayed
— —— — hide a tear;
“All love is dead — ———,” he said.
“———— I’ll —— ——!”

The missing word and groups of words are spelt with the same seven letters.

Solution

16

Some grinding at the ——— must toil,
Down-trodden ——— of to-day;
While other children of the soil
In vast ——— their wealth display.

The missing words are spelt with the same six letters.

Solution

[III-12]

No. XII.—STRIKE A BALANCE

This diagram shows that the odd numbers of the 9 digits add up to 25, and the even numbers to 20.

1	2
3
5	4
7	6
9	8
25	20

Can you arrange the 9 digits in two groups in which the odd numbers and the even will add up to exactly the same sum?

Solution

17

Betrayed by faithless friends, in ——— mood
Man ——— his fellows as the ——— brood.

The missing words are spelt with the same six letters.

Solution

18. HONEST INDIAN

With divers —— his —— is scarred,
He hangs a bangle in his nose;
Such marks secure his —— regard,
Exalt his fame, and —— his foes.

Each missing word is spelt with the same four letters.

Solution

[III-13]

No. XIII.—HKISTA!

MRS LR’S SR
MR LR KRS.
“BLR MR LR!”
MRS LR HRS.

How do you read these lines and their title?

Solution

19. ON THE OCEAN WAVE

———— who, as we ———— roll,
———— for me the foaming bowl,
And ———— off unfriendly spray
With oilskin cape, thou shalt not say
“In vain I’ve ———— my favours here.”
I’ll think of thee when port is near!

The four missing words are spelt with the same seven letters.

Solution

20. THE ZENANA MISSION

With high ——— for hearts and hands,
These ——— ——— for distant lands.

The three missing words are spelt with the same six letters.

Solution

21

The ———— of his speech did not
———— his audience a jot.
They greeted all he said thereafter
With ————, smiles, and open laughter.

The missing words have the same seven letters.

Solution

22

To convent shrine at break of day
With ——— together nuns repair;
Mid gleaming ——— they kneel and pray,
And chanted ——— allays each care.

Spelt with the same five letters.

Solution

[III-14]

No. XIV.—IN MEMORIAM

The following puzzle-epitaph was engraved on a tombstone in Durham Cathedral:—


WEON	.	CEW		.	ERET	.	WO
WET	.	WOM		.	ADEO	.	NE
NON	.	EFIN		.	DUST	.	WO
NO .	WLI	.	F	EB	.EGO	.	NE
WILLIAM and MARGARET TAYLOR
Anno Domini 1665.

Solution

23

Here once, as a hag is bedizened with paint,
A ——— ——— ——’— in the garb of a saint.

The three missing words are spelt with the same five letters.

Solution

24. IN PRAISE OF SUSSEX

Sussex! No ——— of a bygone age
Ride through thy ——— to-day with shield and ———,
And ——— no horseflesh so they may engage
To save some damozel from harm or fear.

Who now would give a thought to ——— or peaches?
He truly farms who ——— a golden store;
And, though he cannot ——— the simplest speeches,
——— down expense, and savings has galore!

Each missing word is spelt with the same five letters.

Solution

[III-15]

No. XV.—A FRENCH WORD SQUARE

Here is an excellent French Word Square of seven letters:—

R	E	N	E	G	A	T
E	T	A	L	A	G	E
N	A	V	I	R	E	S
E	L	I	D	A	N	T
G	A	R	A	N	C	E
A	G	E	N	C	E	R
T	E	S	T	E	R	A

This is a worthy companion to the English seven-letter squares on “Problem” and “Palated,” which are given on other pages.

25

——— in the ——— far away,
Remote alike from heaven and hell,
The silent ———, so poets say,
Who shape the ends of mortals dwell.

Each missing word has the same five letters.

Solution

26

In all our ——— the mechanician’s skill
Now compasses the rogue with artful wile.
The patent ——— and the “tell tale” till
Beset his way who ——— the path of guile,
Besotted youth, who ——— to defy
The rule of right, beware his awful fate
Who, sitting down to eat a stolen pie,
——— the eighth commandment on the plate!

Spelt with the same six letters.

Solution

[III-16]

No. XVI.—A QUAINT EPITAPH

This epitaph, most of it in some sort of dog Latin, tells its own pathetic tale on its tablet.


	IT - OBIT - MORTI - MERA PUBLI - CANO - FACTO - NAM AT - RES - T - M - ANNO - XXX ALETHA - TE - VERITAS TE - DE - QUA - LV - VASTO MI - NE - A - JOVI - ALTO PERAGO - O - DO - NE - AT STO - UT - IN - A - POTOR - AC AN - IV - VAS - NE - VER - A
	R - I - P

Solution

27

The .... with .... importunate
To rule his .... may try;
His .... is so unfortunate
That .... they may reply!

The missing words are spelt with the same four letters.

Solution

28. “TURN AGAIN WHITTINGTON!”

In all the pomp of —— and chains
He lords it o’er the town;
The —— of his hopes he gains
Who —— with half-a-crown.

Each missing word has the same four letters.

Solution

[III-17]

No. XVII.—A TRAGIC CALENDAR


	Jan-et was quite ill one day; Feb-rile troubles came her way. Mar-tyr like, she lay in bed, Apr-oned nurses softly sped. May-be, said the leech judicial, Jun-ket would be beneficial. Jul-eps, too, though freely tried, Aug-ured ill, for Janet died. Sep-ulchre was sadly made, Oct-aves pealed and prayers were said. Nov-ices with many a tear Dec-orated Janet’s bier.

29. A SAUCY JADE

A writer quite devoid of tact,
She valued ——— more than fact.
A wayward ——— she made her muse
On ——— and noble heaped abuse.
Dealt ——— on ——— to prince or peer,
Her ——— wit a paltry jeer.

Each missing word is spelt with the same six letters.

Solution

30. MISSING WORDS

Of all destructive country pests
The farmer ..... ..... least;
He cannot yet the puzzle .....
How to suppress the beast!

The missing words have the same five letters.

Solution

[III-18]

No. XVIII.—A DIAMOND PALINDROME

Within the four corners of this Mystic Diamond the Palindrome, NAME NO ONE MAN, can be traced in 16,376 different directions, in straight lines, or at right angles, starting from the centre or from the borders.

N
NaN
NamaN
NamemaN
NamenemaN
NamenonemaN
NamenooonemaN
NamenoonoonemaN
NamenoonenoonemaN
NamenoonemenoonemaN
NamenoonemamenoonemaN
NamenoonemaNamenoonemaN
NamenoonemamenoonemaN
NamenoonemenoonemaN
NamenoonenoonemaN
NamenoonoonemaN
NamenooonemaN
NamenonemaN
NamenemaN
NamemaN
NamaN
NaN
N

31. TO THE FRESH AIR FUND
OH THE ——— OF THE ———.

The ——— of darkest London are radiant with ———,
You can ——— it in their ——— little faces.
So wherever you ——— let it be your heart’s ———
To ease the ——— and sorrows of all ———.

The missing words in the title and those in the first and third lines each contain six letters. Those in the second four, and in the fourth five.

Solution

[III-19]

No. XIX.—SHAKESPEARE RECAST

If you start with the right letter in this combination, and then take every third letter, a well-known quotation from Shakespeare will be formed.

House.canoe.after.
hour.print.cave.child
sash.sleve.acorn.
ample.sad.tatta.hena
mat.ache.cake.taches.
heliac.sacque.usual.
arbor.see.mulch.jacur.
use.stop.

Solution

32. THE FLIRT THAT FAILED

She ...... in vain, “Men are ......, and as shy
As ...... in October,” she says with a sigh.

The missing words are spelt with the same six letters.

Solution

33

When good men lapse the ....... grins,
When one ....... he swears,
And strives to set his former sins
Against his ....... prayers.

Each missing word is spelt with the same seven letters.

Solution

[III-20]

No. XX.—A DOUBLE ACROSTIC

An old Italian bird we know
Whose heart is ever touched by snow.

1. None can press me without pain

1. Pressure is against the grain.

2. I am a king without my head.

3. Here is another king instead.

It is fair to our readers to say that some knowledge of Latin and French is needed for dealing with this very excellent Acrostic, of which a full explanation is given with the solution.

Solution

34. THE GIPSY LAD

His hands and face were ———, and sad
Upon the ——— a gipsy lad
Lay; as the breeze his temples fanned
He counted ——— on either hand.

Each missing word has the same five letters.

Solution

35. THE OLD DIVINE

In yon grey ——— an old divine
Taught me my ——— to decline,
And verbs with ——— of mood and tense;
But while I plodded on apace
I had to keep the ——— of grace,
And close his prayers with loud ———.

Each missing word is spelt with the same five letters.

Solution

36. BANZAI!

No reckless ——— of the sword,
He ——— his fatherland to save.
Fighting for freedom, not ———,
Now ——— of the eastern seas.

The four missing words contain six letters.

Solution

[III-21]

No. XXI.—HIDDEN PROVERBS

Five familiar proverbs are hidden in this square of 169 letters.

The proverbs are arranged in a regular sequence.

Solution

37. OF DOUBTFUL WORTH

A fair ———, though ——— and frayed,
The critic ——— to own,
And it might interest the trade
If ——— by some one known.

The missing words are spelt with the same six letters.

Solution

38

In his ——— days, as when he was young,
The ——— indulges in ——— of tongue.

Each missing word is spelt with the same six letters.

Solution

[III-22]

No. XXII.—AN ALPHABETICAL TOAST

Lord Duff, who evidently had a turn for puzzles, proposed this alphabetical toast, which became popular among the Jacobites.

A.B.C.	A blessed change.
D.E.F.	Down every foreigner.
G.H.J.	God help James.
K.L.M.	Keep Lord Mar.
N.O.P.	Noble Ormond preserve.
Q.R.S.	Quickly resolve Stuart.
T.U.V.W.	Truss up vile Whigs.
X.Y.Z.	Exert your zeal.

Another quaint and ingenious use of separate letters is recorded of the well-known preacher, Henry Ward Beecher.

Years ago, before his reputation had become world-wide, he was asked to give a lecture without charge, and assured that it would increase his fame. His reply was characteristic and very much to the point: “I will lecture for F.A.M.E.—fifty and my expenses!”

39. MISSING WORDS

(1)	A cylindrical lock
(1)	Where no key can be found,
(2)	An instrument treble
(2)	And ringing in sound.
(3)	In story-land ranging,
(4)	Now chopping and changing;
(5)	Broken up, reunited,
(5)	Quite whole I am found.

Words, spelt with the same eight letters are indicated in these lines. There are two words in (1).

Solution

[III-23]

No. XXIII.—A MORAL PRECEPT

The following obscure legend was worked on an old sampler, in the red cross-stitch that found favour when our grandmothers were girls:—

Elizabeth out
Rue Constantine
Very thin gloves
Way Susan dart.

This was evidently some excellent moral precept, but it hung on its frame, a mere puzzle on the school-room wall, until an expert word juggler came that way, and solved the mystery by reading it off thus:—

“Eliza be thou true, constant in everything. Love sways us, and art.”

40

In the following lines the first missing word has two letters, and the letters are carried on, with one more added each time, and in varied order, throughout the verses, either in single words or in groups of words:—

A lover of .. unkind fair
Were less than ... did he not ....
“Mine is no ..... life, I swear,
It dwells in this ...... alone.
Grant me thy love, like ....... chaste
.. ...... lest thou live unwooed,
..... .. . lowly life to waste
The treasures of sweet ..........”

Solution

[III-24]

No. XXIV.—SHAKESPEARE’S MANTLE

Ingenious cryptic efforts have been made to prove that Bacon was the author of Shakespeare’s plays, but it has been reserved for us to reveal, by a convincing cryptogram, the modern wearer of his mantle.

The secret is disclosed by a line of capital letters shown below:—

Mac	B	eth.
Oth	E	llo.
Comedy of Er	R	ors.
Merchant of Ve	N	ice.
Coriol	A	nus.
Midsummer Night’s D	R	eam.
Merry Wives of Win	D	sor.
Measure for Mea	S	ure.
Much Ado about Not	H	ing.
Antony and Cleop	A	tra.
All’s Well that ends	W	ell.

41. MISSING WORDS

Till a man is as ——— of a ——— as his palm is,
We ——— him from earning his ——— in our armies.

The missing words are spelt with the same five letters.

Solution

42. THE PAUPER’S PLAINT

Pale penury that ——— social bands,
And any link that ——— worth to fame,
Take ye the blame for my inactive hands,
I ——— in vain to build upon the sands,
Without a ——— who can make a name?

The missing words are spelt with the same six letters.

Solution

[III-25]

No. XXV.—CAPITAL SHORT CUTS

The following example of the use of phonetic capitals and figures is fresh and original. It contains more than eighty such symbols in its twenty-four lines:—

A MAID OF ARCADY

A rosy maid of R K D
Is L N in her bower;
Brisk as U C A honey B,
And sweet as N E flower.

Does she S A herself 2 please
(XQQ the saucy miss),
She sings an L E G 2 TT,
Or blows an M T kiss.

“B mine, I say, U bonny J,
B 4 I CC mine L;
When you are gay my hopes D K,
In T sing U X L.”

Without ado she takes the Q,
Her II B 9 and B D,
“O, sir, I do not N V U
I C that U R C D.

“X S of spirits—O D V—
Begins 2 U U U up;
The cure must B a dish of T
With K N in the cup!”

“O L N U I C R true,
Y need I C Q less?
I’ll never D V 8 from U,
But end my cares with S.”
(caress).

43. MISSING WORDS

Mr Backslide, afflicted with weakness of mind,
———— over to Lushington’s inn, where he dined.
He ———— the pledge he had taken as handy,
And emptied forthwith a ———— of brandy.

Each missing word has eight letters.

Solution

44

A ——— sat in his ——— grey,
Watching the moonbeams ——— play
On a keg that in the bushes lay,
And these were the words of his song:—
“Thou ——— the weak, thou ——— the strong,
To thee the ——— of bad deeds doth belong.”
And the leaves with a ——— took up the sad song.

Each of these missing words is spelt with the same six letters.

Solution

[III-26]

No. XXVI.—SIMPLE SCHOLARSHIP

Three hungry scholars came to a wayside inn, and saw this sign over the door:

PLACET    ORE
STAT   ORDINE
ORE     STABIT
ORE  AT   ABIT

One of them eager to show his ready wit, translated these Latin words of welcome roughly into English verse:—

“Good cheer we provide,
Our service is sure;
Their savours abide
Though meats don’t endure!”

The complacent smile faded from his face as a village schoolboy, who had overheard him, broke in with the real rendering of the words:—“Place to rest at or dine; O rest a bit, or eat a bit!”

45

In these lines, where the dots occur, insert words, each of which is longer by one letter than the one before, and so complete the poem. The same letters are carried on each time in varied arrangement:—

Nature . love .. every land,
On burning plain, by wooded rill;
Where ... is girt by coral strand,
Or .... rears her castled hill.

Then ..... from me the tale to hear,
How, true to one ......, the bee
Once ....... out keeps, year by year,
The ........ by her instinct given,
Which teach her, wheresoe’er she roam,
In every clime beneath the heaven,
To build the same ......... home.

Solution

[III-27]

No. XXVII.—WAS IT VOLAPÜK?


FFAH	CHTI	WT
HGU	ACT	ONE
RASD	RIB	DLO

A schoolmaster in the Midlands, who was a bit of a wag, wrote this on the blackboard, as a novel exercise for the boys of Standard VI. Can you decipher it?

Solution

46

Here is another ingenious specimen of missing words, spelt each of them with the same five letters:—

That Samson did a thousand ———
Is not so wondrous strange.
In days like these at ——— such feats
Assume a wider range.
The Press ——— news ——— now,
Enough to scare a sinner,
And any fool who chooses may,
In Samson’s way, his thousands slay
Who chews his ——— at dinner.

Solution

[III-28]

No. XXVIII.—ANOTHER EPITAPH

(On an Old Pie Woman)

BENE AT hint HEDU S.T.T.H. emo Uldy O
L.D.C. RUSTO F.N.E. L.L.B.
AC. hel orl AT Ely
W ASS hove N.W. how ASS Kill’d
Int heart SOF pi escu Star
D. sand Tart Sand K N ewe,
Ver yus E oft he ove N.W. Hens he
’Dliv’ Dlon geno
UG H.S. hem Ade he R la STP uffap
UF FBY HE RHU
S. B an D. M.
Uchp R.A. is ’D no Wheres He dot
H.L. i.e. TOM a Kead I.R.T.P. Iein hop est
Hat he R.C. Rust W I
L.L.B. ERA IS ’D——!

Solution

47. IN A FARM-YARD

All his flock from ——— rough,
To the ——— ran apace,
Where their ———, old and tough,
———, the guardian of his race.

In these lines each missing word is spelt with the same six letters.

Solution

48

This is a bright little specimen of a missing words puzzle:—

Come, landlord, fill the flowing ——
Until their —— run over;
For in this —— to-night I’ll ——,
To-morrow —— to Dover!

Each missing word has the same four letters.

Solution

[III-29]

No. XXIX.—DOG LATIN

An old worn stone, with the inscription given below just legible, was found near to some ancient Roman remains, and was the valued possession of a local antiquarian, who was convinced that it dated back to the days of the Emperor Claudius:—

BENE
AT . HTH . IS . ST
ONERE . POS . ET
H . CLAUD . COS. TERT
R . I . P
ES . ELLE . RO
F . IMP
IN . G . TONAS . DO
TH . HISCO
N . SORTJ
A . N . E

His pride of possession was, however, shattered when a rival collector read it off into excellent English:—“Beneath this stone reposeth Claud Coster, tripe seller, of Impington, as doth his consort Jane.”

49

Here, as quite a novelty, is a double-barrelled missing words puzzle. As a puzzle, Part I. should stand alone, but the second part forms a thinly-veiled solution, which throws light upon the missing words. These are four in number and are spelt differently with the same six letters.

Part I

I tell of voices hushed and still,
I bid men prick their ears,
I help an army’s ranks to fill,
My gleam like gold appears.

Part II

Hushed is the still and ——— voice,
Pricked ears are keen to ———,
Men who ——— make noble choice.
——— like gold will glisten.

Solution

[III-30]

No. XXX.—THE PROBLEM SQUARED

P	R	O	B	L	E	M
R	E	C	E	I	V	E
O	C	T	A	V	E	S
B	E	A	C	O	N	S
L	I	V	O	N	I	A
E	V	E	N	I	N	G
M	E	S	S	A	G	E

This is a singularly perfect specimen of a seven-letter Word Square.

50. MISSING WORDS

Some men their ——— escorted on their way,
When “——— look here!” I heard a driver say:
“It ——— our pluck to toil like ——— all day,
When wanting ——— we starve on wretched pay.”

Each missing word is spelt with the same five letters.

Solution

[III-31]

No. XXXI.—BY LEAPS AND BOUNDS

Can you disentangle the eight-line verse which is scattered over these 64 squares? You must leap always from square to square, as a knight moves on the chess-board.

tle	to	a	cat-	life	and	live	In
By	tle	ow-	bro wse	of	non	tle	fall
ter	tur-	gain	like	land	one’s	quiet	And
of	ar m	Bet-	me ad-	and	Than	a-	bat-
bask	Be t-	lau-	or	tle	ness	done	wan-
rel	let	Than	die	With	der	of	smo ke
ter	in	brain	myr-	on	and	har-	un-
Ch ap-	or	to	sun	with	work	In	heat

The verses begin with “Better to die,” and end with “tle” in the top left-hand corner.

Solution

51. WISDOM WHILE YOU WAIT

As a ———— ———— of facts you’ll find
Our Encyclopedia ———— the mind.

The three missing words are spelt with the same seven letters.

Solution

52. MISSING WORDS

You drink that ———, ——— wine, too lavishly at night,
And say a ——— or a swim next morning puts you right,
When night brings you a sudden ———, and morning devils blue,
Then you’ll ——— your careless boast, and own my warning true.

Each missing word is spelt with the same six letters.

Solution

[III-32]

No. XXXII.—A BROKEN SQUARE

Can you complete this broken Word Square?

	O	E
O			E
	I	O
E			E
	E	E

Solution

53

The missing words in these lines are all spelt with the same six letters:—

— ——— but for rebel act
Without — ——— should be;
But this — — — end, in fact
None find — ——— in me.

Solution

54. MISSING WORDS

“Oh for a ——— in this vast solitude,
This endless rise and fall of ——— and moor!”
Soliloquised a ——— in sad mood,
As through the lonely hills the staff of life he bore.

Spelt with the same five letters.

Solution

[III-33]

No. XXXIII.—A KNIGHT’S TOUR PROVERB

If the letters on these squares are taken in proper sequence they will form the words of a well-known proverb:—


				E
		E				T
			L	H
	E		R		S
		E	A	S
D		E		O		S
			S	P		M

When a starting point has been chosen for trial of this puzzle, the successive letters must occupy the squares which in every case are reached by a knight’s move at chess, until a popular proverb is formed.

Solution

55. “MONSTRUM HORRENDUM INFORME INGENS”

’Twas in ........ that we saw him play
Like a ........ in his sports, and they
Amuse us as a good ........ may.

Each missing word has the same eight letters.

Solution

[III-34]

No. XXXIV.—GUARINI’S PROBLEM

The following curiosity, which is known as Guarini’s Problem, dates back to the year 1512. On a board of 9 squares two white Knights are placed in the top corners, and two black Knights in the bottom corners, thus:—

The problem is to interchange, in as few moves as possible, the positions of the white and black knights.

Solution

56

We call particular attention to the construction of this very curious couplet, in which the spaces are filled by the same seven letters. In every case four of the letters of the missing words or phrases are the same, and keep the same order, and in all but the first the order of the letters is unchanged throughout, though the meaning always alters, as it does in that most perfect old Latin motto, “Persevera, per severa, per se vera,” “persevere through trials, true to thyself.”

Soup is —— ——— for a ———— divine,
Who with —— ——— is —— —— to sit down and dine.

Solution

[III-35]

No. XXXV.—AN ANAGRAM SQUARE

Can you break up and recast the five words in this square, so that the fresh words form a perfect Word Square? The initials are A, M, E, N, D, S.

S	E	N	D	E	R
O	N	I	O	N	S
B	A	B	B	L	E
M	A	N	N	E	R
S	M	I	L	E	D
L	I	N	E	A	L

Solution

57. MISSING WORDS

Sweet as the —— and cruel as its thorn,
—— thy power is great, thy pity scorn.
Swift as the —— that through the forest fly,
Deep as the —— that deepest hidden lie,
Is thine own —— to hapless mortals given,
Semblance of darkest hell or brightest heaven.

These missing words are spelt with the same four letters.

Solution

58. MISSING WORDS
(Dedicated to the Fresh Air Fund)

Good ——— for City ———

My pipe ——— for — —— charms, that yield
Pictures and ——— of a children’s day.
Lest conscience ——— I —— — down to say
My ——— shall send some city ——— afield.

Each word or group is spelt with the same five letters.

Solution

[III-36]

No. XXXVI.—SHAKESPEARE’S PSALM

Quite as cryptic and convincing as any of the curious Shakespeare-Bacon cyphers is the evidence which connects our great English poet with the forty-sixth Psalm of the authorised Bible version.

Shakespear, spelt thus, as it often was, contains four vowels and six consonants. This is the key to the position. If, guided by these figures, we turn to the forty-sixth Psalm and count from the beginning, we find the forty-sixth word is “Shake.”

Then, counting from the end, disregarding the “Selah,” which is no part of the text, we find that the forty-sixth word is “spear.”

Thus, by a startling and perfect succession of affinities, the poet’s name-number is linked again and again with this Psalm, until it reveals his name.

If any sceptic asks why the Book of Psalms should thus be turned to, the answer comes in the curious fact that the actual letters of the name William Shakespere, another of its different spellings, form this sentence as their anagram, and thus afford the necessary clue:—

“We are like his Psalm.”

A final point of interest is made when we notice that Shakespeare himself must have been just forty-six years old when the Psalms were re-translated.

59. MISSING WORDS

He said “You ———” when one lied,
He said “Don’t ———” when one hied,
His glass held ——— at his side,
He can ——— what he denied.

Each missing word is spelt with the same six letters.

Solution

[III-37]

No. XXXVII.—A KNIGHT’S TOUR

The letters on this board, if read aright in the order of a Knight’s moves at chess, will give a popular proverb.

R	L	T	E	Y	L	R	O
Y	H	L	T	O	B	T	A
T	A	A	A		H	T	I
E	L		E	I	N	E	O
D	H	W		Y	E	S	Y
R	T	E	S	D		B	W
Y	N	E	S	N	D	A	E
H	A	A	A	W	I	D	E

Start from the most central E, and you will be able to trace the proverb.

Solution

60. MISSING WORDS

Mr Snip, the ————, was ———— a hill,
With a bag of new ———— for stock;
When a runaway motor-car gave him a spill
Which scattered his doubts with the shock.

Each missing word is spelt with the same eight letters.

Solution

[III-38]

No. XXXVIII.—A WORD SQUARE

The pupils of Dr Puzzlewitz found one morning these vowels printed boldly on the blackboard:—

E	*	A	*	E
*	A	*	E	*
A	*	E	*	*
*	E	*	*	E
E	*	*	E	*

Under it the doctor had written “Fill in the consonants, so that the words read alike from top to bottom, and from side to side.” How is this to be done?

Solution

61. MISSING WORDS

——— her fair cheek, and back o’er all
The ——— of years ——— memory.
Those wedding ——— to her recall
The ——— he urged so tenderly.

Each of these missing words has five letters.

Solution

62. MISSING WORDS

Two burglars attempted to ——— a house,
The ——— was heard, though as still as a mouse.
When challenged at once he a ——— became,
But caught as a ——— he finished his game.

Each word has the same five letters.

Solution

[III-39]

No. XXXIX.—THE SQUAREST WORD

The squarest word in any language is the Latin time, which, in connection with the three other Latin words, item, meti, emit, can be read, when written as a square, in every possible direction. Thus:—

T	I	M	E
I	T	E	M
M	E	T	I
E	M	I	T

As it seems impossible to go one better, we have been seeking, as a new nut for our store, some English word which may be a good second. Can you complete the square which is built up on these lines?

D	E	L	F
*	*	*	*
*	*	*	*
*	*	*	*

Delf is the key word, but it so far falls short of the perfection aimed at, that other letters are used in four of the vacant places. Still, it is so constructed that words which begin with D, E, L, or F appear each of them in four different directions, and is thus quite a notable example.

Solution

[III-40]

No. XL.—A PUZZLE DIAMOND

Can you fill in this diamond with four words that read alike from left to right, and from top to bottom?

			D
		.	I	.
	.	.	A	.	.
D	I	A	M	O	N	D
	.	.	O	.	.
		.	N	.
			D

Solution

63. MISSING WORDS

The ———— fool in olden days
Gave kings advice in jesting phrase;
He’s ———— now; the modern throne
———— all follies but its own.

Each missing word is spelt with the same eight letters.

Solution

64. MISSING WORDS

Days of ——— and times of evil,
Starving girls with ——— do toil,
No man ——— feast or revel,
Hushed is ——— and turmoil.

Each missing word contains the same six letters.

Solution

65. MISSING WORDS

Who ———— in his pride and rage,
To ———— vice a prey,
May hope to reach a green old age,
And find ———— his stay.

Each word has the same seven letters.

Solution

[III-41]

No. XLI.—A DEFECTIVE DIAMOND

				S
			.	.	M
		P	.	.	.			L
	.	.	N	.	.	A	L
S	.	.	.	N	.	.	.	R
	M	.	.	.	C	.	E
		L	A	.	.	E
			L	.	E
				R

The places now occupied by dots are to be filled in with letters so that a complete diamond is formed, of words that read alike from left to right, and from top to bottom.

Solution

66. A POET’S POLITICS

When Limerick once, in idle whim,
Moore as her member gaily courted,
The boys, for fun’s sake, asked of him
To state what party he supported.
When thus to them the answer ran,
“I’m of no party as a man,
But as a poet ———”

What is the missing word?

Solution

67. MISSING WORDS

Is England ———? That this is so
A solemn ——— aspires to show.
By most ignored, the theme — —— to some
Who gravely to the same conclusion come.
Like ——— o’er obstacles they soar,
And if an —— — ’vert they rave the more.

There are six letters in the missing words and phrases.

Solution

[III-42]

No. XLII.—A SPECIMEN MAGIC SQUARE

The following clever word square of the unusual number of seven letters, in which there is no undue straining of words or inflexions, is by a master hand, and would be difficult to match:—

P	A	L	A	T	E	D
A	N	E	M	O	N	E
L	E	V	A	N	T	S
A	M	A	S	S	E	S
T	O	N	S	U	R	E
E	N	T	E	R	E	R
D	E	S	S	E	R	T

68. MISSING WORDS

Off to the links is now their cry,
For golf is man’s ————:
Be not ———— or slow,
———— hit the ball will go.

Each missing word is spelt with the same eight letters.

Solution

69. MISSING WORDS

No maid e’er ———— North, South, East, or West,
More ———— than she who ———— Love’s request.

Each missing word is spelt with the same seven letters.

Solution

70. OUT IN THE COLD

Though in ......... I be,
It is, alas! ... ......
No ...... ... comes nigh to me.

Each word or phrase has the same nine letters.

Solution

[III-43]

No. XLIII.—A LETTER PUZZLE

Can you fill in the places of these 21 asterisks with only 3 different letters, so arranged that they spell a common English word of 5 letters in 12 different directions?

*	*	*	*	*
*	*		*	*
*		*		*
*	*		*	*
*	*	*	*	*

Two of the five letters are vowels.

Solution

71

————— his pride the Royal James
Came down upon the ————— Thames;
Like ————— his court repair
To breathe — ————’s freer air.

Each space has the same nine letters.

Solution

72. DROP LETTER LINES

With lily leaves his oars are ........,
Her eager hands their treasures .......,
To the fair winds all cares . .....,
And echo faintly answers .....!

The first letter is dropped in each case, so that while the word which ends line 1 has eight letters, the last word of line 4 has but five.

Solution

73. ENIGMA WITH MISSING LETTERS

There was no good ... in the d...y, so the klim.

Solution

[III-44]

No. XLIV.—A CANINE CHRONOGRAPH

Some years ago a country parson had the following inscription engraved upon the tombstone of a favourite dog that died in 1885:—

CarLo
Dear DoggIe
LoVIng faIthfVL anD trVe
she Lost her sIght
bVt not her LoVe
for
I. e. V.

If the large capital letters are treated as Roman numerals, they add up to the year of the dog’s death, 1885.

74

If the missing letters, indicated by dots, are supplied, and the words are separated, this will be found to form a line in a well-known poem:—

.u.u.m.r.i.u.d.s.s.e..o.l.w.d.a.t.n.f.l.o.e.f.s.e.

Solution

75

Complete this sentence by filling in five words in the gaps, each spelt with the same five letters:

If you write ——— ——— at ——— do not ——— the ———.

Solution

76. SIX MISSING WORDS

A ..... ..... on ....’. strands
Caught Pat’s heart in her meshes;
He left the ..... in Cupid’s hands,
And watched her ..... her tresses;
Tresses of ..... coloured gold,
That did her fairy form enfold.

Each missing word has the same five letters.

Solution

[III-45]

No. XLV.—A HIDDEN NAME

“Yes,” said the village wit, as a merry party sat round the tap-room fire at Stratford-on-Avon, “some wiseacres have tried to prove that Bacon wrote Shakespeare’s plays, because his name can be found hidden in some of the lines. Let me show you how easily this sort of thing can be arranged to suit our fancy.”

Taking a piece of chalk he wrote upon the door—

“Titus An	d	ronicus”
“All’s Well th	a	t Ends Well”
“The Mercha	n	t of Venice”
“Corio	l	anus”
“Cymb	e	line”
“A Midsummer	N	ight’s Dream”
“Much Ado ab	o	ut Nothing”

“Look down the letters under d of these titles of some of Shakespeare’s plays,” he said, “and you will find the well-known name of one who certainly did not write them.” What name did he mean? What but that of the prince of jokers, Dan Leno!

77. MISSING WORDS

Can you supply the missing words in these lines? Each is spelt with the same five letters:—

A man of ——— had caught a ———,
And it was windy weather;
“Give me my ———,” he cried, “to fix
My fish and ——— together.”

Solution

[III-46]

No. XLVI.—A CRYPTIC INSCRIPTION

The following cryptic inscription was engraved, in his own language, upon a tablet in honour of the great French astronomer and scientist, Arago:—

URE
AR ERIL

It has this interpretation:—

AR	à gauche,
ERIL	à droit,
URE	sur tout.

Arago chérit la droiture sur tout.
Arago cherished integrity above all.

78. ON THE LOOSE

When ....., our puppy, sets out for a run,
Over ..... he ....., all frolic and fun.
For no whistle he ..... in his desperate hurry
The cattle to ....., and the slow sheep to worry.

Each word has the same five letters.

Solution

79. MISSING WORDS

Buy my ripe ———, my ——— who’ll buy?
Don’t look so ———, but take some and try!

The missing words are spelt with the same six letters. What are they?

Solution

[III-47]

No. XLVII.—SQUARE THE CIRCLE

Here is a circle which it is quite possible to square:—

C	I	R	C	L	E
I	.	.	.	E	.
R	.	.	E	.	.
C	.	E	.	.	E
L	E	.	.	E	.
E	.	.	E	.	.

Can you fill it in with English words, that read alike from top to bottom, and from left to right? Try it before you turn to the solution. Every E must be worked in as it stands.

Solution

80. MISSING WORDS ILLUSTRATED

He who .... may .... at last,
How to .... we show;
Take a sixpence, hold it fast,
Press the .... and blow!

Each missing word has the same four letters.

Solution

[III-48]

No. XLVIII.—A BROKEN SQUARE

We give as clues the complete border, and a diagonal in which the same letter persists. Can you construct the whole square?

B	O	A	S	T	E	R
O				E		E
A			E			S
S		E				E
T	E					N
E						T
R	E	S	E	N	T	S

Solution

ANAGRAMS

Anagrams, as a method of divining and illustrating personal destiny and character, were quite a craze in the sixteenth and seventeenth centuries. No specimens of this word juggling have ever been more apt than the perfect pair of political anagrams evolved from the names of two of our greatest statesmen.

When the reins of power changed hands, it was found that the letters which form Gladstone also spell out exactly, “G. leads not,” while the name of his great rival and successor Disraeli itself announces, when recast, “I lead, sir!”

[III-49]

No. XLIX.—A CARD PROBLEM

Here is a pretty card problem, akin in its character and arrangement to a Magic Square.

Take from a pack of cards the four aces, kings, queens, and knaves, and arrange them so that in each horizontal, vertical, and diagonal row, each of the four suits and each of the four denominations shall be represented once, and only once.

Solution

IDEAL ANAGRAMS


	Ave Maria, gratiâ plena, Dominus tecum! Virgo serena, pia, munda et immaculata. Regia nata, evadens luctum amari pomi. Eva secunda, Agni immolati pura mater. Hail, Mary, full of grace, the Lord is with thee! A virgin calm, holy, pure and spotless. Of royal kin, free from the penalty of the bitter apple. A second Eve, pure mother of the slain Lamb.

These wonderful anagrams need no word of praise. Constructed each of them with the same letters, the lines express with startling emphasis the character and special attributes of her whom they describe.

[III-50]

No. L.—TURF-CUTTING

I cut eight narrow strips of turf from my lawn, to form a double rose-border, with sides of the relative lengths shown in the diagram:—

How can I relay these eight pieces, without turning or breaking them, on a piece of level soil, so that they enclose three flower-beds of similar size?

Solution

AN ANAGRAM EPITAPH

This was engraved on a slate monument in memory of Marya Arundell, in Duloe, Cornwall, June 8, 1629:—


	MARYA ARUNDELL—MAN A DRY LAUREL
	Man to the marigold compared may be, Man may be likened to the laurel tree. Both feede the eye, both please the optic sense, Both soon decay, both suddenly fleete hence. What then infer you from her name but this, Man fades away, man a dry laurel is!

[III-51]

No. LI.—A READY RECKONER

Two schoolboys, looking into a small water-butt after a heavy rain, could not agree as to whether it was quite half full.

They appealed to the gardener, as there were no means of measurement at hand, and he, being a shrewd, practical man, was able to decide the point. How did he do this?

Solution

TWIN ANAGRAMS

Paradise lost.
Reap sad toils.

Paradise regained.
Dead respire again!

[III-52]

No. LII.—A TRANSFORMATION

Can you turn this flat-headed 3 into a 5 by one continuous line, without scratching out any portion of the 3?

Solution

ADVANCE AUSTRALIA

What were “The Australian Cricketers?”

ANSWERED BY ANAGRAM
Clinkers! Each a true artist.

BUNYAN’S ANAGRAM

John Bunyan, in the conclusion of the advertisement of his “Holy War,” has these quaint lines (using i for j):—

“Witness my hand, if Anagrammed to thee
The letters make ‘Nu hony in a B.’”

OLD POLITICAL ANAGRAMS

“The Earl of Beaconsfield.”
Chief one of all debaters.

“William Ewart Gladstone.”
Wit so great will lead man.

[III-53]

No. LIII.—A CLEAR COURSE

These diagrams show two of the many ways in which eight pieces of chessmen or draughtsmen can be so placed upon the board that each of them has a clear course in every direction, along straight or diagonal lines.

We will give a table in the solutions which shows a large number of similar possible positions. Meantime our solvers may like to trace some for themselves.

APPOSITE AND OPPOSITE

Three most excellent anagrams are formed with the letters of the great name Thomas Carlyle. Two of them seem to point to the rugged sage of Chelsea in life, and one to his repose in death. They are:—

Mercy! lash a lot.
Cry shame to all!
A calm holy rest.

A ROYAL ANAGRAM
(Adsit omen!)

“Albert Edward and Alexandra.”
All dear bread and war tax end!

[III-54]

No. LIV.—QUARRELSOME NEIGHBOURS

Three families, who were not on speaking terms, lived in three houses within the same enclosing fence. Determined to avoid each other, they built covered ways from the doors of their houses to their gates, so that they might never cross each other’s paths. The family in A had their gate at A, those in B at B, and those in C at C. How were these covered ways arranged so as to secure their complete separation?

Solution

HIS HOBBY

William Ewart Gladstone.
A man will go wild at trees.

A SOLDIER’S ANAGRAM

Lord Kitchener of Khartoum.
Oh firm rod! the knack to rule!

[III-55]

No. LV.—A PRETTY TRICK

Ask some one to place five cards (not court cards) in a row, to add up their pips, and to place two cards representing that number below, for subtraction, as is shown in the diagram.

Let him then place cards to represent the result of subtraction, remove which one he pleases of these, and tell you the sum of the remaining pips.

You can at once tell him the value of the card removed by deducting the number of pips in that remainder from the next highest multiple of 9. Thus, in the instance shown above, if one of the sixes is removed, the sum of the remaining pips is 12, and 18 - 12 = 6. A space must be left for any 0.

BOAT-RACE ANAGRAMS

Here is a batch of anagrams, all letters perfect, which show how, by a little ingenuity, words may be twisted into opposite and appropriate meanings.

“The Oxford and Cambridge annual boat-race.”

ANAGRAMS

Hard race, but Cantab gained lead from Oxon.
Ah! bad rudder line for Cantab cox to manage.
Cantab blue had raced in an extra good form.

[III-56]

No. LVI.—THE CROSS-KEYS

This pretty puzzle can be made at home by anyone who is handy with a fret-saw.

Cut three pieces of hard wood according to the patterns given in this diagram, and try to fit the three sections together so that they form a firm symmetrical figure with six projecting ends.

Solution

ANGLO-JAPANESE ANAGRAMS

“The Anglo-Japanese treaty of Alliance.”
Yea, Fate enjoins to help a gallant race
or
Hail, gallant East! Fear not, enjoy peace
or
A peace angel, then joy to all in far East.

A WONDERFUL ANAGRAM

If the letters which spell the names of the twelve months are shaken up and recast, these appropriate lines and their title are formed—

POEM

Just a jury by number, each a scrap of year,
A number recording every jumble, tumble, tear!

[III-57]

No. LVII.—THE NABOB’S DIAMONDS

An Indian Nabob left a casket of valuable diamonds to his children under the following conditions:—The first was to take a diamond and one-seventh of the remainder; the second was to take two and a seventh of the then remainder; the third three and a seventh of the rest, and so on, on similar lines, till all the diamonds were taken. Each of the children had then exactly an equal share. How many diamonds were there, and how many children?

Solution

A PRIZE ANAGRAM

It would be difficult to find a more ingenious and appropriate anagram than this, which took a prize in Truth in 1902, and connects the King’s recovery with the Coronation.

The sentence was—

“God save our newly crowned King and Queen!
Long life to Edward and Alexandra!”

The letters of this were recast thus—

Can we wonder an anxious devoted England followed drear danger quakingly?

A GOOD ANAGRAM

Sir Francis Bacon, the Lord Keeper.
Is born and elect for rich speaker.

THE DREAMER’S ANAGRAM

“Imagination”—I’m on it again!

A SEASONABLE ANAGRAM

“Spring, Summer, Autumn, Winter.”
We murmur—“Time’s running past!”

[III-58]

No. LVIII.—A CARD CHAIN

The cardboard chain in this diagram is formed of unbroken links cut from one card.

There are no joinings in these links, no paste or gum is used, and the chain is fairly cut from a single card.

Solution

APPROPRIATE

Very apt indeed, in these days of books and papers without end, is the descriptive anagram which we find involved in

“The Alphabet,” That be a help.

A TOUR DE FORCE

Made with the letters which form the names of the twelve months, each being used once, and only once:—

Merry durable just grace
My every future month embrace,
No jars remain, joy bubble up apace!

[III-59]

No. LIX.—STRAY DOTS

These represent the four quarters of a torn design, on which large black dots had been so drawn that no two of them stood on the same row, column, or diagonal.

Can you copy out these four pieces, and place them in close contact, so that the proper edges come together to reproduce the original effect?

Solution

AN OLD POLITICAL ANAGRAM

The initials of Brougham, Russell, Allthorp, and Grey,
If rightly disposed the word “brag” will display;
Transpose them and “grab” will appear to the view,
Which hints at what many assert to be true,
That they, like some others, still follow the plan
To brag what they’ll do, and then grab what they can!

[III-60]

No. LX.—THE OPEN DOOR

A prisoner placed in the cell marked A is promised his release on the condition that he finds his way out of the door at X by passing through all the cells, entering each of them once only.

How can he do this?

Solution

A ROYAL ANAGRAM

The following remarkable anagram is recast from the name and title of the daughter of George IV., who was direct heir to the throne:—

“Princess Charlotte Augusta of Wales.”

ANAGRAM

P. C. her august race is lost, O fatal news!

[III-61]

No. LXI.—THE SHEPHERD’S PUZZLE

When a farmer told his shepherd to put 21 sheep into 4 pens at the fair, and added, “I wish you could put an odd number into each pen, as there is luck in odd numbers, but that is impossible,” he did not take into account the shrewdness of the shepherd, who very cleverly folded them thus:—

Each fold or pen has by this arrangement an odd number of sheep within the hurdles that form its outer boundaries, and in this sense the farmer’s wish was satisfied.

We are familiar, most of us, with what is called Macaronic verse or prose, in which the letters and syllables of Latin words can be read so as to form English sentences.

It would seem to be too much to expect that there could be any connection in meaning between these Latin and English words, but there is one striking exception to this general rule. “Non est” means exactly “it is not,” and “No nest” conveys precisely the same idea, when a bird finds that its home has been destroyed.

[III-62]

No. LXII.—LEAP-FROG

Here is an interesting puzzle which can be worked out with coins or counters on a corner of a chess or a draughtboard.

At starting only the central point is vacant. A piece that is moved to a vacant spot must leap over two other pieces if it goes along the solid black lines, and can only move over one of the dotted diagonals at a time to an adjoining point. Try, on these lines, to enable the frog, now in the second hole of the lowest row, to reach the centre in the fewest possible moves, leaving its own original point vacant, and at the last surrounded by the words “leap-frog” as they now stand.

Moves can only be made to vacant places.

Solution

[III-63]

LXIII.—MUSIC HATH CHARMS

Transpose two letters, and the lad
Who grinds his organ in the Strand,
Can sing “my music is not bad,
I wake it with a master hand!”

How did he justify this ambitious claim?

Solution

[III-64]

No. LXIV.—GRIST FOR THE MILL

If the letters P E A R S O N S are printed on small wafers or buttons, and set at hap-hazard and out of order on the points which they now occupy, a very pretty game of patience will result from the attempt to restore them to their places.

Any letter can be pushed along one of the lines to a vacant place, and those on the mill sails can be moved to or from the central spot. There is no fixed limit to the number of moves, but the puzzle is to restore, in as few moves as possible, the broken and disordered word to its proper reading round the mill.

[III-65]

No. LXV.—YOUR WATCH A COMPASS

We are indebted to Sam Loyd, the famous American problem composer and puzzle king, for the following very practical curiosity, which is so closely akin to a puzzle that it is well worth giving for the benefit of our readers when they are out on holiday. If you are uncertain as to your bearings, lay your watch flat on the palm of your hand so that the hour-hand points in the direction of the sun. The point exactly midway between the hour-hand and the figure 12 will be due south at any time between 6 in the morning and 6 in the afternoon. During any other hours our rule will give the north point, and in the southern hemisphere the rules will be reversed.

In the days of Pope Pio Nono someone extracted from the Papal title “Supremus Pontifex Romanus” an anagram, which cut at the very foundation of the faith. It ran thus: “O non sum super petram fixus”—“O I am not founded on the rock.”

This held its place as a clever topical anagram, until in a moment of happy inspiration a son of the Church discovered that if the first words are recast and rearranged, a splendidly appropriate motto for the then reigning pontiff leaps to sight, “Sum Nono, super petram fixus,” “I am Nono, founded on the rock!”

[III-66]

No. LXVI.—A MYSTIC SQUARE

This is an arrangement of numbers in 9 cells, so that no cell contains the same figure as appear in any other, and the two upper rows, the two side columns, the two long diagonals, and the four short diagonals all add up to 18:—

1 + 1 + 1	5 + 5 + 5 + 55	2 + 22
3 + 3	6	4 + 4 + 44
7 + 7 + 77	9 + 9 + 9 + 99	8 + 88

Though not, strictly speaking, a Magic Square, this is a most ingenious fulfilment of the conditions of the puzzle.

UP-TO-DATE ANAGRAMS

Good up-to-date anagrams are:—Chamberlain, “Rich able man,” and Pierpont Morgan, “Man prone to grip.”

[III-67]

No. LXVII.—A SWARM OF WORDS

In each of the five crosses of this mystic figure the same letters are to be inserted where there are asterisks, so that seven different English words are formed, which can be read altogether in 64 different ways and directions.

There will then be in all the five crosses 320 readings of these seven words, three of them having 80 variations and four of them having 20, and only three different letters are used.

Solution

SEASONABLE ANAGRAMS


	“A Merry Christmas and a Happy New Year.”
	My prayer and wishes reach many a part.
	or
	Many a sad heart can whisper my prayer.

[III-68]

No. LXVIII.—AFTER SOME SAD REVERSE

We admit this most miserable picture of a discontented outcast into our bright pages, to “point a moral,” if it does not “adorn a tale.”

Can our readers gather from it the lesson, that when things seem to be at the worst, a turn of fortune’s wheel may set them on their legs again, and change the merest melancholy to the merriest mirth? A reverse of another sort will set things right. Turn the page round!

Solution

A lady, to whom the momentous question had been put with some diffidence, handed to her lover a slip of paper, telling him that it embodied her reply. Nothing was written but the word “stripes,” which seemed at first to be of sinister omen; but to his relief and joy the fateful letters presently resolved themselves into a message of direct encouragement, and never was an anagram more welcome than this which bade him “persist.”

[III-69]

No. LXIX.—THE EXPLOSIVE RAFT

With eight large wooden matches form a miniature raft, as is shown in the diagram:—

Place the little raft on a wine-glass, and apply a lighted match to one of its corners. The tension on its parts will cause the whole construction to fly asunder as soon as the pressure on any point is removed.

A NOTABLE HISTORIC ANAGRAM

It is very remarkable that the letters which form the sentence—

“The Jubilee Day of Victoria, Queen and Empress,” also exactly spell—

Joys are never quite complete if a husband die.

[III-70]

No. LXX.—A PICTURE PUZZLE

Much is bad, and much is sad,
And life has many woes.

May we keep clear from year to year
Of what this picture shows!

Can you interpret it?

Solution

CONTRADICTION BY ANAGRAM

Logica, Latin for logic, can be resolved into the strangely contradictory anagram, caligo, darkness; and, in seeming support of this perversion, our word logic can be turned into I clog!

Here are two good anagrams connected with the land of the Pharaohs:—

David Livingstone,
“Go and visit Nile, D.V.”

Cleopatra’s Needle on the Thames Embankment,
“An Eastern emblem; then take me to Cheops’ land.”

Danes should be dark men, according to the anagram of “Denmark.”

[III-71]

No. LXXI.—PATCHWORK PICTURES

This is good fun for old and young as a round game. Each player draws on the upper part of a slip of paper some fancy head and folds it back, leaving just enough in sight to guide his left-hand neighbour, who takes it and adds a body. Again the slips are handed on for the final addition of legs of any sort, some continuation being always indicated.

Then these completed patchwork pictures are thrown into a central bowl, shaken up, drawn out, and passed round for inspection and merry comment. The folds are the dotted lines.

A HOUSEHOLD WORD

The wounded and sick soldiers whom Florence Nightingale nursed so tenderly in the Crimea would have acclaimed her beautiful anagram—“Flit on, cheering angel!”

[III-72]

No. LXXII.—A WINTER NIGHT’S DREAM

Mr Jolliboy, chubby and active, had been dancing until the small hours at a house in the suburbs, which was the home of sweet Lucy, the lady of his love.

The full moon shone down upon him as he walked happily to his own modest quarters, and the “man in the moon” seemed to smile and wink at him most knowingly.

Letting himself in presently with his latch-key, Mr Jolliboy was soon in bed and fast asleep, when in his dreams the full moon shone again, showing at one moment a likeness of his own round face, at another two smiling profile views of his Lucy, and at times all the three mixed.

Here, changed by a few touches, are the three moon-faces to be seen in one moon!

When the great Tichborne trial was still dragging its slow length along, a barrister with a turn for anagrams amused himself and his learned friends by constructing the following really remarkable specimen:—Sir Roger Charles Doughty Tichborne, Baronet, “Yon horrid butcher Orton, biggest rascal here.”

[III-73]

No. LXXIII.—POINTS AND PICTURES

Among the many openings for pleasant fun in the home circle, there is none which appeals more easily to young and old than the good old puzzle of drawing off-hand some fanciful figure, based on five dots placed at random, which must fall on the face, hands, and feet of the subject chosen.

This spirited specimen shows how well it may be done, and similar efforts, more or less successful, will provoke much amusement. Try it with pencil or pen and ink.

ANOTHER BOAT-RACE ANAGRAM

Among the many points which have to be taken into account by those who in successive years are responsible for the selection of the Oxford eight, there is one which is thus neatly expressed by an anagram:—

“The Oxford and Cambridge annual boat-race.”

Much extra load on board can bring a defeat.

[III-74]

No. LXXIV.—A NERVOUS SHOCK

This is the astounding portrait of himself, which presented itself to our scientific professor in his dreams. What very poor justice it does to the real lines of his benevolent and shrewd old countenance will be seen in a moment if this weird picture is reversed.

Solution

HOLIDAY HAUNTS
Divination by Name

Whenever we are making our plans, some of us for a holiday abroad, some for a few weeks at the seaside, there is a special interest in these descriptive anagrams:—

Davos Platz, Engadine.
“Stop, gaze, and live!”
Weston-super-Mare, Somerset.
“A sweet open summer’s resort.”

A very appropriate anagram that exactly describes its subject is this:—Cleopatra’s Needle, London—“An old lone stone replaced.” Very suggestive, too, are these short ones, which assure us that skeletons are “not sleek,” and that editors are “so tired!”

[III-75]

No. LXXV.—HOGARTH’S PUZZLE

A soldier, a dog, and a door can be thus drawn by only three strokes of a pen:—

It is said that this originated with Hogarth, who made a bet with his boon companions that he would draw a soldier, a dog, and a door in three strokes. For the bayonet he drew a pike.

[III-76]

No. LXXVI.—A REBUS

Why is this “Joker” like a poor joke?

Because he is in an E (inane).

Here are three ingenious instances of what may be called answers by anagram:—

What is the protector of “wealth?”

The law.

Where would a “cart-horse” be unhandy?

In an orchestra.

What is the “Daily Express?”

Pressa die lux.
Concise daily light.
(u is used for y.)

It is curious that Mary, a name so sweet and simple, has as its anagram “army.” The conflicting thoughts suggested by these two words are very happily harmonised by George Herbert in his quaint style:—

“How well her name an army doth present,
In whom the Lord of Hosts doth pitch His tent!”

[III-77]

No. LXXVII.—THREE SQUARES

Here is quite a simple method of arranging nine matches so that they represent three squares.

The figure also includes at its sides two equilateral triangles.

A ROYAL ANAGRAM

Victoria the First, Queen of Great Britain and Ireland, and Empress of India. These letters also spell exactly:—

Fit for a bard I claim inspiréd strain:—
The sad and even tenor of a quiet reign.

POLITICAL ANAGRAMS

Here are two very perfect specimens:—

Earl Beaconsfield.
An able force is led,
or,
A free lance is bold.

[III-78]

No. LXXVIII.—A TRANSPARENCY

When the plebiscite was taken in France to decide whether Napoleon III. should be Emperor, the number of votes cast in his favour was 7,119,791. Against him there were 1,119,000 votes.

If these numbers are written down quite plainly, as is shown above, with a dividing line, and without the three cyphers, and the paper or card on which they are strongly marked is reversed and held up against the light, the very word with which they were concerned, “empereur,” stands out with startling distinctness.

It can be drawn on thin cardboard with good effect.

Solution

AN IMPERIAL ANAGRAM

A sa Majesté impériale le Tsar Nicolas, souverain et autocrat de toutes les Russies.

The same letters exactly spell—

O, ta vanité sera ta perte. O, elle isole la Russie; tes successeurs te maudiront à jamais!

This most remarkable anagram was published in the early days of the Crimean war.

This curiously apposite anagram was formed letter by letter from the surnames of the Oxford and Cambridge crews:—

April first nineteen hundred and five. How all warm, as arms, strong as light or dark blue crew’s, all ply oars on very smooth Thames! Oh! shall Cam’s boat lose?

[III-79]

No. LXXIX.—FOR THE CHILDREN

Here is an excellent and amusing pastime for the winter evenings. Cover a square of stout cardboard with glazed black paper, and divide it as is shown in this diagram:—

With a little ingenuity and some sense of fun, any number of grotesque figures can be constructed with the pieces, such as those which we give here as samples. Try it.

The truth that there is often much in common between puzzles and politics is borne out by the following up-to-date anagram:—This Eastern question—“Is quite a hornet’s nest.”

Quite a good anagram, appropriate to the name of a great author, and one of his works runs thus:—

Charles Dickens: Oliver Twist.
“Now C. D. strikes till vice hears.”

Confessions of an Opium-Eater

The same letters recast spell—

If so man, refuse poison at once!

[III-80]

No. LXXX.—JUDGING DISTANCE
(For the Children)

Can you, without measuring, say which two of these posts are farthest apart?

A JAPANESE ANAGRAM

“Oyama is Field-Marshal.”
Fame aid his loyal arms!

A TOPICAL ANAGRAM

“North Sea outrage.”
A ghost near route!

APPROPRIATE ANAGRAMS

Madame Rachel.
Deal me a charm.

A. Tennyson.
Any sonnet.

A FOURFOLD ANAGRAM

“Notes and Queries”
A question sender.
Enquires on dates.
Reasoned inquest.
I send on a request.

[III-81]

No. LXXXI.—HIT IT HARD

Place the two parts of a common wooden match-box, empty, and in good condition, in the position shown below.

Now challenge any one to break them with a smart downward blow of the edge of the hand. What will happen? Try it.

It is well to take care that no people are sitting, or children standing, near the box, as it might fly into their faces.

An amusing sequence and a note of warning run through these three anagrams:—Sweetheart, “There we sat;” Matrimony, “Into my arm;” One hug, “Enough.”

[III-82]

No. LXXXII.—A RE-“BUS”

The driver of a London ’bus the other day broke out into florid language as he nearly collided with a brand new motor omnibus.

One of the travesties of “motor-’bus” which he hurled at his rival is depicted in this diagram. What was it?

Solution

A PRIZE ANAGRAM

This letter-perfect anagram could not be more apposite if the words had been chosen from a dictionary:—“Abdul Hamid Khan, Sultan of the Ottoman Empire.”—“Inhuman despot, that maketh Armenia bloodful.”

The words in italics in—

One lovely May morn it chanced that I set
My all on a new speculation;
But the venturesome step I can never regret,
For my prize has surpassed expectation,

find in Matrimony their anagram, which is also the solution of the lines.

[III-83]

No. LXXXIII.—ROUSING DEAD DOGS

A GOOD OLD PUZZLE

These dogs are dead, we all should say;
Give them four strokes, they run away!

A MEAL OF ANAGRAMS

Mute hen.
Your posset.	Try our steak.
One solid lamb.	Steamed or tossed.
Mince sole.

This is solved thus:—

The Menu.
Oyster soup.	Roast turkey.
Boiled salmon.	Dressed tomatoes.
Lemon ices.

Each corresponding sentence is a perfect anagram.

Earl of Beaconsfield is spelt with the same letters as the sentence “O able dealer in scoff!”

If a lion with an ear for music were to hear the sound of an “oratorio,” he might say, as an answer by anagram, I roar too!

[III-84]

No. LXXXIV.—LIKE A BLACK SWAN

(Nigroque simillima cygno.)

Here is quite a good “shadowgraph.”

With a strong light and a little practice, any one may easily produce this effect with the shadow thrown by arms and hands.

ANSWERS BY ANAGRAM

What is Russia?—Russia is ursa (a bear).

What did a Prime Minister say of the Saturday Review?

That it was a very rude periodical.

BEANS AND BACON

What appropriate advice might be given by anagram to those who support the “Shakespeare-Bacon” controversy?

Soak cheaper beans.

[III-85]

No. LXXXV.—CHEQUERS AND STRIPES

Here is a particularly charming domino puzzle:—

Place any twenty stones, as is shown in the diagram, so that in every row their fronts and backs alternate. How can you change the picture by only two movements, so that, retaining its present form, you alter its chequers into stripes?

Solution

The answer by anagram to—What helps to make “bakers fat?” is Breakfast.

[III-86]

No. LXXXVI.—HANG THE MATCHES!

Here is an amusing method of turning wax matches to quaint account:—

If the wax is slightly melted, and perhaps shredded for some effects, all sorts of fanciful figures can be thus contrived.

ANSWER BY ANAGRAM

What does an editor say to each “ream of paper?” Appear for me.

LEWIS CARROLL’S WILL PUZZLE

Here is a most ingenious will puzzle, by Lewis Carroll, which will be new to most of our readers. Each of the following five questions has to be answered by a different sentence, nine letters long, and each sentence is spelt with the same letters used in varied order:—

When are you going to make your will?
Shall I write it for you in pencil?
When may a man leave all his money to charities?
What did the uncle say when he heard this?
What did the nephew say when the uncle made him his heir?

The anagram answers to the five questions in Lewis Carroll’s will puzzle are as follows:—

When are you going to make your will?
Now I think.
Shall I write it for you in pencil?
No, with ink.
When may a man leave all his money to charities?
With no kin.
What did the uncle say when he heard this?
Hint, I know.
What did the nephew say when the uncle made him his heir?
Think I won!

[III-87]

No. LXXXVII.—A PARROT CRY

The good old Rebus—

may stand for the proverb—

“Honesty is the best policy.” (On ST is the best poll I see!)

[III-88]

No. LXXXVIII.—A PICTURE PUZZLE

Can you find eight animals that are concealed in this wood?

Solution

If we may go by its anagram the gardenia needs careful “drainage.”

DEFINITIONS BY ANAGRAM

What is the “soldiers’” anagram?
Lo I dress.

What motto befits “Christianity?”
I cry that I sin.

[III-89]

No. LXXXIX.—A SHADOWGRAPH

Here is a good old sample of an effect produced by supple fingers in a strong light on the wall:—

Adjust the fingers as is shown, so as to secure the bright spot for the eye, and then life-like movements can easily be made with legs and ears.

The characteristic for the moment of the gaol-bird who began to tear his clothing, crying out, “I mean to rend it!” was determination, which contains exactly the same letters.

Those who, according to their anagram, are best equipped for a “sea trip” are Pirates.

AN ANSWER BY ANAGRAM

What is most unlike a festival?—Evil fast.

The three words in italics in the verse below form also a long single word, of which the lines themselves give a vivid description:—

While many greet the friends they meet,
I know no face, I press no hand.
Though busy feet may throng the street,
I sit alone, sirs, in the land.

“Solitariness.”

[III-90]

No. XC.—A REBUS

Can you interpret this word-picture?

It represents the name of a famous man.

Solution

ANSWER BY ANAGRAM

Should you wish to go by rail,
Hasten to the station;
“Train on time” can never fail
To reach its destination.
If you need a further clue
Keep your journey’s end in view.

Termination.

We may expect to find “Anarchists” involved in rash acts according to their anagram.

When his patient has recovered, a “surgeon,” can say by anagram go nurse!

ANSWER BY ANAGRAM

What momentous event of the last century forms in two words an anagram of the three words appropriate to it, “violence run forth?”

French Revolution.

[III-91]

No. XCI.—ON THE WALL

Here is a picturesque head, which in a strong light can be thrown upon the wall by anyone who is handy with his fingers.

The peaked cap seems to suggest a French soldier.

ANSWERS BY ANAGRAM

What manner of men has “Eton” produced?

Men of tone and note.

What worries the “postman?”

No stamp.

What are to be seen at “Epsom Races?”

Some pacers.

[III-92]

No. XCII.—ILLUSTRATED EGGS

As an excellent illustration of how much expression can be given by quite a few simple lines, if the pen or pencil is in artistic hands, we give the outlines of half a dozen eggs, on which by a few deft touches varied emotions of the human face are cleverly depicted.

Here is a hint for fun in the home circle, with a basket of eggs, a sheaf of pencils, and a prize for the best rapid design. There is room for two contrasting faces on each egg.

ANSWERS BY ANAGRAM

What did “Henry Wadsworth Longfellow” do for America?

He Won half the New World’s glory.

What was the happy result of patriotic “sentiment” in our colonies during the Boer war?

It sent men.

[III-93]

No. XCIII.—THE FIVE STRAWS

Take five straws, each about four inches long, and a shilling, and arrange them so that by holding an end of one of the straws you can lift them all.

The diagram given above shows how, by properly interlacing the five straws, the shilling may be so inserted as to form a wedge which locks them all together.

ANSWERS BY ANAGRAM

What can you say when using a “fire-escape?”

I creep safe.

What is the extreme of “slow reading?”

A single word.

How might a “Poorhouse” in olden days have been described by its own letters?—O sour hope!

What is “Old England” to her sons and daughters?—Golden land.

The battle of “Inkermann” tells by its anagram of men in rank.

[III-94]

No. XCIV.—EQUIVALENT REDISTRIBUTION

In the problem known as “The Flighty Nuns,” the Abbess in the central cell was satisfied so long as she could count nine of her charges in the cells on each of the four sides. Here are diagrams which show how the thirty-six inmates could on these terms absent themselves without discovery, 2, 4, 8, 10, 12, 16, and even 18 at a time by re-arrangement of their numbers in the cells.

0	9	0	1	8	0	2	5	2
9	A	9	8	A	8	5	A	5
0	9	0	0	8	1	2	5	2

2	5	2	2	4	3	3	3	3
5	A	5	4	A	4	3	A	3
2	5	2	3	4	2	3	3	3

2	2	5	4	1	4	5	0	4
2	A	2	1	A	1	0	A	0
5	2	2	4	1	4	4	0	5

The clue by anagram to those in search of “hidden treasure” who sought to discover a dish-cover is dish under a tree.

[III-95]

No. XCV.—THE PUZZLED CARPENTER

To stop a serious leak a carpenter sought for a board a foot square. The only piece he could find was two feet square, but it was pierced with sixteen holes, as in the diagram below:—

How did he contrive to cut a square from this of the necessary size?

Solution

The answer by anagram to “What should we all welcome, if the Chancellor of the Exchequer could ‘introduce’ it into his Budget?” is reduction.

Things that we know to be “transient” must be looked at, according to their anagram, instanter.

A MUSICAL ANAGRAM

Sweet Mary, the Maid of the Mill, arranged an ingenious signal by song, by which, in olden days, she could assure her father that all was well when mischief was abroad. If he heard her singing, “Do, re, mi, fa, sol, la, si,” he was sure that nothing was amiss. When these syllables are shaken up, and recast as an anagram, what reassuring sentence do they form?

The musical syllables, sung as a reassuring signal to her father, by Mary, the Maid of the Mill, “Do, re, mi, fa, sol, la, si,” when shaken up and recast as an anagram form the sentence “A mill door is safe.”

[III-96]

No. XCVI.—NOT EASY WHEN YOU KNOW

Of the many “match puzzles” the following seems to be the most confusing to the ordinary solver, and any variation of its original position is enough to create fresh confusion.

Re-arrange three of these matches and form four squares.

Solution

The enigma anagram—

They were orthodox as beadles,
But in business tricks and wheedles
They were “sharp I see” as needles—

is solved by Pharisees.

The question—Where did we buy “our fancy mat?”—is answered by anagram at the manufactory.

[III-97]

No. XCVII.—SIMPLICITY

Construct this figure with five matches:—

Remove three of the matches, and then replace two of them so as to form a similar figure.

Solution

A common and much-appreciated “dose at meat shop” is, according to its anagram, mashed potatoes.

Tiglath-Pileser was the name of the king which can be resolved into the anagram, “I till the grapes.”

“Art? I begin art!” is an anagram for Great Britain.

If heartily administered, nine thumps, the anagram of “punishment,” would fall deservedly upon the shoulders of a wife-beater.

ANSWER BY ANAGRAM

Our strongest “armaments” are men-at-arms.

[III-98]

No. XCVIII.—OVER THE WINE AND WALNUTS

Can you build a bridge with three wooden matches, which shall connect three wine-glasses, and be solid enough to support a fourth set upon it?

This picture shows how it is to be done.

The elephant, according to its anagram, is the animal to which the command “Leap then!” would be the least appropriate.

The answer by anagram to “Whom should we employ to make ‘alterations’ in our overcoats?” is Neat tailors.

Where do we go to remedy “disease?”

To the seaside.

Who should make a good “manager?”

A German.

[III-99]

No. XCIX.—FROM THE MATCHBOX

Here is quite a simple match problem:—

Can you remove eight of these matches, that now form nine squares, so as to leave only two squares upon the table?

Solution

When Cato and Chloe, at the Popular Café, decided to order for their afternoon tea a pot of what is formed by the mixture of the letters of their names, they called for Chocolate.

The answer by anagram to “Why may the scenery round Bournemouth be said to be ‘quite spruce’?” is—because it is picturesque.

Lord Roberts’ motto, “Virtute et Valore,” is by its anagram True to avert evil, a happy indication of his character.

[III-100]

No. C.—LIFT NINE WITH ONE

To arrange ten matches on a table, so that with one hand you can lift nine of them with the tenth, lay them, as is shown in Fig. 1, with the heads of eight pillowed on one, and pointing in opposite directions, and the tenth placed across the ridge at the top.

Fig. 1 Fig. 2

Then lift all, as shown in Fig. 2.

A MAN HIS OWN ANAGRAM

The enigma—

Behold in me a man forlorn,
Who, though with sound limbs he was born,
His anagram alas is!
For he has found out to his cost,
While all his nimbleness is lost,
How slippery wet grass is!

is solved by Male, lame.

The answer by anagram to the question, “Whom do ‘our big hens’ frequently annoy?” is neighbours.

[III-101]

No. CI.—FREEHAND DRAWING

This is the way to draw in three strokes an old woman looking out of a window:—

Here is a puzzle anagram:—

Tell how to spell my name,
As on the stall you spy me,
For the letters are the same
Which bid you how to buy me.

Peach—cheap.

The eglantine is the flower which quite contradicts its anagram, inelegant.

The touching epitaph in memory of little Alice formed from the letters of her name was à ciel!

[III-102]

No. CII.—A NOTABLE ANAGRAM

Treated as an anagram the words “Cats on truck” can be recast into Nuts to crack, and the surrounding motto, “Yes! we sparkle on” into Pearsons Weekly; so that the whole design resolves itself into—Nuts to crack, in Pearson’s Weekly.

The old saying that a man who is his own doctor has a fool for his patient, seems to be borne out by the curious fact that the words, “Dangers of amateur physicking,” resolve themselves into the perfect anagram—“The sick men pay for drugs again.”

A ’VARSITY ANAGRAM

What every “undergraduate” hates—

A great rude dun.

The food for a crocodile which seems to be indicated by its name is cool’d rice!

[III-103]

No. CIII.—WITH DRAWN SWORD

Here is a very simple and ingenious method of representing roughly an officer with drawn sword.

Six wax vestas, shredded to form the hair and sword-belt, are fastened together by the application of a little heat.

Anyone with handy fingers and an ingenious turn of mind can easily construct other quaint figures in this style.

“Time and tide wait for no man.”

ITS ANAGRAMS
A fine mandate to mind, I trow.
and
A firm intent made, a “do it now.”

[III-104]

No. CIV.—SHADOWGRAPHS

Here are three excellent shadowgraphs, which can be produced with good effect by flexible fingers in a strong light on the wall.

“Norway’s Olaf is in old England.”
ITS ANAGRAMS

Elf-lad, so loyal and so winning.
A darling son and noisy fellow.
Of winning lads, lead, royal son!
On London’s air wing safely lad.

ANSWERS BY ANAGRAM

Why should city life be happy?
Because the same letters spell felicity.

What is the best proof that “real stickphast paste sticks?”

The same letters spell—Keep this, stick scraps at last!

[III-105]

ANSWERS BY ANAGRAM

What place have our puzzles “in magic tale?”

They are enigmatical.

What great assembly would seem from its name to consist of “partial men?”

Parliament.

CHARACTER BY ANAGRAM

What did Douglas Jerrold, by his name anagram, declare himself to be?

Sure, a droll dog I!(i for j)

What in the old-fashioned days caused “the wig” to be discarded?

Weight.

The following curious peace anagrams are appropriate in these days of disturbance. Each set of words between inverted commas contain exactly the same letters:—

“To escape fray” I ever “stay for peace,”
In “quiet times,” too, “I’m quite set” at ease:
Let no “vile words” provoke the “evil sword,”
Lest “red war” come, and bring its own “reward.”

Why does the old proverb “Birds of a feather flock together” form a mystic link between us and our cousins in America?

Because the same letters recast spell out the patriotic sentence, It rocks the broad flag of the free!

What, by their anagram, are “platitudes?”

Stupid tales.

[III-106]

Why is there a measure to “disappointment?”

Because it is made in pint pots.

What is the purpose of a “catalogue?”

It is got as a clue.

If “porcus” is Latin for pig, what is Latin for its body?

Corpus.

What may “laudation” easily become?

Adulation.

What is “revolution?”

To love ruin.

Define “The Griffin” (Temple Bar).

Fine fright.

Why is there room for variety in “twelve sentences?”

Because we can select new events.

How do we know that “potatoes” in the singular should not have an “e” at the end?

Because they spell O stop at e!

What should be done to a “misanthrope?”

Spare him not.

What was the owl of “Minerva?”

A vermin!

These, wherever they are found,
Cluster lightly overhead.
Should you chance to turn them round
Blows may tell of weight instead.
[III-107] Twisted in a foreign tongue,
You will see them as they are.
Changed again they need a bung
When you move them full and far.

This is solved by the anagram words nuts, stun, sunt, tuns. (Sunt is Latin for “they are.”)

IPSISSIMA VERBA

A discussion arose one day, in the winter season, between several members of a West-end Club, as to the value of flannel underwear. A London physician, who was appealed to, upheld the need for this, and it was afterwards found that his name, Alfred James Andrew Lennane, treated as an anagram, becomes “Man needs aired flannel wear.” This was singular, but a much more curious coincidence of similar sort was discovered by an expert in anagrams.

Another member took quite an opposite view, and declared that all should wear linen. By a wonderful chance his name, Edward Bernard Kinsila, resolves itself into the actual words that came from his lips—“A d—— bad risk Dr., wear linen!”

A CHRISTMAS CARD


	AN ANAGRAM
	“Christmas comes but once a year.” So by Christ came a rescue to man.

[III-108]

PALINDROMES
OR
SENTENCES THAT READ BOTH WAYS

NAPOLEON’S PALINDROME

Able was I ere I saw Elba.

ADAM AND EVE’S PALINDROME

Madam, I’m Adam!

When Charles Grant, Colonial Secretary, was made Lord Glenelg, in 1835, he was called Mr Facing-both-ways, because his title Glenelg was a perfect palindrome, that could be read with the same result from either end.

It was a member of the same family who sought to prove the antiquity of his race by altering an “i” into an “r” in his family Bible, so that the text ran, “there were Grants on the earth in those days.”

A GOOD PALINDROME

“Roma, ibi tibi sedes, ibi tibi amor,” which may be rendered, “At Rome you live, at Rome you love;” is a sentence which reads alike from either end.

A QUAINT PALINDROME

Eve damned Eden, mad Eve!

This sentence reads alike from either end.

A good specimen of a palindrome is this German saying that can be read from either end:—

Bei Leid lieh stets Heil die Lieb
(In trouble comfort is lent by love.)

[III-109]

Here are some ingenious palindromes, which can be read from either end:—

Repel evil as a live leper.

Dog, as a devil deified, lived as a god.

Do Good’s deeds live never even? Evil’s deeds do O God!

A SCHOOLBOY’S PALINDROME

“Subi dura a rudibus”

“I have, endured roughness from the rod” which can be read alike from either end.

Very notable as a long palindrome, even if it is not true record of the great surgeon’s experience, is this quaint sentence:—“Paget saw an Irish tooth, sir, in a waste gap.”

A PEACE PALINDROME

Snug & raw was I ere I saw war & guns.

This sentence reads alike from either end.

A PALINDROME PUZZLE

A turning point in every day,
Reversed I do not alter.
One half of me says haste away!
The other bids me falter.—Noon.

Very remarkable for its length and good sense combined is the following palindrome, which can be read from either end with the same result:—“No, it is opposed, art sees trades opposition.”

A PERFECT PALINDROME

Perhaps the most perfect of English palindromes is the excellent adage—

“Egad, a base tone denotes a bad age.”

[III-110]

Here is the most remarkable Latin palindrome on record:—

SATOR AREPO TENET OPERA ROTAS

Its distinguishing peculiarity is that the first letters of each successive word unite to form the first word, the second letters spell the second word, and so on throughout the five words; and as the whole sentence is a perfect palindrome, this is also true on reversal.

[III-111]

SOLUTIONS

No. III.—A BOOK AND ITS AUTHOR

The well-known book and its author which are represented by

are “Innocents Abroad,” by Mark Twain. (In no sense A broad, by mark twain.)

Back to Puzzle

No. IV.—ON THE SHUTTERS

No.
John Mar
in atten
from 8 a.m.
Barber
Hair C
The bald cry a
for hi
as displayed
which make hair g
Closes

I
shall
dance
daily
and
utter
loud
s creams
in this window
listen
after 8 p.m.

The shutter on the left blew open, leaving the other to tell its strange tale.

Back to Puzzle

[III-112]

No. VI.—SOLVITUR AMBULANDO

A man, tracing step by step the various readings of ROTATOR on this chequered floor, can exhaust all of them, according to the arrangement on our diagram, in 21,648 steps, spelling out the word as he goes in the many directions 3608 separate times!

This large total is due mainly to the fact that ROTATOR is a palindrome, and lends itself to both backward and forward reading. The man, a veritable rotator, will thus have walked more than four miles within a compass of one hundred and forty-four square feet.

Back to Puzzle

[III-113]

No. VIII.—AN OLD SAMPLER


		AL. IT.
	T.L	EW. O. MA!
	N.T.	Ho! UGH. AVE. Ryli.
	T.T.	Let. Hi! N.G.I.
	S.S.	We. Et. Erf. Art. Ha!
	N.S.	Ug. Ara. N.D.F. Lo!
	W.E.	R.S.T. Ha! TB.
	L.O.	O! Mins. Pri.
		N. G.

The cross-stitch legend on the old sampler, if its letters are read in regular sequence, runs thus:—

A little woman, though a very little thing,
Is sweeter far than sugar, and flowers that bloom in spring.

Back to Puzzle

No. XII.—STRIKE A BALANCE

This diagram shows how, while the odd and even numbers of the nine digits add up to 25 and 20 respectively, they can be arranged in two groups so that the odd and the even add up to exactly the same sum.

1	2
3
5	4	79
7	6	79		84	²⁄₆
9	8	5	¹⁄₃	84	²⁄₆
25	20	84	¹⁄₃	84	¹⁄₃

Back to Puzzle

[III-114]

No. XIII.—PUZZLE LINES

The puzzle lines—

HKISTA!
MRS LR’S SR
MR LR KRS.
“BLR MR LR!”
MRS LR HRS—

when read according to the usual pronunciation of Mr and Mrs, and taking the title from the Greek, become, by affinity of sound—

He kissed her!
Mrs Lister’s sister
Mr Lister kisses.
“Blister Mr Lister!”
Mrs Lister hisses.

Back to Puzzle

No. XIV.—IN MEMORIAM

The puzzle epitaph—


WEON	.	CEW		.	ERET	.	WO
WET	.	WOM		.	ADEO	.	NE
NON	.	EFIN		.	DUST	.	WO
NO .	WLI	.	F	EB	.EGO	.	NE
WILLIAM and MARGARET TAYLOR
Anno Domini 1665.

reads thus—

We once were two,
We two made one.
None find us two
Now life be gone.

Back to Puzzle

[III-115]

No. XVI.—A QUAINT EPITAPH


	IT - OBIT - MORTI - MERA PUBLI - CANO - FACTO - NAM AT - RES - T - M - ANNO - XXX ALETHA - TE - VERITAS TE - DE - QUA - LV - VASTO MI - NE - A - JOVI - ALTO PERAGO - O - DO - NE - AT STO - UT - IN - A - POTOR - AC AN - IV - VAS - NE - VER - A
	R - I - P

reads into English thus:—

“I Tobit Mortimer, a publican of Acton, am at rest. Man, no treble X ale that ever I tasted equal was to mine. A jovial toper, a good one at stout in a pot or a can, I was never a rip!”

Back to Puzzle

No. XIX.—SHAKESPEARE RECAST

If you start with the first T in this combination, and then take every third letter—

HOUSE.CANOE.AFTER.
HOUR.PRINT.CAVE.CHILD
SASH.SLEVE.ACORN.
AMPLE.SAD.TATTA.HENA
MAT.ACHE.CAKE.TACHES.
HELIAC.SACQUE.USUAL.
ARBOR.SEE.MULCH.JACUR.
USE.STOP.

[III-116]

you will form the popular quotation, “Thrice is he armed that hath his quarrel just.”

Back to Puzzle

No. XX.—A DOUBLE ACROSTIC

The excellent double Acrostic—

An old Italian bird we know
Whose heart was ever touched by snow.

1. None can press me without pain,
Pressure is against the grain.
2. I am a king without my head.
3. Here is another king instead.

is solved thus:—

CORNIX
1.		C	or	N
2.	(R)	O	—	I
3.		R	e	X

We may tell those of our readers who have not studied the dead languages that cornix is the Latin for a crow, and that the word can be broken up into cor, heart, and nix, snow, while rex is, of course, a king in Latin, as roi is in French. The double meaning of corn is brought out by “against the grain.”

Back to Puzzle

No. XXI.—HIDDEN PROVERBS

The five hidden proverbs are:—

“A rolling stone gathers no moss.”

“Too many cooks spoil the broth.”

“A live dog is more to be feared than a dead lion.”

“You cannot eat your cake and have it.”

“Peace hath her victories no less renowned than war.”

Start from the central A, and work round and round.

Back to Puzzle

[III-117]

No. XXVII.—WAS IT VOLAPÜK?

Read backwards it becomes “Old birds are not caught with chaff.”

Back to Puzzle

No. XXVIII.—ANOTHER EPITAPH

(On an Old Pie Woman)

BENE AT hint HEDU S.T.T.H. emo Uldy O
L.D.C. RUSTO F.N.E. L.L.B.
AC. hel orl AT Ely
W ASS hove N.W. how ASS Kill’d
Int heart SOF pi escu Star
D. sand Tart Sand K N ewe,
Ver yus E oft he ove N.W. Hens he
’Dliv’ Dlon geno
UG H.S. hem Ade he R la STP uffap
UF FBY HE RHU
S. B an D. M.
Uchp R.A. is ’D no Wheres He dot
H L. i.e. TOM a Kead I.R.T.P. Iein hop est
Hat he R.C. Rust W I
L.L.B. ERA IS ’D——!

This puzzle epitaph, written aright, runs thus:—

Beneath in the dust the mouldy old crust
Of Nell Bachelor lately was shoven,
Who was skilled in the arts of pies, custards, and tarts,
And knew every use of the oven.

[III-118]

When she’d liv’d long enough she made her last puff,
A puff by her husband much prais’d;
Now here she doth lie to make a dirt pie,
In hopes that her crust may be rais’d.

Back to Puzzle

No. XXXI.—BY LEAPS AND BOUNDS

tle	to	a	cat-	life	and	live	In
By	tle	ow-	bro wse	of	non	tle	fall
ter	tur-	gain	like	land	one’s	quiet	And
of	ar m	Bet-	me ad-	and	Than	a-	bat-
bask	Be t-	lau-	or	tle	ness	done	wan-
rel	let	Than	die	With	der	of	smo ke
ter	in	brain	myr-	on	and	har-	un-
Ch ap-	or	to	sun	with	work	In	heat

The “Knight’s Tour” verses run as follows:—

Better to die with harness on
In smoke and heat of battle,
Than wander and browse, and fall anon
In quiet of meadow-land cattle.
Better to gain, by arm or brain,
Chaplet of laurel or myrtle,
Than bask in sun, with work undone,
And live one’s life like a turtle,

beginning with “Bet,” and ending in the top left-hand corner.

Back to Puzzle

[III-119]

No. XXXII.—A BROKEN SQUARE

The Broken Word Square is made perfect thus—

S	O	B	E	R
O	L	I	V	E
B	I	S	O	N
E	V	O	K	E
R	E	N	E	W

Back to Puzzle

No. XXXIII.—A KNIGHT’S TOUR PROVERB


				E
		E				T
			L	H
	E		R		S
		E	A	S
D		E		O		S
			S	P		M

To solve the “Knight’s Tour” proverb start with M, and by a succession of moves, as of a knight on the chess-board, you can spell out the proverb “More haste less speed.”

Back to Puzzle

[III-120]

No. XXXIV.—GUARINI’S PROBLEM

The solution of Guarini’s Problem, to transpose the positions of the white and black knights on the subjoined diagram on which they appear, is made clear by following the moves on the lettered diagram:—

First move the pieces from a to A, from b to B, from c to C, and from d to D. Then move them from A to d, from B to a, from C to b, and from D to c. The effect so far is as if the original square had been rotated through one right angle. Repeat the same sequence of moves, and the required change of positions is completed.

Back to Puzzle

No. XXXV.—AN ANAGRAM SQUARE

This is the solution of the Word Square.

A	M	E	N	D	S
M	I	N	I	O	N
E	N	A	B	L	E
N	I	B	B	L	E
D	O	L	L	A	R
S	N	E	E	R	S

Back to Puzzle

[III-121]

No. XXXVII.—A KNIGHT’S TOUR

The letters on the board below, read aright in the order of a Knight’s moves at chess, starting from the most central E form the following popular proverb:—

R	L	T	E	Y	L	R	O
Y	H	L	T	O	B	T	A
T	A	A	A		H	T	I
E	L		E	I	N	E	O
D	H	W		Y	E	S	Y
R	T	E	S	D		B	W
Y	N	E	S	N	D	A	E
H	A	A	A	W	I	D	E

“Early to bed, and early to rise,
Is the way to be healthy, and wealthy, and wise.”

Back to Puzzle

No. XXXVIII.—A WORD SQUARE

Dr Puzzlewitz completed his Word Square thus:—

E	R	A	S	E
R	A	V	E	N
A	V	E	R	T
S	E	R	V	E
E	N	T	E	R

Back to Puzzle

[III-122]

No. XXXIX.—THE SQUAREST WORD

This is completed thus:—

D	E	L	F
E	V	I	L
L	I	V	E
F	L	E	D

It will be seen that there are four distinct readings of each word.

Back to Puzzle

No. XL.—A PUZZLE DIAMOND

The Diamond is completed thus:—

			D
		T	I	P
	T	I	A	R	A
D	I	A	M	O	N	D
	P	R	O	U	D
		A	N	D
			D

Back to Puzzle

No. XLI.—A DEFECTIVE DIAMOND

The Defective Diamond is completed thus:—

				S
			G	E	M
		P	E	R	I	L
	G	E	N	E	R	A	L
S	E	R	E	N	A	D	E	R
	M	I	R	A	C	L	E
		L	A	D	L	E
			L	E	E
				R

Back to Puzzle

[III-123]

No. XLIII.—LETTER PUZZLE

The word is Level, filled in thus:—

L	E	V	E	L
E	E		E	E
V		V		V
E	E		E	E
L	E	V	E	L

Back to Puzzle

No. XLVII.—THE CIRCLE SQUARED

The Circle can be squared thus:—

C	I	R	C	L	E
I	N	U	R	E	S
R	U	L	E	S	T
C	R	E	A	S	E
L	E	S	S	E	E
E	S	T	E	E	M

Back to Puzzle

No. XLVIII.—A BROKEN SQUARE

This is the completed Square:—

B	O	A	S	T	E	R
O	B	S	C	E	N	E
A	S	S	E	R	T	S
S	C	E	P	T	R	E
T	E	R	T	I	A	N
E	N	T	R	A	N	T
R	E	S	E	N	T	S

Back to Puzzle

[III-124]

No. XLIX.—A CARD PROBLEM

Here is the arrangement of the aces, kings, queens, and knaves of a pack of cards in a kind of Magic Square:—

CLUBS ACE	SPADES KING	HEARTS QUEEN	DIAMONDS KNAVE
HEARTS KNAVE	DIAMONDS QUEEN	CLUBS KING	SPADES ACE
DIAMONDS KING	HEARTS ACE	SPADES KNAVE	CLUBS QUEEN
SPADES QUEEN	CLUBS KNAVE	DIAMONDS ACE	HEARTS KING

In each row, column, and diagonal, one, and one only, of the four suits and of the four denominations is represented.

Back to Puzzle

No. L.—TURF-CUTTING

The eight thin strips of turf, cut from my lawn to form the four sides of two square rose-borders, can be placed on a level surface of soil thus without being broken or bent:—

This forms a framework for the three flower-beds of similar shape and size.

Back to Puzzle

[III-125]

No. LI.—A READY RECKONER

The gardener decided that the water-butt was more than half-full thus:—

He tilted it steadily, and some of the water ran over its edge before the bottom corner A came into sight; but as soon as the water level stood at A B the cask was exactly half full.

Back to Puzzle

No. LII.—A TRANSFORMATION

The flat-headed 3 can be turned into a 5 by one continuous line, without scratching out any portion of the 3, by treating the flat top of the 3 as part of a square drawn round the 5, thus:—

Back to Puzzle

[III-126]

No. LIII.—A CLEAR COURSE

Here is a list of ninety-two positions, in which eight pieces can be placed upon the chess or draughtboard so that each has a clear course in every direction.

1	1586	3724	24	3681	5724	47	5146	8273	70	6318	5247
2	1683	7425	25	3682	4175	48	5184	2736	71	6357	1428
3	1746	8253	26	3728	5146	49	5186	3724	72	6358	1427
4	1758	2463	27	3728	6415	50	5246	8317	73	6372	4815
5	2468	3175	28	3847	1625	51	5247	3861	74	6372	8514
6	2571	3864	29	4158	2736	52	5261	7483	75	6374	1825
7	2574	1863	30	4158	6372	53	5281	4736	76	6415	8273
8	2617	4835	31	4258	6137	54	5316	8247	77	6428	5713
9	2683	1475	32	4273	6815	55	5317	2864	78	6471	3528
10	2736	8514	33	4273	6851	56	5384	7162	79	6471	8253
11	2758	1463	34	4275	1863	57	5713	8642	80	6824	1753
12	2861	3574	35	4285	7136	58	5714	2863	81	7138	6425
13	3175	8246	36	4286	1357	59	5724	8136	82	7241	8536
14	3528	1746	37	4615	2837	60	5726	3148	83	7263	1485
15	3528	6471	38	4682	7135	61	5726	3184	84	7316	8524
16	3571	4286	39	4683	1752	62	5741	3862	85	7382	5164
17	3584	1726	40	4718	5263	63	5841	3627	86	7425	8136
18	3625	8174	41	4738	2516	64	5841	7263	87	7428	6135
19	3627	1485	42	4752	6138	65	6152	8374	88	7531	6824
20	3627	5184	43	4753	1682	66	6271	3584	89	8241	7536
21	3641	8572	44	4813	6275	67	6271	4853	90	8253	1746
22	3642	8571	45	4815	7263	68	6317	5824	91	8316	2574
23	3681	4752	46	4853	1726	69	6318	4275	92	8413	6275

The numbers indicate the position on the eight successive columns of the cells on which the men are to be placed. Of course, many similar arrangements arise from merely turning the board.

Back to Puzzle

[III-127]

No. LIV.—QUARRELSOME NEIGHBOURS

This diagram shows, by the dotted lines, how the three unfriendly neighbours made the covered pathways to their gates, so that they might never meet or cross each other’s paths.

Back to Puzzle

No. LVI.—THE CROSS KEYS

The Cross Keys puzzle when put together takes the form shown below.

The method is as follows:—Hold a upright between forefinger and thumb of left hand. With the right hand push b through the slot until the further edge of the middle slot is nearly even with the outer edge of a. Then lower c, held with the short arm of the cross nearest to you, over the top of a, so that the central portion passes through the cross cut in b. Finally[III-128] push b towards the centre, until the transverse cut is hidden, and the puzzle is completed.

Back to Puzzle

No. LVII.—THE NABOB’S DIAMONDS

When the children of the Indian Nabob divided his diamonds, the first taking one stone and a seventh of the remainder, the second two stones and a seventh of what was left, the third three under similar conditions, and so on till all were taken, there were 36 diamonds and 6 children.

The division is prettily illustrated thus:—

This shows how the first three took their shares, indicated by black dots, the remainder being carried down each time, and by similar process three more claimants would exhaust all the diamonds.

Back to Puzzle

[III-129]

No. LVIII.—A CARD CHAIN

To solve the Card Chain puzzle take a card about 5 in. by 3 in., as shown below, draw a light pencil line from A to B and from C to D, lay the card in water till you can split its edges down to the pencil lines, and put it aside to dry.

With a sharp knife cut quite through the straight lines, but only half through the dotted lines on the split edges. The corresponding figures show the bar of each link, marking its two parts, which are connected by the upper and under halves of the split portion. A little patient ingenuity will now release link after link, and thus complete the chain.

Back to Puzzle

[III-130]

No. LIX.—STRAY DOTS

Back to Puzzle

No. LX.—THE OPEN DOOR

The prisoner who is placed in the cell marked A, and is promised his liberty if he can reach[III-131] the door at X by passing through all the cells, entering each once only, gains his freedom by passing from A to the cell below, and thence returning to A, and leaving it again by the other door; his further course then is quite simple.

Back to Puzzle

No. LXII.—LEAP FROG

Move 9 to 13, 3 to 9, 7 to 3, 22 to 7, 18 to 22, 24 to 18, 9 to 24, 13 to 9, 7 to 13, 3 to 7, 18 to 3, 22 to 18.

Back to Puzzle

No. LXIII.—MUSIC HATH CHARMS

is explained by the couplet—

“From Handel I learn
As my handle I turn.”

Back to Puzzle

[III-132]

No. LXVII.—A SWARM OF WORDS

This is the key

		M
		A
M	A	D	A	M
		A
		M

If these letters form each of the five crosses the conditions are all fulfilled.

In each cross the words Madam, Adam, Ada can be traced in sixteen different directions, and the words Dam, am and a in four directions, so that there are no less than three hundred and twenty readings of these words in the whole mystic cross, and sixty-four in each separate cross, though only three different letters are used.

Back to Puzzle

No. LXVIII.—AFTER SOME SAD REVERSE

Back to Puzzle

No. LXX.—A PICTURE PUZZLE

“A misunderstanding between friends.”

Back to Puzzle

No. LXXIV.—A NERVOUS SHOCK

Back to Puzzle

No. LXXVIII.—A TRANSPARENCY

Back to Puzzle

[III-133]

No. LXXXII.—A RE-BUS

It was Incubus that the driver of a London Road car hurled as a scornful charge, at his rival on a motor car.

Back to Puzzle

No. LXXXV.—CHEQUERS AND STRIPES

Put a finger on one of the black backs in the top row, and move that stone round to the bottom of its column, then push upward, so that each stone rises into the row above it. Repeat this with the other back, and the stripes are formed.

Back to Puzzle

[III-134]

No. LXXXVIII.—A PICTURE PUZZLE

The eight animals hidden in this wood are-- Giraffe, Lion, Camel, Elephant, Hog, Horse, Bear, Hound.

Back to Puzzle

No. XC.—A REBUS

The solution is Wellington.

Back to Puzzle

[III-135]

No. XCV.—THE PUZZLED CARPENTER

The carpenter, anxious to stop a leak, was able to cut a board a foot square from a board two feet square, which was pierced at regular intervals by sixteen holes, by the following ingenious method:—

Back to Puzzle

No. XCVI.—NOT EASY WHEN YOU KNOW

The solution of the puzzling match rearrangement is as follows:—We repeat the original five square diagram, from which four squares were to be formed by rearranging three matches, and its solution below.

Back to Puzzle

[III-136]

No. XCVII.—SIMPLICITY

When we have constructed this figure with five matches, we can remove three of the matches, and then replace two of them so as to form a similar figure, by moving any three of them a short distance, and then replacing the two that are left behind, in their original positions! This “catch” finds many victims.

Back to Puzzle

No. XCIX.—FROM THE MATCHBOX

The diagram below shows how eight matches can be removed from the nine-square arrangement so as to leave two squares on the table.

Back to Puzzle

[III-137]

MISSING WORDS SOLUTIONS

1

What tempting sprite beguiled the boy to sample
Fruit that hung ripest on the parson’s trees?
Stripe upon stripe shall make him an example
When the stern priest has brought him to his knees.

Back to Puzzle

2

Man of the dark room, traces none I find
Upon these cartes of likeness to my features.
Carest thou naught, O man of evil mind,
Who racest thus to libel fellow creatures?

Evil thus done reacts upon the doer,
The carets in thy conduct, sir, are many;
Recast thy life, and let thy crimes be fewer,
Or all thy crates of good won’t fetch a penny!

Back to Puzzle

3

The missing words all spelt with the same
seven letters, are tho’ near, a hornet, or neath, nor
hate, or then a, near hot, than o’er, ten hoar, the
roan, and eat horn.

Back to Puzzle

4

’Neath bluest Indian seas fierce battles spread
’Twixt subtle hermit-crabs and other shellfish!
With horrid bustle when their foes are dead
These crabs declare their shells sublet, so selfish.

Back to Puzzle

5

Though seated secure and sedate in his cage,
Our Polly, when teased, will fly into a rage.

Back to Puzzle

[III-138]

6

All courtly honours are but light
As grains that from a grater fly;
And he who wears the Garter bright
May haply in a garret die.

Back to Puzzle

7

I’d rather from a manger eat,
I give my sacred word,
Than dine in slums where ragmen meet,
And German pedlars herd.

Back to Puzzle

8

A much married grandee of Cadiz
Once angered some riotous ladies.
To derange him they chucked
A grenade, but he ducked,
Which enraged these rude ladies of Cadiz.

Back to Puzzle

9

A lass and her lover were warned by the sky
Not to wander too far where no shelter was nigh.
She lingered behind, and drew an old church,
St. Andrew by name, and was left in the lurch.

She tried a short cut through the park on the grass,
But sternly the warden forbade her to pass.
Then helplessly stood the disconsolate maid,
When the lad she was soon to wed ran to her aid.

Back to Puzzle

10

When weather smiles, and sunbeams play
On flowers that wreathe and deck the green,
Whate’er can match the scene so gay
Whereat they crown the May-day queen?

[III-139]

Back to Puzzle

11

’Tis said of William, while his forces rested
On Albion’s shores, when Harold had been bested,
He made the shoers of his horses fuse
Saxon spear-heads, to fashion into shoes.

Back to Puzzle

12

Happiness, brighter than rubies, is dead;
Life’s battle, sterner and busier now,
Heals the sore bruise that love left as it fled,
Buries remembrance of long-broken vow!

Back to Puzzle

13

Press critics fall on me like sharks:
“A shameless patcher of odds and ends,
No chapter original,” and more remarks
In adverse mood. But stay, my friends,
He carpeth best who hath his record clean;
My faults are published, yours are yet unseen!

Back to Puzzle

14

Plates are his staple, fashion-forms of grace
In pastel deftly hinted.
Pleats soft as petals, crowned by Beauty’s face,
In palest hues are tinted.

Back to Puzzle

15

When Kate no heart nor heat displayed
He ran to hide a tear;
“All love is dead on earth,” he said.
“Another I’ll not hear!”

Back to Puzzle

16

Some grinding at the tholes must toil,
Down-trodden helots of to-day;
While other children of the soil
In vast hotels their wealth display.

Back to Puzzle

[III-140]

17

Betrayed by faithless friends, in sadder mood
Man dreads his fellows as the adder’s brood.

Back to Puzzle

18

With divers inks his skin is scarred,
He hangs a bangle in his nose;
Such marks secure his kin’s regard,
Exalt his fame, and sink his foes.

Back to Puzzle

19

Steward, who, as we west’ard roll,
Drawest for me the foaming bowl,
And wardest off unfriendly spray
With oilskin-cape, thou shalt not say
“In vain I’ve strawed my favours here.”
I’ll think of thee when port is near!

Back to Puzzle

20

With high ideals for hearts and hands,
These ladies sailed for distant lands.

Back to Puzzle

21

The premiss of his speech did not
Impress his audience a jot.
They greeted all he said thereafter
With simpers, smiles, and open laughter.

Back to Puzzle

22

To convent shrine at break of day
With palms together nuns repair;
Mid gleaming lamps they kneel and pray,
And chanted psalm allays each care.

Back to Puzzle

23

Here once, as a hag is bedizened with paint,
A devil lived, veil’d in the garb of a saint.

[III-141]

Back to Puzzle

24

The missing words of the lines “In praise of Sussex,” are apers, rapes, spear, spare, pears, reaps, parse, pares, all spelt with the same letters.

Back to Puzzle

25

The missing words are there, ether, and three.

Back to Puzzle

26

The missing words are trades, daters, treads, darest, and read’st.

Back to Puzzle

27

The Tsar with arts importunate
To rule his tars may try;
His star is so unfortunate
That “rats” they may reply!

Back to Puzzle

28

The missing words are mace, acme, and came.

Back to Puzzle

29

The missing words are esprit, sprite, priest, stripe, and ripest.

Back to Puzzle

30

Of all destructive country pests
The farmer loves voles least;
He cannot yet the puzzle solve
How to suppress the beast!

Back to Puzzle

31

The “Fresh Air Fund” missing words are given below in italics:—

OH THE LUSTRE OF THE RESULT

The slimes of darkest London are radiant with smiles,
You can read it in their dear little faces:
So wherever you reside let it be your heart’s desire
To ease the cares and sorrows of all races!

[III-142]

Back to Puzzle

32

She rouges in vain, “Men are rogues, and as shy As grouse in October,” she says with a sigh.

Back to Puzzle

33

When good men lapse the Serpent grins,
When one repents he swears;
And strives to set his former sins
Against his present prayers.

Back to Puzzle

34

His hands and face were swart, and sad
Upon the straw a gipsy lad
Lay: as the breeze his temples fanned
He counted warts on either hand.

Back to Puzzle

35

In yon grey manse an old divine
Taught me my “mensa” to decline,
And verbs with names of mood and tense;
But while I plodded on apace
I had to keep the means of grace,
And close his prayers with loud amens.

Back to Puzzle

36

No reckless drawer of the sword,
He warred his fatherland to save.
Fighting for freedom, not reward,
Now warder of the eastern seas.

Back to Puzzle

37

A fair design, though singed and frayed,
The critic deigns to own,
And it might interest the trade
If signed by some one known.

Back to Puzzle

[III-143]

38

In his latter days, as when he was young,
The tatler indulges in rattle of tongue.

Back to Puzzle

39

The missing words indicated in the lines which begin

A cylindrical lock
Where no key can be found.

are a ringlet, triangle, relating, altering, and integral, which are all spelt with the same eight letters.

Back to Puzzle

40

The lines with missing words, which are increased each time by one letter, run thus:—

A lover of an unkind fair
Were less than man did he not moan,
“Mine is no nomad life, I swear,
It dwells in this domain alone.
Grant me thy love, like diamond chaste
On diadem, lest thou live unwooed,
Doomed in a lonely life to waste
The treasure of sweet maidenhood.”

Back to Puzzle

41

The missing words are bared, beard, debar, bread.

Back to Puzzle

42
THE PAUPER’S PLAINT

Pale penury that rivest social bands,
And any link that rivets worth to fame,
Take ye the blame for my inactive hands,
I strive in vain to build upon the sands,
Without a stiver, who can make a name?

[III-144]

Back to Puzzle

43

Mr Backslide, afflicted with weakness of mind,
Cantered over to Lushington’s inn, where he dined.
He recanted the pledge he had taken as handy,
And emptied forthwith a decanter of brandy.

Back to Puzzle

44

The missing words are indicated below by italics:—

A sutler sat in his ulster grey,
Watching the moonbeams lustre play
On a keg that in the bushes lay;
And these were the words of his song:—
“Thou rulest the weak, thou lurest the strong,
To thee the result of bad deeds doth belong.”
And the leaves with a rustle took up the sad song.

It would be difficult to find a better specimen than this of seven words spelt with the same letters.

Back to Puzzle

45

In these lines each of the words in italics is longer by one letter than the one before, the same letters being carried on in varied order:—

Nature I love in every land,
On burning plain, by wooded rill;
Where Ind is girt by coral strand,
Or Edin rears her castled hill.
Then deign from me the tale to hear,
How, true to one design, the bee
Once singled out keeps year by year
The leadings by her instinct given,
Which teach her, wheresoe’er she roam,
In every clime beneath the heaven,
To build the same six-angled home.

Back to Puzzle

[III-145]

46

The missing words are smite, times, emits, items, and mites.

Back to Puzzle

47

The missing words of the Farmyard puzzle are printed in italics:—

All his flock from danger rough,
To the garden ran apace,
Where their gander, old and tough,
Ranged, the guardian of his race.

Back to Puzzle

48

Come, landlord, fill the flowing pots,
Until their tops run over;
For in this spot to-night I’ll stop,
To-morrow post to Dover!

Back to Puzzle

49

The four missing words are silent, listen, enlist, and tinsel, which are all spelt with the same letters.

Back to Puzzle

50

Some men their teams escorted on their way,
When “Mates look here!” I heard a driver say:
“It tames our pluck to toil like steam all day,
When, wanting meats, we starve on wretched pay.”

Back to Puzzle

51
WISDOM WHILE YOU WAIT

As a general gleaner of facts you’ll find
Our Encyclopædia enlarge the mind.

Back to Puzzle

52

The missing words are nectar, Cretan, canter, trance, recant.

Back to Puzzle

[III-146]

53

I Satan but for rebel act
Without a stain should be;
But this is at an end, in fact
None find a saint in me.

Back to Puzzle

54

“Oh for a break in this vast solitude,
This endless rise and fall of brake and moor!”
Soliloquised a baker in sad mood,
As through the lonely hills the staff of life he bore.

Back to Puzzle

55
THE SEA SERPENT

’Twas in mid-ocean that we saw him play,
Like a demoniac in his sports, and they
Amused us, as a good comedian may.

Back to Puzzle

56

Soup is on table for a notable divine,
Who with no table is not able to sit down and dine.

Back to Puzzle

57

Sweet as the rose and cruel as its thorn,
Eros thy power is great, thy pity scorn.
Swift as the roes that through the forest fly,
Deep as the ores that deepest hidden lie,
Is thine own sore to hapless mortals given,
Semblance of darkest hell or brightest heaven.

Back to Puzzle

58

The missing words, dedicated to the Fresh Air Fund, read thus:—

[III-147]

GOOD TIMES FOR CITY MITES

My pipe emits for me its charms, that yield
Pictures and items of a children’s day.
Lest conscience smite I sit me down to say
My mites shall send some City mites afield.

Back to Puzzle

59

He said “you Cretan,” when one lied,
He said “don’t canter,” when one hied,
His glass held nectar at his side,
He can recant what he denied.

Back to Puzzle

60

Mr Snip, the agnostic, was coasting a hill,
With a bag of new coatings for stock;
When a runaway motor-car gave him a spill
Which scattered his doubts with the shock.

Back to Puzzle

61

Pales her fair cheek, and back o’er all
The lapse of years leaps memory.
Those wedding peals to her recall
The pleas he urged so tenderly.

Back to Puzzle

62

Two burglars attempted to rifle a house,
But the filer was heard, though as still as a mouse.
When challenged at once he a flier became,
But caught as a lifer he finished his game.

Back to Puzzle

63

The licensed fool in olden days
Gave kings advice in jesting phrase;
He’s silenced now: the modern throne
Declines all follies but its own.

Back to Puzzle

[III-148]

64

Days of dearth, and times of evil,
Starving girls with thread do toil,
No man dareth feast or revel,
Hushed is hatred and turmoil.

Back to Puzzle

65

Who reineth in his pride and rage,
To neither vice a prey,
May hope to reach a green old age,
And find therein his stay.

Back to Puzzle

66

This is the full text of Moore’s witty reply, when Limerick courted him as her member, and the “boys for fun’s sake” asked him to what party he belonged:—

“I’m of no party as a man,
But as a poet am—a—tory!”

Back to Puzzle

67

Is England Israel? That this is so
A solemn serial aspires to show.
By most ignored, the theme is real to some,
Who gravely to the same conclusion come.
Like Ariels o’er obstacles they soar,
And if an earl is ’vert they rave the more.

Back to Puzzle

68

Off to the links is now their cry,
For golf is man’s idolatry:
Be not dilatory or slow,
Adroitly hit the ball will go.

Back to Puzzle

69

No maid e’er resided, North, South, East, or West,
More desired than she who derides Love’s request.

Back to Puzzle

[III-149]

70

Though in adversity I be,
It is, alas! sad verity
No vestry aid comes nigh to me.

Back to Puzzle

71

Mastering his pride the royal James
Came down upon the streaming Thames;
Like emigrants his court repair
To breath St Germain’s freer air.

Back to Puzzle

72

The drop letter lines are as follows:—

With lily leaves his oars are trifling,
Her eager hands their treasures rifling.
To the fair winds all cares I fling,
And echo faintly answers fling!

Back to Puzzle

73

The solution of the enigma with missing letters:—

“There was no good ... in the d...y, so the klim,” is—

There was no good air in the dairy, so the milk turned.

Back to Puzzle

74

But unmerciful disaster followed fast and followed faster.

Back to Puzzle

75

If you write stale tales, at least do not steal the slate.

Back to Puzzle

76

The six missing words are Siren, risen, Erin’s, reins, rinse, resin.

Back to Puzzle

[III-150]

77

A man of parts had caught a sprat,
And it was windy weather;
“Give me my strap,” he cried, “to fix
My fish and traps together.”

Back to Puzzle

78

The missing words are Cesar, acres, races, cares, scare.

Back to Puzzle

79

Buy my ripe melons, my lemons who’ll buy?
Don’t look so solemn, but take some and try!

Back to Puzzle

80

He who nips may snip at last,
How to spin we show;
Take a sixpence, hold it fast,
Press the pins and blow!

Back to Puzzle

PRINTED BY M‘LAREN AND CO., LTD., EDINBURGH.

Transcriber’s Notes

Inconsistent spelling, hyphenation, capitalisation, etc. and lay-out have been retained, except as mentioned below. The same applies to repetitions, factual errors, mistakes, unclarities and contradictions in the puzzles, riddles etc. and in the solutions provided.

Depending on the hard- and software and their settings used to read this text, not all elements may display as intended.

Page I-7, Monster Magic Square: row 2 column 2 should be 48, not 41; row 3 column 9 should be 92, not 72.

Page I-30, magic triangle, bottom row 0 should be 8 (as in the solution on page I-150).

Page I-89, "on opposite sides of the central line": this should be read "on opposite sides of the central lines" (both horizontal and vertical).

Page I-130, mens’ tears: as printed in the source document.

Page I-131, An Illusion of Type: the phenomenon described may not work with every font. Therefore the right-side-up and upside-down text lines have been inserted as an additional illustration.

Page I-136, For the Children, last sentence: the opposite is true: If this is an even quantity the coins or sweets in the right hand are odd, and in the left even; if it is odd the contrary is the case.

Page II-130, number 81: some words were misprinted or missing altogether; these have been added based on the context: ... the man [fe]ll sick ...; [Ho]w ought his estate ...; and ... to [the] widow, son and daughter.

Page II-148, Notable Chronogram: IAVDES should have read LAVDES, which would result in the year 1894 (when the organ was blessed).

Page II-176, Solution LXXX: The positions of the dots are indicated in the text only, not in the diagram.

Page II-204, Solution 65, 12 + ¹⁄₂ = ¹³⁄₂: the calculation only works if the 12 were replaced with ¹²⁄₂ (or 6), which would be in accordance with the description.

Page II-206, Solution 77: two and twenty pence should probably read two and twenty pence.

Page III-3 and III-111, No. III: The illustration in the question is not the same as the one in the answer.

Page III-25, Begins 2 U U U up: possibly an error for Begins 2 UU U up (cf. other repeated letters).

Page III-35, No. XXXV, five words: there are six words in the puzzle (and in the solution).

Page III-77, inspiréd strain: as printed in the source document.

Changes made

Some obvious minor typographical and punctuation errors and misprints have been corrected silently.

Some minor lay-out inconsistencies have been standardised without further remarks; where necessary, table and text-elements have been re-arranged and aligned in accordance with the description given.

The part numbers have been inserted on the blank pages preceding each part.

Throughout the book, items from one category (preceded by an Arabic number) are occasionally printed split over two pages, with one or more items from other categories (often preceded by a Roman numeral) between the several parts. For this text, these split items have been recombined on the page where they originally started, and references to their respective parts have been deleted.

The part numbers (I, II and III) have been added to the page numbers for easier reference.

Items in dotted boxes do not occur as such in the original book but have been transcribed schematically from the illustration.

The illustrations on Page II-63 (No. LXIII) and II-65 (No. LXV) have been flipped horizontally, the illustrations on page II-68 (No. LXVIII) and II-78 (No. LXXVIII) have been rotated, all in order to correctly display the letters and numbers.

Page I-141: "cigars" changed to "cigares" (French, 2x).

Page II-99, 6¹ changed to 6¹⁄₂.

Pages II-113 and II-185, illustration: reference letter "F" added.

Page II-199: "there they sold" changed to "these they sold".

Page II-225, Solution 6: "f on d l over" changed to "a f on d l over".

Page III-7, No. VII: "BVT In trVth" changed to "bVt In trVth".

Page III-41, No. 67: "And if — —— is ’vert" changed to "And if an —— — ’vert".

Page III-46: "chêrit" changed to "chérit".

Page III-54, No. LIV: in the printed document, the doors are marked (left to right) B - A - C, and the gates B - A - C as well. The gates’ marks have been changed to C - A - B in order to agree with the solution provided on page III-127.

Page III-67, illustration: unprinted asterisk added to the right-hand arm of the cross.

Page III-78: "a jamais" replaced with "à jamais".

Page III-108: "stats" replaced with "stets".

Page III-123, Solution XLIII: V inserted in bottom line cf. puzzle.

Page III-124: "stripes" changed to "strips" cf. puzzle.

Page III-128: "86 diamonds and 6 children" changed to "36 diamonds and 6 children".

Page III-132: Solutions LXVIII and LXXIV have been added to show the upside-down illustrations. Solution LXXVIII has been added to show the reversed illustration.

*** END OF THE PROJECT GUTENBERG EBOOK 63884 ***

22	47	16	41	10	35	4
5	23	48	17	42	11	29
30	6	24	49	18	36	12
13	31	7	25	43	19	37
38	14	32	1	26	44	20
21	39	8	33	2	27	45
46	15	40	9	34	3	28

				1
			2		6
		3	20	7	24	11
	4	16	8	25	12	4	16
5		9	21	13	5	17		21
	10	22	14	1	18	10	22
		15	2	19	6	23
			20		24
				25

23	464	459	457	109	111	108	110	132	133	130	131	373	371	357	356	372	382	370	335	30	22
25	41	436	435	433	432	196	195	241	242	200	225	284	287	246	245	288	261	51	58	47	460
27	45	13	474	469	467	82	81	72	90	91	83	401	400	396	398	399	397	20	12	440	458
461	55	15	34	450	449	447	446	156	157	180	181	326	327	306	307	44	37	33	470	430	24
456	56	17	42	3	484	479	477	66	65	68	67	422	421	416	415	10	2	443	468	429	29
137	428	471	41	5	127	126	125	361	362	363	364	365	366	118	117	116	480	444	14	57	348
153	431	466	31	7	347	148	338	339	145	143	342	142	344	345	139	138	478	454	19	54	332
154	439	98	453	481	325	161	169	168	318	319	320	321	163	162	324	160	4	32	387	46	331
384	266	407	445	476	292	293	191	190	299	298	297	186	185	184	302	193	9	40	78	219	101
383	268	406	442	424	270	280	272	273	211	210	209	208	278	279	205	215	61	43	79	217	102
379	265	392	172	60	248	227	250	251	230	232	231	233	256	257	258	237	425	313	93	220	106
378	267	391	173	59	226	249	228	229	252	254	253	255	234	235	236	259	426	312	94	218	107
351	282	405	176	74	204	214	206	207	277	276	275	274	212	213	271	281	411	309	80	203	134
350	263	390	177	73	182	192	301	300	189	187	188	296	295	294	183	303	412	308	95	222	135
334	199	77	330	423	171	315	323	322	164	165	166	167	317	316	170	314	62	155	408	286	151
333	216	96	311	413	149	346	147	146	340	341	144	343	141	140	337	336	72	174	389	269	152
100	221	76	310	414	369	359	360	124	123	122	121	120	119	367	368	358	71	175	409	264	385
99	223	75	291	483	1	6	8	419	420	417	418	63	64	69	70	475	482	194	410	262	386
104	202	97	452	35	36	38	39	329	328	305	304	159	158	179	178	441	448	451	388	283	381
105	238	473	11	16	18	403	404	393	395	394	402	84	85	89	87	86	88	465	472	247	380
136	438	49	50	52	53	289	290	244	243	285	260	201	198	239	240	197	224	434	427	437	349
463	21	26	28	376	374	377	375	353	352	355	354	112	114	128	129	113	103	115	150	455	462

4	5	6	43	39	38	40
49	15	16	33	30	31	1
48	37	22	27	26	13	2
47	36	29	25	21	14	3
8	18	24	23	28	32	42
9	19	34	17	20	35	41
10	45	44	7	11	12	46

5	80	59	73	61	3	63	12	13
1	20	55	30	57	28	71	26	81
4	14	31	50	29	60	35	68	78
76	58	46	38	45	40	36	24	6
7	65	33	43	41	39	49	17	75
74	64	48	42	37	44	31	18	8
67	10	47	32	53	22	51	72	15
66	56	27	52	25	54	11	62	16
69	2	23	9	21	79	19	70	77

18	63	4	61	6	59	8	41
49	32	51	14	53	12	39	10
2	47	36	45	22	27	24	57
33	16	35	46	21	28	55	26
31	50	29	20	43	38	9	40
64	17	30	19	44	37	42	7
15	34	13	52	11	54	25	56
48	1	62	3	60	5	58	23

A	B	C	D
476	469	477	484
E	F	G	H
483	478	470	475
I	J	K	L
471	474	482	479
M	N	O	P
480	481	473	472

2	13	24	10	16	2	13	24	10	16	2
9	20	1	12	23	9	20	1	12	23	9
11	22	8	19	5	11	22	8	19	5	11
18	4	15	21	7	18	4	15	21	7	18
25	6	17	3	14	25	6	17	3	14	25
2	13	24	10	16	2	13	24	10	16	2
9	20	1	12	23	9	20	1	12	23	9
11	22	8	19	5	11	22	8	19	5	11
18	4	15	21	7	18	4	15	21	7	18
25	6	17	3	14	25	6	17	3	14	25
2	13	24	10	16	2	13	24	10	16	2
9	20	1	12	23	9	20	1	12	23	9
11	22	8	19	5	11	22	8	19	5	11

1	2	3	4	5	6	7	8	9	10	11
3	4	5	6	7	8	9	10	11	1	2
5	6	7	8	9	10	11	1	2	3	4
7	8	9	10	11	1	2	3	4	5	6
9	10	11	1	2	3	4	5	6	7	8
11	1	2	3	4	5	6	7	8	9	10
2	3	4	5	6	7	8	9	10	11	1
4	5	6	7	8	9	10	11	1	2	3
6	7	8	9	10	11	1	2	3	4	5
8	9	10	11	1	2	3	4	5	6	7
10	11	1	2	3	4	5	6	7	8	9

0	11	22	33	44	55	66	77	88	99	110
33	44	55	66	77	88	99	110	0	11	22
66	77	88	99	110	0	11	22	33	44	55
99	110	0	11	22	33	44	55	66	77	88
11	22	33	44	55	66	77	88	99	110	0
44	55	66	77	88	99	110	0	11	22	33
77	88	99	110	0	11	22	33	44	55	66
110	0	11	22	33	44	55	66	77	88	99
22	33	44	55	66	77	88	99	110	0	11
55	66	77	88	99	110	0	11	22	33	44
88	99	110	0	11	22	33	44	55	66	77

22	47	16	41	10	35	4
5	23	48	17	42	11	29
30	6	24	49	18	36	12
13	31	7	25	43	19	37
38	14	32	1	26	44	20
21	39	8	33	2	27	45
46	15	40	9	34	3	28

				1
			2		6
		3	20	7	24	11
	4	16	8	25	12	4	16
5		9	21	13	5	17		21
	10	22	14	1	18	10	22
		15	2	19	6	23
			20		24
				25

23	464	459	457	109	111	108	110	132	133	130	131	373	371	357	356	372	382	370	335	30	22
25	41	436	435	433	432	196	195	241	242	200	225	284	287	246	245	288	261	51	58	47	460
27	45	13	474	469	467	82	81	72	90	91	83	401	400	396	398	399	397	20	12	440	458
461	55	15	34	450	449	447	446	156	157	180	181	326	327	306	307	44	37	33	470	430	24
456	56	17	42	3	484	479	477	66	65	68	67	422	421	416	415	10	2	443	468	429	29
137	428	471	41	5	127	126	125	361	362	363	364	365	366	118	117	116	480	444	14	57	348
153	431	466	31	7	347	148	338	339	145	143	342	142	344	345	139	138	478	454	19	54	332
154	439	98	453	481	325	161	169	168	318	319	320	321	163	162	324	160	4	32	387	46	331
384	266	407	445	476	292	293	191	190	299	298	297	186	185	184	302	193	9	40	78	219	101
383	268	406	442	424	270	280	272	273	211	210	209	208	278	279	205	215	61	43	79	217	102
379	265	392	172	60	248	227	250	251	230	232	231	233	256	257	258	237	425	313	93	220	106
378	267	391	173	59	226	249	228	229	252	254	253	255	234	235	236	259	426	312	94	218	107
351	282	405	176	74	204	214	206	207	277	276	275	274	212	213	271	281	411	309	80	203	134
350	263	390	177	73	182	192	301	300	189	187	188	296	295	294	183	303	412	308	95	222	135
334	199	77	330	423	171	315	323	322	164	165	166	167	317	316	170	314	62	155	408	286	151
333	216	96	311	413	149	346	147	146	340	341	144	343	141	140	337	336	72	174	389	269	152
100	221	76	310	414	369	359	360	124	123	122	121	120	119	367	368	358	71	175	409	264	385
99	223	75	291	483	1	6	8	419	420	417	418	63	64	69	70	475	482	194	410	262	386
104	202	97	452	35	36	38	39	329	328	305	304	159	158	179	178	441	448	451	388	283	381
105	238	473	11	16	18	403	404	393	395	394	402	84	85	89	87	86	88	465	472	247	380
136	438	49	50	52	53	289	290	244	243	285	260	201	198	239	240	197	224	434	427	437	349
463	21	26	28	376	374	377	375	353	352	355	354	112	114	128	129	113	103	115	150	455	462

4	5	6	43	39	38	40
49	15	16	33	30	31	1
48	37	22	27	26	13	2
47	36	29	25	21	14	3
8	18	24	23	28	32	42
9	19	34	17	20	35	41
10	45	44	7	11	12	46

5	80	59	73	61	3	63	12	13
1	20	55	30	57	28	71	26	81
4	14	31	50	29	60	35	68	78
76	58	46	38	45	40	36	24	6
7	65	33	43	41	39	49	17	75
74	64	48	42	37	44	31	18	8
67	10	47	32	53	22	51	72	15
66	56	27	52	25	54	11	62	16
69	2	23	9	21	79	19	70	77

18	63	4	61	6	59	8	41
49	32	51	14	53	12	39	10
2	47	36	45	22	27	24	57
33	16	35	46	21	28	55	26
31	50	29	20	43	38	9	40
64	17	30	19	44	37	42	7
15	34	13	52	11	54	25	56
48	1	62	3	60	5	58	23

A	B	C	D
476	469	477	484
E	F	G	H
483	478	470	475
I	J	K	L
471	474	482	479
M	N	O	P
480	481	473	472

2	13	24	10	16	2	13	24	10	16	2
9	20	1	12	23	9	20	1	12	23	9
11	22	8	19	5	11	22	8	19	5	11
18	4	15	21	7	18	4	15	21	7	18
25	6	17	3	14	25	6	17	3	14	25
2	13	24	10	16	2	13	24	10	16	2
9	20	1	12	23	9	20	1	12	23	9
11	22	8	19	5	11	22	8	19	5	11
18	4	15	21	7	18	4	15	21	7	18
25	6	17	3	14	25	6	17	3	14	25
2	13	24	10	16	2	13	24	10	16	2
9	20	1	12	23	9	20	1	12	23	9
11	22	8	19	5	11	22	8	19	5	11

1	2	3	4	5	6	7	8	9	10	11
3	4	5	6	7	8	9	10	11	1	2
5	6	7	8	9	10	11	1	2	3	4
7	8	9	10	11	1	2	3	4	5	6
9	10	11	1	2	3	4	5	6	7	8
11	1	2	3	4	5	6	7	8	9	10
2	3	4	5	6	7	8	9	10	11	1
4	5	6	7	8	9	10	11	1	2	3
6	7	8	9	10	11	1	2	3	4	5
8	9	10	11	1	2	3	4	5	6	7
10	11	1	2	3	4	5	6	7	8	9

0	11	22	33	44	55	66	77	88	99	110
33	44	55	66	77	88	99	110	0	11	22
66	77	88	99	110	0	11	22	33	44	55
99	110	0	11	22	33	44	55	66	77	88
11	22	33	44	55	66	77	88	99	110	0
44	55	66	77	88	99	110	0	11	22	33
77	88	99	110	0	11	22	33	44	55	66
110	0	11	22	33	44	55	66	77	88	99
22	33	44	55	66	77	88	99	110	0	11
55	66	77	88	99	110	0	11	22	33	44
88	99	110	0	11	22	33	44	55	66	77

THE TWENTIETH CENTURY STANDARD PUZZLE BOOK

PART I.

CONTENTS

MAGIC SQUARES

No. I.—FOUR HUNDRED YEARS OLD!

No. II.—A SIMPLE MAGIC SQUARE

No. III.—ANOTHER MAGIC SQUARE

ENIGMAS

1 A MYSTIC ENIGMA

No. IV.—A NEST OF CENTURIES

2

No. V.—THE MAKING OF A MAGIC SQUARE

No. VI.—ANOTHER WAY TO MAKE A MAGIC SQUARE

No. VII.—A MONSTER MAGIC SQUARE

No. VIII.—A NOVEL MAGIC SQUARE

3

No. IX.—TWIN MAGIC SQUARES

4

No. X.—A BORDERED MAGIC SQUARE

5 AN OLD ENIGMA By Hannah More

No. XI.—A LARGER BORDERED MAGIC SQUARE

No. XII.—A CENTURY OF CELLS

6 HALLAM’S UNSOLVED ENIGMA

No. XIII.—A SINGULAR MAGIC SQUARE

No. XIV.—SQUARING THE YEAR

7 RANK TREASON By an Irish Rebel, 1798

No. XV.—SQUARING ANOTHER YEAR

No. XVI.—MANIFOLD MAGIC SQUARES

8 AN ENIGMA FOR CHRISTMAS HOLIDAYS

No. XVII.—LARGER AUXILIARY MAGIC SQUARES

No. XVIII.—SQUARING BY ANNO DOMINI

9

No. XIX.—A MAGIC SQUARE OF SEVEN

10 WHAT MOVED HIM?

No. XX.—CURIOUS SQUARES

11 RINGING THE CHANGES

No. XXI.—A MOORISH MAGIC SQUARE

No. XXII.—A CHOICE MAGIC SQUARE

12 CANNING’S ENIGMA

XXIII.—THE TWIN PUZZLE SQUARES

13

No: XXIV.—MAGIC FRACTIONS

14 “DOUBLE, DOUBLE, TOIL AND TROUBLE!”

No. XXV.—MORE MAGIC FRACTIONS

15

No. XXVI.—A MAGIC OBLONG

16

17

No. XXVII.—A MAGIC CUBE

18

No. XXVIII.—A MAGIC CIRCLE

19

No. XXIX.—MAGIC CIRCLE OF CIRCLES

No. XXX.—THE UNIQUE TRIANGLE

20

21

No. XXXI.—MAGIC TRIANGLES

22

No. XXXII.—TWIN TRIANGLES

No. XXXIII.—A MAGIC HEXAGON

23

No. XXXIV.—MAGIC HEXAGON IN A CIRCLE

24 A PERSONAL ENIGMA

No. XXXV.—A MAGIC CROSS

25

26 By Lord Macaulay

No. XXXVI.—A CHARMING PUZZLE

27 A BROKEN TALE

No. XXXVII.—LEAP-FROG

28

29

No. XXXVIII.—SORTING THE COUNTERS

30

31

No. XXXIX.—A TRANSFORMATION

32

33

No. XL.—DOMINO BUILDING

No. XLI.—FAST AND LOOSE

34

THE TWENTIETH CENTURY
STANDARD PUZZLE
BOOK

1
A MYSTIC ENIGMA

5
AN OLD ENIGMA
By Hannah More

6
HALLAM’S UNSOLVED ENIGMA

7
RANK TREASON
By an Irish Rebel, 1798

8
AN ENIGMA FOR CHRISTMAS HOLIDAYS

10
WHAT MOVED HIM?

11
RINGING THE CHANGES

12
CANNING’S ENIGMA

14
“DOUBLE, DOUBLE, TOIL AND TROUBLE!”

24
A PERSONAL ENIGMA

26
By Lord Macaulay

27
A BROKEN TALE

44
“WHAT THE DICKENS IS HIS NAME?”
Merry Wives of Windsor.

45
A NEW “LIGHT BRIGADE”

48
A DOUBLE SHUFFLE

49
AN ENIGMA BY MUTATION

50
AN ENIGMA BY SWIFT

51
A MEDLEY

52
THE MISSING LINK

56
DR. WHEWELL’S ENIGMA

57
AN ENIGMA FOR MOTORISTS

67
A SINGULAR ENIGMA

68
A PARADOX

22	47	16	41	10	35	4
5	23	48	17	42	11	29
30	6	24	49	18	36	12
13	31	7	25	43	19	37
38	14	32	1	26	44	20
21	39	8	33	2	27	45
46	15	40	9	34	3	28

				1
			2		6
		3	20	7	24	11
	4	16	8	25	12	4	16
5		9	21	13	5	17		21
	10	22	14	1	18	10	22
		15	2	19	6	23
			20		24
				25

23	464	459	457	109	111	108	110	132	133	130	131	373	371	357	356	372	382	370	335	30	22
25	41	436	435	433	432	196	195	241	242	200	225	284	287	246	245	288	261	51	58	47	460
27	45	13	474	469	467	82	81	72	90	91	83	401	400	396	398	399	397	20	12	440	458
461	55	15	34	450	449	447	446	156	157	180	181	326	327	306	307	44	37	33	470	430	24
456	56	17	42	3	484	479	477	66	65	68	67	422	421	416	415	10	2	443	468	429	29
137	428	471	41	5	127	126	125	361	362	363	364	365	366	118	117	116	480	444	14	57	348
153	431	466	31	7	347	148	338	339	145	143	342	142	344	345	139	138	478	454	19	54	332
154	439	98	453	481	325	161	169	168	318	319	320	321	163	162	324	160	4	32	387	46	331
384	266	407	445	476	292	293	191	190	299	298	297	186	185	184	302	193	9	40	78	219	101
383	268	406	442	424	270	280	272	273	211	210	209	208	278	279	205	215	61	43	79	217	102
379	265	392	172	60	248	227	250	251	230	232	231	233	256	257	258	237	425	313	93	220	106
378	267	391	173	59	226	249	228	229	252	254	253	255	234	235	236	259	426	312	94	218	107
351	282	405	176	74	204	214	206	207	277	276	275	274	212	213	271	281	411	309	80	203	134
350	263	390	177	73	182	192	301	300	189	187	188	296	295	294	183	303	412	308	95	222	135
334	199	77	330	423	171	315	323	322	164	165	166	167	317	316	170	314	62	155	408	286	151
333	216	96	311	413	149	346	147	146	340	341	144	343	141	140	337	336	72	174	389	269	152
100	221	76	310	414	369	359	360	124	123	122	121	120	119	367	368	358	71	175	409	264	385
99	223	75	291	483	1	6	8	419	420	417	418	63	64	69	70	475	482	194	410	262	386
104	202	97	452	35	36	38	39	329	328	305	304	159	158	179	178	441	448	451	388	283	381
105	238	473	11	16	18	403	404	393	395	394	402	84	85	89	87	86	88	465	472	247	380
136	438	49	50	52	53	289	290	244	243	285	260	201	198	239	240	197	224	434	427	437	349
463	21	26	28	376	374	377	375	353	352	355	354	112	114	128	129	113	103	115	150	455	462

4	5	6	43	39	38	40
49	15	16	33	30	31	1
48	37	22	27	26	13	2
47	36	29	25	21	14	3
8	18	24	23	28	32	42
9	19	34	17	20	35	41
10	45	44	7	11	12	46

5	80	59	73	61	3	63	12	13
1	20	55	30	57	28	71	26	81
4	14	31	50	29	60	35	68	78
76	58	46	38	45	40	36	24	6
7	65	33	43	41	39	49	17	75
74	64	48	42	37	44	31	18	8
67	10	47	32	53	22	51	72	15
66	56	27	52	25	54	11	62	16
69	2	23	9	21	79	19	70	77

18	63	4	61	6	59	8	41
49	32	51	14	53	12	39	10
2	47	36	45	22	27	24	57
33	16	35	46	21	28	55	26
31	50	29	20	43	38	9	40
64	17	30	19	44	37	42	7
15	34	13	52	11	54	25	56
48	1	62	3	60	5	58	23

A	B	C	D
476	469	477	484
E	F	G	H
483	478	470	475
I	J	K	L
471	474	482	479
M	N	O	P
480	481	473	472

2	13	24	10	16	2	13	24	10	16	2
9	20	1	12	23	9	20	1	12	23	9
11	22	8	19	5	11	22	8	19	5	11
18	4	15	21	7	18	4	15	21	7	18
25	6	17	3	14	25	6	17	3	14	25
2	13	24	10	16	2	13	24	10	16	2
9	20	1	12	23	9	20	1	12	23	9
11	22	8	19	5	11	22	8	19	5	11
18	4	15	21	7	18	4	15	21	7	18
25	6	17	3	14	25	6	17	3	14	25
2	13	24	10	16	2	13	24	10	16	2
9	20	1	12	23	9	20	1	12	23	9
11	22	8	19	5	11	22	8	19	5	11

1	2	3	4	5	6	7	8	9	10	11
3	4	5	6	7	8	9	10	11	1	2
5	6	7	8	9	10	11	1	2	3	4
7	8	9	10	11	1	2	3	4	5	6
9	10	11	1	2	3	4	5	6	7	8
11	1	2	3	4	5	6	7	8	9	10
2	3	4	5	6	7	8	9	10	11	1
4	5	6	7	8	9	10	11	1	2	3
6	7	8	9	10	11	1	2	3	4	5
8	9	10	11	1	2	3	4	5	6	7
10	11	1	2	3	4	5	6	7	8	9

0	11	22	33	44	55	66	77	88	99	110
33	44	55	66	77	88	99	110	0	11	22
66	77	88	99	110	0	11	22	33	44	55
99	110	0	11	22	33	44	55	66	77	88
11	22	33	44	55	66	77	88	99	110	0
44	55	66	77	88	99	110	0	11	22	33
77	88	99	110	0	11	22	33	44	55	66
110	0	11	22	33	44	55	66	77	88	99
22	33	44	55	66	77	88	99	110	0	11
55	66	77	88	99	110	0	11	22	33	44
88	99	110	0	11	22	33	44	55	66	77