
Please see the Transcriber’s Notes at the end of this text.

BY THE SAME AUTHOR
UNIFORM WITH THIS VOLUME
THE TWENTIETH CENTURY
STANDARD PUZZLE BOOK
Crown 8vo. Cloth Extra. Gilt.
FRONTISPIECE

Can you discover by anagram what the ape is saying to the elephant, from this descriptive sentence?
A sly tree-ape, he tries a rum telephone.
Exactly the same letters must be used.
Pictured Puzzles
AND
Word Play
A Companion to
THE TWENTIETH CENTURY STANDARD
PUZZLE BOOK
EDITED BY
A. CYRIL PEARSON, M.A.
AUTHOR OF
“100 Chess Problems,” “Anagrams, Ancient and Modern,”
Etc.
PROFUSELY ILLUSTRATED

LONDON
GEORGE ROUTLEDGE & SONS, LTD.
NEW YORK: E. P. DUTTON & CO.
| Frontispiece Puzzle | |
| PAGE | |
| Pictured Puzzles and Word Play | 1 |
| Enigmas, Charades, Puzzles, &c., &c. | 130 |
| Odds and Ends | 188 |
| Solutions to Pictured Puzzles | 202 |
| Solutions to Word Play | 283 |
| Solutions to Odds and Ends | 375 |
[1]
Here is a nest of magic squares, seven of them within the four corners of one diagram:—
| 149 | 16 | 33 | 196 | 47 | 197 | 44 | 208 | 42 | 203 | 57 | 194 | 38 | 54 | 217 |
| 177 | 62 | 183 | 52 | 213 | 59 | 160 | 15 | 161 | 85 | 156 | 190 | 105 | 28 | 49 |
| 56 | 147 | 201 | 146 | 75 | 155 | 2 | 220 | 3 | 153 | 53 | 26 | 209 | 79 | 170 |
| 162 | 76 | 148 | 180 | 83 | 187 | 41 | 104 | 22 | 195 | 145 | 60 | 78 | 150 | 64 |
| 74 | 176 | 4 | 124 | 119 | 37 | 154 | 48 | 186 | 138 | 109 | 102 | 222 | 50 | 152 |
| 221 | 24 | 175 | 63 | 86 | 116 | 93 | 135 | 94 | 127 | 140 | 163 | 51 | 202 | 5 |
| 10 | 215 | 69 | 159 | 134 | 95 | 98 | 126 | 115 | 131 | 92 | 67 | 157 | 11 | 216 |
| 219 | 19 | 165 | 1 | 136 | 97 | 130 | 113 | 96 | 129 | 90 | 225 | 61 | 207 | 7 |
| 8 | 205 | 84 | 191 | 87 | 158 | 111 | 100 | 128 | 68 | 139 | 35 | 142 | 21 | 218 |
| 214 | 34 | 144 | 27 | 112 | 99 | 133 | 91 | 132 | 110 | 114 | 199 | 82 | 192 | 12 |
| 14 | 123 | 55 | 106 | 117 | 189 | 72 | 178 | 40 | 88 | 107 | 120 | 171 | 103 | 212 |
| 206 | 89 | 181 | 166 | 143 | 39 | 185 | 122 | 204 | 31 | 81 | 46 | 45 | 137 | 20 |
| 58 | 101 | 17 | 80 | 151 | 71 | 224 | 6 | 223 | 73 | 173 | 200 | 25 | 125 | 168 |
| 118 | 198 | 43 | 174 | 13 | 167 | 66 | 211 | 65 | 141 | 70 | 36 | 121 | 164 | 108 |
| 9 | 210 | 193 | 30 | 179 | 29 | 182 | 18 | 184 | 23 | 169 | 32 | 188 | 172 | 77 |
As each border is removed a fresh magic square remains, in which the numbers in the cells of each row, column, and diagonal add up to the same sum, while each of these sums is a multiple of the central 113.
[2]
| 1 | ||||||||||||||||||||||||
| 91 | 117 | |||||||||||||||||||||||
| 3 | 20 | 160 | ||||||||||||||||||||||
| 27 | 25 | 129 | 65 | |||||||||||||||||||||
| 156 | 154 | 42 | 38 | 165 | ||||||||||||||||||||
| 161 | 15 | 138 | 36 | 103 | 26 | |||||||||||||||||||
| 130 | 153 | 136 | 124 | 81 | 54 | 159 | ||||||||||||||||||
| 162 | 147 | 120 | 69 | 75 | 135 | 151 | 52 | |||||||||||||||||
| 39 | 22 | 55 | 112 | 111 | 110 | 33 | 64 | 78 | ||||||||||||||||
| 4 | 152 | 76 | 57 | 56 | 62 | 61 | 63 | 93 | 7 | |||||||||||||||
| 168 | 146 | 139 | 100 | 99 | 98 | 97 | 96 | 102 | 142 | 158 | ||||||||||||||
| 6 | 21 | 29 | 45 | 44 | 43 | 49 | 48 | 47 | 133 | 51 | 104 | |||||||||||||
| 157 | 80 | 30 | 88 | 87 | 86 | 85 | 84 | 83 | 82 | 140 | 90 | 13 | ||||||||||||
| 53 | 41 | 134 | 123 | 122 | 121 | 127 | 126 | 125 | 52 | 145 | 79 | |||||||||||||
| 10 | 132 | 89 | 74 | 73 | 72 | 71 | 70 | 34 | 16 | 167 | ||||||||||||||
| 105 | 67 | 35 | 109 | 108 | 114 | 113 | 50 | 155 | 143 | |||||||||||||||
| 5 | 116 | 137 | 60 | 59 | 58 | 115 | 17 | 14 | ||||||||||||||||
| 144 | 19 | 107 | 95 | 101 | 94 | 23 | 9 | |||||||||||||||||
| 11 | 106 | 68 | 46 | 31 | 148 | 40 | ||||||||||||||||||
| 118 | 77 | 37 | 41 | 18 | 8 | |||||||||||||||||||
| 92 | 38 | 128 | 24 | 131 | ||||||||||||||||||||
| 163 | 148 | 149 | 166 | |||||||||||||||||||||
| 12 | 130 | 2 | ||||||||||||||||||||||
| 66 | 164 | |||||||||||||||||||||||
| 169 | ||||||||||||||||||||||||
It is a perfect magic diamond as it stands, and equally perfect are the diamonds that remain when each border of cells is removed, as is indicated by the lines.
[3]
Here is a magic square of 81 cells.
| 53 | 8 | 71 | 28 | 73 | 10 | 51 | 6 | 69 |
| 62 | 44 | 26 | 19 | 37 | 55 | 60 | 42 | 24 |
| 17 | 80 | 35 | 61 | 1 | 46 | 15 | 78 | 33 |
| 66 | 21 | 30 | 14 | 59 | 50 | 34 | 79 | 16 |
| 3 | 39 | 75 | 77 | 41 | 5 | 25 | 43 | 61 |
| 48 | 57 | 12 | 32 | 23 | 68 | 70 | 7 | 52 |
| 31 | 76 | 13 | 72 | 27 | 36 | 11 | 56 | 47 |
| 22 | 40 | 58 | 9 | 45 | 81 | 74 | 38 | 2 |
| 67 | 4 | 49 | 54 | 63 | 18 | 29 | 20 | 65 |
If divided, as is shown, into 9 small squares, each of these is also a magic square, and yet another magic square is formed by the totals of these 9 squares arranged thus:—
| 396 | 333 | 378 |
| 351 | 369 | 387 |
| 360 | 405 | 342 |
[4]
This magic square, which has in its cells the first sixteen numbers, is so constructed that these add up to 34 in very many ways.
| 4 | 15 | 14 | 1 |
| 9 | 6 | 7 | 12 |
| 5 | 10 | 11 | 8 |
| 16 | 3 | 2 | 13 |
How many of these, in addition to the usual rows, columns, and diagonals, can you discover? They must, of course, be in some sort symmetrical.
Can you fill in the missing letters which are needed to turn the oft-repeated “u” below into rhyming verse:—
[5]
| 106 | ||||||||||||||||||||
| 13 | 109 | |||||||||||||||||||
| 113 | 16 | 14 | ||||||||||||||||||
| 12 | 110 | 107 | 15 | |||||||||||||||||
| 42 | 9 | 11 | 100 | 78 | ||||||||||||||||
| 74 | 81 | 112 | 10 | 56 | 71 | |||||||||||||||
| 67 | 53 | 87 | 111 | 83 | 43 | 34 | ||||||||||||||
| 27 | 49 | 50 | 35 | 59 | 63 | 84 | 6 | |||||||||||||
| 96 | 26 | 46 | 72 | 68 | 39 | 37 | 115 | 7 | ||||||||||||
| 30 | 95 | 97 | 76 | 75 | 33 | 85 | 3 | 116 | 114 | |||||||||||
| 91 | 31 | 28 | 94 | 40 | 61 | 82 | 120 | 2 | 5 | 117 | ||||||||||
| 92 | 90 | 25 | 64 | 89 | 47 | 41 | 119 | 121 | 8 | |||||||||||
| 29 | 93 | 58 | 62 | 54 | 69 | 86 | 4 | 118 | ||||||||||||
| 32 | 66 | 60 | 57 | 73 | 52 | 80 | 1 | |||||||||||||
| 44 | 79 | 65 | 19 | 45 | 48 | 36 | ||||||||||||||
| 51 | 38 | 104 | 18 | 55 | 70 | |||||||||||||||
| 88 | 22 | 103 | 105 | 77 | ||||||||||||||||
| 99 | 23 | 20 | 102 | |||||||||||||||||
| 100 | 98 | 17 | ||||||||||||||||||
| 21 | 101 | |||||||||||||||||||
| 24 | ||||||||||||||||||||
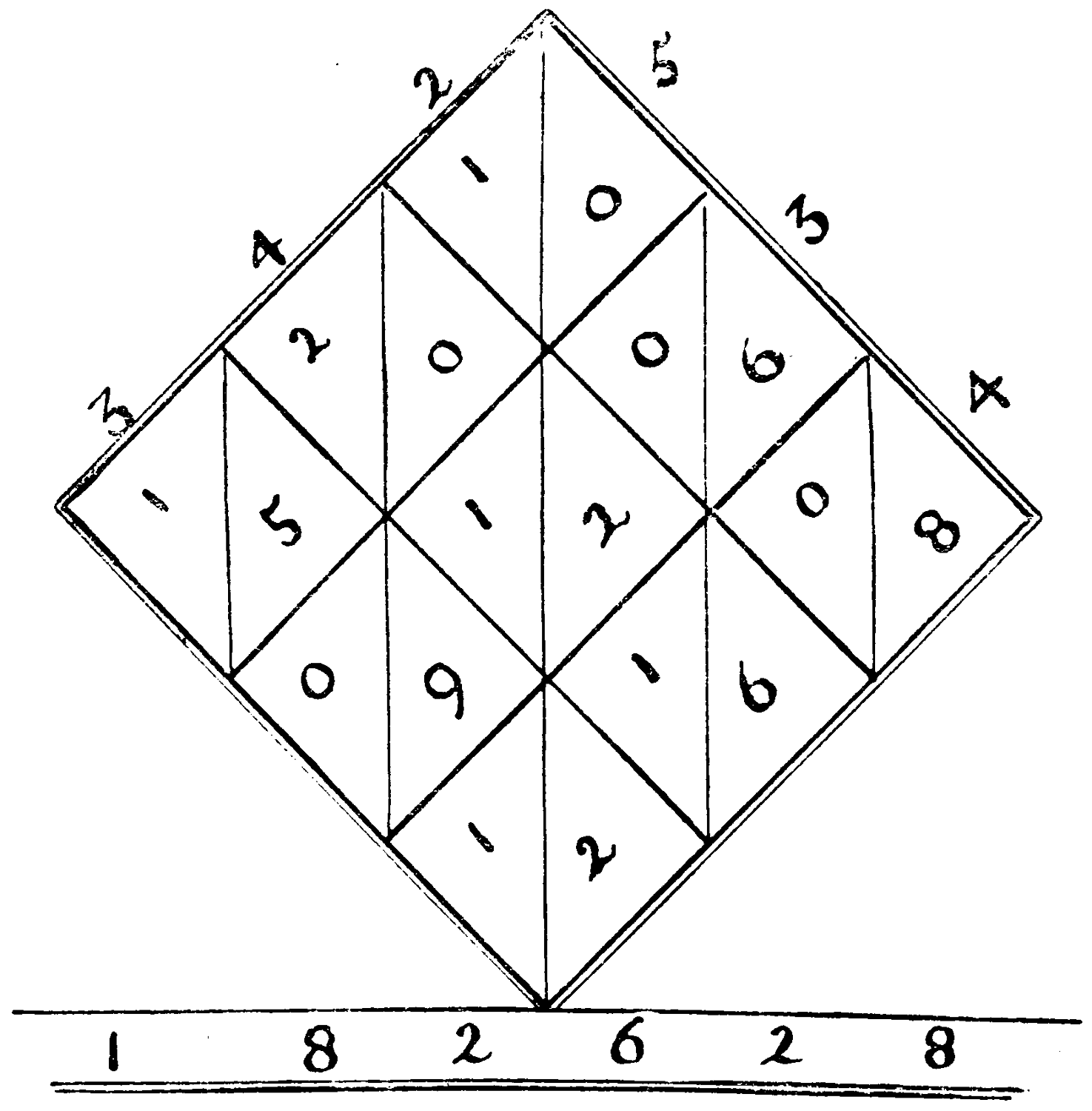
In this ingenious diamond all rows and both diagonals add up to 671; in the four corner diamonds all add up to 244; and in the central diamond, and the 16 rows of threes surrounding it, to 183.
[6]
Here is a magic square, in which the rows, columns, and diagonals yield the same product, 4096, by multiplication:—
| 128 | 1 | 32 |
| 4 | 16 | 64 |
| 8 | 256 | 2 |
It will be seen that the numbers in this square, 1, 2, 4, 8, 16, 32, 64, 128, 256, are in regular progression, and 4096 is also the cube of the central 16.
[7]
Here is quite a good example of a bordered magic square of sixty-four cells:—
| 1 | 56 | 55 | 11 | 53 | 13 | 14 | 57 |
| 63 | 15 | 47 | 22 | 42 | 24 | 45 | 2 |
| 62 | 49 | 25 | 40 | 34 | 31 | 16 | 3 |
| 4 | 48 | 28 | 37 | 35 | 30 | 17 | 61 |
| 5 | 44 | 39 | 26 | 32 | 33 | 21 | 60 |
| 59 | 19 | 38 | 27 | 29 | 36 | 46 | 6 |
| 58 | 20 | 18 | 43 | 23 | 41 | 50 | 7 |
| 8 | 9 | 10 | 54 | 12 | 52 | 51 | 64 |
It is a perfect specimen itself, and as each border is removed a fresh perfect magic square is revealed.
[8]
A magic square can be formed with the 81 numbers from 172 to 252 inclusive, which in all its rows, columns, and diagonals will total 1908. It may interest our solvers to complete the square.
| 216 | 175 | 224 | 240 | 199 | 248 | |||
| 247 | 215 | 174 | 190 | 239 | 207 | |||
| 206 | 246 | 214 | 230 | 198 | 238 | |||
| 213 | 172 | 221 | ||||||
| 244 | 212 | 180 | ||||||
| 203 | 252 | 211 | ||||||
| 186 | 226 | 194 | 210 | 178 | 218 | |||
| 217 | 185 | 234 | 250 | 209 | 177 | |||
| 176 | 225 | 184 | 200 | 249 | 208 |
We have filled in, as a solid start, 45 of the 81 cells.
[9]
This magic square adds up in rows, columns, and diagonals to 1908:—
| 469 | 484 | 472 | 483 |
| 481 | 474 | 478 | 475 |
| 482 | 471 | 485 | 470 |
| 476 | 479 | 473 | 480 |
Can you decide in how many other symmetrical ways the same total is to be made?
[10]
In this magic square the rows, columns, and diagonals add up always to 33.
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | |||||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | |||||||||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||
| ● | ● | ● | ● | |||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | |||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||
| ● | ● | ● | ● | |||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | |||||||||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||
Can you rearrange it so that the first stone (three-ace) shall occupy the centre, now filled by the double six, and it shall still add up in all ways to 33?
[11]
The arrangement of numbers in the 36 cells of this square discloses a very close affinity between chess and arithmetic.
| 30 | 21 | 6 | 15 | 28 | 19 |
| 7 | 16 | 29 | 20 | 5 | 14 |
| 22 | 31 | 8 | 35 | 18 | 27 |
| 9 | 36 | 17 | 26 | 13 | 4 |
| 32 | 23 | 2 | 11 | 34 | 25 |
| 1 | 10 | 33 | 24 | 3 | 12 |
Can you follow this out?
[12]
Those who combine a fancy for “Patience” with some skill in numbers will find amusement in filling the empty cells of this diagram with appropriate numbers, each of which must consist of two figures:—
| 17 | 24 | |||
| 32 | 46 | |||
| 14 | ||||
| 19 | 16 | |||
| 22 | 20 |
It is required that each of the rows across from side to side shall add up, when all the cells are filled, to 143 exactly. No number must be used more than once.
[13]
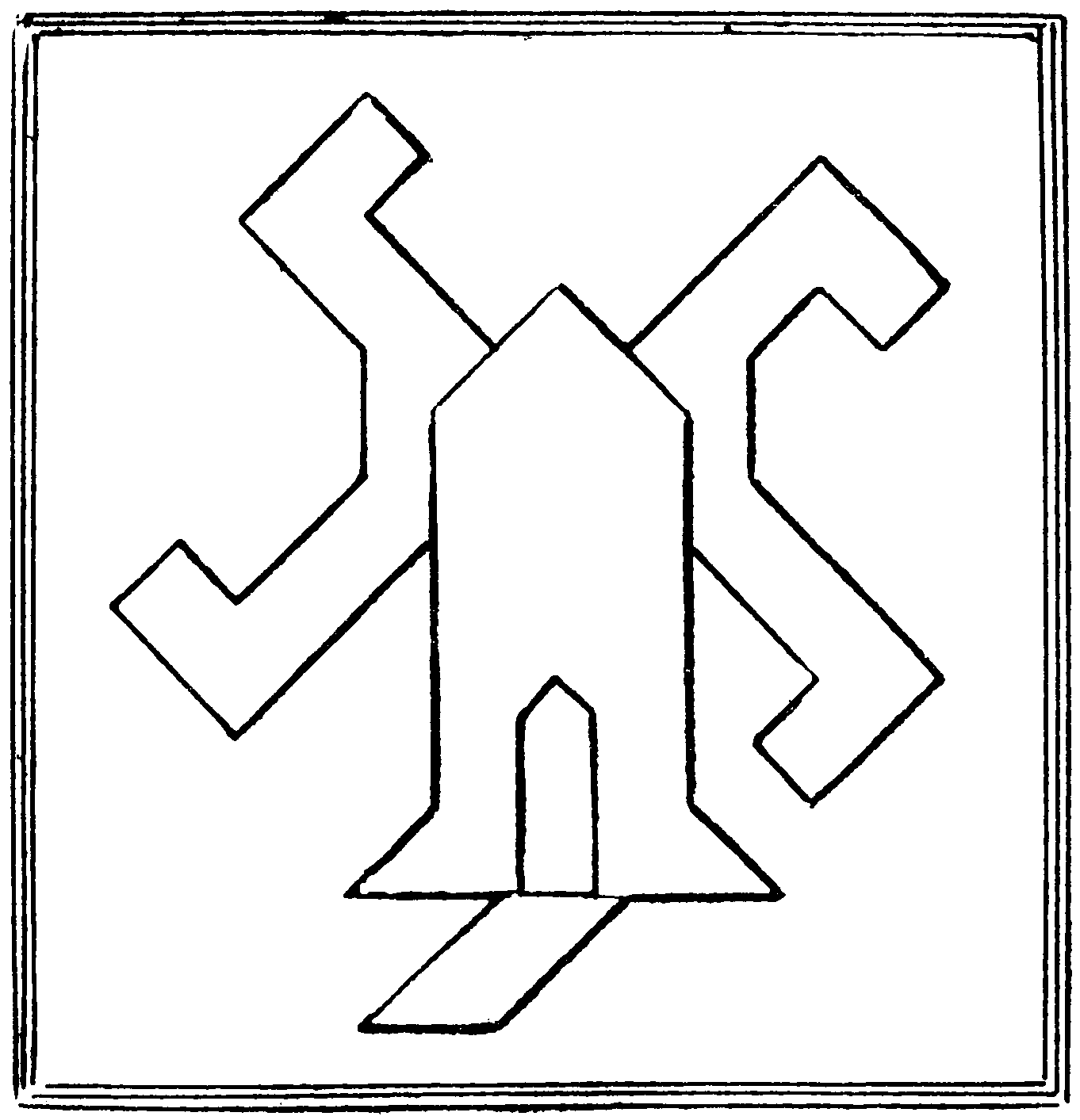
Can you divide a square into 15 parts, which can be built up into this windmill?
[14]
In this nest of 49 squares it is possible to count a great number of distinct and interlacing figures, whose opposite sides are equal, and whose angles are all right angles.
Can you decide exactly the number of these rectangles, and say how many of them are square?
[15]
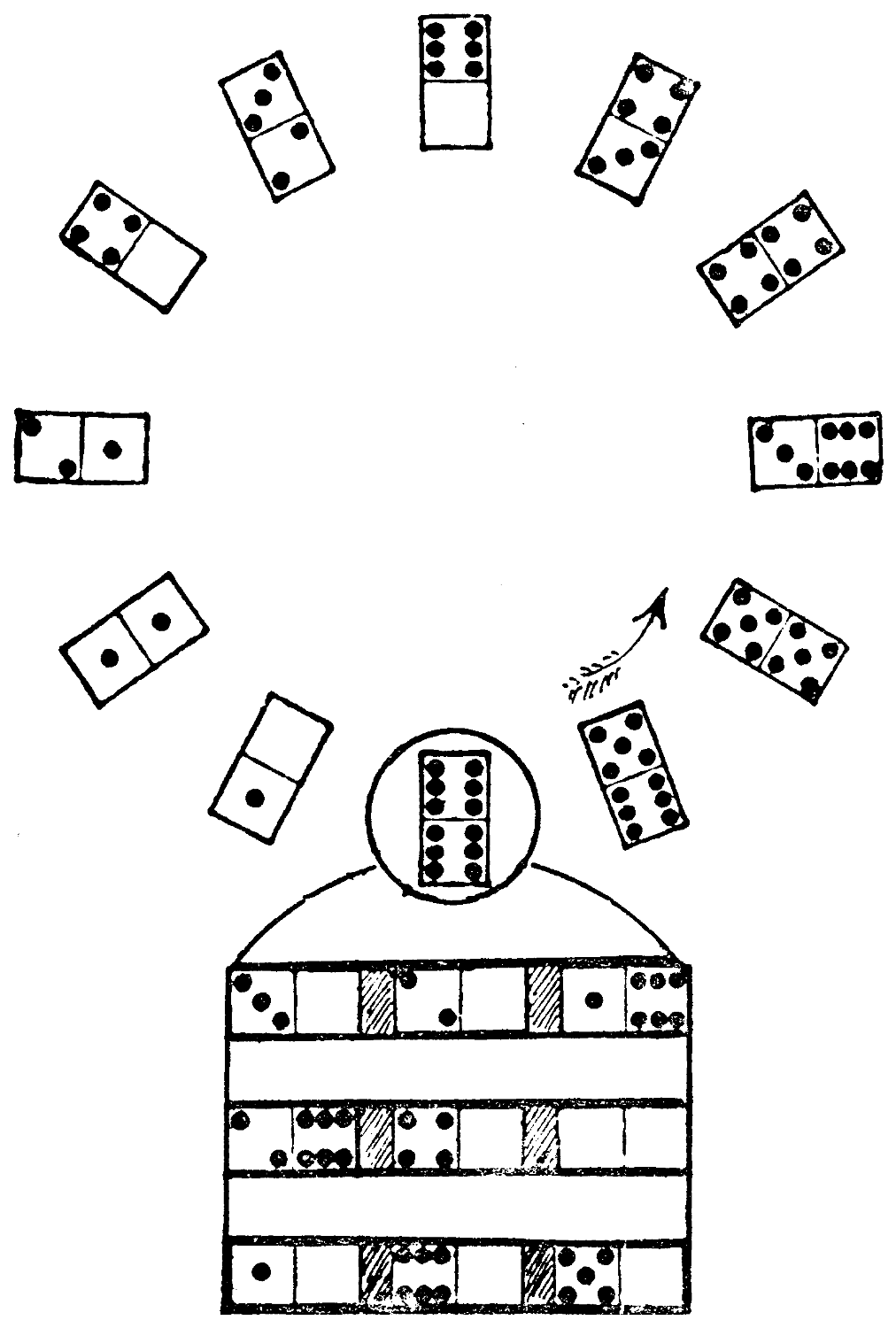
Can you, using all the dominoes except double five, five-six, and double six, construct with the twenty-five stones a magic square that adds up in all rows, columns, and diagonals to 27, and in which the stones in the cells marked by the same figures in this diagram also add up to that number?
| 2 | 1 | 2 | ||
| 4 | 3 | 4 | ||
| 1 | 3 | 3 | 1 | |
| 4 | 3 | 4 | ||
| 2 | 1 | 2 |
[16]
The problem is to construct, with all the twenty-eight stones, a domino pyramid of seven stages, starting with a single stone, and adding one stone on each successive stage.
The stones must be so arranged that the number of pips in any row or column are in all cases exactly three times the number of half-dominoes of which that line or column is composed. There are many solutions to exercise the solver’s patience.
Six horse buses and four motor buses travel each hour from Temple Bar to the Bank. The horses take 15 minutes, and the motors 10 minutes on the journey.
If I come to Temple Bar, and wish to reach the Bank as soon as possible, shall I take the first horse bus that turns up, or wait for a motor? It must be assumed that I can only see a bus as it actually passes me.
[17]
The father of this venturesome lad, who was on the point of breaking out of bounds, came on the scene just in time to warn him in a sentence of nine words, five of which were “Never throw a leg, lad.”

Can you supply the other four words, which are spelt with exactly the same letters?
[18]
In this picture we see that a cat has sprung upon the table to interview the parrot.

The title “Catastrophe” recast by anagram, tells the parrot’s happy thought at this critical moment, and the appropriate sentence,
“New parrot-stand in a house,”
tells, also by anagram, how he put this into instant operation.
[19]
This is the picture of the first prize boy at a baby show. The judge, noticing the position of one chubby fist, said to the proud mother, “Your lad Tommy likes such tit-bits.”

To his amazement the baby, removing the comforting hand, replied in eight words composed of exactly the same letters, “So to-day, sir, . .... .. ...... .....” Can you complete the sentence?
[20]
The lady who is sitting at the back of this overloaded waggonette cries out, in her sympathy with the struggling horse, “This big load quite hinders his pull.”

Her husband, full of holiday spirits and energy, answers her in a sentence of mingled reproof and determination, which forms a perfect anagram of the words of his wife, and describes his feelings and action. Can you recast the letters?
[21]
At the moment when a burly and keen player was in this strange and striking attitude,

a bystander whispered to the marker, “Eh! what a stout player is striking!”
Can you, using exactly the same letters, put into the mouth of the marker a reply appropriate to the position?
[22]
There are two English words which are appropriate to this picture—

One of them has as its anagram the very apposite sentence, “Or not a man first;” the other treated in similar fashion becomes, “O I love nuts!” What are the two words?
Who can turn WHEAT into BREAD with six links, changing one letter each time, and preserving the general order of the letters throughout?
[23]
How can we decide by anagram whether this is a fancy portrait of “William or dear Jack?”

Shake up and recast the words in inverted commas.
Can our readers solve this enigma, which was published in 1811, and to which no answer seems to be known?
[24]
Take this picture in connection with the lines below it, and find out what it represents.

[25]
His wife, who chanced to see Jiggers at the trying moment here depicted, said that he seemed to be in a “sad pet.”

How was this literally true?
[26]
Never was a cow so troublesome at milking-time.
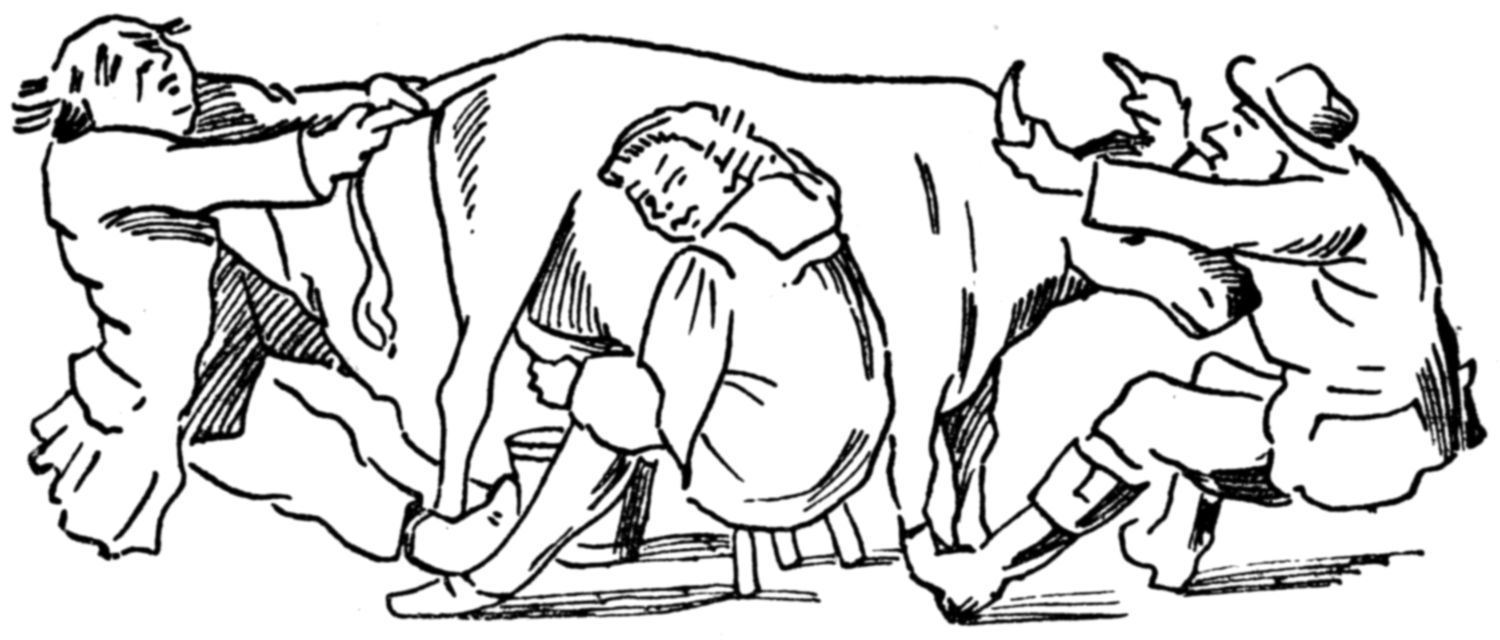
Our picture was taken at the moment when Farmer Hayseed was exclaiming, as he held on behind, “See, we hold this cow’s horns and tail!”
The same letters, recast by anagram, form this sentence spoken by his foreman—
“She cannot toss, ... .... .... .. ..”
Can you fill in the five missing words?
These grave lips chatter no ill.
or
Elephants, all to richest giver!
Can you recast the letters of these sentences so that either of them forms the same homely proverb, to which the first anagram is most akin?
[27]
This very resolute horse and his anxious driver take quite different views of the situation shown in this picture.
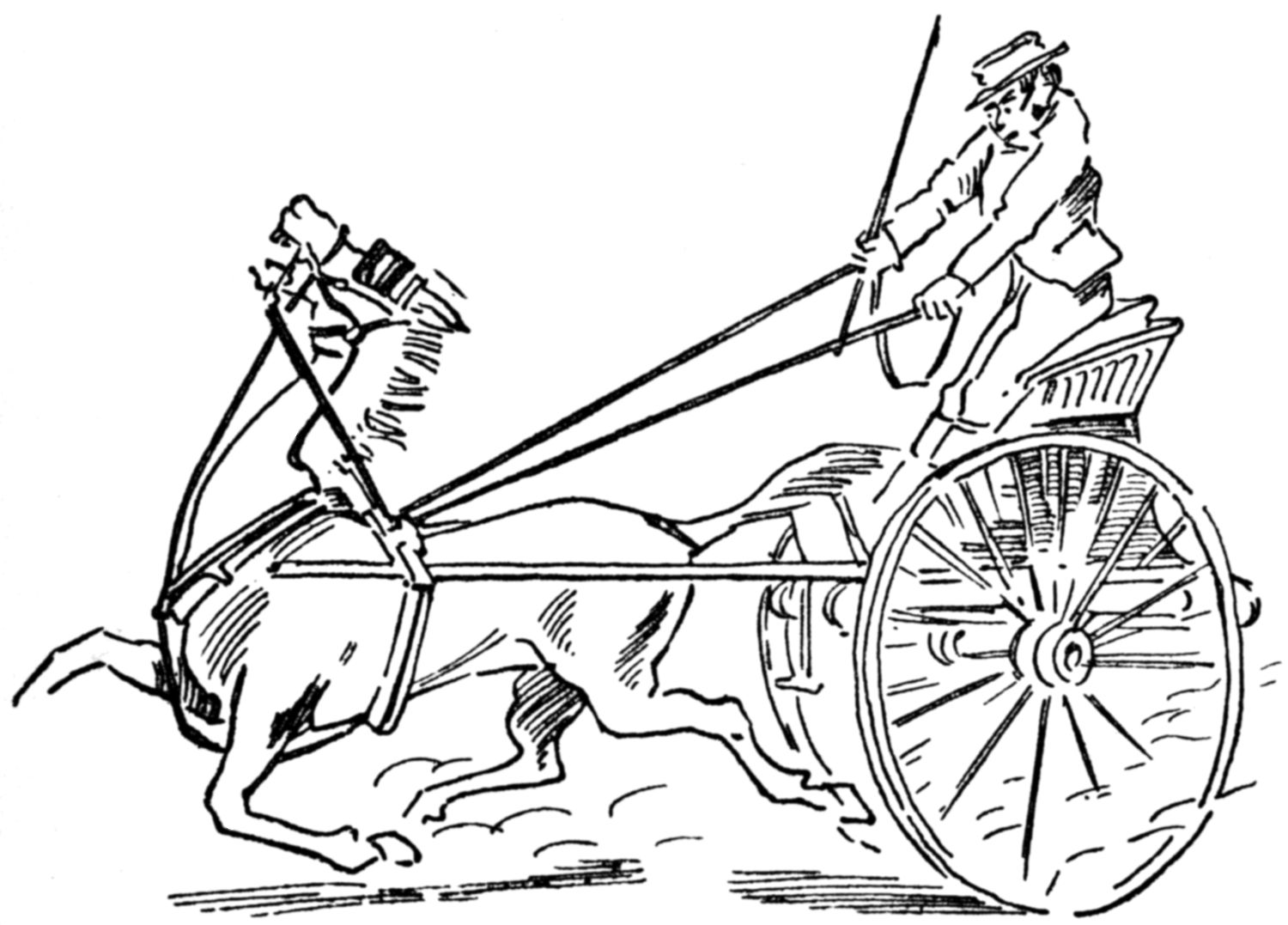
We can fancy that the fast trotter, if he could be endowed with speech, would say, “I’m a train’d stepper!”
Can you take these same letters, and recast them into a sentence which would seem to express the driver’s point of view?
[28]
In this picture a clever artist who has no arms is seen calmly painting with his feet.
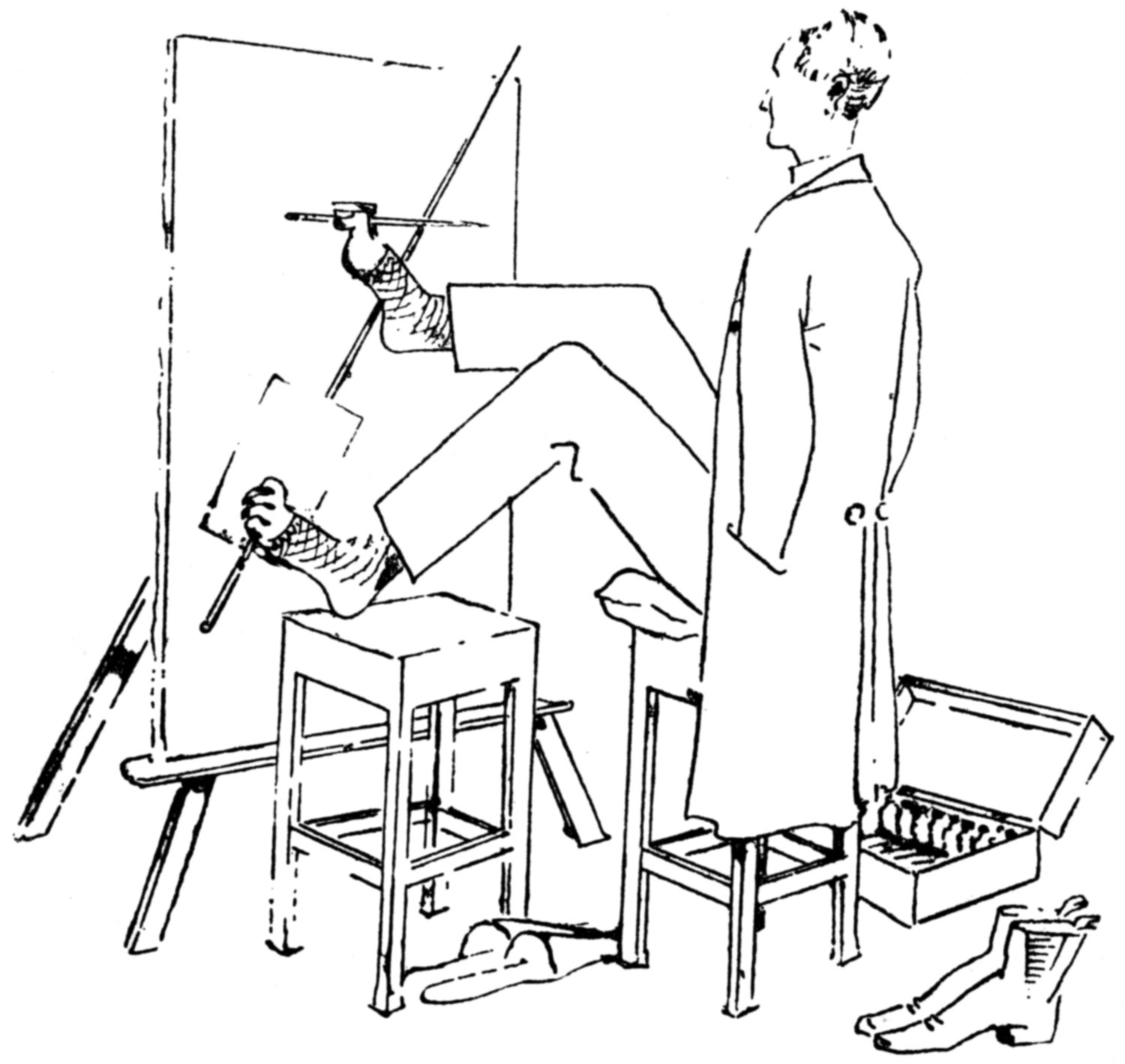
One onlooker says to another, “Why, now I see this fine artist has no hand!” The other replies in a sentence which contains exactly the same letters:
“He draws in any fashion .... ... ... ... .”
Can you fill in the four missing words?
[29]
“This is a wine bottle, dear, on a lure,” said a crafty fisher of men to his better half, who was helping him, as he showed her this illustration of their aims.

1834
PORT
She knew, however, that the fish he sought to catch was not to be tempted in this way, and she replied in words spelt with exactly the same letters, “And see, he will not .... .. ... ....!”
Can you fill in the four missing words?
[30]
This sturdy musical enthusiast, as he settled himself upon his chair, said, “What shall I play?” and some one replied, “Any strains of Beethoven, he charms all!”

This suggestion, however, was not acceptable, and he, as he struck up a piece after his own heart, exclaimed, in a sentence composed of exactly the same letters—
“Nay, for this ’cello ...... .... . ......!”
Can you supply the missing words?
[31]
This picture represents a parsnip lying across a sturdy swede.

Can you so readjust them that they seem to suggest a successful dramatist of the day? We give this broad hint by anagram—
“Here is our parsnip on swede.”
ANAGRAM
Wise and superior person he!
[32]
Can you fill the places of these 21 asterisks with only three different letters, arranging them so that they spell a common English word in twelve different directions?
| ● | ● | ● | ● | ● |
| ● | ● | ● | ● | |
| ● | ● | ● | ||
| ● | ● | ● | ● | |
| ● | ● | ● | ● | ● |
[33]
First form a short sentence with the ten letters that are above the line in this diagram:—
| S | B | |
| R | E | |
| Y | D | |
| O | T | |
| U | O | |
| O | E | E |
Next number the letters of the sentence consecutively 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, and then work out a sum in addition with these numbers substituted for the letters with which they correspond.
[34]
Find within these borders twelve specimens of flowers and foliage:—
| 1L | 2L | 3B | 4H | 5P | 6E | 7F |
| 8L | 9Y | 10E | 11L | 12O | 13R | 14N |
| 15I | 16V | 17B | 18R | 19I | 20V | 21K |
| 22A | 23L | 24E | 25T | 26O | 27N | 28I |
| 29C | 30N | 31A | 32S | 33U | 34L | 35P |
Move in any direction one square at a time, and so spell out their names, using the same square only once in each case.
[35]
To test the powers of his young pupils, Dr Puzzlewitz set the following little problem on his blackboard:—
| A | - | B | = | 4 | ||
| A | ÷ | B | = | 4 | ||
What are the values of A and of B, when 4 is the result of dividing A by B, or of subtracting B from A?
The figures indicate the position of the letters, which spell new words, in the original six-letter word.
[36]
Can you fill in the empty cells with letters, so that they form English words which read alike from top to bottom and from left to right?
| s | ||||||
| s | u | s | ||||
| s | ||||||
Old Couplet.
[37]
Taking the letters as arranged on this diagram for a starting point, can you place in some of the unoccupied cells five more of A, five of E, five of I, and five of O, making eight in all of each letter, so that in no case shall the same vowel be in the same row, column, or diagonal?
| A | I | E | O | ||||
| O | A | ||||||
| I | E | ||||||
| E | O | A | I | ||||
Each vowel is to be regarded without any reference to the other vowels, and, of course, only one may be placed in a cell.
[38]
Mix together the letters which form the eight words on this draught board—
| V | O | T | E | ||||
| W | O | V | E | ||||
| P | R | O | W | ||||
| C | A | L | L | ||||
| S | T | E | W | ||||
| N | E | W | S | ||||
| C | O | R | E | ||||
| N | A | P | E |
and recast them so that they form eight fresh words, which when placed in proper order on the white squares, are a word square in which each word reads alike from left to right, or from top to bottom. The first of the fresh words is CROW.
[39]
Form a short sentence with the letters above the line in this diagram:—
| D | U | |
| E | H | |
| E | D | |
| A | P | |
| S | T | |
| D | E | A |
Number the letters consecutively 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, and then work a sum in addition, substituting these numbers for the letter with which they correspond.
[40]
Shake up the sixteen letters of these four words, and recast them into four other words:—
| S | E | E | K | ||||
| S | L | A | B | ||||
| L | E | E | K | ||||
| M | O | A | N |
These fresh words, placed on the white squares, must read alike from side to side, and zigzag from top to bottom. The first word is MASK.
[41]
Take the letters which form the words in these sixteen cells—
| A | F | A | R |
| T | A | S | K |
| S | E | A | T |
| L | E | A | L |
and recast them so that they form a perfect word square.
[42]
There are five English words in this square:—
| c | h | e | s | s |
| g | r | e | e | d |
| c | a | n | e | s |
| r | e | a | r | s |
| c | h | e | e | r |
Can you shake up their letters, and recast them into five other words which form a perfect word square, and read alike from top to bottom and from left to right? The first fresh word is CRESS.
[43]
Five familiar proverbs are hidden in this square of 169 letters,
| R | E | N | O | W | N | E | D | T | H | A | N | W |
| S | Y | O | U | R | C | A | K | E | A | N | D | A |
| S | T | E | T | O | B | E | F | E | A | R | H | R |
| E | A | R | K | S | S | P | O | I | L | E | A | F |
| L | E | O | O | H | E | R | S | N | T | D | V | O |
| O | T | M | O | T | L | I | N | O | H | T | E | U |
| N | O | S | C | A | L | A | G | M | E | H | I | R |
| S | N | I | Y | G | O | R | S | O | B | A | T | S |
| E | N | G | N | E | N | O | T | S | R | N | P | A |
| I | A | O | A | M | O | O | T | S | O | A | E | W |
| R | C | D | E | V | I | L | A | H | T | D | A | S |
| O | U | O | Y | N | O | I | L | D | A | E | C | A |
| T | C | I | V | R | E | H | H | T | A | H | E | Z |
The proverbs are arranged in a regular sequence.
We are familiar with the anagram that so charmingly points to the ministrations on the battle-field of Florence Nightingale—Flit on, cheering angel—but it is not so well known that her name can also be recast with an appropriate wish for her continuance in our loving memory. Can you frame this?
[44]
A French sentence of 100 letters in twenty-two words is concealed in these 100 cells.
| D | L | A | N | N | E | S | M | P | A |
| L | I | R | D | L | E | E | M | L | H |
| I | L | U | E | E | A | I | N | T | J |
| C | U | R | S | E | M | N | T | U | P |
| E | U | É | S | N | P | R | E | O | S |
| O | L | I | É | D | X | S | M | A | N |
| U | D | E | A | E | É | I | X | N | T |
| T | E | T | P | E | D | N | U | Q | E |
| B | U | U | U | F | L | I | J | I | N |
| Z | U | E | J | I | O | E | U | N | R |
It can be deciphered by means of a cardboard mask of similar size, with circular holes cut out in some of its cells. This is placed squarely over the diagram, turned round in four successive positions. And thus the sequence of letters is found, and falls into words.
[45]
The instant popularity of this clever puzzle was amazing, and its sale is said to have run into millions years ago in America.

Cut the pony into six pieces, as is indicated in the picture, and rearrange these so that they show a trotting horse.
I am
a man
I rate you
a beast
You know me.
Can you put this into shape?
[46]
Here is another of Sam Loyd’s famous trick pictures:—
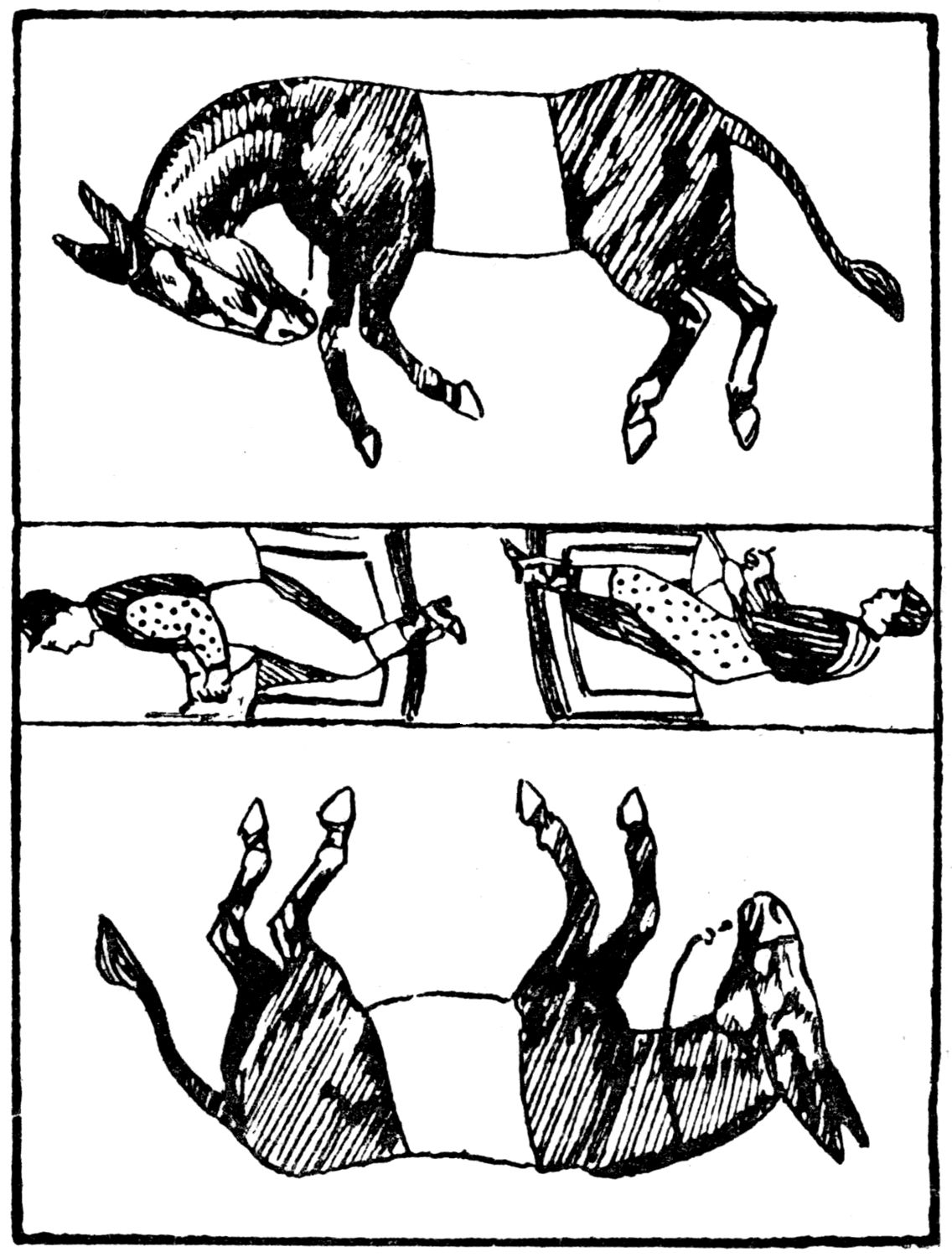
Can you rearrange the parts to show jockeys and horses in racing trim?
[47]
This boy is sure that if he takes his time, and watches his opportunity, he will be able to reach and secure with his mouth the sugar on the chair. Will he?

The names of eight famous British poets are buried in these lines—that is to say, the letters that spell the names form in their proper order parts of different words:—
Can you dig them up?
[48]
Here are six little hoptoads, as our cousins across the water call them, three white and three black, going in opposite directions. A frog may jump, one, two, or three steps, but no two may be together at any time.

In how few jumps can the black frogs be seated to the left of their white brothers? It is obvious that one of the white frogs must jump first to the stool marked 1.
[49]
A very curious old print, of which this might well be the title, was picked up on a bookstall. This picture shows clever designs for two of the digits:

1
Se Pierot or Lun,
A Figure of One.
2
Again he’s to view,
A Figure of Two.
[50]
Here is the second pair of this queer company:—

3
Now ’tis plain you may see,
He’s a Figure of Three.
4
Behold him once more,
A Figure of Four.
[51]
Here is the third pair of these quaint characters:—

5
Now here we contrive
To make him a Five
6
He’s a Six here complete,
With his hands to his feet.
A proverb of eight words is buried here:—
I fancy this Tory outcry, this weary outrageous attempt to show illegality, is as a cat chasing snow-flakes. I must be forgiven if I shun his example.
The six missing words are spelt with the same seven letters.
[52]
Here is another pair of these quaint figures:—

7
With some alteration,
A Seven’s his station.
8
Here not being strait,
He forms a good eight.
[53]
Here is the final pair:—
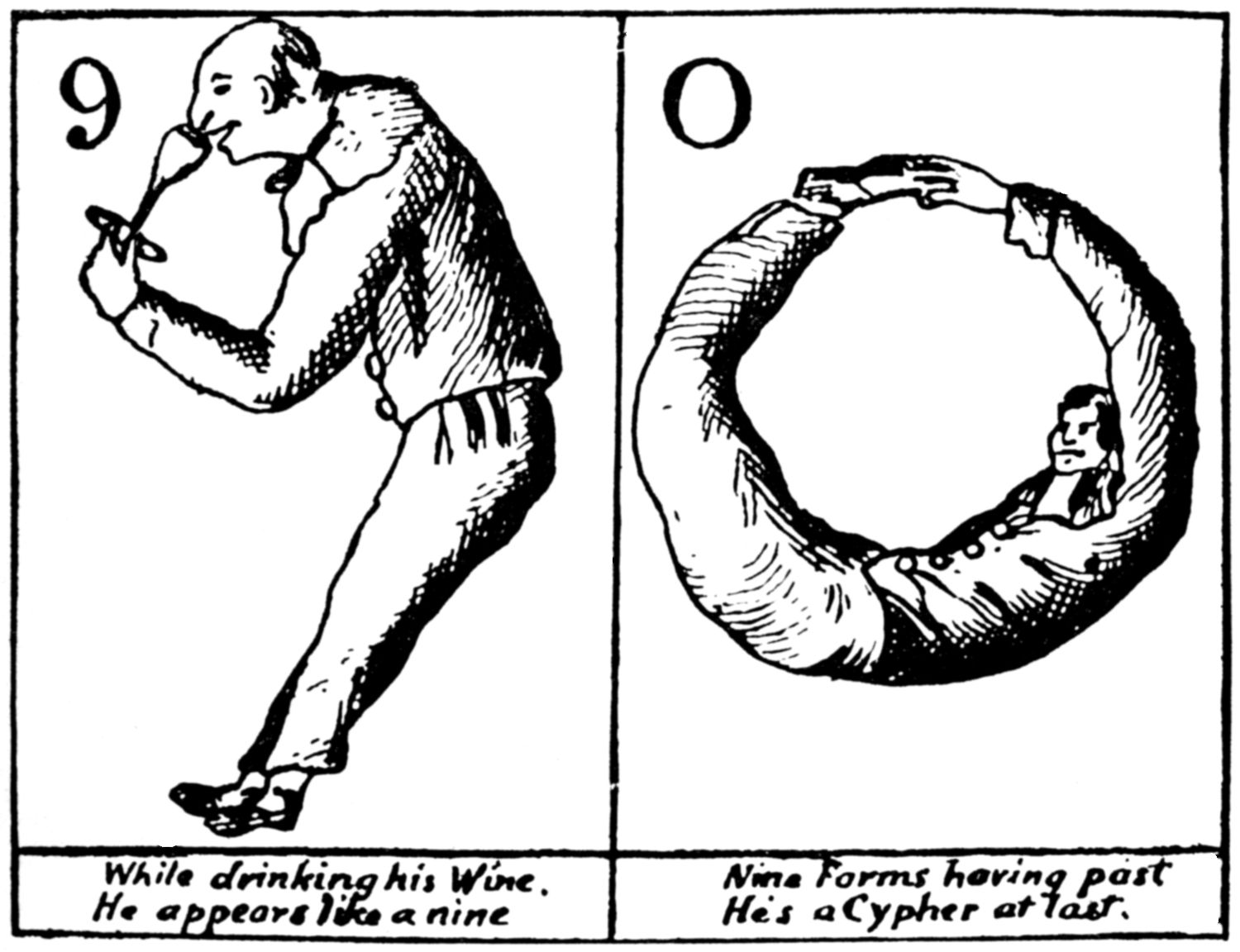
9
While drinking his Wine,
He appears like a nine.
0
Nine Forms having past
He’s a Cypher at last.
If you “resist disasters,” how may this affect one of your home circle?
[54]
1 × 8 + 1 = 9
12 × 8 + 2 = 98
123 × 8 + 3 = 987
1234 × 8 + 4 = 9876
12345 × 8 + 5 = 98765
123456 × 8 + 6 = 987654
1234567 × 8 + 7 = 9876543
12345678 × 8 + 8 = 98765432
123456789 × 8 + 9 = 987654321
If you tell a schoolboy that the longest side of a triangular field measures 100 rods, and that each of the other sides measures 50 rods, and ask him to estimate the value of its grass at £1 per acre, how should he answer?
[55]
What is the smallest number of straight lines which can be drawn within this square so as to enclose each of the wheels within separate boundaries?
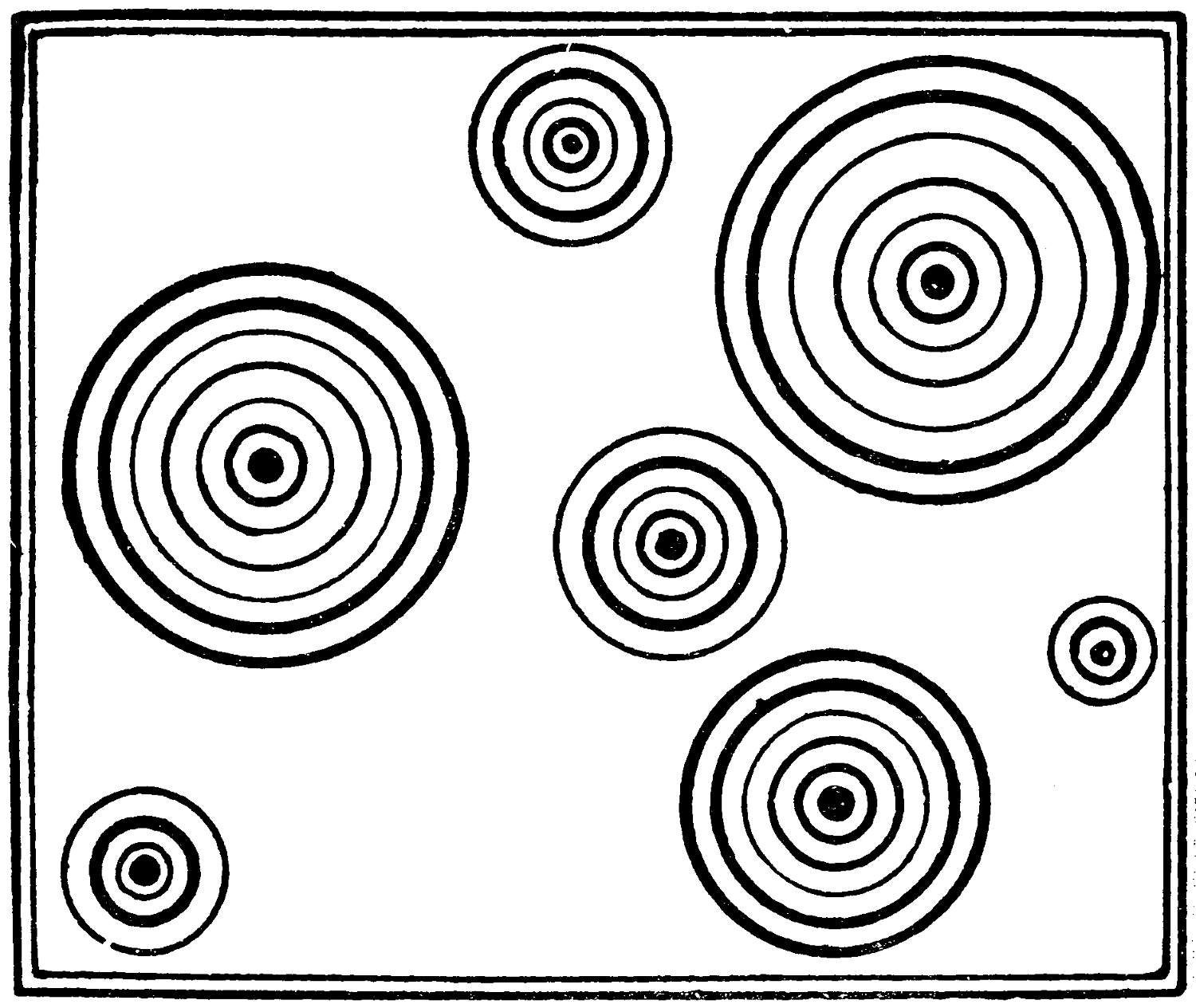
While solving this, rotate the paper in your hand, and see the wheels spin.
[56]
A market gardener who has a large square plot of ground wishes to reserve a fourth of it in the shape of a triangle for himself, as is shown in the diagram—

and to divide the remainder among his four sons, so that each shares equally, with plots of similar shape. How did he mark it out for them?
This appears in a less perfect form in “The Twentieth Century Standard Puzzle Book.”
[57]
Here is a simple little puzzle which may amuse anyone who has paper and pencil at hand:—

Can you combine three figures similar to Fig. A with two similar to Fig. B, so that a perfect Latin cross is formed?
It is, of course, an easier matter to cut out five such pieces in paper or cardboard, and arrange them in the form required.
The missing words are spelt with the same seven letters.
[58]
Four poor men were living in the cottages shown in this diagram, round a central lake well stocked with fish. Four rich men built their houses further afield, and selfishly determined to exclude their neighbours from access to the water.
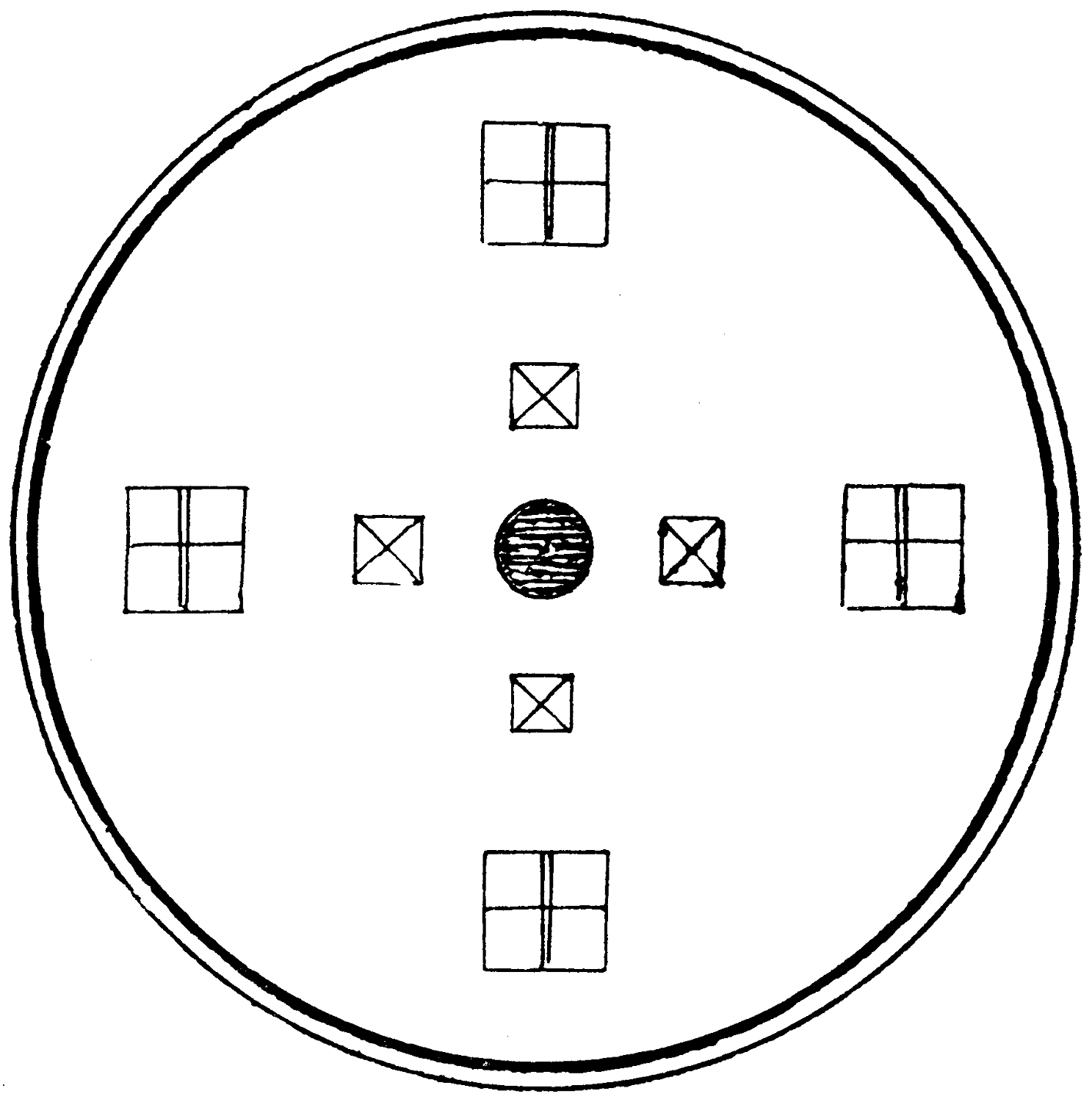
How could they do this effectually without cutting themselves off from the lake?
150 hat robe or tent
Can you form from this the name of a famous British author, treating the 150 as Roman numerals?
[59]
Cut out in cardboard four pieces of the shape and size of each of the large patterns, and two pieces of the small one:—
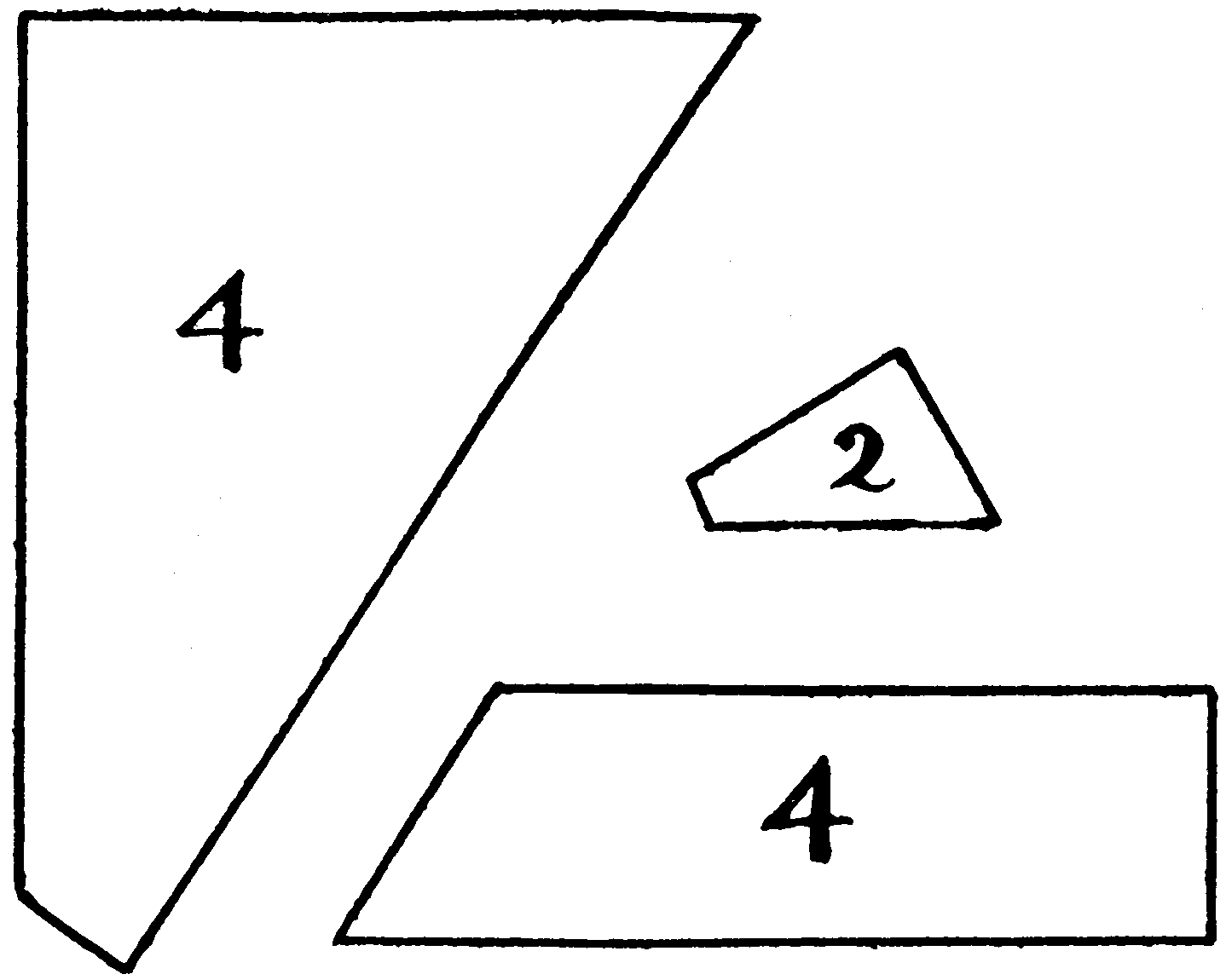
Now arrange these ten pieces so that they form a perfect square.
[60]
The dotted lines in this diagram show how the figure can be divided into nine parts by four straight cuts

which can be reunited to form a perfect cross.
Tom Larkins, proud of his prize for arithmetic, challenged his sisters to show on a blackboard that if 50 is subtracted from the sum of the nine digits, the result is equal to the number obtained by dividing their sum by 3. How did he prove his point?
[61]
Take in paper or cardboard a figure made up of a square and half of a similar square, thus:—
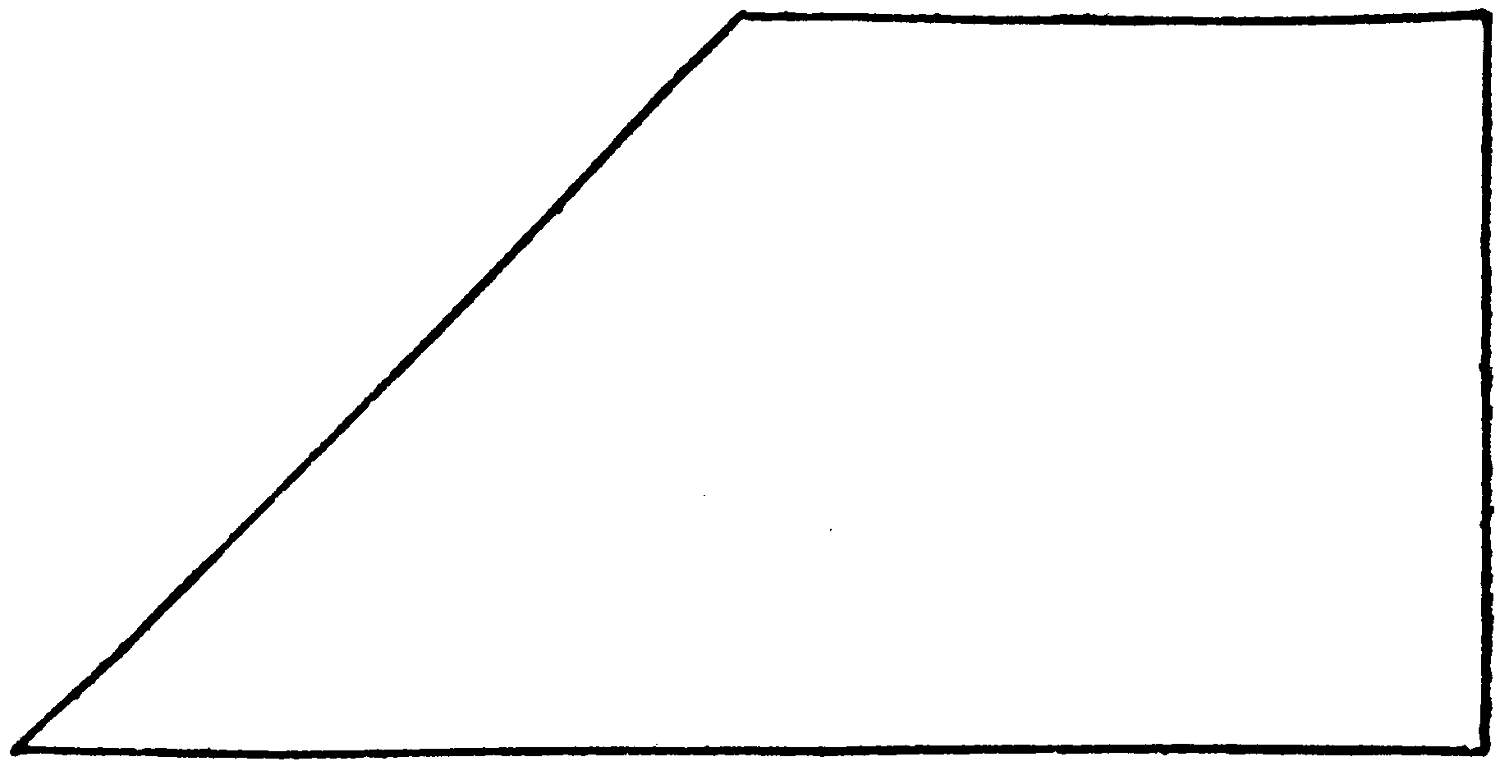
How can you, in the simplest way, divide it into four equal and similar parts by four straight cuts?
[62]
Can you draw twenty-two straight lines within this circle so that they divide it into four similar parts, each having three of the dots within its borders?

Each line must be at right angles to another.
[63]
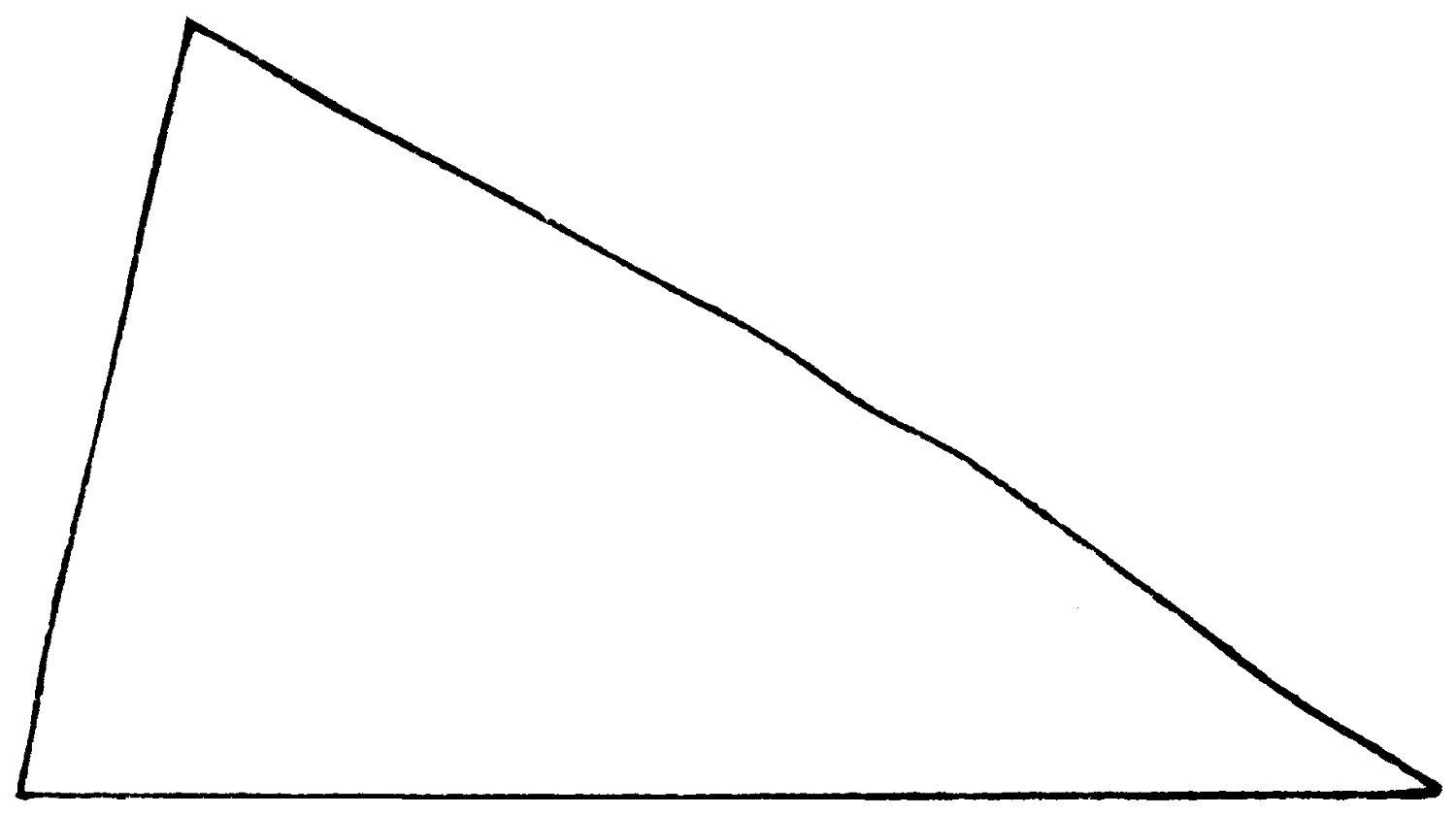
Cut up this triangle into 5 parts,
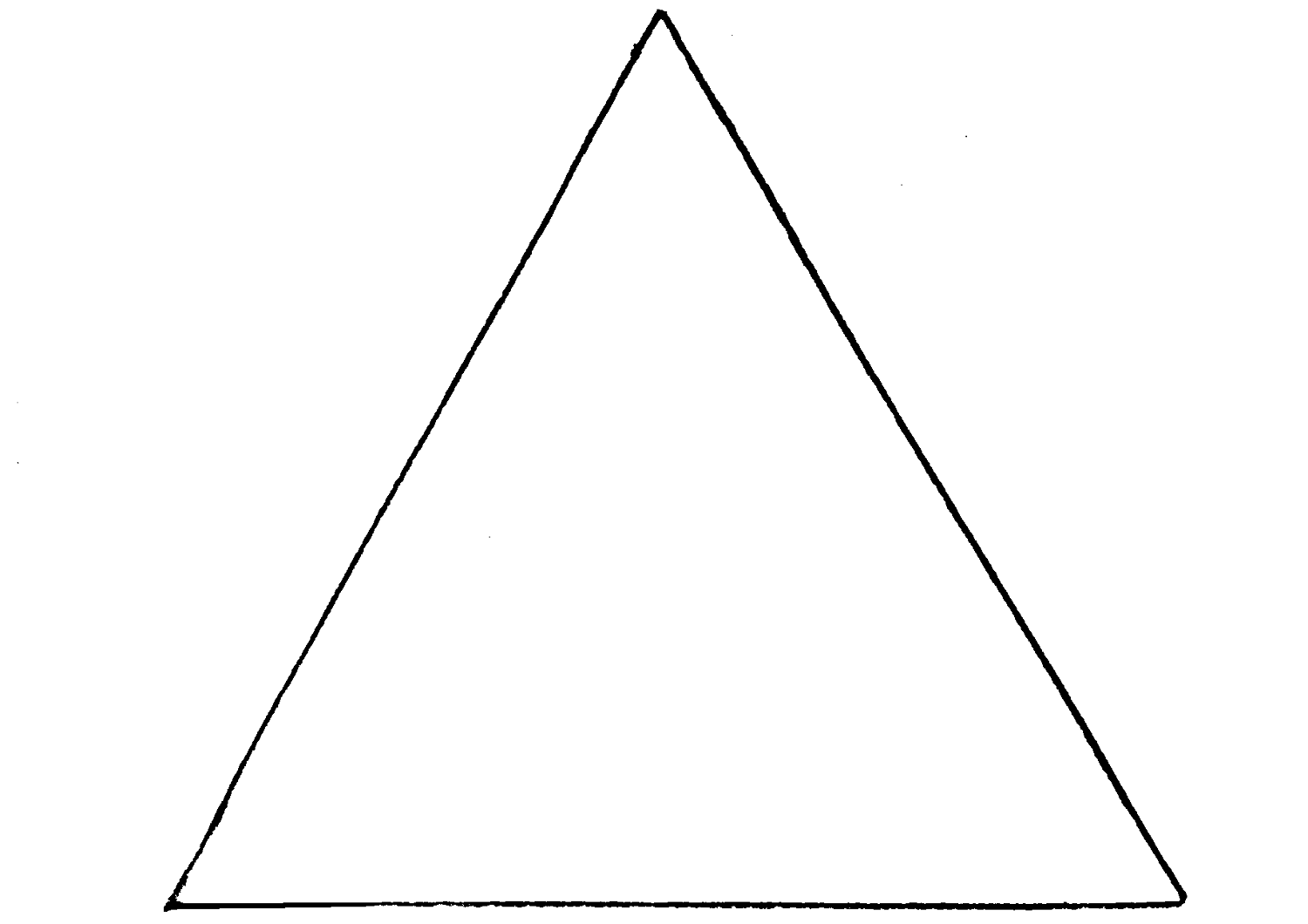
which can be reassembled to form this triangle.
[64]
The peculiar series of numbers, as arranged in this triangular form, is said to have been perfected by Pascal.
| 1 | |||||||
| 2 | 1 | ||||||
| 3 | 3 | 1 | |||||
| 4 | 6 | 4 | 1 | ||||
| 5 | 10 | 10 | 5 | 1 | |||
| 6 | 15 | 20 | 15 | 6 | 1 | ||
| 7 | 21 | 35 | 35 | 21 | 7 | 1 | |
| 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
It has the property of showing, without calculation, how many selections or combinations can be made at a time out of a larger number. Thus to find how many selections of 3 at a time can be made out of 8 we look for the third number on the horizontal row that commences with 8, and find the answer 56.
The series is formed thus: Set down the numbers 1, 2, 3, etc., as far as you please, in a vertical row. To the right of 2 place 1, add them together, and set 3 under the 1. Then add 3 to 3, and set the result below, and so on, always placing the sum of two numbers that are side by side below the one on the right.
[65]
This diagram shows an ancient and curious method of multiplication, which will be novel to most of our readers.
In this instance 534 is multiplied by 342. Draw a square of nine cells with diagonals, fill the three top cells, as is shown, by multiplying the 5 by the 3, the 4 and the 2. Then multiply in similar way the 3 and the 4 by these same figures. Turn the square round so that the diagonals are upright, and add. Of course, placing the numbers thus is the same practically as carrying them by our ordinary rule.
[66]
In this diagram 27 counters are arranged in 9 rows, with 6 in each row.
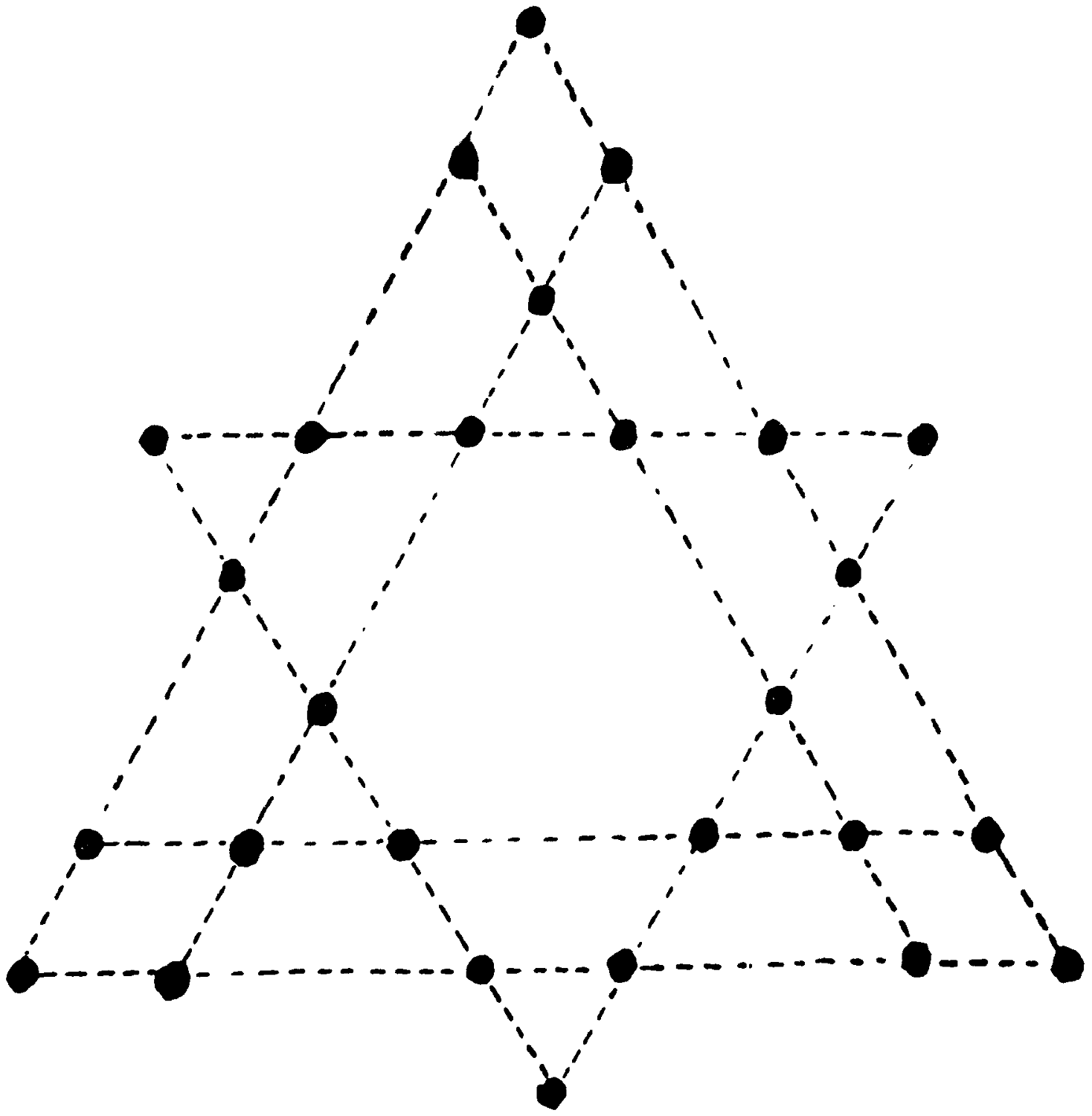
Can you rearrange them so that with similar conditions they all fall within the borders of one equilateral triangle?
Can you discover a very familiar saying that is buried in these lines?
[67]
Place eight cards of two different colours alternately in one row, then with four moves bring all of one colour together.
| A ♠ |
2 ♡ |
3 ♣ |
4 ♢ |
5 ♣ |
6 ♢ |
7 ♣ |
8 ♡ |
Two cards (without altering their relative position) are to be moved at a time, and placed somewhere in the same line, one of them at least touching another card.
The missing words are spelt with the same five letters.
[68]
Cut out this diagram, and paste it on a card. Hand it to anyone, and ask him to fix upon whichever number he pleases, and merely to tell you in which columns this appears.
| I. | II. | III. | IV. | |||||||||||||||
| 1 | 33 | 65 | 97 | 2 | 34 | 66 | 98 | 4 | 36 | 68 | 100 | 8 | 40 | 72 | 104 | |||
| 3 | 35 | 67 | 99 | 3 | 35 | 67 | 99 | 5 | 37 | 69 | 101 | 9 | 41 | 73 | 105 | |||
| 5 | 37 | 69 | 101 | 6 | 38 | 70 | 102 | 6 | 38 | 70 | 102 | 10 | 42 | 74 | 106 | |||
| 7 | 39 | 71 | 103 | 7 | 39 | 71 | 103 | 7 | 39 | 71 | 103 | 11 | 43 | 75 | 107 | |||
| 9 | 41 | 73 | 105 | 10 | 42 | 74 | 106 | 12 | 44 | 76 | 108 | 12 | 44 | 76 | 108 | |||
| 11 | 43 | 75 | 107 | 11 | 43 | 75 | 107 | 13 | 45 | 77 | 109 | 13 | 45 | 77 | 109 | |||
| 13 | 45 | 77 | 109 | 14 | 46 | 78 | 110 | 14 | 46 | 78 | 110 | 14 | 46 | 78 | 110 | |||
| 15 | 47 | 79 | 111 | 15 | 47 | 79 | 111 | 15 | 47 | 79 | 111 | 15 | 47 | 79 | 111 | |||
| 17 | 49 | 81 | 113 | 18 | 50 | 82 | 114 | 20 | 52 | 84 | 116 | 24 | 56 | 88 | 120 | |||
| 19 | 51 | 83 | 115 | 19 | 51 | 83 | 115 | 21 | 53 | 85 | 117 | 25 | 57 | 89 | 121 | |||
| 21 | 53 | 85 | 117 | 22 | 54 | 86 | 118 | 22 | 54 | 86 | 118 | 26 | 58 | 90 | 122 | |||
| 23 | 55 | 87 | 119 | 23 | 55 | 87 | 119 | 23 | 55 | 87 | 119 | 27 | 59 | 91 | 123 | |||
| 25 | 57 | 89 | 121 | 26 | 58 | 90 | 122 | 28 | 60 | 92 | 124 | 28 | 60 | 92 | 124 | |||
| 27 | 59 | 91 | 123 | 27 | 59 | 91 | 123 | 29 | 61 | 93 | 125 | 29 | 61 | 93 | 125 | |||
| 29 | 61 | 93 | 125 | 30 | 62 | 94 | 126 | 30 | 62 | 94 | 126 | 30 | 62 | 94 | 126 | |||
| 31 | 63 | 95 | 127 | 31 | 63 | 95 | 127 | 31 | 63 | 95 | 127 | 31 | 63 | 95 | 127 | |||
| V. | VI. | VII. | |||||||||||
| 16 | 48 | 80 | 112 | 32 | 48 | 96 | 112 | 64 | 80 | 96 | 112 | ||
| 17 | 49 | 81 | 113 | 33 | 49 | 97 | 113 | 65 | 81 | 97 | 113 | ||
| 18 | 50 | 82 | 114 | 34 | 50 | 98 | 114 | 66 | 82 | 98 | 114 | ||
| 19 | 51 | 83 | 115 | 35 | 51 | 99 | 115 | 67 | 83 | 99 | 115 | ||
| 20 | 52 | 84 | 116 | 36 | 52 | 100 | 116 | 68 | 84 | 100 | 116 | ||
| 21 | 53 | 85 | 117 | 37 | 53 | 101 | 117 | 69 | 85 | 101 | 117 | ||
| 22 | 54 | 86 | 118 | 38 | 54 | 102 | 118 | 70 | 86 | 102 | 118 | ||
| 23 | 55 | 87 | 119 | 39 | 55 | 103 | 119 | 71 | 87 | 103 | 119 | ||
| 24 | 56 | 88 | 120 | 40 | 56 | 104 | 120 | 72 | 88 | 104 | 120 | ||
| 25 | 57 | 89 | 121 | 41 | 57 | 105 | 121 | 73 | 89 | 105 | 121 | ||
| 26 | 58 | 90 | 122 | 42 | 58 | 106 | 122 | 74 | 90 | 106 | 122 | ||
| 27 | 59 | 91 | 123 | 43 | 59 | 107 | 123 | 75 | 91 | 107 | 123 | ||
| 28 | 60 | 92 | 124 | 44 | 60 | 108 | 124 | 76 | 92 | 108 | 124 | ||
| 29 | 61 | 93 | 125 | 45 | 61 | 109 | 125 | 77 | 93 | 109 | 125 | ||
| 30 | 62 | 94 | 126 | 46 | 62 | 110 | 126 | 78 | 94 | 110 | 126 | ||
| 31 | 63 | 95 | 127 | 47 | 63 | 111 | 127 | 79 | 95 | 111 | 127 | ||
You can then in a moment, and at a glance, pick out the number that is chosen.
[69]
Let us suppose that these black dots represent a succession of pillar boxes. It will be seen that a postman, starting from the circle, and going along the dotted lines, turns round 18 corners.

Can he take a course which involves fewer turnings?
[70]
Here is an ingenious paper and scissors puzzle:—

Divide a square card into three pieces, so that these can be reunited to form No. 2 or No. 3 of this diagram.
(From an old Sanscrit source, quoted by Longfellow in his “Kavanagh.”)
Ten times the square root of a flock of geese, seeing the clouds collect, flew to the Manus lake. One-eighth of the whole flew from the edge of the water among a tangle of water lilies, and three couples were seen playing in the water. Tell me, my young girl with beautiful locks, what was the whole number of geese?
[71]
| ♚ | |||||||
| ♖ | ♘ | ♖ |
Leaving the Black King in his position, place the three white men so that he stands checkmated.
An American paper published the following:—
Next day this parody appeared in a rival paper:—
Can you fill in the missing words?
[72]
If we look with one eye only, or with eyes half-closed, at these groups of circular dots, they assume the appearance familiar to us in honeycomb. This is an effect of the contrast and opposition of the black and white in the sensation of the retina.

Although the black and the white circles are of the same diameter the irradiation is in their case so intense that the white circles appear to be larger than the black.
[73]
This excellent illusion appeared in a recent number of the “Strand Magazine”:—
Most persons will at first see the passages under these arches as running upwards from left to right, but presently, as their line of vision shifts, the arches will take a downward course from right to left. This very curious effect will well repay a little patience, if it is not realised at once.
I have 91 bananas on my barrow, of two qualities; some I sell at four a penny, and the better sort at three a penny. If I had sold them in mixed lots at seven for twopence, I should have made a penny more. How many were there of each quality?
[74]
The Puzzle Problem—
A passenger in a first-class railway carriage notices that the top of a factory window due S.W. of him coincides with a mark on the carriage window, and does not move from it while the train is running five and a half miles.
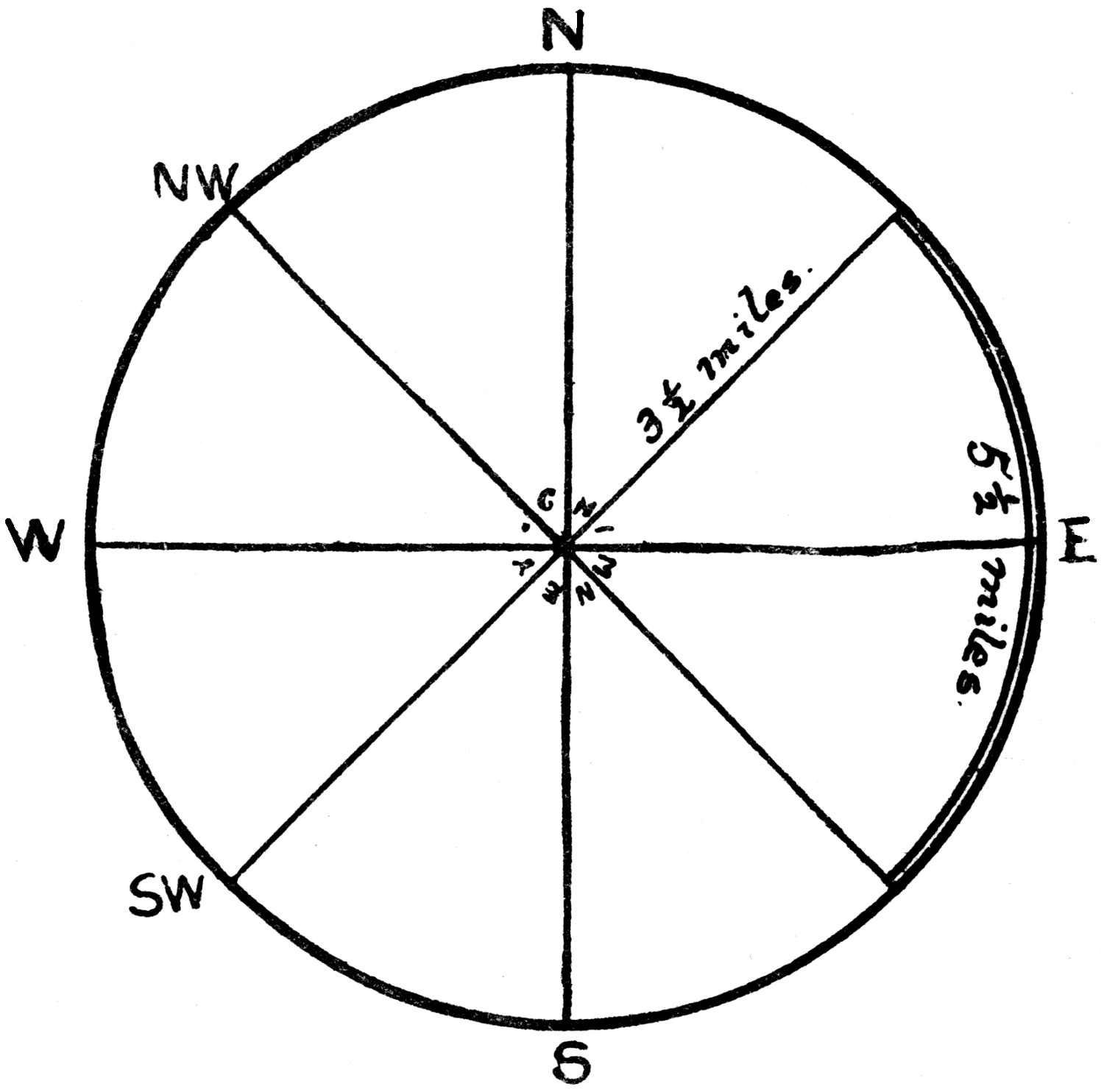
At the end of that distance the compass bearing of the chimney is due N.W. How far was the passenger from the chimney when he first noticed it?
is solved by 31⁄2 miles.
We give a diagram to make the points clear.
As the chimney top does not move from its place on the window, it is clear that the train is running on a segment of a circle having the chimney for its centre. It follows that the observer’s distance throughout is equal to the radius of that circle, and the radius of a circle of which the quadrant measures 51⁄2 miles is 31⁄2 miles within about 11 ft.
[75]
The cross had been taken out from the centre of this flag, and its owner, who had an ingenious turn of mind, found that by cutting what remained into two pieces, and rejoining them, he could make it into a perfect flag without any waste of material.
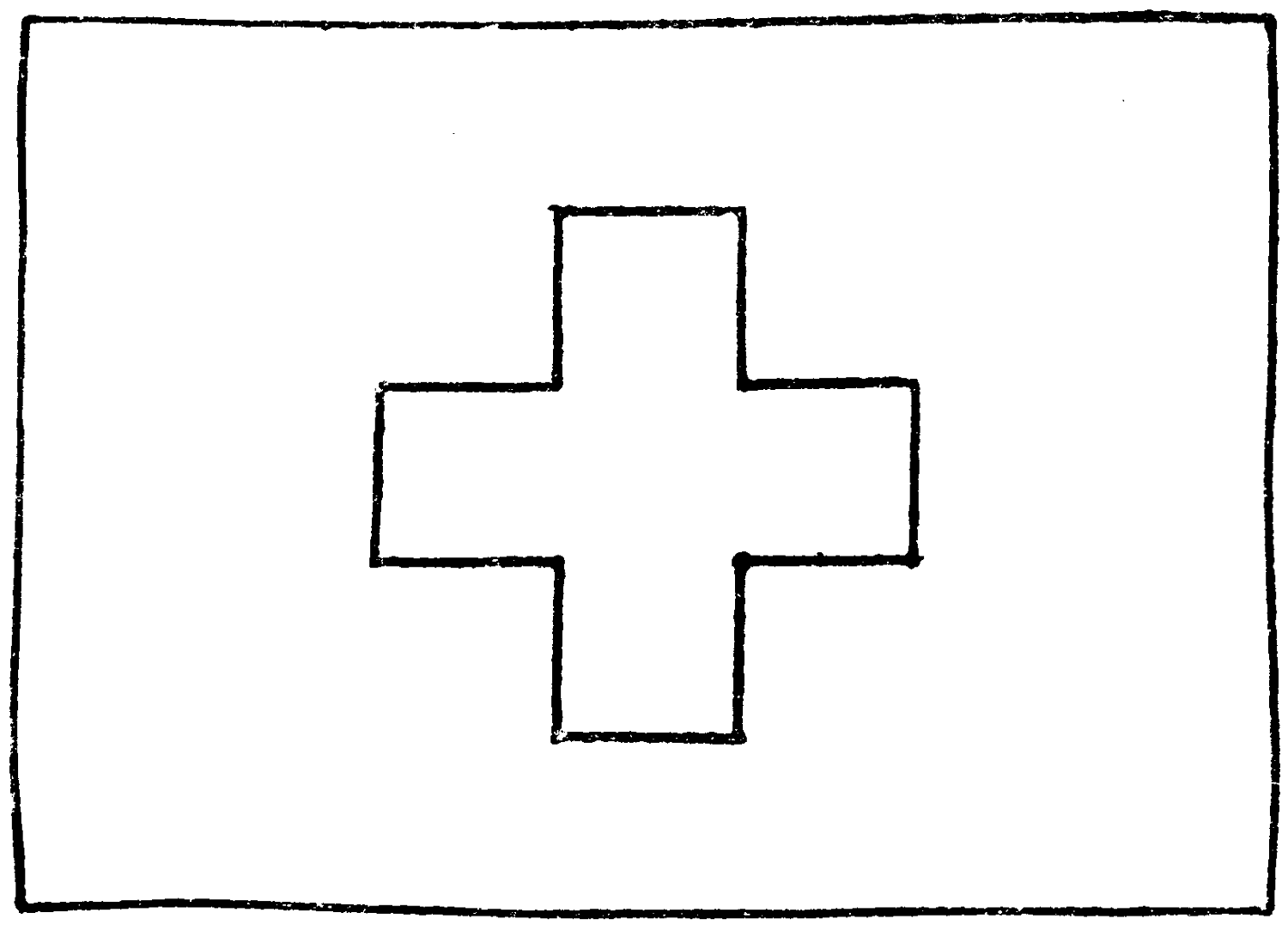
How did he accomplish this?
[76]
Add two more pieces similar in shape and size to that marked A, and one similar to B, C, and D respectively, and then readjust the eleven parts so that they form a perfect square.
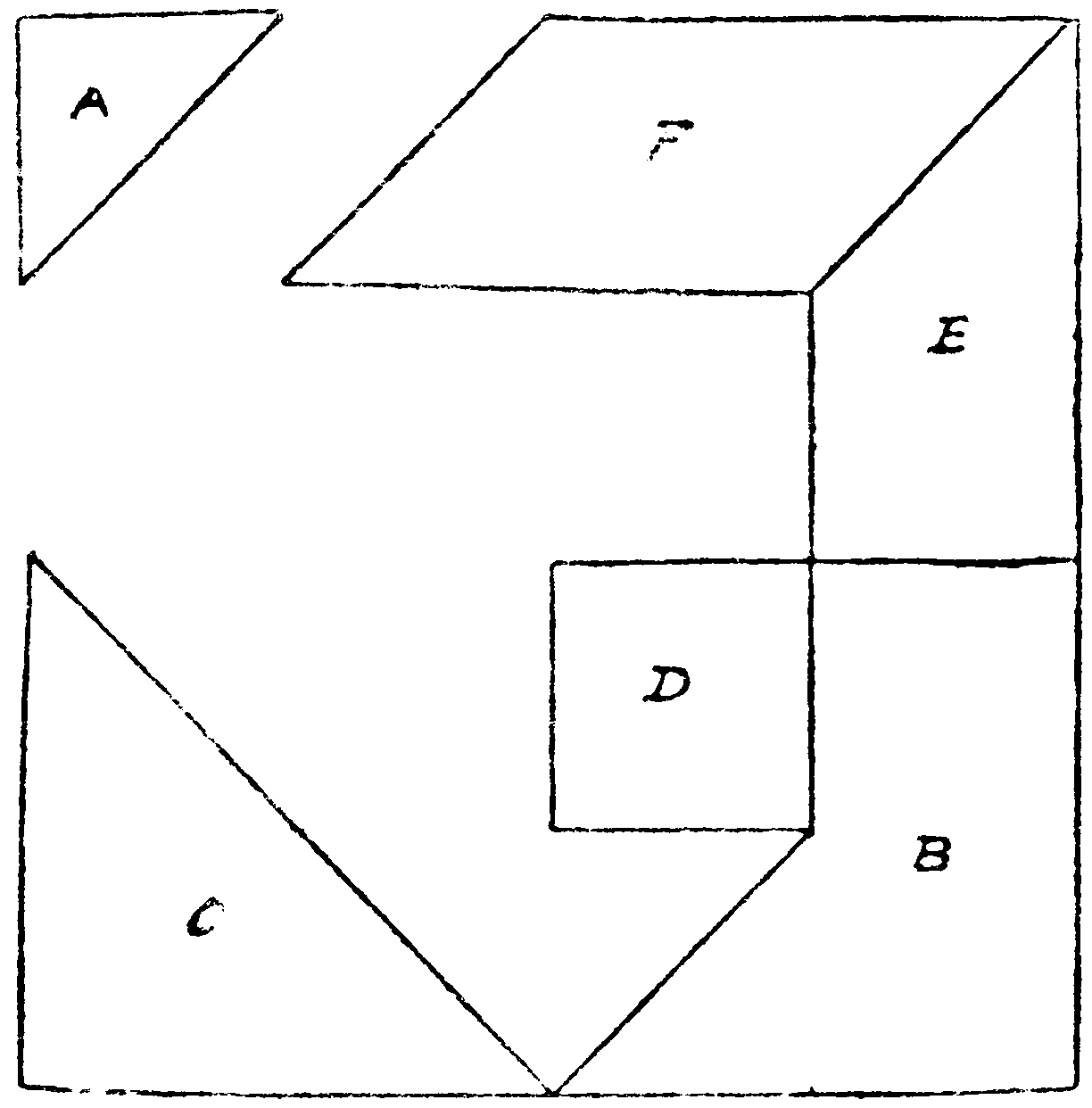
The missing words are spelt with the same letters.
[77]
This is a simple arrangement of eight matches, by which two squares and four similar triangles are formed.
Three towns are buried in these lines.
[78]
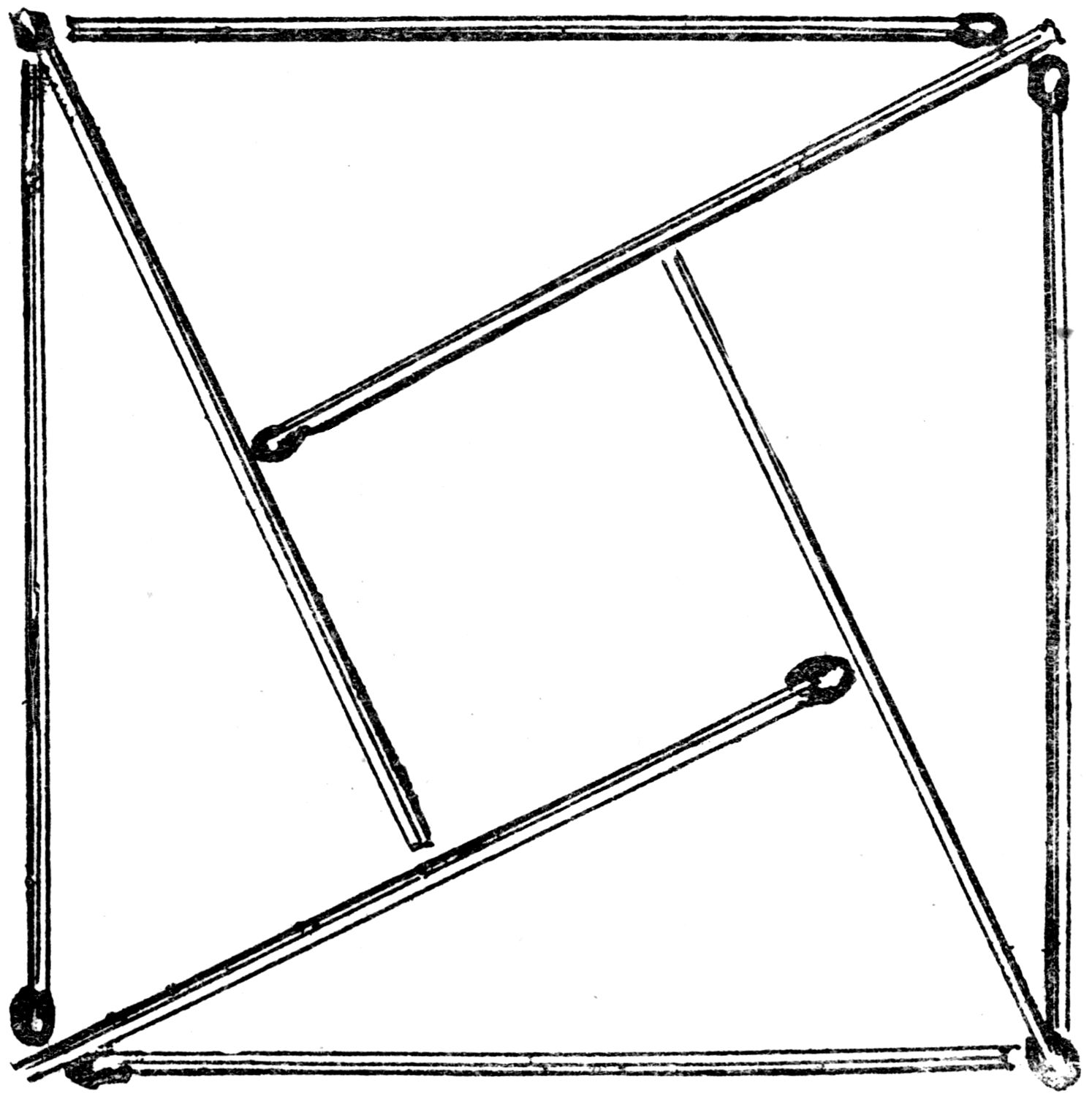
A hospital was built in six detached blocks, and it was the duty of the night watchman to go completely round every block at fixed hours to see that all was safe.
What was his shortest course?
[79]
Can you rearrange the twelve counters on this board of 36 squares so that there are two counters on each row, column, and diagonal?
| ◎ | ◎ | ◎ | ◎ | ◎ | ◎ |
| ◎ | ◎ | ◎ | ◎ | ◎ | ◎ |
There must not be more than these two counters in the same straight line.
[80]
This is a course by which the queen on a chessboard, starting from K R sq., passes over every square in fourteen moves.

“Did you score a score?” said Funniman to his schoolboy nephew, after a local cricket match. “No, uncle,” said the youngster, “but if I had made as many more runs, half as many more, and two runs and a half, I should have made my twenty.” How many runs did he get?
[81]
In the “Twentieth Century Standard Puzzle Book” we gave a figure similar to this, in which there were 653 interlacing triangles in four tiers of this character.
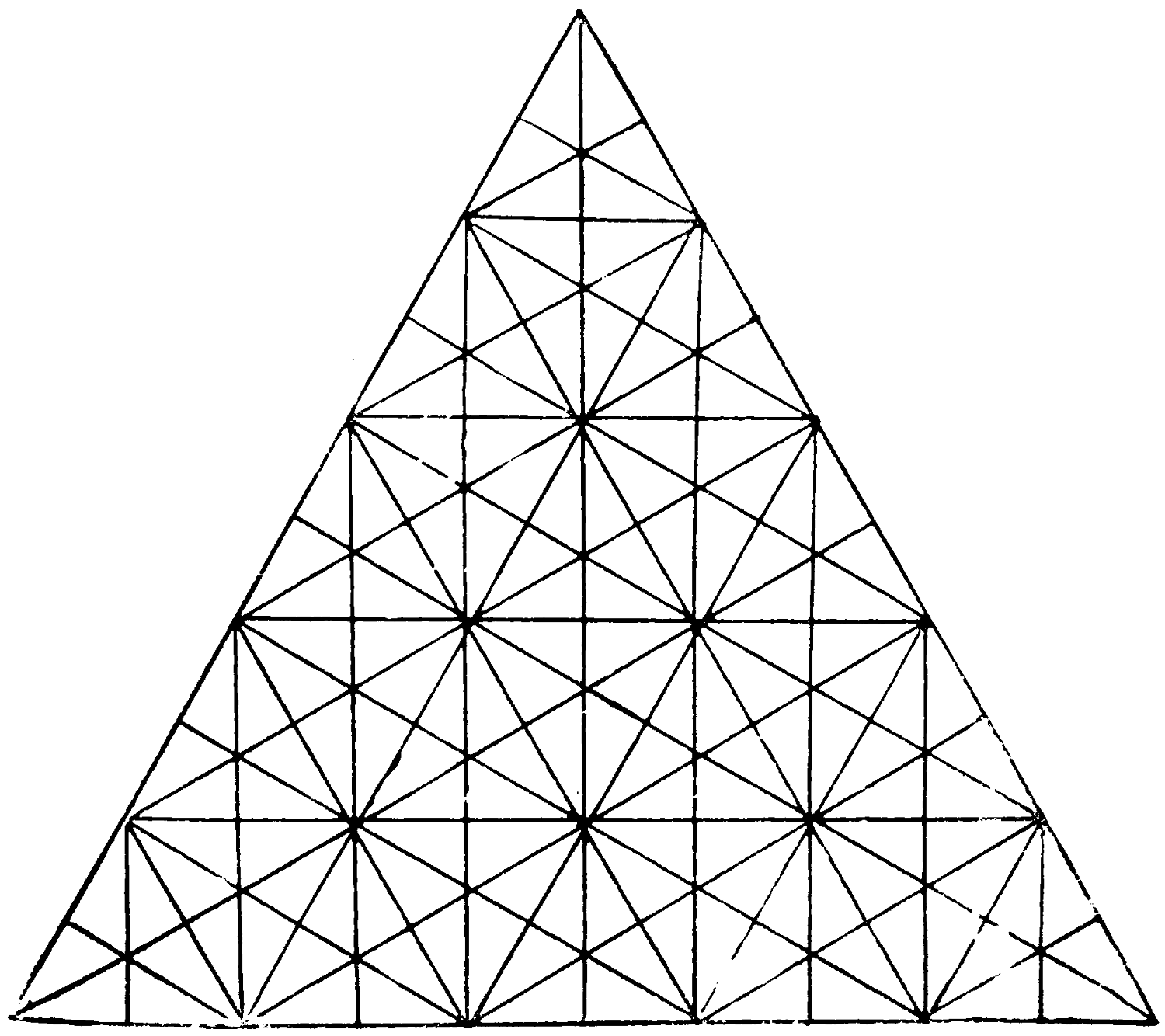
We now add a fifth tier at the base, and ask our solvers to determine how many triangles of all shapes and sizes can be counted within its enlarged borders.
[82]
Place eight matches in a row, about an inch apart, as indicated in the diagram.

The puzzle is to form these into four pairs in four moves, by moving one match clear over two matches every time.
[83]
Place twelve matches, as is shown in the diagram, so that they form four squares.
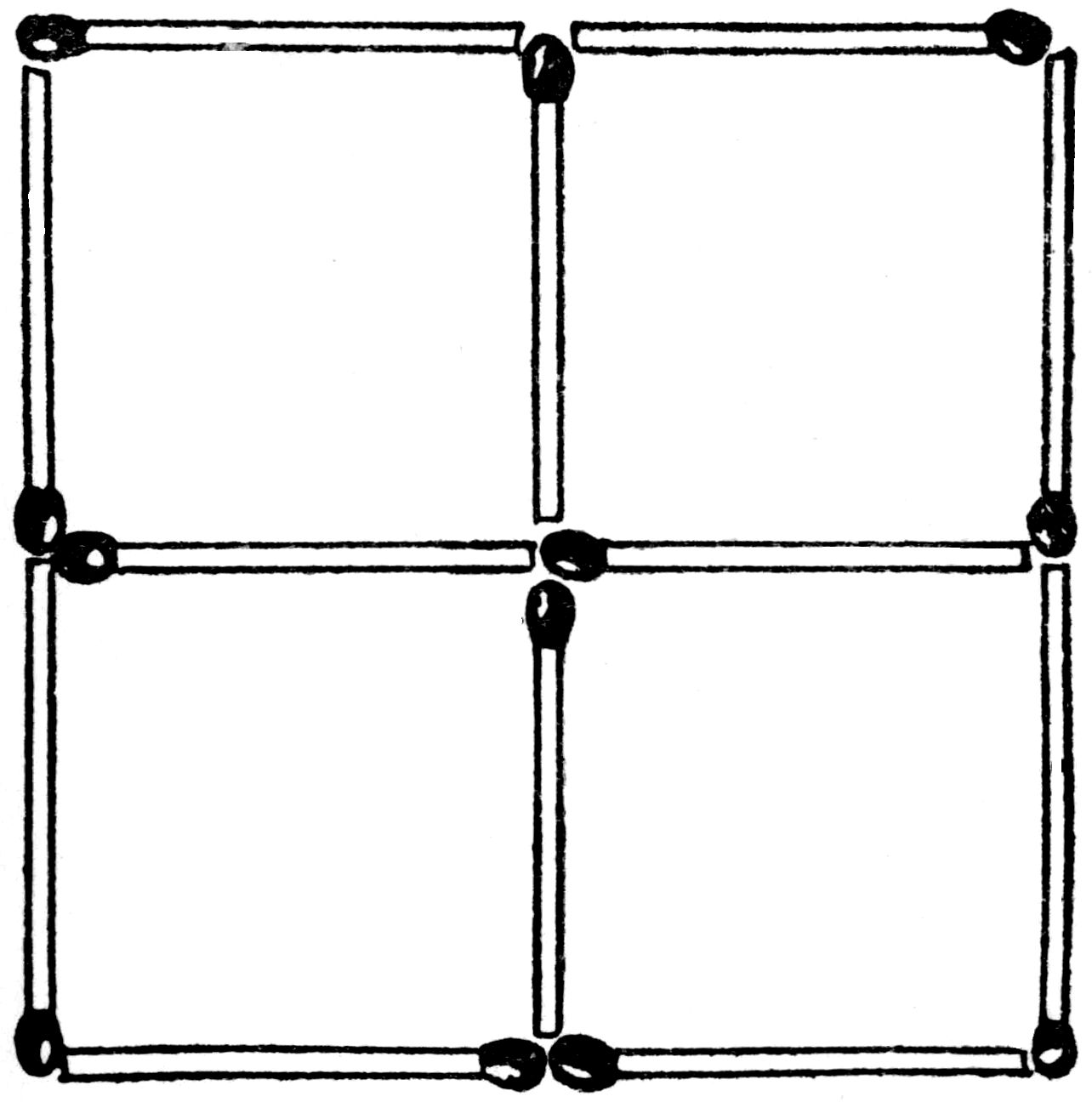
Now remove three of the matches, and readjust the nine that remain so that they represent three squares.
Edwin and Angelina were far apart, when this message, with its touch of jealous resentment, reached her on the wings of a Marconigram—
“No fickle girl is bonnie to my mind!”
Quite equal to the occasion, she flashed back the reply—
“In love inconstant I no pleasure find!”
How did these messages reveal the places from which they were despatched?
[84]
In the four corner and four central cells of this nest of squares four matches are so placed as to represent 1⁄2, 1, 4, 1⁄50, 11, 12, 41, and 49.
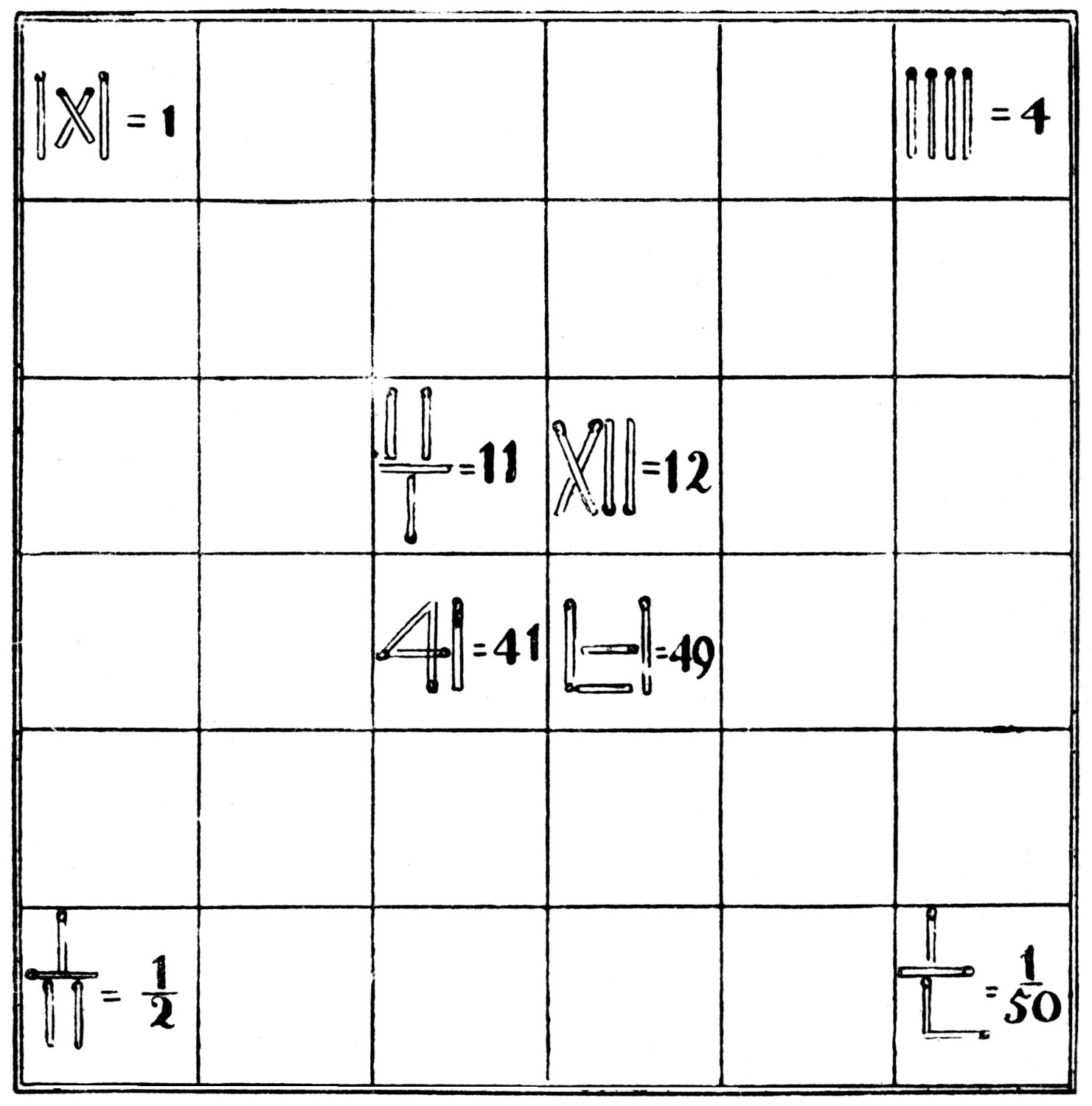
Can you, still using only four matches in each case, fit different whole numbers or fractions in similar fashion into the other 28 cells?
[85]
Can you complete the top and bottom rows, the two side columns, and the two diagonals of this square by forming in each of them the same sentence so that it can be read in twenty different directions?
| R | I | V | I | R | ||||||||
| I | I | I | I | |||||||||
| V | V | V | ||||||||||
| I | I | I | I | |||||||||
| R | I | V | I | R |
There are four words in the sentence of thirteen letters.
[86]
Ask anyone to fix upon a number between 1 and 60 inclusive, and to point out to you the square or squares in which it appears:—
| 3 | 5 | 7 | 9 | 11 | 1 | 5 | 6 | 7 | 13 | 12 | 4 | |
| 13 | 15 | 17 | 19 | 21 | 23 | 14 | 15 | 20 | 21 | 22 | 23 | |
| 25 | 27 | 29 | 31 | 33 | 35 | 28 | 29 | 30 | 31 | 36 | 37 | |
| 37 | 39 | 41 | 43 | 45 | 47 | 52 | 38 | 39 | 44 | 45 | 46 | |
| 49 | 51 | 53 | 55 | 57 | 59 | 47 | 53 | 54 | 55 | 60 | 13 |
| 9 | 10 | 11 | 12 | 13 | 8 | 3 | 6 | 7 | 10 | 11 | 2 | |
| 14 | 15 | 24 | 25 | 26 | 27 | 14 | 15 | 18 | 19 | 22 | 23 | |
| 28 | 29 | 30 | 31 | 40 | 41 | 26 | 27 | 30 | 31 | 34 | 35 | |
| 42 | 43 | 44 | 45 | 46 | 47 | 38 | 39 | 42 | 43 | 46 | 47 | |
| 56 | 57 | 58 | 59 | 60 | 13 | 50 | 51 | 54 | 55 | 58 | 59 |
| 17 | 18 | 19 | 20 | 21 | 16 | 33 | 34 | 35 | 36 | 37 | 32 | |
| 22 | 23 | 24 | 25 | 26 | 27 | 38 | 39 | 40 | 41 | 42 | 43 | |
| 28 | 29 | 30 | 31 | 48 | 49 | 44 | 45 | 46 | 47 | 48 | 49 | |
| 50 | 51 | 52 | 53 | 54 | 55 | 50 | 51 | 52 | 53 | 54 | 55 | |
| 56 | 57 | 58 | 59 | 30 | 60 | 56 | 57 | 58 | 59 | 60 | 41 |
You can find the number at a glance, by simply adding together the numbers in the right-hand top corner cells of the square indicated. Thus, if 45 has been chosen, 32 + 8 + 4 + 1 = 45.
[87]
Here is a little subtraction sum, which is not quite so simple as it appears to be:—
| miles | furlongs | rods | yards | feet | inches | |||||||
| 1 | „ | 0 | „ | 0 | „ | 0 | „ | 0 | „ | 0 | ||
| 7 | „ | 39 | „ | 5 | „ | 1 | „ | 5 | ||||
Try it as it stands, without reducing the distance to inches.
Can you, by supplying the missing words, turn a grilse into a salmon? One letter is changed each time, and, except in one case, the order of the letters varies:—
[88]
These are the arrangements of the nine digits, by which they add up alike in rows, columns, and diagonals in a square; on all sides in a triangle; and from top to bottom and from side to side in a cross:—
|
|
|
The totals are 15, 20, and 27 respectively.
HAATTCEUMSSSS
The question was asked in a puzzle competition—“Why is every angler ipso facto an Ananias?” Although no such method was asked for or expected, we find that the very letters of the question can be recast into a most apposite reply. Our answer by anagram runs thus—
A liar, .. ..... gay fancies to a ..... ....
Can you complete the sentence by filling in the missing words?
[89]
On a board of sixty-seven squares, arranged as is shown in the diagram, place nine counters, so that no two are in the same row, column, or diagonal.
The indentations do not affect the simple conditions.
[90]
Can you arrange these nine cards so that they form ten rows with three cards in each row?
| A ♣ |
||||||
| A ♢ |
10 ♡ |
A ♠ |
||||
| Q ♠ |
K ♣ |
K ♢ |
J ♢ |
|||
| K ♡ |
||||||
This may, of course, be done with any nine cards.
Separate these strings of letters into words that scan and rhyme, adding the same missing letter in 55 places.
[91]
Two ladies and their squires, here represented by the White Knights and the Black, were dressed to impersonate Light, Liberty, Love, and Learning, and took their places on the corners of a pavement chequered to represent a chessboard, as is shown below:—
| ♘ | ♞ | ||||||
| ♞ | ♘ |
They undertook to step a figure which should exhibit at each pause a revolving square, and in three paces bring them together in the centre, by a course traced upon the lines of their combined monograms. What were their successive steps?
[92]
Can you disentangle all this good advice?
| tell | you know | tells | knows | tells | he should not |
| do | you think of | does | thinks of | does | is not good |
| believe | you hear | believes | hears | believes | is false |
| spend | you have | spends | has | spends | he needs |
| judge | you see | judges | sees | judges | is not there |
| never | all | he who | all he | often | what |
It forms 5 excellent maxims in its 36 cells.
[93]
Study this quaint figure carefully, and try to discover how it can be divided into two pieces, so that these can be reunited to form a perfect circle.
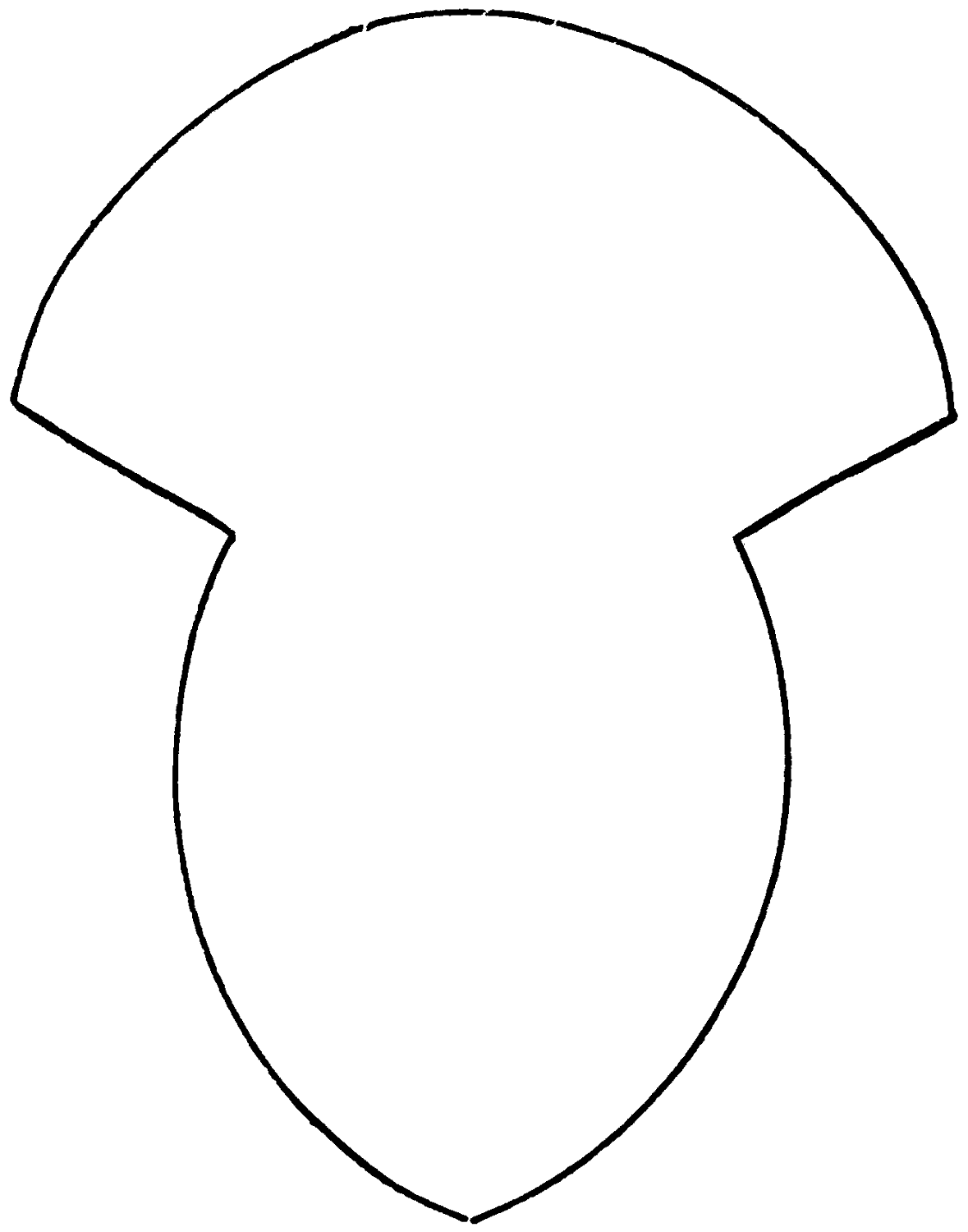
[94]
When Tommy was offered all the money by his uncle if he could place 15 half-crowns and 15 pennies in such order in a circle that, counting always by nines, and starting at a fixed point, he came always upon a penny, and removed it from the circle, he found the key to success in this Latin line, given to him by a school friend, who shared the spoil—“Populeam virgam mater regina ferebat.” The vowels, from a to u, are numbered from 1 to 5, and when they are thus marked in the sentence—
| “ | P | o | p | u | l | e | a | m | v | i | r | g | a | m | m | a | t | e | r | r | e | g | i | n | a | f | e | r | e | b | a | t | , | ” | ||||
| 4 | 5 | 2 | 1 | 3 | 1 | 1 | 2 | 2 | 3 | 1 | 2 | 2 | 1 | |||||||||||||||||||||||||
they show the necessary sequence of half-crowns and pennies.

Start counting with the half-crown marked a, and remove each penny as you come to it on counting up to nine, and the conditions are fulfilled.
[95]
This smart advertisement of a polish known as “Old Dutch Cleanser” appeared in an American paper:—
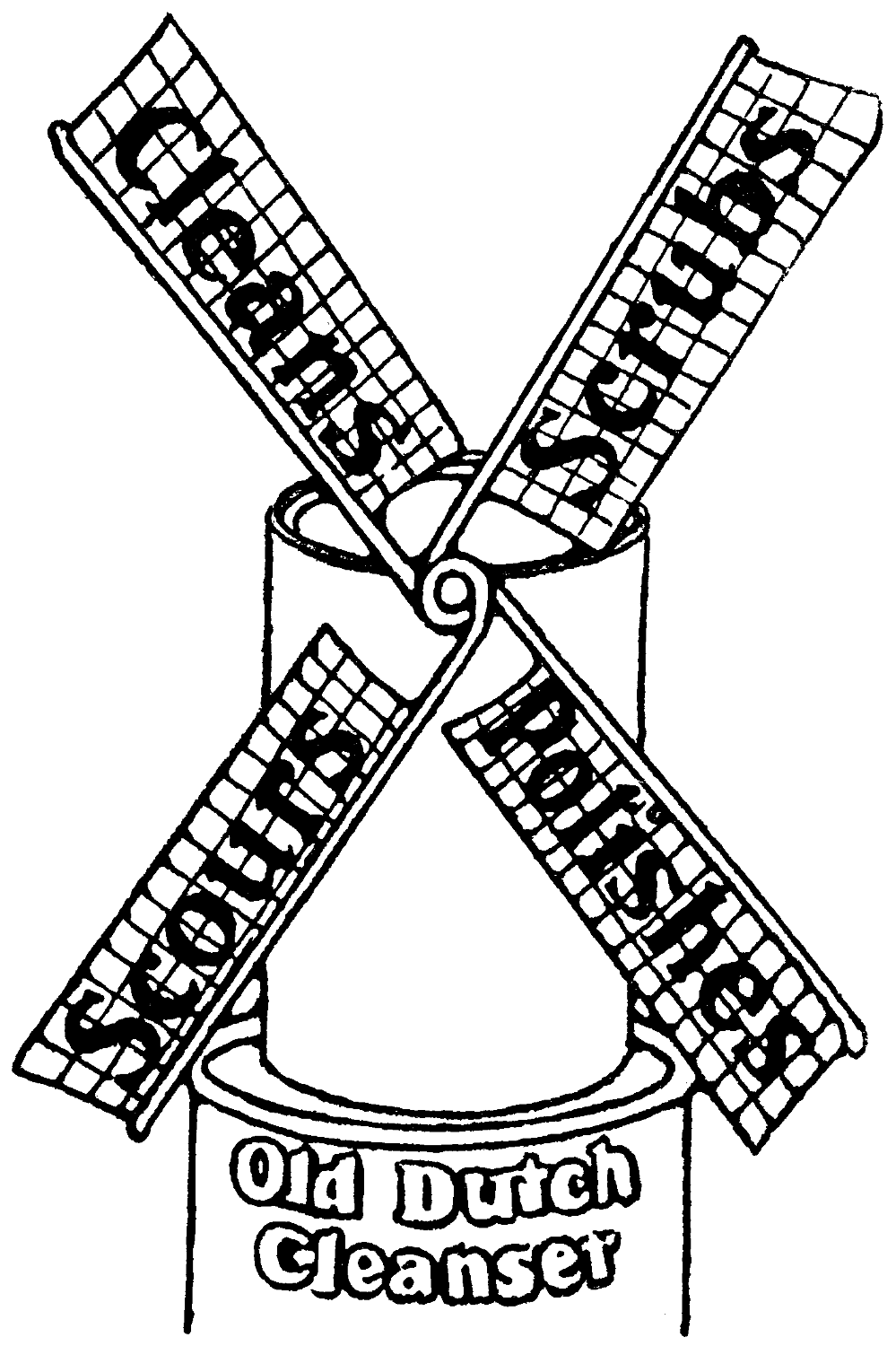
Cleans Scrubs
Scours Polishes
Old Dutch
Cleanser
If the eyes of the proprietor should fall upon this column, he will be surprised to find that his catch words Cleans, Scrubs, Scours, Polishes, can be recast into a perfect anagram, singularly appropriate to the powder advertised.
The opening words of the anagram are “O rub on, sir.”—Can our solvers complete the sentence?
[96]
Replace all these 51 pieces on the chessboard, so that no Queen attacks another Queen, no Rook another Rook, no Bishop another Bishop, and no Knight another Knight.
| Q | Q | Q | Q | Q | Q | Q | Q |
| B | B | B | B | B | B | ||
| B | B | ||||||
| B | B | B | B | B | B | ||
| R | R | R | R | R | R | R | R |
| Kt | Kt | Kt | Kt | Kt | |||
| Kt | Kt | Kt | Kt | Kt | Kt | Kt | Kt |
| Kt | Kt | Kt | Kt | Kt | Kt | Kt | Kt |
No account is to be taken of the intervening pieces, but each type of piece is to be considered as if it stood alone upon the board.
[97]
Here is a beautifully symmetrical specimen of the Knight’s tour:—
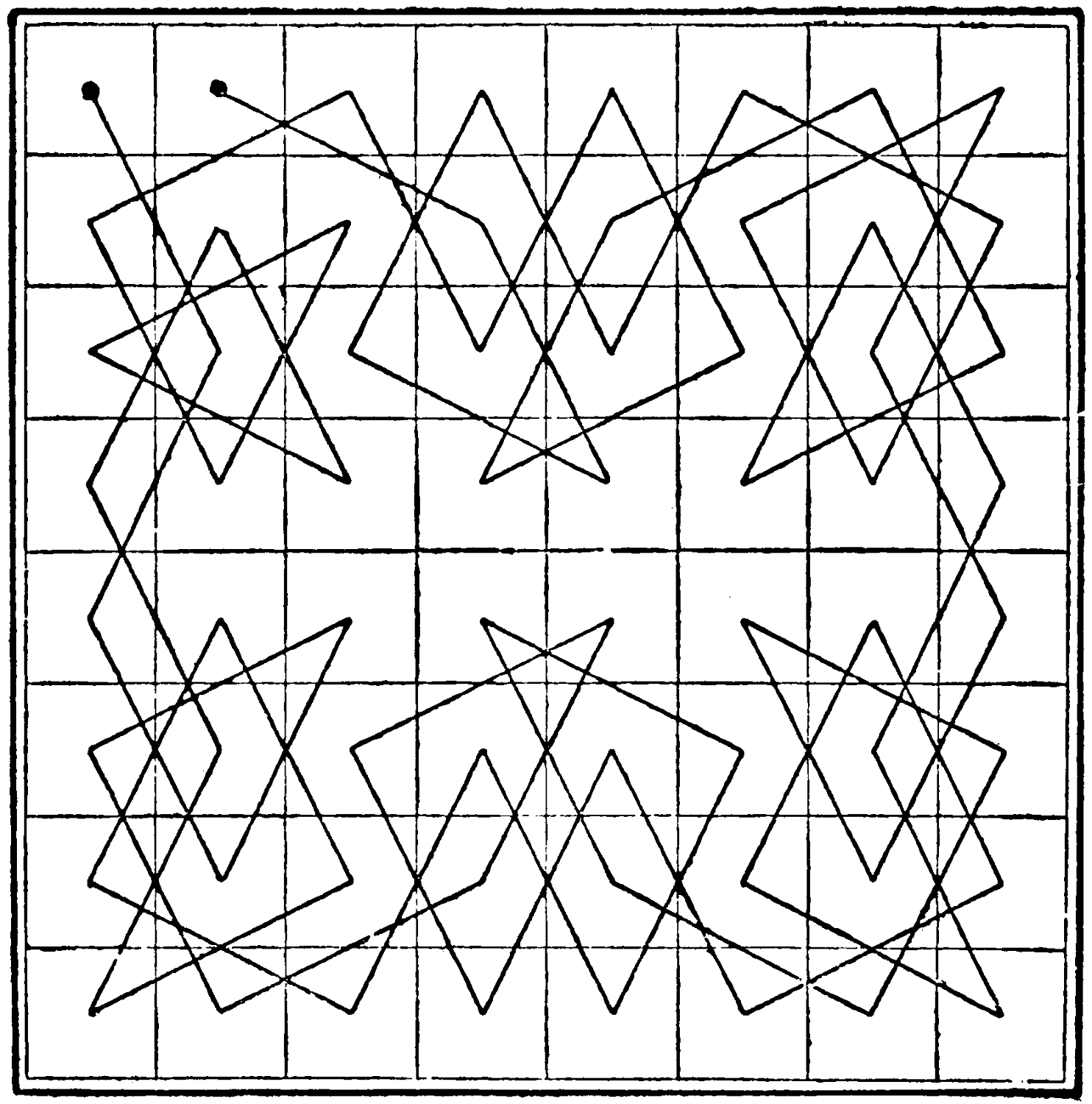
[98]
Here is another beautifully symmetrical Knight’s tour:—

It starts from the corner square, and the second half of the course has dotted lines.
The missing words are spelt with the same six letters.
[99]
Here is quite a curious pattern described by another Knight’s tour:—

[100]
Here is a very symmetrical Knight’s tour, in which half of the moves are indicated by dotted, and half by unbroken lines:—
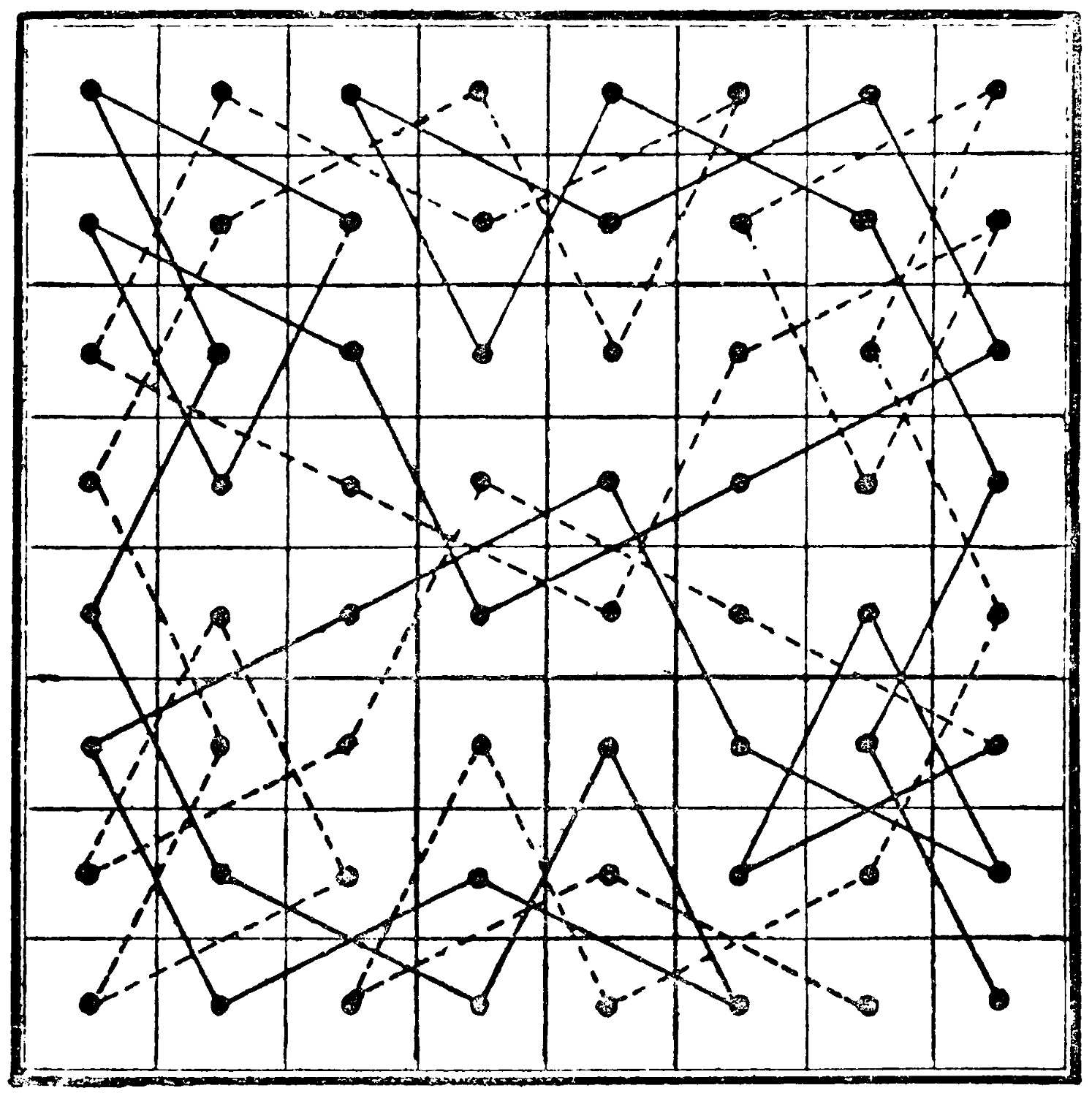
The letters of this sentence “Arrive to vote at it,” can be so recast as to form two palindrome words, or words that read alike from either end. What are they?
[101]
Here is another specimen of the Knight’s tour, which is beautifully symmetrical—
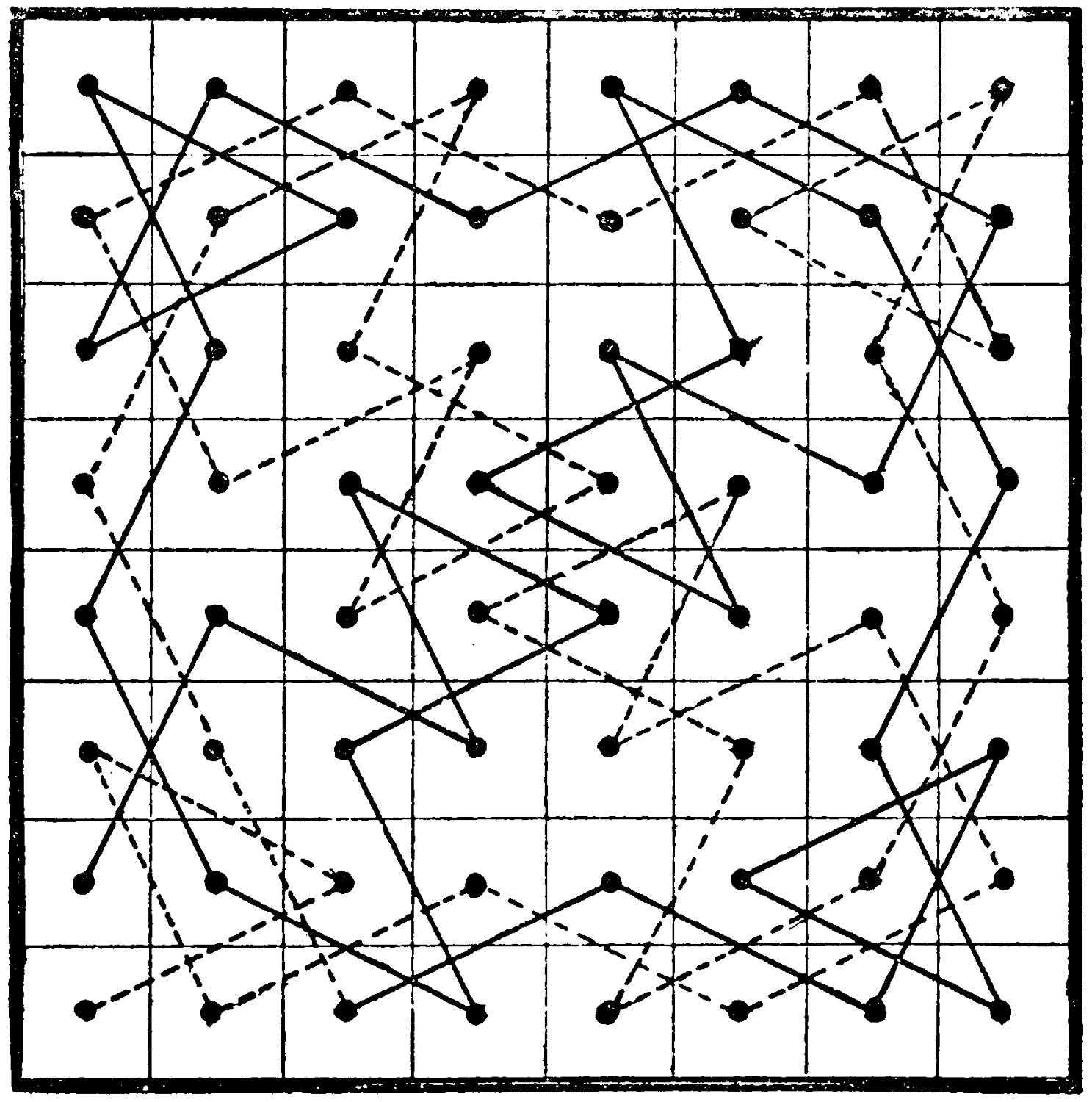
Half of the course is marked with dotted lines.
[102]
On the board below a verse of eight lines runs on the course of a Knight’s move from square to square:—
| sor | to | king | good | say | luck | loy | eth |
| and | moth | a | soon | dis | our | to | bad |
| place | ry | church | his | force | is | hat | al |
| er | queen | him | wight | he | to | may | truth |
| man | his | and | and | chess | es | knight | op’s |
| a | sneer | the | and | un | lawn | of | tates |
| cas | that | at | less | pawn | no | bish | lant |
| eth | faith | tles | hath | the | gal | in | love |
Can you disentangle the little poem?
“Dad,” said little Tommy, “give me as much as I have in my purse, and I will put a shilling in my money-box.” This was done, and the process was repeated for three more days. How much had Tommy originally in his purse, which was now quite empty?
[103]
This is the way to draw three rabbits so that they have but three ears among them all:—

[104]
On this table is shown in ten different ways how exactly 100 can be arrived at by the use of the nine digits, each appearing only once.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 4 | 95 | 3⁄7 | 56 | 98 | 6 | 15 | 15 | ||||||||
| 3 | 45 | 53 | 4 | 16⁄28 | 34 | 1 | 2 | 2 | 36 | ||||||||
| 5 | 7 | 6 | 7 | 3⁄6 | 8 | 79 | 47 | ||||||||||
| 8 | 9 | 8 | 1 | 27⁄54 | 9 | 8⁄4 | 98 | ||||||||||
| 9 | 62 | 71 | 98 | 1 | 6⁄3 | 2 | |||||||||||
| 26 | 38 | 29 | 2 | 3 | |||||||||||||
| 74 | 4 | ||||||||||||||||
| 75 | |||||||||||||||||
| 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |||||||||
| 9 × 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 100. | |||||||||||||||||
“If it were possible, I should choose,” said young Hopeful, “a life double as long.”
“Yes,” said old Sobersides, “and you might turn it to better account if it was also begun old.”
How did their actual words bear this out?
[105]
On a piece of clear tracing paper draw with pen and ink a close network of lines, such as is shown in this diagram, near enough together to conceal type of ordinary size.

Place this on the page of a book, and challenge any one to read a sentence, or even a word, through it, saying that you can do so easily. How can you succeed?
[106]
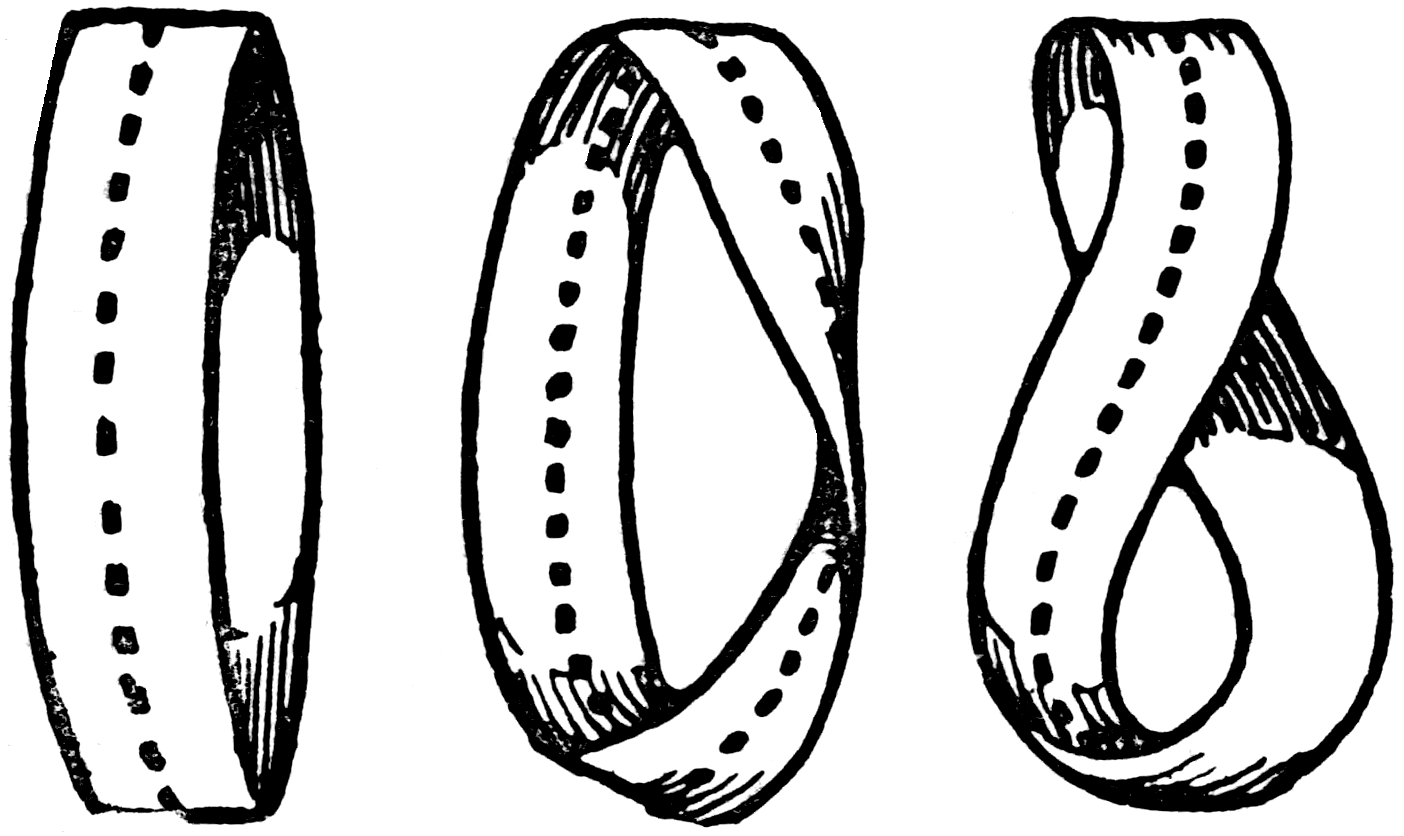
In the diagram a strip of paper is shown (1), with its ends simply gummed together; (2), with a single twist; and (3), with a double twist. Can you decide, without actual experiment, what will be the result in each case if these are cut completely round, as is indicated by the dotted lines?
How do the actual letters of these words in their union prove that anæsthetics are “blessed in pain?”
[107]
Make two parallel cuts with a penknife along the centre of a slip of leather or other material, and below them a hole of the same width. Pass a piece of string under the slit, and through the hole, and tie two buttons, each much larger than the hole, to the ends of the string.

How can the string be released without removing either of the buttons?
[108]
Fasten a pair of scissors securely with a piece of string to some convenient article, as is shown in this diagram:—
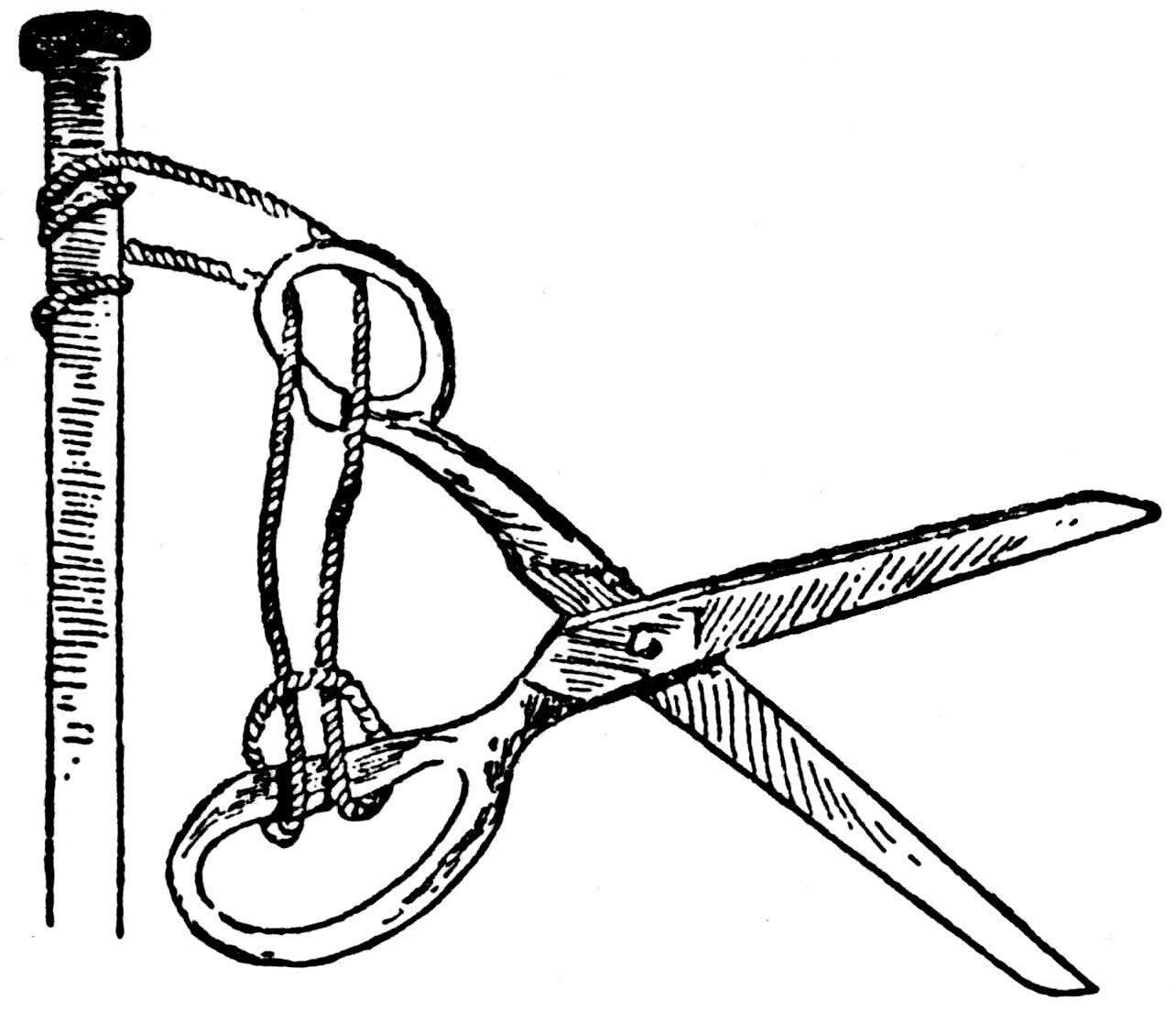
Can you release them without cutting or unfastening the string?
“What sin was it, sonny?” said an American negress to her lover, when she sat on his best hat, which was flattened. Wearily he heard her musical laugh, and arose to go. His hobby was botany, but not hers, for she was then a merry girl. “Bother the flowers! I would prefer this mellow pine-apple, Leonidas,” she said; “I guess we Ethiopians just love fruit!”
[109]
This diagram represents in the simplest outline a primitive wolf-trap.
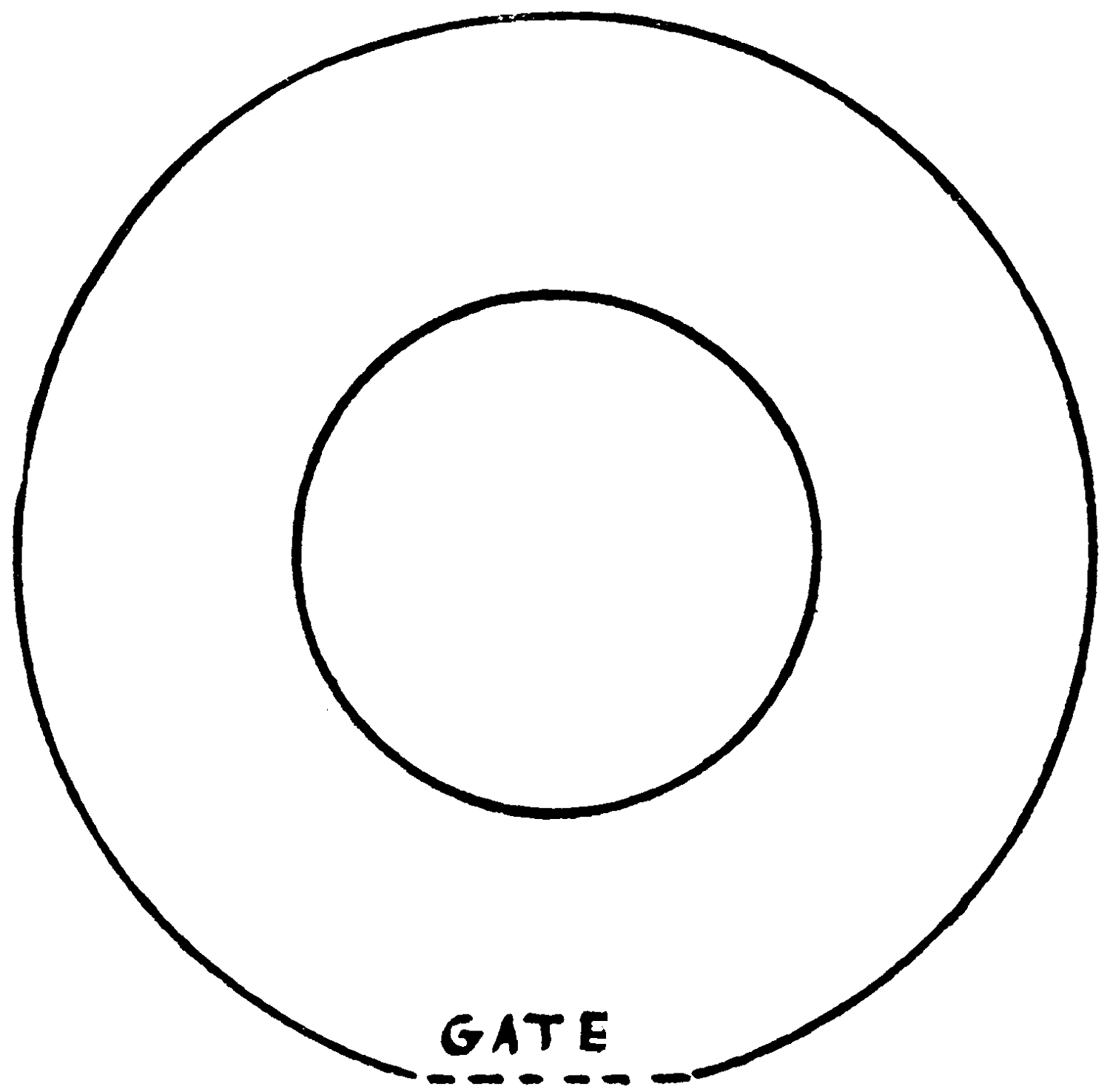
The dotted line is a gate opening into a circular enclosure. How was the trap set and the wolf caught?
What are the missing words?
[110]
To balance a needle on the head of a pin, push the pin into the cork of a wine bottle, and the needle into a separate cork.
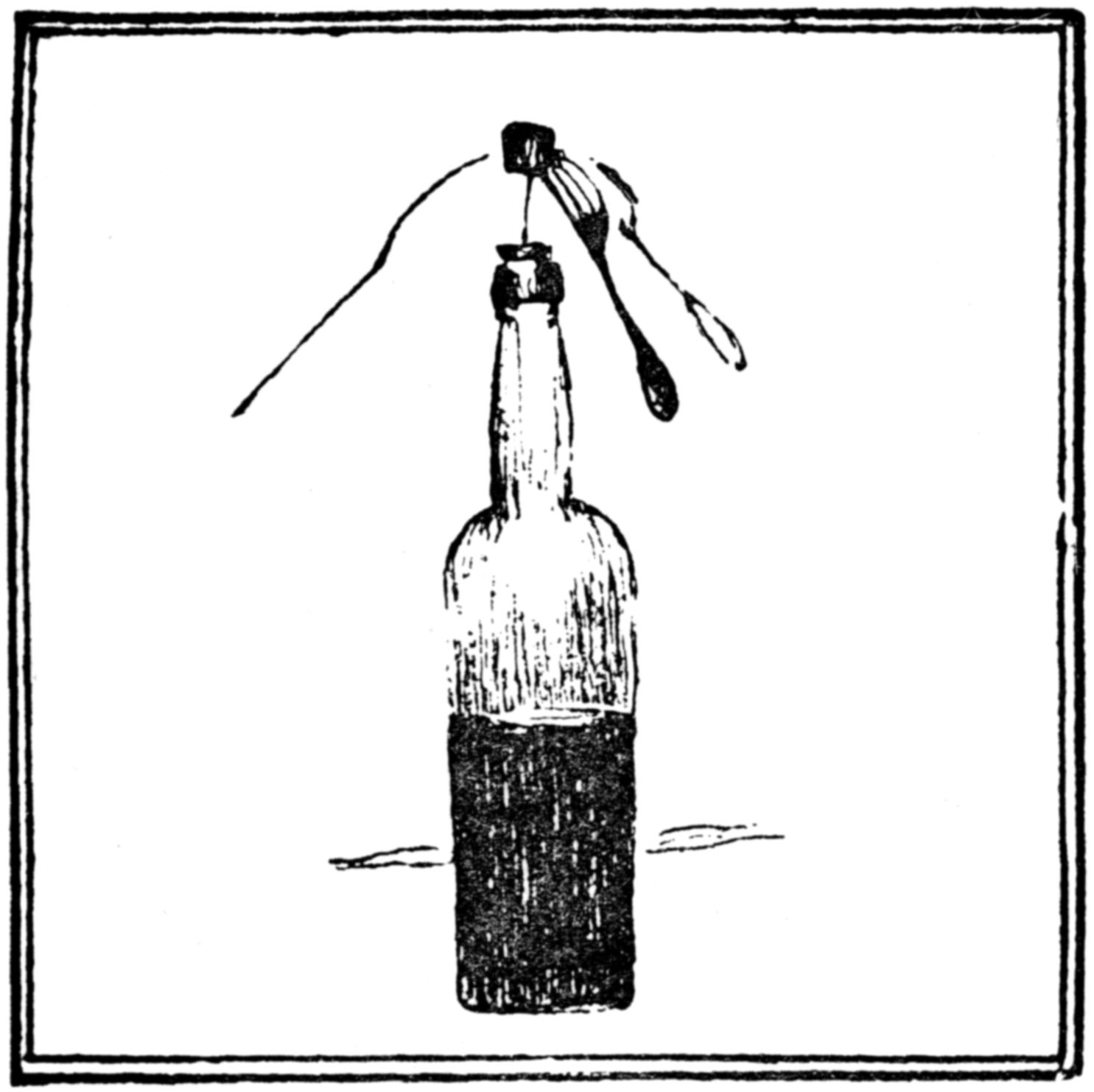
With the aid of three forks, as is shown in the picture, the needle may be balanced and spun round on the head of the pin.
Air—“Three fishers went sailing.”
Each missing word has the same six letters.
[111]
This diagram shows how, as an after-dinner trick, four similar wineglasses can be placed on the table

so that the centres of the lowest parts of their stems are equidistant from each other.
[112]
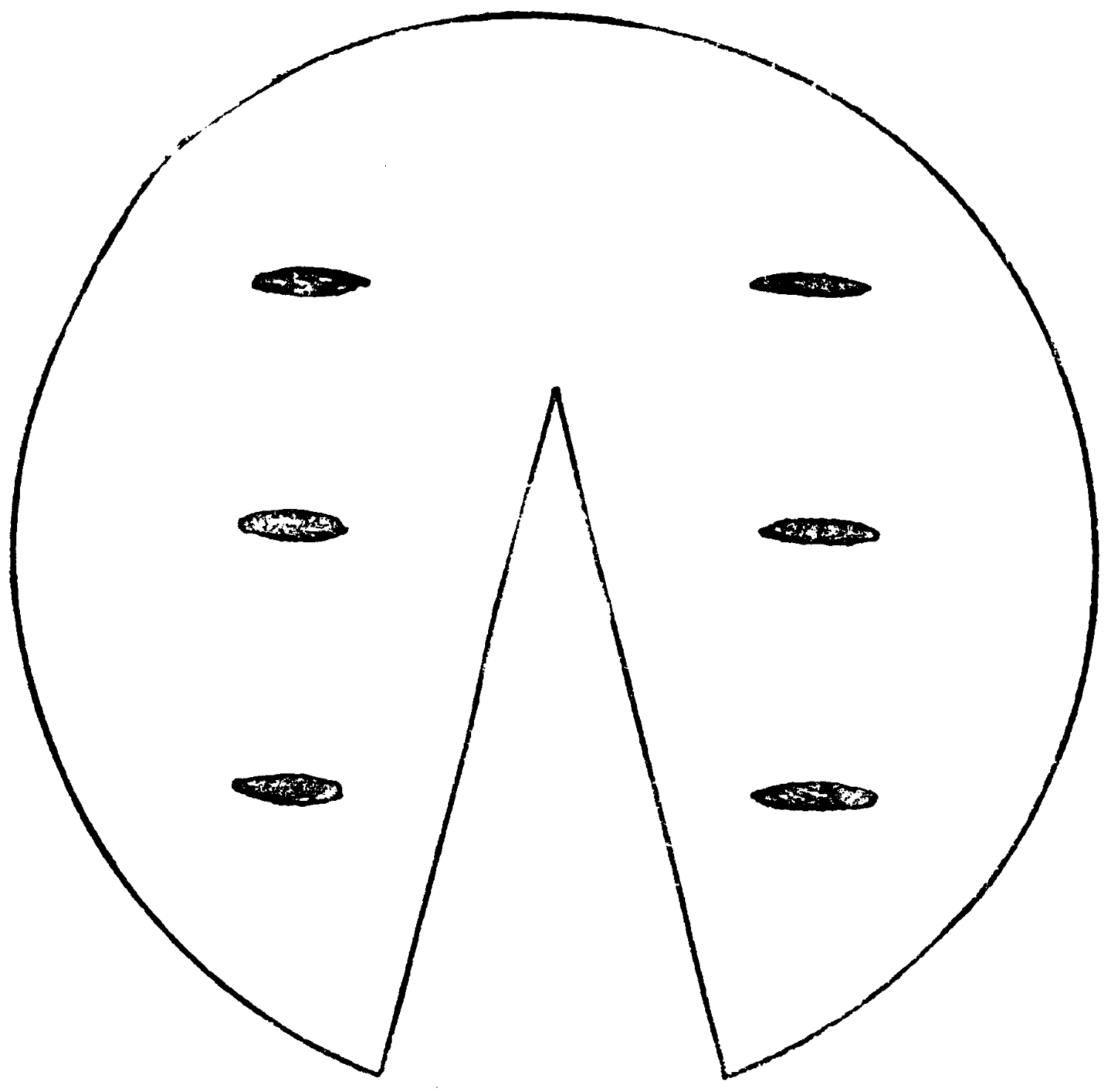
Ask any one, with this diagram to work upon, to think of any number between 5 and 15, and, while your back is turned, to count up to it, beginning at the lowest step, and saying one, two, three, four, and so on, as each step of cards or single card is reached in the direction indicated by the arrow. When the number thought of has been thus arrived at, tell him to stop, and beginning afresh on that card, to count one, two, three, etc., backwards, this time skipping over the double six and the 3 steps until he again reaches the number thought of, and notices which card he has touched last.
How can you, without having seen any of his movements, at once find that card?
[113]
Cut a wedge out of an apple, as is indicated in the diagram, and make six gashes as is shown.
When this has been done, challenge anyone to divide the apple into six pieces by only two straight cuts, so that there shall be one of the gashes in each piece.
[114]
Cut out in cardboard a boomerang as nearly as possible of the size and pattern given here:—

Place it flat on the back of the first three fingers of the left hand, sloping them upward; then flick it smartly with the second finger of the right hand. It will fly off and return to your lap. Try it.
Here are two simple sentences:—
A lamp shines out for thee.
Win me best by tears.
Can you recast the letters, so that they form the names of two of the most important buildings in London?
It was low tide; two children were throwing pebbles into the sea, and sending their excited collie in pursuit of them. The Puzzle Editor, who was on holiday, quickened perhaps by the salt air, bethought him of this appropriate riddle:—What is the difference between that dog and a hungry man?
[115]
Cut a radish in half, press the lower surface firmly against a plate, as is shown in the diagram:—

and you can lift the plate, to which it clings as closely as a boy’s wet leather disc to the pavement.
[116]
The countryman who cut one hole in his door for the cat and another for the kitten would find it difficult to pass a penny through a hole the size of a shilling cut in a stout piece of paper.
This diagram shows how easily it can be done:—
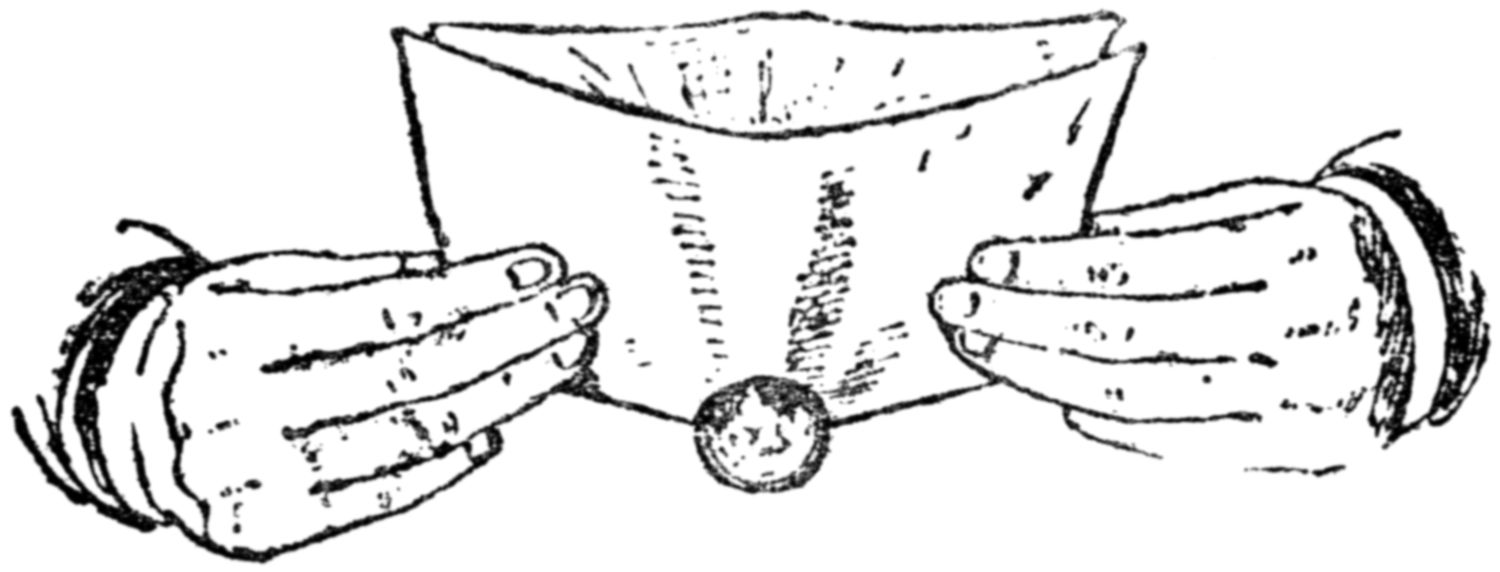
Fold the paper across the centre of the hole, place the penny in the fold, and bend the lower corners of the paper upwards. This elongates the opening, and the coin falls through.
One of the letters of the two short words is used twice in the longer word.
[117]
Place a sixpence on the tablecloth, and over it set a tumbler, as is shown in the picture below.

How can you pocket the sixpence without removing the glass, or having it removed?
abdeefiinnnoopprrrsssttuw
[118]
How can you draw such a spiral as this with very simple appliances?
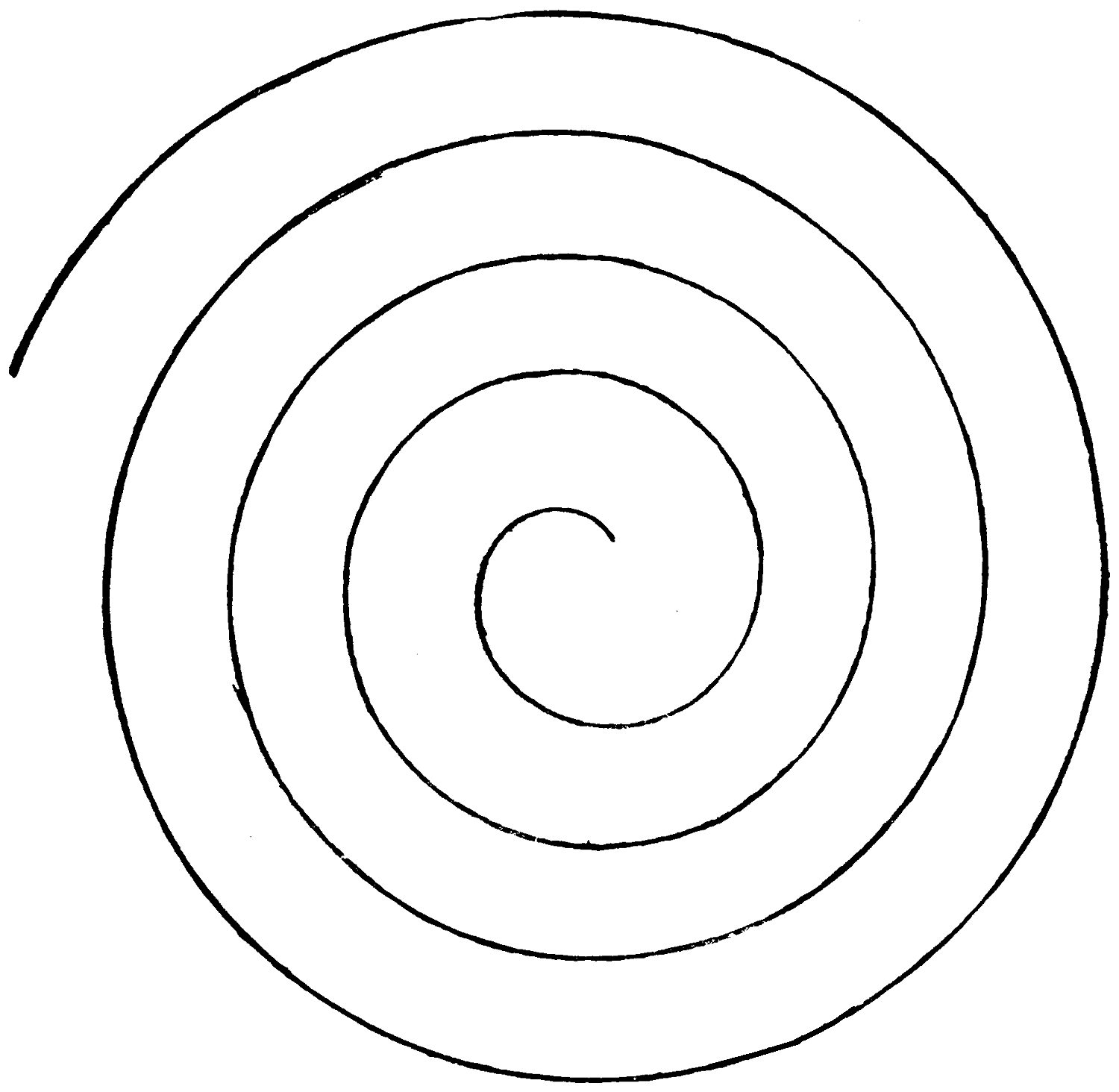
This spiral is drawn rapidly without removing the pencil from the paper.
[119]
Take a piece of stout paper or thin cardboard, about 10 in. by 8 in., and cut it as is shown below, removing the parts that are shaded in the diagram.

If you hold this between a plain wall, or other surface, and a strong light, you will, with a little practice, be able to cast a shadow similar to one or other of these Madonna heads, which will vary in intensity and expression with the positions of the paper and the light.
[120]
This excellent and easy little card trick will commend itself for fireside use in the long evenings.
Take the four Kings from a pack, and two other cards. Hold the Kings thus, in the form of a fan—

hiding the two other cards behind the King of Diamonds.
After showing them, place the six cards at the bottom of the pack. Now move the lowest card to the top, and the two next cards to any part of the pack, apparently leaving but one King at the bottom. Ask some one to cut the pack, and all the Kings will be found together. Some appropriate patter will help the effect.
Can you recast this sentence—
A defeat whose test is very sure—
so that the same letters form an appropriate proverb?
[121]
Its cells add up in columns and rows to 22, and those of the corner squares add up to 10 and 12 respectively.
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | |||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | |||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | |||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | |||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | ● | ● | ● | ● | ● |
[122]
This, though quite an old illusion, may be a mystery to some of our readers, so we give it a place among our many curiosities.

The table is placed on the middle of a platform, well away from the background, and the head, which is very much alive, is prepared to answer questions, or to whistle, or to sing, at the will of the audience. “How it is done” will be explained.
[123]
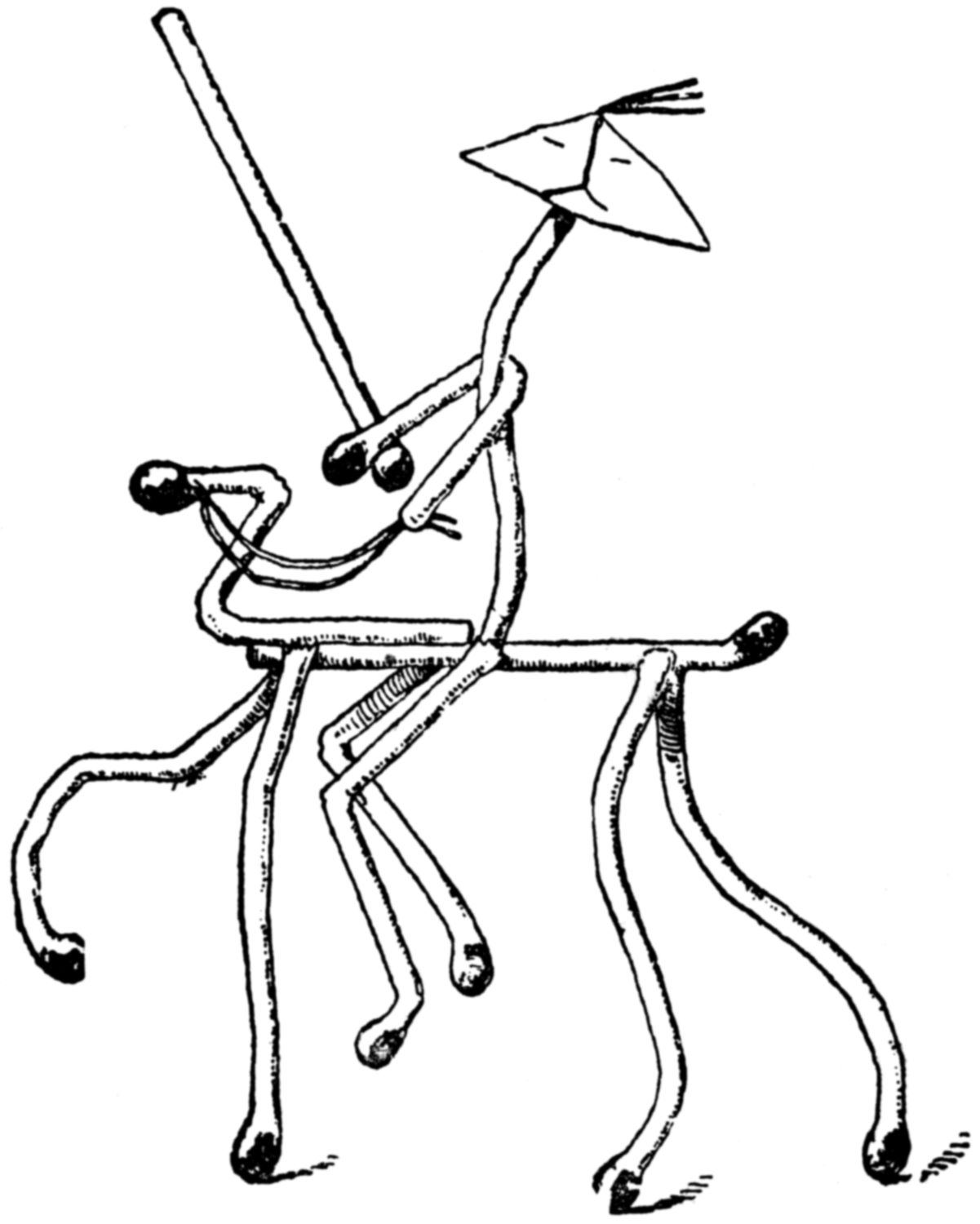
With a little ingenuity, and by slightly warming the wax, and shredding the matches for some effects, all sorts of comical figures can be contrived, similar in character to this dignified general on his high-stepping charger.
[124]
Cut out in cardboard a cross similar to that shown in this diagram:—
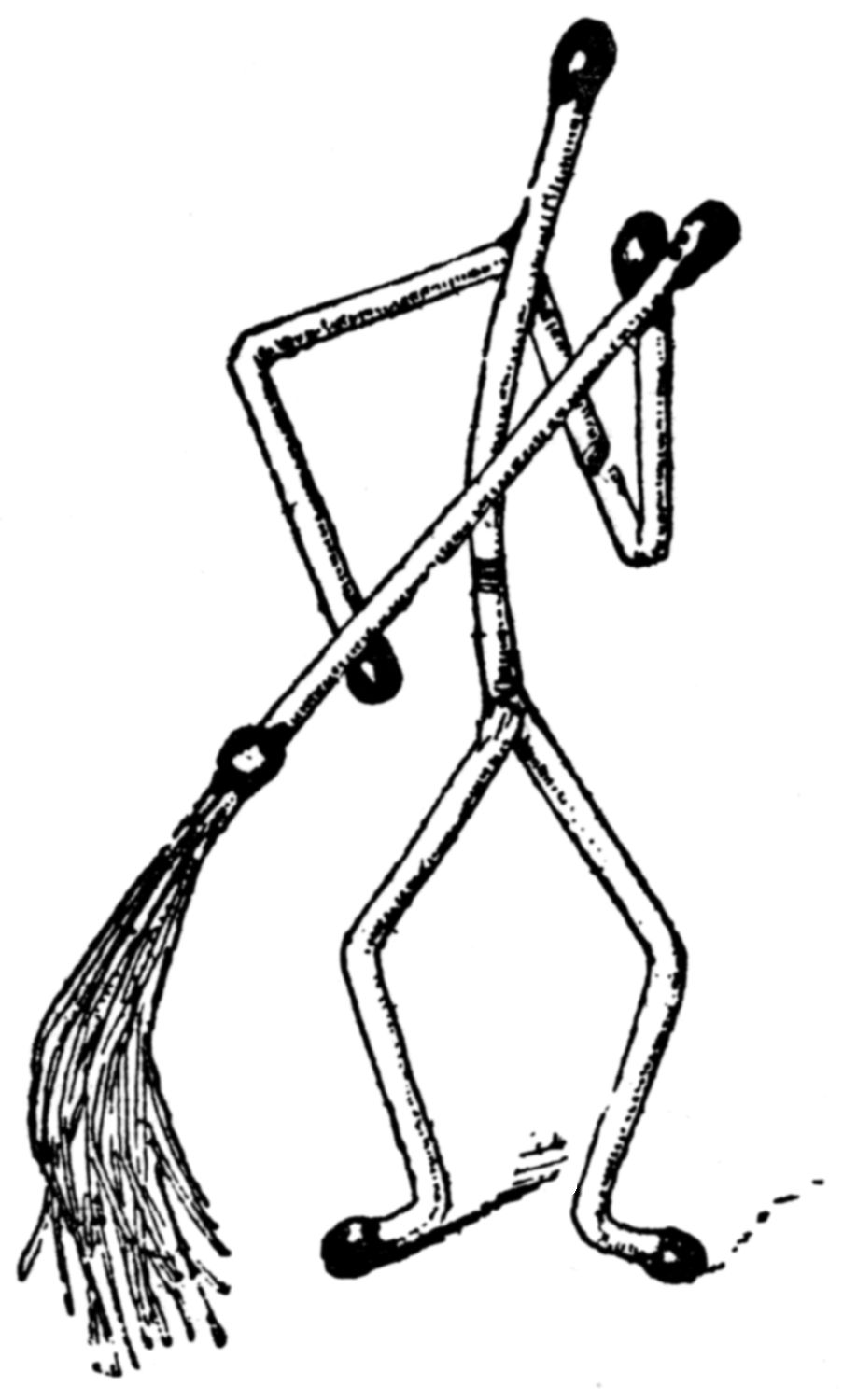
Place one of its limbs under the thumbnail of the left hand, and give the next projecting limb a sharp flick with the middle finger of the right hand. The little boomerang will fly sharply forward, and invariably return rapidly on its tracks. Try it.
Can you fill these gaps with words of similar sound?
The gaps in line 1 take words that sound alike; so do those in line 2; and so do the other three in lines 3 and 4.
[125]
Can you fill in the missing words so as to complete this picture charade?

Can you so deal with this as to form a rhyming couplet?
[126]
A good after dinner trick
Place four walnuts and four cobnuts in a row, as indicated on the diagram.

Now, moving always two that stand together, transfer them to some other positions along the line, and in four such moves leave them so that the large and small nuts range alternately. It may, of course, be done with large and small coins, or with other things that are at hand.
Here is another exercise in Doublets, from Lewis Carroll’s book on the subject:—
Turn ELM into OAK by seven links, introducing the name of another tree as one of them.
[127]
Can you read in this picture the question of our riddle?

1.
2.
[128]
Here is an excellent example of how a characteristic figure may be contrived by shredding, warming, and uniting a few wax matches:—
Many similar figures can be made by handy fingers.
[129]
An old book, published more than 100 years ago, gives the following samples of patterns which may be formed with very simple materials:—

All that is needed for this pastime is a set of 128 coloured triangles, 64 of each colour, with which an endless variety of patterns can be arranged by the exercise of taste and ingenuity.
[130]
How could a Girton girl retort, using the same words?
Can you dig out nineteen beasts that are buried in these lines?—
Ireland’s lot heals slowly. Troubles came long ago—at times in battalions—to attack and harass her. Ambitious democrats now countermine famous enthusiasts nearly akin to heroes. Anarchy enables cowards to sow hot terror and all amazement.
Can you recast the following sentences so that their words form a verse of four lines, which makes good sense, with lines that rhyme alternately, when read from either end?:—
Fading slowly day dies, mournful winds sigh, Stars are waking brightly; owlet holding high revel flies hooting, breaking nightly silence.
[131]
“The Observatory at Greenwich, in England,” has been turned into an excellent anagram, which starts—On landing here begin—Can you complete it?
The missing words are spelt with the same seven letters.
[132]
How was this?
[133]
In each of these sentences a town is buried:—
His sister played the piano while we sang.
I saw Nell out here last evening.
The general rode a large black mare.
I have ordered a cab at half-past one.
Meet me in the lane at half-past nine.
Can you dig them out?
“The leaning tower of Pisa, in Tuscany, Italy.” The first seven words of its anagram are “A funny spot in a sweet city.” Can you complete the anagram by adding four more appropriate words?
[134]
Can you prove by anagram that, whatever may be true of other plays accredited to Shakespeare, Bacon had certainly no hand in “Much Ado About Nothinge,” if we adopt the old spelling of the final word?
Can you recast “Insanitary” and “Sanitary Reform” so as to form two very appropriate anagrams?
[135]
Can you supply the missing letters?
[136]
The following cryptic lines were sent as a reliable tip before a race in which Petronel was to run:—
“Tell me, Ben, who tore it
Seek a plant for it, see Bob.”
Can you discover their hidden meaning?
Can you fill in this broken sentence, first to describe a curse, and then to proclaim its cure:—
A sed end ought eat ease ain.
using 16, and then 17, extra letters.
The deaf and dumb girl began gesticulating with a message, and her delivery was ever neat, with graceful pose in every attitude.
Four rivers are buried here.
[137]
If the “shingle” on the beach at Brighton could speak, what would be its boast?
A May-Day Dirge
The clever play-writer who suggested these words as a phonetic excuse for wife-beating might in another fashion invite a man to beat his wife by merely calling him. What would he say?
| storm? a th |
an umbrella me who |
with alls |
all mud. |
[138]
NRNRMMHDLVLDHMMRNRN.
Can you, keeping these consonants in their order, fill in vowels so as to form a sentence which is a perfect palindrome, and reads alike from either end?
“Can you tell me,” said an undergraduate to his tutor, who was great at Ecclesiastical Law, “whether the Pope would be allowed to bury the Archbishop of Canterbury?” As some slight stress was laid on the syllables Canterbury, the tutor for a moment suspected some trick, but being assured that it was quite a serious question, promised to consider the point. What should he reply?
While there are very many as kind as this, they know no task unkind. Can you dig a proverb out from this sentence?
Strange weather! What could equal it? Yesterday sunshine and soft breezes, to-day a summer cyclone raging noisily; then other changes, as floods of fiercest rain eddy beneath the blast.
[139]
Fill in the necessary vowels, and form thus with these consonants in their present order a perfect palindrome:—
RDRTPTPTRDR
It must read alike from either end.
On the outer wall of a Western college this was written: “Young women should set a good example, for young men .... ...... ....!” What three words will give a most ambiguous sense to the inscription?
Can you supply the missing words?
On the comparatively new organ at Ober Ammergau, on a brass plate above the keyboard, is the following Latin inscription:—
QVI CHRISTI LAVDES CANTANT
SANCTÆ PASSIONIS SVÆ VIRTVTE
IN IPSO ET PATRE VNVM SINT
which may be freely rendered—“May those who sing the praises of Christ be, by virtue of His Sacred Passion, one in the Father and in Him.”
These lines contain a hidden point, beyond their obvious interpretation. Can you discover it?
[141]
Tom, home for the holidays, and in teasing mood, declared that he could give his sister quite a simple sentence of seven common words of one syllable, which she could not produce with her new typewriter. What was his sentence?
[142]
This French charade, ascribed by some to Lady Waterford, and by others to Voltaire, has neat points:—
Sydney Smith, when questioned as to the value and satisfaction of a City feast, said: “I cannot wholly value a dinner by the .... ... ..” Can you supply the finish of his witty reply?
Happy in the possession of a Keen Kut, the newest form of safety razor, and meeting a friend whose chin bore painful traces of a less trusty blade, an undergraduate who had a turn for puzzles propounded this riddle: “What is the difference between my razor and yours?” Can you answer it?
The missing word in the first line has seven letters; its first letter is cut off to form the second missing word, and this process is repeated throughout the seven lines.
[144]
Lines to an owl:—
As a hint, the last line is:—
Or of your hooting howls to know.
Here is an excellent little exercise for patient or quick-witted solvers:—
Each word or group of words in italics forms, when the letters are shuffled and recast as an anagram, a military title. Can you decipher them?
[145]
Can you recast the three words at the end, so that their letters form a word descriptive of the scene?
[146]
Here is another proverb in anagram:—
Behest on thy lips, Society!
Can you recast it, and so recover the proverb, with which it is quite in keeping?
An epidemic of anagrams broke out in a public school, and eight of the prefects, having turned their Christian names into other words, fashioned from them this sentence, which contains them all in order.
“I, thy Tom, am sober and lie or live in dew, but her brain sinned.”
Can you decipher them?
[147]
Why should a man in a rage go to a “shooting gallery?” Each word has its complete anagram.
“I dare not admit faint women.”
Can you recast these words so that their letters form a well-known proverb?
[148]
The missing words are spelt with the same letters.
What is that which is found in the centre of Australia and of America, and in no other place?
“It’s grandfather’s turn,” cried the children at a Christmas party where jokes and riddles have been rife.
With a quiet twinkle in his eye, the old man said, “Do you know why is the fourth of July?” Not one of them could understand or answer his question, which seemed to lack finish and grammar. Can you?
[149]
Can you recast these short sentences into six single words?
See a pug dog.Red paper.
Fat reward.
Stay, O morn.Set on a dish.
[150]
[151]
The missing words are spelt with the same ten letters.
Comes Christmas merry? Hungry birds; no bright berries; rents high, not paid; long bills; empty barns; no peace and prosperity.
How can we amend this gloomy forecast?
Six common plants are concealed by anagram in the following sentence. The letters which spell each plant follow each other, but are in disorder.
O rise love it lad never let this lamb chase trains.
[152]
“Next week,” wrote Funniboy from Naples to his friend, “I am going to ‘plant onions, etc.’ Let me hear from you.” How did his friend gather his destination from these words?
[153]
RPLVLSLVLPR
Can you insert the missing letters, and complete the palindrome so that it reads alike from either end?
“Now, dad,” said Tom Pickles to his father in the Christmas holidays, “take this bottle in your left hand, and when I say ‘three!’ try how far you can blow the cork into it.”
The cork, smaller than the neck of the bottle, was placed just inside, and as Tom cried, “One, two, three!” his father gave a lusty blow. What was the result?
When are acorns as strong as oaken posts?
PTTPBTNTNTBPTTPBTNTNTBPTTP.
Can you add the vowels, and make a palindrome that reads alike from either end?
[154]
A politician used a high-flown phrase, which implied inaccurate wording, though some spoke of it as dust thrown in people’s eyes. Can you recover the two long words which he used, by anagram, from this sentence?
Axiomatic intelligence, or dust.
Woman without her man would be helpless.
Can you recast these short sentences so that each of them forms a single word?
A moment’s cure. The old rocks.
Cod is nice. It lures a cat.
[155]
Many will remember how often the great tenor, Sims Reeves, was prevented from singing by his delicate throat. An excellent anagram can be evolved from his name which, with some exaggeration, proclaims this. Can you discover it?
Here are the bones of a palindrome sentence that might be spoken by some unhappy criminal lunatic. Can you clothe them with their vowels, so that the sentence reads alike from either end?
MNCLVDDVLCNM.
Fruit and flowers are hidden here in anagrams, each in its order separately.
NOW ONE OLD FORT.
What place is this?
RABID OWL.
Change this bird into a beast.
[156]
[157]
Society—how her enthusiasts worship at her Juggernaut car. Cases exist here, proving how illogical are these eagle-sighted, place-hunting beings, scoffing at hereditary position, yet striving to get her smile.
A well-known proverb is buried in this sentence. Can you dig it out?
What should we put on a bird’s tail to catch it without a steel trap?
[158]
Where can you be “in a stone-pine garden”?
[159]
The three missing words are spelt with the same five letters.
What bodily discomfort follows an ague-fit?
Can you readjust the 16 letters in this square so that they form a perfect word square?
| I | E | I | T |
| I | S | A | S |
| A | S | I | S |
| E | D | E | D |
What European rivers are concealed in these eight anagrams:—Set in red robe Henri Le Roi O sell me red pine nerves biter.
Rearrange these letters so that they form a palindrome, or sentence that reads alike from either end:—
F PPPP RRRR SSSS TT
EEEEII OOOO
[160]
What political parrot cry can be evolved by anagram from this sentence, which condemns it?
O fool! O musty cry! O lurid woe!
What statesman’s name was a “terrible poser?”
Can you recast the letters of this sentence into a well-known English proverb?
Yea, a glad sun rose red.
Has there been a poet of unusual solemnity?
“Yes,” said young Biceps of St Boniface, who had failed to satisfy the examiners, “they have ploughed me in Euclid, and yet if I had half a chance I could teach them how to square a circle!”
“Bravo, Biceps!” cried his chum, who was helping him to drown dull care in fruity port, “don’t keep the great secret to yourself!” And so he told him—what?
[161]
When his friend had recovered from the shock of the atrocity described in our last, he retaliated by assuring Biceps that he could extract a circle from a given square. What was his method?
Add two vowels alternately to complete the couplet.
Can you discover by anagram what his brother was when he put “Tim in a pet?”
[162]
In the words welcome to a thirsty toiler, “Mower, I will tap the cask!” are hidden by anagram the names of an English poet and of one of his poems. Can you discover them?
To be
aaaaaaaaaa
tCrIiOfUlSes
standing
is the mark of a mean
[163]
Can you recast the letters that spell RED NUTS AND GIN so that they form one long word?
Can you rearrange these letters so that they form the title of a well-known novel by Charles Dickens?
CDEHHIILOOOPRSSTTUY
The missing words are spelt with the same six letters.
“If father gives us a new dog, it will wake the lazy ones!” Can you discover from these words which of his children were often late for breakfast?
NGOTRDSREAOHR
ETNSVEENUDOEO
Can you decipher the common proverb here concealed?
[164]
How might an oyster, if it could speak, and knew that unda is Latin for wave or water, complain in similar phonetic iteration when disturbed by thunder under unda?
The five missing words are spelt with the same five letters.
Bad hero set by thy door hurt me ma. Army may get ruder daily.
Ten girls’ names are here in anagrams.
Lord Beaconsfield’s statue,
True as old ———
Can you can complete this anagram?
These three lines are perfect anagrams of three consecutive lines in “Romeo and Juliet,” Act II., Scene V.:—
[165]
The tub sold has old rough shelves.
And e’en this fisherman caught best white smelts.
A living lord’s black dress, worn high, I vow!
Can you discover the original lines?
| ◯ | ◯ | ◯ | ◯ |
| ◯ | ● | ● | ● |
| ◯ | ● | ● | ● |
| ◯ | ● | ● | ● |
Can you substitute words which fulfil the conditions?
One letter is dropped each time.
[166]
Can you convert HARE into SOUP, using not more than six links, changing only one letter with each link, and preserving the order of the letters from link to link?
If a “newspaper” could speak, what might it say of the general work of its staff?
How can you turn the positive quantity 1011 into a negative?
What one word can you form from the sentence—
“O, I’m man’s trial!”
EEE and xxx URXXI XXX and eee.
Why may not the owner of a pine forest fell his timber?
[167]
The missing words are spelt with the same seven letters.
Can you change ARMY into NAVY with seven links, changing one letter every time, and preserving their sequence?
When is an onion like music?
What is the bitter cry of “Christianity?”
Show by anagram that a Conservative is constant to his cause.
Christmas Day and New Year’s Day fall as a rule upon the same day of the week. Can any ingenious reader discover why they will not fall upon the same day of the week in the year 1910.
[168]
[169]
[170]
[171]
[172]
[173]
[175]
It is a ...... fact that neither ...... nor ...... grow .. .....
[176]
DRWNDRRDNWRD.
Insert the missing letters, and so form a perfect palindrome, which reads alike from either end.
What person’s name is doubly evil?
The answer may be given in a line that rhymes.
[177]
[178]
In the ’seventies no one was more popular at Simpson’s Chess Room in the Strand than the gentle and brilliant subject of these lines, a clever water-colourist. The charade is by his friend, the well-known problem composer. Both have passed away, but they are not forgotten by those who had the happiness to know them:—
[179]
[180]
[181]
[182]
After officers’ mess, when cigars were well alight, the old conundrum was propounded, “What is most like a cornet of horse?” A sharp sub. was ready with the reply, “A hornet, of course”; it was presently capped by this variant which occurred to a married captain, “a corset of horn”; and yet another reading was suggested by the deaf old colonel, “How much did you say the ..............” Can you complete this?
[184]
What geographical names are buried in these lines?
He has my R. N. as a monogram
I am her stupid sister.
The calmest man is sometimes made irate.
[185]
“We westand fall.”
George Thompson, the zealous anti-slavery advocate, was asked to go into Parliament, the better to press his point and cause. When he hesitated a friend produced, as a conclusive reason, this anagram, spelt with the letters of his name—“O go, the negro’s M.P.!”
[188]
Here is a long-division sum without figures:—
| U | G | I | ) | G | E | V | P | P | N | D | O | ( | I | D | T | P | O |
| G | V | N | I | ||||||||||||||
| D | N | T | P | ||||||||||||||
| U | G | I | |||||||||||||||
| N | E | T | N | ||||||||||||||
| N | E | O | T | ||||||||||||||
| D | U | D | O | ||||||||||||||
| D | U | D | O | ||||||||||||||
These letters form a sentence of three words .... .... .., and represent the figures 1234 5678 90; the puzzle is to discover this key sentence, by working out the sum in the corresponding figures.
At the invitation of a farmer in the country I went out with my gun for a day’s shooting on his farm. “What sport had you?” said a friend afterwards at the Club. “I shot only birds and rabbits,” was my reply, “and the bag showed 36 heads and 100 feet.” How many birds were there, and how many bunnies?
[189]
| D | E | L | F |
| E | V | I | L |
| L | I | V | E |
| F | L | E | D |
How many distinct readings of these four words can you find, taking their letters in any “go as you please” direction, without jumping over any letter?
Can our readers rearrange these letters in the form of a similar cross, so that they form two words familiar to us all?
| A | ||||||
| A | ||||||
| E | ||||||
| D | N | R | E | G | D | N |
| I | ||||||
| T | ||||||
| V | ||||||
| S | ||||||
One of the letters, to be placed where the lower E now stands, is common to both words.
“Take this sovereign, my boy,” said a man to his son who had a turn for arithmetic, “and buy for yourself and for your three sisters the best present possible for each, of different values, expending in each case an aliquot part of the pound, that is to say, a fraction of it whose numerator is one. If there is any change you can give it to the Fresh Air Fund.” How was this commission carried out?
[190]
Can you complete this word-square?
| . | E | . | A | . |
| E | . | A | . | E |
| . | A | . | . | E |
| A | . | . | E | . |
| . | E | E | . | . |
First find a word that is spelt with the ten letters above the line, and number its letters consecutively 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
| A | I | |
| L | C | |
| P | R | |
| U | N | |
| B | E | |
| E | C | C |
Substitute the corresponding figures for the letters, and then work out the addition sum which they represent.
Can you complete this word square?
| T | . | . | . | T |
| . | T | . | . | . |
| . | . | O | . | . |
| . | E | . | S | . |
| T | . | . | . | S |
[191]
Take the twelve first prime numbers, 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, which have no factors but themselves and unity, and write down the value of their product, using no figures but 0, 1, 2, and 3, and of these using 2 and 3 only once.
Can you complete this word square?
| W | . | E | . | S |
| . | . | . | . | . |
| E | . | U | . | E |
| . | . | . | . | . |
| S | . | E | . | R |
Fill a wineglass with water to the brim, and set it on the corner of a table-napkin, which should be in immediate contact with the polished surface of a table, allowing the rest of the napkin to fall over the edge. Can you remove the napkin without touching the glass or spilling any of the water?
[192]
My third and fourth are a quarter of my first and second; my fourth is half of them, and my third is half. What am I?
A London firm, having sent an order by telegram to a manufacturer in Paris for 480 sets of Diabolo, received to their amazement a huge consignment of 6336 sets. How did this mistake arise?
“My husband’s age,” said Mrs Evergreen, “is represented by the figures of my age reversed. He is older than I am, and the difference between our ages is one-eleventh of their sum.” What were their respective ages?
[193]
Can you complete this multiplication sum?
| 4 | * | * | ||
| 3 | * | |||
| 3 | 6 | * | * | |
| * | * | 7 | * | |
| * | * | 3 | * | * |
I bought less than 100 plants for my new rosery, and found that if I set them 3 in a row there would be one over; if 4 in a row there would be two over; if 5 in a row, three over; and if 6 in a row, four over. How many rose trees did I buy?
Can you arrange three nines so that they represent exactly 20?
A house has nine windows on its front. How many signals can be given by merely leaving one or more of them open?
[194]
This arrangement of the digits represents 20, one being a whole number, the others a fraction:—
613258 947 = 20
The battle of Montl’héry was fought in 1465. Its date can be committed to memory in the sentence which might have been a battle-cry—“A cheval, à cheval, gendarmes, à cheval!” For it is arrived at by the addition of the Roman numerals which this contains, thus:—
[195]
| C | = | 100 |
| V | = | 5 |
| L | = | 50 |
| C | = | 100 |
| V | = | 5 |
| L | = | 50 |
| M | = | 1000 |
| C | = | 100 |
| V | = | 5 |
| L | = | 50 |
| Total | = | 1465 |
In this most remarkable sentence of only twenty-eight letters, every letter of the alphabet is used—
IF JACK QUIZ BALD NYMPHS GROW VEXT.
Tom Hood, seeing over the door of a public-house BEAR SOLD HERE, said that it was rightly spelt if it was the landlord’s own bruin!
Here is an ingenious rhyming couplet of only 33 letters, in which every letter of the alphabet is used—
[196]
A sa Majesté impériale le Tsar Nicolas, souverain et autocrate de toutes les Russies.
The same letters exactly spell—
O, ta vanité sera ta perte. O, elle isole la Russie; tes successeurs te maudiront à jamais!
This most remarkable anagram was published in the early days of the Crimean war.
“Notes and Queries.”
A question sender.
Enquires on dates.
Reasoned inquest.
I send on a request.
The name of John Abernethy, a very brusque doctor of bygone days, lends itself to this most apposite anagram—Johnny the bear!
Duchess of Marlborough.
She labours much for God.
Or,
The Duchess of Marlborough.
Lo, she sought much for bread.
French guest to his host after a big shoot:—
“How many braces have you to your bags?”
[197]
It would be difficult to find a more ingenious and appropriate anagram than this, which took a prize in “Truth” in 1902, and connects the King’s recovery with the Coronation.
The sentence set was—
“God save our newly crowned King and Queen! Long life to Edward and Alexandra!”
The letters of this were recast thus—
Can we wonder an anxious devoted England followed drear danger quakingly?
“Truth” offered a prize for the best anagram on the sentence—“‘Truth’ Toy and Doll Fund, Christmas, nineteen hundred and seven.” The winning anagram, by the Editor of these pages, was, “A sunny tender mind understands that the children do love fun!”
In a moment of economy I told my wife that I would put by a farthing the first week of the New Year, a halfpenny the second week, a penny the third, and so on, doubling the sum each week to the end of the year. She had a turn for figures, and staggered me by showing that I should have to provide £4,691,249,611,844, 5s. 33⁄4d. to carry out my plan!
Now that Ellen Terry has written “The Story of My Life,” this anagram has a special interest:—
LYCEUM THEATRE, STRAND.
Teach and melt us, Terry!
[198]
More startling than the well-known calculation of payment by continuously doubling the farthing given for the first nail in a horse’s shoe, is the fact that the possible changes on a peal of 24 bells would not be exhausted if every minute of 4000 years were prolonged to a period of 10,000 years!
Erasmus himself was responsible in one of his lighter moments for the following ingenious play upon his name:—
Quæritur unde mihi sit nomen Erasmus, eras mus;
Si sum mus ego, te judice, summus ero!
“Well!” cried an agitated carpenter to his mate, “of all the saws that I ever saw saw, I never saw a saw saw as this saw saws!”
CONFESSIONS OF AN OPIUM EATER.
The same letters recast spell—
If so, man, refuse poison at once!
[199]
The following curiosity, constructed some years ago for prize purposes by the Editor, shows how, in word or letter juggling, difficulties can be overcome:—
A sentence in which each letter of the alphabet is used exactly twice:
“XLV gruff nymphs jerk XLV jaws,” quoth wag B. Dick, Q.C., to Ben Dizzy, M.P.
If anagrams count, our “ancestor” was not a monkey but a Norse cat!
The name of Randle Holmes, author of a notable book on heraldry, was so recast that it formed the words: “Lo, men’s herald!”
Dog as a devil deified lived as a god.
The Oxford and Cambridge annual Boat-race.
Cantab blue had raced in an extra good form.
Tell a person who holds a sovereign in one hand and a shilling in the other to reckon 4 for the gold, and 3 for the silver. Then bid him triple what is in the right hand, and double what is in the left, and give you the added product. If this is an even number the gold is in the right hand, if odd it is in the left.
[200]
Adelina Patti.
Adept Italian.
Sir Charles Napier’s witty despatch, “Peccavi!” “I have Scinde!” is familiar to us. Not so well known is the happy phrase attributed to Sir Colin Campbell, “Nunc sum fortunatus!” “I am in Lucknow!”
Owen, the Welsh epigrammatist, composed this very clever Latin line:—
In verbis, ubi res postulat, esto brevis.
(“In words, where the matter requires it, be brief.”)
The words in italics are spelt with the same six letters.
Take a long strip of paper, say 9 in. by 2 in., which will have, of course, an upper and an under surface and two edges along its length. How can you arrange this strip, by quite a simple method so that it will have only one surface and one edge?
Can you divide nine into two parts which are together equal to ten?
[201]
A shepherd had a flock of sheep in a fold enclosed by 100 hurdles. His master made a large purchase at the annual fair, and required him to pen some pigs with 16 of the hurdles, and to arrange the remainder so that they could accommodate nine times as many sheep as the 100 hurdles had contained. How was this possible?
Here is a neat final trick, if you have some reputation for sleight of hand. Place three biscuits on the table in a row, and cover each of them with a borrowed hat. Raise each hat in turn, gravely eat the biscuit, and replace the hat. Then undertake that the three biscuits shall be under whichever hat is selected. How can you contrive this?
In how many different ways can 7s. 3d. be paid away in current coin of the realm, without ever using exactly the same set of coins a second time?
[202]
The words which describe this picture can be recast, letter for letter, into the perfect anagram—

“Please, Mister Elephant, are you there?”
Return to description
[203]
It is said that there are 86 ways in which the numbers in this model magic square can be added up so that they make 34.
| 4 | 15 | 14 | 1 |
| 9 | 6 | 7 | 12 |
| 5 | 10 | 11 | 8 |
| 16 | 3 | 2 | 13 |
It is not difficult to discover more than half this number that are symmetrical, including, of course, the 4 rows, 4 columns and 2 diagonals. Here are a dozen samples, from which others can be seen—
| 4, | 1, | 16, | 13. |
| 15, | 14, | 3, | 2. |
| 14, | 12, | 5, | 3. |
| 6, | 7, | 10, | 11. |
| 15, | 8, | 9, | 2. |
| 1, | 6, | 11, | 16. |
| 14, | 8, | 9, | 3. |
| 9, | 15, | 2, | 8. |
| 4, | 5, | 12, | 13. |
| 4, | 5, | 11, | 14. |
| 4, | 9, | 8, | 13. |
| 9, | 14, | 3, | 8. |
Return to description
[204]
Here is the completed magic square—
| 216 | 175 | 224 | 183 | 232 | 191 | 240 | 199 | 248 |
| 247 | 215 | 174 | 223 | 182 | 231 | 190 | 239 | 207 |
| 206 | 246 | 214 | 173 | 222 | 181 | 230 | 198 | 238 |
| 237 | 205 | 245 | 213 | 172 | 221 | 189 | 229 | 197 |
| 196 | 236 | 204 | 244 | 212 | 180 | 220 | 188 | 228 |
| 227 | 195 | 235 | 203 | 252 | 211 | 179 | 219 | 187 |
| 186 | 226 | 194 | 243 | 202 | 251 | 210 | 178 | 218 |
| 217 | 185 | 234 | 193 | 242 | 201 | 250 | 209 | 177 |
| 176 | 225 | 184 | 233 | 192 | 241 | 200 | 249 | 208 |
Every row, column and diagonal adds up to exactly 1908.
Return to description
[205]
This up-to-date magic square adds up to 1908 in quite 56 different symmetrical ways.
| 469 | 484 | 472 | 483 |
| 481 | 474 | 478 | 475 |
| 482 | 471 | 485 | 470 |
| 476 | 479 | 473 | 480 |
Here are 44 of them—
| Rows | 4 |
| Columns | 4 |
| Diagonals | 2 |
| The corners | 1 |
| Corners of squares of 9 cells | 4 |
| Squares of 4 cells | 9 |
| Opposite pairs of outside cells | 6 |
| Opposite pairs of short diagonals | |
| Such combinations as 469, 481, 485, 473 | 8 |
| Such combinations as 482, 484, 472, 470 | |
| Total | 44 |
There are a dozen other ways, more or less symmetrical, such as 481, 474, 483, 470; or 474, 485, 470, 479.
Return to description
[206]
This is the rearrangement of the domino magic square—
| ● | ● | ● | ● | |||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | |||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||
| ● | ● | ● | ● | |||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | |||||||||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | |||||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | |||||||||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | |||||||||||
The three-ace, which was a corner stone in the former diagram now occupies the centre, and the rearrangement was effected by first transferring the two bottom rows to the top, and then the fourth and fifth columns to the extreme left. This method of shifting the stones does not affect the magic quality of the square.
Return to description
[207]
The affinity between chess and numbers is well illustrated by the Knight’s tour on this diagram—

The Knight starts from the square marked 1, and returns at last to it. The constant difference between any opposite and corresponding numbers in cells that are equidistant from the centre is 18.
Return to description
[208]
Here are the cells in the diagram of our Numbers Patience, so filled in that each of the rows across from side to side adds up exactly to 143.
| 17 | 30 | 41 | 31 | 24 |
| 18 | 32 | 13 | 46 | 34 |
| 11 | 12 | 14 | 50 | 56 |
| 51 | 19 | 42 | 16 | 15 |
| 22 | 21 | 35 | 45 | 20 |
Each cell contains, in accordance with the conditions, a different number.
Return to description
[209]
This is the division of a square into fifteen parts, which will form the windmill:—
This puzzle may, of course, be reversed, the parts of the square being given, and the solver asked to form with them a symmetrical windmill.
Return to description
[210]
In this nest of 49 squares it is possible to count 784 distinct interlacing figures, whose opposite sides are equal, and whose angles are all right angles.
Of these 784 rectangles 140 are squares.
Return to description
[211]
This is the domino magic square, in which all the stones are used except double-six, double-five and six-five.
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | |||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ● | |||||||||||||||
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | |||||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | ● | ||||||||||||||||
| ● | ● | ● | ● | ● | ● | |||||||||||||
| ● | ● | ● | ● | |||||||||||||||
| ● | ● | ● | ● | |||||||||||||||
| ● | ● | ● | ● | |||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ||||||||||||||||||
| ● | ● | ● | ● | ● | ||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||
| ● | ● | |||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ||||||||||||
All rows, columns and diagonals add up to 27, as do the stones in the four corner cells and the four central border cells of the full square, and of the square of nine cells in the middle.
Return to description
[212]
Those to whom games of Patience appeal will find an interesting and pretty form of it in the construction of a pyramid with a complete set of dominoes.
| ● | ● | ||||||||||||||||||||||||||||||||||||||||
| ● | ● | ||||||||||||||||||||||||||||||||||||||||
| ● | ● | ||||||||||||||||||||||||||||||||||||||||
| ● | ● | ● | ● | ||||||||||||||||||||||||||||||||||||||
| ● | ● | ● | ● | ||||||||||||||||||||||||||||||||||||||
| ● | ● | ● | ● | ||||||||||||||||||||||||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||||||||||||||||||
| ● | ● | ||||||||||||||||||||||||||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||||||||||||||||
| ● | ● | ● | ● | ||||||||||||||||||||||||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||||||||||||
| ● | ● | ||||||||||||||||||||||||||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||||||||||
| ● | ● | ● | ● | ||||||||||||||||||||||||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||||||||
| ● | ● | ● | ● | ● | |||||||||||||||||||||||||||||||||||||
| ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ||||||||||||||||||||||||
Solvers may like to study the position given, which is one of many that are possible, and to discover for themselves the ruling conditions which are its characteristics.
Return to description
[213]
When the boy’s father came up just in time to stop him from breaking out of bounds, and said, “Never throw a leg, lad,”

the rest of the sentence, spelt with exactly the same letters, was “over the garden wall!”
Return to description
[214]
“Catastrophe,” the title of the tragedy foreshadowed, can be recast into “A cat! stop her!” By similar process the words, “New parrot stand in a house,” become “He turns on a soda-water tap!”

The parrot’s ready resource and triumph is depicted here with striking effect.
Return to description
[215]
When the judge at a baby show said to the mother of the small boy whose thumb was in his mouth, “Your lad Tommy likes such tit-bits,” the precocious child replied, as he removed his comforting hand, in a sentence spelt with exactly the same letters, “So to-day, sir, I suck my little thumb.”

Return to description
[216]
When the lady sitting at the back of this overloaded wagonette said to her husband, “This big load quite hinders his pull,” in her sympathy with the struggling horse,

he made this very practical reply, in a sentence spelt with exactly the same letters: “Do sit quiet, girl; I shall push behind!”
Return to description
[217]
When a bystander whispered to the marker, “Eh! what a stout player is striking!”

an appropriate reply, spelt with exactly the same letters, would have been: “He plays without taking a rest, sir.”
Return to description
The two English words appropriate to this picture—

which have as their anagrams “Or not a man first,” and “O I love nuts!” are Transformation and Evolutions.
Return to description
[218]
This is a fancy portrait of William—

We decide by anagram whether this is William or dear Jack, for these words, when recast, spell “I am Will, a card joker!”
Return to description
[219]
The word indicated by this picture in combination with the lines below it—

is Stout.
Return to description
[220]
The words of Jigger’s wife, when she said that he seemed to be in a “sad pet,” were true by anagram.
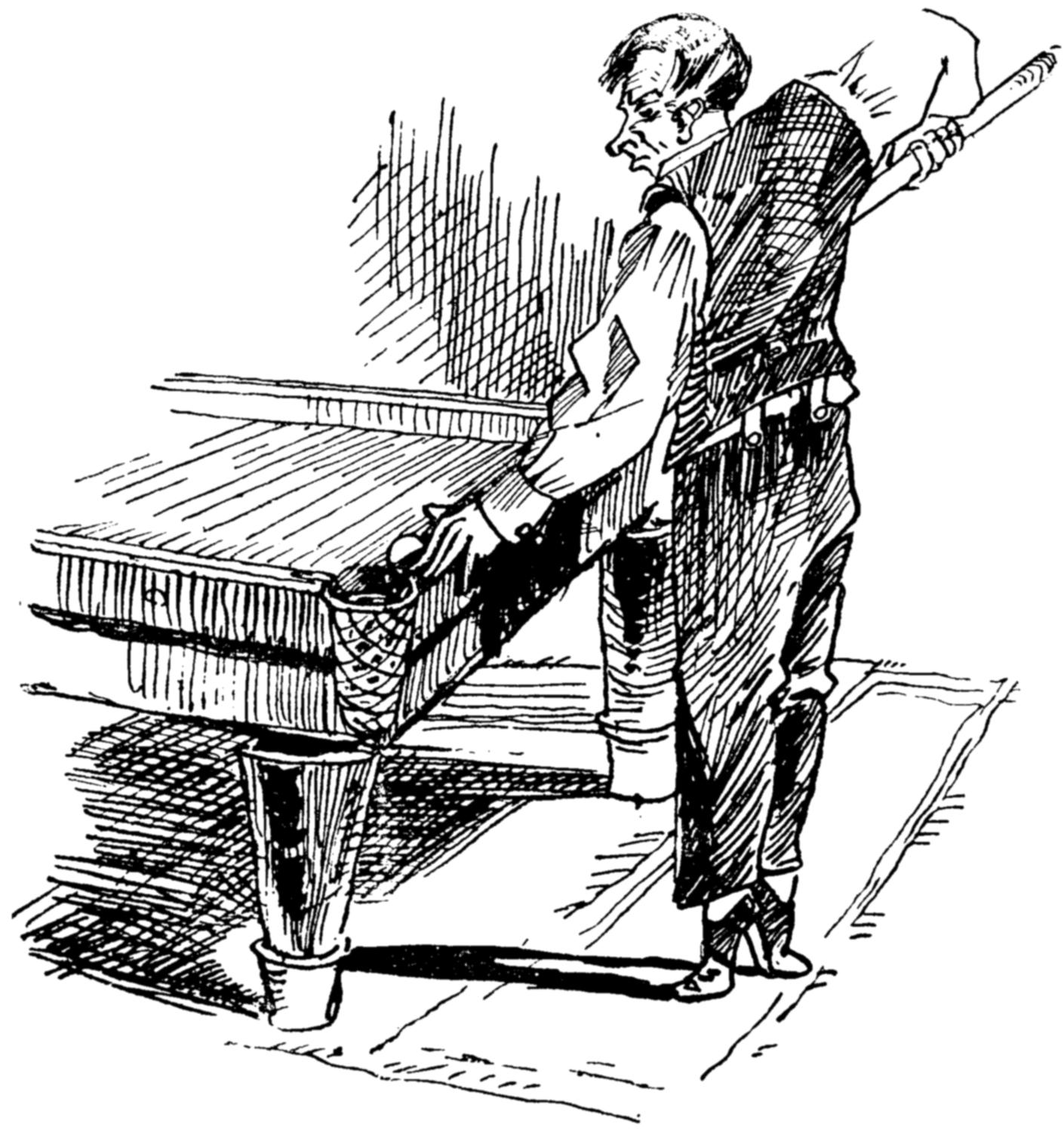
His ball hugs the cushion so closely as to be completely pasted.
Return to description
[221]
When, as they held on to the fractious cow, the farmer exclaimed, “See, we hold this cow’s horns and tail,”
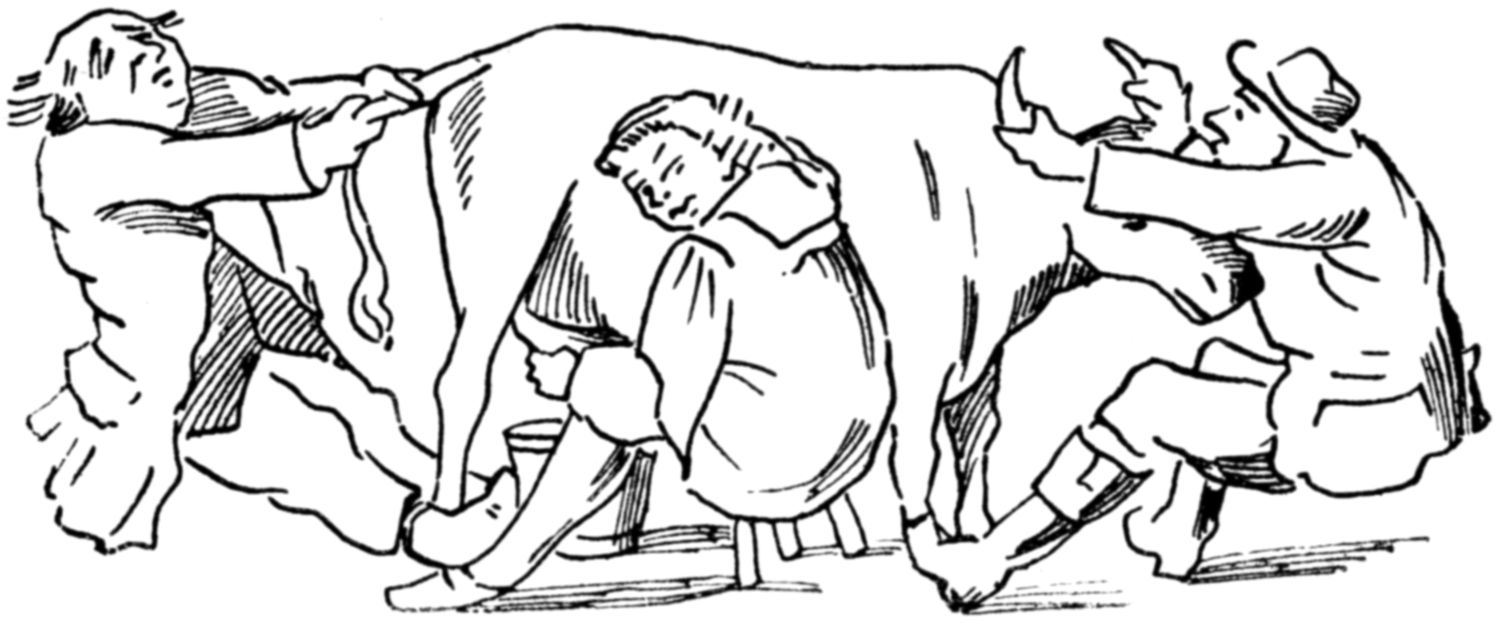
his foreman, using exactly the same letters in his sentence, said—
“She cannot toss, her wild head is low.”
Return to description
[222]
While the horse shown in this picture might be saying, if it could speak, “I’m a train’d stepper!”—
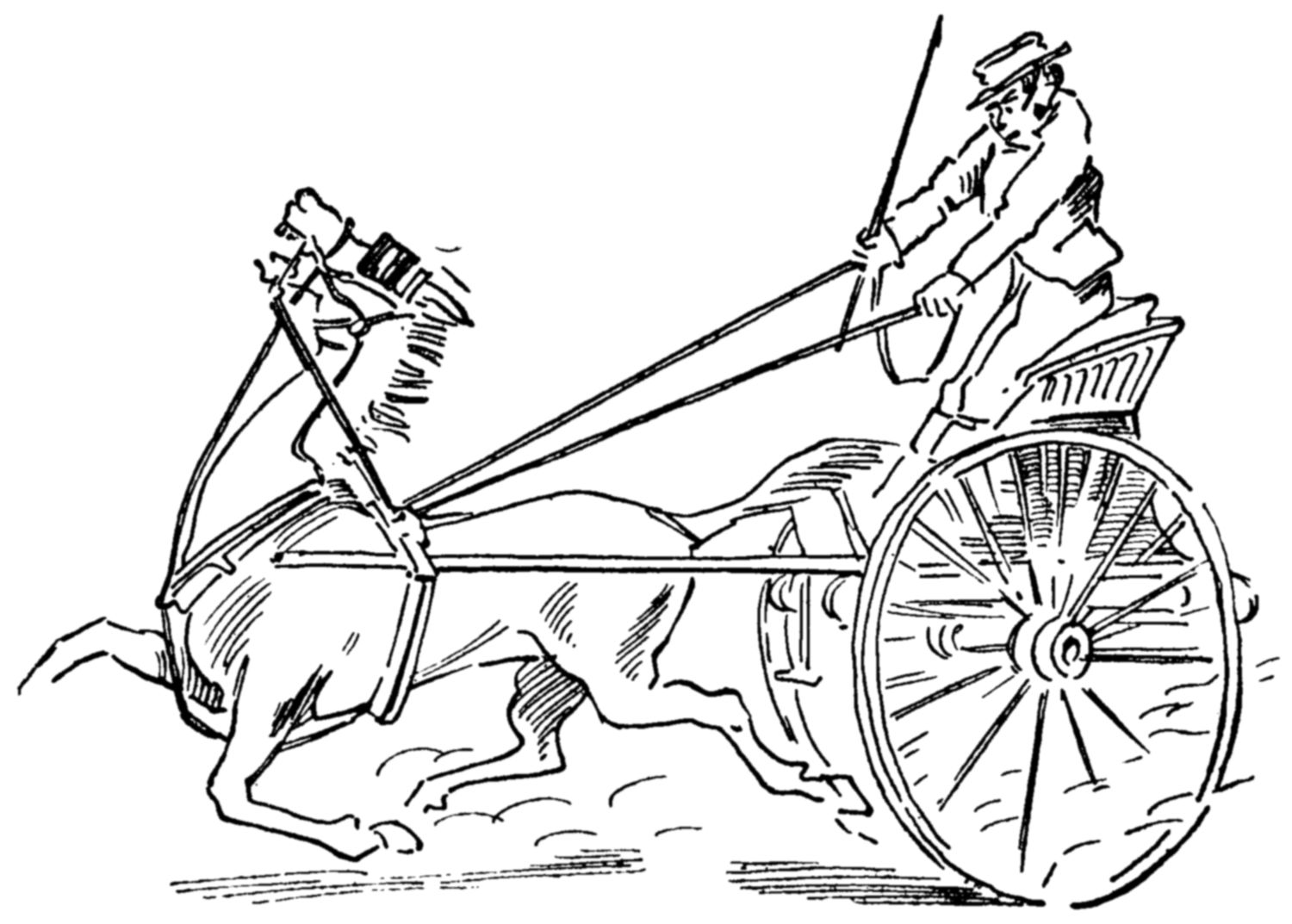
the driver, from his point of view, might say, as he held him in check, “Spirit and a temper!” making use in his words of exactly the same letters.
Return to description
[223]
When one onlooker, seeing the artist working with his feet, said—
“Why, now I see this fine artist has no hand!”
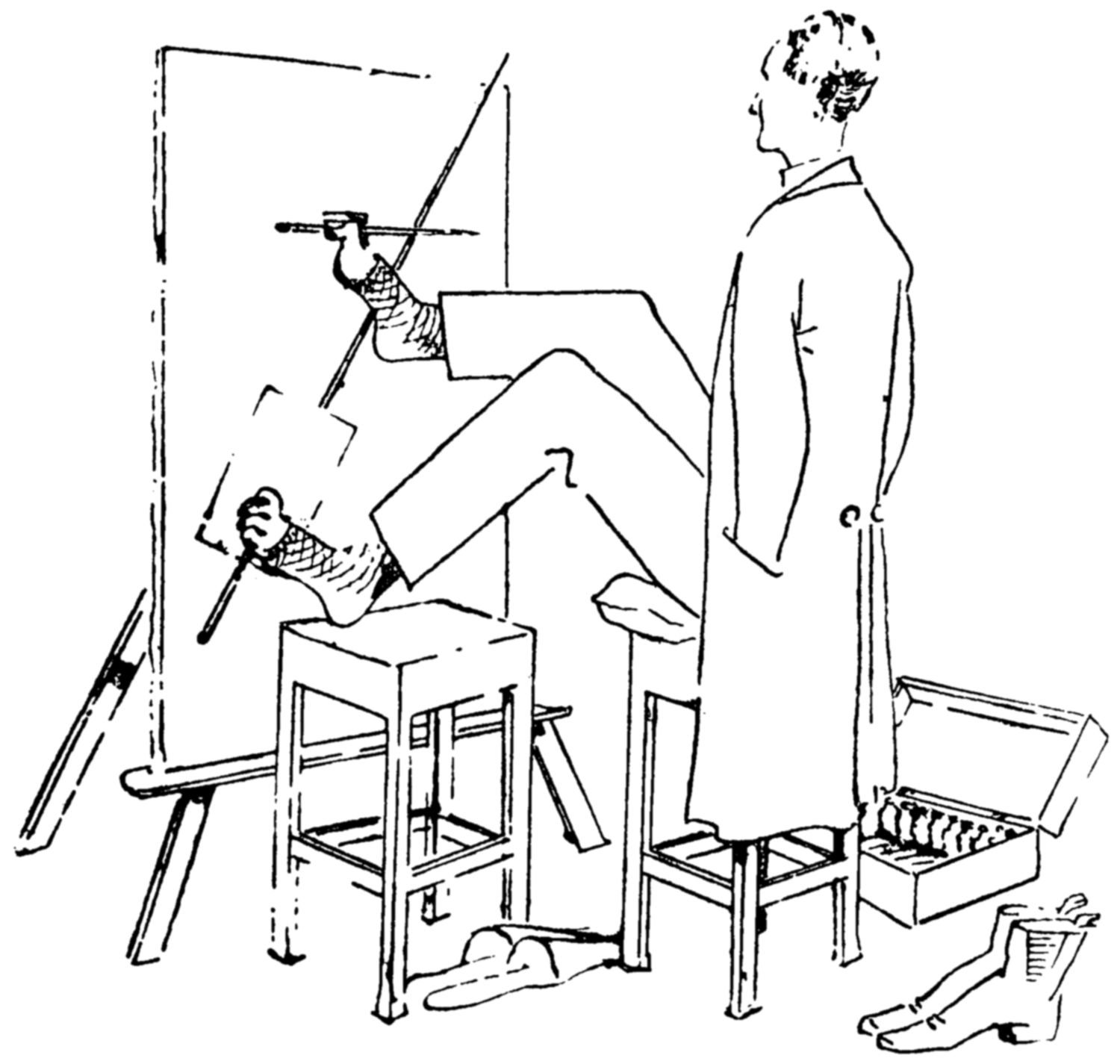
the other replied, using exactly the same letters,
“He draws in any fashion with his ten toes!”
Return to description
[224]
When her husband, showing this picture

said to his wife, “This is a wine bottle, dear, on a lure,” she, knowing that temptation in this form would fail, said, as she glanced at his illustration of their aims, in words spelt with exactly the same letters:—
“And see, he will not rise at our bait!”
Return to description
[225]
The sturdy musician, who had said, “What shall I play?” to which some one replied, “Any strains of Beethoven, he charms all!” as this was not an acceptable suggestion, struck up a piece after his own heart.

He said, as he struck the strings, in a sentence composed of exactly the same letters—“Nay, for this ’cello heaven sent a Brahms!”
Return to description
[226]
Here is the picture of a parsnip lying across a swede readjusted and reversed.
We gave as a clue the anagram—
“Here is our parsnip on swede.”
ANAGRAM
Wise and superior person he!
but this is now hardly needed to show who is thus represented in friendly caricature: (With apologies to G. B. S.)
Return to description
[227]
The letter puzzle is solved thus—
| L | E | V | E | L |
| E | E | E | E | |
| V | V | V | ||
| E | E | E | E | |
| L | E | V | E | L |
Within this square the word LEVEL runs in twelve different directions, being itself a palindrome.
Return to description
[228]
The sentence formed with the ten letters above the line, which is the key to this sum, is Do your best. If these letters are numbered consecutively 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, and the corresponding figures are substituted for the letters, the sum works out as is shown in the second diagram—
| S | B | 9 | 7 | |||
| R | E | 6 | 8 | |||
| Y | D | 3 | 1 | |||
| O | T | 4 | 0 | |||
| U | O | 5 | 2 | |||
| O | E | E | 2 | 8 | 8 |
Return to description
[229]
The twelve names of flowers and foliage that may be gathered within these borders, by moving in any direction one square at a time,
| 1L | 2L | 3B | 4H | 5P | 6E | 7F |
| 8L | 9Y | 10E | 11L | 12O | 13R | 14N |
| 15I | 16V | 17B | 18R | 19I | 20V | 21K |
| 22A | 23L | 24E | 25T | 26O | 27N | 28I |
| 29C | 30N | 31A | 32S | 33U | 34L | 35P |
are 18, 26, 32, 24, Rose; 25, 33, 34, 28, 35, Tulip; 35, 28, 27, 21, Pink; 31, 32, 25, 24, 18, Aster; and, in similar ways, Verbena; Salvia; Ivy; Lily; Lilac; Heliotrope; Fern; and Bell.
Return to description
The solution of this little problem, set by Dr Puzzlewitz on his blackboard to test the powers of his young pupils—“What are the values of A and B, when 4 is the result of dividing A by B, or of subtracting B from A?”—
| A | - | B | = | 4 | ||
| A | ÷ | B | = | 4 | ||
is that A = 51⁄3 and B = 11⁄3.
Return to description
[230]
This is the diamond squared:—
| s | ||||||
| h | i | s | ||||
| h | i | n | t | s | ||
| s | i | n | u | o | u | s |
| s | t | o | r | m | ||
| s | u | m | ||||
| s | ||||||
in which the words read alike from top to bottom, and from left to right.
Return to description
[231]
This is the arrangement of the 32 letters in the 64 cells—
| A | E | I | O | ||||
| E | O | A | I | ||||
| A | I | E | O | ||||
| I | O | A | E | ||||
| O | I | E | A | ||||
| E | O | A | I | ||||
| A | I | E | O | ||||
| E | A | O | I |
No A is in the same column, row, or diagonal with another A, no E with another E, no I with another I, and no O with another O.
Return to description
[232]
This is the anagram square, with the letters, which in the former diagram spelt the words vote, wove, prow, call, stew, news, core, nape, recast into fresh words which now read alike from top to bottom and from left to right of the square.
| C | R | O | W | ||||
| C | L | A | W | ||||
| L | O | V | E | ||||
| R | O | P | E | ||||
| A | P | E | S | ||||
| O | V | E | N | ||||
| W | E | N | T | ||||
| W | E | S | T |
The empty squares and diagonal setting are necessary for this particular puzzle, as the words would not form a word square if their letters were placed below one another in the usual way.
Return to description
[233]
The sentence formed with the ten letters above the line, which is the key to this sum, is—Add these up. If these letters are numbered consecutively 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, and the corresponding figures are substituted for the numbers, the sum works out as is shown below.
| D | U | 2 | 9 | |||
| E | H | 6 | 5 | |||
| E | D | 8 | 3 | |||
| A | P | 1 | 0 | |||
| S | T | 7 | 4 | |||
| D | E | A | 2 | 6 | 1 |
Return to description
[234]
The four words, seek, slab, leek, moan, which were placed on the white squares when recast form the following combination:—
| M | A | S | K | ||||
| A | B | L | E | ||||
| S | L | O | E | ||||
| K | E | E | N |
These fresh words read alike from side to side, and zigzag from top to bottom.
Return to description
[235]
These are the four words, recast by anagram from afar, task, seat, leal, and which now form a perfect word square.
| F | A | S | T |
| A | R | E | A |
| S | E | A | L |
| T | A | L | K |
Return to description
[236]
The word square is recast thus—
| c | r | e | s | s |
| r | e | a | c | h |
| e | a | g | e | r |
| s | c | e | n | e |
| s | h | r | e | d |
Its words are spelt with the same letters as the words chess, greed, canes, rears, cheer, which formed the original square, but did not read alike from top to bottom, and from left to right, as these do.
Return to description
[237]
The five familiar proverbs hidden in this square of 169 letters are: A rolling stone gathers no moss. Too many cooks spoil the broth. A live dog is more to be feared than a dead lion. You cannot eat your cake and have it. Peace hath her victories no less renowned than war.
| R | E | N | O | W | N | E | D | T | H | A | N | W |
| S | Y | O | U | R | C | A | K | E | A | N | D | A |
| S | T | E | T | O | B | E | F | E | A | R | H | R |
| E | A | R | K | S | S | P | O | I | L | E | A | F |
| L | E | O | O | H | E | R | S | N | T | D | V | O |
| O | T | M | O | T | L | I | N | O | H | T | E | U |
| N | O | S | C | A | L | A | G | M | E | H | I | R |
| S | N | I | Y | G | O | R | S | O | B | A | T | S |
| E | N | G | N | E | N | O | T | S | R | N | P | A |
| I | A | O | A | M | O | O | T | S | O | A | E | W |
| R | C | D | E | V | I | L | A | H | T | D | A | S |
| O | U | O | Y | N | O | I | L | D | A | E | C | A |
| T | C | I | V | R | E | H | H | T | A | H | E | Z |
Return to description
[238]

If the shaded circles are cut out and the diagram is placed squarely over the jumbled letters, with the I., II., III., IV. in turn at the top left-hand corner, this sentence is disclosed—
Le premier Supplément du Journal de la Jeunesse a été publié dans le Numéro du Dix-neuf Juin Mil huit cent soixante-quinze.
Return to description
[239]
This is the way to reconstruct Sam Loyd’s black pony—so that, while its legs and tail are strangely misplaced, they form the spirited outline of a white galloping horse.

Return to description
Here is the key to Sam Loyd’s ingenious puzzle—
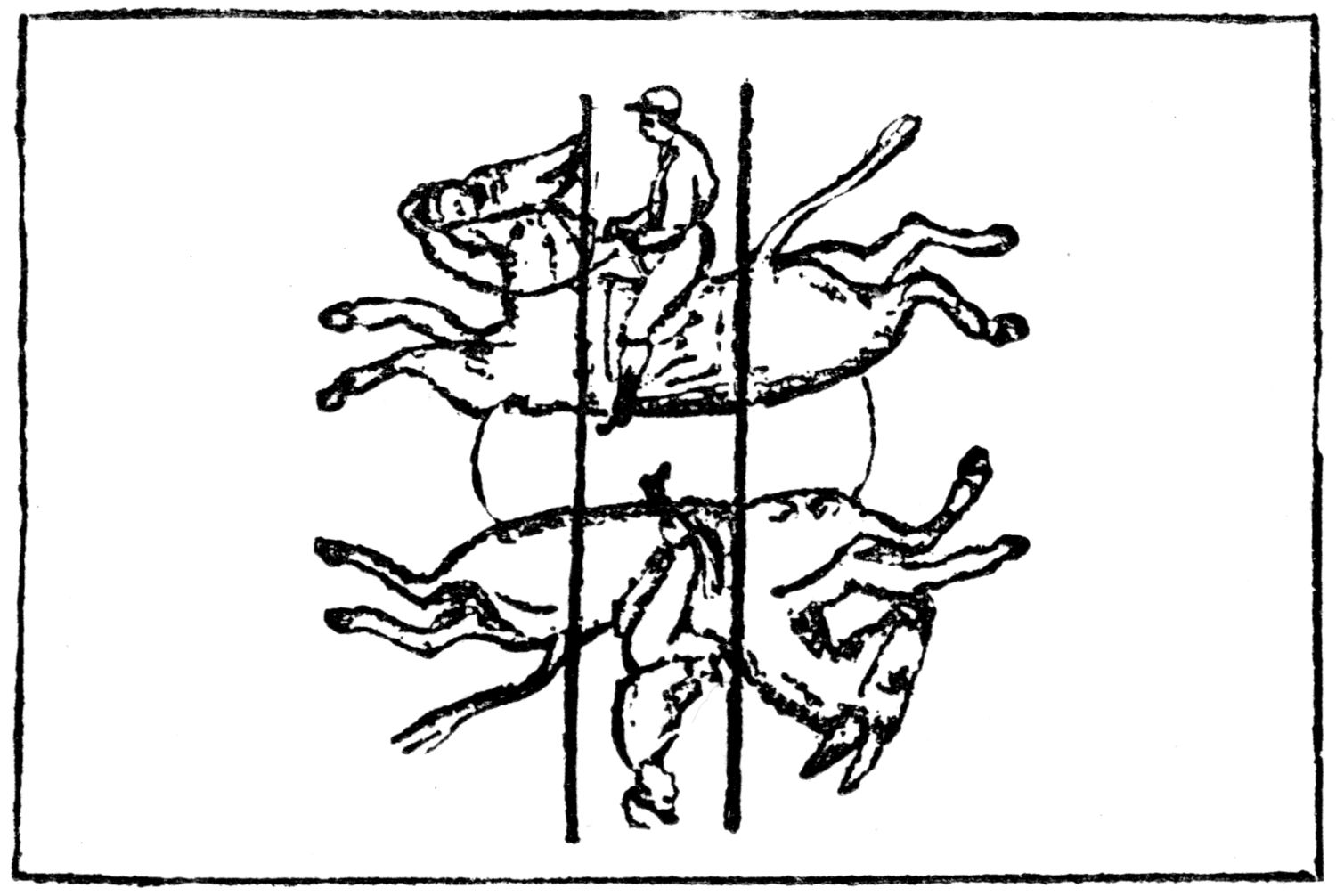
which shows the jockeys and horses in full racing trim.
Return to description
[240]
This is the inevitable result of the boy’s attempt to annex with his mouth the sugar on the chair—

Return to description
The leap-frog puzzle is solved in nine hops thus:—

First jump from stool 2, then from 5, 3, 6, 7, 1, 3, and 6 in turn to the vacant stools.
Return to description
[241]
This diagram shows that the seven wheels, which spin so merrily when the paper is rotated in the hand, can be divided off into separate enclosures by only three straight lines—
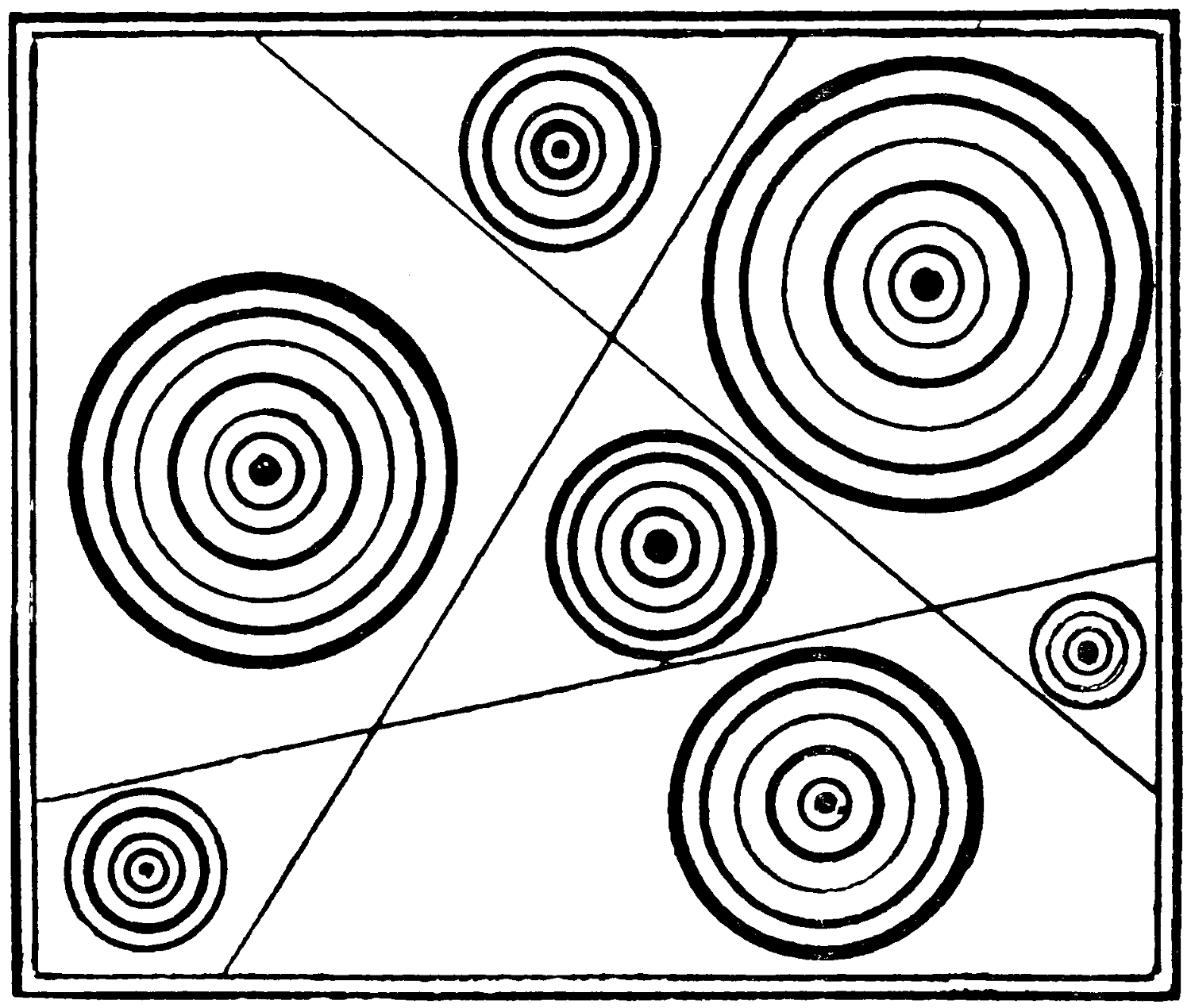
Return to description
[242]
The diagram below shows how the market-gardener, keeping one-fourth of his square field for himself in the shape of a triangle, was able to divide the remainder so that each of his four sons had an equal portion of similar shape—
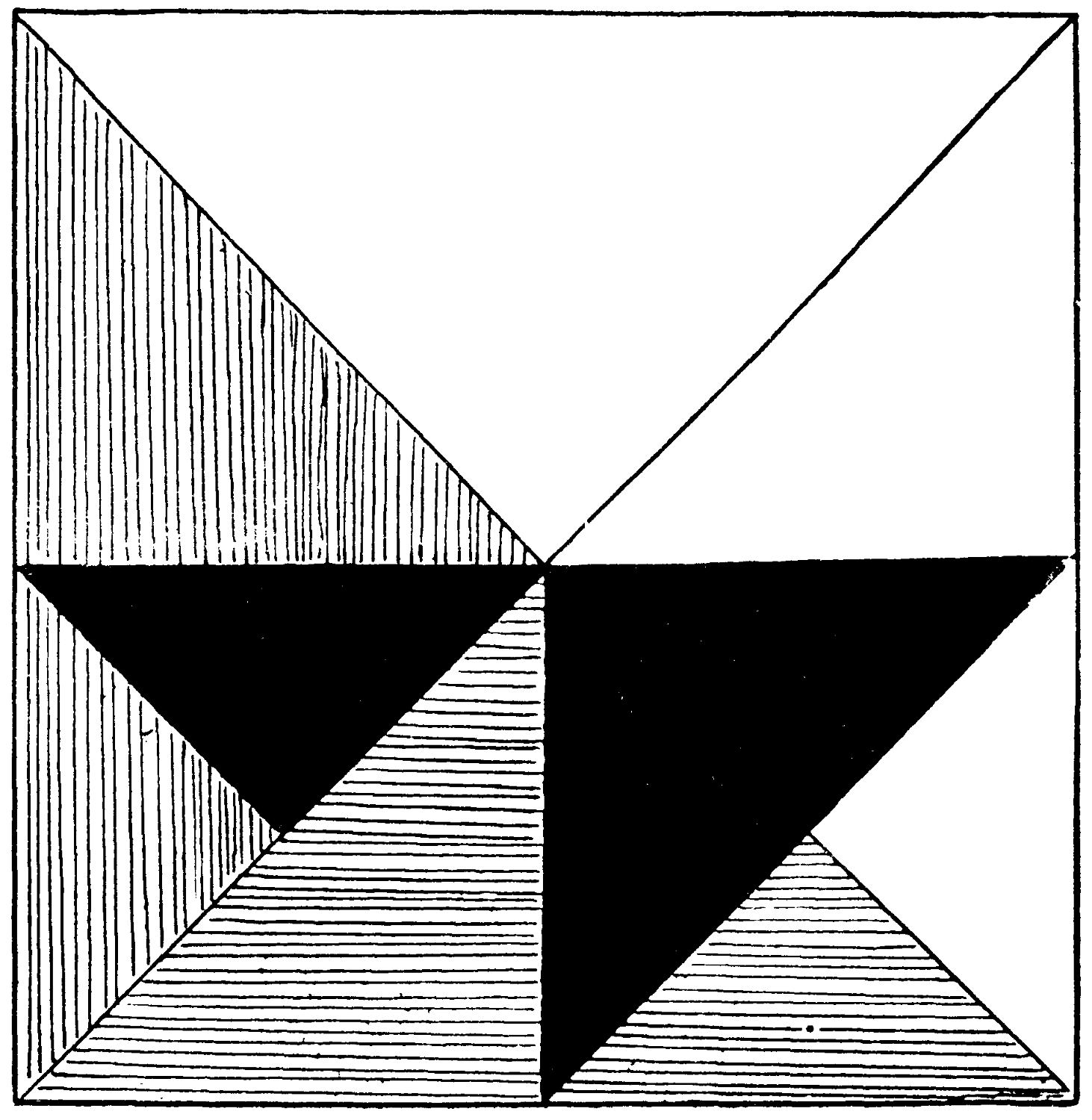
Return to description
[243]
Here is a drawing of the perfect Latin cross—
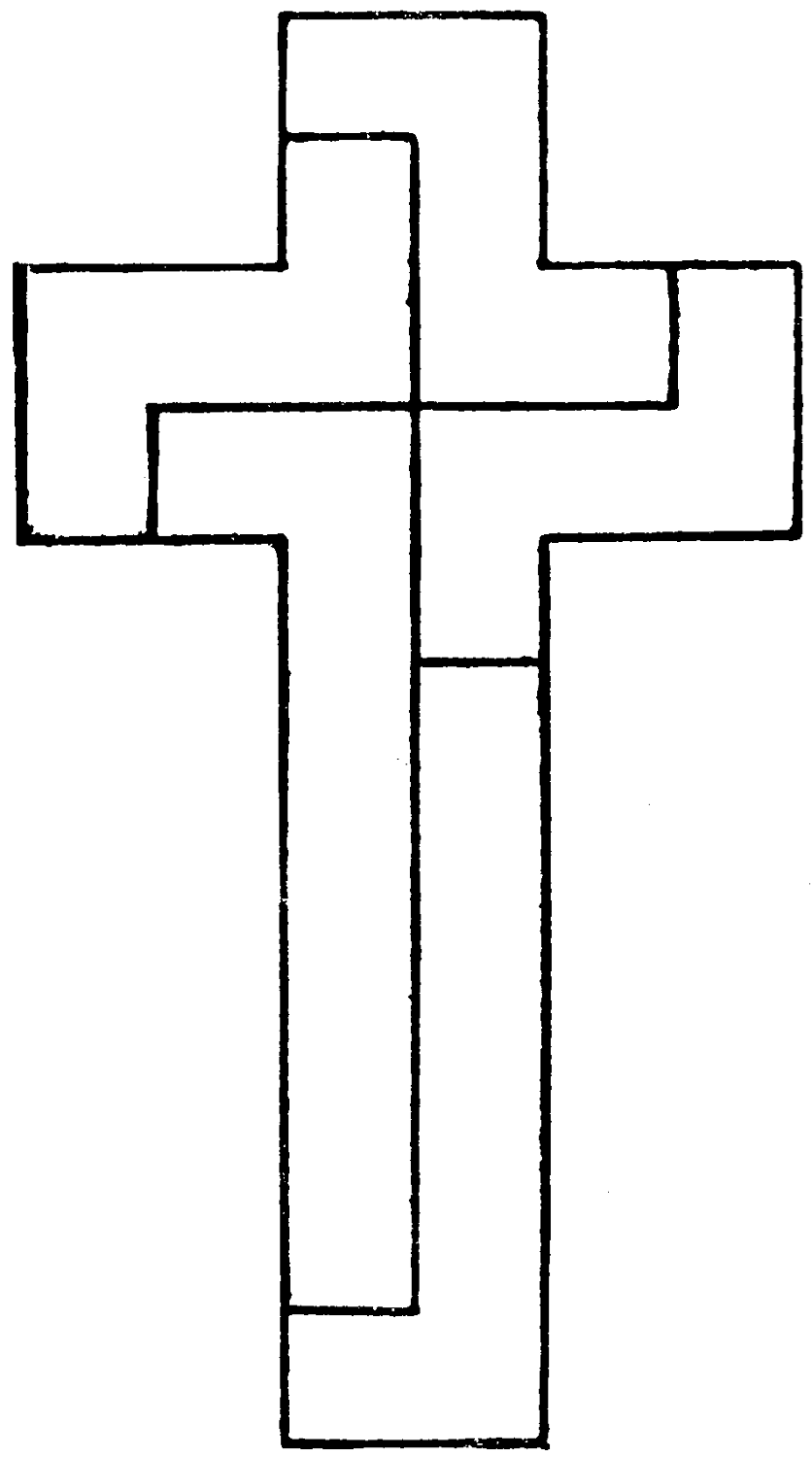
The position of the two long pieces does not readily suggest itself to those who try to arrange the five on paper with a pencil.
Return to description
[244]
This diagram shows the effectual means taken by four rich men, whose houses were further afield, to exclude four poor men from all access to a central lake, that they might reserve the fishing for themselves.
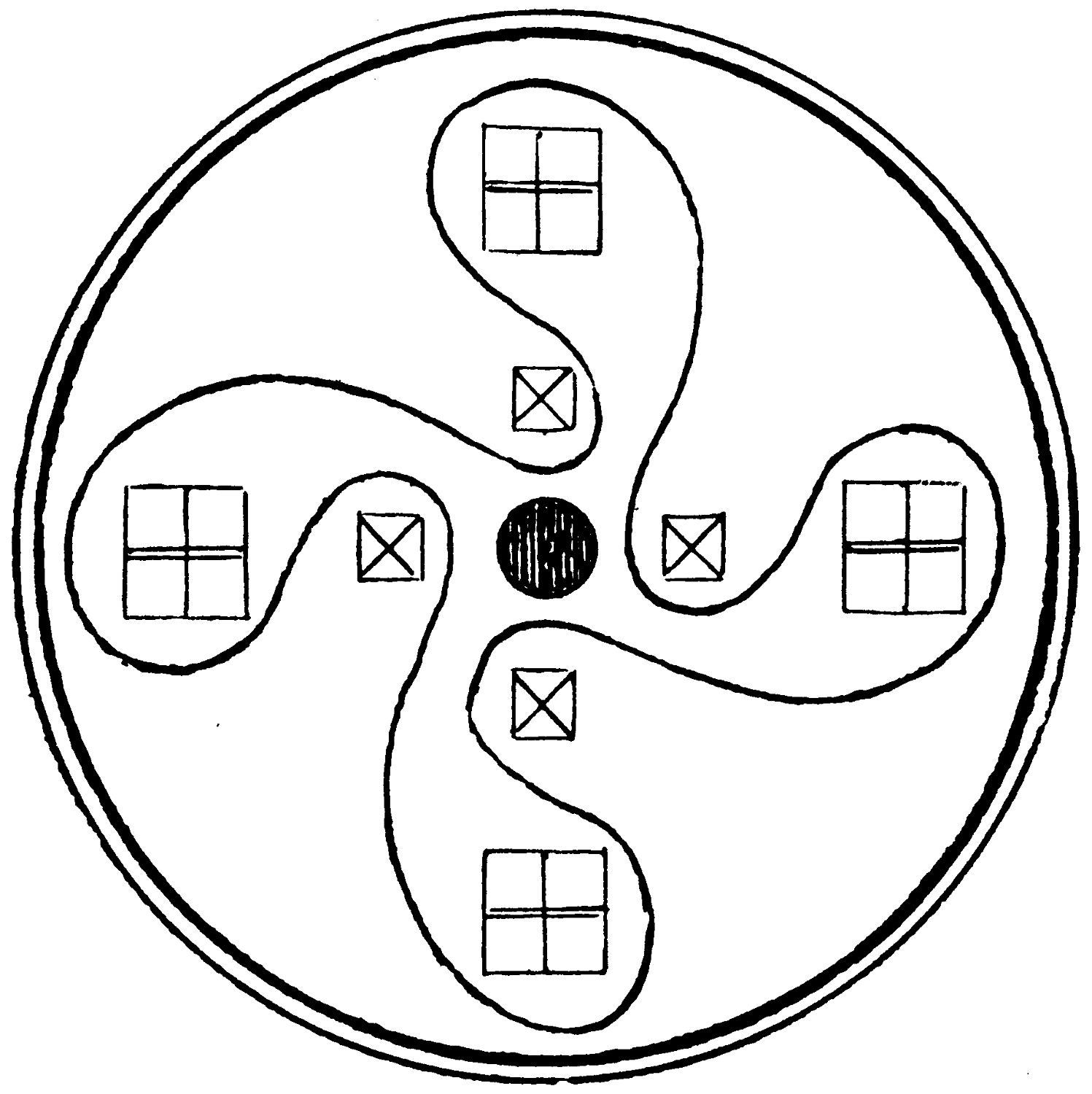
They built a high wall on the lines that are indicated which, while it left a way for each of them to the water, altogether shut it away from their poor neighbours.
Return to description
[245]
This is the square that can be formed with the ten pattern pieces given—
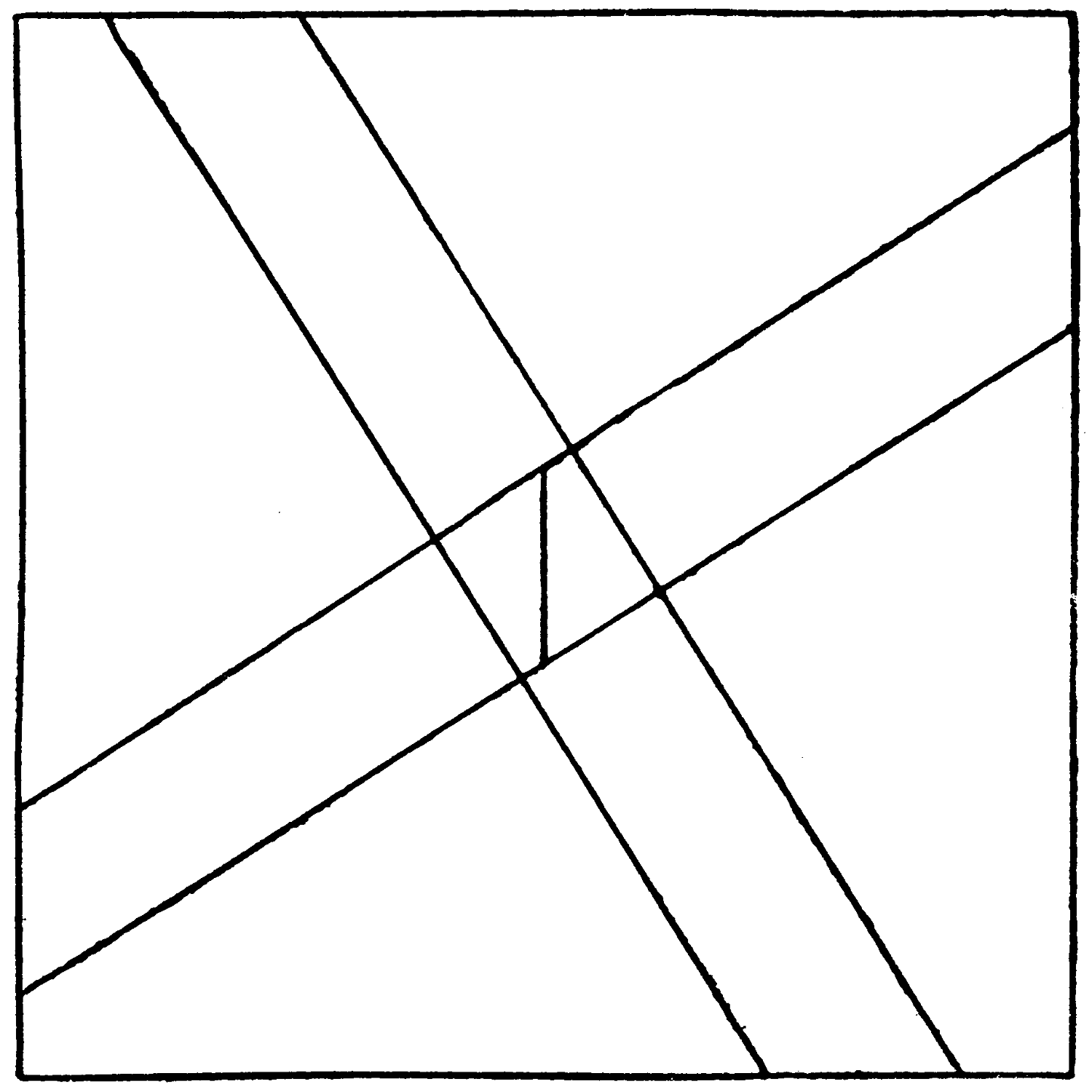
Return to description
[246]
The dotted lines in this diagram show how the figure can be divided into nine parts by four straight cuts
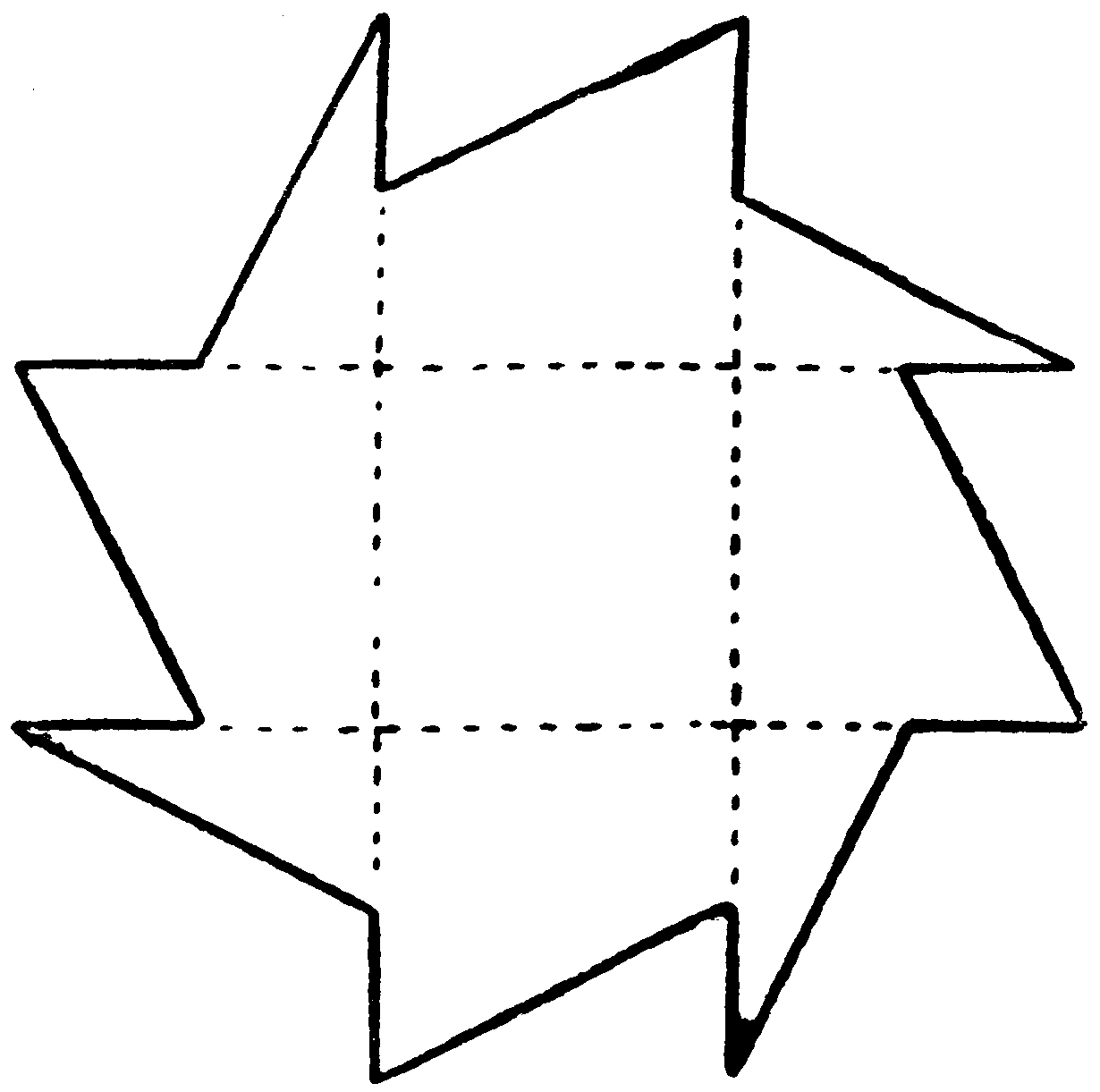
which can be reunited to form a perfect cross.
Return to description
This is a simple way by which the figure given can be divided by four straight cuts into four equal and similar parts—
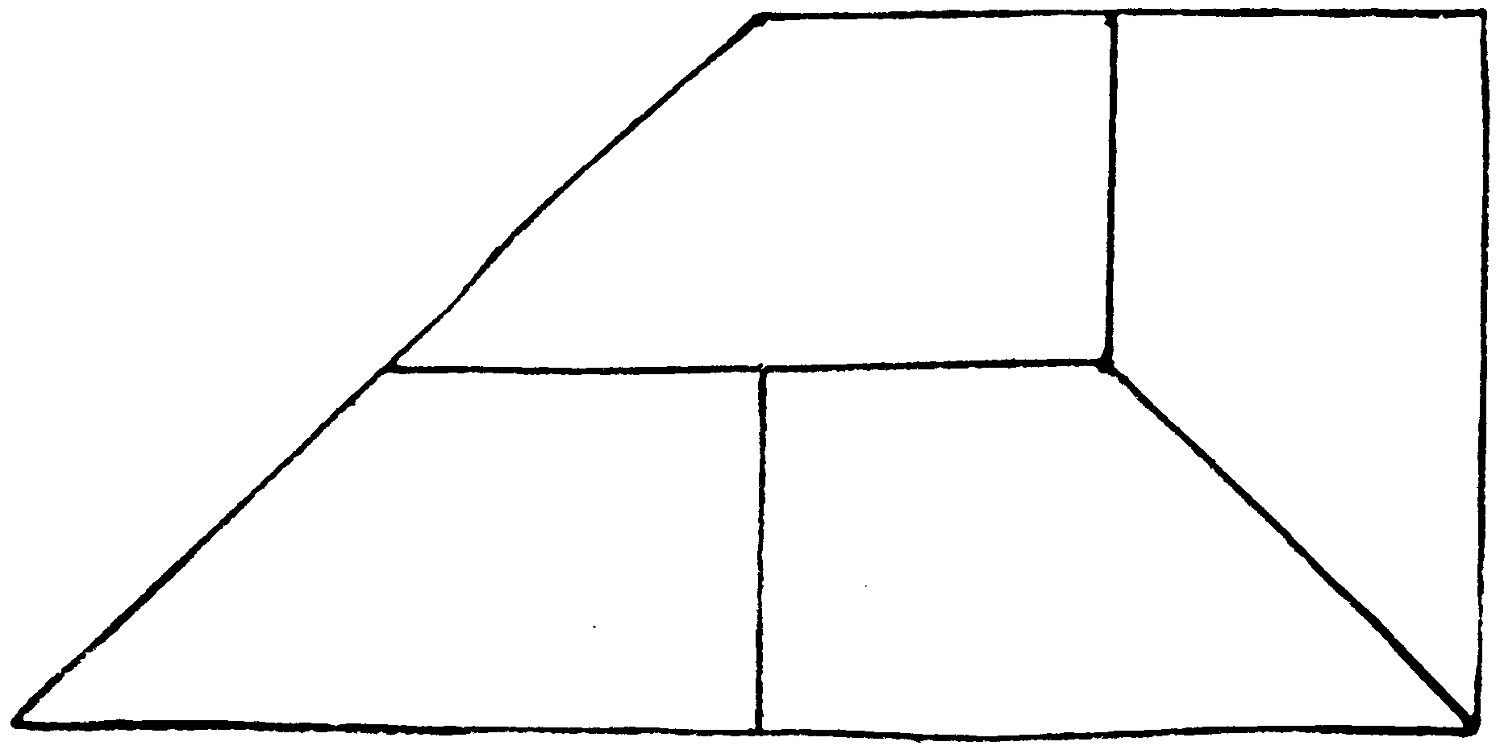
Return to description
[247]
This is the way to draw twenty-two straight lines within the circle at right-angles to each other, so that they divide it into four similar parts—
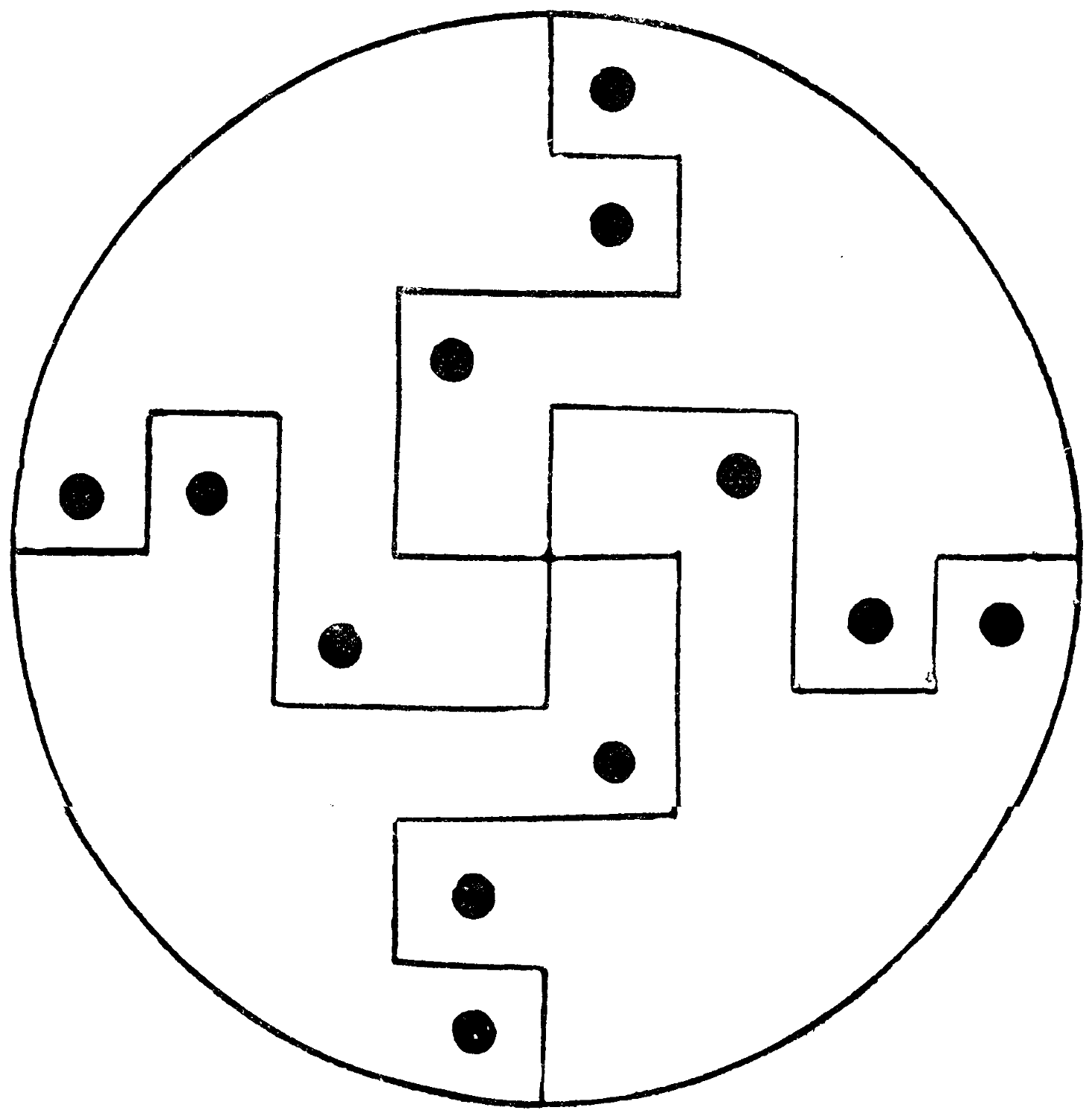
and each part has three dots within its borders.
Return to description
[248]
These diagrams show how the upper triangle is divided into five parts, which can be rearranged to form the equilateral triangle below.
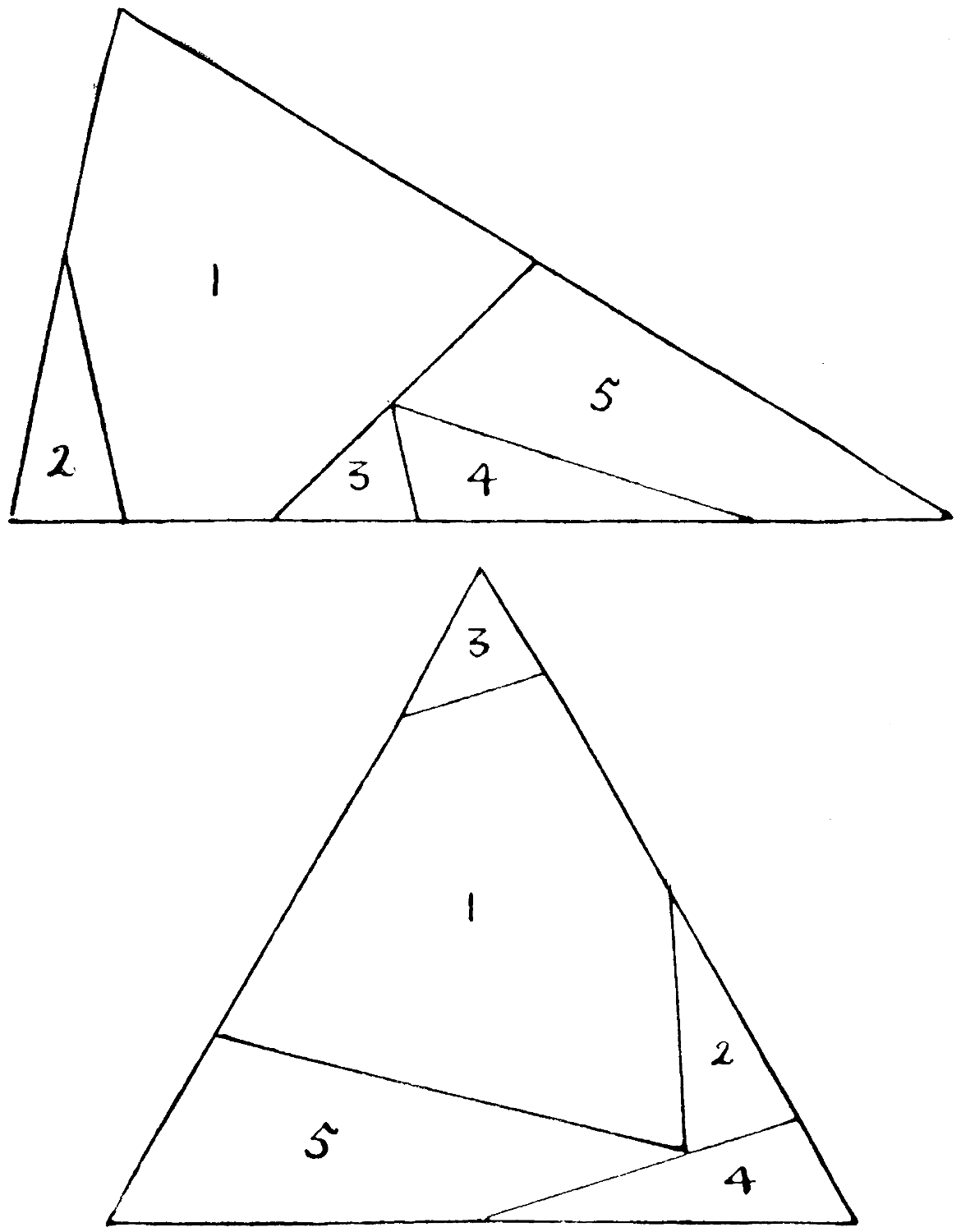
The originator of this ingenious novelty says, “The method of construction is not shown, but its application is general, and the result is easily verified by measurement.”
Return to description
[249]
This is an arrangement of the twenty-seven counters in nine rows, six in a row, within the borders of an equilateral triangle.
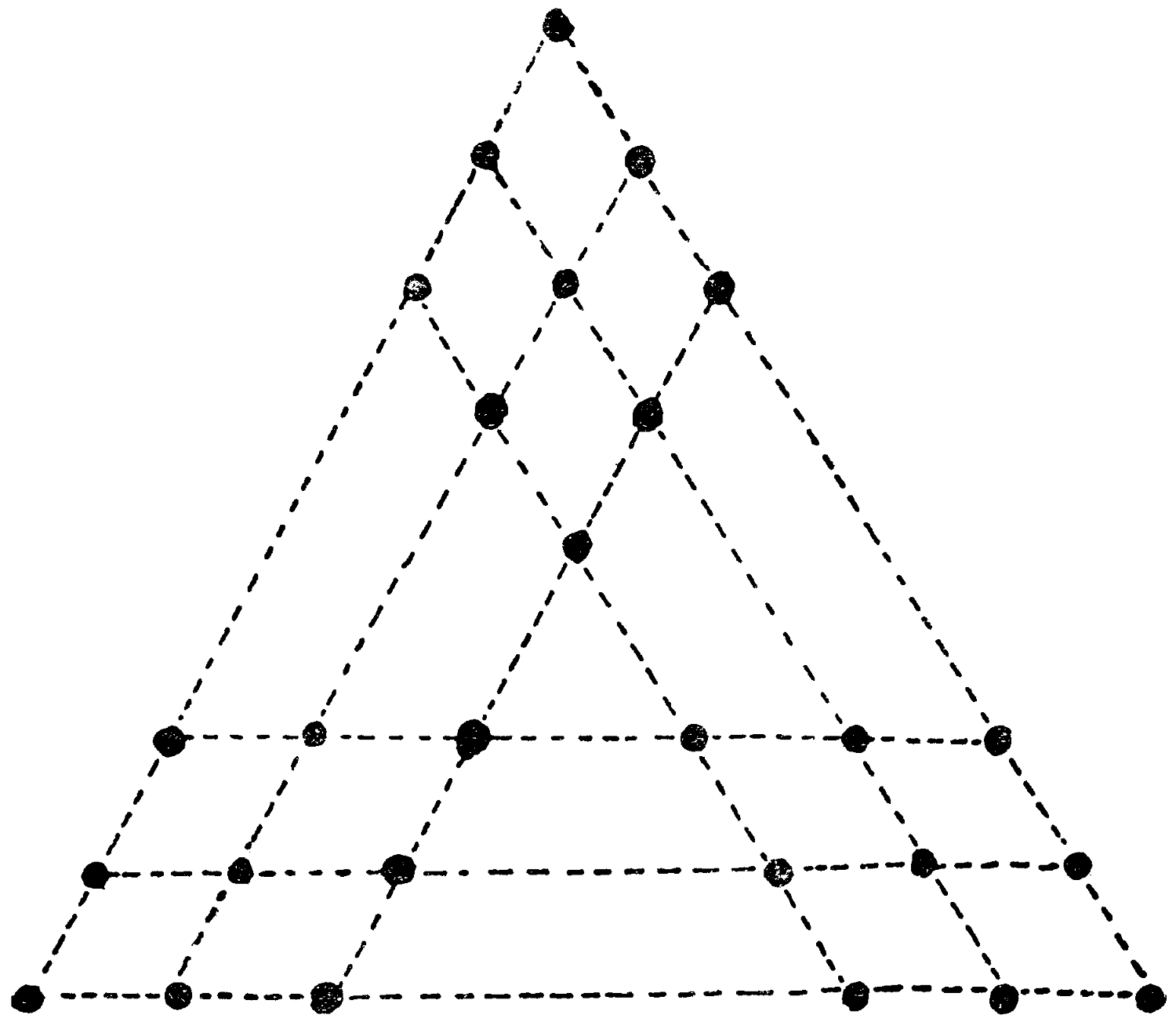
Return to description
All the cards of one colour, when placed alternately, can be brought together in four moves, two at a time, thus—
| A ♠ |
2 ♡ |
3 ♣ |
4 ♢ |
5 ♣ |
6 ♢ |
7 ♣ |
8 ♡ |
Place two and three beyond eight;
Place five and six between one and four;
Place eight and two between four and seven;
Place one and five between seven and three.
Return to description
[250]
You can in a moment tell the number chosen on these cards, when you are told on which of them it appears,
| I. | II. | III. | IV. | |||||||||||||||
| 1 | 33 | 65 | 97 | 2 | 34 | 66 | 98 | 4 | 36 | 68 | 100 | 8 | 40 | 72 | 104 | |||
| 3 | 35 | 67 | 99 | 3 | 35 | 67 | 99 | 5 | 37 | 69 | 101 | 9 | 41 | 73 | 105 | |||
| 5 | 37 | 69 | 101 | 6 | 38 | 70 | 102 | 6 | 38 | 70 | 102 | 10 | 42 | 74 | 106 | |||
| 7 | 39 | 71 | 103 | 7 | 39 | 71 | 103 | 7 | 39 | 71 | 103 | 11 | 43 | 75 | 107 | |||
| 9 | 41 | 73 | 105 | 10 | 42 | 74 | 106 | 12 | 44 | 76 | 108 | 12 | 44 | 76 | 108 | |||
| 11 | 43 | 75 | 107 | 11 | 43 | 75 | 107 | 13 | 45 | 77 | 109 | 13 | 45 | 77 | 109 | |||
| 13 | 45 | 77 | 109 | 14 | 46 | 78 | 110 | 14 | 46 | 78 | 110 | 14 | 46 | 78 | 110 | |||
| 15 | 47 | 79 | 111 | 15 | 47 | 79 | 111 | 15 | 47 | 79 | 111 | 15 | 47 | 79 | 111 | |||
| 17 | 49 | 81 | 113 | 18 | 50 | 82 | 114 | 20 | 52 | 84 | 116 | 24 | 56 | 88 | 120 | |||
| 19 | 51 | 83 | 115 | 19 | 51 | 83 | 115 | 21 | 53 | 85 | 117 | 25 | 57 | 89 | 121 | |||
| 21 | 53 | 85 | 117 | 22 | 54 | 86 | 118 | 22 | 54 | 86 | 118 | 26 | 58 | 90 | 122 | |||
| 23 | 55 | 87 | 119 | 23 | 55 | 87 | 119 | 23 | 55 | 87 | 119 | 27 | 59 | 91 | 123 | |||
| 25 | 57 | 89 | 121 | 26 | 58 | 90 | 122 | 28 | 60 | 92 | 124 | 28 | 60 | 92 | 124 | |||
| 27 | 59 | 91 | 123 | 27 | 59 | 91 | 123 | 29 | 61 | 93 | 125 | 29 | 61 | 93 | 125 | |||
| 29 | 61 | 93 | 125 | 30 | 62 | 94 | 126 | 30 | 62 | 94 | 126 | 30 | 62 | 94 | 126 | |||
| 31 | 63 | 95 | 127 | 31 | 63 | 95 | 127 | 31 | 63 | 95 | 127 | 31 | 63 | 95 | 127 | |||
| V. | VI. | VII. | |||||||||||
| 16 | 48 | 80 | 112 | 32 | 48 | 96 | 112 | 64 | 80 | 96 | 112 | ||
| 17 | 49 | 81 | 113 | 33 | 49 | 97 | 113 | 65 | 81 | 97 | 113 | ||
| 18 | 50 | 82 | 114 | 34 | 50 | 98 | 114 | 66 | 82 | 98 | 114 | ||
| 19 | 51 | 83 | 115 | 35 | 51 | 99 | 115 | 67 | 83 | 99 | 115 | ||
| 20 | 52 | 84 | 116 | 36 | 52 | 100 | 116 | 68 | 84 | 100 | 116 | ||
| 21 | 53 | 85 | 117 | 37 | 53 | 101 | 117 | 69 | 85 | 101 | 117 | ||
| 22 | 54 | 86 | 118 | 38 | 54 | 102 | 118 | 70 | 86 | 102 | 118 | ||
| 23 | 55 | 87 | 119 | 39 | 55 | 103 | 119 | 71 | 87 | 103 | 119 | ||
| 24 | 56 | 88 | 120 | 40 | 56 | 104 | 120 | 72 | 88 | 104 | 120 | ||
| 25 | 57 | 89 | 121 | 41 | 57 | 105 | 121 | 73 | 89 | 105 | 121 | ||
| 26 | 58 | 90 | 122 | 42 | 58 | 106 | 122 | 74 | 90 | 106 | 122 | ||
| 27 | 59 | 91 | 123 | 43 | 59 | 107 | 123 | 75 | 91 | 107 | 123 | ||
| 28 | 60 | 92 | 124 | 44 | 60 | 108 | 124 | 76 | 92 | 108 | 124 | ||
| 29 | 61 | 93 | 125 | 45 | 61 | 109 | 125 | 77 | 93 | 109 | 125 | ||
| 30 | 62 | 94 | 126 | 46 | 62 | 110 | 126 | 78 | 94 | 110 | 126 | ||
| 31 | 63 | 95 | 127 | 47 | 63 | 111 | 127 | 79 | 95 | 111 | 127 | ||
by adding together the numbers at the top left-hand corner of these.
Return to description
[251]
This diagram shows that the postman can take a course which involves fewer turnings than that indicated, when he had to pass round eighteen corners.
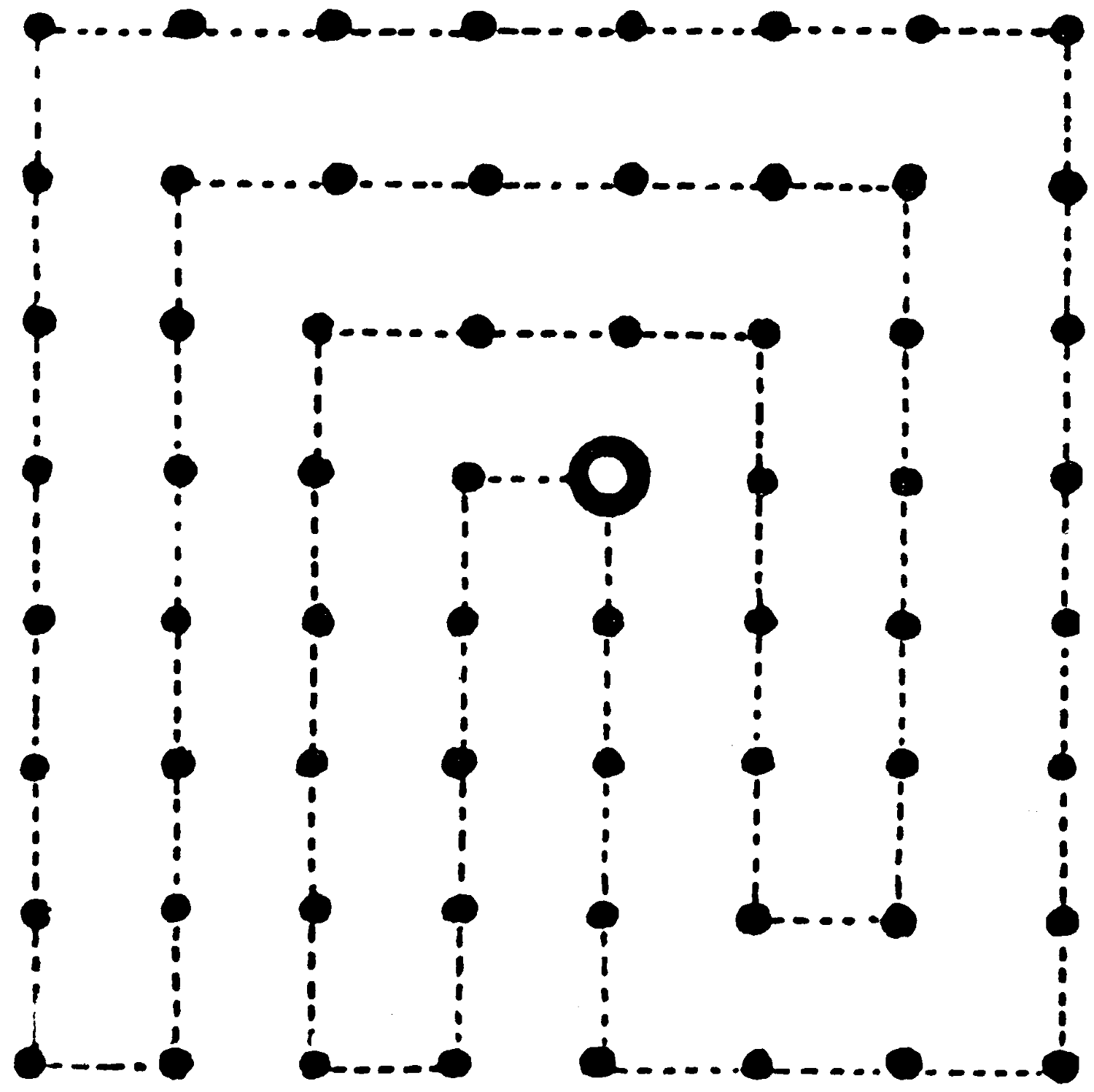
It will be seen that he has to turn only fifteen times.
Return to description
[252]
This shows how a square can be divided into three parts, so that these can be reunited to form No. 2 and No. 3 of the diagram.
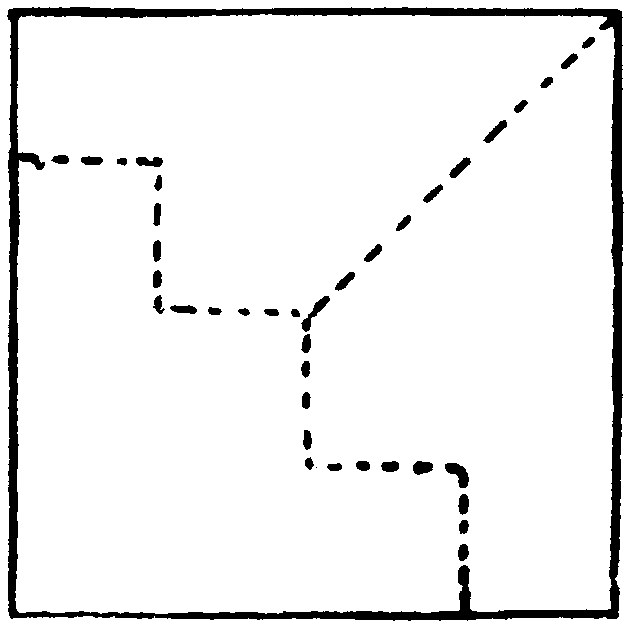
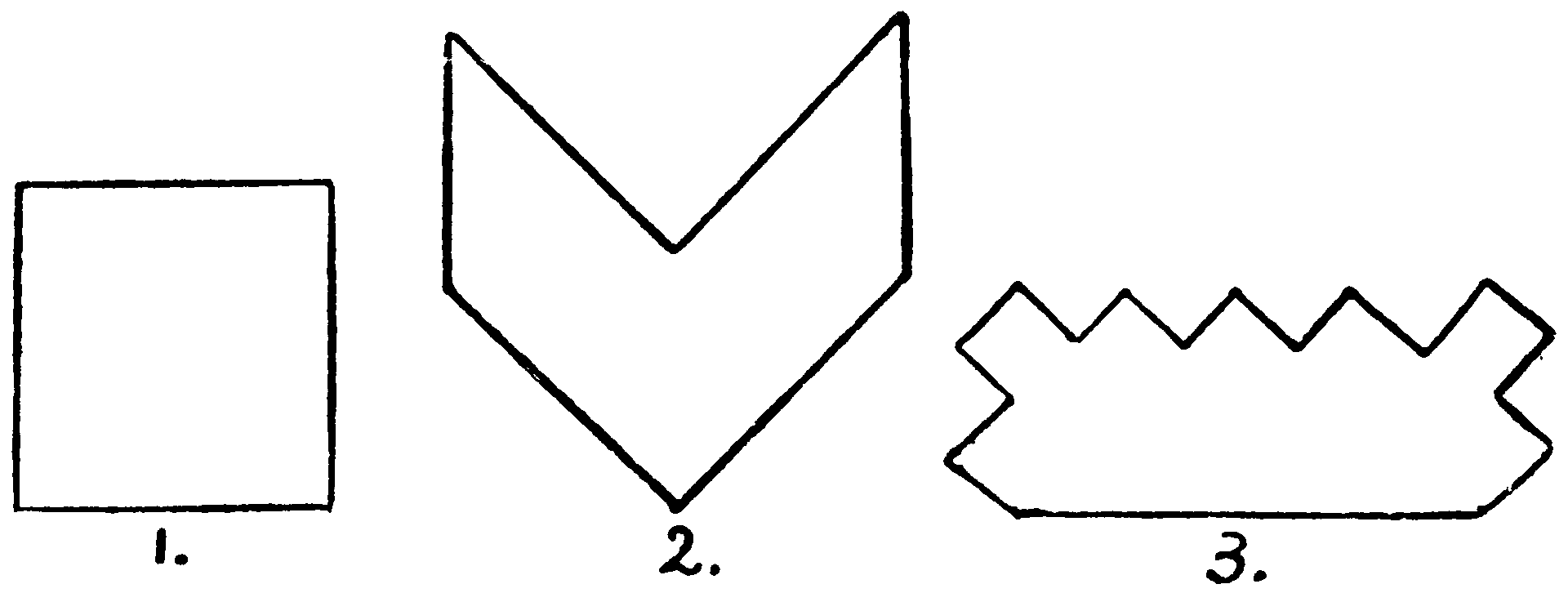
Try it with scissors and paper or cardboard.
Return to description
[253]
| ♘ | ♖ | ♚ | ♖ | ||||
This position fulfils the conditions of the puzzle. Obviously it could not occur in actual play.
Return to description
[254]
The dotted lines in this diagram show where the flag with a cross taken out from its centre must be cut, so that the two pieces can be rejoined to form a perfect flag.
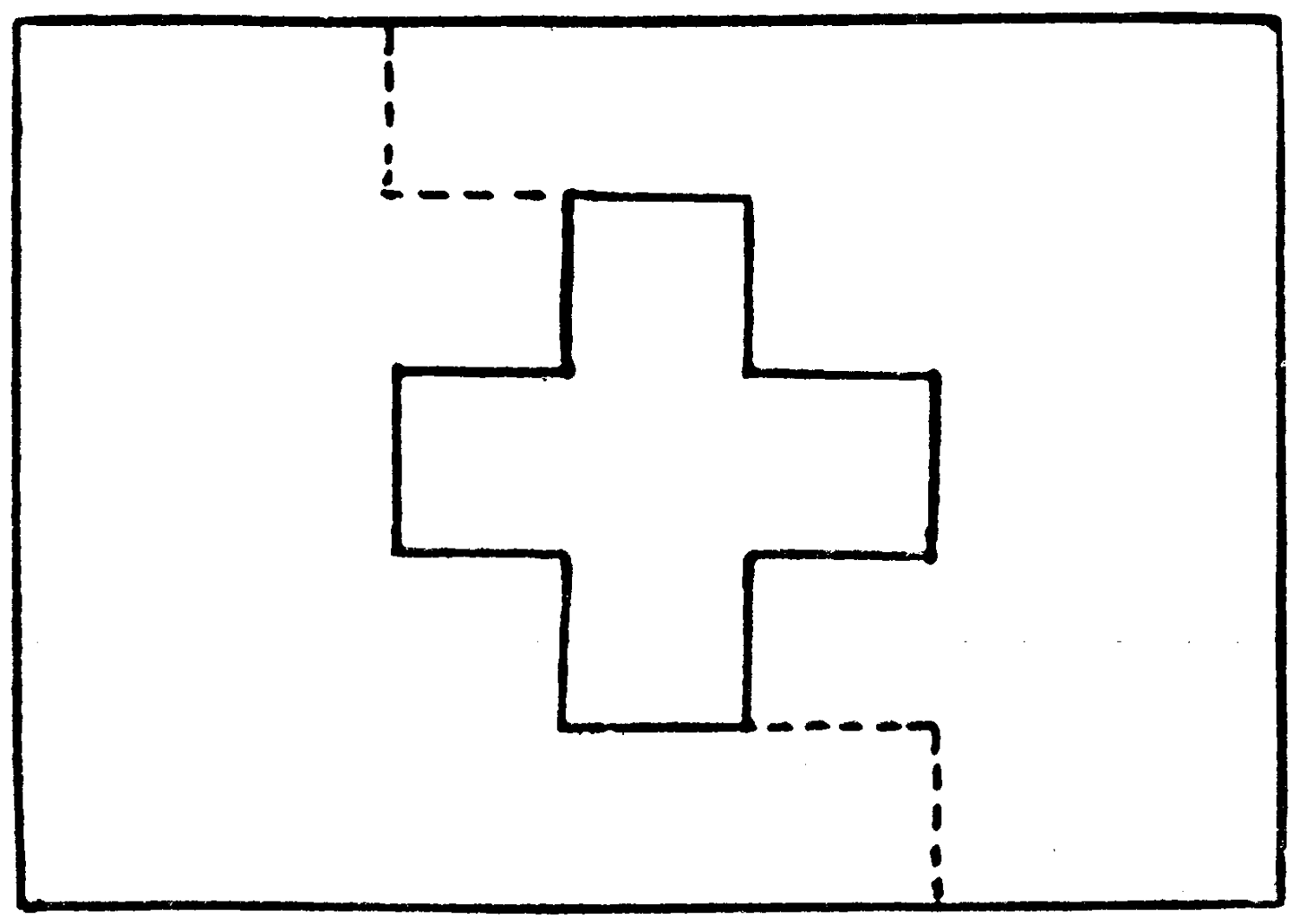
The piece on the right is moved upward, and to the left.
Return to description
[255]
This is a way in which the eleven parts can be readjusted to form a square:—
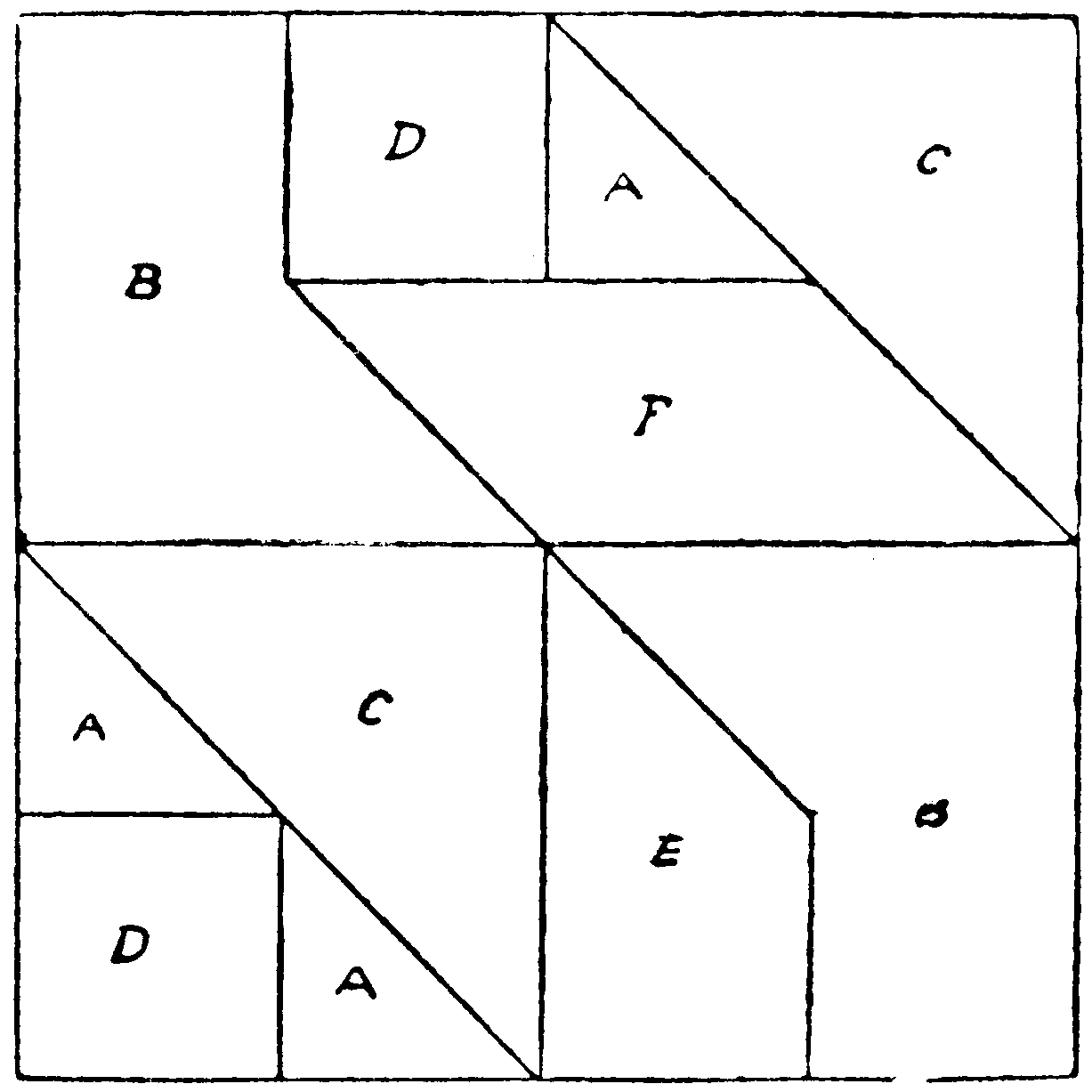
Return to description
This shows the shortest course—
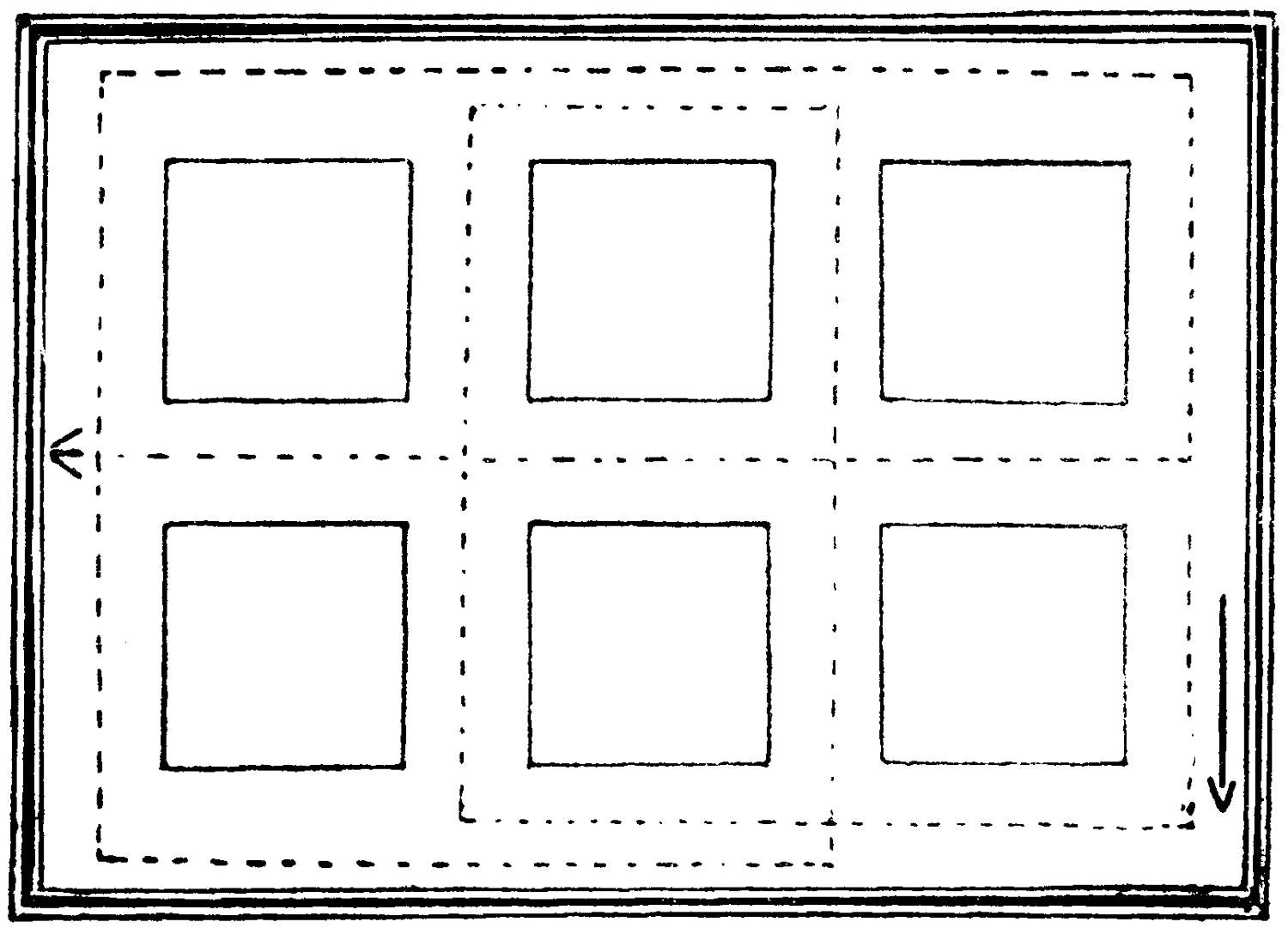
This track takes him completely round every block, passing only once round four of them.
Return to description
[256]
Here is a very simple and symmetrical arrangement, by which on a board of 36 squares twelve counters are so placed that there are two, and two only, on each line, column, and diagonal.
| ◎ | ◎ | ||||
| ◎ | ◎ | ||||
| ◎ | ◎ | ||||
| ◎ | ◎ | ||||
| ◎ | ◎ | ||||
| ◎ | ◎ |
There are other arrangements which fulfil the conditions.
Return to description
[257]
In this nest of triangles of five tiers there are 1196 separate triangles, or nearly double the number (653) of a similar nest of four tiers.

In such a figure with 10,000 tiers there would be 6,992,965,420,332 different triangles!
Return to description
[258]
The match puzzle, in which eight matches set in a row are to be rearranged in four pairs, by passing one match over two four times—

is solved, if the matches are numbered 1, 2, 3, 4, 5, 6, 7, 8, by moving 4 to 7, 6 to 2, 1 to 3, and 5 to 8.
Return to description
The lower diagram shows how, when three matches are removed from the four squares, the[259] remaining nine can be readjusted to represent three squares—
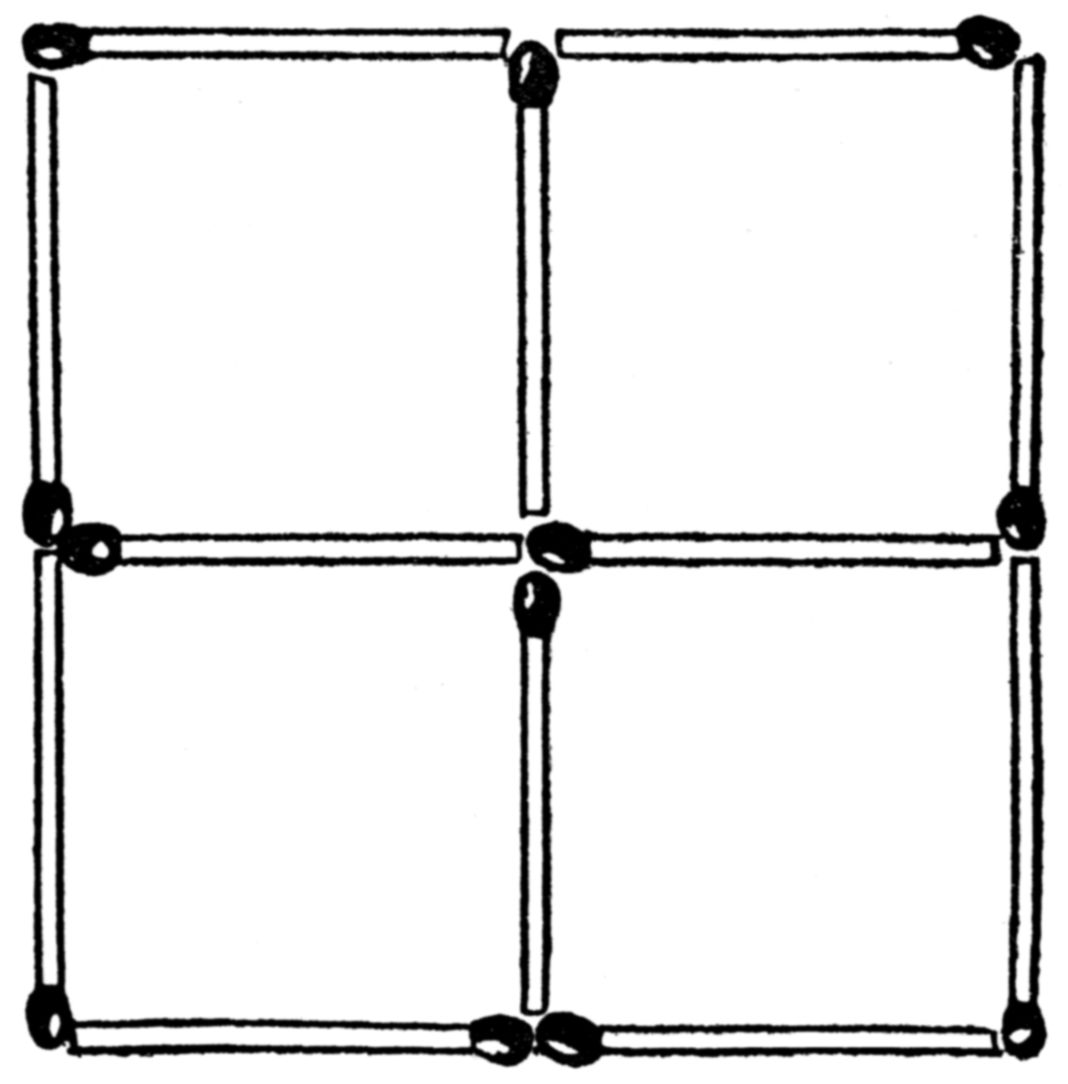

Return to description
[260]
This diagram shows how different arrangements of four matches are possible in all the thirty-six cells of the square.

In every case a whole number or a fraction is represented, with such signs or lines as are necessary, and only four matches are used.
Return to description
[261]
It will be seen from the diagram below that the sentence, when filled in as required, is “Rise to vote, sir.”
| R | I | S | E | T | O | V | O | T | E | S | I | R |
| I | I | I | I | |||||||||
| S | S | S | S | |||||||||
| E | E | E | E | |||||||||
| T | T | T | T | |||||||||
| O | O | O | O | |||||||||
| V | V | V | ||||||||||
| O | O | O | O | |||||||||
| T | T | T | T | |||||||||
| E | E | E | E | |||||||||
| S | S | S | S | |||||||||
| I | I | I | I | |||||||||
| R | I | S | E | T | O | V | O | T | E | S | I | R |
As this sentence is a perfect palindrome, and reads alike from either end, it can be traced in a great number of different directions.
Return to description
[262]
This subtraction sum may be very neatly worked, without reducing the distances to inches, thus:—
| miles | furlongs | rods | yards | feet | inches | |||||||
| 1 | „ | 0 | „ | 0 | „ | 0 | „ | 0 | „ | 0 | ||
| 7 | „ | 39 | „ | 5 | „ | 1 | „ | 5 | ||||
| 0 | „ | 0 | „ | 0 | „ | 0 | „ | 0 | „ | 1 | ||
Instead of borrowing one foot, we borrow half-a-foot—i.e., 6 inches; taking 5 from the 6 we have 1 as a remainder; now carrying the 6 inches to the 1 foot, and borrowing half a yard, and subtracting, we have 0 as remainder; carrying the half-yard to the 5 yards, we borrow the full 51⁄2 yards, which are one rod, and proceed in the usual manner afterwards, with the result that is shown.
Return to description
[263]
This is an arrangement of nine counters on the irregular board of 67 squares.
| ● | ||||||||
| ● | ||||||||
| ● | ||||||||
| ● | ||||||||
| ● | ||||||||
| ● | ||||||||
| ● | ||||||||
| ● | ||||||||
| ● |
No two counters are in the same row, column, or diagonal.
Return to description
[264]
This is the arrangement of nine cards in ten rows, three in each row—
| K ♢ |
Q ♠ |
K ♡ |
||||||
| A ♣ |
A ♢ |
A ♠ |
||||||
| 10 ♡ |
K ♣ |
J ♢ |
||||||
Return to description
The following diagram shows how the two ladies and their squires represented by white Knights and black, and dressed to impersonate Light,[265] Liberty, Love, and Learning, started from the four comer squares, and stepped a figure which exhibited at each pause a revolving square, and in three paces came together in the centre, by a course traced upon the lines of their combined monograms.

Return to description
[266]
The 5 maxims in these 36 cells—
| tell | you know | tells | knows | tells | he should not |
| do | you think of | does | thinks of | does | is not good |
| believe | you hear | believes | hears | believes | is false |
| spend | you have | spends | has | spends | he needs |
| judge | you see | judges | sees | judges | is not there |
| never | all | he who | all he | often | what |
are disentangled by reading the lowest line with each of the upper ones in turn. Thus the first maxim runs:—“Never tell all you know, he who tells all he knows often tells what he should not,” and so on throughout.
Return to description
[267]
The dislocated circle is solved by making a single cut through the dotted line shown in the diagram below, and join up the pieces.
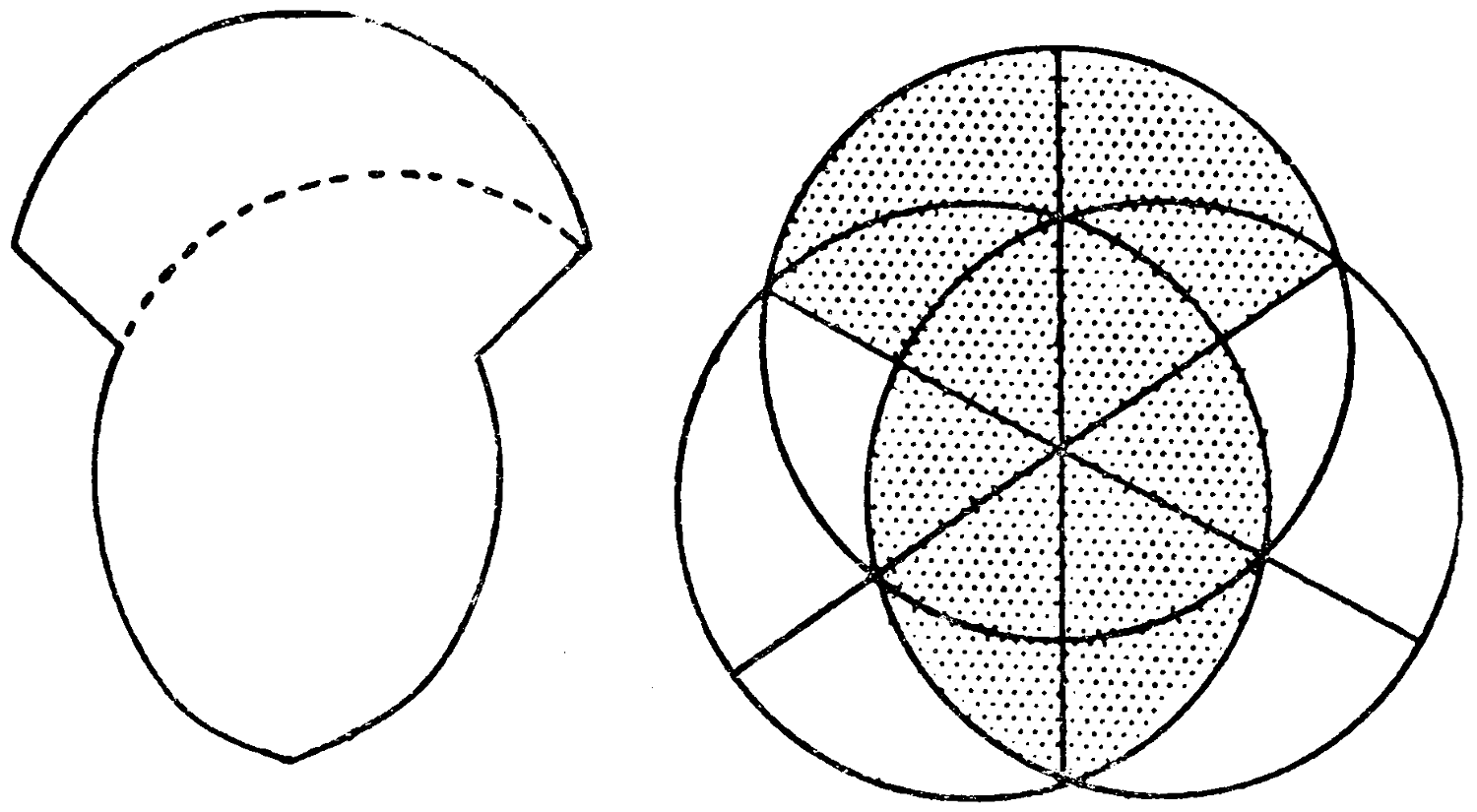
The second diagram shows how this figure is arrived at, by drawing three similar and intersecting circles, which have their centres at the angles of an equilateral triangle. The piece cut off by the dotted line corresponds to the section that completes the circle below.
Return to description
[268]
The catch-words Cleans, Scrubs, Scours, Polishes, which proclaim the merits of an “Old Dutch Cleanser” on the sails of this windmill,
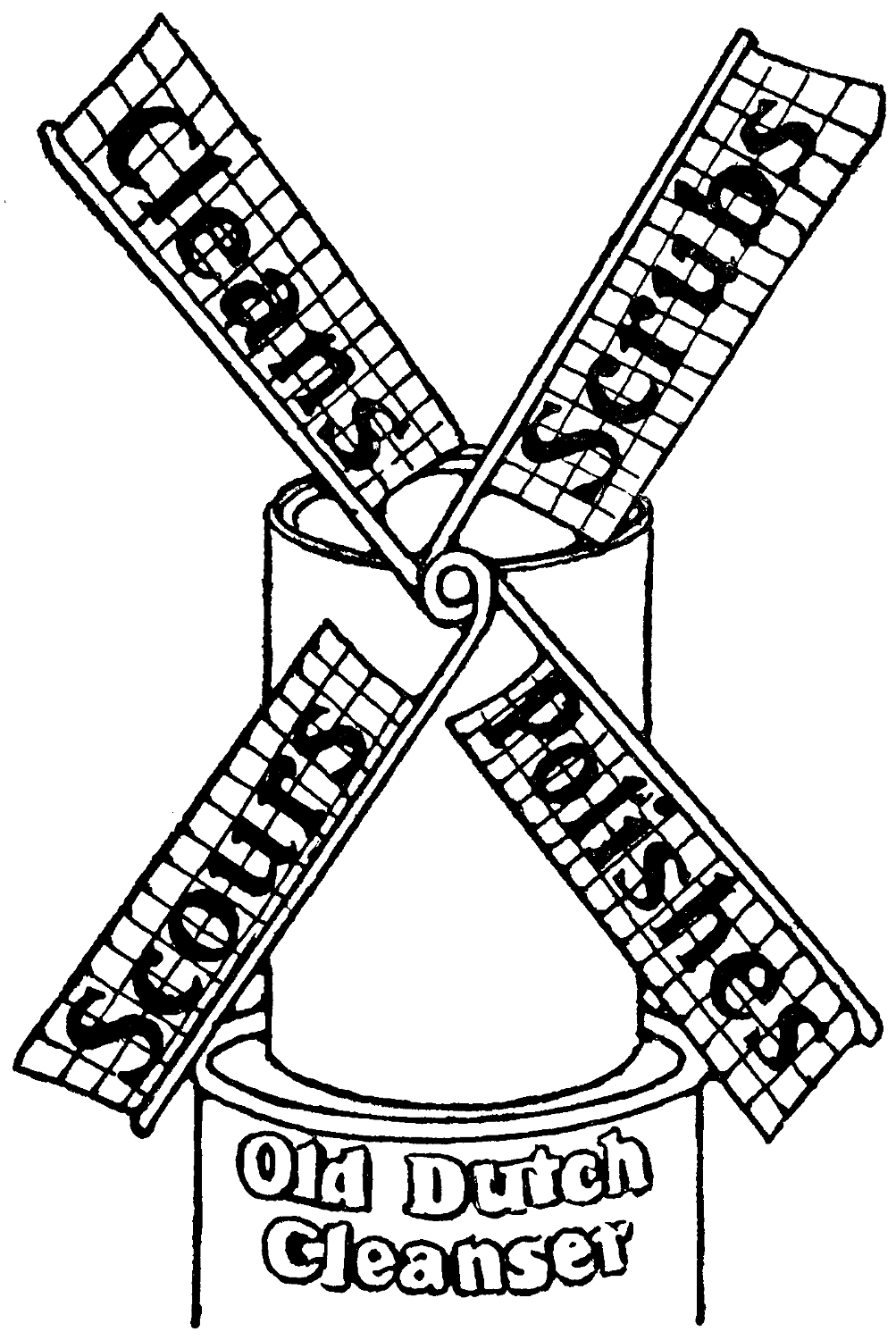
can be recast so that the same letters form the singularly appropriate sentence—
“O rub on, sir, success spells cash!”
Return to description
[269]
The following diagram shows the solution of this new chess puzzle, and fulfils its conditions that no Queen should attack a Queen, no Rook a Rook, no Bishop a Bishop, and no Knight a Knight.
| B | B | B | B | Q | R | B | B |
| Kt | R | Kt | Kt | Q | |||
| Kt | R | Kt | Q | Kt | Kt | B | |
| Q | Kt | Kt | R | Kt | B | ||
| B | Kt | Kt | Q | R | |||
| B | Q | Kt | Kt | R | Kt | ||
| Kt | Kt | R | Kt | Q | Kt | ||
| R | B | Q | Kt | B | B | B | Kt |
Mr Dudeney explains that only 8 Queens or 8 Rooks can be thus placed upon the board, while the greatest number of Bishops is fourteen, and of Knights thirty-two. But as all Knights must be placed on squares of the same colour, while the Queens occupy four of each colour, and the bishops seven of each colour, it follows that only twenty-one Knights can be placed, and the arrangement shown above contains the maximum number of these pieces under the conditions.
Return to description
[270]
This diagram shows the order in which the syllables or words of the eight-line verse are to be read on the course of a Knight’s moves at chess—
| 14 sor |
55 to |
22 king |
37 good |
12 say |
51 luck |
18 loy |
35 eth |
| 23 and |
38 moth |
13 a |
54 soon |
17 dis |
36 our |
11 to |
50 bad |
| 56 place |
15 ry |
40 church |
21 his |
52 force |
9 is |
34 hat |
19 al |
| 39 er |
24 queen |
53 him |
16 wight |
33 he |
20 to |
49 may |
10 truth |
| 2 man |
57 his |
28 and |
41 and |
8 chess |
61 es |
32 knight |
47 op’s |
| 25 a |
42 sneer |
1 the |
60 and |
29 un |
48 lawn |
7 of |
62 tates |
| 58 cas |
3 that |
44 at |
27 less |
64 pawn |
5 no |
46 bish |
31 lant |
| 44 eth |
26 faith |
59 tles |
4 hath |
45 the |
30 gal |
63 in |
6 love |
They run thus:—
Return to description
[271]
If such a network as is shown in the diagram below is drawn on clear tracing-paper and placed on the page of a book, it will conceal the words beneath it.

But if, while lying close to the page, it is moved quickly round and about, the letters and words will be distinctly seen, just as objects on the other side of close lattice-work become visible as we pass them quickly in a train.
Return to description
[272]
These are the results of cutting, in the direction of the dotted lines, completely round a simple paper ring, a ring with one twist, and a ring with a double twist.
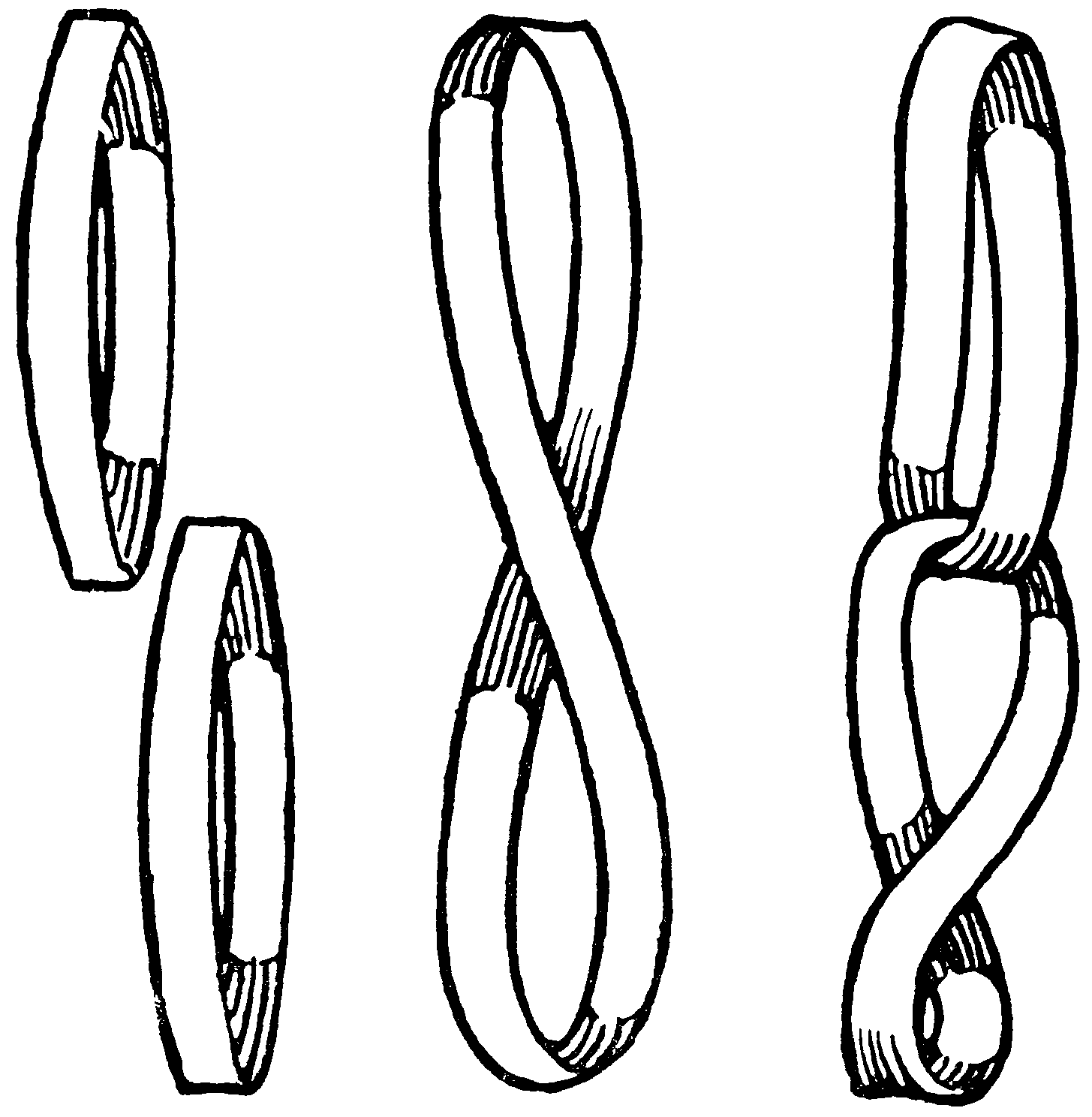
We have (1) two simple rings; (2) one large-twisted ring; (3) two rings linked together. If a third twist is given before cutting, a curious knot is formed.
Return to description
[273]
The string when it has been placed in the position shown in the diagram, and two buttons larger than the hole have been fixed upon its ends can be easily removed if the narrow slip of the leather is drawn through the hole.
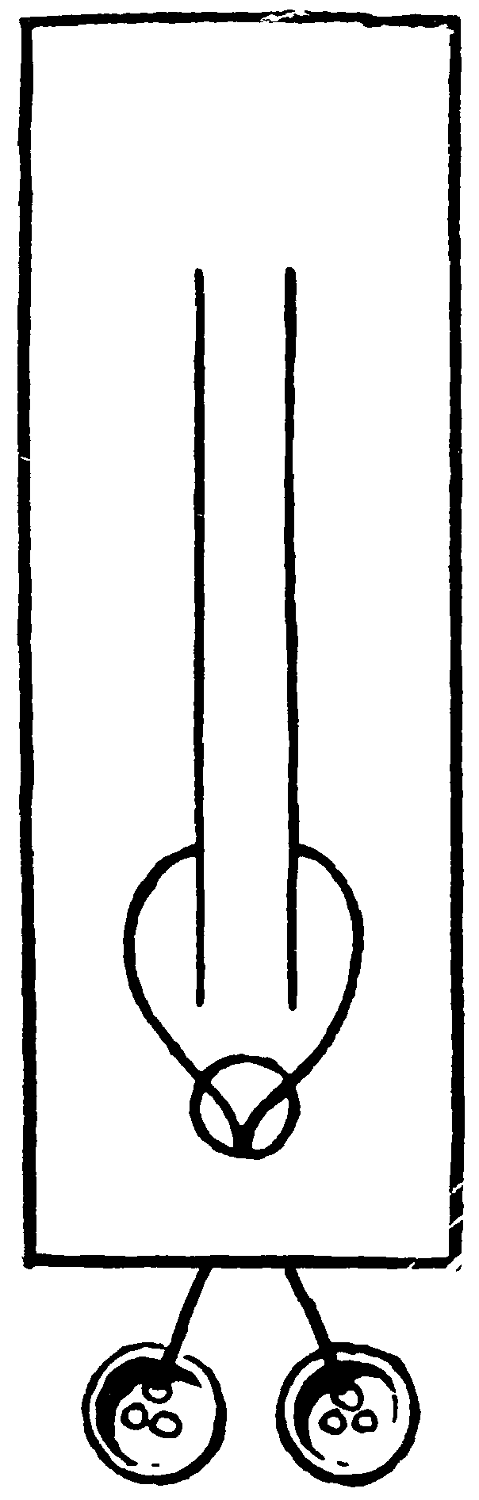
Return to description
[274]
The scissors, when securely fastened, as is shown in the diagram,
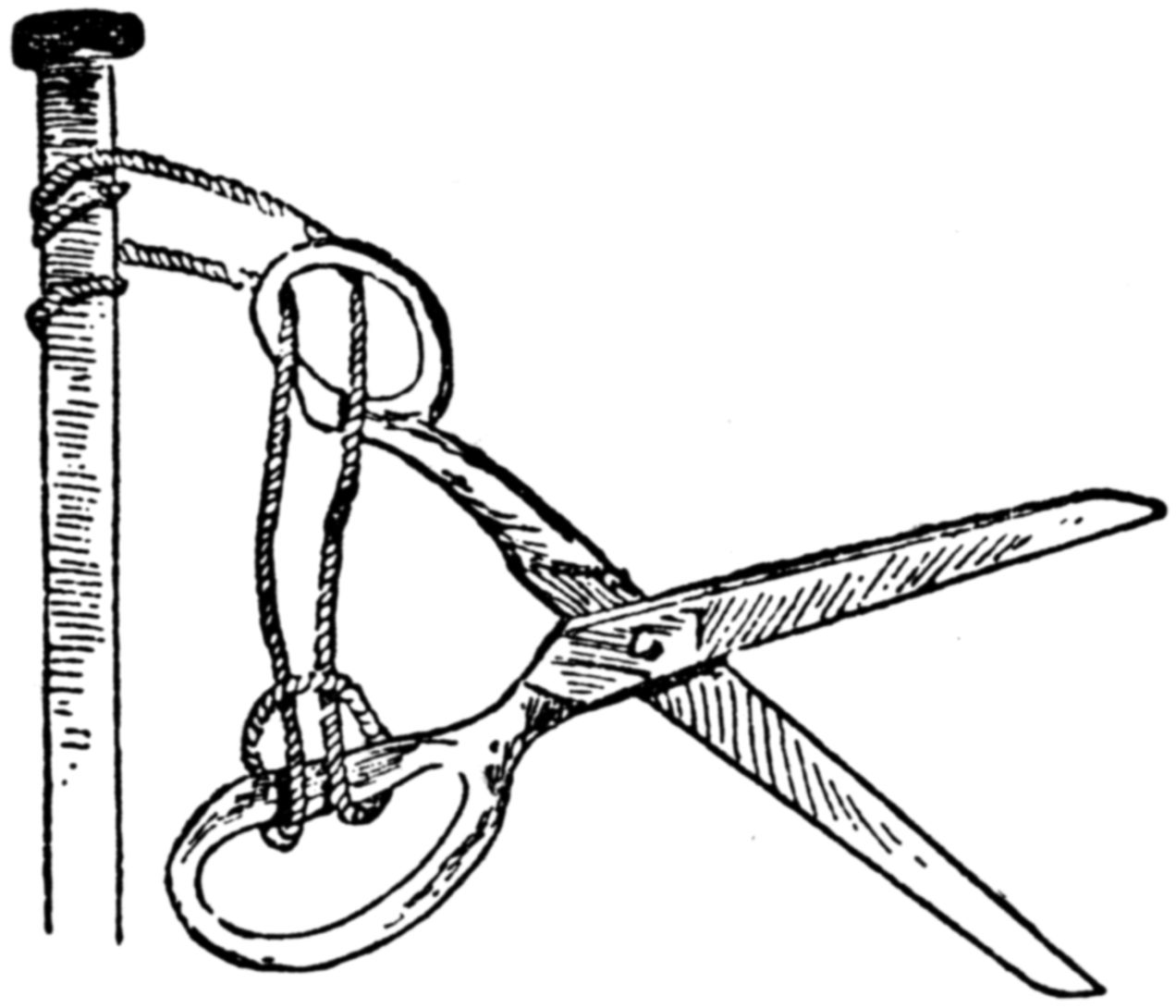
can be easily released by passing the loop upward through the handle, and then completely over them.
Return to description
[275]
The primitive wolf-trap consisted of two circular fences higher than a wolf could scale, with a gate as was shown on the former diagram. To set the trap a lamb was placed in the safe centre, and the gate was opened as is shown below—
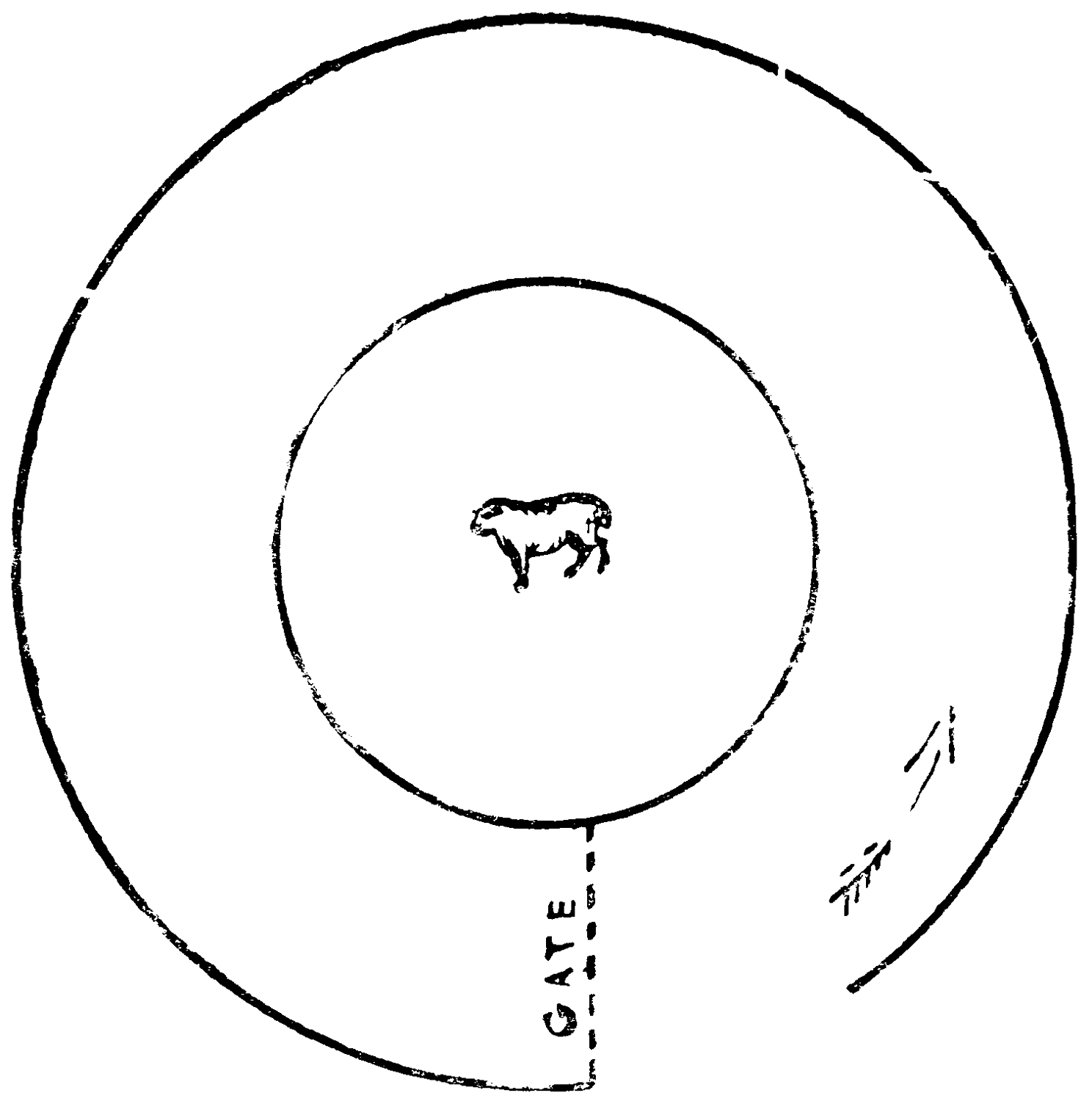
Attracted by the bleating of the lamb, the wolf entered the outer circle, made his way round, and presently pushed aside the gate, which closed with a spring, and shut off all escape.
Return to description
[276]
When you have told someone to think of a number between 5 and 15, and while you are not looking, to count upwards from the lowest card step, and round in the direction indicated by the arrow, until that number is reached, and then, starting afresh with “one” on that card to count backwards round the semi-circle, this time not including the central upright or the steps below it, until the number thought of is again reached,[277] you can tell at once which is the final card arrived at, for it will be as many places upwards on the left as there are step cards and their upright.
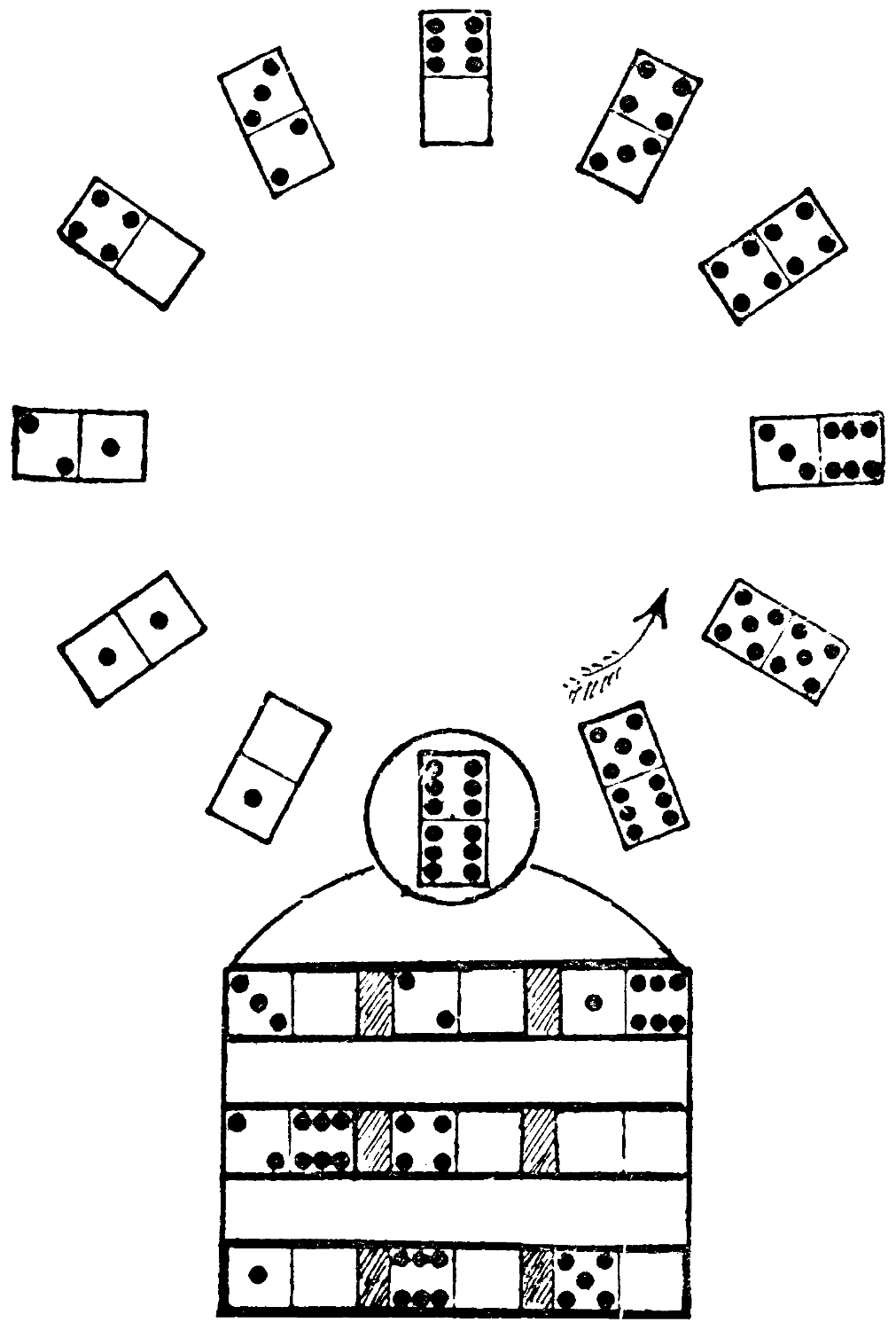
Thus if there are 3 steps, it must always be the fourth card upwards on the left of the semi-circle. To keep up the puzzle, the number of steps should each time be changed, on the pretext that their number does not signify.
Return to description
This diagram shows how the apple may be divided into six pieces by two straight cuts, so that there shall be a gash in each piece.
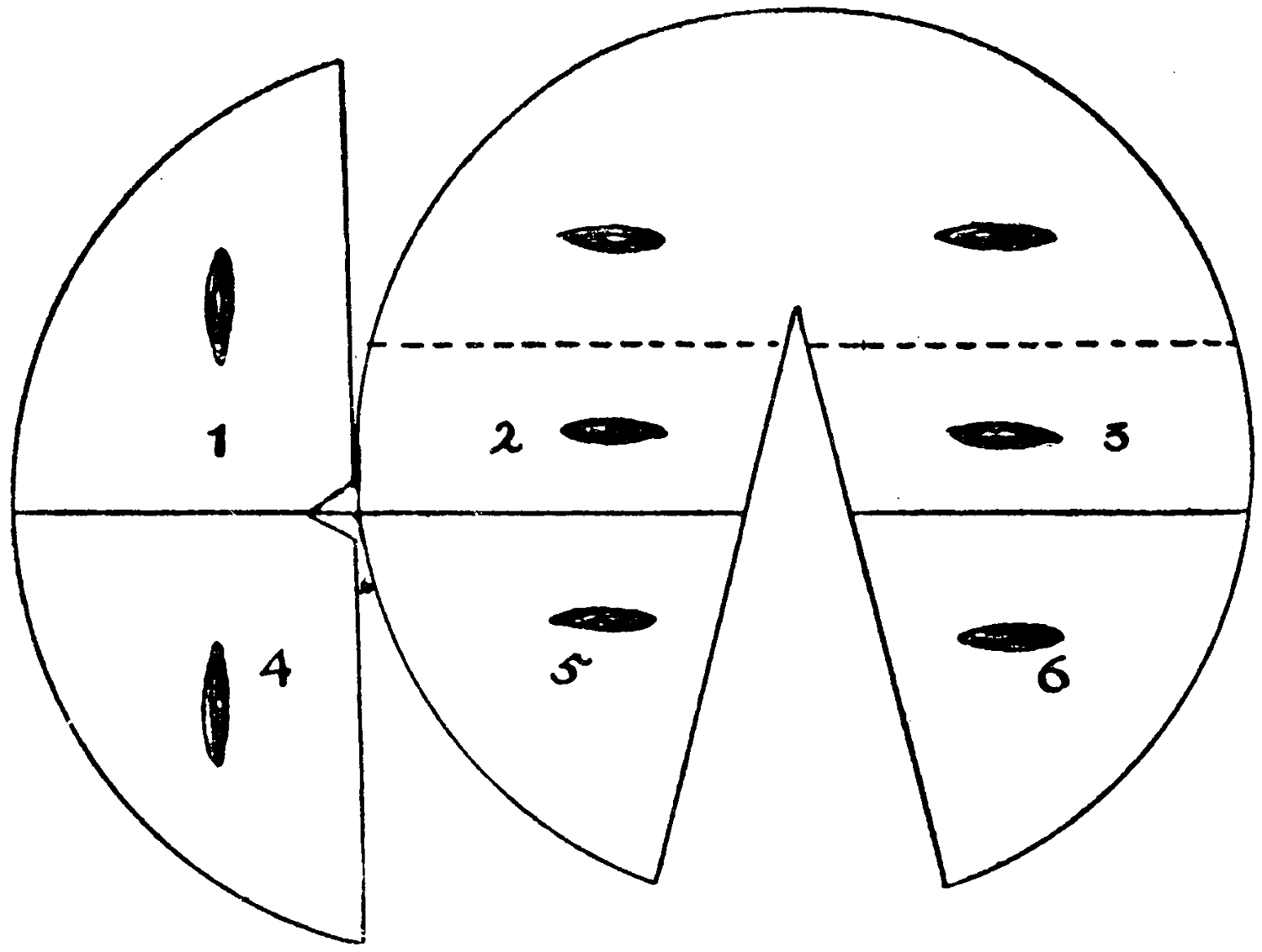
First cut the apple through the dotted line, then place the upper piece shown at the side of the larger piece, and make the second cut straight through, where the line is drawn.
Return to description
[278]
The sixpence under the middle of the tumbler can be easily removed thus—

Slip larger coins under opposite edges of the tumbler to raise it slightly, and then scratch firmly on the cloth, from just outside the rim, in the direction you wish the sixpence to take. It will at once respond, and makes its own way gradually outside the circle that had surrounded it.
Return to description
[279]
This is the way to draw the spiral—
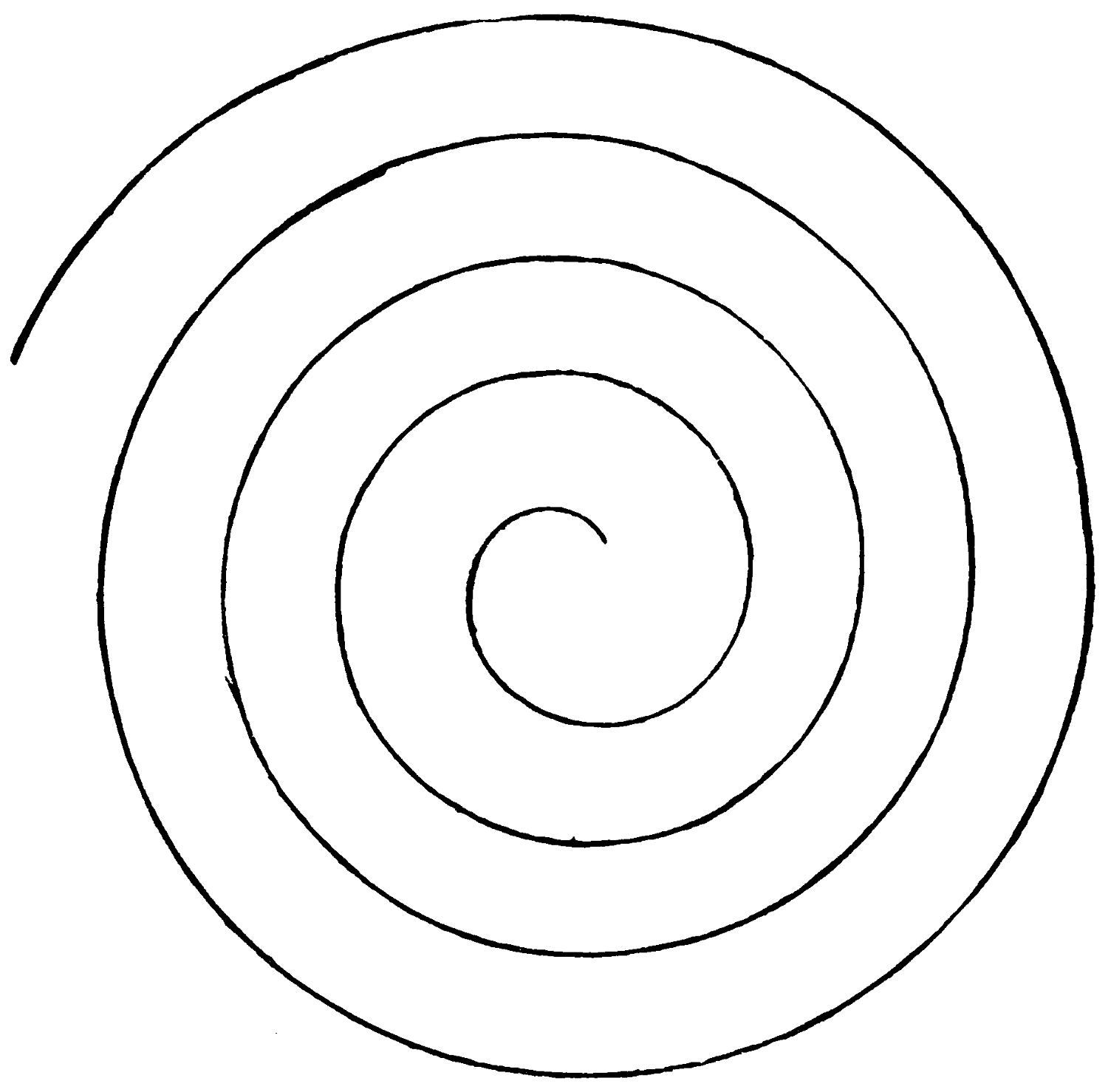
Tie a piece of strong thread with a loop at its end round the upper part of the windings of a screw. Drive the screw into a board, through the middle of a card, wind the thread down the screw so that its loop just reaches the card, place a pencil in this loop, and draw the spiral freely, unwinding the thread from the grooves of the screw, and keeping it always taut. A perfect spiral is the result.
Return to description
[280]
The secret of the talking head is simple indeed when you know it.
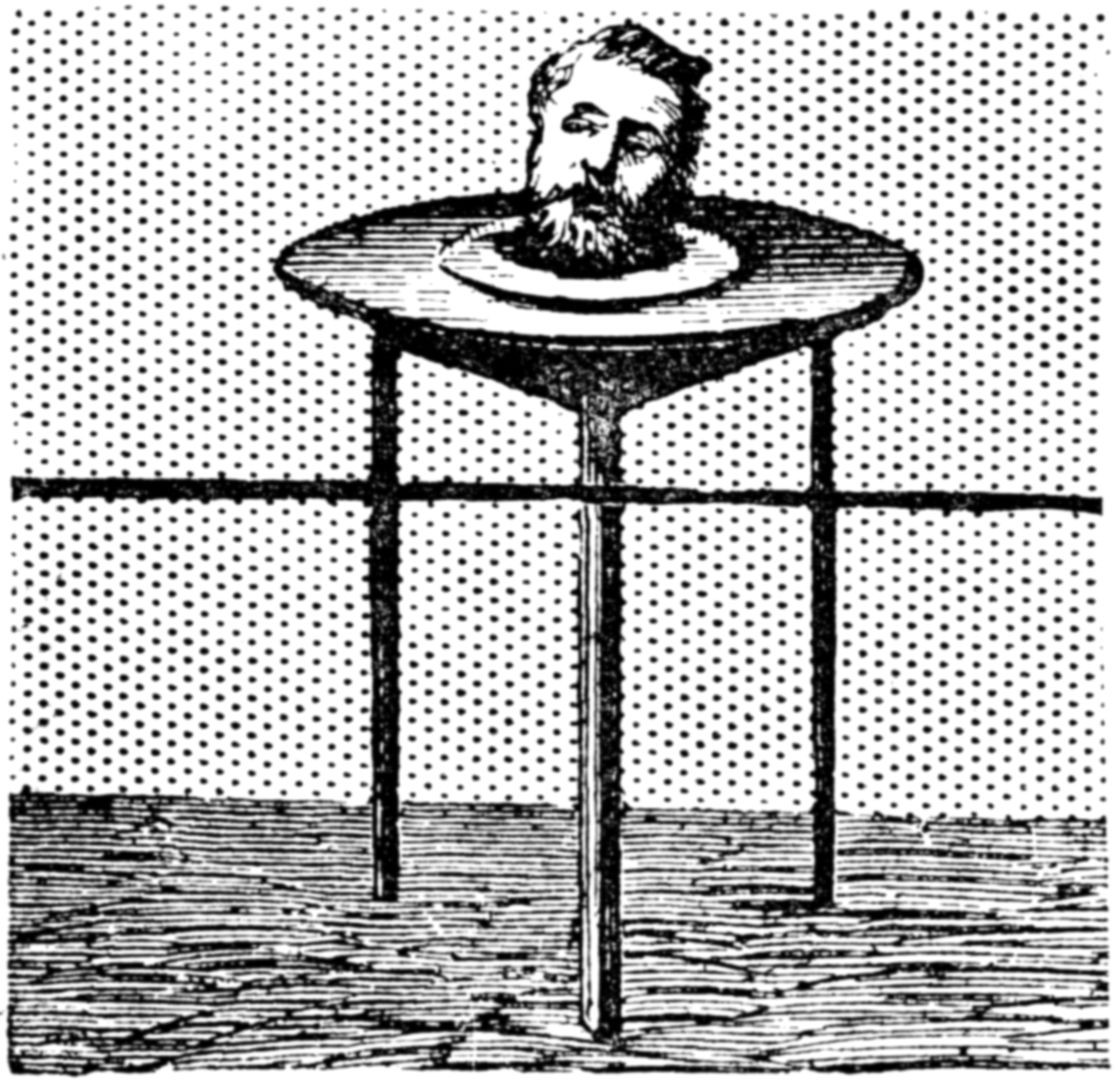
Between the front and two side legs of the table mirrors are fixed, which reflect the similar surroundings, so that the performer, kneeling behind these, and putting his head through a hole in the table top, completely conceals his body and limbs from the audience.
Return to description
[281]
The picture charade is completed thus—

and is solved by Puffin.
Return to description
[282]
When the walnuts and cobnuts have been arranged as is shown on the diagram—

they can be shifted so that they stand alternately, by moving two that are close together at a time, in four moves, as follows:—
(1) Move 2 and 3 beyond 8.
(2) Move 5 and 6 between 1 and 4.
(3) Move what are now 6th and 7th in the gap.
(4) Move what are now 1st and 2nd in the gap, and the alternate arrangement is complete.
Return to description
The question suggested by this picture riddle is: Why is a waiter like a racehorse? And the solution is: Because he runs for cups and plates.

Return to description
[283]
The paradox—
is solved by the lines—
Return to description
The verse is completed thus—
Return to description
The enigma—
is solved by ICICLE.
Return to description
[284]
The charade—
is solved by Pigeon (one becomes eon).
Return to description
Byron’s enigma—
is solved by the letter I.
Return to description
is solved by Star, tar, arts, rats.
Return to description
[285]
Horace Smith’s charade—
is solved by Reformatory.
Return to description
is solved by Nascent, ascent, scent, cent.
Return to description
The enigma—
is solved by Sling, ling, gin, in.
Return to description
[286]
The charade—
is solved by Pleasure.
Return to description
The answer to the problem—
Six horse ’buses and four motor ’buses travel each hour from Temple Bar to the Bank. The horses take 15 minutes, and the motors 10 minutes on the journey.
If I come to Temple Bar, and wish to reach the Bank as soon as possible, shall I take the first horse ’bus that turns up, or wait for a motor? It must be assumed that I can only see a ’bus as it actually passes me—
is (1) Take a motor if it comes first.
is (2) Take a horse ’bus if it comes first, and comes within 21⁄2 minutes of waiting.
is (3) Wait for a motor if a horse ’bus comes first, but does not come till after 21⁄2 minutes.
As I may have to wait 0 minutes or 15 minutes, the average time of waiting will be 71⁄2 minutes.
If I wait x min., and a horse ’bus arrives, I should reach the Bank in 15 mins, if I took it.
If I waited longer for a motor, which, on the average, will now turn up in 71⁄2 - x mins., I should reach the Bank in 171⁄2 - x mins.
If, therefore, x is greater than 21⁄2, the motor is the quicker.
Return to description
[287]
The historical charade—
is solved by Stephen (Step-hen).
Return to description
is solved by Donkey.
Return to description
Lewis Carroll turns WHEAT into BREAD, changing one letter each time, and preserving their general order throughout, thus—
WHEAT; cheat; cheap; cheep; creep; creed; breed; BREAD.
Return to description
[288]
Unity is a probable solution of the old enigma, part of which evidently refers to “a house divided against itself”—
Return to description
The anagram proverbs, “These grave lips chatter no ill,” and “Elephants, all to richest giver,” are both founded on Little pitchers have long ears, and spelt with exactly the same letters.
Return to description
The charade—
is solved by Pertinacity.
Return to description
The buried potentate in the lines—
is King Edward.
Return to description
The charade—
is solved by Clovis (vis in Latin is both power and you wish).
Return to description
is solved by Moat—atom.
Return to description
The puzzle—
is solved by the word Enigma, from which are formed, as is indicated, the words aim, men, game, man, mine, gain, gem, and amen.
Return to description
The enigma—
Old Couplet.
is solved by Dog (Og, go, dog, God).
Return to description
The logograph—
is solved by Stable, table, able.
Return to description
The names that satisfy the conditions of this Single Acrostic—
[291]
are Kennet, Ness, Otter, Xagua, which give Knox.
Return to description
The charade—
is solved by Madam (ma, dam, mad, Adam, Ada).
Return to description
In addition to the singularly appropriate anagram that has been so happily attached to the name of Florence Nightingale, Flit on, cheering angel, the same group of letters can be recast as an aspiration for her continuance in our loving memory, so that they form the sentence, Cling on, feeling heart.
Return to description
[292]
The rebus—
I am
a man
I rate you
a beast
You know me
reads thus:—I rate you lower than a man, above a beast. Know between you and me I am above the rest.
Return to description
The charade—
is solved by Scissors (Lat. scis, thou knowest; sors, a lot).
Return to description
The poets’ names buried in the lines—
are Gray, Moore, Byron, Pope, Dryden, Gay, Keats and Hemans.
[293]
Return to description
The enigma—
is solved by the letter n (me becomes men; one, none; a sty, nasty.)
Return to description
The words in italics have the same letters.
Return to description
The charade—
is solved by Within (Swithin).
Return to description
The puzzle lines—
are solved by Pardon (rap-nod).
Return to description
[294]
The enigma—
is solved by Vixen.
Return to description
The buried proverb—
I fancy this Tory outcry, this weary outrageous attempt to show illegality, is as a cat chasing snow-flakes. I must be forgiven if I shun his example—is—
If you swear you will catch no fish.
Return to description
The six words in italics are spelt with the same letters.
Return to description
is solved by Sonnet.
Return to description
[295]
The lover’s vow—
is solved by Endless.
Return to description
The enigma—
is solved by U, You, Hugh, Yew, How.
Return to description
If you “resist disasters,” this may, by anagram, distress a sister.
Return to description
The charade—
is solved by Archæology.
Return to description
If you ask a schoolboy to estimate the value of the grass in a triangular field, of which the longest side measures 100 rods, and each of the other sides 50 rods, at £1 per acre, it may take him some little time to see that he is being sold, since the condition is not fulfilled that any two sides of a triangle must be greater than the third side.
Return to description
[296]
is solved by waistcoat.
Return to description
The historical charade—
is solved by the battle of Drumclog.
Return to description
The five words in italics are spelt with the same seven letters.
Return to description
The Arithmorem “150 hat robe or tent” forms the name Charlotte Bronte.
Return to description
The Shedding Letters enigma—
is solved by The Postman!
Return to description
When Tom Larkins challenged his sisters to prove on a blackboard that if 50 is subtracted from the sum of the nine digits the result equals the number obtained by dividing their sum by 3, he showed them that the sum of the digits may be written thus: XLV, and that if the L, which represents 50, is removed, XV, or 15, the third of 45, remains.
Return to description
In the “Geese to Market” problem—
B bought 25 geese at 5s. each, and proposed to sell 20 of them at 6s. 3d.
Return to description
[298]
The charade—
is solved by Herring.
Return to description
In the lines—
the familiar adage, “Be it ever so humble, there’s no place like home” is buried.
Return to description
The mutilations in—
are Fox, ox, o, x.
Return to description
Return to description
[299]
The old Sanscrit problem, quoted by Longfellow in his “Kavanagh,”
Ten times the square root of a flock of geese, seeing the clouds collect, flew to the Manus lake. One-eighth of the whole flew from the edge of the water among a tangle of water lilies, and three couple were seen playing in the water. Tell me, my young girl with beautiful locks, what was the whole number of geese?
is solved by 144.
Return to description
The enigma—
is solved by turning the sixes of 660 upside down, when it becomes 990, and satisfies the conditions.
Return to description
The press parody ran thus—
Return to description
is solved by Hebrides.
Return to description
[300]
If I have 91 bananas on my barrow, and find, when I have sold one quality at four a penny, and the other at three a penny, that in mixed lots at seven for twopence I should have made a penny more, I had 64 of inferior and 27 of better sort.
Return to description
The words in italics have the same letters—
Return to description
is solved by Cheque, check (the letter Q).
Return to description
The three towns buried in the lines—
are Leith, Thebes, St Ives.
Return to description
[301]
Return to description
The charade—
is solved by Dietary (Amsterdam is on the River Y).
Return to description
The schoolboy who calculated that if he had made as many more runs at a cricket match, and half as many more, and two runs and a half, he would have made a score, scored seven runs.
Return to description
The enigma—
is solved by United, untied.
Return to description
[302]
The riddle—
is solved by Shackle, Tons, Ant, Arctic Expedition.
[Lieutenant Ernest H. Shackleton, R.N., leader of his South Polar Expedition.]
Return to description
The words in italics have the same letters.
Return to description
When Edwin and Angelina received these mutual Marconigrams—
“No fickle girl is bonnie to my mind.”
“In love inconstant I no pleasure find,”
he was at Lisbon and she was at Constantinople, as is indicated by the fact that the names of these places are “buried” in the messages.
Return to description
The Mental Arithmetic—
is solved by 1.25. In 11⁄4 the figures are not in a line.
Return to description
[303]
The doublet by missing words, in which a grilse is turned into a salmon, is solved thus—
One letter is changed in each link.
Return to description
The enigma—
is solved by Road, which spells also Dora.
Return to description
The Letters—
HAATTCEUMSSSS
form the name of the State Massachusetts.
Return to description
The enigma—
is solved by There: the words are—there, here, her, the, ere, he, re.
Return to description
[304]
The full solution of the answer by anagram to the question, “Why is every angler ipso facto an Ananias?” is—
A liar, he spins gay fancies to a woven yarn.
Question and answer are spelt with the same letters.
Return to description
The quaint riddle—
is solved thus—It would be Askewer (a skewer!)
Return to description
“S” is the missing letter which occurs 55 times, and these are the four lines:—
Return to description
The enigma—
is solved by Patent, paten, pate, pat.
Return to description
[305]
The logogriph—
is solved by feasting, fasting, sting, tin, in.
Return to description
The words in italics are spelt with the same letters.
Return to description
The enigma—
is solved by Coat.
Return to description
The charade—
is solved by Lethe.
Return to description
[306]
The two palindrome words which can be formed from the letters of the sentence “Arrive to vote at it,” are Rotator and Evitative.
Return to description
The enigma—
is solved by Clover, lover, over, ver (Latin for Spring).
Return to description
When Tommy undertook to put a shilling in his money-box if his father would give him as much as he had in his purse, and after repeating the process for three more days found himself penniless, he had elevenpence farthing in his purse at first.
Return to description
is solved by Theatres (tres, Latin for three).
Return to description
When young Hopeful said, “If it were possible I should choose a life double as long,” and old Sobersides answered, “Yes, and you might turn it to better account if it was also begun old,” and the fact that their actual words “double as long,” and “also begun old,” were spelt with exactly the same letters, gave emphasis to the reply.
Return to description
[307]
The charade—
is solved by Drama, ram, a dram.
Return to description
The words in italics have the same letters.
Return to description
The proof by anagram that the words of commendation “blessed in pain,” are properly applied to anæsthetics, is that exactly the same letters spell indispensable.
Return to description
The quotation buried in the sentence—
“What sin was it, sonny?” said an American negress to her lover, when she sat on his best hat, which was flattened. Wearily he heard her musical laugh, and arose to go. His hobby was botany, but not hers, for she was then a merry girl. “Bother the flowers! I would prefer this mellow pineapple, Leonidas,” she said; “I guess we Ethiopians just love fruit!”
is “What’s in a name? That which we call a rose by any other name would smell as sweet.”
Return to description
[308]
The words in italics are spelt with the same four letters.
Return to description
......
The words in italics have the same six letters.
Return to description
The charade—
is solved by Punchestown.
Return to description
The enigma—
is solved by Entrance.
Return to description
[309]
The two sentences—
A lamp shines out for thee,
Win me best by tears,
are anagrams of The Houses of Parliament and Westminster Abbey.
Return to description
When on the Brighton beach an excited collie in pursuit of stones thrown into the sea, suggested the riddle, “What is the difference between that dog and a hungry man?” The appropriate answer was, “The one stops and shakes himself; the other chops and steaks himself!”
Return to description
The hidden animal in—
is Rhinoceros.
Return to description
The smart enigma—
is solved by A Fox.
Return to description
[310]
The words in italics are spelt with the same letters, the t being repeated in toast.
Return to description
The pied proverb is “Fine words butter no parsnips.”
Return to description
The puzzle verse—
is solved by Badinage (bad in age).
Return to description
The hero’s name, hidden in—
is General Wolfe.
Return to description
[311]
Here is the sentence given with its appropriate and perfect anagram—
A defeat whose test is very sure.
Sweet are the uses of adversity.
Return to description
The phonetic missing words are given in italics:—
Return to description
The queer obstacle—
is A turnstile.
Return to description
The old enigma—
is solved thus—
Return to description
[312]
The phonetic gaps are filled thus—
Return to description
is solved by X S—S X.
Return to description
The cryptogram—
is solved by inserting the letter “I” throughout, when this rhyming couplet is formed—
Return to description
The buried proverb in—
is ’Tis a long lane that has no turning.
Return to description
Lewis Carroll’s doublet, which changes ELM into OAK by seven links, introducing the name of another tree as one of them, is solved thus by him—
ELM, ELL, ALL, AIL, AIR, FIR, FAR, OAR, OAK.
[313]
A shorter solution is by these six links—Ely, sly, say, bay, bat, oat; and one of these (bay) is also a tree, as was fir, so that the conditions given are fulfilled.
Return to description
is solved by attendance.
is solved by satiate.
Return to description
The charade—
is solved by Artisan, strain, train, rain.
Return to description
The lines by an old Oxbridge don—
[314]
can be happily met by this retort in the same words, recast by a Girton girl—
Return to description
The enigma—
is solved by Beautify, Beatify.
Return to description
The beasts buried in the lines—
Ireland’s lot heals slowly. Troubles came long ago—at times in battalions—to attack and harass her. Ambitious democrats now countermine famous enthusiasts nearly akin to heroes. Anarchy enables cowards to sow hot terror and all amazement, are—
eland, sloth, camel, goat, bat, lion, stoat, ass, ram, fat, ermine, mouse, yak, roe, hyena, cow, sow, otter and llama.
Return to description
This is the palindrome verse that reads and rhymes from either end—
[315]
Return to description
The anagram recast from “The Observatory at Greenwich in England” is completed thus—
On landing here begin to watch every star.
Return to description
The enigma—
is solved by Nemo, omen, o men.
Return to description
The question—
is solved thus—
FOWL IS FARE.
Return to description
The enigma—
is solved by There.
Return to description
[316]
The words in italics are spelt with the same letters.
Return to description
A Mr Harwood had two daughters by his first wife, the elder of these was married to John Coshick. This Coshick had a daughter by his first wife, whom old Harwood married. Thus Harwood’s daughter could say—
Return to description
The charade—
is solved by Catchword.
Return to description
The paradox—
is solved by the fact that the lines apply to the large and small wheels of a bicycle.
Return to description
[317]
The enigma from Lewis Carroll’s Papers—
is solved by Tablet.
Return to description
The charade—
is solved by Halfpenny.
Return to description
is solved by Honeycomb.
Return to description
The towns buried in the sentences—
are Lewes, Louth, Deal, Bath and Neath.
Return to description
[318]
The anagram on “The leaning tower of Pisa, in Tuscany, Italy,” is completed thus—
A funny spot in a sweet city; I o’erhang it all.
Return to description
The words in italics are spelt with the same letters.
Return to description
The charade—
is solved by Flambeau.
Return to description
If we adopt the old spelling of the final word, we can prove by anagram that Bacon had no hand at anyrate in Shakespeare’s play “Much Ado About Nothinge,” for the same letters exactly spell “Bacon? O, naught due to him!”
Return to description
is solved by Left, felt, let.
Return to description
[319]
“Insanitary” and “sanitary reform” are very happily recast by anagram thus—In nasty air; Former air nasty.
Return to description
The charade—
is solved by Cutlet.
Return to description
These are the completed lines—
It will be seen that “a” was the only missing letter.
Return to description
The charade—
is solved by Honey (honey-moon; hone; Ney; one).
Return to description
[320]
The enigma—
is solved by Attenuate:—at ten, u, Ate, goddess of Revenge.
Return to description
The charade—
is solved by Overcomes.
Return to description
The cryptogram which was sent as a reliable tip before a race in which Petronel was to run—
is deciphered thus—
Take every third letter, and you arrive at Lenortepnoteb. Read this backwards, and you have the tip, “Bet on Petronel!”
Return to description
The enigma—
is solved by Nothing.
[321]
Return to description
The broken sentence—
A sed end ought eat ease ain.
is thus filled in to describe a curse and to proclaim its cure—
A cursed fiend brought death, disease and pain;
A blessed friend brought breath and ease again.
Return to description
The charade—
is solved by Capacity.
Return to description
The four rivers buried in the sentence—
The deaf and dumb girl began gesticulating with a message, and her delivery was ever neat, with graceful pose in every attitude.
are Ganges, Thames, Severn and Seine.
Return to description
If the “shingle” on the Brighton beach could speak, it might boast by anagram, “I am English!”
Return to description
The enigma—
is solved by adding an a to her, which becomes hear.
Return to description
[322]
The missing words in the “Plaint of the Rejected” are—The R.A., hater, heart, earth, Herat.
Return to description
The man who could attach a phonetic meaning to the words “Beta in Greek means letter B,” could in another fashion invite others to beat his wife by merely calling them and saying, “Hither!” (hit her).
Return to description
The rebus—
| storm? a th |
an umbrella me who |
with alls |
all mud |
is solved thus—Who follows me under an umbrella, with overalls all over mud, after a thunderstorm?
Return to description
This is the completed palindrome:—
Nor I nor Emma had level’d a hammer on iron.
It reads alike from either end.
Return to description
The tutor came to the conclusion that there is nothing in Ecclesiastical Law to prevent the Pope from burying the Archbishop of Canterbury, but the undergraduate who had proposed the question demurred to this reply; pressed for his reason he said, as his face broke into a smile, “He cannot do so, because the Archbishop is not dead!”
Return to description
[323]
The proverb buried in the sentence, “While there are very many as kind as this, they know no task unkind,” is, “Let every man skin his own skunk.”
Return to description
is solved by Heather (he, at her).
Return to description
The quotation from Shakespeare buried in—
Strange weather! What could equal it? Yesterday sunshine and soft breezes, to-day a summer cyclone raging noisily; then other changes, as floods of fiercest rain eddy beneath the blast.
is “The quality of mercy is not strained.”
Return to description
The beetroot palindrome, which reads alike from either end is—
RED ROOT PUT UP TO ORDER
Return to description
is solved by Missionaries.
Return to description
[324]
The words written on the walls of a Western college gained their ambiguous sense from the three final words, printed in italics—“Young women should set a good example, for young men will follow them!”
Return to description
The enigma—
is solved by Note.
Return to description
This is the full text—
Return to description
The words in italics have the same letters.
Return to description
[325]
The date of the new organ given by the English is concealed in the lines of this inscription above its keyboard at Ober Ammergau—
QVI CHRISTI LAVDES CANTANT
SANCTÆ PASSIONIS SVÆ VIRTVTE
IN IPSO ET PATRE VNVM SINT.
If the Roman numerals that occur in the words are added together, they amount to 1894, the date of its completion.
Return to description
is solved by Stael, least.
Return to description
The French charade—
is solved by Mari-age.
Return to description
The charade—
is solved by Current.
Return to description
[326]
is solved by Ramrod.
Return to description
The enigma—
is solved by the letters me.
Return to description
When Tom declared that he could give his sister quite a simple sentence of seven common English words of one syllable, which she could not produce on her typewriter, he had in his mind, “We can spell (to, too, two) in three ways,” which cannot, of course, be expressed in seven written words.
Return to description
The French charade—
is solved by Mariage.
Return to description
[327]
Sydney Smith’s conclusion as to the value and satisfaction of a City dinner was completed thus:—“I cannot wholly value a dinner by the test you do!” (Turtle, in Latin, testudo).
Return to description
DEAN SWIFT’S ENIGMA—
is solved by A Goose-quill.
Return to description
The answer to the riddle propounded by the possessor of a new Keen Kut razor to his friend whose chin was disfigured by scars, “What is the difference between my razor and yours?” is—“Mine cuts thoroughly; yours also cuts, tho’ roughly!”
Return to description
[328]
The decapitated words are in italics—
The ern, or erne, is the sea-eagle.
Return to description
is solved by Covering.
Return to description
is solved by vote, veto.
Return to description
The lines to an owl are filled in thus—
The vowel “o” occurs forty-six times in the six lines.
Return to description
[329]
In the Army anagram—
the words in italics spell also soldier, colonel, general, captain, and lieutenant.
Return to description
is solved by Anemone, the wind flower (name, mean, anem, one, o, ne).
Return to description
The anagram enigma—
is solved by snowbound, which contains exactly the same letters as “no buds now.”
Return to description
[330]
The question of time—
is solved by a quarter to four.
Return to description
The Donkey drive—
is solved by Ass-ass-in.
Return to description
The “Eating by Alphabet” enigma—
is solved by A past Y (a pasty).
Return to description
The charade—
is solved by Buskin.
Return to description
[331]
The sentence—
Behest on thy lips, Society;
forms an Anagram of the proverb
“Honesty is the best policy.”
Return to description
This sentence, fashioned by eight schoolboys as anagrams on their Christian names, arranged in order—
“I thy Tom am sober and lie or live in dew, but her brain sinned”—
reveals, when deciphered, the names Timothy, Ambrose, Daniel, Oliver, Edwin, Hubert, Brian and Dennis.
Return to description
The enigma—
is solved by Fright.
Return to description
The double acrostic—
From “Punch,” 1875.
is solved
M. P.
P. M.
Return to description
[332]
A man in a rage should go to a “shooting gallery,” because by its Anagram it is largely soothing.
Return to description
The beatitude—
is solved by A Queen Bee. The Bee is made up of the letter b (let her be), in Greek called Beta (beat her), and two little e’s (ease).
Return to description
The puzzle-lines—
are cleared up by Satisfactory.
Return to description
The English proverb which is concealed under its anagram—
“I dare not admit faint women,”
is Time and tide wait for no man.
Return to description
The charade—
is solved by Asbestos (os is Latin for mouth).
Return to description
[333]
The four words in italics have the same letters.
Return to description
That which is found in the centre of Australia and of America, and in no other place, is the letter “r” (no other place).
Return to description
Grandfather’s riddle, “Do you know why is the fourth of July?” is solved by the fact that the fourth letter of that word is y!
Return to description
is solved by Nightingale.
Return to description
The words in italics have the same letters.
Return to description
The enigma—
is solved by Comfortable.
Return to description
[334]
The charade—
is solved by Wheel, heel, eel.
Return to description
The anagram sentences are recast thus into single words—
See a pug dog.Red paper.
Pedagogues.Prepared.
Fat reward.
Afterward.
Stay, O morn.Set on a dish.
Astronomy.Astonished.
Return to description
The enigma—
is solved by Do-do.
Return to description
The paradox—
is solved by the word heard.
Return to description
The enigma—
is solved by Incomplete.
Return to description
[335]
The words in italics have the same letters.
Return to description
is solved by Two in the shade!
Return to description
The puzzle—
is solved by Love.
Return to description
The missing words are in italics—
Return to description
Read backwards it becomes—
Prosperity and peace; no barns empty; bills long paid; not high rents; berries bright; no birds hungry; merry Christmas comes.
Return to description
[336]
The anagram plants concealed in the sentence—O rise love it lad never let this lamb chase trains, are: Osier, violet, lavender, thistle, balm, china asters.
Return to description
The enigma—
is solved by Sinecure.
Return to description
The paradox—
is solved by TIT.
Return to description
The charade—
is solved by I.O.U.
Return to description
When Funniboy wrote from Naples to his friend, “Next week I am going ‘to plant onions, etc.,’” it was an intimation by anagram that he was bound for Constantinople.
Return to description
[337]
is solved by Fearless.
Return to description
The enigma—
is solved by Thymy (thy, my).
Return to description
This is the completed palindrome—
REPEL EVIL AS A LIVE LEPER,
which reads alike from either end.
Return to description
When Tom Pickles’s father tried with a lusty puff to blow the small cork into the bottle, the sudden compression of the air inside, followed by its expansion, drove the cork in an unexpected direction, so that it flew out and struck him sharply on the mouth.
Return to description
Acorns are as strong as oaken posts when they propagate (prop-a-gate).
Return to description
The completed palindrome runs thus—
“Put it up but not on tub, put it up but not on tub, put it up,” which reads alike from either end.
Return to description
[338]
The words in italics have the same letters.
Return to description
The two long words used recently by a politician which can be recast by anagram to form the sentence, “Axiomatic intelligence, or dust” are—
TERMINOLOGICAL INEXACTITUDES.
Return to description
is solved by Palate (Até, goddess of fate).
Return to description
The sentence “Woman without her man would be helpless” takes on a distinct meaning if the words “without her” are read together, and a comma is placed after “woman.” Thus—“Woman, without her man would be helpless.”
Return to description
[339]
The short sentences are recast into single words thus—
A moment’s cure. The old rocks.
Commensurate. Stockholder.
Cod is nice. It lures a cat.
Coincides. Articulates.
Return to description
The enigma—
is solved by Hearth, earth, heart (transpose eat to ate).
Return to description
Here is a metrical account of the anagram which, with some exaggeration, proclaims that Sims Reeves was often prevented from singing by his delicate throat—
Return to description
The words in italics have the same letters.
Return to description
This is the completed palindrome—
I maniac lived, a devil Cain am I.
Return to description
[340]
The lines—
contain in anagram and in proper order the fruits tamarinds, gooseberries, and the flowers magnolia, daisy, lobelia.
Return to description
These are the anagrams—
Now one old fort
Tower of London.
Rabid owl
Wild Boar.
Return to description
is solved by Knighthood.
Return to description
is solved by Earwig.
Return to description
is solved by A’blowing (n-a-g).
Return to description
[342]
The proverb buried in the sentence—
Society—how her enthusiasts worship at her Juggernaut car. Cases exist here, proving how illogical are these eagle-sighted, place-hunting beings, scoffing at hereditary position, yet striving to get her smile.
is “Where the carcase is there will the eagles be gathered together.”
Return to description
The answer by anagram to—What should we put on a bird’s tail to catch it without a steel-trap? is Saltpetre.
Return to description
The charade—
is solved by Season.
Return to description
The sequel to the Arab and his ass runs thus—
Return to description
The words in italics are spelt with the same letters.
Return to description
The answer by anagram to “Where can you be ‘in a stone-pine garden’?” is Pontresina, Engadine.
Return to description
The words in italics are spelt with the same letters—
Return to description
According to its anagram, the bodily discomfort which follows an ague-fit is fatigue.
Return to description
[344]
This is the adjustment of the tangled square—
| I | S | I | S |
| S | I | D | E |
| I | D | E | A |
| S | E | A | T |
Return to description
The European rivers concealed in the eight anagrams: Set in red robe Henri Le Roi O sell me red pine nerves biter, are Dniester, Ebro, Rhine, Loire, Moselle, Dnieper, Severn, Tiber.
Return to description
The palindrome runs thus—
STOP ROSE, I PREFER PIES OR POTS.
Return to description
“Your food will cost you more!”
is the political parrot cry which can be evolved by anagram from—
O fool! O musty cry! O lurid woe!
Return to description
Sir Robert Peel was the statesman from whose name a “terrible poser” is formed by anagram.
Return to description
The letters of the sentence, “Yea, a glad sun rose red” can be recast into the well-known proverb Delays are dangerous.
Return to description
The question, “Has there been a poet of unusual solemnity?” is answered by “Yes, Milton.”
Return to description
[345]
The anagram enigma—
is solved by Onion (no, no, I).
Return to description
When young Biceps, who had been plucked in Euclid declared that he could teach the examiners how to square a circle, this was his tricky method:—A circle may be aptly described as a “copper” or “Brown.” Having at hand your “copper” (P. C. Brown), when he has caught you on his rounds, proceed to square him in the customary way.
Return to description
As Biceps could not tell how to extract a circle from a square, his friend gave him the following solution: “Let the given square be Sloane Square; find the Inner Circle, and take its lines to any point, at any distance from that square, paying the proper fare. That’s the ticket!”
Return to description
Return to description
[346]
The charade—
is solved by Denounce (16 ozs. = 1 Pound).
Return to description
The cipher—
becomes by the addition of E and O alternately—
Return to description
When his brother put “Tim in a pet,” the explanation by anagram is that he was impatient.
Return to description
The missing words are in italics.
Return to description
[347]
The charade—
is solved by Void.
Return to description
In the words spoken in the hay-field to a thirsty toiler, “Mower, I will tap the cask!” are concealed by anagram the poet and his poem—William Cowper, The task.
Return to description
The charade—
is solved by Important.
Return to description
To be
aaaaaaaaaa
tCrIiOfUlSes
standing
is the mark of a mean
is solved by To be tenacious in the midst of trifles is the mark of a mean understanding.
Return to description
The letters which spell RED NUTS AND GIN can be recast to form the one word UNDERSTANDING.
Return to description
[348]
The novel by Charles Dickens hidden in the pied letters—
CDEHHIILOOOPRSSTTUY
is The Old Curiosity Shop.
Return to description
The words in italics have the same six letters.
Return to description
The charade—
is solved by Nameless.
Return to description
When one of the children said, “If father gives us a new dog it will wake the lazy ones”—the words pointed to Susan and Ethel, whose names are buried in the sentence.
Return to description
The cipher—
NGOTRDSREAOHR
ETNSVEENUDOEO
is solved by starting with last letter of the second line, followed by the first letter of the first line, and so on throughout, taking always the last and first unused letters alternately, and forming thus the proverb “One good turn deserves another!”
Return to description
[349]
The enigma—
is solved by Lot’s wife.
Return to description
The question—
How might an oyster, if it could speak and knew that unda is Latin for wave or water, complain in similar phonetic iteration when disturbed by thunder under unda?
is answered thus—
He could exclaim, “a noise annoys an oyster!”
Return to description
The words in italics have the same five letters—
Return to description
The girls’ names shown by anagram in the sentence—“Bad hero set by thy door hurt me ma. Army may get ruder daily,” are Deborah, Betsy, Dorothy, Ruth, Emma, Mary, Amy, Gertrude, Lydia.
Return to description
The anagram is completed thus—
“Lord Beaconsfield’s statue.”
True as old Ben’s stolid face!
Return to description
[350]
The Shakespeare anagrams—
The tub sold has old rough shelves.
And e’en this fisherman caught best white smelts.
A living lord’s black dress, worn high, I vow!
are formed, letter for letter and line for line, from this passage in “Romeo and Juliet”—
“Love’s heralds should be thoughts,
Which ten times faster glide than the sun’s beams,
Driving black shadows over low’ring hills.”
Return to description
The words in italics are spelt with the same six letters.
Return to description
The Puzzle acrostic—
is solved thus—
| ◯ | ◯ | ◯ | ◯ |
| ◯ | ● | ● | ● |
| ◯ | ● | ● | ● |
| ◯ | ● | ● | ● |
| L | A | R | K |
| A | R | M | Y |
| R | O | O | K |
| K | I | T | E |
Return to description
[351]
One letter is dropped each time.
Return to description
In the doublets puzzle HARE is made into SOUP by the following six links, changing one letter each time, and preserving their order—
HARE, hark, hack, sack, sock, soak, soap, SOUP.
Return to description
The enigma—
is solved by Epigram.
Return to description
If a “newspaper” could speak, it might say by anagram of the general work of its staff, We pen pars.
Return to description
The positive quantity 1011 is turned into a negative thus:—
NO.
Return to description
The one word formed by anagram from “O, I’m man’s trial” is Matrimonials.
Return to description
[352]
The rebus—
EEE and xxx URXXI XXX and eee.
is solved by “Great ease and small crosses before you are twenty-one, great crosses and little ease after that.”
Return to description
The answer to the riddle “Why may not the owner of a pine forest fell his timber?” is—Because no one is allowed to cut when it is his own deal.
Return to description
The words in italics are spelt with the same letters.
Return to description
In the doublet, as solved by Lewis Carroll, ARMY is changed into NAVY with seven links, and preserving the sequence while changing a letter every time—thus: ARMY, arms, aims, dims, dams, dame, name, nave, NAVY.
Return to description
The anagram puzzle—
is solved by Unexceptionably, which contains exactly the same letters.
Return to description
The answer to the strange riddle, “When is an onion like music?” is “When you find it smell odious!” (it’s melodious).
Return to description
[353]
The bitter cry of Christianity is, by its anagram: I cry that I sin.
Return to description
That a Conservative is constant to his cause is shown by the anagram: Not vice versâ.
Return to description
As a rule Christmas Day and New Year’s Day fall upon the same day of the week, but they will not fall upon the same day of the week in 1910 (or indeed in any year), because the New Year’s Day must be after the Christmas Day to fulfil the conditions!
Return to description
is solved by Armstrong.
Return to description
[354]
is solved by Top-mast.
Return to description
is solved by Needles, needless.
Return to description
is solved by Clock, lock.
Return to description
is solved by Mistrust.
Return to description
Mark Lemon’s charade—
is solved by Barrow.
Return to description
is solved by Clover, lover, over, clove, love, cover, cove.
Return to description
is solved by Ten score.
Return to description
is solved by Outline.
Return to description
[357]
is solved by Punch.
Return to description
is solved by Dovetail.
Return to description
is solved by Tobacco.
Return to description
is solved by Vagabond.
Return to description
[358]
is solved by COMIC.
Return to description
Praed’s charade—
is solved by Cambridge.
Return to description
is solved by Justice.
Return to description
[359]
is solved by Fire-irons.
Return to description
is solved by Olive.
Return to description
is solved by Catacomb.
Return to description
is solved by A portrait.
Return to description
is solved by Eye.
Return to description
is solved by Falsehood.
Return to description
[361]
is solved by Charade.
Return to description
is solved by Inoculate.
Return to description
is solved by Horsemanship.
Return to description
It is a fact that neither melons nor lemons grew on elms.
The words in italics have the same letters.
Return to description
The completed palindrome, which reads alike from either end, is—
DRAW NO DRAY A YARD ONWARD.
Return to description
[362]
is solved by Match.
Return to description
Return to description
is solved by Bow.
Return to description
is solved by Weevil.
Return to description
is solved by Heathen.
Return to description
is solved by To-day.
Return to description
is solved by Childhood.
Return to description
is solved by Train, rain, ain, in.
[364]
Return to description
is solved by Out.
Return to description
is solved by A Needle.
Return to description
The Chess charade—
is solved by Boden.
Return to description
[365]
is solved by A coachman.
Return to description
is solved by An umbrella.
Return to description
is solved by Grass.
Return to description
[366]
Fox’s enigma—
is solved by Glass, lass, ass.
Return to description
is solved by Feather.
Return to description
The words in italics have the same letters.
Return to description
is solved by Average.
Return to description
[367]
is solved by Gnat, tang, ant.
Return to description
is solved by The figure 8.
Return to description
is solved by Cocoanut.
Return to description
[368]
is solved by Runagate.
Return to description
is solved by Candid.
Return to description
is solved by Earnest.
Return to description
is solved by Bed-time.
Return to description
[369]
is solved by Chine, niche, chin, inch.
Return to description
is solved by Hatred, hat red, dearth, thread.
Return to description
is solved by Within, Swithin.
Return to description
After officers’ mess, when cigars were well alight, the old conundrum was propounded,[370] “What is most like a cornet of horse?” A sharp sub. was ready with the reply, “A hornet, of course”; it was presently capped by this variant which occurred to a married captain, “a corset of horn”; and yet another reading was suggested by the deaf old colonel, “How much did you say the ‘horse ate of corn’?”
Return to description
is solved by Venice (Venus changes to Venice).
Return to description
The very prosaic reply to the dainty lines—
is: Because they are leg ends (legends)!
Return to description
The words in italics have the same letters.
Return to description
is solved by The letter E.
Return to description
[371]
is solved by Suetonius.
Return to description
The geographical names buried in the sentences—
He has my R.N. as a monogram on all his paper.
I am her stupid sister.
The calmest man is sometimes made irate—
are Smyrna; Amherst; and Madeira.
Return to description
is solved by Date-palm.
Return to description
is solved by A spider’s web.
Return to description
[372]
is solved by Murmur.
Return to description
is solved by Colenso.
Return to description
is solved by Sinking.
Return to description
is solved by trifle, flirt.
Return to description
is solved by Backgammon.
Return to description
The Rebus—“We westand fall,”—is solved by United we stand, divided we fall.
Return to description
is solved by Counterfoil.
Return to description
[374]
is solved by Nothing.
Return to description
[375]
Here is both the sum without figures, and its counterpart in numbers:—
| U | G | I | ) | G | E | V | P | P | N | D | O | ( | I | D | T | P | O |
| G | V | N | I | ||||||||||||||
| D | N | T | P | ||||||||||||||
| U | G | I | |||||||||||||||
| N | E | T | N | ||||||||||||||
| N | E | O | T | ||||||||||||||
| D | U | D | O | ||||||||||||||
| D | U | D | O | ||||||||||||||
| 9 | 5 | 6 | ) | 5 | 8 | 7 | 0 | 0 | 3 | 1 | 2 | ( | 6 | 1 | 4 | 0 | 2 |
| 5 | 7 | 3 | 6 | ||||||||||||||
| 1 | 3 | 4 | 0 | ||||||||||||||
| 9 | 5 | 6 | |||||||||||||||
| 3 | 8 | 4 | 3 | ||||||||||||||
| 3 | 8 | 2 | 4 | ||||||||||||||
| 1 | 9 | 1 | 2 | ||||||||||||||
| 1 | 9 | 1 | 2 | ||||||||||||||
The key sentence is: DON’T GIVE UP, the letters of which correspond to 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Return to description
[376]
When I shot only birds and rabbits, and my bag at the end of the day showed 36 heads and 100 feet, I had killed 22 birds and 14 rabbits.
Return to description
There are no fewer than 40 distinct readings of the four words which form the square—
| D | E | L | F |
| E | V | I | L |
| L | I | V | E |
| F | L | E | D |
DELF and FLED have each four straight readings, while EVIL and LIVE can each be traced in 16 different ways, and the four words run straight from every side of the square.
Return to description
| A | ||||||
| A | ||||||
| E | ||||||
| D | N | R | E | G | D | N |
| I | ||||||
| T | ||||||
| V | ||||||
| S | ||||||
| S | ||||||
| T | ||||||
| A | ||||||
| E | V | E | N | I | N | G |
| D | ||||||
| A | ||||||
| R | ||||||
| D | ||||||
Return to description
When a man gave a sovereign to his son to be spent on presents of different values for him and his three sisters, each to cost an aliquot part of the pound, and each to be as good as possible;[377] and told him to give the change to the Fresh Air Fund, the presents cost 1⁄3, 1⁄4, 1⁄5, 1⁄6 of a pound respectively, or 6s. 8d., 5s., 4s., and 3s. 4d., and there was a shilling over for the Fresh Air Fund.
Return to description
This is the complete word-square—
| M | E | T | A | L |
| E | R | A | S | E |
| T | A | S | T | E |
| A | S | T | E | R |
| L | E | E | R | S |
Return to description
The key word to the addition sum is REPUBLICAN. It works out thus—
| R 1 |
E 2 |
P 3 |
U 4 |
B 5 |
L 6 |
I 7 |
C 8 |
A 9 |
N 0 |
| A | I | |
| L | C | |
| P | R | |
| U | N | |
| B | E | |
| E | C | C |
| 9 | 7 | |
| 6 | 8 | |
| 3 | 1 | |
| 4 | 0 | |
| 5 | 2 | |
| 2 | 8 | 8 |
Return to description
The word square is completed thus—
| T | O | A | S | T |
| O | T | T | E | R |
| A | T | O | N | E |
| S | E | N | S | E |
| T | R | E | E | S |
Return to description
[378]
The product of the first twelve prime numbers, 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, can be written down by using no figures but 0, 1, 2, and 3, and of these 2 and 3 once only, thus—
10 × 1001 × 2001 × 10013:—
or
10 = 1 × 2 × 5
1001 = 7 × 11 × 13
2001 = 3 × 23 × 29
10013 = 17 × 19 × 31
Return to description
The question—
is answered by—Collars, 2d. Cuffs, 3d.
Return to description
The word square is completed thus—
| W | E | E | K | S |
| E | L | L | E | N |
| E | L | U | D | E |
| K | E | D | G | E |
| S | N | E | E | R |
Return to description
[379]
To remove the table-napkin on a corner of which a wine-glass full of water stands near the edge of a polished table, take hold with the left hand of the part that hangs over the edge and raise it to a horizontal position. Then strike hard downward with the right hand, at about six inches from the table, and the cloth will come away, leaving the wineglass altogether undisturbed—an illustration of what is known as the vis inertiæ.
Return to description
My third and fourth are a quarter of my first and second; my fourth is half of them, and my third is half. What am I?
is solved by Twopence-half-penny.
Return to description
The London firm who had sent a telegram to Paris for 480 sets of Diabolo, and received to their surprise a huge consignment of 6336 sets, had worded their order thus: “Send us twenty two-dozen cases of Diabolo,” knowing that they were put up two dozen in a case. The wholesale firm read the order as twenty-two dozen cases—i.e., 264 cases of 24 in a case!
Return to description
When Mrs Evergreen said: “My husband’s age is represented by the figures of mine reversed; he is older than I am, and the difference between our ages is one-eleventh of their sum,” he was 54, and she was 45.
Return to description
[380]
This is the completed multiplication sum—
| 4 | * | * | ||
| 3 | * | |||
| 3 | 6 | * | * | |
| * | * | 7 | * | |
| * | * | 3 | * | * |
| 4 | 5 | 7 | ||
| 3 | 8 | |||
| 3 | 6 | 5 | 6 | |
| 1 | 3 | 7 | 1 | |
| 1 | 7 | 3 | 6 | 6 |
Return to description
is solved by writing 13 in Roman numerals, XIII.; and then drawing a line across their middle, so that the upper half forms VIII.
Return to description
I bought fifty-eight plants for my new rosery, when I found that if I set them three in a row there would be one over; if four in a row two over; if five in a row three over; and if six in a row four over.
Return to description
Three nines arranged thus represent 20—
9 + 9·9
Return to description
If a house has nine windows on its front, as many as 511 signals can be given by merely leaving one or more of them open, including the case in which all are left open.
Return to description
[381]
The birthday puzzle by Sir John Evans is solved thus—
Return to description
This is the way to arrange a strip of paper 9 in. by 2 in. so that it has only one surface and one edge.
Gum the ends together with a half twist in the slip. If a continuous line is now drawn along the middle of the band it will traverse the whole length of the paper and finish at its starting point. Again, if a mark is made on the edge, and the finger or a pencil starting from this runs along the edge, it also will return to its starting point.
Return to description
To divide nine into two parts which shall be together equal to ten, write IX in bold Roman numerals on a sheet of paper, and fold this across the middle of the figures, thus—
IX — IVIɅ
This gives a six on one side of the fold and a four upon the other side.
Return to description
[382]
The shepherd who had folded his flock with 100 hurdles, and whose master bade him the next day use 16 of these to pen some pigs, and to enclose nine times as many sheep with the remaining 84 as the 100 had contained, had originally placed the hurdles in two rows of 49 each, with one hurdle at each end. He made room for nine times as many sheep within 84 hurdles by arranging them in a square, with 21 on every side, thus increasing the area ninefold.
Return to description
When you have lifted three hats that cover three biscuits in a row, eaten the biscuits and replaced the hats, you can carry out your undertaking that the three biscuits shall be under whichever hat is selected by solemnly placing that hat upon your head!
Return to description
The number of different ways in which 7s. 3d. can be paid away in current coin of the realm, without ever using exactly the same set of coins a second time, is 1,062,102!
Return to description
PRINTED AT THE MERCAT PRESS, EDINBURGH.
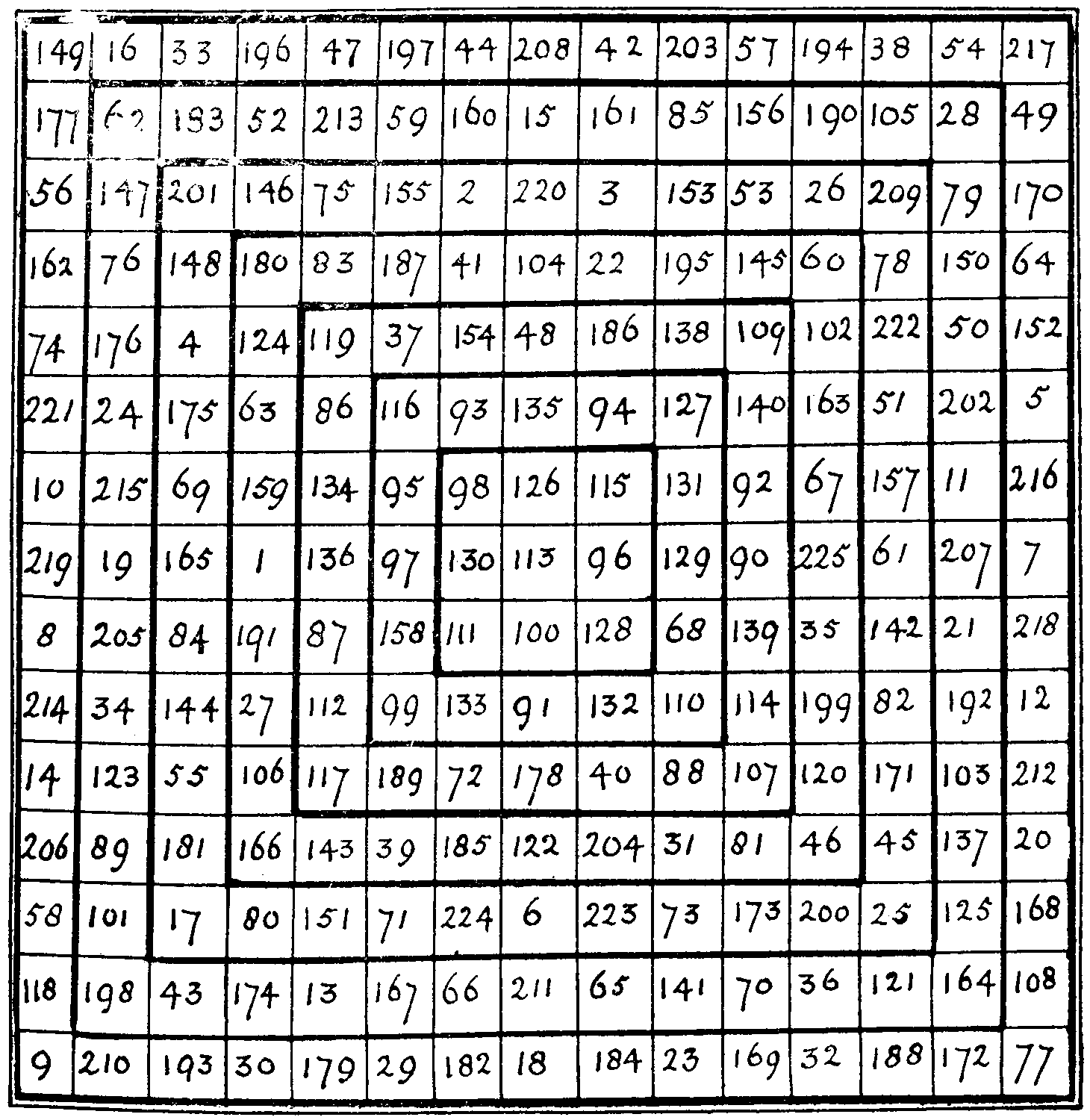
Return to description
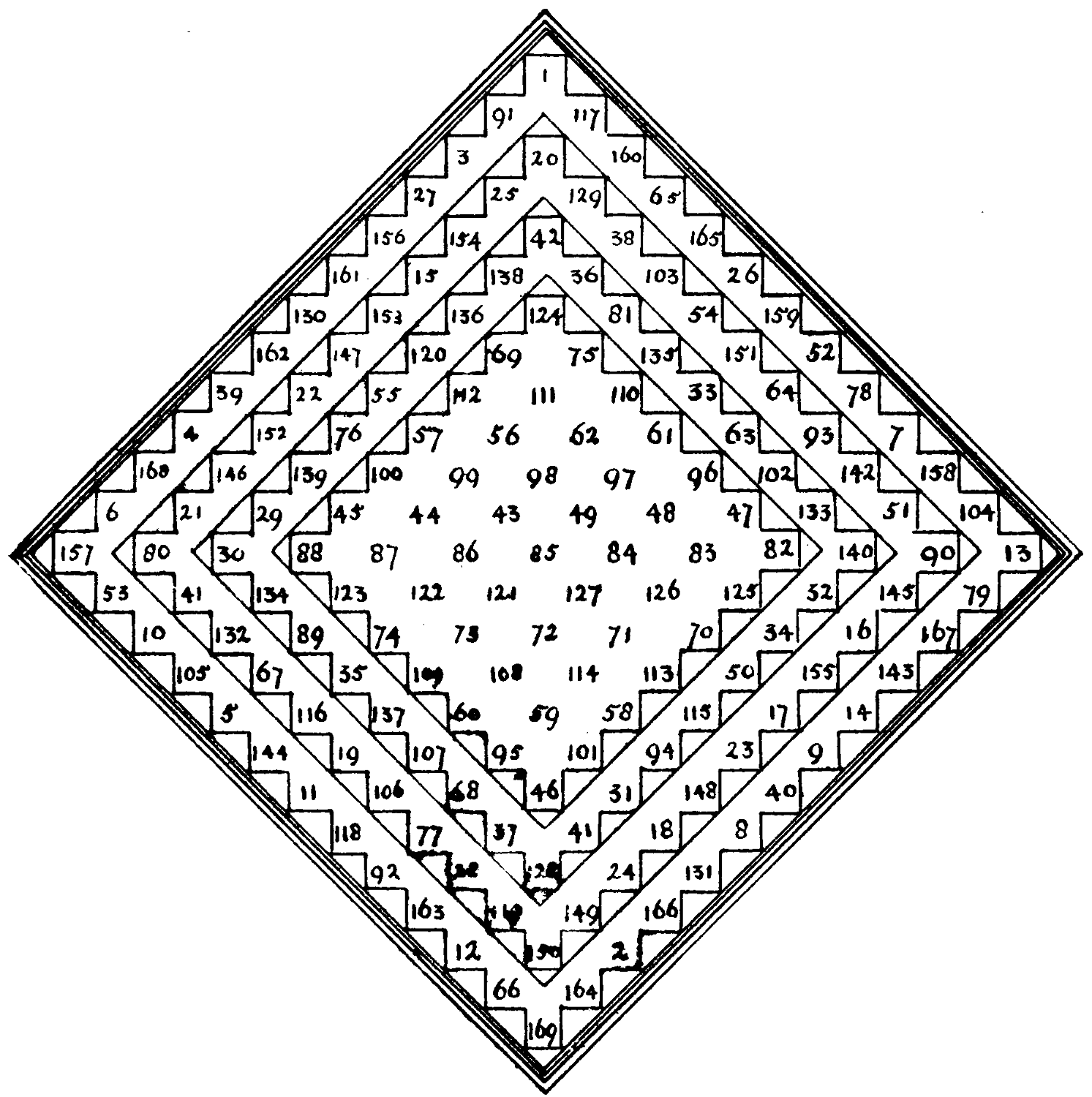
Return to description

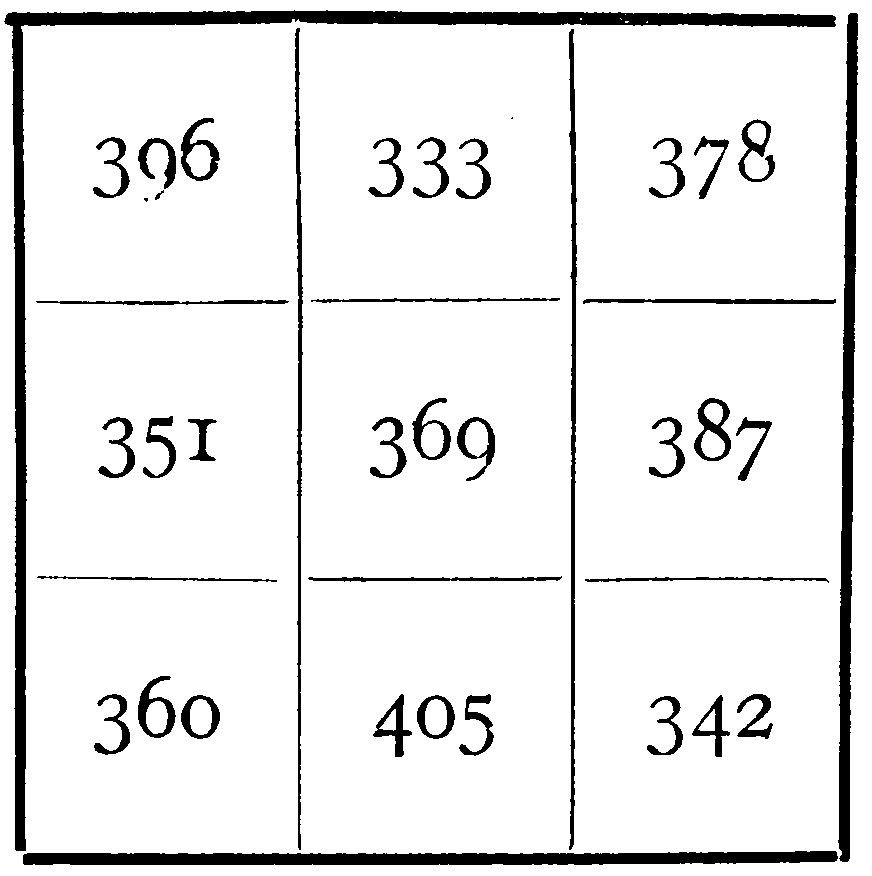
Return to descriptions
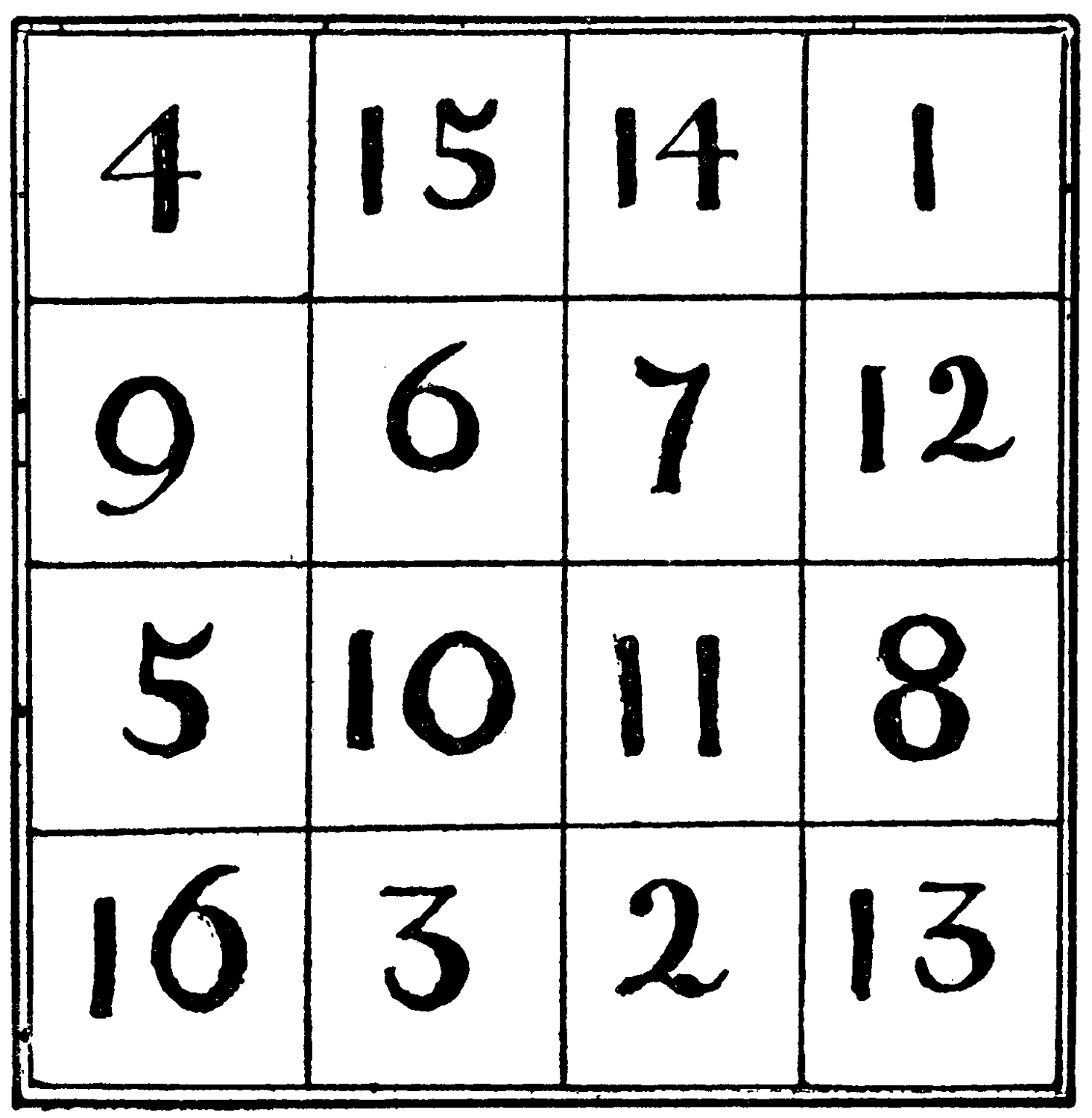
Return to description
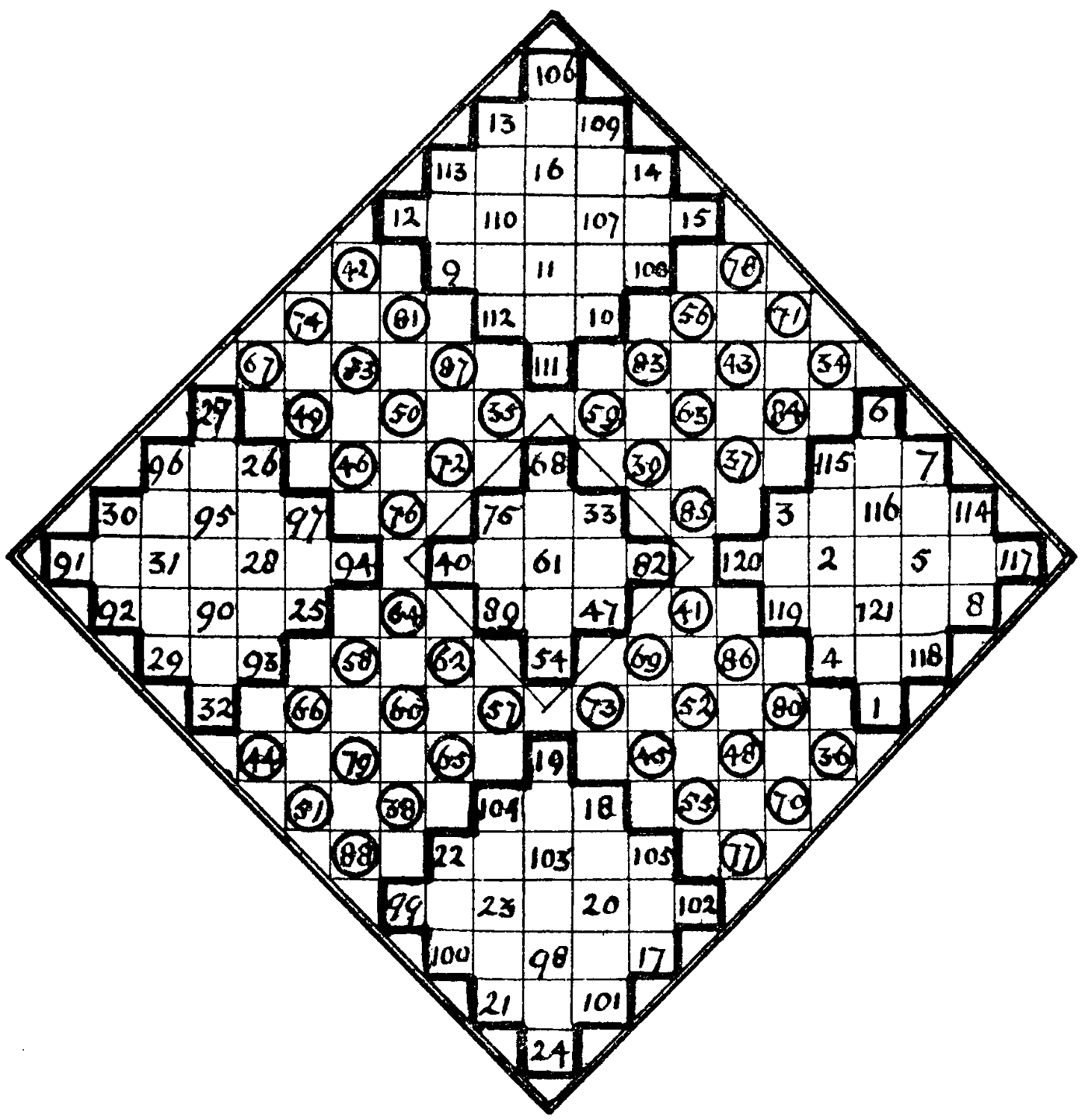
Return to description

Return to description

Return to description
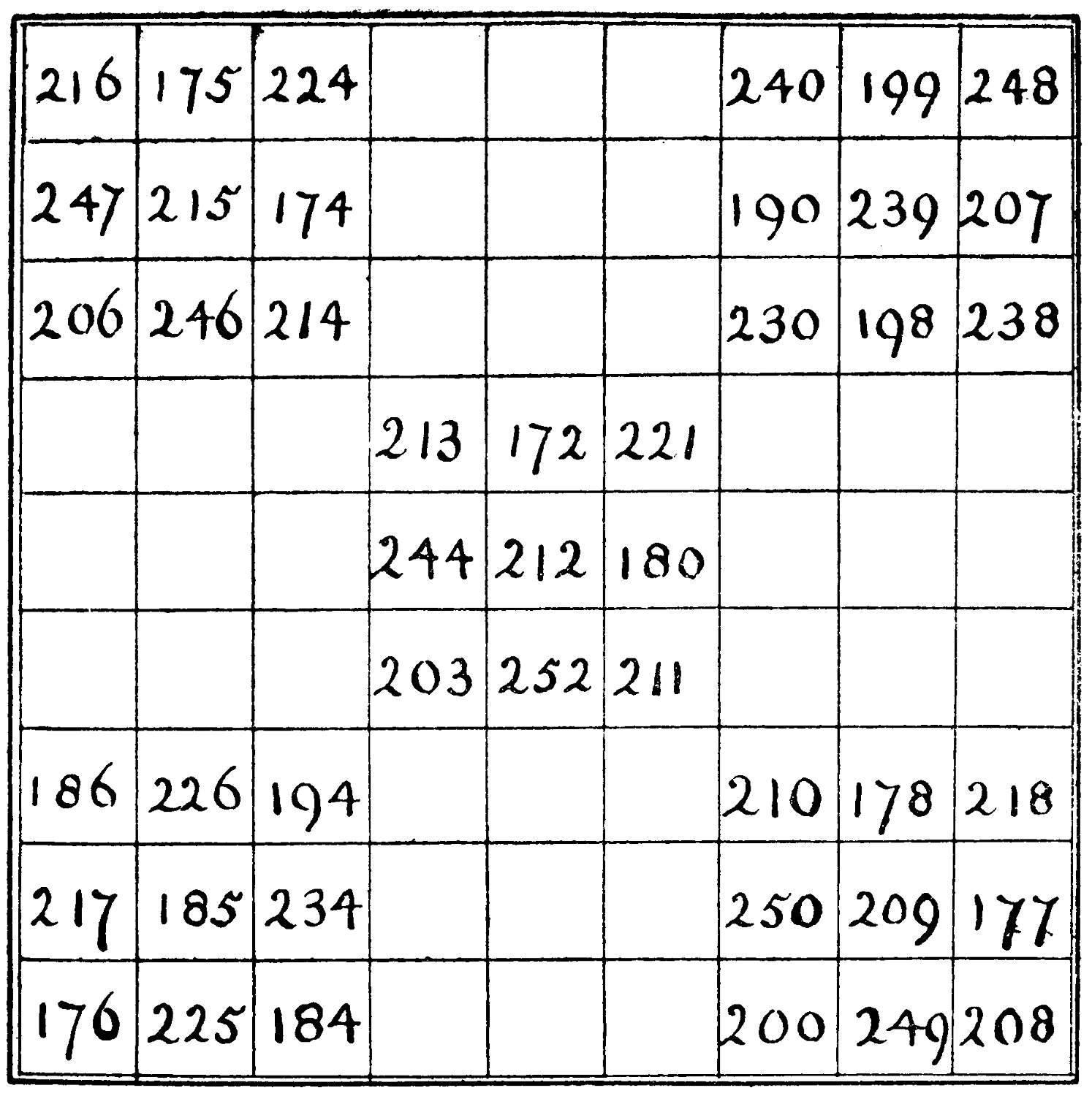
Return to description
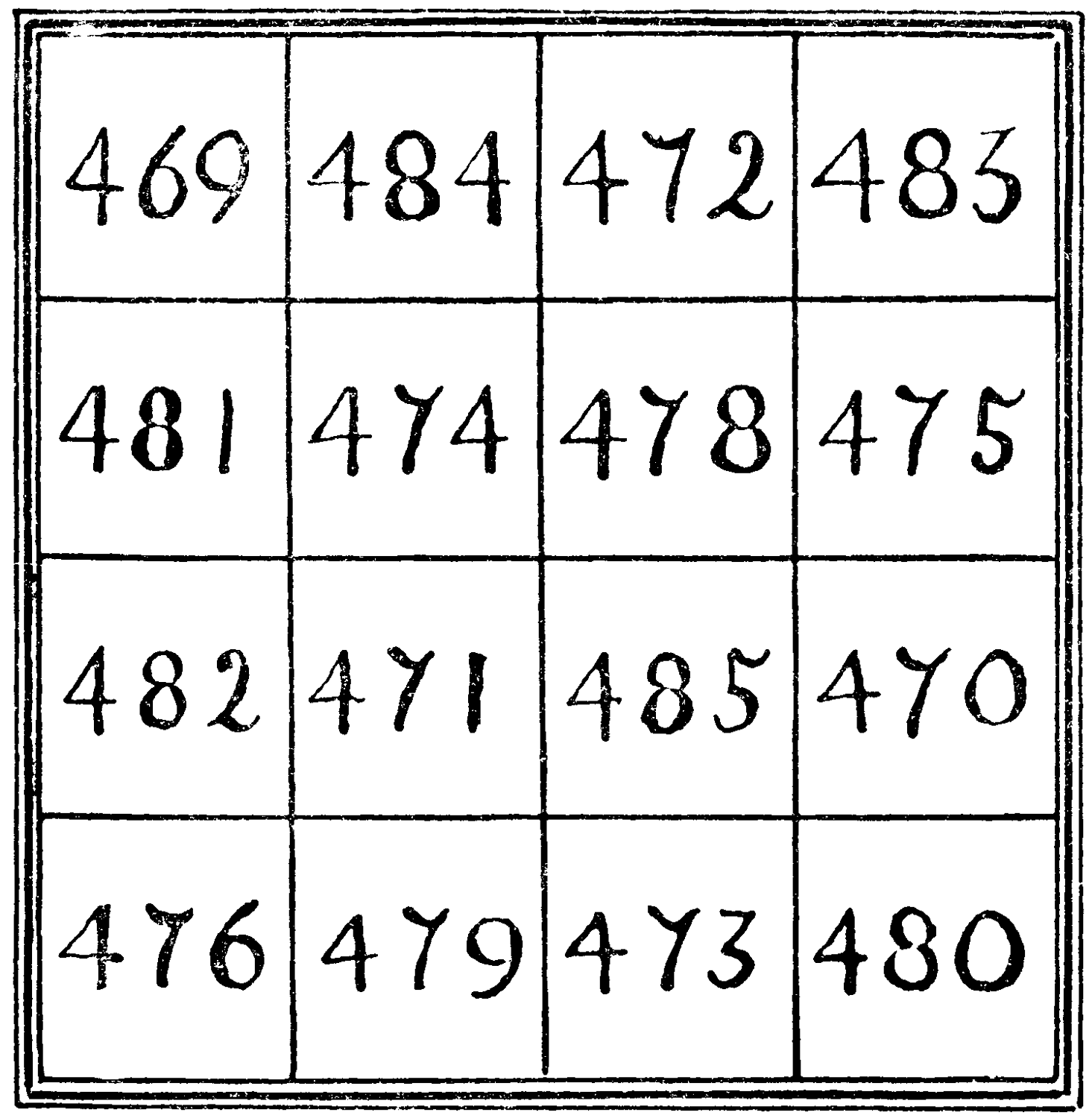
Return to description

Return to description
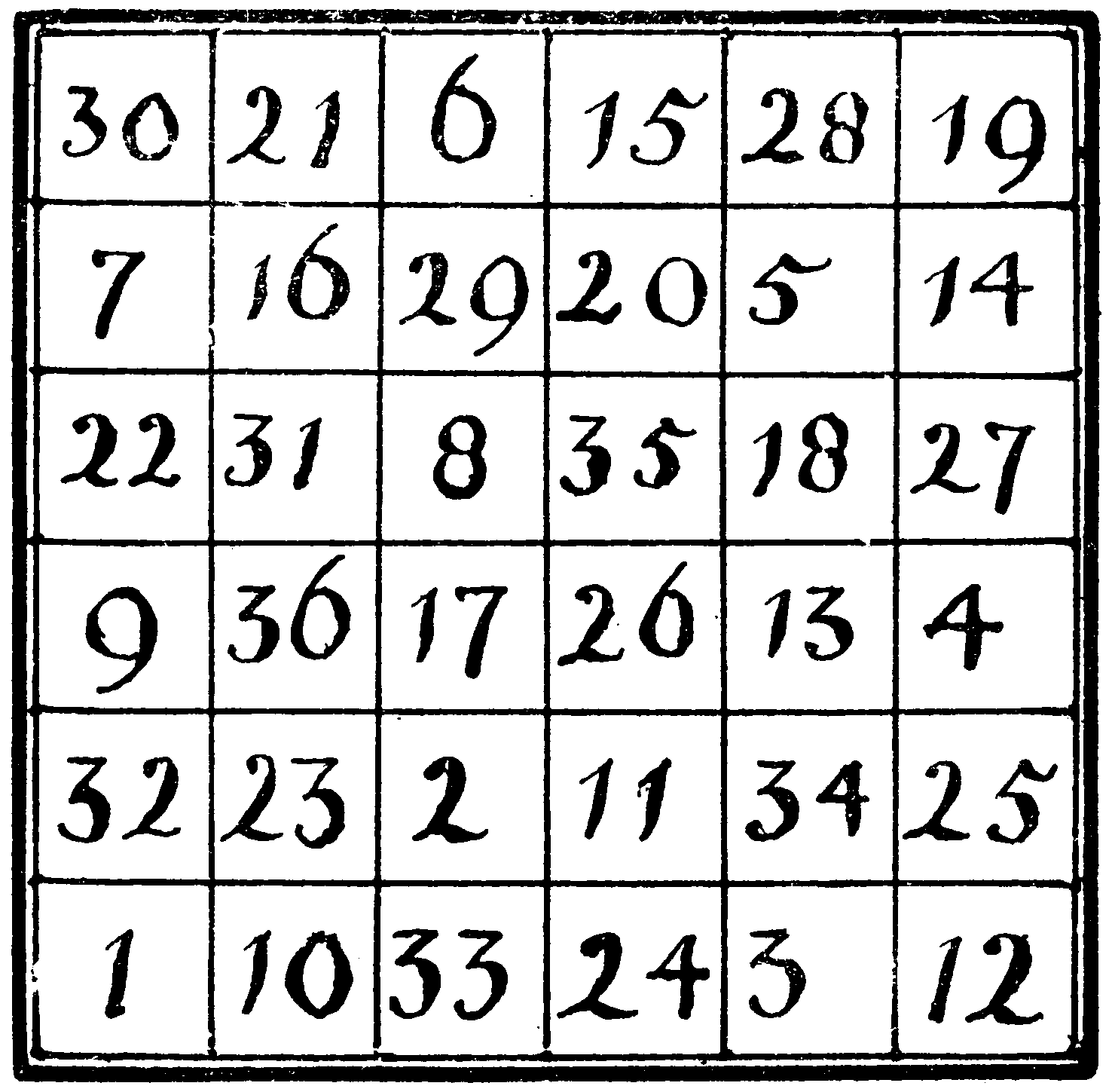
Return to description
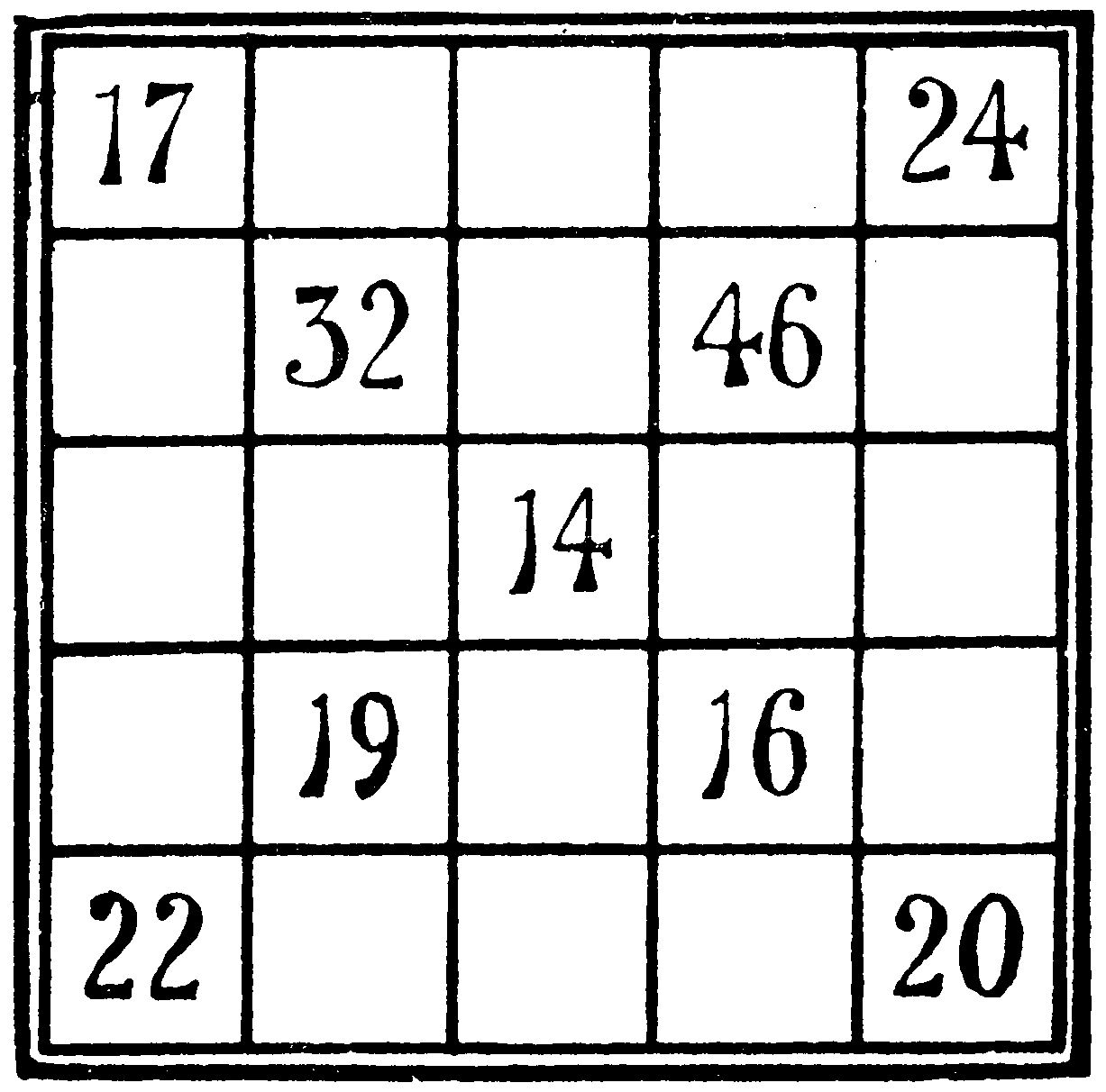
Return to description

Return to description

Return to description

Return to description

Return to description

Return to description
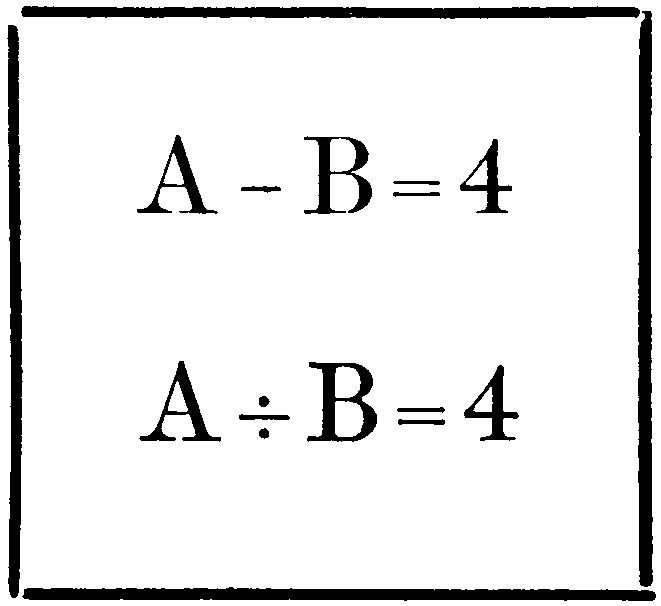
Return to description
Return to description

Return to description

Return to description

Return to description

Return to description
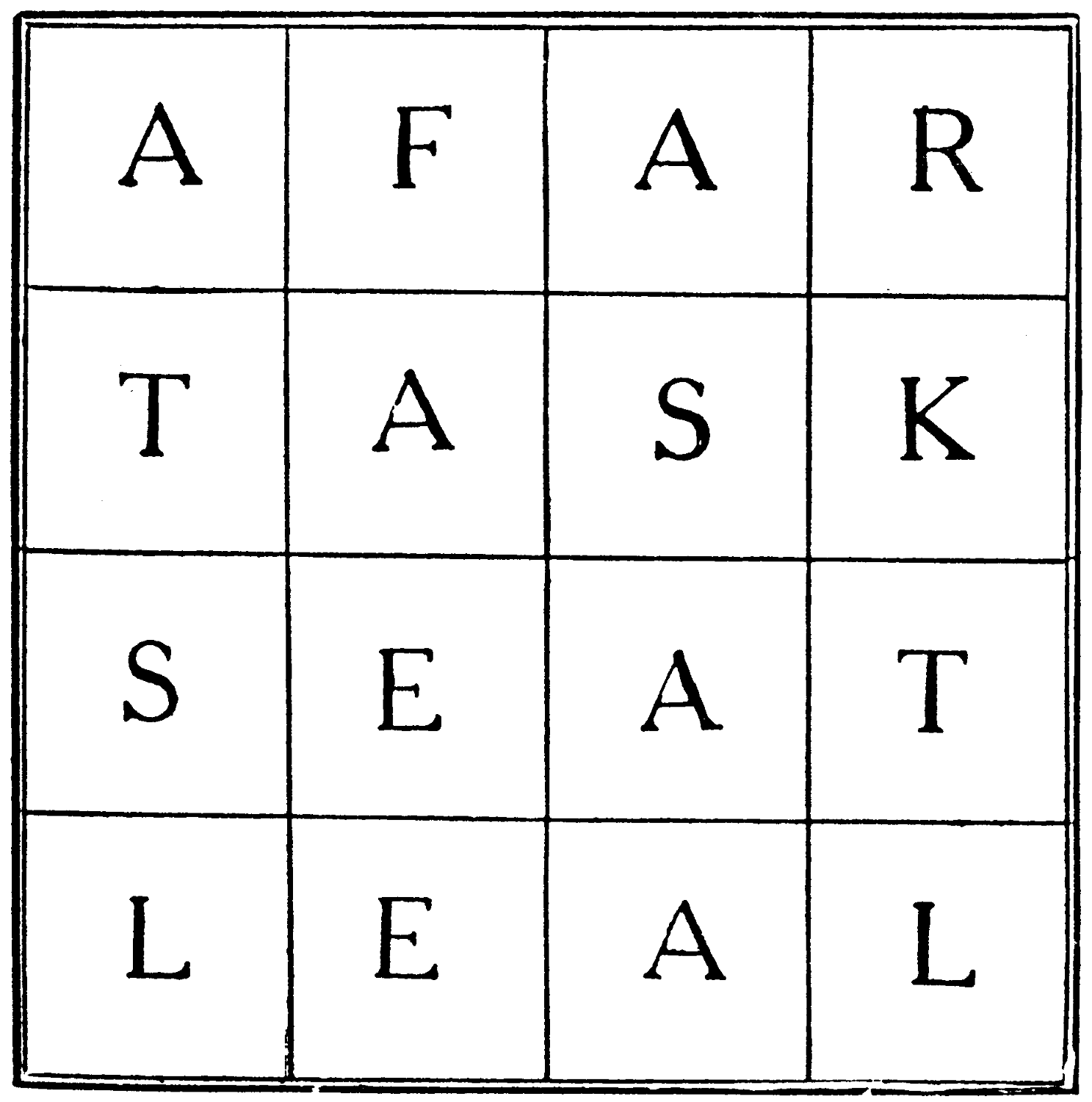
Return to description

Return to description

Return to description
Return to solution

Return to description
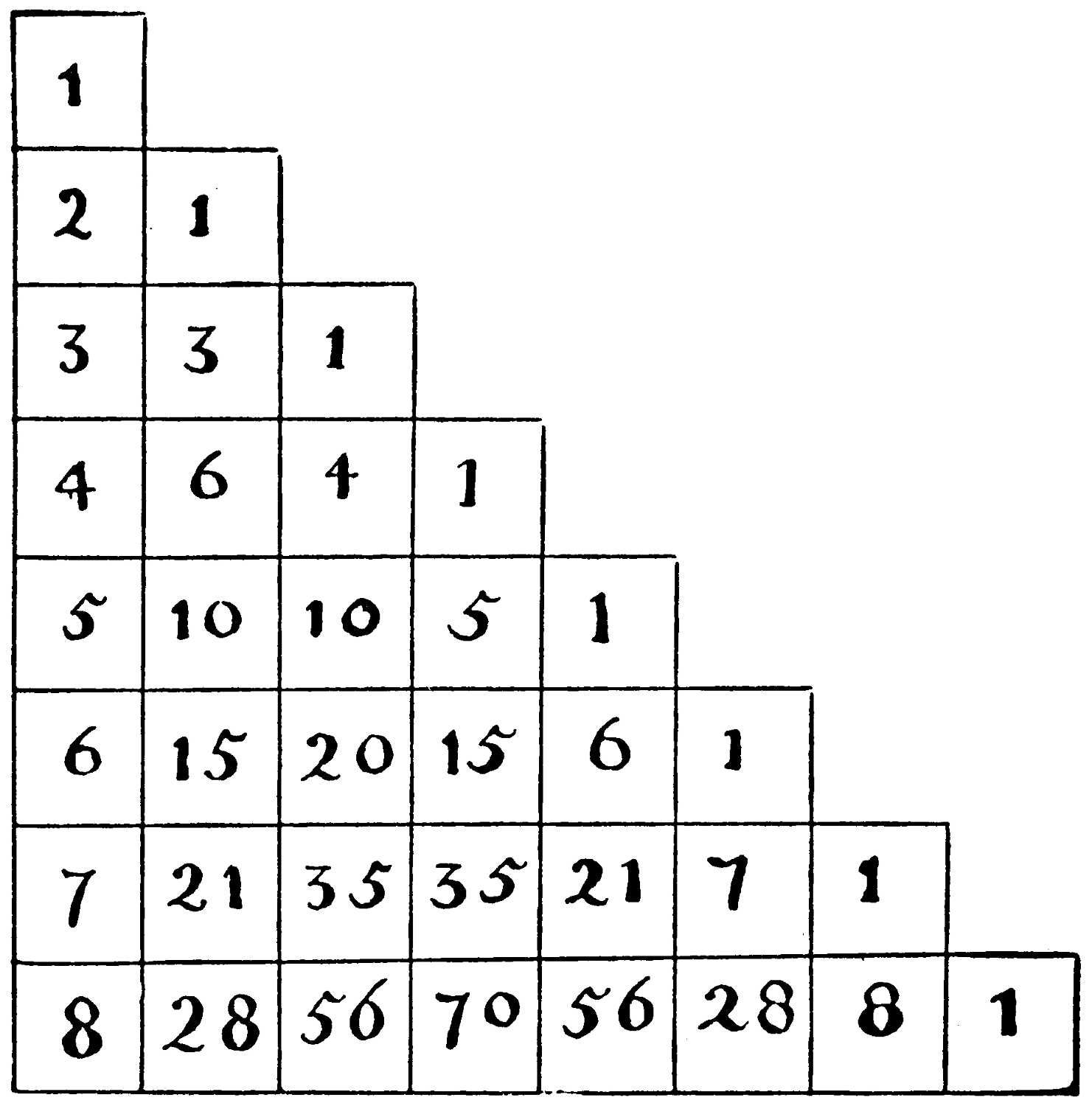
Return to description

Return to description
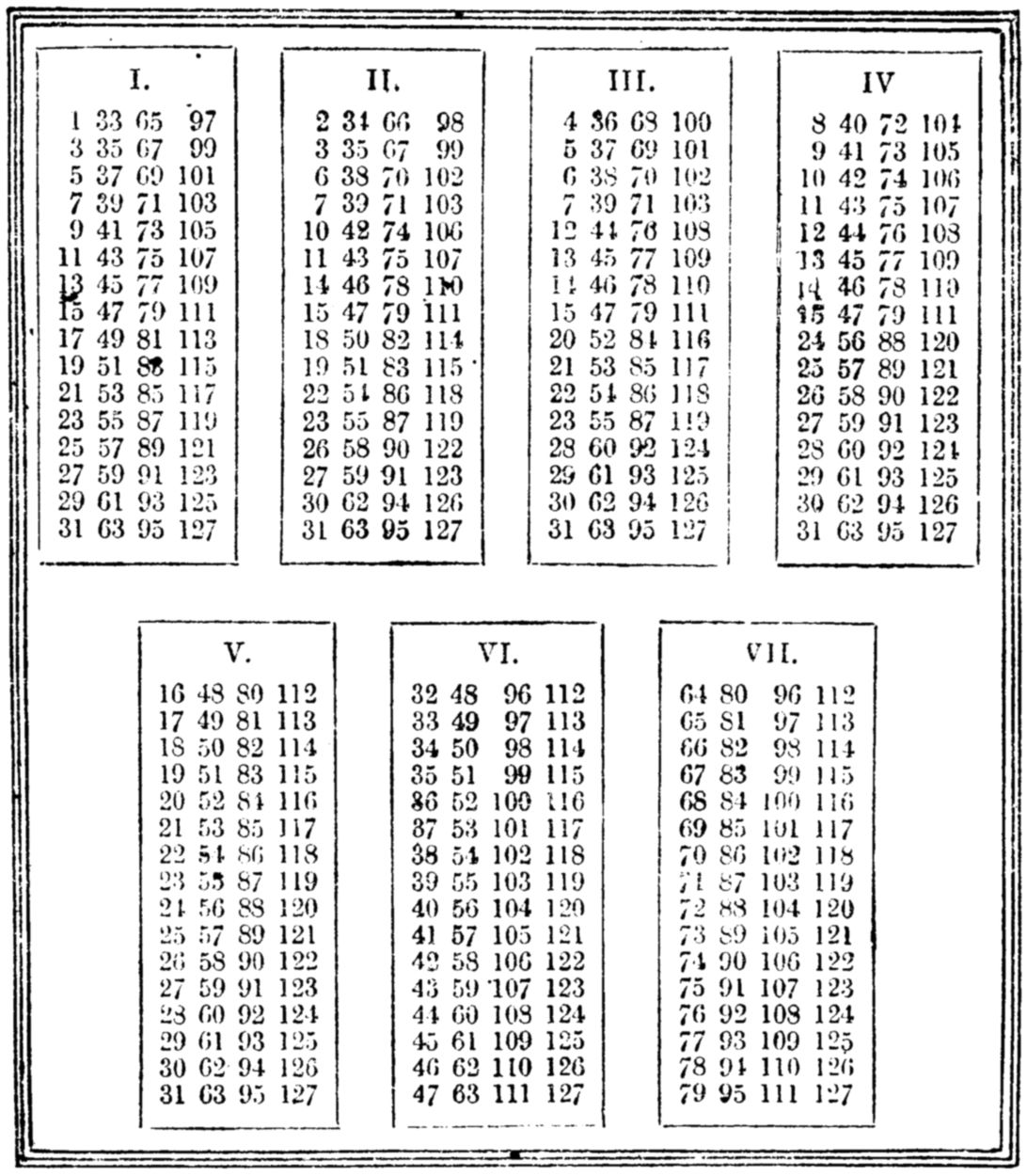
Return to description

Return to description

Return to description

Return to description
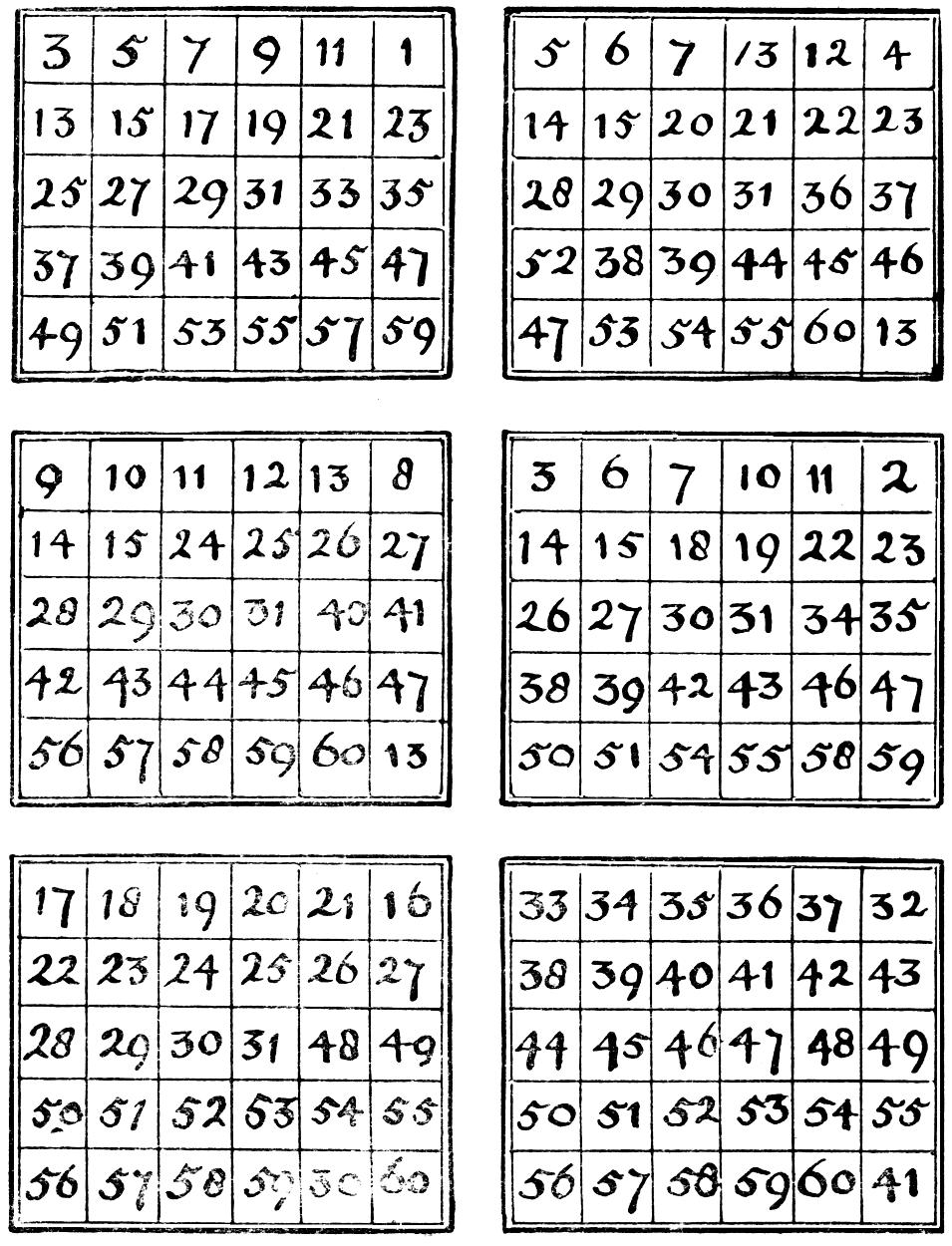
Return to description
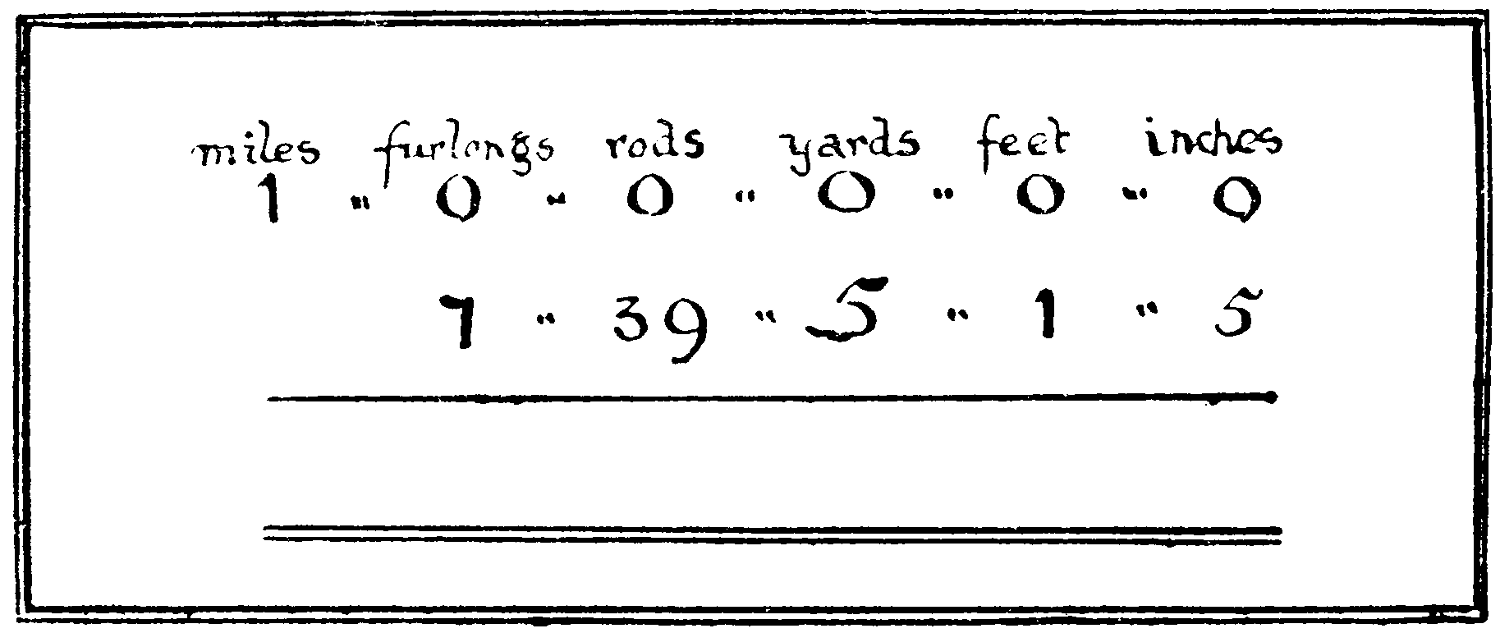
Return to description
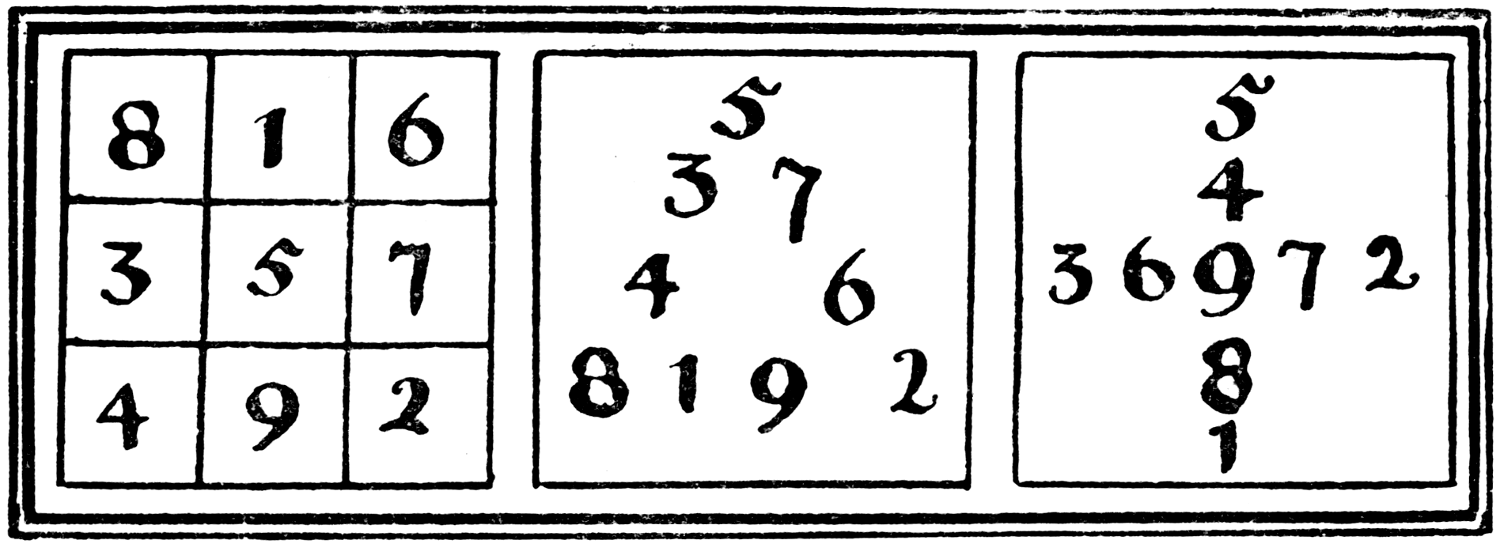
Return to description
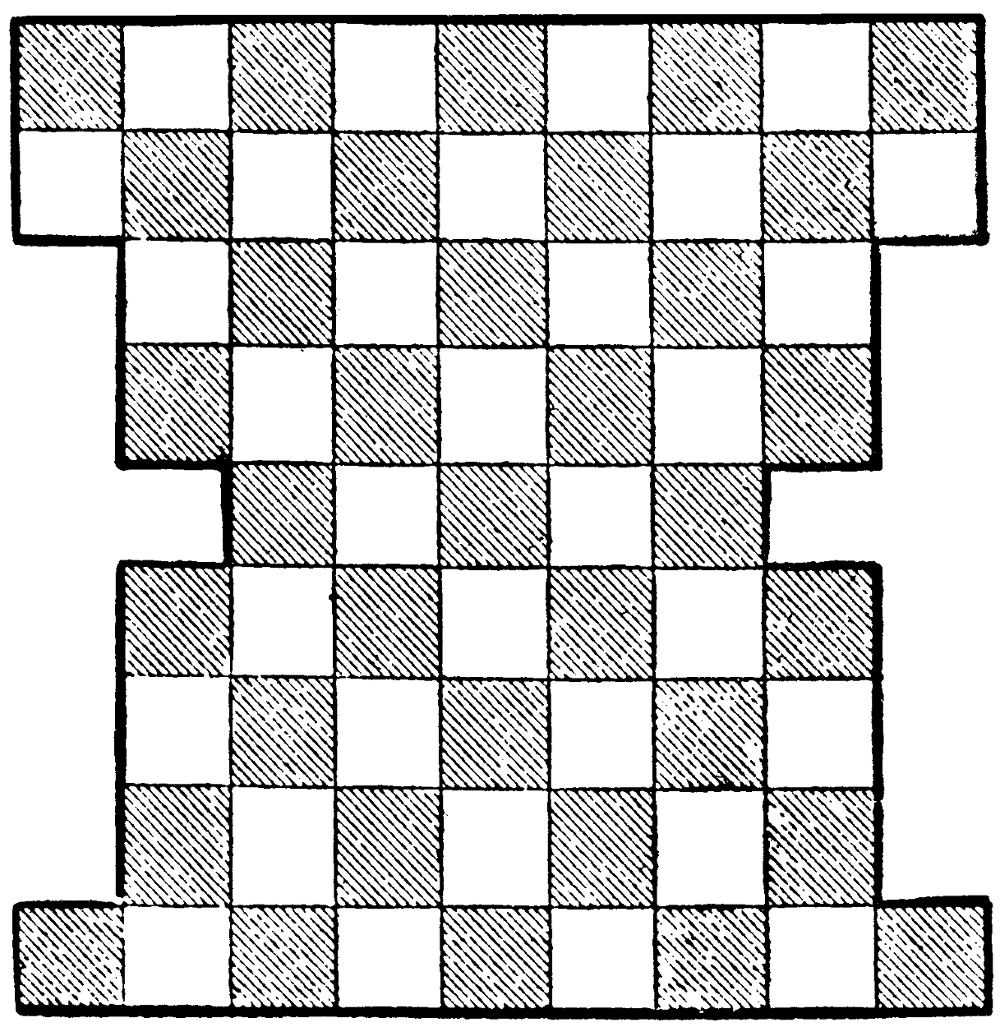
Return to description
Return to description

Return to description

Return to description

Return to description
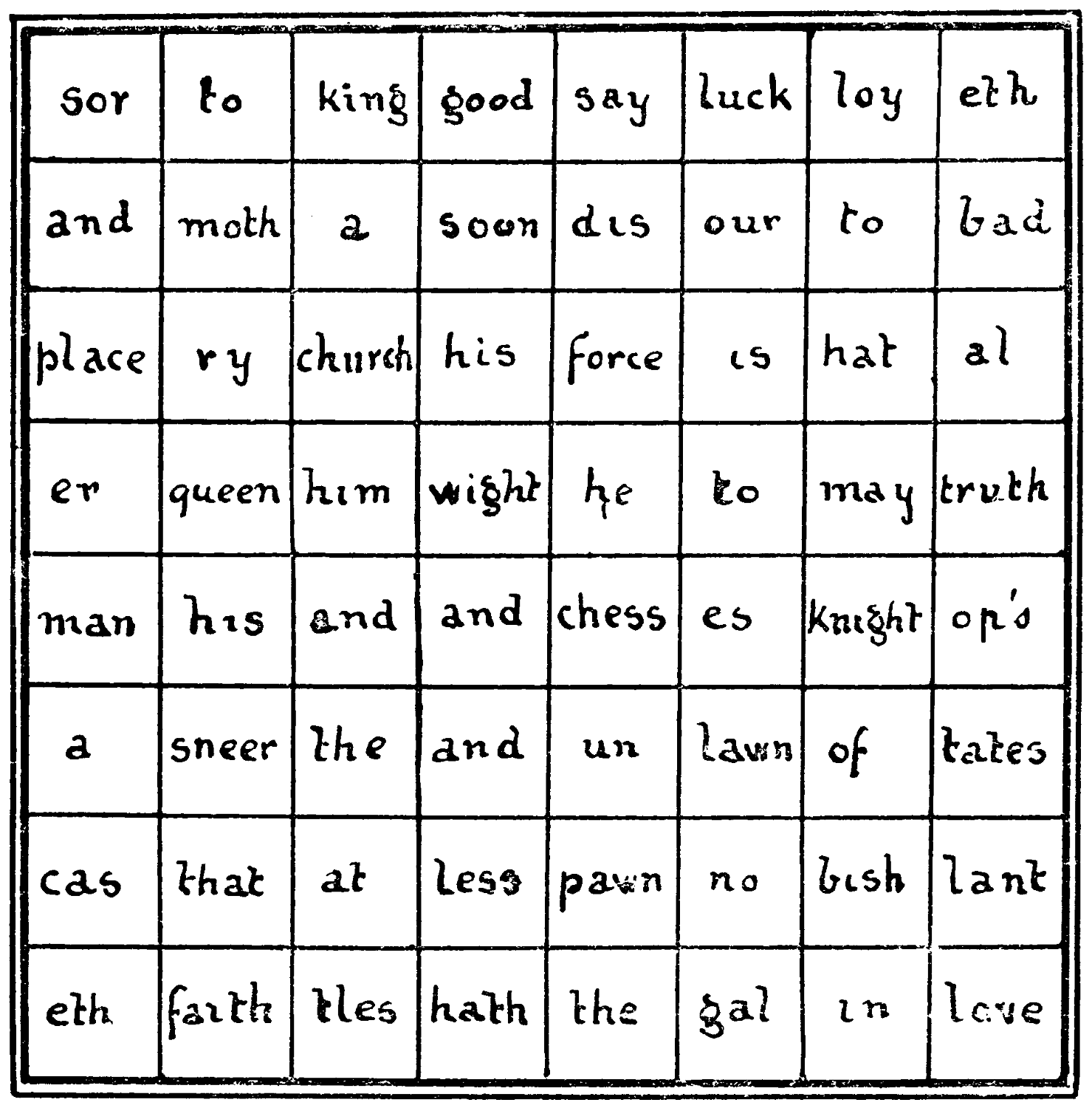
Return to description

Return to description
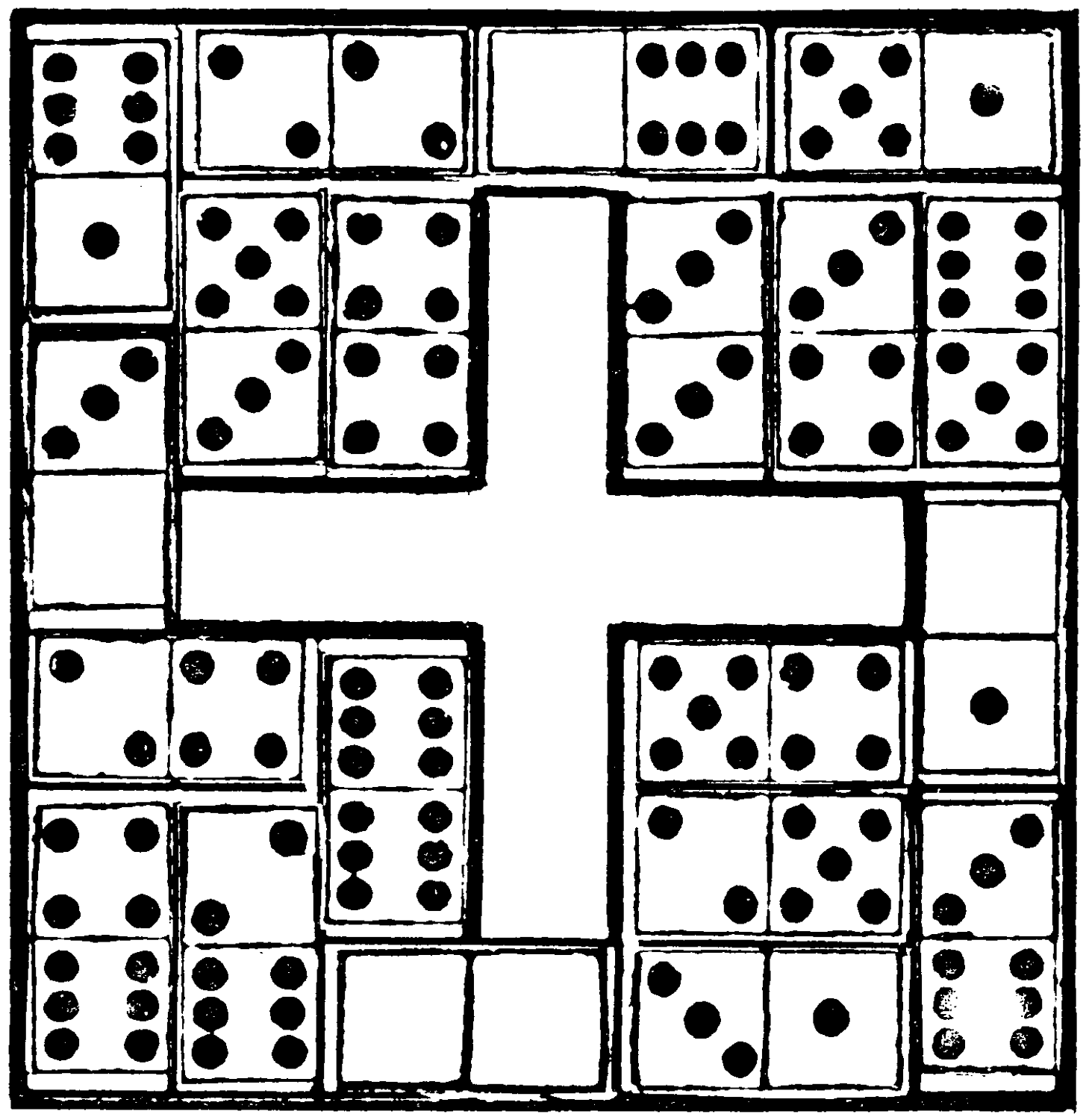
Return to description
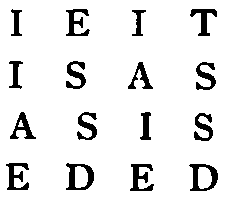
Return to description

Return to description
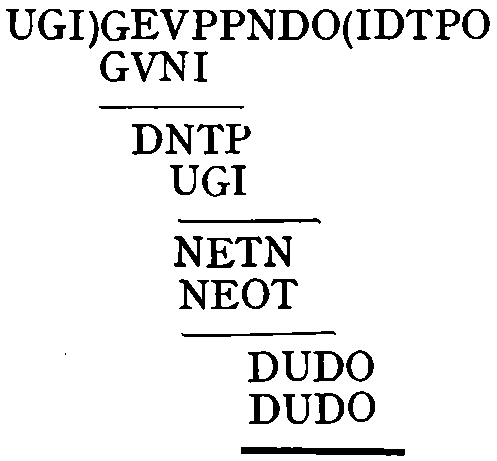
Return to description

Return to description
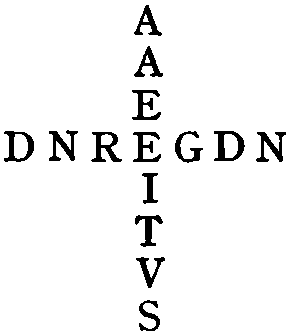
Return to description

Return to description

Return to description

Return to description

Return to description
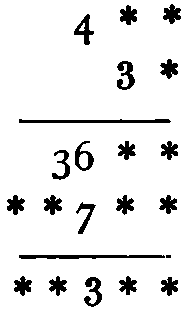
Return to description

Return to solution
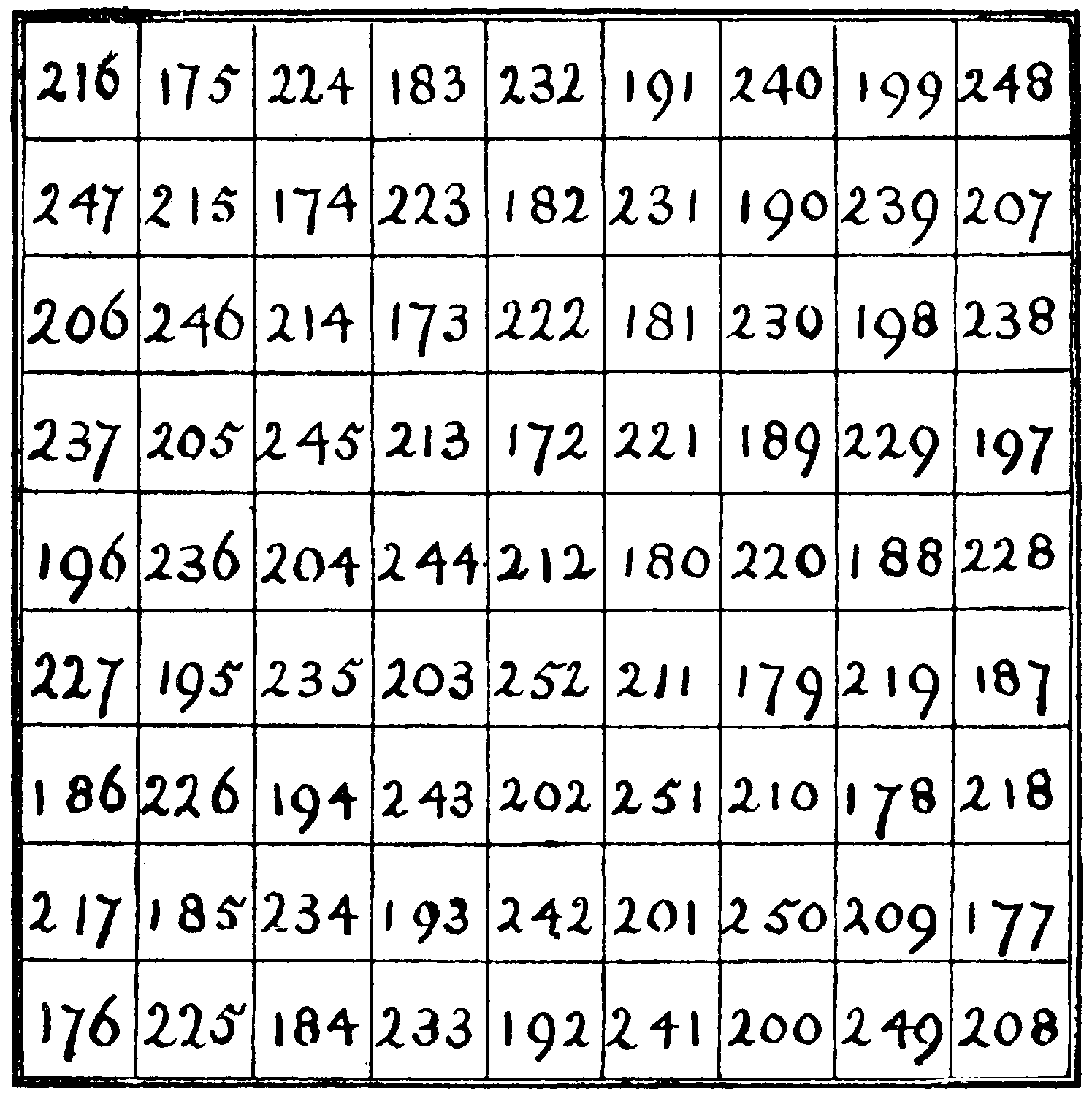
Return to solution
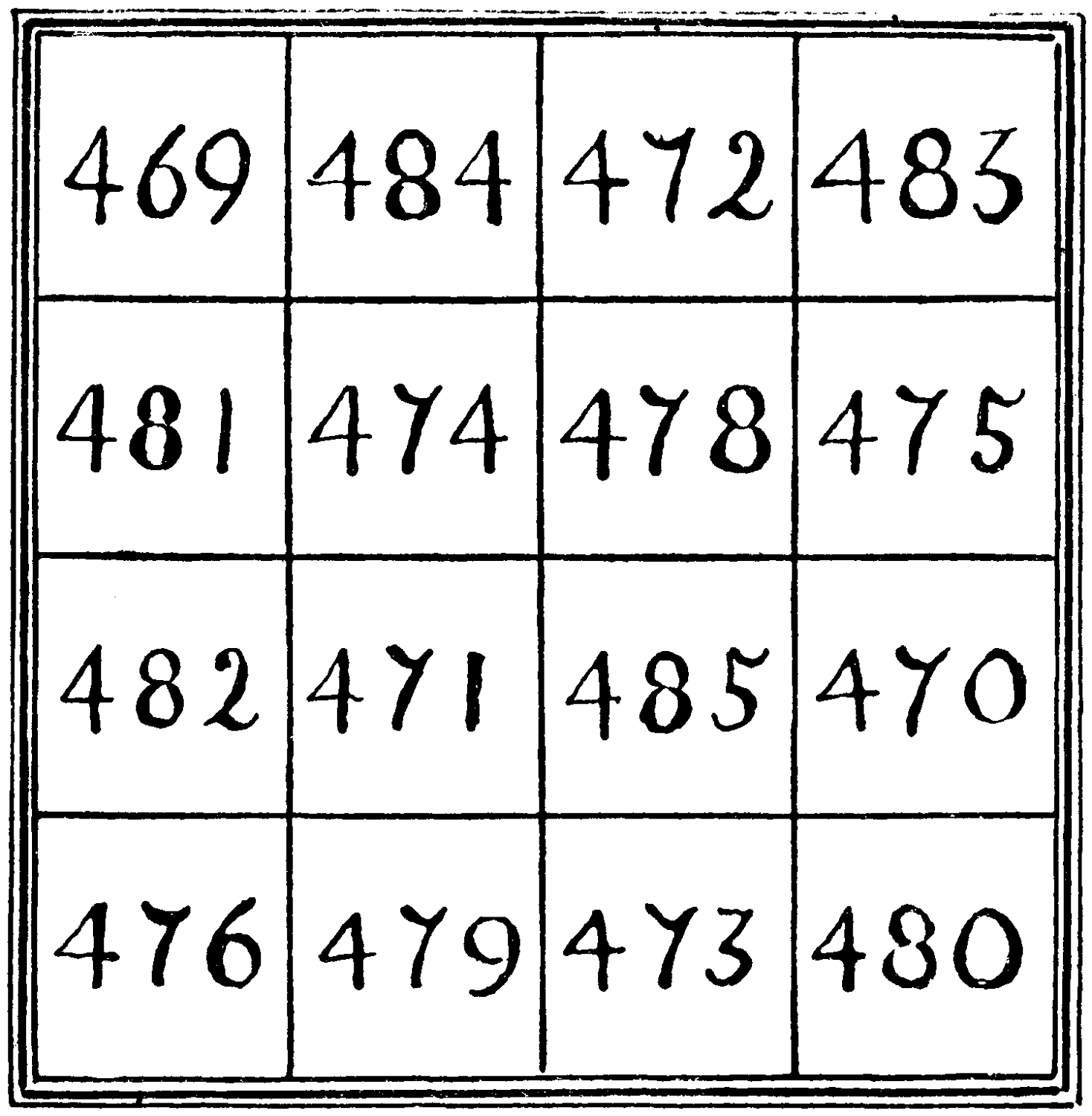
Return to solution

Return to solution
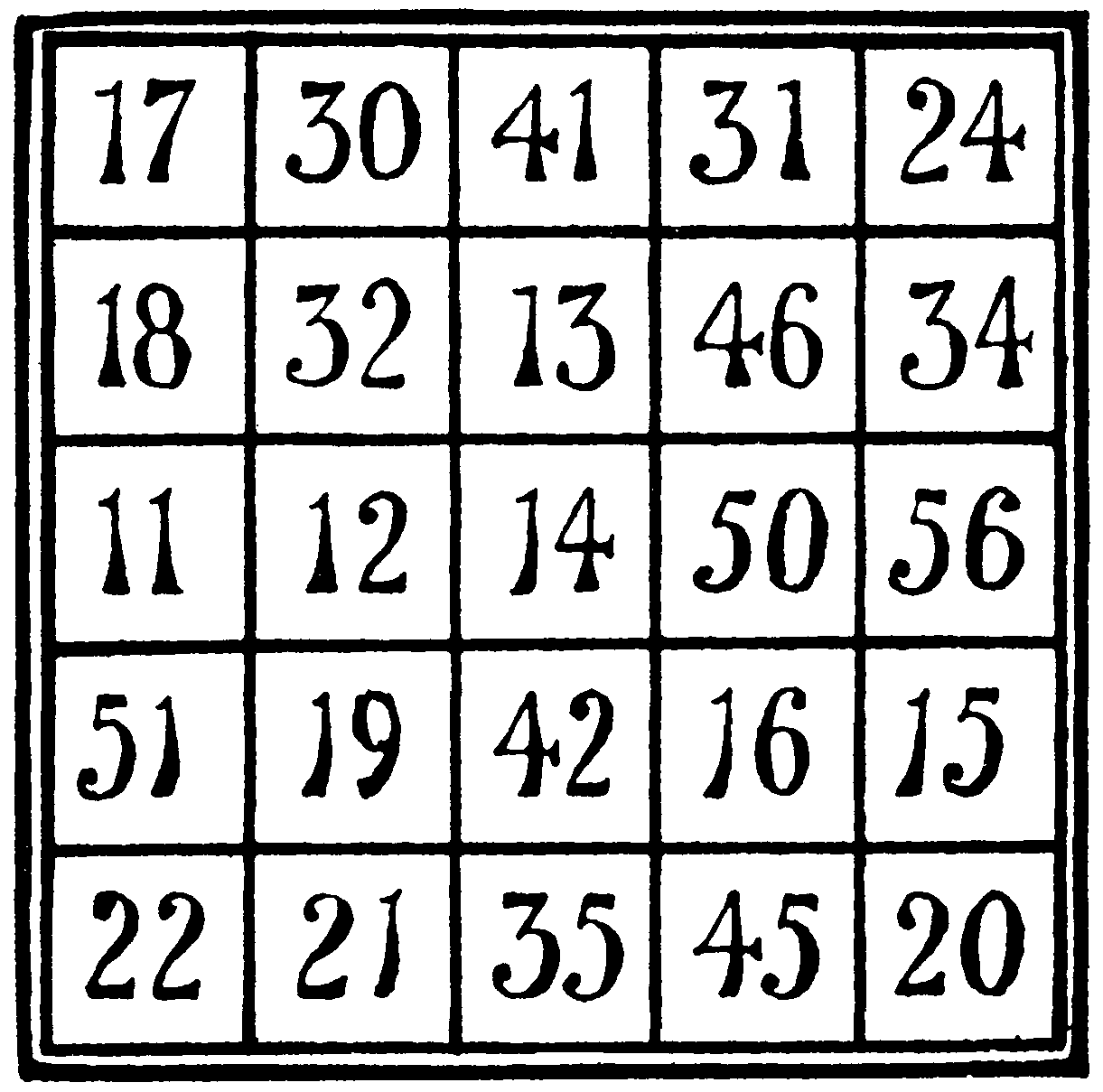
Return to solution

Return to solution
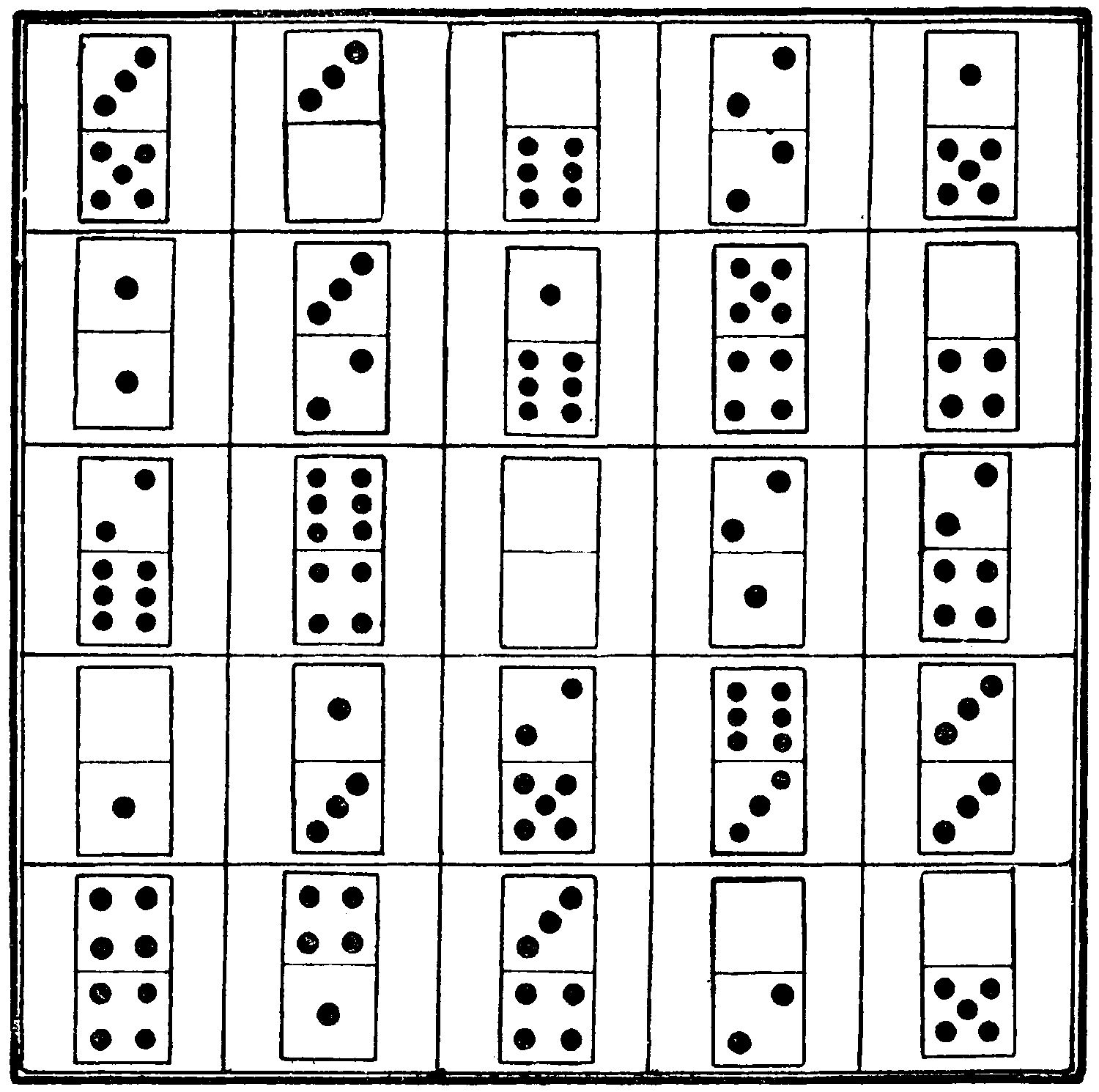
Return to solution

Return to solution

Return to solution
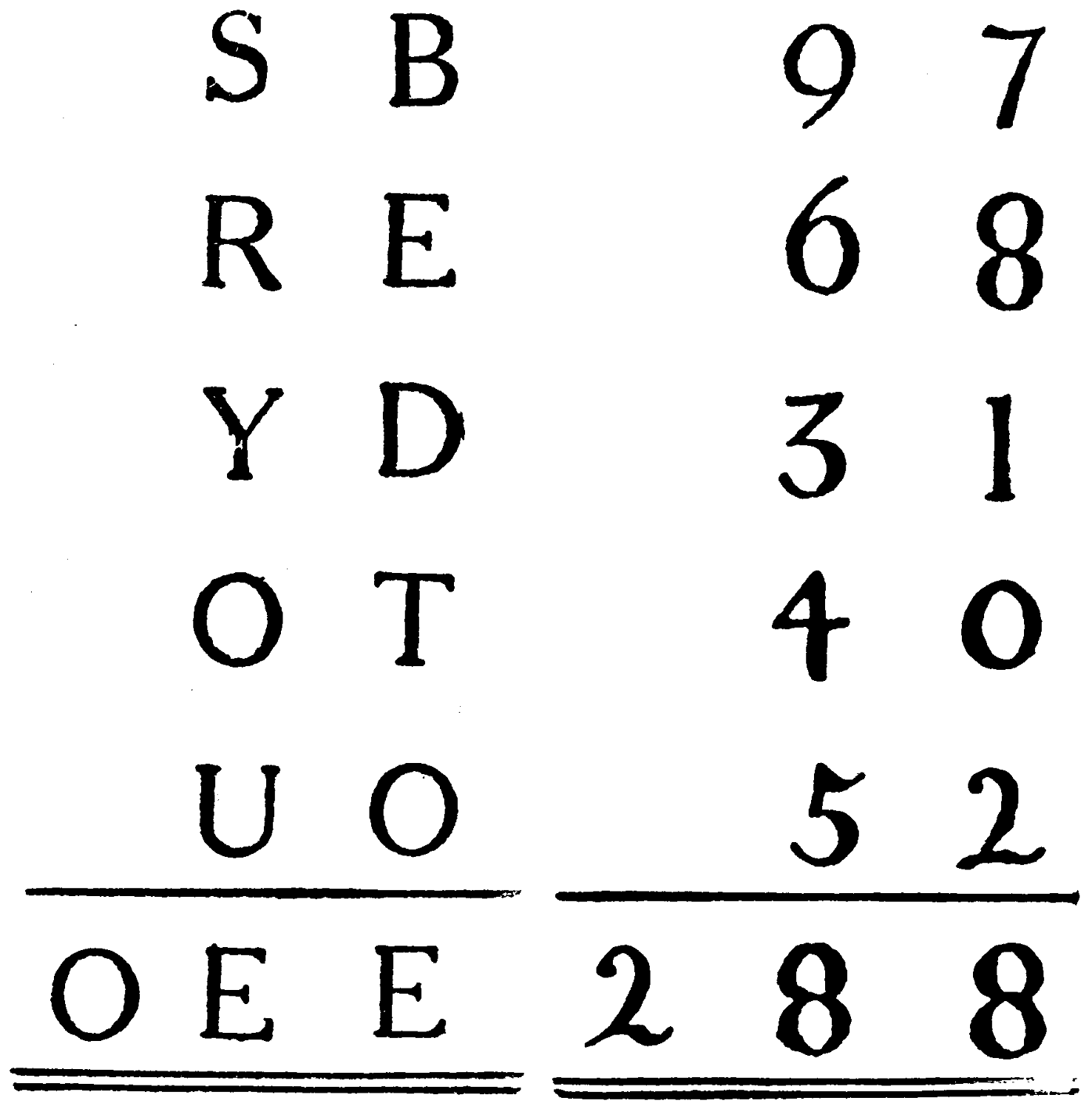
Return to solution

Return to solution
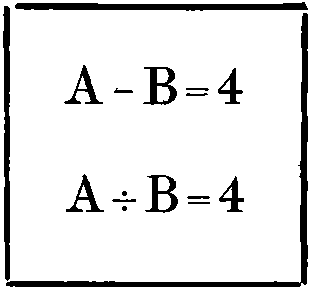
Return to solution

Return to solution

Return to solution

Return to solution

Return to solution

Return to solution
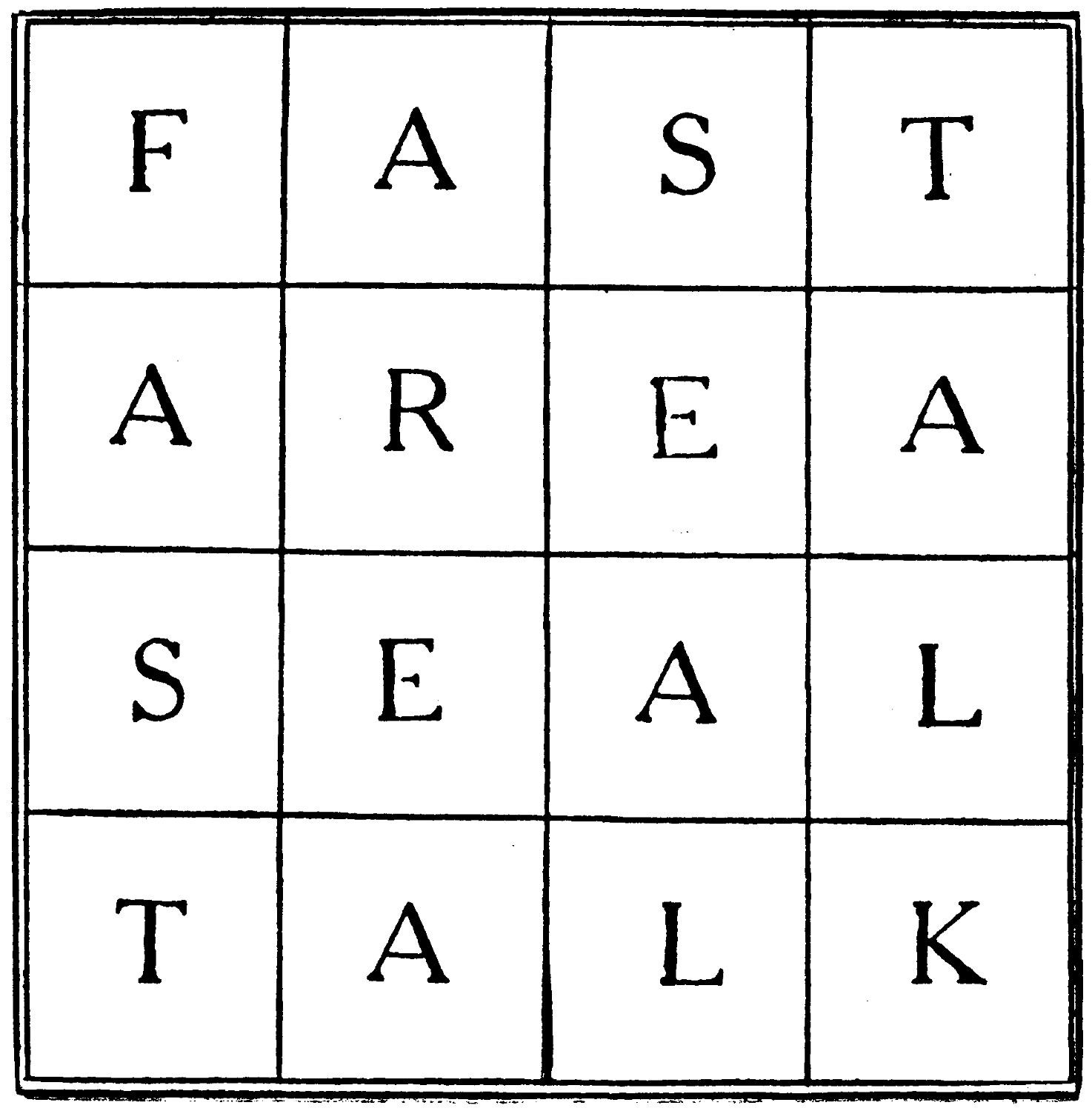
Return to solution

Return to solution

Return to solution
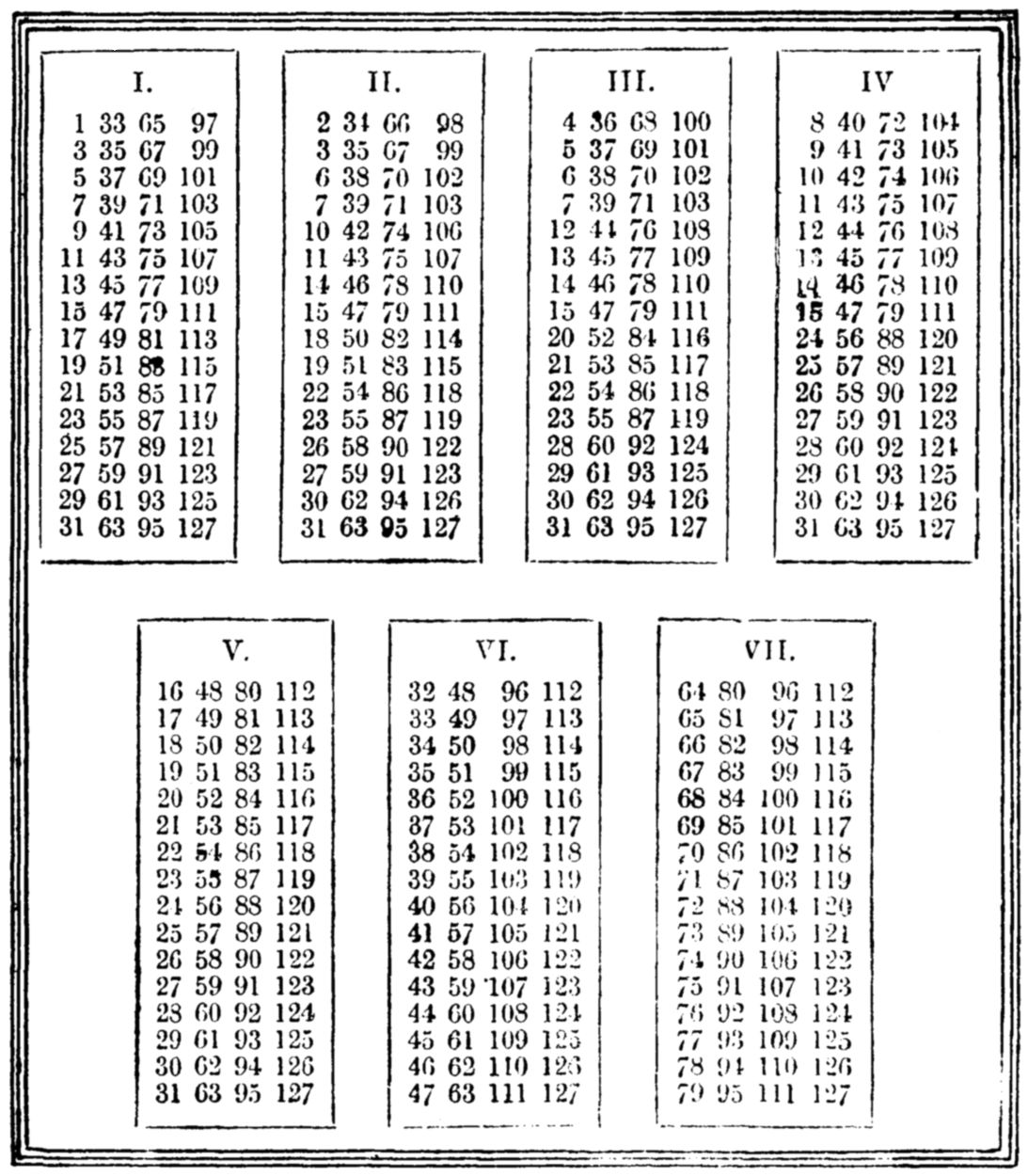
Return to solution
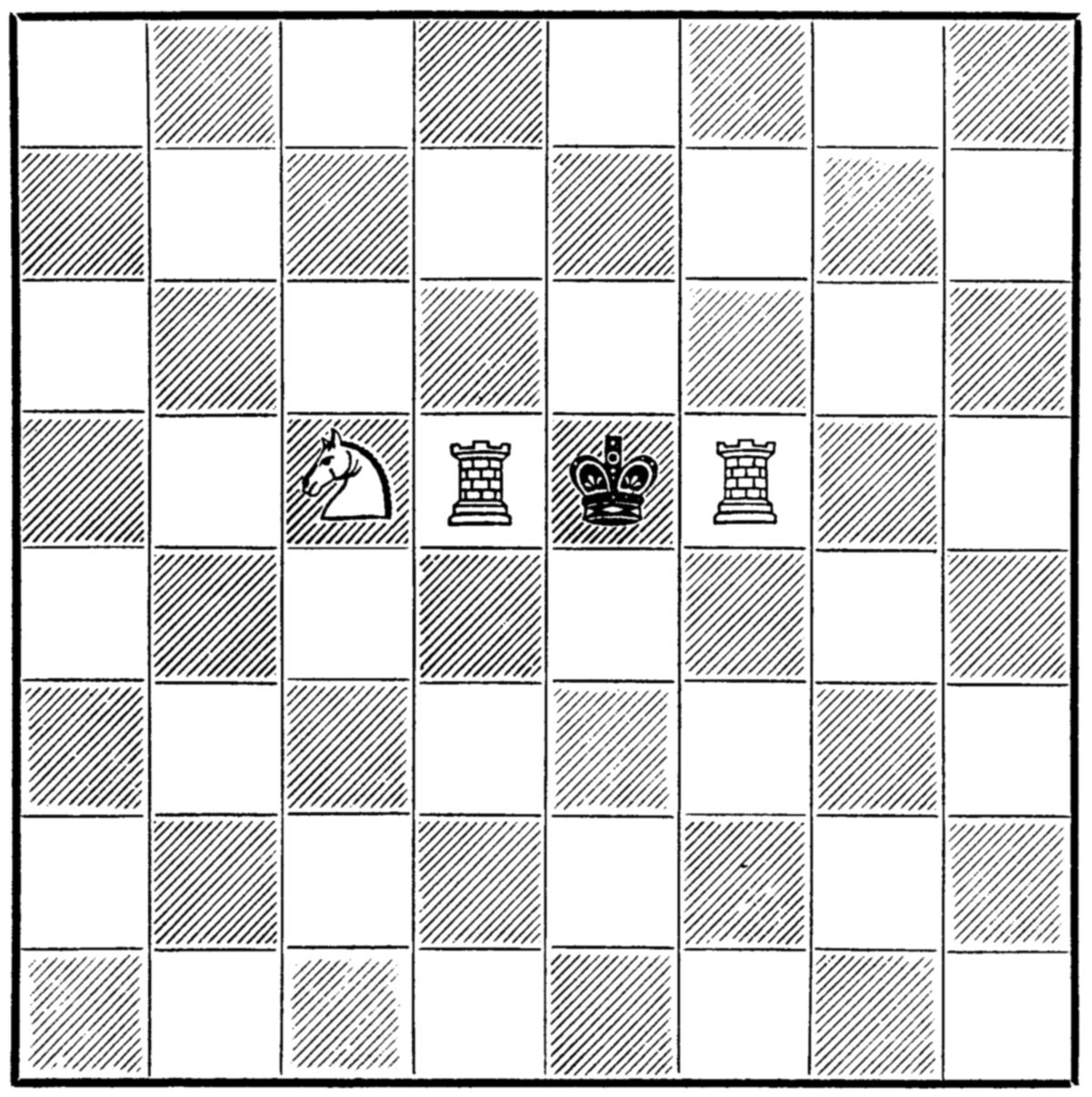
Return to solution
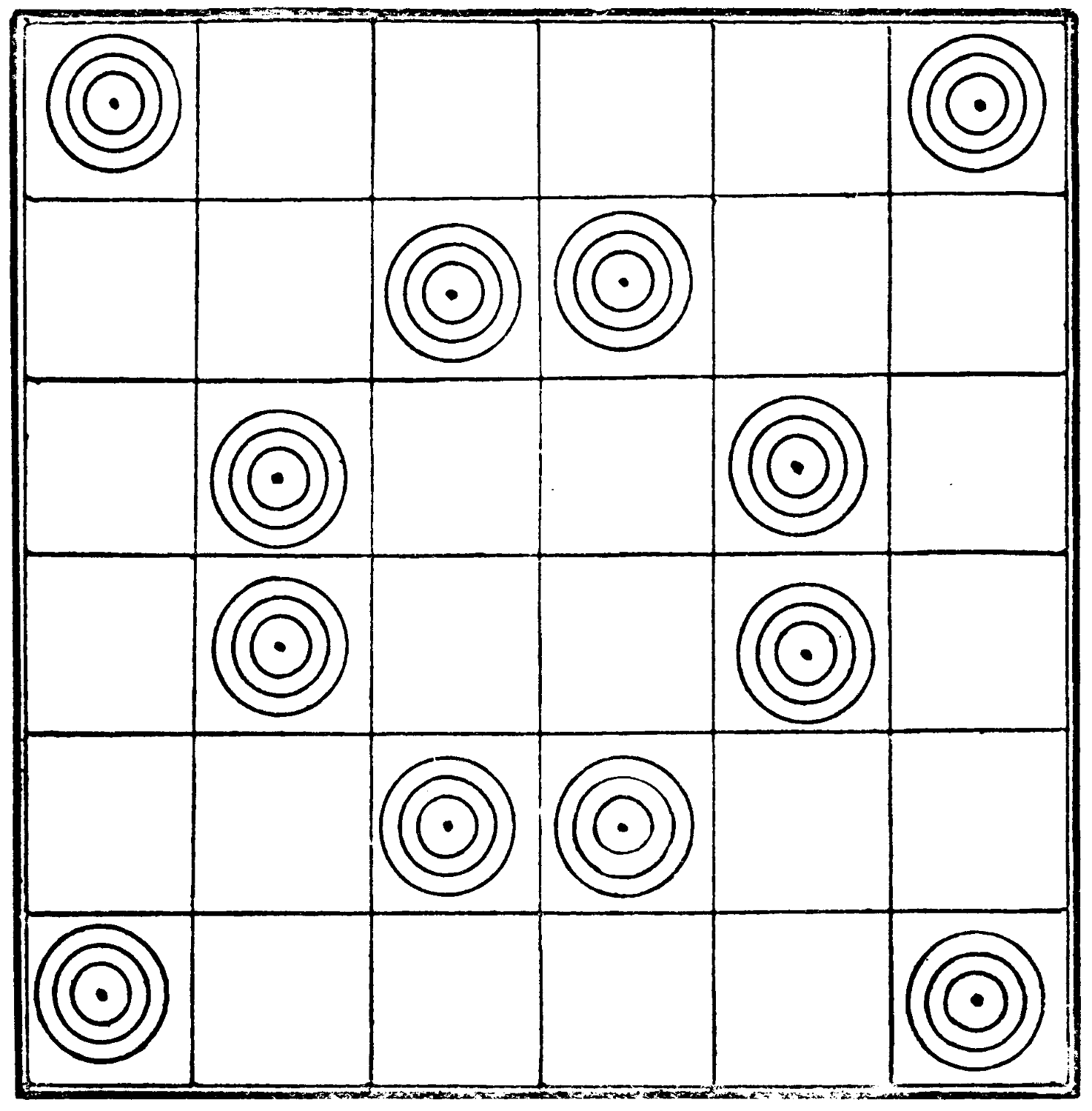
Return to solution
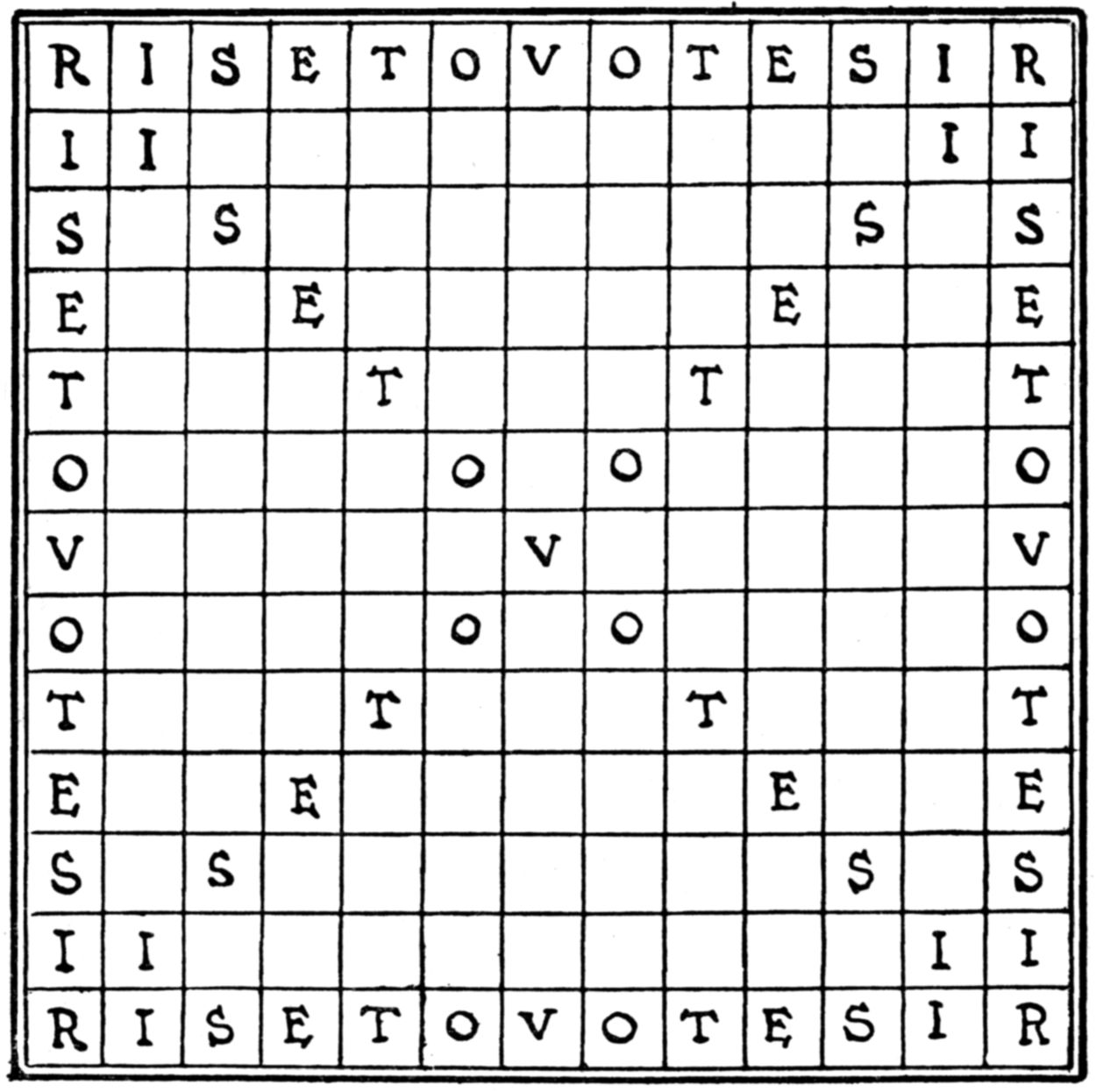
Return to solution
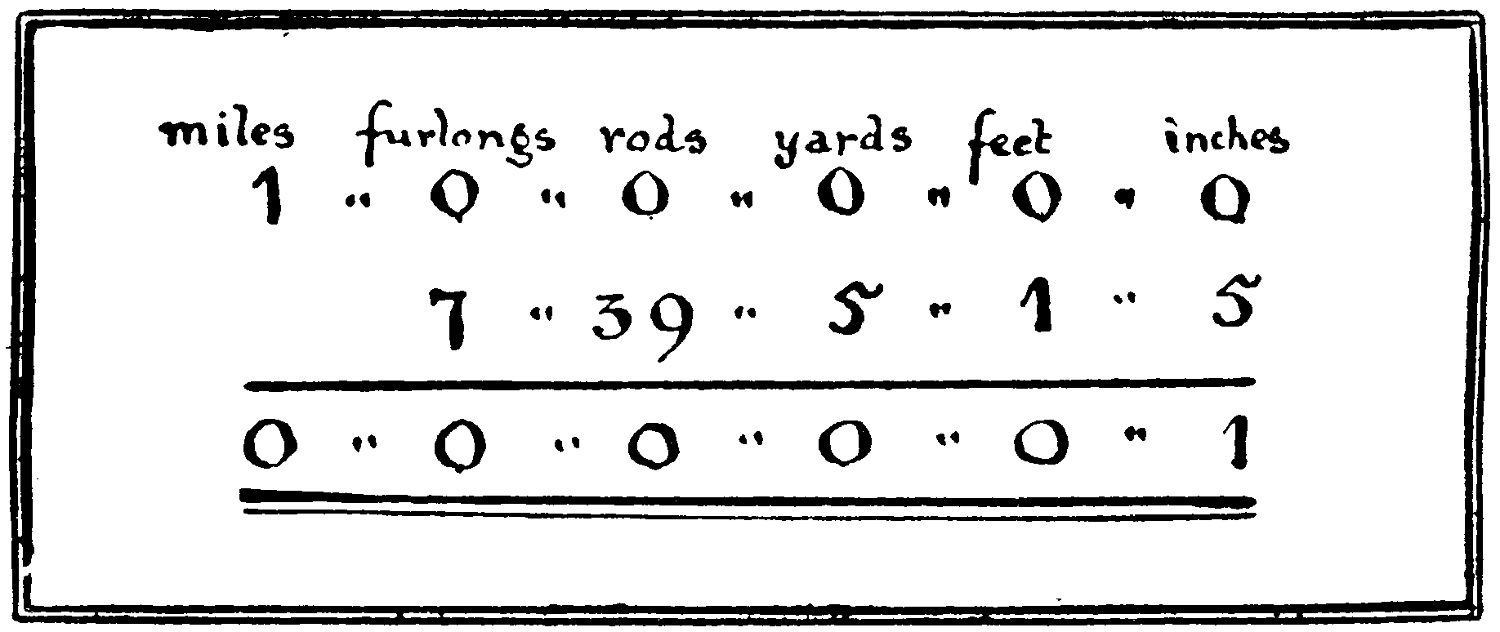
Return to solution

Return to solution
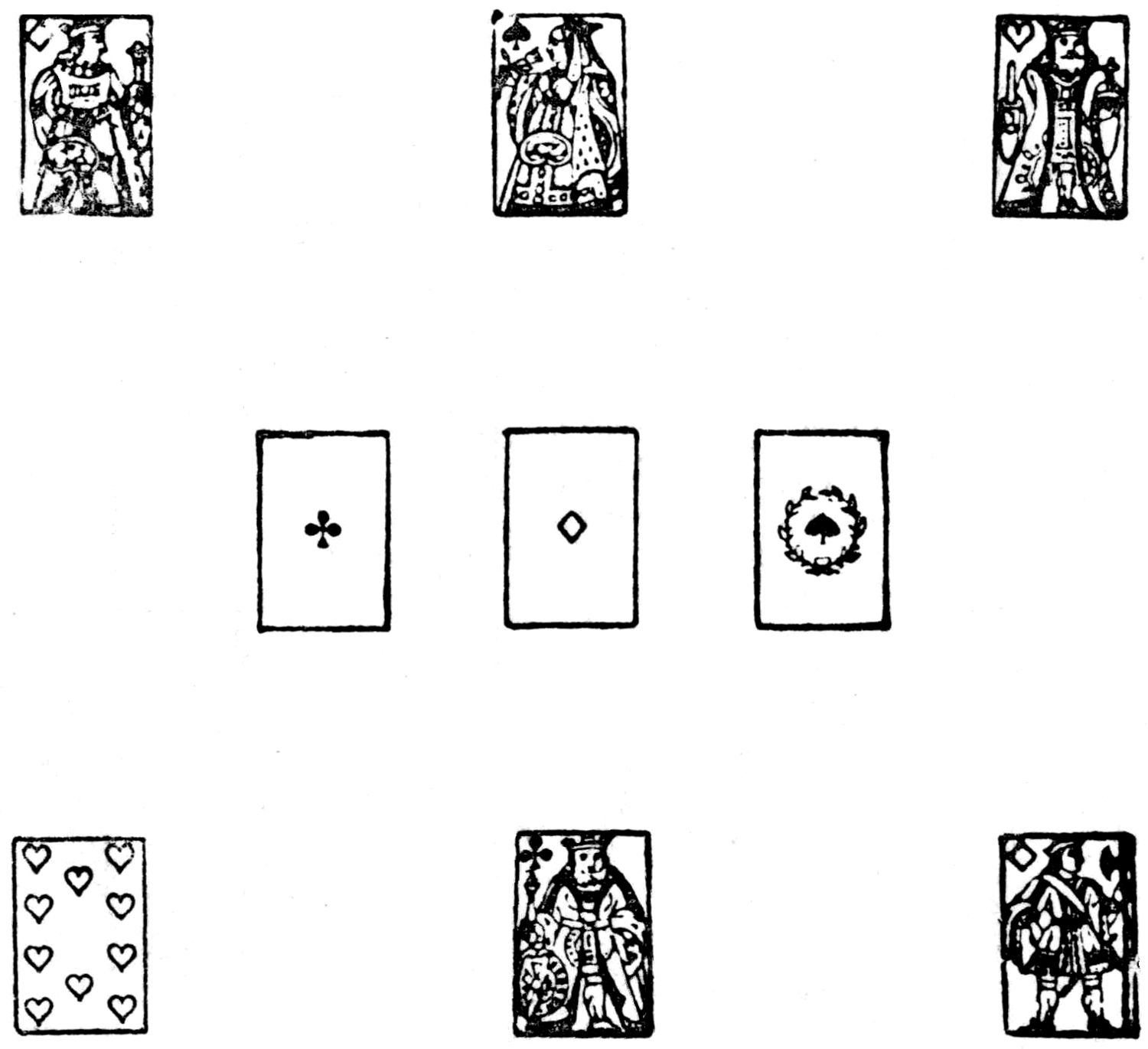
Return to solution
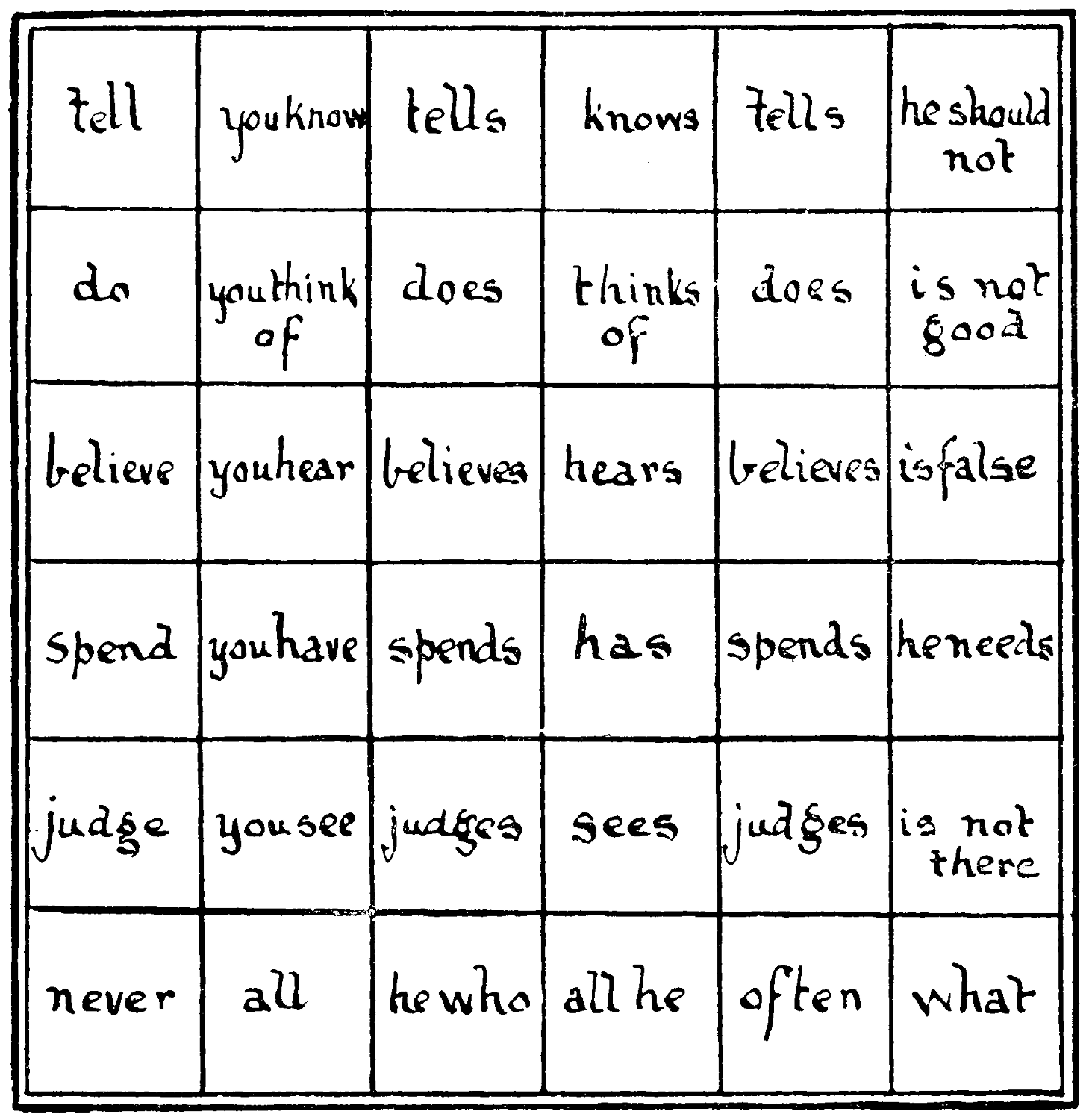
Return to solution

Return to solution
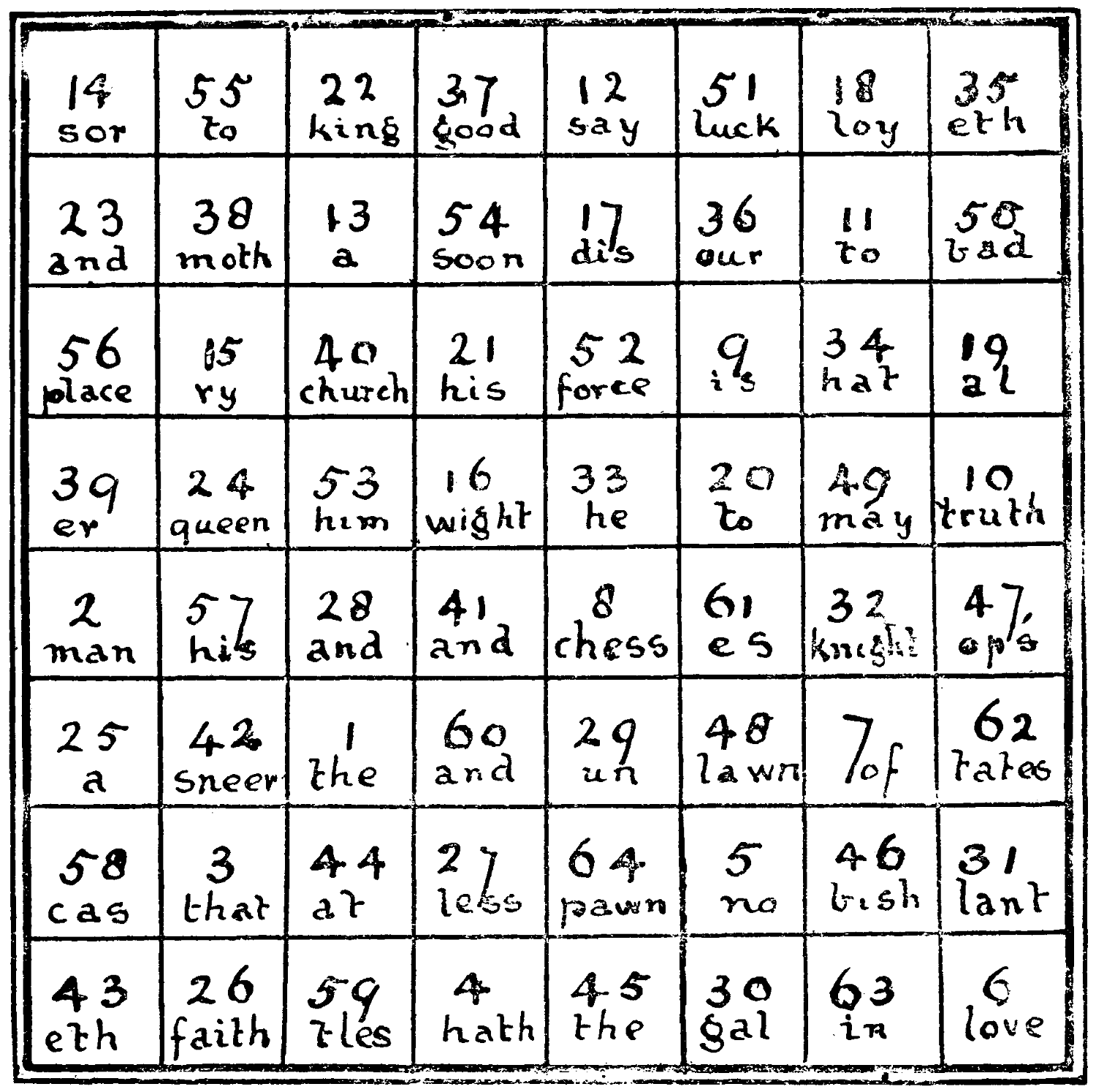
Return to solution
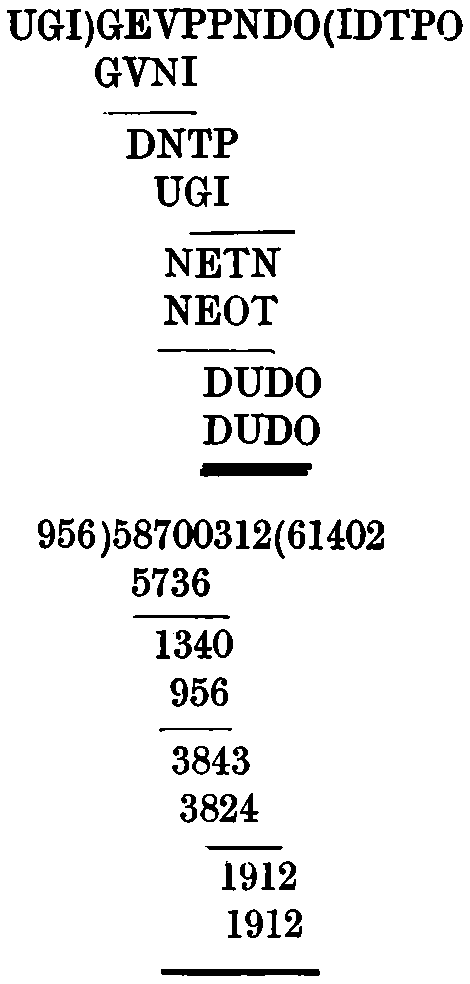
Return to solution
Return to solution
Return to solution
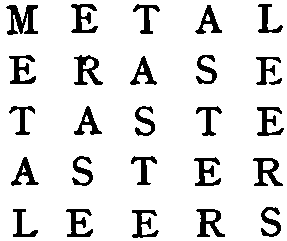
Return to solution
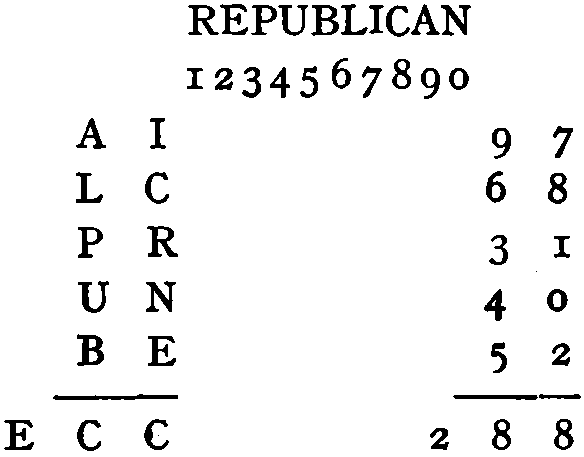
Return to solution

Return to solution
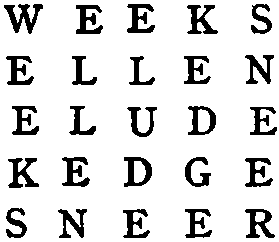
Return to solution
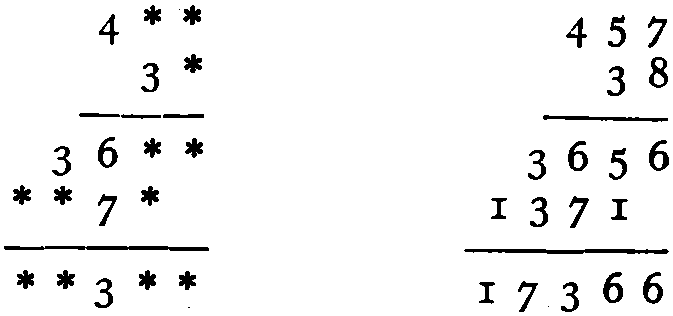
Return to solution
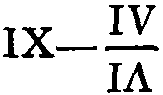
Return to solution
Inconsistent spelling, hyphenation, capitalisation, etcetera have been retained, unless listed under Changes below.
Unless listed below, the riddles, puzzles and tricks and their solutions are given here as printed in the source document, even though some of them arguably contain ambiguities, errors and/or misprints. Inconsistencies in lay-out between the puzzles and their solutions have not been standardised.
The source document has several pages that contain a Pictured Puzzle at the top (Roman numerals) and one or more Word Play puzzles or jokes (Latin numerals). This has been retained in this text; any auto-generated Tables of Contents may therefore look jumbled up with intermixed Roman and Latin numerals.
Depending on the hard- and software used to read this text and on their settings, not all elements may display as intended. The larger diagrams may be illegible on small screens or in small windows.
Where possible and relevant, illustrations have been “transcribed”, occasionally discarding some of the ornamentation. For reference and for the sake of completeness, images of the transcribed illustrations have been provided at the end of this e-book, with hyperlinks (“Image”) pointing to them. Hyperlinks from these images point back to the riddle, puzzle, etc. (“Return to description”) or to its solution (“Return to solution”). In addition, hyperlinks are provided from the puzzles etc. to their solutions (“Solution”) and from the solutions back to the puzzle etc. (“Return to description”).
Table of Contents, page 130: The Enigmas, Charades, Puzzles, &c., &c. do not actually start on this page (they start on page 2), but there are no more Pictured Puzzles and Word Play from this page on.
Page 49, Se Pierot or Lun: possibly an error for See Pierot or L’un or Le Pierot or L’un.
Page 60, No. LX: the description is confusing, as the puzzle consists of drawing the four dotted lines, and they are therefore not given.
Page 89 and 263, Pictured puzzle LXXXIX and solution: either the puzzle or the solution has been printed upside-down in the source document.
Page 114, ... as nearly as possible of the size and pattern ...: based on the size of the physical book (around 7″ or 18 cm tall), the boomerang’s width would be some 3″ or 7.5 cm.
Page 149, ... six single words: the solution provided gives five single words.
Page 205, Solution IX: the table as printed lacks values for Opposite pairs of short diagonals (of which there are four) and Such combinations as 482, 484, 472, 470 (of which there ought to be two in order to reach the given total).
Changes made
In the source document, jokes, riddles and puzzles may be split over multiple pages (for example, Word Play 5 may be found on page 7 (first part) and page 9 (second part)). In this e-text, the second part has been re-combined with the first, and references to the separate first and second parts have been deleted.
Some minor obvious typographical errors have been corrected silently. Similarly, minor discrepancies (such as the number of blanks or periods) have been rectified silently. Fractions (the forms x⁄y, xy and x-y all occur in the source document) have (bar a single exception) been standardised to x⁄y.
Unless they fitted better within the text paragraphs, illustrations, verses, diagrams, etc. have been moved out of the text paragraphs. The footnote has been moved to directly underneath the Word Play in which it is referenced.
Texts in a dashed box has been transcribed from the accompanying diagram or illustration, and does not appear as text in the source document.
Page 10: ... cut of my head; changed to ... cut off my head;
Page 62: ... thought myself happy to win her ... changed to ... I thought myself happy to win her ... (cf. solution).
Page 89: ... indentations do not effect ... changed to ... indentations do not affect ....
Page 93: the logogriph has been laid out as in the solution on page 305.
Page 110-111: Word Play 92 in this text (Missing Words) was erroneously numbered 93 (first part) and 39 (second part) in the source document.
Page 130: “Tis an absurdity to say ... changed to ’Tis an absurdity to say ....
Page 139: !” inserted after the dots cf. solution.
Page 144, Nr. 176, last line: space inserted between F and R in R FR H; H T G changed to H T N G.
Page 152: ... his destination from these words.” changed to ... his destination from these words?
Page 196: ... sa Majéste impériale ... changed to ...sa Majesté impériale ...; ... a jamais! changed to ... à jamais!
Page 197-198: Odds and Ends 38 appears twice; the second one has been renamed 38a.
Page 201: ... a flock of sheep in a fold enclosed by 10 hurdles ... changed to ... a flock of sheep in a fold enclosed by 100 hurdles ....
Page 294: Number 34 inserted before first solution.
Page 309: The Houses of Parliament and Westminster Abbey changed to The Houses of Parliament and Westminster Abbey.
Page 310: The words italics are spelt ... changed to The words in italics are spelt ....
Page 379: vis inertiœ changed to vis inertiæ.